2.17 Matlab em Sistemas de Controle
|
|
|
- Zilda Leveck Bayer
- 10 Há anos
- Visualizações:
Transcrição
1 46 CAPÍTULO 2. INTRODUÇÃO AO MATLAB 2.17 Matlab em Sistemas de Controle Nesta seção, os comandos básicos do CONTROL SYSTEM Toolbox do MATLAB são introduzidos. O comando helpcontrol fornece uma lista das diversas funções disponíveis. Para obter mais detalhes sobre cada uma das funções pode-se usar o comando help < nome da função >. Para a elaboração desta seção as seguintes referências foram utilizadas MathWorks (1997), Ogata (1997a) e Gaspar et al. (22). No MATLAB os sistemas dinâmicos podem ser descritos por uma função de transferência ou por um modelo em espaço de estado. Na representação por função de transferência definemse os coeficientes dos polinômios do numerador e denominador. Na representação em espaço de estado definem-se as quatro matrizes que caracterizam o modelo Função de transferência As funções de transferência no domínio da variável complexa s/z são usadas para caracterizar as relações entre entrada e saída de sistemas contínuos/discretos que possam ser descritos por equações diferenciais/a diferença lineares invariantes no tempo. Para condições iniciais nulas, a partir da aplicação da transformada de Laplace às equações diferenciais lineares obtém-se a relação entre a entrada e a saída descrita por uma relação entre polinômios na variável complexa s. No MATLAB, os polinomios são descritos pelos seus coeficientes. Por exemplo, a função de transferência em s y(s) r(s) = 3s2 2 s 2 + 2s + 4 é introduzida pelos coeficientes dispostos em ordem decrescente das potências dos polinômios do numerador e denominador num=[3-2]; den=[1 2 4]; O comando printsys(num, den) fornece a função de transferência na forma num/den= 3s 2 s 2 + 2s + 4 o comando G=tf(num,den) fornece Transfer function: 3s 2 s 2 + 2s + 4 e o comando G = tf(num,den,ts) gera uma função de transferência para sistemas discretos com TS o tempo de amostragem. A saida G é um objeto do tipo TF. Evidentemente, a função pode ser chamada de outro nome qualquer.
2 2.17. MATLAB EM SISTEMAS DE CONTROLE Espaço de estado Um sistema dinâmico formado por elementos concentrados pode ser representado por equações diferenciais ordinárias em que o tempo é a variável independente. Fazendo uso de notação matricial-vetorial, uma equação diferencial de ordem n pode ser representada por uma equação matricial-vetorial de primeira ordem. Se n elementos do vetor formam um conjunto de variáveis de estado, a descrição matricial vetorial denominada espaço de estado possui a forma ẋ = Ax + Bu y = Cx + Du Considere o seguinte sistemana forma espaço de estado [ ] [ ] ẋ = x + u 3 1 y = [ 3.5 ] x As matrizes são introduzidas no MATLABcomo segue A=[2-1 ; 3-1]; B=[1 ] ; C=[3 -.5]; D=[]; printsys(a,b,c,d); A= O comando printsys fornece o modelo espaço de estado na forma x1 x2 x x B= u1 x1 1. x2 C= x1 x2 y
3 48 CAPÍTULO 2. INTRODUÇÃO AO MATLAB D= u1 y1. O comando ss fornece o modelo espaço de estado contínuo nomeado Gss com matrizes A, B, C, D Gss=ss(A,B,C,D) A= x1 x2 x1 2-1 x2 3-1 B= u1 x1 1 x2 C= x1 x2 y D= u1 y1 Continuous-time model. O comando Gd = c2d(sys,ts,method) converte o sistema continuo Gss para um sistema discreto com Ts o tempo de amostragem e method o metodo de discretização a ser estudo no Capítulo Conversão de representações É possível realizar conversões de representação de sistemas de uma forma para outra
4 2.17. MATLAB EM SISTEMAS DE CONTROLE 49 Função de transferência (transfer function - tf ) Espaço de estado (state space - ss) Zeros, pólos e ganho (zero pole gain - zp) Em todos os tipos de conversões lembrar que a função de transferência é dada por um polinômio no numerador e no denominador, a representação espaço de estado é dada pelas matrizes A, B, C, D e a representação zeros, pólos e ganho é dada pelo conjunto de pólos zeros e ganho. Conversão entre espaço de estado e função de transferência Para a conversão de espaço de estado a função de transferência e vice-versa utilizam-se as funções ss2tf e tf 2ss, respectivamente. Considere o seguinte sistema dado na forma espaço de estado ẋ = A = [-2-1; 1-2]; B = [1 2] ; C = [1 ]; D = []; [num,den] = ss2tf(a, B, C, D) num= 1 den= [ ] 2 1 x y = [ 1 ] x E, a função de transferência do sistema possui a forma G(s) = s s 2 + 4s + 5 [ ] 1 u 2 Conversão entre pólo, zero e ganho e função de transferência No caso do sistema estar descrito por pólos, zeros e ganho, a conversão para função de transferência é dada por z = ; % zero do sistema p1 = -2 + i; % pólo do sistema p2 = -2 - i; % pólo do sistema k = 1; % ganho
5 5 CAPÍTULO 2. INTRODUÇÃO AO MATLAB [num,den]=zp2tf (z, [p1 p2], k); obtendo-se portanto a mesma função de transferência do sistema que anteriormente. No caso do sistema estar na forma pólo, zero e ganho, a conversão para espaço de estado é dada pelas funções tf2ss e zp2ss Considere a seguinte função de transferência G(s) = s s 2 + 4s + 5 As linhas de comando para obter a representação espaço de estado seguem num=[ 1 ] den = [ ] [A, B, C, D]=tf2ss(num,den) A sua representação em espaço de estado é como segue A= B= C= D= Se fossem dados os pólos, zeros e ganho do sistema, a conversão para a representação espaço de estado seguiria os passos usados para obter a função de transferência, mas, obtendo-se as matrizes A,B,C,D e não os coeficientes do numerador e denominador da função de transferência. Conversão para pólo, zero e ganho A conversão para pólos, zeros e ganho pode ser realizada a partir aas seguintes funções
6 2.17. MATLAB EM SISTEMAS DE CONTROLE 51 tf2zp % obtenção pólos, zeros e ganho a partir da função de transferência ss2zp % obtenção pólos, zeros e ganho a partir da forma espaço de estado Os pólos, zeros e ganho dos exemplos anteriores para sistemas na forma espaço de estado e na forma de função de transferência podem ser obtidos da seguinte forma % Sistema representado no espaço de estado A=[-2-1; 1-2] B=[1 2] C=[1 ] D=[] [z, p, k]=ss2zp (A, B, C, D) % Sistema representado na forma de função de transferência num=[ 1 ] den=[1 4 5] [z, p, k]=tf2zp (num, den) z= p= i i k= Sistemas conectados Existe um conjunto de funções que permite obter representações de sistemas formados por diversos subsistemas interligados. O diagrama de blocos de um sistema é uma representação das funções desempenhadas por cada um dos componentes e fluxos de sinais. O diagrama de blocos indica as conexões entre os vários componentes do sistema. Sistemas em cascata O comando series permite a associação de blocos em cascata (Figura 2.12), tendo em consideração que os dois sistemas deverão ser do mesmo tipo (contínuos ou discretos).
7 52 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Aqui e doravante, considera-se que um sistema sys pode estar representado por Função de transferência: sys = (num, den) Espaço de estado: sys=(a, B, C, D) A seguinte função implementa a associação de sistemas em cascata sys=series(sys1,sys2) Figura 2.12: Conecção em cascata. Considere as funções de transferência do sistema nomeado sys num1 = [ 2 ]; den1 = [ ]; num2 = [ 1 1 ]; den2 = [ ]; sys1=tf(num1,den1); sys2=tf(num2,den2); sys=series(sys1,sys2) Transfer function: 2s + 2 4s s s s + 18 Para os sistemas descritos por função de transferência pode-se também utilizar o comando conv para conectar sistemas em cascata num = conv (num1, num2 ) den = conv (den1, den2 ) num = 2 2 den = Assim, utilizando sys = tf(num, den ) obtém-se a função de transferência do sistema resultante. Considere os modelos espaço de estado de um sistema conectado sys
8 2.17. MATLAB EM SISTEMAS DE CONTROLE 53 A1=[2-1 ; 3-1]; B1=[1 ] ; C1=[2 -.5]; D1=[]; sys1=ss(a1,b1,c1,d1); A2 = [ -4-5 ; 1 ]; B2 = [ 1 ] ; C2 = [ 1 ]; D2 = [ ]; sys2=ss(a2,b2,c2,d2); sys=series(sys1,sys2) A = x1 x2 x3 x4 x x2 1 x3 2-1 x4 3-1 B = u1 x1 x2 x3 1 x4 C = x1 x2 x3 x4 y1 1 D = u1 y1 Continuous-time model
9 54 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Sistemas em paralelo A ligação de sistemas em paralelo, (Figura 2.13) com os dois sistemas do mesmo tipo (contínuos ou discretos) pode ser feita usando os comandos sys = parallel (sys1, sys2) Figura 2.13: Conecção em paralelo. O comando parallel é equivalente à soma direta de polinômios no caso dos sistemas estarem representados na forma de função de transferência Realimentação unitária Um sistema de malha fechada com realimentação unitária (Figura 2.14) pode ser obtido com o seguinte comando sys = feedback(g) Considere o sistema de malha aberta G(s) Figura 2.14: Realimentação unitária. G(s) = s 6 s 2 s + 5 A função de transferência de malha fechada com realimentação unitária y(s)/r(s) pode ser obtida a partir das seguintes linhas de comando num = [ 1-6 ] den = [ ]
10 2.17. MATLAB EM SISTEMAS DE CONTROLE 55 G=tf(num,den) sys=feedback(g,-1) Transfer function: s - 6 s 2-1 E, a função de transferência é da forma sys : y(s) r(s) = G(s) 1 + G(s) = s 6 s 2 1 Observação 2.2 Para realimentação não unitária negativa utiliza-se comando feedback (sys1,sys2,-1) e para realimentação não unitária positiva o comando feedback (sys1,sys2,1) Sistemas de 2 a ordem Considere o sistema de 2 a ordem y(s) r(s) = w 2 n s 2 + 2ξw n + w 2 n A sua construção na forma de função de transferência ou espaço de estado pode ser realizada a partir da freqüência natural w n e do coeficiente de amortecimento ξ. No caso de sistema na forma de função de transferência com uma freqüência natural de w n = 2.4rad/s e, com um coeficiente de amortecimento ξ =.4 pode-se utilizar [num, den] = ord2 (2.4,.4) num = 1 den = correspondendo à função de transferência Resposta no tempo y(s) r(s) = 1 s s Em sistemas de controle é usual utilizar entradas de teste típicas para avaliação do desempenho do controlador. As entradas de teste usualmente utilizadas são degrau,
11 56 CAPÍTULO 2. INTRODUÇÃO AO MATLAB rampa e impulso. A escolha do tipo de entrada deve ser pautada nas características da entrada a que o sistema está submetido mais freqüentemente durante sua operação normal. A propriedade principal da dinâmica de um sistema de controle é a estabilidade. Diz-se que um sistema de controle é estável se a saída quando perturbada voltar ao seu estado de equilíbrio. Resposta ao degrau unitário A seguir considera-se a resposta de sistemas 2 a ordem a um degrau unitário. Seja y(s) r(s) = Kw 2 n s 2 + 2ξw n + w 2 n O comportamento dinâmico deste sistema de 2 a ordem pode ser descrito pela freqüência natural w n e pelo coeficiente de amortecimento ξ. A função step fornece a resposta de um sistema no domínio do tempo a uma entrada em degrau unitário para condição inicial nula. Quando o comando é utilizado sem argumentos, esta função fornece graficamente a solução do sistema em resposta ao degrau unitário. A duração da simulação é determinada automaticamente baseada nos pólos e zeros do sistema step (sys) onde sys = tf(num,den) % função de transferência sys = ss(a, B, C, D) % forma espaço de estado Para obter o vetor da saída y e estado x no tempo, deve-se utilizar os argumentos no comando. O comando step, neste formato, não gera qualquer gráfico. O gráfico da resposta do sistema pode ser obtido com a função plot [y, t] = step(sys) %sistema representado por função de transferência [y, x, t] = step(sys) %sistema representado por espaço de estado plot(t, y) O comando [y,t] = step(sys) retorna a saída y e o tempo t gerado. Se sys tiver ny saídas, nu entradas e, comprimento lt = length(t), y é um conjunto de tamanho lt ny nu onde y(:,:,j) fornece a resposta ao degrau da j ésima entrada do sistema. O comando [y,x,t] = step(sys) retorna o estado x de dimensão lt nx nu se o sistema tiver nx variáveis de estado. Do mesmo modo, pode-se estabelecer a duração da simulação através da imposição do tempo t = :.1 : 1 step (sys,t)
12 2.17. MATLAB EM SISTEMAS DE CONTROLE 57 A função step permite a introdução de argumentos distintos para definir vários sistemas, de modo que sejam apresentados os traçados da resposta sobrepostos no mesmo gráfico, podendo os tipos, cores e marcadores das linhas de cada sistema serem definidos como nas funções básicas de criação de gráficos step (sys1, y:,sys2, g- ) Considere a função de transferência de malha fechada do seguinte sistema y(s) r(s) = 25 s 2 + 4s + 25 A resposta do sistema no domínio do tempo a uma entrada em degrau unitário pode ser obtida da seguinte forma y(s) = 25 s 2 + 4s + 25 r(s) com r(s) = 1 s. As linhas de comando para a visualização da resposta do sistema seguem (Figura 2.15) num = [ 25] den = [1 4 25] sys=tf(num,den) step (sys) O sistema também pode estar na forma espaço de estado, sendo a resposta a um degrau unitário obtida com a função expressa do seguinte modo: step(a,b,c,d) Resposta a entrada rampa O MATLAB não dispõe de nenhuma função para obter a resposta de um sistema no domínio do tempo a uma entrada em rampa unitária. Para obter a resposta no tempo a este sinal de entrada particular, utiliza-se a função step aumentando um grau os coeficientes das sucessivas potências do polinômio que traduzem o denominador da função de transferência do sistema. O uso do comando segue o caso anterior. Considerando a mesma função de transferência anterior, a resposta do sistema no domínio do tempo a uma entrada em rampa unitária é obtida como segue y(s) = 25 s 2 + 4s + 25 r(s) com r(s) = 1 s 2. As funções para obter os sistemas e a resposta à ramapa seguem (Figura 2.16)
13 58 CAPÍTULO 2. INTRODUÇÃO AO MATLAB 1.4 Step Response Amplitude Time (sec) Figura 2.15: Resposta do sistema num = [ 25], den = [1 4 25] à uma entrada degrau unitário. num1=[ 25]; den1=[1 4 25]; num2=[ 1]; den2=[ 1 ]; sys1=tf(num1,den1); %função de transferência 25/(s 2 + 4s + 25) sys2=tf(num2,den2); %função de transferência 1/s sys=series(sys1,sys2); step(sys, r,sys2, k ) O erro estacionário para a resposta no domínio do tempo de um sistema de 2 a ordem sujeito a uma entrada em rampa unitária é dado por e ss = 2ξ w n Resposta ao impulso A função impulse fornece a resposta de um sistema no domínio do tempo a uma entrada em impulso. Considere o sistema anterior sujeito a uma entrada impulso. A saída y(s) é da forma 25 y(s) = s 2 r(s) com r(s) = 1 + 4s + 25
14 2.17. MATLAB EM SISTEMAS DE CONTROLE 59 5 Step Response Amplitude Time (sec) Figura 2.16: Resposta sistema G(s) = 25/(s 2 +4s+25) a uma entrada rampa unitária. As linhas de comando para a visualizar a resposta do sistema seguem (Figura 2.17) num = [ 25 ]; den = [ ]; sys=tf(num,den); impulse(sys) Como a resposta a uma entrada impulso corresponde à derivada da resposta a uma entrada em degrau unitário, o sobre-sinal máximo para a resposta a degrau unitário pode ser determinado a partir da correspondente resposta ao impulso, já que a área sob a curva de resposta ao impulso de Dirac desde t = até t p (tempo do primeiro cruzamento com zero) é dada por 1 + M p onde M p corresponde ao sobre-sinal máximo para a resposta a degrau unitário. Resposta a entradas e a condições iniciais A função initial gera a resposta no domínio do tempo de um sistema no espaço de estado com condições iniciais não nulas. Considere um sistema representado no espaço de estado com condições iniciais não nulas ẋ = Ax + Bu,x() = x y = Cx As linhas de comando que possibilitam a obtenção da resposta do sistema a este tipo
15 6 CAPÍTULO 2. INTRODUÇÃO AO MATLAB 3.5 Impulse Response Amplitude Time (sec) Figura 2.17: Resposta do sistema num = [ 25 ], den = [ ] a uma entrada impulso. particular de entrada segue initial(sys, x) Considere o seguinte sistema representado no espaço de estado [ ] ẋ = x.7814 y = [ ] x e as condições [ ] iniciais 1 x() = As linhas de comando para obter a resposta a x seguem (Figura 2.18) A = [ ;.7814 ]; B = [ ] ; C = [ ]; D = []; x = [1 ] ; initial (A, B, C, D, x)
16 2.17. MATLAB EM SISTEMAS DE CONTROLE 61 5 Response to Initial Conditions 4 3 Amplitude Time (sec) Figura 2.18: Resposta do sistema [A,B,C,D] à condição inicial x Resposta a uma entrada arbitrária A função lsim (linear simulation) simula a resposta de um sistema no domínio do tempo a uma entrada arbitrária e possui a mesma estrutura das funções anteriores lsim (sys, u, t) A matriz formada pela entrada u possui tantas colunas quanto a dimensão do vetor u no tempo t(length(t)). A função lsim pode também gerar a resposta a entrada arbitrária de sistemas representados no espaço de estado com condições iniciais não nulas lsim(sys,u,t,x) O comando que gera o sinal arbitrário u é o comando gensig (generate signal). Este comando gera um sinal periódico escalar u da classe type e período τ, para simulações no domínio do tempo através do uso da função lsim. A função gensig suporta as seguintes classes de sinal type = sin : onda senoidal type = square : onda quadrada type = pulse : impulso periódico [u,t] = gensig(type,τ)
17 62 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Considere a seguinte função de transferência y(s) r(s) = s 1 s 2 + s + 5 Pode-se obter a resposta a uma entrada do tipo onda quadrada com um período de 4 segundos da seguinte forma. Inicialmente, gera-se a onda quadrada com a função gensig considerando um tempo de amostragem de.1s durante 1s e posteriormente, simula-se a resposta do sistema (Figura 2.19) [u,t] = gensig ( square,4,1,.1 ); num = [ 1-1 ]; den = [ ]; sys=tf(num,den); lsim(sys, r,u,t) axis([ ]) hold Current plot held plot(t,u, k ) axis([ ]) 1.5 Linear Simulation Results 1.5 Amplitude Time (sec) Figura 2.19: Resposta do sistema a uma entrada quadrada Lugar geométrico das raízes A característica básica da resposta transitória de um sistema em malha fechada está intimamente relacionada com a localização dos pólos de malha fechada. Os pólos de
18 2.17. MATLAB EM SISTEMAS DE CONTROLE 63 malha fechada são as raízes da equação característica δ(s) = 1 + G(s)H(s). O lugar geométrico das raízes é formado pelas raízes da equação característica em função de um parâmetro. O parâmetro usualmente utilizado é o ganho da função de transferência de malha aberta. Pólos e zeros A função pzmap sem argumento fornece um diagrama dos pólos e dos zeros de um sistema contínuo ou discreto. Os pólos são representados por x e os zeros representados por o. Com argumento, pzmap fornece duas colunas correspondentes aos pólos e aos zeros sem gerar qualquer diagrama pzmap(sys) %geração do diagrama de pólos e zeros do sistema [p, z] = pzmap(sys) %obtenção dos valores dos pólos e dos zeros Considere a função de transferência de malha aberta do sistema G(s) = 2s2 + 5s + 1 s 2 + 2s + 3 Pede-se os obter os pólos e os zeros com as linhas de comando como seguem (Figura 2.2) num = [2 5 1]; den = [1 2 3]; sys=tf(num,den); pzmap (sys, r ) 1.5 Pole Zero Map 1.5 Imaginary Axis Real Axis Figura 2.2: Mapa de pólos e zeros.
19 64 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Usando rlocus A função rlocus fornece o lugar geométrico das raízes do polinômio característico de um sistema que correspondem aos pólos do sistema realimentado em função da variação do ganho K desde zero até infinito. O lugar geométrico das raízes indica o lugar dos pólos de malha fechada do sistema em função do ganho de realimentação K para realimentação negativa. O lugar geométrico das raízes é usado no estudo dos efeitos da variação do ganho de realimentação na localização dos pólos de malha fechada. As diferentes funções de transferência de malha aberta de sistemas para implementação da função rlocus, são mostradas na Figura 2.21 Seja G(s) dada por Figura 2.21: Diferentes configurações de realimentação. G(s) = n(s) d(s). Os pólos do sistema realimentado são dados pelas raízes de d(s) + Kn(s) = Quando o comando rlocus é utilizado sem argumentos obtém-se o lugar dos pólos em função do ganho K. Em caso contrário, apresenta duas colunas correspondentes à localização das raízes complexas r e, o respectivo ganho K, sem gerar qualquer gráfico rlocus (sys) %geração do lugar das raízes rlocus (sys,k) %mapa das raízes para um determinado ganho K [r,k] = rlocus(sys) %geração dos vetores das raízes e respectivo ganho r = rlocus (sys,k) %raízes para um ganho fixo K
20 2.17. MATLAB EM SISTEMAS DE CONTROLE 65 Para visualizar o lugar das raízes (Figura 2.22) utilizam-se os seguintes comandos num=conv([1 1],[1 1]); den=conv([1-2],[1 4 68]); sys=tf(num,den) rlocus(sys) 3 Root Locus 2 1 Imaginary Axis Real Axis Figura 2.22: Lugar das raízes de do polinômio característico δ(s) = d(s) + Kn(s) em função de K para num=conv([1 1],[1 1])e den=conv([1-2],[1 4 68]. Ganho estático A função rlocfind utiliza a regra da magnitude do lugar geométrico das raízes para determinar o ganho para uma localização particular das raízes. Trata-se de uma função interativa, já que permite ao usuário selecionar a localização das raízes no traçado do lugar de raízes para as quais pretende determinar o ganho de realimentação. No entanto, pode ser utilizada com argumentos de modo a calcular o ganho de realimentação para uma localização especifica das raízes. [K,poles]= rlocfind (sys) [K,poles] = rlocfind (sys,p) dos pólos. %obtenção do ganho K interativamente %obtenção do ganho K para uma localização especifica
21 66 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Curvas de w n e ξ constantes A função sgrid permite gerar um gráfico no plano s de curvas de freqüência natural constante e de coeficiente de amortecimento constante. O gráfico é gerado sobre o traçado do lugar geométrico das raízes ou sobre o mapa dos pólos e zeros obtido anteriormente, com um espaçamento de.1 desde até 1 para as curvas de coeficiente de amortecimento ξ constante, e com um espaçamento de 1 rad/s desde até 9 rad/s para as curvas de freqüência natural w n constante. Pode-se especificar como argumento as linhas de coeficiente de amortecimento constante ξ e as linhas freqüência natural constante w n sgrid sgrid(xi,wn) Os gráficos mostrados nas Figuras 2.23 e 2.24 ilustram o uso do comando sgrid. Considere a função de transferência de malha aberta do sistema. Para gerar o mapa de pólos e zeros sobre o lugar dos pólos, as linhas no plano s de coeficiente de amortecimento constante e de freqüência natural constante utiliza-se a função sgrid. Seja G(s) = 2s2 + 5s + 1 s 2 + 2s + 3 As linhas de comando para gerar o mapa de pólos e zeros e o lugar das raízes seguem num = [2 5 1]; den = [1 2 3]; sys=tf(num,den); pzmap (sys) sgrid num=conv([1 1],[1 1]); den=conv([1-2],[1 4 68]); sys=tf(num,den) rlocus(sys) sgrid Resposta em frequência Pelo termo resposta em freqüência entende-se a resposta em regime estacionário de um sistema sujeito a uma entrada exponencial complexa. Existe um conjunto de funções no Matlab que permite analisar a resposta no domínio da freqüência de um dado sistema. Os diagramas de Bode, Nyquist e Nichols são usualmente utilizados seja para o sistema descrito por uma função de transferência seja pelo modelo espaço de estado. Diagrama de Bode A função de transferência para s = jw pode ser caracterizada pelo seu módulo e ângulo de fase em função da freqüência em escala logarítmica. A função bode fornece o diagrama de Bode da resposta em freqüência de um dado sistema pela avaliação da função de
22 2.17. MATLAB EM SISTEMAS DE CONTROLE Pole Zero Map Imaginary Axis Real Axis.4 Figura 2.23: Pólos e zeros no plano s com indicando pólo, o zero e curva de w n = 5 e ξ = Root Locus Imaginary Axis System: sys Gain: 33.8 Pole: i Damping:.294 Overshoot (%): 38.1 Frequency (rad/sec): Real Axis Figura 2.24: Lugar das ráizes com o comandos rlocus e sgrid.
23 68 CAPÍTULO 2. INTRODUÇÃO AO MATLAB transferência G(s) no eixo imaginário s = jw. Apenas são consideradas freqüências positivas. Para sistemas na forma espaço de estado, a resposta em freqüência é dada por G(jw) = D + C(jwI A) 1 B, w Quando o comando é utilizado sem argumentos, esta função gera o módulo e do ângulo de fase em função da freqüência. O diagrama de Bode são utilizados para analisar propriedades do sistema, tais como margem de ganho, margem de fase, largura de banda, estabilidade, etc. A faixa de freqüências, em rad/s, é determinada automaticamente baseada nos pólos e zeros do sistema. As diversas sintaxes desta função seguem bode (sys) %geração diagrama de Bode de módulo e fase bode (sys,w ) %geração diagrama de Bode com faixa de freqüência especificada bode (sys1, sys2,..., sysn) %geração do diagrama de Bode diversos sistemas sobrepostos Quando o comando bode é usado com os seus argumentos, obtém-se os vetores do módulo, ângulo de fase e a freqüência w e, o gráfico não é exibido. [mod,fase,w] = bode(sys) %obtenção dos valores do módulo, fase e freqüência [mod,fase] = bode(sys,w) %obtenção dos valores do módulo e fase para a faixa de freqüência especificada Considere a seguinte função de transferência em malha aberta G(s) = s2 +.1s s s 3 + s 2. O diagrama de Bode pode ser obtido com as seguintes linhas de comando (Figura 2.25) num = [ ]; den = [ ]; sys=tf(num,den) bode (sys, r ) Para obter o gráfico da resposta do sistema no domínio da freqüência para uma faixa maior de freqüência, por exemplo de.1 até 1 rad/s, basta introduzir o comando (Figura 2.26) w = logspace (-1, 2); num = [ ]; den = [ ]; sys=tf(num,den) bode (sys, r, w)
24 2.17. MATLAB EM SISTEMAS DE CONTROLE 69 5 Bode Diagram Magnitude (db) 5 1 Phase (deg) Frequency (rad/sec) Figura 2.25: Resposta em freqüencia. 5 Bode Diagram Magnitude (db) Phase (deg) Frequency (rad/sec) Figura 2.26: Resposta em freqüência selecionando a faixa.
25 7 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Margem de ganho e margem de fase Na análise da resposta de sistemas no domínio da freqüência, as margens de ganho e de fase permitem avaliar a estabilidade relativa do sistema. A margem de fase é definida como o atraso de fase adicional na freqüência de cruzamento do ganho (w cg ) necessário para levar o sistema ao limiar da instabilidade. A freqüência de cruzamento do ganho é a freqüência na qual G(jw), o módulo da função de transferência de malha aberta, é unitário ou db no caso do módulo da função de transferência de malha aberta ser representado em db. A margem de fase (MF) pode ser calculada da seguinte forma MF = 18 o + G(w cg ) MF = 18 o + φ Portanto, a MF é 18 o mais o ângulo φ da função transferência de malha aberta na freqüência de cruzamento de ganho denotado (w cg ). Para um sistema de fase mínima (todos os pólos e zeros no semiplano s da esquerda) ser estável, a margem de fase deve ser positiva. A margem de ganho é definida como o inverso do módulo G(jw) na freqüência de cruzamento da fase (w φ ). A freqüência de cruzamento da fase é a freqüência na qual G(jw cg ), o ângulo de fase da função de transferência de malha aberta, é igual a 18o. A margem de ganho (MG) pode ser obtida da seguinte forma MG = 2log G(w φ ) Uma margem de ganho positiva significa que o sistema é estável, e o contrário que o sistema é instável. Para um sistema de fase mínima estável, a margem de ganho indica quanto o ganho pode ser aumentado antes que o sistema se torne instável. Para um sistema instável, a margem de ganho é indicativa de quanto o ganho deve ser diminuído para tornar o sistema estável. A margem de ganho e a margem de fase e respectivas freqüências de cruzamento, são calculadas a partir da função de transferência em malha aberta pela função margin. Indicam a estabilidade relativa do sistema em malha fechada. Quando o comando é usado sem argumentos, exibe os diagramas de Bode de módulo e ângulo de fase com as referidas margens. As sintaxes possíveis para esta função seguem margin(sys) %diagrama de Bode com as margens [Gm, Pm, Wcg, Wcp] = margin(sys) % margens e freqüências de cruzamento margin(mag,fase,w) % diagrama de Bode com as margens [Gm, Pm, Wcg, Wcp]=margin (mag,fase,w) % margens e freqüências de cruzamento allmargin(sys) % todas as margens de ganho e fase Considere a seguinte função de transferência em malha aberta G(s)H(s) = db K s(s + 1)(s + 5)
26 2.17. MATLAB EM SISTEMAS DE CONTROLE 71 Para K = 1 e K = 1 as margens de ganho e fase podem ser obtidas como segue (Figura 2.27) % Para K=1 num=[1]; den1=conv([1 1],[1 5]); den=conv([1 ],den1); sys=tf(num,den) margin(sys) 1 Bode Diagram Gm = 9.54 db (at 2.24 rad/sec), Pm = 25.4 deg (at 1.23 rad/sec) 5 Magnitude (db) Phase (deg) Frequency (rad/sec) Figura 2.27: Margens de estabilidade para K=1. % Para K=1 num=[1]; den1=conv([1 1],[1 5]); den=conv([1 ],den1); sys=tf(num,den) margin(sys) Critério de Nyquist O critério de estabilidade de Nyquist permite investigar a estabilidade absoluta e a estabilidade relativa de sistemas lineares de malha fechada a partir da resposta em freqüência do respectivo sistema em malha aberta. Considere o seguinte sistema representado pela
27 72 CAPÍTULO 2. INTRODUÇÃO AO MATLAB 1 Bode Diagram Gm = 1.5 db (at 2.24 rad/sec), Pm = 23.7 deg (at 3.91 rad/sec) 5 Magnitude (db) Phase (deg) Frequency (rad/sec) Figura 2.28: Margens de estabilidade para K=1. sua função de transferência de malha fechada y(s) r(s) = G(s) 1 + G(s)H(s) Para que este sistema seja estável, todas as raízes da equação característica δ(s) = 1 + G(s)H(s) = devem permanecer no semiplano lateral esquerdo s. O critério de Nyquist estabelece que Z=N+P com Z o número de pólos instáveis do sistema em malha fechada N o número de envolvimentos do gráfico de Nyquist (plano da função G(s)H(s)) no sentido horário em torno do ponto 1 + j e P o número de pólos de G(s)H(s) no semiplano lateral direito. Se o diagrama de Nyquist envolver o ponto 1 + j uma vez no sentido horário, N=1, se no sentido anti-horário N=-1. Do critério pode-se concluir o seguinte 1. Se P, para estabilidade deve-se ter Z = o que implica N = P, ou seja, o número de envolvimentos do gráfico de Nyquist, no sentido anti-horário em torno do ponto 1 + j deve ser igual ao número de pólos de G(s)H(s) no semiplano lateral direito do plano s 2. Se P =, para estabilidade deve-se ter Z = N =, ou seja, não pode haver envolvimento do ponto 1 + j
28 2.17. MATLAB EM SISTEMAS DE CONTROLE 73 A função nyquist fornece o gráfico de G(jw)H(jw) em função da frequência w. O diagrama de Nyquist permite estudar também a estabilidade relativa do sistema em malha fechada, ou seja, a margem de ganho e margem de fase. Quando o comando nyquist é usado com argumentos obtém-se as partes real e imaginárias de G(jw)H(jw) em função de w. As sintaxes possíveis para este comado seguem nyquist (num, den) %diagrama de Nyquist nyquist (num, den, w) %diagrama de Nyquist para faixa de freqüências especificada [re, im, w] = nyquist (num, den) %obtenção partes real e imaginária de G(jw)H(jw) Considere a seguinte função de transferência em malha aberta G(s)H(s) = 2s2 + 5s + 1 s 2 + 2s + 3 Para obter o diagrama de Nyquist utilizar os seguintes comandos (Figura 2.29) num = [2 5 1]; den = [ ]; sys=tf(num,den) nyquist (sys, r ) 2 Nyquist Diagram Imaginary Axis System: sys Real: 1.37 Imag: 1.68 Frequency (rad/sec): Real Axis Figura 2.29: Diagrama de Nyquist para w de a.
29 74 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Diagrama de Nichols A função Nichols fornece a resposta de um sistema no domínio da freqüência e exibe o diagrama nas coordenadas de Nichols. Esta função é útil para analisar as propriedades de sistema em malha aberta e em malha fechada. Quando o comando é usado sem argumentos produz a exibição do diagrama de Nichols. A função ngrid gera as linhas de grade para o traçado de Nichols que correspondem às linhas de módulo e ângulo de fase constantes da função de transferência de malha aberta. A grade e a faixa de freqüências é determinada automaticamente a partir dos pólos e zeros do sistema nichols (sys) %diagrama de Nichols nichols (sys,w) %diagrama de Nichols com faixa de freqüência especificada nichols (sys1, sys2,..., sysn) %diagramas de Nichols sobrepostos de diversos sistemas Quando o comando é usado com os argumentos do módulo, os vetores da resposta são exibidos em lugar do diagrama de Nichols [mod,fase,w]= nichols (sys) %valores do módulo, fase e freqüência [mod,fase,w]= nichols (sys,w) % valores do módulo e fase para faixa de freqüência especificada Considere o seguinte sistema dado pela sua função de transferência em malha aberta G(s)H(s) = 4s2 + 48s 3 18s s + 6 s 2 + 3s 3 18s s + 6 O diagrama de Nichols pode ser obtido a partir dos comandos (Figura 2.3.) num = [ ]; den = [ ]; sys=tf(num,den); nichols (num, den ) ngrid 4 Nichols Chart db 3.25 db.5 db Open Loop Gain (db) db 3 db 6 db 1 db 3 db 6 db 1 12 db 2 db Open Loop Phase (deg) Figura 2.3: Diagrama de Nichols.
30 2.17. MATLAB EM SISTEMAS DE CONTROLE Identificação de modelos simples Os parâmetros de modelos com polos e zeros e um atraso para descrever processos utilizando respostas a entradas típicas podem ser obtidos com o uso de uma interface gráfica denotada ident. A seguir três processos frequentemente utilizados em laboratório são identificados: motor CC, mini-forno e circuito RLC. Para identificar o modelo para o primeiro e segundo processos considera-se a resposta ao degrau e para o terceiro a resposta em frequencia. Identificação dos parâmetros do modelo de um motor CC Identificar as constantes de tempo e ganho constante do modelo de um motor CC a partir da resposta à um degrau de tensão aplicado na armadura. Considere a função de transferência entre a velocidade wrad/s e a tensão aplicada na armadura v a G(s) := w(s)/v a (s) = K m (s + γ)(s + δ) As linhas de comando para chamar e definir dados de entrada e saída do motor CC são mostradas na Tabela 2.1 Tabela 2.1: Linhas de comando para uso do ìdent para obter parâmetros do motor CC clear all; close all; clc; load dados.dat; %carregar dados do ensaio de tensão t = dados(:,1); % tempo (s) % w = dados(:,2); % velocidade angular (rad/s)% Ts = 1/3 %taxa de amostragem motor = iddata;motor.tstart = ; % define objeto motor.ts = Ts motor.inputdata = 12*ones(size(t)); % define entrada degrau motor.outputdata = w; ident motorid.sid ident( motorid.sid % define resposta ao degrau obtida % chamar a interface gráfica % importar dados via objeto motor % escolher modelo % executar o comando Estimate % salvar a seção % chamar a seção salva previamente
31 76 CAPÍTULO 2. INTRODUÇÃO AO MATLAB Identificação do modelo de um miniforno Identificar a constante de tempo, atraso e ganho constante do modelo de um miniforno a partir da resposta à um degrau de tensão aplicado na resistência. Considere a função de transferência entre a temperatura temperatura em o C e a tensão aplicada na resistencia térmica G(s) := Ke sl (1 + st) em que K é o ganho estático, T é a constante de tempo, e L é o atraso. As linhas de comando para chamar e definir dados de entrada e saída do miniforno são apresentadas na Tabela 2.2. Tabela 2.2: Linhas de comando para uso do ìdent para obter parâmetros do miniforno clear all; close all; clc; load dados; y = (dados.y.data*1/.38); tempo = dados.x.data; u = 5*ones(size(y)); % tensão de 5V aplicada D = dados.capture.downsampling; Ts = dados.capture.samplingperiod; Ta = double(d)*ts; % tempo de amostragem f1 = ; f2 = 1; filtro = [ (2*pi)*f2]; % Filtro passa banda [,1Hz] dadoss = iddata(y,u,ta); dadoss.tstart = ; % definindo objeto tempos = dadoss.samplinginstants; disp( Filtrando... ) dadosfilt = idfilt(dadoss,filtro); disp( Filtragem...OK ) disp( Reamostrando... ) P = 1; Q = 1; dadosr = resample(dadosfilt,p,q,25,7); tempor = dadosr.samplinginstants; figure(1) disp( Reamostragem...OK ) saida = dadosr.outputdata; entrada = dadosr.inputdata; ident %chamar a interface gráfica Identificação do modelo de um circuito RLC Identificação das constantes de tempo e ganho constante a partir da resposta em frequência. Seja um circuito RLC série como na Figura 5.3, tendo como entrada uma tensão u(t) e como saída a tensão no capacitor y(t), cuja função de transferência se
32 2.17. MATLAB EM SISTEMAS DE CONTROLE 77 relaciona com a função na forma canônica de um sistema de segunda ordem da seguinte maneira: G(s) = 1 LC s 2 + R L s + 1. LC Considera-se o seguinte modelo autoregressivo com entrada externa (ARX, das iniciais em inglês) para representar os dados A(s)y(s) = B(s)u(s) + e(s) em que A(s) e B(s) denotam os polinômios A(s) = s na + a 1 s na a na e B(s) = b 1 s nb 1 + +b nb, respectivamente. As linhas de comando para chamar e definir dados de entrada e saída do processo 2.3. Tabela 2.3: Linhas de comando para uso do ìdent para obter parâmetros do circuito RLC load dados.dat; %carregar dados da resposta em frequencia An = dados(:,1); % amplitude das oscilações Fn = dados(:,2); % fase das oscilações em graus w=dados(:,3); % frequencia das oscilações em rad/s Ts=; %sistema contínuo RLC=idfrd(resposta,w,Ts); ident RLC.sid ident( RLC.sid ) % define objeto %resposta=an*exp(i*fn*pi/18) % chamar a interface gráfica % importar dados via objeto RLC % escolher modelo ARX de ordem na=2 e nb=1 % executar o comando Estimate % salvar a seção % chamar a seção previamente salva
Toolbox de Sistemas de Controle MATLAB
 Toolbox de Sistemas de Controle MATLAB Control System Toolbox Grupo PET Engenharia Elétrica UFMS Campo Grande MS Junho - 2003 2 Índice Índice 3 1. Introdução 4 2. Representação dos Sistemas 5 2.1. Representação
Toolbox de Sistemas de Controle MATLAB Control System Toolbox Grupo PET Engenharia Elétrica UFMS Campo Grande MS Junho - 2003 2 Índice Índice 3 1. Introdução 4 2. Representação dos Sistemas 5 2.1. Representação
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Estabilidade. Carlos Alexandre Mello. Carlos Alexandre Mello [email protected] 1
 Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Sistemas a Tempo Discreto - Projeto
 Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello [email protected] 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Circuitos Osciladores
 Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
 Resumo Sinais e Sistemas Transformada de aplace [email protected] Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Resumo Sinais e Sistemas Transformada de aplace [email protected] Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação
 Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello [email protected] 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Sessão Prática: Simulação e Controle com LabVIEW
 Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Sistema de excitação
 Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Desempenho de Sistemas de Controle Realimentados
 Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
Aula 13 Análise no domínio da frequência
 Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Introdução AVALIAÇÃO DE DESEMPENHO. No domínio do tempo. No domínio da freqüência. Função de transferência. Módulo e fase da função de transferência
 AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
AULA #12. Estabilidade de Sistemas de Controle por
 AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
Transformada de Laplace. Parte 3
 Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
Controle de Conversores Estáticos Controladores baseados no princípio do modelo interno. Prof. Cassiano Rech [email protected]
 Controle de Conversores Estáticos Controladores baseados no princípio do modelo interno [email protected] 1 Objetivos da aula Projeto de um controlador PID para o controle da tensão de saída de um inversor
Controle de Conversores Estáticos Controladores baseados no princípio do modelo interno [email protected] 1 Objetivos da aula Projeto de um controlador PID para o controle da tensão de saída de um inversor
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech [email protected]
 Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos [email protected] 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos [email protected] 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Departamento de Engenharia Química e de Petróleo UFF. Disciplina: TEQ102- CONTROLE DE PROCESSOS. Diagrama de Bode. Outros Processos de Separação
 Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ102- CONTROLE DE PROCESSOS custo Diagrama de Bode Outros Processos de Separação Prof a Ninoska Bojorge 5.A. Traçado das Assíntotas Traçado
Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ102- CONTROLE DE PROCESSOS custo Diagrama de Bode Outros Processos de Separação Prof a Ninoska Bojorge 5.A. Traçado das Assíntotas Traçado
UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB
 NOME: UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB O que é o Matlab? O Matlab é um sistema para cálculo científico que proporciona um ambiente de fácil utilização com uma notação intuitiva,
NOME: UNIVERSIDADE GAMA FILHO Laboratório de Controle I - MATLAB O que é o Matlab? O Matlab é um sistema para cálculo científico que proporciona um ambiente de fácil utilização com uma notação intuitiva,
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. [email protected] Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. [email protected] Prof. Rafael Concatto Beltrame, Me.
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem
 p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP. Prof. Cassiano Rech [email protected]
 Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP [email protected] 1 Operação como PFP Como a freqüência de comutação do interruptor S é muito maior que a freqüência
Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP [email protected] 1 Operação como PFP Como a freqüência de comutação do interruptor S é muito maior que a freqüência
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, [email protected] Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, [email protected] Campinas, Janeiro de 2007
Análise de Circuitos Elétricos III
 Análise de Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Introdução à Transformada de Laplace A Transformada
Análise de Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Introdução à Transformada de Laplace A Transformada
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle
 Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Modelos Variáveis de Estado
 Modelos Variáveis de Estado Introdução; Variáveis de Estados de Sistemas Dinâmicos; Equação Diferencial de Estado; Função de Transferência a partir das Equações de Estados; Resposta no Domínio do Tempo
Modelos Variáveis de Estado Introdução; Variáveis de Estados de Sistemas Dinâmicos; Equação Diferencial de Estado; Função de Transferência a partir das Equações de Estados; Resposta no Domínio do Tempo
Transformada z. ADL 25 Cap 13. A Transformada z Inversa
 ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
Modelagem de Sistemas Dinâmicos. Eduardo Camponogara
 Equações Diferenciais Ordinárias Modelagem de Sistemas Dinâmicos Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle
Equações Diferenciais Ordinárias Modelagem de Sistemas Dinâmicos Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
MICROMASTER MM4. Usando o Controle de Malha Fechada (PID) Edição 08.2002. IND 1 Drives technology Suporte Técnico Drives Hotline
 s MICROMASTER MM4 Usando o Controle de Malha Fechada (PID) Edição 08.2002 IND 1 Drives technology Suporte Técnico Drives Hotline USANDO O CONTROLE DE MALHA FECHADA NO MM4 O que é controle de malha fechada
s MICROMASTER MM4 Usando o Controle de Malha Fechada (PID) Edição 08.2002 IND 1 Drives technology Suporte Técnico Drives Hotline USANDO O CONTROLE DE MALHA FECHADA NO MM4 O que é controle de malha fechada
Resposta Transitória de Circuitos com Elementos Armazenadores de Energia
 ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
INSTITUTO POLITÉCNICO DE TOMAR. Matlab Tutorials. Principais Funções do Matlab
 Matlab Tutorials Principais Funções do Matlab Funções Básicas do Matlab O Matlab consiste num programa interactivo de computação numérica e visualização de dados. Este programa é muito utilizado na área
Matlab Tutorials Principais Funções do Matlab Funções Básicas do Matlab O Matlab consiste num programa interactivo de computação numérica e visualização de dados. Este programa é muito utilizado na área
Guião do Trabalho Laboratorial Nº 3 Análise do Comportamento de uma Suspensão de Automóvel
 SISEL Sistemas Electromecânicos Guião do Trabalho Laboratorial Nº 3 Análise do Comportamento de uma Suspensão de Automóvel GRIS Group of Robotics and Intelligent Systems Homepage: http://www.dee.isep.ipp.pt/~gris
SISEL Sistemas Electromecânicos Guião do Trabalho Laboratorial Nº 3 Análise do Comportamento de uma Suspensão de Automóvel GRIS Group of Robotics and Intelligent Systems Homepage: http://www.dee.isep.ipp.pt/~gris
Universidade Federal do Rio de Janeiro. Princípios de Instrumentação Biomédica. Módulo 4
 Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
2 - Modelos em Controlo por Computador
 Modelação, Identificação e Controlo Digital 2-Modelos em Controlo por Computador 1 2 - Modelos em Controlo por Computador Objectivo: Introduzir a classe de modelos digitais que são empregues nesta disciplina
Modelação, Identificação e Controlo Digital 2-Modelos em Controlo por Computador 1 2 - Modelos em Controlo por Computador Objectivo: Introduzir a classe de modelos digitais que são empregues nesta disciplina
CAPÍTULO 4 - ANÁLISE DA RESPOSTA EM FREQÜÊNCIA
 CAPÍTULO 4 - ANÁLISE DA RESPOSTA EM FREQÜÊNCIA 4.. Introdução Pelo termo resposta em freqüência, entende-se a resposta em regime estacionário de um sistema com entrada senoidal. Nos métodos de resposta
CAPÍTULO 4 - ANÁLISE DA RESPOSTA EM FREQÜÊNCIA 4.. Introdução Pelo termo resposta em freqüência, entende-se a resposta em regime estacionário de um sistema com entrada senoidal. Nos métodos de resposta
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO
 PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, [email protected]
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, [email protected]
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. [email protected] Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. [email protected] Prof. Rafael Concatto Beltrame, Me.
² Servomecanismo: Sistema de controle realimentado para controle automático de posição, velocidade ou aceleração. Muito empregado na indústria.
 1. Introdução 1.1. De nições Básicas ² Sistema: Interconexão de dispositivos e elementos para cumprir um objetivo desejado. ² Processo: Um sistema ou dispositivo a ser controlado. ² Sistema de controle:
1. Introdução 1.1. De nições Básicas ² Sistema: Interconexão de dispositivos e elementos para cumprir um objetivo desejado. ² Processo: Um sistema ou dispositivo a ser controlado. ² Sistema de controle:
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
 Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
5. Diagramas de blocos
 5. Diagramas de blocos Um sistema de controlo pode ser constituído por vários componentes. O diagrama de blocos é uma representação por meio de símbolos das funções desempenhadas por cada componente e
5. Diagramas de blocos Um sistema de controlo pode ser constituído por vários componentes. O diagrama de blocos é uma representação por meio de símbolos das funções desempenhadas por cada componente e
Aplicações com OpAmp. 1) Amplificadores básicos. Amplificador Inversor
 225 Aplicações com OpAmp A quantidade de circuitos que podem ser implementados com opamps é ilimitada. Selecionamos aqueles circuitos mais comuns na prática e agrupamos por categorias. A A seguir passaremos
225 Aplicações com OpAmp A quantidade de circuitos que podem ser implementados com opamps é ilimitada. Selecionamos aqueles circuitos mais comuns na prática e agrupamos por categorias. A A seguir passaremos
Filtros de sinais. Conhecendo os filtros de sinais.
 Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes
 Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade
 Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Conversão Digital Analógico e Analógico Digital. Disciplina: Eletrônica Básica Prof. Manoel Eusebio de Lima
 Conversão Digital Analógico e Analógico Digital Disciplina: Eletrônica Básica Prof. Manoel Eusebio de Lima Agenda Grandezas Digitais e Analógicas Por que converter? Diagrama básico para conversão Conversores
Conversão Digital Analógico e Analógico Digital Disciplina: Eletrônica Básica Prof. Manoel Eusebio de Lima Agenda Grandezas Digitais e Analógicas Por que converter? Diagrama básico para conversão Conversores
ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS
 ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS 01 - Questão Esta questão deve ser corrigida? SIM NÃO Um transformador de isolação monofásico, com relação de espiras N
ABAIXO ENCONTRAM-SE 10 QUESTÕES. VOCÊ DEVE ESCOLHER E RESPONDER APENAS A 08 DELAS 01 - Questão Esta questão deve ser corrigida? SIM NÃO Um transformador de isolação monofásico, com relação de espiras N
LABORATÓRIO DE CONTROLE I ESTUDO DE COMPENSADORES DE FASE
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 4: ESTUDO DE COMPENSADORES DE FASE COLEGIADO DE ENGENHARIA ELÉTRICA DISCENTES: Lucas
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 4: ESTUDO DE COMPENSADORES DE FASE COLEGIADO DE ENGENHARIA ELÉTRICA DISCENTES: Lucas
Laboratório de Circuitos Elétricos II
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ ESCOLA POLITÉCNICA CURSO DE ENGENHARIA DE COMPUTAÇÃO DISCIPLINA DE CIRCUITOS ELÉTRICOS II NOME DO ALUNO: Laboratório de Circuitos Elétricos II Prof. Alessandro
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ ESCOLA POLITÉCNICA CURSO DE ENGENHARIA DE COMPUTAÇÃO DISCIPLINA DE CIRCUITOS ELÉTRICOS II NOME DO ALUNO: Laboratório de Circuitos Elétricos II Prof. Alessandro
Técnico em Eletrotécnica
 Técnico em Eletrotécnica Caderno de Questões Prova Objetiva 2015 01 Em uma corrente elétrica, o deslocamento dos elétrons para produzir a corrente se deve ao seguinte fator: a) fluxo dos elétrons b) forças
Técnico em Eletrotécnica Caderno de Questões Prova Objetiva 2015 01 Em uma corrente elétrica, o deslocamento dos elétrons para produzir a corrente se deve ao seguinte fator: a) fluxo dos elétrons b) forças
4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92)
 ADL22 4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92) A transformada de Laplace fornece: (4.93) (4.94) A fim de separar X(s), substitua sx(s)
ADL22 4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92) A transformada de Laplace fornece: (4.93) (4.94) A fim de separar X(s), substitua sx(s)
Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros
 Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Capítulo 11 MOTORES ELÉTRICOS DE CORRENTE CONTÍNUA E UNIVERSAL. Introdução
 Capítulo 11 MOTORES ELÉTRICOS DE CORRENTE CONTÍNUA E UNIVERSAL Esta aula apresenta o princípio de funcionamento dos motores elétricos de corrente contínua, o papel do comutador, as características e relações
Capítulo 11 MOTORES ELÉTRICOS DE CORRENTE CONTÍNUA E UNIVERSAL Esta aula apresenta o princípio de funcionamento dos motores elétricos de corrente contínua, o papel do comutador, as características e relações
( ) ( ) ( ( ) ( )) ( )
 Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Métodos de Sintonização de Controladores PID
 3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
SISTEMAS DE CONTROLO. Objectivos Pedagógicos
 SISTEMAS DE CONTROLO Responsável: Prof. Doutor João Miguel Gago Pontes de Brito Lima Atendimento (Gab. 2.63): Terça e Quarta das 11:00 à 13:00 Objectivos Pedagógicos Pretende-se com esta disciplina fornecer
SISTEMAS DE CONTROLO Responsável: Prof. Doutor João Miguel Gago Pontes de Brito Lima Atendimento (Gab. 2.63): Terça e Quarta das 11:00 à 13:00 Objectivos Pedagógicos Pretende-se com esta disciplina fornecer
ACIONAMENTOS ELETRÔNICOS (INVERSOR DE FREQUÊNCIA)
 ACIONAMENTOS ELETRÔNICOS (INVERSOR DE FREQUÊNCIA) 1. Introdução 1.1 Inversor de Frequência A necessidade de aumento de produção e diminuição de custos faz surgir uma grande infinidade de equipamentos desenvolvidos
ACIONAMENTOS ELETRÔNICOS (INVERSOR DE FREQUÊNCIA) 1. Introdução 1.1 Inversor de Frequência A necessidade de aumento de produção e diminuição de custos faz surgir uma grande infinidade de equipamentos desenvolvidos
3) IMPORTÂNCIA DESTE PROGRAMA DE APRENDIZAGEM NA FORMAÇÃO PROFISSIONAL, NESTE MOMENTO DO CURSO
 PROGRAMA DE APRENDIZAGEM NOME: SEL0302 Circuitos Elétricos II PROFESSORES: Azauri Albano de Oliveira Junior turma Eletrônica PERÍODO LETIVO: Quarto período NÚMERO DE AULAS: SEMANAIS: 04 aulas TOTAL: 60
PROGRAMA DE APRENDIZAGEM NOME: SEL0302 Circuitos Elétricos II PROFESSORES: Azauri Albano de Oliveira Junior turma Eletrônica PERÍODO LETIVO: Quarto período NÚMERO DE AULAS: SEMANAIS: 04 aulas TOTAL: 60
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 1
 597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
2 A Derivada. 2.1 Velocidade Média e Velocidade Instantânea
 2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
2 O objetivo geral desse curso de Cálculo será o de estudar dois conceitos básicos: a Derivada e a Integral. No decorrer do curso esses dois conceitos, embora motivados de formas distintas, serão por mais
2.3- DIAGRAMAS DE BLOCOS E DE FLUXO DE SINAL. FÓRMULA DE MASON DIAGRAMA DE BLOCOS DB
 2.3 DIRMS DE BLOOS E DE FLUXO DE SINL. FÓRMUL DE MSON DIRM DE BLOOS DB Os sistemas de controle, geralmente, são constituídos por vários componentes ou partes interligadas. Para mostrar estas interconexões
2.3 DIRMS DE BLOOS E DE FLUXO DE SINL. FÓRMUL DE MSON DIRM DE BLOOS DB Os sistemas de controle, geralmente, são constituídos por vários componentes ou partes interligadas. Para mostrar estas interconexões
CONVERSORES E CONTROLADORES DE FASE. Circuitos de retificação monofásicos
 CONVERSORES E CONTROLADORES DE FASE Um conversor é um equipamento utilizado para converter potência alternada em potência contínua. Num conversor simples, que usa somente diodos retificadores, a tensão
CONVERSORES E CONTROLADORES DE FASE Um conversor é um equipamento utilizado para converter potência alternada em potência contínua. Num conversor simples, que usa somente diodos retificadores, a tensão
Circuitos Elétricos Senoides e Fasores
 Circuitos Elétricos Senoides e Fasores Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Corrente contínua x corrente alternada. Ver War of Currentes
Circuitos Elétricos Senoides e Fasores Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Corrente contínua x corrente alternada. Ver War of Currentes
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 1 A resistência
Circuitos Elétricos III Prof. Danilo Melges ([email protected]) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 1 A resistência
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Função de Transferência de Malha Fechada
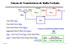 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
DIODO SEMICONDUTOR. Conceitos Básicos. Prof. Marcelo Wendling Ago/2011
 DIODO SEMICONDUTOR Prof. Marcelo Wendling Ago/2011 Conceitos Básicos O diodo semicondutor é um componente que pode comportar-se como condutor ou isolante elétrico, dependendo da forma como a tensão é aplicada
DIODO SEMICONDUTOR Prof. Marcelo Wendling Ago/2011 Conceitos Básicos O diodo semicondutor é um componente que pode comportar-se como condutor ou isolante elétrico, dependendo da forma como a tensão é aplicada
4.2 Produto Vetorial. Orientação sobre uma reta r
 94 4. Produto Vetorial Dados dois vetores u e v no espaço, vamos definir um novo vetor, ortogonal a u e v, denotado por u v (ou u v, em outros textos) e denominado produto vetorial de u e v. Mas antes,
94 4. Produto Vetorial Dados dois vetores u e v no espaço, vamos definir um novo vetor, ortogonal a u e v, denotado por u v (ou u v, em outros textos) e denominado produto vetorial de u e v. Mas antes,
Tutorial de Eletrônica Aplicações com 555 v2010.05
 Tutorial de Eletrônica Aplicações com 555 v2010.05 Linha de Equipamentos MEC Desenvolvidos por: Maxwell Bohr Instrumentação Eletrônica Ltda. Rua Porto Alegre, 212 Londrina PR Brasil http://www.maxwellbohr.com.br
Tutorial de Eletrônica Aplicações com 555 v2010.05 Linha de Equipamentos MEC Desenvolvidos por: Maxwell Bohr Instrumentação Eletrônica Ltda. Rua Porto Alegre, 212 Londrina PR Brasil http://www.maxwellbohr.com.br
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 15
 Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Razão de Rejeição a Fonte de Potência (PSRR)
 215 Outra unidade que expressa de forma direta o efeito da CMRR. Pode ser obtida observando que a tensão de offset V CM é expressa por: V CM = V C. 1/CMRR = V C.CMRR -1 Agora como CMRR -1 expressa-lo em
215 Outra unidade que expressa de forma direta o efeito da CMRR. Pode ser obtida observando que a tensão de offset V CM é expressa por: V CM = V C. 1/CMRR = V C.CMRR -1 Agora como CMRR -1 expressa-lo em
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
Engenharia de Controle
 Engenharia de Controle Prof. Fernando de Oliveira Souza Contato: Sala 2523 (BLOCO 1) e-mail: [email protected] www.cpdee.ufmg.br/ fosouza Terças-feiras (20h55 às 22h35) e Sextas-feiras (19h00 às 20h40)
Engenharia de Controle Prof. Fernando de Oliveira Souza Contato: Sala 2523 (BLOCO 1) e-mail: [email protected] www.cpdee.ufmg.br/ fosouza Terças-feiras (20h55 às 22h35) e Sextas-feiras (19h00 às 20h40)
UNIVERSIDADE FEDERAL DE SANTA MARIA - UFSM CENTRO DE TECNOLOGIA - CT DEPARTAMENTO DE ELETRÔNICA E COMPUTAÇÃO - DELC PROJETO REENGE - ENG.
 UNIVERSIDADE FEDERAL DE SANTA MARIA - UFSM CENTRO DE TECNOLOGIA - CT DEPARTAMENTO DE ELETRÔNICA E COMPUTAÇÃO - DELC PROJETO REENGE - ENG. ELÉTRICA CADERNO DIDÁTICO DE SISTEMAS DE CONTROLE 1 ELABORAÇÃO:
UNIVERSIDADE FEDERAL DE SANTA MARIA - UFSM CENTRO DE TECNOLOGIA - CT DEPARTAMENTO DE ELETRÔNICA E COMPUTAÇÃO - DELC PROJETO REENGE - ENG. ELÉTRICA CADERNO DIDÁTICO DE SISTEMAS DE CONTROLE 1 ELABORAÇÃO:
Ondas Eletromagnéticas. E=0, 1 B=0, 2 E= B t, 3 E
 Ondas Eletromagnéticas. (a) Ondas Planas: - Tendo introduzido dinâmica no sistema, podemos nos perguntar se isto converte o campo eletromagnético de Maxwell em uma entidade com existência própria. Em outras
Ondas Eletromagnéticas. (a) Ondas Planas: - Tendo introduzido dinâmica no sistema, podemos nos perguntar se isto converte o campo eletromagnético de Maxwell em uma entidade com existência própria. Em outras
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
OBJETIVOS: CARGA HORÁRIA MÍNIMA CRONOGRAMA:
 ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
ESTUDO DIRIGIDO COMPONENTE CURRICULAR: Controle de Processos e Instrumentação PROFESSOR: Dorival Rosa Brito ESTUDO DIRIGIDO: Métodos de Determinação de Parâmetros de Processos APRESENTAÇÃO: O rápido desenvolvimento
Video Lecture RF. Laps
 Video Lecture RF Laps Agenda 1. Considerações no projeto de circuitos RF 2. Casamento de impedância 3. Parâmetros S e Carta de Smith 4. Dispositivos/blocos comumente usados 5. Arquiteturas de transceptores
Video Lecture RF Laps Agenda 1. Considerações no projeto de circuitos RF 2. Casamento de impedância 3. Parâmetros S e Carta de Smith 4. Dispositivos/blocos comumente usados 5. Arquiteturas de transceptores
LABORATÓRIO 3 Análise dinâmica do controle do motor PARTE 1. ANÁLISE DO CONTROLE DE VELOCIDADE
 LABORATÓRIO 3 Análise dinâmica do controle do motor OBJETIVOS: - analisar a resposta transitória a mudanças degrau pelas variações de ganho, pela inclusão de atraso e pelo aumento do momento de inércia;
LABORATÓRIO 3 Análise dinâmica do controle do motor OBJETIVOS: - analisar a resposta transitória a mudanças degrau pelas variações de ganho, pela inclusão de atraso e pelo aumento do momento de inércia;
O que você deve saber sobre
 O que você deve saber sobre Além de resistores, os circuitos elétricos apresentam dispositivos para gerar energia potencial elétrica a partir de outros componentes (geradores), armazenar cargas, interromper
O que você deve saber sobre Além de resistores, os circuitos elétricos apresentam dispositivos para gerar energia potencial elétrica a partir de outros componentes (geradores), armazenar cargas, interromper
MODULAÇÃO AM E DEMODULADOR DE ENVELOPE
 204/ MODULAÇÃO AM E DEMODULADOR DE ENVELOPE 204/ Objetivos de Estudo: Desenvolvimento de um modulador AM e um demodulador, utilizando MatLab. Visualização dos efeitos de modulação e demodulação no domínio
204/ MODULAÇÃO AM E DEMODULADOR DE ENVELOPE 204/ Objetivos de Estudo: Desenvolvimento de um modulador AM e um demodulador, utilizando MatLab. Visualização dos efeitos de modulação e demodulação no domínio
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA UNIDADE ACADEMICA DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA UNIDADE ACADEMICA DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCÍCIOS #11 (1) O circuito a seguir é usado como pré-amplificador
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA UNIDADE ACADEMICA DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCÍCIOS #11 (1) O circuito a seguir é usado como pré-amplificador
Uma lei que associa mais de um valor y a um valor x é uma relação, mas não uma função. O contrário é verdadeiro (isto é, toda função é uma relação).
 5. FUNÇÕES DE UMA VARIÁVEL 5.1. INTRODUÇÃO Devemos compreender função como uma lei que associa um valor x pertencente a um conjunto A a um único valor y pertencente a um conjunto B, ao que denotamos por
5. FUNÇÕES DE UMA VARIÁVEL 5.1. INTRODUÇÃO Devemos compreender função como uma lei que associa um valor x pertencente a um conjunto A a um único valor y pertencente a um conjunto B, ao que denotamos por
REAL LACOS: CONTROLE DIGITAL EM TEMPO REAL
 REAL LACOS: CONTROLE DIGITAL EM TEMPO REAL Andreya Prestes da Silva 1, Rejane de Barros Araújo 1, Rosana Paula Soares Oliveira 1 e Luiz Affonso Guedes 1 Universidade Federal do ParáB 1 Laboratório de Controle
REAL LACOS: CONTROLE DIGITAL EM TEMPO REAL Andreya Prestes da Silva 1, Rejane de Barros Araújo 1, Rosana Paula Soares Oliveira 1 e Luiz Affonso Guedes 1 Universidade Federal do ParáB 1 Laboratório de Controle
