Cálculo de Carga dos Rolamentos
|
|
|
- Caio Castelhano Aveiro
- 8 Há anos
- Visualizações:
Transcrição
1 4. Cálculo de carga dos s Para calcular as cargas dos s, deve-se determinar as forças que atuam sobre o eixo que é suportado pelos s. Estas forças incluem o peso morto inerente ao corpo giratório, a carga produzida quando a máquina realiza um trabalho e a carga produzida por ação da força dinâmica de transmissão. Teoricamente, as cargas podem ser calculadas, mas o cálculo é difícil na maioria dos casos. Um método de cálculo de cargas que atuam sobre o eixo que transmite força dinâmica, sendo esta a principal aplicação, é mostrada abaixo. 4. Cargas que atuam no eixo 4.. tor de carga Há inúmeros casos onde a carga operacional real sobre o eixo, é muito maior do que a carga teórica calculada, devido a vibração ou choques. A carga real do eixo, pode ser calculada conforme a formula (4.). K fwkc 4. Onde: K Carga real sobre o eixo Nkgf fw tor de carga (Tabela 4.) KcValor teórico calculado Nkgf Tabela 4. tor de carga fw Intensidade de choque Muito baixo ou sem choque Choques leves..5 Choques pesados fw Aplicação Máquinas elétricas sem choque, máquinas ferramentas, instrumentos de medição. Veículos ferroviários, automóveis, moinhos de rolos, máquinas para trabalhar metal, máquinas para fabricar papel, máquinas para misturar borracha, impressoras, aeronaves, máquinas têxteis, unidades elétricas, máquinas para escritório. Trituradores, equipamentos agrícolas, equipamentos de construção, guindastes. 4.. Cargas de engrenamento As cargas que atuam sobre engrenagens podem dividirse em três tipos principais segundo a direção na qual se aplica a carga: tangencial (Kt), radial (Ks), e axial (Ka). A magnitude e direção dessas cargas variam segundo os tipos de engrenagens. O método de cálculo de cargas, informado a seguir, é para dois tipos de engrenagens e arranjos de uso geral: Engrenagens para eixos paralelos e engrenagens para eixos transversais. Para métodos de cálculo referentes a outros tipos de arranjos de engrenagens e eixos, favor consultar a Engenharia da NTN. () Cargas atuantes em engrenagems sobre eixos paralelos As forças que atuam sobre as engrenagens retas e helicoidais em eixos paralelos, estão indicadas nas figs. 4., 4. e 4.3. A magnitude das cargas pode ser determinada usando as equações (4.) a (4.5). K t 9.06 H D N pn H D kgf pn Ks Kttandentes retos 4.3a K t tan dentes helicoidais cos 4.3b Kr Kt Ks 4.4 Ka Kttandentes retos 4.5 Onde: KtCarga tangencial da engrenagem (força tangencial), N {kgf} KsCarga radial da engrenagem (força de separação), N {kgf} KrCarga do eixo em ângulo reto (força resultante da força tangencial e da força de separação), N {kgf} KaCarga paralela ao eixo, N {kgf} H orça de transmissão, kw n Rotação, rpm DpDiâmetro do passo da engrenagem, mm Ângulo de pressão da engrenagem, Ângulo da hélice, Como a carga real da engrenagem também contém vibrações e cargas de choque, as cargas teóricas obtidas com as equações anteriores devem ser ajustadas pelo fator de engrenagem fz, conforme indicado na tabela 4.. Ks ig. 4. Cargas de engrenagens retas Ks ig. 4. Cargas de engrenagens helicoidais Kt Kr Ks Kt Kt Ka ig. 4.3 orça radial resultante Dp A-
2 Tabela 4. tor de engrenagem fz Tipo de engrenagem Engrenagens com retífica de precisão (Erros no passo e no perfil do dente inferior a 0,0 mm) Engrenagens torneadas de acabamento ordinário (Erros no passo e no perfil do dente inferior a 0, mm) ()Cargas atuantes sobre eixos transversais As cargas que atuam sobre engrenagens cônicas de dentes retos e sobre engrenagens cônicas espirais em eixos transversais estão indicadas nas figs. 4.4 e 4.5. Os métodos de cálculo para se obter estas cargas nas engrenagens estão indicadas na tabela 4.3. Para o cálculo das cargas nas engrenagens cônicas de dentes retos, pode-se aplicar o ângulo da hélice =0. Os símbolos e unidades usados na tabela 4.3 são os seguintes: Kt Carga tangencial da engrenagem (força tangencial), N {kgf} Ks Carga radial da engrenagem (força de separação), N {kgf} Ka Carga paralela ao eixo, N {kgf} H orça de transmissão, kw n Rotação, rpm DpmDiâmetro médio do passo, mm Ångulo de pressão da engrenagem, Ångulo da hélice, Ångulo do passo do cone, Devido à intersecção de dois eixos, a relação de carga entre pinhão e coroa é dada por: fz KspKsgorça de separação do pinhão e da coroa (engrenagem), N {kgf} KapKagCarga axial do pinhão e da coroa (engrenagem), N {kgf} Para engrenagens cônicas espirais, o sentido da carga varia em função da direção do ângulo da hélice, do sentido de rotação, e de qual é o lado motor e o lado movido. O sentido da força de separação (Ks) e da carga axial (Ka), indicado na fig. 4.5 é positivo. O sentido de rotação e de direção do ângulo da hélice são definidos aso serem vistos pelo lado da engrenagem de diâmetro maior. O sentido de rotação da engrenagem da fig. 4.5 é assumido como horário (direito). Kag Ksg Ktg K tp Kap Ksp ig. 4.4 Cargas sobre engrenagens cônicas δ β K s K a K t D pm KspKag4.6 KapKsg4.7 Tabela 4.3 Cargas que atuam sobre as engrenagens cônicas Tipos de cargas Sentido de rotação Direção da hélice ig. 4.5 Diagramas de engrenagens cônicas Horário Anti-horário Horário Anti-horário Direito Esquerdo Esquerdo Direito Carga tangencial Kt Kt 9.06 H Dpmn, H Dpmn Carga Radial (força de separação) Ks Lado motor Lado movido KsKt KsKt tan tansin KsKt tan tansin tan tansin KsKt tan tansin Carga axial Lado motor KaKt tan sin tan KaKt tan sin tan Ka Lado movido KaKt tan sin tan KaKt tan sin tan A-
3 4..3 Carga sobre o eixo devido a correias /correntes As cargas tangenciais sobre as rodas dentadas ou polias podem ser calculadas pela equação (4.8). Kt H N Dpn H kgf Dpn Onde, KtCargas tangenciais, N {kgf} H Potência transmitida, kw DpDiâmetro do passo da roda dentada/polia, mm Para transmissões de potência por correias se aplica uma tensão inicial para manter constante a tensão de operação na polia e na correia. Levando-se em conta esta tensão, as cargas radiais que atuam nas polias são obtidas através da equação (4.9). Para transmissões de potência por corrente, a mesma equação pode ser usada se as cargas de vibração e choque são levadas em consideração. Krf bkt4.9 KrCarga radial na roda dentada ou polia, N {kgf} f btor de corrente ou correia (Tabela 4.4) 4. Distribuição da carga sobre os s Para sistemas de eixos, se considera que a tensão estática é recebida através dos s e qualquer carga atuante sobre o eixo é distribuída sobre os s. Por exemplo, no conjunto de eixo e engrenagem representado na fig. 4.7 as cargas aplicadas sobre os s podem ser determinadas mediante o uso das equações (4.0) e (4.). Este é um exemplo simples, mas normalmente tais cálculos são complexos. ra ab d 4.0 b cd rb a c 4. b cd racarga radial no A, N {kgf} rbcarga radial no B, N {kgf}, Carga radial no eixo, N {kgf} Se as direções de carga radial forem diferentes, a soma vetorial de cada carga deve ser determinada. a b Rolamento A Rolamento B Tabela 4.4 tor de corrente ou correia f b Tipo da corrente ou da correia f b ra rb Corrente simples..5 Correia em V Correia de c d Correia plana (com polia tensionadora) Correia plana ig. 4.7 Eixo de engrenagem Lado frouxo Dp Kr Lado tencionado ig. 4.6 Cargas em correntes / correias A-3
4 4.3 Carga média Em muitos casos, em circunstância normais, a carga sobre os s utilizados em máquinas irá flutuar em função de um período de tempo fixo, ou de uma jornada de trabalho programada. A carga sobre os s que operam sob estas condições pode ser convertida em uma carga média (); esta é uma carga que dá aos s a mesma vida que teriam sob condições de operação constantes. () Carga flutuante escalonada A carga média dos s,, para cargas escalonadas, se calcula através da equação (4.).,... n são as cargas que atuam sobre o ; n, n...nn e t, t... tn são as rotações do e os tempos de operação respectivamente onde: i p ni ti p 4. ni ti p3 p03 para s de esferas para s de rolos (3) Carga flutuante linear A carga média,, pode ser aproximada pela equação (4.4) inax ax in ig. 4.0 Carga linear flutuante (4) Carga flutuante senoidal A carga média, pode ser aproximada pelas equações (4.5) e (4.6). caso (a) caso (b) 0.75ax ax 4.6 t n n t nt nn tn ax ig. 4.8 Carga escalonada () Carga de série consecutiva Quando é possível exprimir a função (t) em termos de carga cíclica to e do tempo t, a carga média é determinada através da equação (4.3) a t where: to t p dt p 4.3 to o p3 p03 para s de esferas para s de rolos ax b t ig. 4. Carga variável senoidal (t) 0 to to t ig. 4.9 Carga de série em função do tempo A-4
5 4.4 Carga equivalente 4.4. Carga dinâmica equivalente Quando as cargas dinâmicas radiais e cargas dinâmicas axiais atuam sobre um ao mesmo tempo, a carga hipotética que atua sobre o centro dos s e que lhes dá a mesma vida como se tivessem somente carga radial ou somente axial, se denomina carga dinâmica equivalente. Para s radiais, esta carga se expressa como carga radial pura e é denominada carga radial dinâmica equivalente. Para s axiais, se expressa como carga axial pura, e é denominada carga axial dinâmica equivalente. () Carga radial dinâmica equivalente A carga radial dinâmica equivalente é expressa pela equação (4.7). PrXrY4.7 PrCarga radial dinâmica equivalente, N {kgf} rcarga radial atuante, N {kgf} Carga axial atuante N {kgf} X tor de carga radial Y tor de carga axial Os valores para X e Y estão listados nas tabelas de s. () Carga axial dinâmica equivalente Como regra geral, os s axiais padronizados com contato angular de 90 não podem suportar cargas radiais. Entretanto, s axiais autocompensadores de rolos podem suportar uma parcela de carga radial. A carga axial dinâmica equivalente para estes s é determinada pela equação (4.8). Pa.r4.8 PaCarga axial dinâmica equivalente, N {kgf} Carga axial atuante, N {kgf} rcarga radial atuante, N {kgf} Desde que r / 0.55 somente Carga estática equivalente A carga estática equivalente é uma carga hipotética que poderia causar a mesma deformação permanente total nos pontos de contato de maior esforço entre os corpos rolantes e as pistas como se fosse sob as condições reais de uma carga atuante; Esta situação se dá quando as cargas radiais estáticas e as cargas axiais estáticas atuam simultaneamente sobre o. Para s radiais esta carga hipotética se refere a cargas radiais puras e para s axiais se refere a cargas axiais puras e centradas. Estas cargas são denominadas cargas radiais estáticas equivalentes e cargas axiais estáticas equivalentes, respectivamente. () Carga radial estática equivalente Para s radiais a carga radial estática equivalente pode ser determinada através das equações (4.9) ou (4.0). O maior dos dois resultados é o valor utilizado para Por. PorXo ryo 4.9 Porr 4.0 PorCarga radial estática equivalente, N {kgf} r Carga radial atuante, N {kgf} Carga axial atuante, N {kgf} Xotor de carga estática radial Yo tor de carga estática axial Os valores para Xo e Yo estão listados nas respectivas tabelas de s. () Carga axial estática equivalente Para s axiais autocompensadores de rolos, a carga axial estática equivalente é expressa pela equação (4.). Poa.7r4. PoaCarga axial estática equivalente, N {kgf} Carga axial atuante, N {kgf} r Carga radial atuante, N {kgf} Desde que r / 0.55 somente Cálculo da carga para s de esferas de contato angular e s de rolos cônicos Para s de esferas de contato angular e s de rolos cônicos, o ápice do cone de pressão (centro de carga) está localizado conforme indicado na fig. 4., e seus valores estão listados nas tabelas de s. Quando cargas radiais atuam sobre estes tipos de s, um componente de força é induzido na direção axial. Por esta razão, estes s são aplicados em pares (arranjo DB ou D). Este componente de força deve ser considerado para o cálculo de carga e se expressa conforme a equação (4.) 0.5r 4. Y : Carga axial dinâmica equivalente, N {kgf} r : Carga radial atuante, N {kgf} Y : tor de carga axial As cargas radiais dinâmicas equivalentes para esses pares de s são dados na tabela 4.5. a r Centro de carga a r Centro de carga ig. 4. Ápice do cone de pressão e componente de carga axial A-5
6 Tabela 4.5 Disposição de s e carga dinâmica equivalente Disposição do Condição de carga Carga axial Carga radial equivalente DB (Costa a costa) r r 0.5r 0.5r 0.5r PrXr Prr 0.5r D (ce a face) r r 0.5r 0.5r 0.5r Prr PrXr 0.5r DB (Costa a costa) r r 0.5r 0.5r 0.5r Prr PrXr 0.5r D (ce a face) r r 0.5r 0.5r 0.5r PrXr Prr 0.5r Nota : Aplicável para pré-carga zero. : orças radiais em sentido oposto ao indicado na ilustração acima também são consideradas como positivas. A-6
7 4.5 Vida nominal e exemplos de cálculo da vida Nos exemplos dados nesta seção, para o propósito de cálculo, todos os fatores de carga hipotética, bem como todos os fatores de carga calculados, podem estar presumidamente inclusos como resultante dos valores de carga. (Exemplo ) Qual é a vida nominal em horas de operação (L0h) para o de esferas 608, operando a velocidade de rotação n = 650 rpm, com uma carga radial r de 3. kn? Conforme a fórmula 4.7, a carga radial dinâmica equivalente é: Prr3.kN36kgf A capacidade de carga dinâmica Cr para o 608 da página B- é 9.kN; O fator de rotação fn para s de esferas n = 650 rpm da figura 3. é fn = Assim sendo, o fator de vida fh, conforme a fórmula é: f hfn Cr P r 3. Portanto, com fh = 3.36 da figura 3., a vida nominal L0h, é de aproximadamente 9,000 horas. Da figura 3. e fórmula (3.), o fator de vida fh é: f h f n Cr Pr 4.38 Portanto, com o fator de vida fh =.46, da figura 3., a vida nominal L0h é de aproximadamente 7,500 horas. (Exemplo 3) Determine o tamanho ótimo para um de rolos cilíndricos que opera a 450 rpm, com uma carga radial, r de 00 kn, e que deve ter uma vida nominal superior a horas. Da fig. 3. o fator de vida fh = 3.0 (L0h para 0,000), E o fator de rotação fn = 0.46 (n = 450 rpm). Para encontrar a capacidade de carga dinâmica Cr, utiliza-se a equação (3.). Cr f h Pr f n 0.46,33kN34,000kgf Da tabela de s página B-06 o menor que segue todos os requisitos é o NU336 (Cr =380 kn). (Exemplo ) Qual é a vida nominal L0h para o mesmo nas mesmas condições do exemplo acima, mas com uma carga axial adicional de.8kn? Para encontrar o valor da carga radial dinâmica equivalente Pr, deve-se utilizar o fator de carga radial X e o fator de carga axial Y. A capacidade de carga estática básica Cor para o 608 informado na página B- é 7.8kN e fo é 4.0. Assim sendo: fo Cor 7.8 Calculando-se pelo método de interpolação proporcional, dado na pág. B-3, e = 0.30 para as operações de carga axial e radial: e=0.30 r 3. Conforme o dado da página B-3, X = 0.56 e Y =.44, portanto, a carga radial equivalente dada pela fórmula (4.7) Pr, é: PrXrY kn447kgf A-7
8 (Exemplo 4) A engrenagem de dentes retos da figura 4.3 (diâmetro do passo Dp 50mm, ângulo de pressão = 0 ) está apoiada em um par de s de rolos cônicos, sendo; 4T-306 (Cr = 54.5 kn) e 4T-305 (Cr = 4kN). Encontre os valores referentes a vida nominal de cada quando a engrenagem transfere a força H = 50 kw a,000 rpm. Rolamento (4T-306) 50 Rolamento (4T-305) Da fórmula (3.5) e figura 3., o fator de vida fh para cada é: Cr f h fn Pr Cr f h fn Pr Portanto, a =.4 (4T- de rolos cônicos da pág. B-44) Lh 3,00a 3,00.4 8,480 horas Lh,600a, ,40 horas A vida combinada do Lh, da fórmula 3.3, é: Lh e ig. 4.3 Diagrama da engrenagem de dentes retos As cargas de engrenamento das fórmulas (4.), (4.3) e (4.4), são: Kt 9.06 H 9,0050 D pn 50, kN974kgf Ks Kttan9.55tan0 3.48kN355kgf Kr Kt Ks kN,040kgf As cargas radiais aplicadas aos s!e@, são: e Lh e Lh 8,480 9/8 6,40 9/8 9,330 horas 8/9 r 00 Kr kN r 70 K kN r r.5 A carga radial equivalente da tabela (4.5): Pr r 5.98kN60kgf Pr Xr 0.5r kN489kgf A-8
9 (Exemplo 5) Encontre a carga media para um de rolos esféricos 393 (La = 30 kn) quando se opera sob condições flutuantes indicas na tabela 4.6. Tabela 4.6 Condição Tempo de Carga radial Carga axial Rotações Nr. operação ri i ni i i kn kgf kn kgf rpm A carga radial equivalente, Pr, para cada condição de operação é encontrada mediante o uso da equação (4.7) e mostrada na tabela 4.7. Como todos os valores de ri e i das tabelas de s são maiores que / r > e 0.8, X 0.67, P Xri i 0.67ri 5.50i Da equação (4.) a carga média,, é: Tabela 4.7 0/3 Pri ni i 3/0 48.kN4,906kgf ni i Condiçao Nr. i Carga radial equivalente Pri kn kgf (Exemplo 6) Encontre a vida nominal e a carga axial permissível do de rolos cilíndricos NUP3 quando operando conforme condições a seguir. Carga axial intermitente e lubrificação com óleo. Carga radial r0kn,00kgf Rotação n,000 rpm A carga radial equivalente é: P0kN O fator de rotação de s de rolos cilíndricos, f, para n,000 rpm, da tabela. 3. fn /0 0.93,000 O fator de vida, f h, da tabela. 3. f h Portanto a vida nominal, L0h, da equação (3.3) L0h /3 37,000 A carga axial permissível para s de rolos cilíndricos é mostrada na página B-93. Na equação () na página B-93, baseado no NUP3 da tabela 4 na página B-93, k = dp6030/95mmn,000 rpm Levando em consideração a carga axial intermitente: dpn Na fig. na página B-93, dpn = A pressão permissível sobre a face do colar é Pt=40 MPa. Portanto a carga axial permissível, Pt, é Pz ,360N Baseado na tabela 4 da página B-93, está dentro do limite max 0.40,000 = 4,000 N. Portanto Pt4,000 N. A-9
Órgãos de Máquinas II
 Órgãos de Máquinas II 7. Estudo Dinâmico de Engrenagens Adaptado e adotado para a unidade curricular por José R. Gomes / Departamento de Engenharia Mecânica a partir de materiais de apoio pedagógico em
Órgãos de Máquinas II 7. Estudo Dinâmico de Engrenagens Adaptado e adotado para a unidade curricular por José R. Gomes / Departamento de Engenharia Mecânica a partir de materiais de apoio pedagógico em
Rolamentos Axiais. 2. Rolamentos Axiais de Esferas de Contato Angular. 1. Rolamentos Axiais de Esferas de Escora Simples
 Rolamentos axiais de esferas de escora simples Rolamentos axiais de esferas de contato angular de escora dupla bidirecional Rolamentos axiais de esferas de contato angular pareado para altas rotações Rolamentos
Rolamentos axiais de esferas de escora simples Rolamentos axiais de esferas de contato angular de escora dupla bidirecional Rolamentos axiais de esferas de contato angular pareado para altas rotações Rolamentos
3. TRANSMISSÃO DE POTÊNCIA
 8 3. TRANSMISSÃO DE POTÊNCIA Os mecanismos de transmissão estão presentes em várias partes das máquinas e implementos agrícolas, transferindo potência e movimento, podendo atuar também como elemento de
8 3. TRANSMISSÃO DE POTÊNCIA Os mecanismos de transmissão estão presentes em várias partes das máquinas e implementos agrícolas, transferindo potência e movimento, podendo atuar também como elemento de
Fig Folga interna radial e axial da série 69 Fig Folga interna radial e axial da série 62
 7. Dados técnicos 7. Folga interna radial e axial de rolamentos rígidos de esferas........8 68 68 68 68 68 68....8 6 6 6 6 6 6.6....... Fig.7.. Folga interna radial e axial da série 68.6....... Fig. 7..
7. Dados técnicos 7. Folga interna radial e axial de rolamentos rígidos de esferas........8 68 68 68 68 68 68....8 6 6 6 6 6 6.6....... Fig.7.. Folga interna radial e axial da série 68.6....... Fig. 7..
Torção. Deformação por torção de um eixo circular. Deformação por torção de um eixo circular. Capítulo 5:
 Capítulo 5: Torção Adaptado pela prof. Dra. Danielle Bond Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal: preocupação no
Capítulo 5: Torção Adaptado pela prof. Dra. Danielle Bond Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal: preocupação no
Resistência dos Materiais. Aula 6 Estudo de Torção, Transmissão de Potência e Torque
 Aula 6 Estudo de Torção, Transmissão de Potência e Torque Definição de Torque Torque é o momento que tende a torcer a peça em torno de seu eixo longitudinal. Seu efeito é de interesse principal no projeto
Aula 6 Estudo de Torção, Transmissão de Potência e Torque Definição de Torque Torque é o momento que tende a torcer a peça em torno de seu eixo longitudinal. Seu efeito é de interesse principal no projeto
Capítulo 5. Torção Pearson Prentice Hall. Todos os direitos reservados.
 Capítulo 5 Torção slide 1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento
Capítulo 5 Torção slide 1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento
SEM DESENHO TÉCNICO MECÂNICO I
 SEM 0564 - DESENHO TÉCNICO MECÂNICO I Notas de Aulas v.2016 Aula 11 Componentes de transmissão e união II: engrenagens, pinos, cavilhas. Prof. Assoc. Carlos Alberto Fortulan Departamento de Engenharia
SEM 0564 - DESENHO TÉCNICO MECÂNICO I Notas de Aulas v.2016 Aula 11 Componentes de transmissão e união II: engrenagens, pinos, cavilhas. Prof. Assoc. Carlos Alberto Fortulan Departamento de Engenharia
Órgãos de Máquinas II Exercícios de Aplicação
 Órgãos de Máquinas II Exercícios de Aplicação Paulo Flores José Gomes Nuno Dourado Universidade do Minho Escola de Engenharia Guimarães 2016 ÍNDICE Órgãos de Máquinas II - Exercícios de Aplicação... 1
Órgãos de Máquinas II Exercícios de Aplicação Paulo Flores José Gomes Nuno Dourado Universidade do Minho Escola de Engenharia Guimarães 2016 ÍNDICE Órgãos de Máquinas II - Exercícios de Aplicação... 1
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Departamento de Engenharia Mecânica
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Departamento de Engenharia Mecânica Elementos de Máquinas II - Engrenagens 61 6.1. Aplicações Moinhos 1 61 6.1. Aplicações Redutores mistos 2 estágios 3 estágios
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Departamento de Engenharia Mecânica Elementos de Máquinas II - Engrenagens 61 6.1. Aplicações Moinhos 1 61 6.1. Aplicações Redutores mistos 2 estágios 3 estágios
Carregamentos Combinados (Projeto de Eixos e Árvores) Mecânica dos Materiais II
 Carregamentos Combinados (Projeto de Eios e Árvores) ecânica dos ateriais II Universidade de Brasília UnB Departamento de Engenharia ecânica EN Grupo de ecânica dos ateriais GAA Definições Eios e árvores
Carregamentos Combinados (Projeto de Eios e Árvores) ecânica dos ateriais II Universidade de Brasília UnB Departamento de Engenharia ecânica EN Grupo de ecânica dos ateriais GAA Definições Eios e árvores
ROLAMENTOS. Prof. Alexandre Augusto Pescador Sardá
 ROLAMENTOS Prof. Alexandre Augusto Pescador Sardá INTRODUÇÃO Há evidências que toras de madeira (rodas ou rolos) foram utilizadas pelos nossos ancestrais para mover objetos pesados em 4000 a.c., ou seja,
ROLAMENTOS Prof. Alexandre Augusto Pescador Sardá INTRODUÇÃO Há evidências que toras de madeira (rodas ou rolos) foram utilizadas pelos nossos ancestrais para mover objetos pesados em 4000 a.c., ou seja,
LISTA DE EXERCÍCIOS ÁREA 3. Disciplina: Elementos de Máquina Semestre: 2016/01
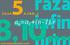 LISTA DE EXERCÍCIOS ÁREA 3 Disciplina: Elementos de Máquina Semestre: 2016/01 Prof: Diego R. Alba 1. O pinhão de 16 dentes da figura move um trem de engrenagem de redução dupla, como mostrado. Todas as
LISTA DE EXERCÍCIOS ÁREA 3 Disciplina: Elementos de Máquina Semestre: 2016/01 Prof: Diego R. Alba 1. O pinhão de 16 dentes da figura move um trem de engrenagem de redução dupla, como mostrado. Todas as
ELEMENTOS DE MÁQUINAS (SEM 0241)
 ELEMENTOS DE MÁQUINAS (SEM 0241) Notas de Aulas v.2018 Lista de exercícios aula 12 Dimensionamento de mancais de rolamentos Professor: Carlos Alberto Fortulan Ex47- aula 23 Dados Mancal esquerdo Mancal
ELEMENTOS DE MÁQUINAS (SEM 0241) Notas de Aulas v.2018 Lista de exercícios aula 12 Dimensionamento de mancais de rolamentos Professor: Carlos Alberto Fortulan Ex47- aula 23 Dados Mancal esquerdo Mancal
Aplicações Mecânicas Aula 3
 Aplicações Mecânicas Aula 3 Ementa CONTEÚDO PROGRAMÁTICO 2. Correias 2.1. Tipos 2.2. Características geométricas da transmissão por correia Elementos flexíveis - Correia A correia é um elemento de transmissão
Aplicações Mecânicas Aula 3 Ementa CONTEÚDO PROGRAMÁTICO 2. Correias 2.1. Tipos 2.2. Características geométricas da transmissão por correia Elementos flexíveis - Correia A correia é um elemento de transmissão
ANÁLISE DE FORÇA - ENGRENAGENS CILÍNDRICAS DE DENTES RETOS. Prof. Alexandre Augusto Pescador Sardá
 ANÁLISE DE FORÇA - ENGRENAGENS CILÍNDRICAS DE DENTES RETOS Prof. Alexandre Augusto Pescador Sardá ENGRENAGENS HELICOIDAIS DE EIXOS PARALELOS Ângulo de hélice é o mesmo em cada engrenagem; Uma engrenagem
ANÁLISE DE FORÇA - ENGRENAGENS CILÍNDRICAS DE DENTES RETOS Prof. Alexandre Augusto Pescador Sardá ENGRENAGENS HELICOIDAIS DE EIXOS PARALELOS Ângulo de hélice é o mesmo em cada engrenagem; Uma engrenagem
APLICAÇÕES. Você vê engrenagens em quase tudo que tem partes giratórias. Transmissão de carro. Redutor de velocidade. Relógios
 APLICAÇÕES Você vê engrenagens em quase tudo que tem partes giratórias.. Transmissão de carro Redutor de velocidade Relógios 1 CURSO ENGENHARIA DE PRODUÇÃO DEFINIÇÃO: Engrenagens são rodas com dentes padronizados
APLICAÇÕES Você vê engrenagens em quase tudo que tem partes giratórias.. Transmissão de carro Redutor de velocidade Relógios 1 CURSO ENGENHARIA DE PRODUÇÃO DEFINIÇÃO: Engrenagens são rodas com dentes padronizados
Engrenagem Cônica Reta. - V <= 1000 pés/min; - Ruído não é importante;
 Engrenagem Cônica Reta - V
Engrenagem Cônica Reta - V
PEM. Projeto de elementos de máquinas - Aula 4
 PEM Projeto de elementos de máquinas - Aula 4 Ementa CONTEÚDO PROGRAMÁTICO 2.1 Esforços na transmissão 2.2. Seleção de correias trapezoidais Esforços Considerando o sistema em rotação constante temos:
PEM Projeto de elementos de máquinas - Aula 4 Ementa CONTEÚDO PROGRAMÁTICO 2.1 Esforços na transmissão 2.2. Seleção de correias trapezoidais Esforços Considerando o sistema em rotação constante temos:
ELEMENTOS DE MÁQUINAS (SEM 0241)
 ELEMENTOS DE MÁQUINAS (SEM 0241) Notas de Aulas v.2018 Aula 11 Mancais de rolamentos Professores: Ernesto Massaroppi Junior Jonas de Carvalho Carlos Alberto Fortulan 11. 2 São Carlos 11 Mancais de Rolamento
ELEMENTOS DE MÁQUINAS (SEM 0241) Notas de Aulas v.2018 Aula 11 Mancais de rolamentos Professores: Ernesto Massaroppi Junior Jonas de Carvalho Carlos Alberto Fortulan 11. 2 São Carlos 11 Mancais de Rolamento
1- Engrenagem Cilíndrica de dentes retos - ECDR
 1 1- Engrenagem Cilíndrica de dentes retos - ECDR Os dentes são dispostos paralelamente entre si e em relação ao eixo. É o tipo mais comum de engrenagem e o de mais baixo custo. É usada em transmissão
1 1- Engrenagem Cilíndrica de dentes retos - ECDR Os dentes são dispostos paralelamente entre si e em relação ao eixo. É o tipo mais comum de engrenagem e o de mais baixo custo. É usada em transmissão
Cálculo de Engrenagens Cónicas
 Instituto Superior de Transportes e Comunicações Cálculo de Engrenagens Cónicas Órgãos de Máquinas Aula 4 3⁰ Ano Eng⁰ Eulices Mabasso Tópicos 1. Conceitos gerais Transmissões por engrenagens cónicas 2.
Instituto Superior de Transportes e Comunicações Cálculo de Engrenagens Cónicas Órgãos de Máquinas Aula 4 3⁰ Ano Eng⁰ Eulices Mabasso Tópicos 1. Conceitos gerais Transmissões por engrenagens cónicas 2.
Seleção de um modelo. Cálculo da carga axial. Fa3= μ mg + f mα 19. Fa4= mg f mα 26 Fa5= mg f 27 Fa6= mg f + mα 28. Fa3= mg + f mα 25.
 Cálculo da carga axial Em montagens horizontais Com sistemas de transporte comuns, a carga axial (Fa n ) aplicada ao alternar o trabalho para a direção horizontal é obtida na equação abaixo. Fa1= μ mg
Cálculo da carga axial Em montagens horizontais Com sistemas de transporte comuns, a carga axial (Fa n ) aplicada ao alternar o trabalho para a direção horizontal é obtida na equação abaixo. Fa1= μ mg
MÁQUINAS DE ELEVAÇÃO E TRANSPORTE
 MÁQUINAS DE ELEVAÇÃO E TRANSPORTE AULA 8 ACIONAMENTO E MECANISMOS DE ELEVAÇÃO PROF.: KAIO DUTRA Acionamento Manual e Alavanca de Comando Um acionamento manual pode ser empregado em mecanismos de baixa
MÁQUINAS DE ELEVAÇÃO E TRANSPORTE AULA 8 ACIONAMENTO E MECANISMOS DE ELEVAÇÃO PROF.: KAIO DUTRA Acionamento Manual e Alavanca de Comando Um acionamento manual pode ser empregado em mecanismos de baixa
APLICAÇÕES. Você vê engrenagens em quase tudo que tem partes giratórias. Transmissão de carro. Redutor de velocidade. Relógios
 APLICAÇÕES Você vê engrenagens em quase tudo que tem partes giratórias.. Transmissão de carro Redutor de velocidade Relógios 1 CURSO ENGENHARIA DE PRODUÇÃO DEFINIÇÃO: Engrenagens são rodas com dentes padronizados
APLICAÇÕES Você vê engrenagens em quase tudo que tem partes giratórias.. Transmissão de carro Redutor de velocidade Relógios 1 CURSO ENGENHARIA DE PRODUÇÃO DEFINIÇÃO: Engrenagens são rodas com dentes padronizados
PROJETO MECÂNICO (SEM 0347)
 PROJETO MECÂNICO (SEM 0347) Notas de Aulas v.2017 Aula 12 Transmissão Professor: Carlos Alberto Fortulan Transmissão A transmissão de potência é um recurso empregado para transmitir energia de um eixo
PROJETO MECÂNICO (SEM 0347) Notas de Aulas v.2017 Aula 12 Transmissão Professor: Carlos Alberto Fortulan Transmissão A transmissão de potência é um recurso empregado para transmitir energia de um eixo
Aula 3 Equilíbrio de uma partícula
 Aula 3 Equilíbrio de uma partícula slide 1 Condição de equilíbrio de uma partícula Para manter o equilíbrio, é necessário satisfazer a primeira lei do movimento de Newton: onde ΣF é a soma vetorial de
Aula 3 Equilíbrio de uma partícula slide 1 Condição de equilíbrio de uma partícula Para manter o equilíbrio, é necessário satisfazer a primeira lei do movimento de Newton: onde ΣF é a soma vetorial de
Flange/Eixo de Entrada. Bucha de Redução. B14 Flange Tipo C-DIN. N Sem Bucha. B5 Flange Tipo FF. B1 Bucha Simples. Flange de Saída 136
 ibr qdr IBR q IBR qdr IBR qp IBR r IBR m IBR c IBR p IBR H IBR x variadores TRANS. ANGULARES motor acopla. Torques de até 1800 N.m Fabricada com a união de dois redutores com engrenagens do tipo coroa
ibr qdr IBR q IBR qdr IBR qp IBR r IBR m IBR c IBR p IBR H IBR x variadores TRANS. ANGULARES motor acopla. Torques de até 1800 N.m Fabricada com a união de dois redutores com engrenagens do tipo coroa
FUSOS DE ESFERAS 1 - FOLGA. 2 - CARGA DINÂMICA (Cd) 3 - CARGA ESTÁTICA (Ce) 4 - CARGA AXIAL PERMITIDA. Fmáx = Ce / Fs 5 - MATERIAL E DUREZA
 1 - FOLGA Axial: É a medida entre o fuso e a castanha no sentido longitudinal ao eixo. Radial: É a folga entre o fuso e a castanha perpendicular ao eixo do fuso. 2 - CARGA DINÂMICA (Cd) É uma carga axial
1 - FOLGA Axial: É a medida entre o fuso e a castanha no sentido longitudinal ao eixo. Radial: É a folga entre o fuso e a castanha perpendicular ao eixo do fuso. 2 - CARGA DINÂMICA (Cd) É uma carga axial
ROLAMENTOS AUTOCOMPENSADORES DE ROLOS ROLAMENTOS AUTOCOMPENSADORES DE ROLOS
 ROLAMENTOS AUTOCOMPENSADORES DE ROLOS ROLAMENTOS AUTOCOMPENSADORES DE ROLOS, Furo Cônico Diâmetro do Furo 20-150 mm... B184 Diâmetro do Furo 160-560 mm... B192 Diâmetro do Furo 600-1400 mm... B202 B 182
ROLAMENTOS AUTOCOMPENSADORES DE ROLOS ROLAMENTOS AUTOCOMPENSADORES DE ROLOS, Furo Cônico Diâmetro do Furo 20-150 mm... B184 Diâmetro do Furo 160-560 mm... B192 Diâmetro do Furo 600-1400 mm... B202 B 182
Rolamento autocompensador de rolos vedado tipo WA
 Rolamento autocompensador de rolos vedado tipo WA Rolamento Autocompensador de Rolos Vedado NTN Tipo WA Longos períodos de operação entre inspeções de manutenção em ambientes contaminados! INTRODUÇÃO A
Rolamento autocompensador de rolos vedado tipo WA Rolamento Autocompensador de Rolos Vedado NTN Tipo WA Longos períodos de operação entre inspeções de manutenção em ambientes contaminados! INTRODUÇÃO A
No license: PDF produced by PStill (c) F. Siegert -
 A maioria das falhas em máquinas são devido a cargas que variam com o tempo do que com cargas estáticas. Estas falhas ocorrem tipicamente a níveis de tensões significantemente menores do que as resistências
A maioria das falhas em máquinas são devido a cargas que variam com o tempo do que com cargas estáticas. Estas falhas ocorrem tipicamente a níveis de tensões significantemente menores do que as resistências
Rolamentos Autocompensadores de Esferas
 Rolamentos Autocompensadores de Esferas Tolerância Página 52 Folga interna Página 64 Modelo Os Rolamentos Autocompensadores de Esferas são particularmente apropriados para aplicações onde ocorram desalinhamentos
Rolamentos Autocompensadores de Esferas Tolerância Página 52 Folga interna Página 64 Modelo Os Rolamentos Autocompensadores de Esferas são particularmente apropriados para aplicações onde ocorram desalinhamentos
Mateus de Almeida Silva. Meca 3º ano. Tipos de Rolamentos e Aplicações. Rolamento
 Mateus de Almeida Silva. Meca 3º ano Tipos de Rolamentos e Aplicações Rolamento A função do rolamento é minimizar a fricção entre as peças móveis da máquina e suportar uma carga. A maioria dos rolamentos
Mateus de Almeida Silva. Meca 3º ano Tipos de Rolamentos e Aplicações Rolamento A função do rolamento é minimizar a fricção entre as peças móveis da máquina e suportar uma carga. A maioria dos rolamentos
ELEMENTOS MECÂNICOS FLEXÍVEIS - CORREIAS. Prof. Alexandre Augusto Pescador Sardá
 ELEMENTOS MECÂNICOS LEXÍVEIS - CORREIAS Prof. Alexandre Augusto Pescador Sardá INTRODUÇÃO ELEMENTOS LEXÍVEIS - UTILIZAÇÃO Transmitem potência através de distâncias relativamente grandes. Substituem engrenagens,
ELEMENTOS MECÂNICOS LEXÍVEIS - CORREIAS Prof. Alexandre Augusto Pescador Sardá INTRODUÇÃO ELEMENTOS LEXÍVEIS - UTILIZAÇÃO Transmitem potência através de distâncias relativamente grandes. Substituem engrenagens,
Torques de até 1400 N.m. IBR q IBR qdr IBR qp IBR r IBR m IBR c IBR p IBR H IBR x variadores TRANS. A Direito. A Direito. N Sem Bucha.
 ibr qp IBR q IBR qdr IBR qp IBR r IBR m IBR c IBR p IBR H IBR x variadores TRANS. ANGULARES motor acopla. Torques de até 1400 N.m Fabricado com a união de dois redutores, sendo um com engrenagens do tipo
ibr qp IBR q IBR qdr IBR qp IBR r IBR m IBR c IBR p IBR H IBR x variadores TRANS. ANGULARES motor acopla. Torques de até 1400 N.m Fabricado com a união de dois redutores, sendo um com engrenagens do tipo
Avaliação de Sistemas de Industriais. Prof. Herbert Oliveira Guimarães
 Avaliação de Sistemas de Industriais 2016-2 1 Aula 11 Noções de elementos de máquinas Elementos de transmissão flexíveis 2 Avaliação de Sistemas de Industriais Elementos de transmissão flexíveis Conceitos
Avaliação de Sistemas de Industriais 2016-2 1 Aula 11 Noções de elementos de máquinas Elementos de transmissão flexíveis 2 Avaliação de Sistemas de Industriais Elementos de transmissão flexíveis Conceitos
Rolamentos Rígidos de Esferas
 Rolamentos Rígidos de Esferas Os rolamentos de esferas são extremamente comuns, pois eles podem lidar com ambas as cargas, radiais e axiais e são os mais amplamente utilizados devido a um conjunto de fatores:
Rolamentos Rígidos de Esferas Os rolamentos de esferas são extremamente comuns, pois eles podem lidar com ambas as cargas, radiais e axiais e são os mais amplamente utilizados devido a um conjunto de fatores:
Conteúdo. Resistência dos Materiais. Prof. Peterson Jaeger. 3. Concentração de tensões de tração. APOSTILA Versão 2013
 Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
MÁQUINAS DE ELEVAÇÃO E TRANSPORTE
 MÁQUINAS DE ELEVAÇÃO E TRANSPORTE AULA 9 MECANISMOS DE TRANSLAÇÃO PROF.: KAIO DUTRA Mecanismos de Translação Estes mecanismos são responsáveis pela locomoção do equipamento em trabalho, e podem ser classificados
MÁQUINAS DE ELEVAÇÃO E TRANSPORTE AULA 9 MECANISMOS DE TRANSLAÇÃO PROF.: KAIO DUTRA Mecanismos de Translação Estes mecanismos são responsáveis pela locomoção do equipamento em trabalho, e podem ser classificados
LISTA DE EXERCÍCIOS ÁREA 2. Disciplina: Elementos de Máquina Semestre: 2016/01
 LISTA DE EXERCÍCIOS ÁREA 2 Disciplina: Elementos de Máquina Semestre: 2016/01 Prof: Diego R. Alba 1. Um mancal de esferas de série 02 de contato angular, com anel interno rotante, é requerido para uma
LISTA DE EXERCÍCIOS ÁREA 2 Disciplina: Elementos de Máquina Semestre: 2016/01 Prof: Diego R. Alba 1. Um mancal de esferas de série 02 de contato angular, com anel interno rotante, é requerido para uma
Clique para editar o estilo do subtítulo mestre
 Capítulo 3 Equilíbrio de uma partícula slide 1 Objetivos do capítulo Introduzir o conceito do diagrama de corpo livre (DCL) para uma partícula. Mostrar como resolver problemas de equilíbrio de uma partícula
Capítulo 3 Equilíbrio de uma partícula slide 1 Objetivos do capítulo Introduzir o conceito do diagrama de corpo livre (DCL) para uma partícula. Mostrar como resolver problemas de equilíbrio de uma partícula
LISTA DE EXERCÍCIOS ÁREA 1. Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02
 LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
4ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO ANÁLISE DE TENSÕES
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
FIS-14 Lista-04 Setembro/2012
 FIS-14 Lista-04 Setembro/2012 1. A posição de uma partícula é descrita por r = 300e 0,500t mm e θ = 0,300t 2 rad, onde t é dado em segundos. Determine as intensidades da velocidade e da aceleração da partícula
FIS-14 Lista-04 Setembro/2012 1. A posição de uma partícula é descrita por r = 300e 0,500t mm e θ = 0,300t 2 rad, onde t é dado em segundos. Determine as intensidades da velocidade e da aceleração da partícula
Órgãos de Máquinas II
 Órgãos de Máquinas II 3. Transmissões por Correntes Adaptado e adotado para a unidade curricular por José R. Gomes / Departamento de Engenharia Mecânica a partir do material de apoio pedagógico em Powerpoint
Órgãos de Máquinas II 3. Transmissões por Correntes Adaptado e adotado para a unidade curricular por José R. Gomes / Departamento de Engenharia Mecânica a partir do material de apoio pedagógico em Powerpoint
Rolamentos Axiais Autocompensadores de Rolos
 s Axiais Autocompensadores de Rolos Tolerância Página 52 Pré-carga Página 95 Este tipo de rolamento tem a capacidade de se auto alinhar, absorvendo possíveis desalinhamentos no eixo. Os rolamentos axiais
s Axiais Autocompensadores de Rolos Tolerância Página 52 Pré-carga Página 95 Este tipo de rolamento tem a capacidade de se auto alinhar, absorvendo possíveis desalinhamentos no eixo. Os rolamentos axiais
ELEMENTOS ORGÂNICOS DE MÁQUINAS II AT-102
 Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira ELEMENTOS ORGÂNICOS DE MÁQUINAS II AT-102 Dr. Alan Sulato de Andrade [email protected] MANCAIS DE ROLAMENTOS E DESLIZAMENTO INTRODUÇÃO:
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira ELEMENTOS ORGÂNICOS DE MÁQUINAS II AT-102 Dr. Alan Sulato de Andrade [email protected] MANCAIS DE ROLAMENTOS E DESLIZAMENTO INTRODUÇÃO:
Instituto Federal de Educação Ciência e Tecnologia. Prof.: Carlos
 Instituto Federal de Educação Ciência e Tecnologia Campos de Presidente Epitácio LIDIANE FERREIRA Trabalho apresentado na disciplina de Elementos de Maquinas do Curso de Automação Industrial 3º módulo
Instituto Federal de Educação Ciência e Tecnologia Campos de Presidente Epitácio LIDIANE FERREIRA Trabalho apresentado na disciplina de Elementos de Maquinas do Curso de Automação Industrial 3º módulo
- MANCAIS - Mancal é um suporte que serve de apoio para eixos e rolamentos que são elementos girantes em máquinas.
 Definição :.. - MANCAIS - Mancal é um suporte que serve de apoio para eixos e rolamentos que são elementos girantes em máquinas. Os mancais classificam-se em duas categorias : Mancais de Deslizamentos
Definição :.. - MANCAIS - Mancal é um suporte que serve de apoio para eixos e rolamentos que são elementos girantes em máquinas. Os mancais classificam-se em duas categorias : Mancais de Deslizamentos
FUSOS DE ESFERAS 1 - FOLGA. 2 - CARGA DINÂMICA (Cd) 3 - CARGA ESTÁTICA (Ce) 4 - CARGA AXIAL PERMITIDA. Fmáx = Ce / Fs 5 - MATERIAL E DUREZA
 s de Esferas 1 - FOLGA Axial: É a medida entre o fuso e a castanha no sentido longitudinal ao eixo. Radial: É a folga entre o fuso e a castanha perpendicular ao eixo do fuso. 2 - CARGA DINÂMICA (Cd) É
s de Esferas 1 - FOLGA Axial: É a medida entre o fuso e a castanha no sentido longitudinal ao eixo. Radial: É a folga entre o fuso e a castanha perpendicular ao eixo do fuso. 2 - CARGA DINÂMICA (Cd) É
ROLAMENTOS PARA EQUIPAMENTOS VIBRATÓRIOS
 ROLAMENTOS PARA EQUIPAMENTOS VIBRATÓRIOS Alta performance em equipamentos vibratórios Rolamentos para Equipamentos Vibratórios Designações dos rolamentos NSK para equipamentos vibratórios Rolamentos para
ROLAMENTOS PARA EQUIPAMENTOS VIBRATÓRIOS Alta performance em equipamentos vibratórios Rolamentos para Equipamentos Vibratórios Designações dos rolamentos NSK para equipamentos vibratórios Rolamentos para
Redutores planetários Alta Precisão Alta Velocidade
 Código de compra SÉRIE AF APEX DYNAMICS BRASIL AF07-00 - S - P / MOTOR Tamanho do redutor Opção de eixo de saída: S: Eixo de saída liso S: Eixo de saída com chaveta Dados do motor: Fabricante e modelo
Código de compra SÉRIE AF APEX DYNAMICS BRASIL AF07-00 - S - P / MOTOR Tamanho do redutor Opção de eixo de saída: S: Eixo de saída liso S: Eixo de saída com chaveta Dados do motor: Fabricante e modelo
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
a-) o lado a da secção b-) a deformação (alongamento) total da barra c-) a deformação unitária axial
 TRAÇÃO / COMPRESSÃO 1-) A barra de aço SAE-1020 representada na figura abaixo, deverá der submetida a uma força de tração de 20000 N. Sabe-se que a tensão admissível do aço em questão é de 100 MPa. Calcular
TRAÇÃO / COMPRESSÃO 1-) A barra de aço SAE-1020 representada na figura abaixo, deverá der submetida a uma força de tração de 20000 N. Sabe-se que a tensão admissível do aço em questão é de 100 MPa. Calcular
Cálculo de Engrenagens Cilíndricas de Dentes Helicoidais
 Instituto Superior de Transportes e Comunicações Cálculo de Engrenagens Cilíndricas de Dentes Helicoidais Órgãos de Máquinas Aula 3 3⁰ Ano Eng⁰ Eulices Mabasso Tópicos 1. Conceitos gerais Transmissões
Instituto Superior de Transportes e Comunicações Cálculo de Engrenagens Cilíndricas de Dentes Helicoidais Órgãos de Máquinas Aula 3 3⁰ Ano Eng⁰ Eulices Mabasso Tópicos 1. Conceitos gerais Transmissões
Exercícios de Resistência dos Materiais A - Área 3
 1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
Torção em eixos de seção circular Análise de tensões e deformações na torção Exercícios. Momento torsor. 26 de setembro de 2016.
 26 de setembro de 2016 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 Este capítulo é dividido em duas partes: 1 Torção em barras
26 de setembro de 2016 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 Este capítulo é dividido em duas partes: 1 Torção em barras
Permissível na instalação
 Acoplamento de corrente KAISHIN consiste em duas engrenagens e uma extensão de corrente de rolo dupla. É muito simples e flexível, com as seguintes características: FÁCIL INSTALAÇÃO: A flexibilidade deste
Acoplamento de corrente KAISHIN consiste em duas engrenagens e uma extensão de corrente de rolo dupla. É muito simples e flexível, com as seguintes características: FÁCIL INSTALAÇÃO: A flexibilidade deste
Carga axial. Princípio de Saint-Venant
 Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
ROLAMENTOS FIXOS DE ESFERAS
 B 4 ROLAMENTOS FIXOS DE ESFERAS ROLAMENTOS FIXOS DE UMA CARREIRA DE ESFERAS Tipo, Tipo Blindado e Tipo Vedado Tipo Diâmetro do Furo 10-240 mm... B8 Diâmetro do Furo 260-800 mm... B20 ROLAMENTOS DE ESFERAS
B 4 ROLAMENTOS FIXOS DE ESFERAS ROLAMENTOS FIXOS DE UMA CARREIRA DE ESFERAS Tipo, Tipo Blindado e Tipo Vedado Tipo Diâmetro do Furo 10-240 mm... B8 Diâmetro do Furo 260-800 mm... B20 ROLAMENTOS DE ESFERAS
Torção Deformação por torção de um eixo circular
 Torção Deformação por torção de um eixo irular Torque é um momento que tende a torer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o omprimento e o raio do eixo permaneerão
Torção Deformação por torção de um eixo irular Torque é um momento que tende a torer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o omprimento e o raio do eixo permaneerão
Rolamentos de rolos cônicos
 Os rolamentos de rolos cônicos são projetados de modo que a capa, o cone e os rolos tenham superfícies cônicas cujos ápices convergem para um ponto comum no eixo do rolamento. Junto com os rolamentos da
Os rolamentos de rolos cônicos são projetados de modo que a capa, o cone e os rolos tenham superfícies cônicas cujos ápices convergem para um ponto comum no eixo do rolamento. Junto com os rolamentos da
Tels.: Campinas-sp Itupeva-sp
 Principais características: Inserção do tipo mandíbula Pode ser entregue a prova de falha ou a favor do rompimento Reduz vibrações Materiais: EN-GJL-250 (GG-25) Alta resistência ao desgaste Desenho compacto
Principais características: Inserção do tipo mandíbula Pode ser entregue a prova de falha ou a favor do rompimento Reduz vibrações Materiais: EN-GJL-250 (GG-25) Alta resistência ao desgaste Desenho compacto
ELEMENTOS DE MÁQUINAS (SEM 0241)
 ELEMENTOS DE MÁQUINAS (SEM 0241) Notas de Aulas v.2015 Aula 10 Uniões Eixo-Eixo Professores: Ernesto Massaroppi Junior Jonas de Carvalho Carlos Alberto Fortulan 10. 2 São Carlos 10 - Uniões Eixo com Eixo
ELEMENTOS DE MÁQUINAS (SEM 0241) Notas de Aulas v.2015 Aula 10 Uniões Eixo-Eixo Professores: Ernesto Massaroppi Junior Jonas de Carvalho Carlos Alberto Fortulan 10. 2 São Carlos 10 - Uniões Eixo com Eixo
TRENS DE ENGRENAGENS. Prof. Alexandre Augusto Pescador Sardá
 TRES E EGREAGES Prof. Alexandre Augusto Pescador Sardá ITROUÇÃO Engrenagens são utilizadas para transmitir movimento de um eixo rotativo para outro ou de um eixo rotativo para outro que translada (rotação
TRES E EGREAGES Prof. Alexandre Augusto Pescador Sardá ITROUÇÃO Engrenagens são utilizadas para transmitir movimento de um eixo rotativo para outro ou de um eixo rotativo para outro que translada (rotação
Universidade Federal do Paraná Setor de Tecnologia Departamento de Engenharia Mecânica. Eixos e árvores
 Universidade Federal do Paraná Setor de Tecnologia Departamento de Engenharia Mecânica Eixos e árvores Introdução 1.1 Conceitos fundamentais 1.2 Considerações sobre fabricação 1.3 Considerações sobre projeto
Universidade Federal do Paraná Setor de Tecnologia Departamento de Engenharia Mecânica Eixos e árvores Introdução 1.1 Conceitos fundamentais 1.2 Considerações sobre fabricação 1.3 Considerações sobre projeto
Tensão. Introdução. Introdução
 Capítulo 1: Tensão Adaptado pela prof. Dra. Danielle Bond Introdução A resistência dos materiais é um ramo da mecânica que estuda as relações entre as cargas externas aplicadas a um corpo deformável e
Capítulo 1: Tensão Adaptado pela prof. Dra. Danielle Bond Introdução A resistência dos materiais é um ramo da mecânica que estuda as relações entre as cargas externas aplicadas a um corpo deformável e
O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal.
 CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial.
 Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Sumário e Objectivos Sumário: Flexão segundo os dois Eixos Principais de Inércia ou Flexão Desviada. Flexão Combinada com Esforço Axial. Objectivos da Aula: Apreensão da forma de Cálculo das Tensões Axiais
Disciplina de Mecânica Geral II. CINEMÁTICA e DINÂMICA de CORPOS RÍGIDOS
 isciplina de Mecânica Geral II CINEMÁTIC e INÂMIC de CORPOS RÍGIOS CINEMÁTIC é o estudo da geometria em movimento, utilizada para relacionar as grandezas de deslocamento, velocidade, aceleração e tempo.
isciplina de Mecânica Geral II CINEMÁTIC e INÂMIC de CORPOS RÍGIOS CINEMÁTIC é o estudo da geometria em movimento, utilizada para relacionar as grandezas de deslocamento, velocidade, aceleração e tempo.
OS ROLAMENTOS BIPARTIDOS IBROL DE ROLOS CILÍNDRICOS AUTOCOMPENSADORES PROPORCIONAM:
 1 OS ROLAMENTOS BIPARTIDOS IBROL AUTOCOMPENSADORES PROPORCIONAM: Economia de tempo e redução de custo para reposição em locais de acesso restrito: Os rolamentos bipartidos de rolos cilíndricos autocompensadores
1 OS ROLAMENTOS BIPARTIDOS IBROL AUTOCOMPENSADORES PROPORCIONAM: Economia de tempo e redução de custo para reposição em locais de acesso restrito: Os rolamentos bipartidos de rolos cilíndricos autocompensadores
SD E SDL CARACTERÍSTICAS
 SD E SDL CARACTERÍSTICAS PB PBL SB SBL SE SEL SD SDL SF SFL ST ENGRENAGENS DE DENTES HELICOIDAIS Mecanismos de redução de primeira linha empregar engrenagens de dentes helicoidais, que fornecem uma taxa
SD E SDL CARACTERÍSTICAS PB PBL SB SBL SE SEL SD SDL SF SFL ST ENGRENAGENS DE DENTES HELICOIDAIS Mecanismos de redução de primeira linha empregar engrenagens de dentes helicoidais, que fornecem uma taxa
FEPI. Fresamento. Surgiu em , Page 1 Tecnologia Mecânica II
 Fresamento A Fresagem ou o Fresamento é um processo de usinagem mecânica, feito através de uma máquina chamada FRESADORA e ferramentas especiais chamadas de FRESAS. Surgiu em 1918 28.09.2009, Page 1 Fresadora
Fresamento A Fresagem ou o Fresamento é um processo de usinagem mecânica, feito através de uma máquina chamada FRESADORA e ferramentas especiais chamadas de FRESAS. Surgiu em 1918 28.09.2009, Page 1 Fresadora
TOLERÂNCIA GEOMÉTRICA
 TOLERÂNCIA GEOMÉTRICA FORMA Um erro de forma corresponde à diferença entre a superfície real da peça e a forma geométrica teórica. POSIÇÃO A tolerância de posição estuda a relação entre dois ou mais elementos.
TOLERÂNCIA GEOMÉTRICA FORMA Um erro de forma corresponde à diferença entre a superfície real da peça e a forma geométrica teórica. POSIÇÃO A tolerância de posição estuda a relação entre dois ou mais elementos.
Circuito Hidráulico Básico:
 Circuito Hidráulico ásico: O circuito hidráulico mais simples consiste no comando de avanço e recuo de um cilindro de dupla ação, utilizando uma bomba de vazão constante e uma válvula direcional de acionamento
Circuito Hidráulico ásico: O circuito hidráulico mais simples consiste no comando de avanço e recuo de um cilindro de dupla ação, utilizando uma bomba de vazão constante e uma válvula direcional de acionamento
Rolamentos. Rolamentos Autocompensadores de Esferas. Rolamentos Rígidos de Esferas
 Rolamentos Desde a invenção da roda as civilizações mais antigas tinham a necessidade de substituir o atrito e o deslizamento provocado pelos contatos que dois materiais causavam. Relatos de que os Romanos
Rolamentos Desde a invenção da roda as civilizações mais antigas tinham a necessidade de substituir o atrito e o deslizamento provocado pelos contatos que dois materiais causavam. Relatos de que os Romanos
VERIFICAÇÃO DE UMA ENGRENAGEM ATRAVÉS DE ELEMENTOS FINITOS
 UNIVERSIDADE FEDERAL DE MINAS GERAIS CURSO DE GRADUAÇÃO EM ENGENHARIA MECÂNICA VERIFICAÇÃO DE UMA ENGRENAGEM ATRAVÉS DE ELEMENTOS FINITOS ADLER SOARES ARAÚJO - 2001016594 VALDÉRIO RODRIGUES SILVA GALVÃO
UNIVERSIDADE FEDERAL DE MINAS GERAIS CURSO DE GRADUAÇÃO EM ENGENHARIA MECÂNICA VERIFICAÇÃO DE UMA ENGRENAGEM ATRAVÉS DE ELEMENTOS FINITOS ADLER SOARES ARAÚJO - 2001016594 VALDÉRIO RODRIGUES SILVA GALVÃO
Exemplo de cálculo da vida nominal
 Condição (instalação horizontal) Número suposto do modelo : KR 5520A Unidade da guia linear (C = 8.00N, C 0 = 6.900N) Unidade do fuso de esferas (C a =.620N, C 0a = 9.290N) Unidade do mancal (lado fi xo)
Condição (instalação horizontal) Número suposto do modelo : KR 5520A Unidade da guia linear (C = 8.00N, C 0 = 6.900N) Unidade do fuso de esferas (C a =.620N, C 0a = 9.290N) Unidade do mancal (lado fi xo)
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
- de dentes helicoidais (ECDH);
 Mecanismos Engrenagens As engrenagens são rodas com dentes. Esses dentes se acoplam de forma a permitir a transmissão de movimento de uma engrenagem para outra. Elas podem ser de vários tipos: Engrenagens
Mecanismos Engrenagens As engrenagens são rodas com dentes. Esses dentes se acoplam de forma a permitir a transmissão de movimento de uma engrenagem para outra. Elas podem ser de vários tipos: Engrenagens
Resistência dos Materiais
 Aula 7 Estudo de Torção, Ângulo de Torção Ângulo de Torção O projeto de um eixo depende de limitações na quantidade de rotação ou torção ocorrida quando o eixo é submetido ao torque, desse modo, o ângulo
Aula 7 Estudo de Torção, Ângulo de Torção Ângulo de Torção O projeto de um eixo depende de limitações na quantidade de rotação ou torção ocorrida quando o eixo é submetido ao torque, desse modo, o ângulo
As molas são usadas, principalmente, nos casos de armazenamento de energia, amortecimento de choques, distribuição de cargas, limitação de vazão,
 MOLAS As molas são usadas, principalmente, nos casos de armazenamento de energia, amortecimento de choques, distribuição de cargas, limitação de vazão, preservação de junçõeses ou contatos. MOLAS HELICOIDAIS
MOLAS As molas são usadas, principalmente, nos casos de armazenamento de energia, amortecimento de choques, distribuição de cargas, limitação de vazão, preservação de junçõeses ou contatos. MOLAS HELICOIDAIS
ENG1200 Mecânica Geral Lista de Exercícios 1 Equilíbrio da Partícula
 ENG1200 Mecânica Geral 2013.2 Lista de Exercícios 1 Equilíbrio da Partícula Questão 1 - Prova P1 2013.1 Determine o máximo valor da força P que pode ser aplicada na estrutura abaixo, sabendo que no tripé
ENG1200 Mecânica Geral 2013.2 Lista de Exercícios 1 Equilíbrio da Partícula Questão 1 - Prova P1 2013.1 Determine o máximo valor da força P que pode ser aplicada na estrutura abaixo, sabendo que no tripé
Elementos de Máquinas
 Professor: Leonardo Leódido Sumário Definição Partes Características Fabricação Definição Definição: Engrenagens são rodas com dentes padronizados que servem para transmitir movimento e força entre dois
Professor: Leonardo Leódido Sumário Definição Partes Características Fabricação Definição Definição: Engrenagens são rodas com dentes padronizados que servem para transmitir movimento e força entre dois
Rendimentos em Transmissões Mecânicas
 Rendimentos em Transmissões Mecânicas NOME: Lucas Ribeiro Machado O que é Transmissões Mecânicas Transmissão mecânica são equipamentos ou mecanismo que tem a função de transmitir potência, torque ou rotação
Rendimentos em Transmissões Mecânicas NOME: Lucas Ribeiro Machado O que é Transmissões Mecânicas Transmissão mecânica são equipamentos ou mecanismo que tem a função de transmitir potência, torque ou rotação
SENSORES E ACTUADORES Grandezas mecânicas
 SENSORES E ACTUADORES Grandezas mecânicas J.R.Azinheira Nov 2008 Bibliografia:, J.R. Azinheira, 2002, IST-DEM (disponível na página da UC em 'Material de Apoio' -> 'Bibliografia Complementar') ÍNDICE Cadeia
SENSORES E ACTUADORES Grandezas mecânicas J.R.Azinheira Nov 2008 Bibliografia:, J.R. Azinheira, 2002, IST-DEM (disponível na página da UC em 'Material de Apoio' -> 'Bibliografia Complementar') ÍNDICE Cadeia
Elementos de Máquinas II. UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Departamento de Engenharia Mecânica
 Elementos de Máquinas II 6. ELEMENTOS DE APOIO - Mancais de Deslizamento TÓPICOS ABORDADOS: 6.1. Introdução 6.. Nomenclatura e Definições 6.3. Projeto de Mancais de Deslizamento 6.4. Lubrificação 6.5.
Elementos de Máquinas II 6. ELEMENTOS DE APOIO - Mancais de Deslizamento TÓPICOS ABORDADOS: 6.1. Introdução 6.. Nomenclatura e Definições 6.3. Projeto de Mancais de Deslizamento 6.4. Lubrificação 6.5.
Escola Politécnica da Universidade de São Paulo Departamento de Engenharia Mecatrônica. Trem de engrenagens. Prof. Chi Nan Pai MS-14
 Escola Politécnica da Universidade de São Paulo Departamento de Engenharia Mecatrônica Trem de engrenagens Prof. Chi Nan Pai MS-14 [email protected] 1 Introdução Transmissão de movimento Engrenagens Médio
Escola Politécnica da Universidade de São Paulo Departamento de Engenharia Mecatrônica Trem de engrenagens Prof. Chi Nan Pai MS-14 [email protected] 1 Introdução Transmissão de movimento Engrenagens Médio
Prof. Willyan Machado Giufrida. Torção Deformação por torção de um eixo circular
 Torção Deformação por torção de um eixo circular Torque: É um movimento que tende a torcer um elemento em torno do seu eixo tangencial -Quando o torque é aplicado os círculos e retas longitudinais originais
Torção Deformação por torção de um eixo circular Torque: É um movimento que tende a torcer um elemento em torno do seu eixo tangencial -Quando o torque é aplicado os círculos e retas longitudinais originais
SF E SFL CARACTERÍSTICAS
 SF E SFL CARACTERÍSTICAS PB PBL SB SBL SE SEL SD SDL SF SFL ST ENGRENAGENS DE DENTES HELICOIDAIS Mecanismos de redução de primeira linha empregar engrenagens de dentes helicoidais, que fornecem uma taxa
SF E SFL CARACTERÍSTICAS PB PBL SB SBL SE SEL SD SDL SF SFL ST ENGRENAGENS DE DENTES HELICOIDAIS Mecanismos de redução de primeira linha empregar engrenagens de dentes helicoidais, que fornecem uma taxa
Rolamentos com duas fileiras. de esferas de contato radial 262
 Rolamentos com duas fileiras de esferas Rolamentos com duas fileiras de esferas de contato radial 262 Definições e aptidões 262 Séries 262 Tolerâncias e jogos 262 Elementos de cálculo 263 Sufixos 263 Características
Rolamentos com duas fileiras de esferas Rolamentos com duas fileiras de esferas de contato radial 262 Definições e aptidões 262 Séries 262 Tolerâncias e jogos 262 Elementos de cálculo 263 Sufixos 263 Características
DIMENSIONAMENTO MOTORREDUTOR DE UM INSTITUTO SUPERIOR DE ENGENHARIA DE LISBOA DEPARTAMENTO DE ENGENHARIA MECÂNICA. Cadeira: Órgãos de Máquinas
 DEPARTAMENTO DE ENGENHARIA MECÂNICA DIMENSIONAMENTO DE UM MOTORREDUTOR Cadeira: Órgãos de Máquinas Docente: Prof. Eng. Gil Quitério Ano Lectivo 2005/2006 Semestre de Inverno Trabalho executado por: André
DEPARTAMENTO DE ENGENHARIA MECÂNICA DIMENSIONAMENTO DE UM MOTORREDUTOR Cadeira: Órgãos de Máquinas Docente: Prof. Eng. Gil Quitério Ano Lectivo 2005/2006 Semestre de Inverno Trabalho executado por: André
SEM-0534 Processos de Fabricação Mecânica. Aula 2. Professor Alessandro Roger Rodrigues
 SEM-0534 Processos de Fabricação Mecânica Aula 2 Professor Alessandro Roger Rodrigues Tipos de Corte no Fresamento (a) Fresamento Tangencial (b) Fresamento Frontal Penetração de trabalho Profundidade de
SEM-0534 Processos de Fabricação Mecânica Aula 2 Professor Alessandro Roger Rodrigues Tipos de Corte no Fresamento (a) Fresamento Tangencial (b) Fresamento Frontal Penetração de trabalho Profundidade de
MESTRADO INTEGRADO EM ENGENHARIA MECÂNICA Órgãos de Máquinas II
 T.01 SISTEMAS DE TRANSMISSÃO DE MOVIMENTO MESTRADO INTEGRADO EM ENGENHARIA MECÂNICA Elaborado e revisto por Paulo Flores, José Gomes, Nuno Dourado e Filipe Marques - 2017 Departamento de Engenharia Mecânica
T.01 SISTEMAS DE TRANSMISSÃO DE MOVIMENTO MESTRADO INTEGRADO EM ENGENHARIA MECÂNICA Elaborado e revisto por Paulo Flores, José Gomes, Nuno Dourado e Filipe Marques - 2017 Departamento de Engenharia Mecânica
Rolamentos de rolos cilíndricos
 Rolamentos de rolos cilíndricos Rolamentos de rolos cilíndricos 292 Definições e aptidões 292 Séries 292 Variantes 293 Tolerâncias e jogos 294 Elementos de cálculo 296 Elementos de montagem 297 Sufixos
Rolamentos de rolos cilíndricos Rolamentos de rolos cilíndricos 292 Definições e aptidões 292 Séries 292 Variantes 293 Tolerâncias e jogos 294 Elementos de cálculo 296 Elementos de montagem 297 Sufixos
ROLAMENTOS AXIAIS DE ESFERAS DE CONTATO ANGULAR
 B 234 ROLAMENTOS AXIAIS DE ESFERAS DE CONTATO ANGULAR ROLAMENTOS AXIAIS DE ESFERAS DE CONTATO ANGULAR DE ESCORA DUPLA ROLAMENTOS PARA SUPORTE DE FUSOS DE ESFERAS Diâmetro do Furo 35-280 mm... B238 Diâmetro
B 234 ROLAMENTOS AXIAIS DE ESFERAS DE CONTATO ANGULAR ROLAMENTOS AXIAIS DE ESFERAS DE CONTATO ANGULAR DE ESCORA DUPLA ROLAMENTOS PARA SUPORTE DE FUSOS DE ESFERAS Diâmetro do Furo 35-280 mm... B238 Diâmetro
Propriedades mecânicas dos materiais
 Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Curso de Manutenção Industrial (Mecânica)
 Curso de Manutenção Industrial (Mecânica) VIBRAÇÕES MECÂNICAS Diagnóstico de avarias através da análise de Vibrações Desalinhamento Existe desalinhamento sempre que as linhas de eixo dos veios e das chumaceiras
Curso de Manutenção Industrial (Mecânica) VIBRAÇÕES MECÂNICAS Diagnóstico de avarias através da análise de Vibrações Desalinhamento Existe desalinhamento sempre que as linhas de eixo dos veios e das chumaceiras
Guia Linear. Tamanho. Patins. Patins --- A. Características Técnicas Material das guias DIN 58 CrMoV4 Material dos patins DIN 16 MnCr5
 Guias Lineares - Série R Guia Linear R - Modelo amanho 07 25 09 30 12 35 15 45 20 Curso Máx. 4000mm Exemplo: R15-200 R15-100 R atins - Modelo amanho 07 25 09 30 12 35 15 45 20 atins --- A ixação Sem Aba
Guias Lineares - Série R Guia Linear R - Modelo amanho 07 25 09 30 12 35 15 45 20 Curso Máx. 4000mm Exemplo: R15-200 R15-100 R atins - Modelo amanho 07 25 09 30 12 35 15 45 20 atins --- A ixação Sem Aba
