Grafos e digrafos com o sagemath
|
|
|
- Isabela Bento Lisboa
- 9 Há anos
- Visualizações:
Transcrição
1 Grafos e digrafos com o sagemath Pedro Patrício Acção de Formação de Grafos, Maio/Junho de 2008 Conteúdo 1 Introdução 1 2 Conceitos iniciais 2 3 Representação com matrizes 3 4 Conexidade 10 5 Grafos orientáveis 16 Referências bibliográficas 18 Anexo Maxima SAGE Introdução Os grafos são uma forma conveniente de representar um fluxo de um certo bem. Imagine uma empresa transportadora que tem a seu cargo o fornecimento de um certo bem a várias localidades (ou filiais, deixo à sua imaginação). Obviamente que a empresa tem como alvo efectuar o serviço de forma competente, reduzindo os custos. Intuitivamente, associa-se cada filial a um vértice, desenhando uma aresta entre dois vértices (aka filiais) se estes estiverem ligados de alguma forma conveniente por auto-estrada, por exemplo. Claro que a cada aresta podemos associar um peso, relativo ao custo de tomar essa estrada (combustível, portagens, horas a serem pagas ao motorista, por exemplo). Podemos também pressupor que existem estradas de sentido único, obtendo assim um digrafo ou grafo dirigido, ou que existem Departamento do Matemática da Universidade do Minho. [email protected] 1
2 vários caminhos possíveis, e neste caso temos um multigrafo. Os grafos tornam-se então numa representação gráfica de possíveis fluxos de bens, o que não significa que constituam um mapa. De facto, não existe obrigatoriedade qualquer em relação a orientação, posição nem distância relativa. 2 Conceitos iniciais Recorde que um digrafo D é um par ordenado (V, A), onde V é um conjunto não vazio finito de vértices e A conjunto de arestas é um subconjunto de {(U, V ) : U, V V}. No caso dos digrafos pesados, as arestas têm a si associadas um peso, e portanto são elementos de V V P, onde P é o conjunto dos pesos. A classe dos multigrafos pode ser definida indexando cada aresta a um conjunto de índices. Ou seja, para I conjunto de índices, o conjunto das arestas é um subconjunto do produto cartesiano V V I. Iremos autorizar a existência de lacetes, ou loops, isto é, (U, U) A, mas não iremos considerar multigrafos. Dada uma aresta (U, V ) A, o vértice U diz-se extremidade inicial e o vértice V extremidade final. Dizemos que os vértices U e V são adjacentes, U V, se (U, V ) A ou (V, U) A. Em qualquer um destes casos, diz-se que o vértice U é vizinho do vértice V. Esta aresta diz-se incidente em cada um desses vértices. O conjunto dos vizinhos de U denota-se por Γ(U). Duas arestas l 1, l 2 são adjacentes se existir X V tal que l 1, l 2 incidem em X. Os antecessores [resp. sucessores] de um vértice V são os elementos do conjunto Γ (V ) = {U V : (U, V ) A} [resp. Γ + (V ) = {U V : (V, U) A}]. O grau (ou valência) de um vértice V, denotado por deg(v ) ou por (V ), é o número de arestas próprias (ou seja, que não sejam lacetes) incidentes em V adicionado ao dobro do número 1 de laços em V. O grau interior de V, (V ), é o número de arestas da forma (, V ), e o grau exterior de V, + (V ), é o número de arestas da forma (V, ). Ou seja, (V ) = #Γ (V ) e + (V ) = #Γ + (V ). A título de exemplo, considere a representação gráfica do digrafo seguinte U V W Temos, então, V = {U, V, W }, A = {(U, V ), (V, U), (V, V ), (V, W )}. Neste digrafo, (U) = + (U) = (W ) = 1, + (W ) = 0, (V ) = 2, + (V ) = 3. Exercício 2.1. Para os grafos representados nas figuras, encontre os graus interior e exterior de cada vértice: 1 que no nosso caso pode ser 0 ou 1. 2
3 3 Representação com matrizes A um (p, q)-grafo G, isto é, um grafo com p vértices e q arestas, podemos associar, de forma única, uma matriz p p, A G = A(G), denominada matriz de adjacência de G, cujas linhas e 3
4 colunas estão indexadas da mesma forma a uma ordenação dos elementos de V, definida por { número de arestas incidentes com u e v se u v A [u,v] = número de lacetes em u se u = v onde u, v V. Claro que ao apenas considerarmos grafos ao invés de multigrafos, então as entradas da matriz de adjacência podem apenas tomar os valores 0 e 1. Considere os grafos u v a b x w c d Ordenando os vértices do primeiro grafo da forma (u, v, w, x), a matriz de adjacência é A = Como exercício, calcule a matriz de adjacência do segundo grafo, ordenando os vértices como (a, b, c, d). Como é óbvio, a matriz de adjacência de um grafo (não dirigido) é simétrica. Vejamos agora o caso dos digrafos. Nas mesmas condições da definição para grafos, a matriz de adjacência de um digrafo D = (V, A), que não é multidigrafo, é a matriz A D definida por { 1 se v Γ + (u) A D [u, v] = 0 caso contrário onde u, v V. Como exemplo, é a matriz de adjacência do digrafo u v x w 4
5 considerando a ordenação dos vértices como (u, v, w, x). Repare que a linha correspondente ao vértice u diz-nos que de u é antecessor de todos os vertices, e que a coluna correspondente ao vértice w diz-nos que w é sucessor de todos os vértices do digrafo. Voltaremos mais tarde a esta noção de alcance. Exercício As matrizes e são de adjacência de cada um dos digrafos. Faça a correspondência. 2. Encontre a matriz de adjacência de cada um dos grafos seguintes, fixando uma ordem para os vértices. 5
6 3. Determine as matrizes de adjacência dos digrafos seguintes, fixando previamente uma ordem para os vértices. 6
7 A um grafo G podemos associar uma matriz, a matriz de incidência, para uma certa ordenação dos vértices (a que se farão corresponder as linhas) e das arestas (a que se farão corresponder as colunas) fixa previamente, da seguinte forma: onde v V e e A. 0 se e não incide em v I G [v, e] = 1 se e incide em v e e não é lacete em v 2 se e é lacete em v Calculemos a matriz de incidência do grafo já visto anteriormente, ordenando os vértices como (u, v, w, x) e as arestas como (a, b, c, d, e, f): f a b u v d x e w c I G =
8 Como é fácil de verificar, uma outra ordenação dos vértices leva a troca de linhas da matriz de incidência, e uma outra ordenação das arestas a troca de colunas da matriz de incidência. Proposição 3.2. A soma das entradas de uma qualquer linha da matriz de incidência de um grafo é igual ao grau do vértice respectivo. Demonstração. Considere um vértice v do grafo de forma arbitrária, bem como as arestas das quais v é extremidade, mas que não são lacete em v. Estas são em número igual (v) 2δ, onde δ = 1 se existe um lacete v e δ = 0 caso contrário. Ora (v) 2δ iguala o número de 1 s na linha correspondente ao vértice v na matrix de incidência. Um lacete f (caso exista) contribui com 2 unidades no cálculo de (v), e 2 é a entrada na linha correspondente ao vértice v e na coluna correspondente à aresta f. Proposição 3.3. A soma das entradas de uma qualquer coluna da matriz de incidência de um grafo é igual a 2. Demonstração. Se a aresta e incide em dois vértices distintos, digamos u e v, então as entradas correspondentes a u, e e v, e são iguais a 1. Uma aresta incide no máximo em dois vértices, pelo que as outras entradas dessa coluna valem 0. Se e é lacete, então incide num só vértice e a entrada correspondente é 2, sendo as restantes nulas. A matriz de incidência de um digrafo é definida de forma análoga. Dado o digrafo D = (V, A), e para uma ordenação dos elementos de V e dos elementos de A fixa previamente, a matriz de incidência I D de D é dada por 0 se e não incide em v 1 se v é extremidade inicial de e e e não é lacete em v I D [v, e] = 1 se v é extremidade final de e e e não é lacete em v 2 se e é lacete em v onde v V e e A. Por exemplo, no digrafo seguinte, ordenando os vértices como (u, v, w, x) e as arestas como (a, b, c, d, e, f, g, h), a b u v I D = c h d x w e f g Proposição 3.4. Num digrafo sem lacetes, a soma das entradas de uma coluna da matriz de incidência é zero. Demonstração. Exercício. 8
9 Exercício Encontre uma ordenação das arestas e dos vértices por forma a que seja a matriz de incidência do digrafo 2. Indique uma matriz de incidência dos digrafos 9
10 4 Conexidade Um caminho dirigido num digrafo G do vértice v para o vértice w é uma sucessão (finita) de vértices e arestas v = v 0, x 1, v 1,... v n 1, x n, v n = w, com v i V G, tais que x i = (v i 1, v i ) A G. Ou seja, v i 1 Γ (v i ). As arestas são tais que a extremidade inicial de x i é v i 1 e a final é v i. Dizemos, neste caso, que existe uma conexão de v para w e escrevemos v w. No digrafo representado por temos, por exemplo, 0 4 e 0 6, mas 4 i, para i = 0,..., 6. Um par de vértices diz-se fortemente conectado se existir uma conexão de cada um deles para o outro. Se existir conexão de apenas um deles para o outro, então teremos um par 10
11 unilateralmente conectado. Um digrafo diz-se fortemente conexo se cada par de vértices for fortemente conectado, e unilateralmente conexo se cada par de vértices for unilateralmente conectado. Um digrafo diz-se fracamente conexo se o grafo suporte 2 for conexo. Exercício 4.1. Indique que par de vértices do digrafo anterior são fortemente conectados. A um caminho dirigido de um vértice para ele mesmo dá-se o nome de caminho fechado dirigido. Um caminho fechado dirigido diz-se um circuito dirigido se os arcos que o compõem forem distintos, e um ciclo dirigido se todos os vértices que o compõem forem distintos. A relação definida por xrw se {v, w} forem fortemente conectados (ou seja, v w ou w v) é uma relação de equivalência, e corresponde à partição de V em classes de equivalência, designadas por componentes fortemente conexas do digrafo. O digrafo seguinte, embora o grafo suporte seja conexo, não é fortemente conexo. Por isso se diz que é fracamente conexo. Este digrafo tem como matriz de adjacência, tomando a ordem natural da enumeração dos vértices, A = Quantas componentes fortemente conexas existem? 2 Ou seja, o grafo obtido do digrafo onde as arestas perdem a orientação. 11
12 Teorema 4.2. Seja A a matriz de adjacência do digrafo G, para uma ordenação fixa previamente dos vértices. A entrada A r [u,v] indica o número de caminhos dirigidos de u para v de comprimento r. Demonstração. A prova é feita por indução sobre r. Para r = 1, o resultado é óbvio. Suponha que é válido para r 1. Ora A r [u,v] = A r 1 [u,p] A [p,v] pela forma como o produto matricial está p V definido. Mas A r 1 [u,p] A [p,v] = { A r 1 [u,p] se (u, p) A 0 caso contrário Como A r 1 [u,p] é um número de r 1-caminhos entre u e p, que iguala o número de r caminhos entre u e v que passam por p Γ (v), temos que A r 1 [u,p] A [p,v] é o número de r-caminhos p V entre u e v. No digrafo representado atrás, e sabendo que A 2 = não existem, por exemplo, caminhos dirigidos de comprimento 2 de 7 para qualquer outro vértice que não o 6. Sabendo ainda que A 6 = não existem caminhos dirigidos de comprimento 6 de qualquer vértice que não o 0 e que termine em 1. E que existem 3 caminhos dirigidos de comprimento 6 de 2 para 5. Corolário 4.3. Se A é a matriz de adjacência de G então a entrada (i, j) de B r = A + A 2 + A A r 12
13 indica o número de caminhos, de comprimento não superior a r, entre v i e v j. Proposição 4.4. Sejam A a matriz de adjacência de G, com m vértices, e B m = A + A 2 + A A m. Então G é fortemente conexo se e só se B m não tiver entradas nulas. Para o digrafo considerado acima, B 8 = Logo, o digrafo não é fortemente conexo. Exercício 4.5. Considere o digrafo Indique uma matriz de adjacência. Ele é fortemente conexo? E o grafo suporte é conexo? A matriz de alcançabilidade de um digrafo com n vértices é uma matriz R = [r ij ] em que r ij = 1 se existir um caminho dirigido de i para j e 0 caso contrário. Como é evidente, um digrafo é fortemente conexo se e sé se os elementos da sua matriz de alcançabilidade forem todos iguais a 1. 13
14 Uma forma alternativa de se definir matriz de alcançabilidade (equivalente, como é óbvio, com a apresentada) de um digrafo com n vértices é a de considerar a matriz de adjacência A como matriz boleana, e tomar R = A + A A m. Recorde que as operações na álgebra de Boole estão definidas como No cálculo proposicional, a operação + corresponde ao OR ou, e a ao AND ou. Seja R uma relação binária num conjunto finito V com m elementos. Ou seja, R V V. O fecho transitivo R de R é o invólucro transitivo de R. Ou seja, é o menor conjunto (para a relação de ordem ) que contém R e é uma relação transitiva 3. A relação R pode ser identificada da forma natural com o digrafo G = (V, R). A relação binária R 2 = R R está definida por R R = {(u, v) V V w R (u, w), (w, v) R}. Ou seja, R 2 pode ser encarado como um digrafo com m vértices e arestas (u, v) se existir um caminho dirigido de comprimento 2 de u para v. De forma análoga, R k = {(u, v) V V existe um caminho de comprimento k de u para v}. O fecho transitivo R de R pode agora ser visto como o conjunto dos elementos (u, v), com u, v V, para os quais u v, ou seja, existe um caminho dirigido de u para v. Teorema 4.6. Seja R uma relação binária num conjunto V com m elementos e considere o digrafo G = (V, R). Então 1. R = R R 2 R m é o fecho transitivo de R. 2. A matriz de alcançabilidade de G iguala a matriz de adjacência de G = (V, R ) Na figura acima, a matriz de adjacência de G é a matriz e a de G é a matriz Exercício 4.7. Encontre o fecho transitivo e a matriz de alcançabilidade dos digrafos seguintes: 3 Recorde que a relação binária é transitiva se a b e b c força necessariamante que a c. 14
15 Figura 1: Um digrafo G e o seu fecho transitivo G 15
16 5 Grafos orientáveis Se G é um grafo, então o digrafo que se obtém substituindo cada aresta de G por um arco é denominado de orientação de G. Uma orientação de um grafo diz-se uma orientação forte se a orientação for fortemente conexa. Um grafo diz-se fortemente orientável se possuir uma orientação forte. O resultado seguinte caracteriza os grafos fortemente orientáveis. Teorema 5.1 (Teorema de Robbins). Um grafo é fortemente orientável se e só se é conexo e não tem pontes. Exercício 5.2. Dos grafos seguintes, indique os que são fortemente orientáveis. 16
17 17
18 Referências [1] Stephen Barnett, Discrete mathematics: numbers and beyond, Addison-Wesley Longman, 1998 (ISBN ). [2] Jonathan Gross, Jay Yellen, Graph theory and its applications, CRC Press, 1999 (ISBN ). [3] Frank Harary, Graph theory, Addison-Wesley Publ., 1972 (ISBN ). [4] Robert E. Hartwig, Directed graphs, notas não publicadas, North Carolina State University, [5] João Patrício, Grafos e Digrafos, notas de apoio à disciplina Lógica e Computação, IPT, 2007/2008. [6] Mario Rodríguez Riotorto, Primeros pasos en Maxima, 2008, disponível em [7] Ilda Perez F. da Silva, Tópicos de Matemática Finita, edição da A.E.F.C.L., [8] William Stein, Sage Reference Manual, Release , 2008, disponível em [9] J. K. Truss, Discrete mathematics for computer scientists, Addison-Wesley Publ., 1999 (ISBN ). 18
19 Anexo 5.1 Maxima O Maxima é uma sistema algébrico computacional de código aberto distribuído de acordo com a licença GPL. Pode ser obtido no endereço A documentação referente ao estudo dos grafos pode ser consultada em Uma versão mais intuitiva no uso do Maxima, o wxmaxima, pode ser obtido em Em [6, pp 37 42] pode consultar como construir e realizar operações simples com grafos e digrafos. Deixamo-lo com algumas implementações muito simples. (%i1) load (graphs)$ (%i2) g : create_graph([1,2,3], [[1,2], [2,3], [1,3]])$ (%i3) print_graph(g)$ 19
20 Graph on 3 vertices with 3 edges. Adjacencies: 3 : : : 3 2 (%i4) d : create_graph( [1,2,3,4], [ [1,3], [1,4], [2,3], [2,4] ], directed = true)$ (%i5) print_graph(d)$ Digraph on 4 vertices with 4 arcs. Adjacencies: 4 : 3 : 2 : : 4 3 (%i6) draw_graph(g)$ (%i7) draw_graph(d)$ 5.2 SAGE As representações gráficas de grafos e digrafos apresentadas neste documento foram, na sua maioria, construidas com um outro sistema computacional, também ele distribuído sob a licença GPL, denominado SAGE. Pode ser obtido no endereço Em [8] pode consultar um manual de utilização, ou visitar Apresentamos uma forma de integrar o SAGE na resolução de alguns dos exercícios propostos nestas notas. 1. Exercício 2.1 sage: D=DiGraph({ 0:[1,2,0], 1:[0]},loops=True) sage: D.show() sage: d = {0: [1,4,5], 1: [2,6], 2: [3,7], 3: [4,8], 4: [9], \...: 5: [7, 8], 6: [8,9], 7: [9]} 20
21 sage: D=DiGraph (d,loops=true) sage: D.show() sage: g = DiGraph({0:[1,2,3], 2:[5]}) sage: G=DiGraph(g) sage: G.show() sage: g=digraph([[1..12],lambda i,j: i!=j and i.divides(j)]) sage: G=DiGraph(g) sage: G.plot().show() sage: D = DiGraph( { 0: [1,2,3], 1: [0,2], 2: [3], 3: [4], 4: [0,5], 5: [1] } ) sage: D.in_degree(vertices = [0,1,2], labels=true) {0: 2, 1: 2, 2: 2} sage: D.in_degree() [2, 2, 2, 2, 1, 1] sage: G = graphs.petersengraph().to_directed() sage: G.in_degree(0) 3 2. Exercício 3.1(1) sage: G = DiGraph( { 0 : [1, 2], 1 : [2], 3 : [4, 5], 4 : [5] } ) sage: G.plot().show() sage: G.add_edge([0,4]) sage: G.plot().show() sage: G.adjacency_matrix () [ ] [ ] [ ] [ ] [ ] [ ] 3. Exercício 3.1(3) sage: g={0:[1,2], 1:[0,2,4], 2:[ 4,0], 3:[1,4]} sage: G=DiGraph (g) sage: G.show() sage: G.adjacency_matrix() 21
22 [ ] [ ] [ ] [ ] [ ] 4. Exercício 4.5 sage: N=matrix([[1,0,1,1,1,0,1],[1,0,0,1,1,0,0],[0,0,0,1,0,1,0],\...: [0,0,0,0,0,0,0],[1,1,0,0,0,0,0],[0,0,0,0,1,0,0],[0,0,1,1,1,0,0]]) sage: G=DiGraph (N,loops=True) sage: G.show(layout= circular ) sage: G.show3d() sage: G.adjacency_matrix () [ ] [ ] [ ] [ ] [ ] [ ] [ ] sage: G.adjacency_matrix ()==N True sage: G.vertices () [0, 1, 2, 3, 4, 5, 6] sage: sum(n^(i+1) for i in range(7)) [ ] [ ] [ ] [ ] [ ] [ ] [ ] sage: N+N^2+N^3+N^4+N^5+N^6+N^7 [ ] [ ] 22
23 [ ] [ ] [ ] [ ] [ ] 5. Exercício 4.7 sage: g1=digraph( {0:[1],1:[2],2:[3],3:[0]}) sage: g1trans=g1.transitive_closure () sage: g1trans.show() sage: g1trans.adjacency_matrix () [ ] [ ] [ ] [ ] 23
MATEMÁTICA DISCRETA. Patrícia Ribeiro 2018/2019. Departamento de Matemática, ESTSetúbal 1 / 47
 1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
1 / 47 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 47 1 Combinatória 2 Aritmética Racional 3 3 / 47 Capítulo 3 4 / 47 não orientados Um grafo não orientado
GRAFOS ORIENTADOS. PSfrag replacements. Figura 1: Exemplo de um grafo orientado.
 Introdução à Teoria dos Grafos Bacharelado em Ciência da Computação UFMS, 2005 GRAFOS ORIENTAOS Resumo Existem ocasiões onde grafos não são apropriados para descrever certas situações. Por exemplo, um
Introdução à Teoria dos Grafos Bacharelado em Ciência da Computação UFMS, 2005 GRAFOS ORIENTAOS Resumo Existem ocasiões onde grafos não são apropriados para descrever certas situações. Por exemplo, um
Grafos Orientados (digrafos)
 Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Grafos Orientados (digrafos) Grafo Orientado ou digrafo Consiste em um grafo G = (V,A) onde V = {v 1,, v n } é um conjunto de vértices e A = {a 1,, a k } é um conjunto de arcos tais que a k, k=1,,m é representado
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 09: Representação de Grafos Preparado a partir do texto: Rangel, Socorro. Teoria
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 09: Representação de Grafos Preparado a partir do texto: Rangel, Socorro. Teoria
Cap. 2 Conceitos Básicos em Teoria dos Grafos
 Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
Teoria dos Grafos e Aplicações 8 Cap. 2 Conceitos Básicos em Teoria dos Grafos 2.1 Grafo É uma noção simples, abstrata e intuitiva, usada para representar a idéia de alguma espécie de relação entre os
CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:
![CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo: CAP4. ELEMENTOS DA TEORIA DE GRAFOS. Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E) , sendo:](/thumbs/54/34072329.jpg) Matemática Discreta ESTiG\IPB Cap4. Elementos da Teoria de Grafos pg 1 CAP4. ELEMENTOS DA TEORIA DE GRAFOS Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E), sendo: Exemplos
Matemática Discreta ESTiG\IPB Cap4. Elementos da Teoria de Grafos pg 1 CAP4. ELEMENTOS DA TEORIA DE GRAFOS Grafo [graph]. Estrutura que consiste num par ordenado de conjuntos, G ( V, E), sendo: Exemplos
01 Grafos: parte 1 SCC0503 Algoritmos e Estruturas de Dados II
 01 Grafos: parte 1 SCC0503 Algoritmos e Estruturas de Dados II Prof. Moacir Ponti Jr. www.icmc.usp.br/~moacir Instituto de Ciências Matemáticas e de Computação USP 2011/1 Moacir Ponti Jr. (ICMCUSP) 01
01 Grafos: parte 1 SCC0503 Algoritmos e Estruturas de Dados II Prof. Moacir Ponti Jr. www.icmc.usp.br/~moacir Instituto de Ciências Matemáticas e de Computação USP 2011/1 Moacir Ponti Jr. (ICMCUSP) 01
Conceitos Básicos da Teoria de Grafos
 Conceitos Básicos da Teoria de Grafos Universidade Federal do Pampa - UNIPAMPA Engenharia da Computação Estrutura de Dados Profª Sandra Piovesan Grafos Uma noção simples, abstrata e intuitiva. Representa
Conceitos Básicos da Teoria de Grafos Universidade Federal do Pampa - UNIPAMPA Engenharia da Computação Estrutura de Dados Profª Sandra Piovesan Grafos Uma noção simples, abstrata e intuitiva. Representa
Estrutura de Dados e Algoritmos e Programação e Computadores II. Aula 10: Introdução aos Grafos
 Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
Estrutura de Dados e Algoritmos e Programação e Computadores II Aula 10: Introdução aos Grafos História O assunto que se constitui no marco inicial da teoria de grafos é na realidade um problema algorítmico.
4.1 Preliminares. No exemplo acima: Dom(R 1 ) = e Im(R 1 ) = Dom(R 2 ) = e Im(R 2 ) = Dom(R 3 ) = e Im(R 3 ) = Diagrama de Venn
 4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
4 Relações 4.1 Preliminares Definição 4.1. Sejam A e B conjuntos. Uma relação binária, R, de A em B é um subconjunto de A B. (R A B) Dizemos que a A está relacionado com b B sss (a, b) R. Notação: arb.
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] Preparado a partir do texto: Rangel, Socorro. Teoria do Grafos,
Teoria dos Grafos Aula 1 - Introdução
 Teoria dos Grafos Aula 1 - Introdução Profa. Sheila Morais de Almeida Mayara Omai Universidade Tecnológica Federal do Paraná - Ponta Grossa 2018 Sheila Almeida e Mayara Omai (UTFPR-PG) Teoria dos Grafos
Teoria dos Grafos Aula 1 - Introdução Profa. Sheila Morais de Almeida Mayara Omai Universidade Tecnológica Federal do Paraná - Ponta Grossa 2018 Sheila Almeida e Mayara Omai (UTFPR-PG) Teoria dos Grafos
Teoria dos Grafos. Teoria dos Grafos. Profa. Sheila Morais de Almeida DAINF-UTFPR-PG. agosto
 Teoria dos Grafos Introdução Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2017 O que é Grafo? Definição formal Um grafo G = (V (G), E(G)) é uma estrutura matemática que consiste de dois conjuntos:
Teoria dos Grafos Introdução Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2017 O que é Grafo? Definição formal Um grafo G = (V (G), E(G)) é uma estrutura matemática que consiste de dois conjuntos:
Teoria dos Grafos. Edson Prestes
 Edson Prestes Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 2001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications, 1993; Kaufmann,
Edson Prestes Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 2001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications, 1993; Kaufmann,
Introdução à Teoria dos Grafos
 Introdução à Teoria dos Grafos Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Introdução à Teoria dos Grafos junho - 2018 1 / 38 Este material é preparado usando
Introdução à Teoria dos Grafos Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Introdução à Teoria dos Grafos junho - 2018 1 / 38 Este material é preparado usando
MATEMÁTICA DISCRETA GRAFOS (1/4) Carlos Luz. EST Setúbal / IPS. 28 Maio - 3 Junho 2012
 MATEMÁTICA DISCRETA GRAFOS (1/4) Carlos Luz EST Setúbal / IPS 28 Maio - 3 Junho 2012 Carlos Luz (EST Setúbal / IPS) Grafos (1/4) 28 Maio - 3 Junho 2012 1 / 34 Noção de Grafo De nição Um grafo não orientado
MATEMÁTICA DISCRETA GRAFOS (1/4) Carlos Luz EST Setúbal / IPS 28 Maio - 3 Junho 2012 Carlos Luz (EST Setúbal / IPS) Grafos (1/4) 28 Maio - 3 Junho 2012 1 / 34 Noção de Grafo De nição Um grafo não orientado
TEORIA DOS GRAFOS TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MATEMÁTICA DISCRETA II PROFº MARCOS NASCIMENTO
 TEORIA DOS GRAFOS TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MATEMÁTICA DISCRETA II PROFº MARCOS NASCIMENTO Por que estudar grafos? Importante ferramenta matemática com aplicação em diversas áreas
TEORIA DOS GRAFOS TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS MATEMÁTICA DISCRETA II PROFº MARCOS NASCIMENTO Por que estudar grafos? Importante ferramenta matemática com aplicação em diversas áreas
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A de Oliveira, Socorro Rangel, Silvio A de Araujo Departamento de Matemática Aplicada Capítulo 12: Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro Teoria do
Teoria dos Grafos Valeriano A de Oliveira, Socorro Rangel, Silvio A de Araujo Departamento de Matemática Aplicada Capítulo 12: Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro Teoria do
Doutorado em Ciência da Computação. Algoritmos e Grafos. Raimundo Macêdo LaSiD/DCC/UFBA
 Doutorado em Ciência da Computação Algoritmos e Grafos Raimundo Macêdo LaSiD/DCC/UFBA Grafo Completo Grafo simples cujos vértices são dois a dois adjacentes. Usa-se a notação K n para um grafo completo
Doutorado em Ciência da Computação Algoritmos e Grafos Raimundo Macêdo LaSiD/DCC/UFBA Grafo Completo Grafo simples cujos vértices são dois a dois adjacentes. Usa-se a notação K n para um grafo completo
GRAFOS E ALGORITMOS TEORIA DE GRAFOS
 GRAFOS E ALGORITMOS TEORIA DE GRAFOS 1a. PARTE Prof. Ronaldo R. Goldschmidt [email protected] [email protected] ROTEIRO 1. INTRODUÇÃO E MOTIVAÇÃO 2. FUNDAMENTOS 3. CONECTIVIDADE 4.
GRAFOS E ALGORITMOS TEORIA DE GRAFOS 1a. PARTE Prof. Ronaldo R. Goldschmidt [email protected] [email protected] ROTEIRO 1. INTRODUÇÃO E MOTIVAÇÃO 2. FUNDAMENTOS 3. CONECTIVIDADE 4.
AULA 11 PROJETO E ANÁLISE DE ALGORITMOS. Conceitos básicos e representação de grafos Karina Valdivia Delgado
 AULA 11 PROJETO E ANÁLISE DE ALGORITMOS Conceitos básicos e representação de grafos Karina Valdivia Delgado Roteiro Motivação Conceitos básicos Representação Motivação Um grafo é uma abstração que permite
AULA 11 PROJETO E ANÁLISE DE ALGORITMOS Conceitos básicos e representação de grafos Karina Valdivia Delgado Roteiro Motivação Conceitos básicos Representação Motivação Um grafo é uma abstração que permite
Revisões de Conjuntos
 Revisões de Conjuntos {, {a}, {b}, {a, b}} a A a pertence a A, a é elemento de A a {a, b, c} a / A a não pertence a A d / {a, b, c} A B A contido em B, A subconjunto de B x A x B {a, b} {b, c, a} A B A
Revisões de Conjuntos {, {a}, {b}, {a, b}} a A a pertence a A, a é elemento de A a {a, b, c} a / A a não pertence a A d / {a, b, c} A B A contido em B, A subconjunto de B x A x B {a, b} {b, c, a} A B A
Matemática Discreta. Aula nº 22 Francisco Restivo
 Matemática Discreta Aula nº 22 Francisco Restivo 2006-05-26 Definição: Um grafo cujos vértices são pontos no plano e cujos lados são linhas no plano que só se encontram nos vértices do grafo são grafos
Matemática Discreta Aula nº 22 Francisco Restivo 2006-05-26 Definição: Um grafo cujos vértices são pontos no plano e cujos lados são linhas no plano que só se encontram nos vértices do grafo são grafos
Teoria dos Grafos Introdu c ao
 Teoria dos Grafos Introdução Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications,
Teoria dos Grafos Introdução Referências P. O. Boaventura Netto, Grafos: Teoria, Modelos e Algoritmos, São Paulo, E. Blucher 001; R. J. Trudeau, Introduction to Graph Theory, New York, Dover Publications,
Teoria dos Grafos. Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo. Departamento de Matemática Aplicada
 Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 14: Conjuntos de Corte e Conectividade Preparado a partir do texto: Rangel,
Teoria dos Grafos Valeriano A. de Oliveira, Socorro Rangel, Silvio A. de Araujo Departamento de Matemática Aplicada Capítulo 14: Conjuntos de Corte e Conectividade Preparado a partir do texto: Rangel,
Parte B Teoria dos Grafos
 45 Parte B Teoria dos Grafos B. Grafos e Subgrafos Um grafo G é uma tripla ordenada (V(G), E(G), ), constituindo de um conjunto não vazio V(G) de vértices, um conjunto disjunto E(G) das arestas e uma função
45 Parte B Teoria dos Grafos B. Grafos e Subgrafos Um grafo G é uma tripla ordenada (V(G), E(G), ), constituindo de um conjunto não vazio V(G) de vértices, um conjunto disjunto E(G) das arestas e uma função
Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 45
 Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 45 Introdução a Grafos Muitos problemas de otimização podem ser analisados utilizando-se uma estrutura denominada grafo ou rede. Problemas
Volmir Eugênio Wilhelm Departamento de Engenharia de Produção UFPR 45 Introdução a Grafos Muitos problemas de otimização podem ser analisados utilizando-se uma estrutura denominada grafo ou rede. Problemas
Teoria dos Grafos AULA 1
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] AULA 1 Introdução, Conceitos Iniciais, Isomorfismo Preparado
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada [email protected], [email protected] AULA 1 Introdução, Conceitos Iniciais, Isomorfismo Preparado
GRAFOS. Introdução Conceitos Fundamentais
 GRAFOS Introdução Conceitos Fundamentais Uma aplicação do produto de matrizes Agora é a sua vez... Considere o diagrama seguinte Determine, o número de formas diferentes de ir de a 1 até e 2 e de a 2
GRAFOS Introdução Conceitos Fundamentais Uma aplicação do produto de matrizes Agora é a sua vez... Considere o diagrama seguinte Determine, o número de formas diferentes de ir de a 1 até e 2 e de a 2
TGR BCC Representação Computacional de Grafos. Prof. Ricardo José Pfitscher
 TGR BCC Representação Computacional de Grafos Prof. Ricardo José Pfitscher Cronograma Representação Matriz de djacências Lista de djacências Matriz de Incidências Representação Como podemos representar
TGR BCC Representação Computacional de Grafos Prof. Ricardo José Pfitscher Cronograma Representação Matriz de djacências Lista de djacências Matriz de Incidências Representação Como podemos representar
Teoria dos Grafos AULA 1
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada [email protected], [email protected], [email protected] AULA 1 Introdução,
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada [email protected], [email protected], [email protected] AULA 1 Introdução,
UNIP - Ciência da Computação e Sistemas de Informação. Estrutura de Dados. AULA 8 Grafos. Estrutura de Dados 1
 UNIP - Ciência da Computação e Sistemas de Informação Estrutura de Dados AULA 8 Grafos Estrutura de Dados 1 Grafos - Motivação Muitas aplicações em computação necessitam considerar conjunto de conexões
UNIP - Ciência da Computação e Sistemas de Informação Estrutura de Dados AULA 8 Grafos Estrutura de Dados 1 Grafos - Motivação Muitas aplicações em computação necessitam considerar conjunto de conexões
Conceito Básicos da Teoria de Grafos
 1 Conceito Básicos da Teoria de Grafos GRAFO Um grafo G(V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w),
1 Conceito Básicos da Teoria de Grafos GRAFO Um grafo G(V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w),
Estruturas de Dados Grafos
 Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
Estruturas de Dados Grafos Prof. Eduardo Alchieri (introdução) Grafo é um conjunto de pontos e linhas que conectam vários pontos Formalmente, um grafo G(V,A) é definido pelo par de conjuntos V e A, onde:
Teoria dos Grafos. Valeriano A. de Oliveira Socorro Rangel Departamento de Matemática Aplicada.
 Teoria dos Grafos Valeriano A de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilceunespbr, socorro@ibilceunespbr Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro
Teoria dos Grafos Valeriano A de Oliveira Socorro Rangel Departamento de Matemática Aplicada antunes@ibilceunespbr, socorro@ibilceunespbr Grafos Hamiltonianos Preparado a partir do texto: Rangel, Socorro
Introdução a Grafos Letícia Rodrigues Bueno
 Introdução a Grafos Letícia Rodrigues Bueno UFABC Teoria dos Grafos - Motivação Objetivo: aprender a resolver problemas; Como: usando grafos para modelar os problemas; Grafos: ferramenta fundamental de
Introdução a Grafos Letícia Rodrigues Bueno UFABC Teoria dos Grafos - Motivação Objetivo: aprender a resolver problemas; Como: usando grafos para modelar os problemas; Grafos: ferramenta fundamental de
Definição e Conceitos Básicos
 Definição e Conceitos Básicos Grafos e Algoritmos Computacionais Prof. Flávio Humberto Cabral Nunes [email protected] 1 Conceitos Básicos Em grafos ocorrem dois tipos de elementos: Vértices ou nós;
Definição e Conceitos Básicos Grafos e Algoritmos Computacionais Prof. Flávio Humberto Cabral Nunes [email protected] 1 Conceitos Básicos Em grafos ocorrem dois tipos de elementos: Vértices ou nós;
Capítulo 2. Conjuntos Infinitos
 Capítulo 2 Conjuntos Infinitos Não é raro encontrarmos exemplos equivocados de conjuntos infinitos, como a quantidade de grãos de areia na praia ou a quantidade de estrelas no céu. Acontece que essas quantidades,
Capítulo 2 Conjuntos Infinitos Não é raro encontrarmos exemplos equivocados de conjuntos infinitos, como a quantidade de grãos de areia na praia ou a quantidade de estrelas no céu. Acontece que essas quantidades,
1.3 Isomorfismo 12 CAP. 1 CONCEITOS BÁSICOS
 12 CAP. 1 CONCEITOS BÁSICOS I i I j. Essa relação de adjacência define um grafo com conjunto de vértices {I 1,...,I k }. Esse é um grafo de intervalos. Faça uma figura do grafo definido pelos intervalos
12 CAP. 1 CONCEITOS BÁSICOS I i I j. Essa relação de adjacência define um grafo com conjunto de vértices {I 1,...,I k }. Esse é um grafo de intervalos. Faça uma figura do grafo definido pelos intervalos
Percursos em um grafo
 Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Combinando relações. Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações
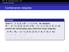 1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/3 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/3 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
GRAFOS. Prof. André Backes. Como representar um conjunto de objetos e as suas relações?
 8/0/06 GRAFOS Prof. André Backes Definição Como representar um conjunto de objetos e as suas relações? Diversos tipos de aplicações necessitam disso Um grafo é um modelo matemático que representa as relações
8/0/06 GRAFOS Prof. André Backes Definição Como representar um conjunto de objetos e as suas relações? Diversos tipos de aplicações necessitam disso Um grafo é um modelo matemático que representa as relações
PCC173 - Otimização em Redes
 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 27 de abril de 2016 Marco Antonio M. Carvalho
PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 27 de abril de 2016 Marco Antonio M. Carvalho
Matemática Discreta 10
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta 10 Prof. Jorge Cavalcanti [email protected] - www.univasf.edu.br/~jorge.cavalcanti 1 Muitas
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Matemática Discreta 10 Prof. Jorge Cavalcanti [email protected] - www.univasf.edu.br/~jorge.cavalcanti 1 Muitas
Doutorado em Ciência da Computação. Algoritmos e Grafos. Raimundo Macêdo LaSiD/DCC/UFBA
 Doutorado em Ciência da Computação Algoritmos e Grafos Raimundo Macêdo LaSiD/DCC/UFBA Grafo Completo Grafo simples cujos vértices são dois a dois adjacentes. Usa-se a notação K n para um grafo completo
Doutorado em Ciência da Computação Algoritmos e Grafos Raimundo Macêdo LaSiD/DCC/UFBA Grafo Completo Grafo simples cujos vértices são dois a dois adjacentes. Usa-se a notação K n para um grafo completo
GRAFOS Aula 03 Representações de Grafos Max Pereira
 Ciência da Computação GRAFOS Aula 03 Representações de Grafos Max Pereira A maior vantagem de um grafo é a sua representação visual da informação. Mas para a manipulação e armazenamento em um computador,
Ciência da Computação GRAFOS Aula 03 Representações de Grafos Max Pereira A maior vantagem de um grafo é a sua representação visual da informação. Mas para a manipulação e armazenamento em um computador,
CAL ( ) MIEIC/FEUP Grafos: Introdução (Março, 2011)
 1 Algoritmos em Grafos: Introdução R. Rossetti, A.P. Rocha, A. Pereira, P.B. Silva, T. Fernandes CAL, MIEIC, FEUP Março de 2011 Índice 2 Revisão de conceitos e definições Exemplificar aplicações Representação
1 Algoritmos em Grafos: Introdução R. Rossetti, A.P. Rocha, A. Pereira, P.B. Silva, T. Fernandes CAL, MIEIC, FEUP Março de 2011 Índice 2 Revisão de conceitos e definições Exemplificar aplicações Representação
Percursos em um grafo
 Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Percursos em um grafo Definição Um percurso ou cadeia é uma seqüência de arestas sucessivamente adjacentes, cada uma tendo uma extremidade adjacente à anterior e a outra a subsequente (à exceção da primeira
Definições Básicas para Grafos
 Definições Básicas para rafos RAFO Um grafo (V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w), v e w V:
Definições Básicas para rafos RAFO Um grafo (V,A) é definido pelo par de conjuntos V e A, onde: V - conjunto não vazio: os vértices ou nodos do grafo; A - conjunto de pares ordenados a=(v,w), v e w V:
grafo nós vértices arcos arestas
 GRAFOS E APLICAÇÕES 1. INTRODUÇÃO 1) Um grafo G = (V, E) consiste num conjunto de nós (ou vértices) V e num conjunto de arcos (ou arestas) E. Cada arco é representado por um par de nós. No seguinte exemplo,
GRAFOS E APLICAÇÕES 1. INTRODUÇÃO 1) Um grafo G = (V, E) consiste num conjunto de nós (ou vértices) V e num conjunto de arcos (ou arestas) E. Cada arco é representado por um par de nós. No seguinte exemplo,
Teoria dos Grafos 1. Teoria dos Grafos
 Teoria dos Grafos Teoria dos Grafos 1 A palavra grafo é um neologismo derivado da palavra graph em inglês. Ela foi usada pela primeira vez no sentido que nos interessa aqui pelo matemático inglês James
Teoria dos Grafos Teoria dos Grafos 1 A palavra grafo é um neologismo derivado da palavra graph em inglês. Ela foi usada pela primeira vez no sentido que nos interessa aqui pelo matemático inglês James
Noções da Teoria dos Grafos. André Arbex Hallack
 Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 1.1 Introdução histórica..................................... 1 1.2 Passeios
Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 1.1 Introdução histórica..................................... 1 1.2 Passeios
Curso: Ciência da Computação Turma: 6ª Série. Teoria da Computação. Aula 2. Conceitos Básicos da Teoria da Computação
 Curso: Ciência da Computação Turma: 6ª Série Aula 2 Conceitos Básicos da Computação pode ser definida como a solução de um problema ou, formalmente, o cálculo de uma função, através de um algoritmo. A
Curso: Ciência da Computação Turma: 6ª Série Aula 2 Conceitos Básicos da Computação pode ser definida como a solução de um problema ou, formalmente, o cálculo de uma função, através de um algoritmo. A
Teoria dos Grafos. Árvores
 Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada [email protected], [email protected], [email protected] Preparado a partir
Teoria dos Grafos Valeriano A. de Oliveira Socorro Rangel Silvio A. de Araujo Departamento de Matemática Aplicada [email protected], [email protected], [email protected] Preparado a partir
Teoria dos Grafos. Edson Prestes
 Edson Prestes Introdução Representação Mostre que todo passeio de u até v contém um caminho de u até v. Considere um passeio de comprimento l de u até v. Se l = 0 então temos um passeio sem nenhuma aresta.
Edson Prestes Introdução Representação Mostre que todo passeio de u até v contém um caminho de u até v. Considere um passeio de comprimento l de u até v. Se l = 0 então temos um passeio sem nenhuma aresta.
ESTRUTURAS DISCRETAS (INF 1631) GRAFOS. 1. O que é um grafo? Defina um grafo orientado. Defina um grafo não-orientado.
 PUC-Rio Departamento de Informática Profs. Marcus Vinicius S. Poggi de Aragão Período: 0. Horário: as-feiras e as-feiras de - horas de maio de 0 ESTRUTURAS DISCRETAS (INF 6) a Lista de Exercícios Procure
PUC-Rio Departamento de Informática Profs. Marcus Vinicius S. Poggi de Aragão Período: 0. Horário: as-feiras e as-feiras de - horas de maio de 0 ESTRUTURAS DISCRETAS (INF 6) a Lista de Exercícios Procure
Teoria dos Grafos. Profa. Alessandra Martins Coelho
 Teoria dos Grafos Profa. Alessandra Martins Coelho fev/2014 Avaliação 2 Provas 30 pontos cada; 3 Implementações 10 pontos cada; 1 Seminário 10 pontos; Listas de exercícios Listas não valem nota, entretanto...
Teoria dos Grafos Profa. Alessandra Martins Coelho fev/2014 Avaliação 2 Provas 30 pontos cada; 3 Implementações 10 pontos cada; 1 Seminário 10 pontos; Listas de exercícios Listas não valem nota, entretanto...
Teoria dos Grafos. Aula 5 - Estruturas de Dados para Grafos. Profª. Alessandra Martins Coelho. março/2013
 Teoria dos Grafos Aula 5 - Estruturas de Dados para Grafos Profª. Alessandra Martins Coelho março/2013 Estrutura é o que caracteriza o próprio grafo e independe da forma como ele é representado. A representação
Teoria dos Grafos Aula 5 - Estruturas de Dados para Grafos Profª. Alessandra Martins Coelho março/2013 Estrutura é o que caracteriza o próprio grafo e independe da forma como ele é representado. A representação
ESTRUTURAS DE DADOS. prof. Alexandre César Muniz de Oliveira. 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8.
 ESTRUTURAS DE DADOS prof. Alexandre César Muniz de Oliveira 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8. Grafos Sugestão bibliográfica: ESTRUTURAS DE DADOS USANDO C Aaron
ESTRUTURAS DE DADOS prof. Alexandre César Muniz de Oliveira 1. Introdução 2. Pilhas 3. Filas 4. Listas 5. Árvores 6. Ordenação 7. Busca 8. Grafos Sugestão bibliográfica: ESTRUTURAS DE DADOS USANDO C Aaron
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/29 5 - RELAÇÕES 5.1) Relações e Dígrafos 5.2) Propriedades
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/29 5 - RELAÇÕES 5.1) Relações e Dígrafos 5.2) Propriedades
CES-11. Algoritmos e Estruturas de Dados. Carlos Alberto Alonso Sanches
 CES-11 Algoritmos e Estruturas de Dados Carlos Alberto Alonso Sanches Juliana de Melo Bezerra CES-11 Grafos Conceitos gerais e representações Algoritmos em grafos Exploração sistemática em largura Caminhos
CES-11 Algoritmos e Estruturas de Dados Carlos Alberto Alonso Sanches Juliana de Melo Bezerra CES-11 Grafos Conceitos gerais e representações Algoritmos em grafos Exploração sistemática em largura Caminhos
Comunicação e redes. Aula 2: Teoria dos Grafos Conceitos básicos. Professor: Guilherme Oliveira Mota.
 Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota [email protected] Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
Comunicação e redes Aula 2: Teoria dos Grafos Conceitos básicos Professor: Guilherme Oliveira Mota [email protected] Aula passada Redes complexas Grafo G: Conjunto de pontos e linhas ligando esses pontos
GRAFOS Conceitos Básicos (Parte 1)
 ALGORITMOS E ESTRUTURAS DE DADOS II GRAFOS Conceitos Básicos (Parte 1) Gustavo Batista Profa. Elaine Parros Machado de Sousa alterações: Cris-na Dutra de Aguiar Ciferri Material baseado em aulas dos professores:
ALGORITMOS E ESTRUTURAS DE DADOS II GRAFOS Conceitos Básicos (Parte 1) Gustavo Batista Profa. Elaine Parros Machado de Sousa alterações: Cris-na Dutra de Aguiar Ciferri Material baseado em aulas dos professores:
Curso: Ciência da Computação Disciplina: Matemática Discreta RELAÇÕES. Prof.: Marcelo Maraschin de Souza
 Curso: Ciência da Computação Disciplina: Matemática Discreta RELAÇÕES Prof.: Marcelo Maraschin de Souza [email protected] Considere o conjunto S={1,2,3}, descreva o conjunto dos pares ordenados
Curso: Ciência da Computação Disciplina: Matemática Discreta RELAÇÕES Prof.: Marcelo Maraschin de Souza [email protected] Considere o conjunto S={1,2,3}, descreva o conjunto dos pares ordenados
Grafos: caminhos (matriz adjacência)
 Grafos: caminhos (matriz adjacência) Algoritmos e Estruturas de Dados 2 Graça Nunes 1 O problema do menor caminho Um motorista deseja encontrar o caminho mais curto possível entre duas cidades do Brasil
Grafos: caminhos (matriz adjacência) Algoritmos e Estruturas de Dados 2 Graça Nunes 1 O problema do menor caminho Um motorista deseja encontrar o caminho mais curto possível entre duas cidades do Brasil
CONCEITOS BÁSICOS EM GRAFOS
 Um grafo (simples) G é formado por um conjunto de vértices, denotado por V(G), e um conjunto de arestas, denotado por E(G). Cada aresta é um par (não ordenado) de vértices distintos. Se xy é uma aresta,
Um grafo (simples) G é formado por um conjunto de vértices, denotado por V(G), e um conjunto de arestas, denotado por E(G). Cada aresta é um par (não ordenado) de vértices distintos. Se xy é uma aresta,
Capítulo 2. Conjuntos Infinitos. 2.1 Existem diferentes tipos de infinito
 Capítulo 2 Conjuntos Infinitos Um exemplo de conjunto infinito é o conjunto dos números naturais: mesmo tomando-se um número natural n muito grande, sempre existe outro maior, por exemplo, seu sucessor
Capítulo 2 Conjuntos Infinitos Um exemplo de conjunto infinito é o conjunto dos números naturais: mesmo tomando-se um número natural n muito grande, sempre existe outro maior, por exemplo, seu sucessor
APLICAÇÕES DA TEORIA DOS GRAFOS
 Universidade de Aveiro Departamento de Matemática 2013 Sandra Maria Pereira dos Santos APLICAÇÕES DA TEORIA DOS GRAFOS Dissertação apresentada à Universidade de Aveiro para cumprimento dos requisitos necessários
Universidade de Aveiro Departamento de Matemática 2013 Sandra Maria Pereira dos Santos APLICAÇÕES DA TEORIA DOS GRAFOS Dissertação apresentada à Universidade de Aveiro para cumprimento dos requisitos necessários
UMA PARTIÇÃO DO CONJUNTO DOS GRAFOS CONEXOS DE ORDEM n EM CLASSES DE GRAFOS (a, b)-lineares
 UMA PARTIÇÃO DO CONJUNTO DOS GRAFOS CONEXOS DE ORDEM n EM CLASSES DE GRAFOS (a, b)-lineares Patricia Erthal de Moraes Colégio Pedro II Campo de São Cristóvão, 77 - São Cristóvão -Rio de Janeiro, CEP: 9-44
UMA PARTIÇÃO DO CONJUNTO DOS GRAFOS CONEXOS DE ORDEM n EM CLASSES DE GRAFOS (a, b)-lineares Patricia Erthal de Moraes Colégio Pedro II Campo de São Cristóvão, 77 - São Cristóvão -Rio de Janeiro, CEP: 9-44
Instituto de Computação Universidade Federal Fluminense. Notas de Aula de Teoria dos Grafos. Prof. Fábio Protti Niterói, agosto de 2015.
 Instituto de Computação Universidade Federal Fluminense Notas de Aula de Teoria dos Grafos Niterói, agosto de 2015. Conteúdo 1 Conceitos Básicos 5 1.1 Grafos, vértices, arestas..................... 5 1.2
Instituto de Computação Universidade Federal Fluminense Notas de Aula de Teoria dos Grafos Niterói, agosto de 2015. Conteúdo 1 Conceitos Básicos 5 1.1 Grafos, vértices, arestas..................... 5 1.2
As Pontes de Königsberg
 As Pontes de Königsberg Anderson Freitas Ferreira e Lívia Minami Borges 13 de junho de 2015 Resumo A teoria de grafos teve seu início em 1736, quando Euler utilizou uma estrutura para resolver o Problema
As Pontes de Königsberg Anderson Freitas Ferreira e Lívia Minami Borges 13 de junho de 2015 Resumo A teoria de grafos teve seu início em 1736, quando Euler utilizou uma estrutura para resolver o Problema
Noções da Teoria dos Grafos
 Noções da Teoria dos Grafos André Arbex Hallack Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 7 3 Árvores 11 4 Emparelhamento em grafos 15 5 Grafos planares: Colorindo
Noções da Teoria dos Grafos André Arbex Hallack Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 7 3 Árvores 11 4 Emparelhamento em grafos 15 5 Grafos planares: Colorindo
Matemática Discreta. Aula 06: Teoria dos Grafos. Tópico 01: Grafos e suas Representações. Observação
 Aula 06: Teoria dos Grafos Tópico 01: Grafos e suas Representações Nesta aula nós passamos a estudar um outro assunto, mas que também tem muita aplicação na vida prática, a Teoria dos Grafos. Para esta
Aula 06: Teoria dos Grafos Tópico 01: Grafos e suas Representações Nesta aula nós passamos a estudar um outro assunto, mas que também tem muita aplicação na vida prática, a Teoria dos Grafos. Para esta
Noções da Teoria dos Grafos. André Arbex Hallack
 Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 5 3 Árvores 7 4 Emparelhamento em grafos 11 5 Grafos planares:
Noções da Teoria dos Grafos André Arbex Hallack Junho/2015 Índice 1 Introdução e definições básicas. Passeios eulerianos 1 2 Ciclos hamiltonianos 5 3 Árvores 7 4 Emparelhamento em grafos 11 5 Grafos planares:
Grafos AULA META. Introduzir noções elementares da teoria dos grafos. OBJETIVOS. Ao final da aula o aluno deverá ser capaz de:
 Grafos META Introduzir noções elementares da teoria dos grafos. OBJETIVOS Ao final da aula o aluno deverá ser capaz de: Representar grafos por meio de matrizes e diagramas; Caracterizar uma árvore; Identificar
Grafos META Introduzir noções elementares da teoria dos grafos. OBJETIVOS Ao final da aula o aluno deverá ser capaz de: Representar grafos por meio de matrizes e diagramas; Caracterizar uma árvore; Identificar
