2 Introdução à Fluorescência

Transcrição

1 2 Introdução à luorecência 2. O fenômeno da fluorecência Luminecência é a emião de luz por alguma ubtância, ocorrendo a partir de etado eletrônico excitado. Para ecrever ee capítulo conultamo principalmente o excelente livro de Valeur, 22, e Lakowicz, 26. A luminecência é formalmente dividida em dua categoria, a fluorecência e a foforecência, dependendo da natureza do etado excitado. luorecência é a emião de luz a partir de um etado excitado ingleto, no qual o elétron excitado não muda a orientação de pin, continuando deemparelhado. Conequentemente, o retorno ao etado fundamental é permitido e ocorre rapidamente via emião de um fóton. A taxa de emião de fluorecência é tipicamente da ordem de 8 -, então o tempo de vida de fluorecência típico é da ordem de -9. Como iremo ver adiante, o tempo de vida () de um fluoróforo é a média de tempo que ele paa no eu etado excitado ante de retornar ao etado fundamental. Para melhor viualizarmo a ecala de tempo de vida de nanoegundo do fluoróforo é importante contextualizarmo com repeito à magnitude da velocidade da luz. Nete entido, temo que a luz trafega 3 cm em n. oforecência é a emião de luz a partir de um etado excitado tripleto, no qual o elétron excitado muda a orientação de pin ficando emparelhado com o elétron que permaneceu no orbital fundamental. Dete modo, temo que a traniçõe para o etado fundamental ão proibida e a taxa de emião ão mai lenta, etando compreendida na faixa de 3 -. Dete modo, o tempo de vida da foforecência é da ordem de miliegundo egundo. Contudo, grande tempo de vida ão poívei. A emião de foforecência não é comumente obervada em oluçõe fluida à temperatura ambiente. Ito porque exitem muito proceo de deativação o quai competem com a emião, tai como decaimento não radioativo e proceo de upreão.

2 6 O fluoróforo ão dividido em dua grande clae o intríneco e o extríneco. luoróforo intríneco ão aquele que emitem luz naturalmente. Já o extríneco ão aquele adicionado à amotra para deempenharem a função onda. O fluoróforo emitem luz geralmente na faixa de comprimento de onda do epectro viível, ou eja, entre o infravermelho e o ultravioleta. igura 2. Indicação da freqüência e do comprimento de onda do epectro eletromagnético. Em compoto orgânico, o fenômeno da fluorecência ocorre tipicamente em etrutura aromática. Algun do fluoróforo típico ão a quinina, a fluoreceína, a rodamina, o POPOP. A quinina, encontrada na água tônica, foi o primeiro fluoróforo etudado e foi o reponável por etimular o deenvolvimento do primeiro epectrofluorímetro que urgiram omente em 95. Muito fluoróforo ão encontrado no dia atuai. Hidrocarboneto aromático polinucleare, tai como o antraceno e o perileno, ão também fluorecente. Em proteína o fluoróforo dominante é o grupo do triptofano que aborve próximo de 28 nm e emite próximo de 34 nm. Em contrate à molécula orgânica aromática, átomo ão geralmente não fluorecente em fae condenada. Uma exceção notável é o grupo do lantanídeo.

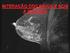
3 7 igura 2.2 Emião fluorecente da fluoreceína em meio aquoo. Laboratório de biofíica e íntee, Intituto de íica, Pontifícia Univeridade Católica do Rio de Janeiro. Uma caracterítica importante da técnica de fluorecência é a alta enibilidade de obervação. Dada eta enibilidade, a fluorecência foi utilizada em 877 para comprovar que o rio Danúbio e Reno eram conectado por correnteza ubterrânea. Eta conexão foi demontrada adicionando-e fluoreceína no rio Danúbio. Apó um período de eenta hora, reíduo verde fluorecente apareceram em um pequeno rio que deaguava no rio Reno. Epectro de fluorecência ão geralmente apreentado como epectro de emião. Um epectro de emião é uma curva de intenidade de fluorecência (I) veru comprimento de onda (λ) em nanômetro ou número de onda (cm - ). O comportamento do epectro de emião é altamente enível à etrutura química do fluoróforo e à polaridade do olvente no qual etão diolvido. O epectro de emião pode, por exemplo, er delocado para o azul e o grupo fluorecente for e aprofundando em uma proteína, bicamada lipídica ou membrana natural. Por outro lado, pode ofrer um delocamento para o vermelho e um dado grupo fluorecente de uma proteína for deenovelado.

4 8 O proceo o quai ocorrem entre a aborção e a emião da luz ão ilutrado pelo Diagrama de Jablonki, também conhecido como Diagrama de Perrin-Jablonki (ig. 2.3). Tai diagrama exitem em uma variedade de forma e ilutram o vário proceo moleculare que ocorrem em etado excitado. O diagrama foram aim nomeado em homenagem ao profeor Alexander Jablonki (898-98), coniderado como o pai da epectrocopia de fluorecência. Dentre a ua contribuiçõe podemo citar ua definição do termo aniotropia para decrever a emião polarizada de oluçõe. O diagrama de Jablonki ão ferramenta eenciai para a decrição do proceo quântico envolvido na aborção e na emião da luz, tai como aborção de fóton, converão interna, cruzamento interitema, foforecência, traniçõe tripleto-tripleto e fluorecência. Com o diagrama podemo melhor viualizar a interaçõe de upreão, energia de tranferência e interação com o olvente. O etado eletrônico ingleto, o fundamental, o primeiro e o egundo ão decrito por S, S e S 2, repectivamente. Em cada um dete nívei energético eletrônico do fluoróforo pode exitir um conjunto de nívei energético vibracionai, denotado por,, 2,... A traniçõe entre etado ão decrito como linha verticai para ilutrar a natureza intantânea da aborção da luz. A traniçõe ocorrem em um tempo da ordem de -5, um tempo muito pequeno para o delocamento do núcleo. O que é conhecido como princípio de ranck-condon. À temperatura ambiente, a energia térmica não é uficiente para ocaionar uma população ignificativa do etado vibracionai excitado. A aborção de fóton ocorre por molécula com energia vibracional mai baixa. Apó a aborção da luz, um fluoróforo é excitado para algum nível vibracional mai alto de eu etado de ingleto S e S 2 e, então, vário proceo ocorrem. Converão interna de energia é uma tranição não radiativa entre doi etado eletrônico de mema multiplicidade de pin. Em olução, ete proceo é eguido por uma relaxação vibracional em direção ao mai baixo nível vibracional do etado eletrônico fundamental. O exceo de energia vibracional pode er tranferido para o olvente durante coliõe entre a molécula excitada e a molécula do olvente. A converão interna ocorre em um tempo de -2 ou meno e eu tempo de vida de fluorecência ão da ordem de -8. A converão interna é completada anteriormente à emião.

5 9 Cruzamento interitema é uma tranição não radiativa entre doi nívei vibracionai ioenergético pertencente a etado eletrônico com diferente multiplicidade. Molécula no etado S podem experimentar uma converão de pin para o primeiro etado de tripleto, T. A emião de T é denominada de foforecência e é delocada para comprimento de onda maiore (energia menore) comparado à fluorecência. A tranição de T para o etado fundamental de ingleto é proibida. Como reultado, a taxa contante de emião para o tripleto é de vária orden de magnitude menore que aquela da fluorecência. Molécula contendo átomo metálico, tai como brometo e iodeto ão freqüentemente foforecente. O átomo metálico facilitam o cruzamento interitema e deta maneira aumentam o rendimento quântico de foforecência. Cruzamento interitema revero, T S, pode ocorrer quando a diferença de energia entre o etado S e T for pequena e quando o tempo de vida de T for grande o uficiente. Ete proceo provoca a fluorecência atraada, onde o epectro é o memo da fluorecência comum, no entanto o tempo de vida de decaimento de fluorecência é maior devido à permanência da molécula no etado tripleto T ante da emião de S. Em oluçõe concentrada, a colião entre dua molécula no etado T pode fornecer energia uficiente para permitir que uma dela retorne ao etado S. Ete proceo é chamado de aniquilação tripleto-tripleto. Por outro lado, uma vez que a molécula é excitada e atinge o etado T, ela pode aborver fóton com outro comprimento de onda, dado que a traniçõe tripleto-tripleto ão permitida. A emião de fluorecência reulta de um equilíbrio térmico do etado excitado, ito é, do etado vibracionai de nívei energético mai baixo de S. Já o retorno ao etado fundamental ocorre para o nível do etado fundamental excitado vibracional mai alto, o qual então rapidamente ( -2 ) alcança eu equilíbrio térmico. Uma vez excitado o fluoróforo é levado ao nível vibracional mai alto do etado eletrônico excitado, S. O exceo de energia é rapidamente diipado, em um tempo da ordem de -2, levando o fluoróforo ao mai baixo nível vibracional de S. Por caua deta rápida relaxação, o epectro de emião ão independente do comprimento de onda de excitação. No entanto, exceçõe exitem, tai como o fluoróforo que exitem em doi etado de ionização, cada qual exibindo ditinto epectro de aborção e emião. Por outro lado, alguma molécula ão

6 2 conhecida por emitirem do nível S 2, ma tal emião é rara e não ão obervada em molécula biológica. Uma intereante coneqüência da emião do mai alto etado vibracionai fundamentai é que o epectro de emião é tipicamente uma imagem epelho do epectro de aborção da tranição S S. Eta imilaridade ocorre devido ao fato de que a excitação eletrônica não altera ignificativamente a geometria do núcleo. Aim, o epaçamento do nívei energético vibracionai do etado excitado é imilar ao do etado fundamental. Como reultado, a etrutura vibracional vita no epectro de emião e de aborção ão imilare. O epectro de algun compoto, tai como o perileno, motram uma ignificativa etrutura devido ao nívei energético vibracionai individuai do etado fundamental e do etado excitado. Outro compoto, por outro lado, podem apreentar um epectro deprovido de etrutura vibracional. Embora a regra da imagem epelho eja frequentemente válida, muita exceçõe a eta regra ocorrem. Dete modo, memo que o epectro de aborção de um dado fluoróforo eja deprovido de etrutura vibracional, eu epectro de emião pode apreentar eta etrutura. Tai devio da regra da imagem epelho indicam um rearranjo diferente da geometria do núcleo no etado excitado comparado ao etado fundamental. Devido ao longo tempo de vida do etado S, delocamento do núcleo podem ocorrer ante da emião de fluorecência. Em reaçõe de etado excitado de complexo e exciplexe também podem ocorrer rearranjo geométrico que impliquem no devio da regra da imagem epelho. Abaixo temo o tempo caracterítico do proceo aociado à aborção e a emião de fóton: Proceo Tempo caracterítico () Aborção -5 Relaxação vibracional -2 - Tempo de vida do etado excitado S - -7 Cruzamento interitema Converão interna - -9 Tempo de vida do etado excitado T -6 -

7 2 Um exame do diagrama de Jablonki (ig. 2.3) no revela que a energia de emião é menor que a energia de aborção. Dete modo, dizemo que a fluorecência ocorre em energia menore ou comprimento de onda maiore. Ete fenômeno foi primeiramente obervado por G. G. Stoke. A diferença de energia entre a excitação e a emião é obervada de maneira univeral para toda a molécula fluorecente em olução. Outra propriedade da fluorecência é que o memo epectro de emião pode er obervado para diferente comprimento de onda de excitação. O epectro de emião de um fluoróforo independe do comprimento de onda da excitação. O tempo de vida de fluorecência e o rendimento quântico ão talvez a mai importante caracterítica de um fluoróforo. O rendimento quântico é a razão do número de fóton emitido pelo número de fóton aborvido. Subtância com um grande rendimento quântico, aproximando-e da unidade, tai como a fluoreceína, apreentam uma emião viivelmente brilhante. O tempo de vida determina o tempo diponível para o fluoróforo interagir com ou difundir-e no meio, e aim diponibilizar a informação de ua emião. O ignificado do rendimento quântico e do tempo de vida de fluorecência pode er melhor viualizado a partir do diagrama de Jablonki. igura 2.3 Diagrama de Jablonki modificado. (A) aborção de um fóton, (S ) etado fundamental de ingleto, (S n ) etado excitado de ingleto, (S ) primeiro etado excitado de ingleto, (RV) relaxação vibracional, (CI) converão interna, (CSI) cruzamento interitema, (T n ) etado excitado de tripleto.

8 A partir do diagrama acima podemo definir a taxa de emião radiativa de um fluoróforo dada por Γ e não radiativa dada por k nr 22. Tanto a taxa de emião radiativa, quando a não radiativa ão reponávei pela depopulação do etado excitado. A fração de fluoróforo que decaem atravé da emião de fóton, e aim o rendimento quântico, é dada por: Γ Φ = (2.) Γ + k nr Da equação (2.) concluímo, naturalmente, que quanto menor a taxa não radiativa, maior o valor do rendimento quântico, de modo que Φ. Dete modo, o rendimento quântico pode er tão próximo da unidade quanto menor for a taxa de decaimento não radiativo. No entanto, o rendimento quântico é empre menor que a unidade devido à perda de Stoke. Por conveniência, todo o poívei proceo não radiativo foram agrupado a uma única taxa k nr. 2.2 luorecência reolvida no tempo Medida de fluorecência podem er claificada em doi tipo: no etado etacionário e reolvida no tempo. Medida no etado etacionário ão aquela realizada com uma iluminação e obervação contante. A amotra é iluminada com um feixe contínuo de luz e a intenidade ou epectro de emião é então regitrado. Quando a amotra é expota à luz, o etado etacionário é alcançado quae que imediatamente. Já o egundo tipo de medida, a reolvida no tempo, é utilizado para medir intenidade e tempo de decaimento de fluorecência. Para eta medida a amotra é expota a um pulo de luz, onde a largura do pulo é tipicamente mai curto que o tempo de decaimento da amotra. Eta intenidade de decaimento é regitrada com um itema de alta velocidade de detecção que permite medir a intenidade e a aniotropia em uma ecala de tempo de nanoegundo. É importante realtar que podemo etabelecer uma relação entre a medida de etado etacionário e a medida de fluorecência reolvida no tempo. A obervação do etado etacionário é tida como uma média do fenômeno reolvido no tempo obre a intenidade de decaimento da amotra. Muito

9 fluoróforo dipõem de tempo de vida de ubnanoegundo. Devido à curta ecala de tempo da fluorecência, medida da emião de fluorecência reolvida no tempo requerem uma ótica e uma eletrônica ofiticada. No entanto, apear da dificuldade experimentai, a técnica da fluorecência reolvida no tempo tem ido cada vez mai utilizada. Dada uma olução diluída de epécie fluorecente com concentração [A] (em mol L - ), um pulo de luz no tempo t = leva certo número de molécula, A, ao etado excitado de ingleto S atravé da aborção de fóton. Eta molécula excitada então retornam ao etado S, atravé do proceo radiativo, não radiativo e cruzamento interitema. A taxa de depopulação do etado excitado pode er decrita com a equação diferencial dada por: d[ A*] = ( kr + knr )[ A*] (2.2) dt Integrando a equação (2.2) obtemo a evolução no tempo da concentração de molécula no etado excitado, [ A *]. Dete modo, temo: 23 A*] = [ A*] [ t exp (2.3) onde [ A *] é a concentração de molécula no etado excitado no tempo t = e é o tempo de vida do etado excitado S, dado por: = (2.4) k + k r nr A intenidade de fluorecência é definida como a quantidade de fóton emitida por unidade de tempo por unidade de volume. Aim podemo ecrever: k A* r A + fóton (2.5) A intenidade de fluorecência i no tempo t apó a excitação da amotra por um pulo de luz no tempo igual a é proporcional, em cada tempo, à concentração intantânea de molécula no etado excitado, [ A*] ; o fator de proporcionalidade é dado pela taxa radiativa = = t i ( t) kr [ A*] kr [ A*] exp (2.6) onde i (t) é a repota do itema, o qual diminui de acordo com uma função exponencial. Cabe realtar que, para o cao de uma medida de intenidade de k r :

10 fluorecência, a quantidade medida é proporcional a i, onde o fator de proporcionalidade depende da condiçõe experimentai. A medida de fluorecência erá denotada por I. O tempo de decaimento de fluorecência é a propriedade mai importante de uma molécula fluorecente, porque define a janela temporal em que podemo obervar o fenômeno dinâmico do itema. Apó a excitação, uma fração de molécula do itema pode alcançar o etado excitado tripleto, de onde retornarão ao etado fundamental via proceo radiativo, emião de fóton, e proceo não radiativo. A concentração de molécula no etado tripleto decai exponencialmente com um tempo caracterítico T, o qual repreenta o tempo de vida do etado tripleto. Dete modo, podemo ecrever: T = (2.7) k + k T r T nr O rendimento quântico de fluorecência Φ é a fração de molécula no etado excitado que retornam ao etado fundamental S com emião de fóton. Aim, temo: r nr kr Φ = = kr (2.8) k + k Por outro lado, o rendimento quântico de fluorecência é a razão do número de fóton emitido (ao longo de toda a duração do decaimento) pelo número de fóton aborvido. De acordo com a equação (2.6), a razão de i (t) pelo número de fóton aborvido é dada por: i ( t) = t k r exp (2.9) [ A*] onde a integração deta relação em toda a duração do decaimento (matematicamente de zero a infinito) no fornece o rendimento quântico, de modo que: 24 [ i t dt = k r A ( ) *] = Φ (2.) Na fluorecência etacionária o epectro de emião e excitação ão regitrado com o uo de um epectrofluorímetro. A fonte de luz é uma lâmpada

11 emitindo um fluxo de fóton contante. Sendo N o número de fóton incidente durante um intervalo de tempo por unidade de volume da amotra com concentração do fluoróforo [A] (N e [A] em mol L - ), temo que α N repreenta a quantidade de fóton aborvido por unidade de volume e o proceo de 25 Ka excitação em quetão é dado por A + hυ A*, onde 5 k a. Sob iluminação contínua, a concentração [ A*] permanece contante. Dete modo, dizemo que o itema etá no etado etacionário. Medida realizada neta condiçõe ão chamada de medida de etado etacionário. A taxa temporal de mudança de [ A*] é dada por: d [ A*] = = ka α N ( kr + knr )[ A*] (2.) dt onde k a α N repreenta o número de fóton aborvido por unidade de volume por unidade de tempo. Podemo reecrever a equação (2.) em termo de α I, onde I repreenta a intenidade de luz incidente (em mol de fóton por litro por egundo). A concentração contante de [ A*] é dada por: [ A*] = α I k r + knr (2.2) A quantidade de fóton fluorecente emitido por unidade de tempo e por unidade de volume, ou eja, a intenidade de fluorecência do etado etacionário e dada por: i k α Φ (2.3) r = kr [ A*] = I = α I kr + knr A equação acima motra que a intenidade de fluorecência do etado etacionário por fóton aborvido i α I é o próprio rendimento quântico de fluorecência. 2.3 Supreão de luorecência A intenidade de fluorecência pode er diminuída por muito proceo. Tai diminuiçõe em intenidade ão chamada de upreão. A upreão reulta do encontro difuivo entre fluoróforo e upreor durante o tempo de vida do etado excitado do fluoróforo. Uma grande variedade de interaçõe moleculare

12 26 pode reultar no fenômeno da upreão. Dentre ela temo a reaçõe de etado excitado, rearranjo moleculare, tranferência de energia, formação de complexo no etado fundamental e upreão coliional ou dinâmica. Por outro lado, outro tipo de upreão, a upreão aparente, pode ocorrer devido à alta denidade ótica na excitação e emião da amotra. A upreão de fluorecência tem ido etudada como um fenômeno fundamental e como fonte de informação obre muito itema bioquímico. Tai aplicaçõe bioquímica ão devida à interaçõe moleculare que reultam na upreão. Tanto a upreão etática quanto a upreão coliional ou dinâmica requerem contato entre o fluoróforo e upreor. No cao da upreão coliional, o upreor e difundirá no fluoróforo durante o tempo de vida de eu etado excitado. Apó o contato, o fluoróforo retorna ao etado fundamental em a emião de um fóton. Em geral, a upreão coliional ocorre em nenhuma alteração permanente na molécula, ou eja, em reação fotoquímica. Já na upreão etática um complexo não fluorecente no etado fundamental é formado entre o fluoróforo e o upreor. Contudo, em ambo o cao, etático e dinâmico, para que ocorra o fenômeno da upreão o fluoróforo e o upreor devem etar em contato. Tal condição de contato implica em numeroa aplicaçõe da upreão. Se coniderarmo um fluoróforo ligado a uma proteína ou a lipídeo de membrana, por exemplo, e a proteína ou a membrana for impermeável ao upreor, e o fluoróforo etiver localizado no interior da macromolécula, nenhuma upreão etática poderá ocorrer. Por eta razão a upreão de fluorecência pode er uada para revelar a localização de fluoróforo em proteína e membrana, a aceibilidade do fluoróforo ao upreore, aim como ua permeabilidade a upreore. Há uma variedade muito grande de ubtância que agem como upreore de fluorecência. Um do mai conhecido upreore coliionai é a molécula de oxigênio. Dependendo do tipo da amotra em invetigação é frequentemente neceário remover o oxigênio diolvido para e obter reultado confiávei na medida de fluorecência etacionária e reolvida no tempo. Outro upreore eficiente ão o aromático, halogênio, acrilamida, amina alifática, dietilanilina, compoto halogênio, purina, pirimidina, etc. Na upreão coliional ou dinâmica, a diminuição da intenidade fluorecência é decrita pela equação de Stern-Volmer:

13 = + k [ Q] = K [ Q] (2.4) q + Neta expreão e ão a intenidade de fluorecência na auência e preença do upreor, repectivamente, k q é a contante bimolecular de upreão; é o tempo de vida do fluoróforo na auência do upreor, K D é contante de upreão de Stern-Volmer e [Q] é a concentração de upreor. A contante de upreão bimolecular, k q, no informa a eficiência da upreão e a aceibilidade do fluoróforo ao upreore. A medida de upreão ão geralmente repreentada em um gráfico de / veru [Q]. Dete modo, eperae que / eja linearmente dependente da concentração de upreor. Um ajute linear é indicado quando exite uma clae única de fluoróforo, etando todo aceívei ao upreor. É importante realtar que a obervação de um ajute linear de Stern-Volmer não prova que a upreão coliional de fluorecência tenha ocorrido. Por outro lado, e dua populaçõe de fluoróforo etão preente e uma dela não etá aceível ao upreor, temo que o gráfico de Stern-Volmer devia-e da linearidade e nova conideraçõe devem er inerida na equação (2.4). Outra importante caracterítica da upreão coliional é a equivalência entre diminuição da intenidade de fluorecência e do tempo de vida, ilutrada pela equaçõe: = + k [ Q q ] (2.5) De modo que, = (2.6) A diminuição do tempo de vida ocorre devido à diminuição da população do etado excitado devido à deexcitação por colião. Já a upreão etática não diminui o tempo de vida porque omente molécula fluorecente ão obervada e o fluoróforo que não formaram complexo pouem o memo tempo de vida. O fenômeno da upreão pode também ocorrer como reultado da formação de um complexo não fluorecente entre o fluoróforo e o upreor. Nete entido, o complexo aborve luz e retorna imediatamente ao etado fundamental em a D 27

14 28 emião de fóton. Quando io ocorre dizemo que a upreão é etática e é decrita por: = + K [ Q] (2.7) S Note que a dependência de / de [Q] é linear, o que é idêntico para a upreão dinâmica, exceto pelo fato de que a contante de upreão agora é a própria contante de aociação. A ditinção entre upreão etática e upreão dinâmica pode er realizada atravé da dependência ditinta em função da temperatura, da vicoidade e atravé de medida de tempo de vida. Em temperatura elevada temo uma difuão rápida, o que implica em um aumento da upreão coliional, em uma diociação da ligaçõe fraca, diminuindo a quantidade de complexo, em uma diminuição da upreão etática. A realização de medida de tempo de vida é a forma mai definitiva de ditinguir upreão etática e dinâmica. A upreão etática remove a fração de fluoróforo da obervação, poi o complexo formado ão não fluorecente. A fração de fluoróforo que não formaram complexo poui então um tempo de vida. Para a upreão etática / =. Em contrate com a upreão dinâmica onde / = /. Outro método para ditinguir upreão etática de upreão dinâmica é examinando o epectro de aborção do fluoróforo. Supreão coliional afeta omente o etado excitado do fluoróforo e, portanto, não altera o epectro de aborção. Em contrate, a formação de complexo no etado fundamental frequentemente reulta em uma perturbação no epectro de aborção do fluoróforo. Em muita ituaçõe a fluorecência pode er uprimida por ambo o tipo de upreão: dinâmica, colidindo com o upreor, e etática, formando complexo. Nete cao, a equação de Stern-Volmer é modificada e poui um termo não linear, de egunda ordem em [Q]. O que reulta em uma concavidade poitiva na curva. Dete modo, temo: = + K [ Q] (2.8) onde K = ( K + K ) K K [ Q] depende da concentração de upreor. app D S + D S app Proteína contêm muito reíduo de triptofano que etão localizado em meio ditinto. Dete modo, podemo fazer uo da upreão para avaliar a

15 29 aceibilidade da proteína ao upreor. Nete cao, a equação de Stern-Volmer modificada é dada por: = + f K [ Q] f a a a (2.9) onde K a é a contante de upreão de Stern-Volmer da fração aceível, [Q] é a concentração de upreor e f a é a fração da fluorecência inicial aceível ao upreor, dada por: f a a = (2.2) b + a onde a e b ão a intenidade de fluorecência totai na auência do upreor do fluoróforo aceívei e inaceívei, repectivamente. A intenidade de fluorecência obervada para um fluoróforo é proporcional à ua concentração no etado excitado, [*]. Sob iluminação contínua, temo que a população de fluoróforo excitado é etabilizada, de modo que, d [ *] dt =. Na auência e na preença do upreor a equaçõe diferenciai que decrevem [*], ão: d[ *] = f ( t) γ [ *] = (2.2) dt d[ *] = f ( t) ( γ + kq [ Q]) [ *] = (2.22) dt onde f(t) é a função de excitação contante, e γ = - é a taxa de decaimento do fluoróforo na auência do upreor. Na auência do upreor a população do etado excitado decai com uma taxa γ = (Γ+ k nr ), onde Γ e k nr ão a taxa de decaimento radiativa e não radiativa, repectivamente. No entanto, na preença do upreor temo uma taxa de decaimento adicional dada por k q [Q]. Dividindo a equação (2.2) pela equação (2.22), temo: [ *] [ *] γ + kq [ Q] = = + kq [ Q] (2.23) γ A equação de Stern-Volmer pode er obtida coniderando a fração de fluoróforo excitado que decaem por emião em relação ao total. Ea fração / é dada pela razão da taxa de decaimento na auência do upreor, γ, pela taxa de decaimento total na preença do upreor γ + k q [Q], de modo que:

16 γ = = (2.24) γ + k Q] + K [ ] q [ q Q A equação (2.24) é jutamente a equação de Stern-Volmer. Como a upreão coliional é um proceo que diminui a população do etado excitado, podemo exprear o tempo de vida na auência e na preença do upreor por: = γ (2.25) = ( γ + k q [ Q]) (2.26) Aim, temo que o tempo e relacionam atravé: = + k q [ Q] (2.27) Tranferência de Energia Tranferência reonante de energia na fluorecência (RET) é um fenômeno eletrodinâmico que pode er explicado atravé da fíica cláica. A RET ocorre entre um doador (D) e uma molécula receptora (A) no etado fundamental. A molécula doadora tipicamente emitem em comprimento de onda que e obrepõem ao epectro de aborção da molécula receptora. A tranferência de energia é um proceo que não envolve a emião e reaborção de fóton, ou eja, não é o reultado da emião de um D endo aborvida por um A. O termo tranferência de energia reonante (RET), portanto, motra-e mai adequado, ao invé de RET. Para que a RET ocorra não é neceário que A eja fluorecente. A teoria da RET baeia-e no conceito do fluoróforo como um dipolo ocilante, o qual pode trocar energia com outro dipolo que poua uma freqüência de reonância imilar. Note que o fenômeno da RET é imilar ao de ociladore acoplado. A taxa de RET depende da extenão da obrepoição entre o epectro de emião do D e de aborção do A, do rendimento quântico do D, da orientação relativa entre o dipolo e da ditância entre a molécula do D e A. RET é comumente utilizada em toda a aplicaçõe da fluorecência, incluindo diagnótico médico, análie de DNA, ecaneamento ótico. O uo mai comum da RET é a determinação da ditância entre doi ítio de uma macromolécula.

17 Por outro lado, RET também é uada para etudar itema macromoleculare mai complexo onde há uma ditribuição de doadore e receptore. A tranferência de energia pode er influenciada pela preença pela difuão do par D_A durante o tempo de vida de fluorecência do D. Embora eta influência poa er obervada na medida de fluorecência etacionária, tai itema ão uualmente etudado atravé da fluorecência reolvida no tempo. A ditância em que a RET poui uma eficiência de 5% é chamada de ditância de rter, que e encontra na faixa de 2 a 6 angtron em oluçõe aquoa. A taxa de tranferência de energia, K t (r), de um D para um A é dada por: K 6 R t ( r) = D r (2.28) onde D é o tempo de decaimento do D na auência do A, R é a ditância de rter e r é a ditância entre o D e o A. Aim, a taxa de tranferência de energia é igual à taxa de decaimento do doador, / D, quando D etá a uma ditância, r, igual à ditância de rter, R, com a eficiência na tranferência de 5%. Dete modo, quando r = R a intenidade de emião de fluorecência do D deverá diminuir em 5% da intenidade na auência do A. Note que a taxa de tranferência depende fortemente da ditância e é proporcional a r -6. Ditância de rter na faixa de 2 a 9 angtrom ão conveniente para e etudar macromolécula biológica, dado que eta ditância ão comparávei ao tamanho da biomolécula e à ditância entre o ítio de proteína. Determinada condiçõe que influem na ditância D A influem conequentemente na taxa de tranferência de energia. Dete modo, podemo uar a RET como uma régua epectrocópica para quantificar ditância entre D A. A eficiência da tranferência de energia, E, é definida como a fração de fóton aborvido pelo D o quai ão tranferido para o A. Eta fração é dada por: kt ( r) E = (2.29) + k ( r) D T onde k T (r) é a taxa de tranferência de energia e D é o tempo de vida do doador na auência do A. Subtituindo a equação (2.28) na equação (2.29), de modo a exprear a eficiência em termo do raio de rter R e da ditância entre o D e A, temo: 3

18 6 R E = (2.3) 6 R + r 6 Eta equação motra que a eficiência de tranferência de energia é fortemente dependente da ditância. Por outro lado, podemo exprear a eficiência em termo da intenidade de fluorecência do D na auência, D, e na preença, DA, do A. Aim, temo que: E DA = (2.3) D A eficiência pode er também calculada diretamente do tempo de vida do D na auência, DA, e na preença, D, de A. Dete modo: E DA = (2.32) D Cabe alientar que eta equaçõe ão válida omente para pare de D A que etão eparado por uma ditância fixa, cao típico de marcadore de proteína. Entretanto, uma ditância fixa única entre doadore e receptore não é encontrada em mitura de doadore e receptore olução, ou para receptore dipero aleatoriamente em membrana. Modelo mai complexo ão neceário nete cao. Modelo que geralmente e baeiam em taxa média de RET obre uma ditribuição epacial de pare de D A. 32