ELEMENTOS DE EUCLIDES.
|
|
|
- Francisco Stachinski Paranhos
- 9 Há anos
- Visualizações:
Transcrição
1 ELEMENTOS DE EUCLIDES. DOS SEIS PRIMEIROS LIVROS, DO UNDECIMO E DUODECIMO DA VERSÃO LATINA DE FREDERICO COMMANDINO COIMBRA Imprensa da Universidade
2 Definições I. Ponto é o, que não tem partes, ou o, que não tem grandeza alguma. II. Linha é o, que tem comprimento sem largura. III. As extremidades da linha são pontos. IV. Linha recta é aquella, que está posta egualmente entre as suas extremidades. V. Superfície é o, que tem comprimento e largura. VI. As extremidades da superfície são linhas. VII. Superfície plana é aquella, sobre a qual assenta toda uma linha recta entre dous pontos quaesquer, que estiverem na mesma superfície. VIII. Angulo plano é a inclinação reciproca de duas linhas, que se tocam em uma superfície plana, sem estarem em direitura uma com a outra. IX. Angulo plano rectilineo é a inclinação reciproca de duas linhas rectas, que se encontram, e não estão em direitura uma com outra. Se alguns angulos existirem no mesmo ponto B, cada um delles vem indicado com tres letras do alfabeto; e a, que estiver no vertice do angulo, isto he, no ponto, no qual se encontram as rectas, que formam o angulo, se põe no meio das outras duas; e destas uma está posta perto de uma das ditas rectas, em alguma parte, e a outra perto da outra linha. Assim o angulo feito pelas rectas AB, CB representarse-ha com as letras ABC, ou CBA; o angulo formado pelas rectas AB, DB, com as letras ABD, ou DBA; e o angulo que fazem as rectas DB, CB, com as letras DBC, ou CBD. Mas, se um angulo estiver separado de outro qualquer, poder-se-ha marcar com a mesma letra, que estiver no vertice, como o angulo no ponto E. X. Quando uma linha recta, caindo sobre outra linha recta, fizer com esta dous angulos eguaes, um de uma, e outro de outra parte, cada um destes angulos eguaes se chama angulo recto; e a linha incidente se diz perpendicular á outra linha, sobre a qual cae. XI. Angulo obtuso é o, que é maior, que o angulo recto. XII. Angulo agudo é o, que é menor, que o angulo recto. XIII. Termo se diz aquillo, que é extremidade de alguma cousa. XIV. Figura é um espaço, fechado por um ou mais termos.
3 XV. Circulo é uma figura plana, fechada por uma só linha, a qual se chama circumferencia: de maneira que todos as linhas rectas, que de um certo ponto existente no meio da figura, se conduzem para a circumferencia, são eguaes entre si. XVI. O dicto ponto se chama centro do circulo. XVII. Diametro do circulo é uma linha recta,que passa pelo centro, e que se termina por ambas as partes na circumferencia. XVIII. Semicirculo é uma figura, comprehendida entre o diametro e aquella parte da circumferencia do circulo, que é cortada pelo diametro. XIX. Segmento de circulo é uma figura, comprehendida entre uma linha recta e uma porção da circumferencia. XX. Figuras rectilineas são as, que são formadas com linhas rectas. XXI. As trilateras são aquellas, que são formadas com tres linhas rectas. XXII. As quadrilateras são aquellas, que são feitas por quatro linhas rectas. XXIII. As multilateras são as, que são feitas por mais de quatro linhas rectas. XXIV. Entre as figuras trilateras o triangulo equilatero é o, que tem os tres lados eguaes. XXV. Triangulo isosceles é o, que tem dous lados eguaes. XXVI. Triangulo scaleno é o, que tem os tres lados desiguaes. XXVII. Triangulo rectangulo é o, que tem um angulo recto. XXVIII. Triangulo obtusangulo é o, que tem um angulo obtuso. XXIX. O triangulo acutangulo é o, que tem todos os angulos agudos.
4 XXX. Entre as figuras quadrilateras o quadrado é o, que é junctamente equilatero e rectangulo. XXXI. E a figura, que de uma parte for mais comprida, pode ser rectangula, mas não equilatera. XXXII. Mas o rhombo é uma figura equilatera, e não rectangula. XXXIII. Rhomboide é uma figura, que, tendo os lados opostos eguaes, nem é equilatera nem equiangula. XXXIV. Todas as mais figuras quadrilateras, que não são as referidas, se chamam trapezios. XXXV. Linhas parallelas ou equidistantes são linhas rectas, que existindo no mesmo plano, e sendo produzidas de ambas as partes, nunca se chegam a tocar.
5 Axiomas I. As cousas, que são eguaes a uma terceira, são eguaes entre si. II. Se a cousas eguaes se junctarem outras eguaes, os todos serão iguaes. III. E, se de cousas eguaes se tirarem outras eguaes, os restos serão iguaes. IV. E, se a cousas deseguaes se ajunctarem outras eguaes, os todos serão deseguaes. V. E, se de cousas deseguaes se tirarem cousas eguaes, os restos serão deseguaes. VI. As quantidades, das quaes cada uma por si faz o dobro de outra quantidade, são eguaes. VII. E aquellas, que são ametades de uma mesma quantidade, são tambem eguaes. VIII. Duas quantidades, que se ajustam perfeitamente uma com outra, são eguaes. IX. O todo é maior do que qualquer das suas partes. X. Duas linhas rectas não comprehendem espaço. XI. Todos os angulos rectos são eguaes. [Postulado 4] XII. E se uma linha recta, encontrando-se com outras duas rectas, fizer os angulos internos da mesma parte menores que dous rectos, estas duas rectas, produzidas ao infinito concorrerão para a mesma parte dos dictos angulos internos. [Postulado 5] Estes sinaes =, >, <, de que os Mathematicos usam frequentemente, servem para maior brevidade. O sinal = significa, que o primeiro termo é egual ao segundo. > Que o primeiro termo é maior que o segundo. < Que o primeiro termo é menor que o segundo. Assim A = B significa, que A é igual a B. A > B que A é maior que B. A < B que A é menor que B. Postulados I. Pede-se como cousa possivel, que se tire de um ponto qualquer para outro qualquer ponto uma linha recta. II. E que uma linha recta determinada se continue em direitura de si mesma, até onde seja necessario. III. E que com qualquer centro e qualquer intervallo se descreva um circulo.
6 PROPOSIÇÕES I. Sobre uma linha recta determinada descrever um triangulo equilatero. II. De um ponto dado tirar uma linha recta igual á outra recta dada. III. Dadas duas linhas rectas deseguaes, cortar da linha maior uma parte egual á linha menor. IV. Se dous triangulos tiverem dous lados eguaes a dous lados, cada um a cada um; e os angulos, comprehendidos por estes lados, forem tambem eguaes, as bases e os triangulos, e os mais angulos, que são oppostos a lados eguaes, serão tambem eguaes. V.Em qualquer triangulo isosceles os angulos, que estão sobre a base, são eguaes; e produzidos os lados eguaes, os angulos, que se formam debaixo da base, são tambem eguaes. VI. Se dous angulos de um triangulo forem eguaes, os lados, oppostos a estes angulos eguaes, serão tambem eguaes. VII.Sobre a mesma base e da mesma parte não se podem construir dous triangulos differentes, que tenham os outros lados eguaes; isto é, os dous, que partem de um mesmo termo da base e os outros dous, que partem do outro, não podem ser eguaes. VIII.Se dous triangulos tiverem dous lados eguaes a dous lados, cada um a cada um, e as bases tambem eguaes, os angulos, comprehendidos pelos lados eguaes, serão tambem eguaes. IX. Dividir em duas partes eguaes um angulo rectilineo dado. X. Dividir em duas partes eguaes uma linha recta de um comprimento dado. XI. De um ponto dado em uma linha recta dada levantar uma perpendicular sobre a mesma recta dada. XII. Conduzir uma perpendicular sobre uma linha recta dada indefinita de um ponto dado fóra d'ella. XIII. Uma linha recta, cahindo sobre outra linha recta, faz com esta, ou dous angulos rectos, ou dous angulos eguaes a dous rectos. XIV.Se um ponto de uma linha recta qualquer concorrerem de partes oppostas duas rectas, fazendo com a primeira recta os angulos adjacentes eguaes a dous rectos, as rectas, que concorrem para o dito ponto, estarão em direitura uma da outra.
7 XV. Se duas linhas rectas reciprocamente se cortarem, farão os angulos verticalmente oppostos eguaes entre si. XVI. Produzido um lado qualquer de qualquer triangulo, o angulo externo sempre é maior, que cada um dos angulos internos e oppostos. XVII. Dous angulos de um triangulo qualquer, tomados de qualquer modo, que se quiser, são menores que dous rectos. XVIII. Em qualquer triangulo o lado maior oppõe-se ao angulo maior. XIX. Em qualquer triangulo o angulo maior fica opposto ao lado maior. XX. Em qualquer triangulo dous lados, tomados de qualquer modo que se quizer, são maiores que o terceiro. XXI.Se sobre os extremos de um lado de um triangulo estiverem postas duas rectas dentro do mesmo triangulo, estas serão menores que os outros dous lados do triangulo, mas comprehenderão um angulo maior do que o angulo, que fica opposto ao lado, sobre cujos extremos estão postas as dictas rectas. XXII.Construir um triangulo com tres linhas rectas eguaes a tres outras dadas, entre as quaes duas, tomadas como se quizer, sejam sempre maiores que a terceira. XXIII. Em um ponto de uma linha recta dada formar um angulo rectilineo dado. XXIV.Se dous triangulos tiverem dous lados eguaes a dous lados, cada um a cada um, e um dos angulos comprehendidos pelos lados eguaes for maior, e o outro menor; a base, que estiver opposta ao angulo maior, será maior que a outra base opposta ao angulo menor. XXV.Se em dous triangulos forem dous lados de um eguaes a dous lados de outro, cada um a cada um, e for a base de um triangulo maior que a base do outro; aquelle dos angulos comprehendidos pelos lados eguaes, que ficar opposto á base maior, será maior que o outro opposto á base menor. XXVI.Se em dous triangulos dous angulos de um forem eguaes a dous angulos do outro, cada um a cada um, e um lado do primeiro egual a um lado do outro, e forem estes lados ou adjacentes, ou oppostos a angulos eguaes; os outros lados dos dous triangulos serão eguaes aos outros lados, cada um a cada um; e tambem o terceiro angulo será egual ao terceiro. XXVII. Se uma recta, cortando outras duas rectas, fizer com ellas os angulos alternos eguaes: as mesmas duas rectas serão parallelas.
8 XXVIII.Se uma recta cortar outras duas, e fizer o angulo externo egual ao interno e opposto da mesma parte; ou tambem os dous internos da mesma parte eguaes a dous rectos; as mesmas rectas serão parallelas. XXIX.Uma linha recta, que corta duas rectas parallelas, faz os angulos alternos eguaes entre si; o angulo externo egual ao interno e opposto da mesma parte, e finalmente os internos da mesma parte eguaes a dous rectos. XXX. As linhas rectas, que são parallelas a uma mesma linha recta, são parallelas entre si. XXXI. De um ponto dado conduzir uma linha recta parellela a outra linha recta dada. XXXII.Em todo o triangulo produzido um lado qualquer, o angulo externo é egual aos dous internos e oppostos; e os tres angulos internos de um triangulo são eguaes a dous rectos. XXXIII.As rectas, que da mesma parte estão postas entre as extremidades de duas outras rectas eguaes e parallelas, são tambem eguaes e parallelas. XXXIV.Os lados e os angulos oppostos dos espaços formados com linhas parallelas, ou parallelogrammos, são eguaes; e todo o espaço parallelogrammo, fica dividido pela diagonal em duas partes eguaes. XXXV. Os parallelogrammos, que estão postos sobre a mesma base, e entre as mesmas parallelas, são eguaes. XXXVI. Os parallelogrammos, que estão postos sobre bases eguaes, e entre as mesmas parallelas, são eguaes. XXXVII. Os triangulos, que estão postos sobre a mesma base, e entre as mesmas parallelas, são eguaes. XXXVIII. Os triangulos, que estão sobre bases eguaes, e entre as mesmas parallelas, são eguaes. XXXIX. Os triangulos eguaes postos sobre a mesma base, e da mesma parte, estão entre as mesmas parallelas. XL. Os triangulos eguaes postos sobre bases eguaes, e da mesma parte, estão entre as mesmas parallelas. XLI.Se um parallelogrammo e um triangulo estiverem sobre a mesma base, e entre as mesmas parallelas; o parallelogrammo será o dobro do triangulo.
9 XLII. Construir um parallelogrammo, que seja egual a um triangulo dado, e que tenha um angulo egual a outro angulo dado. XLIII. Em qualquer parallelogrammo os complementos dos parallelogrammos, que existem ao redor da diagonal, são eguaes entre si. XLIV.Sobre uma linha recta dada construir um parallelogrammo egual a um triangulo dado, e que tenha um angulo egual a outro angulo rectilineo dado. XLV. Construir um parallelogrammo egual a uma figura rectilinea qualquer dada, e com um angulo egual a outro angulo dado. XLVI. Sobre uma linha recta dada descrever em quadrado. XLVII.Em todo o triangulo rectangulo o quadrado feito sobre o lado opposto ao angulo recto, é egual aos quadrados formados sobre os outros lados, que fazem o mesmo angulo recto. XLVIII.Se o quadrado feito sobre um lado de um triangulo for egual aos quadrados dos outros dous lados; o angulo comprehendido por estes dous lados será recto.
LEI Nº 4.035. De: 04 de julho de 2014. A CÂMARA MUNICIPAL DE UMUARAMA, ESTADO DO PARANÁ, aprovou, e eu, Prefeito Municipal, sanciono a seguinte Lei:
 LEI Nº 4.035 De: 04 de julho de 2014. Desafeta do domínio público os imóveis localizados no CONJUNTO HABITACIONAL SONHO MEU, na cidade de Umuarama - PR. A CÂMARA MUNICIPAL DE UMUARAMA, ESTADO DO PARANÁ,
LEI Nº 4.035 De: 04 de julho de 2014. Desafeta do domínio público os imóveis localizados no CONJUNTO HABITACIONAL SONHO MEU, na cidade de Umuarama - PR. A CÂMARA MUNICIPAL DE UMUARAMA, ESTADO DO PARANÁ,
Figura I Experiência prévia em Teatro dos alunos do 1º período do Curso de Graduação em Teatro da EBA/UFMG no 1º semestre de 2009.
 Lista de Figuras Figura I Experiência prévia em Teatro dos alunos do 1º período do Curso de Graduação em Teatro da EBA/UFMG no 1º semestre de 2009. Figura 2- Local onde os alunos, com experiência prévia,
Lista de Figuras Figura I Experiência prévia em Teatro dos alunos do 1º período do Curso de Graduação em Teatro da EBA/UFMG no 1º semestre de 2009. Figura 2- Local onde os alunos, com experiência prévia,
TABELA DE CONTRIBUIÇÃO DO SEGURADO EMPREGADO, DOMÉSTICO E AVULSO
 TABELA DE CONTRIBUIÇÃO DO SEGURADO EMPREGADO, DOMÉSTICO E AVULSO A PARTIR DE 1º DE JANEIRO DE 2010 Salário-de-contribuição (R$) INSS até 1.040,22 8,00% de 1.040,23 até 1.733,70 9,00% de 1.733,71 até 3.467,40
TABELA DE CONTRIBUIÇÃO DO SEGURADO EMPREGADO, DOMÉSTICO E AVULSO A PARTIR DE 1º DE JANEIRO DE 2010 Salário-de-contribuição (R$) INSS até 1.040,22 8,00% de 1.040,23 até 1.733,70 9,00% de 1.733,71 até 3.467,40
PORTARIA CFO-SEC-56, de 25 de fevereiro de 1999
 Página 1 PORTARIA CFO-SEC-56, de 25 de fevereiro de 1999 O Plenário do Conselho Federal de Odontologia, em reunião realizada no dia 25 de fevereiro de 1999, RESOLVE: Art. 1º. Referendar as deliberações
Página 1 PORTARIA CFO-SEC-56, de 25 de fevereiro de 1999 O Plenário do Conselho Federal de Odontologia, em reunião realizada no dia 25 de fevereiro de 1999, RESOLVE: Art. 1º. Referendar as deliberações
Cadeia de caracteres (strings)
 BCC 201 - Introdução à Programação I Cadeia de caracteres (strings) Guillermo Cámara-Chávez UFOP 1/1 Cadeia de caracteres I Definição: são seqüências de letras, números ou símbolos onde o último caracter
BCC 201 - Introdução à Programação I Cadeia de caracteres (strings) Guillermo Cámara-Chávez UFOP 1/1 Cadeia de caracteres I Definição: são seqüências de letras, números ou símbolos onde o último caracter
FACULDADE METODISTA GRANBERY - MATRIZ CURRICULAR - CURSO DE ADMINIS
 FACULDADE METODISTA GRANBERY - MATRIZ CURRICULAR - CURSO DE ADMINIS 1º PERÍODO MÓDULOS (Hora/Aula) TEMAS Teorias da Administração I - EVOLUÇÃO DA ADMINISTRAÇÃO II - RESPONSABILIDADE CORPORATIVA Adm. Contemporânea
FACULDADE METODISTA GRANBERY - MATRIZ CURRICULAR - CURSO DE ADMINIS 1º PERÍODO MÓDULOS (Hora/Aula) TEMAS Teorias da Administração I - EVOLUÇÃO DA ADMINISTRAÇÃO II - RESPONSABILIDADE CORPORATIVA Adm. Contemporânea
Anexo 1 Plan de clase (10º B/F/G; Describir la vivienda)
 Anexo 1 Plan de clase (10º B/F/G; Describir la vivienda) i Anexo 1.1 Trabalhos realizados pelos alunos (Posters) ii Anexo 2 Planificação de unidade didáctica (10º D; La gastronomía española) iii Anexo
Anexo 1 Plan de clase (10º B/F/G; Describir la vivienda) i Anexo 1.1 Trabalhos realizados pelos alunos (Posters) ii Anexo 2 Planificação de unidade didáctica (10º D; La gastronomía española) iii Anexo
MUNICÍPIO DE JUAZEIRO ESTADO DA BAHIA
 LEI Nº 2.293 / 2012 Dispõe sobre a instituição do Bairro Monte Castelo no âmbito urbano do Município de Juazeiro Bahia e dá outras providências. O PREFEITO MUNICIPAL DE JUAZEIRO, Estado da Bahia, no uso
LEI Nº 2.293 / 2012 Dispõe sobre a instituição do Bairro Monte Castelo no âmbito urbano do Município de Juazeiro Bahia e dá outras providências. O PREFEITO MUNICIPAL DE JUAZEIRO, Estado da Bahia, no uso
Índice de Anexos da Ata nº 116 de 26 de Julho de 2016
 Índice de Anexos da Ata nº 116 de 26 de Julho de 2016 Anexo I Documentação Munícipe Ana Isidro Anexo II Documentação Munícipe José Baltazar Anexo III Petição Nº 10_2016 - Pelo fim imediato da utilização
Índice de Anexos da Ata nº 116 de 26 de Julho de 2016 Anexo I Documentação Munícipe Ana Isidro Anexo II Documentação Munícipe José Baltazar Anexo III Petição Nº 10_2016 - Pelo fim imediato da utilização
Capítulo XII - A Comissão Mercantil A comissão mercantil e seu alcance 36. Traços distintivos Contornos legais.
 SUMÁRIO Capítulo I - Os Contratos Comerciais e Seu Regime Jurídico. 1. Observações introdutórias: atividades civis e comerciais. 2. Os contratos comerciais. 3. Regime jurídico. Capítulo II - A Compra e
SUMÁRIO Capítulo I - Os Contratos Comerciais e Seu Regime Jurídico. 1. Observações introdutórias: atividades civis e comerciais. 2. Os contratos comerciais. 3. Regime jurídico. Capítulo II - A Compra e
DAS COORDENAÇÃO DE EIXO_TECNOLÓGICO
 DAS COORDENAÇÃO DE EIXO_TECNOLÓGICO TÍTULO I DA NATUREZA E FINALIDADES Art. 1 - À coordenação de eixo-tecnológico compete: I - Convocar e presidir as reuniões do Colegiado de Curso; II - Submeter à Coordenação
DAS COORDENAÇÃO DE EIXO_TECNOLÓGICO TÍTULO I DA NATUREZA E FINALIDADES Art. 1 - À coordenação de eixo-tecnológico compete: I - Convocar e presidir as reuniões do Colegiado de Curso; II - Submeter à Coordenação
Capítulo I Introdução e objectivo Introdução Objectivos do estudo Motivação para o estudo 2. Capítulo II Revisão da Literatura 4
 Índice geral Capítulo I Introdução e objectivo 1 Pág. 1.0 Introdução 2 1.1 Objectivos do estudo 2 1.2 Motivação para o estudo 2 Capítulo II Revisão da Literatura 4 2.1 O Suicídio na História e na Literatura:
Índice geral Capítulo I Introdução e objectivo 1 Pág. 1.0 Introdução 2 1.1 Objectivos do estudo 2 1.2 Motivação para o estudo 2 Capítulo II Revisão da Literatura 4 2.1 O Suicídio na História e na Literatura:
PÉRICLES ALVES DE OLIVEIRA ANA LISS. Bom Despacho-MG
 ANA LISS PÉRICLES ALVES DE OLIVEIRA ANA LISS Bom Despacho-MG. 2017. Um pouco sobre mim. Algo de poeta. Algo de quântico. Algo de niilista. Algo de sonhos descrentes. Algo de louco. Algo de tudo. E um
ANA LISS PÉRICLES ALVES DE OLIVEIRA ANA LISS Bom Despacho-MG. 2017. Um pouco sobre mim. Algo de poeta. Algo de quântico. Algo de niilista. Algo de sonhos descrentes. Algo de louco. Algo de tudo. E um
Capítulo I Dos Pronunciamentos do Comitê de Pronunciamentos Contábeis - CPC
 LIVRO : PLANO CONTÁBIL DAS ENTIDADES ABERTAS DE PREVIDÊNCIA COMPLEMENTAR, SOCIEDADES SEGURADORAS, SOCIEDADES DE CAPITALIZAÇÃO E RESSEGURADORES LOCAIS ANEXO IV: Título IV - Normas Recepcionadas Capítulo
LIVRO : PLANO CONTÁBIL DAS ENTIDADES ABERTAS DE PREVIDÊNCIA COMPLEMENTAR, SOCIEDADES SEGURADORAS, SOCIEDADES DE CAPITALIZAÇÃO E RESSEGURADORES LOCAIS ANEXO IV: Título IV - Normas Recepcionadas Capítulo
LEI Nº. 34, de 08 de Outubro de Alterada pela Lei Municipal nº 459, de 30 de Setembro de 2005.
 LEI Nº. 34, de 08 de Outubro de 1984. Alterada pela Lei Municipal nº 459, de 30 de Setembro de 2005. DENOMINA VIA URBANAS DA SEDE DO MUNICIPIO. O Prefeito do Município de Ibatiba, Estado do Espírito Santo,
LEI Nº. 34, de 08 de Outubro de 1984. Alterada pela Lei Municipal nº 459, de 30 de Setembro de 2005. DENOMINA VIA URBANAS DA SEDE DO MUNICIPIO. O Prefeito do Município de Ibatiba, Estado do Espírito Santo,
SECRETARIA DE DEFESA AGROPECUÁRIA INSTRUÇÃO NORMATIVA No-36, DE 30 DE DEZEMBRO DE 2010
 Data: 31/12/2010 Nº 029 Pág: 1 de 43 SECRETARIA DE DEFESA AGROPECUÁRIA INSTRUÇÃO NORMATIVA No-36, DE 30 DE DEZEMBRO DE 2010 O SECRETÁRIO SUBSTITUTO DE DEFESA AGROPECUÁRIA DO MINISTÉRIO DA AGRICULTURA,
Data: 31/12/2010 Nº 029 Pág: 1 de 43 SECRETARIA DE DEFESA AGROPECUÁRIA INSTRUÇÃO NORMATIVA No-36, DE 30 DE DEZEMBRO DE 2010 O SECRETÁRIO SUBSTITUTO DE DEFESA AGROPECUÁRIA DO MINISTÉRIO DA AGRICULTURA,
1º Período. Figuras geométricas
 ii 1º Período Figuras geométricas Quadrado polígono com quatro lados iguais e com quatro ângulos rectos. Rectângulo polígono com quatro lados iguais dois a dois e com quatro ângulos rectos. Trapézio rectângulo
ii 1º Período Figuras geométricas Quadrado polígono com quatro lados iguais e com quatro ângulos rectos. Rectângulo polígono com quatro lados iguais dois a dois e com quatro ângulos rectos. Trapézio rectângulo
PADRE ANTÓNIO VIEIRA RTE de FURTAR ESPELHO DE ENGANOS TEATRO DE VERDADES. SUB Hamburg "'" III III Mil IIIII fllfl lllff A/511049
 SUB Hamburg "'" III III Mil IIIII fllfl lllff A/511049 PADRE ANTÓNIO VIEIRA RTE de FURTAR ESPELHO DE ENGANOS TEATRO DE VERDADES FRONTEIRA DO CAOS EDITORES ÍNDICE 9 INTRODUÇÃO 15 DEPRECAÇAO Ao Sereníssimo
SUB Hamburg "'" III III Mil IIIII fllfl lllff A/511049 PADRE ANTÓNIO VIEIRA RTE de FURTAR ESPELHO DE ENGANOS TEATRO DE VERDADES FRONTEIRA DO CAOS EDITORES ÍNDICE 9 INTRODUÇÃO 15 DEPRECAÇAO Ao Sereníssimo
RESOLUÇÃO CSDPE Nº 04/2018
 RESOLUÇÃO CSDPE Nº 04/2018 Altera a Resolução CSDPE nº 03/2016, incluindo a atribuição para atuação no Juizado Especial da Fazenda Pública em seus anexos. O CONSELHO SUPERIOR DA DEFENSORIA PÚBLICA DO ESTADO
RESOLUÇÃO CSDPE Nº 04/2018 Altera a Resolução CSDPE nº 03/2016, incluindo a atribuição para atuação no Juizado Especial da Fazenda Pública em seus anexos. O CONSELHO SUPERIOR DA DEFENSORIA PÚBLICA DO ESTADO
MEDIDA PROVISÓRIA 805, DE 30 DE OUTUBRO DE 2017
 MEDIDA PROVISÓRIA 805, DE 30 DE OUTUBRO DE 2017 Posterga ou cancela aumentos remuneratórios para os exercícios subsequentes, altera a Lei no 8.112, de 11 de dezembro de 1990, que dispõe sobre o regime
MEDIDA PROVISÓRIA 805, DE 30 DE OUTUBRO DE 2017 Posterga ou cancela aumentos remuneratórios para os exercícios subsequentes, altera a Lei no 8.112, de 11 de dezembro de 1990, que dispõe sobre o regime
ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO. 1- Ângulos Definição: Chama-se ângulo à porção de plano limitada por duas semirretas com a mesma origem.
 ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO 1ª Ficha Informativa MATEMÁTICA - A 10º Ano 2012/2013 1- Ângulos Definição: Chama-se ângulo à porção de plano limitada por duas semirretas com a mesma origem. Definição:
ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO 1ª Ficha Informativa MATEMÁTICA - A 10º Ano 2012/2013 1- Ângulos Definição: Chama-se ângulo à porção de plano limitada por duas semirretas com a mesma origem. Definição:
Capitulo I Dos Pronunciamentos do Comitê de Pronunciamentos Contábeis - CPC
 - 792 - LIVRO : PLANO CONTÁBIL DAS ENTIDADES ABERTAS DE PREVIDENCIA COMPLEMENTAR, SOCIEDADES SEGURADORAS, SOCIEDADES DE CAPITALIZAÇÃO E RESSEGURADORES LOCAIS ANEXO IV: Título IV - Normas Recepcionadas
- 792 - LIVRO : PLANO CONTÁBIL DAS ENTIDADES ABERTAS DE PREVIDENCIA COMPLEMENTAR, SOCIEDADES SEGURADORAS, SOCIEDADES DE CAPITALIZAÇÃO E RESSEGURADORES LOCAIS ANEXO IV: Título IV - Normas Recepcionadas
Prefeitura Municipal de Pojuca publica:
 Prefeitura Municipal de Pojuca 1 Quinta-feira Ano VI Nº 1193 Prefeitura Municipal de Pojuca publica: Republicação do Anexo 6 do Relatório Resumido da Execução Orçamentária - 1º Bimestre 2018. Portaria
Prefeitura Municipal de Pojuca 1 Quinta-feira Ano VI Nº 1193 Prefeitura Municipal de Pojuca publica: Republicação do Anexo 6 do Relatório Resumido da Execução Orçamentária - 1º Bimestre 2018. Portaria
RESOLUÇÃO. Gestão de Negócios; Gestão Estratégica de Pessoas, no câmpus de Itatiba, criados pela Resolução CONSEPE 21-A/2003, de 26/6/2003;
 RESOLUÇÃO CONSEPE 69/2004 DISPÕE SOBRE O PROCESSO DE EXTINÇÃO DE CURSOS DE PÓS- GRADUAÇÃO LATO SENSU, DA UNIVERSIDADE SÃO FRANCISCO. O Presidente do Conselho de Ensino, Pesquisa e Extensão - CONSEPE, no
RESOLUÇÃO CONSEPE 69/2004 DISPÕE SOBRE O PROCESSO DE EXTINÇÃO DE CURSOS DE PÓS- GRADUAÇÃO LATO SENSU, DA UNIVERSIDADE SÃO FRANCISCO. O Presidente do Conselho de Ensino, Pesquisa e Extensão - CONSEPE, no
CURSO COMPLETO: PLANEJAMENTO DAS CONTRATAÇÕES
 CURSO EAD CURSO COMPLETO: PLANEJAMENTO DAS CONTRATAÇÕES Com ênfase: Elaboração do Termo de Referência; Cautelas na fase externa: habilitação e julgamento das propostas; Peculiaridades do pregão; Tratamento
CURSO EAD CURSO COMPLETO: PLANEJAMENTO DAS CONTRATAÇÕES Com ênfase: Elaboração do Termo de Referência; Cautelas na fase externa: habilitação e julgamento das propostas; Peculiaridades do pregão; Tratamento
Sumário. Еbгehий Oheгиh / Eugênio Onêguin. Nota dos Tradutores Посвящение / Dedicatória xvi xviii ii...
 Sumário Nota dos Tradutores.... 11 Еbгehий Oheгиh / Eugênio Onêguin Посвящение / Dedicatória.... 17 ГЛАВА ПЕРВАЯ / Capítulo I i... 21 ii... 21 iii.... 23 iv.... 23 v... 25 vi.... 25 vii.... 27 viii...
Sumário Nota dos Tradutores.... 11 Еbгehий Oheгиh / Eugênio Onêguin Посвящение / Dedicatória.... 17 ГЛАВА ПЕРВАЯ / Capítulo I i... 21 ii... 21 iii.... 23 iv.... 23 v... 25 vi.... 25 vii.... 27 viii...
M a n u e l C e l e s t i n o V i l e l a T e i x e i r a d e A l m e i d a
 M a n u e l C e l e s t i n o V i l e l a T e i x e i r a d e A l m e i d a AV A L I A Ç Ã O D O E F E I T O D E F O G O S F L O R E S T A I S N O R E G I M E D E E S C O A M E N T O E N A Q U A L I D
M a n u e l C e l e s t i n o V i l e l a T e i x e i r a d e A l m e i d a AV A L I A Ç Ã O D O E F E I T O D E F O G O S F L O R E S T A I S N O R E G I M E D E E S C O A M E N T O E N A Q U A L I D
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE. Professor: João Carmo
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo DEFINIÇÃO Triângulo ou trilátero é um polígono de três lados. Observações: a) O triângulo não possui diagonais;
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE Professor: João Carmo DEFINIÇÃO Triângulo ou trilátero é um polígono de três lados. Observações: a) O triângulo não possui diagonais;
ATIVIDADES COM VARETAS
 ATIVIDADES COM VARETAS Em todas as atividades é usado o Material: Varetas. Nos casos específicos onde o trabalho é realizado com varetas congruentes será especificado como Material: varetas do mesmo comprimento.
ATIVIDADES COM VARETAS Em todas as atividades é usado o Material: Varetas. Nos casos específicos onde o trabalho é realizado com varetas congruentes será especificado como Material: varetas do mesmo comprimento.
GEOMETRIA PLANA. Segmentos congruentes: Dois segmentos ou ângulos são congruentes quando têm as mesmas medidas.
 PARTE 01 GEOMETRIA PLANA Introdução A Geometria está apoiada sobre alguns postulados, axiomas, definições e teoremas, sendo que essas definições e postulados são usados para demonstrar a validade de cada
PARTE 01 GEOMETRIA PLANA Introdução A Geometria está apoiada sobre alguns postulados, axiomas, definições e teoremas, sendo que essas definições e postulados são usados para demonstrar a validade de cada
RESOLUÇÃO Nº 084/2015 CONSU/IFAC.
 RESOLUÇÃO Nº 084/2015 CONSU/IFAC. Dispõe sobre o Regulamento das Atribuições da Coordenação Técnico Pedagógica COTEP do Instituto Federal de Educação, Ciência e Tecnologia do Acre IFAC. O PRESIDENTE SUBSTITUTO
RESOLUÇÃO Nº 084/2015 CONSU/IFAC. Dispõe sobre o Regulamento das Atribuições da Coordenação Técnico Pedagógica COTEP do Instituto Federal de Educação, Ciência e Tecnologia do Acre IFAC. O PRESIDENTE SUBSTITUTO
PEDIDO PÚBLICO DE PROCURAÇÃO
 PEDIDO PÚBLICO DE PROCURAÇÃO COMUNICADO AO MERCADO PEDIDO PÚBLICO DE PROCURAÇÃO Lojas Renner S.A. ( Companhia ), com apoio no artigo 27 da Instrução nr. 481, de 17 de dezembro de 2009, editada pela Comissão
PEDIDO PÚBLICO DE PROCURAÇÃO COMUNICADO AO MERCADO PEDIDO PÚBLICO DE PROCURAÇÃO Lojas Renner S.A. ( Companhia ), com apoio no artigo 27 da Instrução nr. 481, de 17 de dezembro de 2009, editada pela Comissão
POLÍGONOS TRIÂNGULOS E QUADRILÁTEROS
 7º ANO POLÍGONOS TRIÂNGULOS E QUADRILÁTEROS Ângulos e triângulos Nuno Marreiros Antes de começar O Alfabeto Grego O alfabeto utilizado para escrever a Língua grega teve o seu desenvolvimento por volta
7º ANO POLÍGONOS TRIÂNGULOS E QUADRILÁTEROS Ângulos e triângulos Nuno Marreiros Antes de começar O Alfabeto Grego O alfabeto utilizado para escrever a Língua grega teve o seu desenvolvimento por volta
PORTARIA Nº 475 DE 06 DE ABRIL DE 2016
 PORTARIA Nº 475 DE 06 DE ABRIL DE 2016 Dispõe sobre delegação de competências aos Diretores Gerais dos Campi, Diretores Gerais Pro-Tempore dos Campi e Diretores Pro-Tempore dos Campi Avançados do IFMG.
PORTARIA Nº 475 DE 06 DE ABRIL DE 2016 Dispõe sobre delegação de competências aos Diretores Gerais dos Campi, Diretores Gerais Pro-Tempore dos Campi e Diretores Pro-Tempore dos Campi Avançados do IFMG.
Dados para Audiência Pública Energisa Mato Grosso Distribuidora de Energia S.A
 Cuiabá, 21 de março de 2018. Dados para Audiência Pública Energisa Mato Grosso Distribuidora de Energia S.A 1. Informações sobre os s já realizados/em realização. 1.1. Tipologia - Baixa Renda ( em Andamento)
Cuiabá, 21 de março de 2018. Dados para Audiência Pública Energisa Mato Grosso Distribuidora de Energia S.A 1. Informações sobre os s já realizados/em realização. 1.1. Tipologia - Baixa Renda ( em Andamento)
OBRAS COMPLETAS DE FERNANDO PESSOA III ALBERTO CAEIRO. 12. a EDIÇÃO EDITORIAL NOVA ATIÇA LISBOA
 OBRAS COMPLETAS DE FERNANDO PESSOA III de ALBERTO CAEIRO 12. a EDIÇÃO EDITORIAL NOVA ATIÇA LISBOA ÍNDICE «O GUARDADOR DE REBANHOS» Data das poesias 1911-1912 I Eu nunca guardei rebanhos, (Atena, n. 4,
OBRAS COMPLETAS DE FERNANDO PESSOA III de ALBERTO CAEIRO 12. a EDIÇÃO EDITORIAL NOVA ATIÇA LISBOA ÍNDICE «O GUARDADOR DE REBANHOS» Data das poesias 1911-1912 I Eu nunca guardei rebanhos, (Atena, n. 4,
MINISTÉRIO DA EDUCAÇÃO INSTITUTO NACIONAL DE ESTUDOS E PESQUISAS EDUCACIONAIS ANÍSIO TEIXEIRA PORTARIAS DE 22 DE JUNHO DE 2012
 MINISTÉRIO DA EDUCAÇÃO INSTITUTO NACIONAL DE ESTUDOS E PESQUISAS EDUCACIONAIS ANÍSIO TEIXEIRA PORTARIAS DE 22 DE JUNHO DE 2012 O Presidente do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio
MINISTÉRIO DA EDUCAÇÃO INSTITUTO NACIONAL DE ESTUDOS E PESQUISAS EDUCACIONAIS ANÍSIO TEIXEIRA PORTARIAS DE 22 DE JUNHO DE 2012 O Presidente do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio
O Colégio Militar de Curitiba, em relação ao regulamento Nº 001/13 resolve, complementar os seguintes itens :
 O de Curitiba, em relação ao regulamento Nº 001/13 resolve, complementar os seguintes itens : 2. DAS CONDIÇÕES DE INGRESSO, REMUNERAÇÃO E ATRIBUIÇÕES b. O regime de trabalho será, preferencialmente, o
O de Curitiba, em relação ao regulamento Nº 001/13 resolve, complementar os seguintes itens : 2. DAS CONDIÇÕES DE INGRESSO, REMUNERAÇÃO E ATRIBUIÇÕES b. O regime de trabalho será, preferencialmente, o
RESOLUÇÃO Nº 030/2012 CONSEPE (Vide Resolução nº 007/2013-CONSEPE)
 RESOLUÇÃO Nº 030/2012 CONSEPE (Vide Resolução nº 007/2013-CONSEPE) Aprova alteração curricular do Curso de Licenciatura em Teatro, do Centro de Artes - CEART, da Fundação Universidade do Estado de Santa
RESOLUÇÃO Nº 030/2012 CONSEPE (Vide Resolução nº 007/2013-CONSEPE) Aprova alteração curricular do Curso de Licenciatura em Teatro, do Centro de Artes - CEART, da Fundação Universidade do Estado de Santa
Anexo VIII - Diversos
 Anexo VIII - Diversos lxxxiii Figura I - Plano geral das estruturas de origem islâmica encontradas no Pátio de S. Miguel. (Foto: ERA-Arqueologia, 2012). Figura II - Plano geral das estruturas de origem
Anexo VIII - Diversos lxxxiii Figura I - Plano geral das estruturas de origem islâmica encontradas no Pátio de S. Miguel. (Foto: ERA-Arqueologia, 2012). Figura II - Plano geral das estruturas de origem
CARTA-CIRCULAR Nº 3089
 CARTA-CIRCULAR Nº 3089 Libera módulos do Sistema de Informações sobre Entidades de Interesse do Banco Central - Unicad. Em conformidade com o disposto nas Circulares 3.165 e 3.180, de 4 de dezembro de
CARTA-CIRCULAR Nº 3089 Libera módulos do Sistema de Informações sobre Entidades de Interesse do Banco Central - Unicad. Em conformidade com o disposto nas Circulares 3.165 e 3.180, de 4 de dezembro de
MUNICÍPIO DE SETÚBAL CÂMARA MUNICIPAL
 REUNIÃO Nº : PROPOSTA Nº : 0/0/DCED/DIMUS Realizada em: DELIBERAÇÃO Nº : ASSUNTO : Doação de várias peças de arte ao Município no âmbito da atividade cultural no Museu de Setúbal/Convento de Jesus O Sr.
REUNIÃO Nº : PROPOSTA Nº : 0/0/DCED/DIMUS Realizada em: DELIBERAÇÃO Nº : ASSUNTO : Doação de várias peças de arte ao Município no âmbito da atividade cultural no Museu de Setúbal/Convento de Jesus O Sr.
Coordenadoria de Acórdãos e Resoluções
 Página 139 nº 23.326/2010 - que dispõe sobre as diretrizes para a tramitação de documentos e processos sigilosos no âmbito da Justiça Eleitoral -, vieram-me os autos conclusos. Observo que os documentos
Página 139 nº 23.326/2010 - que dispõe sobre as diretrizes para a tramitação de documentos e processos sigilosos no âmbito da Justiça Eleitoral -, vieram-me os autos conclusos. Observo que os documentos
CARREIRA DO BANCO CENTRAL DO
 ESTUDO SOBRE OS PLANOS DE CARREIRA DO BANCO CENTRAL DO BRASIL PROPOSTA DE REVISÃO A SER SUBMETIDA À XXI ASSEMBLÉIA NACIONAL DELIBERATIVA AND DIAGNÓSTICO O Plano de Carreira do Banco Central do Brasil foi
ESTUDO SOBRE OS PLANOS DE CARREIRA DO BANCO CENTRAL DO BRASIL PROPOSTA DE REVISÃO A SER SUBMETIDA À XXI ASSEMBLÉIA NACIONAL DELIBERATIVA AND DIAGNÓSTICO O Plano de Carreira do Banco Central do Brasil foi
Prefeitura Municipal de Venda Nova do Imigrante
 I - INTRODUÇÃO II - OBJETO III - DOS ÓRGÃOS E UNIDADES INTEGRANTES DO REGISTRO IV - CONDIÇÕES GERAIS PARA PARTICIPAÇÃO V - DO RECEBIMENTO DA DOCUMENTAÇÃO E DA PROPOST VI - ABERTURA DOS ENVELOPES VII -
I - INTRODUÇÃO II - OBJETO III - DOS ÓRGÃOS E UNIDADES INTEGRANTES DO REGISTRO IV - CONDIÇÕES GERAIS PARA PARTICIPAÇÃO V - DO RECEBIMENTO DA DOCUMENTAÇÃO E DA PROPOST VI - ABERTURA DOS ENVELOPES VII -
VI CONGRESSO BRASILEIRO DE GESTÃO AMBIENTAL
 O Biólogo no mercado de trabalho em Gestão Ambiental Prof. Dr. Murilo Damato Conselho Federal de Biologia CONSELHO FEDERAL DE BIOLOGIA -CFBio, Autarquia Federal, com personalidade jurídica de direito público,
O Biólogo no mercado de trabalho em Gestão Ambiental Prof. Dr. Murilo Damato Conselho Federal de Biologia CONSELHO FEDERAL DE BIOLOGIA -CFBio, Autarquia Federal, com personalidade jurídica de direito público,
DOU Seção I 30/09/2013 MINISTÉRIO DA SAÚDE ANSS - AGÊNCIA NACIONAL DE SAÚDE SUPLEMENTAR. PORTARIA No- 1, DE 26 DE FEVEREIRO DE 2016
 DOU Seção I 30/09/2013 MINISTÉRIO DA SAÚDE ANSS - AGÊNCIA NACIONAL DE SAÚDE SUPLEMENTAR PORTARIA No- 1, DE 26 DE FEVEREIRO DE 2016 A DIRETORA DE DESENVOLVIMENTO SETORIAL DA AGÊNCIA NACIONAL DE SAÚDE SUPLEMENTAR,
DOU Seção I 30/09/2013 MINISTÉRIO DA SAÚDE ANSS - AGÊNCIA NACIONAL DE SAÚDE SUPLEMENTAR PORTARIA No- 1, DE 26 DE FEVEREIRO DE 2016 A DIRETORA DE DESENVOLVIMENTO SETORIAL DA AGÊNCIA NACIONAL DE SAÚDE SUPLEMENTAR,
2ª feira 02/Dez/2013 - Edição nº 9097. de Umuarama.
 24 2ª feira 02/Dez/2013 - Edição nº 9097 de Umuarama. 2ª feira 02/Dez/2013 - Edição nº 9097 25 ANEXO I DO REGULAMENTO A QUE SE REFERE O DECRETO Nº 9510/2013 26 2ª feira 02/Dez/2013 - Edição nº 9097 ANEXO
24 2ª feira 02/Dez/2013 - Edição nº 9097 de Umuarama. 2ª feira 02/Dez/2013 - Edição nº 9097 25 ANEXO I DO REGULAMENTO A QUE SE REFERE O DECRETO Nº 9510/2013 26 2ª feira 02/Dez/2013 - Edição nº 9097 ANEXO
Duração: 90 minutos (3 valores) Sabe-se que a b. Atendendo à gura, calcule a medida do ângulo D indicado.
 aculdade de Ciências Departamento de Matemática e Informática Licenciatura em Informática, Diurno 1 0 Teste de undamentos de Geometria. Correcção. ariante Duração: 90 minutos 18.0.01 1. ( valores) Sabe-se
aculdade de Ciências Departamento de Matemática e Informática Licenciatura em Informática, Diurno 1 0 Teste de undamentos de Geometria. Correcção. ariante Duração: 90 minutos 18.0.01 1. ( valores) Sabe-se
GUIA DE FUNCIONAMENTO DA UNIDADE CURRICULAR
 Curso Engenharia civil Ano letivo 2013/2014 Unidade Curricular Tecnologia das construções ECTS 4 Regime Obrigatório Ano 2º Semestre 1º semestre Horas de trabalho globais Docente (s) Maria de Jesus de Almeida
Curso Engenharia civil Ano letivo 2013/2014 Unidade Curricular Tecnologia das construções ECTS 4 Regime Obrigatório Ano 2º Semestre 1º semestre Horas de trabalho globais Docente (s) Maria de Jesus de Almeida
PROC. Nº 3832/07 PR Nº 060/07 EXPOSIÇÃO DE MOTIVOS
 EXPOSIÇÃO DE MOTIVOS Apresentamos aos Senhores Vereadores o presente Projeto de Resolução, que institui premiações a serem conferidas pela Câmara Municipal de Porto Alegre. Este trabalho é resultado da
EXPOSIÇÃO DE MOTIVOS Apresentamos aos Senhores Vereadores o presente Projeto de Resolução, que institui premiações a serem conferidas pela Câmara Municipal de Porto Alegre. Este trabalho é resultado da
NOME: ANO: 3º Nº: PROFESSOR(A):
 NOME: ANO: º Nº: PROFESSOR(A): Ana Luiza Ozores DATA: Algumas definições Triângulos: REVISÃO Lista 06 Triângulos e Quadriláteros Classificação quanto aos lados: Escaleno (todos os lados diferentes), Isósceles
NOME: ANO: º Nº: PROFESSOR(A): Ana Luiza Ozores DATA: Algumas definições Triângulos: REVISÃO Lista 06 Triângulos e Quadriláteros Classificação quanto aos lados: Escaleno (todos os lados diferentes), Isósceles
Definição de Polígono
 Definição de Polígono Figura plana limitada por segmentos de recta, chamados lados dos polígonos onde cada segmento de recta, intersecta exactamente dois outros extremos; se os lados forem todos iguais
Definição de Polígono Figura plana limitada por segmentos de recta, chamados lados dos polígonos onde cada segmento de recta, intersecta exactamente dois outros extremos; se os lados forem todos iguais
PERÍMETRO O perímetro de um triângulo é igual à soma das medidas dos seus lados. Perímetro ABC = AB + AC + BC TRIÂNGULOS
 TRIÂNGULOS Conceito: Triângulo é um polígono de três lados. PERÍMETRO O perímetro de um triângulo é igual à soma das medidas dos seus lados. Perímetro ABC = AB + AC + BC CLASSIFICAÇÃO DOS TRIÂNGULOS Quanto
TRIÂNGULOS Conceito: Triângulo é um polígono de três lados. PERÍMETRO O perímetro de um triângulo é igual à soma das medidas dos seus lados. Perímetro ABC = AB + AC + BC CLASSIFICAÇÃO DOS TRIÂNGULOS Quanto
MATRIZ CURRICULAR DO CURSO DE ENGENHARIA ELÉTRICA
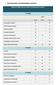 1- BACHARELADO EM ENGENHARIA ELÉTRICA MATRIZ CURRICULAR DO CURSO DE ENGENHARIA ELÉTRICA 1º TERMO Aulas Teóricas Práticas Total Comunicação e Expressão 36-36 Cálculo Diferencial e Integral I 72-72 Informática
1- BACHARELADO EM ENGENHARIA ELÉTRICA MATRIZ CURRICULAR DO CURSO DE ENGENHARIA ELÉTRICA 1º TERMO Aulas Teóricas Práticas Total Comunicação e Expressão 36-36 Cálculo Diferencial e Integral I 72-72 Informática
SECRETARIA DE RECURSOS HUMANOS PORTARIA NORMATIVA Nº 2, DE 8 DE NOVEMBRO DE 2011
 SECRETARIA DE RECURSOS HUMANOS PORTARIA NORMATIVA Nº 2, DE 8 DE NOVEMBRO DE 2011 Dispõe sobre os procedimentos para a aplicação do limite remuneratório de que trata o inciso XI, do art. 37, da Constituição
SECRETARIA DE RECURSOS HUMANOS PORTARIA NORMATIVA Nº 2, DE 8 DE NOVEMBRO DE 2011 Dispõe sobre os procedimentos para a aplicação do limite remuneratório de que trata o inciso XI, do art. 37, da Constituição
LEI N 999, DE 08 DE NOVEMBRO DE 2018.
 Quinta-feira, 22 de Novembro de 2018 Edição N 985 Caderno II 4 LEI N 999, DE 08 DE NOVEMBRO DE 2018. Altera o Quadro de Cargos de provimento efetivo, criando novos cargos, extinguindo vagas e dando novas
Quinta-feira, 22 de Novembro de 2018 Edição N 985 Caderno II 4 LEI N 999, DE 08 DE NOVEMBRO DE 2018. Altera o Quadro de Cargos de provimento efetivo, criando novos cargos, extinguindo vagas e dando novas
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro?
 Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
Equilátero Isósceles Escaleno
 TRIÂNGULOS Triângulo são polígonos formados por três lados. Os polígonos, por sua vez, são figuras geométricas formadas por segmentos de reta que, dois a dois, tocam-se em seus pontos extremos, mas que
TRIÂNGULOS Triângulo são polígonos formados por três lados. Os polígonos, por sua vez, são figuras geométricas formadas por segmentos de reta que, dois a dois, tocam-se em seus pontos extremos, mas que
REGULAMENTO CIRCUTO CIDADES PAULISTAS 5
 REGULAMENTO CIRCUTO CIDADES PAULISTAS 5 I. A 23ª Corrida Cidade de Indaiatuba, tem sua realização no dia 10/12/2017 na cidade de Indaiatuba/SP, com largada e chegada na Av. Fábio Roberto Barnabé, 2800,
REGULAMENTO CIRCUTO CIDADES PAULISTAS 5 I. A 23ª Corrida Cidade de Indaiatuba, tem sua realização no dia 10/12/2017 na cidade de Indaiatuba/SP, com largada e chegada na Av. Fábio Roberto Barnabé, 2800,
O PRESIDENTE DA REPÚBLICA, no uso da atribuição que lhe confere o art. 62 da Constituição, adota a seguinte Medida Provisória, com força de lei:
 MEDIDA PROVISÓRIA N o 805, DE 30 DE OUTUBRO DE 2017 Posterga ou cancela aumentos remuneratórios para os exercícios subsequentes, altera a Lei n o 8.112, de 11 de dezembro de 1990, que dispõe sobre o regime
MEDIDA PROVISÓRIA N o 805, DE 30 DE OUTUBRO DE 2017 Posterga ou cancela aumentos remuneratórios para os exercícios subsequentes, altera a Lei n o 8.112, de 11 de dezembro de 1990, que dispõe sobre o regime
ZALMINO ZIMMERMANN TEORIA DA MEDIUNIDADE
 ZALMINO ZIMMERMANN TEORIA DA MEDIUNIDADE CAMPINAS SP 2011 SUMÁRIO Primeiras palavras... 17 Capítulo I Introdução... 19 Capítulo II O mediunismo na história... 23 Capítulo III Mediunidade Conceito Tipos...
ZALMINO ZIMMERMANN TEORIA DA MEDIUNIDADE CAMPINAS SP 2011 SUMÁRIO Primeiras palavras... 17 Capítulo I Introdução... 19 Capítulo II O mediunismo na história... 23 Capítulo III Mediunidade Conceito Tipos...
CM127 - Lista Mostre que os pontos médios de um triângulo isósceles formam um triângulo também isósceles.
 CM127 - Lista 2 Congruência de Triângulos e Desigualdade Triangular 1. Faça todos os exercícios dados em aula. 2. Em um triângulo ABC a altura do vértice A é perpendicular ao lado BC e divide BC em dois
CM127 - Lista 2 Congruência de Triângulos e Desigualdade Triangular 1. Faça todos os exercícios dados em aula. 2. Em um triângulo ABC a altura do vértice A é perpendicular ao lado BC e divide BC em dois
Triângulos classificação
 Triângulos classificação Quanto aos ângulos Acutângulo: possui três ângulos agudos. Quanto aos lados Equilátero: três lados de mesma medida. Obs.: os três ângulos internos têm medidas de 60º. Retângulo:
Triângulos classificação Quanto aos ângulos Acutângulo: possui três ângulos agudos. Quanto aos lados Equilátero: três lados de mesma medida. Obs.: os três ângulos internos têm medidas de 60º. Retângulo:
ANEXO I. Tabela I Reitoria. Nível Cargo Vagas
 ANEXO I Tabela I Reitoria Nível C Auxiliar em Assuntos Educacionais 1 Nível C Auxiliar de Administração 4 Assistente em Administração 12 Técnico em Arquivo 2 Informática 1 Técnico em Secretariado 3 Técnico
ANEXO I Tabela I Reitoria Nível C Auxiliar em Assuntos Educacionais 1 Nível C Auxiliar de Administração 4 Assistente em Administração 12 Técnico em Arquivo 2 Informática 1 Técnico em Secretariado 3 Técnico
ATIVIDADES COM GEOTIRAS
 ATIVIDADES COM GEOTIRAS 1. Material: Geotiras i. Represente varias retas paralelas. ii. Represente duas retas concorrentes em um ponto. 2. Material: Geotiras Represente as seguintes poligonais: i. Poligonal
ATIVIDADES COM GEOTIRAS 1. Material: Geotiras i. Represente varias retas paralelas. ii. Represente duas retas concorrentes em um ponto. 2. Material: Geotiras Represente as seguintes poligonais: i. Poligonal
MEF LATIN AMERICA CÓDIGO DE CONDUTA SERVIÇOS DE VALOR ADICIONADO BRASIL ANEXO I INFRAÇÕES ÉTICAS E PENALIDADES
 MEF LATIN AMERICA CÓDIGO DE CONDUTA SERVIÇOS DE VALOR ADICIONADO BRASIL ANEXO I INFRAÇÕES ÉTICAS E PENALIDADES Este Anexo I ao Código de Conduta visa organizar e tipificar as infrações éticas e suas respectivas
MEF LATIN AMERICA CÓDIGO DE CONDUTA SERVIÇOS DE VALOR ADICIONADO BRASIL ANEXO I INFRAÇÕES ÉTICAS E PENALIDADES Este Anexo I ao Código de Conduta visa organizar e tipificar as infrações éticas e suas respectivas
Índice. Átrio ou Três Encontros e Duas Notas...17. De Um A Razão Animada por Álvaro Ribeiro...21
 Índice Átrio ou Três Encontros e Duas Notas...17 De Um A Razão Animada por Álvaro Ribeiro...21 Carta I...25 I Domingo do Advento, 3 de Dezembro de 2006 Passeios no campo Carta II...28 II Domingo do Advento,
Índice Átrio ou Três Encontros e Duas Notas...17 De Um A Razão Animada por Álvaro Ribeiro...21 Carta I...25 I Domingo do Advento, 3 de Dezembro de 2006 Passeios no campo Carta II...28 II Domingo do Advento,
RESOLUÇÃO Nº 617 DE 27 DE NOVEMBRO DE 2015
 RESOLUÇÃO Nº 617 DE 27 DE NOVEMBRO DE 2015 Ementa: Dispõe as atribuições e competênciasdo farmacêutico nos Hemocentros Nacional e Regionais bem como em serviços de hemoterapia e/ou bancos de sangue. O
RESOLUÇÃO Nº 617 DE 27 DE NOVEMBRO DE 2015 Ementa: Dispõe as atribuições e competênciasdo farmacêutico nos Hemocentros Nacional e Regionais bem como em serviços de hemoterapia e/ou bancos de sangue. O
