DESENHO DE OBSERVAÇÃO
|
|
|
- Victorio Angelim Ribeiro
- 9 Há anos
- Visualizações:
Transcrição
1
2 QUESTÃO 1 DESENHO DE OBSERVAÇÃO Tendo como motivação as imagens abaixo, desenhe, no espaço reservado da página seguinte, o que está apresentado à sua frente, buscando, sobretudo, registrar o movimento. Na avaliação de seu desenho, serão considerados os seguintes quesitos: as proporções, a qualidade do traço e o enquadramento do desenho no espaço reservado. 1
3 Desenho de observação (valor da questão: 1,5 ponto) 2
4 QUESTÃO 2 DESENHO DE MEMÓRIA Desenhe, no espaço reservado abaixo, um cavalo em movimento. Na avaliação de seu desenho, serão considerados os seguintes quesitos: as proporções, a qualidade do traço e o enquadramento do desenho no espaço reservado. Cavalo em movimento (valor da questão: 1,5 ponto) 3
5 QUESTÃO 3 DESENHO DE IMAGINAÇÃO O TANGRAM é um antigo quebra-cabeça chinês cujo nome significa 7 tábuas da sabedoria. Ele é composto de 7 peças, conforme ilustrado abaixo: 5 triângulos, de vários tamanhos; 1 quadrado; e 1 paralelogramo. As peças, chamadas de tans, podem ser posicionadas de maneira a formar um retângulo, como mostrado abaixo, ou um quadrado. Além disso, diversas outras formas podem ser obtidas, observando-se, sempre, duas regras básicas: todas as peças devem ser usadas e as peças não podem ser sobrepostas. Respeitando as regras acima explicitadas, faça, nos espaços reservados da página seguinte, duas composições plásticas abstratas e coloridas usando as peças do TANGRAM e, no máximo, três cores em cada composição, além do preto e do branco do papel. A primeira composição deverá expressar movimento, e a segunda, ser uma composição estática. Na avaliação do conjunto das composições, serão considerados os seguintes quesitos: criatividade, qualidade da pintura, harmonia de cores e correção do exercício. 4
6 Composição movimentada Composição estática (valor da questão: 2,0 pontos) 5
7 QUESTÃO 4 RACIOCÍNIO ESPACIAL 4.1 Planificação A figura I, abaixo, ilustra um cubo cortado, de modo a formar um hexágono no plano de corte. Na figura II, é apresentado o volume planificado do cubo cortado representado na figura I, incluídas as linhas nele desenhadas. Com base no exemplo do cubo mostrado nas figuras I e II, faça os exercícios 4.1(a), 4.1(b) e 4.1(c) propostos nas páginas seguintes, desenhando sobre o quadrilátero em branco a planificação do volume apresentado em cada exercício. Na avaliação de cada exercício, serão considerados os seguintes quesitos: correção da solução e qualidade do traço. Exemplo: cubo Figura I cubo cortado Figura II volume planificado 6
8 Exercício 4.1(a) tronco de pirâmide hexagonal tronco de pirâmide hexagonal volume planificado (valor do exercício: 1,0 ponto) 7
9 Exercício 4.1(b) forma simétrica forma simétrica volume planificado (valor do exercício: 1,0 ponto) 8
10 Exercício 4.1(c) poliedro de lord Kelvin poliedro de lord Kelvin volume planificado (valor do exercício: 1,0 ponto) 9
11 4.2 TANGRAM (quebra-cabeça) Tendo como base a descrição e as regras do TANGRAM apresentadas na questão 3 e o exemplo ilustrado nas figuras III e IV, a seguir, faça os exercícios 4.2(a) e 4.2(b), que constam na próxima página, da seguinte maneira: em cada exercício, desenhe, na figura da esquerda, as sete peças do TANGRAM identificadas e numeradas na figura da direita; identifique e numere, na figura da esquerda, a peça correspondente a cada forma geométrica indicada na figura da direita, de acordo com a numeração proposta nesta figura. Em cada exercício, será avaliada a correção da solução. Exemplo Figura III Figura IV 10
12 Exercício 4.2(a) Exercício 4.2(b) (valor do exercício: 0,5 ponto) (valor do exercício: 0,5 ponto) 11
13 4.3 Vista inferior Com base no exemplo abaixo, que corresponde ao desenho de um poste, visto de baixo para cima, pelo observador indicado, desenhe, no espaço reservado, um guarda-chuva aberto, visto de baixo para cima, conforme a visão do referido observador. Nesse exercício, serão avaliados os seguintes quesitos: correção da solução e qualidade do traço. Poste visto de baixo para cima pelo observador Guarda-chuva aberto visto de baixo para cima pelo observador (valor do exercício: 1,0 ponto) 12
14 Folha de Rascunho 13
DESENHO DE OBSERVAÇÃO
 QUESTÃO 1 DESENHO DE OBSERVAÇÃO As expressões humanas chamaram a atenção de artistas do século XIX, entre os quais Honoré Daumier, que se ocupou da retratação de tipos populares e curiosos de sua época,
QUESTÃO 1 DESENHO DE OBSERVAÇÃO As expressões humanas chamaram a atenção de artistas do século XIX, entre os quais Honoré Daumier, que se ocupou da retratação de tipos populares e curiosos de sua época,
INSTRUÇÕES. 1 Este caderno é constituído de quatro questões.
 INSTRUÇÕES 1 Este caderno é constituído de quatro questões. 2 Caso o caderno de prova esteja incompleto ou tenha qualquer defeito, solicite ao fiscal de sala mais próximo que tome as providências cabíveis.
INSTRUÇÕES 1 Este caderno é constituído de quatro questões. 2 Caso o caderno de prova esteja incompleto ou tenha qualquer defeito, solicite ao fiscal de sala mais próximo que tome as providências cabíveis.
Alfredo Volpi. Volpi morreu em 1988, em São Paulo.
 1 nasceu em Lucca, Itália, em 1896. Chegou ao Brasil com pouco mais de um ano, fixando-se em São Paulo. Aos 15 anos começou a trabalhar como pintor/decorador de paredes e aos 18 pintou seu primeiro quadro:
1 nasceu em Lucca, Itália, em 1896. Chegou ao Brasil com pouco mais de um ano, fixando-se em São Paulo. Aos 15 anos começou a trabalhar como pintor/decorador de paredes e aos 18 pintou seu primeiro quadro:
Tô na área! Dinâmica 6. Primeira Etapa Compartilhar ideias. Aluno. 9º Ano 4º Bimestre
 Tô na área! Reforço escolar M ate mática Dinâmica 6 9º Ano 4º Bimestre DISCIPLINA Ano CAMPO CONCEITO Matemática 9º do Ensino Fundamental Geométrico. Polígonos regulares e áreas de figuras planas Aluno
Tô na área! Reforço escolar M ate mática Dinâmica 6 9º Ano 4º Bimestre DISCIPLINA Ano CAMPO CONCEITO Matemática 9º do Ensino Fundamental Geométrico. Polígonos regulares e áreas de figuras planas Aluno
Seções de Prismas Julho/ 2009
 Seções de Prismas Heloiza Rangel da Silva Josie Pacheco de Vasconcellos Souza Paula Eveline da Silva dos Santos Orientadora: Gilmara Teixeira Barcelos Julho/ 2009 Apostila de atividades disponível em http://www.es.iff.edu.br/softmat/projeto_tic/prismas
Seções de Prismas Heloiza Rangel da Silva Josie Pacheco de Vasconcellos Souza Paula Eveline da Silva dos Santos Orientadora: Gilmara Teixeira Barcelos Julho/ 2009 Apostila de atividades disponível em http://www.es.iff.edu.br/softmat/projeto_tic/prismas
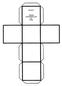 10 11 Escola Municipal Francis Hime SÓLIDOS GEOMÉTRICOS 6º ANO Nome: 1601 Geometria: Uma ciência de muitos povos A geometria, assim como as ciências, nasceu das necessidades e das observações do homem.
10 11 Escola Municipal Francis Hime SÓLIDOS GEOMÉTRICOS 6º ANO Nome: 1601 Geometria: Uma ciência de muitos povos A geometria, assim como as ciências, nasceu das necessidades e das observações do homem.
ESPAÇO E FORMA. CURSO: Pró-Letramento. TURMA: Revezamento. ÁREA: Matemática. CONTEÚDO: Espaço e Forma. TEMA: Dobradura, Tangram e Mosaicos
 ESPAÇO E FORMA CURSO: Pró-Letramento TURMA: Revezamento ÁREA: Matemática CONTEÚDO: Espaço e Forma TEMA: Dobradura, Tangram e Mosaicos DATA DO ENCONTRO: 22/08/2012 a 24/08/2012 PROFESSOR RESPONSÁVEL: Profª
ESPAÇO E FORMA CURSO: Pró-Letramento TURMA: Revezamento ÁREA: Matemática CONTEÚDO: Espaço e Forma TEMA: Dobradura, Tangram e Mosaicos DATA DO ENCONTRO: 22/08/2012 a 24/08/2012 PROFESSOR RESPONSÁVEL: Profª
G eo m et ri a 6º A N O
 G eo m et ri a 6º A N O Plano cartesiano: associação dos vértices de um polígono a pares ordenados Geoplano Atividade 1: reproduzir os polígonos no geoplano, após isso identifique as coordenadas dos vértices
G eo m et ri a 6º A N O Plano cartesiano: associação dos vértices de um polígono a pares ordenados Geoplano Atividade 1: reproduzir os polígonos no geoplano, após isso identifique as coordenadas dos vértices
Nível. Cole aqui a etiqueta com os dados do aluno. Visite nossas páginas na Internet:
 Cole aqui a etiqueta com os dados do aluno. Nível 2 8º e 9º anos do Ensino Fundamental 2ª FASE 14 de setembro de 2013 Nome completo do aluno Endereço completo do aluno (Rua, Av., nº) Complemento Bairro
Cole aqui a etiqueta com os dados do aluno. Nível 2 8º e 9º anos do Ensino Fundamental 2ª FASE 14 de setembro de 2013 Nome completo do aluno Endereço completo do aluno (Rua, Av., nº) Complemento Bairro
Avaliação E. Educação Professor
 Teste de Avaliação Nome N. o Turma Data /jan./2019 Avaliação E. Educação Professor MATEMÁTICA 7. o ANO Duração: 90 minutos Não é permitido o uso de calculadora. Na resposta aos itens de escolha múltipla,
Teste de Avaliação Nome N. o Turma Data /jan./2019 Avaliação E. Educação Professor MATEMÁTICA 7. o ANO Duração: 90 minutos Não é permitido o uso de calculadora. Na resposta aos itens de escolha múltipla,
Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de Matemática de 4ª Série Fundamental
 Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de de 4ª Série Fundamental TEMA I ESPAÇO E FORMA A compreensão do espaço com suas dimensões e formas de constituição são elementos necessários
Comentários e Exemplos sobre os Temas e seus Descritores da Matriz de de 4ª Série Fundamental TEMA I ESPAÇO E FORMA A compreensão do espaço com suas dimensões e formas de constituição são elementos necessários
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL FARROUPILHA CAMPUS ALEGRETE PIBID
 PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Gabriel Prates Brener 1.2 Público alvo: 6º ao 9º ano Ensino Fundamental e Curso Magistério 1.3 Duração: 5 horas 1.4 Conteúdo desenvolvido:
PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do bolsista: Gabriel Prates Brener 1.2 Público alvo: 6º ao 9º ano Ensino Fundamental e Curso Magistério 1.3 Duração: 5 horas 1.4 Conteúdo desenvolvido:
MATEMÁTICA NOTA ENSINO FUNDAMENTAL II ANO: 6º TURMAS: A B C D E TIPO: U PROFESSORA: ALESSANDRA TOLEDO ATIVIDADE DE RECUPERAÇÃO INSTRUÇÕES
 MATEMÁTICA ATIVIDADE DE NOTA ENSINO FUNDAMENTAL II ANO: 6º TURMAS: A B C D E TIPO: U PROFESSORA: ALESSANDRA TOLEDO VALOR: 3,5 PONTOS ALUNO(A): Nº: DATA: /09/2017 ASSINATURA DO RESPONSÁVEL: INSTRUÇÕES 1.
MATEMÁTICA ATIVIDADE DE NOTA ENSINO FUNDAMENTAL II ANO: 6º TURMAS: A B C D E TIPO: U PROFESSORA: ALESSANDRA TOLEDO VALOR: 3,5 PONTOS ALUNO(A): Nº: DATA: /09/2017 ASSINATURA DO RESPONSÁVEL: INSTRUÇÕES 1.
SIMULADO DE GEOMETRIA OBMEP ª FASE. NÍVEL 1 6 e 7 anos do Ensino Fundamental. Nome completo do aluno:
 LEMIN - Laboratório de Educação Matemática Isaac Newton Professor Coordenador: Cristiano Rodolfo Tironi Rua da Integração, 386 - Centro - Massaranduba (SC) www.leminsc.com.br email: [email protected]
LEMIN - Laboratório de Educação Matemática Isaac Newton Professor Coordenador: Cristiano Rodolfo Tironi Rua da Integração, 386 - Centro - Massaranduba (SC) www.leminsc.com.br email: [email protected]
Tangram. Ivany Aparecida Rodrigues da Motta Escola Estadual Professor Luiz Menezes Guaratinguetá SP.
 Tangram Ivany Aparecida Rodrigues da Motta Escola Estadual Professor Luiz Menezes Guaratinguetá SP [email protected] Dezembro de 2006 Público Alvo: 6ª e 8ª Séries do Ensino Fundamental Pré-Requisitos
Tangram Ivany Aparecida Rodrigues da Motta Escola Estadual Professor Luiz Menezes Guaratinguetá SP [email protected] Dezembro de 2006 Público Alvo: 6ª e 8ª Séries do Ensino Fundamental Pré-Requisitos
Universidade Tecnológica Federal do Paraná UTFPR Câmpus Apucarana. Projeto Novos Talentos Edital CAPES 55/12. Professor Responsável Ivan José Coser.
 1 Universidade Tecnológica Federal do Paraná UTFPR Câmpus Apucarana Projeto Novos Talentos Edital CAPES 55/12 Professor Responsável Ivan José Coser. Atividades de Matemática Julho 2014 2 1. TANGRAM O TANGRAM
1 Universidade Tecnológica Federal do Paraná UTFPR Câmpus Apucarana Projeto Novos Talentos Edital CAPES 55/12 Professor Responsável Ivan José Coser. Atividades de Matemática Julho 2014 2 1. TANGRAM O TANGRAM
Tô na área! Dinâmica 6. Professor. 9º Ano 4º Bimestre. DISCIPLINA Ano CAMPO CONCEITO DINÂMICA. 9º do Ensino Fundamental
 Tô na área! Reforço escolar M ate mática Dinâmica 6 9º Ano 4º Bimestre DISCIPLINA Ano CAMPO CONCEITO Matemática 9º do Ensino Fundamental Geométrico. Polígonos regulares e áreas de figuras planas Professor
Tô na área! Reforço escolar M ate mática Dinâmica 6 9º Ano 4º Bimestre DISCIPLINA Ano CAMPO CONCEITO Matemática 9º do Ensino Fundamental Geométrico. Polígonos regulares e áreas de figuras planas Professor
LISTA DE EXERCÍCIO GEOMETRIA PLANA
 QUESTÃO 01 A parte sombreada da malha quadriculada representa um terreno de propriedade do senhor Josias. Ele quer construir algumas casas nesse terreno. LISTA DE EXECÍCIO GEOMETIA PLANA Considere que
QUESTÃO 01 A parte sombreada da malha quadriculada representa um terreno de propriedade do senhor Josias. Ele quer construir algumas casas nesse terreno. LISTA DE EXECÍCIO GEOMETIA PLANA Considere que
Noções de Geometria. Professora: Gianni Leal 6º B.
 Noções de Geometria Professora: Gianni Leal 6º B. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato:
Noções de Geometria Professora: Gianni Leal 6º B. Figuras geométricas no espaço: mundo concreto e mundo abstrato Mundo concreto: é mundo no qual vivemos e realizamos nossas atividades. Mundo abstrato:
Geometria Espacial: Poliedros, Prismas, Pirâmides e Semelhança
 Geometria Espacial: Poliedros, Prismas, Pirâmides e Semelhança Geometria Espacial: Poliedros, Prismas, Pirâmides e Semelhança 1. Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes
Geometria Espacial: Poliedros, Prismas, Pirâmides e Semelhança Geometria Espacial: Poliedros, Prismas, Pirâmides e Semelhança 1. Maria quer inovar sua loja de embalagens e decidiu vender caixas com diferentes
DEPARTAMENTO DE 1º Ciclo - Grupo 110. Planificação Anual /Critérios de avaliação. Disciplina: Matemática 1.º ano 2015/2016
 AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE 1º Ciclo - Grupo 110 Planificação Anual /Critérios de avaliação Disciplina: Matemática 1.º ano 2015/2016 Domínio (Unidade / Tema) Números e Operações
AGRUPAMENTO DE ESCOLAS ANSELMO DE ANDRADE DEPARTAMENTO DE 1º Ciclo - Grupo 110 Planificação Anual /Critérios de avaliação Disciplina: Matemática 1.º ano 2015/2016 Domínio (Unidade / Tema) Números e Operações
1 POLIEDROS 2 ELEMENTOS 4 POLIEDROS REGULARES 3 CLASSIFICAÇÃO. 3.2 Quanto ao número de faces. 4.1 Tetraedro regular. 3.
 Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
Matemática 2 Pedro Paulo GEOMETRIA ESPACIAL II 1 POLIEDROS Na Geometria Espacial, como o nome diz, o nosso assunto são as figuras espaciais (no espaço). Vamos estudar sólidos e corpos geométricos que possuem
OFICINA. Construindo com tangram. Letícia Fonseca Reis F. Castro Matemática e Livro das Formas 13/08/2011
 OFICINA Construindo com tangram Letícia Fonseca Reis F. Castro Matemática e Livro das Formas 13/08/2011 Matemática Uma das finalidades de estudar matemática é aprender como se resolvem problemas, indo
OFICINA Construindo com tangram Letícia Fonseca Reis F. Castro Matemática e Livro das Formas 13/08/2011 Matemática Uma das finalidades de estudar matemática é aprender como se resolvem problemas, indo
QUESTÃO 03 (OBMEP) Os quadrados abaixo tem todos o mesmo tamanho. Em qual deles a região sombreada tem a maior área?
 / /017 QUESTÃO 01 A parte sombreada da malha quadriculada representa um terreno de propriedade do senhor Josias. Ele quer construir algumas casas nesse terreno. Considere que cada quadrícula da malha equivale
/ /017 QUESTÃO 01 A parte sombreada da malha quadriculada representa um terreno de propriedade do senhor Josias. Ele quer construir algumas casas nesse terreno. Considere que cada quadrícula da malha equivale
Geometria Espacial PRISMA RETO DE BASE TRIANGULAR (OU PRISMA TRIANGULAR)
 Espacial 1 PRISMAS Os prismas são sólidos geométricos bastante recorrentes em Espacial. Podemos definir o prisma da seguinte forma: PRISMA RETO DE BASE TRIANGULAR (OU PRISMA TRIANGULAR) Prisma é um sólido
Espacial 1 PRISMAS Os prismas são sólidos geométricos bastante recorrentes em Espacial. Podemos definir o prisma da seguinte forma: PRISMA RETO DE BASE TRIANGULAR (OU PRISMA TRIANGULAR) Prisma é um sólido
CENTRO EDUCACIONAL CHARLES DARWIN ENSINO FUNDAMENTAL. DIRETRIZES CURRICULARES 1º ao 5º ANO MATEMÁTICA
 CENTRO EDUCACIONAL CHARLES DARWIN ENSINO FUNDAMENTAL 2014 DIRETRIZES CURRICULARES 1º ao 5º ANO MATEMÁTICA OBJETIVOS GERAIS Reconhecer a Matemática como instrumento de compreensão e de transformação do
CENTRO EDUCACIONAL CHARLES DARWIN ENSINO FUNDAMENTAL 2014 DIRETRIZES CURRICULARES 1º ao 5º ANO MATEMÁTICA OBJETIVOS GERAIS Reconhecer a Matemática como instrumento de compreensão e de transformação do
OFICINA COGNIÇÃO E LÓGICA
 OFICINA COGNIÇÃO E LÓGICA A metodologia desenvolvida para aplicação destes módulos obedece a uma estratégia de uso progressivo dos jogos lógicos, graduando os estímulos sensoriais e o grau de dificuldade
OFICINA COGNIÇÃO E LÓGICA A metodologia desenvolvida para aplicação destes módulos obedece a uma estratégia de uso progressivo dos jogos lógicos, graduando os estímulos sensoriais e o grau de dificuldade
SOFTWARES EDUCATIVOS
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO NÚCLEO DE COMPUTAÇÃO ELETRÔNICA - NCE PROGRAMA DE PÓS-GRADUAÇÃO EM TECNOLOGIAS DA INFORMAÇÃO APLICADAS À EDUCAÇÃO - PGTIAE SOFTWARES EDUCATIVOS Anne Caroline de Oliveira
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO NÚCLEO DE COMPUTAÇÃO ELETRÔNICA - NCE PROGRAMA DE PÓS-GRADUAÇÃO EM TECNOLOGIAS DA INFORMAÇÃO APLICADAS À EDUCAÇÃO - PGTIAE SOFTWARES EDUCATIVOS Anne Caroline de Oliveira
CLASSIFICAÇÃO DOS POLIEDROS
 COLÉGIO SHALOM 65 Ensino Fundamental II 6º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO 1) Complete os quadros com as respectivas características: TRABALHO DE
COLÉGIO SHALOM 65 Ensino Fundamental II 6º ANO Profº: Sâmia M. Corrêa Disciplina: Geometria Aluno (a):. No. TRABALHO DE RECUPERAÇÃO 1) Complete os quadros com as respectivas características: TRABALHO DE
Revisional 3 Bim - MARCELO
 6º Ano Revisional 3 Bim - MARCELO 1) Represente no papel quatro pontos distintos e, por eles, determine dois segmentos de reta distintos. 2) Observe os segmentos de reta na figura. Escreva quantos são
6º Ano Revisional 3 Bim - MARCELO 1) Represente no papel quatro pontos distintos e, por eles, determine dois segmentos de reta distintos. 2) Observe os segmentos de reta na figura. Escreva quantos são
Poliedros 1 ARESTAS FACES VERTICES. Figura 1.1: Elementos de um poliedro
 Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
Poliedros 1 Os poliedros são sólidos cujo volume é definido pela interseção de quatro ou mais planos (poli + edro). A superfície poliédrica divide o espaço em duas regiões: uma região finita, que é a parte
4º. ano 1º. VOLUME. Projeto Pedagógico de Matemática 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE. Números e operações.
 4º. ano 1º. VOLUME 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE Realização de compreendendo seus significados: adição e subtração (com e sem reagrupamento) Multiplicação (como adição de parcelas
4º. ano 1º. VOLUME 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE Realização de compreendendo seus significados: adição e subtração (com e sem reagrupamento) Multiplicação (como adição de parcelas
1. (Enem 2011) A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.
 1. (Enem 2011) A figura seguinte mostra um modelo de sombrinha muito usado em países orientais. Esta figura é uma representação de uma superfície de revolução chamada de a) pirâmide. b) semiesfera. c)
1. (Enem 2011) A figura seguinte mostra um modelo de sombrinha muito usado em países orientais. Esta figura é uma representação de uma superfície de revolução chamada de a) pirâmide. b) semiesfera. c)
FIGURAS PLANAS. Materiais manipulativos para o ensino de COLEÇÃO MATHEMOTECA. ORGANIZADORAS Katia Stocco Smole Maria Ignez Diniz
 COLEÇÃO MATHEMOTECA ORGANIZADORAS Katia Stocco Smole Maria Ignez Diniz Anos iniciais do ensino fundamental Materiais manipulativos para o ensino de FIGURAS PLANAS 1. Construa em seu geoplano cada uma das
COLEÇÃO MATHEMOTECA ORGANIZADORAS Katia Stocco Smole Maria Ignez Diniz Anos iniciais do ensino fundamental Materiais manipulativos para o ensino de FIGURAS PLANAS 1. Construa em seu geoplano cada uma das
Apostila de Matemática II 3º bimestre/2016. Professora : Cristiane Fernandes
 Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
Apostila de Matemática II 3º bimestre/2016 Professora : Cristiane Fernandes Pirâmide A pirâmide é uma figura geométrica espacial, um poliedro composto por uma base (triangular, pentagonal, quadrada, retangular,
MATEMÁTICA - 3o ciclo Posição relativa de retas e planos (9 o ano)
 MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) xercícios de provas nacionais e testes intermédios 1. O centro geodésico de Portugal continental situa-se na Serra da Melriça, próximo de Vila
MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) xercícios de provas nacionais e testes intermédios 1. O centro geodésico de Portugal continental situa-se na Serra da Melriça, próximo de Vila
SÓLIDOS GEOMÉTRICOS. Materiais manipulativos para o ensino de COLEÇÃO MATHEMOTECA. ORGANIZADORAS Katia Stocco Smole Maria Ignez Diniz
 COLEÇÃO MATHEMOTECA ORGANIZADORAS Katia Stocco Smole Maria Ignez Diniz Anos iniciais do ensino fundamental Materiais manipulativos para o ensino de SÓLIDOS GEOMÉTRICOS ATIVIDADES 1. Faça as construções
COLEÇÃO MATHEMOTECA ORGANIZADORAS Katia Stocco Smole Maria Ignez Diniz Anos iniciais do ensino fundamental Materiais manipulativos para o ensino de SÓLIDOS GEOMÉTRICOS ATIVIDADES 1. Faça as construções
PLANIFICAÇÃO ANUAL
 PLANIFICAÇÃO ANUAL 2015-2016 Agrupamento de Escolas Domingos Sequeira Área Disciplinar: Matemática Ano de Escolaridade: 1.º Mês: setembro / outubro Domínios/ s Números e Operações Números Naturais Adição
PLANIFICAÇÃO ANUAL 2015-2016 Agrupamento de Escolas Domingos Sequeira Área Disciplinar: Matemática Ano de Escolaridade: 1.º Mês: setembro / outubro Domínios/ s Números e Operações Números Naturais Adição
MATEMÁTICA PLANEJAMENTO 2º BIMESTRE º B - 11 Anos
 PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 2º
PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 2º
Exercícios Obrigatórios
 Exercícios Obrigatórios 1) (UFRGS) A figura abaixo, formada por trapézios congruentes e triângulos equiláteros, representa a planificação de um sólido. Esse sólido é um (a) tronco de pirâmide. (b) tronco
Exercícios Obrigatórios 1) (UFRGS) A figura abaixo, formada por trapézios congruentes e triângulos equiláteros, representa a planificação de um sólido. Esse sólido é um (a) tronco de pirâmide. (b) tronco
Matemática 2 LEIA COM ATENÇÃO
 LEI COM TENÇÃO Matemática 2 01. Só abra este caderno após ler todas as instruções e quando for autorizado pelos fiscais da sala. 02. Preencha os dados pessoais. 03. utorizado o início da prova, verifique
LEI COM TENÇÃO Matemática 2 01. Só abra este caderno após ler todas as instruções e quando for autorizado pelos fiscais da sala. 02. Preencha os dados pessoais. 03. utorizado o início da prova, verifique
KITS DIDÁTICOS ÁREA: QUÍMICA
 KITS DIDÁTICOS Os KITS DIDÁTICOS apresentados a seguir foram obtidos a partir de recursos oriundos de parceria firmada em UFPR - Campus Jandaia do Sul e o Rotary Clube local. Os materiais doados possibilitam
KITS DIDÁTICOS Os KITS DIDÁTICOS apresentados a seguir foram obtidos a partir de recursos oriundos de parceria firmada em UFPR - Campus Jandaia do Sul e o Rotary Clube local. Os materiais doados possibilitam
MATEMÁTICA - 3o ciclo Posição relativa de retas e planos (9 o ano)
 MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) xercícios de provas nacionais e testes intermédios 1. onsidera o prisma hexagonal regular KL representado na figura seguinte. Relativamente
MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) xercícios de provas nacionais e testes intermédios 1. onsidera o prisma hexagonal regular KL representado na figura seguinte. Relativamente
COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria. Aluno(a):. Nº.
 COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria Aluno(a):. Nº. Trabalho De Recuperação final E a receita é uma só: fazer as pazes com você mesmo, diminuir a expectativa e entender que
COLÉGIO SHALOM 8 ANO Professora: Bethânia Rodrigues 65 Geometria Aluno(a):. Nº. Trabalho De Recuperação final E a receita é uma só: fazer as pazes com você mesmo, diminuir a expectativa e entender que
FORMAÇÃO SOBRE CONTEÚDOS DE MATEMATICA DOS 4º E 5º ANOS DO ENSINO FUNDAMENTAL FIGURAS PLANAS E ESPACIAIS
 FORMAÇÃO SOBRE CONTEÚDOS DE MATEMATICA DOS 4º E 5º ANOS DO ENSINO FUNDAMENTAL FIGURAS PLANAS E ESPACIAIS Professora: Vanessa Bayerl Cesana PLANA Figuras poligonais e não poligonais. Forma, número de lados,
FORMAÇÃO SOBRE CONTEÚDOS DE MATEMATICA DOS 4º E 5º ANOS DO ENSINO FUNDAMENTAL FIGURAS PLANAS E ESPACIAIS Professora: Vanessa Bayerl Cesana PLANA Figuras poligonais e não poligonais. Forma, número de lados,
Cole aqui a etiqueta com os dados do aluno. Nível
 Cole aqui a etiqueta com os dados do aluno. Nível 1 6.º e 7.º anos do Ensino Fundamental 2.ª FASE 10 de setembro de 2016 Nome completo do aluno Endereço completo do aluno (Rua, Av., n o ) Complemento (casa,
Cole aqui a etiqueta com os dados do aluno. Nível 1 6.º e 7.º anos do Ensino Fundamental 2.ª FASE 10 de setembro de 2016 Nome completo do aluno Endereço completo do aluno (Rua, Av., n o ) Complemento (casa,
PRISMAS E PIRÂMIDES 1. DEFINIÇÕES (PRISMAS) MATEMÁTICA. Prisma oblíquo: as arestas laterais são oblíquas aos planos das bases.
 PRISMAS E PIRÂMIDES. DEFINIÇÕES (PRISMAS) Chama-se prisma todo poliedro convexo composto por duas faces (bases) que são polígonos congruentes contidos em planos paralelos e as demais faces (faces laterais)
PRISMAS E PIRÂMIDES. DEFINIÇÕES (PRISMAS) Chama-se prisma todo poliedro convexo composto por duas faces (bases) que são polígonos congruentes contidos em planos paralelos e as demais faces (faces laterais)
PLANO DE TRABALHO MATEMÁTICA 5º ANO O TANGRAN
 PLANO DE TRABALHO MATEMÁTICA 5º ANO O TANGRAN Coordenação Pedagógica de Matemática Piraquara Junho/2016 - Noção de ângulos. - Triângulos e quadriláteros. - Paralelismo e perpendicularismo. - Simetria.
PLANO DE TRABALHO MATEMÁTICA 5º ANO O TANGRAN Coordenação Pedagógica de Matemática Piraquara Junho/2016 - Noção de ângulos. - Triângulos e quadriláteros. - Paralelismo e perpendicularismo. - Simetria.
Ciência Hoje das Crianças. FNDE; Instituto Ciência Hoje, ano 19, n. 166, mar
 lista de exercícios - 3º ano - matemática Aluno: Série: Turma: Data: Questão 1 É possível usar água ou comida para atrair as aves e observá-las. Muitas pessoas costumam usar água com açúcar, por exemplo,
lista de exercícios - 3º ano - matemática Aluno: Série: Turma: Data: Questão 1 É possível usar água ou comida para atrair as aves e observá-las. Muitas pessoas costumam usar água com açúcar, por exemplo,
PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA - 2.º ano. Proposta Hypatiamat. Ano letivo 2017/2018
 PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA - 2.º ano Proposta Hypatiamat Ano letivo 2017/2018 PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA - 2.º ano Ano letivo 2017/2018 Números e Operações Geometria
PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA - 2.º ano Proposta Hypatiamat Ano letivo 2017/2018 PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA - 2.º ano Ano letivo 2017/2018 Números e Operações Geometria
Palitos - 5 a série Actividade:
 Palitos - 5 a série Actividade: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Disponha sete palitos da seguinte forma. 1 Agora, acrescente seis palitos e obtenha o número 1 000. Utilizando 11 palitos, monte uma
Palitos - 5 a série Actividade: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Disponha sete palitos da seguinte forma. 1 Agora, acrescente seis palitos e obtenha o número 1 000. Utilizando 11 palitos, monte uma
Se os tubos opostos forem de mesmo comprimento, teremos as várias possibilidades de paralelogramos, incluindo o retângulo.
 Ernesto Rosa Poliedros de canudinhos rígidos possuem muitas vantagens: são fáceis de se fazer com sucata como tubinhos de canetas, bambus etc. (mas no mercado há tubos plásticos à venda), são ótimos nas
Ernesto Rosa Poliedros de canudinhos rígidos possuem muitas vantagens: são fáceis de se fazer com sucata como tubinhos de canetas, bambus etc. (mas no mercado há tubos plásticos à venda), são ótimos nas
APOSTILA GEOMETRIA DESCRITIVA
 APOSTILA GEOMETRIA DESCRITIVA 1 GEOMETRIA MÉTRICA E ESPACIAL 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 SISTEMAS DE PROJEÇÃO Conforme o que foi exposto anteriormente, o estudo da Geometria Descritiva está
APOSTILA GEOMETRIA DESCRITIVA 1 GEOMETRIA MÉTRICA E ESPACIAL 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 SISTEMAS DE PROJEÇÃO Conforme o que foi exposto anteriormente, o estudo da Geometria Descritiva está
CATÁLOGOS DE ATIVIDADES DA TENDÊNCIA TIC S. Alesson e Júlio
 CATÁLOGOS DE ATIVIDADES DA TENDÊNCIA TIC S Alesson e Júlio CABRI- GEOMETRY TÍTULO SÉRIE OBJETIVOS ASSUNTO Construção de um 6º ano Identificar as triângulo Equilátero características do Construção de um
CATÁLOGOS DE ATIVIDADES DA TENDÊNCIA TIC S Alesson e Júlio CABRI- GEOMETRY TÍTULO SÉRIE OBJETIVOS ASSUNTO Construção de um 6º ano Identificar as triângulo Equilátero características do Construção de um
MATEMÁTICA - 3o ciclo Posição relativa de retas e planos (9 o ano)
 MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) xercícios de provas nacionais e testes intermédios 1. Na figura ao lado, estão representados um cilindro e um prisma quadrangular regular [
MTMÁT - 3o ciclo Posição relativa de retas e planos (9 o ano) xercícios de provas nacionais e testes intermédios 1. Na figura ao lado, estão representados um cilindro e um prisma quadrangular regular [
1ª Parte SÓLIDOS GEOMÉTRICOS. Prof. Danillo Alves 6º ano Matutino
 1ª Parte SÓLIDOS GEOMÉTRICOS Prof. Danillo Alves 6º ano Matutino "Um monstro ou uma bela senhora, a forma como vemos a Matemática é produto dos nossos esforços." Prof. Jerriomar Ferreira As Formas existentes
1ª Parte SÓLIDOS GEOMÉTRICOS Prof. Danillo Alves 6º ano Matutino "Um monstro ou uma bela senhora, a forma como vemos a Matemática é produto dos nossos esforços." Prof. Jerriomar Ferreira As Formas existentes
EMENTA ESCOLAR I Trimestre Ano 2017 Disciplina: Matemática Professor: Flávio Calônico Júnior Turma: 2 ano do Ensino Médio
 EMENTA ESCOLAR I Trimestre Ano 2017 Disciplina: Matemática Professor: Flávio Calônico Júnior Turma: 2 ano do Ensino Médio Datas 14/fevereiro 17/fevereiro 21/fevereiro 24/fevereiro 28/fevereiro 03/março
EMENTA ESCOLAR I Trimestre Ano 2017 Disciplina: Matemática Professor: Flávio Calônico Júnior Turma: 2 ano do Ensino Médio Datas 14/fevereiro 17/fevereiro 21/fevereiro 24/fevereiro 28/fevereiro 03/março
EXERCICIOS - ÁREAS E ÂNGULOS:
 EXERCICIOS - ÁREAS E ÂNGULOS: 32 - Sabendo-se que um ângulo externo de um triângulo retângulo mede 287, quais os valores dos ângulos internos deste? 37 - Assinale qual dos polígonos abaixo possui todos
EXERCICIOS - ÁREAS E ÂNGULOS: 32 - Sabendo-se que um ângulo externo de um triângulo retângulo mede 287, quais os valores dos ângulos internos deste? 37 - Assinale qual dos polígonos abaixo possui todos
CONHECIMENTOS ESPECÍFICOS
 De acordo com o comando a que cada um dos itens de 51 a 120 se refira, marque, na folha de respostas, para cada item: o campo designado com o código C, caso julgue o item CERTO; ou o campo designado com
De acordo com o comando a que cada um dos itens de 51 a 120 se refira, marque, na folha de respostas, para cada item: o campo designado com o código C, caso julgue o item CERTO; ou o campo designado com
1) Mova 6 fósforos nestes copos, de forma a compor uma casinha.
 Colégio COC Imperatriz IV Mostra de Ciências 5º Ano A Matemática está em tudo Clube de Descobertas matemáticas: lógica e ação Atividade 1: Desafios Matemáticos com Palitinhos 1) Mova 6 fósforos nestes
Colégio COC Imperatriz IV Mostra de Ciências 5º Ano A Matemática está em tudo Clube de Descobertas matemáticas: lógica e ação Atividade 1: Desafios Matemáticos com Palitinhos 1) Mova 6 fósforos nestes
2.ª Certificação de Habilidade Específica de 2014
 sala n.º Prova de Habilidades Específicas - Arquitetura e Urbanismo 2.ª Certificação de Habilidade Específica de 2014 1 Este caderno é constituído de quatro questões. Caso o caderno de prova esteja incompleto
sala n.º Prova de Habilidades Específicas - Arquitetura e Urbanismo 2.ª Certificação de Habilidade Específica de 2014 1 Este caderno é constituído de quatro questões. Caso o caderno de prova esteja incompleto
Escola Secundária com 3º Ciclo D. Dinis. Ficha de Apoio nº2
 Escola Secundária com 3º Ciclo D. Dinis Ano Lectivo 2008 /2009 Matemática B Ano 10º Turma D 1. Observe a figura. 1.1.Indique as coordenadas dos pontos A, B, C, A, B e C. 1.2. Descreva a transformação geométrica
Escola Secundária com 3º Ciclo D. Dinis Ano Lectivo 2008 /2009 Matemática B Ano 10º Turma D 1. Observe a figura. 1.1.Indique as coordenadas dos pontos A, B, C, A, B e C. 1.2. Descreva a transformação geométrica
GEOMETRIA MÉTRICA. As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases.
 GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
GEOMETRIA MÉTRICA 1- I- PRISMA 1- ELEMENTOS E CLASSIFICAÇÃO Considere o prisma: As bases são polígonos congruentes. Os prismas são designados de acordo com o número de lados dos polígonos das bases. BASES
Com base no texto e assuntos ligados a ele, marque a alternativa correta nas questões 02 e 03.
 1º BIM P2 HABILIDADES LISTA DE EXERCÍCIOS MATEMÁTICA 6º ANO Aluno (a): Professor: Turma: Turno:... Data: / /2014 Unidade: ( ) Asa Norte ( ) Águas Lindas ( )Ceilândia ( ) Gama ( )Guará ( ) Pistão Norte
1º BIM P2 HABILIDADES LISTA DE EXERCÍCIOS MATEMÁTICA 6º ANO Aluno (a): Professor: Turma: Turno:... Data: / /2014 Unidade: ( ) Asa Norte ( ) Águas Lindas ( )Ceilândia ( ) Gama ( )Guará ( ) Pistão Norte
Grupo 1 - PIC OBMEP 2011 Módulo 2 - Geometria. Resumo do Encontro 6, 22 de setembro de Questões de geometria das provas da OBMEP
 Grupo 1 - PIC OBMEP 2011 Módulo 2 - Geometria Resumo do Encontro 6, 22 de setembro de 2012 Questões de geometria das provas da OBMEP http://www.obmep.org.br/provas.htm 1. Área: conceito e áreas do quadrado
Grupo 1 - PIC OBMEP 2011 Módulo 2 - Geometria Resumo do Encontro 6, 22 de setembro de 2012 Questões de geometria das provas da OBMEP http://www.obmep.org.br/provas.htm 1. Área: conceito e áreas do quadrado
CADERNO DE QUESTÕES. Nível 2. 1ª Olimpíada de Matemática do Distrito Federal. Segunda Fase - 20 de agosto de º e 9º Anos do Ensino Fundamental
 CADERNO DE QUESTÕES 1ª Olimpíada de Matemática do Distrito Federal Nível 2 8º e 9º Anos do Ensino Fundamental Nome completo Segunda Fase - 20 de agosto de 2017 Endereço completo Complemento (casa, apartamento,
CADERNO DE QUESTÕES 1ª Olimpíada de Matemática do Distrito Federal Nível 2 8º e 9º Anos do Ensino Fundamental Nome completo Segunda Fase - 20 de agosto de 2017 Endereço completo Complemento (casa, apartamento,
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 2.º ano Ano Letivo 2018/2019
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 2.º ano Ano Letivo 2018/2019 Matemática 1º Trimestre Tempo Calendários e horários. Números naturais Números pares
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 2.º ano Ano Letivo 2018/2019 Matemática 1º Trimestre Tempo Calendários e horários. Números naturais Números pares
XXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA Segunda Fase Nível 2 (7 a. ou 8 a. séries)
 XXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA Segunda Fase Nível 2 (7 a. ou 8 a. séries) PROBLEMA 1 As peças de um jogo chamado Tangram são construídas cortando-se um quadrado em sete partes, como mostra o
XXIII OLIMPÍADA BRASILEIRA DE MATEMÁTICA Segunda Fase Nível 2 (7 a. ou 8 a. séries) PROBLEMA 1 As peças de um jogo chamado Tangram são construídas cortando-se um quadrado em sete partes, como mostra o
A PAVIMENTAÇÃO DO PLANO
 1 A PAVIMENTAÇÃO DO PLANO I) O modelo prático : Uma experiência prática muito conhecida por todos é a colocação de azulejos e ladrilhos nas paredes e pisos. É bastante intuitivo o senso comum a respeito
1 A PAVIMENTAÇÃO DO PLANO I) O modelo prático : Uma experiência prática muito conhecida por todos é a colocação de azulejos e ladrilhos nas paredes e pisos. É bastante intuitivo o senso comum a respeito
Alfredo Volpi. Volpi morreu em 1988, em São Paulo.
 1 nasceu em Lucca, Itália, em 1896. Chegou ao Brasil com pouco mais de um ano, fixando-se em São Paulo. Aos 15 anos começou a trabalhar como pintor/decorador de paredes e aos 18 pintou seu primeiro quadro:
1 nasceu em Lucca, Itália, em 1896. Chegou ao Brasil com pouco mais de um ano, fixando-se em São Paulo. Aos 15 anos começou a trabalhar como pintor/decorador de paredes e aos 18 pintou seu primeiro quadro:
MATEMÁTICA - 3 o ANO MÓDULO 53 PIRÂMIDE
 MATEMÁTICA - 3 o ANO MÓDULO 53 PIRÂMIDE Como pode cair no enem (ENEM) Uma indústria fabrica brindes promocionais em forma de pirâmide. A pirâmide é obtida a partir de quatro cortes em um sólido
MATEMÁTICA - 3 o ANO MÓDULO 53 PIRÂMIDE Como pode cair no enem (ENEM) Uma indústria fabrica brindes promocionais em forma de pirâmide. A pirâmide é obtida a partir de quatro cortes em um sólido
Guião 2 Explorando sólidos geométricos - II
 Guião 2 Explorando sólidos geométricos - II cubos, paralelepípedos retângulos, cilindros, esferas, pirâmides, cones,prismas A cadeia de tarefas aqui apresentada tem por objetivo continuar a exploração
Guião 2 Explorando sólidos geométricos - II cubos, paralelepípedos retângulos, cilindros, esferas, pirâmides, cones,prismas A cadeia de tarefas aqui apresentada tem por objetivo continuar a exploração
1º Período MATEMÁTICA 4.º ANO. setembro. Domínios Conteúdos programáticos Objetivos/Descritores de desempenho
 1º Período setembro Números e Operações Dezenas e centenas de milhar. Resolução de problemas. Rever a matéria do ano anterior Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo
1º Período setembro Números e Operações Dezenas e centenas de milhar. Resolução de problemas. Rever a matéria do ano anterior Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo
OS PRISMAS. 1) Definição e Elementos :
 1 OS PRISMAS 1) Definição e Elementos : Dados dois planos paralelos α e β, um polígono contido em um desses planos e um reta r, que intercepta esses planos, chamamos de PRISMA o conjunto de todos os segmentos
1 OS PRISMAS 1) Definição e Elementos : Dados dois planos paralelos α e β, um polígono contido em um desses planos e um reta r, que intercepta esses planos, chamamos de PRISMA o conjunto de todos os segmentos
INSTRUÇÕES CANDIDATO, LEIA COM ATENÇÃO!
 MINISTÉRIO DA DEFESA Manaus, AM, 11 de novembro de 01 EXÉRCITO BRASILEIRO CONCURSO DE ADMISSÃO 01/013 D E C Ex D E P A COLÉGIO MILITAR DE MANAUS MATEMÁTICA 1º Ano Ensino Médio INSTRUÇÕES CANDIDATO, LEIA
MINISTÉRIO DA DEFESA Manaus, AM, 11 de novembro de 01 EXÉRCITO BRASILEIRO CONCURSO DE ADMISSÃO 01/013 D E C Ex D E P A COLÉGIO MILITAR DE MANAUS MATEMÁTICA 1º Ano Ensino Médio INSTRUÇÕES CANDIDATO, LEIA
Возрастная группа: 6º ano, 5 º ano
 1 План урока Composição e Decomposição d e Figuras Geométricas Возрастная группа: 6º ano, 5 º ano Онлайн ресурсы: Co pi ar, c o l ar e de sc o bri r Abert ura Professor apresent a Alunos prat icam Discussão
1 План урока Composição e Decomposição d e Figuras Geométricas Возрастная группа: 6º ano, 5 º ano Онлайн ресурсы: Co pi ar, c o l ar e de sc o bri r Abert ura Professor apresent a Alunos prat icam Discussão
Visite o blog:
 ESCOLA Aluno: Data: / /2011 Professor: 5 ano Descritor 3 1. Um artista plástico está construindo um painel com ladrilhos decorados. Ele fez um esquema desse painel mostrado na figura e utilizou as formas
ESCOLA Aluno: Data: / /2011 Professor: 5 ano Descritor 3 1. Um artista plástico está construindo um painel com ladrilhos decorados. Ele fez um esquema desse painel mostrado na figura e utilizou as formas
CRITÉRIOS DE AVALIAÇÃO 1º CICLO 4.º ANO DE ESCOLARIDADE MATEMÁTICA
 ANO LETIVO 0/06 CRITÉRIOS DE AVALIAÇÃO º CICLO.º ANO DE ESCOLARIDADE MATEMÁTICA Números e Operações Números naturais Contar Reconhece, sem falhas, que se poderia prosseguir a contagem indefinidamente introduzindo
ANO LETIVO 0/06 CRITÉRIOS DE AVALIAÇÃO º CICLO.º ANO DE ESCOLARIDADE MATEMÁTICA Números e Operações Números naturais Contar Reconhece, sem falhas, que se poderia prosseguir a contagem indefinidamente introduzindo
Professor Diego - Tarefa 19
 Professor Diego - Tarefa 9 0. Uma peça tem a forma de uma pirâmide reta, de base quadrada, com 5 cm de altura e é feita de madeira maciça. A partir da base dessa peça, foi escavado um orifício na forma
Professor Diego - Tarefa 9 0. Uma peça tem a forma de uma pirâmide reta, de base quadrada, com 5 cm de altura e é feita de madeira maciça. A partir da base dessa peça, foi escavado um orifício na forma
2 CILINDRO E ESFERA 1 CUBO E ESFERA. 2.1 Cilindro inscrito. 1.1 Cubo inscrito. 2.2 Cilindro circunscrito. 1.2 Cubo circunscrito
 Matemática Pedro Paulo GEOMETRIA ESPACIAL XI A seguir, nós vamos analisar a relação entre alguns sólidos e as esferas. Os sólidos podem estar inscritos ou circunscritos a uma esfera. Lembrando: A figura
Matemática Pedro Paulo GEOMETRIA ESPACIAL XI A seguir, nós vamos analisar a relação entre alguns sólidos e as esferas. Os sólidos podem estar inscritos ou circunscritos a uma esfera. Lembrando: A figura
ÂNGULOS. Dados dois pontos distintos, a reunião do conjunto desses dois pontos com o conjunto dos pontos que estão entre eles é o segmento de reta.
 ÂNGULOS 1 CONSIDERAÇÕES PRELIMINARES 1.1 Notação de ponto, reta e plano: a) Letras: Ponto: letras maiúsculas: A, B, C,... Reta: letras minúsculas: a,b,c... Plano: letras gregas minúsculas: α, β, γ,...
ÂNGULOS 1 CONSIDERAÇÕES PRELIMINARES 1.1 Notação de ponto, reta e plano: a) Letras: Ponto: letras maiúsculas: A, B, C,... Reta: letras minúsculas: a,b,c... Plano: letras gregas minúsculas: α, β, γ,...
BARALHO São usados dois baralhos, JOGO DOS POLIEDROS, de 54 cartas cada, já inclusos os curingas.
 OFICINA: JOGO DOS POLIEDROS INTRODUÇÃO Para proporcionar um ensino compatível com as exigências da sociedade contemporânea são necessárias mudanças nas formas de ensinar. Estas mudanças implicam no repensar
OFICINA: JOGO DOS POLIEDROS INTRODUÇÃO Para proporcionar um ensino compatível com as exigências da sociedade contemporânea são necessárias mudanças nas formas de ensinar. Estas mudanças implicam no repensar
FÁTIMA HELENA COSTA DIAS. institucional: MATEMÁTICA NA ESCOLA, 2ª SÉRIE, 2º BIMESTRE. Tutor: Daiana da Silva Leite
 FÁTIMA HELENA COSTA DIAS e-mail institucional: [email protected] MATEMÁTICA NA ESCOLA, 2ª SÉRIE, 2º BIMESTRE Tutor: Daiana da Silva Leite Grupo: 05 Tarefa 4 Duração Prevista: 290 minutos, distribuídos
FÁTIMA HELENA COSTA DIAS e-mail institucional: [email protected] MATEMÁTICA NA ESCOLA, 2ª SÉRIE, 2º BIMESTRE Tutor: Daiana da Silva Leite Grupo: 05 Tarefa 4 Duração Prevista: 290 minutos, distribuídos
3 ÁREAS E VOLUME DO TRONCO DE PIRÂMIDE 1 TRONCO DE PIRÂMIDE 2 SEMELHANÇA ENTRE AS PIRÂMIDES. 3.1 Área lateral. 3.2 Área das bases. 3.
 Matemática Pedro Paulo GEOMETRIA ESPACIAL VIII 1 TRONCO DE PIRÂMIDE Chamaremos de tronco de pirâmide de bases paralelas a porção da pirâmide limitada por sua base e por uma secção transversal qualquer
Matemática Pedro Paulo GEOMETRIA ESPACIAL VIII 1 TRONCO DE PIRÂMIDE Chamaremos de tronco de pirâmide de bases paralelas a porção da pirâmide limitada por sua base e por uma secção transversal qualquer
Hewlett-Packard PIRÂMIDES. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 Hewlett-Packard PIRÂMIDES Aulas 01 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Sumário PIRÂMIDES... 1 CLASSIFICAÇÃO DE UMA PIRÂMIDE... 1 EXERCÍCIOS FUNDAMENTAIS... 2 ÁREAS EM UMA PIRÂMIDE...
Hewlett-Packard PIRÂMIDES Aulas 01 a 05 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Sumário PIRÂMIDES... 1 CLASSIFICAÇÃO DE UMA PIRÂMIDE... 1 EXERCÍCIOS FUNDAMENTAIS... 2 ÁREAS EM UMA PIRÂMIDE...
MATEMÁTICA PLANEJAMENTO 3º BIMESTRE º B - 11 Anos
 PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 3º
PREFEITURA MUNICIPAL DE IPATINGA ESTADO DE MINAS GERAIS SECRETARIA MUNICIPAL DE EDUCAÇÃO DEPARTAMENTO PEDAGÓGICO/ SEÇÃO DE ENSINO FORMAL Centro de Formação Pedagógica CENFOP MATEMÁTICA PLANEJAMENTO 3º
COLÉGIO OBJETIVO JÚNIOR
 COLÉGIO OBJETIVO JÚNIOR NOME: N. o : DATA: / /2015 FOLHETO DE INFORMÁTICA (V.C. E R.V.) 7. o ANO Ao longo deste ano, aprendemos a operar os comandos e as funções básicas do SCRATCH, por exemplo, utilizando
COLÉGIO OBJETIVO JÚNIOR NOME: N. o : DATA: / /2015 FOLHETO DE INFORMÁTICA (V.C. E R.V.) 7. o ANO Ao longo deste ano, aprendemos a operar os comandos e as funções básicas do SCRATCH, por exemplo, utilizando
ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE 9º ANO ANO LECTIVO
 ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE 9º ANO ANO LECTIVO 2011-2012 Sólidos Geométricos NOME: Nº TURMA: Polígonos Um polígono é uma figura geométrica plana limitada por uma linha fechada.
ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE 9º ANO ANO LECTIVO 2011-2012 Sólidos Geométricos NOME: Nº TURMA: Polígonos Um polígono é uma figura geométrica plana limitada por uma linha fechada.
A Geometria nas Provas de Aferição
 Escola E.B. 2 e 3 de Sande Ficha de Trabalho de Matemática 6.º Ano A Geometria nas Provas de Aferição Nome: N.º Turma: 1. Assinala com um x a figura em que os triângulos representados são simétricos em
Escola E.B. 2 e 3 de Sande Ficha de Trabalho de Matemática 6.º Ano A Geometria nas Provas de Aferição Nome: N.º Turma: 1. Assinala com um x a figura em que os triângulos representados são simétricos em
Prova Final de Matemática
 PROVA FINAL DO 1.º CICLO DO ENSINO BÁSICO Matemática/Prova 42/1.ª Fase/2013 Decreto-Lei n.º 139/2012, de 5 de julho A PREENCHER PELO ESTUDANTE Nome completo Documento de identificação CC n.º ou BI n.º
PROVA FINAL DO 1.º CICLO DO ENSINO BÁSICO Matemática/Prova 42/1.ª Fase/2013 Decreto-Lei n.º 139/2012, de 5 de julho A PREENCHER PELO ESTUDANTE Nome completo Documento de identificação CC n.º ou BI n.º
AGRUPAMENTO de ESCOLAS de PEDRÓGÃO GRANDE CONSELHO de DOCENTES 1.º CEB Planificação Anual Matemática- _ 2.º Ano /2013
 ANUAL 164 dias letivos Números naturais Noção de número natural Números ordinais e cardinais Relações numéricas 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «vigésimo».
ANUAL 164 dias letivos Números naturais Noção de número natural Números ordinais e cardinais Relações numéricas 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «vigésimo».
Formação Continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ. Matemática 2º Ano 3º Bimestre/2012
 Formação Continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2012 Plano de Trabalho 2 Pirâmides e Cones Cursista: Ângela Pereira Cerqueira Halfeld Tutora: Ana Paula
Formação Continuada em Matemática Fundação CECIERJ/Consórcio CEDERJ Matemática 2º Ano 3º Bimestre/2012 Plano de Trabalho 2 Pirâmides e Cones Cursista: Ângela Pereira Cerqueira Halfeld Tutora: Ana Paula
