Faculdade de Informática e Tecnologia de Pernambuco
|
|
|
- Luiz Herman da Rocha Lage
- 9 Há anos
- Visualizações:
Transcrição
1 Faculdade de Informática e Tecnologia de Pernambuco Plano de Ensino Disciplina: INF101 - Álgebra Aplicada à Computação; Professor: Diego Machado Dias; Curso: Ciência da Computação; Carga horária: 72h; Objetivos Geral Familiarizar-se com a escrita matemática formal; Aprender a encontrar modelos matemáticos que representem problemas concretos (noções de modelagem matemática); Desenvolver ferramentas algébricas básicas para o aluno de computação; Ementa Lógica formal; Linguagem e lógica de conjuntos; Relações e funções; Estruturas algébricas e relacionais; Transformações entre estruturas; Noções de tipo abstrato e de especificação algébrica, representação de funções e noção de semântica denotacional; Sistemas ordenados; Metodologia Aulas expositivas com foco na participação dos alunos para melhor entendimento, bem como resolução de exercícios. As aulas serão ministradas com anotações no quadro e eventual uso de projetor multimídia para ilustração dos conceitos.
2 Recursos de Ensino Projetor multimídia; Quadro branco; Página da disciplina disponibilizando as listas de exercícios, materiais para leitura, cronograma e outros recursos. Endereço da página: Avaliação 2 Provas; Listas de ; Pesos: Prova tem 70%; Lista, 30%; Plano de Aula AULA DURAÇÃO DE AULAS CONTEÚDO PROGRAMÁTICO RECURSOS DIDÁTICOS Aula 1 03/08 Aula 2 05/08 Aula 3 10/08 Aula 4 12/08 2 Lógica formal: Proposições Representações simbólicas Tautologia e contradição 2 Lógica formal: Equivalência proposicional Predicados e quantificadores Quantificadores aninhados 2 Lógica formal Regras de inferência Conjuntos Operações com conjuntos Identidades envolvendo conjuntos 2 Conjuntos Lógica e conjuntos Partições Operações binárias Prova por casos [Exemplificação]
3 Aula 5 17/08 Aula 6 19/08 Aula 7 24/08 Aula 8 26/08 Aula 9 31/08 Aula 10 02/09 Aula 11 07/09 2 Conjuntos Operações unárias Relações Definição Propriedades das relações binárias Representação gráfica das relações Representação matricial 2 Fechos de uma relação Relações de equivalência 2 Relações Relação dual Composição de relações Classificação de relações. Teorema envolvendo partições e relações de equivalência. 2 Relações Relações de ordem Ordenação parcial Conjunto parcialmente ordenado Diagrama de Hasse Ordem total Predecessor e sucessor Elemento maximal e minimal 2 Relações Subposet Elemento máximo e mínimo Unicidade do elemento máximo e mínimo Limite superior Limite inferior Menor limite superior Maior limite inferior 2 Reticulados Definição Exemplos 2 Feriado Independência do Brasil Aula 12 09/09 Aula 13 14/09 2 Reticulado Reticulado distributivo Reticulado complementado Definições e exemplos Teorema do complemento único 2 Álgebras de Boole Definição e Propriedades
4 Aula 14 16/09 Aula 15 21/09 Aula 16 23/09 Aula 17 28/09 Aula 18 30/09 Aula 19 05/10 Aula 20 07/10 Aula 21 12/10 Aula 22 14/10 Aula 23 19/10 Aula 24 21/10 Aula 25 26/10 2 Álgebras de Boole Isomorfismos 2 Álgebras de Boole Exemplos Lista de exercícios Discussão da lista Revisão 2 Entrega da lista de exercícios Primeira prova 2 Discussão e resolução da primeira prova em sala 2 Funções Definição Classificação 2 Feriado Feriado de Nossa Senhora Aparecida 2 Funções Composição de funções Gráfico de funções Estruturas Algébricas Associatividade Comutatividade Elemento neutro Elemento inversível Semi-grupos Monóides Grupos Propriedades elementares (Grupos) Exemplos de Grupos Ordem de um grupo Tábua de um grupo Subgrupos Quadro branco.
5 Aula 26 28/10 Aula 27 02/11 Aula 28 04/11 Aula 29 09/11 Aula 30 11/11 Aula 31 16/11 Aula 32 18/11 Aula 33 23/11 Aula 34 25/11 Exemplos de subgrupos 2 Feriado Finados Homomorfismo de Grupos Exemplos de grupos isomorfos Demonstrações Técnicas de demonstrações 2 Demonstrações Sumarização das técnicas de demonstrações usadas na disciplina Lista de exercícios Discussão da lista Revisão 2 Entrega da lista de exercícios Segunda prova 2 Discussão e correção da segunda prova em sala. Entrega das notas Quadro branco. Aula 35 30/11 Aula 36 07/ Prova final Quadro branco.
6 Bibliografia Básica: 1. Fundamentos Matemáticos para a Ciência da Computação. Judith L Gersting 2. Discrete Mathematics (5th Edition). Kenneth A. Ross, Charles R. Wright. Complementar: 1. Álgebra Booleana e Circuitos de Chaveamento. Elliott Mendelson 2. Matemática Discreta para Computação e Informática. Paulo Blauth Menezes. 3. Mathematical Logic for Computer Science. Mordechai Ben-Ari. [Apenas apendice]
Faculdade de Informática e Tecnologia de Pernambuco. Primeira lista de exercícios de Álgebra Aplicada à Computação Prof. Diego Machado Dias
 Faculdade de Informática e Tecnologia de Pernambuco Primeira lista de exercícios de Álgebra Aplicada à Computação Prof. Diego Machado Dias Instruções 1. No início de cada seção da lista há uma sugestão
Faculdade de Informática e Tecnologia de Pernambuco Primeira lista de exercícios de Álgebra Aplicada à Computação Prof. Diego Machado Dias Instruções 1. No início de cada seção da lista há uma sugestão
sumário 1 introdução e conceitos básicos 1 2 noções de lógica e técnicas de demonstração introdução à matemática discreta...
 sumário 1 introdução e conceitos básicos 1 1.1 introdução à matemática discreta... 2 1.2 conceitos básicos de teoria dos conjuntos... 3 1.2.1 conjuntos...3 1.2.2 pertinência...5 1.2.3 alguns conjuntos
sumário 1 introdução e conceitos básicos 1 1.1 introdução à matemática discreta... 2 1.2 conceitos básicos de teoria dos conjuntos... 3 1.2.1 conjuntos...3 1.2.2 pertinência...5 1.2.3 alguns conjuntos
A2. Cada operação é distributiva sobre a outra, isto é, para todo x, y e z em A, x (y + z) = (x y) + (x z) e x + (y z) = (x + y) (x + z)
 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, que é baseada em um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas.
Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, que é baseada em um conjunto de axiomas (ou postulados). Veremos também algumas leis ou propriedades de álgebras booleanas.
Cálculo proposicional
 Notas de aula de MAC0329 (2003) 9 2 Cálculo proposicional Referências para esta parte do curso: capítulo 1 de [Mendelson, 1977], capítulo 3 de [Whitesitt, 1961]. Proposição Proposições são sentenças afirmativas
Notas de aula de MAC0329 (2003) 9 2 Cálculo proposicional Referências para esta parte do curso: capítulo 1 de [Mendelson, 1977], capítulo 3 de [Whitesitt, 1961]. Proposição Proposições são sentenças afirmativas
Lógica Proposicional
 Lógica Proposicional Equivalências Lógicas Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Lógica Proposicional junho - 2018 1 / 36 Este material é preparado
Lógica Proposicional Equivalências Lógicas Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Lógica Proposicional junho - 2018 1 / 36 Este material é preparado
3.4 Álgebra booleana, ordens parciais e reticulados
 Notas de aula de MAC0329 (2003) 23 3.4 Álgebra booleana, ordens parciais e reticulados Seja A um conjunto não vazio. Uma relação binária R sobre A é um subconjunto de A A, isto é, R A A. Se (x, y) R, denotamos
Notas de aula de MAC0329 (2003) 23 3.4 Álgebra booleana, ordens parciais e reticulados Seja A um conjunto não vazio. Uma relação binária R sobre A é um subconjunto de A A, isto é, R A A. Se (x, y) R, denotamos
BACHARELADO EM SISTEMAS DE INFORMAÇÃO MATEMÁTICA DISCRETA Aula 1 - Apresentação da disciplina
 BACHARELADO EM SISTEMAS DE INFORMAÇÃO MATEMÁTICA DISCRETA Aula 1 - Apresentação da disciplina Prof. Marcelo Gama Universidade Federal Rural de Pernambuco - DM 16 de Agosto de 2011 Marcelo Gama (DM - UFRPE)
BACHARELADO EM SISTEMAS DE INFORMAÇÃO MATEMÁTICA DISCRETA Aula 1 - Apresentação da disciplina Prof. Marcelo Gama Universidade Federal Rural de Pernambuco - DM 16 de Agosto de 2011 Marcelo Gama (DM - UFRPE)
(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Reticulados e Álgebras de Boole
 Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Cálculo de Predicados. Matemática Discreta. Profa. Sheila Morais de Almeida DAINF-UTFPR-PG. março
 Matemática Discreta Cálculo de Predicados Profa. Sheila Morais de Almeida DAINF-UTFPR-PG março - 2017 Quantificadores Como expressar a proposição Para todo número inteiro x, o valor de x é positivo. usando
Matemática Discreta Cálculo de Predicados Profa. Sheila Morais de Almeida DAINF-UTFPR-PG março - 2017 Quantificadores Como expressar a proposição Para todo número inteiro x, o valor de x é positivo. usando
Notas de aula de MAC0329 Álgebra Booleana e Aplicações
 Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
Notas de aula de MAC0329 Álgebra Booleana e Aplicações Nina S. T. Hirata Depto. de Ciência da Computação IME / USP Este texto é uma referência-base para o curso de MAC0329 (Álgebra Booleana e Aplicações).
Regras de Inferência. Matemática Discreta. Profa. Sheila Morais de Almeida DAINF-UTFPR-PG. março
 Matemática Discreta Regras de Inferência Profa. Sheila Morais de Almeida DAINF-UTFPR-PG março - 2017 Argumentos Válidos em Lógica Proposicional Considere o argumento: Se João pensa, então João existe.
Matemática Discreta Regras de Inferência Profa. Sheila Morais de Almeida DAINF-UTFPR-PG março - 2017 Argumentos Válidos em Lógica Proposicional Considere o argumento: Se João pensa, então João existe.
Teoria dos Conjuntos. Matemática Discreta. Teoria dos Conjuntos - Parte I. Profa. Sheila Morais de Almeida DAINF-UTFPR-PG.
 Matemática Discreta Teoria dos Conjuntos - Parte I Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 2017 Letras maiúsculas: conjuntos. Letras minúsculas: elementos do conjunto. Pertinência: o símbolo
Matemática Discreta Teoria dos Conjuntos - Parte I Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 2017 Letras maiúsculas: conjuntos. Letras minúsculas: elementos do conjunto. Pertinência: o símbolo
PLANO DE ENSINO DA DISCIPLINA
 PLANO DE ENSINO DA DISCIPLINA Docente: FABIO LUIS BACCARIN Telefones: (43) 3422-0725 / 9116-4048 E-mail: [email protected] Nome da Disciplina: Álgebra Elementar Curso: Licenciatura em Matemática Carga
PLANO DE ENSINO DA DISCIPLINA Docente: FABIO LUIS BACCARIN Telefones: (43) 3422-0725 / 9116-4048 E-mail: [email protected] Nome da Disciplina: Álgebra Elementar Curso: Licenciatura em Matemática Carga
Cálculo proposicional
 Cálculo proposicional Proposição Proposições são sentenças afirmativas declarativas que não sejam ambígüas e que possuem a propriedade de serem ou verdadeiras ou falsas, mas não ambas. Exemplos:. Gatos
Cálculo proposicional Proposição Proposições são sentenças afirmativas declarativas que não sejam ambígüas e que possuem a propriedade de serem ou verdadeiras ou falsas, mas não ambas. Exemplos:. Gatos
Álgebra Booleana: Axiomas, Teoremas e Leis de De Morgan
 Arquitectura de Computadores I Engenharia Informática (11537) Tecnologias e Sistemas de Informação (6616) Álgebra Booleana: Axiomas, Teoremas e Leis de De Morgan Nuno Pombo / Miguel Neto Arquitectura Computadores
Arquitectura de Computadores I Engenharia Informática (11537) Tecnologias e Sistemas de Informação (6616) Álgebra Booleana: Axiomas, Teoremas e Leis de De Morgan Nuno Pombo / Miguel Neto Arquitectura Computadores
(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Arquitetura e Organização de Computadores. Álgebra Booleana
 Arquitetura e Organização de Computadores Álgebra Booleana 1 Histórico e Propriedades Formalizada por George Boole em 1854 Usada por Shannon em 1938 para provar propriedades de circuitos de chaveamento
Arquitetura e Organização de Computadores Álgebra Booleana 1 Histórico e Propriedades Formalizada por George Boole em 1854 Usada por Shannon em 1938 para provar propriedades de circuitos de chaveamento
Abaixo descreveremos 6 portas lógicas: AND, OR, NOT, NAND, NOR e XOR.
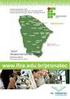 9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
Lógica Computacional
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN CAMPUS NATAL ZONA NORTE LICENCIATURA EM INFORMÁTICA Aula 01: Apresentação da Disciplina Francisco Júnior E-mail: [email protected] Website:
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN CAMPUS NATAL ZONA NORTE LICENCIATURA EM INFORMÁTICA Aula 01: Apresentação da Disciplina Francisco Júnior E-mail: [email protected] Website:
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes [email protected] DCC-FCUP Complexidade 2002/03 1 Teoria de Conjuntos Um conjunto é uma colecção de objectos/elementos/membros. (Cantor
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes [email protected] DCC-FCUP Complexidade 2002/03 1 Teoria de Conjuntos Um conjunto é uma colecção de objectos/elementos/membros. (Cantor
PLANO DE ENSINO. Ano: 2015 Semestre Letivo: ( ) Primeiro ( x ) Segundo Total de Créditos (se for o caso): 4 Carga Horária: 60 horas
 UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO PRÓ-REITORIA DE ENSINO DE GRADUAÇÃO Rua Dom Manoel de Medeiros, s/n Dois Irmãos 52171-900 Recife-PE Fone: 0xx-81-332060-40 [email protected] PLANO DE ENSINO
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO PRÓ-REITORIA DE ENSINO DE GRADUAÇÃO Rua Dom Manoel de Medeiros, s/n Dois Irmãos 52171-900 Recife-PE Fone: 0xx-81-332060-40 [email protected] PLANO DE ENSINO
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções
 Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) [email protected] Álgebra de Boole Binária A Álgebra de Boole binária
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) [email protected] Álgebra de Boole Binária A Álgebra de Boole binária
Prof.Letícia Garcia Polac. 6 de abril de 2017
 Fundamentos de Lógica e Conjuntos Prof.Letícia Garcia Polac Universidade Federal de Uberlândia UFU-MG 6 de abril de 2017 Sumário 1 EMENTA 2 BIBLIOGRAFIA 3 AVALIAÇÕES 4 INTRODUÇÃO EMENTA Ementa 1. Lógica
Fundamentos de Lógica e Conjuntos Prof.Letícia Garcia Polac Universidade Federal de Uberlândia UFU-MG 6 de abril de 2017 Sumário 1 EMENTA 2 BIBLIOGRAFIA 3 AVALIAÇÕES 4 INTRODUÇÃO EMENTA Ementa 1. Lógica
ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN
 ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN No século XIX Georges Boole desenvolveu uma teoria matemática com base nas leis da lógica - a Álgebra de Boole - cuja aplicação nos circuitos digitais e computadores
ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN No século XIX Georges Boole desenvolveu uma teoria matemática com base nas leis da lógica - a Álgebra de Boole - cuja aplicação nos circuitos digitais e computadores
Matemática Discreta. Lógica Proposicional. Profa. Sheila Morais de Almeida. agosto DAINF-UTFPR-PG
 Matemática Discreta Lógica Proposicional Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2016 Tautologias Tautologia é uma fórmula proposicional que é verdadeira para todos os possíveis valores-verdade
Matemática Discreta Lógica Proposicional Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2016 Tautologias Tautologia é uma fórmula proposicional que é verdadeira para todos os possíveis valores-verdade
Álgebra de Boole. Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes
 Álgebra de Boole Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Álgebra de Boole Álgebra Booleana ou Álgebra de Boole Conjunto
Álgebra de Boole Este material é uma adaptação das notas de aula dos professores Edino Fernandes, Juliano Maia, Ricardo Martins e Luciana Guedes Álgebra de Boole Álgebra Booleana ou Álgebra de Boole Conjunto
Lógica Computacional DCC/FCUP 2017/18
 2017/18 Funcionamento da disciplina Docentes: Teóricas: Sandra Alves Práticas: Sandra Alves e Nelma Moreira Página web http://www.dcc.fc.up.pt/~sandra/home/lc1718.html (slides de aulas e folhas de exercícios,
2017/18 Funcionamento da disciplina Docentes: Teóricas: Sandra Alves Práticas: Sandra Alves e Nelma Moreira Página web http://www.dcc.fc.up.pt/~sandra/home/lc1718.html (slides de aulas e folhas de exercícios,
Lógica Computacional Aula 1
 Lógica Computacional Aula 1 DCC/FCUP 2017/18 Funcionamento da disciplina Docentes: Teóricas: Sandra Alves Práticas: Sandra Alves e Nelma Moreira Página web http://www.dcc.fc.up.pt/~sandra/home/lc1718.html
Lógica Computacional Aula 1 DCC/FCUP 2017/18 Funcionamento da disciplina Docentes: Teóricas: Sandra Alves Práticas: Sandra Alves e Nelma Moreira Página web http://www.dcc.fc.up.pt/~sandra/home/lc1718.html
Matemática Discreta. Lógica de Predicados. Profa. Sheila Morais de Almeida. agosto DAINF-UTFPR-PG
 Matemática Discreta Lógica de Predicados Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2016 Quantificadores Como expressar a sentença Para todo número inteiro x, o valor de x é positivo. usando
Matemática Discreta Lógica de Predicados Profa. Sheila Morais de Almeida DAINF-UTFPR-PG agosto - 2016 Quantificadores Como expressar a sentença Para todo número inteiro x, o valor de x é positivo. usando
Invariantes de Laço. Profa. Sheila Morais de Almeida. junho DAINF-UTFPR-PG
 Invariantes de Laço Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Invariantes de Laço junho - 2018 1 / 28 Este material é preparado usando como referências
Invariantes de Laço Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Invariantes de Laço junho - 2018 1 / 28 Este material é preparado usando como referências
Lógica Computacional
 Lógica Computacional Nelma Moreira Departamento de Ciência de Computadores da FCUP Lógica Computacional Aula 1 http://www.dcc.fc.up.pt/~nam/web/teaching/lc2015/ index.html Cursos: LCC, MIERSI e (como Lógica
Lógica Computacional Nelma Moreira Departamento de Ciência de Computadores da FCUP Lógica Computacional Aula 1 http://www.dcc.fc.up.pt/~nam/web/teaching/lc2015/ index.html Cursos: LCC, MIERSI e (como Lógica
Lógica Proposicional
 Lógica Proposicional Lógica Proposicional Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Lógica Proposicional junho - 2018 1 / 55 Este material é preparado
Lógica Proposicional Lógica Proposicional Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Lógica Proposicional junho - 2018 1 / 55 Este material é preparado
Universidade de Caxias do Sul Centro de Ciências Exatas e Tecnologia Departamento de Informática. Matemática Discreta. Márcia Rodrigues Notare
 Universidade de Caxias do Sul Centro de Ciências Exatas e Tecnologia Departamento de Informática Caxias do Sul, julho de. ÍNDICE TEORIA DOS CONJUNTOS...4. RELAÇÃO DE PERTINÊNCIA...4. ALGUNS CONJUNTOS IMPORTANTES...4.
Universidade de Caxias do Sul Centro de Ciências Exatas e Tecnologia Departamento de Informática Caxias do Sul, julho de. ÍNDICE TEORIA DOS CONJUNTOS...4. RELAÇÃO DE PERTINÊNCIA...4. ALGUNS CONJUNTOS IMPORTANTES...4.
Matemática Discreta para Ciência da Computação
 Matemática Discreta para Ciência da Computação P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Ciência da Computação
Matemática Discreta para Ciência da Computação P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Ciência da Computação
Conjuntos parcialmente ordenados, totalmente ordenados e bem ordenados
 Conteúdo Conteúdo 1 1 Conjuntos parcialmente ordenados, totalmente ordenados e bem ordenados 2 1.1 Conjuntos parcialmente ordenados................ 2 1.2 Diagramas de Hasse........................ 4 1.3
Conteúdo Conteúdo 1 1 Conjuntos parcialmente ordenados, totalmente ordenados e bem ordenados 2 1.1 Conjuntos parcialmente ordenados................ 2 1.2 Diagramas de Hasse........................ 4 1.3
PLANO DE ENSINO E APRENDIZAGEM
 SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR (A) DA DISCIPLINA:
SERVIÇO PÚBLICO FEDERAL UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS CURSO DE LICENCIATURA PLENA EM MATEMÁTICA PARFOR PLANO E APRENDIZAGEM I IDENTIFICAÇÃO: PROFESSOR (A) DA DISCIPLINA:
Circuitos Digitais Álgebra de Boole
 Circuitos Digitais Álgebra de Boole Álgebra de Boole (ou Booleana) Desenvolvida pelo matemático britânico George Boole para estudo da lógica. Definida sobre um conjunto de dois elementos: (falso, verdadeiro)
Circuitos Digitais Álgebra de Boole Álgebra de Boole (ou Booleana) Desenvolvida pelo matemático britânico George Boole para estudo da lógica. Definida sobre um conjunto de dois elementos: (falso, verdadeiro)
Lógica Computacional
 Lógica Computacional Nelma Moreira: T, PL02,PL03 Rogério Reis: PL01,PL04 Departamento de Ciência de Computadores da FCUP Lógica Computacional Aula 1 www.dcc.fc.up.pt/~nam/web/teaching/lc16/index.html Cursos:
Lógica Computacional Nelma Moreira: T, PL02,PL03 Rogério Reis: PL01,PL04 Departamento de Ciência de Computadores da FCUP Lógica Computacional Aula 1 www.dcc.fc.up.pt/~nam/web/teaching/lc16/index.html Cursos:
ESTRUTURAS ALGÉBRICAS FICHA DE EXERCÍCIOS
 FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhanguene, Av de Moçambique, km 1, Tel: +58 1401078, Fa: +58 140108, Maputo ESTRUTURAS ALGÉBRICAS -01 FICHA DE EXERCÍCIOS
FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhanguene, Av de Moçambique, km 1, Tel: +58 1401078, Fa: +58 140108, Maputo ESTRUTURAS ALGÉBRICAS -01 FICHA DE EXERCÍCIOS
Notas de aula de MAC0329 Álgebra Booleana e Aplicações (2004)
 Notas de aula de MAC0329 Álgebra Booleana e Aplicações (2004) Nina S. T. Hirata Depto. de Ciência da Computação Instituto de Matemática e Estatística Universidade de São Paulo Página da disciplina: www.vision.ime.usp.br/~nina/cursos/mac0329-04/
Notas de aula de MAC0329 Álgebra Booleana e Aplicações (2004) Nina S. T. Hirata Depto. de Ciência da Computação Instituto de Matemática e Estatística Universidade de São Paulo Página da disciplina: www.vision.ime.usp.br/~nina/cursos/mac0329-04/
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/23 7 - ESTRUTURAS ALGÉBRICAS 7.1) Operações Binárias
INE5403 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/23 7 - ESTRUTURAS ALGÉBRICAS 7.1) Operações Binárias
Aplicações da teoria de conjuntos álgebra booleana. Pontifícia Universidade Católica de Goiás Msc. Gustavo Siqueira Vinhal 2016/1
 Aplicações da teoria de conjuntos álgebra booleana Pontifícia Universidade Católica de Goiás Msc. Gustavo Siqueira Vinhal 2016/1 CONJUNTOS Conjuntos são fundamentais para formalização de qualquer teoria.
Aplicações da teoria de conjuntos álgebra booleana Pontifícia Universidade Católica de Goiás Msc. Gustavo Siqueira Vinhal 2016/1 CONJUNTOS Conjuntos são fundamentais para formalização de qualquer teoria.
A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS.
 A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS. SANDRO MARCOS GUZZO RESUMO. A construção dos conjuntos numéricos é um assunto clássico na matemática, bem como o estudo das propriedades das operações
A DEFINIÇÃO AXIOMÁTICA DO CONJUNTO DOS NÚMEROS NATURAIS. SANDRO MARCOS GUZZO RESUMO. A construção dos conjuntos numéricos é um assunto clássico na matemática, bem como o estudo das propriedades das operações
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES
 MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
Predicados e Quantificadores
 Predicados e Quantificadores Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Predicados e Quantificadores junho - 2018 1 / 57 Este material é preparado usando
Predicados e Quantificadores Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Predicados e Quantificadores junho - 2018 1 / 57 Este material é preparado usando
Lógica para Computação. Álgebra de Boole
 Lógica para Computação Álgebra de Boole Formas Normais Definição: diz-se que uma proposição está na forma normal (FN) se e somente se, quando muito, contém os conectivos ~, ^ e v. - Toda proposição pode
Lógica para Computação Álgebra de Boole Formas Normais Definição: diz-se que uma proposição está na forma normal (FN) se e somente se, quando muito, contém os conectivos ~, ^ e v. - Toda proposição pode
Matemática Discreta. Teoria de Conjuntos - Parte 2. Profa. Sheila Morais de Almeida. abril DAINF-UTFPR-PG
 Matemática Discreta Teoria de Conjuntos - Parte 2 Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 2017 Operações em conjuntos As operações entre conjuntos podem ser unárias, binárias, ternárias,
Matemática Discreta Teoria de Conjuntos - Parte 2 Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 2017 Operações em conjuntos As operações entre conjuntos podem ser unárias, binárias, ternárias,
DIVISÃO DE ASSUNTOS ACADÊMICOS Secretaria Geral de Cursos PROGRAMA DE DISCIPLINA
 DIVISÃO DE ASSUNTOS ACADÊMICOS Secretaria Geral de Cursos PROGRAMA DE DISCIPLINA DEPARTAMENTO DE CIÊNCIAS EXATAS CÓDIGO: EXA804 DISCIPLINA: PROGRAMAÇÃO CARGA HORÁRIA: 180h EMENTA: Estudo aprofundado de
DIVISÃO DE ASSUNTOS ACADÊMICOS Secretaria Geral de Cursos PROGRAMA DE DISCIPLINA DEPARTAMENTO DE CIÊNCIAS EXATAS CÓDIGO: EXA804 DISCIPLINA: PROGRAMAÇÃO CARGA HORÁRIA: 180h EMENTA: Estudo aprofundado de
Lógica Proposicional e Álgebra de Boole
 Lógica Proposicional e Álgebra de Boole A lógica proposicional remonta a Aristóteles, e teve como objectivo modelizar o raciocínio humano. Partindo de frases declarativas ( proposições), que podem ser
Lógica Proposicional e Álgebra de Boole A lógica proposicional remonta a Aristóteles, e teve como objectivo modelizar o raciocínio humano. Partindo de frases declarativas ( proposições), que podem ser
1 Operações com conjuntos
 Notas sobre Conjuntos (2) Anjolina Grisi de Oliveira 1 Operações com conjuntos Definição 1 (União) Sejam A e B dois conjuntos arbitrários. A união dos conjuntos A e B, denotada por A B, é o conjunto que
Notas sobre Conjuntos (2) Anjolina Grisi de Oliveira 1 Operações com conjuntos Definição 1 (União) Sejam A e B dois conjuntos arbitrários. A união dos conjuntos A e B, denotada por A B, é o conjunto que
Álgebras Booleanas e Aplicações
 Álgebras Booleanas e Aplicações Prof. Dr. Clotilzio Moreira dos Santos IBILCE - UNESP São José do Rio Preto Outubro de 2013 Álgebras Booleanas e Aplicações Clotilzio Moreira dos Santos Sumário 1 ÁLGEBRAS
Álgebras Booleanas e Aplicações Prof. Dr. Clotilzio Moreira dos Santos IBILCE - UNESP São José do Rio Preto Outubro de 2013 Álgebras Booleanas e Aplicações Clotilzio Moreira dos Santos Sumário 1 ÁLGEBRAS
ÁLGEBRA DE BOOLE POSTULADOS, TEOREMAS E PROPRIEDADES
 ÁLGEBRA DE BOOLE POSTULADOS, TEOREMAS E PROPRIEDADES A aplicação principal da álgebra de Boole é o estudo e a simplificação algébrica de circuitos lógicos. As variáveis booleanas podem assumir apenas dois
ÁLGEBRA DE BOOLE POSTULADOS, TEOREMAS E PROPRIEDADES A aplicação principal da álgebra de Boole é o estudo e a simplificação algébrica de circuitos lógicos. As variáveis booleanas podem assumir apenas dois
Álgebra de Boole. Nikolas Libert. Aula 4B Eletrônica Digital ET52C Tecnologia em Automação Industrial
 Álgebra de Boole Nikolas Libert Aula 4B Eletrônica Digital ET52C Tecnologia em Automação Industrial Álgebra de Boole Álgebra de Boole Augustus De Morgan (1806-1871) e George Boole (1815-1864). Desenvolvimento
Álgebra de Boole Nikolas Libert Aula 4B Eletrônica Digital ET52C Tecnologia em Automação Industrial Álgebra de Boole Álgebra de Boole Augustus De Morgan (1806-1871) e George Boole (1815-1864). Desenvolvimento
3. Computadores Industriais
 UNIVERSIDADE DO ESTADO DE SANTA CATARINA UDESC CENTRO DE CIÊNCIAS TECNOLÓGICAS CCT DEPARTAMENTO DE ENG. DE PRODUÇÃO E SISTEMAS - DEPS INFORMÁTICA INDUSTRIAL IFD 3. Computadores Industriais Igor Kondrasovas
UNIVERSIDADE DO ESTADO DE SANTA CATARINA UDESC CENTRO DE CIÊNCIAS TECNOLÓGICAS CCT DEPARTAMENTO DE ENG. DE PRODUÇÃO E SISTEMAS - DEPS INFORMÁTICA INDUSTRIAL IFD 3. Computadores Industriais Igor Kondrasovas
Introdução ao Curso. Área de Teoria DCC/UFMG 2019/01. Introdução à Lógica Computacional Introdução ao Curso Área de Teoria DCC/UFMG /01 1 / 22
 Introdução ao Curso Área de Teoria DCC/UFMG Introdução à Lógica Computacional 2019/01 Introdução à Lógica Computacional Introdução ao Curso Área de Teoria DCC/UFMG - 2019/01 1 / 22 Introdução: O que é
Introdução ao Curso Área de Teoria DCC/UFMG Introdução à Lógica Computacional 2019/01 Introdução à Lógica Computacional Introdução ao Curso Área de Teoria DCC/UFMG - 2019/01 1 / 22 Introdução: O que é
Lógica Computacional
 Lógica Computacional 3.ano LCC e LERSI URL: http://www.ncc.up.pt/~nam/aulas/0304/lc Escolaridade: 3.5T e 1P Frequência:Semanalmente serão propostos trabalhos aos alunos, que serão entregues até hora e
Lógica Computacional 3.ano LCC e LERSI URL: http://www.ncc.up.pt/~nam/aulas/0304/lc Escolaridade: 3.5T e 1P Frequência:Semanalmente serão propostos trabalhos aos alunos, que serão entregues até hora e
Aplicar as propriedades imediatas dos homomorfismos de grupos. Aplicar os teoremas dos homomorfismos na relação de problemas.
 Aula 06 HOMOMORFISMOS DE GRUPOS META Apresentar o conceito de homomorfismo de grupos OBJETIVOS Reconhecer e classificar os homomorfismos. Aplicar as propriedades imediatas dos homomorfismos de grupos.
Aula 06 HOMOMORFISMOS DE GRUPOS META Apresentar o conceito de homomorfismo de grupos OBJETIVOS Reconhecer e classificar os homomorfismos. Aplicar as propriedades imediatas dos homomorfismos de grupos.
Introdução à Computação: Álgebra Booleana
 Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza ([email protected]) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza ([email protected]) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
LÓGICA APLICADA - GST0049 LÓGICA APLICADA (20/10/2014) Perfil Docente Especialista em Matemática, preferencialmente com pós-graduação stricto sensu na
 LÓGICA APLICADA - GST0049 LÓGICA APLICADA (20/10/2014) Perfil Docente Especialista em Matemática, preferencialmente com pós-graduação stricto sensu na área. Mestre ou Doutor em áreas afins. Experiência
LÓGICA APLICADA - GST0049 LÓGICA APLICADA (20/10/2014) Perfil Docente Especialista em Matemática, preferencialmente com pós-graduação stricto sensu na área. Mestre ou Doutor em áreas afins. Experiência
UNIVERSIDADE PRESBITERIANA MACKENZIE Faculdade de Computação e Informática
 2 a ETAPA exclusivo de curso (X) Eixo Comum ( ) Eixo Universal ( ) Curso: CIÊNCIA DA COMPUTAÇÃO ALGORITMOS E PROGRAMAÇÃO II ( 02 ) Sala de Aula 04 h/a ( 02 ) Laboratório ALGORITMOS E PROGRAMAÇÃO Estudo
2 a ETAPA exclusivo de curso (X) Eixo Comum ( ) Eixo Universal ( ) Curso: CIÊNCIA DA COMPUTAÇÃO ALGORITMOS E PROGRAMAÇÃO II ( 02 ) Sala de Aula 04 h/a ( 02 ) Laboratório ALGORITMOS E PROGRAMAÇÃO Estudo
Teoria dos Conjuntos MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES. Fundamentos de Lógica Técnicas Elementares de Prova A NOÇÃO DE CONJUNTO
 SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
A B f(a, B) = A + B. A f(a ) = A
 Álgebra de Boole ESTV-ESI-Sistemas Digitais-Álgebra de Boole 1/7 A Álgebra de Boole é uma ferramenta matemática muito utilizada na representação e simplificação de funções binárias (ou lógicas), sendo
Álgebra de Boole ESTV-ESI-Sistemas Digitais-Álgebra de Boole 1/7 A Álgebra de Boole é uma ferramenta matemática muito utilizada na representação e simplificação de funções binárias (ou lógicas), sendo
MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos
 MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos Karina Girardi Roggia [email protected] Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa
MDI0001 Matemática Discreta Aula 04 Álgebra de Conjuntos Karina Girardi Roggia [email protected] Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa
Combinando relações. Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações
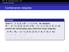 1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
1 / 11 Combinando relações Combinando relações Exemplo Seja A = {1, 2, 3} e B = {1, 2, 3, 4}. As relações R 1 = {(1, 1), (2, 2), (3, 3)} e R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} podem ser combinadas para
Conteúdo. Conceitos e Resultados Gerais. 11 Combinatória. Introdução
 Introdução ix I Conceitos e Resultados Gerais 1 1 Linguagem Matemática e Lógica Informal 1.1 Sistemas matemáticos.. 1.2 Noção de conjunto... 1.3 Linguagem proposicional.. 1.4 Operações sobre conjuntos.
Introdução ix I Conceitos e Resultados Gerais 1 1 Linguagem Matemática e Lógica Informal 1.1 Sistemas matemáticos.. 1.2 Noção de conjunto... 1.3 Linguagem proposicional.. 1.4 Operações sobre conjuntos.
1.1 Conjuntos parcialmente ordenados (c.p.o. s)
 Capítulo 1 PRELIMINARES Neste primeiro capítulo podemos encontrar algumas definições e proposições que para além de nos familiarizar com a notação que iremos utilizar também têm como finalidade a referência
Capítulo 1 PRELIMINARES Neste primeiro capítulo podemos encontrar algumas definições e proposições que para além de nos familiarizar com a notação que iremos utilizar também têm como finalidade a referência
LÓGICA APLICADA A COMPUTAÇÃO
 LÓGICA APLICADA A COMPUTAÇÃO 2009.3 Aquiles Burlamaqui Apresentação da Disciplina Planejamento Conteúdo Programático Metodologia Bibliografia Definição Motivação Planejamento Semestre 2009.3 Local 3B5
LÓGICA APLICADA A COMPUTAÇÃO 2009.3 Aquiles Burlamaqui Apresentação da Disciplina Planejamento Conteúdo Programático Metodologia Bibliografia Definição Motivação Planejamento Semestre 2009.3 Local 3B5
02 Álgebra de Boole elementos físicos e funções lógicas. v0.2
 02 Álgebra de Boole elementos físicos e funções lógicas v0.2 Conteúdo Leis Teoremas Corolários Dualidade Conjunto binário Elementos físicos e funções lógicas 05 November 2014 Sistemas Digitais 2 Definição
02 Álgebra de Boole elementos físicos e funções lógicas v0.2 Conteúdo Leis Teoremas Corolários Dualidade Conjunto binário Elementos físicos e funções lógicas 05 November 2014 Sistemas Digitais 2 Definição
Álgebra de Boole. João Paulo Cerquinho Cajueiro 19 de agosto de 2009
 Álgebra de Boole João Paulo Cerquinho Cajueiro 19 de agosto de 2009 A álgebra de Boole foi desenvolvida por George Boole(1815 1864) em seu livro An Investigation of the Laws of Thought on Which are Founded
Álgebra de Boole João Paulo Cerquinho Cajueiro 19 de agosto de 2009 A álgebra de Boole foi desenvolvida por George Boole(1815 1864) em seu livro An Investigation of the Laws of Thought on Which are Founded
Indução Matemática. Profa. Sheila Morais de Almeida. junho DAINF-UTFPR-PG
 Indução Matemática Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Indução Matemática junho - 2018 1 / 38 Este material é preparado usando como referências os
Indução Matemática Profa. Sheila Morais de Almeida DAINF-UTFPR-PG junho - 2018 Sheila Almeida (DAINF-UTFPR-PG) Indução Matemática junho - 2018 1 / 38 Este material é preparado usando como referências os
Pontifícia Universidade Católica Federal do Rio de Santa Grande Catarina do Sul
 DEPARTAMENTO: Engenharia Elétrica CURSO: Engenharia Elétrica DISCIPLINA: Sistemas Digitais CÓDIGO: EEL 7020 CRÉDITOS: 04 (02 Teoria e 02 Prática) CARGA HORÁRIA: 72 horas-aula REQUISITOS: OFERTA: Pré-requisito:
DEPARTAMENTO: Engenharia Elétrica CURSO: Engenharia Elétrica DISCIPLINA: Sistemas Digitais CÓDIGO: EEL 7020 CRÉDITOS: 04 (02 Teoria e 02 Prática) CARGA HORÁRIA: 72 horas-aula REQUISITOS: OFERTA: Pré-requisito:
George Boole ( ) Claude Shannon
 George Boole (1815 1864) Claude Shannon Da matemática básica temos: Constante = valor fixo Variável = pode assumir qualquer valor Constante booleana = valor fixo (0 ou 1) independente da situação! Variável
George Boole (1815 1864) Claude Shannon Da matemática básica temos: Constante = valor fixo Variável = pode assumir qualquer valor Constante booleana = valor fixo (0 ou 1) independente da situação! Variável
Capítulo 3. Álgebra de Bool
 Capítulo 3 Álgebra de Bool Adaptado dos transparentes das autoras do livro The Essentials of Computer Organization and Architecture Objectivos Compreender a relação entre lógica Booleana e os circuitos
Capítulo 3 Álgebra de Bool Adaptado dos transparentes das autoras do livro The Essentials of Computer Organization and Architecture Objectivos Compreender a relação entre lógica Booleana e os circuitos
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA
 INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/51 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
INE0003 FUNDAMENTOS DE MATEMÁTICA DISCRETA PARA A COMPUTAÇÃO PROF. DANIEL S. FREITAS UFSC - CTC - INE Prof. Daniel S. Freitas - UFSC/CTC/INE/2007 p.1/51 6 - RELAÇÕES DE ORDENAMENTO 6.1) Conjuntos parcialmente
aula 01 (Lógica) Ementa Professor: Renê Furtado Felix Site:
 aula 01 (Lógica) Ementa Professor: Renê Furtado Felix E-mail: [email protected] Site: http://www.renecomputer.net/pdflog.html Plano de Ensino CURSO: Tecnologia em Análise e Desenvolvimento de Sistemas
aula 01 (Lógica) Ementa Professor: Renê Furtado Felix E-mail: [email protected] Site: http://www.renecomputer.net/pdflog.html Plano de Ensino CURSO: Tecnologia em Análise e Desenvolvimento de Sistemas
Matemática Discreta para Ciência da Computação
 Matemática Discreta para Ciência da Computação P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Ciência da Computação
Matemática Discreta para Ciência da Computação P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Ciência da Computação
3.3 Cálculo proposicional clássico
 81 3.3 Cálculo proposicional clássico 3.3.1 Estrutura dedutiva Neste parágrafo serão apresentados, sem preocupação com excesso de rigor e com riqueza de detalhes, alguns conceitos importantes relativos
81 3.3 Cálculo proposicional clássico 3.3.1 Estrutura dedutiva Neste parágrafo serão apresentados, sem preocupação com excesso de rigor e com riqueza de detalhes, alguns conceitos importantes relativos
Noções básicas de álgebra universal para a disciplina de Fundamentos Algébricos de Engenharia da Programação da LMAC
 Noções básicas de álgebra universal para a disciplina de Fundamentos Algébricos de Engenharia da Programação da LMAC Pedro Resende Departamento de Matemática Instituto Superior Técnico Conteúdo 1 Álgebras
Noções básicas de álgebra universal para a disciplina de Fundamentos Algébricos de Engenharia da Programação da LMAC Pedro Resende Departamento de Matemática Instituto Superior Técnico Conteúdo 1 Álgebras
