MATEMÁTICA PARA COMPUTAÇÃO

Transcrição

1 Professor Angelo Gonçalves da Luz MATEMÁTICA PARA COMPUTAÇÃO Teoria de conjuntos

2 Notação e Relação entre elementos Letras maiúsculas denotam Conjuntos. O Símbolo denota que um elemento pertence a um determinado conjunto. Ex.: Se A = {java, php, haskell}, então java A e C# A. Expressando valores de um conjunto (Finito ou Infinito). Ex.: Para expressar os números pares Por amostra: S = {2, 4, 6,...} Problema: Interpretação Caracterização através de propriedades: S = { x x é um inteiro positivo par} Vantagem: Fácil interpretação. Se lê O conjunto de todos os x tais que x é um inteiro positivo par

3 Notação Descreva os conjuntos abaixo listando seus elementos a) S = {x x é um inteiro e 4 < x <= 8} b) S = {x x é a capital do Brasil} c) S = {x x é um tipo primitivo java} Descreve cada um dos conjuntos abaixo através de uma propriedade (compreensão) a) S = {2, 4, 6, 8, 10} b) S = {2, 3, 5, 7, 11, 13,...} c) S = {1, 2, 3, 4, 5}

4 Conjuntos Numéricos Números Naturais N Números Inteiros Z Números Racionais Q Números Irracionais I Números Reais R I Descreva os conjuntos abaixo listando seus elementos ou uma amostra deles. S = { x x N e x < 0} S = { x x Z e x < 0}

5 Relações entre conjuntos É possível que um conjunto tenha relação com outro. A = { 2, 4, 6, 8, 10, 12, 14} B = {4, 8, 12} Pode-se observar que, todos os elementos de B também são elementos de A. Então, B é um subconjunto de A, ou B está contido em A, ou ainda, A contém B. Representação: B A Qual a relação entre int e short (java)?

6 Relações entre conjuntos Subconjuntos Ex.: A B B A Conjunto que faz parte de outro conjunto. Sendo assim, A é um subconjunto de B. Conjunto das Partes Conjunto composto por todos os subconjuntos possíveis de um conjunto. Ex.: A = {1, 2} B= {1,2,3} C= {1, 2, 3, 4} P(A) = {, {1}, {2}, {1,2}} P(B) =? P( C)=? Como saber o total de partes de um conjunto?

7 Exercício Descreva por compreensão e também aponte as relações entre os conjuntos da imagem ao lado.

8 Exercício Seja S = {2, 5, 17, 27} Quais das seguintes afirmações são verdadeiras? a. 5 S b. 2+5 S c. 17 S d. {5,27} S e. S f. S S g. {27} S h. {27} S

9 Teoria de Conjuntos Tipos de Representação: Extensão (listando os elementos) Compreensão (através de propriedades) Diagrama de Venn Euler diagrama de Venn extensão A = {a, b, c} Compreensão(propriedades) A = {x x N e x < 2}

10 Teoria de Conjuntos Operações com Conjuntos União ( ) A B = {x x A ou x B} Interseção ( ) A B =? Subtração (-) A B =?

11 Exercício Considerando os conjuntos A= {1,2,3} e B{2,3,4,5,6}, represente: a. A B b. A B c. A B d. B A Monte o diagrama de Venn para representar os conjuntos acima.

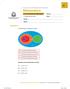
12 Teoria de Conjuntos Em uma pesquisa de mercado, várias pessoas foram entrevistadas acerca de quais suas preferências em relação a 3 Sistemas Operacionais: Windus, Linucs e MecOS. Os resultados apontaram que: 190 pessoas utilizam Windus, 190 o Linucs, 220 o MecOS. 30 utilizam os 3, 120 nenhum, 50 utilizam Windus e Linucs, 70 utilizam Windus e MecOS e, por fim, 40 utilizam Linucs e MecOS. Quantas pessoas foram entrevistadas? Quantos entrevistados utilizam apenas Windus? Quantos entrevistados utilizam apenas MecOS? Quanto entrevistados utilizam mais de 1 sistema operacional?

13 Teoria de Conjuntos Uma pesquisa a respeito de qual o curso mais promissor na área de TI: ADS ou Redes, entrevistou 35 vestibulandos, onde, todos votaram em ADS, Redes, ou ambos. Após a pesquisa, descobriu-se que, 26 acreditam que o curso de ADS seja mais promissor e 14 que o de Redes seja. Quantos votaram em ambos? Monte o diagrama de Venn Euler.

14 Teoria de Conjuntos Solução: A B = A + B - A B Ou seja: ADS Redes = ADS + Redes - ADS REDES ADS Redes = ADS Redes = 5

15 Teoria de Conjuntos Um grupo de estudantes está planejando encomendar pizzas. Se 13 comem linguiça calabresa, 10 comem salame italiano, 12 comem queijo extra, 4 comem tanto calabresa quanto salame, 5 comem tanto salame quanto queijo extra, 7 comem tanto linguiça calabresa quanto queijo extra, e 3 comem tudo. Quantos estudantes tem o grupo? Monte o diagrama de Venn Euler.

16 Teoria de Conjuntos Solução: A B C = A + B + C - A B - A C - B C + A B C

17 Teoria de Conjuntos Feito um levantamento entre os 91 assinantes da revista NERDS, afim de analisar quais as linguagens de programação mais utilizadas pelos seus assinantes. Os resultados do levantamento revelam que 68 programam em java, 34 em php, 30 em C#. Além disso, 19 programam ambos java e php, 11 programam em ambos php e C#, e 13 dominam tanto java quanto C#. Monte o diagrama de Venn Euler. Quantos assinantes dominam as 3 linguagens?

18 Teoria de Conjuntos Um feirante vende apenas brócolis, cenoura e quiabo. Em um dia o feirante atende 207 pessoas. Se 114 pessoas compram brócolis, 152 compram cenoura, 25 compram quiabo, 64 compram brócolis e cenoura, 12 compram cenoura e quiabo e 9 compram os três produtos. Quantas pessoas compram brócolis e quiabo? Monte o diagrama de Venn Euler.

19 Desafio! Implemente um programa que recebe como entrada dois conjuntos e gera como saída a impressão dos conjuntos, os valores da união, interseção e subtração entre os conjuntos.