AULA 03 - TENSÃO E DEFORMAÇÃO
|
|
|
- Edite Pinto Monsanto
- 6 Há anos
- Visualizações:
Transcrição
1 AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito da deformação normal e por cisalhamento. Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele. Essas mudanças são denominadas deformações e podem ser altamente visíveis ou praticamente imperceptíveis se não forem utilizados equipamentos que façam medições precisas. Por exemplo, uma tira de borracha sofrerá uma grande deformação quando esticada. Por outro lado, os elementos estruturais de um edifício sofrem apenas leves deformações quando há muitas pessoas dentro dele. Também pode ocorrer deformação em um corpo quando há mudança de temperatura. Um exemplo típico é a expansão ou contração térmica de um telhado causada pelas condições atmosféricas. Portanto as medições de deformação são experimentais e, uma vez obtidas, podem ser relacionadas com as cargas aplicadas, ou tensões, que agem no interior do corpo. 1. DEFORMAÇÃO NORMAL O alongamento ou contração de um segmento de reta por unidade de comprimento é denominado deformação normal. O alongamento total de uma barra submetida a uma força axial é designado pela letra grega δ (delta), onde δ = L = ( L - Lo ). E a deformação normal, representado pela letra grega ε (epsilon), como: ε = δ L o
2 onde: ε = deformação normal δ = alongamento ou encurtamento Lo = comprimento inicial da barra. Note-se que a deformação ε é uma quantidade adimensional DIAGRAMA DE TENSÃO DEFORMAÇÃO A resistência de um material depende da sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente ao próprio material e deve ser determinada por métodos experimentais. Um dos testes mais importantes nesses casos é o ensaio de tração ou compressão. Embora seja possível determinar muitas propriedades mecânicas importantes de um material por esse teste, ele é usado primariamente para determinar a relação entre a tensão normal média e a deformação normal média em muitos materiais usados na engenharia, como metais, cerâmicas, polímeros e compósitos. Pelos dados obtidos em um ensaio de tração ou compressão, é possível calcular vários valores da tensão e da deformação, correspondentes no corpo de prova e, então, construir um gráfico com esses resultados. A curva resultante é denominada diagrama tensão deformação. O diagrama tensão x deformação varia muito de material para material e, dependendo da temperatura do corpo de prova ou da velocidade de crescimento da carga podem ocorrer resultados diferentes para um mesmo material. Entre os diagramas tensão 2
3 x deformação de vários grupos de materiais é possível, no entanto, distinguir algumas características comuns que nos levam a dividir os materiais em duas importantes categorias: materiais dúcteis e materiais frágeis. Materiais Dúcteis Qualquer Material que possa ser submetido a grandes deformações antes da ruptura é chamado de material dúctil. O aço doce é um exemplo. Os engenheiros escolhem materiais dúcteis para o projeto por que são capazes de absorver choque ou energia e, quando sobrecarregados, exibem, em geral, grande deformação antes de falhar. Materiais Frágeis São materiais que possuem pouco, ou nenhum escoamento. Exemplo: ferro fundido, concreto. O concreto, assim como o ferro fundido cinzento, é classificado como um material frágil e também tem baixa capacidade de resistência à tração. As características de seu diagrama tensão-deformação dependem primariamente da mistura do concreto (água, areia, brita e cimento) e do tempo e temperatura de cura. Um exemplo típico de um diagrama tensão-deformação "completo" para o concreto é dado na figura abaixo. Observamos nesse gráfico que a máxima resistência à compressão do concreto é quase 12,5 vezes maior do que sua resistência à tração, ( c)máx = 34,5 MPa, em comparação com ( t)máx = 2,76 MPa. Por essa razão, o concreto é quase sempre reforçado com barras ou hastes de aço quando projetado para suportar cargas de tração. 3
4 1.2 - DIAGRAMA TENSÃO-DEFORMAÇÃO CONVENCIONAL E REAL PARA MATERIAIS DÚCTEIS REGIÃO ELÁSTICA O trecho da curva tensão-deformação, compreendido entre a origem e o limite de proporcionalidade que representa a tensão máxima que pode ser aplicada à barra sem que apareçam deformações residuais, ou permanentes, após a retirada integral da carga externa. 4
5 Limite de proporcionalidade: Representa o valor máximo da tensão abaixo da qual o material obedece a Lei de Hooke. Para um material frágil, não existe limite de proporcionalidade (o diagrama não apresenta parte reta). Limite de elasticidade: Existe um ponto na curva tensão x deformação ao qual corresponde o limite de elasticidade; representa a tensão máxima que pode ser aplicada a barra sem que apareçam deformações residuais ou permanentes após a retirada integral da carga externa. Para muitos materiais, os valores dos limites de elasticidade e proporcionalidade são praticamente iguais, sendo usados como sinônimos. Na fase elástica do diagrama tensão - deformação, temos um trecho reto. Por consequência, um aumento na tensão provoca um aumento proporcional na deformação. Esse fato foi descoberto por Robert Hooke, em 1676, para molas, e é conhecido como lei de Hooke e pode ser expresso matematicamente como: = E. Nesta expressão, E representa a constante de proporcionalidade, denominada módulo de elasticidade ou módulo de Young, nome que se deve a Thomas Young, que publicou uma explicação sobre o módulo em Alguns valores de E são mostrados na Tabela abaixo. Para a maioria dos materiais, o valor do Módulo de Elasticidade sob compressão ou sob tração são iguais. 5
6 Tabela 1 Propriedades mecânicas típicas de alguns materiais Peso específico Módulo de Elasticidade Material (kn/m 3 ) (GPa) Concreto Simples Concreto Armado Aço Estrutural 78,5 210 Alumínio 26,9 70 Bronze 83,2 98 Cobre 88,8 105 Madeira Estrutural 3 a 12 7 a 14 Quando a barra é carregada por tração simples, a tensão axial é σ = P / A e a deformação específica é ε = δ / L. Combinando estes resultados com a Lei de Hooke, tem-se a seguinte expressão para o alongamento da barra: δ = PL o EA Esta equação mostra que o alongamento de uma barra linearmente elástica é diretamente proporcional à carga e ao comprimento e inversamente proporcional ao módulo de elasticidade e à área da seção transversal. O produto EA é conhecido como rigidez axial da barra. Exemplo: A barra rígida BDE é suspensa por duas barras AB e CD. A barra AB é de alumínio (Ealu = 70 GPa) e com seção transversal de área de 400 mm 2, a barra CD é de aço (Eaço = 200 GPa) com uma seção transversal de área de 500 mm 2. Considerando um comportamento elástico, determine os alongamentos das barras AB e CD. 6
7 1.2.2 REGIÃO PLÁSTICA O trecho da curva entre o limite de proporcionalidade e o ponto de ruptura do material; é chamado de região plástica. Nesta região se retirarmos o carregamento, o corpo não volta à sua forma inicial, havendo um deslocamento residual. a) Escoamento A maioria dos materiais metálicos, ao ser submetida a uma tensão de tração crescente, se comporta dentro do grupo dos que cedem antes de romper. Neste caso, antes de ser atingida a tensão que caracteriza a resistência mecânica do material, a relação entre a força aplicada e o alongamento desvia-se da linearidade elástica na (assim denominada) tensão de escoamento. Para estes materiais, a partir deste ponto em diante, passa a acontecer o processo que se denomina deformação plástica do metal. Quando se atinge o limite de escoamento, o material passa a escoar-se. A partir deste limite, aumentam as deformações sem que se altere praticamente o valor da tensão. 7
8 Observação: Os materiais frágeis e alguns com características de dúcteis, apresentam de modo indefinido, o início do escoamento. Neste casos a Norma Brasileira estabelece uma Tensão Convencional de Escoamento, tomando-se no eixo dos deslocamento específicos o valor = 0,2%. A partir deste ponto traça-se uma reta paralela ao trecho reto do diagrama. A tensão de Escoamento ( e) é obtida pela intersecção com o gráfico. b) Endurecimento por deformação Discordâncias são os defeitos em linha, são imperfeições em uma estrutura cristalina nas quais uma linha de átomos tem uma estrutura local que difere da estrutura circunvizinha. Durante a deformação plástica o número de discordâncias aumenta drasticamente; Esse endurecimento dá-se devido a este aumento de discordâncias e imperfeições promovidas pela deformação, que impedem o escorregamento dos planos atômicos; O escoamento termina e a curva cresce continuamente (endurecimento), até atingir a tensão máxima denominada limite de resistência. 8
9 Desde o início do teste até o limite de resistência, a área da seção transversal decresce uniformemente. Exemplo A figura apresenta o diagrama tensãodeformação para um aço-liga com 12 mm de diâmetro original e comprimento de referência 50 mm. Determine: a) os valores aproximados do módulo de elasticidade para o material; b) a carga aplicada ao corpo de prova que causa escoamento; c) a carga máxima que o corpo de prova suportará. Exemplo 2 A figura apresenta o diagrama tensão-deformação de uma barra de aço. Determine os valores aproximados do módulo de elasticidade, limite de proporcionalidade, limite de resistência e módulo de resiliência. Se a barra for submetida a uma carga de tração de 450 MPa, determine o valor da recuperação da deformação elástica e da deformação permanente na barra quando descarregada. 9
10 c) Estricção Quando a carga de tração aumentar muito, quando se atinge a tensão da resistência mecânica (tensão máxima) a situação torna-se incontrolável, com a formação de uma zona de deformação acentuada, localizada, denominada pescoço, onde a seção da peça diminui de forma visível, prenunciando a ruptura iminente. 10
11 1.2.3 COEFICIENTE DE POISSON As experiências demonstram que um material, quando submetido à tração, sofre além da deformação axial (alongamento), uma deformação transversal (afinamento). duas deformações eram proporcionais uma em relação à outra, dentro dos limites da Lei de Hooke. Poisson demonstrou que estas δ y L y = δ z L z y = z As experiências mostram que y = z e que a relação entre deformação transversal e longitudinal é constante. Essa relação é denominada de Coeficiente de Poisson ( ) (ni) = ε y ε x = ε z ε x = - (εtransversal / εlongitudinal) Essa expressão tem sinal negativo porque o alongamento longitudinal (deformação positiva) provoca contração lateral (deformação negativa) e vice-versa. O coeficiente de Poisson é constante para cada material e seu valor varia entre 0 e 0,5. 11
12 Exemplos: Material Coeficiente de Poisson ( ) Aço 0,3 Concreto 0,15 Pedra 0,20 Exemplo: A barra circular de aço apresentada na figura abaixo possui d = 20 mm e comprimento L = 0,80 m. Encontra-se submetida à ação de uma carga axial de 7,2 kn. Pede-se determinar: a) tensão normal atuante na barra; b) o alongamento; c) a deformação longitudinal; d) a deformação transversal; Dados: Eaço = MPa aço = 0,3 (coeficiente de Poisson) 12
13 1.2.4 ENERGIA DE DEFORMAÇÃO Quando um material é deformado por uma carga externa, tende a armazenar energia internamente em todo o seu volume. Como essa energia está relacionada com as deformações no material, ela é denominada energia de deformação. Por exemplo, quando um corpo de prova de ensaio de tração é submetido a uma carga axial, um elemento de volume do material é submetido a uma tensão uniaxial, como mostra a figura ao lado. Essa tensão desenvolve uma força F = A = ( x. y) nas faces superior e inferior do elemento após ele ter sofrido um deslocamento vertical (. z). Por definição, trabalho é determinado pelo produto entre a força e o deslocamento na direção da força. Visto que a força aumenta uniformemente de zero até seu valor final F quando é obtido odeslocamento (. z), o trabalho realizado pela força sobre o elemento é igual ao valor médio da força ( F/2) vezes o deslocamento (. z). Esse trabalho externo" é equivalente ao "trabalho interno" ou energia de deformação armazenada no elemento, se considerarmos que nenhuma energia é perdida sob a forma de calor. Por consequência, a energia de deformação U é U = (1/2 F). z = (1/2 x..y).. z. Visto que o volume do elemento é V = x. y. z, então U = 1/2 V 13
14 Às vezes, é conveniente formular a energia de deformação por unidade de volume de material, denominada densidade de energia de deformação, a qual pode ser expressa por: Se o comportamento do material for linear elástico, então a lei de Hooke se aplica, = E. e, portanto, podemos expressar a densidade de energia de deformação em termos da tensão uniaxial como: Módulo de resiliência. Em particular, quando a tensão atinge o limite de proporcionalidade, a densidade de energia de deformação é calculada pela Equação: Observe, na região elástica do diagrama tensãodeformação (Figura a), que ur é equivalente à área triangular sombreada sob o diagrama. Em termos físicos, a resiliência de um material representa sua capacidade de absorver energia sem sofrer qualquer dano permanente. Módulo de tenacidade. Outra importante propriedade de um material é o módulo de tenacidade (ut). O trabalho realizado por unidade de volume do material, quando há uma força de tração simples que aumenta gradualmente a partir de zero até atingir o limite de ruptura, é chamado de módulo de tenacidade. Essa quantidade representa a área inteira sob o diagrama tensão-deformação (Figura b), portanto indica a densidade de energia de deformação do material um pouco antes da ruptura. A tenacidade de um material é sua capacidade de absorver energia na região plástica de um material. 14
15 Essa propriedade é importante no projeto de elementos estruturais que possam ser sobrecarregados acidentalmente. Materiais com alto módulo de tenacidade sofrerão grande distorção devido à sobrecarga; contudo, podem ser preferíveis aos que têm baixo valor de módulo de tenacidade, já que os que têm ut baixo podem sofrer ruptura repentina sem dar nenhum sinal dessa ruptura iminente. Exemplo: A figura apresenta o diagrama tensãodeformação para um aço-liga com 12 mm de diâmetro original e 50 mm de comprimento de referência. Determine os valores aproximados do módulo de resiliencia e do módulo de tenacidade para o material 15
16 2. TENSÃO - DEFORMAÇÃO POR CISALHAMENTO. Seja uma partícula submetida a um esforço F com indicado abaixo: A partícula irá sofre uma deformação, onde poderemos observar um deslocamento angular denominado de distorção. A mudança que ocorre no ângulo entre dois segmentos de reta que originalmente eram perpendiculares um ao outro é denominada deformação por cisalhamento. Esse ângulo é representado por (gama) e medido em radianos (rad). = π 2 θ 16
17 Observação: a) As deformações normais causam uma mudança no volume do elemento, ao passo que deformações por cisalhamento provocam uma mudança em sua forma. É claro que ambos os efeitos ocorrem simultaneamente durante a deformação. b) A maioria dos materiais de engenharia sofre pequenas deformações, portanto, uma deformação normal ε << O DIAGRAMA TENSÃO DEFORMAÇÃO DE CISALHAMENTO A forma deste gráfico é semelhante ao gráfico de tensão - deslocamento específico ( - ), mudando apenas a ordem de grandeza dos valores. 17
18 Para os pontos A, B, C e D e para p, e, u, R, vale a mesma nomenclatura anterior (agora no cisalhamento) LEI DE HOOKE NO CISALHAMENTO O trecho AO do diagrama - é uma reta, ou seja, existe uma proporcionalidade entre Tensão de Cisalhamento e Distorção. A maioria dos materiais de engenharia apresenta comportamento elástico linear, portanto a lei de Hooke para cisalhamento pode ser expressa por = G. Essa expressão é a chamada Lei de Hooke no cisalhamento e G é o módulo de Elasticidade Transversal. O valor de G pode ser obtido do diagrama - sendo numericamente igual à tg, com a mesma unidade da Tensão de Cisalhamento, visto que é expresso em radianos. As experiências demonstram que um material, quando submetido à tração, sofre além da deformação axial (alongamento), uma deformação transversal (afinamento). Três constantes do material, E, v e G, na realidade, estão relacionadas pela equação E G 2 1 G = módulo de elasticidade o cisalhamento ou módulo de rigidez. v 18
19 TABELA PROPRIEDADES DE ALGUNS MATERIAIS Aplicando a lei de Hooke para o alongamento, temos: Para pequenos deslocamentos o ângulo de cisalhamento pode ser γ tgγ = δ h Sendo: τ = F A τ = G. γ F A = G. δ h δ = F. h A. G 19
20 Exemplo Qual o valor máximo da carga P a ser aplicada na peça abaixo, sabendo-se que o deslocamento máximo permitido é 20º. Dado: G = 80 kgf/cm 2. BIBLIOGRAFIA ANTÔNIO NETO, Aiello Giuseppe Resistência dos Materiais I - Universidade Presbiteriana Mackenzi. GASPAR, Ricardo MECÂNICA DOS MATERIAIS - Notas de aula da disciplina Resistência dos Materiais ministrada pelo Prof. Leandro Mouta Trautwein. HIBBELER, R. C. Resistencia dos materiais 7ª Ed. Pearson JUDICE, Flávia Moll de Souza e PERLINGEIRO,Mayra Soares Pereira Lima Resistência Dos Materiais IX - Universidade Federal Fluminense BEER, Ferdinand P. JOHNSTON, E. Russel Jr - Resistência dos Materiais -. Ed. PEARSON - 3ª edição VINICIOS, Marcos Notas de Aulas da disciplina Resistência dos Materiais- Universidade Candido Mendes BAÊTA, Fernando da Costa SARTOR, Valmir Resistência dos Materiais e Dimensionamento de Estruturas para Construções Rurais Universidade Federal de Viçosa 1999 GUSTAVO, Luiz - Apostila Resistencia dos Materiais - IFSP 20
AULA 03 - TENSÃO E DEFORMAÇÃO
 AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. A - DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito
AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. A - DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito
Capítulo 3: Propriedades mecânicas dos materiais
 Capítulo 3: Propriedades mecânicas dos materiais O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade
Capítulo 3: Propriedades mecânicas dos materiais O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade
Propriedades mecânicas dos materiais
 Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Objetivo do capítulo. O ensaio de tração e compressão
 Capítulo 3: Propriedades mecânicas dos materiais Adaptado pela prof. Dra. Danielle Bond Objetivo do capítulo Agora que já discutimos os conceitos básicos de tensão e deformação, mostraremos, neste capítulo,
Capítulo 3: Propriedades mecânicas dos materiais Adaptado pela prof. Dra. Danielle Bond Objetivo do capítulo Agora que já discutimos os conceitos básicos de tensão e deformação, mostraremos, neste capítulo,
Capítulo 4 Propriedades Mecânicas dos Materiais
 Capítulo 4 Propriedades Mecânicas dos Materiais Resistência dos Materiais I SLIDES 04 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Propriedades Mecânicas dos Materiais 2 3 Propriedades
Capítulo 4 Propriedades Mecânicas dos Materiais Resistência dos Materiais I SLIDES 04 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Propriedades Mecânicas dos Materiais 2 3 Propriedades
CENTRO UNIVERSITÁRIO PLANALDO DO DISTRITO FEDERAL
 7. Propriedades Mecânicas dos Materiais As propriedades mecânicas de um material devem ser conhecidas para que os engenheiros possam relacionar a deformação medida no material com a tensão associada a
7. Propriedades Mecânicas dos Materiais As propriedades mecânicas de um material devem ser conhecidas para que os engenheiros possam relacionar a deformação medida no material com a tensão associada a
Teste de tração - compressão
 PROPRIEDADES MECÂNICAS DOS MATERIAIS Prof. Renata Machado Soares - REMA I Teste de tração - compressão Resistência capacidade de suportar carga sem deformação excessiva ou ruptura; A partir de um ensaio
PROPRIEDADES MECÂNICAS DOS MATERIAIS Prof. Renata Machado Soares - REMA I Teste de tração - compressão Resistência capacidade de suportar carga sem deformação excessiva ou ruptura; A partir de um ensaio
Conteúdo. Resistência dos Materiais. Prof. Peterson Jaeger. 3. Concentração de tensões de tração. APOSTILA Versão 2013
 Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
RESISTÊNCIA DOS MATERIAIS CONTROLE DE QUALIDADE INDUSTRIAL Aula 03 TENSÃO
 CONTROLE DE QUALIDADE INDUSTRIAL Tensão Tensão é ao resultado da ação de cargas externas sobre uma unidade de área da seção analisada na peça, componente mecânico ou estrutural submetido à solicitações
CONTROLE DE QUALIDADE INDUSTRIAL Tensão Tensão é ao resultado da ação de cargas externas sobre uma unidade de área da seção analisada na peça, componente mecânico ou estrutural submetido à solicitações
Capítulo 3 Propriedades Mecânicas dos Materiais
 Capítulo 3 Propriedades Mecânicas dos Materiais 3.1 O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa
Capítulo 3 Propriedades Mecânicas dos Materiais 3.1 O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa
Estabilidade. Marcio Varela
 Estabilidade Marcio Varela Esforços internos O objetivo principal deste módulo é estudar os esforços ou efeitos internos de forças que agem sobre um corpo. Os corpos considerados não são supostos perfeitamente
Estabilidade Marcio Varela Esforços internos O objetivo principal deste módulo é estudar os esforços ou efeitos internos de forças que agem sobre um corpo. Os corpos considerados não são supostos perfeitamente
Professor: José Junio Lopes
 A - Deformação normal Professor: José Junio Lopes Lista de Exercício - Aula 3 TENSÃO E DEFORMAÇÃO 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada
A - Deformação normal Professor: José Junio Lopes Lista de Exercício - Aula 3 TENSÃO E DEFORMAÇÃO 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada
Ensaios Mecânicos dos Materiais
 Universidade de São Paulo Escola de Engenharia de São Carlos Departamento de Engenharia de Materiais Ensaios Mecânicos dos Materiais Engenharia e Ciência dos Materiais I Prof. Dr. Cassius O. F. T. Ruckert
Universidade de São Paulo Escola de Engenharia de São Carlos Departamento de Engenharia de Materiais Ensaios Mecânicos dos Materiais Engenharia e Ciência dos Materiais I Prof. Dr. Cassius O. F. T. Ruckert
Professor: José Junio Lopes
 Lista de Exercício Aula 3 TENSÃO E DEFORMAÇÃO A - DEFORMAÇÃO NORMAL 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga provocar um deslocamento
Lista de Exercício Aula 3 TENSÃO E DEFORMAÇÃO A - DEFORMAÇÃO NORMAL 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga provocar um deslocamento
Principais propriedades mecânicas
 Principais propriedades mecânicas Resistência à tração Elasticidade Ductilidade Fluência Fadiga Dureza Tenacidade,... Cada uma dessas propriedades está associada à habilidade do material de resistir às
Principais propriedades mecânicas Resistência à tração Elasticidade Ductilidade Fluência Fadiga Dureza Tenacidade,... Cada uma dessas propriedades está associada à habilidade do material de resistir às
MECÂNICA DOS SÓLIDOS PROPRIEDADES MECÂNICAS DOS MATERIAIS. Prof. Dr. Daniel Caetano
 MECÂNICA DOS SÓLIDOS PROPRIEDADES MECÂNICAS DOS MATERIAIS Prof. Dr. Daniel Caetano 2019-1 Objetivos Conhecer o comportamento dos materiais na tração e compressão Compreender o gráfico de tensão x deformação
MECÂNICA DOS SÓLIDOS PROPRIEDADES MECÂNICAS DOS MATERIAIS Prof. Dr. Daniel Caetano 2019-1 Objetivos Conhecer o comportamento dos materiais na tração e compressão Compreender o gráfico de tensão x deformação
Propriedades Geométricas de um seção Plana e Propriedades Mecânicas dos Materiais
 MKT-MDL-05 Versão 00 Propriedades Geométricas de um seção Plana e Propriedades Mecânicas dos Materiais Curso: Bacharelado em Engenharia Civil Turma: 5º Docente: Carla Soraia da Silva Pereira MKT-MDL-05
MKT-MDL-05 Versão 00 Propriedades Geométricas de um seção Plana e Propriedades Mecânicas dos Materiais Curso: Bacharelado em Engenharia Civil Turma: 5º Docente: Carla Soraia da Silva Pereira MKT-MDL-05
PROPRIEDADES MECÂNICAS II
 INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS PROPRIEDADES MECÂNICAS II Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Ensaio de tração Propriedades elásticas Propriedades
INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS PROPRIEDADES MECÂNICAS II Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Ensaio de tração Propriedades elásticas Propriedades
Aula 6 Propriedades dos materiais
 Aula 6 Propriedades Mecânicas dos Materiais E-mail: daniel.boari@ufabc.edu.br Universidade Federal do ABC Princípios de Reabilitação e Tecnologias Assistivas 3º Quadrimestre de 2018 Conceitos fundamentais
Aula 6 Propriedades Mecânicas dos Materiais E-mail: daniel.boari@ufabc.edu.br Universidade Federal do ABC Princípios de Reabilitação e Tecnologias Assistivas 3º Quadrimestre de 2018 Conceitos fundamentais
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
Prof. Willyan Machado Giufrida Curso de Engenharia Química. Ciências dos Materiais. Propriedades Mecânicas dos Materiais
 Ciências dos Materiais Propriedades Mecânicas dos Materiais IMPORTÂNCIA Aplicações onde são necessárias solicitações mecânicas. Atender as exigências de serviço previstas. POR QUÊ ESTUDAR? A determinação
Ciências dos Materiais Propriedades Mecânicas dos Materiais IMPORTÂNCIA Aplicações onde são necessárias solicitações mecânicas. Atender as exigências de serviço previstas. POR QUÊ ESTUDAR? A determinação
Propriedades Geométricas de um seção Plana e Propriedades Mecânicas dos Materiais
 MKT-MDL-05 Versão 00 Propriedades Geométricas de um seção Plana e Propriedades Mecânicas dos Materiais Curso: Bacharelado em Engenharia Civil Turma: 5º Docente: Carla Soraia da Silva Pereira MKT-MDL-05
MKT-MDL-05 Versão 00 Propriedades Geométricas de um seção Plana e Propriedades Mecânicas dos Materiais Curso: Bacharelado em Engenharia Civil Turma: 5º Docente: Carla Soraia da Silva Pereira MKT-MDL-05
COMPORTAMENTO MECÂNICO DOS MATERIAIS
 UNIVERSIDADE FEDERAL DO ABC Centro de Engenharia, Modelagem e Ciências Sociais Aplicadas (CECS) BC-1105: MATERIAIS E SUAS PROPRIEDADES COMPORTAMENTO MECÂNICO DOS MATERIAIS Propriedades Mecânicas dos Materiais
UNIVERSIDADE FEDERAL DO ABC Centro de Engenharia, Modelagem e Ciências Sociais Aplicadas (CECS) BC-1105: MATERIAIS E SUAS PROPRIEDADES COMPORTAMENTO MECÂNICO DOS MATERIAIS Propriedades Mecânicas dos Materiais
Relações entre tensões e deformações
 9 de agosto de 06 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
9 de agosto de 06 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
COMPORTAMENTO MECÂNICO DOS MATERIAIS PARTE I
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia Metalúrgica e de Materiais COMPORTAMENTO MECÂNICO DOS MATERIAIS PARTE I PMT 2100 - Introdução à Ciência dos Materiais para Engenharia
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia Metalúrgica e de Materiais COMPORTAMENTO MECÂNICO DOS MATERIAIS PARTE I PMT 2100 - Introdução à Ciência dos Materiais para Engenharia
Aula 11 - Propriedades Mecânicas dos Materiais / Coeficiente de Poisson.
 Aula 11 - Propriedades Mecânicas dos Materiais / Coeficiente de Poisson. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Propriedades Mecânicas dos Materiais As propriedades mecânicas de um
Aula 11 - Propriedades Mecânicas dos Materiais / Coeficiente de Poisson. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Propriedades Mecânicas dos Materiais As propriedades mecânicas de um
RESISTÊNCIA DOS MATERIAIS II - Notas de Aulas
 RESISTÊNCIA DOS MATERIAIS II - Notas de Aulas Prof. José Junio Lopes BIBLIOGRAFIA BÁSICA HIBBELER, Russell Charles. Resistência dos Materiais ed. São Paulo: Pearson Prentice Hall, 2009. 1 - CONCEITOS FUNDAMENTAIS
RESISTÊNCIA DOS MATERIAIS II - Notas de Aulas Prof. José Junio Lopes BIBLIOGRAFIA BÁSICA HIBBELER, Russell Charles. Resistência dos Materiais ed. São Paulo: Pearson Prentice Hall, 2009. 1 - CONCEITOS FUNDAMENTAIS
AULA 06 PROPRIEDADES MECÂNICAS DOS MATERIAIS
 AULA 06 PROPRIEDADES MECÂNICAS DOS MATERIAIS 1 As propriedades mecânicas de um material devem ser conhecidas para que os engenheiros possam relacionar a deformação medida no material com a tensão associada
AULA 06 PROPRIEDADES MECÂNICAS DOS MATERIAIS 1 As propriedades mecânicas de um material devem ser conhecidas para que os engenheiros possam relacionar a deformação medida no material com a tensão associada
Ensaios dos. Materiais. Ensaios Mecânicos. dos Materiais - Tração. Universidade de São Paulo. Escola de Engenharia de Lorena
 Universidade de São Paulo Escola de Engenharia de Lorena Departamento de Engenharia de Materiais Ensaios dos Ensaios Mecânicos Materiais dos Materiais - Tração Introdução à Ciência dos Materiais Prof.
Universidade de São Paulo Escola de Engenharia de Lorena Departamento de Engenharia de Materiais Ensaios dos Ensaios Mecânicos Materiais dos Materiais - Tração Introdução à Ciência dos Materiais Prof.
Deformação. - comportamento de um material quando carregado
 Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento
 Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento estrutural a partir do qual ele é feito Materiais são frequentemente
Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento estrutural a partir do qual ele é feito Materiais são frequentemente
Estruturas Metálicas PROPRIEDADES DOS AÇOS
 Estruturas Metálicas PROPRIEDADES DOS AÇOS 1. Diagrama Tensão- Deformação Uma propriedade mecânica importante para os materiais em geral é a chamada tensão ( ), definida por: F A o Onde F é a carga aplicada
Estruturas Metálicas PROPRIEDADES DOS AÇOS 1. Diagrama Tensão- Deformação Uma propriedade mecânica importante para os materiais em geral é a chamada tensão ( ), definida por: F A o Onde F é a carga aplicada
MÓDULO 2: Propriedades mecânicas dos metais. Deformação elástica, Deformação plástica
 MÓDULO 2: Propriedades mecânicas dos metais. Deformação elástica, Deformação plástica Propriedades mecânicas dos metais Muitos materiais, quando em serviço, são submetidos a forças ou cargas. O comportamento
MÓDULO 2: Propriedades mecânicas dos metais. Deformação elástica, Deformação plástica Propriedades mecânicas dos metais Muitos materiais, quando em serviço, são submetidos a forças ou cargas. O comportamento
Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio NECE. Experimento de ensino baseado em problemas. Módulo 01: Análise estrutural de vigas
 Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio NECE Experimento de ensino baseado em problemas Módulo 01: Análise estrutural de vigas Aula 02: Estruturas com barras sob corportamento axial
Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio NECE Experimento de ensino baseado em problemas Módulo 01: Análise estrutural de vigas Aula 02: Estruturas com barras sob corportamento axial
Deformação. Deformação. Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele.
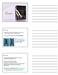 Capítulo 2: Adaptado pela prof. Dra. Danielle Bond Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele. Essas mudanças são denominadas deformações. Note as posições
Capítulo 2: Adaptado pela prof. Dra. Danielle Bond Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele. Essas mudanças são denominadas deformações. Note as posições
Carga axial. Princípio de Saint-Venant
 Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
AULA 4 Materiais de Construção II
 AULA 4 Materiais de Construção II Introdução Para a construção, as propriedades que interessam considerar aos metais são várias, concretamente, a aparência, densidade, dilatação e condutibilidade térmica,
AULA 4 Materiais de Construção II Introdução Para a construção, as propriedades que interessam considerar aos metais são várias, concretamente, a aparência, densidade, dilatação e condutibilidade térmica,
AULA 02 - TENSÃO NORMAL E DE CISALHAMENTO
 AULA 02 - TENSÃO NORMAL E DE CISALHAMENTO Observação: Este texto não deverá ser considerado como apostila, somente como notas de aula. 1 - INTRODUÇÃO O projeto da estrutura de qualquer edificação, máquina
AULA 02 - TENSÃO NORMAL E DE CISALHAMENTO Observação: Este texto não deverá ser considerado como apostila, somente como notas de aula. 1 - INTRODUÇÃO O projeto da estrutura de qualquer edificação, máquina
28/09/2017. Ewaldo Luiz de Mattos Mehl. Departamento de Engenharia Elétrica
 Ewaldo Luiz de Mattos Mehl Departamento de Engenharia Elétrica mehl@ufpr.br 1 Agenda: Arranjos atômicos Estrutura cristalina Tipos de estruturas Influência nas propriedades Defeitos na estrutura cristalina
Ewaldo Luiz de Mattos Mehl Departamento de Engenharia Elétrica mehl@ufpr.br 1 Agenda: Arranjos atômicos Estrutura cristalina Tipos de estruturas Influência nas propriedades Defeitos na estrutura cristalina
Tensões normais. Compressão. Tração. Volumar. Flexão. Tensão e deformação em sólidos MCFZ2. Prof. Osvaldo Canato Jr.
 Tensões normais Coeficiente de Poisson () Y e (alguns exemplos) Y, G e (Alguns exemplos) Relação entre u, e Tração Flexão Compressão Volumar Tensões tangenciais (ou transversais) Coeficiente de Poisson
Tensões normais Coeficiente de Poisson () Y e (alguns exemplos) Y, G e (Alguns exemplos) Relação entre u, e Tração Flexão Compressão Volumar Tensões tangenciais (ou transversais) Coeficiente de Poisson
AULA 4 Materiais de Construção II
 Faculdade de Engenharia - Licenciatura em Engenharia Civil UL 4 Materiais de Construção II Capítulo ula 4 (Teórica/Prática) II ços para Construção Introdução Ensaios sobre os aços: 1) Ensaio de Tracção;
Faculdade de Engenharia - Licenciatura em Engenharia Civil UL 4 Materiais de Construção II Capítulo ula 4 (Teórica/Prática) II ços para Construção Introdução Ensaios sobre os aços: 1) Ensaio de Tracção;
ENSAIO DE TRAÇÃO EM-641
 ENSAIO DE TRAÇÃO DEFINIÇÃO: Aplicação de uma carga uniaxial de tração em um CP geralmente cilíndrico e maciço; Mede-se a variação comprimento como função da aplicação da carga ; Fornece dados quantitativos
ENSAIO DE TRAÇÃO DEFINIÇÃO: Aplicação de uma carga uniaxial de tração em um CP geralmente cilíndrico e maciço; Mede-se a variação comprimento como função da aplicação da carga ; Fornece dados quantitativos
UNIVERSIDADE FEDERAL DE SANTA MARIA Curso de Graduação em Engenharia Civil ECC 1006 Concreto Armado A ESTRUTURAS. Gerson Moacyr Sisniegas Alva
 UNIVERSIDADE FEDERAL DE SANTA MARIA Curso de Graduação em Engenharia Civil ECC 1006 Concreto Armado A COMPORTAMENTO DOS MATERIAIS E DAS ESTRUTURAS Gerson Moacyr Sisniegas Alva A prática sem teoria é cega
UNIVERSIDADE FEDERAL DE SANTA MARIA Curso de Graduação em Engenharia Civil ECC 1006 Concreto Armado A COMPORTAMENTO DOS MATERIAIS E DAS ESTRUTURAS Gerson Moacyr Sisniegas Alva A prática sem teoria é cega
Tensão convencional: P A. σ = Deformação convencional: = l
 Ensaio de Tração Tensão convencional: σ = P A 0 Deformação convencional: ε = l l l 0 0 2 A Amostra Área de medida A Stainless Steel sample is loaded in the tester. This device, called an EXTENSOMETER,
Ensaio de Tração Tensão convencional: σ = P A 0 Deformação convencional: ε = l l l 0 0 2 A Amostra Área de medida A Stainless Steel sample is loaded in the tester. This device, called an EXTENSOMETER,
Resistência dos Materiais Teoria 2ª Parte
 Condições de Equilíbrio Estático Interno Equilíbrio Estático Interno Analogamente ao estudado anteriormente para o Equilíbrio Estático Externo, o Interno tem um objetivo geral e comum de cada peça estrutural:
Condições de Equilíbrio Estático Interno Equilíbrio Estático Interno Analogamente ao estudado anteriormente para o Equilíbrio Estático Externo, o Interno tem um objetivo geral e comum de cada peça estrutural:
2 Fundamentos para a avaliação de integridade de dutos com perdas de espessura e reparados com materiais compósitos
 2 Fundamentos para a avaliação de integridade de dutos com perdas de espessura e reparados com materiais compósitos Este capítulo apresenta um resumo dos fundamentos básicos de avaliação de dutos com e
2 Fundamentos para a avaliação de integridade de dutos com perdas de espessura e reparados com materiais compósitos Este capítulo apresenta um resumo dos fundamentos básicos de avaliação de dutos com e
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I
 LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Ex. 1.40. O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,840
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Ex. 1.40. O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,840
Tema III. TRAÇÃO E COMPRESSÃO 3.1. Introdução. Esforços solicitantes são esforços (efeitos) internos:
 Tema III. TRAÇÃO E COMRESSÃO 3.1. Introdução Esforços solicitantes são esforços (efeitos) internos: Força normal ou axial (N), É definida como força axial ou normal a carga que atua na direção do eixo
Tema III. TRAÇÃO E COMRESSÃO 3.1. Introdução Esforços solicitantes são esforços (efeitos) internos: Força normal ou axial (N), É definida como força axial ou normal a carga que atua na direção do eixo
Sistemas Estruturais. Prof. Rodrigo mero
 Sistemas Estruturais Prof. Rodrigo mero Aula 2 Cargas que Atuam nas estruturas Índice Forças Vetoriais Geometria das Forças Cargas Quanto a Frequência Levantamento de Cargas Simples Equilíbrio Interno
Sistemas Estruturais Prof. Rodrigo mero Aula 2 Cargas que Atuam nas estruturas Índice Forças Vetoriais Geometria das Forças Cargas Quanto a Frequência Levantamento de Cargas Simples Equilíbrio Interno
a) Os três materiais têm módulos de elasticidade idênticos. ( ) Introdução à Ciência dos Materiais para Engenharia PMT 3110
 Lista de Exercícios 06 / 2018 Comportamento mecânico dos materiais - Parte I 1. Um pedaço de arame recozido de aço baixo carbono tem 2 mm de diâmetro, limite de escoamento 210 MPa e módulo de elasticidade
Lista de Exercícios 06 / 2018 Comportamento mecânico dos materiais - Parte I 1. Um pedaço de arame recozido de aço baixo carbono tem 2 mm de diâmetro, limite de escoamento 210 MPa e módulo de elasticidade
13 PROPRIEDADES MECÂNICAS DOS MATERIAIS
 NG01140 Turma C (Prof. Aleandre Pacheco) 39 13 PROPRIDADS MCÂNICAS DOS MATRIAIS Os ensaios de tração e compressão stes ensaios são provavelmente uns dos mais comuns a serem usados em engenharia. les são
NG01140 Turma C (Prof. Aleandre Pacheco) 39 13 PROPRIDADS MCÂNICAS DOS MATRIAIS Os ensaios de tração e compressão stes ensaios são provavelmente uns dos mais comuns a serem usados em engenharia. les são
Universidade Estadual de Campinas Faculdade de Engenharia Civil Departamento de Estruturas. Aços para concreto armado
 Universidade Estadual de Campinas Faculdade de Engenharia Civil Departamento de Estruturas Aços para concreto armado Notas de aula da disciplina AU414 - Estruturas IV Concreto armado Prof. Msc. Luiz Carlos
Universidade Estadual de Campinas Faculdade de Engenharia Civil Departamento de Estruturas Aços para concreto armado Notas de aula da disciplina AU414 - Estruturas IV Concreto armado Prof. Msc. Luiz Carlos
PROPRIEDADES MECÂNICAS III Propriedades de tração
 INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS PROPRIEDADES MECÂNICAS III Propriedades de tração Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Regime plástico Propriedades
INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS PROPRIEDADES MECÂNICAS III Propriedades de tração Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Regime plástico Propriedades
RESISTÊNCIA DOS MATERIAIS
 CAPÍTUO RESISTÊNCIA DOS MATERIAIS Terceira Edição Ferdinand P. Beer E. Russell Johnston Jr. Tensão e Deformação Carregamento Aial Capítulo 2 Tensão e Deformacão: Carregamento Aial 2.1 - Introdução 2.2
CAPÍTUO RESISTÊNCIA DOS MATERIAIS Terceira Edição Ferdinand P. Beer E. Russell Johnston Jr. Tensão e Deformação Carregamento Aial Capítulo 2 Tensão e Deformacão: Carregamento Aial 2.1 - Introdução 2.2
Universidade de Lisboa
 Universidade de Lisboa Instituto Superior Técnico Ciência de Materiais 1º Teste (14. Abril.2014) Cotações Pergunta Cotação 1. (a) 0,50 1. (b) 0,50 1. (c) 0,50 1. (d) 0,50 2. (a) 0,50 2. (b) 0,50 2. (c)
Universidade de Lisboa Instituto Superior Técnico Ciência de Materiais 1º Teste (14. Abril.2014) Cotações Pergunta Cotação 1. (a) 0,50 1. (b) 0,50 1. (c) 0,50 1. (d) 0,50 2. (a) 0,50 2. (b) 0,50 2. (c)
 1) Qual propriedade de um material reproduz a lei de Hooke? Escrever a expressão que traduz a lei. 2) Um cilindro de 90,0 cm de comprimento (figura) está submetido a uma força de tração de 120 kn. Uma
1) Qual propriedade de um material reproduz a lei de Hooke? Escrever a expressão que traduz a lei. 2) Um cilindro de 90,0 cm de comprimento (figura) está submetido a uma força de tração de 120 kn. Uma
Diagrama Tensão Deformação 0,0000 0,0005 0,0010 0,0015 0,0020 0,0025
 . Os dados de um teste tensão-deformação de uma cerâmica são fornecidos na tabela. A curva é linear entre a origem e o primeiro ponto. Construir o diagrama e determinar o módulo de elasticidade e o módulo
. Os dados de um teste tensão-deformação de uma cerâmica são fornecidos na tabela. A curva é linear entre a origem e o primeiro ponto. Construir o diagrama e determinar o módulo de elasticidade e o módulo
Deformação e Mecanismos de Endurecimento Metais DEMEC TM242-B Prof Adriano Scheid
 Deformação e Mecanismos de Endurecimento Metais DEMEC TM242-B Prof Adriano Scheid Tensão Propriedades Mecânicas: Tensão e Deformação Deformação Elástica Comportamento tensão-deformação O grau com o qual
Deformação e Mecanismos de Endurecimento Metais DEMEC TM242-B Prof Adriano Scheid Tensão Propriedades Mecânicas: Tensão e Deformação Deformação Elástica Comportamento tensão-deformação O grau com o qual
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Tensões. Professores: Nádia Forti Marco Carnio
 Tensões Professores: Nádia Forti Marco Carnio SOLICITAÇÃO AXIAL Se uma força tende a alongar o elemento, é chamada de força de tração. Se uma força tende a encurtar o elemento, é chamada de força de compressão.
Tensões Professores: Nádia Forti Marco Carnio SOLICITAÇÃO AXIAL Se uma força tende a alongar o elemento, é chamada de força de tração. Se uma força tende a encurtar o elemento, é chamada de força de compressão.
GMEC7301-Materiais de Construção Mecânica Introdução. Módulo II Ensaios Mecânicos
 GMEC7301-Materiais de Construção Mecânica Introdução Módulo II Ensaios Mecânicos OBJETIVOS DOS ENSAIOS MECÂNICOS Os ensaios são realizados com o objetivo de se obter informações específicas em relação
GMEC7301-Materiais de Construção Mecânica Introdução Módulo II Ensaios Mecânicos OBJETIVOS DOS ENSAIOS MECÂNICOS Os ensaios são realizados com o objetivo de se obter informações específicas em relação
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Aula 06 - Estudo de Deformações, Normal e por Cisalhamento.
 Aula 06 - Estudo de Deformações, Normal e por Cisalhamento. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Deformação Quando uma força é aplicada a um corpo, tende a mudar a forma e o tamanho
Aula 06 - Estudo de Deformações, Normal e por Cisalhamento. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Deformação Quando uma força é aplicada a um corpo, tende a mudar a forma e o tamanho
Resistência dos Materiais
 CONCURSO PETROBRAS TÉCNICO(A) DE MANUTENÇÃO JÚNIOR - MECÂNICA Resistência dos Materiais Questões Resolvidas QUESTÕES RETIRADAS DE PROVAS DA BANCA CESGRANRIO DRAFT Produzido por Exatas Concursos www.exatas.com.br
CONCURSO PETROBRAS TÉCNICO(A) DE MANUTENÇÃO JÚNIOR - MECÂNICA Resistência dos Materiais Questões Resolvidas QUESTÕES RETIRADAS DE PROVAS DA BANCA CESGRANRIO DRAFT Produzido por Exatas Concursos www.exatas.com.br
Ciência e Engenharia dos Materiais. Propriedades Mecânicas. Prof. C. Brunetti
 Ciência e Engenharia dos Materiais Propriedades Mecânicas Prof. C. Brunetti Porque estudar? A determinação e/ou conhecimento das propriedades mecânicas é muito importante para a escolha do material para
Ciência e Engenharia dos Materiais Propriedades Mecânicas Prof. C. Brunetti Porque estudar? A determinação e/ou conhecimento das propriedades mecânicas é muito importante para a escolha do material para
LISTA DE EXERCÍCIOS ÁREA 1. Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02
 LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
RESISTÊNCIA DOS MATERIAIS
 RESISTÊNCIA DOS MATERIAIS Eng. Wanderson S. Paris, MSc MÓDULO 18 TENSÃO TÉRMICA E CONCENTRAÇÃO DE TENSÕES. Tensão Térmica ü Mudança na temperatura pode provocar alterações nas dimensões de um material.
RESISTÊNCIA DOS MATERIAIS Eng. Wanderson S. Paris, MSc MÓDULO 18 TENSÃO TÉRMICA E CONCENTRAÇÃO DE TENSÕES. Tensão Térmica ü Mudança na temperatura pode provocar alterações nas dimensões de um material.
Comportamento Elastoplástico
 Departamento de Engenharia Mecânica Comportamento Elastoplástico Prof. Arthur Braga Projeto Mecânico Estratégia Identificar possíveis modos de falha (escoamento, ruptura, fadiga, fratura, etc.) Definir
Departamento de Engenharia Mecânica Comportamento Elastoplástico Prof. Arthur Braga Projeto Mecânico Estratégia Identificar possíveis modos de falha (escoamento, ruptura, fadiga, fratura, etc.) Definir
Ensaio de compressão
 A UU L AL A Ensaio de compressão Podemos observar o esforço de compressão na construção mecânica, principalmente em estruturas e em equipamentos como suportes, bases de máquinas, barramentos etc. Às vezes,
A UU L AL A Ensaio de compressão Podemos observar o esforço de compressão na construção mecânica, principalmente em estruturas e em equipamentos como suportes, bases de máquinas, barramentos etc. Às vezes,
UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO ENGENHARIA DE REABILITAÇÃO E ACESSIBILIDADES PROCESSOS DE FABRICO
 UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO ENGENHARIA DE REABILITAÇÃO E ACESSIBILIDADES PROCESSOS DE FABRICO DETERMINAÇÃO DAS CARACTERÍSTICAS MECÂNICAS MATERIAIS DE 1. INTRODUÇÃO CONSTRUÇÃO Neste trabalho
UNIVERSIDADE DE TRÁS-OS-MONTES E ALTO DOURO ENGENHARIA DE REABILITAÇÃO E ACESSIBILIDADES PROCESSOS DE FABRICO DETERMINAÇÃO DAS CARACTERÍSTICAS MECÂNICAS MATERIAIS DE 1. INTRODUÇÃO CONSTRUÇÃO Neste trabalho
Introdução a Ciência dos Materiais Relação Microestrutura e Propriedade Deformação Elástica e Plástica
 Introdução a Ciência dos Materiais Relação Microestrutura e Propriedade Deformação Elástica e Plástica Professora: Maria Ismenia Sodero maria.ismenia@usp.br Tópicos abordados 1. Mecanismos atômicos deformação
Introdução a Ciência dos Materiais Relação Microestrutura e Propriedade Deformação Elástica e Plástica Professora: Maria Ismenia Sodero maria.ismenia@usp.br Tópicos abordados 1. Mecanismos atômicos deformação
Ciência de Materiais. LEGI. Ano lectivo PROPRIEDADES MECÂNICAS parte I
 1. Um provete cilíndrico com 1 10-2 m de diâmetro e 10-1 m de comprimento (dimensões iniciais) foi traccionado até à fractura. Ao atingir-se a tensão nominal de 150MPa, o comprimento do provete era 10,5
1. Um provete cilíndrico com 1 10-2 m de diâmetro e 10-1 m de comprimento (dimensões iniciais) foi traccionado até à fractura. Ao atingir-se a tensão nominal de 150MPa, o comprimento do provete era 10,5
Propriedades Mecânicas: O Ensaio de Tração Uniaxial
 Propriedades Mecânicas: O Ensaio de Tração Uniaxial Tensão e deformação Ensaios: Tração Compressão Cisalhamento Torção Tensão e deformação Cálculo da tensão (Para tração e compressão): Onde: σ= Tensão
Propriedades Mecânicas: O Ensaio de Tração Uniaxial Tensão e deformação Ensaios: Tração Compressão Cisalhamento Torção Tensão e deformação Cálculo da tensão (Para tração e compressão): Onde: σ= Tensão
3ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO DIAGRAMA DE ESFORÇO NORMAL
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Professor: Armando Sá Ribeiro Jr. Disciplina: ENG285 - Resistência dos Materiais I-A www.resmat.ufba.br 3ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Professor: Armando Sá Ribeiro Jr. Disciplina: ENG285 - Resistência dos Materiais I-A www.resmat.ufba.br 3ª LISTA
Física dos Materiais FMT0502 ( )
 Física dos Materiais FMT0502 (4300502) 1º Semestre de 2010 Instituto de Física Universidade de São Paulo Professor: Antonio Dominguesdos Santos E-mail: adsantos@if.usp.br Fone: 3091.6886 http://plato.if.usp.br/~fmt0502n/
Física dos Materiais FMT0502 (4300502) 1º Semestre de 2010 Instituto de Física Universidade de São Paulo Professor: Antonio Dominguesdos Santos E-mail: adsantos@if.usp.br Fone: 3091.6886 http://plato.if.usp.br/~fmt0502n/
Caderno de Prova. Resistência dos Materiais. Universidade Federal Fronteira Sul. Edital n o 006/UFFS/ de maio. das 14 às 17 h.
 Universidade Federal Fronteira Sul Edital n o 006/UFFS/2010 Caderno de Prova 23 de maio das 14 às 17 h 3 h* E6P14 Resistência dos Materiais Confira o número que você obteve no ato da inscrição com o que
Universidade Federal Fronteira Sul Edital n o 006/UFFS/2010 Caderno de Prova 23 de maio das 14 às 17 h 3 h* E6P14 Resistência dos Materiais Confira o número que você obteve no ato da inscrição com o que
CORRECÇÃO do 1º Teste de Ciência de Materiais COTAÇÕES. Cotaçãoo
 CORRECÇÃO do 1º Teste de Ciência de Materiais COTAÇÕES Pergunta Cotaçãoo 1. (a) 0,50 1. (b) 0,50 2. (a) 0,50 2. (b) 0,50 2. (c) 0,50 2. (d) 0,50 3. (a) 0,50 3. (b) 0,50 3. (c) 0,50 3. (d) 0,50 3. (e) 0,50
CORRECÇÃO do 1º Teste de Ciência de Materiais COTAÇÕES Pergunta Cotaçãoo 1. (a) 0,50 1. (b) 0,50 2. (a) 0,50 2. (b) 0,50 2. (c) 0,50 2. (d) 0,50 3. (a) 0,50 3. (b) 0,50 3. (c) 0,50 3. (d) 0,50 3. (e) 0,50
MATERIAIS DE CONSTRUÇÃO CIVIL. Propriedades dos MCC s
 Curso Superior de Tecnologia em Construção de Edifícios MATERIAIS DE CONSTRUÇÃO CIVIL Propriedades dos MCC s Prof. Leandro Candido de Lemos Pinheiro leandro.pinheiro@riogrande.ifrs.edu.br PROPRIEDADES
Curso Superior de Tecnologia em Construção de Edifícios MATERIAIS DE CONSTRUÇÃO CIVIL Propriedades dos MCC s Prof. Leandro Candido de Lemos Pinheiro leandro.pinheiro@riogrande.ifrs.edu.br PROPRIEDADES
RESISTÊNCIA DOS MATERIAIS AULAS 02
 Engenharia da Computação 1 4º / 5 Semestre RESISTÊNCIA DOS MATERIAIS AULAS 02 Prof Daniel Hasse Tração e Compressão Vínculos e Carregamentos Distribuídos SÃO JOSÉ DOS CAMPOS, SP Aula 04 Vínculos Estruturais
Engenharia da Computação 1 4º / 5 Semestre RESISTÊNCIA DOS MATERIAIS AULAS 02 Prof Daniel Hasse Tração e Compressão Vínculos e Carregamentos Distribuídos SÃO JOSÉ DOS CAMPOS, SP Aula 04 Vínculos Estruturais
Exercícios de Resistência dos Materiais A - Área 3
 1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
Resistência dos Materiais
 Aula 4 Deformações e Propriedades Mecânicas dos Materiais Tópicos Abordados Nesta Aula Estudo de Deformações, Normal e por Cisalhamento. Propriedades Mecânicas dos Materiais. Coeficiente de Poisson. Deformação
Aula 4 Deformações e Propriedades Mecânicas dos Materiais Tópicos Abordados Nesta Aula Estudo de Deformações, Normal e por Cisalhamento. Propriedades Mecânicas dos Materiais. Coeficiente de Poisson. Deformação
MECÂNICA DOS SÓLIDOS DEFORMAÇÕES
 MECÂNICA DOS SÓLIDOS DEFORMAÇÕES Prof. Dr. Daniel Caetano 2019-1 Objetivos Conhecer os tipos de deformação e deslocamentos Saber estimar valor da deformação nas formas normal/axial e por cisalhamento Calcular
MECÂNICA DOS SÓLIDOS DEFORMAÇÕES Prof. Dr. Daniel Caetano 2019-1 Objetivos Conhecer os tipos de deformação e deslocamentos Saber estimar valor da deformação nas formas normal/axial e por cisalhamento Calcular
LISTA DE EXERCÍCIOS RESISTÊNCIA DOS MATERIAIS 2
 LISTA DE EXERCÍCIOS RESISTÊNCIA DOS MATERIAIS 2 I) TRANSFORMAÇÃO DE TENSÕES 1) Uma única força horizontal P de intensidade de 670N é aplicada à extremidade D da alavanca ABD. Sabendo que a parte AB da
LISTA DE EXERCÍCIOS RESISTÊNCIA DOS MATERIAIS 2 I) TRANSFORMAÇÃO DE TENSÕES 1) Uma única força horizontal P de intensidade de 670N é aplicada à extremidade D da alavanca ABD. Sabendo que a parte AB da
UNIDADE 9 Propriedades Mecânicas I
 UNIDADE 9 Propriedades Mecânicas I 1. Fios de aço carbono com área de seção transversal nominal de 62,9 mm 2 são utilizados para a fabricação de peças pré-moldadas de concreto protendido. Nessas peças,
UNIDADE 9 Propriedades Mecânicas I 1. Fios de aço carbono com área de seção transversal nominal de 62,9 mm 2 são utilizados para a fabricação de peças pré-moldadas de concreto protendido. Nessas peças,
Aço Exercício 2.1. Resolução : A = π D2 4 σ = E.ε. = π(2,54cm)2 4. = 5,067 cm 2. δ L o. ε = δ = NL o AE = 35 kn.350 cm
 Aço Exercício.1 Uma barra de seção circular com diâmetro de 5, mm (1 ) está sujeita a uma tração axial de 35N. Calcular o alongamento da barra supondo seu comprimento inicial o = 3,50 m e que a mesma foi
Aço Exercício.1 Uma barra de seção circular com diâmetro de 5, mm (1 ) está sujeita a uma tração axial de 35N. Calcular o alongamento da barra supondo seu comprimento inicial o = 3,50 m e que a mesma foi
Teoria das Estruturas I - Aula 08
 Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
PROPRIEDADES FÍSICAS, QUÍMICAS E MECÂNICAS DOS MATERIAIS
 CURSO TÉCNICO EM MECÂNICA MATERIAIS PARA CONSTRUÇÃO MECÂNICA PROPRIEDADES FÍSICAS, QUÍMICAS E MECÂNICAS DOS MATERIAIS PROF. M. SC. MARCONI FURTADO 2013 Importância. Propriedades físicas dos materiais Comportamento
CURSO TÉCNICO EM MECÂNICA MATERIAIS PARA CONSTRUÇÃO MECÂNICA PROPRIEDADES FÍSICAS, QUÍMICAS E MECÂNICAS DOS MATERIAIS PROF. M. SC. MARCONI FURTADO 2013 Importância. Propriedades físicas dos materiais Comportamento
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO
 Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
Equações Diferenciais aplicadas à Flexão da Vigas
 Equações Diferenciais aplicadas à Flexão da Vigas Page 1 of 17 Instrutor HEngholmJr Version 1.0 September 21, 2014 Page 2 of 17 Indice 1. CONCEITOS PRELIMINARES DA MECANICA.... 4 1.1. FORÇA NORMAL (N)...
Equações Diferenciais aplicadas à Flexão da Vigas Page 1 of 17 Instrutor HEngholmJr Version 1.0 September 21, 2014 Page 2 of 17 Indice 1. CONCEITOS PRELIMINARES DA MECANICA.... 4 1.1. FORÇA NORMAL (N)...
Carga axial. Princípio de Saint-Venant. Princípio de Saint-Venant
 Capítulo 4: Carga axial Adaptado pela prof. Dra. Danielle Bond Princípio de Saint-Venant Anteriormente desenvolvemos os conceitos de: Tensão (um meio para medir a distribuição de força no interior de um
Capítulo 4: Carga axial Adaptado pela prof. Dra. Danielle Bond Princípio de Saint-Venant Anteriormente desenvolvemos os conceitos de: Tensão (um meio para medir a distribuição de força no interior de um
Ensaios e propriedades Mecânicas em Materiais
 FACULDADE SUDOESTE PAULISTA Ciência e Tecnologia de Materiais Prof. Ms. Patrícia Corrêa Ensaios e propriedades Mecânicas em Materiais Ensaios Mecânicos Os ensaios mecânicos consistem num conjunto de procedimentos
FACULDADE SUDOESTE PAULISTA Ciência e Tecnologia de Materiais Prof. Ms. Patrícia Corrêa Ensaios e propriedades Mecânicas em Materiais Ensaios Mecânicos Os ensaios mecânicos consistem num conjunto de procedimentos
7 RESULTADOS EXPERIMENTAIS
 7 RESULTADOS EXPERIMENTAIS No presente capítulo, é apresentada a aplicação efetiva da metodologia desenvolvida para medição de campos de deformações. Imagens coletadas durante ensaios de tração são analisadas,
7 RESULTADOS EXPERIMENTAIS No presente capítulo, é apresentada a aplicação efetiva da metodologia desenvolvida para medição de campos de deformações. Imagens coletadas durante ensaios de tração são analisadas,
Resistência dos Materiais
 Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
Resistência dos Materiais Prof. Antonio Dias Antonio Dias / Resistência dos Materiais 1 Flexão Diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares
MATERIAIS PARA ENGENHARIA DE PETRÓLEO - EPET069 - Propriedades Mecânicas dos Materiais
 MATERIAIS PARA ENGENHARIA DE PETRÓLEO - EPET069 - Propriedades Mecânicas dos Materiais Materiais Metálicos Um material cristalino pode deformar-se plasticamente por quatro mecanismos: deslizamento de planos
MATERIAIS PARA ENGENHARIA DE PETRÓLEO - EPET069 - Propriedades Mecânicas dos Materiais Materiais Metálicos Um material cristalino pode deformar-se plasticamente por quatro mecanismos: deslizamento de planos
Capítulo 2 Deformação
 Capítulo 2 Deformação 2.1 O conceito de deformação Sob a ação de cargas externas, um corpo sofre mudanças de forma e de volume que são chamadas de deformação. Note as posições antes e depois de três segmentos
Capítulo 2 Deformação 2.1 O conceito de deformação Sob a ação de cargas externas, um corpo sofre mudanças de forma e de volume que são chamadas de deformação. Note as posições antes e depois de três segmentos
PROPRIEDADES MECÂNICAS DE
 DE MATERIAIS METÁLICOS CONCEITO DE TENSÃO E DEFORMAÇÃO Formas de aplicação de carga: 2 1 COMPORTAMENTO ELÁSTICO E PLÁSTICO 3 COMPORTAMENTO ELÁSTICO E PLÁSTICO 4 2 COMPORTAMENTO ELÁSTICO 5 COMPORTAMENTO
DE MATERIAIS METÁLICOS CONCEITO DE TENSÃO E DEFORMAÇÃO Formas de aplicação de carga: 2 1 COMPORTAMENTO ELÁSTICO E PLÁSTICO 3 COMPORTAMENTO ELÁSTICO E PLÁSTICO 4 2 COMPORTAMENTO ELÁSTICO 5 COMPORTAMENTO
