u seja, pode ser escrito como uma combinação linear de.
|
|
|
- Eugénio da Conceição Oliveira
- 7 Há anos
- Visualizações:
Transcrição
1 Toma d Cayly-Hamilo ja x sja d I α... α poliômio caacísico d. Eão: α α... α α I Toda maiz é um zo d su poliômio caacísico., mos qu qu:... I { I,,..., } u sja, pod s scio como uma combiação lia d.
2 Também, muliplicado ambos mmbos d pô, mos qu:... Ou sja, pod s scio como uma combiação lia d {,,..., } qu pô sua vz pod s scio como uma combiação lia d { I,,..., }. ssim, podmos coclui qu paa qualqu poliômio f, idpd do gau, f podá smp s xpssado como: f I... 3
3 Dividido 3 pô obmos: od q é o quoci é o so. Mas sa divisão é complicada s o gau d f é muio maio do qu o gau d. Eao, pod-s ob diam d: fq. Sja: S odos avs. d são disios os is podm s obidos solvdo-s as quaçõs: i,... q q f 4... h 5 i i i i i q f
4 S m avs. pidos ão 5 pod s divada sucssivam d modo a s ob o o. d quaçõs cssáias à obção dos is. Ex : Calcul paa. f Ou sja, paa calcula f. O p.c. d é: os avs. são {,-}. Sja f f f 99 99
5 ssim, I 99I 99 S uma fução f admii o dsvolvimo m séi d MacLaui f qu covg paa <R ão a séi d maizs f ambém covg, dsd qu sja quadada qu cada um dos sus auovalos ha valo absoluo ifio a R. Diz-s qu a fução é bm dfiida. Cada fução bm dfiida pod ambém s psada como m 3.
6 Ex : Paa a maiz do x dmia Eão, fução mais impoa d é. Po séi mos qu: lgumas igualdads: f ; ; ; f f f I I...! I [ ] I d d maiz ula
7 Fomas quadáicas Uma foma quadáica Q é um poliômio al m qu as vaiávis ais x, x,...,x scalas coém som mos da foma αijxixj, ais qu: Q i j α x lgus xmplos d fomas quadáicas: Q 3x ij i x j, α x x x 5 Q α x α x x ij α é al i, x x x 3 j
8 Toda foma quadáica Q pod s xpssada como o poduo io <x,qx> x Qx vic vsa, od Q é uma maiz siméica, iso é, Q Q. Ex : f x, x x x x 5x 6 6 x 5 x [ ] x x Os avs. d uma maiz siméica são ais os auovos associados a avs. disios são oogoais. Msmo com avs. ão disios um cojuo d auovos ooomais pod s coado
9 Poao a psação a foma d Joda d uma maiz siméica é uma maiz diagoal. Dfiição 7 maiz Q é dfiida posiiva s sua foma quadáica associada Q é smp posiiva xco quado x é o vo ulo. Q é dfiida posiiva s é só s odos sus auovalos são maios do qu zo. Dfiição8 maiz Q é smidfiida posiiva s Q ão é gaiva mas poddo s zo paa algum x. Q é smidfiida posiiva s odos sus avs. São maios ou iguais a zo.
10 Uma oua maia d chca s uma maiz é dfiida posiiva é o ciéio d Sylvs: uma maiz Q é dfiida posiiva s só s o odos sus mos picipais são posiivos. Um mo picipal d Q é o dmia da submaiz d Q obida pla limiação das úlimas k lihas k coluas, k,,...,-. Ex 3: Dmi s a foma quadáica do x. é dfiida posiiva. Usado Sylvs: 6 Q ; > q q q q - Como m um mo picipal < ão é dfiida posiiva. - Usado os avs: Os auovalos d Q são: , como m um gaivo Q ão é dfiida posiiva.
11 dcomposição d Cholsky Qualqu maiz dfiida posiiva pod s aoada m LL* od L é uma maiz iagula fio com valos posiivos a diagoal. Exis ambém um algoimo paa ga a maiz L. Toma. Uma maiz H, com m, m ak s só s a maiz x H H m ak ou d H' H. Uma maiz H, com m,m ak m s só s a maiz mxm HH m ak m ou d HH' H H HH são siméicas smidfiidas posiivas poao sus avs. São ais ão gaivos.
12 Dcomposição m valos sigulas - SVD Sja H mx. Eão a maiz H H é x siméica, smidfiida posiiva cosqüm odos sus avs. são ão gaivos. { σ } i, O cojuo i od i é um av d é chamado valos sigulas d H. i... Toma Toda maiz H mx pod s asfomada a foma: od S é m R R H RSQ RR I m, Q Q QQ I com os valos sigulas a diagoal. m,
13 -s coluas d Q são auovos ooomalizados d H H. - s coluas d R são auovos ooomalizados d HH. - O ak d H é igual ao úmo d σis ão ulos. - S o ak d H é, as pimias coluas d R são uma bas ooomal paa o ag d H. - s úlimas - coluas d Q são uma bas ooomal paa o spaço ulo d H. - SVD é usado o malab paa compua o ak, o ag o spaço ulo.
14 Ex 4: Cosid a maiz do Ex. 5. O comado svd do MTLB oa o sulado abaixo. O ak é dois dois valos sigulas ão ulos. a s 3 4 >> [ s q]svda q
15 Excícios paa casa 8 Mos qu o cofici α o oma d Cayly Hamilo α... α α I é zo s som s é sigula. 9 Rfaz os xmplos 3.7, do Ch. Mos qu: a [ ] B B b B B - Mos qu: L si od L é a ivsa da asfomada d Laplac. Faz um sudo diigido im 3.7 do Ch. Vifica o MTLB o comado mlyapa,b,c T cia um xmplo com 3x3, B x C 3x. 3 Rfaz Exs do Ch.
16 4 Pov qu uma maiz M siméica x é dfiida posiiva s som s: a Todos sus avs. são posiivos. b S xis uma maiz N x ão sigula al qu MN N. 5 Vifiqu s a foma quadáica Q x 5 x x x x3 xx 4xx3 6 é dfiida posiiva. 3
17 6 Usado fução d maizs dmi a aiz quadada da maiz : 7 Sja. Dmi a ivsa d usado o oma d Cayly-Hamilo. 6 4 paa b paa a
( ). ( ) ( 2.2 Valor Esperado e Momentos. Função Geratriz de Momentos Seja X uma variável aleatória, então, se o valor esperado de existe
. Valo Espao omnos Função Gaiz omnos Sja uma vaiávl alaóia, não, s o valo spao xis paa oo valo m algum invalo ( h,h, h > 0, l é inio como a Função Gaiz omnos, noaa Fomalmn, x E. ( x x R (. caso isco x
Gabarito Zero de Função
Gabaito Zo d Fução Ecício : Um mlo é -, R A aiz ão od s dtmiada lo Método da Bissção oqu R. Tmos também qu muda d sial quado s aoima d. Ecício : Sja a aiz d. O método d Nwto-Raso od ão covgi s gad. [ U
4. Radiação electromagnética e a sua interacção com matéria.
4. Radiação lomagéia a sua iação om maéia. Equaçõs d Maxwll odas lomagéias Sisma d quaçõs d Maxwll: divd 4 divb o d dsloamo oe B o 4 D uo om as laçõs maiais: D E B dmiam ompoamo spaço-mpoal das ompos léia
TEOREMA DE TAYLOR 2! 1 1. (n) n (n 1) 0 + f x0 x x0 + f (c) x
(Tóp. Tto Complmta) TEOREMA DE TAYLOR TEOREMA DE TAYLOR S uma ução suas pimias divadas istm um itvalo abto I cotdo, sgu-s do toma do valo médio galizado (dado o tópico dsta aula), substituido a ou b po,
Exercícios resolvidos
Excícios solvidos 1 Um paallpípdo ABCDEFGH d bas ABCD m volum igual a 9 unidads Sabndo-s qu A (1,1,1), B(2,1,2), C(1,2,2), o véic E pnc à a d quação : x = y = 2 z (AE, i) é agudo Dmin as coodnadas do véic
Campo Gravítico da Terra
3.9 Camada d G Toma d Stoks Toma d Stoks: sdo S uma supf íci quipotcial d um campo Nwtoiao, cotdo o su itio todas as massas atats, s s modifica a distibuição das massas, sm alta a sua totalidad, po foma
6.15 EXERCÍCIOS pg. 290
56 6.5 EXERCÍCOS pg. 9. Da um mplo d uma fução cotíua po pat dfiida o itvalo ] [. Muito mplo podm ciado. Sgu um dl: ) ( - - f - - - - - - 6 8 y. Calcula a itgal da guit fuçõ cotíua po pat dfiida o itvalo
Sistemas e Sinais 2009/2010
Aálise em espaço de estados Sistemas e Siais 009/010 Repesetação de Sistemas Sistemas descitos po equações difeeciais Sistemas descitos po sistemas de equações difeeciais Repesetação em espaço de estados
Teoria de Controle (sinopse) 4 Função de matriz. J. A. M. Felippe de Souza
Toria d Conrol (sinops) 4 Função d mariz J. A. M. Flipp d Souza Função d mariz Primiramn vamos dfinir polinómio d mariz. Dfinição: Polinómio d mariz (quadrada) Sja p(λ)um polinómio m λd grau n (finio),
3. VIBRAÇÃO FORÇADA - FORÇA HARMÔNICA
VIBAÇÕE MECÂNICA - CAPÍTULO 3 VIBAÇÃO OÇADA 8 3. VIBAÇÃO OÇADA - OÇA HAMÔNICA No apíulo aio sudou-s a vibação liv d sisas o u gau d libdad. A vibação liv é obida aavés da solução hoogêa da quação difial
Transformação de similaridade
Trasformação de similaridade Relembrado bases e represetações, ós dissemos que dada uma base {q, q,..., q} o espaço real - dimesioal, qualquer vetor deste espaço pode ser escrito como:. Ou a forma matricial
TRANSFORMADA DE LAPLACE- PARTE I
TRNSFORMD DE LLE- RTE I Eor. d Barro. INTRODUÇÃO odmo dfiir a Traformada d Laplac como uma opração mamáica qu covr uma fução d variávl ral m uma fução d variávl complxa: Od, F f d i f é uma fução ral da
z 0 0 w = = 1 Grupo A 42. alternativa C det A = Como A é inteiro positivo, então n deve ser par. 43. A comuta com B A B = B A
Resoluções das aividades adicioais Capíulo 6 Grupo A. aleraiva C de A 6 (de A) 8 de A. aleraiva C de A de( A) (de A) de A (de A) de A Como A é ieiro posiivo, eão deve ser par.. A comua com B A B B A y
4. Análise de Sistemas de Controle por Espaço de Estados
Sisma para vrificação Lógica do Corolo Dzmro 3 4. ális d Sismas d Corol por Espaço d Esados No capiulo arior, vimos qu a formulação d um Prolma Básico d Corolo Ópimo Liar, ra cosidrado um sisma diâmico
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
Uivridad Salvador UNIFACS Curo d Egharia Méodo Mmáico Aplicado / Cálculo Avaçado / Cálculo IV Profa: Ilka Rouça Frir A Traformada d Laplac Txo : Irodução. Dfiição. Codiçõ d Exiêcia. Propridad. Irodução
4. VIBRAÇÃO FORÇADA - FORÇAS NÃO SENOIDAIS
VIBRAÇÕES MEÂNIAS - APÍTULO VIBRAÇÃO ORÇADA 3. VIBRAÇÃO ORÇADA - ORÇAS NÃO SENOIDAIS No capíulo ao suou-s a vbação oçaa ssas co u gau lba, subos a oças cação oa soal. Es suo po s so paa aplcaçõs quao as
Análise de Sistemas Lineares
Aáli d Sima iar Dvolvido plo Prof Dr Emilo Rocha d Olivira, EEEC-UFG, 6 Traformada d aplac A ididad d Eulr dfi uma rlação r o ial xpocial o iai oidai a forma ± j = co ( ) ± j ( ) N cao, é dfiido como a
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Retas Cortadas por uma Transversal. Oitavo Ano
Maial Tóico - Módulo Elmno Báico d Gomia Plana - Pa 1 Ra Coada po uma Tanval Oiavo Ano Auo: Pof. Uli Lima Pan Rvio: Pof. Anonio Caminha M. No Poal da OBMEP 1 Ra coada po uma anval Sjam dua a iuada m um
Principais fórmulas. Capítulo 3. Desvio padrão amostral de uma distribuição de frequência: Escore padrão: z = Valor Média Desvio padrão σ
Picipais fómulas De Esaísica aplicada, 4 a edição, de Laso e Fabe, 00 Peice Hall Capíulo Ampliude dos dados Lagua da classe úmeo de classes (Aedode paa cima paa o póimo úmeo coveiee Poo médio (Limie ifeio
por eliminaçaoda linha i e da coluna j
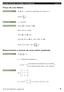ídice Traço de uma Matriz DEFINIÇÃO, B, C,..., matrizes quadradas de ordem tr ( ) = a ii i= MTLB t = trace( ) PROPRIEDDES tr( ± B) = tr( ) ± tr( B) tr tr ( α ) = α tr( ) ( B) = tr( B ) ( B C) = ( B C )
setor 1103 Aula 39 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO Então, 1. INTRODUÇÃO Duas retas r e s de um plano podem ser: Distintas: r s = Exemplo:
to 58 Aula 9 POSIÇÕES RELATIVAS DE DUAS RETAS NO PLANO. INTRODUÇÃO Dua ta d um plano podm : Ditinta: = Emplo: Então, O coficint angula ão iguai. O coficint lina ão difnt. Paalla b) ão PARALELAS COINCIDENTES.
7. Aplicação do Principio do Máximo
7. Aplicação do Principio do Máximo Ns capiulo vamos implmnar um algorimo qu uiliz a oria do Principio do Máximo para drminar o conjuno dos sados aingívis. Com o rsulados obidos vamos nar fazr um parallo
PROCESSO SELETIVO UFES 2013
UNIESIDADE FEDEAL DO ESPÍIO SANO OMISSÃO OODENADOA DO ESIBULA POESSO SELEIO UFES 0 As bacas laboaoas sam ob a maioia os caiaos sosas como as u sgum No ao aa a coção as ovas ouas sosas ambém oão s cosiaas
Soluções das Fichas de trabalho. FICHA DE TRABALHO 1 Propriedades das operações sobre conjuntos
Soluçõs das FICHA DE TRABALHO Popidads das opaçõs sob conjuntos a) {,, 5} {,,, 5} {,, } {,, 5} ) {} f) {} g) {, 5} h) {,,, 5} i) Q j) {} k) {} l) Q m) {,, 5} a) {, 5,, 7, 8, 9, } {, 8, } {, 5} {, 7, 9}
CÁLCULO I 2º Semestre 2011/2012. Duração: 1 hora e 30 minutos
NOVA SCHOOL OF BSINESS AND ECONOMICS CÁLCLO I º Smsr / TESTE INTERMÉDIO Tópi d rsolução Abril Duração: ora miuos Não é prmiido o uso d calculadoras. Não pod dsagraar as olas do uciado. Rspoda d orma jusiicada
03-05-2015. Sumário. Campo e potencial elétrico. Energia potencial elétrica
Sumáio Unidad II Elticidad Magntismo 1- - Engia potncial lética. - Potncial lético. - Supfícis quipotnciais. Movimnto d cagas léticas num campo lético unifom. PS 22 Engia potncial lética potncial lético.
Não serão feitos esclarecimentos individuais sobre questões durante a prova. Não se esqueça que tudo é para justificar.
Eam m 7 d Jairo d 007 Cálculo ATENÇÃO: FOLHAS DE EXAE NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eam fial ª Época 7 Jairo d 007 Duração: horas 0 miutos Rsolva os grupos do am m folhas sparadas O uso
2ª Lei de Newton em forma geral ( p = mv. - momento linear, F = r r dt
Tópios d Físia Moda 4/5 Fomuláio Mdiçõs os ~ < > i i σ i < > i σ < > ± σ < > ± 3σ < > ± g µ σ πσ mlo simaia do alo dadio a pai d mdidas - média aiméia Dsio padão aaiza a dispsão dos sulados d mdidas do
ELECTROMAGNETISMO. TESTE 1 4 de Abril de 2009 RESOLUÇÕES
LTROMAGNTIMO TT 4 d Abil d 009 ROLUÇÕ a Dvido à simtia das cagas, o campo léctico m qualqu ponto no io dos é paallo a ss io, ou sja a componnt é smp nula Paa > 0, o sntido do y campo léctico é o sntido
Exercícios de Cálculo Numérico
Ecícios d Cálculo Numéico Zo d Fução. Dê um mlo d ução, qu ta lo mos uma aiz, qu ão od s dtmiada usado o Método da Bissção.. Dê um mlo d ução, qu ta lo mos uma aiz, od o Método d Nwto-Raso ão covg.. A
1. A TRANSFORMADA DE LAPLACE
Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Transporte Vestiário Higiene Pessoal Poupança
Álgbr Mricil PRTE LGUMS CONSDERÇÕES TEORCS MTRZES Noção d mriz Mrizs formm um impor cocio m mmáic, d spcil uso o sudo d rsformçõs lirs mriiz é um bl d lmos disposos m lih colus Mriz m é um bl d m úmros
Matriz. Matrizes especiais
Mariz Mariz de ipo m sobre um corpo Uma mariz de ipo m sobre um corpo Ω é um quadro com m lihas e coluas cujos elemeos A ij são escalares de Ω. A11 A2 A1 A21 A22 A 2 A= A ij = Am 1 Am2 Am A mariz A ij
Secção 4. Equações lineares de ordem superior.
Scção 4 Equaçõs linas d odm supio Falow: Sc 3 a 35 Vamos agoa analisa como podmos solv EDOs linas d odm supio à pimia Uma vz qu os sultados obtidos paa EDOs d sgunda odm são smp gnalizávis paa odns supios,
Transformada de Laplace Solução de Modelos Lineais
TEQ CONTROE DE PROCESSOS Dmo d Eghi Químic d Pólo UFF Tfomd d lc Solução d Modlo ii Pof Niok Bojog A Tfomd d lc EDO: dy 5 y y d Equção Difcil Odiái Equção Algéic y -,8,5,5 Solução d Equção Difcil - Solução
1- Resolução de Sistemas Lineares.
MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
Ondas - 2EE 2003 / 04
Ondas - 3 / 4 1 Inodução 1.1 Conco d onda móvl Uma função f dscv o pfl d vaação d uma onda móvl vlocdad v no spaço no mpo. Paa qu o pfl d vaação f caac uma onda móvl dv sasfa a quação d onda sgun: f 1
VERSÃO DE TRABALHO. Prova Escrita de Matemática A. 12.º Ano de Escolaridade. Prova 635/2.ª Fase. Critérios de Classificação
EXAME FINAL NACIONAL DO ENSINO SECUNDÁRIO Pova Escita d Matmática A.º Ao d Escolaidad Dcto-Li.º 39/0, d 5 d julho Pova 635/.ª Fas Citéios d Classificação Págias 06 Pova 635/.ª F. CC Págia / CRITÉRIOS GERAIS
7 Solução de um sistema linear
Toria d Conrol (sinops 7 Solução d um sisma linar J. A. M. Flipp d Souza Solução d um sisma linar Dfinição 1 G(,τ mariz cujos lmnos g ij (,τ são as rsposas na i ésima saída ao impulso aplicado na j ésima
Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I. Ano Lectivo º Semestre
aculdad d Ecoomia Uivrsidad Nova d Lisboa EXAME DE CÁLCULO I Ao Lctivo 009-0 - º Smstr Eam ial d ª Época m d Jairo d 00 Duração: horas 0 miutos É proibido usar máquias d calcular ou tlmóvis Não tha o su
log 2, qual o valor aproximado de 0, 70
UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
Prova Escrita de Matemática A
EXAME FINAL NACIONAL DO ENSINO SECUNDÁRIO Pova Escita d Matmática A 1.º Ao d Escolaidad Dcto-Li.º 139/01, d 5 d julho Pova 635/.ª Fas Citéios d Classificação 14 Págias 016 Pova 635/.ª F. CC Págia 1/ 14
NPQV Variável Educação Prof. Responsáv el : Ra ph a el B i c u d o
NPQV Variável Educação Prof. Responsáv v el :: Ra ph aa el BB ii cc uu dd o ATIVIDADES DESENVOLVIDAS NA ÁREA DE EDUCAÇÃO 2º Semestre de 2003 ATIVIDADES DESENVOLVIDAS NA ÁREA DE EDUCAÇÃO As atividades realizadas
Transformada Inversa de Laplace. Prof. Eng. Antonio Carlos Lemos Júnior
Tanfomada Inva d Lalac Pof Eng nonio Calo Lmo Júnio GEND Tanfomada Inva d Lalac Excício Conol d Sima Mcânico Tanfomada Inva d Lalac Obivo: O obivo da ção é faz uma odução à Tanfomada Inva d Lalac ua alicação
1 Eliminação gaussiana com pivotamento parcial
1 Elimiação gaussiaa com pivotamto parcial Exmplo sm pivotamto parcial Costruimos a matriz complta: 0 2 2 1 1 1 6 0 2 2 1 2 1 1 1 1 0 2 2 1 1 1 6 1 2 0 0 2 0 6 x y z = 9 6 0 2 2 0 1 0 3 1 0 0 2 0 2 0 6
DESDOBRAMENTO DA FUNÇÃO QUALIDADE - QFD UM MODELO CONCEITUAL APLICADO EM TREINAMENTO
G 996 DDBM D FUÇÃ QUDD QFD UM MD U D M M h v, M M h h, hd Jã B, M F gh jbá F / D çã D v. B,.0 hh jbá MG 700000 b: h h f g h f y, w, h k f g, whh h h. h Qy F Dy ( QFD ) hq g b f g h h w. Fy, QFD y hw g
Novo Espaço Matemática A 12.º ano Proposta de Teste [janeiro ]
![Novo Espaço Matemática A 12.º ano Proposta de Teste [janeiro ]](/thumbs/80/81607224.jpg "Novo Espaço Matemática A 12.º ano Proposta de Teste [janeiro ]")
Novo Espaço Matmática A.º ao Proposta d Tst [jairo - 08] Nom: Ao / Turma: N.º: Data: / / Não é prmitido o uso d corrtor. Dvs riscar aquilo qu prtds qu ão sja classificado. A prova iclui um formulário.
Capítulo 5 Transformadas de Fourier
Capíulo 5 Trasformadas d Fourir 5. Aális da composição d sismas aravés da rsposa m frquêcia 5. Trasformadas d Fourir propridads Capíulo 5 Trasformadas d Fourir 5. Aális da composição d sismas aravés da
PROFUNDIDADE PELICULAR, REFLEXÃO DE ONDAS, ONDAS ESTACIONÁRIAS
5 PROFUNDIDAD PLICULAR, RFLXÃO D ONDAS, ONDAS STACIONÁRIAS 5. Pofunddad Plcula Mos dsspavos apsnam conduvdad à mdda qu uma onda lomagnéca nl s popaga, sua amplud sof uma anuação, mulplcada plo mo z (quando
MATEMÁTICA. QUESTÃO 1 De quantas maneiras n bolas idênticas podem ser distribuídas em três cestos de cores verde, amarelo e azul?
(9) - www.litcampias.com.br O ELITE RESOLVE IME 8 TESTES MATEMÁTICA MATEMÁTICA QUESTÃO D quatas mairas bolas idêticas podm sr distribuídas m três cstos d cors vrd, amarlo azul? a) b) d) ( )! ) Rsolução
5. Implementação da solução da equação de estados
Sisma para vrifiação Lógia do Corolo Dzmbro 3 5. Implmação da solução da uação d sados No apiulo arior abordamos a aális dsvolvimo mamáio d Sismas d Corol por Espaço d Esados u os prmiiu hgar à Solução
ANALISE DE CIRCUITOS DE 1 a E 2 a. J.R. Kaschny ORDENS
ANAISE DE IRUITOS DE a E a J.R. Kaschny ORDENS Inrodução As caracrísicas nsão-corrn do capacior do induor inroduzm as quaçõs difrnciais na anális dos circuios léricos. As is d Kirchhoff as caracrísicas
+ = x + 3y = x 1. x + 2y z = Sistemas de equações Lineares
Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn
Organização e Arquitetura de computadores
gaização Aquiua compuao oução Pipliigéuma écica implmação m qu váia iuçõ ão obpoa a xcução Exmplo: lavagm oupa Mlhoao o mpho com pipliig Pof. D. Luciao Joé Sg Pipliig abalho é iviio m apa ou ágio Técica
FUNÇÕES DE VÁRIAS VARIÁVEIS REAIS
INTRODUÇÃO FUNÇÕES DE VÁRIAS VARIÁVEIS REAIS Uma ganda ísica pod dpnd d divsas outas gandas Po mplo: a vlocidad do som m um gás idal dpnd da dnsidad do gás d sua pssão Muitas unçõs dpndm d mais d uma vaiávl
Sinais e Sistemas. Env. CS1 Ground Revolute. Sine Wave Joint Actuator. Double Pendulum Two coupled planar pendulums with
-4-6 -8-2 -22-24 -26-28 -3-32 Frqucy (khz) Hammig kaisr Chbyshv Siais Sismas Powr Spcral Dsiy Ev B F CS CS2 B F CS Groud Rvolu Body Rvolu Body Powr/frqucy (db/hz) Si Wav Joi Acuaor Joi Ssor Rvolu.5..5.2.25.3.35.4.45.5-34
Prova Escrita de Matemática A
Eam Final Nacional do Ensino Scundáio Pova Escita d Matmática A 1.º Ano d Escolaidad Dcto-Li n.º 139/01, d 5 d julho Pova 635/1.ª Fas Citéios d Classificação 1 Páginas 014 Pova 635/1.ª F. CC Página 1/
FICHA DE AVALIAÇÃO 1 FICHA DE AVALIAÇÃO 2. Grupo I 1 A 2 D 3 A 4 C 5 B. Grupo II. 6 4 rapazes pontos. 8 a) 5040 b) 720 c) 1260
FICHA DE AVALIAÇÃO A D A C 5 B I 6 apazs 7 5 pontos a) 5 b) 7 c) 6. ( y) 5 5 C 5 5 C y 5 C y 5 C y 5 C y 5 C 5 y 5 ( y) 5 5 C 5 5 C y 5 C y 5 C y 5 C y 5 C 5 y 5 ( y) 5 ( y) 5 ( 5 C 5 5 C y 5 C y ) ( 5
1. Revisão Matemática
Se x é um elemeto do cojuto Notação S: x S Especificação de um cojuto : S = xx satisfaz propriedadep Uião de dois cojutos S e T : S T Itersecção de dois cojutos S e T : S T existe ; para todo f : A B sigifica
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Prof Mc ARMANDO PAULO DA SILVA Prof Mc JOSÉ DONIZETTI DE LIMA INTEGRAIS IMPRÓPRIAS A TRANSFORMADA DE LAPLACE g ()d = lim R R g()d o limit it Qudo o limit it
Definição: Sejam dois números inteiros. Uma matriz real é uma tabela de números reais com m linhas e n colunas, distribuídos como abaixo:
I MTRIZES Elemeos de Álgebr Lier - MTRIZES Prof Emíli / Edmé Defiição: Sem dois úmeros ieiros Um mriz rel é um bel de úmeros reis com m lihs e colus, disribuídos como bixo: ( ) i m m m m Cd elemeo d mriz
TEORIA DE SISTEMAS LINEARES
Ageda. Algebra Liear (Parte II). Atividades V Profa. Dra. Letícia Maria Bolzai Poehls 8// Potifícia Uiversidade Católica do Rio Grade do Sul PUCRS Faculdade de Egeharia FENG Programa de Pós-Graduação em
Microcilindros. Duplo efeito: ø4 / Haste recolhida : ø2.5, ø4. Haste simples 2.5. n. recolhida. Como encomendar/duplo efeito.
Micocilindos Duplo fio: ø / Has colhida : ø, ø Vaiaçõs Séi Funcionamno sandad B Básica mm Duplo fio Simpls Efio Has simpls Has simpls n. colhida sandad, Como ncomnda/duplo fio CJ1B U sandad do cilindo
Secção de Mecânica Estrutural e Estruturas Departamento de Engenharia Civil e Arquitectura ESTÁTICA Arquitectura 2006/07
Scção d Mcâica Estutual Estutuas Dpatamto d Eghaia Civil Aquitctua ESTÁTICA Aquitctua 2006/07 ESTÁTICA 0. Apstação Objctivo (gal): Aális stutual d stutuas isostáticas paa acçõs státicas, cálculo d sfoços
Análise do Processo de Reversão à Média para a Avaliação de Projetos de Investimento
Aális do Pocsso d Rvsão à Média paa a Avaliação d Pojos d Ivsimo Alad Maiho Gaudio Poifícia Uivsidad Caólica do Rio d Jaio. Rua Maquês d São Vic 5 Gáva Rio d Jaio RJ - Basil - 53-9 Maclo Wiskopf Poifícia
KV-29FS150. Manual de instruções. Conexión de equipo adicional 3-210-910-51(2) 2007 Sony Corporation Impresso no Brasil
xó q 3-2-9-5(2 õ K-29F5 L h 27 y B Ê ÇÕ v í hq é, xh v à hv z hq é, z x q j ÇÃ HQ LÉ Ã B ÇÃ v hq é: Ã B v, é q y í ó á õ,, q hq é í ó á q à õ (v õ q h h v ( v óx í ê ÇÃ Ç h v -22 5/6 Hz HQ LÉ, X L L LÉ
Aula 9. Vimos que a freqüência natural de oscilação dos elétrons em torno das suas respectivas posições de equilíbrio, é dada pela expressão 4.2.
Aula 9 Nsta aula, continuamos o capítulo 4 do livo txto, ond agoa invstigamos as fitos do movimnto témico, qu oa dsconsidamos, nas oscilaçõs natuais d létons. 4.3 Ondas Eltônicas d Plasma Vimos qu a fqüência
ELECTROTECNIA TEÓRICA. Transparências das aulas teóricas. Maria Inês Barbosa de Carvalho
LCTROTCNI TÓRIC Tspêis ds uls tóis Mi Iês os d Cvlo 4/5 LCTROTCNI TÓRIC Ods ltomgétis Lis d tsmissão Guis d od ilídios o Guis mtálios Pls plls Rtguls Ciuls o Guis dilétios Pls Fis Óptis GUIS D OND CILÍNDRICOS
sen( x h) sen( x) sen xcos h sen hcos x sen x
MAT00 Cálculo Difrcial Itgral I RESUMO DA AULA TEÓRICA Livro do Stwart: Sçõs 3., 3.4 3.8. DEMONSTRAÇÕES Nssa aula srão aprstadas dmostraçõs, ou sboços d dmostraçõs, d algus rsultados importats do cálculo
XXXI Olimpíada Brasileira de Matemática GABARITO Primeira Fase
XXXI Olimpíada Brasilira d Matmática GABARITO Primira Fas Soluçõs Nívl Uivrsitário Primira Fas PROBLEMA ( x) a) A drivada da fução f é f ( x) =, qu s aula apas para x =, sdo gativa para x < positiva para
Exame - Modelagem e Simulação - 30/01/2004. ( x Xc) + ( y Yc) = r, onde x e y são observações e X c, Y c e r são
Eame - odelagem e Simulação - 0/0/004 ome: )[5] Supoha que voê queia ivesi $0000,00 a bolsa de valoes ompado ações em uma de ompahias e B s pevisões idiam que as ações de deveão e um luo de 50% se as odições
Cinemática e dinâmica da partícula
Sumáio Unia I MECÂNICA 1- a patícula Cinmática inâmica a patícula m moimntos a mais o qu uma imnsão - Rfncial to posição. - Equaçõs paaméticas o moimnto. Equação a tajtóia. - Dslocamnto, locia méia locia.
Aula 11 Mais Ondas de Matéria II
http://www.bugman3.com/physics/ Aula Mais Ondas d Matéia II Física Gal F-8 O átomo d hidogênio sgundo a Mcânica Quântica Rcodando: O modlo atômico d Boh (93) Motivação xpimntal: Nils H. D. Boh (885-96)
5- Método de Elementos Finitos Aplicado às Equações Diferenciais Parciais.
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 5- Método d Elmntos Finitos Aplicado às Equaçõs Difnciais Paciais. 5.- Bv Intodução Históica. 5.- Solução d Equaçõs Difnciais Odináias: 5.3- Solução
TEORIA DE SISTEMAS LINEARES
Ageda. Algebra Liear (Parte I). Ativadades IV Profa. Dra. Letícia Maria Bolzai Poehls /0/00 Potifícia Uiversidade Católica do Rio Grade do Sul PUCRS Faculdade de Egeharia FENG Programa de Pós-Graduação
TÓPICOS. Sinais contínuos e sinais discretos. Função impulso unitário discreto.
Not bm: a litura dsts apotamtos ão dispsa d modo algum a litura atta da bibliografia pricipal da cadira hama-s a atção para a importâcia do trabalho pssoal a ralizar plo aluo rsolvdo os problmas aprstados
5 Modelo financeiro para os ativos
Modelo financeio paa os aivos 51 5 Modelo financeio paa os aivos 5.1. Pemissas A eada de dados de uma pogamação esocásica é caaceizada como o valo que epesea cada fao de isco duae o peíodo de duação de
Sumário Propagação em Meios com perdas Propagação em Meios Dieléctricos e Condutores Energia transportada por uma onda electromagnética
Sumário Propagação m Mios com prdas Propagação m Mios Dilécricos Conduors nrgia ransporada por uma onda lcromagnéica Livro Chng : pp [354 37] [379 385] Propagação d Ondas m Mios sm Prdas k k x x x k C
CÁLCULO I 2º Semestre 2011/2012. Duração: 2 horas e 15 minutos
NOVA SHOOL OF BSINESS AND EONOMIS ÁLLO I º Ssr / EXAME ª ÉOA TÓIOS DE RESOLÇÃO Juho Duração: horas iuos Não é priido o uso d calculadoras Não pod dsagrafar as folhas do uciado Rspoda d fora jusificada
ORBITAIS EM ÁTOMOS E. André Bathista Instituto de Física de São Carlos Universidade de São Paulo
ORBITAIS EM ÁTOMOS E MOLÉCULAS Adré Bathista Istituto d Física d São Carlos Uivrsidad d São Paulo Torias º Toria da Coordação d Wrr. É a mais simpls das torias d orbitais atômicos molculars º Toria dos
2.6 - Conceitos de Correlação para Sinais Periódicos
.6 - Conceios de Correlação para Sinais Periódicos O objeivo é o de comparar dois sinais x () e x () na variável empo! Exemplo : Considere os dados mosrados abaixo y 0 x Deseja-se ober a relação enre x
TÓPICOS. Integração complexa. Integral de linha. Teorema de Cauchy. Fórmulas integrais de Cauchy.
No m, liur dss pomos ão disps d modo lgum liur d iliogri pricipl d cdir hm-s à ção pr imporâci do rlho pssol rlir plo luo rsolvdo os prolms prsdos iliogri, sm ul prévi ds soluçõs proposs, ális compriv
1 a Lista: MTM146: Prof. Paulo Magalhães:
Exercício : Mosre que a solução do sisema de EDO s x y f ( x y y com codições iiciais: x ( ) x() ) ), f saisfazedo x( f ( ) d f ( ) cos( ) d f ( ) cos( ) d f ( ), é dada por Exercício : Resolva o seguie
Ánálise de Fourier tempo discreto
Faculdad d Egharia Áális d Fourir tmpo discrto 4 3.5 3.5.5.5.5.5 -.5 -.5 - - -8-6 -4-4 6 8 - - -5 5 5 5 3 SS MIEIC 8/9 Aális d Fourir m tmpo discrto aula d hoj Faculdad d Egharia Rsposta d SLITs discrtos
2 Fundamentos da Mecânica da Fratura Linear Elástica
Fudamtos da Mcâica da Fatua Lia lástica.. Coctação d tsõs As fómulas clássicas da aális tadicioal d tsõs (ou da sistêcia dos matiais) só svm paa s calculam as chamadas tsõs omiais, as quais dspam os fitos
Ondas Electromagnéticas
Faculdad d ghaa Odas lcomagécas Op - MIB 007/008 Pogama d Ópca lcomagsmo Faculdad d ghaa Aáls Vcoal (vsão) aulas lcosáca Magosáca 8 aulas Odas lcomagécas 6 aulas Ópca Goméca 3 aulas Fbas Ópcas 3 aulas
/ :;7 1 6 < =>6? < 7 A 7 B 5 = CED? = DE:F= 6 < 5 G? DIHJ? KLD M 7FD? :>? A 6? D P
26 a Aula 20065 AMIV 26 Exponncial d matrizs smlhants Proposição 26 S A SJS ntão Dmonstração Tmos A SJS A % SJS SJS SJ % S ond A, S J são matrizs n n ", (com dt S 0), # S $ S, dond ; A & SJ % S SJS SJ
CADERNO 1. (É permitido o uso de calculadora gráfica) N.º de possibilidades de representar os 4 algarismos ímpares e a sequência de pares: 5!
Novo Espaço Matmática A º ao Proposta d Rsolução [jairo - 08] Algarismos ímpars:,,, 7, 9 Algarismos pars:, 4, 6, 8 CADERNO (É prmitido o uso d calculadora gráfica) Nº d possibilidads para o algarismo das
TRANSFORMAÇÕES CONTÍNUAS
TRANSFORMAÇÕES CONTÍNUAS Tscçõs o mo U, 0 0 odo scção o mo odo voução U, 0 HU, 0 Hmoo, H, dd do mo U fução d H U, H 0 0 H gdo do guo ds scçõs o mo [ H, U, ] 0 0 H 0 H 0, 0 H cos do movmo: E, g, cosv-s
EQUAÇÕES DIFERENCIAIS LINEARES DE ORDEM SUPERIOR
Caítlo III EQUAÇÕES DIFERENCIAIS LINEARES DE ORDEM SUPERIOR Caítlo III Eqaçõs Difciais Lias d Odm Sio Caítlo III Eqaçõs Lias Homogéas Rcodmos q ma qação difcial odiáia d -ésima odm é ma qação a qal a divada
. As partículas colidem? Onde? Qual instante?
( ) Pova ( ) Pova Smsal (X) Excícios ( ) Sgunda Chamada ( ) Pova Modula ( ) Pova d Rcupação ( ) Páica d Laboaóio ( ) Exam Final/Exam d Cificação ( ) Apoviamno Exaodináio d Esudos Disciplina: Cálculo 3
Capítulo V Efeito Eletroóptico Linear
Capíul V fi lópic Lia O fi lópic f-s à mudaça as ppidads ópicas d um diléic, iduzidas p um camp léic cuja fquêcia ca-s mui abai da ssâcia cisalia d mi []. O fi lópic quadáic fi bsvad pimiam p K, m 87,
Em termos da fração da renda total da população recebida por cada pessoa, na distribuição dual temos. pessoas
6. Dual do Ídic d hil Dfiição Gral do Dual: Sja x uma variávl alatória com média µ distribuição tal qu o valor d crta mdida d dsigualdad é M. Chama-s dual a distribuição com as sguits caractrísticas: a.
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
Grupo I. 1) Calcule os integrais: (4.5) 2) Mostre que toda a equação do tipo yf( xydx ) xg( xydy ) 0
Mamáica III / ºSmsr Grupo I ) Calcul os ingrais: a) b) D () ( ) dd sndo D d d d d (.) ) Mosr qu oda a quação do ipo f( d ) g( d ) s ransforma numa quação d variávis sparadas fazndo a subsiuição (.) ) A
Unidade XI Análise de correlação e regressão
Uvedade Fedeal do Ro Gade Iuo de Maemáca, Eaíca e Fíca Dcpla Pobabldade e Eaíca Aplcada à Egehaa CÓDIGO: Iodução Poceo de quema de maa ceâmca de pavmeo Udade XI Aále de coelação e egeão Vvae Lee Da de
JOGO. Meio ambiente e ciência: a energia na minha cidade. Fontes consultadas. Para aprender de forma divertida. Aprenda mais em
Ralização coodnação: Fundação AcloMial Dsnvolvimno d conúdo dsign gáfico: Mondana:IB Rvisão: Days Mnds - Maxo Rvisão Edioação www.fundacaoaclomial.og.b Paa apnd d foma divida F Acss as fências complas
Universidade Federal de Pelotas Vetores e Álgebra Linear Prof a : Msc. Merhy Heli Rodrigues Matrizes
Uiversidde Federl de Pelos Veores e Álgebr Lier Prof : Msc. Merhy Heli Rodrigues Mrizes. Mrizes. Defiição: Mriz m x é um bel de m. úmeros reis disposos em m lihs (fils horizois) e colus (fils vericis)..
03. Sejam z = n 2 (cos 45 + i sem 45 ) e w = n(cos 15 + isen15 ), em. igual a. Solução: n = 4 Assim: 04. Se arg z, então um valor para arg(-2iz) é
. Sjam z = (cos + i sm ) w = (cos + is ), m. Dsja-s trocar uma moda d ctavos, usado-s apas modas d, ctavos. Etão, o úmro d difrts mairas m qu a moda d ctavos pod sr trocada é igual a a) b) c) d) ) mairas