260 Direcionamento de Trajetórias
|
|
|
- Eliza Borges da Conceição
- 7 Há anos
- Visualizações:
Transcrição
1 260 Direcionamento de Trajetórias Controle - OGY 0,4 Z 0 Z f V C2-0,1 Direcionamento Posicionamento -0,6-3,0-1,0 1,0 V C1 Figura 8.13: Direcionamento da trajetória da equação (8.6), do ponto inicial dado por (8.10) ao ponto Z f com coordenadas dadas por (8.7), aplicando o nosso método de direcionamento. Após atingido o ponto Z f que é o ponto fixo ξ da equação (7.56), iniciamos a aplicação do método OGY para estabilizar a órbita periódica instável apresentada na figura 7.31A.
2 Capítulo 9 Conclusões 9.1 Introdução As principais conclusões descritas em cada um dos capítulos da tese serão resumidas a seguir. Cada ítem a seguir contém também comentários sobre esses resultados. 9.2 Mapa Logístico Embora o mapa Logístico seja um sistema matemático muito simples, ele descreve um conjunto de órbitas com um comportamento extremamente rico em fenômenos não-lineares [1]. Dos muitos fenômenos presentes neste mapa, destacamos a intermitência tipo I [7], o aparecimento de janelas periódicas (seção 2.4) e as crises [65]. Entretanto, o mais impressionante foi a descoberta da rota para o caos via duplicação de período [1] (rota de Feigenbaum). Este cenário, no qual o caos aparece através da variação de um parâmetro apresenta um comportamento universal e autosimilar na maneira como os períodos das órbitas se duplicam (até aparecer o caos) para determinados valores do parâmetro de controle. Isso também ocorre para qualquer outro sistema unimodal (cuja função tem um único máximo) ao variarmos o seu parâmetro de controle. Assim, qualquer sistema experimental que possa ser modelado por uma função unimodal, e que seja considerada com codimensão 1 (apenas um parâmetro a ser variado), terá o caos aparecendo através do cenário de duplicação de período. Portanto, a identificação de tal cenário é um passo extremamente importante na iden-
3 262 Conclusões tificação da dinâmica do sistema considerado. Outro interesse na identificação dessa rota é a previsibilidade que teremos desse sistema, mesmo que a sua dinâmica seja desconhecida. Com isso, podemos dizer que não só o comportamento caótico é determinista mas também a maneira como ele surge. 9.3 Mapa Logístico Perturbado O mapa Logístico perturbado corresponde ao mapa Logístico com a adição de um termo constante de amplitude q a cada t iteração [8], [9], [10]. Para esse mapa, diferentes bacias de atração (conjuntos de condições iniciais cujas trajetórias se dirigem aos atratores determinados) coexistem [9], [10] (ver seção 3.2). A existência de mais de um atrator pode levar ao aparecimento da crise de transferência que é caracterizada pela mudança brusca na característica do atrator devido a transferência da trajetória para as diferentes bacias de atração que coexistem. O período das órbitas desse mapa são múltiplos do período da perturbação t (seção 3.3). Além disso, essas órbitas periódicas podem ter uma trajetória na qual pelo menos dois pontos apresentam o mesmo valor. Isso se reflete nos diagramas de bifurcação (seção 3.7) que apresentam cruzamentos de ramos, característica não presente no mapa não perturbado. Isso ocorre devido a existência de dois máximos na função do mapa perturbado. Nesse mapa foi determinado que a intermitência existente é do tipo I, similar a que foi vista no mapa Logístico que apresenta uma lei de escala de potência. Esse resultado é importante já que o mapa perturbado, pode ser interpretado como um mapa descontínuo que apresenta intermitência tipo V, cuja lei de escala é logarítmica [36], [33]. O mapa perturbado também não apresenta um cenário de rota para o caos típico de mapas discontínuos, no qual o aparecimento de novos períodos acontece de forma aditiva [35] e não em potência de dois, como no cenário de Feigenbaum. Quando aumentamos a amplitude da perturbação q, presenciamos o surgimento de cascatas inversas, cujo período da trajetória decresce na razão de dois, para um aumento do parâmetro q. As cascatas inversas só aparecem para variações positivas em q.
4 9.4 Diagrama no Espaço de Parâmetros do Mapa Logístico Perturbado e sua Estabilidade Diagrama no Espaço de Parâmetros do Mapa Logístico Perturbado e sua Estabilidade Neste capítulo, realizamos uma análise mais detalhada dos diagramas no espaço de parâmetros, em especial a determinação não só das regiões periódicas, mas na identificação das regiões de diferentes períodos p. Quando em um diagrama mostramos somente as regiões periódicas, este é denominado de diagrama isoperiódico. Demos especial ênfase à estrutura, geometria e estabilidade dos diagramas isoperiódicos. A análise de tal diagrama nós dá condições de afirmar que a introdução de perturbações periódicas e constantes ao mapa Logístico faz este passar de um sistema de codimensão um para um sistema de codimensão dois (número de parâmetros envolvidos). Essa afirmação fica clara analisando-se os diagramas isoperiódicos no espaço de parâmetros (q b), nos quais aparecem as estruturas em forma de camarões, caracterizadas pelo período p que representam (seção 4.2). Camarões com o mesmo perído p aparecem alinhados nos diagramas. A sequência dessa estrutura não é fractal. A existência de diferentes bacias de atração faz com que os diagramas no espaço de parâmetros sejam dependentes da condição inical. Além disso, há regiões para valores de b e q (ver tabela da seção 3.4 do capítulo 3) com atrator não limitado (quando a trajetória sai da região de validade do mapa), além de outros atratores finitos. Para estas regiões observamos que um diagrama de bifurcação pode ter uma estrutura quebrada, ou seja, dependendo do valor do parâmetro, pode haver um atrator finito, identificado visualmente no diagrama, ou um atrator não finito, que não é identificado no diagrama; há uma lacuna no diagrama, correspondente ao parâmetro para o qual o mapa não tem atrator finito. Uma questão a determinar é se a estrutura destes diagramas na região em que aparecem as lacunas (devidas a não existência de um atrator) têm uma estrutura fractal. A análise da estabilidade das órbitas periódicas de período p=2 para perturbações com período t=2, permite determinar a forma da ilha periódica (região que representa os parâmetros b e q para os quais o mapa tem uma trajetória estável) de período p=2, que aparece no diagrama isoperiódico. Isso parece indicar que o formato de qualquer estrutura periódica, que aparece nos diagramas isoperiódicos, pode ser determinado através da análise da estabilidade das órbitas periódicas. Consequentemente, colocamos uma questão: Será possível, analisando a estabilidade dessas órbitas periódicas, provar o alinhamento dos camarões de mesmo período? Acreditamos que o estudo da estabilidade das órbitas periódicas pode nos levar a uma demostração rigorosa dessa característica para sistemas de codimensão 2.
5 264 Conclusões Para b > 3, e q = 0, situação para a qual o mapa não perturbado passa a apresentar comportamento caótico, aparece movimento periódico para determinados intervalos de b, denominados de janelas periódicas. Ao introduzirmos o termo perturbativo (q 0), as regiões no espaço de parâmetros para b > 3, 57, que apresentam comportamento periódico são prolongamentos das janelas periódicas. Ou seja, aparecem faixas cuja extremidade para q = 0 se localizam sobre as janelas periódicas. 9.5 O Circuito de Matsumoto Da mesma maneira que decidimos iniciar o nosso trabalho perturbando o mapa Logístico, devido a sua simplicidade matemática, escolhemos o circuito de Matsumoto por ser o circuito eletrônico mais simples de se montar entre os que apresentam movimento caótico [160]. Nesse circuito, a determinação dos pontos de equilíbrio pode ser realizada de maneira trivial, já que ele pode ser facilmente modelado por um sistema tridimensional de equações diferenciais de primeira ordem. Também toda a sua estrutura geométrica acaba sendo trivialmente determinada, analisando-se o fluxo ao redor desses pontos de equilíbrio, para diferentes valores de um parâmetro de controle, que nesse caso pode ser o valor de um dos componentes eletrônicos desse circuito. Esse circuito apresenta coexistência de atratores e consequêntemente diferentes bacias de atração. Em especial, um desses atratores, denominado de Double Scroll [12], tem uma característica própria de formação (para uma variação do parâmetro de controle), exposta a seguir. Dois pontos de equilíbrio sofrem bifurcação de Hopf e surgem então dois ciclos limites, cada um com a sua bacia de atração, o que faz com que dependendo da condição inicial, só possamos ver um desses ciclos limites. Esses ciclos vão sendo duplicados, via cenário de Feigenbaum, gerando dois atratores (coexistentes) espirais caóticos do tipo Rössler [43]. Quando as bacias desses atratores se tocam, os dois atratores se fundem dando origem ao Double Scroll. No entanto, nesse ponto, acontece a intermitência caos-caos [11], na qual existe uma predominância da trajetória permanecer em um dos dois atratores espirais. E essa predominância diminui com a variação do parâmetro considerado. Outra característica importante desse sistema é a existência da bifurcação de forquilha [28]. A caracterização do caos desse circuito foi feita determinando-se os coeficientes de Lyapunov e, através deles, a caoticidade desse sistema. Além disso, foi apresentado por Chua [12], uma prova da existência de caos baseada na existência de uma órbita homoclínica, o que
6 9.6 Circuito de Matsumoto Perturbado Senoidalmente 265 consequentemente mostraria a existência de um espaço topológico descrito pela ferradura de Smalle (mapa que descreve as propriedades de um atrator caótico). Para nós, esses fatores foram suficientes para considerar que este sistema é caótico. Entretanto, a rigor, devemos lembrar que a existência da órbita homoclínica só pode ser associada com a existência de comportamento caótico quando for provado que não há uma tangência homoclínica (apêndice A) [41], fato que parece existir no circuito de Matsumoto. A existência dessa tangência levaria o sistema a ser definido como um quasi-atrator, entidade que pode apresentar infinitas órbitas periódicas para uma infinitésima variação no parâmetro [41]. Entretanto, para o circuito de Matsumoto, a existência dessas infinitas órbitas periódicas não foi provada. Por enquanto, o que podemos dizer é que nem metricamente (através dos coeficientes de Lyapunov), nem topologicamente (existência da órbita homoclínica) há uma prova rigorosa de comportamento caótico no circuito de Matsumoto. Surge, então, a sugestão de aplicar a caracterização simbólica para essa demonstração, o que seria feito através da determinação da dinâmica simbólica das trajetórias do circuito de Matsumoto. A discussão, acerca da caoticidade do circuito de Matsumoto, vem da importância de podermos divulgar a existência de pelo menos um sistema real com uma prova irrefutável de comportamento caótico. Prova que por enquanto só pôde ser realizada no mapa de Hénon. 9.6 Circuito de Matsumoto Perturbado Senoidalmente No capítulo 6, foram analisadas oscilações do circuito de Matsumoto alteradas por uma perturbação senoidal. Na medida que estamos interessados em controlar esse circuito, consideramos não só a eliminação do caos por essa perturbação, mas também outros efeitos causados por ela. Queremos ainda enfatizar que perturbar um sistema qualquer usando uma onda senoidal é, em geral, simples, econômico e versátil. Esse aspecto realça a importância dos resultados obtidos. A introdução de uma perturbação senoidal, caracterizada pela sua frequência f e pela sua amplitude V g, no circuito de Matsumoto, tem um resultado imediato que é o surgimento de uma frequência a mais em relação as que haviam no circuito não perturbado. Com isso, o circuito perturbado pode passar a apresentar movimento em um toro de duas frequências (toro T 2 ). Uma frequência é a da perturbação f e a outra corresponde a frequência característica do circuito perturbado. Com o surgimento do toro T 2 o movimento passa a ser quasi-periódico ao invés de caótico.
7 266 Conclusões No entanto, sabemos que, além do movimento quasi-periódico em T 2, ocorre, para alguns valores do parâmetro de controle, movimento sincronizado ( phase-locked ) nesse mesmo toro. Uma rota para o caos, investigada nesta tese, é através da quebra desse toro T 2. Verificamos, para este caso, existir duas maneiras dinâmicas de ocorrer essa quebra. Uma maneira é abrupta, onde a destruição total do toro e o caos surgem através da variação infinitesimal de um parâmetro. Isso ocorre pelo surgimento de uma órbita homoclínica. A outra maneira é suave, onde o caos surge deixando o toro rugoso e dobrado, mas sem destruí-lo totalmente. Neste caso, a caoticidade (medida pelo coeficiente de Lyapunov) cresce suavemente com a variação de um parâmetro. Além disso, a determinação exata do valor do parâmetro em que acontece a quebra é difícil porque o caos surge e desaparece para variações ínfimas nesse parâmetro de controle. A caracterização dinâmica dessa quebra pôde ser realizada. Entretando, deixamos como um trabalho futuro a caracterização topológica dessas duas quebras. Sabemos que existem pontos sela-nó e sorvedouros no toro e que o surgimento do caos é determinado pela maneira como as variedades desses pontos se cruzam [76]. Mostramos na tese que os resultados através da simulação são coerentes com os resultados da experiência. Os fenômenos presentes no circuito perturbado podem ser bem descritos através da simulação. Para isso, iremos citá-los e, para uma clara identificação de como aparecem tais fenômenos, usamos o diagrama da figura Esse diagrama, como a maioria dos diagramas no espaço de parâmetros do capítulo 6, foi obtido usando o acumulador da equação 5.22 (capítulo 5). Esse acumulador determina, com uma determinada precisão, se a trajetória estudada é periódica, e o seu período p é fornecido pelo código que determina a função acumuladora. A determinação de órbitas periódicas pelo algorítmo do acumulador é muito mais precisa do que a obtida com o uso do cálculo do expoente de Lyapunov. Em vários testes realizados, a função acumuladora mostrou ser digna de confiança. A definição mostrada nos diagramas isoperiódicos desse capítulo, dificilmente seria obtida calculando-se o espectro de Lyapunov. Outra razão é que, o tempo de computação necessário para a obtenção de um diagrama isoperiódico, usando o cálculo do acumulador, é pelo menos quatro vezes menor do que o que seria necessário calculando o coeficiente de Lyapunov. Entretanto, a função acumuladora pode apresentar uma pequena falha quando a somatória no acumulador considerar um laço (o n da somatória, neste trabalho n=5) não muito grande. E a falha recai na determinação da posição exata das línguas de Arnold
8 9.7 Controle de Caos 267 nos diagramas (ver seção , figura 6.52). Porém, essa imprecisão só deixa incertezas quanto ao formato das bordas externas das línguas. Essa falha na determinação exata do formato das línguas de Arnold é devida ao fato de que a borda de uma língua de Arnold tem um número de rotação aproximadamente racional, fazendo com que um movimento quasi-periódico seja confundido com um movimento periódico. Para resolver esse problema teríamos que aumentar o valor de n e, portanto, o tempo de computação utilizado. No diagrama da figura 6.40, vemos uma grande ilha vermelha no centro deste. Esta ilha corresponde a um ciclo limite de período p=1 e é observada para grandes variações de frequência e amplitude. Nas bordas superiores dessa ilha aparecem as línguas de Arnold, também presentes nas bordas da maioria das ilhas periódicas desse diagrama. Nesse mesmo diagrama, para a região nas proximidades de f=0,3 (próximo à frequência característica f c 0,31), vemos que surgem várias regiões periódicas e regiões quasi-periódicas que podem ser identificadas na figura Isso leva-nos a uma conclusão quase esperada. Podemos eliminar o caos, no sistema de Matsumoto, aplicando uma perturbação com frequência f próxima da frequência característica f c. Frequências f muito acima da frequência f c têm pouco efeito no controle do circuito de Matsumoto. No diagrama da figura 6.40 há uma grande ilha negra, correspondente a uma região para a qual ocorre crise exterior e o atrator é destruído. Neste caso preferimos usar a nomenclatura atrator não finito. No entanto, apesar de pequena, há regiões periódicas presentes nessa ilha do atrator não finito. Caso identificado nos diagramas do mapa Logístico Perturbado (no capítulo 4 nas figuras 4.1, 4.2 e 4.3). Por fim, verificamos que estes diagramas não possuem estruturas fractais [10], [30]. Também não foram encontrados neste diagrama os camarões encontrados nos sistemas de codimensão dois [29], [10]. Entretanto, os camarões existem nos diagramas isoperiódicos do sistema de Matsumoto não perturbado. 9.7 Controle de Caos Mostramos, no capítulo 7, como o caos pode ser suprimido, controlado ou então obtido a partir de um comportamento não caótico. O trabalho referente aos capítulos em que perturbamos o mapa Logístico (capítulos 3, 4) e o circuito de Matsumoto (capítulo 6), pode ser colocado no âmbito do assunto do controle de caos, já que mostramos ser possível eliminar o caos desses sistemas através de perturbações periódicas. No caso do mapa Logístico Perturbado, a geração de caos foi
9 268 Conclusões investigada. Além desses resultados, o capítulo referênte ao direcionamento de trajetórias, onde mostramos como dirigir rapidamento uma trajetória de um sistema caótico para um determinado alvo, deve ser tratado como um tópico integrante do assunto controle de caos. Além desses resultados, aplicamos alguns métodos de controle de caos, que atualmente têm sido vastamente utilizados para aplicações tanto experimentais quanto teóricas. Usando o mapa Logístico, mostramos como a idéia de controle de caos pode ser aplicada perturbando-se o parâmetro de controle b do mapa, ou um parâmetro externo q, adicionado ao sistema [10]. Neste mapa apresentamos adaptações dos métodos de controle de Singer [101], OGY [21], Sinha [127] e Pyragas [90] e, por último, aplicamos o método de Hübbler [89]. Aplicamos o método de Romeiras [117], que é uma generalização do método OGY, ao mapa de Hénon. Esse método foi usado para controlar uma órbita periódica criada para aplicar o nosso método de direcionamento [20] (método apresentado no capítulo 8). Quanto ao sistema de Matsumoto, mostramos como estabilizar uma trajetória periódica aplicando o método OGY [21], e o método de Pyragas [90], [110]. Aplicamos também o método de Sinha [127], para direcionar a trajetória para um ponto de equilíbrio, e o método OPCL [131], para fazer a trajetória do sistema de Matsumoto ser trasferida de um atrator a outro, entre os cinco que coexistem para os parâmetros escolhidos. Devemos salientar que todos os métodos de controle usados neste capítulo usam perturbações lineares e consideram somente um parâmetro a ser perturbado. Entretanto, esses métodos apresentaram resultados satisfatórios para o controle de comportamento caótico dos sistemas considerados. Outros métodos, não aplicados, foram mencionados no decorrer e, principalmente, no final do capítulo. Entre eles citamos métodos que consideram perturbações não lineares [150], [143] ou a perturbação conjunta de mais de um parâmetro [121]. 9.8 Direcionamento de Trajetórias No capítulo 8, nós mostramos que as trajetórias do mapa Logístico, do mapa de Hénon e do sistema de Matsumoto podem ser rapidamente dirigidas de uma posição inicial para um alvo previamente escolhido, aplicando uma sequência de N perturbações constantes em um parâmetro de controle. Nesse método, o parâmetro genérico p assume apenas valores constantes. Neste trabalho, foram considerados somente três valores para o parâmetro de controle: p 0 + δ, p 0 δ e p 0, δ sendo a amplitude da perturbação [20].
10 9.8 Direcionamento de Trajetórias 269 Para determinar a sequência de N perturbações que devem ser aplicadas ao parâmetro, para dirigir a trajetória do ponto inicial para o alvo, uma grande quantidade de memória é necessária. Para evitar esse problema, nós desenvolvemos um método numérico que requer apenas os 3 N pontos que são gerados na (última) iteração N. A sequência escolhida (responsável por fazer o alvo ser atingido) entre as outras 3 N possibilidades, pode não ser única. Entretanto, qualquer uma das sequências faz a trajetória evoluir ao longo da variedade estável do alvo (figura 8.9). O método pode ser experimentalmente aplicado, como mostrado usando o mapa Logístico Perturbado com um ruído (seção 8.2.2). Usando o método de direcionamento, nós podemos criar novas órbitas periódicas que não estão presentes no atrator do sistema não perturbado. Embora essas novas órbitas sejam instáveis, sua estabilização é possível aplicando o método OGY [21] de controle. O método de direcionamento foi aplicado ao sistema de Matsumoto, um sistema de equações tridimensional, sem que esse sistema fosse unidimensionalmente modelado. Algumas adaptações, ao uso inicial (em mapas) do método, foram introduzidas, como o número N de perturbações que deve ser estimado previamente. A relevância de termos aplicado este método a um sistema com mais de uma dimensão, é que isso não é possível nos métodos de direcionamento tradicionais [22], [23], [24]. Para simular um experimento real, nós não ajustamos a condição inicial como pode ser feito quando se trabalha numericamente com um sistema de equações. Entretanto, antes de aplicar nosso método de direcionamento, o sistema precisa ser dirigido para uma determinada trajetória. Então, para isso, uma perturbação senoidal ressonante foi aplicada ao sistema (como feito no capítulo 6), de maneira que a trajetória se comporte periodicamente via sincronização e, então, nós consideramos o ponto inicial como o cruzamento entre a trajetória periódica e alguma seção de Poincaré escolhida (nesta tese a seção escolhida foi aquela com V C1 =-1,5). Para melhorar a performance do método de controle OGY, nós podemos aplicar nosso método de direcionamento. Como o método OGY requer que a trajetória se aproxime da órbita periódica a ser controlada (fato que pode levar algum tempo), nós usamos nosso método para dirigir rapidamente a trajetória do sistema para um ponto localizado nas vizinhanças da órbita periódica escolhida.
11 270 Conclusões
Analisa-se agora o comportamento dinâmico da estrutura sob uma carga harmônica vertical da forma:
 5 Vibração Forçada 5.1 Equações de movimento com carga harmônica Analisa-se agora o comportamento dinâmico da estrutura sob uma carga harmônica vertical da forma: = (Ω ), (5.1) onde é a magnitude da força
5 Vibração Forçada 5.1 Equações de movimento com carga harmônica Analisa-se agora o comportamento dinâmico da estrutura sob uma carga harmônica vertical da forma: = (Ω ), (5.1) onde é a magnitude da força
IV Rotas para o Caos. E-Crises
 IV Rotas para o Caos E-Crises 1-Introdução Mudança abrupta no atrator em um parâmetro crítico. Crises em mapas bidimensionais Crises em sistemas tridimensionais de equações diferenciais 2-Variedades Alterações
IV Rotas para o Caos E-Crises 1-Introdução Mudança abrupta no atrator em um parâmetro crítico. Crises em mapas bidimensionais Crises em sistemas tridimensionais de equações diferenciais 2-Variedades Alterações
Cenário de Ruelle-Takens via Quase-Periodicidade. Iberê L. Caldas Abril de 2009
 Cenário de Ruelle-Takens via Quase-Periodicidade Iberê L. Caldas Abril de 2009 Índice I- Cenário de Landau II- Mapa do Círculo III- Cenário de Ruelle-Takens IV- Janelas Periódicas I- Cenário de Landau
Cenário de Ruelle-Takens via Quase-Periodicidade Iberê L. Caldas Abril de 2009 Índice I- Cenário de Landau II- Mapa do Círculo III- Cenário de Ruelle-Takens IV- Janelas Periódicas I- Cenário de Landau
Caos em Equações Diferenciais. Referência Principal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Springer (1997)
 aos em Equações Diferenciais Referência Principal: haos K. Alligood, T. D. Sauer, J. A. Yorke Springer (997) onvecção em um gradiente de temperatura haos Alligood et al. Sistema de Lorenz x - σ y z - x
aos em Equações Diferenciais Referência Principal: haos K. Alligood, T. D. Sauer, J. A. Yorke Springer (997) onvecção em um gradiente de temperatura haos Alligood et al. Sistema de Lorenz x - σ y z - x
5. ANÁLISE NÃO LINEAR.
 5. ANÁLISE NÃO LINEAR. Após a análise linear, apresentada no capítulo anterior, este capítulo investiga a influência da não linearidade geométrica da estrutura no seu comportamento dinâmico sob cargas
5. ANÁLISE NÃO LINEAR. Após a análise linear, apresentada no capítulo anterior, este capítulo investiga a influência da não linearidade geométrica da estrutura no seu comportamento dinâmico sob cargas
X - Variedades Estáveis e Crises. Referência Principal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Springer (1997)
 X - Variedades Estáveis e Crises Referência Principal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Springer (1997) 1- Introdução Variedade estável (instável): conjunto de pontos iniciais que convergem
X - Variedades Estáveis e Crises Referência Principal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Springer (1997) 1- Introdução Variedade estável (instável): conjunto de pontos iniciais que convergem
Sistemas caóticos simples
 Sistemas caóticos simples Aluna: Simone Bochner de Araújo Orientadora: Celia Anteneodo Introdução Uma grande variedade de sistemas apresenta comportamentos complicados, irregulares, imprevisíveis, em maior
Sistemas caóticos simples Aluna: Simone Bochner de Araújo Orientadora: Celia Anteneodo Introdução Uma grande variedade de sistemas apresenta comportamentos complicados, irregulares, imprevisíveis, em maior
DAFIS/DAQBI - PPGFCET. Sistemas Complexos. [ M.S. Freitas / UTFPR ] Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS.
![DAFIS/DAQBI - PPGFCET. Sistemas Complexos. [ M.S. Freitas / UTFPR ] Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS. DAFIS/DAQBI - PPGFCET. Sistemas Complexos. [ M.S. Freitas / UTFPR ] Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS.](/thumbs/99/141975218.jpg) DAFIS/DAQBI - PPGFCET Sistemas Complexos Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS msergio58@gmail.com [ M.S. Freitas / UTFPR ] Ementa 0 INTRODUÇÃO 1 REDES BOOLEANAS E AUTÔMATOS CELULARES 2 AUTOSSIMILARIDADE
DAFIS/DAQBI - PPGFCET Sistemas Complexos Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS msergio58@gmail.com [ M.S. Freitas / UTFPR ] Ementa 0 INTRODUÇÃO 1 REDES BOOLEANAS E AUTÔMATOS CELULARES 2 AUTOSSIMILARIDADE
II- Mapas Bidimensionais. Referência: Chaos, K. Alligood, T. D. Sauer, J. A. Yorke; Springer (1997).
 II- Mapas Bidimensionais Referência: Chaos, K. Alligood, T. D. Sauer, J. A. Yorke; Springer (997). - Novas CaracterísMcas Dinâmicas Além de pontos fixos, há pontos de selas. Ponto de sela: contração em
II- Mapas Bidimensionais Referência: Chaos, K. Alligood, T. D. Sauer, J. A. Yorke; Springer (997). - Novas CaracterísMcas Dinâmicas Além de pontos fixos, há pontos de selas. Ponto de sela: contração em
Capítulo 3. Intermitência Tipo III. 3.1 Forma Normal
 Capítulo 3 Intermitência Tipo III 3.1 Forma Normal A intermitência classificada por Pomeau e Manneville como tipo III pode ser associada a um mapa discreto da forma x n+1 = (1 + ɛ )x n + α x 2 n + η x
Capítulo 3 Intermitência Tipo III 3.1 Forma Normal A intermitência classificada por Pomeau e Manneville como tipo III pode ser associada a um mapa discreto da forma x n+1 = (1 + ɛ )x n + α x 2 n + η x
Evidências Experimentais. Iberê L. Caldas
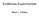 Evidências Experimentais Iberê L. Caldas Sumário I - Torneira Gotejante II - Convecção de Rayleigh-Bénard III Fluido em Rotação IV Reação Química I - Evidências Experimentais de Crises Laboratório de Fenômenos
Evidências Experimentais Iberê L. Caldas Sumário I - Torneira Gotejante II - Convecção de Rayleigh-Bénard III Fluido em Rotação IV Reação Química I - Evidências Experimentais de Crises Laboratório de Fenômenos
Um Estudo da Dinâmica da Equação Logística
 Um Estudo da Dinâmica da Equação Logística Conconi, T.; Silva Lima, M.F. Resumo: Equações diferenciais são adequadas para representar sistemas discretos por grandezas cujos valores variam apenas em determinados
Um Estudo da Dinâmica da Equação Logística Conconi, T.; Silva Lima, M.F. Resumo: Equações diferenciais são adequadas para representar sistemas discretos por grandezas cujos valores variam apenas em determinados
Carlos A. C. Jousseph
 Carlos A. C. Jousseph Universidade Tecnológica Federal do Paraná Campus Medianeira - Departamento Acadêmico de Física 27 de janeiro de 2017 Conteúdo q Características q Introdução Teórica Ø Sistemas Discretos
Carlos A. C. Jousseph Universidade Tecnológica Federal do Paraná Campus Medianeira - Departamento Acadêmico de Física 27 de janeiro de 2017 Conteúdo q Características q Introdução Teórica Ø Sistemas Discretos
Física no computador. Marcio Argollo de Menezes UFF Niterói
 Física no computador Marcio Argollo de Menezes UFF Niterói ... não se pode provar tudo...... determinismo não é previsibilidade! ... não se pode provar tudo... Automata celulares Números no computador
Física no computador Marcio Argollo de Menezes UFF Niterói ... não se pode provar tudo...... determinismo não é previsibilidade! ... não se pode provar tudo... Automata celulares Números no computador
Considerações sobre a Condição Inicial na Construção do Diagrama de Bifurcação para o Mapa Logístico
 Trabalho apresentado no DINCON, Natal - RN, 2015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Considerações sobre a Condição Inicial na Construção do Diagrama de
Trabalho apresentado no DINCON, Natal - RN, 2015. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics Considerações sobre a Condição Inicial na Construção do Diagrama de
Multi-Estabilidade, Diagramas de Fase e Propriedades Estatísticas do Rotor Quicado: Um Mapa Onde Coexistem Muitos Atratores
 Multi-Estabilidade, Diagramas de Fase e Propriedades Estatísticas do Rotor Quicado: Um Mapa Onde Coexistem Muitos Atratores Luciano Camargo Martins Jason Alfredo Carlson Gallas IF-UFRGS 91501-970 Porto
Multi-Estabilidade, Diagramas de Fase e Propriedades Estatísticas do Rotor Quicado: Um Mapa Onde Coexistem Muitos Atratores Luciano Camargo Martins Jason Alfredo Carlson Gallas IF-UFRGS 91501-970 Porto
VII Exemplos de Atratores Estranhos
 VII Exemplos de Atratores Estranhos VII Sistema de Lorenz Primeira Parte onvecção de Rayleigh-Bernard Equação de Navier-Stokes r dv r r r ρ = F p + µ 2 v dt dt dt = κ 2 T Equação de ondução do alor Equação
VII Exemplos de Atratores Estranhos VII Sistema de Lorenz Primeira Parte onvecção de Rayleigh-Bernard Equação de Navier-Stokes r dv r r r ρ = F p + µ 2 v dt dt dt = κ 2 T Equação de ondução do alor Equação
Universalidade. 1.1 Universalidade Estrutural
 Capítulo 1 Universalidade Vimos que os dois sistemas dinâmicos tratados antes (sistemas de equações diferenciais e mapas discretos) podem apresentar um comportamento qualitativo comum: uma série de sucessivas
Capítulo 1 Universalidade Vimos que os dois sistemas dinâmicos tratados antes (sistemas de equações diferenciais e mapas discretos) podem apresentar um comportamento qualitativo comum: uma série de sucessivas
6 Integridade de sistemas não-lineares
 6 Integridade de sistemas não-lineares A avaliação da integridade de uma solução estável (estática ou dinâmica) de um sistema dinâmico não-linear consiste no conhecimento do seu comportamento quando o
6 Integridade de sistemas não-lineares A avaliação da integridade de uma solução estável (estática ou dinâmica) de um sistema dinâmico não-linear consiste no conhecimento do seu comportamento quando o
Análise de Mapeamentos Não Lineares e Aplicações
 UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA Tese de Doutorado Análise de Mapeamentos Não Lineares e Aplicações Wilson Luiz da Costa Façanha Orientador: Prof. Dr. Iberê Luiz Caldas Tese de Doutorado submetida
UNIVERSIDADE DE SÃO PAULO INSTITUTO DE FÍSICA Tese de Doutorado Análise de Mapeamentos Não Lineares e Aplicações Wilson Luiz da Costa Façanha Orientador: Prof. Dr. Iberê Luiz Caldas Tese de Doutorado submetida
5 Análise Dinâmica da Estabilidade
 5 Análise Dinâmica da Estabilidade Neste capítulo é analisado o comportamento dinâmico não-linear da torre estaiada, considerando os modelos apresentados nos capítulos anteriores. Especial atenção é dada
5 Análise Dinâmica da Estabilidade Neste capítulo é analisado o comportamento dinâmico não-linear da torre estaiada, considerando os modelos apresentados nos capítulos anteriores. Especial atenção é dada
Diagramas no Espaço de Parâmetros do Mapa Logístico Perturbado e sua Estabilidade
 Capítulo Diagramas no Espaço de Parâmetros do Mapa Logístico Perturado e sua Estailidade No capítulo, apresentamos o mapa Logístico Perturado analisando vários de seus fenômenos. Através de diagramas de
Capítulo Diagramas no Espaço de Parâmetros do Mapa Logístico Perturado e sua Estailidade No capítulo, apresentamos o mapa Logístico Perturado analisando vários de seus fenômenos. Através de diagramas de
MAT001 Cálculo Diferencial e Integral I
 1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
PGF Mecânica Clássica Prof. Iberê L. Caldas
 PGF 55 - Mecânica Clássica Prof. Iberê L. Caldas Terceiro Estudo Dirigido o semestre de 18 Os estudos dirigidos podem ser realizados em duplas. Apenas os exercícios marcados com asteriscos precisam ser
PGF 55 - Mecânica Clássica Prof. Iberê L. Caldas Terceiro Estudo Dirigido o semestre de 18 Os estudos dirigidos podem ser realizados em duplas. Apenas os exercícios marcados com asteriscos precisam ser
Aula 4 - Experiência 1 Circuitos CA e Caos 2013
 Prof. Antonio Domingues dos Santos adsantos@if.usp.br Ramal: 6886 Mário Schemberg, sala 205 Prof. Leandro Barbosa lbarbosa@if.usp.br Ramal: 7157 Ala1, sala 225 Aula 4 - Experiência 1 Circuitos CA e Caos
Prof. Antonio Domingues dos Santos adsantos@if.usp.br Ramal: 6886 Mário Schemberg, sala 205 Prof. Leandro Barbosa lbarbosa@if.usp.br Ramal: 7157 Ala1, sala 225 Aula 4 - Experiência 1 Circuitos CA e Caos
Notas de Aula - Parte 6. Estabilidade Estrutural e Bifurcações
 FGE417- Fenômenos Não-Lineares em Física: Introdução ao Caos Determinístico e aos Sistemas Dinâmicos Prof. Reynaldo Daniel Pinto Notas de Aula - Parte 6 Estabilidade Estrutural e Bifurcações 1972 - René
FGE417- Fenômenos Não-Lineares em Física: Introdução ao Caos Determinístico e aos Sistemas Dinâmicos Prof. Reynaldo Daniel Pinto Notas de Aula - Parte 6 Estabilidade Estrutural e Bifurcações 1972 - René
período em um laser de semicondutor com
 Horizontes de acumulação e adição de período em um laser de semicondutor com injeção óptica 1/ 22 Horizontes de acumulação e adição de período em um laser de semicondutor com injeção óptica e Jason Gallas
Horizontes de acumulação e adição de período em um laser de semicondutor com injeção óptica 1/ 22 Horizontes de acumulação e adição de período em um laser de semicondutor com injeção óptica e Jason Gallas
na Órbita Terrestre: um Estudo do Caos Thales Agricola Instituto de Física UFRJ
 1 Introdução A Influência de Júpiter na Órbita Terrestre: um Estudo do Caos Thales Agricola Instituto de Física UFRJ Investigar o movimento da Terra ( ) quando submetida aos campos gravitacionais do Sol
1 Introdução A Influência de Júpiter na Órbita Terrestre: um Estudo do Caos Thales Agricola Instituto de Física UFRJ Investigar o movimento da Terra ( ) quando submetida aos campos gravitacionais do Sol
étodos uméricos AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
étodos uméricos AJUSTE DE FUNÇÕES Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA UNIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
Introdução à Neurociência Computacional (Graduação) Prof. Antônio Roque Aula 6
 Variações do modelo integra-e-dispara Nesta aula vamos apresentar algumas variações do modelo LIF visto na aula passada. Modelo integra-e-dispara com adaptação Estudos in vitro mostram que muitos tipos
Variações do modelo integra-e-dispara Nesta aula vamos apresentar algumas variações do modelo LIF visto na aula passada. Modelo integra-e-dispara com adaptação Estudos in vitro mostram que muitos tipos
Experimento 7. Circuitos RC e filtros de frequência. 7.1 Material. 7.2 Introdução. Gerador de funções; osciloscópio;
 Experimento 7 Circuitos RC e filtros de frequência 7.1 Material Gerador de funções; osciloscópio; multímetros digitais (de mão e de bancada); resistor de 1 kω; capacitor de 100 nf. 7.2 Introdução Vimos
Experimento 7 Circuitos RC e filtros de frequência 7.1 Material Gerador de funções; osciloscópio; multímetros digitais (de mão e de bancada); resistor de 1 kω; capacitor de 100 nf. 7.2 Introdução Vimos
Controle de Caos e Saltos entre Atratores em um Sistema com Impactos
 Universidade de São Paulo Instituto de Física Controle de Caos e Saltos entre Atratores em um Sistema com Impactos Everton Santos Medeiros Orientador: Prof. Dr. Iberê Luiz Caldas Dissertação de mestrado
Universidade de São Paulo Instituto de Física Controle de Caos e Saltos entre Atratores em um Sistema com Impactos Everton Santos Medeiros Orientador: Prof. Dr. Iberê Luiz Caldas Dissertação de mestrado
5 Formulação Dinâmica Não Linear no Domínio da Frequência
 129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
129 5 Formulação Dinâmica Não Linear no Domínio da Frequência No Capítulo 2, foram apresentadas as formulações para a análise dinâmica de estruturas reticuladas no domínio do tempo, sendo uma informação
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 04/2014 Zeros reais de funções Parte 1 Objetivo Determinar valores aproximados para as soluções (raízes) de equações da
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 04/2014 Zeros reais de funções Parte 1 Objetivo Determinar valores aproximados para as soluções (raízes) de equações da
Bifurcações da região de estabilidade de sistemas dinâmicos autônomos não lineares: Bifurcação Sela-Nó do Tipo-1
 Bifurcações da região de estabilidade de sistemas dinâmicos autônomos não lineares: Bifurcação Sela-Nó do Tipo-1 Fabíolo Moraes Amaral Departamento de Ensino, IFBA Campus Eunápolis 45.822-000, Eunápolis,
Bifurcações da região de estabilidade de sistemas dinâmicos autônomos não lineares: Bifurcação Sela-Nó do Tipo-1 Fabíolo Moraes Amaral Departamento de Ensino, IFBA Campus Eunápolis 45.822-000, Eunápolis,
Kátia Slodkowski Clerici 2, Cássio L. M. Belusso 3. Projeto de pesquisa PRO-ICT/UFFS 2. Acadêmica do curso de Física da UFFS Campus Cerro Largo 3
 DETECÇÃO DE COMPORTAMENTO REGULAR E CAÓTICO EM UM PULVERIZADOR DE POMARES TIPO TORRE UTILIZANDO DIAGRAMAS DE BIFURCAÇÃO 1 ON APPEARANCE OF REGULAR AND CHAOTIC BEHAVIOR ON THE TOWER ORCHARD SPRAYER USING
DETECÇÃO DE COMPORTAMENTO REGULAR E CAÓTICO EM UM PULVERIZADOR DE POMARES TIPO TORRE UTILIZANDO DIAGRAMAS DE BIFURCAÇÃO 1 ON APPEARANCE OF REGULAR AND CHAOTIC BEHAVIOR ON THE TOWER ORCHARD SPRAYER USING
6 Exemplos Numéricos no Domínio da Frequência
 145 6 Exemplos Numéricos no Domínio da Frequência Neste Capítulo são apresentados exemplos numéricos para validar a formulação apresentada no Capítulo 5, assim como estudar a resposta em frequência de
145 6 Exemplos Numéricos no Domínio da Frequência Neste Capítulo são apresentados exemplos numéricos para validar a formulação apresentada no Capítulo 5, assim como estudar a resposta em frequência de
Circuitos RC e filtros de frequência. 6.1 Material. resistor de 1 kω; capacitor de 100 nf.
 Circuitos RC e filtros de frequência 6 6. Material resistor de kω; capacitor de 00 nf. 6.2 Introdução Vimos que a reatância capacitiva depende da frequência: quanto maior a frequência do sinal que alimenta
Circuitos RC e filtros de frequência 6 6. Material resistor de kω; capacitor de 00 nf. 6.2 Introdução Vimos que a reatância capacitiva depende da frequência: quanto maior a frequência do sinal que alimenta
6 Análise de Sensibilidade do Método LSM
 Análise de Sensibilidade do Método LSM 72 6 Análise de Sensibilidade do Método LSM Para fazer uma análise de sensibilidade do método LSM, tomamos como base exemplos de call e put americanas 1. Para os
Análise de Sensibilidade do Método LSM 72 6 Análise de Sensibilidade do Método LSM Para fazer uma análise de sensibilidade do método LSM, tomamos como base exemplos de call e put americanas 1. Para os
Caos. Apresentado na disciplina Mecânica Cássica (PGF 5005) IFUSP. Iberê L. Caldas
 Caos Iberê L. Caldas Apresentado na disciplina Mecânica Cássica (PGF 5005) IFUSP Caos na Mecânica Clássica Criação da Mecânica. Determinismo. Sensibilidade às condições iniciais. Indeterminismo clássico.
Caos Iberê L. Caldas Apresentado na disciplina Mecânica Cássica (PGF 5005) IFUSP Caos na Mecânica Clássica Criação da Mecânica. Determinismo. Sensibilidade às condições iniciais. Indeterminismo clássico.
5 Resultados Dados artificiais Convergência à mediana e à média com dados artificiais
 5 Resultados Os resultados da aplicação do método proposto estão estruturados de forma a evidenciar: 1. A convergência numérica do algoritmo proposto nesta tese para a mediana e para a média de grupos
5 Resultados Os resultados da aplicação do método proposto estão estruturados de forma a evidenciar: 1. A convergência numérica do algoritmo proposto nesta tese para a mediana e para a média de grupos
Rotor Não Axissimétrico
 104 6 Vídeo e simulação Neste Capítulo comparam-se os resultados numéricos em um ambiente virtual e os vídeos do giroscópio que foram gravados no laboratório. É um método qualitativo de avaliação do modelo
104 6 Vídeo e simulação Neste Capítulo comparam-se os resultados numéricos em um ambiente virtual e os vídeos do giroscópio que foram gravados no laboratório. É um método qualitativo de avaliação do modelo
Bifurcações de Sistemas Dinâmicos Planares e Aplicações em Sistemas de Potência
 Bifurcações de sistemas dinâmicos planares e aplicações em sistemas de potência 1 Bifurcações de Sistemas Dinâmicos Planares e Aplicações em Sistemas de Potência 1. Introdução O estudo global das curvas
Bifurcações de sistemas dinâmicos planares e aplicações em sistemas de potência 1 Bifurcações de Sistemas Dinâmicos Planares e Aplicações em Sistemas de Potência 1. Introdução O estudo global das curvas
Circuitos RC e filtros de frequência. 7.1 Material
 Circuitos RC e filtros de frequência 7 7. Material Gerador de funções; osciloscópio; multímetros digitais (de mão e de bancada); resistor de kω; capacitor de 00 nf. 7.2 Introdução Vimos que a reatância
Circuitos RC e filtros de frequência 7 7. Material Gerador de funções; osciloscópio; multímetros digitais (de mão e de bancada); resistor de kω; capacitor de 00 nf. 7.2 Introdução Vimos que a reatância
Sinais e Sistemas. Tempo para Sistemas Lineares Invariantes no Tempo. Representações em Domínio do. Profª Sandra Mara Torres Müller.
 Sinais e Sistemas Representações em Domínio do Tempo para Sistemas Lineares Invariantes no Tempo Profª Sandra Mara Torres Müller Aula 7 Representações em Domínio do Tempo para Sistemas Lineares e Invariantes
Sinais e Sistemas Representações em Domínio do Tempo para Sistemas Lineares Invariantes no Tempo Profª Sandra Mara Torres Müller Aula 7 Representações em Domínio do Tempo para Sistemas Lineares e Invariantes
Velocidade de uma reação
 Velocidade de uma reação A + 2B 3P Vale lembrar que a lei de velocidade não tem nada a ver com a estequiometria da reação. Cinética de primeira ordem Integrando ln [A] = kt + Se t = 0 temos [A] = [A] 0
Velocidade de uma reação A + 2B 3P Vale lembrar que a lei de velocidade não tem nada a ver com a estequiometria da reação. Cinética de primeira ordem Integrando ln [A] = kt + Se t = 0 temos [A] = [A] 0
5.1. Aspectos gerais Aspectos gerais
 181 5. Análise do movimento acoplado de barras com imperfeições geométricas iniciais Análise do movimento acoplado de barras com imperfeições geométricas iniciais Perfeição significa o constante empenho
181 5. Análise do movimento acoplado de barras com imperfeições geométricas iniciais Análise do movimento acoplado de barras com imperfeições geométricas iniciais Perfeição significa o constante empenho
Resumo das aulas dos dias 4 e 11 de abril e exercícios sugeridos
 MAT 1351 Cálculo para funções uma variável real I Curso noturno de Licenciatura em Matemática 1 semestre de 2016 Docente: Prof. Dr. Pierluigi Benevieri Resumo das aulas dos dias 4 e 11 de abril e exercícios
MAT 1351 Cálculo para funções uma variável real I Curso noturno de Licenciatura em Matemática 1 semestre de 2016 Docente: Prof. Dr. Pierluigi Benevieri Resumo das aulas dos dias 4 e 11 de abril e exercícios
Comportamento caótico em um circuito RLC não-linear
 Comportamento caótico em um circuito RLC não-linear N. Carlin, E.M. Szanto, W.A. Seale, F.O. Jorge, F.A. Souza, I.H. Bechtold e L.R. Gasques Instituto de Física, Universidade de São Paulo, Caixa Postal
Comportamento caótico em um circuito RLC não-linear N. Carlin, E.M. Szanto, W.A. Seale, F.O. Jorge, F.A. Souza, I.H. Bechtold e L.R. Gasques Instituto de Física, Universidade de São Paulo, Caixa Postal
Instituto de Física - USP FGE Laboratório de Física III - LabFlex
 Instituto de Física - USP FGE0213 - Laboratório de Física III - LabFlex Aula 2 Curvas Características Potência e temperatura de uma lâmpada de filamento Manfredo H. Tabacniks agosto 2007 3 assuntos a serem
Instituto de Física - USP FGE0213 - Laboratório de Física III - LabFlex Aula 2 Curvas Características Potência e temperatura de uma lâmpada de filamento Manfredo H. Tabacniks agosto 2007 3 assuntos a serem
CAPÍTULO 4 - ANÁLISE DA RESPOSTA EM FREQÜÊNCIA
 CAPÍTULO 4 - ANÁLISE DA RESPOSTA EM FREQÜÊNCIA 4.. Introdução Pelo termo resposta em freqüência, entende-se a resposta em regime estacionário de um sistema com entrada senoidal. Nos métodos de resposta
CAPÍTULO 4 - ANÁLISE DA RESPOSTA EM FREQÜÊNCIA 4.. Introdução Pelo termo resposta em freqüência, entende-se a resposta em regime estacionário de um sistema com entrada senoidal. Nos métodos de resposta
4 Cálculo de Equivalentes Dinâmicos
 4 Cálculo de Equivalentes Dinâmicos 4.1 Introdução O crescimento do sistema de energia elétrica, o aumento do número de interligações e a sofisticação dos modelos para representação dos componentes de
4 Cálculo de Equivalentes Dinâmicos 4.1 Introdução O crescimento do sistema de energia elétrica, o aumento do número de interligações e a sofisticação dos modelos para representação dos componentes de
MÉTODOS NEWTON E QUASE-NEWTON PARA OTIMIZAÇÃO IRRESTRITA
 MÉTODOS NEWTON E QUASE-NEWTON PARA OTIMIZAÇÃO IRRESTRITA Marlon Luiz Dal Pasquale Junior, UNESPAR/FECILCAM, jr.marlon@hotmail.com Solange Regina dos Santos (OR), UNESPAR/FECILCAM, solaregina@fecilcam.br
MÉTODOS NEWTON E QUASE-NEWTON PARA OTIMIZAÇÃO IRRESTRITA Marlon Luiz Dal Pasquale Junior, UNESPAR/FECILCAM, jr.marlon@hotmail.com Solange Regina dos Santos (OR), UNESPAR/FECILCAM, solaregina@fecilcam.br
3 Identificação de Locutor Usando Técnicas de Múltiplos Classificadores em Sub-bandas Com Pesos Não-Uniformes
 3 Identificação de Locutor Usando Técnicas de Múltiplos Classificadores em Sub-bandas Com Pesos Não-Uniformes Neste capítulo, é apresentada uma nova proposta de combinação de múltiplos classificadores
3 Identificação de Locutor Usando Técnicas de Múltiplos Classificadores em Sub-bandas Com Pesos Não-Uniformes Neste capítulo, é apresentada uma nova proposta de combinação de múltiplos classificadores
MODELAGEM DE UM OSCILADOR NÃO LINEAR OBSERVADO NOS CURSOS DE FÍSICA BÁSICA.
 MODELAGEM DE UM OSCILADOR NÃO LINEAR OBSERVADO NOS CURSOS DE FÍSICA BÁSICA. 1 IFBA, campus Salvador. e-mail: rnaziazeno@ifba.edu.br 2 IFBA, campus Salvador. e-mail: nielsfl@ifba.edu.br 3 IFBA, campus Salvador.
MODELAGEM DE UM OSCILADOR NÃO LINEAR OBSERVADO NOS CURSOS DE FÍSICA BÁSICA. 1 IFBA, campus Salvador. e-mail: rnaziazeno@ifba.edu.br 2 IFBA, campus Salvador. e-mail: nielsfl@ifba.edu.br 3 IFBA, campus Salvador.
4 Cálculo de Equivalentes Dinâmicos
 4 Cálculo de Equivalentes Dinâmicos 4.1. Introdução Os sistemas de potência interligados vêm adquirindo maior tamanho e complexidade, aumentando a dependência de sistemas de controle tanto em operação
4 Cálculo de Equivalentes Dinâmicos 4.1. Introdução Os sistemas de potência interligados vêm adquirindo maior tamanho e complexidade, aumentando a dependência de sistemas de controle tanto em operação
Controle Não LInear. CEFET/RJ Centro Federal de Educação Tecnológica Celso Suckow da Fonseca Rio de Janeiro
 Controle Não LInear CEFET/RJ Centro Federal de Educação Tecnológica Celso Suckow da Fonseca Rio de Janeiro 1 2. SISTEMAS DE 2ª ORDEM 2.1. INTRODUÇÃO 2.2. ANÁLISE QUALITATIVA DOS SISTEMAS LINEARES 2.2.1.
Controle Não LInear CEFET/RJ Centro Federal de Educação Tecnológica Celso Suckow da Fonseca Rio de Janeiro 1 2. SISTEMAS DE 2ª ORDEM 2.1. INTRODUÇÃO 2.2. ANÁLISE QUALITATIVA DOS SISTEMAS LINEARES 2.2.1.
Estabilidade de tensão.. p.1/44
 Estabilidade de tensão p/44 Característica do fenômeno Fenômeno mais recente em sistemas muito carregados Associado ao esgotamento de fontes de potência reativa Caracterizado pela queda descontrolada da
Estabilidade de tensão p/44 Característica do fenômeno Fenômeno mais recente em sistemas muito carregados Associado ao esgotamento de fontes de potência reativa Caracterizado pela queda descontrolada da
2 Hiperbolicidade e estabilidade
 2 Hiperbolicidade e estabilidade Neste capítulo serão apresentados dois novos conceitos que são centrais neste trabalho: Estabilidade estrutural e difeomordfismos Morse-Smale. Para isso, será necessário
2 Hiperbolicidade e estabilidade Neste capítulo serão apresentados dois novos conceitos que são centrais neste trabalho: Estabilidade estrutural e difeomordfismos Morse-Smale. Para isso, será necessário
Pequenas oscilações TÓPICOS FUNDAMENTAIS DE FÍSICA
 Pequenas oscilações 5 - Oscilações TÓPICOS FUNDAMENTAIS DE FÍSICA Aplicações em Acústica, espectros moleculares, vibrações em mecanismos, circuitos elétricos acoplados, etc. Se os desvios do equilíbrio
Pequenas oscilações 5 - Oscilações TÓPICOS FUNDAMENTAIS DE FÍSICA Aplicações em Acústica, espectros moleculares, vibrações em mecanismos, circuitos elétricos acoplados, etc. Se os desvios do equilíbrio
Modelos de Regressão Linear Simples parte I
 Modelos de Regressão Linear Simples parte I Erica Castilho Rodrigues 27 de Setembro de 2017 1 2 Objetivos Ao final deste capítulo você deve ser capaz de: Usar modelos de regressão para construir modelos
Modelos de Regressão Linear Simples parte I Erica Castilho Rodrigues 27 de Setembro de 2017 1 2 Objetivos Ao final deste capítulo você deve ser capaz de: Usar modelos de regressão para construir modelos
PGF Mecânica Clássica Prof. Iberê L. Caldas
 PGF 5005 - Mecânica Clássica Prof Iberê L Caldas Quarto Estudo Dirigido o semestre de 08 Os estudos dirigidos podem ser realizados em duplas Apenas os exercícios marcados com asteriscos precisam ser entregues
PGF 5005 - Mecânica Clássica Prof Iberê L Caldas Quarto Estudo Dirigido o semestre de 08 Os estudos dirigidos podem ser realizados em duplas Apenas os exercícios marcados com asteriscos precisam ser entregues
 Determinismo: Indeterminismo: Existem eventos futuros que não estão pré-estabelecidos, ou o futuro não está fixado, é aberto. Mesmo que o futuro esteja determinado, pode nos ser incerto. Certeza (ou incerteza)
Determinismo: Indeterminismo: Existem eventos futuros que não estão pré-estabelecidos, ou o futuro não está fixado, é aberto. Mesmo que o futuro esteja determinado, pode nos ser incerto. Certeza (ou incerteza)
Modelos de Regressão Linear Simples - parte I
 Modelos de Regressão Linear Simples - parte I Erica Castilho Rodrigues 19 de Agosto de 2014 Introdução 3 Objetivos Ao final deste capítulo você deve ser capaz de: Usar modelos de regressão para construir
Modelos de Regressão Linear Simples - parte I Erica Castilho Rodrigues 19 de Agosto de 2014 Introdução 3 Objetivos Ao final deste capítulo você deve ser capaz de: Usar modelos de regressão para construir
Trabalho 5 Métodos Computacionais da Física B
 Trabalho 5 Métodos Computacionais da Física B Esteban Gerling - 00231223 12 de julho de 2016 Introdução Este trabalho é sobre o estudo de um mapa, em específico sobre o mapa de Arnold tongue[1] descrito
Trabalho 5 Métodos Computacionais da Física B Esteban Gerling - 00231223 12 de julho de 2016 Introdução Este trabalho é sobre o estudo de um mapa, em específico sobre o mapa de Arnold tongue[1] descrito
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 8 04/2014 Zeros reais de funções Parte 2 Voltando ao exemplo da aula anterior, vemos que o ponto médio da primeira iteração
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 8 04/2014 Zeros reais de funções Parte 2 Voltando ao exemplo da aula anterior, vemos que o ponto médio da primeira iteração
EXPERIÊNCIA 08 CIRCUITOS COM AMPLIFICADORES OPERACIONAIS ELABORAÇÃO: PROFS ARIANA S. e VITOR N.
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia de Sistemas Eletrônicos PSI - EPUSP PSI 3212 - LABORATÓRIO DE CIRCUITOS ELÉTRICOS EXPERIÊNCIA 08 CIRCUITOS COM AMPLIFICADORES
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia de Sistemas Eletrônicos PSI - EPUSP PSI 3212 - LABORATÓRIO DE CIRCUITOS ELÉTRICOS EXPERIÊNCIA 08 CIRCUITOS COM AMPLIFICADORES
I Controle Contínuo 1
 Sumário I Controle Contínuo 1 1 Introdução 3 1.1 Sistemas de Controle em Malha Aberta e em Malha Fechada................ 5 1.2 Componentes de um sistema de controle............................ 5 1.3 Comparação
Sumário I Controle Contínuo 1 1 Introdução 3 1.1 Sistemas de Controle em Malha Aberta e em Malha Fechada................ 5 1.2 Componentes de um sistema de controle............................ 5 1.3 Comparação
Análise de Regressão - parte I
 16 de Outubro de 2012 Introdução Objetivos Ao final deste capítulo você deve ser capaz de: Usar modelos de regressão para construir modelos para dados coletados. Entender como método de mínimos é usado
16 de Outubro de 2012 Introdução Objetivos Ao final deste capítulo você deve ser capaz de: Usar modelos de regressão para construir modelos para dados coletados. Entender como método de mínimos é usado
FUNDAMENTOS DE CONTROLE - EEL 7531
 Soluções periódicas e ciclos limite Funções descritivas FUNDAMENTOS DE CONTROLE - EEL 7531 Professor: Aguinaldo S. e Silva LABSPOT-EEL-UFSC 9 de junho de 2015 Professor: Aguinaldo S. e Silva FUNDAMENTOS
Soluções periódicas e ciclos limite Funções descritivas FUNDAMENTOS DE CONTROLE - EEL 7531 Professor: Aguinaldo S. e Silva LABSPOT-EEL-UFSC 9 de junho de 2015 Professor: Aguinaldo S. e Silva FUNDAMENTOS
MÉTODO GALERKIN DE ELEMENTOS FINITOS NA DETERMINAÇÃO DO PERFIL DE TEMPERATURA NA PAREDE DE UM CONTÊINER ESFÉRICO UTILIZANDO MATLAB
 MÉTODO GALERKIN DE ELEMENTOS FINITOS NA DETERMINAÇÃO DO PERFIL DE TEMPERATURA NA PAREDE DE UM CONTÊINER ESFÉRICO UTILIZANDO MATLAB Bruno Avila Farenzena 1 Eliete Biasotto Hauser 2 Resumo: Neste trabalho
MÉTODO GALERKIN DE ELEMENTOS FINITOS NA DETERMINAÇÃO DO PERFIL DE TEMPERATURA NA PAREDE DE UM CONTÊINER ESFÉRICO UTILIZANDO MATLAB Bruno Avila Farenzena 1 Eliete Biasotto Hauser 2 Resumo: Neste trabalho
Métodos de Fourier Prof. Luis S. B. Marques
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
Caos determinístico e mapa logístico num circuito RLD FAP0214 Física Experimental IV 2008/1. Manfredo Harri Tabacniks IFUSP
 Caos determinístico e mapa logístico num circuito RLD FAP0214 Física Experimental IV 2008/1 Manfredo Harri Tabacniks IFUSP Revendo atividade da semana passada Como medir R L a partir da figura de Lissajous?
Caos determinístico e mapa logístico num circuito RLD FAP0214 Física Experimental IV 2008/1 Manfredo Harri Tabacniks IFUSP Revendo atividade da semana passada Como medir R L a partir da figura de Lissajous?
6 Análise Dinâmica. 6.1 Modelagem computacional
 6 Análise Dinâmica O presente capítulo apresenta um estudo do comportamento dinâmico da coluna de aço estaiada, abrangendo análises modais para determinação da freqüência natural, com e sem protensão [32]
6 Análise Dinâmica O presente capítulo apresenta um estudo do comportamento dinâmico da coluna de aço estaiada, abrangendo análises modais para determinação da freqüência natural, com e sem protensão [32]
ANÁLISE DO MÉTODO DA RESPOSTA EM FREQÜÊNCIA
 VIII- CAPÍTULO VIII ANÁLISE DO MÉTODO DA RESPOSTA EM FREQÜÊNCIA 8.- INTRODUÇÃO O método da resposta em freqüência, nada mais é que a observação da resposta de um sistema, para um sinal de entrada senoidal,
VIII- CAPÍTULO VIII ANÁLISE DO MÉTODO DA RESPOSTA EM FREQÜÊNCIA 8.- INTRODUÇÃO O método da resposta em freqüência, nada mais é que a observação da resposta de um sistema, para um sinal de entrada senoidal,
MAT Resumo Teórico e Lista de
 MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
MAT 0132 - Resumo Teórico e Lista de Exercícios April 10, 2005 1 Vetores Geométricos Livres 1.1 Construção dos Vetores 1.2 Adição de Vetores 1.3 Multiplicação de um Vetor por um Número Real 2 Espaços Vetoriais
Passeios Aleatórios. 1 Introdução. 2 Passeio aleatório em uma dimensão. Paulo Matias. 11 de outubro de 2011
 Passeios Aleatórios Paulo Matias 11 de outubro de 11 Resumo O passeio aleatório é um modelo muito conhecido em Mecânica Estatística, comumente identicável em diversos fenômenos da natureza. Este trabalho
Passeios Aleatórios Paulo Matias 11 de outubro de 11 Resumo O passeio aleatório é um modelo muito conhecido em Mecânica Estatística, comumente identicável em diversos fenômenos da natureza. Este trabalho
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 04/2014 Zeros reais de funções Parte 1 Objetivo Determinar valores aproximados para as soluções (raízes) de equações da
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 04/2014 Zeros reais de funções Parte 1 Objetivo Determinar valores aproximados para as soluções (raízes) de equações da
INF Fundamentos da Computação Gráfica Professor: Marcelo Gattass Aluno: Rogério Pinheiro de Souza
 INF2608 - Fundamentos da Computação Gráfica Professor: Marcelo Gattass Aluno: Rogério Pinheiro de Souza Trabalho 02 Visualização de Imagens Sísmicas e Detecção Automática de Horizonte Resumo Este trabalho
INF2608 - Fundamentos da Computação Gráfica Professor: Marcelo Gattass Aluno: Rogério Pinheiro de Souza Trabalho 02 Visualização de Imagens Sísmicas e Detecção Automática de Horizonte Resumo Este trabalho
Comportamentos dinâmicos em dimensão 1 e seus parâmetros em famílias específicas
 Comportamentos dinâmicos em dimensão 1 e seus parâmetros em famílias específicas January 26, 2007 O projeto atual visa proporcionar ao candidato os primeiros contatos com questões e técnicas da área de
Comportamentos dinâmicos em dimensão 1 e seus parâmetros em famílias específicas January 26, 2007 O projeto atual visa proporcionar ao candidato os primeiros contatos com questões e técnicas da área de
aula ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES
 ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
Lista No. 5 Gabarito
 CÁLCULO NUMÉRICO Lista No. 5 Gabarito. (a) Queremos y f() ϕ() α +. Temos então n, as funções bases g (), g (), e m 8. Precisamos resolver o sistema de equações normais correspondente. Este sistema para
CÁLCULO NUMÉRICO Lista No. 5 Gabarito. (a) Queremos y f() ϕ() α +. Temos então n, as funções bases g (), g (), e m 8. Precisamos resolver o sistema de equações normais correspondente. Este sistema para
TREND STRIPS E NÍVEIS DE RUÍDO ADICIONADOS A UM MAPA SENOIDAL
 167 TREND STRIPS E NÍVEIS DE RUÍDO ADICIONADOS A UM MAPA SENOIDAL Antônio Carlos da Silva Filho Uni-FACEF Introdução Trend Strips (TS) são uma nova técnica de análise da dinâmica de um sistema, quando
167 TREND STRIPS E NÍVEIS DE RUÍDO ADICIONADOS A UM MAPA SENOIDAL Antônio Carlos da Silva Filho Uni-FACEF Introdução Trend Strips (TS) são uma nova técnica de análise da dinâmica de um sistema, quando
Algoritmos geométricos
 Algoritmos geométricos introdução a conceitos básicos de geometria computacional que serão abordados de forma mais avançada na disciplina Computação Gráfica disciplina de computação gráfica arquitetura
Algoritmos geométricos introdução a conceitos básicos de geometria computacional que serão abordados de forma mais avançada na disciplina Computação Gráfica disciplina de computação gráfica arquitetura
Modelagem em Sistemas Complexos
 Modelagem em Sistemas Complexos Bifurcação local de campos vetoriais Marcone C. Pereira Escola de Artes, Ciências e Humanidades Universidade de São Paulo São Paulo - Brasil Abril de 2012 Nesta aula discutiremos
Modelagem em Sistemas Complexos Bifurcação local de campos vetoriais Marcone C. Pereira Escola de Artes, Ciências e Humanidades Universidade de São Paulo São Paulo - Brasil Abril de 2012 Nesta aula discutiremos
3 Avaliação da segurança dinâmica de sistemas de energia elétrica: Resultados
 3 Avaliação da segurança dinâmica de sistemas de energia elétrica: Resultados 3.1 Introdução O presente capítulo apresenta os resultados obtidos da aplicação do método de avaliação da segurança dinâmica
3 Avaliação da segurança dinâmica de sistemas de energia elétrica: Resultados 3.1 Introdução O presente capítulo apresenta os resultados obtidos da aplicação do método de avaliação da segurança dinâmica
Estudo Numérico da Dinâmica de Osciladores Forçados no Espaço de Parâmetros
 UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS DEPARTAMENTO DE FÍSICA - DFIS PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA - PPGF JULIO CÉZAR D AMORE CARDOSO Estudo Numérico da Dinâmica
UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS DEPARTAMENTO DE FÍSICA - DFIS PROGRAMA DE PÓS-GRADUAÇÃO EM FÍSICA - PPGF JULIO CÉZAR D AMORE CARDOSO Estudo Numérico da Dinâmica
Aula 1, Experiência 1 Circuitos CA e Caos
 Notas de aula:.fap.if.usp.br/~hbarbosa LabFlex:.dfn.if.usp.br/curso/LabFlex Prof. Henrique Barbosa hbarbosa@if.usp.br Ramal: 6647 Ed. Basílio Jafet, sala 100 Aula 1, Experiência 1 Circuitos CA e Caos Objetivos
Notas de aula:.fap.if.usp.br/~hbarbosa LabFlex:.dfn.if.usp.br/curso/LabFlex Prof. Henrique Barbosa hbarbosa@if.usp.br Ramal: 6647 Ed. Basílio Jafet, sala 100 Aula 1, Experiência 1 Circuitos CA e Caos Objetivos
Experimento 8 Circuitos RC e filtros de freqüência
 Experimento 8 Circuitos C e filtros de freqüência OBJETIO O objetivo desta aula é ver como filtros de freqüência utilizados em eletrônica podem ser construídos a partir de um circuito C Os filtros elétricos
Experimento 8 Circuitos C e filtros de freqüência OBJETIO O objetivo desta aula é ver como filtros de freqüência utilizados em eletrônica podem ser construídos a partir de um circuito C Os filtros elétricos
Descrição do processo de Modelagem e Simulação em quatro etapas no ambiente AMESim
 Descrição do processo de Modelagem e Simulação em quatro etapas no ambiente AMESim Similarmente a outros softwares de modelagem e simulação, a utilização do sistema AMESim está baseada em quatro etapas:
Descrição do processo de Modelagem e Simulação em quatro etapas no ambiente AMESim Similarmente a outros softwares de modelagem e simulação, a utilização do sistema AMESim está baseada em quatro etapas:
UMA INVESTIGAÇÃO HISTÓRICA SOBRE OS LOGARITMOS COM SUGESTÕES DIDÁTICAS PARA A SALA DE AULA
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXATAS E DA TERRA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE CIÊNCIAS NATURAIS E MATEMÁTICA EVANILDO COSTA SOARES UMA INVESTIGAÇÃO HISTÓRICA SOBRE
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE CENTRO DE CIÊNCIAS EXATAS E DA TERRA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE CIÊNCIAS NATURAIS E MATEMÁTICA EVANILDO COSTA SOARES UMA INVESTIGAÇÃO HISTÓRICA SOBRE
DAFIS/DAQBI - PPGFCET. Sistemas Complexos. [ M.S. Freitas / UTFPR ] Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS.
![DAFIS/DAQBI - PPGFCET. Sistemas Complexos. [ M.S. Freitas / UTFPR ] Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS. DAFIS/DAQBI - PPGFCET. Sistemas Complexos. [ M.S. Freitas / UTFPR ] Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS.](/thumbs/88/117059401.jpg) DAFIS/DAQBI - PPGFCET Sistemas Complexos Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS msergio58@gmail.com [ M.S. Freitas / UTFPR ] Ementa 0 INTRODUÇÃO 1 REDES BOOLEANAS E AUTÔMATOS CELULARES 2 AUTOSSIMILARIDADE
DAFIS/DAQBI - PPGFCET Sistemas Complexos Prof. Mário Sérgio Freitas, Dr. - UTFPR/DAFIS msergio58@gmail.com [ M.S. Freitas / UTFPR ] Ementa 0 INTRODUÇÃO 1 REDES BOOLEANAS E AUTÔMATOS CELULARES 2 AUTOSSIMILARIDADE
CAOS E FRACTAIS: UMA INTRODUÇÃO
 SUGESTÃO DE DISCIPLINA CAOS E FRACTAIS: UMA INTRODUÇÃO VIA SISTEMAS DINÂMICOS DISCRETOS PRIMEIRO PERÍODO DE 2015 PROFESSOR OFERTANTE : Marcelo Domingos Marchesin CARGA HORÁRIA : 60 Horas PRÉ-REQUISITO
SUGESTÃO DE DISCIPLINA CAOS E FRACTAIS: UMA INTRODUÇÃO VIA SISTEMAS DINÂMICOS DISCRETOS PRIMEIRO PERÍODO DE 2015 PROFESSOR OFERTANTE : Marcelo Domingos Marchesin CARGA HORÁRIA : 60 Horas PRÉ-REQUISITO
distribuição perto do pico
 Teoria Quântica de Campos I 178 Em espalhamentos relativísticos o mesmo ocorre, as partículas iniciais podem se combinar para formar estados instáveis, que então decaem em outros, por exemplo: Na amplitude
Teoria Quântica de Campos I 178 Em espalhamentos relativísticos o mesmo ocorre, as partículas iniciais podem se combinar para formar estados instáveis, que então decaem em outros, por exemplo: Na amplitude
A Análise de Fourier utilizando o software Proteus Isis: Um estudo de caso sobre as harmônicas
 A Análise de Fourier utilizando o software Proteus Isis: Um estudo de caso sobre as harmônicas José Ailton Batista da Silva 1, Renan Nunes Pinheiro 2 1 Graduando do Curso de Tecnologia em Mecatrônica Industrial
A Análise de Fourier utilizando o software Proteus Isis: Um estudo de caso sobre as harmônicas José Ailton Batista da Silva 1, Renan Nunes Pinheiro 2 1 Graduando do Curso de Tecnologia em Mecatrônica Industrial
6 MÉTODO DE ELEMENTOS FINITOS - MEF
 6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
6 MÉTODO DE ELEMENTOS FINITOS - MEF O Método de Elementos Finitos é uma técnica de discretização de um problema descrito na Formulação Fraca, na qual o domínio é aproximado por um conjunto de subdomínios
SUMÁRIO PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3. PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação...
 PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3 PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação... 7 CAPÍTULO 1 Modelagem matemática e resolução de problemas de engenharia...10
PARTE 1 MODELAGEM, COMPUTADORES E ANÁLISE DE ERROS 3 PT1.1 Motivação... 3 Pt1.2 Fundamentos Matemáticos... 5 Pt1.3 Orientação... 7 CAPÍTULO 1 Modelagem matemática e resolução de problemas de engenharia...10
Capítulo 1 - Erros e Aritmética Computacional
 Capítulo 1 - Erros e Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil e Electrotécnica Carlos Balsa Métodos Numéricos 1/ 21 Sumário
Capítulo 1 - Erros e Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança 2 o Ano - Eng. Civil e Electrotécnica Carlos Balsa Métodos Numéricos 1/ 21 Sumário
3. Limites e Continuidade
 3. Limites e Continuidade 1 Conceitos No cálculo de limites, estamos interessados em saber como uma função se comporta quando a variável independente se aproxima de um determinado valor. Em outras palavras,
3. Limites e Continuidade 1 Conceitos No cálculo de limites, estamos interessados em saber como uma função se comporta quando a variável independente se aproxima de um determinado valor. Em outras palavras,
