Definições Exemplos de gramáticas
|
|
|
- Ricardo Miranda Amorim
- 9 Há anos
- Visualizações:
Transcrição
1 Definições Exemplos de gramáticas 1
2 Gramáticas Conceito introduzido pela lingüística Objetivo de ensinar o inglês pelo computador e conseguir um tradutor de línguas Fracasso da tradução por volta dos anos 50. Sucesso na descrição de LP. Algol 60 foi descrito como uma linguagem livre de contexto na notação BNF. Atualmente, a tradução voltou a ganhar força dado o sucesso da tradução por métodos estatísticos que aprender a tarefa a partir de grandes conjuntos de dados (temos a WEB a disposição!) Antes de vermos a noção formal de uma gramática vamos para algumas definições: 2
3 Alfabeto ou Vocabulário: Conjunto finito não vazio de símbolos. Símbolo é um elemento qualquer de um alfabeto. Ex: {A,B,C,.Z} alfabeto latino {,,,,,, } alfabeto grego {0,1} alfabeto binário {0,1,2,3,4,5,6,7,8,9} alfabeto de digitos {a, b} Cadeia ou palavra: Concatenação de símbolos de um alfabeto. Define-se como cadeia vazia ou nula uma cadeia que não contém nenhum símbolo. Ex: aab l - cadeia nula 3
4 Comprimento de cadeia: Número de símbolos de uma cadeia. Ex: aab = =6 l =0 Concatenação de cadeias: Define-se a concatenação z de uma cadeia x com uma cadeia y, como sendo a concatenação dos símbolos de ambas as cadeias, formando a cadeia xy. z = x + y Ex: x = abaa; y = ba z = abaaba x = ba; y = l z = ba 4
5 Produto de alfabetos: É o produto cartesiano de alfabetos. Ex: V1 = {a,b} V2 = {1, 2, 3} V1.V2 = V1xV2 = {a1, a2, a3, b1, b2, b3} Observe que V1.V2 V2.V1 Exponenciação de alfabetos: São todas as cadeias de comprimento n sobre V (V n ). V 0 ={l}, V 1 =V, V n =V n-1.v Ex: V = {0, 1} V 3 = V 2.V = (V.V).V = {00, 01, 10, 11}.{0, 1} = {000, 001, 010, 011, 100, 101, 110, 111} V n = m n onde V = m 5
6 Fechamento (Clausura) de um Alfabeto: Seja A um alfabeto, então o fechamento de A é definido como A * = A 0 A 1 A 2... A n... Portanto A * = conjunto das cadeias de qualquer comprimento sobre o alfabeto a. Ex: A = {1} A * = {l, 1, 11, 111,...} Fechamento Positivo de A: A + = A * - {l} 6
7 Linguagem é uma coleção/conjunto de cadeias de símbolos sobre um alfabeto/vocabulário. Estas cadeias são denominadas sentenças da linguagem, e são formadas pela justaposição de elementos individuais, os símbolos da linguagem. Ex: V = {0, 1} L1 = {0 n 1 n n >= 1} infinita L1 = {01, 0011, , } L2 = {ab, bc} finita (linguagem formada pelas cadeias ab e bc) L3 = {ab n a n b n>=0} infinita (linguagem formada por todas as cadeias que começam com "a" seguido de um número qualquer de "b"'s OU começam com um número qualquer de "a"'s seguidos de um "b", 7por exemplo ab, abb, aab, aaab,...)
8 Finita ou Infinita? i) L1 = { x x {a, b, c}* e x contém ab} ii) L2 = {w {0,1}* w tem pelo menos um 1} iii) L3 = { x x é uma cadeia de 0 s e 1 s e x >= 2} iv) L1 = {w {a,b}* todo a tem um b imediatamente à sua direita} v) L2 = {w {a,b}* w tem aa como subpalavra} 8
9 sequência de Símbolo item de Cadeia elemento de Linguagem Alfabeto elemento de conjunto de conjunto de 9
10 Vamos analisar uma sentença do Português colocada no contexto da cadeia alimentar O gato comeu o rato. <sentença> <sintagma nominal> <sintagma verbal> <artigo> <substantivo> <verbo> <sintagma nominal> < artigo> <substantivo> O gato comeu o rato 10
11 Regras para analisar a sentença <sentença> -> <sn> <sv> <sn> -> <artigo> <substantivo> <sv> -> <verbo> <sn> <artigo> -> o <substantivo> -> gato rato <verbo> -> comeu dada -> definido por < > para distinguir sentença, sv, sn das palavras do português Com essa gramática poderíamos gerar: 1) O gato comeu o rato 2) O rato comeu o gato que são gramaticalmente corretas mas 2) é inaceitável no contexto dado. 11
12 Para formar essa gramática parcial para o português usamos 4 conceitos: categorias sintáticas como <sentença>, <sn>, <sv>, <artigo>, <substantivo>, <verbo> são chamados de não terminais ou variáveis palavras são chamadas de terminais relação entre terminais e não terminais são chamadas de produções o não terminal que gera todas as cadeias de terminais (<sentença>) é chamado de símbolo inicial 12
13 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática. Este vocabulário corresponde ao conjunto de todos os símbolos dos quais a gramática se vale para definir as leis de formação das sentenças da linguagem. 13
14 Vt é o vocabulário terminal, contendo os símbolos que constituem as sentenças da linguagem. Dá-se o nome de terminais aos elementos de Vt. P representa o conjunto de todas as leis de formação utilizadas pela gramática para definir a linguagem. Para tanto, cada construção parcial, representada por um não-terminal, é definida como um conjunto de regras de formação relativas à definicão do não-terminal a ela referente. A cada uma destas regras de formação que compõem o conjunto P dá-se o nome de produção da gramática. 14
15 Assumimos Vn Vt =. Convencionamos que Vn U Vt = V Cada produção P tem a forma: -> V+; V* S є Vn denota a principal categoria gramatica de G; é dito o símbolo inicial ou o axioma da gramática. Indica onde se inicia o processo de geração de sentenças. Ex.1: G = ({S, A, B}, {a, b}, P, S) P: {S -> AB A -> a B -> b} 15
16 Notação/Convenções Letras do alfabeto latino maiúsculas {A,B,..Z}: variáveis Letras do começo do alfabeto latino minúsculas {a,b,c,...}: terminais Letras do fim do alfabeto latino minúsculas {t,u,v,x,z}: cadeias de terminais Letras gregas minúsculas {,,,,,..., }: cadeias de terminais e não terminais alfa, beta, gama, delta, épsilon, zeta, eta, teta, iota, kapa, lâmbda, mi, ni, xi, ômicron, pi, rô, sigma, tau, úpsilon, fi, qui, psi, ômega 16
17 Exercício Tentem definir uma gramática simples, por exemplo, de algum construtor (definição) ou comando de uma linguagem de programação. 17
18 Comando de atribuição com variáveis simples em Pascal G = ({<atribuição>, <variável>, <expressão>, <identificador>}, {:=, letras, digitos, _, operadores, (,)}, P, <atribuição>) P = { } <atribuição>::= <variável> := <expressão> <variável> ::= <identificador> <expressão> deve ainda ser definida. Veremos isto mais para frente. <identificador> ::= é formado por uma letra, seguido de qualquer número de letras, digitos ou underscore (tem fazer esta regra) 18
19 Definida uma gramática G, qual é a linguagem gerada por ela? Precisaremos das relações => G (deriva diretamente) e => G * (deriva) definidas entre as cadeias de V* Def1. Se -> é uma produção de P e (gama) e (delta) são cadeias quaisquer de V*, então => G (deriva diretamente na gramática G). Dizemos que a produção -> é aplicada à cadeia para obter. A relação => G relaciona cadeias exatamente quando a segunda é obtida a partir da primeira pela aplicação de uma única produção. No Ex.1.: S => G AB ; ab => G ab S => G AB => G ab => G ab ou 19
20 Def2. Suponha que m são cadeias de V* e 1 => G 2, 2 => G 3,, m-1 => G m. Então dizemos que 1 => G * m (deriva). Aplicamos algum número de produções de P. Por convenção => G * para a cadeia. No Ex.1.: S => G * ab; S => G * ab; AB => G * ab; ab => G * ab 20
21 Def3. Forma sentencial: uma cadeia composta de terminais e não terminais se S =>* No Ex.1: ab, AB, S, ab são formas sentenciais. Uma forma sentencial,, é uma sentença de G se S e Vt * (são composta de terminais). Ou seja, as cadeias geradas pela gramática são as sentenças de G. 21
22 Def4. A Linguagem L gerada por uma gramática G é definida como o conjunto de cadeias geradas por G. Ou seja, L(G) = {x x є Vt * e S => G * x} ou {x x é sentença de G} 1. A cadeia consiste somente de terminais 2. A cadeia pode ser derivada a partir do símbolo inicial da gramática Def5. Duas gramáticas G1 e G2 são equivalentes sse L(G1) = L(G2) 22
23 Exemplos de Gramáticas G1 = ({S}, {0,1}, P1, S) P1: { 1. S -> 0S1 2. S -> 01 } Qual é a linguagem gerada por G1? Aplicamos o processo de derivação para saber L(G1), que é o processo de obtenção de cadeias a partir de uma gramática. G2 = ({S,B,C}, {a,b,c}, P2, S) P2: { 1. S -> asbc 2. S -> abc 3. CB -> BC 4. ab -> ab 5. bb -> bb 6. bc -> bc 7. cc -> cc} L(G2) =? 23
24 G1 A menor cadeia gerada é 01: S => 2 01 Se aplicarmos n-1 vezes a produção 1, seguida da produção 2 teremos: S => 0S1 => 00S11 => 0 3 S1 3 =>* 0 n-1 S1 n-1 => 0 n 1 n Portanto, L(G1) = {0 n 1 n n >= 1} ou S =>* 0 n 1 n 24
25 25
26 26
27 27
28 G2 A menor cadeia gerada é abc: S=> 2 abc => 4 abc => 6 abc Usamos 1 n-1 vezes: S=>* a n-1 S(BC) n-1 Usamos a 2 uma vez: S=>* a n (BC) n A 3 permite trocar B com C para que B s precedam os C s Para n = 2 aabcbc => aabbcc (usamos a regras 3 1 vez) Para n = 3 aaabcbcbc => aaabbccbc => aaabbcbcc => aaabbbccc (usamos a regra 3 3 vezes) Para n = 4 aaaabcbcbcbc => aaaabcbcbbcc => aaaabcbbcbcc => aaaabcbbbccc => aaaabbcbbccc => aaaabbbcbccc => aaaabbbbcccc (usamos a regra 3 6 vezes); Para n = 5 usamos a 3 10 vezes. Assim S=>* a n B n C n Usamos a 4 uma vez: S=>* a n bb n-1 C n Aplicamos a 5 n-1 vezes: S=>* a n b n C n Aplicamos a 6 uma vez: S=>* a n b n cc n-1 Aplicamos a 7 n-1 vezes: S=>* a n b n c n L(G2) = {a n b n c n n >= 1} 28
29 Fecho e a definição de Linguagem A definição formal de linguagem é baseada em um subconjunto do fecho de um vocabulário terminal, como já vimos: L(G) = {x x є Vt * e S => G * x} ou {x x é sentença de G} Então, a maior linguagem sobre um vocabulário Vt é Vt*. A menor linguagem sobre um vocabulário Vt é (conjunto vazio) ou seja, a linguagem vazia, composta por zero cadeias/sentenças. Observe que é diferente do conjunto que tem a cadeia vazia { l } O conjunto de todos os subconjuntos possíveis de Vt * é 2 Vt* e representa o conjunto de todas as linguagens que podem ser definidas a partir de Vt *. (conjunto vazio) e também Vt * є 2 Vt* 29
30 Exercício Seja Vt = {a,b,c} e a propriedade todas as cadeias são iniciadas pelo símbolo a 1. Qual a menor linguagem? 2. Qual a maior linguagem? 3. A linguagem {a, ab, ac, abc, acb} satisfaz a propriedade acima? 4. A linguagem {a} {a}* {b}* {c}* satisfaz a propriedade acima? 30
Definições Hierarquia de Chomsky Exemplos de gramáticas. Gramáticas. Objetivo de ensinar o inglês pelo computador e conseguir um tradutor de línguas
 Definições Hierarquia de Chomsky Exemplos de gramáticas 1 Gramáticas Conceito introduzido pela lingüística Objetivo de ensinar o inglês pelo computador e conseguir um tradutor de línguas Fracasso da tradução
Definições Hierarquia de Chomsky Exemplos de gramáticas 1 Gramáticas Conceito introduzido pela lingüística Objetivo de ensinar o inglês pelo computador e conseguir um tradutor de línguas Fracasso da tradução
Definições Hierarquia de Chomsky Exemplos de gramáticas
 Definições Hierarquia de Chomsky Exemplos de gramáticas 1 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática.
Definições Hierarquia de Chomsky Exemplos de gramáticas 1 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática.
Definições Hierarquia de Chomsky Exemplos de gramáticas
 Definições Hierarquia de Chomsky Exemplos de gramáticas 1 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática.
Definições Hierarquia de Chomsky Exemplos de gramáticas 1 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática.
Conceitos Básicos. Vocabulário Cadeias Linguagens Problema
 Conceitos Básicos Vocabulário Cadeias Linguagens Problema Alfabeto ou Vocabulário: Conjunto finito não vazio de símbolos. Símbolo é um elemento qualquer de um alfabeto. Ex: {A,B,C,.Z} alfabeto latino (maiúsculas)
Conceitos Básicos Vocabulário Cadeias Linguagens Problema Alfabeto ou Vocabulário: Conjunto finito não vazio de símbolos. Símbolo é um elemento qualquer de um alfabeto. Ex: {A,B,C,.Z} alfabeto latino (maiúsculas)
Conceitos Básicos. Vocabulário Cadeias Linguagens Expressões Regulares Problema X Linguagem
 Conceitos Básicos Vocabulário Cadeias Linguagens Expressões Regulares Problema X Linguagem Alfabeto ou Vocabulário: Conjunto finito não vazio de símbolos. Símbolo é um elemento qualquer de um alfabeto.
Conceitos Básicos Vocabulário Cadeias Linguagens Expressões Regulares Problema X Linguagem Alfabeto ou Vocabulário: Conjunto finito não vazio de símbolos. Símbolo é um elemento qualquer de um alfabeto.
Linguagens Formais e Autômatos 02/2015. LFA Aula 02. introdução 28/09/2015. Celso Olivete Júnior.
 LFA Aula 02 Linguagens regulares - introdução 28/09/2015 Celso Olivete Júnior [email protected] 1 Na aula passada... Visão geral Linguagens regulares expressões regulares autômatos finitos gramáticas
LFA Aula 02 Linguagens regulares - introdução 28/09/2015 Celso Olivete Júnior [email protected] 1 Na aula passada... Visão geral Linguagens regulares expressões regulares autômatos finitos gramáticas
Linguagens e Gramáticas. Linguagens Formais Hierarquia de Chomsky
 Linguagens e Gramáticas Linguagens Formais Hierarquia de Chomsky Já vimos que Linguagem é um conjunto de cadeias de símbolos sobre um alfabeto/vocabulário, V. É um subconjunto específico de V*. Estas cadeias
Linguagens e Gramáticas Linguagens Formais Hierarquia de Chomsky Já vimos que Linguagem é um conjunto de cadeias de símbolos sobre um alfabeto/vocabulário, V. É um subconjunto específico de V*. Estas cadeias
Exemplo preliminar. Considere a linguagem dos Palíndromos Lpal:
 a n b n 1 Exemplo preliminar Considere a linguagem dos Palíndromos Lpal: radar, Roma é amor, 0110, 11011,... ou seja, quando w = w r Lpal é regular? usando o Lema do Bombeamento: Suponha Lpal regular,
a n b n 1 Exemplo preliminar Considere a linguagem dos Palíndromos Lpal: radar, Roma é amor, 0110, 11011,... ou seja, quando w = w r Lpal é regular? usando o Lema do Bombeamento: Suponha Lpal regular,
Hierarquia de Chomsky Exemplos de gramáticas
 Hierarquia de Chomsky Exemplos de gramáticas 1 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática. Este
Hierarquia de Chomsky Exemplos de gramáticas 1 Formalmente, as gramáticas são caracterizadas como quádruplas ordenadas G = ( Vn, Vt, P, S) onde: Vn representa o vocabulário não terminal da gramática. Este
Gramática. Prof. Yandre Maldonado e Gomes da Costa. Prof. Yandre Maldonado - 1
 Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa [email protected] Prof. Yandre Maldonado - 2 Mecanismo gerador que permite definir formalmente uma linguagem; Através de uma gramática
Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa [email protected] Prof. Yandre Maldonado - 2 Mecanismo gerador que permite definir formalmente uma linguagem; Através de uma gramática
Gramática. Gramática. Gramática
 Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa [email protected] Prof. Yandre Maldonado - 2 Mecanismo gerador que permite definir formalmente uma linguagem; Através de uma gramática
Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa [email protected] Prof. Yandre Maldonado - 2 Mecanismo gerador que permite definir formalmente uma linguagem; Através de uma gramática
Linguagens Formais - Preliminares
 Linguagens Formais - Preliminares Regivan H. N. Santiago DIMAp-UFRN 25 de fevereiro de 2007 Regivan H. N. Santiago (DIMAp-UFRN) Linguagens Formais - Preliminares 25 de fevereiro de 2007 1 / 26 Algumas
Linguagens Formais - Preliminares Regivan H. N. Santiago DIMAp-UFRN 25 de fevereiro de 2007 Regivan H. N. Santiago (DIMAp-UFRN) Linguagens Formais - Preliminares 25 de fevereiro de 2007 1 / 26 Algumas
Teoria da Computação Aula 02 Introdução
 Teoria da Computação Aula 02 Introdução Prof. Esp. Pedro Luís Antonelli Anhanguera Educacional Alfabeto Um alfabeto é um conjunto finito de símbolos ou caracteres, representado pela letra sigma ( ). Portanto:
Teoria da Computação Aula 02 Introdução Prof. Esp. Pedro Luís Antonelli Anhanguera Educacional Alfabeto Um alfabeto é um conjunto finito de símbolos ou caracteres, representado pela letra sigma ( ). Portanto:
Disciplina: LINGUAGENS FORMAIS, AUTÔMATOS E COMPUTABILIDADE Prof. Jefferson Morais
 UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS FACULDADE DE COMPUTAÇÃO CURSO DE BACHARELADO EM CIÊNCIA DA COMPUTAÇÃO Disciplina: LINGUAGENS FORMAIS, AUTÔMATOS E COMPUTABILIDADE Prof.
UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS FACULDADE DE COMPUTAÇÃO CURSO DE BACHARELADO EM CIÊNCIA DA COMPUTAÇÃO Disciplina: LINGUAGENS FORMAIS, AUTÔMATOS E COMPUTABILIDADE Prof.
Compiladores Aula 4. Celso Olivete Júnior.
 Aula 4 Celso Olivete Júnior [email protected] Na aula de hoje... Revisão: gramáticas Relações em uma gramática: Cabeça, Último, Primeiro (First) e Seguinte (Follow) Capítulo 4 (seção 4.4.2) do livro
Aula 4 Celso Olivete Júnior [email protected] Na aula de hoje... Revisão: gramáticas Relações em uma gramática: Cabeça, Último, Primeiro (First) e Seguinte (Follow) Capítulo 4 (seção 4.4.2) do livro
Gramáticas ( [HMU00], Cap. 5.1)
![Gramáticas ( [HMU00], Cap. 5.1) Gramáticas ( [HMU00], Cap. 5.1)](/thumbs/67/57571767.jpg) Gramáticas ( [HMU00], Cap. 5.1) Vimos que a seguinte linguagem não é regular L = {0 n 1 n n 0} Contudo podemos fácilmente dar uma definição indutiva das suas palavras: 1. ɛ L 2. Se x L então 0x1 L L é
Gramáticas ( [HMU00], Cap. 5.1) Vimos que a seguinte linguagem não é regular L = {0 n 1 n n 0} Contudo podemos fácilmente dar uma definição indutiva das suas palavras: 1. ɛ L 2. Se x L então 0x1 L L é
Linguagens Formais. Aula 01 - Conceitos Básicos. Prof. Othon Batista Mestre em Informática
 Linguagens Formais Aula 01 - Conceitos Básicos Prof. Othon Batista Mestre em Informática Sumário Introdução à Linguagem Alfabeto Cadeias de Símbolos, Palavras Tamanho de Palavra Prefixo, Sufixo ou Subpalavra
Linguagens Formais Aula 01 - Conceitos Básicos Prof. Othon Batista Mestre em Informática Sumário Introdução à Linguagem Alfabeto Cadeias de Símbolos, Palavras Tamanho de Palavra Prefixo, Sufixo ou Subpalavra
COMPILADORES. Revisão Linguagens formais Parte 01. Geovane Griesang
 Universidade de Santa Cruz do Sul UNISC Departamento de informática COMPILADORES Revisão Linguagens formais Parte 01 [email protected] Legenda: = sigma (somatório) = delta ε = épsilon λ = lambda
Universidade de Santa Cruz do Sul UNISC Departamento de informática COMPILADORES Revisão Linguagens formais Parte 01 [email protected] Legenda: = sigma (somatório) = delta ε = épsilon λ = lambda
Linguagens Formais e Autômatos P. Blauth Menezes
 Linguagens Formais e Autômatos P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Ciência da Computação - P. Blauth Menezes
Linguagens Formais e Autômatos P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Matemática Discreta para Ciência da Computação - P. Blauth Menezes
Gramáticas e Linguagens independentes de contexto
 Capítulo 6 Gramáticas e Linguagens independentes de contexto 6.1 Gramáticas Nesta secção vamos introduzir gramáticas formais para caracterização das linguagens, estudando fundamentalmente as gramáticas
Capítulo 6 Gramáticas e Linguagens independentes de contexto 6.1 Gramáticas Nesta secção vamos introduzir gramáticas formais para caracterização das linguagens, estudando fundamentalmente as gramáticas
IBM1088 Linguagens Formais e Teoria da
 IBM1088 Linguagens Formais e Teoria da Computação Linguagens e Gramáticas Evandro Eduardo Seron Ruiz [email protected] Universidade de São Paulo E.E.S. Ruiz (USP) LFA 1 / 47 Frase do dia Sofremos muito com
IBM1088 Linguagens Formais e Teoria da Computação Linguagens e Gramáticas Evandro Eduardo Seron Ruiz [email protected] Universidade de São Paulo E.E.S. Ruiz (USP) LFA 1 / 47 Frase do dia Sofremos muito com
LFA Aula 09. Gramáticas e Linguagens Livres de Contexto 18/01/2016. Linguagens Formais e Autômatos. Celso Olivete Júnior.
 LFA Aula 09 Gramáticas e Linguagens Livres de Contexto (Hopcroft, 2002) 18/01/2016 Celso Olivete Júnior [email protected] www.fct.unesp.br/docentes/dmec/olivete/lfa 1 Classes Gramaticais Linguagens
LFA Aula 09 Gramáticas e Linguagens Livres de Contexto (Hopcroft, 2002) 18/01/2016 Celso Olivete Júnior [email protected] www.fct.unesp.br/docentes/dmec/olivete/lfa 1 Classes Gramaticais Linguagens
Gramáticas Sensíveis ao Contexto (GSC) Linguagens Sensíveis ao Contexto (LSC) Autômatos Linearmente Limitados (ALL)
 Gramáticas Sensíveis ao Contexto (GSC) Linguagens Sensíveis ao Contexto (LSC) Autômatos Linearmente Limitados (ALL) 1 Gramática Sensível ao Contexto Definição: Uma gramática G é sensível ao contexto se
Gramáticas Sensíveis ao Contexto (GSC) Linguagens Sensíveis ao Contexto (LSC) Autômatos Linearmente Limitados (ALL) 1 Gramática Sensível ao Contexto Definição: Uma gramática G é sensível ao contexto se
INE5317 Linguagens Formais e Compiladores. AULA 4: Gramáticas
 INE5317 Linguagens Formais e Compiladores AULA 4: Gramáticas bas eado em material produzido pelo prof Olinto Jos é Varela Furtado Ricardo Azambuja Silveira INE-CTC-UFSC E-Mail: [email protected] URL:
INE5317 Linguagens Formais e Compiladores AULA 4: Gramáticas bas eado em material produzido pelo prof Olinto Jos é Varela Furtado Ricardo Azambuja Silveira INE-CTC-UFSC E-Mail: [email protected] URL:
BCC244. Alfabeto, String, Linguagem, Gramática. Registro aqui o agradecimento à Profa. Lucília por ceder slides que fazem parte deste materal.
 BCC244 Alfabeto, String, Linguagem, Gramática Registro aqui o agradecimento à Profa. Lucília por ceder slides que fazem parte deste materal. Exemplo: Máquina de Venda A máquina de venda retorna uma cocacola
BCC244 Alfabeto, String, Linguagem, Gramática Registro aqui o agradecimento à Profa. Lucília por ceder slides que fazem parte deste materal. Exemplo: Máquina de Venda A máquina de venda retorna uma cocacola
Alfabeto, Cadeias, Operações e Linguagens
 Linguagens de Programação e Compiladores - Aula 3 1 Alfabeto, Cadeias, Operações e Linguagens 1.Conjuntos Para representar um determinado conjunto é necessário buscar uma notação para representá-lo e ter
Linguagens de Programação e Compiladores - Aula 3 1 Alfabeto, Cadeias, Operações e Linguagens 1.Conjuntos Para representar um determinado conjunto é necessário buscar uma notação para representá-lo e ter
Linguagens Formais e Autômatos
 Linguagens Formais e Autômatos Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa Introdução Problema: definir um conjunto de cadeias de símbolos; Prof. Yandre Maldonado - 2 Exemplo: conjunto
Linguagens Formais e Autômatos Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa Introdução Problema: definir um conjunto de cadeias de símbolos; Prof. Yandre Maldonado - 2 Exemplo: conjunto
Linguagens Formais e Autômatos
 Linguagens Formais e Autômatos Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa Problema: definir um conjunto de cadeias de símbolos; Prof. Yandre Maldonado - 2 Exemplo: conjunto M dos
Linguagens Formais e Autômatos Prof. Yandre Maldonado - 1 Prof. Yandre Maldonado e Gomes da Costa Problema: definir um conjunto de cadeias de símbolos; Prof. Yandre Maldonado - 2 Exemplo: conjunto M dos
LINGUAGEM LIVRE DE CONTEXTO GRAMÁTICA LIVRE DE CONTEXTO
 LINGUAGEM LIVRE DE CONTEXTO As Linguagens Livres de Contexto é um reconhecedor de linguagens, capaz de aceitar palavras corretas (cadeia, sentenças) da linguagem. Por exemplo, os autômatos. Um gerador
LINGUAGEM LIVRE DE CONTEXTO As Linguagens Livres de Contexto é um reconhecedor de linguagens, capaz de aceitar palavras corretas (cadeia, sentenças) da linguagem. Por exemplo, os autômatos. Um gerador
Python e sua sintaxe LNCC UFRJ
 Python e sua sintaxe LNCC UFRJ Linguagens naturais e formais Linguagens naturais Linguagem formal Um conjunto finito e não-vazio cujos elementos são símbolos Qualquer cadeia finita de símbolos justapostos
Python e sua sintaxe LNCC UFRJ Linguagens naturais e formais Linguagens naturais Linguagem formal Um conjunto finito e não-vazio cujos elementos são símbolos Qualquer cadeia finita de símbolos justapostos
Linguagens Formais e Problemas de Decisão
 Linguagens Formais e Problemas de Decisão Mário S. Alvim ([email protected]) Fundamentos de Teoria da Computação (FTC) DCC-UFMG (2018/02) Mário S. Alvim ([email protected]) Linguagens Formais e Problemas
Linguagens Formais e Problemas de Decisão Mário S. Alvim ([email protected]) Fundamentos de Teoria da Computação (FTC) DCC-UFMG (2018/02) Mário S. Alvim ([email protected]) Linguagens Formais e Problemas
UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO. Prof.ª Danielle Casillo
 UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO TEORIA DA COMPUTAÇÃO Aula 02 Introdução à Teoria da Computação Prof.ª Danielle Casillo Linguagem: é uma forma precisa de expressar
UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO TEORIA DA COMPUTAÇÃO Aula 02 Introdução à Teoria da Computação Prof.ª Danielle Casillo Linguagem: é uma forma precisa de expressar
Gramática regular. IBM1088 Linguagens Formais e Teoria da Computação. Evandro Eduardo Seron Ruiz Universidade de São Paulo
 Gramática regular IBM1088 Linguagens Formais e Teoria da Computação Evandro Eduardo Seron Ruiz [email protected] Universidade de São Paulo E.E.S. Ruiz (USP) LFA 1 / 41 Frase do dia Através de três métodos
Gramática regular IBM1088 Linguagens Formais e Teoria da Computação Evandro Eduardo Seron Ruiz [email protected] Universidade de São Paulo E.E.S. Ruiz (USP) LFA 1 / 41 Frase do dia Através de três métodos
Exemplo preliminar. Considere a linguagem dos Palíndromos Lpal:
 a n b n 1 Exemplo preliminar Considere a linguagem dos Palíndromos Lpal: radar, Roma é amor, 0110, 11011,... ou seja, quando w = w r Lpal é regular? usando o Lema do Bombeamento: Suponha Lpal regular,
a n b n 1 Exemplo preliminar Considere a linguagem dos Palíndromos Lpal: radar, Roma é amor, 0110, 11011,... ou seja, quando w = w r Lpal é regular? usando o Lema do Bombeamento: Suponha Lpal regular,
Capítulo 1: Alfabetos, cadeias, linguagens
 Capítulo 1: Alfabetos, cadeias, linguagens Símbolos e alfabetos. Um alfabeto é, para os nossos fins, um conjunto finito não vazio cujos elementos são chamados de símbolos. Dessa maneira, os conceitos de
Capítulo 1: Alfabetos, cadeias, linguagens Símbolos e alfabetos. Um alfabeto é, para os nossos fins, um conjunto finito não vazio cujos elementos são chamados de símbolos. Dessa maneira, os conceitos de
COMPILADORES. Revisão Linguagens formais Parte 02. Prof. Geovane Griesang
 Universidade de Santa Cruz do Sul UNISC Departamento de informática COMPILADORES Revisão Linguagens formais Parte 02 Prof. [email protected] Legenda: = sigma (somatório) = delta ε = epsilon λ =
Universidade de Santa Cruz do Sul UNISC Departamento de informática COMPILADORES Revisão Linguagens formais Parte 02 Prof. [email protected] Legenda: = sigma (somatório) = delta ε = epsilon λ =
Apostila 01 Fundamentação da Teoria da Computação e Linguagens Formais
 Cursos: Bacharelado em Ciência da Computação e Bacharelado em Sistemas de Informação Disciplinas: (1493A) Teoria da Computação e Linguagens Formais, (4623A) Teoria da Computação e Linguagens Formais e
Cursos: Bacharelado em Ciência da Computação e Bacharelado em Sistemas de Informação Disciplinas: (1493A) Teoria da Computação e Linguagens Formais, (4623A) Teoria da Computação e Linguagens Formais e
Um alfabeto é um conjunto de símbolos indivisíveis de qualquer natureza. Um alfabeto é geralmente denotado pela letra grega Σ.
 Linguagens O conceito de linguagem engloba uma variedade de categorias distintas de linguagens: linguagens naturais, linguagens de programação, linguagens matemáticas, etc. Uma definição geral de linguagem
Linguagens O conceito de linguagem engloba uma variedade de categorias distintas de linguagens: linguagens naturais, linguagens de programação, linguagens matemáticas, etc. Uma definição geral de linguagem
Construção de Compiladores
 Construção de Compiladores Parte 1 Introdução Linguagens e Gramáticas F.A. Vanini IC Unicamp Klais Soluções Motivação Porque compiladores? São ferramentas fundamentais no processo de desenvolvimento de
Construção de Compiladores Parte 1 Introdução Linguagens e Gramáticas F.A. Vanini IC Unicamp Klais Soluções Motivação Porque compiladores? São ferramentas fundamentais no processo de desenvolvimento de
LINGUAGENS FORMAIS Definições. Desenvolveram-se na História em função da necessidade dos grupos humanos que as empregavam
 Linguagens Naturais LINGUAGENS FORMAIS Definições Desenvolveram-se na História em função da necessidade dos grupos humanos que as empregavam São muito ricas, mas também ambíguas e imprecisas. Ex.: João
Linguagens Naturais LINGUAGENS FORMAIS Definições Desenvolveram-se na História em função da necessidade dos grupos humanos que as empregavam São muito ricas, mas também ambíguas e imprecisas. Ex.: João
Expressões Regulares e Gramáticas Regulares
 Universidade Católica de Pelotas Escola de informática 053212 Linguagens Formais e Autômatos TEXTO 2 Expressões Regulares e Gramáticas Regulares Prof. Luiz A M Palazzo Março de 2007 Definição de Expressão
Universidade Católica de Pelotas Escola de informática 053212 Linguagens Formais e Autômatos TEXTO 2 Expressões Regulares e Gramáticas Regulares Prof. Luiz A M Palazzo Março de 2007 Definição de Expressão
Linguagens e Programação Gramáticas. Paulo Proença
 Linguagens e Programação Gramáticas Gramáticas Ferramenta para a descrição e análise de linguagens; Baseada num conjunto de regras que especificam o modo de construção das frases válidas na linguagem;
Linguagens e Programação Gramáticas Gramáticas Ferramenta para a descrição e análise de linguagens; Baseada num conjunto de regras que especificam o modo de construção das frases válidas na linguagem;
Conceitos básicos de Teoria da Computação
 Folha Prática Conceitos básicos de 1 Conceitos básicos de Métodos de Prova 1. Provar por indução matemática que para todo o número natural n: a) 1 + 2 + 2 2 + + 2 n = 2 n+1 1, para n 0 b) 1 2 + 2 2 + 3
Folha Prática Conceitos básicos de 1 Conceitos básicos de Métodos de Prova 1. Provar por indução matemática que para todo o número natural n: a) 1 + 2 + 2 2 + + 2 n = 2 n+1 1, para n 0 b) 1 2 + 2 2 + 3
LFA. Aula 04. Sintaxe e Semântica. Conceitos Básicos Alfabeto Palavra Linguagem
 LFA Aula 04 Sintaxe e Semântica. Conceitos Básicos Alfabeto Palavra Linguagem Linguagens Formais Linguagens formais se preocupam com os problemas sintáticos das linguagens. Sintaxe e Semântica Sintaxe
LFA Aula 04 Sintaxe e Semântica. Conceitos Básicos Alfabeto Palavra Linguagem Linguagens Formais Linguagens formais se preocupam com os problemas sintáticos das linguagens. Sintaxe e Semântica Sintaxe
TEORIA DAS LINGUAGENS 3. GRAMÁTICAS INDEPENDENTES DE CONTEXTO
 LICENCIATURA EM CIÊNCIAS DA COMPUTAÇÃO TEORIA DAS LINGUAGENS 3. GRAMÁTICAS INDEPENDENTES DE CONTEXTO José Carlos Costa Dep. Matemática e Aplicações Universidade do Minho Braga, Portugal 31 de Maio de 2010
LICENCIATURA EM CIÊNCIAS DA COMPUTAÇÃO TEORIA DAS LINGUAGENS 3. GRAMÁTICAS INDEPENDENTES DE CONTEXTO José Carlos Costa Dep. Matemática e Aplicações Universidade do Minho Braga, Portugal 31 de Maio de 2010
Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos
 Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não
Notas de aula: Cálculo e Matemática Aplicados às Notas de aula: Ciências dos Alimentos 1 Conjuntos Um conjunto está bem caracterizado quando podemos estabelecer com certeza se um elemento pertence ou não
Linguagem (formal) de alfabeto Σ
 Linguagem (formal) de alfabeto Σ Linguagem é qualquer subconjunto de Σ, i.e. qualquer conjunto de palavras de Σ Σ = {a, b} {aa, ab, ba, bb} ou {x x {a, b} e x = 2} {a, aa, ab, ba, aaa, aab, aba,...} ou
Linguagem (formal) de alfabeto Σ Linguagem é qualquer subconjunto de Σ, i.e. qualquer conjunto de palavras de Σ Σ = {a, b} {aa, ab, ba, bb} ou {x x {a, b} e x = 2} {a, aa, ab, ba, aaa, aab, aba,...} ou
Modelos de Computação
 Modelos de Computação 2.ano LCC e LERSI URL: http://www.ncc.up.pt/~nam/aulas/0405/mc Escolaridade: 3.5T e 1P Frequência:Semanalmente serão propostos trabalhos aos alunos, que serão entregues nas caixas
Modelos de Computação 2.ano LCC e LERSI URL: http://www.ncc.up.pt/~nam/aulas/0405/mc Escolaridade: 3.5T e 1P Frequência:Semanalmente serão propostos trabalhos aos alunos, que serão entregues nas caixas
Linguagens Formais e Autômatos. Conceitos Básicos Prof. Anderson Belgamo
 Linguagens Formais e Autômatos Conceitos Básicos Prof. Anderson Belgamo Introdução Teoria das Linguagens Formais Originariamente desenvolvida na década de 1950. Objetivo inicial: desenvolver teorias relacionadas
Linguagens Formais e Autômatos Conceitos Básicos Prof. Anderson Belgamo Introdução Teoria das Linguagens Formais Originariamente desenvolvida na década de 1950. Objetivo inicial: desenvolver teorias relacionadas
Prof. Adriano Maranhão COMPILADORES
 Prof. Adriano Maranhão COMPILADORES LINGUAGENS: INTERPRETADAS X COMPILADAS Resumo: Linguagem compilada: Se o método utilizado traduz todo o texto do programa, para só depois executar o programa, então
Prof. Adriano Maranhão COMPILADORES LINGUAGENS: INTERPRETADAS X COMPILADAS Resumo: Linguagem compilada: Se o método utilizado traduz todo o texto do programa, para só depois executar o programa, então
Revisões de Conjuntos
 Revisões de Conjuntos {, {a}, {b}, {a, b}} a A a pertence a A, a é elemento de A a {a, b, c} a / A a não pertence a A d / {a, b, c} A B A contido em B, A subconjunto de B x A x B {a, b} {b, c, a} A B A
Revisões de Conjuntos {, {a}, {b}, {a, b}} a A a pertence a A, a é elemento de A a {a, b, c} a / A a não pertence a A d / {a, b, c} A B A contido em B, A subconjunto de B x A x B {a, b} {b, c, a} A B A
1 INTRODUÇÃO E CONCEITOS BÁSICOS
 1 INTRODUÇÃO E CONCEITOS BÁSICOS Inicia com uma breve história do surgimento e do desenvolvimento dos conceitos, resultados e formalismos nos quais a Teoria da Computação é baseada. Formalização dos conceitos
1 INTRODUÇÃO E CONCEITOS BÁSICOS Inicia com uma breve história do surgimento e do desenvolvimento dos conceitos, resultados e formalismos nos quais a Teoria da Computação é baseada. Formalização dos conceitos
Apostila 05 Assunto: Linguagens dos tipos 0 e 1
 Cursos: Bacharelado em Ciência da Computação e Bacharelado em Sistemas de Informação Disciplinas: (1493A) Teoria da Computação e Linguagens Formais, (4623A) Teoria da Computação e Linguagens Formais e
Cursos: Bacharelado em Ciência da Computação e Bacharelado em Sistemas de Informação Disciplinas: (1493A) Teoria da Computação e Linguagens Formais, (4623A) Teoria da Computação e Linguagens Formais e
Transformações úteis para GLC: (1) eliminação de produções nulas; (2) eliminação de produções unitárias; (3) Eliminação de símbolos estéreis e
 Transformações úteis para GLC: (1) eliminação de produções nulas; (2) eliminação de produções unitárias; (3) Eliminação de símbolos estéreis e inacessíveis; Forma Normal de Chomsky (FNC) e Forma Normal
Transformações úteis para GLC: (1) eliminação de produções nulas; (2) eliminação de produções unitárias; (3) Eliminação de símbolos estéreis e inacessíveis; Forma Normal de Chomsky (FNC) e Forma Normal
Curso: Ciência da Computação Turma: 6ª Série. Teoria da Computação. Aula 3. Autômatos Finitos
 Curso: Ciência da Computação Turma: 6ª Série Aula 3 Autômatos Finitos Alfabeto Alfabeto Conjunto finito de símbolos; Normalmente descrito por ; Exemplos: ={a, b} ={1, 2, 3} ={00, 11} Ø Alfabeto romano
Curso: Ciência da Computação Turma: 6ª Série Aula 3 Autômatos Finitos Alfabeto Alfabeto Conjunto finito de símbolos; Normalmente descrito por ; Exemplos: ={a, b} ={1, 2, 3} ={00, 11} Ø Alfabeto romano
Teoria de Linguagens 1 o semestre de 2018 Professor: Newton José Vieira Primeira Lista de Exercícios Data de entrega: 17/4/2018 Valor: 10 pontos
 Departamento de Ciência da Computação ICEx/UFMG Teoria de Linguagens o semestre de 8 Professor: Newton José Vieira Primeira Lista de Exercícios Data de entrega: 7/4/8 Valor: pontos. Uma versão do problema
Departamento de Ciência da Computação ICEx/UFMG Teoria de Linguagens o semestre de 8 Professor: Newton José Vieira Primeira Lista de Exercícios Data de entrega: 7/4/8 Valor: pontos. Uma versão do problema
Métodos Quantitativos
 Métodos Quantitativos Unidade 4. Estatística inferencial Parte II 1 Sumário Seção Slides 4.1 Correlação entre variáveis quantitativas 03 11 4.2 Teste de significância 12 19 4.3 Regressão linear 20 27 4.4
Métodos Quantitativos Unidade 4. Estatística inferencial Parte II 1 Sumário Seção Slides 4.1 Correlação entre variáveis quantitativas 03 11 4.2 Teste de significância 12 19 4.3 Regressão linear 20 27 4.4
Linguagens Livres de Contexto
 Linguagens Livres de Contexto 1 Roteiro Gramáticas livres de contexto Representação de linguagens livres de contexto Formas normais para gramáticas livres de contexto Gramáticas ambíguas Autômatos de Pilha
Linguagens Livres de Contexto 1 Roteiro Gramáticas livres de contexto Representação de linguagens livres de contexto Formas normais para gramáticas livres de contexto Gramáticas ambíguas Autômatos de Pilha
ACH2043 INTRODUÇÃO À TEORIA DA COMPUTAÇÃO
 ACH2043 INTRODUÇÃO À TEORIA DA COMPUTAÇÃO 2. Linguagens Livres-do-Contexto Referência: SIPSER, M. Introdução à Teoria da Computação. 2ª edição, Ed. Thomson Prof. Marcelo S. Lauretto [email protected]
ACH2043 INTRODUÇÃO À TEORIA DA COMPUTAÇÃO 2. Linguagens Livres-do-Contexto Referência: SIPSER, M. Introdução à Teoria da Computação. 2ª edição, Ed. Thomson Prof. Marcelo S. Lauretto [email protected]
ACH2043 INTRODUÇÃO À TEORIA DA COMPUTAÇÃO
 ACH2043 INTRODUÇÃO À TEORIA DA COMPUTAÇÃO 2. Linguagens Livres-do-Contexto Referência: SIPSER, M. Introdução à Teoria da Computação. 2ª edição, Ed. Thomson Prof. Marcelo S. Lauretto [email protected]
ACH2043 INTRODUÇÃO À TEORIA DA COMPUTAÇÃO 2. Linguagens Livres-do-Contexto Referência: SIPSER, M. Introdução à Teoria da Computação. 2ª edição, Ed. Thomson Prof. Marcelo S. Lauretto [email protected]
Compiladores I Prof. Ricardo Santos (cap 3 Análise Léxica: Introdução, Revisão LFA)
 Compiladores I Prof. Ricardo Santos (cap 3 Análise Léxica: Introdução, Revisão LFA) Análise Léxica A primeira fase da compilação Recebe os caracteres de entrada do programa e os converte em um fluxo de
Compiladores I Prof. Ricardo Santos (cap 3 Análise Léxica: Introdução, Revisão LFA) Análise Léxica A primeira fase da compilação Recebe os caracteres de entrada do programa e os converte em um fluxo de
SCC Capítulo 3 Linguagens Sensíveis ao Contexto e Autômatos Limitados Linearmente
 SCC-505 - Capítulo 3 Linguagens Sensíveis ao Contexto e João Luís Garcia Rosa 1 1 Departamento de Ciências de Computação Instituto de Ciências Matemáticas e de Computação - Universidade de São Paulo http://www.icmc.usp.br/~joaoluis
SCC-505 - Capítulo 3 Linguagens Sensíveis ao Contexto e João Luís Garcia Rosa 1 1 Departamento de Ciências de Computação Instituto de Ciências Matemáticas e de Computação - Universidade de São Paulo http://www.icmc.usp.br/~joaoluis
Teoria da Computação Gramáticas, Linguagens Algébricas e Autómatos de Pilha
 Teoria da Computação Gramáticas, Linguagens Algébricas e Autómatos de Pilha Simão Melo de Sousa 12 de Outubro de 2011 Conteúdo 1 Gramáticas e Definições básicas 1 2 Gramáticas e Linguagens 4 2.1 Gramáticas
Teoria da Computação Gramáticas, Linguagens Algébricas e Autómatos de Pilha Simão Melo de Sousa 12 de Outubro de 2011 Conteúdo 1 Gramáticas e Definições básicas 1 2 Gramáticas e Linguagens 4 2.1 Gramáticas
Segunda Lista de Exercícios 2004/2...
 + + UFLA Universidade Federal de Lavras Departamento de Ciência da Computação COM162 Linguagens Formais e Autômatos Prof. Rudini Sampaio Monitor: Rodrigo Pereira dos Santos Segunda Lista de Exercícios
+ + UFLA Universidade Federal de Lavras Departamento de Ciência da Computação COM162 Linguagens Formais e Autômatos Prof. Rudini Sampaio Monitor: Rodrigo Pereira dos Santos Segunda Lista de Exercícios
Gramáticas Livres de Contexto
 Gramáticas Livres de Contexto IBM1088 Linguagens Formais e Teoria da Computação Evandro Eduardo Seron Ruiz [email protected] Universidade de São Paulo E.E.S. Ruiz (USP) LFA 1 / 42 Frase do dia Quando vires
Gramáticas Livres de Contexto IBM1088 Linguagens Formais e Teoria da Computação Evandro Eduardo Seron Ruiz [email protected] Universidade de São Paulo E.E.S. Ruiz (USP) LFA 1 / 42 Frase do dia Quando vires
Linguagens Formais e Autômatos P. Blauth Menezes
 Linguagens Formais e Autômatos P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Linguagens Formais e Autômatos - P. Blauth Menezes 1 Linguagens
Linguagens Formais e Autômatos P. Blauth Menezes [email protected] Departamento de Informática Teórica Instituto de Informática / UFRGS Linguagens Formais e Autômatos - P. Blauth Menezes 1 Linguagens
Teoria de Linguagens 2 o semestre de 2017 Professor: Newton José Vieira Primeira Lista de Exercícios Data de entrega: 19/9/2017 Valor: 10 pontos
 Departamento de Ciência da Computação ICEx/UFMG Teoria de Linguagens o semestre de 7 Professor: Newton José Vieira Primeira Lista de Exercícios Data de entrega: 9/9/7 Valor: pontos. Uma versão do problema
Departamento de Ciência da Computação ICEx/UFMG Teoria de Linguagens o semestre de 7 Professor: Newton José Vieira Primeira Lista de Exercícios Data de entrega: 9/9/7 Valor: pontos. Uma versão do problema
Histórico e motivação
 Expressões regulares 1. Histórico e motivação 2. Definição a) Sintaxe b) Semântica c) Precedência dos operadores 3. Exemplos 4. Leis algébricas 5. Dialetos 6. Aplicações 7. Exercícios Pré-requisito: básico
Expressões regulares 1. Histórico e motivação 2. Definição a) Sintaxe b) Semântica c) Precedência dos operadores 3. Exemplos 4. Leis algébricas 5. Dialetos 6. Aplicações 7. Exercícios Pré-requisito: básico
Prof. Dr. Marcos Castilho. Departamento de Informática/UFPR. 22 de Fevereiro de 2018
 22 de Fevereiro de 2018 Motivação O que é um computador? O que é um algoritmo? Para que serve um algoritmo? Quando um algoritmo é bom? A análise de um algoritmo depende do computador? Motivação Em teoria
22 de Fevereiro de 2018 Motivação O que é um computador? O que é um algoritmo? Para que serve um algoritmo? Quando um algoritmo é bom? A análise de um algoritmo depende do computador? Motivação Em teoria
Teoria da Computação
 Introdução Março - 2009 1 Noções e Terminologia Matemática Conjuntos Um conjunto é um grupo de objetos, chamados elementos ou membros, representado como uma unidade. O conjunto { 3, 41, 57} possui os elementos
Introdução Março - 2009 1 Noções e Terminologia Matemática Conjuntos Um conjunto é um grupo de objetos, chamados elementos ou membros, representado como uma unidade. O conjunto { 3, 41, 57} possui os elementos
SCC Capítulo 1 Linguagens Regulares e Autômatos Finitos
 SCC-505 - Capítulo 1 Linguagens Regulares e Autômatos Finitos João Luís Garcia Rosa 1 1 Departamento de Ciências de Computação Instituto de Ciências Matemáticas e de Computação Universidade de São Paulo
SCC-505 - Capítulo 1 Linguagens Regulares e Autômatos Finitos João Luís Garcia Rosa 1 1 Departamento de Ciências de Computação Instituto de Ciências Matemáticas e de Computação Universidade de São Paulo
LINGUAGENS FORMAIS E AUTÔMATOS
 LINGUAGENS FORMAIS E AUTÔMATOS O objetivo deste curso é formalizar a idéia de linguagem e definir os tipos de sintaxe e semântica. Para cada sintaxe, analisamos autômatos, ue são abstrações de algoritmos.
LINGUAGENS FORMAIS E AUTÔMATOS O objetivo deste curso é formalizar a idéia de linguagem e definir os tipos de sintaxe e semântica. Para cada sintaxe, analisamos autômatos, ue são abstrações de algoritmos.
LINGUAGENS FORMAIS: Teoria, Modelagem e Implementação. Material adicional, versão do dia 22 de novembro de 2017 às 17:24
 LINGUAGENS FORMAIS: Teoria, Modelagem e Implementação Material adicional, versão do dia 22 de novembro de 2017 às 17:24 1. Página 32, imediatamente depois do Exemplo 1.8: A teoria de conjuntos apresentada
LINGUAGENS FORMAIS: Teoria, Modelagem e Implementação Material adicional, versão do dia 22 de novembro de 2017 às 17:24 1. Página 32, imediatamente depois do Exemplo 1.8: A teoria de conjuntos apresentada
Parte A FÓRMULAS Spiegel_II_01-06.indd 11 Spiegel_II_01-06.indd :17: :17:08
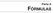 Parte A FÓRMULAS Seção I: Constantes, Produtos e Fórmulas Elementares Alfabeto Grego e Constantes Especiais 1 Alfabeto grego Nome Letras Gregas Grego Minúsculas Maiúsculas Alfa Α Beta Β Gama Γ Delta Δ
Parte A FÓRMULAS Seção I: Constantes, Produtos e Fórmulas Elementares Alfabeto Grego e Constantes Especiais 1 Alfabeto grego Nome Letras Gregas Grego Minúsculas Maiúsculas Alfa Α Beta Β Gama Γ Delta Δ
Análise Léxica. O papel do analisador léxico
 Análise Léxica Compiladores 1 A varredura, ou análise léxica, é a fase de um compilador que lê o programafonte como um arquivo de caracteres e o separa em marcas. Essas marcas são como palavras em uma
Análise Léxica Compiladores 1 A varredura, ou análise léxica, é a fase de um compilador que lê o programafonte como um arquivo de caracteres e o separa em marcas. Essas marcas são como palavras em uma
IV Gramáticas Livres de Contexto
 IV Gramáticas Livres de Contexto Introdução Definições de GLC 1 G = (Vn, Vt, P, S) onde P = {A α A Vn α (Vn Vt) + } 2 GLC ε - LIVRE : S ε pode pertencer a P, desde que: S seja o símbolo inicial de G S
IV Gramáticas Livres de Contexto Introdução Definições de GLC 1 G = (Vn, Vt, P, S) onde P = {A α A Vn α (Vn Vt) + } 2 GLC ε - LIVRE : S ε pode pertencer a P, desde que: S seja o símbolo inicial de G S
AXB = {(x, y) x A e y B}
 CENTRO UNIVERSITÁRIO DO NORTE PAULISTA LÓGICA E MATEMÁTICA DISCRETA 2010 1 Produto Cartesiano Par ordenado: são dois elementos em uma ordem fixa, (x,y) Produto Cartesiano: Dados dois conjuntos A e B, não
CENTRO UNIVERSITÁRIO DO NORTE PAULISTA LÓGICA E MATEMÁTICA DISCRETA 2010 1 Produto Cartesiano Par ordenado: são dois elementos em uma ordem fixa, (x,y) Produto Cartesiano: Dados dois conjuntos A e B, não
Aula 8: Gramáticas Livres de Contexto
 Teoria da Computação Primeiro Semestre, 2015 Aula 8: Gramáticas Livres de Contexto DAINF-UTFPR Prof. Ricardo Dutra da Silva Veremos agora maneira de gerar as strings de um tipo específico de linguagem,
Teoria da Computação Primeiro Semestre, 2015 Aula 8: Gramáticas Livres de Contexto DAINF-UTFPR Prof. Ricardo Dutra da Silva Veremos agora maneira de gerar as strings de um tipo específico de linguagem,
MATEMÁTICA. Aula 2 Teoria dos Conjuntos. Prof. Anderson
 MATEMÁTICA Aula 2 Teoria dos Conjuntos Prof. Anderson CONCEITO Na teoria dos conjuntos, um conjunto é descrito como uma coleção de objetos bem definidos. Estes objetos são chamados de elementos ou membros
MATEMÁTICA Aula 2 Teoria dos Conjuntos Prof. Anderson CONCEITO Na teoria dos conjuntos, um conjunto é descrito como uma coleção de objetos bem definidos. Estes objetos são chamados de elementos ou membros
Gramáticas e Linguagens Independentes de Contexto
 Gramáticas e Linguagens Independentes de Contexto 6.1 Responde às uestões seguintes considerando a gramática independente de contexto G = (V, {a, b}, P, R), onde o conjunto de regras P é: R XRX S S at
Gramáticas e Linguagens Independentes de Contexto 6.1 Responde às uestões seguintes considerando a gramática independente de contexto G = (V, {a, b}, P, R), onde o conjunto de regras P é: R XRX S S at
