Capítulo 1 Carga axial
|
|
|
- Gabriel Henrique de Escobar Cerveira
- 9 Há anos
- Visualizações:
Transcrição
1 Capítulo 1 Carga axial
2 1.1 - Revisão Definição de deformação e de tensão: L Da Lei de Hooke: P A P 1 P E E A E EA Barra homogênea BC, de comprimento L e seção uniforme de área A, submetida a uma força axial centrada P Temos para o deslocamento: PL EA Com variações de carga, seção transversal ou propriedades dos materiais, i PL i i E A i i
3 Força e deslocamento são positivos se provocarem tração e alongamento; e negativos causarão compressão e contração.
4 1.2-Problemas hipestáticos Barra sob carga axial fixada em uma única extremidade: Isostático Este problema é isostático, porque apenas as equações de equilíbrio disponíveis são suficientes para determinar as reações de apoio. Fx 0: RA P2 P1 0 R A P 1 P2
5 Hiperestático Barra sob carga axial fixada nas duas extremidades: Neste caso o problema é hiperestático, porque apenas as equações de equilíbrio não suficientes para determinar as reações de apoio. Fy 0: FA FB P 0 F A F B P (1)
6 1.3-Equação de compatibilidade É preciso criar uma equação adicional que leva em conta a maneira como a estrutura se deforma. Este tipo de equação é chamado de equação de compatibilidade (ou condição cinemática). A 0 B 0 Neste problema como as extremidades A e B são fixas, tem-se que o deslocamento relativo entre A e B deve ser nulo. AB 0
7 Equação de compatibilidade: AB AC CB 0 AB N FA. L E. A. L E. A AC AC AC N FB. L E. A. L E. A CB CB CB 0 0 F B L L AC CB F A (2) F A F B P (1) Substituindo (2) em (1): F A L L CB P e F B L L AC P
8 Procedimento de análise: 1. Desenhar um diagrama de corpo livre da estrutura, indicando todas as reações de apoio e forças externas. 2. Aplicar as equações de equilíbrio disponíveis. 3. Criar uma ou mais equações de compatibilidade adicionais. 4. Resolver o sistema de equações: equilíbrio + compatibilidade.
9 Exercício de fixação 1)A barra de aço é presa a dois apoios fixos A e B. Determine as reações desses apoios quando se aplica o carregamento indicado. E aço = 200 GPa Respostas: R A =323kN e R B =577kN
10 Exemplo 1- A haste de aço tem diâmetro de 5 mm e está presa à parede fixa em A. Antes de ser carregada, há uma folga de 1 mm entre a parede B e a haste. Determine as reações em A e B se a haste for submetida a uma força axial P = 20 kn. Despreze o tamanho do colar em C. (E aço = 200 GPa)
11
12 O equilíbrio da haste exige: AB F F F N 3 x 0; A B (1) A condição de compatibilidade para a haste é. F L F L 1mm EA EA A AC B CB EA F mm F mm A B mm mm N mm F mm F mm 1( ) 2,5 ( ) ( / ) AB A 1mm B 6 400FA 800FB 3,93 10 N.mm (2) F F A B (1) As equações (1) e (2) nos dá F A = 16,6 kn e F B = 3,39 kn
13 Exercício de fixação 2)Calcular as reações em A e B, na barra do exercício anterior, supondo que existe uma distância de 4,5mm entre a barra e o apoio B, quando o carregamento é aplicado. Adotar E aço = 200 GPa Respostas R A =784,6kN R B =115,4kN
14 Exercícios de fixação: 3) As três barras de aço A-36 mostradas abaixo estão conectadas por pinos a um elemento rígido. Se a carga aplicada ao elemento for 15kN, determine a força desenvolvida em cada barra. Cada uma das barras AB e EF tem área de seção transversal de 25mm 2, e a barra CD tem área de seção transversal de 15mm 2. Respostas: F A =9,52kN, F C =3,46kN e F E =2,02kN
15 1.4- Estruturas heterogêneas quanto aos materiais Outro tipo de problema estaticamente indeterminado: qual a deformação da barra e do tubo quando uma força P é aplicada por meio de uma placa rígida? P1P 2 P (1)
16 No entanto, a geometria do problema nos mostra que as deformações e 1 2 = da barra e do tubo devem ser iguais. PL PL E A E 1A1 2 2 P E A P E A (2) Resolvendo o sistema temos o valor de P 1 e P 2. Em seguida calculamos a deformação da barra e do tubo pelas equações de deslocamento citadas acima. P P = e = L E A L E A
17 Exemplo 3- O poste de alumínio mostrado abaixo é reforçado com um núcleo de latão. Se este conjunto suportar uma carga de compressão axial resultante P=45kN, aplicada na tampa rígida, determine a tensão normal média no alumínio e no latão. Considere E 70 GPa e E 105 GPa al lat F 0; 45kN F F 0 (1) y al lat = al estaticamente indeterminado lat Fal L Flat L E A E A al al lat lat
18 2 2 Flat E (0,05 ) (0,025 ) al Aal 70GPa m m al lat 2 E lat Alat GPa m F F 105 (0,025 ) F 2F (2) al lat Resolvendo o sistema: F al 30kN F lat 15kN A tensão normal média no alumínio e no latão é: F 30kN 5,09MPa al al A al (0,05 0,0025 ) m F 15kN 7,64MPa lat lat 2 2 A lat (0,0025 ) m
19 Exercícios de fixação: 4) A coluna é construída de concreto de alta resistência e seis hastes de reforço de aço A-36. Se ela for submetida a uma força axial de 30kip, determine a tensão normal média no concreto e em cada haste. Cada uma tem diâmetro de 0,75in. E ksi e E ksi conc Resposta: aço 3 3 4,2(10 ) aço 29(10 ) 3,14 ksi e 0,46ksi conc
20 Exercícios de fixação: 5) Uma barra trimetálica está comprimida uniformemente por uma força axial P=2000lb aplicada através de uma placa rígida na extremidade. A barra consiste de um núcleo circular de aço circundado por tubos de latão e de cobre. O núcleo de aço tem diâmetro 0,4in, o tubo de latão tem diâmetro externo de 0,6in e o tubo de cobre tem diâmetro externo de 0,8in. Os módulos de elasticidade correspondentes são E aço =30x10 6 psi, E latão =15x10 6 psi e E cobre =18x10 6 psi. Calcule as tensões normais de compressão no aço, latão e cobre devido à força P. Respostas: aço 5,95ksi cob 3,57 ksi lat 2,98ksi
21 1.5- Tensões térmicas A variação de temperatura provoca mudanças nas dimensões de uma peça estrutural. Quando a temperatura aumenta a estrutura sofre uma dilatação. Quando a temperatura diminui a estrutura sofre uma contração.
22 Estudos experimentais demonstraram que a variação de comprimento provocada pela temperatura em uma barra de material homogêneo é dada por:.t T. L = propriedade do material denominada coeficiente de dilatação térmica dado em 1/ o C T = variação de temperatura em o C L = comprimento inicial da barra T = variação algébrica no comprimento da barra
23 Se a estrutura for isostática, e a variação de comprimento provocada pela temperatura for livre, não surgirão tensões causadas pela variação de temperatura.
24 Se a estrutura for hiperestática, a variação de comprimento da barra provocada pela temperatura será impedida e surgirão tensões térmicas. Estas tensões térmicas podem atingir valores elevados, causando danos à estrutura ou mesmo provocando sua ruptura.
25 Por este motivo, em estruturas de grande porte, como pontes, são feitas juntas de dilatação, para permitir a livre movimentação térmica da estrutura.
26 Cálculo do efeito da variação térmica em uma estrutura hiperestática (variação de comprimento impedida). Para a resolução deste tipo de problema, é possível considerar a reação do apoio como reação redundante e aplicar o princípio da superposição Equação de equilíbrio: F 0: R R 0 y A B RA R B (1)
27 Equação de compatibilidade: AB 0 (2) Variação de comprimento provocada pela temperatura: T.T. L Variação de comprimento provocada reação R A : R R A. L E. A
28 Equação de compatibilidade: AB T R 0 (2) R. L. T. L A AB E. A 0 R E. A..T A R B N E. A.. T T N E.. T A Tensão térmica
29 Exemplo 4- A barra de aço mostrada na figura está restringida para caber exatamente entre os dois suportes fixos quando T 1 =30 C. Se a temperatura aumentar até T 2 =60 C, determinar a tensão térmica normal média desenvolvida na barra. Usar E=200GPa e / C
30 Fy 0: FA FB F AB T F T TL FL F AE FL TL- 0 EA F T AE 0
31 F T AE T =60-30=30 C 2 A 10mm 10mm=100mm F / C 30 C 100mm MPa F 7200N 7,2kN F 7200N = 72MPa 2 A 100mm =-72MPa
32 Exercício de fixação: 6) A barra AB é perfeitamente ajustada aos anteparos fixos quando a temperatura é de +25 C. Determinar as tensões atuantes nas partes AC e CB da barra para a temperatura de -50 C. Usar :E=200GPa e / C Respostas: AC 240 MPa 120MPa CB
33 7) Os diâmetros e materiais de fabricação do conjunto são indicados na figura. Se o conjunto estiver bem ajustado entre seus apoios fixos quando a temperatura é T 1 =70 F, determine a tensão normal média em cada material quando a temperatura atingir T 2 =110 F. F F F alum 12,8 10 1/ bronze 9,6 10 1/ açoinox 9,6 10 1/ E ksi ksi ksi alum 10,6(10 ) Ebronze 15(10 ) Eaçoinox 28(10 ) Respostas: 2,5 ksi 5,5 ksi 22,1ksi alum bronze açoinox
34 8) Os dois segmentos de haste circular, um de alumínio e outro de cobre, estão presos às paredes rígidas de modo tal que há uma folga de 0,2mm entre eles quando T 1 = 15 C. Cada haste tem diâmetro de 30mm, determine a tensão normal média em cada haste se T 2 = 150 C. alum C / C cobre / E 70 GPa E 126GPa alum cobre Resposta: 185,6MPa
35 1.6 - Coeficiente de Poisson Quando um corpo deformável é alongado em uma direção, ele sofre uma contração na direção transversal.
36 Quando um corpo deformável sofre um encurtamento em uma direção, ele sofre uma expansão na direção transversal.
37 Nos anos de 1800, o cientista francês S. D. Poisson descobriu que a relação entre a deformação transversal e deformação longitudinal era constante no regime elástico. transversal longitudinal Coeficiente de Poisson (ni) para alguns materiais: Aço: 0,30 Concreto: 0,20 Plástico: 0,34 O valor máximo para é 0,5.
38 A expressão acima tem sinal negativo porque o alongamento longitudinal (deformação positiva) provoca contração lateral (deformação negativa) e vice-versa. longitudinal L transversal ' r
39 1.7- Estados Múltiplos de Carregamento Generalização da Lei de Hooke Até agora, nosso estudo se limitou à análise de barras delgadas submetidas a cargas axiais, isto é, dirigidas ao longo de um eixo somente. Tensão normal em cubo elementar Tensão normal em um elemento plano
40 Passamos agora a considerar elementos estruturais sujeitos à ação de carregamentos que atuam nas direções dos três eixos coordenados, produzindo tensões normais. Temos então um ESTADO MÚLTIPLO DE CARREGAMENTO OU CARREGAMENTO MULTIAXIAL., e x y z Cubo elementar original de arestas de comprimento unitário Cubo elementar deformado
41 Para escrevermos as expressões das componentes de deformação em função das tensões, vamos considerar separadamente o efeito provocado por cada componente de tensão e superpor os resultados (princípio da superposição). Considerando em primeiro lugar a tensão : causa uma deformação específica de valor x / E x y z na direção y e z. x E E E E x x y y E z y E E E z z E x x / E na direção do eixo x e de Generalização da Lei de Hooke para carregamento multiaxial Lembrando: Válido para o regime elástico e deformações pequenas! Deformação positiva expansão Deformação negativa - contração
42 1.8-Dilatação volumétrica Volume : (1 )(1 )(1 ) x y z Mudança de volume: e 1 (1 )(1 )(1 ) 1 Aplicando a Lei de Hooke Generalizada: e e 2 x 1 2 E E y x x y z As deformações específicas são muito menores que a unidade e os produtos entre elas podem ser desprezados. e x y z z y Dilatação volumétrica específica z x E y z V e V
43 Pressão hidrostática uniforme: x y z p z p e 3(1 2 ) E p Módulo de elasticidade de volume: E k 3(1 2 ) x p y p e p k
44 Exercício de fixação: 9) Um círculo de diâmetro d=230mm é desenhado em uma placa de alumínio livre de tensões de espessura t=20mm. Forças atuando no plano da placa posteriormente provocam tensões normais e z 140MPa. Para E=70GPa e ν=0,33, determine a variação (a) do comprimento do diâmetro AB, (b) do comprimento do diâmetro CD, (c) da espessura da placa e (d) a dilatação volumétrica específica. Respostas: (a)δ AB =122,6μm (b)δ CD =368 μm (c) δ t =-21,2 μm (d) 0,00107 x 84MPa
45 Exercício de fixação: 10) A figura mostra um bloco de aço submetido à ação de pressão uniforme em todas as faces. Mediu-se a variação do comprimento AB, que foi de -24μm. Determinar: (a) variação do comprimento das outras duas arestas (b) a pressão p aplicada às faces do bloco. Adotar E=200GPa e ν=0,29. Respostas: (a)δ y =-12μm (b)δ z =-18 μm (c) p=-142,9mpa
46 Exercício de fixação: 11) Um bloco cilíndrico de latão, com 160mm de altura e 120mm de diâmetro é deixado afundar num oceano até a profundidade onde a pressão é de 75MPa (cerca de 7500m abaixo da superfície). Sabendose que E=105GPa e ν=0,35, determinar: (a) variação do altura do bloco (b) sua variação do diâmetro (c) sua dilatação volumétrica específica (d) variação do volume Respostas: (a) δ h =-34,2μm (b)δ d =-25,7 μm (c) e=-6,42(10-4 ) (d)δv= -1161mm 3
Capítulo 1 Carga axial
 Capítulo 1 Carga axial 1.1 - Revisão Definição de deformação e de tensão: L P A Da Lei de Hooke: P 1 P E E A E EA Barra homogênea BC, de comprimento L e seção uniforme de área A, submetida a uma força
Capítulo 1 Carga axial 1.1 - Revisão Definição de deformação e de tensão: L P A Da Lei de Hooke: P 1 P E E A E EA Barra homogênea BC, de comprimento L e seção uniforme de área A, submetida a uma força
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I
 LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a. Se AB tiver diâmetro de 10 mm
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a. Se AB tiver diâmetro de 10 mm
Resistência dos Materiais
 Aula 4 Deformações e Propriedades Mecânicas dos Materiais Tópicos Abordados Nesta Aula Estudo de Deformações, Normal e por Cisalhamento. Propriedades Mecânicas dos Materiais. Coeficiente de Poisson. Deformação
Aula 4 Deformações e Propriedades Mecânicas dos Materiais Tópicos Abordados Nesta Aula Estudo de Deformações, Normal e por Cisalhamento. Propriedades Mecânicas dos Materiais. Coeficiente de Poisson. Deformação
Se a força de tração de cálculo for 110 kn, a área do tirante, em cm 2 é A) 5,0. B) 4,5. C) 3,0. D) 2,5. E) 7,5.
 25.(TRT-18/FCC/2013) Uma barra de aço especial, de seção circular com extremidades rosqueadas é utilizada como tirante em uma estrutura metálica. O aço apresenta f y = 242 MPa e f u = 396 MPa. Dados: Coeficientes
25.(TRT-18/FCC/2013) Uma barra de aço especial, de seção circular com extremidades rosqueadas é utilizada como tirante em uma estrutura metálica. O aço apresenta f y = 242 MPa e f u = 396 MPa. Dados: Coeficientes
Professor: José Junio Lopes
 Aula 2 - Tensão/Tensão Normal e de Cisalhamento Média; Tensões Admissíveis. A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a.
Aula 2 - Tensão/Tensão Normal e de Cisalhamento Média; Tensões Admissíveis. A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a.
Carga axial. Princípio de Saint-Venant
 Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
Carga axial Princípio de Saint-Venant O princípio Saint-Venant afirma que a tensão e deformação localizadas nas regiões de aplicação de carga ou nos apoios tendem a nivelar-se a uma distância suficientemente
Resistência dos Materiais
 Aula 3 Tensão Admissível, Fator de Segurança e rojeto de Acoplamentos Simples Tópicos Abordados Nesta Aula Tensão Admissível. Fator de Segurança. rojeto de Acoplamentos Simples. Tensão Admissível O engenheiro
Aula 3 Tensão Admissível, Fator de Segurança e rojeto de Acoplamentos Simples Tópicos Abordados Nesta Aula Tensão Admissível. Fator de Segurança. rojeto de Acoplamentos Simples. Tensão Admissível O engenheiro
Carga axial. Princípio de Saint-Venant. Princípio de Saint-Venant
 Capítulo 4: Carga axial Adaptado pela prof. Dra. Danielle Bond Princípio de Saint-Venant Anteriormente desenvolvemos os conceitos de: Tensão (um meio para medir a distribuição de força no interior de um
Capítulo 4: Carga axial Adaptado pela prof. Dra. Danielle Bond Princípio de Saint-Venant Anteriormente desenvolvemos os conceitos de: Tensão (um meio para medir a distribuição de força no interior de um
Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/
 Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/ Estrutura Sistema qualquer de elementos ligados, construído para suportar ou transferir
Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/ Estrutura Sistema qualquer de elementos ligados, construído para suportar ou transferir
- 1ª LISTA DE RESISTÊNCIA DOS MATERIAIS II Carga axial
 - 1ª LISTA DE RESISTÊNCIA DOS MATERIAIS II Carga axial 1) O tubo de aço tem raio externo de 20mm e raio interno de 15mm. Se ele se ajustar exatamente entre as paredes fixas antes de ser carregado, determine
- 1ª LISTA DE RESISTÊNCIA DOS MATERIAIS II Carga axial 1) O tubo de aço tem raio externo de 20mm e raio interno de 15mm. Se ele se ajustar exatamente entre as paredes fixas antes de ser carregado, determine
1. TORÇÃO EM BARRAS DE SEÇÃO CIRCULAR
 1. ORÇÃO EM BARRAS DE SEÇÃO CIRCULAR Elementos estruturais sujeitos a torção são amplamente utilizados na engenharia. Podemos citar os seguintes exemplos, entre muitos outros: eixos de transmissão, turbinas
1. ORÇÃO EM BARRAS DE SEÇÃO CIRCULAR Elementos estruturais sujeitos a torção são amplamente utilizados na engenharia. Podemos citar os seguintes exemplos, entre muitos outros: eixos de transmissão, turbinas
Mecânica Geral. Aula 04 Carregamento, Vínculo e Momento de uma força
 Aula 04 Carregamento, Vínculo e Momento de uma força 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
Aula 04 Carregamento, Vínculo e Momento de uma força 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
Capítulo 3 - PROPRIEDADES MECÂNICAS DOS MATERIAIS
 Capítulo 3 - PROPRIEDADES MECÂNICAS DOS MATERIAIS 1*. Um determinado latão, cujo módulo de Young é 1,03x10 5 MPa, apresenta uma tensão de cedência de 345MPa. (a) Considerando um provete desse latão, cuja
Capítulo 3 - PROPRIEDADES MECÂNICAS DOS MATERIAIS 1*. Um determinado latão, cujo módulo de Young é 1,03x10 5 MPa, apresenta uma tensão de cedência de 345MPa. (a) Considerando um provete desse latão, cuja
AULA 03 - TENSÃO E DEFORMAÇÃO
 AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. A - DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito
AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. A - DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito
Mecânica Geral. Aula 05 - Equilíbrio e Reação de Apoio
 Aula 05 - Equilíbrio e Reação de Apoio 1 - Equilíbrio de um Ponto Material (Revisão) Condição de equilíbrio de um Ponto Material Y F 0 F X 0 e F 0 Exemplo 01 - Determine a tensão nos cabos AB e AD para
Aula 05 - Equilíbrio e Reação de Apoio 1 - Equilíbrio de um Ponto Material (Revisão) Condição de equilíbrio de um Ponto Material Y F 0 F X 0 e F 0 Exemplo 01 - Determine a tensão nos cabos AB e AD para
Torção - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA SALETE SOUZA DE OLIVEIRA BUFFONI
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA SALETE SOUZA DE OLIVEIRA BUFFONI RESISTÊNCIA DOS MATERIAIS Torção Definições: Torção se refere ao giro de
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA SALETE SOUZA DE OLIVEIRA BUFFONI RESISTÊNCIA DOS MATERIAIS Torção Definições: Torção se refere ao giro de
TECNOLOGIA DOS MATERIAIS
 TECNOLOGIA DOS MATERIAIS Aula 6: Propriedades Mecânicas Ensaios Propriedades de Tração Dureza CEPEP - Escola Técnica Prof.: Propriedades Mecânicas dos Materiais Muitos materiais, quando em serviço, são
TECNOLOGIA DOS MATERIAIS Aula 6: Propriedades Mecânicas Ensaios Propriedades de Tração Dureza CEPEP - Escola Técnica Prof.: Propriedades Mecânicas dos Materiais Muitos materiais, quando em serviço, são
Pontifícia Universidade Católica do Rio Grande do Sul. Faculdade de Engenharia FACULDADE DE ARQUITETURA E URBANISMO SISTEMAS ESTRUTURAIS II
 Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Engenharia FACULDADE DE ARQUITETURA E URBANISMO SISTEMAS ESTRUTURAIS II COMENTÁRIOS Norma NBR 6118/2007 Prof. Eduardo Giugliani 1 0. COMENTÁRIOS
Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Engenharia FACULDADE DE ARQUITETURA E URBANISMO SISTEMAS ESTRUTURAIS II COMENTÁRIOS Norma NBR 6118/2007 Prof. Eduardo Giugliani 1 0. COMENTÁRIOS
Equilíbrio de uma Partícula
 Apostila de Resistência dos Materiais I Parte 2 Profª Eliane Alves Pereira Turma: Engenharia Civil Equilíbrio de uma Partícula Condição de Equilíbrio do Ponto Material Um ponto material encontra-se em
Apostila de Resistência dos Materiais I Parte 2 Profª Eliane Alves Pereira Turma: Engenharia Civil Equilíbrio de uma Partícula Condição de Equilíbrio do Ponto Material Um ponto material encontra-se em
5 - ENSAIO DE COMPRESSÃO. Ensaios Mecânicos Prof. Carlos Baptista EEL
 5 - ENSAIO DE COMPRESSÃO Informações Iniciais: Teste Uniaxial. Propriedades obtidas analogamente ao ensaio de tração. Exemplos de Normas: - ASTM E 9 (metais) - NBR 5739 (concreto) Razões para o Ensaio:
5 - ENSAIO DE COMPRESSÃO Informações Iniciais: Teste Uniaxial. Propriedades obtidas analogamente ao ensaio de tração. Exemplos de Normas: - ASTM E 9 (metais) - NBR 5739 (concreto) Razões para o Ensaio:
Equilíbrio de um corpo rígido
 Equilíbrio de um corpo rígido Objetivos da aula: Desenvolver as equações de equilíbrio para um corpo rígido. Introduzir o conceito do diagrama de corpo livre para um corpo rígido. Mostrar como resolver
Equilíbrio de um corpo rígido Objetivos da aula: Desenvolver as equações de equilíbrio para um corpo rígido. Introduzir o conceito do diagrama de corpo livre para um corpo rígido. Mostrar como resolver
Capítulo 4 Cisalhamento
 Capítulo 4 Cisalhamento 4.1 Revisão V dm dx 4.2 A fórmula do cisalhamento A fórmula do cisalhamento é usada para encontrar a tensão de cisalhamento na seção transversal. VQ It onde Q yda y' A' A' Q= momento
Capítulo 4 Cisalhamento 4.1 Revisão V dm dx 4.2 A fórmula do cisalhamento A fórmula do cisalhamento é usada para encontrar a tensão de cisalhamento na seção transversal. VQ It onde Q yda y' A' A' Q= momento
Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da massa específica do meio µ, de acordo com a expressão:
 PROVA DE FÍSICA DO VESTIBULAR 96/97 DO INSTITUTO MILITAR DE ENGENHARIA (03/12/96) 1 a Questão: Valor : 1,0 Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da
PROVA DE FÍSICA DO VESTIBULAR 96/97 DO INSTITUTO MILITAR DE ENGENHARIA (03/12/96) 1 a Questão: Valor : 1,0 Suponha que a velocidade de propagação v de uma onda sonora dependa somente da pressão P e da
Conteúdo. Resistência dos Materiais. Prof. Peterson Jaeger. 3. Concentração de tensões de tração. APOSTILA Versão 2013
 Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
ENSAIOS DOS MATERIAIS
 Ensaios Mecânicos dos Materiais Ensaio de tração NBR ISO 6892:2002, Assossiação Brasileira de Normas Técnicas - ABNT Entre os diversos tipos de ensaios existentes para avaliação das propriedades mecânicas
Ensaios Mecânicos dos Materiais Ensaio de tração NBR ISO 6892:2002, Assossiação Brasileira de Normas Técnicas - ABNT Entre os diversos tipos de ensaios existentes para avaliação das propriedades mecânicas
Mecânica dos Sólidos - Colecção de Problemas Resolvidos. 2º ano da Licenciatura em Engenharia Civil
 ALVARO F. M. AZEVEDO Mecânica dos Sólidos - Colecção de Problemas Resolvidos 2º ano da Licenciatura em Engenharia Civil Faculdade de Engenharia da Universidade do Porto - Portugal 1993 Faculdade de Engenharia
ALVARO F. M. AZEVEDO Mecânica dos Sólidos - Colecção de Problemas Resolvidos 2º ano da Licenciatura em Engenharia Civil Faculdade de Engenharia da Universidade do Porto - Portugal 1993 Faculdade de Engenharia
Capítulo 5 Carga Axial
 Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt [email protected] Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Capítulo 5 Carga Axial Resistência dos Materiais I SIDES 05 Prof. MSc. Douglas M. A. Bittencourt [email protected] Objetivos do capítulo Determinar a tensão normal e as deformações em elementos
Física Térmica Exercícios. Dilatação.
 Física Térmica Exercícios. Dilatação. Dilatação linear 1- Uma bobina contendo 2000 m de fio de cobre medido num dia em que a temperatura era de 35 C. Se o fio for medido de novo em um dia que a temperatura
Física Térmica Exercícios. Dilatação. Dilatação linear 1- Uma bobina contendo 2000 m de fio de cobre medido num dia em que a temperatura era de 35 C. Se o fio for medido de novo em um dia que a temperatura
Prof. Michel Sadalla Filho
 MECÂNICA APLICADA Prof. Michel Sadalla Filho MOMENTO DE UMA FORÇA + EQUILÍBRIO DE UMA BARRA (No Plano XY) Referência HIBBELER, R. C. Mecânica Estática. 10 ed. São Paulo: Pearson Education do Brasil, 2005,
MECÂNICA APLICADA Prof. Michel Sadalla Filho MOMENTO DE UMA FORÇA + EQUILÍBRIO DE UMA BARRA (No Plano XY) Referência HIBBELER, R. C. Mecânica Estática. 10 ed. São Paulo: Pearson Education do Brasil, 2005,
ALUNO: Nº SÉRIE: DATA: / / PROF.: VICTOR GERMINIO EXERCÍCIO DE REVISÃO I UNIDADE FÍSICA 2º ANO B ENSINO MÉDIO
 ALUNO: Nº SÉRIE: DATA: / / PROF.: VICTOR GERMINIO EXERCÍCIO DE REVISÃO I UNIDADE FÍSICA 2º ANO B ENSINO MÉDIO 1 ) Considere que o calor específico de um material presente nas cinzas seja c = 0,8 J/g C.
ALUNO: Nº SÉRIE: DATA: / / PROF.: VICTOR GERMINIO EXERCÍCIO DE REVISÃO I UNIDADE FÍSICA 2º ANO B ENSINO MÉDIO 1 ) Considere que o calor específico de um material presente nas cinzas seja c = 0,8 J/g C.
Quarta Lista de Exercícios
 Universidade Católica de Petrópolis Disciplina: Resitência dos Materiais I Prof.: Paulo César Ferreira Quarta Lista de Exercícios 1. O tubo de aço (E s = 210 GPa) tem núcleo de alumínio (E a = 69 GPa)
Universidade Católica de Petrópolis Disciplina: Resitência dos Materiais I Prof.: Paulo César Ferreira Quarta Lista de Exercícios 1. O tubo de aço (E s = 210 GPa) tem núcleo de alumínio (E a = 69 GPa)
RESISTÊNCIA DOS MATERIAIS
 RESISTÊNCIA DOS MATERIAIS Introdução e Conceitos Básicos 1. Mecânica Mecânica dos corpos rígidos: È subdividida em Estática, Cinemática e Dinâmica. A Estática se refere aos corpos em repouso e estuda as
RESISTÊNCIA DOS MATERIAIS Introdução e Conceitos Básicos 1. Mecânica Mecânica dos corpos rígidos: È subdividida em Estática, Cinemática e Dinâmica. A Estática se refere aos corpos em repouso e estuda as
Introdução aos Sistemas Estruturais
 Introdução aos Sistemas Estruturais Noções de Mecânica Estrutural Estuda o comportamento das estruturas frente aos esforços externos. Por definição estrutura é qualquer corpo sólido capaz de oferecer resistência
Introdução aos Sistemas Estruturais Noções de Mecânica Estrutural Estuda o comportamento das estruturas frente aos esforços externos. Por definição estrutura é qualquer corpo sólido capaz de oferecer resistência
EXERCÍCIOS PARA ESTUDOS DILATAÇÃO TÉRMICA
 1. (Unesp 89) O coeficiente de dilatação linear médio de um certo material é = 5,0.10 ( C) e a sua massa específica a 0 C é ³. Calcule de quantos por cento varia (cresce ou decresce) a massa específica
1. (Unesp 89) O coeficiente de dilatação linear médio de um certo material é = 5,0.10 ( C) e a sua massa específica a 0 C é ³. Calcule de quantos por cento varia (cresce ou decresce) a massa específica
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO PIAUÍ DISCIPLINA: Laboratório de Física Professor: Experimento 1: Lei de Hooke. Modelo...
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO PIAUÍ DISCIPLINA: Laboratório de Física Professor: Experimento 1: Lei de Hooke Modelo... Parnaíba/2009 Introdução Estando uma mola no seu estado relaxado
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO PIAUÍ DISCIPLINA: Laboratório de Física Professor: Experimento 1: Lei de Hooke Modelo... Parnaíba/2009 Introdução Estando uma mola no seu estado relaxado
LISTA DE EXERCÍCIOS ÁREA 1. Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02
 LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
LISTA DE EXERCÍCIOS ÁREA 1 Disciplina: Mecânica dos Sólidos MECSOL34 Semestre: 2016/02 Prof: Diego R. Alba 1. O macaco AB é usado para corrigir a viga defletida DE conforme a figura. Se a força compressiva
Resumo. QM - propriedades mecânicas 1
 Resumo tensão e deformação em materiais sólidos ensaios de tracção e dureza deformação plástica de materiais metálicos recristalização de metais encruados fractura fadiga fluência QM - propriedades mecânicas
Resumo tensão e deformação em materiais sólidos ensaios de tracção e dureza deformação plástica de materiais metálicos recristalização de metais encruados fractura fadiga fluência QM - propriedades mecânicas
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 14
 Ondas 5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Introdução: elementos básicos sobre ondas De maneira geral, uma onda é qualquer sinal que se transmite de um ponto a outro
Ondas 5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Introdução: elementos básicos sobre ondas De maneira geral, uma onda é qualquer sinal que se transmite de um ponto a outro
RESISTÊNCIA DOS MATERIAIS - Notas de Aulas
 RESISTÊNCIA DOS MATERIAIS - Notas de Aulas Prof. José Junio 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
RESISTÊNCIA DOS MATERIAIS - Notas de Aulas Prof. José Junio 1 - INTRODUÇÃO A Mecânica é uma ciência física aplicada que trata dos estudos das forças e dos movimentos. A Mecânica descreve e prediz as condições
1 = Pontuação: Os itens A e B valem três pontos cada; o item C vale quatro pontos.
 Física 0. Duas pessoas pegam simultaneamente escadas rolantes, paralelas, de mesmo comprimento l, em uma loja, sendo que uma delas desce e a outra sobe. escada que desce tem velocidade V = m/s e a que
Física 0. Duas pessoas pegam simultaneamente escadas rolantes, paralelas, de mesmo comprimento l, em uma loja, sendo que uma delas desce e a outra sobe. escada que desce tem velocidade V = m/s e a que
Professor: José Junio Lopes
 Lista de Exercício Aula 3 TENSÃO E DEFORMAÇÃO A - DEFORMAÇÃO NORMAL 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga provocar um deslocamento
Lista de Exercício Aula 3 TENSÃO E DEFORMAÇÃO A - DEFORMAÇÃO NORMAL 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga provocar um deslocamento
Resistência dos Materiais
 Capítulo 3: Tensões em Vasos de Pressão de Paredes Finas Coeficiente de Dilatação Térmica Professor Fernando Porto Resistência dos Materiais Tensões em Vasos de Pressão de Paredes Finas Vasos de pressão
Capítulo 3: Tensões em Vasos de Pressão de Paredes Finas Coeficiente de Dilatação Térmica Professor Fernando Porto Resistência dos Materiais Tensões em Vasos de Pressão de Paredes Finas Vasos de pressão
patologias Fissura devida à deformação da laje Fissura Laje δ Deformada da laje
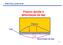 patologias Fissura devida à deformação da laje Laje Fissura δ Deformada da laje 171 patologias Fissura devida a deslocamento horizontal da parede Laje Fissura 172 patologias Fissura devida à rotação da
patologias Fissura devida à deformação da laje Laje Fissura δ Deformada da laje 171 patologias Fissura devida a deslocamento horizontal da parede Laje Fissura 172 patologias Fissura devida à rotação da
Professor: José Junio Lopes
 A - Deformação normal Professor: José Junio Lopes Lista de Exercício - Aula 3 TENSÃO E DEFORMAÇÃO 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada
A - Deformação normal Professor: José Junio Lopes Lista de Exercício - Aula 3 TENSÃO E DEFORMAÇÃO 1 - Ex 2.3. - A barra rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais II. Capítulo 2 Torção
 Capítulo 2 Torção 2.1 Revisão Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e o raio do eixo permanecerão inalterados.
Capítulo 2 Torção 2.1 Revisão Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e o raio do eixo permanecerão inalterados.
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I
 LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Ex. 1.40. O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,840
LISTA DE EXERCÍCIOS MECÂNICA DOS SÓLIDOS I A - Tensão Normal Média 1. Ex. 1.40. O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,840
MÉTODOS BÁSICOS DA ANÁLISE DE ESTRUTURAS
 MÉTODOS BÁSICOS DA ANÁLISE DE ESTRUTURAS Luiz Fernando Martha Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio Departamento de Engenharia Civil Rua Marquês de São Vicente, 225 - Gávea CEP 22453-900
MÉTODOS BÁSICOS DA ANÁLISE DE ESTRUTURAS Luiz Fernando Martha Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio Departamento de Engenharia Civil Rua Marquês de São Vicente, 225 - Gávea CEP 22453-900
LISTA DE EXERCÍCIOS Trabalho, Calor e Primeira Lei da Termodinâmica para Sistemas
 - 1 - LISTA DE EXERCÍCIOS Trabalho, Calor e Primeira Lei da Termodinâmica para Sistemas 1. Um aquecedor de ambientes a vapor, localizado em um quarto, é alimentado com vapor saturado de água a 115 kpa.
- 1 - LISTA DE EXERCÍCIOS Trabalho, Calor e Primeira Lei da Termodinâmica para Sistemas 1. Um aquecedor de ambientes a vapor, localizado em um quarto, é alimentado com vapor saturado de água a 115 kpa.
As constantes a e b, que aparecem nas duas questões anteriores, estão ligadas à constante ρ, pelas equações: A) a = ρs e b = ρl.
 9.3. Representando a constante de proporcionalidade por ρ, podemos reunir as equações R = a L e R = b S 1 (vistas nas duas questões anteriores) da seguinte maneira: L R = ρ (segunda lei de Ohm). S As constantes
9.3. Representando a constante de proporcionalidade por ρ, podemos reunir as equações R = a L e R = b S 1 (vistas nas duas questões anteriores) da seguinte maneira: L R = ρ (segunda lei de Ohm). S As constantes
FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO
 FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO Fixação 1) O bloco da figura, de peso P = 50N, é arrastado ao longo do plano horizontal pela força F de intensidade F = 100N. A força de
FÍSICA - 1 o ANO MÓDULO 27 TRABALHO, POTÊNCIA E ENERGIA REVISÃO Fixação 1) O bloco da figura, de peso P = 50N, é arrastado ao longo do plano horizontal pela força F de intensidade F = 100N. A força de
Campo Magnético Girante de Máquinas CA
 Apostila 3 Disciplina de Conversão de Energia B 1. Introdução Campo Magnético Girante de Máquinas CA Nesta apostila são descritas de forma sucinta as equações e os princípios relativos ao campo magnético
Apostila 3 Disciplina de Conversão de Energia B 1. Introdução Campo Magnético Girante de Máquinas CA Nesta apostila são descritas de forma sucinta as equações e os princípios relativos ao campo magnético
RESISTÊNCIA DOS MATERIAIS CONTROLE DE QUALIDADE INDUSTRIAL Aula 05 TRAÇÃO, COMPRESSÃO E CISALHAMENTO
 CONTROLE DE QUALIDADE INDUSTRIAL TRAÇÃO, COMPRESSÃO E CISALHAMENTO. No Sistema Internacional, a força é expressa em Newtons (N), a área em metros quadrados (m 2 ). A tensão (σ) será expressa, então, em
CONTROLE DE QUALIDADE INDUSTRIAL TRAÇÃO, COMPRESSÃO E CISALHAMENTO. No Sistema Internacional, a força é expressa em Newtons (N), a área em metros quadrados (m 2 ). A tensão (σ) será expressa, então, em
TENSÃO NORMAL e TENSÃO DE CISALHAMENTO
 TENSÃO NORMAL e TENSÃO DE CISALHAMENTO 1) Determinar a tensão normal média de compressão da figura abaixo entre: a) o bloco de madeira de seção 100mm x 120mm e a base de concreto. b) a base de concreto
TENSÃO NORMAL e TENSÃO DE CISALHAMENTO 1) Determinar a tensão normal média de compressão da figura abaixo entre: a) o bloco de madeira de seção 100mm x 120mm e a base de concreto. b) a base de concreto
Resposta Questão 2. a) O N O b) Linear
 GABARITO DA PROVA DO PROCESSO DE SELEÇÃO PARA O PROGRAMA DE PÓS-GRADUAÇÃO 1 SEMESTRE DE 2016 FÍSICA E QUÍMICA DE MATERIAIS UNIVERSIDADE FEDERAL DE SÃO JOÃO DEL REI Resposta Questão 1. A amônia apresenta
GABARITO DA PROVA DO PROCESSO DE SELEÇÃO PARA O PROGRAMA DE PÓS-GRADUAÇÃO 1 SEMESTRE DE 2016 FÍSICA E QUÍMICA DE MATERIAIS UNIVERSIDADE FEDERAL DE SÃO JOÃO DEL REI Resposta Questão 1. A amônia apresenta
Introdução ao Projeto de Aeronaves. Aula 34 Cálculo Estrutural da Fuselagem
 Introdução ao Projeto de Aeronaves Aula 34 Cálculo Estrutural da Fuselagem Tópicos Abordados Estrutura da Fuselagem. Projeto da Fuselagem. Estrutura da Fuselagem A fuselagem inclui a cabine de comandos,
Introdução ao Projeto de Aeronaves Aula 34 Cálculo Estrutural da Fuselagem Tópicos Abordados Estrutura da Fuselagem. Projeto da Fuselagem. Estrutura da Fuselagem A fuselagem inclui a cabine de comandos,
FATEC - SP Faculdade de Tecnologia de São Paulo. ESTACAS DE CONCRETO PARA FUNDAÇÕES - carga de trabalho e comprimento
 FATEC - SP Faculdade de Tecnologia de São Paulo ESTACAS DE CONCRETO PARA FUNDAÇÕES - carga de trabalho e comprimento Prof. Manuel Vitor Curso - Edifícios ESTACAS PRÉ-MOLDADAS DE CONCRETO NBR 6122/1996
FATEC - SP Faculdade de Tecnologia de São Paulo ESTACAS DE CONCRETO PARA FUNDAÇÕES - carga de trabalho e comprimento Prof. Manuel Vitor Curso - Edifícios ESTACAS PRÉ-MOLDADAS DE CONCRETO NBR 6122/1996
Propriedades mecânicas dos materiais
 Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Precisão do fuso de esferas
 Precisão do ângulo de avanço A precisão do fuso de esferas no ângulo de avanço é controlado de acordo com os padrões JIS (JIS B 1192-1997). As classes de precisão C0 a C5 são defi nidas na linearidade
Precisão do ângulo de avanço A precisão do fuso de esferas no ângulo de avanço é controlado de acordo com os padrões JIS (JIS B 1192-1997). As classes de precisão C0 a C5 são defi nidas na linearidade
f (x) = a n x n + a n - 1 x n - 1 +... + a 0 = 0 (a n > 0)
 Lista de Exercícios Resolução de Equações Não Lineares 1) Para a delimitação das raízes reais de uma equação polinomial, além do teorema de Lagrange, existem vários outros como, por exemplo, o apresentado
Lista de Exercícios Resolução de Equações Não Lineares 1) Para a delimitação das raízes reais de uma equação polinomial, além do teorema de Lagrange, existem vários outros como, por exemplo, o apresentado
Pressão INSTRUMENTAÇÃO E CONTROLE. Unidades usuais de pressão. Conversão de Unidades de Pressão. Tipos de pressão. Quanto a referência utilizada
 Pressão É a razão entre a força exercida sobre uma superfície e a área desta superfície. INSTRUMENTAÇÃO E CONTROLE Medidores de pressão Unidades SI P: pressão em N/m 2 = Pa = Pascal F: força normal (ortogonal)
Pressão É a razão entre a força exercida sobre uma superfície e a área desta superfície. INSTRUMENTAÇÃO E CONTROLE Medidores de pressão Unidades SI P: pressão em N/m 2 = Pa = Pascal F: força normal (ortogonal)
FESP Faculdade de Engenharia São Paulo. CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Duração: 85 minutos
 FESP Faculdade de Engenharia São Paulo Avaliação: S1 Data: 16/jun/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Duração: 85 minutos Nome: Matrícula ORIENTAÇÕES PARA PROVA a b c
FESP Faculdade de Engenharia São Paulo Avaliação: S1 Data: 16/jun/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Duração: 85 minutos Nome: Matrícula ORIENTAÇÕES PARA PROVA a b c
PROBLEMAS DE TERMOLOGIA
 PROBLEMAS DE TERMOLOGIA 1 - Numa estação meteorológica, foi registrada uma temperatura máxima de 25ºC. Qual é a indicação da máxima na escala Fahrenheit? 2 - Numa escala termométrica X, marca-se -10ºX
PROBLEMAS DE TERMOLOGIA 1 - Numa estação meteorológica, foi registrada uma temperatura máxima de 25ºC. Qual é a indicação da máxima na escala Fahrenheit? 2 - Numa escala termométrica X, marca-se -10ºX
TRELIÇAS ISOSTÁTICAS
 86 TRELIÇAS ISOSTÁTICAS I. DEFINIÇÃO: Treliça ideal é um sistema reticulado indeformável cujas barras possuem todas as suas extremidades rotuladas e cujas cargas estão aplicadas nestas rótulas. Obs 1 :
86 TRELIÇAS ISOSTÁTICAS I. DEFINIÇÃO: Treliça ideal é um sistema reticulado indeformável cujas barras possuem todas as suas extremidades rotuladas e cujas cargas estão aplicadas nestas rótulas. Obs 1 :
3ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO DIAGRAMA DE ESFORÇO NORMAL
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Professor: Armando Sá Ribeiro Jr. Disciplina: ENG285 - Resistência dos Materiais I-A www.resmat.ufba.br 3ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Professor: Armando Sá Ribeiro Jr. Disciplina: ENG285 - Resistência dos Materiais I-A www.resmat.ufba.br 3ª LISTA
4ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO ANÁLISE DE TENSÕES
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
Capítulo 3 Propriedades Mecânicas dos Materiais
 Capítulo 3 Propriedades Mecânicas dos Materiais 3.1 O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa
Capítulo 3 Propriedades Mecânicas dos Materiais 3.1 O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa
FÍSICA - 1 o ANO MÓDULO 10 EQUILÍBRIO DE CORPOS EXTENSOS
 FÍSICA - 1 o ANO MÓDULO 10 EQUILÍBRIO DE CORPOS EXTENSOS F d M 0 F = Fd O + - A C α B Q F at T N α P B P Q F at T T sen α N A T cos α α B P B PQ Como pode cair no enem? Desde muito cedo, bem antes do início
FÍSICA - 1 o ANO MÓDULO 10 EQUILÍBRIO DE CORPOS EXTENSOS F d M 0 F = Fd O + - A C α B Q F at T N α P B P Q F at T T sen α N A T cos α α B P B PQ Como pode cair no enem? Desde muito cedo, bem antes do início
8kN/m V C V A V B. 3 m 1 5 m. 3 m 5 m. 3 m 5 m. 1 - Calcule as reações de apoio da viga hiperestática representada pela figura abaixo: X 1.
 Lista de Eercícios - alcule as reações de apoio da viga hiperestática representada pela figura abaio: m m kn/m M z ( ) 4 6 ( ) m m kn/m Na tabela: ( ) 4 ( 4 9 () ) m m Pb Na tabela: ( b ) 6 X ( 6 9,7 X
Lista de Eercícios - alcule as reações de apoio da viga hiperestática representada pela figura abaio: m m kn/m M z ( ) 4 6 ( ) m m kn/m Na tabela: ( ) 4 ( 4 9 () ) m m Pb Na tabela: ( b ) 6 X ( 6 9,7 X
Neste tipo de medidor o elemento sensível é um fole que pode ser interno ou externo.
 O Manómetro de Fole é um medidor de pressão em que a medição se faz por equilíbrio da força produzida numa área conhecida com a tensão actuante num meio elástico. Neste tipo de medidor o elemento sensível
O Manómetro de Fole é um medidor de pressão em que a medição se faz por equilíbrio da força produzida numa área conhecida com a tensão actuante num meio elástico. Neste tipo de medidor o elemento sensível
1) Cálculo do tempo de subida do objeto: V y. = V 0y. + γt s 0 = 4 10t s. t s. = 0,4s. 2) Cálculo do tempo total de vôo : t total.
 46 e FÍSICA No interior de um ônibus que trafega em uma estrada retilínea e horizontal, com velocidade constante de 90 km/h, um passageiro sentado lança verticalmente para cima um pequeno objeto com velocidade
46 e FÍSICA No interior de um ônibus que trafega em uma estrada retilínea e horizontal, com velocidade constante de 90 km/h, um passageiro sentado lança verticalmente para cima um pequeno objeto com velocidade
Problema Experimental 1
 41ª Olimpíada Internacional de Física, Croácia Prova Experimental, 21 de Julho de 2010 1/4 Problema Experimental 1 Há dois problemas experimentais. O material que se encontra sobre a mesa é utilizado em
41ª Olimpíada Internacional de Física, Croácia Prova Experimental, 21 de Julho de 2010 1/4 Problema Experimental 1 Há dois problemas experimentais. O material que se encontra sobre a mesa é utilizado em
Relações entre tensões e deformações
 9 de agosto de 06 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
9 de agosto de 06 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
Pelo que foi exposto no teorema de Carnot, obteve-se a seguinte relação:
 16. Escala Absoluta Termodinâmica Kelvin propôs uma escala de temperatura que foi baseada na máquina de Carnot. Segundo o resultado (II) na seção do ciclo de Carnot, temos que: O ponto triplo da água foi
16. Escala Absoluta Termodinâmica Kelvin propôs uma escala de temperatura que foi baseada na máquina de Carnot. Segundo o resultado (II) na seção do ciclo de Carnot, temos que: O ponto triplo da água foi
1.38. A luminária de 50 lb é suportada por duas hastes de aço acopladas por um anel em
 1.36. A luminária de 50 lb é suportada por duas hastes de aço acopladas por um anel em A. Determinar qual das hastes está sujeita à maior tensão normal média e calcular seu valor. Suponha que θ = 60º.
1.36. A luminária de 50 lb é suportada por duas hastes de aço acopladas por um anel em A. Determinar qual das hastes está sujeita à maior tensão normal média e calcular seu valor. Suponha que θ = 60º.
2. TRANSFERÊNCIA OU TRANSFORMAÇÃO DE ENERGIA
 Física: 1º ano Jair Júnior Nota de aula (7/11/014) 1. ENERGIA Um dos princípios básicos da Física diz que a energia pode ser transformada ou transferida, mas nunca criada ou destruída. Então, o que é energia?
Física: 1º ano Jair Júnior Nota de aula (7/11/014) 1. ENERGIA Um dos princípios básicos da Física diz que a energia pode ser transformada ou transferida, mas nunca criada ou destruída. Então, o que é energia?
ESTRUTURAS DE MADEIRA
 UNEMAT Universidade do Estado de Mato Grosso ESTRUTURAS DE MADEIRA Professora: Engª Civil Silvia Romfim AULA 03 1. INTRODUÇÃO: Madeira e suas características. 1.4 - PROPRIEDADES MECÂNICAS: 1.4.1 - Propriedades
UNEMAT Universidade do Estado de Mato Grosso ESTRUTURAS DE MADEIRA Professora: Engª Civil Silvia Romfim AULA 03 1. INTRODUÇÃO: Madeira e suas características. 1.4 - PROPRIEDADES MECÂNICAS: 1.4.1 - Propriedades
Capítulo 3: Propriedades mecânicas dos materiais
 Capítulo 3: Propriedades mecânicas dos materiais O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade
Capítulo 3: Propriedades mecânicas dos materiais O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade
MAC-015 Resistência dos Materiais Unidade 02
 MAC-015 Resistência dos Materiais Unidade 02 Engenharia Elétrica Engenharia de Produção Engenharia Sanitária e Ambiental Leonardo Goliatt, Michèle Farage, Alexandre Cury Departamento de Mecânica Aplicada
MAC-015 Resistência dos Materiais Unidade 02 Engenharia Elétrica Engenharia de Produção Engenharia Sanitária e Ambiental Leonardo Goliatt, Michèle Farage, Alexandre Cury Departamento de Mecânica Aplicada
EQUILÍBRIO DA PARTÍCULA
 Questão 1 - As cordas A, B e C mostradas na figura a seguir têm massa desprezível e são inextensíveis. As cordas A e B estão presas no teto horizontal e se unem à corda C no ponto P. A corda C tem preso
Questão 1 - As cordas A, B e C mostradas na figura a seguir têm massa desprezível e são inextensíveis. As cordas A e B estão presas no teto horizontal e se unem à corda C no ponto P. A corda C tem preso
FÍSICA (Eletromagnetismo) CAMPOS ELÉTRICOS
 FÍSICA (Eletromagnetismo) CAMPOS ELÉTRICOS 1 O CONCEITO DE CAMPO Suponhamos que se fixe, num determinado ponto, uma partícula com carga positiva, q1, e a seguir coloquemos em suas proximidades uma segunda
FÍSICA (Eletromagnetismo) CAMPOS ELÉTRICOS 1 O CONCEITO DE CAMPO Suponhamos que se fixe, num determinado ponto, uma partícula com carga positiva, q1, e a seguir coloquemos em suas proximidades uma segunda
Prof. Michel Sadalla Filho
 Referências MECÂNICA APLICADA Prof. Michel Sadalla Filho Centros de Gravidade, Centro de Massa, Centróides de uma figura plana DOC 06 14 Fev 2013 Ver. 01 HIBBELER, R. C. Mecânica Estática. 10 ed. São Paulo:
Referências MECÂNICA APLICADA Prof. Michel Sadalla Filho Centros de Gravidade, Centro de Massa, Centróides de uma figura plana DOC 06 14 Fev 2013 Ver. 01 HIBBELER, R. C. Mecânica Estática. 10 ed. São Paulo:
Faculdades Oswaldo Cruz ESQ (Física I Profº Ito Lista de Torque)
 1. Um ponto material está parado sobre uma prancha rígida horizontal, de massa desprezível, apoiada nas extremidades. O comprimento da prancha é de 3,0 m. O peso do ponto material é de 60 N e este está
1. Um ponto material está parado sobre uma prancha rígida horizontal, de massa desprezível, apoiada nas extremidades. O comprimento da prancha é de 3,0 m. O peso do ponto material é de 60 N e este está
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
XXVII CPRA LISTA DE EXERCÍCIOS FÍSICA (CINEMÁTICA)
 XXVII CPRA LISTA DE EXERCÍCIOS FÍSICA (CINEMÁTICA) 1) Na Figura 1, uma esfera lisa pode ser lançada por três escorregadores polidos. Ordene os escorregadores de acordo com o trabalho que a força gravitacional
XXVII CPRA LISTA DE EXERCÍCIOS FÍSICA (CINEMÁTICA) 1) Na Figura 1, uma esfera lisa pode ser lançada por três escorregadores polidos. Ordene os escorregadores de acordo com o trabalho que a força gravitacional
Dobramento e flexão. Imagine-se sentado à beira de uma piscina, Nossa aula. Da flexão ao dobramento
 A U A UL LA Dobramento e flexão Introdução Imagine-se sentado à beira de uma piscina, numa bela tarde ensolarada, completamente relaxado, apenas observando o movimento. De repente, você vê alguém dando
A U A UL LA Dobramento e flexão Introdução Imagine-se sentado à beira de uma piscina, numa bela tarde ensolarada, completamente relaxado, apenas observando o movimento. De repente, você vê alguém dando
Capítulo 20: Entropia e segunda Lei da Termodinâmica
 Capítulo 20: Entropia e segunda Lei da ermodinâmica Resumo Processos irreversíveis e Entropia A xícara a transfere calor para sua mão. Processo irreversível. Mão Q Q Xícara(Quente) Como saber se um processo
Capítulo 20: Entropia e segunda Lei da ermodinâmica Resumo Processos irreversíveis e Entropia A xícara a transfere calor para sua mão. Processo irreversível. Mão Q Q Xícara(Quente) Como saber se um processo
Lista de Exercícios - Aula 02 Aplicações das Leis de Newton
 Lista de Exercícios - Aula 02 Aplicações das Leis de Newton 1 - Equilíbrio Estático 1 - Um garoto, apoiando-se em uma bengala, encontra-se em cima de uma balança que marca 40 Kg. Se o garoto empurrar fortemente
Lista de Exercícios - Aula 02 Aplicações das Leis de Newton 1 - Equilíbrio Estático 1 - Um garoto, apoiando-se em uma bengala, encontra-se em cima de uma balança que marca 40 Kg. Se o garoto empurrar fortemente
ESTABILIDADE DAS ESTRUTURAS GEODÉSICAS
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS DA TERRA DEPARTAMENTO DE GEOMÁTICA CURSO DE GRADUAÇÃO EM ENGENHARIA CARTOGRÁFICA ESTABILIDADE DAS ESTRUTURAS GEODÉSICAS Marcelo Carvalho dos Santos, Ph.D.
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS DA TERRA DEPARTAMENTO DE GEOMÁTICA CURSO DE GRADUAÇÃO EM ENGENHARIA CARTOGRÁFICA ESTABILIDADE DAS ESTRUTURAS GEODÉSICAS Marcelo Carvalho dos Santos, Ph.D.
LOM Introdução à Mecânica dos Sólidos
 LOM 3081 - CAP. 2 ANÁLISE DE TENSÃO E DEFORMAÇÃO PARTE 2 ANÁLISE DE DEFORMAÇÃO COEFICIENTE DE POISSON Para uma barra delgada submetida a uma carga aial: 0 E A deformação produida na direção da força é
LOM 3081 - CAP. 2 ANÁLISE DE TENSÃO E DEFORMAÇÃO PARTE 2 ANÁLISE DE DEFORMAÇÃO COEFICIENTE DE POISSON Para uma barra delgada submetida a uma carga aial: 0 E A deformação produida na direção da força é
PROGRAMAÇÃO DE COMPUTADORES I - BCC701-2015 Lista de Exercícios do Módulo 1 - Preparação para a Prova 1
 PROGRAMAÇÃO DE COMPUTADORES I - BCC701-2015 Lista de Exercícios do Módulo 1 - Preparação para a Prova 1 Exercício 1 Apesar da existência do Sistema Internacional (SI) de Unidades, ainda existe a divergência
PROGRAMAÇÃO DE COMPUTADORES I - BCC701-2015 Lista de Exercícios do Módulo 1 - Preparação para a Prova 1 Exercício 1 Apesar da existência do Sistema Internacional (SI) de Unidades, ainda existe a divergência
LISTA DE EXERCÍCIOS - PRA FENÔMENOS DE TRANSPORTE
 LISTA DE EXERCÍCIOS - PRA FENÔMENOS DE TRANSPORTE A - Viscosidade 1. (Exercício 1.1, pág. 11, Brunetti) A viscosidade cinemática ν de um óleo é de 0,028 m 2 /s e o seu peso específico relativo r é de 0,85.
LISTA DE EXERCÍCIOS - PRA FENÔMENOS DE TRANSPORTE A - Viscosidade 1. (Exercício 1.1, pág. 11, Brunetti) A viscosidade cinemática ν de um óleo é de 0,028 m 2 /s e o seu peso específico relativo r é de 0,85.
TENSÃO NORMAL e TENSÃO DE CISALHAMENTO
 TENSÃO NORMAL e TENSÃO DE CISALHAMENTO 1) Determinar a tensão normal média de compressão da figura abaixo entre: a) o bloco de madeira de seção 100mm x 120mm e a base de concreto. b) a base de concreto
TENSÃO NORMAL e TENSÃO DE CISALHAMENTO 1) Determinar a tensão normal média de compressão da figura abaixo entre: a) o bloco de madeira de seção 100mm x 120mm e a base de concreto. b) a base de concreto
MECÂNICA DOS SÓLIDOS
 MECÂNICA DOS SÓLIDOS Cláudio Messias da Silva O principal objetivo de um curso básico de mecânica deveria se o de desenvolver no estudante de engenharia a habilidade de analisar um dado problema, de maneira
MECÂNICA DOS SÓLIDOS Cláudio Messias da Silva O principal objetivo de um curso básico de mecânica deveria se o de desenvolver no estudante de engenharia a habilidade de analisar um dado problema, de maneira
Terceira Lista de Exercícios
 Universidade Católica de Petrópolis Disciplina: Resitência dos Materiais I Prof.: Paulo César Ferreira Terceira Lista de Exercícios 1. Calcular o diâmetro de uma barra de aço sujeita a ação de uma carga
Universidade Católica de Petrópolis Disciplina: Resitência dos Materiais I Prof.: Paulo César Ferreira Terceira Lista de Exercícios 1. Calcular o diâmetro de uma barra de aço sujeita a ação de uma carga
Bibliografia referência para esta aula. Propriedades dos materiais. Propriedades. Solicitações. Propriedades mecânicas. Carga X deformação
 Propriedades dos materiais Prof. Maristela Gomes da Silva Departamento de Engenharia Civil Bibliografia referência para esta aula ISAIA, G. C. (editor) Materiais de Construção Civil e Princípios de ciência
Propriedades dos materiais Prof. Maristela Gomes da Silva Departamento de Engenharia Civil Bibliografia referência para esta aula ISAIA, G. C. (editor) Materiais de Construção Civil e Princípios de ciência
Capítulo 3 Esforço Normal. 1ª. Questão
 Capítulo 3 Esforço Normal 1ª. Questão A estaca da figura possui 60 mm de diâmetro e está submetida a uma carga de 20 kn. O solo tem a capacidade de resistir lateralmente, por meio de uma carga que varia
Capítulo 3 Esforço Normal 1ª. Questão A estaca da figura possui 60 mm de diâmetro e está submetida a uma carga de 20 kn. O solo tem a capacidade de resistir lateralmente, por meio de uma carga que varia
O que é Histerese? Figura 1. A deformação do elemento elástico de um tubo tipo Bourdon.
 O que é Histerese? Por Gilberto Carlos Fidélis Você já deve ter sentido o efeito da histerese quando dirige. Quando estamos em uma certa velocidade e de repente tiramos o pé do acelerador percebemos que
O que é Histerese? Por Gilberto Carlos Fidélis Você já deve ter sentido o efeito da histerese quando dirige. Quando estamos em uma certa velocidade e de repente tiramos o pé do acelerador percebemos que
Lista de Exercícios Campo Elétrico
 Considere k o = 9,0. 10 9 N. m 2 /C 2 Lista de Exercícios Campo Elétrico 1. Uma partícula de carga q = 2,5. 10-8 C e massa m = 5,0. 10-4 kg, colocada num determinado ponto P de uma região onde existe um
Considere k o = 9,0. 10 9 N. m 2 /C 2 Lista de Exercícios Campo Elétrico 1. Uma partícula de carga q = 2,5. 10-8 C e massa m = 5,0. 10-4 kg, colocada num determinado ponto P de uma região onde existe um
A Equação de Onda em Uma Dimensão (continuação)
 A Equação de Onda em Uma Dimensão (continuação) Energia em uma onda mecânica Consideremos novamente o problema da onda transversal propagando-se em uma corda vibrante em uma dimensão (lembrese, a corda
A Equação de Onda em Uma Dimensão (continuação) Energia em uma onda mecânica Consideremos novamente o problema da onda transversal propagando-se em uma corda vibrante em uma dimensão (lembrese, a corda
