Canguru Matemático sem Fronteiras 2013
|
|
|
- Victor Gabriel Azevedo Silveira
- 9 Há anos
- Visualizações:
Transcrição
1 Destinatários: alunos do 9. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis: Problemas de 3 pontos, Problemas de 4 pontos e Problemas de 5 pontos. Inicialmente tens 30 pontos. Por cada questão correta ganhas tantos pontos quantos os do nível da questão, no entanto, por cada questão errada és penalizado em 1/4 dos pontos correspondentes a essa questão. Não és penalizado se não responderes a uma questão, mas infelizmente também não adicionas pontos. Problemas de 3 pontos 1. O maior triângulo da figura é um triângulo equilátero com medida de área igual a 9. As linhas no interior do triângulo são paralelas aos lados do triângulo e dividem os lados do triângulo em três partes iguais. Qual é a medida da área da região sombreada? (A) 1 (B) 4 (C) 5 (D) 6 (E) 7 2. Sabendo que = 11, qual é o valor de ? (A) 5 (B) 9 (C) 11 (D) 55 (E) As massas de sal e de água doce na água do mar de Protaras (Chipre) estão na razão de 7 para 193. Quantos quilogramas de sal existem em 1000 kg de água do mar de Protaras? (A) 35 (B) 186 (C) 193 (D) 200 (E) A Ana tem uma folha quadrada de papel quadriculado (ver figura da esquerda) e resolveu cortá-la ao longo das linhas traçadas na folha, de modo a obter pedaços de papel com a forma representada na figura da direita. Qual é o menor número de quadrículas que podem sobrar? (A) 0 (B) 2 (C) 4 (D) 6 (E) 8 DEPARTAMENTO DE MATEMÁTICA
2 5. O Rui quer dizer ao Cristiano um número natural em que o produto dos seus algarismos é igual a 24. Qual é a soma dos algarismos do menor número que o Rui pode dizer ao Cristiano? (A) 6 (B) 8 (C) 9 (D) 10 (E) Um saco contém bolas de cinco cores diferentes. Duas são vermelhas, três são azuis, dez são brancas, quatro são verdes e três são pretas. O João resolveu tirar bolas do saco sem olhar e sem as repor no saco. Qual é o menor número de bolas que o João terá de tirar para ter a garantia de que tira pelo menos duas bolas da mesma cor? (A) 2 (B) 12 (C) 10 (D) 5 (E) 6 7. O Alexandre acende uma vela a cada dez minutos. Cada vela fica acesa exatamente durante 40 minutos. Quantas velas estão acesas 55 minutos após o Alexandre ter acendido a primeira vela? (A) 2 (B) 3 (C) 4 (D) 5 (E) 6 8. Qual dos seguintes valores não pode ser a média aritmética do número de filhos de cinco famílias? (A) 0,2 (B) 1,2 (C) 2,2 (D) 2,4 (E) 2,5 9. O Marco e a Catarina estão em lados opostos de uma fonte circular. Eles decidiram correr no sentido dos ponteiros do relógio à volta da fonte. A velocidade do Marco é 9/8 da velocidade da Catarina. Quantas voltas tinha dado a Catarina à fonte quando o Marco a apanhou pela primeira vez? (A) 4 (B) 8 (C) 9 (D) 2 (E) Os inteiros positivos x, y e z satisfazem as igualdades x y = 14, y z = 10 e z x = 35. Qual é o valor de x + y + z? (A) 10 (B) 12 (C) 14 (D) 16 (E) 18 Problemas de 4 pontos 11. A Margarida e um amigo estão a jogar à Batalha Naval num tabuleiro de dimensões 5 5. A Margarida já colocou dois navios representados a sombreado na figura. Ela ainda tem de colocar um navio de dimensões 3 1 que ocupará exatamente três quadrículas. Os navios não podem ter pontos de contacto entre si. Quantas posições existem para ela colocar o navio de dimensões 3 1? (A) 4 (B) 5 (C) 6 (D) 7 (E) 8 Alunos do 9. o ano de escolaridade 2
3 12. Na figura estão representados os ângulos α, β, γ e δ. Sabendo que as amplitudes de α, β e γ são 55, 40 e 35, respetivamente, qual é a amplitude de δ? γ δ α β (A) 100 (B) 105 (C) 120 (D) 125 (E) A medida do perímetro de um trapézio é 5 e as medidas dos lados são números naturais. Quais são as duas menores amplitudes para dois dos ângulos do trapézio? (A) 30 e 30 (B) 60 e 60 (C) 45 e 45 (D) 30 e 60 (E) 45 e Qual dos seguintes moldes de papel, dobrado ao longo das linhas marcadas, nunca dá origem a um cubo? (A) (B) (C) (D) (E) 15. A Constança escreveu vários números naturais consecutivos numa folha em branco. Qual dos seguintes valores não pode ser a percentagem de números ímpares escritos nessa folha? (A) 40 (B) 45 (C) 48 (D) 50 (E) Os lados de um retângulo [ABCD] são paralelos aos eixos das coordenadas do referencial xoy. O retângulo [ABCD] está abaixo do eixo das abcissas e à direita do eixo das ordenadas, como representado na figura. Para cada um dos vértices do retângulo calculamos o valor da fração ordenada. Qual é o vértice que dá origem ao menor valor? abcissa (A) A (B) B (C) C (D) D (E) Depende do retângulo y D A C B x 17. No quadro da escola, o Gonçalo escreveu todos os números de quatro algarismos, por ordem crescente, formados apenas com os algarismos do número Qual é o maior valor possível para a diferença entre dois dos números consecutivos escritos no quadro? (A) 702 (B) 703 (C) 693 (D) 793 (E) 198 Alunos do 9. o ano de escolaridade 3
4 18. Na tabela 6 8, representada na figura, 24 das quadrículas não são intersetadas pelas diagonais da tabela. Se considerarmos uma tabela 6 10, quantas quadrículas da tabela é que não serão intersetadas pelas diagonais? (A) 28 (B) 29 (C) 30 (D) 31 (E) O André, a Beatriz, a Cátia, o Dinis e o Eduardo nasceram nas seguintes datas: 20/02/2001, 12/03/2000, 20/03/2001, 12/04/2000 e 23/04/2001 (dia/mês/ano). O André e o Eduardo nasceram no mesmo mês. A Beatriz e a Cátia também nasceram no mesmo mês. O André e a Cátia nasceram no mesmo dia, mas de meses diferentes. O Dinis e o Eduardo também nasceram no mesmo dia, mas de meses diferentes. Qual é a criança mais nova? (A) O André (B) A Beatriz (C) A Cátia (D) O Dinis (E) O Eduardo 20. O João construiu 16 torres de cubos sobre um tabuleiro 4 4. Na tabela ao lado estão representados o número de cubos usados em cada torre. Quando o João olha para a construção da parte de trás, o que é que ele vê? (A) (B) (C) (D) (E) Problemas de 5 pontos 21. A Margarida desenhou numa folha de papel quadriculado o quadrilátero [KLMN]. Cada quadrícula do papel tem 2 cm de lado. Qual é a área de [KLMN]? K PARTE DE TRÁS PARTE DA FRENTE (A) 96 cm 2 (B) 84 cm 2 (C) 76 cm 2 (D) 88 cm 2 (E) 104 cm O Afonso listou no seu computador todos os números de 1 a Seja S o número de quadrados perfeitos entre os números listados e seja Q o número de cubos perfeitos entre os mesmos números. Qual das seguintes igualdades é verdadeira? (A) S = Q (B) 2S = 3Q (C) 3S = 2Q (D) S = 2013Q (E) S 3 = Q 2 N L M 23. O Ivo escolheu um número inteiro positivo com 5 algarismos e resolveu eliminar um dos algarismos de modo a obter um número de 4 algarismos. A soma do número de 4 algarismos com o número inicial de 5 algarismos é Qual é a soma dos 5 algarismos do número inicial? (A) 26 (B) 20 (C) 23 (D) 19 (E) 17 Alunos do 9. o ano de escolaridade 4
5 24. Um jardineiro quer plantar vinte árvores, carvalhos e tílias, ao longo de uma avenida. O número de árvores entre quaisquer dois carvalhos não pode ser três. Qual é o maior número de carvalhos que o jardineiro poderá plantar? (A) 8 (B) 10 (C) 12 (D) 14 (E) O André e o Daniel participaram recentemente numa maratona. Quando terminaram a maratona, verificou-se que o André ficou à frente do dobro do número de atletas que ficaram à frente do Daniel, e o Daniel ficou à frente de 1,5 vezes o número de atletas que terminaram à frente do André. O André terminou no vigésimo primeiro lugar. Quantos atletas participaram na maratona? (A) 31 (B) 41 (C) 51 (D) 61 (E) Na rotunda representada na figura entram, ao mesmo tempo, quatro carros vindos de direções distintas. Cada um dos carros dá menos de uma volta à rotunda e não há dois que saiam na mesma direção. De quantas maneiras distintas pode isto acontecer? (A) 9 (B) 12 (C) 15 (D) 24 (E) Uma sequência começa com os números 1, 1, 1, 1, 1. Depois do quinto termo, cada termo é o produto dos dois termos anteriores. Por exemplo, o sexto termo é igual ao produto do quarto termo com o quinto termo. Qual é a soma dos primeiros 2013 termos da sequência? (A) 1006 (B) 671 (C) 0 (D) 671 (E) A Susana está a fazer 6 tartes de framboesa, umas a seguir às outras, ordenadas e numeradas de 1 a 6, sendo a primeira a ser cozinhada a número 1. Enquanto ela está a fazer as tartes, os seus filhos entram às vezes na cozinha e comem sempre a tarte mais quente. Qual das seguintes ordenações não pode representar a ordem em que as tartes são comidas? (A) (B) (C) (D) (E) Cada um dos quatro vértices e cada uma das seis arestas de um tetraedro estão marcados com um dos dez números 1, 2, 3, 4, 5, 6, 7, 8, 9 e 11 (o número 10 não faz parte da lista). Cada número é usado apenas uma vez. O número marcado em cada aresta do tetraedro é a soma dos números marcados nos vértices unidos por esta aresta. A aresta [P Q] está marcada com o número 9. Qual é o número que marca a aresta [RS]? (A) 4 (B) 5 (C) 6 (D) 8 (E) Um número inteiro positivo N é menor do que a soma dos seus três maiores divisores (excluindo o próprio número N). Qual das seguintes afirmações é verdadeira? (A) Todos os números N nessas condições são divisíveis por 4 (B) Todos os números N nessas condições são divisíveis por 5 (C) Todos os números N nessas condições são divisíveis por 6 (D) Todos os números N nessas condições são divisíveis por 7 (E) Não existe um número N nessas condições P 9 Q S? R Alunos do 9. o ano de escolaridade 5
Canguru Matemático sem Fronteiras 2017
 Destinatários: alunos do 9. o ano de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Destinatários: alunos do 9. o ano de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Canguru Brasil 2013 Nível C - Soluções
 Canguru Brasil 013 Nível C - Soluções Problemas de 3 pontos 01. Na figura, o triângulo maior é equilátero e tem área igual a 9. Os três segmentos paralelos aos lados dividem os lados em três partes iguais.
Canguru Brasil 013 Nível C - Soluções Problemas de 3 pontos 01. Na figura, o triângulo maior é equilátero e tem área igual a 9. Os três segmentos paralelos aos lados dividem os lados em três partes iguais.
Canguru Matemático sem Fronteiras 2013
 Canguru atemático sem Fronteiras 2013 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 30min Nome: Turma: Canguru atemático. Todos os direitos reservados.
Canguru atemático sem Fronteiras 2013 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 30min Nome: Turma: Canguru atemático. Todos os direitos reservados.
Canguru Matemático sem Fronteiras 2012
 Canguru Matemático sem Fronteiras 0 http://www.mat.uc.pt/canguru/ Destinatários: alunos do. o ano de escolaridade Nome: Turma: Duração: h 0min Não podes usar calculadora. Em cada questão deves assinalar
Canguru Matemático sem Fronteiras 0 http://www.mat.uc.pt/canguru/ Destinatários: alunos do. o ano de escolaridade Nome: Turma: Duração: h 0min Não podes usar calculadora. Em cada questão deves assinalar
(A) 389 (B) 399 (C) 409 (D) 419 (E) 429
 Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru Matemático sem Fronteiras 2010
 Canguru Matemático sem Fronteiras 2010 Duração: 1h30min Destinatários: alunos do 12 Ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões
Canguru Matemático sem Fronteiras 2010 Duração: 1h30min Destinatários: alunos do 12 Ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões
Canguru Matemático sem Fronteiras 2011
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 0. e. anos de escolaridade Nome: Turma: Duração: h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 0. e. anos de escolaridade Nome: Turma: Duração: h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões
Canguru Matemático sem Fronteiras 2016
 Destinatários: alunos do 9. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Destinatários: alunos do 9. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2017
 Canguru Matemático sem Fronteiras 07 Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
Canguru Matemático sem Fronteiras 07 Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
Canguru Matemático sem Fronteiras 2014
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
Canguru sem fronteiras 2006
 Duração: 1h15 Destinatários: alunos dos 7º e 8º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és
Duração: 1h15 Destinatários: alunos dos 7º e 8º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és
Canguru Matemático sem Fronteiras 2016
 estinatários: alunos do 12. o ano de escolaridade uração: 1h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. s questões estão agrupadas em três níveis:
estinatários: alunos do 12. o ano de escolaridade uração: 1h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. s questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2009
 Destinatários: alunos dos 7 e 8 anos de Escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis:
Destinatários: alunos dos 7 e 8 anos de Escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2016
 Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru Matemático sem Fronteiras 2009
 Duração: 1h30min Destinatários: alunos do 9 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis: Problemas
Duração: 1h30min Destinatários: alunos do 9 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis: Problemas
Canguru Matemático sem fronteiras 2008
 Destinatários: alunos do 12º ano de Escolaridade Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Destinatários: alunos do 12º ano de Escolaridade Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem Fronteiras 2011
 Canguru Matemático sem Fronteiras 20 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 2. ano de escolaridade Nome: Turma: Duração: h30min Não podes usar calculadora. Há apenas uma resposta correcta
Canguru Matemático sem Fronteiras 20 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 2. ano de escolaridade Nome: Turma: Duração: h30min Não podes usar calculadora. Há apenas uma resposta correcta
Canguru Matemático sem Fronteiras 2011
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 9. ano de escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 9. ano de escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão
Canguru Matemático sem Fronteiras 2017
 Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru Matemático sem Fronteiras 2013
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As
Canguru Matemático sem Fronteiras 2012
 http://wwwmatucpt/canguru/ Destinatários: alunos dos 10 o e 11 o anos de escolaridade Nome: Turma: Duração: 1h 0min Não podes usar calculadora Em cada questão deves assinalar a resposta correta As questões
http://wwwmatucpt/canguru/ Destinatários: alunos dos 10 o e 11 o anos de escolaridade Nome: Turma: Duração: 1h 0min Não podes usar calculadora Em cada questão deves assinalar a resposta correta As questões
Canguru Matemático sem Fronteiras 2017
 Destinatários: alunos do 12. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Destinatários: alunos do 12. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2009
 Duração: 1h30min Destinatários: alunos dos 10 e 11 anos de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis:
Duração: 1h30min Destinatários: alunos dos 10 e 11 anos de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2018
 Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru Matemático sem fronteiras 2008
 Destinatários: alunos do 9º ano de Escolaridade Duração:1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Destinatários: alunos do 9º ano de Escolaridade Duração:1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem Fronteiras 2018
 Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 10. o e 11. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru Matema tico sem Fronteiras 2019
 Canguru Matema tico sem Fronteiras 019 Destinata rios: alunos do 1.o ano de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa o deves assinalar a resposta correta.
Canguru Matema tico sem Fronteiras 019 Destinata rios: alunos do 1.o ano de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa o deves assinalar a resposta correta.
Canguru Matemático sem Fronteiras 2016
 Destinatários: alunos dos 7. o e 8. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 7. o e 8. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru sem fronteiras 2005
 Duração: 1h30mn Destinatários: alunos dos 10 e 11 anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada,
Duração: 1h30mn Destinatários: alunos dos 10 e 11 anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada,
Canguru sem fronteiras 2007
 Canguru sem fronteiras 2007 Duração: 1h15mn Destinatários: alunos do 9 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30
Canguru sem fronteiras 2007 Duração: 1h15mn Destinatários: alunos do 9 ano de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30
Canguru Matemático sem Fronteiras 2018
 Destinatários: alunos do 9. o ano de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Destinatários: alunos do 9. o ano de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Canguru sem fronteiras 2007
 Duração: 1h15mn Destinatários: alunos dos 7 e 8 anos de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão
Duração: 1h15mn Destinatários: alunos dos 7 e 8 anos de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão
Canguru Matemático sem Fronteiras 2018
 Destinatários: alunos do 12. o ano de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Destinatários: alunos do 12. o ano de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2019
 Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três
Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três
Canguru Matemático sem Fronteiras 2017
 Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três
Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três
Canguru Matema tico sem Fronteiras 2013
 Canguru Matema tico sem Fronteiras 2013 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 7.o e 8.o anos de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa
Canguru Matema tico sem Fronteiras 2013 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 7.o e 8.o anos de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa
Canguru Matemático sem fronteiras 2008
 Destinatários: alunos dos 7º e 8º anos de Escolaridade Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada,
Destinatários: alunos dos 7º e 8º anos de Escolaridade Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada,
Prova da segunda fase - Nível 3
 Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Canguru sem fronteiras 2006
 Canguru sem fronteiras 006 Duração: 1h15 Destinatários: alunos dos 10º e 11º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos.
Canguru sem fronteiras 006 Duração: 1h15 Destinatários: alunos dos 10º e 11º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos.
Canguru sem fronteiras 2006
 Duração: 1h15 Destinatários: alunos do 9º ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Duração: 1h15 Destinatários: alunos do 9º ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem Fronteiras 2018
 Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Canguru Matema tico sem Fronteiras 2012
 Canguru Matema tico sem Fronteiras 2012 http://www.mat.uc.pt/canguru/ Destinata rios: alunos do 9.o ano de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa o deves
Canguru Matema tico sem Fronteiras 2012 http://www.mat.uc.pt/canguru/ Destinata rios: alunos do 9.o ano de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa o deves
Canguru Matemático sem Fronteiras 2013
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 4. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 4. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
EXTERNATO JOÃO ALBERTO FARIA ARRUDA DOS VINHOS maio 2014
 EXTERNATO JOÃO ALBERTO FARIA ARRUDA DOS VINHOS maio 2014 Matemática 6.º Ano O Professor, (Luís Melícias) Nome do(a) aluno(a) N.º Turma 6.º. Classificação % por cento. Observações: O Enc. de Educação Deve
EXTERNATO JOÃO ALBERTO FARIA ARRUDA DOS VINHOS maio 2014 Matemática 6.º Ano O Professor, (Luís Melícias) Nome do(a) aluno(a) N.º Turma 6.º. Classificação % por cento. Observações: O Enc. de Educação Deve
Prova da primeira fase - Nível 2
 1. Quantos números inteiros existem entre 20,12 e 201,2? a) 180. d) 183. b) 181. e) 184. c) 182. 2. O conjunto dos números inteiros pares é: {... 4; 2; 0; 2; 4;...} Se o produto de quatro inteiros pares
1. Quantos números inteiros existem entre 20,12 e 201,2? a) 180. d) 183. b) 181. e) 184. c) 182. 2. O conjunto dos números inteiros pares é: {... 4; 2; 0; 2; 4;...} Se o produto de quatro inteiros pares
Canguru sem fronteiras 2005
 Duração: 1h30mn Destinatários: alunos do 12 ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Duração: 1h30mn Destinatários: alunos do 12 ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem Fronteiras 2012
 Canguru Matemático sem Fronteiras 0 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves
Canguru Matemático sem Fronteiras 0 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: h 0min Nome: Turma: Não podes usar calculadora. Em cada questão deves
Canguru sem fronteiras 2005
 Duração: 1h30mn Destinatários: alunos do 9 ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Duração: 1h30mn Destinatários: alunos do 9 ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem Fronteiras 2009
 Duração: 1h30min Destinatários: alunos dos 5 e 6 anos de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. s questões estão agrupadas em três níveis:
Duração: 1h30min Destinatários: alunos dos 5 e 6 anos de Escolaridade Nome: Turma: Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. s questões estão agrupadas em três níveis:
Canguru Matemático sem Fronteiras 2011
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 7. e 8. anos de escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 7. e 8. anos de escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro?
 Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
Canguru Matemático sem Fronteiras 2014
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
Canguru Matemático sem Fronteiras 2015
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
Matemática. Questão 1. 7 o ano do Ensino Fundamental Turma. 2 o Bimestre de 2016 Data / / Escola Aluno RESOLUÇÃO:
 EF AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 7 o ano do Ensino Fundamental Turma GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO 2 o Bimestre de 2016 Data / / Escola Aluno Questão 1 Qual é
EF AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 7 o ano do Ensino Fundamental Turma GOVERNO DO ESTADO DE SÃO PAULO SECRETARIA DA EDUCAÇÃO 2 o Bimestre de 2016 Data / / Escola Aluno Questão 1 Qual é
PROVA DE MATEMÁTICA QUESTÃO 31 QUESTÃO 32
 PROVA DE MATEMÁTICA QUESTÃO 31 Dona Margarida comprou terra adubada para sua nova jardineira, que tem a forma de um paralelepípedo retângulo, cujas dimensões internas são: 1 m de comprimento, 25 cm de
PROVA DE MATEMÁTICA QUESTÃO 31 Dona Margarida comprou terra adubada para sua nova jardineira, que tem a forma de um paralelepípedo retângulo, cujas dimensões internas são: 1 m de comprimento, 25 cm de
Canguru sem fronteiras 2006
 Duração:1h15 Destinatários: alunos do 1º ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 0 pontos. Por cada questão errada, és penalizado
Duração:1h15 Destinatários: alunos do 1º ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 0 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem Fronteiras 2012
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 4. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 4. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
INSTRUÇÕES. Esta prova é individual e sem consulta à qualquer material.
 OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
Canguru Matemático sem Fronteiras 2014 R U. Problemas de 3 pontos. Destinatários: alunos dos 7. o e 8. o anos de escolaridade
 anguru Matemático sem Fronteiras 2014 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 7. o e 8. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão
anguru Matemático sem Fronteiras 2014 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 7. o e 8. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão
XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 2. 1 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP
 XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 2 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP - A duração da prova é de horas. - Não é permitido o uso de calculadoras nem
XXI OLIMPÍADA BRASILEIRA DE MATEMÁTICA Primeira Fase Nível 2 a. Fase Olimpíada Regional BA - ES - GO - RJ - RN - RS - SC - SP - A duração da prova é de horas. - Não é permitido o uso de calculadoras nem
Canguru Matemático sem Fronteiras 2013
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
Canguru Matemático sem Fronteiras 2015
 anguru Matemático sem Fronteiras 2015 http://www.mat.uc.pt/canguru/ ategoria: Escolar Destinatários: alunos dos 5. o e 6. o anos de escolaridade ome: Turma: Duração: 1h 30min anguru Matemático. Todos os
anguru Matemático sem Fronteiras 2015 http://www.mat.uc.pt/canguru/ ategoria: Escolar Destinatários: alunos dos 5. o e 6. o anos de escolaridade ome: Turma: Duração: 1h 30min anguru Matemático. Todos os
Canguru Matemático sem Fronteiras 2015
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
Instruções para a realização da Prova Leia com muita atenção!
 Nível 3 Instruções para a realização da Prova Leia com muita atenção! Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima segunda edição da Olimpíada de Matemática de São José do
Nível 3 Instruções para a realização da Prova Leia com muita atenção! Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima segunda edição da Olimpíada de Matemática de São José do
Prova da segunda fase - Nível 2
 Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Canguru Matemático sem Fronteiras 2012
 http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
http://www.mat.uc.pt/canguru/ Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões
Instruções para a realização da Prova Leia com muita atenção!
 Nível 2 Instruções para a realização da Prova Leia com muita atenção! Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima segunda edição da Olimpíada de Matemática de São José do
Nível 2 Instruções para a realização da Prova Leia com muita atenção! Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima segunda edição da Olimpíada de Matemática de São José do
Canguru Matema tico sem Fronteiras 2017
 Canguru Matema tico sem Fronteiras 207 Categoria: Mini-Escolar - nı vel III Destinata rios: alunos do 4.o ano de escolaridade Durac a o: h 30min Turma: Nome: Na o podes usar calculadora. Em cada questa
Canguru Matema tico sem Fronteiras 207 Categoria: Mini-Escolar - nı vel III Destinata rios: alunos do 4.o ano de escolaridade Durac a o: h 30min Turma: Nome: Na o podes usar calculadora. Em cada questa
1. Na figura está representada uma pavimentação feita apenas com trapézios isósceles, geometricamente iguais. Os trapézios têm cores diferentes.
 Nome: Ano / Turma: N. o : Data - - 1. Na figura está representada uma pavimentação feita apenas com trapézios isósceles, geometricamente iguais. Os trapézios têm cores diferentes. 1.1. Determina, em graus,
Nome: Ano / Turma: N. o : Data - - 1. Na figura está representada uma pavimentação feita apenas com trapézios isósceles, geometricamente iguais. Os trapézios têm cores diferentes. 1.1. Determina, em graus,
Teste de Matemática A 2016 / 2017
 Teste de Matemática A 2016 / 2017 Teste N.º 5 Matemática A Duração do Teste: 90 minutos 10.º Ano de Escolaridade Nome do aluno: N.º: Turma: Grupo I Os cinco itens deste grupo são de escolha múltipla. Em
Teste de Matemática A 2016 / 2017 Teste N.º 5 Matemática A Duração do Teste: 90 minutos 10.º Ano de Escolaridade Nome do aluno: N.º: Turma: Grupo I Os cinco itens deste grupo são de escolha múltipla. Em
Canguru Matemático sem Fronteiras 2017
 Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em três níveis:
UFRGS MATEMÁTICA
 - MATEMÁTICA 6) O Estádio Nacional de Pequim, construído para a realização dos Jogos Olímpicos de 008, teve um custo de 500 milhões de dólares, o que representa 1,5% do investimento total feito pelo país
- MATEMÁTICA 6) O Estádio Nacional de Pequim, construído para a realização dos Jogos Olímpicos de 008, teve um custo de 500 milhões de dólares, o que representa 1,5% do investimento total feito pelo país
Canguru de Matemática Brasil 2017
 Canguru de Matemática Brasil 2017 Prova Nível C Respostas Problemas de 3 pontos Questão 1 Que horas são 17 horas depois das 17h? (a) 8h (B) 10h (C) 11h (D) 12h (E) 13h 1. Alternativa B Das 17h até 24h
Canguru de Matemática Brasil 2017 Prova Nível C Respostas Problemas de 3 pontos Questão 1 Que horas são 17 horas depois das 17h? (a) 8h (B) 10h (C) 11h (D) 12h (E) 13h 1. Alternativa B Das 17h até 24h
Canguru Matemático sem Fronteiras 2014
 Canguru Matemático sem Fronteiras 014 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão
Canguru Matemático sem Fronteiras 014 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 5. o e 6. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão
Prova Escrita de Matemática
 ESCOLA SECUNDÁRIA DE LOUSADA Prova Escrita de Matemática.º Ciclo do ensino Básico ; 7ºAno de escolaridade Duração da Prova: 90 minutos Versão 1 2012 A PREENCHER PELO ALUNO Nome completo do aluno Nº Turma:
ESCOLA SECUNDÁRIA DE LOUSADA Prova Escrita de Matemática.º Ciclo do ensino Básico ; 7ºAno de escolaridade Duração da Prova: 90 minutos Versão 1 2012 A PREENCHER PELO ALUNO Nome completo do aluno Nº Turma:
1. Encontre a equação das circunferências abaixo:
 Nome: nº Professor(a): Série: 2ª EM. Turma: Data: / /2013 Nota: Sem limite para crescer Exercícios de Matemática II 2º Ano 2º Trimestre 1. Encontre a equação das circunferências abaixo: 2. Determine o
Nome: nº Professor(a): Série: 2ª EM. Turma: Data: / /2013 Nota: Sem limite para crescer Exercícios de Matemática II 2º Ano 2º Trimestre 1. Encontre a equação das circunferências abaixo: 2. Determine o
Canguru Matemático sem Fronteiras 2016
 Canguru Matemático sem Fronteiras 206 Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As
Canguru Matemático sem Fronteiras 206 Destinatários: alunos do 3. o ano de escolaridade Nome: Turma: Duração: h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: Observe os dados do quadro a seguir.
 MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x cos x : cosseno de x x : módulo de x log x : logaritmo de x na base 10 6. Um
MATEMÁTICA NESTA PROVA SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS: sen x : seno de x cos x : cosseno de x x : módulo de x log x : logaritmo de x na base 10 6. Um
Matemática. x : módulo do número x. 29. Com base nos dados do gráfico, que fração das mulheres viviam na zona rural do Brasil em 1996?
 Matemática Nesta prova serão utilizados os seguintes símbolos com seus respectivos significados: x : módulo do número x i: unidade imaginária sen x: seno de x 9. Com base nos dados do gráfico, que fração
Matemática Nesta prova serão utilizados os seguintes símbolos com seus respectivos significados: x : módulo do número x i: unidade imaginária sen x: seno de x 9. Com base nos dados do gráfico, que fração
,12 2, = , ,12 = = (2012) 2.
 1 QUESTÃO 1 Usando a comutatividade da multiplicação, podemos escrever 1000 0,1,01 100 = 1000,01 00 0,1 = 01 01 = (01). QUESTÃO Observe que para obter o primeiro retângulo foi necessário escrever quatro
1 QUESTÃO 1 Usando a comutatividade da multiplicação, podemos escrever 1000 0,1,01 100 = 1000,01 00 0,1 = 01 01 = (01). QUESTÃO Observe que para obter o primeiro retângulo foi necessário escrever quatro
Prova da UFRGS
 Prova da UFRGS - 2013 01. Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como a) 10 9. b) 10 10. c) 10 11.
Prova da UFRGS - 2013 01. Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como a) 10 9. b) 10 10. c) 10 11.
Unidade 6 Geometria: quadriláteros
 Sugestões de atividades Unidade 6 Geometria: quadriláteros 8 MTEMÁTI 1 Matemática 1. onsidere o retângulo representado a seguir. Indique o valor da medida do ângulo correspondente a α 1 β. 40 β 4. onsidere
Sugestões de atividades Unidade 6 Geometria: quadriláteros 8 MTEMÁTI 1 Matemática 1. onsidere o retângulo representado a seguir. Indique o valor da medida do ângulo correspondente a α 1 β. 40 β 4. onsidere
Prova Final de Matemática. Caderno 1: 45 minutos. Tolerância: 15 minutos. 1.º Ciclo do Ensino Básico. Prova 42/Época Especial
 Prova Final de Matemática 1.º Ciclo do Ensino Básico Prova 42/Época Especial/2015 Decreto-Lei n.º 139/2012, de 5 de julho A PREENCHER PELO ALUNO Nome completo Documento de identificação Assinatura do Aluno
Prova Final de Matemática 1.º Ciclo do Ensino Básico Prova 42/Época Especial/2015 Decreto-Lei n.º 139/2012, de 5 de julho A PREENCHER PELO ALUNO Nome completo Documento de identificação Assinatura do Aluno
38 a OLIMPÍADA BRASILEIRA DE MATEMÁTICA 2 a Fase Nível 1 (6 o ou 7 o ano)
 38 a OLIMPÍADA BRASILEIRA DE MATEMÁTICA a Fase Nível 1 (6 o ou 7 o ano) GABARITO PARTE A - Cada problema vale 5 pontos CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta
38 a OLIMPÍADA BRASILEIRA DE MATEMÁTICA a Fase Nível 1 (6 o ou 7 o ano) GABARITO PARTE A - Cada problema vale 5 pontos CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta
QUESTÕES OBJETIVAS. 2. O número de divisores de 9800 que são múltiplos de 5 é (A) 36 (B) 27 (C) 12 (D) 24 (E) 2
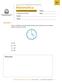
 QUESTÕES OBJETIVAS 1. Um relógio de ponteiros atrasa-se 30 segundos em cada hora. Sabendo que às 12 horas de hoje indica a hora exata, em que dia o relógio voltará a marcar a hora correta? (A) 09 de Outubro
QUESTÕES OBJETIVAS 1. Um relógio de ponteiros atrasa-se 30 segundos em cada hora. Sabendo que às 12 horas de hoje indica a hora exata, em que dia o relógio voltará a marcar a hora correta? (A) 09 de Outubro
Instruções para a realização da Prova Leia com muita atenção. Prova da segunda fase
 Nível 3 Instruções para a realização da Prova Leia com muita atenção Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima primeira edição da Olimpíada de Matemática de São José do
Nível 3 Instruções para a realização da Prova Leia com muita atenção Prova da segunda fase Caro Aluno, Parabéns pela sua participação na décima primeira edição da Olimpíada de Matemática de São José do
a. 0 b. 1 c. 2 d. 3 e. 5
 X OM NÍVEL ª OPM. Maria foi à feira e comprou duas dúzias de laranjas, duas dúzias de bananas e uma dúzia de maçãs, gastando R$ 5,80. Na outra semana, quando voltou à feira, comprou três dúzias de laranjas,
X OM NÍVEL ª OPM. Maria foi à feira e comprou duas dúzias de laranjas, duas dúzias de bananas e uma dúzia de maçãs, gastando R$ 5,80. Na outra semana, quando voltou à feira, comprou três dúzias de laranjas,
1. A imagem da função real f definida por f(x) = é a) R {1} b) R {2} c) R {-1} d) R {-2}
 1. A imagem da função real f definida por f(x) = é R {1} R {2} R {-1} R {-2} 2. Dadas f e g, duas funções reais definidas por f(x) = x 3 x e g(x) = sen x, pode-se afirmar que a expressão de (f o g)(x)
1. A imagem da função real f definida por f(x) = é R {1} R {2} R {-1} R {-2} 2. Dadas f e g, duas funções reais definidas por f(x) = x 3 x e g(x) = sen x, pode-se afirmar que a expressão de (f o g)(x)
Caderno 1: 30 minutos. Tolerância: 10 minutos. (com recurso à calculadora)
 PROVA FINAL DO 2.º CICLO DO ENSINO BÁSICO Matemática/Prova 62/2.ª Chamada/2013 Decreto-Lei n.º 139/2012, de 5 de julho A PREENCHER PELO ESTUDANTE Nome completo Documento de identificação CC n.º ou BI n.º
PROVA FINAL DO 2.º CICLO DO ENSINO BÁSICO Matemática/Prova 62/2.ª Chamada/2013 Decreto-Lei n.º 139/2012, de 5 de julho A PREENCHER PELO ESTUDANTE Nome completo Documento de identificação CC n.º ou BI n.º
B) R$ 6, 50 C) R$ 7, 00 D) R$ 7, 50 E) R$ 8, 00
 1 Matemática Q1. (OBMEP) Joãozinho escreveu os números 1, 2 e 3 como resultados de operações envolvendo exatamente quatro algarismos 4, como nos exemplos a seguir: 1 = (4 + 4) (4 + 4) 2 = 4 4 + 4 4 3 =
1 Matemática Q1. (OBMEP) Joãozinho escreveu os números 1, 2 e 3 como resultados de operações envolvendo exatamente quatro algarismos 4, como nos exemplos a seguir: 1 = (4 + 4) (4 + 4) 2 = 4 4 + 4 4 3 =
Prova Final de Matemática
 PROVA FINAL DO 2.º CICLO DO ENSINO BÁSICO Matemática/Prova 62/2.ª Chamada/2012 Decreto-Lei n.º 6/2001, de 18 de janeiro A PREENCHER PELO ESTUDANTE Nome completo Documento de identificação CC n.º ou BI
PROVA FINAL DO 2.º CICLO DO ENSINO BÁSICO Matemática/Prova 62/2.ª Chamada/2012 Decreto-Lei n.º 6/2001, de 18 de janeiro A PREENCHER PELO ESTUDANTE Nome completo Documento de identificação CC n.º ou BI
