3 Modelos Não-Lineares
|
|
|
- Heitor Sanches
- 5 Há anos
- Visualizações:
Transcrição
1 3 Modelos Não-Lineares 3.1. Modelos Não-Lineares Univariados Modelo TAR O modelo Auto-regressivo com limiar (TAR Threshold Autoregressive) foi proposto inicialmente por Tong (1978). Um pouco mais trabalhado, foi mais bem desenvolvido por Tong e Lim (1980) e Tong (1983). Conforme os avanços das pesquisas, este modelo se popularizou com inúmeras aplicações em séries temporais não-lineares. As análises tornaram-se interessantes pelo fato deste modelo atribuir um modelo linear diferente para distintas regiões onde se encontram os valores de uma variável determinada variável de transição. Definiuse que se a variável de transição for uma defasagem da variável endógena, o modelo é, então, denominado modelo auto-regressivo com limiar auto-excitante SETAR (Self-Exciting Threshold Autoregressive) Formulação Matemática caso, Defina como uma série temporal. Esta série segue um processo TAR (3.1) onde, os termos,,, e,,, =1,,h, são os coeficientes reais do modelo; ~ 0, ;. é uma função indicadora, definida por
2 30 = 1, 0, á O modelo pode ser reescrito na forma vetorial, (3.2) onde, os coeficientes do modelo são os vetores =,,, e =,,, e, ainda, = 1,,,,. Esta representação do modelo permite verificar que, dependendo do valor assumido pela variável, o modelo ativa um dos h+1 modelos lineares autoregressivos de ordem p, AR(p). Conforme dito, caso = o modelo TAR é denominado SETAR, e tem a seguinte representação matricial: (3.3) onde, o escalar d é conhecido como tamanho do limiar ou parâmetro de defasamento Modelo STAR Uma generalização do modelo SETAR com dois regimes, incorporando uma transição suave entre eles, foi proposta por Chan e Tong (1986). Este modelo foi denominado modelo STAR (Smooth Threshold Autoregressive). Para uma revisão, consulte Teräsvirta (1994) Formulação matemática Considere uma série temporal univariada. A expressão matemática representada pelo modelo com dois regimes é dada por: onde, = x ;, + x 1 ;, + (3.4)
3 31 o vetor ϕ =,,,,,, ; =1,2 são os coeficientes dos modelos lineares ligados aos regimes o vetor x = 1,,,,, é formado por 1 na posição inicial indicando o intercepto do modelo e nas demais posições as defasagens da variável endógena a função. é uma função limitada no intervalo [0,1], aqui determinada como a função logística, dada por: ;, = 1 1+ (3.5) O vetor de parâmetros =, dessa função contém os parâmetros de suavidade e locação, respectivamente, com a restrição >0. O primeiro é o responsável pelo grau de suavidade da função de transição, e o segundo representa o limiar entre os dois regimes. Para o mesmo valor de, a distância entre o valor de e c determina o grau de pertinência dos regimes do modelo. Na situação em que =, a observação pertence a ambos os regimes com igual grau de pertinência. Obtemos o modelo TAR se definirmos a função de transição. como uma função indicadora do tipo:. = 1, 0, > Neste caso, o limiar entre os dois regimes é abrupto e determinado por c, o parâmetro de limiar ou locação. Uma das grandes vantagens na utilização dos modelos de transição suave é a possibilidade de especificar a função de transição de forma a evitar este problema da busca por um limiar rígido entre os regimes. A escolha mais comum para a função de transição é a função logística. O modelo com esta função de transição é denominado modelo LSTAR (Logistic Smooth Transition AutoRegressive). A fim de experimentar a função logística, fixou-se alguns parâmetros e avaliou-se o seu comportamento através do Gráfico 3.1. O parâmetro de suavidade
4 32 assumiu os valores do conjunto {1, 2.5, 5, 50}, para representar diferentes níveis de suavidade da função logística, e o parâmetro de locação c assumiu o valor zero. Gráfico 3.1: Função logística com parâmetros fixos Quando tende para zero, a função logística torna-se uma constante igual a 0,5 e o modelo LSTAR se reduz a uma média de dois modelos lineares AR(p). Este comportamento permite concluir que não existe distinção entre os regimes. Conforme aumentamos o valor do parâmetro de suavidade, ou seja, com tendendo para infinito, a função logística aproxima-se de uma função do tipo degrau e a transição de um regime para o outro se torna uma transição abrupta. Neste caso, a função logística torna-se uma função indicadora e o modelo é denominado TAR. E ainda, caso a variável de transição seja uma defasagem da variável endógena, =, o modelo é então denominado SETAR (Self- Exciting Threshold Autoregression). Para valores no intervalo (0,1) assumidos pela função logística., o modelo LSTAR com dois regimes é definido como uma média ponderada de dois modelos AR(p), onde os pesos das observações são determinados por esses valores da função de transição, ;, e 1 ;,. O modelo STAR citado anteriormente possui 2 regimes. Porém, este pode ser estendido para um número maior de regimes. Neste caso, denomina-se como
5 33 MRSTAR (Multiple Regime Smooth Transition AutoRegression). Por exemplo, a representação de um modelo MRSTAR de 4 regimes pode ser escrita da seguinte forma: = ;, + 1 ;, ;, + ;, + 1 ;, 1 ;, + (3.6) Considerando conhecidas as variáveis de transição e, nota-se que os regimes na equação são ponderados por uma composição de funções logísticas (. e. ). Essa composição soma a unidade, por isso podem ser vista como funções de pertinência. O conceito de pertinência é largamente utilizado na teoria da Lógica Fuzzy (Zadeh, 1965). Maiores detalhes referentes aos modelos MRSTAR podem ser obtidos em van Dijk e Franses (1999) Especificação do modelo Esta seção apresenta uma estratégia de especificação do modelo STAR. Estratégia esta, definida como específica-para-geral. Este procedimento inicia com um modelo simples e, de acordo com os resultados dos testes estatísticos aplicados, o modelo tem sua complexidade aumentada. A primeira preocupação refere-se à seleção das variáveis que irá compor o modelo, tanto as variáveis que formarão o vetor quanto aquelas denominadas variáveis de transição, que formam o vetor. A modelagem STAR parte de um modelo simples e aumenta sua complexidade de acordo com os resultados dos testes aplicados. van Dijk, Terasvirta e Franses (2002) em seu trabalho, propuseram um processo de construção destes modelos, o qual segue um ciclo de modelagem. Os passos são: 1) Especificação de um modelo AR(p) Diversos modelos lineares são estimados, começando com um modelo AR(1) e aumentando a ordem p do modelo, com =1,2,,. Aquele modelo que minimizar os critérios de informação AIC (Akaike, 1974) ou BIC (Schwarz, 1978) deve ser selecionado. Todas as
6 34 propriedades dos modelos lineares AR(p) devem ser verificadas, incluindo a que se refere aos resíduos do modelo, definindo-os como aproximadamente um ruído branco. 2) Teste da hipótese de linearidade contra uma alternativa da família STAR Na construção do modelo STAR, o teste de linearidade tem duas funções. A primeira verifica a adequação do modelo linear para descrever os dados. A hipótese nula do teste é a de linearidade. No caso em que esta não for rejeitada, não é necessário estimar um modelo não-linear para os dados. A segunda determina as variáveis que formam o vetor de transição. Tsay (1989) propôs a aplicação do teste de linearidade para cada uma das defasagens da variável endógena ( ) e selecionar como variável de transição aquela que apresentar o menor p-valor do teste. 3) Estimação dos parâmetros do modelo STAR selecionado Para estimar os parâmetros do modelo, utiliza-se o método de Mínimos Quadrados Ordinários (MQO) para os parâmetros lineares e o método de Mínimos Quadrados Não-Lineares (MQNL) para os parâmetros não-lineares do modelo STAR. Este último, sob a normalidade dos erros, é equivalente ao método de Máxima Verossimilhança (MV). 4) Análise de diagnóstico do modelo O modelo STAR selecionado e estimado deve apresentar resíduos com boas propriedades. Basicamente, verifica-se a correlação dos resíduos de forma que eles se comportem como ruído branco. 5) Re-especificação do modelo de acordo com os resultados do diagnóstico No caso de selecionar um modelo STAR que não produza resíduos com boas propriedades, deve-se voltar a etapa 1 e re-especificar um modelo AR(p) e, assim, seguir todas as etapas.
7 35 6) Utilização do modelo com fins descritivos ou de previsão Com todas as etapas acima verificadas, determina-se este modelo como o modelo final e este deve ser utilizado de acordo com os seus fins Modelos Não-Lineares Multivariados Modelo TVAR Tsay (1998) estendeu a abordagem dos modelos TAR (Threshold Autoregressive) para modelos multivariados, definindo-os como modelos TVAR (Threshold Vector Autoregressive). Este modelo teve como motivação uma aplicação no mercado financeiro, onde um ativo foi negociado em dois mercados, simultaneamente Formulação matemática Considere que os modelos lineares locais dependam de algumas variáveis exógenas. Seja =,, uma série temporal k-dimensional e =,, uma série temporal v-dimensional de variáveis exógenas. Seja = < < < < =, então segue um modelo multivariado de limiar com variável de limiar e um lag d dado pela seguinte expressão: (3.7) onde, =1,, ; são vetores de constantes; p e q são inteiros não negativos. A inovação satisfaz onde, o primeiro termo é uma matriz positiva definida simétrica;
8 36 o segundo é uma seqüência de vetores descorrelatados aleatórios com média zero e matriz de covariância I, a matriz identidade. O modelo apresentado tem s regimes e é um modelo linear com relação ao espaço de limiar, mas é não linear no tempo se s >1. Assume-se que a variável de limiar é conhecida, estacionária e apresenta uma distribuição contínua e o lag d, o número de regimes s, e os limiares são desconhecidos Teste de Linearidade Primeiramente, Tsay (1998) propôs um teste estatístico para detectar a necessidade de estimar o modelo TVAR ao invés de um modelo linear, isto é, testou s =1 contra s > 1. O teste é simples e apresenta um bom desempenho em amostras finitas. Este teste é uma generalização do proposto em Tsay (1989) para o caso univariado, e apresenta uma distribuição assintótica Qui-Quadrado. A generalização também leva em conta a presença de variáveis exógenas e heterocedasticidade condicional. Em seguida, o autor considerou o teste LM com a hipótese nula que é linear contra a hipótese alternativa que segue um modelo TVAR definido anteriormente. O teste LM usa a variável de limiar para construir uma regressão arranjada. Este regressão baseada no crescimento da ordem da variável de limiar é: (3.8) onde é o índice temporal de. É importante notar que a dinâmica da série não mudou. O que mudou foi a ordem que cada dado entra na regressão, isto é, a ordem das linhas, se víssemos a regressão em um contexto matricial. A idéia do teste é simples: se é linear, então o estimador de mínimos quadrados recursivo da regressão arranjada é consistente, logo os resíduos previstos são aproximadamente um ruído branco. Conseqüentemente, os resíduos previstos são descorrelatados do regressor. Por outro lado, se seguir um modelo de limiar, os resíduos previstos
9 37 não serão ruído branco, pois o estimador de mínimos quadrados será viesado. Neste caso, os resíduos previstos serão correlatados com o regressor. Após a aplicação do teste o autor descreve um procedimento de construção do modelo incluindo a estimação de s e dos limiares. O método de estimação aplicado é o de mínimos quadrados condicional e a seleção do modelo é realizada com base no critério de informação de Akaike Estimação Considerando estimação por mínimos quadrados condicional e assumindo que p, q e s são conhecidos, e que a variável de limiar é dada, escrevemos o modelo para o caso de s = 2 da seguinte forma: Os parâmetros do modelo são e a sua estimação pode ser obtida em dois passos. Primeiro, para um dado d e, o modelo acima nada mais é do que duas regressões lineares multivariadas separadas, cujas estimativas de mínimos quadrados dos seus parâmetros são um resultado conhecido: Define-se a soma do quadrado dos resíduos como onde, é o traço de No passo 2, as estimativas de mínimos quadrados condicional de d e são obtidas fazendo
10 38 Os estimadores de mínimos quadrados condicionais são estimadores consistentes dos coeficientes, do lag e dos limiares e da matriz de covariâncias Identificação do modelo O problema de identificação e especificação de um modelo de limiar multivariado envolve a seleção de muitos parâmetros. Os problemas mais difíceis são: a identificação da variável de limiar e a especificação do número de regimes. A identificação de s pode levar em consideração experiências passadas e informações a priori sobre o conjunto de dados, ou a complexidade computacional pode restringir s a um número pequeno. Assumindo que e s são dados, o autor usa o critério AIC para selecionar um modelo. Dados p, q, d e s, o critério AIC do modelo de limiar multivariado é dado por: (3.9) onde,,, é a função de verossimilhança do regime j avaliado na estimativa de máxima verossimilhança de,, Modelo STVAR O modelo STVAR (Smooth Transition Vector Autoregressive) é a versão multivariada do modelo STAR descrito na seção Este modelo é severamente utilizado para modelar vetores de séries temporais, citando aqui o campo da Macroeconomia Formulação matemática Considere =,,, como um vetor (K x 1) de séries temporais. Uma analogia K-dimensional da expressão matemática representada pelo modelo STAR com dois regimes é dada por:
11 39 =Φ X ;, +Φ X 1 ;, + (3.10) onde, os vetores Φ,, i =1,2 são vetores (K x 1) dos coeficientes interceptos ligados aos regimes; a matriz Φ = Φ,,,Φ, i =1,2 tem dimensão (K x K) e é formada pelos coeficientes dos modelos lineares ligados aos regimes; o vetor ε = ε,,ε é o vetor k-dimensional de ruído branco com média zero e matriz de variância-covariância positiva definida Σ ; a matriz X = 1,,1,,,,, é formada por 1 na posição inicial indicando o intercepto do modelo e nas demais posições as defasagens das variáveis endógenas; a função. é a função logística. Observe que no modelo STVAR os regimes são comuns às K variáveis, no sentido de que uma mesma função de transição determina o regime e a troca de regimes de todas as K equações do modelo Teste de Linearidade Para realizar os testes de linearidade enfrentamos o mesmo problema do caso univariado. Isto é, o STVAR contém parâmetros que não são identificáveis sob a hipótese nula. Para solucionar o problema de identificação os autores usam uma aproximação de Taylor adequada para a função de transição. Por exemplo no caso da função logística utiliza-se a aproximação de Taylor de terceira ordem em torno de =0, resultando em um modelo re-parametrizado: (3.11) Desta forma, a hipótese nula original é equivalente à de que =0, = 1,2,3. A estatística do teste de multiplicador de Lagrange (LM) resultante tem uma distribuição assintótica qui-quadrada com 3 graus de liberdade sob a hipótese nula.
12 Estimação Quando a linearidade é rejeitada e a variável e a função de transição foram selecionadas, os parâmetros do modelo STVAR podem ser estimados através de mínimos quadrados não lineares (MQNL). Sob algumas condições de regularidade, os estimadores são consistentes e com distribuição assintoticamente Normal Adequação Como proposto em Eitrheim e Teräsvirta (1996), três testes são realizados com o objetivo de checar se o modelo estimado é adequado. Testa-se se os resíduos apresentam auto-correlação, se os dados ainda apresentam alguma não linearidade e se os parâmetros são constantes. Camacho (2004) descreve esses testes detalhadamente Modelo SBTVAR O modelo TVAR proposto por Tsay (1998) é um modelo linear local com matrizes auto-regressivas diferentes em cada regime, determinados por uma variável de limiar (uma das variáveis endógenas), um lag e um limiar. O modelo SBTVAR (Structural Break Threshold Vector Autoregressive) proposto por Galvão (2006) também divide a amostra em dois períodos, determinados por um ponto de quebra, o qual permite diferentes dinâmicas antes e depois desta quebra. O que mostra que este modelo caracteriza em mudanças abruptas de um regime para o outro. Apesar dos modelos não-lineares capturarem algumas características de modelos de quebras estruturais, pode ser que a quebra também implique em mudanças nos parâmetros que determinam a não-linearidade.
13 Formulação matemática Defina x = x,,x como um vetor (m x 1) de m variáveis endógenas e defina x = 1,x,,x como uma matriz (m x (mp+1)), onde p é a ordem auto-regressiva. O modelo SBTVAR pode ser escrito como: (3.12) onde,, é uma função indicadora, a qual depende de uma variável de transição, do limiar e do lag, e é uma função indicadora que depende do ponto de quebra. O SBTVAR tem um TVAR em cada subconjunto determinado pelo ponto de quebra, ou seja, a quebra também afeta os parâmetros da função indicadora que determina os regimes. Se não houver limiar, o VAR com quebra estrutural (SBVAR) é dado por: (3.13) Por outro lado, se houver limiar, mas não quebra estrutural, temos o VAR com limiar (TVAR), que pode ser escrito como: (3.14) Estimação A estimação do SBTVAR pode seguir duas abordagens, a de mínimos quadrados condicionais, usada em Tsay (1998), apresentada na seção 2.3, ou máxima verossimilhança, sugerida em Hansen and Seo (2002). Usando os resíduos, a matriz de covariância é computada de forma consistente como
14 42 O estimador de mínimos quadrados condicionais (MQC) é obtido fazendo fazendo Da mesma forma, o estimador de máxima verossimilhança (ML) é obtido O estimador de ML é construído assumindo que as matrizes de covariância são as mesmas em cada regime. Essa hipótese pode não ser válida quando aplicada a dados macroeconômicos com variância não constante no tempo, mas o estimador pode ser modificado para este caso Seleção do modelo Em Galvão (2006) é apresentado um procedimento de seleção entre modelos de limiar. A questão a ser estudada é qual modelo é mais adequado ao conjunto de dados, um VAR, TVAR, SBVAR ou um SBTVAR. Mesmo se podendo estimar modelos SBTVAR s, não fica claro a necessidade de ter limiares ou transições que variam no tempo para capturar a estrutura dinâmica dos dados. Testes para limiar em um SBVAR ou para quebra estrutural em um TVAR são complicados devido à descontinuidade das mudanças e da presença de parâmetros mal comportados. A autora propõe um método de especificação do modelo baseado nos limites assintóticos para os testes LM e de Wald, derivados por Altissimo e Corradi (2002). A regra de decisão para a seleção do modelo usa limites assintóticos e os valores máximos das estatísticas de Wald e LM em uma grade de possíveis valores para os parâmetros mal comportados, como proposto por Altissimo e Corradi (2002). As estatísticas de Wald e LM são calculadas usando a soma do quadrado dos resíduos (SSR) sob a hipótese nula e alternativa:
15 43 O vetor contém parâmetros como limiares e quebras do modelo sob a hipótese nula, e o vetor contêm os mesmos parâmetros sob a hipótese alternativa Modelo TVEC Lo e Zivot (2001) definiram um modelo de co-integração com limiar multivariado, chamado TVEC (Threshold Vector Error Correction), que é um caso especial do TVAR do Tsay (1998) Formulação matemática De acordo com todas as considerações e suposições feitas no modelo TVAR, Tsay (1998), define-se um modelo de limiar bivariado com 3 regimes pela expressão: (3.15) Pode-se reescrever este modelo como: onde (3.16) Se, em cada regime j, é I(1) e co-integrado com o vetor de co-integração comum = 1,, então o rank =1 e
16 44 Desta forma, a representação do modelo TVEC é dada por: (3.17) Teste de co-integração Lo e Zivot (2001) consideram testes de não co-integração contra cointegração linear e co-integração com limiar, além de testes de linearidade depois de determinado que existe co-integração nos dados. Balke e Fomby (1997) discutiram alguns problemas associados a testes de co-integração com limiar. Os autores notaram que testar a hipótese nula de não co-integração contra a hipótese alternativa de co-integração com limiar é complicado. Além disso, para construir testes com alto poder para um tipo específico de TVEC, é preciso especificar e estimar a forma do modelo de limiar sob a hipótese alternativa, e isto pode ser difícil, uma vez que existem muitos tipos de modelos de limiar. Baseados em resultados de simulações de Monte Carlo, Balke e Fomby (1997) sugeriram a seguinte estratégia, que Lo e Zivot (2001) estenderam: 1) Testa a hipótese nula de não co-integração contra a alternativa de cointegração linear. 2) Se a hipótese de não co-integração for rejeitada, testa a hipótese nula de co-integração linear contra a alternativa de co-integração nãolinear (com limiar). 3) Se a hipótese de linearidade for rejeitada, é realizada a especificação e estimação do modelo de limiar Teste de linearidade Para testar a linearidade, os autores usaram o teste generalizado apresentado em Tsay (1998), que também é válido para processos co-integrados. Para implementar esse teste, foi considerada uma regressão arranjada multivariada para VEC.
17 Especificação do modelo Após a realização dos testes e de rejeitar a não co-integração e linearidade, é necessário determinar que tipo de modelo de limiar é mais apropriado para o conjunto de dados. Algumas questões a serem respondidas são o número de regimes do modelo, se os valores dos limiares são simétricos, qual modelo é mais apropriado, entre outras. Duas linhas gerais foram seguidas para determinar a especificação do modelo de limiar apropriada. A primeira, adotada por Tong (1990), Clements e Krolzig (1998), e Tsay (1998), usa um critério de seleção como AIC para determinar a melhor especificação do modelo. A segunda, recentemente revisada por Hansen (1999), usa um procedimento de testes seqüenciais baseados em modelos aninhados. Lo e Zivot (2001) seguiram Hansen (1999) e consideraram testes de hipóteses em ninhos baseadas em estimação irrestrita do modelo TVEC Estimação A estimação do modelo é realizada usando mínimos quadrados condicional seqüenciais, como em Hansen (1999) Modelo STVEC O modelo STVEC (Smooth Transition Vector Error Correction) é a versão não-linear do modelo VEC (Vector Error Correction). A julgar pelas aplicações destes modelos multivariados não-lineares que estão atualmente disponíveis, um modelo de particular interesse é aquele em que os componentes do linear estão ligados por uma relação de equilíbrio de longo prazo, enquanto a adaptação para este equilíbrio é não-linear e pode ser caracterizado como troca de regimes, com os regimes determinados pelo tamanho e/ou o desvio de sinal de equilíbrio. Em modelos lineares de séries temporais, este tipo de comportamento é capturado pelo modelo vetorial de correção de erros, consulte Johansen (1995) para os
18 46 tratamentos em profundidade. Recentemente, extensões não-lineares destes conceitos foram consideradas na literatura Formulação matemática Concentrando-se na incorporação do mecanismo de transição suave em um VEC para permitir a não-linearidade ou assimetria dos dados, define-se como um modelo vetorial de correção de erros com transição suave (Smooth Transition Vector Error Correction STVEC) dado por: (3.18) onde, os vetores α, i =1,2 são vetores (K x 1) e = para algum vetor (K x 1); é o termo de correção de erro, isto é, é o desvio da relação de equilíbrio a qual é dada por =0; a matriz Φ = Φ,,,Φ, i =1,2 tem dimensão (K x K) e é formada pelos coeficientes dos modelos lineares ligados aos regimes; o vetor ε = ε,,ε é o vetor k-dimensional de ruído branco com média zero e matriz de variância-covariância positiva definida Σ ; a matriz X = 1,,1,,,,, é formada por 1 na posição inicial indicando o intercepto do modelo e nas demais posições as defasagens das variáveis endógenas. Afigura-se que as formas de correção de erros não-lineares freqüentemente afetam diferentes ajustes para desvios positivos e negativos, ou para desvios grandes e pequenos do equilíbrio. Efeitos assimétricos de desvios positivos e negativos do equilíbrio podem ser obtidos definindo a função. como a função logística e =. No modelo resultante, a força de reversão de ao seu atrator muda monotonicamente para valores crescentes de. A constante de locação pode ser reduzida a zero para tornar a mudança simétrica em torno do valor de equilíbrio zero.
19 47 Já os efeitos assimétricos de desvios grandes e pequenos do equilíbrio podem ser obtidos definindo a função. como a função exponencial, dada por: ;, =1, >0. com = e novamente com a constante de locação reduzida a zero para centrar a força de equilíbrio em zero Teste de Linearidade A seleção da variável de transição é feita testando a linearidade do modelo. A hipótese nula é de que o conjunto de dados segue um modelo VEC e a alternativa é de que seguem um STVEC. Para isso, preparam-se uma seqüência de candidatas a variáveis de transição. Para solucionar o problema de identificação dos parâmetros sob a hipótese nula, segue-se a abordagem de Luukkonen, Saikkonen, Teräsvirta (1988) e substitui-se a função de transição por uma aproximação de Taylor adequada. Desta forma, a metodologia aplicada no teste é a mesma da aplicada em modelos STVAR. O teste proposto por Luukkonen, Saikkonen, Teräsvirta (1988) vem sendo usado em muitos estudos empíricos. Mas esse teste estatístico é baseado em uma aproximação polinomial, e os erros de aproximação podem afetar a inferência estatística. Além disso, os testes não são diretamente relacionados com o modelo de transição suave, logo não pode apontar o que causa a rejeição da linearidade. Com esta motivação, Seo (2004) considerou testes diretos para ajuste não-linear em um modelo STVEC, baseados na especificação exata da transição suave. Hansen e Seo (2002) consideraram os testes para não-linearidade de limiar em um VEC e Seo (2004) estendeu para VEC de transição suave (STVEC). Os testes são baseados na estatística LM, que pode ser calculada sob a hipótese nula Metodologia CART Introdução A metodologia Classification and Regression Tree (CART), proposta por Breiman, Friedman, Olshen e Stone (1984), é um método de particionamento
20 48 recursivo, o qual estrutura os modelos definidos para sub-amostra dos dados, dividindo de forma conveniente o problema em partes. Isto define a estruturação por árvores de decisão, servindo de alternativa aos métodos tradicionais de classificação (variável dependente binária) e regressão (variável dependente contínua). O modelo CART é não-paramétrico, sendo, portanto, não-probabilístico, pois não assume uma distribuição de probabilidade e não seguem suposições sobre componentes aleatórios e a forma do modelo. A principal vantagem do CART vem da facilidade de interpretação da estrutura de árvore de decisão. As variáveis envolvidas na definição da árvore formam um conjunto de sentenças lógicas do modelo final. O ciclo da modelagem envolve o crescimento da árvore a partir da raiz (nó inicial), que contém todas as observações do conjunto de dados, até as folhas (nós terminais), cada qual contendo parte das observações. Primeiramente, realiza-se um teste no nó inicial, o qual só admite resposta do tipo binário {0,1}, sendo então um teste lógico. Este teste é realizado em cada observação de cada uma das variáveis preditoras e, de acordo com as respostas lógicas obtidas, a raiz dará origem a dois filhos (novos nós), contendo parte das observações originais. Por convenção, se a resposta for 1, aloca-se a observação no nó esquerdo, caso contrário, no nó direito. Para cada nó gerado, este procedimento de teste lógico deve ser repetido até que não seja mais possível dividir a árvore. Desta forma, cada um dos nós que não geraram novos nós são os chamados nós terminais. E cada nó que gerou dois filhos são denominados nós ancestrais, ou nós de divisão, ou ainda nós intermediários. O modelo final estimado é representado por um gráfico com o formato de uma árvore binária de decisão, com os nós ancestrais (ou nós de divisão) e os nós terminais (ou folhas). Um procedimento importante de numeração dos nós deve ser adotado. A raiz é sempre o nó 0. E cada nó gerado a partir do nó 0 segue uma seqüência numérica crescente da esquerda para a direita. Quando os nós não forem gerados, deve-se saltar os seus números correspondentes e prosseguir a numeração com o nó à direita mais próximo. A Figura 3.1 ilustra um exemplo de árvore com ausência de alguns nós.
21 Formulação matemática Figura 3.1: Exemplo de árvore com ausência de alguns nós Seja =,,, R um vetor com variáveis preditoras de uma determinada resposta univariada e contínua R. Defina. como uma função desconhecida através da expressão: = x + (3.19) tal que, não há suposições sobre o termo aleatório. Define-se, conforme Lewis,Stevens (1991), um modelo estruturado por árvore com K folhas por uma função geral não-linear x ; de x e definida pelo vetor de parâmetros R, onde r é o número total de parâmetros, através da expressão: x x ; = x ; (3.20) onde,. é uma função indicadora, dada por: x ; = 1, x 0,. e =,,,,, é o vetor de parâmetros envolvidos na árvore.
22 50 Usualmente, H(.) é uma função constante definida por K sub-regiões, =1,,, de algum domínio K R. A Figura 3.2 é um exemplo de um modelo gerado por uma árvore de regressão que explica a relação entre a variável resposta y e um conjunto de duas variáveis preditoras x 1 e x 2 (q = 2). Define-se c j, j = 0,1,...,N, como o valor limite da partição k i que determinará a inclusão da observação na região. Figura 3.2: Exemplo de um modelo gerado por uma árvore de regressão Algoritmo de crescimento A arquitetura da árvore é definida a partir de um ciclo iterativo que escolhe um nó a cada passo para ser subdividido e gerar mais 2 nós. A cada iteração, além do nó a ser dividido, também é especificada uma variável de transição e o limiar desta divisão (c j ). A escolha desta especificação visa minimizar a soma dos erros quadráticos de previsão. Para a raiz da árvore (primeira divisão), a equação a ser minimizada é dada por: SQE = ;, + 1 ;, (3.21)
23 51 Após a especificação, estimam-se os parâmetros dos modelos locais para as observações alocadas dentro dos nós gerados pela divisão. Esse ciclo se repete até que não haja mais ganho em efetuar subdivisões na árvore. Com o modelo final estimado, é possível realizar cortes de algumas folhas, técnica conhecida como podagem (prunning), a partir de medidas de custo e complexidade, ou da capacidade preditiva do modelo.
2 Modelos Não Lineares
 Modelos Não Lineares 17 2 Modelos Não Lineares 2.1. Introdução Nos últimos anos, muitos modelos não-lineares para a análise de séries temporais têm sido propostos. Na econometria clássica, os modelos de
Modelos Não Lineares 17 2 Modelos Não Lineares 2.1. Introdução Nos últimos anos, muitos modelos não-lineares para a análise de séries temporais têm sido propostos. Na econometria clássica, os modelos de
Neste capítulo apresentam-se os modelos STVAR-Tree, o principal da dissertação, além dos modelos competidores PAR(p) e Neuro-Fuzzy.
 4 Metodologia 4.1. Introdução Neste capítulo apresentam-se os modelos STVAR-Tree, o principal da dissertação, além dos modelos competidores PAR(p) e Neuro-Fuzzy. 4.2. Modelo STVAR-Tree O modelo vetorial
4 Metodologia 4.1. Introdução Neste capítulo apresentam-se os modelos STVAR-Tree, o principal da dissertação, além dos modelos competidores PAR(p) e Neuro-Fuzzy. 4.2. Modelo STVAR-Tree O modelo vetorial
2 Modelos STAR-Tree 2.1 CART
 2 Modelos STAR-Tree Este capítulo apresenta os principais conceitos envolvidos na denição do modelo STAR-Tree. Sua origem foi marcada pelos processos autoregressivos com limiar, TAR (Threshold AutoRegressive),
2 Modelos STAR-Tree Este capítulo apresenta os principais conceitos envolvidos na denição do modelo STAR-Tree. Sua origem foi marcada pelos processos autoregressivos com limiar, TAR (Threshold AutoRegressive),
3 Metodologia. resenha de VAN DIJK et al. (2002). 12 Para uma exposição extensiva do uso do modelo STR aplicado a séries macroeconômicas, ver a
 3 Metodologia Como explicado acima, o modelo novo-keynesiano não fornece bases teóricas que motivem a existência de não-linearidades na CPNKH. Por isso, optamos por utilizar uma estratégia empírica flexível
3 Metodologia Como explicado acima, o modelo novo-keynesiano não fornece bases teóricas que motivem a existência de não-linearidades na CPNKH. Por isso, optamos por utilizar uma estratégia empírica flexível
4 Modelos de Regressão Dinâmica
 4 Modelos de Regressão Dinâmica Nos modelos de regressão linear (Johnston e Dinardo, 1998) estudados comumente na literatura, supõe-se que os erros gerados pelo modelo possuem algumas características como:
4 Modelos de Regressão Dinâmica Nos modelos de regressão linear (Johnston e Dinardo, 1998) estudados comumente na literatura, supõe-se que os erros gerados pelo modelo possuem algumas características como:
Aula 2 Uma breve revisão sobre modelos lineares
 Aula Uma breve revisão sobre modelos lineares Processo de ajuste de um modelo de regressão O ajuste de modelos de regressão tem como principais objetivos descrever relações entre variáveis, estimar e testar
Aula Uma breve revisão sobre modelos lineares Processo de ajuste de um modelo de regressão O ajuste de modelos de regressão tem como principais objetivos descrever relações entre variáveis, estimar e testar
Séries Temporais e Modelos Dinâmicos. Econometria. Marcelo C. Medeiros. Aula 9
 em Econometria Departamento de Economia Pontifícia Universidade Católica do Rio de Janeiro Aula 9 Data Mining Equação básica: Amostras finitas + muitos modelos = modelo equivocado. Lovell (1983, Review
em Econometria Departamento de Economia Pontifícia Universidade Católica do Rio de Janeiro Aula 9 Data Mining Equação básica: Amostras finitas + muitos modelos = modelo equivocado. Lovell (1983, Review
A Metodologia de Box & Jenkins
 A Metodologia de Box & Jenins Aula 03 Bueno, 0, Capítulo 3 Enders, 009, Capítulo Morettin e Toloi, 006, Capítulos 6 a 8 A Metodologia Box & Jenins Uma abordagem bastante utilizada para a construção de
A Metodologia de Box & Jenins Aula 03 Bueno, 0, Capítulo 3 Enders, 009, Capítulo Morettin e Toloi, 006, Capítulos 6 a 8 A Metodologia Box & Jenins Uma abordagem bastante utilizada para a construção de
Análise de Dados Longitudinais Aula
 1/35 Análise de Dados Longitudinais Aula 08.08.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/35 Sumário 1 Revisão para dados transversais 2 Como analisar dados longitudinais 3 Perspectiva
1/35 Análise de Dados Longitudinais Aula 08.08.2018 José Luiz Padilha da Silva - UFPR www.docs.ufpr.br/ jlpadilha 2/35 Sumário 1 Revisão para dados transversais 2 Como analisar dados longitudinais 3 Perspectiva
Análise Multivariada Aplicada à Contabilidade
 Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Econometria em Finanças e Atuária
 Ralph S. Silva http://www.im.ufrj.br/ralph/especializacao.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Maio-Junho/2013 Modelos condicionalmente
Ralph S. Silva http://www.im.ufrj.br/ralph/especializacao.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Maio-Junho/2013 Modelos condicionalmente
CONHECIMENTOS ESPECÍFICOS
 CONHECIMENTOS ESPECÍFICOS 2003 2004 2005 2006 2007 2008 2009 2010 X 39,0 39,5 39,5 39,0 39,5 41,5 42,0 42,0 Y 46,5 65,5 86,0 100,0 121,0 150,5 174,0 203,0 A tabela acima mostra as quantidades, em milhões
CONHECIMENTOS ESPECÍFICOS 2003 2004 2005 2006 2007 2008 2009 2010 X 39,0 39,5 39,5 39,0 39,5 41,5 42,0 42,0 Y 46,5 65,5 86,0 100,0 121,0 150,5 174,0 203,0 A tabela acima mostra as quantidades, em milhões
Ralph S. Silva
 ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
ANÁLISE ESTATÍSTICA MULTIVARIADA Ralph S Silva http://wwwimufrjbr/ralph/multivariadahtml Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Sumário Revisão:
Referências Bibliográcas
 Referências Bibliográcas [1] BOX, G.; JENKINS, G. ; REINSEL, G.. Time Series Analysis, Forecasting and Control. Prentice Hall, New Jersey, 1994. [2] BREIMAN, L.; FRIEDMAN, J.; OLSHEN, R. ; STONE, C. J..
Referências Bibliográcas [1] BOX, G.; JENKINS, G. ; REINSEL, G.. Time Series Analysis, Forecasting and Control. Prentice Hall, New Jersey, 1994. [2] BREIMAN, L.; FRIEDMAN, J.; OLSHEN, R. ; STONE, C. J..
Econometria IV Modelos Lineares de Séries Temporais. Fernando Chague
 Econometria IV Modelos Lineares de Séries Temporais Fernando Chague 2016 Estacionariedade Estacionariedade Inferência estatística em séries temporais requer alguma forma de estacionariedade dos dados Intuição:
Econometria IV Modelos Lineares de Séries Temporais Fernando Chague 2016 Estacionariedade Estacionariedade Inferência estatística em séries temporais requer alguma forma de estacionariedade dos dados Intuição:
3 Modelos Comparativos: Teoria e Metodologia
 3 Modelos Comparativos: Teoria e Metodologia Para avaliar o desempenho do modelo STAR-Tree, foram estimados os modelos Naive, ARMAX e Redes Neurais. O ajuste dos modelos ARMAX e das redes neurais foi feito
3 Modelos Comparativos: Teoria e Metodologia Para avaliar o desempenho do modelo STAR-Tree, foram estimados os modelos Naive, ARMAX e Redes Neurais. O ajuste dos modelos ARMAX e das redes neurais foi feito
Análise da Regressão múltipla: MQO Assintótico y = β 0 + β 1 x 1 + β x +... β k x k + u 3. Propriedades assintóticas Antes, propriedades sobre amostra
 Análise da Regressão múltipla: MQO Assintótico Capítulo 5 do Wooldridge Análise da Regressão múltipla: MQO Assintótico y = β 0 + β 1 x 1 + β x +... β k x k + u 3. Propriedades assintóticas Antes, propriedades
Análise da Regressão múltipla: MQO Assintótico Capítulo 5 do Wooldridge Análise da Regressão múltipla: MQO Assintótico y = β 0 + β 1 x 1 + β x +... β k x k + u 3. Propriedades assintóticas Antes, propriedades
Análise de Regressão Linear Simples e
 Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Análise de Regressão Linear Simples e Múltipla Carla Henriques Departamento de Matemática Escola Superior de Tecnologia de Viseu Introdução A análise de regressão estuda o relacionamento entre uma variável
Introdução a Modelos VAR
 Introdução a Modelos VAR Henrique Dantas Neder - Professor Associado Universidade Federal de Uberlândia July 24, 2014 Um VAR é um modelo no qual K variáveis são especicadas como funções lineares de p de
Introdução a Modelos VAR Henrique Dantas Neder - Professor Associado Universidade Federal de Uberlândia July 24, 2014 Um VAR é um modelo no qual K variáveis são especicadas como funções lineares de p de
CONHECIMENTOS ESPECÍFICOS
 CONHECIMENTOS ESPECÍFICOS Em uma grande escola, 10% dos alunos são comprovadamente fracos. Um teste educacional conseguiu identificar corretamente 80% entre aqueles que são fracos e 85% entre aqueles que
CONHECIMENTOS ESPECÍFICOS Em uma grande escola, 10% dos alunos são comprovadamente fracos. Um teste educacional conseguiu identificar corretamente 80% entre aqueles que são fracos e 85% entre aqueles que
Transformações e Ponderação para corrigir violações do modelo
 Transformações e Ponderação para corrigir violações do modelo Diagnóstico na análise de regressão Relembrando suposições Os erros do modelo tem média zero e variância constante. Os erros do modelo tem
Transformações e Ponderação para corrigir violações do modelo Diagnóstico na análise de regressão Relembrando suposições Os erros do modelo tem média zero e variância constante. Os erros do modelo tem
Testes de Raiz Unitária para Dados em Painel
 Aula 7 Bibliografia: Stata, 2017. help xtunitroot. From Stata/SE 13 (accessed on Oct. 23, 2018). Pesaran, M.H. (2015). Time series and panel data econometrics. Oxford: Oxford University Press. Rafael S.
Aula 7 Bibliografia: Stata, 2017. help xtunitroot. From Stata/SE 13 (accessed on Oct. 23, 2018). Pesaran, M.H. (2015). Time series and panel data econometrics. Oxford: Oxford University Press. Rafael S.
'HVFULomRH$QiOLVH([SORUDWyULDGRV'DGRV
 69 'HVFULomRH$QiOLVH([SORUDWyULDGRV'DGRV O presente capítulo objetiva entender o comportamento das séries de retorno financeiras para as carteiras de investimento elaboradas no capítulo anterior. Tal análise
69 'HVFULomRH$QiOLVH([SORUDWyULDGRV'DGRV O presente capítulo objetiva entender o comportamento das séries de retorno financeiras para as carteiras de investimento elaboradas no capítulo anterior. Tal análise
Os Mínimos Quadrados Ordinários Assintóticos
 Os Mínimos Quadrados Ordinários Assintóticos Enquadramento 1. A analise assintótica, é o método matemático que descreve a limitação de um determinado comportamento. O termo assintótico significa aproximar-se
Os Mínimos Quadrados Ordinários Assintóticos Enquadramento 1. A analise assintótica, é o método matemático que descreve a limitação de um determinado comportamento. O termo assintótico significa aproximar-se
Econometria. Econometria MQO MQO. Resíduos. Resíduos MQO. 1. Exemplo da técnica MQO. 2. Hipóteses do Modelo de RLM. 3.
 3. Ajuste do Modelo 4. Modelo Restrito Resíduos Resíduos 1 M = I- X(X X) -1 X Hipóteses do modelo Linearidade significa ser linear nos parâmetros. Identificação: Só existe um único conjunto de parâmetros
3. Ajuste do Modelo 4. Modelo Restrito Resíduos Resíduos 1 M = I- X(X X) -1 X Hipóteses do modelo Linearidade significa ser linear nos parâmetros. Identificação: Só existe um único conjunto de parâmetros
θ depende de um parâmetro desconhecido θ.
 73 Método de Máxima Verosimilhança (Maximum Likelihood) Seja uma variável aleatória (v. a.) cuja densidade de probabilidade depende de um parâmetro desconhecido. Admite-se conhecida a forma de Exemplo
73 Método de Máxima Verosimilhança (Maximum Likelihood) Seja uma variável aleatória (v. a.) cuja densidade de probabilidade depende de um parâmetro desconhecido. Admite-se conhecida a forma de Exemplo
CONHECIMENTOS ESPECÍFICOS
 fonte de graus de soma de quadrado variação liberdade quadrados médio teste F regressão 1 1,4 1,4 46,2 resíduo 28 0,8 0,03 total 2,2 A tabela de análise de variância (ANOVA) ilustrada acima resulta de
fonte de graus de soma de quadrado variação liberdade quadrados médio teste F regressão 1 1,4 1,4 46,2 resíduo 28 0,8 0,03 total 2,2 A tabela de análise de variância (ANOVA) ilustrada acima resulta de
AULA 09 Regressão. Ernesto F. L. Amaral. 17 de setembro de 2012
 1 AULA 09 Regressão Ernesto F. L. Amaral 17 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario F. 2008. Introdução à
1 AULA 09 Regressão Ernesto F. L. Amaral 17 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario F. 2008. Introdução à
Métodos Quantitativos para Avaliação de Políticas Públicas
 ACH3657 Métodos Quantitativos para Avaliação de Políticas Públicas Aula 11 Análise de Resíduos Alexandre Ribeiro Leichsenring alexandre.leichsenring@usp.br Alexandre Leichsenring ACH3657 Aula 11 1 / 26
ACH3657 Métodos Quantitativos para Avaliação de Políticas Públicas Aula 11 Análise de Resíduos Alexandre Ribeiro Leichsenring alexandre.leichsenring@usp.br Alexandre Leichsenring ACH3657 Aula 11 1 / 26
4 Modelos Lineares Generalizados
 4 Modelos Lineares Generalizados Neste capítulo, serão apresentados arcabouços teóricos dos modelos lineares generalizados (MLGs) e como casos particulares desses modelos são aplicáveis ao problema da
4 Modelos Lineares Generalizados Neste capítulo, serão apresentados arcabouços teóricos dos modelos lineares generalizados (MLGs) e como casos particulares desses modelos são aplicáveis ao problema da
A análise de séries temporais é uma área da estatística dedicada ao estudo de dados orientados no tempo (MONTGOMERY, 2004).
 3 Séries temporais A análise de séries temporais é uma área da estatística dedicada ao estudo de dados orientados no tempo (MONTGOMERY, 2004). 3.1. Princípios fundamentais Conforme Box et al. (1994), uma
3 Séries temporais A análise de séries temporais é uma área da estatística dedicada ao estudo de dados orientados no tempo (MONTGOMERY, 2004). 3.1. Princípios fundamentais Conforme Box et al. (1994), uma
Vetores Auto-Regressivos (VAR) Cristian Rafael Pelizza Estágio de docência
 Vetores Auto-Regressivos (VAR) Cristian Rafael Pelizza Estágio de docência Forma estrutural e reduzida O método VAR busca capturar a interdependência entre múltiplas séries de tempo. Estrutura-se equações
Vetores Auto-Regressivos (VAR) Cristian Rafael Pelizza Estágio de docência Forma estrutural e reduzida O método VAR busca capturar a interdependência entre múltiplas séries de tempo. Estrutura-se equações
Disciplina de Modelos Lineares Professora Ariane Ferreira
 Disciplina de Modelos Lineares 2012-2 Regressão Logística Professora Ariane Ferreira O modelo de regressão logístico é semelhante ao modelo de regressão linear. No entanto, no modelo logístico a variável
Disciplina de Modelos Lineares 2012-2 Regressão Logística Professora Ariane Ferreira O modelo de regressão logístico é semelhante ao modelo de regressão linear. No entanto, no modelo logístico a variável
AULA 13 Análise de Regressão Múltipla: MQO Assimptótico
 1 AULA 13 Análise de Regressão Múltipla: MQO Assimptótico Ernesto F. L. Amaral 15 de abril de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução
1 AULA 13 Análise de Regressão Múltipla: MQO Assimptótico Ernesto F. L. Amaral 15 de abril de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução
Modelos de Regressão Linear Simples - Análise de Resíduos
 Modelos de Regressão Linear Simples - Análise de Resíduos Erica Castilho Rodrigues 1 de Setembro de 2014 3 O modelo de regressão linear é dado por Y i = β 0 + β 1 x i + ɛ i onde ɛ i iid N(0,σ 2 ). O erro
Modelos de Regressão Linear Simples - Análise de Resíduos Erica Castilho Rodrigues 1 de Setembro de 2014 3 O modelo de regressão linear é dado por Y i = β 0 + β 1 x i + ɛ i onde ɛ i iid N(0,σ 2 ). O erro
Modelos de Regressão Linear Simples - Análise de Resíduos
 1 Modelos de Regressão Linear Simples - Análise de Resíduos Erica Castilho Rodrigues 27 de Setembro de 2016 2 3 O modelo de regressão linear é dado por 3 O modelo de regressão linear é dado por Y i = β
1 Modelos de Regressão Linear Simples - Análise de Resíduos Erica Castilho Rodrigues 27 de Setembro de 2016 2 3 O modelo de regressão linear é dado por 3 O modelo de regressão linear é dado por Y i = β
4 Mecanismo gerador dos dados, quebras estruturais e cointegração
 4 Mecanismo gerador dos dados, quebras estruturais e cointegração 4.1. Mecanismo gerador de dados Eis alguns fatos destacados na literatura: A teoria da PPC prevê que a taxa de câmbio real deve convergir
4 Mecanismo gerador dos dados, quebras estruturais e cointegração 4.1. Mecanismo gerador de dados Eis alguns fatos destacados na literatura: A teoria da PPC prevê que a taxa de câmbio real deve convergir
Modelo de Regressão Múltipla
 Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Modelo de Regressão Múltipla Modelo de Regressão Linear Simples Última aula: Y = α + βx + i i ε i Y é a variável resposta; X é a variável independente; ε representa o erro. 2 Modelo Clássico de Regressão
Markov Switching Models. Profa. Airlane Alencar. Depto de Estatística - IME-USP. lane. Ref: Kim e Nelson (1999) e Hamilton (1990)
 Markov Switching Models Profa. Airlane Alencar Depto de Estatística - IME-USP www.ime.usp.br/ lane Ref: Kim e Nelson (1999) e Hamilton (1990) 1 Objetivo Mudança nos parâmetros de um modelo de regressão
Markov Switching Models Profa. Airlane Alencar Depto de Estatística - IME-USP www.ime.usp.br/ lane Ref: Kim e Nelson (1999) e Hamilton (1990) 1 Objetivo Mudança nos parâmetros de um modelo de regressão
Notas de Aulas Econometria I ** Eduardo P. Ribeiro, 2010 PARTE II
 Notas de Aulas Econometria I ** Eduardo P Ribeiro, 00 PARTE II Autocorrelação Autocorrelação: violação da hipótese: E [ε t ε t-s ] = 0, para s > 0, como por exemplo, ε t = ε t- + υ t, onde υ t é ruído
Notas de Aulas Econometria I ** Eduardo P Ribeiro, 00 PARTE II Autocorrelação Autocorrelação: violação da hipótese: E [ε t ε t-s ] = 0, para s > 0, como por exemplo, ε t = ε t- + υ t, onde υ t é ruído
AULA 11 Heteroscedasticidade
 1 AULA 11 Heteroscedasticidade Ernesto F. L. Amaral 30 de julho de 2012 Análise de Regressão Linear (MQ 2012) www.ernestoamaral.com/mq12reg.html Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
1 AULA 11 Heteroscedasticidade Ernesto F. L. Amaral 30 de julho de 2012 Análise de Regressão Linear (MQ 2012) www.ernestoamaral.com/mq12reg.html Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
3 Filtro de Kalman Discreto
 3 Filtro de Kalman Discreto As medidas realizadas por sensores estão sujeitas a erros, como pode ser visto no Capítulo 2. Os filtros são aplicados aos sinais medidos pelos sensores para reduzir os erros,
3 Filtro de Kalman Discreto As medidas realizadas por sensores estão sujeitas a erros, como pode ser visto no Capítulo 2. Os filtros são aplicados aos sinais medidos pelos sensores para reduzir os erros,
AULAS 25 E 26 Heteroscedasticidade
 1 AULAS 25 E 26 Heteroscedasticidade Ernesto F. L. Amaral 10 e 15 de junho de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
1 AULAS 25 E 26 Heteroscedasticidade Ernesto F. L. Amaral 10 e 15 de junho de 2010 Métodos Quantitativos de Avaliação de Políticas Públicas (DCP 030D) Fonte: Wooldridge, Jeffrey M. Introdução à econometria:
4. Modelagem Proposta
 Modelagem roposta 4. Modelagem roposta Uma das conseqüências da privatização dos mercados de energia foi a maior ênfase que passou a ser dada à previsão da curva de carga, isto é, o valor da série de cargas
Modelagem roposta 4. Modelagem roposta Uma das conseqüências da privatização dos mercados de energia foi a maior ênfase que passou a ser dada à previsão da curva de carga, isto é, o valor da série de cargas
5 Avaliação dos estimadores propostos
 5 valiação dos estimadores propostos Este capítulo apresenta as medidas estatísticas usuais para avaliar a qualidade de estimadores e as expressões utilizadas para a estimação destas medidas, a partir
5 valiação dos estimadores propostos Este capítulo apresenta as medidas estatísticas usuais para avaliar a qualidade de estimadores e as expressões utilizadas para a estimação destas medidas, a partir
REGRESSÃO E CORRELAÇÃO
 REGRESSÃO E CORRELAÇÃO A interpretação moderna da regressão A análise de regressão diz respeito ao estudo da dependência de uma variável, a variável dependente, em relação a uma ou mais variáveis explanatórias,
REGRESSÃO E CORRELAÇÃO A interpretação moderna da regressão A análise de regressão diz respeito ao estudo da dependência de uma variável, a variável dependente, em relação a uma ou mais variáveis explanatórias,
(iv) Ausência de correlação serial nos erros, dados dois valores quaisquer de X, X i e X j (i j), a correlação entre ε i e ε j é zero,, /,
 4 Metodologia O método de estimação por mínimos quadrados está fundamentado em algumas premissas, que são necessárias para realizar inferências estatísticas sobre a variável dependente Y. As principais
4 Metodologia O método de estimação por mínimos quadrados está fundamentado em algumas premissas, que são necessárias para realizar inferências estatísticas sobre a variável dependente Y. As principais
CC-226 Aula 07 - Estimação de Parâmetros
 CC-226 Aula 07 - Estimação de Parâmetros Carlos Henrique Q. Forster - Instituto Tecnológico de Aeronáutica 2008 Estimação de Parâmetros Para construir o classificador bayesiano, assumimos as distribuições
CC-226 Aula 07 - Estimação de Parâmetros Carlos Henrique Q. Forster - Instituto Tecnológico de Aeronáutica 2008 Estimação de Parâmetros Para construir o classificador bayesiano, assumimos as distribuições
Disciplina de Modelos Lineares
 Disciplina de Modelos Lineares 2012-2 Seleção de Variáveis Professora Ariane Ferreira Em modelos de regressão múltipla é necessário determinar um subconjunto de variáveis independentes que melhor explique
Disciplina de Modelos Lineares 2012-2 Seleção de Variáveis Professora Ariane Ferreira Em modelos de regressão múltipla é necessário determinar um subconjunto de variáveis independentes que melhor explique
RESUMO DO CAPÍTULO 3 DO LIVRO DE WOOLDRIDGE ANÁLISE DE REGRESSÃO MÚLTIPLA: ESTIMAÇÃO
 RESUMO DO CAPÍTULO 3 DO LIVRO DE WOOLDRIDGE ANÁLISE DE REGRESSÃO MÚLTIPLA: ESTIMAÇÃO Regressão simples: desvantagem de apenas uma variável independente explicando y mantendo ceteris paribus as demais (ou
RESUMO DO CAPÍTULO 3 DO LIVRO DE WOOLDRIDGE ANÁLISE DE REGRESSÃO MÚLTIPLA: ESTIMAÇÃO Regressão simples: desvantagem de apenas uma variável independente explicando y mantendo ceteris paribus as demais (ou
Análise de Séries Temporais. Modelos estacionários Processos puramente aleatórios, AR(p), MA(q) ARIMA(p,q)
 UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Análise de Séries Temporais. Modelos estacionários Processos puramente aleatórios, AR(p), MA(q) ARIMA(p,q)
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Análise de Séries Temporais. Modelos estacionários Processos puramente aleatórios, AR(p), MA(q) ARIMA(p,q)
Mais Informações sobre Itens do Relatório
 Mais Informações sobre Itens do Relatório Amostra Tabela contendo os valores amostrados a serem utilizados pelo método comparativo (estatística descritiva ou inferencial) Modelos Pesquisados Tabela contendo
Mais Informações sobre Itens do Relatório Amostra Tabela contendo os valores amostrados a serem utilizados pelo método comparativo (estatística descritiva ou inferencial) Modelos Pesquisados Tabela contendo
3 Aprendizado por reforço
 3 Aprendizado por reforço Aprendizado por reforço é um ramo estudado em estatística, psicologia, neurociência e ciência da computação. Atraiu o interesse de pesquisadores ligados a aprendizado de máquina
3 Aprendizado por reforço Aprendizado por reforço é um ramo estudado em estatística, psicologia, neurociência e ciência da computação. Atraiu o interesse de pesquisadores ligados a aprendizado de máquina
Econometria. Econometria ( ) O modelo de regressão linear múltipla. O modelo de regressão linear múltipla. Aula 2-26/8/2010
 Aula - 6/8/010 Econometria Econometria 1. Hipóteses do Modelo de RLM O modelo de regressão linear múltipla Estudar a relação entre uma variável dependente e uma ou mais variáveis independentes. Forma genérica:
Aula - 6/8/010 Econometria Econometria 1. Hipóteses do Modelo de RLM O modelo de regressão linear múltipla Estudar a relação entre uma variável dependente e uma ou mais variáveis independentes. Forma genérica:
O uso de Máquina de Suporte Vetorial para Regressão (SVR) na Estimação da Estrutura a Termo da Taxa de Juros do Brasil 12
 1 Introdução No Brasil, o grande aumento na adesão a planos de previdência privada nos últimos tempos implicou em maiores preocupações de bancos e seguradoras em fazer investimentos visando garantir o
1 Introdução No Brasil, o grande aumento na adesão a planos de previdência privada nos últimos tempos implicou em maiores preocupações de bancos e seguradoras em fazer investimentos visando garantir o
Correlação e Regressão
 Correlação e Regressão Vamos começar com um exemplo: Temos abaixo uma amostra do tempo de serviço de 10 funcionários de uma companhia de seguros e o número de clientes que cada um possui. Será que existe
Correlação e Regressão Vamos começar com um exemplo: Temos abaixo uma amostra do tempo de serviço de 10 funcionários de uma companhia de seguros e o número de clientes que cada um possui. Será que existe
Correlação Serial e Heterocedasticidade em Regressões de Séries Temporais. Wooldridge, Cap. 12
 Correlação Serial e Heterocedasticidade em Regressões de Séries Temporais Wooldridge, Cap. 1 Porto Alegre, 11 de novembro de 010 1 CORRELAÇÃO SERIAL Ocorrência Conseqüência Análise gráfica Autocorrelação
Correlação Serial e Heterocedasticidade em Regressões de Séries Temporais Wooldridge, Cap. 1 Porto Alegre, 11 de novembro de 010 1 CORRELAÇÃO SERIAL Ocorrência Conseqüência Análise gráfica Autocorrelação
Tópicos de Estatística Espacial Geoestatística
 Tópicos de Estatística Espacial Geoestatística Anderson Castro Soares de Oliveira Geoestatística A geoestatística é uma análise espacial que considera que a variável em estudo se distribui continuamente
Tópicos de Estatística Espacial Geoestatística Anderson Castro Soares de Oliveira Geoestatística A geoestatística é uma análise espacial que considera que a variável em estudo se distribui continuamente
Multicolinariedade e Autocorrelação
 Multicolinariedade e Autocorrelação Introdução Em regressão múltipla, se não existe relação linear entre as variáveis preditoras, as variáveis são ortogonais. Na maioria das aplicações os regressores não
Multicolinariedade e Autocorrelação Introdução Em regressão múltipla, se não existe relação linear entre as variáveis preditoras, as variáveis são ortogonais. Na maioria das aplicações os regressores não
AULAS 14 E 15 Modelo de regressão simples
 1 AULAS 14 E 15 Modelo de regressão simples Ernesto F. L. Amaral 18 e 23 de outubro de 2012 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem
1 AULAS 14 E 15 Modelo de regressão simples Ernesto F. L. Amaral 18 e 23 de outubro de 2012 Avaliação de Políticas Públicas (DCP 046) Fonte: Wooldridge, Jeffrey M. Introdução à econometria: uma abordagem
7 Conclusões e desenvolvimentos futuros
 7 Conclusões e desenvolvimentos futuros 7.1 Conclusões Este trabalho apresentou novas soluções para a determinação da posição de terminais de comunicações móveis com base em medidas de ToA. Nos métodos
7 Conclusões e desenvolvimentos futuros 7.1 Conclusões Este trabalho apresentou novas soluções para a determinação da posição de terminais de comunicações móveis com base em medidas de ToA. Nos métodos
Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação
 Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação Francisco A. Rodrigues Departamento de Matemática Aplicada e Estatística - SME Objetivo Dada M classes ω 1, ω 2,..., ω M e um
Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação Francisco A. Rodrigues Departamento de Matemática Aplicada e Estatística - SME Objetivo Dada M classes ω 1, ω 2,..., ω M e um
AULA 11 - Normalidade e Inferência em Regressão Múltipla - Parte 1
 AULA 11 - Normalidade e Inferência em Regressão Múltipla - Parte 1 Susan Schommer Econometria I - IE/UFRJ Distribuições amostrais dos estimadores MQO Nas aulas passadas derivamos o valor esperado e variância
AULA 11 - Normalidade e Inferência em Regressão Múltipla - Parte 1 Susan Schommer Econometria I - IE/UFRJ Distribuições amostrais dos estimadores MQO Nas aulas passadas derivamos o valor esperado e variância
Metodologia de Box-Jenkins. Metodologia de Box-Jenkins. Metodologia de Box-Jenkins
 Programa de Pós-graduação em Engenharia de Produção Análise de séries temporais: Modelos de Box-Jenkins Profa. Dra. Liane Werner Metodologia de Box-Jenkins Para os modelos de decomposição e os modelos
Programa de Pós-graduação em Engenharia de Produção Análise de séries temporais: Modelos de Box-Jenkins Profa. Dra. Liane Werner Metodologia de Box-Jenkins Para os modelos de decomposição e os modelos
Séries Temporais e Modelos Dinâmicos. Econometria. Marcelo C. Medeiros. Aula 12
 em Econometria Departamento de Economia Pontifícia Universidade Católica do Rio de Janeiro Aula 12 Regressão com Variáveis Não-Estacionárias Considere três processos estocásticos definidos pelas seguintes
em Econometria Departamento de Economia Pontifícia Universidade Católica do Rio de Janeiro Aula 12 Regressão com Variáveis Não-Estacionárias Considere três processos estocásticos definidos pelas seguintes
COKRIGAGEM. Aplicação da cokrigagem
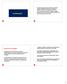 COKRIGAGEM Procedimento geoestatístico segundo o qual diversas variáveis regionalizadas podem ser estimadas em conjunto, com base na correlação espacial entre si. É uma extensão multivariada do método
COKRIGAGEM Procedimento geoestatístico segundo o qual diversas variáveis regionalizadas podem ser estimadas em conjunto, com base na correlação espacial entre si. É uma extensão multivariada do método
Carga Horária: 80 horas (correspondem a aulas e atividades extra-classe)
 Curso: Economia Disciplina: ECONOMETRIA Turma 4ECO Carga Horária: 80 horas (correspondem a aulas e atividades extra-classe) Período Letivo: 2014/1 Professor: Hedibert Freitas Lopes (www.hedibert.org) OBJETIVO:
Curso: Economia Disciplina: ECONOMETRIA Turma 4ECO Carga Horária: 80 horas (correspondem a aulas e atividades extra-classe) Período Letivo: 2014/1 Professor: Hedibert Freitas Lopes (www.hedibert.org) OBJETIVO:
i j i i Y X X X i j i i i
 Mario de Andrade Lira Junior lira.pro.br\wordpress lira.pro.br\wordpress Diferença Regressão - equação ligando duas ou mais variáveis Correlação medida do grau de ligação entre duas variáveis Usos Regressão
Mario de Andrade Lira Junior lira.pro.br\wordpress lira.pro.br\wordpress Diferença Regressão - equação ligando duas ou mais variáveis Correlação medida do grau de ligação entre duas variáveis Usos Regressão
Aula 6. Modelo de Correção de Erros Vetorial. Wilson Correa. August 23, Wilson Correa August 23, / 16
 Aula 6 Modelo de Correção de Erros Vetorial Wilson Correa August 23, 2017 Wilson Correa August 23, 2017 1 / 16 Equações Simultâneas e Modelos VAR/VEC Frequentemente o interesse em economia é centrado na
Aula 6 Modelo de Correção de Erros Vetorial Wilson Correa August 23, 2017 Wilson Correa August 23, 2017 1 / 16 Equações Simultâneas e Modelos VAR/VEC Frequentemente o interesse em economia é centrado na
Análise de regressão linear simples. Diagrama de dispersão
 Introdução Análise de regressão linear simples Departamento de Matemática Escola Superior de Tecnologia de Viseu A análise de regressão estuda o relacionamento entre uma variável chamada a variável dependente
Introdução Análise de regressão linear simples Departamento de Matemática Escola Superior de Tecnologia de Viseu A análise de regressão estuda o relacionamento entre uma variável chamada a variável dependente
ANÁLISE DE SÉRIES TEMPORAIS
 ANÁLISE DE SÉRIES TEMPORAIS Ralph S. Silva http://www.im.ufrj.br/ralph/seriestemporais.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Estimação
ANÁLISE DE SÉRIES TEMPORAIS Ralph S. Silva http://www.im.ufrj.br/ralph/seriestemporais.html Departamento de Métodos Estatísticos Instituto de Matemática Universidade Federal do Rio de Janeiro Estimação
EAE0325 Econometria II. Professora: Fabiana Fontes Rocha. Gabarito Primeira Lista Teórica de Exercícios
 EAE0325 Econometria II Professora: Fabiana Fontes Rocha Gabarito Primeira Lista Teórica de Exercícios Bloco 1 Assinalar se as afirmativas a seguir são verdadeiras V) ou falsas F) Exercício 1 Sobre o modelo
EAE0325 Econometria II Professora: Fabiana Fontes Rocha Gabarito Primeira Lista Teórica de Exercícios Bloco 1 Assinalar se as afirmativas a seguir são verdadeiras V) ou falsas F) Exercício 1 Sobre o modelo
Prova de Estatística
 Prova de Estatística 1. Para um número-índice ser considerado um índice ideal, ele precisa atender duas propriedades: reversão no tempo e o critério da decomposição das causas. Desta forma, é correto afirmar
Prova de Estatística 1. Para um número-índice ser considerado um índice ideal, ele precisa atender duas propriedades: reversão no tempo e o critério da decomposição das causas. Desta forma, é correto afirmar
Estimação e Testes de Hipóteses
 Estimação e Testes de Hipóteses 1 Estatísticas sticas e parâmetros Valores calculados por expressões matemáticas que resumem dados relativos a uma característica mensurável: Parâmetros: medidas numéricas
Estimação e Testes de Hipóteses 1 Estatísticas sticas e parâmetros Valores calculados por expressões matemáticas que resumem dados relativos a uma característica mensurável: Parâmetros: medidas numéricas
INFERÊNCIA EM MODELOS LINEARES GENERALIZADOS ANÁLISE DE DEVIANCE
 INFERÊNCIA EM MODELOS LINEARES GENERALIZADOS ANÁLISE DE DEVIANCE A análise de deviance é uma generalização, para modelos lineares generalizados, da análise de variância. No caso de modelos lineares, utiliza-se
INFERÊNCIA EM MODELOS LINEARES GENERALIZADOS ANÁLISE DE DEVIANCE A análise de deviance é uma generalização, para modelos lineares generalizados, da análise de variância. No caso de modelos lineares, utiliza-se
Modulo I. Séries Temporais: ARIMA
 UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS FACULDADE DE ESTATÍSTICA Modulo I Séries Temporais: ARIMA Curso: Bacharelado em Estatística Disciplina: Estatística Aplicada Nome: Verena
UNIVERSIDADE FEDERAL DO PARÁ INSTITUTO DE CIÊNCIAS EXATAS E NATURAIS FACULDADE DE ESTATÍSTICA Modulo I Séries Temporais: ARIMA Curso: Bacharelado em Estatística Disciplina: Estatística Aplicada Nome: Verena
Testes de Hipóteses. Curso de Introdução à Econometria usando o R. Vítor Wilher. 1 de Dezembro de analisemacro.com.br
 Testes de Hipóteses Curso de Introdução à Econometria usando o R Vítor Wilher analisemacro.com.br 1 de Dezembro de 2016 Vítor Wilher (analisemacro.com.br) Testes de Hipóteses 1 de Dezembro de 2016 1 /
Testes de Hipóteses Curso de Introdução à Econometria usando o R Vítor Wilher analisemacro.com.br 1 de Dezembro de 2016 Vítor Wilher (analisemacro.com.br) Testes de Hipóteses 1 de Dezembro de 2016 1 /
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Intervalo Amostragem e inferência estatística População: consiste na totalidade das observações em que estamos interessados. Nº de observações na população é denominado tamanho=n.
Cap. 4 - Estimação por Intervalo Amostragem e inferência estatística População: consiste na totalidade das observações em que estamos interessados. Nº de observações na população é denominado tamanho=n.
5 Filtro de Kalman Aplicado ao Modelo de Schwartz e Smith (2000)
 5 Filtro de Kalman Aplicado ao Modelo de Schwartz e Smith (2000) A primeira parte deste capítulo, referente à passagem dos modelos estocásticos para as equações do Filtro de Kalman, já foi previamente
5 Filtro de Kalman Aplicado ao Modelo de Schwartz e Smith (2000) A primeira parte deste capítulo, referente à passagem dos modelos estocásticos para as equações do Filtro de Kalman, já foi previamente
)XQGDPHQWRVGHSUREDELOLGDGHHHVWDWtVWLFD
 )XQGDPHQWRVGHUREDELOLGDGHHHVWDWtVWLFD,QWURGXomR A história da estatística pode ser dividida em três fases. De acordo com PEANHA (00), a estatística inicialmente não mantinha nenhuma relação com a probabilidade,
)XQGDPHQWRVGHUREDELOLGDGHHHVWDWtVWLFD,QWURGXomR A história da estatística pode ser dividida em três fases. De acordo com PEANHA (00), a estatística inicialmente não mantinha nenhuma relação com a probabilidade,
Capítulo 9 - Regressão Linear Simples (RLS): Notas breves
 Capítulo 9 - Regressão Linear Simples RLS: Notas breves Regressão Linear Simples Estrutura formal do modelo de Regressão Linear Simples RLS: Y i = β 0 + β 1 x i + ε i, 1 onde Y i : variável resposta ou
Capítulo 9 - Regressão Linear Simples RLS: Notas breves Regressão Linear Simples Estrutura formal do modelo de Regressão Linear Simples RLS: Y i = β 0 + β 1 x i + ε i, 1 onde Y i : variável resposta ou
Define-se o regressor,ϕ,como. e o vector de parâmetros a estimar, θ,como. O modelo escreve-se:
 22 Mínimos Quadrados - Notação matricial Se quisermos resolver o problema de estimação para um número arbitrário de parâmetros temos de usar a notação matricial. Define-se o regressor,,como [ ] e o vector
22 Mínimos Quadrados - Notação matricial Se quisermos resolver o problema de estimação para um número arbitrário de parâmetros temos de usar a notação matricial. Define-se o regressor,,como [ ] e o vector
FICHA DE DISCIPLINA/PROGRAMA
 Programa de Pós-Graduação em Economia Mestrado/Doutorado Av. João Naves de Ávila, nº 2121 Campus Stª Mônica Bloco J. CEP 38.400-902 Uberlândia/MG. Telefax: (034) 3239-4315 E-Mail: ppge@ufu.br FICHA DE
Programa de Pós-Graduação em Economia Mestrado/Doutorado Av. João Naves de Ávila, nº 2121 Campus Stª Mônica Bloco J. CEP 38.400-902 Uberlândia/MG. Telefax: (034) 3239-4315 E-Mail: ppge@ufu.br FICHA DE
4 Informação auxiliar
 89 4 Informação auxiliar para Segundo D Orazio et al., 2006, p. 11, o conjunto de modelos identificáveis A B é pequeno e pode ser inapropriado para o fenômeno em estudo. Para resolver esse problema, conforme
89 4 Informação auxiliar para Segundo D Orazio et al., 2006, p. 11, o conjunto de modelos identificáveis A B é pequeno e pode ser inapropriado para o fenômeno em estudo. Para resolver esse problema, conforme
3 Modelo estocástico para os fatores de risco
 Modelo estocástico para os fatores de risco 35 3 Modelo estocástico para os fatores de risco 3.1. Conceitos básicos Um dos principais problemas de um ALM é a modelagem da incerteza sobre os valores futuros
Modelo estocástico para os fatores de risco 35 3 Modelo estocástico para os fatores de risco 3.1. Conceitos básicos Um dos principais problemas de um ALM é a modelagem da incerteza sobre os valores futuros
Utilização de modelos marginais na análise de dados longitudinais irregulares em relação ao tempo
 Utilização de modelos marginais na análise de dados longitudinais irregulares em relação ao tempo César Gonçalves de Lima 1 Michele Barbosa 2 Valdo Rodrigues Herling 3 1. Introdução Dados longitudinais
Utilização de modelos marginais na análise de dados longitudinais irregulares em relação ao tempo César Gonçalves de Lima 1 Michele Barbosa 2 Valdo Rodrigues Herling 3 1. Introdução Dados longitudinais
3 Dados e metodologia
 3 Dados e metodologia 3.1 Apresentação de Dados Para a realização dessa pesquisa foram utilizados os dados da série histórica dos preços da soja (em grão) do Estado do Paraná, obtidos da base de dados
3 Dados e metodologia 3.1 Apresentação de Dados Para a realização dessa pesquisa foram utilizados os dados da série histórica dos preços da soja (em grão) do Estado do Paraná, obtidos da base de dados
Redes Neurais. A Rede RBF. Redes RBF: Função de Base Radial. Prof. Paulo Martins Engel. Regressão não paramétrica. Redes RBF: Radial-Basis Functions
 Redes RBF: Função de Base Radial Redes Neurais A Rede RBF O LP é baseado em unidades que calculam uma função não-linear do produto escalar do vetor de entrada e um vetor de peso. A rede RBF pertence a
Redes RBF: Função de Base Radial Redes Neurais A Rede RBF O LP é baseado em unidades que calculam uma função não-linear do produto escalar do vetor de entrada e um vetor de peso. A rede RBF pertence a
PARTE 1 ANÁLISE DE REGRESSÃO COM DADOS DE CORTE TRANSVERSAL CAPÍTULO 2 O MODELO DE REGRESSÃO SIMPLES
 PARTE 1 ANÁLISE DE REGRESSÃO COM DADOS DE CORTE TRANSVERSAL CAPÍTULO 2 O MODELO DE REGRESSÃO SIMPLES 2.1 DEFINIÇÃO DO MODELO DE REGRESSÃO SIMPLES Duas variáveis: y e x Análise explicar y em termos de x
PARTE 1 ANÁLISE DE REGRESSÃO COM DADOS DE CORTE TRANSVERSAL CAPÍTULO 2 O MODELO DE REGRESSÃO SIMPLES 2.1 DEFINIÇÃO DO MODELO DE REGRESSÃO SIMPLES Duas variáveis: y e x Análise explicar y em termos de x
Métodos Numéricos Interpolação / Aproximação. Renato S. Silva, Regina C. Almeida
 Métodos Numéricos Interpolação / Aproximação Renato S. Silva, Regina C. Almeida Interpolação / Aproximação situação: uma fábrica despeja dejetos no leito de um rio; objetivo: determinar a quantidade de
Métodos Numéricos Interpolação / Aproximação Renato S. Silva, Regina C. Almeida Interpolação / Aproximação situação: uma fábrica despeja dejetos no leito de um rio; objetivo: determinar a quantidade de
Coeficiente de determinação R 2 no modelo de regressão linear normal
 Coeficiente de determinação R 2 no modelo de regressão linear normal Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Curitiba/PR, 81531 990, Brasil email: lucambio@ufpr.br
Coeficiente de determinação R 2 no modelo de regressão linear normal Fernando Lucambio Departamento de Estatística Universidade Federal do Paraná Curitiba/PR, 81531 990, Brasil email: lucambio@ufpr.br
Estimação de Variáveis Instrumentais e Mínimos Quadrados de Dois Estágios. Wooldridge, Cápítulo 15
 Estimação de Variáveis Instrumentais e Mínimos Quadrados de Dois Estágios Wooldridge, Cápítulo 5 Variáveis Instrumentais () 2 Variáveis Instrumentais Considere o seguinte modelo de regressão linear múltipla
Estimação de Variáveis Instrumentais e Mínimos Quadrados de Dois Estágios Wooldridge, Cápítulo 5 Variáveis Instrumentais () 2 Variáveis Instrumentais Considere o seguinte modelo de regressão linear múltipla
Econometria II. Equações simultâneas
 Eco monitoria Leandro Anazawa Econometria II Este não é um resumo extensivo. O intuito deste resumo é de servir como guia para os seus estudos. Procure desenvolver as contas e passos apresentados em sala
Eco monitoria Leandro Anazawa Econometria II Este não é um resumo extensivo. O intuito deste resumo é de servir como guia para os seus estudos. Procure desenvolver as contas e passos apresentados em sala
CÁLCULO NUMÉRICO. Profa. Dra. Yara de Souza Tadano
 CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 04/2014 Zeros reais de funções Parte 1 Objetivo Determinar valores aproximados para as soluções (raízes) de equações da
CÁLCULO NUMÉRICO Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 7 04/2014 Zeros reais de funções Parte 1 Objetivo Determinar valores aproximados para as soluções (raízes) de equações da
Métodos Numéricos e Estatísticos Parte II-Métodos Estatísticos
 Métodos Numéricos e Estatísticos Parte II-Métodos Estatísticos Lic. Eng. Biomédica e Bioengenharia-2009/2010 Modelos de regressão É usual estarmos interessados em estabelecer uma relação entre uma variável
Métodos Numéricos e Estatísticos Parte II-Métodos Estatísticos Lic. Eng. Biomédica e Bioengenharia-2009/2010 Modelos de regressão É usual estarmos interessados em estabelecer uma relação entre uma variável
9 Correlação e Regressão. 9-1 Aspectos Gerais 9-2 Correlação 9-3 Regressão 9-4 Intervalos de Variação e Predição 9-5 Regressão Múltipla
 9 Correlação e Regressão 9-1 Aspectos Gerais 9-2 Correlação 9-3 Regressão 9-4 Intervalos de Variação e Predição 9-5 Regressão Múltipla 1 9-1 Aspectos Gerais Dados Emparelhados há uma relação? se há, qual
9 Correlação e Regressão 9-1 Aspectos Gerais 9-2 Correlação 9-3 Regressão 9-4 Intervalos de Variação e Predição 9-5 Regressão Múltipla 1 9-1 Aspectos Gerais Dados Emparelhados há uma relação? se há, qual
Análise Multivariada Aplicada à Contabilidade
 Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
Mestrado e Doutorado em Controladoria e Contabilidade Análise Multivariada Aplicada à Contabilidade Prof. Dr. Marcelo Botelho da Costa Moraes www.marcelobotelho.com mbotelho@usp.br Turma: 2º / 2016 1 Agenda
6 Geração de Cenários
 6 Geração de Cenários O planejamento do setor elétrico para operações hidrotérmicas de longo prazo de cada subsistema, atualmente, está fundamentado na avaliação dos resultados da simulação de diversos
6 Geração de Cenários O planejamento do setor elétrico para operações hidrotérmicas de longo prazo de cada subsistema, atualmente, está fundamentado na avaliação dos resultados da simulação de diversos
Comparação entre intervalos de confiança calculados com métodos bootstrap e intervalos assintóticos
 Comparação entre intervalos de confiança calculados com métodos strap e intervalos assintóticos Selene Loibel Depto. de Estatística, Matemática Aplicada e Computação, IGCE, UNESP, Rio Claro, SP E-mail:sloibel@rc.unesp.br,
Comparação entre intervalos de confiança calculados com métodos strap e intervalos assintóticos Selene Loibel Depto. de Estatística, Matemática Aplicada e Computação, IGCE, UNESP, Rio Claro, SP E-mail:sloibel@rc.unesp.br,
