PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO CDM MODIFICADO
|
|
|
- Maria Júlia Barateiro Belmonte
- 5 Há anos
- Visualizações:
Transcrição
1 DISSERTAÇÃO DE MESTRADO PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO CDM MODIFICADO Por, ALEXANDRE GONÇALVES DE SOUZA Brasília, 5 de Fevereiro de 08 UNIVERSIDADE DE BRASILIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECANICA UNIVERSIDADE DE BRASILIA
2 Faculdade de Tecnologia Departamento de Engenharia Mecânica DISSERTAÇÃO DE MESTRADO PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO CDM MODIFICADO POR, ALEXANDRE GONÇALVES DE SOUZA Dissertação de Mestrado submetida ao Departamento de Engenharia Mecânica da Faculdade de Tecnologia da Universidade de Brasília como requisito parcial para obtenção do grau de Mestre em Ciências Mecânicas. Banca Examinadora Prof. Lucival Malcher, PhD, UnB/ ENM (Orientador) Prof. Jorge Luiz de Almeida Ferreira UnB/ ENM (Examinador Interno) Prof. Luis Augusto Veloso, UnB/ ENM (Examinador Externo) Prof. Fábio Comes de Castro, UnB/ ENM (Suplente) Brasília, 5 de fevereiro de 08
3 FICHA CATALOGRÁFICA SOUZA, ALEXANDRE GONÇALVES DE PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO CDM MODIFICADO 04p., 0 x 97 mm (ENM/FT/UnB, Mestre, Ciências Mecânicas, 08) Dissertação de Mestrado Universidade de Brasília. Faculdade de Tecnologia. Departamento de Engenharia Mecânica.. Fadiga. Plasticidade. Mecânica do Dano Contínuo 4. Denominador de dano I. ENM/FT/UnB II. Título (ENM.DM-76/08) REFERÊNCIA BIBLIOGRÁFICA SOUZA, A. G., (08), Previsão de vida à fadiga através de modelo CDM modificado. Dissertação de mestrado, Publicação ENM.DM-76/08, Departamento de Engenharia Mecânica, Universidade de Brasília, DF, 04p. CESSÃO DE DIREITOS AUTOR: Alexandre Gonçalves de Souza. TÍTULO: Previsão de vida à fadiga através de modelo CDM modificado. GRAU: Mestre ANO: 08 É concedida à Universidade de Brasília permissão para reproduzir cópias desta dissertação de mestrado e para emprestar ou vender tais cópias somente para propósitos acadêmicos e científicos. O autor reserva outros direitos de publicação e nenhuma parte dessa dissertação de mestrado pode ser reproduzida sem autorização por escrito do autor. Alexandre Gonçalves de Souza Correio Eletrônico: alexandregz@hotmail.com
4 Dedico esta dissertação ao meu querido filho Caio Miguel e a minha eterna e amada companheira, Bárbara Saviani. Alexandre Gonçalves de Souza
5 Agradecimentos Agradeço aos Professores Jorge Luiz e José Alexander pelo convívio e ótima oportunidade de aprimorar ainda na graduação, nossos conhecimentos sobre fadiga através de trabalhos desenvolvidos no Laboratório de Ensaios Mecânicos. Essas experiências gratificantes, aliadas ao entusiasmo transmitido pelo querido amigo Marcus Sá, nos motivaram a trilhar o caminho rumo ao Mestrado em Ciências Mecânicas. Agradeço também ao meu orientador, o Professor Lucival Malcher, pela amizade, orientação acadêmica, disponibilidade em atender a dúvidas e inclusive pelo suporte material, ao nos fornecer ferramentas de trabalho que permitiram o pleno desenvolvimento desta dissertação. Agradeço a minha mãe, Fátima Cristina, e minha avó, Ermelinda Cândido, que tenho como exemplo de mulheres aguerridas e pelo papel maravilhoso que tem desempenhado em minha vida, sempre com muito amor e dedicação. Agradeço imensamente a minha amada esposa, Bárbara Letícia, e ao meu filho querido, Caio Miguel, pelo amor incondicional que sempre nos impulsiona a superar de maneira positiva os desafios apresentados pela vida. Muito obrigado também por compreenderem a grandeza deste momento em que tive que me manter por diversas vezes ausente para me dedicar ao Mestrado. Por fim, agradeço imensamente a Deus pelo dom da vida! Alexandre Gonçalves de Souza
6 RESUMO Neste trabalho, busca-se comparar os resultados experimentais apresentados por Jiang (007) com os obtidos a partir dos modelos de Lemaitre e CDM modificado, ambos com a lei de evolução de Chaboche para o endurecimento cinemático. Para tanto, elaborou-se modelos matemáticos e em seguida implementou-se em linguagem FORTRAN os modelos numéricos. Na solução das equações constitutivas, levou-se em consideração as propriedades mecânicas do aço S460N, trajetórias com carregamentos multiaxiais proporcionais e não-proporcionais, a lei de Chaboche com três termos e a discretização implícita de Euler. Com base nos dados aferidos foi possível calibrar os parâmetros de tensão, de dano e os denominadores de dano para alta e baixa triaxialidade. Na sequência, realizou-se a análise comparativa das amplitudes de tensão, vida em fadiga e evolução do dano. Analisando os resultados, nota-se que de um modo geral o modelo CDM modificado previu a vida em fadiga do aço S460N com maior precisão que o modelo de Lemaitre para trajetórias axiais, cisalhantes, proporcionais e não proporcionais. ABSTRACT In this work, the experimental results presented by Jiang (007) are compared with those obtained from the Lemaitre and modified CDM models, both with the Chaboche evolution law for kinematic hardening. For that, mathematical models were elaborated and then the numerical models were implemented in FORTRAN language. In the solution of the constitutive equations, the mechanical properties of S460N steel, proportional and non-proportional multiaxial loading trajectories, Chaboche's three-law law, and Euler's implicit discretization were considered. Based on the data, it was possible to calibrate the voltage, damage and denominator parameters for high and low triaxiality. Then, the comparative analysis of tension amplitudes, life in fatigue and evolution of the damage was performed. Analyzing the results, it is noted that in general the modified CDM model predicted the fatigue life of S460N steel with greater precision than the Lemaitre model for axial, shear, proportional and non-proportional trajectories.
7 SUMÁRIO INTRODUÇÃO.... MOTIVAÇÃO.... OBJETIVOS ORGANIZAÇÃO DO TRABALHO... 4 ASPECTOS TEÓRICOS INTRODUÇÃO NATUREZA FÍSICA DO DANO POR FADIGA FADIGA MULTIAXIAL TEORIA DA PLASTICIDADE MODELOS DE PLASTICIDADE CÍCLICA PRAGER ARMSTRONG-FREDERICK CHABOCHE CRITÉRIO DE ESCOAMENTO DE MISES MECÂNICA DO DANO VARIÁVEL DE DANO UNIDIMENSIONAL TENSÃO EFETIVA E PRINCÍPIO DE EQUIVALÊNCIA DE DEFORMAÇÃO CRITÉRIO DE RUPTURA DANO ISOTRÓPICO TRIDIMENSIONAL LEIS DE EVOLUÇÃO DO DANO MODELO DE LEMAITRE COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE MODELO CDM MODIFICADO COM ENDURECIMENTO CINEMÁTICO... 7 MODELOS NUMÉRICOS.... INTRODUÇÃO.... MODELO DE VON MISES COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE.... MODELO DE LEMAITRE COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE MODELO CDM MODIFICADO COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE ESTRATÉGIA DE IDENTIFICAÇÃO DE PARÂMETROS INTRODUÇÃO CALIBRAÇÃO DOS PARÂMETROS DO MATERIAL CALIBRAÇÃO DOS PARÂMETROS DE TENSÃO CALIBRAÇÃO DO DANO CRÍTICO E DOS DENOMINADORES DE DANO RESULTADOS E DISCUSSÃO ANÁLISE DOS RESULTADOS CARREGAMENTOS VIDA EM FADIGA EVOLUÇÃO DO DANO CONCLUSÕES E TRABALHOS FUTUROS REFERÊNCIAS BIBLIOGRÁFICAS ANEXOS A. ALGORITMO DE IDENTIFICAÇÃO DOS PARÂMETROS ELASTOPLÁSTICOS B. ALGORITMO PARA O MODELO DE LEMAITRE COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE... 8 C. ALGORITMO PARA O MODELO CDM MODIFICADO COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE... 87
8 LISTA DE FIGURAS. Análise estrutural de um braço de suspensão inferior de um carro através do método de elementos finitos (Compass Automotive Groupe, 0)..... Deslizamento em metais dúcteis devido a carregamentos cíclicos (NDT Centro de Pesquisa) Formação de intrusões e extrusões, captado por microscópio eletrônico de varredura (MEV) (Ma & Laird, 989) Formação de PSBs em apenas alguns grãos. (Meyers & Chawla, 009) Estrias de fadiga em liga de alumínio 04-T6 visto em MEV (Meyers & Chawla, 009) Falha por fadiga de um parafuso de porca em razão de flexão unidirecional repetida. A falha começou na raiz da rosca em A, propagou-se ao longo da maior parte da seção transversal como evidenciado pelas marcas de praia em B, antes da fratura rápida final em C (Shigley, 005) Endurecimento isotrópico (KACHANOV, 97) Endurecimento cinemático (KACHANOV, 97) Resultados do modelo de Prager (Bari e Hassan, 000) Resultados do modelo de Prager para laço de histerese em tensão controlada com tensão média sobreposta (Bari e Hassan, 000)....0 Curvas de histerese para os modelos de endurecimento Redução da área efetiva da seção devido à formação de microtrincas ou microcavidades Dependência entre o denominador de dano e a razão de triaxialidade (Malcher, 0)..... Algoritmo de atualização das tensões e variáveis internas Algoritmo de calibração dos parâmetros do modelo constitutivo Comparação entre dados experimentais e valores obtidos com regressão Variação do dano com o denominador de dano, número de ciclos e amplitudes de deformação normal Variação do dano com o denominador de dano, número de ciclos e amplitudes de deformação cisalhante Históricos de carregamento impostos para o aço S460N (Jiang et al., 007) Comparação entre a vida observada experimentalmente e a vida calculada pelo modelo de Lemaitre com endurecimento cinemático de Chaboche, S 0. = 5., D c = Comparação entre a vida observada experimentalmente e a vida calculada pelo modelo de Lemaitre com endurecimento cinemático de Chaboche, S 0. = 0.8, D c = Comparação entre a vida observada experimentalmente e a vida calculada pelo modelo CDM modificado com endurecimento cinemático de Chaboche e S 0. = 5., S 0.00 = 86.67, D c = Comparação entre a vida observada experimentalmente e a vida calculada pelo modelo CDM modificado com endurecimento cinemático de Chaboche e S 0. = 0.8, S 0.00 = 60.00, D c = Comparação entre a vida observada experimentalmente e a vida calculada pelos modelos de Lemaitre (S 0. = 5.) e CDM modificado (S 0. = 5. e S 0.00 = 86.67), D c = 0,0, ambos com endurecimento cinemático de Chaboche Comparação entre a vida observada experimentalmente e a vida calculada pelos modelos de Lemaitre (S 0. = 0.8) e CDM modificado (S 0. = 0.8 e S 0.00 = 60.00), D c = 0,0, ambos com endurecimento cinemático de Chaboche... 7
9 5.8 Evolução do dano para o aço S460N para trajetórias axiais e modelo de dano de Lemaitre com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias cisalhantes e modelo de dano de Lemaitre com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias proporcionais e modelo de dano de Lemaitre com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias não proporcionais e modelo de dano de Lemaitre com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias axiais e modelo de dano CDM modificado com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias cisalhantes e modelo de dano CDM modificado com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias proporcionais e modelo de dano CDM modificado com endurecimento cinemático de Chaboche Evolução do dano para o aço S460N para trajetórias não proporcionais e modelo de dano CDM modificado com endurecimento cinemático de Chaboche
10 LISTA DE TABELAS. Modelo Matemático para o critério de Von Mises com endurecimento cinemático de Chaboche Variáveis de estado e forças termodinâmicas associadas Modelo Matemático para o modelo de Lemaitre com endurecimento cinemático de Chaboche Modelo Matemático para o modelo associativo modificado de Lemaitre com endurecimento cinemático de Chaboche Modelo Numérico - Algoritmo de atualização das tensões e variáveis internas para o modelo de Von Mises com endurecimento cinemático de Chaboche Algoritmo de resolução do sistema não linear para o modelo de Von Mises com endurecimento cinemático de Chaboche Modelo Numérico - Algoritmo de atualização das tensões e variáveis internas para o modelo elastoplástico de Lemaitre com endurecimento cinemático de Chaboche Algoritmo de resolução do sistema não linear para o modelo elastoplástico de Lemaitre com endurecimento cinemático de Chaboche Modelo Numérico - Algoritmo de atualização das tensões e variáveis internas para o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche Algoritmo de resolução do sistema não linear para o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche Parâmetros de Ramberg-Osgood, módulo de elasticidade e coeficiente de Poisson para o aço S460N (Jiang et al., 007) Resultados da calibração por amplitude para o modelo de Chaboche e parâmetros da curva de Ramberg-Osgood obtidos da literatura para o aço S460N Ensaios de fadiga conduzidos utilizando espécimes cilíndricos (Jiang et al., 007) Relação de valores obtidos para o dano a partir da variação do denominador de dano, número de ciclos e amplitude de deformação normal Relação de valores obtidos para o dano a partir da variação do denominador de dano, número de ciclos e amplitude de deformação cisalhante (continuação) Denominadores de dano obtidos a partir de simulações com tensões normais e utilizados na previsão de vida em fadiga com os modelos de Lemaitre e CDM modificado Denominadores de dano obtidos a partir de simulações com tensões cisalhantes e utilizados na previsão de vida em fadiga com o modelo CDM modificado Amplitudes de deformação impostas com S 0. = 5., vida experimental e vida calculada obtidas para o aço S460N Amplitudes de deformação impostas com S 0. = 0.8, vida experimental e vida calculada obtidas para o aço S460N Amplitudes de deformação impostas com S 0. = 5. e S 0.00 = 86.67, vida experimental e vida calculada obtidas para o aço S460N Amplitudes de deformação impostas com S 0. = 0.8 e S 0.00 = 60.00, vida experimental e vida calculada obtidas para o aço S460N... 68
11 LISTA DE SÍMBOLOS β β n+ β i n Tensor das tensões cinemáticas Tensão de endurecimento cinemático no pseudo-tempo t n+ Termo i da tensão de endurecimento cinemático no pseudo-tempo t n i β n+ Termo i da tensão de endurecimento cinemático no pseudo-tempo t n+ β Lei de evolução para o tensor das tensões cinemáticas β i Termo i da taxa de evolução do tensor das tensões cinemáticas Γ Razão de triaxialidade γ Taxa de evolução do multiplicador plástico γ Incremento do multiplicador plástico Δε p Incremento de deformação plástica ε p Incremento de deformação plástica equivalente E Módulo de elasticidade ε e Deformação elástica e Tensor das deformações elásticas no pseudo-tempo t n+ ε n+ e trial ε n+ Tensor das deformações elásticas tentativa no pseudo-tempo t n+ p ε Taxa de evolução da deformação plástica p ε n Deformação plástica equivalente no pseudo-tempo t n p ε n+ Deformação plástica equivalente no pseudo-tempo t n+ H Coeficiente de endurecimento cíclico H k Módulo de endurecimento cinemático k H i Termo i do módulo de endurecimento cinemático η Tensor relativo N Vida sob fadiga N Vetor de fluxo N n+ Vetor de fluxo no pseudo-tempo t n+ N Vetor de fluxo efetivo N n+ Vetor de fluxo normalizado no pseudo-tempo t n+ ν Coeficiente de Poisson ξ Terceiro invariante normalizado do tensor desviador σ máx Tensão máxima σ mín Tensão mínima σ r Gama de tensão σ m Tensão média σ a Tensão alternante σ Tensor tensão de Cauchy σ n+ Tensor tensão no pseudo-tempo t n+ trial σ n+ Tensor tensão tentativa no pseudo-tempo t n+ σ y0 Tensão de escoamento inicial Y Força termodinâmica associada ao dano Y n+ Força termodinâmica associada ao dano no pseudo-tempo t n+ ψ ed Contribuição devido a elasticidade-dano na energia livre
12 a Constante b Constante do material relativa ao endurecimento cinemático b i Termo i da constante do material relativa ao endurecimento cinemático D Variável isotrópica de dano D n+ Variável de dano no pseudo-tempo t n+ D c Dano crítico D Lei de evolução para a variável isotrópica de dano D e Tensor constitutivo f Fração G Módulo de cisalhamento I Matriz identidade de segunda ordem I Matriz identidade J Segundo invariante do tensor tensão desviador K Módulo volumétrico n Fator de segurança n Expoente de endurecimento cíclico m Número de termos não lineares no somatório da lei de Chaboche p Pressão hidrostática p n+ Pressão hidrostática no pseudo-tempo t n+ q Tensão equivalente de Von Mises q n+ Tensão equivalente de Von Mises no pseudo-tempo t n+ R Razão de variação das tensões r Terceiro invariante S ut Limite de resistência a tração S y Limite de resistência ao escoamento Se Limite de resistência a fadiga S f Resistência a fadiga S 0.00 Denominador de dano para baixa triaxialidade S 0. Denominador de dano para alta triaxialidade S(Γ, ξ) Função denominador de dano S Tensor das tensões desviadoras S n+ Tensor desviador no pseudo-tempo t n+ s Expoente de dano φ Função de escoamento φ n+ Função de escoamento segundo Lemaitre no pseudo-tempo t n+ ρ Densidade do material ρ Densidade do material na configuração de referência ( ) Estado real Estado tentativa ( ) trial
13 INTRODUÇÃO. MOTIVAÇÃO O projeto de produtos tem demandado dos Engenheiros análises de viabilidade rápidas, que levem em consideração a economia de insumos e o uso de estruturas mais leves. De acordo com Jiang (007), nem sempre é possível utilizar-se de um teste experimental para avaliar novos protótipos devido a considerações que envolvem custo e tempo de execução. Portanto, as dificuldades associadas a um ensaio exclusivamente experimental tem estimulado a implementação de modelos numéricos que contam com parâmetros obtidos a partir de ensaios e produzem resultados ágeis no que diz respeito ao comportamento elastoplástico de materiais selecionados e expostos a carregamentos, principalmente devido aos progressos computacionais recentes. A figura., por exemplo, ilustra a análise de fadiga por elementos finitos de um braço de suspensão inferior de um carro. O cálculo em questão visa estimar a vida em fadiga deste componente a partir dos valores das tensões flutuantes. Figura. Análise estrutural de um braço de suspensão inferior de um carro através do método de elementos finitos (Compass Automotive Groupe, 0). Jiang (007) argumenta também que as simulações computacionais possibilitam a análise de vida em fadiga de componentes submetidos a tensões multiaxiais não-proporcionais. A seguir apresentaremos um breve histórico dos trabalhos e principais fatos relativos ao estudo da fadiga, plasticidade e mecânica do dano em materiais:
14 Em 87 Wilhelm desenvolveu uma máquina para ensaio de correntes transportadoras utilizadas em minas e publicou um artigo sobre fadiga mostrando a correlação entre a carga aplicada e a durabilidade das correntes (Schu tz, 996). De acordo com Schu tz (996), Poncelet cunhou em 89 o termo fadiga em um livro sobre mecânica. Wohler, por sua vez, com base nos resultados obtidos a partir de ensaios em eixos mecânicos ferroviários (realizados ao longo de 0 anos), concluiu em 870 que o intervalo de tensão cíclica é mais importante que o pico de tensão e introduziu os conceitos de Curva S-N e limite de fadiga (Schu tz, 996). Segundo Socie & Marquis (000), Lanza elaborou em 887 o primeiro trabalho em fadiga multiaxial, além de desenvolver a primeira máquina de teste de fadiga rotativa de flexãotorção. Ewing, após realizar estudos da microestrutura dos metais, propôs em 90 que as falhas por fadiga eram devidas a bandas de deslizamento persistentes e que a fratura de componentes mecânicos estava relacionada a uma única trinca dominante. (Schu tz, 996). Em 90, após analisar os dados obtidos por Wohler em ensaios de fadiga, Basquin indicou uma relação log-log entre a tensão (S) e a vida (N) para representar a curva S-N, tendo em vista a constatação de que o número de ciclos se relacionava potencialmente com a tensão aplicada. Ao combinar os resultados apresentados em pesquisas de Bauschinger e Ewing, bem como realizar ensaios com carregamentos cíclicos acima do limite de escoamento do material, Bairstow identificou em 9 o fenômeno conhecido por laços de histerese (Schu tz, 996). Miner contribuiu através de seus estudos em 945 para que a hipótese de acúmulo de dano linear em fadiga, inicialmente pesquisada por Palmgreen (94), se consolidasse como a Regra de Palmgreen-Miner. Com o objetivo de identificar se as falhas por fadiga ocorreram devido a carregamentos cíclicos multiaxiais, Gough (950) e Pollard (95) propuseram equações tanto para materiais dúcteis quanto para materiais frágeis. Coffin (954) e Manson (95) estabeleceram um novo conceito de análise de fadiga em materiais ao obter de forma independente curvas ε N, ao invés das curvas S-N propostas por Wohler. Em 959 Findley desenvolveu a ideia de plano crítico para determinar a vida em fadiga de componentes mecânicos expostos a carregamentos cíclicos multiaxiais. Paris criou em 96 a Teoria de Propagação de Trincas que utiliza os conceitos de fator de intensidade de tensões em carregamentos cíclicos para prever a taxa de crescimento de uma trinca individual (Schu tz, 996). O método de contagem de ciclos Rainflow, com autoria de Matsuishi e Endo relativa ao ano de 968, possibilitou a estimativa de vida em fadiga de componentes mecânicos sujeitos a carregamentos cíclicos com amplitude variável (Schu tz, 996). Elber pesquisou em 970 o fenômeno de fechamento da trinca e ao introduzi-lo, obteve melhora significativa dos resultados relacionados a previsão de vida em fadiga com a Mecânica da Fratura (Schu tz, 996).
15 Conforme exposto por Malcher (0), desde o trabalho pioneiro de Kachanov (958), inúmeros outros desenvolvimentos em mecânica aplicada foram feitos, no sentido de formular novos modelos constitutivos que sejam capazes de descrever a degradação interna de sólidos, de acordo com os princípios da mecânica do continuo. Segundo Lemaitre (985), a Mecânica do Dano Contínuo (MDC) surgiu como uma formulação alternativa para a introdução de novas variáveis de estado dentro dos modelos constitutivos. O comportamento elastoplástico do material relaciona-se ao modelo constitutivo e ao dano interno, que se inicia através de micro-trincas e pode ser corretamente representado através de variáveis internas com grandezas de natureza escalar, vetorial ou tensorial. Para mensurar as variáveis de dano, podemos considerar os defeitos no interior de um volume representativo elementar (VRE). Ainda de acordo com Malcher (0), sua evolução deve ser definida através das relações termodinâmicas constitutivas, normalmente representadas por um sistema de equações diferenciais no tempo. Lemaitre, Chaboche, Paas e outros pesquisadores, propuseram modelos de acúmulo de dano em fadiga baseados na Mecânica do Dano Contínuo (Desmorat, 006). H. C. Wang e M. W. Brown (996) foram os responsáveis por propor um método que ficou conhecido como versão multiaxial da Regra de Palmgreen-Miner. De acordo com Socie (000), no século XX ocorreu uma disseminação e utilização intensa de ferramentas computacionais na resolução de problemas de engenharia, principalmente no âmbito industrial. Segundo Malcher (0), isto se deve a significativa ampliação da capacidade de processamento e consequente redução dos custos de implementação de modelos robustos e confiáveis a partir de computadores, corroborando desta forma para uma ampla aceitação de técnicas numéricas tanto no meio acadêmico como na iniciativa privada. O emprego de métodos de elementos finitos por projetistas na resolução de problemas não-lineares da mecânica dos sólidos tem se consolidado devido ao fato destes estarem continuamente serem desenvolvidos e aperfeiçoados por pesquisadores diversos. De acordo com Malcher (0), apesar dos avanços constatados, questões como o desenvolvimento de modelos relativos a falha (fratura) de material, com progressiva deterioração em nível microestrutural a partir de grandes deformações ainda representam excelentes áreas de pesquisa e desenvolvimento. Uma maior eficiência em processos tecnológicos aplicados na fabricação de superfícies maquinadas depende, portanto, da ampliação do conhecimento e da quantificação dos diferentes fenômenos físicos que ocorrem próximos da ruptura de materiais dúcteis.
16 . OBJETIVOS Este trabalho tem como objetivo implementar o modelo associativo modificado de Lemaitre com endurecimento cinemático de Chaboche para estimar a vida em fadiga do aço S460N quando submetido a carregamentos uniaxiais ou multiaxiais. Os históricos de tensões para diferentes amplitudes de deformação e números de ciclos foram obtidos com o uso de algoritmos implementados em linguagem FORTRAN a partir de modelos numéricos. Durante a pesquisa trabalhamos com trajetórias uniaxiais, multiaxiais proporcionais e multiaxiais não-proporcionais, contabilizando uma série de quatro históricos de deformações cíclicas diferentes para o aço S460N. Os dados obtidos foram aplicados ao modelo clássico de dano de Lemaitre com endurecimento cinemático de Chaboche, permitindo desta forma comparar sua capacidade preditiva com o modelo baseado na mecânica dos danos contínuos (CDM) desenvolvido por Malcher (0) e com resultados provenientes de ensaios experimentais para fadiga de baixo e alto ciclo. Além disso, pretende-se a partir das curvas de evolução de dano avaliar a influência da calibração do dano crítico e dos denominadores de alta e baixa triaxialidade sobre os resultados aferidos com os modelos elastoplásticos.. ORGANIZAÇÃO DO TRABALHO Este trabalho foi dividido em 5 capítulos de forma a permitir a comparação dos resultados experimentais obtidos por Jiang (007) com aqueles aferidos tanto pelo modelo de Lemaitre quanto pelo modelo CDM modificado, ambos com endurecimento cinemático de acordo com a lei de evolução proposta por Chaboche. No capítulo, formalizamos as motivações e definimos os objetivos que norteiam esta dissertação. No capítulo, com o intuito de oferecer subsídios para implementar e calibrar os modelos elastoplásticos, bem como analisar os resultados aferidos e propor novos estudos, realiza-se uma revisão bibliográfica a partir de tópicos relativos a fadiga, plasticidade e mecânica do dano. Além disso, são apresentados os modelos matemáticos de acordo com as premissas estabelecidas por von Mises, Lemaitre e para o CDM modificado. No capítulo, desenvolve-se a partir da discretização de Euler e aplicação do método de Newton-Raphson, a solução do conjunto de equações dos modelos constitutivos de Lemaitre e CDM modificado para o aço S460N, considerando o critério de von Mises para a função de escoamento. 4
17 No capítulo 4, discorre-se sobre a estratégia de calibração dos modelos elastoplásticos para o aço S460N, a qual compreende a identificação tanto dos parâmetros de tensão quanto do dano crítico e dos denominadores de dano para alta e baixa triaxialidade. No capítulo 5 compara-se os resultados de ensaios experimentais disponíveis na literatura para o aço S460N quando exposto a carregamentos com trajetórias uniaxiais, multiaxiais proporcionais ou multiaxiais não proporcionais, com a vida calculada através dos modelos de Lemaitre ou CDM modificado. Também são analisadas as curvas de evolução do dano. Em seguida apresenta-se as conclusões e propostas para eventuais trabalhos futuros. 5
18 ASPECTOS TEÓRICOS. INTRODUÇÃO Segundo Lemaitre (985), os conceitos estabelecidos na mecânica dos danos baseiam-se na metalurgia e permitem uma melhor compreensão de fraturas em estruturas expostas a carregamentos multiaxiais. Isso torna-se possível ao estabelecermos correlações entre uma variável de dano e a deterioração dos materiais antes do surgimento de trincas. Para descrever o comportamento elastoplástico do material e implementar corretamente a modelagem numérica do modelo, faz-se necessário uma revisão bibliográfica de conceitos relacionados a fadiga, plasticidade e mecânica do dano.. NATUREZA FÍSICA DO DANO POR FADIGA A maioria dos metais estruturais são policristalinos, ou seja, constituídos por um grande número de cristais individuais ordenados (grãos). As propriedades mecânicas, as direções de ordenação assim como outras características diferem de um para outro grão. Alguns grãos são orientados de tal forma que planos de deslizamento estão na direção da máxima tensão de cisalhamento aplicada. O deslizamento pode ser verificado tanto em carregamentos cíclicos quanto em carregamentos estáticos. Em metais dúcteis, o deslizamento ocorre no interior dos grãos individuais ao longo de planos cristalográficos. De acordo com Fatemi et. al (000), Forsyth mostrou através da microscopia eletrônica que ambas as bandas de deslizamento por intrusões e extrusões ocorrem na superfície dos metais quando estes são submetidos a carregamentos cíclicos. As Figuras. e. representam as considerações apresentadas. Figura. - Deslizamento em metais dúcteis devido a carregamentos cíclicos (NDT Centro de Pesquisa). 6
19 Figura. Formação de intrusões e extrusões, captado por microscópio eletrônico de varredura (MEV) (Ma & Laird, 989). Faixas de deslizamento relacionadas a intrusões são responsáveis por uma grande concentração de tensões, que pode vir a ser o local a partir do qual trincas irão se desenvolver. Dentre as várias condições que podem acelerar a formação de trincas, podemos citar: tensões residuais de tração, temperaturas elevadas, ciclagem térmica, ambientes corrosivos assim como ciclagem de alta frequência. A maioria das bandas de deslizamento pode ser eliminada através do eletropolimento. A vida à fadiga será substancialmente melhorada se estas forem suprimidas. Isto significa que as fases iniciais da fadiga são essencialmente um fenômeno de superfície. Entretanto, uma pequena quantidade das faixas de deslizamento não poderá ser eliminada através desse processo de forma que estas são conhecidas como "bandas de deslizamento persistente". O surgimento das trincas por fadiga está relacionado a bandas locais de deslizamento ao passo que o crescimento das mesmas tende a ocorrer num plano de máxima amplitude de tensão cisalhante. Esse crescimento é extremamente pequeno, geralmente da ordem de vários grãos. Como o número de ciclos aumenta com o passar do tempo, as trincas tendem a fundir-se e crescer ao longo de planos de máxima amplitude de tração. O mecanismo de fadiga em metais frágeis ou de alta resistência não ocorre devido a bandas de deslizamento persistentes (PSBs). Microtrincas surgem imediatamente em descontinuidades, tais como inclusões ou vazios e, em seguida crescem ao longo dos planos de tensões máximas de tração. Podemos dividir o processo de falha devido à fadiga em três etapas principais: () nucleação da trinca de fadiga; () propagação segundo os estágios I e II; () ruptura final (Dowling,99). 7
20 De uma forma geral, os mecanismos que podem caracterizar a propagação da trinca em materiais dúcteis são a estricção e a coalescência de microcavidades ao passo que em materiais frágeis frequentemente surgem microclivagens (Crooker et al, 976). O estágio III diz respeito ao ciclo de carga final, quando a integridade física do material foi severamente comprometida e este, não suportando os esforços aplicados, irá falhar de forma súbita. Uma falha de estágio III poderá ser frágil, dúctil ou uma combinação de ambas. As fases da vida à fadiga foram ilustradas através das Fig.. a.5. Figura. Formação de PSBs em apenas alguns grãos. (Meyers & Chawla, 009). Figura.4 Estrias de fadiga em liga de alumínio 04-T6 visto em MEV (Meyers & Chawla, 009). A vida de um componente exposto à fadiga está relacionada com o número de ciclos necessários para que ocorra a ruptura do mesmo em determinado nível de tensão. Apesar de certas abordagens não considerarem a presença de trincas de fadiga, podemos definir a falha da estrutura através da soma do número de ciclos até a nucleação das trincas com o número de ciclos para sua propagação até que o componente falhe (Moura Branco, 985). 8
21 Figura.5 - Falha por fadiga de um parafuso de porca em razão de flexão unidirecional repetida. A falha começou na raiz da rosca em A, propagou-se ao longo da maior parte da seção transversal como evidenciado pelas marcas de praia em B, antes da fratura rápida final em C (Shigley, 005).. FADIGA MULTIAXIAL Falha por fadiga multiaxial é um dos principais modos de falha de componentes e tem sido amplamente estudado. Entretanto, apresenta desafios adicionais quando comparada a fadiga uniaxial, uma vez que envolve endurecimento do material e efeitos decorrentes de tensões normais e cisalhantes médias. De acordo com Liu et. al (07), devido ao nível de complexidade de mecanismos de falha em fadiga multiaxial e a relação com a microestrutura do material, os diferentes modelos aplicados na previsão de falha em fadiga podem ser resumidos nas seguintes categorias: modelos de tensão/deformação equivalente, modelos baseados em critérios de energia, modelos baseados em mecanismos de dano e em planos críticos. Os modelos de Fatemi-Socie, Wang-Brown e Findley representam abordagens baseadas no plano crítico. Por vezes, faz-se necessário determinar constantes materiais que dependem do número de ciclos até a falha. Esta etapa desenvolve-se através da realização de ensaios dos materiais, regressão dos dados de fadiga e a partir de fórmulas. Dessa forma, de acordo Liu et. al (07), o processo de determinação da vida em fadiga torna-se em alguns casos inconveniente. Malcher & Balthazar (007) ressaltam que a ideia principal na abordagem baseada nos invariantes do tensor tensão é relacionar diretamente a resistência a fadiga com o segundo invariante do tensor desviador e o primeiro invariante do tensor. Os modelos de Sines, Crossland e Kakuno-Kawada podem ser considerados como uma combinação da abordagem de tensão equivalente, uma vez que utilizam a tensão cisalhante equivalente para tensões multiaxiais aplicadas, além da abordagem do plano crítico para 9
22 encontrar os valores máximos de seus parâmetros, em planos com a maior interseção com o caminho do tensor tensão desviador (Malcher, 006)..4 TEORIA DA PLASTICIDADE Nos tópicos.8. a.8.4 será apresentada uma breve revisão com as principais características dos modelos de plasticidade cíclica comumente empregados em análises e simulações computacionais. Em seguida, desenvolveremos no tópico.8.5 o modelo matemático para o critério de von Mises, o qual traz conceitos fundamentais para a plena compreensão de modelos elastoplásticos com dano acoplado..4. MODELOS DE PLASTICIDADE CÍCLICA De acordo com Kachanov (97), qualquer alteração no tamanho da superfície de escoamento pode ser relacionada a taxas de deformação plástica, comumente mensuradas através do trabalho plástico total por unidade de volume, deformação plástica acumulada ou taxa de deformação plástica volumétrica, por exemplo. A Figura.6 representa uma expansão uniforme da superfície de escoamento após a aplicação de um incremento de tensão entre as etapas i e i +. Figura.6 - Endurecimento isotrópico (KACHANOV, 97). Uma vez que a superfície de escoamento depende da deformação plástica (ε p ), esta pode ser matematicamente expressa da seguinte forma: f(σ, ε p ) = 0 (.0) 0
23 O tamanho da superfície em qualquer estágio do carregamento é determinado através de uma lei de evolução. Conforme o nível de deformação plástica inicialmente aplicado e o histórico de carregamentos, poderá ocorrer a contração da superfície de escoamento e o consequente amolecimento do material. Por outro lado, o endurecimento ou encruamento será verificado para processos com expansão do limite de escoamento. Por fim, o material em análise será denominado perfeitamente plástico quando for submetido a carregamentos cíclicos e não houver alterações em sua superfície de escoamento. A lei de endurecimento isotrópico estabelece que durante o processo de fluxo plástico ocorrem expansões ou contrações da superfície de escoamento. Por outro lado, são mantidos o centro, formato e orientação da superfície em questão. Ao submetermos um espécime a cargas de tração que ultrapassem o limite de elasticidade do material metálico e em seguida invertermos a direção de deformação, observaremos uma menor resistência a novo carregamento na direção inicial. Este fenômeno é conhecido como efeito de Bauschinger e descreve a dependência direcional após deformações plásticas. Isso ocorre devido a adições e bloqueamentos de discordâncias (falhas) no material. O termo endurecimento cinemático foi introduzido por Prager em 955 com o intuito inicial de modelar o efeito de Bauschinger, comumente observado em ensaios com carregamentos cíclicos. Conforme podemos constatar através da Fig..7, durante o fluxo plástico ocorre uma translação da superfície de escoamento no espaço das tensões, na direção da taxa de deformação plástica. O formato e tamanho da superfície, entretanto, não sofrem alterações. Figura.7 - Endurecimento cinemático (KACHANOV, 97)..4. PRAGER A seguir apresentamos a lei de evolução do endurecimento cinemático proposta por Prager em 956. O modelo em questão prevê o comportamento plástico de materiais através da
24 relação linear entre as taxas de variação do tensor cinemático e da deformação plástica equivalente, onde a proporcionalidade é obtida através do módulo de endurecimento cinemático H k. β = H kε p (.) onde, β é a taxa de evolução da tensão de endurecimento cinemático, H k é o módulo de endurecimento cinemático e ε p corresponde a taxa de evolução da deformação plástica. Apesar de representar bem o efeito de Bauschinger, a lei proposta por Prager não contempla de maneira adequada à parte inicial não linear da curva de histerese experimental, o que pode ser constatado através da imagem abaixo. De acordo com Bari e Hassan (000), o modelo também não contempla o fenômeno conhecido por ratcheting que corresponde ao colapso incremental do material, uma vez que este não diferencia as curvas de histerese, resultando em laços fechados, independente do carregamento ser reverso ou não (Bari e Hassan, 000), conforme apresentado na Fig..8. Figura.8 - Resultados do modelo de Prager (Bari e Hassan, 000).
25 Figura.9 - Resultados do modelo de Prager para laço de histerese em tensão controlada com tensão média sobreposta (Bari e Hassan, 000)..4. ARMSTRONG-FREDERICK Armstrong & Frederick (966) introduziram o efeito de saturação a lei de Prager através da inclusão de um termo não linear composto pela tensão de endurecimento cinemático (β), uma constante do material (b) e a taxa de variação da deformação plástica equivalente (ε p ). De acordo com Chaboche (986), verifica-se uma descrição mais efetiva de cargas cíclicas através da lei de Armstrong-Frederick, uma vez que esta permite correções relativas à forma do laço de histerese, estabilização do ciclo, relações entre as amplitudes do ciclo estabilizado, modelagem do efeito de Bauschinger e a não linearidade das evoluções de tensãodeformação. β = Hkε p ε p bβ (.) onde, β é a taxa de evolução da tensão de endurecimento cinemático, β é a tensão de endurecimento cinemático, H k é o módulo de endurecimento cinemático, ε p é a taxa de evolução da deformação plástica, ε p é a taxa de evolução da deformação plástica equivalente e b corresponde a um parâmetro do material relativo ao endurecimento cinemático. Segundo Armstrong & Frederick (966) o material apresentará comportamento perfeitamente plástico caso tenhamos o valor máximo para o termo de saturação, ou seja, quanto maior β, menor será sua evolução.
26 .4.4 CHABOCHE A Fig..0 apresentada a seguir, traz as curvas tensão-deformação de ciclo estabilizado uniaxial para os modelos de endurecimento isotrópico linear, cinemático linear (Prager) e cinemático não linear (Armstrong-Frederick ou Chaboche). Figura.0 - Curvas de histerese para os modelos de endurecimento. Devido o modelo de Armstrong-Frederick superestimar os efeitos de ratchetting, Chaboche (986) propôs sua generalização, com maior flexibilidade no ajuste dos parâmetros materiais (b e H k ), conforme pode ser verificado através da Eq.., na qual m representa o número de termos do somatório. m β = ( H i k ε p ε p b i β i ) i= (.) onde, β é a taxa de evolução da tensão de endurecimento cinemático, β i é o termo i da tensão de endurecimento cinemático, H k i é o termo i do módulo de endurecimento cinemático, ε p é a taxa de evolução da deformação plástica, ε p é a taxa de evolução da deformação plástica equivalente, b i é o termo i do parâmetro do material relativo ao endurecimento cinemático e m corresponde ao número de termos da lei de evolução de Chaboche..4.5 CRITÉRIO DE ESCOAMENTO DE MISES Neste tópico apresentaremos o critério de escoamento de von Mises com o endurecimento cinemático de acordo com a lei de evolução de Chaboche. Além disso, consideraremos que a evolução do vetor de fluxo plástico ocorre em direção normal à superfície de escoamento no espaço das tensões, conforme estabelecido pela plasticidade associativa. Importante frisar também que o modelo independe do tempo. 4
27 A resolução do modelo desenvolve-se através da definição da função de escoamento, do vetor de fluxo plástico e das leis de evolução das variáveis internas. ) Função de escoamento φ = q σ y0 (.4) onde, φ é a função de escoamento, q é a tensão equivalente de Von Mises e σ y0 é o limite de tensão de escoamento inicial. A tensão equivalente é matematicamente determinada por: q (η) = η: η (.5) onde, η é o tensor relativo, cujo cálculo é realizado através da expressão abaixo: η = S β (.6) onde, β é o tensor das tensões cinemáticas e S é o tensor das tensões desviadoras. ) Vetor de fluxo N φ σ = η q = η η (.7) onde, N é o vetor de fluxo. ) Lei de fluxo plástico ε p γ N (.8) onde, ε p e γ representam as taxas de evolução, respectivamente, da deformação plástica e do multiplicador plástico. 5
28 4) Lei de evolução para outras variáveis internas ε p ε p : ε p = γ (.9) onde, ε p é a taxa de evolução da deformação plástica equivalente. A seguir iremos definir β, ou seja, a lei de evolução para o tensor das tensões cinemáticas. m β = β i i= m = γ ( H i k N b i β i ) i= (.0) onde, m é o número de termos não lineares no somatório da lei de evolução de Chaboche, β i é o termo i da taxa de evolução do tensor das tensões cinemáticas, H k é módulo de endurecimento cinemático e b i corresponde ao termo i da constante do material relativa ao endurecimento cinemático. 5) Lei de Hooke generalizada O tensor tensão, por sua vez, é dado segundo a lei de Hooke generalizada, conforme apresentado a seguir: σ = D e : ε e (.) A Tabela., por sua vez, apresenta um resumo das equações que governam o modelo elastoplástico de von Mises com endurecimento cinemático de Chaboche. 6
29 Tabela. - Modelo Matemático para o critério de Von Mises com endurecimento cinemático de Chaboche. i) Decomposição aditiva da deformação: ε = ε e + ε p ii) Lei de Hooke: σ = D e : ε e iii) Função de escoamento: φ = η: η σ y 0 vi) Lei de fluxo plástico: ε p γ N N = η q = η η e leis de evolução para outras variáveis internas ε p ε p : ε p = γ m β = β i i= m = γ ( H i k N b i β i ) i= v) Regra da Complementariedade γ 0 φ 0 γ φ = 0.5 MECÂNICA DO DANO O processo físico que ocorre simultaneamente a deformação do material e resulta em sua falha é denominado dano. A mecânica do dano estuda o fenômeno da degradação do material submetido a carregamentos, desde a etapa inicial até o desenvolvimento da trinca. Há três diferentes estágios ou escalas de interesse quando consideramos o dano de materiais: Microescala: o dano é considerado como uma acumulação de microtrincas na vizinhança de defeitos ou interfaces. 7
30 Mesoescala: o dano é considerado como o crescimento e coalescência de microtrincas e microvazios que dão início a trinca. Macroescala: o dano é considerado como uma descontinuidade na escala macro que conduz a uma falha global (fratura). Os dois primeiros estágios são geralmente estudados através de variáveis de dano definidas no nível da mesoescala a partir da mecânica do contínuo. O terceiro estágio, por sua vez, é comumente analisado através da mecânica da fratura, com as variáveis de dano definidas no nível da macroescala..5. VARIÁVEL DE DANO UNIDIMENSIONAL A abordagem fenomenológica para modelagem do dano originou-se a partir do trabalho de Kachanov (968) e Rabotnov (966). Lazar Kachanov introduziu o conceito de parâmetro de dano (D) conforme representado na Fig.., ou seja, definido como a razão entre a área efetiva das interseções de todas as microtrincas ou microcavidades (A D ) em uma seção de um elemento de volume representativo (RVE) com um plano dado pela área da seção (S) do RVE: D = A D /A (.) Figura. Redução da área efetiva da seção devido à formação de microtrincas ou microcavidades. De acordo com Mishnaevsky (007), a iniciação e acumulação de microtrincas (danos) são descritas pela lei de evolução do dano, que apresenta (em um caso geral) uma relação entre a taxa de crescimento do parâmetro de danos, as condições de carregamento, o dano acumulado e as propriedades do material. 8
31 .5. TENSÃO EFETIVA E PRINCÍPIO DE EQUIVALÊNCIA DE DEFORMAÇÃO A tensão de tração para um corpo cilíndrico de seção transversal com área A, submetido a cargas uniaxiais através da aplicação de uma força F, é dada por: σ = F A (.) Para um corpo danificado onde a área dos microdefeitos corresponde a A D, verifica-se que a área efetiva que resiste ao carregamento equivale a (A A D ). A partir desta definição temos a seguinte expressão matemática relativa à tensão efetiva σ : σ = F (A A D ) (.4) Uma vez que D = A D /A, tem-se: σ = σ ( D) (.5) Rabotnov (968) propôs a expressão acima, válida somente para carregamentos de tração, uma vez que para materiais submetidos à compressão não se verifica a ampliação da seção transversal relativa aos microdefeitos, ou seja, neste caso a tensão efetiva (σ ) e a tensão usual (σ) são idênticas. Segundo o Princípio de Equivalência de Lemaitre, entretanto, ao substituirmos a tensão usual (σ) pela tensão efetiva (σ ), é possível obtermos qualquer equação constitutiva para determinado material danificado. Para exemplificarmos este conceito, apresentamos a seguira Lei de Hooke unidimensional para um material danificado: σ = Eε e ( D) = E ε e (.6).5. CRITÉRIO DE RUPTURA A ideia fenomenológica do parâmetro de dano D levar em consideração na escala macroscópica deteriorações microscópicas (vazios, microtrincas, etc.) é geralmente aceita (Krempl, 977) com as seguintes limitações: Para um material que não foi submetido a carregamentos temos D = 0. A iniciação da trinca macroscópica ocorre para D = D c. A falha pode ser constatada para D <, devido a processos de instabilidade. A ruptura do material ocorre quando D =. O dano crítico pode ser definido através das características intrínsecas ao material e das condições de carregamento como D c 0 para fratura puramente frágil e D c para fratura 9
32 puramente dúctil. De acordo com Lemaitre (996), comumente verifica-se, entretanto, que 0. < D c < DANO ISOTRÓPICO TRIDIMENSIONAL Para modelar a elasticidade, plasticidade e o dano em um processo isotérmico, as variáveis apresentadas na tabela abaixo devem ser introduzidas. Dessa forma é possível definir tanto as equações de estado quanto às constitutivas. Tabela. Variáveis de estado e forças termodinâmicas associadas. Mecanismo Variáveis de Estado Força Termodinâmica Observáveis Internas Associada Elasticidade ε e σ Plasticidade ε p σ Endurecimento Cinemático β X Dano D Y A energia livre de Helmholtz (Ψ) corresponde a um potencial termodinâmico no qual a elasticidade e a plasticidade não estão acopladas, conforme Eq..7. Ψ(ε e, D, β) = Ψ ed (ε e, D) + Ψ p (β) (.7) De acordo com Lemaitre (996), a equação acima pode ser reescrita da seguinte maneira: Ψ(ε e, D, β) = ρ [ εe : D: ε e ( D) + bh k β: β] (.8) A partir da Eq..8 verifica-se que não há dependência entre a componente plástica da energia livre de Helmholtz (Ψ p ), a deformação elástica (ε e ) e o dano (D). Portanto, sabendo que as derivadas de Ψ p com relação à ε e e D são nulas, é possível obter a partir da segunda lei da termodinâmica a seguinte expressão σ: σ = ρ Ψ Ψed = ρ εe ε e = D: εe ( D) (.9) Modificando a Lei de Hooke expressa pela Eq..9 com a aplicação do tensor efetivo, temos as seguintes equações: σ = D: ε e (.0) σ = σ (.) ( D) 0
33 Desenvolvendo raciocínio semelhante para a variável interna de dano (D), temos: Y = ρ Ψ Ψed = ρ D D = εe : D: ε e (.) Levando em consideração a Lei de Hooke para a Eq.., temos: Y = σ: D : σ (.) onde, Y corresponde a densidade de energia de deformação liberada devido ao dano, sendo igual a metade da variação da densidade da energia de Lemaitre (Malcher, 0). A Eq.., por sua vez, pode ser reescrita em termos das constantes de Lamé (G e K), módulo de elasticidade (E), coeficiente de Poisson (ν), pressão hidrostática (p) e da tensão equivalente de von Mises (q ), conforme verifica-se através ad Eq..4. Y = q 6G( D) + p K( D) (.4).5.5 LEIS DE EVOLUÇÃO DO DANO A seguir apresentamos através da Eq..5 a lei de evolução de dano proposta por Lemaitre em 985. Conforme pode ser observado, no cálculo da taxa de variação de dano (D ) considera-se a densidade de energia de deformação ( Y), a deformação plástica equivalente (ε p ), bem como o denominador (S) e o expoente de dano (s). D = ε p ( Y s S ) (.5) Ao analisar diversas pesquisas publicadas nas últimas décadas, Malcher (0) constatou que a capacidade preditiva de modelos elastoplásticos com dano acoplado era fortemente dependente da condição de calibração utilizada para determinação dos parâmetros materiais. De acordo com Bai et al. (007 e 008), a razão entre a pressão hidrostática (p) e a tensão equivalente de von Mises (q) é denominada triaxialidade (Γ). Trata-se de importante parâmetro nos estudos da elasto-plasticidade, uma vez que está relacionado ao tamanho do regime elástico do material. Γ = p q (.6) Segundo Malcher (0), outro parâmetro elasto-plástico bastante relevante é o terceiro invariante do tensor desviador (r), expresso matematicamente da seguinte forma: r = ( 7 dets) (.7)
34 onde, S corresponde ao tensor das tensões desviadoras. Ao normalizarmos o terceiro invariante do tensor desviador, temos: ξ = ( r q ) = 7 dets q (.8) Com base na Mecânica do Dano Continuo, Malcher (0) propõe em seu trabalho o aperfeiçoamento da lei de evolução de dano de Lemaitre para materiais dúcteis, ao tratar o denominador de dano como uma função relacionada ao nível de triaxialidade (Γ) e ao terceiro invariante normalizado (ξ). D = ε p ( Y s S(Γ, ξ) ) (.9) Através da Fig.. é possível observar que o denominador de dano decresce com o aumento da triaxialidade, independentemente da região estudada. A aplicação da função denominadora de dano garante uma maior representatividade das regiões de alta (tração predominante) e baixa triaxialidade (cisalhamento predominante). Além disso, outra vantagem é a necessidade de um menor número de pontos para calibração do modelo (Malcher, 0). Figura. - Dependência entre o denominador de dano e a razão de triaxialidade (Malcher, 0). Na região de alta triaxialidade, aplicam-se os resultados experimentais obtidos com base em um ensaio de tração pura (Γ 0.) em um corpo de prova cilíndrico liso. Por sua vez, para a região de baixa triaxialidade, utiliza-se a condição de cisalhamento puro (Γ = 0) como segundo ponto de calibração. Portanto, é possível distinguir a partir da razão de triaxialidade o tipo de carregamento aplicado.
35 Para que a função denominadora de dano seja aplicável simultaneamente em ambas às regiões, as expressões fenomenológicas sugeridas por Malcher (0) para as faixas de alta e baixa triaxialidade deverão ser acopladas. Como resultado temos a Eq..40, apresentada a seguir. S(Γ, ξ) = S 0. Γ + S 0. S 0.00 ( ξ ) (.40) onde, S 0. e S 0.00 representam, respectivamente, os denominadores de dano calibrados através ensaios sob tração e cisalhamento puros..5.6 MODELO DE LEMAITRE COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE Seguindo os passos apresentados na seção anterior, define-se o algoritmo de atualização para o modelo de dano de Lemaitre com endurecimento cinemático de Chaboche, com m=, ou seja, três termos não lineares no somatório da lei de evolução de Chaboche. Primeiramente, o estado tentativa é dado por: ) Função de escoamento φ = q D σ y 0 (.4) onde, φ é a função de escoamento segundo Lemaitre, q é a tensão equivalente de Von Mises, D é a variável isotrópica de dano e σ y0 é a tensão de escoamento inicial. A tensão equivalente é matematicamente determinada por: q (η) = η: η (.4) onde, η é o tensor relativo, cujo cálculo é realizado através da expressão abaixo: η = S β (.4) onde, β é o tensor das tensões cinemáticas e S é o tensor das tensões desviadoras. ) Vetor de fluxo
36 N φ σ = η q ( D) = η η ( D) (.44) onde, N é o vetor de fluxo. A seguir definimos o vetor de fluxo efetivo N : N = η = q η η (.45) O vetor de fluxo pode ser reescrito ao substituirmos a variável N na Eq..45: N φ σ = N ( D) (.46) ) Lei de fluxo plástico ε p γ N = γ N ( D) (.47) onde, ε p e γ representam respectivamente, a taxa de evolução da deformação plástica e do multiplicador plástico. 4) Lei de evolução para outras variáveis internas ε p ε p : ε p = γ D (.48) onde, ε p é a taxa de evolução da deformação plástica equivalente. A seguir iremos definir β, ou seja, a lei de evolução para o tensor das tensões cinemáticas. m β = β i i= m = γ D ( H i k N b i β i ) i= (.49) onde, m é o número de termos não lineares no somatório da lei de evolução de Chaboche, β i é o termo i da taxa de evolução do tensor das tensões cinemáticas, H k é módulo de endurecimento cinemático e b i corresponde ao termo i da constante do material relativa ao endurecimento cinemático. A Eq..50, por sua vez, traz a lei de evolução para a variável isotrópica de dano. D = γ D ( Y S )s (.50) 4
37 onde, Y é força termodinâmica associada ao dano e s é o expoente de dano. A força termodinâmica associada a variável interna de dano, Y, deriva do potencial de estado devido à elasticidade-dano e pode ser escrita como: ψ ed (ε e, D) Y = ρ = D εe : ( D)D: ε e (.5) onde, ρ é a densidade do material na configuração de referência, ψ ed é a contribuição devido a elasticidade-dano na energia livre, ε e é a deformação elástica e D é o tensor constitutivo. Após algumas manipulações matemáticas, é possível escrever Y em função da pressão hidrostática, p, da tensão equivalente de Von Mises (independe do endurecimento cinemático), q, do módulo de cisalhamento, G, e do módulo volumétrico, K: Y = q 6G( D) + p K( D) (.5) 5) Lei de Hooke generalizada O tensor tensão, por sua vez, é dado segundo a lei de Hooke generalizada, conforme apresentado a seguir: σ = ( D)D e : ε e (.5) A Tabela., por sua vez, apresenta um resumo das equações que governam o modelo elastoplástico de Lemaitre com endurecimento cinemático de Chaboche. 5
38 Tabela. - Modelo Matemático para o modelo de Lemaitre com endurecimento cinemático de Chaboche. i) Decomposição aditiva da deformação: ii) Lei de Hooke: iii) Função de escoamento: ε = ε e + ε p σ = ( D)D e : ε e φ = D η: η σ y 0 vi) Lei de fluxo plástico: ε p γ N = γ N ( D) N = η q = η η e leis de evolução para outras variáveis internas ε p ε p : ε p = γ D m β = β i i= m = γ D ( H i k N b i β i ) i= D = γ s D ( Y S ) Y = q 6G( D) + p K( D) v) Regra da Complementariedade γ 0 φ 0 γ φ = 0 6
39 .5.7 MODELO CDM MODIFICADO COM ENDURECIMENTO CINEMÁTICO ) Função de escoamento φ = q D σ y 0 (.54) onde, φ é a função de escoamento segundo Lemaitre, q é a tensão equivalente de Von Mises, D é a variável isotrópica de dano e σ y0 é a tensão de escoamento inicial. A tensão equivalente é matematicamente determinada por: q (η) = η: η (.55) onde, η é o tensor relativo, cujo cálculo é realizado através da expressão abaixo: η = S β (.56) onde, β é o tensor das tensões cinemáticas e S é o tensor das tensões desviadoras. ) Vetor de fluxo N φ σ = η q ( D) = η η ( D) (.57) onde, N é o vetor de fluxo. A seguir definimos o vetor de fluxo efetivo N : N = η = q η η (.58) O vetor de fluxo pode ser reescrito ao substituirmos a variável N na Eq..58: N φ σ = N ( D) (.59) ) Lei de fluxo plástico ε p γ N = γ N ( D) (.60) 7
40 onde, ε p e γ representam respectivamente, a taxa de evolução da deformação plástica e do multiplicador plástico. 4) Lei de evolução para outras variáveis internas ε p ε p : ε p = γ D (.6) onde, ε p é a taxa de evolução da deformação plástica equivalente. A seguir iremos definir β, ou seja, a lei de evolução para o tensor das tensões cinemáticas. m β = β i i= m = γ D ( H i k N b i β i ) i= (.6) onde, m é o número de termos não lineares no somatório da lei de evolução de Chaboche, β i é o termo i da taxa de evolução do tensor das tensões cinemáticas, H k é módulo de endurecimento cinemático e b i corresponde ao termo i da constante do material relativa ao endurecimento cinemático. A Eq..6, por sua vez, traz a lei de evolução para a variável isotrópica de dano. D = γ D ( Y S(Γ,ξ) )s (.6) onde, Y é força termodinâmica associada ao dano, s é o expodente de dano e S(Γ, ξ) é a função denominador de dano. Conforme pode ser constatado através da Eq..64, a última variável mencionada depende do terceiro invariante normalizado do tensor desviador ξ, da razão de triaxialidade Γ, do denominador de dano para baixa triaxialidade S 0.00 e do denominador de dano para alta triaxialidade S 0.. S(Γ, ξ) = S 0. Γ + S 0. S 0.00 ( ξ ) (.64) O terceiro invariante normalizado do tensor desviador ξ, por sua vez, está relacionado ao tensor das tensões desviadoras S e a tensão equivalente de Von Mises q. Matematicamente, temos: ξ = (7 ) det S q (.65) 8
41 A tensão equivalente de Von Mises na Eq..66 independe do endurecimento cinemático. Dessa forma, temos a seguinte expressão matemática para q: q = J (S) = S: S (.66) onde, J é o segundo invariante do tensor tensão desviador S. Na Eq..6 observamos também a variável denominada triaxialidade, definida matematicamente pela razão entre dois parâmetros elastoplásticos, conforme apresentado a seguir: Γ = p q (.67) onde, p é conhecido por tensão hidrostática e q por tensão equivalente de Von Mises (independe do endurecimento cinemático). A força termodinâmica associada a variável interna de dano, Y, deriva do potencial de estado devido à elasticidade-dano e pode ser escrita como: ψ ed (ε e, D) Y = ρ = D εe : ( D)D: ε e (.68) onde, ρ é a densidade do material na configuração de referência, ψ ed é a contribuição devido a elasticidade-dano na energia livre, ε e é a deformação elástica e D é o tensor constitutivo. Após algumas manipulações matemáticas, é possível escrever Y em função da pressão hidrostática, p, da tensão equivalente de Von Mises (independe do endurecimento cinemático), q, do módulo de cisalhamento, G, e do módulo volumétrico, K: Y = q 6G( D) + p K( D) (.69) 5) Lei de Hooke generalizada O tensor tensão, por sua vez, é dado segundo a lei de Hooke generalizada, conforme apresentado a seguir: σ = ( D)D e : ε e (.70) A Tabela.4 apresenta um resumo das equações que governam o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche. 9
42 Tabela.4 - Modelo Matemático para o modelo associativo modificado de Lemaitre com endurecimento cinemático de Chaboche. i) Decomposição aditiva da deformação: ii) Lei de Hooke: iii) Função de escoamento: vi) Lei de fluxo plástico: ε = ε e + ε p σ = ( D)D e : ε e φ = D η: η σ y 0 ε p γ N = γ N ( D), com N = η η = q η e leis de evolução para outras variáveis internas ε p ε p : ε p = γ D m β = β i i= m = γ D ( H i k N b i β i ) i= D = γ D ( Y S(Γ,ξ) )s S(Γ, ξ) = S 0. Γ + S 0. S 0.00 ( ξ ) Y = q 6G( D) + p K( D) v) Regra da Complementariedade γ 0 φ 0 γ φ = 0 0
43 MODELOS NUMÉRICOS. INTRODUÇÃO Para materiais e modelos elastoplásticos cujo comportamento é dependente da trajetória, a solução do conjunto de equações do modelo constitutivo requer a formulação de um algoritmo de integração numérica. Este procedimento será detalhado a seguir para os modelos de Von Mises, Lemaitre e CDM modificado. Nestes casos teremos três termos não lineares no somatório da lei de evolução de Chaboche para a tensão de endurecimento cinemático, ou seja, m =. Inicialmente, estabelece-se um pseudo-intervalo de tempo [t n, t n+ ], em que o estado n é conhecido e deseja-se obter o estado n +. Dentro do pseudotempo o algoritmo numérico deverá ser capaz de atualizar a tensão σ n+ e as variáveis internas α n+ através de metodologia amplamente utilizada na plasticidade computacional e conhecida por decomposição do operador. Posteriormente, é realizada a discretização das equações constitutivas no pseudo-tempo, com base no algoritmo de Euler implícito. A atualização das tensões e das variáveis internas é realizada em duas partes: i. Preditor elástico: o problema é assumido como completamente elástico; ii. Corretor plástico: um sistema de equações residuais não-lineares e discretizado é resolvido com o método de Newton-Raphson, considerando os valores obtidos a partir do preditor elástico como valores iniciais. Figura. - Algoritmo de atualização das tensões e variáveis internas. Na Figura. temos o algoritmo o algoritmo de mapeamento de retorno ou de atualização das tensões e das variáveis internas. Assume-se que um incremento de deformação
44 Δε completamente elástico foi aplicado. A partir disso, obtém-se o estado tentativa ( ) trial. Em seguida é realizada a avaliação da função de escoamento para o estado tentativa φ trial. Caso tenhamos φ trial 0, o passo dado será puramente elástico, e o estado real ( ) n+ será idêntico ao estado tentativa ( ) trial. Caso contrário teremos φ trial > 0 e será necessário corrigir o estado tentativa aplicando o corretor plástico. Para este comportamento, o incremento de deformação plástica será removido da deformação elástica tentativa.. MODELO DE VON MISES COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE Nesta seção será tratada a formulação dos modelos numéricos considerando a abordagem de Von Mises com endurecimento cinemático de Chaboche. Para tanto, serão desenvolvidos o algoritmo de atualização das tensões e variáveis internas bem como o algoritmo de resolução do sistema não linear. ) Atualização de variáveis internas Para o modelo de Von Mises com lei de evolução do tensor de endurecimento cinemático dado por Chaboche, temos a seguinte atualização do tensor deformação elástica: e ε n+ e ε n+ e = ε trial n+ Δε p e = ε trial n+ γn n+ e = ε trial n+ γn n+ (.) e e trial onde, ε n+ é o tensor das deformações elásticas no pseudo-tempo t n+, ε n+ é o tensor das deformações elásticas tentativa no pseudo-tempo t n+, Δε p é o incremento de deformação plástica, γ é o incremento do multiplicador plástico, N n+ é o vetor de fluxo no pseudo-tempo t n+, N n+ é o vetor de fluxo normalizado no pseudo-tempo t n+ e q n+ é a tensão equivalente de Von Mises no pseudo-tempo t n+. A seguir temos atualização do tensor tensão com a aplicação da lei de Hooke: σ n+ = σ trial n+ G γn n+ e σ n+ = D: ε trial n+ G γn n+ (.) trial onde, σ n+ é o tensor tensão no pseudo-tempo t n+, σ n+ é o tensor tensão tentativa no pseudo-tempo t n+, G é o módulo de cisalhamento e D é o tensor constitutivo.
45 ) Atualização de outras variáveis internas De forma discretizada, a atualização da deformação plástica equivalente é dada pela Eq... Ao invés de remover o incremento de deformação plástica equivalente, este deve ser adicionado. Matematicamente, temos: p ε n+ = ε n p + ε p p ε n+ = ε n p + γ (.) p onde, ε p é o incremento de deformação plástica, ε n+ é a deformação plástica equivalente no pseudo-tempo t n+ e ε n p é a deformação plástica equivalente no pseudotempo t n. Para o tensor das tensões cinemáticas é necessário definir o valor de m, ou seja, o número de termos não lineares no somatório da lei de evolução de Chaboche. Com m =, temos: i β n+ = β n+ i= = β n+ + β n+ + β n+ (.4) i onde, β n+ é a tensão de endurecimento cinemático no pseudo-tempo t n+ e β n+ é o termo i da tensão de endurecimento cinemático no pseudo-tempo t n+. Analisando a i Eq,.4, verifica-se que é necessário atualizar cada termo β n+ separadamente, para em seguida considerar o somatório de forma a obter β n+. Portanto, com base na lei de evolução de Chaboche, temos: β i n+ = βi n + γ ( H i k N n+ b i β i n+ ) (.5) onde, β i n é o termo i da tensão de endurecimento cinemático no pseudo-tempo t n, H k i é o termo i do módulo de endurecimento cinemático e b i é termo i da constante do material relativa ao endurecimento cinemático. Finalmente, a função de escoamento no estado real é dada segundo a Eq..6. φ n+ = q n+ σ y0 (.6) onde, q n+ é a tensão equivalente de Von Mises normalizada (independe do endurecimento cinemático) no pseudo-tempo t n+ e φ n+ é a função de escoamento segundo no pseudo-tempo t n+.
46 ) Sistema de equações não-lineares Verifica-se a formação de um sistema não linear de equações cujos valores para as variáveis σ n+, γ, β n+, β n+ e β n+ são desconhecidos no estado real. e σ n+ = D: ε trial n+ G γn n+ φ n+ = q n+ σ y0 β n+ = β n + γ ( H k N n+ b β n+ ) β n+ = β n + γ ( H k N n+ b β n+ ) (.7) { β n+ = β n + γ ( H k N n+ b β n+ ) 4) Sistema de equações não-lineares na forma de equações residuais As equações de atualização na forma de resíduos são dadas por: e R σn+ = σ n+ D: ε trial n+ + G γn n+ R γ = q n+ σ y0 R β n+ = β n+ β n γ ( H k N n+ b β n+ ) R β n+ = β n+ β n γ ( H k N n+ b β n+ ) (.8) { R β = β n+ n+ β n γ ( H k N n+ b β n+ ) 5) Linearização do sistema A Tabela. apresenta de forma resumida o algoritmo de atualização das tensões e variáveis internas para o modelo de Von Mises com endurecimento cinemático de Chaboche. Para a aplicação do método de Newton-Raphson, o sistema deve ser reescrito na forma linearizada, conforme apresentado através da Eq..9. R σn+ σ n+ R σn+ Δγ R σn+ R σn+ R σn+ k R Δγ σ n+ σ n+ σ n+ R Δγ Δγ Δγ Δγ R Δγ R Δγ R Δγ k+ δσ n+ [ δδγ δβ n+ δβ n+ δβ n+ ] = [ R σn+ R Δγ R βn+ R βn+ R βn+ ] k (.9) [ σ n+ Δγ ] 4
47 6) Derivada das equações residuais A Tabela. mostra, de forma resumida, a aplicação do método de Newton-Raphson para a resolução do sistema não linear. O estado inicial, ou seja, para k = 0, é tomado como sendo o estado tentativa. Para a primeira equação residual, temos: R σn+ σ n+ R σn+ Δγ = I + GΔγ N n+ S n+ = GN n+ R σn+ = GΔγ N n+ R σn+ = GΔγ N n+ (.0) R σn+ = GΔγ N n+ Para a segunda equação residual, temos: R Δγ σ n+ = N n+ R Δγ Δγ = 0 R Δγ = N n+ R Δγ = N n+ (.) R Δγ = N n+ Para a terceira equação residual, temos: σ n+ Δγ = Δγ H k N n+ σ n+ = H k N n+ b β n+ = I Δγ ( H k N n+ b I) = Δγ H k N n+ (.) = Δγ H k N n+ 5
48 Para a quarta equação residual, temos: σ n+ Δγ = Δγ H k N n+ σ n+ = H k N n+ b β n+ = Δγ H k N n+ (.) = I Δγ ( H k N n+ b I) = Δγ H k N n+ Para a quinta equação residual, temos: σ n+ Δγ = Δγ H k N n+ σ n+ = H k N n+ b β n+ = Δγ H k N n+ = Δγ H k N n+ (.4) = I Δγ ( H k N n+ b I) Outras derivadas: N n+ = [I I I η σ n+ q n+ (q n+ ) n+ η n+ ] N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] (.5) N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] 6
49 Tabela. - Modelo Numérico - Algoritmo de atualização das tensões e variáveis internas para o modelo de Von Mises com endurecimento cinemático de Chaboche i) Dado um incremento de deformação Δε, determinar o estado tentativa: e ε trial n+ = ε e n + Δε p ε trial p n+ = ε n p ε n+ trial p = ε n q n+ trial = ( )η n+ : η n+ σ trial n+ = ( D n )D e e trial : ε n+ β trial n+ = β n β trial n+ = β n β trial n+ = β n ii) Verificar a admissibilidade plástica: φ trial = q n+ trial σ y0 Se φ trial 0, então (passo elástico): ( ) trial n+ = ( ) n+ Se φ trial > 0, então (passo plástico): algoritmo de retorno. iii) Algoritmo de retorno: Resolver o sistema de equações não lineares pelo método de Newton-Raphson, tendo como variáveis σ n+, γ, β n+, β n+ e β n+. e R σn+ = σ n+ D: ε trial n+ + G γn n+ R γ = q n+ σ y0 R β n+ = β n+ β n γ ( H k N n+ b β n+ ) R β n+ = β n+ β n γ ( H k N n+ b β n+ ) { R β = β n+ n+ β n γ ( H k N n+ b β n+ ) iv) Atualizar as outras variáveis internas. v) Fim. 7
50 Tabela. - Algoritmo de resolução do sistema não linear para o modelo de Von Mises com endurecimento cinemático de Chaboche. i) Dado o estado tentativa como parâmetros iniciais: (0) σ n+ trial = σ n+ Δγ (0) = 0 (0) β n+ = trial (0) βn+ β n+ = trial (0) βn+ β n+ = trial βn+ i ii) Resolver o sistema de equações para σ n+, β n+ e Δγ: [ R σn+ σ n+ R Δγ σ n+ σ n+ σ n+ σ n+ R σn+ Δγ R Δγ Δγ Δγ Δγ Δγ R σn+ β n+ R Δγ β n+ β n+ β n+ β n+ R σn+ β n+ R Δγ β n+ β n+ β n+ β n+ R k σn+ β n+ R Δγ k+ β δσ n+ n+ β n+ β n+ β n+ ] [ δδγ δβ n+ δβ n+ δβ n+ ] = [ R σn+ R Δγ R βn+ R βn+ R βn+ ] k iii) Calcular: (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) σ n+ = σn+ + δσn+ (k+) (k) (k+) Δγ n+ = Δγn+ + δδγn+ iv) Verificar a convergência: φ (k+) = q (k+) σ y0 erro = φ(k+) σ y0 tolerância v) Fim. 8
51 . MODELO DE LEMAITRE COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE Nesta seção será tratada a formulação dos modelos numéricos considerando a abordagem de Lemaitre com endurecimento cinemático de Chaboche. Para tanto, serão desenvolvidos o algoritmo de atualização das tensões e variáveis internas bem como o algoritmo de resolução do sistema não linear. ) Atualização de variáveis internas Para o modelo de Lemaitre com lei de evolução do tensor de endurecimento cinemático dado por Chaboche, temos a seguinte atualização do tensor deformação elástica: e ε n+ e = ε trial n+ Δε p e = ε trial n+ γn n+ e ε n+ e = ε trial n+ γn n+ ( D n+ ) (.6) e e trial onde, ε n+ é o tensor das deformações elásticas no pseudo-tempo t n+, ε n+ é o tensor das deformações elásticas tentativa no pseudo-tempo t n+, Δε p é o incremento de deformação plástica, γ é o incremento do multiplicador plástico, N n+ é o vetor de fluxo no pseudo-tempo t n+, N n+ é o vetor de fluxo normalizado no pseudo-tempo t n+, q n+ é a tensão equivalente de Von Mises no pseudo-tempo t n+ e D n+ é a variável de dano no pseudo-tempo t n+. Atualização do tensor tensão com a aplicação da lei de Hooke danificada: σ n+ = σ trial n+ ( D n+ )G γn n+ e σ n+ = ( D n+ )D: ε trial n+ ( D n+ )G γ N n+ ( D n+ ) (.7) e σ n+ = ( D n+ )D: ε trial n+ G γn n+ trial onde, σ n+ é o tensor tensão no pseudo-tempo t n+, σ n+ é o tensor tensão tentativa no pseudo-tempo t n+, G é o módulo de cisalhamento e D é o tensor constitutivo. ) Atualização de outras variáveis internas De forma discretizada, a atualização da deformação plástica equivalente é dada pela Eq..8. Ao invés de remover o incremento de deformação plástica equivalente, este deve ser adicionado. Matematicamente, temos: p ε n+ = ε n p + ε p D n+ (.8) 9
52 p ε n+ = ε n p + γ D n+ p onde, ε p é o incremento de deformação plástica, ε n+ é a deformação plástica equivalente no pseudo-tempo t n+ e ε n p é a deformação plástica equivalente no pseudotempo t n. Para o tensor das tensões cinemáticas é necessário definir o valor de m, ou seja, o número de termos não lineares no somatório da lei de evolução de Chaboche. Com m =, temos: i β n+ = β n+ i= = β n+ + β n+ + β n+ (.9) i onde, β n+ é a tensão de endurecimento cinemático no pseudo-tempo t n+ e β n+ é o termo i da tensão de endurecimento cinemático no pseudo-tempo t n+. i Analisando a Eq..9, verifica-se que é necessário atualizar cada termo β n+ separadamente, para em seguida considerar o somatório de forma a obter β n+. Portanto, com base na lei de evolução de Chaboche, temos: β i n+ = βi n + γ ( D n+ ) ( H i k N n+ b i β i n+ ) (.0) onde, β i n é o termo i da tensão de endurecimento cinemático no pseudo-tempo t n, H i k é o termo i do módulo de endurecimento cinemático e b i é termo i da constante do material relativa ao endurecimento cinemático. Com relação a evolução da variável isotrópica de dano, temos: D n+ = D n + γ ( D n+ ) ( Y n+ S s ) (.) Na Eq.. o termo Y n+ corresponde à força termodinâmica associada ao dano no pseudo-tempo t n+. q n+ p n+ Y n+ = 6G( D n+ ) + K( D n+ ) (.) onde, q n+ é a tensão equivalente de Von Mises (independe do endurecimento cinemático) no pseudo-tempo t n+ e p n+ é a pressão hidrostática no pseudo-tempo t n+. Finalmente, a função de escoamento no estado real é dada segundo a Eq... 40
53 φ n+ = q n+ ( D n+ ) σ y 0 (.) onde, φ n+ é a função de escoamento segundo Lemaitre no pseudo-tempo t n+. ) Sistema de equações não-lineares Verifica-se a formação de um sistema não linear de equações cujos valores para as variáveis σ n+, γ, D n+, β n+, β n+ e β n+ são desconhecidos no estado real. e σ n+ = ( D n+ )D: ε trial n+ G γn n+ q n+ φ n+ = ( D n+ ) σ y 0 s γ D n+ = D n + ( D n+ ) ( Y n+ ) S β n+ = β n + γ ( D n+ ) ( H k N n+ b β n+ ) β n+ = β n + γ ( D n+ ) ( H k N n+ b β n+ ) β { n+ = β n + γ ( D n+ ) ( H k N n+ b β n+ ) (.4) 4) Sistema de equações não-lineares na forma de equações residuais As equações de atualização na forma de resíduos são dadas por: e R σn+ = σ n+ ( D n+ )D: ε trial n+ + G γn n+ q n+ R γ = ( D n+ ) σ y 0 s γ R Dn+ = D n+ D n ( D n+ ) ( Y n+ ) S R β = β n+ n+ β n γ ( D n+ ) ( H k N n+ b β n+ ) R β = β n+ n+ β n γ ( D n+ ) ( H k N n+ b β n+ ) R { β = β n+ n+ β n γ ( D n+ ) ( H k N n+ b β n+ ) (.5) 5) Linearização do sistema A Tabela. apresenta de forma resumida o algoritmo de atualização das tensões e variáveis internas para o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche. Para a aplicação do método de Newton-Raphson, o sistema deve ser reescrito na forma linearizada, conforme apresentado na Eq..6. 4
54 R σn+ σ n+ R σn+ Δγ R σn+ D n+ R σn+ R σn+ R σn+ k R Δγ σ n+ R Dn+ σ n+ σ n+ σ n+ R Δγ Δγ R Dn+ Δγ Δγ Δγ R Δγ D n+ R Dn+ D n+ D n+ D n+ R Δγ R Dn+ R Δγ R Dn+ R Δγ R Dn+ [ δσ n+ δδγ δd n+ δβ n+ δβ n+ δβ n+ ] k+ (.6) [ σ n+ Δγ D n+ ] = R σn+ R Δγ R Dn+ R βn+ R βn+ R βn+ ] [ k 6) Derivada das equações residuais A Tabela.4 mostra, de forma resumida, a aplicação do método de Newton-Raphson para a resolução do sistema não linear. O estado inicial, ou seja, para k = 0, é tomado como sendo o estado tentativa. Para a primeira equação residual, temos: R σn+ σ n+ R σn+ Δγ = I + GΔγ N n+ S n+ = GN n+ R σn+ D n+ R σn+ e trial = D: ε n+ = GΔγ N n+ (.7) R σn+ = GΔγ N n+ R σn+ = GΔγ N n+ Para a segunda equação residual, temos: 4
55 R Δγ σ n+ = D n+ N n+ R Δγ Δγ = 0 R Δγ = q n+ D n+ ( D n+ ) R Δγ β = N n+ D n+ n+ (.8) R Δγ β = N n+ D n+ n+ R Δγ β = N n+ D n+ n+ Para a terceira equação residual, temos: R D n+ σ n+ = s γ R D n+ Δγ = S( D n+ ) ( Y n+ ) s ( Y n+ ) S σ n+ ( D n+ ) ( Y n+ ) s S R D n+ D n+ R D n+ = = 0 ( D n+ ) ( Y n+ S ) s s γ S( D n+ ) ( Y n+ ) s ( Y n+ ) S σ n+ (.9) R D n+ = 0 R D n+ = 0 Para a quarta equação residual, temos: = Δγ H σ n+ D n+ k N n+ σ n+ Δγ = ( H D n+ k N n+ b β n+ ) = D n+ γ ( D n+ ) ( H k N n+ b β n+ ) β = I Δγ n+ ( H D n+ k N n+ b I) (.0) β = Δγ n+ D n+ β = Δγ n+ D n+ H k N n+ β n+ H k N n+ β n+ 4
56 Tabela. - Modelo Numérico - Algoritmo de atualização das tensões e variáveis internas para o modelo elastoplástico de Lemaitre com endurecimento cinemático de Chaboche. i) Dado um incremento de deformação Δε, determinar o estado tentativa: e ε trial n+ = ε e n + Δε p ε trial p n+ = ε n p ε n+ trial p = ε n q n+ trial = η n+: η n+ D trial n+ = D n σ trial n+ = ( D n )D e e trial : ε n+ β trial n+ = β n β trial n+ = β n β trial n+ = β n ii) Verificar a admissibilidade plástica: φ trial = trial q n+ ( D trial n+ ) σ y 0 Se φ trial 0, então (passo elástico): ( ) trial n+ = ( ) n+ Se φ trial > 0, então (passo plástico): algoritmo de retorno. iii) Algoritmo de retorno: Resolver o sistema de equações não lineares pelo método de Newton-Raphson, tendo como variáveis σ n+, γ, D n+, β n+, β n+ e β n+. e R σn+ = σ n+ ( D n+ )D: ε trial n+ + G γn n+ R γ = q n+ ( D n+ ) σ y 0 R Dn+ = D n+ D n γ ( D n+ ) ( Y n+ ) s S γ R β = β n+ n+ β n ( D n+ ) ( H k N n+ b β n+ ) R β = β n+ n+ β n ( D n+ ) ( H k N n+ b β n+ ) { R β = β n+ n+ β n ( D n+ ) ( H k N n+ b β n+ ) γ γ iv) Atualizar as outras variáveis internas. v) Fim. 44
57 Tabela.4 - Algoritmo de resolução do sistema não linear para o modelo elastoplástico de Lemaitre com endurecimento cinemático de Chaboche. i) Dado o estado tentativa como parâmetros iniciais: (0) σ n+ trial = σ n+ Δγ (0) (0) trial = 0 D n+ = D n+ (0) β n+ = trial (0) βn+ β n+ = trial (0) βn+ β n+ = trial βn+ i ii) Resolver o sistema de equações para σ n+, β n+, Δγ e D n+ : R σn+ σ n+ R σn+ Δγ R σn+ D n+ R σn+ R σn+ R σn+ k R Δγ σ n+ R Dn+ σ n+ σ n+ σ n+ R Δγ Δγ R Dn+ Δγ Δγ Δγ R Δγ D n+ R Dn+ D n+ D n+ D n+ R Δγ R Dn+ R Δγ R Dn+ R Δγ R Dn+ [ δσ n+ δδγ δd n+ δβ n+ δβ n+ δβ n+ ] k+ = R σn+ R Δγ R Dn+ R βn+ R βn+ R βn+ ] [ k [ R βn+ σ n+ R βn+ Δγ R βn+ D n+ R βn+ R βn+ R βn+ ] iii) Calcular: (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) σ n+ = σn+ + δσn+ (k+) (k) (k+) Δγ n+ = Δγn+ + δδγn+ (k+) (k) (k+) D n+ = Dn+ + δdn+ iv) Verificar a convergência: φ (k+) = q (k+) (k+) D σ y 0 n+ erro = φ(k+) σ y0 tolerância v) Fim. 45
58 Para a quinta equação residual, temos: = Δγ H σ n+ D n+ k N n+ σ n+ Δγ = ( H D n+ k N n+ b β n+ ) = D n+ γ ( D n+ ) ( H k N n+ b β n+ ) β = Δγ n+ D n+ H k N n+ β n+ (.) β = I Δγ n+ β = Δγ n+ D n+ ( H D n+ k N n+ b I) H k N n+ β n+ Para a sexta equação residual, temos: = Δγ H σ n+ D n+ k N n+ σ n+ Δγ = ( H D n+ k N n+ b β n+ ) = D n+ γ ( D n+ ) ( H k N n+ b β n+ ) β = Δγ n+ D n+ H k N n+ β n+ (.) β = Δγ n+ D n+ β = I Δγ n+ H k N n+ β n+ ( H D n+ k N n+ b I) Outras derivadas: N n+ = [I I I η σ n+ q n+ (q n+ ) n+ η n+ ] N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] (.) N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] 46
59 ( Y n+ ) σ n+ = ( Y n+ ) D n+ = ( D n+ ) [S n+ + p n+i ] G K q n+ + p n+ G( D n+ ) K( D n+ ) ( Y n+ ) = 0 (.4) ( Y n+ ) = 0 ( Y n+ ) = 0.4 MODELO CDM MODIFICADO COM ENDURECIMENTO CINEMÁTICO DE CHABOCHE Nesta seção será tratada a formulação dos modelos numéricos considerando a abordagem associativa modificada de Lemaitre com endurecimento cinemático de Chaboche. Para tanto, serão desenvolvidos o algoritmo de atualização das tensões e variáveis internas bem como o algoritmo de resolução do sistema não linear. ) Atualização do tensor deformação elástica: e ε n+ e = ε trial n+ Δε p e = ε trial n+ γn n+ e ε n+ e = ε trial n+ γn n+ ( D n+ ) (.5) e e trial onde, ε n+ é o tensor das deformações elásticas no pseudo-tempo t n+, ε n+ é o tensor das deformações elásticas tentativa no pseudo-tempo t n+, Δε p é o incremento de deformação plástica, γ é o incremento do multiplicador plástico, N n+ é o vetor de fluxo no pseudo-tempo t n+, N n+ é o vetor de fluxo normalizado no pseudo-tempo t n+, q n+ é a tensão equivalente de Von Mises no pseudo-tempo t n+ e D n+ é a variável de dano no pseudo-tempo t n+. Atualização do tensor tensão com a aplicação da lei de Hooke danificada: σ n+ = σ trial n+ ( D n+ )G γn n+ N n+ e σ n+ = ( D n+ )D: ε trial n+ ( D n+ )G γ ( D n+ ) (.6) e σ n+ = ( D n+ )D: ε trial n+ G γn n+ 47
60 trial onde, σ n+ é o tensor tensão no pseudo-tempo t n+, σ n+ é o tensor tensão tentativa no pseudo-tempo t n+, G é o módulo de cisalhamento e D é o tensor constitutivo. ) Atualização das variáveis internas De forma discretizada, a atualização da deformação plástica equivalente é dada pela Eq..7. Ao invés de remover o incremento de deformação plástica equivalente, este deve ser adicionado. Matematicamente, temos: p ε n+ = ε n p + γ D n+ (.7) p onde, ε p é o incremento de deformação plástica, ε n+ é a deformação plástica equivalente no pseudo-tempo t n+ e ε n p é a deformação plástica equivalente no pseudotempo t n. Para o tensor das tensões cinemáticas é necessário definir o valor de m, ou seja, o número de termos não lineares no somatório da lei de evolução de Chaboche. Com m =, temos: i β n+ = β n+ i= = β n+ + β n+ + β n+ (.8) i onde, β n+ é a tensão de endurecimento cinemático no pseudo-tempo t n+ e β n+ é o termo i da tensão de endurecimento cinemático no pseudo-tempo t n+. i Analisando a Eq..8, verifica-se que é necessário atualizar cada termo β n+ separadamente, para em seguida considerar o somatório de forma a obter β n+. Portanto, com base na lei de evolução de Chaboche, temos: β i n+ = βi n + γ ( D n+ ) ( H i k N n+ b i β i n+ ) (.9) onde, β i n é o termo i da tensão de endurecimento cinemático no pseudo-tempo t n, H k i é o termo i do módulo de endurecimento cinemático e b i é termo i da constante do material relativa ao endurecimento cinemático. Com relação a evolução da variável isotrópica de dano, temos: s γ D n+ = D n + ( D n+ ) ( Y n+ S(Γ, ξ) ) (.40) 48
61 Na Eq..40 o termo Y n+ corresponde à força termodinâmica associada ao dano no pseudo-tempo t n+. As grandezas E, v e ρ, por sua vez, são respectivamente, o módulo de elasticidade, o coeficiente de Poisson e a densidade do material. q n+ p n+ Y n+ = 6G( D n+ ) + K( D n+ ) (.4) onde, q n+ é a tensão equivalente de Von Mises (independe do endurecimento cinemático) no pseudo-tempo t n+ e p n+ é a pressão hidrostática no pseudo-tempo t n+. Finalmente, a função de escoamento no estado real é dada segundo a Eq..4. φ n+ = q n+ ( D n+ ) σ y 0 (.4) onde, φ n+ é a função de escoamento segundo Lemaitre no pseudo-tempo t n+. ) Sistema de equações não-lineares Verifica-se a formação de um sistema não linear de equações cujos valores para as variáveis σ n+, γ, D n+, β n+, β n+ e β n+ são desconhecidos no estado real. e σ n+ = ( D n+ )D: ε trial n+ G γn n+ q n+ φ n+ = ( D n+ ) σ y 0 s γ D n+ = D n + ( D n+ ) ( Y n+ S(Γ, ξ) ) β n+ = β n + γ ( D n+ ) ( H k N n+ b β n+ ) β n+ = β n + γ ( D n+ ) ( H k N n+ b β n+ ) β { n+ = β n + γ ( D n+ ) ( H k N n+ b β n+ ) (.4) 49
62 4) Sistema de equações não-lineares na forma de equações residuais As equações de atualização na forma de resíduos são dadas por: e R σn+ = σ n+ ( D n+ )D: ε trial n+ + G γn n+ q n+ R γ = ( D n+ ) σ y 0 s γ R Dn+ = D n+ D n ( D n+ ) ( Y n+ S(Γ, ξ) ) R β = β n+ n+ β n γ ( D n+ ) ( H k N n+ b β n+ ) R β = β n+ n+ β n γ ( D n+ ) ( H k N n+ b β n+ ) R { β = β n+ n+ β n γ ( D n+ ) ( H k N n+ b β n+ ) (.44) 5) Linearização do sistema A Tabela.5 apresenta de forma resumida o algoritmo de atualização das tensões e variáveis internas para o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche. Para a aplicação do método de Newton-Raphson, o sistema deve ser reescrito na forma linearizada, conforme apresentado na Eq..45. R σn+ σ n+ R σn+ Δγ R σn+ D n+ R σn+ R σn+ R σn+ k [ R Δγ σ n+ R Dn+ σ n+ σ n+ σ n+ R βn+ σ n+ R Δγ Δγ R Dn+ Δγ Δγ Δγ R βn+ Δγ R Δγ D n+ R Dn+ D n+ D n+ D n+ R βn+ D n+ R Δγ R Dn+ R βn+ R Δγ R Dn+ R βn+ R Δγ R Dn+ R βn+ ] [ δσ n+ δδγ δd n+ δβ n+ δβ n+ δβ n+ ] k+ (.45) = R σn+ R Δγ R Dn+ R βn+ R βn+ k R βn+ ] [ 50
63 6) Derivadas das equações residuais A Tabela.6 mostra, de forma resumida, a aplicação do método de Newton-Raphson para a resolução do sistema não linear. O estado inicial, ou seja, para k = 0, é tomado como sendo o estado tentativa. Para a primeira equação residual, temos: R σn+ σ n+ R σn+ Δγ = I + GΔγ N n+ S n+ = GN n+ R σn+ D n+ R σn+ e trial = D: ε n+ = GΔγ N n+ (.46) R σn+ = GΔγ N n+ R σn+ = GΔγ N n+ Para a segunda equação residual, temos: R Δγ σ n+ = D n+ N n+ R Δγ Δγ = 0 R Δγ = q n+ D n+ ( D n+ ) R Δγ β = N n+ D n+ n+ (.47) R Δγ β = N n+ D n+ n+ R Δγ β = N n+ D n+ n+ Para a terceira equação residual, temos: R D n+ σ n+ = s γ ( D n+ ) ( Y n+ R D n+ Δγ = ( D n+ ) ( Y n+ S(Γ,ξ) )s S(Γ,ξ) )s ( Y n+ σ n+ S(Γ,ξ) ) R D n+ D n+ = γ ( D n+ ) ( Y n+ S(Γ,ξ) )s s γ ( D n+ ) ( Y n+ S(Γ,ξ) )s ( Y n+ S(Γ,ξ) ) D n+ (.48) R D n+ = 0 R D n+ = 0 5
64 R D n+ = 0 Para a quarta equação residual, temos: = Δγ H σ n+ D n+ k N n+ σ n+ Δγ = ( H D n+ k N n+ b β n+ ) = D n+ γ ( D n+ ) ( H k N n+ b β n+ ) β = I Δγ n+ ( H D n+ k N n+ b I) (.49) β = Δγ n+ D n+ β = Δγ n+ D n+ H k N n+ β n+ H k N n+ β n+ Para a quinta equação residual, temos: = Δγ H σ n+ D n+ k N n+ σ n+ Δγ = ( H D n+ k N n+ b β n+ ) = D n+ γ ( D n+ ) ( H k N n+ b β n+ ) β = Δγ n+ D n+ H k N n+ β n+ (.50) β = I Δγ n+ β = Δγ n+ D n+ ( H D n+ k N n+ b I) H k N n+ β n+ Para a sexta equação residual, temos: = Δγ H σ n+ D n+ k N n+ σ n+ Δγ = ( H D n+ k N n+ b β n+ ) = D n+ γ ( D n+ ) ( H k N n+ b β n+ ) (.5) β = Δγ n+ D n+ β = Δγ n+ D n+ H k N n+ β n+ H k N n+ β n+ 5
65 β = I Δγ n+ ( H D n+ k N n+ b I) Outras derivadas: N n+ = [I I I η σ n+ q n+ (q n+ ) n+ η n+ ] N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] (.5) N n+ = [I I I η q n+ (q n+ ) n+ η n+ ] ( Y n+ S(Γ,ξ) ) σ n+ = σ n+ ( Y n+ )S(Γ, ξ) ( Y n+ S(Γ,ξ) ) = S(Γ, ξ) Y n+ S(Γ,ξ) ( Y σ n+ σ n+ )S(Γ, ξ) n+ σ n+ ( Y n+ S(Γ,ξ) ) D n+ = D n+ ( Y n+ )S(Γ, ξ) = S(Γ, ξ) Y n+ D n+ ( Y n+ S(Γ,ξ) ) = 0 (.5) ( Y n+ S(Γ,ξ) ) = 0 ( Y n+ S(Γ,ξ) ) = 0 Y n+ σ n+ = Y n+ D n+ = ( D n+ ) [S n+ n+i G K ] (.54) q n+ + p n+ G( D n+ ) K( D n+ ) S(Γ,ξ) σ n+ = Γ = σ n+ ξ σ n+ = ξ S 0. ( Γ [ Γ + S 0. S0.00 ( ξ )] Γ q n+ I r σ n+ Γ S q n+ n+ q n+ r σ n+ q Γ ξs 0. σ n+ S 0.00 ξ ) σ n+ (.55) 5
66 Tabela.5 - Modelo Numérico - Algoritmo de atualização das tensões e variáveis internas para o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche. i) Dado um incremento de deformação Δε, determinar o estado tentativa: e ε trial n+ = ε e n + Δε p ε trial p n+ = ε n p ε n+ trial p = ε n q n+ trial = η n+: η n+ D trial n+ = D n σ trial n+ = ( D n )D e e trial : ε n+ β trial n+ = β n β trial n+ = β n β trial n+ = β n ii) Verificar a admissibilidade plástica: φ trial = trial q n+ ( D trial n+ ) σ y 0 Se φ trial 0, então (passo elástico): ( ) trial n+ = ( ) n+ Se φ trial > 0, então (passo plástico): algoritmo de retorno. iii) Algoritmo de retorno: Resolver o sistema de equações não lineares pelo método de Newton-Raphson, tendo como variáveis σ n+, γ, D n+, β n+, β n+ e β n+. { e R σn+ = σ n+ ( D n+ )D: ε trial n+ + G γn n+ R γ = q n+ ( D n+ ) σ y 0 R Dn+ = D n+ D n γ ( D n+ ) ( Y n+ S(Γ,ζ) )s γ R β = β n+ n+ β n ( D n+ ) ( H k N n+ b β n+ ) γ R β = β n+ n+ β n ( D n+ ) ( H k N n+ b β n+ ) γ R β = β n+ n+ β n ( D n+ ) ( H k N n+ b β n+ ) iv) Atualizar as outras variáveis internas. v) Fim. 54
67 Tabela.6 - Algoritmo de resolução do sistema não linear para o modelo elastoplástico associativo modificado de Lemaitre com endurecimento cinemático de Chaboche. i) Dado o estado tentativa como parâmetros iniciais: (0) σ n+ trial = σ n+ Δγ (0) (0) trial = 0 D n+ = D n+ (0) β n+ = trial (0) βn+ β n+ = trial (0) βn+ β n+ = trial βn+ i ii) Resolver o sistema de equações para σ n+, β n+, Δγ e D n+ : R σn+ σ n+ R σn+ Δγ R σn+ D n+ R σn+ R σn+ R σn+ k R Δγ σ n+ R Dn+ σ n+ σ n+ σ n+ R Δγ Δγ R Dn+ Δγ Δγ Δγ R Δγ D n+ R Dn+ D n+ D n+ D n+ R Δγ R Dn+ R Δγ R Dn+ R Δγ R Dn+ [ δσ n+ δδγ δd n+ δβ n+ δβ n+ δβ n+ ] k+ = R σn+ R Δγ R Dn+ R βn+ R βn+ R βn+ ] [ k [ R βn+ σ n+ R βn+ Δγ R βn+ D n+ R βn+ R βn+ R βn+ ] iii) Calcular: (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) β n+ = βn+ + δβn+ (k+) (k) (k+) σ n+ = σn+ + δσn+ (k+) (k) (k+) Δγ n+ = Δγn+ + δδγn+ (k+) (k) (k+) D n+ = Dn+ + δdn+ iv) Verificar a convergência: φ (k+) = q (k+) (k+) D σ y 0 n+ erro = φ(k+) σ y0 tolerância v) Fim. 55
68 onde, r σ n+ e q n+ σ n+ representam as derivadas, respectivamente, do terceiro invariante e da tensão equivalente de Von Mises, em relação ao tensor tensão, que são determinadas como: q n+ σ n+ = S n+ S n+ r = 9 dets n+ σ n+ r σ n+ (.56) onde, dets n+ σ n+ representa a derivada do determinante do tensor desviador S n+ em relação ao tensor tensão, que pode ser escrita como: dets n+ σ n+ = dets n+ : S n+ (.57) S n+ σ n+ As Eq..58 e.59, por sua vez, estão relacionadas respectivamente, a derivada do determinante do tensor desviador S n+ com relação ao tensor desviador e a derivada do tensor desviador com relação ao tensor tensão σ n+. dets n+ S n+ = det(s n+ S n+ T ) (.58) S n+ = I I I (.59) σ n+ 56
69 4 ESTRATÉGIA DE IDENTIFICAÇÃO DE PARÂMETROS 4. INTRODUÇÃO Os problemas numéricos diretos ocorrem quando o modelo constitutivo, a geometria inicial e as condições de contorno são conhecidas. Trata-se de um problema clássico de elementos finitos onde o objetivo é determinar a geometria final, as tensões e deformações bem como a evolução das grandezas do processo. Os problemas de otimização de pré-forma e problemas de identificação de parâmetros, por sua vez, correspondem a classes dos problemas numéricos inversos. No primeiro caso, espera-se identificar a geometria inicial após especificarmos a deformação e geometria final de determinada estrutura ou componente. A outra classe trata da aplicação de modelos constitutivos para identificar parâmetros a partir de resultados experimentais. A Fig. 4. resume o processo de calibração dos parâmetros de tensão e de dano dos modelos constitutivos elastoplásticos. Nos tópicos seguintes iremos detalhar, portanto, a referida estratégia de identificação do dano crítico, denominadores de dano, módulos e constantes de endurecimento cinemático, bem como do limite de escoamento inicial. Figura 4. Algoritmo de calibração dos parâmetros de tensão e de dano do modelo constitutivo. 57
70 4. CALIBRAÇÃO DOS PARÂMETROS DO MATERIAL Para definir os parâmetros materiais do aço S460N foi utilizado o modelo de Lemaitre com endurecimento cinemático conforme teoria proposta por Chaboche para dois termos não lineares e um termo linear, resultando na lei de evolução do tensor tensão de endurecimento cinemático conforme descrito pela equação abaixo: β = H k ε p γ b β + H k ε p γ b β + H k ε p (4.) Dessa forma, os seguintes parâmetros deverão ser obtidos: σ y0, H k, H k, H k, b, b e S. Considera-se o expoente de dano s = para a maioria dos materiais metálicos dúcteis como o aço S460N (Malcher, 0). Verifica-se que o denominador de dano (S) está relacionado a taxa de crescimento da variável de dano. Os parâmetros σ y0, H k i e b i, por sua vez, estão relacionados aos níveis de tensão do material. Dessa forma, verifica-se que uma calibração dos parâmetros elencados de forma simultânea não seria o ideal. O processo de calibração dos denominadores de dano consistiu na identificação dos parâmetros de tensão (σ y0, H k i e b i ) e na identificação dos parâmetros de dano (S 0. e S 0.00 ). Uma vez que estas análises levam em consideração níveis de tensão diferentes, dividiu-se o processo de calibração em duas etapas. 4.. CALIBRAÇÃO DOS PARÂMETROS DE TENSÃO Observa-se uma relação analítica entre as amplitudes de deformação aplicadas em estado uniaxial e as amplitudes de tensão obtidas na análise dos parâmetros de tensão. De acordo com Chaboche (986), considerando um carregamento uniaxial cíclico com amplitude de deformação plástica ε p a e amplitude de tensão σ a, verifica-se que a lei de endurecimento cinemático de Chaboche é composta por dois termos não lineares e um termo linear, conforme exposto através da Eq σ a = H k k p H tanh(b b ε a ) + p tanh(b b ε a ) + k H ε p a + σ y0 (4.) Os parâmetros materiais H e n presentes na Eq. 4. foram obtidos para o aço S460N a partir da literatura (Jiang et al, 007). Considerando também as amplitudes de deformação plástica e de tensão, é possível definir os parâmetros de tensão (H i k, b i e σ y0 ) com um ajuste da 58
71 curva de Ramberg-Osgood, uma vez que esta relaciona σ a e ε a p. Importante frisar que ao aplicarmos na regressão dados experimentais relativos ao aço S460N, os resultados para a calibração dos parâmetros de tensão deverão ser mais precisos. ε p a = ( σ a n H ) (4.) Através de um algoritmo (anexo A) desenvolvido no programa Matlab, realizou-se um ajuste linear, considerando a função nlinfit e uma tolerância de 0 8 para cada parâmetro. A seguir apresentamos, respectivamente, nas Tabelas 4. e 4. os parâmetros relativos à equação de Ramberg-Osgood e os resultados aferidos para a lei de endurecimento cinemático proposta por Chaboche. Tabela 4. Parâmetros de Ramberg-Osgood, módulo de elasticidade e coeficiente de Poisson para o aço S460N (Jiang et al., 007). Parâmetro S460N (Jiang et al., 007) H (MPa) 5 n 0,6 E (GPa) 08 v 0,0 Tabela 4. Resultados da calibração por amplitude para o modelo de Chaboche e parâmetros da curva de Ramberg-Osgood obtidos da literatura para o aço S460N. Parâmetro S460N (Jiang et al., 007) k H (MPa) k H (MPa) k H (MPa) 60 b 6,5 b 98,50 σ y0 (MPa) 70 Através da Fig. 4. é possível comparar os dados relativos à equação de Ramberg- Osgood com os valores aferidos através da regressão com a função nlinfit, que relaciona a amplitude de tensão e a amplitude de deformação plástica para o modelo de Chaboche. 59
72 Figura 4. Comparação entre dados experimentais e valores obtidos com regressão. 4.. CALIBRAÇÃO DO DANO CRÍTICO E DOS DENOMINADORES DE DANO A tabela 4. contém dados extraídos do trabalho desenvolvido por Jiang (007), onde espécimes cilíndricos fabricados a partir do aço S460N foram submetidos a ensaios de fadiga com carregamentos uniaxiais normais ou cisalhantes. Definido o número de ciclos e a amplitude de deformações, foi possível identificar o valor do dano para diferentes denominadores de dano, conforme apresentado na tabela 4.4. Tabela 4. Ensaios de fadiga conduzidos utilizando espécimes cilíndricos (Jiang et al., 007). Carregamento ε (%) γ (%) σ (MPa) τ (MPa) N (ciclos) Normal Cisalhante Ainda com relação à tabela abaixo, em verde e azul, respectivamente, foram destacados os valores de dano crítico próximos a 0.0 e 0.0. Com base na Figura 4. é possível verificar 60
73 que a tendência no limite é de convergência para o dano com a ampliação do denominador de dano, independentemente do nível de deformação aplicado. Tabela 4.4 Relação de valores obtidos para o dano a partir da variação do denominador de dano, número de ciclos e amplitude de deformação normal. Denominador Dano N (ciclos) ε (%) Figura 4. Variação do dano com o denominador de dano, número de ciclos e amplitudes de deformação normal. 6
74 A Figura 4., por sua vez, mostra de que forma o dano variou com a alteração do denominador de dano entre 0. e 0 bem como do número de ciclos e amplitude de deformação cisalhante aplicada ao aço S460N. Todos os dados obtidos foram relacionados na tabela 4.5 e novamente destacou-se em verde e azul, respectivamente, os valores de dano crítico próximos a 0.0 e 0.0. Figura 4.4 Variação do dano com o denominador de dano, número de ciclos e amplitudes de deformação cisalhante. Tabela 4.5 Relação de valores obtidos para o dano a partir da variação do denominador de dano, número de ciclos e amplitude de deformação cisalhante. Denominador Dano
75 N (ciclos) γ (%) A tabela 4.6, além de resumir a tabela 4.4, traz os denominadores de dano para alta triaxialidade (S 0. ). Considerando a média dos denominadores aferidos para um dano crítico de 0.0, temos S 0. igual a 5.. Por sua vez, para um dano de 0.0, S 0. corresponde a 0.8. Tabela 4.6 Denominadores de dano obtidos a partir de simulações com tensões normais e utilizados na previsão de vida em fadiga com os modelos de Lemaitre e CDM modificado. Dano S [MPa] S / [MPa] ε (%) N (ciclos) Conforme pode ser observado abaixo, a tabela 4.7 traz os denominadores de dano de baixa triaxialidade (S 0.00 ) para os danos críticos de 0.0 e 0.0, os quais equivalem respectivamente a e Importante ressaltar que o algoritmo implementado em MATLAB e utilizado para identificação dos danos a partir da definição das amplitudes de deformação cisalhantes e normais bem como do número de ciclos e do denominador de dano, encontra-se no Anexo A. 6
76 Tabela 4.7 Denominadores de dano obtidos a partir de simulações com tensões cisalhantes e utilizados na previsão de vida em fadiga com o modelo CDM modificado. Dano S [MPa] S 0 [MPa] ϒ (%) N (ciclos) 64
77 5 RESULTADOS E DISCUSSÃO 5. ANÁLISE DOS RESULTADOS Neste capítulo, serão apresentados os resultados referentes à implementação do modelo de dano de Lemaitre com endurecimento cinemático de Chaboche para o aço S460N, submetido a carregamentos uniaxiais e multiaxiais. Em seguida, os dados aferidos serão comparados ao modelo CDM modificado com endurecimento cinemático de Chaboche. Os parâmetros do material analisado foram apresentados no Capítulo 4. Com o objetivo de comparar a capacidade dos modelos apresentados de prever o comportamento elastoplástico do aço S460N quando submetido a carregamentos axiais e cisalhantes, proporcionais ou não proporcionais, implementou-se o algoritmo de atualização de tensões aplicado em um ponto material com o uso da linguagem computacional FORTRAN. Na seção 5. os históricos de carregamentos aplicados ao material em estudo são apresentados. Na seção 5., por sua vez, realiza-se uma comparação entre os resultados aferidos de vida em fadiga e os disponíveis em literatura. A seção 5.4 traz as curvas de evolução de dano, ao passo que na seção 5.5 observa-se as conclusões referentes aos tópicos elencados neste capítulo. 5. CARREGAMENTOS No trabalho desenvolvido por Jiang et. al (007), foram aplicados ao aço S460N os carregamentos com trajetórias uniaxiais (A e B), multiaxiais proporcionais (C) e multiaxiais não proporcionais (D), conforme apresentado através da Fig. 5.. Os anexos B e C trazem as rotinas de carregamento desenvolvidas em linguagem FORTRAN. Figura 5. Históricos de carregamento impostos para o aço S460N (Jiang et al., 007). 65
IMPLEMENTAÇÃO IMPLÍCITA DO MODELO DE PLASTICIDADE CÍCLICA DE CHABOCHE
 PROJETO DE GRADUAÇÃO IMPLEMENTAÇÃO IMPLÍCITA DO MODELO DE PLASTICIDADE CÍCLICA DE CHABOCHE Por Jhonatan da Ponte Lopes Brasília, 9 de Dezembro de 04 UNIVERSIDADE DE BRASILIA FACULDADE DE TECNOLOGIA DEPARTAMENTO
PROJETO DE GRADUAÇÃO IMPLEMENTAÇÃO IMPLÍCITA DO MODELO DE PLASTICIDADE CÍCLICA DE CHABOCHE Por Jhonatan da Ponte Lopes Brasília, 9 de Dezembro de 04 UNIVERSIDADE DE BRASILIA FACULDADE DE TECNOLOGIA DEPARTAMENTO
IMPLEMENTAÇÃO E VALIDAÇÃO DE MODELOS CONSTITUTIVOS PARA PLASTICIDADE CÍCLICA
 UNIVERSIDADE DE BRASÍLIA FACULDADE GAMA/FACULDADE DE TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM INTEGRIDADE DE MATERIAIS DA ENGENHERIA IMPLEMENTAÇÃO E VALIDAÇÃO DE MODELOS CONSTITUTIVOS PARA PLASTICIDADE
UNIVERSIDADE DE BRASÍLIA FACULDADE GAMA/FACULDADE DE TECNOLOGIA PROGRAMA DE PÓS-GRADUAÇÃO EM INTEGRIDADE DE MATERIAIS DA ENGENHERIA IMPLEMENTAÇÃO E VALIDAÇÃO DE MODELOS CONSTITUTIVOS PARA PLASTICIDADE
Cap. 1: INTRODUÇÃO AO ESTUDO DA FADIGA. Fadiga dos Materiais Metálicos - Prof. Carlos Baptista EEL
 Cap. 1: INTRODUÇÃO AO ESTUDO DA FADIGA John Braithwaite (1797-1870) OS PIONEIROS August Wöhler (1819-1914) OS PIONEIROS OS PIONEIROS James Alfred Ewing (1855-1935) O FENÔMENO DA FADIGA Ocorrência - Processo
Cap. 1: INTRODUÇÃO AO ESTUDO DA FADIGA John Braithwaite (1797-1870) OS PIONEIROS August Wöhler (1819-1914) OS PIONEIROS OS PIONEIROS James Alfred Ewing (1855-1935) O FENÔMENO DA FADIGA Ocorrência - Processo
Comportamento Elastoplástico
 Departamento de Engenharia Mecânica Comportamento Elastoplástico Prof. Arthur Braga Projeto Mecânico Estratégia Identificar possíveis modos de falha (escoamento, ruptura, fadiga, fratura, etc.) Definir
Departamento de Engenharia Mecânica Comportamento Elastoplástico Prof. Arthur Braga Projeto Mecânico Estratégia Identificar possíveis modos de falha (escoamento, ruptura, fadiga, fratura, etc.) Definir
PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO BASEADO NA MICROMECÂNICA DE DEFEITOS
 PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO BASEADO NA MICROMECÂNICA DE DEFEITOS TIAGO DE BORTOLI LUCIANO MESTRADO EM CIÊNCIAS MECÂNICAS DEPARTAMENTO DE ENGENHARIA MECÂNICA UNIVERSIDADE DE BRASÍLIA UnB
PREVISÃO DE VIDA À FADIGA ATRAVÉS DE MODELO BASEADO NA MICROMECÂNICA DE DEFEITOS TIAGO DE BORTOLI LUCIANO MESTRADO EM CIÊNCIAS MECÂNICAS DEPARTAMENTO DE ENGENHARIA MECÂNICA UNIVERSIDADE DE BRASÍLIA UnB
MODELOS INCREMENTAIS PARA PLASTICIDADE CÍCLICA: UM ESTUDO NUMÉRICO
 MODELOS INCREMENTAIS PARA PLASTICIDADE CÍCLICA: UM ESTUDO NUMÉRICO Por Carlos Magno Lopes da Silva Filho DISSERTAÇÃO DE MESTRADO EM CIÊNCIAS MECÂNICAS UNIVERSIDADE DE BRASILIA FACULDADE DE TECNOLOGIA DEPARTAMENTO
MODELOS INCREMENTAIS PARA PLASTICIDADE CÍCLICA: UM ESTUDO NUMÉRICO Por Carlos Magno Lopes da Silva Filho DISSERTAÇÃO DE MESTRADO EM CIÊNCIAS MECÂNICAS UNIVERSIDADE DE BRASILIA FACULDADE DE TECNOLOGIA DEPARTAMENTO
5 Mecanismo de dano para modelagem de corte em rocha por erosão
 5 Mecanismo de dano para modelagem de corte em rocha por erosão Devido ao modelo de dano isotrópico ser usado na modelagem da interação rocha-cortador, os conceitos envolvidos para a descrição deste modelo
5 Mecanismo de dano para modelagem de corte em rocha por erosão Devido ao modelo de dano isotrópico ser usado na modelagem da interação rocha-cortador, os conceitos envolvidos para a descrição deste modelo
UMA ANÁLISE COMPARATIVA ENTRE MODELOS DE DANO CONTÍNUO DEPENDENTES DO TERCEIRO INVARIANTE E COM MÚLTIPLOS PONTOS DE CALIBRAÇÃO JOÃO DE ALMEIDA NETO
 UNIVERSIDADE DE BRASÍLIA UnB FACULDADE DE TECNOLOGIA FT DEPARTAMENTO DE ENGENHARIA MECÂNICA UnB UMA ANÁLISE COMPARATIVA ENTRE MODELOS DE DANO CONTÍNUO DEPENDENTES DO TERCEIRO INVARIANTE E COM MÚLTIPLOS
UNIVERSIDADE DE BRASÍLIA UnB FACULDADE DE TECNOLOGIA FT DEPARTAMENTO DE ENGENHARIA MECÂNICA UnB UMA ANÁLISE COMPARATIVA ENTRE MODELOS DE DANO CONTÍNUO DEPENDENTES DO TERCEIRO INVARIANTE E COM MÚLTIPLOS
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos
 2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
2 Análise do Colapso de Estruturas através do Método dos Elementos Finitos Neste capítulo, através do método dos elementos finitos baseado em deslocamentos, são apresentadas três técnicas de análise do
Capítulo 4 Propriedades Mecânicas dos Materiais
 Capítulo 4 Propriedades Mecânicas dos Materiais Resistência dos Materiais I SLIDES 04 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Propriedades Mecânicas dos Materiais 2 3 Propriedades
Capítulo 4 Propriedades Mecânicas dos Materiais Resistência dos Materiais I SLIDES 04 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Propriedades Mecânicas dos Materiais 2 3 Propriedades
1. Introdução Objetivo
 21 1. Introdução 1.1. Objetivo O objetivo desta tese é avaliar modelos de plasticidade incremental em fadiga multiaxial. Para isso, nesta, desenvolveu-se uma máquina biaxial tração-torção servindo-se de
21 1. Introdução 1.1. Objetivo O objetivo desta tese é avaliar modelos de plasticidade incremental em fadiga multiaxial. Para isso, nesta, desenvolveu-se uma máquina biaxial tração-torção servindo-se de
MATERIAIS ELASTOPLÁSTICOS
 MATERIAIS ELASTOPLÁSTICOS - DESCRIÇÃO DO COMPORTAMENTO ELASTOPLÁSTICO Alguns elementos característicos dos ensaios de tração simples são analisados a seguir para identificar os fenômenos que devem ser
MATERIAIS ELASTOPLÁSTICOS - DESCRIÇÃO DO COMPORTAMENTO ELASTOPLÁSTICO Alguns elementos característicos dos ensaios de tração simples são analisados a seguir para identificar os fenômenos que devem ser
Estudo das equações aplicáveis em teoria de plasticidade independente do tempo. Study of equations applied in theory of plasticity independent of time
 61 Estudo das equações aplicáveis em teoria de plasticidade independente do tempo Study of equations applied in theory of plasticity independent of time Horácio Delgado Júnior 1,2 Alexandre Alvarenga Palmeira
61 Estudo das equações aplicáveis em teoria de plasticidade independente do tempo Study of equations applied in theory of plasticity independent of time Horácio Delgado Júnior 1,2 Alexandre Alvarenga Palmeira
Critérios de Escoamento
 Departamento de Engenharia Mecânica Mecânica dos Sólidos I Critérios de Escoamento Prof. Arthur Braga Projeto Mecânico Estratégia Identificar possíveis modos de falha (escoamento, ruptura, fadiga, fratura,
Departamento de Engenharia Mecânica Mecânica dos Sólidos I Critérios de Escoamento Prof. Arthur Braga Projeto Mecânico Estratégia Identificar possíveis modos de falha (escoamento, ruptura, fadiga, fratura,
2 Fundamentos para a avaliação de integridade de dutos com perdas de espessura e reparados com materiais compósitos
 2 Fundamentos para a avaliação de integridade de dutos com perdas de espessura e reparados com materiais compósitos Este capítulo apresenta um resumo dos fundamentos básicos de avaliação de dutos com e
2 Fundamentos para a avaliação de integridade de dutos com perdas de espessura e reparados com materiais compósitos Este capítulo apresenta um resumo dos fundamentos básicos de avaliação de dutos com e
ESTIMATIVA DE VIDA À FADIGA POR FRETTING EM CABOS CONDUTORES BASEADA NA MICROMECÂNICA DE DEFEITOS
 DISSERTAÇÃO DE MESTRADO EM CIÊNCIAS MECÂNICAS ESTIMATIVA DE VIDA À FADIGA POR FRETTING EM CABOS CONDUTORES BASEADA NA MICROMECÂNICA DE DEFEITOS FELIPE AZEVEDO CANUT Brasília, 30 de Setembro de 2016 UNIVERSIDADE
DISSERTAÇÃO DE MESTRADO EM CIÊNCIAS MECÂNICAS ESTIMATIVA DE VIDA À FADIGA POR FRETTING EM CABOS CONDUTORES BASEADA NA MICROMECÂNICA DE DEFEITOS FELIPE AZEVEDO CANUT Brasília, 30 de Setembro de 2016 UNIVERSIDADE
Principais propriedades mecânicas
 Principais propriedades mecânicas Resistência à tração Elasticidade Ductilidade Fluência Fadiga Dureza Tenacidade,... Cada uma dessas propriedades está associada à habilidade do material de resistir às
Principais propriedades mecânicas Resistência à tração Elasticidade Ductilidade Fluência Fadiga Dureza Tenacidade,... Cada uma dessas propriedades está associada à habilidade do material de resistir às
4 Modelo Constitutivo de Drucker-Prager para materiais rochosos
 4 Modelo Constitutivo de Drucker-Prager para materiais rochosos Os modelos constitutivos são parte essencial nas análises de distribuição de tensões e deformações em problemas complexos de Engenharia Geotécnica.
4 Modelo Constitutivo de Drucker-Prager para materiais rochosos Os modelos constitutivos são parte essencial nas análises de distribuição de tensões e deformações em problemas complexos de Engenharia Geotécnica.
Propagação de trincas por fadiga:
 O contorno de grão também pode se tornar uma importante posição para a nucleação de trincas em carregamentos de grandes amplitudes de deformação. Além disso, impurezas que induzam a fragilização localizada
O contorno de grão também pode se tornar uma importante posição para a nucleação de trincas em carregamentos de grandes amplitudes de deformação. Além disso, impurezas que induzam a fragilização localizada
LOM Teoria da Elasticidade Aplicada
 Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte - Critérios de Falha Prof. Dr. João Paulo
Departamento de Engenharia de Materiais (DEMAR) Escola de Engenharia de Lorena (EEL) Universidade de São Paulo (USP) LOM310 - Teoria da Elasticidade Aplicada Parte - Critérios de Falha Prof. Dr. João Paulo
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 2 Tensão e deformação: Carregamento axial Conteúdo Tensão e Deformação: Carregamento Axial Deformação Normal
5. Critérios de falha
 5. Critérios de falha Determinam a segurança do componente. Coeficientes de segurança arbitrários não garantem projeto seguro. Compreensão clara do(s) mecanismo(s) de falha (modos de falha). Aspectos de
5. Critérios de falha Determinam a segurança do componente. Coeficientes de segurança arbitrários não garantem projeto seguro. Compreensão clara do(s) mecanismo(s) de falha (modos de falha). Aspectos de
ESTUDO DO MODELO ELASTO-PLÁSTICO DE GAO E DESENVOLVIMENTO DE ROTINA UMAT PARA IMPLEMENTAÇÃO NO ABAQUS
 PROJETO DE GRADUAÇÃO ESTUDO DO MODELO ELASTO-PLÁSTICO DE GAO E DESENVOLVIMENTO DE ROTINA UMAT PARA IMPLEMENTAÇÃO NO ABAQUS Por, Jônatas Pinheiro de Oliveira Brasília, 02 de Julho de 2015 UNIVERSIDADE DE
PROJETO DE GRADUAÇÃO ESTUDO DO MODELO ELASTO-PLÁSTICO DE GAO E DESENVOLVIMENTO DE ROTINA UMAT PARA IMPLEMENTAÇÃO NO ABAQUS Por, Jônatas Pinheiro de Oliveira Brasília, 02 de Julho de 2015 UNIVERSIDADE DE
Aula 6 Propriedades dos materiais
 Aula 6 Propriedades Mecânicas dos Materiais E-mail: daniel.boari@ufabc.edu.br Universidade Federal do ABC Princípios de Reabilitação e Tecnologias Assistivas 3º Quadrimestre de 2018 Conceitos fundamentais
Aula 6 Propriedades Mecânicas dos Materiais E-mail: daniel.boari@ufabc.edu.br Universidade Federal do ABC Princípios de Reabilitação e Tecnologias Assistivas 3º Quadrimestre de 2018 Conceitos fundamentais
Fadiga Um metal rompe-se por fadiga quando submetido a tensões cíclicas.
 Fadiga Um metal rompe-se por fadiga quando submetido a tensões cíclicas. Fratura é de aparência frágil, mesmo que em materiais dúcteis, com formação de uma série de anéis que se desenvolvem do início da
Fadiga Um metal rompe-se por fadiga quando submetido a tensões cíclicas. Fratura é de aparência frágil, mesmo que em materiais dúcteis, com formação de uma série de anéis que se desenvolvem do início da
Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento
 Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento estrutural a partir do qual ele é feito Materiais são frequentemente
Muitos materiais, quando em serviço, são submetidos a forças ou cargas É necessário conhecer as características do material e projetar o elemento estrutural a partir do qual ele é feito Materiais são frequentemente
3. Materiais e Métodos
 34 3. Materiais e Métodos A literatura apresenta vários trabalhos que adotam o método de elementos finitos para análise da distribuição de tensões em diversos equipamentos, elementos de máquinas, peças
34 3. Materiais e Métodos A literatura apresenta vários trabalhos que adotam o método de elementos finitos para análise da distribuição de tensões em diversos equipamentos, elementos de máquinas, peças
Teste de tração - compressão
 PROPRIEDADES MECÂNICAS DOS MATERIAIS Prof. Renata Machado Soares - REMA I Teste de tração - compressão Resistência capacidade de suportar carga sem deformação excessiva ou ruptura; A partir de um ensaio
PROPRIEDADES MECÂNICAS DOS MATERIAIS Prof. Renata Machado Soares - REMA I Teste de tração - compressão Resistência capacidade de suportar carga sem deformação excessiva ou ruptura; A partir de um ensaio
COMPORTAMENTO MECÂNICO DOS MATERIAIS
 UNIVERSIDADE FEDERAL DO ABC Centro de Engenharia, Modelagem e Ciências Sociais Aplicadas (CECS) BC-1105: MATERIAIS E SUAS PROPRIEDADES COMPORTAMENTO MECÂNICO DOS MATERIAIS Propriedades Mecânicas dos Materiais
UNIVERSIDADE FEDERAL DO ABC Centro de Engenharia, Modelagem e Ciências Sociais Aplicadas (CECS) BC-1105: MATERIAIS E SUAS PROPRIEDADES COMPORTAMENTO MECÂNICO DOS MATERIAIS Propriedades Mecânicas dos Materiais
Capítulo 3: Propriedades mecânicas dos materiais
 Capítulo 3: Propriedades mecânicas dos materiais O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade
Capítulo 3: Propriedades mecânicas dos materiais O ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade
Falhas. Fraturas. Tipos de fraturas: a) Fratura Dúctil b) Fratura moderadamente dúctil c) Fratura frágil
 Falhas Fraturas Tipos de fraturas: a) Fratura Dúctil b) Fratura moderadamente dúctil c) Fratura frágil Estágios da fratura dúctil, tipo taça e cone: a) Empescoçamento inicial b) Formação de cavidades c)
Falhas Fraturas Tipos de fraturas: a) Fratura Dúctil b) Fratura moderadamente dúctil c) Fratura frágil Estágios da fratura dúctil, tipo taça e cone: a) Empescoçamento inicial b) Formação de cavidades c)
CONTEÚDOS PROGRAMADOS. (Análise Computacional de Tensões EEK 533)
 (Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
(Análise Computacional de Tensões EEK 533) - AULAS POR UNIDADE 1 - Princípios Variacionais 1.1 - Princípio dos Trabalhos Virtuais 1.2 - Princípios da Mínima Energia Total e da Mínima energia complementar.
3 Implementação Computacional
 3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
3 Implementação Computacional Neste trabalho considerou-se o estudo da instabilidade elástica e inelástica de estruturas planas como vigas, colunas, pórticos e arcos. No estudo deste tipo de estruturas
Escoamento Plástico. Instituto Tecnológico de Aeronáutica Divisão de Engenharia Mecânica MT-717: Introdução a materiais e processos de fabricação
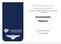 Instituto Tecnológico de Aeronáutica Divisão de Engenharia Mecânica MT-717: Introdução a materiais e processos de fabricação Escoamento Plástico Dr. Alfredo R. de Faria Dr. Ronnie Rego Agenda 1. 2. 3.
Instituto Tecnológico de Aeronáutica Divisão de Engenharia Mecânica MT-717: Introdução a materiais e processos de fabricação Escoamento Plástico Dr. Alfredo R. de Faria Dr. Ronnie Rego Agenda 1. 2. 3.
CARGA HORÁRIA TOTAL: 60 TEORIA: 60 PRÁTICA:-x- CÓDIGO: 245 E M E N T A
 DEPARTAMENTO: Engenharia Mecânica DISCIPLINA: Tópicos Especiais - Comportamento Mecânico e Seleção dos Materiais de Engenharia SIGLA: CMS CARGA HORÁRIA TOTAL: 60 TEORIA: 60 PRÁTICA:-x- CÓDIGO: 245 CURSO:
DEPARTAMENTO: Engenharia Mecânica DISCIPLINA: Tópicos Especiais - Comportamento Mecânico e Seleção dos Materiais de Engenharia SIGLA: CMS CARGA HORÁRIA TOTAL: 60 TEORIA: 60 PRÁTICA:-x- CÓDIGO: 245 CURSO:
Propriedades mecânicas dos materiais
 Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Propriedades mecânicas dos materiais Ensaio de tração e compressão A resistência de um material depende de sua capacidade de suportar uma carga sem deformação excessiva ou ruptura. Essa propriedade é inerente
Projeto de Máquina para Ensaios de Fadiga
 Universidade Santa Cecília Faculdade de Engenharia Engenharia Industrial Mecânica Objetivo Executar o projeto de uma máquina para ensaios de fadiga. Projeto de Máquina para Ensaios de Fadiga Allan Carlo
Universidade Santa Cecília Faculdade de Engenharia Engenharia Industrial Mecânica Objetivo Executar o projeto de uma máquina para ensaios de fadiga. Projeto de Máquina para Ensaios de Fadiga Allan Carlo
Fundamentos da mecânica de fratura e suas potenciais. Falhas
 Fundamentos da mecânica de fratura e suas potenciais aplicações na Análise de Falhas Docente: Prof. Willy Ank de Morais Faculdade de Engenharia / Engenharia Industrial Mecânica UNISANTA Grupo de Estudos
Fundamentos da mecânica de fratura e suas potenciais aplicações na Análise de Falhas Docente: Prof. Willy Ank de Morais Faculdade de Engenharia / Engenharia Industrial Mecânica UNISANTA Grupo de Estudos
Simulação computacional de estruturas de concreto por meio da mecânica do dano. Resumo
 1 Simulação computacional de estruturas de concreto por meio da mecânica do dano Guello, Gustavo de Assis. (1); Bittencourt, Túlio Nogueira (2) (1) Mestrando, Departamento de Engenharia de Estruturas e
1 Simulação computacional de estruturas de concreto por meio da mecânica do dano Guello, Gustavo de Assis. (1); Bittencourt, Túlio Nogueira (2) (1) Mestrando, Departamento de Engenharia de Estruturas e
Conteúdo. Resistência dos Materiais. Prof. Peterson Jaeger. 3. Concentração de tensões de tração. APOSTILA Versão 2013
 Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
Resistência dos Materiais APOSTILA Versão 2013 Prof. Peterson Jaeger Conteúdo 1. Propriedades mecânicas dos materiais 2. Deformação 3. Concentração de tensões de tração 4. Torção 1 A resistência de um
Propriedades dos Materiais Fadiga INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS FADIGA
 INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS FADIGA Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Introdução Carregamento Ensaio Fratura Variáveis 2 de 18 1 de 9 INTRODUÇÃO
INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS FADIGA Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Introdução Carregamento Ensaio Fratura Variáveis 2 de 18 1 de 9 INTRODUÇÃO
Acidentes causados a partir de trincas/fissuras em estruturas são comuns na história da engenharia (Figura 1.1).
 1 Introdução 1.1 Considerações iniciais Acidentes causados a partir de trincas/fissuras em estruturas são comuns na história da engenharia (Figura 1.1). Figura 1.1: Acidente gerado por fadiga propagação
1 Introdução 1.1 Considerações iniciais Acidentes causados a partir de trincas/fissuras em estruturas são comuns na história da engenharia (Figura 1.1). Figura 1.1: Acidente gerado por fadiga propagação
13 PROPRIEDADES MECÂNICAS DOS MATERIAIS
 NG01140 Turma C (Prof. Aleandre Pacheco) 39 13 PROPRIDADS MCÂNICAS DOS MATRIAIS Os ensaios de tração e compressão stes ensaios são provavelmente uns dos mais comuns a serem usados em engenharia. les são
NG01140 Turma C (Prof. Aleandre Pacheco) 39 13 PROPRIDADS MCÂNICAS DOS MATRIAIS Os ensaios de tração e compressão stes ensaios são provavelmente uns dos mais comuns a serem usados em engenharia. les são
3 Metodologia. 3.1 Dados experimentais da literatura
 3 Metodologia Resultados numéricos e experimentais disponíveis na literatura [31] sobre fadiga em tubos com escala real serão usados para comparar as previsões de vida à fadiga dos métodos selecionados
3 Metodologia Resultados numéricos e experimentais disponíveis na literatura [31] sobre fadiga em tubos com escala real serão usados para comparar as previsões de vida à fadiga dos métodos selecionados
UNIVERSIDADE FEDERAL DO ABC MATERIAIS E SUAS PROPRIEDADES (BC 1105) ENSAIOS MECÂNICOS ENSAIOS DE TRAÇÃO E FLEXÃO
 1 UNIVERSIDADE FEDERAL DO ABC CENTRO DE ENGENHARIA, MODELAGEM E CIÊNCIAS SOCIAIS APLICADAS MATERIAIS E SUAS PROPRIEDADES (BC 1105) ENSAIOS MECÂNICOS ENSAIOS DE TRAÇÃO E FLEXÃO 2 1. INTRODUÇÃO Algumas das
1 UNIVERSIDADE FEDERAL DO ABC CENTRO DE ENGENHARIA, MODELAGEM E CIÊNCIAS SOCIAIS APLICADAS MATERIAIS E SUAS PROPRIEDADES (BC 1105) ENSAIOS MECÂNICOS ENSAIOS DE TRAÇÃO E FLEXÃO 2 1. INTRODUÇÃO Algumas das
COMPORTAMENTO MECÂNICO DOS MATERIAIS PARTE I
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia Metalúrgica e de Materiais COMPORTAMENTO MECÂNICO DOS MATERIAIS PARTE I PMT 2100 - Introdução à Ciência dos Materiais para Engenharia
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia Metalúrgica e de Materiais COMPORTAMENTO MECÂNICO DOS MATERIAIS PARTE I PMT 2100 - Introdução à Ciência dos Materiais para Engenharia
Ensaios Mecânicos dos Materiais
 Universidade de São Paulo Escola de Engenharia de São Carlos Departamento de Engenharia de Materiais Ensaios Mecânicos dos Materiais Engenharia e Ciência dos Materiais I Prof. Dr. Cassius O. F. T. Ruckert
Universidade de São Paulo Escola de Engenharia de São Carlos Departamento de Engenharia de Materiais Ensaios Mecânicos dos Materiais Engenharia e Ciência dos Materiais I Prof. Dr. Cassius O. F. T. Ruckert
Relações entre tensões e deformações
 9 de agosto de 06 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
9 de agosto de 06 As relações entre tensões e deformações são estabelecidas a partir de ensaios experimentais simples que envolvem apenas uma componente do tensor de tensões. Ensaios complexos com tensões
3. Metodologia utilizada na modelagem numérica dos conglomerados
 52 3. Metodologia utilizada na modelagem numérica dos conglomerados Neste capítulo apresenta-se a metodologia utilizada para a determinação das propriedades mecânicas dos conglomerados, utilizando a interpretação
52 3. Metodologia utilizada na modelagem numérica dos conglomerados Neste capítulo apresenta-se a metodologia utilizada para a determinação das propriedades mecânicas dos conglomerados, utilizando a interpretação
RESISTÊNCIA DOS MATERIAIS CONTROLE DE QUALIDADE INDUSTRIAL Aula 03 TENSÃO
 CONTROLE DE QUALIDADE INDUSTRIAL Tensão Tensão é ao resultado da ação de cargas externas sobre uma unidade de área da seção analisada na peça, componente mecânico ou estrutural submetido à solicitações
CONTROLE DE QUALIDADE INDUSTRIAL Tensão Tensão é ao resultado da ação de cargas externas sobre uma unidade de área da seção analisada na peça, componente mecânico ou estrutural submetido à solicitações
10 CRITÉRIOS DE RUPTURA 10.1 MATERIAIS FRÁGEIS 0 0,5 1 1,5 2 2,5
 tensão (GPa) 10 CRITÉRIOS DE RUPTURA A avaliação das tensões e deformações sempre é feita em função de certas condições do material. Após o cálculo dessas variáveis existe a necessidade de confrontar os
tensão (GPa) 10 CRITÉRIOS DE RUPTURA A avaliação das tensões e deformações sempre é feita em função de certas condições do material. Após o cálculo dessas variáveis existe a necessidade de confrontar os
DA MECÂNICA DO DANO CONTÍNUO: UMA EVOLUÇÃO DO MODELO DE LEMAITRE PARA REDUÇÃO DA DEPENDÊNCIA DO PONTO DE CALIBRAÇÃO
 UNIVERSIDADE DE BRASÍLIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA DA MECÂNICA DO DANO CONTÍNUO: UMA EVOLUÇÃO DO MODELO DE LEMAITRE PARA REDUÇÃO DA DEPENDÊNCIA DO PONTO DE CALIBRAÇÃO
UNIVERSIDADE DE BRASÍLIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA DA MECÂNICA DO DANO CONTÍNUO: UMA EVOLUÇÃO DO MODELO DE LEMAITRE PARA REDUÇÃO DA DEPENDÊNCIA DO PONTO DE CALIBRAÇÃO
Ensaios e propriedades Mecânicas em Materiais
 FACULDADE SUDOESTE PAULISTA Ciência e Tecnologia de Materiais Prof. Ms. Patrícia Corrêa Ensaios e propriedades Mecânicas em Materiais Ensaios Mecânicos Os ensaios mecânicos consistem num conjunto de procedimentos
FACULDADE SUDOESTE PAULISTA Ciência e Tecnologia de Materiais Prof. Ms. Patrícia Corrêa Ensaios e propriedades Mecânicas em Materiais Ensaios Mecânicos Os ensaios mecânicos consistem num conjunto de procedimentos
FLUÊNCIA I. Generalidades II. Comportamento em Fluência deformação X tempo
 Deformação 1 FLUÊNCIA I. Generalidades Materiais que são freqüentemente submetidos a condições de trabalho em elevadas temperaturas sob carregamento estático podem apresentar deformação por fluência. Por
Deformação 1 FLUÊNCIA I. Generalidades Materiais que são freqüentemente submetidos a condições de trabalho em elevadas temperaturas sob carregamento estático podem apresentar deformação por fluência. Por
2 ANÁLISE LIMITE NUMÉRICA
 AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
AÁLISE LIMIE UMÉRICA O objetivo principal da Análise Limite é determinar a carga que leva uma estrutura ao colapso (carga de colapso). As formulações existentes na Análise Limite para o cálculo da carga
7 RESULTADOS EXPERIMENTAIS
 7 RESULTADOS EXPERIMENTAIS No presente capítulo, é apresentada a aplicação efetiva da metodologia desenvolvida para medição de campos de deformações. Imagens coletadas durante ensaios de tração são analisadas,
7 RESULTADOS EXPERIMENTAIS No presente capítulo, é apresentada a aplicação efetiva da metodologia desenvolvida para medição de campos de deformações. Imagens coletadas durante ensaios de tração são analisadas,
5 Resultados Experimentais
 5 Resultados Experimentais 5.1. Introdução Neste capítulo são apresentados os resultados medidos dos dois testes experimentais em escala real realizados para a comparação dos resultados teóricos. 5.2.
5 Resultados Experimentais 5.1. Introdução Neste capítulo são apresentados os resultados medidos dos dois testes experimentais em escala real realizados para a comparação dos resultados teóricos. 5.2.
Projeto de Risers Flexíveis Fadiga
 Projeto de Risers Flexíveis Fadiga Carlos Alberto D. de Lemos (Beto) Petrobras/Cenpes/Tec.. Submarina caolemos@petrobras.com.br Tubos Flexíveis Bonded Cabos Umbilicais Unbonded Tubos Flexíveis Carcaça
Projeto de Risers Flexíveis Fadiga Carlos Alberto D. de Lemos (Beto) Petrobras/Cenpes/Tec.. Submarina caolemos@petrobras.com.br Tubos Flexíveis Bonded Cabos Umbilicais Unbonded Tubos Flexíveis Carcaça
MATERIAIS PARA ENGENHARIA DE PETRÓLEO - EPET069 - Propriedades Mecânicas dos Materiais
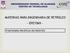 MATERIAIS PARA ENGENHARIA DE PETRÓLEO - EPET069 - Propriedades Mecânicas dos Materiais Materiais Metálicos Um material cristalino pode deformar-se plasticamente por quatro mecanismos: deslizamento de planos
MATERIAIS PARA ENGENHARIA DE PETRÓLEO - EPET069 - Propriedades Mecânicas dos Materiais Materiais Metálicos Um material cristalino pode deformar-se plasticamente por quatro mecanismos: deslizamento de planos
UNIVERSIDADE DE BRASILIA
 PROJETO DE GRADUAÇÃO PREDIÇÃO DE VIDA À FADIGA DE EIXO ENTALHADO SOB FLEXÃO-TORÇÃO BASEADA NA ABORDAGEM DEFORMAÇÃO-VIDA Por, Luiz Henrique Bresser Cardoso de Mello Brasília, 14 de Outubro de 2013 UNIVERSIDADE
PROJETO DE GRADUAÇÃO PREDIÇÃO DE VIDA À FADIGA DE EIXO ENTALHADO SOB FLEXÃO-TORÇÃO BASEADA NA ABORDAGEM DEFORMAÇÃO-VIDA Por, Luiz Henrique Bresser Cardoso de Mello Brasília, 14 de Outubro de 2013 UNIVERSIDADE
GMEC7301-Materiais de Construção Mecânica Introdução. Módulo II Ensaios Mecânicos
 GMEC7301-Materiais de Construção Mecânica Introdução Módulo II Ensaios Mecânicos OBJETIVOS DOS ENSAIOS MECÂNICOS Os ensaios são realizados com o objetivo de se obter informações específicas em relação
GMEC7301-Materiais de Construção Mecânica Introdução Módulo II Ensaios Mecânicos OBJETIVOS DOS ENSAIOS MECÂNICOS Os ensaios são realizados com o objetivo de se obter informações específicas em relação
UNIVERSIDADE FEDERAL DO ABC CENTRO DE ENGENHARIA, MODELAGEM E CIÊNCIAS SOCIAIS APLICADAS MATERIAIS E SUAS PROPRIEDADES (BC 1105)
 UNIVERSIDADE FEDERAL DO ABC CENTRO DE ENGENHARIA, MODELAGEM E CIÊNCIAS SOCIAIS APLICADAS MATERIAIS E SUAS PROPRIEDADES (BC 1105) ENSAIOS MECÂNICOS PARTE A ENSAIOS DE TRAÇÃO E FLEXÃO 2 1. INTRODUÇÃO Algumas
UNIVERSIDADE FEDERAL DO ABC CENTRO DE ENGENHARIA, MODELAGEM E CIÊNCIAS SOCIAIS APLICADAS MATERIAIS E SUAS PROPRIEDADES (BC 1105) ENSAIOS MECÂNICOS PARTE A ENSAIOS DE TRAÇÃO E FLEXÃO 2 1. INTRODUÇÃO Algumas
I. Fazer uma revisão dos modelos poroelásticos de Biot e Rice & Cleary
 1. Introdução 1.1 Objetivos Os objetivos deste trabalho são: I. Fazer uma revisão dos modelos poroelásticos de Biot e Rice & Cleary 64 buscando o entendimento de suas formulações, bem como, dos parâmetros
1. Introdução 1.1 Objetivos Os objetivos deste trabalho são: I. Fazer uma revisão dos modelos poroelásticos de Biot e Rice & Cleary 64 buscando o entendimento de suas formulações, bem como, dos parâmetros
Fadiga dos Materiais Metálicos Prof. Carlos Baptista. Cap. 2 ABORDAGEM TENSÃO-VIDA LEITURA 2: ESTIMATIVA DA CURVA S-N
 Fadiga dos Materiais Metálicos Prof. Carlos Baptista Cap. 2 ABORDAGEM TENSÃO-VIDA LEITURA 2: ESTIMATIVA DA CURVA S-N Na ausência de dados experimentais S-N, métodos para estimar o comportamento em fadiga
Fadiga dos Materiais Metálicos Prof. Carlos Baptista Cap. 2 ABORDAGEM TENSÃO-VIDA LEITURA 2: ESTIMATIVA DA CURVA S-N Na ausência de dados experimentais S-N, métodos para estimar o comportamento em fadiga
1 Introdução. Solos não saturados. Reconstituídos. Figura 1.1: Origem dos solos não saturados.
 1 Introdução Poderia-se afirmar que solos são como pessoas, se comportam e reagem segundo a sua formação e experiência prévia, isto é, de acordo com a própria história. Esta idéia leva-nos a pensar nos
1 Introdução Poderia-se afirmar que solos são como pessoas, se comportam e reagem segundo a sua formação e experiência prévia, isto é, de acordo com a própria história. Esta idéia leva-nos a pensar nos
PARTE 6: FADIGA POR FRETTING. Fadiga dos Materiais Metálicos - Prof. Carlos Baptista EEL
 PARTE 6: FADIGA POR FRETTING 0 2 2 0 1 1 0 2 2 0 1 1 V V v V V v A y y A x x A da y x q Q da y x q Q da y x p P ), ( ), ( ), ( MECÂNICA DO CONTATO Quadro de referência centrado no ponto de contato entre
PARTE 6: FADIGA POR FRETTING 0 2 2 0 1 1 0 2 2 0 1 1 V V v V V v A y y A x x A da y x q Q da y x q Q da y x p P ), ( ), ( ), ( MECÂNICA DO CONTATO Quadro de referência centrado no ponto de contato entre
Estabilidade. Marcio Varela
 Estabilidade Marcio Varela Esforços internos O objetivo principal deste módulo é estudar os esforços ou efeitos internos de forças que agem sobre um corpo. Os corpos considerados não são supostos perfeitamente
Estabilidade Marcio Varela Esforços internos O objetivo principal deste módulo é estudar os esforços ou efeitos internos de forças que agem sobre um corpo. Os corpos considerados não são supostos perfeitamente
Tensão convencional: P A. σ = Deformação convencional: = l
 Ensaio de Tração Tensão convencional: σ = P A 0 Deformação convencional: ε = l l l 0 0 2 A Amostra Área de medida A Stainless Steel sample is loaded in the tester. This device, called an EXTENSOMETER,
Ensaio de Tração Tensão convencional: σ = P A 0 Deformação convencional: ε = l l l 0 0 2 A Amostra Área de medida A Stainless Steel sample is loaded in the tester. This device, called an EXTENSOMETER,
UNIVERSIDADE FEDERAL DE SANTA MARIA Curso de Graduação em Engenharia Civil ECC 1006 Concreto Armado A ESTRUTURAS. Gerson Moacyr Sisniegas Alva
 UNIVERSIDADE FEDERAL DE SANTA MARIA Curso de Graduação em Engenharia Civil ECC 1006 Concreto Armado A COMPORTAMENTO DOS MATERIAIS E DAS ESTRUTURAS Gerson Moacyr Sisniegas Alva A prática sem teoria é cega
UNIVERSIDADE FEDERAL DE SANTA MARIA Curso de Graduação em Engenharia Civil ECC 1006 Concreto Armado A COMPORTAMENTO DOS MATERIAIS E DAS ESTRUTURAS Gerson Moacyr Sisniegas Alva A prática sem teoria é cega
Tabela 1 Características gerais dos corpos de prova escolhidos. RI=Rocha intacta; ZD=Zona de dano; NF=Núcleo da falha
 50 3 Material e método Este capítulo aborda os matérias e métodos utilizados neste estudo. Apresenta os corpos de prova utilizados, interpretação das imagens tomográficas e o método de construção do modelo
50 3 Material e método Este capítulo aborda os matérias e métodos utilizados neste estudo. Apresenta os corpos de prova utilizados, interpretação das imagens tomográficas e o método de construção do modelo
O que é Resistência dos Materiais?
 Roteiro de aula O que é Resistência dos Materiais? Definições Resistência x Rigidez Análise x Projeto Áreas de Aplicação Forças externas Esforços internos Elementos estruturais Hipóteses básicas Unidades
Roteiro de aula O que é Resistência dos Materiais? Definições Resistência x Rigidez Análise x Projeto Áreas de Aplicação Forças externas Esforços internos Elementos estruturais Hipóteses básicas Unidades
Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio NECE. Experimento de ensino baseado em problemas. Módulo 01: Análise estrutural de vigas
 Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio NECE Experimento de ensino baseado em problemas Módulo 01: Análise estrutural de vigas Aula 02: Estruturas com barras sob corportamento axial
Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio NECE Experimento de ensino baseado em problemas Módulo 01: Análise estrutural de vigas Aula 02: Estruturas com barras sob corportamento axial
2 Critérios de Resistência
 2 Critérios de Resistência O critério de resistência de solos sempre foi um foco de interesse na engenharia geotécnica, porque ele é responsável pela determinação do fator de segurança ao colapso. Como
2 Critérios de Resistência O critério de resistência de solos sempre foi um foco de interesse na engenharia geotécnica, porque ele é responsável pela determinação do fator de segurança ao colapso. Como
Objetivo do capítulo. O ensaio de tração e compressão
 Capítulo 3: Propriedades mecânicas dos materiais Adaptado pela prof. Dra. Danielle Bond Objetivo do capítulo Agora que já discutimos os conceitos básicos de tensão e deformação, mostraremos, neste capítulo,
Capítulo 3: Propriedades mecânicas dos materiais Adaptado pela prof. Dra. Danielle Bond Objetivo do capítulo Agora que já discutimos os conceitos básicos de tensão e deformação, mostraremos, neste capítulo,
O Fenômeno da Fadiga. Causa de falha mais comum (50%-90%) Normalmente falha súbita
 O Fenômeno da Fadiga Redução gradual da capacidade de carga do componente, pela ruptura lenta do material, consequência do avanço quase infinitesimal das fissuras (deformações plásticas) formadas no interior
O Fenômeno da Fadiga Redução gradual da capacidade de carga do componente, pela ruptura lenta do material, consequência do avanço quase infinitesimal das fissuras (deformações plásticas) formadas no interior
Fractura em Metais Dúcteis Modelação Numérica do Dano em Metais Dúcteis
 Modelação Numérica do Dano em Metais Dúcteis Fábio José Pinho Reis Dissertação para obtenção do Mestrado Integrado em Engenharia Mecânica Orientador: Prof. Francisco Pires Faculdade de Engenharia da Universidade
Modelação Numérica do Dano em Metais Dúcteis Fábio José Pinho Reis Dissertação para obtenção do Mestrado Integrado em Engenharia Mecânica Orientador: Prof. Francisco Pires Faculdade de Engenharia da Universidade
MODELOS ELASTO-PLÁSTICOS E SUA INFLUÊNCIA NO PROCESSO DE DIMENSIONAMENTO DE COMPONENTES MECÂNICOS
 UNIVERSIDADE DE BRASÍLIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA MODELOS ELASTO-PLÁSTICOS E SUA INFLUÊNCIA NO PROCESSO DE DIMENSIONAMENTO DE COMPONENTES MECÂNICOS CAROLINA FERNANDA
UNIVERSIDADE DE BRASÍLIA FACULDADE DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA MODELOS ELASTO-PLÁSTICOS E SUA INFLUÊNCIA NO PROCESSO DE DIMENSIONAMENTO DE COMPONENTES MECÂNICOS CAROLINA FERNANDA
AULA 4 Materiais de Construção II
 AULA 4 Materiais de Construção II Introdução Para a construção, as propriedades que interessam considerar aos metais são várias, concretamente, a aparência, densidade, dilatação e condutibilidade térmica,
AULA 4 Materiais de Construção II Introdução Para a construção, as propriedades que interessam considerar aos metais são várias, concretamente, a aparência, densidade, dilatação e condutibilidade térmica,
AULA 03 - TENSÃO E DEFORMAÇÃO
 AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. A - DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito
AULA 03 - TENSÃO E DEFORMAÇÃO Observação: Esse texto não deverá ser considerado como apostila, somente como notas de aula. A - DEFORMAÇÃO Em engenharia, a deformação de um corpo é especificada pelo conceito
Seleção dos Materiais
 Sumário Fatores gerais de influência na seleção de materiais 1 Critérios de 2 Matriz de Decisão............................... 3 Índice de Mérito................................ 4 2 Fatores gerais de influência
Sumário Fatores gerais de influência na seleção de materiais 1 Critérios de 2 Matriz de Decisão............................... 3 Índice de Mérito................................ 4 2 Fatores gerais de influência
Por fim, deve-se mencionar o problema da geometria 2D complexa. Segundo a MFLE, as taxas de propagação das trincas por fadiga dependem
 1 Introdução Este trabalho trata da simulação numérica, com verificação experimental, do processo de trincamento de componentes estruturais bi-dimensionais (2D) por fadiga sob cargas de amplitude variável.
1 Introdução Este trabalho trata da simulação numérica, com verificação experimental, do processo de trincamento de componentes estruturais bi-dimensionais (2D) por fadiga sob cargas de amplitude variável.
DISSERTAÇÃO DE MESTRADO
 DISSERTAÇÃO DE MESTRADO ESTUDO DO MÉTODO DE INTEGRAÇÃO NUMÉRICA DE DOGHRI: APLICAÇÃO AO MODELO ELASTOPLÁSTICO DE CHABOCHE Por, Edson José Alves de Souza Júnior Brasília, 02 de julho de 2018 UNIVERSIDADE
DISSERTAÇÃO DE MESTRADO ESTUDO DO MÉTODO DE INTEGRAÇÃO NUMÉRICA DE DOGHRI: APLICAÇÃO AO MODELO ELASTOPLÁSTICO DE CHABOCHE Por, Edson José Alves de Souza Júnior Brasília, 02 de julho de 2018 UNIVERSIDADE
1. Introdução 1.1. Considerações Gerais
 1. Introdução 1.1. Considerações Gerais O desenvolvimento tecnológico das últimas décadas tem influenciado intensamente a dinâmica de crescimento das cidades, evidenciando novas técnicas de construção,
1. Introdução 1.1. Considerações Gerais O desenvolvimento tecnológico das últimas décadas tem influenciado intensamente a dinâmica de crescimento das cidades, evidenciando novas técnicas de construção,
ENSAIO DE TRAÇÃO EM-641
 ENSAIO DE TRAÇÃO DEFINIÇÃO: Aplicação de uma carga uniaxial de tração em um CP geralmente cilíndrico e maciço; Mede-se a variação comprimento como função da aplicação da carga ; Fornece dados quantitativos
ENSAIO DE TRAÇÃO DEFINIÇÃO: Aplicação de uma carga uniaxial de tração em um CP geralmente cilíndrico e maciço; Mede-se a variação comprimento como função da aplicação da carga ; Fornece dados quantitativos
AVALIAÇÃO DA COMPRESSÃO DE UMA LIGA DE ALUMÍNIO: EXPERIMENTAL X NUMÉRICO
 AVALIAÇÃO DA COMPRESSÃO DE UMA LIGA DE ALUMÍNIO: EXPERIMENTAL X NUMÉRICO Alexandre da Silva Scari, alexandrescari@gmail.com 1 Bruno Cesar Pockszevnicki, brupock@yahoo.com.br 1 Daniel Miranda Horta, danieldmh@gmail.com
AVALIAÇÃO DA COMPRESSÃO DE UMA LIGA DE ALUMÍNIO: EXPERIMENTAL X NUMÉRICO Alexandre da Silva Scari, alexandrescari@gmail.com 1 Bruno Cesar Pockszevnicki, brupock@yahoo.com.br 1 Daniel Miranda Horta, danieldmh@gmail.com
Os modelos numéricos propostos foram elaborados a partir do elemento Shell 63 disponibilizado na biblioteca do programa ANSYS.
 5 Modelagem numérica Neste trabalho foram desenvolvidos modelos numéricos bidimensionais e tridimensionais. O modelo bidimensional foi adotado na simulação do conector T- Perfobond, e o tridimensional
5 Modelagem numérica Neste trabalho foram desenvolvidos modelos numéricos bidimensionais e tridimensionais. O modelo bidimensional foi adotado na simulação do conector T- Perfobond, e o tridimensional
Construir o elo de ligação entre o estado de tensão e o estado de deformação.
 Universidade Federal de Alagoas Centro de Tecnologia Curso de ngenharia Civil Disciplina: Mecânica dos Sólidos 2 Código: CIV3 Professor: duardo Nobre Lages Relações Constitutivas Maceió/AL Objetivo stado
Universidade Federal de Alagoas Centro de Tecnologia Curso de ngenharia Civil Disciplina: Mecânica dos Sólidos 2 Código: CIV3 Professor: duardo Nobre Lages Relações Constitutivas Maceió/AL Objetivo stado
AULA 4 Materiais de Construção II
 Faculdade de Engenharia - Licenciatura em Engenharia Civil UL 4 Materiais de Construção II Capítulo ula 4 (Teórica/Prática) II ços para Construção Introdução Ensaios sobre os aços: 1) Ensaio de Tracção;
Faculdade de Engenharia - Licenciatura em Engenharia Civil UL 4 Materiais de Construção II Capítulo ula 4 (Teórica/Prática) II ços para Construção Introdução Ensaios sobre os aços: 1) Ensaio de Tracção;
Deformação. - comportamento de um material quando carregado
 Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
Deformação - comportamento de um material quando carregado : tipos de deformação Deformação - deformação normal variação do comprimento de uma fibra em relação a uma direção. : tipos de deformação Deformação
1 Introdução 3. 2 Estática de partículas Corpos rígidos: sistemas equivalentes SUMÁRIO. de forças 67. xiii
 SUMÁRIO 1 Introdução 3 1.1 O que é a mecânica? 4 1.2 Conceitos e princípios fundamentais mecânica de corpos rígidos 4 1.3 Conceitos e princípios fundamentais mecânica de corpos deformáveis 7 1.4 Sistemas
SUMÁRIO 1 Introdução 3 1.1 O que é a mecânica? 4 1.2 Conceitos e princípios fundamentais mecânica de corpos rígidos 4 1.3 Conceitos e princípios fundamentais mecânica de corpos deformáveis 7 1.4 Sistemas
Métodos de Seleção de Materiais
 Métodos de Seleção de Materiais Materiais de Construção Aeroespacial (10368/10388/10408) 2015 Tópicos Análise de requisitos de projeto. Métodos qualitativos e quantitativos. Caso de estudo. 2 1. Introdução
Métodos de Seleção de Materiais Materiais de Construção Aeroespacial (10368/10388/10408) 2015 Tópicos Análise de requisitos de projeto. Métodos qualitativos e quantitativos. Caso de estudo. 2 1. Introdução
7 Análise Método dos Elementos Finitos
 168 7 Análise Método dos Elementos Finitos No presente capítulo estão apresentados os resultados da análise do problema geotécnico ilustrado no capítulo 5 realizada a partir do método dos elementos finitos.
168 7 Análise Método dos Elementos Finitos No presente capítulo estão apresentados os resultados da análise do problema geotécnico ilustrado no capítulo 5 realizada a partir do método dos elementos finitos.
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Palavras-chave: Triaxial, Argamassa, Alvenaria Estrutural, compressão.
 Anais das XXXII Jornadas Sulamericanas de Engenharia Estrutural Maio / 2006 ISBN 85-99956-01-9 Projetos Estruturais Trabalho JOR0001 - p. 2954-2963 PROPRIEDADES MECÂNICAS DAS ARGAMASSAS SOB COMPRESSÃO
Anais das XXXII Jornadas Sulamericanas de Engenharia Estrutural Maio / 2006 ISBN 85-99956-01-9 Projetos Estruturais Trabalho JOR0001 - p. 2954-2963 PROPRIEDADES MECÂNICAS DAS ARGAMASSAS SOB COMPRESSÃO
Parte 3 Comportamento mecânico de materiais e estruturas
 Parte 3 Comportamento mecânico de materiais e estruturas Capítulo 2 Proposta de superfícies de plastificação para materiais dúcteis porosos dentro de uma abordagem multi-escala Wanderson Ferreira dos
Parte 3 Comportamento mecânico de materiais e estruturas Capítulo 2 Proposta de superfícies de plastificação para materiais dúcteis porosos dentro de uma abordagem multi-escala Wanderson Ferreira dos
Introdução à Mecânica da Fratura. Universidade de Brasília UnB Departamento de Engenharia Mecânica ENM Mecânica dos Materiais II
 Introdução à Mecânica da Fratura Universidade de Brasília UnB Departamento de Engenharia Mecânica ENM Mecânica dos Materiais II Tópicos da Aula Motivação Conceitos básicos Trincas como intensificadores
Introdução à Mecânica da Fratura Universidade de Brasília UnB Departamento de Engenharia Mecânica ENM Mecânica dos Materiais II Tópicos da Aula Motivação Conceitos básicos Trincas como intensificadores
Propriedades dos Materiais Fluência INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS FLUÊNCIA
 INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS FLUÊNCIA Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Métodos Comportamento em fluência Tipos de ensaios Avaliação da fluência
INSTITUTO MILITAR DE ENGENHARIA PROGRAMA DE CIÊNCIA DOS MATERIAIS FLUÊNCIA Propriedades dos Materiais Ten Cel Sousa Lima, D. C. SUMÁRIO Métodos Comportamento em fluência Tipos de ensaios Avaliação da fluência
Estruturas Metálicas PROPRIEDADES DOS AÇOS
 Estruturas Metálicas PROPRIEDADES DOS AÇOS 1. Diagrama Tensão- Deformação Uma propriedade mecânica importante para os materiais em geral é a chamada tensão ( ), definida por: F A o Onde F é a carga aplicada
Estruturas Metálicas PROPRIEDADES DOS AÇOS 1. Diagrama Tensão- Deformação Uma propriedade mecânica importante para os materiais em geral é a chamada tensão ( ), definida por: F A o Onde F é a carga aplicada
