Aula Teórica 14 Matrizes
|
|
|
- Júlio César Ferrão Sales
- 9 Há anos
- Visualizações:
Transcrição
1 Programação de Computadores I Universidade Federal de Ouro Preto Departamento de Ciência da Computação Aula Teórica 14 Matrizes Material Didático Proposto 1
2 Agenda Introdução; Declaração de Matrizes; Algumas operações com matrizes; Algumas funções aplicadas a matrizes; Exercícios. 2
3 Introdução; Declaração de matrizes; Algumas operações com matrizes; Algumas funções aplicadas a matrizes; Exercícios. INTRODUÇÃO 3
4 Introdução Conjunto de variáveis Ao estudar vetores observamos que, em determinadas situações, é necessário utilizar muitas variáveis com um propósito comum. Relembrando exemplos: Para armazenar três notas de um aluno: Nota1 = input( Digite a nota 1: ); Nota2 = input( Digite a nota 2: ); Nota3 = input( Digite a nota 3: ); Ler e imprimir cinco números: for i = 1 : 5 Num = input( Digite um numero: ); printf( Numero digitado: %g, num); end 4
5 Introdução Relembrando Vetor Nestes casos, todas as variáveis representam um conjunto de valores, possuem um objetivo em comum e são do mesmo tipo de dados; Um vetor representa conjuntos ordenados de valores homogêneos (do mesmo tipo), que podem ser números, strings e booleanos; A palavra ordenado é empregada no sentido dos valores estarem localizados em posições ordenadas de memória, e não no sentido de estarem respeitando uma relação (<, <=, >, ou >=). 5
6 Introdução Relembrando Vetor Os itens contidos em um vetor são chamados de elementos; A posição do elemento no vetor é chamado de índice ou subscrito, e é usado para individualizar um elemento do vetor; O vetor nota = [ ], pode ser representado na memória como uma sequência de variáveis distintas, com o mesmo nome, mas diferenciadas pelo índice: 6
7 Introdução O tipo de dados Matriz Agora imagine a seguinte situação: Desejo armazenar 3 notas para 5 alunos; Para isto eu preciso de 3 vetores ou de 5 vetores? 7
8 Introdução O tipo de dados Matriz Agora imagine a seguinte situação: Desejo armazenar 3 notas para 5 alunos; Para isto eu preciso de 3 vetores ou de 5 vetores? Nenhum dos dois: podemos utilizar uma matriz em que cada linha representa um aluno e cada coluna representa uma nota: Nota 1 Nota 2 Nota 3 Aluno 1 : : Aluno
9 Introdução O tipo de dados Matriz Matrizes são variáveis que contêm uma quantidade potencialmente grande de valores; Assim como nos vetores, elementos da matriz são acessados através de índices; Uma matriz bidimensional A, com dimensão m x n (ou seja, de m linhas e n colunas: 9 OBS: Um vetor corresponde a uma matriz m x 1 (no caso de um vetor coluna), ou uma matriz 1 x n (no caso de um vetor linha).
10 Introdução O tipo de dados Matriz Além das matrizes serem muito úteis para o armazenamento e manipulação de um grande volume de dados, elas também são muito utilizadas em diversas áreas: Para se resolver sistemas de equações lineares; Translação, rotação, escala de objetos em computação gráfica; Para resolver problemas de circuitos elétricos e linhas de transmissão de energia elétrica; Algoritmos para determinar rotas entre dois pontos; E muito mais; É no tratamento de matrizes que o Scilab mostra grande superioridade sobre linguagens como C, Fortran ou Java; 10
11 Introdução Exemplos de uso de Matriz Para se ter uma pequena ideia do poder das matrizes, vejamos alguns exemplos simples do nosso cotidiano que envolvem a multiplicação de matrizes: 1. Uma lanchonete prepara três tipos de salgados utilizando diferentes tipos de ingredientes, conforme as tabelas abaixo. Qual o preço de custo de cada salgado? Ovos Farinha Açúcar Carne Pastéis Empadas Quibes Ingredientes Preço (R$) Ovos 0,20 Farinha 0,30 Açúcar 0,50 Carne 0,80 11
12 Introdução Exemplos de uso de Matriz Solução: ,20 0,30 x = 0,50 0,80 5,30 4,60 5,80 Custos: Pastéis: R$ 5,30; Empadas: R$ 4,60; Quibes: R$ 5,80. 12
13 Introdução Exemplos de uso de Matriz 2. Uma fábrica de automóveis deseja produzir uma certa quantidade de carros de dois modelos (X e Y) em três diferentes versões, utilizando três tipos de peças. Quantas peças serão necessárias para executar o plano de produção representado nas tabelas abaixo? Carro X Carro Y Peça A 4 3 Peça B 3 5 Peça C 6 2 Standard Luxo Super Luxo Carro X Carro Y
14 Introdução Exemplos de uso de Matriz Solução: x = Assim, a quantidades de peças será: Peça A: = 66; Peça B: = 77; Peça C: = 74; Calcule quantas peças cada modelo demandará no total. 14
15 Introdução Exemplos de uso de Matriz Na resolução de sistemas de equações lineares: Dado um sistema linear do tipo: A * X = B; A solução é obtida resolvendo: X = A -1 * B; Exemplo: 3x + y + 2z = 13 x + y -8z = -1 -x + 2y + 5z = 13 15
16 Introdução Exemplos de uso de Matriz Na resolução de sistemas de equações lineares: Exemplo: 3x + y + 2z = 13 x + y -8z = -1 -x + 2y + 5z = 13 --> A = [3, 1, 2; 1, 1, -8; -1, 2, 5]; --> B = [13; -1; 13]; --> X = inv(a) * B X = Assim, chega-se à solução: x = 2, y = 5, z = 1. 16
17 Introdução; Declaração de matrizes; Algumas operações com matrizes; Algumas funções aplicadas a matrizes; Exercícios. DECLARAÇÃO DE MATRIZES 17
18 Declaração de matrizes Definindo todos os elementos Utiliza-se colchetes para delimitar todos os elementos; Cada elemento de uma linha é separado por espaço ou vírgula; Cada linha é separada por um ponto-e-vírgula; Exemplo: --> M = [1, 2, 3; 4, 5, 6; 7, 8, 9] M = --> <tópicos>
19 Declaração de matrizes A partir de matrizes A definição pode ser feita a partir de matrizes já existentes; Exemplos: --> A = [1 2; 3 4] A = > B = [5 6; 7 8] B = > C = [A B] C = >D = [A; B] D = > <tópicos> 19
20 Declaração de matrizes Matriz de 1 s Todos os elementos assumirão valor inicial 1: Matriz = ones(<linhas>, <colunas>) Matriz: nome da variável do tipo matriz; ones: função que retorna uma matriz com valores 1; <linhas>: número de linhas; <colunas>: número de colunas. 20 <tópicos>
21 Declaração de matrizes Matriz de 1 s Exemplos: --> M1 = ones(2, 5) M1 = > --> M2 = ones(5, 2) M1 = > 21 <tópicos>
22 Declaração de matrizes Matriz de 0 s Todos os elementos assumirão valor inicial 0: Matriz = zeros(<linhas>, <colunas>) Matriz: nome da variável do tipo matriz; zeros: função que retorna uma matriz com valores 0; <linhas>: número de linhas; <colunas>: número de colunas. 22 <tópicos>
23 Declaração de matrizes Matriz de 0 s Exemplos: --> M1 = zeros(2, 5) M1 = > --> M2 = zeros (5, 2) M1 = > 23 <tópicos>
24 Declaração de matrizes Matriz identidade Todos os elementos da diagonal principal assumirão valor inicial 1, e os demais elementos assumirão 0: Matriz = eye(<linhas>, <colunas>) Matriz = eye(<matriz parâmetro>) Matriz: nome da variável do tipo matriz; <linhas>: número de linhas; <colunas>: número de colunas; <matriz parâmetro>: matriz que definirá as dimensões da matriz resultante. 24 <tópicos>
25 Declaração de matrizes Matriz identidade Exemplos: --> Id1 = eye(4,3) Id1 = > Id2 = eye(a) Id2 = > Id3 = eye(10) // 10 é uma matriz com um elemento (a 11 = 10) Id3 = 1. --> 25 <tópicos>
26 Declaração de matrizes Modificando o formato Pode-se declarar uma matriz modificando o formato de uma matriz conhecida: Matriz = matrix(<matriz parâmetro>, <linhas>, <colunas>) Matriz: nome da variável do tipo matriz; <matriz parâmetro>: matriz que definirá os elementos da matriz resultante; <linhas>: número de linhas da matriz resultante; <colunas>: número de colunas da matriz resultante. 26 <tópicos>
27 Declaração de matrizes Valores randômicos Pode-se declarar uma matriz com valores randômicos (gerados aleatoriamente): Matriz = rand(<linhas>, <colunas>) Matriz: nome da variável do tipo matriz; <linhas>: número de linhas da matriz resultante; <colunas>: número de colunas da matriz resultante; Gera valores entre 0 e 1; A cada chamada são gerados valores diferentes. 27 <tópicos>
28 Declaração de matrizes Valores randômicos Exemplos: --> Mr1 = rand(2,3) Mr1 = >Mr2 = rand(2,3) Mr2 = > Mr3 = int(rand(2,3) * 10) // Matriz com valores inteiros entre 0 e 10 Mr3 = > 28 <tópicos>
29 Algumas operações com matrizes Acesso aos elementos Para acessar um elemento específico: Matriz(<índice de linha>, <índice de coluna>) Exemplo: --> M = [1, 2, 3; 4, 5, 6]; --> E1 = M(2, 3) E1 = 6. --> E2 = M(1, 2) E2 = 2. --> Pode ser usado para modificar o valor: M(1, 3) = 300, modifica o valor da linha 1 e coluna 3 de 3 para 300. OBS.: Utilizando este recurso é possível definir uma matriz definindo o valor de cada um dos seus elementos individualmente. 29 <tópicos>
30 Algumas operações com matrizes Transposição de matrizes Operador apóstrofo ( ): Matriz Transforma linhas em colunas e colunas em linhas; Exemplo: x = > y = x y = <tópicos> 30
31 Algumas operações com matrizes Dimensões [a, b] = size(m) b = 4. a = 2. -->M M = <tópicos>
32 Algumas operações com matrizes Adição e subtração de matrizes --> A = [1 2 3; 4 5 6] A = >B = [1 2 3; 4 5 6] B = >C = A + B C = >C = A - B C = <tópicos>
33 Algumas operações com matrizes Multiplicação por um escalar Uma matriz pode ser multiplicada por um valor escalar; -->A A = >C = 2*A C = <tópicos>
34 Algumas operações com matrizes Multiplicação entre matrizes --> A = [1 2 3; 4 5 6] A = >B = [1 2 3; 4 5 6] B = >C = A*B!--error 10 Multiplicação incoerente. -->C = A'*B C = >C = A*B' C = <tópicos> 34
Introdução a Matrizes
 Programação de Computadores I UFOP DECOM 2013 2 Tutorial Introdução a Matrizes Resumo Neste tutorial você irá aprender como criar matrizes, como realizar operações aritméticas básicas sobre matrizes e
Programação de Computadores I UFOP DECOM 2013 2 Tutorial Introdução a Matrizes Resumo Neste tutorial você irá aprender como criar matrizes, como realizar operações aritméticas básicas sobre matrizes e
Introdução ao Scilab
 Universidade do Estado do Rio de Janeiro Faculdade de Engenharia Laboratório de Engenharia Elétrica Introdução ao Scilab (Aula 2) Elaine de Mattos Silva Orientador: Prof. José Paulo Vilela Soares da Cunha
Universidade do Estado do Rio de Janeiro Faculdade de Engenharia Laboratório de Engenharia Elétrica Introdução ao Scilab (Aula 2) Elaine de Mattos Silva Orientador: Prof. José Paulo Vilela Soares da Cunha
Introdução ao Scilab 3.0 Parte 2
 Introdução ao Scilab 3.0 Parte 2 Paulo S. Motta Pires [email protected] Departamento de Engenharia de Computação e Automação Universidade Federal do Rio Grande do Norte NATAL - RN Paulo Motta (DCA-UFRN)
Introdução ao Scilab 3.0 Parte 2 Paulo S. Motta Pires [email protected] Departamento de Engenharia de Computação e Automação Universidade Federal do Rio Grande do Norte NATAL - RN Paulo Motta (DCA-UFRN)
Algoritmos e Programação
 Algoritmos e Programação Aula 8 Matrizes Profa. Marina Gomes [email protected] 30/05/2017 Engenharia de Computação - Unipampa 1 Matrizes As variáveis vetores declarados até o momento possuem
Algoritmos e Programação Aula 8 Matrizes Profa. Marina Gomes [email protected] 30/05/2017 Engenharia de Computação - Unipampa 1 Matrizes As variáveis vetores declarados até o momento possuem
LINGUAGEM C: ARRAY: VETORES E MATRIZES
 LINGUAGEM C: ARRAY: VETORES E MATRIZES Prof. André Backes POR QUE USAR ARRAY? As variáveis declaradas até agora são capazes de armazenar um único valor por vez. Sempre que tentamos armazenar um novo valor
LINGUAGEM C: ARRAY: VETORES E MATRIZES Prof. André Backes POR QUE USAR ARRAY? As variáveis declaradas até agora são capazes de armazenar um único valor por vez. Sempre que tentamos armazenar um novo valor
Vetores. e o programa deverá ler os valores separadamente:
 Vetores Vetor é um tipo de dado usado para representar uma certa quantidade de variáveis de valores homogêneos (do mesmo tipo). Imagine o seguinte problema: calcular a média das notas da prova de 5 alunos.
Vetores Vetor é um tipo de dado usado para representar uma certa quantidade de variáveis de valores homogêneos (do mesmo tipo). Imagine o seguinte problema: calcular a média das notas da prova de 5 alunos.
Computação Eletrônica. Vetores e Matrizes. Prof: Luciano Barbosa. CIn.ufpe.br
 Computação Eletrônica Vetores e Matrizes Prof: Luciano Barbosa Recapitulando: Funções 2 Recapitulando: Função Void 3 Recapitulando: Escopo das Variáveis Referência à variável global A variável de escopo
Computação Eletrônica Vetores e Matrizes Prof: Luciano Barbosa Recapitulando: Funções 2 Recapitulando: Função Void 3 Recapitulando: Escopo das Variáveis Referência à variável global A variável de escopo
Aula 03 Introdução à Java. Disciplina: Fundamentos de Lógica e Algoritmos Prof. Bruno Gomes
 Aula 03 Introdução à Java Disciplina: Fundamentos de Lógica e Algoritmos Prof. Bruno Gomes http://www3.ifrn.edu.br/~brunogomes Agenda da Aula Representação de Algoritmos em Pseudocódigo: Tipos de Dados;
Aula 03 Introdução à Java Disciplina: Fundamentos de Lógica e Algoritmos Prof. Bruno Gomes http://www3.ifrn.edu.br/~brunogomes Agenda da Aula Representação de Algoritmos em Pseudocódigo: Tipos de Dados;
Exercícios. Faça um programa para calcular o valor de S, dado por:
 Exercício Escreva um programa que determine se dois valores inteiros e positivos A e B são primos entre si. (dois números inteiros são ditos primos entre si, caso não exista divisor comum aos dois números).
Exercício Escreva um programa que determine se dois valores inteiros e positivos A e B são primos entre si. (dois números inteiros são ditos primos entre si, caso não exista divisor comum aos dois números).
Matrizes (Vetores Bidimensionais)
 (Vetores Bidimensionais) Objetivos Conceituação de Vetores Bidimensionais Manipulação de Vetores Bidimensionais Entender a diferença entre uso dos diferentes vetores Entender como manipular entrada, saída
(Vetores Bidimensionais) Objetivos Conceituação de Vetores Bidimensionais Manipulação de Vetores Bidimensionais Entender a diferença entre uso dos diferentes vetores Entender como manipular entrada, saída
Aula 10: Introdução a Vetores e Matrizes
 Aula 10: Introdução a Vetores e Matrizes Fernanda Passos Universidade Federal Fluminense Programação de Computadores IV Fernanda Passos (UFF) Vetores e Matrizes Programação de Computadores IV 1 / 50 Agenda
Aula 10: Introdução a Vetores e Matrizes Fernanda Passos Universidade Federal Fluminense Programação de Computadores IV Fernanda Passos (UFF) Vetores e Matrizes Programação de Computadores IV 1 / 50 Agenda
Material Didático Unificado.
 Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Comissão da Disciplina Programação de Computadores I CDPCI Programação de Computadores I BCC701 www.decom.ufop.br/bcc701 Material
Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Comissão da Disciplina Programação de Computadores I CDPCI Programação de Computadores I BCC701 www.decom.ufop.br/bcc701 Material
Aula 06 Introdução à Programação Matrizes
 Aula 06 Introdução à Programação Matrizes Prof. Gustavo Callou [email protected] [email protected] Roteiro Matrizes Unidimensionais (Vetor) Bidimensionais String Exercícios Gustavo Callou DEINFO/UFRPE
Aula 06 Introdução à Programação Matrizes Prof. Gustavo Callou [email protected] [email protected] Roteiro Matrizes Unidimensionais (Vetor) Bidimensionais String Exercícios Gustavo Callou DEINFO/UFRPE
Murilo F. Tomé ICMC-USP
 INTRODUÇÃO AO MATLAB Murilo F. Tomé ICMC-USP Pré-requisitos: Utilização de editor de texto; Atribuição de valores e manuseio de variáveis; Manuseio de loops; Números reais e complexos; Vetores e matrizes.
INTRODUÇÃO AO MATLAB Murilo F. Tomé ICMC-USP Pré-requisitos: Utilização de editor de texto; Atribuição de valores e manuseio de variáveis; Manuseio de loops; Números reais e complexos; Vetores e matrizes.
SCS Sistemas de Controle / Servomecanismos. Aula 01 Introdução ao software MATLAB
 Aula 01 Introdução ao software MATLAB O MATLAB (Matrix Laboratory) é um ambiente de programação de alto desempenho voltado para a resolução de problemas expressos em notação matemática, projeto e simulação
Aula 01 Introdução ao software MATLAB O MATLAB (Matrix Laboratory) é um ambiente de programação de alto desempenho voltado para a resolução de problemas expressos em notação matemática, projeto e simulação
Revisão: Matrizes e Sistemas lineares. Parte 01
 Revisão: Matrizes e Sistemas lineares Parte 01 Definição de matrizes; Tipos de matrizes; Operações com matrizes; Propriedades; Exemplos e exercícios. 1 Matrizes Definição: 2 Matrizes 3 Tipos de matrizes
Revisão: Matrizes e Sistemas lineares Parte 01 Definição de matrizes; Tipos de matrizes; Operações com matrizes; Propriedades; Exemplos e exercícios. 1 Matrizes Definição: 2 Matrizes 3 Tipos de matrizes
Variáveis Compostas. Vanessa Braganholo
 Variáveis Compostas Vanessa Braganholo [email protected] Aula de hoje } Veremos os diferentes tipos de variáveis compostas (arrays) } Com uma dimensão (vetores) } Com duas ou mais dimensões (matrizes)
Variáveis Compostas Vanessa Braganholo [email protected] Aula de hoje } Veremos os diferentes tipos de variáveis compostas (arrays) } Com uma dimensão (vetores) } Com duas ou mais dimensões (matrizes)
Universidade Federal de Uberlândia Faculdade de Computação. Linguagem C: ponteiros e alocação dinâmica
 Universidade Federal de Uberlândia Faculdade de Computação Linguagem C: ponteiros e alocação dinâmica Prof. Renato Pimentel 1 Ponteiros 2 Prof. Renato Pimentel 1 Ponteiros: introdução Toda a informação
Universidade Federal de Uberlândia Faculdade de Computação Linguagem C: ponteiros e alocação dinâmica Prof. Renato Pimentel 1 Ponteiros 2 Prof. Renato Pimentel 1 Ponteiros: introdução Toda a informação
Inteligência Computacional Aula 2 - Introdução ao MatLab Graduação /2
 Universidade Federal do Rio de Janeiro Instituto de Matemática / DCC Inteligência Computacional Aula 2 - Introdução ao MatLab Graduação - 2003/2 Prof. A. C. G. Thomé, PhD [email protected] Airam C. P.
Universidade Federal do Rio de Janeiro Instituto de Matemática / DCC Inteligência Computacional Aula 2 - Introdução ao MatLab Graduação - 2003/2 Prof. A. C. G. Thomé, PhD [email protected] Airam C. P.
Estruturas de Dados Estáticas Cont.
 Estruturas de Dados Estáticas 1 Estruturas de Dados Estáticas Cont. Matriz (arrays multidimensionais) Uma matriz é uma variável composta homogênea bidimensional formada por uma sequência de variáveis,
Estruturas de Dados Estáticas 1 Estruturas de Dados Estáticas Cont. Matriz (arrays multidimensionais) Uma matriz é uma variável composta homogênea bidimensional formada por uma sequência de variáveis,
Algoritmos e Lógica de Programação 80 horas // 4 h/semana. Para começar... Matrizes. Para começar... Matrizes. Matrizes
 Algoritmos e Lógica de Programação 80 horas // 4 h/semana Aula 13 Prof. Piva Para começar... Vamos considerar um algoritmo que foi elaborado para para armazenar os Nomes e as Médias Finais dos 20 alunos
Algoritmos e Lógica de Programação 80 horas // 4 h/semana Aula 13 Prof. Piva Para começar... Vamos considerar um algoritmo que foi elaborado para para armazenar os Nomes e as Médias Finais dos 20 alunos
Ambiente Scilab Variáveis, expressões, comando de atribuição Entrada e Saída básica
 Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Programação de Computadores I BCC701 www.decom.ufop.br/moodle Ambiente Scilab Variáveis, expressões, comando de atribuição Entrada
Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Programação de Computadores I BCC701 www.decom.ufop.br/moodle Ambiente Scilab Variáveis, expressões, comando de atribuição Entrada
PROGRAMAÇÃO de COMPUTADORES: LINGUAGEM FORTRAN 90/95
 PROGRAMAÇÃO de COMPUTADORES: LINGUAGEM FORTRAN 90/95 Exercícios de revisão Lista 01: a) Monte um mapa conceitual indicando as relações entre os seguintes conceitos, no contexto do assunto visto em aula:
PROGRAMAÇÃO de COMPUTADORES: LINGUAGEM FORTRAN 90/95 Exercícios de revisão Lista 01: a) Monte um mapa conceitual indicando as relações entre os seguintes conceitos, no contexto do assunto visto em aula:
Material Didático Proposto
 Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Comissão para Coordenação das Atividades Pedagógicas da Disciplina BCC701 CAP-BCC701 www.decom.ufop.br/bcc701 2014-1 Material
Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Comissão para Coordenação das Atividades Pedagógicas da Disciplina BCC701 CAP-BCC701 www.decom.ufop.br/bcc701 2014-1 Material
Programação Estruturada Comandos Condicionais (Decisão) Operadores Relacionais
 Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Comissão para Coordenação das Atividades Pedagógicas da Disciplina BCC701 CAP-BCC701 www.decom.ufop.br/bcc701 2014-1 Material
Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Comissão para Coordenação das Atividades Pedagógicas da Disciplina BCC701 CAP-BCC701 www.decom.ufop.br/bcc701 2014-1 Material
Algoritmo e Programação Matemática
 Algoritmo e Programação Matemática Fundamentos de Algoritmos Parte 1 Renato Dourado Maia Instituto de Ciências Agrárias Universidade Federal de Minas Gerais Dados A funcionalidade principal de um computador
Algoritmo e Programação Matemática Fundamentos de Algoritmos Parte 1 Renato Dourado Maia Instituto de Ciências Agrárias Universidade Federal de Minas Gerais Dados A funcionalidade principal de um computador
Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Programação de Computadores I - BCC701
 Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Programação de Computadores I - BCC701 www.decom.ufop.br/red AULA TEÓRICA 02 1 Prof. Marcelo Luiz Silva Red CONTEÚDOS DA AULA
Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM Programação de Computadores I - BCC701 www.decom.ufop.br/red AULA TEÓRICA 02 1 Prof. Marcelo Luiz Silva Red CONTEÚDOS DA AULA
CURSO BÁSICO DE PROGRAMAÇÃO AULA 15. Revisão Vetores e Matrizes Trabalho
 CURSO BÁSICO DE PROGRAMAÇÃO AULA 15 Revisão Vetores e Matrizes Trabalho Definição: Introdução a Linguagem C Vetores Estrutura que permite armazenar um conjunto de dados do mesmo tipo na mesma variável;
CURSO BÁSICO DE PROGRAMAÇÃO AULA 15 Revisão Vetores e Matrizes Trabalho Definição: Introdução a Linguagem C Vetores Estrutura que permite armazenar um conjunto de dados do mesmo tipo na mesma variável;
Vetores, Matrizes e Gráficos
 Programação de Computadores I UFOP DECOM 2013 2 Aula prática 3 Vetores, Matrizes e Gráficos Resumo Nesta aula você irá utilizar vetores para resolver diversos tipos de problemas. Para expressar a solução
Programação de Computadores I UFOP DECOM 2013 2 Aula prática 3 Vetores, Matrizes e Gráficos Resumo Nesta aula você irá utilizar vetores para resolver diversos tipos de problemas. Para expressar a solução
-->A = [1 2 3; 4 5 6] A = Matrizes
![-->A = [1 2 3; 4 5 6] A = Matrizes -->A = [1 2 3; 4 5 6] A = Matrizes](/thumbs/56/38572394.jpg) Matrizes Matrizes são variáveis que contêm uma quantidade potencialmente grande de valores. É no tratamento de matrizes que o Scilab mostra grande superioridade sobre linguagens como C, Fortran ou Java.
Matrizes Matrizes são variáveis que contêm uma quantidade potencialmente grande de valores. É no tratamento de matrizes que o Scilab mostra grande superioridade sobre linguagens como C, Fortran ou Java.
Mini curso básico. Gilberto A. S. Segundo Fábio Carmo. Programa de Educação Tutorial
 Programa de Educação Tutorial Mini curso básico Universidade Federal do Espírito Santo Departamento de Informática Gilberto A. S. Segundo Fábio Carmo Agenda Apresentação Vetores e matrizes em matlab Comandos
Programa de Educação Tutorial Mini curso básico Universidade Federal do Espírito Santo Departamento de Informática Gilberto A. S. Segundo Fábio Carmo Agenda Apresentação Vetores e matrizes em matlab Comandos
CURSO SUPERIOR DE TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS DISCIPLINA : INTRODUÇÃO À LÓGICA DE PROGRAMAÇÃO ASSUNTO: ALGORITMOS
 CURSO SUPERIOR DE TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS DISCIPLINA : INTRODUÇÃO À LÓGICA DE PROGRAMAÇÃO ASSUNTO: ALGORITMOS PROFESSOR : Romilson Lopes Sampaio Introdução a Lógica de Programação
CURSO SUPERIOR DE TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS DISCIPLINA : INTRODUÇÃO À LÓGICA DE PROGRAMAÇÃO ASSUNTO: ALGORITMOS PROFESSOR : Romilson Lopes Sampaio Introdução a Lógica de Programação
Algoritmos e Programação
 Algoritmos e Programação Aula 7 Vetores Profa. Marina Gomes [email protected] 19/05/2017 Engenharia de Computação - Unipampa 1 Motivação Problema: Leia as notas de uma turma de cinco estudantes
Algoritmos e Programação Aula 7 Vetores Profa. Marina Gomes [email protected] 19/05/2017 Engenharia de Computação - Unipampa 1 Motivação Problema: Leia as notas de uma turma de cinco estudantes
Disciplina de Algoritmos e Programação. Vetor e Matriz
 Disciplina de Algoritmos e Programação Vetor e Matriz Definição de Vetor Vetor é uma variável composta homogênea unidimensional Conjunto de variáveis de mesmo tipo que possuem mesmo identificador (nome)
Disciplina de Algoritmos e Programação Vetor e Matriz Definição de Vetor Vetor é uma variável composta homogênea unidimensional Conjunto de variáveis de mesmo tipo que possuem mesmo identificador (nome)
Introdução ao Scilab. Comandos de entrada e saída de dados.
 BCC701 Programação de Computadores I Universidade Federal de Ouro Preto Departamento de Ciência da Computação www.decom.ufop.br/bcc701 2012/01 Semana 02: Introdução ao Scilab. Comandos de entrada e saída
BCC701 Programação de Computadores I Universidade Federal de Ouro Preto Departamento de Ciência da Computação www.decom.ufop.br/bcc701 2012/01 Semana 02: Introdução ao Scilab. Comandos de entrada e saída
Algoritmos II Aula 2 Vetores
 Algoritmos II Aula 2 Vetores Professor: Max Pereira [email protected] Ciência da Computação Variável Representação simbólica dos elementos de memória de um computador. Cada variável corresponde a uma
Algoritmos II Aula 2 Vetores Professor: Max Pereira [email protected] Ciência da Computação Variável Representação simbólica dos elementos de memória de um computador. Cada variável corresponde a uma
Material Didático Unificado. Variáveis correspondem a nomes para endereços de memória que são gerenciados pelo Scilab.
 Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Comissão da Disciplina Programação de Computadores I CDPCI Programação de Computadores I BCC701 www.decom.ufop.br/bcc701 Material
Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Comissão da Disciplina Programação de Computadores I CDPCI Programação de Computadores I BCC701 www.decom.ufop.br/bcc701 Material
Algoritmos e Estruturas de Dados. Prof. Marcos Quinet Universidade Federal Fluminense UFF Pólo Universitário de Rio das Ostras PURO
 Programação de Computadores I Algoritmos e Estruturas de Dados Prof. Marcos Quinet Universidade Federal Fluminense UFF Pólo Universitário de Rio das Ostras PURO Estruturas de dados Vetor (array): trata-se
Programação de Computadores I Algoritmos e Estruturas de Dados Prof. Marcos Quinet Universidade Federal Fluminense UFF Pólo Universitário de Rio das Ostras PURO Estruturas de dados Vetor (array): trata-se
Breve Introdução à Programação em Scilab 6.0
 Universidade Federal do Paraná UFPR Departamento de Engenharia Química Breve Introdução à Programação em Scilab 6.0 Prof. Éliton Fontana 2018/2 2 Conteúdo 1 Conceitos Básicos 4 2 Operando Vetores e Matrizes
Universidade Federal do Paraná UFPR Departamento de Engenharia Química Breve Introdução à Programação em Scilab 6.0 Prof. Éliton Fontana 2018/2 2 Conteúdo 1 Conceitos Básicos 4 2 Operando Vetores e Matrizes
Unidade 3: Linguagem de programação
 Unidade 3: Linguagem de programação 3.5. Trabalhando com polinômios, vetores e matrizes O programa Scilab trabalha com polinômios, vetores e matrizes de forma similar a vários pacotes computacionais disponíveis
Unidade 3: Linguagem de programação 3.5. Trabalhando com polinômios, vetores e matrizes O programa Scilab trabalha com polinômios, vetores e matrizes de forma similar a vários pacotes computacionais disponíveis
Linguagem de Programação
 Linguagem de Programação Matrizes Gil Eduardo de Andrade Introdução Uma matriz pode ser definida, assim como um vetor, como um conjunto de elementos (variáveis) que apresentam um mesmo tipo e são referenciados
Linguagem de Programação Matrizes Gil Eduardo de Andrade Introdução Uma matriz pode ser definida, assim como um vetor, como um conjunto de elementos (variáveis) que apresentam um mesmo tipo e são referenciados
PROGRAMAÇÃO DE COMPUTADORES I BCC Aula Prática 15
 Exercício 1 PROGRAMAÇÃO DE COMPUTADORES I BCC701 2017-1 Aula Prática 15 No jogo Inventei, cada posição do tabuleiro é representada por suas coordenadas x e y e contém um número. O tabuleiro pode ser representado
Exercício 1 PROGRAMAÇÃO DE COMPUTADORES I BCC701 2017-1 Aula Prática 15 No jogo Inventei, cada posição do tabuleiro é representada por suas coordenadas x e y e contém um número. O tabuleiro pode ser representado
1ª Lista de Exercícios
 Universidade Federal do Rio de Janeiro Data: 26/04/05 Disciplina: Computação I 1ª Lista de Exercícios 1) Faça um programa, em pseudo-código, que peça ao usuário que informe n números reais e então calcule
Universidade Federal do Rio de Janeiro Data: 26/04/05 Disciplina: Computação I 1ª Lista de Exercícios 1) Faça um programa, em pseudo-código, que peça ao usuário que informe n números reais e então calcule
Aula 03 - Introdução ao Scilab (p2)
 BCC701- Programação de Computadores I Aula 03 - Introdução ao Scilab (p2) Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM http://www.decom.ufop.br/bcc701 BCC701-2019-01 DECOM
BCC701- Programação de Computadores I Aula 03 - Introdução ao Scilab (p2) Universidade Federal de Ouro Preto - UFOP Departamento de Computação - DECOM http://www.decom.ufop.br/bcc701 BCC701-2019-01 DECOM
n. 1 Matrizes Cayley (1858) As matrizes surgiram para Cayley ligadas às transformações lineares do tipo:
 n. Matrizes Foi um dos primeiros matemáticos a estudar matrizes, definindo a ideia de operarmos as matrizes como na Álgebra. Historicamente o estudo das Matrizes era apenas uma sombra dos Determinantes.
n. Matrizes Foi um dos primeiros matemáticos a estudar matrizes, definindo a ideia de operarmos as matrizes como na Álgebra. Historicamente o estudo das Matrizes era apenas uma sombra dos Determinantes.
CI208 - Programação de Computadores. Aula 24: Arrays. Prof. MSc. Diego Roberto Antunes
 CI208 - Programação de Computadores Aula 24: Arrays Prof. MSc. Diego Roberto Antunes [email protected] www.inf.ufpr.br/diegor Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Informática
CI208 - Programação de Computadores Aula 24: Arrays Prof. MSc. Diego Roberto Antunes [email protected] www.inf.ufpr.br/diegor Universidade Federal do Paraná Setor de Ciências Exatas Departamento de Informática
Introdução à Programação Estruturada Parte 3. Material da Prof. Ana Eliza
 Introdução à Programação Estruturada Parte 3 Material da Prof. Ana Eliza Arquitetura do Computador Digital MEMÓRIA Armazena dados e comandos UNIDADE DE ENTRADA UNIDADE DE CONTROLE UNIDADE LÓGICA E ARITMÉTICA
Introdução à Programação Estruturada Parte 3 Material da Prof. Ana Eliza Arquitetura do Computador Digital MEMÓRIA Armazena dados e comandos UNIDADE DE ENTRADA UNIDADE DE CONTROLE UNIDADE LÓGICA E ARITMÉTICA
PROGRAMAÇÃO ESTRUTURADA E ORIENTADA A OBJETOS
 INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE PROGRAMAÇÃO ESTRUTURADA E ORIENTADA A OBJETOS Docente: Éberton da Silva Marinho e-mail: [email protected] [email protected]
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RIO GRANDE DO NORTE PROGRAMAÇÃO ESTRUTURADA E ORIENTADA A OBJETOS Docente: Éberton da Silva Marinho e-mail: [email protected] [email protected]
Exercícios: Vetores e Matrizes
 Universidade Federal de Uberlândia - UFU Faculdade de Computação - FACOM Lista de exercícios de programação em linguagem C Exercícios: Vetores e Matrizes 1 Vetores 1. Faça um programa que possua um vetor
Universidade Federal de Uberlândia - UFU Faculdade de Computação - FACOM Lista de exercícios de programação em linguagem C Exercícios: Vetores e Matrizes 1 Vetores 1. Faça um programa que possua um vetor
MATRIZES - PARTE Definição e Manipulação de Matrizes AULA 21
 AULA 21 MATRIZES - PARTE 1 21.1 Definição e Manipulação de Matrizes Sabemos como definir variáveis de um novo tipo de dados, denominado vetor, que representam seqüências de valores de um mesmo tipo. Por
AULA 21 MATRIZES - PARTE 1 21.1 Definição e Manipulação de Matrizes Sabemos como definir variáveis de um novo tipo de dados, denominado vetor, que representam seqüências de valores de um mesmo tipo. Por
Lista 2 TP060. Exercícios Vetores
 Lista 2 TP060 Esta lista auxilia nos estudos da disciplina, porém é dever do aluno estudar além do que foi visto em sala de aula e procurar resolver exercícios que não estão em listas elaboradas pelo professor
Lista 2 TP060 Esta lista auxilia nos estudos da disciplina, porém é dever do aluno estudar além do que foi visto em sala de aula e procurar resolver exercícios que não estão em listas elaboradas pelo professor
EXERCÍCIOS DE RECORDAÇÃO DE ALGORITMOS
 UNIVERSIDADE SALGADO DE OLIVEIRA CURSO DE SISTEMAS DE INFORMAÇÃO DISCIPLINA: LINGUAGEM DE PROGRAMAÇÃO I PROF: GIULIANO PRADO DE MORAIS GIGLIO EXERCÍCIOS DE RECORDAÇÃO DE ALGORITMOS 0) Faça um algoritmo
UNIVERSIDADE SALGADO DE OLIVEIRA CURSO DE SISTEMAS DE INFORMAÇÃO DISCIPLINA: LINGUAGEM DE PROGRAMAÇÃO I PROF: GIULIANO PRADO DE MORAIS GIGLIO EXERCÍCIOS DE RECORDAÇÃO DE ALGORITMOS 0) Faça um algoritmo
Estruturas Indexadas Vetores e Matrizes
 Estruturas Indexadas Vetores e Matrizes Profa Jacqueline 1 Estruturas Indexadas Vetores e Matrizes Objetivo: Estudar as estruturas de dados estáticas e homogêneas (vetores e matrizes); Estudar as operações
Estruturas Indexadas Vetores e Matrizes Profa Jacqueline 1 Estruturas Indexadas Vetores e Matrizes Objetivo: Estudar as estruturas de dados estáticas e homogêneas (vetores e matrizes); Estudar as operações
Variáveis, Expressões Aritméticas e Entrada e Saída de Dados
 Escola de Ciências e Tecnologia UFRN Variáveis, Expressões Aritméticas e Entrada e Saída de Dados ECT1103 INFORMÁTICA FUNDAMENTAL Manter o telefone celular sempre desligado/silencioso quando estiver em
Escola de Ciências e Tecnologia UFRN Variáveis, Expressões Aritméticas e Entrada e Saída de Dados ECT1103 INFORMÁTICA FUNDAMENTAL Manter o telefone celular sempre desligado/silencioso quando estiver em
Grupo de Usuários Java do Noroeste Paulista. Tópicos Avançados em Java
 Grupo de Usuários Java do Noroeste Paulista Tópicos Avançados em Java Aula 1 Objetivos Programa exemplo; Programação Orientada a Objetos. Conceitos Orientada a Objetos Mundo real Conceitos Orientada a
Grupo de Usuários Java do Noroeste Paulista Tópicos Avançados em Java Aula 1 Objetivos Programa exemplo; Programação Orientada a Objetos. Conceitos Orientada a Objetos Mundo real Conceitos Orientada a
Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Programação de Computadores I BCC701
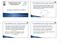 Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Programação de Computadores I BCC701 www.decom.ufop.br/moodle No circuito abaixo, temos uma fonte de voltagem V=120V, com uma
Universidade Federal de Ouro Preto -UFOP Departamento de Computação - DECOM Programação de Computadores I BCC701 www.decom.ufop.br/moodle No circuito abaixo, temos uma fonte de voltagem V=120V, com uma
GFM015 Introdução à Computação. Plano de Curso e Introdução. Ilmério Reis da Silva UFU/FACOM
 GFM015 Introdução à Computação Plano de Curso e Introdução Ilmério Reis da Silva [email protected] www.facom.ufu.br/~ilmerio/ic UFU/FACOM Plano de Curso Ementa Noções básicas sobre os componentes de
GFM015 Introdução à Computação Plano de Curso e Introdução Ilmério Reis da Silva [email protected] www.facom.ufu.br/~ilmerio/ic UFU/FACOM Plano de Curso Ementa Noções básicas sobre os componentes de
AULA 2 1) Comando linspace 2) Indexação de matriz
 AULA 2 1 1) Comando linspace >> linspace(0,10,5) ans = 0 2.5000 5.0000 7.5000 10.0000 Espaça linearmente um determinado número de elementos entre um valor final e um inicial. 2) Indexação de matriz >>
AULA 2 1 1) Comando linspace >> linspace(0,10,5) ans = 0 2.5000 5.0000 7.5000 10.0000 Espaça linearmente um determinado número de elementos entre um valor final e um inicial. 2) Indexação de matriz >>
Aula 8 Oficina de Programação Vetores. Profa. Elaine Faria UFU
 Aula 8 Oficina de Programação Vetores Profa. Elaine Faria UFU - 2017 Variáveis Compostas Homogêneas O que uma variável composta homogênea? - Conjunto de variáveis do mesmo tipo - É chamada de forma geral
Aula 8 Oficina de Programação Vetores Profa. Elaine Faria UFU - 2017 Variáveis Compostas Homogêneas O que uma variável composta homogênea? - Conjunto de variáveis do mesmo tipo - É chamada de forma geral
Aula 25 - Espaços Vetoriais
 Espaço Vetorial: Aula 25 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Espaço Vetorial: Aula 25 - Espaços Vetoriais Seja V um conjunto não vazio de objetos com duas operações definidas: 1. Uma adição que associa a cada par de objetos u, v em V um único objeto u + v, denominado
Programação: Vetores
 Programação de Computadores I Aula 09 Programação: Vetores José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/62 Motivação Problema Faça um programa que leia
Programação de Computadores I Aula 09 Programação: Vetores José Romildo Malaquias Departamento de Computação Universidade Federal de Ouro Preto 2011-1 1/62 Motivação Problema Faça um programa que leia
Vetores e Matrizes. Vetores
 Vetores e Matrizes José Gustavo de Souza Paiva Vetores Também conhecidos como variáveis compostas homogêneas unidimensionais É um tipo de dado que representa um conjunto de valores do mesmo tipo É como
Vetores e Matrizes José Gustavo de Souza Paiva Vetores Também conhecidos como variáveis compostas homogêneas unidimensionais É um tipo de dado que representa um conjunto de valores do mesmo tipo É como
Arrays. Professor: Ricardo Luis dos Santos IFSUL Campus Sapucaia do Sul
 Professor: Ricardo Luis dos Santos IFSUL 2015 Arrays ou vetores são estruturas de dados que armazenam usualmente uma quantidade fixa de dados de um determinado tipo Também são conhecidos como estruturas
Professor: Ricardo Luis dos Santos IFSUL 2015 Arrays ou vetores são estruturas de dados que armazenam usualmente uma quantidade fixa de dados de um determinado tipo Também são conhecidos como estruturas
Computação Gráfica. Engenharia de Computação. CEFET/RJ campus Petrópolis. Prof. Luis Retondaro. Aula 3. Transformações Geométricas
 Computação Gráfica Engenharia de Computação CEFET/RJ campus Petrópolis Prof. Luis Retondaro Aula 3 Transformações Geométricas no plano e no espaço Introdução (Geometria) 2 Pontos, Vetores e Matrizes Dado
Computação Gráfica Engenharia de Computação CEFET/RJ campus Petrópolis Prof. Luis Retondaro Aula 3 Transformações Geométricas no plano e no espaço Introdução (Geometria) 2 Pontos, Vetores e Matrizes Dado
ALGORITMOS 3ª Aula. 3. Introdução Tipos de dados, variáveis e operadores Tipos de dados
 3. Introdução Segundo alguns especialistas, qualquer programa de computador pode ser escrito utilizando apenas três estruturas básicas: Seqüência, Condição e Repetição. Isto significa que, na construção
3. Introdução Segundo alguns especialistas, qualquer programa de computador pode ser escrito utilizando apenas três estruturas básicas: Seqüência, Condição e Repetição. Isto significa que, na construção
Introdução a programação Vetores
 Instituto Federal de Minas Gerais Campus Ponte Nova Introdução a programação Vetores Professor: Saulo Henrique Cabral Silva Vetores 2 Como funciona Em qual variável está a oitava nota... Notas 5 2 1 9
Instituto Federal de Minas Gerais Campus Ponte Nova Introdução a programação Vetores Professor: Saulo Henrique Cabral Silva Vetores 2 Como funciona Em qual variável está a oitava nota... Notas 5 2 1 9
