III. Jogo de Lógica
|
|
|
- Alexandre de Lacerda Azenha
- 7 Há anos
- Visualizações:
Transcrição
1 III Jogo de Lógica
2 x. y. m. y'. x'. O Jogo de L ógica As instruções para se jogar encontram-se neste trabalho. y. x. y'. O jogo é constituído por 2 tabuleiros (trilateral e bilateral), e, 9 contas (5 cinzentas e 4 vermelhas). x'
3 Lew is Carroll ( ) DIAGRAMA BILATERAL xy xy x y x y O Jogo de L ógica DIAGRAMA TRILATERAL xy xy m m x y m xy m x y m xy m x y m x y m Vazio Ocupado/ um ou mais
4 O Jogo de Lógica 9 0 x. 2 y. m. y'. 3 4 x'. 5 6 CORES PARA OS CALCULADORES Vejam, o sol está lá em cima, Brilhando em nós, cheio e VERMELHO! Agora, que o sol se pôs E o céu vazio está CINZENTO! 5 6 x. y. y'. x'
5 Capítulo I Para os velhos novas lâmpadas A luz tal como vem, também vai. Proposições Alguns bolos novos são bons. Nenhum bolo novo é bom. Todos os bolos novos são bons. Aqui estão três Proposições Neste jogo usam-se apenas estes três tipos. A primeira coisa a fazer é aprender como expressá-las notabuleiro. Iniciemos por Alguns bolos novos são bons. O mundo contém muitas Coisas, (tais como: Ossos, Bebés, Baratas, Raquetes ), e estas Coisas possuem muitos atributos (tais como: lindo, preto, partido ) De facto, seja o que for, pode possuir atributos, isto é, ditos pertencentes a, qualquer Coisa é um Atributo. Para mencionar uma coisa usa-se um substantivo. Para mencionar um atributo usa-se um Adjectivo. As pessoas perguntam Pode uma Coisa existir sem possuir qualquer atributo? É uma pergunta enigmática, à qual não se irá tentar responder. Contempla-se com silêncio, como se não valesse ser reparado. Mas, se fosse colocada a questão ao contrário: Pode um atributo existir sem ter que pertencer a alguma Coisa? Pode dizer-se de uma vez só: Não. Nem um bebé poderia ir viajar sem que ninguém tomasse conta dele! Nunca ninguém viu bonito a pairar no ar ou atirado ao chão, sem que alguma coisa seja bonita, ou já viu? Continuando esta condução. Pode usar-se o verbo ser (é, são) entre nomes de duas Coisas (exemplo: alguns porcos são animais gordos), ou no meio de nomes de dois atributos (ex. cor-de-rosa é vermelho-vivo) e faz sentido nos dois exemplos. Mas se põe o verbo ser entre o nome de uma Coisa e o nome de um atributo (ex. Alguns porcos são rosas) não faz sentido. Como pode ser uma Coisa um Atributo. A não ser que já se conheça a pessoa com quem se está a falar e ambas estarem dentro do contexto. Senão teria de completar a frase, i. e., o substantivo deveria repetir-se no final da frase ex. Alguns porcos são porcos corde-rosa
6 Portanto, para fazer sentido, a Proposição Alguns dos bolos novos são bons, é obrigatório escrever a frase completa. Alguns dos bolos novos são (bolos) bons. Agora a frase contém dois termos bolos novos sendo um deles e (bolos) bons o outro. Bolos novos é o chamado Sujeito da Proposição e (bolos) bons o Predicado. Esta Proposição é Particular, visto que não fala de todo o Sujeito, mas apenas de uma parte. Os outros dois tipos são designados por Universais, pois referem-se a todo o Sujeito um que nega ser bom e o outro afirma que sim, em toda a Classe de bolos novos. Por fim, pode tomar como definição de Proposição, uma frase declarando que alguns, ou nenhum, ou todos, das Coisas pertencentes a uma certa Classe, chama-se Sujeito, são também coisas que pertencem a outra determinada Classe, chamada Predicado. Ao longo deste estudo usam-se estas sete palavras: Proposição; Atributo; Termo; Sujeito; Predicado; Particular e Universal Serão charmosamente úteis. 5 6 x y y ' x ' 7 8 Ao observar o Diagrama menor, suponha-se que se trata de um armário, feito para ter todos os bolos do mundo. Todos os novos serão colocados na metade de cima (marcado com x), e todos os outros (não novos) na metade de baixo (marcado x ). Então a metade de baixo irá conter os bolos mais velhos, (bolos velhos, bolos antigos, bolos pré-diluvianos). Os bolos bons são colocados na metade esquerda (marcada y) e todos os outros (i.e., não bons) na metade do lado direito (marcado y ). Neste momento tem que se entender: 5 6 x x como novo y y ' x como não novo x ' y como bom 7 8 y como não bom Qual o tipo de bolos que estaria à espera de encontrar no compartimento n.º 5? Na metade superior se tiver alguns bolos têm de ser novos e, é na metade do lado esquerdo, logo eles têm de ser bons. Se existem alguns bolos neste compartimento, têm dois Atributos novos e bons, ou então ao usar as letras, têm de ser xy
7 Observe-se que as letras x, y estão escritas nas margens deste compartimento. Esta regra é conveniente para saber quais os atributos que pertencem às coisas em qualquer compartimento. Tome-se o n.º 7 por exemplo. Se existirem lá alguns bolos, têm de ser x y, isto é, têm de ser não novos e bons. Designando: - As Contas Vermelhas num compartimento significam ocupado, i. e., existem alguns bolos, a palavra alguns em Lógica significa um ou mais. Para referir um único bolo no compartimento seria suficiente dizer Existem alguns bolos aqui. - As Contas Cinzentas num compartimento significam vazio, i. e., ali não há bolos. Nos próximos diagramas, coloca-se para designar um ou mais, equivalente a colocar uma conta vermelha; e 0 para designar nenhum equivalente a colocar uma conta cinzenta. Como o Sujeito da proposição é bolos novos, interessa a parte superior do tabuleiro, onde todos os bolos têm o Atributo x, i.e., novos. Agora, fixando a atenção na metade superior, supomos que se encontra marcada assim, i.e., com uma conta vermelha no n.º 5. Tendo como referência a Classe dos bolos novos, o que diz esta situação? Quererá dizer que alguns deles estão no compartimento-xy? Isto é, alguns deles (para além de ter o Atributo x, que pertence aos dois compartimentos) tem o Atributo y (i.e., bom ). Isto pode-se expressar como, Alguns bolos-x são bolos-y ou pondo em palavras em vez de letras Alguns bolos novos são bons (bolos), mais abreviado, Alguns bolos novos são bons. Por fim, encontrou-se a maneira de como representar a º proposição desta secção. A Classe da totalidade das Coisas designa-se por Universo, sendo a finalidade do Tabuleiro. Então poderia-se ter iniciado dizendo, considere-se o universo dos Bolos. É claro que qualquer outra Coisa ficaria tão bem como Bolos. Poderia-se ter feito proposições sobre Universo dos Lagartos ou até Universo das Vespas. Já se aprendeu que
8 Significa alguns x são y, i.e., alguns novos são bons. Logo Significa Alguns x são y, i.e., alguns novos são não bons. Coloca-se agora uma Conta cinzenta no n.º 5, que significará? Isto diz que o compartimento xy está vazio, o qual poderemos exprimir por nenhum x é y, ou, nenhum bolo novo é bom. Esta é a segunda das três Proposições importantes desta secção. Da mesma maneira Significa nenhum x é y, ou, nenhum bolo novo é não bom. Qual a interpretação de Representa uma dupla proposição, sendo alguns x são y, e alguns são y, i.e., alguns novos são bons, e são não bons. Seja Significa nenhum x é y e nenhum é y, i.e., nenhum novo é bom e nenhum é não bom. O que conduz ao resultado Não existem novos, i.e., nenhum bolo é novo. Isto porque bom e não bom faz o que se chama de exaustiva divisão de Classe bolos novos, i.e., entre estes, eles esvaziaram toda a Classe. Tal que todos os bolos que existiam, tem de ser encontrados na outra ou na outra das divisões. Tendo de representar o contrário de nenhum dos bolos é novo, o qual seria Alguns bolos são novos ou usando as letras em vez de palavras alguns bolos são x. Evidentemente que se terá de colocar algures na parte x do tabuleiro uma Conta vermelha, visto que lá está alguns bolos novos. Mas não se sabe de que lado, direito ou esquerdo, visto não saber se são bons ou não bons. Coloca-se então a Conta vermelha na linha de divisão entre os compartimentos-xy e dos compartimentos-xy : A posição da conta vermelha, na linha de divisão, tanto está no n.º 5 como no n.º6, e não se sabe para que lado irá saltar. O que quer dizer isto? Isto é claramente uma Proposição dupla. Diz não apenas que alguns x são y, mas também que nenhum x é não y. Em suma o resultado é Todo x é y, i.e., todos os bolos novos são bons, a qual é a última das três proposições mais importantes desta secção. Então a Proposição Universal Todos os bolos são bons. Consiste em duas proposições juntas, que são Alguns bolos novos são bons e Nenhum novo bolo é não bom
9 Da mesma maneira, Quer dizer Todos os x são y, i.e., Todos os bolos novos são não bons. Considere-se a seguinte proposição O bolo que me deste é bom, será Particular ou Universal? Particular, com certeza seria uma resposta impulsiva, esta é Universal. Pois divide-se o Universo de bolos em duas Classes os bolos que me deram (os quais se designa para a parte superior do tabuleiro), e aqueles que não me deram (os quais vão para a parte de baixo). A metade inferior encontra-se quase cheia e a parte superior está praticamente, possivelmente vazia. Então, mantendo os bolos bons na esquerda e os não bons na direita, começa-se por juntar todos os bolos que se deram, empilhando-os no compartimento do lado esquerdo. Aqui está outra proposição Universal: Barzillai Beckalegg é um homem honesto, o que significa que Todos os Barzillai Beckalegg, que se estão a considerar, são homens honestos. Este tipo de Proposições Universais (onde o Sujeito é uma coisa singular) é designado por Proposição Indivídual. Considere-se bolos bons como Sujeito da nossa proposição, i.e., fixa-se os pensamentos na metade do lado esquerdo do tabuleiro, onde todos os bolos têm o Atributo y, i.e., bons. Suponha-se que se encontra fixado como: Significa alguns y são x, i.e., alguns bolos bons são novos. Mas pode perecer que este caso tenha sido analisado anteriormente. Onde se colocou uma Conta Vermelha no n.º 5, que significava alguns bolos novos são bons e, agora significa alguns bolos bons são novos! Poderá querer dizer ambos? Quer dizer ambos. Se tomar x (i.e., bolos novos) como seu Sujeito, e com respeito ao n.º 5 como parte do rectângulo horizontal, pode-se ler Alguns x são y, i.e., Alguns bolos novos são bons. Mas se tomar y (i.e., bolos bons) como Sujeito, e tomando o n.º5 como parte do rectângulo vertical esquerdo, então pode-se ler Alguns y são x, i.e., Alguns bolos bons são novos. Elas são simplesmente duas maneiras diferentes para expressar a mesma verdade
10 Para uma melhor compreensão aconselha-se que se vá comparando com os vários casos do rectângulo horizontal. Símbolos Significado Alguns y são x ; i.e., Alguns bons são não novos Nenhum y é x ; i.e., Nenhum bom é novo [outra forma de expressar é, Nenhum novo é bom ] Nenhum y é x ; i.e., Nenhum bom é não novo. Alguns y são x e alguns são x ; i.e., Alguns bons são novos e alguns são não novos. Nenhum y é x, e nenhum é x ; i.e., Nenhum y existe ; i.e., Nenhum bolo é bom Todo y é x ; i.e., Todos os bons são novos. Todo o y é x ; i.e., Todos os bons são não novos. Em relação ao Diagrama maior, este pode ser considerado como o tabuleiro anterior, dividido da mesma maneira, mas também dividido em duas porções, para o atributo m. Tome-se o m com o significado de saudável e supõe-se que todos os bolos saudáveis são colocados dentro do quadrado central, e todos aqueles não saudáveis fora dele, i.e., num ou noutro dos quatro compartimentos exteriores ao quadrado central. Consegue-se ver, tal como no diagrama menor os bolos em cada compartimento têm dois atributos, então aqui os bolos em cada compartimento têm três atributos e, tal com as letras representam dois atributos, estavam a ser escritas nas arestas do compartimento, e agora elas estão escritas nos cantos
11 Observe que m, suposto estar escrito em cada um dos quatro cantos exteriores. Assim pode-se dizer num só momento apenas olhando para um compartimento, quais dos três atributos pertencem às coisas dele. Por exemplo tome-se o n.º 2, aqui tem-se x, y, m nos cantos, por isso sabe-se que os bolos ali, caso existam, têm três atributos, «xy m», i.e., novos, não-bons e saudáveis. Novamente, tome-se n.º 6, aqui encontra-se nos cantos x, y, m portanto os bolos aqui são não-novos, não-bons, não-saudáveis (os bolos não são nada tentadores). Levaria muito tempo para averiguar todo o tipo de proposições, contendo x, y e m, que podem ser representadas neste diagrama. (Existem 96 ao todo) Considere-se apenas a metade superior, sendo o Sujeito bolos novos, como representamos: Nenhum dos bolos novos são saudáveis? Escrevendo letras em vez de palavras nenhum x é m. Isto diz que nenhum dos bolos, pertencentes à metade superior do tabuleiro, serão encontrados dentro do quadrado central, i.e., os dois compartimentos n.º e n.º 2 estão vazios, isto é representado obviamente por: E agora como se representa a Proposição contraditória: Alguns x são m? Pensa-se que a melhor maneira seria colocar uma conta vermelha na linha de divisão entre n.º e o n.º 2, e para compreender isto, significa que um dos dois compartimentos está ocupado, mas presentemente não sabemos qual. Representa-se então por Considere-se a expressão Todo x é m Isto consiste em saber duas Proposições: Alguns x são m e Nenhum x é m Primeiro analisa-se a parte negativa. Isto diz que nenhum bolo, pertencente à metade superior do tabuleiro é para ser posto fora do quadrado central, i.e., nos dois compartimentos n.º 9 e n.º 0 estão vazios. É claramente representado por Mas ainda tem que se representar Alguns x são m. Isto diz que existem alguns bolos no rectângulo do n.º e n.º 2, portanto coloca-se a conta vermelha, como no exemplo anterior na linha de divisão entre n.º e n.º 2, e o resultado é: O que se deve fazer a x e a y? Isto diz, em relação ao quadrado-xy, que está todo vazio, visto que ambos os compartimentos estão assim marcados
12 Considerando o quadrado-xy, diz que está ocupado. Verdade é que só um compartimento está ocupado. Mas é quase suficiente quer o outro esteja ocupado ou vazio, para constatar que existe algo naquele quadrado. Se, então se transferir estas marcas para o diagrama menor, para nos livrar da subdivisão-m tem-se o direito a marcar Que significa, Todo o x é y. O resultado seria exactamente o mesmo caso o rectângulo fosse marcado Mais uma vez, como se deve interpretar isto, tendo em conta x e y? Em relação ao quadrado-xy, isto diz que um dos seus compartimentos está vazio. Mas esta informação é praticamente nula, visto que não tem nada marcado no outro compartimento. Se o outro compartimento estivesse marcado vazio também, o quadrado estaria vazio e se estivesse ocupado, o quadrado estaria ocupado. Como não sabemos qual o caso, nada se pode dizer deste quadrado. O outro quadrado, quadrado-xy, sabemos (como no exemplo anterior) estar ocupado. Se, então transferirmos as marcas para o diagrama menor apenas obtemos o qual significa Alguns x são y. Estes princípios podem ser aplicados a todos os rectângulos. Por exemplo, para representar Todos os y são m. Marca-se o rectângulo do lado direito ao alto (aquele que tem o atributo y ) como e, se for pedido para interpretar a metade abaixo do tabuleiro, marcada da seguinte maneira, tendo em conta x e y. Deveremos transferir para o diagrama menor, vem E ler Todo x é y. Mais dois comentários sobre as proposições, é necessário fazer uma delas é que, em todas as proposições começadas em Alguns ou Todas a existência actual do Sujeito é afirmado se por exemplo, disser Todos os infelizes são egoístas
13 Garanto que infelizes realmente existem. Se desejar evitar estas afirmações e, meramente para declarar a lei que infelizes necessariamente envolve egoísmo, dever-se- -ía dizer, nenhum infeliz é generoso o que não afirma que existe qualquer infeliz, mas meramente que se algum existisse eles poderiam ser egoístas. Quando uma Proposição começa por algum ou nenhum e, contém mais que dois Atributos, podem ser re-arranjados e movidos de um termo para o outro. Por exemplo Alguns abc são def pode ser re-arranjado como Alguns bf são acde o qual seria equivalente a Algumas coisas são abcdef. Outra vez Nenhuns homens velhos sábios são jogadores apressados e descuidados pode ser re-arranjado como Nenhum jogador velho apressado é sábio e descuidado o que será equivalente Nenhum homem é um jogador velho apressado, descuidado e sábio. 2. Silogismos Agora supõe-se que se divide o Universo de Coisas em três, tendo em consideração três Atributos diferentes. Fora desses três Atributos, nós podemos fazer três pares diferentes (por exemplo, se eles são a, b, c, nós podemos fazer três pares, ab, ac, bc). Também supondo que se tem duas Proposições dadas, contendo dois destes três pares e que deles se pode provar uma terceira Proposição contendo o terceiro par. (Por exemplo, se dividir o Universo em m, x, e y; e se as duas Proposições dadas, "nenhum m é x " e "todo m é y", contendo os dois pares mx e my, pode ser possível provar a partir deles uma terceira Proposição, contendo x e y.) Em tal caso chamamos às Proposições dadas 'Premissas', à terceira 'Conclusão e ao conjunto inteiro Silogismo'. No primeiro caso quando, por ex. as Premissas são Alguns m são x e Nenhum m é y. O termo, que ocorre duas vezes, é chamado o termo do meio, porque serve de ligação entre os outros dois termos. No segundo caso (quando, por exemplo, as Premissas estão "nenhum m é x " e "todo m é y" os dois Termos, que contêm esses Atributos contraditórios, podem ser chamados 'os Meios Termos '. Assim, no primeiro caso, a classe de "coisas-m" é o Meio Termo e, no segundo caso as duas classes de "coisas-m " e "coisas-m " são o Meio Termo. O Atributo, que ocorre no Meio Termo ou Termos, desaparece na Conclusão e é "eliminado", que literalmente significa excluído
14 Agora tenta-se desenhar uma Conclusão a partir das Premissas "Alguns bolos novos são saudáveis; Nenhuns Bolos bons são não saudáveis." A fim de os expressar com as peças, necessitasse dividir os Bolos de três formas diferentes, com consideração aos novos, aos bons e aos saudáveis. Para este fim tem-se que usar o Diagrama maior, fazendo o x significar "novo", y "bom", e m "saudável". (Tudo no interior do Quadrado central é suposto ter o atributo m e, tudo no exterior dele o atributo m, i.e. "não-m".) Tinha-se adoptado a regra de fazer m significar o Atributo que ocorre no Termo Meio ou Termos. (Tendo escolhido m como o símbolo, porque meio começa com m.). Ao representar as duas Premissas, é preferível começar com a negativa (aquela que começa com "não"), porque as peças cinzentas podem sempre ser colocadas com certeza, e vai então ajudar a fixar a posição das peças vermelhas, que estão às vezes em dúvida.a expressão "Nenhum Bolo bom é saudável (Bolo)", i.e. "nenhum bolo-y é m (Bolos)". Isto diz que nenhum Bolo pertencendo à metade de y do tabuleiro está no compartimento m (i.e. aquele exterior ao Quadrado central). Os dois compartimentos, Número 9 e Número 5, estão ambos vazios ; e nós devemos colocar uma peça cinzenta em cada um deles, assim: Tem-se agora de expressar a outra premissa, que é, "Alguns bolos novos são não-saudáveis (Bolos)", i.e. "Alguns bolos-x são m (Bolos)". Isto diz que alguns dos Bolos na metade x do tabuleiro está no compartimento-m. Um dos dois compartimentos, Número 9 e Número 0, está ocupado e, como não foi dito em qual destes dois compartimentos, coloca-se a peça vermelha, a regra usual poderá ser pôr a peça na linha-divisão entre eles, mas, neste caso, a outra Premissa tem afirmado o Sujeito, ao declarar que o Número 9 está vazio, a peça vermelha não tem escolha, e deve ir para dentro do compartimento Número 0, assim. Agora quais as peças que esta informação não nos deixa coloca no Diagrama menor, afim de que obter alguma Proposição envolvendo x e y unicamente, deixando de fora o m? Vamos considerar os quatro compartimentos, um por um. Primeiro, Número 5, tudo o que sabemos sobre isto é que a porção exterior está vazia, mas não sabemos nada sobre sua porção interior. Assim o Quadrado pode estar vazio,
15 ou isto pode ter alguma coisa nele. Quem pode dizer? Por isso atrevemo-nos a não colocar qualquer peça neste Quadrado. Secundariamente, o que se passa no Número 6? Aqui estamos um pouco melhor sabe-se que há alguma coisa lá dentro, lá está uma peça vermelha na porção exterior. É verdade que não se sabe onde na sua porção interior está vazio ou ocupado, mas para que isso interessa? Um Bolo solitário, num canto do Quadrado, é suficiente desculpa para dizer, este Quadrado é ocupado, e para marcar isto usa-se a peça vermelha. Quanto ao Número 7, está na mesma condição que o Número 5, encontra-se parcialmente vazio, mas não se sabe se a outra parte está vazia ou ocupada, assim atrevemo-nos a marcar neste Quadrado. Quanto ao Número 8, simplesmente não se tem a informação de tudo. O resultado é. A nossa conclusão, deve retirar-se da informação que há uma peça vermelha no Quadrado x y. A nossa conclusão é alguns x são y, i.e. alguns Bolos novos são nãobons (Bolos) ou, se prefere tomar o y como Sujeito, alguns bolos não-bons são novos (Bolos) ; mas o outro parece mais claro. Escreve-se agora o silogismo, colocando o símbolo para portanto, e omitindo Bolos para poder abreviar no fim de cada proposição. Alguns Bolos novos são não-saudáveis; Nenhuns Bolos bons são não-saudáveis. Alguns Bolos novos são não-bons. O primeiro silogismo foi bem trabalhado. Vejamos o que se pode fazer com as duas Premissas Todos Dragões são ferozes; Todos Escoceses são inofensivos. Recorde, que não se garante que as Premissas sejam factos. Como lógicos sejam as Premissas falsas ou verdadeiras, tudo o que se tem de fazer é compreender quando elas nos levam a conclusões lógicas, de modo, se elas forem verdadeiras isto poderá ser verdadeiro também. Para que o tabuleiro tenha uma maior utilidade deixamos o exemplo dos Bolos. Tomemos como Universo alguma classe de coisa as quais incluem Dragões e HomensEscoceses, dever-se-á dizer animais? E tal como inofensivo é o atributo
16 Pertencente ao termo do meio representar-se-á inofensivo por m, Dragões por x e Escoceses por y. As premissas Todos os Animais-Dragões são ferozes (Animais); Todos os Animais-HomensEscoceses são inofensivos (Animais) Isto pode ser expresso, usando letras, ao invés de palavras, Todos os x são m ; Todos os y são m. A primeira premissa consiste em, como se sabe, duas partes, Alguns x são m e Nenhum x é m. A segunda também consiste em duas partes, Alguns y são m e Nenhum y é m. Analisando primeiramente as porções negativas, temos de marcar no diagrama mais largo, primeiro Nenhum x é m e segundo Nenhum y é m, o resultado é, e estas duas combinadas obtemos, temos agora que representar as duas partes positivas, Alguns x são m e Alguns y são m. O único compartimento disponível para coisas as quais são xm, é o número 9 e o número 0. Destas, o número 9 já está marcada como vazia por isso a peça vermelha tem mesmo de ser marcada no número 0. Analogamente, as duas disponíveis para ym, são o número e o número 3. Destas, o número já está marcada como vazia por isso a peça vermelha tem mesmo de ser marcada no número 3. O resultado final é, Qual desta informação pode ser transferida para o diagrama menor? Vejamos os quatro compartimentos, um a um. No número 5, podemos verificar que está vazio, desta forma marca-se com a peça cinzenta. O número 6, vemos que está ocupado, assim sendo marca-se com uma peça vermelha. O número 7? Idem. No número 8, não há informação. Agora o Diagrama menor está devidamente marcado
17 Agora, que conclusão tiramos após a sua leitura? É impossível empacotar tanta informação abundante numa só preposição, teremos que a dividir em duas. Primeiro, tomando x como Sujeito, temos Todo x é y, Todos Dragões são não- HomensEscoceses. Segundo, tomando y como Sujeito, temos Todo y é x, isto é, Todo Homens Escoceses é não-dragão. Ao escrever tudo junto, as duas premissas e a nossa chave da conclusão. Todos os Dragões são ferozes, Todos os HomensEscoceses são inofensivos, Todos Dragões são não-homensescoceses; Todos HomensEscoceses são não-dragões. Deve-se mencionar na conclusão, que porventura se encontre com o estudo de lógica, o qual não é assumido que qualquer coisa existe de tudo, mas Alguns x são y é interpretado como o Atributo de x, y são compatíveis de modo que uma coisa possa ter ambas de uma vez só, e Nenhum x é y representa os Atributos x, y são compatíveis, de modo que nada pode ter ambos ao mesmo tempo. Neste estudo, as proposições têm diferentes significados do que têm para o nosso Jogo de Lógica e será correcto compreender exactamente quais as diferenças. Primeiro tomemos, Alguns x são y. Aqui compreende-se são como são, como um facto real que certamente implica que algumas coisas x existem. Mas os escritores destes estudos unicamente compreendem são como pode ser, o que não implica de todo a sua existência. Assim para estes significa menos do que para nós. O nosso significado inclui o deles, certamente Alguns x são y inclui Alguns x podem ser y, mas o deles não inclui o nosso. Por exemplo, Alguns Hipopótamos-Galeses são pesados seria verdade segundo estes escritores, dado que os atributos Galeses e pesado serem compatíveis com hipopótamos, mas seria falso no nosso jogo visto que não há Hipopótamos-Galeses serem pesados. Segundo, tomemos Nenhum x é y. Aqui unicamente compreendemos são como são, como facto actual o que não implica que nenhum x possa ser y. Mas interpretam a proposição como, não apenas como nenhum é y, mas que nenhum possa ser y, como tal interpretam mais do que nós. O significado dos escritores inclui o nosso, certamente
18 Nenhum x pode ser y inclui Nenhum x é y, mas a nossa não inclui a deles. Por exemplo Nenhum policia mede 2,4 m seria verdade no jogo, pois, como um facto actual, não se encontrou ainda tal espécie. Mas seria falso, segundo estes autores, visto que os atributos pertencem à Força-Policia e altura 2,4m é compatível. Não há nada que previna um polícia de crescer até aquela altura, se suficientemente esfregado com um óleo Olex, que passa por fazer crescer o cabelo quando esfregamos a cabeça e claro que fará um polícia crescer quando esfregado com óleo Olex. Consideremos todo o x é y, o qual consiste em duas proposições parciais, alguns x são y e nenhum x é y. Aqui certamente que para os estudiosos significa menos do que para nós na º parte, e mais do que para nós na 2º. Mas as duas operações não se equilibram uma à outra, mais do que quando se oferece um degrau extra a um homem cuja chaminé caiu. Ao encontrar silogismos deste género, pode-se trabalhá-los, facilmente, pelo sistema já fornecido. Tem que se fazer unicamente são como ser capaz de existir, e tudo seguirá suavemente. Para alguns x são y será alguns x são capazes de ser y, i.e., o atributo x e y são compatíveis. E nenhum x é y será nenhum x é capaz de ser y, i.e., os atributos x e y, são incompatíveis E certamente todo o x é y será Alguns x são capazes de ser y e nenhum é capaz de ser y,i.e., os atributos x,y são compatíveis e os atributos x,y são incompatíveis. Ao usar diagramas para este sistema, tem de entender que a peça vermelha significa É possível que existe qualquer coisa neste compartimento, e uma cinzenta significa lá não pode possivelmente existir qualquer coisa neste compartimento. 3. Falácias Para um par de premissas práticas (um par que conduza a uma conclusão lógica) as quais se podem encontrar ao ler o jornal ou revista, pode-se encontrar provavelmente 5 que não leve a nenhuma conclusão de todo: e, até mesmo quando as premissas são práticas, por exemplo, onde o escritor desenha uma conclusão correcta, provavelmente existem 0 onde ele desenha uma incorrecta. No º caso, pode dizer-se as premissas são enganadoras. No 2º, a conclusão é enganadora Com tal habilidade lógica como este jogo poderá ensinar a detectar Enganos dos 2 géneros
19 A primeira espécie de enganos Premissas enganadoras são detectáveis após marcar no Diagrama Maior, ao tentar transferir para o diagrama menor, tendo em conta os seus quatro compartimentos, um por um, e perguntará para cada vez, Qual a marca que coloco aqui?, e em todas elas a resposta será Nenhuma informação. Mostrando que não há nenhuma conclusão de todo. Por exemplo, Todos os soldados são corajosos; Alguns ingleses são corajosos. Alguns ingleses são soldados. Parece um silogismo pouco comum, e era capaz de enganar um lógico menos experiente. Mas não nos deixemos apanhar por tal truque! Marcaria como Premissas Enganadoras. (qualquer coisa está errada). O outro tipo de engano é Conclusões enganadoras só são detectáveis após marcar em ambos os diagramas, e ter chegado à conclusão correcta e ter comparado com a conclusão que o escritor escreveu. Não se pode dizer conclusão enganadora simplesmente porque não é idêntica à correcta: pode ser uma parte da conclusão correcta, e ser um pouco correcta, até onde vai. Neste caso poderia-se comentar com um sorriso conclusão defeituosa. Supondo por exemplo, encontrava este silogismo, Todas as pessoas não egoístas são generosas; Nenhum desgraçado é generoso. Nenhum desgraçado é não egoísta. A premissa pode ser expressa por letras, Todo x é m; Nenhum y é m. Aqui a conclusão verdadeira é Todo o x é y. Isto é, Todas as pessoas não egoístas são não desgraçadas Enquanto a conclusão do escritor é Nenhum y é x. o que é o mesmo Nenhum x é y. e por isso é uma parte de Todo o x é y. Aqui pode dizer-se Conclusão Defeituosa. Mas se o escritor tivesse escrito a conclusão Todos os desgraçados são egoístas i.e., Todo o y é x (isto assegura a existência de y o que não é assegurado uma premissa) Ao que se diz Conclusão Enganadora Quando ler outros estudos de lógica, poderá encontrar vários tipos de enganos, o que nem sempre o significa. Por exemplo,
20 Se tivesse que por um uma só estas duas premissas lógicas: Nenhum homem honesto faz batotice; Nenhum homem desonesto é confiável. E se perguntar qual a conclusão que se segue? Provavelmente respondesse nenhum de qualquer modo. Estas premissas vão contra duas regras distintas, são tão enganadoras até onde possam ser. Supondo que mesmo assim se diria Nenhum homem que faça batotice é confiável, o seu parceiro de jogo, amigo lógico, iria depressa embora talvez zangado e desrespeitado, não se aconselha tal experiência. Mas porquê é isto? Dir-se-á. Quer dizer que todos estes lógicos estão errados? Longe disso. Do ponto de vista deles, eles estão perfeitamente correctos. Mas eles não incluem no seu sistema, qualquer coisa como todas as formas possíveis de silogismos. Tomemos o nosso sistema. Capítulos II/III Perguntas Variadas/ Respostas O Homem do mundo selvagem perguntou-me Quantos morangos crescem no mar? Eu respondi-lhe, como achava melhor, São tantos como os arenques crescem na madeira. Elementar. O que é um Atributo? Dê exemplos. Qualquer coisa pode ser atributo de, isto é, diz-se que pertence a, uma Coisa é designada por Atributo. Por exemplo, assado o qual pode (frequentemente) ser o atributo de bolos bonito o qual pode (raramente) ser o atributo de Bebés 2. Quando é que é de bom censo colocar é ou são entre dois nomes? Dê exemplos. Quando eles são o nome de duas coisas (por exemplo; Estes porcos são animais gordos, ou para dois atributos, por exemplo: cor de rosa é vermelho claro 3. Quando é que não é no bom sentido? Dê exemplos. É quando um é nome de uma Coisa, e o outro é o nome de um atributo (exemplo: Estes porcos são cor de rosa ) visto que uma coisa não pode eventualmente ser um atributo. 4. Quando não está no bom sentido, qual é o arranjo simplista a fazer, de modo que faça bom censo? Que o substantivo é suposto ser repetitivo no final da frase por exemplo Estes porcos são (porcos) cor-de-rosa
21 5. Explique: Proposição, Termo, Sujeito e Predicado. Dê exemplos. Proposição é uma frase declarando que, alguma, ou nenhuma, ou toda, de uma coisa pertencente a uma certa classe, chamada Sujeito, são coisas pertencentes a uma outra certa classe chamada Predicado. Por exemplo, Alguns bolos novos não são bons, i. e., escrito totalmente: Alguns bolos novos não são bolos bons, onde a classe dos bolos novos é o Sujeito e a classe bolos não bons é o predicado. 6. O que são Proposições Particular e Universal? Dê exemplos. Uma proposição, declarando que algumas das coisas pertencentes ao seu Sujeito é assim-e-assim, é designada Particular ex.: Alguns bolos novos são bons. Uma proposição declarando que nenhuma das coisas pertencentes ao Sujeito, ou todas elas, são assim-e-assim, designa-se Universal, ex.: Nenhum bolo novo é bom todos os bolos novos são não bons. 7. Indique uma regra para saber, quando nós olhamos para o Diagrama menor, quais os atributos que pertencem às coisas de cada compartimento. As coisas em cada compartimento possuem 2 atributos, cujos símbolos se encontram escritos em cada aresta do respectivo compartimento. 8. O que é que alguns, algumas significa em Lógica? Um ou mais. 9. Em que sentido se usa a palavra Universo neste jogo? Com o nome da classe de coisas para as quais todo o Diagrama está atribuído. 0. O que é uma proposição dupla? Dê exemplos. Proposição contendo duas declarações. Ex.: Alguns bolos novos são bons e alguns são não-bons. Quando é que uma classe de coisas é dividida exaustivamente? Dê exemplos. Quando toda a classe, assim dividida, é exaustivamente dentro de conjuntos nos quais está dividida, lá não está nenhum membro o qual não pertence a alguma delas. Por ex.: a classe bolos novos é exaustivamente dividida em bons e não-bons desde que todo o novo bolo tem de ser ou uma ou outra. 2. Explique a frase Sentado na cerca. Quando um homem não é capaz de se decidir para qual das duas partes ele irá escolher, diz-se que ele está sentado na cerca (na fronteira) ele não é capaz de decidir para qual lado irá saltar (escolher). 3. O que é que duas proposições parciais fazem quando tomadas juntamente, todo x é y? alguns x são y e nenhum x é y. 4. O que é proposição Indivíduo? Dá exemplos. Uma proposição, cujo Sujeito é uma coisa única é chamada de Indivíduo. Por ex.: Eu sou feliz, O João não está em casa. Estas são proposições universais, sendo
22 as mesmas como Todos os Eu que existem são felizes, todos os Joãos, que eu estou agora a considerar, não estão em casa. 5. Que tipo de proposição implicam, neste jogo, a existência do seu Sujeito. Proposições que iniciam com alguns ou todos. 6. Quando uma proposição contém mais do que dois atributos, estes atributos podem em certos casos re-arranjados e movidos de um termo para o outro. Em que casos pode isto ser feito? Quando eles iniciam com algum ou nenhum. Por ex.: alguns abc são def pode ser re-arranjado como alguns bf são acde o qual é equivalente a alguns abcdef existem. Separe cada uma das seguintes em duas proposições parciais 7. Todos os tigres são ferozes. Alguns tigres são ferozes, Nenhum tigre é não-feroz 8. Todos os ovos cozidos são não-saudáveis. Alguns ovos cozidos são não-saudáveis Nenhum ovo cozido é saudável. 9. Eu estou feliz. Alguns eus estão felizes Nenhum eu é infeliz. 20. João não está em casa. Alguns Joãos não estão em casa, Nenhum João está em casa. 2. Dê uma regra para conhecer, quando nós olhamos para o diagrama maior, quais os atributos que pertencem ás coisas contidas em cada compartimento. As coisas, em cada compartimento do diagrama maior possuem três atributos, cujos símbolos são encontrados escritos nos 3 cantos dos compartimentos (excepto no caso m, o qual actualmente não está inscrito no diagrama, mas é suposto estar em cada um dos outros 4 cantos. 22. Explique: Premissas, Conclusão e Silogismos. Dê exemplos. Se o Universo das coisas estiver dividido em consideração a 3 diferentes atributos, e dadas 2 proposições, contendo 2 pares diferentes destes atributos, e se destes nós podermos provar uma terceira proposição, contendo os dois atributos que ainda não ocorreram juntamente; As proposições dadas designam-se por premissas. A terceira é a conclusão, e todo o conjunto o Silogismo. Por exemplo, as premissas podem ser nenhum m é x e todo m é y ; e poderá ser possível provar a partir delas uma conclusão contendo x e y. 23. Explica as frases: Termo do meio e termos do meio. Se um atributo ocorreu em ambas as premissas, o termo contido é designado por o termo do meio. Por ex. se a premissa for alguns m são x e nenhum m é y a classe de Coisas-m é o termo do meio
23 Se um atributo ocorrer numa premissa, e a sua contraditória na outra, os termos contendo-as podem ser chamadas de termos do meio por ex. Se as premissas forem nenhum m é x 2 e todo m é y, as duas classes de m-coisas e m - Coisas podem ser chamadas de termos do meio. 24. Ao marcar um par de Premissas no Diagrama maior, porque é que é melhor marcar primeiro as proposições negativas e depois as afirmativas? Porque elas podem ser marcadas com certezas, ao passo que as proposições afirmativas (i.e., aqueles que começam por alguns ou todo ) por vezes requeremnos que coloquemos uma peça vermelha sentados na cerca 25. Porque é que para os lógicos o não ter consequência, quer as premissas sejam verdadeiras ou falsas? Porque a única questão que interessa é quando se chega a uma conclusão lógica a partir das premissas, portanto, se elas fossem verdadeiras, ela seria também verdadeira. 26. Como se trabalha silogismo quando é dito que alguns x são y é entendido como dizendo os atributos x,y são compatíveis, e nenhum x é y significa os atributos x,y são incompatíveis? Entendendo que uma peça vermelha significa este compartimento poderá estar ocupado e uma peça cinzenta significa este compartimento não pode estar ocupado ou este compartimento tem de estar vazio. 27. Quais são os dois tipos de enganos? Premissas enganosas e conclusões enganosas 28. Como se poderá detectar Premissas enganosas? Ao tentar transferir as peças do Diagrama maior para o menor e não se ter nenhuma informação para qualquer dos seus 4 compartimentos 29. Como se detecta conclusões enganosas? Descobrindo a conclusão verdadeira, e então observando que a conclusão dada, não é nem idêntica à nossa nem a uma parte dela. 30. Por vezes a conclusão dada, não é idêntica à conclusão correcta, e ainda não pode ser chamada de Enganosa, Quando é que isto acontece? E qual o nome que se dá a tal conclusão? Quando a conclusão dada é parte da conclusão certa, neste caso designa-se por conclusão defeituosa. 2. Metade do Diagrama Menor Proposições para representar.. Alguns x são não-y. 2. Todo x é não-y. x y y'
24 3. Alguns x são y, e alguns são não-y. 4. Nenhum x existe. 5. Alguns x existem. 6. Nenhum x é não-y. 7. Alguns x são não-y, e alguns x existem. Poderiam pensar que o diagrama seria mais próprio, de modo a expressar Alguns x existem, mas isto está realmente contido em alguns x são y. Por a peça vermelha na linha-de-divisão simplesmente nos diria um dos dois compartimentos está ocupado, o que já sabemos, pelo conhecimento dado é que um está ocupado. Tomar: x = juízes ; y = justo 8. Nenhum juiz é justo. Nenhum x é y. 9. Alguns juizes são injustos. Alguns x são y 0. Todos os juizes são justos. Todo o x é y Tomar: x = ameixas ; y = saudáveis. Algumas ameixas são saudáveis. Alguns x são y 2. Não há ameixas saudáveis. Nenhum x é y. 3. Ameixas são algumas delas saudáveis, e algumas não. Alguns x são y, e alguns são y. 4. Todas as ameixas são não-saudáveis. Todo y é y
25 Tomar: x = estudantes diligentes ; y = com sucesso 5. Nenhum estudante diligente é mal-sucedido. Nenhum y é x. 6. Todo o estudante diligente é bem sucedido. Todo y é x. 7. Nenhum estudante é diligente. Nenhum y existe. 8. Existem alguns diligentes, mas mal-sucedidos, estudantes. Alguns y são x. 9. Alguns estudantes são diligentes. Alguns y existem. y x x' 3. Metade do Diagrama Menor Interpretar símbolos. Nenhum x é y x y y 2. Nenhum x existe 3. Alguns x existem. 4. Todo x é y. Tomando: x = bons enigmas ; y = difícil 5. Alguns x são y, i. e., Alguns bons enigmas são difíceis. 6. Todo x é y. Todos os bons enigmas são difíceis
26 7. Nenhum x existe. Nenhum enigma é bom. 8. Nenhum x é y. Nenhum bom enigma é difícil. Tomando: x = lagosta ; y = egoísta 9. Alguns x são y. Algumas lagostas são não-egoistas. 0. Nenhum x é y. Nenhuma lagosta é egoísta.. Todo x é y. Toda a lagosta é não-egoísta. 2. Alguns x são y e alguns são y. Algumas lagostas e alguns são não-egoístas. Tomando: x = pessoas saudáveis ; y = feliz 3. Todas as pessoas inválidas são infelizes. Todo y é x. x x Y 4. Alguns y existem. Algumas pessoas são não-saudáveis. 5. Alguns y são x e alguns são x. Alguns inválidos são felizes e alguns são não-felizes
27 6. Ninguém é não-saudável
28 4. Diagrama Menor Proposições para representar y x y'. Todo y é x. x' 2. Alguns y são não-x. 3. Nenhum não-x é não-y. 4. Alguns x são não-y. 5. Alguns não-y são x. 6. Nenhum não-x é y. 7. Alguns não-x são não-y. 8. Todo não-x é não-y. 9. Alguns não-u existem. 0. Nenhum não-x existe
29 . Alguns y são x, e alguns são não-x. 2. Todo x é y, e todo não-y é não-x. Tomando: nações como Universo; x = civilizadas ; y = guerreiras 3. Nenhuma nação não-civilizada é guerreira. Nenhum x é y. 4. Toda a nação guerreira é não-civilizada. Todo y é x. 5. Algumas nações são não-guerreiras. Alguns y existem. 6. Toda a nação guerreira é civilizada, e toda a nação civilizada é guerreira. Todo y é x, e todo x é y. 7. Nenhuma nação b é não-civilizada. Nenhum x existe
30 Tomando: crocodilos como Universo; x = faminto ; y = amável 8. Todo o crocodilo faminto é não-amável. Todo x é y. 9. Nenhum crocodilo é amável quando faminto. Nenhum x é y. 20. Alguns crocodilos, quando não estão famintos, são amáveis; mas alguns não são. Alguns x são y, e alguns são y. 2. Nenhum crocodilo é amável, e alguns são famintos. Nenhum y existe, e alguns são x. 22. Todos os crocodilos, quando não famintos, são amáveis; e todos os crocodilos não amáveis são famintos. Todo x é y a todo y é x. 23. Alguns crocodilos famintos são amáveis. E alguns que não são famintos são não-amáveis. Alguns x são y, e alguns x são y
31 5. Diagrama Menor Interpretação símbolos x. y. y'. x'.. Alguns y são não-x. Ou, Alguns não-x são y. 2. Nenhum não-x é não-y, Ou, Nenhum não-y é não-x. 3. Nenhum não-y é x. 4. Nenhum não-x existe. i. e. Nenhuma Coisa é não-x. Tomando: casas como Universo; x = construído de tijolos ; y = doisandares 5. Nenhum y existe. i. e. Nenhuma casa é dois-andares. 6. Alguns x existem. I. e. Algumas casas são não construídas de tijolos
32 7. Nenhum x é y. Ou, nenhum y é x. i e. Nenhuma casa, construída de tijolos, é de dois-andares. Ou, Nenhuma casa, que não é de dois andares, é construída de tijolos. 8. Todo x é y. I. e., Todos as casas eu não são construídas de tijolo, não são de dois andares. Tomando: rapazes como Universo; x = gordos ; y = activos 9. Alguns x são y, e alguns são y. i. e., Alguns rapazes gordos são activos, e Resp alguns não são. 0. Todo y é x. I. e., Todos os rapazes preguiçosos são magros. Resp. Todo x é y, e todo y é x. I. e. Todos os rapazes gordos são preguiçosos. E Resp todos os preguiçosos são gordos. 2. Todo o y é x, e todo o x é y. I. e. Todos os rapazes activos são gordos, e Resp todos os magros são preguiçosos. Tomando: gatos como Universo; x = olhos verdes ; y = bom feitio 3. Nenhum x existe e nenhum y existe. i. e. Nenhum gato tem olhos verdes, Resp e nenhum tem mau-feitio
33 4. Alguns x são y, e alguns x são y. Ou, alguns y são x, e alguns y são x. i. e. Alguns gatos de olhos verdes têm mau-feitio, e alguns, que não têm olhos verdes, têm bom-feitio. Ou, alguns gatos com bom-feitio não têm olhos verdes, e alguns com mau-feitio têm olhos verdes. Resp 5. Alguns x são y, e nenhum x é y. Ou, alguns y são x, e nenhum y é x. i. e. Alguns gatos de olhos verdes têm bom-feitio, e nenhum, que não tem olhos verdes tem mau-feitio. Ou, alguns gatos com mau-feitio têm olhos verdes, e nenhum, que seja com mau-feitio, não tem olhos verdes. Resp 6. Todo x é y, e todo x é y. Ou, Todo y é x, e todo y é x. I. e. Todo o gato de olhos verdes tem mau-feitio, e todos os que não têm olhos verdes, têm bom-feitio. Ou, todos com bom-feitio têm olhos que não são verdes. E todos com mau-feitio têm olhos verdes. Resp
34 6. Diagrama Maior Proposições para representar x. Nenhum x é m. y m y' x' 2. Alguns y são m. 3. Todo m é x. 4. Nenhum m é y. 5. Nenhum m é x; Todo y é m. 6. Alguns x são m; Nenhum y é m
35 7. Todo m é x. Nenhum m é y. 8. Nenhum x é m; Nenhum y é m. Universo, coelhos m = ávido ; x = velho ; y = preto ; 9. Nenhum coelho velho é ávido. Nenhum x é m. 0. Alguns coelhos não-ávidos são pretos. Alguns m são y.. Todos os coelhos brancos são sem avidez. Todo y é m. 2. Todos os coelhos ávidos são jovens
36 Todo m é x. Nenhum coelho velho é ávido; Todos os coelhos pretos são ávidos. Nenhum x é m; Todo y é m. 3. Todos os coelhos que não são ávidos, são pretos; Nenhum coelho está livre de ser ávido. Todo m é y; Nenhum x é m. Universo, pássaros ; m = cantam alto ; x = bem-alimentado ; y = feliz ; 4. Todos os pássaros bem alimentados cantam alto; Nenhum pássaro, que cante alto, é infeliz. Todo x é m; Nenhum m é y. Todos os pássaros, que não cantam alto, são infelizes; Nenhum pássaro bem alimentado deixa de cantar alto. Todo m é y ; Nenhum x é m. Universo, pessoas ; m = dentro de casa ; x = João ; y = têm uma dor de dentes ;
37 5. O João está dentro de casa; Todos os que estão em casa sofrem de dor de dentes. Todo x é m; Nenhum x é m. 6. Ninguém está em casa a não ser o João. Ninguém, fora de casa, tem uma dor de dentes. Nenhum x é m. Nenhum m é y. Universo, pessoas ; m = eu ; x = que tenha dado um passeio ; y = que se sente melhor 7. Eu estive fora a dar um passeio; Eu sinto-me muito melhor. Todo m é x; Todo m é y. Escolha o seu próprio Universo e represente. 8. Eu pedi-lhe um gatinho (kitten). Ele trouxe-me uma panela (kettle) por engano. Deve-se tomar o Universo pessoas pode-se escolher eu como termo médio e neste caso as premissas serão, Eu sou uma pessoa que lhe pediu um gatinho; Eu sou a pessoa a quem ele trouxe uma panela por engano. Ou, pode-se escolher ele como termo médio, e neste caso a premissa vem na forma, Ele é a pessoa a quem eu pedi para trazer um gatinho; - 0 -
38 Ele é a pessoa que me trouxe uma panela por engano. Esta última maneira parece ser a melhor, visto que o interesse da anedota depende da sua estupidez - e não no que aconteceu a mim. Toma-se m= ele ; x= pessoas que eu pedi, ; e y= pessoas que trouxeram, Então, Todo m é x; e o Diagrama requerido é Todo m é y. 7. Usar ambos os diagramas - Aplicar x x y m y' y y' x' x' Nota: Em cada questão, o diagrama menor deveria ser desenhado, para x e y unicamente, e marcado em conformidade com o diagrama maior dado, e então as proposições possíveis realizar o máximo de proposições possíveis para x e y, deverá ser lido a partir do Diagrama menor.. Todo y é x. - -
39 2. Alguns x são y. Ou Alguns y são x. 3. Alguns y são x. Ou Alguns x são y. 4. Nenhum x é y. Ou Nenhum y são x. Marque, no Diagrama Maior, os seguintes pares de proposições da secção anterior. Então marque o diagrama menor em conformidade com isso. 5. Nenhum coelho velho é ávido; Todos os coelhos pretos são ávidos. Todo y é x, i.e., Todos os coelhos pretos são jovens
40 6. Todos os coelhos que não são ávidos, são pretos; Nenhum coelho está livre de ser ávido. Alguns y são x, i. e., Alguns coelhos pretos são jovens. 7. Todos os pássaros bem alimentados cantam alto; Nenhum pássaro, que cante alto, é infeliz. Ou Nenhum x é y ; Alguns x são y. Todo x é y, i. e., Todos os pássaros bem alimentados são felizes. 8. Todos os pássaros, que não cantam alto, são infelizes; Nenhum pássaro bem alimentado deixa de cantar alto. Alguns x é y, i. e., Alguns pássaros que não são bem alimentados, são infelizes; Ou Alguns pássaros infelizes são mal alimentados
41 9. O João está dentro de casa; Todos os que estão em casa sofrem de dor de dentes. Todo x é y, i. e., O João tem uma dor de dentes. 0. Ninguém está em casa a não ser o João. Ninguém, fora de casa, tem uma dor de dentes. Nenhum x é y, i. e., Ninguém a não ser o João tem dor de dentes.. Eu estive fora a dar um passeio; Eu sinto-me muito melhor. Alguns x são y, i. e., Alguém, que foi caminhar, sente-se melhor. 2. Eu pedi-lhe um gatinho (kitten). Ele trouxe-me uma panela (kettle) por engano. Alguns x são y, i. e., Alguém, que eu pedi para me trazer um gatinho, trouxe-me uma panela por engano. Marque no Diagrama maior, os seguintes pares de proposições: Então marque o diagrama menor. Estes são, de facto Pares de Premissas de Silogismos e os resultados, lidos a partir do Diagrama menor são conclusões
42 3. Nenhum livro excitante é apropriado para doentes febris; Livros não excitantes provocam sonolência. Universo = livros m= excitantes x = apropriado para doentes febris y = que provocam sonolência Nenhum m é x; Todo m é y. Nenhum y é x. i. e., Nenhum livro é apropriado para doentes febris, excepto os que provocam sonolência. 4. Alguns, que merecem a justiça, obtêm a sua sobremesa; Ninguém, a não ser os bravos merece a justiça. Universo = pessoas ; m= que merecem a justiça ; x = que obtêm a sua sobremesa ; y = bravos Alguns m são x; Nenhum y é m. Alguns y são x. i. e., Algumas pessoas bravas obtêm a suas sobremesa
43 5. Nenhuma criança é paciente; Nenhuma pessoa impaciente é capaz de se sentar quieta. Universo = pessoas ; m= paciência ; x = crianças ; y = que saiba sentar quieta ; Nenhum x é m; Nenhum m é y. Nenhum x é y. i. e., Nenhuma criança é capaz de se sentar quieta. 6. Todos os porcos são gordos; Nenhum esqueleto é gordo. Universo = Coisas ; m= gordos x = porcos ; y = esqueletos ; Todo x é m; Nenhum y é m. Todo x é y. i. e., Todos os porcos são não-esqueletos
44 7. Nenhum macaco é soldado; Todos os macacos são malandros. Universo = Criaturas ; m= macacos x = soldados ; y = malandros ; Nenhum m é x; Todo m é y. Alguns y são x. i. e., Algumas criaturas malandras não são soldados. 8. Nenhum dos meus primos é justo; Nenhum Juiz é injusto. Universo = pessoas ; m= justo ; x = meus primos ; y = juízes ; Nenhum x é m; Nenhum y é m. Nenhum x é y. i. e., Nenhum dos meus primos é juiz. 9. Alguns dias são chuvosos; Dias chuvosos são cansativos. Universo = períodos ; m= dias ; x = chuvosos; y = cansativos ; Alguns m são x; Todo xm é y. Alguns x são y
Livro VIII. Exemplos, Respostas e Soluções
 Livro V Exemplos, Respostas e Soluções 1. Proposições de Relação a ser reduzidas á Forma normal 1. Estive fora a dar um passeio. O Universo é pessoas. O ndividual Eu pode ser considerado como a Classe
Livro V Exemplos, Respostas e Soluções 1. Proposições de Relação a ser reduzidas á Forma normal 1. Estive fora a dar um passeio. O Universo é pessoas. O ndividual Eu pode ser considerado como a Classe
Semáforo Autor: Alan Parr. Avanço Autor: Dan Troyka, Material Um tabuleiro quadrado 7 por peças brancas e 14 peças negras.
 Avanço Autor: Dan Troyka, 2000 Material Um tabuleiro quadrado 7 por 7. 14 peças brancas e 14 peças negras. Objectivo posição inicial Um jogador ganha se chegar com uma das suas peças à primeira linha do
Avanço Autor: Dan Troyka, 2000 Material Um tabuleiro quadrado 7 por 7. 14 peças brancas e 14 peças negras. Objectivo posição inicial Um jogador ganha se chegar com uma das suas peças à primeira linha do
Livro I. Coisas e seus atributos. [Por exemplo, eu, Londres, rosas, vermelhão, velhos livros ingleses, a carta aquela que eu recebi ontem.
 Livro Coisas e seus atributos Capítulo ntrodução O Universo contém Coisas. [Por exemplo, eu, Londres, rosas, vermelhão, velhos livros ingleses, a carta aquela que eu recebi ontem.] Coisas têm Atributos.
Livro Coisas e seus atributos Capítulo ntrodução O Universo contém Coisas. [Por exemplo, eu, Londres, rosas, vermelhão, velhos livros ingleses, a carta aquela que eu recebi ontem.] Coisas têm Atributos.
Método de indução. José Carlos Santos
 Método de indução José Carlos Santos O termo «indução» tem origem na Filosofia. A entrada do Dicionário de Filosofia de Simon Blackburn que lhe diz respeito começa do seguinte modo: Indução Termo usado
Método de indução José Carlos Santos O termo «indução» tem origem na Filosofia. A entrada do Dicionário de Filosofia de Simon Blackburn que lhe diz respeito começa do seguinte modo: Indução Termo usado
Afirmação verdadeira: frase, falada ou escrita, que declara um facto que é aceite no momento em que é ouvido ou lido.
 Matemática Discreta ESTiG\IPB 2011.12 Cap1 Lógica pg 1 I- Lógica Informal Afirmação verdadeira: frase, falada ou escrita, que declara um facto que é aceite no momento em que é ouvido ou lido. Afirmação
Matemática Discreta ESTiG\IPB 2011.12 Cap1 Lógica pg 1 I- Lógica Informal Afirmação verdadeira: frase, falada ou escrita, que declara um facto que é aceite no momento em que é ouvido ou lido. Afirmação
Canguru Matemático sem Fronteiras 2014
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 10. o e 11. o anos de escolaridade Nome: Turma: Duração: 1h 30min Não podes usar calculadora. Em cada questão deves assinalar a resposta correta.
Vimos que a todo o argumento corresponde uma estrutura. Por exemplo ao argumento. Se a Lua é cúbica, então os humanos voam.
 Matemática Discreta ESTiG\IPB 2012/13 Cap1 Lógica pg 10 Lógica formal (continuação) Vamos a partir de agora falar de lógica formal, em particular da Lógica Proposicional e da Lógica de Predicados. Todos
Matemática Discreta ESTiG\IPB 2012/13 Cap1 Lógica pg 10 Lógica formal (continuação) Vamos a partir de agora falar de lógica formal, em particular da Lógica Proposicional e da Lógica de Predicados. Todos
JOGOS Bruno Holanda, Fortaleza CE
 JOGOS Bruno Holanda, Fortaleza CE Nível Iniciante Problemas sobre jogos estão entre os mais atrativos para a maioria dos alunos que estão iniciando o seu gosto pela matemática e, por isso, vêm ganhando
JOGOS Bruno Holanda, Fortaleza CE Nível Iniciante Problemas sobre jogos estão entre os mais atrativos para a maioria dos alunos que estão iniciando o seu gosto pela matemática e, por isso, vêm ganhando
Material Extra Aula 6 Raciocínio Lógico Prof. Edgar Abreu
 Auditor Fiscal Material Extra Aula 6 Raciocínio Lógico Prof. Edgar Abreu Raciocínio Lógico SILOGISMO Silogismo Categórico é uma forma de raciocínio lógico na qual há duas premissas e uma conclusão distinta
Auditor Fiscal Material Extra Aula 6 Raciocínio Lógico Prof. Edgar Abreu Raciocínio Lógico SILOGISMO Silogismo Categórico é uma forma de raciocínio lógico na qual há duas premissas e uma conclusão distinta
Canguru Matemático sem Fronteiras 2009
 Destinatários: alunos dos 7 e 8 anos de Escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis:
Destinatários: alunos dos 7 e 8 anos de Escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão agrupadas em três níveis:
Canguru sem fronteiras 2005
 Duração: 1h30mn Destinatários: alunos do 12 ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Duração: 1h30mn Destinatários: alunos do 12 ano de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Canguru Matemático sem fronteiras 2008
 Destinatários: alunos do 9º ano de Escolaridade Duração:1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Destinatários: alunos do 9º ano de Escolaridade Duração:1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A. 5º Teste de avaliação versão2. Grupo I
 Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A 5º Teste de avaliação versão Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A 5º Teste de avaliação versão Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
Canguru Matemático sem Fronteiras 2011
 http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 9. ano de escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão
http://www.mat.uc.pt/canguru/ Destinatários: alunos dos 9. ano de escolaridade Nome: Turma: Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. As questões estão
Escola Secundária da Sobreda. Análise Combinatória e Probabilidades. Actividade 4
 Escola Secundária da Sobreda Análise Combinatória e Probabilidades Actividade 4 Os vinte alunos de uma turma de uma escola secundária resolveram formar uma comissão de três de entre eles para organizar
Escola Secundária da Sobreda Análise Combinatória e Probabilidades Actividade 4 Os vinte alunos de uma turma de uma escola secundária resolveram formar uma comissão de três de entre eles para organizar
Canguru Brasil 2014 Nível PE - Soluções
 3 pontos Canguru Brasil 2014 Nível PE - Soluções 1. A joaninha irá assentar na flor que tiver cinco pétalas e três folhas. Qual das flores a seguir será escolhida pela joaninha? 1. Alternativa B A flor
3 pontos Canguru Brasil 2014 Nível PE - Soluções 1. A joaninha irá assentar na flor que tiver cinco pétalas e três folhas. Qual das flores a seguir será escolhida pela joaninha? 1. Alternativa B A flor
O JOGO DE XADREZ. Vamos conhecer as peças que compõe o jogo: O Tabuleiro
 O JOGO DE XADREZ O xadrez é um esporte intelectual, disputado entre duas pessoas que possuem forças iguais (peças) sobre um tabuleiro. Este jogo representa uma batalha em miniatura, onde cada lado comanda
O JOGO DE XADREZ O xadrez é um esporte intelectual, disputado entre duas pessoas que possuem forças iguais (peças) sobre um tabuleiro. Este jogo representa uma batalha em miniatura, onde cada lado comanda
REGRAS DOS JOGOS do CNJM15
 REGRAS DOS JOGOS do CNJM15 Semáforo Autor: Alan Parr 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores. Ser o primeiro a conseguir uma linha de três peças da mesma cor na horizontal,
REGRAS DOS JOGOS do CNJM15 Semáforo Autor: Alan Parr 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores. Ser o primeiro a conseguir uma linha de três peças da mesma cor na horizontal,
Canguru sem fronteiras 2006
 Canguru sem fronteiras 006 Duração: 1h15 Destinatários: alunos dos 10º e 11º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos.
Canguru sem fronteiras 006 Duração: 1h15 Destinatários: alunos dos 10º e 11º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos.
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A TEMA 1 GEOMETRIA NO PLANO E NO ESPAÇO I
 Escola Secundária com º ciclo D. Dinis 10º Ano de Matemática A TEMA 1 GEOMETRIA NO PLANO E NO ESPAÇO I TPC nº entregar no dia 25 02 201 1. Uma jovem, sentada num baloiço, é largada de uma certa altura.
Escola Secundária com º ciclo D. Dinis 10º Ano de Matemática A TEMA 1 GEOMETRIA NO PLANO E NO ESPAÇO I TPC nº entregar no dia 25 02 201 1. Uma jovem, sentada num baloiço, é largada de uma certa altura.
Olimpíada Pernambucana de Matemática Caderno de Questões Com Resoluções
 Olimpíada Pernambucana de Matemática 017 NÍVEL Caderno de Questões Com Resoluções LEIA COM ATENÇÃO 01. Só abra este caderno após ler todas as instruções e quando for autorizado pelos fiscais da sala. 0.
Olimpíada Pernambucana de Matemática 017 NÍVEL Caderno de Questões Com Resoluções LEIA COM ATENÇÃO 01. Só abra este caderno após ler todas as instruções e quando for autorizado pelos fiscais da sala. 0.
CEDERJ MÉTODOS DETERMINÍSTICOS 1 - EP4. Prezado Aluno,
 CEDERJ MÉTODOS DETERMINÍSTICOS 1 - EP4 Prezado Aluno, Neste EP daremos sequência ao nosso estudo da linguagem da lógica matemática. Aqui veremos o conectivo que causa mais dificuldades para os alunos e
CEDERJ MÉTODOS DETERMINÍSTICOS 1 - EP4 Prezado Aluno, Neste EP daremos sequência ao nosso estudo da linguagem da lógica matemática. Aqui veremos o conectivo que causa mais dificuldades para os alunos e
Prog A B C A e B A e C B e C A,B e C Nenhum Pref
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 2 Lógica II Quando lemos um problema de matemática imediatamente podemos ver que ele está dividido em duas partes:
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 2 Lógica II Quando lemos um problema de matemática imediatamente podemos ver que ele está dividido em duas partes:
MD Lógica de Proposições Quantificadas Cálculo de Predicados 1
 Lógica de Proposições Quantificadas Cálculo de Predicados Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br http://www.dcc.ufmg.br/~loureiro MD Lógica de Proposições Quantificadas Cálculo de Predicados
Lógica de Proposições Quantificadas Cálculo de Predicados Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br http://www.dcc.ufmg.br/~loureiro MD Lógica de Proposições Quantificadas Cálculo de Predicados
Raciocínio Lógico. Quantificadores Lógicos: Todo, Nenhum e Existente. Professor Edgar Abreu.
 Raciocínio Lógico Quantificadores Lógicos: Todo, Nenhum e Existente Professor Edgar Abreu www.acasadoconcurseiro.com.br Raciocínio Lógico QUANTIFICADORES LÓGICOS Chama-se argumento a afirmação de que
Raciocínio Lógico Quantificadores Lógicos: Todo, Nenhum e Existente Professor Edgar Abreu www.acasadoconcurseiro.com.br Raciocínio Lógico QUANTIFICADORES LÓGICOS Chama-se argumento a afirmação de que
CAPÍTULO 1. Os elementos. O jogo de xadrez é um desafio para a mente. J. W. von Goethe O TABULEIRO DE XADREZ
 CAPÍTULO 1 Os elementos O jogo de xadrez é um desafio para a mente. J. W. von Goethe O TABULEIRO DE XADREZ Joga-se xadrez sobre um tabuleiro quadrado, formado por 64 casas quadradas, sendo sua cor, alternadamente,
CAPÍTULO 1 Os elementos O jogo de xadrez é um desafio para a mente. J. W. von Goethe O TABULEIRO DE XADREZ Joga-se xadrez sobre um tabuleiro quadrado, formado por 64 casas quadradas, sendo sua cor, alternadamente,
SOLUÇÕES N item a) Basta continuar os movimentos que estão descritos no enunciado:
 N1Q1 Solução SOLUÇÕES N1 2015 Basta continuar os movimentos que estão descritos no enunciado: Basta continuar por mais dois quadros para ver que a situação do Quadro 1 se repete no Quadro 9. Também é possível
N1Q1 Solução SOLUÇÕES N1 2015 Basta continuar os movimentos que estão descritos no enunciado: Basta continuar por mais dois quadros para ver que a situação do Quadro 1 se repete no Quadro 9. Também é possível
Semáforo. Um tabuleiro retangular 4 por 3. 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores.
 Semáforo Autor: Alan Parr Um tabuleiro retangular por. 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores. Ser o primeiro a conseguir uma linha de três peças da mesma cor na horizontal,
Semáforo Autor: Alan Parr Um tabuleiro retangular por. 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores. Ser o primeiro a conseguir uma linha de três peças da mesma cor na horizontal,
Já falamos que, na Matemática, tudo se baseia em axiomas. Já estudamos os números inteiros partindo dos seus axiomas.
 Teoria dos Conjuntos Já falamos que, na Matemática, tudo se baseia em axiomas. Já estudamos os números inteiros partindo dos seus axiomas. Porém, não é nosso objetivo ver uma teoria axiomática dos conjuntos.
Teoria dos Conjuntos Já falamos que, na Matemática, tudo se baseia em axiomas. Já estudamos os números inteiros partindo dos seus axiomas. Porém, não é nosso objetivo ver uma teoria axiomática dos conjuntos.
Expandindo o Vocabulário. Tópicos Adicionais. Autor: Prof. Francisco Bruno Holanda Revisor: Prof. Antônio Caminha Muniz Neto. 12 de junho de 2019
 Material Teórico - Módulo de INTRODUÇÃO À LÓGICA MATEMÁTICA Expandindo o Vocabulário Tópicos Adicionais Autor: Prof. Francisco Bruno Holanda Revisor: Prof. Antônio Caminha Muniz Neto 12 de junho de 2019
Material Teórico - Módulo de INTRODUÇÃO À LÓGICA MATEMÁTICA Expandindo o Vocabulário Tópicos Adicionais Autor: Prof. Francisco Bruno Holanda Revisor: Prof. Antônio Caminha Muniz Neto 12 de junho de 2019
Argumentos e Validade Petrucio Viana
 GAN00166: Lógica para Ciência da Computação Texto da Aula 7 Argumentos e Validade Petrucio Viana Departamento de Análise, IME UFF Sumário 1 Argumentos 1 1.1 Observações................................
GAN00166: Lógica para Ciência da Computação Texto da Aula 7 Argumentos e Validade Petrucio Viana Departamento de Análise, IME UFF Sumário 1 Argumentos 1 1.1 Observações................................
Olimpíada Pernambucana de Matemática Caderno de Questões Com Resoluções
 Olimpíada Pernambucana de Matemática 07 NÍVEL Caderno de Questões Com Resoluções LEIA COM ATENÇÃO 0. Só abra este caderno após ler todas as instruções e quando for autorizado pelos fiscais da sala. 0.
Olimpíada Pernambucana de Matemática 07 NÍVEL Caderno de Questões Com Resoluções LEIA COM ATENÇÃO 0. Só abra este caderno após ler todas as instruções e quando for autorizado pelos fiscais da sala. 0.
Técnicas de Inteligência Artificial
 Universidade do Sul de Santa Catarina Ciência da Computação Técnicas de Inteligência Artificial Aula 02 Representação do Conhecimento Prof. Max Pereira Para que um computador possa solucionar um problema
Universidade do Sul de Santa Catarina Ciência da Computação Técnicas de Inteligência Artificial Aula 02 Representação do Conhecimento Prof. Max Pereira Para que um computador possa solucionar um problema
Soluções Simulado OBMEP 2017 Nível 1 6º e 7º anos do Ensino Fundamental. = 7 cm. Logo, ela parou na marca de = 13 cm.
 Soluções Simulado OBMEP 2017 Nível 1 6º e 7º anos do Ensino Fundamental 1. ALTERNATIVA C Alvimar recebeu de troco 5,00 3,50 = 1,50 reais. Dividindo 1,50 por 0,25, obtemos o número de moedas de 25 centavos
Soluções Simulado OBMEP 2017 Nível 1 6º e 7º anos do Ensino Fundamental 1. ALTERNATIVA C Alvimar recebeu de troco 5,00 3,50 = 1,50 reais. Dividindo 1,50 por 0,25, obtemos o número de moedas de 25 centavos
1 Lógica de primeira ordem
 1 Lógica de primeira ordem 1.1 Sintaxe Para definir uma linguagem de primeira ordem é necessário dispor de um alfabeto. Este alfabeto introduz os símbolos à custa dos quais são construídos os termos e
1 Lógica de primeira ordem 1.1 Sintaxe Para definir uma linguagem de primeira ordem é necessário dispor de um alfabeto. Este alfabeto introduz os símbolos à custa dos quais são construídos os termos e
JOGOS LIVRO REGRAS M AT E M Á T I CO S. 11.º Campeonato Nacional
 Vila Real JOGOS M AT E M Á T I CO S.º Campeonato Nacional LIVRO DE REGRAS Semáforo Autor: Alan Parr Material Um tabuleiro retangular por. 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores.
Vila Real JOGOS M AT E M Á T I CO S.º Campeonato Nacional LIVRO DE REGRAS Semáforo Autor: Alan Parr Material Um tabuleiro retangular por. 8 peças verdes, 8 amarelas e 8 vermelhas partilhadas pelos jogadores.
Canguru Matema tico sem Fronteiras 2013
 Canguru Matema tico sem Fronteiras 2013 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 7.o e 8.o anos de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa
Canguru Matema tico sem Fronteiras 2013 http://www.mat.uc.pt/canguru/ Destinata rios: alunos dos 7.o e 8.o anos de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa
Ficha de Trabalho nº 11 Matemática 7º ano Maio / 2011 INTRODUÇÃO AO ESTUDO DA ESTATÍSTICA
 Ficha de Trabalho nº 11 Matemática 7º ano Maio / 2011 INTRODUÇÃO AO ESTUDO DA ESTATÍSTICA Recorda: A Estatística é um ramo da Matemática que nos ajuda a recolher, organizar e interpretar dados para tirar
Ficha de Trabalho nº 11 Matemática 7º ano Maio / 2011 INTRODUÇÃO AO ESTUDO DA ESTATÍSTICA Recorda: A Estatística é um ramo da Matemática que nos ajuda a recolher, organizar e interpretar dados para tirar
Faz a tua própria história
 Faz a tua própria história! Faz a tua própria história, Página 1 Estou aqui para vos falar de uma história muito simples. E a história não é sobre um rei, um príncipe, um elefante, ou um rato. A história
Faz a tua própria história! Faz a tua própria história, Página 1 Estou aqui para vos falar de uma história muito simples. E a história não é sobre um rei, um príncipe, um elefante, ou um rato. A história
5º Teste de avaliação versão1. Grupo I
 Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A 5º Teste de avaliação versão1 Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
Escola Secundária com 3º ciclo D. Dinis 10º Ano de Matemática A 5º Teste de avaliação versão1 Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
Raciocínio Lógico I. Solução. Primeiramente vamos listar todos os números de dois algarismos que são múltiplos de 7 ou 13.
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 1 Prof. Bruno Holanda Aula 3 Raciocínio Lógico I O estudo da Lógica é essencial para os alunos que desejam participar de olimpíadas de matemática.
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 1 Prof. Bruno Holanda Aula 3 Raciocínio Lógico I O estudo da Lógica é essencial para os alunos que desejam participar de olimpíadas de matemática.
PACRU SÉRIE 302. Linguagens e Informação Extra. Três Jogos: Shacru, Azacru & Pacru
 PACRU SÉRIE 302 Linguagens e Informação Extra Se esta informação não está na sua linguagem, vá a www.pacru.com, seleccione a linguagem e imprima as regras. Neste folheto estão todas as informações necessárias
PACRU SÉRIE 302 Linguagens e Informação Extra Se esta informação não está na sua linguagem, vá a www.pacru.com, seleccione a linguagem e imprima as regras. Neste folheto estão todas as informações necessárias
XXVIII OLIMPÍADA DE MATEMATICA DO RIO GRANDE DO NORTE PRIMEIRA FASE SOLUÇÃO DA PROVA DO NÍVEL I
 XXVIII OLIMPÍADA DE MATEMATICA DO RIO GRANDE DO NORTE 2017- PRIMEIRA FASE SOLUÇÃO DA PROVA DO NÍVEL I PARA CADA QUESTÃO, ASSINALE UMA ALTERNATIVA COMO A RESPOSTA CORRETA NOME DO(A) ESTUDANTE: ESCOLA: 1
XXVIII OLIMPÍADA DE MATEMATICA DO RIO GRANDE DO NORTE 2017- PRIMEIRA FASE SOLUÇÃO DA PROVA DO NÍVEL I PARA CADA QUESTÃO, ASSINALE UMA ALTERNATIVA COMO A RESPOSTA CORRETA NOME DO(A) ESTUDANTE: ESCOLA: 1
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Canguru sem fronteiras 2005
 Duração: 1h30mn Destinatários: alunos dos 10 e 11 anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada,
Duração: 1h30mn Destinatários: alunos dos 10 e 11 anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada,
ESCOLA EMEF PROFª MARIA MARGARIDA ZAMBON BENINI - PIBID 08/10/2014, 29/10/2014 e 05/11/2014
 ESCOLA EMEF PROFª MARIA MARGARIDA ZAMBON BENINI - PIBID 08/10/2014, 29/10/2014 e 05/11/2014 Bolsistas: Mévelin Maus, Milena Poloni Pergher e Odair José Sebulsqui. Supervisora: Marlete Basso Roman Disciplina:
ESCOLA EMEF PROFª MARIA MARGARIDA ZAMBON BENINI - PIBID 08/10/2014, 29/10/2014 e 05/11/2014 Bolsistas: Mévelin Maus, Milena Poloni Pergher e Odair José Sebulsqui. Supervisora: Marlete Basso Roman Disciplina:
OBMEP a Fase Soluções Nível 2. N2Q1 Solução
 1 N2Q1 Solução a) Com o número 92653 Mônica obteve a expressão 9 + 2 6 5 3. Efetuando primeiro a multiplicação e, em seguida, a divisão (ou então a divisão seguida da multiplicação), temos 9 + 2 6 5 3
1 N2Q1 Solução a) Com o número 92653 Mônica obteve a expressão 9 + 2 6 5 3. Efetuando primeiro a multiplicação e, em seguida, a divisão (ou então a divisão seguida da multiplicação), temos 9 + 2 6 5 3
Combinatória I. Sumário Introdução Princípios Básicos... 2
 11 Combinatória I Sumário 11.1 Introdução....................... 2 11.2 Princípios Básicos................... 2 1 Unidade 11 Introdução 11.1 Introdução Combinatória é um vasto e importante campo da matemática
11 Combinatória I Sumário 11.1 Introdução....................... 2 11.2 Princípios Básicos................... 2 1 Unidade 11 Introdução 11.1 Introdução Combinatória é um vasto e importante campo da matemática
Gatos & Cães Simon Norton, 1970s
 Gatos & Cães Simon Norton, 1970s Um tabuleiro quadrado 8 por 8. 28 peças gato e 28 peças cão (representadas respectivamente por peças negras e brancas). Ganha o jogador que realizar a última jogada. zona
Gatos & Cães Simon Norton, 1970s Um tabuleiro quadrado 8 por 8. 28 peças gato e 28 peças cão (representadas respectivamente por peças negras e brancas). Ganha o jogador que realizar a última jogada. zona
XXI Olimpíada de Matemática do Estado do Rio Grande do Norte. Prova do Nível I Em 25/09/2010
 XXI Olimpíada de Matemática do Estado do Rio Grande do Norte Prova do Nível I Em 25/09/2010 Problema 1 Um professor de Matemática definiu a seguinte operação entre dois números naturais: Ele exemplificou
XXI Olimpíada de Matemática do Estado do Rio Grande do Norte Prova do Nível I Em 25/09/2010 Problema 1 Um professor de Matemática definiu a seguinte operação entre dois números naturais: Ele exemplificou
MA21 (2015) - Teste - Gabarito comentado. Problema 1 (OBM 2005) Na sequência de números
 MA21 (2015) - Teste - Gabarito comentado Problema 1 (OBM 2005) Na sequência de números 1, a, 2, b, c, d,... dizemos que o primeiro termo é 1, o segundo é a, o terceiro é 2, o quarto é b, o quinto é c e
MA21 (2015) - Teste - Gabarito comentado Problema 1 (OBM 2005) Na sequência de números 1, a, 2, b, c, d,... dizemos que o primeiro termo é 1, o segundo é a, o terceiro é 2, o quarto é b, o quinto é c e
Canguru Matema tico sem Fronteiras 2012
 Canguru Matema tico sem Fronteiras 2012 http://www.mat.uc.pt/canguru/ Destinata rios: alunos do 9.o ano de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa o deves
Canguru Matema tico sem Fronteiras 2012 http://www.mat.uc.pt/canguru/ Destinata rios: alunos do 9.o ano de escolaridade Durac a o: 1h 30min Nome: Turma: Na o podes usar calculadora. Em cada questa o deves
Por que o teste estrela funciona?
 Por que o teste estrela funciona? Observações preliminares A lógica silogística estuda argumentos cuja validade dependem de "todo", "nenhum", "algum" e noções similares. Ao simbolizar esses argumentos,
Por que o teste estrela funciona? Observações preliminares A lógica silogística estuda argumentos cuja validade dependem de "todo", "nenhum", "algum" e noções similares. Ao simbolizar esses argumentos,
Prova da segunda fase - Nível 2
 Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Caro Aluno, Parabéns pela sua participação na nona edição da Olimpíada de Matemática de São José do Rio Preto! Lembre-se de que uma Olimpíada é diferente de uma prova escolar. Muitas vezes, as questões
Canguru Matemático sem fronteiras 2008
 Destinatários: alunos do 12º ano de Escolaridade Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Destinatários: alunos do 12º ano de Escolaridade Duração: 1h30min Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 30 pontos. Por cada questão errada, és penalizado
Silogismos Categóricos e Hipotéticos
 Silogismos Categóricos e Hipotéticos Resumo elaborado por Francisco Cubal Apenas para publicação em Resumos.tk Primeiros objectivos a alcançar: Reconhecer os quatro tipos de proposições categóricas. Enunciar
Silogismos Categóricos e Hipotéticos Resumo elaborado por Francisco Cubal Apenas para publicação em Resumos.tk Primeiros objectivos a alcançar: Reconhecer os quatro tipos de proposições categóricas. Enunciar
Aulas 5 e 6 / 28 e 30 de março
 Aulas 5 e / 8 e 30 de março 1 Notação de soma e produto Como expressar a seguinte soma de uma maneira mais concisa? 1 + + 3 3 + + 10? Note que as parcelas são semelhantes, e que a única coisa que varia
Aulas 5 e / 8 e 30 de março 1 Notação de soma e produto Como expressar a seguinte soma de uma maneira mais concisa? 1 + + 3 3 + + 10? Note que as parcelas são semelhantes, e que a única coisa que varia
Teste de Funções por Partição do Espaço de Entrada
 Teste de Funções por Partição do Espaço de Entrada Programação II Universidade de Lisboa Faculdade de Ciências Departamento de Informática Licenciatura em Tecnologias da Informação Vasco Thudichum Vasconcelos
Teste de Funções por Partição do Espaço de Entrada Programação II Universidade de Lisboa Faculdade de Ciências Departamento de Informática Licenciatura em Tecnologias da Informação Vasco Thudichum Vasconcelos
Introdução à Programação. João Manuel R. S. Tavares
 Introdução à Programação João Manuel R. S. Tavares Sumário 1. Ciclo de desenvolvimento de um programa; 2. Descrição de algoritmos; 3. Desenvolvimento modular de programas; 4. Estruturas de controlo de
Introdução à Programação João Manuel R. S. Tavares Sumário 1. Ciclo de desenvolvimento de um programa; 2. Descrição de algoritmos; 3. Desenvolvimento modular de programas; 4. Estruturas de controlo de
livro das regras (provisório)
 livro das regras (provisório) Avanço Autor: Dan Troyka, 2000 Um tabuleiro quadrado 7 por 7; 14 peças brancas e 14 peças negras. Um jogador ganha se chegar com uma das suas peças à primeira linha do adversário,
livro das regras (provisório) Avanço Autor: Dan Troyka, 2000 Um tabuleiro quadrado 7 por 7; 14 peças brancas e 14 peças negras. Um jogador ganha se chegar com uma das suas peças à primeira linha do adversário,
Introdução à Programação
 Introdução à Program João Manuel R. S. Tavares Sumário 1. Ciclo de desenvolvimento de um programa; 2. Descrição de algoritmos; 3. Desenvolvimento modular de programas; 4. Estruturas de controlo de um programa.
Introdução à Program João Manuel R. S. Tavares Sumário 1. Ciclo de desenvolvimento de um programa; 2. Descrição de algoritmos; 3. Desenvolvimento modular de programas; 4. Estruturas de controlo de um programa.
Gatos & Cães Simon Norton, 1970s
 Gatos & Cães Simon Norton, 970s Um tabuleiro quadrado 8 por 8. 8 peças gato e 8 peças cão (representadas respectivamente por peças negras e brancas). Ganha o jogador que realizar a última jogada. zona
Gatos & Cães Simon Norton, 970s Um tabuleiro quadrado 8 por 8. 8 peças gato e 8 peças cão (representadas respectivamente por peças negras e brancas). Ganha o jogador que realizar a última jogada. zona
Divisibilidade e Restos. Caio Hermano Maia
 Divisibilidade e Restos Caio Hermano Maia 1 Introdução Neste material iremos introduzi-lo à Teoria dos Números, uma área da matemática focada exclusivamente no estudo dos números inteiros e suas diversas
Divisibilidade e Restos Caio Hermano Maia 1 Introdução Neste material iremos introduzi-lo à Teoria dos Números, uma área da matemática focada exclusivamente no estudo dos números inteiros e suas diversas
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória
 Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória Tarefa nº 1 1. Verdadeiro ou Falso? 1.1. É pouco provável tirar um rei ao acaso de um baralho de 52
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória Tarefa nº 1 1. Verdadeiro ou Falso? 1.1. É pouco provável tirar um rei ao acaso de um baralho de 52
Canguru sem fronteiras 2006
 Duração: 1h15 Destinatários: alunos dos 5º e 6º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 24 pontos. Por cada questão errada, és
Duração: 1h15 Destinatários: alunos dos 5º e 6º anos de Escolaridade Não podes usar calculadora. Há apenas uma resposta correcta em cada questão. Inicialmente tens 24 pontos. Por cada questão errada, és
XXVII Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 Soluções Nível 1 Segunda Fase Parte A XXVII Olimpíada Brasileira de Matemática GABARITO Segunda Fase CRITÉRIO DE CORREÇÃO: PARTE A Cada questão vale pontos se, e somente se, para cada uma o resultado escrito
Soluções Nível 1 Segunda Fase Parte A XXVII Olimpíada Brasileira de Matemática GABARITO Segunda Fase CRITÉRIO DE CORREÇÃO: PARTE A Cada questão vale pontos se, e somente se, para cada uma o resultado escrito
Advérbios. Os advérbios modificam o sentido de um verbo, de um adjectivo, de outro advérbio ou de uma oração inteira.
 Advérbios Os advérbios modificam o sentido de um verbo, de um adjectivo, de outro advérbio ou de uma oração inteira. Advérbios de tempo: quando? agora, ainda, amanhã, antes, antigamente, cedo, dantes,
Advérbios Os advérbios modificam o sentido de um verbo, de um adjectivo, de outro advérbio ou de uma oração inteira. Advérbios de tempo: quando? agora, ainda, amanhã, antes, antigamente, cedo, dantes,
RECEITA FEDERAL ANALISTA
 SENTENÇAS OU PROPOSIÇÕES São os elementos que expressam uma idéia, mesmo que absurda. Estudaremos apenas as proposições declarativas, que podem ser classificadas ou só como verdadeiras (V), ou só como
SENTENÇAS OU PROPOSIÇÕES São os elementos que expressam uma idéia, mesmo que absurda. Estudaremos apenas as proposições declarativas, que podem ser classificadas ou só como verdadeiras (V), ou só como
Soluções. Nível 2 7 a e 8 a séries (8º e 9º anos) do Ensino Fundamental
 1. (alternativa A) No diagrama ao lado cada quadradinho tem 1 km de lado e o ponto C indica a casa de Carlos. Representando o trajeto descrito no enunciado pelas flechas em traço fino, vemos que a escola
1. (alternativa A) No diagrama ao lado cada quadradinho tem 1 km de lado e o ponto C indica a casa de Carlos. Representando o trajeto descrito no enunciado pelas flechas em traço fino, vemos que a escola
Indiscernibilidade de Idênticos. Atitudes Proposicionais e indiscernibilidade de idênticos
 Indiscernibilidade de Idênticos Atitudes Proposicionais e indiscernibilidade de Consideremos agora o caso das atitudes proposicionais, das construções epistémicas e psicológicas, e perguntemo-nos se é
Indiscernibilidade de Idênticos Atitudes Proposicionais e indiscernibilidade de Consideremos agora o caso das atitudes proposicionais, das construções epistémicas e psicológicas, e perguntemo-nos se é
Canguru Matemático sem Fronteiras 2018
 Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Destinatários: alunos dos 7. o e 8. o anos de escolaridade Duração: 1h 30min Nome: Turma: Não podes usar calculadora. Em cada questão deves assinalar a resposta correta. As questões estão agrupadas em
Teste de avaliação (Versão B) Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 0º ANO DE MATEMÁTICA A 2-03 - 2007 Teste de avaliação (Versão B) Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 0º ANO DE MATEMÁTICA A 2-03 - 2007 Teste de avaliação (Versão B) Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
Canguru de Matemática Brasil 2016 Nível E Soluções
 Problemas de 3 pontos Canguru de Matemática Brasil 2016 Nível E Soluções 1. Ana, Bruna, Cris, Dora e Edna jogaram dois dados cada uma. Qual das meninas obteve a maior soma do número de pontos? (A) Ana
Problemas de 3 pontos Canguru de Matemática Brasil 2016 Nível E Soluções 1. Ana, Bruna, Cris, Dora e Edna jogaram dois dados cada uma. Qual das meninas obteve a maior soma do número de pontos? (A) Ana
Tarefa : Vamos contar narizes, olhos, pernas, braços, mão, pés e dedos
 Tarefa : Vamos contar narizes, olhos, pernas, braços, mão, pés e dedos 1. Na tua sala de aula há alunos. Quantos são os narizes? 2. E quantos são os olhos? E os dedos?... Tarefa : Rodas de motas, automóveis
Tarefa : Vamos contar narizes, olhos, pernas, braços, mão, pés e dedos 1. Na tua sala de aula há alunos. Quantos são os narizes? 2. E quantos são os olhos? E os dedos?... Tarefa : Rodas de motas, automóveis
Lógica Dedutiva e Falácias
 Lógica Dedutiva e Falácias Aula 3 Prof. André Martins Lógica A Lógica é o ramo do conhecimento humano que estuda as formas pelas quais se pode construir um argumento correto. O que seria um raciocínio
Lógica Dedutiva e Falácias Aula 3 Prof. André Martins Lógica A Lógica é o ramo do conhecimento humano que estuda as formas pelas quais se pode construir um argumento correto. O que seria um raciocínio
ZSRest. Manual de Configuração. Centros de Produção. V2011-Certificado
 Manual de Configuração Centros de Produção V2011-Certificado 1 1. Índice 2. Introdução... 2 3. Criar um Centro de Produção... 3 4. Definir Impressoras de Pedidos... 4 5. Opções de Impressão... 6 6. Impressão
Manual de Configuração Centros de Produção V2011-Certificado 1 1. Índice 2. Introdução... 2 3. Criar um Centro de Produção... 3 4. Definir Impressoras de Pedidos... 4 5. Opções de Impressão... 6 6. Impressão
Polos Olímpicos de Treinamento. Aula 1. Curso de Combinatória - Nível 2. Prof. Bruno Holanda
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 1 Lógica Nos últimos anos, a participação brasileira em competições internacionais de matemática vem melhorado significamente.
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 1 Lógica Nos últimos anos, a participação brasileira em competições internacionais de matemática vem melhorado significamente.
Distribuição de Jogos por Ciclo
 REGRAS DOS JOGOS Distribuição de Jogos por Ciclo 1º CEB 2º CEB 3º CEB Sec. Semáforo x Gatos & Cães x x Rastros x x x Produto x x x Avanço x x Flume x 2 Semáforo Autor: Alan Parr 8 peças verdes, 8 amarelas
REGRAS DOS JOGOS Distribuição de Jogos por Ciclo 1º CEB 2º CEB 3º CEB Sec. Semáforo x Gatos & Cães x x Rastros x x x Produto x x x Avanço x x Flume x 2 Semáforo Autor: Alan Parr 8 peças verdes, 8 amarelas
COMO FORMATAR UM ROTEIRO PARA HQ
 COMO FORMATAR UM ROTEIRO PARA HQ A primeira coisa que você deve se lembrar é que um roteiro vai ser lido por alguém. Para ser mais exato, o seu roteiro será lido por um desenhista. E, creia-me, os desenhistas
COMO FORMATAR UM ROTEIRO PARA HQ A primeira coisa que você deve se lembrar é que um roteiro vai ser lido por alguém. Para ser mais exato, o seu roteiro será lido por um desenhista. E, creia-me, os desenhistas
Reference to English Interconnections Lesson Changes at School p. 14 Social Studies Standard(s): Standard 1, Objective 1
 1ª Série Lição: As mudanças na escola - Igual e diferente Reference to English Interconnections Lesson Changes at School p. 14 Social Studies Standard(s): Standard 1, Objective 1 Objetivo(s) do Conteúdo
1ª Série Lição: As mudanças na escola - Igual e diferente Reference to English Interconnections Lesson Changes at School p. 14 Social Studies Standard(s): Standard 1, Objective 1 Objetivo(s) do Conteúdo
Lógica Proposicional Parte 2
 Lógica Proposicional Parte 2 Como vimos na aula passada, podemos usar os operadores lógicos para combinar afirmações criando, assim, novas afirmações. Com o que vimos, já podemos combinar afirmações conhecidas
Lógica Proposicional Parte 2 Como vimos na aula passada, podemos usar os operadores lógicos para combinar afirmações criando, assim, novas afirmações. Com o que vimos, já podemos combinar afirmações conhecidas
CAPÍTULO II NOÇÕES TOPOLÓGICAS EM R
 CAPÍTULO II NOÇÕES TOPOLÓGICAS EM R 1. Distância e vizinhanças Ao número real não negativo d(x, y) = x y chama-se distância entre os números reais x e y. São imediatas as seguintes propriedades: P1 : d(x,
CAPÍTULO II NOÇÕES TOPOLÓGICAS EM R 1. Distância e vizinhanças Ao número real não negativo d(x, y) = x y chama-se distância entre os números reais x e y. São imediatas as seguintes propriedades: P1 : d(x,
Etiqueta de Identificação. TIMSS e PIRLS Questionário ao Aluno. 4.º ano. GAVE Gabinete de Avaliação Educacional Lisboa, Portugal
 Etiqueta de Identificação TIMSS e PIRLS 2011 Questionário ao Aluno 4.º ano GAVE Gabinete de Avaliação Educacional Lisboa, Portugal IEA, 2011 Instruções Neste caderno, vais encontrar perguntas sobre ti
Etiqueta de Identificação TIMSS e PIRLS 2011 Questionário ao Aluno 4.º ano GAVE Gabinete de Avaliação Educacional Lisboa, Portugal IEA, 2011 Instruções Neste caderno, vais encontrar perguntas sobre ti
Material Teórico - Módulo O Plano Cartesiano e Sistemas de Equações. O Plano Cartesiano. Sétimo Ano do Ensino Fundamental
 Material Teórico - Módulo O Plano Cartesiano e Sistemas de Equações O Plano Cartesiano Sétimo Ano do Ensino undamental Autor: Prof. rancisco Bruno Holanda Revisor: Prof. Antonio Caminha Muniz Neto Introdução
Material Teórico - Módulo O Plano Cartesiano e Sistemas de Equações O Plano Cartesiano Sétimo Ano do Ensino undamental Autor: Prof. rancisco Bruno Holanda Revisor: Prof. Antonio Caminha Muniz Neto Introdução
Soluções dos Exercícios do Capítulo 2
 A MATEMÁTICA DO ENSINO MÉDIO Volume 1 Soluções dos Exercícios do Capítulo 2 2.1. Seja X = {n N; a + n Y }. Como a Y, segue-se que a + 1 Y, portanto 1 X. Além disso n X a + n Y (a + n) + 1 Y n + 1 X. Logo
A MATEMÁTICA DO ENSINO MÉDIO Volume 1 Soluções dos Exercícios do Capítulo 2 2.1. Seja X = {n N; a + n Y }. Como a Y, segue-se que a + 1 Y, portanto 1 X. Além disso n X a + n Y (a + n) + 1 Y n + 1 X. Logo
Tema I Introdução à lógica bivalente e à teoria de conjuntos
 Tema I Introdução à lógica bivalente e à teoria de conjuntos Unidade 1 Proposições Páginas 13 a 9 1. a) 3 é uma designação. b) 3 = 6 é uma proposição. c) é o único número primo par é uma proposição. d)
Tema I Introdução à lógica bivalente e à teoria de conjuntos Unidade 1 Proposições Páginas 13 a 9 1. a) 3 é uma designação. b) 3 = 6 é uma proposição. c) é o único número primo par é uma proposição. d)
Teorema de Gerschgorin...
 Texto da palestra Teorema de Gerschgorin... ou será Ger sgorin? ou ainda Gerŝhgorin? Gersgorin? Geršgorin? Gershgorin? Gerŝgorin? Jaime Gaspar 2004/09/19 1 Introdução 1 Vamos falar um pouco sobre o Teorema
Texto da palestra Teorema de Gerschgorin... ou será Ger sgorin? ou ainda Gerŝhgorin? Gersgorin? Geršgorin? Gershgorin? Gerŝgorin? Jaime Gaspar 2004/09/19 1 Introdução 1 Vamos falar um pouco sobre o Teorema
Capítulo 4 LEITURA E INTERPRETAÇÃO DE DESENHOS
 Capítulo 4 LEITURA E INTERPRETAÇÃO DE DESENHOS Definição e Pré-Requisitos Ler um desenho significa entender a forma espacial do objeto representado no desenho bidimensional resultante das projeções ortogonais.
Capítulo 4 LEITURA E INTERPRETAÇÃO DE DESENHOS Definição e Pré-Requisitos Ler um desenho significa entender a forma espacial do objeto representado no desenho bidimensional resultante das projeções ortogonais.
a 11 a a 1n a 21 a a 2n A = a m1 a m2... a mn
 Matrizes Definição Definição Uma matriz m n é uma tabela de mn números dispostos em m linhas e n colunas a 11 a 1 a 1n a 1 a a n a m1 a m a mn Embora a rigor matrizes possam ter quaisquer tipos de elementos,
Matrizes Definição Definição Uma matriz m n é uma tabela de mn números dispostos em m linhas e n colunas a 11 a 1 a 1n a 1 a a n a m1 a m a mn Embora a rigor matrizes possam ter quaisquer tipos de elementos,
fragmentos dos diálogos categorias e obras da exortativas interpretação aristóteles introdução, tradução e notas ricardo santos tradução ( universidad
 fragmentos dos diálogos categorias e obras da exortativas interpretação aristóteles introdução, tradução e notas ricardo santos tradução ( universidade e textos introdutórios de lisboa) antónio de castro
fragmentos dos diálogos categorias e obras da exortativas interpretação aristóteles introdução, tradução e notas ricardo santos tradução ( universidade e textos introdutórios de lisboa) antónio de castro
Representação decimal dos números racionais
 Representação decimal dos números racionais Alexandre Kirilov Elen Messias Linck 21 de março de 2018 1 Introdução Um número é racional se puder ser escrito na forma a/b, com a e b inteiros e b 0; esta
Representação decimal dos números racionais Alexandre Kirilov Elen Messias Linck 21 de março de 2018 1 Introdução Um número é racional se puder ser escrito na forma a/b, com a e b inteiros e b 0; esta
LISTA 29 - PROBABILIDADE 1
 LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
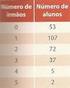 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
Números pares e ímpares
 Números pares e ímpares 1 O que tem neste Capítulo Todos os números inteiros são divididos em dois grupos pares e ímpares. Eles se seguem um ao outro em ordem ímpar, par, ímpar, par, como os números das
Números pares e ímpares 1 O que tem neste Capítulo Todos os números inteiros são divididos em dois grupos pares e ímpares. Eles se seguem um ao outro em ordem ímpar, par, ímpar, par, como os números das
3. Ana Júlia, tia de Alfredo, vende trufas de chocolate...
 1. Para construir uma estante completa... Nível 1 O marceneiro possui pranchas grandes suficientes para montar 6 estantes e pranchas pequenas suficientes para 5, os demais materiais são mais abundantes
1. Para construir uma estante completa... Nível 1 O marceneiro possui pranchas grandes suficientes para montar 6 estantes e pranchas pequenas suficientes para 5, os demais materiais são mais abundantes
