3 CONSEQUÊNCIAS DA TEORIA DE CAUCHY
|
|
|
- Giulia Vilaverde
- 5 Há anos
- Visualizações:
Transcrição
1 3 CONSEQUÊNCIAS DA TEORIA DE CAUCHY A teoria de Cauchy-Goursat, desenvolvida na secção 2 (TEORIA DE CAUCHY- GOUR- SAT), permite-nos tirar algumas propriedades importantes sobre as funções f que são diferenciáveis num conjunto aberto U: Uma primeira consequência surge do facto de considerando u Re f(x + iy) e v Im f(x + iy); a função derivada de f; ser dada para qualquer x + iy 2 U; através de qualquer uma das igualdades seguintes: f 0 (x + iy) = + i i : Mas como f 0 é contínua em U; por ser também diferenciável em U; podemos concluir que então são igualmente funções contínuas no aberto = f : x + iy 2 Ug ; e que, por conseguinte, f é uma função holomorfa em U: Logo ter f diferenciável em U é equivalente a que f seja holomorfa em U: 3. FUNÇÕES HARMÓNICAS Uma função real que seja de classe C 2 num conjunto aberto R 2 ; e que satisfaça para cada 2 ; a equação de 0; 2 2 diz-se uma função harmónica em : Casos concretos de funções harmónicas são-nos dados pelas funções que são parte real ou parte imaginária de uma função, f; que seja holomorfa num dado conjunto aberto, U C; isto é, pelas funções u Re f(x + iy) e v Im f(x + iy); de nidas no aberto = f : x + iy 2 Ug R 2 : Para isso tenhamos em conta que Re f 0 (x + iy) = Im f 0 (x + iy) = e que o Teorema 7 da secção 2.2 (FÓRMULAS INTEGRAIS DE CAUCHY) garante que f 0 também é diferenciável em U: Então destas relações podemos concluir que existirão necessariamente em ; todas as derivadas parcias de segunda ordem, quer de u; quer de
2 v; e que as correspondentes equações de Cauchy-Riemann são veri cadas. Assim, para qualquer ou v 2 2 u : 2 Além disso, ainda por ser uma função diferenciável em U; f 00 é uma função contínua neste conjunto, podendo-se então a rmar que também todas as derivadas de segunda ordem são funções contínuas em ; ou seja que u e v são funçõess de classe C 2 em : Então a igualdade entre as derivadas parciais cruzadas de segunda ordem permite-nos concluir que, para qualquer 2 ; u u 0; 2 2 v v 0: 2 2 Logo, em tais circunstâncias, podemos a rmar que, na verdade, u e v são funções harmónicas. Dada uma função harmónica num dado conjunto R 2 ; se existir uma função complexa de variável complexa, f; holomorfa em U = fx + iy : 2 g tal que a função Re f(x + iy); Im f(x + iy) é chamada de harmónica conjugada de u: Notemos ainda que a diferenciabilidade de f 0 leva a que para qualquer x + iy 2 U; f 00 (x + iy)
3 ou seja que f 00 (x + iy) u + v 2 v 2 2 v = u 2 2 u v : 2 Mas como ainda pelo Teorema 7 da secção 2.2 (FÓRMULAS INTEGRAIS DE CAUCHY) também f 00 também é holomorfa, existem igualmente todas as derivadas parciais de terceira ordem de qualquer das funções u e v: Prosseguindo continuamente este processo, podemos assim concluir que quer u; quer v; admitem no conjunto ; todas derivadas parciais de todas as ordens. Logo u e v são ambas funções de classe C em : 3.2 TEOREMA DE LIOUVILLE Uma outra consequência simples das fórmulas integrais de Cauchy reporta-se ao teorema seguinte, comummente atribuído ao francês Joseph Liouville ( ). Teorema (Teorema de Liouville) Qualquer função inteira limitada é constante. Dem.: Com z 2 C; temos para qualquer circunferência, C r (z); de centro em z e raio r > 0; simples e positivamente orientada, f 0 (z) = f(w) 2i (w z) dw: 2 C r(z) Então supondo que jf(z)j M; para qualquer z 2 C; obtemos que jf 0 (z)j M 2 r 2r = M 2 r : Da arbitrariedade de r > 0; concluímos que f 0 é identicamente nula em C: Logo f é constante em C: 3.3 TEOREMA FUNDAMENTAL DA ÁLGEBRA Teorema 2 (Teorema Fundamental da Álgebra) Qualquer polinómio de grau superior a um tem pelo menos uma raiz. Dem.: Seja p(z) = a n z n + ::: + a z + a 0 um polinómio de grau n > e suponhamos que p(z) não admite qualquer raiz. Nestas circunstâncias, temos que p(z) 6= 0; qualquer que seja z 2 C; e por conseguinte a função é uma função inteira. f (z) = p(z) 3
4 De jp(z)j = z n a n + a n + ::: + a z z + a 0 n z n = jzj n an + a n z + ::: + a z n + a 0 z n ; podemos concluir que jp(z)j! +; quando jzj! + e consequentemente que jf (z)j! 0; quando jzj! +: Ou seja, existe R > 0 su cientemente grande tal que jf (z)j < ; quando jzj > R: Porém, sendo f inteira, em particular f é contínua em C; e como tal limitada na bola fechada B R = fz : jzj Rg : Em suma, f é uma função inteira limitada. Mas em tais circunstâncias, o teorema de Liouville, leva-nos a a rmar que f é uma função constante. Mas isto implica que todos os coe cientes do polinómio a; :::; a ; são nulos, e que portanto p(z) é um polinómio de grau zero, o que é absurdo. 3.4 TEORIA DE CAUCHY GLOBAL A teoria de Cauchy permanece válida em condições mais gerais, como mostraremos a seguir com base no conceito de homologia, o qual é construído através do índice de uma linha em C, relativamente a um ponto w =2 im, I(; w) = 2i z w dz: Duas linhas fechadas no aberto U; dizem-se homólogas em U sempre que, I(; w) = I(; w), para cada w =2 U: Se se reduzir a um ponto de U; será homóloga a em U se I(; w) = 0, para cada w =2 U; caso em que se diz homóloga a um ponto de U; ou 0-homóloga em U. O conceito de homologia pode ser estendido de uma maneira formal a conjuntos de linhas, com alguma vantagem prática. A um conjunto nito de linhas = f ; :::; n g chamaremos uma cadeia. Uma cadeia diz-se um ciclo se cada linha que compõe for fechada. Por im = im [ ::: [ im n ; designaremos a imagem da cadeia. Se f for uma função contínua em im, ao valor f = nx k= chamaremos integral de f ao longo de : Por comprimento de entenderemos o valor k f c( ) = nx c( k ): k= 4
5 Se for um ciclo, consideraremos o índice de em relação a um ponto w =2 im, como sendo o número inteiro nx I( ; w) = I( k ; w): k= Deste modo, diremos que dois ciclos e 2 são homólogos no aberto U, se I( ; w) = I( 2 ; w) para cada w =2 U. Um ciclo dir-se-á homólogo a um ponto de U ou 0-homólogo em U se I( ; w) = 0; para cada w =2 U: Posto isto, podemos enunciar a seguinte versão do teorema de Cauchy. Teorema 3 (Teorema de Cauchy Global) Seja f uma função holomorfa no aberto U e um ciclo 0-homólogo em U. Então: (i) f(z)i( ; z) = f(w) dw; para cada z 2 Unim ; 2i w z (ii) f = 0: Dem.: Comecemos por observar que (i) ) (ii): Na verdade, tomando um ponto z 0 2 Unim ; através de F (z) = (z z 0 )f(z), constituímos uma função diferenciável em U e, por (i), f(z)dz = F (z) dz = F (z 0 )I( ; z 0 ) = 0: 2i 2i z z 0 ) Iniciemos a demonstração de (i) com a formulação da função auxiliar g : U U! C, dada por 8 < f(w) f(z) ; se w 6= z; g(w; z) = : w z f 0 (z); se w = z: Trata-se de uma função contínua em U U: Na verdade, a esse respeito, apenas os pontos do tipo (u; u); u 2 U, poderão merecer dúvidas. Ora, qualquer que seja " > 0; pela continuidade de f 0 ; existe > 0; tal que jz uj < ) jf 0 (z) f 0 (u)j < "; facto que mostra ser jg(w; z) g(u; u)j < "; sempre que jz uj < e w = z: Por outro lado, para z e w tais que 0 < jz uj < ; 0 < jw uj < ; de f(w) f(z) = f 0 (v)dv e f 0 (u) = f 0 (u)dv: w z [z;w] [z;w] obtemos, jg(w; z) g(u; u)j = w z [z;w] (f 0 (v) f 0 (u)) dv < " c([z; w]) = "; jw zj o que prova a continuidade de g em U U: Deste facto resulta que, para cada w 2 U; xo, a função de nida por (z) = g(w; z); é diferenciável em U: Na verdade, possuirá, quando muito uma singularidade em z = w; mas por aplicação do teorema de Goursat, atendendo a que é contínua, teremos = 0; para cada triângulo, ; contido em U; permitindo então o teorema de Morera concluir a diferenciabilidade de em U: 5
6 2) Tomemos agora a função, de nida em U, através de h(z) = g(w; z)dw: 2i Para z 2 Unim ; temos h(z) = 2i f(w) dw f(z)i( ; z); w z pelo que (i) equivale a mostrar que h é identicamente nula em Unim : A função h é contínua em U: Na verdade com z 0 2 U; se B(z 0 ; r) for uma bola fechada de centro em z 0 e raio r > 0; contida em U; atendendo a que, pela sua continuidade, g é uniformemente contínua no limitado e fechado im B(z 0 ; r); temos que para cada " > 0; existe 0 < r tal que jg(w; z) g(w; z 0 )j < 2" c( ) ; para (w; z) 2 im B(z 0 ; ). Como tal, jh(z) h(z 0 )j < 2" c( ) = ": 2 c( ) Além de contínua, h é holomorfa em U; já que é holomorfa em cada bola aberta contida em U: De facto, se for uma linha qualquer fechada contida nessa bola; temos h(z)dz = g(w; z)dw dz = g(w; z)dz dw; 2i 2i por aplicação do teorema de Fubini, atendendo à continuidade de g e a que os integrais em causa se resumem a integrais em intervalos fechados ou somas nitas de integrais deste tipo. Mas como para cada w 2 U, a função (z) = g(w; z) é, como vimos, diferenciável em U; e a bola considerada é um conjunto convexo, temos pelo teorema de Cauchy que R h(z)dz = 0; o que permite concluir por aplicação do teorema de Morera que h é holomorfa em U: 3) Seja agora W = fz 2 Cnim : I( ; z) = 0g : W é um conjunto aberto porque I( ; z) é uma função contínua na variável z que apenas toma valores inteiros e como é um ciclo homólogo a um ponto em U; temos que CnU W; o que implica, em particular que U [ W = C. Por outro lado, sabemos que a função F (z) = f(w) 2i w z dw é holomorfa em Cnim e, por conseguinte, também em W; além de que F (z) = h(z); se z 2 U \ W: Deste modo a função h(z); se z 2 U; H(z) = F (z); se z 2 W; 6
7 encontra-se bem de nida em todo o plano complexo e nessa qualidade é mesmo uma função inteira. 4) Se mostrarmos que H(z)! 0 quando jzj! +; provamos, em particular que H é limitada, e como tal constante, pelo teorema de Liouville. Da própria condição no in nito resulta então que H é identicamente nula em C, o que prova ser h = 0 em U: Para tal, comecemos por notar que sendo im um conjunto limitado, qualquer ponto z 2 U com jzj su cientemente grande se acha em W. Assim, para z tal que jzj > r; é H(z) = F (z) e, por conseguinte, Ora, se r > max w2im jh(z)j 2 max w2im jf(w)j max w2im jw zj c( ) jwj ; temos para w 2 im ; qualquer, jw zj jzj r; donde jh(z)j 2 max jf(w)j c( ): w2im jzj r Logo fazendo jzj! +; obtemos H(z)! 0; o que completa a demonstração do teorema. Observemos que este teorema é válido quando o ciclo é constituído por uma única linha fechada homóloga a um ponto em U. Nestas circunstâncias (ii) exprime um resultado mais geral que a versão indicada do teorema de Cauchy, o mesmo sucedendo a (i) relativamente à primeira fórmula integral de Cauchy. Notando que uma linha de Jordan, ; num aberto U; tal que int U; é homóloga a um ponto de U, pois CnU ext; obtemos a seguinte versão do teorema de Cauchy para linhas de Jordan: Corolário 4 Se f é uma função holomorfa no aberto U e é uma linha de Jordan em U; cujo interior se encontra contido em U, então f = 0: Para a homologia entre ciclos temos: Corolário 5 Se f é uma função holomorfa no aberto U e e 2 são dois ciclos homólogos em U então f(z)dz = f(z)dz: Dem.: Se = f ; :::; n g e 2 = f 2 ; :::; 2n g ; basta tomar o ciclo = ; :::; n ; 2 ; :::; 2n ; o qual é homólogo a um ponto de U, pois I( ; z) = I( ; z) I( 2 ; z) = 0; para cada z =2 U: Então pelo teorema vem f(z)dz = 0 = f(z)dz f(z)dz: 2 2 7
8 3.5 EXERCÍCIOS RESOLVIDOS. Sejam e duas funções harmónicas num conjunto aberto R 2 : Mostre que a função complexa de variável complexa @ f (x + iy) = + i é holomorfa em U = fx + iy : 2 g : 2. Seja u x 3 3xy 2 5y: a) Veri que que u é uma função harmónica em R 2 : b) Determine, v a harmónica conjugada de u tal que v (0; 0) = 0: 3. Considere a função v e x2 y 2 cos (2xy) : a) Veri que que v é harmónica em R 2 : b) Determine uma função inteira f; tal que f (0) = i e Im f (x + iy) = v : 4. Justi que que em R 2 ; v 2xy é harmónica conjugada de u x 2 y 2 : 5. Mostre que não existe uma função holomorfa, f; tal que Re f (x + iy) = y 4 + x 2 : 6. Sabendo que num conjunto R 2 ; v é harmónica conjugada de u; determine uma harmónica conjugada de v em : 7. Seja p (z) um polinómio de grau n: Para que valores de n é possível que =p (z) seja uma função inteira? 8. Considere as seguintes linhas do plano complexo: (t) = 2 ei2t ; t 2 [0; 2] ; 2 (t) = 3e i2t ; t 2 [0; 2] ; 3 (t) = e i2t ; t 2 [0; 2] : Quais destas linhas são homólogas entre si nos seguintes conjuntos abertos do plano complexo: a) U = fz : jzj > =3g : b) U = fz : jz 2j > =2g \ fz : jz + 2j > =2g : 8
9 9. Sejam z 0 ; z 2 C e r < jz z 0 j =2 e C r (z 0 ) ; C r (z ) circunferências de raio r e centros em z 0 e z ; respectivamente, simples e positivamente orientadas. Seja uma linha de Jordan contendo no seu interior C r (z 0 ) e C r (z ) : Justi que que: (z z 0 ) (z z ) dz = C r(z 0 ) (z z 0 ) (z z ) dz + C r(z ) (z z 0 ) (z z ) dz: 0. Seja f uma função holomorfa no conjunto aberto U = fz : jzj > g e designe-se por E a elipse simples e positivamente orientada dada pela equação x2 + = : 4 9 Justi que que f (z) E z dz = f (z) dz (n 2 ) n C r zn para qualquer circunferência, C r ; simples e positivamente orientada de centro na origem e raio r > : 3.5. RESOLUÇÕES. Como e são de classe C 2 ; as v + são ambas de classe C : Além disso são veri cadas as equações de Cauchy-Riemann. Na verdade de atendendo à igualdade das derivadas cruzadas e a que, por se harmónica, se tem Analogamente, de resulta : : Logo f é holomorfa em U = fx + iy : 2 g : 9
10 2.a) Veri quemos que 8 2 R 2 se tem Ora por diferenciação obtemos Logo u 0: 3x2 3y 2 u ; 6x; 2 6xy 2 u 6x: 2 u u 6x 6x = 0: b) Procuremos uma função inteira f tal que A função Re f (x + iy) = u : v Im f (x + iy) será então uma harmónica conjugada de u: Tendo a atenção a diferenciabilidade de f; as funções u e v relacionam-se entre si pelas equações de Cauchy-Riemann. Isto é, v será tal que Assim, temos que e 3x2 3y 2 ; 6xy + 5: 8 2 R2 : Então por primitivação em ordem a y e a x; respectivamente, concluímos que v 3x 2 y y 3 + c (x) ; v 3x 2 y + 5x + c 2 (y) onde c (x) e c 2 (y) designam funções exclusivamente dependentes das variáveis x e y; respectivamente. Por comparação podemos então concluir que v 3x 2 y + 5x y 3 + K; onde K é uma qualquer constante real. Da condição v (0; 0) = 0 podemos a rmar que K = 0 e que portanto v 3x 2 y + 5x y 3 : 3.a) Pelas regras de derivação temos que 2xex2 cos (2xy) e x2 y 2 2y sin (2xy) ; 0
11 @ 2 v 2ex2 2 cos (2xy)+4x 2 e x2 y 2 cos (2xy) 8xye x2 y 2 sin (2xy) e x2 y 2 4y 2 cos (2xy) ; 2yex2 cos (2xy) e x2 y 2 2x sin (2xy) 2 v 2ex2 cos (2xy)+4y 2 e x2 y 2 cos (2xy)+8xye x2 y 2 sin (2xy) e x2 y 2 4x 2 cos (2xy) : 2 Logo, na verdade v e x2 y 2 cos (2xy) : v v 0: b) Procuremos uma função u tal que f (x + iy) = u + iv seja uma função inteira. As equações de Cauchy-Riemann indicam-nos que u deverá ser tal que Assim temos que e 8 2 R2 : 2yex2 cos (2xy) 2xe x2 y 2 sin (2xy) ; 2xcex2 cos (2xy) + e x2 y 2 2y sin (2xy) : Da primeira destas relações, observemos que pela regra de derivação do produto de funções o que implica que 2yex2 = e x2 2 e x2 cos (2xy) 2xe x2 y 2 sin (2xy) sin (2xy) ex2 y 2 sin (2xy) ; u e x2 y 2 sin (2xy) + c (y) ; sin (2xy) ; onde c (y) é uma qualquer função dependente apenas da variável y: Analogamente da segunda relação temos que 2xex2 cos (2xy) + 2ye x2 = e x2 2 sin (2xy) e x2 y 2 sin (2xy) ; y 2 sin e x2 y 2 sin (2xy)
12 e que por conseguinte u e x2 y 2 sin (2xy) + c 2 (x) ; para uma qualquer função c 2 (x) que apenas dependa da variável x: Comparando os dois resultados obtidos podemos então concluir que para uma qualquer constante real u e x2 y 2 sin (2xy) + K; e que f (x + iy) = e x2 y 2 sin (2xy) + K + ie x2 y 2 cos (2xy) : Por m a condição f (0) = i ca equivalente a K + i = i; donde resulta que K = 0: Logo f (x + iy) = e x2 y 2 sin (2xy) + ie x2 y 2 cos (2xy) : 4. Facilmente se observa que f (x + iy) = u + iv = x 2 y 2 + i2xy = x 2 + i2xy + i 2 y 2 = (x + iy) 2 : Como f (z) = z 2 é obviamente uma função holomorfa, de u Re f (x + iy) ; v Im f (x + iy) concluímos que u e v são de facto harmónicas conjugadas. 5. Supondo que existia uma função holomorfa, f; tal que Re f (x + iy) = y 4 + x 2 : num certo conjunto U C; então a função y 4 + x 2 teria de ser necessariamente harmónica em = f : x + iy 2 Ug : Ora por derivação temos que o que implica y3 ; : Ora como 6= 0; 8 2 R 2 ; temos que não é harmónica em nenhum conjunto R 2 : Logo não existe nenhuma função holomorfa, f; tal que Re f (x + iy) = y 4 + x 2 : 2
13 6. Se v é harmónica conjugada de u; num certo conjunto R 2 ; então existe uma função f; holomorfa em U = fx + iy : 2 g ; tal que u Re f (x + iy) ; v Im f (x + iy) ; 8 2 : Assim, além de serem harmónicas temos que u; v 2 C em e que são veri cadas as equações de Cauchy-Riemann e 8 2 : O que se pretende é determinar uma função w 2 C em para a qual exista uma função g holomorfa em U tal que v Re g (x + iy) ; w Im g (x + iy) ; 8 2 : Nestas condições devem igualmente ser satisfeitas as equações de ; 8 2 : Assim w será tal que, para qualquer 2 ; o que : w u + K: Logo w = u é uma harmónica conjugada de v: 7. Se n > 0 então pelo teorema fundamental da Álgebra, p (z) possui pelo menos uma raíz z 0 : Nessas circunstâncias não pode de nir-se em z 0 um valor para =p (z) ; já que lim z!z 0 p (z) = ; facto que não permite que aquela função seja diferenciável em z 0 : Quando n = 0; tem-se p (z) = c e este entrave não acontece se for c 6= 0: Logo =p (z) será uma função inteira se e só se p (z) for um polinómio de grau zero não identicante nulo. 8.a) Seja w =2 U; isto é w tal que jwj =3: Temos que I ( ; w) = I ( 2 ; w) = 2; I ( 3 ; w) = 2: Logo em U; apenas e 2 são homólogas. 8.b) Seja w =2 U; isto é w tal que jw + j =2 ou jw j =2: Temos agora I ( ; w) = 0; I ( 2 ; w) = 2; I ( 3 ; w) = 0: Logo em U; apenas e 3 são homólogas. 3
14 9. A função f (z) = (z z 0 ) (z z ) é holomorfa em U = Cn fz 0 ; z g : Os ciclos = fg e 2 = fc r (z 0 ) ; C r (z )g são homólogos pois e I ( ; z 0 ) = I (; z 0 ) = ; I ( 2 ; z 0 ) = I (C r (z 0 ) ; z 0 ) + I (C r (z ) ; z 0 ) = + 0 = ; I ( ; z ) = I (; z ) = I ( 2 ; z ) = I (C r (z 0 ) ; z ) + I (C r (z ) ; z ) = 0 + = Como tal, pelo Corolário 5 temos (z z 0 ) (z z ) dz = 2 (z z 0 ) (z z ) dz; ou seja, (z z 0 ) (z z ) dz = C r(z 0 ) (z z 0 ) (z z ) dz + C r(z ) (z z 0 ) (z z ) dz: 0. Para qualquer n 2 ; a função f (z) =z n é holomorfa em U: Além disso E e C r são linhas homólogas em U já que I (E; w) = I (C r ; w) = ; para cada w =2 U: Logo pelo Corolário 5 temos que f (z) z dz = f (z) n C r z n E dz: 4
2 TEORIA DE CAUCHY-GOURSAT
 TEORIA DE CAUCHY-GOURSAT Quando é uma unção primitivável num dado conjunto aberto U; isto é, sempre que exista uma unção, F; dierenciável em U; tal que F 0 = ; então para qualquer linha em U; : [a; b]!
TEORIA DE CAUCHY-GOURSAT Quando é uma unção primitivável num dado conjunto aberto U; isto é, sempre que exista uma unção, F; dierenciável em U; tal que F 0 = ; então para qualquer linha em U; : [a; b]!
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Problemas Singulares e Métodos Assimptóticos Desenvolvimento da solução de uma EDO em série de potências na vizinhança de uma singularidade regular
 Problemas Singulares e Métodos Assimptóticos Desenvolvimento da solução de uma EDO em série de potências na vizinhança de uma singularidade regular Consideremos uma EDO linear de segunda ordem com a forma
Problemas Singulares e Métodos Assimptóticos Desenvolvimento da solução de uma EDO em série de potências na vizinhança de uma singularidade regular Consideremos uma EDO linear de segunda ordem com a forma
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
RESOLUÇÃO DO PRIMEIRO TESTE 31 DE OUTUBRO DE 2015 MEMEC,LEAN. f(x + iy) = x + x 3 + i(1 + y + y 2 )
 ANÁLISE COMPLEXA E EQUAÇÕES DIFEENCIAIS ESOLUÇÃO DO PIMEIO TESTE 3 DE OUTUBO DE 205 MEMEC,LEAN Considere a função f : C C definida pela expressão fx + iy = x + x 3 + i + y + y 2 a Determine o domínio de
ANÁLISE COMPLEXA E EQUAÇÕES DIFEENCIAIS ESOLUÇÃO DO PIMEIO TESTE 3 DE OUTUBO DE 205 MEMEC,LEAN Considere a função f : C C definida pela expressão fx + iy = x + x 3 + i + y + y 2 a Determine o domínio de
6 SINGULARIDADES E RESÍDUOS
 6 SINGULARIDADES E RESÍDUOS Quando uma função f (z) não é diferenciável num complexo z 0 ; diremos que z 0 é uma singularidade de f (z) ; z 0 dir-se-á uma singularidade isolada de f (z) se, contudo, f
6 SINGULARIDADES E RESÍDUOS Quando uma função f (z) não é diferenciável num complexo z 0 ; diremos que z 0 é uma singularidade de f (z) ; z 0 dir-se-á uma singularidade isolada de f (z) se, contudo, f
Invariância da integral por homotopia, fórmula de Cauchy e séries de Taylor
 Invariância da integral por homotopia, fórmula de Cauchy e séries de Taylor Roberto Imbuzeiro Oliveira 6 de Abril de 20 Preliminares Nestas notas, U C sempre será um aberto e f : U C é contínua. Duas curvas
Invariância da integral por homotopia, fórmula de Cauchy e séries de Taylor Roberto Imbuzeiro Oliveira 6 de Abril de 20 Preliminares Nestas notas, U C sempre será um aberto e f : U C é contínua. Duas curvas
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Análise Complexa e Equações Diferenciais Guia 3 João Pedro Boavida. 21 a 28 de Setembro
 2 de Setembro de 211 21 a 28 de Setembro A secção Números complexos e matrizes 2 2 indica algumas das conclusões da discussão no final do guia 1 As secções Derivação em C e Integração em C resumem algumas
2 de Setembro de 211 21 a 28 de Setembro A secção Números complexos e matrizes 2 2 indica algumas das conclusões da discussão no final do guia 1 As secções Derivação em C e Integração em C resumem algumas
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Fichas de Análise Matemática III
 Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
Fichas de Análise Matemática III Fernando Lobo Pereira, João Borges de Sousa Depto de Engenharia Electrotécnica e de Computadores Faculdade de Engenharia da Universidade do Porto Instituto de Sistemas
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1. (1) Descreva as regiões do plano complexo definidas por z i c z, onde c é um número real não negativo.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
3 ā Prova de MAT Cálculo IV - IFUSP 2 ō semestre de /12/2009 Prof. Oswaldo Rio Branco de Oliveira
 3 ā Prova de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009 - /2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : Q 2 3 4 5 E E2 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Para cada
3 ā Prova de MAT0220 - Cálculo IV - IFUSP 2 ō semestre de 2009 - /2/2009 Prof. Oswaldo Rio Branco de Oliveira Nome : N ō USP : Q 2 3 4 5 E E2 Total N JUSTIFIQUE TODAS AS PASSAGENS BOA SORTE. Para cada
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
1 Primeira lista de exercícios
 1 Primeira lista de exercícios Números complexos, derivadas e integrais. 1. Ache todos os valores das seguintes raízes: (a) (2i) 1=2 (b) ( i) 1=3 (c) 8 1=6 2. Descreva geometricamente cada uma das regiões
1 Primeira lista de exercícios Números complexos, derivadas e integrais. 1. Ache todos os valores das seguintes raízes: (a) (2i) 1=2 (b) ( i) 1=3 (c) 8 1=6 2. Descreva geometricamente cada uma das regiões
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 2018
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE MATEMÁTICA IV FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Análise Complexa e Equações Diferenciais 1 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
Análise Complexa e Equações Diferenciais 1 ō Semestre 1/14 1 ō Teste Versão A (Cursos: LEIC-A, LEMat, MEAmbi, MEBiol, MEQ) de Novembro de 1, 11h 1. Seja v(x,y) = (x+1)α(y), em que α : R R é uma função
Análise Matemática IV Problemas para as Aulas Práticas
 Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
Análise Matemática IV Problemas para as Aulas Práticas 4 de Abril de 5 Semana 3. Determine os valores dos seguintes integrais: a) z dz em que é o semicírculo percorrido em sentido directo unindo i a i.
1.1 Função Exponencial
 VARIÁVEL COMPLEXA 3. AS FUNÇÕES ELEMENTARES 1.1 Função Exponencial 1. Escreva as funções abaixo sob a forma u (x; y) + iv (x; y) : (a) w = exp (2z) (b) w = exp z 2 (c) w = exp (iz) : 2. Em cada caso, determine
VARIÁVEL COMPLEXA 3. AS FUNÇÕES ELEMENTARES 1.1 Função Exponencial 1. Escreva as funções abaixo sob a forma u (x; y) + iv (x; y) : (a) w = exp (2z) (b) w = exp z 2 (c) w = exp (iz) : 2. Em cada caso, determine
(x, y) = 0. Análise Complexa e Equações Diferenciais 2 o Semestre 2016/ de abril de 2017, às 9:00 Teste 1 versão A
 Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
4.1 Função Complexa de uma Variável Real. 4.2 Contornos. 1. Calcule as seguintes integrais: Z =4 e it dt. Z 1 e wt dt; (Re w > 0) (c)
 VAIÁVEL COMPLEXA 4. INTEGAÇÃO COMPLEXA 4. Função Complexa de uma Variável eal. Calcule as seguintes integrais: =4 e it dt e wt dt; (e w > ) (c) 2 e imt e int dt; m; n 2 : 2. Calcule as integrais trigonométricas:
VAIÁVEL COMPLEXA 4. INTEGAÇÃO COMPLEXA 4. Função Complexa de uma Variável eal. Calcule as seguintes integrais: =4 e it dt e wt dt; (e w > ) (c) 2 e imt e int dt; m; n 2 : 2. Calcule as integrais trigonométricas:
Análise Complexa e Equações Diferenciais 2 ō Semestre 2009/2010
 Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais ō Semestre 9/ ō Teste - Versão A (Cursos: Todos) 4 de Abril de, h Duração: h 3m. Seja u(x,y) = xe x cos(y) e x y sen(y)+β(x), em que β : R R é uma função de classe
Análise Complexa e Equações Diferenciais Guia 6 João Pedro Boavida. 19 a 28 de Outubro
 19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
Análise Matemática II - 1 o Semestre 2001/ o Exame - 25 de Janeiro de h
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
3.1 Limite & Continuidade
 3. FUNÇÕES CONTÍNUAS ANÁLISE NO CORPO R - 2018.1 3.1 Limite & Continuidade 1. Mostre que a função valor absoluto f (x) = jxj é contínua em qualquer ponto x 2 R: 2. A função de Dirichlet ' : R! R é de nida
3. FUNÇÕES CONTÍNUAS ANÁLISE NO CORPO R - 2018.1 3.1 Limite & Continuidade 1. Mostre que a função valor absoluto f (x) = jxj é contínua em qualquer ponto x 2 R: 2. A função de Dirichlet ' : R! R é de nida
1.1 Números Complexos
 . O PLANO COMPLEXO VARIÁVEL COMPLEXA - 07.. Números Comlexos. Em cada caso, reduza a exressão à forma a + ib; a; b R: (a) ( i) + (3 + 4i) (b) ( + i) i (3 + 4i) (c) ( + i) ( + i) (d) ( i) (e) ( i) 3 + i
. O PLANO COMPLEXO VARIÁVEL COMPLEXA - 07.. Números Comlexos. Em cada caso, reduza a exressão à forma a + ib; a; b R: (a) ( i) + (3 + 4i) (b) ( + i) i (3 + 4i) (c) ( + i) ( + i) (d) ( i) (e) ( i) 3 + i
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 1 o Teste Versão A Cursos: LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - o Semestre de / MEEC EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Método de Eliminação de Gauss Sistemas de equações lineares Uma equação linear nas variáveis (ou incógnitas) x ; ; x n ; é uma equação do
IST - o Semestre de / MEEC EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Método de Eliminação de Gauss Sistemas de equações lineares Uma equação linear nas variáveis (ou incógnitas) x ; ; x n ; é uma equação do
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral II 1 o Teste (Versão A)
 Cálculo Diferencial e Integral II 1 o Teste (ersão A) LEIC-TP, LETI, LEE, LEGI 11 de Abril de 015 Justifique adequadamente todas as respostas. (5,0) 1. Seja = {(, y, z) [ 1, 1] [0, 1] R 3 : 0 z, 0 y 1}
Cálculo Diferencial e Integral II 1 o Teste (ersão A) LEIC-TP, LETI, LEE, LEGI 11 de Abril de 015 Justifique adequadamente todas as respostas. (5,0) 1. Seja = {(, y, z) [ 1, 1] [0, 1] R 3 : 0 z, 0 y 1}
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 5 28 DE FEVEREIRO DE 2018
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 5 8 DE FEVEREIRO DE 018 Para o logaritmo complexo, nem sempre são válidas as propriedades conecidas do logaritmo real. Por exemplo: log 0 ( i) = 3π
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 5 8 DE FEVEREIRO DE 018 Para o logaritmo complexo, nem sempre são válidas as propriedades conecidas do logaritmo real. Por exemplo: log 0 ( i) = 3π
GABARITO. 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan
 GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
17 a Aula AMIV LEAN, LEC Apontamentos
 7 a Aula 004.0. AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 7. Definições de polinómio e fracção racional Comecemos por adoptar uma definição de polinómio de grau n. Definição 7. Uma
7 a Aula 004.0. AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 7. Definições de polinómio e fracção racional Comecemos por adoptar uma definição de polinómio de grau n. Definição 7. Uma
1 Números Complexos e Plano Complexo
 UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
13 AULA. Regra da Cadeia e Derivação Implícita LIVRO. META Derivar funções compostas e funções definidas implicitamente.
 1 LIVRO Regra da Cadeia e Derivação Implícita 13 AULA META Derivar funções compostas e funções definidas implicitamente. OBJETIVOS Estender os conceitos da regra da cadeia e da derivação implícita de funções
1 LIVRO Regra da Cadeia e Derivação Implícita 13 AULA META Derivar funções compostas e funções definidas implicitamente. OBJETIVOS Estender os conceitos da regra da cadeia e da derivação implícita de funções
Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
 UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE MATEMÁTICA Campus Apucarana Prof. Dr. Márcio Hiran Simões Apostila de Cálculo Diferencial e Integral 3 - Funções de uma Variável Complexa.
12 AULA. ciáveis LIVRO. META Estudar derivadas de funções de duas variáveis a valores reais.
 1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
4.1 Preliminares. 1. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = 1=x; x 6= 0 (c) f (x) = 1= p x; x > 0:
 4. FUNÇÕES DERIVÁVEIS ANÁLISE NO CORPO R - 208. 4. Preinares. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = =x; x 6= 0 (c) f (x) = = p x; x > 0: 2. Mostre que
4. FUNÇÕES DERIVÁVEIS ANÁLISE NO CORPO R - 208. 4. Preinares. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = =x; x 6= 0 (c) f (x) = = p x; x > 0: 2. Mostre que
Cálculo Diferencial e Integral II 2012/13 1 o semestre
 Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 2 ANÁLISE COMPLEXA Para cada um dos seguintes conjuntos Z C, esboce o conjunto dos seus logaritmos.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 2 ANÁLISE COMPLEXA Para cada um dos seguintes conjuntos Z C, esboce o conjunto dos seus logaritmos.
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
7 temos que e u =
 Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
Capítulo 1 Complementos de Álgebra Linear 11 Introdução Seja A = [a ij ] uma matriz quadrada de ordem n e pensemos na transformação linear R n! R n que a cada cada vector u R n faz corresponder um vector
Funções analíticas LISTA DE EXERCÍCIOS
 LISTA DE EXERCÍCIOS Funções analíticas. Suponha que f : Ω C é C-diferenciável. Denote por r (Ω) o conjunto { z; z Ω}. Mostre que g : r (Ω) C dada por g (z) := f ( z) é ainda C-diferenciável. Recíproca?
LISTA DE EXERCÍCIOS Funções analíticas. Suponha que f : Ω C é C-diferenciável. Denote por r (Ω) o conjunto { z; z Ω}. Mostre que g : r (Ω) C dada por g (z) := f ( z) é ainda C-diferenciável. Recíproca?
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ
 Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Cálculo II Exame de 2 a Época, 28 de Junho de 2000
 Faculdade de Economia Universidade Nova de Lisboa Cálculo II Exame de a Época, 8 de Junho de 000 O exame é constítuido por cinco perguntas. Responda a cada questão em folhas separadas. Não se esqueça de
Faculdade de Economia Universidade Nova de Lisboa Cálculo II Exame de a Época, 8 de Junho de 000 O exame é constítuido por cinco perguntas. Responda a cada questão em folhas separadas. Não se esqueça de
ANÁLISE MATEMÁTICA IV 1 o Teste (LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ) Justifique cuidadosamente todas as respostas.
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA IV o Teste LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ Justifique cuidadosamente todas as respostas.
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise ANÁLIE MATEMÁTICA IV o Teste LEAM, LEBL, LEC, LEEC, LEM, LEGM, LEMAT, LEN, LEQ, LQ Justifique cuidadosamente todas as respostas.
Sobre Desenvolvimentos em Séries de Potências, Séries de Taylor e Fórmula de Taylor
 Sobre Desenvolvimentos em Séries de Potências, Séries de Taylor e Fórmula de Taylor Pedro Lopes Departamento de Matemática Instituto Superior Técnico o. Semestre 004/005 Estas notas constituem um material
Sobre Desenvolvimentos em Séries de Potências, Séries de Taylor e Fórmula de Taylor Pedro Lopes Departamento de Matemática Instituto Superior Técnico o. Semestre 004/005 Estas notas constituem um material
Universidade Federal do Espírito Santo Prova de Álgebra II Prof. Lúcio Fassarella DMA/CEUNES/UFES Data: 07/05/2015
 Universidade Federal do Espírito Santo Prova de Álgebra II Prof. Lúcio Fassarella DMA/CEUNES/UFES Data: 07/05/2015 Aluno: Matrícula. Nota: : :.Observações: I A prova tem duração de 100 min; não é permitido
Universidade Federal do Espírito Santo Prova de Álgebra II Prof. Lúcio Fassarella DMA/CEUNES/UFES Data: 07/05/2015 Aluno: Matrícula. Nota: : :.Observações: I A prova tem duração de 100 min; não é permitido
Análise Complexa e Equações Diferenciais
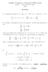 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Revisão do Teorema de Green
 Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Curso: MAT 0- CÁLCULO DIFERENCIAL E INTEGRAL IV - IFUSP Professor Oswaldo Rio Branco de Oliveira Período: Segundo Semestre de 009 A Terceira Prova: - Não cobrirá questões sobre sequências numericas nem
Primitivas e a integral de Riemann Aula 26
 Primitivas e a integral de Riemann Aula 26 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 13 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica
Primitivas e a integral de Riemann Aula 26 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 13 de Maio de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica
Mais Alguns Aspectos da Derivação Complexa
 Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA
 ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA Maria do Rosário de Pinho e Maria Margarida Ferreira Agosto 2004 Faculdade de Engenharia da Universidade do Porto Licenciatura
ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA Maria do Rosário de Pinho e Maria Margarida Ferreira Agosto 2004 Faculdade de Engenharia da Universidade do Porto Licenciatura
Análise Complexa e Equações Diferenciais 1 o Semestre de 2011/ o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2011, 10h,
 Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Instituto Superior Técnico Departamento de Matemática (Cursos: Análise Complexa e Equações Diferenciais o Semestre de 2/22 o Teste - Versão A LEAN, LEIC-A, MEAer, MEEC, MEMec) 5 de Novembro de 2, h, Duração:
Máximos e mínimos UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 22. Assunto: Máximos e mínimos
 Assunto: Máximos e mínimos UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos Sejam f uma função a valores
Assunto: Máximos e mínimos UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos Sejam f uma função a valores
Integrais. ( e 12/ )
 Integrais (21-04-2009 e 12/19-05-2009) Já estudámos a determinação da derivada de uma função. Revertamos agora o processo de derivação, isto é, suponhamos que nos é dada uma função F e que pretendemos
Integrais (21-04-2009 e 12/19-05-2009) Já estudámos a determinação da derivada de uma função. Revertamos agora o processo de derivação, isto é, suponhamos que nos é dada uma função F e que pretendemos
n=1 a n converge e escreveremos a n = s n=1 n=1 a n. Se a sequência das reduzidas diverge, diremos que a série
 Séries Numéricas Nosso maior objetivo agora é dar um sentido a uma soma de infinitas parcelas, isto é, estudar a convergência das chamadas séries numéricas. Inicialmente, seja (a n ) uma sequência e formemos
Séries Numéricas Nosso maior objetivo agora é dar um sentido a uma soma de infinitas parcelas, isto é, estudar a convergência das chamadas séries numéricas. Inicialmente, seja (a n ) uma sequência e formemos
Exercícios de revisão
 Exercícios de revisão Roberto Imbuzeiro Oliveira 7 de Abril de 20 Vários exercícios apresentados aqui vêm do livro David Ullrich, Complex Made Simple, ou dos livros de Ahlfors e Churchill. Em alguns casos,
Exercícios de revisão Roberto Imbuzeiro Oliveira 7 de Abril de 20 Vários exercícios apresentados aqui vêm do livro David Ullrich, Complex Made Simple, ou dos livros de Ahlfors e Churchill. Em alguns casos,
Sucessões. , ou, apenas, u n. ,u n n. Casos Particulares: 1. Progressão aritmética de razão r e primeiro termo a: o seu termo geral é u n a n1r.
 Sucessões Definição: Uma sucessão de números reais é uma aplicação u do conjunto dos números inteiros positivos,, no conjunto dos números reais,. A expressão u n que associa a cada n a sua imagem designa-se
Sucessões Definição: Uma sucessão de números reais é uma aplicação u do conjunto dos números inteiros positivos,, no conjunto dos números reais,. A expressão u n que associa a cada n a sua imagem designa-se
Um espaço métrico incompleto 1
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Um espaço métrico incompleto
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Um espaço métrico incompleto
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Séries de Laurent e Teoremas de Cauchy
 Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Concluímos esta secção apresentando alguns exemplos que constituirão importantes limites de referência. tan θ. sin θ
 aula 08 Funções reais de variável real Limites e continuidade (Continuação) A definição de limite segundo Heine permite, como já vimos anteriormente no caso da álgebra de limites, transpor quase imediatamente
aula 08 Funções reais de variável real Limites e continuidade (Continuação) A definição de limite segundo Heine permite, como já vimos anteriormente no caso da álgebra de limites, transpor quase imediatamente
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
c + 1+t 2 (1 + t 2 ) 5/2 dt e 5 2 ln(1+t2 )dt (1 + t 2 ) 5/2 dt (c 5/2 + (1 + t 2 ) 5/2 (1 + t 2 ) 5/2 dt ϕ(t) = (1 + t 2 ) 5/2 (1 + t).
 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
1 o Semestre 2018/2019 MEC
 ACED Análise Complea e Equações Diferenciais o Semestre 208/209 MEC Conteúdo I. Números compleos, funções compleas........... II. Transformações conformes e diferenciabilidade de funções compleas.............................
ACED Análise Complea e Equações Diferenciais o Semestre 208/209 MEC Conteúdo I. Números compleos, funções compleas........... II. Transformações conformes e diferenciabilidade de funções compleas.............................
Notas Sobre Sequências e Séries Alexandre Fernandes
 Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Valores e vectores próprios
 Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Análise Matemática I 1 o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI)
 Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Análise Matemática II TESTE/EXAME
 Instituto Superior Técnico Departamento de Matemática o Semestre 4-5 a Data Análise Matemática II TESTE/EXAME CURSOS: LEAMB, LEEC, LCI, LQ, LEQ, LEBL Obtenha uma primitiva de cada uma das funções definidas
Instituto Superior Técnico Departamento de Matemática o Semestre 4-5 a Data Análise Matemática II TESTE/EXAME CURSOS: LEAMB, LEEC, LCI, LQ, LEQ, LEBL Obtenha uma primitiva de cada uma das funções definidas
Exercícios Complementares 6.3
 Exercícios Complementares 6.3 6.3A Usando a De nição 6.1.3 ou o Teorema 6.1.9, mostre que as funções dadas são soluções LI da edo indicada. y 1 (x) = sen x; y (x) = cos x; y 00 + y = 0; y 1 (x) = ; y (x)
Exercícios Complementares 6.3 6.3A Usando a De nição 6.1.3 ou o Teorema 6.1.9, mostre que as funções dadas são soluções LI da edo indicada. y 1 (x) = sen x; y (x) = cos x; y 00 + y = 0; y 1 (x) = ; y (x)
Álgebra. Exercícios de auto-avaliação
 Universidade Eduardo Mondlane Faculdade de Ciências Departamento de Matemática e Informática Álgebra Para Estudantes do Ensino à Distância do Curso de Licenciatura em Matemática, ano 01 Unidade 1 Números
Universidade Eduardo Mondlane Faculdade de Ciências Departamento de Matemática e Informática Álgebra Para Estudantes do Ensino à Distância do Curso de Licenciatura em Matemática, ano 01 Unidade 1 Números
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS Como vimos no Capítulo 4, no Volume I, um dos principais usos da derivada ordinária é na determinação dos valores máximo e mínimo. DERIVADAS PARCIAIS 14.7
1.1 Teorema fundamental da álgebra
 Motivação. Teorema fundamental da álgebra Vivamos num mundo sem os complexos. Um dia, resolvendo um problema real do nosso mundo, nos deparamos com a equação 3x + : () Fácil ver que, neste nosso mundo
Motivação. Teorema fundamental da álgebra Vivamos num mundo sem os complexos. Um dia, resolvendo um problema real do nosso mundo, nos deparamos com a equação 3x + : () Fácil ver que, neste nosso mundo
Exame de Matemática II - Curso de Arquitectura
 Exame de Matemática II - Curso de ruitectura o semestre de 8 7 de Junho de 8 esponsável Henriue Oliveira a Parte. Considere a seguinte função f! de nida por f(x ; x ; x ) (x cos (x ) ; x sin (x ) ; x ).
Exame de Matemática II - Curso de ruitectura o semestre de 8 7 de Junho de 8 esponsável Henriue Oliveira a Parte. Considere a seguinte função f! de nida por f(x ; x ; x ) (x cos (x ) ; x sin (x ) ; x ).
Espaços vectoriais reais
 Espaços Vectoriais - Matemática II - 2004/05 40 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o
Espaços Vectoriais - Matemática II - 2004/05 40 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o
Cap. 5 Estabilidade de Lyapunov
 Cap. 5 Estabilidade de Lyapunov 1 Motivação Considere as equações diferenciais que modelam o oscilador harmônico sem amortecimento e sem força aplicada, dada por: M z + Kz = 0 Escolhendo-se x 1 = z e x
Cap. 5 Estabilidade de Lyapunov 1 Motivação Considere as equações diferenciais que modelam o oscilador harmônico sem amortecimento e sem força aplicada, dada por: M z + Kz = 0 Escolhendo-se x 1 = z e x
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática. Notas de Aulas de
 Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
Universidade Estadual de Montes Claros Departamento de Ciências Exatas Curso de Licenciatura em Matemática Notas de Aulas de Cálculo Rosivaldo Antonio Gonçalves Notas de aulas que foram elaboradas para
Notas sobre primitivas
 Análise Matemática I - Engenharia Topográ ca - 9/- Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo
Análise Matemática I - Engenharia Topográ ca - 9/- Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo
Bola Aberta UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 10. Assuntos: Continuidade de funções e limite
 Assuntos: Continuidade de funções e limite UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 10 Palavras-chaves: continuidade, funções contínuas, limite Bola Aberta Sejam p R n e r R com r
Assuntos: Continuidade de funções e limite UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 10 Palavras-chaves: continuidade, funções contínuas, limite Bola Aberta Sejam p R n e r R com r
MAT146 - Cálculo I - Extremos Locais e Globais. Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira
 Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos que a derivada de uma função em um ponto é a inclinação da reta tangente ao gráfico da função neste ponto. Usaremos agora a derivada
Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos que a derivada de uma função em um ponto é a inclinação da reta tangente ao gráfico da função neste ponto. Usaremos agora a derivada
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas
 Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas LCE0176 - Cálculo e Matemática Aplicados às Ciências Biológicas Professora: Clarice G. B. Demétrio
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas LCE0176 - Cálculo e Matemática Aplicados às Ciências Biológicas Professora: Clarice G. B. Demétrio
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Critérios de Avaliação A avaliação ao longo das actividades lectivas será periódica, sendo efectuados dois testes. Os testes serão nos dias 7 de Abril
 Cálculo II Mestrado Integrado em Engenharia Aeronáutica Mestrado Integrado em Engenharia Civil António Bento bento@ubi.pt Departamento de Matemática Universidade da Beira Interior 2014/2015 António Bento
Cálculo II Mestrado Integrado em Engenharia Aeronáutica Mestrado Integrado em Engenharia Civil António Bento bento@ubi.pt Departamento de Matemática Universidade da Beira Interior 2014/2015 António Bento
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Proposta de Resolução do Exame do 12º ano Matemática A (Prova 635) Grupo I
 Proposta de Resolução do Exame do 1º ano Matemática A (Prova 635) Grupo I 1. Como só existem bolas de dois tipos na caixa e a probabilidade de sair bola azul é 1, existem tantas bolas roxas quantas as
Proposta de Resolução do Exame do 1º ano Matemática A (Prova 635) Grupo I 1. Como só existem bolas de dois tipos na caixa e a probabilidade de sair bola azul é 1, existem tantas bolas roxas quantas as
QUESTÕES ABERTAS ESPECÍFICAS PARA OS FORMANDOS DE BACHARELADO. b) cos (α + β) = cos (α) cos (β) sen (α) sen (β) e (valor: 10,0 pontos)
 Questão nº QUESTÕES ABERTAS ESPECÍFICAS PARA OS FORMANDOS DE BACHARELADO i( + β) e = cos( + β) + isen( + β ) () i iβ e. e = (cos + isen ). (cos β + isen β) = =coscos β +i sensen β +isencos β +icossen β
Questão nº QUESTÕES ABERTAS ESPECÍFICAS PARA OS FORMANDOS DE BACHARELADO i( + β) e = cos( + β) + isen( + β ) () i iβ e. e = (cos + isen ). (cos β + isen β) = =coscos β +i sensen β +isencos β +icossen β
Revisão : máximo, minimo em dimensão 1
 Revisão : máximo, minimo em dimensão 1 ( de Rolle) Seja f uma função que satisfaça as seguintes hipóteses: 1 f é contínua no intervalo fechado [a, b], 2 f é diferenciável no intervalo aberto (a, b), 3
Revisão : máximo, minimo em dimensão 1 ( de Rolle) Seja f uma função que satisfaça as seguintes hipóteses: 1 f é contínua no intervalo fechado [a, b], 2 f é diferenciável no intervalo aberto (a, b), 3
7.3 Diferenciabilidade
 CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
CAPÍTULO 7. INTRODUÇÃO À ANÁLISE EM RN 7.18 Estude quanto a continuidade a função f de R 2 com valores em R definida por: x 2, se x 2 + y 2 < 2y, f(x, y) = x, se x 2 + y 2 = 2y, y 2, se x 2 + y 2 > 2y.
