Transformada de Laplace
|
|
|
- Esther Bergler Varejão
- 5 Há anos
- Visualizações:
Transcrição
1 rorm plc Crcríic pricipl: Algrizor EDO lir, ou j, rorm um EDO lir um qução lgéric Méoo: ] PVI : I ] p q Vg: Exim u rzõ pricipi pr uilizção rorm plc ; i O méoo riciol rolução um PVI volvo um EDO ão homogê rqur rê p: rolvr homogê oci rvé oção um cojuo uml, or um olução priculr, 3 impor coiçõ iicii A rorm plc rolv EDO icorporo imulm coiçõ iicii ii Rolv PVI com orç xr mi gri qu impo plo méoo o coici irmio iii Rolv quçõ igri igro-ircii Dvg: i Só plic PVI` volvo EDO lir, priciplm à coici co ii No co EDO ão-homogê, ão-homogi m qu izr cr rriçõ Diição: D :], ii- rorm plc como o ução por ] OBS: Um oção lriv é F ] OBS: Um juiiciv oprciol pr ruur rorm plc é plo gui o: pr qu um opror igrl uclr ] K, F pou propri rormr um EDO m um qução lgéric volvo F coiçõ iicii, orvmo qu ] K, K, K, lim K, K, K, K, Pulo Mrclo Di Mglhã - DEMA-UFOP
2 D qu h K,, quo é um coição iciol qu v impor A qução lgéric mi impl volvo F ri orm p F, com p um poliômio m Pr qu h um compiili r orm EDO o gru qução lgéric corrpo, impõ- qu o gru p j O poliômio o primiro gru mi impl é p, com R Pr uo io j io, impor qu h K, K, o riv é m rlção vriávl Rolvo om- qu K, C Como rorm u or uçõ ii pr ci o compormo ióico K,, quo, ão é cário omr, o mi impl omrmo C, quirmo qu o omíio ução F coh o mi-ixo poiivo, ou j, K, OBS: A igrl imprópri cim é ii como o lim Quo pr lgum o limi cim xi, iz- qu igrl covrg vlor OBS: Qui vm r coiçõ or pr qu j covrg quo pr o mo lgu vlor? Primirm, ução m qu r igrávl vriávl m qulqur irvlo, ], Como é coíu,ão qu j igrávl, por xmplo j coíu por pr m qulqur irvlo, ], Já quão covrgêci quo é muio mi lic, vr, ão cohc um coição cári Ero, um coição uici é qu j omi por lgum xpocil l moo qu h o gui cimo, quo Diição: :, ] é coíu por pr ou cciolm coíu m, ] : i C, ] {,, } io é ó ão é coíu o cojuo iio {,, }, ] ii Exim o limi lri o poo,,, ou j, coiui ão p lo, ou j, lim lim lim lim Pulo Mrclo Di Mglhã - DEMA-UFOP
3 Noção: C, ] { :, ] : é coíu por pr m, ]} p Exmplo: / / ão ão coíu por pr m hum irvlo coo origm Propri uçõ coíu por pr P C, ] P g p m, ] xco o poo coiui P3, g C, ] g C, ] p P4 C, ] C, ] p p g Pulo Mrclo Di Mglhã - DEMA-UFOP 3
4 Diição: :], é orm xpocil m ], C,, C,q: C, Exmplo: é orm xpocil m ], com C, é orm xpocil m, ] com C, é orm xpocil m ], com C, é orm xpocil m ], com C, co co é orm xpocil m ], com C, co é orm xpocil m ], com C, Exmplo: ão é orm xpocil m ],, poi lim lim, Diição: E { :], R : éccoíu orm xpocil m ], } Propri: E é um pço voril rl orm : S E ão xi l qu covrg Prov: Uilizrmo o gui criério comprção m: S g ão igrávi m oo irvlo,], o é ixo, g,, ão Como covrg g covrg E, C,, C,l qu: C, Por ouro lo, C C C lim C Pulo Mrclo Di Mglhã - DEMA-UFOP 4 lim D moo qu, plo criério comprção plico C, covrg C g C lim, om- qu
5 Coqüêci: O omíio rorm plc um ução coém um mi-ixo poiivo ], E mpr Exmplo: Cálculo lgum rorm ] lim lim lim, ] lim, co ] ó lim co lim co co lim co Pulo Mrclo Di Mglhã - DEMA-UFOP 5
![Diição: Dii- como ci covrgêci ] o úmro o por Com io qur- izr qu i, i{ : ], } ii S :, Po- morr qu ] ão covrg pr, moo qu D ] ], OBS: S ou ão Prgu: Já mo qu E ão ] Srá qu vl rcíproc? S ],, ão E?](/docs-images/82/85790971/images/6-1.jpg "A rpo é ão, poi, por xmplo, / E, m ], A rorm plc como rormção ir Coorm vimo E é um pço voril o mpr xi ] Poro, é um om omíio pr Agor, vmo chr um pço voril rl qu irv coromíio pr Diição: S { F : I : I")
6 Diição: Dii- como ci covrgêci ] o úmro o por Com io qur- izr qu i, i{ : ], } ii S :, Po- morr qu ] ão covrg pr, moo qu D ] ], OBS: S ou ão Prgu: Já mo qu E ão ] Srá qu vl rcíproc? S ],, ão E? A rpo é ão, poi, por xmplo, / E, m ], A rorm plc como rormção ir Coorm vimo E é um pço voril o mpr xi ] Poro, é um om omíio pr Agor, vmo chr um pço voril rl qu irv coromíio pr Diição: S { F : I : I ], ou, ou } Com ição muliplicção por clr poo poo, S é um pço voril rl Além io, : E S Prgu: g] ] g],, g E? Rpo: Nm mpr, poi co g co, ão ] g], m ], Pulo Mrclo Di Mglhã - DEMA-UFOP 6
7 M ão á ii pr Por ouro lo, g] ] m ],!? Covção: Iiicrmo F, G S quo ivrmo F G m lgum mi-ixo poiivo ], Aim oém qu g] ] g],, g E,, Prgu: Núclo = { E }? Ou j, é ijiv, poro ivrívl or u imgm? Rpo: Não, poi coorm já mo pl propri P,, g E ó irm m u poo coiui, ão ] g, ro g orm : rch D, g E i qu Rizo: ] g, ], Eão, xcuo o poívi poo coiui, m- qu g, ], Cocluão: : E S é um rormção lir qu, covciormo iiicr uçõ m E qu coicim o poo coiui, iz ] F S F] E Diição: F] é omi rorm ivr plc ução F S Prgu: : E S é orjiv, ou j, E S? Rpo: Não! Io por cu o gui rulo orm 3: E lim ] Prov: Plo orm, ] C C, Cocluão: Fuçõ como,,,co,, prcm S, m ão poum rorm ivr m E Pulo Mrclo Di Mglhã - DEMA-UFOP 7
8 orm 4: Sj C], l qu E Eão, ] ] o lim Grlizo,,,, C], ão ] ] ] ] E, Prov: Ap pr o co, o ouro co gum por iução ii ] ] lim Agor vmo ur o gui o m: S C], com E, ão E Prov: Como E ão C, R, C l qu C,, ou j C C Igro przo co igrção, oém- qu D moo qu,, qo, Poro, ] ] lim lim ] C Exmplo: ogo, co ] co ] co ],! Exmplo:! D ]!]! ], Pulo Mrclo Di Mglhã - DEMA-UFOP 8
9 Pulo Mrclo Di Mglhã - DEMA-UFOP 9 Por ouro lo, ] ] ] D ogo,,! ] ]! OBS: D úlim igul oém qu, ]!, m priculr pr =, omo grlizção o oril um úmro url pr qulqur úmro rl qu ão j um iiro givo, o pl ução pcil ução Gm Eulr! x x x Aplicção rorm plc um PVI Co Priculr: I PVI ] ] ] ] : ou j, ] ] ] ], Qu é, xm, úic olução o PVI Co Grl: Do,,, R, E,,,,, j o ] ] ] : I PVI Uo propri, omo qu ] ] ] ] ] ] ] ] ] ] ] ] ] p q i i i i i i i i i i i i
10 orm 5: S E,ão x x D um moo grl ] x x x x x ] x x x Prov: A prov i o o qu x x x x x x x x x xx E ão x x E D moo qu, x x A órmul grl é prov iro rulo x x ] x Exmplo: Como co xx Eão, ] co ] ], Exmplo: ]? m- qu x x x x x x x x x D moo qu, x ] x x] ] M ão ] ] ] O qu rul m ], OBS: ] ] Coiciêci? Pulo Mrclo Di Mglhã - DEMA-UFOP
11 Pulo Mrclo Di Mglhã - DEMA-UFOP º orm rlção:,, ] ] R Prov: ] ] Corolário:,, ] ] - R, ] ] R Exmplo: m- qu ] co D moo qu,,, ] co R Exmplo: Clculr ] D moo qu, co 4 ] 4 3 Diição: A ução gru uiário ou ução Hvii é gui ução:,, H
12 Aplicção: D um ução g : R R po- coruir gui ução H g, R A irprção íic i uçõ é qu l rprm impulo com rrmo m im íico, poi ó pm ur o im pó = º orm rlção: S H g E, ão ] g], Prov: ] H g g g g] Corolário: g] ] H g, Pulo Mrclo Di Mglhã - DEMA-UFOP
13 Exmplo: H ] H co co ] co co ] ] ] co ] co i Exmplo: Sj um ução qu poui o gui gráico Pomo clculr ] uilizo o orm cim B orvr qu Aim m- qu D moo qu, ], ] 3,,,, 3, H, H 3 ] ] 3 Exmplo: ]? 6 Vmo ur o corolário: g] ] H g, N co, mo qu crim 3 D moo qu, 3 ] H g 3 o g] Por ouro lo, 3 g ] ] Poro, ] H orm 6: ] ] Pulo Mrclo Di Mglhã - DEMA-UFOP 3
14 Prov: =: ] >: iução or ] Corolário: ] ] ] Exmplo: ] ] Exmplo: ]? Vmo ur propri x x ] N co, oém- qu ] ] D moo qu, ] ] ] Por ouro lo, ] ] Aim, ] xx x x cox co O próximo rulo é muio impor áli ii prióico, o qui ão muio rqü lrôic orm 7: S E é prióic príoo, ão Prov: ] ] Fzo muç x +-éim igrl oém- qu x x x Pulo Mrclo Di Mglhã - DEMA-UFOP 4 x x x
15 D moo qu, ] x x x x x x x Um vz qu, x x x x x Exmplo: Oh rorm plc o gui il m- qu D moo qu, Exmplo: Or m- qu,, ] ] co ] Aplicçõ EDO Coici Poliomii: A gu ução pcil qu ó ormo rá ução Bl ª péci orm zro, J, pl olução o gui PVI :, Aplico plc à EDO omo Pulo Mrclo Di Mglhã - DEMA-UFOP 5
16 ] ] ] ] Ou j ] ] ] ] Ou j ] ] ] ] A qul é um EDO lir ª orm com or igr / l / D moo qu, C C / C 3! ] 4!! OBS: Por lor om- qu 3 x x x x, R! 3! So im, ão! ] C! Proco ormlm plico rorm ivr plc, omo!! C ] C C!!!! Agor, impoo coição iicil, coclui- qu J! Grlizção: A qução Bl ª péci orm é por Poui como um oluçõ ução Bl ª péci orm por J,!! Aplicção PVI com coiçõ iicii m Coirmo o gui PVI :, Fzo muç x omo qu ~ x x iz gui coiçõ Pulo Mrclo Di Mglhã - DEMA-UFOP 6
17 ~, ~, ~ x D moo qu, o PVI origil rorm o gui ~ ~ PVI : ~, ~ E ó pomo plicr plc pr or ~ x ~ ] x] ] ~ ] ~ ~ ] ~ ] ou j ~ ~ ] ] D moo qu, ~ x ] x ] x Agor, co x, co x x D moo qu, ~ x co x x Roro vriávl iicil, om- qu olução o PVI origil é por co Fução Impulo Uiário Dl Dirc A orç impuliv prcm grlm como orç xr m EDO o ipo c g o g é zro xco um irvlo, o qul é muio gr, ou j g é um orç cocr m Diição: A igrl imprópri g I é o impulo ol plico pl orç impuliv g Pulo Mrclo Di Mglhã - DEMA-UFOP 7 Exmplo: Coirmo gui orç impuliv,, N co o impulo ol é o por I,
18 Cocrção orç impuliv : é quo z m- qu lim Por ouro lo, lim I D moo qu, o limi oém um ojo mmáico urpr!, izo,!? E ovo ojo impô um grlizção o cocio uul ução Diição: A ução l Dirc ou ução impulo uiário,, é crcriz pl gui propri,, OBS: Não xi ução o Cálculo Elmr izo i propri O é o primiro xmplo um ução grliz ou iriuição Diição: O impulo uiário m é o por oo por D moo qu,, com, Apr ão r um ução, po- or rorm plc rvé um proco limi Do- por Diição: ] lim ], D moo qu, ] lim lim lim lim lim Aplico hopil, om- qu h OBS: Surprm, ],, OBS: Po o limi ] S, m E!, om- qu Pulo Mrclo Di Mglhã - DEMA-UFOP 8
19 ] Diição: lim, C Uilizo o VM pr igri, om- qu * * pr lgum ], ogo,, quo, moo qu * *, C Exmplo: Rolv o gui PVI : Aplico omo qu ] ] ] ou j ] ] Aplico ] ] H H Covolução: Prgu: g] ] g]? Rpo: Não! Cor-Exmplo:, g ], g] ] g] 3 Ero, g] ] Por ouro lo, pl ª propri rlção, m- qu OBS: D o, g] H g ] g, Pulo Mrclo Di Mglhã - DEMA-UFOP 9
20 Por ouro lo, g] H g ] g g, ] g g g g Como g E,ão D g ], g,,], D moo qu, ] g g g], Poro,, g E poum rorm ii m ],, ão ] ou j, g] g ] g] g g g g ] g] lim g Um vz qu, ], g], OBS: Fixo, R,m- qu o igro m é coíuo m u-rgiõ coi o râgulo R :, R Um vz qu, o lo m, ] ocorrm o poo,,, m o lo g m, R] ocorrm o poo i, i,,, ão o lo o igro ocorrm r;, i Pulo Mrclo Di Mglhã - DEMA-UFOP
21 orm: M Wirr pr covrgêci uiorm igri o ipo F x x,, x c Hipó: H x, coíu m rgiõ poligoi º iio coi m râgulo: x c, HExi um ução cciolm coíu M izo x, M, x c, M : A igrl Fx é uiormm covrg m rlção o prâmro x, c] OBS: Pr pormo ivrr orm igrção m é cário lcr covrgêci uiorm igrl imprópri m m rlção o prâmro, ] Ero, vio à, g E, xi C, R l qu g C C : M o M iz o M Wirr, poi ip o prâmro D moo qu, po r rcrio como o M, ] g] lim g lim I I D, om- qu g I I g Pulo Mrclo Di Mglhã - DEMA-UFOP
22 D moo qu, I C C, lim I Por ouro lo, rgião igrção I é o quro:,, o qu g ão á ii pr poo, poro, r ii igul zro rgião Com io, om- qu D moo qu, g I g ] g] lim I Diição: A covolução u uçõ g, o por gui ução g : g g, é pl orm: Hipó: :, g E com ], g] ii m ] g] g] Corolário: g F G ] Propri: P g g P g h g h P3 g h g h P4 P5, ~,, OBS: C C Prgu:, g E g E? Rpo: Sim! g D o,, g E C, C g,, g R: C, g Cg, D moo qu, g g C C, o C C C g, mx{, g } ogo, Pulo Mrclo Di Mglhã - DEMA-UFOP g g C C, Por ouro lo, o, iio
23 Pulo Mrclo Di Mglhã - DEMA-UFOP 3 M mx Omo qu M C C o CM M Aplicção Equçõ Igri Covoluiv g EIC Proco ormlm, plicmo m mo o lo oo ] G F Y Y G F g F Y o ], ], ] g G F Y Aplico omo qu G F G ] ] Exmplo: Aplicção Equçõ Igro - Dircii Covoluiv coici co ª orm g Aplico om- Y G F Y ogo G p F Y Aplico om- G p G p ] ] Aplicção EDO ir com coici poliomii
24 PVI :, I OBS: F ] ] F D moo qu, ] Y Y Y Aplico mo o lo EDO om- Y Y Y Y ou j Y Y Qu é um EDO ir ª orm D moo qu, l Y Y C OBS: Poro, Ero, quirmo Y C E ão crim C Cocluão: Aplico, om- qu olução o PVI m E é por Exmplo: PVI :, I Aplico mo o lo EDO om- Ou j Y Y Y Y Pulo Mrclo Di Mglhã - DEMA-UFOP 4
25 Y Y N co, / / / / Y Y C Novm, como qurmo D moo qu, E, ão crim C / / Y Ero, plicrmo ormo qu / /? OBS: Não xi covolução E l qu ] / D moo qu, ão po plicr orm: Vlor Iicil Hipó:, E : lim ] lim Prov: ] ] E lim ] Poro, lim ] lim orm: Vlor Fil Hipó:, cciolm coíu limi or,, com igrávl m, : lim ] lim Prov: ] lim ] lim Pl covrgêci uiorm oi plo Wirr, um vz qu,, mo qu Pulo Mrclo Di Mglhã - DEMA-UFOP 5
26 lim lim D moo qu, lim ] lim lim Poro, lim ] lim ] lim orm: Hipó: : F, olum covrg F ],! Além io, é coíu orm xpocil, Aplicção o cálculo igri prmriz Exmplo: Fução Gm Eulr oril grlizo: O oril um úmro iiro poiivo é por iição o por! 3 D moo qu ução oril iz gui qução uciol!! Aim, pr omo qu!!! S izrmo ormo qu!!! lim M ão quo ormo qu!!! Alogm, quo ormo qu! 3! 3! E im ucivm Ou j, o oril qulqur iiro givo rá iiio! Por ouro lo, mo qu! ], D moo qu, ]! E o lvou Eulr iir gui grlizção ução oril Pulo Mrclo Di Mglhã - DEMA-UFOP 6
27 Diição: A Fução Gm ou oril grlizo, o por x, é por x x, x Propri P x x x, x P P3!, Gráico x x - - Com ução Gm pomo or r ], r Io prmi grlizr oção riv orm N pr orm rcioári! OBS: r r r ] ], r, r r orm: Do r R, r>-, m- qu Prov: r r r! ], r r r r u ] u r u r r Exmplo: Um xmplo igrl ão rivil qu oo u Cálculo I cohc é o gui x x Arvé rorm plc pomo clculr l igrl D o, iio gui ução míli prmriz igri imprópri Pulo Mrclo Di Mglhã - DEMA-UFOP 7
28 m- qu, x x x x x ] x x x x x x lim x lim x x x x x / x lim rc g x/ x/ D moo qu, OBS: Plo orm rior, ] / / ] / ] Plo xrcício li, mo qu /, o qu implic m / Poro, OBS: Solução pr por plc: Por ouro lo, x x x x x x x x ] x x x rcgx] x x / x u x u / OBS: u : x x u / x u OBS: / x u x u / / v : v vv v u u x v u x v u D moo qu, Pulo Mrclo Di Mglhã - DEMA-UFOP 8
29 x x ] x x Exmplo: Avlir míli igri h cox x x,, Aplico rorm lplc à, om- qu OBS: m- qu cox x H x h x, x o x, M x com M x x D moo qu, plo x M Wirr h é uiormm covrg, poro po- rocr orm igrção m or- qu H x x x co x x Uo rçõ prcii A B A / x x B / x x D moo qu, x H So im, Poro, x x x h H ] ] cox x,, x Pulo Mrclo Di Mglhã - DEMA-UFOP 9
30 Aplicção à oluçõ umi quçõ ircii prcii Molo Mmáico pr iuão o clor uiimiol um io mi-iiio mril homogêo com mprur iicil = igul zro, com xrmi x = mi à mprur co u O Prolm Vlor Iicil Froir PVIF é o por u uxx PVIF : u x, u, u, x,, x, O K / c é o coici iuivi, o K couivi érmic, c o clor pcíico o mril o io i o io Como ão xim o muo rl mprur iii, impõ- gui coição limição or mprur u x, M, x, Como mprur á ii, m c vriávl, m omíio mi-iiio, po plicr rorm plc o m rlção o pço vriávl x quo m rlção o mpo vriávl Apliqumo m rlção à vriávl Com io omo qu u ] x, u x, u] x, u x, U x, uxx ] x, u x, u x, U x, x x x D moo qu, omo gui EDO U x, U x, x OBS: N vr r- um míli EDO prmriz plo prâmro rl Pl ori EDO, pr ormo um olução úic um EDO ª orm prcimo impor u coiçõ iicii Ero, ó mo um coição iicil vriávl x! Rlm, coição roir é rorm m um coição iicil pr ução rorm U x,, um vz qu u U, u, ] u, u u ] A olução grl EDO é por x C C U x, Aqui é qu rá uml rmo impoo coição Io uprirá l um gu coição iicil D o, om- qu x Pulo Mrclo Di Mglhã - DEMA-UFOP 3
31 M U x, u x, u x, M, D moo qu, crim lim U x, Poro, U x, C x Agor im pomo impor o úic coição iicil or olução grl pr ormo um olução úic Fzo io, omo qu u U, C Poro, úic olução o prolm mio É Eão, olução o PVIF rá por U x, U x,, x x U, u / ~ U x, M u x U x, x u x, U x, ] x, u ] x, 3 Pr ormo rorm ivr prcirmo lgu rulo Propoição: 4 ], 4 ], 3 Prov: Erégi: rormr m um im EDO Diio vriávi Y,, Z,, m- qu Pulo Mrclo Di Mglhã - DEMA-UFOP 3
32 Pulo Mrclo Di Mglhã - DEMA-UFOP 3 Y Z Y Y Z OBS: D o, / 3 3 / Z Y Y Y Y D moo qu, omo o gui im Y Z Z Y Y Aplico, omo lvo o im 4 z z z z OBS: ] ] ] ] ] Y Y Y Y A qul é um EDO lir ª orm, cujo or igr é o por 4 4 Poro, om- qu C 4 C z 4 3 S, ão, ] / Y ogo, pr, mo qu
33 Pulo Mrclo Di Mglhã - DEMA-UFOP 33 C Rumio, ov- qu,, 4,, 4 3 z OBS: E morção á corr qu co C j ip Um morção ir po r gui orm Primiro provmo pr poi uilizmo o º orm rlção D o, como,,, 4 / é coíu limi, ão 4 4 / Y zo muç om- qu c Y zo muç om- qu Y Somo c om- qu Y Film zo primir igrl om- qu x Y x D moo qu,
34 ou j, Y / 4 ] Pr ormo pr,, uilizr o gui rulo º orm rlção: Hipó: ] F, pr : F c ],, c c c c Aim, / 4 Y ] ], / ou j, / 4 ],, Pr provr, orvmo qu ução / 4 z,, z, 3 é coíu limi Além io, z Aplico o gui rulo orm: Hipó: E, lim : ] ], Prov: Orvo qu F iz coiçõ o orm Wirr ão, om- qu r F r r r r r Pulo Mrclo Di Mglhã - DEMA-UFOP 34
35 Pulo Mrclo Di Mglhã - DEMA-UFOP 35 OBS: E E lim, D moo qu, ] lim Poro, zo r, om- qu ] F Coclui- ão qu lim lim ] ] ] Y z ou j,,, ] 4 / 3 Agor já mo qu uo qu prcimo pr or olução o PVIF pl rorm ivr 3 Ero, i cimo iir u uçõ pcii muio impor Fíic-Mmáic; uçõ rro rro complmr Como moivção, lmrmo qu, ] r r r r Por ouro lo, ] G F g Priculrm, mo qu r r r / ] Diição: A ução pcil rro proili igrl é por, : r r r D moo qu, ] r Por ouro lo, plo º orm rlção, mo qu F, ] R Com io omo qu
36 Pulo Mrclo Di Mglhã - DEMA-UFOP 36, ] r mro mém qu, ] ] x x, omo qu x x x x x x x x z Z 3 / 4 / 3 / 4 / ] ] ] zo muç x 4 /, omo qu / / 4 ] Aim omo lvo gui Diição: A ução pcil rro complmr é ii como o, : r rc r Propri:, rc r Gráico: D moo qu, ] / r r r r r ou j,,, ] rc
37 Cocluão: A olução o PVIF é por x x u x, U x, ] x, u ] x, u rc Aplicção Sim Corol uomáico Srvomcimo Ojivo: Corolr roção um h h rvé um poiro corol Noção: o âgulo giro h oupu i âgulo giro o poiro ipu Hipó: A h poui um momo iérci I >> momo iérci o poiro Diição: h, poiro o i Procimo: Um im uxilir rvomcimo é projo pr mir rrolimr h rvé um orqu qu j proporciol o vio Além io, pr prouzir um mpig o im o rvomcimo mém prouzirá um orqu proporciol à vrição o vio OBS: O rvomcimo po cor u própri o rgi rvé moor, gror ou quipmo lérico Molo mmáico: O molo mmáico é coqüêci gui li Fíic: O prouo I pl clrção gulr é igul o orqu plico h, ou j, xpro mmicm om- I o c OBS: S uilizrmo prcrmo qu EDO qu á por rá é Io o i c o i o co i ci ou j, I c c o o Ou j, é um EDO ª orm lir coici co, poro o ipo o c Hipó icioi:, c, i, i coíu m, Coiçõ iicii: Como h á iicilm m rpouo, ão 3 o o Pulo Mrclo Di Mglhã - DEMA-UFOP 37 i i
38 Cocluão: O molo mmáico é o plo gui I o c, PVI : o o Aplico plc qução, om- I o c ci 3 OBS: i Por ouro lo, plico plc m, om- D 3 4, gu- o i 4 I i c ci Do I i ci I c Poro, o vio h rá o por I c i i I c Em priculr,, om- qu i I I c c I I c c o, I I 4I D moo qu, OBS: Supô- mpig c N co, é um ocilção ucríic um I 4I Pulo Mrclo Di Mglhã - DEMA-UFOP 38
39 Fórmul Complx Ivrão S pouirmo o rrml mmáico cário pr ormo ivrão iv rorm plc ivrão rá oi rvé Fórmul Igrl Mli Diição: S F ], ão i z i F z z, FI i OBS: m- qu F Complxiico vriávl ip, ou j, zo = z = x+i, om- qu xi x x co F z i x x co i u x, iv x, Como E ão C >, α q x co x C C, C, x x x ogo, u v ão m iio ix z > Por ouro lo, uo iiz x x ux x, co co x x x u x, co x x vx x, x x x v x, co D moo qu, u v ão coíu m ], izm quçõ Cuch- Rim Poro, Fz é líic m z > FI é o méoo iro pr oção F z] A igrção é u o logo r z =, o é l qu igulri Fz ão à qur z = Pulo Mrclo Di Mglhã - DEMA-UFOP 39
40 Origm Fórmul FI: r- um grlizção Fórmul Igrl Cuch pr r z = o co m l ão roir o mi-plo o z é líic Pr io cirmo r lgum iormção or o compormo z pr z rirrim gr Diição: z é orm z quo z Noção: z = Oz z M z, z r, M, r > i qu; orm: Igrl Imprópri Cuch Hip: z líic or o mi-plo z z = Oz, > : S z >, ão z i z z i i i z z i z D moo qu, Fz é líic m z, Fz = Oz, >, z >>, m qu i F z F i z,, i z Prov: Sj C R o rco o círculo z = R: x, o R > R > z D moo qu, z ic R {x = } Diio m-, pl Fórmul Igrl Cuch, qu Pulo Mrclo Di Mglhã - DEMA-UFOP 4
41 i i z z z z z z i z i z z i z z z z { } z z z z z z z z CR x CR i CR i Quo zc R m- qu ; z z z = R, R uicim gr R >>, om- qu como z<mz, ão z M M z z z z R R z z, R > r,p/lgum r >> O igro m z xprão cim ão coíuo O comprimo C R é mor qu R Poro, como z M M z z z z M z R z z R R z R z / R C C CR Quo R, poi > Além io, como R = + igrl Covrg pr quo + D moo qu, omo o limi + om- qu i z i i i i z z i i z i i z z lim z lim Eão, proco ormlm, om- qu i Fz i F ] i z] i F z ] z i z i z i i i z F z z Cooro Bromwich: N práic igrl m FI é rorm um igrl cooro Pulo Mrclo Di Mglhã - DEMA-UFOP 4
42 o C B = z F z z i C é o cooro Bromwich; B m- qu = o é R, o i z z z lim i F z z lim i F z z i F z z R i R C B OBS: Coição uici pr qu igrl or covirj pr zro quo R: F z O z CS pr lgum > E coição mpr ocorr quo, por xmplo, Fz=pz/qz, pr p q poliômio com grup < gruq Aplicção o orm o Ríuo à Ivrão rorm plc: S igulri F ão pólo orm ii à qur um r, lém io, ivrmo o cooro Bromwich, ão z F z z, qo R z R F z : z, z pólo F z Exmplo: Clcul z z Pólo Fz : 3 z z ] 3 Pulo Mrclo Di Mglhã - DEMA-UFOP 4
43 z z z z orm 3 R F z : lim! ] z z z z z z z z z z z z z z z z lim ] 4 lim ] z 4 z z z z z 3 z z z z z z lim 4 ] z z z z z z ] z z z z ]4 z z z z 4 z 3 lim z ] 4 ] z z z 3 z z z z z 3 z z z orm R F z : lim ] lim ] z 3 6 z z z z D moo qu, ] Pulo Mrclo Di Mglhã - DEMA-UFOP 43
44 Pulo Mrclo Di Mglhã - DEMA-UFOP 44
Transformada de Laplace
No ul: MM6 rorm plc Crcríic pricipl: Algrizor EDO lir ou j rorm um EDO lir um qução lgéric Méoo: PVI : I ] p q Vg: Exim u rzõ pricipi pr uilizção rorm plc ; i O méoo riciol rolução um PVI volvo um EDO
Transformada de Laplace
No ul: MM6 rorm plc Crcríic pricipl: Algrizor EDO lir ou j rorm um EDO lir um qução lgéric Méoo: PVI ] : I ] p q Vg: Exim u rzõ pricipi pr uilizção rorm plc ; i O méoo riciol rolução um PVI volvo um EDO
Transformada de Laplace. Prof. Eng. Antonio Carlos Lemos Júnior
Trormd d plc Pro. Eg. oio Crlo mo Júior GEND Diição d Trormd d plc Trormd d plc d lgu ii Propridd d Trormd d plc Exrcício Corol d Sm Mcâico Trormd d plc Obivo: O obivo d ção é zr um irodução à Trormd d
SÉRIES - TRANSFORMADAS NOTAS DE AULA
SÉRIES - TRANSFORMADAS NOTAS DE AUA Não é proo ir qu o oo momo ipirção mi óric pomo r o mi próimo poívl o plicçõ mi práic A N Whih (86-97) E obr é um compêio o ul, orgi ur () mr livo 7/, pr icipli Cálculo
SÉRIES - TRANSFORMADAS
UTFPR Uivri Tcológic Frl o Prá DAMAT Dprmo Acêmico Mmáic Cálculo Dircil Igrl (MA6A) SÉRIES - TRANSFORMADAS NOTAS DE AUA Ruimr ui Nó o mr/ Não é proo ir qu o oo momo ipirção mi óric pomo r o mi próimo
TÓPICOS. Integração complexa. Integral de linha. Teorema de Cauchy. Fórmulas integrais de Cauchy.
No m, liur dss pomos ão disps d modo lgum liur d iliogri pricipl d cdir hm-s à ção pr imporâci do rlho pssol rlir plo luo rsolvdo os prolms prsdos iliogri, sm ul prévi ds soluçõs proposs, ális compriv
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
Uivridad Salvador UNIFACS Curo d Egharia Méodo Mmáico Aplicado / Cálculo Avaçado / Cálculo IV Profa: Ilka Rouça Frir A Traformada d Laplac Txo : Irodução. Dfiição. Codiçõ d Exiêcia. Propridad. Irodução
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Prof Mc ARMANDO PAULO DA SILVA Prof Mc JOSÉ DONIZETTI DE LIMA INTEGRAIS IMPRÓPRIAS A TRANSFORMADA DE LAPLACE g ()d = lim R R g()d o limit it Qudo o limit it
MATEMÁTICA. 01. Sejam os conjuntos P 1, P 2, S 1 e S 2 tais que (P 2 S 1) P 1, (P 1 S 2) P 2 e (S 1 S 2) (P 1 P 2). Demonstre que (S 1 S 2) (P 1 P 2).
GGE RESOE - VESTIBULAR IME MATEMÁTICA) MATEMÁTICA Sj o ojuo S S qu S ) S ) S S ) ) or qu S S ) ) : Sj S S Coo S S ão ou l r o rol oo uor r grl) qu oo S ão logo oo qurío orr F F F F F ) Crufrê ro -) ro
Sistemas Lineares Entrada/Saída 30
Sim Lir Erd/Síd 3 3- Sim Lir Erd/Síd 3.- Fuçõ Sigulr (Sii Elmr Hyi) Muio ii d xcição uilizdo o udo d im diâmico ão uçõ impl o domíio do mpo, xpro mmicm por um couo d uçõ domid uçõ igulr, qu coium um couo
SISTEMAS DE CONTROLE I
UNIVERSIDDE FEDERL DO RIO GRNDE DO NORTE CENTRO DE TECNOLOGI DEPRTMENTO DE ENG. DE COMPUTÇÃO E UTOMÇÃO SISTEMS DE CONTROLE I Proor: Fáio Mghi Ugulio rújo Nl-RN, mrço ÍNDICE INTRODUÇÃO...4. DEFINIÇÕES...4.
CMC INTRODUÇÃO AO ESTUDO DE SISTEMAS DE CONTROLE. Aulas: 3 e 4 SISTEMAS LINEARES E EQUAÇÕES DIFERENCIAIS (ED)
CMC-- - INTRODUÇÃO AO ESTUDO DE SISTEMAS DE CONTROLE Auls: 3 4 SISTEMAS LINEARES E EQUAÇÕES DIFERENCIAIS (ED). Iroução Sisms, sisms físico sisms ghri Excição & rspos um sism Diâmic - Aális iâmic sus ságios:
Espaço de Estados. Modelo de Estado: y(t) = saída u(t) = entrada. função de transferência em cadeia fechada (f.t.c.f) :
Epço Eo Eqo or corolo covcol - rlção r í-r, o fção rfrêc, o corolo moro - crção qçõ o m m rmo qçõ frc ªorm q pom r com m qção frcl ª orm form mrcl. O o oção mrcl mplfc m mo rprção mmác m qçõ. O mo úmro
0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:
![0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:](/thumbs/95/123353134.jpg "0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:")
- Rção orm zro: Es ipo rção ão po sr lmr (., ão há rção!), so poro ipo ν, logo, mos qu, i Igrção, pr 4 ) (, cocrção m um mpo é: 5 6 7 Eq. () 8 (Nos mplos i supori qu ). 9 - Rçõs orm : S loci rção é rmi
Unidade 4 - Vibrações Forçadas sob Condições Gerais
Ui 4 Vibrçõs Forçs sob Coiçõs Gris Ui 4 - Vibrçõs Forçs sob Coiçõs Gris 4. - Iroução Ui 3, foi su vibrção forç sisms um gru libr sob ção forçs hrmôics. s cpíulo, s suo srá sio pr forçs qulqur urz. Iicilm
TRANSFORMADA DE LAPLACE 9.1 INTRODUÇÃO
9 TANSFOMADA DE APAE 9. INTODUÇÃO A rformd d Fourir prmi rprr qulqur il fíico pl om, fii ou ifii, d u compo, gudo um rfrcil m qu vriávl ω d b é rl. Tl rprção d ii dmph um ppl impor o udo d im lir ivri,
Análises de sistemas no domínio da frequência
prmno d Engnhri Químic d Prólo UFF iciplin: TEQ0- COTROLE E PROCESSOS náli d im no domínio d frquênci Prof inok Boorg Rpo d Frquênci Cliqu pr dir o ilo do xo mr COCEITO: Coni d um méodo gráfico-nlíico
Transformada de Laplace Solução de Modelos Lineais
TEQ CONTROE DE PROCESSOS Dmo d Eghi Químic d Pólo UFF Tfomd d lc Solução d Modlo ii Pof Niok Bojog A Tfomd d lc EDO: dy 5 y y d Equção Difcil Odiái Equção Algéic y -,8,5,5 Solução d Equção Difcil - Solução
TÓPICOS. Números complexos. Plano complexo. Forma polar. Fórmulas de Euler e de Moivre. Raízes de números complexos.
Not m: litur dsts potmtos ão disps d modo lgum litur tt d iliogrfi pricipl d cdir Chm-s tção pr importâci do trlho pssol rlir plo luo rsolvdo os prolms prstdos iliogrfi, sm cosult prévi ds soluçõs proposts,
MECANISMOS DE REAÇÕES
/4/7 MECSMS DE REÇÕES rof. Hrly. Mrins Filho Rçõs lmnrs Rçõs qu concm m pns um p são rçõs lmnrs. molculri rção lmnr é o númro moléculs qu rgm. Rção lmnr unimolculr: C molécul m um proili inrínsc s compor
GRAVITAÇÃO UNIVERSAL
GVIÇÃO UNIVESL z- u ci féric u fr chubo rio, l qu u uprfíci ngnci uprfíci xrn fr chubo p plo cnro priii fr chubo r D coro co Li Grição Unirl, qul rá forç co qu fr chubo rirá u pqun fr locliz à iânci, o
1. A TRANSFORMADA DE LAPLACE
Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Transporte Vestiário Higiene Pessoal Poupança
Álgbr Mricil PRTE LGUMS CONSDERÇÕES TEORCS MTRZES Noção d mriz Mrizs formm um impor cocio m mmáic, d spcil uso o sudo d rsformçõs lirs mriiz é um bl d lmos disposos m lih colus Mriz m é um bl d m úmros
Escola Politécnica Universidade de São Paulo
Ecol Poliécic Uiveridde de São Pulo PSI323 Circuio Elérico II Bloco 3 Fuçõe de rede e Regime Permee Seoidl Prof Deie Cooi PSI323- Prof Deie Bloco 3 DESCRIÇÃO ENTRADA-SAÍDA DE UM CIRCUITO R, LINEAR E INVARIANTE
Princípios de Telecomunicações
UNVERSDADE FEDERAL DE PERNAMBUO ro d cologi Gociêcis urso d Eghri Eléric Elrôic ODE Grupo d Psquis m omuicçõs Pricípios d lcomuicçõs élio MAGALÃES DE OLVERA, BEE, MEE, Docur, MEEE Lis d Exrcício 9 d Novmbro
CAPÍTULO 3. Exercícios é contínua, decrescente e k 2 positiva no intervalo [ 3, [. De ln x 1 para x 3, temos. dx 3.
CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)
Módulo 03. Determinantes. [Poole 262 a 282]
![Módulo 03. Determinantes. [Poole 262 a 282]](/thumbs/74/70829060.jpg "Módulo 03. Determinantes. [Poole 262 a 282]")
Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
Métodos Computacionais em Engenharia DCA0304 Capítulo 4
Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d
PROVA NACIONAL ESCRITA DE MATEMÁTICA
PROVA NACIONAL ESCRITA DE MATEMÁTICA Equip Rsposávl Pl Elorção Corrção d Prov: Prof. Douor Sérgio Brrir Prof.ª Douor Cri Lmos Durção d Prov: 0 miuos. Tolrâci: 30 miuos Coção: 00 PONTOS Escol d Proviêci
CÁLCULO I 1º Semestre 2011/2012. Duração: 2 horas e 30 minutos
NOVA SCHOOL OF USINESS AND ECONOMICS CÁLCULO I º Smsr / EXAME ª ÉOCA Jiro Durção: hors miuos Não é prmiido o uso d luldors. Não pod dsgrfr s folhs do uido. O uido ds m é omposo por págis. Rspod d form
Análise de Sistemas Lineares
Aáli d Sima iar Dvolvido plo Prof Dr Emilo Rocha d Olivira, EEEC-UFG, 6 Traformada d aplac A ididad d Eulr dfi uma rlação r o ial xpocial o iai oidai a forma ± j = co ( ) ± j ( ) N cao, é dfiido como a
RESOLUÇÃO DE EQUAÇÕES POR MEIO DE DETERMINANTES
RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.
3. TRANSFORMADA DE LAPLACE. Prof. JOSÉ RODRIGO DE OLIVEIRA
3 TRNSFORMD DE LPLCE Prof JOSÉ RODRIGO DE OLIVEIR CONCEITOS BÁSICOS Númro complxo: ond α β prncm ao nº rai Módulo fa d um númro complxo Torma d Eulr: b a an a co co n n Prof Joé Rodrigo CONCEITOS BÁSICOS
8 REPRESENTAÇÃO NO ESPAÇO DE ESTADOS
8 REPRESENÇÃO NO ESPÇO DE ESDOS 8. Cocio d sdo ( prsção srá fi o domíio do mpo coíuo; s difrçs com o cso discro são pqus srão prsds posriorm. rprsção rd/síd d um sism só é álid qudo, o mpo iicil, o sism
TRANSFORMADA DE LAPLACE- PARTE I
TRNSFORMD DE LLE- RTE I Eor. d Barro. INTRODUÇÃO odmo dfiir a Traformada d Laplac como uma opração mamáica qu covr uma fução d variávl ral m uma fução d variávl complxa: Od, F f d i f é uma fução ral da
# D - D - D - - -
1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
1 Capítulo 2 Cálc l u c lo l I ntegra r l l em m R
píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos
b a c v g g g t a n m p o i a a a m i o t f m p b a m p e l x m x o a a i o r a r n r c h a a s l u u u v m u c a a s n u g r l l i a a e l
x x x z f f h h q h f z X x x x z f f h h q h f z Pó C S C Cí Nzó Lüí Aí Aó G Oá Xé Ró Lóz Bó X Mqé V Mí Lz Méz Fáz Gz Nz B Có E P C, S. L. D R Hz C ISBN13 978-84-694-1518-4 DL C 634-2011 X : TOP X : TOP
5 ANÁLISE EM TERMOS DE MODELOS ENTRADA/SAÍDA DO TIPO FUNÇÃO DE TRANSFERÊNCIA. 5.1 Respostas a Perturbações Típicas dos Sistemas Contínuos
5 ANÁLISE EM ERMOS DE MODELOS ENRADA/SAÍDA DO IPO FUNÇÃO DE RANSFERÊNCIA Arovio lhç ooro r i oío iro o o, iiil rá rli áli r o o o i oío. O ooro o i iro o irio rá lio o fil o ílo, ro riii ifrç oo o i oío.
Capítulo 4: Derivada A Reta Tangente. y = uma curva definida no intervalo ( a, ) e sejam ( x, y ) e Q( x y ) P dois pontos
Isio d Ciêcis Es - Dprmo d Mmáic Cálclo I Proª Mri Jli Vr Crlo d Arjo Cpílo : Drid - A R T Sj b disios d cr Sj s r sc q pss plos poos P Q Cosidrdo o riâlo râlo PMQ, ir o ldo, mos q iclição d r s, o coici
1 Introdução e Base Matemática
J. A. M. Flipp Souz Iroução Bs Mmáic Iroução Bs Mmáic Iroução Bs Mmáic 3. O úmro imgiário 3. Númros complxos 4.3 Oprçõs com úmros complxos 9.4 O so o co-so.5 A qução Eulr 5.6 A g 7.7 As ivrss so, co-so
Prgrmçã O Mu s u Év r, p r l ém f rcr s s i g ns «vi s i t s cl áss i cs» qu cri m s p nt s c nt ct nt r s di v rs s p úb l ic s qu vi s it m s c nt ú d s d s u ri c s p ó l i, p r cu r, c nc m i t nt
Valoração de Grafos. Fluxo em Grafos. Notas. Teoria dos Grafos - BCC 204, Fluxo em Grafos. Notas. Exemplos. Fluxo em Grafos. Notas.
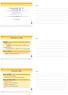Teori o Grfo - BCC 204 Fluxo em Grfo Hrolo Gmini Sno Univerie Feerl e Ouro Preo - UFOP 19 e ril e 2011 1 / 19 Vlorção e Grfo Exemplo vlore eáio: iâni roovi que lig ie e ie é e 70 kilômero vlore inâmio:
1 a Lista: MTM146: Prof. Paulo Magalhães:
Exercício : Mosre que a solução do sisema de EDO s x y f ( x y y com codições iiciais: x ( ) x() ) ), f saisfazedo x( f ( ) d f ( ) cos( ) d f ( ) cos( ) d f ( ), é dada por Exercício : Resolva o seguie
Tópicos Especiais em Identificação Estrutural. Representação de sistemas mecânicos dinâmicos
Tópicos Espciais m Idiicação Esruural Rprsação d sismas mcâicos diâmicos O problma diro... rada Sisma rsposa rsposa y() rada x() Problma diro: rada x() Cohcimo + rsposa do sisma y() O problma ivrso...
Análise de Sistemas Contínuos por Série de Fourier
ES 43 Aális d Sisms oíuos por Séri d Fourir Prof. Aluizio Fuso Ribiro Arúo po. of Sisms d ompução ro d Iformáic - UFPE píulo 6 Irodução oúdo Rprsção d Sil Priódico por Séri d Fourir rigooméric Eisêci ovrgêci
8 = 1 GRUPO II. = x. 1 ln x
Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim
Definição: Sejam dois números inteiros. Uma matriz real é uma tabela de números reais com m linhas e n colunas, distribuídos como abaixo:
I MTRIZES Elemeos de Álgebr Lier - MTRIZES Prof Emíli / Edmé Defiição: Sem dois úmeros ieiros Um mriz rel é um bel de úmeros reis com m lihs e colus, disribuídos como bixo: ( ) i m m m m Cd elemeo d mriz
Questionário sobre o Ensino de Leitura
ANEXO 1 Questionário sobre o Ensino de Leitura 1. Sexo Masculino Feminino 2. Idade 3. Profissão 4. Ao trabalhar a leitura é melhor primeiro ensinar os fonemas (vogais, consoantes e ditongos), depois as
1 a Lista: MTM146: Prof. Paulo Magalhães:
a Lisa: MTM46: Prof Paulo Magalhães: Exercício : Mosre que a solução do sisema de EDO s x y f ( x y y com codições iiciais: x ( x(, f saisfazedo f (, é dada por x( f ( d Exercício : Resolva o seguie y
PROGRAD / COSEAC ENGENHARIAS MECÂNICA E PRODUÇÃO VOLTA REDONDA - GABARITO
Prov de Cohecietos Especíicos QUESTÃO:, poto Deterie os vlores de e pr os quis ução dd sej cotíu e R. =,,, é cotíu e :.. li li li li. li li é cotíu e :.. li li li li Obteos Resolvedo equções θ e β: Respost:.
( ) 2. Eletromagnetismo I Prof. Dr. Cláudio S. Sartori - CAPÍTULO VIII Exercícios 1 ˆ ˆ ( ) Idl a R. Chamando de: x y du. tg θ
Elromgnismo Prof. Dr. Cláudio S. Srori - CPÍTUO V Ercícios Emplo Cálculo do cmpo mgnéico d um fio d comprimno prcorrido por um corrn léric num pono P(,,. dl - r + + r dl d P(,, r r + + ( ( r r + + r r
Uniforme Exponencial Normal Gama Weibull Lognormal. t (Student) χ 2 (Qui-quadrado) F (Snedekor)
Prof. Lorí Vili, Dr. vili@pucrs.br vili@m.ufrgs.br hp://www.pucrs.br/fm/vili/ hp://www.m.ufrgs.br/~vili/ Uniform Exponncil Norml Gm Wibull Lognorml (Sudn) χ (Qui-qudrdo) F (Sndkor) Um VAC X é uniform no
O E stado o d o o Solo
O Etdo do Solo Índic Fíico Elmnto Contituint d um olo O oloéummtril contituídoporum conjunto d prtícul ólid, dixndo ntr i vzio qu podrão tr prcil ou totlmnt prnchido pl águ. É poi no co mi grl, um itm
= 1, independente do valor de x, logo seria uma função afim e não exponencial.
6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0
UMA CONTRIBUIÇÃO AO ESTUDO DAS REDES MUTUAMENTE CONECTADAS DE DPLLS USANDO MODELOS DE TEMPO DISCRETO
RCUS VINÍCIUS RICHRDELLE UNZUE U CONRIBUIÇÃO O ESUDO DS REDES UUENE CONECDS DE DPLLS USNDO ODELOS DE EPO DISCREO o pro à Eol Polé Uvr São Pulo pr oção o íulo r m Eghr. Ár Corção: Eghr Elér Oror: Pro. Dr.
Sinais e Sistemas Mecatrónicos
Sinis Sistms Mctrónicos Anális d Sistms no Domínio do Tmpo José Sá d Cost José Sá d Cost T11 - Anális d Sistms no Tmpo - Rsp. stcionári 1 Crctrizção d rspost stcionário A crctrizção d rspost stcionári
Transformadas de Laplace
Trformd de plce O MÉTODO O méodo de rformd de plce é um méodo muio úil pr reolver equçõe diferecii ordiári EDO. Com rformd de plce, pode-e coverer mui fuçõe comu, i como, eoidi e morecid, em equçõe lgébric
= n + 1. a n. n 1 =,,,,,, K,,K. K descreve uma sequência finita.
DICIPINA: CÁCUO A CONTEÚDO: EQUÊNCIA PROFEORA: NEYVA ROMEIRO PERÍODO: BIMETRE EQUÊNCIA Um squêc um fução f cujo domío o cojuo dos ros posvos su gráfco o plo y do po, ou d, squêc um cojuo d prs orddos do
Compreendendo placas de interface de voz do escritório de câmbio internacional (FXO)
Cm lc ifc z ciói câmbi icil FO I cm: Aliz m: g 6 fêci PF Imimi Fbck P Rlci Plc ifc z Cic Cic 6 Si liic Plfm Íic Iç Péqii Rqii Cm Uiliz Cç úm Rc Cfigç S à lfm Ifmç Rlci Cic lci i ic cmi Iç A ifc Fig Exchg
REVISÃO MATEMÁTICA &$3Ì78/2,, 2.1- INTRODUÇÃO 2.2- DEFINIÇÃO DE VARIÁVEL COMPLEXA E FUNÇÃO COMPLEXA. - Variável Complexa 2.3- FUNÇÕES ANALÍTICAS
posil isms Conrol I II- &$Ì78/,, REVIÃO MTEMÁTIC.- INTRODUÇÃO Es cpíulo m por objivo rvisr lguns funmnos mmáicos ncssários pr o suo ori conrol. Inicilmn, fini-s o qu vm sr um vriávl complx um função complx.
Procedimento do U.S.HCM2010
Eh Táo Poo o U.S.HM1 ál oo o, l (oo l o HM/1). íl ço o ção o ool zão /. íl ço /l ção o j (LoS So) V Tl 18-4,5 (HM1 ão l oo íl l ço o j é l ço lo áo) ál oção xl o oolo o EUA. o ção EMA, l à çõ áoo. oo o
conjunto dos números inteiros. conjunto dos números que podem ser representados como quociente de números inteiros.
Cpítulo I Noçõs Eltrs d Mtátic. Oprçõs co frcçõs, Equçõs Iquçõs Tipos d úros {,,,,,6, } cojuto dos úros turis. 0 { 0} {,,,, 0,,,, } cojuto dos úros itiros., 0 0 p : p, q q cojuto dos úros rciois ou frccioários,
Primeira Prova de CTC-20 Estruturas Discretas 24/09/2009 Prof. Carlos Henrique Q. Forster
Primir Prov CTC-0 Estruturs Disrts 4/09/009 Pro Crlos nriqu Q Forstr om: GABARITO 40 pontos Consir Z n { 0 n } Z é um grupo on é oprção ou-xlusivo Mostr qu oprção ou-xlusivo it--it m plvrs 3 its orm um
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química 2014/1 1
Univrsidd Fdrl do Rio d Jniro COPPE Progrm d Engnhri Químic COQ 79 ANÁLISE DE SISEMAS DA ENGENHARIA QUÍMICA AULA : Rprsnção m Espço d Esdos 4/ Rprsnção m Espço d Esdos Esdo: O sdo d um sism no mpo é o
E v o lu ç ã o d o c o n c e i t o d e c i d a d a n i a. A n t o n i o P a i m
E v o lu ç ã o d o c o n c e i t o d e c i d a d a n i a A n t o n i o P a i m N o B r a s i l s e d i me nt o u - s e u ma v is ã o e r r a d a d a c id a d a n ia. D e u m mo d o g e r a l, e s s a c
Lista 3 - Resolução. 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os.
GN7 Introução à Álgr Linr Prof n Mri Luz List - Rsolução Vrifiqu s os proutos ixo stão m finios, m so firmtivo, lul-os ) [ / ] / ) / [ / ] ) ) Solução ) orm primir mtriz é x sgun é x, logo o prouto stá
UNIDADE 1 Conteúdos UNIDADE 2 Conteúdos UNIDADE 3 Conteúdos UNIDADE 4 Conteúdos
PROGRAMAÇÃO CURRICULAR UNIDADE 1 1 ọ ano - 1.º volume Símbolos Alfabeto UNIDADE 2 Crachá Vogais Consoantes UNIDADE 3 1 ọ ano - 2.º volume Vogais e consoantes Encontro de vogais Palavras com til (~) Palavras
Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e :
INSCRIÇÕES ABERTAS ATÉ 13 DE JULH DE 2015! Ac esse o sit e w w w. d e ca c lu b.c om.br / es t u dos 2 0 1 5 e f a ç a s u a insc riçã o cl ica nd o e m Pa r t i c i p e : Caso vo cê nunca t e nh a pa
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Geometria Ficha de Trabalho Nº 02 10º Ano
AGUPAMENO DE EOLA DE MOÁGUA Gomti Fih lho Nº 0 0º Ano Osv igu o lo... Ini so istm: ois plnos ppniuls us ts plls um t post um plno um t snt o plno FIH us ts não omplns. s oons os vétis... Qul posição ltiv
Capítulo IV TRANSFORMADAS DE LAPLACE
Cpíulo IV TRANSFORMADAS DE LAPLACE Cpíulo IV Trnormd d Lplc Cpíulo IV O méodo d rnormd d Lplc rolv quçõ dirncii corrpondn problm d vlor inicil problm d vlor ronir O proco d olução coni m rê po principi:
ESTE FORMULÁRIO É SOMENTE PARA CONSULTA. NÃO O UTILIZE COMO RASCUNHO.
Uvrdd Tcológc drl do Prá DAMAT Dprmo Acdêmco d Mmác Dcpl: álculo Drcl grl 4 Proor: Rudmr u Nó ORMUÁRO ETE ORMUÁRO É OMENTE PARA ONUTA. NÃO O UTZE OMO RAUNHO.. ér d ourr/oc d ourr b co d b d co d. A orm
Problema do Caixeiro Viajante. Solução força bruta. Problema do Caixeiro Viajante. Projeto e Análise de Algoritmos. Problema do Caixeiro Viajante
Projto Anális Aloritmos Prolm o Cixiro Vijnt Altirn Sors Silv Univrsi Frl o Amzons Instituto Computção Prolm o Cixiro Vijnt Um vim (tour) m um ro é um ilo qu pss por toos os vértis. Um vim é simpls quno
MATEMÁTICA ATUARIAL DE VIDA Modelos de Sobrevivência
EAC 44 Maáica Auaria II Ciêcia Auariai Nouro FEA USP Prof. Dr. Ricaro Pachco MAEMÁICA AUARIAL DE VIDA Moo Sobrvivêcia Uivria São Pauo º Sr 5 A ábua oraia u oo icro obrvivêcia. Daa a ábua Moraia hipoéica:
1 - SINAIS PERIÓDICOS NÃO SENOIDAIS
Frqüêcis hrmôics - INI PEIÓDIO NÃO ENOIDI m dois siis soidis d rqüêcis rspcis. rqüêci é hrmôic d rqüêci qudo or sisi iguldd: od é qulqur úmro iiro posiio, iclusi zro. rqüêci é chmd, ormlm, d rqüêci udml.
Correção da fuvest ª fase - Matemática feita pelo Intergraus
da fuvest 009 ª fase - Matemática 08.0.009 MATEMÁTIA Q.0 Na figura ao lado, a reta r tem equação y x no plano cartesiano Oxy. Além dis so, os pontos 0,,, estão na reta r, sendo 0 = (0,). Os pontos A 0,
P i s cina s : 2 P i s ci n a e x te rior de á g u a d e m a r a q u e cida P i s ci n a i n te ri or d e á g u a
E M P R IM E I R A MÃO T h e O i ta v os é o e x c lu s i v o h o te l d e 5 e s tre la s q u e co m p le t a e v a l ori za a ofe rta d a Q u i n ta d a M a ri n h a, co n s olid a n d o -a c om o d e
TRANSFORMADA DE LAPLACE
TRANSFORMADA DE LAPLACE Nt cpítulo trtmo d um método d rolução d quçõ difrncii linr d ordm n com coficint contnt condiçõ inici, ou j, trnformd d Lplc.. Dfinição Sj f(t) um função dd pr t, uponhmo qu f
4. Análise de Sistemas de Controle por Espaço de Estados
Sisma para vrificação Lógica do Corolo Dzmro 3 4. ális d Sismas d Corol por Espaço d Esados No capiulo arior, vimos qu a formulação d um Prolma Básico d Corolo Ópimo Liar, ra cosidrado um sisma diâmico
CCI-22 CCI-22. Ajuste de Curvas. Matemática Computacional. Regressão Linear. Ajuste de Curvas
CCI- CCI- eá Copuol Ause e Curvs Crlos Herque Q. Forser Nos opleeres Ause e Curvs Apl-se os seues sos: Erpolção: vlores or o ervlo elo Vlores o erros proveees e oservções Cosse e: Deerr prâeros que ee
CAPÍTULO 1. , e o vetor r representa a posição desta mesma partícula no instante t, indicado por. r P(t)
1 CPÍTULO 1 CINEMÁTIC VETORIL D PRTÍCUL Feqüeemee eg lei e Newo é eci fom cláic qe elcio foç ele com celeção pícl. O eo ciemáic pícl em como objeio obe elçõe memáic ee ge poição, elocie e celeção, m eemio
Física Computacional 5
Física Computacioal 5. Drivaas com irças iitas a. O cocito rivaa mos simpls qu o itgral b. Cálculo umérico a rivaa com irças iitas c. Um outro cocito Equação Dircial Oriária. Solução aalítica as EDO liars.
Capítulo 9. Chopper(conversor CC-CC)
píulo 9 onrsor nrodução hoppr(conrsor rg Alimnção: nsão ix rg: nsão riál Equiln d um rnsormdor A A nsão d síd do conrsor pod sr mior ou mnor qu nsão d nrd Normlmn uilizdos m limnção d disposiios lromcânicos
CD CORAÇÃO DA NOIVA - 1. O SENHOR É BOM INTR:E D A/C# C7+ B E D A/C# O SENHOR É BOM C7+ B E SEU AMOR DURA PARA SEMPRE ELE É BOM...
C CORÇÃO NOIV - 1. O SNHOR É OM INTR: /C# C7+ /C# O SNHOR É OM C7+ SU MOR UR PR SMPR L É OM... Letra e Música: avi Silva C CORÇÃO NOIV - 2. SNTO É O TU NOM M TO TRR S OUVIRÁ UM NOVO SOM UM CNÇÃO MOR PRCORRRÁ
que indica que, através do operador H, pode-se determinar y(t) para qualquer u(t).
8. REPRESENÇÃO NO ESPÇO DE ESDOS 8. Coco so ( prsção srá f o omío o mpo coío; s frçs com o cso scro são pqs srão prss posrorm). rprsção r/sí m ssm lr só é ál qo, o mpo cl, o ssm sá o so scoáro. ssm é ál
u seja, pode ser escrito como uma combinação linear de.
Toma d Cayly-Hamilo ja x sja d I α... α poliômio caacísico d. Eão: α α... α α I Toda maiz é um zo d su poliômio caacísico., mos qu qu:... I { I,,..., } u sja, pod s scio como uma combiação lia d. Também,
soluções sustentáveis soluções sustentáveis
soluções sustentáveis 1 1 1 2 3 KEYAS S OCIADOS UNIDADES DE NEGÓCIO ALGUNS CLIENTES 2 2 1 2 3 KEYAS S OCIADOS UNIDADES DE NEGÓCIO ALGUNS CLIENTES 3 3 APRES ENTAÇÃO A KEYAS S OCIADOS a tu a d e s d e 1
Matrizes 2. Notação de uma matriz 2 Matriz Quadrada 2 Matriz Diagonal 2 Matriz linha 2 Matriz coluna 2 Matrizes iguais 2. Matriz Transposta 3
//, :: Mrizes Defiição Noção de u riz Mriz Qudrd Mriz Digol Mriz lih Mriz colu Mrizes iguis Eercício Mriz Trspos Proprieddes d riz rspos Mriz Opos Mriz Nul Mriz ideidde ou Mriz uidde dição de Mrizes Eercício
Revista Bioética ISSN: Conselho Federal de Medicina Brasil
Revista Bioética ISSN: 1983-8042 bioetica@portalmedico.org.br Conselho Federal de Medicina Brasil de Pontes Regis, Arthur Henrique; Cornelli, Gabriele Situação jurídica dos animais e propostas de alterações
Com muito carinho para minha querida amiga e super profissional. Ale Del Vecchio
Com muito carinho para minha querida amiga e super profissional. BA BE BI BO BU BÃO ba be bi bo bu bão BA ba boi BE be bebê BI bi Bia BO bo boi BU bu buá Nome: BA BE BI BO BU BÃO ba be bi bo bu bão BA
Análise de Sistemas Contínuos por Transformada de Laplace
ES 4 Análi d Sim Conínuo por Trnformd d Lplc Prof. Aluizio Fuo Riiro Arújo Dpo. of Sim d Compução Cnro d Informáic - UFPE Cpíulo 4 Inrodução Conúdo A Trnformd d Lplc A Trnformd Invr Propridd d Trnformd
Cálculo I 3ª Lista de Exercícios Limites
Cálculo I ª List de Eercícios Liites Clcule os liites: 9 / /8 Resp.: 6 li li li li li li e d c e d c Clcule os liites io: Clcule: 8 6 li 8 li e d li li c li li / /.: Resp e d c Resp.: li li li li li li
EQUAÇÕES DIFERENCIAIS NOTAS DE AULA
Miisério d Educção Uivrsidd Tcológic Fdrl do Prá mpus urii Grêci d Esio Psquis Dprmo Acdêmico d Mmáic EQUAÇÕES DIFERENIAIS NOTAS DE AULA Prof. Pul Frcis Bvids Equçõs Difrcis Prof Pul Frcis Bvids oúdo AULA...
+12V. 0.1uF/ 100V RL4 :A ULN2003A C3 3 U1:D LIGA/ DESLIGA CARREGADOR. 10uF/ 16V C2 4 1N4148 D1 1 1N K GND 10K BC337 R2 5 CRISTAL DE 2 0 MHZ
ДХILUIR P/ LRR RL_ R To l. er a l es. Num. QU M PRVR IOO P O RROR MIOR V R LMJ U: UZZR R 0 ILUIR P M PRLLO OM ONTTO O RL 0.u/ 00V V R 0 0 R 0 verm elho U: ULN00 U: LMJ 0 ULN00 U: LI/ LI RROR V N R 0u/
6ª COPA NOVE DE JULHO FUTEBOL AMADOR 2016 RODADA SEDE LESTE BOTAFOGO - GUAIANASES 30/01/2016 (SABADO) 31/01/2016 ( DOMINGO) 13/02/2016 (SABADO)
14:00 LIRÃO. - VIL NOUN 0 X 1 OMNO. - J RORU 15:30 VM QU TM. - ITIM PULIST 2 X 1. GUPIR - JNÃ 13:00 ORO. - ONJ JOS ONIIO 1 X 2. 1 MIO - GUINSS 14:30 NINGUM OM. - ITQUR 3 X 0.R. SÃO JORG - VIL URUÇ 14:00
+ = x + 3y = x 1. x + 2y z = Sistemas de equações Lineares
Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn
Disciplina: Programação 1 Professor: Paulo César Fernandes de Oliveira, BSc, PhD. Lista de Exercícios JavaScript 8 (revisão)
Disiplin: Progrmção 1 Profssor: Pulo Césr Frnns Olivir, BS, PhD List Exríios JvSript 8 (rvisão) 1. O qu ont o s xutr progrm ixo? jvsript: - funtion utorizr(snh){ if(snh == "luno"){ lrt("bm-vino!"); ls{
Escola Básica e Secundária D. Filipa de Lencastre
cl Báic cári ilip Lcr 2º icl - cr Li 39/202 cl irr() r cl Báic cári ilip Lcr, Lib li bl bri çlv LÇÃ U 5º - r i lic ri ix 9 X X X X X X X X X X X X X X 23042 2 chk 9 X X X X X X X X X X X X X X 23043 3
RESPOSTA TEMPORAL. 1. Motivação. 2. Solução homogênea. Calcular a resposta temporal de sistemas dinâmicos LIT na forma SS.
Euaro Lobo Luoa Cabral RESPOST TEMPORL. Moiação Calcular a rpoa mporal ima inâmico LT na forma SS. Rpoa mporal prmi analiar comporamno inâmico o ima no omínio o mpo. Dua oluçõ: Solução homogêna rpoa à
Associação de Resistores e Resistência Equivalente
Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos