Transformadas de Laplace
|
|
|
- Luna Lombardi Zagalo
- 8 Há anos
- Visualizações:
Transcrição
1 Transformadas de Laplace Notas de aulas - material compilado no dia 6 de Maio de 23 Computação, Engenharia Elétrica e Engenharia Civil Prof. Ulysses Sodré
2 ii Copyright c 22 Ulysses Sodré. Todos os direitos reservados. <ulysses@sercomtel.com.br> <ulysses@matematica.uel.br> Material compilado no dia 6 de Maio de 23. Este material pode ser usado por docentes e alunos desde que citada a fonte, mas não pode ser vendido e nem mesmo utilizado por qualquer pessoa ou entidade para auferir lucros. Para conhecer centenas de aplicações da Matemática, visite a Home Page: Filho meu, se aceitares as minhas palavras, e entesourares contigo os meus mandamentos, para fazeres atento à sabedoria o teu ouvido, e para inclinares o teu coração ao entendimento; sim, se clamares por discernimento, e por entendimento alçares a tua voz; se o buscares como a prata e o procurares como a tesouros escondidos; então entenderás o temor do Senhor, e acharás o conhecimento de Deus. Porque o Senhor dá a sabedoria; da sua boca procedem o conhecimento e o entendimento; ele reserva a verdadeira sabedoria para os retos; e escudo para os que caminham em integridade, guardando-lhes as veredas da justiça, e preservando o caminho dos seus santos. Então entenderás a retidão, a justiça, a eqüidade, e todas as boas veredas. [PROVÉRBIOS 2:1-9, Bíblia Sagrada.]
3 CONTEÚDO iii Conteúdo 1 Introdução às transformadas de Laplace 1 2 Definição de transformada de Laplace 1 3 Função de ordem (tipo) exponencial 3 4 Existência da Transformada de Laplace 4 5 Pares de Transformadas de Laplace 5 6 Propriedades lineares das Transformadas de Laplace 5 7 Tabela de algumas transformadas de Laplace 7 8 Translação na Transformada de Laplace 7 9 Escala (homotetia) na Transformada de Laplace 8 1 Transformadas de Laplace de derivadas de funções 9 11 Derivadas de Transformadas de Laplace 1 12 Resolução de EDO Linear com Transformadas de Laplace 1 13 Convolução de funções Convolução e Transformadas de Laplace Tabela de propriedades das Transformadas de Laplace O Método das frações parciais através de exemplos Denominador tem m fatores lineares distintos Divisão de polinômio p n por fator linear repetido Divisão de polinômio p n por um fator linear e outro repetido
4 CONTEÚDO iv 16.4 Divisão de polinômio p n por fatores lineares repetidos Completando quadrados em uma função quadrática Divisão de p(s) = ds + e por fator quadrático sem raízes reais Divisão de p n por fator quadrático sem raízes reais e outro linear Refinando a decomposição em frações parciais O denominador tem um fator linear não repetido (s a) O denominador tem um fator linear repetido (s a) m O denominador tem fator linear complexo (s a) não repetido O denominador possui um fator complexo (s a) Resolução de uma equação integro-diferencial 3 2 Resolução de Sistemas de EDO lineares Resolução de Equações com coeficientes variáveis Transformada de Laplace de uma função periódica A função Gama e a Transformada de Laplace 37
5 1 Introdução às transformadas de Laplace 1 1 Introdução às transformadas de Laplace Oliver Heaviside, quando estudava processos simples para obter soluções de Equações Diferenciais, vislumbrou um método de Cálculo Operacional que leva ao conceito matemático da Transformada de Laplace, que é um método simples para transformar um Problema com Valores Iniciais (PVI) 1, em uma equação algébrica, de modo a obter uma solução deste PVI de uma forma indireta, sem o cálculo de integrais e derivadas para obter a solução geral da Equação Diferencial. Pela utilidade deste método em Matemática, na Computação, nas Engenharias, na Física e outras ciências aplicadas, o método representa algo importante neste contexto. As transformadas de Laplace são muito usadas em diversas situações, porém, aqui trataremos de suas aplicações na resolução de Equações Diferenciais Ordinárias Lineares. Figura 1: Solução de Equação Diferencial com Transformadas de Laplace 2 Definição de transformada de Laplace Se f = f(t) é uma função real ou complexa, definida para todo t e o parâmetro z é um número complexo da forma z = s + iv de modo que para cada para s >, ocorre a convergência da integral imprópria 1 PVI: Problema com Valores Iniciais formado por uma equação diferencial e condições iniciais.
6 2 Definição de transformada de Laplace 2 F (z) = [ M ] f(t)e zt dt = lim M f(t)e zt dt então a função F = F (z) definida pela integral acima, recebe o nome de transformada de Laplace da função f = f(t). Se o parâmetro z é um número real, isto é, a parte imaginária v =, usamos z = s > e a definição fica simplesmente na forma F (s) = f(t)e st dt A transformada de Laplace depende de s, é representada por uma letra maiúscula F = F (s), enquanto que a função original que sofreu a transformação depende de t é representada por uma letra minúscula f = f(t). Para representar a transformada de Laplace da função f, é comum usar a notação L[f(t)] = F (s) Exemplo: A função degrau unitário é muito importante neste contexto e é definida por u(t) = { 1 se t se t < Para a função degrau unitário e considerando s >, temos que L[u(t)] = = lim M u(t)e st dt = lim [ e st s ] M M = lim M M e st dt [ e sm s 1 ] = 1 s s Identidade de Euler: Para todo número complexo α, vale a relação: e iα cos(α) + i sin(α)
7 3 Função de ordem (tipo) exponencial 3 A partir desta identidade, podemos escrever cos(α) = 1 2 [eiα + e iα ] e sin(α) = 1 2i [eiα e iα ] Exercício: Demonstrar que para 1. s > : 2. s, a R com s > a: 3. z, α C com Re(z α) > : 4. Re(z) > : L[1] = 1 s, L[t] = 1 s 2 e L[t 2 ] = 2 s 3 L[cos(kt)] = L[e at ] = 1 s a L[e αt ] = 1 z α z z 2 + k 2, L[sin(kt)] = k z 2 + k 2 Exercícios: Calcular as transformadas de Laplace das funções reais 1. f(t) = cosh(kt) = 1 2 [ekt + e kt ] 2. f(t) = sinh(kt) = 1 2 [ekt e kt ] 3. f(t) = t e at 4. f(t) = e at cos(bt) 3 Função de ordem (tipo) exponencial Uma função f = f(t) é de ordem (tipo) exponencial α sobre [, ), se existem constantes M > e α R, tal que para todo t > se tem: f(t) Me αt
8 4 Existência da Transformada de Laplace 4 o que é equivalente a Exemplos: lim t e αt f(t) = 1. f(t) = t 2 é de ordem exponencial pois f(t) 2e t. 2. f(t) = t 2 cos(at) é de ordem exponencial pois f(t) 2e (1+a)t. 3. f(t) = exp(t 3/2 ) não é de ordem exponencial. 4. f(t) = t n e at cos(bt) é de ordem exponencial 5. g(t) = t n e at sin(bt) é de ordem exponencial 4 Existência da Transformada de Laplace Se f = f(t) é seccionalmente contínua 2 para todo intervalo finito de [, ), e além disso f = f(t) é de tipo exponencial de ordem α quando t, então a transformada de Laplace F = F (s), definida para s > α por: F (s) = existe e converge absolutamente. f(t)e st dt A partir deste ponto, assumiremos que todas as funções f = f(t) serão seccionalmente contínuas em todos os intervalos finitos de [, ) e que todas serão de ordem exponencial quando t. Para este tipo de função f = f(t) podemos obter a transformada de Laplace F = F (s), assim, dada uma função G = G(s) poderemos questionar se existe uma função g = g(t) tal que G(s) = L[g(t)]? 2 Contínua por pedaços = Contínua por partes.
9 5 Pares de Transformadas de Laplace 5 Se existir esta função, ela será a transformada inversa de Laplace de G = G(s) e esta inversa será denotada por L 1 [G(s)] = g(t) 5 Pares de Transformadas de Laplace Na realidade, duas transformadas inversas de Laplace para a mesma função F = F (s) são iguais, a menos de uma constante, mas aqui não levaremos isto em consideração tendo em vista que estamos procurando soluções particulares para equações diferenciais ordinárias lineares. Assumindo que as transformadas de Laplace direta e inversa são inversas uma da outra, isto é: L L 1 = I d = L 1 L, usaremos a notação com duas setas em sentidos opostos e o par de funções (f, F ) na forma f(t) F (s) para indicar que F = F (s) é a Transformada de Laplace de f = f(t) e que f = f(t) é a transformada inversa de Laplace de F = F (s). Exemplos: Dois importantes pares de transformadas são u(t) 1 s e at 1 s a (s > ) (s > a) 6 Propriedades lineares das Transformadas de Laplace A Transformada de Laplace é uma transformação linear, isto é: L[f + g] = L[f] + L[g] e L[kf] = k L[f]
10 6 Propriedades lineares das Transformadas de Laplace 6 Exemplo: Pode-se demonstrar que L[a+bt+ct 2 ] = al[1]+bl[t]+cl[t 2 ]. Exercício: Calcular as transformadas de Laplace das funções reais: f(t) = 1 + t + t 2 e g(t) = sin(t) + cos(t) A Transformada inversa de Laplace é uma transformação linear, i.e.: L 1 [F + G] = L 1 [F ] + L 1 [G] e L 1 [kf ] = k L 1 [F ] Exemplo: Pode-se mostrar que L 1 [ 8 s 16 s 2 ] = 8 L 1 [ 1 s ] 16 L 1 [ 1 s 2] Exercícios: Calcular as transformadas inversas de Laplace de: F (s) = 3 s a + 5 s b e G(s) = 2s + 5 s 2 25 Embora sejam necessárias algumas propriedades para facilitar o cálculo da transformada inversa de Laplace, um modo prático para obter transformadas inversas de Laplace é através de tabelas.
11 7 Tabela de algumas transformadas de Laplace 7 7 Tabela de algumas transformadas de Laplace N função L[f] N função L[f] Condição 1 u(t) 1 1/s 2 t 1/s 2 s > 3 t 2 2/s 3 4 t n n!/s n+1 s > 5 e at 1, a R 6 e at 1, a C Re(z a) > s a z a s a 7 cos(at) 8 sin(at) s > s 2 + a 2 s 2 + a 2 9 e at s a cos(bt) 1 e at b sin(bt) s > a (s a) 2 + b 2 (s a) 2 + b s a 2 11 cosh(at) 12 sinh(at) s > a 13 t cos(at) s 2 a 2 s 2 a 2 14 t sin(at) (s 2 + a 2 ) 2 s 2 a 2 2as s > (s 2 + a 2 ) 2 8 Translação na Transformada de Laplace Se a Transformada de Laplace de f = f(t) é dada por L[f(t)] = F (s) = então f(t)e st dt L[e bt f(t)] = F (s b) Demonstração: L[e bt f(t)] = [e bt f(t)]e st dt = Substituindo s b = σ, seguirá que L[e bt f(t)] = e (s b)t f(t)dt e σt f(t)dt = F (σ) = F (s b)
12 9 Escala (homotetia) na Transformada de Laplace 8 Exercício: Seja a função f(t) = u(t) cos(t). Obter a transformada de Laplace da translação de f deslocada b unidades para a direita. 9 Escala (homotetia) na Transformada de Laplace Se a Transformada de Laplace de f = f(t) é dada por L[f(t)] = F (s) = e λ >, então f(t)e st dt L[f(λt)] = 1 λ F ( s λ ) Demonstração: L[f(λt)] = [f(λt)]e st dt Substituindo λt = u e depois substituindo σ = s λ poderemos escrever L[f(λt)] = 1 λ f(u)e su λ du (1) = 1 λ f(u)e σu du (2) = F (σ) (3) = 1 λ F ( s λ ) (4) Exercício: Obter a transformada de Laplace da função f(t) = cos(12t) e determinar a conexão entre a transformada obtida e a transformada de Laplace de f(t) = cos(t).
13 1 Transformadas de Laplace de derivadas de funções 9 1 Transformadas de Laplace de derivadas de funções Uma propriedade muito útil na resolução de um PVI é Demonstração: L[y ] = L[y ] = s L[y] y() M y (t)e st dt = lim y (t)e st dt M Usando o método de integração por partes com u = e st e dv = y (t)dt, poderemos escrever [ L[y ] = L[y ] = lim ] M y(t)e st M M y(t)( s)e st dt [ = lim y(m)e sm y() ] M + s y(t)e st dt M = lim M = y() + s = s Y (s) y() [ ] y(m)e sm y() + s y(t)e st dt y(t)e st dt sendo que lim M [y(m)e sm ] = pois a função y = y(t) é de ordem exponencial quando t, assim L[y ] = s Y (s) y() Exercício: Se Y (s) = L[y(t)], demonstrar que e que em geral L[y ] = s 2 Y (s) s y() y ()
14 11 Derivadas de Transformadas de Laplace 1 L[y (n) ] = s n Y (s) s n 1 y() s n 2 y () s n 3 y ()... y (n 1) () 11 Derivadas de Transformadas de Laplace Se tomarmos a Transformada de Laplace: F (s) = f(t)e st dt e derivarmos ambos os membros desta igualdade em relação à variável s, obteremos: df ds = que também pode ser escrito como ( t)f(t)e st dt df ds = L[( t).f(t)] Tomando as derivadas sucessivas de F = F (s), teremos a regra geral L[t n f(t)] = ( 1) n dn dsnf (s) 12 Resolução de EDO Linear com Transformadas de Laplace Exemplo: Para obter a solução do PVI y + y = e t, y() = 5 aplicamos a Transformada de Laplace a esta EDO Linear para obter:
15 12 Resolução de EDO Linear com Transformadas de Laplace 11 L[y + y] = L[e t ] Pela fórmula 5 da tabela da seção 7 e pela linearidade da transformada de Laplace, segue que L[y ] + L[y] = 1 s + 1 Usando a fórmula da transformada da derivada, obtemos que podemos reescrever como sy (s) y() + Y (s) = 1 s + 1 sy (s) 5 + Y (s) = 1 s + 1 Extraindo o valor de Y (s), obtemos Y (s) = 1 (s + 1) s + 1 Aplicando a transformada inversa de Laplace a esta equação e observando na tabela que L[t e t ] = obtemos a solução do PVI 1 e L[e t ] = 1 (s + 1) 2 s + 1 y(t) = te t + 5e t = (t + 5)e t Exemplo: Para obter a solução do PVI y 2y 3y = 6e t, y() = 1, y () = 3
16 13 Convolução de funções 12 aplicamos a Transformada de Laplace a esta equação, para obter Pela linearidade, temos L[y 2y 3y] = L[6e t ] que pode ser escrito como L[y ] 2L[y ] 3L[y] = L[6e t ] [s 2 Y (s) s 3] 2[sY (s) 1] 3Y (s) = 6 s 1 Extraindo o valor Y (s), obtemos Y (s) = 6 (s 1)(s + 1)(s 3) + 1 (s + 1)(s 3) Como esta última função pode ser escrita na forma: Y (s) = s s s 3 então, aplicando as transformadas inversas de Laplace através do uso das tabelas, obtemos a solução do PVI: y(t) = 3 2 et e t e3t 13 Convolução de funções Sejam f = f(t) e g = g(t) funções integráveis para as quais o produto destas funções também é uma função integrável. Definimos a convolução (ou produto de convolução) de f e g, denotada por f g, como a função
17 13 Convolução de funções 13 (f g)(t) = t f(t u)g(u)du Com a mudança de variáveis v = t u, teremos que v t e a integral acima poderá ser escrita como (f g)(t) = t g(t v)f(v)dv = (g f)(t) significando que a convolução é comutativa: f g = g f Em cursos mais avançados, podemos estudar outras propriedades da convolução de funções. Por exemplo, quando temos uma função f com uma propriedade fraca relacionada com a suavidade e outra função g com propriedade forte relacionada com a suavidade, então a convolução f g é uma outra função com propriedades melhores que as propriedades de f e g. Para a convolução de funções valem as seguintes propriedades: 1. Comutatividade: f g = g f 2. Associatividade: f (g h) = (f g) h 3. Distributividade: f (g + h) = f g + f h 4. Nulidade: f = 5. Identidade: f δ = f onde δ é a distribuição delta de Dirac. Exercício: Calcular cada convolução indicada 1. u 2 (t) = (u u)(t) onde u = u(t) é a função degrau unitário. 2. u n (t) = (u u... u)(t) (n vezes). 3. f g sendo f(t) = e at e g(t) = e bt. 4. f g sendo f(t) = e at e u = u(t).
18 14 Convolução e Transformadas de Laplace Convolução e Transformadas de Laplace O produto das transformadas de Laplace não é igual à transformada de Laplace do produto de funções, mas se tomarmos F (s) = L[f(t)] e G(s) = L[g(t)], então poderemos escrever L[f g] = F (s) G(s) Em particular, se g(t) = u(t), então G(s) = 1/s para s >, teremos L[f u] = F (s) s Como u(w) = 1 para w >, segue que [ t ] [ t ] [ t ] L[f u] = L f(t w)u(w)dw = L f(t w)dw = L f(w)dw então [ t ] L f(w)dw = F (s) s Tomando as transformadas de f = f(t), g(t) = h(t) = u(t), respectivamente dadas por F = F (s) e G(s) = H(s) = 1/s (s > ), teremos F (s) s 2 [ t ( w ) ] = L f(v)dv dw Exercício: Usando o Princípio da Indução Finita (PIF), mostre que [ ] t n L = 1 ] [ ] [e n! s n+1, L at tn 1 1 at tn = L 1 n! (s a) n+1, = e (s a) n+1 n!
19 15 Tabela de propriedades das Transformadas de Laplace Tabela de propriedades das Transformadas de Laplace T n Propriedades da Transformada In Propriedades da Inversa T 1 L[f + g] = L[f] + L[g] I1 L 1 [F + G] = L 1 [F ] + L 1 [G] T 2 L[kf] = kl[f] I2 L 1 [kf ] = kl 1 [F ] T 3 L[e at f(t)] = F (s + a) I3 L 1 [F (s + a)] = e at f(t) T 4 L[f g] = F (s).g(s) I4 L 1 [F (s).g(s)] = f g T 5 L[( t)f(t)] = F (s) I5 L 1 [F (s)] = ( t)f(t) T 6 L[( t) n f(t)] = F (n) (s) I6 L 1 [F (n) (s)] = ( t) n f(t) [ t ] T 7 L f(w)dw = F (s) [ ] F (s) t I7 L 1 = f(w)dw s s 16 O Método das frações parciais através de exemplos O Método das frações parciais é utilizado para decompor uma função racional f(s) = p(s) q(s) que é a divisão de dois polinômios p = p(s) e q = q(s), ambos na variável s, para obter frações mais simples, com o objetivo de facilitar processos de integração ou obter as transformadas inversas de Laplace. Para realizar tal tarefa, necessitamos de três hipóteses essenciais sobre os polinômios p = p(s) e q = q(s): 1. p = p(s) e q = q(s) só possuem coeficientes reais; 2. p = p(s) e q = q(s) não possuem fatores em comum; 3. O grau de p = p(s) é sempre menor que o grau de q = q(s). Apresentaremos alguns exemplos e o mínimo necessário de teoria relacionado com cada método. Um polinômio de grau n na variável s
20 16.1 Denominador tem m fatores lineares distintos 16 será representado por p n = p n (s), enquanto p = p(s) será um polinômio conhecido, sendo o seu grau indicado por gr(p). Dentre os casos importantes, quatro serão analisados: 16.1 Denominador tem m fatores lineares distintos Aqui n = gr(p n ) e cada um dos m fatores lineares possuirá a forma (s a k ) (k = 1, 2,..., m), sendo m > n. Exemplo: Para decompor a função racional f(s) = em frações parciais, devemos escrever 2s 2 s + 1 (s 1)(s 2)(s 3) 2s 2 s + 1 (s 1)(s 2)(s 3) C 1 s 1 + C 2 s 2 + C 3 s 3 multiplicar todos os termos desta identidade por (s 1)(s 2)(s 3) para obter uma outra identidade sem frações: 2s 2 s + 1 C 1 (s 2)(s 3) + C 2 (s 1)(s 3) + C 3 (s 1)(s 2) Substituir nesta última identidade, respectivamente, os valores s = 1, s = 2 e s = 3, para obter: 2 = C 1 (1 2)(1 3) 7 = C 2 (2 1)(2 3) 16 = C 3 (3 1)(3 2) Assim C 1 = 1, C 2 = 7 e C 3 = 8, logo 2s 2 s + 1 (s 1)(s 2)(s 3) = 1 s 1 7 s s 3
21 16.1 Denominador tem m fatores lineares distintos 17 Método geral: Para decompor a função racional f(s) = p n (s) (s a 1 )(s a 2 )...(s a m ) em m fatores lineares da forma (s a 1 ), (s a 2 ),..., (s a m ), sendo m > n, escreveremos a identidade p n (s) (s a 1 )(s a 2 )...(s a m ) C 1 s a 1 + C 2 s a C m s a m Multiplicamos agora todos os termos desta identidade pelo produto de todos os m fatores lineares: m (s a j ) = (s a 1 )(s a 2 )...(s a m ) j=1 para obter uma outra identidade sem frações: p n (s) C 1 (s a 2 )(s a 3 )...(s a m ) + C 2 (s a 1 )(s a 3 )...(s a m ) + C 3 (s a 1 )(s a 2 )(s a 4 )...(s a m ) C k (s a 1 )(s a 2 )...(s a k 1 )(s a k )(s a k+1 )...(s a m ) C n (s a 1 )(s a 2 )...(s a m 1 ) Para obter cada constante C k, basta substituir s = a k nesta última identidade, para obter a igualdade: p n (a k ) = C k m j=1,(j k) (a k a j )
22 16.2 Divisão de polinômio p n por fator linear repetido 18 Observamos que a expressão da direita contém o produto de todos os fatores da forma (a k a j ) com j = 1, 2,..., m exceto o que tem índice j = k. Dessa forma, para cada k = 1, 2,..., m temos que C k = p n (a k ) m j=1,(j k) (a k a j ) 16.2 Divisão de polinômio p n por fator linear repetido Consideremos uma situação em que m é o número de vezes que ocorre a repetição de um fator linear (s a) sendo m > n. Exemplo: Para decompor a função racional em frações parciais, escreveremos f(s) = 2s2 s + 1 (s 2) 3 2s 2 s + 1 (s 2) 3 C 1 s 2 + C 2 (s 2) 2 + C 3 (s 2) 3 Multiplicamos os termos da identidade por (s 2) 3 para obter 2s 2 s + 1 C 1 (s 2) 2 + C 2 (s 2) + C 3 Como necessitamos de três identidades, ainda faltam duas, as quais podem ser obtidas através das duas primeiras derivadas desta última: 4s 1 2C 1 (s 2) + C 2 4 = 2C 1 Da última relação, obtemos C 1 = 2. Na penúltima, tomamos s = 2 para obter C 2 = 7 e na primeira, obtemos C 3 = 7. Concluímos que
23 16.3 Divisão de polinômio p n por um fator linear e outro repetido 19 2s 2 s + 1 (s 2) 3 2 s (s 2) (s 2) 3 Método: Para decompor a função racional f(s) = p n(s) (s a) m em m frações parciais, sendo m > n, escreveremos p n (s) (s a) m C 1 s a + C 2 (s a) C m (s a) m Multiplicamos todos os termos da identidade por (s a) m para obter p n (s) C 1 (s a) m 1 + C 2 (s a) m C m Como necessitamos de m equações, devemos calcular as m 1 primeiras derivadas sucessivas desta identidade e depois substituir s = a em todas as m identidades para obter os coeficientes C k para cada k = 1, 2,..., m Divisão de polinômio p n por um fator linear e outro repetido Seja m é o número de vezes que ocorre a repetição do fator linear (s a) com m > n e vamos considerar que ocorre apenas um fator linear (s b) no denominador da expressão racional. Exemplo: Para decompor a função racional em frações parciais, escreveremos f(s) = 2s2 s + 1 (s 2) 3 (s 1) 2s 2 s + 1 (s 2) 3 (s 1) C 1 s 2 + C 2 (s 2) 2 + C 3 (s 2) 3 + C 4 s 1
24 16.3 Divisão de polinômio p n por um fator linear e outro repetido 2 Multiplicando os termos da identidade por (s 2) 3 (s 1), obteremos 2s 2 s + 1 C 1 (s 1)(s 2) 2 + C 2 (s 1)(s 2) + C 3 (s 1) + C 4 (s 2) 3 Como o fator linear (s 1) aparece somente uma vez, basta tomar s = 1 nesta identidade para obter C 4 = 2. Para s = 2 obtemos C 3 = 7, mas ainda necessitamos de duas outras identidades. Basta realizar as duas primeiras derivadas da identidade acima em relação à variável s para obter: 4s 1 C 1 [2(s 1)(s 2)+(s 2) 2 ]+C 2 [(s 1)+(s 2)]+C 3 +C 4 (s 2) 2 e 4 C 1 [2(s 1) + 4(s 2)] + 2C 2 + 6C 4 (s 2) e depois substituir s = 2 em ambas. Não fizemos qualquer esforço para reunir os termos semelhantes pois esta forma é altamente simplificadora, pois para s = 2, segue que C 2 = e C 1 = 2, logo 2s 2 s + 1 (s 2) 3 (s 1) 2 s (s 2) 2 3 s 1 Método geral: Para decompor a função racional f(s) = em frações parciais, escreveremos p n (s) (s a) m (s b) p n (s) (s a) m (s b) C 1 s a + C 2 (s a) C m (s a) m + C s b Multiplicando os termos da identidade por (s a) m (s b), obteremos p n (s) (s b)[c 1 (s a) m 1 + C 2 (s a) m C m ] + C (s a) m
25 16.4 Divisão de polinômio p n por fatores lineares repetidos 21 Como o fator linear (s b) aparece somente uma vez, basta tomar s = b nesta identidade para obter C. Para s = a obtemos C m, mas ainda necessitamos de m 1 outras identidades. Basta realizar as m 1 primeiras derivadas sucessivas da identidade acima em relação à variável s para obter as outras constantes Divisão de polinômio p n por fatores lineares repetidos Seja q o número de vezes que ocorre a repetição do fator linear (s a) e r o número de vezes que ocorre a repetição do fator linear (s b), sendo q + r > n. Exemplo: Para decompor a função racional em frações parciais, escreveremos f(s) = 2s2 s + 1 (s 2) 3 (s 1) 2 2s 2 s + 1 (s 2) 3 (s 1) 2 C 1 s 2 + C 2 (s 2) 2 + C 3 (s 2) 3 + C 4 s 1 + C 5 (s 1) 2 Multiplicando os termos da identidade por (s 2) 3 (s 1) 2, obteremos 2s 2 s + 1 (s 1) 2 [C 1 (s 2) 2 + C 2 (s 2) + C 3 ] +(s 2) 3 [C 4 (s 1) + C 5 ] Como o fator linear (s 1) aparece duas vezes, devemos ter duas identidades relacionadas com ele, assim devemos derivar esta identidade mais uma vez para obter a segunda identidade. Como o fator linear (s 2) aparece três vezes, devemos ter três identidades relacionadas com este fator, assim, devemos realizar ainda as duas primeiras derivadas desta identidade para que tenhamos três identidades relacionadas com este outro fator. Substituindo s = 2 e s = 1 nas cinco identidades, obtemos as constantes.
26 17 Completando quadrados em uma função quadrática 22 Método geral: Podemos decompor a função racional f(s) = em frações parciais, para escrever p n (s) (s a) q (s b) r p n (s) (s a) q (s b) r C 1 s a + C 2 (s a) C q (s a) q + D 1 s b + D 2 (s b) D r (s b) r Multiplicando os termos da identidade por (s a) q (s b) r, obteremos uma identidade sem frações: p n (s) (s b) r [C 1 (s a) q 1 + C 2 (s a) q C q ] +(s a) q [D 1 (s b) r 1 + D 2 (s b) r D r ] Como o fator linear s a aparece q vezes na função racional, devemos ainda realizar as primeiras q 1 derivadas sucessivas desta identidade para ter ao final q identidades associadas ao fator s a. Como o fator linear s b aparece r vezes na função racional, devemos ainda realizar as primeiras r 1 derivadas sucessivas desta identidade para ter ao final r identidades associadas ao fator s b. Substituindo s = a e s = b nas q+r identidades, obtemos as constantes C j com j = 1, 2,..., q e D k com k = 1, 2,..., r. 17 Completando quadrados em uma função quadrática Se uma função quadrática q(s) = as 2 + bs + c não possui zeros (raízes) reais, e este fato ocorre quando o discriminante = b 2 4ac <, é vantajoso reescrever esta função como uma soma de quadrados. Para
27 17 Completando quadrados em uma função quadrática 23 realizar isto, devemos por em evidência o valor a, que é o coeficiente do termo dominante: q(s) = a[s 2 + b a s + c a ] Somamos e subtraímos o valor ( b 2a )2 dentro das chaves, que corresponde ao quadrado da metade do coeficiente do termo em s: para escrever q(s) = a[s 2 + b a s + ( b 2a )2 ( b 2a )2 + c a ] q(s) = a[(s + b a )2 + 4ac b2 4a 2 ] que representa a soma de dois quadrados, pois 4ac b 2 >. Exemplo: Seja q(s) = 2s 2 s + 1. Como = 7, pomos em evidência a constante 2 para obter q(s) = 2[s s ] A metade do coeficiente do termo em s é 1 4 que elevado ao quadrado fornece Somando e subtraindo 1, segue que 16 q(s) = 2[s s ] ou seja q(s) = 2[(s 1 2 ) ] que é uma soma de quadrados multiplicada por uma constante
28 17.1 Divisão de p(s) = ds + e por fator quadrático sem raízes reais 24 q(s) = 2 [ (s 1 2 )2 + ( ] 7 4 ) Divisão de p(s) = ds + e por fator quadrático sem raízes reais Seja a função p(s) = ds+e dividida por um fator quadrático as 2 +bs+c que não tem zeros reais, isto é f(s) = ds + e as 2 + bs + c Uma forma útil de decompor esta função racional é usar o fato que o denominador pode ser escrito como uma soma de quadrados multiplicada por uma constante: f(s) = ds + e a[(s + b a )2 + 4ac b2 4a 2 ] Com a mudança de variável v = s + b a, a função racional fica na forma f(v) = d a [ f(v) = d(v b a ) + e a[v 2 + 4ac b2 v v 2 + 4ac b2 4a 2 ] + 4a 2 ] ae db a 2 Voltando a usar a variável s, podemos escrever: [ 1 v 2 + 4ac b2 4a 2 ] [ ] f(s) = d s + b a + a (s + b a )2 + 4ac b2 4a 2 ae db a 2 [ 1 (s + b a )2 + 4ac b2 4a 2 ] Exemplo: Seja a função racional f(s) = s s 2 4s + 13
29 17.2 Divisão de p n por fator quadrático sem raízes reais e outro linear 25 Assim f(s) = s s 2 4s = s (s 2) que também pode ser escrito na conveniente forma f(s) = s 2 (s 2) (s 2) Divisão de p n por fator quadrático sem raízes reais e outro linear Exemplo: Seja a função racional f(s) = 2s + 5 (s 2 4s + 13)(s 3) Esta função pode ser reescrita na forma f(s) = que pode ser decomposta como 2s + 5 (s 2 4s + 13)(s 3) 2(s 2 + 2) + 5 [(s 2) ](s 3) = 2(s 2) + 9 [(s 2) ](s 3) A(s 2) (s 2) B (s 2) C s 3 Multiplicando os termos da identidade por (s 2 4s + 13)(s 3), obteremos 2s + 5 A(s 2)(s 3) + B(s 3) + C[(s 2) ] Com s = 3 na identidade acima, obtemos C = 11 1 mesma identidade, obtemos B = 9 1. e com s = 2 na
30 18 Refinando a decomposição em frações parciais 26 Ainda falta obter a constante A. Derivaremos então a identidade acima em relação à variável s para obter 2 A[(s 2) + (s 3)] + B + 2C(s 2) Com s = 2 nesta identidade adicional, obtemos A = Refinando a decomposição em frações parciais 18.1 O denominador tem um fator linear não repetido (s a) Neste caso, temos que q(a) = e a decomposição fica na forma p(s) q(s) A s a + r(s) Multiplicando os termos da identidade acima por (s a), obtemos: (s a)p(s) q(s) A + (s a) r(s) Sabemos que q(a) =, assim, se definirmos ϕ 1 (s) = (s a)p(s) q(s) = p(s) q(s) q(a) s a escreveremos ϕ 1 (s) A + (s a) r(s) Tomando agora o limite em ambos os membros desta identidade, quando s a, obtemos
31 18.2 O denominador tem um fator linear repetido (s a) m 27 A = lim s a ϕ 1 (s) = lim s a lim p(s) s a q(s) q(a) s a = p(a) q (a) Obtemos assim a constante A, e a transformada inversa de Laplace aplicada à identidade, nos dará: L 1 [ p(s) q(s) ] = Aeat + L 1 [r(s)] Exercício: Usando as transformadads de Laplace, mostrar que se F (s) = então f(t) = 2e 3t e 2t e t. 7s 1 (s 3)(s + 2)(s 1) 18.2 O denominador tem um fator linear repetido (s a) m Neste caso: p(s) q(s) A m (s a) m + A m 1 (s a) m A 1 s a + r(s) Multiplicando a identidade acima por (s a) m, obtemos (s a) m p(s) q(s) A m + A m 1 (s a) A 1 (s a) m 1 + r(s) É interessante definir O coeficiente A m é dado por ϕ m (s) = (s a)m p(s) q(s)
32 18.3 O denominador tem fator linear complexo (s a) não repetido 28 A m = lim s a ϕ m (s) e os coeficiente A m 1, A m 2,..., são obtidos, respectivamente pelas relações obtidas pelos limites das derivadas sucessivas de ϕ multiplicadas por algumas constantes, isto é: A m 1 = 1 1! lim s a dϕ m (s), A m 2 = 1 ds 2! lim d 2 ϕ m (s),... s a ds 2 Em geral, cada A k (k = 1, 2,..., m), pode ser obtido por 1 A k = (m k)! lim d m k ϕ m (s) s a ds m k e a transformada inversa de Laplace nos dará: L 1 [ p(s) [ q(s) ] = Am t m 1 eat (m 1)! + A m 1t m 2 (m 2)! A 1 ] + L 1 [r(s)] Exercício: Obter a função f = f(t) cuja transformada de Laplace é F (s) = 1 (s 4).(s 3) 3 Resposta: f(t) = e 3t ( 1 2 t2 t 1) + e 4t. Em momento algum nos preocupamos se o número a deveria ser real ou complexo. Se a é complexo, isto é, a = c + di, então podemos decompor a função racional em frações parciais de uma forma um pouco diferente, pois sabemos da Álgebra que se a = c + di é um zero de q = q(s), então o conjugado de a, dado por a = c di também é um zero de q = q(s), uma vez que os coeficientes do polinômio q = q(s) são números reais. Temos assim, o terceiro caso O denominador tem fator linear complexo (s a) não repetido Neste caso:
33 18.4 O denominador possui um fator complexo (s a) 2 29 p(s) q(s) A s a + r(s) Aqui usaremos a = c+di e multiplicaremos tanto o numerador como o denominador da fração do segundo membro da identidade pelo conjugado de (s a) = s a, para obter p(s) q(s) A s a (s a)s a + r(s) e esta última identidade pode ser escrita como p(s) q(s) = A(s c) + B (s c) 2 + d 2 + r(s) onde agora A e B são números reais, ou ainda na forma p(s) q(s) = A s c (s c) 2 + d + D d 2 (s c) 2 + d + r(s) 2 A transformada inversa de Laplace nos dá então L 1 [ p(s) q(s) ] = Aect cos(dt) + De ct sin(dt) + L 1 [r(s)] 18.4 O denominador possui um fator complexo (s a) 2 Aqui, usaremos a = c + di e escreveremos p(s) q(s) A (s a) 2 + r(s) Multiplicaremos tanto o numerador como o denominador da fração do segundo membro da identidade pelo conjugado de (s a) 2, para obter uma identidade da forma
34 19 Resolução de uma equação integro-diferencial 3 p(s) q(s) As + B [(s c) 2 + d 2 ] 2 + onde agora A, B, C e D são números reais. Cs + D (s c) 2 + d 2 + r(s) O restante segue de forma similar aos casos anteriores. Exercício: Obter a função f = f(t) tal que Resposta: F (s) = s (s 2 + 2s + 5) 2 [ t f(t) = 2e t 16 cos(2t) + ( t ] 32 ) sin(2t) 19 Resolução de uma equação integro-diferencial Uma equação integro-diferencial é uma equação diferencial em que a função incógnita está sob o sinal de integração. Consideremos o PVI dado pela equação integro-diferencial t y + 2y 3 y(u)du = 5(1 + t), y() = 2 Aplicando a Transformada de Laplace a ambos os membros da igualdade desta equação, obtemos: assim [ t ] L[y ] + 2L[y] 3L y(u)du = 5L[1 + t] s Y (s) 2 + 2Y (s) 3 Y (s) s = 5 s + 5 s 2
35 2 Resolução de Sistemas de EDO lineares 31 Isolando o valor de Y (s), obtemos Y (s) = s + 5 s 2 s 2 + 2s 3 = 2s2 + 5s + 5 s 2 (s 1)(s + 3) Usando frações parciais, podemos escrever Y (s) = A s + B s 2 + C s 1 + D s + 3 Após obter as constantes A, B, C e D, podemos usar as transformadas inversas de Laplace para escrever y(t) = et e 3t Exercícios: Resolver as Equações integro-diferenciais: 1. y + t 2. y y 6 3. y + t y(u)du = 1, y() = 2 t y(u)du = 12e 3t, y(u)du = sin(2t) y() = 3 2 Resolução de Sistemas de EDO lineares Para resolver sistemas com duas equações diferenciais nas funções incógnitas x = x(t) e y = y(t), podemos aplicar a Transformada de Laplace a cada EDO de forma que L[x] = X(s) e L[y] = Y (s) e fazer com que o sistema recaia num sistema algébrico com duas equações nas duas incógnitas X(s) e Y (s). Veremos como isto funciona com um exemplo relativamente simples mas suficientemente amplo para mostrar a funcionalidade do método.
36 2 Resolução de Sistemas de EDO lineares 32 Exemplo: Para determinar a solução do PVI x (t) + x(t) + y (t) y(t) = 2 x (t) + x (t) y (t) = cos(t) sujeito às condições: x() =, x () = 2 e y() = 1, devemos usar as fórmulas que envolvem as transformadas de Laplace das derivadas de primeira e segunda ordem. Como L[x (t)] = s 2 X(s) s x() x () = s 2 X(s) x () L[x (t)] = sx(s) x() = sx(s) L[y (t)] = sy (s) y() = sy (s) 1 L[2] = 2 s s L[cos(t)] = s podemos aplicar a transformada de Laplace às equações para obter L[x (t) + x(t) + y (t) y(t)] = L[2] L[x (t) + x (t) y (t)] = L[cos(t)] (s + 1) X(s) + (s 1) Y (s) = s (s 2 + s) X(s) s Y (s) = 1 + s s Este sistema de equações algébricas pode ser posto na forma matricial
37 21 Resolução de Equações com coeficientes variáveis 33 ( ) ( ) s + 1 s 1 X(s) = s Y (s) s + 2 s 1 s + 1 s Resolvendo este sistema pela regra de Cramer, obtemos X(s) = 1 s s Y (s) = 1 s 2 + s s Com as transformadas inversas de Laplace destas funções, obtemos x(t) = t + sin(t) y(t) = t + cos(t) 21 Resolução de Equações com coeficientes variáveis Já mostramos antes que e que em geral: d ds L[f(t)] = F (s) = L[( t) f(t)] F (n) (s) = L[( t) n f(t)] o que significa que a n-ésima derivada da transformada de Laplace de f em relação à variável s, é igual à transformada de Laplace da função ( t) n f(t), isto é: d n ds nl[f(t)] = L[( t)n f(t)]
38 21 Resolução de Equações com coeficientes variáveis 34 Se, em particular, tomarmos f(t) = y (t), teremos: que pode ser escrito na forma: d ds L[y (t)] = L[ t y (t)] e como L[y ] = sy (s) y(), então L[t y (t)] = d ds L[y ] L[t y (t)] = d ds [sy (s) y()] = sy (s) Y (s) Resumindo, temos para a primeira derivada: L[t y (t)] = s Y (s) Y (s) Repetindo o processo para a função f(t) = y (t), temos: L[t y (t)] = s 2 Y (s) 2s Y (s) + y() Exemplo: Para resolver o Problema com Valor Inicial com uma EDO linear com coeficientes variáveis: y + ty 2y = 7, y () =, y() = aplicaremos a transformada de Laplace a ambos os membros da igualdade para obter Como L[y + ty 2y] = L[4] L[y (t)] = s 2 Y (s) s y() y () = s 2 Y (s)
39 22 Transformada de Laplace de uma função periódica 35 L[t y ] = s Y (s) Y (s) então L[4] = 4 s Y (s) + 3 s2 Y (s) = 4 s s 2 e resolvendo esta Equação Diferencial Ordinária Linear, teremos: Y (s) = 4 s 3 + C 1 s 3 exp(s2 2 ) e obtendo a transformada inversa de Laplace desta função com C =, temos a solução: y(t) = 2t 2 22 Transformada de Laplace de uma função periódica Consideremos uma função periódica de período p >, isto é, uma função tal que f(t + p) = f(t) para todo t >. Como a transformada de Laplace de f é dada por: L[f(t)] = f(t)e st dt então, decompondo esta integral em infinitas integrais realizadas sobre os sub-intervalos de comprimento p, obteremos p 2p 3p 4p F (s) = ( )f(t)e st dt p 2p 3p que pode ser escrito em uma forma sintética
40 22 Transformada de Laplace de uma função periódica 36 F (s) = k= kp (k+1)p f(t)e st dt Em cada integral dada acima, temos que kp t (k+1)p. Realizando uma mudança de variável t = v + kp, teremos que dt = dv e dessa forma a variável v estará no domínio v p. F (s) = p k= f(v + kp) e s(v+kp) dv Como f é p-periódica, f(v) = f(v + kp) para todo v e assim F (s) = p k= f(v) e sv e skp dv que também pode ser posto na forma [ ] p F (s) = e skp f(v)e sv dv k= e como a expressão dentro dos colchetes é uma série geométrica de razão e skp < 1, segue que: F (s) = 1 p f(v)e sv dv 1 e sp Exemplo: Seja f(t) = sin(t) para t [, 2π]. Então L[u(t)f(t)] = 1 2π sin(v)e sv dv 1 e 2πs Exemplo: Seja f(t) = t para < t < 6 e f(t + 6) = f(t) para todo t. Assim
41 23 A função Gama e a Transformada de Laplace 37 L[u(t)f(t)] = 1 6 ve sv dv 1 e 6s 23 A função Gama e a Transformada de Laplace A função gama, denotada por Γ = Γ(z), é definida por: Γ(z) = e t t z 1 dt Se na integral acima tomarmos t = sv, poderemos escrever Γ(z) = e sv (sv) z 1 sdv = s z v z 1 e sv dv Tomando em particular, z = n, observamos que esta última integral é a transformada de Laplace de f(v) = v n 1 e segue que Γ(n) = s n L[v n 1 ] Acontece que para cada n natural, temos que logo L[v n 1 ] = (n 1)! s n Γ(n) = s n(n 1)! s n Assim, para todo n natural, podemos tomar a função gama como Γ(n) = (n 1)!
42 23 A função Gama e a Transformada de Laplace 38 A função Γ = Γ(z) é usada como extensão da função fatorial válida para todo número natural e tal extensão vale para todo número real onde esta integral converge. Uma situação muito difícil de ser demonstrada no âmbito do Ensino Básico é que! = 1, mas pela identificação da função Γ com a função fatorial, podemos mostrar que! = Γ(1) = e t t 1 1 dt = e t dt = 1 Para a função f(t) = t n 1, a transformada de Laplace é dada por logo L[t n 1 ] = (n 1)! s n = Γ(n) s n L[t n ] = n! Γ(n + 1) = sn+1 s n+1 A propriedade L[tf(t)] = F (s) aplicada à função f(t) = t n 1 fornece L[t n ] = L[t t n 1 ] = d ds L[tn 1 ] = d Γ(n) ds s n = nγ(n) s n+1 assim, a função Γ = Γ(n) pode ser definida recursivamente para cada n natural, pelas duas relações Γ(n + 1) = n Γ(n), Γ(1) = 1 Na verdade, em estudos mais avançados, a função Γ = Γ(x) pode ser definida para todo x R, exceto para os x que são números inteiros não positivos, isto é, x / {, 1, 2, 3,...}.
43 REFERÊNCIAS BIBLIOGRÁFICAS 39 Referências bibliográficas [1] Ditkine,V e Proudnikov,A., Transformations Intégrales et Calcul Opérationnel, Éditions MIR, (1978), Moscou [2] Hille, Einar, Analysis, vol.1 e 2. Blaisdell Publ. Co., (1966), Waltham, Mass., USA. [3] Kaplan, Wilfred, Cálculo Avançado, vol.1 e 2. Edgard Blücher Editora e EDUSP, (1972), São Paulo, Brasil. [4] Quevedo, Carlos P., Circuitos Elétricos, LTC Editora, (1988), Rio de Janeiro, Brasil. [5] Moore, Douglas, Heaviside Operational Calculus, American Elsevier Publ. Co., (1971), New York. [6] Spiegel, Murray, Análise de Fourier, Coleção Schaum, McGraw- Hill do Brasil, (1976), São Paulo, Brasil.
Transformada de Laplace
 Capítulo 8 Transformada de Laplace A transformada de Laplace permitirá que obtenhamos a solução de uma equação diferencial ordinária de coeficientes constantes através da resolução de uma equação algébrica.
Capítulo 8 Transformada de Laplace A transformada de Laplace permitirá que obtenhamos a solução de uma equação diferencial ordinária de coeficientes constantes através da resolução de uma equação algébrica.
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.
 Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92)
 ADL22 4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92) A transformada de Laplace fornece: (4.93) (4.94) A fim de separar X(s), substitua sx(s)
ADL22 4.10 Solução das Equações de Estado através da Transformada de Laplace Considere a equação de estado (4.92) A transformada de Laplace fornece: (4.93) (4.94) A fim de separar X(s), substitua sx(s)
Análise de Circuitos Elétricos III
 Análise de Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Introdução à Transformada de Laplace A Transformada
Análise de Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Introdução à Transformada de Laplace A Transformada
Resposta Transitória de Circuitos com Elementos Armazenadores de Energia
 ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias
 Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Capítulo 2 - Problemas de Valores Fronteira para Equações Diferenciais Ordinárias Departamento de Matemática balsa@ipb.pt Mestrados em Engenharia da Construção Métodos de Aproximação em Engenharia 1 o
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Somatórias e produtórias
 Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
por séries de potências
 Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
MATERIAL MATEMÁTICA I
 MATERIAL DE MATEMÁTICA I CAPÍTULO I REVISÃO Curso: Administração 1 1. Revisão 1.1 Potência de Epoente Inteiro Seja a um número real e m e n números inteiros positivos. Podemos observar as seguintes propriedades
MATERIAL DE MATEMÁTICA I CAPÍTULO I REVISÃO Curso: Administração 1 1. Revisão 1.1 Potência de Epoente Inteiro Seja a um número real e m e n números inteiros positivos. Podemos observar as seguintes propriedades
PARTE 2 FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL
 PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS
 INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS Terminologia e Definições Básicas No curso de cálculo você aprendeu que, dada uma função y f ( ), a derivada f '( ) d é também, ela mesma, uma função de e
INTRODUÇÃO AO ESTUDO DE EQUAÇÕES DIFERENCIAIS Terminologia e Definições Básicas No curso de cálculo você aprendeu que, dada uma função y f ( ), a derivada f '( ) d é também, ela mesma, uma função de e
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
 Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
a 1 x 1 +... + a n x n = b,
 Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
MATEMÁTICA. Aula 1 Revisão. Prof. Anderson
 MATEMÁTICA Aula 1 Revisão Prof. Anderson Assuntos Equação do 1º grau com uma variável. Sistemas de equações do 1º grau com duas variáveis. Equação do º grau com uma variável. Equação do 1º grau com uma
MATEMÁTICA Aula 1 Revisão Prof. Anderson Assuntos Equação do 1º grau com uma variável. Sistemas de equações do 1º grau com duas variáveis. Equação do º grau com uma variável. Equação do 1º grau com uma
Definição. A expressão M(x,y) dx + N(x,y)dy é chamada de diferencial exata se existe uma função f(x,y) tal que f x (x,y)=m(x,y) e f y (x,y)=n(x,y).
 PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
PUCRS FACULDADE DE ATEÁTICA EQUAÇÕES DIFERENCIAIS PROF. LUIZ EDUARDO OURIQUE EQUAÇÔES EXATAS E FATOR INTEGRANTE Definição. A diferencial de uma função de duas variáveis f(x,) é definida por df = f x (x,)dx
Aula: Equações polinomiais
 Aula: Equações polinomiais Turma 1 e 2 Data: 05/09/2012-12/09/2012 Tópicos Equações polinomiais. Teorema fundamental da álgebra. Raízes reais e complexas. Fatoração e multiplicação de raízes. Relações
Aula: Equações polinomiais Turma 1 e 2 Data: 05/09/2012-12/09/2012 Tópicos Equações polinomiais. Teorema fundamental da álgebra. Raízes reais e complexas. Fatoração e multiplicação de raízes. Relações
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
x0 = 1 x n = 3x n 1 x k x k 1 Quantas são as sequências com n letras, cada uma igual a a, b ou c, de modo que não há duas letras a seguidas?
 Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Recorrências Muitas vezes não é possível resolver problemas de contagem diretamente combinando os princípios aditivo e multiplicativo. Para resolver esses problemas recorremos a outros recursos: as recursões
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
CÁLCULO DE ZEROS DE FUNÇÕES REAIS
 15 CÁLCULO DE ZEROS DE FUNÇÕES REAIS Um dos problemas que ocorrem mais frequentemente em trabalhos científicos é calcular as raízes de equações da forma: f() = 0. A função f() pode ser um polinômio em
15 CÁLCULO DE ZEROS DE FUNÇÕES REAIS Um dos problemas que ocorrem mais frequentemente em trabalhos científicos é calcular as raízes de equações da forma: f() = 0. A função f() pode ser um polinômio em
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.
 Matemática Essencial Equações do Primeiro grau Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ Resumo: Notas de
Matemática Essencial Equações do Primeiro grau Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ Resumo: Notas de
2. Modelos Lineares de Espaço de Estados. e resposta ao impulso. Método para o cálculo das soluções: através do uso de transformadas de Laplace
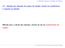 2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
Sequências e Séries. Capítulo Exercícios
 Capítulo Sequências e Séries Exercícios Encontre uma fórmula para o termo geral da sequência a n } n= assumindo que o padrão dos primeiros termos continua (a), 4, 8, 6, } (b), 4, 6, 8, } (c), 7,, 7, }
Capítulo Sequências e Séries Exercícios Encontre uma fórmula para o termo geral da sequência a n } n= assumindo que o padrão dos primeiros termos continua (a), 4, 8, 6, } (b), 4, 6, 8, } (c), 7,, 7, }
Capítulo 1. x > y ou x < y ou x = y
 Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
COLÉGIO ETIP NIVELAMENTO BÁSICO DE MATEMÁTICA ENSINO MÉDIO INTEGRADO À INFORMÁTICA PROFESSOR RUBENS SOARES
 COLÉGIO ETIP NIVELAMENTO BÁSICO DE MATEMÁTICA ENSINO MÉDIO INTEGRADO À INFORMÁTICA PROFESSOR RUBENS SOARES SANTO ANDRÉ 2012 MEDIDAS DE SUPERFÍCIES (ÁREA): No sistema métrico decimal, devemos lembrar que,
COLÉGIO ETIP NIVELAMENTO BÁSICO DE MATEMÁTICA ENSINO MÉDIO INTEGRADO À INFORMÁTICA PROFESSOR RUBENS SOARES SANTO ANDRÉ 2012 MEDIDAS DE SUPERFÍCIES (ÁREA): No sistema métrico decimal, devemos lembrar que,
Equação do 1º Grau. Maurício Bezerra Bandeira Junior
 Maurício Bezerra Bandeira Junior Introdução às equações de primeiro grau Para resolver um problema matemático, quase sempre devemos transformar uma sentença apresentada com palavras em uma sentença que
Maurício Bezerra Bandeira Junior Introdução às equações de primeiro grau Para resolver um problema matemático, quase sempre devemos transformar uma sentença apresentada com palavras em uma sentença que
Uma lei que associa mais de um valor y a um valor x é uma relação, mas não uma função. O contrário é verdadeiro (isto é, toda função é uma relação).
 5. FUNÇÕES DE UMA VARIÁVEL 5.1. INTRODUÇÃO Devemos compreender função como uma lei que associa um valor x pertencente a um conjunto A a um único valor y pertencente a um conjunto B, ao que denotamos por
5. FUNÇÕES DE UMA VARIÁVEL 5.1. INTRODUÇÃO Devemos compreender função como uma lei que associa um valor x pertencente a um conjunto A a um único valor y pertencente a um conjunto B, ao que denotamos por
INSTITUTO TECNOLÓGICO
 PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
Material Teórico - Módulo de Divisibilidade. MDC e MMC - Parte 1. Sexto Ano. Prof. Angelo Papa Neto
 Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Prof. Angelo Papa Neto 1 Máximo divisor comum Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum
Material Teórico - Módulo de Divisibilidade MDC e MMC - Parte 1 Sexto Ano Prof. Angelo Papa Neto 1 Máximo divisor comum Nesta aula, definiremos e estudaremos métodos para calcular o máximo divisor comum
Exp e Log. Roberto Imbuzeiro Oliveira. 21 de Fevereiro de 2014. 1 O que vamos ver 1. 2 Fatos preliminares sobre espaços métricos 2
 Funções contínuas, equações diferenciais ordinárias, Exp e Log Roberto Imbuzeiro Oliveira 21 de Fevereiro de 214 Conteúdo 1 O que vamos ver 1 2 Fatos preliminares sobre espaços métricos 2 3 Existência
Funções contínuas, equações diferenciais ordinárias, Exp e Log Roberto Imbuzeiro Oliveira 21 de Fevereiro de 214 Conteúdo 1 O que vamos ver 1 2 Fatos preliminares sobre espaços métricos 2 3 Existência
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
 Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
3 Matemática financeira e atuarial
 3 Matemática financeira e atuarial A teoria dos juros compostos em conjunto com a teoria da probabilidade associada à questão da sobrevivência e morte de um indivíduo são os fundamentos do presente trabalho.
3 Matemática financeira e atuarial A teoria dos juros compostos em conjunto com a teoria da probabilidade associada à questão da sobrevivência e morte de um indivíduo são os fundamentos do presente trabalho.
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
 Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Conceitos Fundamentais
 Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Capítulo 1 Conceitos Fundamentais Objetivos: No final do Capítulo o aluno deve saber: 1. distinguir o uso de vetores na Física e na Matemática; 2. resolver sistema lineares pelo método de Gauss-Jordan;
Aluno: Fatorar é transformar uma expressão num produto indicado, ou seja, numa multiplicação de dois ou mais fatores.
 8º ANO LISTA 1 de fatoração AV 1 3º Bim. Escola adventista de Planaltina Professor: Celmo Xavier. Aluno: Fatorar é transformar uma expressão num produto indicado, ou seja, numa multiplicação de dois ou
8º ANO LISTA 1 de fatoração AV 1 3º Bim. Escola adventista de Planaltina Professor: Celmo Xavier. Aluno: Fatorar é transformar uma expressão num produto indicado, ou seja, numa multiplicação de dois ou
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
 Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
[a11 a12 a1n 4. SISTEMAS LINEARES 4.1. CONCEITO. Um sistema de equações lineares é um conjunto de equações do tipo
 4. SISTEMAS LINEARES 4.1. CONCEITO Um sistema de equações lineares é um conjunto de equações do tipo a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 11 x 1 + a 12 x 2 +... + a 1n x n = b 2... a n1 x 1 + a
4. SISTEMAS LINEARES 4.1. CONCEITO Um sistema de equações lineares é um conjunto de equações do tipo a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 11 x 1 + a 12 x 2 +... + a 1n x n = b 2... a n1 x 1 + a
9. Derivadas de ordem superior
 9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
Transformada z. ADL 25 Cap 13. A Transformada z Inversa
 ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES
 MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES VERSÃO 1.0.2 Resumo. Este texto resume e complementa alguns assuntos dos Capítulo 9 do Boyce DiPrima. 1. Sistemas autônomos
MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES VERSÃO 1.0.2 Resumo. Este texto resume e complementa alguns assuntos dos Capítulo 9 do Boyce DiPrima. 1. Sistemas autônomos
Números Complexos. Capítulo 1. 1.1 Unidade Imaginária. 1.2 Números complexos. 1.3 O Plano Complexo
 Capítulo 1 Números Complexos 11 Unidade Imaginária O fato da equação x 2 + 1 = 0 (11) não ser satisfeita por nenhum número real levou à denição dos números complexos Para solucionar (11) denimos a unidade
Capítulo 1 Números Complexos 11 Unidade Imaginária O fato da equação x 2 + 1 = 0 (11) não ser satisfeita por nenhum número real levou à denição dos números complexos Para solucionar (11) denimos a unidade
Matemática para Engenharia
 Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Aritmética Binária e. Bernardo Nunes Gonçalves
 Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
Aritmética Binária e Complemento a Base Bernardo Nunes Gonçalves Sumário Soma e multiplicação binária Subtração e divisão binária Representação com sinal Sinal e magnitude Complemento a base. Adição binária
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
13 ÁLGEBRA Uma balança para introduzir os conceitos de Equação do 1ºgrau
 MATEMATICA 13 ÁLGEBRA Uma balança para introduzir os conceitos de Equação do 1ºgrau ORIENTAÇÃO PARA O PROFESSOR OBJETIVO O objetivo desta atividade é trabalhar com as propriedades de igualdade, raízes
MATEMATICA 13 ÁLGEBRA Uma balança para introduzir os conceitos de Equação do 1ºgrau ORIENTAÇÃO PARA O PROFESSOR OBJETIVO O objetivo desta atividade é trabalhar com as propriedades de igualdade, raízes
TEMPO DE PROVA: 2h. y 4y +5y = g(t), y(0) = 0, y (0) = 0. 0, se 0 t < 3; 7, se t 3. g(t) = s 2 4s+5 ) (s 2) 2 +1 +2 1. f : [0,1] R x 1 x. 1 (2m+1) 2.
![TEMPO DE PROVA: 2h. y 4y +5y = g(t), y(0) = 0, y (0) = 0. 0, se 0 t < 3; 7, se t 3. g(t) = s 2 4s+5 ) (s 2) 2 +1 +2 1. f : [0,1] R x 1 x. 1 (2m+1) 2. TEMPO DE PROVA: 2h. y 4y +5y = g(t), y(0) = 0, y (0) = 0. 0, se 0 t < 3; 7, se t 3. g(t) = s 2 4s+5 ) (s 2) 2 +1 +2 1. f : [0,1] R x 1 x. 1 (2m+1) 2.](/thumbs/25/5567556.jpg) Página Instituto de Matemática - IM/UFRJ Segunda prova unificada - Escola Politécnica / Escola de Química - 25/6/25 TEMPO DE PROVA: 2h Questão : (3. pontos) Resolva o problema de valor inicial onde y 4y
Página Instituto de Matemática - IM/UFRJ Segunda prova unificada - Escola Politécnica / Escola de Química - 25/6/25 TEMPO DE PROVA: 2h Questão : (3. pontos) Resolva o problema de valor inicial onde y 4y
CIRCUITOS ELÉTRICOS RESOLUÇÃO DE CIRCUITOS TRANSITÓRIOS NO DOMÍNIO DA FREQÜÊNCIA
 1 CIRCUITOS ELÉTRICOS RESOLUÇÃO DE CIRCUITOS TRANSITÓRIOS NO DOMÍNIO DA FREQÜÊNCIA Simulação de chaves utilizando a função degrau a) Fonte de tensão que entra em operação em t = 0 Substituindo a chave
1 CIRCUITOS ELÉTRICOS RESOLUÇÃO DE CIRCUITOS TRANSITÓRIOS NO DOMÍNIO DA FREQÜÊNCIA Simulação de chaves utilizando a função degrau a) Fonte de tensão que entra em operação em t = 0 Substituindo a chave
Movimentos Periódicos: representação vetorial
 Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Álgebra Linear. Mauri C. Nascimento Departamento de Matemática UNESP/Bauru. 19 de fevereiro de 2013
 Álgebra Linear Mauri C. Nascimento Departamento de Matemática UNESP/Bauru 19 de fevereiro de 2013 Sumário 1 Matrizes e Determinantes 3 1.1 Matrizes............................................ 3 1.2 Determinante
Álgebra Linear Mauri C. Nascimento Departamento de Matemática UNESP/Bauru 19 de fevereiro de 2013 Sumário 1 Matrizes e Determinantes 3 1.1 Matrizes............................................ 3 1.2 Determinante
REFLEXÃO DA LUZ: ESPELHOS 412EE TEORIA
 1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
Notas de Cálculo Numérico
 Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ. 1º. semestre de 2010 Aula 2 Ref. Butkov, cap. 8, seção 8.2
 Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 2 Ref. Butkov, cap. 8, seção 8.2 O Método de Separação de Variáveis A ideia central desse método é supor que a solução
Métodos de Física Teórica II Prof. Henrique Boschi IF - UFRJ 1º. semestre de 2010 Aula 2 Ref. Butkov, cap. 8, seção 8.2 O Método de Separação de Variáveis A ideia central desse método é supor que a solução
94 (8,97%) 69 (6,58%) 104 (9,92%) 101 (9,64%) 22 (2,10%) 36 (3,44%) 115 (10,97%) 77 (7,35%) 39 (3,72%) 78 (7,44%) 103 (9,83%)
 Distribuição das 1.048 Questões do I T A 94 (8,97%) 104 (9,92%) 69 (6,58%) Equações Irracionais 09 (0,86%) Equações Exponenciais 23 (2, 101 (9,64%) Geo. Espacial Geo. Analítica Funções Conjuntos 31 (2,96%)
Distribuição das 1.048 Questões do I T A 94 (8,97%) 104 (9,92%) 69 (6,58%) Equações Irracionais 09 (0,86%) Equações Exponenciais 23 (2, 101 (9,64%) Geo. Espacial Geo. Analítica Funções Conjuntos 31 (2,96%)
Karine Nayara F. Valle. Métodos Numéricos de Euler e Runge-Kutta
 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
EQUAÇÃO DO 1º GRAU. 2 melancias + 2Kg = 14Kg 2 x + 2 = 14
 EQUAÇÃO DO 1º GRAU EQUAÇÃO: Para resolver um problema matemático, quase sempre devemos transformar uma sentença apresentada com palavras em uma sentença que esteja escrita em linguagem matemática. Esta
EQUAÇÃO DO 1º GRAU EQUAÇÃO: Para resolver um problema matemático, quase sempre devemos transformar uma sentença apresentada com palavras em uma sentença que esteja escrita em linguagem matemática. Esta
Lista de Exercícios 4: Soluções Sequências e Indução Matemática
 UFMG/ICEx/DCC DCC Matemática Discreta Lista de Exercícios : Soluções Sequências e Indução Matemática Ciências Exatas & Engenharias o Semestre de 05 O conjunto dos números racionais Q é enumerável, ou seja,
UFMG/ICEx/DCC DCC Matemática Discreta Lista de Exercícios : Soluções Sequências e Indução Matemática Ciências Exatas & Engenharias o Semestre de 05 O conjunto dos números racionais Q é enumerável, ou seja,
GAAL - 2013/1 - Simulado - 1 Vetores e Produto Escalar
 GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO
 E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
E A D - S I S T E M A S L I N E A R E S INTRODUÇÃO Dizemos que uma equação é linear, ou de primeiro grau, em certa incógnita, se o maior expoente desta variável for igual a um. Ela será quadrática, ou
Transformada de Laplace. Parte 3
 Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Seja D R. Uma função vetorial r(t) com domínio D é uma correspondência que associa a cada número t em D exatamente um vetor r(t) em R 3
 1 Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire Cálculo Vetorial Texto 01: Funções Vetoriais Até agora nos cursos de Cálculo só tratamos de funções cujas imagens
1 Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire Cálculo Vetorial Texto 01: Funções Vetoriais Até agora nos cursos de Cálculo só tratamos de funções cujas imagens
Equações do primeiro grau
 Módulo 1 Unidade 3 Equações do primeiro grau Para início de conversa... Você tem um telefone celular ou conhece alguém que tenha? Você sabia que o telefone celular é um dos meios de comunicação que mais
Módulo 1 Unidade 3 Equações do primeiro grau Para início de conversa... Você tem um telefone celular ou conhece alguém que tenha? Você sabia que o telefone celular é um dos meios de comunicação que mais
EQUAÇÕES E INEQUAÇÕES DE 1º GRAU
 1 EQUAÇÕES E INEQUAÇÕES DE 1º GRAU Equação do 1º grau Chamamos de equação do 1º grau em uma incógnita x, a qualquer expressão matemática que pode ser escrita sob a forma: em que a e b são números reais,
1 EQUAÇÕES E INEQUAÇÕES DE 1º GRAU Equação do 1º grau Chamamos de equação do 1º grau em uma incógnita x, a qualquer expressão matemática que pode ser escrita sob a forma: em que a e b são números reais,
CURSO ONLINE RACIOCÍNIO LÓGICO
 AULA QUINZE: Matrizes & Determinantes (Parte II) Olá, amigos! Pedimos desculpas por não ter sido possível apresentarmos esta aula na semana passada. Motivos de força maior nos impediram de fazê-lo, mas
AULA QUINZE: Matrizes & Determinantes (Parte II) Olá, amigos! Pedimos desculpas por não ter sido possível apresentarmos esta aula na semana passada. Motivos de força maior nos impediram de fazê-lo, mas
NIVELAMENTO MATEMÁTICA 2012
 NIVELAMENTO MATEMÁTICA 202 Monitor: Alexandre Rodrigues Loures Monitor: Alexandre Rodrigues Loures SUMÁRIO. LOGARITMOS... 3.. Mudança de base... 3.2. Propriedades dos logaritmos... 4 2. DERIVADAS... 4
NIVELAMENTO MATEMÁTICA 202 Monitor: Alexandre Rodrigues Loures Monitor: Alexandre Rodrigues Loures SUMÁRIO. LOGARITMOS... 3.. Mudança de base... 3.2. Propriedades dos logaritmos... 4 2. DERIVADAS... 4
Equações do segundo grau
 Módulo 1 Unidade 4 Equações do segundo grau Para início de conversa... Nesta unidade, vamos avançar um pouco mais nas resoluções de equações. Na unidade anterior, você estudou sobre as equações de primeiro
Módulo 1 Unidade 4 Equações do segundo grau Para início de conversa... Nesta unidade, vamos avançar um pouco mais nas resoluções de equações. Na unidade anterior, você estudou sobre as equações de primeiro
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional. n=1
 Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA Números e Funções Reais Avaliação - GABARITO 3 de abril de 203. Determine se as afirmações a seguir são verdadeiras
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA Números e Funções Reais Avaliação - GABARITO 3 de abril de 203. Determine se as afirmações a seguir são verdadeiras
REVISÃO E AVALIAÇÃO DA MATEMÁTICA
 2 Aula 45 REVISÃO E AVALIAÇÃO DA 3 Vídeo Arredondamento de números. 4 Arredondamento de números Muitas situações cotidianas envolvendo valores destinados à contagem, podem ser facilitadas utilizando o
2 Aula 45 REVISÃO E AVALIAÇÃO DA 3 Vídeo Arredondamento de números. 4 Arredondamento de números Muitas situações cotidianas envolvendo valores destinados à contagem, podem ser facilitadas utilizando o
FUNÇÃO DO 1º GRAU. Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência:
 FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
. Determine os valores de P(1) e P(22).
 Resolução das atividades complementares Matemática M Polinômios p. 68 Considere o polinômio P(x) x x. Determine os valores de P() e P(). x x P() 0; P() P(x) (x x)? x (x ) x x x P()? 0 P() ()? () () 8 Seja
Resolução das atividades complementares Matemática M Polinômios p. 68 Considere o polinômio P(x) x x. Determine os valores de P() e P(). x x P() 0; P() P(x) (x x)? x (x ) x x x P()? 0 P() ()? () () 8 Seja
Figura 2.1: Carro-mola
 Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
FRAÇÕES TERMOS DE UMA FRAÇÃO NUMERADOR 2 TRAÇO DE FRAÇÃO DENOMINADOR. DENOMINADOR Indica em quantas partes o todo foi dividido.
 FRAÇÕES TERMOS DE UMA FRAÇÃO NUMERADOR TRAÇO DE FRAÇÃO DENOMINADOR DENOMINADOR Indica em quantas partes o todo foi dividido. NUMERADOR - Indica quantas partes foram consideradas. TRAÇO DE FRAÇÃO Indica
FRAÇÕES TERMOS DE UMA FRAÇÃO NUMERADOR TRAÇO DE FRAÇÃO DENOMINADOR DENOMINADOR Indica em quantas partes o todo foi dividido. NUMERADOR - Indica quantas partes foram consideradas. TRAÇO DE FRAÇÃO Indica
Modelos Variáveis de Estado
 Modelos Variáveis de Estado Introdução; Variáveis de Estados de Sistemas Dinâmicos; Equação Diferencial de Estado; Função de Transferência a partir das Equações de Estados; Resposta no Domínio do Tempo
Modelos Variáveis de Estado Introdução; Variáveis de Estados de Sistemas Dinâmicos; Equação Diferencial de Estado; Função de Transferência a partir das Equações de Estados; Resposta no Domínio do Tempo
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
AULA 6 LÓGICA DOS CONJUNTOS
 Disciplina: Matemática Computacional Crédito do material: profa. Diana de Barros Teles Prof. Fernando Zaidan AULA 6 LÓGICA DOS CONJUNTOS Intuitivamente, conjunto é a coleção de objetos, que em geral, tem
Disciplina: Matemática Computacional Crédito do material: profa. Diana de Barros Teles Prof. Fernando Zaidan AULA 6 LÓGICA DOS CONJUNTOS Intuitivamente, conjunto é a coleção de objetos, que em geral, tem
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto
 Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto Maria Angélica Araújo Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação
Um estudo sobre funções contínuas que não são diferenciáveis em nenhum ponto Maria Angélica Araújo Universidade Federal de Uberlândia - Faculdade de Matemática Graduanda em Matemática - Programa de Educação
Aula 3. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
O B. Podemos decompor a pirâmide ABCDE em quatro tetraedros congruentes ao tetraedro BCEO. ABCDE tem volume igual a V = a2.oe
 GABARITO - QUALIFICAÇÃO - Setembro de 0 Questão. (pontuação: ) No octaedro regular duas faces opostas são paralelas. Em um octaedro regular de aresta a, calcule a distância entre duas faces opostas. Obs:
GABARITO - QUALIFICAÇÃO - Setembro de 0 Questão. (pontuação: ) No octaedro regular duas faces opostas são paralelas. Em um octaedro regular de aresta a, calcule a distância entre duas faces opostas. Obs:
Simulado OBM Nível 2
 Simulado OBM Nível 2 Gabarito Comentado Questão 1. Quantos são os números inteiros x que satisfazem à inequação? a) 13 b) 26 c) 38 d) 39 e) 40 Entre 9 e 49 temos 39 números inteiros. Questão 2. Hoje é
Simulado OBM Nível 2 Gabarito Comentado Questão 1. Quantos são os números inteiros x que satisfazem à inequação? a) 13 b) 26 c) 38 d) 39 e) 40 Entre 9 e 49 temos 39 números inteiros. Questão 2. Hoje é
Introdução ao estudo de equações diferenciais
 Matemática (AP) - 2008/09 - Introdução ao estudo de equações diferenciais 77 Introdução ao estudo de equações diferenciais Introdução e de nição de equação diferencial Existe uma grande variedade de situações
Matemática (AP) - 2008/09 - Introdução ao estudo de equações diferenciais 77 Introdução ao estudo de equações diferenciais Introdução e de nição de equação diferencial Existe uma grande variedade de situações
ESCOLA ESTADUAL DE ENSINO MÉDIO RAUL PILLA COMPONENTE CURRICULAR: Matemática PROFESSORA: Maria Inês Castilho. Conjuntos
 ESCOL ESTDUL DE ENSINO MÉDIO UL PILL COMPONENTE CUICUL: Matemática POFESSO: Maria Inês Castilho Noções básicas: Conjuntos 1º NOS DO ENSINO MÉDIO Um conjunto é uma coleção qualquer de objetos, de dados,
ESCOL ESTDUL DE ENSINO MÉDIO UL PILL COMPONENTE CUICUL: Matemática POFESSO: Maria Inês Castilho Noções básicas: Conjuntos 1º NOS DO ENSINO MÉDIO Um conjunto é uma coleção qualquer de objetos, de dados,
Cap. 7 - Fontes de Campo Magnético
 Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
Resolução de sistemas lineares
 Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Resolução de sistemas lineares J M Martínez A Friedlander 1 Alguns exemplos Comecemos mostrando alguns exemplos de sistemas lineares: 3x + 2y = 5 x 2y = 1 (1) 045x 1 2x 2 + 6x 3 x 4 = 10 x 2 x 5 = 0 (2)
Uma e.d.o. de segunda ordem é da forma
 Equações Diferenciais de Ordem Superior Uma e.d.o. de segunda ordem é da forma ou então d 2 y ( dt = f t, y, dy ) 2 dt y = f(t, y, y ). (1) Dizemos que a equação (1) é linear quando a função f for linear
Equações Diferenciais de Ordem Superior Uma e.d.o. de segunda ordem é da forma ou então d 2 y ( dt = f t, y, dy ) 2 dt y = f(t, y, y ). (1) Dizemos que a equação (1) é linear quando a função f for linear
A equação do 2º grau
 A UA UL LA A equação do 2º grau Introdução Freqüentemente, ao equacionarmos um problema, obtemos uma equação na qual a incógnita aparece elevada ao quadrado. Estas são as chamadas equações do 2º grau.
A UA UL LA A equação do 2º grau Introdução Freqüentemente, ao equacionarmos um problema, obtemos uma equação na qual a incógnita aparece elevada ao quadrado. Estas são as chamadas equações do 2º grau.
MD Sequências e Indução Matemática 1
 Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
