Revista Brasileira de Ensino de Fsica, vol. 21, no. 1, Marco, Simetrias e Leis de Conservac~ao na. Mec^anica Classica
|
|
|
- Bento Frade de Oliveira
- 8 Há anos
- Visualizações:
Transcrição
1 Revsta Braslera e Ensno e Fsca, vol. 21, no. 1, Marco, Smetras e Les e Conservac~ao na Mec^anca Classca Arano e Souza Martns Dep. e Fsca o Estao Solo - UFRJ Cx. Postal 68528, CEP , (Ro e Janero) Recebo em 26 e Junho, 1998 A conex~ao entre les e conservac~ao e smetras o sstema s~ao analsaas entro o formalsmo lagrangeano. Apos uma breve exposc~ao os concetos acma ctaos, apresentaremos a conex~ao entre estes sob o ponto e vsta o teorema e Noether, cuja euc~ao sera apresentaa. Dscutremos uma amplac~ao este teorema, e moo a nclur a varac~ao e calbre as lagrangeanas, e moo a lancar luz em novas smetras o sstema. The connecton between conservaton laws an symmetres propertes of physcal systems are showe n Lagrangan formalsm. After a short exposton of symmetres an conserve quanttes concepts, we wll explore ther connecton n the Noether Theorem frame. We also scuss one amplaton of ths theorem to nclue the gauge varant Lagrangans. I Introuc~ao O estuo as propreaes e smetra e um sstema nos a precosas nformac~oes sobre o mesmo, como a forma e suas soluc~oes (Teorema e Bloch), reuc~ao e graus e lberaec... Dentro este contexto, quero examnar o papel as smetras entro o formalsmo lagrangeano a mec^anca e sua relac~ao com quantaes fscas conservaas, sob o ponto e vsta o teorema e Noether. Este teorema, e grane mport^anca e rqueza, quase n~ao e tratao nos cursos convenconas e mec^anca classca, apesar e sua forma smples. Hstorcamente, a conex~ao entre les e conservac~ao e smetras fo nvestgaa prmeramente por Schutz [6] no caso e smetra translaconal. Uma formulac~ao mas precsa e aa pelo teorema e Noether [5], que estabelece o elo entre as les e conservac~ao e as transformac~oes o grupo e Galle. O que preteno neste texto e apresentar uma espece e revs~ao os concetos e smetras na fsca classca e sua conex~ao com a conservac~ao e quantaes fscas, sob o ponto e vsta o Teorema e Noether. Este Teorema e pouco comentao em lvros atcos, apesar e sua aparente popularae. Com vsta a enrquecer mas a scuss~ao, veremos como estener a aplcablae o teorema e Noether e moo a nclur o fato que lagrangeanas que ferem por uma ervaa total no tempo e uma func~ao s~ao equvalentes, ou seja, escrevem o mesmo sstema fsco [4]. A segur apresentare um breve resumo os concetos e smetra e les e conservac~ao, com as respectvas analogas entre os formalsmos Newtonano e lagrangeano. II Smetras O termo smetra em Fsca refere-se a um conjunto e transformac~oes enas num grupo que levam uma express~ao ser nvarante na sua forma: zemos ent~ao que o sstema e nvarante sob aquela transformac~ao ou que ele apresenta uma smetra no par^ametro a transformac~ao. As operac~oes aqu ser~ao aquelas enas no grupo e Galle, pos tuo que aqu sera analsao sera entro o lmte n~ao relatvstco. Vamos tomar o formalsmo Newtonano como exemplo: F = 2 r 2 (1) F =,r U (r ); (2) e-mal: asm@f.ufrj.br
2 34 Arano e Souza Martns para forcas este tpo, as equac~oes e movmento o tpo 1,s~ao nvarantes sob transformac~oes e Galle o tpo: t 0 = t + ; r 0 = r + + t (3) Aqu, ao referr-me ao termo nvar^anca, estare me referno a nvar^anca a lagrangeana sob operac~oes e eslocamento em suas coorenaas generalzaas, n~ao em sua equac~ao e movmento. Como lustrac~ao basta lembrarmos que sempre assoca-se a conservac~ao o momento lnear a translac~oes espacas e a energa a translac~oes temporas. Mas esta nvar^anca referese a lagrangeana L que escreve o sstema, pos uma partcula submeta a uma forca frcconal moveno-se seguno a equac~ao r =,k n~ao conserva momento nem energa, (4) apesar esta equac~ao ser nvarante sob translac~oes temporas e espacas. Vemos assm que n~ao exste uma relac~ao bunvoca entre as smetras a equac~ao e movmento com as a lagrangeana L. Para uma scuss~ao mas aprofunaa, sugro a letura o artgo o Havas [2]. III Les e Conservac~ao Na mec^anca classca, uma graneza fsca G e conservaa se: G =0 (5) O termo conservac~ao e utlzao aqu no sento que uma partcular express~ao que caracterza um sstema, efetuaa num nstante t 0,e nepenente e e t, ou seja, e uma constante e movmento. Na mec^anca newtonana, se temos um sstema e partculas n partculas, a forca sobre a -esma partcula na aus^enca e forcas externas e aa por: F = X 6=k F k ; F =,r V; (6) Se estas forcas obeecem a tercera Le e Newton, F k =, F k, obtemos as les e conservac~ao usuas para um sstema e partculas: E =0; P =0; E = X (T + V ); (7) X P = p ; (8) G L =0; =0; X L = r p ; (9) X G = m r, Pt; (10) que expressam, respectvamente, a conservac~ao a energa, o momento lnear, o momento angular e o movmento o centro e massa o sstema. No formalsmo lagrangeano, o sstema e escrto pela sua func~ao lagrangeana L: L = L(q; _q; t) (11) e as equac~oes e movmento s~ao aas pelas equac~oes e Euler-Lagrange:, =0 k Se a lagrangeana L n~ao epene explctamente e uma coorenaa q, zemos que esta coorenaa e cclca ou gnoravel. q k : Para uma coorenaa k =0 (13) levano (13) para a equac~ao (12) obtemos: p k = = const: (14) Na equac~ao acma, p k echamao e momento generalzao conjugao a coorenaa q k. A equac~ao (12) expressa a conservac~ao o momento generalzao. IV Teorema e Noether Vmos que a aus^enca explcta a epen^enca a lagrangeana L em uma coorenaa leva a nepen^enca esta frente a uma transformac~ao que altere o valor a varavel, nos ano a conservac~ao o momento generalzao. Pctoramente, poemos vsualsar o Teorema e Noether como uma espece e maquna, one entramos com a transformac~ao e smetra na varavel q k e tramos a graneza conservaa G:
3 Revsta Braslera e Ensno e Fsca, vol. 21, no. 1, Marco, Fgura 1. Estrutura pctora o Teorema (maquna) e Noether. Para uma lagrangeana o tpo (11), o teorema e Noether e ao pela express~ao _q k, L t + q k =0 (15) A emonstrac~ao este, assm como as conc~oes necessaras para a sua euc~ao est~ao no ap^ence este texto. Sugro sua letura para a melhor compreens~ao n~ao so a conex~ao que queremos explorar, assm como a extens~ao que se faz a este teorema e moo a se levar em conta a varac~ao as lagrangeanas frente a transformac~oes e calbre. A. Translac~ao temporal Uma translac~ao temporal e ena como e t = t, ; q k =0 (16) Levano estas transformac~oes para o teorema (15) teremos _q k, L =0! E = _q k, L = const:; (17) one a constante E resulta ser a energa total o sstema. Veremos no ap^ence uma extens~ao o teorema e Noether que permtra obter a conservac~ao a energa e e outra quantaes n~ao prevstas pela forma par~ao o teorema. B. Translac~ao espacal A mas smples transformac~ao e smetra neste caso e a translac~ao a orgem e um sstema cartesano ao longo e apenas uma as tr^es rec~oes que o forma. Escolheno o exo x no qual a translac~ao e feta: et = t; ex = x, x 0 ; ey = y; ez = z (18) Levano estas transformac~oes em (15) teremos x _x = p x = const:; (19) que e a express~ao usual para a conservac~ao o momento lnear ao longo a rec~ao em que e feta a translac~ao. C. Rotac~ao em torno e um exo Para uma rotac~ao nntesmal e um ^angulo em torno o exo z e um sstema e coorenaas cartesanas, as novas coorenaas s~ao conectaas as antgas pelas seguntes transformac~oes ex = x + y ; ey = y, x ; ez = z e _x = _x +_y ; e _y =_y, _x ; e _z =_z (20) one mplctamente e assumo que e t = t: Levano as express~oes acma na express~ao o teorema e Noether resulta que _y, y =[xp x, yp y ]=const: _x A express~ao (21) nos a a conservac~ao usual a componente z o momento angular. Aqu encerramos os exemplos, porem estes n~ao se esgotam nestes poucos aqu apresentaos. Vale a pena tambem ressaltar que ha uma formulac~ao analoga o Teorema e Noether para campos, one ele se mostra ana mas poeroso. Uma boa scuss~ao esta extens~ao poemos encontrar num artgo evo a Hll [3]. V Les e conservac~ao para lagrangeanas que apresentam varac~ao e calbre A. Introuc~ao Nesta sec~ao quero apresentar uma extens~ao natural a anteror. Quano um sstema fsco apresenta alguma propreae e smetra, ele e escrto por equac~oes e movmento nvarantes sob o grupo corresponente e transformac~oes. A lagrangeana que o escreve porem n~ao eve necessaramente o ser. Na emonstrac~ao o Teorema e Noether, etalhaa no ap^ence, uma as hpoteses levaa em conta fo que a lagrangeana evera ter a mesma forma funconal apos as transformac~oes e smetra, ou seja: L = L (q; _q; t), e L eq; e _q; e t =0 (22) Com sto, exclu-se uma classe e sstemas cujas lagrangeanas s~ao tas varantes e calbre [4]. Dzemos que uma lagrangeana sofre uma varac~ao e calbre se ao realzarmos sobre a mesma uma transformac~ao e smetra, ela varar apenas e uma ervaa total no tempo
4 36 Arano e Souza Martns e uma func~ao (q k ;t). Da mec^anca classca, sabemos que uas lagrangeanas que ferem apenas por uma ervaa total no tempo s~ao equvalentes. Como exemplo, vejamos o caso o campo eletromagnetco. Uma partcula e massa m e carga eletrca e num campo eletrco E e magnetco B e escrta pela lagrangeana L = 1 2 m _q2 + e _q A, ev; (23) one A e V s~ao, respectvamente, o potencal vetor e o escalar os campos, tas que e 0 1 A A,rV (24) B = r A (25) Sabemos a teora eletromagnetca que estes potencas n~ao s~ao uncamente enos, pos para transformac~oes e calbre (gauge) o tpo A! A + r V! ; (26) os campos, que contem a fsca o problema, n~ao se alteram. Apos esta transformac~ao, a lagrangeana se transformara a segunte forma: L! L +2e ; (27) e como sabemos, o sstema fsco e o mesmo, ou seja, as uas lagrangeanas s~ao equvalentes. B. Teorema e Noether Generalzao A raz~ao fsca a equval^eca e lagrangeanas que ferem por ervaas totas no tempo e func~oes o tpo (q k ;t)vem o prncpo e mnma ac~ao e Hamlton. Seja uma lagrangeana L (q; _q; t), num ntervalo e tempo t = t 1 a t = t 2 o sstema move-se e tal forma que a ntegral e ac~ao S = 2 t1 L (q; _q; t) (28) assuma o menor valor possvel, ou seja, S = 0. Assm, se uas lagrangeanas ferem entre s apenas pela ervaa total e uma func~ao (q k ;t) L 0 eq; e _q; e t = L (q; _q; t)+ (q k;t) (29) ovalor a ac~ao e L 0 sera h S 0 = S + q (2) ;t 2, cuja varac~ao S 0 tambem sera nula. q (1) ;t 1 ; (30) Para um sstema com N graus e lberae sua lagrangeana L que epenera as N coorenaas generalzaas q k, k = 1:::N, e suas velocaes generalzaas _q k e possvelmente o tempo. Vamos mpor agora uma transformac~ao e coorenaas o tpo q k = "f k (q k ; _q k ;t) ; (31) cujo efeto maxmoe fazer a lagrangeana varar por uma ervaa total no tempo e uma func~ao que epene apenas as coorenaas q k eet: L = " (q k;t) (32) Em termo as transformac~oes (46) a varac~ao L a lagrangeana (omtno o subscrto k) sera L = q + _q; one L fo assuma ser nepenente o tempo. Usano as equac~oes e Lagrange, poemos reescrever (48) como: e assm L = q + L = " (q) ; f (34) Comparano com a hpotese (37) a varac~ao e gauge a lagrangeana nos obtemos a le e conservac~ao F =0 (35) para a quantae F, que sera aa por X F f k, (q k ;t) (36) k O resultao (41) fere o resultao obto anterormente pela ac~ao o termo. Vamos a segur lustrar a mport^anca este termo para o caso e uma partcula carregaa num campo eletromagnetco. 1. Conservac~ao a energa
5 Revsta Braslera e Ensno e Fsca, vol. 21, no. 1, Marco, Se a lagrangeana L n~ao epene explctamente o tempo t, =0 (37) ent~ao, sua varac~ao sob uma translac~ao temporal nntesmal t L = L t (38) somente vra atraves a varac~ao as coorenaas q k =_q k t (39) Se fazemos a entcac~ao f k = _q k e=l, obtemos e()aleeconservac~ao corresponente X F = _q k, L = energa (40) k 2. Movmento num campo eletromagnetco Vmos que a lagrangeana e uma partcula carregaa num campo eletromagnetco e L = 1 2 m _q2 + e _q A, ev (41) Vamos conserar um campo eletrco E unforme e constante. Este campo e nvarante sob translac~oes espacas e temporas. Escolheno o potencal escalar a forma V =, E q, que e temporalmente nvarante. A lagrangeana assocaa L 1 = 1 2 m _q2 + e E q (42) n~ao e nvarante sob translac~oes espacas q k = a ja que L 1 = e E a = e Et a (43) e e acoro com o teorma e Noether generalzao a express~ao acma mplca a conservac~ao e F m _q, e Et= const; (44) mostrano a natureza unformemente aceleraa o movmento. VI Conclus~oes Preteno ser breve nas conclus~oes este trabalho, vsto que ele ja representa um corpo bem eno e eas. Expomos e uma manera sstematca como uas eas bascas na fsca, que s~ao as e smetra e e conservac~ao e granezas fscas, s~ao conectaas. Apesar e ter passao ao largo o aspecto hstorco, julgo tambem mportante enfatzar como estes concetos foram surgno com o tempo, que poe ser vsto as ferentes formas com que os formalsmos Newtonano e Lagrangeano aboram o problema. Do ponto e vsta atco, julgo mportante a aboragem este Teorema em cursos e grauac~ao, e forma a ar uma vs~ao e conjunto as les e conservac~ao em fsca, trataas mutas vezes e forma fragmentara nestes cursos, como se caa le e conservac~ao n~ao guara relac~oes entre s. Para quem se nteressa, sugro a letura a extens~ao este teorema para o formalsmo e campos, no lvro o Golsten. Ap^ence: Demonstrac~ao o Teorema e Noether Smetra sobre transformac~oes e coorenaas toca ao efeto e transformac~oes nntesmas o tpo: t! e t = t + t (45) q k (t)! eq k = qk (t)+q k ; (46) one t eq k poem ser func~oes arbtraras as coorenaas generalzaas. Ja asvelocaes generalzaas ter~ao a segunte transformac~ao: _q k (t)! e _qk =_qk (t)+ _q k : (47) Sob transformac~oes o tpo (45), (46) e (47), a lagrangeana se transformara a segunte manera: L (q k (t) ; _q k (t) ;t)! L eqk ; e _qk ; e t (48) A partr este ponto, omtre o subscrto k por smplcae, cano subteno que ele subscreve caa coorenaa generalzaa. Tr^es conc~oes s~ao assumas a valer: 1. Estaremos conserano um espaco-tempo euclano; 2. A lagrangeana L tem a mesma forma funconal tanto em termo as quantaes transformaas quanto as quantaes orgnas, sto e, vale a express~ao (48).
6 38 Arano e Souza Martns 3. A magntue a ntegral e ac~ao e nvarante sob a transformac~ao ei = Z et ele t = L: (49) e Isto representa uma extens~ao as propreaes as coorenaas gnoraves. Se a lagrangeana n~ao mua sob transformac~oes nessas coorenaas n~ao ha motvo que ela possa assm alterar o valor a ntegral e ac~ao I. c Combnano (18) e (19) Z et e el eq ; e _qk ; e t e t, L (q (t) ; _q (t) ;t) =0: (50) Na prmera ntegral e t representa uma falsa varavel e ntegrac~ao, poeno ser rebatzaa e t, mas o omno e ntegrac~ao n~ao se altera. Omtremos tambem a partr aqu os t's as coorenaas, assm Z et e el eq; e _q; e t, L (q; _q; t) =0: (51) Sob transformac~oes nntesmas o tpo (45) e (46), a ferenca entre as ntegras em (51) sera = +t + L + [L + L], +t t [L + L], L (52) Z + [L + L] Em 1 a orem os os ultmos termos em (52) poem ser escrtos como: Com sto, a equac~ao (52) torna-se: +t L, t Z + L = tl(t), t 0 L (t 0 ) (53) +t [L + L], + L = = L + Lt j t (54) L(t)+ (tl(t)) Vale a pena relembrar que L = L eq; e _q; e t, L (q; _q; t) e, em 1 a orem, poemos escrever esta ferenca acma como L (~), L () k q k + _q k ; (55) one representa uma varac~ao os q k 0 s e e suas ervaas num ponto xo o espaco, ferente a varac~ao. Seno assm, ela comuta com = e a equac~ao (55) ca L = L (~), L () = Substtuno (56) na eq. (54) q k + tl(t) q k (56) =0; (57) que e uma forma e corrente conservaa. As varac~oes e e se relaconam a segunte forma: q k = q k k t (58)
7 Revsta Braslera e Ensno e Fsca, vol. 21, no. 1, Marco, Levano a express~ao acma para a equac~ao (57) Refer^encas _q k, L t + q k =0 (59) 1. H.A. Buchhal, L. J. Tasse, Austr. J. Phys. 17, 431 (1964). Assm obtemos o resultao esperao _q k, L t + q k =0 (60) A equac~ao (59) e a forma nal o teorema e Noether, que relacona as transformac~oes e smetra na lagrangeana com suas equvalentes quantaes fscas conservaas. Deve car claro que o teorema na forma apresentaa acma sup~oe que as tr^es conc~oes vstas no nco a emonstrac~ao sejam valas. 2. P. Havas, Acta Physca Austraca 38, 145 (1973). 3. E. L. Hll, Revews of Moern Physcs, vol. 23, n L. Leblon, J. Marc, Amercan Journal of Physcs, vol. 23, n3. 5. E. Noether, Nachr. Aka. Wss. Gottngen, Math.-Phys. K1. (1918), J. R. Schutz, Nachr. Aka. Wss. Gottngen, Math.-Phys. K1. (1897), 110.
Capítulo 4 CONSERVAÇÃO DA MASSA E DA ENERGIA
 Capítulo 4 COSERAÇÃO DA MASSA E DA EERGIA 4.1. Equações para um Sstema Fechao 4.1.1. Defnções Consere o volume materal e uma aa substânca composta por espéces químcas lustrao na Fgura 4.1, one caa espéce
Capítulo 4 COSERAÇÃO DA MASSA E DA EERGIA 4.1. Equações para um Sstema Fechao 4.1.1. Defnções Consere o volume materal e uma aa substânca composta por espéces químcas lustrao na Fgura 4.1, one caa espéce
Fenômenos de Transporte I
 Prof. Carlos Ruberto Fragoso Jr. Fenômenos e Transporte I 1. Funamentos e Cnemátca os Fluos 1.1 Defnções Escoamento é a eformação contínua e um fluo que sofre a ação e uma força tangencal, por menor que
Prof. Carlos Ruberto Fragoso Jr. Fenômenos e Transporte I 1. Funamentos e Cnemátca os Fluos 1.1 Defnções Escoamento é a eformação contínua e um fluo que sofre a ação e uma força tangencal, por menor que
Classificação das Equações de Conservação
 Angela Neckele PUC-Ro Classcação as Equações e Conservação Equação erencal parcal lnear e seguna orem, com uas varáves nepenentes (x, y) ou (x, t) B AC 0 elíptca Classcação: B AC 0 parabólca B AC 0 perbólc
Angela Neckele PUC-Ro Classcação as Equações e Conservação Equação erencal parcal lnear e seguna orem, com uas varáves nepenentes (x, y) ou (x, t) B AC 0 elíptca Classcação: B AC 0 parabólca B AC 0 perbólc
1 Princípios da entropia e da energia
 1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
Aula 7: Circuitos. Curso de Física Geral III F-328 1º semestre, 2014
 Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
1 Curso PIBID: Os Alicerces da Mecânica Clássica
 1 Curso PIBID: Os Alcerces a Mecânca Clássca Prof. Sérgo Augusto Caras e Olvera Profa. Debora Profa. Fabane Prncípo Varaconal Um problema hstórco e bem nteressante, avém a procura por uma função ou curva,
1 Curso PIBID: Os Alcerces a Mecânca Clássca Prof. Sérgo Augusto Caras e Olvera Profa. Debora Profa. Fabane Prncípo Varaconal Um problema hstórco e bem nteressante, avém a procura por uma função ou curva,
.FL COMPLEMENTOS DE MECÂNICA. Mecânica. Recuperação de doentes com dificuldades motoras. Desempenho de atletas
 COMPLEMENTOS DE MECÂNICA Recuperação e oentes com fculaes motoras Mecânca Desempenho e atletas Construção e prótese e outros spostvos CORPOS EM EQUILÍBRIO A prmera conção e equlíbro e um corpo correspone
COMPLEMENTOS DE MECÂNICA Recuperação e oentes com fculaes motoras Mecânca Desempenho e atletas Construção e prótese e outros spostvos CORPOS EM EQUILÍBRIO A prmera conção e equlíbro e um corpo correspone
7. Resolução Numérica de Equações Diferenciais Ordinárias
 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
Curso de Engenharia Física Tecnológica 2014/2015. sin 2 θ ϕ 2. 3x 2 1 ), P 3 = 1 2
 Mecânca Quântca Sére 7 Curso e Engenhara Físca Tecnológca 2014/2015 Vers~ao e 12 e Novembro e 2014) 7.1 Mostre que, em coorenaas esfércas, se tem L ± = e ±ϕ ± θ +cotθ ) ϕ e L 2 = 2 2 θ +cotθ 2 θ + 1 )
Mecânca Quântca Sére 7 Curso e Engenhara Físca Tecnológca 2014/2015 Vers~ao e 12 e Novembro e 2014) 7.1 Mostre que, em coorenaas esfércas, se tem L ± = e ±ϕ ± θ +cotθ ) ϕ e L 2 = 2 2 θ +cotθ 2 θ + 1 )
E-mails: damasceno1204@yahoo.com.br damasceno@interjato.com.br damasceno12@hotmail.com http://www. damasceno.info www. damasceno.info damasceno.
 Matemátca Fnancera 007. Prof.: Luz Gonzaga Damasceno E-mals: amasceno04@yahoo.com.br amasceno@nterjato.com.br amasceno@hotmal.com 5. Taxa Over mensal equvalente. Para etermnar a rentablae por a útl one
Matemátca Fnancera 007. Prof.: Luz Gonzaga Damasceno E-mals: amasceno04@yahoo.com.br amasceno@nterjato.com.br amasceno@hotmal.com 5. Taxa Over mensal equvalente. Para etermnar a rentablae por a útl one
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
UNIVERSIDADE PRESBITERIANA MACKENZIE CCSA - Centro de Ciências Sociais e Aplicadas Curso de Economia
 CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
Trabalho e Energia. Definimos o trabalho W realizado pela força sobre uma partícula como o produto escalar da força pelo deslocamento.
 Trabalho e Energa Podemos denr trabalho como a capacdade de produzr energa. Se uma orça eecutou um trabalho sobre um corpo ele aumentou a energa desse corpo de. 1 OBS: Quando estudamos vetores vmos que
Trabalho e Energa Podemos denr trabalho como a capacdade de produzr energa. Se uma orça eecutou um trabalho sobre um corpo ele aumentou a energa desse corpo de. 1 OBS: Quando estudamos vetores vmos que
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
Física. Física Módulo 1 Vetores, escalares e movimento em 2-D
 Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Capítulo. Capacitores Resoluções dos exercícios propostos. P.283 a) Dados: ε 0 8,8 10 12 F/m; A (0,30 0,50) m 2 ; d 2 10 3 m 0,30 0,50 2 10 3
 apítulo a físca xercícos propostos nae apítulo apactores apactores Resoluções os exercícos propostos P.8 a) aos: ε 0 8,8 0 F/m; (0,0 0,50) m ; 0 m ε 0 8,8 0 0,0 0,50 0 6,6 0 0 F b) ao:.000 V 6,6 00.000,
apítulo a físca xercícos propostos nae apítulo apactores apactores Resoluções os exercícos propostos P.8 a) aos: ε 0 8,8 0 F/m; (0,0 0,50) m ; 0 m ε 0 8,8 0 0,0 0,50 0 6,6 0 0 F b) ao:.000 V 6,6 00.000,
CQ110 : Princípios de FQ
 CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
MECÂNICA CLÁSSICA. AULA N o 7. Teorema de Liouville Fluxo no Espaço de Fases Sistemas Caóticos Lagrangeano com Potencial Vetor
 1 MECÂNICA CLÁSSICA AULA N o 7 Teorema de Louvlle Fluo no Espaço de Fases Sstemas Caótcos Lagrangeano com Potencal Vetor Voltando mas uma ve ao assunto das les admssíves na Físca, acrescentamos que, nos
1 MECÂNICA CLÁSSICA AULA N o 7 Teorema de Louvlle Fluo no Espaço de Fases Sstemas Caótcos Lagrangeano com Potencal Vetor Voltando mas uma ve ao assunto das les admssíves na Físca, acrescentamos que, nos
Por efeito da interação gravitacional, a partícula 2 exerce uma força F sobre a partícula 1 e a partícula 1 exerce uma força F sobre a partícula 2.
 Interação Gravitacional Vimos que a mola é esticaa quano um corpo é suspenso na sua extremiae livre. A força que estica a mola é e origem eletromagnética e tem móulo igual ao móulo o peso o corpo. O peso
Interação Gravitacional Vimos que a mola é esticaa quano um corpo é suspenso na sua extremiae livre. A força que estica a mola é e origem eletromagnética e tem móulo igual ao móulo o peso o corpo. O peso
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Leis de Newton. 1.1 Sistemas de inércia
 Capítulo Leis e Newton. Sistemas e inércia Supomos a existência e sistemas e referência, os sistemas e inércia, nos quais as leis e Newton são válias. Um sistema e inércia é um sistema em relação ao qual
Capítulo Leis e Newton. Sistemas e inércia Supomos a existência e sistemas e referência, os sistemas e inércia, nos quais as leis e Newton são válias. Um sistema e inércia é um sistema em relação ao qual
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
PEF Projeto de Estruturas Marítimas ESFORÇOS NA PLATAFORMA FIXA
 PEF 506 - Projeto e Estruturas Marítmas ESFORÇOS NA PLATAFORMA FIXA 1. Introução O prncpal esorço agente em uma plataorma xa é aquele avno o movmento o meo luo. evo à complexae o movmento as partículas
PEF 506 - Projeto e Estruturas Marítmas ESFORÇOS NA PLATAFORMA FIXA 1. Introução O prncpal esorço agente em uma plataorma xa é aquele avno o movmento o meo luo. evo à complexae o movmento as partículas
1 a Lei de Kirchhoff ou Lei dos Nós: Num nó, a soma das intensidades de correntes que chegam é igual à soma das intensidades de correntes que saem.
 Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
CURSO ON-LINE PROFESSOR: VÍTOR MENEZES
 O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Data: / / LISTA DE FÍSICA. Um ímã permanente é colocado verticalmente sobre uma base magnética como mostra a figura abaixo.
 Ensno Funamental II Unae São Juas Taeu Professor (a): Aluno (a): Ano: 9º Pero Paulo S. Arras Data: / / 2014. LISTA DE FÍSICA Questão 01 - (PUC RJ/2011) Um ímã permanente é colocao vertcalmente sobre uma
Ensno Funamental II Unae São Juas Taeu Professor (a): Aluno (a): Ano: 9º Pero Paulo S. Arras Data: / / 2014. LISTA DE FÍSICA Questão 01 - (PUC RJ/2011) Um ímã permanente é colocao vertcalmente sobre uma
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
1 Curso PIBID: Os Alicerces da Mecânica Clássica
 1 Curo PIBID: O Alcerce a Mecânca Cláca Pro. Sérgo Auguto Cara e Olvera Proa. Debora Proa. Fabane Prncípo Varaconal Um problema htórco e bem ntereante, avém a procura por uma unção ou curva, atravé a qual
1 Curo PIBID: O Alcerce a Mecânca Cláca Pro. Sérgo Auguto Cara e Olvera Proa. Debora Proa. Fabane Prncípo Varaconal Um problema htórco e bem ntereante, avém a procura por uma unção ou curva, atravé a qual
2003/2004. então o momento total das forças exercidas sobre o sistema é dado por. F ij = r i F (e)
 Resolução da Frequênca de Mecânca Clássca I/Mecânca Clássca 2003/2004 I Consdere um sstema de N partículas de massas m, =,..., N. a Demonstre que, se a força nterna exercda sobre a partícula pela partícula
Resolução da Frequênca de Mecânca Clássca I/Mecânca Clássca 2003/2004 I Consdere um sstema de N partículas de massas m, =,..., N. a Demonstre que, se a força nterna exercda sobre a partícula pela partícula
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
Associação de resistores em série
 Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
4 Sistemas de partículas
 4 Sstemas de partículas Nota: será feta a segunte convenção: uma letra em bold representa um vector,.e. b b Nesta secção estudaremos a generalzação das les de Newton a um sstema de váras partículas e as
4 Sstemas de partículas Nota: será feta a segunte convenção: uma letra em bold representa um vector,.e. b b Nesta secção estudaremos a generalzação das les de Newton a um sstema de váras partículas e as
Leis de conservação em forma integral
 Les de conservação em forma ntegral J. L. Balño Departamento de Engenhara Mecânca Escola Poltécnca - Unversdade de São Paulo Apostla de aula Rev. 10/08/2017 Les de conservação em forma ntegral 1 / 26 Sumáro
Les de conservação em forma ntegral J. L. Balño Departamento de Engenhara Mecânca Escola Poltécnca - Unversdade de São Paulo Apostla de aula Rev. 10/08/2017 Les de conservação em forma ntegral 1 / 26 Sumáro
Nota Técnica Médias do ENEM 2009 por Escola
 Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
Aluno (a): Ano: 9º V Data: / / LISTA DE FÍSICA
 Ensno Funamental II Unae Parque Atheneu Professor (a): Pero Paulo S. Arras Aluno (a): Ano: 9º V Data: / / 2014. LISTA DE FÍSICA 1) (PUC RJ/2011) Um ímã permanente é colocao vertcalmente sobre uma base
Ensno Funamental II Unae Parque Atheneu Professor (a): Pero Paulo S. Arras Aluno (a): Ano: 9º V Data: / / 2014. LISTA DE FÍSICA 1) (PUC RJ/2011) Um ímã permanente é colocao vertcalmente sobre uma base
APLICAÇÃO DA TÉCNICA DA TRANSFORMADA INTEGRAL GENERALIZADA NA ANÁLISE DO COMPORTAMENTO DE CÉLULAS DE COMBUSTÍVEL NUCLEAR EM GEOMETRIAS RETANGULARES
 APLICAÇÃO DA TÉCNICA DA TRANSFORMADA INTEGRAL GENERALIZADA NA ANÁLISE DO COMPORTAMENTO DE CÉLULAS DE COMBUSTÍVEL NUCLEAR EM GEOMETRIAS RETANGULARES Mateus Calegar Paulque Thago Antonn Alves Casso Roberto
APLICAÇÃO DA TÉCNICA DA TRANSFORMADA INTEGRAL GENERALIZADA NA ANÁLISE DO COMPORTAMENTO DE CÉLULAS DE COMBUSTÍVEL NUCLEAR EM GEOMETRIAS RETANGULARES Mateus Calegar Paulque Thago Antonn Alves Casso Roberto
Texto 03: Campos Escalares e Vetoriais. Gradiente. Rotacional. Divergência. Campos Conservativos.
 1 Unversdade Salvador UNIFACS Crsos de Engenhara Cálclo IV Profa: Ila Reboças Frere Cálclo Vetoral Teto 03: Campos Escalares e Vetoras. Gradente. Rotaconal. Dvergênca. Campos Conservatvos. Campos Escalares
1 Unversdade Salvador UNIFACS Crsos de Engenhara Cálclo IV Profa: Ila Reboças Frere Cálclo Vetoral Teto 03: Campos Escalares e Vetoras. Gradente. Rotaconal. Dvergênca. Campos Conservatvos. Campos Escalares
Trabalho e Energia. Curso de Física Básica - Mecânica J.R. Kaschny (2005)
 Trabalho e Energa Curso de Físca Básca - Mecânca J.R. Kaschny (5) Lembrando nosso epermento de queda lvre... z z 1 v t 1 z = z - v t - gt ( ) z- z v = g = t Contudo, se consderarmos obtemos: v z z 1 t
Trabalho e Energa Curso de Físca Básca - Mecânca J.R. Kaschny (5) Lembrando nosso epermento de queda lvre... z z 1 v t 1 z = z - v t - gt ( ) z- z v = g = t Contudo, se consderarmos obtemos: v z z 1 t
Mecânica. Sistemas de Partículas
 Mecânca Sstemas de Partículas Mecânca» Sstemas de Partículas Introdução A dnâmca newtonana estudada até aqu fo utlzada no entendmento e nas prevsões do movmento de objetos puntformes. Objetos dealzados,
Mecânca Sstemas de Partículas Mecânca» Sstemas de Partículas Introdução A dnâmca newtonana estudada até aqu fo utlzada no entendmento e nas prevsões do movmento de objetos puntformes. Objetos dealzados,
Custo de Capital. O enfoque principal refere-se ao capital de longo prazo, pois este dá suporte aos investimentos nos ativos permanentes da empresa.
 Custo e Captal 1 Custo e Captal Seguno Gtman (2010, p. 432) o custo e Captal é a taxa e retorno que uma empresa precsa obter sobre seus nvestmentos para manter o valor a ação nalterao. Ele também poe ser
Custo e Captal 1 Custo e Captal Seguno Gtman (2010, p. 432) o custo e Captal é a taxa e retorno que uma empresa precsa obter sobre seus nvestmentos para manter o valor a ação nalterao. Ele também poe ser
Prof. Dr. Alfredo Takashi Suzuki
 JORNADA DE FÍSICA TEÓRICA INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 3-07-010 CAMPOS: CLÁSSICOS, QUÂNTICOS, DE GAUGE E POR AÍ AFORA Jornada de Físca Teórca 010 Insttuto de Físca Teórca/UNESP Prof. Dr.
JORNADA DE FÍSICA TEÓRICA INSTITUTO DE FÍSICA TEÓRICA U.N.E.S.P. 19 a 3-07-010 CAMPOS: CLÁSSICOS, QUÂNTICOS, DE GAUGE E POR AÍ AFORA Jornada de Físca Teórca 010 Insttuto de Físca Teórca/UNESP Prof. Dr.
5.1 Seleção dos melhores regressores univariados (modelo de Índice de Difusão univariado)
 5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
TE210 FUNDAMENTOS PARA ANÁLISE DE CIRCUITOS ELÉTRICOS
 TE0 FUNDAMENTOS PARA ANÁLISE DE CIRCUITOS ELÉTRICOS Números Complexos Introdução hstórca. Os números naturas, nteros, raconas, rraconas e reas. A necessdade dos números complexos. Sua relação com o mundo
TE0 FUNDAMENTOS PARA ANÁLISE DE CIRCUITOS ELÉTRICOS Números Complexos Introdução hstórca. Os números naturas, nteros, raconas, rraconas e reas. A necessdade dos números complexos. Sua relação com o mundo
Sistemas de Campo Magnético
 Sstemas e ampo Magnétco 1. onsere o segunte sstema electromagnétco. Amta que não há spersão. A peça a sombreao tem um grau e lberae seguno a recção. 12 cm 8 cm N y z 6 cm 12 cm N 120 esp. rfe 800 4 10
Sstemas e ampo Magnétco 1. onsere o segunte sstema electromagnétco. Amta que não há spersão. A peça a sombreao tem um grau e lberae seguno a recção. 12 cm 8 cm N y z 6 cm 12 cm N 120 esp. rfe 800 4 10
2 Principio do Trabalho Virtual (PTV)
 Prncpo do Trabalho rtual (PT)..Contnuo com mcroestrutura Na teora que leva em consderação a mcroestrutura do materal, cada partícula anda é representada por um ponto P, conforme Fgura. Porém suas propredades
Prncpo do Trabalho rtual (PT)..Contnuo com mcroestrutura Na teora que leva em consderação a mcroestrutura do materal, cada partícula anda é representada por um ponto P, conforme Fgura. Porém suas propredades
Plano de Aula Leitura obrigatória Mecânica Vetorial para Engenheiros, 5ª edição revisada, Ferdinand P. Beer, E. Russell Johnston, Jr.
 UC - Goás Curso: Engenhara Cvl Dscplna: Mecânca Vetoral Corpo Docente: Gesa res lano e Aula Letura obrgatóra Mecânca Vetoral para Engenheros, 5ª eção revsaa, ernan. Beer, E. ussell Johnston, Jr. Etora
UC - Goás Curso: Engenhara Cvl Dscplna: Mecânca Vetoral Corpo Docente: Gesa res lano e Aula Letura obrgatóra Mecânca Vetoral para Engenheros, 5ª eção revsaa, ernan. Beer, E. ussell Johnston, Jr. Etora
Eletromagnetismo Indutores e Indutância
 Eletromagnetsmo Indutores e Indutânca Eletromagnetsmo» Indutores e Indutânca Introdução Indutores são elementos muto útes, pos com eles podemos armazenar energa de natureza magnétca em um crcuto elétrco.
Eletromagnetsmo Indutores e Indutânca Eletromagnetsmo» Indutores e Indutânca Introdução Indutores são elementos muto útes, pos com eles podemos armazenar energa de natureza magnétca em um crcuto elétrco.
7.4 Precificação dos Serviços de Transmissão em Ambiente Desregulamentado
 64 Capítulo 7: Introdução ao Estudo de Mercados de Energa Elétrca 7.4 Precfcação dos Servços de Transmssão em Ambente Desregulamentado A re-estruturação da ndústra de energa elétrca que ocorreu nos últmos
64 Capítulo 7: Introdução ao Estudo de Mercados de Energa Elétrca 7.4 Precfcação dos Servços de Transmssão em Ambente Desregulamentado A re-estruturação da ndústra de energa elétrca que ocorreu nos últmos
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
ANÁLISE E CARACTERIZAÇÃO DE MODELOS DE CUSTOS QUE UTILIZAM O VALOR DE SHAPLEY PARA ALOCAÇÃO DE CUSTOS ENTRE DEPARTAMENTOS
 ANÁLISE E CARACTERIZAÇÃO DE MODELOS DE CUSTOS QUE UTILIZAM O VALOR DE SHAPLEY PARA ALOCAÇÃO DE CUSTOS ENTRE DEPARTAMENTOS Autores: FRANCISCO ANTONIO BEZERRA (FUNDAÇÃO UNIVERSIDADE REGIONAL DE BLUMENAU)
ANÁLISE E CARACTERIZAÇÃO DE MODELOS DE CUSTOS QUE UTILIZAM O VALOR DE SHAPLEY PARA ALOCAÇÃO DE CUSTOS ENTRE DEPARTAMENTOS Autores: FRANCISCO ANTONIO BEZERRA (FUNDAÇÃO UNIVERSIDADE REGIONAL DE BLUMENAU)
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS
 Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
(note que não precisa de resolver a equação do movimento para responder a esta questão).
 Mestrado Integrado em Engenhara Aeroespacal Mecânca e Ondas 1º Ano -º Semestre 1º Teste 31/03/014 18:00h Duração do teste: 1:30h Lea o enuncado com atenção. Justfque todas as respostas. Identfque e numere
Mestrado Integrado em Engenhara Aeroespacal Mecânca e Ondas 1º Ano -º Semestre 1º Teste 31/03/014 18:00h Duração do teste: 1:30h Lea o enuncado com atenção. Justfque todas as respostas. Identfque e numere
INTRODUÇÃO SISTEMAS. O que é sistema? O que é um sistema de controle? O aspecto importante de um sistema é a relação entre as entradas e a saída
 INTRODUÇÃO O que é sstema? O que é um sstema de controle? SISTEMAS O aspecto mportante de um sstema é a relação entre as entradas e a saída Entrada Usna (a) Saída combustível eletrcdade Sstemas: a) uma
INTRODUÇÃO O que é sstema? O que é um sstema de controle? SISTEMAS O aspecto mportante de um sstema é a relação entre as entradas e a saída Entrada Usna (a) Saída combustível eletrcdade Sstemas: a) uma
9. Derivadas de ordem superior
 9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
Aula 1- Distâncias Astronômicas
 Aula - Distâncias Astronômicas Área 2, Aula Alexei Machao Müller, Maria e Fátima Oliveira Saraiva & Kepler e Souza Oliveira Filho Ilustração e uma meição e istância a Terra (à ireita) à Lua (à esquera),
Aula - Distâncias Astronômicas Área 2, Aula Alexei Machao Müller, Maria e Fátima Oliveira Saraiva & Kepler e Souza Oliveira Filho Ilustração e uma meição e istância a Terra (à ireita) à Lua (à esquera),
Notas de Aula de Física
 Versão prelmnar 7 de setembro de Notas de Aula de Físca 7. TRABAO E ENERGIA CINÉTICA... MOVIMENTO EM UMA DIMENSÃO COM FORÇA CONSTANTE... TRABAO EXECUTADO POR UMA FORÇA VARIÁVE... Análse undmensonal...
Versão prelmnar 7 de setembro de Notas de Aula de Físca 7. TRABAO E ENERGIA CINÉTICA... MOVIMENTO EM UMA DIMENSÃO COM FORÇA CONSTANTE... TRABAO EXECUTADO POR UMA FORÇA VARIÁVE... Análse undmensonal...
UNIVERSIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE CIÊNCIAS INTEGRADAS DO PONTAL
 UNIVERIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE CIÊNCIA INTEGRADA DO PONTAL Físca Expermental IV Lentes Cmpstas Objetv Determnar as stâncas cas e lentes e um sstema e lentes cmpstas. Intruçã utas vezes
UNIVERIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE CIÊNCIA INTEGRADA DO PONTAL Físca Expermental IV Lentes Cmpstas Objetv Determnar as stâncas cas e lentes e um sstema e lentes cmpstas. Intruçã utas vezes
AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA
 CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
CAPÍTULO 1 AS LEIS DE NEWTON PROFESSOR ANDERSON VIEIRA Talvez o conceito físico mais intuitivo que carregamos conosco, seja a noção do que é uma força. Muito embora, formalmente, seja algo bastante complicado
EDITORIAL MODULO - WLADIMIR
 1. Um os granes problemas ambientais ecorrentes o aumento a proução inustrial munial é o aumento a poluição atmosférica. A fumaça, resultante a queima e combustíveis fósseis como carvão ou óleo, carrega
1. Um os granes problemas ambientais ecorrentes o aumento a proução inustrial munial é o aumento a poluição atmosférica. A fumaça, resultante a queima e combustíveis fósseis como carvão ou óleo, carrega
Despacho Econômico de. Sistemas Termoelétricos e. Hidrotérmicos
 Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Física Geral I - F Aula 12 Momento Angular e sua Conservação. 2º semestre, 2012
 Físca Geral I - F -18 Aula 1 Momento Angular e sua Conservação º semestre, 01 Momento Angular Como vmos anterormente, as varáves angulares de um corpo rígdo grando em torno de um exo fxo têm sempre correspondentes
Físca Geral I - F -18 Aula 1 Momento Angular e sua Conservação º semestre, 01 Momento Angular Como vmos anterormente, as varáves angulares de um corpo rígdo grando em torno de um exo fxo têm sempre correspondentes
Física. Setor B. Índice-controle de Estudo. Prof.: Aula 23 (pág. 86) AD TM TC. Aula 24 (pág. 87) AD TM TC. Aula 25 (pág.
 Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
3 Modelagem computacional do escoamento com superfícies livres e deformáveis
 3 Moelagem comptaconal o escoamento com sperfíces lres e eformáes Para resoler o escoamento em processos e reestmentos por Etrsão, se fzeram so o sstema e eqações e Naer-Stokes na forma bmensonal e as
3 Moelagem comptaconal o escoamento com sperfíces lres e eformáes Para resoler o escoamento em processos e reestmentos por Etrsão, se fzeram so o sstema e eqações e Naer-Stokes na forma bmensonal e as
Cap. 6 - Energia Potencial e Conservação da Energia Mecânica
 Unversdade Federal do Ro de Janero Insttuto de Físca Físca I IGM1 014/1 Cap. 6 - Energa Potencal e Conservação da Energa Mecânca Prof. Elvs Soares 1 Energa Potencal A energa potencal é o nome dado a forma
Unversdade Federal do Ro de Janero Insttuto de Físca Físca I IGM1 014/1 Cap. 6 - Energa Potencal e Conservação da Energa Mecânca Prof. Elvs Soares 1 Energa Potencal A energa potencal é o nome dado a forma
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
S.A. 1. 2002; TIPLER, P. A.; MOSCA, G.
 Rotação Nota Alguns sldes, fguras e exercícos pertencem às seguntes referêncas: HALLIDAY, D., RESNICK, R., WALKER, J. Fundamentos da Físca. V 1. 4a.Edção. Ed. Lvro Técnco Centífco S.A. 00; TIPLER, P. A.;
Rotação Nota Alguns sldes, fguras e exercícos pertencem às seguntes referêncas: HALLIDAY, D., RESNICK, R., WALKER, J. Fundamentos da Físca. V 1. 4a.Edção. Ed. Lvro Técnco Centífco S.A. 00; TIPLER, P. A.;
Capítulo 4 Trabalho e Energia
 Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Capítulo 4 Trabalho e Energia Este tema é, sem dúvidas, um dos mais importantes na Física. Na realidade, nos estudos mais avançados da Física, todo ou quase todos os problemas podem ser resolvidos através
Universidade Estadual do Sudoeste da Bahia
 Unversdade Estadual do Sudoeste da Baha Departamento de Cêncas Exatas e Naturas 5 - Rotações, Centro de Massa, Momento, Colsões, Impulso e Torque Físca I Ferrera Índce 1. Movmento Crcular Unformemente
Unversdade Estadual do Sudoeste da Baha Departamento de Cêncas Exatas e Naturas 5 - Rotações, Centro de Massa, Momento, Colsões, Impulso e Torque Físca I Ferrera Índce 1. Movmento Crcular Unformemente
10 DIMENSIONAMENTO DE SECÇÕES RETANGULARES COM ARMADURA DUPLA
 10 DIMENSIONAMENTO DE SECÇÕES RETANGULARES COM ARMADURA DUPLA 10.1 INTRODUÇÃO A armaura posicionaa na região comprimia e uma viga poe ser imensionaa a fim e se reuzir a altura e uma viga, caso seja necessário.
10 DIMENSIONAMENTO DE SECÇÕES RETANGULARES COM ARMADURA DUPLA 10.1 INTRODUÇÃO A armaura posicionaa na região comprimia e uma viga poe ser imensionaa a fim e se reuzir a altura e uma viga, caso seja necessário.
Energia de deformação na flexão
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
SOLENÓIDE E INDUTÂNCIA
 EETROMAGNETSMO 105 1 SOENÓDE E NDUTÂNCA 1.1 - O SOENÓDE Campos magnéticos prouzios por simples conutores ou por uma única espira são bastante fracos para efeitos práticos. Assim, uma forma e se conseguir
EETROMAGNETSMO 105 1 SOENÓDE E NDUTÂNCA 1.1 - O SOENÓDE Campos magnéticos prouzios por simples conutores ou por uma única espira são bastante fracos para efeitos práticos. Assim, uma forma e se conseguir
MAPEAMENTO DA VARIABILIDADE ESPACIAL
 IT 90 Prncípos em Agrcultura de Precsão IT Departamento de Engenhara ÁREA DE MECANIZAÇÃO AGRÍCOLA MAPEAMENTO DA VARIABILIDADE ESPACIAL Carlos Alberto Alves Varella Para o mapeamento da varabldade espacal
IT 90 Prncípos em Agrcultura de Precsão IT Departamento de Engenhara ÁREA DE MECANIZAÇÃO AGRÍCOLA MAPEAMENTO DA VARIABILIDADE ESPACIAL Carlos Alberto Alves Varella Para o mapeamento da varabldade espacal
Capítulo 4: Equações e Considerações Adicionais para Projeto
 68 Capítulo 4: Equações e Conserações Aconas para Projeto Bem feto é melhor que bem to. Benjamn Frankln (106-190) 4.1. Apresentação A partr a análse matemátca o crcuto retfcaor apresentao no Capítulo,
68 Capítulo 4: Equações e Conserações Aconas para Projeto Bem feto é melhor que bem to. Benjamn Frankln (106-190) 4.1. Apresentação A partr a análse matemátca o crcuto retfcaor apresentao no Capítulo,
Hoje não tem vitamina, o liquidificador quebrou!
 A U A UL LA Hoje não tem vtamna, o lqudfcador quebrou! Essa fo a notíca dramátca dada por Crstana no café da manhã, lgeramente amenzada pela promessa de uma breve solução. - Seu pa dsse que arruma à note!
A U A UL LA Hoje não tem vtamna, o lqudfcador quebrou! Essa fo a notíca dramátca dada por Crstana no café da manhã, lgeramente amenzada pela promessa de uma breve solução. - Seu pa dsse que arruma à note!
Mecânica Analítica REVISÃO
 Mecânica Analítica REVISÃO Prof. Nelson Luiz Reyes Marques Vínculos São limitações às possíveis posições e velociaes as partículas e um sistema mecânico, restringino a priori o seu movimento. É importante
Mecânica Analítica REVISÃO Prof. Nelson Luiz Reyes Marques Vínculos São limitações às possíveis posições e velociaes as partículas e um sistema mecânico, restringino a priori o seu movimento. É importante
Polos Olímpicos de Treinamento. Aula 10. Curso de Teoria dos Números - Nível 2. Divisores. Prof. Samuel Feitosa
 Polos Olímpcos de Trenamento Curso de Teora dos Números - Nível 2 Prof. Samuel Fetosa Aula 10 Dvsores Suponha que n = p α 1 2...pα é a fatoração em prmos do ntero n. Todos os dvsores de n são da forma
Polos Olímpcos de Trenamento Curso de Teora dos Números - Nível 2 Prof. Samuel Fetosa Aula 10 Dvsores Suponha que n = p α 1 2...pα é a fatoração em prmos do ntero n. Todos os dvsores de n são da forma
1 A Integral por Partes
 Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
GABARITO ERP19. impedância total em pu. impedância linha em pu; impedância carga em pu; tensão no gerador em pu.
 GABARITO ERP9 Questão mpedânca total em pu. mpedânca lnha em pu; mpedânca carga em pu; tensão no gerador em pu. Assm, tem-se que: ( ). Mas, ou seja: : ( ).. Logo: pu. () A mpedânca da carga em pu,, tem
GABARITO ERP9 Questão mpedânca total em pu. mpedânca lnha em pu; mpedânca carga em pu; tensão no gerador em pu. Assm, tem-se que: ( ). Mas, ou seja: : ( ).. Logo: pu. () A mpedânca da carga em pu,, tem
Questões de Vestibulares
 Cnemátca: movmento retlíneo, movmento curvlíneo Questões e Vestbulares. (UFRJ) Heloísa, sentaa na poltrona e um ônbus, afrma que o passagero sentao à sua frente não se move, ou seja, está em repouso. o
Cnemátca: movmento retlíneo, movmento curvlíneo Questões e Vestbulares. (UFRJ) Heloísa, sentaa na poltrona e um ônbus, afrma que o passagero sentao à sua frente não se move, ou seja, está em repouso. o
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO PROGRAMA DE EDUCAÇÃO TUTORIAL - MATEMÁTICA PROJETO FUNDAMENTOS DE MATEMÁTICA ELEMENTAR Assuntos: Matrizes; Matrizes Especiais; Operações com Matrizes; Operações Elementares
O USO DA INTEGRAL DEFINIDA NO CÁLCULO DA ÁREA ALAGADA DA BARRAGEM DO RIO BONITO
 O USO DA INTEGRAL DEFINIDA NO CÁLCULO DA ÁREA ALAGADA DA BARRAGEM DO RIO BONITO Crstna Martns Paraol crstna@hotmal.com Insttuto Federal Catarnense Rua Prefeto Francsco Lummertz Júnor, 88 88960000 Sombro
O USO DA INTEGRAL DEFINIDA NO CÁLCULO DA ÁREA ALAGADA DA BARRAGEM DO RIO BONITO Crstna Martns Paraol crstna@hotmal.com Insttuto Federal Catarnense Rua Prefeto Francsco Lummertz Júnor, 88 88960000 Sombro
ESTUDO DA MÁQUINA SIMÉTRICA TRIFÁSICA
 CAPÍTUO ETUDO DA ÁQUINA IÉTICA TIFÁICA. INTODUÇÃO A máquna de ndução trfásca com rotor bobnado é smétrca. Apresenta estruturas magnétcas clíndrcas tanto no rotor quanto no estator. Os enrolamentos, tanto
CAPÍTUO ETUDO DA ÁQUINA IÉTICA TIFÁICA. INTODUÇÃO A máquna de ndução trfásca com rotor bobnado é smétrca. Apresenta estruturas magnétcas clíndrcas tanto no rotor quanto no estator. Os enrolamentos, tanto
3 Metodologia de Avaliação da Relação entre o Custo Operacional e o Preço do Óleo
 3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
CAPÍTULO V CÁLCULO DOS ESFORÇOS INTERNOS RESISTENTES DADOS a, 1/R a E e O
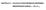 CAPÍTULO V CÁLCULO DOS ESFOÇOS ITEOS ESISTETES DADOS a / a E e O Cálculo os Esforços Internos esstentes Daos /r e εo 5 Cálculo os Esforços Internos esstentes Daos a /r a e e o 5 Introução A etermnação
CAPÍTULO V CÁLCULO DOS ESFOÇOS ITEOS ESISTETES DADOS a / a E e O Cálculo os Esforços Internos esstentes Daos /r e εo 5 Cálculo os Esforços Internos esstentes Daos a /r a e e o 5 Introução A etermnação
8- Controlador PID. PID = Proporcional + Integral + Derivativo
 Controlaor PID 154 8- Controlaor PID PID = Proporcional + Integral + Derivativo É interessante assinalar que mais a metae os controlaores inustriais em uso nos ias atuais utiliza estratégias e controle
Controlaor PID 154 8- Controlaor PID PID = Proporcional + Integral + Derivativo É interessante assinalar que mais a metae os controlaores inustriais em uso nos ias atuais utiliza estratégias e controle
Um modelo nada mais é do que uma abstração matemática de um processo real (Seborg et al.,1989) ou
 Dscplna - MR070 INTRODUÇÃO À MODELAGEM DE SISTEMAS LINEARES POR EQUAÇÕES DIFERENCIAIS Os modelos de um determnado sstema podem ser físcos ou matemátcos. Neste curso focaremos a modelagem pela dentfcação
Dscplna - MR070 INTRODUÇÃO À MODELAGEM DE SISTEMAS LINEARES POR EQUAÇÕES DIFERENCIAIS Os modelos de um determnado sstema podem ser físcos ou matemátcos. Neste curso focaremos a modelagem pela dentfcação
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
AULA 10 Entropia e a Segunda Lei da Termodinâmica
 UFABC - BC0205 - Prof. Germán Lugones AULA 10 Entropa e a Segunda Le da ermodnâmca Sad Carnot [1796-1832] R. Clausus [1822-1888] W. homson (Lord Kelvn) [1824-1907] Quando um saco de ppocas é aquecdo em
UFABC - BC0205 - Prof. Germán Lugones AULA 10 Entropa e a Segunda Le da ermodnâmca Sad Carnot [1796-1832] R. Clausus [1822-1888] W. homson (Lord Kelvn) [1824-1907] Quando um saco de ppocas é aquecdo em
MECÂNICA CLÁSSICA. AULA N o 9. Colchetes de Poisson Simetrias Espaço de Fases Transformações Canônicas (Hamiltoniano)
 1 MECÂNICA CLÁSSICA AULA N o 9 Colchetes de Posson Smetras Esaço de Fases Transformações Canôncas (amltonano) O Esaço de Fases tem uma estrutura assocada a s. Esaços ossuem estruturas, que se referem aos
1 MECÂNICA CLÁSSICA AULA N o 9 Colchetes de Posson Smetras Esaço de Fases Transformações Canôncas (amltonano) O Esaço de Fases tem uma estrutura assocada a s. Esaços ossuem estruturas, que se referem aos
AS COMPONENTES SIMÉTRICAS INSTANTÂNEAS E A MÁQUINA SIMÉTRICA
 CAPÍTULO 5 A COMPONENTE IMÉTICA INTANTÂNEA E A MÁQUINA IMÉTICA 5. INTODUÇÃO O emprego das componentes smétrcas nstantâneas permte a obtenção de modelos mas smples que aqueles obtdos com a transformação
CAPÍTULO 5 A COMPONENTE IMÉTICA INTANTÂNEA E A MÁQUINA IMÉTICA 5. INTODUÇÃO O emprego das componentes smétrcas nstantâneas permte a obtenção de modelos mas smples que aqueles obtdos com a transformação
ASSOCIAÇÃO DE RESISTORES
 Prof(a) Stela Mara de arvalho Fernandes SSOIÇÃO DE ESISTOES ssocação de esstores em Sére Dos ou mas resstores estão assocados em sére quando são percorrdos pela mesma corrente elétrca. omo U D Somando
Prof(a) Stela Mara de arvalho Fernandes SSOIÇÃO DE ESISTOES ssocação de esstores em Sére Dos ou mas resstores estão assocados em sére quando são percorrdos pela mesma corrente elétrca. omo U D Somando
O degrau de potencial. Caso II: energia maior que o degrau
 O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
Metodologia IHFA - Índice de Hedge Funds ANBIMA
 Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Conteúdo 4 - Impulsos elétricos e fenômenos biológicos
 Conteúdo 4 - Impulsos elétrcos e fenômenos bológcos 4.1 Introdução Os seres vvos, em sua grande maora, são compostos majortaramente por água. A água é uma materal que na presença de certos sas se comporta
Conteúdo 4 - Impulsos elétrcos e fenômenos bológcos 4.1 Introdução Os seres vvos, em sua grande maora, são compostos majortaramente por água. A água é uma materal que na presença de certos sas se comporta
