Transformada de Laplace. Transformada de Laplace (CP1) DEQ/UFSCar 1 / 76
|
|
|
- Lucinda Araújo de Miranda
- 6 Há anos
- Visualizações:
Transcrição
1 Transformada de Laplace Transformada de Laplace (CP) DEQ/UFSCar / 76
2 Roteiro I Introdução Definição da Transformada Transformada de Laplace de Algumas Funções Transformada de Derivadas Solução de Equações Diferenciais Lineares 2 Inversão por Frações Parciais Raízes Distintas, Reais ou Complexas Raízes Múltiplas 3 Solução de Equações Diferenciais Lineares com a Transformada de Laplace 4 Natureza Qualitativa das Soluções 5 Propriedades Adicionais das Transformadas de Laplace 6 Exemplos Equação Diferencial de Primeira Ordem (Geral) Equação Diferencial de Primeira Ordem Equação Diferencial de Segunda Ordem (Geral) Transformada de Laplace (CP) DEQ/UFSCar 2 / 76
3 Roteiro II Equação Diferencial de Segunda Ordem (Raízes Reais Diferentes) Equação Diferencial de Segunda Ordem (Raízes Complexas) Equação Diferencial de Segunda Ordem (Raízes Múltiplas) Sistema com Interação 7 Atividades Complementares Transformada de Laplace (CP) DEQ/UFSCar 3 / 76
4 Introdução à Transformada de Laplace O método da Transformada de Laplace é uma ferramenta que proporciona a solução de equações diferenciais lineares com coeficientes constantes, de maneira sistemática e relativamente simples. Uma classe importante do controle se restringe à resolução desses tipos de equações. Portanto, destaca-se a importância da Transformada de Laplace no controle de processos. A transformação de uma equação diferencial resulta em uma equação algébrica, onde a variável s substitui a variável independente (como o tempo, t). Transformada de Laplace (CP) DEQ/UFSCar 4 / 76
5 Introdução à Transformada de Laplace - I F = H E C E = 6 H = I B H A = F =? A - G K =, E B A H A? E = E A I E? E = E I A + J H 5 2 H > A = H E C E = 6 H = I B H = L A H I A = F =? A - I F = 6 H = I B H A = F =? A - G K = ) C > H E? = 5 K Figura: Esquema da transformação e solução da equação diferencial Transformada de Laplace (CP) DEQ/UFSCar 5 / 76
6 Definição da Transformada de Laplace A Transformada de Laplace de uma função f (t) é F (s) = L{f (t)} = A Transformada de Laplace é linear 0 f (t)e st dt L{a f (t) + a 2 f 2 (t)} = a L{f (t)} + a 2 L{f 2 (t)} Transformada de Laplace (CP) DEQ/UFSCar 6 / 76
7 Transformada de Laplace de Algumas Funções Item F(s) f (t) δ(t), impulso unitário 2 u (t), degrau unitário s s 2 s n (n = 3, 4,...) s+a τs+ (s+a) n (n = 2, 3,...) (τs+) n (n = 2, 3,...) s (s+a) 2 s(s+a) s(τs+) s(τs+) n t, rampa t n (n )! e at τ e t/τ t n e at (n )! t n e t/τ τ n (n )! e at ( at) a ( e at ) e t/τ e t/τ n i=0 (t/τ) i i! Transformada de Laplace (CP) DEQ/UFSCar 7 / 76
8 Transformada de Laplace de Algumas Funções Item F (s) f (t) (s+a)(s+b) (b a) (e at e bt ) (τ s+)(τ 2 s+) (τ 2 τ ) (e t/τ e t/τ 2) s (s+a)(s+b) (a b) (ae at be bt ) s+c (c a) (s+a)(s+b) (b a) e at + (c b) (a b) e bt τ 3 s+ (τ τ 3 ) (τ s+)(τ 2 s+) τ (τ τ 2 ) e t/τ + (τ 2 τ 3 ) τ 2 (τ 2 τ ) e t/τ 2 [ ] s(s+a)(s+b) ab + (a b) (be at ae bt ) e at (s+a)(s+b)(s+c) (b a)(c a) + e bt (a b)(c b) + e ct (a c)(b c) (s+d) (d a)e at (s+a)(s+b)(s+c) (b a)(c a) + (d b)e bt (a b)(c b) + (d c)e ct (a c)(b c) s 2 +a 2 a sen(at) [ cos(at)] s(s 2 +a 2 ) a 2 Transformada de Laplace (CP) DEQ/UFSCar 8 / 76
9 Transformada de Laplace de Algumas Funções Item F(s) f (t) s s 2 +a 2 a cos(φ)+s sen(φ) cos(at) s 2 +a 2 sen(at + φ) (s+a) 2 +b 2 s+a (s+a) 2 +b 2 b e at sen(bt) e at cos(bt) 27 e as δ(t a), impulso unitário em t = a e as s w (τs+)(s 2 +w 2 ) s 2 (τs+) ( wτ τ 2 w 2 + u (t a), degrau unitário em t = a ) e t/τ + sen(wt + θ) τ 2 w 2 + onde θ = arctg( wτ) τ(e t/τ + t/τ ) s(τ s+)(τ 2 s+) + (τ 2 τ ) (τ e t/τ τ 2 e t/τ 2) τ 3 s+ s(τ s+)(τ 2 s+) + (τ 3 τ ) (τ τ 2 ) e t/τ + (τ 3 τ 2 ) (τ 2 τ ) e t/τ 2 33 f (s)e as f (t a) Transformada de Laplace (CP) DEQ/UFSCar 9 / 76
10 Transformada de Laplace de Algumas Funções Inversões que Apresentam Respostas com Decaimento Oscilatório ξ < ; A = ( ξ 2 ); B = ( ξ 2 )/τ; C = ξ/τ Item F(s) f (t) τ 2 s 2 +2ξτs+ s(τ 2 s 2 +2ξτs+) τ s+ τ 2 s 2 +2ξτs+ Aτ e ct sen(bt) A e ct sen(bt + φ) onde φ = arctg ( ) B C [ Aτ 2τ C + ( τ ) ] 2 /2 τ e ct sen(bt + φ) ) onde φ = arctg ( τ B τ C Transformada de Laplace (CP) DEQ/UFSCar 0 / 76
11 Transformada de Derivadas A Transformada de Laplace tem a propriedade singular de transformar a operação de diferenciação em relação a t em uma multiplicação por s: { } df (t) L = sf(s) f (0), f (0) = f (t = 0) dt { d 2 } f (t) L dt 2 = s 2 F(s) sf (0) f (0), f (0) = f (t = 0) { d n } f (t) L dt n = s n F (s) s n f (0) s n 2 f (0) sf n 2 (0) f n (0), f (i) (0) = f (i) (t = 0) Transformada de Laplace (CP) DEQ/UFSCar / 76
12 Solução de Equações Diferenciais Lineares Na resolução de equações diferenciais por Transformada de Laplace, as funções f i (t) são convertidas em suas transformadas e as equações algébricas resultantes são resolvidas para as funções F i (s) desconhecidas. Segue-se o seguinte procedimento: obter a Transformada de Laplace de ambos os membros da equação (as condições iniciais são incorporadas neste passo nas transformadas das derivadas) 2 resolver algebricamente a equação resultante para a Transformada de Laplace da função desconhecida 3 achar a função de t que possui a Transformada de Laplace obtida no passo 2. Esta função satisfaz a equação diferencial e as condições iniciais e, conseqüentemente, é a função desejada (obter a Transformada Inversa de Laplace, L ) Transformada de Laplace (CP) DEQ/UFSCar 2 / 76
13 Inversão por Frações Parciais As equações diferenciais a serem resolvidas são todas da forma geral a n d n y dt n + a d n y n dt n + + a dy dt + a 0y = b m d m u dt m + b m onde y (i) (0) = y (i) (t = 0) e u (i) (0) = u (i) (t = 0). d m u dt m + + b du dt + b 0u () A função desconhecida é y(t) (resposta do sistema). A função u(t) é chamada de função perturbação (entrada do sistema). a n, a n,, a, a 0, b m, b m,, b, b 0 são coeficientes constantes. Transformada de Laplace (CP) DEQ/UFSCar 3 / 76
14 Inversão por Frações Parciais Quando a Transformada de Laplace é aplicada em ambos os lados da equação (), as condições iniciais são introduzidas e, então Y (s) = c ms m + c m s m + + c s + c 0 s n + d n s n U(s) = N(s) + + d s + d 0 D(s) onde N(s) e D(s) são polinômios em s que representam o numerador e o denominador, com graus m e n, respectivamente. Transformada de Laplace (CP) DEQ/UFSCar 4 / 76
15 Inversão por Frações Parciais Sendo o grau de D(s) maior do que o de N(s), Y (s) pode ser expandida em frações parciais, após fatorar o polinômio D(s), tal que Y (s) = N(s) (s p )(s p 2 ) (s p n ) U(s) onde p, p 2,, p n são as raízes reais ou complexas do polinômio D(s). D(s) é conhecido como a equação característica ou polinômio característico e [p, p 2,, p n ] são os pólos do sistema representado por Y (s)/u(s). Determinadas essas raízes, o próximo passo depende da natureza de seus valores e da frequência em que elas aparecem. Transformada de Laplace (CP) DEQ/UFSCar 5 / 76
16 Inversão por Frações Parciais Raízes Distintas, Reais ou Complexas Quando as raízes são reais ou complexas, mas distintas, pode-se escrever Y (s) como a soma de frações parciais, com um termo para cada raiz p i : Y (s) = N(s) D(s) = N(s) (s p )(s p 2 ) (s p n ) U(s) para U(s) = (impulso unitário) (2) Y (s) = A + A A n s p s p 2 s p n (3) Para calcular o coeficiente A i, multiplique ambos os lados da equação (3) por (s p i ). Após substituir s por p i, todos os termos do lado direito da equação (3) desaparecem, com exceção de A i. Portanto, A i = [ (s p i ) N(s) D(s) ] s=p i = N(p i ) (p i p )(p i p 2 ) (p i p n ) Procedimento análogo é utilizado para encontrar os demais coeficientes. Transformada de Laplace (CP) DEQ/UFSCar 6 / 76
17 Inversão por Frações Parciais Raízes Distintas, Reais ou Complexas () Cada termo da expansão em frações parciais com uma raiz real resultará em um termo no domínio do tempo, tal que a Transformada Inversa de Laplace será A i s p i = L A i e p i t Existindo uma raiz complexa, necessariamente uma outra raiz é complexa conjugada da primeira: p j = a j + ıb j e p k = a k ıb k, onde a j = a k e b j = b k. A Transformada Inversa de Laplace dos pares complexos forma a expressão A j s (a j + ıb j ) + A k s (a k ıb k ) L = A j e (a j +ıb j )t + A k e (a k ıb k )t Transformada de Laplace (CP) DEQ/UFSCar 7 / 76
18 Inversão por Frações Parciais Raízes Distintas, Reais ou Complexas () Aplicando a identidade trigonométrica e x+ıy = e x (cos y + ı seny) no resultado da transformada inversa, esta resulta em (A j + A k )e a j t cos(b j t) + (A j A k )e a j t ı sen(b j t) Utilizando uma outra identidade trigonométrica a cos b + a 2 senb = a 3 sen(b + φ), onde a 3 e φ são calculados de a 3 = a 2 + a2 2 e φ = tan (a /a 2 ), obtém-se 2e a j t A j A k sen(b j t + φ), com [ ] φ = tan Aj + A k (A j A k )ı Transformada de Laplace (CP) DEQ/UFSCar 8 / 76
19 Inversão por Frações Parciais Raízes Múltiplas Se o polinômio D(s) apresentar raízes múltiplas, o fator (s p i ) n do denominador de Y (s) dará origem a n termos na expansão em frações parciais, tal que Y (s) = N(s) D(s) = A i, (s p i ) n + A i,2 (s p i ) n + + A i,n (s p i ) + (4) A constante A i, pode ser determinada da forma usual, pela multiplicação por (s p i ) n e fazendo s = p i. As outras constantes são determinadas por sucessivas multiplicações do resultado da diferenciação da equação (4), após substituir s por p i. Os termos apresentados na equação (4) conduzem à seguinte expressão como transformada inversa: [ Ai, (n )! tn + A ] i,2 (n 2)! tn A i,n t + A i,n e p i t Transformada de Laplace (CP) DEQ/UFSCar 9 / 76
20 Solução de Equações Diferenciais Lineares com a Transformada de Laplace Resumindo: as seguintes etapas são executadas obter a Transformada de Laplace de ambos os membros da equação 2 resolver algebricamente a equação resultante 3 inversão da transformada técnica da expansão em frações parciais Transformada de Laplace (CP) DEQ/UFSCar 20 / 76
21 Solução de Equações Diferenciais Lineares com a Transformada de Laplace Forma Geral: modelo LTI Em notação vetorial { ẋ = Ax + Bu, x0 = 0 y = Cx + Du Aplica-se a Transformada de Laplace em ambos os lados das duas equações do modelo LTI, substituindo X(s) obtido da resolução da primeira equação na equação da saída Y(s). Ao final obtém-se uma relação entre a saída e a entrada, Y(s)/U(s), conhecida como Função de Transferência (ou Matriz Função de Transferência), denominada de G(s): Y(s) = [C(s A) B + D]U(s) }{{} G(s) Transformada de Laplace (CP) DEQ/UFSCar 2 / 76
22 Solução de Equações Diferenciais Lineares com a Transformada de Laplace Essa equação permite a conversão entre a representação do sistema da forma em Espaço de Estado (LTI: domínio do t) para o da forma Função de Transferência (domínio s). Transformada de Laplace (CP) DEQ/UFSCar 22 / 76
23 Natureza Qualitativa das Soluções F F A informação sobre a forma da solução y(t) pode ser diretamente obtida das raízes (pólos) do denominador de Y (s) chamado de equação característica. A natureza qualitativa da solução de y(t) está relacionada à localização das raízes (pólos) da equação característica no plano complexo: = > A E N E = C E H E F! F " >! = " > " F F $ F # = = # F " >! F! = > = " > " A E N H A = Pólos Termos em y(t) para t > 0 p A e a t p 2, p2 e a2t [A cos(b 2 t) + A 2 sen(b 2 t)] p 3, p3 A cos(b 3 t) + A 2 sen(b 3 t) p 4, p4 e a4t [A cos(b 4 t) + A 2 sen(b 4 t)] p 5 A e a 5t p 6 A A I J L A E I J L A Transformada de Laplace (CP) DEQ/UFSCar 23 / 76
24 Natureza Qualitativa das Soluções Observa-se, então, que: pólos à esquerda do eixo imaginágio (semi-plano esquerdo) correspondem a respostas que decrescem exponencialmente com o tempo: sistemas estáveis pólos à direita do eixo imaginágio (semi-plano direito) correspondem a respostas que crescem exponencialmente com o tempo: sistemas instáveis pólos complexos conjugados fazem a resposta oscilar com o tempo com amplitudes decrescentes (sistemas estáveis) quando localizados no semi-plano esquerdo com amplitudes crescentes (sistemas instáveis) quando localizados no semi-plano direito com amplitudes constantes (no limite de estabilidade) quando localizados sobre o eixo imaginário Transformada de Laplace (CP) DEQ/UFSCar 24 / 76
25 Natureza Qualitativa das Soluções pólos sobre a origem indicam uma resposta constante no tempo é óbvio que para uma dada entrada, u(t), deve-se considerar as raízes adicionais introduzidas pelo denominador de U(s) para se ter um quadro completo da resposta qualitativa do sistema Transformada de Laplace (CP) DEQ/UFSCar 25 / 76
26 Conversão Entre LTI e Função de Transferência estudo de caso Tanque de Aquecimento com Agitação O modelo LTI (espaço de estado) (ḣ ) ( ) ( ) 0, 0 0 h = + Ṫ 0, 30 T }{{}}{{}}{{} ẋ A x Fi ( ) Ti, 00 0, Fi2 86, 52 0, 0 84, 52 0, 0 90, 04, 0 }{{} Ti2, x 0 = 0 Fst B Tst }{{} u ( ) ( ) ( ) h 0 h = T 0 T }{{}}{{}}{{} y C x Transformada de Laplace (CP) DEQ/UFSCar 26 / 76
27 Conversão Entre LTI e Função de Transferência estudo de caso () Tanque de Aquecimento com Agitação pode ser transformado em modelo na forma função de transferência, utilizando Y(s) = [C(s A) B + D]U(s) }{{} G(s) cuja Matriz Função de Transferência, G(s), é calculada utilizando as instruções no MATLAB sysss=ss(a,b,c,d) % cria modelo em espaço de estado systf=tf(sysss) % cria modelo em função de transferência ou instruções equivalentes no SCILAB sysss=syslin( c,a,b,c) // cria modelo contínuo (c) em espaço de estado com D = 0 systf=ss2tf(sysss) // cria modelo em função de transferência Transformada de Laplace (CP) DEQ/UFSCar 27 / 76
28 Conversão Entre LTI e Função de Transferência estudo de caso () Tanque de Aquecimento com Agitação ( ) h(s) = T (s) }{{} Y(s) ( s+0,0 0 86,52 0,0 84,52 s+,30 s+,30 s+,30 s+0, ,0 s+,30 90,04 s+,30,0 s+,30 } {{ } G(s) Fi(s) ) Ti(s) Fi2(s) Ti2(s) Fst(s) Tst(s) }{{} U(s) Transformada de Laplace (CP) DEQ/UFSCar 28 / 76
29 Conversão Entre LTI e Função de Transferência estudo de caso () Tanque de Aquecimento com Agitação mostrando as 2 6 funções de transferências entre as 2 saídas [h(s)t (s)] T e as 6 entradas [Fi(s)Ti(s)Fi2(s)Ti2(s) Fst(s)Tst(s)] T, Y i (s) U j (s) : h(s) Fi(s) = s + 0, 0 h(s) Ti(s) = 0 h(s) Fi2(s) = s + 0, 0 h(s) Ti2(s) = 0 h(s) Fst(s) = 0 h(s) Tst(s) = 0 T (s) 86, 52 = Fi(s) s +, 30 T (s) 0, 0 = Ti(s) s +, 30 T (s) 84, 52 = Fi2(s) s +, 30 T (s) 0, 0 = Ti2(s) s +, 30 T (s) 90, 04 = Fst(s) s +, 30 T (s), 0 = Tst(s) s +, 30 Transformada de Laplace (CP) DEQ/UFSCar 29 / 76
30 Propriedades Adicionais das Transformadas de Laplace Propriedades selecionadas de acordo com sua aplicabilidade em teoria de controle, lembrando que F (s) = L{f (t)}: Teorema do Valor Final lim [f (t)] = lim [sf(s)] t s 0 desde que sf(s) seja finita. Caso contrário, f (t) não apresenta limite quando t. Teorema do Valor Inicial Translação da Transformada lim[f (t)] = lim [sf(s)] t 0 s L{e at f (t)} = F (s + a) Transformada de Laplace (CP) DEQ/UFSCar 30 / 76
31 Propriedades Adicionais das Transformadas de Laplace B J Transformada de uma Integral Translação da Função B J { t } L f (t)dt = F (s) 0 s L{f (t t 0 )} = e t 0s F(s) B J J J Transformada de Laplace (CP) DEQ/UFSCar 3 / 76
32 Equação Diferencial de Primeira Ordem Exemplo Obtenha a solução da seguinte equação diferencial linear de primeira ordem a dy dt + a 0y = b 0 u, y(t = 0) = y(0) com a, a 0, b 0 0, y(0) = 0 e u é um degrau de amplitude A. Transformada de Laplace (CP) DEQ/UFSCar 32 / 76
33 Equação Diferencial de Primeira Ordem Solução a dy dt + a 0y = b 0 u, y(0) = 0 Aplicando a Transformada de Laplace em ambos os lados da equação: { } dy L a dt + a 0y = L{b 0 u} a sy (s) y(0) }{{} + a 0Y (s) = b 0 U(s) =0 Transformada de Laplace (CP) DEQ/UFSCar 33 / 76
34 Equação Diferencial de Primeira Ordem Resolvendo a equação no domínio da Transformada: a sy (s) + a 0 Y (s) = b 0 U(s) (a s + a 0 ) Y (s) = b 0 U(s) Y (s) = b 0 U(s) Y (s) a s + a 0 U(s) = b 0 a s + a 0 ou Y (s) U(s) = b 0 a 0 Substituindo u pelo degrau de amplitude A: Y (s) U(s) = Y (s) = a a 0 s + (a 0 0 e pólo p = a 0 /a ) b 0 a 0 a a 0 s + Y (s) = b 0 a 0 A s( a a 0 s + ) b 0 a 0 a a 0 s + Transformada de Laplace (CP) DEQ/UFSCar 34 / 76 A s
35 Equação Diferencial de Primeira Ordem Costuma-se chamar b 0 a 0 = K p e a a 0 = τ p. Calculando a transformada inversa de Y (s) utilizando uma tabela de Transformada de Laplace: Y (s) = K p A s(τ p s + ) L = y(t) = K p A ( e t/τp) Transformada de Laplace (CP) DEQ/UFSCar 35 / 76
36 Equação Diferencial de Primeira Ordem Exemplo Obtenha a solução da seguinte equação diferencial linear de primeira ordem a dy dt + a 0y = b 0 u, y(t = 0) = y(0) com a = a 0 = b 0 =, y(0) = 0 e u é um degrau de amplitude unitário. Transformada de Laplace (CP) DEQ/UFSCar 36 / 76
37 Equação Diferencial de Primeira Ordem Solução a dy dt + a 0y = b 0 u, y(0) = 0 Aplicando a Transformada de Laplace em ambos os lados da equação: { } dy L a dt + a 0y = L{b 0 u} a sy (s) y(0) }{{} + a 0Y (s) = b 0 U(s) =0 Transformada de Laplace (CP) DEQ/UFSCar 37 / 76
38 Equação Diferencial de Primeira Ordem Resolvendo a equação no domínio da Transformada: a sy (s) + a 0 Y (s) = b 0 U(s) (a s + a 0 ) Y (s) = b 0 U(s) Y (s) = b 0 U(s) Y (s) a s + a 0 U(s) = b 0 a s + a 0 ou Y (s) U(s) = b 0 a 0 a a 0 s + (a 0 0 e pólo p = a 0 /a ) Substituindo os coeficientes a = a 0 = b 0 = e u pelo degrau unitário: Y (s) U(s) = Y (s) = b 0 a 0 s + s a a 0 s + Y (s) = s(s + ) Transformada de Laplace (CP) DEQ/UFSCar 38 / 76
39 Equação Diferencial de Primeira Ordem Calculando a transformada inversa de Y (s) utilizando uma tabela de Transformada de Laplace: Y (s) = s(s + ) L = y(t) = e t Transformada de Laplace (CP) DEQ/UFSCar 39 / 76
40 Equação Diferencial de Segunda Ordem Exemplo Obtenha a solução da seguinte equação diferencial linear de segunda ordem d 2 y a 2 dt 2 + a dy dt + a 0y = b 0 u, y(t = 0) = y(0) e y (t = 0) = y (0) com a 2, a, a 0, b 0 0 e y(0) = y (0) = 0 e u é um degrau de amplitude A. Transformada de Laplace (CP) DEQ/UFSCar 40 / 76
41 Equação Diferencial de Segunda Ordem Solução d 2 y a 2 dt 2 + a dy dt + a 0y = b 0 u, y(0) = y (0) = 0 Aplicando a Transformada de Laplace em ambos os lados da equação: { d 2 y L a 2 a 2 } dy dt + a 0y dt 2 + a = L {b 0 u} s2 Y (s) s y(0) y (0) }{{}}{{} + a sy (s) y(0) }{{} + a 0Y (s) = b 0 U(s) =0 =0 =0 Transformada de Laplace (CP) DEQ/UFSCar 4 / 76
42 Equação Diferencial de Segunda Ordem Resolvendo a equação no domínio da Transformada: a 2 s 2 Y (s) + a sy (s) + a 0 Y (s) = b 0 U(s) (a 2 s 2 + a s + a 0 ) Y (s) = b 0 U(s) Y (s) = ou Y (s) U(s) = b 0 a 2 s 2 U(s) Y (s) + a s + a 0 U(s) = b 0 a 2 s 2 + a s + a 0 b 0 a 0 a 2 a 0 s 2 + a a 0 s + com a 0 0 e pólos p = p 2 = ( a + ( ) a a 2 4a 2a 0 /a a 2 4a 2a 0 ) /a e Transformada de Laplace (CP) DEQ/UFSCar 42 / 76
43 Equação Diferencial de Segunda Ordem Substituindo u pelo degrau de amplitude A: Y (s) U(s) = Y (s) = b 0 a 0 a 2 a 0 s 2 + a a 0 s + Y (s) = b 0 a 0 A s( a 2 a 0 s 2 + a a 0 s + ) b 0 a 0 a 2 a 0 s 2 + a a 0 s + A s Costuma-se chamar b 0 a 0 = K p, a 2 a 0 = τp 2 e a a 0 = 2ζτ p. Neste caso, os pólos são descritos como p = ( p 2 = ζ ) ζ 2 /τ p. ( ζ + ζ 2 ) /τ p e Transformada de Laplace (CP) DEQ/UFSCar 43 / 76
44 Equação Diferencial de Segunda Ordem Quando ζ =, os pólos são reais e iguais a p = p 2 = /τ p. Calculando a transformada inversa de Y (s) utilizando uma tabela de Transformada de Laplace: Y (s) = Y (s) = K p A s(τ 2 p s 2 + 2ζτ p s + ) = K p A s(τ p s + ) 2 L = y(t) = K p A K p A s(τ p s + )(τ p s + ) [ ( + t τ p ) e t/τp ] Transformada de Laplace (CP) DEQ/UFSCar 44 / 76
45 Equação Diferencial de Segunda Ordem Quando ζ >, os pólos são reais e distintos: p = ( e p 2 = ζ ) ζ 2 /τ p. ( ζ + ) ζ 2 /τ p Calculando a transformada inversa de Y (s) utilizando uma tabela de Transformada de Laplace: Y (s) = K p A s(τ 2 p s 2 + 2ζτ p s + ) = Y (s) = L y(t) = K p A onde τ p = ( ζ + ζ 2 K p A s(τ p s + )(τ p2 s + ) [ ( τ p τ τp p2 e t/τ p τ p2 e t/τ ) ] p2 ) ) τ p e τ p2 = ( ζ ζ 2 τ p Transformada de Laplace (CP) DEQ/UFSCar 45 / 76
46 Equação Diferencial de Segunda Ordem Quando ( ζ <, os pólos são complexos conjugados: p = ζ + ) ( ζ 2 /τ p e p 2 = ζ ) ζ 2 /τ p. Calculando a transformada inversa de Y (s) utilizando uma tabela de Transformada de Laplace: K p A Y (s) = s(τp 2 s 2 + 2ζτ p s + ) Y (s) = L y(t) = K p A w = ζ 2 τ p φ = arctg ( ) ζ 2 ζ [ ζ 2 e ζt/τp sen(wt + φ) ], onde Transformada de Laplace (CP) DEQ/UFSCar 46 / 76
47 Inversão por Frações Parciais: raízes reais diferentes Exemplo Obtenha a solução da seguinte equação diferencial linear de segunda ordem d 2 x a 2 dt 2 + a dx dt + a 0x = b 0 u, x(t = 0) = x(0) e x (t = 0) = x (0) com a 2 =, a = 5, a 0 = 4, b 0 = e x(0) = x (0) = e u é um impulso unitário. Transformada de Laplace (CP) DEQ/UFSCar 47 / 76
48 Inversão por Frações Parciais: raízes reais diferentes Solução d 2 x dt 2 + 5dx dt + 4x = u, x(0) = x (0) = Aplicando a Transformada de Laplace em ambos os lados da equação: { d 2 } x L dt 2 + 5dx dt + 4x = L{δ(t)} s2 X(s) s x(0) x (0) }{{}}{{} + 5 sx(s) x(0) + 4X(s) }{{} = = = = Transformada de Laplace (CP) DEQ/UFSCar 48 / 76
49 Inversão por Frações Parciais: raízes reais diferentes Resolvendo a equação no domínio da Transformada: s 2 X(s) + 5sX(s) + 4X(s) = s (s 2 + 5s + 4)X(s) = s + 5 X(s) = s + 5 s 2 + 5s + 4 Após fatorar o denominador de X(s), pode-se expandir X(s) em duas frações parciais X(s) = s 2 + 5s + 4 = (s + 4)(s + ) s + 5 A = (s + 4)(s + ) s A 2 s + Transformada de Laplace (CP) DEQ/UFSCar 49 / 76
50 Inversão por Frações Parciais: raízes reais diferentes Os coeficientes A e A 2 podem ser determinados da seguinte maneira: A : multiplicam-se ambos os lados da expansão em frações parciais por s + 4, simplificam-se os termos semelhantes e faz-se s = 4 (uma das raízes do denominador de X(s)) s + 5 (s + 4)(s + ) (s + 4) = A s + 4 (s + 4) + A 2 (s + 4) s + s + 5 s + = A + A 2 (s + 4) s + s = 4 A = = 3 Transformada de Laplace (CP) DEQ/UFSCar 50 / 76
51 Inversão por Frações Parciais: raízes reais diferentes A 2 : de maneira análoga, multiplicam-se ambos os lados da expansão em frações parciais por s +, simplificam-se os termos semelhantes e faz-se s = (uma das raízes do denominador de X(s)) s + 5 (s + 4)(s + ) (s + ) = A s + 4 (s + ) + A 2 (s + ) s + s + 5 s + 4 = A s + 4 (s + ) + A 2 s = A 2 = = 4 3 Transformada de Laplace (CP) DEQ/UFSCar 5 / 76
52 Inversão por Frações Parciais: raízes reais diferentes Calculando a transformada inversa de cada termo de X(s) utilizando uma tabela de Transformada de Laplace: Desta forma, /3 s + 4 4/3 s + L = 3 e 4t L = 4 3 e t x(t) = 3 e t [ 4 e 3t] Transformada de Laplace (CP) DEQ/UFSCar 52 / 76
53 Inversão por Frações Parciais: raízes complexas Exemplo Obtenha a solução da seguinte equação diferencial linear de segunda ordem d 2 x a 2 dt 2 + a dx dt + a 0x = b 0 u, x(t = 0) = x(0) e x (t = 0) = x (0) com a 2 =, a = 2, a 0 = 5, b 0 = 2 e x(0) = x (0) = e u é um impulso unitário. Transformada de Laplace (CP) DEQ/UFSCar 53 / 76
54 Inversão por Frações Parciais: raízes complexas Solução d 2 x dt 2 2dx dt + 5x = 2u, x(0) = x (0) = Aplicando a Transformada de Laplace em ambos os lados da equação: { d 2 } x L dt 2 2dx dt + 5x = 2L{δ(t)} s2 X(s) s x(0) x (0) }{{}}{{} 2 [sx(s) x(0) }{{} + 5X(s) = 2 = = = Transformada de Laplace (CP) DEQ/UFSCar 54 / 76
55 Inversão por Frações Parciais: raízes complexas Resolvendo a equação no domínio da Transformada: s 2 X(s) 2sX(s) + 5X(s) = s (s 2 2s + 5)X(s) = s + X(s) = s + s 2 2s + 5 Após fatorar o denominador de X(s), pode-se expandir X(s) em duas frações parciais X(s) = s 2 2s + 5 = [s ( + ı2)][s ( ı2)] s + A = [s ( + ı2)][s ( ı2)] s ( + ı2) + A 2 s ( ı2) Transformada de Laplace (CP) DEQ/UFSCar 55 / 76
56 Inversão por Frações Parciais: raízes complexas Os coeficientes A e A 2 podem ser determinados da seguinte maneira: A : multiplicam-se ambos os lados da expansão em frações parciais por s ( + ı2), simplificam-se os termos semelhantes e faz-se s = + ı2 (uma das raízes do denominador de X(s)) s + [s ( + ı2)] = [s ( + ı2)][s ( ı2)] A s ( + ı2) [s ( + ı2)] + A 2 [s ( + ı2)] s ( ı2) s + s ( ı2) = A A 2 + [s ( + ı2)] s ( ı2) + ı2 + s = + ı2 A = + ı2 ( ı2) = 2 + ı2 2ı2 = ı 2 Transformada de Laplace (CP) DEQ/UFSCar 56 / 76
57 Inversão por Frações Parciais: raízes complexas A 2 : de maneira análoga, multiplicam-se ambos os lados da expansão em frações parciais por s ( ı2), simplificam-se os termos semelhantes e faz-se s = ı2 (uma das raízes do denominador de X(s)) s + [s ( ı2)] = [s ( + ı2)][s ( ı2)] A s ( + ı2) [s ( ı2)] + A 2 [s ( ı2)] s ( ı2) s + s ( + ı2) = A s ( + ı2) [s ( ı2)] + A 2 s = ı2 A 2 = ı2 + ı2 ( + ı2) = 2 ı2 2ı2 = + ı 2 Transformada de Laplace (CP) DEQ/UFSCar 57 / 76
58 Inversão por Frações Parciais: raízes complexas Calculando a transformada inversa de cada termo de X(s) utilizando uma tabela de Transformada de Laplace: ( ı)/2 s ( + ı2) ( + ı)/2 s ( ı2) L = ı 2 e(+ı2)t L = + ı 2 e( ı2)t Assim, x(t) = ı 2 e(+ı2)t + + ı 2 e( ı2)t Transformada de Laplace (CP) DEQ/UFSCar 58 / 76
59 Inversão por Frações Parciais: raízes complexas Utilizando a identidade trigonométrica e x+ıy = e x (cos y + ı seny): x(t) = ı 2 x(t) = et 2 + ı 2 { e t [cos(2t) + ı sen(2t)] } + et cos( 2t) +ı sen( 2t) } {{ } =cos(2t) }{{} = sen(2t) {( ı)[cos(2t) + ı sen(2t)] + ( + ı)[cos(2t) ı sen(2t)]} x(t) = e t [cos(2t) + sen(2t)] Transformada de Laplace (CP) DEQ/UFSCar 59 / 76
60 Inversão por Frações Parciais: raízes complexas Utilizando a identidade trigonométrica a cos b + a 2 senb = a 3 sen(b + φ), onde a 3 e φ são calculados de a 3 = a 2 + a2 2 e φ = tan (a /a 2 ): x(t) = e t 2 sen(2t + φ) ( ) φ = arctg = 45 o Transformada de Laplace (CP) DEQ/UFSCar 60 / 76
61 Inversão por Frações Parciais: raízes múltiplas Exemplo Obtenha a transformada inversa de X(s) = (s + 2)(s + ) 3 Transformada de Laplace (CP) DEQ/UFSCar 6 / 76
62 Inversão por Frações Parciais: raízes múltiplas Solução Pode-se expandir X(s) em suas frações parciais: X(s) = (s + 2)(s + ) 3 = A s A 2 (s + ) 3 + A 3 (s + ) 2 + A 4 s + Os coeficientes A e A 4 podem ser determinados da seguinte maneira: A : multiplicam-se ambos os lados da expansão em frações parciais por s + 2, simplificam-se os termos semelhantes e faz-se s = 2 (uma das raízes do denominador de X(s)) (s + 2)(s + ) (s + 2) = A 3 s + 2 (s + 2) + A 2 (s + 2) (s + ) 3 A 3 (s + ) (s + 2) + A 4 (s + 2) 2 s + (s + ) = A A (s + ) (s + 2) + A 3 3 (s + ) (s + 2) + A 4 (s + 2) 2 s + s = 2 A = ( 2 + ) = 3 Transformada de Laplace (CP) DEQ/UFSCar 62 / 76
63 Inversão por Frações Parciais: raízes múltiplas A 2 : multiplicam-se ambos os lados da expansão em frações parciais por (s + ) 3, simplificam-se os termos semelhantes e faz-se s = (uma das raízes do denominador de X(s)) (s + 2)(s + ) 3 (s + )3 = A s + 2 (s + )3 + A 2 (s + ) 3 (s + )3 + A 3 (s + ) 2 (s + )3 + A 4 (s + )3 s + s + 2 = A s + 2 (s + )3 + A 2 + A 3 (s + ) + A 4 (s + ) 2 (5) s = A 2 = + 2 = Transformada de Laplace (CP) DEQ/UFSCar 63 / 76
64 Inversão por Frações Parciais: raízes múltiplas A 3 : derivam-se ambos os lados da equação (5) com relação a s e faz-se s = (uma das raízes do denominador de X(s)) na equação resultante (s + 2) 2 = A (s + ) 2 (2s + 5) (s + 2) 2 + A 3 + 2A 4 (s + ) (6) s = A 3 = ( + 2) 2 = A 4 : derivam-se ambos os lados da equação (6) com relação a s e faz-se s = (uma das raízes do denominador de X(s)) na equação resultante 2 (s + 2) 3 = A 2(s + ) s2 + 5s + 7 (s + 2) 3 + 2A 4 s = A 4 = 2 2( + 2) 3 = Transformada de Laplace (CP) DEQ/UFSCar 64 / 76
65 Inversão por Frações Parciais: raízes múltiplas Calculando a transformada inversa de cada termo de X(s) utilizando uma tabela de Transformada de Laplace: Desta forma, L = e 2t s + 2 L (s + ) 3 = t2 e t 2 L (s + ) 2 = te t s + L = e t x(t) = e t ( t + t2 2 e t ) Transformada de Laplace (CP) DEQ/UFSCar 65 / 76
66 Sistema com Interação Exemplo Obtenha a solução do conjunto de equações diferenciais lineares dx dt dx 2 dt = 2x + 3x 2 +, x (0) = 0 = 2x + x 2 + e t, x 2 (0) = 0 Transformada de Laplace (CP) DEQ/UFSCar 66 / 76
67 Sistema com Interação Solução Aplicando a Transformada de Laplace em ambos os lados das equações: { dx dt = 2x + 3x 2 +, x (0) = 0 dx 2 dt = 2x + x 2 + e t, x 2 (0) = 0 { } L dx dt = L{2x + 3x 2 + } { } L dx2 dt = L{2x + x 2 + e t } sx (s) x (0) = 2X }{{} (s) + 3X 2 (s) + s =0 sx 2 (s) x 2 (0) }{{} =0 = 2X (s) + X 2 (s) + s Transformada de Laplace (CP) DEQ/UFSCar 67 / 76
68 Sistema com Interação Resolvendo o sistema de equações no domínio da Transformada: { sx (s) 2X (s) 3X 2 (s) = s sx 2 (s) 2X (s) X 2 (s) = s { (s 2)X (s) 3X 2 (s) = s 2X (s) + (s )X 2 (s) = s ] [ (s 2) 3 2 (s ) [ X (s) X 2 (s) ] = ] [ X (s) X 2 (s) [ (s 2) 3 2 (s ) = [ s s ] [ s s ] ] Transformada de Laplace (CP) DEQ/UFSCar 68 / 76
69 Sistema com Interação A matriz inversa de [ (s 2) 3 2 (s ) Portanto, [ X (s) X 2 (s) ] = X (s) = X 2 (s) = ] = [ (s ) 3 (s 2)(s ) 6 2 (s 2) [ (s ) 3 (s 2)(s ) 6 2 (s 2) s s + 3 s (s 2)(s ) 6 = (s ) 2 +3s 2 s + s 2 s (s 2)(s ) 6 = ] [ s s (s 2 3s 4)s(s ) = s 2 +s+ s(s )(s 4)(s+) 2(s )+s(s 2) (s 2 3s 4)s(s ) = s 2 2 s(s )(s 4)(s+) ] ] Transformada de Laplace (CP) DEQ/UFSCar 69 / 76
70 Sistema com Interação Pode-se expandir X (s) e X 2 (s) em suas frações parciais { s X (s) = 2 +s+ s(s )(s 4)(s+) = A s + A 2 s + A 3 s 4 + A 4 s+ s X 2 (s) = 2 2 s(s )(s 4)(s+) = B s + B 2 s + B 3 s 4 + B 4 s+ Os coeficientes A a A 4 e B a B 4 podem ser determinados da seguinte maneira: Transformada de Laplace (CP) DEQ/UFSCar 70 / 76
71 Sistema com Interação A e B : multiplicam-se ambos os lados das expansões em frações parciais por s, simplificam-se os termos semelhantes e faz-se s = 0 (uma das raízes do denominador de X (s) e X 2 (s)): { s 2 +s+ s(s )(s 4)(s+) s = A s s + A 2 s s + A 3 s 4 s + A 4 s 2 2 s(s )(s 4)(s+) s = B s s + B 2 s s + B 3 s 4 s + B 4 s+ s { s 2 +s+ (s )(s 4)(s+) = A + A 2 s s + A 3 s 4 s + A 4 s 2 2 (s )(s 4)(s+) = B + B 2 s s + B 3 s 4 s + B 4 { A = s = 0 B = ( )( 4)() = 4 2 ( )( 4)() = 2 s+ s s+ s s+ s Transformada de Laplace (CP) DEQ/UFSCar 7 / 76
72 Sistema com Interação A 2 e B 2 : multiplicam-se ambos os lados das expansões em frações parciais por s, simplificam-se os termos semelhantes e faz-se s = (uma das raízes do denominador de X (s) e X 2 (s)): s 2 +s+ s(s )(s 4)(s+) (s ) = A s (s ) + A 2 s (s ) + A 3 s 4 (s )+ A 4 s+ (s ) s 2 2 s(s )(s 4)(s+) (s ) = B s (s ) + B 2 { s 2 +s+ s(s 4)(s+) = A B 4 s+ (s ) s (s ) + B 3 s 4 s (s ) + A 2 + A 3 s 4 (s ) + A 4 s+ (s ) s 2 2 s(s 4)(s+) = B s (s ) + B 2 + B 3 s 4 (s ) + B 4 s+ (s ) { ++ A2 = ()( 4)(+) s = = 2 B 2 = 2 ()( 4)(+) = 6 (s )+ Transformada de Laplace (CP) DEQ/UFSCar 72 / 76
73 Sistema com Interação A 3 e B 3 : multiplicam-se ambos os lados das expansões em frações parciais por s 4, simplificam-se os termos semelhantes e faz-se s = 4 (uma das raízes do denominador de X (s) e X 2 (s)): s 2 +s+ s(s )(s 4)(s+) (s 4) = A s (s 4) + A 2 s (s 4) + A 3 s 4 (s 4)+ A 4 s+ (s 4) s 2 2 s(s )(s 4)(s+) (s 4) = B s (s 4) + B 2 { s 2 +s+ s(s )(s+) = A B 4 s+ (s 4) s (s 4) + B 3 s 4 (s 4)+ s (s 4) + A 2 s (s 4) + A 3 + A 4 s+ (s 4) s 2 2 s(s )(s+) = B s (s 4) + B 2 s (s 4) + B 3 + B 4 s+ (s 4) { A3 = 6+4+ s = 4 B 3 = (4)(4 )(4+) = (4)(4 )(4+) = 7 30 Transformada de Laplace (CP) DEQ/UFSCar 73 / 76
74 Sistema com Interação A 4 e B 4 : multiplicam-se ambos os lados das expansões em frações parciais por s +, simplificam-se os termos semelhantes e faz-se s = (uma das raízes do denominador de X (s) e X 2 (s)): s 2 +s+ s(s )(s 4)(s+) (s + ) = A s (s + ) + A 2 s (s + ) + A 3 s 4 (s + )+ A 4 s+ (s + ) s 2 2 s(s )(s 4)(s+) (s + ) = B s (s + ) + B 2 { s 2 +s+ s(s )(s 4) = A B 4 s+ (s + ) s (s + ) + B 3 s 4 (s + )+ s (s + ) + A 2 s (s + ) + A 3 s 4 (s + ) + A 4 s 2 2 s(s )(s 4) = B s (s + ) + B 2 s (s + ) + B 3 s 4 (s + ) + B 4 { +( )+ A4 = s = 0 ( )( )( 4) = B 4 = 2 ( )( )( 4) = 0 Transformada de Laplace (CP) DEQ/UFSCar 74 / 76
75 Sistema com Interação Calculando a transformada inversa de cada termo de X (s) e X 2 (s) utilizando uma tabela de Transformada de Laplace: /4 L s = /2 L 4 s = 2 /2 L X (s) s = et /6 L 2 X L = 2 (s) s = et 6 7e4t 7/30 L = 7e4t Desta forma, 7/20 s 4 /0 s+ 20 L = e t 0 s 4 /0 s+ x (t) = 4 et 2 + 7e4t 20 e t 0 x 2 (t) = 2 + et 6 + 7e4t 30 + e t 0 30 L = e t 0 Transformada de Laplace (CP) DEQ/UFSCar 75 / 76
76 Leitura I Leitura Complementar Próxima aula: apostila do Prof. Wu a, capítulo 0 (volume I). livro do Stephanopoulos b, capítulo 0. livro do Seborg et al. c, capítulo 5. a Kwong, W. H., Introdução ao Controle de Processos Químicos com MATLAB. Volumes I e II, EdUFSCar, São Carlos, Brasil, b Stephanopoulos, G., Chemical Process Control. An Introduction to Theory and Practice. Prentice Hall, Englewood Cliffs, USA, 984. c Seborg, D. E., Edgar, T. F., Mellichamp, D. A., Process Dynamics and Control. st Edition, John Wiley, New York, USA, 989. Transformada de Laplace (CP) DEQ/UFSCar 76 / 76
Comportamento Dinâmico de Sistemas de Primeira Ordem. Sistemas de Primeira Ordem (CP1) DEQ/UFSCar 1 / 46
 Comportamento Dinâmico de Sistemas de Primeira Ordem Sistemas de Primeira Ordem (CP1) www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 46 Roteiro 1 Sistemas de Primeira Ordem Função de Transferência
Comportamento Dinâmico de Sistemas de Primeira Ordem Sistemas de Primeira Ordem (CP1) www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 46 Roteiro 1 Sistemas de Primeira Ordem Função de Transferência
Aula 3. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Sistemas lineares. Aula 7 Transformada Inversa de Laplace
 Sistemas lineares Aula 7 Transformada Inversa de Laplace Transformada Inversa de Laplace Transformada Inversa de Laplace e RDC x(t) única Metódos Inversão pela Definição Inversão pela Expansão em Frações
Sistemas lineares Aula 7 Transformada Inversa de Laplace Transformada Inversa de Laplace Transformada Inversa de Laplace e RDC x(t) única Metódos Inversão pela Definição Inversão pela Expansão em Frações
Aspectos do Projeto de um Sistema de Controle de Processos. Aspectos do Projeto (CP1) DEQ/UFSCar 1 / 25
 Aspectos do Projeto de um Sistema de Controle de Processos Aspectos do Projeto (CP1) wwwprofessoresdequfscarbr/ronaldo/cp1 DEQ/UFSCar 1 / 25 Roteiro 1 Classificação das Variáveis em um Processo Químico
Aspectos do Projeto de um Sistema de Controle de Processos Aspectos do Projeto (CP1) wwwprofessoresdequfscarbr/ronaldo/cp1 DEQ/UFSCar 1 / 25 Roteiro 1 Classificação das Variáveis em um Processo Químico
Variáveis de Estado e Equações de Estado Desenvolvimento de Modelos Matemáticos
 Variáveis de Estado e Equações de Estado Desenvolvimento de Modelos Matemáticos Modelos Matemáticos (CP1) www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 40 Roteiro 1 Variáveis de Estado e Equações
Variáveis de Estado e Equações de Estado Desenvolvimento de Modelos Matemáticos Modelos Matemáticos (CP1) www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 40 Roteiro 1 Variáveis de Estado e Equações
Aula 6 Transformada de Laplace
 Aula 6 Transformada de Laplace Introdução Propriedades da Transformada de Laplace Tabela Transformada ade Laplace Transformada Inversa de Laplace Função de transferência Definição: X s = L x t = s é uma
Aula 6 Transformada de Laplace Introdução Propriedades da Transformada de Laplace Tabela Transformada ade Laplace Transformada Inversa de Laplace Função de transferência Definição: X s = L x t = s é uma
Transformada de Laplace
 Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Sistemas de Controle 1
 Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap2 - Modelagem no Domínio de Frequência Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 1 Prof. Dr. Marcos
Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap2 - Modelagem no Domínio de Frequência Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 1 Prof. Dr. Marcos
Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros
 107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial
 Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Transformadas de Laplace Engenharia Mecânica - FAENG. Prof. Josemar dos Santos
 Engenharia Mecânica - FAENG SISTEMAS DE CONTROLE Prof. Josemar dos Santos Sumário Transformadas de Laplace Teorema do Valor Final; Teorema do Valor Inicial; Transformada Inversa de Laplace; Expansão em
Engenharia Mecânica - FAENG SISTEMAS DE CONTROLE Prof. Josemar dos Santos Sumário Transformadas de Laplace Teorema do Valor Final; Teorema do Valor Inicial; Transformada Inversa de Laplace; Expansão em
Capítulo 2 Dinâmica de Sistemas Lineares
 Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Controle de Processos Aula: Sistemas de 1ª e 2ª ordem
 107484 Controle de Processos Aula: Sistemas de 1ª e 2ª ordem Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
107484 Controle de Processos Aula: Sistemas de 1ª e 2ª ordem Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
Sistemas de Controle
 Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
2. Modelos Lineares de Espaço de Estados. e resposta ao impulso. Método para o cálculo das soluções: através do uso de transformadas de Laplace
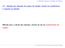 2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
II. REVISÃO DE FUNDAMENTOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
Controle de Processos
 17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 217 E. S. Tognetti (UnB) Controle
17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 217 E. S. Tognetti (UnB) Controle
Controle de Processos Aula: Função de transferência, diagrama de blocos e pólos
 107484 Controle de Processos Aula: Função de transferência, diagrama de blocos e pólos Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016
107484 Controle de Processos Aula: Função de transferência, diagrama de blocos e pólos Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle
 Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Representação e Análise de Sistemas Dinâmicos Lineares Componentes Básicos de um Sistema de Controle
 Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
V. ANÁLISE NO DOMÍNIO DO TEMPO
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
TRANSFORMADA DE LAPLACE E OPERADORES LINEARES
 TRANSFORMADA DE LAPLACE E OPERADORES LINEARES O DOMÍNIO DE LAPLACE Usualmente trabalhamos com situações que variam no tempo (t), ou seja, trabalhamos no domínio do tempo. O domínio de Laplace é um domínio
TRANSFORMADA DE LAPLACE E OPERADORES LINEARES O DOMÍNIO DE LAPLACE Usualmente trabalhamos com situações que variam no tempo (t), ou seja, trabalhamos no domínio do tempo. O domínio de Laplace é um domínio
Circuitos Elétricos II
 Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada inversa de Laplace Definição Funções racionais Expansão em frações parciais
Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada inversa de Laplace Definição Funções racionais Expansão em frações parciais
Controle de Processos
 17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 216 E. S. Tognetti (UnB) Controle
17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 216 E. S. Tognetti (UnB) Controle
O Papel dos Pólos e Zeros
 Departamento de Engenharia Mecatrônica - EPUSP 27 de setembro de 2007 1 Expansão em frações parciais 2 3 4 Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q i=1(s + z i )(s + p m ),
Departamento de Engenharia Mecatrônica - EPUSP 27 de setembro de 2007 1 Expansão em frações parciais 2 3 4 Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q i=1(s + z i )(s + p m ),
A Transformada de Laplace
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Entradas sinusoidais
 Carla C. Pinheiro e F. Lemos Dinâmica de Sistemas e Controlo de Processos DEQB - IST Entradas sinusoidais U(s) G(s) Y(s) Estudar a resposta de um sistema linear estável para alterações do tipo sinusoidal
Carla C. Pinheiro e F. Lemos Dinâmica de Sistemas e Controlo de Processos DEQB - IST Entradas sinusoidais U(s) G(s) Y(s) Estudar a resposta de um sistema linear estável para alterações do tipo sinusoidal
Transformada de Laplace
 Transformada de Laplace Monitoria de Sinais e Sistemas Lineares 04/11/09 Monitoria de Sinais e Sistemas Lineares () Transformada de Laplace 04/11/09 1 / 19 Transformadas Transformada de Laplace X(s) =
Transformada de Laplace Monitoria de Sinais e Sistemas Lineares 04/11/09 Monitoria de Sinais e Sistemas Lineares () Transformada de Laplace 04/11/09 1 / 19 Transformadas Transformada de Laplace X(s) =
Estabilidade de sistemas de controle lineares invariantes no tempo
 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
Aula 11. Revisão de Fasores e Introdução a Laplace
 Aula Revisão de Fasores e Introdução a Laplace Revisão - Fasor Definição: Fasor é a representação complexa da magnitude e fase de uma senoide. V = V m e jφ = V m φ v t = V m cos(wt + φ) = R(V e jwt ) Impedância
Aula Revisão de Fasores e Introdução a Laplace Revisão - Fasor Definição: Fasor é a representação complexa da magnitude e fase de uma senoide. V = V m e jφ = V m φ v t = V m cos(wt + φ) = R(V e jwt ) Impedância
Estabilidade de sistemas de controle lineares invariantes no tempo
 Capítulo 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2. Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no
Capítulo 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2. Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no
4.1 Pólos, Zeros e Resposta do Sistema
 ADL17 4.1 Pólos, Zeros e Resposta do Sistema A resposta de saída de um sistema é a soma de duas respostas: a resposta forçada e a resposta natural. Embora diversas técnicas, como a solução de equações
ADL17 4.1 Pólos, Zeros e Resposta do Sistema A resposta de saída de um sistema é a soma de duas respostas: a resposta forçada e a resposta natural. Embora diversas técnicas, como a solução de equações
COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 10: Domínio Discreto; Transformada Z.
 Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 10: Domínio Discreto; Transformada Z. 2014/1 Introdução ao Domínio Discreto
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 10: Domínio Discreto; Transformada Z. 2014/1 Introdução ao Domínio Discreto
Transformada de Laplace Inversa Expansão em Frações Parciais
 Transformada de Laplace Inversa Expansão em Frações Parciais 1 Introdução Estamos interessados em determinar a transformada inversa de uma função da forma D(s) = a ms m + a m 1 s m 1 +... + a 1 s + a 0
Transformada de Laplace Inversa Expansão em Frações Parciais 1 Introdução Estamos interessados em determinar a transformada inversa de uma função da forma D(s) = a ms m + a m 1 s m 1 +... + a 1 s + a 0
TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER
 TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER Transformada integral Em Física Matemática há pares de funções que satisfazem uma expressão na forma: F α = a b f t K α, t dt f t = A função F( ) é denominada
TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER Transformada integral Em Física Matemática há pares de funções que satisfazem uma expressão na forma: F α = a b f t K α, t dt f t = A função F( ) é denominada
Caderno de Exercícios
 Caderno de Exercícios Orlando Ferreira Soares Índice Caracterização de Sinais... Caracterização de Sistemas...0 Sistemas LIT - Convolução...5 Série de Fourier para Sinais Periódicos Contínuos...0 Transformada
Caderno de Exercícios Orlando Ferreira Soares Índice Caracterização de Sinais... Caracterização de Sistemas...0 Sistemas LIT - Convolução...5 Série de Fourier para Sinais Periódicos Contínuos...0 Transformada
Transformada de Laplace
 Transformada de aplace Nas aulas anteriores foi visto que as ferramentas matemáticas de Fourier (série e transformadas) são de extrema importância na análise de sinais e de sistemas IT. Isto deve-se ao
Transformada de aplace Nas aulas anteriores foi visto que as ferramentas matemáticas de Fourier (série e transformadas) são de extrema importância na análise de sinais e de sistemas IT. Isto deve-se ao
Fundamentos de Controle
 Fundamentos de Controle Modelagem matemática de sistemas de controle Prof. Juliano G. Iossaqui Engenharia Mecânica Universidade Tecnológica Federal do Paraná (UTFPR) Londrina, 2017 Prof. Juliano G. Iossaqui
Fundamentos de Controle Modelagem matemática de sistemas de controle Prof. Juliano G. Iossaqui Engenharia Mecânica Universidade Tecnológica Federal do Paraná (UTFPR) Londrina, 2017 Prof. Juliano G. Iossaqui
Pontifícia Universidade Católica de Goiás. Engenharia de Controle e Automação. Prof: Marcos Lajovic Carneiro Aluno (a):
 Pontifícia Universidade Católica de Goiás Departamento de Engenharia Laboratório ENG 3502 Controle de Processos 01 Prof: Marcos Lajovic Carneiro Aluno (a): Aula Prática 01 Polinômios, frações parciais,
Pontifícia Universidade Católica de Goiás Departamento de Engenharia Laboratório ENG 3502 Controle de Processos 01 Prof: Marcos Lajovic Carneiro Aluno (a): Aula Prática 01 Polinômios, frações parciais,
Transformada de Laplace
 Capítulo 8 Transformada de Laplace A transformada de Laplace permitirá que obtenhamos a solução de uma equação diferencial ordinária de coeficientes constantes através da resolução de uma equação algébrica.
Capítulo 8 Transformada de Laplace A transformada de Laplace permitirá que obtenhamos a solução de uma equação diferencial ordinária de coeficientes constantes através da resolução de uma equação algébrica.
Transformada de Laplace. Definição. O processo inverso de obter a função temporal f(t) a partir da
 Prof. Raimundo Nonato das Mercês Machado O processo inverso de obter a função temporal f(t) a partir da transformada de Laplace F(s) é chamado transformada de Laplace inversa. A notação para a transformada
Prof. Raimundo Nonato das Mercês Machado O processo inverso de obter a função temporal f(t) a partir da transformada de Laplace F(s) é chamado transformada de Laplace inversa. A notação para a transformada
Aula 12. Transformada de Laplace II
 Aula 12 Transformada de Laplace II Matérias que serão discutidas Nilsson Circuitos Elétricos Capítulos 12, 13 e 14 LAPLACE Capítulo 8 Circuitos de Segunda ordem no domínio do tempo Revisão A transformada
Aula 12 Transformada de Laplace II Matérias que serão discutidas Nilsson Circuitos Elétricos Capítulos 12, 13 e 14 LAPLACE Capítulo 8 Circuitos de Segunda ordem no domínio do tempo Revisão A transformada
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Controle de Processos Aula: Atraso no tempo e obtenção de modelos empíricos
 107484 Controle de Processos Aula: Atraso no tempo e obtenção de modelos empíricos Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E.
107484 Controle de Processos Aula: Atraso no tempo e obtenção de modelos empíricos Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E.
5 Descrição entrada-saída
 Teoria de Controle (sinopse) 5 Descrição entrada-saída J. A. M. Felippe de Souza Descrição de Sistemas Conforme a notação introduzida no capítulo 1, a função u( ) representa a entrada (ou as entradas)
Teoria de Controle (sinopse) 5 Descrição entrada-saída J. A. M. Felippe de Souza Descrição de Sistemas Conforme a notação introduzida no capítulo 1, a função u( ) representa a entrada (ou as entradas)
Sistemas lineares. Aula 6 Transformada de Laplace
 Sistemas lineares Aula 6 Transformada de Laplace Introdução Transformada de Laplace Convergência da transformada de laplace Exemplos Região de Convergência Introdução Transformações matemáticas: Logaritmo:
Sistemas lineares Aula 6 Transformada de Laplace Introdução Transformada de Laplace Convergência da transformada de laplace Exemplos Região de Convergência Introdução Transformações matemáticas: Logaritmo:
Organização da Disciplina Controle de Processos 1
 Organização da Disciplina Controle de Processos 1 Ronaldo Guimarães Corrêa Departamento de Engenharia Química Universidade Federal de São Carlos 2 o Sem. 2017 Organização da Disciplina (CP1) www.professores.deq.ufscar.br/ronaldo/cp1
Organização da Disciplina Controle de Processos 1 Ronaldo Guimarães Corrêa Departamento de Engenharia Química Universidade Federal de São Carlos 2 o Sem. 2017 Organização da Disciplina (CP1) www.professores.deq.ufscar.br/ronaldo/cp1
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Circuitos Elétricos II
 Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada de Laplace Definição da Transformada de Laplace Propriedades da Transformada
Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada de Laplace Definição da Transformada de Laplace Propriedades da Transformada
ELT062 - OFICINA DE SIMULAÇÃO ANALÓGICA E DIGITAL EM CONTROLE LINEARIZAÇÃO DE SISTEMAS
 ELT062 - OFICINA DE SIMULAÇÃO ANALÓGICA E DIGITAL EM CONTROLE LINEARIZAÇÃO DE SISTEMAS 1. INTRODUÇÃO Sistemas dinâmicos lineares são aqueles que obedecem ao princípio da superposição, isto é, um sistema
ELT062 - OFICINA DE SIMULAÇÃO ANALÓGICA E DIGITAL EM CONTROLE LINEARIZAÇÃO DE SISTEMAS 1. INTRODUÇÃO Sistemas dinâmicos lineares são aqueles que obedecem ao princípio da superposição, isto é, um sistema
X. MÉTODOS DE ESPAÇO DE ESTADOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE X. MÉTODOS DE ESPAÇO DE ESTADOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE X. MÉTODOS DE ESPAÇO DE ESTADOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Transformada de Laplace aplicada a circuitos elétricos
 Escola Politécnica da USP Departamento de Engenharia de Sistemas Eletrônicos Transformada de Laplace aplicada a circuitos elétricos Magno T. M. Silva Junho de 25 Sumário Introdução 2 2 Definição 4 3 Existência
Escola Politécnica da USP Departamento de Engenharia de Sistemas Eletrônicos Transformada de Laplace aplicada a circuitos elétricos Magno T. M. Silva Junho de 25 Sumário Introdução 2 2 Definição 4 3 Existência
Controle de Processos Aula: Estabilidade e Critério de Routh
 107484 Controle de Processos Aula: Estabilidade e Critério de Routh Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB)
107484 Controle de Processos Aula: Estabilidade e Critério de Routh Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB)
PMR3404 Controle I Aula 2
 PMR3404 Controle I Aula 2 Pólos e zeros, Estabilidade, Critério de Estabilidade de Routh-Hurwitz Newton Maruyama 16 de março de 2017 PMR-EPUSP Introdução Introdução O cálculo da resposta no domínio do
PMR3404 Controle I Aula 2 Pólos e zeros, Estabilidade, Critério de Estabilidade de Routh-Hurwitz Newton Maruyama 16 de março de 2017 PMR-EPUSP Introdução Introdução O cálculo da resposta no domínio do
Transformada Z. Transformada Z
 Semelhante ao apresentado anteriormente, entre a relação das transformadas de Fourier e de Laplace, será visto que a generalização da representação senoidal complexa de um sinal de tempo discreto pela
Semelhante ao apresentado anteriormente, entre a relação das transformadas de Fourier e de Laplace, será visto que a generalização da representação senoidal complexa de um sinal de tempo discreto pela
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química 2014/1
 Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 8: Sistemas de Primeira Ordem (Continuação): Sistema Lead-Lag; Sistemas
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 8: Sistemas de Primeira Ordem (Continuação): Sistema Lead-Lag; Sistemas
AULA 3. CRITÉRIO DE ESTABILIDADE DE Routh-Hurwitz. Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I
 Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 3 CRITÉRIO DE ESTABILIDADE DE Routh-Hurwitz PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA Critério de estabilidade de Routh A questão
Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 3 CRITÉRIO DE ESTABILIDADE DE Routh-Hurwitz PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA Critério de estabilidade de Routh A questão
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Controle. Transformada Laplace básico
 Controle Transformada Laplace básico REQUISITOS Para perfeita compreensão do conteúdo desta aula é desejável o entendimento dos seguintes assuntos (eventualmente disponíveis em outros vídeos neste canal):
Controle Transformada Laplace básico REQUISITOS Para perfeita compreensão do conteúdo desta aula é desejável o entendimento dos seguintes assuntos (eventualmente disponíveis em outros vídeos neste canal):
Modelação e Simulação 4.Sistemas lineares Sistemas lineares
 Modelação e Simulação 4.Sistemas lineares. 4.Sistemas lineares Objectivo: Após completar este módulo o aluno deverá ser capaz de relacionar o tipo de resposta no tempo com a estrutura do sistema linear,
Modelação e Simulação 4.Sistemas lineares. 4.Sistemas lineares Objectivo: Após completar este módulo o aluno deverá ser capaz de relacionar o tipo de resposta no tempo com a estrutura do sistema linear,
1. Sinais de teste. 2. Sistemas de primeira ordem. 3. Sistemas de segunda ordem. Especificações para a resposta
 Desempenho de Sistemas de Controle Realimentados 1. Sinais de teste. Sistemas de primeira ordem 3. Sistemas de segunda ordem Especificações para a resposta Fernando de Oliveira Souza pag.1 Engenharia de
Desempenho de Sistemas de Controle Realimentados 1. Sinais de teste. Sistemas de primeira ordem 3. Sistemas de segunda ordem Especificações para a resposta Fernando de Oliveira Souza pag.1 Engenharia de
O método do lugar das raízes
 4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada em função
4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada em função
Universidade Federal do Rio de Janeiro. Circuitos Elétricos I EEL 420. Módulo 11
 Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Universidade Federal do Rio de Janeiro. Circuitos Elétricos I EEL 420. Módulo 11
 Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Indice. Resposta forçada (condições iniciais nulas)
 Indice 3.3 Inversão da TLP Fracções parciais Resolução equações diferenciais Polinómio característico Estabilidade resposta natural 3.4 Função de Transferência Estabilidade devido à entrada (resposta forçada)
Indice 3.3 Inversão da TLP Fracções parciais Resolução equações diferenciais Polinómio característico Estabilidade resposta natural 3.4 Função de Transferência Estabilidade devido à entrada (resposta forçada)
Modelagem no Domínio do Tempo
 CAPÍTULO TRÊS Modelagem no Domínio do Tempo SOLUÇÕES DE DESAFIOS DOS ESTUDOS DE CASO Controle de Antena: Representação no Espaço de Estados Para o amplificador de potência, E s a() V () s 150. Usando a
CAPÍTULO TRÊS Modelagem no Domínio do Tempo SOLUÇÕES DE DESAFIOS DOS ESTUDOS DE CASO Controle de Antena: Representação no Espaço de Estados Para o amplificador de potência, E s a() V () s 150. Usando a
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE MAIO DE 2017
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
EN2607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 2 2 quadrimestre 2011
 EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares quadrimestre 0 (P-0003D) (HAYKIN, 00, p 9) Use a equação de definição da TF para obter a representação no domínio da
EN607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares quadrimestre 0 (P-0003D) (HAYKIN, 00, p 9) Use a equação de definição da TF para obter a representação no domínio da
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Transformadas Inversas Transformada Inversa de Laplace V(s) é
Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais Transformadas Inversas Transformada Inversa de Laplace V(s) é
Disciplina: Instrumentação e Controle de Sistemas Mecânicos. Teoria de Controle Parte 2
 Disciplina: Instrumentação e Controle de Sistemas Mecânicos Teoria de Controle Parte 2 Sistemas de Primeira Ordem: Função de Transferência Pelo o que já foi dito, devido aos diferentes tipos de atraso,
Disciplina: Instrumentação e Controle de Sistemas Mecânicos Teoria de Controle Parte 2 Sistemas de Primeira Ordem: Função de Transferência Pelo o que já foi dito, devido aos diferentes tipos de atraso,
1 [30] A figura ao lado mostra o zoom da discretização de uma função
![1 [30] A figura ao lado mostra o zoom da discretização de uma função 1 [30] A figura ao lado mostra o zoom da discretização de uma função](/thumbs/92/110361962.jpg) TT9 Matemática Aplicada I Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P, 3 mar 22 Prof. Nelson Luís Dias NOME: GABARITO Assinatura: 3] A figura ao lado mostra o zoom da discretização
TT9 Matemática Aplicada I Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P, 3 mar 22 Prof. Nelson Luís Dias NOME: GABARITO Assinatura: 3] A figura ao lado mostra o zoom da discretização
RESPOSTA EM FREQUÊNCIA: DIAGRAMA DE BODE
 RESPOSTA EM FREQUÊNCIA: DIAGRAMA DE BODE CCL Profa. Mariana Cavalca Baseado em: MAYA, Paulo Álvaro; LEONARDI, Fabrizio. Controle essencial. São Paulo: Pearson, 2011. OGATA, Katsuhiko. Engenharia de controle
RESPOSTA EM FREQUÊNCIA: DIAGRAMA DE BODE CCL Profa. Mariana Cavalca Baseado em: MAYA, Paulo Álvaro; LEONARDI, Fabrizio. Controle essencial. São Paulo: Pearson, 2011. OGATA, Katsuhiko. Engenharia de controle
Sistemas e Sinais. Universidade Federal do Rio Grande do Sul Departamento de Engenharia Elétrica
 O método das frações parciais usa o conhecimento de diversos pares de transformada Z básicos e as propriedades da transformada Z para obtenção da transformada Z inversa das funções de interesse Admite-se
O método das frações parciais usa o conhecimento de diversos pares de transformada Z básicos e as propriedades da transformada Z para obtenção da transformada Z inversa das funções de interesse Admite-se
Introdução aos Circuitos Elétricos
 Introdução aos Circuitos Elétricos A Transformada de Laplace Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia A Transformada de Laplace História Pierri
Introdução aos Circuitos Elétricos A Transformada de Laplace Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia A Transformada de Laplace História Pierri
Modelos Matemáticos de Sistemas
 Modelos Matemáticos de Sistemas Introdução; Equações Diferenciais de Sistemas Físicos; Aproximações ineares de Sistemas Físicos; Transformada de aplace; Função de Transferência de Sistemas ineares; Modelos
Modelos Matemáticos de Sistemas Introdução; Equações Diferenciais de Sistemas Físicos; Aproximações ineares de Sistemas Físicos; Transformada de aplace; Função de Transferência de Sistemas ineares; Modelos
CONTROLE LINEAR CONTÍNUO: PRINCÍPIOS E LUGAR DAS RAÍZES
 PETROBRAS ENGENHEIRO(A) DE EQUIPAMENTOS JÚNIOR - ELETRÔNICA ENGENHEIRO(A) DE EQUIPAMENTOS JÚNIOR - ELÉTRICA ENGENHEIRO(A) JÚNIOR - ÁREA: AUTOMAÇÃO CONTROLE LINEAR CONTÍNUO: PRINCÍPIOS E LUGAR DAS RAÍZES
PETROBRAS ENGENHEIRO(A) DE EQUIPAMENTOS JÚNIOR - ELETRÔNICA ENGENHEIRO(A) DE EQUIPAMENTOS JÚNIOR - ELÉTRICA ENGENHEIRO(A) JÚNIOR - ÁREA: AUTOMAÇÃO CONTROLE LINEAR CONTÍNUO: PRINCÍPIOS E LUGAR DAS RAÍZES
Modelagem de Sistemas de Controle por Espaço de Estados
 Modelagem de Sistemas de Controle por Espaço de Estados A modelagem por espaço de estados possui diversas vantagens. Introduz a teoria conhecida como Controle Moderno ; Adequada para sistemas de múltiplas
Modelagem de Sistemas de Controle por Espaço de Estados A modelagem por espaço de estados possui diversas vantagens. Introduz a teoria conhecida como Controle Moderno ; Adequada para sistemas de múltiplas
ESPAÇO DE ESTADOS. Capítulo 4. Objectivos do capítulo. Espaço de estados Plano de fase Estabilidade. Sistemas não lineares.
 Capítulo 4 EPAÇO DE ETADO Objectivos do capítulo Espaço de estados Plano de fase Estabilidade valores próprios istemas não lineares linearização Indice 4. Exemplos 4. Caso Geral 4.3 Plano de fase 4.4 Resolução
Capítulo 4 EPAÇO DE ETADO Objectivos do capítulo Espaço de estados Plano de fase Estabilidade valores próprios istemas não lineares linearização Indice 4. Exemplos 4. Caso Geral 4.3 Plano de fase 4.4 Resolução
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2
 FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Resposta no espaço de estados Representações
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Resposta no espaço de estados Representações
INTRODUÇÃO À ANALISE DE SINAIS ELT 032
 INTRODUÇÃO À ANALISE DE SINAIS ELT 032 Prof. Jeremias Barbosa Machado Introdução Neste capítulo estudaremos as Transformadas de Laplace. Elas apresentam uma representação de sinais no domínio da frequência
INTRODUÇÃO À ANALISE DE SINAIS ELT 032 Prof. Jeremias Barbosa Machado Introdução Neste capítulo estudaremos as Transformadas de Laplace. Elas apresentam uma representação de sinais no domínio da frequência
EES-20: Sistemas de Controle II. 31 Julho 2017
 EES-20: Sistemas de Controle II 31 Julho 2017 1 / 41 Folha de informações sobre o curso 2 / 41 O que é Controle? Controlar: Atuar sobre um sistema físico de modo a obter um comportamento desejado. 3 /
EES-20: Sistemas de Controle II 31 Julho 2017 1 / 41 Folha de informações sobre o curso 2 / 41 O que é Controle? Controlar: Atuar sobre um sistema físico de modo a obter um comportamento desejado. 3 /
Introdução ao Controle de Processos. Introdução ao Controle de Processos (CP1) DEQ/UFSCar 1 / 49
 Introdução ao Controle de Processos Introdução ao Controle de Processos (CP1) www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 49 Roteiro 1 Incentivos ao Controle de Processos 2 Principais Objetivos
Introdução ao Controle de Processos Introdução ao Controle de Processos (CP1) www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 49 Roteiro 1 Incentivos ao Controle de Processos 2 Principais Objetivos
Controle de Processos Aula: Sistema em malha fechada
 107484 Controle de Processos Aula: Sistema em malha fechada Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2017 E. S. Tognetti (UnB) Controle
107484 Controle de Processos Aula: Sistema em malha fechada Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2017 E. S. Tognetti (UnB) Controle
Controle e Sistemas Não lineares
 Controle e Sistemas Não lineares Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 01 de dezembro de 2016. Sumário Objetivos Introduzir
Controle e Sistemas Não lineares Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 01 de dezembro de 2016. Sumário Objetivos Introduzir
CONTROLO LINEAR. Mestrado em Matemática e Aplicações. Universidade de Aveiro
 CONTROLO LINEAR Mestrado em Matemática e Aplicações Universidade de Aveiro Sistemas dinâmicos de controlo u - entrada y - saída x - estado - memória do sistema (condições iniciais) x(t ) u(t), t t y(t),
CONTROLO LINEAR Mestrado em Matemática e Aplicações Universidade de Aveiro Sistemas dinâmicos de controlo u - entrada y - saída x - estado - memória do sistema (condições iniciais) x(t ) u(t), t t y(t),
Circuitos Elétricos II
 Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Introdução Definição da Transformada de aplace Propriedades da Transformada de aplace
Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Introdução Definição da Transformada de aplace Propriedades da Transformada de aplace
EES-49/2012 Correção do Exame. QBM1 Esboce o diagrama de Nyquist para a seguinte função de transferência:
 EES-49/2012 Correção do Exame QBM1 Esboce o diagrama de Nyquist para a seguinte função de transferência: Analise a estabilidade do sistema em malha fechada (dizendo quantos polos instáveis o sistema tem
EES-49/2012 Correção do Exame QBM1 Esboce o diagrama de Nyquist para a seguinte função de transferência: Analise a estabilidade do sistema em malha fechada (dizendo quantos polos instáveis o sistema tem
Sequências e Séries. Capítulo Exercícios
 Capítulo Sequências e Séries Exercícios Encontre uma fórmula para o termo geral da sequência a n } n= assumindo que o padrão dos primeiros termos continua (a), 4, 8, 6, } (b), 4, 6, 8, } (c), 7,, 7, }
Capítulo Sequências e Séries Exercícios Encontre uma fórmula para o termo geral da sequência a n } n= assumindo que o padrão dos primeiros termos continua (a), 4, 8, 6, } (b), 4, 6, 8, } (c), 7,, 7, }
Fundamentos de Controlo
 Fundamentos de Controlo 3 a Série Estabilidade e Desempenho, Critério de Routh-Hurwitz, Rejeição de Perturbações, Sensibilidade à Variação de Parâmetros, Erros em Regime Estacionário. S3. Exercícios Resolvidos
Fundamentos de Controlo 3 a Série Estabilidade e Desempenho, Critério de Routh-Hurwitz, Rejeição de Perturbações, Sensibilidade à Variação de Parâmetros, Erros em Regime Estacionário. S3. Exercícios Resolvidos
