PMR3404 Controle I Aula 2
|
|
|
- Maria Clara Rafaela Lage Campelo
- 6 Há anos
- Visualizações:
Transcrição
1 PMR3404 Controle I Aula 2 Pólos e zeros, Estabilidade, Critério de Estabilidade de Routh-Hurwitz Newton Maruyama 16 de março de 2017 PMR-EPUSP
2 Introdução
3 Introdução O cálculo da resposta no domínio do tempo y(t) de um sistema g(t) pode ser calculado através da integral de convolução: y(t) = 0 g(τ)u(t τ)dτ, onde u(t) é o sinal de excitação do sistema. 1
4 Usualmente, utiliza-se a transformada de Laplace para a conversão do sistema para o domínio da freqüência: Y(s) = G(s)U(s). 2
5 Posteriormente, para o cálculo de y(t), pode-se realizar a anti-transformada de Laplace. Para isto, é mais fácil transformar Y(s) utilizando a técnica de expansão em frações parciais, já que cada fração parcial tem anti-transformada facilmente conhecida. 3
6 Neste caso, é possível evidenciar o efeito de cada pólo do sistema e do sinal de entrada u(t). Os zeros de Y(s) desaparecem na expansão em frações parciais. O efeito dos zeros afeta apenas os coeficentes das frações parciais. A conclusão que devemos chegar é que os zeros do sistema atuam como filtros evidenciando ou anulando o efeito dos pólos do sistema. 4
7 Algumas questões básicas
8 Seja um sistema linear e invariante no tempo representado por: a ny (n) (t) + a n 1y (n 1) (t) a 1y (1) (t) + a 0y(t) = b mu (m) (t) + b m 1u (m 1) (t) b 1u (1) (t) + b 0u(t), onde, y (i) (t) d(i) y(t) dt (i), u (i) (t) d(i) u(t) dt (i), 5
9 Podemos definir: D(p) a np n + a n 1p n a 1p + a 0, e onde, N(p) b mp m + b m 1p m b 1p + b 0, p (i) d(i) dt (i). 6
10 Utilizando esta notação podemos escrever: D(p)y(t) = N(p)u(t). (1) A solução para y(t) envolve dois termos. O primeiro, corresponde a resposta do sistema D(p)y(t) = N(p)u(t) considerando uma entrada nula, i.e., u(t) = 0. Neste caso, a Equação 1 se reduz a equação denominada Homogênea, D(p)y(t) = 0. 7
11 A sua transformada de Laplace pode ser expressa como: Y(s) = I(s) D(s), onde I(s) é um polinômio cujos coeficientes dependem das condições iniciais. D(s) é denominado polinômio característico de 1 porque caracteriza a resposta denominada livre, não forçada ou resposta natural. As raízes de D(s) são denominadas modos do sistema. 8
12 Por exemplo, se: D(s) = (s 2)(s + 1) 2 (s + 2 j3)(s j3). Os modos do sistema nesse caso são: 2, 1, 2 + j3, 2 j3. Os pólos tem multiplicidade unitária, com exceção de 1 que possui multiplicidade igual a dois. 9
13 Desta forma, para quaisquer condições iniciais, Y(s) pode ser expandido em frações parciais como: Y(s) = K1 (s 2) + K 2 (s + 2 j3) + K 3 (s j3) + C1 (s + 1) + C2 (s + 1) 2. (2) 10
14 A resposta no tempo pode ser escrita como: y(t) = K 1 exp 2t +K 2 exp (2 j3)t +K 3 exp (2+j3)t + C 1 exp t +C 2t exp t, onde K 1, K 2, K 3, C 1 e C 2 dependem das condições iniciais. 11
15 Se todas as condições iniciais forem nulas a resposta de 1 pode ser escrita como: Y(s) U(s) = N(s) D(s) = G(s), onde G(s) é a transformada de Laplace quando as condições iniciais são nulas (c.i.n.): G(s) = Y(s) U(s) = L[saída] c.i.n. L[entrada]. c.i.n. 12
16 Logo a solução geral da Equação 1 pode ser escrita como: Y(s) = I(s) N(s) + D(s) D(s) U(s). }{{}}{{} Resposta a Entrada-Zero Resposta a Estado-Zero 13
17 Considere por exemplo a seguinte equação diferencial: d 2 y(t) dt dy(t) dt + 2y(t) = 3 du(t) dt u(t). (3) A utilização da transformada de Laplace considerando condições iniciais não nulas, resulta em: s 2 Y(s) sy(0 ) ẏ(0 ) + 3[sY(s) y(0 )] + 2Y(s) = 3[sU(s) u(0 )] U(s), onde ẏ = dy/dt e as letras maiúsculas denotam as transformadas de Laplace das variáveis representadas pelas letras minúsculas correspondentes. 14
18 Fazendo um reagrupamento dos termos podemos escrever a equação acima da seguinte forma: (s + 3)y(0 ) + ẏ(0 ) 3u(0 ) Y(s) = + (s 2 + 3s + 2) }{{} Resposta a Entrada-Zero 3s 1 (s 2 + 3s + 2) U(s). }{{} Resposta a Estado-Zero 15
19 Esta equação revela que a solução da Equação 3 é parcialmente excitada por u(t), t > 0, o que resulta numa parcela denominada de Resposta a Estado-Zero, e parcialmente excitada pelas condições iniciais y(0 ), ẏ(0 ), e u(0 ), o que resulta na parcela denominada Resposta a Entrada-Zero. Tais condições iniciais serão denominadas aqui de estado inicial. O estado inicial pode ser entendido como o resultado da entrada u(t) para t 0. 16
20 Expansão em frações parciais
21 Expansão em frações parciais Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q (s + p i=1 i)(s + p, m) r one i = 1,..., q e n = q + r. A expansão em frações parciais de G(s) pode ser escrita como: q i=1 K i (s + p i ) + A 1 (s + p m) + A 2 (s + p m) A r (s + p m) r, 17
22 onde: K i = (s + p i )G(s) s= pi, A r = [(s + p m) r G(s)] s= pm, A r 1 = d ds [(s + pm)r G(s)], s= pm A r 2 = 1 d 2 2! ds [(s + 2 pm)r G(s)], s= pm. A 1 = 1 d r 1 (r 1)! ds [(s + r 1 pm)r G(s)]. s= pm 18
23 A função no domínio do tempo pode ser escrita como: q g(t) = K i exp p i t +A 1 exp pmt +A 2t exp pmt + (4) i= A rt r 1 exp pmt. 19
24 Pólos e zeros A seguir, uma definição formal para pólos e zeros é estabelecida. Pólo número real ou complexo finito λ tal que G(λ) =. Zero número real ou complexo finito λ tal que G(λ) = 0. 20
25 Um primeiro questionamento de ordem teórica que pode ser feito é se todas as raízes do polinômio D(s) são polos de G(s). Considere a seguinte função de transferência: G(s) = N(s) D(s) = 2(s3 + 3s 2 s 3) (s 1)(s + 2)(s + 1) 3. Para λ = 2 temos: G( 2) = 6 0 =. Portanto, λ = 2 é um pólo e também λ = 2 é uma raiz de D(s). Agora vamos fazer λ = 1, dessa forma: o que torna o resultado indefinido. G(1) = N(1) D(1) = 0 0, 21
26 Entretanto, utilizando a regra de L Hôpital 1 obtemos: G(1) = N(s) D(s) = N (s) s=1 D (s), s=1 2(3s 2 + 6s 1) = 5s s s 2 4s 5, s=1 = Dessa forma, λ = 1 não é um pólo de G(s). 1 A regra de L Hôpital pode ser utilizada quando existe uma indeterminação do tipo f(p) lim x p g(p) = 0 0. Dado f(x) e g(x) funções diferenciáveis e g (p) 0 então: f(x) lim x p g(x) = lim f (x) x p g (x). (5) 22
27 Portanto, nem toda raiz de D(s) é um pólo de G(s). No exemplo acima, o fato se deve ao fato que N(s) e D(s) possuem um fator comum. Na verdade, a função de transferência pode ser escrita como: 2(s + 3)(s 1)(s + 1) (s 1)(s + 2)(s + 1) 3 = 2(s + 3) (s + 2)(s + 1) 2. G(s) tem um zero em s = 3 e três pólos: s = 2, 1, 1. 23
28 Através deste exemplo, concluímos que se os polinômios N(s) e D(s) não possuem fatores comums, então todas as raízes de N(s) e D(s) são respectivamente zeros e pólos de G(s). Se N(s) e D(s) não possuem um fator comum eles são denominados co-primos e G(s) é denominado irredutível. 24
29 Resposta a estado-zero
30 Resposta a estado-zero A resposta a estado-zero é estabelecida pela seguinte equação: Y(s) = G(s)U(s). (6) Computa-se inicialmente a transformada de Laplace de u(t), U(s), e posteriomente podemos obter Y(s). Uma expansão em frações parciais de Y(s) pode facilmente levar a transformada de Laplace inversa para obtenção da resposta do sistema no domínio do tempo y(t). A seguir são apresentados alguns exemplos. 25
31 Exemplo 1 Dado o sistema G(s) = 3s 1 (s + 1)(s + 2), calcular a resposta para um entrada a degrau unitário u(t) = 1 para t 0. 26
32 Podemos escrever Y(s) como: 3s 1 1 Y(s) = G(s)U(s) = (s + 1)(s + 2) s. 27
33 A expansão em frações parciais pode ser representada como: Y(s) = 3s 1 (s + 1)(s + 2)s = K1 (s + 1) + K2 (s + 2) + K3 s, 28
34 onde os coeficientes podem ser calculados como: K 1 = Y(s)(s + 1) s= 1 = 3s 1 ( 4) (s + 2)s = s= 1 (1) ( 1) = 4, K 2 = Y(s)(s + 1) s= 2 = 3s 1 (s + 1)s = s= 2 ( 7) ( 1) ( 2) = 3.5, 3s 1 K 3 = Y(s)s s=0 = (s + 1)(s + 2) = ( 1) s=0 (2) =
35 Y(s) pode então ser representada como: 3s 1 Y(s) = (s + 1)(s + 2)s = 4 (s + 1) (s + 2) + 0.5, s A resposta no tempo pode então ser calculada como: y(t) = 4 exp t 3.5 exp 2t }{{} 0.5 }{{}. Devido aos pólos de G(s) Devido ao pólo de U(s) 30
36 Podemos observar através do Exemplo Anterior que os termos relativos aos pólos do sistema podem ser divididos em duas partes, uma relativa aos pólos do sistema G(s) e um relativo ao pólo de U(s). A resposta deste sistema poderia ser escrita genericamente como: y(t) = K 1 exp t +K 2 exp 2t + (7) termos devidos aos pólos de U(s). 31
37 Importante!!!!!!! Uma questão importante é que dependendo de u(t), os pólos de G(s) podem não ser excitados. O exemplo a seguir ilustra esta questão. 32
38 Exemplo 2 Considere por exemplo U(s) = s + 1. Neste caso, 3s 1 Y(s) = G(s)U(s) = (s + 1), (s + 1)(s + 2) = 3s 1 3(s + 2) 7 7 = = 3 (s + 2) (s + 2) (s + 2). O que implica em: y(t) = 3δ(t) 7 exp 2t. 33
39 Exemplo 3 Vamos supor agora que: u(t) = exp 3t, 3 34
40 A transformada de Laplace é dada por: U(s) = (s + 1) s(s + 3), dessa forma, 3s 1 s + 1 Y(s) = (s + 2)(s + 1) s(s + 3) = 3s 1 (s + 2)(s + 3)s 7 = 2(s + 2) 10 3(s + 3) 1 6s. 35
41 A resposta do sistema no domínio do tempo y(t) é dada por: y(t) = 7 2 exp 2t 10 3 exp 3t 1 6. Neste exemplo, é possível observar que a excitação ou não do pólo depende se U(s) possui um zero para cancelá-lo. 36
42 Pólos e suas características no domínio do tempo
43 Pólo real negativo s = σ Função de transferência: Resposta no domínio do tempo: K (s + σ). K exp σt. 37
44 Pólo real positivo s = +σ Função de transferência: Resposta no domínio do tempo: K (s σ). K exp σt. 38
45 Pólos complexos conjugados com parte real negativa s = σ ± jω Função de transferência: Onde K i = K i+1. Resposta no domínio do tempo: K i (s + σ jω) + K i+1 (s + σ + jω). K i exp (σ jω)t +K i+1 exp (σ+jω)t, A exp σt sin(ωt + Φ). 39
46 Pólos complexos conjugados com parte real positiva s = +σ ± jω Função de transferência: Onde K i = K i+1. Resposta no domínio do tempo: K i (s σ jω) + K i+1 (s σ + jω). K i exp ( σ jω)t +K i+1 exp ( σ+jω)t, A exp σt sin(ωt + Φ). 40
47 Pólos reais negativos com multiplicidade 2 s = σ Função de transferência: Resposta no domínio do tempo: Ki (s + σ) + K i+1 (s + σ) 2. K i exp σt +K i+1 t exp σt. 41
48 Pólos imaginários s = ±jω Função de transferência: Onde K i = K i+1. Resposta no domínio do tempo: k i s jω + K i+1 s + jω. K i exp jωt +K i+1 exp jωt, (8) A sin(ωt + Φ). 42
49 Pólos imaginários duplos s = ±jω Função de transferência: K (s 2 + ω 2 ) = 2 K (s + jω) 2 (s jω) = 2 K 1 (s + jω) + K 2 (s + jω) + K 3 2 (s jω) + K 4 (s jω). 2 Resposta no domínio do tempo: g(t) = A 1 sin(ωt + Φ 1) + A 2t sin(ωt + Φ 2). 43
50 O efeito dos zeros
51 O efeito dos zeros O efeito dos zeros sobre a resposta do sistema é mais difícil de ser inferido. Apesar da localização dos pólos determinar a natureza dos modos do sistema, é a localização dos zeros que determina a proporção que os modos são combinados. Estas combinações podem fazer com que os resultados sejam bastante diferentes quando comparados com os modos individuais relativos a cada pólo. 44
52 Da mesma forma como nos pólos, também podemos definir zeros rápidos e zeros lentos. Zeros rápidos são aqueles que estão bastante afastados em relação ao eixo imaginário quando comparado com os pólos dominantes. Por outro lado, zeros lentos são aqueles que estão bem mais próximos do eixo imaginário do que os pólos dominantes. 45
53 Exemplo 1 Para ilustrar a influência dos zeros na resposta do sistema a resposta a degrau de vários sistemas com pólos iguais mas com zeros diferentes são comparados. Os sistemas definidos pelas funções de transferência G 1(s), G 2(s), G 3(s) e G 4(s) e suas respectivas expansões em frações parciais podem ser observados na Tabela. A expansão em frações parciais de qualquer um desses sistemas pode ser representada por: Y(s) = K1 (s + 1) + K 2 (s j) + K 3 (s + 1 j) + K4 s. 46
54 Tabela 1: Respostas a degrau dos sistemas. K 1 K 2 K 3 K 4 2 G 1 (s) = (s+1)(s+1+j)(s+1 j) j j (s+10) G 2 (s) = (s+1)(s+1+j)(s+1 j) j j (s+10) G 3 (s) = (s+1)(s+1+j)(s+1 j) j j0.5 1 G 4 (s) = 10(s2 +0.1s+0.2) (s+1)(s+1+j)(s+1 j) j4.5 5 j
55 G 1(s) = G 2(s) = G 3(s) = G 4(s) = 2 (s+1)(s+1+j)(s+1 j) 0.2(s+10) (s+1)(s+1+j)(s+1 j) 0.2(s+10) (s+1)(s+1+j)(s+1 j) 10(s2 +0.1s+0.2) (s+1)(s+1+j)(s+1 j) 2 y(t) t(s) 48
56 Exemplo 2 Considere, por exemplo, a seguinte função de transferência: H(s) = s + c c(s + 1)(0.5s + 1), Nesse sistema é possível verificar a variação da resposta y(t) através da variação do parâmetro c sem a mudança dos valores dos pólos e do ganho do sistema. 49
57 s + c H(s) = c(s + 1)(0.5s + 1), c = 0.1, 0.1 c 0.25, 0.25 c = 10, y(t) t(s) 50
58 Os dois modos naturais do sistema são representados por, exp 1t e exp 2t, que são relacionados aos pólos 1 e 2 respectivamente. 51
59 O efeito do primeiro modo natural exp 1t pode gradativamente ser anulado a medida que c 1. O mesmo acontece para exp 2t quando c 2. Uma situação mais geral, pode ser observada na Figura onde é apresentado a resposta a degrau do sistema H(s) considerando c = 0.1, 0.1, 0.25, 0.25, 10,
60 Pode ser observado que, para um zero rápido, por exemplo c 1, não existe um impacto significativo na resposta transitória. Quando o zero é lento e estável o sistema possui sobresinal significativo. Quando o zero é lento e instável então o sistema exibe um undershoot significativo. 53
61 Estabilidade
62 Sistema bola e barra (Ball and Beam) Objetivo: equilibrar a bola numa posição específica. 54
63 [ ] Jb r + m + mg sin θ(t) mp(t) θ(t) 2 = 0 (9) 2 [ mp(t) 2 ] + J + J b θ(t) + 2mp(t)ṗ(t) θ + mgp(t) cos θ(t) = τ(t) (10) J b momento de inércia da bola m massa da bola r raio da bola J momento de inércia da haste θ ângulo da haste p(t) distância da bola ao centro da haste 55
64 G 1(s) = P(s) T(s) = mg (11) J E1 J E2 s 4 m 2 g 2 J E1 = J b r 2 + m (12) J E2 = ml2 4 + J + J b (13) 56
65 A importância do modelo Muitos sistemas, especialmente sistemas aeronáuticos e aerospaciais, possuem este comportamento dinâmico. Por exemplo: mísseis, foguetes, aviões, etc. 57
66 Supermaneuverability Super-manobrabilidade. Aviões de combate são intencionalmente feito instáveis ou quase instáveis. Por exemplo, o avião deve ser capaz de realizar a manobra Pugachev s Cobra. 58
67 Eurofighter Typhoon 59
68 Pêndulo invertido 60
69 Parâmetros massa do pêndulo m = 0.5Kg, massa do carro M = 0.5Kg, comprimento do pêndulo l = 0.3m, coeficiente de atrito viscoso b = 0.1N/m/s, momento de inércia do pêndulo I p = 0.006Kgm 2, cte gravitacional I p = 9.81m/s 2. 61
70 modelo linearizado Modelo linearizado em θ = 0 o (sin θ = θ,cos θ = 0), Θ(s) F(s) = s 3 + b(ip+ml2 q where q = [(M + m)(i pml 2 ) (ml) 2 ]. ml q s s 2 (M+m)mgl q, (14) s bmgl q 62
71 modelo linearizado Função de transferência: Θ(s) F(s) = s s s (15) Pólos: s 1 = , s 2 = , s 3 = 0.1. Pólo s 1 é instável. Um problema mais desafiador seria controlar θ(t) e x(t) simultaneamente utilizando f(t). 63
72 Estabilidade: algumas definições Definition (Estabilidade absoluta) se refere a condição se um sistema é estável ou instável. Definition (Estabilidade relativa) se o sistema é estável, pode-se determinar o grau de estabilidade deste sistema. 64
73 Estabilidade Entrada-Saída Seja: u(t): entrada do sistema, y(t): saída do sistema, g(t) resposta impulsiva. Definition (Estabilidade Entrada-Saída) com condições iniciais nulas, o sistema é dito ser Entrada-Saída estável, ou simplesmente estável, se a saída y(t) é limitada para uma entrada u(t) limitada. Ou ainda, para um número 0 < Q < : 0 g(t) dt Q <. (16) A condição dada pela Equação 16 implica que a área sobre a curva g(t) t deve ser finita. 65
74 Sistema marginalmente estável Um sistema é marginalmente estável se o sistema não for assintoticamente estável e se for possível escolher constantes A, B < tal que: 0 g(t) dt < A + BT, T (17) Interpretação: O sistema é marginalmente estável se a integral cresce linearmente com o tempo T. Exemplos: 1. G(s) = 1 s (18) 2. Sistema marginalmente estável G(s) = 1 s 2 (19) Sistema instável 66
75 Relação entre estabilidade e as raízes da equação característica Theorem Um sistema SISO com uma função de transferência própria G(s) é estável, se e somente se cada pólo de G(s) possui parte real negativa. 67
76 Estabilidade com entrada nula, estabilidade assintótica ou estabilidade interna A estabilidade com entrada nula se refere à condição de estabilidade quando a entrada é nula e o sistema é dirigido pelas condições iniciais não nulas x 0. Definition A resposta com entrada nula do sistema ẋ(t) = Ax(t) é marginalmente estável se para cada estado inicial finito x 0 excita uma resposta x(t) limitada. Definition A resposta com entrada nula do sistema ẋ(t) = Ax(t) é assintoticamente estável se para cada estado inicial finito x 0 excita uma resposta x(t) limitada e ainda lim t x = 0. 68
77 Exemplo Vamos supor, o seguinte sistema de 1a. ordem: ẏ(t) = ay(t) + bu(t). (20) Este sistema pode ser escrito, da seguinte forma: ẋ(t) = ax(t) + bu(t); y(t) = x(t), (21) o que corresponde à representação em espaço de estados. 69
78 Fazendo o sinal de entrada u(t) = 0, obtemos: ẋ(t) = ax(t). (22) Utilizando a propriedade da Transformada de Laplace para a derivada de um sinal, temos: sx(s) x(0) = ax(s). (23) Logo: X(s) = x(0) L = 1 x(t) = e at x(0). (24) s a 70
79 Observando a Equação 24 podemos concluir que: Se o pólo é positivo (a > 0) então x(t) cresce indefinidamente, ou seja: lim x(t) =. (25) t Se o pólo é negativo (a < 0) então x(t) decresce exponencialmente, ou seja: lim x(t) = 0. (26) t Obviamente, a estabilidade assintótica do estado x(t) implica na estabilidade assintótica da saída y(t). 71
80 Sistemas de ordem n O mesmo resultado, pode ser extrapolado para sistemas de ordem n: ẋ(t) = Ax(t), (27) onde A é uma matriz n n. Neste caso, poderíamos escrever: x(t) = e At x(0), (28) e da mesma forma, o vetor de estados x(t) decresce exponencialmente se e somente se os pólos do sistema tiverem parte real negativa. 72
81 Pólos e suas respostas impulsivas m=1 jω y(t) y(t) t(s) 1 t(s) y(t) σ y(t) t(s) t(s) y(t) y(t) t(s) t(s) 73
82 Pólos e suas respostas impulsivas m=2 jω y(t) y(t) t(s) t(s) y(t) σ y(t) t(s) t(s) y(t) y(t) t(s) t(s) 74
83 Condição de Estabilidade Valores de s = σ i + jω i (i = 1,..., n) Assintoticamente Estável/ Estável Marginalmente estável ou Marginalmente instável σ i < 0 para i = 1,..., n pelo menos algum σ i = 0, nenhum valor σ i > 0, nenhum pólo múltiplo no eixo jω. Instável Pelo menos algum σ i > 0 ou algum pólo σ i = 0 de ordem múltipla (pólo de ordem múltipla no eixo jω) Tabela 2: Condições de estabilidade de sistemas SISO invariantes no tempo. 75
84 Exemplos G(s) = 20 (s + 1)(s + 2)(s + 3). (29) Obviamente trata-se de um sistema estável. Os pólos são: s = 1, s = 2 e s = Resposta a impulso G1(s)=20/(s+1)(s+2)(s+3) 3.5 Resposta a Degrau G1(s)=20/(s+1)(s+2)(s+3) Amplitude Amplitude Time (sec) (a) Resposta a Impulso Time (sec) (b) Resposta a Degrau 76
85 20(s + 1) G 2(s) = (s 1)(s 2 + 2s + 2). (30) O sistema é instável porque existe um pólo em s = 1. Resposta a Impulso G2(s)=20(s+1)/(s 1)(s 2 +2s+2) Resposta a Degrau G2(s)=20(s+1)/(s 1)(s 2 +2s+2) Amplitude 50 Amplitude Time (sec) (c) Resposta a Impulso Time (sec) (d) Resposta a Degrau 77
86 20(s 1) G 3(s) = (s + 2)(s 2 + 4). (31) O sistema é marginalmente estável devido ao par de pólos complexos conjugados ±j2. 8 Resposta a Impulso G3(s)=20(s 1)/(s+2)(s 2 +4) 2 Resposta a Degrau G3(s)=20(s 1)/(s+2)(s 2 +4) Amplitude 0 2 Amplitude Time (sec) (e) Resposta a Impulso Time (sec) (f) Resposta a Degrau 78
87 10 G 4(s) (s 2 + 4) 2 (s + 10). (32) O sistema é instável devido aos pólo complexos de ordem múltipla s = ±j2 3 Resposta a Impulso G4(s)=10/(s 2 +4) 2 (s+10) 2 Resposta a Degrau G4(s)=10/(s 2 +4) 2 (s+10) Amplitude 0 Amplitude Time (sec) (g) Resposta a Impulso Time (sec) (h) Resposta a Degrau 79
88 O Critério de estabilidade de Routh-Hurwitz O método de Routh-Hurwitz permite definir a estabilidade de um sistema a partir da equação característica do sistema. A equação característica de um sistema SISO (Single Input Single Output) invariante no tempo pode ser escrita como: F(s) = a ns n + a n 1s n a 1s + a 0. (33) Para se determinar a estabilidade ou não de um sistema é necessário determinar se alguma das raízes de F(s) pertence ao semi-plano direito de s. Se a Equação 33 é escrita na forma fatorada obtemos: F(s) = a n(s r 1)(s r 2)... (s r n), (34) onde r i é a i-ésima raiz da equação característica. 80
89 Multiplicando todos os fatores, podemos escrever: F(s) =a ns n a n(r 1 + r r n)s n 1 + a n(r 1r 2 + r 2r 3 + r 1r )s n 2 a n(r 1r 2r 3 + r 1r 2r )s n (35) + a n( 1) n r 1r 2r 3... r n 81
90 Em outras palavras, para uma equação de ordem n, obtemos: F(s) =a ns n a n(soma de todas as raízes)s n 1 + a n(soma de todos os produtos de raízes duas a duas)s n 2 a n(soma de todos os produtos de raízes três a três)s n a n(produto de todas as raízes) = 0 82
91 Examinando a Equação 35, podemos notar que todos os coeficientes do polinômio devem ter o mesmo sinal se todas as raízes estão no semi-plano esquerdo. Além disso, é necessário que todos os coeficientes sejam não nulos. Esses requisitos são necessários mas não suficientes. Isto é, se estes requisitos não forem satisfeitos, já podemos afirmar que o sistema não é estável. Entretanto, se os requisitos forem satisfeitos, não necessariamente temos um sistema estável. 83
92 Por exemplo, para a seguinte equação característica: F(s) = (s + 2)(s 2 s + 4) = (s 3 + s 2 + 2s + 8). Este sistema é instável, mesmo tendo todos os coeficientes de mesmo sinal. 84
93 O critério de Hurwitz A condição necessária e suficiente para que todas as raízes da equação característica estejam no semi-plano esquerdo é satisfeita quando todos os determinantes de Hurwitz D k, k = 1, 2,... sejam positivos. Os determinantes de Hurwitz para a equação característica são dados por: D 1 = an 1 D 2 = an 1 an 3 a n a n 2 a n 1 a n 3 a n 5 D 3 = a n a n 2 a n 4 0 a n 1 a n 3... (36) 85
94 D n = a n 1 a n 3 a n 5 0 a n a n 2 a n a n 1 a n a 0 (37) 86
95 A tabulação de Routh Felizmente, não é necessário calcular os determinantes de Hurwitz. Um método equivalente foi desenvolvido por Routh e é comumente denominado tabulação de Routh. Inicialmente, arranja-se os coeficientes da seguinte forma: a n a n 2 a n 4 a n 6 a n 8... a n 1 a n 3 a n 5 a n 7 a n 9 87
96 Vamos utilizar como exemplo uma equação de 6a. ordem: F(s) = a 6s 6 + a 5s 5 + a 4s 4 + a 3s 3 + a 2s 2 + a 1s + a 0. (38) Para este caso a Tabulação de Routh é calculada como: 88
97 Cálculos para ordem 6 s 6 a 6 a 4 a 2 a 0 s 5 a 5 a 3 a 1 0 s 4 a 5a 4 a 6a 3 a 5 = A a 5a 2 a 6a 1 a 5 = B a 5a 0 a 60 a 5 = a 0 0 s 3 Aa 3 a 5B A = C Aa 1 a 5a 0 A = D A0 a 50 A = 0 0 s 2 BC AD C = E Ca 0 A0 C = a 0 C0 A0 C = 0 0 s 1 ED Ca 0 E = F s 0 Fa 0 E0 F = a
98 O critério de estabilidade de Routh-Hurwitz estabelece que o número de pólos do sistema com parte real positiva é igual ao número de trocas de sinal dos elementos da primeira coluna da tabela. 90
99 Exemplo 1 Considere a equação: F(s) = (s 2)(s + 1)(s 3) = s 3 4s 2 + s + 6 = 0. (39) A equação acima possui um coeficiente negativo, o que significa que não satisfaz as condições necessárias para a estabilidade. Através da forma fatorada, sabemos que existem duas raízes no semi-plano direito: s = 2, s = 3. 91
100 Exemplo1 Vamos examinar quais seriam os cálculos do método de Routh-Hurwitz: s s s 1 ( 4)(1) (6)(1) 4 = s 0 (2.5)(6) ( 4)(0) 2.5 = 6 0 Existem duas mudanças de sinal na coluna 1, indicando a presença de duas raízes no semi-plano direito. 92
101 Exemplo 2 Considere a equação: F(s) = 2s 4 + s 3 + 3s 2 + 5s + 10 = 0. (40) Neste caso, as condições necessárias são satisfeitas, i.e., todos os termos estão presentes e de mesmo sinal. 93
102 A tabulação de Routh-Hurwitz é calculada como: s s s 2 s 1 (1)(3) (2)(5) 1 = ( 7)(5) (1)(10) 7 = s Como existem duas mudanças de sinal na primeira coluna existem duas raízes no semi-plano direito. As quatro raízes do sistema são dadas por: s = ± j0.9311, s = ± j
103 Caso Especial 1 Se o primeiro elemento de qualquer linha for zero e os outros forem diferentes de zero, os elementos da próxima linha serão todos infinitos. Para solucionar este problema, dev-se substituir o elemento nulo por um número positivo ɛ arbitrariamente pequeno. 95
104 Exemplo 3 F(s) = s 4 + s 3 + 2s 2 + 2s + 3 = 0 (41) s s s 2 0 ɛ 3 Como a linha correspondente a s 2 possui o primeiro elemento nulo, devemos substituí-lo por ɛ. 96
105 Exemplo 3 s s s 2 ɛ 3 s 1 2ɛ 3 ɛ = 3 ɛ 0 s Existem duas mudanças de sinal o que significa que existem duas raízes no semi-plano direito. As raízes são: s = ± j0.902, s = ± j OBS: O método pode não funcionar se o sistema possui raízes imaginárias puras. 97
106 Caso Especial 2 Se todos os elementos de uma linha são zeros as seguintes condições podem existir: A equação possui pelo menos um par de raízes reais iguais mas de sinais opostos, A equação tem um ou mais pares de raízes imaginárias, A equação tem pares de raízes complexas conjugadas formando uma simetria em relação à origem. Ex: s = 1 ± j1, s = 1 ± j1. 98
107 Caso Especial 2 Uma possível solução consiste em utilizar uma equação auxiliar A(s) = 0 que corresponde à linha anterior de zeros. A equação auxiliar sempre contêm apenas termos de ordem par. As raízes da equação auxiliar também satisfazem a equação original. O método consiste nos seguintes passos: Escreva a Equação A(s) utilizando os coeficientes da linha anterior nula, Calcule a derivada da equação A(s): da(s) ds = 0, (42) Substitua a linha de zeros pelos coeficientes de da(s)/ds = 0. 99
108 Exemplo 4 Vamos tentar determinar a estabilidade absoluta de um sistema que possua a seguinte equação característica: F(s) = s 5 + 4s 4 + 8s 3 + 8s 2 + 7s + 4 = 0. (43) A tabulação de Routh-Hurwitz é calculada como: s s s s s
109 Exemplo 4 Como podemos observar a linha correspondente à linha s 1 é nula. Os polinômios A(s) E da(s)/ds neste caso seriam dados por: A(S) = 4s2 + 4 = 0 da(s) ds = 8s = 0. (44) 101
110 Exemplo 4 A tabulação de Routh-Hurwitz seria agora dada por: s s s s (45) s s 0 4 Como não há mudanças de sinal não há raízes no semi-plano direito. As raízes de A(s) são s = ±j o que indica que o sistema é marginalmente estável. 102
O Papel dos Pólos e Zeros
 Departamento de Engenharia Mecatrônica - EPUSP 27 de setembro de 2007 1 Expansão em frações parciais 2 3 4 Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q i=1(s + z i )(s + p m ),
Departamento de Engenharia Mecatrônica - EPUSP 27 de setembro de 2007 1 Expansão em frações parciais 2 3 4 Suponha a seguinte função de transferência: m l=1 G(s) = (s + z l) q i=1(s + z i )(s + p m ),
Estabilidade de sistemas de controle lineares invariantes no tempo
 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
Estabilidade de sistemas de controle lineares invariantes no tempo
 Capítulo 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2. Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no
Capítulo 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2. Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no
Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros
 Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Controle de Processos Aula: Estabilidade e Critério de Routh
 107484 Controle de Processos Aula: Estabilidade e Critério de Routh Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB)
107484 Controle de Processos Aula: Estabilidade e Critério de Routh Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB)
IV. ESTABILIDADE DE SISTEMAS LIT
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE IV. ESTABILIDADE DE SISTEMAS LIT Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE IV. ESTABILIDADE DE SISTEMAS LIT Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
AULA 3. CRITÉRIO DE ESTABILIDADE DE Routh-Hurwitz. Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I
 Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 3 CRITÉRIO DE ESTABILIDADE DE Routh-Hurwitz PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA Critério de estabilidade de Routh A questão
Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 3 CRITÉRIO DE ESTABILIDADE DE Routh-Hurwitz PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA Critério de estabilidade de Routh A questão
Modelagem Matemática de Sistemas
 Modelagem Matemática de Sistemas 1. Descrição Matemática de Sistemas 2. Descrição Entrada-Saída 3. Exemplos pag.1 Teoria de Sistemas Lineares Aula 3 Descrição Matemática de Sistemas u(t) Sistema y(t) Para
Modelagem Matemática de Sistemas 1. Descrição Matemática de Sistemas 2. Descrição Entrada-Saída 3. Exemplos pag.1 Teoria de Sistemas Lineares Aula 3 Descrição Matemática de Sistemas u(t) Sistema y(t) Para
Estabilidade de Sistemas Lineares Realimentados
 Estabilidade de Sistemas Lineares Realimentados 1. Conceito de estabilidade 2. Critério de estabilidade de Routh-Hurwitz p.1 Engenharia de Controle Aula 6 Estabilidade de Sistemas Lineares Realimentados
Estabilidade de Sistemas Lineares Realimentados 1. Conceito de estabilidade 2. Critério de estabilidade de Routh-Hurwitz p.1 Engenharia de Controle Aula 6 Estabilidade de Sistemas Lineares Realimentados
Sistemas lineares. Aula 7 Transformada Inversa de Laplace
 Sistemas lineares Aula 7 Transformada Inversa de Laplace Transformada Inversa de Laplace Transformada Inversa de Laplace e RDC x(t) única Metódos Inversão pela Definição Inversão pela Expansão em Frações
Sistemas lineares Aula 7 Transformada Inversa de Laplace Transformada Inversa de Laplace Transformada Inversa de Laplace e RDC x(t) única Metódos Inversão pela Definição Inversão pela Expansão em Frações
Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros
 107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
Capítulo 2 Dinâmica de Sistemas Lineares
 Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Representação e Análise de Sistemas Dinâmicos Lineares Componentes Básicos de um Sistema de Controle
 Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
O método do lugar das raízes
 4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada em função
4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada em função
Controle e Sistemas Não lineares
 Controle e Sistemas Não lineares Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 01 de dezembro de 2016. Sumário Objetivos Introduzir
Controle e Sistemas Não lineares Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 01 de dezembro de 2016. Sumário Objetivos Introduzir
Critério de Estabilidade: Routh-Hurwitz
 Critério de Estabilidade: Routh-Hurwitz O Critério de Nyquist foi apresentado anteriormente para determinar a estabilidade de um sistema em malha fechada analisando-se sua função de transferência em malha
Critério de Estabilidade: Routh-Hurwitz O Critério de Nyquist foi apresentado anteriormente para determinar a estabilidade de um sistema em malha fechada analisando-se sua função de transferência em malha
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
O lugar das raízes p. 1/54. O lugar das raízes. Newton Maruyama
 O lugar das raízes p. 1/54 O lugar das raízes Newton Maruyama O lugar das raízes p. 2/54 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização
O lugar das raízes p. 1/54 O lugar das raízes Newton Maruyama O lugar das raízes p. 2/54 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização
SC1 Sistemas de Controle 1. Cap. 2 - Estabilidade Prof. Tiago S Vítor
 SC1 Sistemas de Controle 1 Cap. 2 - Estabilidade Prof. Tiago S Vítor Sumário 1. Introdução 2. Critério de Routh-Hurwitz 3. Critério de Routh-Hurwitz: Casos Especiais 4. Projeto de Estabilidade via Routh-Hurwitz
SC1 Sistemas de Controle 1 Cap. 2 - Estabilidade Prof. Tiago S Vítor Sumário 1. Introdução 2. Critério de Routh-Hurwitz 3. Critério de Routh-Hurwitz: Casos Especiais 4. Projeto de Estabilidade via Routh-Hurwitz
Aula 9. Carlos Amaral Cristiano Quevedo Andrea. UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica
 Aula 9 Carlos Amaral Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Abril de 2012. Resumo 1 Introdução - Estabilidade
Aula 9 Carlos Amaral Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Abril de 2012. Resumo 1 Introdução - Estabilidade
Controle de Processos Aula: Função de transferência, diagrama de blocos e pólos
 107484 Controle de Processos Aula: Função de transferência, diagrama de blocos e pólos Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016
107484 Controle de Processos Aula: Função de transferência, diagrama de blocos e pólos Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016
Aula 6 Transformada de Laplace
 Aula 6 Transformada de Laplace Introdução Propriedades da Transformada de Laplace Tabela Transformada ade Laplace Transformada Inversa de Laplace Função de transferência Definição: X s = L x t = s é uma
Aula 6 Transformada de Laplace Introdução Propriedades da Transformada de Laplace Tabela Transformada ade Laplace Transformada Inversa de Laplace Função de transferência Definição: X s = L x t = s é uma
II. REVISÃO DE FUNDAMENTOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
Aula 3. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
PMR3404 Controle I Aula 3
 PMR3404 Controle I Aula 3 Resposta estática Ações de controle PID Newton Maruyama 23 de março de 2017 PMR-EPUSP Classificação de sistemas de acordo com o seu desempenho em regime estático Seja o seguinte
PMR3404 Controle I Aula 3 Resposta estática Ações de controle PID Newton Maruyama 23 de março de 2017 PMR-EPUSP Classificação de sistemas de acordo com o seu desempenho em regime estático Seja o seguinte
5 Descrição entrada-saída
 Teoria de Controle (sinopse) 5 Descrição entrada-saída J. A. M. Felippe de Souza Descrição de Sistemas Conforme a notação introduzida no capítulo 1, a função u( ) representa a entrada (ou as entradas)
Teoria de Controle (sinopse) 5 Descrição entrada-saída J. A. M. Felippe de Souza Descrição de Sistemas Conforme a notação introduzida no capítulo 1, a função u( ) representa a entrada (ou as entradas)
A Transformada de Laplace
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
Pólos, Zeros e Estabilidade
 Pólos, Zeros e Estabilidade Definindo Estabilidade A condição para estabilidade pode também ser expressa da seguinte maneira: se um sistema é estável quando sujeito a um impulso, a saída retoma a zero.
Pólos, Zeros e Estabilidade Definindo Estabilidade A condição para estabilidade pode também ser expressa da seguinte maneira: se um sistema é estável quando sujeito a um impulso, a saída retoma a zero.
Estabilidade. Samir A. M. Martins 1. Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre UFSJ e CEFET MG
 Interna Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre UFSJ e CEFET MG O que nos espera? Interna 1 em sistemas multivariáveis
Interna Samir A. M. Martins 1 1 UFSJ / Campus Santo Antônio, MG Brasil Programa de Pós-Graduação em Engenharia Elétrica Associação ampla entre UFSJ e CEFET MG O que nos espera? Interna 1 em sistemas multivariáveis
PROJETO DE CONTROLADORES A PARTIR DO PLANO S. critério Routh-Hurwitz análise de estabilidade análise de desempenho
 PROJETO DE CONTROLADORES A PARTIR DO PLANO S critério Routh-Hurwitz análise de estabilidade análise de desempenho Critério Routh-Hurwitz: análise da estabilidade Sistemas de primeira ordem: 1 x o (t)=
PROJETO DE CONTROLADORES A PARTIR DO PLANO S critério Routh-Hurwitz análise de estabilidade análise de desempenho Critério Routh-Hurwitz: análise da estabilidade Sistemas de primeira ordem: 1 x o (t)=
Controle de Processos Aula: Sistemas de 1ª e 2ª ordem
 107484 Controle de Processos Aula: Sistemas de 1ª e 2ª ordem Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
107484 Controle de Processos Aula: Sistemas de 1ª e 2ª ordem Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
Transformada de Laplace
 Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Sinais e Sistemas Transformada de Laplace lco@ist.utl.pt Instituto Superior Técnico Sinais e Sistemas p.1/60 Resumo Definição da transformada de Laplace. Região de convergência. Propriedades da transformada
Circuitos Elétricos II
 Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada inversa de Laplace Definição Funções racionais Expansão em frações parciais
Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada inversa de Laplace Definição Funções racionais Expansão em frações parciais
Sistemas de Controle 1
 Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap6 Estabilidade Prof. Filipe Fraga Sistemas de Controle 1 6. Estabilidade 6.1 Introdução 6.2 Critério de Routh-Hurwitz
Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap6 Estabilidade Prof. Filipe Fraga Sistemas de Controle 1 6. Estabilidade 6.1 Introdução 6.2 Critério de Routh-Hurwitz
Análise no Domínio do Tempo de Sistemas em Tempo Contínuo
 Análise no Domínio do Tempo de Sistemas em Tempo Contínuo Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise no Domínio do Tempo de Sistemas em Tempo Contínuo Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Instrumentação e Controle Aula 7. Estabilidade. Prof. Renato Watanabe ESTO004-17
 Instrumentação e Controle Aula 7 Estabilidade Prof. Renato Watanabe ESTO004-17 Onde estamos no curso Sistema Obtenção das Equações Diferenciais que descrevem o comportamento do sistema Representação no
Instrumentação e Controle Aula 7 Estabilidade Prof. Renato Watanabe ESTO004-17 Onde estamos no curso Sistema Obtenção das Equações Diferenciais que descrevem o comportamento do sistema Representação no
Estabilidade. 1. Estabilidade Entrada-Saída Sistemas LIT. 2. Estabilidade BIBO Sistemas LIT. 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT
 Estabilidade 1. Estabilidade Entrada-Saída Sistemas LIT 2. Estabilidade BIBO Sistemas LIT 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT 4. Sistemas Discretos LIT 5. Estabilidade BIBO Sistemas
Estabilidade 1. Estabilidade Entrada-Saída Sistemas LIT 2. Estabilidade BIBO Sistemas LIT 3. Estabilidade BIBO de Equações Dinâmicas Sistemas LIT 4. Sistemas Discretos LIT 5. Estabilidade BIBO Sistemas
Indice. Resposta forçada (condições iniciais nulas)
 Indice 3.3 Inversão da TLP Fracções parciais Resolução equações diferenciais Polinómio característico Estabilidade resposta natural 3.4 Função de Transferência Estabilidade devido à entrada (resposta forçada)
Indice 3.3 Inversão da TLP Fracções parciais Resolução equações diferenciais Polinómio característico Estabilidade resposta natural 3.4 Função de Transferência Estabilidade devido à entrada (resposta forçada)
Técnicas de Lugar das Raízes. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Técnicas de Lugar das Raízes Carlos Alexandre Mello 1 Introdução Lugar das raízes é um método de análise e projeto para estabilidade e resposta de transiente É uma representação gráfica dos polos de um
Técnicas de Lugar das Raízes Carlos Alexandre Mello 1 Introdução Lugar das raízes é um método de análise e projeto para estabilidade e resposta de transiente É uma representação gráfica dos polos de um
Transformadas de Laplace Engenharia Mecânica - FAENG. Prof. Josemar dos Santos
 Engenharia Mecânica - FAENG SISTEMAS DE CONTROLE Prof. Josemar dos Santos Sumário Transformadas de Laplace Teorema do Valor Final; Teorema do Valor Inicial; Transformada Inversa de Laplace; Expansão em
Engenharia Mecânica - FAENG SISTEMAS DE CONTROLE Prof. Josemar dos Santos Sumário Transformadas de Laplace Teorema do Valor Final; Teorema do Valor Inicial; Transformada Inversa de Laplace; Expansão em
Sistemas de Controle
 Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
Transformada de Laplace
 Transformada de aplace Nas aulas anteriores foi visto que as ferramentas matemáticas de Fourier (série e transformadas) são de extrema importância na análise de sinais e de sistemas IT. Isto deve-se ao
Transformada de aplace Nas aulas anteriores foi visto que as ferramentas matemáticas de Fourier (série e transformadas) são de extrema importância na análise de sinais e de sistemas IT. Isto deve-se ao
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
Estabilidade entrada-saída (externa).
 Estabilidade entrada-saída (externa) ENGC33: Sinais e Sistemas II Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 05 de junho de 2019 Prof Tito Luís Maia Santos 1/ 38 Sumário
Estabilidade entrada-saída (externa) ENGC33: Sinais e Sistemas II Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 05 de junho de 2019 Prof Tito Luís Maia Santos 1/ 38 Sumário
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial
 Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
Resumo Sinais e Sistemas Transformada de aplace uís Caldas de Oliveira lco@istutlpt Instituto Superior Técnico Definição da transformada de aplace Região de convergência Propriedades da transformada de
INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA. Sistemas
 INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA Sistemas Dinâmicos Para controlar é preciso conhecer Sistemas dinâmicos Modificam-se no decorrer do tempo Modelos matemáticos Método analítico (Leis físicas)
INSTITUTO FEDERAL DO ESPÍRITO SANTO - CAMPUS SERRA Sistemas Dinâmicos Para controlar é preciso conhecer Sistemas dinâmicos Modificam-se no decorrer do tempo Modelos matemáticos Método analítico (Leis físicas)
SCILAB: MÓDULO 4 SISTEMAS E CONTROLE
 SCILAB: MÓDULO 4 SISTEMAS E CONTROLE Scilab 5.3.3 Dr.ª Eng.ª Mariana Santos Matos Cavalca O que é controlar? Função de Transferência: breve definição u(t) Sistema LIT y(t) Usualmente (sistemas próprios)
SCILAB: MÓDULO 4 SISTEMAS E CONTROLE Scilab 5.3.3 Dr.ª Eng.ª Mariana Santos Matos Cavalca O que é controlar? Função de Transferência: breve definição u(t) Sistema LIT y(t) Usualmente (sistemas próprios)
Circuitos Elétricos II
 Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Ganho e Deslocamento de Fase Função de Rede (ou de Transferência) Estabilidade 1 Definições
Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Ganho e Deslocamento de Fase Função de Rede (ou de Transferência) Estabilidade 1 Definições
1. Sinais de teste. 2. Sistemas de primeira ordem. 3. Sistemas de segunda ordem. Especificações para a resposta
 Desempenho de Sistemas de Controle Realimentados 1. Sinais de teste. Sistemas de primeira ordem 3. Sistemas de segunda ordem Especificações para a resposta Fernando de Oliveira Souza pag.1 Engenharia de
Desempenho de Sistemas de Controle Realimentados 1. Sinais de teste. Sistemas de primeira ordem 3. Sistemas de segunda ordem Especificações para a resposta Fernando de Oliveira Souza pag.1 Engenharia de
INTRODUÇÃO À ANALISE DE SINAIS ELT 032
 INTRODUÇÃO À ANALISE DE SINAIS ELT 032 Prof. Jeremias Barbosa Machado Introdução Neste capítulo estudaremos as Transformadas de Laplace. Elas apresentam uma representação de sinais no domínio da frequência
INTRODUÇÃO À ANALISE DE SINAIS ELT 032 Prof. Jeremias Barbosa Machado Introdução Neste capítulo estudaremos as Transformadas de Laplace. Elas apresentam uma representação de sinais no domínio da frequência
Aula 04 Representação de Sistemas
 Aula 04 Representação de Sistemas Relação entre: Função de Transferência Transformada Laplace da saída y(t) - Transformada Laplace da entrada x(t) considerando condições iniciais nulas. Pierre Simon Laplace,
Aula 04 Representação de Sistemas Relação entre: Função de Transferência Transformada Laplace da saída y(t) - Transformada Laplace da entrada x(t) considerando condições iniciais nulas. Pierre Simon Laplace,
Ações de controle básicas: uma análise do desempenho em regime
 Capítulo 3 Ações de controle básicas: uma análise do desempenho em regime estático 3. Introdução Neste capítulo, as ações de controle básicas utilizadas em controladores industriais e o seu desempenho
Capítulo 3 Ações de controle básicas: uma análise do desempenho em regime estático 3. Introdução Neste capítulo, as ações de controle básicas utilizadas em controladores industriais e o seu desempenho
Transformada de Laplace
 Transformada de Laplace Monitoria de Sinais e Sistemas Lineares 04/11/09 Monitoria de Sinais e Sistemas Lineares () Transformada de Laplace 04/11/09 1 / 19 Transformadas Transformada de Laplace X(s) =
Transformada de Laplace Monitoria de Sinais e Sistemas Lineares 04/11/09 Monitoria de Sinais e Sistemas Lineares () Transformada de Laplace 04/11/09 1 / 19 Transformadas Transformada de Laplace X(s) =
ANÁLISE DO MÉTODO DA RESPOSTA EM FREQÜÊNCIA
 VIII- CAPÍTULO VIII ANÁLISE DO MÉTODO DA RESPOSTA EM FREQÜÊNCIA 8.- INTRODUÇÃO O método da resposta em freqüência, nada mais é que a observação da resposta de um sistema, para um sinal de entrada senoidal,
VIII- CAPÍTULO VIII ANÁLISE DO MÉTODO DA RESPOSTA EM FREQÜÊNCIA 8.- INTRODUÇÃO O método da resposta em freqüência, nada mais é que a observação da resposta de um sistema, para um sinal de entrada senoidal,
Transformada de Laplace. Transformada de Laplace (CP1) DEQ/UFSCar 1 / 76
 Transformada de Laplace Transformada de Laplace (CP) www.professores.deq.ufscar.br/ronaldo/cp DEQ/UFSCar / 76 Roteiro I Introdução Definição da Transformada Transformada de Laplace de Algumas Funções Transformada
Transformada de Laplace Transformada de Laplace (CP) www.professores.deq.ufscar.br/ronaldo/cp DEQ/UFSCar / 76 Roteiro I Introdução Definição da Transformada Transformada de Laplace de Algumas Funções Transformada
6-Análise de estabilidade de sistemas feedback 6.1- Noções de estabilidade
 6-Análise de estabilidade de sistemas feedback 6.- Noções de estabilidade Nos capítulos anteriores examinamos as características dinâmicas da resposta de sistemas em malha fechada e desenvolvemos a função
6-Análise de estabilidade de sistemas feedback 6.- Noções de estabilidade Nos capítulos anteriores examinamos as características dinâmicas da resposta de sistemas em malha fechada e desenvolvemos a função
CRITÉRIO DE ESTABILIDADE DE ROUTH
 ENGENHARIA ELETRÔNICA DAELN UTFPR Prof. Paulo R. Brero de Campos CRITÉRIO DE ESTABILIDADE DE ROUTH Um sistema será estável quando todos os polos estiverem no semiplano esquerdo do plano S. Exemplo: G(s)
ENGENHARIA ELETRÔNICA DAELN UTFPR Prof. Paulo R. Brero de Campos CRITÉRIO DE ESTABILIDADE DE ROUTH Um sistema será estável quando todos os polos estiverem no semiplano esquerdo do plano S. Exemplo: G(s)
EES-49/2012 Prova 1. Q1 Dado o seguinte conjunto de equações:
 Q1 Dado o seguinte conjunto de equações: EES-49/2012 Prova 1 Onde: h C é o sinal de entrada do sistema; θ é o sinal de saída do sistema; T P é uma entrada de perturbação; T T, T R e h R são variáveis intermediárias;
Q1 Dado o seguinte conjunto de equações: EES-49/2012 Prova 1 Onde: h C é o sinal de entrada do sistema; θ é o sinal de saída do sistema; T P é uma entrada de perturbação; T T, T R e h R são variáveis intermediárias;
4.1 Pólos, Zeros e Resposta do Sistema
 ADL17 4.1 Pólos, Zeros e Resposta do Sistema A resposta de saída de um sistema é a soma de duas respostas: a resposta forçada e a resposta natural. Embora diversas técnicas, como a solução de equações
ADL17 4.1 Pólos, Zeros e Resposta do Sistema A resposta de saída de um sistema é a soma de duas respostas: a resposta forçada e a resposta natural. Embora diversas técnicas, como a solução de equações
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2
 FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Resposta no espaço de estados Representações
FUNDAMENTOS DE SISTEMAS LINEARES PARTE 2 Prof. Iury V. de Bessa Departamento de Eletricidade Faculdade de Tecnologia Universidade Federal do Amazonas Agenda Resposta no espaço de estados Representações
2. Modelos Lineares de Espaço de Estados. e resposta ao impulso. Método para o cálculo das soluções: através do uso de transformadas de Laplace
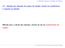 2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
Aula 11. Revisão de Fasores e Introdução a Laplace
 Aula Revisão de Fasores e Introdução a Laplace Revisão - Fasor Definição: Fasor é a representação complexa da magnitude e fase de uma senoide. V = V m e jφ = V m φ v t = V m cos(wt + φ) = R(V e jwt ) Impedância
Aula Revisão de Fasores e Introdução a Laplace Revisão - Fasor Definição: Fasor é a representação complexa da magnitude e fase de uma senoide. V = V m e jφ = V m φ v t = V m cos(wt + φ) = R(V e jwt ) Impedância
Erros de Estado Estacionário. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
SISTEMAS DE CONTROLE I Capítulo 6 - Estabilidade. Prof. M.e Jáder de Alencar Vasconcelos
 SISTEMAS DE CONTROLE I Capítulo 6 - Estabilidade Prof. M.e Jáder de Alencar Vasconcelos CAPÍTULO 6 INTRODUÇÃO INTRODUÇÃO No Capítulo 1, vimos que três requisitos fazem parte do projeto de um sistema de
SISTEMAS DE CONTROLE I Capítulo 6 - Estabilidade Prof. M.e Jáder de Alencar Vasconcelos CAPÍTULO 6 INTRODUÇÃO INTRODUÇÃO No Capítulo 1, vimos que três requisitos fazem parte do projeto de um sistema de
Universidade Federal do Rio de Janeiro. Circuitos Elétricos I EEL 420. Módulo 11
 Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Resposta no Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Resposta no Tempo Carlos Alexandre Mello 1 Resposta no Tempo - Introdução Como já discutimos, após a representação matemática de um subsistema, ele é analisado em suas respostas de transiente e de estadoestacionário
Resposta no Tempo Carlos Alexandre Mello 1 Resposta no Tempo - Introdução Como já discutimos, após a representação matemática de um subsistema, ele é analisado em suas respostas de transiente e de estadoestacionário
TRANSFORMADA DE LAPLACE E OPERADORES LINEARES
 TRANSFORMADA DE LAPLACE E OPERADORES LINEARES O DOMÍNIO DE LAPLACE Usualmente trabalhamos com situações que variam no tempo (t), ou seja, trabalhamos no domínio do tempo. O domínio de Laplace é um domínio
TRANSFORMADA DE LAPLACE E OPERADORES LINEARES O DOMÍNIO DE LAPLACE Usualmente trabalhamos com situações que variam no tempo (t), ou seja, trabalhamos no domínio do tempo. O domínio de Laplace é um domínio
V. ANÁLISE NO DOMÍNIO DO TEMPO
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
Aula 9. Diagrama de Bode
 Aula 9 Diagrama de Bode Hendrik Wade Bode (americano,905-98 Os diagramas de Bode (de módulo e de fase são uma das formas de caracterizar sinais no domínio da frequência. Função de Transferência Os sinais
Aula 9 Diagrama de Bode Hendrik Wade Bode (americano,905-98 Os diagramas de Bode (de módulo e de fase são uma das formas de caracterizar sinais no domínio da frequência. Função de Transferência Os sinais
Aula 18: Projeto de controladores no domínio da frequência
 Aula 18: Projeto de controladores no domínio da frequência prof. Dr. Eduardo Bento Pereira Universidade Federal de São João del-rei ebento@ufsj.edu.br 26 de outubro de 2017. prof. Dr. Eduardo Bento Pereira
Aula 18: Projeto de controladores no domínio da frequência prof. Dr. Eduardo Bento Pereira Universidade Federal de São João del-rei ebento@ufsj.edu.br 26 de outubro de 2017. prof. Dr. Eduardo Bento Pereira
Controle de Processos
 17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 217 E. S. Tognetti (UnB) Controle
17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 217 E. S. Tognetti (UnB) Controle
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
J. A. M. Felippe de Souza 10 Estabilidade. 10 Estabilidade
 J. A. M. Felippe de Souza 10 Estabilidade 10 Estabilidade 10.1 Introdução à Estabilidade 3 Definição 10.1 Estabilidade 3 Definição 10.2 - BIBO-estável 3 Teorema 10.1 Localização dos polos 4 Exemplo 10.1
J. A. M. Felippe de Souza 10 Estabilidade 10 Estabilidade 10.1 Introdução à Estabilidade 3 Definição 10.1 Estabilidade 3 Definição 10.2 - BIBO-estável 3 Teorema 10.1 Localização dos polos 4 Exemplo 10.1
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
RESPOSTA EM FREQUÊNCIA: DIAGRAMA DE BODE
 RESPOSTA EM FREQUÊNCIA: DIAGRAMA DE BODE CCL Profa. Mariana Cavalca Baseado em: MAYA, Paulo Álvaro; LEONARDI, Fabrizio. Controle essencial. São Paulo: Pearson, 2011. OGATA, Katsuhiko. Engenharia de controle
RESPOSTA EM FREQUÊNCIA: DIAGRAMA DE BODE CCL Profa. Mariana Cavalca Baseado em: MAYA, Paulo Álvaro; LEONARDI, Fabrizio. Controle essencial. São Paulo: Pearson, 2011. OGATA, Katsuhiko. Engenharia de controle
Fundamentos de Controlo
 Fundamentos de Controlo 3 a Série Estabilidade e Desempenho, Critério de Routh-Hurwitz, Rejeição de Perturbações, Sensibilidade à Variação de Parâmetros, Erros em Regime Estacionário. S3. Exercícios Resolvidos
Fundamentos de Controlo 3 a Série Estabilidade e Desempenho, Critério de Routh-Hurwitz, Rejeição de Perturbações, Sensibilidade à Variação de Parâmetros, Erros em Regime Estacionário. S3. Exercícios Resolvidos
Controle de Processos
 17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 216 E. S. Tognetti (UnB) Controle
17484 Controle de Processos Aula: Função de Transferência Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 216 E. S. Tognetti (UnB) Controle
14 Estimador assintótico
 Teoria de Controle (sinopse) 4 J. A. M. Felippe de Souza Neste capítulo continuaremos no estudo de que foi iniciado no capítulo anterior. Estimadores de Estado, A exemplo dos capítulos anteriores será
Teoria de Controle (sinopse) 4 J. A. M. Felippe de Souza Neste capítulo continuaremos no estudo de que foi iniciado no capítulo anterior. Estimadores de Estado, A exemplo dos capítulos anteriores será
Introdução aos Circuitos Elétricos
 Introdução aos Circuitos Elétricos A Transformada de Laplace Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia A Transformada de Laplace História Pierri
Introdução aos Circuitos Elétricos A Transformada de Laplace Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia A Transformada de Laplace História Pierri
Aula 15. Derivadas Direcionais e Vetor Gradiente. Quando u = (1, 0) ou u = (0, 1), obtemos as derivadas parciais em relação a x ou y, respectivamente.
 Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Aula 15 Derivadas Direcionais e Vetor Gradiente Seja f(x, y) uma função de variáveis. Iremos usar a notação D u f(x 0, y 0 ) para: Derivada direcional de f no ponto (x 0, y 0 ), na direção do vetor unitário
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
VI. MÉTODO DO LUGAR GEOMÉTRICO DAS RAÍZES
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE VI. MÉTODO DO LUGAR GEOMÉTRICO DAS RAÍZES Prof. Davi Antônio dos Santos (davists@ita.br) Departamento
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE VI. MÉTODO DO LUGAR GEOMÉTRICO DAS RAÍZES Prof. Davi Antônio dos Santos (davists@ita.br) Departamento
R + b) Determine a função de transferência de malha fechada, Y (s)
 FUP IC Teoria do Controlo xercícios Análise de Sistemas ealimentados Teoria do Controlo xercícios Análise de Sistemas ealimentados AS Considere o sistema da figura ao lado: a) Determine a função de transferência
FUP IC Teoria do Controlo xercícios Análise de Sistemas ealimentados Teoria do Controlo xercícios Análise de Sistemas ealimentados AS Considere o sistema da figura ao lado: a) Determine a função de transferência
Universidade Federal do Rio de Janeiro. Circuitos Elétricos I EEL 420. Módulo 11
 Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Universidade Federal do Rio de Janeiro Circuitos Elétricos I EEL 420 Módulo Laplace Bode Fourier Conteúdo - Transformada de Laplace.... - Propriedades básicas da transformada de Laplace....2 - Tabela de
Métodos Matemáticos para Engenharia
 Métodos Matemáticos para Engenharia Transformada de Laplace Docentes: > Prof. Fabiano Araujo Soares, Dr. Introdução Muitos parâmetros em nosso universo interagem através de equações diferenciais; Por exemplo,
Métodos Matemáticos para Engenharia Transformada de Laplace Docentes: > Prof. Fabiano Araujo Soares, Dr. Introdução Muitos parâmetros em nosso universo interagem através de equações diferenciais; Por exemplo,
O método do lugar das raízes
 Capítulo 4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada
Capítulo 4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada
Modelagem de Sistemas de Controle por Espaço de Estados
 Modelagem de Sistemas de Controle por Espaço de Estados A modelagem por espaço de estados possui diversas vantagens. Introduz a teoria conhecida como Controle Moderno ; Adequada para sistemas de múltiplas
Modelagem de Sistemas de Controle por Espaço de Estados A modelagem por espaço de estados possui diversas vantagens. Introduz a teoria conhecida como Controle Moderno ; Adequada para sistemas de múltiplas
Introdução aos Sinais e Sistemas
 Introdução aos Sinais e Sistemas Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco Colegiado de Engenharia
Introdução aos Sinais e Sistemas Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco Colegiado de Engenharia
I Controle Contínuo 1
 Sumário I Controle Contínuo 1 1 Introdução 3 1.1 Sistemas de Controle em Malha Aberta e em Malha Fechada................ 5 1.2 Componentes de um sistema de controle............................ 5 1.3 Comparação
Sumário I Controle Contínuo 1 1 Introdução 3 1.1 Sistemas de Controle em Malha Aberta e em Malha Fechada................ 5 1.2 Componentes de um sistema de controle............................ 5 1.3 Comparação
Sistemas lineares. Aula 6 Transformada de Laplace
 Sistemas lineares Aula 6 Transformada de Laplace Introdução Transformada de Laplace Convergência da transformada de laplace Exemplos Região de Convergência Introdução Transformações matemáticas: Logaritmo:
Sistemas lineares Aula 6 Transformada de Laplace Introdução Transformada de Laplace Convergência da transformada de laplace Exemplos Região de Convergência Introdução Transformações matemáticas: Logaritmo:
I Controle Contínuo 1
 Sumário I Controle Contínuo 1 1 Introdução 3 1.1 Sistemas de Controle em Malha Aberta e em Malha Fechada................ 5 1.2 Componentes de um sistema de controle............................ 5 1.3 Comparação
Sumário I Controle Contínuo 1 1 Introdução 3 1.1 Sistemas de Controle em Malha Aberta e em Malha Fechada................ 5 1.2 Componentes de um sistema de controle............................ 5 1.3 Comparação
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química 2014/1
 Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 8: Sistemas de Primeira Ordem (Continuação): Sistema Lead-Lag; Sistemas
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química COQ 790 ANÁLISE DE SISTEMAS DA ENGENHARIA QUÍMICA AULA 8: Sistemas de Primeira Ordem (Continuação): Sistema Lead-Lag; Sistemas
Sistemas de Controle 1
 Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap6 Estabilidade Prof. Filipe Fraga Sistemas de Controle 1 6. Estabilidade 6.1 Introdução 6.2 Critério de Routh-Hurwitz
Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 1 Cap6 Estabilidade Prof. Filipe Fraga Sistemas de Controle 1 6. Estabilidade 6.1 Introdução 6.2 Critério de Routh-Hurwitz
Controle. Transformada Laplace básico
 Controle Transformada Laplace básico REQUISITOS Para perfeita compreensão do conteúdo desta aula é desejável o entendimento dos seguintes assuntos (eventualmente disponíveis em outros vídeos neste canal):
Controle Transformada Laplace básico REQUISITOS Para perfeita compreensão do conteúdo desta aula é desejável o entendimento dos seguintes assuntos (eventualmente disponíveis em outros vídeos neste canal):
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Aula 8. Cristiano Quevedo Andrea 1. Curitiba, Abril de DAELT - Departamento Acadêmico de Eletrotécnica
 Classificaçã dos Sistemas de Controle Especificaçõe do Estado Estacionário de Erro Aula 8 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico
Classificaçã dos Sistemas de Controle Especificaçõe do Estado Estacionário de Erro Aula 8 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico
EES-20: Sistemas de Controle II
 EES-: Sistemas de Controle II 14 Agosto 17 1 / 49 Recapitulando: Estabilidade interna assintótica Modelo no espaço de estados: Equação de estado: ẋ = Ax + Bu Equação de saída: y = Cx + Du Diz-se que o
EES-: Sistemas de Controle II 14 Agosto 17 1 / 49 Recapitulando: Estabilidade interna assintótica Modelo no espaço de estados: Equação de estado: ẋ = Ax + Bu Equação de saída: y = Cx + Du Diz-se que o
