5 Análise Dinâmica da Estabilidade
|
|
|
- Nathalia Bennert Cortês
- 6 Há anos
- Visualizações:
Transcrição
1 5 Análise Dinâmica da Estabilidade Neste capítulo é analisado o comportamento dinâmico não-linear da torre estaiada, considerando os modelos apresentados nos capítulos anteriores. Especial atenção é dada ao estudo paramétrico das freqüências naturais e à correlação entre o comportamento dinâmico não-linear e a energia do sistema. Como se sabe [6, 7], a existência de múltiplas posições de equilíbrio para um dado nível de carregamento estático, sempre presente nas estruturas, pode acarretar uma grande complexidade no comportamento dinâmico, dando origem a diversos tipos de oscilações não-lineares e bifurcações. Esta análise é feita no domínio do tempo. 5.. Critério dinâmico da estabilidade O critério dinâmico da estabilidade diz que uma estrutura, só está em um estado de equilíbrio estável se suas freqüências naturais de vibração forem todas reais [3]. Para se calcular a freqüência natural de vibração é necessário obter a equação de movimento. A equação de movimento pode ser obtida a partir da função de Lagrange ou Lagrangiano, que é dado pela diferença entre a variação de energia cinética e a variação de energia potencial total, a saber L = T π (5.) 5.. Energia Cinética y x=s senθ ds θ s y=s cosθ Figura 5.: Posição de um elemento da barra de comprimento infinitesimal, ds. x
2 8 dada por A massa de um elemento infinitesimal da coluna de comprimento ds é dm = ρ dv = ρads (5.) onde ρ é a densidade do material e A é área da seção transversal da coluna. A energia cinética é dada por: ρ T = L v Ads onde L é o comprimento da coluna e v a velocidade. (5.3) Inicialmente é necessário determinar a posição do elemento infinitesimal de massa dm e comprimento ds segundo as direções x e y. Conforme a Figura 5., tem-se que: x = s senθ (5.) y = s cosθ (5.5) onde s é a distância do ponto à base da torre e θ a rotação da coluna que, neste caso, é uma função do tempo. Derivando as equações 5. e 5.5 em relação ao tempo, obtêm-se as r r r componentes do vetor velocidade nas direções x e y ( v = ( dx / dt) i + ( dy / dt) j ), ou seja v r r v = s cosθ θ& i s senθ θ& j (5.6) Inserindo (5.6) em (5.) e integrando ao longo de s chega-se à seguinte expressão que descreve a energia cinética para uma coluna de seção transversal constante. 6 & 3 T = ρ AL θ (5.7) sendo que L na equação (5.7) refere-se ao comprimento da barra Equação do movimento A energia potencial total é obtida a partir das parcelas de energia interna de deformação e do potencial das cargas externas dadas nos Capítulos 3 e para cada modelo aqui estudado. De posse da energia potencial total e da energia cinética, obtém-se o Lagrangiano (equação 5.). Aplicando o princípio de Hamilton, chega-se à equação de movimento. Se o sistema for conservativo, a equação de movimento é dada por:
3 8 L L t θ& θ = (5.8) Para um sistema conservativo, tem-se, pelo princípio da conservação da energia, que a soma da energia cinética com a energia potencial total do sistema é uma constante, ou seja T + π = C (5.9) onde C depende apenas das condições iniciais do sistema, ou seja, o deslocamento inicial, θ (), e da velocidade inicial, θ & (), da torre. No caso de um sistema com amortecimento, apenas uma parcela da energia cinética é transformada em energia potencial e vice-versa, o restante é dissipado pelo amortecimento. Para sistemas não conservativos, a equação de movimento é obtida igualando a equação (5.8) à força de amortecimento, ao invés de iguala-la a zero. Para amortecimento do tipo viscoso e proporcional à velocidade, tem-se: L L θ& θ& = c t θ (5.) A seguir apresenta-se a equação de movimento para os quatro modelos apresentados nos capítulo anteriores, considerando o modelo imperfeito Modelo de molas A equação que descreve o movimento da barra quando a mesma está conectada a molas é dada por d π m θ& + cθ& + = (5.) dθ onde a massa m é dada por 3 m = ρal (5.) Modelo de cabos No caso de um modelo de cabos, chega-se à equação de movimento mlθ&& + cθ& + 3 np i= nc / i= P Γ (senθ + e i i γ T i i xi ( θ)cosθ nc γ T ( θ)cosθ i xi i= nc / + L cosθ cosθ) + py senθ + q( t) nc i= γ T i yi ( θ)senθ = (5.3)
4 8 Em cada uma das equações de movimento, o termo que multiplica θ & é a massa equivalente e os termos que estão em função de θ, quando somados, resultam em uma força. Estas equações podem ser escritas na forma m eq Lcosθ θ & + cθ & + f ( θ) = q( t ) (5.) Onde f (θ ) é a força elástica, função da rigidez e da rotação, θ, da barra. 5.. Freqüência natural Retirando o carregamento externo da equação, (5.) tem-se o sistema autônomo que permite o estudo da vibração livre. Na dinâmica, a freqüência circular natural de vibração é dada pela raiz quadrada da rigidez equivalente dividida pela massa equivalente, conforme a equação keq ω = (5.5) m eq Para obter a freqüência circular natural, ω, é necessário tomar a parcela linear da força f (θ) (eq. 5.), ou seja, tomar o termo linear da série de Taylor que a representa, que é a rigidez equivalente da equação (5.5). Esta linearização só é possível analiticamente no modelo de molas, já que no modelo de cabos as componentes das forças que atuam nos cabos somente são determinadas numericamente. A Figura 5.a exibe a variação da freqüência natural circular, ω, da torre, em radianos por segundo, em função de α, para diferentes valores de ξ e ξ. Em todas as curvas, ξ =, 95. Na Figura 5.b, exibe-se à variação de ω em p função do parâmetro de carga λ. Para todas as curvas tomou-se ξ =. Quando λ é igual à carga crítica a freqüência se anula. A Figura 5.3 mostra a variação da freqüência natural em função do parâmetro de pré-tensionamento, ξ, e do parâmetro geométrico, ξ. A Figura 5. mostra que existe, como acontece em muitas estruturas, uma relação linear entre o quadrado da freqüência e o parâmetro de carga λ. p
5 α = 3 ; ξ = ; ξ = ; α = 5 ; ξ = ; ξ = ; α = 5 ; ξ =,; ξ = ; α = 5 ; ξ =,; ξ =,8; ω ω ξ = ; ξ = ; ξ =,5; ξ = ; ξ =,; ξ = ; ξ =,; ξ =,8; α [ ] (a) (b) Figura 5.: Variação da freqüência natural circular: (a) em função de α. (b) em função de λ. λ 6 α = 5 ; ξ = ; α = 5 ; ξ =,8; α = 3 ; ξ =,8; 8 6 α = 5 ; ξ =,; α = 5 ; ξ = ; α = ; ξ = ; ω ω ξ (a) (b) Figura 5.3: Variação da freqüência natural circular: (a) em função do parâmetro de prétensionamento, (b) em função do parâmetro de geometria. ξ Analisando as Figuras 5., 5.3 e 5., percebe-se que os diversos parâmetros adimensionais influenciam a freqüência de uma forma semelhante à carga crítica.
6 8 3 α = 5 ; ξ = ; ξ = ; ω² λ Figura 5.: Variação do quadrado da freqüência natural circular em função do parâmetro de carga Máxima freqüência natural O comportamento exibido na seção anterior para o modelo de molas, revela que as configurações apresentadas no Capítulo 3 que geram uma carga crítica máxima são as mesmas que causam uma freqüência natural máxima. Para o modelo de cabos, a Figura 5.5 exibe a variação da freqüência natural, obtida através da solução numérica das equações de movimento do sistema autônomo, em função da inclinação do cabo. Para isso consideram-se pequenas perturbações iniciais, integram-se as equações no tempo e mede-se o período para cada valor de α. Para um modelo de cabos, a maior freqüência natural foi obtida para α = 53, enquanto que a análise estática para o mesmo modelo indicou uma carga crítica máxima em α = 39 (Figura.3b)..6. f [ Hz ] α Figura 5.5: Variação da Freqüência natural em função de α.
7 Solução numérica da equação de movimento Em sistemas não lineares raramente é possível uma solução exata para a equação diferencial de movimento. Em tais casos, a mesma deve ser obtida pela integração da equação ao longo do tempo, através de um método numérico. Neste trabalho, utiliza-se o Runge Kutta de a ordem. Para usar este algoritmo é necessário transformar a equação diferencial de a ordem, eq. (5.) em um sistema de equações diferenciais de primeira ordem e, então, este sistema é integrado no tempo. O algoritmo pode ser encontrado, por exemplo, na referência [8]. A transformação é feita tomando-se x = θ e x = θ &. Assim temse x& x & = x = L cos x k ( ) + eq x cx q( ) meq t (5.6) A Figura 5.6a apresenta uma comparação entre o modelo de molas lineares e o de molas não lineares sob vibração livre, a única diferença entre os dois modelos é o pequeno valor da constante de mola k, que é zero no modelo de molas lineares. Não foi considerado o pré-tensionamento das molas. A Figura 5.6b apresenta uma comparação da solução numérica do modelo de cabos e molas. Percebe-se que há uma pequena diferença no período das soluções. A diferença na parte (a) é imperceptível dentro do intervalo adotado..8 p=,98 kn; y=5,m ; L= m ; α=6 ; mola linear mola não linear mo la linea r F = ; k = N/ m; mo la n ão line ar k = N/m; k = 5N/m³; l = ;.8 cabos molas p=8,6 kn; y=, m; f=, ; s=7, 5m ; L = m ; α= ; w=, 7kN/m t [ s ] t [ s ] (a) (b) Figura 5.6: Vibração livre: (a) comparação entre o modelo de molas lineares e o modelo de molas não lineares; (b) comparação entre o modelo de cabos e o modelo de molas usado para representar cabos. -.8
8 Amortecimento crítico O amortecimento considerado neste trabalho é do tipo viscoso, retirando do sistema uma parcela de energia que é proporcional à velocidade. Dada a equação diferencial: m eq θ& + cθ& + K θ = (5.7) eql O coeficiente de amortecimento, c, que faz com a resposta do sistema deixe de ser um movimento oscilatório é chamado de amortecimento crítico. Para uma equação como a (5.8), o amortecimento crítico vale: c = K m (5.8) cri eql Nas análises de vibração forçada adotou-se um amortecimento de 5% do amortecimento crítico. eq 5.7. Análise da estabilidade e natureza do movimento A análise da estabilidade de sistemas autônomos ou não autônomos está toda baseada na superfície de energia. No caso em que não há amortecimento, a superfície de energia é dada pela equação (5.9). Quando considera-se o amortecimento, o que é uma necessidade em problemas não-autônomos, não é possível traçar a superfície de energia, então aproveita-se a relação existente entre a superfície de energia e o plano fase, e a estabilidade é analisada no espaço fase e no domínio do tempo. A relação entre a superfície de energia e o plano fase para sistemas autônomos é exibida na Figura 5.7, retirada do livro de Leipholz (referência [9]). Verifica-se que as órbitas do sistema são as curvas de nível da superfície de energia.
9 87 Figura 5.7: Relação entre a superfície de energia e o plano fase. Quando uma carga variando no tempo é considerada, o sistema é dito não-autônomo Análise do sistema autônomo O modelo aqui analisado é uma torre de m de altura, presa a duas molas em sua extremidade superior. A torre possui seção uniforme, sendo sua massa, distribuída uniformemente ao longo da coluna ρa = kg/m. A Figura 5.8 apresenta o caminho pós-crítico de equilíbrio para o modelo com α=3. Em 5.8a varia-se θ de -9 a 9 e em 5.9b varia-se de - a para uma melhor visualização do comportamento na vizinhança da carga de bifurcação. O valor de λ cri para o modelo é,389. São considerados dois casos de carregamento axial: no primeiro caso adota-se uma carga levemente inferior à carga crítica (λ=,375), e, para o segundo caso, um valor imediatamente superior ao crítico, λ=,389. Os parâmetros de carga estão representados pela linha tracejada na Figura 5.8. Nos pontos em que ocorre o cruzamento do caminho com a linha tracejada, tem-se um ponto de equilíbrio, que é uma sela ou um centro, no caso do sistema autônomo. A consideração do amortecimento transforma este centro em um foco ou nó.
10 88.6 λ caso λ caso λ.8 λ (a) Figura 5.8: Caminho pós -crítico (b) No caso, em que a torre está sujeita a um carregamento axial menor que o valor crítico, há somente um ponto de equilíbrio estável, associado justamente à configuração inicial não perturbada. Ao aplicar-se uma pequena perturbação, o amortecimento dissipa a energia até o sistema atingir o repouso na configuração inicial. Nesta análise, como não está sendo considerado o amortecimento, o sistema permanece oscilando em torno de uma posição de equilíbrio estável. A Figura 5.9 apresenta o primeiro caso. Em 5.9a tem-se a superfície de energia, e em 5.9b sua projeção no plano fase, obtida pela integração numérica ao longo do tempo do sistema (5.6), para algumas condições iniciais. Tanto em 5.9a ou em 5.9b é possível identificar facilmente os pontos estáveis e os instáveis. O campo vetorial mostrado no plano fase ajuda a entender o comportamento global da estrutura. Nota-se que, para pequenas perturbações, a resposta do sistema é praticamente linear. A medida que a perturbação inicial cresce, a resposta se torna cada vez mais não-linear até que a fronteira de estabilidade, dada pelas órbitas heteroclínicas que ligam os dois pontos de sela é atingida e o sistema, para uma perturbação imediatamente superior à perturbação limite, perde a estabilidade, escapando do vale potencial préflambagem. Este comportamento é típico de estruturas sujeitas a bifurcação instável.
11 89 (a) (b) Figura 5.9: Parâmetro de carga menor que o crítico: (a) Superfície de energia (b) plano fase. No caso específico da Figura 5., tem-se cinco pontos de equilíbrio, dois centros e três pontos de sela, como mostra o plano fase apresentado na mesma. Para cargas superiores à carga pós-crítica máxima, o plano fase se reduz a um ponto de sela, associado à configuração fundamental de equilíbrio. Figura 5. Plano fase para um valor de λ levemente maior que o crítico. Tomando uma inclinação para a mola um pouco maior (α=5 ), repete-se a análise. Neste caso, tem-se, como esperado, uma bifurcação simétrica estável. O λcri para o modelo passa a ser,95 e são adotados no primeiro caso, λ=,85, e no segundo caso, λ=,6. De acordo com a Figura 5., para qualquer nível de carregamento estático, desde que seja maior que o crítico, há três pontos de equilíbrio, dois centros associados às configurações pós-críticas estáveis e uma sela associada à configuração não-perturbada, enquanto que para valores menores que o crítico, tem-se apenas um único ponto de equilíbrio (estável).
12 9.6 λ..8 λ caso λ caso Figura 5.: Caminho pós -crítico e parâmetro de carga utilizado em cada caso. Para a superfície exibida na Figura 5., o parâmetro de carga utilizado é o correspondente ao caso, indicado na Figura 5.. Em 5.3 apresenta-se a superfície de energia e o plano fase para o segundo caso de carregamento, sendo λ % superior ao parâmetro de carga crítico. Nota-se na Figura 5. que nenhum par de condições iniciais pertence a uma órbita instável. O Ponto de coordenadas (;) no plano fase é um centro estável. Figura 5. Superfície de energia para carregamento inferior ao crítico Na Figura 5.3 há dois centros estáveis, pontos no plano fase de coordenadas P(-,8;) e P(,8;), e um ponto de sela, P(;).
13 9 (a) (b) Figura 5.3: Parâmetro de carga maior que o crítico: (a) Superfície de energia (b) plano fase Análise do sistema não autônomo Apresenta-se a seguir a análise para o modelo com cabos inclinados a 5, com uma carga lateral variando no tempo de forma senoidal, com o período igual ao período natural da estrutura (região de ressonância). A estrutura encontra-se inicialmente em repouso. O parâmetro de carga no primeiro caso é maior que o parâmetro crítico, posteriormente se considera uma carga menor que a crítica. A amplitude da carga é variada até o sistema atingir o escape. Para o modelo em que a inclinação é 5 e o parâmetro de carga λ=,6, a variação das trajetórias do sistema em função do parâmetro de carga lateral é apresentada na Figura 5.. O amortecimento utilizado é de 5% do amortecimento crítico. O sistema oscila inicialmente em torno de uma configuração de equilíbrio pós-crítica. Para ξq =,7 ocorre um salto dinâmico e o sistema passa a oscilar em torno de outra configuração de equilíbrio, conforme mostra a Figura 5.b, que apresenta o diagrama de bifurcação associado ao problema. Neste caso não houve dobramento de período próximo à fronteira da bacia de atração, como acontece comumente neste tipo de problema. O período da resposta permanece igual ao período da força até o momento da bifurcação.
14 ξq,7,5,,5,, ξq (a) (b) Figura 5.: Plano fase para diversos níveis de carga lateral, com λ maior que λ crítico. Analisando o mesmo modelo, porém com λ menor que o λ crítico (λ =,85), percebe-se que não há bifurcação ou escape. A resposta permanente tem sempre o mesmo período da força. 8 ξq,5,5,3, Figura 5.5: Plano fase para diversos níveis de carga lateral, com λ menor que λ crítico Bifurcação por dobramento de período Sistemas dinâmicos não lineares quando sujeitos a um carregamento harmônico com uma freqüência Tq podem não apresentar uma resposta na fase permanente de mesmo período que a excitação. Quando isto acontece diz-se que houve uma bifurcação. A Figura 5.6 exibe a variação da posição do ponto fixo em função da amplitude do carregamento lateral, para um modelo de molas não lineares e com um carregamento maior que o crítico.
15 q [ kn/m ] Figura 5.6: Diagrama de bifurcação do sistema não-autônomo para valores crescentes da amplitude do carregamento harmônico. Variação da coordenada generalizada θ da seção de Poincaré em função do parâmetro q. Observa-se que o sistema dinâmico exibe respostas com diferentes períodos, além de saltos. Sucessivos dobramentos do período da resposta podem levar o sistema a um regime caótico, onde é impossível prever o comportamento do sistema a longo prazo. Uma possível região caótica está no diagrama de bifurcação apresentado na Figura 5.6. A Figura 5.7 exibe o plano fase e o mapeamento de Poincaré para alguns valores de carregamento extraídos da Figura 5.6. O mapeamento consiste em dividir a trajetória da solução em várias seções, espaçadas igualmente no tempo. Cada seção é na verdade um plano fase. A seção correspondente ao tempo inicial é chamada de seção de Poincaré. Em trajetórias estáveis, o número de pontos fixos no mapeamento de Poincaré revela o período da solução permanente, que é igual ao número de pontos fixos multiplicado pelo período da carga. Na Figura 5.7a, tem-se uma solução permanente de período, e conseqüentemente um único ponto fixo no mapa de Poincaré (Fig 5.7b). Na Fig. 5.7d, o mapeamento revela que o período da solução é o dobro do período da excitação, passando a ser quatro vezes superior para o carregamento indicado na Figura 5.7e, e finalmente, nas partes (g) e (h) da figura percebe-se claramente o aparecimento de caos, tornando o período da solução infinito.
16 9 q = 6,5 kn (a) (b) q = 6,7 kn (c) (d) q = 6,9 kn (e) (f)
17 95 5 q = 7 kn (g) Figura 5.7: Plano fase e mapeamento de Poincaré para diferentes carregamentos extraídos da Figura 5.6. (h) As Figuras 5., 5.5 e 5.6 ilustram o comportamento dinâmico de torres estaiadas em vibração forçada. Verifica-se que o comportamento dinâmico da torre está intimamente relacionado com a geometria da superfície de energia associada ao problema e, conseqüentemente, ao tipo de bifurcação exibido pelo sistema sob cargas estáticas. Os resultados mostram que torres estaiadas podem apresentar diversos fenômenos típicos de sistemas não-lineares como, por exemplo, escape de um vale potencial (instabilidade dinâmica), bifurcações de diversos tipos e até mesmo caos. Este comportamento caótico é devido à não-linearidade dos estais expressa pela presença do termo cúbico no modelo de molas. Caminhos de equilíbrio, como o exibido em 5.8b, permite haver escape, até mesmo para carregamentos menores que o crítico. Com base na análise estática, verifica-se que, em modelos de mola não linear e cabos, o escape do vale de potencial associado a uma posição de equilíbrio fundamental é mais difícil de ocorrer do que no modelo de molas lineares. Entretanto, como mostrado neste trabalho, a ruptura de um estai pode provocar mudanças bruscas no comportamento da estrutura e esta possibilidade deve ser futuramente incluída na análise dinâmica. Assim sendo, deve haver um rigoroso cuidado com o nível de carregamento presente na torre, para que sob alguma tormenta, a mesma não venha a apresentar colapso.
APLICAÇÕES DAS EQUAÇÕES DE EULER-LAGRANGE
 APLICAÇÕES DAS EQUAÇÕES DE EULER-LAGRANGE Eliomar Corrêa Caetano Universidade Católica de Brasília Orientador: Cláudio Manoel Gomes de Sousa RESUMO Neste trabalho estudamos três aplicações das equações
APLICAÇÕES DAS EQUAÇÕES DE EULER-LAGRANGE Eliomar Corrêa Caetano Universidade Católica de Brasília Orientador: Cláudio Manoel Gomes de Sousa RESUMO Neste trabalho estudamos três aplicações das equações
MECÂNICA DOS FLUIDOS 2 ME262
 UNIVERSIDADE FEDERAL DE PERNAMBUCO CENTRO DE TECNOLOGIA E GEOCIÊNCIAS (CTG) DEPARTAMENTO DE ENGENHARIA MECÂNICA (DEMEC) MECÂNICA DOS FLUIDOS ME6 Prof. ALEX MAURÍCIO ARAÚJO (Capítulo 5) Recife - PE Capítulo
UNIVERSIDADE FEDERAL DE PERNAMBUCO CENTRO DE TECNOLOGIA E GEOCIÊNCIAS (CTG) DEPARTAMENTO DE ENGENHARIA MECÂNICA (DEMEC) MECÂNICA DOS FLUIDOS ME6 Prof. ALEX MAURÍCIO ARAÚJO (Capítulo 5) Recife - PE Capítulo
Resolução Comentada CEFET/MG - 2 semestre 2014
 Resolução Comentada CEFET/MG - 2 semestre 2014 01 - A figura mostra um sistema massa-mola que pode oscilar livremente, sem atrito, sobre a superfície horizontal e com resistência do ar desprezível. Nesse
Resolução Comentada CEFET/MG - 2 semestre 2014 01 - A figura mostra um sistema massa-mola que pode oscilar livremente, sem atrito, sobre a superfície horizontal e com resistência do ar desprezível. Nesse
FÍSICA. Questões de 01 a 04
 GRUPO 1 TIPO A FÍS. 1 FÍSICA Questões de 01 a 04 01. Considere uma partícula presa a uma mola ideal de constante elástica k = 420 N / m e mergulhada em um reservatório térmico, isolado termicamente, com
GRUPO 1 TIPO A FÍS. 1 FÍSICA Questões de 01 a 04 01. Considere uma partícula presa a uma mola ideal de constante elástica k = 420 N / m e mergulhada em um reservatório térmico, isolado termicamente, com
Excitação dos modos normais de um sistema usando um motor desbalanceado
 Revista Brasileira de Ensino de Física, v. 29, n. 1, p. 5-10, (2007) www.sbfisica.org.br Artigos Gerais Excitação dos modos normais de um sistema usando um motor desbalanceado (Excitation of normal modes
Revista Brasileira de Ensino de Física, v. 29, n. 1, p. 5-10, (2007) www.sbfisica.org.br Artigos Gerais Excitação dos modos normais de um sistema usando um motor desbalanceado (Excitation of normal modes
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 1
 597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES
 1 INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES 1.1 - Instrumentação Importância Medições experimentais ou de laboratório. Medições em produtos comerciais com outra finalidade principal. 1.2 - Transdutores
1 INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES 1.1 - Instrumentação Importância Medições experimentais ou de laboratório. Medições em produtos comerciais com outra finalidade principal. 1.2 - Transdutores
5. EXEMPLOS NUMÉRICOS: ANÁLISE ESTRUTURAL DINÂMICA
 5. EXEMPLOS NUMÉRICOS: ANÁLISE ESTRUTURAL DINÂMICA 5.1 INTRODUÇÃO Este capítulo apresenta a aplicação dos procedimentos numéricos apresentados no Capítulo 4 na solução de problemas de vibração livre e
5. EXEMPLOS NUMÉRICOS: ANÁLISE ESTRUTURAL DINÂMICA 5.1 INTRODUÇÃO Este capítulo apresenta a aplicação dos procedimentos numéricos apresentados no Capítulo 4 na solução de problemas de vibração livre e
Forças internas. Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro.
 Forças internas Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro. Generalizar esse procedimento formulando equações que podem ser representadas de
Forças internas Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro. Generalizar esse procedimento formulando equações que podem ser representadas de
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Análise Dinâmica do Sistema de Suspensão Swing Axle para veículos off-road
 Anais do XIV ENCITA 008, ITA, Outubro, 19-, 009 Análise inâmica do Sistema de Suspensão Swing Axle para veículos off-road Fábio Antônio Teixeira Sabóia Filho Instituto Tecnológico de Aeronáutica Praça
Anais do XIV ENCITA 008, ITA, Outubro, 19-, 009 Análise inâmica do Sistema de Suspensão Swing Axle para veículos off-road Fábio Antônio Teixeira Sabóia Filho Instituto Tecnológico de Aeronáutica Praça
Caso (2) X 2 isolado no SP
 Luiz Fernando artha étodo das Forças 6 5.5. Exemplos de solução pelo étodo das Forças Exemplo Determine pelo étodo das Forças o diagrama de momentos fletores do quadro hiperestático ao lado. Somente considere
Luiz Fernando artha étodo das Forças 6 5.5. Exemplos de solução pelo étodo das Forças Exemplo Determine pelo étodo das Forças o diagrama de momentos fletores do quadro hiperestático ao lado. Somente considere
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle
 Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Representação de Modelos Dinâmicos em Espaço de Estados Graus de Liberdade para Controle Espaço de Estados (CP1 www.professores.deq.ufscar.br/ronaldo/cp1 DEQ/UFSCar 1 / 69 Roteiro 1 Modelo Não-Linear Modelo
Capítulo 7 Conservação de Energia
 Função de mais de uma variável: Capítulo 7 Conservação de Energia Que para acréscimos pequenos escrevemos Onde usamos o símbolo da derivada parcial: significa derivar U parcialmente em relação a x, mantendo
Função de mais de uma variável: Capítulo 7 Conservação de Energia Que para acréscimos pequenos escrevemos Onde usamos o símbolo da derivada parcial: significa derivar U parcialmente em relação a x, mantendo
Movimento Harmônico Simples: Exemplos (continuação)
 Movimento Harmônico Simples: Exemplos (continuação) O Pêndulo Físico O chamado pêndulo físico é qualquer pêndulo real. Ele consiste de um corpo rígido (com qualquer forma) suspenso por um ponto O e que
Movimento Harmônico Simples: Exemplos (continuação) O Pêndulo Físico O chamado pêndulo físico é qualquer pêndulo real. Ele consiste de um corpo rígido (com qualquer forma) suspenso por um ponto O e que
Resistência dos Materiais. Prof. Carmos Antônio Gandra, M. Sc.
 Resistência dos Materiais Prof. Carmos Antônio Gandra, M. Sc. Unidade 01 Conceitos Fundamentais Objetivo da unidade Estabelecer um embasamento conceitual, de modo que o aluno possa prosseguir ao longo
Resistência dos Materiais Prof. Carmos Antônio Gandra, M. Sc. Unidade 01 Conceitos Fundamentais Objetivo da unidade Estabelecer um embasamento conceitual, de modo que o aluno possa prosseguir ao longo
OSCILAÇÕES: Movimento Harmônico Simples - M. H. S.
 Por Prof. Alberto Ricardo Präss Adaptado de Física de Carlos Alberto Gianotti e Maria Emília Baltar OSCILAÇÕES: Movimento Harmônico Simples - M. H. S. Todo movimento que se repete em intervelos de tempo
Por Prof. Alberto Ricardo Präss Adaptado de Física de Carlos Alberto Gianotti e Maria Emília Baltar OSCILAÇÕES: Movimento Harmônico Simples - M. H. S. Todo movimento que se repete em intervelos de tempo
22/Abr/2015 Aula 15. 17/Abr/2015 Aula 14
 17/Abr/2015 Aula 14 Introdução à Física Quântica Radiação do corpo negro; níveis discretos de energia. Efeito foto-eléctrico: - descrições clássica e quântica - experimental. Efeito de Compton. 22/Abr/2015
17/Abr/2015 Aula 14 Introdução à Física Quântica Radiação do corpo negro; níveis discretos de energia. Efeito foto-eléctrico: - descrições clássica e quântica - experimental. Efeito de Compton. 22/Abr/2015
p A = p B = = ρgh = h = Por outro lado, dado que a massa total de fluido despejada foi m, temos M 1 m = ρ(v 1 + V 2 ) = ρ 4 H + πd2 4 h = H = 4
 Q1 (,5) Um pistão é constituído por um disco ao qual se ajusta um tubo oco cilíndrico de diâmetro d. O pistão está adaptado a um recipiente cilíndrico de diâmetro D. massa do pistão com o tubo é M e ele
Q1 (,5) Um pistão é constituído por um disco ao qual se ajusta um tubo oco cilíndrico de diâmetro d. O pistão está adaptado a um recipiente cilíndrico de diâmetro D. massa do pistão com o tubo é M e ele
Lista 4. 2 de junho de 2014
 Lista 4 2 de junho de 24 Seção 5.. (a) Estime a área do gráfico de f(x) = cos x de x = até x = π/2 usando quatro retângulos aproximantes e extremidades direitas. Esboce os gráficos e os retângulos. Sua
Lista 4 2 de junho de 24 Seção 5.. (a) Estime a área do gráfico de f(x) = cos x de x = até x = π/2 usando quatro retângulos aproximantes e extremidades direitas. Esboce os gráficos e os retângulos. Sua
UNIVERSIDADE CATÓLICA DE GOIÁS. DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201) Prof.
 01 UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201) Prof. EDSON VAZ NOTA DE AULA III (Capítulo 7 e 8) CAPÍTULO 7 ENERGIA CINÉTICA
01 UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201) Prof. EDSON VAZ NOTA DE AULA III (Capítulo 7 e 8) CAPÍTULO 7 ENERGIA CINÉTICA
3.1. Representação de Velocidade de um Corpo Rígido:
 3. CINEMÁTICA DIFERENCIAL Neste capítulo abordamos a descrição do movimento do robô manipulador sem levar em conta os esforços que o produzem. Um importante problema cinemático associado ao movimento do
3. CINEMÁTICA DIFERENCIAL Neste capítulo abordamos a descrição do movimento do robô manipulador sem levar em conta os esforços que o produzem. Um importante problema cinemático associado ao movimento do
1 Analise a figura a seguir, que representa o esquema de um circuito com a forma da letra U, disposto perpendicularmente à superfície da Terra.
 FÍSIC 1 nalise a figura a seguir, que representa o esquema de um circuito com a forma da letra U, disposto perpendicularmente à superfície da Terra. Esse circuito é composto por condutores ideais (sem
FÍSIC 1 nalise a figura a seguir, que representa o esquema de um circuito com a forma da letra U, disposto perpendicularmente à superfície da Terra. Esse circuito é composto por condutores ideais (sem
Elementos de Máquinas
 Professor: Leonardo Leódido Aula 2 Revisão: Análise de alhas Aula 2 Análise de alhas Instituto ederal de Brasília Sumário Sistemas de orças Resistência dos Materiais lambagem alhas Estáticas alhas Dinâmicas
Professor: Leonardo Leódido Aula 2 Revisão: Análise de alhas Aula 2 Análise de alhas Instituto ederal de Brasília Sumário Sistemas de orças Resistência dos Materiais lambagem alhas Estáticas alhas Dinâmicas
LISTA 3 - Prof. Jason Gallas, DF UFPB 10 de Junho de 2013, às 14:14. Jason Alfredo Carlson Gallas, professor titular de física teórica,
 Exercícios Resolvidos de Física Básica Jason Alfredo Carlson Gallas, professor titular de física teórica, Doutor em Física pela Universidade Ludwig Maximilian de Munique, Alemanha Universidade Federal
Exercícios Resolvidos de Física Básica Jason Alfredo Carlson Gallas, professor titular de física teórica, Doutor em Física pela Universidade Ludwig Maximilian de Munique, Alemanha Universidade Federal
RESOLUÇÕES DA PROVA DE FÍSICA UFC 2006. PROFESSOR Célio Normando
 RESOLUÇÕES DA PROVA DE FÍSICA UFC 006 Ari Duque de Caxias Ari Washington Soares Ari Aldeota Da 5ª Série ao Pré-Vestibular Sede Hildete de Sá Cavalcante (da Educação Infantil ao Pré-Vestibular) Rua Monsenhor
RESOLUÇÕES DA PROVA DE FÍSICA UFC 006 Ari Duque de Caxias Ari Washington Soares Ari Aldeota Da 5ª Série ao Pré-Vestibular Sede Hildete de Sá Cavalcante (da Educação Infantil ao Pré-Vestibular) Rua Monsenhor
Universidade do Vale do Paraíba Faculdade de Engenharias, Arquitetura e Urbanismo - FEAU. Fundamentos Física Prof. Dra. Ângela Cristina Krabbe
 Universidade do Vale do Paraíba Faculdade de Engenharias, Arquitetura e Urbanismo - FEAU Fundamentos Física Prof. Dra. Ângela Cristina Krabbe Lista de exercícios 1. Considerando as grandezas físicas A
Universidade do Vale do Paraíba Faculdade de Engenharias, Arquitetura e Urbanismo - FEAU Fundamentos Física Prof. Dra. Ângela Cristina Krabbe Lista de exercícios 1. Considerando as grandezas físicas A
Lei de Coulomb: Campo Elétrico:
 Lei de Coulomb: Método para distribuição de cargas: Dividir a distribuição em infinitos dq Analisar feito por dq Dividir em suas componentes dfx e dfy Analisar se há alguma forma de simetria que simplifica
Lei de Coulomb: Método para distribuição de cargas: Dividir a distribuição em infinitos dq Analisar feito por dq Dividir em suas componentes dfx e dfy Analisar se há alguma forma de simetria que simplifica
Elipses e Gravitação
 Elipses e Gravitação Cássio dos Santos Sousa 6 de novembro de 2013 Sumário 1 Introdução 3 2 Definição 3 3 Nomenclaturas 3 4 Equação da elipse na forma cartesiana 4 5 Semi-latus rectum 5 6 Excentricidade
Elipses e Gravitação Cássio dos Santos Sousa 6 de novembro de 2013 Sumário 1 Introdução 3 2 Definição 3 3 Nomenclaturas 3 4 Equação da elipse na forma cartesiana 4 5 Semi-latus rectum 5 6 Excentricidade
Movimentos Periódicos: representação vetorial
 Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Licenciatura em Engenharia de Telecomunicações e Informática. 1ª Parte Frequência
 ISCTE Ano Lectivo 2005/2006 Licenciatura em Engenharia de Telecomunicações e Informática Física Frequência / 2º Teste Duração: Frequência 3h, Teste 1h 30min. Não é permitido o uso de telemóveis durante
ISCTE Ano Lectivo 2005/2006 Licenciatura em Engenharia de Telecomunicações e Informática Física Frequência / 2º Teste Duração: Frequência 3h, Teste 1h 30min. Não é permitido o uso de telemóveis durante
Disciplina : Termodinâmica. Aula 5 ANÁLISE DA MASSA E ENERGIA APLICADAS A VOLUMES DE CONTROLE
 Curso: Engenharia Mecânica Disciplina : Aula 5 ANÁLISE DA MASSA E ENERGIA APLICADAS A VOLUMES DE CONTROLE Prof. Evandro Rodrigo Dário, Dr. Eng. Vazão mássica e vazão volumétrica A quantidade de massa que
Curso: Engenharia Mecânica Disciplina : Aula 5 ANÁLISE DA MASSA E ENERGIA APLICADAS A VOLUMES DE CONTROLE Prof. Evandro Rodrigo Dário, Dr. Eng. Vazão mássica e vazão volumétrica A quantidade de massa que
TIPO-A FÍSICA. r 1200 v média. Dado: Aceleração da gravidade: 10 m/s 2. Resposta: 27
 1 FÍSICA Dado: Aceleração da gravidade: 10 m/s 01. Considere que cerca de 70% da massa do corpo humano é constituída de água. Seja 10 N, a ordem de grandeza do número de moléculas de água no corpo de um
1 FÍSICA Dado: Aceleração da gravidade: 10 m/s 01. Considere que cerca de 70% da massa do corpo humano é constituída de água. Seja 10 N, a ordem de grandeza do número de moléculas de água no corpo de um
Questão 57. Questão 58. alternativa D. alternativa C. seu mostrador deverá indicar, para esse mesmo objeto, o valor de
 OBSERVAÇÃO (para todas as questões de Física): o valor da aceleração da gravidade na superfície da Terra é representado por g. Quando necessário, adote: para g, o valor 10 m/s ; para a massa específica
OBSERVAÇÃO (para todas as questões de Física): o valor da aceleração da gravidade na superfície da Terra é representado por g. Quando necessário, adote: para g, o valor 10 m/s ; para a massa específica
Questão 1. Resposta. b) Estime o intervalo de tempo t 2, em segundos, que a bola levou para ir do ponto A ao ponto B.
 Questão 1 Durante um jogo de futebol, um chute forte, a partir do chão, lança a bola contra uma parede próxima. Com auxílio de uma câmera digital, foi possível reconstituir a trajetória da bola, desde
Questão 1 Durante um jogo de futebol, um chute forte, a partir do chão, lança a bola contra uma parede próxima. Com auxílio de uma câmera digital, foi possível reconstituir a trajetória da bola, desde
ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04
 ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 15 Sumário Trabalho e EP Energia potencial Forças conservativas Calculando
ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 15 Sumário Trabalho e EP Energia potencial Forças conservativas Calculando
1.5 O oscilador harmónico unidimensional
 1.5 O oscilador harmónico unidimensional A energia potencial do oscilador harmónico é da forma U = 2 2, (1.29) onde é a constante de elasticidade e a deformação da mola. Substituindo (1.29) em (1.24) obtemos
1.5 O oscilador harmónico unidimensional A energia potencial do oscilador harmónico é da forma U = 2 2, (1.29) onde é a constante de elasticidade e a deformação da mola. Substituindo (1.29) em (1.24) obtemos
POTENCIAL ELÉTRICO. por unidade de carga
 POTENCIAL ELÉTRICO A lei de Newton da Gravitação e a lei de Coulomb da eletrostática são matematicamente idênticas, então os aspectos gerais discutidos para a força gravitacional podem ser aplicadas para
POTENCIAL ELÉTRICO A lei de Newton da Gravitação e a lei de Coulomb da eletrostática são matematicamente idênticas, então os aspectos gerais discutidos para a força gravitacional podem ser aplicadas para
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
Modelos Variáveis de Estado
 Modelos Variáveis de Estado Introdução; Variáveis de Estados de Sistemas Dinâmicos; Equação Diferencial de Estado; Função de Transferência a partir das Equações de Estados; Resposta no Domínio do Tempo
Modelos Variáveis de Estado Introdução; Variáveis de Estados de Sistemas Dinâmicos; Equação Diferencial de Estado; Função de Transferência a partir das Equações de Estados; Resposta no Domínio do Tempo
3.5 Sistemas de referência não-inerciais
 3.5-1 3.5 Sistemas de referência não-inerciais A primeira lei de Newton não é válida em todos os sistemas de referência, ver 2.1.2, mas, sempre podemos achar sistemas de referência nos quais ela (e o resto
3.5-1 3.5 Sistemas de referência não-inerciais A primeira lei de Newton não é válida em todos os sistemas de referência, ver 2.1.2, mas, sempre podemos achar sistemas de referência nos quais ela (e o resto
Capítulo 1 - Flambagem de Colunas
 Capítulo 1 - Flambagem de Colunas 1.1. Introdução Em que se constitui a falha de uma estrutura? Como um engenheiro, você deve considerar diversos modos de falha possíveis quando estiver projetando uma
Capítulo 1 - Flambagem de Colunas 1.1. Introdução Em que se constitui a falha de uma estrutura? Como um engenheiro, você deve considerar diversos modos de falha possíveis quando estiver projetando uma
AULA #12. Estabilidade de Sistemas de Controle por
 AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
UNIVERSIDADE SANTA CECÍLIA
 010 UNIVERIDDE NT CECÍLI ETÁTIIC N ETRUTUR José Carlos Morilla Estática nas Estruturas 1. Estruturas... 3 1.1. arras... 3 1.1.1. Classificação das barras... 4. Esforços que atuam nas estruturas... 4.1.
010 UNIVERIDDE NT CECÍLI ETÁTIIC N ETRUTUR José Carlos Morilla Estática nas Estruturas 1. Estruturas... 3 1.1. arras... 3 1.1.1. Classificação das barras... 4. Esforços que atuam nas estruturas... 4.1.
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
FÍSICA. Dados: Velocidade da luz no vácuo: 3,0 x 10 8 m/s Aceleração da gravidade: 10 m/s 2 1 4πε. Nm 2 /C 2
 Dados: FÍSICA Velocidade da luz no vácuo: 3,0 x 10 8 m/s Aceleração da gravidade: 10 m/s 1 4πε 0 = 9,0 10 9 Nm /C Calor específico da água: 1,0 cal/g o C Calor latente de evaporação da água: 540 cal/g
Dados: FÍSICA Velocidade da luz no vácuo: 3,0 x 10 8 m/s Aceleração da gravidade: 10 m/s 1 4πε 0 = 9,0 10 9 Nm /C Calor específico da água: 1,0 cal/g o C Calor latente de evaporação da água: 540 cal/g
UNIVERSIDADE DE MARÍLIA
 UNIVERSIDADE DE MARÍLIA Faculdade de Engenharia, Arquitetura e Tecnologia SISTEMAS ESTRUTURAIS (NOTAS DE AULA) Professor Dr. Lívio Túlio Baraldi MARILIA, 2007 1. DEFINIÇÕES FUNDAMENTAIS Força: alguma causa
UNIVERSIDADE DE MARÍLIA Faculdade de Engenharia, Arquitetura e Tecnologia SISTEMAS ESTRUTURAIS (NOTAS DE AULA) Professor Dr. Lívio Túlio Baraldi MARILIA, 2007 1. DEFINIÇÕES FUNDAMENTAIS Força: alguma causa
Mecânica dos Materiais
 Mecânica dos Materiais Esforços axiais Tensões e Deformações Esforços multiaxiais Lei de Hooke generalizada 2 Tradução e adaptação: Victor Franco Correia (versão 1/2013) Ref.: Mechanics of Materials, Beer,
Mecânica dos Materiais Esforços axiais Tensões e Deformações Esforços multiaxiais Lei de Hooke generalizada 2 Tradução e adaptação: Victor Franco Correia (versão 1/2013) Ref.: Mechanics of Materials, Beer,
Física 1 DINÂMICA. Jaime E. Villate
 Física 1 DINÂMICA Jaime E. Villate Física 1. Dinâmica Jaime E. Villate Faculdade de Engenharia Universidade do Porto http://www.villate.org/livros Física 1. Dinâmica Copyright c 2009-2012 Jaime E. Villate
Física 1 DINÂMICA Jaime E. Villate Física 1. Dinâmica Jaime E. Villate Faculdade de Engenharia Universidade do Porto http://www.villate.org/livros Física 1. Dinâmica Copyright c 2009-2012 Jaime E. Villate
Resistência. dos Materiais II
 Resistência Prof. MSc Eng Halley Dias dos Materiais II Material elaborado pelo Prof. MSc Eng Halley Dias Instituto Federal de Educação Ciência e Tecnologia de Santa Catarina Aplicado ao Curso Técnico de
Resistência Prof. MSc Eng Halley Dias dos Materiais II Material elaborado pelo Prof. MSc Eng Halley Dias Instituto Federal de Educação Ciência e Tecnologia de Santa Catarina Aplicado ao Curso Técnico de
Processos em Engenharia: Modelagem Matemática de Sistemas Fluídicos
 Processos em Engenharia: Modelagem Matemática de Sistemas Fluídicos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101
Processos em Engenharia: Modelagem Matemática de Sistemas Fluídicos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101
PLANO DE ESTUDOS DE MATEMÁTICA 8.º ANO
 DE MATEMÁTICA 8.º ANO Ano Letivo 2015 2016 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de relacionar números racionais e dízimas, completar a reta numérica e ordenar números
DE MATEMÁTICA 8.º ANO Ano Letivo 2015 2016 PERFIL DO ALUNO No domínio dos Números e Operações, o aluno deve ser capaz de relacionar números racionais e dízimas, completar a reta numérica e ordenar números
UNIVERSIDADE FEDERAL FLUMINENSE
 UNIVERSIDADE FEDERAL FLUMINENSE Escola de Engenharia Industrial Metalúrgica de Volta Redonda PROVAS RESOLVIDAS DE CÁLCULO VETORIAL Professora Salete Souza de Oliveira Aluna Thais Silva de Araujo P1 Turma
UNIVERSIDADE FEDERAL FLUMINENSE Escola de Engenharia Industrial Metalúrgica de Volta Redonda PROVAS RESOLVIDAS DE CÁLCULO VETORIAL Professora Salete Souza de Oliveira Aluna Thais Silva de Araujo P1 Turma
RESISTÊNCIA DOS MATERIAIS AMB 28 AULA 7. Professor Alberto Dresch Webler
 Resistências dos Materiais dos Materiais - Aula 5 - Aula 7 RESISTÊNCIA DOS MATERIAIS AMB 28 AULA 7 Professor Alberto Dresch Webler 1 Aula 7 Tensão e deformação de cisalhamento; Tensões e cargas admissíveis;
Resistências dos Materiais dos Materiais - Aula 5 - Aula 7 RESISTÊNCIA DOS MATERIAIS AMB 28 AULA 7 Professor Alberto Dresch Webler 1 Aula 7 Tensão e deformação de cisalhamento; Tensões e cargas admissíveis;
Conservação de Massa. A quantidade de fluido entrando no cubo pela face y z intervalo t
 Conservação de Massa Em um fluido real, massa deve ser conservada não podendo ser destruída nem criada. Se a massa se conserva, o que entrou e não saiu ficou acumulado. Matematicamente nós formulamos este
Conservação de Massa Em um fluido real, massa deve ser conservada não podendo ser destruída nem criada. Se a massa se conserva, o que entrou e não saiu ficou acumulado. Matematicamente nós formulamos este
Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta
 Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
Métodos computacionais
 Métodos computacionais Métodos Computacionais: Dependem de computadores para o cálculo de recurso/reserva e fazem uso de funções matemática de interpolação, as quais são aplicadas para o cálculo de teor
Métodos computacionais Métodos Computacionais: Dependem de computadores para o cálculo de recurso/reserva e fazem uso de funções matemática de interpolação, as quais são aplicadas para o cálculo de teor
A experiência de Oersted
 Os pólos de um ímã á séculos, o homem observou que determinadas pedras têm a propriedade de atrair pedaços de ferro ou interagir entre si. Essas pedras foram chamadas de ímãs e os fenômenos, que de modo
Os pólos de um ímã á séculos, o homem observou que determinadas pedras têm a propriedade de atrair pedaços de ferro ou interagir entre si. Essas pedras foram chamadas de ímãs e os fenômenos, que de modo
7] As polias indicadas na figura se movimentam em rotação uniforme, ligados por um eixo fixo.
![7] As polias indicadas na figura se movimentam em rotação uniforme, ligados por um eixo fixo. 7] As polias indicadas na figura se movimentam em rotação uniforme, ligados por um eixo fixo.](/thumbs/19/212732.jpg) Colégio Militar de Juiz de Fora Lista de Exercícios C PREP Mil Prof.: Dr. Carlos Alessandro A. Silva Cinemática: Vetores, Cinemática Vetorial, Movimento Circular e Lançamento de Projéteis. Nível I 1] Dois
Colégio Militar de Juiz de Fora Lista de Exercícios C PREP Mil Prof.: Dr. Carlos Alessandro A. Silva Cinemática: Vetores, Cinemática Vetorial, Movimento Circular e Lançamento de Projéteis. Nível I 1] Dois
LISTA 3 - Prof. Jason Gallas, DF UFPB 10 de Junho de 2013, às 18:19. Jason Alfredo Carlson Gallas, professor titular de física teórica,
 ISTA 3 - Prof. Jason Gallas, DF UFPB 10 de Junho de 2013, às 18:19 Exercícios Resolvidos de Física Básica Jason Alfredo Carlson Gallas, professor titular de física teórica, Doutor em Física pela Universidade
ISTA 3 - Prof. Jason Gallas, DF UFPB 10 de Junho de 2013, às 18:19 Exercícios Resolvidos de Física Básica Jason Alfredo Carlson Gallas, professor titular de física teórica, Doutor em Física pela Universidade
EFEITO COMPTON. J.R. Kaschny
 EFEITO COMPTON J.R. Kaschny Os Experimentos de Compton Das diversas interações da radiação com a matéria, um destaque especial é dado ao efeito, ou espalhamento, Compton - Arthur Holly Compton (93, Nobel
EFEITO COMPTON J.R. Kaschny Os Experimentos de Compton Das diversas interações da radiação com a matéria, um destaque especial é dado ao efeito, ou espalhamento, Compton - Arthur Holly Compton (93, Nobel
Mecânica Geral Básica
 Mecânica Geral Básica Conceitos Básicos Prof. Nelson Luiz Reyes Marques Unidades - o sistema métrico O sistema internacional de unidades (SI) o sistema MKS Baseado em potências de 10 de unidades de base
Mecânica Geral Básica Conceitos Básicos Prof. Nelson Luiz Reyes Marques Unidades - o sistema métrico O sistema internacional de unidades (SI) o sistema MKS Baseado em potências de 10 de unidades de base
Prof. André Motta - mottabip@hotmail.com_ 4.O gráfico apresentado mostra a elongação em função do tempo para um movimento harmônico simples.
 Eercícios Movimento Harmônico Simples - MHS 1.Um movimento harmônico simples é descrito pela função = 7 cos(4 t + ), em unidades de Sistema Internacional. Nesse movimento, a amplitude e o período, em unidades
Eercícios Movimento Harmônico Simples - MHS 1.Um movimento harmônico simples é descrito pela função = 7 cos(4 t + ), em unidades de Sistema Internacional. Nesse movimento, a amplitude e o período, em unidades
Capítulo 8. Conservação do momento. Recursos com copyright incluídos nesta apresentação:
 Capítulo 8 Conservação do momento Recursos com copyright incluídos nesta apresentação: Até agora consideramos o movimento de uma única partícula submetida à ação de uma força resultante. Esta descrição
Capítulo 8 Conservação do momento Recursos com copyright incluídos nesta apresentação: Até agora consideramos o movimento de uma única partícula submetida à ação de uma força resultante. Esta descrição
b) Calcule as temperaturas em Kelvin equivalentes às temperaturas de 5,0 ºC e 17,0 ºC.
 Questão 1 A pressão P no interior de um fluido em equilíbrio varia com a profundidade h como P = P 0 + ρgh. A equação dos gases ideais relaciona a pressão, o volume e a temperatura do gás como PV = nrt,
Questão 1 A pressão P no interior de um fluido em equilíbrio varia com a profundidade h como P = P 0 + ρgh. A equação dos gases ideais relaciona a pressão, o volume e a temperatura do gás como PV = nrt,
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I Estruturas II. Capítulo 5 Torção
 Capítulo 5 Torção 5.1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e
Capítulo 5 Torção 5.1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e
Fuvest 2005 2ª fase FÍSICA
 Fuvest 2005 2ª fase FÍSICA 1. Procedimento de segurança, em auto-estradas, recomenda que o motorista mantenha uma distância de 2 segundos do carro que está à sua frente, para que, se necessário, tenha
Fuvest 2005 2ª fase FÍSICA 1. Procedimento de segurança, em auto-estradas, recomenda que o motorista mantenha uma distância de 2 segundos do carro que está à sua frente, para que, se necessário, tenha
Prof. Rogério Porto. Assunto: Eletrostática
 Questões COVEST Física Elétrica Prof. Rogério Porto Assunto: Eletrostática 1. Duas esferas condutoras A e B possuem a mesma carga Q. Uma terceira esfera C, inicialmente descarregada e idêntica às esferas
Questões COVEST Física Elétrica Prof. Rogério Porto Assunto: Eletrostática 1. Duas esferas condutoras A e B possuem a mesma carga Q. Uma terceira esfera C, inicialmente descarregada e idêntica às esferas
3 - Sistemas em Corrente Alternada. 1 Considerações sobre Potência e Energia. Carlos Marcelo Pedroso. 18 de março de 2010
 3 - Sistemas em Corrente Alternada Carlos Marcelo Pedroso 18 de março de 2010 1 Considerações sobre Potência e Energia A potência fornecida a uma carga à qual está aplicada um tensão instantânea u e por
3 - Sistemas em Corrente Alternada Carlos Marcelo Pedroso 18 de março de 2010 1 Considerações sobre Potência e Energia A potência fornecida a uma carga à qual está aplicada um tensão instantânea u e por
Seção de choque diferencial
 Seção de choque diferencial Em uma postagem anterior, Seções de choque, apresentei o conceito de seção de choque como sendo uma medida da probabilidade de colisão entre uma partícula incidente e uma partícula
Seção de choque diferencial Em uma postagem anterior, Seções de choque, apresentei o conceito de seção de choque como sendo uma medida da probabilidade de colisão entre uma partícula incidente e uma partícula
CAMPO MAGNÉTICO. Definição de B
 Em 1822, durante uma aula experimental, o professor de física dinamarquês Hans Christian Oersted descobriu que uma corrente elétrica passando por um fio deslocava a agulha de uma bússola que estava por
Em 1822, durante uma aula experimental, o professor de física dinamarquês Hans Christian Oersted descobriu que uma corrente elétrica passando por um fio deslocava a agulha de uma bússola que estava por
Probabilidade de Colapso de Muro de Solo Reforçado e Considerações de Projeto
 Probabilidade de Colapso de Muro de Solo Reforçado e Considerações de Projeto Marcus Vinicius Weber de Campos Escola de Engenharia de São Carlos da Universidade de São Paulo, EESC-USP, São Carlos, Brasil,
Probabilidade de Colapso de Muro de Solo Reforçado e Considerações de Projeto Marcus Vinicius Weber de Campos Escola de Engenharia de São Carlos da Universidade de São Paulo, EESC-USP, São Carlos, Brasil,
Mecânica. Forças Conservativas e a Energia Mecânica
 Mecânica Forças Conservativas e a Energia Mecânica Mecânica» Forças Conservativas e a Energia Mecânica 1 Forças Conservativas O trabalho realizado por uma força, quando do deslocamento de uma partícula
Mecânica Forças Conservativas e a Energia Mecânica Mecânica» Forças Conservativas e a Energia Mecânica 1 Forças Conservativas O trabalho realizado por uma força, quando do deslocamento de uma partícula
Álgebra Linear I Solução da 5ª Lista de Exercícios
 FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Engenharia de Produção Curso de Graduação em Engenharia Ambiental e Sanitária
FUNDAÇÃO EDUCACIONAL SERRA DOS ÓRGÃOS CENTRO UNIVERSITÁRIO SERRA DOS ÓRGÃOS Centro de Ciências e Tecnologia Curso de Graduação em Engenharia de Produção Curso de Graduação em Engenharia Ambiental e Sanitária
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 15
 Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Diferenciais Parciais
 Capítulo Solução Numérica de Equações Diferenciais Parciais. Introdução Uma equações diferencial parcial (EDP) pode ser escrita na forma geral a φ x + b φ x y + φ c y + d φ x + e φ + fφ+ g = 0 (.) y onde
Capítulo Solução Numérica de Equações Diferenciais Parciais. Introdução Uma equações diferencial parcial (EDP) pode ser escrita na forma geral a φ x + b φ x y + φ c y + d φ x + e φ + fφ+ g = 0 (.) y onde
a) Estime o intervalo de tempo t 1 , em segundos, que a bola levou para ir do ponto A ao ponto B. b) Estime o intervalo de tempo t 2
 1 FÍSICA Durante um jogo de futebol, um chute forte, a partir do chão, lança a bola contra uma parede próxima. Com auxílio de uma câmera digital, foi possível reconstituir a trajetória da bola, desde o
1 FÍSICA Durante um jogo de futebol, um chute forte, a partir do chão, lança a bola contra uma parede próxima. Com auxílio de uma câmera digital, foi possível reconstituir a trajetória da bola, desde o
Notas de Mecânica e Campo Electromagnético. Carlos A. R. Herdeiro
 Notas de Mecânica e Campo Electromagnético Carlos A. R. Herdeiro Departamento de Física Universidade de Aveiro v2.0 2012/2013 Conteúdo 1 Fundamentos de Mecânica Clássica 2 1.1 Cinemática da partícula............................
Notas de Mecânica e Campo Electromagnético Carlos A. R. Herdeiro Departamento de Física Universidade de Aveiro v2.0 2012/2013 Conteúdo 1 Fundamentos de Mecânica Clássica 2 1.1 Cinemática da partícula............................
Análise Dimensional Notas de Aula
 Primeira Edição Análise Dimensional Notas de Aula Prof. Ubirajara Neves Fórmulas dimensionais 1 As fórmulas dimensionais são formas usadas para expressar as diferentes grandezas físicas em função das grandezas
Primeira Edição Análise Dimensional Notas de Aula Prof. Ubirajara Neves Fórmulas dimensionais 1 As fórmulas dimensionais são formas usadas para expressar as diferentes grandezas físicas em função das grandezas
EXERCÍCIOS DE RECUPERAÇÃO PARALELA 4º BIMESTRE
 EXERCÍCIOS DE RECUPERAÇÃO PARALELA 4º BIMESTRE NOME Nº SÉRIE : 1º EM DATA : / / BIMESTRE 3º PROFESSOR: Renato DISCIPLINA: Física 1 VISTO COORDENAÇÃO ORIENTAÇÕES: 1. O trabalho deverá ser feito em papel
EXERCÍCIOS DE RECUPERAÇÃO PARALELA 4º BIMESTRE NOME Nº SÉRIE : 1º EM DATA : / / BIMESTRE 3º PROFESSOR: Renato DISCIPLINA: Física 1 VISTO COORDENAÇÃO ORIENTAÇÕES: 1. O trabalho deverá ser feito em papel
Análise de procedimentos para medida de rotações e curvaturas em vigas de concreto armado
 BE8 Encontro Nacional Betão Estrutural 8 Guimarães 5, 6, 7 de Novembro de 8 Análise de procedimentos para medida de rotações e curvaturas em vigas de concreto armado Bruna Catoia 1, Carlos A.T. Justo,
BE8 Encontro Nacional Betão Estrutural 8 Guimarães 5, 6, 7 de Novembro de 8 Análise de procedimentos para medida de rotações e curvaturas em vigas de concreto armado Bruna Catoia 1, Carlos A.T. Justo,
Aula 18. Sistemas de conversão AD e DA
 Aula 18 Sistemas de conversão AD e DA Introdução A maior parte dos sistemas eletrônicos tem em seu núcleo um processamento digital; desde os sistemas mais familiares como Televisão, Computadores Pessoais,
Aula 18 Sistemas de conversão AD e DA Introdução A maior parte dos sistemas eletrônicos tem em seu núcleo um processamento digital; desde os sistemas mais familiares como Televisão, Computadores Pessoais,
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
Capítulo 22: Campos Elétricos
 1 Campos létricos Capítulo : Campos létricos Campo létrico: é um campo vetorial, constituído por uma distribuição de vetores, um para cada ponto de uma região em torno de um objeto eletricamente carregado.
1 Campos létricos Capítulo : Campos létricos Campo létrico: é um campo vetorial, constituído por uma distribuição de vetores, um para cada ponto de uma região em torno de um objeto eletricamente carregado.
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 3
 Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
1 Descrição do Trabalho
 Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
Departamento de Informática - UFES 1 o Trabalho Computacional de Algoritmos Numéricos - 13/2 Métodos de Runge-Kutta e Diferenças Finitas Prof. Andréa Maria Pedrosa Valli Data de entrega: Dia 23 de janeiro
1 Solução geral para equação de ondas
 1 2.1. SOLUÇÃO GERAL PARA EQUAÇÃO DE ONDAS 1.138J/2.062J, PROPAGAÇÃO DE ONDAS Outono, 2000 MIT Observações de C. C. Mei CAPÍTULO DOIS ONDAS MONODIMENSIONAIS 1 Solução geral para equação de ondas É fácil
1 2.1. SOLUÇÃO GERAL PARA EQUAÇÃO DE ONDAS 1.138J/2.062J, PROPAGAÇÃO DE ONDAS Outono, 2000 MIT Observações de C. C. Mei CAPÍTULO DOIS ONDAS MONODIMENSIONAIS 1 Solução geral para equação de ondas É fácil
PROGRAD / COSEAC ENGENHARIAS (CIVIL, DE PRODUÇÃO, MECÂNICA, PETRÓLEO E TELECOMUNICAÇÕES) NITERÓI - GABARITO
 Prova de Conhecimentos Específicos 1 a QUESTÃO: (1,0 ponto) Considere uma transformação linear T(x,y) em que, 5 autovetores de T com relação aos auto valores -1 e 1, respectivamente. e,7 são os Determine
Prova de Conhecimentos Específicos 1 a QUESTÃO: (1,0 ponto) Considere uma transformação linear T(x,y) em que, 5 autovetores de T com relação aos auto valores -1 e 1, respectivamente. e,7 são os Determine
4 As Leis de Conservaçaõ
 4.1-1 4 As Leis de Conservaçaõ Temos que voltar ao capítulo 2, onde falamos sobre a interpretação da mecânica Newtoniâna pelo físico austríaco Ernst Mach. Um ponto central nessa interpretação ocupam os
4.1-1 4 As Leis de Conservaçaõ Temos que voltar ao capítulo 2, onde falamos sobre a interpretação da mecânica Newtoniâna pelo físico austríaco Ernst Mach. Um ponto central nessa interpretação ocupam os
Governador Cid Ferreira Gomes. Vice Governador Domingos Gomes de Aguiar Filho. Secretária da Educação Maria Izolda Cela de Arruda Coelho
 Governador Cid Ferreira Gomes Vice Governador Domingos Gomes de Aguiar Filho Secretária da Educação Maria Izolda Cela de Arruda Coelho Secretário Adjunto Maurício Holanda Maia Secretário Executivo Antônio
Governador Cid Ferreira Gomes Vice Governador Domingos Gomes de Aguiar Filho Secretária da Educação Maria Izolda Cela de Arruda Coelho Secretário Adjunto Maurício Holanda Maia Secretário Executivo Antônio
MOVIMENTO CIRCULAR UNIFORME MOVIMENTO HARMÔNICO SIMPLES E ONDAS
 UNIVERSIDADE FEDERAL DE SANTA MARIA DEPARTAMENTO DE FÍSICA GRUPO DE ENSINO DE FÍSICA MOVIMENTO CIRCULAR UNIFORME MOVIMENTO HARMÔNICO SIMPLES E ONDAS Joecir Palandi Dartanhan Baldez Figueiredo João Carlos
UNIVERSIDADE FEDERAL DE SANTA MARIA DEPARTAMENTO DE FÍSICA GRUPO DE ENSINO DE FÍSICA MOVIMENTO CIRCULAR UNIFORME MOVIMENTO HARMÔNICO SIMPLES E ONDAS Joecir Palandi Dartanhan Baldez Figueiredo João Carlos
FRANCIELE ALVES DA SILVEIRA GONZAGA PEREIRA. Existência e Estabilidade de Órbitas Periódicas da Equação de van der Pol-Mathieu
 FRANCIELE ALVES DA SILVEIRA GONZAGA PEREIRA Existência e Estabilidade de Órbitas Periódicas da Equação de van der Pol-Mathieu UNIVERSIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE MATEMÁTICA 1 i ii FRANCIELE
FRANCIELE ALVES DA SILVEIRA GONZAGA PEREIRA Existência e Estabilidade de Órbitas Periódicas da Equação de van der Pol-Mathieu UNIVERSIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE MATEMÁTICA 1 i ii FRANCIELE
MÓDULO 03 - PROPRIEDADES DO FLUIDOS. Bibliografia
 MÓDULO 03 - PROPRIEDADES DO FLUIDOS Bibliografia 1) Estática dos Fluidos Professor Dr. Paulo Sergio Catálise Editora, São Paulo, 2011 CDD-620.106 2) Introdução à Mecânica dos Fluidos Robert W. Fox & Alan
MÓDULO 03 - PROPRIEDADES DO FLUIDOS Bibliografia 1) Estática dos Fluidos Professor Dr. Paulo Sergio Catálise Editora, São Paulo, 2011 CDD-620.106 2) Introdução à Mecânica dos Fluidos Robert W. Fox & Alan
Modelo de Solow: Efeitos de Transição Dinâmica
 Capítulo 4 Modelo de Solow: Efeitos de Transição Dinâmica No capítulo anterior vimos que, quando a economia atinge o seu equilíbrio de longo prazo, todas as variáveis endógenas passam a crescer a uma taxa
Capítulo 4 Modelo de Solow: Efeitos de Transição Dinâmica No capítulo anterior vimos que, quando a economia atinge o seu equilíbrio de longo prazo, todas as variáveis endógenas passam a crescer a uma taxa
ENGENHARIA DE FORTIFICAÇÃO E CONSTRUÇÃO CADERNO DE QUESTÕES
 CONCURSO DE ADMISSÃO AO CURSO DE FORMAÇÃO ENGENHARIA DE FORTIFICAÇÃO E CONSTRUÇÃO CADERNO DE QUESTÕES 2014 1 a QUESTÃO Valor: 1,00 O núcleo central de inércia é o lugar geométrico da seção transversal
CONCURSO DE ADMISSÃO AO CURSO DE FORMAÇÃO ENGENHARIA DE FORTIFICAÇÃO E CONSTRUÇÃO CADERNO DE QUESTÕES 2014 1 a QUESTÃO Valor: 1,00 O núcleo central de inércia é o lugar geométrico da seção transversal
FUNDAMENTOS DE ONDAS, Prof. Emery Lins Curso Eng. Biomédica
 FUNDAMENTOS DE ONDAS, RADIAÇÕES E PARTÍCULAS Prof. Emery Lins Curso Eng. Biomédica Questões... O que é uma onda? E uma radiação? E uma partícula? Como elas se propagam no espaço e nos meios materiais?
FUNDAMENTOS DE ONDAS, RADIAÇÕES E PARTÍCULAS Prof. Emery Lins Curso Eng. Biomédica Questões... O que é uma onda? E uma radiação? E uma partícula? Como elas se propagam no espaço e nos meios materiais?
Linguagem da Termodinâmica
 Linguagem da Termodinâmica Termodinâmica N A = 6,022 10 23 Ramo da Física que estuda sistemas que contêm um grande nº de partículas constituintes (átomos, moléculas, iões,...), a partir da observação das
Linguagem da Termodinâmica Termodinâmica N A = 6,022 10 23 Ramo da Física que estuda sistemas que contêm um grande nº de partículas constituintes (átomos, moléculas, iões,...), a partir da observação das
OE Seminário Aplicação do Eurocódigo 8 ao Projecto de Edifícios Projecto de estruturas para resistência aos sismos EC8-1
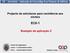 Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 2 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 2 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
Introdução à Máquina Síncrona
 Apostila 2 Disciplina de Conversão de Energia B 1. Introdução Introdução à Máquina Síncrona Esta apostila descreve resumidamente as principais características construtivas e tecnológicas das máquinas síncronas.
Apostila 2 Disciplina de Conversão de Energia B 1. Introdução Introdução à Máquina Síncrona Esta apostila descreve resumidamente as principais características construtivas e tecnológicas das máquinas síncronas.
Equipe de Física FÍSICA
 Aluno (a): Série: 3ª Turma: TUTORIAL 8B Ensino Médio Equipe de Física Data: FÍSICA Estática de um ponto Para que um ponto esteja em equilíbrio precisa satisfazer a seguinte condição: A resultante de todas
Aluno (a): Série: 3ª Turma: TUTORIAL 8B Ensino Médio Equipe de Física Data: FÍSICA Estática de um ponto Para que um ponto esteja em equilíbrio precisa satisfazer a seguinte condição: A resultante de todas
