META: Introduzir o conceito de derivada de funções de variáveis complexas.
|
|
|
- Ian Pedroso Viveiros
- 6 Há anos
- Visualizações:
Transcrição
1 AULA 3 META: Introduzir o conceito de derivada de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir derivada de funções de variáveis complexas e determinar a derivada de algumas funções de variáveis complexas. PRÉ-REQUISITOS Aula02 de Variáveis Complexas e os conhecimentos básicos, da disciplina Cálculo II.
2 3.1 Introdução Caros alunos em nossa aula de hoje veremos a Derivação Complexa. Em muitos aspectos a derivação complexa tem as mesmas propriedades da derivação real. Em outros porém a derivação complexa é peculiar e estas peculiaridades serão parte do tema de nossa aula. 3.2 Derivação Complexa Iniciaremos pela definição de derivada de uma função complexa. Definição 3.1. Sejam D C aberto, z 0 D e f : D C C uma função complexa. Definimos a derivada de f( ) no ponto z 0, denotada f (z 0 ), por: f (z 0 ) def = lim z z0 f(z) f(z 0 ) z z 0 (3.7) OBS 3.1. Está implícito na definição acima que a derivada de f( ) é dada pela expressão à direita se, somente se o limite existe. Podemos expressar também o limite usando uma nova variável = z z 0, z = z 0 +, onde é escolhido de modo que tenhamos z D. f (z 0 ) def = lim z z0 f(z 0 + ) f(z 0 ) (3.8) OBS 3.2. Para que a derivada de f( ) exista em um ponto z 0 D é necessário que o limite da definição seja independente da maneira como z se aproxima de z 0. Vejamos, agora, dois exemplos: 40
3 Variáveis Complexas Exemplo 3.1. Seja f : C C dada por f(z) = z 3. Calculemos sua derivada. SOLUÇÃO: Seja z 0 C temos: AULA 3 f(z 0 + ) f(z 0 ) = (z 0 + ) 3 z 3 0 = z z z 0() 2 + () 3 z 3 0 = 3z z 0() 2 + () 3 = 3z z 0 + () 2 Passando o limite 0 e usando a definição de derivada eqn 3.8 temos: f(z 0 + ) f(z 0 ) lim = lim 0 0 (3z z 0 + () 2 ) f (z 0 ) = 3z 2 0 Vamos ao segundo exemplo: Exemplo 3.2. Seja f : C C dada por f(z) = z 2. Calculemos sua derivada. SOLUÇÃO: Seja z 0 C temos: f(z 0 + ) f(z 0 ) = z z 0 2 = (z 0 + )(z 0 + ) z 0 z 0 = z 0 z 0 + z 0 + z 0 + z 0 z 0 = z 0 + z 0 + = z 0 + z 0 + Vamos passar o limite 0 por dois caminhos distintos. Caminho 1: Vamos fazer 0 seguindo um caminho paralelo ao eixo real. Neste caso = x+0ı = x, = x 0ı = x. 41
4 Daí, = 1. E passando o limite 0 que é equivalente, neste caso a x 0 temos: f (z 0 ) = z 0 + z 0 Caminho 2: Vamos fazer 0 seguindo um caminho paralelo ao eixo imaginário. Neste caso = 0 + yı = ı y, = 0 yı = ı y. Daí, = 1. E passando o limite 0 que é equivalente, neste caso a y 0 temos: f (z 0 ) = z 0 z 0 Daí, f(z) = z 2 não é derivável em ponto nenhum do plano complexo, exceto em z 0 = Regras de Derivação Complexa Se f( ) e g( ) são funções deriváveis em um ponto z 0 C então valem as seguintes regras de derivação: 1. (f + g) (z 0 ) = f (z 0 ) + g (z 0 ) 2. (f g) (z 0 ) = f (z 0 ) g (z 0 ) 3. (f.g) (z 0 ) = f(z 0 ).g (z 0 ) + g(z 0 ).f (z 0 ) 4. ( f g ) (z 0 ) = f(z 0).g (z 0 ) g(z 0 ).f (z 0 ) g 2 (z 0 ) se g(z 0 ) 0 Demonstraremos, agora, uma das regras de derivação complexa. A saber. Se f( ) e g( ) são funções deriváveis em um ponto z 0 C então vale ( ) a seguinte regra de derivação: f (z 0 ) = f(z 0).g (z 0 ) g(z 0 ).f (z 0 ) g g 2 (z 0 ) se g(z 0 ) 0. 42
5 Variáveis Complexas PROVA: Para simplificar trocaremos por λ. Usando a definição de derivada complexa temos: AULA 3 ( ) f (z 0 ) = lim g = lim = lim ( ) f (z 0 + λ) g λ f(z 0 + λ) g(z 0 + λ) f(z 0) g(z 0 ) λ ( ) f (z 0 ) g f(z 0 + λ)g(z 0 ) f(z 0 )g(z 0 + λ) g(z 0 + λ)g(z 0 ) λ = lim f(z 0 + λ)g(z 0 ) f(z 0 )g(z 0 + λ) g(z 0 + λ)g(z 0 )λ (3.9) Adicionando o termo nulo f(z 0 )g(z 0 ) + f(z 0 )g(z 0 ) ao denominador da equação eqn acima temos: ( ) f f(z 0 + λ)g(z 0 ) f(z 0 )g(z 0 ) (z 0 ) = lim g g(z 0 + λ)g(z 0 )λ f(z 0 )g(z 0 + λ) f(z 0 )g(z 0 ) lim g(z 0 + λ)g(z 0 )λ g(z 0 ) f(z 0 + λ) f(z 0 ) = lim g(z 0 + λ)g(z 0 ) λ f(z 0 ) g(z 0 + λ) g(z 0 ) lim g(z 0 + λ)g(z 0 ) λ g(z 0 ) = lim g(z 0 + λ)g(z 0 ) lim f(z 0 + λ) f(z 0 ) λ lim f(z 0 ) g(z 0 + λ)g(z 0 ) lim g(z 0 + λ) g(z 0 ) λ (3.10) Como as funções f( ) e g( ) são deriváveis, são também contínuas e da definição de derivada complexa temos: 43
6 lim lim g(z 0 ) g(z 0 + λ)g(z 0 ) = g(z 0) gr(z 0 ) f(z 0 ) g(z 0 + λ)g(z 0 ) = f(z 0) g 2 (z 0 ) f f(z 0 + λ) f(z 0 ) (z 0 ) = lim λ g g(z 0 + λ) g(z 0 ) (z 0 ) = lim λ Logo a última equação eqn passa a: ( ) f (z 0 ) = g(z 0) g g 2 (z 0 ) f (z 0 ) f(z 0) g 2 (z 0 ) g (z 0 ) = g(z 0)f (z 0 ) f(z 0 )g (z 0 ) g 2 (z 0 ) 3.4 Equações de Cauchy-Riemann Nesta seção estabeleceremos condições necessárias e suficiente para garantir a existência da derivada de uma função de variáveis complexas em um ponto do plano complexo. Teorema 3.1. Seja D C aberto e suponhamos que f : D C C, f(z) = u(x, y) + v(x, y)ı e f (z) existam na vizinhança de um ponto z 0 = x 0 + y 0 ı C. Então as derivadas parciais de primeira ordem de u e v com relação a x e a y existem e satisfazem: x (x 0, y 0 ) = x (x 0, y 0 ) = (3.11) PROVA: Da hipótese do teorema f(z) = u(x, y)+v(x, y)ı e f (z) estão definidas em uma vizinhança do ponto z 0 = x 0 + y 0 ı C. Da definição de derivada temos: f (z 0 ) def = lim z z0 f(z) f(z 0 ) z z 0 (3.12) 44
7 Variáveis Complexas Podemos tomar dois casos (caminhos): Caso 1 podemos fazer z z 0 seguindo o caminho z = x + y 0 ı, AULA 3 z z 0 = x + y 0 ı (x 0 + y 0 ı) = x x 0 que é equivalente a x x 0 e temos: f(z) f(z 0 ) = u(x, y 0) + v(x, y 0 )ı u(x 0 +, y 0 ) v(x 0, y 0 )ı z z 0 x x 0 = u(x, y 0) u(x 0, y 0 ) + ı v(x, y 0) v(x 0, y 0 ) x x 0 x x 0 Passando o limite z z 0 (de forma equivalente) x x 0 temos: f(z) f(z 0 ) u(x, y 0 ) u(x 0, y 0 ) lim = lim z z 0 z z 0 x x 0 x x 0 f (z 0 ) = x (x 0, y 0 ) + x (x 0, y 0 )ı (3.13) Caso 2 podemos fazer z z 0 seguindo o caminho z = x 0 + yı, z z 0 = x 0 + yı (x 0 + y 0 ı) = (y y 0 )ı que é equivalente a y y 0 e temos: f(z) f(z 0 ) z z 0 = u(x 0, y) + v(x 0, y)ı u(x 0 +, y 0 ) v(x 0, y 0 )ı x x 0 = u(x 0, y) u(x 0, y 0 ) (y y 0 )ı = ı u(x 0, y) u(x 0, y 0 ) (y y 0 ) + ı v(x 0, y) v(x 0, y 0 ) (y y 0 )ı + v(x 0, y) v(x 0, y 0 ) (y y 0 ) Passando o limite z z 0 (de forma equivalente) x x 0 temos: f(z) f(z 0 ) lim = lim ı u(x 0, y) u(x 0, y 0 ) z z 0 z z 0 y y 0 (y y 0 ) f (z 0 ) = ı + = ı (3.14) Comparando as equações eqn e eqn temos: x (x 0, y 0 ) + x (x 0, y 0 )ı = ı 45
8 Da igualdade de números complexos temos: x (x 0, y 0 ) = x (x 0, y 0 ) = Antes de provar a suficiência, provaremos um lema que será muito útil. Lema 3.1. Sejam D R 2 um aberto e f : D R 2 R uma função com derivadas parciais e D, contínuas em (x 0, y 0 ) D. Então: f(x 0 + λ, y 0 + η) f(x 0, y 0 ) = f x (x 0, y 0 )λ + f η + ξλ + ζη onde ξ 0 e ζ 0 quando λ 0 e η 0. PROVA: Começamos por escrever a diferença f(x 0 + λ, y 0 + η) f(x 0, y 0 ) como: f(x 0 + λ, y 0 + η) f(x 0, y 0 ) = f(x 0 + λ, y 0 + η) f(x 0, y 0 + η) + f(x 0, y 0 + η) f(x 0, y 0 ) (3.15) Do teorema do valor médio para funções de uma variável real existe t (0, 1) tal que: f(x 0 + λ, y 0 + η) f(x 0, y 0 + η) = f x (x 0 + tλ, y 0 + η)λ Como f é contínua em D a diferença: x ξ(λ, η) = f x (x 0 + tλ, y 0 + η) f x (x 0, y 0 ) tende a zero quando λ 0 e η 0. Daí, temos: ( ) f f(x 0 + λ, y 0 + η) f(x 0, y 0 + η) = x (x 0, y 0 ) + ξ λ (3.16) 46
9 Do mesmo modo temos: Variáveis Complexas f(x 0, y 0 + η) f(x 0, y 0 ) = ( ) f + ζ η (3.17) AULA 3 portanto das equações eqn 3.15, eqn 3.16 e eqn 3.17 temos f(x 0 + λ, y 0 + η) f(x 0, y 0 ) = f x (x 0, y 0 )λ + f η + ξλ + ζη e fica provado o lema. Vamos, agora, provar a suficiência. Teorema 3.2. Seja D C aberto e suponhamos que f : D C C seja uma função complexa tal que as derivadas parciais x, x, y e y existam em D e são contínuas em z 0 = x 0 + y 0 ı. Se as condições de Cauchy-Riemann são satisfeitas em z 0, x (x 0, y 0 ) = x (x 0, y 0 ) = então f é derivável em z 0. PROVA: Como, da hipótese, x e y o lema a u(x, y), temos: u = u(x 0 + λ, y 0 + η) u(x 0, y 0 ) = x (x 0, y 0 )λ + η + ξ 1 λ + ζ 1 η são contínuas, aplicando (3.18) onde ξ 1 0 e ζ 1 0 quando λ 0 e η 0. Do mesmo modo, Como, da hipótese, x e são contínuas, y aplicando o lema a v(x, y), temos: v = v(x 0 + λ, y 0 + η) v(x 0, y 0 ) = x (x 0, y 0 )λ + η + ξ 2 λ + ζ 2 η (3.19) 47
10 onde ξ 2 0 e ζ 2 0 quando λ 0 e η 0. Das equações eqn 3.18 e eqn 3.19 temos: w = u + vı ( = x + ) ( x ı λ + y + ) y ı η + ξλ + ζη (3.20) onde omitimos o argumento (x 0, y 0 ) das derivadas parciais e ξ = ξ 1 + ξ 2 e ζ = ζ 1 + ζ 2. Das equações de Cauchy-Riemann podemos reescrever a equação eqn 3.20 como: ( w = x + ( = x + x ı ) x ı ) ( λ + x + ) x ı η + ξλ + ζη (λ + ηı) + ξλ + ζη Dividindo a equação eqn 3.21 por = λ + ηı temos: ( w = x + ) x ı ξλ + ζη + λ + ηı (3.21) (3.22) Antes de fazer 0 em eqn 3.22 temos que mostrar que ξλ + ζη lim 0 λ + ηı = 0. Para isto tomando o módulo da expressão e usando a desigualdade triangular temos: ξλ + ζη λ + ηı ξ λ λ + ηı η λ + ηı (3.23) Como λ λ + ηı λ λ 2 + η 1 e η 2 λ + ηı η λ 2 + η 2 1 podemos reescrever eqn 3.23 como: 0 ξλ + ζη λ + ηı ξ + ζ (3.24) Passando o limite 0 em eqn 3.24 lembrando que ξ 0 e ζ 0 quando 0 temos: 0 ξλ + ζη λ + ηı 0 48
11 Variáveis Complexas ξλ + ζη e portanto lim = 0 e passando o limite 0 em eqn 0 λ + ηı 3.22 temos: f w (z 0 ) = lim 0 = x + x ı Portanto a derivada f (z 0 ) existe e é única. Agora um exemplo de aplicação das equações de Cauchy-Riemann. Em seção anterior vimos que a função f(z) = z 3 era derivável usando para isso a definição de derivada complexa. Por outro lado podemos expressar a função em suas componentes reais e imaginárias da seguinte forma: AULA 3 f(z) = z 3 = f(x + yı) = (x + yı) 3 = (x + yı) 2 (x + yı) = (x 2 y2 + 2xyı)(x + yı) = x 3 3xy 2 + (3x 2 y y 3 )ı Temos então u(x, y) = x 3 3xy 3 e v(x, y) = 3x 2 y 3. Derivando com relação a x e a y temos: x = 3x2 3y 2 y = 6xy x = 6xy y = 3x2 3y 2 Vemos pois, que as equações de Cauchy-Riemann: x = y y = x são satisfeitas para todo z = x + yı C. 49
12 3.5 Conclusão Na aula de hoje, vimos que derivação de funções complexas em alguns aspectos é semelhante à derivação de funções reais enquanto que em outros aspectos diferem sensivelmente. RESUMO No nosso resumo da Aula 03 constam os seguintes tópicos: Derivação Complexa Definição da derivação complexa: DEFINIÇÃO: Sejam D C aberto, z 0 D e f : D C C uma função complexa. Definimos a derivada de f( ) no ponto z 0, denotada f (z 0 ), por: f (z 0 ) def = lim z z0 f(z) f(z 0 ) z z 0 Regras de Derivação Complexa Para a derivação complexa temos, entre outras, as seguintes regras: 1. (f + g) (z 0 ) = f (z 0 ) + g (z 0 ) 2. (f g) (z 0 ) = f (z 0 ) g (z 0 ) 3. (f.g) (z 0 ) = f(z 0 ).g (z 0 ) + g(z 0 ).f (z 0 ) 4. ( f g ) (z 0 ) = f(z 0).g (z 0 ) g(z 0 ).f (z 0 ) g 2 (z 0 ) se g(z 0 ) 0 Equações de Cauchy-Riemann Os seguintes teoremas constituem condições necessária e suficiente (respectivamente) para a derivabilidade de uma função complexa: 50
13 Variáveis Complexas TEOREMA: (condição necessária) Seja D C aberto e suponhamos que f : D C C, f(z) = u(x, y) + v(x, y)ı e f (z) existam na vizinhança de um ponto z 0 = x 0 + y 0 ı C. Então as derivadas parciais de primeira ordem de u e v com relação a x e a y existem e satisfazem: AULA 3 x (x 0, y 0 ) = x (x 0, y 0 ) = TEOREMA: (condição suficiente) Seja D C aberto e suponhamos que f : D C C seja uma função complexa tal que as derivadas parciais x, x, y e y existam em D e são contínuas em z 0 = x 0 + y 0 ı. Se as condições de Cauchy-Riemann são satisfeitas em z 0, x (x 0, y 0 ) = x (x 0, y 0 ) = PRÓXIMA AULA Em nossa próxima aula veremos mais alguns aspectos da derivação de funções complexas. Em particular funções holomorfas e a ligação de funções harmonicas com a derivação complexa. 51
14 ATIVIDADES Deixamos como atividades o cálculo de algumas integrais duplas. ATIV Se f( ) e g( ) são funções deriváveis em um ponto z 0 C então vale a seguinte regra de derivação: (f.g) (z 0 ) = f(z 0 ).g (z 0 ) + g(z 0 ).f (z 0 ). Comentário: Volte ao texto e reveja com calma e atenção a demonstração de uma das regras de derivação complexa, ela lhe servirá de guia. ATIV Mostre que as componentes da função complexa f(x+ yı) = sin(x) cosh(y) + cos(x) sinh(y)ı satisfazem as equações de Cauchy-Riemann. Comentário: Reveja as derivadas das funções trigonométricas e das funções hiperbólicas. LEITURA COMPLEMENTAR SPIEGEL, Murray R., Variáveis Complexas, Coleção Schaum, Editora McGraw-Hill do Brasil, SOARES, Márcio G., Cálculo em uma Variável Complexa, Coleção Matemática Universitária, Editora SBM, BROWN, James W. and CHURCHILL, Ruel R., Complex Variables and Applications Editora McGraw Hill, FERNANDEZ, Cecília S. e BERNARDES Jr, Nilson C. Introdução às Funções de uma Variável Complexa. Editora SBM,
Mais Alguns Aspectos da Derivação Complexa
 Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Mais Alguns Aspectos da Derivação Complexa META: Introduzir o conceito de funções holomorfas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir funções holomorfas e determinar se uma
Limites de Funções de Variáveis Complexas
 Limites de Funções de Variáveis Complexas AULA 2 META: Introduzir o conceito de limite de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir limites de
Limites de Funções de Variáveis Complexas AULA 2 META: Introduzir o conceito de limite de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir limites de
Convergência de Séries de Números Complexos
 Convergência de Séries de Números Complexos META: Apresentar o conceito de convergência de séries de números complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir convergência
Convergência de Séries de Números Complexos META: Apresentar o conceito de convergência de séries de números complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir convergência
Funções Elementares do Cálculo Complexos 1
 Funções Elementares do Cálculo Complexos 1 META: Definir algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir algumas funções elementares
Funções Elementares do Cálculo Complexos 1 META: Definir algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir algumas funções elementares
Cálculo de Resíduos AULA 12
 AULA 2 META: Apresentar cálculo de resíduos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir resíduo de uma função de variáveis complexas em um ponto dado e calcular o resíduo de uma
AULA 2 META: Apresentar cálculo de resíduos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir resíduo de uma função de variáveis complexas em um ponto dado e calcular o resíduo de uma
Transformações Conformes: 15 Aplicações
 AULA Transformações Conformes: 15 Aplicações META: Aplicar transformações conformes. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Aplicar transformações conformes na determinação da distribuição
AULA Transformações Conformes: 15 Aplicações META: Aplicar transformações conformes. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Aplicar transformações conformes na determinação da distribuição
Funções Elementares do Cálculo Complexos 2
 Funções Elementares do Cálculo Complexos AULA 6 META: Definir mais algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir mais algumas funções
Funções Elementares do Cálculo Complexos AULA 6 META: Definir mais algumas funções elementares no campo dos complexos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir mais algumas funções
Teoremas de Cauchy AULA 8
 Teoremas de auchy META: Introduzir os principais teoremas de auchy sobre integração de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Enunciar os principais
Teoremas de auchy META: Introduzir os principais teoremas de auchy sobre integração de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Enunciar os principais
14 AULA. Funções LIVRO. META: Apresentar o conceitos de funções.
 2 LIVRO Funções META: Apresentar o conceitos de funções. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Identificar se uma dada relção é uma função. Determinar a imagem direta e a imagem inversa
2 LIVRO Funções META: Apresentar o conceitos de funções. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Identificar se uma dada relção é uma função. Determinar a imagem direta e a imagem inversa
10 AULA. Operações com Conjuntos: Produto Cartesiano LIVRO. META: Introduzir propriedades para o produto cartesiano de conjuntos.
 1 LIVRO Operações com Conjuntos: Produto Cartesiano META: Introduzir propriedades para o produto cartesiano de conjuntos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Demonstrar propriedades
1 LIVRO Operações com Conjuntos: Produto Cartesiano META: Introduzir propriedades para o produto cartesiano de conjuntos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Demonstrar propriedades
Transformações Conformes
 META: Introduzir o conceito de transformações conforme. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir transformações conformes e exemplificar transformações conformes. PRÉ-REQUISITOS
META: Introduzir o conceito de transformações conforme. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir transformações conformes e exemplificar transformações conformes. PRÉ-REQUISITOS
Uma demonstração elementar de um resultado sobre a noção de diferencial em espaços normados
 Uma demonstração elementar de um resultado sobre a noção de diferencial em espaços normados Cecília S. Fernandez UFF Neste trabalho vamos apresentar uma demonstração elementar de um resultado envolvendo
Uma demonstração elementar de um resultado sobre a noção de diferencial em espaços normados Cecília S. Fernandez UFF Neste trabalho vamos apresentar uma demonstração elementar de um resultado envolvendo
Singularidades de Funções de Variáveis Complexas
 Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
META: Introduzir o conceito de integração de funções de variáveis complexas.
 Integrção omplex AULA 7 META: Introduzir o conceito de integrção de funções de vriáveis complexs. OBJETIVOS: Ao fim d ul os lunos deverão ser cpzes de: Definir integrl de um função complex. lculr integrl
Integrção omplex AULA 7 META: Introduzir o conceito de integrção de funções de vriáveis complexs. OBJETIVOS: Ao fim d ul os lunos deverão ser cpzes de: Definir integrl de um função complex. lculr integrl
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 2018
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 7 5 DE MARÇO DE 08 Condições Suficientes de Diferenciabilidade Teorema Seja f(z) = u(, y) + iv(, y). Se u e v têm derivadas parciais contínuas em torno
Universidade Federal de Goiás. Plano de Ensino
 01: Dados de Identificação da Disciplina: Plano de Ensino Disciplina: Funções de uma Variável Complexa Cod. da Disciplina: 2733 Curso: Matematica Licenciatura Cod. do Curso: Turma: Matemática: Licenciatura
01: Dados de Identificação da Disciplina: Plano de Ensino Disciplina: Funções de uma Variável Complexa Cod. da Disciplina: 2733 Curso: Matematica Licenciatura Cod. do Curso: Turma: Matemática: Licenciatura
6.1.2 Derivada de ordem superior e derivação implícita
 6.1. DERIVABILIDADE E DIFERENCIABILIDADE 111 6.1.2 Derivada de ordem superior e derivação implícita Observe que se f é derivável num subconjunto A de seu domínio D, obtemos então uma nova função g = f
6.1. DERIVABILIDADE E DIFERENCIABILIDADE 111 6.1.2 Derivada de ordem superior e derivação implícita Observe que se f é derivável num subconjunto A de seu domínio D, obtemos então uma nova função g = f
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 16, 2011 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Variáveis Complexas. José Carlos Leite
 Variáveis Complexas José Carlos Leite São Cristóvão/SE 2011 Variaveis Complexas Elaboração de Conteúdo José Carlos Leite Projeto Gráfico Neverton Correia da Silva Nycolas Menezes Melo Capa Hermeson Alves
Variáveis Complexas José Carlos Leite São Cristóvão/SE 2011 Variaveis Complexas Elaboração de Conteúdo José Carlos Leite Projeto Gráfico Neverton Correia da Silva Nycolas Menezes Melo Capa Hermeson Alves
Variável Complexa
 Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2015.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Convergência, séries de potência e funções analíticas
 Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Convergência, séries de potência e funções analíticas Roberto Imbuzeiro Oliveira March 13, 2015 1 Algumas palavras sobre convergência em C Tudo o que descreveremos aqui é análogo ao que se define e prova
Sumário Algumas Demonstrações CONCLUSÃO RESUMO ATIVIDADES... 34
 Sumário Aula 11: Relações Binárias 9 11.1 Introdução... 10 11.2 Relações Binárias... 10 11.2.1 Propriedades das Relações Binárias... 13 11.3 Algumas Demonstrações... 16 11.4 CONCLUSÃO... 18 11.5 RESUMO....
Sumário Aula 11: Relações Binárias 9 11.1 Introdução... 10 11.2 Relações Binárias... 10 11.2.1 Propriedades das Relações Binárias... 13 11.3 Algumas Demonstrações... 16 11.4 CONCLUSÃO... 18 11.5 RESUMO....
12 AULA. ciáveis LIVRO. META Estudar derivadas de funções de duas variáveis a valores reais.
 1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
4 Existência da Derivada
 4 4.1 Continuidade As seções precedentes serviram para nos fornecer o conceito de derivada de uma função. Muito embora os conceitos de velocidade instantânea e de inclinação da curva num ponto tenham sido
4 4.1 Continuidade As seções precedentes serviram para nos fornecer o conceito de derivada de uma função. Muito embora os conceitos de velocidade instantânea e de inclinação da curva num ponto tenham sido
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas
 Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas LCE0176 - Cálculo e Matemática Aplicados às Ciências Biológicas Professora: Clarice G. B. Demétrio
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas LCE0176 - Cálculo e Matemática Aplicados às Ciências Biológicas Professora: Clarice G. B. Demétrio
Aula 26 A regra de L Hôpital.
 MÓDULO - AULA 6 Aula 6 A regra de L Hôpital Objetivo Usar a derivada para determinar certos ites onde as propriedades básicas de ites, vistas nas aulas 3, 4, e 5, não se aplicam Referência: Aulas 3, 4,
MÓDULO - AULA 6 Aula 6 A regra de L Hôpital Objetivo Usar a derivada para determinar certos ites onde as propriedades básicas de ites, vistas nas aulas 3, 4, e 5, não se aplicam Referência: Aulas 3, 4,
Aula 05 - Limite de uma Função - Parte I Data: 30/03/2015
 bras.png Cálculo I Logonewton.png Aula 05 - Limite de uma Função - Parte I Data: 30/03/2015 Objetivos da Aula: Definir limite de uma função Definir limites laterias Apresentar as propriedades operatórias
bras.png Cálculo I Logonewton.png Aula 05 - Limite de uma Função - Parte I Data: 30/03/2015 Objetivos da Aula: Definir limite de uma função Definir limites laterias Apresentar as propriedades operatórias
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
15 AULA. Tipos de Funções LIVRO. META: Introduzir os diversos tipos de funções.
 2 LIVRO Tipos de Funções META: Introduzir os diversos tipos de funções. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Determinar se uma dada função é injetora, sobrejetora ou bijetora. PRÉ-REQUISITOS
2 LIVRO Tipos de Funções META: Introduzir os diversos tipos de funções. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Determinar se uma dada função é injetora, sobrejetora ou bijetora. PRÉ-REQUISITOS
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
Capítulo 7. Operadores Normais. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 7 Operadores Normais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 7: Operadores Normais Meta
Capítulo 7 Operadores Normais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 7: Operadores Normais Meta
Análise Complexa e Equações Diferenciais Guia 6 João Pedro Boavida. 19 a 28 de Outubro
 19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
19 a 28 de Outubro Nestas teóricas, estamos a falar das últimas ideias de análise complexa. Veremos algumas aplicações do teorema dos resíduos e algumas propriedades das funções holomorfas. No livro, falta-vos
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
GABARITO. 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan
 GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
GABARITO 1 a PROVA - DISCIPLINA MTM 5186: CÁLCULO IV Professor: Matheus C. Bortolan (Valor 3.) Questão 1: Responda às seguintes questões, usando as equações de Cauchy-Riemann. (1.5) (a) Mostre que a função
13 AULA. Relações de Equivalência LIVRO. META: Introduzir o conceito de relações de equivalência e suas propriedades.
 2 LIVRO Relações de Equivalência META: Introduzir o conceito de relações de equivalência e suas propriedades. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Identificar se uma dada relação
2 LIVRO Relações de Equivalência META: Introduzir o conceito de relações de equivalência e suas propriedades. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Identificar se uma dada relação
A Equivalência entre o Teorema do Ponto Fixo de Brouwer e o Teorema do Valor Intermediário
 A Equivalência entre o Teorema do Ponto Fixo de Brouwer e o Teorema do Valor Intermediário Renan de Oliveira Pereira, Ouro Preto, MG, Brasil Wenderson Marques Ferreira, Ouro Preto, MG, Brasil Eder Marinho
A Equivalência entre o Teorema do Ponto Fixo de Brouwer e o Teorema do Valor Intermediário Renan de Oliveira Pereira, Ouro Preto, MG, Brasil Wenderson Marques Ferreira, Ouro Preto, MG, Brasil Eder Marinho
Algumas Aplicações das Integrais tríplas
 Algumas Aplicações das Integrais tríplas META: Apresentar algumas aplicações das integrais triplas de funções de valores reais e domínio em R 3. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes
Algumas Aplicações das Integrais tríplas META: Apresentar algumas aplicações das integrais triplas de funções de valores reais e domínio em R 3. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1. (1) Descreva as regiões do plano complexo definidas por z i c z, onde c é um número real não negativo.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
1 Números Complexos e Plano Complexo
 UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
UNIVERSIDADE FEDERAL DE SANTA CATARINA Centro de Ciências Físicas e Matemáticas Departamento de Matemática SEMESTRE CÓDIGO DISCIPLINA TURMA 09-1 MTM5327 Variável Complexa 0549 Professor Lista de Exercícios
Lista 1 - Métodos Matemáticos II Respostas
 Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
Lista 1 - Métodos Matemáticos II Respostas Prof. Jorge Delgado Importante: As resoluções não pretendem ser completas mas apenas uma indicação para o aluno consultar caso seja necessário, cabendo a ele
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
Aula 22 O teste da derivada segunda para extremos relativos.
 O teste da derivada segunda para extremos relativos. MÓDULO 2 - AULA 22 Aula 22 O teste da derivada segunda para extremos relativos. Objetivo: Utilizar a derivada segunda para determinar pontos de máximo
O teste da derivada segunda para extremos relativos. MÓDULO 2 - AULA 22 Aula 22 O teste da derivada segunda para extremos relativos. Objetivo: Utilizar a derivada segunda para determinar pontos de máximo
4.1 Preliminares. 1. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = 1=x; x 6= 0 (c) f (x) = 1= p x; x > 0:
 4. FUNÇÕES DERIVÁVEIS ANÁLISE NO CORPO R - 208. 4. Preinares. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = =x; x 6= 0 (c) f (x) = = p x; x > 0: 2. Mostre que
4. FUNÇÕES DERIVÁVEIS ANÁLISE NO CORPO R - 208. 4. Preinares. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = =x; x 6= 0 (c) f (x) = = p x; x > 0: 2. Mostre que
Objetivos. Estudar a derivada de certas funções.
 Funções deriváveis MÓDULO 1 - AULA 9 Aula 9 Funções deriváveis Objetivos Compreender a noção de função derivável Referências: Aulas 15 e 16, de Pré-Cálculo, e aulas 2, 3, 4 e 5 Estudar a derivada de certas
Funções deriváveis MÓDULO 1 - AULA 9 Aula 9 Funções deriváveis Objetivos Compreender a noção de função derivável Referências: Aulas 15 e 16, de Pré-Cálculo, e aulas 2, 3, 4 e 5 Estudar a derivada de certas
GEOMETRIAS NÃO- EUCLIDIANAS E SUAS MÉTRICAS
 GEOMETRIAS NÃO- EUCLIDIANAS E SUAS MÉTRICAS Fernando da Costa Gomes (bolsista do PIBIC/UFPI), Newton Luís Santos (Orientador, Depto. de Matemática UFPI) RESUMO Neste trabalho, exibimos os modelos clássicos,
GEOMETRIAS NÃO- EUCLIDIANAS E SUAS MÉTRICAS Fernando da Costa Gomes (bolsista do PIBIC/UFPI), Newton Luís Santos (Orientador, Depto. de Matemática UFPI) RESUMO Neste trabalho, exibimos os modelos clássicos,
 Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Capítulo 1 Como motivação para a construção dos números complexos aconselha-se o visionamento do quinto do capítulo do documentário Dimensions, disponível em http://www.dimensions-math.org/ Slides de apoio
Aula 7 Os teoremas de Weierstrass e do valor intermediário.
 Os teoremas de Weierstrass e do valor intermediário. MÓDULO - AULA 7 Aula 7 Os teoremas de Weierstrass e do valor intermediário. Objetivo Compreender o significado de dois resultados centrais a respeito
Os teoremas de Weierstrass e do valor intermediário. MÓDULO - AULA 7 Aula 7 Os teoremas de Weierstrass e do valor intermediário. Objetivo Compreender o significado de dois resultados centrais a respeito
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Material Teórico - Módulo de Função Exponencial. Primeiro Ano - Médio. Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M.
 Material Teórico - Módulo de Função Exponencial Gráfico da Função Exponencial Primeiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 0 de dezembro de 018 1 Funções convexas
Material Teórico - Módulo de Função Exponencial Gráfico da Função Exponencial Primeiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 0 de dezembro de 018 1 Funções convexas
9 AULA. Operações com Conjuntos: Diferença e Complementar LIVRO. META: Apresentar algumas propriedades da diferença e do complementar de conjuntos.
 1 LIVRO Operações com Conjuntos: Diferença e Complementar META: Apresentar algumas propriedades da diferença e do complementar de conjuntos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de:
1 LIVRO Operações com Conjuntos: Diferença e Complementar META: Apresentar algumas propriedades da diferença e do complementar de conjuntos. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de:
Derivadas 1
 www.matematicaemexercicios.com Derivadas 1 Índice AULA 1 Introdução 3 AULA 2 Derivadas fundamentais 5 AULA 3 Derivada do produto e do quociente de funções 7 AULA 4 Regra da cadeia 9 www.matematicaemexercicios.com
www.matematicaemexercicios.com Derivadas 1 Índice AULA 1 Introdução 3 AULA 2 Derivadas fundamentais 5 AULA 3 Derivada do produto e do quociente de funções 7 AULA 4 Regra da cadeia 9 www.matematicaemexercicios.com
Capítulo 2. Ortogonalidade e Processo de Gram-Schmidt. Curso: Licenciatura em Matemática
 Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Capítulo 2 Ortogonalidade e Processo de Gram-Schmidt Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves de Melo Disciplina: Álgebra Linear II Unidade II Aula
Séries de Laurent e Teoremas de Cauchy
 Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Séries de Laurent e Teoremas de Cauchy Roberto Imbuzeiro Oliveira 3 de Abril de 20 A maior parte destas notas tem como refererência o livro de David Ullrich, Complex Made Simple. Preliminares sobre séries
Polinômio Mínimo e Operadores Nilpotentes
 Capítulo 9 Polinômio Mínimo e Operadores Nilpotentes Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula
Capítulo 9 Polinômio Mínimo e Operadores Nilpotentes Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula
Álgebra Linear I - Aula 2. Roteiro
 Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
Álgebra Linear I - Aula 2 1. Produto escalar. Ângulos. 2. Desigualdade triangular. 3. Projeção ortugonal de vetores. Roteiro 1 Produto escalar Considere dois vetores = (u 1, u 2, u 3 ) e v = (v 1, v 2,
Análise Complexa e Equações Diferenciais Guia 3 João Pedro Boavida. 21 a 28 de Setembro
 2 de Setembro de 211 21 a 28 de Setembro A secção Números complexos e matrizes 2 2 indica algumas das conclusões da discussão no final do guia 1 As secções Derivação em C e Integração em C resumem algumas
2 de Setembro de 211 21 a 28 de Setembro A secção Números complexos e matrizes 2 2 indica algumas das conclusões da discussão no final do guia 1 As secções Derivação em C e Integração em C resumem algumas
Capítulo 6. Operadores Ortogonais. Curso: Licenciatura em Matemática. Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo
 Capítulo 6 Operadores Ortogonais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 6: Operadores Ortogonais
Capítulo 6 Operadores Ortogonais Curso: Licenciatura em Matemática Professor-autor: Danilo Felizardo Barboza Wilberclay Gonçalves Melo Disciplina: Álgebra Linear II Unidade II Aula 6: Operadores Ortogonais
A TRANSFORMADA DE LAPLACE E ALGUMAS APLICAÇÕES. (UFG) RESUMO
 A TRANSFORMADA DE LAPLACE E ALGUMAS APLICAÇÕES Fernando Ricardo Moreira 1, Esdras Teixeira Costa 2, Marcio Koetz 3, Samanta Andressa Santos Dumke Teixeira 4, Henrique Bernardes da Silva 5 1 Professor Mestre
A TRANSFORMADA DE LAPLACE E ALGUMAS APLICAÇÕES Fernando Ricardo Moreira 1, Esdras Teixeira Costa 2, Marcio Koetz 3, Samanta Andressa Santos Dumke Teixeira 4, Henrique Bernardes da Silva 5 1 Professor Mestre
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Teoria da Medida e Integração (MAT505)
 Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
Teoria da Medida e Integração (MAT505) Modos de convergência V. Araújo Mestrado em Matemática, UFBA, 2014 1 Modos de convergência Modos de convergência Neste ponto já conhecemos quatro modos de convergência
(versão preliminar) exceto possivelmente para x = a. Dizemos que o limite de f(x) quando x tende para x = a é um numero L, e escrevemos
 LIMITE DE FUNÇÕES REAIS JOSÉ ANTÔNIO G. MIRANDA versão preinar). Revisão: Limite e Funções Continuas Definição Limite de Seqüências). Dizemos que uma seqüência de números reais n convergente para um número
LIMITE DE FUNÇÕES REAIS JOSÉ ANTÔNIO G. MIRANDA versão preinar). Revisão: Limite e Funções Continuas Definição Limite de Seqüências). Dizemos que uma seqüência de números reais n convergente para um número
Vamos revisar alguns fatos básicos a respeito de séries de potências
 Seção 4 Revisão sobre séries de potências Vamos revisar alguns fatos básicos a respeito de séries de potências a n (x x ) n, que serão úteis no estudo de suas aplicações à resolução de equações diferenciais
Seção 4 Revisão sobre séries de potências Vamos revisar alguns fatos básicos a respeito de séries de potências a n (x x ) n, que serão úteis no estudo de suas aplicações à resolução de equações diferenciais
Aula 17 Superfícies quádricas - parabolóides
 Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
Objetivos Aula 17 Superfícies quádricas - parabolóides Apresentar os parabolóides elípticos e hiperbólicos identificando suas seções planas. Estudar os parabolóides regrados e de revolução. Nas superfícies
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Números e Funções Reais, E. L. Lima, Coleção PROFMAT.
 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 8 - Seções 8.9 e 8.10 do livro texto da disciplina: Números e Funções
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 8 - Seções 8.9 e 8.10 do livro texto da disciplina: Números e Funções
Derivadas 1 DEFINIÇÃO. A derivada é a inclinação da reta tangente a um ponto de uma determinada curva, essa reta é obtida a partir de um limite.
 Derivadas 1 DEFINIÇÃO A partir das noções de limite, é possível chegarmos a uma definição importantíssima para o Cálculo, esta é a derivada. Por definição: A derivada é a inclinação da reta tangente a
Derivadas 1 DEFINIÇÃO A partir das noções de limite, é possível chegarmos a uma definição importantíssima para o Cálculo, esta é a derivada. Por definição: A derivada é a inclinação da reta tangente a
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
CÁLCULO I. 1 Derivada de Funções Elementares
 CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o : Derivada das Funções Elementares. Regras de Derivação. Objetivos da Aula Apresentar a derivada das funções elementares; Apresentar
CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o : Derivada das Funções Elementares. Regras de Derivação. Objetivos da Aula Apresentar a derivada das funções elementares; Apresentar
Análise Complexa e Equações Diferenciais
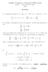 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Aula 6 Produto interno
 MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
MÓDULO 1 - AULA 6 Objetivos Aula 6 Produto interno Estabelecer os conceitos de norma de um vetor e de ângulo entre dois vetores do espaço. Definir o produto interno de vetores no espaço e estabelecer suas
Teoria da Medida e Integração (MAT505)
 Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Modos de convergência Teoria da Medida e Integração (MAT505) Modos de convergência. V. Araújo Instituto de Matemática, Universidade Federal da Bahia Mestrado em Matemática, UFBA, 2014 Modos de convergência
Prof. Doherty Andrade. 25 de outubro de 2005
 Funções Hiperbólicas - Resumo Prof. Doherty Andrade 5 de outubro de 005 Sumário Funções Transcendentes. Função Logaritmo Natural............................ Funções Trigonométricas Hiperbólicas.....................
Funções Hiperbólicas - Resumo Prof. Doherty Andrade 5 de outubro de 005 Sumário Funções Transcendentes. Função Logaritmo Natural............................ Funções Trigonométricas Hiperbólicas.....................
RESOLUÇÃO DO PRIMEIRO TESTE 31 DE OUTUBRO DE 2015 MEMEC,LEAN. f(x + iy) = x + x 3 + i(1 + y + y 2 )
 ANÁLISE COMPLEXA E EQUAÇÕES DIFEENCIAIS ESOLUÇÃO DO PIMEIO TESTE 3 DE OUTUBO DE 205 MEMEC,LEAN Considere a função f : C C definida pela expressão fx + iy = x + x 3 + i + y + y 2 a Determine o domínio de
ANÁLISE COMPLEXA E EQUAÇÕES DIFEENCIAIS ESOLUÇÃO DO PIMEIO TESTE 3 DE OUTUBO DE 205 MEMEC,LEAN Considere a função f : C C definida pela expressão fx + iy = x + x 3 + i + y + y 2 a Determine o domínio de
Variável Complexa
 Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
Variável Complexa 2017.2 Aula1 Utilizamos o símbolo C para denotar o plano real R 2 equipado com as seguintes operações: z 1 + z 2 = (x 1 + x 2, y 1 + y 2 ) adição z 1 z 2 = (x 1 x 2 y 1 y 2,, x 1 y 2
MAT CÁLCULO 2 PARA ECONOMIA. Geometria Analítica
 MT0146 - CÁLCULO PR ECONOMI SEMESTRE DE 016 LIST DE PROBLEMS Geometria nalítica 1) Sejam π 1 e π os planos de equações, respectivamente, x + y + z = e x y + z = 1. Seja r a reta formada pela interseção
MT0146 - CÁLCULO PR ECONOMI SEMESTRE DE 016 LIST DE PROBLEMS Geometria nalítica 1) Sejam π 1 e π os planos de equações, respectivamente, x + y + z = e x y + z = 1. Seja r a reta formada pela interseção
Diferenciais em Série de Potências
 Existência de Soluções de Equações Diferenciais em Série de Potências Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/ regi 0 de julho de
Existência de Soluções de Equações Diferenciais em Série de Potências Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/ regi 0 de julho de
Concluímos esta secção apresentando alguns exemplos que constituirão importantes limites de referência. tan θ. sin θ
 aula 08 Funções reais de variável real Limites e continuidade (Continuação) A definição de limite segundo Heine permite, como já vimos anteriormente no caso da álgebra de limites, transpor quase imediatamente
aula 08 Funções reais de variável real Limites e continuidade (Continuação) A definição de limite segundo Heine permite, como já vimos anteriormente no caso da álgebra de limites, transpor quase imediatamente
13 AULA. Regra da Cadeia e Derivação Implícita LIVRO. META Derivar funções compostas e funções definidas implicitamente.
 1 LIVRO Regra da Cadeia e Derivação Implícita 13 AULA META Derivar funções compostas e funções definidas implicitamente. OBJETIVOS Estender os conceitos da regra da cadeia e da derivação implícita de funções
1 LIVRO Regra da Cadeia e Derivação Implícita 13 AULA META Derivar funções compostas e funções definidas implicitamente. OBJETIVOS Estender os conceitos da regra da cadeia e da derivação implícita de funções
Método de Gauss-Jordan e Sistemas Homogêneos
 Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA
 ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA Maria do Rosário de Pinho e Maria Margarida Ferreira Agosto 2004 Faculdade de Engenharia da Universidade do Porto Licenciatura
ANÁLISE MATEMÁTICA 3 APONTAMENTOS DAS AULAS TEÓRICAS PARTE A ANÁLISE COMPLEXA Maria do Rosário de Pinho e Maria Margarida Ferreira Agosto 2004 Faculdade de Engenharia da Universidade do Porto Licenciatura
Máximos e mínimos (continuação)
 UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 3 Assunto: Máximos e mínimos Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos (continuação) Sejam f
UNIVERSIDADE FEDERAL DO PARÁ CÁLCULO II - PROJETO NEWTON AULA 3 Assunto: Máximos e mínimos Palavras-chaves: máximos e mínimos, valores máximos e valores mínimos Máximos e mínimos (continuação) Sejam f
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Fórmulas de Taylor - Notas Complementares ao Curso de Cálculo I
 Fórmulas de Taylor - Notas Complementares ao Curso de Cálculo I Gláucio Terra Sumário 1 Introdução 1 2 Notações 1 3 Notas Preliminares sobre Funções Polinomiais R R 2 4 Definição do Polinômio de Taylor
Fórmulas de Taylor - Notas Complementares ao Curso de Cálculo I Gláucio Terra Sumário 1 Introdução 1 2 Notações 1 3 Notas Preliminares sobre Funções Polinomiais R R 2 4 Definição do Polinômio de Taylor
A Projeção e seu Potencial
 A Projeção e seu Potencial Rolci Cipolatti Departamento de Métodos Matemáticos Instituto de Matemática, Universidade Federal do Rio de Janeiro C.P. 68530, Rio de Janeiro, Brasil e-mail: cipolatti@im.ufrj.br
A Projeção e seu Potencial Rolci Cipolatti Departamento de Métodos Matemáticos Instituto de Matemática, Universidade Federal do Rio de Janeiro C.P. 68530, Rio de Janeiro, Brasil e-mail: cipolatti@im.ufrj.br
A derivada da função inversa
 A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
Cursos: Análise Complexa e Equações Diferenciais 2 ō Semestre 23/24 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi) 5 de Abril de 24, h3m Duração: h 3m. Seja α C 2 R) e u : R 2 R uma função
LIMITES E CONTINUIDADE
 LIMITES E CONTINUIDADE 1 LIMITE Marina Vargas R. P. Gonçalves a a Departamento de Matemática, Universidade Federal do Paraná, marina.vargas@gmail.com, http:// www.estruturas.ufpr.br Definição 1.1 O limite
LIMITES E CONTINUIDADE 1 LIMITE Marina Vargas R. P. Gonçalves a a Departamento de Matemática, Universidade Federal do Paraná, marina.vargas@gmail.com, http:// www.estruturas.ufpr.br Definição 1.1 O limite
Geometria Analítica II - Aula 4 82
 Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Geometria Analítica II - Aula 4 8 IM-UFF K. Frensel - J. Delgado Aula 5 Esferas Iniciaremos o nosso estudo sobre superfícies com a esfera, que já nos é familiar. A esfera S de centro no ponto A e raio
Material Teórico - Módulo Cônicas. Hipérboles. Terceiro Ano do Ensino Médio
 Material Teórico - Módulo Cônicas Hipérboles Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução Já vimos que as hipérboles são as
Material Teórico - Módulo Cônicas Hipérboles Terceiro Ano do Ensino Médio Autor: Prof. Fabrício Siqueira Benevides Revisor: Prof. Antonio Caminha M. Neto 1 Introdução Já vimos que as hipérboles são as
Aula 5 Derivadas parciais
 Aula 5 Derivadas parciais MÓDULO 1 AULA 5 Objetivos Aprender a calcular as derivadas parciais de funções de várias variáveis. Conecer a interpretação geométrica desse conceito. Introdução Ao longodas quatro
Aula 5 Derivadas parciais MÓDULO 1 AULA 5 Objetivos Aprender a calcular as derivadas parciais de funções de várias variáveis. Conecer a interpretação geométrica desse conceito. Introdução Ao longodas quatro
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Objetivos. Expressar o vértice da parábola em termos do discriminante e dos
 MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
MÓDULO 1 - AULA 17 Aula 17 Parábola - aplicações Objetivos Expressar o vértice da parábola em termos do discriminante e dos coeficientes da equação quadrática Expressar as raízes das equações quadráticas
Comprimento de Arco, o Número π e as Funções Trigonométricas
 Comprimento de Arco, o Número π e as Funções Trigonométricas J. A. Verderesi Apresentaremos a seguir a medida de um ângulo como limite de poligonais inscritas e circunscritas à circunfêrencia unitária,
Comprimento de Arco, o Número π e as Funções Trigonométricas J. A. Verderesi Apresentaremos a seguir a medida de um ângulo como limite de poligonais inscritas e circunscritas à circunfêrencia unitária,
Definição 3.1: Seja x um número real. O módulo de x, denotado por x, é definido como: { x se x 0 x se x < 0
 Capítulo 3 Módulo e Função Módular A função modular é uma função que apresenta o módulo na sua lei de formação. No entanto, antes de falarmos sobre funções modulares devemos definir o conceito de módulo,
Capítulo 3 Módulo e Função Módular A função modular é uma função que apresenta o módulo na sua lei de formação. No entanto, antes de falarmos sobre funções modulares devemos definir o conceito de módulo,
Área e Teorema Fundamental do Cálculo
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área e Teorema Fundamental
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área e Teorema Fundamental
