Capítulo 8 Teste de Hipótese. Seção 8-1 Visão Geral. Definições
|
|
|
- Fátima Barreiro Imperial
- 6 Há anos
- Visualizações:
Transcrição
1 Capítulo 8 Teste de Hipótese 8-1 Visão Geral 8-2 Fundamentos do Teste de Hipótese 8-3 Testando Afirmações sobre uma Proporção 8-4 Testando Afirmações sobre uma Média: σ Conhecido 8-5 Testando Afirmações sobre uma Média: σ Desconhecido 8-6 Testando Afirmações sobre o Desvio Padrão ou Variância Slide 2 Seção 8-1 Visão Geral 1 Created by Erin Hodgess, Houston, Texas Revised to accompany 10 th Edition, Tom Wegleitner, Centreville, VA Slide 3 Definições Em estatística, uma hipótese é uma afirmação ou setença sobre as propriedades de uma população. Um Teste de hipótese (ou teste de significância) é um procedimento padronizado para testar uma afirmação sobre as propriedades de uma população. Slide 4
2 Regra do Evento Raro para a Inferência Estatística Se, sob uma dada suposição, a probabilidade de um evento particular observado é excepcionalmente pequena, nós concluímos que a suposição provavelmente não é correta. Slide 5 Exemplo: As Indústrias ProCare Ltda. forneceram, certa vez, um produto chamado Gender Choice (Escolha o Sexo) que, de acordo com a propaganda, permitia aos casais aumentar em até 80% as suas chances de ter uma menina. Suponha que façamos um experimento com 100 casais que querem ter meninas e que eles sigam o Gender Choice, um sistema fácil de usar em casa descrito na embalagem cor de rosa para meninas. Com o propósito de testar a afirmação de que há um acréscimo na proporção de meninas vamos assumir que o Gender Choice não tem efeito. Usando o bom senso e nenhum método formal de estatística, o que podemos concluir sobre a suposição de nenhum efeito do Gender Choice se 100 casais usando Gender Choice tiverem 100 bebês sendo: a) 52 meninas? b) 97 meninas? 2 Slide 6 Exemplo: Indústrias ProCare Industries Ltda.: Parte a) a) Nós em geral esperamos cerca de 50 meninas em 100 nascimentos. O resultado de 52 meninas é bastante próximo de 50, então não podemos concluir que o Gender Choice é realmente eficaz. Se os 100 casais não usaram nenhum método especial para seleção de gênero, o resultado de 52 meninas pode ocorrer facilmente. A suposição de não efeito do Gender Choice aparenta ser correta. Não temos evidência para afirmar que p Gender Choice é eficiente. Slide 7
3 Exemplo: Indústrias ProCare Industries Ltda.: Parte b) b) O resultado de 97 meninas em 100 nascimentos é extremamente improvável de acontecer. Podemos explicar este fato por duas maneiras: Um evento extremamente raro ocorreu devido a fatores aleatórios, ou o Gender Choice é eficiente. A probabilidade extremamente baixa em termos 97 meninas em 100 nascimentos é uma forte evidência contra a suposição inicial de que o Gender Choice não funciona. Slide 8 Seção 8-2 Fundamentos de Teste de Hipótese 3 Created by Erin Hodgess, Houston, Texas Revised to accompany 10 th Edition, Tom Wegleitner, Centreville, VA Slide 9 Pontos Chave Esta seção apresenta os componentes individuais de um teste de hipótese, e as seções seguintes usarão estes componentes em um procedimento claro e objetivo. A função de cada um deles deve ser bem compreendido: Hipótese Nula Hipótese Alternativa Estatística do Teste Região Crítica Nível de Significância Valor Crítico P-valor Erro Tipo I e II Slide 10
4 Seção 8-2 Objetivos Dada uma afirmação, identificar as hipóteses nula e alternativa, e expressá-las em forma simbólica. Dada uma afirmação e uma amostra, calcular o valor da estatística do teste. Dado um nível de significância. Identificar o(s) valor(es) crítico(s). Dado o valor da estatística do teste, identificar o P-valor. Formar uma conclusão a respeito do teste de hipótese em uma linguagem simples e não técnica. Slide 11 Exemplo: Vamos usar novamente o exemplo do Gender Choice que foi distribuido pelaws Indústrias ProCare. As Indústrias ProCare afirmaram que os casais que usarem a caixa rosa do Gender Choice terão as chances de terem meninas maiores que 50%, ou 0,5. Vamos novamente considerar o experimento onde 100 casais usam o Gender Choice com a intenção de terem uma menina. Vamos assumir que nos 100 nascimentos temos exatamente 52 meninas, e vamos formalizar algumas análises: Sob circunstâncias normais a proporção de meninas é de 0,5, então a afirmação de que o Gender Choice é funcional pode ser expressa como p > 0,5. Usando a distribuição normal como uma aproximação à binomial nós achamos que P(52 ou mais meninas em 100 nascimentos) = 0,3821. A Figura 8-1 a seguir mostra que com uma probabilidade de 0,5, a ocorrência de 52 meninas em 100 nascimentos não é incomum. Slide 12 4 Figura 8-1 Nós não podemos excluir o efeito aleatório como uma possível explicação. Concluímos, então, que a proporção de meninas que nasceram de casais que usaram o Gender Choice não é significantemente maior do que o número esperado devido a fatores aleatórios. Slide 13
5 Observações Afirmação: Para casais que usam Gender Choice, a proporção de meninas é p > 0.5. Suposição de trabalho: A proporção de meninas é p = 0.5 (com o Gender Choice sem surtir efeito). A amostra apresenta 52 meninas em 100 nascimentos, então a proporção amostral é p = 52/100 = ˆ Assumindo que p = 0.5, nós usamos a distribuição normal como uma aproximação à distribuição binomial para achar que P (Pelo menos 52 meninas em 100 nascimentos) = Há duas possíveis explicações para o resultado de 52 meninas em 100 nascimentos: Ou uma variação aleatória ocorreu (com probabilidade igual a ), ou a proporção de meninas nascidas de casais que usaram Gender Choice é maior que 0.5. Não há evidência suficiente para basear afirmação do Gender Choice. Slide 14 Componentes de um Teste de Hipótese Formal 5 Slide 15 Hipótese Nula: H 0 A hipótese nula (denotada por H 0 ) é uma suposição de que o valor de um parâmetro populacional (tal como a proporção, média ou desvio padrão) é igual a algum valor pré-fixado. Nós testamos a hipótese nula diretamente. Podemos rejeitar H 0 ou não rejeitar H 0. Slide 16
6 Hipótese Alternativa: H 1 A hipótese alternativa (denotada por H 1 ou H a ou H A ) é a suposição de que o parâmetro populacional tem um valor que difere do apresentado na hipótese nula. A forma simbólica para a hipótese alternativa deve usar um destes sinais:, <, >. Slide 17 Notas sobre Como Formar suas Próprias Afirmações (Hipóteses) Se você está executando um estudo e quer usar um teste de hipótese para basear a sua afirmação, esta afirmação dever ser escrita de tal forma que se torne a hipótese alternativa. 6 Slide 18 Notas sobre Como Identificar H 0 e H 1 Figura 8-2 Slide 19
7 Exemplo: Identifique as hipóteses nulas e alternativas. Use a Figura 8-2 e com base nas afirmações dadas expresse as hipóteses nula e alternativa correspondentes em forma simbólica. a) A proporção de motoristas que admitem passar em sinal vermelho é maior que 0,5. b) A altura média dos jogadores de basquetes da liga profissional é de no máximo 2,14m. c) O desvio padrão do escore de QI dos atores é igual a 15. Slide 20 Exemplo: Identifique as hipóteses nulas e alternativas. Use a Figura 8-2 e com base nas afirmações dadas expresse as hipóteses nula e alternativa correspondentes em forma simbólica. a) A proporção de motoristas que admitem ultrapassar o sinal vermelho é maior que 0,5. No passo 1 da Figura 8-2, nós expressamos a afirmação dada como p > 0.5. No passo 2I, nós vemos que se p > 0.5 é falso, então p 0.5 deve ser verdadeiro. No passo 3, observamos que a expressão p > 0.5 não contém a igualdade, então nós determinamos a hipótese alternativa H 1 como p > 0.5, e a hipótese nula H 0 como p = Slide 21 Exemplo: Identifique as hipóteses nulas e alternativas. Use a Figura 8-2 e com base nas afirmações dadas expresse as hipóteses nula e alternativa correspondentes em forma simbólica. b) A altura média dos jogadores de basquetes da liga profissional é de no máximo 2,14m. No passo 1 da Figura 8-2 nós expressamos a média é de no máximo 2,14m simbolicamente como µ 2,14. No passo 2, nós vemos que se µ 2,14 é falsam então µ > 2,14 deve ser verdadeiro. No passo 3, nós vemos que se a expressão µ > 2,14 não contém a igualdade, então a hipótese alternativa H 1 será µ > 2,14, e H 0 será µ = 2,14. Slide 22
8 Exemplo: Identifique as hipóteses nulas e alternativas. Use a Figura 8-2 e com base nas afirmações dadas expresse as hipóteses nula e alternativa correspondentes em forma simbólica. c) O desvio padrão do escore de QI dos atores é igual a 15. No passo 1 da Figura 8-2 nós representamos esta afirmação como σ = 15. No passo 2, vemos que se σ = 15 é falso, então σ 15 deve ser verdadeiro. No passo 3, temos que a hipótese alternativa H 1 será σ 15, e que H 0 será σ = 15. Slide 23 Estatística de Teste A estatística do teste é um valor usado para tomar a decisão sobre a hipótese nula, e é calculada convertendo a estatística amostral em um escore com a suposição de que a hipótese nula é verdadeira. 8 Slide 24 Estatística do Teste - Fórmulas /\ z = p - p pq n z = x - µ x σ n χ 2 = (n 1)s2 σ 2 Estatística do teste para proporções Estatística do teste para média Estatística do teste para desvio padrão Slide 25
9 Exemplo: Uma pesquisa com uma amostra aleatória de 880 motoristas adultos mostrou que 56% (ou p = 0.56) destes respondentes admitiram que ultrapassavam o sinal fechado. Encontre o valor da estatística do teste para a afirmação de que a maioria dos adultos admitem ultrapassar o sinal fechado. (Na Seção 8-3 nós veremos que há algumas suposições a serem observadas. Para este exemplo, admitamos que estas suposições são obedecidas e vamos nos focar em encontrar a estatística do teste adequada.) Slide 26 Solução: O exemplo anterior mostrou que a afirmação dada resulta nas seguintes hipóteses nula e alternativa: H 0 : p=0.5 e H 1 : p>0.5. Devido a trabalharmos sob a suposição de que a hipótese nula é verdadeira, ou seja, p=0.5, nós temos a seguinte estatística do teste: /\ z = p p = pq n (0.5)(0.5) 880 = Slide 27 Interpretação: Nós sabemos dos capítulos anteriores que o valor de z=3,56 é excepcionalmente alto. Isto indica que mais que ser maior que 50%, o resultado amostral de 56% é significativamente maior que 50%. Veja figura abaixo: Slide 28
10 Região Crítica, Valor Crítico, Estatística do Teste Slide 29 Região Crítica A região crítica (ou região de rejeição) é o conjunto de valores para a estatística do teste que nos faz rejeitar a hipótese nula. Por exemplo, veja a região sombreada em vermelho na figura anterior. 10 Slide 30 Nível de Significância O nível de significância (denotado por α) é a probabilidade de que a estatística do teste irá pertencer à região crítica quando a hipótese nula for verdadeira. Este é o mesmo α que introduzimos na Seção 7-2. Valores comuns para α são 0.05, 0.01, e Slide 31
11 Valor Crítico Um valor crítico é qualquer valor que separa a região crítica (onde rejeitamos a hipótese nula) dos valores da estatística do teste que não nos faz rejeitar a H 0. O valor crítico depende da natureza da hipótese nula, da distribuição amostral que é utilizada, e do nível de significância α. Veja na figura anterior que o valor crítico de z=1.645 corresponde ao nível de significância de α=0.05. Slide 32 Testes Bilateral, Unilateral à Esquerda e Unilateral à Direita As caudas em uma distribuição são regiões nos extremos das mesmas limitados por valores críticos. 11 Slide 33 H 0 : = H 1 : Teste Bilateral Significa menor ou maior que α é dividido igualmente entre as duas caudas da região crítica Slide 34
12 Teste Unilateral à Direita H 0 : = H 1 : > Pontos à Direita Slide 35 Teste Unilateral à Esquerda H 0 : = Pontos à Esquerda H 1 : < 12 Slide 36 P-Valor O P-valor (ou p-valor ou valor de probabilidade) é a probabilidade de ter um valor da estatística de teste que está pelo menos tão extremo como a estatística calculada para a amostra em questão, assumindo que a hipótese nula é verdadeira. A hipótese nula é rejeitado se o P-valor é muito pequeno, tal como 0,05 ou menos. Slide 37
13 Conclusões em Testes de Hipótese Nós sempre testamos a hipótese nula; A conclusão inicial será sempre uma das abaixo: 1. Rejeitar a hipótese nula. 2. Falhar em rejeitar a hipótese nula. Slide 38 Regra de Decisão Método Tradicional: Rejeitamos H 0 se a estatística de teste pertence à região crítica. Falhamos em rejeitar H 0 se a estatística de teste não pertence à região crítica. 13 Slide 39 Regra de Decisão - cont Método do P-valor: Rejeitamos H 0 se o P-valor α (onde α é o nível de significância, como 0,05, por exemplo.). Falhamos em rejeitar H 0 se o P- valor>α. Slide 40
14 Regra de Decisão - cont Uma outra opção: Ao invés de usar um nível de significância (feito 0,05, por exemplo), simplesmente identifique o P-valor e deixe a decisão para o leitor. Slide 41 Regra de Decisão - cont Intervalos de Confiança: Devido ao IC para um parâmetro populacional conter os valores mais prováveis para este parâmetro, rejeitamos a afirmação de que o parâmetro não é igual a um determinado valor se ele não estiver contido no IC. 14 Slide 42 Procedimento para Encontrar o P-Valor Figura 8-6 Slide 43
15 Exemplo: Como calcular o P-valor: Primeiro, verifique se as condições dadas resultam em um teste bilateral ou unilateral à esquerda ou à direita. Em seguida, calcule o P-valor e formule sua conclusão a respeito da hipótese nula. a) Um nível de significância α=0.05 é usado para testar a afirmação de que p>0.25, e os dados amostrais resultaram em uma estatística de teste z=1.18. b) Um nível de significância α=0.05 é usado para testar a afirmação de que p 0.25, e os dados amostrais resultaram em uma estatística de teste z = Slide 44 Exemplo: Como calcular o P-valor: Primeiro, verifique se as condições dadas resultam em um teste bilateral ou unilateral à esquerda ou à direita. Em seguida, calcule o P-valor e formule sua conclusão a respeito da hipótese nula. a) Com a afirmação de que p>0.25, temos que o teste é unilateral à direita. Assim, de acordo com a Figura 8-6, temos que o P-valor é a área à direita da estatística do teste z=1.18. Usando a Tabela A-2 encontramos que a área à direita é Assim, temos que o P-valor=0.1190, sendo maior que o nível de significância, e não podemos rejeitar a hipótese nula. O P-valor é relativamente alto, o que indica que este resultado amostral pode ocorrer facilmente devido à aleatoriedade do processo. Slide Exemplo: Como calcular o P-valor: Primeiro, verifique se as condições dadas resultam em um teste bilateral ou unilateral à esquerda ou à direita. Em seguida, calcule o P-valor e formule sua conclusão a respeito da hipótese nula. b) Com a afirmação de que p 0.25, o teste é bilateral, e como a estatística do teste z=2.34 está à direita do centro da distribuição, de acordo com a Figura 8-6 temos que o P-valor é igual ao dobro da área à direita de z=2.34. Utilizando a Tabela A-2 nós vemos que a área à direita de z=2.34 é , assim, temos que P- valor=2x0.0096= O P-valor é menor que o nível de significância, assim rejeitamos a hipótese nula. O valor pequeno do P-valor indica que este resultado amostral é bastante raro, considerando H 0 válida. Slide 46
16 Escrevendo as Conclusões Finais Figura 8-7 Slide 47 Aceitar Versus Não Rejeitar Alguns autores usam aceitar a hipótese nula. Nós não estamos provando a hipótese nula. 16 A amostra evidencia que não temos força para rejeitar a hipótese nula (Assim como não temos evidência de que a hipótese é verdadeira). Slide 48 Erro Tipo I Um Erro Tipo I é o erro cometido ao rejeitarmos H 0 quando ela é verdadeira. A letra grega α é usada para representar a probabilidade de se cometer o Erro Tipo I. Slide 49
17 Erro Tipo II Um Erro Tipo II é o erro cometido quando não rejeitamos H 0 e ela é falsa. A letra grega β é usada para representar a probabilidade de se cometer o Erro Tipo II. Slide 50 Exemplo: Assuma que estamos realizando um teste de hipótese para p>0.5. Aqui, temos que as hipóteses nula e alternativa são: H 0 :p=0.5, e H 1 :p>0.5 a) Identifique um erro tipo I. b) Identifique um erro tipo II. 17 Slide 51 Exemplo: Assuma que estamos realizando um teste de hipótese para p>0.5. Aqui, temos que as hipóteses nula e alternativa são: H 0 :p=0.5, e H 1 :p>0.5. a) Um erro tipo I é o erro de se rejeitar uma hipótese nula verdadeira, então neste caso, o erro tipo I ocorrerá quando tivermos evidências de que p>0.5, quando na verdade temos p=0.5. Slide 52
18 Exemplo: Assuma que estamos realizando um teste de hipótese para p>0.5. Aqui, temos que as hipóteses nula e alternativa são: H 0 :p=0.5, e H 1 :p>0.5 b) Um erro tipo II é o erro de não rejeitarmos uma hipótese nula falsa, ou seja, para este exemplo seria não rejeitar p=0.5 (e por conseqüência não aceitar que p>0.5) quando na verdade temos p>0.5. Slide 53 Erro Tipo I e Erro Tipo II 18 Slide 54 Controlando os Erros Tipo I e Tipo II Para qualquer α fixado, um aumento no tamanho da amostra n causa uma diminuição em β. Para qualquer tamanho de amostra n fixo, uma diminuição de α causará em aumento de β. Inversamente, um acréscimo em α causará uma dimnuição em β. Para diminuir tanto α quanto β, temos que aumentar o tamanho da amostra. Slide 55
19 Definição O poder do teste de hipótese é a probabilidade (1 - β ) de rejeitar uma hipótese nula falsa, que é calculada usando um valor fixo para o nível de significância α e um valor fixo para o parâmetro populacional que é uma alternativa ao valor assumido como verdadeiro na hipótese nula. Em outras palavras, o poder do teste de hipótese é a probabilidade de aceitar uma hipótese alternativa verdadeira. Slide 56 Metodologia Detalhada do Teste de Hipótese Método do P- valor 19 Slide 57 Metodologia Detalhada do Teste de Hipótese Método Tradicional Slide 58
20 Metodologia Detalhada do Teste de Hipótese - cont Um IC para um parâmetro populacional contém os valores mais verossímeis para este parâmetro. Nós podemos então rejeitar uma afirmação de que o parâmetro populacional não está incluído bo IC. Veja na Tabela 8-2 abaixo os níveis de confiança do IC para os níveis de significância de acordo com o tipo do teste (bilateral ou unilateral): Slide 59 Metodologia Detalhada do Teste de Hipótese - cont Cuidado: Em alguns casos, a conclusão baseada no IC pode diferir da conclusão do teste de hipótese. Veja os comentários presentes em cada uma das seções seguinte. 20 Slide 60 Recapitulando In this section we have discussed: Hipótese Nula Hipótese Alternativa Estatística do Teste Região Crítica Nível de Significância e P-valor Valor Crítico Erro Tipo I e II Poder de um Teste de Hipótese Slide 61
21 Seção 8-3 Testando uma Afirmação sobre uma Proporção Created by Erin Hodgess, Houston, Texas Revised to accompany 10 th Edition, Tom Wegleitner, Centreville, VA Slide 62 Pontos Chave Esta seção apresenta o procedimento completo para testar a hipótese feita sobre uma proporção populacional. Esta seção utiliza os componentes apresentados na seção anterior para os métodos do P-valor, tradicional ou uso do I.C. 21 Slide 63 Requisitos para Testar Afirmações sobre uma Proporção Populacional p 1) As observações devem vir de um plano de amostra aleatória simples. 2) As condições para a distribuição binomial são satisfeitas (Seção 5-3). 3) As condições np 5 e nq 5 são satisfeitas, então a distribuição binomial pode ser aproximada pela distribuição normal com µ = np and σ = npq. Slide 64
22 Notação n = número de tentativas p = x (proporção amostral) n p = proporção populacional (usada na hipótese nula) q = 1 p Slide 65 Estatística de Teste para Testar uma Afirmação sobre uma Proporção z = p p pq n 22 Slide 66 Método do P-Valor Use a mesma metodologia descrita na Seção 8-2 e na Figura 8-8. Use a distribuição normal padronizada (Tabela A-2). Slide 67
23 Método Tradicional Use a mesma metodologia descrita na Seção 8-2 e na Figura 8-9. Slide 68 Método do Intervalo de Confiança Use a mesma metodologia descrita na Seção 8-2 e na Tabela Slide 69 Exemplo: Um artigo distribuído pela Associated Press incluía estes resultados de relativos a uma pesquisa nacional: De 880 motoristas selecionados aleatoriamente, 56% deles admitiam que ultrapassavam o sinal vermelho. A afirmação é que a maioria dos americanos avançam no sinal fechado, ou seja, p>0.5. Os dados amostrais são n=880, e p=0,56. np = (880)(0,5) = nq = (880)(0,5) = Slide 70
24 Exemplo: Um artigo distribuído pela Associated Press incluía estes resultados de relativos a uma pesquisa nacional: De 880 motoristas selecionados aleatoriamente, 56% deles admitiam que ultrapassavam o sinal vermelho. A afirmação é que a maioria dos americanos avançam no sinal fechado, ou seja, p>0.5. Os dados amostrais são n=880, e p=0,56. Nós usaremos o Método do P-valor. z = p p = = 3.56 H 0 : p = 0.5 H 1 : p > 0.5 pq (0.5)(0.5) α = 0.05 n 880 De acordo com a Tabela A-2, observamos que para valores de z = 3.50 ou maiores, nós usamos para a área acumulada à esquerda da estatística do teste. O P-valor é = Como o P-valor é menor que α = 0.05, rejeitamos a hipótese nula. Não temos evidências suficientes para admitirmos a hipótese nula como válida. Slide 71 Exemplo: Um artigo distribuído pela Associated Press incluía estes resultados de relativos a uma pesquisa nacional: De 880 motoristas selecionados aleatoriamente, 56% deles admitiam que ultrapassavam o sinal vermelho. A afirmação é que a maioria dos americanos avançam no sinal fechado, ou seja, p>0.5. Os dados amostrais são n=880, e p=0,56. Nós usaremos o Método do P-valor. H 0 : p = 0.5 H 1 : p > 0.5 α = 0.05 z = Slide 72 Exemplo: Um artigo distribuído pela Associated Press incluía estes resultados de relativos a uma pesquisa nacional: De 880 motoristas selecionados aleatoriamente, 56% deles admitiam que ultrapassavam o sinal vermelho. A afirmação é que a maioria dos americanos avançam no sinal fechado, ou seja, p>0.5. Os dados amostrais são n=880, e p=0,56. Nós usaremos o Método Tradicional. z = p p = = 3.56 H 0 : p = 0.5 H 1 : p > 0.5 pq (0.5)(0.5) α = 0.05 n 880 Este é um teste bilateral à direita, então a região crítica é uma área de 0,05. Assim, temos que z=1,645 é o valor crítico da região crítica. Portanto, rejeitamos a hipótese nula. Não temos evidências suficientes para admitirmos a afirmação como válida. Slide 73
25 Exemplo: Um artigo distribuído pela Associated Press incluía estes resultados de relativos a uma pesquisa nacional: De 880 motoristas selecionados aleatoriamente, 56% deles admitiam que ultrapassavam o sinal vermelho. A afirmação é que a maioria dos americanos avançam no sinal fechado, ou seja, p>0.5. Os dados amostrais são n=880, e p=0,56. Nós usaremos o Método do IC. Para testar uma hipótese unilateral com nível de significância α, nós iremos construir um intervalo de confiança com 1 2α de nível de confiança. Nós contruimos um IC com 90% de confiança. Nós obtemos < p < Estamos 90% confiantes que o valor verdadeiro de p está contido no intervalo de limites e Assim, não podemos afirmar que p>0.5, já que esse valor não pertence ao IC. Slide 74 CUIDADO Quando testamos afirmações sobre proporção populacional, o método tradicional e o método do P- valor são equivalentes e terão os mesmos resultados desde que usem o mesmo desvio padrão baseado na proporção suposta p. Por outro lado, o IC usa um desvio padrão estimado baseado na proporção amostral p. Consequentimente, é possível que os métodos tradicional e P-valor tenham uma conclusão diferente do que o método do IC. 25 Uma boa tática é utilizar o IC para estimar a proporção populacional, mas utilizar os métodos tradicional ou P- valor para teste de hipótese. Slide 75 Obtendo P p algumas vezes é informado diretamente: 10% dos carros esportivos observados são vermelho é expresso como p = 0.10 p algumas vezes é calculado: 96 residências pesquisadas têm TV a cabo e 54 não é calculado usando x 96 p = n = = 0.64 (96+54) (determinando a proporção amostral de residências com TV a cabo) Slide 76
26 Exemplo: Quando Gregory Mendel realizou seu famoso experimento de hibridação com ervilhas, um dos experimentos resultou em uma geração constituída de 428 ervilhas com vagens verdes e 152 com vagens amarelos. Segundo a teoria de Mendel, 1/4 das ervilhas desta geração teria bagos amarelos. Use 5% de significância com o método do P-valor para testar a afirmação de Mendel. Nós notamos que n= =580, então p = 0.262, e p = Slide 77 Exemplo: Quando Gregory Mendel realizou seu famoso experimento de hibridação com ervilhas, um dos experimentos resultou em uma geração constituída de 428 ervilhas com vagens verdes e 152 com vagens amarelos. Segundo a teoria de Mendel, 1/4 das ervilhas desta geração teria bagos amarelos. Use 5% de significância com o método do P-valor para testar a afirmação de Mendel. H 0 : p = 0.25 H 1 : p 0.25 n = 580 α = 0.05 p = z = p p pq n = = 0.67 (0.25)(0.75) 580 Já que este é um teste bilateral, o P-valor será o dobro da área à direita da estatística do teste. Usando a Tabela A-2, o P-valor para z = 0.67 é = Slide Exemplo: Quando Gregory Mendel realizou seu famoso experimento de hibridação com ervilhas, um dos experimentos resultou em uma geração constituída de 428 ervilhas com vagens verdes e 152 com vagens amarelos. Segundo a teoria de Mendel, 1/4 das ervilhas desta geração teria bagos amarelos. Use 5% de significância com o método do P-valor para testar a afirmação de Mendel. H 0 : p = 0.25 H 1 : p 0.25 n = 580 α = 0.05 p = z = p p pq O P-valor é 2x0.2514= Assim, não podemos rejeitar a hipótese nula, ou seja, não há evidência suficiente para refutar a afirmação de que ¼ das ervilhas desta geração tenham vagens amarelos. Slide 79 n = = 0.67 (0.25)(0.75) 580
27 Recapitulando Nesta seção nós vimos: Teste estatístico para afirmações sobre uma proporção. Método do P-valor. Método do IC. Obtendo p. Slide 80 Seção 8-4 Testando Afirmações sobre uma Média: σ Conhecido 27 Created by Erin Hodgess, Houston, Texas Revised to accompany 10 th Edition, Tom Wegleitner, Centreville, VA Slide 81 Pontos Chave Esta seção apresenta os métodos para se testar afirmações sobre a média de uma população, dado que o desvio padrão desta população é conhecido. Esta seção utiliza a distribuição normal com os mesmos componentes introduzidos na Seção 8-2. Slide 82
28 Requisitos para Testar Afirmações sobre uma Média Populacional (com σ Conhecido) 1) A amostra foi extraída segundo um plano de amostra aleatória simples. 2) O valor do desvio padrão populacional σ é conhecido. 3) Pelo menos uma destas condições deve ser satisfeita: a população é normalmente distribuída ou n>30. Slide 83 Estatística do Teste para Testar Afirmações sobre uma Média (com σ Conhecido) z = x µ x σ n 28 Slide 84 Exemplo: Temos uma amostra da temperatura corporal de 106 pessoas, tendo média F. Assuma que esta amostra veio de uma amostra aleatória simples e que o desvio padrão populacional σ é conhecido e igual a 0.62 F. Teste com 5% de significância a idéia popular de que a temperatura corporal média de adultos sadios é igual a 98.6 F. Use o método do P-valor. H 0 : µ = 98.6 H 1 : µ 98.6 α = 0.05 x = 98.2 σ = 0.62 z = x µ x Este é um teste bilateral e a estatística do teste está à esquerda do centro da distribuição, logo o P-valor é igual ao dobro da área à esquerda de z= Utilizando a Tabela A-2 calculamos que a área à esquerda de z= 6.64 é , assim o P-valor é igual a 2x(0.0001) = Slide 85 σ n = =
29 Exemplo: Temos uma amostra da temperatura corporal de 106 pessoas, tendo média F. Assuma que esta amostra veio de uma amostra aleatória simples e que o desvio padrão populacional σ é conhecido e igual a 0.62 F. Teste com 5% de significância a idéia popular de que a temperatura corporal média de adultos sadios é igual a 98.6 F. Use o método do P-valor. H 0 : µ = 98.6 H 1 : µ 98.6 α = 0.05 x = 98.2 σ = 0.62 z = 6.64 Slide 86 Exemplo: Temos uma amostra da temperatura corporal de 106 pessoas, tendo média F. Assuma que esta amostra veio de uma amostra aleatória simples e que o desvio padrão populacional σ é conhecido e igual a 0.62 F. Teste com 5% de significância a idéia popular de que a temperatura corporal média de adultos sadios é igual a 98.6 F. Use o método do P-valor. H 0 : µ = 98.6 H 1 : µ 98.6 z = 6.64 α = 0.05 x = 98.2 σ = Como o P-valor é igual a , e como este valor é menor que o nível de significância α=0.05, nós rejeitamos a hipótese nula. Assim, temos evidência suficiente para concluir que a temperatura corporal média de adultos saudáveis é diferente de 98.6 F. Slide 87 Exemplo: Temos uma amostra da temperatura corporal de 106 pessoas, tendo média F. Assuma que esta amostra veio de uma amostra aleatória simples e que o desvio padrão populacional σ é conhecido e igual a 0.62 F. Teste com 5% de significância a idéia popular de que a temperatura corporal média de adultos sadios é igual a 98.6 F. Use o método tradicional. H 0 : µ = 98.6 H 1 : µ 98.6 α = 0.05 x = 98.2 σ = 0.62 z = 6.64 Nós encontramos como valores críticos z= 1.96 e z=1.96. Nós rejeitamos a hipótese nula, pois a estatística do teste z= 6.64 pertence à região crítica. Temos evidência suficiente para concluir que a temperatura corporalmédia de adultos saudáveis é diferente de 98.6 F. Slide 88
30 Exemplo: Temos uma amostra da temperatura corporal de 106 pessoas, tendo média F. Assuma que esta amostra veio de uma amostra aleatória simples e que o desvio padrão populacional σ é conhecido e igual a 0.62 F. Teste com 5% de significância a idéia popular de que a temperatura corporal média de adultos sadios é igual a 98.6 F. Use o método do intervalo de confiança. H 0 : µ = 98.6 H 1 : µ 98.6 α = 0.05 x = 98.2 σ = 0.62 Para um teste de hipótese bilateral com 5% de significância, construímos um IC com 95% de confiabilidade. Assim, temos: < µ < Nós estamos 95% confiantes de que o intervalo de a contém o valor verdadeiro de µ, assim, aparentemente 98.6 nãopode ser o valor verdadeiro de µ. Slide 89 Relações Subjacentes ao Teste de Hipótese Se, sob uma dada suposição, temos uma probabilidade extremamente pequena de obtermos um resultado amostral tão extremo como o que observamos, podemos concluir que a suposição inicial provavelmente não é correta. 30 Quando testamos uma afirmação, fazemos uma suposição de igualdade (com a hipótese nula). A seguir, comparamos esta suposição com o resultado obtido com a amostra e tomamos uma destas conclusões: Slide 90 Relações Subjacentes ao Teste de Hipótese - cont Se o resultado amostral (ou resultado mais extremo) pode ocorrer facilmente quando a suposição (hipótese nula) é verdadeira, podemos atribuir a relativamente curta discrepância entre a suposição e o resultado amostral ter ocorrido devido a fatores aleatórios. Se o resultado amostral não pode ocorrer facilmente quando a suposição (hipótese nula) é verdadeira, nós explicamos a relativamente grande discrepância entre a suposição e o resultado amostral concluindo que a suposição inicial não é verdadeira, rejeitando, assim, esta suposição. Slide 91
31 Recapitulando Nesta seção nós apresentamos: Requisitos para testar afirmações sobre médias populacionais, com σ conhecido. Método do P-valor. Método Tradicional. Método do Intervalo de Confiança. Relações para os testes de hipótese. Slide 92 Seção 8-5 Testando Afirmações sobre uma Média : σ Desconhecido 31 Created by Erin Hodgess, Houston, Texas Revised to accompany 10 th Edition, Tom Wegleitner, Centreville, VA Slide 93 Pontos Chave Esta seção apresenta a metodologia para testar afirmações sobre a média populacional quando não temos o valor de σ. Os métodos desta seção utilizam a distribuição t de Student vista anteriormente. Slide 94
32 Requisitos para Testar Afirmações sobre a Média com σ Desconhecido 1) A amostra foi extraída segundo um plano de amostra aleatória simples. 2) O valor do desvio padrão populacional σ não é conhecido. 3) Pelo menos uma destas condições deve ser satisfeita: a população é normalmente distribuída ou n>30. Slide 95 Estatística do Teste para Testar Afirmações sobre uma Média (com σ Desconhecido) x µ t = x sn 32 P-valor e Valores Críticos Usar a Tabela A-3 Graus de Liberdade (GL) = n 1 Slide 96 Propriedades Importantes da Distribuição t de Student 1. A distribuição t de Student t é diferente para cada tamanho de amostra (veja Figura 7-5 na Seção 7-4). 2. A distribuição t de Student t tem a mesma forma que a distribuição normal (forma de sino); Sua forma mais alongada reflete uma maior variabilidade que é esperada quando usamos s para estimar σ. 3. A distribuição t de Student tem média t=0 (identicamente à distribuição normal padronizada que tem média z=0). 4. TO desvio padrão da distribuição t de Student varia de acordo com o tamanho da amostra e é maior que 1 (ao contrário da distribuição normal padronizada onde temos σ=1). 5. Para tamanhos de amostra suficientemente grande, temos que a distribuição t de Student se aproxima da distribuição normal padronizada. Slide 97
33 Escolhendo entre as Distribuições Normal e t de Student t ao testar afirmações sobre uma média populacional µ Use a distribuição t de Student quando σ é desconhecido e ao menos uma destas condições são satisfeitas: A população é normalmente distribuída ou n>30. Slide 98 Exemplo: O conjunto de dados 13 no Apêndice B do texto inclui os pesos de 13 confeitos M&M vermelhos aleatoriamente selecionado de um pacote com 465 M&M s. O peso (em gramas) tem média x=0.8635g e desvio padrão s=0.0576g. O pacote afirma que o peso líquido total é de 396.9g. Assim, de acordo com o afirmado no pacote, um confeito M&M deve ter peso médio 396.9/465=0.8535g. Use os dados amostrais para ao nível de 5% testar a afirmação de um gerente de produção que está suspeitando falha no processo, fazendo com que os confeitos saiam com peso médio maior que g. Use o método tradicional. Temos que a amostragem utilizada é a aleatória simples, e não temos um valor conhecido de σ. O tamanho da amostra é n=13 e um gráfico quartilquartil sugere normalidade na distribuição dos dados. 33 Slide 99 Exemplo: O conjunto de dados 13 no Apêndice B do texto inclui os pesos de 13 confeitos M&M vermelhos aleatoriamente selecionado de um pacote com 465 M&M s. O peso (em gramas) tem média x=0.8635g e desvio padrão s=0.0576g. O pacote afirma que o peso líquido total é de 396.9g. Assim, de acordo com o afirmado no pacote, um confeito M&M deve ter peso médio 396.9/465=0.8535g. Use os dados amostrais para ao nível de 5% testar a afirmação de um gerente de produção que está suspeitando falha no processo, fazendo com que os confeitos saiam com peso médio maior que g. Use o método tradicional. H 0 : µ = H 1 : µ > α = 0.05 x = s = n = 13 t = x µ x s n = = O valor crítico, de acordo com a Tabela A-3, é t=1.782 Slide 100
34 Exemplo: O conjunto de dados 13 no Apêndice B do texto inclui os pesos de 13 confeitos M&M vermelhos aleatoriamente selecionado de um pacote com 465 M&M s. O peso (em gramas) tem média x=0.8635g e desvio padrão s=0.0576g. O pacote afirma que o peso líquido total é de 396.9g. Assim, de acordo com o afirmado no pacote, um confeito M&M deve ter peso médio 396.9/465=0.8535g. Use os dados amostrais para ao nível de 5% testar a afirmação de um gerente de produção que está suspeitando falha no processo, fazendo com que os confeitos saiam com peso médio maior que g. Use o método tradicional. H 0 : µ = H 1 : µ > α = 0.05 x = s = n = 13 t = Como a estatística do teste t=0.626 não pertence à região crítica, não podemos rejeitar H 0. Não temos evidência suficiente para afirmar que o peso médio dos confeitos M&M é maior que g. Valor Crítico t=1.782 Slide 101 Distribução Normal Versus t de Student O valor crítico usado no exemplo anterior foi t=1.782, porém, se a distribuição normal fosse utilizada, teríamos o valor crítico z= O valor crítico da distribuição t de Student é maior (ou mais à direita), demonstrando que com a distribuição t, a evidência amostral deve ser mais extrema antes de considerá-la significante. 34 Slide 102 Método do P-Value Neste caso, temos que usar um software estatístico ou uma calculadora TI-83/84 Plus. Alternativamente, podemos usar a Tabela A-3 para identificar a variação do P-valor. Slide 103
35 Exemplo: Assumindo que não temos acesso nem a um pacote estatístico ou a uma calculadora TI-83 Plus, use a Tabela A-3 para encontrar o range de variação do P-valor para cada um dos exemplos abaixo: a) Se temos uma hipótese unilateral à esquerda, o tamanho amostral é n=12, e a estatística de teste é t= b) Se temos uma hipótese unilateral à direita, o tamanho amostral é n=12, e a estatística de teste é t=1.222 c) Se temos uma hipótese bilateral, o tamanho amostral é n=12, e a estatística de teste é t= Slide 104 Exemplo: Assumindo que não temos acesso nem a um pacote estatístico ou a uma calculadora TI-83 Plus, use a Tabela A-3 para encontrar o range de variação do P-valor para cada um dos exemplos abaixo: 35 Slide 105 Exemplo: Assumindo que não temos acesso nem a um pacote estatístico ou a uma calculadora TI-83 Plus, use a Tabela A-3 para encontrar o range de variação do P-valor para cada um dos exemplos abaixo: a) O teste é unilateral à esquerda com estatística de teste t= 2.007, assim o P-valor é a área à esquerda de Devido à simetria da distribuição t, esta é a mesma área à direita de Qualquer estatística de teste entre e tem um P-valor entre e Podemos concluir que < P-valor < Slide 106
36 Exemplo: Assumindo que não temos acesso nem a um pacote estatístico ou a uma calculadora TI-83 Plus, use a Tabela A-3 para encontrar o range de variação do P-valor para cada um dos exemplos abaixo: b) O teste é unilateral à esquerda com estatística de teste t=1.222, assim o P-valor é a área à direita de Qualquer estatística de teste menor que terá um P-valor que será maior que Podemos concluir que P-valor > Slide 107 Exemplo: Assumindo que não temos acesso nem a um pacote estatístico ou a uma calculadora TI-83 Plus, use a Tabela A-3 para encontrar o range de variação do P-valor para cada um dos exemplos abaixo: c) O teste é bilateral com estatística de teste t= O P-valor é igual ao dobro da área à esquerda de 3.456, ou à direita de Qualquer estatística de teste maior que tem um P- valor menor que 0.01 para testes bilaterais. Podemos concluir que P-valor < Slide 108 Recapitulando Nesta seção nós discutimos: Requisitos para testar afirmações sobre a média populacional com σ desconhecido. A distribuição t de Student. O Método do P-valor. Slide 109
37 Seção 8-6 Testando Afirmações sobre o Desvio Padrão ou Variância Created by Erin Hodgess, Houston, Texas Revised to accompany 10 th Edition, Tom Wegleitner, Centreville, VA Slide 110 Pontos Chave Esta seção introduz a metodologia para testar uma afirmação sobre o desvio padrão σ ou variância de uma população σ 2. Estes métodos usam a distribuição qui-quadrado como referência. Esta distribuição foi utilizada anteriormente na Seção Slide 111 Requisitos para Testar Afirmações sobre σ ou σ 2 1. O plano amostral utilizado é amostra aleatória simples. 2. A população tem distribuição normal. Esta suposição é mais restritiva neste teste do que nos testes para médias. Slide 112
38 Distribuição Qui-quadrado Estatística do Teste χ 2 = (n 1) s 2 σ 2 n s 2 σ 2 = tamanho da amostra = variância amostral = variância populacional (dada na hipótese nula) Slide 113 P-Valor e Valores Críticos para Distribuição Qui-quadrado Use a Tabela A-4. Graus de Liberdade: G.L.=n Slide 114 Propriedades da Distribuição Qui-quadrado Todos os valores de χ 2 são nãonegativos, e a distribuição não é simétrica (veja a Figura 8-13 a seguir). Há uma distribuição para cada número de graus de liberdade (veja a Figura 8-14 a seguir). Os valores críticos são encontrados com base na Tabela A-4 usando n-1 graus de liberdade. Slide 115
39 Propriedades da Distribuição Qui-quadrado - cont Propriedades da Distribuição Qui-quadrado Qui-quadrado com 10 e 20 graus de liberdade. Temos uma distribuição diferente para cada valor de graus de liberdade. Figura 8-13 Figura 8-14 Slide 116 Exemplo: Para uma amostra aleatória simples de adultos o escore QI é normalmente distribuído com média 100 e desvio padrão 15. Uma amostra aleatória de 13 professores de estatística forneceu um desvio padrão s=7.2. Assuma que o escore QI dos professores de estatística é normalmente distribuído e use5% de significância para testar a afirmação de que σ = 15. H 0 : σ = 15 H 1 : σ 15 α = 0.05 n = 13 s = 7.2 χ 2 = (n 1)s 2 = (13 1)(7.2) 2 σ = Slide 117 Exemplo: Para uma amostra aleatória simples de adultos o escore QI é normalmente distribuído com média 100 e desvio padrão 15. Uma amostra aleatória de 13 professores de estatística forneceu um desvio padrão s=7.2. Assuma que o escore QI dos professores de estatística é normalmente distribuído e use5% de significância para testar a afirmação de que σ = 15. H 0 : σ = 15 H 1 : σ 15 α = 0.05 n = 13 s = 7.2 χ 2 = Slide 118
40 Exemplo: Para uma amostra aleatória simples de adultos o escore QI é normalmente distribuído com média 100 e desvio padrão 15. Uma amostra aleatória de 13 professores de estatística forneceu um desvio padrão s=7.2. Assuma que o escore QI dos professores de estatística é normalmente distribuído e use5% de significância para testar a afirmação de que σ = 15. H 0 : σ = 15 H 1 : σ 15 α = 0.05 n = 13 s = 7.2 χ 2 = Os valores críticos e são encontrados na Tabela A-4 na 12ª linha (graus de liberdade= n 1) nas colunas correspondentes à e Slide 119 Exemplo: Para uma amostra aleatória simples de adultos o escore QI é normalmente distribuído com média 100 e desvio padrão 15. Uma amostra aleatória de 13 professores de estatística.forneceu um desvio padrão s=7.2. Assuma que o escore QI dos professores de estatística é normalmente distribuído e use5% de significância para testar a afirmação de que σ = 15. H 0 : σ = 15 χ 2 = H 1 : σ 15 α = 0.05 n = 13 Como a estatística do teste pertence à região s = 7.2 crítica, nós rejeitamos a hipótese nula. Temos evidência suficiente para rejeitar a afirmação de que o desvio padrão é igual à Slide 120 Recapitulando Nesta seção nós discutimos: Testes para afirmações sobre desvio padrão e variância. Estatística de teste. Distribuição qui-quadrado. Valores críticos. Slide 121
Testes de Hipóteses Estatísticas
 Capítulo 5 Slide 1 Testes de Hipóteses Estatísticas Resenha Hipótese nula e hipótese alternativa Erros de 1ª e 2ª espécie; potência do teste Teste a uma proporção; testes ao valor médio de uma v.a.: σ
Capítulo 5 Slide 1 Testes de Hipóteses Estatísticas Resenha Hipótese nula e hipótese alternativa Erros de 1ª e 2ª espécie; potência do teste Teste a uma proporção; testes ao valor médio de uma v.a.: σ
Probabilidade e Estatística
 Probabilidade e Estatística TESTES DE HIPÓTESES (ou Testes de Significância) Estimação e Teste de Hipóteses Estimação e teste de hipóteses (ou significância) são os aspectos principais da Inferência Estatística
Probabilidade e Estatística TESTES DE HIPÓTESES (ou Testes de Significância) Estimação e Teste de Hipóteses Estimação e teste de hipóteses (ou significância) são os aspectos principais da Inferência Estatística
AULA 07 Distribuições Discretas de Probabilidade
 1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
1 AULA 07 Distribuições Discretas de Probabilidade Ernesto F. L. Amaral 31 de agosto de 2010 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro:
Modelos de Regressão Linear Simples - Erro Puro e Falta de Ajuste
 Modelos de Regressão Linear Simples - Erro Puro e Falta de Ajuste Erica Castilho Rodrigues 2 de Setembro de 2014 Erro Puro 3 Existem dois motivos pelos quais os pontos observados podem não cair na reta
Modelos de Regressão Linear Simples - Erro Puro e Falta de Ajuste Erica Castilho Rodrigues 2 de Setembro de 2014 Erro Puro 3 Existem dois motivos pelos quais os pontos observados podem não cair na reta
AULA 19 Análise de Variância
 1 AULA 19 Análise de Variância Ernesto F. L. Amaral 18 de outubro de 2012 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro: LTC. Capítulo
1 AULA 19 Análise de Variância Ernesto F. L. Amaral 18 de outubro de 2012 Metodologia de Pesquisa (DCP 854B) Fonte: Triola, Mario F. 2008. Introdução à estatística. 10 ª ed. Rio de Janeiro: LTC. Capítulo
Métodos Estatísticos Avançados em Epidemiologia
 Métodos Estatísticos Avançados em Epidemiologia Análise de Variância - ANOVA Cap. 12 - Pagano e Gauvreau (2004) - p.254 Enrico A. Colosimo/UFMG Depto. Estatística - ICEx - UFMG 1 / 39 Introdução Existem
Métodos Estatísticos Avançados em Epidemiologia Análise de Variância - ANOVA Cap. 12 - Pagano e Gauvreau (2004) - p.254 Enrico A. Colosimo/UFMG Depto. Estatística - ICEx - UFMG 1 / 39 Introdução Existem
DISTRIBUIÇÕES ESPECIAIS DE PROBABILIDADE DISCRETAS
 VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADES 1 1. VARIÁVEIS ALEATÓRIAS Muitas situações cotidianas podem ser usadas como experimento que dão resultados correspondentes a algum valor, e tais situações
VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES DE PROBABILIDADES 1 1. VARIÁVEIS ALEATÓRIAS Muitas situações cotidianas podem ser usadas como experimento que dão resultados correspondentes a algum valor, e tais situações
Teste de Hipótese e Intervalo de Confiança. Parte 2
 Teste de Hipótese e Intervalo de Confiança Parte 2 Questões para discutirmos em sala: O que é uma hipótese estatística? O que é um teste de hipótese? Quem são as hipóteses nula e alternativa? Quando devemos
Teste de Hipótese e Intervalo de Confiança Parte 2 Questões para discutirmos em sala: O que é uma hipótese estatística? O que é um teste de hipótese? Quem são as hipóteses nula e alternativa? Quando devemos
Distribuição Normal de Probabilidade
 Distribuição Normal de Probabilidade 1 Aspectos Gerais 2 A Distribuição Normal Padronizada 3 Determinação de Probabilidades 4 Cálculo de Valores 5 Teorema Central do Limite 1 1 Aspectos Gerais Variável
Distribuição Normal de Probabilidade 1 Aspectos Gerais 2 A Distribuição Normal Padronizada 3 Determinação de Probabilidades 4 Cálculo de Valores 5 Teorema Central do Limite 1 1 Aspectos Gerais Variável
Estimação. Como definir um estimador. Como obter estimativas pontuais. Como construir intervalos de confiança
 Estimação Como definir um estimador. Como obter estimativas pontuais. Como construir intervalos de confiança Motivação A partir da média de uma a amostra em uma colheita recente, o conselho de qualidade
Estimação Como definir um estimador. Como obter estimativas pontuais. Como construir intervalos de confiança Motivação A partir da média de uma a amostra em uma colheita recente, o conselho de qualidade
Probabilidade. Evento (E) é o acontecimento que deve ser analisado.
 Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
Consideremos os seguintes exemplos de hipóteses cuja veracidade interessa avaliar:
 Consideremos os seguintes exemplos de hipóteses cuja veracidade interessa avaliar: o tempo médio de efeito de dois analgésicos não é o mesmo; a popularidade de determinado partido político aumentou; uma
Consideremos os seguintes exemplos de hipóteses cuja veracidade interessa avaliar: o tempo médio de efeito de dois analgésicos não é o mesmo; a popularidade de determinado partido político aumentou; uma
Capítulo 4 Inferência Estatística
 Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a variância de
Capítulo 4 Inferência Estatística Slide 1 Resenha Intervalo de Confiança para uma proporção Intervalo de Confiança para o valor médio de uma variável aleatória Intervalo de Confiança para a variância de
Pressuposições à ANOVA
 UNIVERSIDADE FEDERAL DE RONDÔNIA CAMPUS DE JI-PARANÁ DEPARTAMENTO DE ENGENHARIA AMBIENTAL Estatística II Aula do dia 09.11.010 A análise de variância de um experimento inteiramente ao acaso exige que sejam
UNIVERSIDADE FEDERAL DE RONDÔNIA CAMPUS DE JI-PARANÁ DEPARTAMENTO DE ENGENHARIA AMBIENTAL Estatística II Aula do dia 09.11.010 A análise de variância de um experimento inteiramente ao acaso exige que sejam
Módulo de Equações do Segundo Grau. Equações do Segundo Grau: Resultados Básicos. Nono Ano
 Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
Módulo de Equações do Segundo Grau Equações do Segundo Grau: Resultados Básicos. Nono Ano Equações do o grau: Resultados Básicos. 1 Exercícios Introdutórios Exercício 1. A equação ax + bx + c = 0, com
Modelos de Probabilidade e Inferência Estatística
 Modelos de Probabilidade e Inferência Estatística Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Distribuições Qui-quadrado, t-student e F de Snedecor 04/14
Modelos de Probabilidade e Inferência Estatística Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Distribuições Qui-quadrado, t-student e F de Snedecor 04/14
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR. Prof. Angelo Augusto Frozza, M.Sc.
 PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 2 do livro de Taha (2008): Introdução O modelo de PL de duas variáveis Propriedades
Pós-Graduação em Computação Distribuída e Ubíqua
 Pós-Graduação em Computação Distribuída e Ubíqua INF612 - Aspectos Avançados em Engenharia de Software Engenharia de Software Experimental [Head First Statistics] Capítulos 10, 11, 12 e 13 [Experimentation
Pós-Graduação em Computação Distribuída e Ubíqua INF612 - Aspectos Avançados em Engenharia de Software Engenharia de Software Experimental [Head First Statistics] Capítulos 10, 11, 12 e 13 [Experimentation
3º Ano do Ensino Médio. Aula nº06
 Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº06 Assunto: Noções de Estatística 1. Conceitos básicos Definição: A estatística é a ciência que recolhe, organiza, classifica, apresenta
Nome: Ano: º Ano do E.M. Escola: Data: / / 3º Ano do Ensino Médio Aula nº06 Assunto: Noções de Estatística 1. Conceitos básicos Definição: A estatística é a ciência que recolhe, organiza, classifica, apresenta
OPERAÇÕES COM FRAÇÕES
 OPERAÇÕES COM FRAÇÕES Adição A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Se inicialmente todas as frações já possuírem um denominador comum, basta que
OPERAÇÕES COM FRAÇÕES Adição A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Se inicialmente todas as frações já possuírem um denominador comum, basta que
Modelos Lineares Generalizados - Verificação do Ajuste do Modelo
 Modelos Lineares Generalizados - Verificação do Ajuste do Modelo Erica Castilho Rodrigues 21 de Junho de 2013 3 Uma outra medida usada para verificar o ajuste do modelo. Essa estatística é dada por X
Modelos Lineares Generalizados - Verificação do Ajuste do Modelo Erica Castilho Rodrigues 21 de Junho de 2013 3 Uma outra medida usada para verificar o ajuste do modelo. Essa estatística é dada por X
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS
 Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
Cap. II EVENTOS MUTUAMENTE EXCLUSIVOS E EVENTOS NÃO- EXCLUSIVOS Dois ou mais eventos são mutuamente exclusivos, ou disjuntos, se os mesmos não podem ocorrer simultaneamente. Isto é, a ocorrência de um
Técnicas de Contagem I II III IV V VI
 Técnicas de Contagem Exemplo Para a Copa do Mundo 24 países são divididos em seis grupos, com 4 países cada um. Supondo que a escolha do grupo de cada país é feita ao acaso, calcular a probabilidade de
Técnicas de Contagem Exemplo Para a Copa do Mundo 24 países são divididos em seis grupos, com 4 países cada um. Supondo que a escolha do grupo de cada país é feita ao acaso, calcular a probabilidade de
P R O G R A M A TERCEIRA FASE. DISCIPLINA: Estatística Aplicada à Pesquisa Educacional Código: 3EAPE Carga Horária: 54h/a (crédito 03)
 UNIVERSIDADE DO ESTADO DE SANTA CATARINA - UDESC CENTRO DE CIÊNCIAS DA SAÚDE E DO ESPORTE - CEFID DEPARTAMENTO DE EDUCAÇÃO FÍSICA - DEF CURSO: LICENCIATURA EM EDUCAÇÃO FÍSICA CURRÍCULO: 2008/2 P R O G
UNIVERSIDADE DO ESTADO DE SANTA CATARINA - UDESC CENTRO DE CIÊNCIAS DA SAÚDE E DO ESPORTE - CEFID DEPARTAMENTO DE EDUCAÇÃO FÍSICA - DEF CURSO: LICENCIATURA EM EDUCAÇÃO FÍSICA CURRÍCULO: 2008/2 P R O G
UM JOGO BINOMIAL 1. INTRODUÇÃO
 1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
1. INTRODUÇÃO UM JOGO BINOMIAL São muitos os casos de aplicação, no cotidiano de cada um de nós, dos conceitos de probabilidade. Afinal, o mundo é probabilístico, não determinístico; a natureza acontece
WWW.RENOVAVEIS.TECNOPT.COM
 Energia produzida Para a industria eólica é muito importante a discrição da variação da velocidade do vento. Os projetistas de turbinas necessitam da informação para otimizar o desenho de seus geradores,
Energia produzida Para a industria eólica é muito importante a discrição da variação da velocidade do vento. Os projetistas de turbinas necessitam da informação para otimizar o desenho de seus geradores,
Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios
 Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios O Método Intuitivo de elaboração de circuitos: As técnicas de elaboração de circuitos eletropneumáticos fazem parte
Comandos de Eletropneumática Exercícios Comentados para Elaboração, Montagem e Ensaios O Método Intuitivo de elaboração de circuitos: As técnicas de elaboração de circuitos eletropneumáticos fazem parte
Usando potências de 10
 Usando potências de 10 A UUL AL A Nesta aula, vamos ver que todo número positivo pode ser escrito como uma potência de base 10. Por exemplo, vamos aprender que o número 15 pode ser escrito como 10 1,176.
Usando potências de 10 A UUL AL A Nesta aula, vamos ver que todo número positivo pode ser escrito como uma potência de base 10. Por exemplo, vamos aprender que o número 15 pode ser escrito como 10 1,176.
Estatística Analítica
 Teste de Hipótese Testes Estatísticos 2 Teste de Hipótese Testes Estatísticos 3 1 Teste de Hipótese Testes Estatísticos 4 Principais Testes: Teste Qui-quadrado Teste T de Student Teste ANOVA Teste de Correlação
Teste de Hipótese Testes Estatísticos 2 Teste de Hipótese Testes Estatísticos 3 1 Teste de Hipótese Testes Estatísticos 4 Principais Testes: Teste Qui-quadrado Teste T de Student Teste ANOVA Teste de Correlação
ActivALEA. ative e atualize a sua literacia
 ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL
ActivALEA ative e atualize a sua literacia N.º 26 A FREQUÊNCIIA RELATIIVA PARA ESTIIMAR A PROBABIILIIDADE Por: Maria Eugénia Graça Martins Departamento de Estatística e Investigação Operacional da FCUL
A dependência entre a inflação cabo-verdiana e a portuguesa: uma abordagem de copulas.
 A dependência entre a inflação cabo-verdiana e a portuguesa: uma abordagem de copulas. Jailson da Conceição Teixeira Oliveira 1 Murilo Massaru da Silva 2 Robson Oliveira Lima 3 Resumo: Cabo Verde é um
A dependência entre a inflação cabo-verdiana e a portuguesa: uma abordagem de copulas. Jailson da Conceição Teixeira Oliveira 1 Murilo Massaru da Silva 2 Robson Oliveira Lima 3 Resumo: Cabo Verde é um
MOQ-14 Projeto e Análise de Experimentos
 Instituto Tecnológico de Aeronáutica Divisão de Engenharia Mecânica-Aeronáutica MOQ-14 Projeto e Análise de Experimentos Profa. Denise Beatriz Ferrari www.mec.ita.br/ denise denise@ita.br Regressão Linear
Instituto Tecnológico de Aeronáutica Divisão de Engenharia Mecânica-Aeronáutica MOQ-14 Projeto e Análise de Experimentos Profa. Denise Beatriz Ferrari www.mec.ita.br/ denise denise@ita.br Regressão Linear
Aula 12 Teste de hipótese sobre proporções amostras grandes
 Aula 12 Teste de hipótese sobre proporções amostras grandes Objetivos Na aula anterior, você aprendeu a construir testes de hipóteses sobre a média de uma população normal com variância σ 2 conhecida.
Aula 12 Teste de hipótese sobre proporções amostras grandes Objetivos Na aula anterior, você aprendeu a construir testes de hipóteses sobre a média de uma população normal com variância σ 2 conhecida.
Métodos Estatísticos Avançados em Epidemiologia
 Métodos Estatísticos Avançados em Epidemiologia Análise de Sobrevivência - Conceitos Básicos Enrico A. Colosimo Departamento de Estatística Universidade Federal de Minas Gerais http://www.est.ufmg.br/
Métodos Estatísticos Avançados em Epidemiologia Análise de Sobrevivência - Conceitos Básicos Enrico A. Colosimo Departamento de Estatística Universidade Federal de Minas Gerais http://www.est.ufmg.br/
Resolução da Lista de Exercício 6
 Teoria da Organização e Contratos - TOC / MFEE Professor: Jefferson Bertolai Fundação Getulio Vargas / EPGE Monitor: William Michon Jr 10 de novembro de 01 Exercícios referentes à aula 7 e 8. Resolução
Teoria da Organização e Contratos - TOC / MFEE Professor: Jefferson Bertolai Fundação Getulio Vargas / EPGE Monitor: William Michon Jr 10 de novembro de 01 Exercícios referentes à aula 7 e 8. Resolução
Avaliação de Empresas Profa. Patricia Maria Bortolon
 Avaliação de Empresas RISCO E RETORNO Aula 2 Retorno Total É a variação total da riqueza proporcionada por um ativo ao seu detentor. Fonte: Notas de Aula do Prof. Claudio Cunha Retorno Total Exemplo 1
Avaliação de Empresas RISCO E RETORNO Aula 2 Retorno Total É a variação total da riqueza proporcionada por um ativo ao seu detentor. Fonte: Notas de Aula do Prof. Claudio Cunha Retorno Total Exemplo 1
MAE116 - Noções de Estatística
 MAE116 - Noções de Estatística Grupo A - 1 semestre de 2015 Gabarito da Lista de exercícios 10 - Introdução à Estatística Descritiva - CASA Exercício 1. (2 pontos) Sabe-se que, historicamente, 18% dos
MAE116 - Noções de Estatística Grupo A - 1 semestre de 2015 Gabarito da Lista de exercícios 10 - Introdução à Estatística Descritiva - CASA Exercício 1. (2 pontos) Sabe-se que, historicamente, 18% dos
Probabilidade. Luiz Carlos Terra
 Luiz Carlos Terra Nesta aula, você conhecerá os conceitos básicos de probabilidade que é a base de toda inferência estatística, ou seja, a estimativa de parâmetros populacionais com base em dados amostrais.
Luiz Carlos Terra Nesta aula, você conhecerá os conceitos básicos de probabilidade que é a base de toda inferência estatística, ou seja, a estimativa de parâmetros populacionais com base em dados amostrais.
MBA em Gerenciamento de Projetos. Teoria Geral do Planejamento. Professora: Maria Erileuza do Nascimento de Paula
 MBA em Gerenciamento de Projetos Teoria Geral do Planejamento Professora: Maria Erileuza do Nascimento de Paula SOBRAL - CE 2014 O que é Planejamento É um processo contínuo e dinâmico que consiste em um
MBA em Gerenciamento de Projetos Teoria Geral do Planejamento Professora: Maria Erileuza do Nascimento de Paula SOBRAL - CE 2014 O que é Planejamento É um processo contínuo e dinâmico que consiste em um
Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Raciocínio Lógico Professor: Custódio Nascimento
 Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Professor: Custódio Nascimento 1- Análise da prova Análise e Resolução da prova de Agente / PF Neste artigo, farei a análise das questões
Análise e Resolução da prova de Agente de Polícia Federal Disciplina: Professor: Custódio Nascimento 1- Análise da prova Análise e Resolução da prova de Agente / PF Neste artigo, farei a análise das questões
INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA. Prof. Anderson Rodrigo da Silva anderson.silva@ifgoiano.edu.br
 INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA Prof. Anderson Rodrigo da Silva anderson.silva@ifgoiano.edu.br Tipos de Pesquisa Censo: é o levantamento de toda população. Aqui não se faz inferência e sim uma descrição
INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA Prof. Anderson Rodrigo da Silva anderson.silva@ifgoiano.edu.br Tipos de Pesquisa Censo: é o levantamento de toda população. Aqui não se faz inferência e sim uma descrição
Fundamentos de Teste de Software
 Núcleo de Excelência em Testes de Sistemas Fundamentos de Teste de Software Módulo 1- Visão Geral de Testes de Software Aula 2 Estrutura para o Teste de Software SUMÁRIO 1. Introdução... 3 2. Vertentes
Núcleo de Excelência em Testes de Sistemas Fundamentos de Teste de Software Módulo 1- Visão Geral de Testes de Software Aula 2 Estrutura para o Teste de Software SUMÁRIO 1. Introdução... 3 2. Vertentes
Se A =, o evento é impossível, por exemplo, obter 7 no lançamento de um dado.
 PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
Probabilidade e Estatística, 2009/2
 Probabilidade e Estatística, 2009/2 CCT - UDESC Prof. Fernando Deeke Sasse Problemas Resolvidos - Testes de Hipóteses 1. Uma empresa de manufatura têxtil está testando rolos de fio que o fornecedor afirma
Probabilidade e Estatística, 2009/2 CCT - UDESC Prof. Fernando Deeke Sasse Problemas Resolvidos - Testes de Hipóteses 1. Uma empresa de manufatura têxtil está testando rolos de fio que o fornecedor afirma
MANUAL DO AVALIADOR O que é uma Feira de Ciência? Por que avaliar os trabalhos? Como os avaliadores devem proceder?
 MANUAL DO AVALIADOR O que é uma Feira de Ciência? É uma exposição que divulga os resultados de experimentos ou de levantamentos realizados, com rigor científico, por alunos, sob a orientação de um professor.
MANUAL DO AVALIADOR O que é uma Feira de Ciência? É uma exposição que divulga os resultados de experimentos ou de levantamentos realizados, com rigor científico, por alunos, sob a orientação de um professor.
CONFIGURAçÃO E GERAÇÃO DO LALUR. Parâmetros
 CONFIGURAçÃO E GERAÇÃO DO LALUR Parâmetros *O campo Limite para compensação de prejuízos anteriores, é utilizado pelas empresas que em um determinado período de apuração, obtiveram prejuízo, e sobre esse
CONFIGURAçÃO E GERAÇÃO DO LALUR Parâmetros *O campo Limite para compensação de prejuízos anteriores, é utilizado pelas empresas que em um determinado período de apuração, obtiveram prejuízo, e sobre esse
Álgebra Linear Aplicada à Compressão de Imagens. Universidade de Lisboa Instituto Superior Técnico. Mestrado em Engenharia Aeroespacial
 Álgebra Linear Aplicada à Compressão de Imagens Universidade de Lisboa Instituto Superior Técnico Uma Breve Introdução Mestrado em Engenharia Aeroespacial Marília Matos Nº 80889 2014/2015 - Professor Paulo
Álgebra Linear Aplicada à Compressão de Imagens Universidade de Lisboa Instituto Superior Técnico Uma Breve Introdução Mestrado em Engenharia Aeroespacial Marília Matos Nº 80889 2014/2015 - Professor Paulo
AULA 11 Experimentos Multinomiais e Tabelas de Contingência
 1 AULA 11 Experimentos Multinomiais e Tabelas de Contingência Ernesto F. L. Amaral 24 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG)
1 AULA 11 Experimentos Multinomiais e Tabelas de Contingência Ernesto F. L. Amaral 24 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG)
ANOVA (Analysis of Variance)
 Tópicos Avançados em Avaliação e Desempenho de Sistemas ANOVA (Analysis of Variance) Aleciano Júnior aflj@cin.ufpe.br Carlos Melo casm3@cin.ufpe.br Charles Bezerra cbm3@cin.ufpe.br Tópicos Introdução História,
Tópicos Avançados em Avaliação e Desempenho de Sistemas ANOVA (Analysis of Variance) Aleciano Júnior aflj@cin.ufpe.br Carlos Melo casm3@cin.ufpe.br Charles Bezerra cbm3@cin.ufpe.br Tópicos Introdução História,
AULA 4 DELINEAMENTO EM QUADRADO LATINO (DQL)
 AULA 4 DELINEAMENTO EM QUADRADO LATINO (DQL) Características Utiliza-se de três princípios básicos da experimentação: repetição, casualização e controle local. Possui um controle local mais eficiente que
AULA 4 DELINEAMENTO EM QUADRADO LATINO (DQL) Características Utiliza-se de três princípios básicos da experimentação: repetição, casualização e controle local. Possui um controle local mais eficiente que
IND 1115 Inferência Estatística Aula 8
 Conteúdo IND 5 Inferência Estatística Aula 8 Setembro 4 Mônica Barros O - aproximação da Binomial pela Este teorema é apenas um caso particular do teorema central do limite, pois uma variável aleatória
Conteúdo IND 5 Inferência Estatística Aula 8 Setembro 4 Mônica Barros O - aproximação da Binomial pela Este teorema é apenas um caso particular do teorema central do limite, pois uma variável aleatória
Resolução da Prova de Raciocínio Lógico da ANS (Técnico Administrativo) de 2016, aplicada em 21/02/2016.
 Raciocínio Lógico p/ NS Resolução da Prova de Raciocínio Lógico da NS (Técnico dministrativo) de 2016, aplicada em 21/02/2016. 11 - De acordo com o raciocínio lógico-matemático, a negação da frase: o obstetra
Raciocínio Lógico p/ NS Resolução da Prova de Raciocínio Lógico da NS (Técnico dministrativo) de 2016, aplicada em 21/02/2016. 11 - De acordo com o raciocínio lógico-matemático, a negação da frase: o obstetra
1 Visão Geral. 2 Instalação e Primeira Utilização. Manual de Instalação do Gold Pedido
 Manual de Instalação do Gold Pedido 1 Visão Geral Programa completo para enviar pedidos e ficha cadastral de clientes pela internet sem usar fax e interurbano. Reduz a conta telefônica e tempo. Importa
Manual de Instalação do Gold Pedido 1 Visão Geral Programa completo para enviar pedidos e ficha cadastral de clientes pela internet sem usar fax e interurbano. Reduz a conta telefônica e tempo. Importa
Observando embalagens
 Observando embalagens A UUL AL A O leite integral é vendido em caixas de papelão laminado por dentro. Essas embalagens têm a forma de um paralelepípedo retângulo e a indicação de que contêm 1000 ml de
Observando embalagens A UUL AL A O leite integral é vendido em caixas de papelão laminado por dentro. Essas embalagens têm a forma de um paralelepípedo retângulo e a indicação de que contêm 1000 ml de
Prof. Daniela Barreiro Claro
 O volume de dados está crescendo sem parar Gigabytes, Petabytes, etc. Dificuldade na descoberta do conhecimento Dados disponíveis x Análise dos Dados Dados disponíveis Analisar e compreender os dados 2
O volume de dados está crescendo sem parar Gigabytes, Petabytes, etc. Dificuldade na descoberta do conhecimento Dados disponíveis x Análise dos Dados Dados disponíveis Analisar e compreender os dados 2
Teste de hipótese em modelos normais lineares: ANOVA
 Teste de hipótese em modelos normais lineares: ANOVA Prof Caio Azevedo Prof Caio Azevedo Exemplo 1 No primeiro modelo, o interesse primário, de certa forma, é testar se a carga não contribui para explicar
Teste de hipótese em modelos normais lineares: ANOVA Prof Caio Azevedo Prof Caio Azevedo Exemplo 1 No primeiro modelo, o interesse primário, de certa forma, é testar se a carga não contribui para explicar
Relatório do Experimento 1 Sistema Massa - Mola. Fernando Henrique Ferraz Pereira da Rosa
 FEP0111 - Física I Relatório do Experimento 1 Sistema Massa - Mola Fernando Henrique Ferraz Pereira da Rosa 4 de novembro de 2005 Sumário 1 Introdução 2 2 Objetivos 2 3 Procedimento experimental 2 3.1
FEP0111 - Física I Relatório do Experimento 1 Sistema Massa - Mola Fernando Henrique Ferraz Pereira da Rosa 4 de novembro de 2005 Sumário 1 Introdução 2 2 Objetivos 2 3 Procedimento experimental 2 3.1
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. São Paulo, Editora Atlas, 2002....
 GIL, Antonio Carlos. Como elaborar projetos de pesquisa. São Paulo, Editora Atlas, 2002.... 1 Como encaminhar uma Pesquisa? A pesquisa é um projeto racional e sistemático com objetivo de proporcionar respostas
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. São Paulo, Editora Atlas, 2002.... 1 Como encaminhar uma Pesquisa? A pesquisa é um projeto racional e sistemático com objetivo de proporcionar respostas
Teste de Hipótese para uma Amostra Única
 Teste de Hipótese para uma Amostra Única OBJETIVOS DE APRENDIZAGEM Depois de um cuidadoso estudo deste capítulo, você deve ser capaz de: 1.Estruturar problemas de engenharia de tomada de decisão, como
Teste de Hipótese para uma Amostra Única OBJETIVOS DE APRENDIZAGEM Depois de um cuidadoso estudo deste capítulo, você deve ser capaz de: 1.Estruturar problemas de engenharia de tomada de decisão, como
Uso de escalas logaritmicas e linearização
 Uso de escalas logaritmicas e linearização Notas: Rodrigo Ramos 1 o. sem. 2015 Versão 1.0 Obs: Esse é um texto de matemática, você deve acompanhá-lo com atenção, com lápis e papel, e ir fazendo as coisas
Uso de escalas logaritmicas e linearização Notas: Rodrigo Ramos 1 o. sem. 2015 Versão 1.0 Obs: Esse é um texto de matemática, você deve acompanhá-lo com atenção, com lápis e papel, e ir fazendo as coisas
Aula 5. Uma partícula evolui na reta. A trajetória é uma função que dá a sua posição em função do tempo:
 Aula 5 5. Funções O conceito de função será o principal assunto tratado neste curso. Neste capítulo daremos algumas definições elementares, e consideraremos algumas das funções mais usadas na prática,
Aula 5 5. Funções O conceito de função será o principal assunto tratado neste curso. Neste capítulo daremos algumas definições elementares, e consideraremos algumas das funções mais usadas na prática,
Aula 6 Medidas de Tendência Central
 1 Estatística e Probabilidade Aula 6 Medidas de Tendência Central Professor Luciano Nóbrega Somatório Quando queremos representar uma soma de valores que obedecem à uma sequência, podemos codificá-la através
1 Estatística e Probabilidade Aula 6 Medidas de Tendência Central Professor Luciano Nóbrega Somatório Quando queremos representar uma soma de valores que obedecem à uma sequência, podemos codificá-la através
Testes Qui-Quadrado - Teste de Aderência
 Testes Qui-Quadrado - Teste de Aderência Consideremos uma tabela de frequências com k frequências, k 2 k: total de categorias frequências observadas: O 1,, O k seja p 1 = p 01,, p k = p 0k as probabilidades
Testes Qui-Quadrado - Teste de Aderência Consideremos uma tabela de frequências com k frequências, k 2 k: total de categorias frequências observadas: O 1,, O k seja p 1 = p 01,, p k = p 0k as probabilidades
COMENTÁRIO DA PROVA DO BANCO DO BRASIL
 COMENTÁRIO DA PROVA DO BANCO DO BRASIL Prezados concurseiros, segue abaixo os comentários das questões de matemática propostas pela CESPE no último concurso para o cargo de escriturário do Banco do Brasil
COMENTÁRIO DA PROVA DO BANCO DO BRASIL Prezados concurseiros, segue abaixo os comentários das questões de matemática propostas pela CESPE no último concurso para o cargo de escriturário do Banco do Brasil
EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros exercícios)
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros eercícios) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Eercícios
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA EXERCÍCIOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (sistemas de equações lineares e outros eercícios) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Eercícios
Graphing Basic no Excel 2007
 Graphing Basic no Excel 2007 Tabela de Conteúdos 1. Inserindo e formatando os dados no Excel 2. Criando o gráfico de dispersão inicial 3. Criando um gráfico de dispersão de dados de titulação 4. Adicionando
Graphing Basic no Excel 2007 Tabela de Conteúdos 1. Inserindo e formatando os dados no Excel 2. Criando o gráfico de dispersão inicial 3. Criando um gráfico de dispersão de dados de titulação 4. Adicionando
Gerenciamento dos Riscos do Projeto (PMBoK 5ª ed.)
 Gerenciamento dos Riscos do Projeto (PMBoK 5ª ed.) Esta é uma área essencial para aumentar as taxas de sucesso dos projetos, pois todos eles possuem riscos e precisam ser gerenciados, ou seja, saber o
Gerenciamento dos Riscos do Projeto (PMBoK 5ª ed.) Esta é uma área essencial para aumentar as taxas de sucesso dos projetos, pois todos eles possuem riscos e precisam ser gerenciados, ou seja, saber o
QUESTÕES PARA A 3ª SÉRIE ENSINO MÉDIO MATEMÁTICA 2º BIMESTE SUGESTÕES DE RESOLUÇÕES
 QUESTÕES PARA A 3ª SÉRIE ENSINO MÉDIO MATEMÁTICA 2º BIMESTE QUESTÃO 01 SUGESTÕES DE RESOLUÇÕES Descritor 11 Resolver problema envolvendo o cálculo de perímetro de figuras planas. Os itens referentes a
QUESTÕES PARA A 3ª SÉRIE ENSINO MÉDIO MATEMÁTICA 2º BIMESTE QUESTÃO 01 SUGESTÕES DE RESOLUÇÕES Descritor 11 Resolver problema envolvendo o cálculo de perímetro de figuras planas. Os itens referentes a
Aula 8. Teste Binomial a uma proporção p
 Aula 8. Teste Binomial a uma proporção p Métodos Estadísticos 2008 Universidade de Averio Profª Gladys Castillo Jordán Teste Binomial a uma Proporção p Seja p ˆ = X n a proporção de indivíduos com uma
Aula 8. Teste Binomial a uma proporção p Métodos Estadísticos 2008 Universidade de Averio Profª Gladys Castillo Jordán Teste Binomial a uma Proporção p Seja p ˆ = X n a proporção de indivíduos com uma
Função. Adição e subtração de arcos Duplicação de arcos
 Função Trigonométrica II Adição e subtração de arcos Duplicação de arcos Resumo das Principais Relações I sen cos II tg sen cos III cotg tg IV sec cos V csc sen VI sec tg VII csc cotg cos sen Arcos e subtração
Função Trigonométrica II Adição e subtração de arcos Duplicação de arcos Resumo das Principais Relações I sen cos II tg sen cos III cotg tg IV sec cos V csc sen VI sec tg VII csc cotg cos sen Arcos e subtração
Tópicos Avançados em Banco de Dados Dependências sobre regime e controle de objetos em Banco de Dados. Prof. Hugo Souza
 Tópicos Avançados em Banco de Dados Dependências sobre regime e controle de objetos em Banco de Dados Prof. Hugo Souza Após vermos uma breve contextualização sobre esquemas para bases dados e aprendermos
Tópicos Avançados em Banco de Dados Dependências sobre regime e controle de objetos em Banco de Dados Prof. Hugo Souza Após vermos uma breve contextualização sobre esquemas para bases dados e aprendermos
Métricas de Software
 Métricas de Software Plácido Antônio de Souza Neto 1 1 Gerência Educacional de Tecnologia da Informação Centro Federal de Educação Tecnologia do Rio Grande do Norte 2006.1 - Planejamento e Gerência de
Métricas de Software Plácido Antônio de Souza Neto 1 1 Gerência Educacional de Tecnologia da Informação Centro Federal de Educação Tecnologia do Rio Grande do Norte 2006.1 - Planejamento e Gerência de
Matrizes. matriz de 2 linhas e 2 colunas. matriz de 3 linhas e 3 colunas. matriz de 3 linhas e 1 coluna. matriz de 1 linha e 4 colunas.
 Definição Uma matriz do tipo m n (lê-se m por n), com m e n, sendo m e n números inteiros, é uma tabela formada por m n elementos dispostos em m linhas e n colunas. Estes elementos podem estar entre parênteses
Definição Uma matriz do tipo m n (lê-se m por n), com m e n, sendo m e n números inteiros, é uma tabela formada por m n elementos dispostos em m linhas e n colunas. Estes elementos podem estar entre parênteses
Introdução. Ou seja, de certo modo esperamos que haja uma certa
 UNIVERSIDADE FEDERAL DA PARAÍBA Teste de Independência Luiz Medeiros de Araujo Lima Filho Departamento de Estatística Introdução Um dos principais objetivos de se construir uma tabela de contingência,
UNIVERSIDADE FEDERAL DA PARAÍBA Teste de Independência Luiz Medeiros de Araujo Lima Filho Departamento de Estatística Introdução Um dos principais objetivos de se construir uma tabela de contingência,
Capítulo 5. Inferência no Modelo de Regressão Simples: Estimação de Intervalos, Teste de Hipóteses e Previsão
 Capítulo 5 Inferência no Modelo de Regressão Simples: Estimação de Intervalos, Teste de Hipóteses e Previsão Hipóteses do Modelo de Regressão Linear Simples RS1. y x e t 1 t t RS. RS3. RS4. RS5. RS6. Ee
Capítulo 5 Inferência no Modelo de Regressão Simples: Estimação de Intervalos, Teste de Hipóteses e Previsão Hipóteses do Modelo de Regressão Linear Simples RS1. y x e t 1 t t RS. RS3. RS4. RS5. RS6. Ee
UMA ANÁLISE BAYESIANA DO PERFIL COR/RAÇA DOS INDIVÍDUOS QUE TEM CURSO SUPERIOR NO BRASIL
 ISSN 2175-6295 Rio de Janeiro- Brasil, 08 e 09 novembro de 2007. SPOLM 2007 UMA ANÁLISE BAYESIANA DO PERFIL COR/RAÇA DOS INDIVÍDUOS QUE TEM CURSO SUPERIOR NO BRASIL Giovani Glaucio de Oliveira Costa Universidade
ISSN 2175-6295 Rio de Janeiro- Brasil, 08 e 09 novembro de 2007. SPOLM 2007 UMA ANÁLISE BAYESIANA DO PERFIL COR/RAÇA DOS INDIVÍDUOS QUE TEM CURSO SUPERIOR NO BRASIL Giovani Glaucio de Oliveira Costa Universidade
números decimais Inicialmente, as frações são apresentadas como partes de um todo. Por exemplo, teremos 2 de um bolo se dividirmos esse bolo
 A UA UL LA Frações e números decimais Introdução Inicialmente, as frações são apresentadas como partes de um todo. Por exemplo, teremos de um bolo se dividirmos esse bolo em cinco partes iguais e tomarmos
A UA UL LA Frações e números decimais Introdução Inicialmente, as frações são apresentadas como partes de um todo. Por exemplo, teremos de um bolo se dividirmos esse bolo em cinco partes iguais e tomarmos
Figura 4.1: Diagrama de representação de uma função de 2 variáveis
 1 4.1 Funções de 2 Variáveis Em Cálculo I trabalhamos com funções de uma variável y = f(x). Agora trabalharemos com funções de várias variáveis. Estas funções aparecem naturalmente na natureza, na economia
1 4.1 Funções de 2 Variáveis Em Cálculo I trabalhamos com funções de uma variável y = f(x). Agora trabalharemos com funções de várias variáveis. Estas funções aparecem naturalmente na natureza, na economia
Registro de Retenções Tributárias e Pagamentos
 SISTEMA DE GESTÃO DE PRESTAÇÃO DE CONTAS (SiGPC) CONTAS ONLINE Registro de Retenções Tributárias e Pagamentos Atualização: 20/12/2012 A necessidade de registrar despesas em que há retenção tributária é
SISTEMA DE GESTÃO DE PRESTAÇÃO DE CONTAS (SiGPC) CONTAS ONLINE Registro de Retenções Tributárias e Pagamentos Atualização: 20/12/2012 A necessidade de registrar despesas em que há retenção tributária é
AULA 04 Estimativas e Tamanhos Amostrais
 1 AULA 04 Estimativas e Tamanhos Amostrais Ernesto F. L. Amaral 27 de agosto de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario
1 AULA 04 Estimativas e Tamanhos Amostrais Ernesto F. L. Amaral 27 de agosto de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola, Mario
números decimais Inicialmente, as frações são apresentadas como partes de um todo. Por exemplo, teremos 2 de um bolo se dividirmos esse bolo
 A UA UL LA Frações e números decimais Introdução Inicialmente, as frações são apresentadas como partes de um todo. Por exemplo, teremos de um bolo se dividirmos esse bolo em cinco partes iguais e tomarmos
A UA UL LA Frações e números decimais Introdução Inicialmente, as frações são apresentadas como partes de um todo. Por exemplo, teremos de um bolo se dividirmos esse bolo em cinco partes iguais e tomarmos
Análise Qualitativa no Gerenciamento de Riscos de Projetos
 Análise Qualitativa no Gerenciamento de Riscos de Projetos Olá Gerente de Projeto. Nos artigos anteriores descrevemos um breve histórico sobre a história e contextualização dos riscos, tanto na vida real
Análise Qualitativa no Gerenciamento de Riscos de Projetos Olá Gerente de Projeto. Nos artigos anteriores descrevemos um breve histórico sobre a história e contextualização dos riscos, tanto na vida real
FERRAMENTAS DA QUALIDADE FOLHA DE VERIFICAÇÃO
 FERRAMENTAS DA QUALIDADE FOLHA DE VERIFICAÇÃO 1 A Folha de Verificação é utilizada para permitir que um grupo registre e compile sistematicamente dados de fontes com experiência na área (históricos), ou
FERRAMENTAS DA QUALIDADE FOLHA DE VERIFICAÇÃO 1 A Folha de Verificação é utilizada para permitir que um grupo registre e compile sistematicamente dados de fontes com experiência na área (históricos), ou
COBRANÇA BANCÁRIA CAIXA
 COBRANÇA BANCÁRIA CAIXA ESPECIFICAÇÃO DE CÓDIGO DE BARRAS PARA BLOQUETOS DE COBRANÇA COBRANÇAS RÁPIDA E SEM REGISTRO GESER NOVEMBRO/2000 ÍNDICE PÁGINA 1 INTRODUÇÃO... 3 2 ESPECIFICAÇÕES...4 2.1 FORMATO......
COBRANÇA BANCÁRIA CAIXA ESPECIFICAÇÃO DE CÓDIGO DE BARRAS PARA BLOQUETOS DE COBRANÇA COBRANÇAS RÁPIDA E SEM REGISTRO GESER NOVEMBRO/2000 ÍNDICE PÁGINA 1 INTRODUÇÃO... 3 2 ESPECIFICAÇÕES...4 2.1 FORMATO......
Aula 6 Propagação de erros
 Aula 6 Propagação de erros Conteúdo da aula: Como estimar incertezas de uma medida indireta Como realizar propagação de erros? Exemplo: medimos A e B e suas incertezas. Com calcular a incerteza de C, se
Aula 6 Propagação de erros Conteúdo da aula: Como estimar incertezas de uma medida indireta Como realizar propagação de erros? Exemplo: medimos A e B e suas incertezas. Com calcular a incerteza de C, se
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA DEPARTAMENTO DE ENGENHARIA QUÍMICA ENG 008 Fenômenos de Transporte I A Profª Fátima Lopes
 Equações básicas Uma análise de qualquer problema em Mecânica dos Fluidos, necessariamente se inicia, quer diretamente ou indiretamente, com a definição das leis básicas que governam o movimento do fluido.
Equações básicas Uma análise de qualquer problema em Mecânica dos Fluidos, necessariamente se inicia, quer diretamente ou indiretamente, com a definição das leis básicas que governam o movimento do fluido.
Vantagens e desvantagens da utilização do patrimônio líquido pelo seu valor de mercado na avaliação de empresas
 Vantagens e desvantagens da utilização do patrimônio líquido pelo seu valor de mercado na avaliação de empresas! Quais as vantagem da utilização do valor de mercado em relação a utilização do patrimônio
Vantagens e desvantagens da utilização do patrimônio líquido pelo seu valor de mercado na avaliação de empresas! Quais as vantagem da utilização do valor de mercado em relação a utilização do patrimônio
Análise de Regressão Linear Simples III
 Análise de Regressão Linear Simples III Aula 03 Gujarati e Porter Capítulos 4 e 5 Wooldridge Seção.5 Suposições, Propriedades e Teste t Suposições e Propriedades RLS.1 O modelo de regressão é linear nos
Análise de Regressão Linear Simples III Aula 03 Gujarati e Porter Capítulos 4 e 5 Wooldridge Seção.5 Suposições, Propriedades e Teste t Suposições e Propriedades RLS.1 O modelo de regressão é linear nos
Orientações para Inscrição do Grupo e Projeto de Pesquisa
 1 Orientações para Inscrição do Grupo e Projeto de Pesquisa O primeiro passo é criar um login de acesso que será com um e-mail e uma senha única para o grupo. Ao entrar no ambiente de Inscrição e selecionar
1 Orientações para Inscrição do Grupo e Projeto de Pesquisa O primeiro passo é criar um login de acesso que será com um e-mail e uma senha única para o grupo. Ao entrar no ambiente de Inscrição e selecionar
Circuitos de Comunicação. Prática 1: PWM
 Circuitos de Comunicação Prática 1: PWM Professor: Hélio Magalhães Grupo: Geraldo Gomes, Paulo José Nunes Recife, 04 de Maio de 2014 SUMÁRIO Resumo 3 Parte I PWM - Teoria 3 Geração do PWM 5 Parte II Prática
Circuitos de Comunicação Prática 1: PWM Professor: Hélio Magalhães Grupo: Geraldo Gomes, Paulo José Nunes Recife, 04 de Maio de 2014 SUMÁRIO Resumo 3 Parte I PWM - Teoria 3 Geração do PWM 5 Parte II Prática
Inferência sobre duas proporções
 Teste para duas populações duas populações Amostra :,,,, alor comum para delta 0 Amostra 2:,,,, Tamanho Tamanho Média amostral x Média amostral x Desvio-padrão Desvio-padrão Teste para duas populações
Teste para duas populações duas populações Amostra :,,,, alor comum para delta 0 Amostra 2:,,,, Tamanho Tamanho Média amostral x Média amostral x Desvio-padrão Desvio-padrão Teste para duas populações
12 26, 62, 34, 43 21 37, 73 30 56, 65
 1 Questão 1 Solução a) Primeiro multiplicamos os algarismos de 79, obtendo 7 9 = 63, e depois somamos os algarismos desse produto, obtendo 6 + 3 = 9. Logo o transformado de é 79 é 9. b) A brincadeira de
1 Questão 1 Solução a) Primeiro multiplicamos os algarismos de 79, obtendo 7 9 = 63, e depois somamos os algarismos desse produto, obtendo 6 + 3 = 9. Logo o transformado de é 79 é 9. b) A brincadeira de
Se inicialmente, o tanque estava com 100 litros, pode-se afirmar que ao final do dia o mesmo conterá.
 ANÁLISE GRÁFICA QUANDO y. CORRESPONDE A ÁREA DA FIGURA Resposta: Sempre quando o eio y corresponde a uma taa de variação, então a área compreendida entre a curva e o eio do será o produto y. Isto é y =
ANÁLISE GRÁFICA QUANDO y. CORRESPONDE A ÁREA DA FIGURA Resposta: Sempre quando o eio y corresponde a uma taa de variação, então a área compreendida entre a curva e o eio do será o produto y. Isto é y =
cuja distribuição é t de Student com n 1 graus de liberdade.
 Aula 13 Teste de hipótese sobre a média de uma população normal σ 2 desconhecida Objetivos: Nesta aula você completará seu estudo básico sobre testes de hipóteses, analisando a situação relativa a uma
Aula 13 Teste de hipótese sobre a média de uma população normal σ 2 desconhecida Objetivos: Nesta aula você completará seu estudo básico sobre testes de hipóteses, analisando a situação relativa a uma
BALANÇO PATRIMONIAL AMBIENTAL - EXERCÍCIO COMENTADO Prof Alan
 FACULDADE EVANGÉLICA CIÊNCIAS CONTÁBEIS DISCIPLINA: CONTABILIDADE AMBIENTAL E SOCIAL TURMA: 3º, 4º e 5º PERÍODOS BALANÇO PATRIMONIAL AMBIENTAL - EXERCÍCIO COMENTADO Prof Alan Considere os fatos contábeis
FACULDADE EVANGÉLICA CIÊNCIAS CONTÁBEIS DISCIPLINA: CONTABILIDADE AMBIENTAL E SOCIAL TURMA: 3º, 4º e 5º PERÍODOS BALANÇO PATRIMONIAL AMBIENTAL - EXERCÍCIO COMENTADO Prof Alan Considere os fatos contábeis
CURSO DE MATEMÁTICA BÁSICA PROGRAMA DE EDUCAÇÃO TUTORIAL CENTRO DE ENGENHARIA DA MOBILIDADE
 CURSO DE MATEMÁTICA BÁSICA Aula 01 Introdução a Geometria Plana Ângulos Potenciação Radiciação Introdução a Geometria Plana Introdução: No estudo da Geometria Plana, consideraremos três conceitos primitivos:
CURSO DE MATEMÁTICA BÁSICA Aula 01 Introdução a Geometria Plana Ângulos Potenciação Radiciação Introdução a Geometria Plana Introdução: No estudo da Geometria Plana, consideraremos três conceitos primitivos:
Processamento Digital de Sinais. Conversão A/D e D/A. Prof. Dr. Carlos Alberto Ynoguti
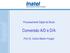 Processamento Digital de Sinais Conversão A/D e D/A Prof. Dr. Carlos Alberto Ynoguti Introdução A maioria dos sinais encontrados na natureza é contínua Para processá los digitalmente, devemos: Converter
Processamento Digital de Sinais Conversão A/D e D/A Prof. Dr. Carlos Alberto Ynoguti Introdução A maioria dos sinais encontrados na natureza é contínua Para processá los digitalmente, devemos: Converter
Ondas EM no Espaço Livre (Vácuo)
 Secretaria de Educação Profissional e Tecnológica Instituto Federal de Santa Catarina Campus São José Área de Telecomunicações ELM20704 Eletromagnetismo Professor: Bruno Fontana da Silva 2014-1 Ondas EM
Secretaria de Educação Profissional e Tecnológica Instituto Federal de Santa Catarina Campus São José Área de Telecomunicações ELM20704 Eletromagnetismo Professor: Bruno Fontana da Silva 2014-1 Ondas EM
ANÁLISE DE CIRCUITOS I ( AULA 03)
 ANÁLISE DE CIRCUITOS I ( AULA 03) 1.0 O CAPACÍMETRO É o instrumento usado para medir o valor dos capacitores comuns e eletrolíticos. Há dois tipos de capacímetro: o analógico (de ponteiro) e o digital
ANÁLISE DE CIRCUITOS I ( AULA 03) 1.0 O CAPACÍMETRO É o instrumento usado para medir o valor dos capacitores comuns e eletrolíticos. Há dois tipos de capacímetro: o analógico (de ponteiro) e o digital
