CÁLCULO E DETALHAMENTO DE LAJES E VIGAS EM CONCRETO ARMADO DO ANDAR TIPO DE UM EDIFÍCIO RESIDENCIAL
|
|
|
- Anderson da Silva Chagas
- 6 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE MINAS GERIAIS ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA DE ESTRUTURAS CURSO DE ESPECIALIZAÇÃO EM ESTRUTURAS CÁLCULO E DETALHAMENTO DE LAJES E VIGAS EM CONCRETO ARMADO DO ANDAR TIPO DE UM EDIFÍCIO RESIDENCIAL SHIRLEI COSTA DE OLIVEIRA 1
2 ÍNDICE ITEM DESCRIÇÃO FOLHA 1 INTRODUÇÃO 3 2 OBJETIVO 3 3 PROGRAMAS UTILIZADOS 3 4 DESENVOLVIMENTO 4 5 CONCLUSÃO 39 6 NORMAS / BIBLIOGRAFIA ADOTADAS 40 7 ANEXO 40 2
3 1. INTRODUÇÃO A UNIÃO DO CONCRETO COM O AÇO FORMA, ATRAVÉS DA ADERÊNCIA, UMA PEÇA EM CONCRETO ARMADO QUE RESISTE TANTO AOS ESFORÇOS DE COMPRESSÃO QUANTO DE TRAÇÃO. APESAR DO PESO ESPECÍFICO ELEVADO EM RELAÇÃO AO AÇO, DA DIFICULDADE DE EXECUÇÃO DE REFORMAS E ADAPTAÇÕES, DA FACILIDADE EM CONDUZIR CALOR E DA NECESSIDADE DE FÔRMAS E ESCORAMENTOS (QUANDO NÃO PREMOLDADOS), O CONCRETO ARMADO APRESENTA VANTAGENS COMO: BOA RESISTÊNCIA À MAIORIA DAS SOLICITAÇÕES, BOA TRABALHABILIDADE, EXECUÇÃO DOMINADA NO PAÍS, ECONOMIA EM DIVERSAS SITUAÇÕES EM RELAÇÃO AO AÇO E DURABILIDADE, SE EXECUTADO DE ACORDO COM A NORMA. AS ESTRUTURAS USUAIS DE CONCRETO ARMADO SÃO SISTEMAS COMPOSTOS POR ELEMENTOS ESTRUTURAIS COMO LAJES, VIGAS, PILARES E FUNDAÇÕES. A DISCRETIZAÇÃO EM ELEMENTOS FACILITA O CÁLCULO PARA O DIMENSIONAMENTO. SE NÃO ADOTADA, REQUER A NECESSIDADE DE PROGRAMAS ESPECÍFICOS PARA TAL FIM. LOGO, UMA SIMPLES ESTRUTURA PODE SER ANALISADA CONSIDERANDO QUE A LAJE DE CONCRETO SUPORTA SEU PESO, OS REVESTIMENTOS E MAIS ALGUMA CARGA ACIDENTAL; AS VIGAS RECEBEM OS ESFORÇOS DA LAJE E OS TRANSMITEM, COM SEU PRÓPRIO PESO E ALVENARIA (SE HOUVER), PARA OS PILARES; ESTES RECEBEM TODAS AS CARGAS E AS TRANSMITEM, TAMBÉM COM SEU PESO, PARA AS FUNDAÇÕES. 2. OBJETIVO O PRESENTE TRABALHO TEM COMO OBJETIVO APRESENTAR, COM BASE EM ESTUDOS QUE SIMPLIFICAM OS PROCESSOS FÍSICOS E MATEMÁTICOS DISPONÍVEIS, O CÁLCULO E DETALHAMENTO DAS LAJES E DAS VIGAS V1, V5 E V6 DA FÔRMA ABAIXO. 3. PROGRAMAS UTILIZADOS FTOOL - PARA A DETERMINAÇÃO DOS DIAGRAMAS DE ESFORÇO CORTANTE E MOMEN- TO FLETOR. CAD TQS - PARA O DESENHO DE DETALHAMENTO DOS ELEMENTOS. 3
4 4. DESENVOLVIMENTO A PLANTA DE FORMAS APRESENTA QUATRO LAJES (L1, L2, L3 E L4) QUE SERÃO APOIADAS NAS VIGAS V1 À V6. DIMENSÕES ESTIMADAS PARA LAJES E VIGAS LAJES (cm) VIGAS (cm) L1=10 V1=20/90 L2=12 V2=20/40 L3=12 V3=20/90 L4=10 V4=20/40 V5=20/50 V6=20/90 4
5 DADOS: fck=25 MPa AÇO CA-50/60 OBRA RESIDENCIAL SOBRECARGA = 2kN/M2 REVESTIMENTO = 1kN/M2 ALVENARIA 0,15x2,80 TIJOLOS FURADOS SOBRE TODAS AS VIGAS LAJE EM BALANÇO: ALVENARIA 0,15x1,20 TIJOLO FURADO REGIME ELÁSTICO N = DOIS ÚLTIMOS ALGARIMOS DA MATRÍCULA = 44 γconc = 25 kn/m3 γtijolo = 13 kn/m3 ES = MPa = kn/cm² LAJES AS LAJES DEVEM SER CALCULADAS PARA SUPORTAR TODO CARREGAMENTO ATUANTE SOBRE ELAS E RESISTIR AOS ESFORÇOS PROVOCADO POR ESSE CARREGAMENTO. O CÁLCULO ENGLOBA O DIMENSIONAMENTO DA SUA ESPESSURA, A QUANTIDADE DE AÇO PARA AS ARMADURAS E A DIMENSÃO DE CADA BARRA. TODO PROCEDIMENTO DEVE LEVAR EM CONTA PARÂMETROS INICIAIS COMO: CARGAS, CONDIÇÕES DE APOIO, MATERIAIS UTILIZADOS, INTERAÇÃO ENTRE LAJES E CONDIÇÕES DE ESTABILIDADE. REAÇÕES E MOMENTOS DAS LAJES PARA A LAJE L1 CARGAS: PP = 1x1x0,10x25 = 2,5 kn (CADA m² DE LAJE PESA 2,5 kn) REVESTIMENTO: 1,0 kn/m² CARGA ACIDENTAL (q) = 2,0 kn/m² ALVENARIA: 0,15x2,8x(3,8+1,85)x13 = 30,85/(4x3,7) = 2,08 kn/m² CARGA PERMANENTE (g) = 2,5+1+2,08 = 5,58 kn/m² CARGA TOTAL (P) = g + q = 5,58+2 = 7,58 kn/m² 5
6 REAÇÕES E MOMENTOS: b a = 4 = 1,08 < 2 laje armada em 2 direções 3,7 p. a = 7,58x3,7 = 28,05 kn/m p. a 2 = 7,58x3,7 2 = 28,05 kn/m DE ACORDO COM A TABELA EM ANEXO: R=r(p.a) r'a = 0,183 r"a = 0,317 r'b = 0,1968 (VALOR INTERPOLADO) r"b = 0,34 (VALOR INTEROLADO) R'a = 0,183x28,05 = 5,13 kn/m R"a = 0,317x28,05 = 8,89 kn/m R'b = 0,1968x28,05 = 5,52 kn/m R"b = 0,34x28,05 = 9,54 kn/m 6
7 DE ACORDO COM A TABELA EM ANEXO: p. a2 M = m ma = 32,48 (VALOR INTERPOLADO) mb = 37,36 (VALOR INTERPOLADO) na = 13,02 (VALOR INTERPOLADO) nb = 13,74 (VALOR INTERPOLADO) p. a2 e X = n Ma = 7,58x3,72 32,48 Xa = 7,58x3,72 13,02 = 3,2 kn. m e Mb = 7,58x3,72 37,36 = 7,97 kn. m e Xb = 7,58x3,72 13,74 = 2,78 kn. m = 7,55 kn. m CARGAS: PARA A LAJE L2 PP = 1x1x0,12x25 = 3,0 kn (CADA m² DE LAJE PESA 3,0 kn) REVESTIMENTO: 1,0 kn/m² CARGA ACIDENTAL (q) = 2,0 kn/m² ALVENARIA: 0,15x2,8x(3+1,5+2,74)x13 = 39,53/(4,44x7,5) =1,19kN/m² 7
8 CARGA PERMANENTE (g) = 3+1+1,19 = 5,19 kn/m² CARGA TOTAL (P) = g + q = 5,19+2 = 7,19 kn/m² REAÇÕES E MOMENTOS: b a = 7,40 = 1,67 < 2 laje armada em 2 direções 4,44 p. a = 7,19x4,44 = 31,92 kn/m p. a 2 = 7,19x4,44 2 = 141,74 kn/m DE ACORDO COM A TABELA EM ANEXO: R=r(p.a) r'a = 0,183 r'b = 0,287 r"b = 0,497 R'a = 0,183x31,92 = 5,84 kn/m R'b = 0,287x31,92 = 9,16 kn/m R"b = 0,497x31,92 = 15,86 kn/m 8
9 DE ACORDO COM A TABELA EM ANEXO: ma = 17,8 mb = 55,8 na = 8,6 M = p. a2 m p. a2 e X = n Ma = 7,19x4,442 17,8 Xa = 7,19x4,442 8,6 = 7,96 kn. m e Mb = 7,19x4,442 55,8 = 16,48 kn. m = 2,54 kn. m PARA A LAJE L3 CARGAS: PP = 1x1x0,12x25 = 3,0 kn (CADA m² DE LAJE PESA 3,0 kn) REVESTIMENTO: 1,0 kn/m² CARGA ACIDENTAL (q) = 2,0 kn/m² ALVENARIA(7,40m): 0,15x1,2x13 = 2,34 kn/m 9
10 ALVENARIA(1,30): [2x(0,15x1,3x1,2x13)]/(7,4x1,3) = 0,63 kn/m² CARGA PERMANENTE (g) = 3+1+0,63 = 4,63 kn/m² CARGA TOTAL (P) = g + q = 4,63+2 = 6,63 kn/m² REAÇÕES E MOMENTOS: b a = 7,40 = 5,69 > 2 laje armada em 1 direção 1,30 OBS.: AO LONGO DOS PARAPEITOS E BALCÕES DEVEM SER CONSIDERADOS APLICADAS, UMA CARGA HORIZONAL DE 0,8 kn/m NA ALTURA DO CORRIMÃO E UMA CARGA MÍNIMA DE 2 kn/m. 10
11 V = 0 Re-6,63x1,3-4,34= 0 R 13 kn M = 0 Me+[(6,63x1,3)x(1,3/2)]+(4,34x1,3)+0,96= 0 Me -12,20 kn.m PARA A LAJE L4 CARGAS: PP = 1x1x0,10x25 = 2,5 kn (CADA m² DE LAJE PESA 2,5 kn) REVESTIMENTO: 1,0 kn/m² CARGA ACIDENTAL (q) = 2,0 kn/m² 11
12 CARGA PERMANENTE (g) = 2,5+1 = 3,5 kn/m² CARGA TOTAL (P) = g + q = 3,5+2 = 5,5 kn/m² REAÇÕES E MOMENTOS: b a = 4 = 1,08 < 2 laje armada em 2 direções 3,7 20,35 kn/m p. a 2 = 5,5x3,7 2 = 75,29 kn/m DE ACORDO COM A TABELA EM ANEXO: R=r(p.a) r'a = 0,183 r"a = 0,317 r'b = 0,1968 (VALOR INTERPOLADO) r"b = 0,34 (VALOR INTEROLADO) R'a = 0,183x20,35 = 3,72 kn/m R"a = 0,317x20,35 = 6,45 kn/m R'b = 0,1968x20,35 = 4 kn/m p. a = 5,5x3,7 = 12
13 R"b = 0,34x20,35 = 6,92 kn/m DE ACORDO COM A TABELA EM ANEXO: p. a2 M = m ma = 32,48 (VALOR INTERPOLADO) mb = 37,36 (VALOR INTERPOLADO) na = 13,02 (VALOR INTERPOLADO) nb = 13,74 (VALOR INTERPOLADO) p. a2 e X = n Ma = 5,5x3,72 32,48 = 2,32 kn. m e Mb = 5,5x3,72 37,36 = 2,0 kn. m Xa = 5,5x3,72 13,02 = 5,78 kn. m e Xb = 5,5x3,72 13,74 = 5,48 kn. m 13
14 DESENHO ESQUEMÁTICO DAS REAÇÕES NAS LAJES: COMPENSAÇÃO DOS NEGATIVOS: 0,8x1648 = 1318,4 kn. cm X final(l1,l2) { ( ) X med = = 1201,5 kn. cm 2 X final(l1,l2) = 1318,4 kn. cm 0,8x797 = 637,6 kn. cm X final(l1,l4) { ( ) X med = = 687,5 kn. cm 2 X final(l1,l4) = 687,5 kn. cm 0,8x1648 = 1318,4 kn. cm X final(l4,l2) { ( ) X med = = 1098 kn. cm 2 X final(l4,l2) = 1318,4 kn. cm 14
15 CÁLCULO DAS ARMADURAS E DETALHAMENTO: AÇO CA-60 f yd = 60 = 52,17 kn/cm² 1,15 f c = σ cd = 0,85 f ck 2,5 = 0,85 = 1,52 kn/cm² 1,4 1,4 PARA A LAJE L1 E L4: d=h-2,5= 10-2,5= 7,5cm bw.h= 100x10 cm² PARA A LAJE L2 E L3: d=h-2,5= 12-2,5= 9,5cm bw.h= 100x12 cm² * M= 320 kn.cm K = M d f c bd 2 = 320x1,4 1,52x100x7,5 2 = 0,05 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 1,12 cm² (1 1 2K ) = 1,52x100x7,5 (1 1 2x0,05) 52,17 * ARMADURA MÍNIMA PARA MOMENTO POSITIVO E LAJE ARMADA EM DUAS DIREÇÕES: ASMÍN= 0,10%x100x10 = 1 cm²/m OK! * X= 1318,4 kn.cm K = M d f c bd 2 = A S = A S1 = f cbd f yd AS = 5,50 cm² 1318,4x1,4 1,52x100x7,5 2 = 0,22 < K L = 0,32 K = K (1 1 2K ) = 1,52x100x7,5 (1 1 2x0,22) 52,17 * ARMADURA MÍNIMA PARA MOMENTO NEGATIVO: ASMÍN= 0,15%x100x10 = 1,5 cm²/m OK! 15
16 * X= 687,5 kn.cm K = M d f c bd 2 = A S = A S1 = f cbd f yd AS = 2,55 cm² 687,5x1,4 1,52x100x7,5 2 = 0,11 < K L = 0,32 K = K (1 1 2K ) = 1,52x100x7,5 (1 1 2x0,11) 52,17 * ARMADURA MÍNIMA PARA MOMENTO NEGATIVO: ASMÍN= 0,15%x100x10 = 1,5 cm²/m OK! * M= 200 kn.cm K = M d f c bd 2 = 200x1,4 1,52x100x7,5 2 = 0,033 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 0,73 cm² (1 1 2K ) = 1,52x100x7,5 (1 1 2x0,033) 52,17 * ARMADURA MÍNIMA PARA MOMENTO POSITIVO E LAJE ARMADA EM DUAS DIREÇÕES: ASMÍN= 0,10%x100x10 = 1 cm²/m ADOTAR AS = 1,0 cm² * M= 232 kn.cm K = M d f c bd 2 = 232x1,4 1,52x100x7,5 2 = 0,038 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 0,85 cm² (1 1 2K ) = 1,52x100x7,5 (1 1 2x0,038) 52,17 * ARMADURA MÍNIMA PARA MOMENTO POSITIVO E LAJE ARMADA EM DUAS DIREÇÕES: ASMÍN= 0,10%x100x10 = 1 cm²/m ADOTAR AS = 1,0 cm² * M= 254 kn.cm K = M d f c bd 2 = 254x1,4 1,52x100x9,5 2 = 0,026 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 0,73 cm² (1 1 2K ) = 1,52x100x9,5 (1 1 2x0,026) 52,17 16
17 * ARMADURA MÍNIMA PARA MOMENTO POSITIVO E LAJE ARMADA EM DUAS DIREÇÕES: ASMÍN= 0,10%x100x12 = 1,2 cm²/m ADOTAR AS = 1,2 cm² * M= 796 kn.cm K = M d f c bd 2 = 796x1,4 1,52x100x9,5 2 = 0,081 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 2,34 cm² (1 1 2K ) = 1,52x100x9,5 (1 1 2x0,081) 52,17 * ARMADURA MÍNIMA PARA MOMENTO POSITIVO E LAJE ARMADA EM DUAS DIREÇÕES: ASMÍN= 0,10%x100x12 = 1,2 cm²/m OK! * X= 1220 kn.cm K = M d f c bd 2 = 1220x1,4 1,52x100x9,5 2 = 0,124 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 3,68 cm² (1 1 2K ) = 1,52x100x9,5 (1 1 2x0,124) 52,17 * ARMADURA MÍNIMA PARA MOMENTO NEGATIVO: ASMÍN= 0,15%x100x10 = 1,5 cm²/m OK! RESUMO: M (KN.cm) K As (cm²) Φ A C/ 320,0 0,050 1,12 Φ5 C/15 278,0 0,046 1,03 Φ5 C/ ,4 0,220 5,50 Φ8 C/10-687,5 0,110 2,55 Φ6.3 C/10 200,0 0,033 1,00 Φ5 C/15 232,0 0,038 1,00 Φ5 C/15 254,0 0,026 1,20 Φ5 C/ ,0 0,081 2,34 Φ6.3 C/ ,0 0,124 3,68 Φ8 C/
18 DETALHAMENTO DE TODAS AS LAJES: VERIFICAÇÃO DA FLECHA MÁXIMA DAS LAJES FLECHA MÁXIMA: PARA A LAJE L1: f = f 1 p a 4 E cs h³ 18
19 ψ2 = 0,3 (EDIFÍCIO RESIDENCIAL) pi = g + ψ2.q = 5,58+0,3x2= 6,18 kn/m² p = 2,46. pi = 2,46x6,18= 15,2 kn/m² = 15,2x10 4 kn/cm² f1=0,029 (TABELA PARA b/a=1,08 - LAJE TIPO C) DE ACORDO COM TABELA EM ANEXO: a=3,70m ma=32,48 M serv = pa2 ma = 6,18x3,72 = 2,60 kn. m = 260 kn. cm 32,48 M r = 150. f ctm. h 2 6 = 150x0,256x102 6 f ctm = 0,3(f ck ) 2/3 = 0,3x25 2/3 = 2,56 MPa = 0,256 kn/cn² EI eq =E cs. I c e h = h eq = 640 kn. cm M r = 640 kn. cm > M serv = 260 kn. cm estádio I E cs = 0,85x5600x f ck = 0,85x5600x 25 = MPa = 2380 kn/cm² f = 0,029x 15,2x10 4 x x10³ = 0,35cm < l 250 = 370 = 1,48 cm OK! 250 FLECHA MÁXIMA: ψ2 = 0,3 (EDIFÍCIO RESIDENCIAL) pi = g + ψ2.q = 5,19+0,3x2= 5,79 kn/m² PARA A LAJE L2: f = f 1 p a 4 E cs h³ p = 2,46. pi = 2,46x5,79= 14,24 kn/m² = 14,24x10 4 kn/cm² f1=0,053 (TABELA PARA b/a=1,67 1,70 - LAJE TIPO B) DE ACORDO COM TABELA EM ANEXO: a=4,44m ma=17,8 M serv = pa2 ma = 5,79x4,442 = 6,41 kn. m = 641 kn. cm 17,8 M r = 150. f ctm. h 2 6 = 150x0,256x122 6 f ctm = 0,3(f ck ) 2/3 = 0,3x25 2/3 = 2,56 MPa = 0,256 kn/cn² EI eq =E cs. I c e h = h eq 19 = 921,6 kn. cm M r = 921,6 kn. cm > M serv = 641 kn. cm estádio I
20 E cs = 0,85x5600x f ck = 0,85x5600x 25 = MPa = 2380 kn/cm² f = 0,053 14,24x10 4 x x12³ = 0,71cm < l 250 = 444 = 1,77 cm OK! 250 FLECHA MÁXIMA: PARA A LAJE L3: p = 2,46. pi = 2,46x5,23= 12,87 kn/m = 12,87x10 2 kn/cm I = b. h3 12 = = cm 4 * FLECHA DEVIDO À CARGA DISTRIBUÍDA δ = pl4 8EI = 12,87x10 2 x130 4 = 0,134 cm 8x2380x
21 * FLECHA DEVIDO À CARGA CONCENTRADA δ = pl3 3EI = 10,68x1303 = 0,23 cm 3x2380x14400 * FLECHA DEVIDO AO MOMENTO δ = Ml2 2EI = 236x1302 = 0,058 cm 2x2380x14400 f total = 0, ,23 + 0,058 = 0,42 cm f lim = 2. l 250 = 2x130 = 1,04 cm OK! 250 FLECHA MÁXIMA: ψ2 = 0,3 (EDIFÍCIO RESIDENCIAL) pi = g + ψ2.q = 3,5+0,3x2= 4,10 kn/m² PARA A LAJE L4: f = f 1 p a 4 E cs h³ p = 2,46. pi = 2,46x4,10= 10,09 kn/m² = 10,09x10 4 kn/cm² 21
22 f1=0,029 (TABELA PARA b/a=1,08 1,10 - LAJE TIPO C) DE ACORDO COM TABELA EM ANEXO: a=3,70m ma=32,48 M serv = pa2 ma = 4,10x3,72 = 1,73 kn. m = 173 kn. cm 32,48 M r = 150. f ctm. h 2 6 = 150x0,256x102 6 f ctm = 0,3(f ck ) 2/3 = 0,3x25 2/3 = 2,56 MPa = 0,256 kn/cn² EI eq =E cs. I c e h = h eq = 640 kn. cm M r = 640 kn. cm > M serv = 173 kn. cm estádio I E cs = 0,85x5600x f ck = 0,85x5600x 25 = MPa = 2380 kn/cm² f = 0,029 10,09x10 4 x x10³ = 0,23cm < VIGAS l 250 = 370 = 1,48 cm OK! 250 O CÁLCULO DE VIGAS ENGLOBA O DIMENSIONAMENTO DA SUA ALTURA E LARGURA DE SUA SEÇÃO RETA, A QUANTIDADE DE AÇO PARA AS ARMADURAS E A DIMENSÃO DE CADA BARRA. TODO PROCEDIMENTO DEVE LEVAR EM CONTA PARÂMETROS INICIAIS COMO: CARGAS, CONDIÇÕES DE APOIO, NÚMERO DE VÃOS, MATERIAIS UTILIZADOS, INTERAÇÃO ENTRE VÃOS E CONDIÇÕES DE ESTABILIDADE. CÁLCULO, DETALHAMENTO (FLEXÃO E CISALHAMENTO)E VERIFICAÇÃO À FISSURAÇÃO DAS VIGAS V1, V5 E V6. VIGA V5 CARGAS: PP = 0,2x0,5x25 = 2,5 kn/m ALVENARIA: 0,15x2,8x13 = 5,46 kn/m REAÇÕES TRAMO A = 6,45+15,86 = 22,31 kn/m REAÇÕES TRAMO B = 8,89+15,86 = 24,75 kn/m CARGA TOTAL TRAMO A = 5,46+2,5+22,31 = 30,27 kn/m CARGA TOTAL TRAMO B = 5,46+2,5+24,75 = 32,71 kn/m 22
23 CARREGAMENTO: DIAGRAMA DA FORÇA CORTANTE: DIAGRAMA DO MOMENTO FLETOR E REAÇÕES: * M= 28,4 kn.m K = CÁLCULO DA ARMADURA DE FLEXÃO M d f c bd 2 = 28,4x100x1,4 1,52x20x45 2 = 0,0646 < K L = 0,32 K = K A S = A S1 = f cbd f yd (1 1 2K ) = 1,52x20x45 (1 1 2x0,0646) 43,5 AS = 2,10 cm² 3 Φ10 = 2,36 cm² * ARMADURA MÍNIMA: ASMÍN= 0,15%x20x50 = 1,5 cm² OK! 23
24 * M= 32,3 kn.m K = M d f c bd 2 = 32,3x100x1,4 1,52x20x45 2 = 0,0735 < K L = 0,32 K = K A S = A S1 = f cbd f yd (1 1 2K ) = 1,52x20x45 (1 1 2x0,0735) 43,5 AS = 2,40 cm² 2 Φ12.5 = 2,45 cm² * ARMADURA MÍNIMA: ASMÍN= 0,15%x20x50 = 1,5 cm² OK! * X= 53,9 kn.m K = M d f c bd 2 = 53,9x100x1,4 1,52x20x45 2 = 0,122 < K L = 0,32 K = K A S = A S1 = f cbd f yd (1 1 2K ) = 1,52x20x45 (1 1 2x0,122) 43,5 AS = 4,10 cm² 4 Φ12.5 = 4,91 cm² * ARMADURA MÍNIMA: ASMÍN= 0,15%x20x50 = 1,5 cm² OK! * PARA MOMENTO X= 53,9 kn.m VERIFICAÇÃO DA FISSURAÇÃO 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = σ s = f yd. A scal = 43,5 γ f A sef 1,4. 4,10 = 25,95 kn/cm² 4,91 Acr=(5+7,5x1,25)x20 = 287,5 cm² ρ r = A e A cr = 4,91 287,5 = 0, ,5. η 1. σ s1 E s1. ( 4 ρ r + 45) w 1 = 12,5 12,5x2,25. 25, ( 4 0, ) = 0,153 mm < w k = 0,3mm OK! * PARA MOMENTO M= 32,3 kn.m 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = σ s = f yd. A scal = 43,5 γ f A sef 1,4. 2,4 = 30,44 kn/cm² 2, ,5. η 1. σ s1 E s1. ( 4 ρ r + 45)
25 Acr=(5+7,5x1,25)x20 = 287,5 cm² ρ r = A e A cr = 2,45 287,5 = 0,009 2a. VERIFICAÇÃO: w 2 = w 1 = 12,5 12,5x2,25. 30, ( 4 0, ) = 0,315 mm > w k = 0,3mm 12,5. η 1. σ s2 E s2. 3σ s2 f ctm = 12,5 12,5x2,25 x 3x30, x0,256 = 0,230 < w k = 0,3mm OK! * PARA MOMENTO M= 28,4 kn.m 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = σ s = f yd. A scal = 43,5 γ f A sef 1,4. 2,10 = 27,65 kn/cm² 2,36 Acr=(5+7,5x1)x20 = 250 cm² ρ r = A e A cr = 2, = 0,009 w 1 = 12,5. η 1. σ s1 E s1. ( 4 ρ r + 45) 10 12,5x2,25. 27, ( 4 0, ) = 0,229 mm < w k = 0,3mm OK! PARA fck=25 MPa: Vmáx = 75 kn CÁLCULO DA ARMADURA DE CISALHAMENTO - VERIFICAÇÃO DO CONCRETO: τ wd2 = 4,34 MPa = 0,434 kn/cm² τ wd = V d b w. d = 75x1,4 = 0,105 kn/cm² 20x50 τ wd < τ wd2 O CONCRETO ESTÁ VERIFICADO, OU SEJA, A BIELA COMPRIMIDA DE CONCRETO NÃO ROMPERÁ. - ARMADURA: PARA O ESTRIBO SIMPLES: τ wd min = 0,117 kn/cm² τ wd < τ wd min ρ w = ρ w min = 0,103 A sw = A sw min = ρ w min. b w = 0,103x20 = 2,06 cm²/m 25
26 A sw 2 = 2,06 = 1,03 cm²/m 2 ESPAÇAMENTO: 1, = 5,15 estribos = 5 c/ 17,5 0,2 5 5,15 ESPAÇAMENTO MÁXIMO: τ wd = 0,07 kn cm 2 < 0,67. τ wd2 = 0,67x0,434 = 0,29 kn cm 2 s = 0,67d 0,6. d = 0,6x50 = 30 cm s = 17,5 cm OK! { 30 cm * MOMENTO POSITIVO - VÃO 1 DETALHAMENTO: l b = 37,67. = 40 cm l b nec = α 1. l b. A s cal = 1x40x 2,10 = 36 cm A se 2,36 0,3. l b = 0,3x40 = 12 cm OK! l b min > { 10. = 10x1 = 10 cm 10 cm - VÃO 2 l b = 37,67. = 50 cm - APOIO INTERNO V = 75 kn l b nec = α 1. l b. A s cal = 1x50x 2,40 = 49 cm A se 2,45 0,3. l b = 0,3x50 = 15 cm OK! l b min > { 10. = 10x1,25 = 12,5 cm 10 cm A s cal = 0,5. V d = 0,50x 75x1,4 = 1,21 cm² f yd 43,5 NÚMERO DE BARRAS: Nb,vao/4 2 BARRAS NÚMERO DE BARRAS = 2 PARA BITOLA DE 12.5: l b 12.5 = 37,67. = 50 cm l b nec = α 1. l b. A s cal = 1x50x 1,21 = 25 cm A se 2,45 0,3. l b = 0,3x50 = 15 cm OK! l b min > { 10. = 10x1,25 = 12,5 cm 10 cm 26
27 PARA BITOLA DE 10: ADOTAR 3 φ 10: l b 10 = 37,67. = 40 cm l b nec = α 1. l b. A s cal = 1x40x 1,21 = 21 cm A se 2,36 0,3. l b = 0,3x40 = 12 cm OK! l b min > { 10. = 10x1 = 10 cm 10 cm - APOIO EXTERNO DIREITO V = 46 kn A s cal = 0,5. V d = 0,50x 46x1,4 = 0,74 cm² f yd 43,5 NÚMERO DE BARRAS: Nb,vao/4 2 BARRAS NÚMERO DE BARRAS = 2 - APOIO EXTERNO ESQUERDO V = 41,4 kn l b 10 = 37,67. = 50 cm l b nec = α 1. l b. A s cal = 1x50x 0,74 = 15 cm A se 2,45 0,3. l b = 0,3x50 = 15 cm OK! l b min > { 10. = 10x1,25 = 12,5 cm 10 cm A s cal = 0,5. V d = 0,50x 41,4x1,4 = 0,67 cm² f yd 43,5 NÚMERO DE BARRAS: Nb,vao/4 2 BARRAS NÚMERO DE BARRAS = 2 l b 10 = 37,67. = 40 cm * MOMENTO NEGATIVO l b nec = α 1. l b. A s cal = 1x40x 0,67 = 17 cm A se 1,57 0,3. l b = 0,3x40 = 12 cm OK! l b min > { 10. = 10x1 = 10 cm 10 cm l b = 37,67. = 50 cm 27
28 l b nec = 50 0,7 x 4,10 = 60 cm 4,91 0,3. l b = 0,3x50 = 15 cm OK! l b min > { 10. = 10x1,25 = 12,5 cm 10 cm VIGA V1 CARGAS: PP = 0,2x0,9x25 = 4,5 kn/m ALVENARIA: 0,15x2,8x13 = 5,46 kn/m REAÇÕES TRAMO ESQUERDO = 5,52 kn/m REAÇÕES TRAMO DIREITO = 5,84 kn/m CARGA TOTAL TRAMO ESQUERDO = 5,46+4,5+5,52 = 15,48 kn/m CARGA TOTAL TRAMO DIREITO = 5,46+4,5+5,84 = 15,8 kn/m 28
29 CARREGAMENTO: DIAGRAMA DA FORÇA CORTANTE: 29
30 DIAGRAMA DO MOMENTO FLETOR: * M= 219 kn.m CÁLCULO DA ARMADURA DE FLEXÃO 30
31 K = M d f c bd 2 = 219x100x1,4 1,52x20x85 2 = 0,14 < K L = 0,32 K = K A S = A S1 = f cbd f yd (1 1 2K ) = 1,52x20x85 (1 1 2x0,14) 43,5 AS = 9,0 cm² 3 Φ20 = 9,42 cm² * ARMADURA MÍNIMA: ASMÍN= 0,15%x20x90 = 2,7 cm² OK! * X= 16,6 kn.m (APOIO DIREITO E ESQUERDO) K = M d f c bd 2 = 16,6x100x1,4 1,52x20x85 2 = 0,01 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 0,60 cm² * ARMADURA MÍNIMA: (1 1 2K ) = 1,52x20x85 (1 1 2x0,01) 43,5 ASMÍN= 0,15%x20x90 = 2,7 cm² As= 2,7 cm² 4 Φ10 = 3,14 cm² * PARA MOMENTO X= 16,6 kn.m VERIFICAÇÃO DA FISSURAÇÃO 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = σ s = f yd. A scal = 43,5 γ f A sef 1,4. 2,7 = 26,72 kn/cm² 3,14 Acr=(7,5+5)x20 = 250 cm² ρ r = A e A cr = 3, = 0,0126 w 1 = 12,5. η 1. σ s1 E s1. ( 4 ρ r + 45) 10 12,5x2,25. 26, ( 4 0, ) = 0,164 mm < w k = 0,3mm OK! * PARA MOMENTO M= 219 kn.m 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = σ s = f yd. A scal = 43,5 γ f A sef 1,4. 9 = 29,69 kn/cm² 9,42 Acr=(5+7,5x2)x20 = 400 cm² 12,5. η 1. σ s1 E s1. ( 4 ρ r + 45) 31
32 ρ r = A e A cr = 9, = 0,0236 w 1 = 20 12,5x2,25. 26, ( 4 0, ) = 0,216 mm < w k = 0,3mm OK! CÁLCULO DA ARMADURA DE CISALHAMENTO PARA fck=25 MPa: Vmáx = 89,87 kn τ wd2 = 4,34 MPa = 0,434 kn/cm² - VERIFICAÇÃO DO CONCRETO: τ wd = V d b w. d = 89,87x1,4 = 0,07 kn/cm² 20x85 τ wd < τ wd2 O CONCRETO ESTÁ VERIFICADO, OU SEJA, A BIELA COMPRIMIDA DE CONCRETO NÃO ROMPERÁ. - ARMADURA: τ wd min = 0,117 kn/cm² τ wd < τ wd min ρ w = ρ w min = 0,103 A sw = A sw min = ρ w min. b w = 0,103x20 = 2,06 cm²/m PARA O ESTRIBO SIMPLES: ESPAÇAMENTO: A sw 2 = 2,06 = 1,03 cm²/m 2 1, = 5,15 estribos = 5 c/ 17,5 0,2 5 5,15 ESPAÇAMENTO MÁXIMO: τ wd = 0,07 kn cm 2 < 0,67. τ wd2 = 0,67x0,434 = 0,29 kn cm 2 s = 0,67d 0,6. d = 0,6x85 = 51 cm s = 17,5 cm OK! { 30 cm DETALHAMENTO: * MOMENTO POSITIVO l b = 37,67. = 80 cm 32
33 l b nec = α 1. l b. A s cal = 1x80x 9 = 77 cm A se 9,42 0,3. l b = 0,3x80 = 24 cm OK! l b min > { 10. = 10x2 = 20 cm 10 cm - APOIO EXTERNO DIREITO V = 88,1 kn A s cal = 0,5. V d = 0,50x 88,1x1,4 = 1,42 cm² f yd 43,5 NÚMERO DE BARRAS: Nb,vao/4 2 BARRAS NÚMERO DE BARRAS = 2 l b = 37,67. = 80 cm l b nec = α 1. l b. A s cal = 1x80x 1,42 = 18 cm A se 6,28 0,3. l b = 0,3x80 = 24 cm l b nec = 24 cm l b min > { 10. = 10x2 = 20 cm 10 cm - APOIO EXTERNO ESQUERDO V = 89,9 kn A s cal = 0,5. V d = 0,50x 89,9x1,4 = 1,45 cm² f yd 43,5 NÚMERO DE BARRAS: Nb,vao/4 2 BARRAS NÚMERO DE BARRAS = 2 * MOMENTO NEGATIVO l b 10 = 37,67. = 80 cm l b nec = α 1. l b. A s cal = 1x80x 1,45 = 19 cm A se 6,28 0,3. l b = 0,3x80 = 24 cm l b nec = 24 cm l b min > { 10. = 10x2 = 20 cm 10 cm l b = 37,67. = 40 cm * COSTELA A s,costela = 0,10% x face l b nec = 40 0,7 x 2,7 = 50 cm 3,14 0,3. l b = 0,3x40 = 12 cm OK! l b min > { 10. = 10x1 = 10 cm 10 cm A c = 0,10% x 20x90 face = 1,8 cm²
34 VIGA V6 CARGAS: PP = 0,2x0,9x25 = 4,5 kn/m ALVENARIA: 0,15x2,8x13 = 5,46 kn/m REAÇÕES DA LAJE L3= 9,16+13= 22,16 CARGA TOTAL = 5,46+4,5+22,16 = 32,12 kn/m CARREGAMENTO: 34
35 DIAGRAMA DA FORÇA CORTANTE: 35
36 DIAGRAMA DO MOMENTO FLETOR: CÁLCULO DA ARMADURA DE FLEXÃO * M= 204,6 kn.m 36
37 K = M d f c bd 2 = 204,6x100x1,4 1,52x20x85 2 = 0,13 < K L = 0,32 K = K A S = A S1 = f cbd f yd (1 1 2K ) = 1,52x20x85 (1 1 2x0,13) 43,5 AS = 8,30 cm² 3 Φ20 = 9,42 cm² * ARMADURA MÍNIMA: ASMÍN= 0,15%x20x90 = 2,7 cm² OK! * X= 15,2 kn.m (APOIO DIREITO E ESQUERDO) K = M d f c bd 2 = 15,2x100x1,4 1,52x20x85 2 = 0,01 < K L = 0,32 K = K A S = A S1 = f cbd f yd AS = 0,60 cm² (1 1 2K ) = 1,52x20x85 (1 1 2x0,01) 43,5 * ARMADURA MÍNIMA: ASMÍN= 0,15%x20x90 = 2,7 cm² As= 2,7 cm² 4 Φ10 = 3,14 cm² * PARA MOMENTO X= 15,2 kn.m VERIFICAÇÃO DA FISSURAÇÃO 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = σ s = f yd. A scal = 43,5 γ f A sef 1,4. 0,60 = 26,72 kn/cm² 3,14 Acr=(7,5+5)x20 = 250 cm² ρ r = A e A cr = 3, = 0,0126 w 1 = 12,5. η 1. σ s1 E s1. ( 4 ρ r + 45) 10 12,5x2,25. 26, ( 4 0, ) = 0,164 mm < w k = 0,3mm OK! * PARA MOMENTO M= 204,6 kn.m 1a. VERIFICAÇÃO: CONSIDERANDO CAA II wk 0,3 mm w 1 = 12,5. η 1. σ s1 E s1. ( 4 ρ r + 45) σ s = f yd. A scal = 43,5 γ f A sef 1,4. 8,3 = 27,4 kn/cm² 9,42 37
38 Acr=(5+7,5x2)x20 = 400 cm² ρ r = A e A cr = 9, = 0,0236 w 1 = 20 12,5x2,25. 27, ( 4 0, ) = 0,199 mm < w k = 0,3mm OK! CÁLCULO DA ARMADURA DE CISALHAMENTO PARA fck=25 MPa: Vmáx = 118,9 kn τ wd2 = 4,34 MPa = 0,434 kn/cm² - VERIFICAÇÃO DO CONCRETO: τ wd = V d b w. d = 118,9x1,4 = 0,098 kn/cm² 20x85 τ wd < τ wd2 O CONCRETO ESTÁ VERIFICADO, OU SEJA, A BIELA COMPRIMIDA DE CONCRETO NÃO ROMPERÁ. - ARMADURA: τ wd min = 0,117 kn/cm² τ wd < τ wd min ρ w = ρ w min = 0,103 A sw = A sw min = ρ w min. b w = 0,103x20 = 2,06 cm2 m PARA O ESTRIBO SIMPLES: ESPAÇAMENTO: A sw 2 = 2,06 = 1,03 cm²/m 2 1, = 5,15 estribos = 5 c/ 17,5 0,2 5 5,15 ESPAÇAMENTO MÁXIMO: τ wd = 0,07 kn cm 2 < 0,67. τ wd2 = 0,67x0,434 = 0,29 kn cm 2 s = 0,67d 0,6. d = 0,6x85 = 51 cm s = 17,5 cm OK! { 30 cm * MOMENTO POSITIVO DETALHAMENTO: 38
39 l b = 37,67. = 80 cm l b nec = α 1. l b. A s cal = 1x80x 8,30 = 71 cm A se 9,42 0,3. l b = 0,3x80 = 24 cm OK! l b min > { 10. = 10x2 = 20 cm 10 cm - APOIO EXTERNO DIREITO = ESQUERDO V = 118,8 kn A s cal = 0,5. V d = 0,50x 118,8x1,4 = 1,91 cm² f yd 43,5 NÚMERO DE BARRAS: Nb,vao/4 2 BARRAS NÚMERO DE BARRAS = 2 l b = 37,67. = 80 cm * MOMENTO NEGATIVO l b nec = α 1. l b. A s cal = 1x80x 1,91 = 25 cm A se 6,28 0,3. l b = 0,3x80 = 24 cm OK! l b min > { 10. = 10x2 = 20 cm 10 cm l b = 37,67. = 40 cm l b nec = 40 0,7 x 2,7 = 50 cm 3,14 0,3. l b = 0,3x40 = 12 cm OK! l b min > { 10. = 10x1 = 10 cm 10 cm * COSTELA A c A s,costela = 0,10% x face = 0,10% x 20x90 face = 1,8 cm²
40 5. CONCLUSÃO DE ACORDO COM O DETALHAMENTO DAS LAJES E VIGAS PODE SER DEDUZIDO QUE A ÁREA DA SEÇAO DE CONCRETO E ARMADURA UTILIZADAS ATENDEM AO CARREGAMENTO SOLICITANTE COM UM CONSUMO DE MATERIAIS CONSIDERADO MODERADO. ALÉM DISSO, É IMPORTANTE FRISAR, QUE O CÁLCULO FOI DESENVOLVIDO DE FORMA MANUAL E DE ACORDO COM A NORMA BRASILEIRA NBR 6118/2003. ATUALMENTE, AS ESTRUTURAS PODEM SER PROJETADAS COM O AUXÍLIO DE SOFTWARES QUE OFERECEM ALTO GRAU DE COMPLEXIDADE E SOFISTIFICAÇÃO DAS ANÁLISES. A UTILIZAÇÃO DE UMA FERRAMENTA COMPUTACIONAL, QUANDO FEITA DE MANEIRA RESPONSÁVEL E CRITERIOSA, TRAZ ENORMES VANTAGENS À ELABORAÇÃO DE UM PROJETO, TAIS COMO: PRODUTIVIDADE, QUALIDADE E SEGURANÇA. PORTANTO, É IMPORTANTE RECONHECER O APERFEIÇOAMENTO DA ENGENHARIA DE ESTRUTURAS ATRAVÉS DA INFORMÁTICA, MAS COM A CIÊNCIA QUE O SOFTWARE JAMAIS SUBSTITUIRÁ O PAPEL DO ENGENHEIRO. 40
41 6. NORMAS/BIBLIOGRAFIA ADOTADAS: - INFORMÁTICA APLICADA EM ESTRUTURAS DE CONCRETO ARMADO - ALIO KIMURA - CÁLCULO E DETALHAMENTO DE ESTRUTURAS USUAIS DE CONCRETO ARMADO - 3a. EDIÇÃO - ROBERTO CHUST CARVALHO E JASSON RODRIGUES DE FIGUEIREDO FILHO - APOSTILA DO CURSO DE ESPECIALIZAÇÃO EM ESTRUTURAS - PROJETO DE ESTRUTURAS DE CONCRETO I DO PROFESSOR: NEY AMORIM SILVA - NBR-6118/ PROJETO DE ESTRUTURAS DE CONCRETO - PROCEDIMENTO 7. ANEXO: ANEXO 41
42 42
43 43
44 44
45 45
e-mail: ederaldoazevedo@yahoo.com.br
 Assunto: Cálculo de Lajes Prof. Ederaldo Azevedo Aula 3 e-mail: ederaldoazevedo@yahoo.com.br 3.1. Conceitos preliminares: Estrutura é a parte ou o conjunto das partes de uma construção que se destina a
Assunto: Cálculo de Lajes Prof. Ederaldo Azevedo Aula 3 e-mail: ederaldoazevedo@yahoo.com.br 3.1. Conceitos preliminares: Estrutura é a parte ou o conjunto das partes de uma construção que se destina a
4. DIMENSIONAMENTO DE ESCADAS EM CONCRETO ARMADO
 4. DIMENSIONAMENTO DE ESCADAS EM CONCRETO ARMADO 4.1 Escada com vãos paralelos O tipo mais usual de escada em concreto armado tem como elemento resistente uma laje armada em uma só direção (longitudinalmente),
4. DIMENSIONAMENTO DE ESCADAS EM CONCRETO ARMADO 4.1 Escada com vãos paralelos O tipo mais usual de escada em concreto armado tem como elemento resistente uma laje armada em uma só direção (longitudinalmente),
ESTRUTURAS DE FUNDAÇÕES RASAS
 Universidade Federal de Ouro Preto - Escola de Minas Departamento de Engenharia Civil CIV620-Construções de Concreto Armado ESTRUTURAS DE FUNDAÇÕES RASAS Profa. Rovadávia Aline Jesus Ribas Ouro Preto,
Universidade Federal de Ouro Preto - Escola de Minas Departamento de Engenharia Civil CIV620-Construções de Concreto Armado ESTRUTURAS DE FUNDAÇÕES RASAS Profa. Rovadávia Aline Jesus Ribas Ouro Preto,
Universidade Estadual de Campinas Faculdade de Engenharia Civil Departamento de Estruturas. Elementos estruturais. Prof. MSc. Luiz Carlos de Almeida
 Universidade Estadual de Campinas Faculdade de Engenharia Civil Departamento de Estruturas Elementos estruturais Notas de aula da disciplina AU405 Concreto Prof. MSc. Luiz Carlos de Almeida Agosto/2006
Universidade Estadual de Campinas Faculdade de Engenharia Civil Departamento de Estruturas Elementos estruturais Notas de aula da disciplina AU405 Concreto Prof. MSc. Luiz Carlos de Almeida Agosto/2006
CÁLCULO DE VIGAS. - alvenaria de tijolos cerâmicos furados: γ a = 13 kn/m 3 ; - alvenaria de tijolos cerâmicos maciços: γ a = 18 kn/m 3.
 CAPÍTULO 5 Volume 2 CÁLCULO DE VIGAS 1 1- Cargas nas vigas dos edifícios peso próprio : p p = 25A c, kn/m ( c A = área da seção transversal da viga em m 2 ) Exemplo: Seção retangular: 20x40cm: pp = 25x0,20x0,40
CAPÍTULO 5 Volume 2 CÁLCULO DE VIGAS 1 1- Cargas nas vigas dos edifícios peso próprio : p p = 25A c, kn/m ( c A = área da seção transversal da viga em m 2 ) Exemplo: Seção retangular: 20x40cm: pp = 25x0,20x0,40
Módulo 5 Lajes: Estados Limites Últimos Estados Limites de Serviço Detalhamento Exemplo. Dimensionamento de Lajes à Punção
 NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo ELU e ELS Força Cortante em Dimensionamento de à Punção - Detalhamento - - Conclusões Estado Limite Último
NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo ELU e ELS Força Cortante em Dimensionamento de à Punção - Detalhamento - - Conclusões Estado Limite Último
CAPÍTULO 4 4. ELEMENTOS ESTRUTURAIS. 4.1 Classificação Geométrica dos Elementos Estruturais
 Elementos Estruturais 64 CAPÍTULO 4 4. ELEMENTOS ESTRUTURAIS 4.1 Classificação Geométrica dos Elementos Estruturais Neste item apresenta-se uma classificação dos elementos estruturais com base na geometria
Elementos Estruturais 64 CAPÍTULO 4 4. ELEMENTOS ESTRUTURAIS 4.1 Classificação Geométrica dos Elementos Estruturais Neste item apresenta-se uma classificação dos elementos estruturais com base na geometria
11 - PROJETO ESTRUTURAL DO EDIFÍCIO DA ENGENHARIA CIVIL
 11 - PROJETO ESTRUTURAL DO EDIFÍCIO DA ENGENHARIA CIVIL Fernando Musso Junior musso@npd.ufes.br Estruturas de Concreto Armado 216 11.1 - ARQUITETURA DO EDIFÍCIO Fernando Musso Junior musso@npd.ufes.br
11 - PROJETO ESTRUTURAL DO EDIFÍCIO DA ENGENHARIA CIVIL Fernando Musso Junior musso@npd.ufes.br Estruturas de Concreto Armado 216 11.1 - ARQUITETURA DO EDIFÍCIO Fernando Musso Junior musso@npd.ufes.br
2.0 O PROJETO DE LAJES PROTENDIDAS - SÍNTESE
 LAJES PLANAS PROTENDIDAS: DETERMINAÇÃO DA FORÇA DE PROTENSÃO E PRÉ-DIMENSIONAMENTO DOS CABOS UM PROCESSO PRÁTICO 1.0 - INTRODUÇÃO Nos projetos de lajes protendidas, as armaduras a serem determinadas resultam
LAJES PLANAS PROTENDIDAS: DETERMINAÇÃO DA FORÇA DE PROTENSÃO E PRÉ-DIMENSIONAMENTO DOS CABOS UM PROCESSO PRÁTICO 1.0 - INTRODUÇÃO Nos projetos de lajes protendidas, as armaduras a serem determinadas resultam
e-mail: ederaldoazevedo@yahoo.com.br
 Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Disciplina: Sistemas Estruturais em Concreto Armado Disciplina: Sistemas Estruturais em Concreto Armado Assunto: Dimensionamento de
Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Disciplina: Sistemas Estruturais em Concreto Armado Disciplina: Sistemas Estruturais em Concreto Armado Assunto: Dimensionamento de
Módulo 4 Vigas: Estados Limites Últimos Estados Limites de Serviço Detalhamento Exemplo. Segurança em Relação aos ELU e ELS
 NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo Segurança em Relação aos ELU e ELS ELU Solicitações Normais ELU Elementos Lineares Sujeitos à Força Cortante
NBR 6118 : Estados Limites Últimos Estados Limites de Serviço Detalhamento P R O M O Ç Ã O Conteúdo Segurança em Relação aos ELU e ELS ELU Solicitações Normais ELU Elementos Lineares Sujeitos à Força Cortante
Estribos verticais: 2 Largura X: 45.0 cm Ø10 CA-50-A P9, P10, P11, Largura Y: 45.0 cm
 1 MEMÓRIA DE CÁLCULO - ESTRUTURAL 4.1 MEMÓRIA DE CÁLCULO FUNDAÇÕES 4.1.1 DESCRIÇÃO Referências Estacas Material Geometria Armadura P1, P2, P3, P4, Tipo: 18x18 Concreto: C25, Bloco de 1 estaca Estribos
1 MEMÓRIA DE CÁLCULO - ESTRUTURAL 4.1 MEMÓRIA DE CÁLCULO FUNDAÇÕES 4.1.1 DESCRIÇÃO Referências Estacas Material Geometria Armadura P1, P2, P3, P4, Tipo: 18x18 Concreto: C25, Bloco de 1 estaca Estribos
Resumo. Palavras-chave. Concreto Armado; Pórtico Plano; Dimensionamento; Otimização. Introdução
 Procedimento Numérico para Busca do Dimensionamento Otimizado de Pórticos Planos de Concreto Armado Wilson T. Rosa Filho 1, Maria Cecilia A. Teixeira da Silva 2, Francisco A. Menezes 3 1 Universidade Estadual
Procedimento Numérico para Busca do Dimensionamento Otimizado de Pórticos Planos de Concreto Armado Wilson T. Rosa Filho 1, Maria Cecilia A. Teixeira da Silva 2, Francisco A. Menezes 3 1 Universidade Estadual
Tecnologia da Construção Civil - I Fundações. Roberto dos Santos Monteiro
 Tecnologia da Construção Civil - I Fundações Após a execução da sondagem, iremos definir qual o tipo de fundação mais adequada a ser utilizado no nosso empreendimento. As Fundações são elementos estruturais
Tecnologia da Construção Civil - I Fundações Após a execução da sondagem, iremos definir qual o tipo de fundação mais adequada a ser utilizado no nosso empreendimento. As Fundações são elementos estruturais
LAJES MACIÇAS DE CONCRETO ARMADO
 CAPÍTULOS 1 A 4 Volume LAJES MACIÇAS DE CONCRETO ARMADO 1 1- Tipos usuais de lajes dos edifícios Laje h Laje maciça apoiada em vigas Vigas h Lajes nervuradas nervuras aparentes material inerte Laje Laje
CAPÍTULOS 1 A 4 Volume LAJES MACIÇAS DE CONCRETO ARMADO 1 1- Tipos usuais de lajes dos edifícios Laje h Laje maciça apoiada em vigas Vigas h Lajes nervuradas nervuras aparentes material inerte Laje Laje
Detalhamento de Concreto Armado
 Detalhamento de Concreto Armado (Exemplos Didáticos) José Luiz Pinheiro Melges Ilha Solteira, março de 2009 Exercícios - Detalhamento 1 1. DIMENSIONAR E DETALHAR A VIGA ABAIXO. 1.1 DADOS A princípio, por
Detalhamento de Concreto Armado (Exemplos Didáticos) José Luiz Pinheiro Melges Ilha Solteira, março de 2009 Exercícios - Detalhamento 1 1. DIMENSIONAR E DETALHAR A VIGA ABAIXO. 1.1 DADOS A princípio, por
Matrizes de Transferência de Forças e Deslocamentos para Seções Intermediárias de Elementos de Barra
 Matrizes de Transferência de Forças e Deslocamentos para Seções Intermediárias de Elementos de Barra Walter Francisco HurtaresOrrala 1 Sílvio de Souza Lima 2 Resumo A determinação automatizada de diagramas
Matrizes de Transferência de Forças e Deslocamentos para Seções Intermediárias de Elementos de Barra Walter Francisco HurtaresOrrala 1 Sílvio de Souza Lima 2 Resumo A determinação automatizada de diagramas
ESCADAS USUAIS DOS EDIFÍCIOS
 Volume 4 Capítulo 3 ESCDS USUIS DOS EDIFÍCIOS 1 3.1- INTRODUÇÃO patamar lance a b c d e Formas usuais das escadas dos edifícios armada transversalmente armada longitudinalmente armada em cruz V3 V4 Classificação
Volume 4 Capítulo 3 ESCDS USUIS DOS EDIFÍCIOS 1 3.1- INTRODUÇÃO patamar lance a b c d e Formas usuais das escadas dos edifícios armada transversalmente armada longitudinalmente armada em cruz V3 V4 Classificação
APÊNDICE 2 TABELAS PARA O CÁLCULO DE LAJES
 APÊNDICE 2 TABELAS PARA O CÁLCULO DE LAJES 338 Curso de Concreto Armado 1. Lajes retangulares apoiadas no contorno As tabelas A2.1 a A2.6 correspondem a lajes retangulares apoiadas ao longo de todo o contorno
APÊNDICE 2 TABELAS PARA O CÁLCULO DE LAJES 338 Curso de Concreto Armado 1. Lajes retangulares apoiadas no contorno As tabelas A2.1 a A2.6 correspondem a lajes retangulares apoiadas ao longo de todo o contorno
Exemplo de Análise de Tabuleiro com duas Vigas
 Exemplo de Análise de Tabuleiro com duas Vigas 1 Introdução Mostra-se no que segue um exemplo de determinação das solicitações permanentes e móveis das longarinas que formam juntamente com a laje e a transversina
Exemplo de Análise de Tabuleiro com duas Vigas 1 Introdução Mostra-se no que segue um exemplo de determinação das solicitações permanentes e móveis das longarinas que formam juntamente com a laje e a transversina
Cálculo de Lajes Retangulares de Concreto Armado MANUAL DO USUÁRIO. Apresentação 2. Observações gerais sobre o software 2. Formas de trabalho 3
 ÍNDICE Assunto Página Apresentação 2 Observações gerais sobre o software 2 Formas de trabalho 3 Fluxo das informações 4 Laje isolada 4 Geometria 6 Vinculação 6 Cargas 7 Configuração 8 Resultados 10 Impressão
ÍNDICE Assunto Página Apresentação 2 Observações gerais sobre o software 2 Formas de trabalho 3 Fluxo das informações 4 Laje isolada 4 Geometria 6 Vinculação 6 Cargas 7 Configuração 8 Resultados 10 Impressão
1 ESTRUTURAS DE CONCRETO ARMANDO 1.1 INTRODUÇÃO
 1 ESTRUTURAS DE CONCRETO ARMANDO 1.1 INTRODUÇÃO Estrutura de concreto armado é a denominação de estruturas compostas de concreto, cimento + água + agregados (e às vezes + aditivos) com barras de aço no
1 ESTRUTURAS DE CONCRETO ARMANDO 1.1 INTRODUÇÃO Estrutura de concreto armado é a denominação de estruturas compostas de concreto, cimento + água + agregados (e às vezes + aditivos) com barras de aço no
UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil. Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV
 UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV NOTAS DE AULA MARQUISES Prof. Dr. PAULO SÉRGIO DOS SANTOS
UNIVERSIDADE ESTADUAL PAULISTA UNESP Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1365 - ESTRUTURAS DE CONCRETO IV NOTAS DE AULA MARQUISES Prof. Dr. PAULO SÉRGIO DOS SANTOS
Fau USP PEF 604. Estruturas em aço. Prof. Francisco Paulo Graziano. Baseado em anotações e apresentações do Prof. Waldir Pignata
 Fau USP PEF 604 Estruturas em aço Baseado em anotações e apresentações do Prof. Waldir Pignata Disponibilidade de produtos Tipo de Aço f y f u (MPa) (MPa) ASTM A-36 250 400 ASTM A-570 250 360 (Gr 36) COS-AR-COR
Fau USP PEF 604 Estruturas em aço Baseado em anotações e apresentações do Prof. Waldir Pignata Disponibilidade de produtos Tipo de Aço f y f u (MPa) (MPa) ASTM A-36 250 400 ASTM A-570 250 360 (Gr 36) COS-AR-COR
Capítulo1 Tensão Normal
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Referências Bibliográficas:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Referências Bibliográficas:
UNIVERSIDADE DE SÃO PAULO
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS Departamento de Engenharia de Estruturas CONCRETO ARMADO: ESCADAS José Luiz Pinheiro Melges Libânio Miranda Pinheiro José Samuel Giongo Março
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS Departamento de Engenharia de Estruturas CONCRETO ARMADO: ESCADAS José Luiz Pinheiro Melges Libânio Miranda Pinheiro José Samuel Giongo Março
MODOS DE RUÍNA EM VIGA (COLAPSO)
 MODOS DE RUÍNA EM VIGA (COLAPSO) É NECESSÁRIO GARANTIR O ELU ESTADO LIMITE ÚLTIMO 1. RUÍNA POR FLEXÃO (MOMENTO FLETOR ARMADURA LONGITUDINAL); 2. RUPTURA POR ESMAGAMENTO DA BIELA DE CONCRETO; 3. RUPTURA
MODOS DE RUÍNA EM VIGA (COLAPSO) É NECESSÁRIO GARANTIR O ELU ESTADO LIMITE ÚLTIMO 1. RUÍNA POR FLEXÃO (MOMENTO FLETOR ARMADURA LONGITUDINAL); 2. RUPTURA POR ESMAGAMENTO DA BIELA DE CONCRETO; 3. RUPTURA
Lajes de Edifícios de Concreto Armado
 Lajes de Edifícios de Concreto Armado 1 - Introdução As lajes são elementos planos horizontais que suportam as cargas verticais atuantes no pavimento. Elas podem ser maciças, nervuradas, mistas ou pré-moldadas.
Lajes de Edifícios de Concreto Armado 1 - Introdução As lajes são elementos planos horizontais que suportam as cargas verticais atuantes no pavimento. Elas podem ser maciças, nervuradas, mistas ou pré-moldadas.
Distribuição de Cargas Verticais
 Distribuição de Cargas Verticais Disponível em http://www.chasqueweb.ufrgs.br/~jeanmarie/eng01208/eng01208.html jean.marie@ufrgs.br Funções das paredes de alvenaria Compressão axial Transmite as cargas
Distribuição de Cargas Verticais Disponível em http://www.chasqueweb.ufrgs.br/~jeanmarie/eng01208/eng01208.html jean.marie@ufrgs.br Funções das paredes de alvenaria Compressão axial Transmite as cargas
As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados.
 LAJES DE CONCRETO ARMADO 1. Unidirecionais As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados. 1.1 Lajes em balanço Lajes em balanço são unidirecionais
LAJES DE CONCRETO ARMADO 1. Unidirecionais As lajes de concreto são consideradas unidirecionais quando apenas um ou dois lados são considerados apoiados. 1.1 Lajes em balanço Lajes em balanço são unidirecionais
3.6.1. Carga concentrada indireta (Apoio indireto de viga secundária)
 cisalhamento - ELU 22 3.6. rmadura de suspensão para cargas indiretas 3.6.1. Carga concentrada indireta (poio indireto de viga secundária) ( b w2 x h 2 ) V 1 ( b w1 x h 1 ) V d1 - viga com apoio ndireto
cisalhamento - ELU 22 3.6. rmadura de suspensão para cargas indiretas 3.6.1. Carga concentrada indireta (poio indireto de viga secundária) ( b w2 x h 2 ) V 1 ( b w1 x h 1 ) V d1 - viga com apoio ndireto
6 Vigas: Solicitações de Flexão
 6 Vigas: Solicitações de Fleão Introdução Dando seqüência ao cálculo de elementos estruturais de concreto armado, partiremos agora para o cálculo e dimensionamento das vigas à fleão. Ações As ações geram
6 Vigas: Solicitações de Fleão Introdução Dando seqüência ao cálculo de elementos estruturais de concreto armado, partiremos agora para o cálculo e dimensionamento das vigas à fleão. Ações As ações geram
PROJETO DE ESCADAS DE CONCRETO ARMADO
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE ESCADAS DE CONCRETO ARMADO AMÉRICO CAMPOS FILHO 04 SUMÁRIO Introdução... Escadas com vãos paralelos...
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE ESCADAS DE CONCRETO ARMADO AMÉRICO CAMPOS FILHO 04 SUMÁRIO Introdução... Escadas com vãos paralelos...
Prof. Wendell Diniz Varela, D.Sc.
 Universidade Federal do Rio de Janeiro Curso: Arquitetura e Urbanismo Disciplina: Estruturas de Concreto Armado II Prof. Wendell Diniz Varela, D.Sc. Contatos Prof. Wendell Diniz Varela Departamento de
Universidade Federal do Rio de Janeiro Curso: Arquitetura e Urbanismo Disciplina: Estruturas de Concreto Armado II Prof. Wendell Diniz Varela, D.Sc. Contatos Prof. Wendell Diniz Varela Departamento de
Recomendações para a Elaboração do Projeto Estrutural
 Universidade Estadual de Maringá - Centro de Tecnologia Departamento de Engenharia Civil Disciplina: Estruturas em Concreto I Professor: Rafael Alves de Souza Recomendações para a Elaboração do Projeto
Universidade Estadual de Maringá - Centro de Tecnologia Departamento de Engenharia Civil Disciplina: Estruturas em Concreto I Professor: Rafael Alves de Souza Recomendações para a Elaboração do Projeto
Projetos na construção civil. Projetos na construção civil. Projeto Arquitetônico. Projeto Arquitetônico Planta Baixa. Projeto Arquitetônico
 Universidade Federal do Espírito Santo Centro Tecnológico Departamento de Engenharia Civil Tecnologia da Construção Civil I Elementos constitutivos de um projeto interpretação, exame e análise Projeto
Universidade Federal do Espírito Santo Centro Tecnológico Departamento de Engenharia Civil Tecnologia da Construção Civil I Elementos constitutivos de um projeto interpretação, exame e análise Projeto
PROJETO DE ESCADAS DE CONCRETO ARMADO
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE ESCADAS DE CONCRETO ARMADO AMÉRICO CAMPOS FILHO 0 SUMÁRIO Introdução... Escadas com vãos paralelos...
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL ESCOLA DE ENGENHARIA DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE ESCADAS DE CONCRETO ARMADO AMÉRICO CAMPOS FILHO 0 SUMÁRIO Introdução... Escadas com vãos paralelos...
CÁLCULO DE ESTAQUEAMENTO PLANO POR MEIO DE
 CÁLCULO DE ESTAQUEAMENTO PLANO POR MEIO DE PLANILHAS ELETRÔNICAS T. R. Ferreira 1, B. C. S. Lopes 2, R. K. Q. Souza 3, R. G. Delalibera 4 Engenharia Civil Campus Catalão 1. tobias.trf@hotmail.com; 2. bcs_90@hotmail.com;
CÁLCULO DE ESTAQUEAMENTO PLANO POR MEIO DE PLANILHAS ELETRÔNICAS T. R. Ferreira 1, B. C. S. Lopes 2, R. K. Q. Souza 3, R. G. Delalibera 4 Engenharia Civil Campus Catalão 1. tobias.trf@hotmail.com; 2. bcs_90@hotmail.com;
cs-41 RPN calculator Mac OS X CONCRETO ARMADO J. Oliveira Arquiteto Baseado nas normas ABNT NBR-6118 e publicações de Aderson Moreira da Rocha
 cs-41 RPN calculator Mac OS X CONCRETO ARMADO J. Oliveira Arquiteto Baseado nas normas ABNT NBR-6118 e publicações de Aderson Moreira da Rocha MULTIGRAFICA 2010 Capa: foto do predio do CRUSP em construção,
cs-41 RPN calculator Mac OS X CONCRETO ARMADO J. Oliveira Arquiteto Baseado nas normas ABNT NBR-6118 e publicações de Aderson Moreira da Rocha MULTIGRAFICA 2010 Capa: foto do predio do CRUSP em construção,
Fundações Diretas Rasas
 Fundações Diretas Rasas Grupo: Anderson Martens Daniel Pereira Ricardo N. Lima Ronaldo Guedes Vitor A. Teruya Vivian R. Pestana Professor Manoel Vitor O que são fundações? Elementos estruturais cuja função
Fundações Diretas Rasas Grupo: Anderson Martens Daniel Pereira Ricardo N. Lima Ronaldo Guedes Vitor A. Teruya Vivian R. Pestana Professor Manoel Vitor O que são fundações? Elementos estruturais cuja função
Professor: José Junio Lopes
 Aula 2 - Tensão/Tensão Normal e de Cisalhamento Média; Tensões Admissíveis. A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a.
Aula 2 - Tensão/Tensão Normal e de Cisalhamento Média; Tensões Admissíveis. A - Tensão Normal Média 1. Exemplo 1.17 - A luminária de 80 kg é sustentada por duas hastes, AB e BC, como mostra a Figura 1.17a.
LT 500kV MARIMBONDO - ASSIS MEMORIAL DO PROJETO BÁSICO DE FUNDAÇÕES
 24/09/2013 Complementação torres MF SA 0A 03/05/2013 Emissão Inicial MF SA Rev. Data Descrição Por Aprovação Nome da Obra Título do Documento Projeto MARCOS F. 24/09/2013 Nº Rev Folha 1/13 Aprovação SÉRGIO
24/09/2013 Complementação torres MF SA 0A 03/05/2013 Emissão Inicial MF SA Rev. Data Descrição Por Aprovação Nome da Obra Título do Documento Projeto MARCOS F. 24/09/2013 Nº Rev Folha 1/13 Aprovação SÉRGIO
CISALHAMENTO EM VIGAS CAPÍTULO 13 CISALHAMENTO EM VIGAS
 CISALHAMENTO EM VIGAS CAPÍTULO 13 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 25 ago 2010 CISALHAMENTO EM VIGAS Nas vigas, em geral, as solicitações predominantes são o momento fletor e
CISALHAMENTO EM VIGAS CAPÍTULO 13 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 25 ago 2010 CISALHAMENTO EM VIGAS Nas vigas, em geral, as solicitações predominantes são o momento fletor e
PERFIL COLABORANTE. Dimensionamento
 PERFIL COLABORANTE Dimensionamento O dimensionamento da laje mista, usando o perfil COLABORANTE, pode ser feito através da consulta, por parte do projectista, de tabelas de dimensionamento de uso directo,
PERFIL COLABORANTE Dimensionamento O dimensionamento da laje mista, usando o perfil COLABORANTE, pode ser feito através da consulta, por parte do projectista, de tabelas de dimensionamento de uso directo,
Exemplo de projeto estrutural
 Planta de formas do pavimento tipo Exemplo de projeto estrutural P1-30x30 P2-20x50 P3-30x30 V1 L1 L2 P4-20x50 P5-40x40 P-20x50 V2 Estruturas de Concreto Armado Prof. José Milton de Araújo L3 480 cm 480
Planta de formas do pavimento tipo Exemplo de projeto estrutural P1-30x30 P2-20x50 P3-30x30 V1 L1 L2 P4-20x50 P5-40x40 P-20x50 V2 Estruturas de Concreto Armado Prof. José Milton de Araújo L3 480 cm 480
Laje de concreto com esferas plásticas
 Laje de concreto com esferas plásticas Augusto Freire, engenheiro civil, diretor técnico da BubbleDeck Brasil BubbleDeck é um sistema construtivo formado por esferas plásticas contidas entre uma pré-laje
Laje de concreto com esferas plásticas Augusto Freire, engenheiro civil, diretor técnico da BubbleDeck Brasil BubbleDeck é um sistema construtivo formado por esferas plásticas contidas entre uma pré-laje
Estruturas de Concreto Armado. Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com
 Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
Vão Livre ( o ): distância entre faces internas dos apoios. (No geral: = distância entre os eixos dos apoios). EXEMPLO 01:
 01. DEFINIÇÃO Modulo 02-1 Módulo 02 - Lajes Placa: elem//tos de superfície plana, em geral horizontais, sujeitos principalmente a ações perpendiculares ao seu plano. Lajes: são placas de concreto armado
01. DEFINIÇÃO Modulo 02-1 Módulo 02 - Lajes Placa: elem//tos de superfície plana, em geral horizontais, sujeitos principalmente a ações perpendiculares ao seu plano. Lajes: são placas de concreto armado
ES015 - Projeto de Estruturas Assistido por Computador: Cálculo e Detalhamento
 Escola Politécnica da Universidade de São Paulo Departamento de Engenharia de Estruturas e Fundações ES015 - Projeto de Estruturas Assistido por Computador: Cálculo e Detalhamento Prof. Túlio Nogueira
Escola Politécnica da Universidade de São Paulo Departamento de Engenharia de Estruturas e Fundações ES015 - Projeto de Estruturas Assistido por Computador: Cálculo e Detalhamento Prof. Túlio Nogueira
Módulo 6 Pilares: Estados Limites Últimos Detalhamento Exemplo. Imperfeições Geométricas Globais. Imperfeições Geométricas Locais
 NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
Artigo submetido ao Curso de Engenharia Civil da UNESC - como requisito parcial para obtenção do Título de Engenheiro Civil
 ANÁLISE DO DIMENSIONAMENTO DE PILARES DE CONCRETO ARMADO PELO MÉTODO DO PILAR PADRÃO COM RIGIDEZ κ APROXIMADA E PELO MÉTODO DO PILAR PADRÃO COM CURVATURA APROXIMADA PARA EFEITOS DE 2º ORDEM Augusto Figueredo
ANÁLISE DO DIMENSIONAMENTO DE PILARES DE CONCRETO ARMADO PELO MÉTODO DO PILAR PADRÃO COM RIGIDEZ κ APROXIMADA E PELO MÉTODO DO PILAR PADRÃO COM CURVATURA APROXIMADA PARA EFEITOS DE 2º ORDEM Augusto Figueredo
TQS - SISEs Parte 10 Fundações em bloco sobre 3 estacas sem baldrame e sobre 1 estaca com baldra
 Palavras-chave: SISEs, bloco sobre estacas, pórtico espacial, baldrames. Seguindo o assunto da Interação entre estrutura, fundação e solo, vamos apresentar agora out ras duas possíveis soluções, tendo
Palavras-chave: SISEs, bloco sobre estacas, pórtico espacial, baldrames. Seguindo o assunto da Interação entre estrutura, fundação e solo, vamos apresentar agora out ras duas possíveis soluções, tendo
1.1 Conceitos fundamentais... 19 1.2 Vantagens e desvantagens do concreto armado... 21. 1.6.1 Concreto fresco...30
 Sumário Prefácio à quarta edição... 13 Prefácio à segunda edição... 15 Prefácio à primeira edição... 17 Capítulo 1 Introdução ao estudo das estruturas de concreto armado... 19 1.1 Conceitos fundamentais...
Sumário Prefácio à quarta edição... 13 Prefácio à segunda edição... 15 Prefácio à primeira edição... 17 Capítulo 1 Introdução ao estudo das estruturas de concreto armado... 19 1.1 Conceitos fundamentais...
1 INTRODUÇÃO 3 2 DIRETRIZES DE CÁLCULO 3 3 MATERIAIS 3 4 DOCUMENTOS DE REFERÊNCIA 3 5 GERADOR DE IMPULSO E DIVISOR DE TENSÃO DE 6,4 MV 4
 Documento: Cliente: MEMÓRIA DE CÁLCULO CEPEL CENTRO DE PESQUISAS DE ENERGIA ELÉTRICA SISTEMA ELETROBRAS LDIST-ST-A4-002-0 Pag: 1 of 32 Título: EQUIPAMENTOS E FUNDAÇÕES PARA PÓRTICOS TECHNIP ENGENHARIA
Documento: Cliente: MEMÓRIA DE CÁLCULO CEPEL CENTRO DE PESQUISAS DE ENERGIA ELÉTRICA SISTEMA ELETROBRAS LDIST-ST-A4-002-0 Pag: 1 of 32 Título: EQUIPAMENTOS E FUNDAÇÕES PARA PÓRTICOS TECHNIP ENGENHARIA
detalhamento da armadura longitudinal da viga
 conteúdo 36 detalhamento da armadura longitudinal da viga 36.1 Decalagem do diagrama de momentos fletores (NBR6118/2003 Item 17.4.2.2) Quando a armadura longitudinal de tração for determinada através do
conteúdo 36 detalhamento da armadura longitudinal da viga 36.1 Decalagem do diagrama de momentos fletores (NBR6118/2003 Item 17.4.2.2) Quando a armadura longitudinal de tração for determinada através do
UNIVERSIDADE DE SÃO PAULO
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS Departamento de Engenharia de Estruturas CONCRETO ARMADO: ESCADAS José Luiz Pinheiro Melges Libânio Miranda Pinheiro José Samuel Giongo Março
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS Departamento de Engenharia de Estruturas CONCRETO ARMADO: ESCADAS José Luiz Pinheiro Melges Libânio Miranda Pinheiro José Samuel Giongo Março
Efeito do comportamento reológico do concreto
 Efeito do comportamento reológico do concreto FLECHAS E ELEENTOS DE CONCRETO ARADO 1 - INTRODUÇÃO Todo o cálculo das deformações de barras, devidas à fleão, tem por base a clássica equação diferencial
Efeito do comportamento reológico do concreto FLECHAS E ELEENTOS DE CONCRETO ARADO 1 - INTRODUÇÃO Todo o cálculo das deformações de barras, devidas à fleão, tem por base a clássica equação diferencial
e-mail: ederaldoazevedo@yahoo.com.br
 Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
A dissertação é dividida em 6 capítulos, incluindo este capítulo 1 introdutório.
 1 Introdução A escolha racional dos sistemas estruturais em projetos de galpões industriais é um fator de grande importância para o desenvolvimento de soluções padronizadas e competitivas. No mercado brasileiro
1 Introdução A escolha racional dos sistemas estruturais em projetos de galpões industriais é um fator de grande importância para o desenvolvimento de soluções padronizadas e competitivas. No mercado brasileiro
2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 2012 Duração prevista: até 4 horas.
 2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 212 Duração prevista: até 4 horas. Esta prova tem oito (8) questões e três (3) laudas. Consulta permitida somente ao formulário básico.
2 a Prova de EDI-49 Concreto Estrutural II Prof. Flávio Mendes Junho de 212 Duração prevista: até 4 horas. Esta prova tem oito (8) questões e três (3) laudas. Consulta permitida somente ao formulário básico.
Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/
 Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/ Estrutura Sistema qualquer de elementos ligados, construído para suportar ou transferir
Aula 09 Análise Estrutural - Treliça Capítulo 6 R. C. Hibbeler 10ª Edição Editora Pearson - http://www.pearson.com.br/ Estrutura Sistema qualquer de elementos ligados, construído para suportar ou transferir
Ancoragem e Emenda de Armaduras
 UNESP - Bauru/SP Disciplina 1309 - Estruturas de Concreto II - Ancoragem e Emenda de Armaduras 1 Ancoragem e Emenda de Armaduras 1. ADERÊNCIA ENTRE CONCRETO E ARMADURA Uma ótima aderência entre a armadura
UNESP - Bauru/SP Disciplina 1309 - Estruturas de Concreto II - Ancoragem e Emenda de Armaduras 1 Ancoragem e Emenda de Armaduras 1. ADERÊNCIA ENTRE CONCRETO E ARMADURA Uma ótima aderência entre a armadura
Instruções básicas para a análise de um pórtico 2D com o programa ROBOT Estruturas de Betão 2
 Instruções básicas para a análise de um pórtico 2D com o programa ROBOT Mário Pimentel Pretende-se analisar um dos pórticos intermédios do Bloco B da Residência Universitária do Campo Alegre no Porto.
Instruções básicas para a análise de um pórtico 2D com o programa ROBOT Mário Pimentel Pretende-se analisar um dos pórticos intermédios do Bloco B da Residência Universitária do Campo Alegre no Porto.
UNIDADE 2 DIMENSIONAMENTO DE ESTRUTURAS DE CONCRETO ARMADO
 Universidade Federal de Pelotas Centro de Engenharias Curso de Engenharia Civil e Engenharia Agrícola UNIDADE 2 DIMENSIONAMENTO DE ESTRUTURAS DE CONCRETO ARMADO (AULA 3 HIPÓTESES DE CÁLCULO) Prof. Estela
Universidade Federal de Pelotas Centro de Engenharias Curso de Engenharia Civil e Engenharia Agrícola UNIDADE 2 DIMENSIONAMENTO DE ESTRUTURAS DE CONCRETO ARMADO (AULA 3 HIPÓTESES DE CÁLCULO) Prof. Estela
DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T
 DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T Hevânio D. de Almeida a b, Rafael A. Guillou a,, Cleilson F. Bernardino
DESENVOLVIMENTO DE PROGRAMA COMPUTACIONAL PARA CÁLCULO E DIMENSIONAMENTO DE POSTES DE CONCRETO ARMADO COM SEÇÃO TRANSVERSAL DUPLO T Hevânio D. de Almeida a b, Rafael A. Guillou a,, Cleilson F. Bernardino
A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO
 A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO Marcos Alberto Ferreira da Silva (1) ; Jasson Rodrigues de Figueiredo Filho () ; Roberto Chust Carvalho ()
A UTILIZAÇÃO DA ANALOGIA DE GRELHA PARA ANÁLISE DE PAVIMENTOS DE EDIFÍCIOS EM CONCRETO ARMADO Marcos Alberto Ferreira da Silva (1) ; Jasson Rodrigues de Figueiredo Filho () ; Roberto Chust Carvalho ()
AÇO PARA CONSTRUÇÃO CIVIL
 AÇO PARA CONSTRUÇÃO CIVIL GG 0 O vergalhão que está por dentro das melhores obras. VERGALHÃO GERDAU GG 0 Para o seu projeto sair do papel com segurança e qualidade, use o Vergalhão Gerdau GG 0. Produzido
AÇO PARA CONSTRUÇÃO CIVIL GG 0 O vergalhão que está por dentro das melhores obras. VERGALHÃO GERDAU GG 0 Para o seu projeto sair do papel com segurança e qualidade, use o Vergalhão Gerdau GG 0. Produzido
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny
 Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
ESTUDO COMPARATIVO ENTRE AÇO E CONCRETO PROTENDIDO NO DIMENSIONAMENTO DA SUPERESTRUTURA DE UMA PONTE FERROVIÁRIA
 ESTUDO COPARATIVO ENTRE AÇO E CONCRETO PROTENDIDO NO DIENSIONAENTO DA SUPERESTRUTURA DE UA PONTE FERROVIÁRIA Glauco José de Oliveira Rodrigues, D.Sc. Cooenação de Pós Graduação e Pesquisa / Engenharia
ESTUDO COPARATIVO ENTRE AÇO E CONCRETO PROTENDIDO NO DIENSIONAENTO DA SUPERESTRUTURA DE UA PONTE FERROVIÁRIA Glauco José de Oliveira Rodrigues, D.Sc. Cooenação de Pós Graduação e Pesquisa / Engenharia
ANÁLISE COMPARATIVA ENTRE DOIS SOFTWARES COMERCIAIS PARA DIMENSIONAMENTO DE ESTRUTURAS EM CONCRETO ARMADO.
 Artigo submetido ao Curso de Engenharia Civil da UNESC ANÁLISE COMPARATIVA ENTRE DOIS SOFTWARES COMERCIAIS PARA DIMENSIONAMENTO DE ESTRUTURAS EM CONCRETO ARMADO. Marcos Roberto de Souza (1), Alexandre
Artigo submetido ao Curso de Engenharia Civil da UNESC ANÁLISE COMPARATIVA ENTRE DOIS SOFTWARES COMERCIAIS PARA DIMENSIONAMENTO DE ESTRUTURAS EM CONCRETO ARMADO. Marcos Roberto de Souza (1), Alexandre
TORÇÃO EM VIGAS DE CONCRETO ARMADO
 UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 33 - ESTRUTURAS DE CONCRETO II Notas de Aula TORÇÃO EM VIGAS DE CONCRETO ARMADO
UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 33 - ESTRUTURAS DE CONCRETO II Notas de Aula TORÇÃO EM VIGAS DE CONCRETO ARMADO
VIGAS E LAJES DE CONCRETO ARMADO
 UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Curso: Arquitetura e Urbanismo Disciplina: 6033 - SISTEMAS ESTRUTURAIS I Notas de Aula
UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Curso: Arquitetura e Urbanismo Disciplina: 6033 - SISTEMAS ESTRUTURAIS I Notas de Aula
Resumidamente, vamos apresentar o que cada item influenciou no cálculo do PumaWin.
 Software PumaWin principais alterações O Software PumaWin está na versão 8.2, as principais mudanças que ocorreram ao longo do tempo estão relacionadas a inclusão de novos recursos ou ferramentas, correção
Software PumaWin principais alterações O Software PumaWin está na versão 8.2, as principais mudanças que ocorreram ao longo do tempo estão relacionadas a inclusão de novos recursos ou ferramentas, correção
Tabela 1.1 FLEXÃO SIMPLES EM SEÇÃO RETANGULAR - ARMADURA SIMPLES
 Tabela. FLEXÃO SIMPLES EM SEÇÃO RETANGULAR - ARMADURA SIMPLES β x c = d k c = bd M (cm / kn) C0 C5 C0 C5 C30 C35 C40 C45 d 0,0 03, 69, 5,9 4,5 34,6 9,7 5,9 3, 0, 0,046 0,03 0,09 0,04 5,3 34,9 6, 0,9 7,4
Tabela. FLEXÃO SIMPLES EM SEÇÃO RETANGULAR - ARMADURA SIMPLES β x c = d k c = bd M (cm / kn) C0 C5 C0 C5 C30 C35 C40 C45 d 0,0 03, 69, 5,9 4,5 34,6 9,7 5,9 3, 0, 0,046 0,03 0,09 0,04 5,3 34,9 6, 0,9 7,4
Sistemas mistos aço-concreto viabilizando estruturas para Andares Múltiplos
 viabilizando estruturas para Andares Múltiplos Vantagens Com relação às estruturas de concreto : -possibilidade de dispensa de fôrmas e escoramentos -redução do peso próprio e do volume da estrutura -aumento
viabilizando estruturas para Andares Múltiplos Vantagens Com relação às estruturas de concreto : -possibilidade de dispensa de fôrmas e escoramentos -redução do peso próprio e do volume da estrutura -aumento
Artigo submetido ao Curso de Engenharia Civil da UNESC - Como requisito parcial para obtenção do Título de Engenheiro Civil
 Como requisito parcial para obtenção do Título de Engenheiro Civil AVALIAÇÃO DO COMPORTAMENTO DE UMA ESTRUTURA DE CONCRETO ARMADO ANALISANDO A RIGIDEZ DO ENGASTAMENTO ENTRE VIGAS E PILARES E UTILIZANDO
Como requisito parcial para obtenção do Título de Engenheiro Civil AVALIAÇÃO DO COMPORTAMENTO DE UMA ESTRUTURA DE CONCRETO ARMADO ANALISANDO A RIGIDEZ DO ENGASTAMENTO ENTRE VIGAS E PILARES E UTILIZANDO
tecfix ONE quartzolit
 Pág. 1 de 8 Adesivo para ancoragem à base de resina epóxi-acrilato 1. Descrição: Produto bicomponente disposto numa bisnaga com câmaras independentes, projetada para realizar a mistura adequada dos constituintes
Pág. 1 de 8 Adesivo para ancoragem à base de resina epóxi-acrilato 1. Descrição: Produto bicomponente disposto numa bisnaga com câmaras independentes, projetada para realizar a mistura adequada dos constituintes
RELATÓRIO VISTORIA NA ESTRUTURA DO CARTÓRIO ELEITORAL DE GURINHÉM - SEARQ
 PODER JUDICIÁRIO TRIBUNAL REGIONAL ELEITORAL DA PARAÍBA Secretaria de Administração e Orçamento Seção de Engenharia e Arquitetura / COSEG RELATÓRIO VISTORIA NA ESTRUTURA DO CARTÓRIO ELEITORAL DE GURINHÉM
PODER JUDICIÁRIO TRIBUNAL REGIONAL ELEITORAL DA PARAÍBA Secretaria de Administração e Orçamento Seção de Engenharia e Arquitetura / COSEG RELATÓRIO VISTORIA NA ESTRUTURA DO CARTÓRIO ELEITORAL DE GURINHÉM
ANÁLISE DE LAJES E VIGAS DE UM EDIFÍCIO USANDO O SISTEMA CAD/TQS
 ANÁLISE DE LAJES E VIGAS DE UM EDIFÍCIO USANDO O SISTEMA CAD/TQS Ricardo Jaques Benzecry Projeto de Graduação apresentado ao Curso de Engenharia Civil da Escola Politécnica, Universidade Federal do Rio
ANÁLISE DE LAJES E VIGAS DE UM EDIFÍCIO USANDO O SISTEMA CAD/TQS Ricardo Jaques Benzecry Projeto de Graduação apresentado ao Curso de Engenharia Civil da Escola Politécnica, Universidade Federal do Rio
O conhecimento das dimensões permite determinar os vãos equivalentes e as rigidezes, necessários no cálculo das ligações entre os elementos.
 PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
Mecânica Geral. Aula 05 - Equilíbrio e Reação de Apoio
 Aula 05 - Equilíbrio e Reação de Apoio 1 - Equilíbrio de um Ponto Material (Revisão) Condição de equilíbrio de um Ponto Material Y F 0 F X 0 e F 0 Exemplo 01 - Determine a tensão nos cabos AB e AD para
Aula 05 - Equilíbrio e Reação de Apoio 1 - Equilíbrio de um Ponto Material (Revisão) Condição de equilíbrio de um Ponto Material Y F 0 F X 0 e F 0 Exemplo 01 - Determine a tensão nos cabos AB e AD para
INFLUÊNCIA DO TIPO DE LAJE NO DIMENSIONAMENTO DE VIGAS MISTAS.
 UNIVERSIDADE ESTADUAL DE FEIRA DE SANTANA DEPARTAMENTO DE TECNOLOGIA COLEGIADO ENGENHARIA CIVIL RAPHAEL LIMA DE SOUZA INFLUÊNCIA DO TIPO DE LAJE NO DIMENSIONAMENTO DE VIGAS MISTAS. FEIRA DE SANTANA 2011
UNIVERSIDADE ESTADUAL DE FEIRA DE SANTANA DEPARTAMENTO DE TECNOLOGIA COLEGIADO ENGENHARIA CIVIL RAPHAEL LIMA DE SOUZA INFLUÊNCIA DO TIPO DE LAJE NO DIMENSIONAMENTO DE VIGAS MISTAS. FEIRA DE SANTANA 2011
OE Seminário Aplicação do Eurocódigo 8 ao Projecto de Edifícios Projecto de estruturas para resistência aos sismos EC8-1
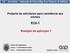 Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 1 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 1 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
UTILIZAÇÃO DE GEOTÊXTIL BIDIM EM MURO MISTO DE SOLO REFORÇADO E SOLO GRAMPEADO NA BASE SÃO JOSÉ DOS CAMPOS SP
 UTILIZAÇÃO DE GEOTÊXTIL BIDIM EM MURO MISTO DE SOLO REFORÇADO E SOLO GRAMPEADO NA BASE SÃO JOSÉ DOS CAMPOS SP Autor: Departamento Técnico - Atividade Bidim PERÍODO 2005 Revisado ABRIL 2011 - Departamento
UTILIZAÇÃO DE GEOTÊXTIL BIDIM EM MURO MISTO DE SOLO REFORÇADO E SOLO GRAMPEADO NA BASE SÃO JOSÉ DOS CAMPOS SP Autor: Departamento Técnico - Atividade Bidim PERÍODO 2005 Revisado ABRIL 2011 - Departamento
TORÇÃO EM VIGAS DE CONCRETO ARMADO
 UNESP(Bauru/SP) 1309 - Estruturas de Concreto II - Torção em Vigas de Concreto rmado 1 TORÇÃO EM VIGS DE CONCRETO RMDO 1. INTRODUÇÃO Um conjugado que tende a torcer uma peça fazendo-a girar sobre o seu
UNESP(Bauru/SP) 1309 - Estruturas de Concreto II - Torção em Vigas de Concreto rmado 1 TORÇÃO EM VIGS DE CONCRETO RMDO 1. INTRODUÇÃO Um conjugado que tende a torcer uma peça fazendo-a girar sobre o seu
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA POLITÉCNICA Curso de Engenharia Civil Departamento de Mecânica Aplicada e Estruturas
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA POLITÉCNICA Curso de Engenharia Civil Departamento de Mecânica Aplicada e Estruturas PROJETO DE ESTRUTURAS COM GRANDES VARANDAS EDUARDO VIEIRA DA COSTA Projeto
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ESCOLA POLITÉCNICA Curso de Engenharia Civil Departamento de Mecânica Aplicada e Estruturas PROJETO DE ESTRUTURAS COM GRANDES VARANDAS EDUARDO VIEIRA DA COSTA Projeto
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL MARCOS ANDREW RABELO SOEIRO
 i UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL MARCOS ANDREW RABELO SOEIRO PÓS-PROCESSADOR PARA DIMENSIONAMENTO E VERIFICAÇÃO DE BARRAS DE
i UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA ESTRUTURAL E CONSTRUÇÃO CIVIL MARCOS ANDREW RABELO SOEIRO PÓS-PROCESSADOR PARA DIMENSIONAMENTO E VERIFICAÇÃO DE BARRAS DE
DIMENSIONAMENTO DE ELEMENTOS DE ESTRUTURAS DE AÇO USANDO MÉTODOS
 Contribuição técnica nº 5 ESTUDO NUMÉRICO-EXPERIMENTAL DE LIGAÇÕES PARAFUSADAS COM CHAPA DE TOPO ENTRE VIGA METÁLICA DE SEÇÃO I E PILAR MISTO PREENCHIDO COM CONCRETO NUMÉRICOS DE SEÇÃO QUADRADA DIMENSIONAMENTO
Contribuição técnica nº 5 ESTUDO NUMÉRICO-EXPERIMENTAL DE LIGAÇÕES PARAFUSADAS COM CHAPA DE TOPO ENTRE VIGA METÁLICA DE SEÇÃO I E PILAR MISTO PREENCHIDO COM CONCRETO NUMÉRICOS DE SEÇÃO QUADRADA DIMENSIONAMENTO
Fundações e Estruturas Especiais. Módulo III. Pavimentos Industriais BASES PARA DIMENSIONAMENTO. Fundações e Estruturas Especiais
 Módulo III Pavimentos Industriais BASES PARA DIMENSIONAMENTO João Veludo 1 Índice 1. Materiais. Cargas 3. Determinação da espessura do pavimento 4. Juntas 5. Exemplos de dimensionamento João Veludo 1 Índice
Módulo III Pavimentos Industriais BASES PARA DIMENSIONAMENTO João Veludo 1 Índice 1. Materiais. Cargas 3. Determinação da espessura do pavimento 4. Juntas 5. Exemplos de dimensionamento João Veludo 1 Índice
Pontifícia Universidade Católica do Rio Grande do Sul. Faculdade de Engenharia FACULDADE DE ARQUITETURA E URBANISMO SISTEMAS ESTRUTURAIS II
 Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Engenharia FACULDADE DE ARQUITETURA E URBANISMO SISTEMAS ESTRUTURAIS II COMENTÁRIOS Norma NBR 6118/2007 Prof. Eduardo Giugliani 1 0. COMENTÁRIOS
Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Engenharia FACULDADE DE ARQUITETURA E URBANISMO SISTEMAS ESTRUTURAIS II COMENTÁRIOS Norma NBR 6118/2007 Prof. Eduardo Giugliani 1 0. COMENTÁRIOS
Referências Bibliográficas
 Referências Bibliográficas 1 KAEFER, L. F. Desenvolvimento de uma ferramenta gráfica para análise de pórticos de concreto armado. São Paulo, 2000. Dissertação de Mestrado Escola Politécnica da Universidade
Referências Bibliográficas 1 KAEFER, L. F. Desenvolvimento de uma ferramenta gráfica para análise de pórticos de concreto armado. São Paulo, 2000. Dissertação de Mestrado Escola Politécnica da Universidade
Lajes pré-fabricadas em situação de incêndio Ms. Kleber Aparecido Gomide Prof. Dr. Armando Lopes Moreno Jr
 Lajes pré-fabricadas em situação de incêndio Ms. Kleber Aparecido Gomide Prof. Dr. Armando Lopes Moreno Jr Universidade Estadual de Campinas UNICAMP Faculdade de Engenharia Civil, Arquitetura e Urbanismo
Lajes pré-fabricadas em situação de incêndio Ms. Kleber Aparecido Gomide Prof. Dr. Armando Lopes Moreno Jr Universidade Estadual de Campinas UNICAMP Faculdade de Engenharia Civil, Arquitetura e Urbanismo
ANÁLISE COMPARATIVA DE UMA ESTRUTURA DE EDIFÍCIO EM LAJE LISA PELOS PROGRAMAS SAP2000 E EBERICK
 Universidade Federal do Rio de Janeiro ANÁLISE COMPARATIVA DE UMA ESTRUTURA DE EDIFÍCIO EM LAJE LISA PELOS PROGRAMAS SAP2000 E EBERICK Danilo de Araujo Canaes 2013 ANÁLISE COMPARATIVA DE UMA ESTRUTURA
Universidade Federal do Rio de Janeiro ANÁLISE COMPARATIVA DE UMA ESTRUTURA DE EDIFÍCIO EM LAJE LISA PELOS PROGRAMAS SAP2000 E EBERICK Danilo de Araujo Canaes 2013 ANÁLISE COMPARATIVA DE UMA ESTRUTURA
PROJETO DE DIMENSIONAMENTO DE UM EDIFÍCIO CONTENDO UM LABORATÓRIO DE ENSAIOS MECÂNICOS LOCALIZADO NA UENF, NO MUNICÍPIO DE CAMPOS DOS GOYTACAZES
 PROJETO DE DIMENSIONAMENTO DE UM EDIFÍCIO CONTENDO UM LABORATÓRIO DE ENSAIOS MECÂNICOS LOCALIZADO NA UENF, NO MUNICÍPIO DE CAMPOS DOS GOYTACAZES ANA BEATRIZ CARVALHO E SILVA THAIS RIBEIRO BARROSO UNIVERSIDADE
PROJETO DE DIMENSIONAMENTO DE UM EDIFÍCIO CONTENDO UM LABORATÓRIO DE ENSAIOS MECÂNICOS LOCALIZADO NA UENF, NO MUNICÍPIO DE CAMPOS DOS GOYTACAZES ANA BEATRIZ CARVALHO E SILVA THAIS RIBEIRO BARROSO UNIVERSIDADE
ABNT NBR 7680:2015 Concreto Extração, preparo, ensaio e análise de testemunhos de estruturas de concreto Parte 1: Resistência à compressão
 ABNT NBR 7680:2015 Concreto Extração, preparo, ensaio e análise de testemunhos de estruturas de concreto Parte 1: Resistência à compressão Eng.º Felipe C. Bungenstab, M.Sc. Brascontec Engenharia e Tecnologia
ABNT NBR 7680:2015 Concreto Extração, preparo, ensaio e análise de testemunhos de estruturas de concreto Parte 1: Resistência à compressão Eng.º Felipe C. Bungenstab, M.Sc. Brascontec Engenharia e Tecnologia
INDICE 3.CÁLCULO PELO MÉTODO SIMPLIFICADO X CÁLCULO COMO PLACAS ISOLADAS...5
 INDICE 1.INTRODUÇÃO 3 2.OBJETIVO 4 3.CÁLCULO PELO MÉTODO SIMPLIFICADO X CÁLCULO COMO PLACAS ISOLADAS...5 3.1 Caixa d`água Vazia...... 6 3.1.1 Parede XZ (Par 1 e Par 3)... 7 3.1.2. Parede YZ (Par 4 e Par
INDICE 1.INTRODUÇÃO 3 2.OBJETIVO 4 3.CÁLCULO PELO MÉTODO SIMPLIFICADO X CÁLCULO COMO PLACAS ISOLADAS...5 3.1 Caixa d`água Vazia...... 6 3.1.1 Parede XZ (Par 1 e Par 3)... 7 3.1.2. Parede YZ (Par 4 e Par
TORÇÃO EM VIGAS DE CONCRETO ARMADO
 UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1309 - ESTRUTURAS DE CONCRETO II Notas de Aula TORÇÃO EM VIGAS DE CONCRETO
UNIVERSIDADE ESTADUAL PAULISTA UNESP - Campus de Bauru/SP FACULDADE DE ENGENHARIA Departamento de Engenharia Civil Disciplina: 1309 - ESTRUTURAS DE CONCRETO II Notas de Aula TORÇÃO EM VIGAS DE CONCRETO
ESPECIFICAÇÃO DE SERVIÇO
 ESPECIFICAÇÃO DE SERVIÇO BUEIROS CELULARES DE CONCRETO Grupo de Serviço DRENAGEM Código DERBA-ES-D-010/01 1. OBJETIVO Esta especificação de serviço tem por objetivo definir e orientar a execução de bueiros
ESPECIFICAÇÃO DE SERVIÇO BUEIROS CELULARES DE CONCRETO Grupo de Serviço DRENAGEM Código DERBA-ES-D-010/01 1. OBJETIVO Esta especificação de serviço tem por objetivo definir e orientar a execução de bueiros
VERIFICAÇÃO VERIFICAÇÃO DE FLECHAS EM VIGAS CONCRETO ARMADO
 5 VRIFICAÇÃO VRIFICAÇÃO D FCHAS VIGAS CONCRTO ARADO 1/79 111 5.1 DSOCANTOS TS NBR 6118:2003/13.3 5.1.1 ACITABIIDAD SNSORIA RAZÕS DA TAÇÃO XPOS DSOCA. T DSOCANTO A CONSIDRAR Visual Deslocamentos em elementos
5 VRIFICAÇÃO VRIFICAÇÃO D FCHAS VIGAS CONCRTO ARADO 1/79 111 5.1 DSOCANTOS TS NBR 6118:2003/13.3 5.1.1 ACITABIIDAD SNSORIA RAZÕS DA TAÇÃO XPOS DSOCA. T DSOCANTO A CONSIDRAR Visual Deslocamentos em elementos
Practical formulas for calculation of deflections of reinforced concrete beams
 Teoria e Prática na Engenharia Civil, n.18, p.6-70 Novembro, 011 Fórmulas práticas para cálculo de flechas de vigas de concreto armado Practical formulas for calculation of deflections of reinforced concrete
Teoria e Prática na Engenharia Civil, n.18, p.6-70 Novembro, 011 Fórmulas práticas para cálculo de flechas de vigas de concreto armado Practical formulas for calculation of deflections of reinforced concrete
