8. Síntese de Imagens: Cálculo de Cor
|
|
|
- Diana Fagundes Estrada
- 8 Há anos
- Visualizações:
Transcrição
1 8. Síntese de Imagens: Cálculo de Cor O processo de determinar a aparência (ou seja, a textura e a cor) das superfícies visíveis é chamado de shading. Essa aparência da superfície depende das propriedades da superfície (textura, reflectância, etc.), do tipo de fonte de luz que ilumina o objeto, e da sua posição relativa à fonte de luz e ao observador. Apesar da existência de diversos algoritmos, não existe uma solução geral para o problema do realismo visual, incluindo-se aí o ocultamento das faces e o shading. Devemos buscar soluções específicas, em função dos requisitos das aplicações, evitando a busca de soluções generalíssimas. Cor e Iluminação A iluminação é uma técnica importante em objetos gráficos criados através do computador. Sem iluminação os objetos tendem a não apresentar características realistas. O princípio da iluminação consiste em simular como os objetos refletem as luzes. Alguns modelos de iluminação de uma cena envolvem basicamente três aspectos: -propriedades dos materiais que formam as superfícies dos objetos -propriedades de luzes, definidas a partir das fontes de luz inseridas na cena -parâmetros globais de iluminação, que depende do ambiente no qual os objetos estão inseridos. Apesar de o estudo e descrição de cor ser um assunto amplo, podemos simplificar uma cor com sendo matematicamente um vetor 3D formado por três componentes R, G e B que indicam respectivamente a quantidade de vermelho, verde e azul que compôem tal cor. Esta definição de cor será necessária pois todo o cálculo de iluminação envolve o uso de cores. O modelo de iluminação aqui descrito é baseado em um modelo chamado de iluminação de Phong. Em cada vértice da primitiva, uma cor é calculada usando as propriedades dos materiais junto com as propriedades das luzes envolvidas. Para este cálculo é utilizado um modelo geométrico semelhante ao da figura 8.3 para a incidência e reflexão da luz sobre os objetos.
2 Fig. 8.3 Geometria do Modelo de Iluminação A cor para o vértice é calculada como sendo a soma de quatro outras cores. Estas quatro cores que contribuem para a cor final do vértice são: Iluminação Ambiente, Componente Difusa, Luz Especular e Emissião. A) Iluminação Ambiente: representa a luz do ambiente no qual se encontram os objetos. Não é resultante de nenhum fonte de luz especificamente, mas é o resultado global de toda iluminação do ambiente (luz solar, reflexão indireta de todos os objetos da cena, etc). Com isto ela vem de todas as direções. Normalmente é muito difícil calcular esta luz computacionalmente. Uma solução simples é fornecer o valor desta luz como um dado de entrada. Fig. 8.4 Iluminação Global B) Luz Difusa: é a luz que vem de uma direção, ou seja, de uma determinada fonte de luz que se encontra na cena. Uma vez que esta luz incida em uma superfície, é difundida igualmente em todas as direções, assim a superfície aparece igualmente luminosa, não importando de onde é visualizada. Qualquer luz vindo de uma posição particular ou direção tem provavelmente uma componente difusa. Fig. 8.5 Iluminação Difusa. C) Luz Especular: luz que vem de uma direção, ou seja de uma fonte de luz, e tende a ser refletida numa única direção;
3 Fig. 8.6 Iluminação Esécular. D) Luz Emissiva: simula a luz que se origina do próprio objeto; a cor emissiva de uma superfície adiciona intensidade ao objeto, mas não é afetada por qualquer fonte de luz; ela também não introduz luz adicional da cena. É importante destacar que as propriedades globais de iluminação incluem a definição da luz ambiente resultante (independente das fontes de luz que se encontram na cena). Já as propriedades locais de cada fonte de luz podem incluir a sua cor (contribuição) ambiental, sua contribuição difusa e sua contribuição especular, dentre outras propriedades. As propriedades locais do material que forma os objetos também indicam como eles refletem a luz ambiente, a luz difusa e a luz especular, além de definir como deve ser este brilho especular, e como eles emitem sua própria luz, etc Como o OpenGL simula a Iluminação Para adicionar luz a uma cena são necessários os seguintes passos : Definir os vetores normais para cada vértice do objeto Criar, selecionar, e posicionar uma ou mais fontes de luz. Criar e selecionar um modelo de iluminação que define a luz ambiente global e a localização efetiva do ponto de visão. Definir as propriedades dos materiais que compõem os objetos na cena A) Definição do Vetores Normais Os vetores normais devem ser definidos para cada vértice de todos os objetos. Estes vetores determinam a orientação do objeto relativo às fontes de luz. A última seção deste capítulo mostra como calcular os vetores normais. Uma vez calculada a normal de um vértice, ela dirá ao OpenGL como o objeto reflete luz ao redor deste vértice. Imaginando que exista um espelho pequeno no vértice, a normal descreve como o espelho é orientado, e por conseguinte como a luz é refletida. A função glnormal3f recebe as três coordenadas do vetor normal que é usada no calculo de iluminação para todos os vertices até uma nova normal ser configurada. void glnormal3f (float nx, flota ny, floatr nz);
4 Este função deve ser chamada antes de desenhar o vértice (glvertex). Lembre-se que OpenGl é uma máquina de estado, logo se um próximo vértice tiver outra normal, então deve-se fazer outra chamada de glnormal. B) Criação, Seleção e Posicionamento de Fontes de Luz Lembremos que cada fonte de luz possui propriedades locais como contribuição ambiental, difusa e especular. Estas contrinuições na verdade são cores (vetor 3D). Outras propriedades incluem posição da fonte de luz e atenuação da luz à medida em que se afasta da fonte. A função gllightf é usada para fixar essas propriedade ou parâmetros para uma fonte de luz. O OpenGL permite a implementação de até oito luzes que são nomeadas como GL_LIGHT0 até GL_LIGHTn onde n é um menos o número máximo suportado. As propriedades de cores (ambiental, difusa, especular) permitem interações separadas com as diferentes propriedades dos materiais. Propriedades de posicionamento controlam a localização e o tipo da luz e a atenuação controla a tendência natural da luz deteriorar-se sobre a distância. A função gllightf tem a seguinte definição: void gllightf(int light, int pname, float param); ou void gllightfv(int light, int pname, float *param); A diferença entre gllightf e gllightfv é que enquanto o parâmetro param do primeiro é um float, o parâmetro param do segundo deve ser um vetor de floats. Ambas as funções criam uma luz especificada pelo parâmetro light que pode ser GL_LIGHT0 GL_LIGHT1,..., ou GL_LIGHT7. A propriedade da luz que está sendo setada é definida por pname que determina uma propriedade nomeada conforme tabela abaixo. param indica os valores para os quais a propriedade pname é fixada; param é um ponteiro para um grupo de valores se a versão de vetor é usada (gllightfv, com v no final), ou o próprio valor se a versão não vetorial for usada (gllightf, sem v no final).
5 Perceba, na tabela, que as propriedades GL_AMBIENT, GL_DIFFUSE,GL_SPECULAR, GL_POSITION e GL_SPOT_EXPOENT requerem um vetor de floats, logo devem ser especificadas com aversão vetorial da função, ou seja, com gllightfv (com v no final). Já as demias propriedades requerem apenas um valor e desvem ser setadas com a versão não vetorial, ou seja, com gllightf. Exemplo: Neste exemplo uma cor possui 4 parametros: alem do R,G e B, há um parametro para inidicar transparencia, mas nao se preocupe com este ultimo agora. float luz_ambiente[]= {0.0,0.0,0.0,1.0}; //Cor preta R=0.0,G=0.0,B=0.0 float luz_difusa[] = {1.0,1.0,1.0,1.0}; //Cor branca R=1.0,G=1.0,B=1.0 float luz_epecular[] = {1.0,1.0,1.0,1.0};//Cor branca R=1.0,G=1.0,B=1.0 float luz_posicao[] = { 1.0, 1.0, 1.0, 0.0 }; gllightfv(gl_light0, GL_AMBIENT, luz_ambiente); gllightfv(gl_light0, GL_DIFFUSE, luz_difusa); gllightfv(gl_light0, GL_SPECULAR, luz_epecular); gllightfv(gl_light0, GL_POSITION, luz_posicao); C) Criação e Seleção de Modelo de Iluminação Estas propriedades incluem as que não são diretamente conectadadas com materiais ou luzes. Estas propriedades incluem : Cor ambiente global, que inicia a contribuição global do ambiente na equação de iluminação.
6 Modo de visualização local, que desabilita a otimização mas que provê mais rapidamente os cálculos de iluminação. Iluminação de um ou dos dois lados de cada face do objeto. O comando usado para especificar todas as propriedades do modelo de iluminação é gllightmodelf. Esta função tem dois argumentos: a propriedade do modelo de iluminação e o valor desejado para aquela propriedade. void gllightmodelf(int pname, float param); ou void gllightmodelfv(int pname, float *param); A versão terminada em v indica que o segundo parâmetro é um vetor de floats em vez de um só valor. Estas funções especificam as propriedades do modelo de iluminação. O parâmetro pname indica uma das propriedades especificadas na tabela abaixo. O parâmetro param indica os valores que a propriedade de pname assume; param é um ponteiro a um grupo de valores se a versão de vetor for usada (gllightmodelfv, terminada em v), ou o próprio valor se a versão não vetorial for utilizada (gllightmodelf, sem v). A versão não vetorial pode ser usada para fixar as propriedades GL_LIGHT_MODEL_LOCAL_VIEWER e GL_LIGHT_MODEL_TWO_SIDE, que requerem apenas um valor. Mas a propriedade GL_LIGHT_MODEL_AMBIENT requer a versão vetorial (com v) pois esta propriedade requer um vetor com as coordenadas da luz ambiente. D) Propriedades de Materiais Estas propriedades descrevem a cor e propriedades de superfície de um material. OpenGL suporta que as propriedades de materiais sejam definidas na frente e nas costas dos objetos. Algumas das propriedades definidas pelo OpenGL são: GL_DIFFUSE - cor básica de objeto GL_SPECULAR - cor de destaques do objeto GL_AMBIENT - cor do objeto quando não diretamente iluminado GL_EMISSION - cor emitida pelo objeto GL_SHININESS - concentração de brilhos em objetos. Valores variam de 0 (superfície muito áspera - nenhum destaque) até 128 (muito brilhante). A tabela a seguir mostra todas as propriedades. A função responsável por setar as propriedades do material é: void glmaterialf(int face, int pname, float param); ou void glmaterialfv(int face, int pname, float *param);
7 O parâmetro face indica se a propriedade é aplicada na parte frontal, na parte de trás ou em ambos os lados das faces do objeto. Para tal, este parâmetro deve assumir respectivamente os valores GL_FRONT, GL_BACK ou GL_FRONT_AND_BACK. O parâmetro pname indica uma das propriedades da tabela abaixo e o parâmetros param indica os valores que estas propriedades podem assumir. Perceba que param pode ser um valor (glmaterialf) ou um vetor de valores reais (glmaterialfv). Vetores Unitários e Produto Vetorial (Revisão) Produto Vetorial Chama-se produto vetorial de dois vetores a um outro vetor, cujo comprimento ou módulo, é igual ao produto dos módulos dos dois vetores pelo seno do ângulo por eles formado, cuja direção é perpendicular ao plano determinado pelos dois vetores e o sentido é o determinado pela regra da mão direita. Vetores Unitários Fig. 8.7 O Produto Vetorial. Dado um vetor a=(a x,a y,a z ), definimos o vetor unitário u como sendo o vetor de comprimento igual a uma unidade e tendo a mesma direção e sentido de a. O vetor u é definido como
8 u = (1/ a ). a, onde a é o comprimento ou norma do vetor a. Vetores Fundamentais Unitários: sejam (X,Y,Z) as coordenadas de um vetor a. Chamemos de os três vetores unitários localizados sobre os eixos fundamentais de um sistema de coordenadas cartesianas (estes vetores também são representados por e 1 =(1,0,0), e 2 =(0,1,0) e e 3 =(0,0,1) respectivamente). Então, Fig. 8.8 Os Vetores Fundamentais Unitários. são vetores localizados sobre os eixos fundamentais e de comprimento igual a X, Y, Z respectivamente. Sendo o vetor a, a soma desses três vetores, podemos escrever: o que constitui a representação analítica do vetor. Voltando ao produto vetorial, devemos lembrar que são válidas as regras ordinárias do cálculo algébrico (exceto a comutativa) e que o produto vetorial de dois vetores unitários fundamentais é sempre igual ao outro vetor unitário, com sentido determinado pela regra da mão direita. Assim, considerando dois vetores na forma analítica,
9 efetuamos o produto vetorial dos dois vetores, e que desenvolvendo algebricamente, obedecidas as propriedades relativas aos produtos vetoriais dos vetores unitários, obtemos: e que se pode resumir, em termos de fórmulas, para o produto vetorial 3D em um sistema de coordenadas da mão direita, como se segue: O que se pode também escrever sob a forma matricial, em termos de determinantes: Definição de Vetor Normal a uma Face e um Vértice Vimos que os objetos são modelados como um conjunto de faces, mais especificamente triângulos ou quadriláteros. Por exemplo, podemos modelar um cubo unitário através das seguintes listas de vértices e faces (fig 8.9): V 1= (0,0,0),V 2= (1,0,0),V 3= (1,0,1),V 4= (0,0,1),V 5= (1,1,0),V 6= (1,1,0),V 7= (1,1,1),V 8= (0,1,1); F 1 =V 1 V 2 V 3 V 4, F 2 =V 2 V 6 V 7 V 3, F 3 =V 1 V 5 V 6 V 2, F 4 =V 1 V 4 V 8 V 5, F 5 =V 3 V 7 V 8 V 4, F 6 =V 5 V 8 V 7 V 5,
10 Fig. 8.9 Modelagem do Cubo Unitário. É importante perceber que a definição de cada face da lista requer que os vértices estejam ordenados. Neste exemplo a ordenação está no sentido anti-horário. Esta ordenação é essencial para possibilitar a cálculo correto das normais às faces. Vimos que as normais são necessárias para o cálculo da iluminação. E como calcular o vetor normal a uma face F? Basta tomar dois vetores não colineares da face F e calcular o produto vetorial destes vetores. Por exemplo, a normal n à face F2 do cubo pode ser calculada a partir do produto vetorial n = u x v, onde os vetores u e v são u=v 6 -V 2 e v=v 2 -V 3. Perceba que há outras possibilidades de se calcular os vetores u e v. O cálculo do vetor normal a um vértice pode ser simulado computacionalmente fazendo-se a média dos vetores normais às faces que compartilham aquele vértice, ponderada pelas áreas destas faces.
Como Fazer um Programa, simples, em OpenGL para Trabalhar com Iluminação (exemplo do site da Isabel Mansour)
 Como Fazer um Programa, simples, em OpenGL para Trabalhar com Iluminação (exemplo do site da Isabel Mansour) 1) Crie um Programa Simples que desenhe qualquer sólido na Tela. Há um exemplo Há Novo na Página
Como Fazer um Programa, simples, em OpenGL para Trabalhar com Iluminação (exemplo do site da Isabel Mansour) 1) Crie um Programa Simples que desenhe qualquer sólido na Tela. Há um exemplo Há Novo na Página
Computação Gráfica - 13
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 13 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 13 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
Curso de Computação Gráfica (CG) 2014/2- Unidade 1- Modelagem de objetos. Exercício 1 (individual) - Entrega: quarta 13/08
 Curso de Computação Gráfica (CG) 2014/2- Unidade 1- Modelagem de objetos Exercício 1 (individual) - Entrega: quarta 13/08 Escolha um objeto entre os que possivelmente compõem uma clínica médica de exames
Curso de Computação Gráfica (CG) 2014/2- Unidade 1- Modelagem de objetos Exercício 1 (individual) - Entrega: quarta 13/08 Escolha um objeto entre os que possivelmente compõem uma clínica médica de exames
4.2 Produto Vetorial. Orientação sobre uma reta r
 94 4. Produto Vetorial Dados dois vetores u e v no espaço, vamos definir um novo vetor, ortogonal a u e v, denotado por u v (ou u v, em outros textos) e denominado produto vetorial de u e v. Mas antes,
94 4. Produto Vetorial Dados dois vetores u e v no espaço, vamos definir um novo vetor, ortogonal a u e v, denotado por u v (ou u v, em outros textos) e denominado produto vetorial de u e v. Mas antes,
TIPOS DE REFLEXÃO Regular Difusa
 Reflexão da luz TIPOS DE REFLEXÃO Regular Difusa LEIS DA REFLEXÃO RI = raio de luz incidente i normal r RR = raio de luz refletido i = ângulo de incidência (é formado entre RI e N) r = ângulo de reflexão
Reflexão da luz TIPOS DE REFLEXÃO Regular Difusa LEIS DA REFLEXÃO RI = raio de luz incidente i normal r RR = raio de luz refletido i = ângulo de incidência (é formado entre RI e N) r = ângulo de reflexão
RESUMO 2 - FÍSICA III
 RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
Computação Gráfica - 13
 Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 13 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Universidade Federal do Vale do São Francisco Curso de Engenharia da Computação Computação Gráfica - 13 Prof. Jorge Cavalcanti jorge.cavalcanti@univasf.edu.br www.univasf.edu.br/~jorge.cavalcanti www.twitter.com/jorgecav
Iluminação e sombreamento
 OpenGL Iluminação e sombreamento Sombreamento OpenGL calcula a cor de cada pixel e parte disso depende de qual é a iluminação usada no cenário e de como os objetos no cenário refletem ou absorvem a luz
OpenGL Iluminação e sombreamento Sombreamento OpenGL calcula a cor de cada pixel e parte disso depende de qual é a iluminação usada no cenário e de como os objetos no cenário refletem ou absorvem a luz
Iluminaçao. Os modelos de Iluminação são técnicas usadas para calcular a intensidade da cor de um ponto a ser exibido.
 Iluminaçao Os modelos de Iluminação são técnicas usadas para calcular a intensidade da cor de um ponto a ser exibido. Também chamados modelos de reflexão, utilizam: a cor do objeto a cor da luz a posição
Iluminaçao Os modelos de Iluminação são técnicas usadas para calcular a intensidade da cor de um ponto a ser exibido. Também chamados modelos de reflexão, utilizam: a cor do objeto a cor da luz a posição
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 3
 Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Ponto, reta e plano no espaço tridimensional, cont.
 Ponto, reta e plano no espaço tridimensional, cont. Matemática para arquitetura Ton Marar 1. Posições relativas Posição relativa entre pontos Dois pontos estão sempre alinhados. Três pontos P 1 = (x 1,
Ponto, reta e plano no espaço tridimensional, cont. Matemática para arquitetura Ton Marar 1. Posições relativas Posição relativa entre pontos Dois pontos estão sempre alinhados. Três pontos P 1 = (x 1,
Objetivos. Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas e
 MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
MÓDULO 2 - AULA 13 Aula 13 Superfícies regradas e de revolução Objetivos Apresentar as superfícies regradas e superfícies de revolução. Analisar as propriedades que caracterizam as superfícies regradas
Dadas a base e a altura de um triangulo, determinar sua área.
 Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Modelos de Iluminação
 C A P Í T U L O 4 Modelos de Iluminação Um modelo de iluminação é um conjunto de equações que determinam quantitativamente qual é a cor sobre um ponto da superfície de um objeto em função das propriedades
C A P Í T U L O 4 Modelos de Iluminação Um modelo de iluminação é um conjunto de equações que determinam quantitativamente qual é a cor sobre um ponto da superfície de um objeto em função das propriedades
GAAL - 2013/1 - Simulado - 1 Vetores e Produto Escalar
 GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
Capítulo 1. x > y ou x < y ou x = y
 Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
CorelDRAW 11 1. UM PROGRAMA DE DESIGN
 CorelDRAW 11 1. UM PROGRAMA DE DESIGN Com o Corel você vai trabalhar com um dos aplicativos mais usados no campo do design e da auto-edição, já que permite operar com dois tipos de gráficos (vetoriais
CorelDRAW 11 1. UM PROGRAMA DE DESIGN Com o Corel você vai trabalhar com um dos aplicativos mais usados no campo do design e da auto-edição, já que permite operar com dois tipos de gráficos (vetoriais
Projeção ortográfica da figura plana
 A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
A U L A Projeção ortográfica da figura plana Introdução As formas de um objeto representado em perspectiva isométrica apresentam certa deformação, isto é, não são mostradas em verdadeira grandeza, apesar
REFLEXÃO DA LUZ: ESPELHOS 412EE TEORIA
 1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
1 Módulo ou norma de um vetor
 Álgebra Linear I - Aula 3-2005.2 Roteiro 1 Módulo ou norma de um vetor A norma ou módulo do vetor ū = (u 1, u 2, u 3 ) de R 3 é ū = u 2 1 + u2 2 + u2 3. Geometricamente a fórmula significa que o módulo
Álgebra Linear I - Aula 3-2005.2 Roteiro 1 Módulo ou norma de um vetor A norma ou módulo do vetor ū = (u 1, u 2, u 3 ) de R 3 é ū = u 2 1 + u2 2 + u2 3. Geometricamente a fórmula significa que o módulo
Simulado OBM Nível 2
 Simulado OBM Nível 2 Gabarito Comentado Questão 1. Quantos são os números inteiros x que satisfazem à inequação? a) 13 b) 26 c) 38 d) 39 e) 40 Entre 9 e 49 temos 39 números inteiros. Questão 2. Hoje é
Simulado OBM Nível 2 Gabarito Comentado Questão 1. Quantos são os números inteiros x que satisfazem à inequação? a) 13 b) 26 c) 38 d) 39 e) 40 Entre 9 e 49 temos 39 números inteiros. Questão 2. Hoje é
MANUAL DE UTILIZAÇÃO SISTEMA DE CADASTRO INTRANET
 MANUAL DE UTILIZAÇÃO SISTEMA DE CADASTRO INTRANET I Sumário 1. Objetivo do Documento... 1 2. Início... 1 3. Cadastro de Pessoa Física... 3 3.1. Preenchimentos Obrigatórios.... 4 3.2. Acesso aos Campos
MANUAL DE UTILIZAÇÃO SISTEMA DE CADASTRO INTRANET I Sumário 1. Objetivo do Documento... 1 2. Início... 1 3. Cadastro de Pessoa Física... 3 3.1. Preenchimentos Obrigatórios.... 4 3.2. Acesso aos Campos
Copiright de todos artigos, textos, desenhos e lições. A reprodução parcial ou total desta aula só é permitida através de autorização por escrito de
 1 No início do nível intermediário, falamos brevemente sobre a perspectiva e a aplicação de alguns dos seus elementos, como o ponto de fuga, a linha de horizonte e a relação dos objetos com o olho do observador.
1 No início do nível intermediário, falamos brevemente sobre a perspectiva e a aplicação de alguns dos seus elementos, como o ponto de fuga, a linha de horizonte e a relação dos objetos com o olho do observador.
OBJETIVO Verificar as leis da Reflexão Verificar qualitativamente e quantitativamente a lei de Snell. Observar a dispersão da luz em um prisma.
 UNIVERSIDADE CATÓLICA DE BRASÍLIA CURSO DE FÍSICA LABORATÓRIO ÓPTICA REFLEXÃO E REFRAÇÃO OBJETIVO Verificar as leis da Reflexão Verificar qualitativamente e quantitativamente a lei de Snell. Observar a
UNIVERSIDADE CATÓLICA DE BRASÍLIA CURSO DE FÍSICA LABORATÓRIO ÓPTICA REFLEXÃO E REFRAÇÃO OBJETIVO Verificar as leis da Reflexão Verificar qualitativamente e quantitativamente a lei de Snell. Observar a
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
Curso: Ensino Fundamental II Disciplina: MATEMÁTICA Professor: Álvaro / Leandro
 Nome do aluno: nº série/turma 9 Curso: Ensino Fundamental II Disciplina: MATEMÁTICA Professor: Álvaro / Leandro Data: De 17 a 21/08/2009 Bimestre: 3º Tipo de atividade: Lista de Exercícios A REFLEXÃO DA
Nome do aluno: nº série/turma 9 Curso: Ensino Fundamental II Disciplina: MATEMÁTICA Professor: Álvaro / Leandro Data: De 17 a 21/08/2009 Bimestre: 3º Tipo de atividade: Lista de Exercícios A REFLEXÃO DA
AULA 6 - Operações Espaciais
 6.1 AULA 6 - Operações Espaciais Essa aula descreve as operações espaciais disponíveis no TerraView. Antes de iniciar sua descrição é necessário importar alguns dados que serão usados nos exemplos. Exercício:
6.1 AULA 6 - Operações Espaciais Essa aula descreve as operações espaciais disponíveis no TerraView. Antes de iniciar sua descrição é necessário importar alguns dados que serão usados nos exemplos. Exercício:
3.4 Movimento ao longo de uma curva no espaço (parte segunda)
 3.4-17 3.4 Movimento ao longo de uma curva no espaço (parte segunda) 3.4.4 Mais exemplos sobre curvas no espaço. No parágrafo anterior discutimos os elementos que entram na descrição de uma trajetória
3.4-17 3.4 Movimento ao longo de uma curva no espaço (parte segunda) 3.4.4 Mais exemplos sobre curvas no espaço. No parágrafo anterior discutimos os elementos que entram na descrição de uma trajetória
Dicas de uso - Render Up
 Dicas de uso - Render Up (versão 3.6.7 ou superior) Desenvolvido por: Promob Software Solutions Rua dos Cinamomos - 517 - Cinquentenário CEP 95012-140 - Caxias do Sul - RS Brasil Fone/Fax: 54 3209 9200
Dicas de uso - Render Up (versão 3.6.7 ou superior) Desenvolvido por: Promob Software Solutions Rua dos Cinamomos - 517 - Cinquentenário CEP 95012-140 - Caxias do Sul - RS Brasil Fone/Fax: 54 3209 9200
Manual de Relação de Pontos por Indicação
 Manual de Relação de Pontos por Indicação Sumário 1. Verificando se o parâmetro das funções está ativo... 3 2. Efetuando o cadastro da faixa de indicação... 5 2.1. Cadastro de faixas com intervalos...
Manual de Relação de Pontos por Indicação Sumário 1. Verificando se o parâmetro das funções está ativo... 3 2. Efetuando o cadastro da faixa de indicação... 5 2.1. Cadastro de faixas com intervalos...
Movimentos Periódicos: representação vetorial
 Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Aula 5 00 Movimentos Periódicos: representação vetorial A experiência mostra que uma das maneiras mais úteis de descrever o movimento harmônico simples é representando-o como uma projeção perpendicular
Usando o Excel ESTATÍSTICA. A Janela do Excel 2007. Barra de título. Barra de menus. Barra de ferramentas padrão e de formatação.
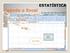 Barra de deslocamento ESTATÍSTICA Barra de menus Barra de título Barra de ferramentas padrão e de formatação Barra de fórmulas Conjuntos e Células (Intervalos) Área de trabalho Separador de folhas Barra
Barra de deslocamento ESTATÍSTICA Barra de menus Barra de título Barra de ferramentas padrão e de formatação Barra de fórmulas Conjuntos e Células (Intervalos) Área de trabalho Separador de folhas Barra
Contagem I. Figura 1: Abrindo uma Porta.
 Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 4 Contagem I De quantos modos podemos nos vestir? Quantos números menores que 1000 possuem todos os algarismos pares?
Polos Olímpicos de Treinamento Curso de Combinatória - Nível 2 Prof. Bruno Holanda Aula 4 Contagem I De quantos modos podemos nos vestir? Quantos números menores que 1000 possuem todos os algarismos pares?
Atividade: matrizes e imagens digitais
 Atividade: matrizes e imagens digitais Aluno(a): Turma: Professor(a): Parte 01 MÓDULO: MATRIZES E IMAGENS BINÁRIAS 1 2 3 4 5 6 7 8 Indique, na tabela abaixo, as respostas dos 8 desafios do Jogo dos Índices
Atividade: matrizes e imagens digitais Aluno(a): Turma: Professor(a): Parte 01 MÓDULO: MATRIZES E IMAGENS BINÁRIAS 1 2 3 4 5 6 7 8 Indique, na tabela abaixo, as respostas dos 8 desafios do Jogo dos Índices
2. Representação Numérica
 2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
2. Representação Numérica 2.1 Introdução A fim se realizarmos de maneira prática qualquer operação com números, nós precisamos representa-los em uma determinada base numérica. O que isso significa? Vamos
Visualização Científica. Pedro de Botelho Marcos Março/2008. Núcleo de Computação Científica Tópicos Avançados em Computação II
 Pedro de Botelho Marcos Março/2008 1 Sumário Introdução Ciclo de Visualização Dados 3D Dados Vetoriais Referências 2 Introdução O que? Representação visual de dados. Para? Facilitar a análise de grandes
Pedro de Botelho Marcos Março/2008 1 Sumário Introdução Ciclo de Visualização Dados 3D Dados Vetoriais Referências 2 Introdução O que? Representação visual de dados. Para? Facilitar a análise de grandes
Como consolidar dados nas planilhas utilizando o comando CONSOLIDAR do Excel
 Como consolidar dados nas planilhas utilizando o comando CONSOLIDAR do Excel! Como utilizar o comando Consolidar do Excel?! Quais são os diferenciais em relação ao cálculo aritmético normal?! Quais são
Como consolidar dados nas planilhas utilizando o comando CONSOLIDAR do Excel! Como utilizar o comando Consolidar do Excel?! Quais são os diferenciais em relação ao cálculo aritmético normal?! Quais são
ESTRUTURAS CRISTALINAS - TEORIA
 ESTRUTURAS CRISTALINAS - TEORIA Introdução Sólidos são compostos que apresentam uma alta regularidade estrutural. Com exceção dos sólidos amorfos, nos quais essa regularidade só existe em um curto espaço,
ESTRUTURAS CRISTALINAS - TEORIA Introdução Sólidos são compostos que apresentam uma alta regularidade estrutural. Com exceção dos sólidos amorfos, nos quais essa regularidade só existe em um curto espaço,
Paulo Sérgio Rodrigues. Exercícios de Laboratório
 Paulo Sérgio Rodrigues Exercícios de Laboratório Iluminação São Bernardo do Campo, SP Abril de 2010 Iluminação Como é possível observar na Fig. 1, a imagem gerada não possui uma qualidade satisfatória.
Paulo Sérgio Rodrigues Exercícios de Laboratório Iluminação São Bernardo do Campo, SP Abril de 2010 Iluminação Como é possível observar na Fig. 1, a imagem gerada não possui uma qualidade satisfatória.
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES
 CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
CAPÍTULO 3 - TIPOS DE DADOS E IDENTIFICADORES 3.1 - IDENTIFICADORES Os objetos que usamos no nosso algoritmo são uma representação simbólica de um valor de dado. Assim, quando executamos a seguinte instrução:
Reflexão. A reflexão ocorre quando a luz incide sobre a superfície de separação entre dois meios com propriedades distintas.
 Ótica Reflexão A reflexão ocorre quando a luz incide sobre a superfície de separação entre dois meios com propriedades distintas. A reflexibilidade é a tendência dos raios de voltarem para o mesmo meio
Ótica Reflexão A reflexão ocorre quando a luz incide sobre a superfície de separação entre dois meios com propriedades distintas. A reflexibilidade é a tendência dos raios de voltarem para o mesmo meio
PARTE 2 FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL
 PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
Nesta aula iremos continuar com os exemplos de revisão.
 Capítulo 8 Nesta aula iremos continuar com os exemplos de revisão. 1. Exemplos de revisão Exemplo 1 Ache a equação do círculo C circunscrito ao triângulo de vértices A = (7, 3), B = (1, 9) e C = (5, 7).
Capítulo 8 Nesta aula iremos continuar com os exemplos de revisão. 1. Exemplos de revisão Exemplo 1 Ache a equação do círculo C circunscrito ao triângulo de vértices A = (7, 3), B = (1, 9) e C = (5, 7).
ÓPTICA GEOMÉTRICA PREGOLINI
 ÓPTICA GEOMÉTRICA PREGOLINI ÓPTICA GEOMÉTRICA É a parte da Física que estuda os fenômenos relacionados com a luz e sua interação com meios materiais quando as dimensões destes meios é muito maior que o
ÓPTICA GEOMÉTRICA PREGOLINI ÓPTICA GEOMÉTRICA É a parte da Física que estuda os fenômenos relacionados com a luz e sua interação com meios materiais quando as dimensões destes meios é muito maior que o
Iluminando o Cenário
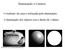 Iluminando o Cenário O realismo da cena é reforçada pela iluminação; A iluminação dos objetos cria a ilusão de volume: http://mech.fsv.cvut.cz/~dr/papers/habil/node51.html Fundamentos: Fisicamente: a percepção
Iluminando o Cenário O realismo da cena é reforçada pela iluminação; A iluminação dos objetos cria a ilusão de volume: http://mech.fsv.cvut.cz/~dr/papers/habil/node51.html Fundamentos: Fisicamente: a percepção
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,...
 Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Por que o quadrado de terminados em 5 e ta o fa cil? Ex.: 15²=225, 75²=5625,... 0) O que veremos na aula de hoje? Um fato interessante Produtos notáveis Equação do 2º grau Como fazer a questão 5 da 3ª
Valores eternos. MATÉRIA PROFESSOR(A) ---- ----
 Valores eternos. TD Recuperação ALUNO(A) MATÉRIA Física II PROFESSOR(A) Fernando ANO SEMESTRE DATA 2º 1º Julho/2013 TOTAL DE ESCORES ESCORES OBTIDOS ---- ---- 1. Considere a figura ao lado. Com base no
Valores eternos. TD Recuperação ALUNO(A) MATÉRIA Física II PROFESSOR(A) Fernando ANO SEMESTRE DATA 2º 1º Julho/2013 TOTAL DE ESCORES ESCORES OBTIDOS ---- ---- 1. Considere a figura ao lado. Com base no
Unidade: Vetores e Forças. Unidade I:
 Unidade I: 0 Unidade: Vetores e Forças 2.VETORES 2.1 Introdução Os vetores são definidos como entes matemáticos que dão noção de intensidade, direção e sentido. De forma prática, o conceito de vetor pode
Unidade I: 0 Unidade: Vetores e Forças 2.VETORES 2.1 Introdução Os vetores são definidos como entes matemáticos que dão noção de intensidade, direção e sentido. De forma prática, o conceito de vetor pode
Imagem e Gráficos. vetorial ou raster?
 http://computacaografica.ic.uff.br/conteudocap1.html Imagem e Gráficos vetorial ou raster? UFF Computação Visual tem pelo menos 3 grades divisões: CG ou SI, AI e OI Diferença entre as áreas relacionadas
http://computacaografica.ic.uff.br/conteudocap1.html Imagem e Gráficos vetorial ou raster? UFF Computação Visual tem pelo menos 3 grades divisões: CG ou SI, AI e OI Diferença entre as áreas relacionadas
Projetos. Universidade Federal do Espírito Santo - UFES. Mestrado em Informática 2004/1. O Projeto. 1. Introdução. 2.
 Pg. 1 Universidade Federal do Espírito Santo - UFES Mestrado em Informática 2004/1 Projetos O Projeto O projeto tem um peso maior na sua nota final pois exigirá de você a utilização de diversas informações
Pg. 1 Universidade Federal do Espírito Santo - UFES Mestrado em Informática 2004/1 Projetos O Projeto O projeto tem um peso maior na sua nota final pois exigirá de você a utilização de diversas informações
Aula do Curso Noic de Física, feito pela parceria do Noic com o Além do Horizonte
 Espelhos esféricos são superfícies refletoras muito comuns e interessantes de se estudar. Eles são capazes de formar imagens maiores ou menores, inversas ou direitas, dependendo do tipo de espelho, suas
Espelhos esféricos são superfícies refletoras muito comuns e interessantes de se estudar. Eles são capazes de formar imagens maiores ou menores, inversas ou direitas, dependendo do tipo de espelho, suas
CÁLCULO DE ADIANTAMENTO SALARIAL
 CÁLCULO DE ADIANTAMENTO SALARIAL O cálculo de adiantamento salarial no Cordilheira Recursos Humanos é bem flexível e consegue atender muitas situações diferenciadas. Para que o cálculo seja efetuado de
CÁLCULO DE ADIANTAMENTO SALARIAL O cálculo de adiantamento salarial no Cordilheira Recursos Humanos é bem flexível e consegue atender muitas situações diferenciadas. Para que o cálculo seja efetuado de
Engenharia Informática. Física II. 1º Ano 2º Semestre. Instituto politécnico de Bragança Escola Superior de Tecnologia e de Gestão
 1º no º Semestre 1. Cálculo vectorial 1.1. Introdução análise vectorial é um assunto do âmbito da matemática e não propriamente da Engenharia. No entanto, é quase impossível estudar Electrostática e Magnetismo
1º no º Semestre 1. Cálculo vectorial 1.1. Introdução análise vectorial é um assunto do âmbito da matemática e não propriamente da Engenharia. No entanto, é quase impossível estudar Electrostática e Magnetismo
O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem.
 TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta
 Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
Aula 03: Movimento em um Plano Tópico 02: Movimento Circular Uniforme; Aceleração Centrípeta Caro aluno, olá! Neste tópico, você vai aprender sobre um tipo particular de movimento plano, o movimento circular
Levantamento topográfico
 MA092 - Geometria plana e analítica - Segundo projeto Levantamento topográfico Francisco A. M. Gomes Outubro de 2014 1 Descrição do projeto Nessa atividade, vamos usar a lei dos senos e a lei dos cossenos
MA092 - Geometria plana e analítica - Segundo projeto Levantamento topográfico Francisco A. M. Gomes Outubro de 2014 1 Descrição do projeto Nessa atividade, vamos usar a lei dos senos e a lei dos cossenos
LENTES E ESPELHOS. O tipo e a posição da imagem de um objeto, formada por um espelho esférico de pequena abertura, é determinada pela equação
 LENTES E ESPELHOS INTRODUÇÃO A luz é uma onda eletromagnética e interage com a matéria por meio de seus campos elétrico e magnético. Nessa interação, podem ocorrer alterações na velocidade, na direção
LENTES E ESPELHOS INTRODUÇÃO A luz é uma onda eletromagnética e interage com a matéria por meio de seus campos elétrico e magnético. Nessa interação, podem ocorrer alterações na velocidade, na direção
Capítulo 3. Avaliação de Desempenho. 3.1 Definição de Desempenho
 20 Capítulo 3 Avaliação de Desempenho Este capítulo aborda como medir, informar e documentar aspectos relativos ao desempenho de um computador. Além disso, descreve os principais fatores que influenciam
20 Capítulo 3 Avaliação de Desempenho Este capítulo aborda como medir, informar e documentar aspectos relativos ao desempenho de um computador. Além disso, descreve os principais fatores que influenciam
Orientação a Objetos
 1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
1. Domínio e Aplicação Orientação a Objetos Um domínio é composto pelas entidades, informações e processos relacionados a um determinado contexto. Uma aplicação pode ser desenvolvida para automatizar ou
Computação Gráfica Interativa
 Computação Gráfica Interativa conceitos, fundamentos geométricos e algoritmos 1. Introdução Computação Gráfica é a criação, armazenamento e a manipulação de modelos de objetos e suas imagens pelo computador.
Computação Gráfica Interativa conceitos, fundamentos geométricos e algoritmos 1. Introdução Computação Gráfica é a criação, armazenamento e a manipulação de modelos de objetos e suas imagens pelo computador.
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
Projeção ortográfica
 Instituto Federal de Educação Ciências e Tecnologia IFCE Sobral Eixo de Controle e Processos Industriais Curso: Tecnologia em Mecatrônica Industrial Disciplina: Desenho Técnico e Mecânico Projeção ortográfica
Instituto Federal de Educação Ciências e Tecnologia IFCE Sobral Eixo de Controle e Processos Industriais Curso: Tecnologia em Mecatrônica Industrial Disciplina: Desenho Técnico e Mecânico Projeção ortográfica
Clip-art Retrieval using Sketches PTDC/EIA-EIA/108077/2008
 PROJECTOS DE INVESTIGAÇÃO CIENTÍFICA E DESENVOLVIMENTO TECNOLÓGICO Clip-art Retrieval using Sketches PTDC/EIA-EIA/108077/2008 Deliverable: D1 - Clip-art Simplification Tool Task: T1 - Clip-art Simplification
PROJECTOS DE INVESTIGAÇÃO CIENTÍFICA E DESENVOLVIMENTO TECNOLÓGICO Clip-art Retrieval using Sketches PTDC/EIA-EIA/108077/2008 Deliverable: D1 - Clip-art Simplification Tool Task: T1 - Clip-art Simplification
MÉTODOS DE REPRESENTAÇÃO
 MARIA DO CÉU SIMÕES TERENO 2011 EUROPEU E AMERICANO SISTEMAS DE PROJEÇÕES ORTOGONAIS Ângulos Diedros A representação de objectos tridimensionais por meio de desenhos bidimensionais, utilizando projecções
MARIA DO CÉU SIMÕES TERENO 2011 EUROPEU E AMERICANO SISTEMAS DE PROJEÇÕES ORTOGONAIS Ângulos Diedros A representação de objectos tridimensionais por meio de desenhos bidimensionais, utilizando projecções
Arquitetura de Rede de Computadores
 TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
Forças internas. Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro.
 Forças internas Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro. Generalizar esse procedimento formulando equações que podem ser representadas de
Forças internas Objetivos da aula: Mostrar como usar o método de seções para determinar as cargas internas em um membro. Generalizar esse procedimento formulando equações que podem ser representadas de
Função. Definição formal: Considere dois conjuntos: o conjunto X com elementos x e o conjunto Y com elementos y. Isto é:
 Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
Manual do Usuário. Plano de Corte
 Manual do Usuário Plano de Corte Sumário Gigatron Plano de Corte...2 Versão...2 Plano de Corte...2 Edição de Atributos de Peças...3 Atributos de Linhas de Corte...4 Estilos de Entrada e Saída...8 Contorno...8
Manual do Usuário Plano de Corte Sumário Gigatron Plano de Corte...2 Versão...2 Plano de Corte...2 Edição de Atributos de Peças...3 Atributos de Linhas de Corte...4 Estilos de Entrada e Saída...8 Contorno...8
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 8 FUNÇÕES CRESCENTES OU DECRESCENTES... 9 SINAL DE UMA
www.educandusweb.com.br
 Sistema Terra-Lua-Sol Índice 1. Introdução... 3 2. Simulador... 3 2.1 Painel Principal... 3 O que ocorreu com dimensões e distâncias dos corpos estudados?... 5 2.2 Visualização - Wireframe/Texturizada...
Sistema Terra-Lua-Sol Índice 1. Introdução... 3 2. Simulador... 3 2.1 Painel Principal... 3 O que ocorreu com dimensões e distâncias dos corpos estudados?... 5 2.2 Visualização - Wireframe/Texturizada...
Análise de Dados do Financeiro
 Análise de Dados do Financeiro Introdução Para reunir em um só local as informações de contas a pagar e receber cadastradas e/ou geradas no sistema TTransp existe a interface de análise de dados do financeiro.
Análise de Dados do Financeiro Introdução Para reunir em um só local as informações de contas a pagar e receber cadastradas e/ou geradas no sistema TTransp existe a interface de análise de dados do financeiro.
N1Q1 Solução. a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas.
 1 N1Q1 Solução a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas. b) Há várias formas de se cobrir o tabuleiro com peças dos tipos A e B, com pelo
1 N1Q1 Solução a) Há várias formas de se cobrir o tabuleiro usando somente peças do tipo A; a figura mostra duas delas. b) Há várias formas de se cobrir o tabuleiro com peças dos tipos A e B, com pelo
Busca. Pesquisa sequencial
 Busca Banco de dados existem para que, de tempos em tempos, um usuário possa localizar o dado de um registro, simplesmente digitando sua chave. Uma tabela ou um arquivo é um grupo de elementos, cada um
Busca Banco de dados existem para que, de tempos em tempos, um usuário possa localizar o dado de um registro, simplesmente digitando sua chave. Uma tabela ou um arquivo é um grupo de elementos, cada um
Laboratório Virtual Kit Óptico
 Laboratório Virtual Kit Óptico Reflexão A luz nem sempre se propaga indefinidamente em linha reta: em algumas situações eles podem se quebrar, como acontece quando um espelho é colocado em seu caminho.
Laboratório Virtual Kit Óptico Reflexão A luz nem sempre se propaga indefinidamente em linha reta: em algumas situações eles podem se quebrar, como acontece quando um espelho é colocado em seu caminho.
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Localização dos inquéritos de rua para Arroios e Gulbenkian
 Project IAAPE Pedestrian Accessibility and Attractiveness Indicators: Tool for Urban Walkability Assessment and Management Working Paper No. WP-8 Localização dos inquéritos de rua para Arroios e Gulbenkian
Project IAAPE Pedestrian Accessibility and Attractiveness Indicators: Tool for Urban Walkability Assessment and Management Working Paper No. WP-8 Localização dos inquéritos de rua para Arroios e Gulbenkian
Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.
 Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
Matemática Essencial Equações do Segundo grau Conteúdo Matemática - UEL - 2010 - Compilada em 18 de Março de 2010. Prof. Ulysses Sodré Matemática Essencial: http://www.mat.uel.br/matessencial/ 1 Introdução
Ciências da Natureza I Ensino Médio Oficina Espelhos Material do aluno
 Caro aluno, Este material foi produzido objetivando que você aprofunde seus conhecimentos sobre os espelhos planos e os espelhos esféricos côncavos e convexos. Antes de iniciar as atividades desta oficina
Caro aluno, Este material foi produzido objetivando que você aprofunde seus conhecimentos sobre os espelhos planos e os espelhos esféricos côncavos e convexos. Antes de iniciar as atividades desta oficina
 MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
MODELAGEM DIGITAL DE SUPERFÍCIES
 MODELAGEM DIGITAL DE SUPERFÍCIES Prof. Luciene Delazari Grupo de Pesquisa em Cartografia e SIG da UFPR SIG 2012 Introdução Os modelo digitais de superficie (Digital Surface Model - DSM) são fundamentais
MODELAGEM DIGITAL DE SUPERFÍCIES Prof. Luciene Delazari Grupo de Pesquisa em Cartografia e SIG da UFPR SIG 2012 Introdução Os modelo digitais de superficie (Digital Surface Model - DSM) são fundamentais
4 Segmentação. 4.1. Algoritmo proposto
 4 Segmentação Este capítulo apresenta primeiramente o algoritmo proposto para a segmentação do áudio em detalhes. Em seguida, são analisadas as inovações apresentadas. É importante mencionar que as mudanças
4 Segmentação Este capítulo apresenta primeiramente o algoritmo proposto para a segmentação do áudio em detalhes. Em seguida, são analisadas as inovações apresentadas. É importante mencionar que as mudanças
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO)
 Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 1 Prof. Cristóvão Cunha Objetivos de aprendizagem
Análise e Desenvolvimento de Sistemas ADS Programação Orientada a Obejeto POO 3º Semestre AULA 03 - INTRODUÇÃO À PROGRAMAÇÃO ORIENTADA A OBJETO (POO) Parte: 1 Prof. Cristóvão Cunha Objetivos de aprendizagem
4. Curvas planas. T = κn, N = κt, B = 0.
 4. CURVAS PLANAS 35 4. Curvas planas Nesta secção veremos que no caso planar é possível refinar a definição de curvatura, de modo a dar-lhe uma interpretação geométrica interessante. Provaremos ainda o
4. CURVAS PLANAS 35 4. Curvas planas Nesta secção veremos que no caso planar é possível refinar a definição de curvatura, de modo a dar-lhe uma interpretação geométrica interessante. Provaremos ainda o
5 Equacionando os problemas
 A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
A UA UL LA Equacionando os problemas Introdução Nossa aula começará com um quebra- cabeça de mesa de bar - para você tentar resolver agora. Observe esta figura feita com palitos de fósforo. Mova de lugar
MÓDULO 9. A luz branca, que é a luz emitida pelo Sol, pode ser decomposta em sete cores principais:
 A COR DE UM CORPO MÓDULO 9 A luz branca, que é a luz emitida pelo Sol, pode ser decomposta em sete cores principais: luz branca vermelho alaranjado amarelo verde azul anil violeta A cor que um corpo iluminado
A COR DE UM CORPO MÓDULO 9 A luz branca, que é a luz emitida pelo Sol, pode ser decomposta em sete cores principais: luz branca vermelho alaranjado amarelo verde azul anil violeta A cor que um corpo iluminado
GUIA DO PROFESSOR ATIVIDADES MATEMÁTICAS COM O SCRATCH
 ATIVIDADES MATEMÁTICAS COM O SCRATCH Conteúdos: Geometria, espaço e forma, grandezas e medidas. Tempo: 2 aulas de 50 minutos. Objetivos: Desenvolver a análise de espaço e forma dentro de ambientes simulados,
ATIVIDADES MATEMÁTICAS COM O SCRATCH Conteúdos: Geometria, espaço e forma, grandezas e medidas. Tempo: 2 aulas de 50 minutos. Objetivos: Desenvolver a análise de espaço e forma dentro de ambientes simulados,
Construindo a câmara escura
 Construindo a câmara escura Shizue Introdução Captar e registrar imagens tornou-se possível com a câmara escura de orifício. Essa câmara nada mais é do que uma lata, preta por dentro para não refletir
Construindo a câmara escura Shizue Introdução Captar e registrar imagens tornou-se possível com a câmara escura de orifício. Essa câmara nada mais é do que uma lata, preta por dentro para não refletir
Seno de 30 é um meio?
 Seno de 30 é um meio? Adaptado do artigo de Renate Watanabe Acontecem fatos estranhos quando se ensina Trigonometria: Observe as tabelas abaixo, contendo alguns valores de duas funções f e g. x f(x) x
Seno de 30 é um meio? Adaptado do artigo de Renate Watanabe Acontecem fatos estranhos quando se ensina Trigonometria: Observe as tabelas abaixo, contendo alguns valores de duas funções f e g. x f(x) x
Aplicações de Escritório Electrónico
 Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
Universidade de Aveiro Escola Superior de Tecnologia e Gestão de Águeda Curso de Especialização Tecnológica em Práticas Administrativas e Tradução Aplicações de Escritório Electrónico Folha de trabalho
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 4
 Lei de Gauss Considere uma distribuição arbitrária de cargas ou um corpo carregado no espaço. Imagine agora uma superfície fechada qualquer envolvendo essa distribuição ou corpo. A superfície é imaginária,
Lei de Gauss Considere uma distribuição arbitrária de cargas ou um corpo carregado no espaço. Imagine agora uma superfície fechada qualquer envolvendo essa distribuição ou corpo. A superfície é imaginária,
GeoMafra Portal Geográfico
 GeoMafra Portal Geográfico Nova versão do site GeoMafra Toda a informação municipal... à distância de um clique! O projecto GeoMafra constitui uma ferramenta de trabalho que visa melhorar e homogeneizar
GeoMafra Portal Geográfico Nova versão do site GeoMafra Toda a informação municipal... à distância de um clique! O projecto GeoMafra constitui uma ferramenta de trabalho que visa melhorar e homogeneizar
Exercícios Teóricos Resolvidos
 Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
Universidade Federal de Minas Gerais Instituto de Ciências Exatas Departamento de Matemática Exercícios Teóricos Resolvidos O propósito deste texto é tentar mostrar aos alunos várias maneiras de raciocinar
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
Serviço Público Federal Universidade Federal do Pará - UFPA Centro de Tecnologia da Informação e Comunicação - CTIC S I E
 Serviço Público Federal Universidade Federal do Pará - UFPA Centro de Tecnologia da Informação e Comunicação - CTIC S I E SISTEMA DE INFORMAÇÕES PARA O ENSINO (*) Módulo: Produção Institucional Guia de
Serviço Público Federal Universidade Federal do Pará - UFPA Centro de Tecnologia da Informação e Comunicação - CTIC S I E SISTEMA DE INFORMAÇÕES PARA O ENSINO (*) Módulo: Produção Institucional Guia de
Usando o Excel ESTATÍSTICA. Funções
 Funções Podemos usar no Excel fórmulas ou funções. Anteriormente já vimos algumas fórmulas. Vamos agora ver o exemplo de algumas funções que podem ser úteis para o trabalho de Excel. Para começar podemos
Funções Podemos usar no Excel fórmulas ou funções. Anteriormente já vimos algumas fórmulas. Vamos agora ver o exemplo de algumas funções que podem ser úteis para o trabalho de Excel. Para começar podemos
Lista 2 Espelhos Planos Construções Extensivo Noite
 1. (Fuvest 2007) A janela de uma casa age como se fosse um espelho e reflete a luz do Sol nela incidente, atingindo, às vezes, a casa vizinha. Para a hora do dia em que a luz do Sol incide na direção indicada
1. (Fuvest 2007) A janela de uma casa age como se fosse um espelho e reflete a luz do Sol nela incidente, atingindo, às vezes, a casa vizinha. Para a hora do dia em que a luz do Sol incide na direção indicada
A função do primeiro grau
 Módulo 1 Unidade 9 A função do primeiro grau Para início de conversa... Já abordamos anteriormente o conceito de função. Mas, a fim de facilitar e aprofundar o seu entendimento, vamos estudar algumas funções
Módulo 1 Unidade 9 A função do primeiro grau Para início de conversa... Já abordamos anteriormente o conceito de função. Mas, a fim de facilitar e aprofundar o seu entendimento, vamos estudar algumas funções
6.3 Equivalência entre Autômatos com Pilha Não-Determinísticos e Gramáticas Livre do Contexto
 Capítulo 6. Autômatos com Pilha 6.3 Equivalência entre Autômatos com Pilha Não-Determinísticos e Gramáticas Livre do Contexto Nos exemplos da seção anterior, vimos que os autômatos com pilha existem para
Capítulo 6. Autômatos com Pilha 6.3 Equivalência entre Autômatos com Pilha Não-Determinísticos e Gramáticas Livre do Contexto Nos exemplos da seção anterior, vimos que os autômatos com pilha existem para
