INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios
|
|
|
- Talita Caires Pais
- 6 Há anos
- Visualizações:
Transcrição
1 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. VII Interpretação económica do modelo de PL António Carlos Morais da Silva Professor de I.O. i
2 Cap. VII - Interpretação económica do modelo de PL - Exercícios VII. Interpretação económica do modelo de PL Utilize o software do autor para obter a solução óptima em algumas das questões propostas.. Uma empresa utiliza o seguinte modelo linear para optimizar o lucro ( ) da produção dos bens A, B e C utilizando, 5 e horas de trabalho de 3 máquinas (M, M e M3): Max f(x) 3x + 3x + x 3 s.a. x + 3x + 4x 3 3x + x + 3x 3 5 4x + x + 3x 3 x, x, x 3 As variáveis x, x e x 3 representam o nível de produção (em litros) de A, B e C respectivamente. O valor do lucro óptimo é de 56 (são produzidas 46 litros de A e 6 litros de B ). a. Calcule o contributo óptimo, para a formação do lucro, de uma hora de cada uma das máquinas utilizadas. b. Que designação se dá, na programação matemática, aos valores indicados na alínea anterior? c. Os valores calculados na primeira alínea serão válidos se operar apenas com 8 horas de M? Justifique a resposta. d. Exponha as consequências na produção óptima se resolver produzir o bem C. Apresente o cálculo em que baseia a resposta.. No modelo de uma nova linha de produção : Max f(x) 9x + 8x + 5x 3 s.a. x + 3x + x 3 4 5x + 4x + 3x 3 x, x, x 3 x, x, x 3 representam a produção mensal de 3 novos tipos de aglomerado (A, A, A3 ) vendidos com margens de lucro unitário de 9, 8, 5 u.m. respectivamente. a ª restrição materializa o limite de venda no mercado a ª restrição limita a capacidade produtiva ( unidades) a. Visando a competitividade do aglomerado do tipo A qual a margem mínima de lucro a considerar, mantendo a estrutura do plano óptimo de produção (aglomerados A e A 3 )? Justifique a resposta. b. Actuando apenas na margem de lucro, que modificação é necessário introduzir para que o plano óptimo de produção inclua o aglomerado do tipo A sem alterar o lucro total (9 u.m.) do plano óptimo corrente? c. De quanto é possível aumentar o lucro total à custa do aumento da capacidade produtiva, sem alterar a estrutura da base óptima corrente? VII-
3 Cap. VII - Interpretação económica do modelo de PL - Exercícios 3. Numa exploração de suinicultura, estuda-se a alimentação diária de um animal com base nos dados seguintes: a. g do nutriente A kg de grão fornece ao animal : 4 g do nutriente B g do nutriente C kg de farinha fornece ao animal : 4 g do nutriente A g do nutriente C Custos kg de grão : kg de farinha : u.m. 5 u.m. Diariamente, o animal necessita de, pelo menos, g do nutriente A, 6 g do nutriente B e g do nutriente C. O modelo de PL para optimizar o custo da alimentação diária, é o seguinte: Min f(x) x + 5x s.a. x + 4x 4x 6 x + x em que a f(x) minimiza o custo da ração diária e as variáveis decisionais significam : x : quantidade (kg) de grão a considerar na ração diária x : quantidade (kg) de farinha a considerar na ração diária A solução óptima é a seguinte : x 4 kg ; x 6.5 kg ; Min f(x) 7.5 u.m., ou seja, a dieta do animal será constituída por 4 kg de grão e 6.5 kg de farinha com o custo de 7.5 u.m./dia. Pretende-se efectuar um estudo sumário dos resultados obtidos, recorrendo exclusivamente ás relações Primal- Dual e à versão matricial do Simplex. b. Qual ou quais dos nutrientes mais encarece, internamente, a ração diária? c. Se pretender que a dieta passe a ser mais rica em nutriente B, de quanto pode aumentar, no máximo, a quantidade deste sem alterar a estrutura corrente da base óptima? d. Uma empresa de cereais recomenda o uso de Soja para este tipo de ração oferecendo as seguintes condições: Custo de kg : 8 u.m. kg de Soja fornece ao animal: 5 g de A ; g de B ; 4 g de C. Verifique se, utilizando Soja, é possível reduzir o actual custo óptimo da ração (7.5 u.m. por dia). VII-
4 Cap. VII - Interpretação económica do modelo de PL - Exercícios 4. Uma empresa produz 4 tipos de bens (A, B, C, D) que coloca no mercado com lucro de 5, 7, 4 e 8 u.m. respectivamente. A produção envolve Aquecimento, Centrifugação e Filtragem. Para o próximo mês, a disponibilidade de tempo para a produção é a seguinte: Actividade Horas disponíveis Aquecimento 3 Centrifugação 4 Filtragem Os tempos (horas) associados à produção de cada um dos tipos de bens são os seguintes: Tipo Aquecimento Centrifugação Filtragem A 5 3 B 3 5 C D 4 Admita que os custos por hora (u.m.) são os seguintes: Aquecimento Centrifugação Filtragem 8 5 Da solução óptima do modelo de PL associado à situação exposta, sabe-se que: são produzidas unidades do bem A e 7 do bem D. há um excesso 6 horas para Centrifugação. a. Calcule os preços unitários de venda para A, B, C e D. b. Considere que o custo do Aquecimento passa a ser de u.m./hora. Admitindo que pretende manter os Preços de Venda calculados e a base óptima corrente, indique a alteração que é necessário fazer nos lucros unitários de venda dos produtos. 5. Uma empresa tem 3 fábricas (F, F, F3 ) onde produz os bens A e/ou B que vende com lucro unitário de 3 e 5 u.m., respectivamente. A disponibilidade de matéria-prima e os consumos unitários na produção em cada uma das fábricas são os seguintes: Fábricas Matéria-prima disponível A B (unidades) F 4 F F VII-3
5 Cap. VII - Interpretação económica do modelo de PL - Exercícios O modelo de PL para optimizar a produção, é o seguinte: Max f(x) 3x A + 5x B + 3x 3A + 5x 3B s.a. x A 4 x B 3x 3A + x 3B 8 em que a função objectivo maximiza o lucro da venda e as variáveis decisionais significam : x A : nível da produção do bem A em F x B : nível da produção do bem B em F x 3A : nível da produção do bem A em F3 x 3B : nível da produção do bem B em F3 O quadro óptimo da produção é o seguinte: VB x A x B x 3A x 3B F F F 3 VSM x A 4 x B / 6 x 3B 3/ / 9 f(x) 9/ 3 5/ 5/ 87 a. A fábrica F3 não produz o bem A. Será por escassez de matéria-prima? Justifique. b. Do ponto de vista interno, em qual das fábricas é de maior interesse produzir B? Justifique. c. Admita uma variação marginal na disponibilidade de matéria-prima em F. Qual é o impacto nos valores da função e das variáveis básicas? Justifique algebricamente a resposta. d. Mantendo o valor óptimo do lucro total (87 u.m.), qual deve ser, no mínimo, o lucro unitário da venda de A para rentabilizar a sua produção em F3? Justifique algebricamente. 6. Uma empresa usa o seguinte modelo linear para optimizar o lucro ( ) da produção dos bens A e B utilizando kg e 5 kg das matérias-primas MP e MP respectivamente. Max f(x) 3x + 4x s.a. x + x 3x + x 5 x, x As variáveis x e x representam o nível de produção (em litros) de A e B respectivamente. O valor do lucro óptimo é de 46 (são produzidas 6 litros de A e 7 litros de B ). Considere k e k os custos unitários de MP e MP respectivamente e v e v os preços unitários de venda de A e B. VII-4
6 Cap. VII - Interpretação económica do modelo de PL - Exercícios a. Apresente as expressões de cálculo de v e v em ordem a k! e k. b. Apresente a expressão geral da receita total da venda em ordem a k e k. c. Admita a redução de. /kg no custo de aquisição dos 5 kg de MP e a seguinte decisão: Incorporar no lucro total o desconto de.5 Manter as margens correntes de lucro Reflectir nos preços de venda o desconto na aquisição de MP Calcule a quantidade adicional de MP que deve ser adquirida nestas condições. d. Para a quantidade de MP calculada na alínea anterior, apresente a expressão geral da receita total da venda em ordem a k e k. e. Considere: k 5 /kg k /kg v 38 /litro v 4 /litro Para os dois modelos anteriores (com 5 kg e 3.5 kg de MP, respectivamente) e suas soluções óptimas apresente um relatório comparativo onde constem: e.. Custo dos recursos por litro produzido de A e B, Preço e Lucro unitários de venda. e.. Custo total de aquisição das matérias-primas, Receita e Lucro totais da venda. 7. Uma empresa produz os bens A, B, C e D. Entre outras, participam na produção as secções de Acabamento, Montagem e Corte. Prevê-se que estas secções tenham disponíveis para o plano de produção, respectivamente 48 horas, 8 horas e horas. O tempo (horas) utilizado por cada secção para os trabalhos de uma unidade de cada tipo é o seguinte: Tipo Secção A B C D Acabamento 8 4 Montagem Corte O lucro unitário da venda é de 9, 6, 4 e u.m. para os bens A, B, C e D respectivamente. VII-5
7 Cap. VII - Interpretação económica do modelo de PL - Exercícios O modelo de PL desenvolvido para optimizar a produção, maximizando o lucro da venda, é o seguinte: Max f(x) 9x + 6x + 4x 3 + x 4 s.a. x + 8x + 4x 3 + x x + 4x + 8x 3 + 5x 4 8 7x + 8x + 3x 3 + 5x 4 x, x, x 3, x 4 e Inteiro (x, x, x 3, x 4 representam o nível da produção de A, B, C e D expresso em unidades) a. Admita a possibilidade de obter uma redução de.5 /h nas 48 horas de Acabamento e que se pretende: Incorporar no lucro total a redução associada às 48 horas Manter as margens correntes de lucro Reflectir nos preços de venda a redução referida Nestas condições quantas horas cativa para o Acabamento? Qual é o novo plano óptimo de produção? b. São necessários cenários de rentabilização da produção do bem A harmonizando o tempo unitário de produção em todas as secções. Apresente o conjunto de condições a observar que permitem rentabilizar a produção do bem A com a base óptima corrente e sem alterar os lucros unitários de venda e efectue um teste das mesmas. 8. Uma empresa utiliza 3 máquinas no fabrico de 3 produtos (A, B e C). O tempo de operação em cada máquina para produzir uma unidade de cada um dos bens referidos e as disponibilidades de tempo para planeamento são as seguintes: M (h) M (h) M3(h) A 3 B 4 3 C Disponível (h) A margem de lucro unitário é de 3, 4 e 35 u.m. para A, B e C, respectivamente. O modelo de PL desenvolvido é o seguinte: Max f(x) 3x + 4x + 35x 3 s.a. 3x + 4x + x 3 9 x + x + x 3 54 x + 3x + x 3 93 x, x, x 3 VII-6
8 Cap. VII - Interpretação económica do modelo de PL - Exercícios Sendo x, x e x 3 os níveis de produção de A, B e C, o quadro óptimo da produção é o seguinte: VB x x x 3 F F F 3 VSM x /3 /3 -/3 x 3 5/6 -/6 /3 F 3-5/3 -/3 -/3 5 f(x) 5/ 5/ 5 a. Qual é o valor marginal de hora em M? Que limites de validade impõe? b. Se alterar a disponibilidade de tempo nas máquinas para, 5 e 88 horas, a base óptima corrente mantém-se? c. Qual é o valor do custo de oportunidade associado ao bem A? Como interpretá-lo? d. Se a margem de lucro de venda do bem A for alterada para 43 u.m. mantém-se a base óptima corrente? e. Estude o cenário de produção de outro bem cuja produção unitária carece de 4 horas em M, horas em M, 3 horas em M3 e se planeia vender com margem de lucro de 55 u.m. 9. Uma fábrica de têxteis produz 3 tipos de tecido (Tramas Ligeira, Normal e Densa, respectivamente). O modelo de PL para estudo da produção optimizada é o seguinte: Max f(x) 5x + x + 4x 3 s.a. x + x + x 3 5 x - x +3x 3 x, x, x 3 (toneladas de algodão) (relação de mercado) (níveis de produção em milhares de metros) Os lucros de venda para m de cada tecido foram obtidos do seguinte modo: Trama Ligeira Trama Normal Trama Densa Algodão necessário para m ton. ton. ton. Custo de ton. algodão 5 u.m. Custo de algodão para m 5 u.m. u.m. 5 u.m. Outros custos para m u.m. u.m. 9 u.m. Custo Total para m 5 u.m. u.m. 4 u.m. Preço de Venda de m u.m. 34 u.m. 8 u.m. Lucro por m 5 u.m. u.m. 4 u.m. VII-7
9 Cap. VII - Interpretação económica do modelo de PL - Exercícios O quadro óptimo (método Simplex) do modelo de PL é o seguinte: x x x 3 F A VSM x 7 / 5 / 5 / 5 9 / 5 x - / 5 / 5 - / 5 8 / 5 f(x) 3 / 5 9 / 5 - / 5 4 / 5 (F e A são variáveis auxiliares das ª e ª restrições técnicas, respectivamente) A produção óptima é: x 9 / 5 milhares de metros 8 m de tecido de trama ligeira ; x 8 / 5 milhares de metros 6 m de tecido de trama normal ; a que está associado o lucro máximo de 4 / 5 8. u.m. a. Se pretender rentabilizar a produção de tecido de Trama densa de quanto é necessário reduzir, no mínimo, o consumo de Algodão necessário à produção de m? b. Admita a possibilidade de adquirir Algodão com custo de 3.84 u.m./ton. e que pretende: Incorporar no lucro total a redução associada a 5 toneladas Manter as margens correntes de lucro Reflectir nos preços de venda dos tecidos a redução referida Nestas condições quantas toneladas de Algodão adquire? Quais os novos preços de venda?. Uma empresa para optimizar a produção dos bens A, B e C em quantidades x, x, e x 3 utiliza o seguinte modelo de PL: x x x 3 f(x) 3 Restrição 3 3 Restrição Restrição 3 O objectivo é maximizar o lucro da venda (u.m.), estando a produção condicionada às disponibilidades de matéria-prima MP e MP (3 e 4 ton respectivamente) e à necessidade de a produção total ser, no mínimo, unidades. A produção óptima é de toneladas do bem A e 7 toneladas do bem B com lucro máximo de 43 u.m. a. Estude o cenário de rentabilização da produção do bem C alterando conjuntamente o lucro unitário e os consumos das matérias-primas MP e MP por forma a que estas alterações tenham, respectivamente, o valor de %, 5% e 3% da anti economia corrente associada à produção deste bem. VII-8
10 INVESTIGAÇÃO OPERACIONAL Programação Linear Soluções dos Exercícios Cap. VII Interpretação económica do modelo de PL António Carlos Morais da Silva Professor de I.O. i
11 . Modelo proposto: Max f(x) 3x + 3x + x 3 s.a. x + 3x + 4x 3 3x + x + 3x 3 5 4x + x + 3x 3 x, x, x 3 a. Usando o método Simplex obtém-se o quadro óptimo: O contributo de uma hora (de cada uma das máquinas) para a formação do lucro é igual ao valor da variável de decisão do problema Dual, associada à respectiva restrição técnica. No quadro óptimo lê-se: y 3/5 euros por hora da máquina M y 3/5 euros por hora da máquina M y 3 euros por hora da máquina M3 Veja-se que o contributo total é de y + 5y + y Max f(x) b. Preços-sombra ou Custos de Oportunidade. c. É necessário verificar se a afectação de 8 horas na máquina M mantém a admissibilidade da base corrente em que as VB são x, x e F 3. Para tal calcula-se a nova solução: A m B A solução Primal não é admissível (x - ; F 3-8) pelo que a base corrente deixa de ser óptima e, consequentemente, os valores óptimos indicados para as variáveis de decisão do Dual deixam de ser válidos. d. Se um bem não é produzido em optimalidade tal indicia a existência de anti economia. No quadro óptimo o coeficiente, em f(x), da variável x 3 (nível da produção de C ) é /5 expresso em euros por litro de C. S/ VII-
12 Para estudar o impacto na produção de um litro de C estuda-se a solução corrente em ordem à variável x 3 : x 6-6/5x 3 x 46 - /5x 3 Produzindo litro de C (x 3 ) as consequências são as seguintes: Redução da produção de B em 6/5. litros Redução da produção de A em /5. litros Impacto no lucro: redução em resultante de: + (produção de litro de C ) -.(3) -3.6 (redução da produção de B ) -.(3) -. 6 (redução da produção de A ) O valor desta redução é evidente lendo a equação de f(x) em ordem à variável x 3 : f(x) 56 - /5 x 3 A produção de um litro de C (x 3 ) degrada o valor de f(x) em /5. (quantificador da anti economia unitária de C ).. a. É necessário calcular a sensibilidade do modelo à variação do coeficiente de x, em f(x). Considerando tal coeficiente igual a c a base óptima mantém-se se e só se: c 8 5 c 5 5c c - 5 -c c 35 8 c 5 5 3c 5 c 3 c + c Conclusão : 43/5 c Margem mínima de lucro unitário 43/5 8.6 u.m. b. A anti economia associada à produção de uma unidade de A é de u.m. (coeficiente, em f(x), da variável x ) pelo que para rentabilizar a sua produção é necessário que o lucro unitário aumente u.m., passando a ser u.m. lucro corrente + anti economia. S/ VII-
13 c. É necessário calcular a sensibilidade do modelo à variação de b : 4 3 A m B 5 b b b + b b A base óptima corrente mantém-se admissível se a capacidade produtiva aumentar unidade ficando em unidades. 3. a. Comecemos por calcular os preços-sombra de cada um dos nutrientes. As VB do quadro óptimo são x, x e E (veja que há excesso na ª restrição técnica). Atendendo a que o problema Dual tem 3 variáveis de Decisão (y, y, y 3 ) e restrições técnicas (tipo ) a que são associadas variáveis de Folga (y 4 e y 5 ), as relações de complementaridade Primal-Dual são as seguintes: x.y 4 y 4 x.y 5 y 5 E.y y E.y y? E 3.y 3 y 3? Resolvendo o sistema de equações técnicas do problema Dual obtêm-se os valores óptimos das restantes variáveis Duais: y /8.5 ; y 3 /4.5 Do ponto de vista interno, o nutriente mais caro é o nutriente C ( preço sombra.5 u.m. por grama) b. É necessário calcular a sensibilidade do modelo à variação de b o que exige conhecer a matriz inversa da base: A 4 4 m A m / 4 / 4 / / A m B Am b / 4( b ) b / 4( b ) + / b 4 S/ VII-3
14 A estrutura da base óptima corrente não se altera se a quantidade máxima de nutriente B for 4 gramas pelo que o aumento máximo é de gramas. c. O modelo de PL, modificado com a introdução de x 3 quilos de Soja, é o seguinte: Min f(x) x + 5x + 8x 3 s.a. x + 4x + 5x 3 4x + x 3 6 x + x + 4x 3 A base óptima corrente mantém-se se e só se a nova restrição Dual 5y + y + 4y 3 8 for satisfeita pela solução óptima corrente do problema Dual, já calculada: y ; y.5 ; y 3.5. Substituindo valores constata-se que a restrição é violada pelo que é necessário reoptimizar para obter outra solução óptima em que a Soja será usada na produção da ração. O quadro óptimo corrente (equações técnicas) é o seguinte (use as matrizes já calculadas): VB x x E E E 3 A A A 3 VSM x - / 4 / 4 4 x / 4 - / - / 4 / 3/ E / / 4 O vector da Soja neste quadro é O quadro aumentado com A m P3 5 / A m P3 A m 3/ 4 45 e com o coeficiente reduzido de x 3, em f(x), é o seguinte: VB x x x 3 E E E 3 A A A 3 VSM x / - / 4 / 4 4 x 3/ / 4 - / - / 4 / 3/ E 45 / / 4 f(x) 9/ -/8 -/4 /8 /4 7.5 A solução não é óptima. Entra para a base a variável x 3 por troca com a variável E : VB x x x 3 E E E 3 A A A 3 VSM x 3 /45 /9 -/45 -/45 -/9 /45 8/9 x -/9 -/36 /9 /9 /36 -/45 /9 x -/3 / /6 /3 -/ -/6 /6 f(x) -/ -7/4 -/ / 7/4 / 58.5 S/ VII-4
15 Da leitura do novo quadro-óptimo conclui-se: É possível reduzir o custo da dieta em 4 u.m./dia ( ) A nova dieta é obtida com /9 kg de Grão, /6 kg de Farinha e 8/9 kg de Soja. 4. a. Horas por unidade produzida Tipo Aquecimento Centrifugação Filtragem A 5 3 B 3 5 C D 4 Tipo Aquecimento Centrifugação Filtragem Total Custos Lucro unitário Preço de Venda ( u.m./h) (8 u.m./h) (5 u.m./h) (u.m./unidade) (u.m./unidade) (u.m./unidade) A B C D b. Considerando x, x, x 3 e x 4 os níveis de produção de A, B, C e D respectivamente, temos: Tipo Aquecimento Aumento de custo Lucro unitário corrente Novo Lucro unitário (horas) (u.m.) (u.m.) (u.m.) A B C D Calculemos os preços-sombra correntes recorrendo ao modelo Dual: Problema Primal Max f(x) 5x + 7x + 4x 3 + 8x 4 s.a. x + 3x + 5x 3 + 4x 4 3 5x + x + 4x 3 + x 4 4 3x + 5x + 4x 3 + x 4 x, x, x 3, x 4 Problema Dual Min g(y) 3y + 4y + y 3 s.a. y + 5y + 3y 3 5 3y + y + 5y 3 7 5y + 4y + 4y 3 4 4y + y + y 3 8 y, y, y 3 Sabendo que as VB da base óptima corrente são x, x 4 e F (não nulas) obtém-se nas relações de complementaridade Primal-Dual, o valor óptimo dos preços-sombra y.4 ; y ; y 3.. S/ VII-5
16 Se o custo da hora de Aquecimento aumenta de u.m. e são mantidos os preços de venda, então o respectivo preço sombra y.4 diminui de u.m. passando ser de.4 u.m./hora. A nova função objectivo é f(x) 4x + 4x - x 3 + 4x 4 sendo necessário verificar se atinge o máximo com a base corrente. Para tal testam-se as restrições técnicas do Dual com o novo preço-sombra da hora de Aquecimento e com os novos lucros unitários: Problema Dual (novos lucros) Verificação Min g(y) 3y + 4y + y 3 g(y) 3(.4) + 4 () + (.) 36 y + 5y + 3y 3 4 (.4) + + 3(.) Saturada (x é VB) 3y + y + 5y 3 4 3(.4) + + 5(.) Não saturada (x é VNB) 5y + 4y + 4y 3-5(.4) + + 4(.) Não saturada (x 3 é VNB) 4y + y + y 3 4 4(.4) + + (.) Saturada (x 4 é VB) Todas as restrições Duais são satisfeitas pelo que o novo lucro máximo (36 u.m.) é atingido com a base óptima corrente. De facto, aplicando o método Simplex, obtém-se: Notar o novo preço-sombra da hora de Aquecimento (y / ) 5. a. O bem A não é produzido porque o seu custo de oportunidade (medida da anti economia) é de 4.5 u.m. por unidade produzida (a produção de unidade diminui em 4.5 u.m. o valor óptimo do lucro). b. Em ambas, pois a anti economia associada é nula nas fábricas F e F3. S/ VII-6
17 c. No óptimo, os valores das VB em ordem a F são: VB x A x B x 3A x 3B F F F 3 Solução em ordem a F x A 4 - F x B 6 x 3B 9 f 87 3F Da restrição técnica x A + F 4, temos x A 4 - F onde podemos simular, no º membro, a variação de matéria-prima actuando no valor de F. F A disponibilidade de matéria-prima passa de 4 para 3 unidades (redução), a produção de A na fábrica F é reduzida de unidade (x 3) e o valor do lucro total é reduzido de 3 u.m. ficando f(x) 84 u.m. F - A disponibilidade de matéria-prima passa de 4 para 5 unidades (aumento), a produção de A na fábrica F é aumentada de unidade (x 5) e o valor do lucro total é aumentado de 3 u.m. ficando f(x) 9 u.m. Resta saber, para a base óptima corrente, qual o intervalo de variação da matéria-prima na fábrica F em que são válidas estas conclusões. Para tal analisa-se a sensibilidade do modelo à variação da matéria-prima na fábrica F recorrendo à equação x A 4 - F, obtendo-se: b Ilimitado Os resultados apresentados são válidos para valores de matéria-prima (na ª restrição técnica) não negativos. d. Sendo a anti economia de 9/ u.m. por unidade de A produzida em F3 então o lucro unitário que rentabiliza a sua produção deve ser, no mínimo: Lucro actual + Custo de oportunidade u.m. (solução óptima indeterminada). 6. a. Cálculo dos preços de venda de litro (quadro ): MP (kg) MP (kg) Custo MP ( ) Custo MP ( ) Total Custos ( ) Lucro ( ) Preço Venda ( /litro) A 3 k 3K k + 3k 3 v k + 3k + 3 B k k k + k 4 v k + k + 4 S/ VII-7
18 b. Plano óptimo de produção: 6 litros de A e 7 litros de B (quadro ): Preço Venda Produção Receita total da venda ( /litro) (litros) ( ) A v k + 3k (k + 3k + 3) 6k + 8k + 8 B v k + k (k + k + 4) 4k + 7k + 8 Expressão geral da receita total da venda ( ) k + 5k + 46 Custos de aquisição k + 5k Lucro 46 c. A manutenção das margens de lucro garante a manutenção dos preços-sombra das matérias-primas. O desconto total para 5kg é de.5 pelo que o novo lucro total óptimo será de Usando as relações de complementaridade Prima-Dual obtêm-se os valores óptimos dos preços-sombra: y.8 ; y.4 Recorrendo à função objectivo do problema Dual calcula-se a quantidade de MP a adquirir (α): (y ) + α(y ) 48.5 α 3.5 kg (adquirir 3.5 kg de MP). Adquirir a quantidade adicional de 6.5 kg de MP ( ). d. Quadro óptimo com 3.5 kg de MP: Plano óptimo de produção: 8.5 litros de A e 5.75 litros de B (matérias-primas totalmente consumidas). Notar a manutenção dos preços-sombra (porque se mantiveram os lucros unitários e a quantidade de MP está no intervalo admissível) e o novo lucro total (48.5) já calculado na alínea anterior. MP (kg) MP (kg) Custo MP ( /litro) Custo MP ( /litro) Total custos ( /litro) Lucro ( /litro) Produção (litros) Receita total da venda ( ) A 3 k 3(K -.) k + 3k (k + 3k ) B k k -. k + k (k + k -.+ 4) S/ VII-8
19 Expressão geral da receita total da venda ( ) k + 3.5k e. e.. Custo dos recursos por unidade produzida, Preço e Lucro unitários de venda: MP e MP adquiridos a 5 /kg e /kg, respectivamente MP (kg) MP (kg) Custo Total ( /litro) Preço de Venda ( /litro) Lucro ( /litro) A B 4 4 MP e MP adquiridos a 5 /kg e 9.9 /kg, respectivamente MP (kg) MP (kg) Custo Total ( /litro) Preço de Venda ( /litro) Lucro ( /litro) A B (Notar a manutenção do lucro e a redução dos PV) e.. Custo total de aquisição das matérias-primas, Receita total e Lucro total da venda: A B MP (kg) MP (kg) Custo Total das MP ( ) Receita Venda ( ) (38) + 7(4) Lucro ( ) A B MP (kg) MP (kg) Custo Total das MP ( ) Receita Venda ( ) Lucro ( ) (37.7) (3.9) a. Comecemos por calcular o quadro óptimo para conhecermos as soluções óptimas dos problemas Primal e Dual. S/ VII-9
20 A manutenção das margens de lucro garante a manutenção dos preços-sombra das horas de cada uma das secções. O desconto total para 48 horas de Acabamento é de 48(.5) 7 pelo que o novo lucro total óptimo deverá ser de (incorporação do desconto no novo lucro total). Recorrendo à função objectivo do problema Dual calcula-se o número de horas a cativar: b (y ) + 8(y ) + (y 3 ) 87 b (.5) + 8(5) + () 87 b horas (valor óptimo para aquisição) Deve ser cativado um adicional de 57.6 horas ( ) se e só se não afectar a admissibilidade da base corrente. O plano óptimo de produção com horas é: A m B x x 64 F Trata-se de uma solução admissível pelo que devem ser cativadas horas obtendo-se o lucro máximo de: 34(6) + 3.8() 87 (valor de referência inicial) b. Comecemos por identificar o vector P A com o consumo de tempo, por unidade produzida, em cada uma das secções: 4 3 P A 5 7 Para rentabilizar a produção do bem A é necessário anular a anti economia associada ( /un. de A), ou seja, é necessário que a restrição Dual associada seja verificada na forma de igualdade (a admissibilidade da base mantém-se pois a variável x é VNB). Considere-se então a seguinte formalização para o vector P A : P A a a a 3 Para anular a anti economia corrente é necessário satisfazer a restrição Dual associada, na forma de igualdade (saturação): a (y ) + a (y ) + a 3 (y 3 ) 9.5a + 5a + a 3 9 (restrição para cenários) S/ VII-
21 Qualquer cenário válido deverá satisfazer esta restrição que, graficada, facilitará a tarefa do analista: (Notar que a 3 tem valor livre pois y 3 tem valor nulo) TESTE Bem A : Redução do tempo de Acabamento para.5 horas O valor admissível para a horas de Montagem deverá ser:.5(.5) + 5(a ) + a 3 9 a 4.75 horas.5 Calculando a solução óptima com P A o quadro óptimo para estes novos consumos é: Notar a manutenção da solução óptima corrente mas em que é nula a anti economia associada à produção do bem A (solução indeterminada). Podemos agora mudar de base para obter outra solução em que o bem A é produzido: Notar a manutenção dos preços-sombra. Notar que a base óptima não se altera para qualquer valor de a 3 (horas de Corte para uma unidade de A ). S/ VII-
22 Dispondo das duas soluções óptima calculadas estabelece-se a expressão geral das solução óptimas para o cenário em estudo:, 55/ * * * α α α α α α α α e com X X F F F x x x x X 8. a. Quadro óptimo e Análise de sensibilidade: O valor marginal de hora em M (preço-sombra) é de 7.5 u.m. Limites de Validade: variação independente de segundos membros nos intervalos acima indicados variação independente de c no intervalo indicado (notar que x é VNB do óptimo) não alteração dos coeficientes c e c 3 (notar que x e x 3 são VB do óptimo) S/ VII-
23 b. Usando a Regra dos % : Valor Corrente (horas) Subida Máxima (horas) Descida máxima (horas) Novo Valor (horas) Variação (horas) Alteração percentual (valor absoluto) b %.5 b % 3.5 b 3 93 Ilimitada % 5 Soma das alterações percentuais 9.4% A soma das variações percentuais é inferior a % pelo que a base corrente permanece óptima. Idêntica conclusão pode obter-se recorrendo à versão matricial: A m B / 3 / 6 / 3 / 3 / 3 / A solução básica é admissível pelo que a base corrente permanece óptima. c. No quadro óptimo conclui-se que a anti economia associada à produção de unidade de A é de.5 u.m que deriva do seguinte (ver quadro óptimo): x x 3 Produzindo unidade de A (x ) as consequências são: Aumenta o lucro em 3 u.m. ( unidade de A ) x x Reduz o lucro /3(4) u.m. (redução de /3 na produção de B ) Reduz o lucro 5/6(35) u.m. (redução de 5/6 na produção de C ) No total o impacto no lucro é de: 3 - /3(4) - 5/6(35) -.5 u.m. d. Consultando a tabela apresentada em alínea anterior a resposta é negativa pois o limite superior do intervalo de variação de c é 4.5 u.m. S/ VII-3
24 e. Consideremos k o nível de produção deste novo bem. O modelo aumentado passa a ser: Max f(x) 3x + 4x + 35x k s.a. 3x + 4x + x 3 + 4k 9 x + x + x 3 + k 54 x + 3x + x 3 + 3k 93 x, x, x 3, k A nova restrição Dual associada à variável k é 4y + y + 3y 3 55 u.m. Substituindo o valor das variáveis Duais tem-se: 4 (7.5) + () + 3 () (falso) A restrição Dual é violada (coeficiente de k em f(x) é negativo) pelo que a variável deve entrar para a base. Para registar no quadro óptimo corrente calcula-se para k : A 4 / 3 / 3 3 / m Pk Am 3 No quadro calcula-se o coeficiente da variável K, em f(x), ficando: VB x x x 3 k F F F 3 VSM x / 3 /3 / 3 - / 3 x 3 5/ 6 /3 - / 6 / 3 F 3-5/ 3 -/3 - / 3 - / 3 5 f (X) 5/ -5 5/ 5 Reoptimizando obtém-se a nova solução óptima : VB x x x 3 k F F F 3 VSM k / 3/ / - / 8 x 3 / - - / 9 F 3-3/ / - / - / f(x) 5 5/ 5/ 35 Novo plano de produção: 9 unidades de C e 8 unidades do novo produto. Lucro máximo 35 u.m. O valor do lucro aumenta de 9 u.m. (35 5 9). S/ VII-4
25 9. a. É necessário calcular o valor de a 3 (coeficiente de x 3 na ª restrição técnica) que torna rentável a produção deste tipo de tecido (anular a anti economia corrente). Para tal recorre-se à restrição Dual associada que deverá ser satisfeita na forma de igualdade: a 3 y + 3y 4 a 3 ( 9 / 5 ) + (3) ( - / 5 ) 4 a 3 6 / 9 ton / m Consumo corrente para m ton Consumo máximo que rentabiliza a produção 6 / 9 ton. Redução mínima 3 / 9 ton. Conclusão: se, pelo menos, for possível efectuar esta redução, a produção do tecido de Trama Densa passa a ser rentável (verifique com o software do autor). b. A manutenção das margens de lucro garante a manutenção dos preços-sombra correntes. O desconto na aquisição de Algodão é de.6 u.m. por tonelada, ou seja, 5.8 u.m. para as 5 toneladas correntes. O lucro total óptimo passará a ser de u.m. (incorporação do desconto no novo lucro total). Recorrendo à função objectivo do problema Dual calcula-se a quantidade de algodão a adquirir: b (y ) + (y ) 34 u.m. b ( 9 / 5 ) + () ( - / 5 ) 34 b 6 ton. de algodão (valor óptimo para aquisição) O plano de produção com 6 toneladas de algodão é: x A m B 5 5 x com lucro máximo de 34 u.m. Os preços de venda a praticar serão 8.84, 3.68 e 6.84 u.m. por milhar de metros para cada um dos tecidos. Os quadros apresentados, no enunciado, rectificam-se ficando: Trama Ligeira Trama Normal Trama Densa Algodão necessário para m ton. ton. ton. Custo de ton. Algodão (u.m.) 3.84 Custo de algodão para m (u.m Outros custos para m (u.m.) 9 Custo Total para m (u.m.) Preço de Venda de m Lucro por m (u.m.) 5 4 S/ VII-5
26 . a. Recorrendo ao sistema de equações técnicas, de que se conhecem os valores x e x 7, conclui-se que E 3 6 (variável excedentária da 3ª restrição). Considerando y, y e y 3 os preços sombra associados, respectivamente, às ª, ª e 3ª restrições técnicas e y 4, y 5 e y 6 os valores da anti economia associada aos bens A, B e C, respectivamente, as relações de complementaridade são: x y 4 x y 5 x 3 y 6 F y F y E 3 y 3 Nestas relações, atendendo a que x, x e E 3 são diferentes de zero, conclui-se que y 4 y 5 y 3. Resolvendo o sistema de equações do Dual: y + 3y + y3 y4 y + 3y 3y + y + y3 y5 3 3y + y 3 y + 3y + y3 y6 y + 3y y 6 y y y 6 7 / 8 3/ 8 7 / 8 obtém-se o valor da anti economia unitária de C que é y 6 7/8.875 u.m. O lucro unitário de venda deve absorver % da anti economia (.75 u.m.) pelo que deve ser rectificado para: c u.m. por unidade vendida O consumo unitário de MP deve absorver 5% da anti economia (.4375 u.m.) Dado que o preço sombra de tonelada de MP é de y 7/8.875 u.m., para reduzir, em custo de produção,.4375 u.m. é necessário reduzir o consumo de.4375/ toneladas por unidade de C, ou seja: a ton. O consumo unitário de MP deve absorver os restantes 3% da anti economia (.65 u.m.). Dado que o preço sombra de tonelada de MP é de y 3/8.375 u.m., para reduzir, em custo de produção,.65 u.m. é necessário reduzir o consumo de.65/ toneladas por unidade de C, ou seja: a ton. S/ VII-6
27 O vector técnico de C deverá ser: P C.5.3 e, em f(x), o coeficiente unitário de lucro deverá ser c.75 u.m. por unidade vendida. Em resumo, para rentabilizar a produção de C o novo modelo deve ser o seguinte: x x x 3 Max f(x) 3.75 Restrição Restrição Restrição 3 Neste novo modelo a solução óptima é múltipla (indeterminada). Os resultados obtidos também podem obter-se recorrendo à restrição Dual associada à variável x 3 (nível da produção de C ). Situação corrente (anti economia.875) y + 3y + y 3 - y 6 (7/8) + 3(3/8) Margem de Lucro Anular.75 u.m. da anti economia (7/8) + 3(3/8) + - ( ) +.75 (7/8) + 3(3/8) Consumo de MP Anular.4375 u.m. da anti economia a 3 (7/8) + 3(3/8) + - ( ).75 a 3 (7/8) + 3(3/8) a 3.5 ton. Consumo de MP Anular.65 u.m. da anti economia.5(7/8) + a 3 (3/8) a 3.3 ton. Teste (com anti economia nula).5y +.3y + y (correcto) S/ VII-7
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios. Cap. IV Modelo Dual
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
sujeito a: 30x x (madeira) 5x x (horas de trabalho) x 1, x 2 0
 IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não tendo pois qualquer interesse prático. O método gráfico permite visualizar um conjunto
IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não tendo pois qualquer interesse prático. O método gráfico permite visualizar um conjunto
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios. Cap. X Programação por Metas
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. X Programação por Metas António Carlos Morais da Silva Professor de I.O. i Cap. X Programação por Metas - Exercícios X. Programação por Metas.
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. X Programação por Metas António Carlos Morais da Silva Professor de I.O. i Cap. X Programação por Metas - Exercícios X. Programação por Metas.
Universidade da Beira Interior Departamento de Matemática. Ficha de exercícios nº3: Dualidade. Interpretação Económica.
 Ano lectivo: 2008/2009; Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº3: Dualidade. Interpretação Económica. Cursos: Economia 1. Formule o problema
Ano lectivo: 2008/2009; Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº3: Dualidade. Interpretação Económica. Cursos: Economia 1. Formule o problema
No eixo das ordenadas o ponto B tem abcissa nula (x 1 = 0) pelo que a equação se reduz a 20x 2 = 300. Madeira. C(10,10) não é admissível.
 IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não sendo pois de considerar para resolução de problemas da vida real. Porque a determinação
IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não sendo pois de considerar para resolução de problemas da vida real. Porque a determinação
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 15. Dualidade Interpretação económica. Problema dual: preços sombra e perdas de oportunidade. Propriedade dos desvios complementares 2 Formulação do Problema de PL em termos
1 Programação Linear (PL) Aula 15. Dualidade Interpretação económica. Problema dual: preços sombra e perdas de oportunidade. Propriedade dos desvios complementares 2 Formulação do Problema de PL em termos
Pesquisa Operacional
 Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Investigação Operacional
 Métodos de Programação Linear: Big M, Fases, S Dual (Licenciatura) Tecnologias e Sistemas de Informação http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Simplex
Métodos de Programação Linear: Big M, Fases, S Dual (Licenciatura) Tecnologias e Sistemas de Informação http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Simplex
Simplex. Investigação Operacional José António Oliveira Simplex
 18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
Investigação Operacional
 Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Universidade da Beira Interior Departamento de Matemática. Ficha de exercícios nº4 Pós-Optimização e Análise de Sensibilidade
 Ano lectivo: 2008/2009 Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº4 Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia 1.
Ano lectivo: 2008/2009 Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº4 Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia 1.
IX - A N Á L I S E D E S E N S I B I L I D A D E
 IX - A N Á L I S E D E S E N S I B I L I D A D E A N Á L I S E P Ó S - O P T I M A L I D A D E Recordemos o exercício apresentado para ilustrar a aplicação do Algoritmo Simplex Revisto: Consideremos o
IX - A N Á L I S E D E S E N S I B I L I D A D E A N Á L I S E P Ó S - O P T I M A L I D A D E Recordemos o exercício apresentado para ilustrar a aplicação do Algoritmo Simplex Revisto: Consideremos o
Investigação Operacional
 Ano lectivo: /6 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia. Uma fábrica
Ano lectivo: /6 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia. Uma fábrica
Optimização/Matemática II (Eco)
 Optimização/Matemática II (Eco) Frequência/ Exame 1ª Época 1º Ano 2º Semestre 2013 / 2014 Licenciaturas em Gestão, Finanças e Contabilidade, Gestão de Marketing e Economia 02-06-2014 Duração da Frequência:
Optimização/Matemática II (Eco) Frequência/ Exame 1ª Época 1º Ano 2º Semestre 2013 / 2014 Licenciaturas em Gestão, Finanças e Contabilidade, Gestão de Marketing e Economia 02-06-2014 Duração da Frequência:
Investigação Operacional
 Investigação Operacional Licenciatura em Gestão 3.º Ano Ano Lectivo 2013/14 Programação Linear Texto elaborado por: Maria João Cortinhal (Coordenadora) Anabela Costa Maria João Lopes Ana Catarina Nunes
Investigação Operacional Licenciatura em Gestão 3.º Ano Ano Lectivo 2013/14 Programação Linear Texto elaborado por: Maria João Cortinhal (Coordenadora) Anabela Costa Maria João Lopes Ana Catarina Nunes
Investigação Operacional
 Modelos de Programação Linear (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Modelação Matemática As técnicas e algoritmos
Modelos de Programação Linear (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Modelação Matemática As técnicas e algoritmos
Faculdade de Engenharia Investigação Operacional. Prof. Doutor Engº Jorge Nhambiu
 1 Aula 3 Definição de Problemas de Investigação Operacional (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema
1 Aula 3 Definição de Problemas de Investigação Operacional (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema
Método do Big M. Análise de Sensibilidade
 A 5 =A 4 +C 5 B 5 =B 3 +C 5 C 5 =C 4 /2 E 5 =E 4 +C 5 Método do Big M.5.5 4 -.5.5 6 -.5.5 2 -G.5.5 2 i 2/- 4/- 4/2=2 max = 2 Nuno Moreira - 22/23 x 2 R 3 5 G=2 R 2 R 5 x 3 Análise de Sensibilidade Nuno
A 5 =A 4 +C 5 B 5 =B 3 +C 5 C 5 =C 4 /2 E 5 =E 4 +C 5 Método do Big M.5.5 4 -.5.5 6 -.5.5 2 -G.5.5 2 i 2/- 4/- 4/2=2 max = 2 Nuno Moreira - 22/23 x 2 R 3 5 G=2 R 2 R 5 x 3 Análise de Sensibilidade Nuno
2º Semestre 2002/2003 Problemas Resolvidos
 RESOLUÇÂO DO PROBLEMA Nº 19 Determinado problema de Programação Linear depois de formulado permitiu obter as seguintes expressões: Max L = 4x 1-2x 2 + 2x 3 -x 4 s.a. R 1: x 1 - x 2 + 2x 3 +x 4 10 R 2:
RESOLUÇÂO DO PROBLEMA Nº 19 Determinado problema de Programação Linear depois de formulado permitiu obter as seguintes expressões: Max L = 4x 1-2x 2 + 2x 3 -x 4 s.a. R 1: x 1 - x 2 + 2x 3 +x 4 10 R 2:
A Dualidade em Programação Linear
 Investigação Operacional- 2009/10 - Programas Lineares 14 A Dualidade em Programação Linear Para melhor ilustrar este conceito vamos estudar dois problemas intimamente relacionadas: o problema da dona
Investigação Operacional- 2009/10 - Programas Lineares 14 A Dualidade em Programação Linear Para melhor ilustrar este conceito vamos estudar dois problemas intimamente relacionadas: o problema da dona
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Aula 3 Definição de Problemas de Optimização (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema 3.1 Uma empresa
1 Aula 3 Definição de Problemas de Optimização (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema 3.1 Uma empresa
CAPÍTULO 3. Método Simplex
 CAPÍTULO 3 1. Soluções Básicas Admissíveis Considere um problema de PL representado nas suas formas padrão e matricial. Uma base é um conjunto de m variáveis, tais que a matriz dos coeficientes do sistema
CAPÍTULO 3 1. Soluções Básicas Admissíveis Considere um problema de PL representado nas suas formas padrão e matricial. Uma base é um conjunto de m variáveis, tais que a matriz dos coeficientes do sistema
O Problema de Transportes
 Investigação Operacional- 00/0 - Problemas de Transportes 8 O Problema de Transportes O problema geral de transportes consiste em determinar a forma mais económica de enviar um bem que está disponível
Investigação Operacional- 00/0 - Problemas de Transportes 8 O Problema de Transportes O problema geral de transportes consiste em determinar a forma mais económica de enviar um bem que está disponível
Investigação Operacional
 Ano lectivo: 0/06 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Algoritmo Simplex Cursos: Gestão e Economia. Considere o seguinte conjunto
Ano lectivo: 0/06 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Algoritmo Simplex Cursos: Gestão e Economia. Considere o seguinte conjunto
X - D U A L I D A D E
 X - D U A L I D A D E 1 - Introdução. Regras de transformação "Primal - Dual" Consideremos os dois problemas P1 e P2 de Programação Linear seguintes: P1 : n Maximizar F = Σ ck. Xk k = 1 n Σ aik. Xk bi
X - D U A L I D A D E 1 - Introdução. Regras de transformação "Primal - Dual" Consideremos os dois problemas P1 e P2 de Programação Linear seguintes: P1 : n Maximizar F = Σ ck. Xk k = 1 n Σ aik. Xk bi
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 10: Método Simplex Técnica das variáveis artificias Método das penalidades ( Big M ). Método das duas fases. 2 Modificando o Exemplo Protótipo. Suponha-se que é modificado
1 Programação Linear (PL) Aula 10: Método Simplex Técnica das variáveis artificias Método das penalidades ( Big M ). Método das duas fases. 2 Modificando o Exemplo Protótipo. Suponha-se que é modificado
Programação Linear/Inteira - Aula 5
 Unidade de Matemática e Tecnologia - RC/UFG Programação Linear/Inteira - Aula 5 Prof. Thiago Alves de Queiroz Aula 5 Thiago Queiroz (IMTec) Aula 5 Aula 5 1 / 43 Análise de Sensibilidade Estudar o efeito
Unidade de Matemática e Tecnologia - RC/UFG Programação Linear/Inteira - Aula 5 Prof. Thiago Alves de Queiroz Aula 5 Thiago Queiroz (IMTec) Aula 5 Aula 5 1 / 43 Análise de Sensibilidade Estudar o efeito
CAPÍTULO 4. Teoria da Dualidade
 CAPÍTULO 4 1. Introdução Uma dos conceitos mais importantes em programação linear é o de dualidade. Qualquer problema de PL tem associado um outro problema de PL, chamado o Dual. Neste contexto, o problema
CAPÍTULO 4 1. Introdução Uma dos conceitos mais importantes em programação linear é o de dualidade. Qualquer problema de PL tem associado um outro problema de PL, chamado o Dual. Neste contexto, o problema
Graduação em Engenharia Elétrica MÉTODOS DE OTIMIZAÇÃO ENE081. PROF. IVO CHAVES DA SILVA JUNIOR
 UNIVERSIDADE FEDERAL DE JUIZ DE FORA Graduação em Engenharia Elétrica MÉTODOS DE OTIMIZAÇÃO ENE081 PROF. IVO CHAVES DA SILVA JUNIOR E-mail: ivo.junior@ufjf.edu.br Aula Número: 07 Programação Linear Últimas
UNIVERSIDADE FEDERAL DE JUIZ DE FORA Graduação em Engenharia Elétrica MÉTODOS DE OTIMIZAÇÃO ENE081 PROF. IVO CHAVES DA SILVA JUNIOR E-mail: ivo.junior@ufjf.edu.br Aula Número: 07 Programação Linear Últimas
Professor João Soares 20 de Setembro de 2004
 Teoria de Optimização (Mestrado em Matemática) Texto de Apoio 2A Universidade de Coimbra 57 páginas Professor João Soares 20 de Setembro de 2004 Optimização Linear Considere o problema (1) abaixo, que
Teoria de Optimização (Mestrado em Matemática) Texto de Apoio 2A Universidade de Coimbra 57 páginas Professor João Soares 20 de Setembro de 2004 Optimização Linear Considere o problema (1) abaixo, que
Cap ıtulo 1 Exerc ıcios de Formula c ao Enunciados
 Capítulo 1 Exercícios de Formulação Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo
Capítulo 1 Exercícios de Formulação Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo
Cap ıtulo 1 Exerc ıcios de Formula c Enunciados
 Capítulo 1 Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo se não houver atrasos.
Capítulo 1 Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo se não houver atrasos.
Problemas de Transportes e de Afectação
 CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
Índice. Prefácio Os modelos de programação linear e a investigação operacional 17
 Índice Prefácio 13 Capítulo 1 Introdução 1. Os modelos de programação linear e a investigação operacional 17 2. O problema de programação linear 18 2.1. O problema de programação linear em substituição
Índice Prefácio 13 Capítulo 1 Introdução 1. Os modelos de programação linear e a investigação operacional 17 2. O problema de programação linear 18 2.1. O problema de programação linear em substituição
Matemática. C. Requejo (UA) Métodos de Investigação Operacional MIO / 34
 Modelação em Programação Matemática C. Requejo (UA) Métodos de Investigação Operacional MIO 2016-2017 1 / 34 Modelação de problemas simples Problema da compra de bilhetes Nas próximas 5 semanas vou, de
Modelação em Programação Matemática C. Requejo (UA) Métodos de Investigação Operacional MIO 2016-2017 1 / 34 Modelação de problemas simples Problema da compra de bilhetes Nas próximas 5 semanas vou, de
max z = 10x 1 + 4x 2 s.a x 1 + x x 1 + 4x x 1 + 6x 2 300
 Escola Superior de Tecnologia de Tomar Área de Matemática Investigação Operacional / Técnicas de Optimização e Decisão Engenharia Química, Engenharia do Ambiente, Engenharia Informática e Engenharia Civil
Escola Superior de Tecnologia de Tomar Área de Matemática Investigação Operacional / Técnicas de Optimização e Decisão Engenharia Química, Engenharia do Ambiente, Engenharia Informática e Engenharia Civil
Prof.: Eduardo Uchoa.
 Análise de sensibilidade Prof.: Eduardo Uchoa http://www.logis.uff.br/~uchoa/poi 1 Análise de Sensibilidade Uma vez que já se tenha resolvido um PL, existem técnicas para avaliar como pequenas alterações
Análise de sensibilidade Prof.: Eduardo Uchoa http://www.logis.uff.br/~uchoa/poi 1 Análise de Sensibilidade Uma vez que já se tenha resolvido um PL, existem técnicas para avaliar como pequenas alterações
Programação Linear. (4ª parte) Informática de Gestão Maria do Rosário Matos Bernardo 2016
 Programação Linear (4ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Análise de sensibilidade Relatório de reposta Relatório de sensibilidade Relatório de limites Desafio:
Programação Linear (4ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Análise de sensibilidade Relatório de reposta Relatório de sensibilidade Relatório de limites Desafio:
Programação Linear - Parte 5
 Matemática Industrial - RC/UFG Programação Linear - Parte 5 Prof. Thiago Alves de Queiroz 1/2016 Thiago Queiroz (IMTec) Parte 5 1/2016 1 / 29 Dualidade Os parâmetros de entrada são dados de acordo com
Matemática Industrial - RC/UFG Programação Linear - Parte 5 Prof. Thiago Alves de Queiroz 1/2016 Thiago Queiroz (IMTec) Parte 5 1/2016 1 / 29 Dualidade Os parâmetros de entrada são dados de acordo com
PROGRAMAÇÃO LINEAR 1. A TEORIA DA PROGRAMAÇÃO LINEAR 2. MÉTODO GRÁFICO 3. MÉTODO SIMPLEX 4. ANÁLIDE DE SENSIBILIDADE 5. APLICAÇÕES
 UNIVERSIDADE FEDERAL DA BAHIA - UFBA ESCOLA POLITÉCNICA DEPARTAMENTO DE ENGENHARIA MECÂNICA DEM CURSO DE ENGENHARIA DE PRODUÇÃO PROGRAMAÇÃO LINEAR PESQUISA OPERACIONAL PARTE II 1. A TEORIA DA PROGRAMAÇÃO
UNIVERSIDADE FEDERAL DA BAHIA - UFBA ESCOLA POLITÉCNICA DEPARTAMENTO DE ENGENHARIA MECÂNICA DEM CURSO DE ENGENHARIA DE PRODUÇÃO PROGRAMAÇÃO LINEAR PESQUISA OPERACIONAL PARTE II 1. A TEORIA DA PROGRAMAÇÃO
Vânio Correia Domingos Massala
 Optimização e Decisão 06/0/008 Método do Simplex Vânio Correia - 5567 Domingos Massala - 58849 INSTITUTO SUPERIOR TÉCNICO Generalidades do Método do Simplex Procedimento algébrico iterativo para resolver
Optimização e Decisão 06/0/008 Método do Simplex Vânio Correia - 5567 Domingos Massala - 58849 INSTITUTO SUPERIOR TÉCNICO Generalidades do Método do Simplex Procedimento algébrico iterativo para resolver
Pesquisa Operacional
 Pesquisa Operacional Casos Especiais do Método Simplex e Gráfica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG setembro - 2015 1 Casos Especiais do Método Simplex Degeneração Múltiplas soluções ótimas
Pesquisa Operacional Casos Especiais do Método Simplex e Gráfica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG setembro - 2015 1 Casos Especiais do Método Simplex Degeneração Múltiplas soluções ótimas
Investigação Operacional 2004/05 2º Mini-teste. 26 de Novembro, 9:00h 10:30h. Sem consulta, sem máquina de calcular Justifique todas as respostas
 Investigação Operacional 004/05 º Mini-teste 6 de Novembro, 9:00h 0:h Sem consulta, sem máquina de calcular Justifique todas as respostas Departamento de Engenharia Civil Secção de Planeamento do Território
Investigação Operacional 004/05 º Mini-teste 6 de Novembro, 9:00h 0:h Sem consulta, sem máquina de calcular Justifique todas as respostas Departamento de Engenharia Civil Secção de Planeamento do Território
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios
 INVESTIGÇÃO OPERIONL Prograação Linear Exercícios ap. VI nálise de Sensiilidade e Pós-Optiização ntónio arlos Morais da Silva Professor de I.O. INVESTIGÇÃO OPERIONL (MS edição de 6) i ap. VI nálise de
INVESTIGÇÃO OPERIONL Prograação Linear Exercícios ap. VI nálise de Sensiilidade e Pós-Optiização ntónio arlos Morais da Silva Professor de I.O. INVESTIGÇÃO OPERIONL (MS edição de 6) i ap. VI nálise de
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Recursos críticos disponíveis: Madeira 300 metros Horas de trabalho 110 horas
 I. Programação Linear (PL) 1. Introdução A Programação Linear é, no campo mais vasto da Programação Matemática, uma das variantes de aplicação generalizada em apoio da Decisão. O termo "Programação" deve
I. Programação Linear (PL) 1. Introdução A Programação Linear é, no campo mais vasto da Programação Matemática, uma das variantes de aplicação generalizada em apoio da Decisão. O termo "Programação" deve
Análise de Sensibilidade. Investigação Operacional. Análise de Sensibilidade aos coeficientes da FO. Análise de Sensibilidade
 nálise de Sensibilidade Investigação Operacional rogramação Linear (arte II) 2/2 Nuno Moreira/milcar rantes/ui Marques/Marta Gomes Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território
nálise de Sensibilidade Investigação Operacional rogramação Linear (arte II) 2/2 Nuno Moreira/milcar rantes/ui Marques/Marta Gomes Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território
INVESTIGAÇÃO OPERACIONAL. Modelo de Transporte. Exercícios. Cap. II Soluções Inicial e Óptima
 INVESTIGAÇÃO OPERACIONAL Modelo de Transporte Exercícios Cap. II Soluções Inicial e Óptima António Carlos Morais da Silva Professor de I.O. i Recomendações 1. É possível aprender a matéria fazendo apenas
INVESTIGAÇÃO OPERACIONAL Modelo de Transporte Exercícios Cap. II Soluções Inicial e Óptima António Carlos Morais da Silva Professor de I.O. i Recomendações 1. É possível aprender a matéria fazendo apenas
Aula 10: Revisão Otimização Linear e Inteira Túlio A. M. Toffolo
 Aula 10: Revisão Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br 2018/2 - PCC174/BCC464 Aula Prática - Laboratório COM30!1 Breve Revisão Modelagem Método gráfico O Algoritmo Simplex
Aula 10: Revisão Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br 2018/2 - PCC174/BCC464 Aula Prática - Laboratório COM30!1 Breve Revisão Modelagem Método gráfico O Algoritmo Simplex
PESQUISA OPERACIONAL 11. SOLUÇÃO ALGEBRICA O MÉTODO SIMPLEX ( ) DEFINIÇÕES REGRAS DE TRANSFORMAÇÃO. Prof. Edson Rovina Página 16
 11. SOLUÇÃO ALGEBRICA O MÉTODO SIMPLEX Página 16 Após o problema ter sido modelado, pode-se resolvê-lo de forma algébrica. A solução algébrica é dada pelo método simplex elaborado por Dantzig. Antes da
11. SOLUÇÃO ALGEBRICA O MÉTODO SIMPLEX Página 16 Após o problema ter sido modelado, pode-se resolvê-lo de forma algébrica. A solução algébrica é dada pelo método simplex elaborado por Dantzig. Antes da
OTIMIZAÇÃO. O processo de otimização normalmente involve a procura de pontos de máximos e mínimos de uma função.
 OTIMIZAÇÃO O processo de otimização normalmente involve a procura de pontos de máximos e mínimos de uma função. Pontos de máximos e mínimos de uma função são pontos onde a derivada da função é nula. A
OTIMIZAÇÃO O processo de otimização normalmente involve a procura de pontos de máximos e mínimos de uma função. Pontos de máximos e mínimos de uma função são pontos onde a derivada da função é nula. A
Transparências de apoio à lecionação de aulas teóricas. c 2012, 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP
 Programação Linear Transparências de apoio à lecionação de aulas teóricas Versão 4 c 2012, 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear Problema de planeamento
Programação Linear Transparências de apoio à lecionação de aulas teóricas Versão 4 c 2012, 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear Problema de planeamento
Aula 07: Análise de sensibilidade (2)
 Aula 07: Análise de sensibilidade (2) Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Departamento de Computação UFOP Previously Aulas anteriores: Dualidade
Aula 07: Análise de sensibilidade (2) Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Departamento de Computação UFOP Previously Aulas anteriores: Dualidade
Complementos de Investigação Operacional. Folha nº 2 Programação Multiobjectivo 2006/07
 Complementos de Investigação Operacional Folha nº 2 Programação Multiobjectivo 2006/07 1- x2 D(7,6) C(4,5) E(11,5) F(12,4) B(2,3) X G(13,2) A(1,1) H(10,1) max f 1 (x) = x 1 max f 2 (x) = x 2 (a) Represente
Complementos de Investigação Operacional Folha nº 2 Programação Multiobjectivo 2006/07 1- x2 D(7,6) C(4,5) E(11,5) F(12,4) B(2,3) X G(13,2) A(1,1) H(10,1) max f 1 (x) = x 1 max f 2 (x) = x 2 (a) Represente
Dualidade e Análise de Sensibilidade
 Dualidade e Análise de Sensibilidade 33. Considere o seguinte problema de programação linear: Min Z = 4x 1 + 3x 2 + 6x 3 2x 1 + 2x 2 + 3x 3 4 3x 1 + x 2 + 3x 3 3 x 1, x 2, x 3 0 a) Escreva o dual associado
Dualidade e Análise de Sensibilidade 33. Considere o seguinte problema de programação linear: Min Z = 4x 1 + 3x 2 + 6x 3 2x 1 + 2x 2 + 3x 3 4 3x 1 + x 2 + 3x 3 3 x 1, x 2, x 3 0 a) Escreva o dual associado
Pesquisa Operacional. Prof. José Luiz
 Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Faculdade de Engenharia Investigação Operacional. Prof. Doutor Engº Jorge Nhambiu
 1 Aula 2 Definição de Problemas de Investigação Operacional Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problemas de Investigação
1 Aula 2 Definição de Problemas de Investigação Operacional Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problemas de Investigação
EAD 350 Pesquisa Operacional Aula 03 Parte 1 Revisão Preço-Sombra e Análise de Sensibilidade
 ED 30 Pesquisa Operacional ula 03 Parte Revisão Preço-Sombra e nálise de Sensibilidade Profa. driana ackx Noronha Viana (Participação Prof. Cesar lexandre de Souza) backx@usp.br FE/USP ibliografia para
ED 30 Pesquisa Operacional ula 03 Parte Revisão Preço-Sombra e nálise de Sensibilidade Profa. driana ackx Noronha Viana (Participação Prof. Cesar lexandre de Souza) backx@usp.br FE/USP ibliografia para
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010
 DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
PROGRAMAÇÃO LINEAR. Tipo de problemas: cálculo do plano óptimo de distribuição de mercadorias; minimiação de desperdícios no corte de materiais;
 PROGRAMAÇÃO LINEAR Atribuição de recursos limitados a actividades concorrentes de modo a atingir-se um objectivo. Tipo de problemas: estrutura ideal das fabricações atendendo ao equipamento, mão de obra,
PROGRAMAÇÃO LINEAR Atribuição de recursos limitados a actividades concorrentes de modo a atingir-se um objectivo. Tipo de problemas: estrutura ideal das fabricações atendendo ao equipamento, mão de obra,
Problemas em Programação Linear Resolução e Análise de Sensibilidade
 Problemas em Programação Linear Resolução e Análise de Sensibilidade 24-25 Junho 2014 Metodologias de apoio à decisão nas Ciências Agrárias Eemplo: Formulação Um agricultor pretende cultivar 80 ha de terra
Problemas em Programação Linear Resolução e Análise de Sensibilidade 24-25 Junho 2014 Metodologias de apoio à decisão nas Ciências Agrárias Eemplo: Formulação Um agricultor pretende cultivar 80 ha de terra
Investigação Operacional E-FÓLIO A. Ano lectivo 2015/2016. Proposta de Resolução
 Investigação Operacional - 07 E-FÓLIO A Ano lectivo 0/0 Proposta de Resolução. Variáveis: Sejam percentagem de M / Kg de mistura percentagem de M / Kg de mistura percentagem de M / Kg de mistura Tomando
Investigação Operacional - 07 E-FÓLIO A Ano lectivo 0/0 Proposta de Resolução. Variáveis: Sejam percentagem de M / Kg de mistura percentagem de M / Kg de mistura percentagem de M / Kg de mistura Tomando
Frequência / Exame de 1. a Época
 ISCTE - Instituto Universitário de Lisboa Licenciaturas: Gestão, Finanças e Contabilidade, Gestão e Engenharia Industrial, Marketing e Economia Frequência / Exame de 1. a Época OPTIMIZAÇÃO / MATEMÁTICA
ISCTE - Instituto Universitário de Lisboa Licenciaturas: Gestão, Finanças e Contabilidade, Gestão e Engenharia Industrial, Marketing e Economia Frequência / Exame de 1. a Época OPTIMIZAÇÃO / MATEMÁTICA
Aula 02: Algoritmo Simplex (Parte 1)
 Aula 02: Algoritmo Simplex (Parte 1) Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Slides baseados no material de Haroldo Gambini Previously... Aula anterior:
Aula 02: Algoritmo Simplex (Parte 1) Otimização Linear e Inteira Túlio A. M. Toffolo http://www.toffolo.com.br BCC464/PCC174 2018/2 Slides baseados no material de Haroldo Gambini Previously... Aula anterior:
2. Soluções do sistema de equações da forma-padrão. A mudança de base Considere-se o seguinte modelo de PL: Max f(x) = 6x 1 + 8x 2 + 0F 1 + 0F 2
 Método do Simple V. MÉTODO DO SIMPLEX. Introdução No capítulo III foram apresentadas as bases teóricas do método do Simple sendo de interesse recordar o seguinte: a solução óptima do PPL (quando eiste)
Método do Simple V. MÉTODO DO SIMPLEX. Introdução No capítulo III foram apresentadas as bases teóricas do método do Simple sendo de interesse recordar o seguinte: a solução óptima do PPL (quando eiste)
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
5 Análise de Sensibilidade
 MAC-35 - Programação Linear Primeiro semestre de 00 Prof. Marcelo Queiroz http://www.ime.usp.br/~mqz Notas de Aula 5 Análise de Sensibilidade Neste capítulo consideramos o problema de programação linear
MAC-35 - Programação Linear Primeiro semestre de 00 Prof. Marcelo Queiroz http://www.ime.usp.br/~mqz Notas de Aula 5 Análise de Sensibilidade Neste capítulo consideramos o problema de programação linear
Tópicos Especiais em Computação I
 Tópicos Especiais em Computação I Pesquisa Operacional Exercícios (Simplex) Prof. Fabio Henrique N. Abe Fabio.henrique.abe@gmail.comd Método Simplex Desenvolvido por George Dantzig em 1947 É um procedimento
Tópicos Especiais em Computação I Pesquisa Operacional Exercícios (Simplex) Prof. Fabio Henrique N. Abe Fabio.henrique.abe@gmail.comd Método Simplex Desenvolvido por George Dantzig em 1947 É um procedimento
Instituto Universitário de Lisboa
 Instituto Universitário de Lisboa Departamento de Matemática Exercícios de Extremos 1 Extremos Livres 1. Dada uma função f : R n R e a R n, (a) Qual a propriedade que f(a) deve vericar para ser um máximo
Instituto Universitário de Lisboa Departamento de Matemática Exercícios de Extremos 1 Extremos Livres 1. Dada uma função f : R n R e a R n, (a) Qual a propriedade que f(a) deve vericar para ser um máximo
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA INVESTIGAÇÃO OPERACIONAL
 INSTITUTO POLITÉCNICO DE SETÚBL ESCOL SUPERIOR DE TECNOLOGI DEPRTMENTO DE MTEMÁTIC INVESTIGÇÃO OPERCIONL TESTE CURSOS: EMP, EEM e EME 2005/2006 Data: 4 de Novembro de 2005 Duração: 19:0 às 21:0 Instruções:
INSTITUTO POLITÉCNICO DE SETÚBL ESCOL SUPERIOR DE TECNOLOGI DEPRTMENTO DE MTEMÁTIC INVESTIGÇÃO OPERCIONL TESTE CURSOS: EMP, EEM e EME 2005/2006 Data: 4 de Novembro de 2005 Duração: 19:0 às 21:0 Instruções:
ADA 1º BIMESTRE CICLO I 2018 MATEMÁTICA 2ª SÉRIE DO ENSINO MÉDIO
 ADA º BIMESTRE CICLO I 08 MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO ITEM DA ADA Um sistema de equações pode ser usado para representar situações-problemas da matemática ou do dia-a-dia. Assinale a alternativa
ADA º BIMESTRE CICLO I 08 MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO ITEM DA ADA Um sistema de equações pode ser usado para representar situações-problemas da matemática ou do dia-a-dia. Assinale a alternativa
Investigação Operacional
 Investigação Operacional Programação Linear Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território Problema Uma firma fabrica dois produtos P e P em três máquinas M, M e M. P é processado
Investigação Operacional Programação Linear Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território Problema Uma firma fabrica dois produtos P e P em três máquinas M, M e M. P é processado
Optimização em Redes e Não Linear
 Departamento de Matemática da Universidade de Aveiro Optimização em Redes e Não Linear Ano Lectivo 005/006, o semestre Folha - Optimização em Redes - Árvores de Suporte. Suponha que uma dada companhia
Departamento de Matemática da Universidade de Aveiro Optimização em Redes e Não Linear Ano Lectivo 005/006, o semestre Folha - Optimização em Redes - Árvores de Suporte. Suponha que uma dada companhia
Gestão. Investigação Operacional. Teste / Exame 3.º ano / 1.º Semestre 2009 / 2010
 Gestão Investigação Operacional Teste / Exame 3.º ano / 1.º Semestre 2009 / 2010 Data: Segunda-feira, 4 de Janeiro de 2010 Duração: 1h30m + 30m./ 2h30 m + 30m. Nome: Instruções: 1 Responda a todas as questões
Gestão Investigação Operacional Teste / Exame 3.º ano / 1.º Semestre 2009 / 2010 Data: Segunda-feira, 4 de Janeiro de 2010 Duração: 1h30m + 30m./ 2h30 m + 30m. Nome: Instruções: 1 Responda a todas as questões
Investigação Operacional
 Licenciatura em Engenharia Electrotécnica e de Computadores Investigação Operacional Recurso 2004.02.09 Duração: 2 horas Nome: Teórica Responda a cada afirmação com (V) Verdadeira ou (F) Falsa. Por cada
Licenciatura em Engenharia Electrotécnica e de Computadores Investigação Operacional Recurso 2004.02.09 Duração: 2 horas Nome: Teórica Responda a cada afirmação com (V) Verdadeira ou (F) Falsa. Por cada
EAD 350 Pesquisa Operacional Aula 03 Parte 2
 EAD 350 Pesquisa Operacional Aula 03 Parte 2 Profa. Adriana Backx Noronha Viana (Participação Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Método Simplex (item 4.1 do Hillier e Lieberman) - apenas
EAD 350 Pesquisa Operacional Aula 03 Parte 2 Profa. Adriana Backx Noronha Viana (Participação Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Método Simplex (item 4.1 do Hillier e Lieberman) - apenas
Resolução de PL usando o método Simplex
 V., V.Lobo, EN / ISEGI, 28 Resolução de PL usando o método Simplex Método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 947 Muito utilizado Facilmente implementado como
V., V.Lobo, EN / ISEGI, 28 Resolução de PL usando o método Simplex Método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 947 Muito utilizado Facilmente implementado como
EXAME MODELO 11 DE JUNHO DE 2008 Duração: 2 horas. Grupo I [10 valores]
![EXAME MODELO 11 DE JUNHO DE 2008 Duração: 2 horas. Grupo I [10 valores] EXAME MODELO 11 DE JUNHO DE 2008 Duração: 2 horas. Grupo I [10 valores]](/thumbs/101/148257693.jpg) INSTITUTO SUPERIOR DE CONTABILIDADE E ADMINISTRAÇÃO DO PORTO MICROECONOMIA EXAME MODELO 11 DE JUNHO DE 2008 Duração: 2 horas Nome Nº informático Turma Professor(a) Preencha o cabeçalho e, para cada uma
INSTITUTO SUPERIOR DE CONTABILIDADE E ADMINISTRAÇÃO DO PORTO MICROECONOMIA EXAME MODELO 11 DE JUNHO DE 2008 Duração: 2 horas Nome Nº informático Turma Professor(a) Preencha o cabeçalho e, para cada uma
Investigação Operacional 2004/05 2º Mini-teste Extra. 9 de Dezembro, 11:00h 12:30h
 Investigação Operacional 00/0 º Mini-teste Extra 9 de Dezembro, :00h :0h Sem consulta, sem máquina de calcular Justifique todas as respostas Departamento de Engenharia Civil Secção de Planeamento do Território
Investigação Operacional 00/0 º Mini-teste Extra 9 de Dezembro, :00h :0h Sem consulta, sem máquina de calcular Justifique todas as respostas Departamento de Engenharia Civil Secção de Planeamento do Território
Programação Linear M É T O D O S : E S T A T Í S T I C A E M A T E M Á T I C A A P L I C A D A S D e 1 1 d e m a r ç o a 2 9 d e a b r i l d e
 Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Pesquisa Operacional. Introdução à Pesquisa Operacional Programação Linear
 Pesquisa Operacional Introdução à Pesquisa Operacional Programação Linear 1 Sumário Modelagem e limitações da Programação Linear. Resolução Gráfica. Forma padrão de um modelo de Programação Linear. Definições
Pesquisa Operacional Introdução à Pesquisa Operacional Programação Linear 1 Sumário Modelagem e limitações da Programação Linear. Resolução Gráfica. Forma padrão de um modelo de Programação Linear. Definições
Ministério da Educação Universidade Tecnológica Federal do Paraná. Campus Apucarana Departamento Acadêmico de Matemática
 Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Apucarana Departamento Acadêmico de Matemática Edital 21-2013/PROGRAD Apoio à Produção de Recursos Educacionais Digitais Autores:
Ministério da Educação Universidade Tecnológica Federal do Paraná Campus Apucarana Departamento Acadêmico de Matemática Edital 21-2013/PROGRAD Apoio à Produção de Recursos Educacionais Digitais Autores:
Método Simplex V 1.1, V.Lobo, EN / ISEGI, 2008
 .,.Lobo, EN / ISEGI, 8 Método Simplex Resolução de PL usando o método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 97 Muito utilizado Facilmente implementado como programa
.,.Lobo, EN / ISEGI, 8 Método Simplex Resolução de PL usando o método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 97 Muito utilizado Facilmente implementado como programa
VERSÃO RESPOSTAS PROVA DE MÉTODOS QUANTITATIVOS
 UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DE RIBEIRÃO PRETO PROGRAMA DE PÓS-GRADUAÇÃO EM ADMINISTRAÇÃO DE ORGANIZAÇÕES PROCESSO SELETIVO DOUTORADO - TURMA 20 VERSÃO
UNIVERSIDADE DE SÃO PAULO FACULDADE DE ECONOMIA, ADMINISTRAÇÃO E CONTABILIDADE DE RIBEIRÃO PRETO PROGRAMA DE PÓS-GRADUAÇÃO EM ADMINISTRAÇÃO DE ORGANIZAÇÕES PROCESSO SELETIVO DOUTORADO - TURMA 20 VERSÃO
Economia I; 2012/2013; 2º sem. Prova da Época Recurso 3 de Julho de Antes de iniciar a sua prova tenha em atenção os seguintes aspectos:
 Economia I; 2012/2013; 2º sem. Prova da Época Recurso 3 de Julho de 2013 Antes de iniciar a sua prova tenha em atenção os seguintes aspectos: A duração da prova é de duas horas e trinta minutos (2h 30m).
Economia I; 2012/2013; 2º sem. Prova da Época Recurso 3 de Julho de 2013 Antes de iniciar a sua prova tenha em atenção os seguintes aspectos: A duração da prova é de duas horas e trinta minutos (2h 30m).
Pesquisa Operacional Aula 3 Modelagem em PL
 Pesquisa Operacional Aula 3 Modelagem em PL Prof. Marcelo Musci aula@musci.info www.musci.info Programação Linear Programação Linear: Preocupação em encontrar a melhor solução para problemas associados
Pesquisa Operacional Aula 3 Modelagem em PL Prof. Marcelo Musci aula@musci.info www.musci.info Programação Linear Programação Linear: Preocupação em encontrar a melhor solução para problemas associados
optimiza a produção? Para formular o modelo de PL é de interesse organizar a informação disponível no quadro seguinte: Produto A B C
 II. Exemplos Típicos de Formulação Matemática do Modelo de PL Nota: Os exemplos apresentados devem ser resolvidos recorrendo ao software do autor. Faça sempre um boneco que ajude a fixar as variáveis de
II. Exemplos Típicos de Formulação Matemática do Modelo de PL Nota: Os exemplos apresentados devem ser resolvidos recorrendo ao software do autor. Faça sempre um boneco que ajude a fixar as variáveis de
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear 2016/I 1. Escreva os seguintes sistemas na forma matricial: 2x 1
1 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear 2016/I 1. Escreva os seguintes sistemas na forma matricial: 2x 1
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Forma geral de um problema Em vários problemas que formulamos, obtivemos: Um objetivo de otimização
Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Forma geral de um problema Em vários problemas que formulamos, obtivemos: Um objetivo de otimização
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Unidade: Modelo Simplex e Modelo Dual. Unidade I:
 Unidade: Modelo Simplex e Modelo Dual Unidade I: 0 Unidade: Modelo Simplex e Modelo Dual Segundo Wikipédia (2008), em teoria da otimização matemática, o algoritmo simplex de George Dantiz é uma técnica
Unidade: Modelo Simplex e Modelo Dual Unidade I: 0 Unidade: Modelo Simplex e Modelo Dual Segundo Wikipédia (2008), em teoria da otimização matemática, o algoritmo simplex de George Dantiz é uma técnica
II. Programação Linear (PL)
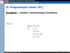 II. Programação Linear (PL) Dualidade revisão e interpretação econômica Seja o pl max Z x x x x 4 x, x 5x x 0 8 000-00 Prof.ª Gladys Castillo Formulação do Problema de PL em termos de Atividades. Exemplo
II. Programação Linear (PL) Dualidade revisão e interpretação econômica Seja o pl max Z x x x x 4 x, x 5x x 0 8 000-00 Prof.ª Gladys Castillo Formulação do Problema de PL em termos de Atividades. Exemplo
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Revisão Método Simplex Solução básica factível: xˆ xˆ, xˆ N em que xˆ N 0 1 xˆ b 0 Solução geral
Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Revisão Método Simplex Solução básica factível: xˆ xˆ, xˆ N em que xˆ N 0 1 xˆ b 0 Solução geral
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR MÉTODO SIMPLEX. Prof. Angelo Augusto Frozza, M.Sc.
 PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR MÉTODO SIMPLEX Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 3 do livro de Taha (2008): Motivação Conceitos Matemáticos Iniciais
PESQUISA OPERACIONAL -PROGRAMAÇÃO LINEAR MÉTODO SIMPLEX Prof. Angelo Augusto Frozza, M.Sc. ROTEIRO Esta aula tem por base o Capítulo 3 do livro de Taha (2008): Motivação Conceitos Matemáticos Iniciais
Modelos de Apoio à Decisão. Programação Linear. Rui Cunha Marques
 Modelos de Apoio à Decisão Programação Linear Rui Cunha Marques / Metodologia: Análise Sistémica Modelo: representação adequada (face aos objectivos do estudo) do sistema em análise que sendo passível
Modelos de Apoio à Decisão Programação Linear Rui Cunha Marques / Metodologia: Análise Sistémica Modelo: representação adequada (face aos objectivos do estudo) do sistema em análise que sendo passível
Técnicas de Planeamento e Gestão. Folha nº. 1 Introdução à Programação Linear 2007/08
 Técnicas de Planeamento e Gestão Folha nº. 1 Introdução à Programação Linear 2007/08 1- A fábrica de gelados Derretem-se na Boca SARL fabrica duas qualidades de gelados: cassata de nozes (C) e pistachio
Técnicas de Planeamento e Gestão Folha nº. 1 Introdução à Programação Linear 2007/08 1- A fábrica de gelados Derretem-se na Boca SARL fabrica duas qualidades de gelados: cassata de nozes (C) e pistachio
Análise de Sensibilidade
 Análise de Sensiilidade Prof. Fernando Augusto Silva Marins Departamento de Produção Faculdade de Engenharia Campus de Guaratinguetá UNESP www.feg.unesp.r/~fmarins fmarins@feg.unesp.r Introdução Dados
Análise de Sensiilidade Prof. Fernando Augusto Silva Marins Departamento de Produção Faculdade de Engenharia Campus de Guaratinguetá UNESP www.feg.unesp.r/~fmarins fmarins@feg.unesp.r Introdução Dados
Matemática A - 10 o Ano
 Matemática A - 10 o Ano Resolução da Ficha de Trabalho Álgebra - Divisão Inteira de Polinómios Grupo I 1. Considerando os polinómios p e b no enunciado temos que o termo de maior grau de p b é a nx n b
Matemática A - 10 o Ano Resolução da Ficha de Trabalho Álgebra - Divisão Inteira de Polinómios Grupo I 1. Considerando os polinómios p e b no enunciado temos que o termo de maior grau de p b é a nx n b
