Q05. Ainda sobre os eventos A, B, C e D do exercício 03, quais são mutuamente exclusivos?
|
|
|
- Lucinda Fragoso Pinho
- 6 Há anos
- Visualizações:
Transcrição
1 LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo das probabilidades. A teoria das probabilidades permite que se calcule a chance de ocorrência de um número em um experimento aleatório. EXPERIMENTO ALEATÓRIO É a situação que, quando repetida em iguais condições, pode fornecer resultados diferentes, ou seja, resultados que ocorrem ao acaso ou aleatoriamente. ESPAÇO AMOSTRAL É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral é U. EVENTO É o resultado desejado dentre todos os possíveis do espaço amostral. O evento será um conjunto indicado por E. PROBABILIDADE Se num fenômeno aleatório não há condições externas ou qualquer tipo de manipulação interna associada que favoreça o acontecimento de um evento, as possibilidades de ocorrência se tornam igualmente prováveis. Nesta situação, a probabilidade é a chance de ocorrer um evento. Q04. Sobre os eventos do exercício anterior, indique o evento em que: A) E = {A ou B ocorrem}; B) F = {B e C ocorrem}; C) G = {somente B ocorre}; D) H = {ocorre B, mas não ocorre D}. Q05. Ainda sobre os eventos A, B, C e D do exercício 03, quais são mutuamente exclusivos? Q06. No lançamento de um dado, qual a probabilidade de ocorrer um número maior que 4? Q07. No lançamento de duas moedas, qual a probabilidade de as faces voltadas para cima serem iguais? Q08. Lança-se um dado e uma moeda. Qual a probabilidade de se ter cara na moeda e um número primo no dado? Q09. Um casal planeja ter três filhos. Qual a probabilidade de que dois deles sejam do mesmo sexo? Q10. Escolhe-se um número natural menor que 100. Qual a probabilidade que tenha dois algarismos distintos? Q11. Escolhe-se um número natural de dois algarismos. Qual a probabilidade de que o número escolhido seja primo? CÁLCULO DA PROBABILIDADE Se A é um evento, a chance de A ocorrer é dada por: Q12. Uma caixa possui três parafusos e três porcas. Qual a probabilidade de, na retirada de dois objetos, um ser parafuso e o outro, porca? EXERCÍCIOS BLOCO I Q01. Escreva o Espaço amostral para os seguintes experimentos. A) Lançamento de uma moeda. B) Lançamento de um dado. C) Nascimento de uma criança. D) Lançamento de duas moedas. E) Lançamento de dois dados. F) Lançamento de um dado e uma moeda. G) Nascimento de três crianças. H) Sorteio de um número primo menor que 30. Q02. Escreva o número de elementos do Espaço amostral para os seguintes experimentos A) Lançamento de três moedas. B) Lançamento de três dados. C) Nascimento de quatro crianças. D) Lançamento de dois dados e uma moeda. E) Lançamento de um dado e duas moedas. F) Escolha de um número de dois algarismos. Q03. Considere o lançamento de um dado e de uma moeda. Escreva, explicitamente, os seguintes eventos: A) A = {aparecer cara e número par}. B) B = {aparecer um número primo}. C) C = {aparecem coroas e um número ímpar}. D) D = {não aparecer cara ou número primo}. Q13. O grupo A de um torneio de Futebol possui Ajax, Barcelona, Benfica, Chelsea, Milan e Porto. Qual a probabilidade de que Chelsea e Milan sejam os dois primeiros colocados do grupo? Q14. O grupo B de um torneio de Vôlei possui Minas, Sesi, Pinheiros, Osasco, Praia Clube e Rio de Janeiro. Qual a probabilidade de que Osasco e Rio de Janeiro sejam, nesta ordem, o primeiro e segundo colocados do grupo? Q15. Um torneio é realizado com dez equipes que ficam divididas em dois grupos. As equipes jogam entre si uma única vez e os dois primeiros colocados de cada grupo se enfrentam nas semifinais, de forma que o primeiro colocado de um grupo enfrente o segundo colocado do outro grupo, em jogo único. Os vencedores disputam a final, também em um único jogo. A) Quantos jogos serão disputados no torneio? B) Qual a probabilidade de que a final seja entre equipes que estavam no mesmo grupo? Q16. Uma pesquisa feita com 1200 alunos de uma escola de idiomas constatou que 600 alunos falam inglês, 500 falam espanhol e 300 não falam qualquer um desses idiomas. Escolhendo-se ao acaso um aluno dessa escola, qual a probabilidade de que esse aluno: A) Fale espanhol? B) Não fale espanhol? C) Fale inglês e espanhol.
2 PROPRIEDADES IMPORTANTES I. Dizemos que um espaço amostral U (finito) é equiprovável quando seus eventos elementares têm probabilidades iguais de ocorrência. II. Se A e A' são eventos complementares, então P(A) + P(A') = 1. III. A probabilidade de um evento é sempre um número entre 0 (probabilidade de evento impossível) e 1 (probabilidade do evento certo). PROBABILIDADE CONDICIONAL Muitas vezes, antes da realização de um experimento, já se tem alguma informação sobre um evento ocorrido e que influencia no resultado que se deseja observar. Nesse caso, o espaço amostral é modificado e o evento tem a sua probabilidade de ocorrência condicionada à informação dada. P(A B) = P(A B) = P(A) P(B/A) = Q02. Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se sortearmos 2 bolas, 1 de cada vez e repondo a sorteada na urna, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul? Como os eventos são independentes, a probabilidade de sair vermelha na primeira retirada e azul na segunda retirada é igual ao produto das probabilidades de cada condição, ou seja, P(A e B) = P(A) P(B). Note que a probabilidade de sair vermelha na primeira retirada é e a de sair azul na segunda retirada. Daí, usando a regra do produto, mostrada anteriormente, temos: P(A B) = = FÓRMULA DE PROBABILIDADE CONDICIONAL Sendo é a probabilidade condicional de ocorrer A, tendo ocorrido B, temos: ou Observe que na segunda retirada foram consideradas todas as bolas, pois houve reposição. Assim, P(B/A) =P(B), porque o fato de sair bola vermelha na primeira retirada não influenciou a segunda retirada, já que ela foi reposta na urna. Daí serem eventos independentes. PROBABILIDADE DE EVENTOS INDEPENDENTES Dizemos que A, B, C,..., N são eventos independentes quando a probabilidade de ocorrer um deles não depende do fato de os outros terem ocorrido. A probabilidade de ocorrerem todos eles é dada por: P(A B C N) = P(A) P(B) P(C) P(N) PROBABILIDADE DA UNIÃO DE EVENTOS P(A B) = P(A) + P(B) P(A B) De fato, se existirem elementos comuns a A e B, estes eventos estarão computados no cálculo de P(A) e P(B). Para que sejam considerados uma vez só, subtraímos P(A B). PROBABILIDADE DA UNIÃO DE EVENTOS MUTUAMEN- TE EXCLUSIVOS: P(A B C N) = P(A) + P(B) + + P(N) Só pra lembrar, os eventos mutuamente exclusivos não têm pontos comuns ou intersecção. EXERCÍCIOS BLOCO II Q01. Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se ocorrer um sorteio de 2 bolas, uma de cada vez e sem reposição, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul? Seja o espaço amostral U, onde N(U) = 30 bolas, e consideraremos os seguintes eventos: A: vermelha na primeira retirada e P(A) = B: azul na segunda retirada e P(B) = Assim: Q03. Se dois dados, azul e branco, forem lançados, qual a probabilidade de sair 5 no azul e 3 no branco? Considerando os eventos: A: Tirar 5 no dado azul P(A) = 1/6 B: Tirar 3 no dado branco P(B) = 1/6 Sendo U o espaço amostral de todos os possíveis resultados, temos: n(u) = 6 6 = 36 possibilidades. Daí, temos: P(A B) = Q04. Se retirarmos aleatoriamente uma carta de baralho com 52 cartas, qual a probabilidade de ser um 8 ou um rei? Sendo U o espaço amostral de todos os resultados possíveis para o baralho, temos: n(u) = 52 cartas. Agora consideremos os eventos: A: sair 8 P(A) = B: sair um rei P(B) = Assim, P(A B) =. Note que P(A B) = 0, pois uma carta não pode ser 8 e rei ao mesmo tempo. Quando isso ocorre, dizemos que os eventos A e B são mutuamente exclusivos. Q05. Uma moeda é viciada, de forma que as caras são três vezes mais prováveis de aparecer do que as coroas. Determine a probabilidade de num lançamento sair coroa. Q06. Três estudantes A, B e C estão em uma competição de natação. A e B têm as mesmas chances de vencer e, cada um, tem duas vezes mais chances de vencer do que C. Calcule a probabilidade de A ou C vencer.
3 Q07. Um dado é viciado, de modo que cada número par tem duas vezes mais chances de aparecer num lançamento que qualquer número ímpar. Determine a probabilidade de num lançamento aparecer um número primo. Q08. Um cartão é retirado aleatoriamente de um conjunto de 50 cartões numerados de 1 a 50. Determine a probabilidade de o cartão retirado ser de um número primo. Q09. Das 10 alunas de uma classe, 3 têm olhos azuis. Se duas delas são escolhidas ao acaso, qual é a probabilidade de ambas terem os olhos azuis? Q10. Oito pessoas incluindo um casal e seu filho são colocados aleatoriamente em fila. Qual é a probabilidade de que a família fique junta? Q11. Três livros de Álgebra, três de Geometria e três de Estatística são colocados ao acaso numa estante. Qual a probabilidade de que os livros fiquem ordenados por temas? QUESTÕES BÁSICAS Q01. (Cesgranrio) Uma urna contém 4 bolas brancas e 5 bolas pretas. Duas bolas escolhidas ao acaso são sacadas dessa urna, sucessivamente e sem reposição. A probabilidade de que ambas sejam brancas é: A) 1/6 C) 4/9 E) 20/81 B) 2/9 D) 16/81 Q02. (FATEC) Considere todos os números de cinco algarismos distintos obtidos pela permutação dos algarismos 4, 5,6, 7 e 8. Escolhendo-se um desses números, ao acaso, a probabilidade de ele ser um número ímpar é: A) 1 C) 2/5 E) 1/5 B) 1/2 D) 1/4 Q03. (FEI SP) Uma caixa contém 3 bolas verdes, 4 bolas amarelas e 2 bolas pretas. Duas bolas são retiradas ao acaso e sem reposição. A probabilidade de ambas serem da mesma cor é: A) 13/72 C) 5/18 E) 1/4 B) 1/18 D) 1/9 Q04. (FEI SP) Em uma pesquisa realizada em uma Faculdade foram feitas duas perguntas aos alunos. Cento e vinte responderam sim a ambas; 300 responderam sim à primeira; 250 responderam sim à segunda e 200 responderam não a ambas. Se um aluno for escolhido ao acaso, qual é a probabilidade de ele ter respondido não à primeira pergunta? A) 1/7 C) 3/8 E) 4/25 B) 1/2 D) 11/21 Q05. (FUVEST) Escolhem-se ao acaso três vértices distintos de um cubo. A probabilidade de que estes vértices pertençam a uma mesma face é: A) 3/14 C) 5/14 E) 13/18 B) 2/7 D) 3/7 Q06. (FUVEST) Em certo jogo de loteria seis números distintos são sorteados dentre os números 1, 2,..., 50. A probabilidade de que, numa extração, os seis números sorteados sejam todos ímpares vale aproximadamente: A) 50% C) 25% E) 5% B) 1% D) 10% Q07. (Mackenzie) Num grupo de 12 professores, somente 5 são de matemática. Escolhidos ao acaso 3 professores do grupo, a probabilidade de no máximo um deles ser de matemática é: A) 3/11. C) 7/11. E) 9/11. B) 5/11. D) 8/11. Q08. (PUC Campinas) O número de fichas de certa urna é igual ao número de anagramas da palavra VESTIBULAR. Se em cada ficha escrevermos apenas um dos anagramas, a probabilidade de sortearmos uma ficha dessa urna e no anagrama marcado as vogais estarem juntas é: A) 1/5040 C) 1/60 E) 1/15 B) 1/1260 D) 1/30 Q09. O número de fichas em certa urna é igual ao número de anagramas da palavra POIA. Se em cada ficha está escrito apenas um dos anagramas, a probabilidade de sortearmos uma ficha dessa urna e no anagrama marcado as vogais estarem todas juntas é: A) 1/4 C) 2/3 E) 4/5 B) 1/2 D) 3/4 Q10. A probabilidade de um homem estar vivo daqui a 20 anos é de 10% e a de seu filho é 50%. A probabilidade de esse filho ser órfão de pai daqui a 20 anos é: A) 10% C) 25% E) 45% B) 20% D) 40% Q11. Um jogo de crianças consiste em lançar uma caixa de fósforos sobre uma mesa. Ganha quem conseguir fazer com que a caixa fique apoiada sobre sua menor face. Suponha que a probabilidade de uma face ficar apoiada sobre a mesa é proporcional à sua área e que a constante de proporcionalidade é a mesma para cada face. Se as dimensões da caixa são 2 cm, 4 cm e 8 cm, qual é a probabilidade de a caixa ficar apoiada sobre sua face menor? Q12. Uma caixa contém 11 bolas idênticas, numeradas de 01 a 11. Retira-se uma bola desta caixa e verifica-se que é um número ímpar. Qual a probabilidade de esse número ser menor que 7? QUESTÕES COMPLEMENTARES Q01. (MACK) Em um determinado jogo, são sorteados 3 números entre os 30 que estão no volante de apostas. O apostador, que assinala 6 números no volante, ganha, se todos os 3 números sorteados estiverem entre os 6 assinalados. A probabilidade de o apostador ganhar é: A) 1/203 C) 1/456 E) 1/98 B) 1/507 D) 1/280 Q02. (MACK) Considere todos os números de 3 algarismos formados com os algarismos 1, 2, 3, 5, 7 e 9. Dentre eles, a quantidade de números pares com exatamente 2 algarismos iguais é: A) 17 C) 15 E) 24 B) 18 D) 22
4 Q03. (UNB) Uma criança entra em um elevador de um edifício no andar térreo. Os botões do painel do elevador estão dispostos como ilustrado na figura a seguir, em que o número zero representa o andar térreo e os números negativos representam os três subsolos do edifício. A criança aperta um botão ao acaso, mas, por ser ainda muito pequena, a probabilidade de ela apertar qualquer botão correspondente a um dos números do conjunto { 3, 2, 1, 0, 1, 2} é o triplo da probabilidade de ela apertar qualquer botão correspondente a um dos números do conjunto {3, 4, 5, 6, 7, 8}, a qual, por sua vez, é o dobro da probabilidade de ela apertar qualquer botão correspondente a um dos números do conjunto {9, 10, 11, 12} Nessas condições, julgue os itens que se seguem. I. A probabilidade de a criança apertar um dos botões correspondentes a um dos números do conjunto { 1, 2, 3 } é igual a 1/3. II. A probabilidade de ela apertar o botão correspondente ao número 5 ou o botão correspondente ao número 2 é igual a 1/6. III. A probabilidade de ela apertar o botão correspondente ao número 0 é menor que 1/10. Q04. (COVEST) Três dados perfeitos A, B e C têm suas faces numeradas da seguinte forma: Dado A: Duas faces numeradas com 1 e quatro com 5; Dado B: Seis faces numeradas com 4; Dado C: Quatro faces numeradas com 2 e duas com 6. Lançando-se dois destes dados, diremos que é ganhador aquele que apresenta o maior número na face voltada para cima. De posse destas informações, analise as afirmativas abaixo: 1) O dado A ganha do dado B com probabilidade 2/3. 2) O dado B ganha do dado C com probabilidade 2/3. 3) O dado C ganha do dado A com probabilidade 5/9. Está(ão) correta(s): A) 1 e 2 apenas D) 1 e 3 apenas B) 1 apenas E) 2 e 3 apenas C) 1, 2 e 3 Q05. (COVEST) Um saco contém 12 bolas verdes e 8 bolas amarelas. Quantas bolas azuis devem ser colocadas no saco, de modo que a probabilidade de retirarmos do mesmo, aleatoriamente, uma bola azul, seja 2/3? A) 5 C) 20 E) 40 B) 10 D) 30 Q06. Num grupo de 12 professores, somente 5 são de Matemática. Escolhendo ao acaso, três professores desse grupo, a probabilidade de que, no máximo um deles seja de Matemática é: A) 2/11 C) 5/11 E) 8/11 B) 4/11 D) 6/11 Q07. (UNEAL) Em uma festa de rua, existe um jogo onde, em cada extração, são sorteados quatro, dentre os números de 1 a 40. Se João aposta em oito números, e Pedro aposta em dez números, qual a razão entre as probabilidades de Pedro ganhar e de João ganhar? A) 2 C) 4 E) 6 B) 3 D) 5 Q08. (UNEAL) Cada um de dois dados perfeitos têm suas faces numeradas de 1 a 6. Os dados são lançados, e os números das faces voltadas para cima são subtraídos, de modo a se obter um inteiro não negativo. Qual dos números abaixo ocorre com maior probabilidade? A) 1 C) 3 E) 5 B) 2 D) 4 Q09. (UNEAL) Uma pesquisa realizada nos Estados Unidos revelou que, quando querem esclarecer dúvidas a respeito de temas cotidianos, 58% da população consultam a internet, e 53% buscam profissionais especializados. Qual o percentual mínimo da população que recorre às duas fontes de informação? A) 8% C) 10% E) 12% B) 9% D) 11% Q10. (UNEAL) Das balas de determinada marca, uma em cada 100 está amassada. Se você escolhe duas destas balas aleatoriamente, de um saco contendo 100 delas, qual a probabilidade percentual de, pelo menos uma das duas, estar amassada? A) 1,99% B) 19,9% C) 0,199% D) 1,98% E) 19,8% Q11. (UFAL) Realizada uma pesquisa 200 dos alunos de uma escola de idiomas, concluiu-se que 130 deles estudam inglês, 80 deles estudam espanhol e 30 deles estudam as duas línguas. Selecionando-se ao acaso um dos alunos pesquisados, a probabilidade de ele A) não estudar essas duas línguas é 12,5%; B) estudar espanhol e não estudar inglês é 15%; C) estudar espanhol e não estudar inglês é 20%; D) estudar inglês e não estudar espanhol é 20%; E) estudar inglês e não estudar espanhol é 50%. Q12. (UFAL) Sabe-se que de um lote de peças produzidas por uma máquina, 10 estavam perfeitas, 4 com pequenos defeitos e 2 com defeitos graves. Retirando-se ao acaso duas dessas peças, sem reposição, determine a probabilidade de: A) ambas serem perfeitas; B) nenhuma delas ter defeitos graves. Q13. A probabilidade de um casal ter um filho do sexo masculino é 1/4. Então, supondo que o casal venha a ter três filhos, a probabilidade de serem exatamente dois do mesmo sexo é: A) 3/16 C) 1/8 E) 9/16 B) 1/16 D) 3/8 Q14. Uma prova apresenta 8 questões objetivas (com alternativas de A até E). Qual a probabilidade de pelo menos 5 acertos, no chute?
5 GABARITO PROBABILIDADES Q BLOCO I BLOCO II BÁSICAS COMPLEMENTARES /4 06 3/5 07 4/9 08 3/ / ,71% 11 1/
PROBABILIDADE. É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral, é S.
 PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade.
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade.
PROBABILIDADE PROPRIEDADES E AXIOMAS
 PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
Lista de exercícios de Matemática Eventos, espaço amostral e definição de probabilidade. Probabilidade condicional. Exercícios gerais.
 p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
PROBABILIDADES PROBABILIDADE DE UM EVENTO EM UM ESPAÇO AMOSTRAL FINITO
 PROBABILIDADES Probabilidade é um conceito filosófico e matemático que permite a quantificação da incerteza, permitindo que ela seja aferida, analisada e usada para a realização de previsões ou para a
PROBABILIDADES Probabilidade é um conceito filosófico e matemático que permite a quantificação da incerteza, permitindo que ela seja aferida, analisada e usada para a realização de previsões ou para a
MATEMÁTICA MÓDULO 4 PROBABILIDADE
 PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
PROBABILIDADE Consideremos um experimento com resultados imprevisíveis e mutuamente exclusivos, ou seja, cada repetição desse experimento é impossível prever com certeza qual o resultado que será obtido,
1 Definição Clássica de Probabilidade
 Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Estatística Aplicada. Prof. Carlos Alberto Stechhahn EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE. Administração. p(a) = n(a) / n(u)
 Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
Exercícios de Probabilidade - Lista 1. Profa. Ana Maria Farias
 Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
2. Nas Figuras 1a a 1d, assinale a área correspondente ao evento indicado na legenda. Figura 1: Exercício 2
 GET00116 Fundamentos de Estatística Aplicada Lista de exercícios Probabilidade Profa. Ana Maria Lima de Farias Capítulo 1 Probabilidade: Conceitos Básicos 1. Lançam-se três moedas. Enumere o espaço amostral
GET00116 Fundamentos de Estatística Aplicada Lista de exercícios Probabilidade Profa. Ana Maria Lima de Farias Capítulo 1 Probabilidade: Conceitos Básicos 1. Lançam-se três moedas. Enumere o espaço amostral
Chama-se evento todo subconjunto de um espaço amostral. PROBABILIDADE. Introdução
 Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Prof.: Joni Fusinato
 Introdução a Teoria da Probabilidade Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Introdução a Teoria da Probabilidade Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
LISTA 29 - PROBABILIDADE 1
 LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
2. Nas Figuras 1a a 1d, assinale a área correspondente ao evento indicado na legenda. Figura 1: Exercício 2
 GET00189 Probabilidade I Lista de exercícios - Capítulo 1 Profa. Ana Maria Lima de Farias SEÇÃO 1.1 Experimento aleatório, espaço amostral e evento 1. Lançam-se três moedas. Enumere o espaço amostral e
GET00189 Probabilidade I Lista de exercícios - Capítulo 1 Profa. Ana Maria Lima de Farias SEÇÃO 1.1 Experimento aleatório, espaço amostral e evento 1. Lançam-se três moedas. Enumere o espaço amostral e
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística. Probabilidades
 Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
3. Probabilidade P(A) =
 7 3. Probabilidade Probabilidade é uma medida numérica da plausibilidade de que um evento ocorrerá. Assim, as probabilidades podem ser usadas como medidas do grau de incerteza e podem ser expressas de
7 3. Probabilidade Probabilidade é uma medida numérica da plausibilidade de que um evento ocorrerá. Assim, as probabilidades podem ser usadas como medidas do grau de incerteza e podem ser expressas de
AULA 08 Probabilidade
 Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
Cursinho Pré-Vestibular da UFSCar São Carlos Matemática Professora Elvira e Monitores Ana Carolina e Bruno AULA 08 Conceitos e assuntos envolvidos: Espaço amostral Evento Combinação de eventos Espaço Amostral
CAPÍTULO 3 PROBABILIDADE
 CAPÍTULO 3 PROBABILIDADE 1. Conceitos 1.1 Experimento determinístico Um experimento se diz determinístico quando repetido em mesmas condições conduz a resultados idênticos. Exemplo 1: De uma urna que contém
CAPÍTULO 3 PROBABILIDADE 1. Conceitos 1.1 Experimento determinístico Um experimento se diz determinístico quando repetido em mesmas condições conduz a resultados idênticos. Exemplo 1: De uma urna que contém
PROBABILIDADE. Numero de Resultados Desejado Numero de Resultados Possiveis EXERCÍCIOS DE AULA
 PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
3. (Apostila 1 - ex.1.4) Defina um espaço amostral para cada um dos seguintes experimentos
 Primeira Lista de Exercícios Introdução à probabilidade e à estatística Prof Patrícia Lusié Assunto: Probabilidade. 1. (Apostila 1 - ex.1.1) Lançam-se três moedas. Enumerar o espaço amostral e os eventos
Primeira Lista de Exercícios Introdução à probabilidade e à estatística Prof Patrícia Lusié Assunto: Probabilidade. 1. (Apostila 1 - ex.1.1) Lançam-se três moedas. Enumerar o espaço amostral e os eventos
Matemática & Raciocínio Lógico
 Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur PROBABILIDADE No estudo das probabilidades estamos interessados em estudar o experimento
Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur PROBABILIDADE No estudo das probabilidades estamos interessados em estudar o experimento
TEORIA DAS PROBABILIDADES
 TEORIA DAS PROBABILIDADES 1.1 Introdução Ao estudarmos um fenômeno coletivo, verificamos a necessidade de descrever o próprio fenômeno e o modelo matemático associado ao mesmo, que permita explicá-lo da
TEORIA DAS PROBABILIDADES 1.1 Introdução Ao estudarmos um fenômeno coletivo, verificamos a necessidade de descrever o próprio fenômeno e o modelo matemático associado ao mesmo, que permita explicá-lo da
Aula 16 - Erivaldo. Probabilidade
 Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Probabilidade em espaços discretos. Prof.: Joni Fusinato
 Probabilidade em espaços discretos Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
Probabilidade em espaços discretos Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
ELEMENTOS DE PROBABILIDADE. Prof. Paulo Rafael Bösing 25/11/2015
 ELEMENTOS DE PROBABILIDADE Prof. Paulo Rafael Bösing 25/11/2015 ELEMENTOS DE PROBABILIDADE Def.: Um experimento é dito aleatório quando o seu resultado não for previsível antes de sua realização, ou seja,
ELEMENTOS DE PROBABILIDADE Prof. Paulo Rafael Bösing 25/11/2015 ELEMENTOS DE PROBABILIDADE Def.: Um experimento é dito aleatório quando o seu resultado não for previsível antes de sua realização, ou seja,
Aula 10 - Erivaldo. Probabilidade
 Aula 10 - Erivaldo Probabilidade Experimento determinístico Dizemos que um experimento é determinístico quando repetido em condições semelhantes conduz a resultados idênticos. Experimento aleatório Dizemos
Aula 10 - Erivaldo Probabilidade Experimento determinístico Dizemos que um experimento é determinístico quando repetido em condições semelhantes conduz a resultados idênticos. Experimento aleatório Dizemos
Roteiro D. Nome do aluno: Número: Revisão. Combinações;
 Faculdade Tecnológica de Carapicuíba Tecnologia em Logística Ênfase em Transportes Roteiro D Nome do aluno: Número: Periodo: Grupo: Revisão Tópicos Tarefa Pesquisar história do Fatorial e outros tipos
Faculdade Tecnológica de Carapicuíba Tecnologia em Logística Ênfase em Transportes Roteiro D Nome do aluno: Número: Periodo: Grupo: Revisão Tópicos Tarefa Pesquisar história do Fatorial e outros tipos
Matemática. Probabilidade Básica. Professor Dudan.
 Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan
 Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
Noções sobre Probabilidade
 Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
Noções sobre Probabilidade Introdução Vimos anteriormente como apresentar dados em tabelas e gráficos, e também como calcular medidas que descrevem características específicas destes dados. Mas além de
T o e r o ia a da P oba ba i b lida d de
 Teoria da Probabilidade Prof. Joni Fusinato Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso cotidiano. Usa o princípio básico do aprendizado humano que
Teoria da Probabilidade Prof. Joni Fusinato Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso cotidiano. Usa o princípio básico do aprendizado humano que
COLEÇÃO DARLAN MOUTINHO VOL. 01 RESOLUÇÕES
 COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
Teoria das Probabilidades
 08/06/07 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto
08/06/07 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto
Probabilidade Parte 1. Camyla Moreno
 Probabilidade Parte 1 Camyla Moreno Probabilidade A teoria das probabilidades é um ramo da Matemática que cria, elabora e pesquisa modelos para estudar experimentos ou fenômenos aleatórios. Principais
Probabilidade Parte 1 Camyla Moreno Probabilidade A teoria das probabilidades é um ramo da Matemática que cria, elabora e pesquisa modelos para estudar experimentos ou fenômenos aleatórios. Principais
Teoria das Probabilidades
 Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica 08:8 ESTATÍSTICA APLICADA I - Teoria das
Universidade Federal do Pará Instituto de Tecnologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica 08:8 ESTATÍSTICA APLICADA I - Teoria das
Estatística. Aula : Probabilidade. Prof. Ademar
 Estatística Aula : Probabilidade Prof. Ademar TEORIA DAS PROBABILIDADES A teoria das probabilidades busca estimar as chances de ocorrer um determinado acontecimento. É um ramo da matemática que cria, elabora
Estatística Aula : Probabilidade Prof. Ademar TEORIA DAS PROBABILIDADES A teoria das probabilidades busca estimar as chances de ocorrer um determinado acontecimento. É um ramo da matemática que cria, elabora
ESCOLA SUPERIOR DE TECNOLOGIA
 Departamento Matemática Curso Engenharia e Gestão Industrial 2º Semestre 1º Folha Nº2 1. Na inspecção final a um produto este é classificado como aceitável para lançamento no mercado ou não. O produto
Departamento Matemática Curso Engenharia e Gestão Industrial 2º Semestre 1º Folha Nº2 1. Na inspecção final a um produto este é classificado como aceitável para lançamento no mercado ou não. O produto
Aulas particulares. Conteúdo
 Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Apresentado ao Curso de Capacitação para Professores da Rede Estadual do Rio de Janeiro
 Apresentado ao Curso de Capacitação para Professores da Rede Estadual do Rio de Janeiro Matemática no 3º ano do ensino médio Probabilidade Por: Jerônimo Pereira Vilela Tutor: Edeson dos Anjos Silva INTRODUÇÃO
Apresentado ao Curso de Capacitação para Professores da Rede Estadual do Rio de Janeiro Matemática no 3º ano do ensino médio Probabilidade Por: Jerônimo Pereira Vilela Tutor: Edeson dos Anjos Silva INTRODUÇÃO
Tópicos. Conjuntos Fatorial Combinações Permutações Probabilidade Binômio de Newton triângulo de Pascal
 Probabilidade Tópicos Conjuntos Fatorial Combinações Permutações Probabilidade Binômio de Newton triângulo de Pascal Conjuntos Conjunto: Na matemática, um conjunto é uma coleção de elementos com características
Probabilidade Tópicos Conjuntos Fatorial Combinações Permutações Probabilidade Binômio de Newton triângulo de Pascal Conjuntos Conjunto: Na matemática, um conjunto é uma coleção de elementos com características
UNIVERSIDADE FEDERAL DA PARAÍBA. Cálculo das Probabilidades e Estatística I. Segunda Lista de Exercícios
 UNIVERSIDADE FEDERAL DA PARAÍBA Cálculo das Probabilidades e Estatística I Professora: Juliana Freitas Pires Segunda Lista de Exercícios Questão 1. Descreva o espaço amostral para cada um dos seguintes
UNIVERSIDADE FEDERAL DA PARAÍBA Cálculo das Probabilidades e Estatística I Professora: Juliana Freitas Pires Segunda Lista de Exercícios Questão 1. Descreva o espaço amostral para cada um dos seguintes
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a
 Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Prof. Luiz Alexandre Peternelli
 Exercícios propostos 1. Numa prova há 7 questões do tipo verdadeiro-falso ( V ou F ). Calcule a probabilidade de acertarmos todas as 7 questões se: a) Escolhermos aleatoriamente as 7 respostas. b) Escolhermos
Exercícios propostos 1. Numa prova há 7 questões do tipo verdadeiro-falso ( V ou F ). Calcule a probabilidade de acertarmos todas as 7 questões se: a) Escolhermos aleatoriamente as 7 respostas. b) Escolhermos
Se A =, o evento é impossível, por exemplo, obter 7 no lançamento de um dado.
 PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
Escola Secundária/2,3 da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 2011/12 Distribuição de probabilidades 12.º Ano
 Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
ESCOLA SUPERIOR DE TECNOLOGIA
 Departamento Matemática Disciplina Estatística Aplicada Curso Engenharia Mec. Gest. Industrial 4º Semestre 2º Folha Nº2: Probabilidades 1. Na inspecção final a uma componente electrónica esta é classificada
Departamento Matemática Disciplina Estatística Aplicada Curso Engenharia Mec. Gest. Industrial 4º Semestre 2º Folha Nº2: Probabilidades 1. Na inspecção final a uma componente electrónica esta é classificada
Nome: n o : Recuperação de Matemática 3ª. E.M. 2017
 Nome: n o : Ensino: Médio Série: 3ª. Turma: Data: Professor: Márcio Recuperação de Matemática 3ª. E.M. 017 Números Complexos 1. Sejam os números complexos z 1 = x 5 + ( + y)i e z = 4 3i. Determine x e
Nome: n o : Ensino: Médio Série: 3ª. Turma: Data: Professor: Márcio Recuperação de Matemática 3ª. E.M. 017 Números Complexos 1. Sejam os números complexos z 1 = x 5 + ( + y)i e z = 4 3i. Determine x e
3 NOÇÕES DE PROBABILIDADE
 3 NOÇÕES DE PROILIDDE 3.1 Conjuntos Um conjunto pode ser considerado como uma coleção de objetos chamados elementos do conjunto. Em geral denota-se conjunto por letras maiúsculas,, C,... e a sua representação
3 NOÇÕES DE PROILIDDE 3.1 Conjuntos Um conjunto pode ser considerado como uma coleção de objetos chamados elementos do conjunto. Em geral denota-se conjunto por letras maiúsculas,, C,... e a sua representação
Introdução à Estatística
 Introdução à Estatística Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Introdução a Probabilidade Existem dois tipos de experimentos:
Introdução à Estatística Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Introdução a Probabilidade Existem dois tipos de experimentos:
01 - (UEM PR) um resultado "cara sobre casa preta" é (MACK SP)
 ALUNO(A): Nº TURMA: 2º ANO PROF: Claudio Saldan CONTATO: saldan.mat@gmail.com LISTA DE EXERCÍCIOS PROBABILIDADE 0 - (UEM PR) Considere a situação ideal na qual uma moeda não-viciada, ao ser lançada sobre
ALUNO(A): Nº TURMA: 2º ANO PROF: Claudio Saldan CONTATO: saldan.mat@gmail.com LISTA DE EXERCÍCIOS PROBABILIDADE 0 - (UEM PR) Considere a situação ideal na qual uma moeda não-viciada, ao ser lançada sobre
PROBABILIDADE - INTRODUÇÃO
 E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
INTRODUÇÃO À PROBABILIDADE
 INTRODUÇÃO À PROBABILIDADE Foto extraída em http://www.alea.pt Profª Maria Eliane Universidade Estadual de Santa Cruz USO DE PROBABILIDADES EM SITUAÇÕES DO COTIDIANO Escolhas pessoais Previsão do tempo
INTRODUÇÃO À PROBABILIDADE Foto extraída em http://www.alea.pt Profª Maria Eliane Universidade Estadual de Santa Cruz USO DE PROBABILIDADES EM SITUAÇÕES DO COTIDIANO Escolhas pessoais Previsão do tempo
PROBABILIDADE. Luciana Santos da Silva Martino. PROFMAT - Colégio Pedro II. 01 de julho de 2017
 Sumário PROBABILIDADE Luciana Santos da Silva Martino PROFMAT - Colégio Pedro II 01 de julho de 2017 Sumário 1 Conceitos Básicos 2 Probabildade Condicional 3 Espaço Amostral Infinito Outline 1 Conceitos
Sumário PROBABILIDADE Luciana Santos da Silva Martino PROFMAT - Colégio Pedro II 01 de julho de 2017 Sumário 1 Conceitos Básicos 2 Probabildade Condicional 3 Espaço Amostral Infinito Outline 1 Conceitos
Resposta: Resposta: 4 ou seja, 1.
 1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
c) 17 b) 4 17 e) 17 21
 Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
EXERCÍCIOS REVISIONAIS SOBRE BINÔMIO DE NEWTON SISTEMAS LINEARES PROBABILIDADE 2 ANO
 QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
QUESTÃO 1: Uma urna contém 4 bolas vermelhas, 6 pretas e 5 azuis. Retirando-se dessa urna, ao acaso, uma bola, CALCULE a probabilidade de ela: ser vermelha. ser vermelha ou preta. não ser azul. QUESTÃO
BANCO DE QUESTÕES TURMA PM-PE PROBABILIDADE
 01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
ESPAÇO AMOSTRAL E EVENTO. 2) Jogando um dado ideal e anotando a face voltada para cima, teremos o espaço amostral E= {1,2,3,4,5,6}
 NOÇÕES DE PROBABILIDADE O estudo da probabilidade vem da necessidade de em certas situações, prevermos a possibilidade de ocorrência de determinados fatos. EXPERIMENTOS ALEATÓRIOS Experimentos aleatórios
NOÇÕES DE PROBABILIDADE O estudo da probabilidade vem da necessidade de em certas situações, prevermos a possibilidade de ocorrência de determinados fatos. EXPERIMENTOS ALEATÓRIOS Experimentos aleatórios
ESCOLA SUPERIOR DE TECNOLOGIA E GESTÃO
 Área Científica Matemática Probabilidades e Estatística Curso Engenharia do Ambiente º Semestre º Ficha n.º: Probabilidades e Variáveis Aleatórias. Lançam-se ao acaso moedas. a) Escreva o espaço de resultados
Área Científica Matemática Probabilidades e Estatística Curso Engenharia do Ambiente º Semestre º Ficha n.º: Probabilidades e Variáveis Aleatórias. Lançam-se ao acaso moedas. a) Escreva o espaço de resultados
Lista de exercícios Defina o espaço amostral para cada um dos seguintes experimentos aleatórios:
 UNIVERSIDADE FEDERAL DE SÃO CARLOS Centro de Ciências Agrárias Departamento de Tecnologia Agroindustrial e Socioeconomia Rural Disciplina: Noções de Probabilidade e Estatística (221171) - 2019 Prof. a
UNIVERSIDADE FEDERAL DE SÃO CARLOS Centro de Ciências Agrárias Departamento de Tecnologia Agroindustrial e Socioeconomia Rural Disciplina: Noções de Probabilidade e Estatística (221171) - 2019 Prof. a
PROBABILIDADE. c) 1/4 d) 1/12 e) nda MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS
 MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
Estatística Aplicada. Prof. Carlos Alberto Stechhahn PARTE I ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE PROBABILIDADE CONDICIONAL.
 Estatística Aplicada Administração p(a) = n(a) / n(u) PARTE I ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE PROBABILIDADE CONDICIONAL Prof. Carlos Alberto Stechhahn 2014 1. Noções de Probabilidade Chama-se experimento
Estatística Aplicada Administração p(a) = n(a) / n(u) PARTE I ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE PROBABILIDADE CONDICIONAL Prof. Carlos Alberto Stechhahn 2014 1. Noções de Probabilidade Chama-se experimento
Estatística Planejamento das Aulas
 7 de outubro de 2018 Fatorial Para n inteiro não negativo. O fatorial de n é definido por: Convenciona-se: Para n = 0, 0! = 1 Para n = 1, 1! = 1 Exemplos: 1. 6! = 6.5.4.3.2.1 = 720 2. 4! = 4.3.2.1 = 24
7 de outubro de 2018 Fatorial Para n inteiro não negativo. O fatorial de n é definido por: Convenciona-se: Para n = 0, 0! = 1 Para n = 1, 1! = 1 Exemplos: 1. 6! = 6.5.4.3.2.1 = 720 2. 4! = 4.3.2.1 = 24
Probabilidade Condicional (grupo 2)
 page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
Probabilidade Condicional
 18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
Probabilidade. Professora Ana Hermínia Andrade. Universidade Federal do Amazonas Faculdade de Estudos Sociais Departamento de Economia e Análise
 Probabilidade Professora Ana Hermínia Andrade Universidade Federal do Amazonas Faculdade de Estudos Sociais Departamento de Economia e Análise Período 2016.2 Você reconhece algum desses experimentos? Alguns
Probabilidade Professora Ana Hermínia Andrade Universidade Federal do Amazonas Faculdade de Estudos Sociais Departamento de Economia e Análise Período 2016.2 Você reconhece algum desses experimentos? Alguns
ESCOLA SUPERIOR DE TECNOLOGIA
 Departamento Matemática Probabilidades e Estatística Curso Engenharia do Ambiente 2º Semestre 1º Ficha n.º1: Probabilidades e Variáveis Aleatórias 1. Lançam- ao acaso 2 moedas. a) Escreva o espaço de resultados
Departamento Matemática Probabilidades e Estatística Curso Engenharia do Ambiente 2º Semestre 1º Ficha n.º1: Probabilidades e Variáveis Aleatórias 1. Lançam- ao acaso 2 moedas. a) Escreva o espaço de resultados
Probabilidade e Estatística Probabilidade Condicional
 Introdução Probabilidade e Estatística Probabilidade Condicional Em algumas situações, a probabilidade de ocorrência de um certo evento pode ser afetada se tivermos alguma informação sobre a ocorrência
Introdução Probabilidade e Estatística Probabilidade Condicional Em algumas situações, a probabilidade de ocorrência de um certo evento pode ser afetada se tivermos alguma informação sobre a ocorrência
A B e A. Calcule as suas respectivas probabilidades.
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA LISTA 2-BIOESTATÍSTICA II (CE020) Prof. Benito Olivares Aguilera 1 o Sem./17 1. Expresse em termos de operações entre eventos:
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA LISTA 2-BIOESTATÍSTICA II (CE020) Prof. Benito Olivares Aguilera 1 o Sem./17 1. Expresse em termos de operações entre eventos:
1. (Meyer,2000) Suponha que o conjunto fundamental seja formado pelos inteiros positivos
 Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Disciplina: LCE0211-Estatística Geral Prof. Idemauro Antonio Rodrigues de Lara 4 a lista de exercícios 1. (Meyer,2000) Suponha que
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Disciplina: LCE0211-Estatística Geral Prof. Idemauro Antonio Rodrigues de Lara 4 a lista de exercícios 1. (Meyer,2000) Suponha que
Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema.
 PROBABILIDADE CONDICIONAL E DISTRIBUIÇÃO BINOMINAL 1. PROBABILIDADE CONDICIONAL Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema. Suponha que um redator
PROBABILIDADE CONDICIONAL E DISTRIBUIÇÃO BINOMINAL 1. PROBABILIDADE CONDICIONAL Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema. Suponha que um redator
Matemática E Extensivo V. 5
 Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades
 Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA
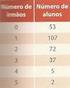 Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine
Disciplina de Estatística Prof. Msc Quintiliano Siqueira Schroden Nomelini LISTA DE PROBABILIDADES
 Disciplina de Estatística Prof. Msc Quintiliano Siqueira Schroden Nomelini LISTA DE PROBABILIDADES 1) Determine a probabilidade de cada evento: a) Um nº par aparece no lançamento de um dado; b) Uma figura
Disciplina de Estatística Prof. Msc Quintiliano Siqueira Schroden Nomelini LISTA DE PROBABILIDADES 1) Determine a probabilidade de cada evento: a) Um nº par aparece no lançamento de um dado; b) Uma figura
Módulo de Introdução à Probabilidade. Ferramentas Básicas. 2 a série E.M.
 Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
Noção de fenómeno aleatório e de experiência aleatória
 Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
Se a bola retirada da urna 1 for branca temos, pelo princípio da multiplicação:
 Livro: Probabilidade - Aplicações à Estatística Paul L. Meyer Capitulo 3 Probabilidade Condicionada e Independência. 1. Probabilidade Condicionada. Definição: Definição. Dizemos que os representam uma
Livro: Probabilidade - Aplicações à Estatística Paul L. Meyer Capitulo 3 Probabilidade Condicionada e Independência. 1. Probabilidade Condicionada. Definição: Definição. Dizemos que os representam uma
3. A probabilidade do evento de números pares. 4. O evento formado por número menor que três. 5. A probabilidade do evento número menor que três.
 1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
1 a Lista de Exercício - Estatística (Probabilidade) Profa. Ms. Ulcilea A. Severino Leal Algumas considerações importantes sobre a resolução dos exercícios. (i) Normas da língua culta, sequência lógica
PROBABILIDADE. Curso: Logística e Transportes Disciplina: Estatística Profa. Eliane Cabariti
 Curso: Logística e Transportes Disciplina: Estatística Profa. Eliane Cabariti PROBABILIDADE Dizemos que a probabilidade é uma medida da quantidade de incerteza que existe em um determinado experimento.
Curso: Logística e Transportes Disciplina: Estatística Profa. Eliane Cabariti PROBABILIDADE Dizemos que a probabilidade é uma medida da quantidade de incerteza que existe em um determinado experimento.
Contagem e Probabilidade Exercícios Adicionais. Paulo Cezar Pinto Carvalho
 Contagem e Probabilidade Exercícios Adicionais Paulo Cezar Pinto Carvalho Exercícios Adicionais Contagem e Probabilidade Para os alunos dos Grupos 1 e 2 1. Um grupo de 4 alunos (Alice, Bernardo, Carolina
Contagem e Probabilidade Exercícios Adicionais Paulo Cezar Pinto Carvalho Exercícios Adicionais Contagem e Probabilidade Para os alunos dos Grupos 1 e 2 1. Um grupo de 4 alunos (Alice, Bernardo, Carolina
UNIVERSIDADE FEDERAL DA PARAÍBA Departamento de Estatística. Probabilidade
 UNIVERSIDADE FEDERAL DA PARAÍBA Departamento de Estatística Probabilidade Disciplina: Cálculo das Probabilidades e Estatística I Prof. Tarciana Liberal Existem muitas situações que envolvem incertezas:
UNIVERSIDADE FEDERAL DA PARAÍBA Departamento de Estatística Probabilidade Disciplina: Cálculo das Probabilidades e Estatística I Prof. Tarciana Liberal Existem muitas situações que envolvem incertezas:
b) 35 c) 14 d) 35 Gab: D
 0 - (PUC SP/006) Em um ônibus há apenas bancos vazios, cada qual com lugares. Quatro rapazes e quatro moças entram nesse ônibus e devem ocupar os bancos vagos. Se os lugares forem escolhidos aleatoriamente,
0 - (PUC SP/006) Em um ônibus há apenas bancos vazios, cada qual com lugares. Quatro rapazes e quatro moças entram nesse ônibus e devem ocupar os bancos vagos. Se os lugares forem escolhidos aleatoriamente,
Universidade Federal da Paraíba Departamento de Estatística Lista 1 - Julho de 2016
 1. Suponha que o conjunto fundamental seja formado pelos inteiros positivos de 1 a 10. Sejam A = {2, 3, 4}, B = {3, 4, 5} e C = {5, 6, 7}. Enumere os elementos dos seguintes conjuntos: (a) A c B. (b) A
1. Suponha que o conjunto fundamental seja formado pelos inteiros positivos de 1 a 10. Sejam A = {2, 3, 4}, B = {3, 4, 5} e C = {5, 6, 7}. Enumere os elementos dos seguintes conjuntos: (a) A c B. (b) A
Prof. Janete Pereira Amador 1. 1 Introdução
 Prof. Janete Pereira Amador 1 1 Introdução A ciência manteve-se até pouco tempo atrás, firmemente apegada à lei da causa e efeito. Quando o efeito esperado não se concretizava, atribuía-se o fato ou a
Prof. Janete Pereira Amador 1 1 Introdução A ciência manteve-se até pouco tempo atrás, firmemente apegada à lei da causa e efeito. Quando o efeito esperado não se concretizava, atribuía-se o fato ou a
Atividade extra. Exercício 1. Exercício 2. Exercício 3. Matemática e suas Tecnologias Matemática
 Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente
Atividade extra Exercício 1 Um teste de múltipla escolha e composto de 12 questões, com 5 alternativas de resposta, sendo que somente uma, é correta. Qual a probabilidade de uma pessoa, marcando aleatoriamente
24 de outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Teoria das probabilidades
 Teoria das probabilidades Prof. Dr. Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 25 de abril de 2018 Londrina 1 / 22 Conceitos probabiĺısticos são necessários para se
Teoria das probabilidades Prof. Dr. Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 25 de abril de 2018 Londrina 1 / 22 Conceitos probabiĺısticos são necessários para se
Sumário. 2 Índice Remissivo 12
 i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
i Sumário 1 Definições Básicas 1 1.1 Fundamentos de Probabilidade............................. 1 1.2 Noções de Probabilidade................................ 3 1.3 Espaços Amostrais Finitos...............................
Ciclo 3 Encontro 2 PROBABILIDADE. Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr.
 1 Ciclo 3 Encontro 2 PROBABILIDADE Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Probabilidade 2 Texto: Módulo Introdução à Probabilidade O que é probabilidade? parte 1 de Fabrício Siqueira
1 Ciclo 3 Encontro 2 PROBABILIDADE Nível 3 PO: Márcio Reis 11º Programa de Iniciação Científica Jr. Probabilidade 2 Texto: Módulo Introdução à Probabilidade O que é probabilidade? parte 1 de Fabrício Siqueira
PROBABILIDADE. Aula 2 Probabilidade Básica. Fernando Arbache
 PROBABILIDADE Aula 2 Probabilidade Básica Fernando Arbache Probabilidade Medida da incerteza associada aos resultados do experimento aleatório Deve fornecer a informação de quão verossímil é a ocorrência
PROBABILIDADE Aula 2 Probabilidade Básica Fernando Arbache Probabilidade Medida da incerteza associada aos resultados do experimento aleatório Deve fornecer a informação de quão verossímil é a ocorrência
Coordenadoria de Matemática. Apostila de Probabilidade
 Coordenadoria de Matemática Apostila de Probabilidade Vitória ES 1. INTRODUÇÃO CAPÍTULO 03 Quando investigamos algum fenômeno, verificamos a necessidade de descrevê-lo por um modelo matemático que permite
Coordenadoria de Matemática Apostila de Probabilidade Vitória ES 1. INTRODUÇÃO CAPÍTULO 03 Quando investigamos algum fenômeno, verificamos a necessidade de descrevê-lo por um modelo matemático que permite
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa.
 A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
Módulo de Introdução à Probabilidade. Ferramentas Básicas. 2 a série E.M.
 Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
Módulo de Introdução à Probabilidade Ferramentas Básicas. a série E.M. Probabilidade Ferramentas Básicas Exercícios Introdutórios Exercício. Uma prova é composta por 5 questões de múltipla escolha com
Probabilidade. Evento (E) é o acontecimento que deve ser analisado.
 Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
Probabilidade Definição: Probabilidade é uma razão(divisão) entre a quantidade de eventos e a quantidade de amostras. Amostra ou espaço amostral é o conjunto formado por todos os elementos que estão incluídos
PROBABILIDADE E ESTATÍSTICA PROBABILIDADES
 PROBABILIDADE E ESTATÍSTICA PROBABILIDADES Bruno Baierle Maurício Furigo Prof.ª Sheila Regina Oro (orientadora) Edital 06/2013 - Produção de Recursos Educacionais Digitais Revisando - Análise combinatória
PROBABILIDADE E ESTATÍSTICA PROBABILIDADES Bruno Baierle Maurício Furigo Prof.ª Sheila Regina Oro (orientadora) Edital 06/2013 - Produção de Recursos Educacionais Digitais Revisando - Análise combinatória
