ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE ABRIL DE 2011
|
|
|
- Ana Luiza Lombardi Quintanilha
- 6 Há anos
- Visualizações:
Transcrição
1 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE ABRIL DE 2011 y 2y + y 2y = 0 O polinómio característico é r 3 2r 2 + r 2, que tem r = 2 como raiz. Obtemos então r 3 2r 2 + r 2 = (r 2) (r 2 + 1). As três raízes são r 1 = 2, r 2 = i e r 3 = i, e temos três soluções dadas por y 1 = e 2t, y 2 = cos(t) e y 3 = sen(t). Podemos ver tal como no exemplo anterior que estas soluções têm wronskiano não nulo, e portanto são linearmente independentes. A solução geral é y = c 1 e 2t + c 2 cos(t) + c 3 sen(t), c i R. Pode acontecer também que haja raízes complexas múltiplas. y (iv) + 2y + y = 0 O polinómio característico é r 4 + 2r 2 + 1, que pode ser escrito como (r 2 + 1) 2, donde r = ±i são raízes complexas duplas. Temos como soluções y 1 = cos t, y 2 = sen t, y 3 = t cos t e y 4 = t sen t. A solução geral é portanto 1
2 2 y = c 1 cos t + c 2 sen t + c 3 t cos t + c 4 t sen t, (c i R). y + 3y + 3y + y = 0 tem polinómio característico r 3 + 3r 2 + 3r + 1 Por inspecção, notamos que r 1 = 1 é raiz do polinómio. Temos r 3 + 3r 2 + 3r + 1 = (r + 1) (r 2 + 2r + 1) e este último polinómio tem como raízes r 2 = r 3 = 1 e portanto o polinómio característico original tem 1 como raiz tripla. São soluções y 1 = e t, y 2 = t e t e y 3 = t 2 e t. A solução geral é y = c 1 e t + c 2 t e t + c 3 t 2 e t, (c i R). Em geral: Uma raiz real r de multiplicidade m dá lugar a m soluções linearmente independentes y 1 = e rt, y 2 = t e rt,, y m = t m 1 e rt Duas raízes complexas conjugadas α ± iβ de multiplicidade m dão lugar a 2m soluções linearmente independentes y 1 = e αt cos(βt), y 2 = t e αt cos(βt),, y m = t m 1 e αt cos(βt) y m+1 = e αt sen(βt), y m+2 = t e αt sen(βt),, y 2m = t m 1 e αt sen(βt) Uma equação linear homogénea com coeficientes constantes tem três soluções, dadas por y 1 = t e t sen t, y 2 = e 2t e y 3 = t 3.
3 3 Pergunta-se: qual é a menor ordem possível para a equação? Qual é a sua solução geral? Como é uma equação possível que tenha tal solução geral? Se a equação tem as soluções dadas, o polinómio característico tem que ter pelo menos 1 + i como raiz dupla ( 1 i também é raiz dupla) 2 como raiz simples 0 como raiz quádrupla e a equação tem que ter (pelo menos) as soluções t e t sen t e 2t t 3 t e t cos t t 2 e t sen t t e t cos t 1 A mínima ordem é 9. Um polinómio característico é, por exemplo, (r (1 + i)) 2 (r (1 i)) 2 (r 2)(r 0) 4 Os coeficientes deste polinómio de grau 9 dão os coeficientes de uma equação possível. EQUAÇÕES LINEARES NÃO HOMOGÉNEAS DE ORDEM 2 Voltemos à equação não homogénea geral y + p(t)y + q(t)y = g(t). Escrevemos esta equação como L[y] = g(t). Se y 1 e y 2 são duas soluções da equação não homogénea, temos L[y 1 y 2 ] = L[y 1 ] L[y 2 ] = g(t) g(t) = 0,
4 4 e por isso y 1 y 2 é solução da equação homogénea correspondente. Donde, se y p for uma solução particular da equação não homogénea e y h for a solução geral da equação homogénea, temos que y = y p + y h é a solução geral da equação não homogénea. y + y = 2e t A equação homogénea correspondente é y + y = 0. O polinómio característico desta equação é r 2 + 1, que tem como raízes r = ±i. A solução geral da homogénea é portanto y h = c 1 cos t + c 2 sen t (c i R) Para a equação não homogénea, vemos por inspecção que y p = e t é solução. Logo, todas as soluções da equação são da forma y = y p + y h = e t + c 1 cos t + c 2 sen t (c i R) Em geral, para resolver y + p(t)y + q(t)y = g(t) devemos resolver primeiro y + p(t)y + q(t)y = 0 e obter y h = c 1 y 1 + c 2 y 2 (c 1, c 2 R) e procurar apenas uma solução particular y p da não homogénea. Depois, a solução geral da não homogénea é y = y p + y h = y p + c 1 y 1 + c 2 y 2 (c 1, c 2 R) Para obter um y p, vamos desenvolver dois métodos: O método dos coeficientes indeterminados é fácil de utilizar, mas serve apenas para equações com coeficientes constantes e para alguns tipos de g(t). O método de variação dos parâmetros (também chamado método de variação das constantes) serve para equações sem coeficientes constantes e para todos os tipos de
5 5 g(t), mas não é em geral fácil de aplicar (conduz a primitivas difíceis ou impossíveis de resolver.) MÉTODO DOS COEFICIENTES INDETERMINADOS y + y = 2e t A homogénea tem como solução geral y h = c 1 cos t + c 2 sen t. Para a solução particular, tentamos adivinhar que tipo pode ter a partir da forma de g(t). Neste caso, g(t) = 2e t sugere que procuremos y p = Ae t. O valor de A obtém-se substituindo na equação original: (Ae t ) + Ae t = 2e t 2Ae t = 2e t A = 1, e por isso y p = e t. Em geral, procuramos y p do mesmo tipo de g(t). Isto funciona para certas funções exponenciais, trigonométricas, e para polinómios. É preciso ter algum cuidado com as escolhas, como se vê no exemplo seguinte. y y = e t Para a homogénea, fazemos r 2 1 = 0 e obtemos r = ±1. y h = c 1 e t + c 2 e t, (c 1, c 2 R) Como g(t) = e t, procuramos, tal como no exemplo anterior, y p = Ae t. Mas (Ae t ) (Ae t ) = 0 e t seja qual for o A. Ou seja, y p não pode ser desta forma. Para evitar este tipo de enganos, podemos usar este método recorrendo a aniquiladores.
6 6 y y = e t A equação homogénea correspondente tem solução geral y h = c 1 e t + c 2 e t (c i R). Definindo D como o operador de derivada, escrevemos a equação não homogénea como (D 2 1)y = e t. Um aniquilador para e t é um operador dado por um polinómio em D que, quando aplicado a e t, produz uma função nula. Por exemplo, D 1 aniquila e t, porque (D 1)e t = De t e t = 0. Aplicamos este aniquilador aos dois termos da equação não homogénea, e obtemos (D 1)(D 2 1)y = (D 1)e t = 0 Ou seja, transformamos deste modo a equação original numa equação homogénea de ordem 3, cujo polinómio característico é (r 1)(r 2 1). A solução geral desta equação é Ae t + Be t + Cte t, que deve portanto ser a forma da solução particular y p que devemos procurar. Substituimos então esta função na equação original de modo a descobrir os valores de A, B e C. Não precisamos de considerar os termos que já estejam na solução y h da equação homogénea, e por isso tomamos apenas y p = Cte t. Substituindo na equação, vem (Cte t ) Cte t = e t Isto implica 2Ce t = e t, ou seja, C = 1/2. Assim, y p = 1 2 tet. A solução geral da equação não homogénea é portanto y = y h + y p = c 1 e t + c 2 e t tet (c 1, c 2 R) Procuramos com este método transformar uma equação não homogénea numa equação homogénea de ordem superior de modo a podermos descobrir uma forma possível para y p.
7 7 y + y = 2e t (D 2 + 1)y = 2e t (D 1)(D 2 + 1)y = 0 O polinómio característico tem como raízes r = 1, r = i e r = i. As soluções são portanto da forma Ae t + Bcos t + Csen t Como os dois últimos termos fazem parte da solução da homogénea correspondente, procuramos y p = Ae t. Substituímos então y p na equação original para determinar o valor de A, e obtemos A = 1. O método só funciona para aqueles g(t) de que conhecemos o aniquilador, e que são funções que tenham a mesma natureza das suas derivadas. Aniquiladores A tabela seguinte mostra aniquiladores para diversas funções elementares. e αt D α (α R) t e αt (D α) 2 (α R) t m e αt (D α) m+1 (α R, m N) cos (βt) D 2 + β 2 (β R) sen (βt) D 2 + β 2 (β R) t m cos (βt) (D 2 + β 2 ) m+1 (β R, m N) t m sen (βt) (D 2 + β 2 ) m+1 (β R, m N) e αt cos (βt) (D α) 2 + β 2 (α, β R) e αt sen (βt) (D α) 2 + β 2 (α, β R)
8 8 t m e αt cos (βt) [(D α) 2 + β 2 ] m+1 (α, β R, m N) t m e αt sen (βt) [(D α) 2 + β 2 ] m+1 (α, β R, m N) Note-se que todos as aniquiladores desta lista são casos particulares dos dois últimos. No entanto, usando esse último aniquilador, a ordem da derivada obtida pode ser superior ao realmente necessário. Por exemplo: e αt = t m e αt cos (βt) (com m = 0 e β = 0) teria como aniquilador [(D α) 2 +0] 1, mas já vimos que para aniquilar e αt é suficiente apenas D α.
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE NOVEMBRO DE dt + a 0(t)y = 0
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 24 16 DE NOVEMBRO DE 2016 EQUAÇÕES LINEARES HOMOGÉNEAS DE ORDEM SUPERIOR A DOIS São da forma a n (t) dn y dt n + a n 1(t) dn 1 y dt n 1 + + a 1(t)
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 24 16 DE NOVEMBRO DE 2016 EQUAÇÕES LINEARES HOMOGÉNEAS DE ORDEM SUPERIOR A DOIS São da forma a n (t) dn y dt n + a n 1(t) dn 1 y dt n 1 + + a 1(t)
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE ABRIL DE 2016
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 25 27 DE ABRIL DE 2016 Aniquiladores A tabela seguinte mostra aniquiladores para diversas funções elementares. e αt D α (α R) t e αt (D α) 2 (α R)
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 25 27 DE ABRIL DE 2016 Aniquiladores A tabela seguinte mostra aniquiladores para diversas funções elementares. e αt D α (α R) t e αt (D α) 2 (α R)
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE ABRIL DE Se y representa a posição de um corpo, o seu movimento é dado por
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 24 27 DE ABRIL DE 2018 EQUAÇÕES DIFERENCIAIS LINEARES DE SEGUNDA ORDEM São da forma d 2 y dt 2 + p(t)dy + q(t)y = g(t) dt Um exemplo destas equações
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 24 27 DE ABRIL DE 2018 EQUAÇÕES DIFERENCIAIS LINEARES DE SEGUNDA ORDEM São da forma d 2 y dt 2 + p(t)dy + q(t)y = g(t) dt Um exemplo destas equações
Aula 5 Equação Diferencial de Segunda Ordem Linear e Coeficientes constantes:
 Aula 5 Equação Diferencial de Segunda Ordem Linear e Coeficientes constantes: caso não Homogêneo Vamos estudar as equações da forma: ay + by + cy = G(x), onde G(x) é uma função polinomial, exponencial,
Aula 5 Equação Diferencial de Segunda Ordem Linear e Coeficientes constantes: caso não Homogêneo Vamos estudar as equações da forma: ay + by + cy = G(x), onde G(x) é uma função polinomial, exponencial,
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Equações Diferenciais de Segunda Ordem. Copyright Cengage Learning. Todos os direitos reservados.
 17 Equações Diferenciais de Segunda Ordem Copyright Cengage Learning. Todos os direitos reservados. 17.2 Equações Lineares Não Homogêneas Copyright Cengage Learning. Todos os direitos reservados. Equações
17 Equações Diferenciais de Segunda Ordem Copyright Cengage Learning. Todos os direitos reservados. 17.2 Equações Lineares Não Homogêneas Copyright Cengage Learning. Todos os direitos reservados. Equações
de Coeficientes Constantes
 Seção 12: Equações Diferenciais Lineares não Homogêneas de Coeficientes Constantes O objetivo desta seção é estudar as equações lineares não homogêneas de coeficientes constantes No entanto, a versão do
Seção 12: Equações Diferenciais Lineares não Homogêneas de Coeficientes Constantes O objetivo desta seção é estudar as equações lineares não homogêneas de coeficientes constantes No entanto, a versão do
Seção 11: EDOLH com coeficientes constantes
 Seção 11: EDOLH com coeficientes constantes Observação fundamental: Se L(y) = y + py + qy, com p, q constantes então L(e λt ) = ( λ + pλ + q ) e λt. Portanto a EDO L(y) = 0 pode ter solução da forma y
Seção 11: EDOLH com coeficientes constantes Observação fundamental: Se L(y) = y + py + qy, com p, q constantes então L(e λt ) = ( λ + pλ + q ) e λt. Portanto a EDO L(y) = 0 pode ter solução da forma y
ORDINÁRIAS. Víctor Arturo Martínez León
 INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE MAIO DE 2017
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
Introdução às Equações Diferenciais e Ordinárias
 Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS LINEARES
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS LINEARES Na disciplina de Análise Matemática, logo ao início de certos cursos de licenciatura, é usual tratar, entre outros temas, o das equações diferenciais, sejam ordinárias
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS LINEARES Na disciplina de Análise Matemática, logo ao início de certos cursos de licenciatura, é usual tratar, entre outros temas, o das equações diferenciais, sejam ordinárias
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes
 Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
EDO III. por Abílio Lemos. 07, 09 e 14 de novembro de Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
 EDO III por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 07, 09 e 14 de novembro de 2018 Teorema (D Alembert): Sejam y 1 (x) uma solução, não nula, da EDO y + p(x)y
EDO III por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 07, 09 e 14 de novembro de 2018 Teorema (D Alembert): Sejam y 1 (x) uma solução, não nula, da EDO y + p(x)y
1.1 Conceitos Básicos
 1 Zeros de Funções 1.1 Conceitos Básicos Muito frequentemente precisamos determinar um valor ɛ para o qual o valor de alguma função é igual a zero, ou seja: f(ɛ) = 0. Exemplo 1.1 Suponha que certo produto
1 Zeros de Funções 1.1 Conceitos Básicos Muito frequentemente precisamos determinar um valor ɛ para o qual o valor de alguma função é igual a zero, ou seja: f(ɛ) = 0. Exemplo 1.1 Suponha que certo produto
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
EQUAÇÕES ÀS DIFERENÇAS ORDINÁRIAS LINEARES
 EQUAÇÕES ÀS DIFERENÇAS ORDINÁRIAS LINEARES Na disciplina de Análise Matemática, em geral no final do segundo semestre do primeiro ano dos cursos de licenciatura em Economia, Gestão e Engenharia, é usual
EQUAÇÕES ÀS DIFERENÇAS ORDINÁRIAS LINEARES Na disciplina de Análise Matemática, em geral no final do segundo semestre do primeiro ano dos cursos de licenciatura em Economia, Gestão e Engenharia, é usual
Na posição de equilíbrio, temos como forças que actuam sobre o corpo: Fora da posição de equilíbrio, as forças que podem actuar são:
 APLICAÇÕES DAS EQUAÇÕES DIFERENCIAIS DE SEGUNDA ORDEM Como aplicação das equações diferenciais de segunda ordem, vamos considerar o movimento oscilatório de uma mola de comprimento l e constante de elasticidade
APLICAÇÕES DAS EQUAÇÕES DIFERENCIAIS DE SEGUNDA ORDEM Como aplicação das equações diferenciais de segunda ordem, vamos considerar o movimento oscilatório de uma mola de comprimento l e constante de elasticidade
Método de Gauss-Jordan e Sistemas Homogêneos
 Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
8.1-Equação Linear e Homogênea de Coeficientes Constantes
 8- Equações Diferenciais Lineares de 2 a Ordem e Ordem Superior As equações diferenciais lineares de ordem n são aquelas da forma: y (n) + a 1 (x) y (n 1) + a 2 (x) y (n 2) + + a n 1 (x) y + a n (x) y
8- Equações Diferenciais Lineares de 2 a Ordem e Ordem Superior As equações diferenciais lineares de ordem n são aquelas da forma: y (n) + a 1 (x) y (n 1) + a 2 (x) y (n 2) + + a n 1 (x) y + a n (x) y
31 a Aula AMIV LEAN, LEC Apontamentos
 31 a Aula 20041126 AMIV LEAN, LEC Apontamentos (RicaroCoutinho@mathistutlpt) 311 Métoo os coeficientes ineterminaos 3111 Funamentação Vamos agora aborar a EDO e coeficientes constantes, mas não homogénea:
31 a Aula 20041126 AMIV LEAN, LEC Apontamentos (RicaroCoutinho@mathistutlpt) 311 Métoo os coeficientes ineterminaos 3111 Funamentação Vamos agora aborar a EDO e coeficientes constantes, mas não homogénea:
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Márcio Nascimento. 19 de fevereiro de 2018
 Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.2 19 de fevereiro de 2018 1 / 16 Considere
Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.2 19 de fevereiro de 2018 1 / 16 Considere
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Seção 9: EDO s lineares de 2 a ordem
 Seção 9: EDO s lineares de a ordem Equações Homogêneas Definição. Uma equação diferencial linear de segunda ordem é uma equação da forma onde fx, gx e rx são funções definidas em um intervalo. y + fx y
Seção 9: EDO s lineares de a ordem Equações Homogêneas Definição. Uma equação diferencial linear de segunda ordem é uma equação da forma onde fx, gx e rx são funções definidas em um intervalo. y + fx y
Aula: Equações diferenciais lineares de ordem superior
 Aula: Equações diferenciais lineares de ordem superior Profa. Ariane Piovezan Entringer DMA - UFV Problema de Valor Inicial - EDO de ordem n Problema de Valor Inicial - EDO de ordem n a n (x) d n y dx
Aula: Equações diferenciais lineares de ordem superior Profa. Ariane Piovezan Entringer DMA - UFV Problema de Valor Inicial - EDO de ordem n Problema de Valor Inicial - EDO de ordem n a n (x) d n y dx
Curso: Engenharia Ambiental. Disciplina: Equações Diferenciais Ordinárias. Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2
 Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes
 Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
1 Diagonalização de Matrizes 2 2. Sistemas de Equações Diferenciais Lineares
 Diagonalização de Matrizes e Sistemas de Equações Diferenciais Lineares Reginaldo J Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 3 de setembro de
Diagonalização de Matrizes e Sistemas de Equações Diferenciais Lineares Reginaldo J Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://wwwmatufmgbr/~regi 3 de setembro de
Integral na reta com Álgebra Linear: caso particular
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 20 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Integral na reta com
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 20 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Integral na reta com
2 ō Semestre 2015/2016
 Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
! " # $ % & ' # % ( # " # ) * # +
 a Aula 69 AMIV ' * + Fórmula de De Moivre Dado z = ρe e Concluímos por indução que = ρ cos θ + i sen θ C temos z = ρe ρe = ρ e z = zz = ρe ρ e = ρ e z = ρ e para qualquer n N e como ρ e ρ e = ρ e pôr n
a Aula 69 AMIV ' * + Fórmula de De Moivre Dado z = ρe e Concluímos por indução que = ρ cos θ + i sen θ C temos z = ρe ρe = ρ e z = zz = ρe ρ e = ρ e z = ρ e para qualquer n N e como ρ e ρ e = ρ e pôr n
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA. MATEMÁTICA APLICADA 1 o SEMESTRE 2016/2017
 3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
Equação algébrica Equação polinomial ou algébrica é toda equação na forma anxn + an 1 xn 1 + an 2 xn a 2 x 2 + a 1 x + a 0, sendo x
 EQUAÇÃO POLINOMIAL Equação algébrica Equação polinomial ou algébrica é toda equação na forma a n x n + a n 1 x n 1 + a n 2 x n 2 +... + a 2 x 2 + a 1 x + a 0, sendo x C a incógnita e a n, a n 1,..., a
EQUAÇÃO POLINOMIAL Equação algébrica Equação polinomial ou algébrica é toda equação na forma a n x n + a n 1 x n 1 + a n 2 x n 2 +... + a 2 x 2 + a 1 x + a 0, sendo x C a incógnita e a n, a n 1,..., a
Seção 10: Redução de ordem de EDOLH s de 2 a ordem se for conhecida uma solução não trivial
 Seção 0: Redução de ordem de EDOLH s de a ordem se for conhecida uma solução não trivial Método de D Alembert Se for conhecida uma solução não trivial de uma EDOLH de a ordem, empregando o método de D
Seção 0: Redução de ordem de EDOLH s de a ordem se for conhecida uma solução não trivial Método de D Alembert Se for conhecida uma solução não trivial de uma EDOLH de a ordem, empregando o método de D
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Sistemas Lineares. Juliana Pimentel. juliana.pimentel. Sala Bloco A, Torre 2
 Sistemas Lineares Juliana Pimentel juliana.pimentel@ufabc.edu.br http://hostel.ufabc.edu.br/ juliana.pimentel Sala 507-2 - Bloco A, Torre 2 O que é uma equação linear? O que é uma equação linear? Ex: 1)
Sistemas Lineares Juliana Pimentel juliana.pimentel@ufabc.edu.br http://hostel.ufabc.edu.br/ juliana.pimentel Sala 507-2 - Bloco A, Torre 2 O que é uma equação linear? O que é uma equação linear? Ex: 1)
Álgebra Linear
 Álgebra Linear - 09 Lista - Sistemas lineares ) Descreva todas as possíveis matrizes, que estão na forma escada reduzida por linha De acordo com a definição de uma matriz na forma escada reduzida por linhas
Álgebra Linear - 09 Lista - Sistemas lineares ) Descreva todas as possíveis matrizes, que estão na forma escada reduzida por linha De acordo com a definição de uma matriz na forma escada reduzida por linhas
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Solução Comentada Prova de Matemática
 18. Se f é uma função real de variável real definida por f() = a + b + c, onde a, b e c são números reais negativos, então o gráfico que melhor representa a derivada de f é: A) y B) y C) y D) y E) y Questão
18. Se f é uma função real de variável real definida por f() = a + b + c, onde a, b e c são números reais negativos, então o gráfico que melhor representa a derivada de f é: A) y B) y C) y D) y E) y Questão
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
EDO I. por Abílio Lemos. 16 e 18 de outubro de Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
 EDO I por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2017 16 e 18 de outubro de 2017 Definição 1 Uma equação diferencial é qualquer relação entre uma função e suas derivadas.
EDO I por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2017 16 e 18 de outubro de 2017 Definição 1 Uma equação diferencial é qualquer relação entre uma função e suas derivadas.
32 a Aula AMIV LEAN, LEC Apontamentos
 32 a Aula 2429 AMIV LEAN, LEC Apontamentos (RicardoCoutinho@mathistutlpt) 32 Fórmula da variação das constantes Temos então pela fórmula dos da variação das constantes (para sistemas de equações - Teorema
32 a Aula 2429 AMIV LEAN, LEC Apontamentos (RicardoCoutinho@mathistutlpt) 32 Fórmula da variação das constantes Temos então pela fórmula dos da variação das constantes (para sistemas de equações - Teorema
Entre os pontos A e B temos uma d.d.p. no indutor dada por V L = L d i e entre os pontos C e D da d.d.p. no capacitor é dada por V L V C = 0
 Um circuito elétrico LC é composto por um indutor de mh e um capacitor de 0,8 μf. A carga inicial do capacitor é de 5 μc e a corrente no circuito é nula, determine: a) A variação da carga no capacitor;
Um circuito elétrico LC é composto por um indutor de mh e um capacitor de 0,8 μf. A carga inicial do capacitor é de 5 μc e a corrente no circuito é nula, determine: a) A variação da carga no capacitor;
30 a Aula AMIV LEAN, LEC Apontamentos
 30 a Aula 20041124 AMIV LEAN, LEC Apontamentos (RicaroCoutinho@mathistutlpt) 301 Equações iferenciais e orem n Comecemos com consierações gerais sobre equações e orem n; nomeaamente sobre a sua relação
30 a Aula 20041124 AMIV LEAN, LEC Apontamentos (RicaroCoutinho@mathistutlpt) 301 Equações iferenciais e orem n Comecemos com consierações gerais sobre equações e orem n; nomeaamente sobre a sua relação
Sistemas de equações lineares
 Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Exponencial de uma matriz
 Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
Exponencial de uma matriz Ulysses Sodré Londrina-PR, 21 de Agosto de 2001; Arquivo: expa.tex Conteúdo 1 Introdução à exponencial de uma matriz 2 2 Polinômio característico, autovalores e autovetores 2
OUTRAS TÉCNICAS DE INTEGRAÇÃO
 8 OUTRAS TÉCNICAS DE INTEGRAÇÃO Gil da Costa Marques 8. Integração por partes 8. Integrais de funções trigonométricas 8.3 Uso de funções trigonométricas 8.4 Integração de Quociente de Polinômios 8.5 Alguns
8 OUTRAS TÉCNICAS DE INTEGRAÇÃO Gil da Costa Marques 8. Integração por partes 8. Integrais de funções trigonométricas 8.3 Uso de funções trigonométricas 8.4 Integração de Quociente de Polinômios 8.5 Alguns
um polinômio de grau menor ou igual a n. Consideremos a edo na variável t
 MAT 216 - Cálculo III - 1 o SEMESTRE de 2014 - IFUSP EQUAÇÕES DIFERENCIAIS COM COEFICIENTES CONSTANTES Referência: A Formula Substituting the Undetermined Coefficients and the Annihilator Methods, Oswaldo
MAT 216 - Cálculo III - 1 o SEMESTRE de 2014 - IFUSP EQUAÇÕES DIFERENCIAIS COM COEFICIENTES CONSTANTES Referência: A Formula Substituting the Undetermined Coefficients and the Annihilator Methods, Oswaldo
Funções Polinomiais com Coeficientes Complexos. Quantidade de Raízes e Consequências. 3 ano E.M. Professores Cleber Assis e Tiago Miranda
 Funções Polinomiais com Coeficientes Complexos Quantidade de Raízes e Consequências 3 ano E.M. Professores Cleber Assis e Tiago Miranda Funções Polinomiais com Coeficientes Complexos Quantidade de Raízes
Funções Polinomiais com Coeficientes Complexos Quantidade de Raízes e Consequências 3 ano E.M. Professores Cleber Assis e Tiago Miranda Funções Polinomiais com Coeficientes Complexos Quantidade de Raízes
Seção 27: Pontos Singulares Método de Frobenius
 Seção 27: Pontos Singulares Método de Frobenius Definição. Seja x 0 um ponto singular para a equação diferencial y + P x y + Qx y = 0. Dizemos que x 0 é um ponto singular regular se P x é analítica em
Seção 27: Pontos Singulares Método de Frobenius Definição. Seja x 0 um ponto singular para a equação diferencial y + P x y + Qx y = 0. Dizemos que x 0 é um ponto singular regular se P x é analítica em
Synergismus Scyentifica UTFPR. XIII ERMAC Mini Curso. Diferenciais
 Synergismus Scyentifica UTFPR Mini Curso Aplicações da Álgebra Linear a Equações Diferenciais Gilson Tumelero Marieli Musial Colegiado de Matemática - FAFIUV Pato Branco, setembro de 2009 Sumário Introdução
Synergismus Scyentifica UTFPR Mini Curso Aplicações da Álgebra Linear a Equações Diferenciais Gilson Tumelero Marieli Musial Colegiado de Matemática - FAFIUV Pato Branco, setembro de 2009 Sumário Introdução
Parte II. Análise funcional II
 Parte II Análise funcional II 12 Capítulo 5 Produto de Operadores. Operadores inversos Neste capítulo vamos introduzir a noção de produto de operadores assim como a de operador invertível. Para tal precisamos
Parte II Análise funcional II 12 Capítulo 5 Produto de Operadores. Operadores inversos Neste capítulo vamos introduzir a noção de produto de operadores assim como a de operador invertível. Para tal precisamos
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
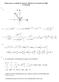 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
17.1 multiplicidade de um ponto da curva
 Aula 17 multiplicidades de interseção (Anterior: C é fecho algébrico de R ) Voltamos ao estudo de curvas planas O assunto agora diz respeito à compreensão das multiplicidades O exemplo modelo bem conhecido
Aula 17 multiplicidades de interseção (Anterior: C é fecho algébrico de R ) Voltamos ao estudo de curvas planas O assunto agora diz respeito à compreensão das multiplicidades O exemplo modelo bem conhecido
Aula 3. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Lista de exercícios 11 Representação Matricial de Aplicações Lineares
 Universidade Federal do Paraná Algebra Linear Olivier Brahic Lista de exercícios Representação Matricial de Aplicações Lineares Exercício : Para cada transformação linear seguinte, encontre a representação
Universidade Federal do Paraná Algebra Linear Olivier Brahic Lista de exercícios Representação Matricial de Aplicações Lineares Exercício : Para cada transformação linear seguinte, encontre a representação
3 a Lista para auto-avaliação (com um exercício resolvido)
 Álgebra Linear Cursos: Engenharia Civil, Engenharia de Minas, Engenharia do Território 1 ō ano/1 ō Semestre 21/211 3 a Lista para auto-avaliação (com um exercício resolvido) 1. Indique a característica
Álgebra Linear Cursos: Engenharia Civil, Engenharia de Minas, Engenharia do Território 1 ō ano/1 ō Semestre 21/211 3 a Lista para auto-avaliação (com um exercício resolvido) 1. Indique a característica
Teoremas e Propriedades Operatórias
 Capítulo 10 Teoremas e Propriedades Operatórias Como vimos no capítulo anterior, mesmo que nossa habilidade no cálculo de ites seja bastante boa, utilizar diretamente a definição para calcular derivadas
Capítulo 10 Teoremas e Propriedades Operatórias Como vimos no capítulo anterior, mesmo que nossa habilidade no cálculo de ites seja bastante boa, utilizar diretamente a definição para calcular derivadas
Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula
 59070 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 6 00 Superposição de Movimentos Periódicos Há muitas situações em física que envolvem a ocorrência simultânea de duas ou mais
59070 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 6 00 Superposição de Movimentos Periódicos Há muitas situações em física que envolvem a ocorrência simultânea de duas ou mais
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Capítulo 9. Circuitos de Segunda Ordem
 EA-53 Circuitos Elétricos I Capítulo 9 Circuitos de Segunda Ordem EA-53 Circuitos Elétricos I 9. Circuitos com Dois Elementos Armazenadores Circuito com dois indutores, onde deseja-se obter a corrente
EA-53 Circuitos Elétricos I Capítulo 9 Circuitos de Segunda Ordem EA-53 Circuitos Elétricos I 9. Circuitos com Dois Elementos Armazenadores Circuito com dois indutores, onde deseja-se obter a corrente
Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Física III Escola Politécnica GABARITO DA P3 13 de junho de 2019
 Física III - 43303 Escola Politécnica - 019 GABARITO DA P3 13 de junho de 019 Questão 1 Considere um fio infinito transportando uma corrente elétrica I(t = I 0 cos(ωt ao longo do eixo x e uma espira quadrada
Física III - 43303 Escola Politécnica - 019 GABARITO DA P3 13 de junho de 019 Questão 1 Considere um fio infinito transportando uma corrente elétrica I(t = I 0 cos(ωt ao longo do eixo x e uma espira quadrada
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
PSI.3031 LABORATÓRIO DE CIRCUITOS ELETRICOS INTRODUÇÃO TEÓRICA EXPERIÊNCIA 10: REDES DE SEGUNDA ORDEM
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia de Sistemas Eletrônicos PSI - EPUSP PSI.3031 LABORATÓRIO DE CIRCUITOS ELETRICOS INTRODUÇÃO TEÓRICA Edição 2017 E.Galeazzo / L.Yoshioka
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia de Sistemas Eletrônicos PSI - EPUSP PSI.3031 LABORATÓRIO DE CIRCUITOS ELETRICOS INTRODUÇÃO TEÓRICA Edição 2017 E.Galeazzo / L.Yoshioka
Circuitos de Primeira Ordem
 Circuitos de Primeira Ordem Magno T. M. Silva e Flávio R. M. Pavan, 5 Introdução Em geral, um circuito de primeira ordem tem um único elemento armazenador de energia (um capacitor ou um indutor) e é descrito
Circuitos de Primeira Ordem Magno T. M. Silva e Flávio R. M. Pavan, 5 Introdução Em geral, um circuito de primeira ordem tem um único elemento armazenador de energia (um capacitor ou um indutor) e é descrito
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE ABRIL DE 2017
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 21 17 DE ABRIL DE 2017 EQUAÇÕES DIFERENCIAIS Equações iferenciais são equações (algébricas) one figuram funções e erivaas e várias orens e funções.
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 21 17 DE ABRIL DE 2017 EQUAÇÕES DIFERENCIAIS Equações iferenciais são equações (algébricas) one figuram funções e erivaas e várias orens e funções.
Representação e Análise de Sistemas Dinâmicos Lineares Componentes Básicos de um Sistema de Controle
 Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Mecânica Quântica. Spin 1/2 e a formulação da M. Q. Parte II. A C Tort 1. Instituto Física Universidade Federal do Rio de Janeiro
 Mecânica Quântica Spin 1/ e a formulação da M. Q. Parte II A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 10 de Maio de 01 Mais dois postulados, agora
Mecânica Quântica Spin 1/ e a formulação da M. Q. Parte II A C Tort 1 1 Departmento de Física Teórica Instituto Física Universidade Federal do Rio de Janeiro 10 de Maio de 01 Mais dois postulados, agora
33 a Aula AMIV LEAN, LEC Apontamentos
 33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
Exame Oral. Segunda Fase do Exame de Seleção para a École Polytechnique Alessandro T. M. Gagliardi
 Exame Oral Segunda Fase do Exame de Seleção para a École Polytechnique - 2012 Alessandro T. M. Gagliardi Depto. de Física Matemática, Universidade de São Paulo, Brasil 2 de Dezembro de 2012 Conteúdo 1
Exame Oral Segunda Fase do Exame de Seleção para a École Polytechnique - 2012 Alessandro T. M. Gagliardi Depto. de Física Matemática, Universidade de São Paulo, Brasil 2 de Dezembro de 2012 Conteúdo 1
Aula 27 - Álgebra II. x (m(x)), x 2 + x + (m(x)), x 2 + x (m(x)) operações deste corpo são as seguintes:
 Já vimos maneiras de codificar mensagens de modo a que, no caso de ocorrerem alguns erros na sua transmissão, o receptor possa ser capaz de corrigir esses erros. Esses códigos, chamados códigos lineares
Já vimos maneiras de codificar mensagens de modo a que, no caso de ocorrerem alguns erros na sua transmissão, o receptor possa ser capaz de corrigir esses erros. Esses códigos, chamados códigos lineares
PARTE I EQUAÇÕES DE UMA VARIÁVEL REAL
 PARTE I EQUAÇÕES DE UMA VARIÁVEL REAL. Introdução Considere f uma função, não constante, de uma variável real ou complexa, a equação f(x) = 0 será denominada equação de uma incógnita. EXEMPLO e x + senx
PARTE I EQUAÇÕES DE UMA VARIÁVEL REAL. Introdução Considere f uma função, não constante, de uma variável real ou complexa, a equação f(x) = 0 será denominada equação de uma incógnita. EXEMPLO e x + senx
u t = c 2 u xx, (1) u(x, 0) = 1 (0 < x < L) Solução: Utilizando o método de separação de variáveis, começamos procurando uma solução u(x, t) da forma
 Seção 9: Equação do Calor Consideremos um fluxo de calor em uma barra homogênea, construída de um material condutor de calor, em que as dimensões da seção lateral são pequenas em relação ao comprimento.
Seção 9: Equação do Calor Consideremos um fluxo de calor em uma barra homogênea, construída de um material condutor de calor, em que as dimensões da seção lateral são pequenas em relação ao comprimento.
d [xy] = x cos x. dx y = sin x + cos x + C, x
![d [xy] = x cos x. dx y = sin x + cos x + C, x d [xy] = x cos x. dx y = sin x + cos x + C, x](/thumbs/66/55981826.jpg) Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Sistemas de equações lineares
 ALGA- / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b
ALGA- / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b
Capítulo Equações da reta no espaço. Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
 Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Capítulo 11 1. Equações da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que AP = t AB Fig. 1: Reta r passando por A e B. Como o ponto
Autovetor e Autovalor de um Operador Linear
 Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
Autovetor e Autovalor de um Operador Linear Definição Seja T : V V um operador linear. Um vetor v V, v 0, é dito um autovetor de T se existe um número real λ tal que T (v) = λv. O número real λ acima é
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Capítulo 3 Equações Diferenciais. O Wronskiano (de Josef Hoëné-Wronski, polonês, )
 Capítulo 3 Equações Diferenciais O Wronskiano (de Josef Hoëné-Wronski, polonês, 1776 1853) Seja a equação diferencial, ordinária, linear e de 2ª. ordem Podemos dividir por os 2 membros e escrever a equação
Capítulo 3 Equações Diferenciais O Wronskiano (de Josef Hoëné-Wronski, polonês, 1776 1853) Seja a equação diferencial, ordinária, linear e de 2ª. ordem Podemos dividir por os 2 membros e escrever a equação
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Se a população está isolada (ou seja, se não há outras espécies que com ela interajam),
 APLICAÇÕES DE EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM Modelos Populacionais Denotemos por p(t) o número de elementos de uma certa população no instante t e por r(t, p) a taxa de crescimento da população
APLICAÇÕES DE EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM Modelos Populacionais Denotemos por p(t) o número de elementos de uma certa população no instante t e por r(t, p) a taxa de crescimento da população
GABARITO P MAT1154. PUC Que Pariu!
 GABARITO P2 2012.2 - MAT1154 PUC Que Pariu! Questão 1: a Utilizaremos cálculo funcional para calcularmos A n : A n = α n A + β n Isto é válido se e somente se: λ n = α n.λ + β n I nλ n 1 = α n Onde λ é
GABARITO P2 2012.2 - MAT1154 PUC Que Pariu! Questão 1: a Utilizaremos cálculo funcional para calcularmos A n : A n = α n A + β n Isto é válido se e somente se: λ n = α n.λ + β n I nλ n 1 = α n Onde λ é
F = m d 2 x d t 2. temos que as forças a única força que atua no bloco é a força elástica da mola ( F E ), dada por. F E = k x
 Um bloco de massa m = 0,5 kg é ligado a uma mola de constante elástica k = 1 N/m. O bloco é deslocado de sua posição de equilíbrio O até um ponto P a 0,5 m e solto a partir do repouso, determine: a) A
Um bloco de massa m = 0,5 kg é ligado a uma mola de constante elástica k = 1 N/m. O bloco é deslocado de sua posição de equilíbrio O até um ponto P a 0,5 m e solto a partir do repouso, determine: a) A
3 ā Prova de MAT Cálculo II - Química 2 ō Semestre - 11/12/2009 Prof. Oswaldo Rio Branco de Oliveira. Boa Sorte!
 3 ā Prova de MAT212 - Cálculo II - Química 2 ō Semestre - 11/12/2009 Prof. Oswaldo Rio Branco de Oliveira Boa Sorte! Nome : N ō USP : Q 1 2 3 5 6 Total N JUSTIFIQUE TODAS AS PASSAGENS 1. Seja w = f(x,y)
3 ā Prova de MAT212 - Cálculo II - Química 2 ō Semestre - 11/12/2009 Prof. Oswaldo Rio Branco de Oliveira Boa Sorte! Nome : N ō USP : Q 1 2 3 5 6 Total N JUSTIFIQUE TODAS AS PASSAGENS 1. Seja w = f(x,y)
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
Material Teórico - Módulo Matrizes e Sistemas Lineares. Sistemas Lineares - Parte 2. Terceiro Ano do Ensino Médio
 Material Teórico - Módulo Matrizes e Sistemas Lineares Sistemas Lineares - Parte 2 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto 1 A representação
Material Teórico - Módulo Matrizes e Sistemas Lineares Sistemas Lineares - Parte 2 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto 1 A representação
Processo de ortogonalização de Gram-Schmidt. Mudança de Base. Doherty Andrade. DMA - F67 - Sala 205
 DMA - F67 - Sala 205 e-mail:doherty@uem.br Em muitas situações trabalhar com uma base particular de V 3 pode simplificar o trabalho. Dado uma base β = { u 1, u 2, u 3 } e outra base β = { w 1, w 2, w 3
DMA - F67 - Sala 205 e-mail:doherty@uem.br Em muitas situações trabalhar com uma base particular de V 3 pode simplificar o trabalho. Dado uma base β = { u 1, u 2, u 3 } e outra base β = { w 1, w 2, w 3
Material Básico: Calculo A, Diva Fleming
 1 Limites Material Básico: Calculo A, Diva Fleming O conceito de Limite é importante na construção de muitos outros conceitos no cálculo diferencial e integral, por exemplo, as noções de derivada e de
1 Limites Material Básico: Calculo A, Diva Fleming O conceito de Limite é importante na construção de muitos outros conceitos no cálculo diferencial e integral, por exemplo, as noções de derivada e de
Capítulo Regra da cadeia
 Cálculo 2 - Capítulo 28 - Regra da cadeia 1 Capítulo 28 - Regra da cadeia 281 - Introdução 283 - Generalização 282 - Regra da cadeia Este capítulo trata da chamada regra da cadeia para funções de duas
Cálculo 2 - Capítulo 28 - Regra da cadeia 1 Capítulo 28 - Regra da cadeia 281 - Introdução 283 - Generalização 282 - Regra da cadeia Este capítulo trata da chamada regra da cadeia para funções de duas
( ) ( ) 60 ( ) ( ) ( ) ( ) R i. Método de Newton. Método de Newton = Substituindo i por x, teremos: 1.Introdução 2.
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I R A = + i ( i ) n
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I R A = + i ( i ) n
