Resolução Estrutural por Difração de Raios X de Tiouréias com Potencial Atividade Biológica
|
|
|
- David Figueira Festas
- 8 Há anos
- Visualizações:
Transcrição
1 Universidade Federal de Goiás Instituto de Física Resolução Estrutural por Difração de Raios X de Tiouréias com Potencial Atividade Biológica Fernando Pereira de Sá Dissertação apresentada ao Instituto de Física da Universidade Federal de Goiás, para a obtenção do título de Mestre em Física. Orientador: Prof. Dr. Carlito Lariucci Co-Orientador: Prof. Dr. Ivo Vencato Goiânia 2006
2 Agradecimentos À Deus por ter permitido alcançar meus objetivos. Ao Prof. Dr. Carlito Lariucci pela orientação do trabalho e amizade demonstrada. Ao Prof. Dr. Ivo Vencato pelas sugestões, incentivo e grande apoio. Ao Prof. Dr. José Ricardo pela ajuda na parte final deste trabalho. Ao Prof. Dr. Silvio do Desterro Cunha pelas discussões da parte química deste trabalho. Ao Instituto de Física da Universidade Federal de Goiás pelo apoio institucional. Aos colegas da Saneago Júlio Cesar e João Gonçalves, pelo apoio durante este trabalho. Aos meus pais Jordelino e Marina, pelo incentivo e apoio que sempre me deram. Aos meus irmãos Márcio e Marcelo, pelo apoio nos momentos difíceis. Aos meus familiares e amigos pelo incentivo. Em especial à Fernanda Dorneles, minha esposa, pelo carinho e dedicação constante.
3 Conteúdo Lista de Figuras Lista de Tabelas Resumo Abstract iii v vii ix Introdução 1 1 Tiouréias Introdução Farmacologia das Tiouréias Método de Patterson Introdução Difração de Raios X A Rede Recíproca Fator de Espalhamento Atômico Fatores de Estrutura e o Problema da Fase Densidade Eletrônica Teorema da Convolução A Função de Patterson Interpretação da Função de Patterson Método do Átomo Pesado Seções de Harker Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O Estrutura Cristalina das Tiouréias Introdução Medidas Difratométricas, Solução e Refinamento das Estruturas N-benzoil, N -tercbutil-tiouréia (T1) N-benzoil, N -(4-metilfenil)-tiouréia (T2) N-benzoil, N -(2-hidroxietil)-tiouréia (T3) Análise das Estruturas Cristalinas Conclusão 66 i
4 A Programa para o Cálculo da Densidade Eletrônica Unidimensional 68 B Programa para o Cálculo da Densidade Eletrônica Bidimensional 71 C Programa para o Cálculo do Mapa de Patterson 74 D Tabelas Adicionais das Estruturas Resolvidas 77 E Compostos Relacionados: Busca no CCD 84 Bibliografia 90 ii
5 Lista de Figuras 1.1 Representação do grupamento uréia e tiouréia Tiouréias ativas biologicamente Representação bidimensional do composto (T1) Representação bidimensional do composto (T2) Representação bidimensional do composto (T3) Esfera de Ewald Fator de espalhamento atômico: (a) átomo estacionário. (b) Correção por vibração térmica Projeção unidimensional da densidade eletrônica para C 18 H 14 - Br 1 N 5 O 1. As duas linhas verticais mostram as coordenadas do Br 1 e Br 2, relacionadas por um centro de inversão Projeção bidimensional da densidade eletrônica para o composto C 18 H 14 Br 1 N 5 O Átomos com simetria relacionadas e com simetria independentes na função de Patterson Diagrama de Argand com um átomo pesado e seis átomos leves Gráfico da função de Patterson bidimensional, l = Projeção plana do mapa de Patterson Representação ORTEP do composto C 18 H 14 N 5 O 1 Br Representação ORTEP do composto T Formação de dímeros em torno de centros de inversão para o composto T1. As linhas tracejadas indicam as ligações de hidrogênio intramoleculares e intermoleculares. Somente os hidrogênios envolvidos nas ligações estão representados. Os demais foram omitidos por motivo de clareza Projeção ao longo do eixo a (representado na Figura por X) mostrando dois dímeros formando um arranjo tipo espinha de peixe, para o composto T Representação ORTEP do composto T Formação de dímeros em torno de centros de inversão para o composto T2. As linhas tracejadas indicam as ligações intermoleculares. Somente os hidrogênios envolvidos nas ligações estão representados. Os demais foram omitidos por motivo de clareza Projeção ao longo do eixo a mostrando o arranjo tipo espinha de peixe (herringbone) para o composto T Representação ORTEP do composto T iii
6 3.8 As linhas tracejadas indicam as ligações intermoleculares. Somente os hidrogênios envolvidos nas ligações estão representados. Os demais foram omitidos por motivo de clareza Projeção ao longo da direção [1 0 1] mostrando o arranjo quase planar em planos formando um ângulo de 75,8 entre si, resultando em arranjo tipo espinha de peixe para o composto T Alguns parâmetros dos compostos encontrados na busca ao CCD, utilizando o programa VISTA Variação de valores para o parâmetro N(1)-C(13) Correlação entre os parâmetros C4-O6 e C2-S5 para os 18 compostos encontrados no CCD E.1 Compostos Relacionados: Busca no CCD, de 1 a E.2 Compostos Relacionados: Busca no CCD, de 5 a E.3 Compostos Relacionados: Busca no CCD, de 9 a E.4 Compostos Relacionados: Busca no CCD, de 13 a E.5 Compostos Relacionados: Busca no CCD, de 17 a iv
7 Lista de Tabelas 2.1 Os 7 sistemas cristalinos e os 14 retículos de Bravais Relações entre os parâmetros de cela no espaço direto e no espaço recíproco Valores de hkl, Fc e φ para o composto C 18 H 14 Br 1 N 5 O Vetores inter-atômicos para o composto C 18 H 14 Br 1 N 5 O Dados cristalográficos do composto C 18 H 14 N 5 O 1 Br Parâmetros posicionais e de vibração térmica isotrópica do composto C 18 H 14 N 5 O 1 Br Distâncias (Å) intramoleculares dos hidrogênios colocados geometricamente Dados Cristalográficos do composto T Picos de Patterson para o composto T Parâmetros posicionais e de vibração térmica isotrópica equivalente do composto T Ligações de hidrogênio intramoleculares e intermolecular do composto T Equações dos planos, distância dos átomos aos planos e ângulo diedro entre planos para o composto T Dados Cristalográficos do composto T Picos de Patterson para o composto T Parâmetros posicionais e de vibração térmica isotrópica equivalente do composto T Equações dos planos, distância dos átomos aos planos e ângulos diedros entre planos para o composto T Ligações de hidrogênio intra e intermoleculares do composto T Dados Cristalográficos do composto T Picos de Patterson para o composto T Parâmetros posicionais e de vibração térmica isotrópica equivalente do composto T Equações dos planos, distância dos átomos aos planos e ângulo diedro entre planos para o composto T Ligações de hidrogênio intra e intermoleculares do composto T Comparação entre os parâmetros dos três compostos resolvidos e os 18 compostos encontrados no CCD Distâncias intramoleculares (Å) e os respectivos desvios padrão dos compostos estudados v
8 3.19 Ângulos intramoleculares ( ) e os respectivos desvios padrão dos compostos estudados A.1 Modelo de arquivo de entrada e de saída do programa desenvolvido para o cálculo da densidade eletrônica unidimensional. 70 B.1 Modelo de arquivo de entrada e de saída do programa desenvolvido para o cálculo da densidade eletrônica bidimensional.. 73 C.1 Modelo de arquivo de entrada e de saída do programa desenvolvido para o cálculo da função de Patterson bidimensional.. 76 D.1 Parâmetros posicionais e de vibração térmica isotrópica dos hidrogênios do composto T D.2 Parâmetros térmicos anisotrópicos (Å 2 x10 3 ) e seus respectivos desvios padrão do composto T D.3 Ângulos de torção ( ) do composto T D.4 Parâmetros posicionais e de vibração térmica isotrópica dos hidrogênios do composto T D.5 Parâmetros térmicos anisotrópicos (Å 2 x10 3 ) e seus respectivos desvios padrão do composto T D.6 Ângulos de torção ( ) do composto T D.7 Parâmetros posicionais e de vibração térmica isotrópica dos hidrogênios do composto T D.8 Parâmetros térmicos anisotrópicos (Å 2 x10 3 ) e seus respectivos desvios padrão do composto T D.9 Ângulos de torção ( ) do composto T vi
9 Resumo Neste trabalho foram resolvidas as estruturas cristalinas e moleculares de três tiouréias com potencial atividade antibacteriana, a partir da difração de raios X. O método de Patterson foi usado para a solução das estruturas e para o refinamento usou-se o método dos mínimos quadrados. A obtenção de dados foi feita em um difratômetro CAD4, utilizando radiação CuKα (λ = 1,54180 Å). A solução, refinamento anisotrópico, cálculos geométricos, empacotamento molecular e desenhos foram feitos com o programa WINGX. 1) C 12 H 16 N 2 O 1 S 1 (T1): a = 11,6226(9), b = 5,7852(4), c = 19,800(7) Å, β = 105,49(1), sistema monoclínico, grupo espacial P2 1 /c, Z = 4, V = 1283,0(5) Å 3, Dc = 1,220 Mgm 3. Foram medidas 2850 reflexões, sendo 2284 únicas e 1898 observadas [I 2σ(I)]. Índices de discordâncias finais R1 = 0,061 (observadas) e ωr2 = 0,162 (únicas), para 152 parâmetros refinados. A estrutura apresenta duas ligações de hidrogênio intramoleculares. Uma ligação de hidrogênio intermolecular do tipo N H S forma um dímero com outra molécula em torno de um centro de inversão. Os dímeros estão empilhados ao longo do eixo b, resultando num arranjo tipo espinha de peixe (herringbone). 2) C 15 H 14 N 2 O 1 S 1 (T2): a = 13,021(2), b = 5,424(1), c = 19,861(3) Å, β = 98,78(1), sistema monoclínico, grupo espacial P2 1 /c, Z = 4, V = 1386,3(3) Å 3, Dc = 1,300 Mgm 3. Foram medidas 3114 reflexões, sendo 2466 únicas e 1862 observadas [I 2σ(I)]. Índices de discordâncias finais R1 = 0,0456 (observadas) vii
10 e ωr2 = 0,158 (únicas), para 183 parâmetros refinados. O composto apresenta duas ligações de hidrogênio intramoleculares. Duas ligações de hidrogênio intermoleculares dos tipos N H S e C H O formam dímeros em torno do centro de inversão, resultando num arranjo tipo espinha de peixe (herringbone). 3) C 10 H 12 N 2 O 2 S 1 (T3): a = 17,088(2), b = 4,583(2), c = 14,283(2) Å, β = 102,61(1), sistema monoclínico, grupo espacial P2 1 /c, Z = 4, V = 1091,6(3) Å 3, Dc = 1,360 Mgm 3. Foram medidas 2473 reflexões, sendo 1877 únicas e 1781 observadas [I 2σ(I)]. Índices finais R1 = 0,060 (observadas) e ωr2 = 0,148 (únicas), para 146 parâmetros refinados. O composto apresenta uma ligação de hidrogênio intramolecular. As quatro ligações de hidrogênio intermoleculares produzem dois arranjos planares formando um ângulo de 75,8 entre si. Visto ao longo da direção [1 0 1], o conjunto lembra espinha de peixe (herringbone). viii
11 Abstract In this work, the crystal and molecular structures of three thiourea compounds with potential antimicrobial activities, where resolved using X rays diffraction. The method of Patterson was used for the solution of the structures and the refinement was performed with the least-squares method. Data were colleted with in a CAD4 diffractometer using CuKα radiation (λ = 1,54180 Å). The solution, anisotropic refinement, geometrical calculations, molecular packings and drawings were done with the WINGX program package. 1) C 12 H 16 N 2 O 1 S 1 (T1): a = (9), b = (4), c = (7) Å, β = (1), monoclinic system, space group P2 1 /c, Z = 4, V = (5) Å 3, Dc = Mgm measured reflections, with 2284 unique and 1898 observed [I 2σ(I)]. Final indices R1 = (observed) and ωr2 = (unique) were obtained for 152 refined parameters. The structure presents two intramolecular hydrogen bonds and an intermolecular hydrogen bond of the type N H O, which forms a dimer with other molecule related by an inversion center. The dimers are stacked along the b axis, resulting in an herringbone arrangement. 2) C 15 H 14 N 2 O 1 S 1 (T2): a = (2), b = 5.424(1), c = (3) Å, β = 98.78(1), monoclinic system, space group P2 1 /c, Z = 4, V = (3) Å 3, Dc = Mgm measured reflections, with 2466 unique and 1862 observed [I 2σ(I)]. Final indices R1 = (observed) and ωr2 = (unique) were obtained for 183 refined parameters. The compound presents two intramolecular hydrogen bonds and two intermolecular hydrogen bonds of the ix
12 types N H S and C H O form dimers about the inversion center, resulting in an herringbone arrangement. 3) C 10 H 12 N 2 O 2 S 1 (T3): a = (2), b = 4.583(2), c = (2) Å, β = (1), monoclinic system, space group P2 1 /c, Z = 4, V = (3) Å 3, Dc = Mgm measured reflections, with 1877 unique and 1781 observed [I 2σ(I)]. Final indices R1 = (observed) and ωr2 = (unique) were obtained for 146 refined parameters. The compound shows an intramolecular hydrogen bond and four intermolecular hydrogen bonds which result in two planar arrangements forming an angle of 75.8 to each other. When viewed along the direction [1 0 1]. The group reminds a fish spine (herringbone). x
13 Introdução Os raios X são radiações eletromagnéticas assim como a luz mas com um comprimento de onda muito menor, da ordem de 0,5 a 100 Å. De acordo com a teoria quântica, a radiação pode ser considerada como um fluxo de partículas, chamados quanta ou fótons, onde cada fóton tem associada uma energia hν [1]. A Cristalografia de raios X é uma técnica experimental que explora o fato de que a radiação X é difratada através de cristais. Estes raios são espalhados pela nuvem eletrônica do arranjo periódico de moléculas, átomos ou íons no cristal e, a partir do padrão de difração pode-se encontrar as densidades eletrônicas. Deve-se obter informações das fases das ondas espalhadas para obter a solução. O conhecimento de estruturas moleculares é uma condição prévia ao estudo de estruturas funcionais para ajudar o desenvolvimento de agentes terapêuticos efetivos. A Cristalografia pode dar respostas confiáveis a muitas perguntas relacionadas à estrutura. O requisito principal para a alta precisão na solução de estruturas em cristalografia é a obtenção de um bom cristal. Neste trabalho, utilizou-se a técnica da difração de raios X por cristais, para a determinação da estrutura cristalina e molecular de três tiouréias com potencial atividade biológica. Foi observado a posição cis ou trans do grupo benzoila em relação ao grupo tiocarbonila pela ligação C2-N3, presente em todas as tiouréias estudadas. A proposta do estudo das tiouréias, surgiu primeiramente do Instituto de Química da Universidade Federal da Bahia, na ocasião em que o Grupo de 1
14 Cristalografia e Materiais do Instituto de Física da UFG, estava iniciando uma colaboração com o IQ-UFBa para efetuar coletas de dados difratométricas para a obtenção de estruturas de uma série de compostos, entre eles, tiouréias. Esta proposta foi circunstancial, tendo em vista que já haviam sido cristalizadas uma grande quantidade destas substâncias, viabilizando então o seu estudo. A metodologia usada para a solução das estruturas foi a do método de Patterson, e para o refinamento foi utilizada a técnica de mínimos quadrados. O estudo cristalográfico destas substâncias tem por objetivo obter as características geométricas presentes, para comparação com outros compostos com atividade biológica comprovada. Esta Dissertação é composta de quatro capítulos e cinco apêndices. No primeiro capítulo faz-se uma abordagem sobre as tiouréias. No segundo descrevese a teoria do método de Patterson, abordando apenas os principais tópicos necessários para a compreensão da técnica de soluções de estruturas contendo átomo pesado. No terceiro apresenta-se os dados da solução e discussão das estruturas estudadas. No último capítulo aborda-se as considerações finais, correlacionando os parâmetros geométricos dessas moléculas com os testes de atividade bacteriana. Nos apêndices A e B são mostrados os desenvolvimentos dos programas usados para o cálculo de densidade eletrônica unidimensional e bidimensional, respectivamente. No apêndice C é mostrado o desenvolvimento do programa para a geração do mapa de Patterson, utilizado no segundo capítulo. No apêndice D são agrupadas as tabelas referentes aos parâmetros posicionais dos hidrogênios, parâmetros térmicos anisotrópicos e ângulos de torção, para as três tiouréias estudadas. E o apêndice E agrupa os compostos relacionados na busca ao Cambridge Crystallographic Database (CCD). 2
15 Capítulo 1 Tiouréias 1.1 Introdução Nos últimos anos, tem-se observado o interesse de alguns grupos de pesquisa no estudo das tiouréias, entre eles os Institutos de Química das Universidades Federais de Goiás e da Bahia. Isto se deve ao fato de que estes compostos apresentam potencial para numerosas aplicações químicas e farmacêuticas [2]. Algumas tiouréias apresentam potencial para atuar no combate a um número considerável de doenças inflamatórias [3] ou cardiovasculares [4]. Outras atuam como agente antioxidante em combustíveis, como a gasolina, inibindo a corrosão [5]. A atividade antimicrobiana tem atraído a atenção, devido à resistência desenvolvida por importantes agentes patogênicos ter aumentado nas últimas décadas e este é reconhecido como um sério problema de saúde pública. A doença de Chagas, a malária e a Leishmaniose são as maiores doenças parasitárias nos países em desenvolvimento. A primeira é a causa de um número considerável de mortes na América Latina. Pelo menos 16 a 18 milhões de pessoas estão infectadas com o Trypanosoma Cruzi, parasita causador da doença de Chagas, resultando em mais de mortes a cada ano [6]. Esta doença é 3
16 1.1 Introdução 4 transmitida ao ser humano através da corrente sangüínea pela picada de barbeiro e introdução do protozoário parasita T. Cruzi. Verifica-se que algumas tiouréias exibem potencial atividade no combate ao Trypanosoma Cruzi. A natureza não peptídica destes compostos, adicionado ao seu baixo custo de síntese, faz desta classe de inibidores covalentes, candidatos promissores para o desenvolvimento de novas drogas eficazes no combate à doença de Chagas. Para a verificação da atividade antibacteriana de uma série de substâncias, entre elas aquelas descritas neste trabalho, foram feitos testes para a Determinação da concentração inibitória mínima (MIC), usando para este fim o método da microdiluição. As culturas de bactérias usadas foram crescidas por 24 h a 35 C em nutriente agar. Os fungos foram cultivados por 72 h a 26 C em meio de cultura malte agar. Para comparação dos resultados com drogas já conhecidas e eficazes foram usados Clorafenicol e Loprox em relação as bactérias e fungos respectivamente. Após incubação, o crescimento dos microorganismos foi observado pela presença de turvação na placa. A MIC foi definida como a menor concentração das substâncias que inibem um visível crescimento da colônia de microorganismos. Entre as bactérias avaliadas estão: Staphylococcus Aureus e Escherichia Coli, importante organismo presente no intestino dos animais de sangue quente, inclusive o homem, sendo por isso muito importante para avaliação de contaminação fecal. Os resultados mostraram que, em geral, os compostos testados foram mais ativos para fungos, havendo um modesto crescimento de inibição em concentrações variando entre µg/ml para todas as bactérias testadas. Os testes em relação as bactérias foram feitos pelo IQ-UFG enquanto que para os fungos pelo IPTSP-UFG. Recentemente, foi observado que algumas tiouréias poderiam ser usadas
17 1.2 Farmacologia das Tiouréias 5 como organocatalisadores em diversas transformações orgânicas. Embora alguns grupos usem uréias e tiouréias como ácidos simples, suas aplicações para este fim são bem menores do que aquelas dos ácidos metálicos de Lewis [7]. 1.2 Farmacologia das Tiouréias Tiouréias são compostos orgânicos que apresentam em sua constituição o grupamento uréia, em que o átomo de oxigênio é substituído por um átomo de enxofre. A Figura 1.1 ilustra o grupamento uréia e a correspondente tiouréia derivada. Observa-se que os átomos de nitrogênio presentes no grupamento tiouréia são capazes de formar ligações de hidrogênio intermoleculares do tipo N-H S e C-H O. É conhecido que a atividade biológica desta classe de substâncias está associada à presença deste tipo de ligação. Lipinski [8] descreve certas propriedades que acredita serem importantes para o desenvolvimento de drogas eficazes no tratamento da doença de Chagas. Elas são: (i) mínima toxicidade celular, (ii) propriedades físicas conhecidas ser compatíveis com desejáveis fármacos (número de ligações de hidrogênio doador 5, número de ligação de hidrogênio receptor 10 e peso molecular < 500) e (iii) simples acesso sintético e portanto baixo custo de produção. A atividade antimicrobiana de uma classe de tiouréias tem sido investigada através de testes farmacológicos, os quais estão relacionados com a evolução de uma colônia de microorganismos, em contato com a solução da substância a ser estudada. Estes testes são feitos pelo Instituto de Química e Instituto de Patologia Tropical e Saúde Pública (IPTSP), ambos da Universidade Federal de Goiás. Os compostos mostrados na Figura 1.2 são ativos no combate ao T. Cruzi. Foram identificadas nestas tiouréias as características necessárias para a ativi-
18 1.2 Farmacologia das Tiouréias 6 Uréia Tiouréia Figura 1.1: Representação do grupamento uréia e tiouréia. dade biológica [6]. N N NH 2 S N NH NH 2 S CF 3 Br Figura 1.2: Tiouréias ativas biologicamente. Alguns compostos apresentando potencial atividade biológica, destacandose as tiouréias, tem sido sintetizados no Laboratório de Bioatividade Molecular do Instituto de Química da Universidade Federal da Bahia. As tiouréias estudadas nesta dissertação foram sintetizadas pela reação de aminas primárias e secundárias com isotiocianato de benzoíla: N-benzoil, N -tercbutil-tiouréia (C 12 H 16 N 2 O 1 S 1 ) (T1), Figura 1.3, N-benzoil, N -(4-metilfenil)-tiouréia (C 15 H 14 - N 2 O 1 S 1 ) (T2), Figura 1.4 e N-benzoil, N -(2-hidroxietil)-tiouréia (C 10 H 12 N 2 O 2 - S 1 ) (T3), Figura 1.5. O S N H N H Figura 1.3: Representação bidimensional do composto (T1).
19 1.2 Farmacologia das Tiouréias 7 O S N H N H Figura 1.4: Representação bidimensional do composto (T2). O N H S N H OH Figura 1.5: Representação bidimensional do composto (T3).
20 Capítulo 2 Método de Patterson 2.1 Introdução O objetivo de uma análise da estrutura cristalina, por difração de raios X, é o de obter informações do conteúdo dos cristais em nível atômico, como se estivéssemos olhando por um microscópio extremamente poderoso. Quando estas informações são disponíveis, e as posições dos átomos individuais são conhecidas precisamente, pode-se calcular distâncias inter-atômicas, ângulos de ligações e outras características da geometria molecular que são de interesse, como a planaridade de um grupo particular de átomos, os ângulos entre planos e ângulos de torção ao redor das ligações. A característica fundamental do estado cristalino é a ordem interna, ou seja, os átomos, moléculas ou íons, dos quais o cristal é composto, são arranjados de um modo regular que é repetido em todas as direções. Existe uma diferença fundamental entre os cristais, os gases e os líquidos. Esta diferença deve-se principalmente à não periodicidade destes dois últimos. Nem todos os sólidos são cristalinos, sendo alguns amorfos, como o vidro, que não tem qualquer arranjo periódico de átomos. Esta é a diferença entre um sólido amorfo e um cristalino. 8
21 2.1 Introdução 9 Pode-se descrever um cristal como um conjunto de pontos que possuem uma relação fixa no espaço, que pode ser considerado como uma moldura em que o cristal é construído. O conjunto de pontos formado constituirá uma rede puntual [9]. As celas formadas neste processo são idênticas, sendo possível escolher qualquer uma delas como a cela unitária. A cela unitária é definida por três vetores a, b e c ou através de seus comprimentos a, b, c e os ângulos entre eles α, β e γ, denominados parâmetros de cela [9]. Existem sete sistemas cristalinos em que os cristais podem ser classificados, os quais são definidos pelos parâmetros de cela (Tabela 2.1). Todas as redes tridimensionais possíveis podem ser classificadas em 14 tipos, denominadas redes de Bravais [9]. A invariância de um objeto ou de uma estrutura com respeito à alguma operação é denominado simetria [9]. Tabela 2.1: Os 7 sistemas cristalinos e os 14 retículos de Bravais Sistemas Eixos e Ângulos Retículos de Bravais P Cúbico a = b = c, α = β = γ = 90 I F Hexagonal a = b c, α = β = 90, γ = 120 P Trigonal a = b = c, α = β = γ 90 R Tetragonal a = b c, α = β = γ = 90 P I P Ortorrômbico a b c, α = β = γ = 90 I C F Monoclínico a b c, α = γ = 90 β P C Triclínico a b c, α β γ 90 P É conveniente expressar a localização de qualquer ponto na cela unitária de uma estrutura cristalina por meio de coordenadas nas direções dos eixos da cela e que suas magnitudes são frações destes eixos. Tais coordenadas são chamadas
22 2.2 Difração de Raios X 10 coordenadas fracionárias [9]. Se X, Y e Z são as coordenadas absolutas, relativas aos eixos a, b e c, respectivamente, então suas coordenadas fracionárias relativas aos mesmos eixos são: x = X/a, y = Y/b e z = Z/c, estas são referidas para uma origem conveniente, usualmente em um canto da cela. 2.2 Difração de Raios X Para executar uma experiência de difração de raios X, precisa-se de uma fonte de raios X, comumente é usado um gerador de ânodo metálico que produz um feixe de comprimento de onda característico do material metálico. O feixe de raios X primário é monocromatizado usando monocromadores cristalinos. O cristal é colocado em uma agulha fixa em um goniômetro, o qual permite posicioná-lo em orientações diferentes em relação ao feixe de raios X. A amostra é completamente banhada por este feixe. Os raios difratados são registrados em chapas fotográficas, detectores cintiladores ou câmaras de CCD. Neste experimento são medidas um grande número de reflexões provenientes de diferentes orientações cristalinas e que resultam numa lista de intensidades indexadas. O termo reflexão, é muito usado em cristalografia por analogia ao processo de reflexão da luz por espelhos, na interpretação de Bragg para a difração. Quando um cristal é colocado no caminho de um feixe de raios X, os átomos atuam, devido à vibração forçada dos elétrons, como uma fonte secundária de raios X. A freqüência e o comprimento de onda (λ) destes raios emitidos são idênticos aos do feixe incidente. Em analogia com a difração óptica, pode-se esperar que em certas direções, o espalhamento individual poderá recombinar em fase, para produzir reflexões, fortes. Isto acontecerá quando a equação de Bragg for satisfeita [10].
23 2.3 A Rede Recíproca 11 nλ = 2dsenθ (2.1) onde θ é o ângulo de espalhamento, d é a distância interplanar da família de planos cristalinos que refletem a radiação e n é um número inteiro correspondente à n-ésima ordem de difração. 2.3 A Rede Recíproca Re-arranjando a equação de Bragg, para n = 1, senθ = λ 2d (2.2) pode-se construir uma esfera, denominada esfera de Ewald [11], de raio de curvatura R = 1/λ, de tal forma que o feixe de raios X incidente no cristal colocado no centro da esfera e o feixe espalhado formam um ângulo 2θ, tal como representado na Figura 2.1. A condição de difração é alcançada quando uma reflexão hkl intercepta a superfície da esfera de Ewald. O ponto onde o feixe transmitido emerge da esfera define a origem da rede recíproca. A distância do ponto onde emerge o feixe espalhado e a origem chama-se vetor recíproco r. O módulo de r é r = 1/d hkl = (2senθ)/λ = (ha + kb + lc ), onde a, b, c são os três vetores que definem a rede recíproca e são definidos por: a = b c/v ; b = c a/v ; c = a b/v ; V = a (b c). Também valem as relações: a = (b c )/V ; b = (c a )/V ; c = (a b )/V ; V = a (b c ), onde a, b, c são os parâmetros de cela no espaço direto e V é o volume da cela unitária. É possível mostrar que V = 1/V. Na tabela 2.2 apresenta-se as relações entre os parâmetros de cela no espaço direto e no espaço recíproco, para
24 2.4 Fator de Espalhamento Atômico 12 uma cela unitária geral. 2 θ Feixe espalhado 1/d RX Plano (hkl) θ Cristal Feixe transmitido O Origem da rede recíproca R=1/λ Figura 2.1: Esfera de Ewald. Tabela 2.2: Relações entre os parâmetros de cela no espaço direto e no espaço recíproco a = bcsenα V b = acsenβ V c = absenγ V ; a = b c senα V ; b = a c senβ V ; c = a b senγ V cosα = cosβ = cosγ = cosβ cos γ cosα senβsenγ cosα cos γ cosβ senαsenγ cosα cos β cosγ senαsenβ ; cosα = cosβ cosγ cosα senβ senγ ; cosβ = cosα cosγ cosβ senα senγ ; cosγ = cosα cosβ cosγ senα senβ V = 1 = abc 1 cos V 2 α cos 2 β cos 2 γ + 2cosα cos β cos γ V = 1 = V a b c 1 cos 2 α cos 2 β cos 2 γ + 2cosα cosβ cosγ 1 d hkl = h 2 a 2 +k 2 b 2 +l 2 c 2 +2hka b cosγ +2hla c cosβ +2klb c cosα 2.4 Fator de Espalhamento Atômico O poder de espalhamento de raios X de um átomo diminui com o aumento do ângulo de espalhamento e é maior para átomos mais pesados. Um gráfico do fator de espalhamento f em função de sen(θ)/λ, mostra este comportamento,
25 2.4 Fator de Espalhamento Atômico 13 Figura 2.2. Para o ângulo de espalhamento zero o valor de f é normalizado ao número de elétrons, que coincide com o número atômico para átomos de carga nula. f Z j f j, θ (a) f j, θ T j, θ (b) (senθ ) / λ Figura 2.2: Fator de espalhamento atômico: (a) átomo estacionário. (b) Correção por vibração térmica. As curvas de espalhamento atômico normalizadas são ajustadas à uma equação de nove parâmetros (equação 2.3) [12]. Conhecendo-se os nove coeficientes e o comprimento de onda, pode-se calcular o fator de espalhamento de cada átomo para qualquer ângulo de espalhamento. f 0 (sin θ/λ) = 4 a i exp[ b i (sin θ/λ) 2 ] + c (2.3) i=0 Estes fatores de espalhamento atômico são funções matemáticas conhecidas e incorporadas nos programas de cristalografia utilizados para o cálculo estrutural. Entretanto, o fator de espalhamento contém contribuições adicionais de efeitos de dispersão anômala (essencialmente absorção de ressonância) que ficam significativos na região da borda de absorção de raios X. Em casos reais haverá um enfraquecimento adicional do poder de espalhamento dos átomos pelo denominado fator de temperatura B, ou fator de Debye-Waller [12]. Este fator exponencial também depende do ângulo de espalhamento θ, Figura 2.2b.
26 2.5 Fatores de Estrutura e o Problema da Fase 14 f j (T ) = f j exp[ B j (sin θ/λ) 2 ] (2.4) O fator B j é dependente da temperatura e pode ser relacionado ao deslocamento irregular de um átomo vibrando, dado por B j = 8π 2 u j 2, onde u j 2 é a amplitude quadrática média de vibração do j-ésimo átomo a partir de sua posição de equilíbrio, na direção normal ao plano de reflexão. Como u j é determinado em Å, a unidade para B j deve ser Å Fatores de Estrutura e o Problema da Fase Em uma experiência de difração obtém-se as intensidades e a posição das reflexões, representada por quatro ângulos medidos com difratômetro de 4 círculos (tipo CAD4). Esta intensidade é proporcional ao quadrado da amplitude do fator de estrutura, F(hkl). Normalmente existem algumas dezenas de milhares de reflexões para cada cristal. O fator de estrutura F(hkl) é um número complexo [12], F(hkl) = N f j exp[2πi(hx j + ky j + lz j )] (2.5) j=1 onde f j é o fator de espalhamento atômico para o j-ésimo átomo da cela unitária, que tem coordenadas fracionárias x j, y j, z j. Para h,k,l = 0, F(000) será normalizado ao número de elétrons na cela unitária. Logo F(hkl) é dado em número de elétrons. Em estudos de cristalografia lida-se com o problema inverso, são conhecidos os fatores de estrutura e deseja-se conhecer a estrutura. A equação 2.5 pode ser representada por uma notação mais compacta F (h) = j f j exp[2πi(h r)] (2.6)
27 2.5 Fatores de Estrutura e o Problema da Fase 15 onde h r=hx+ky+lz. O fator de estrutura pode ser considerado como a soma de ondas espalhadas por todos os átomos da cela unitária. Sendo ρ, a densidade eletrônica, expresso como o número de elétrons por unidade de volume, então o número de elétrons num volume elementar dv é dado por ρ(xyz)dv. A forma exponencial da onda espalhada por este elemento de volume é: ρ(xyz) exp[2πi(hx + ky + lz)]dv (2.7) A integração na cela unitária conduz a F(hkl) = V ρ(xyz) exp[2πi(hx + ky + lz)]dv (2.8) Ou a forma mais compacta F (h) = V ρ(r) exp[2πi(h r)]dv (2.9) As equações 2.8 e 2.9 representam a transformada de Fourier da densidade eletrônica da cela unitária, que é o fator de estrutura. Representados como F (h) = T [ρ(r)] (2.10) resulta A transformada inversa, representada por T 1 [F (h)] = T 1 T [ρ(r)] = ρ(r), ρ(r) = F (h) exp[ 2πi(h r)]dv V (2.11) Observa-se que há uma correspondência entre as equações 2.9 e 2.11: a integração foi no espaço direto V e no espaço recíproco V, havendo troca de
28 2.5 Fatores de Estrutura e o Problema da Fase 16 sinal na parte exponencial. A equação 2.11 deve ser modificada para atender ao fato de que, no espalhamento de raios X, o padrão de difração é discreto devido à periodicidade do cristal. Desta maneira, a integral é substituída pelo somatório ρ(xyz) = 1 V F(hkl) exp[ 2πi(hx + ky + lz)] (2.12) hkl Como F(hkl) é expresso em números de elétrons e a soma é dividida pelo volume da cela, percebe-se que o resultado da transformação ρ(xyz) deve ser uma densidade eletrônica, expressa em número de elétrons por unidade de volume [e/å 3 ]. Nota-se, entretanto, o sinal de menos que precede o expoente, está transformando um espaço inverso em um espaço real ou direto. É uma característica geral da transformada de Fourier transformar um espaço em seu espaço inverso. Assim, o padrão de difração (uma imagem do espaço recíproco) transformou-se no espaço real de densidade eletrônica. Este formato evidencia as amplitudes e fases dos fatores de estrutura como símbolos separados, a partir dos quais percebe-se o problema, as amplitudes F(hkl) são medidas no difratômetro, mas as fases φ(hkl) são desconhecidas, de tal forma que não é possível efetuar uma síntese de Fourier diretamente para obter ρ(xyz). A equação 2.12 também pode ser representada por ρ(r) = 1 V F (h) exp[ 2πi(h r)] (2.13) h Como a equação 2.12 é essencialmente somada em toda a estrutura, é também denominada uma síntese de Fourier ou soma de Fourier. A equação 2.12 revela um detalhe muito importante. Para executar a transformada de Fourier, precisase dos fatores de estrutura F(hkl) mas são conhecidos apenas seus módulos F(hkl). Em termos físicos, isto significa que apenas o valor absoluto do vetor
29 2.6 Densidade Eletrônica 17 complexo F(hkl) é conhecido, mas não sua fase φ(hkl). Esta limitação é denominada O Problema da Fase [13]. Por muitos anos a opinião era que a solução direta de estruturas cristalinas por raios X, em geral, seria impossível, embora as amplitudes das ondas difratadas pudessem ser determinadas experimentalmente, mas suas fases não [14]. 2.6 Densidade Eletrônica Como os raios X são espalhados por elétrons ligados aos átomos em um cristal, os átomos com grandes números atômicos possuem maior número de elétrons e espalham melhor a radiação incidente. Esta concentração de elétrons e sua distribuição ao redor do átomo é chamada de densidade eletrônica e é medida em elétrons por Å 3. Sendo esta em geral uma função da posição, especifica-se a densidade eletrônica no ponto x, y e z como ρ(xyz). A função densidade eletrônica, equação 2.12, é expressa como uma série de Fourier tridimensional. O somatório, na prática, estende-se por todo um conjunto finito de valores h, k, l, que são limitados pela natureza do cristal e pelo arranjo experimental. A forma exponencial da equação 2.12 implica ser a densidade eletrônica uma função complexa, enquanto que, de fato, ela é real ao longo da cela unitária. Como o fator de estrutura é um número complexo, F(hkl) = F(hkl) exp[iφ(hkl)], ou então, F(hkl) = A(hkl) + ib(hkl) e F(hkl) = A(hkl) ib(hkl), a equação 2.12 pode ser representada em formas alternativas como ρ(xyz) = 1 V F(hkl) exp[iφ(hkl)]exp[ 2πi(hx + ky + lz)] (2.14)
30 2.6 Densidade Eletrônica 18 ou, ρ(xyz) = 1 V [A(hkl)cos2π(hx+ky+lz)+iB(hkl)sen2π(hx+ky+lz)] (2.15) Considerando a lei de Friedel que para estruturas centro-simétricas, F(hkl) 2 = F(hkl) 2, e utilizando o fato de que os termos contendo seno se cancelam para pares F(hkl) e F(hkl), resulta [15] ρ(xyz) = 1 V F(hkl) cos[2π(hx + ky + lz) φ(hkl)] (2.16) Para uma soma feita em metade da esfera do espaço recíproco, um dos índices varia de 0 a, e a equação 2.16 fica ρ(xyz) = 2 V h=0,k=,l F(hkl) cos[2π(hx + ky + lz) φ(hkl)] (2.17) Nesta, e em equações similares, o termo F(000), que representa o número total de elétrons na cela unitária, é multiplicado por 1/V e, na prática, o termo F(000)/V é adicionado separadamente ao resultado do somatório. Não importa qual dos índices h, k ou l tenha zero como seu limite inferior no somatório. A equação 2.17 mostra claramente a dependência de ρ(xyz) da fase φ(hkl). Um modelo unidimensional pode ser proposto se, na equação 2.14, considerarse y = 0, z = 0, k = 0 e l = 0, o volume da cela unitária seria reduzido à dimensão a. A contribuição para o h-ésimo fator de estrutura é dado por ρ(x) = 1 F (h) exp[iφ(h)]exp[ 2πihx] (2.18) a h A função densidade eletrônica unidimensional mostrada na Figura 2.3, foi
31 2.6 Densidade Eletrônica 19 gerada com o programa em Fortran desenvolvido para o cálculo de densidade eletrônica unidimensional, apêndice A. Tendo acesso aos arquivos contendo os fatores de estrutura observados e as coordenadas finais da estrutura do composto C 18 H 14 Br 1 N 5 O 1 [16], utilizou-se o programa SHELXL-97 [17] para gerar uma lista contendo os índices h, k, l, os fatores de estrutura observados Fo, os fatores de estrutura calculados Fc e as fases φ em graus. Para o modelo unidimensional, somente os Fc correspondentes aos índices h, 0, 0 foram utilizados para o cálculo da densidade eletrônica, conforme mostrado na Tabela 2.3. Tabela 2.3: Valores de hkl, Fc e φ para o composto C 18 H 14 Br 1 N 5 O 1 h k l Fc φ Observam-se dois picos mal definidos nas coordenadas fracionárias aproximadas x 1 = 0,45 e x 2 = 0,55. Estas são as coordenadas do Br 1 e Br 2, relacionadas por um centro de inversão. A Figura 2.4 é uma projeção bidimensional com l = 0, na equção 2.17 da densidade eletrônica para a estrutura do composto C 18 H 14 Br 1 N 5 O 1 [16]. Para este propósito foi desenvolvido um programa para o cálculo de densidade eletrônica bidimensional, apêndice B. Para o modelo bidimensional, foram utilizados os fatores de estrutura calculados Fc com índices h, k, 0. Este gráfico mostra em
32 2.6 Densidade Eletrônica Densidade eletrônica (e/a) ,0 0,2 0,4 0,6 0,8 1,0 Coordenadas fracionárias x Figura 2.3: Projeção unidimensional da densidade eletrônica para C 18 H 14 Br 1 N 5 - O 1. As duas linhas verticais mostram as coordenadas do Br 1 e Br 2, relacionadas por um centro de inversão D en s ida de E le trôn ic a (e/a o2 ) ,00 0,2 0,4 0,6 Coordenada fracionária x 0,8 1,0 0,0 0,4 0,2 0,8 1,0 0,6 Coordenada fracionária y Figura 2.4: Projeção bidimensional da densidade eletrônica para o composto C 18 - H 14 Br 1 N 5 O 1. destaque dois grandes picos de densidade, ocasionados pelos dois átomos de bromo na cela unitária, relacionados pelo centro de inversão. Neste gráfico, as coordenadas dos átomos de bromo são:
33 2.7 Teorema da Convolução 21 Br 1 x 1 = 0,45; y 1 = 0,78 Br 2 x 2 = 0,55; y 2 = 0, Teorema da Convolução A convolução de duas funções f(r) e g(r), pode ser definida pela integral C(u) = f(r) g(r) = V f(r)g(u r)dv (2.19) onde V é o volume no espaço de r. Observa-se que o integrando é uma função de u e de r, ao passo que a integral é função apenas de u. A relação entre f(r) e g(r) é simétrica ao formar uma convolução [18], o que pode ser mostrado ao substituir, na equação 2.19, r por R = u - r e depois R por r, resultando f(r) g(r) = g(r) f(r) (2.20) Uma propriedade importante de interesse na cristalografia é que a transformada de Fourier da convolução de duas funções f(r) e g(r) é igual ao produto das transformadas de Fourier das duas funções, teorema da convolução, T [f(r) g(r)] = T [f(r)]t [g(r)] (2.21) De maneira similar, a transformada de Fourier do produto de duas funções é igual à convolução das transformadas de Fourier destas funções T [f(r).g(r)] = T [f(r)] T [g(r)] (2.22)
34 2.8 A Função de Patterson A Função de Patterson É interessante notar que a conexão entre teoria de Fourier e difração de raios X, registrada primeiramente em 1915, não era até o início da década de 30 usada na prática. Diante do desenvolvimento computacional, o cálculo de projeções de Fourier envolvendo considerável tempo e esforço, adicionando a isto o problema da fase, foi encarado com mais facilidade. Em 1934, Patterson informava uma nova série de Fourier que poderia ser calculada diretamente de dados de intensidades experimentais [19], porém, devido à informação da fase não ser usada na série de Patterson, o resultado não poderia ser interpretado como um conjunto de posições atômicas, mas algo como uma coleção de vetores inter-atômicos, todos tendo uma origem comum. Na análise de estruturas cristalinas, sempre é possível preparar uma síntese de Patterson. Isto é, uma síntese dos dados originais, obtidos do experimento de difração [20]. Se f(r) for a densidade eletrônica ρ(r) e g(r) a densidade eletrônica invertida na origem ρ(-r), então a equação 2.19 fica P (u) = ρ(r) ρ(-r) = V ρ(r)ρ(u+r)dv (2.23) onde P(u) é a função de Patterson. De forma similar, a função de Patterson pode ser escrita como a autoconvolução de ρ(r): P (u) = ρ(r) ρ(r) = V ρ(r)ρ(u-r)dv (2.24) ou, de outra forma, P (uvw) = ρ(xyz)ρ(u x, v y, w z)dxdydz (2.25) V
35 2.8 A Função de Patterson 23 Sabendo que o fator de estrutura F(h) é um número complexo com a forma A(h)+iB(h) e seu complexo conjugado F (h) = F(-h) é A(h)-iB(h), da equação 2.9, tem-se F (h) = F (-h) = V ρ(-r) exp[2πi(h r)]dv (2.26) F (h) = T [ρ(r)] (2.27) e F (h) = T [ρ(-r)] (2.28) T [P (u)] = T [ρ(r)]t [ρ(-r)] = F (h)f ( h) = [A(h) + ib(h)][a(h) ib(h)] (2.29) T [P (u)] = F (h) 2 (2.30) T 1 T [P (u)] = T 1 [ F (h) 2 ] = F (h) 2 exp[ 2πi(h u)]dv V (2.31) Como tem sido apontado, o problema da fase é o problema central em análise cristalina. Isto se dá pela impossibilidade de calcular a transformada de Fourier para obter ρ sem as fases dos F s. Para evitar esta dificuldade, os F s podem ser substituídos por FF, para qual a transformada de Fourier é possível. O resultado é a função de Patterson
36 2.9 Interpretação da Função de Patterson 24 P (u) = F (h)f (h)exp[ 2πi(h u)]dv (2.32) V onde u é um vetor no espaço direto com componentes (uvw), F(h) é o fator de estrutura, F (h) é o complexo conjugado do fator de estrutura, V é o volume da cela unitária no espaço recíproco e h u = hu + kv + lw [21]. Na equação 2.32, tem-se um produto de um número complexo F(h) pelo seu complexo conjugado F (h), o que resultará em um número real, F (h) 2, com os termos contendo seno se cancelando. Relembrando que: F (h) F (h) = F (h) F (-h) = F (h) 2 = F (hkl) 2 (2.33) Então a integral estendida ao volume da cela no espaço recíproco corresponde ao inverso do volume da cela no espaço real (V = 1/V). Logo P (uvw) = 1 V F (hkl) 2 cos[2π(hu + kv + lw)] (2.34) hkl 2.9 Interpretação da Função de Patterson Podem ser derivadas interpretações geométricas úteis da propriedade de ser P(u) o quadrado da convolução de ρ(r), as quais permitem a solução do problema da fase em estruturas que possuem algumas propriedades especiais. Supondo que a estrutura seja representada por átomos puntuais com peso dado pelos seus números atômicos, a integral na equação 2.24 então se transforma em uma soma P (u) átomos ρ(r)ρ(r u) (2.35)
37 2.9 Interpretação da Função de Patterson 25 P(u) será diferente de zero somente se u for o vetor diferença de algum par de vetores posição de átomos da estrutura, apenas sob esta condição é possível um átomo puntual da estrutura coincidir com um átomo do modelo original. O peso de P(u) é então proporcional ao produto dos pesos dos átomos contribuintes. Se u não satisfaz esta condição, tem-se P(u) = 0. Claro que é possível mais de um par de vetores de posição coincidirem para um vetor u especial, neste caso, u terá uma multiplicidade maior que um, e P(u) terá um peso proporcional à soma dos pesos do produto dos átomos contribuintes. Da interpretação do quadrado da convolução, pode-se dizer que a função de Patterson representa todos os vetores diferença de uma determinada estrutura com um peso proporcional à freqüência de ocorrência e ao peso dos átomos contribuintes. Para uma estrutura real, que possui em vez de pontos atômicos, densidade contínua de elétrons com máximo nos centros atômicos, não há nenhuma diferença fundamental. A função de Patterson de uma densidade eletrônica real tem em princípio as mesmas propriedades que o modelo do átomo puntual. O problema de determinação de estrutura pode ser expresso como o de encontrar a distribuição de todos os vetores diferença entre cada par de posições atômicas, esta em geral não é uma tarefa fácil. Haverá uma boa chance para uma solução se a estrutura possuir uma geometria muito simples ou contiver um ou dois átomos com um número atômico significativamente maior que a maioria dos outros. Comparando a equação 2.34 com a equação 2.16, observa-se que ela é uma série de Fourier com fase zero e F 2 como coeficientes. Na prática, pode ser manipulada como a correspondente equação da densidade eletrônica, com u, v, w substituindo x, y, z, mas deve ser lembrado que ambas funções exploram o mesmo campo, a cela unitária. Agora o vetor é especificado por três coorde-
38 2.9 Interpretação da Função de Patterson 26 nadas, u, v, e w, e P(uvw) é a função de Patterson para estas coordenadas. As posições dos picos na função P(uvw) podem ser esboçadas em três dimensões colocando cada átomo da cela unitária de uma estrutura em torno da origem do espaço de Patterson, na orientação paralela, e traçando as posições de todos os outros átomos sobre a cela unitária de Patterson. Exemplos destes processos são ilustrados graficamente na Figura 2.5 onde, por simplicidade, o pico da origem não é mostrado na Figura 2.5d. Na Figura 2.5a todos os átomos e suas translações equivalentes produzem picos de vetores que são pontos de uma rede idêntica à rede cristalina, por exemplo, o átomo 1 em x, y, z e sua translação equivalente, 1, em x, 1 + y, z sobre a extremidade do vetor em 0, 1, 0 no mapa de Patterson. Picos desta natureza se acumulam nos cantos da cela unitária de Patterson do mesmo modo como os picos da origem, P(000). Da equação 2.34 pode-se derivar a altura do pico na origem: P (000) = 2 V F 0 (hkl) 2 (2.36) h=0 k= l= Em geral, a equação 2.36 é equivalente a uma superposição na origem de todos os N produtos ρ(x j, y j, z j ) ρ(x j, y j, z j ), onde N é o número de átomos na cela unitária. Sendo (x j, y j, z j ) proporcional ao número atômico Z j do j-ésimo átomo, tem-se P (000) = N Zj 2 (2.37) j=1 Um único vetor inter-atômico entre dois átomos j e k, Figura 2.5b terá um pico de Patterson de altura proporcional à Z j Z k. Conseqüentemente, a altura H(j, k) deste pico será dada por
39 2.9 Interpretação da Função de Patterson 27 y v O 1 1' 1 O 1 (x, y, z) (x, 1 + y, z) (a) x u 1 1 (b) (c) (d) Figura 2.5: Átomos com simetria relacionadas e com simetria independentes na função de Patterson. H(j, K) P (000)Z jz k N j=1 (2.38) onde P(000) é calculado com a equação Numa estrutura com N átomos por cela unitária, cada átomo forma um vetor com os restantes N-1 átomos. Então, são N(N-1) picos fora da origem. Da equação 2.34, substituindo u, v, w, por -u, -v, -w, respectivamente, torna P(uvw) inalterado, que é uma manifestação do centro de inversão da função de Patterson. A cela unitária de Patterson é do mesmo tamanho e forma que a cela unitária
40 2.10 Método do Átomo Pesado 28 cristalina, mas tendo que acomodar N 2 e não N picos e é, então muito mais preenchida. Assim, picos no espaço de Patterson tendem a se sobrepor quando existem muitos átomos na cela unitária. Esta característica introduz dificuldades no processo de encontrar a função em termos de corretas distribuições de átomos no cristal Método do Átomo Pesado Para o composto C 18 H 14 Br 1 N 5 O 1 [16], que possui um átomo de número atômico elevado, bromo, a estratégia de solução desta estrutura depende em detalhes da simetria do grupo espacial, contudo, algumas observações gerais podem ser feitas. Se o grupo espacial contiver um centro de inversão, a função de Patterson não só mostrará os vetores diferença dentro de uma molécula (intramolecular) mas também entre cada par de átomos em moléculas diferentes (intermolecular). Os pesos destes vetores estão mostrados na Tabela 2.4. Tabela 2.4: Vetores inter-atômicos para o composto C 18 H 14 Br 1 N 5 O 1 Vetor Pesos H-H 1 x 1 = 1 H-C 1 x 6 = 6 H-Br 1 x 35 = 35 H-N 1 x 7 = 7 H-O 1 x 8 = 8 C-C 6 x 6 = 36 C-Br 6 x 35 = 210 C-N 6 x 7 = 42 C-O 6 x 8 = 48 Br-Br 35 x 35 = 1225 Br-N 35 x 7 = 245 Br-O 35 x 8 = 280 N-O 7 x 8 = 56 O vetor Br-Br terá o pico mais alto na função de Patterson, com exceção
41 2.10 Método do Átomo Pesado 29 do pico na origem. Este vetor, porém, combina o vetor posição r(br) com seu centro-simétrico -r(br), de tal forma que u(br-br) = r(br) - [-r(br)] = 2r(Br). Entretanto, é provável que o vetor que possui o pico mais alto seja duas vezes o vetor posição do átomo de bromo. Portanto a localização deste átomo na cela unitária é determinada. Esta derivação foi possível porque apenas um átomo pesado estava presente na estrutura, resultando em um único pico significativo da função de Patterson. Com a posição do átomo pesado conhecida, é possível, em casos favoráveis, fazer a completa determinação da estrutura. Isto é feito usando o princípio da diferença da densidade eletrônica calculada (Fourier diferença). É costume, em cristalografia, denotar o cálculo numérico da transformada de Fourier do espaço recíproco para o espaço direto como uma síntese. Assim, o termo síntese de Patterson freqüentemente é uma expressão usada. Supondo alguma parte da estrutura, denotada por ρ c (r), já conhecida deste modelo parcial, ou da posição de um átomo pesado, a transformada de Fourier pode ser calculada (conforme as equações 2.6 e 2.10) e obtém-se [21] F c (h) = T [ρ c (r)] (2.39) onde o subscrito c indica que estas quantidades são calculadas a partir de um dado modelo. Escrito como uma soma, F c (h) é dado por N c F c (h) = f j exp[2πih r j ]exp[ T j ] (2.40) j=1 onde N c < N e T j é a expressão para o fator de temperatura isotrópico ou anisotrópico do modelo. O princípio de Fourier diferença está baseado na suposição de que se Nc não difere muito de N, a fase φ(f c ) é próxima de F(h), conforme se pode observar no diagrama de Argand, Figura 2.6.
42 2.10 Método do Átomo Pesado 30 F( h) φ FC φ C o Eixo real Figura 2.6: Diagrama de Argand com um átomo pesado e seis átomos leves. As fases de F c (h) calculadas com a equação 2.40 são atribuídas a F(h), os fatores de estruturas obtidos experimentalmente. Os dois conjuntos, F c (h) e F(h), devem ser colocados numa mesma escala usando o quociente h F c(h) = c (2.41) F (h) h Resultando em um fator c, denominado fator de escala. A quantidade F o, definida por F o (h) = cf (h) (2.42) é denominada amplitude observada de estrutura, sendo que ela é derivada diretamente de observações experimentais. Agora com F o (h) e F c (h) sendo introduzidos, pode-se expressar o cálculo da diferença de densidade eletrônica como ρ(r) = T 1 [F o (h) F c (h)] (2.43) Outra representação da equação 2.43, também conhecida por Fourier diferença, é dada por
43 2.10 Método do Átomo Pesado 31 ρ(r) = 1 V ( F o (h) F c (h) ) exp(iφ c ) exp[ 2πi(h r)] (2.44) h onde φ c = φ(f c ), a fase do modelo. Com φ[f o (h)] sendo aproximado por φ[f c (h)], da propriedade de transformadas de Fourier, segue que ρ(r) = T 1 [F o (h)] T 1 [F c (h)] (2.45) denotando por ρ o (r) a densidade eletrônica observada sendo esta dada pelos dados experimentais junto com as fases verdadeiras. Note que ρ o (r) não é igual à ρ(r), que jamais pode ser obtido diretamente (sendo que nem todos os F s podem ser medidos e os erros experimentais não podem ser completamente excluídos). Além disso, definindo ρ c (r) = T 1 [F c (h)] (2.46) E considerando a aproximação ρ o (r) T 1 [F o (h)] (2.47) Então tem-se ρ(r) ρ o (r) ρ c (r) (2.48) Que significa ter pela aplicação da equação 2.45, uma distribuição de densidade eletrônica para a qual os átomos conhecidos são removidos e o resíduo restante deverá mostrar a parte que falta da estrutura.
44 2.11 Seções de Harker 32 Antes de tentar identificar a porção do átomo pesado da estrutura por interpretação da função de Patterson, deve-se considerar se a parte da estrutura do átomo pesado é significativa o bastante para um sucesso na solução. Para isto, usa-se a regra do quociente ; isto é: Q = p Z2 p l Z2 l (2.49) onde os Z s são os números atômicos dos átomos na cela unitária e o somatório em p no numerador engloba todos os átomos já conhecidos, enquanto a soma em l no denominador é feita sobre todos os átomos não conhecidos. Se Q>1 então a aplicação do método do átomo pesado será provavelmente um sucesso. Porém, com muitos dados difratométricos precisos, o critério da equação 2.49 pode ser ignorado. Uma boa chance de obter sucesso com o método do átomo pesado, será quando a soma dos quadrados dos números atômicos dos átomos pesados não for significativamente menor que dos átomos leves. Um valor para Q igual a 0,5 ainda teria uma razoável chance de sucesso. A estrutura do composto C 18 H 14 Br 1 N 5 O 1 [16] é um bom exemplo para testar esta regra. Com o átomo de bromo sendo um átomo pesado, tem-se um quociente: Q = = = , 3 (2.50) Como mencionado, este valor é suficiente para que o método do átomo pesado possa ser aplicado Seções de Harker Primeiramente apontado por Harker [22] em 1936, que a simetria do grupo
45 2.11 Seções de Harker 33 espacial resulta em seções especiais de uma síntese de Patterson que pode ser interpretada como projeções da estrutura sobre um plano ou uma linha. Estas seções denominadas planos ou linhas de Harker, ou geralmente seções de Harker, são muito usadas para interpretação da função de Patterson. Por exemplo, para o grupo espacial P 2 1 /c, a operação de simetria representando o eixo de rotação é -x, y, 1 2 -z. Cada átomo possuindo o vetor r = (xyz) tem seu equivalente em r = (-x, y, z). Sendo que a função de Patterson contém os vetores diferença entre cada par de átomos, u(r) = r - r = (2x, - 1 2, 2z ) = (u, - 1 2, w). Este resultado pode ser interpretado como uma projeção da estrutura no plano y = 1 2. Neste plano de Harker, um pico em (u, 1 2, w) resulta nas coordenadas atômicas x = u/2 e z = (w + 1 )/2, sendo isto verdadeiro para cada átomo, em 2 princípio pode ser obtida uma completa projeção bidimensional da estrutura. Uma outra seção de Harker para o grupo espacial P 2 1 /c é uma linha de Harker causada pelo elemento de simetria, espelho com deslizamento. O vetor diferença de r = (x, y, z) e r = (x, y, z) será u(r) = (0, 2y - 1 2, ) = (0, 2y + 1 2, 1 2 ). Isto pode ser interpretado como uma projeção da estrutura na linha (0, v, 1 ). Geralmente, a projeção de uma estrutura completa 2 em uma única linha não é muito útil mas em combinação com um plano de Harker, poderá dar informações úteis. Se as coordenadas x e z, da posição de um átomo pesado, foi determinada de um plano de Harker, pode ser possível obter a terceira coordenada da linha de Harker. Embora um plano de Harker possa conter uma projeção da estrutura completa, e informações sobre a terceira dimensão possam ser derivadas da linha de Harker, na prática isto é difícil, porque picos de Harker podem ser superpostos por outros vetores que correspondem aos vetores entre átomos que não estão simetricamente relacionados. Contudo, seções de Harker devem sempre
46 2.12 Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O 1 34 ser inspecionadas com muito cuidado, apesar de algumas ambigüidades, sua interpretação é freqüentemente possível se a geometria da estrutura for simples (especialmente para moléculas planas) ou se a posição de um único átomo pesado tiver sido determinada. Pode ser generalizado, do exemplo do grupo espacial P 2 1 /c, que elementos de simetria derivados de eixos de rotação resultam em planos de Harker, enquanto que elementos de simetria derivados de espelhos planos causam linhas de Harker. Se, por exemplo, mais de um elemento de simetria rotacional está presente, temos mais de um plano de Harker e a informação derivada do plano de Harker pode ser completada e confirmada por aquelas dos outros. Então, em grupos espaciais de alta simetria, a informação de todos os planos e linhas de Harker podem permitir a interpretação de uma parte significante da estrutura. Seções de Harker são particularmente usadas em cristalografia de proteínas, onde é necessária para determinação da fase de alguns átomos pesados derivados de uma proteína. Se o grupo espacial for centro-simétrico, cada vetor r = (x, y, z) possui seu equivalente em r = (-x, -y, -z) e obtém-se um vetor de Patterson u(r) para cada vetor atômico r, u(r) = (2x, 2y, 2z). Segue que o vetor 2r para cada vetor r está presente na síntese de Patterson Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O 1 Da mesma forma que foi feito para o cálculo da densidade eletrônica unidimensional e bidimensional, obteve-se inicialmente a lista dos fatores de estrutura observados Fo. Foi desenvolvido um programa, apêndice C, para o cálculo do mapa de Patterson em projeção bidimensional o qual utiliza-se da equação 2.34,
47 2.12 Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O 1 35 com l = 0, resultando a Figura P (u v) 500 0,0 0 0,1 0,2 0,3 0,4 0,5 Coordenada u 0,6 0,7 0,8 0,9 0,0 0,2 0,8 0,6 0,4 Coordenada v 1,0 Figura 2.7: Gráfico da função de Patterson bidimensional, l = 0. Uma projeção plana do mapa de Patterson mostrada na Figura 2.8, permite obter as coordenadas u e v para o pico Br-Br. 1,0 Coordenada v 0,8 0,6 0, ,2 0,0 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 Coordenada u Figura 2.8: Projeção plana do mapa de Patterson. Estas coordenadas são:
48 2.12 Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O 1 36 u = 0,908; v = 0,574; Através destas coordenadas obtêm-se para a cela real: x = u/2; y = v/2; x = 0,454; y = 0,287 y = y + 0,5 = 0,787; Conhecidas as coordenadas iniciais do bromo, a aplicação de sucessivos mapas de Fourier diferença forneceu as coordenadas posicionais dos demais átomos da estrutura. Os hidrogênios foram colocados geometricamente. Após o refinamento feito por mínimos quadrados obteve-se as coordenadas finais de todos os átomos da estrutura, Tabela 2.6, em concordância com os valores publicados. A Tabela 2.5, mostra um resumo dos dados cristalográficos para este composto e a Figura 2.9 mostra o desenho ORTEP da estrutura obtida com o programa WingX, em concordância com os dados publicados. O exemplo citado ilustra a técnica de Patterson para a obtenção das coordenadas iniciais dos átomos de enxofre para as três estruturas propostas neste trabalho. Tabela 2.5: Dados cristalográficos do composto C 18 H 14 N 5 O 1 Br 1 Sistema cristalino Triclínico Grupo espacial P 1 a 9,274 (2) Å b 9,488 (2) Å c 10,034 (2) Å V 834,5 (5) Å 3 α 75,44 (2) β 78,77 (2) γ 82,07 (2) Z 2 F(000) 399,9 Peso molecular 396,20
49 2.12 Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O 1 37 Tabela 2.6: Parâmetros posicionais e de vibração térmica isotrópica do composto C 18 H 14 N 5 O 1 Br 1 Átomo x y z U(eq) Br 0,4541(1) 0,7870(0) 0,4875(0) 0,0657(3) N(1) 0,8136(3) 0,4014(3) 0,1331(3) 0,0392(6) C(2) 0,9535(3) 0,3318(3) 0,1152(3) 0,0329(6) N(3) 1,0020(3) 0,2682(3) 0,0067(2) 0,0331(5) C(4) 0,9157(3) 0,2623(3) -0,0847(3) 0,0336(6) O(5) 0,7817(2) 0,3060(3) -0,0829(3) 0,0512(6) N(6) 1,0376(3) 0,3348(3) 0,2073(3) 0,0372(6) N(7) 1,1774(3) 0,2585(3) 0,1806(2) 0,0340(5) C(8) 1,2956(4) 0,3328(4) 0,1593(4) 0,0476(8) C(9) 1,4337(4) 0,2629(5) 0,1370(5) 0,068(1) C(10) 1,4516(4) 0,1168(5) 0,1365(5) 0,066(1) C(11) 1,3291(4) 0,0430(4) 0,1611(4) 0,0562(9) C(12) 1,1912(4) 0,1151(3) 0,1840(3) 0,0427(7) C(13) 0,7421(3) 0,4867(3) 0,2238(3) 0,0366(6) N(14) 0,6080(3) 0,5430(3) 0,1948(3) 0,0460(7) C(15) 0,5269(4) 0,6282(4) 0,2736(4) 0,0499(8) C(16) 0,5744(4) 0,6609(4) 0,3818(4) 0,0456(7) C(17) 0,7123(4) 0,6006(4) 0,4143(4) 0,0463(7) C(18) 0,7979(3) 0,5128(3) 0,3338(3) 0,0418(7) C(19) 0,9947(3) 0,1944(3) -0,2012(3) 0,0327(6) C(20) 1,1180(3) 0,0937(3) -0,1860(3) 0,0391(7) C(21) 1,1875(4) 0,0302(4) -0,2954(4) 0,0489(8) C(22) 1,1369(4) 0,0704(4) -0,4221(4) 0,0529(8) C(23) 1,0154(4) 0,1706(4) -0,4383(4) 0,0506(8) C(24) 0,9433(3) 0,2311(3) -0,3285(3) 0,0404(7)
50 2.12 Solução pelo Método de Patterson do Composto C 18 H 14 Br 1 N 5 O 1 38 Figura 2.9: Representação ORTEP do composto C 18 H 14 N 5 O 1 Br 1.
51 Capítulo 3 Estrutura Cristalina das Tiouréias 3.1 Introdução Neste capítulo é discutida a solução das estruturas cristalinas dos compostos N-benzoil, N -tercbutil-tiouréia (T1), N-benzoil, N -(4-metilfenil)-tiouréia (T2) e N-benzoil, N -(2-hidroxietil)-tiouréia (T3). O interesse maior é obter informações estruturais e conformacionais do grupamento tiouréia presente em cada um dos compostos. 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas Após a obtenção dos cristais pelos pesquisadores do Laboratório de Bioatividade Molecular do IQ-UFBA para os três compostos estudados, os mesmos foram colocados no difratômetro automático CAD4 da Enraf-Nonius [23], para a busca de dados em temperatura ambiente. A matriz de orientação e parâmetros 39
52 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 40 de cela unitária foram determinados por mínimos quadrados, a partir da medida das intensidades e posições de 25 reflexões. Estas medidas foram feitas usando a radiação Kα do Cobre, de comprimento de onda 1,54180 Å, monocromatizada por cristal de grafite. O intervalo de variação de θ foi de 2 a 67,2, com varredura do tipo ω - 2θ, no modo zig-zag. Durante a coleta de dados foram usadas três reflexões padrão para controle de intensidade, as quais eram medidas a cada 60 minutos, não sendo observadas alterações significativas nas intensidades destas reflexões. Os dados de intensidade foram reduzidos a fatores de estrutura, após terem sido corrigidos pelos fatores de Lorentz e polarização. Para proceder às correções por absorção, foram feitas também, para todos os compostos, coletas de dados específicas PSI. Para este propósito, foi usado o programa de correção semiempírica conhecido por PSI-SCAN [24]. Para a solução das estruturas utilizou-se do método de Patterson através do programa SHELXS-86 [25] e sucessivas Fourier diferença. Após a localização dos átomos, excluídos os hidrogênios, as estruturas foram refinadas usando o programa SHELXL-97 [17], pelo o método dos mínimos quadrados [26], onde a função minimizada foi M = m i=1 ϖ i[ F (h) 2 obs F (h) 2 cal ]2 sendo ϖ i o fator peso. Foi avaliado o fator de discordância R1, que pode ser escrito da seguinte forma R1 = Fo F c Fo (3.1) E também o índice de discordância ponderado ωr2, dado por ωr2 = (ω Fo 2 F c 2 ) 2 (ω Fo 2 ) 2 (3.2) Os átomos foram mantidos com fatores de vibração isotrópico até o momento
53 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 41 em que não se observou nenhuma modificação para os fatores de discordância R1 e ωr2 após o refinamento, passando a partir daí ao refinamento anisotrópico. Os átomos de hidrogênio foram colocados assumindo a geometria dos carbonos a que estavam ligados, com parâmetros de vibração térmica isotrópicos igual a 1,2 vezes a do átomo ao qual está ligado, exceto para os grupos metil o qual foi de 1,5 vezes, e os hidrogênios ligados ao grupamento tiouréia foram obtidos por Fourier diferença. A Tabela 3.1 mostra as distâncias intramoleculares para os hidrogênios colocados geometricamente. O refinamento foi feito até o momento em que as alterações nos parâmetros tornaram-se menores que seus respectivos desvios padrão. Tabela 3.1: Distâncias (Å) intramoleculares dos hidrogênios colocados geometricamente C-H 0,9300 C-H 2 0,9700 C-H 3 0, N-benzoil, N -tercbutil-tiouréia (T1) Obteve-se um cristal incolor do composto, medindo 0,30 x 0,30 x 0,40 mm, o qual foi usado para coleta de dados. As reflexões (4, -2, -4), (2, -3, -2) e (1, -3, -3) foram usadas para controle de intensidade. A coleta de dados foi feita no sistema monoclínico com os índices h, k, l variando de -13 a 13; -1 a 6 e 0 a 23, respectivamente. Finalizou-se a coleta obtendo 2850 reflexões medidas, sendo 2284 independentes e 2138 consideradas observadas [I 2σ(I)]. O coeficiente de absorção obtido foi µ = 2,092 mm 1. O resumo dos dados cristalográficos para este composto é mostrado na Tabela 3.2 (Código interno IF-UFG: 043-RMT101).
54 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 42 Tabela 3.2: Dados Cristalográficos do composto T1 Sistema cristalino Monoclínico Grupo espacial P2 1 /c a 11,6226 (9) Å b 5,7852 (4) Å c 19,800 (7) Å V 1283,0 (5) Å 3 β 105,49 (1) Z 4 Peso molecular 236,30 Densidade calculada 1,22 Mg/m 3 F(000) 503,9 λ(cukα) 1,54180 Å Número de reflexões medidas 2850 Número de reflexões independentes 2284 Número de reflexões com I 2σ(I) 2138 R int 0,0218 Fatores de transmissão Tmin e Tmax 0,5175 e 0,6203 Obteve-se o valor de 0,968 para a distribuição estatística E(h) 2 1 para este composto, conduzindo a uma estrutura cêntrica. As extinções sistemáticas h0l: l = 2n+1 e 0k0: k = 2n+1 definiram o grupo espacial P2 1 /c [nr:14]. O mapa de Patterson, obtido com o programa SHELXS-86 [25], forneceu os seguintes 7 primeiros picos, listados na Tabela 3.3. Tabela 3.3: Picos de Patterson para o composto T1 u v w Pico Vetor Inter-atômico 1 0,0000 0,0000 0, ,00 2 0,0000 0,2048 0, ,97 3 0,7720 0,5000 0, ,06 4 0,6731 0,5000 0, ,57 5 0,2277 0,3162 0, ,20 6 0,8974 0,0000 0, ,75 7 0,0000 0,5000 0, ,31 O primeiro pico corresponde à superposição de todos os picos na origem.
55 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 43 Os picos de n 2 até 4 são planos e linhas de Harker. O pico n 5, que é um pico geral, poderia ser resultado de um vetor inter-atômico entre dois átomos de enxofre, de uma posição geral x, y, z e o correspondente gerado pela operação centro de inversão, ou seja, -x, -y, -z. Desta maneira, u = 2x, v = 2y, w = 2z, o que forneceria as coordenadas do enxofre S5: x = 0, = 0,1139; y = 0, = 0,1581 e z = 0, = 0,0883. Selecionando a unidade assimétrica 0 < x < 0,5; 0 < y < 0,5 e 0 < z < 0,5, bastaria fazer uma translação de 1/2 cela para a coordenada y (a simetria do grupo espacial P2 1 /c permite isto) resultando em x = 0,1139; y = 0,3419 e z = 0,0883 Outra possibilidade seria considerar o pico n 2 como uma linha de Harker, resultante do vetor inter-atômico entre um átomo de enxofre em uma posição geral x, y, z e o correspondente gerado pela operação de simetria espelho com deslizamento, ou seja, x, 1/2 - y, 1/2 + z. Com esta suposição: u = [x - (x)] = 0 v = [y - (1/2 - y)] = 2y - 1/2 w = [z - (1/2 + z)] = -1/2 A coordenada y do enxofre S5 será: y = 0,2048+1/2 2 = 0,3524 O Pico n 3 pode ser um plano de Harker, resultante do vetor inter-atômico entre um átomo de enxofre gerado pela operação centro de inversão, com coordenadas x, y, z e o seu correspondente gerado pela operação espelho com deslizamento x, 1/2 - y, 1/2 + z. As coordenadas inter-atômicas são: u = [x - (x)] = -2x; v = [y - (1/2 - y)] = -1/2;
56 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 44 w = [z - (1/2 + z)] = -2z - 1/2, que levam às coordenadas x e z do átomo de enxofre S5: x = 0, = -0,3860 z = (0,3215+1/2) 2 = -0,4108 Fazendo uma translação de 1/2 cela para as coordenadas x e z, resulta x = 0,1140; y = 0,3524; z = 0,0892, que são as coordenadas utilizadas para o início do refinamento. Os demais átomos foram obtidos por sucessivas Fourier diferença [21], sendo que no primeiro mapa encontrou-se 27 picos de densidade eletrônica, dos quais os 4 primeiros eram 2 átomos de nitrogênio, 1 átomo de oxigênio e 1 átomo de carbono. Os átomos foram mantidos com fatores de vibração isotrópico até R1 = 0,191 e passando ao refinamento anisotrópico obteve-se R1 = 0,092. Os hidrogênios ligados aos átomos N1 e N3 foram obtidos por Fourier diferença e refinados isotropicamente com fator de temperatura 1,2 vezes o do átomo ao qual está ligado. O fator de discordância final foi R1 = 0,061 (ωr2 = 0,162), para um total de 152 parâmetros refinados. Os parâmetros posicionais, com os respectivos fatores de vibração térmica isotrópica equivalentes de todos os átomos, estão listados na Tabela 3.4. Na Tabela 3.5 são apresentadas as ligações de hidrogênio intramoleculares e intermolecular para o composto T1. Por conveniência, as Tabelas contendo as distâncias e ângulos intramoleculares para esta estrutura e para as duas seguintes, foram agrupadas nas Tabelas 3.18 e 3.19 para simplificar a análise das estruturas, no item 3.3. Encontra-se na Figura 3.1, a representação ORTEP [27] da estrutura molecular, com os átomos identificados, do composto T1. Os elipsóides estão repre-
57 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 45 Tabela 3.4: Parâmetros posicionais e de vibração térmica isotrópica equivalente do composto T1 x y z U(eq) N(1) 0,3174(2) 0,2575(4) 0,0544(1) 0,0452(5) C(2) 0,2121(2) 0,3605(4) 0,0415(1) 0,0392(1) N(3) 0,1817(2) 0,4987(3) -0,0184(1) 0,0425(4) C(4) 0,2485(2) 0,5513(4) -0,0642(1) 0,0462(5) S(5) 0,1143(1) 0,3472(1) 0,0895(0) 0,0591(3) O(6) 0,3447(2) 0,4598(4) -0,0610(1) 0,0689(6) C(7) 0,1965(2) 0,7282(4) -0,1181(1) 0,0435(5) C(8) 0,2190(2) 0,7083(5) -0,1835(1) 0,0529(6) C(9) 0,1759(3) 0,8742(5) -0,2341(1) 0,0578(6) C(10) 0,1125(3) 1,060(5) -0,2203(1) 0,0580(6) C(11) 0,0905(3) 1,0824(4) -0,1550(1) 0,0558(6) C(12) 0,1329(2) 0,9170(4) -0,1042(1) 0,0479(5) C(13) 0,3806(2) 0,1162(4) 0,1156(1) 0,0461(5) C(14) 0,3060(3) -0,0845(6) 0,1278(2) 0,081(1) C(15) 0,4186(4) 0,2693(6) 0,1787(2) 0,091(1) C(16) 0,4899(3) 0,0202(8) 0,0964(2) 0,088(1) Tabela 3.5: Ligações de hidrogênio intramoleculares e intermolecular do composto T1 D-H...A D-H(Å) H...A(Å) D...A(Å) DHA( ) N(1)-H(1)...O(6) 0,86(3) 1,96(3) 2,660(3) 137(3) C(14)-H(14B)...S(5) 0,96 2,63 3,298(4) 127 N(3)-H(3)...S(5)i 0,85(3) 2,64(3) 3,467(2) 165(2) (i) = 2 - x, 1 - y, -z sentados com 30% de probabilidade para vibração térmica. Os planos calculados por mínimos quadrados, passando pelos átomos N1- C2-N3-C4-O6 (plano 1) e C7-C8-C9-C10-C11-C12 (plano 2), formam um ângulo diedro de 32,5(1), mostrando que os átomos envolvidos formam planos, como se pode observar na Tabela 3.6. Pode-se observar na Figura 3.2 três ligações de hidrogênio para o composto T1, sendo duas ligações intramoleculares e uma intermolecular. A ligação intramolecular N1 H1 O6 contribui para a planaridade do pseudo-anel N1-C2-
58 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 46 Figura 3.1: Representação ORTEP do composto T1. Tabela 3.6: Equações dos planos, distância dos átomos aos planos e ângulo diedro entre planos para o composto T1 Plano 1: 3,4250x + 4,5091y + 8,9911z - 2,7264 = 0 Plano 2: 9,1913x + 2,9851y + 2,0994z - 3,7370 = 0 Ângulo diedro entre os planos 1 e 2 = 32,5(1) Plano 1 Plano 2 átomos distância (Å) átomos distância (Å) N(1) 0,010(1) C(7) -0,006(2) C(2) -0,001(1) C(8) 0,006(2) N(3) -0,021(2) C(9) -0,002(2) C(4) 0,033(2) C(10) -0,001(2) O(6) -0,021(1) C(11) 0,001(2) S(5) 0,035(3) C(12) 0,003(2) Átomo não incluído no cálculo do plano. N3-C4-O6. A ligação intermolecular forma um dímero com outra molécula em torno de um centro de inversão. Os dímeros interagem por forças de Van der Waals e se repetem por operações de translação ao longo do eixo b, resultando num empilhamento tipo espinha de peixe (herringbone), conforme se pode observar na projeção de cela unitária ao longo do eixo a, Figura 3.3. As coordenadas dos hidrogênios, os fatores de temperatura anisotrópicos e ângulos de torção, estão no apêndice D. Os fatores de estrutura observados e calculados e o arquivo com todos os dados cristalográficos estão disponíveis
59 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 47 Figura 3.2: Formação de dímeros em torno de centros de inversão para o composto T1. As linhas tracejadas indicam as ligações de hidrogênio intramoleculares e intermoleculares. Somente os hidrogênios envolvidos nas ligações estão representados. Os demais foram omitidos por motivo de clareza. Figura 3.3: Projeção ao longo do eixo a (representado na Figura por X) mostrando dois dímeros formando um arranjo tipo espinha de peixe, para o composto T1. junto ao coordenador do Grupo de Cristalografia e Materiais, Prof. Dr. Carlito Lariucci, através do endereço eletrônico: lariucci@if.ufg.br.
60 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas N-benzoil, N -(4-metilfenil)-tiouréia (T2) Um cristal incolor deste composto medindo 0,35 x 0,28 x 0,20 mm foi escolhido para coleta de dados. Para medida de controle de intensidades usou-se as reflexões (-5, 0, 4), (-3, 1, 6) e (-4, 0, 6). A coleta foi feita no sistema monoclínico com os índices variando de -15 a 15 para h; -1 a 6 para k e 0 a 23 para l. Ao final encontrou-se 3114 reflexões medidas, sendo 2466 independentes e 1862 consideradas observadas [I 2σ(I)]. A Tabela 3.7 mostra o resumo dos dados cristalográficos para este composto (Código interno IF-UFG: 052-RMT17). Tabela 3.7: Dados Cristalográficos do composto T2 Sistema cristalino Monoclínico Grupo espacial P2 1 /c a 13,021 (2) Å b 5,424 (1) Å c 19,861 (3) Å V 1386,3 (3) Å 3 β 98,78 (2) Z 4 Peso molecular 270,40 Densidade calculada 1,30 Mg/m 3 F(000) 567,9 λ(cukα) 1,54180 Å Número de reflexões medidas 3114 Número de reflexões independentes 2466 Número de reflexões com I 2σ(I) 1862 R int 0,0737 Fatores de transmissão Tmin e Tmax 0,5392 e 0,9060 Para a distribuição estatística E(h) 2 1 obteve-se o valor de 0,8722, conduzindo a uma estrutura cêntrica de grupo espacial P2 1 /c [nr:14]. Os 5 primeiros picos do mapa de Patterson, obtido com o programa SHELXS-86 [25], estão listados na Tabela 3.8. O pico n 2, é uma linha de Harker ocasionada pelo elemento de simetria,
61 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 49 Tabela 3.8: Picos de Patterson para o composto T2 u v w Pico Vetor Inter-atômico 1 0,0000 0,0000 0, ,00 2 0,0000 0,1573 0, ,97 3 0,7878 0,5000 0, ,31 4 0,3407 0,0000 0, ,24 5 0,1220 0,5000 0, ,05 espelho com deslizamento. O vetor inter-atômico entre dois átomos de enxofre, de uma posição geral x, y, z e o correspondente gerado pela operação espelho com deslizamento, com coordenadas x, 1/2 - y, 1/2 + z, é dado por u(r) = (0, 2y - 1/2, -1/2) = (0, 2y + 1/2, 1/2). Desta maneira, v = 2y + 1/2, o que forneceria a coordenada y = 0,1573 1/2 2 = -0,1714 do enxofre S5, que é equivalente a y = 0,1714. Considerando o pico n 3 como um plano de Harker, ocasionado pelo vetor inter-atômico entre um átomo de enxofre em uma posição geral x, y, z e o seu correspondente gerado pela operação de simetria eixo de rotação, com coordenadas -x, 1/2 + y, 1/2 - z, pode-se obter as duas coordenadas x e z do átomo de enxofre S5. O vetor inter-atômico é dado por u(r) = (2x, -1/2, 2z - 1/2), desta maneira, u = 2x e w = 2z - 1/2, o que fornece as coordenadas x = 0, = 0,3939 e z = 0,3496+1/2 2 = 0,4248. Para a unidade assimétrica 0 < x < 0,5; 0 < y < 0,5 e 0 < z < 0,5, é suficiente fazer uma translação de 1/2 cela para a coordenada z, resultando em x = 0,3939; y = 0,1714 e z = 0,9248, que são as coordenadas utilizadas para o início do refinamento. Os demais átomos foram obtidos por sucessivas Fourier diferença [21], sendo que no primeiro mapa encontrou-se 28 picos de densidade eletrônica, dos quais os 2 primeiros eram 1 átomo de nitrogênio e 1 átomo de oxigênio. Os átomos
62 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 50 foram mantidos com fatores de vibração isotrópico até R1 = 0,145 e passando ao refinamento anisotrópico obtendo R1 = 0,0456. Os hidrogênios ligados aos átomos N1 e N3 foram obtidos por Fourier diferença [21] e refinados isotropicamente com fator de temperatura 1,2 vezes o do átomo ao qual cada um está ligado. Foi encontrado um fator de discordância final de R1 = 0,0456 (ωr2 = 0,158) para um total de 183 parâmetros refinados. Estão listados na Tabela 3.9 os parâmetros posicionais, com os respectivos fatores de vibração térmica isotrópica equivalentes de todos os átomos. Tabela 3.9: Parâmetros posicionais e de vibração térmica isotrópica equivalente do composto T2 x y z U(eq) N(1) 0,2145(2) 0,2000(5) 0,9760(1) 0,0579(6) C(2) 0,3087(2) 0,1043(5) 0,9773(1) 0,0513(6) N(3) 0,3365(2) -0,0722(5) 1,0283(1) 0,0537(6) C(4) 0,2784(2) -0,1601(5) 1,0750(1) 0,0580(7) S(5) 0,3938(1) 0,1737(2) 0,9261(0) 0,0698(4) 0(6) 0,1896(2) -0,0877(5) 1,0771(1) 0,0847(7) C(7) 0,3269(2) -0,3469(5) 1,1245(1) 0,0539(6) C(8) 0,4020(2) -0,5120(5) 1,1107(1) 0,0585(7) C(9) 0,4403(2) -0,6855(5) 1,1588(2) 0,0691(8) C(10) 0,4051(2) -0,6973(6) 1,2203(2) 0,0718(8) C(11) 0,3311(2) -0,5329(7) 1,2342(2) 0,0772(9) C(12) 0,2921(2) -0,3584(6) 1,1869(1) 0,0678(8) C(13) 0,1574(2) 0,3747(5) 0,9324(1) 0,0519(6) C(14) 0,1995(2) 0,5536(6) 0,8954(2) 0,0691(8) C(15) 0,1337(3) 0,7168(6) 0,8563(2) 0,0743(9) C(16) 0,0279(2) 0,7098(5) 0,8526(1) 0,0599(7) C(17) -0,0120(2) 0,5343(6) 0,8910(1) 0,0676(8) C(18) 0,0512(2) 0,3683(6) 0,9302(1) 0,0647(8) C(19) -0,0425(3) 0,8820(6) 0,8077(2) 0,082(1) Encontra-se na Figura 3.4, a representação ORTEP [27] da estrutura molecular, com os átomos identificados, do composto T2. Os elipsóides estão representados com 30% de probabilidade para vibração térmica.
63 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 51 Figura 3.4: Representação ORTEP do composto T2. Os dois anéis fenila, C7-C8-C9-C10-C11-C12 e C13-C14-C15-C16-C17-C18 formam ângulos diedros com o agrupamento N1-C2-N3-C4-O6 de 27,4(2) e 20,8(1), respectivamente, conforme os cálculos de planos de mínimos quadrados mostrados na Tabela Tabela 3.10: Equações dos planos, distância dos átomos aos planos e ângulos diedros entre planos para o composto T2 Plano 1: 3,5823x + 3,8798y + 11,7748z - 13,0287 = 0 Plano 2: 8,6820x + 3,4562y + 5,5651z - 7,9006 = 0 Plano 3: -0,6394x + 3,4130y + 15,3738z - 15,5222 = 0 Ângulo diedro entre os planos 1 e 2 = 27,4(2) Ângulo diedro entre os planos 1 e 3 = 20,8(1) Plano 1 Plano 2 Plano 3 átomos distância (Å) átomos distância (Å) átomos distância (Å) N(1) 0,008(1) C(7) -0,003(2) C(13) -0,010(2) C(2) -0,011(2) C(8) 0,001(2) C(14) 0,006(2) N(3) 0,005(2) C(9) 0,002(2) C(15) 0,004(2) C(4) 0,005(2) C(10) -0,003(2) C(16) -0,010(2) O(6) -0,007(1) C(11) 0,000(2) C(17) 0,007(2) S(5) -0,039(4) C(12) 0,003(2) C(18) 0,003(2) Átomo não incluído no cálculo do plano. Para o composto T2, observam-se duas ligações intramoleculares e duas ligações intermoleculares, conforme a Tabela A ligação intramolecular
64 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 52 Tabela 3.11: Ligações de hidrogênio intra e intermoleculares do composto T2 D-H...A D-H(Å) H...A(Å) D...A(Å) DHA( ) N(1)-H(1)...O(6) 0,79(3) 1,88(3) 2,602(3) 150(3) C(14)-H(14)...S(5) 0,94(4) 2,63(4) 3,247(3) 123(3) N(3)-H(3)...S(5)i 0,85(3) 2,73(3) 3,534(2) 160(3) C(19)-H(19B)...O(6)ii 0,96 2,46 3,389(4) 163 (i) 1 - x, -y, -z; (ii) -x, 1 - y, -z. Figura 3.5: Formação de dímeros em torno de centros de inversão para o composto T2. As linhas tracejadas indicam as ligações intermoleculares. Somente os hidrogênios envolvidos nas ligações estão representados. Os demais foram omitidos por motivo de clareza. N1 H1 O6 contribui para a planaridade do pseudo-anel N1-C2-N3-C4-O6 e a segunda ligação intramolecular C14 H14 S5 pode ser responsável pelo pequeno ângulo de torção entre o pseudo-anel e o anel C13-C14-C15-C16-C17-C18, indicado por C2-N1-C13-C14 = -25,3(5). A ligação intermolecular N3 H3 S5 [operação de simetria: (i) 1 - x, -y, -z], forma um dímero em torno do centro de inversão em ( 1, 0, 0) resultando num empilhamento molecular na direção [ ]. A outra ligação intermolecular C19 H19B O6 [operação de simetria: (ii) -x, 1 - y, -z], ocorre entre dímeros relacionados por centro de inversão em (0, 1 2,
65 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 53 0) resultando num empilhamento molecular na direção [1 1 0]. O empilhamento resultante lembra uma espinha de peixe, Figura 3.6, na projeção ao longo do eixo a. Os parâmetros geométricos de todas estas ligações estão listados na Tabela Figura 3.6: Projeção ao longo do eixo a mostrando o arranjo tipo espinha de peixe (herringbone) para o composto T2. As coordenadas dos hidrogênios, os fatores de temperatura anisotrópicos e ângulos de torção, estão no apêndice D. Os fatores de estrutura observados e calculados e o arquivo com todos os dados cristalográficos estão disponíveis junto ao coordenador do Grupo de Cristalografia e Materiais, Prof. Dr. Carlito Lariucci, através do endereço eletrônico: lariucci@if.ufg.br N-benzoil, N -(2-hidroxietil)-tiouréia (T3) Um cristal incolor deste composto com dimensões 0,37 x 0,35 x 0,20 mm, foi
66 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 54 usado para coleta de dados de intensidade. As reflexões padrão (5, 1, -4), (3, 1, -6) e (3, 1, -11) foram usadas para controle de intensidade, sendo o intervalo para medida de -17 a 17 em h; -1 a 5 em k e 0 a 20 em l. Obteve-se no final da coleta um total de 2473 reflexões medidas, sendo 1877 independentes e 1781 consideradas observadas [I 2σ(I)]. É mostrado na Tabela 3.12 o resumo dos dados cristalográficos para este composto (Código interno IF-UFG: 062-RMQ8). Tabela 3.12: Dados Cristalográficos do composto T3 Sistema cristalino Monoclínico Grupo espacial P2 1 /c a 17,088 (2) Å b 4,583 (2) Å c 14,283 (2) Å V 1091,6 (3) Å 3 β 102,61 (1) Z 4 Peso molecular 224,3 Densidade calculada 1,36 Mg/m 3 F(000) 471,9 λ(cukα) 1,54180 Å Número de reflexões medidas 2473 Número de reflexões independentes 1877 Número de reflexões com I 2σ(I) 1781 R int 0,0278 Fatores de transmissão Tmin e Tmax 0,6344 e 0,4578 O valor médio da distribuição estatística encontrado para este composto é de E(h) 2 1 = 0,902, conduzindo a uma estrutura cêntrica de grupo espacial P2 1 /a. O programa SHELXS-86 [25] forneceu o mapa de Patterson, sendo listados na Tabela 3.13 os 6 primeiros picos. O grupo espacial P2 1 /a possui 4 posições gerais, são elas: (1) x, y, z; (2) x, y, z;
67 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 55 Tabela 3.13: Picos de Patterson para o composto T3 u v w Pico Vetor Inter-atômico 1 0,0000 0,0000 0, ,00 2 0,5000 0,3913 0, ,36 3 0,4022 0,5000 0, ,28 4 0,1346 0,5000 0, ,88 5 0,8935 0,0000 0, ,56 6 0,5000 0,0561 0, ,15 (3) 1/2 - x, 1/2 + y, -z; (4) 1/2 + x, 1/2 - y, z. O vetor inter-atômico entre dois átomos de enxofre, de uma posição geral (1) e o correspondente gerado pela operação de simetria espelho com deslizamento (4), é dado por u(r) = (1/2, 2y - 1/2, 0) = (1/2, -2y + 1/2, 0). Supondo que o pico n 2, do mapa de Patterson, é uma linha de Harker resultante deste vetor inter-atômico, a coordenada y do átomo de enxofre será: y = (0,3913 1/2) 2 = 0,0544 O pico n 3 pode ser considerando como um plano de Harker, resultante do vetor inter-atômico entre um átomo de enxofre em uma posição geral (1) e o seu correspondente gerado pela operação eixo de rotação (3). Desta maneira, pode-se obter as duas coordenadas x e z do átomo de enxofre S5, são elas: x = (0,4022+1/2) 2 = 0,4511 e z = 0, = 0,0857 Escolhendo a unidade assimétrica 0 < x < 0,5; 0 < y < 0,5 e 0 < z < 0,5, faz-se uma translação de 1/2 cela para a coordenada y, obtendo x = 0,4511; y = 0,5544 e z = 0,0857, que são as coordenadas utilizadas para o início do refinamento. A seguinte matriz, foi usada para a transformação do grupo espacial não convencional P2 1 /a para o grupo espacial P2 1 /c [nr:14].
68 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas Os demais átomos foram obtidos por Fourier diferença [21], sendo que no primeiro mapa encontrou-se 24 picos de intensidade dos quais os 2 primeiros eram 1 átomo de oxigênio e 1 átomo de nitrogênio. A estrutura foi refinada mantendo os átomos com fatores de vibração isotrópico até R1 = 0,188 e a partir deste momento passou-se ao refinamento anisotrópico finalizando com R1 = 0,066. Os átomos de hidrogênio ligados aos átomos N1 e N3 foram obtidos por Fourier diferença e refinados isotropicamente com fator de temperatura 1,2 vezes o do átomo ao qual estava ligado. Ao final do refinamento foi encontrado um fator de discordância de R1 = 0,060 (ωr2 = 0,148) para um total de 146 parâmetros refinados. A Tabela 3.14 lista os parâmetros posicionais, com os respectivos fatores de vibração térmica isotrópica equivalentes de todos os átomos. É mostrado na Figura 3.7, a representação ORTEP [27] da estrutura molecular, com os átomos identificados, para este composto. Os elipsóides estão representados com 30% de probabilidade para vibração térmica. A Figura 3.7 mostra que os átomos C8, C9, C10, C11 e C12 apresentam uma agitação térmica relativamente grande, o que pode ser verificado na Tabela D.8 do apêndice D. Os valores dos parâmetros térmicos U11 e U22 são consistentemente maiores que os outros, evidenciando uma libração do anel fenila em torno da ligação C7-C4. O anel fenila C7-C8-C9-C10-C11-C12 forma um ângulo de 4,7(2) com N1- C2-N3-C4-O6, resultando num agrupamento quase planar, conforme a Tabela 3.15.
69 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 57 Tabela 3.14: Parâmetros posicionais e de vibração térmica isotrópica equivalente do composto T3 x y z U(eq) N(1) 0,1887(1) -0,5106(4) 0,33761(1) 0,0503(5) C(2) 0,1670(1) -0,4250(4) 0,4165(1) 0,0456(5) N(3) 0,2179(1) -0,2280(4) 0,4743(1) 0,0498(5) C(4) 0,2887(1) -0,1147(5) 0,4611(1) 0,0508(5) S(5) 0,0854(0) -0,5413(1) 0,4518(0) 0,0624(3) O(6) 0,3154(1) -0,1723(4) 0,3905(1) 0,0697(5) C(7) 0,3326(1) 0,0830(5) 0,5381(2) 0,0541(5) C(8) 0,4058(2) 0,1852(7) 0,5291(2) 0,0778(8) C(9) 0,4506(2) 0,3634(8) 0,5995(2) 0,094(1) C(10) 0,4224(2) 0,4400(7) 0,6763(2) 0,0871(9) C(11) 0,3500(2) 0,3438(9) 0,6854(3) 0,109(1) C(12) 0,3048(2) 0,1641(8) 0,6161(2) 0,092(1) C(13) 0,1404(1) -0,6984(5) 0,2653(1) 0,0564(5) C(14) 0,0860(1) -0,5225(5) 0,1888(2) 0,0607(6) O(15) 0,1345(1) -0,3406(4) 0,1442(1) 0,0666(5) Figura 3.7: Representação ORTEP do composto T3. A Figura 3.8, evidencia duas ligações de hidrogênio intramoleculares e quatro intermoleculares para o composto T3. As ligações de hidrogênio intermoleculares produzem um arranjo com a forma de espinhas de peixe estendendo-se ao longo da direção [1 0 1], como ilustrado na Figura 3.9. As regiões planares
70 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 58 Tabela 3.15: Equações dos planos, distância dos átomos aos planos e ângulo diedro entre planos para o composto T3 Plano 1: 6,925x - 3,5079y + 5,7044z - 5,0219 = 0 Plano 2: 5,7153x - 3,6876y + 5,7955z - 4,7083 = 0 Ângulo diedro entre os planos 1 e 2 = 4,7(2) Plano 1 Plano 2 átomos distância (Å) átomos distância (Å) N(1) 0,002(1) C(7) 0,005(2) C(2) 0,001(1) C(8) -0,005(2) N(3) -0,007(1) C(9) 0,001(2) C(4) 0,010(1) C(10) 0,003(3) O(6) -0,006(1) C(11) -0,003(3) S(5) 0,045(3) C(12) -0,001(3) Átomo não incluído no cálculo do plano. Figura 3.8: As linhas tracejadas indicam as ligações intermoleculares. Somente os hidrogênios envolvidos nas ligações estão representados. Os demais foram omitidos por motivo de clareza. das moléculas envolvidas no referido arranjo formam um ângulo de 75,8. Os parâmetros geométricos de todas estas ligações estão listados na Tabela As coordenadas dos hidrogênios, os fatores de temperatura anisotrópicos e
71 3.2 Medidas Difratométricas, Solução e Refinamento das Estruturas 59 Figura 3.9: Projeção ao longo da direção [1 0 1] mostrando o arranjo quase planar em planos formando um ângulo de 75,8 entre si, resultando em arranjo tipo espinha de peixe para o composto T3. Tabela 3.16: Ligações de hidrogênio intra e intermoleculares do composto T3 D-H...A D-H(Å) H...A(Å) D...A(Å) DHA( ) N(1)-H(1)...O(6) 0,84(3) 1,94(3) 2,636(3) 140(3) C(13)-H(13A)...S(5) 0,97 2,69 3,096(3) 106 N(3)-H(3)...O(15)i 0,80(3) 2,31(3) 3,087(3) 163(2) O(15)-H(15)...S(5)ii 0,75(3) 2,53(3) 3,211(2) 153(3) C(11)-H(11)...O(6)iii 0,93 2,57 3,456(5) 160 C(12)-H(12)...O(15)i 0,93 2,45 3,368(4) 170 (i) 1/2 + x, 1/2 - y, z; (ii) -1/2 + x, 1/2 - y, z; (iii) 1/2 + x, -1/2 - y, z. ângulos de torção, estão no apêndice D. Os fatores de estrutura observados e calculados e o arquivo com todos os dados cristalográficos estão disponíveis junto ao coordenador do Grupo de Cristalografia e Materiais, Prof. Dr. Carlito Lariucci, através do endereço eletrônico: lariucci@if.ufg.br.
72 3.3 Análise das Estruturas Cristalinas Análise das Estruturas Cristalinas Algumas estruturas apresentando o grupamento tiouréia foram encontradas através de uma busca feita no Cambridge Crystallographic Database, Version 5.27 (CCD) [28]. O critério usado para efetuar a busca foi manter a parte comum às três moléculas pesquisadas, de tal forma que apenas os substituintes do carbono C13 fossem aceitos. Da busca foram eliminadas as estruturas contendo metais ou formando complexos. Foram encontrados 29 compostos, dos quais 18 foram selecionados, apêndice E, e alguns de seus parâmetros foram tabelados, usando o programa VISTA, um novo software incorporado ao pacote de programas CCD, Figura Figura 3.10: Alguns parâmetros dos compostos encontrados na busca ao CCD, utilizando o programa VISTA. Esta Figura mostra a janela principal do programa. A primeira coluna lista o número total de compostos tabelados e na primeira linha são enumerados os
DIFRAÇÃO DE RAIOS X DRX
 DIFRAÇÃO DE RAIOS X DRX O espectro eletromagnético luz visível raios-x microondas raios gama UV infravermelho ondas de rádio Comprimento de onda (nm) Raios Absorção, um fóton de energia é absorvido promovendo
DIFRAÇÃO DE RAIOS X DRX O espectro eletromagnético luz visível raios-x microondas raios gama UV infravermelho ondas de rádio Comprimento de onda (nm) Raios Absorção, um fóton de energia é absorvido promovendo
UNIDADE 4 - ESTRUTURA CRISTALINA
 UNIDADE 4 - ESTRUTURA CRISTALINA 4.1. INTRODUÇÃO Em geral, todos os metais, grande parte dos cerâmicos e certos polímeros cristalizam-se quando se solidificam. Os átomos se arranjam em uma estrutura tridimensional
UNIDADE 4 - ESTRUTURA CRISTALINA 4.1. INTRODUÇÃO Em geral, todos os metais, grande parte dos cerâmicos e certos polímeros cristalizam-se quando se solidificam. Os átomos se arranjam em uma estrutura tridimensional
DRIFRAÇÃO DE RAIOS-X
 DRIFRAÇÃO DE RAIOS-X Prof. Márcio Antônio Fiori Prof. Jacir Dal Magro O espectro eletromagnético luz visível raios-x microondas raios gama UV infravermelho ondas de rádio Comprimento de onda (nm) Absorção,
DRIFRAÇÃO DE RAIOS-X Prof. Márcio Antônio Fiori Prof. Jacir Dal Magro O espectro eletromagnético luz visível raios-x microondas raios gama UV infravermelho ondas de rádio Comprimento de onda (nm) Absorção,
Difração. Espectrometria por Raios X 28/10/2009. Walmor Cardoso Godoi, M.Sc. http://ww.walmorgodoi.com
 Difração Espectrometria por Raios X Fenômeno encontrado enquanto ondas (sísmicas, acústicas, ondas de água, ondas eletromagnéticos, luz visível, ondas de rádio, raios X) encontram um obstáculo teia de
Difração Espectrometria por Raios X Fenômeno encontrado enquanto ondas (sísmicas, acústicas, ondas de água, ondas eletromagnéticos, luz visível, ondas de rádio, raios X) encontram um obstáculo teia de
Arranjos Atômicos 26/3/2006 CM I 1
 Arranjos Atômicos 26/3/2006 CM I 1 26/3/2006 CM I 2 Arranjo Periódico de Átomos Sólido: constituído por átomos (ou grupo de átomos) que se distribuem de acordo com um ordenamento bem definido; Esta regularidade:»
Arranjos Atômicos 26/3/2006 CM I 1 26/3/2006 CM I 2 Arranjo Periódico de Átomos Sólido: constituído por átomos (ou grupo de átomos) que se distribuem de acordo com um ordenamento bem definido; Esta regularidade:»
ESTRUTURAS CRISTALINAS - TEORIA
 ESTRUTURAS CRISTALINAS - TEORIA Introdução Sólidos são compostos que apresentam uma alta regularidade estrutural. Com exceção dos sólidos amorfos, nos quais essa regularidade só existe em um curto espaço,
ESTRUTURAS CRISTALINAS - TEORIA Introdução Sólidos são compostos que apresentam uma alta regularidade estrutural. Com exceção dos sólidos amorfos, nos quais essa regularidade só existe em um curto espaço,
Formas regulares e simétricas assim como a ordenação das partículas que os formam. Cristalografia e Difração em Raio X - Michele Oliveira
 Formas regulares e simétricas assim como a ordenação das partículas que os formam. Cristalografia e Difração em Raio X - Michele Oliveira 2 Cristais são arranjos atômicos ou moleculares cuja estrutura
Formas regulares e simétricas assim como a ordenação das partículas que os formam. Cristalografia e Difração em Raio X - Michele Oliveira 2 Cristais são arranjos atômicos ou moleculares cuja estrutura
2015 Dr. Walter F. de Azevedo Jr. Lei de Bragg e Espaço Recíproco
 2015 Dr. Walter F. de Azevedo Jr. 000000000000000000000000000000000000000 000000000000000000000000000000000000000 000000000000111111111110001100000000000 000000000001111111111111111111000000001 000000000111111111111111111111111000000
2015 Dr. Walter F. de Azevedo Jr. 000000000000000000000000000000000000000 000000000000000000000000000000000000000 000000000000111111111110001100000000000 000000000001111111111111111111000000001 000000000111111111111111111111111000000
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 3
 Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
Linhas de Força Mencionamos na aula passada que o físico inglês Michael Faraday (79-867) introduziu o conceito de linha de força para visualizar a interação elétrica entre duas cargas. Para Faraday, as
1. 3 2. 4 3. 4 4. 5 5. 6 6. 8 7. 9 8. 12 9. 16 10. 17 11. O
 1 DIFRAÇÃO DE RAIOS X Prof. Dr. Walter Filgueira de Azevedo Jr. Laboratório de Sistemas Biomoleculares. Departamento de Física-Instituto de Biociências, Letras e Ciências Exatas-UNESP, São José do Rio
1 DIFRAÇÃO DE RAIOS X Prof. Dr. Walter Filgueira de Azevedo Jr. Laboratório de Sistemas Biomoleculares. Departamento de Física-Instituto de Biociências, Letras e Ciências Exatas-UNESP, São José do Rio
Estrutura de Sólidos Cristalinos. Profa. Dra Daniela Becker
 Estrutura de Sólidos Cristalinos Profa. Dra Daniela Becker Bibliografia Callister Jr., W. D. Ciência e engenharia de materiais: Uma introdução. LTC, 5ed., cap 3, 2002. Shackelford, J.F. Ciências dos Materiais,
Estrutura de Sólidos Cristalinos Profa. Dra Daniela Becker Bibliografia Callister Jr., W. D. Ciência e engenharia de materiais: Uma introdução. LTC, 5ed., cap 3, 2002. Shackelford, J.F. Ciências dos Materiais,
Prof. João Maria Soares UERN/DF/Mossoró E-mail: joaomsoares@gmail.com
 Prof. João Maria Soares UERN/DF/Mossoró E-mail: joaomsoares@gmail.com 1. Estrutura cristalina redes de Bravais 2. Principais estruturas cristalinas 3. Sistemas cristalinos 4. Simetria e grupos de simetria
Prof. João Maria Soares UERN/DF/Mossoró E-mail: joaomsoares@gmail.com 1. Estrutura cristalina redes de Bravais 2. Principais estruturas cristalinas 3. Sistemas cristalinos 4. Simetria e grupos de simetria
Cristalização e Caracterização Estrutural por Difração de Raios X do composto β-ciclodextrina com um agonista do receptor D2 da dopamina
 Cristalização e Caracterização Estrutural por Difração de Raios X do composto β-ciclodextrina com um agonista do receptor D2 da dopamina Rosane de Paula CASTRO, José Ricardo SABINO, Carlos Alberto Mansour
Cristalização e Caracterização Estrutural por Difração de Raios X do composto β-ciclodextrina com um agonista do receptor D2 da dopamina Rosane de Paula CASTRO, José Ricardo SABINO, Carlos Alberto Mansour
SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO
 SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO Respostas breves: 1.1) 9,063 N 1.2) norte, pois é positiva. 1.3) São José (Costa Rica). 2) Não, porque Santa Maria não está localizada sobre ou entre os dois
SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO Respostas breves: 1.1) 9,063 N 1.2) norte, pois é positiva. 1.3) São José (Costa Rica). 2) Não, porque Santa Maria não está localizada sobre ou entre os dois
RESUMO 2 - FÍSICA III
 RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
Espectometriade Fluorescência de Raios-X
 FRX Espectometriade Fluorescência de Raios-X Prof. Márcio Antônio Fiori Prof. Jacir Dal Magro FEG Conceito A espectrometria de fluorescência de raios-x é uma técnica não destrutiva que permite identificar
FRX Espectometriade Fluorescência de Raios-X Prof. Márcio Antônio Fiori Prof. Jacir Dal Magro FEG Conceito A espectrometria de fluorescência de raios-x é uma técnica não destrutiva que permite identificar
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
OBJETIVO Verificar as leis da Reflexão Verificar qualitativamente e quantitativamente a lei de Snell. Observar a dispersão da luz em um prisma.
 UNIVERSIDADE CATÓLICA DE BRASÍLIA CURSO DE FÍSICA LABORATÓRIO ÓPTICA REFLEXÃO E REFRAÇÃO OBJETIVO Verificar as leis da Reflexão Verificar qualitativamente e quantitativamente a lei de Snell. Observar a
UNIVERSIDADE CATÓLICA DE BRASÍLIA CURSO DE FÍSICA LABORATÓRIO ÓPTICA REFLEXÃO E REFRAÇÃO OBJETIVO Verificar as leis da Reflexão Verificar qualitativamente e quantitativamente a lei de Snell. Observar a
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS DEPARTAMENTO DE ENGENHARIA MECÂNICA TÉCNICAS DE ANÁLISE
 UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS DEPARTAMENTO DE ENGENHARIA MECÂNICA TÉCNICAS DE ANÁLISE CMA CIÊNCIA DOS MATERIAIS 2º Semestre de 2014 Prof. Júlio César Giubilei
UNIVERSIDADE DO ESTADO DE SANTA CATARINA CENTRO DE CIÊNCIAS TECNOLÓGICAS DEPARTAMENTO DE ENGENHARIA MECÂNICA TÉCNICAS DE ANÁLISE CMA CIÊNCIA DOS MATERIAIS 2º Semestre de 2014 Prof. Júlio César Giubilei
Física IV. Difração. Sears capítulo 36. Prof. Nelson Luiz Reyes Marques. Capítulo 36 Difração
 Física IV Difração Sears capítulo 36 Prof. Nelson Luiz Reyes Marques Difração e a Teoria Ondulatória da Luz Difração e a Teoria Ondulatória da Luz A difração é um fenômeno essencialmente ondulatório, ou
Física IV Difração Sears capítulo 36 Prof. Nelson Luiz Reyes Marques Difração e a Teoria Ondulatória da Luz Difração e a Teoria Ondulatória da Luz A difração é um fenômeno essencialmente ondulatório, ou
ARRANJOS ATÔMICOS. Química Aplicada
 ARRANJOS ATÔMICOS Química Aplicada Sólidos Sólidos 1. Arranjo Periódico de Átomos SÓLIDO: Constituído por átomos (ou grupo de átomos) que se distribuem de acordo com um ordenamento bem definido; Esta regularidade:
ARRANJOS ATÔMICOS Química Aplicada Sólidos Sólidos 1. Arranjo Periódico de Átomos SÓLIDO: Constituído por átomos (ou grupo de átomos) que se distribuem de acordo com um ordenamento bem definido; Esta regularidade:
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA Primeira Edição junho de 2005 CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA ÍNDICE 5.1- Postulados
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA Primeira Edição junho de 2005 CAPÍTULO 5 PROPRIEDADES ONDULATÓRIAS DA MATÉRIA ÍNDICE 5.1- Postulados
( ) ( ) ( ( ) ( )) ( )
 Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Física 0 Duas partículas A e, de massa m, executam movimentos circulares uniormes sobre o plano x (x e representam eixos perpendiculares) com equações horárias dadas por xa ( t ) = a+acos ( ωt ), ( t )
Prof. Eduardo Loureiro, DSc.
 Prof. Eduardo Loureiro, DSc. Transmissão de Calor é a disciplina que estuda a transferência de energia entre dois corpos materiais que ocorre devido a uma diferença de temperatura. Quanta energia é transferida
Prof. Eduardo Loureiro, DSc. Transmissão de Calor é a disciplina que estuda a transferência de energia entre dois corpos materiais que ocorre devido a uma diferença de temperatura. Quanta energia é transferida
Universidade Federal do Rio de Janeiro. Princípios de Instrumentação Biomédica. Módulo 4
 Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
Tópicos de Física Moderna ano 2005/2006
 Trabalho Prático Nº 3 ESTUDO DA DIFRAÇÃO Tópicos de Física Moderna ano 005/006 Objectivos: Familiarização com os fenómenos de interferência e difracção da luz, com utilização de uma rede de difracção para
Trabalho Prático Nº 3 ESTUDO DA DIFRAÇÃO Tópicos de Física Moderna ano 005/006 Objectivos: Familiarização com os fenómenos de interferência e difracção da luz, com utilização de uma rede de difracção para
EXPERIMENTO N o 6 LENTES CONVERGENTES INTRODUÇÃO
 EXPERIMENTO N o 6 LENTES CONVERGENTES INTRODUÇÃO Ao incidir em uma lente convergente, um feixe paralelo de luz, depois de passar pela lente, é concentrado em um ponto denominado foco (representado por
EXPERIMENTO N o 6 LENTES CONVERGENTES INTRODUÇÃO Ao incidir em uma lente convergente, um feixe paralelo de luz, depois de passar pela lente, é concentrado em um ponto denominado foco (representado por
4 Orbitais do Átomo de Hidrogênio
 4 Orbitais do Átomo de Hidrogênio A aplicação mais intuitiva e que foi a motivação inicial para desenvolver essa técnica é a representação dos orbitais do átomo de hidrogênio que, desde então, tem servido
4 Orbitais do Átomo de Hidrogênio A aplicação mais intuitiva e que foi a motivação inicial para desenvolver essa técnica é a representação dos orbitais do átomo de hidrogênio que, desde então, tem servido
UNIDADE 3 - COORDENAÇÃO ATÔMICA
 A força de repulsão entre os elétrons de dois átomos, quando estão suficientemente próximos, é responsável, em conjunto com as forças de atração, pela posição de equilíbrio dos átomos na ligação química
A força de repulsão entre os elétrons de dois átomos, quando estão suficientemente próximos, é responsável, em conjunto com as forças de atração, pela posição de equilíbrio dos átomos na ligação química
Reflexão. A reflexão ocorre quando a luz incide sobre a superfície de separação entre dois meios com propriedades distintas.
 Ótica Reflexão A reflexão ocorre quando a luz incide sobre a superfície de separação entre dois meios com propriedades distintas. A reflexibilidade é a tendência dos raios de voltarem para o mesmo meio
Ótica Reflexão A reflexão ocorre quando a luz incide sobre a superfície de separação entre dois meios com propriedades distintas. A reflexibilidade é a tendência dos raios de voltarem para o mesmo meio
REFLEXÃO DA LUZ: ESPELHOS 412EE TEORIA
 1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
1 TEORIA 1 DEFININDO ESPELHOS PLANOS Podemos definir espelhos planos como toda superfície plana e polida, portanto, regular, capaz de refletir a luz nela incidente (Figura 1). Figura 1: Reflexão regular
EFEITO FOTOELÉTRICO. J.R. Kaschny
 EFEITO FOTOELÉTRICO J.R. Kaschny Histórico 1886-1887 Heinrich Hertz realizou experimentos que pela primeira vez confirmaram a existência de ondas eletromagnéticas e a teoria de Maxwell sobre a propagação
EFEITO FOTOELÉTRICO J.R. Kaschny Histórico 1886-1887 Heinrich Hertz realizou experimentos que pela primeira vez confirmaram a existência de ondas eletromagnéticas e a teoria de Maxwell sobre a propagação
Óptica. Estudo da luz, como sendo a onda eletromagnética pertencentes à faixa do espectro visível (comprimento de 400 nm até 700 nm).
 Óptica Estudo da luz, como sendo a onda eletromagnética pertencentes à faixa do espectro visível (comprimento de 400 nm até 700 nm). Fenômenos ópticos Professor: Éder (Boto) Sobre a Luz O que emite Luz?
Óptica Estudo da luz, como sendo a onda eletromagnética pertencentes à faixa do espectro visível (comprimento de 400 nm até 700 nm). Fenômenos ópticos Professor: Éder (Boto) Sobre a Luz O que emite Luz?
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
EFEITO COMPTON. J.R. Kaschny
 EFEITO COMPTON J.R. Kaschny Os Experimentos de Compton Das diversas interações da radiação com a matéria, um destaque especial é dado ao efeito, ou espalhamento, Compton - Arthur Holly Compton (93, Nobel
EFEITO COMPTON J.R. Kaschny Os Experimentos de Compton Das diversas interações da radiação com a matéria, um destaque especial é dado ao efeito, ou espalhamento, Compton - Arthur Holly Compton (93, Nobel
18 a QUESTÃO Valor: 0,25
 6 a A 0 a QUESTÃO FÍSICA 8 a QUESTÃO Valor: 0,25 6 a QUESTÃO Valor: 0,25 Entre as grandezas abaixo, a única conservada nas colisões elásticas, mas não nas inelásticas é o(a): 2Ω 2 V 8Ω 8Ω 2 Ω S R 0 V energia
6 a A 0 a QUESTÃO FÍSICA 8 a QUESTÃO Valor: 0,25 6 a QUESTÃO Valor: 0,25 Entre as grandezas abaixo, a única conservada nas colisões elásticas, mas não nas inelásticas é o(a): 2Ω 2 V 8Ω 8Ω 2 Ω S R 0 V energia
DIODOS. Professor João Luiz Cesarino Ferreira
 DIODOS A união de um cristal tipo p e um cristal tipo n, obtém-se uma junção pn, que é um dispositivo de estado sólido simples: o diodo semicondutor de junção. Figura 1 Devido a repulsão mútua os elétrons
DIODOS A união de um cristal tipo p e um cristal tipo n, obtém-se uma junção pn, que é um dispositivo de estado sólido simples: o diodo semicondutor de junção. Figura 1 Devido a repulsão mútua os elétrons
9. Derivadas de ordem superior
 9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
9. Derivadas de ordem superior Se uma função f for derivável, então f é chamada a derivada primeira de f (ou de ordem 1). Se a derivada de f eistir, então ela será chamada derivada segunda de f (ou de
www.fisicanaveia.com.br
 www.fisicanaveia.com.br Lentes Esféricas Lentes Esféricas: construção Biconvexa Lentes Esféricas: construção PLANO-CONVEXA Lentes Esféricas: construção CÔNCAVO-CONVEXA Lentes Esféricas: construção BICÔNCAVA
www.fisicanaveia.com.br Lentes Esféricas Lentes Esféricas: construção Biconvexa Lentes Esféricas: construção PLANO-CONVEXA Lentes Esféricas: construção CÔNCAVO-CONVEXA Lentes Esféricas: construção BICÔNCAVA
Roteiro 23 Difração e Interferência de ondas bidimensionais num meio líquido
 Roteiro 23 Difração e Interferência de ondas bidimensionais num meio líquido 1 INTRODUÇÃO As ondas podem sofrer o efeito de diversos fenômenos, dentre eles estão a difração e a interferência. A difração
Roteiro 23 Difração e Interferência de ondas bidimensionais num meio líquido 1 INTRODUÇÃO As ondas podem sofrer o efeito de diversos fenômenos, dentre eles estão a difração e a interferência. A difração
Biologia Estrutural. Simetria. Prof. Dr. Walter Filgueira de Azevedo Jr. wfdaj.sites.uol.com.br. 2006 Dr. Walter F. de Azevedo Jr.
 Biologia Estrutural Simetria Prof. Dr. Walter Filgueira de Azevedo Jr. Resumo Características dos Cristais Características dos Cristais de Proteínas Elementos de Simetria Rede, Retículo e Empacotamento
Biologia Estrutural Simetria Prof. Dr. Walter Filgueira de Azevedo Jr. Resumo Características dos Cristais Características dos Cristais de Proteínas Elementos de Simetria Rede, Retículo e Empacotamento
Tópico 3. Limites e continuidade de uma função (Parte 2)
 Tópico 3. Limites e continuidade de uma função (Parte 2) Nessa aula continuaremos nosso estudo sobre limites de funções. Analisaremos o limite de funções quando o x ± (infinito). Utilizaremos o conceito
Tópico 3. Limites e continuidade de uma função (Parte 2) Nessa aula continuaremos nosso estudo sobre limites de funções. Analisaremos o limite de funções quando o x ± (infinito). Utilizaremos o conceito
Água e Solução Tampão
 União de Ensino Superior de Campina Grande Faculdade de Campina Grande FAC-CG Curso de Fisioterapia Água e Solução Tampão Prof. Dra. Narlize Silva Lira Cavalcante Fevereiro /2015 Água A água é a substância
União de Ensino Superior de Campina Grande Faculdade de Campina Grande FAC-CG Curso de Fisioterapia Água e Solução Tampão Prof. Dra. Narlize Silva Lira Cavalcante Fevereiro /2015 Água A água é a substância
APLICAÇÕES DE NÚMEROS COMPLEXOS
 http://hermes.ucs.br/ccet/deme/emsoares/inipes/complexos/ APLICAÇÕES DE NÚMEROS COMPLEXOS Silvia Carla Menti Propicio Universidade de Caxias do Sul Centro de Ciências Exatas e Tecnologia Departamento de
http://hermes.ucs.br/ccet/deme/emsoares/inipes/complexos/ APLICAÇÕES DE NÚMEROS COMPLEXOS Silvia Carla Menti Propicio Universidade de Caxias do Sul Centro de Ciências Exatas e Tecnologia Departamento de
Física IV. Interferência
 Física IV Interferência Sears capítulo 35 Prof. Nelson Luiz Reyes Marques Interferência Arco-íris = Bolha de sabão refração interferência Princípio da superposição Quando duas ou mais ondas se superpõem,
Física IV Interferência Sears capítulo 35 Prof. Nelson Luiz Reyes Marques Interferência Arco-íris = Bolha de sabão refração interferência Princípio da superposição Quando duas ou mais ondas se superpõem,
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
 Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS
 REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
REPRESENTAÇÃO FASORIAL DE SINAIS SENOIDAIS Neste capítulo será apresentada uma prática ferramenta gráfica e matemática que permitirá e facilitará as operações algébricas necessárias à aplicação dos métodos
ÓPTICA GEOMÉTRICA PREGOLINI
 ÓPTICA GEOMÉTRICA PREGOLINI ÓPTICA GEOMÉTRICA É a parte da Física que estuda os fenômenos relacionados com a luz e sua interação com meios materiais quando as dimensões destes meios é muito maior que o
ÓPTICA GEOMÉTRICA PREGOLINI ÓPTICA GEOMÉTRICA É a parte da Física que estuda os fenômenos relacionados com a luz e sua interação com meios materiais quando as dimensões destes meios é muito maior que o
 MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
Simetria Externa. Universidade de São Paulo. Instituto de Química de São Carlos. Departamento de Química e Física Molecular. SQM 409 - Cristalografia
 Universidade de São Paulo Instituto de Química de São Carlos Departamento de Química e Física Molecular Simetria Externa SQM 09 - Cristalografia Prof. Dr. Maria Teresa do Prado Gambardella . Simetria Externa
Universidade de São Paulo Instituto de Química de São Carlos Departamento de Química e Física Molecular Simetria Externa SQM 09 - Cristalografia Prof. Dr. Maria Teresa do Prado Gambardella . Simetria Externa
LEI DE OHM. Professor João Luiz Cesarino Ferreira. Conceitos fundamentais
 LEI DE OHM Conceitos fundamentais Ao adquirir energia cinética suficiente, um elétron se transforma em um elétron livre e se desloca até colidir com um átomo. Com a colisão, ele perde parte ou toda energia
LEI DE OHM Conceitos fundamentais Ao adquirir energia cinética suficiente, um elétron se transforma em um elétron livre e se desloca até colidir com um átomo. Com a colisão, ele perde parte ou toda energia
Espectroscopia de Raios X
 Espectroscopia de Raios X 1. Introdução Raios X O conhecimento da estrutura dos materiais, a maioria dos quais são cristalinos no estado sólido, s é fundamental para a caracterização das propriedades físicas
Espectroscopia de Raios X 1. Introdução Raios X O conhecimento da estrutura dos materiais, a maioria dos quais são cristalinos no estado sólido, s é fundamental para a caracterização das propriedades físicas
Do ponto de vista da Termodinâmica, gás ideal é aquele para o qual vale, para quaisquer valores de P e T, a equação de estado de Clapeyron:
 Equação de Estado de Van der Waals Do ponto de vista da Termodinâmica, gás ideal é aquele para o qual vale, para quaisquer valores de P e T, a equação de estado de Clapeyron: P i V i = nrt em que colocamos
Equação de Estado de Van der Waals Do ponto de vista da Termodinâmica, gás ideal é aquele para o qual vale, para quaisquer valores de P e T, a equação de estado de Clapeyron: P i V i = nrt em que colocamos
3 Espectroscopia no Infravermelho 3.1. Princípios Básicos
 3 Espectroscopia no Infravermelho 3.1. Princípios Básicos A espectroscopia estuda a interação da radiação eletromagnética com a matéria, sendo um dos seus principais objetivos o estudo dos níveis de energia
3 Espectroscopia no Infravermelho 3.1. Princípios Básicos A espectroscopia estuda a interação da radiação eletromagnética com a matéria, sendo um dos seus principais objetivos o estudo dos níveis de energia
DETERMINAÇÃO DA ESTRUTURA TRIDIMENSIONAL DE PROTEÍNAS POR DIFRAÇÃO DE RAIOS-X
 DETERMINAÇÃO DA ESTRUTURA TRIDIMENSIONAL DE PROTEÍNAS POR DIFRAÇÃO DE RAIOS-X Disciplina: Engenharia de Proteínas Ma. Flávia Campos Freitas Vieira NÍVEIS ESTRUTURAIS DAS PROTEÍNAS Fonte: Lehninger, 2010.
DETERMINAÇÃO DA ESTRUTURA TRIDIMENSIONAL DE PROTEÍNAS POR DIFRAÇÃO DE RAIOS-X Disciplina: Engenharia de Proteínas Ma. Flávia Campos Freitas Vieira NÍVEIS ESTRUTURAIS DAS PROTEÍNAS Fonte: Lehninger, 2010.
a 1 x 1 +... + a n x n = b,
 Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
LENTES E ESPELHOS. O tipo e a posição da imagem de um objeto, formada por um espelho esférico de pequena abertura, é determinada pela equação
 LENTES E ESPELHOS INTRODUÇÃO A luz é uma onda eletromagnética e interage com a matéria por meio de seus campos elétrico e magnético. Nessa interação, podem ocorrer alterações na velocidade, na direção
LENTES E ESPELHOS INTRODUÇÃO A luz é uma onda eletromagnética e interage com a matéria por meio de seus campos elétrico e magnético. Nessa interação, podem ocorrer alterações na velocidade, na direção
Aula 8 Fótons e ondas de matéria II. Física Geral F-428
 Aula 8 Fótons e ondas de matéria II Física Geral F-428 1 Resumo da aula anterior: Planck e o espectro da radiação de um corpo negro: introdução do conceito de estados quantizados de energia para os osciladores
Aula 8 Fótons e ondas de matéria II Física Geral F-428 1 Resumo da aula anterior: Planck e o espectro da radiação de um corpo negro: introdução do conceito de estados quantizados de energia para os osciladores
LIGAÇÃO COVALENTE APOLAR ELEMENTOS COM MESMA ELETRONEGATIVIDADE
 LIGAÇÃO COVALENTE APOLAR ELEMENTOS COM MESMA ELETRONEGATIVIDADE LIGAÇÃO COVALENTE POLAR ELEMENTOS COM ELETRONEGATIVIDADES DIFERENTES MOLÉCULA APOLAR VETORES SE ANULAM ///// µ R = 0 MOLÉCULA APOLAR VETORES
LIGAÇÃO COVALENTE APOLAR ELEMENTOS COM MESMA ELETRONEGATIVIDADE LIGAÇÃO COVALENTE POLAR ELEMENTOS COM ELETRONEGATIVIDADES DIFERENTES MOLÉCULA APOLAR VETORES SE ANULAM ///// µ R = 0 MOLÉCULA APOLAR VETORES
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Reações a altas temperaturas. Diagrama de Equilíbrio
 Reações a altas temperaturas Diagrama de Equilíbrio Propriedades de um corpo cerâmico Determinadas pelas propriedades de cada fase presente e pelo modo com que essas fases (incluindo a porosidade) estão
Reações a altas temperaturas Diagrama de Equilíbrio Propriedades de um corpo cerâmico Determinadas pelas propriedades de cada fase presente e pelo modo com que essas fases (incluindo a porosidade) estão
MÓDULO DE RECUPERAÇÃO
 DISCIPLINA Física II 2º ANO ENSINO MÉDIO MÓDULO DE RECUPERAÇÃO ALUNO(A) Nº TURMA TURNO Manhã 1º SEMESTRE DATA / / 01- A figura representa um feixe de raios paralelos incidentes numa superfície S e os correspondentes
DISCIPLINA Física II 2º ANO ENSINO MÉDIO MÓDULO DE RECUPERAÇÃO ALUNO(A) Nº TURMA TURNO Manhã 1º SEMESTRE DATA / / 01- A figura representa um feixe de raios paralelos incidentes numa superfície S e os correspondentes
O degrau de potencial. Caso II: energia maior que o degrau
 O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
O degrau de potencial. Caso II: energia maior que o degrau U L 9 Meta da aula plicar o formalismo quântico ao caso de uma partícula quântica que incide sobre o degrau de potencial, definido na ula 8. Vamos
UNIVERSIDADE FEDERAL DO ABC BC-1105: MATERIAIS E SUAS PROPRIEDADES
 UNIVERSIDADE FEDERAL DO ABC Centro de Engenharia, Modelagem e Ciências Sociais Aplicadas (CECS) BC-1105: MATERIAIS E SUAS PROPRIEDADES Estrutura Cristalina - arranjo (organização espacial) - simetria -
UNIVERSIDADE FEDERAL DO ABC Centro de Engenharia, Modelagem e Ciências Sociais Aplicadas (CECS) BC-1105: MATERIAIS E SUAS PROPRIEDADES Estrutura Cristalina - arranjo (organização espacial) - simetria -
22/Abr/2015 Aula 15. 17/Abr/2015 Aula 14
 17/Abr/2015 Aula 14 Introdução à Física Quântica Radiação do corpo negro; níveis discretos de energia. Efeito foto-eléctrico: - descrições clássica e quântica - experimental. Efeito de Compton. 22/Abr/2015
17/Abr/2015 Aula 14 Introdução à Física Quântica Radiação do corpo negro; níveis discretos de energia. Efeito foto-eléctrico: - descrições clássica e quântica - experimental. Efeito de Compton. 22/Abr/2015
PRINCÍPIOS DA ESTRUTURA EM SÓLIDOS. QFL-4010 Prof. Gianluca C. Azzellini
 PRINCÍPIOS DA ESTRUTURA EM SÓLIDOS Estrutura dos Sólidos Tipo Exemplo Unidades Natureza Estruturais da ligação Iônico NaCl, CaCl 2 Íons positivos Iônica - Atração e negativos Eletrostática forte Metálico
PRINCÍPIOS DA ESTRUTURA EM SÓLIDOS Estrutura dos Sólidos Tipo Exemplo Unidades Natureza Estruturais da ligação Iônico NaCl, CaCl 2 Íons positivos Iônica - Atração e negativos Eletrostática forte Metálico
Faculdade Sagrada Família
 AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
B) (até três pontos) Para os pares de espécies apresentados em i, ii e iii, tem-se, respectivamente, Al +, F - e Li.
 Química 1. O raio atômico (ou iônico) é uma propriedade periódica que exerce grande influência na reatividade dos átomos (ou dos íons). A) Explique, em termos de carga nuclear efetiva, a variação apresentada
Química 1. O raio atômico (ou iônico) é uma propriedade periódica que exerce grande influência na reatividade dos átomos (ou dos íons). A) Explique, em termos de carga nuclear efetiva, a variação apresentada
GAAL - 2013/1 - Simulado - 1 Vetores e Produto Escalar
 GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
GAAL - 201/1 - Simulado - 1 Vetores e Produto Escalar SOLUÇÕES Exercício 1: Determinar os três vértices de um triângulo sabendo que os pontos médios de seus lados são M = (5, 0, 2), N = (, 1, ) e P = (4,
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
CAP. I ERROS EM CÁLCULO NUMÉRICO 0. Introdução Por método numérico entende-se um método para calcular a solução de um problema realizando apenas uma sequência finita de operações aritméticas. A obtenção
30 cm, determine o raio da esfera.
 1. (Ufes 015) Enche-se uma fina esfera, feita de vidro transparente, com um líquido, até completar-se exatamente a metade de seu volume. O resto do volume da esfera contém ar (índice de refração n 1).
1. (Ufes 015) Enche-se uma fina esfera, feita de vidro transparente, com um líquido, até completar-se exatamente a metade de seu volume. O resto do volume da esfera contém ar (índice de refração n 1).
Que imagens têm ou não têm simetria?
 O mundo da simetria Que imagens têm ou não têm simetria? Isometrias Isometria: Transformação geométrica que preserva as distâncias; as figuras do plano são transformadas noutras geometricamente iguais.
O mundo da simetria Que imagens têm ou não têm simetria? Isometrias Isometria: Transformação geométrica que preserva as distâncias; as figuras do plano são transformadas noutras geometricamente iguais.
Apostila de Química Geral
 Cursinho Vitoriano UNESP - Universidade Estadual Paulista "Júlio de Mesquita Filho" Câmpus de São José do Rio Preto Apostila de Química Geral Período noturno Ligações químicas interatômicas Vanessa R.
Cursinho Vitoriano UNESP - Universidade Estadual Paulista "Júlio de Mesquita Filho" Câmpus de São José do Rio Preto Apostila de Química Geral Período noturno Ligações químicas interatômicas Vanessa R.
FUNDAMENTOS DE ONDAS, Prof. Emery Lins Curso Eng. Biomédica
 FUNDAMENTOS DE ONDAS, RADIAÇÕES E PARTÍCULAS Prof. Emery Lins Curso Eng. Biomédica Questões... O que é uma onda? E uma radiação? E uma partícula? Como elas se propagam no espaço e nos meios materiais?
FUNDAMENTOS DE ONDAS, RADIAÇÕES E PARTÍCULAS Prof. Emery Lins Curso Eng. Biomédica Questões... O que é uma onda? E uma radiação? E uma partícula? Como elas se propagam no espaço e nos meios materiais?
MÓDULO 6 INTRODUÇÃO À PROBABILIDADE
 MÓDULO 6 INTRODUÇÃO À PROBBILIDDE Quando estudamos algum fenômeno através do método estatístico, na maior parte das vezes é preciso estabelecer uma distinção entre o modelo matemático que construímos para
MÓDULO 6 INTRODUÇÃO À PROBBILIDDE Quando estudamos algum fenômeno através do método estatístico, na maior parte das vezes é preciso estabelecer uma distinção entre o modelo matemático que construímos para
Aula do Curso Noic de Física, feito pela parceria do Noic com o Além do Horizonte
 Espelhos esféricos são superfícies refletoras muito comuns e interessantes de se estudar. Eles são capazes de formar imagens maiores ou menores, inversas ou direitas, dependendo do tipo de espelho, suas
Espelhos esféricos são superfícies refletoras muito comuns e interessantes de se estudar. Eles são capazes de formar imagens maiores ou menores, inversas ou direitas, dependendo do tipo de espelho, suas
ESTUDO DA CINÉTICA DE HIDRÓLISE ÁCIDA DO COMPOSTO Trans-[(Co(en) 2 Cl 2 )Cl]
![ESTUDO DA CINÉTICA DE HIDRÓLISE ÁCIDA DO COMPOSTO Trans-[(Co(en) 2 Cl 2 )Cl] ESTUDO DA CINÉTICA DE HIDRÓLISE ÁCIDA DO COMPOSTO Trans-[(Co(en) 2 Cl 2 )Cl]](/thumbs/26/8060460.jpg) TRABALHO 3 ESTUDO DA CINÉTICA DE HIDRÓLISE ÁCIDA DO COMPOSTO Trans-[(Co(en) 2 Cl 2 )Cl] 1. OBJECTIVO Estudo da cinética da reacção de hidrólise ácida do composto Trans-[Co(en) 2 Cl 2 ]Cl. Determinação
TRABALHO 3 ESTUDO DA CINÉTICA DE HIDRÓLISE ÁCIDA DO COMPOSTO Trans-[(Co(en) 2 Cl 2 )Cl] 1. OBJECTIVO Estudo da cinética da reacção de hidrólise ácida do composto Trans-[Co(en) 2 Cl 2 ]Cl. Determinação
ESTRUTURA DOS MATERIAIS CERÂMICOS
 ESTRUTURA DOS MATERIAIS CERÂMICOS Os sólidos são caracterizados por uma associação muito próxima de átomos, em geral representados por esferas rígidas, em contato uns com os outros e mantidos juntos por
ESTRUTURA DOS MATERIAIS CERÂMICOS Os sólidos são caracterizados por uma associação muito próxima de átomos, em geral representados por esferas rígidas, em contato uns com os outros e mantidos juntos por
Cotagens especiais. Você já aprendeu a interpretar cotas básicas
 A UU L AL A Cotagens especiais Você já aprendeu a interpretar cotas básicas e cotas de alguns tipos de elementos em desenhos técnicos de modelos variados. Mas, há alguns casos especiais de cotagem que
A UU L AL A Cotagens especiais Você já aprendeu a interpretar cotas básicas e cotas de alguns tipos de elementos em desenhos técnicos de modelos variados. Mas, há alguns casos especiais de cotagem que
Correlação e Regressão Linear
 Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
Correlação e Regressão Linear A medida de correlação é o tipo de medida que se usa quando se quer saber se duas variáveis possuem algum tipo de relação, de maneira que quando uma varia a outra varia também.
Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar)
 Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar) 1. OBJETIVOS DA EXPERIÊNCIA 1) Esta aula experimental tem como objetivo o estudo do movimento retilíneo uniforme
Tópico 8. Aula Prática: Movimento retilíneo uniforme e uniformemente variado (Trilho de ar) 1. OBJETIVOS DA EXPERIÊNCIA 1) Esta aula experimental tem como objetivo o estudo do movimento retilíneo uniforme
PARTE 2 FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL
 PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
CÁLCULO DE ZEROS DE FUNÇÕES REAIS
 15 CÁLCULO DE ZEROS DE FUNÇÕES REAIS Um dos problemas que ocorrem mais frequentemente em trabalhos científicos é calcular as raízes de equações da forma: f() = 0. A função f() pode ser um polinômio em
15 CÁLCULO DE ZEROS DE FUNÇÕES REAIS Um dos problemas que ocorrem mais frequentemente em trabalhos científicos é calcular as raízes de equações da forma: f() = 0. A função f() pode ser um polinômio em
Medida da velocidade de embarcações com o Google Earth
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Física Programa de Pós-Graduação em Ensino de Física Mestrado Profissional em Ensino de Física Medida da velocidade de embarcações com o Google Earth
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Física Programa de Pós-Graduação em Ensino de Física Mestrado Profissional em Ensino de Física Medida da velocidade de embarcações com o Google Earth
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
 FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
ESTRUTURA E PROPRIEDADES DOS MATERIAIS ESTRUTURA CRISTALINA
 ESTRUTURA E PROPRIEDADES DOS MATERIAIS ESTRUTURA CRISTALINA Prof. Rubens Caram 1 POR QUE CRISTAL? Antigos gregos: pedaços de quartzo encontrados em regiões frias era um tipo especial de gelo - Krystallos
ESTRUTURA E PROPRIEDADES DOS MATERIAIS ESTRUTURA CRISTALINA Prof. Rubens Caram 1 POR QUE CRISTAL? Antigos gregos: pedaços de quartzo encontrados em regiões frias era um tipo especial de gelo - Krystallos
5/Dez/2012 Aula 21. 21. Polarização das ondas EM 21.1 Por absorção 21.2 Por reflexão 21.3 Por birrefringência 21.4 Equações de Fresnell
 5/Dez/2012 Aula 21 21. Polarização das ondas EM 21.1 Por absorção 21.2 Por reflexão 21.3 Por birrefringência 21.4 Equações de Fresnell 7/Dez/2012 Aula 22 22. Óptica geométrica 22.1 Espelhos planos 22.2
5/Dez/2012 Aula 21 21. Polarização das ondas EM 21.1 Por absorção 21.2 Por reflexão 21.3 Por birrefringência 21.4 Equações de Fresnell 7/Dez/2012 Aula 22 22. Óptica geométrica 22.1 Espelhos planos 22.2
O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:
![O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:](/thumbs/27/10931177.jpg) 4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
FICHA N.º1:Isometrias: Reflexão, rotação e translação ISOMETRIAS
 FICHA N.º1:Isometrias: Reflexão, rotação e translação Matemática 8º Ano Aluno: Data: / /2013 Nº Ano/Turma: 8º ISOMETRIAS Uma ISOMETRIA (iso = igual, metria = medição) é uma transformação geométrica que
FICHA N.º1:Isometrias: Reflexão, rotação e translação Matemática 8º Ano Aluno: Data: / /2013 Nº Ano/Turma: 8º ISOMETRIAS Uma ISOMETRIA (iso = igual, metria = medição) é uma transformação geométrica que
Capítulo UM Bases Numéricas
 Capítulo UM Bases Numéricas 1.1 Introdução Quando o homem aprendeu a contar, ele foi obrigado a desenvolver símbolos que representassem as quantidades e grandezas que ele queria utilizar. Estes símbolos,
Capítulo UM Bases Numéricas 1.1 Introdução Quando o homem aprendeu a contar, ele foi obrigado a desenvolver símbolos que representassem as quantidades e grandezas que ele queria utilizar. Estes símbolos,
O AMPLIFICADOR LOCK-IN
 O AMPLIFICADOR LOCK-IN AUTORES: MARCELO PORTES DE ALBUQUERQUE LEONARDO CORREIA RESENDE JORGE LUÍS GONZALEZ RAFAEL ASTUTO AROUCHE NUNES MAURÍCIO BOCHNER FEVEREIRO 2008 SUMÁRIO RESUMO... 3 1. INTRODUÇÃO...
O AMPLIFICADOR LOCK-IN AUTORES: MARCELO PORTES DE ALBUQUERQUE LEONARDO CORREIA RESENDE JORGE LUÍS GONZALEZ RAFAEL ASTUTO AROUCHE NUNES MAURÍCIO BOCHNER FEVEREIRO 2008 SUMÁRIO RESUMO... 3 1. INTRODUÇÃO...
Como escrever um bom RELATÓRIO
 Como escrever um bom RELATÓRIO Mas o que é uma EXPERIÊNCIA? e um RELATÓRIO? Profa. Ewa W. Cybulska Profa. Márcia R. D. Rodrigues Experiência Relatório Pergunta à Natureza e a procura da Resposta Divulgação
Como escrever um bom RELATÓRIO Mas o que é uma EXPERIÊNCIA? e um RELATÓRIO? Profa. Ewa W. Cybulska Profa. Márcia R. D. Rodrigues Experiência Relatório Pergunta à Natureza e a procura da Resposta Divulgação
Simetria de Figuras Planas e Espaciais
 Simetria de Figuras Planas e Espaciais Introdução A maioria das pessoas acreditam que a simetria está ligada mais a pensamentos sobre Arte e Natureza do que sobre Matemática. De fato, nossas ideias de
Simetria de Figuras Planas e Espaciais Introdução A maioria das pessoas acreditam que a simetria está ligada mais a pensamentos sobre Arte e Natureza do que sobre Matemática. De fato, nossas ideias de
As estações do ano acontecem por causa da inclinação do eixo da Terra em relação ao Sol. O movimento do nosso planeta em torno do Sol, dura um ano.
 PROFESSORA NAIANE As estações do ano acontecem por causa da inclinação do eixo da Terra em relação ao Sol. O movimento do nosso planeta em torno do Sol, dura um ano. A este movimento dá-se o nome de movimento
PROFESSORA NAIANE As estações do ano acontecem por causa da inclinação do eixo da Terra em relação ao Sol. O movimento do nosso planeta em torno do Sol, dura um ano. A este movimento dá-se o nome de movimento
O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem.
 TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
TRIDIMENSIONALIDADE O mundo à nossa volta é povoado de formas as mais variadas tanto nos elementos da natureza como nos de objetos construídos pelo homem. As formas tridimensionais são aquelas que têm
INTERAÇÃO DOS RAIOS-X COM A MATÉRIA
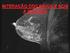 INTERAÇÃO DOS RAIOS-X COM A MATÉRIA RAIOS-X + MATÉRIA CONSEQUÊNCIAS BIOLÓGICAS EFEITOS DAZS RADIAÇÕES NA H2O A molécula da água é a mais abundante em um organismo biológico, a água participa praticamente
INTERAÇÃO DOS RAIOS-X COM A MATÉRIA RAIOS-X + MATÉRIA CONSEQUÊNCIAS BIOLÓGICAS EFEITOS DAZS RADIAÇÕES NA H2O A molécula da água é a mais abundante em um organismo biológico, a água participa praticamente
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
