Prova 3 Matemática. N ọ DE INSCRIÇÃO:
|
|
|
- Luiz Felipe Botelho Caminha
- 7 Há anos
- Visualizações:
Transcrição
1 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta fixada em sua carteira.. Confira se o número do gabarito deste caderno corresponde ao constante na etiqueta fixada em sua carteira. Se houver divergência, avise, imediatamente, o fiscal.. É proibido folhear o Caderno de Provas antes do sinal, às 9 horas. 4. Após o sinal, confira se este caderno contém 0 questões objetivas e/ou qualquer tipo de defeito. Qualquer problema, avise, imediatamente, o fiscal. 5. O tempo mínimo de permanência na sala é de horas após o início da resolução da prova. 6. No tempo destinado a esta prova (4 horas), está incluído o de preenchimento da Folha de Respostas. 7. Transcreva as respostas deste caderno para a Folha de Respostas. A resposta correta será a soma dos números associados às proposições verdadeiras. Para cada questão, preencha sempre dois alvéolos: um na coluna das dezenas e um na coluna das unidades, conforme exemplo ao lado: questão, resposta 09 (soma das proposições 0 e 08). 8. Se desejar, transcreva as respostas deste caderno no para Anotação das Respostas constante nesta prova e destaque-o, para retirá-lo hoje, nesta sala, no horário das h5min às h0min, mediante apresentação do documento de identificação do candidato. Após esse período, não haverá devolução. 9. Ao término da prova, levante o braço e aguarde atendimento. Entregue ao fiscal este caderno, a Folha de Respostas e o para Anotação das Respostas. Corte na linha pontilhada.... RASCUNHO PARA ANOTAÇÃO DAS RESPOSTAS PROVA VERÃO 0 N ọ DE ORDEM: NOME: UEM Comissão Central do Vestibular Unificado GABARITO
2 MATEMÁTICA Questão 0 Considerando dois números complexos, z= + i na forma algébrica e w= (cos θ+ isenθ ) na forma trigonométrica, onde 0 θ< π, assinale o que for correto. 0) z w z = w. 0) Se θ= π, então w= z. 4 04) z = 7 z. 0 08) Se θ= π, então z w z 0. = w 9 9 6) w ( z) ( w) z = w z. Questão 0 Em um triângulo ABC, sejam t a medida do lado AB, u a medida do lado BC, v a medida do lado AC, e seja α a medida do ângulo ABC ˆ, sabendo que t u v, assinale o que for correto. 0) Se v = u, então u < t. u t 0) A área do triângulo ABC é menor ou igual a ut. 04) Se M é o ponto médio do lado AB, e os triângulos AMC e BMC são congruentes, então ABC é um triângulo isósceles. 08) Se α=π/rad, então v = ( t+ u) + tu. 6) Se t + v= u e ABC é acutângulo, então u < 4 t. GABARITO Vestibular de Verão/0 Prova
3 Questão 0 Considere uma sala de aula composta por 48 alunos, sendo meninos e 7 meninas. Na primeira prova de, 5 alunos da sala tiraram nota menor que 6, sendo 8 meninos, e, na primeira prova de Língua Portuguesa, alunos tiraram nota menor que 6, sendo 6 meninas. Dentre esses que tiraram nota inferior a 6, houve ainda alunos que ficaram com nota menor que 6 em ambas as disciplinas. De acordo com os dados fornecidos, assinale o que for correto. 0) A probabilidade de um menino ter tirado nota menor que 6 em ambas as disciplinas é de 5%. 0) Escolhido ao acaso um aluno (menino ou menina), a probabilidade de este ter tirado nota maior ou igual a 6, em ambas as disciplinas, é de 50%. 04) A probabilidade de um menino ter tirado nota maior ou igual a 6 em é. 08) Se os alunos que tiraram nota menor que 6 em ambas as disciplinas são meninos, então a probabilidade de uma menina ter tirado pelo menos uma nota maior ou igual a 6 é de 00%. 6) A probabilidade de uma menina ter tirado nota menor que 6 em é 8. GABARITO Vestibular de Verão/0 Prova
4 Questão 04 Considere uma cidade com população atual de habitantes dos quais 0500 estão com suspeita de infecção pelo vírus da dengue. Esta cidade foi dividida em três regiões: região A com habitantes, região B com 0000 habitantes e região C com o restante dos habitantes. Considere, ainda, as seguintes informações: 0% da população da cidade já estiveram infectados pelo vírus da dengue; na região B, o índice de suspeitas de infecção é 0% superior à média da cidade. Baseando-se nessas informações, assinale o que for correto. 0) O número de pessoas da região B com suspeita de dengue é de, aproximadamente, 4% da população total da cidade. 0) O número total de casos suspeitos de dengue nas regiões A e C é de ) A probabilidade de uma pessoa que já teve dengue estar no grupo dos suspeitos de infecção é menor ou igual a 5%. 08) Se a população da cidade aumenta % ao mês e a taxa de suspeitas de infecção permanece inalterada, então, daqui a três meses, o número de pessoas com suspeita de infecção será maior que ) Se 5% da população da cidade é de crianças e 5% de pessoas têm mais de 50 anos, a probabilidade de uma pessoa desses dois grupos estar no grupo suspeito de infecção é de 0%. Questão 05 Duas matrizes quadradas A e B, de mesma ordem, são semelhantes, se existir uma matriz C, possuindo a mesma ordem de A e B, de determinante não-nulo, tal que A = C BC. Com relação a matrizes semelhantes, é correto afirmar que 0) matrizes com determinantes distintos podem ser semelhantes. 0) a matriz identidade de ordem n n só é semelhante a si mesma. 04) se A é semelhante a B, então, necessariamente, A é semelhante a B. 08) se C 0 = e B = 0, então C BC = 0. 6) se A é semelhante a B, então, A é semelhante a B. GABARITO Vestibular de Verão/0 Prova 4
5 Questão 06 Um número natural é chamado quadrado perfeito, se ele for o quadrado de algum número natural. Sabendo disso, assinale o que for correto. 0) Existem quadrados perfeitos cuja diferença é 70. 0) Todo quadrado perfeito que é múltiplo de 7 é múltiplo de ) A multiplicação de um quadrado perfeito por outro quadrado perfeito é sempre um quadrado perfeito. 08) O resultado da soma de quadrados perfeitos é sempre um quadrado perfeito 6) 0570 é um quadrado perfeito. Questão 07 Uma pirâmide ABCDE possui base quadrada ABCD e o vértice E é equidistante dos demais vértices. Seja O a interseção das diagonais do quadrado ABCD, assinale o que for correto. 0) Todas as faces triangulares dessa pirâmide são triângulos isósceles. 0) Se o comprimento do segmento OE é igual ao comprimento do segmento OA, todas as arestas da pirâmide possuem o mesmo comprimento. 5 04) Se o comprimento de OE é vezes o comprimento do lado do quadrado ABCD, a área da face triangular ABE é maior do que a área de ABCD. 08) Se dobrar-se a medida do lado do quadrado e reduzirse pela metade a medida da altura relativa à base quadrada, o volume da pirâmide permanecerá constante. 6) Se o volume da pirâmide, em centímetros cúbicos, é numericamente igual à área do quadrado ABCD, em centímetros quadrados, a altura da pirâmide é cm. GABARITO Vestibular de Verão/0 Prova 5
6 Questão 08 Considerando o seguinte polinômio px ( ) = ( ax + x+ )( bx+ c), em que abc,, são números reais e b 0 em relação à equação polinomial px ( ) = 0, assinale o que for correto. 0) Se c = 0 e a >, então a equação tem duas raízes 8 não reais. 0) A equação tem pelo menos uma raiz real. 04) Se a 0, então a equação terá todas as raízes reais. 08) Se a= b=, então as raízes da equação são: x = + i 7, x = i 7 e x = c. 6) Se a= b= c=, então a equação terá três raízes distintas. Questão 09 João e Pedro decidiram treinar para competir na Corrida de São Silvestre, mas cada um está fazendo um treinamento diferente: João está correndo 40 minutos por dia e consegue percorrer uma distância de 6 km em cada dia; já Pedro está correndo 0 minutos por dia, do seguinte modo: no primeiro dia, ele percorreu uma distância de km, no segundo dia percorreu,5 km, no terceiro dia percorreu 4 km, assim sucessivamente até o décimo quinto dia, e reinicia o processo percorrendo, novamente km. Com essas informações, assinale o que for correto. 0) A sequência numérica formada pelas velocidades médias de Pedro, nos quinze primeiros dias de treinamento, forma uma progressão geométrica. 0) No quarto dia, a velocidade média que Pedro correu foi igual à velocidade média que João correu. 04) No décimo dia, Pedro percorreu a distância de 7,5 km. 08) A distância total percorrida por Pedro, desde o primeiro até o décimo terceiro dia, foi a mesma percorrida por João no mesmo período. 6) A diferença entre as distâncias totais percorridas por Pedro e João, nos quinze primeiros dias de treinamento, é maior que 0 km. GABARITO Vestibular de Verão/0 Prova 6
7 Questão 0 Considere as funções f e g, ambas com domínio e contradomínio real, dadas por f( x) = 5x e g( x) = x 6x+, para qualquer x real. A respeito dessas funções, assinale o que for correto. 0) A imagem de qualquer número racional, pela função f, é um número irracional. 0) A função g possui uma única raiz real. 04) Ambas as funções são crescentes no intervalo [0, + [ do domínio. 08) O gráfico da função f g é uma parábola. 6) Ambas as funções possuem inversas. Questão O lucro de uma empresa em um período de 5 meses foi modelado matematicamente por meio da seguinte função f ( x) = ax + bx+ c, em que a variável x indica o mês e f ( x ) o lucro, em milhões de reais, obtido no mês x. Sabe-se que no início desse período, digamos mês zero, a empresa tinha um lucro de milhões de reais; no primeiro mês, o lucro foi de milhões de reais; e, no décimo quinto mês, o lucro foi de 7 milhões de reais. Com base nessas informações, assinale o que for correto. 0) O lucro obtido no décimo quarto mês foi igual ao lucro obtido no oitavo mês. 0) O lucro máximo foi obtido no décimo mês. 04) O lucro máximo obtido foi superior a 7,5 milhões de reais. 08) O lucro da empresa nesse período de 5 meses oscilou de a 7 milhões de reais. 6) O gráfico da função que modela o lucro é uma parábola com concavidade para baixo. GABARITO Vestibular de Verão/0 Prova 7
8 Questão Sabendo que r, s e t são três retas no espaço tridimensional com r e s paralelas distintas, assinale o que for correto. 0) Se a reta r é perpendicular a um plano α, então a reta s também é perpendicular ao plano α. 0) Se a reta t é concorrente com a reta s, então t também é concorrente com a reta r. 04) Se um plano β contém a reta s, então o plano β também contém a reta r. 08) Se a reta t é perpendicular à reta r, então t é perpendicular ou ortogonal à reta s. 6) Se as três retas r, s e t são paralelas distintas, então existe um plano α que contém as três retas. Questão Um determinado funil de plástico tem a forma de um tronco de cone cujas circunferências dos furos que o delimitam possuem raios cm e 0,5 cm, e a altura do funil é de 6 cm. Considerando essas informações, e desprezando a espessura do funil, assinale o que for correto. 0) O volume (capacidade) do funil é maior do que 0 cm. 0) A área lateral do funil é superior a 60 cm. 04) Se o funil estiver em posição vertical, com o furo menor voltado para baixo e tampado, para encher o funil até metade da altura com água, serão necessários menos de 0 cm de água. 08) Se o funil foi obtido de um cone, removendo-se sua ponta, a altura do cone original era de 0 cm. 6) A razão entre as áreas respectivas do círculo maior e menor que formam os furos do funil é igual a 8. GABARITO Vestibular de Verão/0 Prova 8
9 Questão 4 Considere a seguinte função f( x) = 4 x x cujo domínio é conjunto dos números reais. Com relação a essa função, assinale o que for correto. 0) O mínimo da função f ocorre em x = 0. 0) O conjunto solução da inequação f( x ) < é S = { x < x< }. 04) Para x = 0, tem-se log f( x ) =. 08) O conjunto solução da inequação f( x ) > 8 é S = { x x< ou x> + } ) log f () não existe. Questão 5 Sejam A, B e C os vértices de um triângulo retângulo, sendo  o ângulo reto e AC medindo o triplo de AB. Considererando agora os pontos D e E no segmento AC, de modo que AD= DE = EC, e F sendo o ponto médio do segmento BC, assinale o que for correto. 0 0) cos( B ˆ) =. 0 0) Os triângulos BDC e FEC são congruentes. 04) sen( BDC ˆ ) =. 08) Os triângulos EDF e BDF são semelhantes. 5 6) cos( EFC ˆ ) =. 5 GABARITO Vestibular de Verão/0 Prova 9
10 Questão 6 Em um sistema ortogonal de coordenadas cartesianas xoy, considere três retas: r a reta que contém os pontos (,0) e (0,); r dada por sua equação na forma segmentária x y = ; e r 4 4 : α x+ y 4= 0, em que α é algum número real. Em relação ao exposto, assinale o que for correto. 0) Se α= 8, então as três retas se interceptam em um mesmo ponto. 0) As retas r e r são perpendiculares. 04) Se α=, então a área do triângulo formado pelas intersecções das retas, duas a duas, é ua... 08) Não existe número real α de modo que as retas r e r sejam paralelas. 6) Para α=, o ângulo agudo entre as retas r e r é de 75. Questão 7 Uma empresa embala quatro tipos de produtos: ABC,, e D. Cada um desses produtos tem um prazo de validade diferente do outro, obedecendo às seguintes relações: o produto B tem um prazo de validade maior que o prazo de validade do produto C ; o prazo de validade do produto D é 7 do prazo de validade do produto ; 0 A o prazo de validade do produto C é do prazo de 5 validade do produto A. Entenda-se como prazo de validade o número de dias entre a data na qual o produto foi embalado e a data máxima para a sua utilização. Com base nessas informações, assinale o que for correto. 0) Se o produto C tem prazo de validade de 60 dias, então o prazo de validade do produto A é de 00 dias. 0) O prazo de validade do produto D é menor que o prazo de validade do produto C. 04) O produto A é o que possui maior prazo de validade dentre os quatro produtos. 08) A soma dos prazos de validade dos produtos A e C é maior que soma dos prazos de validade dos produtos B e D. 6) Se o produto B tem prazo de validade de 80 dias, então o produto D tem prazo de validade de 75 dias. GABARITO Vestibular de Verão/0 Prova 0
11 Questão 8 Sobre uma circunferência com raio de 6 cm, marcam-se os pontos A, B e C, equidistantes entre si, e um ponto D diferente dos anteriores. Sobre essa situação, é correto afirmar que 0) a área do triângulo ABC supera metade da área do círculo delimitado pela circunferência na qual ele está inscrito. 0) o triângulo ABD possui, necessariamente, área menor do que a do triângulo ABC. 04) o triângulo ABC é isósceles. 08) se o triângulo ABD é isósceles seu maior lado é o lado AB. 6) a área da circunferência é menor do que 00 cm. Questão 9 Em um sistema ortogonal de coordenadas cartesianas xoy, considere uma circunferência λ de centro C (,) que contém a origem O do sistema de coordenadas e seja A o outro ponto de intersecção de λ com o eixo Oy. Agora, considere um circunferência λ com centro na origem O, cujo raio é o dobro do raio de λ e sejam B e D os pontos de intersecção de λ com o eixo Ox. Considerando que π,4 e,4 e as informações expostas, assinale o que for correto. 0) A área limitada pela circunferência λ é o dobro da área limitada pela circunferência λ. 0) As circunferências λ são tangentes no ponto λ e E (,). 04) A área do triângulo ABD é maior do que a área limitada pela circunferência λ. 08) A equação geral (ou normal) da circunferência λ é x + y x y = 0. 6) As áreas dos triângulos COB e COD são iguais. GABARITO Vestibular de Verão/0 Prova
12 Questão 0 É cada vez mais comum, em propagandas veiculadas em revistas e outras mídias, o uso de códigos QR. Um código QR é uma espécie de código de barras bidimensional, que é utilizado para armazenar informações diversas. Após codificada, a informação é armazenada sob a forma de um mosaico quadrado quadriculado formado por quadradinhos brancos e pretos, cuja dimensão (número de quadradinhos em cada linha e coluna) depende do tamanho da informação a ser armazenada. Levando-se em consideração as informações fornecidas e supondo que qualquer coloração dos quadrados do mosaico pelas cores preta ou branca forneça um código QR válido, e seus conhecimentos matemáticos, assinale o que for correto. 0) É possível construir exatamente 00 códigos QR de dimensão distintos. 0) O número de códigos QR de dimensão 7 7 que possuem os quatro quadradinhos dos quais um vértice é um vértice do mosaico, coloridos com a mesma cor (preta ou branca) corresponde exatamente a /8 do total de mosaicos possíveis. 04) Se em um mosaico QR 0 0, 70% dos quadradinhos são brancos e 0% são pretos, a probabilidade de, escolhendo-se ao acaso dois quadradinhos distintos, escolher dois da mesma cor é inferior a 70%. 08) Se as cores dos quadradinhos de dois mosaicos QR 0 0 coincidem em exatamente 40% dos quadradinhos e 60% dos quadradinhos cuja cor coincide em ambos os mosaicos possuem a cor branca, os quadradinhos pretos coincidentes em ambos os mosaicos representam 6% dos quadradinhos de um mosaico. 6) Só é possível construir, no máximo, dois mosaicos distintos, de mesma dimensão, de modo que quaisquer dois quadrados com um lado em comum possuam cores distintas. GABARITO Vestibular de Verão/0 Prova
13 MATEMÁTICA Formulário Trigonometria sen(x ± y) = sen(x)cos(y) ± sen(y)cos(x) cos(x ± y) = cos(x)cos(y) sen(x)sen(y) tg(x) ± tg(y) tg(x ± y) = tg(x)tg(y) B c ˆB A Â a b Ĉ C Lei dos senos: a = b = sen(â) sen(bˆ ) Lei dos cossenos: c sen(ĉ) a = b + c bc cos(â) Análise Combinatória P n = n! A n, r = n! (n r)! C n, r = n! (n r)!r! n n n (a + b) = Cn, a i b i i i= 0 Geometria Plana e Espacial Comprimento da circunferência: C= π R d D Área do losango: A= Área do trapézio: Área do círculo: A = πr (b + B)h A= Área lateral do cilindro: A = πrh Área do setor circular: Área lateral do cone: A A = R α =π RG Área da superfície esférica: A = 4πR Volume do paralelepípedo: V=B.h Volume do cubo: V = a Volume do prisma: V = B h B h Volume da pirâmide: V= Volume do cilindro: V = πr h Volume do cone: R V = π h Volume da esfera: V = 4 πr Área total do tetraedro regular: A= a Progressões Geometria Analítica Conversão de unidades Progressão Aritmética (P. A.): an = a + (n )r (a a )n S + = n n Ponto Médio do segmento de extremidades A( x, y ) e B (x, y ): x + x y + y M, Área do triângulo de vértices P(x, y ), Q(x, y ) e R(x, y ) : A = D, onde m = 000 l x D = x x y y y Progressão Geométrica (P. G.): a = a qn n Distância de um ponto a a qn S n = q, q a S =, q < q d = P,r P(x, y ) à reta r: ax + by + c = 0 : 0 0 ax 0 + by 0 + c a + b GABARITO Vestibular de Verão/0 Prova
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
PROVA 3 conhecimentos específicos
 PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA 3 conhecimentos específicos
 PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA 3 conhecimentos específicos
 PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA 3 conhecimentos específicos
 PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
PROVA conhecimentos específicos MATEMÁTICA QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Central do Vestibular Unificado GABARITO
... GABARITO 4 NOME DO CANDIDATO: UEM Comissão Central do Vestibular Unificado
 CADERNO DE QUESTÕES -- PAS--UEM//0 -- ETAPA N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam
CADERNO DE QUESTÕES -- PAS--UEM//0 -- ETAPA N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
... GABARITO 1 NOME DO CANDIDATO: UEM Comissão Central do Vestibular Unificado
 CADERNO DE QUESTÕES -- PAS--UEM//01 -- ETAPA N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam
CADERNO DE QUESTÕES -- PAS--UEM//01 -- ETAPA N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
... GABARITO 2 NOME DO CANDIDATO: UEM Comissão Central do Vestibular Unificado
 N ọ DE ORDEM: NOME DO CANDIDATO: CADERNO DE QUESTÕES N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta fixada
N ọ DE ORDEM: NOME DO CANDIDATO: CADERNO DE QUESTÕES N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta fixada
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Vestibular de Inverno Prova 3 Matemática
 Vestibular de Inverno Prova N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME DO CANDIDATO, que constam na
Vestibular de Inverno Prova N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME DO CANDIDATO, que constam na
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova Matemática QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que
Prova Matemática QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova Matemática QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que
Prova Matemática QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova 3 Matemática. N ọ DE INSCRIÇÃO:
 Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Prova QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, conforme o que consta na etiqueta
Vestibular de Verão Prova 3 Matemática
 Vestibular de Verão Prova N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME DO CANDIDATO, que constam na etiqueta
Vestibular de Verão Prova N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME DO CANDIDATO, que constam na etiqueta
Prova Objetiva - Matemática
 Prova Objetiva - Matemática CADERNO DE QUESTÕES -- VESTIIBULAR EAD 013 N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ
Prova Objetiva - Matemática CADERNO DE QUESTÕES -- VESTIIBULAR EAD 013 N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES I PARA A REALIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ
Prova 3 Matemática ... RASCUNHO PARA ANOTAÇÃO DAS RESPOSTAS PROVA 3 INVERNO 2018 GABARITO 1 INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA NOME DO CANDIDATO:
 Vestibular de Inverno 08 Prova N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME DO CANDIDATO, que constam
Vestibular de Inverno 08 Prova N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME DO CANDIDATO, que constam
TD GERAL DE MATEMÁTICA 2ª FASE UECE
 Fundação Universidade Estadual do Ceará - FUNECE Curso Pré-Vestibular - UECEVest Fones: 3101.9658 / E-mail: uecevest_itaperi@yahoo.com.br Av. Dr. Silas Munguba, 1700 Campus do Itaperi 60714-903 Fone: 3101-9658/Site:
Fundação Universidade Estadual do Ceará - FUNECE Curso Pré-Vestibular - UECEVest Fones: 3101.9658 / E-mail: uecevest_itaperi@yahoo.com.br Av. Dr. Silas Munguba, 1700 Campus do Itaperi 60714-903 Fone: 3101-9658/Site:
Prova 3 - Matemática
 Prova 3 - QUESTÕES OBJETIIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME DO CANDIDATO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta
Prova 3 - QUESTÕES OBJETIIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME DO CANDIDATO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta
Teste de Avaliação. Nome N. o Turma Data /mar./2019. Avaliação E. Educação Professor. Duração (Caderno 1 + Caderno 2): 90 minutos. MATEMÁTICA 9.
 Teste de Avaliação Nome N. o Turma Data /mar./2019 Avaliação E. Educação Professor MATEMÁTICA 9. o ANO Duração (Caderno 1 + Caderno 2): 90 minutos O teste é constituído por dois cadernos (Caderno 1 e Caderno
Teste de Avaliação Nome N. o Turma Data /mar./2019 Avaliação E. Educação Professor MATEMÁTICA 9. o ANO Duração (Caderno 1 + Caderno 2): 90 minutos O teste é constituído por dois cadernos (Caderno 1 e Caderno
NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.
![NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo. NOTAÇÕES. R N C i z. ]a, b[ = {x R : a < x < b} (f g)(x) = f(g(x)) n. = a 0 + a 1 + a a n, sendo n inteiro não negativo.](/thumbs/74/70891793.jpg) R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
R N C i z det A d(a, B) d(p, r) AB Â NOTAÇÕES : conjunto dos números reais : conjunto dos números naturais : conjunto dos números complexos : unidade imaginária: i = 1 : módulo do número z C : determinante
Prova 3 - Matemática
 Prova 3 - QUESTÕES OBJETIIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME DO CANDIDATO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta
Prova 3 - QUESTÕES OBJETIIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME DO CANDIDATO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta
Prova 3 - Matemática
 Prova 3 - QUESTÕES OBJETIIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME DO CANDIDATO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta
Prova 3 - QUESTÕES OBJETIIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME DO CANDIDATO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam na etiqueta
NOTAÇÕES. R : conjunto dos números reais C : conjunto dos números complexos
 NOTAÇÕES R : conjunto dos números reais C : conjunto dos números complexos i : unidade imaginária: i = 1 z : módulo do número z C Re(z) : parte real do número z C Im(z) : parte imaginária do número z C
NOTAÇÕES R : conjunto dos números reais C : conjunto dos números complexos i : unidade imaginária: i = 1 z : módulo do número z C Re(z) : parte real do número z C Im(z) : parte imaginária do número z C
UPE/VESTIBULAR/2002 MATEMÁTICA
 UPE/VESTIBULAR/00 MATEMÁTICA 01 Os amigos Neto, Maria Eduarda, Daniela e Marcela receberam um prêmio de R$ 1000,00, que deve ser dividido, entre eles, em partes inversamente proporcionais às respectivas
UPE/VESTIBULAR/00 MATEMÁTICA 01 Os amigos Neto, Maria Eduarda, Daniela e Marcela receberam um prêmio de R$ 1000,00, que deve ser dividido, entre eles, em partes inversamente proporcionais às respectivas
1 35. b) c) d) 8. 2x 1 8x 4. 3x 3 8x 8. 4 tgα ˆ MAN é igual a 4. . e) Sendo x a medida do segmento CN, temos a seguinte figura:
 7. Considere um retângulo ABCD em que o comprimento do lado AB é o dobro do comprimento do lado BC. Sejam M o ponto médio de BC e N o ponto médio de CM. A tangente do ângulo MAN ˆ é igual a a) 5. b) 5.
7. Considere um retângulo ABCD em que o comprimento do lado AB é o dobro do comprimento do lado BC. Sejam M o ponto médio de BC e N o ponto médio de CM. A tangente do ângulo MAN ˆ é igual a a) 5. b) 5.
MATEMÁTICA SARGENTO DA FAB
 MATEMÁTICA BRUNA PAULA 1 COLETÂNEA DE QUESTÕES DE MATEMÁTICA DA EEAr (QUESTÕES RESOLVIDAS) QUESTÃO 1 (EEAr 2013) Se x é um arco do 1º quadrante, com sen x a e cosx b, então é RESPOSTA: d QUESTÃO 2 (EEAr
MATEMÁTICA BRUNA PAULA 1 COLETÂNEA DE QUESTÕES DE MATEMÁTICA DA EEAr (QUESTÕES RESOLVIDAS) QUESTÃO 1 (EEAr 2013) Se x é um arco do 1º quadrante, com sen x a e cosx b, então é RESPOSTA: d QUESTÃO 2 (EEAr
Prova Final de Matemática a Nível de Escola Prova 82/1ª Fase 2018 Caderno Único: Página 1/9
 Prova Final de Matemática a Nível de Escola 3º Ciclo do Ensino Básico Decreto-Lei nº139/01, de 5 de julho Prova 8/1ª Fase 9 Páginas Duração da Prova (CADERNO ÚNICO): 90 minutos. Tolerância: 30 minutos.
Prova Final de Matemática a Nível de Escola 3º Ciclo do Ensino Básico Decreto-Lei nº139/01, de 5 de julho Prova 8/1ª Fase 9 Páginas Duração da Prova (CADERNO ÚNICO): 90 minutos. Tolerância: 30 minutos.
As cotações dos itens de cada caderno encontram-se no final do respetivo caderno.
 Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
REVISÃO UNIOESTE 2016 MATEMÁTICA GUSTAVO
 REVISÃO UNIOESTE 01 MATEMÁTICA GUSTAVO 1 Considere a figura: Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de metros de lado, conforme a figura
REVISÃO UNIOESTE 01 MATEMÁTICA GUSTAVO 1 Considere a figura: Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas quadradas de metros de lado, conforme a figura
Caderno 1: (É permitido o uso de calculadora.) Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado.
 Nome: Ano / Turma: N.º: Data: - - Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Nome: Ano / Turma: N.º: Data: - - Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou
O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta.
 Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Escola Naval 2010 ( ) ( ) 8 ( ) 4 ( ) 4 (
 Escola Naval 0 1. (EN 0) Os gráficos das funções reais f e g de variável real, definidas por f(x) = x e g(x) = 5 x interceptam-se nos pontos A = (a,f(a)) e B = (b,f(b)), a b. Considere os polígonos CAPBD
Escola Naval 0 1. (EN 0) Os gráficos das funções reais f e g de variável real, definidas por f(x) = x e g(x) = 5 x interceptam-se nos pontos A = (a,f(a)) e B = (b,f(b)), a b. Considere os polígonos CAPBD
n! (n r)!r! P(A/B) = 1 q, 0 < q < 1
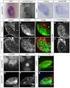 FORMULÁRIO DE MATEMÁTICA Análise Combinatória P n = n! = n A n,r = n! (n r)! Probabilidade número de resultados favoráveis a A P(A) = número de resultados possíveis Progressões aritméticas a n = a +(n
FORMULÁRIO DE MATEMÁTICA Análise Combinatória P n = n! = n A n,r = n! (n r)! Probabilidade número de resultados favoráveis a A P(A) = número de resultados possíveis Progressões aritméticas a n = a +(n
1. A imagem da função real f definida por f(x) = é a) R {1} b) R {2} c) R {-1} d) R {-2}
 1. A imagem da função real f definida por f(x) = é R {1} R {2} R {-1} R {-2} 2. Dadas f e g, duas funções reais definidas por f(x) = x 3 x e g(x) = sen x, pode-se afirmar que a expressão de (f o g)(x)
1. A imagem da função real f definida por f(x) = é R {1} R {2} R {-1} R {-2} 2. Dadas f e g, duas funções reais definidas por f(x) = x 3 x e g(x) = sen x, pode-se afirmar que a expressão de (f o g)(x)
a) 6% b) 7% c) 70% d) 600% e) 700%
 - MATEMÁTICA 01) Supondo-se que o número de vagas em um concurso vestibular aumentou 5% e que o número de candidatos aumentou 35%, o número de candidatos por vaga para esse curso aumentou: a) 8% b) 9%
- MATEMÁTICA 01) Supondo-se que o número de vagas em um concurso vestibular aumentou 5% e que o número de candidatos aumentou 35%, o número de candidatos por vaga para esse curso aumentou: a) 8% b) 9%
Caderno 1: (É permitido o uso de calculadora.) Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado.
 Proposta de Resolução [dezembro - 017] Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul
Proposta de Resolução [dezembro - 017] Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul
Prova Vestibular ITA 2000
 Prova Vestibular ITA Versão. ITA - (ITA ) Sejam f, g : R R definidas por f ( ) = e g cos 5 ( ) =. Podemos afirmar que: f é injetora e par e g é ímpar. g é sobrejetora e f é bijetora e g é par e f é ímpar
Prova Vestibular ITA Versão. ITA - (ITA ) Sejam f, g : R R definidas por f ( ) = e g cos 5 ( ) =. Podemos afirmar que: f é injetora e par e g é ímpar. g é sobrejetora e f é bijetora e g é par e f é ímpar
04) 4 05) 2. ˆ B determinam o arco, portanto são congruentes, 200π 04)
 RESOLUÇÃO DA PROVA FINAL DE MATEMÁTICA - ANO 007 a SÉRIE DO E.M. _ COLÉGIO ANCHIETA BA ELABORAÇÃO: PROF. OCTAMAR MARQUES. PROFA. MARIA ANTÔNIA GOUVEIA. QUESTÃO 0) Na figura, o raio do círculo é igual a
RESOLUÇÃO DA PROVA FINAL DE MATEMÁTICA - ANO 007 a SÉRIE DO E.M. _ COLÉGIO ANCHIETA BA ELABORAÇÃO: PROF. OCTAMAR MARQUES. PROFA. MARIA ANTÔNIA GOUVEIA. QUESTÃO 0) Na figura, o raio do círculo é igual a
Caderno 1: (É permitido o uso de calculadora.) Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado.
 Proposta de Resolução [maio - 018] Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Proposta de Resolução [maio - 018] Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Proposta de Prova Final de Matemática
 Proposta de Prova Final de Matemática 3. o Ciclo do Ensino Básico Duração da Prova (CADERNO 1 + CADERNO ): 90 minutos Tolerância: 30 minutos Data: Caderno 1: 35 minutos. Tolerância: 10 minutos (é permitido
Proposta de Prova Final de Matemática 3. o Ciclo do Ensino Básico Duração da Prova (CADERNO 1 + CADERNO ): 90 minutos Tolerância: 30 minutos Data: Caderno 1: 35 minutos. Tolerância: 10 minutos (é permitido
INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA
 Prova 3 Matemática QUESTÕES DISCURSIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA. Verifique se este caderno contém 05 questões discursivas e/ou qualquer tipo de defeito.
Prova 3 Matemática QUESTÕES DISCURSIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA. Verifique se este caderno contém 05 questões discursivas e/ou qualquer tipo de defeito.
A Matemática no Vestibular do ITA. Material Complementar: Coletânea de Questões Isoladas ITA 1970
 A Matemática no Vestibular do ITA Material Complementar: Coletânea de Questões Isoladas ITA 1970 Essas 24 questões foram coletadas isoladamente em diversas fontes bibliográficas. Seguindo sugestão de uma
A Matemática no Vestibular do ITA Material Complementar: Coletânea de Questões Isoladas ITA 1970 Essas 24 questões foram coletadas isoladamente em diversas fontes bibliográficas. Seguindo sugestão de uma
As cotações dos itens de cada caderno encontram-se no final do respetivo caderno.
 Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Nome: Ano / Turma: N.º: Data: - - O teste é constituído por dois cadernos (Caderno 1 e Caderno 2). Utiliza apenas caneta ou esferográfica, de tinta azul ou preta. É permitido o uso de calculadora no Caderno
Provas de Acesso ao Ensino Superior Para Maiores de 23 Anos
 Provas de Acesso ao Ensino Superior Para Maiores de 23 Anos Candidatura de 207 EXAME DE MATEMÁTICA Tempo para realização da prova: 2 horas Tolerância: 30 minutos Material admitido: material de escrita
Provas de Acesso ao Ensino Superior Para Maiores de 23 Anos Candidatura de 207 EXAME DE MATEMÁTICA Tempo para realização da prova: 2 horas Tolerância: 30 minutos Material admitido: material de escrita
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE
 EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
EXERCÍCIOS DE REVISÃO ENSINO MÉDIO 4º. BIMESTRE 1ª. SÉRIE Exercícios de PA e PG 1. Determinar o 61º termo da PA ( 9,13,17,21,...) Resp. 249 2. Determinar a razão da PA ( a 1,a 2, a 3,...) em que o primeiro
{ } Questão 1. Considere as seguintes afirmações sobre o conjunto U = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Questão 2. Seja o conjunto = { : 0 e 2 2
 NOTAÇÕES : conjunto dos números complexos. : conjunto dos números racionais. : conjunto dos números reais. : conjunto dos números inteiros. = 0,,,,.... { } { } * =,,,.... i : unidade imaginária; i =. z=x+iy,
NOTAÇÕES : conjunto dos números complexos. : conjunto dos números racionais. : conjunto dos números reais. : conjunto dos números inteiros. = 0,,,,.... { } { } * =,,,.... i : unidade imaginária; i =. z=x+iy,
Questão 03 Sejam os conjuntos: A) No conjunto A B C, existem 5 elementos que são números inteiros.
 Questão 0 Dada a proposição: Se um quadrilátero é um retângulo então suas diagonais cortam-se ao meio, podemos afirmar que: A) Se um quadrilátero tem as diagonais cortando-se ao meio então ele é um retângulo.
Questão 0 Dada a proposição: Se um quadrilátero é um retângulo então suas diagonais cortam-se ao meio, podemos afirmar que: A) Se um quadrilátero tem as diagonais cortando-se ao meio então ele é um retângulo.
NOTAÇÕES. Obs.: São cartesianos ortogonais os sistemas de coordenadas considerados
 ITA006 NOTAÇÕES : conjunto dos números complexos : conjunto dos números racionais i: unidade imaginária; i z = x+ iy, x, y = 1 : conjunto dos números reais : conjunto dos números inteiros = {0, 1,, 3,...
ITA006 NOTAÇÕES : conjunto dos números complexos : conjunto dos números racionais i: unidade imaginária; i z = x+ iy, x, y = 1 : conjunto dos números reais : conjunto dos números inteiros = {0, 1,, 3,...
Novo Espaço Matemática A 11.º ano Proposta de Teste Intermédio [janeiro 2015]
![Novo Espaço Matemática A 11.º ano Proposta de Teste Intermédio [janeiro 2015] Novo Espaço Matemática A 11.º ano Proposta de Teste Intermédio [janeiro 2015]](/thumbs/82/85114770.jpg) Proposta de Teste Intermédio [janeiro 015] Nome: Ano / Turma: N.º: Data: - - GRUPO I Na resposta a cada um dos itens deste grupo, seleciona a única opção correta. Escreve, na folha de respostas: o número
Proposta de Teste Intermédio [janeiro 015] Nome: Ano / Turma: N.º: Data: - - GRUPO I Na resposta a cada um dos itens deste grupo, seleciona a única opção correta. Escreve, na folha de respostas: o número
Caderno 1: 35 minutos. Tolerância: 10 minutos. (é permitido o uso de calculadora)
 Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/1.ª Fase Caderno 1: 7 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/1.ª Fase Caderno 1: 7 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
RaizDoito. 1. Num referencial o.m. do plano, considere a reta r de equação x = -5.
 1. Num referencial o.m. do plano, considere a reta r de equação x = -5. Qual dos seguintes pares de pontos define uma reta perpendicular à reta r? (A) (B) ( C) (D) 2. A condição que define o domínio plano
1. Num referencial o.m. do plano, considere a reta r de equação x = -5. Qual dos seguintes pares de pontos define uma reta perpendicular à reta r? (A) (B) ( C) (D) 2. A condição que define o domínio plano
BANCO DE QUESTÕES MATEMÁTICA A 11. O ANO
 BANCO DE QUESTÕES MATEMÁTICA A 11. O ANO DOMÍNIO: Trigonometria e funções trigonométricas 1. Considera o triângulo PQR e as medidas apresentadas na figura ao lado. O comprimento do lado QR é: (A) 4 (C)
BANCO DE QUESTÕES MATEMÁTICA A 11. O ANO DOMÍNIO: Trigonometria e funções trigonométricas 1. Considera o triângulo PQR e as medidas apresentadas na figura ao lado. O comprimento do lado QR é: (A) 4 (C)
Universidade Federal dos Vales do Jequitinhonha e Mucuri.
 INSTRUÇÕES Ministério da Educação Universidade Federal dos Vales do Jequitinhonha e Mucuri Pró-Reitoria de Pesquisa e Pós-Graduação Diretoria de Educação Aberta e a Distância Especialização em Matemática
INSTRUÇÕES Ministério da Educação Universidade Federal dos Vales do Jequitinhonha e Mucuri Pró-Reitoria de Pesquisa e Pós-Graduação Diretoria de Educação Aberta e a Distância Especialização em Matemática
2 Uma caixa d'água cúbica, de volume máximo, deve ser colocada entre o telhado e a laje de uma casa, conforme mostra a figura ao lado.
 MATEMÁTICA Uma pessoa possui a quantia de R$7.560,00 para comprar um terreno, cujo preço é de R$5,00 por metro quadrado. Considerando que os custos para obter a documentação do imóvel oneram o comprador
MATEMÁTICA Uma pessoa possui a quantia de R$7.560,00 para comprar um terreno, cujo preço é de R$5,00 por metro quadrado. Considerando que os custos para obter a documentação do imóvel oneram o comprador
Caderno 1: (É permitido o uso de calculadora.) Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado.
 Nome: Ano / Turma: N.º: Data: - - Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Nome: Ano / Turma: N.º: Data: - - Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Caderno 1: 35 minutos. Tolerância: 10 minutos. É permitido o uso de calculadora.
 Prova Final de Matemática Prova 92 1.ª Fase 3.º Ciclo do Ensino Básico 2017 Decreto-Lei n.º 139/2012, de 5 de julho Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30 minutos. Caderno
Prova Final de Matemática Prova 92 1.ª Fase 3.º Ciclo do Ensino Básico 2017 Decreto-Lei n.º 139/2012, de 5 de julho Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30 minutos. Caderno
Prova Vestibular ITA 1995
 Prova Vestibular ITA 1995 Versão 1.0 ITA - 1995 01) (ITA-95) Seja A = n ( 1) n!. π + sen ; n ℵ n! 6 a) (- 1) n n. b) n. c) (- 1) n n. d) (- 1) n+1 n. e) (- 1) n+1 n. Qual conjunto abaixo é tal que sua
Prova Vestibular ITA 1995 Versão 1.0 ITA - 1995 01) (ITA-95) Seja A = n ( 1) n!. π + sen ; n ℵ n! 6 a) (- 1) n n. b) n. c) (- 1) n n. d) (- 1) n+1 n. e) (- 1) n+1 n. Qual conjunto abaixo é tal que sua
Caderno 1: 35 minutos. Tolerância: 10 minutos. É permitido o uso de calculadora.
 Prova Final de Matemática Prova 92 1.ª Fase 3.º Ciclo do Ensino Básico 2017 Decreto-Lei n.º 139/2012, de 5 de julho Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30 minutos. Caderno
Prova Final de Matemática Prova 92 1.ª Fase 3.º Ciclo do Ensino Básico 2017 Decreto-Lei n.º 139/2012, de 5 de julho Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30 minutos. Caderno
Prova 3 Matemática ... GABARITO 1 NOME DO CANDIDATO:
 Prova 3 QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam da etiqueta
Prova 3 QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam da etiqueta
Caderno 1: 35 minutos. Tolerância: 10 minutos. (é permitido o uso de calculadora)
 Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/01, de 5 de julho Prova 9/1.ª Chamada Caderno 1: 7 Páginas Duração da Prova (CADERNO 1 + CADERNO ): 90 minutos. Tolerância: 30 minutos.
Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/01, de 5 de julho Prova 9/1.ª Chamada Caderno 1: 7 Páginas Duração da Prova (CADERNO 1 + CADERNO ): 90 minutos. Tolerância: 30 minutos.
6. Considere. igual a : (A) f (x) + 2x f(x) = 0 (B) f (x) x f(x) = 0 (C) f (x) + f(x) = 0 (D) f (x) f(x) = 0 (E) f (x) 2x f(x) = 0
 QUESTÃO ÚNICA 0,000 pontos distribuídos em 50 itens Marque no cartão de respostas a única alternativa que responde de maneira correta ao pedido de cada item.. O valor da área, em unidades de área, limitada
QUESTÃO ÚNICA 0,000 pontos distribuídos em 50 itens Marque no cartão de respostas a única alternativa que responde de maneira correta ao pedido de cada item.. O valor da área, em unidades de área, limitada
Prova 3 Matemática ... GABARITO 2 NOME DO CANDIDATO:
 Prova 3 QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam da etiqueta
Prova 3 QUESTÕES OBJETIIVAS N ọ DE ORDEM: NOME DO CANDIDATO: N ọ DE INSCRIÇÃO: IINSTRUÇÕES PARA A REALIIZAÇÃO DA PROVA 1. Confira os campos N ọ DE ORDEM, N ọ DE INSCRIÇÃO e NOME, que constam da etiqueta
Caderno 1: 35 minutos. Tolerância: 10 minutos. (é permitido o uso de calculadora)
 Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/2.ª Fase Caderno 1: 6 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/2.ª Fase Caderno 1: 6 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Final de Matemática
 PROVA FINAL DO 3.º CICLO do Ensino BÁSICO Decreto-Lei n.º 39/0, de 5 de julho Prova Final de Matemática 3.º Ciclo do Ensino Básico Prova 9/.ª Chamada 8 Páginas Duração da Prova: 90 minutos. Tolerância:
PROVA FINAL DO 3.º CICLO do Ensino BÁSICO Decreto-Lei n.º 39/0, de 5 de julho Prova Final de Matemática 3.º Ciclo do Ensino Básico Prova 9/.ª Chamada 8 Páginas Duração da Prova: 90 minutos. Tolerância:
Entrelinha 1,5. Utiliza apenas caneta ou esferográfica de tinta indelével, azul ou preta.
 Teste Intermédio de Matemática Entrelinha 1,5 Teste Intermédio Matemática Entrelinha 1,5 (Versão única igual à Versão 1) Duração do Teste: 90 minutos 10.05.2012 9.º Ano de Escolaridade Decreto-Lei n.º
Teste Intermédio de Matemática Entrelinha 1,5 Teste Intermédio Matemática Entrelinha 1,5 (Versão única igual à Versão 1) Duração do Teste: 90 minutos 10.05.2012 9.º Ano de Escolaridade Decreto-Lei n.º
Caderno 1: 35 minutos. Tolerância: 10 minutos. (é permitido o uso de calculadora)
 Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/2.ª Fase Caderno 1: 6 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/2.ª Fase Caderno 1: 6 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Caderno 1: 35 minutos. Tolerância: 10 minutos. É permitido o uso de calculadora.
 Prova Final de Matemática Prova 92 2.ª Fase 3.º Ciclo do Ensino Básico 2017 Decreto-Lei n.º 139/2012, de 5 de julho Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30 minutos. Caderno
Prova Final de Matemática Prova 92 2.ª Fase 3.º Ciclo do Ensino Básico 2017 Decreto-Lei n.º 139/2012, de 5 de julho Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30 minutos. Caderno
Versão 2. Utiliza apenas caneta ou esferográfica de tinta indelével, azul ou preta.
 Teste Intermédio de Matemática Versão Teste Intermédio Matemática Versão Duração do Teste: 90 minutos 10.05.01 9.º Ano de Escolaridade Decreto-Lei n.º 6/001, de 18 de janeiro Identifica claramente, na
Teste Intermédio de Matemática Versão Teste Intermédio Matemática Versão Duração do Teste: 90 minutos 10.05.01 9.º Ano de Escolaridade Decreto-Lei n.º 6/001, de 18 de janeiro Identifica claramente, na
x 1. Em cada uma das figuras, eles são apenas os primeiros elementos dos
 0) Nas figuras a seguir, a curva é o gráfico da função x retângulos hachurados para infinitos que possuem as mesmas características. f x. Observe atentamente o que ocorre com os x. Em cada uma das figuras,
0) Nas figuras a seguir, a curva é o gráfico da função x retângulos hachurados para infinitos que possuem as mesmas características. f x. Observe atentamente o que ocorre com os x. Em cada uma das figuras,
Avaliação E. Educação Professor
 Teste de Avaliação Nome N. o Turma Data /jan./2019 Avaliação E. Educação Professor MATEMÁTICA 9. o ANO Duração (Caderno 1 + Caderno 2): 90 minutos O teste é constituído por dois cadernos (Caderno 1 e Caderno
Teste de Avaliação Nome N. o Turma Data /jan./2019 Avaliação E. Educação Professor MATEMÁTICA 9. o ANO Duração (Caderno 1 + Caderno 2): 90 minutos O teste é constituído por dois cadernos (Caderno 1 e Caderno
Avaliação E. Educação Professor
 Teste de Avaliação Nome N. o Turma Data /nov./2018 Avaliação E. Educação Professor MATEMÁTICA 9. o ANO Duração (Caderno 1 + Caderno 2): 90 minutos O teste é constituído por dois cadernos (Caderno 1 e Caderno
Teste de Avaliação Nome N. o Turma Data /nov./2018 Avaliação E. Educação Professor MATEMÁTICA 9. o ANO Duração (Caderno 1 + Caderno 2): 90 minutos O teste é constituído por dois cadernos (Caderno 1 e Caderno
Caderno 1: (É permitido o uso de calculadora.) Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja classificado.
 Nome: Ano / Turma: N.º: Data: - - Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Nome: Ano / Turma: N.º: Data: - - Caderno 1: (É permitido o uso de calculadora.) O teste é constituído por dois cadernos (Caderno 1 e Caderno ). Utiliza apenas caneta ou esferográfica, de tinta azul ou
Geometria Analítica - AFA
 Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
Geometria Analítica - AFA x = v + (AFA) Considerando no plano cartesiano ortogonal as retas r, s e t, tais que (r) :, (s) : mx + y + m = 0 e (t) : x = 0, y = v analise as proposições abaixo, classificando-
TD GERAL DE MATEMÁTICA 2ª FASE UECE
 Fundação Universidade Estadual do Ceará - FUNECE Curso Pré-Vestibular - UECEVest Fones: 101.968 / E-mail: uecevest_itaperi@yahoo.com.br Av. Dr. Silas Munguba, 1700 Campus do Itaperi 60714-90 Fone: 101-968/Site:
Fundação Universidade Estadual do Ceará - FUNECE Curso Pré-Vestibular - UECEVest Fones: 101.968 / E-mail: uecevest_itaperi@yahoo.com.br Av. Dr. Silas Munguba, 1700 Campus do Itaperi 60714-90 Fone: 101-968/Site:
INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA
 Prova 3 Matemática QUESTÕES DISCURSIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA 1. Verifique se este caderno contém 05 questões discursivas e/ou qualquer tipo de defeito.
Prova 3 Matemática QUESTÕES DISCURSIVAS N ọ DE ORDEM: N ọ DE INSCRIÇÃO: NOME: INSTRUÇÕES PARA A REALIZAÇÃO DA PROVA 1. Verifique se este caderno contém 05 questões discursivas e/ou qualquer tipo de defeito.
a) b) 5 3 sen 60 o = x. 2 2 = 5. 3 x = x = No triângulo da figura abaixo, o valor do x é igual a: a) 7 c) 2 31 e) 7 3 b) 31 d) 31 3
 Matemática a. série do Ensino Médio Frentes e Eercícios propostos AULA FRENTE Num triângulo ABC em que AB = 5, B^ = º e C^ = 5º, a medida do lado AC é: a) 5 b) 5 c) 5 d) 5 e) 5 Sabendo-se que um dos lados
Matemática a. série do Ensino Médio Frentes e Eercícios propostos AULA FRENTE Num triângulo ABC em que AB = 5, B^ = º e C^ = 5º, a medida do lado AC é: a) 5 b) 5 c) 5 d) 5 e) 5 Sabendo-se que um dos lados
NOTAÇÕES. : inversa da matriz M : produto das matrizes M e N : segmento de reta de extremidades nos pontos A e B
 NOTAÇÕES R C : conjunto dos números reais : conjunto dos números complexos i : unidade imaginária i = 1 det M : determinante da matriz M M 1 MN AB : inversa da matriz M : produto das matrizes M e N : segmento
NOTAÇÕES R C : conjunto dos números reais : conjunto dos números complexos i : unidade imaginária i = 1 det M : determinante da matriz M M 1 MN AB : inversa da matriz M : produto das matrizes M e N : segmento
