Equações Diferenciais Ordinárias de 1 a ordem - II AM3D
|
|
|
- Octavio Estrela Gusmão
- 7 Há anos
- Visualizações:
Transcrição
1 20 2 Equações Diferenciais Ordinárias de a ordem - II AM3D EDOs de a ordem lineares Definição Uma equação diferencial ordinária de a ordem diz-se linear se for da forma y (x)+p(x)y(x) = b(x). Se p(x) = p R, a equação diz-se linear de coeficientes constantes. Se b(x) = 0, a equação diz-se linear homogénea. Por exemplo, v (t) = 0 2v(t) v (t)+2v(t) = 0 é linear não homogénea de coeficientes constantes. Como podemos resolver analiticamente esta equação? Multiplicando por e 2t obtém-se a equação equivalente e 2t v (t)+2e 2t v(t) = 0e 2t (e 2t v(t)) = 0e 2t e 2t v(t) = 5e 2t +C. Obtemos a solução geral v(t) = 5+Ce 2t. Confirmamos pois que a solução de equilíbrio v = 5 é estável, uma vez que lim v(t) = 5. t + Este método de resolução aplica-se na verdade a qualquer equação linear y (x)+p(x)y(x) = b(x). Supondo que as funções p e b são por exemplo contínuas, e denotando por P(x) uma qualquer primitiva de p(x), y (x)+p(x)y(x) = b(x) y (x)e P(x) +e P(x) p(x)y(x) = e P(x) b(x) (e P(x) y(x)) = e P(x) b(x). Obtemos assim a solução geral y(t) = e P(x) e P(x) b(x)dx. Ao factor µ(x) = e P(x) chama-se factor integrante.
2 Como todas as primitivas de e P(x) b(x) diferem de uma constante, fica claro que se p e b são contínuas em R, o problema de valores iniciais y (x)+p(x)y(x) = b(x) possui uma única solução global. Exemplo y = xy ou seja, y(x 0 ) = y 0, y (x) = xy(x) e x2 2 y (x) e x2 2 xy(x) = 0 ( e x2 2 y(x) ) = 0, y(x) = Ce x2 2, C R. Confirmámos que as soluções já conhecidas eram de facto as únicas. Exemplo xy +2y = 4x 2 Começamos por colocar esta equação na forma canónica y + 2 y = 4x. O factor integrante é x dado por 2dx µ(x) = e x = e 2ln x = x 2. Assim, y + 2 x y = 4x x2 y +2xy = 4x 3 (x 2 y) = 4x 3 x 2 y = x 4 +C y = x 2 + C x2, C R. Note que para C 0, as soluções são válidas para x I =]0;+ [ ou x I 2 =] ;0[. A equação admita ainda (C = 0) uma solução válida em R: y = x 2. Figura : Algumas soluções da EDO xy +2y = 4x 2 2
3 Equações diferenciais separáveis Soluções implícitas Muitas vezes apenas podemos resolver equações diferenciais de forma implícita, ou seja, conhecemos uma relação H(x,y(x)) = C entre x e y(x), apesar de não conseguirmos exprimir esta segunda quantidade em função da primeira. Vejamos um exemplo: y = 2xy x 2 +e y. Trata-se de uma equação diferencial não linear muito complexa. À partida, pouco mais podemos fazer do que traçar o seu campo de direcções: Observemos no entanto o seguinte: Figura 2: Campo de direções v = ( ) 2xy, x 2 +e y y = 2xy x 2 +e y x2 y +y e y +2xy = 0 (x 2 y +e y ) = 0 x 2 y +e y = C, C R. Sabemos agora que as soluções da equação diferencial verificam a equação H(x,y) = x 2 y(x)+e y(x) = C, C R, não parecendo no entanto possível exprimir explicitamente y(x) em função. Diremos então que H(x,y) = C é uma solução implícita da equação diferencial y = 2xy x 2 +e y. É possível, com a ajuda de um computador, traçar os pontos (x,y) que verificam H(x,y) = C. Vemos então aparecer as curvas integrais do campo anterior: 3
4 Figura 3: H(x,y) = C para C = 0,20,30,50. Uma importante família de equações diferenciais que podem ser resolvidas implicitamente são as equações diferenciais separáveis: Definição 2, Uma equação diferencial ordinária de primeira ordem diz-se separável se for do tipo y = M(x) N(y), o que, se N(y) 0, é equivalente a y N(y) = M(x). Notação à físico Escrevendo y = dy, podemos escrever esta equação diferencial na forma dx N(y)dy = M(x)dx. Chama-se a esta formulação a forma diferencial da equação diferencial. Tem, como veremos, uma grande utilidade. É desta escrita que vem o termo separável, já que de um lado da igualdade apenas temos a variável dependente y e do outro lado a variável independente x. Como se obtém facilmente uma solução implícita de uma equação diferencial separável? Se Ñ é uma primitiva de N e M é uma primitiva de M, então pelo que (Ñ(y(x)) M(x)) = y (x)ñ (y(x)) M (x) = y (x)m(y(x)) N(x), y (x)n(y(x)) M(x) = 0 Ñ(y(x)) M(x) = C, C R. 4
5 Por outras palavras, H(x,y) = Ñ(y) M(x) = C é uma solução ímplicita da equação y N(y) M(x) = 0. Exemplo y 2 y = e 3x. Podemos começar por traçar o campo de direcções associado. Em vez de tomar v(x,y) = (, e3x ), é preferível, para ultrapassar a dificuldade dos pontos y2 em que y = 0, escolher v(x,y) = (y 2,e 3x ). Figura 4: Campo de direcções v(x,y) = (y 2,e 3x ). Vamos agora obter a solução implícita. Aqui, N(y) = y 2 e M(x) = e 3x. Tomando as primitivas Ñ(y) = 3 y3 e M(x) = 3 e3x, obtemos a solução implícita y 3 e 3x = 3C. 5
6 Figura 5: y 3 e 3x = 3C para C =,4,6,0,2,20,30. Contrariamente ao nosso primeiro exemplo, nesta situação é possível exibir soluções explícitas: y(x) = 3 3C +e 3x, C R. Utilizando as notações à físico, torna-se ainda mais prático resolver esta equação diferencial: y 2 y = e 3x y 2 dy = e 3x dx y 2 dy = e 3x dx 3 y3 = 3 e3x +C y 3 = e 3x +3C. Caso se pretenda resolver um problema de valores iniciais, y(y 0 ) = x 0 : Pode determinar-se a constante C a partir desta nova condição: de onde se obtém y(x) = 3 e 3x e 3x 0 +y 3 0. y0 3 = e 3x 0 +3C C = y3 0 e3x 0, 3 Uma outra possibilidade é, utilizando o método à físico, integrar directamente as variáveis x e y nos intervalos [x 0 ;x] e [y 0 ;y(x)] directamente: y 2 y = e 3x y 2 dy = e 3x dx y(x) y 0 y 2 dy = o que fornece naturalmente a mesma solução. x x 0 e 3x dx 3 (y3 y 3 0) = 3 (e3x e 3x 0 ) Exemplo: Lei de Torricelli Figura 3: Lei de Torricelli. Um depósito de secção S tem um pequeno buraco de secção s. Pretende-se saber como evolui a altura h do líquido em função do tempo. A lei de Torricelli afirma que a água é ejectada à velocidade que teria adquirido uma gota de àgua após uma queda de h, ou seja, 2 mv2 = mgh v = 2gh. 6
7 Durante um curto instante dt, a equação de continuidade (a quantidade de líquido é constante) escreve-se Sdh = sv(t)dt. Obtemos assim a equação diferencial separável h h + s 2g S = 0. Com a condição inicial h(0) = h 0. Obtém-se assim dh = s 2g h(t) h S dt dh t s 2g = h 0 h 0 S dt 2( h(t) h 0 ) = s 2g S t h(t) = 4 ( h0 s ) 2 2g S t. Equações homogéneas Mudanças de variáveis Definição 3 Uma equação diferencial de primeira ordem da forma ( y y = φ(x,y) = f. x) diz-se equação diferencial homogénea. Note que neste caso, para todo α 0, φ(αx,αy) = f ( αy ) ( y = f = φ(x,y) αx x) pelo que esta poderá ser uma boa forma de reconhecer equações homogéneas. As equações homogéneas podem ser transformadas em equações separáveis pela mudança da variável dependente v(x) = y(x) x. Isto significa que a partir da equação diferencial verificada por y(x) vamos deduzir uma equação diferencial equivalente verificada por v(x). Depois de resolvida, poderemos recuperar as soluções da equação inicial fazendo simplesmente y(x) = xv(x). 7
8 Tem-se y (x) = xv (x)+v(x) pelo que ( y y = f x) o que é uma equação separável. Exemplo y = y2 x 2 2xy Fazendo a mudança de variáveis anunciada, xv +v = f(v) f(v) v v = x, Obtemos a equação separável xv +v = x2 v 2 x 2 2x 2 v = v2 2v = 2 v 2v. xv = 2 v 2v = v 2 + 2vdv 2 v v 2 + = dx x. Integrando, vem Voltando às variáveis iniciais, ln(v 2 +) = ln x +C v 2 + = C x, C = ±e C R. y 2 +x 2 C x = 0 ) 2 (X C +y 2 = C Trata-se de uma solução implícita: as curvas integrais do campo são circunferências centradas nos pontos do eixo das abcissas e que passam pela origem. Figura 4: Algumas curvas integrais da equação y = y2 x 2 2xy. 8
9 Equações de Bernoulli Definição 4 Uma equação de Bernoulli é uma equação diferencial da forma y +p(x)y = q(x)y n. Quando n = 0, trata-se simplesmente de uma equação linear, e quando n = de uma equação linear homogénea. Para n 2, mediante a mudança de variável v = y n, estas equações tornam-se lineares: v = y n v = ( n)y y n. Multiplicando a equação inicial por y n obtém-se n v +p(x)v = q(x) v +( n)p(x)v = ( n)q(x). Exemplo Curva logística y = ry ky 2, r,k > 0, constantes positivas fixas. Fazendo a mudança de variável v = y, v = y (y 0): y2 y = ry ky 2 y y 2 = r y k v = rv +k. O factor integrante é e rx, calculando-se assim a solução geral (ve rx ) = ke rx v(x) = k r +Ce rx, ou em termos de y, y(x) = k r +Ce rx. Figura 5: Curvas logísticas 9
10 Equações Exactas Definição 5 Uma equação diferencial da forma diz-se exacta se M e N são de classe C e N(x,y)y +M(x,y) = 0 M y = N x. Por outras palavras, o campo vectorial (M(x,y),N(x,y) é fechado. Dado um ponto (x 0,y 0 ) R 2 e uma vizinhança V simplesmente conexa, (por exemplo uma região rectangular), o campo é conservativo em V, pelo que existe uma função F C (V) tal que Temos então o seguinte resultado: M(x,y) = F F (x,y) e N(x,y) = x y (x,y). Propriedade As soluções da equação diferencial exacta N(x,y)y +M(x,y) = 0 são dadas implicitamente por F(x,y(x)) = C, C R. De facto, basta observar que F(x,y(x)) = F x (x,y)+y (x) F y (x,y) = M(x,y)y (x)+n(x,y) = 0. Exemplo 2xyy +y 2 +2x = 0 Aqui, N(x,y) = 2xy e M(x,y) = y 2 +2x são de classe C (R 2 ) e M N (x,y) = 2y = y x (x,y). Vamos então determinar F, o potencial do campo (M(x,y),N(x,y)) pelo método habitual: F F (x,y) = M(x,y) x x (x,y) = y2 +2x F(x,y) = xy 2 +x 2 +φ(y). 0
11 Diferenciando em ordem a y, 2xy = N(x,y) = F x (x,y) = 2xy +φ (y) pelo que φ (y) = 0: φ(y) = C R. Finalmente, obtemos a solução implícita F(x,y(x)) = xy 2 +x 2 = C, C R. Nesta situação, é possível fornecer as soluções explicitamente (em intervalos convenientes:) Factores integrantes y(x) = x C x 2, C R. Definição 6 Seja uma equação diferencial, N.M C. Se µ(x,y) C for tal que N(x,y)y +M(x,y) = 0 µ(x,y)n(x,y)y +µ(x,y)m(x,y) = 0 é exacta, µ diz-se um factor integrante da equação diferencial. É por vezes possível determinar um factor integrante e assim resolver a respectiva equação diferencial pelo método das equações exactas que acabámos de ver. A função µ é um factor integrante se x (µn) = y (µm), ou seja, se µ verifica a Equação de Derivadas Parciais N µ x M µ y + ( N x M y ) µ = 0. Esta equação é em geral mais difícil de resolver do que a equação diferencial original. No entanto, se µ apenas depender de uma variável (digamos x), esta equação é então uma EDO linear homogénea. É pois interessante obter um critério que permita determinar a existência de factores integrantes que apenas dependem de uma variável.
12 Propriedade 2 Seja N(x,y)y +M(x,y) = 0 uma equação diferencial, N.M C. Se ( M N y N ) = ψ(x) x depende apenas da variável x, então a equação diferencial admite um factor integrante µ(x) que verifica µ (x) ψ(x)µ(x) = 0. Basta observar que, em geral, µ x M µ N y N Exemplo (x 2 +xy)y +(3xy +y 2 ) = 0 Tem-se ( ) M N (x,y) N(x,y) y x (x,y) = Assim, existe um factor integrante µ(x) que verifica ( M y N ) µ = 0. x µ (x) µ(x) = 0. x x 2 +xy (3x+2y 2x y) = x. Resolvendo por exemplo para x > 0, o factor integrante desta equação é e dx x = x : Assim, a equação x µ (x) x 2µ(x) = ( ) µ(x) = 0 : µ(x) = x. x(x 2 +xy)y +x(3xy +y 2 ) = 0 é exacta. Pelo método estudado. as suas soluções são dadas implicitamente por F(x,y(x)) = x 3 y + 2 x2 y 2 = C, C R. x 2
EDO I. por Abílio Lemos. 16 e 18 de outubro de Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
 EDO I por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2017 16 e 18 de outubro de 2017 Definição 1 Uma equação diferencial é qualquer relação entre uma função e suas derivadas.
EDO I por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2017 16 e 18 de outubro de 2017 Definição 1 Uma equação diferencial é qualquer relação entre uma função e suas derivadas.
3xy +y 2 +(x 2 +xy) dy dx = 0 (1)
 2. Determine um factor integrante da forma µ(x). 3xy +y 2 +(x 2 +xy) dy (1) 3. Determine a solução da equação que verifica y(1) = 1. Sendo tem-se M(x,y) = 3xy +y 2 e N(x,y) = x 2 +xy M/ y = 3x+2y e N/
2. Determine um factor integrante da forma µ(x). 3xy +y 2 +(x 2 +xy) dy (1) 3. Determine a solução da equação que verifica y(1) = 1. Sendo tem-se M(x,y) = 3xy +y 2 e N(x,y) = x 2 +xy M/ y = 3x+2y e N/
xy + y = 0. (1) Portanto a solução geral de (1) é a família de hipérboles y = C x,
 Seção 4: Equações Exatas Fator Integrante Introduzimos a idéia de equação exata, através de dois exemplos simples. Note que nesses dois exemplos, além de exata, a EDO também é separável, podendo alternativamente
Seção 4: Equações Exatas Fator Integrante Introduzimos a idéia de equação exata, através de dois exemplos simples. Note que nesses dois exemplos, além de exata, a EDO também é separável, podendo alternativamente
d [xy] = x cos x. dx y = sin x + cos x + C, x
![d [xy] = x cos x. dx y = sin x + cos x + C, x d [xy] = x cos x. dx y = sin x + cos x + C, x](/thumbs/66/55981826.jpg) Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec
 Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
7 Equações Diferenciais. 7.1 Classificação As equações são classificadas de acordo como tipo, a ordem e a linearidade.
 7 Equações Diferenciais Definição: Uma equação diferencial é uma equação em que as incógnitas são funções e a equação envolve derivadas dessas funções. : = 5x + 3 4 d3 3 + (sen x) d2 2 + 5x = 0 2 t 2 4
7 Equações Diferenciais Definição: Uma equação diferencial é uma equação em que as incógnitas são funções e a equação envolve derivadas dessas funções. : = 5x + 3 4 d3 3 + (sen x) d2 2 + 5x = 0 2 t 2 4
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
MAT Cálculo Diferencial e Integral para Engenharia IV
 MAT456 - Cálculo Diferencial e Integral para Engenharia IV Parte A: Equações Diferenciais de 1 a Ordem o Semestre de 018-3 a Lista de exercícios 1) Os gráficos de duas soluções de y = x + y podem se cruzar
MAT456 - Cálculo Diferencial e Integral para Engenharia IV Parte A: Equações Diferenciais de 1 a Ordem o Semestre de 018-3 a Lista de exercícios 1) Os gráficos de duas soluções de y = x + y podem se cruzar
d [xy] = x arcsin x. dx + 4x
![d [xy] = x arcsin x. dx + 4x d [xy] = x arcsin x. dx + 4x](/thumbs/65/53462517.jpg) Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Secção 2. Equações diferenciais de primeira ordem
 . Equações diferenciais de primeira ordem Secção. Equações diferenciais de primeira ordem (Farlow: Sec..,.) Vamos nesta secção analisar como podem ser resolvidos diferentes tipos de EDOs de primeira ordem.
. Equações diferenciais de primeira ordem Secção. Equações diferenciais de primeira ordem (Farlow: Sec..,.) Vamos nesta secção analisar como podem ser resolvidos diferentes tipos de EDOs de primeira ordem.
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
ANÁLISE MATEMÁTICA IV EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN. tet + t
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
Instituto Tecnológico de Aeronáutica / Departamento de Matemática / 2 o Fund / a LISTA DE MAT-32
 1 Instituto Tecnológico de Aeronáutica / Departamento de Matemática / 2 o Fund / 2012. 1 a LISTA DE MAT-32 Nos exercícios de 1 a 9, classi car e apresentar, formalmente, solução (ou candidata a solução)
1 Instituto Tecnológico de Aeronáutica / Departamento de Matemática / 2 o Fund / 2012. 1 a LISTA DE MAT-32 Nos exercícios de 1 a 9, classi car e apresentar, formalmente, solução (ou candidata a solução)
y (n) (x) = dn y dx n(x) y (0) (x) = y(x).
 Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Capítulo 1 Introdução 1.1 Definições Denotaremos por I R um intervalo aberto ou uma reunião de intervalos abertos e y : I R uma função que possua todas as suas derivadas, a menos que seja indicado o contrário.
Equações Ordinarias 1ªOrdem - Lineares
 Nome: Nº Curso: Licenciatura em Matemática Disciplina: Equações Diferenciais Ordinárias 7ºPeríodo Prof. Leonardo Data: / /2018 Equações Ordinarias 1ªOrdem - Lineares 1. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Nome: Nº Curso: Licenciatura em Matemática Disciplina: Equações Diferenciais Ordinárias 7ºPeríodo Prof. Leonardo Data: / /2018 Equações Ordinarias 1ªOrdem - Lineares 1. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Exercícios. de Equações Diferenciais Ordinárias. Tatiana Tchemisova Cordeiro Vera Kharlamova Adelaide Valente Freitas
 Exercícios de Equações Diferenciais Ordinárias Tatiana Tchemisova Cordeiro Vera Kharlamova Adelaide Valente Freitas Departamento de Matemática UNIVERSIDADE DE AVEIRO 2 Prefácio A presente publicação tem
Exercícios de Equações Diferenciais Ordinárias Tatiana Tchemisova Cordeiro Vera Kharlamova Adelaide Valente Freitas Departamento de Matemática UNIVERSIDADE DE AVEIRO 2 Prefácio A presente publicação tem
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
2 ō Semestre 2015/2016
 Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Instituto Universitário de Lisboa
 Instituto Universitário de Lisboa Departamento de Matemática Exercícios de Equações Diferenciais Ordinárias 1 Exercícios 1.1 EDO de Variáveis Separáveis Diz-se que uma equação diferencial ordinária (EDO)
Instituto Universitário de Lisboa Departamento de Matemática Exercícios de Equações Diferenciais Ordinárias 1 Exercícios 1.1 EDO de Variáveis Separáveis Diz-se que uma equação diferencial ordinária (EDO)
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Lista I
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Lista I 1. Desenhe um campo de direções para a equação diferencial dada. Determine o comportamento de y quando t +. Se esse comportamento depender do valor inicial de
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS - Lista I 1. Desenhe um campo de direções para a equação diferencial dada. Determine o comportamento de y quando t +. Se esse comportamento depender do valor inicial de
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática
 Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 3 a Lista MAT 146 - Cálculo I 218/I APLICAÇÃO DE DERIVADAS: OTIMIZAÇÃO Otimização é outra aplicação de derivadas. Em
Universidade Federal de Viçosa Centro de Ciências Exatas Departamento de Matemática 3 a Lista MAT 146 - Cálculo I 218/I APLICAÇÃO DE DERIVADAS: OTIMIZAÇÃO Otimização é outra aplicação de derivadas. Em
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Prof. Guilherme Jahnecke Wemar AULA 03 Equações diferenciais de primeira ordem Equações separáveis Fonte: Material Daniela Buske, Boce, Bronson, Zill, diversos internet
Equações Diferenciais Ordinárias Prof. Guilherme Jahnecke Wemar AULA 03 Equações diferenciais de primeira ordem Equações separáveis Fonte: Material Daniela Buske, Boce, Bronson, Zill, diversos internet
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
EQUAÇÕES DIFERENCIAIS LINEARES SEGUNDA ORDEM
 EQUAÇÕES DIFERENCIAIS LINEARES SEGUNDA ORDEM 02/04/2014 Prof. Geraldine Revisão de Álgebra Linear Definição de conjunto Linearmente Independente Dizemos que as funções f ( x), f ( x) são LI, em um 1 2
EQUAÇÕES DIFERENCIAIS LINEARES SEGUNDA ORDEM 02/04/2014 Prof. Geraldine Revisão de Álgebra Linear Definição de conjunto Linearmente Independente Dizemos que as funções f ( x), f ( x) são LI, em um 1 2
CÁLCULO III - MAT Encontre as soluções das seguintes equações com condições iniciais:
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO III - MAT0021 7 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e da Natureza Centro Interdisciplinar de Ciências da Natureza CÁLCULO III - MAT0021 7 a Lista de exercícios
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Edo s de Primeira Ordem
 Capítulo 3 Edo s de Primeira Ordem 3.1 Introdução Neste capítulo estamos interessados em obter e analisar as soluções das edo s de primeira ordem. Isto é, edo s que podem ser escritas na forma: F(y, y,
Capítulo 3 Edo s de Primeira Ordem 3.1 Introdução Neste capítulo estamos interessados em obter e analisar as soluções das edo s de primeira ordem. Isto é, edo s que podem ser escritas na forma: F(y, y,
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
 Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
c + 1+t 2 (1 + t 2 ) 5/2 dt e 5 2 ln(1+t2 )dt (1 + t 2 ) 5/2 dt (c 5/2 + (1 + t 2 ) 5/2 (1 + t 2 ) 5/2 dt ϕ(t) = (1 + t 2 ) 5/2 (1 + t).
 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Trabalho de Equações Diferenciais Ordinárias
 Universidade Tecnológica Federal do Paraná Diretoria de Graduação e Educação Prossional Departamento Acadêmico de Matemática Trabalho de Equações Diferenciais Ordinárias Data de Entrega: 16/12/2015 Nome:
Universidade Tecnológica Federal do Paraná Diretoria de Graduação e Educação Prossional Departamento Acadêmico de Matemática Trabalho de Equações Diferenciais Ordinárias Data de Entrega: 16/12/2015 Nome:
Frações Parciais e Crescimento Logístico
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Frações Parciais e
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Frações Parciais e
Departamento de Matemática da Universidade de Aveiro. Cálculo II. - Texto de Apoio - Alexandre Almeida
 Departamento de Matemática da Universidade de Aveiro Cálculo II - Texto de Apoio - Alexandre Almeida fevereiro de 2017 Nota prévia Este texto foi escrito com o propósito de apoiar as aulas de Cálculo II
Departamento de Matemática da Universidade de Aveiro Cálculo II - Texto de Apoio - Alexandre Almeida fevereiro de 2017 Nota prévia Este texto foi escrito com o propósito de apoiar as aulas de Cálculo II
Sessão 1: Generalidades
 Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Sessão 1: Generalidades Uma equação diferencial é uma equação envolvendo derivadas. Fala-se em derivada de uma função. Portanto o que se procura em uma equação diferencial é uma função. Em lugar de começar
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
LISTA dy dx y x + y3 cos x = y = ky ay 3. dizemos que F (x, y) é homogênea de grau 0. Neste caso a equação diferencial y =
 MAT 01167 LISTA Equações Diferenciais Resolva: 1. y = y x + x y, y ( ) 1 8 =. (1 x ) dy dx (1 + x) y = y. dy dx y x + y cos x = 0 4. y = ky ay. Se uma função F (x, y) satisfaz a condição F (t x, t y) =
MAT 01167 LISTA Equações Diferenciais Resolva: 1. y = y x + x y, y ( ) 1 8 =. (1 x ) dy dx (1 + x) y = y. dy dx y x + y cos x = 0 4. y = ky ay. Se uma função F (x, y) satisfaz a condição F (t x, t y) =
Introdução às Equações Diferenciais e Ordinárias
 Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
g(s, X n s )ds + t f (s, X s ) 2 ds <, P-q.s. t f (s, X s )db s, t 0.
 CHAPTER 3. INTEGRAIS ESTOCÁSTICOS 88 2. Quais são as propriedades destas soluções? 3. Como podemos resolver uma dada equação? O método usual para provar a existência de uma solução da equação diferencial
CHAPTER 3. INTEGRAIS ESTOCÁSTICOS 88 2. Quais são as propriedades destas soluções? 3. Como podemos resolver uma dada equação? O método usual para provar a existência de uma solução da equação diferencial
Cálculo Diferencial e Integral II
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral II Ficha de trabalho 1 (versão de 6/0/009 (Esboço de Conjuntos. Topologia. Limites. Continuidade
2 Equações Diferenciais Ordinárias (EDOs)
 2 Equações Diferenciais Ordinárias (EDOs) 2.1 Introdução Neste capítulo vamos tratar de um dos tópicos da Matemática mais usados na resolução de certos problemas de engenharia e de ciências (incluindo
2 Equações Diferenciais Ordinárias (EDOs) 2.1 Introdução Neste capítulo vamos tratar de um dos tópicos da Matemática mais usados na resolução de certos problemas de engenharia e de ciências (incluindo
1 Definição de uma equação diferencial linear de ordem n
 Equações diferenciais lineares de ordem superior 1 1 Definição de uma equação diferencial linear de ordem n Equação diferencial linear de ordem n é uma equação da forma: a n (x) dn y dx n + a n 1(x) dn
Equações diferenciais lineares de ordem superior 1 1 Definição de uma equação diferencial linear de ordem n Equação diferencial linear de ordem n é uma equação da forma: a n (x) dn y dx n + a n 1(x) dn
Equações Diferenciais: Um Curso para Engenharias, Física, Matemática e Química
 Notas de Aula da Disciplina Cálculo 3 Equações Diferenciais: Um Curso para Engenharias, Física, Matemática e Química André Luiz Galdino Departamento de Matemática do Campus Catalão da Universidade Federal
Notas de Aula da Disciplina Cálculo 3 Equações Diferenciais: Um Curso para Engenharias, Física, Matemática e Química André Luiz Galdino Departamento de Matemática do Campus Catalão da Universidade Federal
EQUAÇÕES DIFERENCIAIS
 EQUAÇÕES DIFERENCIAIS Uma equação diferencial é aquela em que a função incógnita aparece sob a forma da sua derivada. Havendo uma só variável independente as derivadas são ordinárias e a equação é denominada
EQUAÇÕES DIFERENCIAIS Uma equação diferencial é aquela em que a função incógnita aparece sob a forma da sua derivada. Havendo uma só variável independente as derivadas são ordinárias e a equação é denominada
Equações Diferenciais Ordinárias Lineares de Segunda Ordem
 Universidade Federal de Mato Grosso do Sul Departamento de Ciências Exatas - Câmpus de Três Lagoas Programa de Mestrado Profissional em Rede Nacional - PROFMAT WESLEN XAVIER DE MORAES Solução em Série
Universidade Federal de Mato Grosso do Sul Departamento de Ciências Exatas - Câmpus de Três Lagoas Programa de Mestrado Profissional em Rede Nacional - PROFMAT WESLEN XAVIER DE MORAES Solução em Série
Análise Complexa e Equações Diferenciais Guia 8 João Pedro Boavida. 16 a 23 de Novembro
 Análise Complexa e Equações Diferenciais Guia 8 Este guia explica como resolver os problemas do guia 7 Explica também vários aspectos mais técnicos sobre equações lineares em R n, com os quais eu prefiro
Análise Complexa e Equações Diferenciais Guia 8 Este guia explica como resolver os problemas do guia 7 Explica também vários aspectos mais técnicos sobre equações lineares em R n, com os quais eu prefiro
32 a Aula AMIV LEAN, LEC Apontamentos
 32 a Aula 2429 AMIV LEAN, LEC Apontamentos (RicardoCoutinho@mathistutlpt) 32 Fórmula da variação das constantes Temos então pela fórmula dos da variação das constantes (para sistemas de equações - Teorema
32 a Aula 2429 AMIV LEAN, LEC Apontamentos (RicardoCoutinho@mathistutlpt) 32 Fórmula da variação das constantes Temos então pela fórmula dos da variação das constantes (para sistemas de equações - Teorema
EDO III. por Abílio Lemos. 07, 09 e 14 de novembro de Universidade Federal de Viçosa. Departamento de Matemática UFV. Aulas de MAT
 EDO III por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 07, 09 e 14 de novembro de 2018 Teorema (D Alembert): Sejam y 1 (x) uma solução, não nula, da EDO y + p(x)y
EDO III por Universidade Federal de Viçosa Departamento de Matemática-CCE Aulas de MAT 147-2018 07, 09 e 14 de novembro de 2018 Teorema (D Alembert): Sejam y 1 (x) uma solução, não nula, da EDO y + p(x)y
Métodos Matemáticos 2012 Notas de Aula Equações Diferenciais Ordinárias II. A C Tort. 25 de setembro de y (x) + p(x)y(x) = g(x).
 Métodos Matemáticos 2012 Notas de Aula Equações Diferenciais Ordinárias II A C Tort 25 de setembro de 2012 1 O fator integrante Suponha que a EDO de primeira ordem seja da forma: Multiplicando a EDO por
Métodos Matemáticos 2012 Notas de Aula Equações Diferenciais Ordinárias II A C Tort 25 de setembro de 2012 1 O fator integrante Suponha que a EDO de primeira ordem seja da forma: Multiplicando a EDO por
DERIVADAS PARCIAIS. y = lim
 DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
DERIVADAS PARCIAIS Definição: Seja f uma função de duas variáveis, x e y (f: D R onde D R 2 ) e (x 0, y 0 ) é um ponto no domínio de f ((x 0, y 0 ) D). A derivada parcial de f em relação a x no ponto (x
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari amanda@fcav.unesp.br CONSIDERAÇÕES INICIAIS Considere a função f x : R R tal que y = f(x). Então: Derivada: Mede a taxa de variação de
MATEMÁTICA II Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari amanda@fcav.unesp.br CONSIDERAÇÕES INICIAIS Considere a função f x : R R tal que y = f(x). Então: Derivada: Mede a taxa de variação de
Curso: Engenharia Ambiental. Disciplina: Equações Diferenciais Ordinárias. Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2
 Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Análise Complexa e Equações Diferenciais
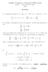 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
7- Equações Diferenciais Ordinárias de 1 a Ordem Redutíveis
 7- Equações Diferenciais Ordinárias de 1 a Ordem Redutíveis 7.1-Equação de Bernoulli A equação de Bernoulli é uma equação diferencial de primeira ordem do tipo: onde é uma constante sendo e e e quaisquer
7- Equações Diferenciais Ordinárias de 1 a Ordem Redutíveis 7.1-Equação de Bernoulli A equação de Bernoulli é uma equação diferencial de primeira ordem do tipo: onde é uma constante sendo e e e quaisquer
3 Equacões de Bernoulli e Riccati Equação de Bernoulli Equação de Riccati Exercícios... 24
 Conteúdo 3 Equacões de Bernoulli e Riccati 18 3.1 - Equação de Bernoulli.................... 18 3.2 - Equação de Riccati..................... 20 3.3 - Exercícios.......................... 24 1 Equações
Conteúdo 3 Equacões de Bernoulli e Riccati 18 3.1 - Equação de Bernoulli.................... 18 3.2 - Equação de Riccati..................... 20 3.3 - Exercícios.......................... 24 1 Equações
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 5 de Fevereiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utiliação de máquina de calcular O tempo para a realiação desta prova é de horas
LEEC Exame de Análise Matemática 3 5 de Fevereiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utiliação de máquina de calcular O tempo para a realiação desta prova é de horas
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Patrícia Nunes da Silva Este livro está registrado no EDA da Fundação Biblioteca Nacional/MinC sob número 350.448, Livro 646, folha 108. i PREFÁCIO As equações diferenciais
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Patrícia Nunes da Silva Este livro está registrado no EDA da Fundação Biblioteca Nacional/MinC sob número 350.448, Livro 646, folha 108. i PREFÁCIO As equações diferenciais
Séries e Equações Diferenciais Lista 04 EDO s de Primeira Ordem e Aplicações
 Séries e Equações Diferenciais Lista 04 EDO s de Primeira Ordem e Aplicações Professor: Daniel Henrique Silva Introdução às Equações Diferenciais 1) Defina equação diferencial. 2) Seja f(x; y) uma função
Séries e Equações Diferenciais Lista 04 EDO s de Primeira Ordem e Aplicações Professor: Daniel Henrique Silva Introdução às Equações Diferenciais 1) Defina equação diferencial. 2) Seja f(x; y) uma função
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Derivada de ordem n. Equação da recta tangente e da recta normal. Polinómio de Taylor
 Equação da recta tangente e da recta normal Como já vimos este ano a equação de uma recta na forma reduzida édadapor y y 0 = m(x x 0 ) Também sabemos que o declive da recta tangente ao gráfico de f no
Equação da recta tangente e da recta normal Como já vimos este ano a equação de uma recta na forma reduzida édadapor y y 0 = m(x x 0 ) Também sabemos que o declive da recta tangente ao gráfico de f no
ANÁLISE MATEMÁTICA IV FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
MÉTODOS MATEMÁTICOS. Prof. Dr. Paulo H. D. Santos.
 MÉTODOS MATEMÁTICOS Prof. Dr. Paulo H. D. Santos psantos@utfpr.edu.br AULA 1 10/03/2015 Apresentação do Plano de Ensino; EDOs de 1ª Ordem Parte 1. Sumário Conteúdo Programático Metodologia Avaliação Critério
MÉTODOS MATEMÁTICOS Prof. Dr. Paulo H. D. Santos psantos@utfpr.edu.br AULA 1 10/03/2015 Apresentação do Plano de Ensino; EDOs de 1ª Ordem Parte 1. Sumário Conteúdo Programático Metodologia Avaliação Critério
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
QUADRADO DA SOMA DE DOIS TERMOS
 Lista 8 ano Observe: (a + b)² = ( a + b). (a + b) = a² + ab+ ab + b² = a² + 2ab + b² QUADRADO DA SOMA DE DOIS TERMOS Conclusão: (primeiro termo)² + 2.(primeiro termo). (segundo termo) + (segundo termo)²
Lista 8 ano Observe: (a + b)² = ( a + b). (a + b) = a² + ab+ ab + b² = a² + 2ab + b² QUADRADO DA SOMA DE DOIS TERMOS Conclusão: (primeiro termo)² + 2.(primeiro termo). (segundo termo) + (segundo termo)²
MAP2310. Análise Numérica e Equações Diferenciais I. 1 Equações Diferenciais Ordinárias
 MAP2310 14/03/2005 Análise Numérica e Equações Diferenciais I 1 o Semestre de 2005 1 1 Equações Diferenciais Ordinárias 1.1 Introdução Equações envolvendo uma variável independente real t, uma função desconhecida
MAP2310 14/03/2005 Análise Numérica e Equações Diferenciais I 1 o Semestre de 2005 1 1 Equações Diferenciais Ordinárias 1.1 Introdução Equações envolvendo uma variável independente real t, uma função desconhecida
Continuidade e Limite
 Continuidade e Limite Antônio Calixto de Souza Filho Escola de Artes, Ciências e Humanidades Universidade de São Paulo 20 de maio de 2013 1 Remoção da indeterminação 0 0 2 3 Propriedades da derivada Derivada
Continuidade e Limite Antônio Calixto de Souza Filho Escola de Artes, Ciências e Humanidades Universidade de São Paulo 20 de maio de 2013 1 Remoção da indeterminação 0 0 2 3 Propriedades da derivada Derivada
Uma Equação Diferencial Ordinária (abrevia-se EDO) de primeira ordem se apresenta sob duas formas equivalentes: (i) FORMA NORMAL:
 5. EDO DE PRIMEIRA ORDEM SÉRIES & EDO - 2017.2 5.1. :::: :::::::::::::::::::::::::::: FUNDAMENTOS GERAIS Uma Equação Diferencial Ordinária (abrevia-se EDO) de primeira ordem se apresenta sob duas formas
5. EDO DE PRIMEIRA ORDEM SÉRIES & EDO - 2017.2 5.1. :::: :::::::::::::::::::::::::::: FUNDAMENTOS GERAIS Uma Equação Diferencial Ordinária (abrevia-se EDO) de primeira ordem se apresenta sob duas formas
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
5 AULA. em Séries de Potências LIVRO. META Apresentar os principais métodos de representação de funções em séries de potências.
 LIVRO Métodos de Representação de Funções em Séries de AULA META Apresentar os principais métodos de representação de funções em séries de potências. OBJETIVOS Representar funções em séries de potências.
LIVRO Métodos de Representação de Funções em Séries de AULA META Apresentar os principais métodos de representação de funções em séries de potências. OBJETIVOS Representar funções em séries de potências.
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de 2010
 Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
EQUAÇÕES DIFERENCIAIS PARA FÍSICOS E ENGENHEIROS
 EQUAÇÕES DIFERENCIAIS PARA FÍSICOS E ENGENHEIROS Paulo Sérgio Costa Lino EQUAÇÕES DIFERENCIAIS PARA FÍSICOS E ENGENHEIROS Universidade Aberta do Brasil - UAB Licenciatura em Física Paulo Sérgio Costa Lino
EQUAÇÕES DIFERENCIAIS PARA FÍSICOS E ENGENHEIROS Paulo Sérgio Costa Lino EQUAÇÕES DIFERENCIAIS PARA FÍSICOS E ENGENHEIROS Universidade Aberta do Brasil - UAB Licenciatura em Física Paulo Sérgio Costa Lino
IST-TAGUS PARQUE-2007/08-2 o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO
 IST-TAGUS PARQUE-007/08- o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM. Diga, justi cando, se as seguintes
IST-TAGUS PARQUE-007/08- o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM. Diga, justi cando, se as seguintes
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes
 Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
Diferenciabilidade de funções reais de várias variáveis reais
 Diferenciabilidade de funções reais de várias variáveis reais Cálculo II Departamento de Matemática Universidade de Aveiro 2018-2019 Cálculo II 2018-2019 Diferenciabilidade de f.r.v.v.r. 1 / 1 Derivadas
Diferenciabilidade de funções reais de várias variáveis reais Cálculo II Departamento de Matemática Universidade de Aveiro 2018-2019 Cálculo II 2018-2019 Diferenciabilidade de f.r.v.v.r. 1 / 1 Derivadas
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
EDP: Método das Características
 EDP: Método das Características Lucio S. Fassarella DMA/CEUNES/UFES August 27, 2018 Contents 0 Introdução 1 0.1 Denições, Terminologia e Notação................................. 2 1 Método das Características
EDP: Método das Características Lucio S. Fassarella DMA/CEUNES/UFES August 27, 2018 Contents 0 Introdução 1 0.1 Denições, Terminologia e Notação................................. 2 1 Método das Características
Capítulo 1.1: Modelos Matemáticos Básicos; Campo de Direções
 Capítulo 1.1: Modelos Matemáticos Básicos; Campo de Direções As Equações Diferenciais são equações que contêm derivadas. Os seguintes exemplos são fenômenos físicos que envolvem taxas de variação: Movimento
Capítulo 1.1: Modelos Matemáticos Básicos; Campo de Direções As Equações Diferenciais são equações que contêm derivadas. Os seguintes exemplos são fenômenos físicos que envolvem taxas de variação: Movimento
Cálculo Infinitesimal II / Cálculo II - Apontamentos de Apoio Capítulo 3 - Funções de n Variáveis
 Cálculo Infinitesimal II / Cálculo II - Apontamentos de Apoio Capítulo 3 - Funções de n Variáveis Neste capítulo vamos estender as noções do cálculo diferencial a funções que dependem de mais de uma variável
Cálculo Infinitesimal II / Cálculo II - Apontamentos de Apoio Capítulo 3 - Funções de n Variáveis Neste capítulo vamos estender as noções do cálculo diferencial a funções que dependem de mais de uma variável
Primitivação de funções reais de variável real
 Capítulo 3 Sugere-se a seguinte bibliografia adicional que completa o estudo a efectuar nas aulas teóricas e nas aulas práticas: Maria Aldina C. Silva e M. dos Anjos F. Saraiva. Primitivação. Edições Asa,
Capítulo 3 Sugere-se a seguinte bibliografia adicional que completa o estudo a efectuar nas aulas teóricas e nas aulas práticas: Maria Aldina C. Silva e M. dos Anjos F. Saraiva. Primitivação. Edições Asa,
Equações Diferenciais A. Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG
 Equações Diferenciais A Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG Sumário Motivação e Algumas Definições 6 Equações Diferenciais de Primeira Ordem. Equações Diferenciais Lineares...............................
Equações Diferenciais A Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG Sumário Motivação e Algumas Definições 6 Equações Diferenciais de Primeira Ordem. Equações Diferenciais Lineares...............................
Cálculo Diferencial e Integral II 2012/13 1 o semestre
 Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
Cálculo Diferencial e Integral II 212/13 1 o semestre Modelo do 1 o Teste LEIC-TP, LEGI, LERC, LEE 6 de Novembro de 212 Justifique adequadamente todas as respostas. 1. Calcule V y dx dy dz em que V = {(x,
BANCO DE EXERCÍCIOS - 24 HORAS
 BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
BANCO DE EXERCÍCIOS - HORAS 9º ANO ESPECIALIZADO/CURSO ESCOLAS TÉCNICAS E MILITARES FOLHA Nº GABARITO COMENTADO ) A função será y,5x +, onde y (preço a ser pago) está em função de x (número de quilômetros
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
24 a Aula AMIV LEAN, LEC Apontamentos
 24 a Aula 2004.11.10 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 24.1 Método de Euler na aproximação de EDO s Métodos numéricos para a determinação de soluções de EDO s podem ser analisados
24 a Aula 2004.11.10 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 24.1 Método de Euler na aproximação de EDO s Métodos numéricos para a determinação de soluções de EDO s podem ser analisados
Cálculo Numérico P2 EM33D
 Cálculo Numérico P EM33D 8 de Abril de 03 Início: 07h30min (Permanência mínima: 08h40min) Término: 0h00min Nome: GABARITO LER ATENTAMENTE AS OBSERVAÇÕES, POIS SERÃO CONSIDERADAS NAS SUA AVALIAÇÃO ) detalhar
Cálculo Numérico P EM33D 8 de Abril de 03 Início: 07h30min (Permanência mínima: 08h40min) Término: 0h00min Nome: GABARITO LER ATENTAMENTE AS OBSERVAÇÕES, POIS SERÃO CONSIDERADAS NAS SUA AVALIAÇÃO ) detalhar
MAP2223 Introdução às Equações Diferenciais Ordinárias e Aplicações
 MAP3 Introdução às Equações Diferenciais Ordinárias e Aplicações Lista 1 o semestre de 18 Prof. Claudio H. Asano 1 Classificação das Equações Diferenciais 1.1 Classifique as equações diferenciais a seguir.
MAP3 Introdução às Equações Diferenciais Ordinárias e Aplicações Lista 1 o semestre de 18 Prof. Claudio H. Asano 1 Classificação das Equações Diferenciais 1.1 Classifique as equações diferenciais a seguir.
Introdução Generalização
 Cálculo 2 - Capítulo 2.9 - Derivação implícita 1 Capítulo 2.9 - Derivação implícita 2.9.1 - Introdução 2.9.3 - Generalização 2.9.2 - Derivação implícita Veremos agora uma importante aplicação da regra
Cálculo 2 - Capítulo 2.9 - Derivação implícita 1 Capítulo 2.9 - Derivação implícita 2.9.1 - Introdução 2.9.3 - Generalização 2.9.2 - Derivação implícita Veremos agora uma importante aplicação da regra
Índice. AULA 5 Derivação implícita 3. AULA 6 Aplicações de derivadas 4. AULA 7 Aplicações de derivadas 6. AULA 8 Esboço de gráficos 9
 www.matematicaemexercicios.com Derivadas Vol. 2 1 Índice AULA 5 Derivação implícita 3 AULA 6 Aplicações de derivadas 4 AULA 7 Aplicações de derivadas 6 AULA 8 Esboço de gráficos 9 www.matematicaemexercicios.com
www.matematicaemexercicios.com Derivadas Vol. 2 1 Índice AULA 5 Derivação implícita 3 AULA 6 Aplicações de derivadas 4 AULA 7 Aplicações de derivadas 6 AULA 8 Esboço de gráficos 9 www.matematicaemexercicios.com
z = y 1 n. (3) Conclusão. A equação de Bernoulli (1) se transforma em uma equação linear através da 1 n, y = 1 1 n z 1
 Seção 6: Equação de Bernoulli Definição. Uma equação de Bernoulli é uma equação diferencial ordinária de a ordem da forma y + fx) y = gx) y n, ) onde n é um número real não precisa ser inteiro nem positivo).
Seção 6: Equação de Bernoulli Definição. Uma equação de Bernoulli é uma equação diferencial ordinária de a ordem da forma y + fx) y = gx) y n, ) onde n é um número real não precisa ser inteiro nem positivo).
Equações Diferenciais A. Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG
 Equações Diferenciais A Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG Sumário Equações Diferenciais Ordinárias 6 2 Equações Diferenciais de Primeira Ordem 2 2. Equações Diferenciais Lineares..............................
Equações Diferenciais A Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG Sumário Equações Diferenciais Ordinárias 6 2 Equações Diferenciais de Primeira Ordem 2 2. Equações Diferenciais Lineares..............................
Modelagem Computacional. Parte 8 2
 Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
Mestrado em Modelagem e Otimização - RC/UFG Modelagem Computacional Parte 8 2 Prof. Thiago Alves de Queiroz 2/2016 2 [Cap. 10 e 11] BURDEN, R. L.; FAIRES, J. D. Numerical Analysis (9th ed). Cengage Learning,
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LICENCIATURA EM ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES. Apontamentos das Aulas Teóricas
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LICENCIATURA EM ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES Análise Matemática 3 Equações Diferenciais Apontamentos das Aulas Teóricas Maria do Rosário
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LICENCIATURA EM ENGENHARIA ELECTROTÉCNICA E DE COMPUTADORES Análise Matemática 3 Equações Diferenciais Apontamentos das Aulas Teóricas Maria do Rosário
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
SEGUNDA CHAMADA CALCULO 2 2/2017
 9/11/017 SEGUNDA CHAMADA CALCULO /017 PROF: RENATO FERREIRA DE VELLOSO VIANNA Questão 1,5 pontos). Resolva os problemas de valor inicial: y + 4y + 4y = e x {, y = xyy + 4), a) = y0) = 0, b) = y0) = 5.
9/11/017 SEGUNDA CHAMADA CALCULO /017 PROF: RENATO FERREIRA DE VELLOSO VIANNA Questão 1,5 pontos). Resolva os problemas de valor inicial: y + 4y + 4y = e x {, y = xyy + 4), a) = y0) = 0, b) = y0) = 5.
