Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 3. Círculos: elementos, arcos e ângulos inscritos
|
|
|
- Maria de Fátima Conceição Cabral
- 7 Há anos
- Visualizações:
Transcrição
1 Material eórico - Módulo Elementos ásicos de Geometria lana - arte 3 írculos: elementos, arcos e ângulos inscritos itavo ano do Ensino Fundamental utor: rof. Jocelino Sato Revisor: rof. ntonio aminha M. Neto ortal da ME
2 1 Elementos de um círculo Sejam um ponto do plano e r um número real positivo. onforme vimos anteriormente, o círculo de centro e raio r, denotado por (, r), é o subconjunto do plano formado por todos os pontos que estão à mesma distância r do ponto (veja a figura abaixo). círculo (, r) Reservamos o termo circunferência para nos referirmos ao comprimento de um círculo. or vezes, a palavra raio também será usada para denotar um segmento, com (, r). ssociados a um círculo temos vários conceitos geométricos. seguir, apresentamos os principais, bem como suas respectivas notações. Um ponto do plano, com < r, é denominado um ponto interior ao círculo (, r); o conjunto formado pelos pontos interiores a um círculo é chamado de interior do círculo. or outro lado, um ponto Q do plano tal que Q > r é dito um ponto exterior a (, r); o conjunto formado pelos pontos exteriores a um círculo é o exterior do círculo. união de um círculo com seu interior é chamado de disco. interior de (, r) Q ponto exterior a (, r) Um segmento cujas extremidades são pontos pertencentes ao círculo (, r) é denominado uma corda de (, r). Qualquer corda de um círculo que contenha seu centro é denominada um diâmetro do círculo. é um diâmetro é corda, mas não diâmetro ortal da ME Se e são pontos de um círculo (, r), a reta é denominada a reta secante a (, r) pelos pontos e. Uma reta secante R que contém o centro recebe o nome especial de reta normal ao círculo. Neste caso, ela fica totalmente caracteriza pelos pontos e e, também, pelos pontos e R, pois a reta que passa por dois pontos distintos é única. Uma tangente a um círculo é uma reta que intersecta o círculo em apenas um ponto. Este ponto é chamado de ponto de tangência e dizemos que o círculo e a reta se tangenciam em. Na próxima seção, mostraremos como construir a tangente a um círculo passando por um de seus pontos, bem como daremos interpretações geométricas para os conceitos acima. R S é uma reta secante R é uma reta normal S é uma reta tangente odo diâmetro de um círculo (, r) o divide em duas partes congruentes (iguais), denominadas semicírculos. Reciprocamente, se uma corda divide um círculo em duas partes iguais, é possível mostrar que ela é, necessariamente, um diâmetro. s extremidades de uma corda de um círculo o dividem em duas partes, chamadas de arcos de círculo. Sempre que não houver perigo de confusão, denotaremos uma qualquer dessas partes por. Se não é um diâmetro, o arco menor é a porção do círculo formada pelos pontos e, juntamente com os pontos do mesmo que estão no interior do ângulo 1 (veja a figura a seguir); por outro lado, o arco maior é a porção do círculo formada pelos pontos e, juntamente com os pontos do mesmo que pertencem ao exterior do ângulo (veja novamente a próxima figura). Um maneira de especificar um desses arcos sem ambiguidade é tomar um terceiro ponto sobre o mesmo, escrevendo então para denotá-lo. ssim, é o arco menor (respectivamente maior) se for um ponto no interior (respectivamente exterior) do ângulo. 1 Recorde que, pelo ângulo, entendemos a região convexa delimitada pelas semirretas e, de sorte que Ô < matematica@obmep.org.br
3 Q é o arco menor Q é o arco maior ângulo associado ao arco menor é denominado um ângulo central de (, r); a medida (em graus ou radianos) do arco menor é, por definição, igual à medida do ângulo central correspondente (em graus ou radianos). medida do arco maior em graus (respectivamente em radianos) é, por definição, igual a 360 (respectivamente 2π) menos a medida do arco menor. bservamos que um arco unitário (isto é, um arco de uma unidade de medida) de um círculo (0, r) é um arco cujo ângulo central associado é um ângulo unitário (isto é, um ângulo de uma unidade de medida). ssim, as noções de congruência, adição e subtração de arcos ficam estabelecidas a partir das noções correspondentes de congruência, adição e subtração dos ângulos centrais associados. Logo, é imediato verificar que dois arcos menores e de círculos de mesmo raio (ou de um mesmo círculo (, r)) possuem a mesma medida se, e somente se, as cordas e possuem a mesma medida. (, ) e (, ) têm o mesmo raio = r =. 2 osições relativas de uma reta e um círculo Entre os resultados apresentados nesta seção, alguns são de fundamental importância para o estudo da construção com régua e compasso. Um exemplo é o teorema da interseção reta-círculo. ntes, contudo, precisamos de outro resultado, importante em si. ortal da ME eorema 1. reta perpendicular a um raio de um círculo, passando pela extremidade que pertence ao círculo, é tangente a ele nesse ponto. Reciprocamente, toda reta tangente a um círculo é perpendicular ao raio do círculo que contém o ponto de tangência. Q Q é uma reta tangente em rova. Sejam λ = (, r) um círculo de centro e raio r e um de seus raios. Seja t a reta perpendicular a em (veja a figura abaixo). Q λ = (, r) Se Q é um ponto de t distinto de, então Q é a hipotenusa do triângulo retângulo Q, de forma que Q >. ortanto, Q não pertence a λ, e concluímos que é o único ponto em comum a λ e t. Mas, isso é o mesmo que dizer que t é tangente a λ. Reciprocamente, seja t uma reta que passa por um ponto de λ, mas tal que t não é perpendicular ao raio em (veja a figura abaixo). Q λ = (, r) Seja o pé da perpendicular a t passando pelo centro de λ. unicidade da perpendicular baixada de um ponto a uma reta garante que. onsidere um ponto Q sobre t, situado na semirreta oposta à semirreta e com = Q. Em relação aos triângulos Q e, temos que é um lado de ambos, Q = = 90 e Q = (por construção); portanto, tais triângulos são congruentes pelo critério LL. ssim, Q = = r, o que mostra que o ponto Q também pertence a λ. ortanto, t não é tangente a λ em. resultado anterior fornece imediatamente o resultado ao qual aludimos no início desta seção (veja também a figura subsequente ao enunciado a seguir). 2 matematica@obmep.org.br
4 eorema 2 (Interseção reta-círculo). Sejam m uma reta e λ = (, r) o círculo de centro e raio r. Se é o pé da perpendicular à reta m baixada do ponto, então uma das seguintes situações ocorre: (a) está situado no exterior de λ e, assim, o mesmo ocorre com os outros pontos de m. (b) está situado no círculo λ e, assim, a reta m e o círculo são tangentes no ponto. (c) está situado no interior de λ e, assim, a reta m intersecta o círculo em exatamente dois pontos. λ = (, r) m λ = (, r) m λ = (, r) Recordemos que a mediatriz de um segmento é o lugar geométrico dos pontos equidistantes das extremidade do segmento. Esse fato dá uma prova imediata para o seguinte resultado. eorema 3. mediatriz de qualquer corda de um círculo passa pelo centro do mesmo. demonstração do resultado seguinte faz uso dos critérios de congruência de triângulos e será deixada a cargo do leitor. eorema 4. Uma condição necessária e suficiente para que a reta passando pelo centro de um círculo seja perpendicular a uma corda do mesmo é que ela intersecte a corda em seu ponto médio. Finalizamos esta seção com o seguinte resultado. eorema 5. Sejam λ um círculo de centro e um ponto no exterior de λ. Se e são pontos de λ tais que as retas e são tangentes a λ, então: (a) s segmentos tangentes e são congruentes; (b) reta é a bissetriz do ângulo e, também, a mediatriz da corda. m ortal da ME I rova. eorema 1 diz que e são ângulos retos. lém disso, como e são pontos de λ, temos que =. omo é hipotenusa comum aos triângulos e, segue do critério cateto hipotenusa de congruência entre triângulos retângulos que. ortanto, = e, da igualdade =, concluímos que é a bissetriz do ângulo. ara o que falta, basta ver que, como = e =, os pontos e pertencem à mediatriz do segmento. Mas, como uma reta é unicamente determinada por dois de seus pontos, concluímos que tal mediatriz é, precisamente, a reta. 3 rcos e ângulos num círculo Um ângulo está inscrito num arco de um círculo λ = (, r) quando seu vértice é um ponto do arco, distinto de e, e seus lados passam por e. Usualmente, quando dizemos que é um ângulo inscrito em λ, fica subentendido que e são as extremidades do arco ao qual pertence. Nesta situação, os segmentos e são cordas de λ e dizemos que o arco de λ ao qual não pertence é o arco subentendido por (veja a figura abaixo, na qual o arco subentendido é o arco menor de λ). inscrito em λ. medida de um ângulo inscrito está relacionada com a medida do arco subentendido. recisamente, temos o importante resultado a seguir. eorema 6 (do Ângulo Inscrito). Se e são cordas de um círculo λ, então a medida do ângulo inscrito é igual à metade da medida do arco subentendido de λ. rova. Sejam um ângulo inscrito num círculo λ de centro e o arco subentendido. Vamos considerar três casos distintos: aso I: Um dos lados do ângulo é um diâmetro de λ: suponha, sem perda de generalidade, que seja um diâmetro de λ (veja a figura abaixo). 3 matematica@obmep.org.br
5 inscrito em λ, sendo um diâmetro. Nesse caso, segue da definição que a medida do arco, correspondente ao ângulo, é igual a Ô < 180. omo o triângulo é isósceles de base temos: Ô =  + Ĉ = 2Â, o que demonstra o teorema neste caso particular. aso II: os lados e estão em semiplanos opostos relativamente à reta (veja a figura abaixo, na qual, por simplicidade, ilustramos somente o caso Ô < 180 ). inscrito em λ, com no seu interior. Seja a interseção da semirreta com o arco. plicando o caso já demonstrado aos ângulos inscritos e, obtemos: Ô = Ô + Ô = 2( + Â) = 2Â. aso III: os lados e estão em um mesmo semiplano relativamente à reta. inscrito em λ, com em seu exterior. ortal da ME Seja a interseção da semirreta com λ. plicando o caso I aos ângulos inscritos e, obtemos: Ô = Ô Ô = 2( Â) = 2Â. Uma consequência imediata do eorema anterior é a seguinte afirmação. orolário 7. odos os ângulos inscritos que subentendem um mesmo arco têm uma mesma medida. omo caso limite ao de um ângulo inscrito, temos aquele em que um dos segmentos ou é tangente a λ. Este tipo de ângulo recebe o nome de ˆangulo de segmento, ou seja, um ângulo é um ângulo de segmento quando seu vértice é um ponto do círculo, um dos segmentos ou é uma corda de λ e o outro é tangente a λ. ara esse tipo de ângulo vale um resultado análogo ao visto para ângulos inscritos, o qual colecionamos a seguir. eorema 8 (do Ângulo de Segmento). Se é um ângulo de segmento de um círculo λ = (0, r), tal que o segmento é uma corda de λ e o segmento é tangente a λ, então a medida de é igual à metade da medida do arco nele contido. Em particular, no caso em que  < 90, sua medida é igual à metade da medida do ângulo central correspondente. rova. or simplicidade, analisemos somente o caso em que  < 90 (a análise do outro caso é análoga e será deixada como exercício para o leitor). Então (veja a figura abaixo), é exterior ao ângulo e, assim, o arco contido em é um arco menor de λ. or definição de ângulo de segmento, temos que é perpendicular a. lém disso, a corda é a base do triângulo isósceles. ssim, sendo α = Â, temos =  = 90 α. omo a soma dos ângulos internos de vale 180, obtemos Ô = 180 2(90 α) = 2α = 2Â. gora, consideremos uma generalização dada pelo caso em que o vértice de não está sobre o círculo λ = (0, r). Este tipo de ângulo recebe o nome de ˆangulo ex-cḙntrico 2. Há duas situações distintas a considerar, quais sejam: (i) vértice está no interior de λ: neste caso, dizemos que é um ˆangulo ex-cḙntrico interior (veja a figura abaixo). 2 Essa nomenclatura, apesar de usual em ortuguês, é um tanto infeliz, haja vista que, antes de mais nada, pode coincidir com o centro de λ! 4 matematica@obmep.org.br
6 é um ângulo ex-cêntrico interior a λ. (ii) vértice está no exterior de λ: aqui, dizemos que é um ˆangulo ex-cḙntrico exterior (novamente, veja a figura a seguir). é um ângulo ex-cêntrico exterior a λ. bserve que, quando coincide com, o ângulo excêntrico interior nada mais é que um ângulo central. or outro lado, quando tende para um ponto de (, r), o ângulo ex-cêntrico correspondente tende para um ângulo inscrito. e qualquer forma, os próximos resultados mostram que as fórmulas para o cálculo das medidas de ângulos ex-cêntricos são compatíveis com essas possibilidades! nalisemos, inicialmente, o caso de ângulos ex-cêntricos interiores. ara tanto, observe que um ângulo ex-cêntrico interior de um círculo (, r) determina as cordas e E que concorrem no vértice e, consequentemente, os arcos e E como mostrado na figura 1. E Figura 1: é um ângulo ex-cêntrico interior a λ. e posse das observações acima, temos o seguinte resultado. ortal da ME eorema 9 (do Ângulo Ex-cêntrico Interior). Seja um ângulo ex-cêntrico interior de um círculo λ. Nas notações da figura acima, se e E são as cordas de λ que concorrem no vértice, então a medida de é igual à média aritmética das medidas dos arcos de λ contidos nos ângulos e E. rova. asta aplicar o eorema do Ângulo Inscrito para os ângulos inscritos E e E, juntamente com o eorema do Ângulo Externo, aplicado ao ângulo externo do triângulo E. e fato, podemos escrever: Â = Ê + EĈ = 1 2 Ô EÔ = 1 (Ô ) 2 + EÔ. Voltemo-nos, agora, ao caso dos ângulos ex-cêntricos exteriores. ara tanto, na figura a seguir, observamos que um ângulo ex-cêntrico exterior determina cordas e E, as quais estão contidas nos segmentos e, respectivamente. onsequentemente, os arcos e E de λ e contidos em são aparentemente tais que a medida de é maior do que a medida de E. Uma consequência da demonstração do resultado a seguir é que esse será, de fato, o caso. E é um ângulo ex-cêntrico exterior a λ. ara ângulos ex-cêntricos exteriores vale o seguinte resultado. eorema 10 (do Ângulo Ex-cêntrico Exterior). Seja um ângulo ex-cêntrico exterior de um círculo λ. Se e E são as cordas de λ contidas nos segmentos e, respectivamente, então a medida de é igual à semidiferença entre as medidas dos arcos e E, nessa ordem. rova. prova deste teorema é bastante similar àquela do teorema anterior, e será deixada para o leitor fazer. omo sugestão, aplique o eorema do Ângulo Inscrito aos ângulos inscritos E e E, juntamente com o eorema do Ângulo Externo ao ângulo externo E do triângulo E. e posse dos teoremas do ângulo inscrito e dos ângulos ex-inscritos interior e exterior, podemos apresentar a condição necessária e suficiente usual para que um triângulo seja retângulo, com ângulo reto no vértice. eorema 11. Um ângulo está inscrito num semicírculo se, e somente se, ele é um ângulo reto. ortanto, 5 matematica@obmep.org.br
7 um triângulo está inscrito num semicírculo se, e somente se, ele é um triângulo retângulo com ângulo reto no vértice. rova. Inicialmente, suponha que está inscrito em um semicírculo do círculo λ = (, r) (veja a figura abaixo). Então, é um diâmetro de λ, de sorte que subentende um arco de λ de medida 180. Segue do eorema do Ângulo inscrito que 180  = = Reciprocamente, suponha que  = 90, seja o ponto médio de e λ = (, r), onde r = 1 2. segmento, sendo um diâmetro de λ, o divide em dois arcos de 180 cada. Se não está sobre λ, então há duas possibilidades: (i) é interior a λ: pelo eorema 9, o ângulo teria medida maior que = 90, o que é uma contradição. (ii) é exterior a λ: pelo eorema 10, o ângulo teria medida menor que = 90, o que também é uma contradição. or fim, uma vez que ambas as possibilidades acima geram contradições, a única possibilidade factível é que esteja sobre λ. corolário a seguir explicita uma consequência imediata, já vista no tópico aralelogramos Especiais e bastante útil, da prova da segunda parte do teorema anterior. orolário 12. Em todo triângulo retângulo, a mediana relativa à hipotenusa tem comprimento igual a metade do comprimento da hipotenusa. ortal da ME rova. Se é retângulo em, então a segunda parte da demonstração do resultado anterior garante que está sobre λ = (, r), onde é o ponto médio de e r = 1 2 (veja a figura abaixo). ortanto, é a mediana relativa à hipotenusa e = r = 1 2. Finalizamos este material observando que os resultados desta seção serão usados, futuramente, na obtenção dos conjuntos usuais de condições necessárias e suficientes para que um quadrilátero seja inscritível num círculo. icas para o rofessor conteúdo dessa aula pode ser visto em dois encontros de 50 minutos cada. primeira seção traz vários conceitos associados a um círculo que devem ser bem assimilados. Na seção dois, sugerimos trabalhar com algumas construções geométricas (compasso e régua), abordando problemas que permitam aplicar os principais resultados vistos. pós estudar o corolário 12 da terceira seção é importante retomar o resultado do eorema 5 da seção 2 e apresentar soluções para os problemas clássicos de construções geométricas de tangências a círculos. referência [2] contém vários exercícios simples envolvendo o eorema do Ângulo Inscrito e suas consequências. Na referência [1] encontramos problemas mais conceituais, incluindo alguns que tratam de construções geométricas. Sugestões de Leitura omplementar 1.. aminha. ópicos de Matemática Elementar, Volume 2: Geometria Euclidiana lana, 2 a edição. Rio de Janeiro, Editora S..M., olce e J. N. ompeu. s Fundamentos da Matemática Elementar, Volume 9: Geometria lana. São aulo, tual Editora, matematica@obmep.org.br
Material Teórico - Módulo Elementos básicos de geometria plana - Parte 3. Quadriláteros Inscritíveis e Circunscritíveis
 Material Teórico - Módulo lementos básicos de geometria plana - Parte 3 Quadriláteros Inscritíveis e ircunscritíveis itavo ano do nsino Fundamental utor: Prof. Jocelino Sato evisor: Prof. ntonio aminha
Material Teórico - Módulo lementos básicos de geometria plana - Parte 3 Quadriláteros Inscritíveis e ircunscritíveis itavo ano do nsino Fundamental utor: Prof. Jocelino Sato evisor: Prof. ntonio aminha
Material Teórico - Módulo Elementos básicos de geometria plana - Parte 3. Quadriláteros. Oitavo ano do Ensino Fundamental
 Material Teórico - Módulo Elementos básicos de geometria plana - arte 3 Quadriláteros Oitavo ano do Ensino Fundamental utor: rof. Jocelino Sato Revisor: rof. ntonio aminha M. Neto ortal da OME 1 Quadriláteros
Material Teórico - Módulo Elementos básicos de geometria plana - arte 3 Quadriláteros Oitavo ano do Ensino Fundamental utor: rof. Jocelino Sato Revisor: rof. ntonio aminha M. Neto ortal da OME 1 Quadriláteros
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 2. Congruência de Triângulos e Aplicações - Parte 1.
 aterial Teórico - ódulo Elementos ásicos de Geometria lana - arte 2 ongruência de Triângulos e plicações - arte 1 Oitavo no utor: rof. Ulisses Lima arente Revisor: rof. ntonio aminha. Neto ortal da OE
aterial Teórico - ódulo Elementos ásicos de Geometria lana - arte 2 ongruência de Triângulos e plicações - arte 1 Oitavo no utor: rof. Ulisses Lima arente Revisor: rof. ntonio aminha. Neto ortal da OE
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 3. Paralelogramos Especiais. Oitavo ano do Ensino Fundamental
 aterial Teórico - ódulo Elementos ásicos de Geometria Plana - Parte 3 Paralelogramos Especiais Oitavo ano do Ensino Fundamental utor: Prof. Jocelino Sato Revisor: Prof. ntonio aminha. Neto Portal da OEP
aterial Teórico - ódulo Elementos ásicos de Geometria Plana - Parte 3 Paralelogramos Especiais Oitavo ano do Ensino Fundamental utor: Prof. Jocelino Sato Revisor: Prof. ntonio aminha. Neto Portal da OEP
Material Teórico - Módulo de Semelhança de Triângulos e Teorema de Tales. Semelhança entre triângulos. Nono ano do Ensino Fundamental
 Material Teórico - Módulo de Semelhança de Triângulos e Teorema de Tales Semelhança entre triângulos Nono ano do Ensino Fundamental utor: Prof. Jocelino Sato Revisor: Prof. ntonio aminha M. Neto 1 Figuras
Material Teórico - Módulo de Semelhança de Triângulos e Teorema de Tales Semelhança entre triângulos Nono ano do Ensino Fundamental utor: Prof. Jocelino Sato Revisor: Prof. ntonio aminha M. Neto 1 Figuras
Material Teórico - Módulo Elementos básicos de geometria plana - Parte 3. Mais Pontos Notáveis de um Triângulo. Oitavo ano do Ensino Fundamental
 Material Teórico - Módulo Elementos básicos de geometria plana - Parte 3 Mais Pontos Notáveis de um Triângulo itavo ano do Ensino Fundamental utor: Prof. Jocelino Sato Revisor: Prof. ntonio aminha M. Neto
Material Teórico - Módulo Elementos básicos de geometria plana - Parte 3 Mais Pontos Notáveis de um Triângulo itavo ano do Ensino Fundamental utor: Prof. Jocelino Sato Revisor: Prof. ntonio aminha M. Neto
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Ângulos - Parte 1. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 1 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha 1 Ângulos Uma região R do plano é convexa
Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 1 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha 1 Ângulos Uma região R do plano é convexa
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Ângulos - Parte 1. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 1 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha Portal da MEP 1 Ângulos Uma região R do
Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 1 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha Portal da MEP 1 Ângulos Uma região R do
Material Teórico - Módulo Elementos Básicos de Geometria Plana Parte 2. A Desigualdade Triangular. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana Parte 2 esigualdade Triangular Oitavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha M. Neto Portal da OMEP 1 desigualdade
Material Teórico - Módulo Elementos ásicos de Geometria Plana Parte 2 esigualdade Triangular Oitavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha M. Neto Portal da OMEP 1 desigualdade
Lugares geométricos básicos I
 Lugares geométricos básicos I M13 - Unidade 5 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Definição Lugar Geométrico da propriedade P é o conjunto
Lugares geométricos básicos I M13 - Unidade 5 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Definição Lugar Geométrico da propriedade P é o conjunto
Material Teórico - Módulo de Semelhança de Triângulos e Teorema de Tales. Teorema de Tales - Parte II. Nono Ano do Ensino Fundamental
 Material Teórico - Módulo de Semelhança de Triângulos e Teorema de Tales Teorema de Tales - Parte II Nono no do Ensino Fundamental Prof. Marcelo Mendes de Oliveira Prof. ntonio aminha Muniz Neto Portal
Material Teórico - Módulo de Semelhança de Triângulos e Teorema de Tales Teorema de Tales - Parte II Nono no do Ensino Fundamental Prof. Marcelo Mendes de Oliveira Prof. ntonio aminha Muniz Neto Portal
Círculos ou circunferências
 Círculos ou circunferências O terceiro postulado de Euclides diz que é possível traçar um círculo com qualquer centro e com qualquer raio. Com os nossos axiomas, este postulado é simplesmente uma consequência.
Círculos ou circunferências O terceiro postulado de Euclides diz que é possível traçar um círculo com qualquer centro e com qualquer raio. Com os nossos axiomas, este postulado é simplesmente uma consequência.
Material Teórico - Módulo Elementos Básicos de Geometria Plana Parte 1. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana Parte 1 Triângulos Oitavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha M. Neto Portal da OMEP 1 Intrudução ados três pontos
Material Teórico - Módulo Elementos ásicos de Geometria Plana Parte 1 Triângulos Oitavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha M. Neto Portal da OMEP 1 Intrudução ados três pontos
Revisão de Círculos. Geometria Básica Profa Lhaylla Crissaff
 Revisão de Círculos Geometria Básica Profa Lhaylla Crissaff 2017.2 1 Definição Circunferência é uma figura geométrica formada por todos os pontos que estão a uma mesma distância de um ponto fixado no plano.
Revisão de Círculos Geometria Básica Profa Lhaylla Crissaff 2017.2 1 Definição Circunferência é uma figura geométrica formada por todos os pontos que estão a uma mesma distância de um ponto fixado no plano.
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 2. Congruência de Triângulos e Aplicações - Parte 2.
 Material Teórico - Módulo lementos ásicos de Geometria Plana - Parte 2 ongruência de Triângulos e plicações - Parte 2 Oitavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha M. Neto Portal
Material Teórico - Módulo lementos ásicos de Geometria Plana - Parte 2 ongruência de Triângulos e plicações - Parte 2 Oitavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio aminha M. Neto Portal
Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas. Redução ao Primeiro Quadrante. Primeiro Ano do Ensino Médio
 Material Teórico - Redução ao rimeiro uadrante e Funções Trigonométricas Redução ao rimeiro uadrante rimeiro Ano do Ensino Médio Autor: rof. Fabrício Siqueira enevides Revisor: rof. Antonio Caminha M.
Material Teórico - Redução ao rimeiro uadrante e Funções Trigonométricas Redução ao rimeiro uadrante rimeiro Ano do Ensino Médio Autor: rof. Fabrício Siqueira enevides Revisor: rof. Antonio Caminha M.
Questões da 1ª avaliação de MA 13 Geometria, 2016
 uestões da 1ª avaliação de M 13 Geometria, 26 1. região na figura abaixo representa um lago. Descreva um processo pelo qual será possível medir a distância entre os pontos e (só medição fora do lago é
uestões da 1ª avaliação de M 13 Geometria, 26 1. região na figura abaixo representa um lago. Descreva um processo pelo qual será possível medir a distância entre os pontos e (só medição fora do lago é
Congruência de triângulos II
 ongruência de triângulos II M13 - Unidade 2 Resumo elaborado por Eduardo Wagner baseado no texto:. aminha M. Neto. Geometria. oleção PROFMT Triângulo isósceles Os ângulos da base de um triângulo isósceles
ongruência de triângulos II M13 - Unidade 2 Resumo elaborado por Eduardo Wagner baseado no texto:. aminha M. Neto. Geometria. oleção PROFMT Triângulo isósceles Os ângulos da base de um triângulo isósceles
Áreas de Figuras Planas: Exercícios da OBMEP. Nono Ano. Autor: Prof. Ulisses Lima Parente Revisor: Prof. Antonio Caminha M. Neto
 Material Teórico - Módulo Áreas de Figuras lanas Áreas de Figuras lanas: Exercícios da OME Nono no utor: rof. Ulisses Lima arente Revisor: rof. ntonio aminha M. Neto de dezembro de 018 1 roblemas da OME
Material Teórico - Módulo Áreas de Figuras lanas Áreas de Figuras lanas: Exercícios da OME Nono no utor: rof. Ulisses Lima arente Revisor: rof. ntonio aminha M. Neto de dezembro de 018 1 roblemas da OME
Polígonos PROFESSOR RANILDO LOPES 11.1
 Polígonos PROFESSOR RANILDO LOPES 11.1 Polígonos Polígono é uma figura geométrica plana e fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano. Exemplos 11.1 Elementos de um polígono
Polígonos PROFESSOR RANILDO LOPES 11.1 Polígonos Polígono é uma figura geométrica plana e fechada formada apenas por segmentos de reta que não se cruzam no mesmo plano. Exemplos 11.1 Elementos de um polígono
Axiomas e Proposições
 Axiomas e Proposições Axiomas: I Incidência I.1 Existem infinitos pontos no plano. I.2 Por dois pontos distintos (ou seja, diferentes) passa uma única reta. I.3 Dada uma reta, existem infinitos pontos
Axiomas e Proposições Axiomas: I Incidência I.1 Existem infinitos pontos no plano. I.2 Por dois pontos distintos (ou seja, diferentes) passa uma única reta. I.3 Dada uma reta, existem infinitos pontos
Módulo de Triângulo Retângulo, Lei dos Senos e Cossenos, Poĺıgonos Regulares. 9 o ano E.F.
 Módulo de Triângulo Retângulo, Lei dos Senos e ossenos, Poĺıgonos Regulares. Relações Métricas em Poĺıgonos Regulares 9 o ano.. Triângulo Retângulo, Lei dos Senos e ossenos, Polígonos Regulares. Relações
Módulo de Triângulo Retângulo, Lei dos Senos e ossenos, Poĺıgonos Regulares. Relações Métricas em Poĺıgonos Regulares 9 o ano.. Triângulo Retângulo, Lei dos Senos e ossenos, Polígonos Regulares. Relações
CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES
 CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES CÍRCULO E CIRCUNFERÊNCIA Circunferência: é uma linha. Exemplos: argola, roda de bicicleta... Círculo: é uma superfície. Exemplos: moeda, mesa redonda... CIRCUNFERÊNCIA
CIRCUNFERÊNCIA E CÍRCULO 1ª PARTE DEFINIÇÕES CÍRCULO E CIRCUNFERÊNCIA Circunferência: é uma linha. Exemplos: argola, roda de bicicleta... Círculo: é uma superfície. Exemplos: moeda, mesa redonda... CIRCUNFERÊNCIA
Os problemas em Desenho Geométrico resumem-se em encontrar pontos. E para determinar um ponto basta obter o cruzamento entre duas linhas.
 31 4 LUGARES GEOMÉTRICOS Os problemas em Desenho Geométrico resumem-se em encontrar pontos. E para determinar um ponto basta obter o cruzamento entre duas linhas. Definição: Um conjunto de pontos do plano
31 4 LUGARES GEOMÉTRICOS Os problemas em Desenho Geométrico resumem-se em encontrar pontos. E para determinar um ponto basta obter o cruzamento entre duas linhas. Definição: Um conjunto de pontos do plano
Ortocentro, Reta de Euler e a Circunferência dos 9 pontos
 Prof. ícero Thiago - cicerothmg@gmail.com rtocentro, Reta de uler e a ircunferência dos 9 pontos Propriedade 1. Seja o centro da circunferência circunscrita ao triângulo acutângulo e seja a projeção de
Prof. ícero Thiago - cicerothmg@gmail.com rtocentro, Reta de uler e a ircunferência dos 9 pontos Propriedade 1. Seja o centro da circunferência circunscrita ao triângulo acutângulo e seja a projeção de
Circunferência. MA092 Geometria plana e analítica. Interior e exterior. Circunferência e círculo. Francisco A. M. Gomes
 Circunferência MA092 Geometria plana e analítica Francisco A. M. Gomes UNICAMP - IMECC Setembro de 2016 A circunferência é o conjunto dos pontos de um plano que estão a uma mesma distância (denominada
Circunferência MA092 Geometria plana e analítica Francisco A. M. Gomes UNICAMP - IMECC Setembro de 2016 A circunferência é o conjunto dos pontos de um plano que estão a uma mesma distância (denominada
Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas. A Lei dos Cossenos Revisitada. Primeiro Ano do Ensino Médio
 Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas Lei dos ossenos Revisitada Primeiro no do Ensino Médio utor: Prof. Farício Siqueira enevides Revisor: Prof. ntonio aminha M. Neto
Material Teórico - Redução ao Primeiro Quadrante e Funções Trigonométricas Lei dos ossenos Revisitada Primeiro no do Ensino Médio utor: Prof. Farício Siqueira enevides Revisor: Prof. ntonio aminha M. Neto
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 2. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 2 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto Nesta segunda parte, veremos
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 2 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto Nesta segunda parte, veremos
Hewlett-Packard CIRCUNFERÊNCIA. AULAS 01 e 02. Prof. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 Hewlett-Packard CIRCUNFERÊNCIA AULAS 01 e 0 Prof. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Sumário Circunferência... 1 CIRCUNFERÊNCIA E CÍRCULO... 1 CIRCUNFERÊNCIA... 1 CÍRCULO... 1 CORDA DE
Hewlett-Packard CIRCUNFERÊNCIA AULAS 01 e 0 Prof. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Sumário Circunferência... 1 CIRCUNFERÊNCIA E CÍRCULO... 1 CIRCUNFERÊNCIA... 1 CÍRCULO... 1 CORDA DE
Desenho Técnico Página 11
 Exercício 16 Concordância Interna de Circunferências Dada uma circunferência de centro O 1 conhecido, determine a circunferência de centro O 2 de tal forma que sejam concordantes internamente. Marque o
Exercício 16 Concordância Interna de Circunferências Dada uma circunferência de centro O 1 conhecido, determine a circunferência de centro O 2 de tal forma que sejam concordantes internamente. Marque o
Material Teórico - Círculo Trigonométrico. Seno, cosseno e tangente. Primeiro Ano do Ensino Médio
 Material Teórico - Círculo Trigonométrico Seno, o e tangente. rimeiro Ano do Ensino Médio Autor: rof. Fabrício Siqueira Benevides Revisor: rof. Antonio Caminha M. Neto 0 de outubro de 08 Seno, o e tangente
Material Teórico - Círculo Trigonométrico Seno, o e tangente. rimeiro Ano do Ensino Médio Autor: rof. Fabrício Siqueira Benevides Revisor: rof. Antonio Caminha M. Neto 0 de outubro de 08 Seno, o e tangente
Matemática. Nesta aula iremos aprender as. 1 Ponto, reta e plano. 2 Posições relativas de duas retas
 Matemática Aula 5 Geometria Plana Alexandre Alborghetti Londero Nesta aula iremos aprender as noções básicas de Geometria Plana. 1 Ponto, reta e plano Estes elementos primitivos da geometria euclidiana
Matemática Aula 5 Geometria Plana Alexandre Alborghetti Londero Nesta aula iremos aprender as noções básicas de Geometria Plana. 1 Ponto, reta e plano Estes elementos primitivos da geometria euclidiana
Material Teórico - Módulo: Vetores em R 2 e R 3. Módulo e Produto Escalar - Parte 1. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Material Teórico - Módulo: Vetores em R 2 e R 3 Módulo e Produto Escalar - Parte 1 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 1 Módulo de um vetor O módulo
Teorema do ângulo externo e sua consequencias
 Teorema do ângulo externo e sua consequencias Definição. Os ângulos internos de um triângulo são os ângulos formados pelos lados do triângulo. Um ângulo suplementar a um ângulo interno do triângulo é denominado
Teorema do ângulo externo e sua consequencias Definição. Os ângulos internos de um triângulo são os ângulos formados pelos lados do triângulo. Um ângulo suplementar a um ângulo interno do triângulo é denominado
MATEMÁTICA 3 GEOMETRIA PLANA
 MATEMÁTICA 3 GEOMETRIA PLANA Professor Renato Madeira MÓDULO 13 Circunferência e Círculo Circunferência é o lugar geométrico dos pontos do plano cujas distâncias a um ponto fixo (centro) são iguais a uma
MATEMÁTICA 3 GEOMETRIA PLANA Professor Renato Madeira MÓDULO 13 Circunferência e Círculo Circunferência é o lugar geométrico dos pontos do plano cujas distâncias a um ponto fixo (centro) são iguais a uma
Coordenadas Cartesianas
 1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
CIRCUNFERÊNCIA E CÍRCULO
 IRUNFRÊNI ÍRUL 01 ( FUVST) medida do ângulo ˆ inscrito na circunferência de centro é, em graus, ) 100 ) 110 ) 10 ) 15 35º 0 0 ( U ) bserve a figura. la mostra dois círculos de mesmo raio com centros em
IRUNFRÊNI ÍRUL 01 ( FUVST) medida do ângulo ˆ inscrito na circunferência de centro é, em graus, ) 100 ) 110 ) 10 ) 15 35º 0 0 ( U ) bserve a figura. la mostra dois círculos de mesmo raio com centros em
III.2 Se os segmentos A B e A B são congruentes ao segmento AB então os segmentos A B e A B também são congruentes.
 1 Grupo III xiomas de ongruência onsidere o conjunto SEG de todos segmentos e o conjunto NG de todos os ângulos. Vamos admitir a existência de duas relações binárias, uma em SEG (e portanto, entre segmentos)
1 Grupo III xiomas de ongruência onsidere o conjunto SEG de todos segmentos e o conjunto NG de todos os ângulos. Vamos admitir a existência de duas relações binárias, uma em SEG (e portanto, entre segmentos)
Propriedades do ortocentro
 Programa límpico de Treinamento Curso de Geometria - Nível 3 Prof. Rodrigo ula 4 Propriedades do ortocentro ortocentro é o ponto de encontro das três alturas de um triângulo arbitrário. Se o triângulo
Programa límpico de Treinamento Curso de Geometria - Nível 3 Prof. Rodrigo ula 4 Propriedades do ortocentro ortocentro é o ponto de encontro das três alturas de um triângulo arbitrário. Se o triângulo
LUGARES GEOMÉTRICOS Geometria Euclidiana e Desenho Geométrico PROF. HERCULES SARTI Mestre
 LUGARES GEOMÉTRICOS Geometria Euclidiana e Desenho Geométrico PROF. HERCULES SARTI Mestre Lugar Geométrico Lugar geométrico é uma figura cujos pontos e somente eles satisfazem determinada condição. Todos
LUGARES GEOMÉTRICOS Geometria Euclidiana e Desenho Geométrico PROF. HERCULES SARTI Mestre Lugar Geométrico Lugar geométrico é uma figura cujos pontos e somente eles satisfazem determinada condição. Todos
Polos Olímpicos de Treinamento. Aula 16. Curso de Geometria - Nível 2. Pontos Notáveis 2: Incentro. Prof. Cícero Thiago
 Polos Olímpicos de Treinamento urso de Geometria - Nível Prof. ícero Thiago ula 16 Pontos Notáveis : ncentro Teorema 1. Seja XOY umângulodadoep umpontoemseuinterior. Então, adistância de P a XO é igual
Polos Olímpicos de Treinamento urso de Geometria - Nível Prof. ícero Thiago ula 16 Pontos Notáveis : ncentro Teorema 1. Seja XOY umângulodadoep umpontoemseuinterior. Então, adistância de P a XO é igual
Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos. Pontos, Retas e Planos - Parte 2. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos Pontos, Retas e Planos - Parte 2 Terceiro no - Médio utor: Prof. ngelo Papa Neto Revisor: Prof. ntonio Caminha 1 Ângulo entre retas no espaço.
Material Teórico - Módulo de Geometria Espacial 1 - Fundamentos Pontos, Retas e Planos - Parte 2 Terceiro no - Médio utor: Prof. ngelo Papa Neto Revisor: Prof. ntonio Caminha 1 Ângulo entre retas no espaço.
Material Teórico - Módulo: Geometria Espacial 3 - Volumes e Áreas de Cilindros, Cones e Esferas. Esfera - Parte 2. Terceiro Ano - Médio
 Material Teórico - Módulo: Geometria Espacial - Volumes e Áreas de Cilindros, Cones e Esferas Esfera - Parte 2 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto
Material Teórico - Módulo: Geometria Espacial - Volumes e Áreas de Cilindros, Cones e Esferas Esfera - Parte 2 Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto
Material Teórico - Elementos Básicos de Geometria Plana - Parte 3. Oitavo Ano
 Material Teórico - Elementos ásicos de Geometria Plana - Parte 3 Número π e o Comprimento do Círculo itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha M. Neto Portal da MEP 1 número
Material Teórico - Elementos ásicos de Geometria Plana - Parte 3 Número π e o Comprimento do Círculo itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha M. Neto Portal da MEP 1 número
CONSTRUÇÕES GEOMÉTRICAS FUNDAMENTAIS
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE EXPRESSÃO GRÁFICA CONSTRUÇÕES GEOMÉTRICAS FUNDAMENTAIS 2 1 NOÇÕES DE GEOMETRIA PLANA 1.1 GEOMETRIA A necessidade de medir terras
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE EXPRESSÃO GRÁFICA CONSTRUÇÕES GEOMÉTRICAS FUNDAMENTAIS 2 1 NOÇÕES DE GEOMETRIA PLANA 1.1 GEOMETRIA A necessidade de medir terras
MATEMÁTICA APLICADA À AGRIMENSURA PROF. JORGE WILSON
 MATEMÁTICA APLICADA À AGRIMENSURA PROF. JORGE WILSON PROFJWPS@GMAIL.COM DEFINIÇÕES GEOMETRIA PLANA Ponto: Um elemento do espaço que define uma posição. Reta: Conjunto infinito de pontos. Dois pontos são
MATEMÁTICA APLICADA À AGRIMENSURA PROF. JORGE WILSON PROFJWPS@GMAIL.COM DEFINIÇÕES GEOMETRIA PLANA Ponto: Um elemento do espaço que define uma posição. Reta: Conjunto infinito de pontos. Dois pontos são
Axiomas de Incidência Axiomas de Ordem Axiomas de Congruência Axioma das paralelas Axiomas de Continuidade
 1 GEOMETRIA PLANA Atualizado em 04/08/2008 www.mat.ufmg.br/~jorge Bibliografia 1. Pogorélov, A.V. Geometria Elemental Editora Mir. 2. Dolce, Osvaldo e Nicolau, Pompeu Geometria Plana Volume 9 da Coleção
1 GEOMETRIA PLANA Atualizado em 04/08/2008 www.mat.ufmg.br/~jorge Bibliografia 1. Pogorélov, A.V. Geometria Elemental Editora Mir. 2. Dolce, Osvaldo e Nicolau, Pompeu Geometria Plana Volume 9 da Coleção
Geometria Euclidiana Espacial e Introdução à Geometria Descritiva
 UNIVERSIDDE ESTDUL PULIST DEPRTMENTO DE MTEMÁTIC Geometria Euclidiana Espacial e Introdução à Geometria Descritiva Material em preparação!! Última atualização: 28.04.2008 Luciana F. Martins e Neuza K.
UNIVERSIDDE ESTDUL PULIST DEPRTMENTO DE MTEMÁTIC Geometria Euclidiana Espacial e Introdução à Geometria Descritiva Material em preparação!! Última atualização: 28.04.2008 Luciana F. Martins e Neuza K.
C A r. GABARITO MA13 Geometria I - Avaliação /2. A área de um triângulo ABC será denotada por (ABC).
 GRITO 13 Geometria I - valiação 3-01/ área de um triângulo será denotada por (). Questão 1. (pontuação: ) figura abaio mostra as semirretas perpendiculares r e s, três circunferências pequenas cada uma
GRITO 13 Geometria I - valiação 3-01/ área de um triângulo será denotada por (). Questão 1. (pontuação: ) figura abaio mostra as semirretas perpendiculares r e s, três circunferências pequenas cada uma
da circunferência. Os lados deste ângulo, as semirretas e são raios da circunferência. Dizemos então, que o ângulo AOB é um ângulo ao centro.
 Ângulo ao centro Consideremos a seguinte circunferência de centro O onde está desenhado o ângulo AOB. Observando a figura podemos concluir que o vértice do ângulo AOB coincide com o centro.. da circunferência.
Ângulo ao centro Consideremos a seguinte circunferência de centro O onde está desenhado o ângulo AOB. Observando a figura podemos concluir que o vértice do ângulo AOB coincide com o centro.. da circunferência.
Paralelismo. MA13 - Unidade 3. Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria.
 Paralelismo M13 - Unidade 3 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Nomes tradicionais reta t corta as retas r e s. Dizemos que a reta t é uma
Paralelismo M13 - Unidade 3 Resumo elaborado por Eduardo Wagner baseado no texto:. Caminha M. Neto. Geometria. Coleção PROFMT Nomes tradicionais reta t corta as retas r e s. Dizemos que a reta t é uma
Polos Olímpicos de Treinamento. Aula 10. Curso de Geometria - Nível 2. Potência de ponto. Prof. Cícero Thiago
 olos límpicos de Treinamento Curso de Geometria - Nível 2 rof. Cícero Thiago ula 10 otência de ponto 1. Definição Seja Γ uma circunferência de centro e raio R. Seja um ponto que está a uma distância d
olos límpicos de Treinamento Curso de Geometria - Nível 2 rof. Cícero Thiago ula 10 otência de ponto 1. Definição Seja Γ uma circunferência de centro e raio R. Seja um ponto que está a uma distância d
GEOMETRIA PLANA. 1) (UFRGS) Na figura abaixo, o vértice A do retângulo OABC está a 6 cm do vértice C. O raio do círculo mede
 GEOMETRI PLN 1) (UFRGS) Na figura abaixo, o vértice do retângulo O está a 6 cm do vértice. O raio do círculo mede O (a) 5 cm (b) 6 cm (c) 8 cm (d) 9 cm (e) 10 cm ) (UFRGS) Na figura abaixo, é o centro
GEOMETRI PLN 1) (UFRGS) Na figura abaixo, o vértice do retângulo O está a 6 cm do vértice. O raio do círculo mede O (a) 5 cm (b) 6 cm (c) 8 cm (d) 9 cm (e) 10 cm ) (UFRGS) Na figura abaixo, é o centro
Posição relativa entre retas e círculos e distâncias
 4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
4 Posição relativa entre retas e círculos e distâncias Sumário 4.1 Distância de um ponto a uma reta.......... 2 4.2 Posição relativa de uma reta e um círculo no plano 4 4.3 Distância entre duas retas no
POTÊNCIA DE PONTO, EIXO RADICAL, CENTRO RADICAL E APLICAÇÕES Yuri Gomes Lima, Fortaleza - CE
 PTÊNI PNT, IX RIL, NTR RIL PLIÇÕS Yuri Gomes Lima, Fortaleza - Nível INTRUÇÃ Muitas vezes na Geometria Plana nos deparamos com problemas em que não temos muitas informações a respeito de ângulos e comprimentos,
PTÊNI PNT, IX RIL, NTR RIL PLIÇÕS Yuri Gomes Lima, Fortaleza - Nível INTRUÇÃ Muitas vezes na Geometria Plana nos deparamos com problemas em que não temos muitas informações a respeito de ângulos e comprimentos,
Geometria Espacial Curso de Licenciatura em Matemática parte II. Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR
 Geometria Espacial Curso de Licenciatura em Matemática parte II Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR - 2014 1. Paralelismo de Retas L20 Postulado das Paralelas ( de Euclides )
Geometria Espacial Curso de Licenciatura em Matemática parte II Prof.a Tânia Preto Departamento Acadêmico de Matemática UTFPR - 2014 1. Paralelismo de Retas L20 Postulado das Paralelas ( de Euclides )
Av. João Pessoa, 100 Magalhães Laguna / Santa Catarina CEP
 Disciplina: Matemática Curso: Ensino Médio Professor(a): Flávio Calônico Júnior Turma: 3ª Série E M E N T A II Trimestre 2013 Conteúdos Programáticos Data 21/maio 28/maio Conteúdo FUNÇÃO MODULAR Interpretação
Disciplina: Matemática Curso: Ensino Médio Professor(a): Flávio Calônico Júnior Turma: 3ª Série E M E N T A II Trimestre 2013 Conteúdos Programáticos Data 21/maio 28/maio Conteúdo FUNÇÃO MODULAR Interpretação
Polos Olímpicos de Treinamento. Aula 18. Curso de Geometria - Nível 3. Transformações geométricas II - Simetria e rotação. Prof.
 olos límpicos de Treinamento urso de Geometria - Nível 3 rof. ícero Thiago ula 18 Transformações geométricas II - Simetria e rotação. 1. Simetria com relação a um ponto. Dizemos que o ponto é o simétrico
olos límpicos de Treinamento urso de Geometria - Nível 3 rof. ícero Thiago ula 18 Transformações geométricas II - Simetria e rotação. 1. Simetria com relação a um ponto. Dizemos que o ponto é o simétrico
Resoluções NÍVEL 3. Classe
 00 www.cursoanglo.com.br Treinamento para Olimpíadas de atemática NÍVL 3 Resoluções ULS 4 6 m lasse. as paralelas traçadas aos bastões pelos pontos,,, e (ver figura) e da propriedade dos ângulos alternos
00 www.cursoanglo.com.br Treinamento para Olimpíadas de atemática NÍVL 3 Resoluções ULS 4 6 m lasse. as paralelas traçadas aos bastões pelos pontos,,, e (ver figura) e da propriedade dos ângulos alternos
Soluções dos Problemas do Capítulo 4
 Soluções do apítulo 4 155 Soluções dos Problemas do apítulo 4 Problema 1 h 10 14 Figura 57 x Seja h a altura do Pão de çúcar em relação ao plano horizontal de medição e seja x a distância de ao pé da altura
Soluções do apítulo 4 155 Soluções dos Problemas do apítulo 4 Problema 1 h 10 14 Figura 57 x Seja h a altura do Pão de çúcar em relação ao plano horizontal de medição e seja x a distância de ao pé da altura
ÂNGULOS. Ângulos no círculo
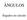 ÂNGULOS Ângulos no círculo A circunferência:. Diâmetro Semicircunferên cia Diâmetro - é o segmento de recta que une 2 pontos da circunferência passando pelo centro. Raio - é o segmento de recta que une
ÂNGULOS Ângulos no círculo A circunferência:. Diâmetro Semicircunferên cia Diâmetro - é o segmento de recta que une 2 pontos da circunferência passando pelo centro. Raio - é o segmento de recta que une
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
76 Capítulo 4 Distâncias no plano e regiões no plano 1. Distância de um ponto a uma reta Dados um ponto P e uma reta r no plano, já sabemos calcular a distância de P a cada ponto P r. Definição 1 Definimos
Geometria Plana. Exterior do ângulo Ô:
 Geometria Plana Ângulo é a união de duas semiretas de mesma origem, não sendo colineares. Interior do ângulo Ô: Exterior do ângulo Ô: Dois ângulos são consecutivos se, e somente se, apresentarem um lado
Geometria Plana Ângulo é a união de duas semiretas de mesma origem, não sendo colineares. Interior do ângulo Ô: Exterior do ângulo Ô: Dois ângulos são consecutivos se, e somente se, apresentarem um lado
Aula 9 Triângulos Semelhantes
 MUL 1 - UL 9 ula 9 Triângulos Semelhantes efinição: ois triângulos são semelhantes se os três ângulos são ordenadamente congruentes e se os lados homólogos são proporcionais. figura mostra dois triângulos
MUL 1 - UL 9 ula 9 Triângulos Semelhantes efinição: ois triângulos são semelhantes se os três ângulos são ordenadamente congruentes e se os lados homólogos são proporcionais. figura mostra dois triângulos
» Teorema (CROSSBAR) Seja ABC um triângulo e seja X um ponto em seu interior. Então todo raio AX corta o lado BC.
 » Teorema (CROSSBAR) Seja ABC um triângulo e seja X um ponto em seu interior. Então todo raio AX corta o lado BC. Iniciamos, nesta seção, o estudo sistemático da geometria dos quadriláteros. Dentre os
» Teorema (CROSSBAR) Seja ABC um triângulo e seja X um ponto em seu interior. Então todo raio AX corta o lado BC. Iniciamos, nesta seção, o estudo sistemático da geometria dos quadriláteros. Dentre os
O Quadrilátero de Saccheri
 O Quadrilátero de Saccheri 1 efinição (Quadrilátero de Saccheri) Na figura abaixo se tem um quadrilátero com ângulos retos em e, os segmentos e denominados hastes são congruentes isto é, e os segmentos
O Quadrilátero de Saccheri 1 efinição (Quadrilátero de Saccheri) Na figura abaixo se tem um quadrilátero com ângulos retos em e, os segmentos e denominados hastes são congruentes isto é, e os segmentos
Lista 5. Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 4.1, pág. 147 em diante.
 MA13 Exercícios das Unidades 8, 9 e 10 2014 Lista 5 Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 4.1, pág. 147 em diante. 1) As retas r, s e t são paralelas com s entre r e t. As transversais
MA13 Exercícios das Unidades 8, 9 e 10 2014 Lista 5 Geometria, Coleção Profmat, SBM. Problemas selecionados da seção 4.1, pág. 147 em diante. 1) As retas r, s e t são paralelas com s entre r e t. As transversais
Aula 11 Conseqüências da semelhança de
 onseqüências da semelhança de triângulos MÓULO 1 - UL 11 ula 11 onseqüências da semelhança de triângulos Objetivos presentar o Teorema de Pitágoras presentar o teorema da bissetriz interna. O Teorema de
onseqüências da semelhança de triângulos MÓULO 1 - UL 11 ula 11 onseqüências da semelhança de triângulos Objetivos presentar o Teorema de Pitágoras presentar o teorema da bissetriz interna. O Teorema de
Pontos notáveis de um triângulo
 MÓULO 1 - UL 9 ula 9 ontos notáveis de um triângulo Objetivos presentar os pontos notáveis de um triângulo. stabelecer alguns resultados envolvendo esses elementos. ontos notáveis de um triângulo Nesta
MÓULO 1 - UL 9 ula 9 ontos notáveis de um triângulo Objetivos presentar os pontos notáveis de um triângulo. stabelecer alguns resultados envolvendo esses elementos. ontos notáveis de um triângulo Nesta
Teorema de Tales. MA13 - Unidade 8. Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria.
 Teorema de Tales MA13 - Unidade 8 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Proporcionalidade 1. Dizemos que o segmento x é a quarta proporcional
Teorema de Tales MA13 - Unidade 8 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Proporcionalidade 1. Dizemos que o segmento x é a quarta proporcional
Expressões Algébricas
 META: Resolver geometricamente problemas algébricos. AULA 11 OBJETIVOS: Introduzir a 4 a proporcional. Construir segmentos que resolvem uma equação algébrica. PRÉ-REQUISITOS O aluno deverá ter compreendido
META: Resolver geometricamente problemas algébricos. AULA 11 OBJETIVOS: Introduzir a 4 a proporcional. Construir segmentos que resolvem uma equação algébrica. PRÉ-REQUISITOS O aluno deverá ter compreendido
Curso: Engenharia Disciplina: Desenho Técnico Prof.ª Me. Aline Ribeiro CONSTRUÇÕES GEOMÉTRICAS 1. DESENHO GEOMÉTRICO
 1 Curso: Engenharia Disciplina: Desenho Técnico Prof.ª Me. Aline Ribeiro CONSTRUÇÕES GEOMÉTRICAS 1. DESENHO GEOMÉTRICO 1.1. O que é desenho geométrico Desenho Geométrico é o conjunto de técnicas utilizadas
1 Curso: Engenharia Disciplina: Desenho Técnico Prof.ª Me. Aline Ribeiro CONSTRUÇÕES GEOMÉTRICAS 1. DESENHO GEOMÉTRICO 1.1. O que é desenho geométrico Desenho Geométrico é o conjunto de técnicas utilizadas
GAD = 180º 75º 60º = 45º
 009 www.cursoanglo.com.br Treinamento para Olimpíadas de Matemática NÍVL 3 Resoluções ULS 4 a 6 m lasse. omo e são triângulos eqüiláteros, cada um de seus ângulos internos mede 60º. No triângulo G temos
009 www.cursoanglo.com.br Treinamento para Olimpíadas de Matemática NÍVL 3 Resoluções ULS 4 a 6 m lasse. omo e são triângulos eqüiláteros, cada um de seus ângulos internos mede 60º. No triângulo G temos
Circunferências tangentes entre si e o Lema da estrela da morte
 Circunferências tangentes entre si e o Lema da estrela da morte emana Olímpica/2018 - Nível 2 rof. rmando Barbosa Maceió, 25 de janeiro de 2018 m algumas questões de olimpíada de matemática, aparecem questões
Circunferências tangentes entre si e o Lema da estrela da morte emana Olímpica/2018 - Nível 2 rof. rmando Barbosa Maceió, 25 de janeiro de 2018 m algumas questões de olimpíada de matemática, aparecem questões
Material Teórico - Módulo de Geometria Anaĺıtica 2. Áreas de Poĺıgonos. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria naĺıtica Áreas de Poĺıgonos Terceiro no - Médio utor: Prof ngelo Papa Neto Revisor: Prof ntonio Caminha M Neto 1 Área de um triângulo Na aula Equação da Reta Módulo
Material Teórico - Módulo de Geometria naĺıtica Áreas de Poĺıgonos Terceiro no - Médio utor: Prof ngelo Papa Neto Revisor: Prof ntonio Caminha M Neto 1 Área de um triângulo Na aula Equação da Reta Módulo
Turma preparatória para Olimpíadas.
 p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br Turma preparatória para Olimpíadas. TRIÂNGULOS - V01 DEFINIÇÃO Sejam três pontos não colineares A, B e C, o triângulo ABC é uma figura
p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br Turma preparatória para Olimpíadas. TRIÂNGULOS - V01 DEFINIÇÃO Sejam três pontos não colineares A, B e C, o triângulo ABC é uma figura
Portal da OBMEP. Material Teórico - Módulo de Geometria Anaĺıtica 1. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Material Teórico - Módulo de Geometria Anaĺıtica 1. Terceiro Ano - Médio. Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M.
 Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Material Teórico - Módulo de Geometria Anaĺıtica 1 Equação da Reta Terceiro Ano - Médio Autor: Prof Angelo Papa Neto Revisor: Prof Antonio Caminha M Neto 1 Condição de alinhamento de três pontos Consideremos
Aula 7 Complementos. Exercício 1: Em um plano, por um ponto, existe e é única a reta perpendicular
 MODULO 1 - AULA 7 Aula 7 Complementos Apresentamos esta aula em forma de Exercícios Resolvidos, mas são resultados importantes que foram omitidos na primeira aula que tratou de Conceitos Básicos. Exercício
MODULO 1 - AULA 7 Aula 7 Complementos Apresentamos esta aula em forma de Exercícios Resolvidos, mas são resultados importantes que foram omitidos na primeira aula que tratou de Conceitos Básicos. Exercício
Geometria (euclidiana)
 Geometria (euclidiana) Professor: jair.donadelli@ufabc.edu.br página da disciplina na web: http://professor.ufabc.edu.br/~jair.donadelli/geometria Professor: jair.donadelli@ufabc.edu.br MA13 Geometria
Geometria (euclidiana) Professor: jair.donadelli@ufabc.edu.br página da disciplina na web: http://professor.ufabc.edu.br/~jair.donadelli/geometria Professor: jair.donadelli@ufabc.edu.br MA13 Geometria
CONSTRUÇÕES GEOMÉTRICAS E DEMONSTRAÇÕES nível 2
 Prof. Élio Mega ONSTRUÇÕES GEOMÉTRIS E DEMONSTRÇÕES nível 2 partir do século V a, os matemáticos gregos desenvolveram uma parte da Matemática, intimamente ligada à Geometria, conhecida como onstruções
Prof. Élio Mega ONSTRUÇÕES GEOMÉTRIS E DEMONSTRÇÕES nível 2 partir do século V a, os matemáticos gregos desenvolveram uma parte da Matemática, intimamente ligada à Geometria, conhecida como onstruções
1. Posição de retas 11 Construindo retas paralelas com régua e compasso 13
 Sumário CAPÍTULO 1 Construindo retas e ângulos 1. Posição de retas 11 Construindo retas paralelas com régua e compasso 13 2. Partes da reta 14 Construindo segmentos congruentes com régua e compasso 15
Sumário CAPÍTULO 1 Construindo retas e ângulos 1. Posição de retas 11 Construindo retas paralelas com régua e compasso 13 2. Partes da reta 14 Construindo segmentos congruentes com régua e compasso 15
 Geometria Plana 1 (UEM-2013) Em um dia, em uma determinada região plana, o Sol nasce às 7 horas e se põe às 19 horas. Um observador, nessa região, deseja comparar a altura de determinados objetos com o
Geometria Plana 1 (UEM-2013) Em um dia, em uma determinada região plana, o Sol nasce às 7 horas e se põe às 19 horas. Um observador, nessa região, deseja comparar a altura de determinados objetos com o
CONSTRUÇÕES GEOMÉTRICAS E DEMONSTRAÇÕES nível 1
 Prof. Élio Mega ONSTRUÇÕES GEOMÉTRIS E DEMONSTRÇÕES nível 1 partir do século V a, os matemáticos gregos desenvolveram uma parte da Matemática, intimamente ligada à Geometria, conhecida como onstruções
Prof. Élio Mega ONSTRUÇÕES GEOMÉTRIS E DEMONSTRÇÕES nível 1 partir do século V a, os matemáticos gregos desenvolveram uma parte da Matemática, intimamente ligada à Geometria, conhecida como onstruções
Aula 2 A distância no espaço
 MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MÓDULO 1 - AULA 2 Objetivos Aula 2 A distância no espaço Determinar a distância entre dois pontos do espaço. Estabelecer a equação da esfera em termos de distância. Estudar a posição relativa entre duas
MATEMÁTICA Polígonos e circunferências. Circunferência
 MTEMÁTI ircunferência hama-se circunferência de centro e raio r ao conjuntos de pontos do plano cuja a distância ao ponto é igual a r. Uma circunferência de centro e raio r designa-se geralmente por (,
MTEMÁTI ircunferência hama-se circunferência de centro e raio r ao conjuntos de pontos do plano cuja a distância ao ponto é igual a r. Uma circunferência de centro e raio r designa-se geralmente por (,
Material Teórico - Módulo de Geometria Espacial 2 - Volumes e Áreas de Prismas e Pirâmides. Terceiro Ano - Médio
 Material Teórico - Módulo de Geometria Espacial 2 - Volumes e Áreas de Prismas e Pirâmides Pirâmides Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 12 de agosto
Material Teórico - Módulo de Geometria Espacial 2 - Volumes e Áreas de Prismas e Pirâmides Pirâmides Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto 12 de agosto
Objetivos. em termos de produtos internos de vetores.
 Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
Aula 5 Produto interno - Aplicações MÓDULO 1 - AULA 5 Objetivos Calcular áreas de paralelogramos e triângulos. Calcular a distância de um ponto a uma reta e entre duas retas. Determinar as bissetrizes
LISTA DE EXERCÍCIOS MAT GEOMETRIA E DESENHO GEOMÉTRICO I
 LISTA DE EXERCÍCIOS MAT 230 - GEOMETRIA E DESENHO GEOMÉTRICO I 1. Numa geometria de incidência, o plano tem 5 pontos. Quantas retas tem este plano? A resposta é única? 2. Exibir um plano de incidência
LISTA DE EXERCÍCIOS MAT 230 - GEOMETRIA E DESENHO GEOMÉTRICO I 1. Numa geometria de incidência, o plano tem 5 pontos. Quantas retas tem este plano? A resposta é única? 2. Exibir um plano de incidência
Polos Olímpicos de Treinamento. Aula 15. Curso de Geometria - Nível 2. Pontos Notáveis 1: Baricentro. Prof. Cícero Thiago
 olos Olímpicos de Treinamento urso de Geometria - Nível rof. ícero Thiago ula 15 ontos Notáveis 1: aricentro ropriedade 1. s três medianas de um triângulo intersectam - se num mesmo ponto, chamado baricentro,
olos Olímpicos de Treinamento urso de Geometria - Nível rof. ícero Thiago ula 15 ontos Notáveis 1: aricentro ropriedade 1. s três medianas de um triângulo intersectam - se num mesmo ponto, chamado baricentro,
Polos Olímpicos de Treinamento. Aula 15. Curso de Geometria - Nível 3. Quádruplas harmônicas e circunferência de Apolônio. Prof.
 olos Olímpicos de Treinamento urso de Geometria - Nível 3 rof. ícero Thiago ula 15 Quádruplas harmônicas e circunferência de polônio Teorema 1. (issetriz interna) bissetriz interna L do ângulo de um triângulo
olos Olímpicos de Treinamento urso de Geometria - Nível 3 rof. ícero Thiago ula 15 Quádruplas harmônicas e circunferência de polônio Teorema 1. (issetriz interna) bissetriz interna L do ângulo de um triângulo
Equilátero Isósceles Escaleno
 TRIÂNGULOS Triângulo são polígonos formados por três lados. Os polígonos, por sua vez, são figuras geométricas formadas por segmentos de reta que, dois a dois, tocam-se em seus pontos extremos, mas que
TRIÂNGULOS Triângulo são polígonos formados por três lados. Os polígonos, por sua vez, são figuras geométricas formadas por segmentos de reta que, dois a dois, tocam-se em seus pontos extremos, mas que
Polos Olímpicos de Treinamento. Aula 17. Curso de Geometria - Nível 2. Pontos Notáveis 3: Circuncentro e Ortocentro. Prof.
 Polos Olímpicos de Treinamento urso de Geometria - Nível 2 Prof. ícero Thiago ula 17 Pontos Notáveis 3: ircuncentro e Ortocentro Teorema 1. Sejam, e P três pontos distintos no plano. Temos que P = P se,
Polos Olímpicos de Treinamento urso de Geometria - Nível 2 Prof. ícero Thiago ula 17 Pontos Notáveis 3: ircuncentro e Ortocentro Teorema 1. Sejam, e P três pontos distintos no plano. Temos que P = P se,
Elementos de Lógica Matemática. Uma Breve Iniciação
 Elementos de Lógica Matemática Uma Breve Iniciação Proposições Uma proposição é uma afirmação passível de assumir valor lógico verdadeiro ou falso. Exemplos de Proposições 2 > 1 (V); 5 = 1 (F). Termos
Elementos de Lógica Matemática Uma Breve Iniciação Proposições Uma proposição é uma afirmação passível de assumir valor lógico verdadeiro ou falso. Exemplos de Proposições 2 > 1 (V); 5 = 1 (F). Termos
MATEMÁTICA A - 12o Ano N o s Complexos - Conjuntos e condições Propostas de resolução
 MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Analisando cada uma das afirmações temos (A) z z = z z é uma afirmação verdadeira
MATEMÁTICA A - o Ano N o s Complexos - Conjuntos e condições Propostas de resolução Exercícios de exames e testes intermédios. Analisando cada uma das afirmações temos (A) z z = z z é uma afirmação verdadeira
Desenho Geométrico e Concordâncias
 UnB - FGA Desenho Geométrico e Concordâncias Disciplina: DIAC-1 Prof a Eneida González Valdés CONSTRUÇÕES GEOMÉTRICAS Todas as construções da geometria plana são importantes, há, entretanto algumas, que
UnB - FGA Desenho Geométrico e Concordâncias Disciplina: DIAC-1 Prof a Eneida González Valdés CONSTRUÇÕES GEOMÉTRICAS Todas as construções da geometria plana são importantes, há, entretanto algumas, que
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Ângulos - Parte 2. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 2 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha 1 Submúltiplos do grau Na aula anterior,
Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 2 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha 1 Submúltiplos do grau Na aula anterior,
Material Teórico - Módulo Elementos Básicos de Geometria Plana - Parte 1. Ângulos - Parte 2. Oitavo Ano
 Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 2 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha 1 Submúltiplos do grau Na aula anterior,
Material Teórico - Módulo Elementos ásicos de Geometria Plana - Parte 1 Ângulos - Parte 2 itavo no utor: Prof. Ulisses Lima Parente Revisor: Prof. ntonio Caminha 1 Submúltiplos do grau Na aula anterior,
Aula 1. Exercício 1: Exercício 2:
 Aula 1 Exercício 1: Com centro em A e raio de medida m achamos dois pontos B e C na reta, esses dois pontos são os centros das circunferências pedidas (2 soluções ). Exercício 2: Com centro em B e raio
Aula 1 Exercício 1: Com centro em A e raio de medida m achamos dois pontos B e C na reta, esses dois pontos são os centros das circunferências pedidas (2 soluções ). Exercício 2: Com centro em B e raio
