Quadrilátero convexo

Tamanho: px

Começar a partir da página:

Download "Quadrilátero convexo"

Victorio Olivares Quintão
7 Há anos
Visualizações:

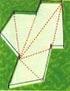
1 EMBAP ESCOLA DE MÚSICA E BELAS ARTES DO PARANÁ DISCIPLINA DE DESENHO GEOMÉTRICO E GEOMETRIA DESCRITIVA Profª Eliane Dumke eliane.dumke@gmail.com Aula 10 (material didático produzido por Paula Rigo) Estudo de propriedades dos quadriláteros e construções Quadrilátero é a figura constituída por quatro pontos do plano, os vértices, e pelos seis segmentos que os unem. Supõe-se que dos quatro pontos não há três que sejam colineares. Diagonais de um quadrilátero são os segmentos de reta que unem dois vértices opostos. Apótema de um quadrilátero regular é a designação dada à linha que partindo do centro geométrico da figura é perpendicular a um dos seus lados. Nomenclatura 4 Vértices: A, B, C, D 4 Lados: [AB], [BC], [CD], [AD] 4 Ângulos internos: ABC, BCD, CDA, DAB 2 Diagonais: [AC], [BD] Vértices consecutivos: A e B, B e C, C e D, D e A Vértices opostos: A e C, B e D Lados consecutivos: [AB] e [BC], [BC] e [CD], [CD] e [AD], [AD] e [AB] Lados opostos: [AB] e [CD], [AD] e [BC] Relações entre os ângulos de um Quadrilátero A soma dos ângulos internos de um quadrilátero é geometricamente igual a um ângulo de 360º. α + β + γ + δ = 360º Classificação dos Quadriláteros Quadrilátero convexo Quadrilátero côncavo Quadrilátero estrelado Chama-se quadrilátero convexo, àquele que define um domínio convexo (1). Quadrilátero côncavo é aquele que define um domínio côncavo (1). Observa-se que o quadrilátero estrelado também é um quadrilátero côncavo. (1) Um domínio plano diz-se convexo quando o segmento de reta definido por dois quaisquer dos seus pontos interiores é um subconjunto do domínio; no caso contrário diz-se côncavo.

2 Propriedades dos Trapézios Trapézios, no sentido lato, são quadriláteros em que dois lados opostos são paralelos. Os lados são as bases e se forem desiguais uma é a base maior e a outra a base menor. Classificação dos Trapézios Trapézio isósceles Trapézio retângulo AB = CD α = β α = 90º Trapézio escaleno Um trapézio isósceles é aquele cujos lados opostos não paralelos são iguais. Um trapézio retângulo é aquele em que um dos lados opostos não paralelos é perpendicular às bases. Um trapézio escaleno é aquele cujos lados opostos não paralelos são desiguais. Relações de um Trapézio Isósceles 1 - Num trapézio isósceles os ângulos adjacentes à mesma base são geometricamente iguais: a = δ e β = γ 2 - As diagonais de um trapézio isósceles são geometricamente iguais: [AC] [BD] 3 - A mediana de um trapézio isósceles é paralela às bases do trapézio e o seu comprimento é igual à semi-soma das bases: AD//BC//EF EF = AD + BC 2 Linhas notáveis de um Trapézio Bases de um trapézio são os lados opostos paralelos. Diagonal de um trapézio é o segmento de reta cujos extremos são dois vértices opostos do quadrilátero. Altura de um trapézio é o segmento de reta perpendicular às bases e compreendido entre elas. Mediana do trapézio é o segmento de reta cujos extremos são os pontos médios dos lados opostos não paralelos.

3 Propriedades dos Paralelogramos Paralelogramos são trapézios cujos lados opostos são paralelos e geometricamente iguais. Classificação dos Paralelogramos Paralelogramo Retângulo AB = CD e AD = BC (todos os ângulos são geometricamente iguais) α = γ e β = δ α = β = γ = δ = 90º Losango (todos os lados são geometricamente iguais) AB = BC = CD = DA Quadrado (todos os lados e ângulos são geometricamente iguais) AB = BC = CD = DA α = γ e β = δ α = β = γ = δ = 90º Retângulo é o quadrilátero cujos lados consecutivos são perpendiculares. Losango é o quadrilátero cujos lados são todos iguais. Quadrado é o retângulo cujos lados são todos iguais. Relações de um Paralelogramo 1 - Os ângulos opostos de um paralelogramo são geometricamente iguais e os ângulos internos consecutivos de cada lado são suplementares: BAD BCD ( ABC) + ( BCD) = 180º ABC ADC ( BAD) + ( ADC) = 180º 2 - Os lados opostos de um paralelogramo são geometricamente iguais: [AB] [CD] [AD] [BC] 3 - As diagonais de um paralelogramo dividem-se em duas partes geometricamente iguais: [AO] [OC] [BO] [OD] O é o ponto médio de [AC] e [BD]

4 4 - Uma diagonal de um paralelogramo divide-o em dois triângulos geometricamente iguais: [ABC] [ACD] Linhas notáveis de um Paralelogramo Base de um paralelogramo é qualquer um dos seus lados. Diagonal de um paralelogramo é o segmento de reta cujos extremos são dois vértices opostos do quadrilátero. Altura de um paralelogramo é o segmento de reta perpendicular à base e compreendida entre ela e o lado paralelo oposto. Exercícios para a pasta continuação Exercício nº45 Construir um quadrado sendo conhecido seu lado AB=4,5cm. 1. Seja o lado AB=4,5cm. 2. Traça-se uma horizontal indefinida e marca-se nela a medida do lado AB. 3. Pelos pontos A e B levantam-se duas perpendiculares, e, em seguida, com centro em A e raio AB corta-se a perpendicular que passa por A no ponto D. 4. Com o mesmo raio e já agora com centro em B corta-se a perpendicular que passa por B no ponto C. 5. Unindo-se os pontos A, B, C e D entre si, teremos construído o quadrado pedido. Exercício nº46 Construir um quadrado conhecendo-se sua diagonal=6cm. 1. Seja esta diagonal AB=6cm 2. Sobre uma horizontal, marca-se o segmento AB. 3. Levanta-se uma perpendicular pelo meio do segmento (mediatriz), e marcando-se nela para cima e para baixo do ponto O as distâncias OC e OD, que são justamente a metade de AB. 4. Unindo os pontos A, B, C e D teremos o quadrado pedido. Exercício nº47 Construir um quadrado conhecendo-se seu apótema=3cm. 1. Seja o apótema OX=3cm. 2. Sobre uma horizontal indefinida marca-se AB igual à duas vezes OX. Este segmento é o lado do quadrado pedido. 3. Repetir procedimento de construção de quadrado, dado seu lado.

5 Exercício nº48 Construir um quadrado conhecendo-se a soma da sua diagonal com um lado=5cm. 1. Seja esta soma o segmento r=5cm 2. Constrói-se um quadrado qualquer 1E2A e prolonga-se a sua diagonal. 3. Marca-se sobre a diagonal a distância AC igual ao segmento r. 4. Centro em E, e com raio E2, descreve-se um arco que vai cortar AC em D. 5. Une-se D a 2. Traça-se uma paralela a 2D pelo ponto C; esta paralela corta o prolongamento do lado do quadrado no ponto B. 6. A distância AB é o lado do quadrado pedido. 7. Repetir procedimento de construção de quadrado, dado seu lado. Exercício nº49 Construir um losango conhecendo-se seu lado e a sua diagonal. AB=5cm e AC=3,5cm. 1. Sejam AB a diagonal e AC o lado do losango. 2. Sobre uma reta horizontal marca-se o segmento AB. Em seguida, com centro em A e raio igual a distância AC traça-se o arco de círculo 1 e Centro em B e mesmo raio, descreve-se o arco que vai cortar o anterior nos pontos C e D. 4. Unindo os pontos A, C, B e D, teremos o losango procurado. Exercício nº50 Construir um losango sendo dados um lado e um ângulo AB=3,5cm e ângulo de 45º. 1. Traça-se uma reta e sobre esta marca-se o segmento AB, que é o lado. 2. Em uma de suas extremidades (no caso, A) constrói-se o ângulo α, de modo que seu vértice coincida com A e o seu lado com o segmento AB. 3. Em seguida, prolonga-se o outro lado do ângulo e marca-se sobre ele a distância AB, com centro em A, raio AB. 4. Agora, traça-se uma paralela a AC passando por B, e outra paralela a AB passando por C. Estas duas linhas encontramse no ponto D. Assim, teremos o losango ABCD. Exercício nº51 Construir um trapézio isósceles sendo dadas as duas bases assim como sua altura. AB=6cm, CD=2,5cm e h=4cm. 1. Sobre uma reta horizontal marca-se a distância AB, que será a base maior do trapézio. 2. Em seguida traça-se uma perpendicular pelo meio de AB. Nesta reta marcamos a altura h. 3. Agora traça-se uma paralela a AB pelo ponto da altura e marcam-se sobre esta a distância CD de modo que este segmento esteja centralizado pela altura. Teremos assim o trapézio pedido. Exercício nº52 Construir um retângulo sendo conhecidos um de seus lados e a sua diagonal. AB=7cm e AC=8cm. 1. Sobre uma linha horizontal marca-se o segmento AB, que é o lado do retângulo. 2. A seguir levantam-se duas perpendiculares ao segmento AB pelas extremidades A e B. 3. Com centro em qualquer uma das extremidades, e com raio igual ao comprimento AC da diagonal, descreve-se um arco que cortará a perpendicular oposta ao ponto centrado. 4. Traça-se então uma paralela à AB passando por este ponto e determina-se assim os vértices do retângulo pedido.

Documentos relacionados

Geometria plana. Índice. Polígonos. Triângulos. Congruência de triângulos. Semelhança de triângulos. Relações métricas no triângulo retângulo

Geometria plana. Índice. Polígonos. Triângulos. Congruência de triângulos. Semelhança de triângulos. Relações métricas no triângulo retângulo Índice Geometria plana Polígonos Triângulos Congruência de triângulos Semelhança de triângulos Relações métricas no triângulo retângulo Quadriláteros Teorema de Tales Esquadros de madeira www.ser.com.br