Sequência da apresentação
|
|
|
- João Batista Sales Assunção
- 7 Há anos
- Visualizações:
Transcrição
1
2 Sequência da apresentação Mal entendidos dos alunos relativos às frações. Os diferentes significados das frações. Diferentes tipos de unidade. Exemplos de tarefas para a reconstrução da unidade e exploração dos diferentes significados da fração. A multiplicação e divisão: Mal entendidos, significados e tarefas.
3 Mal entendidos dos alunos Relativos às frações: 1/3 < ¼, porque 4 é maior que 3. ½ = 1,2. Na adição de números representados por frações os alunos adicionam numeradores e denominadores, precisamente porque generalizam os algoritmos das operações com números inteiros. Alguns destes erros revelam que o sistema de numeração decimal não está entendido e que as representações estão desligadas das quantidades a que dizem respeito. Estas situações enraízam no facto dos alunos serem submetidos a um ensino essencialmente mecanicista baseado em símbolos como realidades próprias, sem terem ainda desenvolvido imagens e modelos que os sustentem.
4 Diferentes significados das frações Uma fração é uma representação versátil e muito rica, porque permite expressar diferentes relações. Por exemplo: A fração 3/5 pode ser interpretada como: 3/5 de um bolo; A razão entre o número de rapazes (3) e de raparigas (5) existentes numa sala de aula; O quociente resultante de se dividir 3 chocolates iguais por cinco pessoas.
5 Quociente entre dois números inteiros Surge em situações de partilha equitativa: O numerador representa o número de algo a ser partilhado e o denominador o número de recetores dessa partilha; É pois uma relação entre duas quantidades, mas que também tem o significado de uma quantidade, que é a quantidade com que cada um dos recetores ficou.
6 Quociente entre dois números inteiros Por exemplo: "três chocolates a dividir por cinco crianças representa a relação entre o número de chocolates e o número de crianças, mas também representa o resultado dessa divisão, ou seja, a fração de chocolate com que cada criança ficou. 3 5
7 Relação parte-todo Como uma unidade continua - três das cinco partes de uma folha de papel estão pintadas. Nestes casos a fração surge da comparação entre a parte e o todo, considerado este a unidade. 3 5 Como uma unidade discreta - três quintos dos cinco berlindes são cinzentos. 3 5
8 Operador partitivo multiplicativo Para obter um meio de dez caricas: O aluno terá de dividir as 10 caricas em dois grupos iguais para saber o número de caricas de um grupo.
9 Medida Nesta situação compara-se uma grandeza com outra tomada como unidade. Por exemplo: Para medir com a unidade AB o comprimento CD, há que dividir a unidade em partes tais, que um número inteiro dessas partes corresponda ao comprimento que se quer medir. A C D B 3 CD = AB 5
10 Diferentes tipos de unidades Uma das grandes dificuldadesinerentes ao estudo das frações prende-se com a questão da unidade tomada como o todo a ser fracionado: Metade de um quilo de laranjas não é o mesmo que metade de uma dúzia de ovos; ou Um terço de uma folha de papel A4 não é o mesmo que um terço de um folha de papel A5.
11 Diferentes tipos de unidades Por exemplo, relativamente à seguinte figura podemos considerar várias frações: 1 ¼ se cada grupo de 4 círculos é uma unidade. 5/8 se o conjunto das 8 círculos é a unidade. 5/3 se considerada a razão entre o número de círculos azuis e o número de círculos brancos. 2 ½ se cada 2 círculos é a unidade.
12 Diferentes tipos de unidades Podem considerar-se vários tipos de unidades: Discretas ou contínuas Simples ou compostas Uma dúzia de maçãs pode ser considerada uma unidade composta pois resulta de se agrupar um conjunto discreto de objetos, uma maça será uma unidade simples. Uma centena integra dez dezenasque por sua vez integra dez unidadessimples. A construção de uma unidade composta, como a centena, implica que a criança coordene diferentes tipos de unidades ao mesmo tempo.
13 Tarefas para a reconstrução da unidade Se duas bolas representam um quarto de uma coleção de bolas, quantas bolas tem a coleção? Se um retângulo representa a décima parte de uma tira de papel qual é o comprimento da tira completa?
14 Tarefas para os diferentes significados das frações Tarefa - Os chocolates O João trouxe para comer no intervalo três chocolates. Resolveu dividi-los com 4 colegas de forma justa: com o Diogo, a Rita, a Inês e o Pedro. Que quantidade de chocolate vai cada um receber? Para resolverem este problema podem usar palavras, desenhos, esquemas ou cálculos.
15 Tarefas para os diferentes significados das frações Planificar a exploração da tarefa Que ideias fundamentais do tópico números racionais não negativos podem surgir durante a exploração desta tarefa? Que vantagens pode trazer para o processo de ensinoaprendizagem este tipo de tarefas e a sua exploração em pequenos grupos? Que desafios adicionais para o professor traz este tipo de exploração? Será possível predefinir a exploração que irá surgir?
16 Produções dos alunos
17 Produções dos alunos
18 Tarefas para os diferentes significados das frações A partir das diferentes estratégias apresentadas que ideias fundamentais pode explorar? Que desafios adicionais traz para o professor este tipo de exploração em sala de aula? Quais as vantagens do confronto de várias resoluções? De vários modos de demonstrar o mesmo resultado? Como é que o professor pode organizar a apresentação e discussão no grupo turma?
19 Multiplicação e divisão de frações Mal entendidos mais frequentes: (os relativos ao efeito das operações sobre um par de números) Multiplicar aumenta sempre; Dividir diminui sempre; O dividendo tem de ser sempre maior que o divisor. Dados da investigação sugerem que estes mal entendidos estão associados ao facto de se trabalhar essencialmente um dos significados da multiplicação a multiplicação como adição sucessiva, e um dos significados da divisão a divisão como partilha.
20 Diferentes significados Isomorfismo de medidas proporção direta simples entre medidas de duas grandezas M1 e M2 (por exemplo, pessoas e objetos, bem e custos, tempo e distância), descrevendo um grande número de situações quer diárias, quer técnicas. Multiplicação Situações que envolvem uma relação quaternária de onde os alunos têm de extrair uma relação terciária. Adição sucessiva Relação multiplicativa
21 Multiplicação: Adição sucessiva A Maria foi à padaria comprar pão. Cada pão pesava 3/4 kg. Quantos quilos de pão trouxe a Maria sabendo que comprou 4 pães?
22 Multiplicação: Relação multiplicativa A Maria está a bordar um quadro. Durante as férias bordou metade do quadro. Desde que começaram as aulas bordou ¼ do que faltava bordar. Que parte do quadro bordou a Maria depois das férias?
23 Multiplicação: Relação multiplicativa A distância da casa da Sofia à escola é ½ da distância da casa do Tiago à escola. O Tiago mora a 2 ½ km da escola. Qual dos dois colegas mora mais próximo da escola. Justifica a tua resposta recorrendo à reta numérica para explicares o teu raciocínio
24 Diferentes significados Isomorfismo de medidas proporção direta simples entre medidas de duas grandezas M1 e M2 (por exemplo, pessoas e objetos, bem e custos, tempo e distância), descrevendo um grande número de situações quer diárias quer técnicas. Divisão: medida Situações cujo objetivo é determinar o número de grupos, sabendo a dimensão de cada grupo. O dividendo e o divisor são da mesma natureza.
25 Divisão: medida O pai do Tiago comprou 5 litros de azeite e quer guardá-lo em garrafas de meio litro. Quantas garrafas serão necessárias? I.: Mas, começaste por dividir e depois multiplicaste cinco por dois. Porquê? A.: Porque fiz o inverso! Multipliquei pelo inverso de 1/2! I.: Não percebi! Mas tens 5 litros a dividir por garrafas de 1/2 litro! A.: Pois! Mas, são precisas duas garrafas de meio litro para levar 1 litro, por isso, são cinco vezes duas!
26 Divisão: medida Um grupo de amigos costuma fazer uma caminhada no final da tarde. Se numa hora percorrem 3 ½ km, quanto tempo será necessário para percorrerem 1 ¾ km? A.: 1 hora igual a 3 ½ km e agora quero saber quanto tempo vai ser preciso para fazerem 1 ¾ km. ( ). Quantas vezes 3 ½ cabem em 1 ¾ para saber quanto tempo é necessário!
27 Diferentes significados Isomorfismo de medidas proporção direta simples entre medidas de duas grandezas M1 e M2 (por exemplo, pessoas e objetos, bem e custos, tempo e distância), descrevendo um grande número de situações quer diárias quer técnicas. Divisão: partilha Situações cujo objetivo é encontrar o valor unitário, ou seja, o valor que cabe a cada um dos elementos do divisor. O Dividendo e o divisor são de natureza diferente.
28 Divisão: partilha Numa caminhada que fez durante o fim-de-semana, a Sofia percorreu 1 ½ km em 1/4 de hora. Dado que manteve a mesma velocidade média, quantos quilómetros terá percorrido numa hora? A. : Se percorreu um quilómetro e meio num quarto de hora, numa hora vai percorrer mais! Um quarto é metade de metade, então é 4 vezes uma hora e meia, que é o mesmo que dividir [1 ½ ] por 1/4!
29 Divisão: partilha Se 4/5 de uma coleção de cromos fossem 48 cromos, quantos cromos teria a coleção completa?
30 Diferentes significados Produto de medidas composição cartesiana de dois espaços métricos, M1 e M2, para encontrar um terceiro espaço métrico, M3. Multiplicação Situações onde são dadas duas grandezas elementares e se pede o valor do produto dessas grandezas.
31 Multiplicação: produto de medidas Qual é a área de um retângulo que tem ¼ m de largura e 2/3 m de comprimento?
32 Diferentes significados Produto de medidas composição cartesiana de dois espaços métricos, M1 e M2, para encontrar um terceiro espaço métrico, M3. Divisão Situações onde se pretende encontrar o valor de uma grandeza elementar, dado o valor da grandeza de um produto e o valor de outra grandeza elementar. Medida em falta Fator em falta
33 Divisão: medida em falta Um retângulo tem ½ m 2 de área e ¾ m de comprimento. Calcula a sua largura?
34 Divisão: fator em falta Qual é o número que multiplicado por 3/4 é igual a 6?
35 Em suma Tarefas exploratórias que comtemplem os diferentes significados das frações e das operações com frações, em contextos significativos para os alunos, promovem a modelação e por conseguinte, aprendizagens significativas dos números racionais, bem como das suas operações, ou seja, o desenvolvimento do sentido de número e de operação.
Ideias associadas à aprendizagem dos números racionais PROF. RANILDO LOPES
 Ideias associadas à aprendizagem dos números racionais PROF. RANILDO LOPES REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS
Ideias associadas à aprendizagem dos números racionais PROF. RANILDO LOPES REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS RACIONAIS FRACCIONÁRIOS REPRESENTAÇÕES DOS NÚMEROS
LOS SIGNIFICADOS DE LOS NÚMEROS FRACCIONÁRIOS
 LOS SIGNIFICADOS DE LOS NÚMEROS FRACCIONÁRIOS Prof. Maria José Ferreira da Silva zeze@pucsp.br Porque as dificuldades no ensino? Porque as dificuldades na aprendizagem? GRANDEZAS Quantificar significa
LOS SIGNIFICADOS DE LOS NÚMEROS FRACCIONÁRIOS Prof. Maria José Ferreira da Silva zeze@pucsp.br Porque as dificuldades no ensino? Porque as dificuldades na aprendizagem? GRANDEZAS Quantificar significa
AGRUPAMENTO DE ESCOLAS DE PAREDE
 GESTÃO DE CONTEÚDOS Ensino Básico 1.º Ciclo Matemática 3.º Ano Domínios Subdomínios Conteúdos Programáticos Nº Tempos previstos (Horas) 1º Período Geometria Medida naturais Adição e subtração Ler e interpretar
GESTÃO DE CONTEÚDOS Ensino Básico 1.º Ciclo Matemática 3.º Ano Domínios Subdomínios Conteúdos Programáticos Nº Tempos previstos (Horas) 1º Período Geometria Medida naturais Adição e subtração Ler e interpretar
Domínio: Geometria. CONSELHO de DOCENTES 1.º Ciclo Página 1
 Domínio: Geometria Subdomínio/Conteúdos Localização e orientação no espaço - Ângulo formado por duas direções; vértice de um ângulo; - Ângulos com a mesma amplitude; - A meia volta e o quarto de volta
Domínio: Geometria Subdomínio/Conteúdos Localização e orientação no espaço - Ângulo formado por duas direções; vértice de um ângulo; - Ângulos com a mesma amplitude; - A meia volta e o quarto de volta
AGRUPAMENTO de ESCOLAS de PEDRÓGÃO GRANDE
 Números e Operações ANUAL 164 dias letivos Números naturais Relações numéricas 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «centésimo». 2. Contar até um milhão 1.
Números e Operações ANUAL 164 dias letivos Números naturais Relações numéricas 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «centésimo». 2. Contar até um milhão 1.
Planificação Anual de Matemática 2017 / ºAno
 Planificação Anual de Matemática 2017 / 2018 3ºAno NÚMEROS E Aulas Previstas: 1º período: 64 aulas 2º período: 55 aulas 3º período: 52 aulas DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Utilizar corretamente
Planificação Anual de Matemática 2017 / 2018 3ºAno NÚMEROS E Aulas Previstas: 1º período: 64 aulas 2º período: 55 aulas 3º período: 52 aulas DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Utilizar corretamente
Planificação Anual de Matemática 2016 / ºAno
 Planificação Anual de Matemática 2016 / 2017 3ºAno NÚMEROS E Aulas Previstas: 1º período: 63 aulas 2º período: 63 aulas 3º período: 45 aulas DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Conhecer os numerais
Planificação Anual de Matemática 2016 / 2017 3ºAno NÚMEROS E Aulas Previstas: 1º período: 63 aulas 2º período: 63 aulas 3º período: 45 aulas DOMÍNIOS OBJETIVOS ATIVIDADES Números naturais Conhecer os numerais
PLANIFICAÇÃO ANUAL MATEMÁTICA 3º ANO
 PLANIFICAÇÃO ANUAL MATEMÁTICA 3º ANO Domínios Subdomínios Objetivos Descritores de Desempenho/ Metas de Aprendizagem NÚMEROS OPERAÇÕES E Números naturais Conhecer os números ordinais Contar até um milhão
PLANIFICAÇÃO ANUAL MATEMÁTICA 3º ANO Domínios Subdomínios Objetivos Descritores de Desempenho/ Metas de Aprendizagem NÚMEROS OPERAÇÕES E Números naturais Conhecer os números ordinais Contar até um milhão
PLANIFICAÇÃO ANUAL 2016/2017 MATEMÁTICA- 3ºANO
 Direção Geral dos Estabelecimentos Escolares Direção de Serviços da Região do Algarve Agrupamento de Escolas José Belchior Viegas (Sede: Escola Secundária José Belchior Viegas) PLANIFICAÇÃO ANUAL 2016/2017
Direção Geral dos Estabelecimentos Escolares Direção de Serviços da Região do Algarve Agrupamento de Escolas José Belchior Viegas (Sede: Escola Secundária José Belchior Viegas) PLANIFICAÇÃO ANUAL 2016/2017
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2016/2017 PLANIFICAÇÃO ANUAL
 AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2016/2017 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Programa Atual da Disciplina e Metas Curriculares 1º CICLO MATEMÁTICA 2º ANO TEMAS/DOMÍNIOS
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2016/2017 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Programa Atual da Disciplina e Metas Curriculares 1º CICLO MATEMÁTICA 2º ANO TEMAS/DOMÍNIOS
Matriz Curricular 1º Ciclo / 2016 Ano de Escolaridade: 3.º Ano Matemática
 Ano letivo 2015 / 16 Matriz Curricular 1º Ciclo Ano Letivo: 2015 / 2016 Ano de Escolaridade: 3.º Ano Matemática Nº total de dias letivos 164 dias Nº de dias letivos 1º período - 64 dias 2º período - 52
Ano letivo 2015 / 16 Matriz Curricular 1º Ciclo Ano Letivo: 2015 / 2016 Ano de Escolaridade: 3.º Ano Matemática Nº total de dias letivos 164 dias Nº de dias letivos 1º período - 64 dias 2º período - 52
Geometria e Medida. Números e Operações. Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação. - Atenção.
 Conselho de Docentes do 3º Ano PLANIFICAÇÃO Anual de Matemática Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Geometria e Medida Localização e orientação no espaço Coordenadas
Conselho de Docentes do 3º Ano PLANIFICAÇÃO Anual de Matemática Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Geometria e Medida Localização e orientação no espaço Coordenadas
Roteiro de trabalho para o 3o ano
 Roteiro de trabalho para o 3o ano No volume do 3º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Os números e sua história
Roteiro de trabalho para o 3o ano No volume do 3º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Os números e sua história
CURRÍCULO DA DISCIPLINA MATEMÁTICA / CRITÉRIOS DE AVALIAÇÃO 2013/2014 1º Ciclo Matemática 2º Ano Metas / Objetivos
 de Avaliação Números e Operações Números Sistema de numeração decimal Adição e subtração Multiplicação Conhecer os numerais ordinais Contar até mil Reconhecer a paridade Descodificar o sistema de numeração
de Avaliação Números e Operações Números Sistema de numeração decimal Adição e subtração Multiplicação Conhecer os numerais ordinais Contar até mil Reconhecer a paridade Descodificar o sistema de numeração
MATEMÁTICA PROF. JOSÉ LUÍS FRAÇÕES
 FRAÇÕES I- INTRODUÇÃO O símbolo a / b significa a : b, sendo a e b números naturais e b diferente de zero. Chamamos: a / b de fração; a de numerador; b de denominador. Se a é múltiplo de b, então a / b
FRAÇÕES I- INTRODUÇÃO O símbolo a / b significa a : b, sendo a e b números naturais e b diferente de zero. Chamamos: a / b de fração; a de numerador; b de denominador. Se a é múltiplo de b, então a / b
NÚMEROS E OPERAÇÕES Números naturais
 CRITÉRIOS ESPECÍFICOS DE AVALIAÇÃO (Aprovados em Conselho Pedagógico de 16 outubro de 2012) No caso específico da disciplina de MATEMÁTICA, do 3.º ano de escolaridade, a avaliação incidirá ainda ao nível
CRITÉRIOS ESPECÍFICOS DE AVALIAÇÃO (Aprovados em Conselho Pedagógico de 16 outubro de 2012) No caso específico da disciplina de MATEMÁTICA, do 3.º ano de escolaridade, a avaliação incidirá ainda ao nível
Plano Curricular de Matemática 3.º Ano - Ano Letivo 2016/2017
 Plano Curricular de Matemática 3.º Ano - Ano Letivo 2016/2017 1.º Período Conteúdos Programados Previstas Dadas Números e Operações Utilizar corretamente os numerais ordinais até vigésimo. Ler e representar
Plano Curricular de Matemática 3.º Ano - Ano Letivo 2016/2017 1.º Período Conteúdos Programados Previstas Dadas Números e Operações Utilizar corretamente os numerais ordinais até vigésimo. Ler e representar
CURRÍCULO DA DISCIPLINA MATEMÁTICA / CRITÉRIOS DE AVALIAÇÃO 2013/2014 1º Ciclo Matemática 3º Ano Metas / Objetivos Instrumentos de Domínios e
 de Avaliação Números e Operações Números Sistema de decimal Adição e subtração Multiplicação Conhecer os numerais ordinais Contar até ao milhão Conhecer a romana Descodificar o sistema de decimal Adicionar
de Avaliação Números e Operações Números Sistema de decimal Adição e subtração Multiplicação Conhecer os numerais ordinais Contar até ao milhão Conhecer a romana Descodificar o sistema de decimal Adicionar
MÊS DOMÍNIO SUBDOMÍNIO OBJETIVOS GERAIS DESCRITORES DE DESEMPENHO
 2017-2018_ Planificação Mensal Português 3 º ano MÊS DOMÍNIO SUBDOMÍNIO OBJETIVOS GERAIS DESCRITORES DE DESEMPENHO setembro outubro História da numeração Numeração romana Recorda a dezena e a centena Números
2017-2018_ Planificação Mensal Português 3 º ano MÊS DOMÍNIO SUBDOMÍNIO OBJETIVOS GERAIS DESCRITORES DE DESEMPENHO setembro outubro História da numeração Numeração romana Recorda a dezena e a centena Números
NÚMEROS RACIONAIS. FRAÇÕES. Ano letivo
 NÚMEROS RACIONAIS. FRAÇÕES Ano letivo 203-4 Fração é um número que exprime uma ou mais partes, em que foi dividida a unidade. Numerador 2 Denominador Termos da fracção é o numerador, representa o número
NÚMEROS RACIONAIS. FRAÇÕES Ano letivo 203-4 Fração é um número que exprime uma ou mais partes, em que foi dividida a unidade. Numerador 2 Denominador Termos da fracção é o numerador, representa o número
Matemática - 4º ano. Números racionais não negativos. Tarefa : O passeio da turma da Rita
 Números racionais não negativos Tarefa : O passeio da turma da Rita No final do ano, a turma da Rita foi passear à Serra da Arrábida. 1. A Rita e quatro dos seus amigos decidiram partilhar igualmente entre
Números racionais não negativos Tarefa : O passeio da turma da Rita No final do ano, a turma da Rita foi passear à Serra da Arrábida. 1. A Rita e quatro dos seus amigos decidiram partilhar igualmente entre
PLANIFICAÇÃO MENSAL/ANUAL Matemática 3.ºano
 PLANIFICAÇÃO MENSAL/ANUAL Matemática 3.ºano Domínio/ Subdomínio Números Naturais Sistema de numeração decimal Adição e subtração Multiplicação MATEMÁTICA Metas a atingir 3.º ANO DE ESCOLARIDADE Meses do
PLANIFICAÇÃO MENSAL/ANUAL Matemática 3.ºano Domínio/ Subdomínio Números Naturais Sistema de numeração decimal Adição e subtração Multiplicação MATEMÁTICA Metas a atingir 3.º ANO DE ESCOLARIDADE Meses do
CONHECIMENTOS CAPACIDADES OBJETIVOS / METAS CURRICULARES
 Escola Secundária 2-3 de Clara de Resende COD. 346 779 Critérios de Avaliação Perfil de Aprendizagens Específicas (Aprovado em Conselho Pedagógico de 18 julho de 2016) AGRU P A M E N T O DE No caso específico
Escola Secundária 2-3 de Clara de Resende COD. 346 779 Critérios de Avaliação Perfil de Aprendizagens Específicas (Aprovado em Conselho Pedagógico de 18 julho de 2016) AGRU P A M E N T O DE No caso específico
PLANO CURRICULAR DISCIPLINAR. MATEMÁTICA 4.º Ano. Números e Operações. Relações numéricas. Números Naturais. Numeração Romana.
 PLANO CURRICULAR DISCIPLINAR MATEMÁTICA 4.º Ano 1.º Período 64 Realizar contagens progressivas e regressivas a partir de números dados. Comparar números e ordenálos em sequências crescentes e decrescentes.
PLANO CURRICULAR DISCIPLINAR MATEMÁTICA 4.º Ano 1.º Período 64 Realizar contagens progressivas e regressivas a partir de números dados. Comparar números e ordenálos em sequências crescentes e decrescentes.
Planificação Matemática
 EB/JI José Joaquim Rita Sei Agrupamento de Escolas Alfredo da Silva - Barreiro Ano Letivo 2018/2019 Ano de Escolaridade: 3.º ano Planificação Matemática 1. o PERÍODO Medir o tempo! Ler e interpretar calendários.
EB/JI José Joaquim Rita Sei Agrupamento de Escolas Alfredo da Silva - Barreiro Ano Letivo 2018/2019 Ano de Escolaridade: 3.º ano Planificação Matemática 1. o PERÍODO Medir o tempo! Ler e interpretar calendários.
Disciplina: Matemática. Período: I. Professor (a): Maria Aparecida Holanda Veloso e Liliane Cristina de Oliveira Vieira
 COLÉGIO LA SALLE BRASILIA Associação Brasileira de Educadores Lassalistas ABEL SGAS Q. 906 Conj. E C.P. 320 Fone: (061) 3443-7878 CEP: 70390-060 - BRASÍLIA - DISTRITO FEDERAL Disciplina: Matemática Período:
COLÉGIO LA SALLE BRASILIA Associação Brasileira de Educadores Lassalistas ABEL SGAS Q. 906 Conj. E C.P. 320 Fone: (061) 3443-7878 CEP: 70390-060 - BRASÍLIA - DISTRITO FEDERAL Disciplina: Matemática Período:
MULTIPLICAÇÃO E DIVISÃO DE DECIMAIS
 MULTIPLICAÇÃO E DIVISÃO DE DECIMAIS Multiplicação com números decimais Há duas maneiras de efetuarmos a multiplicação envolvendo números decimais: multiplicação de número natural por decimal e multiplicação
MULTIPLICAÇÃO E DIVISÃO DE DECIMAIS Multiplicação com números decimais Há duas maneiras de efetuarmos a multiplicação envolvendo números decimais: multiplicação de número natural por decimal e multiplicação
PLANIFICAÇÃO TRIMESTRAL DE MATEMÁTICA 2.º ANO 1.º PERÍODO
 Unidade 2 -outubro Unidade 1 - setembro PLANIFICAÇÃO TRIMESTRAL DE MATEMÁTICA 2.º ANO 1.º PERÍODO Domínio Subdomínio Objetivo geral Descritores Conteúdos Organização e Tratamento de Dados Organização e
Unidade 2 -outubro Unidade 1 - setembro PLANIFICAÇÃO TRIMESTRAL DE MATEMÁTICA 2.º ANO 1.º PERÍODO Domínio Subdomínio Objetivo geral Descritores Conteúdos Organização e Tratamento de Dados Organização e
Plano Curricular de Matemática 2.º Ano - Ano Letivo 2017/2018
 Plano Curricular de Matemática 2.º Ano - Ano Letivo 2017/2018 1.º Período Números e Operações Conteúdos Programados Aulas Previstas Aulas Dadas Números naturais Conhecer os numerais ordinais Utilizar corretamente
Plano Curricular de Matemática 2.º Ano - Ano Letivo 2017/2018 1.º Período Números e Operações Conteúdos Programados Aulas Previstas Aulas Dadas Números naturais Conhecer os numerais ordinais Utilizar corretamente
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática3º ano Ano Letivo 2016/2017
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática3º ano Ano Letivo 2016/2017 1º Período Domínios Números e Operações Números naturais Numerais ordinais até centésimo;
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática3º ano Ano Letivo 2016/2017 1º Período Domínios Números e Operações Números naturais Numerais ordinais até centésimo;
Agrupamento de Escolas Eugénio de Castro Critérios de Avaliação. Ano Letivo 2017/18 Disciplina MATEMÁTICA 3.º Ano
 Agrupamento de Escolas Eugénio de Castro Critérios de Avaliação Ano Letivo 2017/18 Disciplina MATEMÁTICA 3.º Ano Números e Operações Números naturais Utilizar corretamente os numerais ordinais até centésimo.
Agrupamento de Escolas Eugénio de Castro Critérios de Avaliação Ano Letivo 2017/18 Disciplina MATEMÁTICA 3.º Ano Números e Operações Números naturais Utilizar corretamente os numerais ordinais até centésimo.
Plano Geral de Trabalho da Disciplina de Matemática 2016/ º ANO Aulas previstas: 1º Período: 88 aulas 2º Período: 88 aulas 3º Período: 63 aulas
 AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA Plano Geral de Trabalho da Disciplina de Matemática 2016/ 2017 2º ANO Aulas previstas: 1º Período: 88 aulas 2º Período: 88 aulas 3º Período: 63 aulas Gestão dos
AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA Plano Geral de Trabalho da Disciplina de Matemática 2016/ 2017 2º ANO Aulas previstas: 1º Período: 88 aulas 2º Período: 88 aulas 3º Período: 63 aulas Gestão dos
PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO
 PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO Domínios Subdomínios Objetivos Descritores/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Tratamento dados de Representar e interpretar dados e situações
PLANIFICAÇÃO ANUAL MATEMÁTICA 4º ANO Domínios Subdomínios Objetivos Descritores/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Tratamento dados de Representar e interpretar dados e situações
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 3º ano Ano Letivo 2015/2016
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 3º ano Ano Letivo 2015/2016 1º Trimestre Domínios Números e Operações Números naturais Numerais ordinais até centésimo;
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 3º ano Ano Letivo 2015/2016 1º Trimestre Domínios Números e Operações Números naturais Numerais ordinais até centésimo;
Disciplina: MATEMÁTICA
 PLANIFICAÇÃO AGRUPAMENTO DE ESCOLAS DE AVEIRO ANO LETIVO 2018/2019 Disciplina: MATEMÁTICA 3º ANO Horas semanais: 7h Tempo 1.º período Domínios Números e Operações Conteúdos Atividades de diagnóstico Números
PLANIFICAÇÃO AGRUPAMENTO DE ESCOLAS DE AVEIRO ANO LETIVO 2018/2019 Disciplina: MATEMÁTICA 3º ANO Horas semanais: 7h Tempo 1.º período Domínios Números e Operações Conteúdos Atividades de diagnóstico Números
Disciplina: Matemática DIAGNÓSTICO PROF. REGENTE DOMÍNIOS / CONTEÚDOS DESCRIÇÃO DO CONTEÚDO ACOMPANHAMENTO DO PROFESSOR DA SAA. Não At.
 Escola: Nome do Aluno: Professor Regente: Tempo de Permanência no Programa: Disciplina: Matemática Turma: Data Nasc.: / / Professor da Sala de Apoio: Entrada / / Saída / / DOMÍNIOS / CONTEÚDOS DESCRIÇÃO
Escola: Nome do Aluno: Professor Regente: Tempo de Permanência no Programa: Disciplina: Matemática Turma: Data Nasc.: / / Professor da Sala de Apoio: Entrada / / Saída / / DOMÍNIOS / CONTEÚDOS DESCRIÇÃO
NÚMEROS RACIONAIS. operações
 UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: 2018.2 NÚMEROS RACIONAIS operações Prof. Adriano Vargas Freitas Noção de número
UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: 2018.2 NÚMEROS RACIONAIS operações Prof. Adriano Vargas Freitas Noção de número
AGRUPAMENTO DE ESCOLAS MARTIM DE FREITAS 1º CICLO DO ENSINO BÁSICO
 AGRUPAMENTO DE ESCOLAS MARTIM DE FREITAS 1º CICLO DO ENSINO BÁSICO PLANO DE TRABALHO ANUAL MATEMÁTICA* 3º Ano de escolaridade Domínios/Subdomínios Objetivos/Descritores de desempenho Meses GEOMERIA E MEDIDA
AGRUPAMENTO DE ESCOLAS MARTIM DE FREITAS 1º CICLO DO ENSINO BÁSICO PLANO DE TRABALHO ANUAL MATEMÁTICA* 3º Ano de escolaridade Domínios/Subdomínios Objetivos/Descritores de desempenho Meses GEOMERIA E MEDIDA
PLANIFICAÇÃO DE MATEMÁTICA- setembro/outubro
 PLANIFICAÇÃO DE MATEMÁTICA- setembro/outubro Recorda os números até 100 Estratégias de cálculo Adição e subtração Números ordinais Números pares e números ímpares Sólidos geométricos - Saber de memória
PLANIFICAÇÃO DE MATEMÁTICA- setembro/outubro Recorda os números até 100 Estratégias de cálculo Adição e subtração Números ordinais Números pares e números ímpares Sólidos geométricos - Saber de memória
NÚMEROS RACIONAIS OPERAÇÕES
 UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: 2016.2 NÚMEROS RACIONAIS OPERAÇÕES Prof. Adriano Vargas Freitas Noção de número
UNIVERSIDADE FEDERAL FLUMINENSE INSTITUTO DE EDUCAÇÃO DE ANGRA DOS REIS DISCIPLINA: MATEMÁTICA CONTEÚDO E MÉTODO Período: 2016.2 NÚMEROS RACIONAIS OPERAÇÕES Prof. Adriano Vargas Freitas Noção de número
Objetivos Gerais Descritores Conteúdos. 1.Utilizar corretamente os números ordinais até "centésimo
 AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 3.º ANO DE ESCOLARIDADE - 2016-2017 Domínio/ Números naturais Objetivos Gerais Descritores Conteúdos 1.Conhecer os números ordinais
AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 3.º ANO DE ESCOLARIDADE - 2016-2017 Domínio/ Números naturais Objetivos Gerais Descritores Conteúdos 1.Conhecer os números ordinais
Predisposição para procurar e explorar padrões geométricos e o gosto por investigar propriedades e relações geométricas.
 Metas de Isometrias Noção e propriedades da reflexão, da rotação e da translação Simetrias axial e rotacional Resolve problemas utilizando as propriedades das figuras geométricas no plano. Identifica o
Metas de Isometrias Noção e propriedades da reflexão, da rotação e da translação Simetrias axial e rotacional Resolve problemas utilizando as propriedades das figuras geométricas no plano. Identifica o
MATEMÁTICA 3º ANO. Novo programa de matemática Objetivos específicos. Currículo Paulo VI. Números naturais. Relações numéricas Múltiplos e divisores
 MATEMÁTICA 3º ANO NÚMEROS E OPERAÇÕES Tópicos Números naturais Relações numéricas Múltiplos e divisores Novo programa de matemática Objetivos específicos Realizar contagens progressivas e regressivas a
MATEMÁTICA 3º ANO NÚMEROS E OPERAÇÕES Tópicos Números naturais Relações numéricas Múltiplos e divisores Novo programa de matemática Objetivos específicos Realizar contagens progressivas e regressivas a
Plano Curricular de Matemática 2.º Ano - Ano Letivo 2015/2016
 Plano Curricular de Matemática 2.º Ano - Ano Letivo 2015/2016 1.º Período Números e Operações Conteúdos Programados Aulas Previstas Aulas Dadas Números naturais Conhecer os numerais ordinais Utilizar corretamente
Plano Curricular de Matemática 2.º Ano - Ano Letivo 2015/2016 1.º Período Números e Operações Conteúdos Programados Aulas Previstas Aulas Dadas Números naturais Conhecer os numerais ordinais Utilizar corretamente
4º. ano 1º. VOLUME. Projeto Pedagógico de Matemática 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE. Números e operações.
 4º. ano 1º. VOLUME 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE Realização de compreendendo seus significados: adição e subtração (com e sem reagrupamento) Multiplicação (como adição de parcelas
4º. ano 1º. VOLUME 1. AS OPERAÇÕES E AS HABILIDADES DE CALCULAR MENTALMENTE Realização de compreendendo seus significados: adição e subtração (com e sem reagrupamento) Multiplicação (como adição de parcelas
OPERAÇÕES COM FRAÇÕES. Neste caso, adicionamos ou subtraímos os numeradores e conservamos os mesmos denominadores.
 ADIÇÃO E SUBTRAÇÃO Há dois casos possíveis: º) Frações com denominadores iguais OPERAÇÕES COM FRAÇÕES Neste caso, adicionamos ou subtraímos os numeradores e conservamos os mesmos denominadores. Exemplos:
ADIÇÃO E SUBTRAÇÃO Há dois casos possíveis: º) Frações com denominadores iguais OPERAÇÕES COM FRAÇÕES Neste caso, adicionamos ou subtraímos os numeradores e conservamos os mesmos denominadores. Exemplos:
MATEMÁTICA 1º ANO Objetivo Geral CONTEÚDOS: OBJETIVOS
 MATEMÁTICA 1º ANO Objetivo Geral: Reconhecer o fazer matemático em situações rotineiras a fim deste se familiarizar com tais situações, favorecendo o desenvolvimento de seu raciocínio lógico-matemático
MATEMÁTICA 1º ANO Objetivo Geral: Reconhecer o fazer matemático em situações rotineiras a fim deste se familiarizar com tais situações, favorecendo o desenvolvimento de seu raciocínio lógico-matemático
AGRUPAMENTO de ESCOLAS de PEDRÓGÃO GRANDE CONSELHO de DOCENTES 1.º CEB Planificação Anual Matemática- _ 2.º Ano /2013
 ANUAL 164 dias letivos Números naturais Noção de número natural Números ordinais e cardinais Relações numéricas 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «vigésimo».
ANUAL 164 dias letivos Números naturais Noção de número natural Números ordinais e cardinais Relações numéricas 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «vigésimo».
Preparação para a Prova Final de Matemática 2.º Ciclo do Ensino Básico Olá, Matemática! 6.º Ano
 Números e operações Números racionais não negativos Noção e representação de número racional Comparação e ordenação de números racionais Operações com números racionais Valores aproximados Percentagens
Números e operações Números racionais não negativos Noção e representação de número racional Comparação e ordenação de números racionais Operações com números racionais Valores aproximados Percentagens
TEMA / CONTEÚDOS OBJETIVOS / DESCRITORES DE DESEMPENHO AVALIAÇÃO GESTÃO DO TEMPO Contar até ao bilião (mil milhões).
 Números naturais Relações numéricas Operações com números naturais Adição Subtração Números naturais Múltiplos e divisores Operações com números naturais Multiplicação Regularidades Sequências ANO LETIVO
Números naturais Relações numéricas Operações com números naturais Adição Subtração Números naturais Múltiplos e divisores Operações com números naturais Multiplicação Regularidades Sequências ANO LETIVO
PLANIFICAÇÃO ANUAL Documentos Orientadores: Programa e Metas Curriculares
 Disciplina: Matemática /Ano de escolaridade: 2º Ano Página 1 de 7 PLANIFICAÇÃO ANUAL Documentos Orientadores: Programa e Metas Curriculares Os números até 100 Estratégias de cálculo - Adição e subtração
Disciplina: Matemática /Ano de escolaridade: 2º Ano Página 1 de 7 PLANIFICAÇÃO ANUAL Documentos Orientadores: Programa e Metas Curriculares Os números até 100 Estratégias de cálculo - Adição e subtração
Pró-letramento Matemática Estado de Minas Gerais
 Pró-letramento Matemática Estado de Minas Gerais Diferentes significados de um mesmo conceito: o caso das frações. 1 Cleiton Batista Vasconcelos e Elizabeth Belfort Muitos conceitos matemáticos podem ser
Pró-letramento Matemática Estado de Minas Gerais Diferentes significados de um mesmo conceito: o caso das frações. 1 Cleiton Batista Vasconcelos e Elizabeth Belfort Muitos conceitos matemáticos podem ser
PLANIFICAÇÃO ANUAL DE MATEMÁTICA 2.º ANO
 PLANIFICAÇÃO ANUAL DE MATEMÁTICA 2.º ANO Domínios Subdomínios / Conteúdos programáticos Objetivos / Descritores de desempenho Números e Operações Números naturais Numerais ordinais até vigésimo; Números
PLANIFICAÇÃO ANUAL DE MATEMÁTICA 2.º ANO Domínios Subdomínios / Conteúdos programáticos Objetivos / Descritores de desempenho Números e Operações Números naturais Numerais ordinais até vigésimo; Números
PLANIFICAÇÃO ANUAL MATEMÁTICA 2º ANO
 PLANIFICAÇÃO ANUAL MATEMÁTICA 2º ANO Domínios Subdomínios Objetivos Descritores de Desempenho/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Representação conjuntos de Reunião e interseção de
PLANIFICAÇÃO ANUAL MATEMÁTICA 2º ANO Domínios Subdomínios Objetivos Descritores de Desempenho/ Metas de Aprendizagem ORGANIZAÇÃO E TRATAMENTO DE DADOS Representação conjuntos de Reunião e interseção de
Sentidos da divisão e algoritmos da divisão de números representados sob a forma de fracção
 Sentidos da divisão e algoritmos da divisão de números representados sob a forma de fracção Nos primeiros anos de escolaridade, a divisão de números representados sob a forma de fracção é, muito frequentemente,
Sentidos da divisão e algoritmos da divisão de números representados sob a forma de fracção Nos primeiros anos de escolaridade, a divisão de números representados sob a forma de fracção é, muito frequentemente,
Frações. Números Racionais. Conceito de Fração:
 Frações Números Racionais Consideremos a operação 4 : 5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números naturais porque
Frações Números Racionais Consideremos a operação 4 : 5 =? onde o dividendo não é múltiplo do divisor. Vemos que não é possível determinar o quociente dessa divisão no conjunto dos números naturais porque
Roteiro de trabalho para o 4o ano
 Roteiro de trabalho para o 4o ano No volume do 4º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
Roteiro de trabalho para o 4o ano No volume do 4º ano estão assim organizados os conteúdos e as habilidades a serem desenvolvidos no decorrer do ano. LIÇÃO CONTEÚDO OBJETOS 1. Vamos recordar 2. Sistema
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática2º ano Ano Letivo 2016/2017
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática2º ano Ano Letivo 2016/2017 1º Período Domínios Números e Operações Números naturais Numerais ordinais até vigésimo;
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática2º ano Ano Letivo 2016/2017 1º Período Domínios Números e Operações Números naturais Numerais ordinais até vigésimo;
Agrupamento de Escolas de Portela e Moscavide
 Domínio: NÚMEROS E OPERAÇÕES (NO2) Números Naturais (Conhecer os numerais ordinais) 1.Utilizar corretamente os numerais ordinais até vigésimo. Números Naturais ( Contar até mil) 1.Estender as regars de
Domínio: NÚMEROS E OPERAÇÕES (NO2) Números Naturais (Conhecer os numerais ordinais) 1.Utilizar corretamente os numerais ordinais até vigésimo. Números Naturais ( Contar até mil) 1.Estender as regars de
PLANEJAMENTO ANUAL / TRIMESTRAL 2014 Conteúdos Habilidades Avaliação
 Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2014 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2014 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
Exemplo: Algoritmo fundamental da divisão: Exemplo:
 RAZÃO E PROPORÇÃO Vamos revisar o conceito de divisão. A divisão é uma das quatro operações fundamentais da Matemática que pode ser representada da seguinte forma: Algoritmo da divisão: Exemplo: Algoritmo
RAZÃO E PROPORÇÃO Vamos revisar o conceito de divisão. A divisão é uma das quatro operações fundamentais da Matemática que pode ser representada da seguinte forma: Algoritmo da divisão: Exemplo: Algoritmo
à situação. à situação.
 Unidade 1 Números naturais 1. Números naturais 2. Sistemas de numeração 3. Tabela simples Reconhecer os números naturais. Identificar o antecessor e o sucessor numa sequência de números naturais. Identificar
Unidade 1 Números naturais 1. Números naturais 2. Sistemas de numeração 3. Tabela simples Reconhecer os números naturais. Identificar o antecessor e o sucessor numa sequência de números naturais. Identificar
Agrupamento de Escolas de Vale de Milhaços Planificação Anual de Matemática: 2.º Ano de Escolaridade
 Domínio/ Subdomínio Números naturais Agrupamento de Escolas de Vale de Milhaços Planificação Anual de Matemática: 2.º Ano de Escolaridade - 2016-2017 Metas Programa Objetivos Gerais Descritores Conteúdos
Domínio/ Subdomínio Números naturais Agrupamento de Escolas de Vale de Milhaços Planificação Anual de Matemática: 2.º Ano de Escolaridade - 2016-2017 Metas Programa Objetivos Gerais Descritores Conteúdos
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro?
 Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
Qual o raio de um círculo com 53,38 cm de perímetro? (considera = 3,14) Qual o diâmetro de um círculo com 37,68 cm de perímetro? (considera = 3,14) Qual o perímetro de um círculo com 18 cm de raio? (considera
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2017/2018 PLANIFICAÇÃO ANUAL
 AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2017/2018 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Programa Atual da Disciplina e Metas Curriculares 1º CICLO MATEMÁTICA 2º ANO TEMAS/DOMÍNIOS
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2017/2018 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Programa Atual da Disciplina e Metas Curriculares 1º CICLO MATEMÁTICA 2º ANO TEMAS/DOMÍNIOS
1º período. Conhecer os algarismos que compõem o SND (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Diferenciar algarismos e números.
 1º período Os números naturais: Sistema de Numeração Decimal. (SND). Pág.30 a 32. Um pouco de história: sistema de numeração dos romanos. Pág. 33 a 35 Os números naturais. Pág. 36 e 37 Sistema de Numeração
1º período Os números naturais: Sistema de Numeração Decimal. (SND). Pág.30 a 32. Um pouco de história: sistema de numeração dos romanos. Pág. 33 a 35 Os números naturais. Pág. 36 e 37 Sistema de Numeração
MULTIPLICAÇÃO DE NÚMEROS RACIONAIS. Exemplo:
 Números Racionais MULTIPLICAÇÃO DE NÚMEROS RACIONAIS Exemplo: A Susana comprou ¾ de uma tarte. À hora do almoço colocou no forno ½ da porção de tarte para aquecer. Que fração do total da tarte colocou
Números Racionais MULTIPLICAÇÃO DE NÚMEROS RACIONAIS Exemplo: A Susana comprou ¾ de uma tarte. À hora do almoço colocou no forno ½ da porção de tarte para aquecer. Que fração do total da tarte colocou
PLANEJAMENTO ANUAL / TRIMESTRAL 2013 Conteúdos Habilidades Avaliação
 Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2013 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
Disciplina: Matemática Trimestre: 1º PLANEJAMENTO ANUAL / TRIMESTRAL 2013 Conteúdos Fundamentais de Matemática Sistema de Numeração decimal As quatro operações fundamentais Compreender problemas Números
Matemática - 2 o Ano. Planejamento Anual. Objetos de conhecimento
 www.apoioaaula.com.br Matemática - 2 o Ano Planejamento Anual 1 o Bimestre LINHAS Linha reta, linha curva e linha poligonal Polígonos Identificar figuras geométricas planas, considerando algumas características
www.apoioaaula.com.br Matemática - 2 o Ano Planejamento Anual 1 o Bimestre LINHAS Linha reta, linha curva e linha poligonal Polígonos Identificar figuras geométricas planas, considerando algumas características
AGRUPAMENTO DE ESCOLAS GARCIA DE ORTA
 ANO LETIVO - 2018-19 ESCOLA BÁSICA DO 1º CICLO DEPARTAMENTO DE 1º CICLO DO ENSINO BÁSICO PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA DO 2º ANO DE ESCOLARIDADE TEMA / CONTEÚDOS OBJETIVOS / DESCRITORES
ANO LETIVO - 2018-19 ESCOLA BÁSICA DO 1º CICLO DEPARTAMENTO DE 1º CICLO DO ENSINO BÁSICO PLANIFICAÇÃO ANUAL DA DISCIPLINA DE MATEMÁTICA DO 2º ANO DE ESCOLARIDADE TEMA / CONTEÚDOS OBJETIVOS / DESCRITORES
MATEMÁTICA - 2º ANO. Novo programa de matemática Objetivos específicos
 MATEMÁTICA - 2º ANO NÚMEROS E OPERAÇÕES Números naturais Noção de número natural Relações numéricas Sistema de numeração decimal Classificar e ordenar de acordo com um dado critério. Realizar contagens
MATEMÁTICA - 2º ANO NÚMEROS E OPERAÇÕES Números naturais Noção de número natural Relações numéricas Sistema de numeração decimal Classificar e ordenar de acordo com um dado critério. Realizar contagens
Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015
 Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015 Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Números e Operações Números Naturais Extensão
Conselho de Docentes do 4.º Ano PLANIFICAÇÃO Anual de Matemática Ano letivo de 2014/2015 Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Números e Operações Números Naturais Extensão
PROJETO KALI MATEMÁTICA B AULA 3 FRAÇÕES
 PROJETO KALI - 20 MATEMÁTICA B AULA FRAÇÕES Uma ideia sobre as frações Frações são partes de um todo. Imagine que, em uma lanchonete, são vendidos pedaços de pizza. A pizza é cortada em seis pedaços, como
PROJETO KALI - 20 MATEMÁTICA B AULA FRAÇÕES Uma ideia sobre as frações Frações são partes de um todo. Imagine que, em uma lanchonete, são vendidos pedaços de pizza. A pizza é cortada em seis pedaços, como
Matriz Curricular 1º Ciclo. Ano Letivo: 2015 / 2016 Ano de Escolaridade: 2.º MATEMÁTICA
 Ano Letivo: 2015 / 2016 Ano de Escolaridade: 2.º MATEMÁTICA N total de dias letivos 164 dias N de dias letivos - 1 período 64 dias - 2 período 52 dias - 3 período 48 dias N total de horas 221h N total
Ano Letivo: 2015 / 2016 Ano de Escolaridade: 2.º MATEMÁTICA N total de dias letivos 164 dias N de dias letivos - 1 período 64 dias - 2 período 52 dias - 3 período 48 dias N total de horas 221h N total
- Planificação Anual - 2º Ano -
 - Planificação Anual - 2º Ano - Matemática Números e Operações (NO2) Números Naturais - Numerais ordinais até vigésimo; - Números naturais até 1000; - Contagens de 2 em 2, de 5 em 5, de 10 em 10 e de 100
- Planificação Anual - 2º Ano - Matemática Números e Operações (NO2) Números Naturais - Numerais ordinais até vigésimo; - Números naturais até 1000; - Contagens de 2 em 2, de 5 em 5, de 10 em 10 e de 100
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 2.º ano Ano Letivo 2018/2019
 AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 2.º ano Ano Letivo 2018/2019 Matemática 1º Trimestre Tempo Calendários e horários. Números naturais Números pares
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO 1º Ciclo Planificação Anual de Matemática 2.º ano Ano Letivo 2018/2019 Matemática 1º Trimestre Tempo Calendários e horários. Números naturais Números pares
1º Período MATEMÁTICA 4.º ANO. setembro. Domínios Conteúdos programáticos Objetivos/Descritores de desempenho
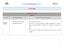 1º Período setembro Números e Operações Dezenas e centenas de milhar. Resolução de problemas. Rever a matéria do ano anterior Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo
1º Período setembro Números e Operações Dezenas e centenas de milhar. Resolução de problemas. Rever a matéria do ano anterior Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo
Representação: 2 5. Resposta: Cada pessoa receberá R$ 6,25 (seis reais e vinte e cinco centavos)
 MATEMÁTICA FRAÇÕES E NÚMEROS DECIMAIS Fração quer dizer pedaços do mesmo tamanho. Você tem um chocolate dividido em 5 partes iguais. Dessas 5 partes você comeu 2. A fração que representa essa situação
MATEMÁTICA FRAÇÕES E NÚMEROS DECIMAIS Fração quer dizer pedaços do mesmo tamanho. Você tem um chocolate dividido em 5 partes iguais. Dessas 5 partes você comeu 2. A fração que representa essa situação
REVISÃO DE MATEMÁTICA BÁSICA
 REVISÃO DE MATEMÁTICA BÁSICA AULA 2 Frações Profe. Kátia FRAÇÕES Uma fração é a representação de uma ou mais partes de algo que foi dividido em partes iguais. Partes de um inteiro. Todo objeto original
REVISÃO DE MATEMÁTICA BÁSICA AULA 2 Frações Profe. Kátia FRAÇÕES Uma fração é a representação de uma ou mais partes de algo que foi dividido em partes iguais. Partes de um inteiro. Todo objeto original
4 º Ano Matemática. METAS Domínios/Conteúdos Objetivos Descritores de Desempenho
 METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Ao longo do ano Números e Operações 3. Resolver problemas 3.1. Resolver problemas de vários passos envolvendo as quatro operações. setembro/
METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Ao longo do ano Números e Operações 3. Resolver problemas 3.1. Resolver problemas de vários passos envolvendo as quatro operações. setembro/
Planificação Anual Departamento 1.º Ciclo
 Modelo Dep-01 Agrupamento de Escolas do Castêlo da Maia Planificação Anual Departamento 1.º Ciclo Ano 2.º Ano letivo 2013.2014 Disciplina Matemática Turmas: 2º ano Professores: todos os docentes do 2.º
Modelo Dep-01 Agrupamento de Escolas do Castêlo da Maia Planificação Anual Departamento 1.º Ciclo Ano 2.º Ano letivo 2013.2014 Disciplina Matemática Turmas: 2º ano Professores: todos os docentes do 2.º
PLANIFICAÇÃO ANUAL 2015/ º Ano Matemática. METAS Domínios/Conteúdos Objetivos Descritores de Desempenho
 METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Número e Operações - Números naturais 1. Contar 1.1. Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de
METAS Domínios/Conteúdos Objetivos Descritores de Desempenho Número e Operações - Números naturais 1. Contar 1.1. Reconhecer que se poderia prosseguir a contagem indefinidamente introduzindo regras de
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2016/2017 PLANIFICAÇÃO ANUAL
 AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2016/2017 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Metas Curriculares e Programa de Matemática 1º CICLO MATEMÁTICA 3º ANO TEMAS/DOMÍNIOS CONTEÚDOS
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2016/2017 PLANIFICAÇÃO ANUAL Documento(s) Orientador(es): Metas Curriculares e Programa de Matemática 1º CICLO MATEMÁTICA 3º ANO TEMAS/DOMÍNIOS CONTEÚDOS
Unidade I MATEMÁTICA APLICADA. Profa. Ana Carolina Bueno
 Unidade I MATEMÁTICA APLICADA Profa. Ana Carolina Bueno Números reais Fonte: http://infomaticando.blogspot.com.br/2012/12/numeros-irracionais.html Expressões algébricas São expressões matemáticas que apresentam
Unidade I MATEMÁTICA APLICADA Profa. Ana Carolina Bueno Números reais Fonte: http://infomaticando.blogspot.com.br/2012/12/numeros-irracionais.html Expressões algébricas São expressões matemáticas que apresentam
Planificação anual matemática
 Planificação anual matemática 1º e 2º anos Tópicos Objetivos específicos Números naturais Noção de número natural Relações numéricas Sistema de numeração decimal Classificar e ordenar de acordo com um
Planificação anual matemática 1º e 2º anos Tópicos Objetivos específicos Números naturais Noção de número natural Relações numéricas Sistema de numeração decimal Classificar e ordenar de acordo com um
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: 1.º Ciclo DISCIPLINA: Matemática CURSO: Ensino Básico ANO: 3º ANO LETIVO: 2017/2018 MANUAL: A Grande Aventura Unidade Didática/Domínio Geometria e Medida
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: 1.º Ciclo DISCIPLINA: Matemática CURSO: Ensino Básico ANO: 3º ANO LETIVO: 2017/2018 MANUAL: A Grande Aventura Unidade Didática/Domínio Geometria e Medida
Frações Se dividirmos um objecto, ou seja, uma unidade em várias partes iguais, a cada uma dessas partes dá-se o nome de fração.
 Frações Se dividirmos um objecto, ou seja, uma unidade em várias partes iguais, a cada uma dessas partes dá-se o nome de fração. numerador 1 6 traço de fração ( : ) denominador Uma fração envolve a seguinte
Frações Se dividirmos um objecto, ou seja, uma unidade em várias partes iguais, a cada uma dessas partes dá-se o nome de fração. numerador 1 6 traço de fração ( : ) denominador Uma fração envolve a seguinte
CRITÉRIOS ESPECÍFICOS DE AVALIAÇÃO 3º ANO (1º CICLO) MATEMÁTICA
 CRTÉRO EPECÍCO DE AVALAÇÃO 3º ANO (1º CCLO) MATEMÁTCA DOMÍNO/ UDOMÍNO Números e Operações Números naturais OJETVO DECRTORE DE DEEMPENHO MENÇÕE 1. Conhecer os numerais ordinais 2. Contar até um milhão 3.
CRTÉRO EPECÍCO DE AVALAÇÃO 3º ANO (1º CCLO) MATEMÁTCA DOMÍNO/ UDOMÍNO Números e Operações Números naturais OJETVO DECRTORE DE DEEMPENHO MENÇÕE 1. Conhecer os numerais ordinais 2. Contar até um milhão 3.
AGRUPAMENTO de ESCOLAS de PEDRÓGÃO GRANDE CONSELHO de DOCENTES 1.º CEB Planificação Anual Matemática- _ 2.º Ano /2017
 Números e Operações NO2 ANUAL 168 dias letivos Números naturais 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «vigésimo». - Numerais ordinais até vigésimo; - Números
Números e Operações NO2 ANUAL 168 dias letivos Números naturais 1. Conhecer os numerais ordinais 1. Utilizar corretamente os numerais ordinais até «vigésimo». - Numerais ordinais até vigésimo; - Números
AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 4.º ANO DE ESCOLARIDADE
 Domínio/ NO4/ Números naturais NO4/ Números racionais não negativos AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 4.º ANO DE ESCOLARIDADE - 2016-2017 1. Contar 1. Reconhecer
Domínio/ NO4/ Números naturais NO4/ Números racionais não negativos AGRUPAMENTO DE ESCOLAS DE VALE DE MILHAÇOS PLANIFICAÇÃO ANUAL DE MATEMÁTICA 4.º ANO DE ESCOLARIDADE - 2016-2017 1. Contar 1. Reconhecer
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM Ano Letivo 2015/2016 PLANIFICAÇÃO ANUAL
 AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM 1º CICLO Ano Letivo 2015/2016 PLANIFICAÇÃO ANUAL MATEMÁTICA 3º ANO Documento(s) Orientador(es): Clique aqui para indicar os documentos que serviram de base à
AGRUPAMENTO de ESCOLAS de SANTIAGO do CACÉM 1º CICLO Ano Letivo 2015/2016 PLANIFICAÇÃO ANUAL MATEMÁTICA 3º ANO Documento(s) Orientador(es): Clique aqui para indicar os documentos que serviram de base à
PLANIFICAÇÃO MENSAL/ANUAL Matemática 4.ºano
 PLANIFICAÇÃO MENSAL/ANUAL Matemática 4.ºano MATEMÁTICA 4.º ANO DE ESCOLARIDADE Domínio/ Subdomínio Números Naturais Operações com números naturais Números racionais não negativos Metas a atingir Contar
PLANIFICAÇÃO MENSAL/ANUAL Matemática 4.ºano MATEMÁTICA 4.º ANO DE ESCOLARIDADE Domínio/ Subdomínio Números Naturais Operações com números naturais Números racionais não negativos Metas a atingir Contar
PLANIFICAÇÃO ANUAL DE MATEMÁTICA
 AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA- Cantanhede DEPARTAMENTO CURRICULAR DO 1.º CICLO 4.º ANO DE ESCOLARIDADE PLANIFICAÇÃO ANUAL DE MATEMÁTICA Domínios Subdomínios / Conteúdos programáticos METAS
AGRUPAMENTO DE ESCOLAS MARQUÊS DE MARIALVA- Cantanhede DEPARTAMENTO CURRICULAR DO 1.º CICLO 4.º ANO DE ESCOLARIDADE PLANIFICAÇÃO ANUAL DE MATEMÁTICA Domínios Subdomínios / Conteúdos programáticos METAS
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: 1.º Ciclo DISCIPLINA: Matemática ANO: 3º ANO LETIVO: 2018/2019 MANUAL: A Grande Aventura avaliação A avaliação dos alunos poderá ser realizada através de:
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: 1.º Ciclo DISCIPLINA: Matemática ANO: 3º ANO LETIVO: 2018/2019 MANUAL: A Grande Aventura avaliação A avaliação dos alunos poderá ser realizada através de:
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 99 / 00 MÚLTIPLA ESCOLHA
 MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 0. Sejam os conjuntos: A = Conjunto dos números no quadrado B = Conjunto dos números no pentágono C =
MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 0. Sejam os conjuntos: A = Conjunto dos números no quadrado B = Conjunto dos números no pentágono C =
CONCEITOS BÁSICOS PARA COMPREENSÃO DA FÍSICA
 CONCEITOS BÁSICOS PARA COMPREENSÃO DA FÍSICA Números decimais Números decimais são todos aqueles números que possuem uma vírgula. Cada número escrito após a virgula é considerado como casa decimal, ou
CONCEITOS BÁSICOS PARA COMPREENSÃO DA FÍSICA Números decimais Números decimais são todos aqueles números que possuem uma vírgula. Cada número escrito após a virgula é considerado como casa decimal, ou
