Elementos de Matemática
|
|
|
- Zaira Alcaide Quintão
- 7 Há anos
- Visualizações:
Transcrição
1 Elementos de Matemática Álgebra de Boole Roteiro no Atividades didáticas de de Outubro de Arq: elementos10.tex Departamento de Matemática - UEL Prof. Ulysses Sodré ulysses(at)matematica(pt)uel(pt)br Matemática Essencial: Resumo: Notas de aulas para as nossas aulas na Universidade Estadual de Londrina. Desejo que elas sejam um roteiro para as aulas e não espero que estas notas venham a substituir qualquer livro sobre o assunto. Algum material foi obtido em livros citados na Bibliografia, mas os assuntos foram bastante modificados. Sugerimos que o leitor pesquise a Interbet para obter materiais gratuitos para os seus estudos. Mensagem: Melhor é serem dois do que um, porque têm melhor paga do seu trabalho. Pois se caírem, um levantará o seu companheiro; mas ai do que estiver só, pois, caindo, não haverá outro que o levante. Também, se dois dormirem juntos, eles se aquentarão; mas um só como se aquentará? E, se alguém quiser prevalecer contra um, os dois lhe resistirão; e o cordão de três dobras não se quebra tão depressa. A Bíblia Sagrada, Eclesiastes 4:9-12
2 Álgebra de Boole 1 1 Álgebra de Boole Definição 1 (Álgebra de Boole). Uma Álgebra Booleana é uma estrutura matemática denotada por B = (B, s, p, c, θ, I), onde os seis objetos são: B: Um conjunto B não vazio. s: Uma operação binária s : B B B que associa a cada par de elementos (a, b) B B um elemento s(a, b) = a + b B, denominado a soma dos elementos a, b B. p: Uma operação binária p : B B B que associa a cada par de elementos (a, b) B B um elemento p(a, b) = a b B, denominado o produto dos elementos a, b B. c: Uma operação unária c : B B B que associa a cada elemento a B um elemento c(a) B, denominado o complemento do elemento a B. θ: Um elemento nulo θ B, I: Um elemento unidade I B que é diferente de θ B. que, para quaisquer a, b, c B, satisfazem aos oito axiomas: 1. Comutativa: a + b = b + a 2. Distributiva: a + (b c) = (a + b) (a + c) 3. Elemento nulo: a + θ = a 4. Complemento: a + c(a) = I 5. Comutativa: a b = b a 6. Distributiva: a (b + c) = (a b) + (a c) 7. Elemento unidade: a I = a 8. Complemento: a c(a) = θ Exemplo 1 (Álgebra de Boole). A estrutura (B, +,, c, 0, 1), onde B = {0, 1}, θ = 0 e I = 1, com as operações definidas pelas tabelas *
3 Álgebra de Boole 2 Observação 1 (Precedência nas operações). Em uma Álgebra de Boole, embora os parênteses possam alterar a precedência, as operações matemáticas são realizadas na seguinte ordem: 1. Complemento, 2. Produto, 3. Soma. Observação 2 (Precedência nas operações). Na Álgebra de Boole do exemplo anterior, (B, +,, c, 0, 1), onde B = {0, 1}, θ = 0 e I = 1, a expressão booleana x = 1 (1 + 0) + c(1) tem valor x = 1, pois x = 1 (1 + 0) + c(1) = 1 (1 + 0) + 0 = 1 * = = 1 Exemplo 2 (Álgebra de Boole de Conjuntos). A estrutura (X,,, c,, U) formada pela coleção X de todos os conjuntos que é fechada para as operações de reunião, interseção e complementar, sendo o elemento nulo θ = (conjunto vazio), o elemento unidade I = U (universo) e c(a) = U A = A c que é complemento, pois, quaisquer que sejam A, B, C X, tem-se: 1. A B = B A 2. A (B C) = (A B) (A C) 3. A = A 4. A A c = U 5. A B = B A 6. A (B C) = (A B) (A C) 7. A U = A 8. A A c = Observação 3. A palavra fechada em X significa que a reunião, a interseção e o complementar de conjuntos em X ainda está em X.
4 Álgebra de Boole 3 Exemplo 3 (Divisores de 12). Seja a estrutura (D(12),,, c, θ, I), formada pelo conjunto D(12) = {1, 2, 3, 4, 6, 12} dos divisores naturais do número 12, o elemento nulo θ = 1 e o elemento unidade I = 12, com as operações definidas pelas tabelas: a b = MMC(a,b) Mínimo Múltiplo Comum entre a e b a b = MDC(a,b) Máximo Divisor Comum entre a e b c(a) = 12/a Divisão de 12 por a A estrutura (D(12),,, c, θ, I) não representa uma Álgebra de Boole, pois 2 D(12) e c(2) = 6 D(12), mas 2 c(2) = 2 6 = MMC(2, 6) = 6 12 = I 2 c(2) = 2 6 = MDC(2, 6) = 2 1 = θ Exemplo 4 (Álgebra de Boole Z2). A estrutura (Z 2, +,, c, P, I) sendo que Z 2 = {P, I}, P é conjunto dos números pares inteiros, I é o conjunto dos números ímpares inteiros, o elemento nulo θ = P, o elemento unidade é o conjunto I dos números ímpares e o complemento definido no universo Z do conjunto dos números inteiros, com as operações definidas pelas tabelas a P I c(a) I P * P I P P P I P I + P I P P I I I I Exemplo 5 (Z3). Seja z um número inteiro. Se a divisão do número z por 3 tem resto r, escrevemos z [r] (z pertence à classe [r]). O conjunto das classes Z 3 = {[0], [1], [2]} é bem conhecido na Álgebra, mas a estrutura (Z 3, +,, c, [0], [1]) com o elemento nulo θ = [0] e o elemento unidade I = [1], Não é uma Álgebra de Boole com as operações definidas pelas tabelas: [0] [1] [1] [0] [2] [2] * [0] [1] [2] [0] [0] [0] [0] [1] [0] [1] [2] [2] [0] [2] [1] + [0] [1] [2] [0] [0] [1] [2] [1] [1] [2] [0] [2] [2] [0] [1] Se (Z 3, +,, c, [0], [1]) fosse uma Álgebra de Boole, poderíamos tomar a = [2], c(a) = [2] e seguiria que [0] = θ = a c(a) = [2] [2] = [1], o que é falso.
5 Álgebra de Boole 4 Exemplo 6 (Álgebra de Boole {(0,0),(1,1)}). Seja B = {0, 1} e o produto cartesiano B 2 = {(0, 0), (0, 1), (1, 0), (1, 1)}. A estrutura (B 2, +,, c, θ, I)) onde θ = (0, 0) e I = (1, 1) é uma Álgebra de Boole, com as operações: (0,0) (1,1) (0,1) (1,0) (1,0) (0,1) (1,1) (0,0) * (0,0) (0,1) (1,0) (1,1) (0,0) (0,0) (0,0) (0,0) (0,0) (0,1) (0,0) (0,1) (0,0) (0,1) (1,0) (0,0) (0,0) (1,0) (1,0) (1,1) (0,0) (0,1) (1,0) (1,1) + (0,0) (0,1) (1,0) (1,1) (0,0) (0,0) (0,1) (1,0) (1,1) (0,1) (0,1) (0,1) (1,1) (1,1) (1,0) (1,0) (1,1) (1,0) (1,1) (1,1) (1,1) (1,1) (1,1) (1,1) Exemplo 7. Seja o conjunto B = {0, 1, 2, 3}. Escrevemos um elemento a B na base 2, dividindo a por 2, para obter o quociente q e o resto r. A notação a 2 = qr indica o valor do número a B na base 2. Formamos assim um novo conjunto B 2 = {00, 01, 10, 11}. Se o elemento nulo é θ = 00, o elemento unidade é I = 11 e as operações são definidas pelas tabelas * segue que a estrutura (B 2, +,, c, 00, 11) é uma Álgebra de Boole. Exemplo 8 (Álgebra de Boole das Proposições lógicas ). A estrutura formada por (P,,,, F, V ), em que P é a coleção de todas as proposições lógicas, é a operação de disjunção, é a operação de conjunção, é a operação de negação, θ = F é a contradição representando o elemento nulo e I = V é a tautologia representando o elemento unidade, é uma Álgebra de Boole. Neste caso, duas proposições lógicas equivalentes são tomadas como iguais.
6 Seção 2 Símbolos superior e inferior de Sheffer 5 Definição 2 (Dualidade). Em uma Álgebra de Boole, o dual de uma afirmação é uma outra afirmação obtida da primeira pela troca das operações de soma (+) pelo produto ( ) e pela troca do elementos nulo (θ) pela unidade (I). Exemplo 9 (Dualidade). A afirmação dual corespondente a é a afirmação (a + θ) (b + c(b)) = a (a I) + (b c(b)) = a Observação 4 (Sobre dualidade). Um Teorema é verdadeiro em uma Álgebra de Boole, se e somente se, o Teorema dual correspondente é verdadeiro. Observação 5 (Dualidade no teorema). No próximo teorema, as afirmações (1,2,3,4,5,6), respectivamente, são duais às afirmações (7,8,9,10,11,12), significando que basta demonstrar o primeiro grupo ou o segundo grupo. Teorema 1 (Propriedades). Se B é uma Álgebra de Boole e a, b, c B, então 1. a + a = a 2. a + I = I 3. a + (a b) = a 4. a + (b + c) = (a + b) + c 5. c(θ) = I 6. c(a + b) = c(a) c(b) 7. a a = a 8. a θ = θ 9. a (a + b) = a 10. a (b c) = (a b) c 11. c(i) = θ 12. c(a b) = c(a) + c(b) Exercício: Se B é uma Álgebra de Boole e a, b, c B, mostrar que 1. c(c(a)) = a 2. Se a + x = 1 e a x = 0 então x = c(a). 2 Símbolos superior e inferior de Sheffer Definição 3. Define-se o símbolo superior de Sheffer por p q = ( p) ( q) = p q
7 Seção 2 Símbolos superior e inferior de Sheffer 6 Exemplo 10 (Negação de p). Usando o símbolo superior de Sheffer, obtemos p p = p p = p Exemplo 11 (Conjunção de p e q). Com o símbolo superior de Sheffer aplicado a duas proposições iguais a p q, obtemos (p q) (p q) = ( ( p q)) ( ( p q)) = (p q) (p q) = p q Exemplo 12 (Disjunção de p e q). Com o símbolo superior de Sheffer aplicado às proposições p p e q q, obtemos (p q) (q q) = ( p p) ( q q) = ( p) ( q) = p q Definição 4. Define-se o símbolo inferior de Sheffer por p q = ( p) ( q) = p q Exemplo 13 (Negação de p). Usando o símbolo inferior de Sheffer, obtemos p p = p p = p Exemplo 14 (Disjunção de p e q). Com o símbolo inferior de Sheffer aplicado a duas proposições iguais a p q, obtemos (p q) (p q) = ( ( p q)) ( ( p q)) = (p q) (p q) = p q Exemplo 15 (Conjunção de p e q). Com o símbolo inferior de Sheffer aplicado às proposições p p e q q, obtemos (p p) (q q) = ( p p) ( q q) = ( p) ( q) = p q Complete a tabela com as operações com os símbolos de Sheffer: Proposição Símbolo Símbolo superior Símbolo inferior Negação p p p p p Conjunção p q (p q) (p q) (p p) (q q) Disjunção p q (p p) (q q) (p q) (p q) Condicional p q Bicondicional p q Podemos construir uma Tabela-Verdade com os símbolos de Sheffer: p q p q p q V V V V V F F V F V F V F F V V
ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN
 ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN No século XIX Georges Boole desenvolveu uma teoria matemática com base nas leis da lógica - a Álgebra de Boole - cuja aplicação nos circuitos digitais e computadores
ÁLGEBRA DE BOOLE B.1 - DIAGRAMA DE VENN No século XIX Georges Boole desenvolveu uma teoria matemática com base nas leis da lógica - a Álgebra de Boole - cuja aplicação nos circuitos digitais e computadores
UNIP Ciência da Computação Prof. Gerson Pastre de Oliveira
 Aula 6 Lógica Matemática Álgebra das proposições e método dedutivo As operações lógicas sobre as proposições possuem uma série de propriedades que podem ser aplicadas, considerando os conectivos inseridos
Aula 6 Lógica Matemática Álgebra das proposições e método dedutivo As operações lógicas sobre as proposições possuem uma série de propriedades que podem ser aplicadas, considerando os conectivos inseridos
é uma proposição verdadeira. tal que: 2 n N k, Φ(n) = Φ(n + 1) é uma proposição verdadeira. com n N k, tal que:
 Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Elementos de Matemática
 Elementos de Matemática Exercícios de Lógica para as atividades didáticas de 2007 Versão compilada no dia 27 de Abril de 2007. Departamento de Matemática - UEL Prof. Ulysses Sodré E-mail: ulysses@matematica.uel.br
Elementos de Matemática Exercícios de Lógica para as atividades didáticas de 2007 Versão compilada no dia 27 de Abril de 2007. Departamento de Matemática - UEL Prof. Ulysses Sodré E-mail: ulysses@matematica.uel.br
Lógica Proposicional e Álgebra de Boole
 Lógica Proposicional e Álgebra de Boole A lógica proposicional remonta a Aristóteles, e teve como objectivo modelizar o raciocínio humano. Partindo de frases declarativas ( proposições), que podem ser
Lógica Proposicional e Álgebra de Boole A lógica proposicional remonta a Aristóteles, e teve como objectivo modelizar o raciocínio humano. Partindo de frases declarativas ( proposições), que podem ser
DISCIPLINA: MATEMÁTICA DISCRETA I PROFESSOR: GISLAN SILVEIRA SANTOS CURSO: SISTEMAS DE INFORMAÇÃO SEMESTRE: TURNO: NOTURNO
 DISCIPLINA: MATEMÁTICA DISCRETA I PROFESSOR: GISLAN SILVEIRA SANTOS CURSO: SISTEMAS DE INFORMAÇÃO SEMESTRE: 2018-2 TURNO: NOTURNO ALUNO a): 1ª Lista de Exercícios - Introdução à Lógica Matemática, Teoria
DISCIPLINA: MATEMÁTICA DISCRETA I PROFESSOR: GISLAN SILVEIRA SANTOS CURSO: SISTEMAS DE INFORMAÇÃO SEMESTRE: 2018-2 TURNO: NOTURNO ALUNO a): 1ª Lista de Exercícios - Introdução à Lógica Matemática, Teoria
Cálculo proposicional
 Notas de aula de MAC0329 (2003) 9 2 Cálculo proposicional Referências para esta parte do curso: capítulo 1 de [Mendelson, 1977], capítulo 3 de [Whitesitt, 1961]. Proposição Proposições são sentenças afirmativas
Notas de aula de MAC0329 (2003) 9 2 Cálculo proposicional Referências para esta parte do curso: capítulo 1 de [Mendelson, 1977], capítulo 3 de [Whitesitt, 1961]. Proposição Proposições são sentenças afirmativas
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES
 MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Newton José Vieira 21 de agosto de 2007 SUMÁRIO Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova 1 CONJUNTOS A NOÇÃO
Álgebra Linear e Geometria Analítica
 Álgebra Linear e Geometria Analítica Engenharia Electrotécnica Escola Superior de Tecnologia de Viseu www.estv.ipv.pt/paginaspessoais/lucas lucas@mat.estv.ipv.pt 2007/2008 Álgebra Linear e Geometria Analítica
Álgebra Linear e Geometria Analítica Engenharia Electrotécnica Escola Superior de Tecnologia de Viseu www.estv.ipv.pt/paginaspessoais/lucas lucas@mat.estv.ipv.pt 2007/2008 Álgebra Linear e Geometria Analítica
Como primeira e indispensável parte da Lógica Matemática temos o Cálculo Proporcional ou Cálculo Sentencial ou ainda Cálculo das Sentenças.
 NE-6710 - SISTEMAS DIGITAIS I LÓGICA PROPOSICIONAL, TEORIA CONJUNTOS. A.0 Noções de Lógica Matemática A,0.1. Cálculo Proposicional Como primeira e indispensável parte da Lógica Matemática temos o Cálculo
NE-6710 - SISTEMAS DIGITAIS I LÓGICA PROPOSICIONAL, TEORIA CONJUNTOS. A.0 Noções de Lógica Matemática A,0.1. Cálculo Proposicional Como primeira e indispensável parte da Lógica Matemática temos o Cálculo
Ciência da Computação A&P
 Algoritmos e Programação Informática II Ciência da Computação Prof. Dr. Leandro Alves Neves Prof. Dr. Adriano M. Cansian 1 Sumário Operações e Expressões Definição Operadores: Aritméticos. Relacionais.
Algoritmos e Programação Informática II Ciência da Computação Prof. Dr. Leandro Alves Neves Prof. Dr. Adriano M. Cansian 1 Sumário Operações e Expressões Definição Operadores: Aritméticos. Relacionais.
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções
 Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) joao.carvalho@inesc.pt Álgebra de Boole Binária A Álgebra de Boole binária
Sistemas Digitais Álgebra de Boole Binária e Especificação de Funções João Paulo Baptista de Carvalho (Prof. Auxiliar do IST) joao.carvalho@inesc.pt Álgebra de Boole Binária A Álgebra de Boole binária
3 Cálculo Proposicional
 3 Cálculo Proposicional O Cálculo Proposicional é um dos tópicos fundamentais da Lógica e consiste essencialmente da formalização das relações entre sentenças (ou proposições), de nidas como sendo frases
3 Cálculo Proposicional O Cálculo Proposicional é um dos tópicos fundamentais da Lógica e consiste essencialmente da formalização das relações entre sentenças (ou proposições), de nidas como sendo frases
Notas de Aula de Probabilidade A
 I- CONCEITOS INICIAIS. 1.1- INTRODUÇÃO. PROBABILIDADE POPULAÇÃO AMOSTRA ESTATÍSTICA 1.2- CONJUNTOS. 1.2.1- DEFINIÇÃO. Conjunto é uma coleção de objetos chamados de elementos do conjunto. Em geral denota-se
I- CONCEITOS INICIAIS. 1.1- INTRODUÇÃO. PROBABILIDADE POPULAÇÃO AMOSTRA ESTATÍSTICA 1.2- CONJUNTOS. 1.2.1- DEFINIÇÃO. Conjunto é uma coleção de objetos chamados de elementos do conjunto. Em geral denota-se
Referências e materiais complementares desse tópico
 Notas de aula: Análise de Algoritmos Centro de Matemática, Computação e Cognição Universidade Federal do ABC Profa. Carla Negri Lintzmayer Conceitos matemáticos e técnicas de prova (Última atualização:
Notas de aula: Análise de Algoritmos Centro de Matemática, Computação e Cognição Universidade Federal do ABC Profa. Carla Negri Lintzmayer Conceitos matemáticos e técnicas de prova (Última atualização:
Circuitos Digitais Álgebra de Boole
 Circuitos Digitais Álgebra de Boole Álgebra de Boole (ou Booleana) Desenvolvida pelo matemático britânico George Boole para estudo da lógica. Definida sobre um conjunto de dois elementos: (falso, verdadeiro)
Circuitos Digitais Álgebra de Boole Álgebra de Boole (ou Booleana) Desenvolvida pelo matemático britânico George Boole para estudo da lógica. Definida sobre um conjunto de dois elementos: (falso, verdadeiro)
MATEMÁTICA 1 MÓDULO 2. Divisibilidade. Professor Matheus Secco
 MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MA14 - Aritmética Unidade 1 Resumo. Divisibilidade
 MA14 - Aritmética Unidade 1 Resumo Divisibilidade Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
MA14 - Aritmética Unidade 1 Resumo Divisibilidade Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
Linguagem Computacional
 Informática II Linguagem Computacional Algoritmos e Programação Parte 3 Prof. Dr. Adriano Cansian Prof. Dr. Leandro Alves Neves 1 Sumário Operações e Expressões q Definição q Operadores: Aritméticos. Relacionais.
Informática II Linguagem Computacional Algoritmos e Programação Parte 3 Prof. Dr. Adriano Cansian Prof. Dr. Leandro Alves Neves 1 Sumário Operações e Expressões q Definição q Operadores: Aritméticos. Relacionais.
(A1) As operações + e são comutativas, ou seja, para todo x e y em A, x + y = y + x e x y = y x
 Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Notas de aula de MAC0329 (2003) 17 3 Álgebra Booleana Nesta parte veremos uma definição formal de álgebra booleana, a qual é feita via um conjunto de axiomas (ou postulados). Veremos também algumas leis
Programa Combinatória Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 52
 1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
Módulo 2 Álgebra e Lógica Booleana
 1 Sistemas Digitais e Arquitetura de Computadores Módulo 2 Álgebra e Lógica Booleana 0. Álgebra de Boole 2017/2018 2 Introdução A álgebra de Boole, como a álgebra tradicional, tem, em princípio, como objeto,
1 Sistemas Digitais e Arquitetura de Computadores Módulo 2 Álgebra e Lógica Booleana 0. Álgebra de Boole 2017/2018 2 Introdução A álgebra de Boole, como a álgebra tradicional, tem, em princípio, como objeto,
Lógica Proposicional Parte I. Raquel de Souza Francisco Bravo 11 de outubro de 2016
 Lógica Proposicional Parte I e-mail: raquel@ic.uff.br 11 de outubro de 2016 Lógica Matemática Cáculo Proposicional Uma aventura de Alice Alice, ao entrar na floresta, perdeu a noção dos dias da semana.
Lógica Proposicional Parte I e-mail: raquel@ic.uff.br 11 de outubro de 2016 Lógica Matemática Cáculo Proposicional Uma aventura de Alice Alice, ao entrar na floresta, perdeu a noção dos dias da semana.
22. Análise Combinatória - Permutação - Repetição - Circular - Condicional Análise Combinatória - Combinação e Arranjo
 Conteúdo 1. Conceitos Iniciais... 6 2. Proposições [1]... 7 3. Proposições [2] Tautologia - Contradição - Contigência... 8 4. Não são Proposições... 9 5. Lógica argumentativa Negação... 10 6. Lógica argumentativa
Conteúdo 1. Conceitos Iniciais... 6 2. Proposições [1]... 7 3. Proposições [2] Tautologia - Contradição - Contigência... 8 4. Não são Proposições... 9 5. Lógica argumentativa Negação... 10 6. Lógica argumentativa
Lógica Boolena. Aula 05. Prof. Msc. Arthur G. Bartsch
 Lógica Boolena Aula 05 Prof. Msc. Arthur G. Bartsch Departamento de engenharia elétrica DEE Centro de ciências tecnológicas CCT Universidade do estado de Santa Catarina UDESC Álgebra de Boole ALB0001 arthur.bartsch@udesc.br
Lógica Boolena Aula 05 Prof. Msc. Arthur G. Bartsch Departamento de engenharia elétrica DEE Centro de ciências tecnológicas CCT Universidade do estado de Santa Catarina UDESC Álgebra de Boole ALB0001 arthur.bartsch@udesc.br
Tecnologia dos Computadores 2002/2003. Exercícios
 Introdução à Álgebra de Boole 1 Introdução Em 1854, George Boole, um matemático inglês, inventou um sistema algébrico de dois valores, cujo resultado da sua evolução até aos dias de hoje se dá o nome de
Introdução à Álgebra de Boole 1 Introdução Em 1854, George Boole, um matemático inglês, inventou um sistema algébrico de dois valores, cujo resultado da sua evolução até aos dias de hoje se dá o nome de
Faculdade de Informática e Tecnologia de Pernambuco. Primeira lista de exercícios de Álgebra Aplicada à Computação Prof. Diego Machado Dias
 Faculdade de Informática e Tecnologia de Pernambuco Primeira lista de exercícios de Álgebra Aplicada à Computação Prof. Diego Machado Dias Instruções 1. No início de cada seção da lista há uma sugestão
Faculdade de Informática e Tecnologia de Pernambuco Primeira lista de exercícios de Álgebra Aplicada à Computação Prof. Diego Machado Dias Instruções 1. No início de cada seção da lista há uma sugestão
RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03
 RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03 PEDRO A. TONELLI 1. Introdução: o esqueleto do espírito E ainda mais remoto que o tempo em que as coisas não tinham nome, é o tempo em que as coisas nem existiam,
RETICULADOS: NOTAS DO SEMINÁRIO DE 7/03/03 PEDRO A. TONELLI 1. Introdução: o esqueleto do espírito E ainda mais remoto que o tempo em que as coisas não tinham nome, é o tempo em que as coisas nem existiam,
Álgebra Booleana: Axiomas, Teoremas e Leis de De Morgan
 Arquitectura de Computadores I Engenharia Informática (11537) Tecnologias e Sistemas de Informação (6616) Álgebra Booleana: Axiomas, Teoremas e Leis de De Morgan Nuno Pombo / Miguel Neto Arquitectura Computadores
Arquitectura de Computadores I Engenharia Informática (11537) Tecnologias e Sistemas de Informação (6616) Álgebra Booleana: Axiomas, Teoremas e Leis de De Morgan Nuno Pombo / Miguel Neto Arquitectura Computadores
Teoria Elementar dos Conjuntos
 Teoria Elementar dos Conjuntos Última revisão em 27 de fevereiro de 2009 Este texto é uma breve revisão sobre teoria elementar dos conjuntos. Em particular, importam-nos os aspectos algébricos no estudo
Teoria Elementar dos Conjuntos Última revisão em 27 de fevereiro de 2009 Este texto é uma breve revisão sobre teoria elementar dos conjuntos. Em particular, importam-nos os aspectos algébricos no estudo
Teoria Elementar dos Conjuntos
 Teoria Elementar dos Conjuntos Este capítulo visa oferecer uma breve revisão sobre teoria elementar dos conjuntos. Além de conceitos básicos importantes em matemática, a sua imprtância reside no fato da
Teoria Elementar dos Conjuntos Este capítulo visa oferecer uma breve revisão sobre teoria elementar dos conjuntos. Além de conceitos básicos importantes em matemática, a sua imprtância reside no fato da
Teoria dos Conjuntos MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES. Fundamentos de Lógica Técnicas Elementares de Prova A NOÇÃO DE CONJUNTO
 SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
SUMÁRIO MATEMÁTICA DISCRETA CONCEITOS PRELIMINARES Teoria dos Conjuntos Relações e Funções Fundamentos de Lógica Técnicas Elementares de Prova Newton José Vieira 21 de agosto de 2007 1 A NOÇÃO DE CONJUNTO
Introdução à Automação
 Núcleo de Mecânica Introdução à Automação Prof. Wander Gaspar wandergaspar@gmail.com Sistemas Analógicos Um sistema analógico contém dispositivos que manipulam quantidades físicas que variam de forma contínua
Núcleo de Mecânica Introdução à Automação Prof. Wander Gaspar wandergaspar@gmail.com Sistemas Analógicos Um sistema analógico contém dispositivos que manipulam quantidades físicas que variam de forma contínua
Observação: Todas as letras em negrito abaixo (x, y, z, a e b) representam números reais.
 Para mostrar que menos vezes menos dá mais precisamos admitir alguns fatos relacionados aos números reais. Vamos chamá-los de axiomas e simplesmente aceitá-los como sendo válidos: Observação: Todas as
Para mostrar que menos vezes menos dá mais precisamos admitir alguns fatos relacionados aos números reais. Vamos chamá-los de axiomas e simplesmente aceitá-los como sendo válidos: Observação: Todas as
Métodos para a construção de algoritmo
 Métodos para a construção de algoritmo Compreender o problema Identificar os dados de entrada e objetos desse cenário-problema Definir o processamento Identificar/definir os dados de saída Construir o
Métodos para a construção de algoritmo Compreender o problema Identificar os dados de entrada e objetos desse cenário-problema Definir o processamento Identificar/definir os dados de saída Construir o
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO Álgebra de Boole Disciplina: Lógica Professora Dr.ª: Donizete
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E DA TERRA BACHARELADO EM SISTEMAS DE INFORMAÇÃO Álgebra de Boole Disciplina: Lógica Professora Dr.ª: Donizete
Unidade II. A notação de que a proposição P (p, q, r,...) implica a proposição Q (p, q, r,...) por:
 LÓGICA Objetivos Apresentar regras e estruturas adicionais sobre o uso de proposições. Conceituar implicação lógica, tautologias, e as propriedade sobre proposições. Apresentar os fundamentos da dedução,
LÓGICA Objetivos Apresentar regras e estruturas adicionais sobre o uso de proposições. Conceituar implicação lógica, tautologias, e as propriedade sobre proposições. Apresentar os fundamentos da dedução,
Computação e Programação
 Computação e Programação 1ª Aula de 2008-2009 Instituto Superior Técnico, Dep. de Engenharia Mecânica - Sistemas O Visual C++ Para Casa (se possível antes da aula!): Veja o video e o screencast que se
Computação e Programação 1ª Aula de 2008-2009 Instituto Superior Técnico, Dep. de Engenharia Mecânica - Sistemas O Visual C++ Para Casa (se possível antes da aula!): Veja o video e o screencast que se
Lógica Computacional
 Aula Teórica 2: Sintaxe da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática,
Aula Teórica 2: Sintaxe da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática,
Proposições. Belo Horizonte é uma cidade do sul do Brasil = 4. A Terra gira em torno de si mesma. 5 < 3
 Proposições Lógicas Proposições O principal conceito usado nos estudos da lógica matemática é o de uma proposição. Uma proposição é essencialmente uma afirmação, transmite pensamentos completos, afirmando
Proposições Lógicas Proposições O principal conceito usado nos estudos da lógica matemática é o de uma proposição. Uma proposição é essencialmente uma afirmação, transmite pensamentos completos, afirmando
MATEMÁTICA I. Ana Paula Figueiredo
 I Ana Paula Figueiredo Números Reais IR O conjunto dos números Irracionais reunido com o conjunto dos números Racionais (Q), formam o conjunto dos números Reais (IR ). Assim, os principais conjuntos numéricos
I Ana Paula Figueiredo Números Reais IR O conjunto dos números Irracionais reunido com o conjunto dos números Racionais (Q), formam o conjunto dos números Reais (IR ). Assim, os principais conjuntos numéricos
Reticulados e Álgebras de Boole
 Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Capítulo 3 Reticulados e Álgebras de Boole 3.1 Reticulados Recorde-se que uma relação de ordem parcial num conjunto X é uma relação reflexiva, anti-simétrica e transitiva em X. Um conjunto parcialmente
Fundamentos 1. Lógica de Predicados
 Fundamentos 1 Lógica de Predicados Predicados e Quantificadores Estudamos até agora a lógica proposicional Predicados e Quantificadores Estudamos até agora a lógica proposicional A lógica proposicional
Fundamentos 1 Lógica de Predicados Predicados e Quantificadores Estudamos até agora a lógica proposicional Predicados e Quantificadores Estudamos até agora a lógica proposicional A lógica proposicional
ENFOQUE USANDO CORTES DE DEDEKIND
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação eletrônica do KIT http://www.dma.uem.br/kit CONSTRUÇÃO DOS REAIS: UM ENFOQUE
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência c Publicação eletrônica do KIT http://www.dma.uem.br/kit CONSTRUÇÃO DOS REAIS: UM ENFOQUE
Lógica Computacional DCC/FCUP 2017/18
 2017/18 Raciocínios 1 Se o André adormecer e alguém o acordar, ele diz palavrões 2 O André adormeceu 3 Não disse palavrões 4 Ninguém o acordou Será um raciocínio válido? Raciocínios Forma geral do raciocínio
2017/18 Raciocínios 1 Se o André adormecer e alguém o acordar, ele diz palavrões 2 O André adormeceu 3 Não disse palavrões 4 Ninguém o acordou Será um raciocínio válido? Raciocínios Forma geral do raciocínio
Capítulo 1. Os Números. 1.1 Notação. 1.2 Números naturais não nulos (inteiros positivos) Última atualização em setembro de 2017 por Sadao Massago
 Capítulo 1 Os Números Última atualização em setembro de 2017 por Sadao Massago 1.1 Notação Números naturais: Neste texto, N = {0, 1, 2, 3,...} e N + = {1, 2, 3, }. Mas existem vários autores considerando
Capítulo 1 Os Números Última atualização em setembro de 2017 por Sadao Massago 1.1 Notação Números naturais: Neste texto, N = {0, 1, 2, 3,...} e N + = {1, 2, 3, }. Mas existem vários autores considerando
Lógica e Matemática Discreta
 Lógica e Matemática Discreta Teoria Elementar dos Conjuntos Prof Clezio 04 de Junho de 2010 Curso de Ciência da Computação Noções básicas Um conjunto designa-se geralmente por uma letra latina maiúscula:
Lógica e Matemática Discreta Teoria Elementar dos Conjuntos Prof Clezio 04 de Junho de 2010 Curso de Ciência da Computação Noções básicas Um conjunto designa-se geralmente por uma letra latina maiúscula:
Uma proposição é uma frase que pode ser apenas verdadeira ou falsa. Exemplos:
 1 Noções Básicas de Lógica 1.1 Proposições Uma proposição é uma frase que pode ser apenas verdadeira ou falsa. 1. Os sapos são anfíbios. 2. A capital do Brasil é Porto Alegre. 3. O tomate é um tubérculo.
1 Noções Básicas de Lógica 1.1 Proposições Uma proposição é uma frase que pode ser apenas verdadeira ou falsa. 1. Os sapos são anfíbios. 2. A capital do Brasil é Porto Alegre. 3. O tomate é um tubérculo.
Arquitetura e Organização de Computadores. Álgebra Booleana
 Arquitetura e Organização de Computadores Álgebra Booleana 1 Histórico e Propriedades Formalizada por George Boole em 1854 Usada por Shannon em 1938 para provar propriedades de circuitos de chaveamento
Arquitetura e Organização de Computadores Álgebra Booleana 1 Histórico e Propriedades Formalizada por George Boole em 1854 Usada por Shannon em 1938 para provar propriedades de circuitos de chaveamento
Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 42
 1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
Prof. Leonardo Augusto Casillo
 UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 1 Sistemas de numeração posicional Aula 2 Modificadores e conectores lógicos Prof. Leonardo Augusto Casillo OBJETIVOS DO CURSO
UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 1 Sistemas de numeração posicional Aula 2 Modificadores e conectores lógicos Prof. Leonardo Augusto Casillo OBJETIVOS DO CURSO
PCS 3115 (PCS2215) Sistemas Digitais I. Módulo 05 Álgebra Booleana. Prof. Dr. Edison Spina. Sobre o material do Prof. Dr. Marcos A. Simplicio Jr.
 PCS 35 (PCS225) Sistemas Digitais I Módulo 5 Álgebra Booleana Prof. Dr. Edison Sobre o material do Prof. Dr. Marcos A. Simplicio Jr. versão: 5 (Mar/28) Conceitos básicos Conteúdo Teoremas de variável Teoremas
PCS 35 (PCS225) Sistemas Digitais I Módulo 5 Álgebra Booleana Prof. Dr. Edison Sobre o material do Prof. Dr. Marcos A. Simplicio Jr. versão: 5 (Mar/28) Conceitos básicos Conteúdo Teoremas de variável Teoremas
Lógica Matemática UNIDADE II. Professora: M. Sc. Juciara do Nascimento César
 Lógica Matemática UNIDADE II Professora: M. Sc. Juciara do Nascimento César 1 1 - Álgebra das Proposições 1.1 Propriedade da Conjunção Sejam p, q e r proposições simples quaisquer e sejam t e c proposições
Lógica Matemática UNIDADE II Professora: M. Sc. Juciara do Nascimento César 1 1 - Álgebra das Proposições 1.1 Propriedade da Conjunção Sejam p, q e r proposições simples quaisquer e sejam t e c proposições
n. 3 Construção de Tabelas-Verdade
 n. 3 Construção de Tabelas-Verdade Dadas várias proposições simples: p, q, r, s,..., podemos combiná-las pelos conectivos lógicos: Negação (~) ou ( ) Conjunção ( ) Disjunção ( ) Condicional ( ) Bicondicional
n. 3 Construção de Tabelas-Verdade Dadas várias proposições simples: p, q, r, s,..., podemos combiná-las pelos conectivos lógicos: Negação (~) ou ( ) Conjunção ( ) Disjunção ( ) Condicional ( ) Bicondicional
Aula 1 Aula 2. Ana Carolina Boero. Página:
 Elementos de lógica e linguagem matemática E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Linguagem matemática A linguagem matemática
Elementos de lógica e linguagem matemática E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Linguagem matemática A linguagem matemática
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA:
 DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (10º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (18 de setembro a 17 de dezembro) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
DEPARTAMENTO DE MATEMÁTICA E INFORMÁTICA DISCIPLINA: Matemática A (10º Ano) METAS CURRICULARES/CONTEÚDOS... 1º Período (18 de setembro a 17 de dezembro) Metas/ Objetivos Conceitos/ Conteúdos Aulas Previstas
MATEMÁTICA Questões comentadas Daniela Arboite
 MATEMÁTICA Questões comentadas Daniela Arboite TODOS OS DIREITOS RESERVADOS. É vedada a reprodução total ou parcial deste material, por qualquer meio ou processo. A violação de direitos autorais é punível
MATEMÁTICA Questões comentadas Daniela Arboite TODOS OS DIREITOS RESERVADOS. É vedada a reprodução total ou parcial deste material, por qualquer meio ou processo. A violação de direitos autorais é punível
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Introdução à Computação: Álgebra Booleana
 Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza (bfmartins@inf.ufes.br) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Introdução à Computação: Álgebra Booleana Beatriz F. M. Souza (bfmartins@inf.ufes.br) http://inf.ufes.br/~bfmartins/ Computer Science Department Federal University of Espírito Santo (Ufes), Vitória, ES
Matemática discreta e Lógica Matemática
 AULA 2 - Proposicionais Prof. Dr. Hércules A. Oliveira UTFPR - Universidade Tecnológica Federal do Paraná, Ponta Grossa Departamento Acadêmico de Matemática Lógicas Proposições compostas - Definição 1
AULA 2 - Proposicionais Prof. Dr. Hércules A. Oliveira UTFPR - Universidade Tecnológica Federal do Paraná, Ponta Grossa Departamento Acadêmico de Matemática Lógicas Proposições compostas - Definição 1
A = B, isto é, todo elemento de A é também um elemento de B e todo elemento de B é também um elemento de A, ou usando o item anterior, A B e B A.
 Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
Teoria Ingênua dos Conjuntos (naive set theory)
 Teoria Ingênua dos Conjuntos (naive set theory) MAT 131-2018 II Pouya Mehdipour 5 de outubro de 2018 Pouya Mehdipour 5 de outubro de 2018 1 / 22 Referências ALENCAR FILHO, E. Iniciação à Lógica Matemática,
Teoria Ingênua dos Conjuntos (naive set theory) MAT 131-2018 II Pouya Mehdipour 5 de outubro de 2018 Pouya Mehdipour 5 de outubro de 2018 1 / 22 Referências ALENCAR FILHO, E. Iniciação à Lógica Matemática,
Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c.
 Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Divisores Definição. Diremos que um número inteiro d é um divisor de outro inteiro a, se a é múltiplo de d; ou seja, se a = d c, para algum inteiro c. Quando a é múltiplo de d dizemos também que a é divisível
Gestão Empresarial Prof. Ânderson Vieira
 NOÇÕES DE LÓGICA Gestão Empresarial Prof. Ânderson ieira A maioria do texto apresentado neste arquivo é do livro Fundamentos de Matemática Elementar, ol. 1, Gelson Iezzi e Carlos Murakami (eja [1]). Algumas
NOÇÕES DE LÓGICA Gestão Empresarial Prof. Ânderson ieira A maioria do texto apresentado neste arquivo é do livro Fundamentos de Matemática Elementar, ol. 1, Gelson Iezzi e Carlos Murakami (eja [1]). Algumas
Lógica Matemática. Prof. Gerson Pastre de Oliveira
 Lógica Matemática Prof. Gerson Pastre de Oliveira Programa da Disciplina Proposições e conectivos lógicos; Tabelas-verdade; Tautologias, contradições e contingências; Implicação lógica e equivalência lógica;
Lógica Matemática Prof. Gerson Pastre de Oliveira Programa da Disciplina Proposições e conectivos lógicos; Tabelas-verdade; Tautologias, contradições e contingências; Implicação lógica e equivalência lógica;
Aula 4: Álgebra booleana
 Aula 4: Álgebra booleana Circuitos Digitais Rodrigo Hausen CMCC UFABC 01 de fevereiro de 2013 http://compscinet.org/circuitos Rodrigo Hausen (CMCC UFABC) Aula 4: Álgebra booleana 01 de fevereiro de 2013
Aula 4: Álgebra booleana Circuitos Digitais Rodrigo Hausen CMCC UFABC 01 de fevereiro de 2013 http://compscinet.org/circuitos Rodrigo Hausen (CMCC UFABC) Aula 4: Álgebra booleana 01 de fevereiro de 2013
Notas de aulas. álgebra abstrata
 1 Notas de aulas de álgebra abstrata UEMA LICENCIATURA EM MATEMATICA Elaborada por : Raimundo Merval Morais Gonçalves Licenciado em Matemática/UFMA Professor Assistente/UEMA Especialista em Ensino de Ciências/UEMA
1 Notas de aulas de álgebra abstrata UEMA LICENCIATURA EM MATEMATICA Elaborada por : Raimundo Merval Morais Gonçalves Licenciado em Matemática/UFMA Professor Assistente/UEMA Especialista em Ensino de Ciências/UEMA
MA14 - Aritmética Unidade 3. Divisão nos Inteiros (Divisibilidade)
 MA14 - Aritmética Unidade 3 Divisão nos Inteiros (Divisibilidade) Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 3 Divisão nos Inteiros (Divisibilidade) Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Lóg L ica M ca at M em e ática PROF.. J EAN 1
 Lógica Matemática PRO. JEAN 1 LÓGICA MATEMÁTICA - CONTEÚDO Definição de Termo e Proposição alor Lógico Proposição Simples e Proposição Composta Conectivos Tabela-erdade 2 LÓGICA MATEMÁTICA INTRODUÇÃO ao
Lógica Matemática PRO. JEAN 1 LÓGICA MATEMÁTICA - CONTEÚDO Definição de Termo e Proposição alor Lógico Proposição Simples e Proposição Composta Conectivos Tabela-erdade 2 LÓGICA MATEMÁTICA INTRODUÇÃO ao
Exercícios e Respostas Lógica Matemática Prof. Jacson Rodrigues
 Exercícios e Respostas Lógica Matemática Prof. Jacson Rodrigues As respostas encontram-se em itálico. 1. Quais das frases a seguir são sentenças? a. A lua é feita de queijo verde. erdadeira, pois é uma
Exercícios e Respostas Lógica Matemática Prof. Jacson Rodrigues As respostas encontram-se em itálico. 1. Quais das frases a seguir são sentenças? a. A lua é feita de queijo verde. erdadeira, pois é uma
Lógica Computacional
 Aula Teórica 2: da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática, Faculdade
Aula Teórica 2: da Lógica Proposicional António Ravara Simão Melo de Sousa Departamento de Informática, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa Departamento de Informática, Faculdade
Matemática Discreta. Fundamentos e Conceitos da Teoria dos Números. Universidade do Estado de Mato Grosso. 4 de setembro de 2017
 Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Prof. Leonardo Augusto Casillo
 UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 6 Álgebra de Boole Prof. Leonardo Augusto Casillo Álgebra de Boole (ou Boleana) Desenvolvida pelo matemático britânico George
UNIVERSIDADE FEDERAL RURAL DO SEMI-ÁRIDO CURSO: CIÊNCIA DA COMPUTAÇÃO Aula 6 Álgebra de Boole Prof. Leonardo Augusto Casillo Álgebra de Boole (ou Boleana) Desenvolvida pelo matemático britânico George
Atenção: Esse conectivo transmite a ideia de e / ou e não apenas a de exclusão como muitas pessoas imaginam.
 CONCEITO DE PROPOSIÇÃO É todo conjunto de palavras ou símbolos que exprimem uma ideia de sentido completo e que, além disso, pode ser julgado como verdadeiro (V) ou falso (F). NÃO SÃO PROPOSIÇÕES Frases
CONCEITO DE PROPOSIÇÃO É todo conjunto de palavras ou símbolos que exprimem uma ideia de sentido completo e que, além disso, pode ser julgado como verdadeiro (V) ou falso (F). NÃO SÃO PROPOSIÇÕES Frases
Demonstrações. Terminologia Métodos
 Demonstrações Terminologia Métodos Técnicas de Demonstração Uma demonstração é um argumento válido que estabelece a verdade de uma sentença matemática. Técnicas de Demonstração Demonstrações servem para:
Demonstrações Terminologia Métodos Técnicas de Demonstração Uma demonstração é um argumento válido que estabelece a verdade de uma sentença matemática. Técnicas de Demonstração Demonstrações servem para:
ÁLGEBRA LINEAR. Subespaços Vetoriais. Prof. Susie C. Keller
 ÁLGEBRA LINEAR Subespaços Vetoriais Prof. Susie C. Keller Às vezes, é necessário detectar, dentro de um espaço vetorial V, subconjuntos S que sejam espaços vetoriais menores. Tais conjuntos S são chamados
ÁLGEBRA LINEAR Subespaços Vetoriais Prof. Susie C. Keller Às vezes, é necessário detectar, dentro de um espaço vetorial V, subconjuntos S que sejam espaços vetoriais menores. Tais conjuntos S são chamados
Bases Matemáticas. Aula 1 Elementos de Lógica e Linguagem Matemática. Prof. Rodrigo Hausen. 24 de junho de 2014
 Aula 1 Elementos de Lógica e Linguagem Matemática Prof. Rodrigo Hausen 24 de junho de 2014 Definição Uma proposição é uma sentença declarativa que é verdadeira ou falsa, mas não simultaneamente ambas.
Aula 1 Elementos de Lógica e Linguagem Matemática Prof. Rodrigo Hausen 24 de junho de 2014 Definição Uma proposição é uma sentença declarativa que é verdadeira ou falsa, mas não simultaneamente ambas.
Professor conteudista: Ricardo Holderegger
 Lógica Professor conteudista: Ricardo Holderegger Sumário Lógica Unidade I 1 SISTEMAS DICOTÔMICOS...3 1.1 Proposições...3 1.1.1 Proposições lógicas...3 1.1.2 Símbolos da lógica matemática...4 1.1.3 A negação...4
Lógica Professor conteudista: Ricardo Holderegger Sumário Lógica Unidade I 1 SISTEMAS DICOTÔMICOS...3 1.1 Proposições...3 1.1.1 Proposições lógicas...3 1.1.2 Símbolos da lógica matemática...4 1.1.3 A negação...4
SMA Elementos de Matemática Notas de Aulas
 Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação SMA 341 - Elementos de Matemática Notas de Aulas Ires Dias Sandra Maria Semensato de Godoy São Carlos 2009 Sumário 1 Noções
Universidade de São Paulo Instituto de Ciências Matemáticas e de Computação SMA 341 - Elementos de Matemática Notas de Aulas Ires Dias Sandra Maria Semensato de Godoy São Carlos 2009 Sumário 1 Noções
Aula 1 Aula 2 Aula 3. Ana Carolina Boero. Página:
 Elementos de lógica e linguagem matemática E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Linguagem matemática A linguagem matemática
Elementos de lógica e linguagem matemática E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Linguagem matemática A linguagem matemática
Teste de Matemática A 2015 / 2016
 Teste de Matemática A 2015 / 2016 Teste N.º 2 Matemática A Duração do Teste: 90 minutos 10.º Ano de Escolaridade Nome do aluno: Turma: Grupo I Os cinco itens deste grupo são de escolha múltipla. Em cada
Teste de Matemática A 2015 / 2016 Teste N.º 2 Matemática A Duração do Teste: 90 minutos 10.º Ano de Escolaridade Nome do aluno: Turma: Grupo I Os cinco itens deste grupo são de escolha múltipla. Em cada
DIVISÃO NOS INTEIROS. Luciana Santos da Silva Martino. lulismartino.wordpress.com PROFMAT - Colégio Pedro II
 Sumário DIVISÃO NOS INTEIROS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 18 de agosto de 2017 Sumário 1 Divisibilidade 2 Divisão Euclidiana
Sumário DIVISÃO NOS INTEIROS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 18 de agosto de 2017 Sumário 1 Divisibilidade 2 Divisão Euclidiana
Abaixo descreveremos 6 portas lógicas: AND, OR, NOT, NAND, NOR e XOR.
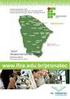 9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
9. Apêndice - Portas e Operações Lógicas Uma porta lógica é um circuito eletrônico (hardware) que se constitui no elemento básico de um sistema de computação. A CPU, as memórias, as interfaces de E/S são
Números Reais. Víctor Arturo Martínez León b + c ad + bc. b c
 Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
Números Reais Víctor Arturo Martínez León (victor.leon@unila.edu.br) 1 Os números racionais Os números racionais são os números da forma a, sendo a e b inteiros e b 0; o conjunto b dos números racionais
CM Funções. Notas de Aula PSE Departamento de Matemática - UFPR
 1. CM 128 - Funções Notas de Aula PSE 2017 Departamento de Matemática - UFPR Sumário 1 Conjuntos 4 1.1 Aula 1 - Operações entre conjuntos................................... 4 1.1.1 Conjuntos.............................................
1. CM 128 - Funções Notas de Aula PSE 2017 Departamento de Matemática - UFPR Sumário 1 Conjuntos 4 1.1 Aula 1 - Operações entre conjuntos................................... 4 1.1.1 Conjuntos.............................................
aula 01 (Lógica) Ementa Professor: Renê Furtado Felix Site:
 aula 01 (Lógica) Ementa Professor: Renê Furtado Felix E-mail: rffelix70@yahoo.com.br Site: http://www.renecomputer.net/pdflog.html Plano de Ensino CURSO: Tecnologia em Análise e Desenvolvimento de Sistemas
aula 01 (Lógica) Ementa Professor: Renê Furtado Felix E-mail: rffelix70@yahoo.com.br Site: http://www.renecomputer.net/pdflog.html Plano de Ensino CURSO: Tecnologia em Análise e Desenvolvimento de Sistemas
MATEMÁTICA MÓDULO 1 TEORIA DOS NÚMEROS 1. DIVISIBILIDADE 1.1. DEFINIÇÃO 1.2. CRITÉRIOS DE DIVISIBILIDADE
 TEORIA DOS NÚMEROS 1. DIVISIBILIDADE Neste momento inicial, nosso interesse será em determinar quando a divisão entre dois números inteiros é exata, ou seja, quando o resto da divisão é 0. Antes de mais
TEORIA DOS NÚMEROS 1. DIVISIBILIDADE Neste momento inicial, nosso interesse será em determinar quando a divisão entre dois números inteiros é exata, ou seja, quando o resto da divisão é 0. Antes de mais
Teoria da Computação
 Introdução Março - 2009 1 Noções e Terminologia Matemática Conjuntos Um conjunto é um grupo de objetos, chamados elementos ou membros, representado como uma unidade. O conjunto { 3, 41, 57} possui os elementos
Introdução Março - 2009 1 Noções e Terminologia Matemática Conjuntos Um conjunto é um grupo de objetos, chamados elementos ou membros, representado como uma unidade. O conjunto { 3, 41, 57} possui os elementos
Lógica Computacional
 Aula Teórica 2: da Lógica Proposicional Departamento de Informática 17 de Fevereiro de 2011 Descrição informal Lógica proposicional Objecto Ocupa-se do estudo do comportamento dos conectivos lógicos (negação,
Aula Teórica 2: da Lógica Proposicional Departamento de Informática 17 de Fevereiro de 2011 Descrição informal Lógica proposicional Objecto Ocupa-se do estudo do comportamento dos conectivos lógicos (negação,
MDI0001 Matemática Discreta Aula 01
 MDI0001 Matemática Discreta Aula 01 e Karina Girardi Roggia karina.roggia@udesc.br Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa Catarina 2016 Karina
MDI0001 Matemática Discreta Aula 01 e Karina Girardi Roggia karina.roggia@udesc.br Departamento de Ciência da Computação Centro de Ciências Tecnológicas Universidade do Estado de Santa Catarina 2016 Karina
Espaços quase topológicos: o caso em que cada conjunto fechado é também aberto. Introdução. Hércules de A. Feitosa, Mauri C.
 Espaços quase topológicos: o caso em que cada conjunto fechado é também aberto Hércules de A. Feitosa, Mauri C. do Nascimento, Departamento de Matemática, FC, UNESP, 17033-360, Bauru, SP E-mail: haf@fc.unesp.br,
Espaços quase topológicos: o caso em que cada conjunto fechado é também aberto Hércules de A. Feitosa, Mauri C. do Nascimento, Departamento de Matemática, FC, UNESP, 17033-360, Bauru, SP E-mail: haf@fc.unesp.br,
Elementos de Matemática
 Elementos de Matemática Roteiro no.1 para as atividades didáticas de 2007 Versão compilada no dia 27 de Abril de 2007. Departamento de Matemática - UEL Prof. Ulysses Sodré E-mail: ulysses@matematica.uel.br
Elementos de Matemática Roteiro no.1 para as atividades didáticas de 2007 Versão compilada no dia 27 de Abril de 2007. Departamento de Matemática - UEL Prof. Ulysses Sodré E-mail: ulysses@matematica.uel.br
Operações Lógicas sobre Proposições
 Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Operações Lógicas sobre Proposições Lógica Computacional 1 Site: http://jeiks.net E-mail: jacsonrcsilva@gmail.com
Universidade Federal do Espírito Santo Centro de Ciências Agrárias CCA UFES Departamento de Computação Operações Lógicas sobre Proposições Lógica Computacional 1 Site: http://jeiks.net E-mail: jacsonrcsilva@gmail.com
Dado um inteiro positivo n, definimos U(n) como sendo o conjunto dos inteiros positivos menores que n e primos com n. Não é difícil ver que a
 Exemplo (U(n)) Dado um inteiro positivo n, definimos U(n) como sendo o conjunto dos inteiros positivos menores que n e primos com n. Não é difícil ver que a multiplicação módulo n é uma operação binária
Exemplo (U(n)) Dado um inteiro positivo n, definimos U(n) como sendo o conjunto dos inteiros positivos menores que n e primos com n. Não é difícil ver que a multiplicação módulo n é uma operação binária
MAT Álgebra I para Licenciatura 2 a Lista de exercícios
 MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
Universidade Federal de Viçosa Departamento de Matemática III LISTA DE MAT INTRODUÇÃO À ÁLGEBRA
 Universidade Federal de Viçosa Departamento de Matemática III LISTA DE MAT 131 - INTRODUÇÃO À ÁLGEBRA 1. Seja A = {1, 3, 5, 7, 11}. Verifique quais das seguintes proposições são verdadeiras ou falsas.
Universidade Federal de Viçosa Departamento de Matemática III LISTA DE MAT 131 - INTRODUÇÃO À ÁLGEBRA 1. Seja A = {1, 3, 5, 7, 11}. Verifique quais das seguintes proposições são verdadeiras ou falsas.
Ficha 1 (permanente)
 Ficha 1 (permanente) Disciplina: Complementos de Matemática Código: CM100 Natureza: ( x ) Obrigatória ( ) Optativa ( x ) Semestral ( ) Anual ( ) Modular Pré-requisito: Não há Co-requisito: - Modalidade:
Ficha 1 (permanente) Disciplina: Complementos de Matemática Código: CM100 Natureza: ( x ) Obrigatória ( ) Optativa ( x ) Semestral ( ) Anual ( ) Modular Pré-requisito: Não há Co-requisito: - Modalidade:
ÁLGEBRA. AULA 1 _ Conjuntos Professor Luciano Nóbrega. Maria Auxiliadora
 1 ÁLGEBRA AULA 1 _ Conjuntos Professor Luciano Nóbrega Maria Auxiliadora 2 Pode-se dizer que a é, em grande parte, trabalho de um único matemático: Georg Cantor (1845-1918). A noção de conjunto não é suscetível
1 ÁLGEBRA AULA 1 _ Conjuntos Professor Luciano Nóbrega Maria Auxiliadora 2 Pode-se dizer que a é, em grande parte, trabalho de um único matemático: Georg Cantor (1845-1918). A noção de conjunto não é suscetível
Para Computação. Aula de Monitoria - Miniprova
 Para Computação Aula de Monitoria - Miniprova 1 2013.1 Roteiro Provas e Proposições Conjuntos Provas e Proposições Proposição - Sentença que ou é verdadeira ou é falsa. ex: Hoje é sábado. -> É uma proposição.
Para Computação Aula de Monitoria - Miniprova 1 2013.1 Roteiro Provas e Proposições Conjuntos Provas e Proposições Proposição - Sentença que ou é verdadeira ou é falsa. ex: Hoje é sábado. -> É uma proposição.
