Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA
|
|
|
- Armando Fartaria Brunelli
- 7 Há anos
- Visualizações:
Transcrição
1 Matemática 9.º ano PROBABILIDADES + ESTATÍSTICA 01. Num saco estão 10 bolas indistinguíveis ao tato, das quais 6 são azuis e 4 são verdes. Retiram-se, sucessivamente e sem reposição duas bolas. Determine a probabilidade de saírem duas bolas da mesma cor. Campo Amostral será 10 bolas, total. Para saírem 2 bolas da mesma cor, estas podem ser ambas azuis ou ambas verdes. A probabilidade de tirar ambas azuis é. A probabilidade de tirar ambas verdes é de. Logo, a probabilidade pedida é de: 02. Uma equipa de futebol é composta por 5 jogadores portugueses, 3 brasileiros, 2 angolanos e 1 espanhol. Escolhido um jogador ao acaso a probabilidade de ser: a) português é 5. b) europeu é 0,54 c) espanhol é 1% d) angolano é 0,5. Campo Amostral será: 11 jogadores, total. Como 5 portugueses e 1 espanhol são europeus. Então: P = E/A >>>> P = 6/11 >>> P = 0, Numa turma de 28 alunos, 9 só praticam natação, 12 praticam apenas futebol e os restantes praticam as duas modalidades. Escolhido um aluno ao acaso, a probabilidade de: a) praticar natação é 4/7. b) praticar natação é 9/28. c) praticar futebol é 12/28. d) não praticar natação é 19/28. as duas modalidades : = = 7 natação : = 16 probabilidade : p = 16/28 = 4/7 04. Num saco estão bolas azuis e vermelhas, num total de 50 bolas. Sabendo que a probabilidade de tirar bola azul é 0,34 podemos concluir que o número de bolas vermelhas é: a) 33. b) 16. c) 25. d) 17. Vamos chamar de a o número de bolas azuis e v a quantidade de bolas vermelhas nesse saco. Como há 50 bolas no total, temos: a + v = 50. Além disso, sabemos que, a probabilidade de tirar uma bola azul é 0,34. Como há a bolas azuis entre 50, podemos afirmar que,. Daí, concluímos que,. Lembrando que, temos, donde. Logo, a quantidade de bolas vermelhas nesse saco é.
2 05. Num frasco temos 17 rebuçados de limão, 5 de laranja e 10 de mentol. Retiram-se, sucessivamente e sem reposição 3 rebuçados. Sabendo que os dois primeiros são de limão, escolhe a opção correta: a) a probabilidade do terceiro ser de laranja é 5/32. b) a probabilidade do terceiro ser de limão é 17/30. c) a probabilidade do terceiro ser de laranja é 3/30. d) a probabilidade do terceiro ser de limão é 1/2. Tirando os 2 primeiros rebuçados que são limão, fica apenas 15 de limão. Somando os outros tem 30 rebuçados no total, e se ainda falta um rebuçado para tirar, vai ser 1 em 30, ou seja, e pelas alternativas, o único certo é o limão, pois ele das 30 chances, ocupa 15, ou seja, meio:1/2 05. Perguntou-se a 200 pessoas se viam telenovelas. Os resultados foram registados na tabela: Escolhida uma pessoa ao acaso: a) P ( " ser homem " ) = 80 b) P ( " ser mulher ou ver telenovelas " ) = 17/20 c) P ( " não ser mulher " ) = 60% d) P ( " não ser mulher nem ver telenovelas " ) = 2/5 200 pessoas % 120 mulheres X % X = / 200 X = 60 % 06. Numa algibeira estão guardadas 2 moedas de 20 cêntimos e duas moedas de 50 cêntimos. Tira-se uma moeda ao acaso, e em seguida, tira-se uma segunda moeda sem ter reposto a primeira. Podemos afirmar que: a) A probabilidade de as duas moedas serem de 20 cêntimos é 1/6. b) A probabilidade de terem valores diferentes é 4/15. c) A probabilidade de ambas serem de 50 cêntimos é 1/15. d) A probabilidade de ambas serem de 20 cêntimos é 1/3. Analisando as combinações Homem e Mulheres, teremos. 20 cêntimos: = 2 12 = 1 6 e 50 cêntimos: = 2 12 = 1 6 Logo: = 2 6 = Um casal está a pensar ter 3 filhos. Supondo que a probabilidade de nascer rapaz é igual à probabilidade de nascer rapariga, podemos afirmar que: a) a probabilidade de os três serem rapazes é 1/2. b) a probabilidade de serem dois rapazes e uma rapariga é 30% c) a probabilidade dos dois mais velhos serem do mesmo sexo é 1/4. d) a probabilidade de não serem todos do mesmo sexo é 3/4. Analisando as combinações Homem e Mulheres, teremos. HHH HHM HMH MHH Logo: P = 2/8 >>> P = 1/4 MMH MHM Não poderia ser: HHH ou MMM pois o terceiro teria mesmo sexo. MMM HMM
3 08. A turma T de uma certa escola tem vinte e três alunos, com números em uma lista de 1 a 23. Em algumas aulas, os alunos estão divididos em dois turnos: os alunos com número ímpar pertencem ao primeiro turno e os restantes alunos pertencem ao segundo turno. Escolhe-se ao acaso, um aluno do primeiro turno. Qual a probabilidade de o aluno escolhido ter um número na lista superior a 17? a) 1/3 b) 1/4 c) 1/6 d) 1/7 Dados: 23 alunos 1º turno { 1,3,5,7,9,11,13,15,17,19,21,23} =12 alunos 2º turno = 11 alunos Superior a 17 do primeiro turno { 19,21,23} P= 3 Casos favoráveis / 12 casos possíveis P= 3/ 12 P= 1/4 09. Na primeira quinzena de março, hospedaram-se no hotel Paraiso 100 turistas: 40 portugueses e 60 estrangeiros. O gráfico seguinte apresenta a distribuição dos turistas estrangeiros, por nacionalidade. Escolhendo-se ao acaso, um dos 100 turistas hospedados no hotel Paraiso na primeira quinzena de março. Qual é a probabilidade de o turista escolhido ser francês? a) 16% b) 18% c) 22% d) 24% Como são 100 turistas no total = 40 portugueses + 60 estrangeiros, temos 60 estrangeiros para serem distribuídos no percentual, logo: 50 % espanhóis = 30 pessoas 30% dos estrangeiros franceses = 18 20% dos estrangeiros ingleses = 12 Daí os estrangeiros serão: 18% >>>> 18 de 100 é 18% 10. O João tem num saco, 9 bolas numeradas de 1 a 9. As bolas são indistinguíveis ao tato. O João retira ao acaso uma bola do saco. Qual a probabilidade de a bola retirada ter um número que admita exatamente dos divisores? a) 2/9 b) 3/9 c) 4/9 d) 5/9 Sabemos que números que tem apenas dois divisores, são chamados de números primos: ( 1; 2; 3; 4; 5; 6; 7; 8; 9 ) dos quais são primos: ( 2; 3; 5; 7 ) P = 4/7 11. Um certo conjunto de cartas de jogar é constituído de dozes cartas vermelhas e por algumas cartas pretas. Escolhese, ao acaso, uma carta desse baralho. Sabe-se que a probabilidade dessa carta ser vermelha é 75%. Quantas cartas pretas há neste baralho? a) 3 b) 4 c) 6 d) 9
4 Temos um total de 12(vermelhas) + X cartas pretas. Se a chance é de 75% ser vermelha então 12 que são as vermelhas sobre o total, que é: 12 + X = 0,75 12 / (12+x) = 0,75 0,75. (12+x) = 12 x = Uma certa turma de 9 o ano é constituída por rapazes e por moças. Nessa turma há 6 meninas. Sabendo que, escolhendo ao acaso um dos alunos da turma a probabilidade de esse aluno ser rapaz é de 2/3. Quantos rapazes há nessa turma? a) 6 b) 9 c) 12 d) Um tratador de animais de um jardim zoológico é responsável pela limpeza de três jaulas: a de um tigre, a de uma pantera e a de um leopardo. O tratador tem de lavar a jaula de cada um destes animais, uma vez por dia. De quantas maneiras diferentes pode o tratador realizar a sequência da lavagem das três jaulas? Assinala a opção correta. a) 2 b) 3 c) 4 d) Pediu-se a 210 pessoas, cada uma delas dona de um cão e de um gato, que respondessem a seguinte questão: Como classifica a relação entre o seu cão e o seu gato. Havia 3 opções de resposta: Boa; Indiferente e Agressiva. A tabela apresenta os totais de cada uma das opções de resposta. Escolhida ao acaso uma das pessoas entrevista, qual é a probabilidade de essa pessoa ter respondido que a relação entre o seu cão e o seu gato é boa? 15. A comissão organizadora de um arraial fez 250 rifas para um sorteio. Apenas uma dessas rifas é premiada. As rifas foram todas vendidas. A Alice comprou algumas rifas. Sabe-se que a probabilidade de a Alice ganhar o prêmio é 1/25. Quantas rifas comprou a Alice? a) 25 b) 10 c) 5 d) A Teresa tem três irmãs: Maria, Inês e Joana. A Teresa vai escolher, ao acaso, uma das irmãs para ir com ela a um arraial no máximo fim de semana. A Teresa vai escolher, também ao acaso, se vai ao arraial no próximo sábado ou no próximo domingo. Qual é a probabilidade de a Teresa escolher ir ao arraial no sábado com a Maria? a) 1/2 b) 1/3 c) 1/5 d) 1/6 17. A mãe, o pai e o filho mais velho da família Coelho ganharam três automóveis num concurso de TV: 1 carro cinza, um carro branco e um carro preto. Todos queriam o automóvel preto, por isso decidiram distribuir aleatoriamente os três automóveis. Qual a probabilidade de o automóvel preto não ser atribuído a mãe? a) 1/3 b) 2/3 c) 1/6 d) 5/6 18. O Scrabble é um jogo em que os jogadores têm de retirar, ao acaso, peças de dentro de um saco. Em cada peça está inscrita uma letra. Os jogadores usam essas letras para tentar construir palavras. Num determinado momento de um jogo de Scrabble ente o Martim e a Leonor estavam, dentro do saco 28 peças. Na tabela seguinte indica-se a frequência absoluta de cada letra. Retirando, ao acaso, uma peça do saco, qual dos seguintes valores é a probabilidade de sair uma vogal?
5 a) 2/7 b) 3/7 c) 4/7 d) 5/7 19. No clube desportivo Os Medalhados vai ser sorteado uma viagem aos próximos Jogos Olímpicos. As 90 rifas para o sorteio foram numeradas de 1 a 90 e foram todas vendidas. O João tem 14 anos. Qual é a probabilidade de a rifa premiada ter um número múltiplo da sua idade? a) 1/15 b) 2/15 c) 1/2 d) 1/ Numa Faculdade, realizou-se um estudo sobre o número de alunos da turma de Beatriz que já doaram sangue. O gráfico que se segue mostra o número de doadores de sangue, por sexos. Relativamente aos dados do gráfico, qual das seguintes afirmação é verdadeira? a) 30% dos alunos nunca doaram sangue. b) 30% dos alunos doaram sangue duas vezes. c) 65% dos alunos doaram sangue mais do que uma vez. d) 75% dos alunos doaram sangue menos do que duas vezes. 20. Numa escola com 1000 alunos, fez-se um estudo sobre o número de vezes que, em média, as meninas e os meninos da escola iam ao cinema por mês. Com os dados recolhidos contraíram a tabela que se segue: Qual dos gráficos que se seguem representa os dados da tabela? 21. Os alunos da turma da Marta combinaram de encontrar-se no Parque das Nações. Cada um deles utilizou um meio de transporte para chegar ao parque. Na tabela que se segue, pode observar os meios de transporte usados e o número de alunos que utilizou cada um deles.
6 Escolhendo, ao acaso, um aluno da turma da Marta, qual dos seguintes valores é o da probabilidade de esse aluno não ter ido de autocarro? a) 60% b) 70% c) 80% d) 90% 22. Na escola de Rita, fez-se um estudo sobre o gosto dos alunos pela leitura. Uma pesquisa realizada incluía a questão seguinte: Quantos livros lestes desde o início do ano letivo?. As respostas obtidas na turma da Rita, relativamente a esta pergunta, estão representadas no gráfico de barras que se segue. Escolhendo, ao acaso, um aluno da turma da Rita, qual dos seguintes acontecimentos é o mais provável? a) ter lido menos do que 1 livro. b) ter lido menos do que 2 livros. c) ter lido menos do que 3 livros. d) ter lido menos do que 4 livros. 23. Jogamos dois dados comuns. Qual a probabilidade de que o total de pontos seja igual a 10? a) 1/12 b) 1/11 c) 1/10 d) 2/23 e) 1/6 24. A probabilidade de um casal com quatro filhos ter dois do sexo masculino e dois do sexo feminino é: a) 60% b) 50% c) 45% d) 37,5% e) 25% 25. Dois jovens partiram, do acampamento em que estavam, em direção à Cachoeira Grande e à Cachoeira Pequena, localizadas na região, seguindo a trilha indicada neste esquema: Em cada bifurcação encontrada na trilha, eles escolhiam, com igual probabilidade, qualquer um dos caminhos e seguiam adiante. Então, é CORRETO afirmar que a probabilidade de eles chegarem à Cachoeira Pequena é: a) 1/2 b) 2/3 c) 3/4 d) 5/6 e) 1/6 26. Dois dados cúbicos, não viciados, com faces numeradas de 1 a 6, serão lançados simultaneamente. A probabilidade de que sejam sorteados dois números consecutivos, cuja soma seja um número primo, é de: a) 2/9 b) 1/3 c) 4/9 d) 5/9 e) 2/3 27. As cinco cartelas numeradas representadas a seguir foram colocadas numa caixa.
7 Se forem retiradas duas cartelas da caixa, simultaneamente e ao acaso, a probabilidade de que a soma dos valores das cartelas retiradas seja 5 ou 6 é: a) 1/5 b) 2/5 c) 3/5 d) 4/5 e) 5/6 28. No lançamento de uma moeda há 50% de chance de sair cara e outros 50% de chance de sair coroa. A chance de sair cara no lançamento de uma moeda é de: a) 1/5 b) 1/2 c) 50/10 d) 50/2 e) 2/ A população de uma pequena cidade do interior de Minas Gerais variou entre 1987 e 1996 segundo o gráfico a seguir. A população dessa cidade era de habitantes: a) Entre 1987 e 1990 b) Entre 1990 e 1993 c) Entre 1993 e 1996 d) Após Numa turma as notas a Matemática foram as seguintes: Ao escolher um aluno, ao acaso, qual a probabilidade da sua nota a Matemática ter sido 2? 31. Lança-se um dado não viciado. Qual é a probabilidade de: a) sair múltiplo de 3; b) sair um 7; c) não sair um 2; d) sair um número menor que 5; e) sair um número par; f) sair um Num saco estão 5 bolas iguais, duas pretas e três brancas. Qual a probabilidade de tirar (sem repor): a) uma bola branca; b) uma bola preta; c) três bolas pretas (3 extrações); d) uma bola branca ou preta. 33. Na lista de chamada de uma turma, os 30 alunos são numerados de 1 a 30. Em certo dia, quando faltaram os alunos de 11 e 26, o professor sorteou um aluno para resolver umas atividades no quadro. Qual é a probabilidade do número sorteado ser:
8 a) Par? b) Menor que 9? c) Múltiplo de 4? d) Primo? e) Maior que 12 e menor que 25? 34. Em uma escola estudam alunos de dois segmentos: no ensino médio são 400 meninos e 200 meninas, e no ensino fundamental são 400 meninas e 300 meninos. Ao sortear um aluno dessa escola, calcule a probabilidade de ser: a) Menino, sabendo que é aluno do ensino médio b) Aluno do ensino médio, sabendo que é menino 35. Um grupo de 1000 pessoas apresenta, conforme sexo e qualificação profissional, a composição: Escolhendo uma dessas pessoas ao acaso: a) Qual a probabilidade de ser homem? b) Qual a probabilidade de ser mulher não especialista? c) Qual porcentagem de não especializados? d) Qual a porcentagem de homens especializados? e) Se for especializado, qual a chance de ser mulher?
(D) 1 (A) 1 (C) 1 2 (B) 2
 20 No clube desportivo Os Medalhados vai ser sorteada uma viagem aos próximos Jogos Olímpicos. As 90 rifas para o sorteio foram numeradas de 1 a 90 e foram todas vendidas. 20.1. O João tem 14 anos. Qual
20 No clube desportivo Os Medalhados vai ser sorteada uma viagem aos próximos Jogos Olímpicos. As 90 rifas para o sorteio foram numeradas de 1 a 90 e foram todas vendidas. 20.1. O João tem 14 anos. Qual
1. Um saco contém várias bolas com o número 1, várias bolas com o número 2 e várias
 Questões Exame Probabilidades (U1) Matemática 9º Ano ANO LECTIVO 2012 / 2013 1. Um saco contém várias bolas com o número 1, várias bolas com o número 2 e várias bolas com o número 3. As bolas são indistinguíveis
Questões Exame Probabilidades (U1) Matemática 9º Ano ANO LECTIVO 2012 / 2013 1. Um saco contém várias bolas com o número 1, várias bolas com o número 2 e várias bolas com o número 3. As bolas são indistinguíveis
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano)
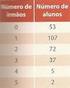
 MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Exercícios de provas nacionais e testes intermédios. A turma da Ana tem 9 alunos, distribuídos, por género e por idade, de acordo com a tabela seguinte. 5
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Exercícios de provas nacionais e testes intermédios. A turma da Ana tem 9 alunos, distribuídos, por género e por idade, de acordo com a tabela seguinte. 5
MÃES D ÁGUA AGRUPAMENTO DE ESCOLAS
 Direção Regional de Lisboa e Vale do Tejo MÃES D ÁGUA AGRUPAMENTO DE ESCOLAS Ficha 4 Probabilidades, Equações do 2º Grau e Sistemas de Equações (1ª) (Exercícios Retirados dos Testes Intermédios) Matemática
Direção Regional de Lisboa e Vale do Tejo MÃES D ÁGUA AGRUPAMENTO DE ESCOLAS Ficha 4 Probabilidades, Equações do 2º Grau e Sistemas de Equações (1ª) (Exercícios Retirados dos Testes Intermédios) Matemática
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano)
 MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Exercícios de provas nacionais e testes intermédios. Num saco, A, estão três bolas numeradas de a 3, indistinguíveis ao tato... Retira-se, ao acaso, uma bola
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Exercícios de provas nacionais e testes intermédios. Num saco, A, estão três bolas numeradas de a 3, indistinguíveis ao tato... Retira-se, ao acaso, uma bola
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Propostas de resolução
 MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
MATEMÁTICA A - 1o Ano Probabilidades - Noções gerais Propostas de resolução Exercícios de exames e testes intermédios 1. Organizando todos os resultados possíveis para os dois números possíveis de observar,
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Observando que o número de rapazes da turma da Ana é 3+8+2 = 13, e que existem
MATEMÁTICA - 3o ciclo Probabilidades (9 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Observando que o número de rapazes da turma da Ana é 3+8+2 = 13, e que existem
AGRUPAMENTO DE ESCOLAS DR. ANTÓNIO AUGUSTO LOURO ESCOLA DOS 2.º E 3.º CICLOS DR. ANTÓNIO AUGUSTO LOURO
 AGRUPAMENTO DE ESCOLAS DR. ANTÓNIO AUGUSTO LOURO ESCOLA DOS 2.º E 3.º CICLOS DR. ANTÓNIO AUGUSTO LOURO FICHA DE TRABALHO 2 REVISÕES PARA O 1º TESTE Ano Letivo 2014/2015 1. Considera as seguintes experiências
AGRUPAMENTO DE ESCOLAS DR. ANTÓNIO AUGUSTO LOURO ESCOLA DOS 2.º E 3.º CICLOS DR. ANTÓNIO AUGUSTO LOURO FICHA DE TRABALHO 2 REVISÕES PARA O 1º TESTE Ano Letivo 2014/2015 1. Considera as seguintes experiências
 Escola Básica de Ribeirão (Sede) ANO LETIVO 2012/201 Ficha de Trabalho dezembro 2012 Nome: N.º: Turma: Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Probabilidades
Escola Básica de Ribeirão (Sede) ANO LETIVO 2012/201 Ficha de Trabalho dezembro 2012 Nome: N.º: Turma: Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Probabilidades
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Uma pessoa lança um dado cúbico, com as faces numeradas de 1 a 6, e regista o número da face que ficou
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais
 MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
MATEMÁTICA A - 12o Ano Probabilidades - Noções gerais Exercícios de exames e testes intermédios 1. Considere um dado cúbico, com as faces numeradas de 1 a 6, e um saco que contém cinco bolas, indistinguíveis
Tema: Probabilidades e Estatística
 Escola Básica de Ribeirão (Sede) ANO LETIVO 2011/2012 Ficha de Trabalho Janeiro 2012 Nome: N.º: Turma: Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Probabilidades
Escola Básica de Ribeirão (Sede) ANO LETIVO 2011/2012 Ficha de Trabalho Janeiro 2012 Nome: N.º: Turma: Compilação de Exercícios de Exames Nacionais (EN) e de Testes Intermédios (TI) Tema: Probabilidades
LISTA 29 - PROBABILIDADE 1
 LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
LISTA 9 - PROBABILIDADE ) Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o próprio seria guardado na casa de um deles. Todos quiseram guardar a taça em suas
Chama-se evento todo subconjunto de um espaço amostral. PROBABILIDADE. Introdução
 Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
Introdução PROBABILIDADE Há certos fenômenos (ou experimentos) que, embora sejam repetidos muitas vezes e sob condições idênticas, não apresentam os mesmos resultados. Por exemplo, no lançamento de uma
c) 17 b) 4 17 e) 17 21
 Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
Probabilidade I Exercícios. Dois jogadores A e B vão lançar um par de dados. Eles combinam que se a soma dos números dos dados for 5, A ganha e se a soma for 8, B é quem ganha. Os dados são lançados. Sabe-se
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades
 Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
Bem Explicado Centro de Explicações Lda. Matemática 9º Ano Probabilidades Nome: Data: / / 1. Das seguintes experiências diz, justificando, quais são as aleatórias: 1.1. Deitar um berlinde num copo de água
MATEMÁTICA A - 12o Ano Probabilidades - Distribuições de probabilidades
 MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
MATEMÁTICA A - o Ano Probabilidades - Distribuições de probabilidades Exercícios de exames e testes intermédios. A tabela de distribuição de probabilidades de uma variável aleatória X é a seguinte. x i
Matemática. Probabilidade Básica. Professor Dudan.
 Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
Matemática Probabilidade Básica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROBABILIDADE Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan
 Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
Matéria: Matemática Assunto: Probabilidade básica Prof. Dudan Matemática Probabilidade Denifinição 0 P 1 Eventos favoráveis Probabilidade = Total de eventos 1. Se a probabilidade de chover num dia de
Teste de Avaliação de MATEMÁTICA 12º ano
 Teste de Avaliação de MATEMÁTICA º ano º Período de 0/ duração 90 min. Prof. Josué Baptista Turma: e º teste A 4 de Outubro Classificação: Nº Nome GRUPO I O Professor: As cinco questões deste grupo são
Teste de Avaliação de MATEMÁTICA º ano º Período de 0/ duração 90 min. Prof. Josué Baptista Turma: e º teste A 4 de Outubro Classificação: Nº Nome GRUPO I O Professor: As cinco questões deste grupo são
Escola Secundária/2,3 da Sé-Lamego Ficha de Trabalho de Matemática 04/10/2011 Estatística e probabilidades 9.º Ano
 Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática 04/0/0 Estatística e probabilidades 9.º Ano Nome: N.º: Turma:. Assinala a alternativa correta Para cada uma das questões seguintes, assinala
Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática 04/0/0 Estatística e probabilidades 9.º Ano Nome: N.º: Turma:. Assinala a alternativa correta Para cada uma das questões seguintes, assinala
PROBABILIDADE - INTRODUÇÃO
 E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
E.E. Dona Antônia Valadares MATEMÁTICA 1º ANO ANÁLISE COMBINATÓRIA PROBABILIDADE - INTRODUÇÃO PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net TEORIA DAS PROBABILIDADES A teoria
PROBABILIDADE PROPRIEDADES E AXIOMAS
 PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
PROBABILIDADE ESPAÇO AMOSTRAL É o conjunto de todos os possíveis resultados de um experimento aleatório. A este conjunto de elementos denominamos de espaço amostral ou conjunto universo, simbolizado por
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω o espaço amostral (espaço de resultados) associado a uma certa experiência
COLEÇÃO DARLAN MOUTINHO VOL. 01 RESOLUÇÕES
 COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
COLEÇÃO DARLAN MOUTINHO VOL. 0 RESOLUÇÕES Me ta PÁGINA 8 0 0 Havendo apenas bolas verdes e azuis na urna, segue que a resposta é dada por Basta dividirmos o número de ocorrências, pelo número total de
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística. Probabilidades
 Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
Universidade Estadual de Londrina Centro de Ciências Exatas Departamento de Estatística Probabilidades Aluna(o): Aluna(o): Turma: Responsável: Prof. Silvano Cesar da Costa L O N D R I N A Estado do Paraná
01 - (UEM PR) um resultado "cara sobre casa preta" é (MACK SP)
 ALUNO(A): Nº TURMA: 2º ANO PROF: Claudio Saldan CONTATO: saldan.mat@gmail.com LISTA DE EXERCÍCIOS PROBABILIDADE 0 - (UEM PR) Considere a situação ideal na qual uma moeda não-viciada, ao ser lançada sobre
ALUNO(A): Nº TURMA: 2º ANO PROF: Claudio Saldan CONTATO: saldan.mat@gmail.com LISTA DE EXERCÍCIOS PROBABILIDADE 0 - (UEM PR) Considere a situação ideal na qual uma moeda não-viciada, ao ser lançada sobre
Exercícios de exames e provas oficiais
 mata Exercícios de exames e provas oficiais. Seja Ω, o conjunto finito, o espaço de resultados associado a uma experiência aleatória. Sejam A e B dois acontecimentos ( A e B ). A e B são acontecimentos
mata Exercícios de exames e provas oficiais. Seja Ω, o conjunto finito, o espaço de resultados associado a uma experiência aleatória. Sejam A e B dois acontecimentos ( A e B ). A e B são acontecimentos
1. Num universo S os acontecimentos A e B são incompatíveis.
 12ºANO ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO Matemática B Probabilidades 2007/08 1. Num universo S os acontecimentos A e B são incompatíveis. Sabe-se que: P( B ) = 0,1 e que P( A B ) = 0,6. Determina P(
12ºANO ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO Matemática B Probabilidades 2007/08 1. Num universo S os acontecimentos A e B são incompatíveis. Sabe-se que: P( B ) = 0,1 e que P( A B ) = 0,6. Determina P(
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014
 AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014 1. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Ficha de Trabalho nº4 - Probabilidades - 12º ano Exames de 2011 a 2014 1. Seja o espaço de resultados associado a uma certa experiência aleatória. Sejam A e B dois acontecimentos
PROBABILIDADE. c) 1/4 d) 1/12 e) nda MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS
 MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
MATQUEST PROBABILIDADE PROF.: JOSÉ LUÍS PROBABILIDADE 1- (Osec-SP) Foram preparadas noventa empadinhas de camarão, sendo que, a pedido, sessenta delas deveriam ser bem mais apimentadas. Por pressa e confusão
24 de outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 24 de outubro de 2012 A PREENCHER PELO ALUNO 9ºano 90m Nome: nº Turma C A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do
Lista de exercícios de Matemática Eventos, espaço amostral e definição de probabilidade. Probabilidade condicional. Exercícios gerais.
 p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
p: João Alvaro w: www.matemaniacos.com.br e: joao.baptista@iff.edu.br. No lançamento de dois dados, D e D 2, tem-se o seguinte espaço amostral, dado em forma de tabela de dupla entrada. Lista de exercícios
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
PROBABILIDADE A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios. Os experimentos
1 Definição Clássica de Probabilidade
 Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
Centro de Ciências e Tecnologia Agroalimentar - Campus Pombal Disciplina: Estatística Básica - 2013 Aula 4 Professor: Carlos Sérgio UNIDADE 2 - Probabilidade: Definições (Notas de aula) 1 Definição Clássica
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa.
 A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
A tabela abaixo apresenta a distribuição dos equipamentos de uma grande empresa. Qual é a probabilidade de que um equipamento selecionado aleatoriamente esteja inativo ou seja do tipo A? a) 6/27 b) 14/27
Nome do aluno: Nº. Classificação: E.Educação:
 9º Ano ESCOLA SECUNDÁRIA/3 DE SANTA MARIA DA FEIRA Ano Letivo 2012/13 TURMA: A TESTE DE MATEMÁTICA Professora Lourdes Fonseca Nome do aluno: Nº Classificação: E.Educação: 1. Observa a roleta da sorte representada
9º Ano ESCOLA SECUNDÁRIA/3 DE SANTA MARIA DA FEIRA Ano Letivo 2012/13 TURMA: A TESTE DE MATEMÁTICA Professora Lourdes Fonseca Nome do aluno: Nº Classificação: E.Educação: 1. Observa a roleta da sorte representada
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Exercícios de exames e testes intermédios 1. Seja Ω, conjunto finito, o espaço de resultados associado a uma certa experiência
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Probabilidade Parte 2. Iva Emanuelly P. Lima
 Probabilidade Parte 2 Iva Emanuelly P. Lima Probabilidade Condicional É um segundo evento que ocorre depois que já tenha ocorrido o primeiro de um mesmo espaço amostral. É uma condição. Ou seja, a probabilidade
Probabilidade Parte 2 Iva Emanuelly P. Lima Probabilidade Condicional É um segundo evento que ocorre depois que já tenha ocorrido o primeiro de um mesmo espaço amostral. É uma condição. Ou seja, a probabilidade
Os experimentos que repetidos sob as mesmas condições produzem resultados geralmente diferentes serão chamados experimentos aleatórios.
 PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
PROBABILIDADE Prof. Aurimenes A teoria das Probabilidades é o ramo da Matemática que cria, desenvolve e em geral pesquisa modelos que podem ser utilizados para estudar experimentos ou fenômenos aleatórios.
Estatística Aplicada. Prof. Carlos Alberto Stechhahn EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE. Administração. p(a) = n(a) / n(u)
 Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Estatística Aplicada Administração p(a) = n(a) / n(u) EXERCÍCIOS - REVISÃO ESPAÇO AMOSTRAL - EVENTOS PROBABILIDADE Prof. Carlos Alberto Stechhahn 2014 1. Tema: Noções de Probabilidade 1) Considere o lançamento
Exercícios Obrigatórios
 Exercícios Obrigatórios ) (UFRGS/20) Observe a figura abaixo. Na figura, um triângulo equilátero está inscrito em um círculo, e um hexágono regular está circunscrito ao mesmo círculo. Quando se lança um
Exercícios Obrigatórios ) (UFRGS/20) Observe a figura abaixo. Na figura, um triângulo equilátero está inscrito em um círculo, e um hexágono regular está circunscrito ao mesmo círculo. Quando se lança um
4. Seja A o acontecimento associado a uma experiência aleatória em que o espaço amostral é Quais as igualdades necessariamente falsas?
 mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
mata. Lançou-se 70 vezes um dado em forma de tetraedro com as faces numeradas de a e obteve-se vezes a face, 0 vezes a face, vezes a face e as restantes a face. Determine a frequência relativa dos acontecimentos:
Prof.: Joni Fusinato
 Introdução a Teoria da Probabilidade Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Introdução a Teoria da Probabilidade Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Teoria da Probabilidade Consiste em utilizar a intuição humana para estudar os fenômenos do nosso
Noção de fenómeno aleatório e de experiência aleatória
 Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
Muitas vezes deparamo-nos com situações de incerteza, fenómenos aleatórios, em que não se pode prever o resultado. Pelo contrário, nos fenómenos deterministas conseguimos dizer antecipadamente o que vai
Se A =, o evento é impossível, por exemplo, obter 7 no lançamento de um dado.
 PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
PROBABILIDADE Espaço amostral Espaço amostral é o conjunto universo U de todos os resultados possíveis de um experimento aleatório. O número de elementos desse conjunto é indicado por n(u). Exemplos: No
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução
 MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução Exercícios de exames e testes intermédios 1. Como P (B) = 1 P ( B ) = P (B) P (A B) vem que P (B) = 1 0,7
MATEMÁTICA A - 12o Ano Probabilidades - Teoremas e operações com conjuntos Propostas de resolução Exercícios de exames e testes intermédios 1. Como P (B) = 1 P ( B ) = P (B) P (A B) vem que P (B) = 1 0,7
b) 35 c) 14 d) 35 Gab: D
 0 - (PUC SP/006) Em um ônibus há apenas bancos vazios, cada qual com lugares. Quatro rapazes e quatro moças entram nesse ônibus e devem ocupar os bancos vagos. Se os lugares forem escolhidos aleatoriamente,
0 - (PUC SP/006) Em um ônibus há apenas bancos vazios, cada qual com lugares. Quatro rapazes e quatro moças entram nesse ônibus e devem ocupar os bancos vagos. Se os lugares forem escolhidos aleatoriamente,
2. Se A e B são acontecimentos incompatíveis, a sua interseção é o conjunto vazio, pelo que
 reparar o Exame 0 06 Matemática ágina 6. nalisemos cada opção: : e não são contrários pois a sua união não é o espaço amostral. Há, ainda, bolas pretas. : e não são contrários pois a sua união não é o
reparar o Exame 0 06 Matemática ágina 6. nalisemos cada opção: : e não são contrários pois a sua união não é o espaço amostral. Há, ainda, bolas pretas. : e não são contrários pois a sua união não é o
Exercícios de provas oficiais
 mata Exercícios de provas oficiais. Considere duas caixas, C e C. A caixa C tem bolas, das quais cinco são brancas e as restantes são pretas, A caixa C tem sete bolas, umas brancas e outras pretas. Considere
mata Exercícios de provas oficiais. Considere duas caixas, C e C. A caixa C tem bolas, das quais cinco são brancas e as restantes são pretas, A caixa C tem sete bolas, umas brancas e outras pretas. Considere
TESTE DE PROBABILIDADES E COMBINATÓRIA 12.º ANO
 TESTE DE PROBABILIDADES E COMBINATÓRIA 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / AVALIAÇÃO: PROFESSOR: ENC. EDUCAÇÃO: DURAÇÃO DO TESTE: 90 MINUTOS O teste é constituído por dois grupos. O Grupo I é constituído
TESTE DE PROBABILIDADES E COMBINATÓRIA 2.º ANO NOME: N.º: TURMA: ANO LETIVO: / AVALIAÇÃO: PROFESSOR: ENC. EDUCAÇÃO: DURAÇÃO DO TESTE: 90 MINUTOS O teste é constituído por dois grupos. O Grupo I é constituído
( ) ( ) Questões tipo exame. O número pedido é: Questões tipo exame Pág Os algarismos 1 e 2 podem ocupar 5 A. posições diferentes.
 Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
Questões tipo exame Pág. 6.. Os algarismos e podem ocupar A posições diferentes. Os restantes lugares são ocupados por três algarismos escolhidos de entre oito, portanto, existem A maneiras diferentes
Aula 16 - Erivaldo. Probabilidade
 Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
Aula 16 - Erivaldo Probabilidade Probabilidade Experimento aleatório Experimento em que não pode-se afirmar com certeza o resultado final, mas sabe-se todos os seus possíveis resultados. Exemplos: 1) Lançar
MATEMÁTICA A - 12o Ano Probabilidades - Probabilidade condicionada Propostas de resolução
 MATEMÁTICA A - o Ano Probabilidades - Probabilidade condicionada Propostas de resolução Exercícios de exames e testes intermédios. No contexto do problema P ( B A ) é a probabilidade de retirar uma bola
MATEMÁTICA A - o Ano Probabilidades - Probabilidade condicionada Propostas de resolução Exercícios de exames e testes intermédios. No contexto do problema P ( B A ) é a probabilidade de retirar uma bola
PROBABILIDADE. Numero de Resultados Desejado Numero de Resultados Possiveis EXERCÍCIOS DE AULA
 PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
PROBABILIDADE São duas as questões pertinentes na resolução de um problema envolvendo probabilidades. Primeiro, é preciso quantificar o conjunto de todos os resultados possíveis, que será chamado de espaço
Matemática E Extensivo V. 5
 Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
Extensivo V. Exercícios 0) Casos possíveis: {,,,,, } Casos favoráveis: {,, } Assim, a probabilidade é: 0) 70% P Casos possíveis: 7 + 0 possibilidades Casos favoráveis: 7 (7 bolas pretas) P 7 0,7 70% 0
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Proposta de teste de avaliação Matemática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Grupo I Na resposta aos itens deste grupo, selecione a opção correta. Escreva, na folha de respostas, o número
Escola Secundária/2,3 da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 2011/12 Distribuição de probabilidades 12.º Ano
 Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
Escola Secundária/, da Sé-Lamego Ficha de Trabalho de Matemática A Ano Lectivo 0/ Distribuição de probabilidades.º Ano Nome: N.º: Turma:. Numa turma do.º ano, a distribuição dos alunos por idade e sexo
Probabilidade Condicional (grupo 2)
 page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
page 39 Capítulo 5 Probabilidade Condicional (grupo 2) Veremos a seguir exemplos de situações onde a probabilidade de um evento émodificadapelainformação de que um outro evento ocorreu, levando-nos a definir
Ano lectivo Ficha de trabalho nº 3
 Disciplina Ano M.A.C.S. 11º Ano lectivo Ficha de trabalho nº 3 2014/2015 Probabilidades 1. Um estojo tem 5 marcadores, 5 canetas e 3 lapiseiras. Retiram-se dois objectos do estojo, ao acaso, sucessivamente
Disciplina Ano M.A.C.S. 11º Ano lectivo Ficha de trabalho nº 3 2014/2015 Probabilidades 1. Um estojo tem 5 marcadores, 5 canetas e 3 lapiseiras. Retiram-se dois objectos do estojo, ao acaso, sucessivamente
ESCOLA SECUNDÁRIA DE CASQUILHOS
 ESCOLA SECUNDÁRIA DE CASQUILHOS 12º Ano Turma B - C.C.H. de Ciências e Tecnologias - 1ª Teste de Avaliação de Matemática A V1 Duração: 90 min 04 Nov. 09 Prof.: Na folha de respostas, indicar de forma legível
ESCOLA SECUNDÁRIA DE CASQUILHOS 12º Ano Turma B - C.C.H. de Ciências e Tecnologias - 1ª Teste de Avaliação de Matemática A V1 Duração: 90 min 04 Nov. 09 Prof.: Na folha de respostas, indicar de forma legível
Resposta: Resposta: 4 ou seja, 1.
 1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
1. (Unicamp 2016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a a) 1. 4 b). 8 c) 1. 2 d). 4
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO. Matemática
 ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO (NO PERÍODO DE FÉRIAS ESCOLARES) ANO 2014/20 PROFESSOR (a) DISCIPLINA Matemática ALUNO (a) SÉRIE 2º ano 1. OBJETIVO
ESCOLA ESTADUAL DR JOSÉ MARQUES DE OLIVEIRA PLANO DE ESTUDOS INDEPENDENTES DE RECUPERAÇÃO (NO PERÍODO DE FÉRIAS ESCOLARES) ANO 2014/20 PROFESSOR (a) DISCIPLINA Matemática ALUNO (a) SÉRIE 2º ano 1. OBJETIVO
Portal da OBMEP. Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE. Fração como Probabilidade. Sexto Ano do Ensino Fundamental
 Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio Caminha Muniz Neto 1 Introdução
Material Teórico - Módulo de FRAÇÃO COMO PORCENTAGEM E COMO PROBABILIDADE Fração como Probabilidade Sexto Ano do Ensino Fundamental Prof. Francisco Bruno Holanda Prof. Antonio Caminha Muniz Neto 1 Introdução
Probabilidade em espaços discretos. Prof.: Joni Fusinato
 Probabilidade em espaços discretos Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
Probabilidade em espaços discretos Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Probabilidade em espaços discretos Definições de Probabilidade Experimento Espaço Amostral Evento Probabilidade
ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO
 ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO Teste 1 Matemática 9.º C Nome: n.º Data: 14/10/2016 Classificação: Professor: Instruções gerais Não é permitido o uso de corretor. É permitido a utilização
ESCOLA BÁSICA DOS 2º E 3º CICLOS DE SANTO ANTÓNIO Teste 1 Matemática 9.º C Nome: n.º Data: 14/10/2016 Classificação: Professor: Instruções gerais Não é permitido o uso de corretor. É permitido a utilização
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a
 Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Lista 2 Estatística 1. Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade se sair bola: a. azul; b. vermelha; c. amarela. 2.
Ficha de trabalho - Combinatória. a) De quantas maneiras distintas se podem colocar os sete sabores no recipiente?
 12º Ano - Matemática A Ficha de trabalho - Combinatória 1. No balcão de uma geladaria existe um recipiente com dez compartimentos, cinco à frente e cinco atrás, para colocar gelado. Em cada compartimento
12º Ano - Matemática A Ficha de trabalho - Combinatória 1. No balcão de uma geladaria existe um recipiente com dez compartimentos, cinco à frente e cinco atrás, para colocar gelado. Em cada compartimento
BANCO DE QUESTÕES TURMA PM-PE PROBABILIDADE
 01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
01. (UNICAMP 016) Uma moeda balanceada é lançada quatro vezes, obtendo-se cara exatamente três vezes. A probabilidade de que as caras tenham saído consecutivamente é igual a A) 1. B). 8 C) 1. D). 0. (UNESP
Teste de Avaliação Escrita
 Teste de Avaliação Escrita Duração: 9 minutos 8 de outubro de Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo /4 Matemática 9.º B Nome: N.º Classificação: Fraco (% 9%) Insuficiente (% 49%) Suficiente
Teste de Avaliação Escrita Duração: 9 minutos 8 de outubro de Escola E.B., Eng. Nuno Mergulhão Portimão Ano Letivo /4 Matemática 9.º B Nome: N.º Classificação: Fraco (% 9%) Insuficiente (% 49%) Suficiente
LISTA DE EXERCÍCIOS 1 ESTATÍSTICA E PROBABILIDADES
 LISTA DE EXERCÍCIOS 1 ESTATÍSTICA E PROBABILIDADES 1- Ordene os dados indicando o 1º, 2º e 3º quartil 45, 56, 62, 67, 48, 51, 64, 71, 66, 52, 44, 58, 55, 61, 48, 50, 62, 51, 61, 55 2- Faça a análise da
LISTA DE EXERCÍCIOS 1 ESTATÍSTICA E PROBABILIDADES 1- Ordene os dados indicando o 1º, 2º e 3º quartil 45, 56, 62, 67, 48, 51, 64, 71, 66, 52, 44, 58, 55, 61, 48, 50, 62, 51, 61, 55 2- Faça a análise da
Escola Secundária com 3º ciclo D. Dinis 12º Ano de Matemática A Tema I Probabilidades e Combinatória. 1º Teste de avaliação.
 Escola Secundária com º ciclo D. Dinis 1º Ano de Matemática A Tema I Probabilidades e Combinatória 1º Teste de avaliação Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas
Escola Secundária com º ciclo D. Dinis 1º Ano de Matemática A Tema I Probabilidades e Combinatória 1º Teste de avaliação Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas
UNIVERSIDADE FEDERAL DA PARAÍBA. Cálculo das Probabilidades e Estatística I. Segunda Lista de Exercícios
 UNIVERSIDADE FEDERAL DA PARAÍBA Cálculo das Probabilidades e Estatística I Professora: Juliana Freitas Pires Segunda Lista de Exercícios Questão 1. Descreva o espaço amostral para cada um dos seguintes
UNIVERSIDADE FEDERAL DA PARAÍBA Cálculo das Probabilidades e Estatística I Professora: Juliana Freitas Pires Segunda Lista de Exercícios Questão 1. Descreva o espaço amostral para cada um dos seguintes
Universidade Federal de Goiás Instituto de Matemática e Estatística
 Universidade Federal de Goiás Instituto de Matemática e Estatística Prova 1 de Probabilidade I Prof.: Fabiano F. T. dos Santos Goiânia, 15 de setembro de 2014 Aluno: Nota: Descreva seu raciocínio e desenvolva
Universidade Federal de Goiás Instituto de Matemática e Estatística Prova 1 de Probabilidade I Prof.: Fabiano F. T. dos Santos Goiânia, 15 de setembro de 2014 Aluno: Nota: Descreva seu raciocínio e desenvolva
Q05. Ainda sobre os eventos A, B, C e D do exercício 03, quais são mutuamente exclusivos?
 LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo
LISTA BÁSICA POIA PROBABILIDADES A história da teoria das probabilidades teve início com os jogos de cartas, de dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo
Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema.
 PROBABILIDADE CONDICIONAL E DISTRIBUIÇÃO BINOMINAL 1. PROBABILIDADE CONDICIONAL Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema. Suponha que um redator
PROBABILIDADE CONDICIONAL E DISTRIBUIÇÃO BINOMINAL 1. PROBABILIDADE CONDICIONAL Para iniciar o conceito do que é probabilidade condicional, vamos considerar o seguinte problema. Suponha que um redator
A B e A. Calcule as suas respectivas probabilidades.
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA LISTA 2-BIOESTATÍSTICA II (CE020) Prof. Benito Olivares Aguilera 1 o Sem./17 1. Expresse em termos de operações entre eventos:
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA LISTA 2-BIOESTATÍSTICA II (CE020) Prof. Benito Olivares Aguilera 1 o Sem./17 1. Expresse em termos de operações entre eventos:
Matemática & Raciocínio Lógico
 Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur PROBABILIDADE No estudo das probabilidades estamos interessados em estudar o experimento
Matemática & Raciocínio Lógico para concursos Prof. Me. Jamur Silveira www.professorjamur.com.br facebook: Professor Jamur PROBABILIDADE No estudo das probabilidades estamos interessados em estudar o experimento
Regras de seleção. MATEMÁTICA- 9.º ANO Setembro Escolas João de Araújo Correia
 Escolas João de Araújo Correia ESCOLA SECUNDÁRIA DR. JOÃO DE ARAÚJO CORREIA MATEMÁTICA- 9.º ANO Setembro 0 TEMA: Organização e tratamento de dados exercícios saídos em TI e exames. A Associação de Estudantes
Escolas João de Araújo Correia ESCOLA SECUNDÁRIA DR. JOÃO DE ARAÚJO CORREIA MATEMÁTICA- 9.º ANO Setembro 0 TEMA: Organização e tratamento de dados exercícios saídos em TI e exames. A Associação de Estudantes
4 3 10! Resposta pedida: 3! x 4! = 144 Resposta: C
 ágina 80. reparar o Exame 0 07 Matemática A 4 0! 4 x x 0!. Devemos escolher, das oito posições, duas para as letras A: temos 8 formas de o fazer. Das seis posições restantes, uma tem de ser para a letra
ágina 80. reparar o Exame 0 07 Matemática A 4 0! 4 x x 0!. Devemos escolher, das oito posições, duas para as letras A: temos 8 formas de o fazer. Das seis posições restantes, uma tem de ser para a letra
Atividade extra. Exercício 1. Exercício 2. Exercício 3. Matemática e suas Tecnologias Matemática
 Atividade extra Exercício 1 João queria sair de casa, mas não sabia qual era a previsão do tempo. Ao ligar a TV no canal do tempo, a jornalista anunciou que existia a possibilidade de chuva no fim da tarde
Atividade extra Exercício 1 João queria sair de casa, mas não sabia qual era a previsão do tempo. Ao ligar a TV no canal do tempo, a jornalista anunciou que existia a possibilidade de chuva no fim da tarde
ANÁLISE COMBINATÓRIA
 ANÁLISE COMBINATÓRIA 1) (PUC) A soma das raízes da equação (x + 1)! = x 2 + x é (a) 0 (b) 1 (c) 2 (d) 3 (e) 4 2) (UFRGS) Um painel é formado por dois conjuntos de sete lâmpadas cada um, dispostos como
ANÁLISE COMBINATÓRIA 1) (PUC) A soma das raízes da equação (x + 1)! = x 2 + x é (a) 0 (b) 1 (c) 2 (d) 3 (e) 4 2) (UFRGS) Um painel é formado por dois conjuntos de sete lâmpadas cada um, dispostos como
Probabilidade Condicional
 18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
18 Probabilidade Condicional Sumário 18.1 Introdução....................... 2 18.2 Probabilidade Condicional............... 2 1 Unidade 18 Introdução 18.1 Introdução Nessa unidade, é apresentada mais uma
PROBABILIDADES PROBABILIDADE DE UM EVENTO EM UM ESPAÇO AMOSTRAL FINITO
 PROBABILIDADES Probabilidade é um conceito filosófico e matemático que permite a quantificação da incerteza, permitindo que ela seja aferida, analisada e usada para a realização de previsões ou para a
PROBABILIDADES Probabilidade é um conceito filosófico e matemático que permite a quantificação da incerteza, permitindo que ela seja aferida, analisada e usada para a realização de previsões ou para a
Exercícios de Probabilidade - Lista 1. Profa. Ana Maria Farias
 Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
Exercícios de Probabilidade - Lista 1 Profa. Ana Maria Farias 1. Lançam-se três moedas. Enumere o espaço amostral e os eventos A = faces iguais ; B = cara na primeira moeda ; C = coroa na segunda e terceira
Lista de exercícios Defina o espaço amostral para cada um dos seguintes experimentos aleatórios:
 UNIVERSIDADE FEDERAL DE SÃO CARLOS Centro de Ciências Agrárias Departamento de Tecnologia Agroindustrial e Socioeconomia Rural Disciplina: Noções de Probabilidade e Estatística (221171) - 2019 Prof. a
UNIVERSIDADE FEDERAL DE SÃO CARLOS Centro de Ciências Agrárias Departamento de Tecnologia Agroindustrial e Socioeconomia Rural Disciplina: Noções de Probabilidade e Estatística (221171) - 2019 Prof. a
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 12º ANO DE ESCOLARIDADE DE MATEMÁTICA A. TESTE Nº 1 Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A TESTE Nº Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A TESTE Nº Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
22 de Outubro de 2012
 Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Escola Básica de Santa Catarina Ficha de Avaliação de Matemática 22 de Outubro de 2012 A PREENCHER PELO ALUNO 9ºano Nome: nº Turma A PREENCHER PELO PROFESSOR Classificação: Nível: ( ) Rubrica do professor:
Matemática E Extensivo V. 5
 Extensivo V Exercícios 0) a) / b) / c) / a) N(E) N(A), logo P(A) b) N(E) N(A), logo P(A) c) N(E) N(A), logo P(A) 0) a) 0 b) / % c) 9/0 90% d) /0 % 0) E a) N(E) 0 + + + 0 b) N(E) 0 N(A), logo P(A) 0, %
Extensivo V Exercícios 0) a) / b) / c) / a) N(E) N(A), logo P(A) b) N(E) N(A), logo P(A) c) N(E) N(A), logo P(A) 0) a) 0 b) / % c) 9/0 90% d) /0 % 0) E a) N(E) 0 + + + 0 b) N(E) 0 N(A), logo P(A) 0, %
Aulas particulares. Conteúdo
 Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Conteúdo Capítulo 6...2 Probabilidade...2 Exercícios...4 Restpostas...9 Capítulo 7... 12 Análise combinatória... 12 Fatorial... 12 Arranjo... 13 Combinação... 16 Exercícios... 17 Respostas... 22 1 Capítulo
Probabilidades Aulas 55 e 56 prof. Aguiar
 Probabilidades Aulas 55 e 56 prof. Aguiar - 2013 Extra 1: Uma urna contém 3 bolas brancas, 2 bolas vermelhas e 2 bolas pretas. Sorteamos 4 bolas, sucessivamente e sem reposição. Qual é a probabilidade
Probabilidades Aulas 55 e 56 prof. Aguiar - 2013 Extra 1: Uma urna contém 3 bolas brancas, 2 bolas vermelhas e 2 bolas pretas. Sorteamos 4 bolas, sucessivamente e sem reposição. Qual é a probabilidade
REDE ISAAC NEWTON ENSINO FUNDAMENTAL 2º ano PROFESSORA: LUCIANO VIEIRA / F LUCIANO ALUNO(A): Nº: MATEMÁTICA
 REDE ISAAC NEWTON ENSINO FUNDAMENTAL 2º ano PROFESSORA: LUCIANO VIEIRA / F LUCIANO DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul MATEMÁTICA 0. (UFRGS - VESTIBULAR 205) Escolhe-se
REDE ISAAC NEWTON ENSINO FUNDAMENTAL 2º ano PROFESSORA: LUCIANO VIEIRA / F LUCIANO DATA: / / TURMA: ALUNO(A): Nº: UNIDADE: ( ) Riacho Fundo ( ) Taguatinga Sul MATEMÁTICA 0. (UFRGS - VESTIBULAR 205) Escolhe-se
No lançamento de uma moeda, a probabilidade de ocorrer cara ou coroa é a mesma. Como se calcula a probabilidade de determinado evento?
 Probabilidade Introdução Dentro de certas condições, é possível prever a que temperatura o leite ferve. Esse tipo de experimento, cujo resultado é previsível, recebe o nome de determinístico. No entanto,
Probabilidade Introdução Dentro de certas condições, é possível prever a que temperatura o leite ferve. Esse tipo de experimento, cujo resultado é previsível, recebe o nome de determinístico. No entanto,
Proposta de teste de avaliação
 Proposta de teste de avaliação Matemática A 1.º ANO DE ESCOLARIDADE Duração: 90 minutos Data: O teste é constituído por dois grupos, I e II. O Grupo I inclui quatro questões de escolha múltipla. O Grupo
Proposta de teste de avaliação Matemática A 1.º ANO DE ESCOLARIDADE Duração: 90 minutos Data: O teste é constituído por dois grupos, I e II. O Grupo I inclui quatro questões de escolha múltipla. O Grupo
Probabilidade 2. Fascículo 11. Unidade 34
 Probabilidade 2 Fascículo 11 Unidade 34 Probabilidade 2 Para início de conversa... Na unidade anterior observamos uma introdução ao estudo das probabilidades. Como exemplos, utilizamos o lançamento de
Probabilidade 2 Fascículo 11 Unidade 34 Probabilidade 2 Para início de conversa... Na unidade anterior observamos uma introdução ao estudo das probabilidades. Como exemplos, utilizamos o lançamento de
