Graduação em Engenharia Civil Mestrado Acadêmico Faculdade de Engenharia FEN/UERJ
|
|
|
- Luís Caldeira Gil
- 7 Há anos
- Visualizações:
Transcrição
1 orção Programa de Pó-GraduaP Graduação em Engenharia Civil Metrado Acadêmico Faculdade de Engenharia FEN/UERJ Profeor: Luciano Rodrigue Ornela de Lima 1. Introdução Momento toror () ecundário Combinado com outro tipo de eforço o flexão pode e tornar preponderante 1
2 1. Introdução Exemplo Prático 1. Introdução Exemplo Prático
3 5 1. Introdução Importância: eçõe de parede fina aberta FL flambagem lateral por torção de viga FLA flambagem lateral da alma de coluna viga-coluna Seçõe de parede fina coniderar o efeito do momento toror e então adicionar o efeito de outro carregamento conideração da eçõe aberta (para a grande maioria) membro de parede fina (d/t 1) 6 1. Introdução Procedimento a er adotado Calcular a tenõe provocada pelo momento toror Avaliar a reitência a torção e aumentá-la, e neceário Certo carregamento e eçõe tranverai intabilidade por torção orção Empenamento Exceçõe:.c.L eçõe tranverai fechada circulare τ e φ J GJ certo cao prático onde a eçõe de parede fina ão feita com elemento de placa que e encontram em um ponto (muito fraco torionalmente) (torção em parte)
4 7 1. Introdução Melhor eção tranveral para membro ubmetido à torção eção circular oca ditância de qualquer elemento deta eção poui a mema ditância até o centróide que coincide com o centro de cialhamento (erá comentado poteriormente) eçõe circulare inicialmente plana permanecem plana não havendo ditorção da eção tranveral orção Pura ou orção de St. Venant ( SV ) ocorre rotação θ da eção tranveral em torno do eixo longitudinal do elemento 8 1. Introdução Membro com eção tranveral Perfil I empenamento da eção tranveral além m da torção muito ignificante em perfi com eçõe aberta orção Empenamento ( Warping( Warping ) - SV + W
5 9. orção Pura ou de St. Venant ( ( SV ) membro com eção circular torção pura (St. Venant) ituação onde a tenõe em qualquer ponto podem er repreentada como cialhamento puro a linha ab,, apó a aplicação do toror paa para a poição a ba coniderando-e e o elemento infiniteimal d 1. orção Pura ou de St. Venant ( ( SV ) taxa de modificação do ângulo de torção φ dθ φ d r. φ γ elemento d linha radial da eção é rotacionada de um ângulo dθ enquanto a linha na uperfície ofre uma rotação de γ r.dθ γ.d dθ γ r γ d r. atravé do módulo m de cialhamento G, a Lei de Hooke fornece para a tenão cialhante unitária ν γ.g φ 5
6 11. orção Pura ou de St. Venant ( da figura torque elementar ( SV ) dθ d r. ν.da r. γ.g.da r..g.da d momento toror total obtenção do equilíbrio A dθ r..g.da d como dθ/dd e G ão contante dθ.g r da d A SV dθ GJ d J (momento polar de inércia) 1. orção Pura ou de St. Venant ( SV ) Eta equação é análoga a de flexão onde o momento fletor M é igual a rigide EI multiplicada pela curvatura d /dx. Aqui, o momento toror é igual a rigide à torção GJ vee a curvatura torional (taxa de mudança a do ângulo θ) Finalmente, pode-e ecrever, dθ ν γ.g r..g d M EI SV ma d dx dθ GJ d dθ SV d GJ SV.r ν J onde r é a ditância do ponto coniderado até o centróide 6
7 1. orção Pura ou de St. Venant ( SV ) Seçõe Circulare Para eçõe circulare com diâmetro t, não ocorre empenamento da eção e J repreenta o momento polar de inércia e a tenão cialhante máxima m ocorre em r t / J πt Seçõe Retangulare A ν 16. π.t SV máx J r da (x + )da x da + da Ix + I I Ponto A p Ponto B A B d d τ 1. orção Pura ou de St. Venant ( SV ) Conideração inconitente Para eçõe retangulare deformaçõe proveniente do cialhamento devem variar de forma não-linear J deve er reavaliado A eção tranveral não permanece plana como previto por St. Venant eoria da Elaticidade tenão cialhante máxima m ocorre no ponto médio ao longo do lado do retângulo e atua paralelamente a ete Magnitude função da raão b / t (comprimento / largura) ν máx k 1. b.t SV b/t k 1 1,,81 1,,57 1,5,,,7,5,88,,75,,55 5,,, J k.b. t k,11,166,196,9,9,6,81,91, 7
8 15. orção Pura ou de St. Venant ( SV ) Para eçõe retangulare a tenõe de cialhamento provocada por deenvolvem-e paralelamente à face do retângulo 16. orção Pura ou de St. Venant ( SV ) Quando vário v retângulo ão aociado para compor a eção tranveral, o fluxo cialhante torna-e mai complexo. Máxima tenão cialhante torção pura, em cada retângulo ocorre no ponto médio m do maior lado do retângulo ν f máx t f SV bt e ν máx t SV bt 8
9 17. orção Pura ou de St. Venant ( Para um perfil I alma + mea ( SV ) SV b t dθ b f t f dθ bt dθ G +. G G d d d ν fm ν fm ν m ν m ν fm ν fm 18. Analogia de Membrana orção de barra eçõe não circulare olução analítica complicada método indireto de olução Método de Analogia Problema diferente (naturea fíica) f reduem-e à mema equaçõe diferenciai analogia entre ete problema Pode-e afirmar que a variávei vei x 1 e 1 de um problema tem a mema dependência que a variávei vei x e de outro problema Prandtl (19) orção eção qualquer mema equaçõe diferenciai que uma membrana eticada obre um contorno de mema configuração e ubmetida a uma preão q 9
10 19. Analogia de Membrana Analogia da tenão cialhante ângulo da tangente à uperfície da membrana Analogia do momento toror volume entre o plano do contorno e a uperfície da membrana τ x τ F q F. Analogia de Membrana Definiçõe q preão uniforme na membrana F força a no aro da membrana por unidade de comprimento G módulo de cialhamento elático: ν coeficiente de Poion φ ângulo de torção E G (1+ ν) dφ/dd taxa de torção ângulo de torção por unidade de comprimento 1
11 1. Analogia de Membrana Equação Diferencial Membrana Deflexão: q + x F orção Função de enão: φ φ φ dφ + G x d Derivada x, φ τ x x, φ τ Volume dx d v φ dx d Portanto, ângulo da tangente da membrana tenõe cialhante. Analogia de Membrana Volume abaixo da membrana v / B x A b A B t Corte AA Corte BB F q F F q F 11
12 . Analogia de Membrana Preão uniforme delocamento equação parabólica (a) F t (b) inclinação: t/ q α d 8 τ d t (c) ΣF : q.t.b.f.b.enα para ângulo pequeno, en α tan α (d/d) máx F (d) k t k k t d 8 t en α d t t máx q 8 q.t.b.f.b. (e) t F t q dφ (f) ma G por analogia e o volume F d V / V t.b. v v / (g) (h) (i). Analogia de Membrana t.b. v.v.t.b q 8 6.v dφ G Gφ' F t t b d t.b.g. φ' v b.t Definindo J GJφ' v e a rigide à torção v C φ' t, tem-e C t GJ Comparando-e com a equação M -EIv onde M é comparado com M v, ( v ), E com G, I com J e φ com v. Da equação (b), tem-e, 8 τ t v τmáx τ. t / t t b.t b.t.t. v τmáx b.t τ t. v máx J Para qualquer configuração de retângulo 1 J tij. τ J b t ij ij v v 1
13 5. Seçõe de Parede Fina Aberta enõe normai flexão ΣF ( τt) σ d d t + d d ( τt) σ ou - t 1. Aumindo-e e que o momento eja apena no plano,, ou eja, M,, tem- e a tenõe de flexão: σ Mx I I I x x (I I x x) e σ Mx / (I I I I I x x x x) 6. Seçõe de Parede Fina Aberta Lembrando-e que V M x /, tem-e τt t V I I I x x (I I Integrando-e para encontrar τt a uma ditância da face livre, tem-e o fluxo de cialhamento τt dado por, V τt I I I x x x x) [ I t d I xt d] x 1
14 7. Seçõe de Parede Fina Aberta. Aumindo-e e que o momento é aplicado no plano x,, ito é, M x, tem-e a tenõe de flexão dada por: M σ ( Ix + I I I I x x x x) omando-e σ /, lembrando que V. e integrando-e para x M / obter o fluxo de cialhamento, tem-e, + Vx τt [ I t d I xt d]. Momento aplicado em ambo o plano e x a tenõe podem er calculada por uperpoição do efeito. O cortante V na direção deve er igual a componente τt na direção omada ao longo de toda a eção. Similarmente, para V x e τt na direção x. I I x I x x x 8. Seçõe de Parede Fina Aberta O equilíbrio rotacional também m deve er atifeito, ou eja, o momento em relação ao centróide da eção n ( τt) r d deve er igual a ero em cao de perfi com eçõe tranverai em I ou Z. Se ete equilíbrio é automaticamente atifeito quando o cialhamento atua no centróide, nenhuma eforço o de torção atuará imultaneamente com o eforço o de flexão. 1
15 9 5. Centro de Cialhamento Para e evitar que ocorra torção da eção tranveral aplicação da carga na linha que paa pelo centro de cialhamento em eçõe duplamente imétrica coincidência com o centróide odavia, ito nem empre é poível tendo em vita que em algun tipo de eção tranveral, o C.S. fica fora da eção tranveral n ( τt) r d 5. Centro de Cialhamento Coniderando-e e o eforço o cortante V x e V atuante em ditância de e x do centróide ide, repectivamente e que o momento toror em n relação ao centróide é o memo que ( τt) r d, tem-e, V x V x n ( τt) r d Em outra palavra, o momento toror é igual a V. x Vx quando a carga ão aplicada em plano que paam atravé do centróide ma igual a ero e a carga ão aplicada em plano que paam atravé do centro de cialhamento coordenada x e 15
16 1 5. Centro de Cialhamento Para e determinar a poição do centro de cialhamento, primeiro fa-e o cortante er igual a ero em uma da direçõe (V( ), lembrando-e que τt foi determinado anteriormente + V com x τt [ Ix t d Ix x t d] 1 n ( τt) r d V x Alternativamente, para V x, tem-e, V x com τt [ I t d I x t d] 1 n ( τt) r d V I I x I I x I I x x x 5. Centro de Cialhamento 16
17 5. Centro de Cialhamento 5. Centro de Cialhamento 17
18 5 5. Centro de Cialhamento 6 6. orção de Empenamento ( Warping( Warping ) Coniderando-e e uma viga em balanço, ubmetida a um momento toror V V+dV empenamento retringido da figura, tem-e empenamento livre h du h dθ d u h d θ d u h d θ u θ. ;. ;.. u d d d d d d a mea do perfil é que reitem ao empenamento V.h f d d V f V f h d hd-tf 18
19 7 6. orção de Empenamento ( Warping( Warping ) Da teoria de viga, dm Vf d Logo, e d u Vf EIf. d M f d u EIf. d onde I f (momento de inércia da mea em relação ao eixo de maior inércia) é tomado igual a I / porque a influência da alma pode er depreada Subtituindo-e e V f na equação de e tomando h d t f, tem-e EI d u.. d ( d t f ).( d t f ). d d EI I. d t d θ. d h θ ( ) ma C f d θ EC d 8 6. orção de Empenamento ( Warping( Warping ) Finalmente, o momento toror total erá dado pela equação: dθ d θ SV + GJ EC d d Reecrevendo a equação acima apó dividir ambo o termo por EC, tem-e, d θ - λ d dθ d EC onde A olução da equação diferencial acima é dada por onde 1 λ a φ A + B.coh( λ) + C.enh( λ) + φ φ p GJ EC é a olução particular para torque aplicado p 19
20 9 7. Condiçõe de Contorno (Idealiada) φ rotação φ empenamento φ empenamento livre 7. Condiçõe de Contorno (Idealiada)
21 1 7. Condiçõe de Contorno (Idealiada) 8. Combinaçõe de enõe τ SV t.sv J t.g. φ' E.b E.b.(d t f ) τ W (d t f ). φ" ' σ ± φ" 16 1
22 9. Procedimento para Dimenionamento Obter a propriedade mecânica e geométrica da eção tranveral J, C, E e G Ecrever a equação diferencial para o problema a er reolvido Reolver a equação diferencial olução exata aplicação da condiçõe de contorno método aproximado Determinar a parcela de tenõe Saint Venant Empenamento Superpoição do efeito 1. Exemplo eórico empenamento retringido φ (rotação) φ (empenamento) 1. equação diferencial empenamento livre Ebh σ φ" φ" GJ SV + GJφ' ECφ"' φ" ' - φ' EC EC olução da forma φ A + B.coh( λ) + C.enh( λ) + φp tentativa ' " "' φ F.; φ F; φ e φ p p p p
23 5 1. Exemplo logo, GJ EC.F EC da condiçõe de contorno lembrando que F GJ. φ A + B.coh( λ) + C.enh( λ) + GJ ' φ ; φ e φl e coh( λ) e enh( λ) λ λ + e e " λ λ e e d d d d coh( λ) λ.inh( λ) coh() 1 enh( λ) λ.coh( λ) enh() 6 1. Exemplo então, φ' B. λ.enh( λ) + C. λ.coh( λ) + GJ φ" B. λ.coh( λ) + C. λ.enh( λ) φ"' B. λ.enh( λ) + C. λ.coh( λ) que para a condiçõe de contorno do problema, valem φ( ) A + B ' φ () C. λ + C ma GJ λ EC GJ λgj '' φ (L) B. λ.coh( λ) + C. λ.enh( λ) B.coh( λl) enh( λl) λ EC B tanh( λl) A λ EC C λ EC
24 7 1. Exemplo finalmente, φ tanh( λl) + tanh( λl).coh( λ) + λ EC λ EC λ EC enh( λl) + λ EC. a partir de φ,, obter φ, φ e φ e determinar τ SV, σ W e τ W τ SV t.sv J t.g. φ' E.b E.b.(d t f ) τ W (d t f ). φ" ' σ ± φ" Exemplo Numérico (Ábaco( AISC) 6, m E MPa G 77 MPa Perfil W1x7 mm J 75x1 9 C 55x1 mm EC mm e L 6, 5 GJ a 17 a 9 do ábaco (novo) CASO 9 (α( 1,) página 88 e 89 φ'gj máx φ "GJ.a ' 1, 1, em em L φ"gj.5a 5, φgj 1.,6 a 6 em (página 88) (página 89) (página 89) em L (página 88) t 9,1 mm t f 16, mm
25 9 11. Exemplo Numérico (Ábaco( AISC) φ"gj.5a 5, em φ"gj.5a φgj 1.,6 a em L φgj 1. a L,5 a φgj 1. a φ"gj.5a Exemplo Numérico (Ábaco( AISC) φ'gj máx 1, em L φ'gj φ"'gj.a φ "GJ.a ' 1, em 5
26 Exemplo Numérico (Ábaco( AISC) A. enão Cialhante - St. Venant τsv máx t.g. φ' em Z L φ ' máx 1,. GJ τ G. t. GJ SV máx.t J.t.9,1 6 τsv máx alma 1,.1. (N/ mm ) J 75.1.t f.16, 6 τsv máx mea 1,9.1. (N / mm ) J ,. (kn.m) 1,9. (kn.m) Exemplo Numérico (Ábaco( AISC) B. enão Normal - Empenamento σ W em Z σ máx E.b.(d t f ) σ W máx. φ 1 φ" 5,.. GJ 5a GJ W máx alma E. G " máx 1. a b.(d t f ). J 1. a 5.(1 16,) , ,6. (kn.m) 6
27 5 11. Exemplo Numérico (Ábaco( AISC) C. enão Cialhante - Empenamento E.b (d t f ) τ W máx. φ"' em Z 16 φ'"gj 1.a 1,.. GJ a τ W máx E b (d t f ) 1.( 1,). G 16 J a τ τ W máx (5) (1 16,) W máx 1,5.1. 1,5. ( em kn.m) 1. (17) 5 1. Seçõe de Parede Fina Fechada Analogia de Membrana h t τ h / t e t é pequeno área fechada limitada pela linha média A Logo, volume V A. h Portanto, A h τ t A q A 7
28 55 1. Seçõe de Parede Fina Fechada Maior rigide à torção Em tubo de parede fina tenõe cialhante uniformemente ditribuída da ao longo da epeura t tenão cialhante τ τt é a força cialhante por unidade de comprimento ao longo da parede fluxo cialhante Apena tenõe cialhante proveniente da torção enõe normai (σ ) τt contante (q) Seçõe de Parede Fina Fechada O incremento de momento toror em cada elemento vale: d τ t ρ d Integrando-e, tem-e, τ t ρ d Obervando-e que ½ ρ d repreenta a área do triângulo hachurado ρ d A E finalmente, τ t A q A onde A repreenta a área da parede fechada 8
29 57 1. Seçõe de Parede Fina Fechada Se uma abertura é feita na parede movimento relativo entre o doi lado na direção axial do membro deformação unitária provocada pelo cialhamento ao longo do perímetro γ τ / G A energia de deformação interna para qualquer elemento de comprimento d ao longo do perímetro vale 1 1 dw i τ t γ d A τ d G 58 O momento toror em torno do ponto pode er ubtituído por um binário / r e o trabalho externo feito pelo binário vale 1 θ dw e n r Igualando-e W i com W e por unidade de comprimento, tem- e θ 1. Seçõe de Parede Fina Fechada AG τ d τ t d/t τ d θ AG AG (com τt contante) Com o objetivo de e obter equaçõe mai uuai GJθ τ t d/t GJ AG E finalmente, eliminando-e entre a equaçõe τ t A e a anterior e reolvendo-e e para a contante de torção J, tem-e A J d/t 9
30 59 1. Seçõe de Parede Fina Fechada Exemplo Comparar a reitência ao momento toror e a contante de torção J para a eçõe a eguir abendo-e e que a tenão cialhante τ 1 ki: 6 1. Seçõe de Parede Fina Fechada a) eção circular de parede fina b) eção caixão retangular τ t A (1) (,5) A (5π) J 9 in d/t π onde d/t π(5) /,5 π τ t A (1) (,5) 1 [ π(1) / ] 91,6 ft kip 1 1 A J (.6 /,5) 88 in d/t 1 [ 7] 8 ft kip
31 61 1. Seçõe de Parede Fina Fechada c) eção aberta Como 1 t τ J, a máxima tenão cialhante ocorrerá na mea. 1 [ 1(,5) + (5,5)(1) ],8 in J bt Jτ t f,8(1) (1)(1),8 ft - kip A partir do reultado obtido, conclui-e que a eção circular poui maior reitência à torção, endo eguida pela eção caixão retangular O J deta eçõe igual a 96 e 71 vee da eção aberta e iguai a 19 e 18 vee ao da eção aberta, repectivamente 6 1. Exemplo CS omando-e V x e faendo- e o momento em relação ao ponto A, b Vq Vfh ( τt) h d Onde V τt I x V t d I x t Para eta eçõe de parede fina, o comprimento utiliado na integração é medido na linha média m da epeura 1
32 6 1. Exemplo CS Subtituindo-e e na primeira equação e uando -h h / com t t f, tem- e, b V h Vq t f h d I x x V t f h I b d f I x V t h b E a poição do centro de cialhamento na direção poitiva do eixo x é Para e obter a coordenada do centro de cialhamento em relação ao eixo, aplica-e V x e toma-e V h b Vx ( τt) d Onde Vx τt x t d I q t f h b I x 6 1. Exemplo CS Para ilutrar numericamente b,, h 1 e t t Cálculo do centróide A. x b(b / )t ()() x A (h + b)t 1 + () Então, x +. in 1 I (). (.8) t 9.87 t V τt I x.8 in - V x (,) d, h d 9,87 Subtituindo-e e τt,, tem-e, τt V x h - Vx 9,87, h d
33 65 1. Exemplo CS Continuação - x + x V h, 9,87 6 V h Com io, motra-e e que. O centro de cialhamento pode er localiado eguindo-e o procedimento abaixo: 1.Calcular, atravé da integral da tenõe em cada lado da eção, a força a cortante atuante;.o O centro de cialhamento é localiado de forma que V x ou V equilibrem a força atuante na eção Obervaçõe Flambagem Lateral por orção M cr E I C b π L G I + π L E I dθ d θ SV + GJ EC d d M cr E I C b π L G J + π L E C
Considere as seguintes expressões que foram mostradas anteriormente:
 Demontração de que a linha neutra paa pelo centro de gravidade Foi mencionado anteriormente que, no cao da flexão imple (em eforço normal), a linha neutra (linha com valore nulo de tenõe normai σ x ) paa
Demontração de que a linha neutra paa pelo centro de gravidade Foi mencionado anteriormente que, no cao da flexão imple (em eforço normal), a linha neutra (linha com valore nulo de tenõe normai σ x ) paa
3 Equações de movimentos
 3 Equaçõe de movimento A formulação da equaçõe governante e da condiçõe de contorno, memo que para um cao geral, é uualmente muito direta. ontudo, a olução analítica do problema, em muito cao é impoível
3 Equaçõe de movimento A formulação da equaçõe governante e da condiçõe de contorno, memo que para um cao geral, é uualmente muito direta. ontudo, a olução analítica do problema, em muito cao é impoível
2. FLEXO-TORÇÃO EM PERFIS DE SEÇÃO ABERTA E PAREDES DELGADAS.
 2. FLEXO-TORÇÃO EM PERFIS DE SEÇÃO BERT E PREDES DELGDS. Nete capítulo ão apreentado, de forma concia, com bae no trabalho de Mori e Munaiar Neto (2009), algun conceito báico neceário ao entendimento do
2. FLEXO-TORÇÃO EM PERFIS DE SEÇÃO BERT E PREDES DELGDS. Nete capítulo ão apreentado, de forma concia, com bae no trabalho de Mori e Munaiar Neto (2009), algun conceito báico neceário ao entendimento do
6 Previsões teóricas Cálculo segundo procedimento de Leon et al. (1996) Momento resistente da ligação
 Previõe teórica Ete capítulo apreentada a previõe de reultado teórico do comportamento da ligação etudada, egundo o modelo analítico utilizado nete trabalho. O primeiro procedimento decrito é referente
Previõe teórica Ete capítulo apreentada a previõe de reultado teórico do comportamento da ligação etudada, egundo o modelo analítico utilizado nete trabalho. O primeiro procedimento decrito é referente
2 Cargas Móveis, Linhas de Influência e Envoltórias de Esforços
 2 Carga óvei, Linha de Influência e Envoltória de Eforço 21 Introdução Para o dimenionamento de qualquer etrutura é neceário conhecer o eforço máximo e mínimo que ela apreentará ao er ubmetida ao carregamento
2 Carga óvei, Linha de Influência e Envoltória de Eforço 21 Introdução Para o dimenionamento de qualquer etrutura é neceário conhecer o eforço máximo e mínimo que ela apreentará ao er ubmetida ao carregamento
ESTRUTURAS DE BETÃO ARMADO I 14 ESTADO LIMITE ÚLTIMO DE RESISTÊNCIA À TORÇÃO
 ESRUURS DE BEÃO RMDO I ESRUURS DE BEÃO RMDO I 14 ESDO LIMIE ÚLIMO DE RESISÊNCI À ORÇÃO 14 ESDO LIMIE ÚLIMO DE RESISÊNCI À ORÇÃO PROGRM 1 Introdução ao betão armado 2 Bae de Projecto e cçõe 3 Propriedade
ESRUURS DE BEÃO RMDO I ESRUURS DE BEÃO RMDO I 14 ESDO LIMIE ÚLIMO DE RESISÊNCI À ORÇÃO 14 ESDO LIMIE ÚLIMO DE RESISÊNCI À ORÇÃO PROGRM 1 Introdução ao betão armado 2 Bae de Projecto e cçõe 3 Propriedade
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2014-2 Objetivos Compreender a deformação por torção Compreender os esforços de torção Determinar distribuição de tensões de cisalhamento
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2014-2 Objetivos Compreender a deformação por torção Compreender os esforços de torção Determinar distribuição de tensões de cisalhamento
MECÂNICA DO CONTÍNUO. Tópico 2. Cont. Elasticidade Linear Cálculo Variacional
 MECÂNICA DO CONTÍNUO Tópico 2 Cont. Elaticidade Linear Cálculo Variacional PROF. ISAAC NL SILVA Lei de Hooke Até o limite elático, a tenão é diretamente proporcional à deformação: x E. e x e e y z n E
MECÂNICA DO CONTÍNUO Tópico 2 Cont. Elaticidade Linear Cálculo Variacional PROF. ISAAC NL SILVA Lei de Hooke Até o limite elático, a tenão é diretamente proporcional à deformação: x E. e x e e y z n E
Torção em eixos de seção circular Análise de tensões e deformações na torção Exercícios. Momento torsor. 26 de setembro de 2016.
 26 de setembro de 2016 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 Este capítulo é dividido em duas partes: 1 Torção em barras
26 de setembro de 2016 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 00 11 0000 1111 000000 111111 0 1 0 1 000000 111111 0000 1111 Este capítulo é dividido em duas partes: 1 Torção em barras
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2012-2 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2012-2 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2013-1 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2013-1 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
ESTADOS LIMITES DE UTILIZAÇÃO
 CAPÍTULO 6 Volume ESTADOS LIMITES DE UTILIZAÇÃO Prof. Joé Milton de Araújo - FURG 1 1- Combinaçõe da açõe de erviço a) combinaçõe quae permanente: atuam durante um período maior ou igual à metade da vida
CAPÍTULO 6 Volume ESTADOS LIMITES DE UTILIZAÇÃO Prof. Joé Milton de Araújo - FURG 1 1- Combinaçõe da açõe de erviço a) combinaçõe quae permanente: atuam durante um período maior ou igual à metade da vida
Lista 4 Prof. Diego Marcon
 Lita 4 Prof. Diego Marcon Método Aplicado de Matemática I 6 de Junho de 07 Lita de exercício referente ao retante da primeira área da noa diciplina: Exponencial de matrize Tranformada de Laplace Delocamento
Lita 4 Prof. Diego Marcon Método Aplicado de Matemática I 6 de Junho de 07 Lita de exercício referente ao retante da primeira área da noa diciplina: Exponencial de matrize Tranformada de Laplace Delocamento
Critério de Resistência
 CAPÍTULO 1 INTRODUÇÃO À RESISTÊNCIA DOS MATERIAIS I. OBJETIVOS FUNDAMENTAIS Um corpo em equilíbrio, ujeito a carga externa ativa e reativa, poui em eu interior eforço. Ete eforço interno ou olicitaçõe
CAPÍTULO 1 INTRODUÇÃO À RESISTÊNCIA DOS MATERIAIS I. OBJETIVOS FUNDAMENTAIS Um corpo em equilíbrio, ujeito a carga externa ativa e reativa, poui em eu interior eforço. Ete eforço interno ou olicitaçõe
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RETÊNCA DO MATERA Ferdinand P. Beer E. Russell Johnston, Jr. Carregamento Transversal Capítulo 5 Carregamento Transversal 5.1 ntrodução 5.2 Carregamento Transversal 5.3 Distribuição
Terceira Edição CAPÍTULO RETÊNCA DO MATERA Ferdinand P. Beer E. Russell Johnston, Jr. Carregamento Transversal Capítulo 5 Carregamento Transversal 5.1 ntrodução 5.2 Carregamento Transversal 5.3 Distribuição
Departamento de Engenharia Mecânica ENG Mecânica dos Sólidos II. Teoria de Vigas. Prof. Arthur Braga
 Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
Departamento de Engenharia Mecânica ENG 174 - Teoria de Vigas Prof. rthur Braga Tensões de Fleão em Barras (vigas Deformação do segmento IJ M N ρ Δφ I J ( ρ y Δφ Compresão ρ ρ y I J y M N Eio Neutro (deformação
Equações diferenciais
 Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Equações diferenciais Equações diferenciais Equação diferencial de 2ª ordem 2 d 2 Mz x q x dx d Mz x Vy x q x C dx Mz x q x C x C 1 2 1 Equações diferenciais Equação do carregamento q0 q x 2 d 2 Mz x q
Efeitos de 2ª 2 Ordem
 Prof. uciano ima - lucianolima@uerj.br Eq.. Diferencial Efeitos 2ª 2 Ordem Programa de Pós-GraduaP Graduação em Engenharia Civil estrado Acadêmico Faculdade de Engenharia FEN/UERJ Professor: uciano Rodrigues
Prof. uciano ima - lucianolima@uerj.br Eq.. Diferencial Efeitos 2ª 2 Ordem Programa de Pós-GraduaP Graduação em Engenharia Civil estrado Acadêmico Faculdade de Engenharia FEN/UERJ Professor: uciano Rodrigues
Resistência dos. Materiais. Capítulo 3. - Flexão
 Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais - Flexão cetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Flexão Pura Flexão Simples Flexão
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
Mecânica dos Sólidos I Parte 5 Tensões de Flexão
 Departamento de Engenharia ecânica Parte 5 Tensões de Fleão Prof. Arthur. B. Braga 8.1 ecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos forças, momentos, etc. F 7 F 8 F F 3 Determinar
Departamento de Engenharia ecânica Parte 5 Tensões de Fleão Prof. Arthur. B. Braga 8.1 ecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos forças, momentos, etc. F 7 F 8 F F 3 Determinar
1 Introdução 3. 2 Estática de partículas Corpos rígidos: sistemas equivalentes SUMÁRIO. de forças 67. xiii
 SUMÁRIO 1 Introdução 3 1.1 O que é a mecânica? 4 1.2 Conceitos e princípios fundamentais mecânica de corpos rígidos 4 1.3 Conceitos e princípios fundamentais mecânica de corpos deformáveis 7 1.4 Sistemas
SUMÁRIO 1 Introdução 3 1.1 O que é a mecânica? 4 1.2 Conceitos e princípios fundamentais mecânica de corpos rígidos 4 1.3 Conceitos e princípios fundamentais mecânica de corpos deformáveis 7 1.4 Sistemas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 06 TORÇÃO Augusto Romanini Sinop - MT 2017/1 AULAS
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 06 TORÇÃO Augusto Romanini Sinop - MT 2017/1 AULAS
Objetivo: Determinar a equação da curva de deflexão e também encontrar deflexões em pontos específicos ao longo do eixo da viga.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
PROJETO ESTRUTURAL. Márcio R. S. Corrêa ASSOCIAÇÃO BRASILEIRA DE CIMENTO PORTLAND
 PROJETO ESTRUTURAL Márcio R. S. Corrêa Exemplo de Dimenionamento de Elemento CAE / Compreão imple Determinar a reitência mínima de bloco que deve ter a parede de alvenaria não-armada, indicada na igura,
PROJETO ESTRUTURAL Márcio R. S. Corrêa Exemplo de Dimenionamento de Elemento CAE / Compreão imple Determinar a reitência mínima de bloco que deve ter a parede de alvenaria não-armada, indicada na igura,
No dimensionamento à flexão simples, os efeitos do esforço cortante podem
 FLEXÃO SIMPLES NA RUÍNA: EQUAÇÕES CAPÍTULO 7 Libânio M. Pinheiro, Caiane D. Muzardo, Sandro P. Santo. 12 maio 2003 FLEXÃO SIMPLES NA RUÍNA: EQUAÇÕES 7.1 HIPÓTESES No dimenionamento à flexão imple, o efeito
FLEXÃO SIMPLES NA RUÍNA: EQUAÇÕES CAPÍTULO 7 Libânio M. Pinheiro, Caiane D. Muzardo, Sandro P. Santo. 12 maio 2003 FLEXÃO SIMPLES NA RUÍNA: EQUAÇÕES 7.1 HIPÓTESES No dimenionamento à flexão imple, o efeito
Sumário e Objectivos. Mecânica dos Sólidos 8ªAula. Lúcia M.J.S. Dinis 2007/2008
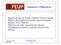 Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Perfis Tubulares Objectivos da Aula: Apreensão dos conceitos
Sumário e Objectivos Sumário: Função de Prandtl. Torção de Veios de Secção Elíptica e Rectangular e de Secções Abertas de paredes delgadas. Perfis Tubulares Objectivos da Aula: Apreensão dos conceitos
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais I. Capítulo 6 Flexão
 Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
Capítulo 6 Flexão 6.1 Deformação por flexão de um elemento reto A seção transversal de uma viga reta permanece plana quando a viga se deforma por flexão. Isso provoca uma tensão de tração de um lado da
RESISTÊNCIA DE MATERIAIS II
 INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
INSTITUTO SUPERIOR TÉCNICO Departamento de Engenharia Civil e Arquitectura Secção de Mecânica Estrutural, Estruturas e Construção Ano lectivo de 2003/2004 2 o teste e o exame Lisboa, 23 de Junho de 2004
Resistência dos Materiais I - Caderno de Consultas
 Resistência dos Materiais I - Caderno de Consultas Instruções: Resolva as questões com clareza e ordem. A interpretação dos enunciados faz parte da prova. Não sendo indicado o contrário, use aproximações
Resistência dos Materiais I - Caderno de Consultas Instruções: Resolva as questões com clareza e ordem. A interpretação dos enunciados faz parte da prova. Não sendo indicado o contrário, use aproximações
Programa. Centroide Momentos de Inércia Teorema dos Eixos Paralelos. 2 Propriedades Geométricas de Áreas Planas
 Propriedades Geométricas de Áreas Planas Programa 2 Propriedades Geométricas de Áreas Planas Centroide Momentos de Inércia Teorema dos Eixos Paralelos L Goliatt, M Farage, A Cury (MAC/UFJF) MAC-015 Resistência
Propriedades Geométricas de Áreas Planas Programa 2 Propriedades Geométricas de Áreas Planas Centroide Momentos de Inércia Teorema dos Eixos Paralelos L Goliatt, M Farage, A Cury (MAC/UFJF) MAC-015 Resistência
Deflexão em vigas de eixo reto
 10 de novembro de 2016 Linha elástica da flexão é a curva formada pelo eixo de uma viga inicialmente retilíneo, devido à aplicação de momentos de flexão. Figura : Exemplo de viga em flexão Antes da aplicação
10 de novembro de 2016 Linha elástica da flexão é a curva formada pelo eixo de uma viga inicialmente retilíneo, devido à aplicação de momentos de flexão. Figura : Exemplo de viga em flexão Antes da aplicação
Resistência dos Materiais
 Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Resistência dos Materiais Eng. Mecânica, Produção UNIME 2016.1 Lauro de Freitas, Março, 2016. 3 Torção Conteúdo Introdução Cargas de Torção em Eixos Circulares Torque Puro Devido a Tensões Internas Componentes
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Capítulo 5. Torção Pearson Prentice Hall. Todos os direitos reservados.
 Capítulo 5 Torção slide 1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento
Capítulo 5 Torção slide 1 Deformação por torção de um eixo circular Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
 Q1: ESCOA POITÉCNICA DA UNIVERSIDADE DE SÃO PAUO Q: Q3: Nota: PME310 Mecânica dos Sólidos I Prova Substitutiva 04/07/018 Duração: 10 minutos Não é permitido o uso de equipamentos eletrônicos durante a
Q1: ESCOA POITÉCNICA DA UNIVERSIDADE DE SÃO PAUO Q: Q3: Nota: PME310 Mecânica dos Sólidos I Prova Substitutiva 04/07/018 Duração: 10 minutos Não é permitido o uso de equipamentos eletrônicos durante a
1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional = 4200 knm²
 CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
6 TORÇÃO SIMPLES. Equação 6.1. Ou, uma vez que df = da, com sendo a tensão de cisalhamento do elementos de área da, Equação 6.2
 6 TORÇÃO SIMPLES Torção simples ocorre quando a resultante na seção for um binário cujo plano de ação é o da própria seção. Considerando a barra de seção circular AB submetida em A e B a toques iguais
6 TORÇÃO SIMPLES Torção simples ocorre quando a resultante na seção for um binário cujo plano de ação é o da própria seção. Considerando a barra de seção circular AB submetida em A e B a toques iguais
Momento torsor. Torção em Eixos de Seção Retangular. 26 de setembro de 2016
 Torção em Eixos de Seção Retangular 26 de setembro de 2016 Torção em Eixos de Seção Retangular Quando um torque é aplicado a um eixo de seção transversal circular, as deforamções por cisalhamento variam
Torção em Eixos de Seção Retangular 26 de setembro de 2016 Torção em Eixos de Seção Retangular Quando um torque é aplicado a um eixo de seção transversal circular, as deforamções por cisalhamento variam
Física I. Oscilações - Resolução
 Quetõe: Fíica I Ocilaçõe - Reolução Q1 - Será que a amplitude eacontantenafae de um ocilador, podem er determinada, e apena for epecificada a poição no intante =0? Explique. Q2 - Uma maa ligada a uma mola
Quetõe: Fíica I Ocilaçõe - Reolução Q1 - Será que a amplitude eacontantenafae de um ocilador, podem er determinada, e apena for epecificada a poição no intante =0? Explique. Q2 - Uma maa ligada a uma mola
MAC-015 Resistência dos Materiais Unidade 03
 MAC-015 Resistência dos Materiais Unidade 03 Engenharia Elétrica Engenharia de Produção Engenharia Sanitária e Ambiental Leonardo Goliatt, Michèle Farage, Alexandre Cury Departamento de Mecânica Aplicada
MAC-015 Resistência dos Materiais Unidade 03 Engenharia Elétrica Engenharia de Produção Engenharia Sanitária e Ambiental Leonardo Goliatt, Michèle Farage, Alexandre Cury Departamento de Mecânica Aplicada
3. Modelagem Numérica
 67 3. Modelagem Numérica Nete capítulo realiza-e um etudo ervindo-e de imulaçõe numérica com o método do elemento finito para conhecer o comportamento e otimizar o dimenionamento do reparo tipo luva, aim
67 3. Modelagem Numérica Nete capítulo realiza-e um etudo ervindo-e de imulaçõe numérica com o método do elemento finito para conhecer o comportamento e otimizar o dimenionamento do reparo tipo luva, aim
(NBR 8800, Tabela C.1)
 CE Estabilidade das Construções II FESP Faculdade de Engenharia São Paulo Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Nome: Matrícula ORIENTAÇÕES PARA PROVA Avaliação: A1 Data: 13/abr/
CE Estabilidade das Construções II FESP Faculdade de Engenharia São Paulo Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Nome: Matrícula ORIENTAÇÕES PARA PROVA Avaliação: A1 Data: 13/abr/
Mecânica dos Sólidos I Parte 3 Estado Plano de Tensão
 Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
Departamento de Engenharia Mecânica Parte 3 Estado Plano de Tensão Prof. Arthur M. B. Braga 15.1 Mecânica dos Sólidos Problema F 1 Corpo sujeito a ação de esforços eternos (forças, momentos, etc.) F 7
Placas Largura Efetiva
 Placas Largura Efetiva Programa de Pós-Graduação em Engenharia Civil PGECIV - Mestrado Acadêmico Faculdade de Engenharia FEN/UERJ Disciplina: Fundamentos Estruturais I Professor: Luciano Rodrigues Ornelas
Placas Largura Efetiva Programa de Pós-Graduação em Engenharia Civil PGECIV - Mestrado Acadêmico Faculdade de Engenharia FEN/UERJ Disciplina: Fundamentos Estruturais I Professor: Luciano Rodrigues Ornelas
ESCOAMENTOS VARIÁVEIS EM PRESSÃO (Choque Hidráulico)
 ECOAMENTO VARIÁVEI EM PREÃO (Choque Hidráulico) Equações Fundamentais 26-5-2003 Equações Fundamentais 1 Escoamentos variáveis em pressão: regime gradualmente variado (ou quase-permanente) ou regime rapidamente
ECOAMENTO VARIÁVEI EM PREÃO (Choque Hidráulico) Equações Fundamentais 26-5-2003 Equações Fundamentais 1 Escoamentos variáveis em pressão: regime gradualmente variado (ou quase-permanente) ou regime rapidamente
5 CISALHAMENTO SIMPLES
 5 CISALHAMENTO SIMPLES Conforme visto anteriormente, sabe-se que um carregamento transversal aplicado em uma viga resulta em tensões normais e de cisalhamento em qualquer seção transversal dessa viga.
5 CISALHAMENTO SIMPLES Conforme visto anteriormente, sabe-se que um carregamento transversal aplicado em uma viga resulta em tensões normais e de cisalhamento em qualquer seção transversal dessa viga.
TEORIA DAS ESTRUTURAS II PROF.: VICTOR MACHADO
 TEORIA DAS ESTRUTURAS II PROF.: VICTOR MACHADO APRESENTAÇÃO Contatos: victor.silva@progeto.com.br victormsilva.com PLANO DE AULA Apresentação do Plano de Aula Forma de Avaliação Faltas e Atrasos UNIDADE
TEORIA DAS ESTRUTURAS II PROF.: VICTOR MACHADO APRESENTAÇÃO Contatos: victor.silva@progeto.com.br victormsilva.com PLANO DE AULA Apresentação do Plano de Aula Forma de Avaliação Faltas e Atrasos UNIDADE
Resistência dos Materiais. Aula 6 Estudo de Torção, Transmissão de Potência e Torque
 Aula 6 Estudo de Torção, Transmissão de Potência e Torque Definição de Torque Torque é o momento que tende a torcer a peça em torno de seu eixo longitudinal. Seu efeito é de interesse principal no projeto
Aula 6 Estudo de Torção, Transmissão de Potência e Torque Definição de Torque Torque é o momento que tende a torcer a peça em torno de seu eixo longitudinal. Seu efeito é de interesse principal no projeto
Resistência dos Materiais
 - Torção Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva Índice Tensões de corte nas secções circulares Rotação das secções Torção em veios circulares
- Torção Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e V. Dias da Silva Índice Tensões de corte nas secções circulares Rotação das secções Torção em veios circulares
Estacas sob acções sísmicas
 Etaca ob acçõe ímica - 1 Metrado em Engenharia de Etrutura Fundaçõe de Etrutura Etaca ob acçõe ímica Jaime A. Santo Dimenionamento de etaca ob acçõe ímica Etaca ob acçõe ímica - 2 AASHTO(1983); JSCE(1988);
Etaca ob acçõe ímica - 1 Metrado em Engenharia de Etrutura Fundaçõe de Etrutura Etaca ob acçõe ímica Jaime A. Santo Dimenionamento de etaca ob acçõe ímica Etaca ob acçõe ímica - 2 AASHTO(1983); JSCE(1988);
Cálculo Diferencial e Integral II. Lista 8 - Exercícios/ Resumo da Teoria
 Cálculo Diferencial e Integral II Lita 8 - Exercício/ Reumo da Teoria Derivada Direcionai Definição Derivada Direcional. A derivada da função f x, no ponto P x, na direção do veror u u 1, u é o número
Cálculo Diferencial e Integral II Lita 8 - Exercício/ Reumo da Teoria Derivada Direcionai Definição Derivada Direcional. A derivada da função f x, no ponto P x, na direção do veror u u 1, u é o número
DEPARTAMENTO DE ENGENHARIA MECÂNICA. ) uma base ortonormal positiva de versores de V. Digamos que a lei de transformação do operador T seja dada por:
 PME-00 - Mecânica dos Sólidos a ista de Exercícios Apresentar as unidades das seguintes grandezas, segundo o Sistema nternacional de Unidades (S..: a comprimento (l; i rotação (θ; b força concentrada (P;
PME-00 - Mecânica dos Sólidos a ista de Exercícios Apresentar as unidades das seguintes grandezas, segundo o Sistema nternacional de Unidades (S..: a comprimento (l; i rotação (θ; b força concentrada (P;
Sumário e Objectivos. Lúcia M.J.S. Dinis 2007/2008. Mecânica dos Sólidos 7ª Aula
 Sumário e Objectivos Sumário: Torção de Veios de Secção Circular Objectivos da Aula: Apreensão dos conceitos Fundamentais associados à torção de veios de Secção Circular. 1 2 Torção 3 Vigas 4 Torção de
Sumário e Objectivos Sumário: Torção de Veios de Secção Circular Objectivos da Aula: Apreensão dos conceitos Fundamentais associados à torção de veios de Secção Circular. 1 2 Torção 3 Vigas 4 Torção de
Curso de Engenharia Civil. Universidade Estadual de Maringá Centro de Tecnologia Departamento de Engenharia Civil CAPÍTULO 3: FLEXÃO
 Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
Curso de Engenharia Civil Universidade Estadual de aringá Centro de Tecnologia Departamento de Engenharia Civil CÍTULO 3: FLEXÃO 3. Revisão de Esforços nternos étodo das Seção: 3. Revisão de Esforços nternos
Universidade Federal de Pelotas Centro de Engenharias. Resistência dos Materiais II. Capítulo 2 Torção
 Capítulo 2 Torção 2.1 Revisão Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e o raio do eixo permanecerão inalterados.
Capítulo 2 Torção 2.1 Revisão Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal. Se o ângulo de rotação for pequeno, o comprimento e o raio do eixo permanecerão inalterados.
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. eer E. Russell Johnston, Jr. Deflexão de Vigas por Integração Capítulo 7 Deflexão de Vigas por Integração 7.1 Introdução 7. Deformação de
Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. eer E. Russell Johnston, Jr. Deflexão de Vigas por Integração Capítulo 7 Deflexão de Vigas por Integração 7.1 Introdução 7. Deformação de
PSI3213 CIRCUITOS ELÉTRICOS II
 PSI33 CIRCUITOS ELÉTRICOS II Solução do Exercício Complementare Correpondente à Matéria da a Prova a) il ( ) = ( não há geradore independente ) Reitência equivalente vita pelo indutor: i i 5 i E i = i
PSI33 CIRCUITOS ELÉTRICOS II Solução do Exercício Complementare Correpondente à Matéria da a Prova a) il ( ) = ( não há geradore independente ) Reitência equivalente vita pelo indutor: i i 5 i E i = i
4ª LISTA DE EXERCÍCIOS PROBLEMAS ENVOLVENDO ANÁLISE DE TENSÕES
 Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
Universidade Federal da Bahia Escola Politécnica Departamento de Construção e Estruturas Disciplina: ENG285 - Resistência dos Materiais I-A Professor: Armando Sá Ribeiro Jr. www.resmat.ufba.br 4ª LISTA
TORÇÃO. Prof. Dr. Carlos A. Nadal
 TORÇÃO Prof. Dr. Carlos A. Nadal Tipo de esforços a) Tração b) Compressão c) Flexão d) Torção e) Compressão f) flambagem Esforços axiais existe uma torção quando uma seção transversal de uma peça está
TORÇÃO Prof. Dr. Carlos A. Nadal Tipo de esforços a) Tração b) Compressão c) Flexão d) Torção e) Compressão f) flambagem Esforços axiais existe uma torção quando uma seção transversal de uma peça está
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
 Univeridade Salvador UNIFACS Curo de Engenharia Método Matemático Aplicado / Cálculo Avançado / Cálculo IV Profa: Ila Rebouça Freire A Tranformada de Laplace Texto 0: A Tranformada Invera. A Derivada da
Univeridade Salvador UNIFACS Curo de Engenharia Método Matemático Aplicado / Cálculo Avançado / Cálculo IV Profa: Ila Rebouça Freire A Tranformada de Laplace Texto 0: A Tranformada Invera. A Derivada da
III- FLEXÃO SIMPLES 1- EQUAÇÕES DE COMPATIBILIDADE DE DEFORMAÇÃO
 III- FLEXÃO SIMPLES - EQUAÇÕES DE COMPATIBILIDADE DE DEFORMAÇÃO A eormaçõe na lexão imple correponem ao omínio, 3 e 4. O valore e x que limitam ete omínio poem er obtio acilmente a equaçõe e compatibiliae
III- FLEXÃO SIMPLES - EQUAÇÕES DE COMPATIBILIDADE DE DEFORMAÇÃO A eormaçõe na lexão imple correponem ao omínio, 3 e 4. O valore e x que limitam ete omínio poem er obtio acilmente a equaçõe e compatibiliae
2 TORÇÃO EM VIGAS Notas Iniciais
 2 TORÇÃO EM VIGAS 2.1. Notas Iniciais As teorias clássicas para torção em materiais homogêneos isótropos, e posteriormente para elementos de concreto de seção retangular são analisadas e discutidas neste
2 TORÇÃO EM VIGAS 2.1. Notas Iniciais As teorias clássicas para torção em materiais homogêneos isótropos, e posteriormente para elementos de concreto de seção retangular são analisadas e discutidas neste
MAC-015 Resistência dos Materiais Unidade 02
 MAC-015 Resistência dos Materiais Unidade 02 Engenharia Elétrica Engenharia de Produção Engenharia Sanitária e Ambiental Leonardo Goliatt, Michèle Farage, Alexandre Cury Departamento de Mecânica Aplicada
MAC-015 Resistência dos Materiais Unidade 02 Engenharia Elétrica Engenharia de Produção Engenharia Sanitária e Ambiental Leonardo Goliatt, Michèle Farage, Alexandre Cury Departamento de Mecânica Aplicada
Torção de uma Barra Prismática
 Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Torção de uma Barra Prismática 1 Torção de uma Barra Prismática Torção Uniforme ou de Saint Venant; Aplicação do método semi-inverso. 2 Figura 1. Barra prismática genérica. Barra submetida a momentos de
Exercícios de linha elástica - prof. Valério SA Universidade de São Paulo - USP
 São Paulo, dezembro de 2015. 1. Um pequeno veículo de peso P se move ao longo de uma viga de seção retangular de largura e altura de, respectivamente, 2 e 12 cm. Determinar a máxima distância s, conforme
São Paulo, dezembro de 2015. 1. Um pequeno veículo de peso P se move ao longo de uma viga de seção retangular de largura e altura de, respectivamente, 2 e 12 cm. Determinar a máxima distância s, conforme
Estacas sob acções sísmicas
 Etaca ob acçõe ímica - 1 Metrado em Geotecnia para Engenharia Civil Fundaçõe Etaca ob acçõe ímica Jaime A. Santo Dimenionamento de etaca ob acçõe ímica Etaca ob acçõe ímica - 2 AASHTO(1983); JSCE(1988);
Etaca ob acçõe ímica - 1 Metrado em Geotecnia para Engenharia Civil Fundaçõe Etaca ob acçõe ímica Jaime A. Santo Dimenionamento de etaca ob acçõe ímica Etaca ob acçõe ímica - 2 AASHTO(1983); JSCE(1988);
Tensões de Flexão nas Vigas
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões de Flexão nas Vigas
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões de Flexão nas Vigas
Sumário. Introdução O conceito de tensão 1. Tensão e deformação Carregamento axial 49
 1 Introdução O conceito de tensão 1 Introdução 2 1.1 Um breve exame dos métodos da estática 2 1.2 Tensões nos elementos de uma estrutura 4 1.3 Tensão em um plano oblíquo sob carregamento axial 25 1.4 Tensão
1 Introdução O conceito de tensão 1 Introdução 2 1.1 Um breve exame dos métodos da estática 2 1.2 Tensões nos elementos de uma estrutura 4 1.3 Tensão em um plano oblíquo sob carregamento axial 25 1.4 Tensão
Vibrações Mecânicas. Sistemas Contínuos. DEMEC UFPE Ramiro Willmersdorf
 Vibrações Mecânicas DEMEC UFPE Ramiro Willmersdorf ramiro@willmersdor.net Sistemas contínuos ou distribuídos Equações diferenciais parciais; Cabos, cordas, vigas, etc.; Membranas, placas, etc; Processo
Vibrações Mecânicas DEMEC UFPE Ramiro Willmersdorf ramiro@willmersdor.net Sistemas contínuos ou distribuídos Equações diferenciais parciais; Cabos, cordas, vigas, etc.; Membranas, placas, etc; Processo
MECÂNICA DO CONTÍNUO. Tópico 3. Método dos Trabalhos Virtuais
 MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
MECÂNICA DO CONTÍNUO Tópico 3 Método dos Trabalhos Virtuais PROF. ISAAC NL SILVA Aspecto físico do equilíbrio Instável Estável P y1 y2 P Indiferente P Aspecto matemático: Eq. Instável d 2 V/dx 2
Sumário e Objectivos. Sumário: Resolução de Problemas. Objectivos da Aula: Ser Capaz de resolver problemas com perfis tubulares
 Sumário e Objectivos Sumário: Resolução de Problemas. Objectivos da Aula: Ser Capaz de resolver problemas com perfis tubulares 1 Vigas 2 Camião 3 Bicicleta 4 Função de Tensão de Prandtl A solução do problema
Sumário e Objectivos Sumário: Resolução de Problemas. Objectivos da Aula: Ser Capaz de resolver problemas com perfis tubulares 1 Vigas 2 Camião 3 Bicicleta 4 Função de Tensão de Prandtl A solução do problema
Projeto do compensador PID no lugar das raízes
 Projeto do compenador PID no lugar da raíze 0 Introdução DAELN - UTFPR - Controle I Paulo Roberto Brero de Campo Neta apotila erão etudado o projeto do compenadore PI, PD e PID atravé do lugar da raíze
Projeto do compenador PID no lugar da raíze 0 Introdução DAELN - UTFPR - Controle I Paulo Roberto Brero de Campo Neta apotila erão etudado o projeto do compenadore PI, PD e PID atravé do lugar da raíze
ENG285 4ª Unidade 1. Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais.
 ENG285 4ª Unidade 1 Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para seção retangular: I =. Para
ENG285 4ª Unidade 1 Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para seção retangular: I =. Para
São as vigas que são fabricadas com mais de um material.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões em Vigas Tópicos
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões em Vigas Tópicos
O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal.
 CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
CENTRÓIDES E MOMENTO DE INÉRCIA Centróide O centróide de área é definido como sendo o ponto correspondente ao centro de gravidade de uma placa de espessura infinitesimal. De uma maneira bem simples: centróide
ANEXO A6.1. Determinação do esforço axial atuante na tábua de madeira definida na Secção
 ANEXO A6.1 Determinação do esforço axial atuante na tábua de madeira definida na Secção 6.4.2.1. As ações permanentes e variáveis consideradas no sótão e na cobertura do edifício de tabique são as indicadas
ANEXO A6.1 Determinação do esforço axial atuante na tábua de madeira definida na Secção 6.4.2.1. As ações permanentes e variáveis consideradas no sótão e na cobertura do edifício de tabique são as indicadas
RESISTÊNCIA DOS MATERIAIS II CISALHAMENTO TRANSVERSAL PARTE I
 RESISTÊNCIA DOS MATERIAIS II CISALHAMENTO TRANSVERSAL PARTE I Prof. Dr. Daniel Caetano 2012-2 Objetivos Conceituar cisalhamento transversal Compreender quando ocorre o cisalhamento transversal Determinar
RESISTÊNCIA DOS MATERIAIS II CISALHAMENTO TRANSVERSAL PARTE I Prof. Dr. Daniel Caetano 2012-2 Objetivos Conceituar cisalhamento transversal Compreender quando ocorre o cisalhamento transversal Determinar
Convecção Natural. v (N 1) x T (N 3)
 Introdução Convecção Natural Convecção Natural em Placa Vertical O problema de convecção natural em placa verticai pode er analiado a partir da equação de quantidade de movimento na direcção vertical.
Introdução Convecção Natural Convecção Natural em Placa Vertical O problema de convecção natural em placa verticai pode er analiado a partir da equação de quantidade de movimento na direcção vertical.
MECSOL34 Mecânica dos Sólidos I
 MECSOL34 Mecânica dos Sólidos I Curso Superior em Tecnologia Mecatrônica Industrial 3ª fase Prof.º Gleison Renan Inácio Sala 9 Bl 5 joinville.ifsc.edu.br/~gleison.renan Tópicos abordados Conceito de Tensão
MECSOL34 Mecânica dos Sólidos I Curso Superior em Tecnologia Mecatrônica Industrial 3ª fase Prof.º Gleison Renan Inácio Sala 9 Bl 5 joinville.ifsc.edu.br/~gleison.renan Tópicos abordados Conceito de Tensão
Pressão Interna + Momento Fletor e Esforço Axial.
 3 Método Anaĺıtico Este capítulo apresenta o desenvolvimento analítico para determinação das tensões atuantes no tubo da bancada de ensaios descrita anteriormente, causadas pelos carregamentos de pressão
3 Método Anaĺıtico Este capítulo apresenta o desenvolvimento analítico para determinação das tensões atuantes no tubo da bancada de ensaios descrita anteriormente, causadas pelos carregamentos de pressão
Coeficientes de dilatação térmica - linear
 Cálculo da junta Coeficiente de dilatação térmica - linear MATERIAL 10-6 (mm / mm / ºC) Alv. de tijolo e emboço 6 Alv. de tijolo e cerâmica 5 Concreto etrutural 9 Vidro 9 Acrílico 81 PVC 60 Granito 11
Cálculo da junta Coeficiente de dilatação térmica - linear MATERIAL 10-6 (mm / mm / ºC) Alv. de tijolo e emboço 6 Alv. de tijolo e cerâmica 5 Concreto etrutural 9 Vidro 9 Acrílico 81 PVC 60 Granito 11
4 SOLUÇÕES ANALÍTICAS
 4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
4 SOLUÇÕES ANALÍTICAS 4 Desenvolvimento Dentre os mais diversos tipos de estruturas que fazem uso de materiais compósitos, os tubos cilindricos laminados são um caso particular em que soluções analíticas,
APRESENTAÇÃO TÓPICOS FUNDAMENTAIS HIPÓTESES ADMITIDAS COMPONENTES DE TENSÃO Componentes de tensão médias...
 SUMÁRIO APRESENTAÇÃO... 11 1. INTRODUÇÃO... 13 2. TÓPICOS FUNDAMENTAIS...17 2.1 HIPÓTESES ADMITIDAS...17 2.2 COMPONENTES DE TENSÃO...17 2.2.1 Componentes de tensão médias...17 2.2.2 Componentes de tensão
SUMÁRIO APRESENTAÇÃO... 11 1. INTRODUÇÃO... 13 2. TÓPICOS FUNDAMENTAIS...17 2.1 HIPÓTESES ADMITIDAS...17 2.2 COMPONENTES DE TENSÃO...17 2.2.1 Componentes de tensão médias...17 2.2.2 Componentes de tensão
Exercícios de Resistência dos Materiais A - Área 3
 1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
1) Os suportes apóiam a vigota uniformemente; supõe-se que os quatro pregos em cada suporte transmitem uma intensidade igual de carga. Determine o menor diâmetro dos pregos em A e B se a tensão de cisalhamento
Escoamento potencial
 Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
Escoamento potencial J. L. Baliño Escola Politécnica - Universidade de São Paulo Apostila de aula 2017, v.1 Escoamento potencial 1 / 26 Sumário 1 Propriedades matemáticas 2 Escoamento potencial bidimensional
Introdução cargas externas cargas internas deformações estabilidade
 TENSÃO Introdução A mecânica dos sólidos estuda as relações entre as cargas externas aplicadas a um corpo deformável e a intensidade das cargas internas que agem no interior do corpo. Esse assunto também
TENSÃO Introdução A mecânica dos sólidos estuda as relações entre as cargas externas aplicadas a um corpo deformável e a intensidade das cargas internas que agem no interior do corpo. Esse assunto também
FESP Faculdade de Engenharia São Paulo. Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr.
 FESP Faculdade de Engenharia São Paulo Avaliação: A2 Data: 15/set/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Duração: 85 minutos Nome: Matrícula
FESP Faculdade de Engenharia São Paulo Avaliação: A2 Data: 15/set/ 2014 CE2 Estabilidade das Construções II Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Duração: 85 minutos Nome: Matrícula
CÁLCULO DE ARMADURAS LONGITUDINAIS DE VIGAS RECTANGULARES DE BETÃO ARMADO SUJEITAS A FLEXÃO SIMPLES PLANA DE ACORDO COM O EUROCÓDIGO 2
 Nº 6 NOV. 008 VOL. 6 ISSN 645-5576 CÁLCULO DE ARMADURAS LONGITUDINAIS DE VIGAS RECTANGULARES DE BETÃO ARMADO SUJEITAS A FLEXÃO SIMPLES PLANA DE ACORDO COM O EUROCÓDIGO E. JÚLIO Profeor Auxiliar DEC FCTUC
Nº 6 NOV. 008 VOL. 6 ISSN 645-5576 CÁLCULO DE ARMADURAS LONGITUDINAIS DE VIGAS RECTANGULARES DE BETÃO ARMADO SUJEITAS A FLEXÃO SIMPLES PLANA DE ACORDO COM O EUROCÓDIGO E. JÚLIO Profeor Auxiliar DEC FCTUC
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE III
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE III Prof. Dr. Daniel Caetano 2012-2 Objetivos Conceituar e capacitar paa a resolução de problemas estaticamente indeterminados na torção Compreender as limitações
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE III Prof. Dr. Daniel Caetano 2012-2 Objetivos Conceituar e capacitar paa a resolução de problemas estaticamente indeterminados na torção Compreender as limitações
DIMENSIONAMENTO PLÁSTICO DE PÓRTICOS METÁLICOS. Vítor José Fernandes Félix Vitorino Paulo de Oliveira Ribeiro Leal SUMÁRIO
 DIMESIOAMETO PLÁSTICO DE PÓRTICOS METÁLICOS Vítor Joé Fernande Félix Vitorino Paulo de Oliveira Ribeiro Leal SUMÁRIO O preente trabalho foi realizado no âmbito do programa da diciplina de Seminário de
DIMESIOAMETO PLÁSTICO DE PÓRTICOS METÁLICOS Vítor Joé Fernande Félix Vitorino Paulo de Oliveira Ribeiro Leal SUMÁRIO O preente trabalho foi realizado no âmbito do programa da diciplina de Seminário de
Departamento de Ciências Aeroespaciais - Universidade da Beira Interior. Cascas. Cascas
 Placa e Placa e 764 3º Ano da Licenciatura em Engenharia Aeronáutica Placa e. Tenõe de Membrana em Uma caca é um corpo tridimenional com: uma da ua dimenõe muito menor do que a outra dua; a curvatura da
Placa e Placa e 764 3º Ano da Licenciatura em Engenharia Aeronáutica Placa e. Tenõe de Membrana em Uma caca é um corpo tridimenional com: uma da ua dimenõe muito menor do que a outra dua; a curvatura da
Disciplina: Resistência dos Materiais Unidade V - Flexão. Professor: Marcelino Vieira Lopes, Me.Eng.
 Disciplina: Resistência dos Materiais Unidade V - Flexão Professor: Marcelino Vieira Lopes, Me.Eng. http://profmarcelino.webnode.com/blog/ Referência Bibliográfica Hibbeler, R. C. Resistência de materiais.
Disciplina: Resistência dos Materiais Unidade V - Flexão Professor: Marcelino Vieira Lopes, Me.Eng. http://profmarcelino.webnode.com/blog/ Referência Bibliográfica Hibbeler, R. C. Resistência de materiais.
3 Avaliação do campo de deformações em torno de uma estaca
 3 valiação do campo de deformaçõe em torno de uma etaca 3.1. Método teórico 3.1.1. Método aeado na funçõe de tranferência de carga Um método aeado na funçõe de tranferência de carga foi inicialmente propoto
3 valiação do campo de deformaçõe em torno de uma etaca 3.1. Método teórico 3.1.1. Método aeado na funçõe de tranferência de carga Um método aeado na funçõe de tranferência de carga foi inicialmente propoto
Mecânica Geral. Prof. Evandro Bittencourt (Dr.) Engenharia de Produção e Sistemas UDESC. 27 de fevereiro de 2008
 Mecânica Geral Prof Evandro Bittencourt (Dr) Engenharia de Produção e Sistemas UDESC 7 de fevereiro de 008 Sumário 1 Prof Evandro Bittencourt - Mecânica Geral - 007 1 Introdução 11 Princípios Fundamentais
Mecânica Geral Prof Evandro Bittencourt (Dr) Engenharia de Produção e Sistemas UDESC 7 de fevereiro de 008 Sumário 1 Prof Evandro Bittencourt - Mecânica Geral - 007 1 Introdução 11 Princípios Fundamentais
ENG285 TORÇÃO. =. á. = G. (material linear-elástico) Adriano Alberto
 ENG285 1 Adriano Alberto Fonte: Hibbeler, R.C., Resistência dos Materiais 5ª edição; Beer 5ª Ed; Barroso, L.C., Cálculo Numérico (com aplicações) 2ª edição; slides do Prof. Alberto B. Vieira Jr.; http://pessoal.sercomtel.com.br/matematica/geometria/geom-areas/geomareas-circ.htm
ENG285 1 Adriano Alberto Fonte: Hibbeler, R.C., Resistência dos Materiais 5ª edição; Beer 5ª Ed; Barroso, L.C., Cálculo Numérico (com aplicações) 2ª edição; slides do Prof. Alberto B. Vieira Jr.; http://pessoal.sercomtel.com.br/matematica/geometria/geom-areas/geomareas-circ.htm
CAPÍTULO 3 ESFORÇO CORTANTE
 CAPÍTULO 3 ESFORÇO CORTANTE 1 o caso: O esforço cortante atuando em conjunto com o momento fletor ao longo do comprimento de uma barra (viga) com cargas transversais. É o cisalhamento na flexão ou cisalhamento
CAPÍTULO 3 ESFORÇO CORTANTE 1 o caso: O esforço cortante atuando em conjunto com o momento fletor ao longo do comprimento de uma barra (viga) com cargas transversais. É o cisalhamento na flexão ou cisalhamento
Transformada de Laplace
 Sinai e Sitema - Tranformada de Laplace A Tranformada de Laplace é uma importante ferramenta para a reolução de equaçõe diferenciai. Também é muito útil na repreentação e análie de itema. É uma tranformação
Sinai e Sitema - Tranformada de Laplace A Tranformada de Laplace é uma importante ferramenta para a reolução de equaçõe diferenciai. Também é muito útil na repreentação e análie de itema. É uma tranformação
