defi departamento de física
|
|
|
- Gabriela Batista Bandeira
- 7 Há anos
- Visualizações:
Transcrição
1 def deparameno de físca Laboraóros de Físca Equações de Fresnel Insuo Superor de Engenhara do Poro Deparameno de Físca Rua Dr. Anóno Bernardno de Almeda, Poro. Tel Fax:
2 Laboraóros de Físca Les de Fresnel Objecvos: Les de Fresnel Compreender o conceo de polarzação da luz; Deermnar o ângulo de Brewser; Traçar expermenalmene as les de Fresnel. Inrodução eórca Segundo as les da reflexão e da refracção, quando um fexe lumnoso ncde na superfíce de separação enre dos meos com dferenes caraceríscas, uma pare desse fexe é reflecdo numa drecção smérca em relação à normal da superfíce, com um ângulo gual ao ângulo de ncdênca Le da Reflexão. O resane fexe é refracado, propagando-se no segundo meo com índce de refracção n, numa drecção que obedece à le da refracção desgnada por Le de Snell (1): n snθ 1 = n snθ (1) A nensdade dos város fexes é deermnada a parr dos coefcenes de reflexão e de ransmssão (), que correspondem à razão enre as ampludes dos campos elécrcos dos fexes reflecdo e ransmdo (ou refracado) relavamene à amplude do fexe ncdene, respecvamene. Sabendo que qualquer po de polarzação pode ser sempre decomposo em duas componenes perpendculares enre s, dever-se-ão dsngur esas duas suações quano ao fexe ncdene, pos as condções fronera mposas na zona de separação enre os meos esão condconadas pela drecção de osclação do campo elécrco ncdene. Assm, dsnguem-se os coefcenes de reflexão e de ransmssão para os dos casos (Fgura 1). E r = E r E = E () Fgura 1 Indcação do plano de ncdênca e das drecções de polarzação para os dferenes fexes: ncdene, reflecdo e refracado. Deparameno de Físca Págna /6
3 Laboraóros de Físca Les de Fresnel a) Quando o fexe ncdene em polarzação perpendcular ao plano de ncdênca, er-se-á: r n1cosθ ncosθ = n cosθ + n cosθ 1 n1 cos = θ n cosθ + n cosθ 1 (3) b) Quando o fexe ncdene em polarzação paralela ao plano de ncdênca, er-se-á: ncosθ n1cosθ r = n cosθ + n cosθ 1 n1 cosθ = n cosθ + n cosθ (4) 1 A nensdade dos fexes reflecdo e ransmdo é deermnada a parr das suas poêncas relavamene ao fexe ncdene. As quandades assm deermnadas são desgnadas por Reflecânca R e Transmânca T. Sendo a reflecânca R a razão enre as respecvas nensdades, esa será gual ao quadrado do coefcene de reflexão, r (5), uma vez que o meo de propagação é o mesmo para os fexes reflecdo e ncdene. Em conraparda, o fexe ransmdo ao propagar-se num meo com índce de refracção dferene numa drecção de propagação ambém dferene, va sofrer expansão,.e., o dâmero do fexe no segundo meo é maor (se n > n 1 ). Nese caso, a ransmânca T é proporconal ao quadrado do coefcene de ransmssão,, com um facor de proporconaldade desgnado por facor de expansão do fexe e represenado em (6). R I I r = = r (5) T I I n n = = 1 cosθ cosθ (6) De acordo com as duas suações de polarzação do campo elécrco ncdene, ambém se dsnguem as reflecâncas e as ransmâncas em função dessa polarzação, conforme as expressões segunes ndcam: R I = = = = I sen ( θ r θ ) Ir g ( ) R θ θ sen ( θ + θ) I g ( θ + θ) (7) T nwi n cosθ 4sen θ cos θ = = nwi 1 n1 cosθ sen ( θ+ θ) wi n cosθ 4sen θ cos θ T = = wi θ θ θ θ θ n1 cos sen cos ( + ) ( ) (8) onde, w w represenam respecvamene, as larguras dos fexes ncdene e ransmdo. Deparameno de Físca Págna 3/6
4 Laboraóros de Físca Les de Fresnel Ângulo de Brewser Quando θ + θ = 90º, a onda reflecda va emergr lnearmene polarzada, apenas com a componene do campo elécrco perpendcular ao plano de ncdênca, pos a sua componene paralela anula-se. O ângulo de ncdênca para o qual se verfca esa suação é desgnado por ângulo de Brewser, podendo ser calculado a parr da le de Snell, resulando em: g B n n θ = (9) 1 Incdênca normal Quando o fexe ncde com drecção normal à superfíce,.e., θ θ 0º e perpendcular são dêncas e as equações de Fresnel escrevem-se como: = =, as componenes paralela n n 1 = = e n1+ n R R R 4nn 1 T = T T = ( n + n ) (10) 1 Nesa suação a reflexão é mínma. A reflexão aumena com a amplude do ângulo de ncdênca. Para θ = 90º a reflexão é oal para ambas as componenes da onda,.e., R = 1. Na Fgura esão represenados dos gráfcos referenes às reflecâncas observadas em função do ângulo de ncdênca, para dferenes meos, nas duas suações de polarzação. A parr deses gráfcos pode-se deermnar o valor do ângulo de Brewser para os nerfaces represenados. Verfca-se que para meos de ransmssão com índces de refracção maores, o ângulo de Brewser aumena. Fgura - Coefcenes de reflexão para n 1 =1 e n = 1.3 (cma) e para n 1 =1 e n = (baxo) em função do ângulo de ncdênca (θ). Deparameno de Físca Págna 4/6
5 Laboraóros de Físca Les de Fresnel Maeral Necessáro Laser Foodíodo Volímero Polarod Transferdor Placa espessa ransparene Procedmeno expermenal 1. Verfque se a monagem expermenal esá de acordo com o esquema represenado na Fgura 3.. Coloque a placa espessa ransparene em cma do ransferdor graduado. Faça ncdr a luz laser rasane ao ransferdor e aponada para o cenro do mesmo de forma a ler a escala correcamene. Laser Polarod Foodíodo Fgura 3 Esquema de monagem. Deermnação do ângulo de Brewser 3. Com a ajuda do Polarod, orene o fexe laser de forma a er o exo de polarzação paralelo ao plano de ncdênca. 4. Vá rodando a placa de plásco sobre o ransferdor de forma ao fexe laser ncdr com um ângulo cada vez maor. Procure o ângulo de Brewser,.e., procure a ncdênca para a qual o fexe reflecdo pela placa ransparene ver um mínmo de nensdade. ATENÇÃO: Exsem pelos menos dos fexes reflecdos na placa, orgnados pela reflexão em cada uma das suas superfíces. Deve consderar somene o fexe reflecdo na prmera superfíce. Deparameno de Físca Págna 5/6
6 Laboraóros de Físca Les de Fresnel 5. Use o valor obdo para deermnar o índce de refracção da placa ransparene, consderando que o índce de refracção do ar é n ar = 1. Verfcação das equações de Fresnel 6. Ajuse o Polarod à saída do laser e rode o laser de forma ao fexe er polarzação horzonal. 7. Coloque o foodíodo orenado para o fexe reflecdo na superfíce da frene da placa (reflexão prncpal ou prmára). 8. Deve er cudado para usar correcamene a fenda que proege o foodíodo da radação ambene. Verfque ambém se o fexe laser esá a ncdr no cenro do foodíodo. NOTA IMPORTANTE: O foodíodo possu uma resposa aproxmadamene lnear de 4mV/lux. A sauração é angda para 450 mv. 9. Faça varar os ângulos de ncdênca, começando por um valor baxo (~10º) aé 90º, em nervalos de 10º. Com o volímero lgado ao foodíodo e usando a escala mas baxa de ensão DC, regse os valores de ensão para cada ângulo. 10. Repa o procedmeno aneror mas com a luz do laser polarzada vercalmene. 11. Represene grafcamene as reflecâncas obdas expermenalmene, comparando-as com as curvas eórcas, usando o índce de refracção meddo anerormene. 1. Represene grafcamene a reflecânca oal R = R + R T. 13. Represene grafcamene a curva da ransmânca para cada uma dos casos de polarzação, a parr dos resulados expermenas. Verfque se exse conservação de energa. Ouras nformações Deverá regsar odas as medções que efecuar, bem como as caraceríscas dos aparelhos de medda ulzados. Todos os cálculos deverão esar ndcados de forma clara, ulzando undades conssenes para as váras grandezas. Referêncas Bblográfcas Physcs Laboraory Expermens (5h edon), Jerry D. Wlson, 1998, Houghon Mffln Company, U.S.A. Laboraory Expermens n College Physcs (7h edon), Ccero H. Bernard & Chrold D. Epp, 1995, John Wley & Sons, Inc. Deparameno de Físca Págna 6/6
7 Laboraóros de Físca Les de Fresnel Anexo A Curso: Les de Fresnel Anexo A Dscplna: Ano: Turma: Grupo #: Daa da realzação: Daa de enrega: Tabelas Tabela 1: Regso dos Aparelhos de Medção Aparelhos Undades Resolução Erro de Leura Tabela : Meddas do fexe reflecdo polarzação horzonal polarzação vercal Ângulo θ V // [mv] R // V [mv] R 10º 0º 30º 40º 50º 60º 70º 80º <90º - -
8 Laboraóros de Físca Les de Fresnel Anexo B Quesões sobre os conceos de: Conceo de polarzação da luz; Ângulo de Brewser; Les de Fresnel. Les de Fresnel Anexo B Quesões - -
Física Experimental IV Polarização por Reflexão ângulo de Brewster. Prof. Alexandre Suaide Prof. Manfredo Tabacniks
 Físca xpermenal IV - 008 Polarzação por Reflexão ângulo de Brewser Prof. Alexandre Suade Prof. Manfredo Tabacnks Reflexão e Refração da Luz fsca.ufpr.br/edlson/cap34.pdf fsca.ufpr.br/edlson/cap34.pdf prsma
Físca xpermenal IV - 008 Polarzação por Reflexão ângulo de Brewser Prof. Alexandre Suade Prof. Manfredo Tabacnks Reflexão e Refração da Luz fsca.ufpr.br/edlson/cap34.pdf fsca.ufpr.br/edlson/cap34.pdf prsma
AGG-232 SÍSMICA I 2011 SÍSMICA DE REFLEXÃO ANÁLISE DE VELOCIDADES
 AGG-3 SÍSMICA I 0 SÍSMICA DE REFLEXÃO AÁLISE DE ELOCIDADES O objevo da análse de velocdades é deermnar as velocdades sísmcas das camadas geológcas em subsuperfíce. As velocdades sísmcas são ulzadas em
AGG-3 SÍSMICA I 0 SÍSMICA DE REFLEXÃO AÁLISE DE ELOCIDADES O objevo da análse de velocdades é deermnar as velocdades sísmcas das camadas geológcas em subsuperfíce. As velocdades sísmcas são ulzadas em
UNIVERSIDADE ESTADUAL PAULISTA UNESP FACULDADE DE ENGENHARIA DE ILHA SOLTEIRA FEIS QUARTA SÉRIE DE EXERCÍCIOS DE ONDAS E LINHAS DE COMUNICAÇÃO
 UNIVERSIDADE ESTADUAL PAULISTA UNESP FACULDADE DE ENGENHARIA DE ILHA SOLTEIRA FEIS QUARTA SÉRIE DE EXERCÍCIOS DE ONDAS E LINHAS DE COMUNICAÇÃO 1) Traçar os gráfcos de magnude e fase do coefcene de reflexão,
UNIVERSIDADE ESTADUAL PAULISTA UNESP FACULDADE DE ENGENHARIA DE ILHA SOLTEIRA FEIS QUARTA SÉRIE DE EXERCÍCIOS DE ONDAS E LINHAS DE COMUNICAÇÃO 1) Traçar os gráfcos de magnude e fase do coefcene de reflexão,
2. FUNDAMENTOS DE CORRENTE ALTERNADA
 Fundamenos de CA 14. FUNDAENTOS DE CORRENTE ALTERNADA Aé o momeno nos preocupamos somene com ensões e correnes conínuas, ou seja, aquelas que possuem módulo e sendo consanes no empo, conforme exemplos
Fundamenos de CA 14. FUNDAENTOS DE CORRENTE ALTERNADA Aé o momeno nos preocupamos somene com ensões e correnes conínuas, ou seja, aquelas que possuem módulo e sendo consanes no empo, conforme exemplos
Módulo 2: Métodos Numéricos. (problemas de valores iniciais e problemas de condições-fronteira)
 Módulo : Méodos Numércos Equações dferencas ordnáras problemas de valores ncas e problemas de condções-fronera Modelação Compuaconal de Maeras -5. Equações dferencas ordnáras - Inrodução Uma equação algébrca
Módulo : Méodos Numércos Equações dferencas ordnáras problemas de valores ncas e problemas de condções-fronera Modelação Compuaconal de Maeras -5. Equações dferencas ordnáras - Inrodução Uma equação algébrca
CAPÍTULO 4. Vamos partir da formulação diferencial da lei de Newton
 9 CPÍTUL 4 DINÂMIC D PRTÍCUL: IMPULS E QUNTIDDE DE MVIMENT Nese capíulo será analsada a le de Newon na forma de negral no domíno do empo, aplcada ao momeno de parículas. Defne-se o conceo de mpulso e quandade
9 CPÍTUL 4 DINÂMIC D PRTÍCUL: IMPULS E QUNTIDDE DE MVIMENT Nese capíulo será analsada a le de Newon na forma de negral no domíno do empo, aplcada ao momeno de parículas. Defne-se o conceo de mpulso e quandade
LISTA DE EXERCÍCIOS DE RECUPERAÇÃO 1º TRIMESTRE MATEMÁTICA
 LISTA DE EXERCÍCIOS DE RECUPERAÇÃO º TRIMESTRE MATEMÁTICA ALUNO(a): Nº: SÉRIE: ª TURMA: UNIDADE: VV JC JP PC DATA: / /07 Obs.: Esa lsa deve ser enregue resolvda no da da prova de recuperação. Valor: 5,0
LISTA DE EXERCÍCIOS DE RECUPERAÇÃO º TRIMESTRE MATEMÁTICA ALUNO(a): Nº: SÉRIE: ª TURMA: UNIDADE: VV JC JP PC DATA: / /07 Obs.: Esa lsa deve ser enregue resolvda no da da prova de recuperação. Valor: 5,0
1 Equações de Maxwell. Corrente de deslocamento.
 1 Equações de Maxwell. Correne de deslocameno. 1.1 Inrodução As equações de Maxwell que formam a base da Teora Elecromagnéca clássca escrevem-se sob a forma (em undades gaussanas): No vácuo [] 1 no S.I.
1 Equações de Maxwell. Correne de deslocameno. 1.1 Inrodução As equações de Maxwell que formam a base da Teora Elecromagnéca clássca escrevem-se sob a forma (em undades gaussanas): No vácuo [] 1 no S.I.
Iluminação e FotoRealismo: Radiosidade
 Ilumnação e oorealsmo: Radosdade Luís Paulo Pexoo dos Sanos hp://gec.d.umnho.p/mcgav/fr Premssas Todas as neracções dos obecos com a luz são dfusas L( x Θ) = L( x), Θ Ω Podemos enão quanfcar a radosdade
Ilumnação e oorealsmo: Radosdade Luís Paulo Pexoo dos Sanos hp://gec.d.umnho.p/mcgav/fr Premssas Todas as neracções dos obecos com a luz são dfusas L( x Θ) = L( x), Θ Ω Podemos enão quanfcar a radosdade
Experiência IV (aulas 06 e 07) Queda livre
 Experênca IV (aulas 06 e 07) Queda lvre 1. Obevos. Inrodução 3. Procedmeno expermenal 4. Análse de dados 5. Quesões 6. Referêncas 1. Obevos Nesa experênca esudaremos o movmeno da queda de um corpo, comparando
Experênca IV (aulas 06 e 07) Queda lvre 1. Obevos. Inrodução 3. Procedmeno expermenal 4. Análse de dados 5. Quesões 6. Referêncas 1. Obevos Nesa experênca esudaremos o movmeno da queda de um corpo, comparando
Conceitos Básicos de Circuitos Elétricos
 onceos Báscos de rcuos lércos. nrodução Nesa aposla são apresenados os conceos e defnções fundamenas ulzados na análse de crcuos elércos. O correo enendmeno e nerpreação deses conceos é essencal para o
onceos Báscos de rcuos lércos. nrodução Nesa aposla são apresenados os conceos e defnções fundamenas ulzados na análse de crcuos elércos. O correo enendmeno e nerpreação deses conceos é essencal para o
Instituto de Física USP. Física V Aula 30. Professora: Mazé Bechara
 Insuo de Físca USP Físca V Aula 30 Professora: Maé Bechara Aula 30 Tópco IV - Posulados e equação básca da Mecânca quânca 1. Os posulados báscos da Mecânca Quânca e a nerpreação probablísca de Ma Born.
Insuo de Físca USP Físca V Aula 30 Professora: Maé Bechara Aula 30 Tópco IV - Posulados e equação básca da Mecânca quânca 1. Os posulados báscos da Mecânca Quânca e a nerpreação probablísca de Ma Born.
Díodo: Regime Dinâmico
 Díodo: eme Dnâmco (exo apoo ao laboraóro) Inrodução Quando se esabelece m crcuo uma ensão ou correne varáves no empo o pono de funconameno em repouso do díodo ambém va varar no empo. A frequênca e amplude
Díodo: eme Dnâmco (exo apoo ao laboraóro) Inrodução Quando se esabelece m crcuo uma ensão ou correne varáves no empo o pono de funconameno em repouso do díodo ambém va varar no empo. A frequênca e amplude
Introdução à Computação Gráfica
 Inrodução à Compuação Gráfca Desenho de Consrução Naval Manuel Venura Insuo Superor Técnco Secção Auónoma de Engenhara Naval Sumáro Represenação maemáca de curvas Curvas polnomas e curvas paramércas Curvas
Inrodução à Compuação Gráfca Desenho de Consrução Naval Manuel Venura Insuo Superor Técnco Secção Auónoma de Engenhara Naval Sumáro Represenação maemáca de curvas Curvas polnomas e curvas paramércas Curvas
Módulo I Ondas Planas. Reflexão e Transmissão com incidência normal Reflexão e Transmissão com incidência oblíqua
 Módulo I Ondas Planas Reflexão e Transmssão com ncdênca normal Reflexão e Transmssão com ncdênca oblíqua Equações de Maxwell Teorema de Poyntng Reflexão e Transmssão com ncdênca normal Temos consderado
Módulo I Ondas Planas Reflexão e Transmssão com ncdênca normal Reflexão e Transmssão com ncdênca oblíqua Equações de Maxwell Teorema de Poyntng Reflexão e Transmssão com ncdênca normal Temos consderado
UFGD 2015 DANIEL KICHESE
 Quesão 59: º) Deermnação dos ponos de nerseção: 5 5 º Pono : B 5 5 º Pono : C 5 5 º Pono : B C C º) Deermnação da Área: B 5 5 5 / e 0 e 5 5 5 5 e 0 5 5/ 5 5 0 0 0 5 5 Resposa: E Quesão 60: Número de blhees
Quesão 59: º) Deermnação dos ponos de nerseção: 5 5 º Pono : B 5 5 º Pono : C 5 5 º Pono : B C C º) Deermnação da Área: B 5 5 5 / e 0 e 5 5 5 5 e 0 5 5/ 5 5 0 0 0 5 5 Resposa: E Quesão 60: Número de blhees
Parte III. Objetivo: estudar o deslocamento de um corpo quando esta rolando
 Pare Objevo: esudar o deslocameno de um corpo quando esa rolando 1 Coneúdo programáco: 6. Movmeno de Roação Varáves da roação, Relação enre Cnemáca Lnear e Cnemáca Angular, Energa cnéca de roação, nérca
Pare Objevo: esudar o deslocameno de um corpo quando esa rolando 1 Coneúdo programáco: 6. Movmeno de Roação Varáves da roação, Relação enre Cnemáca Lnear e Cnemáca Angular, Energa cnéca de roação, nérca
5 Avaliação do Título Conversível pelo Método de Diferenças Finitas Implícito (DFI)
 5 Avalação do Tíulo Conversível pelo Méodo de Dferenças Fnas Implíco (DFI) 5. Meodologa - Premssas Ese modelo desenvolvdo para apreçameno do LYON faz uso da eora de opções desenvolvda por Black and Scholes
5 Avalação do Tíulo Conversível pelo Méodo de Dferenças Fnas Implíco (DFI) 5. Meodologa - Premssas Ese modelo desenvolvdo para apreçameno do LYON faz uso da eora de opções desenvolvda por Black and Scholes
Iluminação e FotoRealismo: Radiosidade
 Ilumnação e oorealsmo: Radosdade Luís Paulo Pexoo dos Sanos hp://gec.d.umnho.p/mcgav/fr Premssas Todas as neracções da luz com os obecos são dfusas L x Θ L x, Θ Ω Expressa em ermos de radosdade W/m 2 r
Ilumnação e oorealsmo: Radosdade Luís Paulo Pexoo dos Sanos hp://gec.d.umnho.p/mcgav/fr Premssas Todas as neracções da luz com os obecos são dfusas L x Θ L x, Θ Ω Expressa em ermos de radosdade W/m 2 r
EN3604 FILTRAGEM ADAPTATIVA
 EN3604 FILTRAGEM ADAPTATIVA Processameno de Snas em Arranjos Técncas de processameno consderando snas provenenes de um grupo de sensores espacalmene dsrbuídos. Poencal para melhorar SNR/ Cancelameno de
EN3604 FILTRAGEM ADAPTATIVA Processameno de Snas em Arranjos Técncas de processameno consderando snas provenenes de um grupo de sensores espacalmene dsrbuídos. Poencal para melhorar SNR/ Cancelameno de
F-128 Física Geral I. Aula exploratória-10a UNICAMP IFGW
 F-8 Físca Geral I Aula exploraóra-a UNICAMP IFGW username@f.uncamp.br Varáves roaconas Cada pono do corpo rígdo execua um movmeno crcular de rao r em orno do exo. Fgura: s=r Deslocameno angular: em radanos
F-8 Físca Geral I Aula exploraóra-a UNICAMP IFGW username@f.uncamp.br Varáves roaconas Cada pono do corpo rígdo execua um movmeno crcular de rao r em orno do exo. Fgura: s=r Deslocameno angular: em radanos
MECÂNICA CLÁSSICA. AULA N o 4. Carga de Noether- Simetrias e Conservação
 MECÂNIC CLÁSSIC UL N o 4 Carga de Noeher- Smeras e Conservação Vamos ver o caso de uma parícula movendo-se no plano, porém descrevendo-a agora em coordenadas polares: r r d dr T T m dr m d r d d m r m
MECÂNIC CLÁSSIC UL N o 4 Carga de Noeher- Smeras e Conservação Vamos ver o caso de uma parícula movendo-se no plano, porém descrevendo-a agora em coordenadas polares: r r d dr T T m dr m d r d d m r m
Física I. 2º Semestre de Instituto de Física- Universidade de São Paulo. Aula 5 Trabalho e energia. Professor: Valdir Guimarães
 Físca I º Semesre de 03 Insuo de Físca- Unversdade de São Paulo Aula 5 Trabalho e energa Proessor: Valdr Gumarães E-mal: valdrg@.usp.br Fone: 309.704 Trabalho realzado por uma orça consane Derenemene
Físca I º Semesre de 03 Insuo de Físca- Unversdade de São Paulo Aula 5 Trabalho e energa Proessor: Valdr Gumarães E-mal: valdrg@.usp.br Fone: 309.704 Trabalho realzado por uma orça consane Derenemene
CAPÍTULO 2 PLANEJAMENTO DA OPERAÇÃO E FORMAÇÃO DO PREÇO SPOT EM UM MERCADO COMPETITIVO DE ENERGIA ELÉTRICA
 CAPÍTULO 2 PLANEJAMEO DA OPERAÇÃO E FORMAÇÃO DO PREÇO SPOT EM UM MERCADO COMPETITIO DE ENERIA ELÉTRICA 2. IRODUÇÃO Ese capíulo apresena um resumo dos prncpas conceos relaconados ao planeameno da operação
CAPÍTULO 2 PLANEJAMEO DA OPERAÇÃO E FORMAÇÃO DO PREÇO SPOT EM UM MERCADO COMPETITIO DE ENERIA ELÉTRICA 2. IRODUÇÃO Ese capíulo apresena um resumo dos prncpas conceos relaconados ao planeameno da operação
TE-289 Dispositivos e Sensores Fotônicos Integrados Aula FEV 2018
 T-89 Dsposvos e Sensores Foôncos Inegrados Aula 6 FV 8 RSUMO: Revsão Geral quações de Mawell Onda Plana em Meo Delérco Propredades geras em Inerfaces Delércas Guas de ondas delércos Gua Slab Smérco: abordagem
T-89 Dsposvos e Sensores Foôncos Inegrados Aula 6 FV 8 RSUMO: Revsão Geral quações de Mawell Onda Plana em Meo Delérco Propredades geras em Inerfaces Delércas Guas de ondas delércos Gua Slab Smérco: abordagem
5 Avaliação da Eficiência Computacional
 5 Avalação da fcênca Compuaconal 5.1 Inrodução É desejado ncorporar o cálculo dos índces de adequação de ações de conrole de ensão ao programa SAN. O programa SAN esá sendo mplemenado com a esruura aual
5 Avalação da fcênca Compuaconal 5.1 Inrodução É desejado ncorporar o cálculo dos índces de adequação de ações de conrole de ensão ao programa SAN. O programa SAN esá sendo mplemenado com a esruura aual
É a parte da mecânica que descreve os movimentos, sem se preocupar com suas causas.
 1 INTRODUÇÃO E CONCEITOS INICIAIS 1.1 Mecânca É a pare da Físca que esuda os movmenos dos corpos. 1. -Cnemáca É a pare da mecânca que descreve os movmenos, sem se preocupar com suas causas. 1.3 - Pono
1 INTRODUÇÃO E CONCEITOS INICIAIS 1.1 Mecânca É a pare da Físca que esuda os movmenos dos corpos. 1. -Cnemáca É a pare da mecânca que descreve os movmenos, sem se preocupar com suas causas. 1.3 - Pono
2 Estabilidade de Tensão
 Esabldade de Tensão. Inrodução O objevo desa seção é mosrar a possbldade de exsênca de fenômenos que se possa assemelhar a aqueles observados na operação de ssemas elércos, e assocados ao colapso de ensão.
Esabldade de Tensão. Inrodução O objevo desa seção é mosrar a possbldade de exsênca de fenômenos que se possa assemelhar a aqueles observados na operação de ssemas elércos, e assocados ao colapso de ensão.
figura 1 Vamos encontrar, em primeiro lugar, a velocidade do som da explosão (v E) no ar que será dada pela fórmula = v
 Dispara-se, segundo um ângulo de 6 com o horizone, um projéil que explode ao aingir o solo e oue-se o ruído da explosão, no pono de parida do projéil, 8 segundos após o disparo. Deerminar a elocidade inicial
Dispara-se, segundo um ângulo de 6 com o horizone, um projéil que explode ao aingir o solo e oue-se o ruído da explosão, no pono de parida do projéil, 8 segundos após o disparo. Deerminar a elocidade inicial
5 Sistemas Lineares com Coecientes Periódicos
 5 Ssemas Lneares com Coecenes Peródcos Ese capíulo raa de forma suscna do esudo da esabldade de soluções peródcas de ssemas dnâmcos não-lneares. Segundo Rand [83], a eora de Floque é a eora mas geral que
5 Ssemas Lneares com Coecenes Peródcos Ese capíulo raa de forma suscna do esudo da esabldade de soluções peródcas de ssemas dnâmcos não-lneares. Segundo Rand [83], a eora de Floque é a eora mas geral que
CAPÍTULO 9 MODELOS DE REGRESSÃO COM VARIÁVEIS BINÁRIAS
 Economera Semesre 200.0 40 CAPÍTULO 9 MODELOS DE REGRESSÃO COM VARIÁVEIS BINÁRIAS OBJETIVOS Consderar modelos em que uma ou mas varáves explcavas são varáves nomnas (ambém chamadas de ndcadores, varáves
Economera Semesre 200.0 40 CAPÍTULO 9 MODELOS DE REGRESSÃO COM VARIÁVEIS BINÁRIAS OBJETIVOS Consderar modelos em que uma ou mas varáves explcavas são varáves nomnas (ambém chamadas de ndcadores, varáves
2. Circuitos de rectificação monofásicos
 EECTÓNICA E POTÊNCIA Crcuos de recfcação monofáscos Colecção de Problemas 2.1 2. Crcuos de recfcação monofáscos Exercíco nº2.1 eermne a expressão da ensão na ressênca e o seu dagrama emporal, em função
EECTÓNICA E POTÊNCIA Crcuos de recfcação monofáscos Colecção de Problemas 2.1 2. Crcuos de recfcação monofáscos Exercíco nº2.1 eermne a expressão da ensão na ressênca e o seu dagrama emporal, em função
MECÂNICA CLÁSSICA. AULA N o 3. Lagrangeano Princípio da Mínima Ação Exemplos
 MECÂNICA CÁSSICA AUA N o 3 agrangeano Prncípo da Mínma Ação Exemplos Todas as les da Físca êm uma esruura em comum: as les de uma parícula em movmeno sob a ação da gravdade, o movmeno dado pela equação
MECÂNICA CÁSSICA AUA N o 3 agrangeano Prncípo da Mínma Ação Exemplos Todas as les da Físca êm uma esruura em comum: as les de uma parícula em movmeno sob a ação da gravdade, o movmeno dado pela equação
Curso de Óptica Aplicada
 Curso de Ópca Aplcada Faculdade de Cêcas e Tecologa Uversdade Nova de Lsboa AT 4 Propagação Deparameo Aula Teórca de Físca 5 Ópca Geomérca Curso de Ópca Aplcada Aula Teórca 4 Propagação Curso de Ópca Aplcada
Curso de Ópca Aplcada Faculdade de Cêcas e Tecologa Uversdade Nova de Lsboa AT 4 Propagação Deparameo Aula Teórca de Físca 5 Ópca Geomérca Curso de Ópca Aplcada Aula Teórca 4 Propagação Curso de Ópca Aplcada
Caracterização ótica de soluções
 Caracterzação ótca de soluções Físca Expermental IV - 2016 - Prof. Dr. Valmr Antono Chtta 1. Resumo O projeto tem como objetvo prncpal determnar o comportamento da luz ao passar por meos delétrcos e translúcdos,
Caracterzação ótca de soluções Físca Expermental IV - 2016 - Prof. Dr. Valmr Antono Chtta 1. Resumo O projeto tem como objetvo prncpal determnar o comportamento da luz ao passar por meos delétrcos e translúcdos,
CIRCULAR Nº 3.634, DE 4 DE MARÇO DE 2013. Padrão. Padrão. max i. I - F = fator estabelecido no art. 4º da Resolução nº 4.
 CIRCULAR Nº 3.634, DE 4 DE MARÇO DE 2013 Esabelece os procedmenos para o cálculo da parcela dos avos ponderados pelo rsco (RWA) referene às exposções sueas à varação de axas de uros prefxadas denomnadas
CIRCULAR Nº 3.634, DE 4 DE MARÇO DE 2013 Esabelece os procedmenos para o cálculo da parcela dos avos ponderados pelo rsco (RWA) referene às exposções sueas à varação de axas de uros prefxadas denomnadas
PRIMEIRO RELATÓRIO DE FÍSICA EXPERIMENTAL PROCESSOS DE ANÁLISE GRÁFICA E NUMÉRICA
 UIVERSIDDE DE PERMUCO / ESCOL POLITÉCIC DE PERMUCO EPP/UPE DEPRTMETO ITERDISCIPLIR ESIO ÁSICO ÍSIC EPERIMETL LUO(): TURM: OT: PROESSOR(): DT: / / PRIMEIRO RELTÓRIO DE ÍSIC EPERIMETL PROCESSOS DE ÁLISE
UIVERSIDDE DE PERMUCO / ESCOL POLITÉCIC DE PERMUCO EPP/UPE DEPRTMETO ITERDISCIPLIR ESIO ÁSICO ÍSIC EPERIMETL LUO(): TURM: OT: PROESSOR(): DT: / / PRIMEIRO RELTÓRIO DE ÍSIC EPERIMETL PROCESSOS DE ÁLISE
t c L S Troço 1 S 1 = 3 km = 3000 m
 . DETERMINAÇÃO DO TEMPO DE CONCENTRAÇÃO Para o cálculo do empo de concenração ( c ) da baca hdrográfca eudada recorreu-e ao valore obdo no rabalho práco (Quadro ). Am, emo que, Quadro Parâmero do rabalho
. DETERMINAÇÃO DO TEMPO DE CONCENTRAÇÃO Para o cálculo do empo de concenração ( c ) da baca hdrográfca eudada recorreu-e ao valore obdo no rabalho práco (Quadro ). Am, emo que, Quadro Parâmero do rabalho
Tratamento de Dados 2º Semestre 2005/2006 Tópicos de Resolução do Trabalho 2 = 12
 Traaeno de Dados º Seesre 5/6 Tópcos de Resolução do Trabalho Quesão a Para agrupar os dados e classes ora consderados os valores das rendas aé 5. ua vez que a parr dese valor os dados se enconra basane
Traaeno de Dados º Seesre 5/6 Tópcos de Resolução do Trabalho Quesão a Para agrupar os dados e classes ora consderados os valores das rendas aé 5. ua vez que a parr dese valor os dados se enconra basane
Gripe: Época de gripe; actividade gripal; cálculo da linha de base e do respectivo intervalo de confiança a 95%; e área de actividade basal.
 Grpe: Época de grpe; acvdade grpal; cálculo da lnha de ase e do respecvo nervalo de confança a 95%; e área de acvdade asal. ÉPOCA DE GRPE Para maor facldade de compreensão será desgnado por época de grpe
Grpe: Época de grpe; acvdade grpal; cálculo da lnha de ase e do respecvo nervalo de confança a 95%; e área de acvdade asal. ÉPOCA DE GRPE Para maor facldade de compreensão será desgnado por época de grpe
Nota Técnica sobre a Circular nº 2.972, de 23 de março de 2000
 Noa Técnca sobre a rcular nº 2.972, de 23 de março de 2000 Meodologa ulzada no processo de apuração do valor da volaldade padrão e do mulplcador para o da, dvulgados daramene pelo Banco enral do Brasl.
Noa Técnca sobre a rcular nº 2.972, de 23 de março de 2000 Meodologa ulzada no processo de apuração do valor da volaldade padrão e do mulplcador para o da, dvulgados daramene pelo Banco enral do Brasl.
Projeto de Inversores e Conversores CC-CC
 eparameno de Engenhara Elérca Aula. onversor Buck Prof. João Amérco lela Bblografa BAB, vo. & MANS enzar ruz. onversores - Báscos Não-solados. ª edção, UFS,. MOHAN Ned; UNEAN ore M.; OBBNS Wllam P. Power
eparameno de Engenhara Elérca Aula. onversor Buck Prof. João Amérco lela Bblografa BAB, vo. & MANS enzar ruz. onversores - Báscos Não-solados. ª edção, UFS,. MOHAN Ned; UNEAN ore M.; OBBNS Wllam P. Power
Departamento de Informática. Modelagem Analítica. Modelagem Analítica do Desempenho de Sistemas de Computação. Disciplina:
 Deparameno de Informáca Dscplna: Modelagem Analíca do Desempenho de Ssemas de Compuação Fluxos de Enrada Fluxos de Saída Le de Lle Faor de Ulzação rof. Sérgo Colcher colcher@nf.puc-ro.br rocesso de Chegada
Deparameno de Informáca Dscplna: Modelagem Analíca do Desempenho de Ssemas de Compuação Fluxos de Enrada Fluxos de Saída Le de Lle Faor de Ulzação rof. Sérgo Colcher colcher@nf.puc-ro.br rocesso de Chegada
SISMICA DE REFRACÇÃO
 SISMICA DE REFRACÇÃO Ondas elástcas e parâmetros de propagação As elocdades das ondas P e S respectamente, p e s estão relaconadas com as constantes elástcas e a densdade do materal. As relações são: k
SISMICA DE REFRACÇÃO Ondas elástcas e parâmetros de propagação As elocdades das ondas P e S respectamente, p e s estão relaconadas com as constantes elástcas e a densdade do materal. As relações são: k
Laboratório de Mecânica Aplicada I Estática: Roldanas e Equilíbrio de Momentos
 Laboratóro de Mecânca Aplcada I Estátca: Roldanas e Equlíbro de Momentos 1 Introdução O conhecmento das condções de equlíbro de um corpo é mprescndível em númeras stuações. Por exemplo, o estudo do equlíbro
Laboratóro de Mecânca Aplcada I Estátca: Roldanas e Equlíbro de Momentos 1 Introdução O conhecmento das condções de equlíbro de um corpo é mprescndível em númeras stuações. Por exemplo, o estudo do equlíbro
3.1 Método Ground Penetrating Radar GPR
 Capíulo 3 Para abordar nosso problema em esudo empregamos o GPR e a sísmca de refração. Aqu apresenamos os prncpas ópcos dos fundamenos eórcos e nsrumenas deses méodos. Como exse uma asa bblografa sobre
Capíulo 3 Para abordar nosso problema em esudo empregamos o GPR e a sísmca de refração. Aqu apresenamos os prncpas ópcos dos fundamenos eórcos e nsrumenas deses méodos. Como exse uma asa bblografa sobre
ÓPTICA GEOMÉTRICA ÓPTICA REFLEXÃO MEIOS DE PROPAGAÇÃO DA LUZ. Estuda os fenômenos luminosos, sem se interessar com sua natureza.
 12. Num calorímetro de capacdade térmca 8,0 cal/ o C ncalmente a 10º C são colocados 200g de um líqudo de calor específco 0,40 cal/g. o C. Verfca-se que o equlíbro térmco se estabelece a 50º C. Determne
12. Num calorímetro de capacdade térmca 8,0 cal/ o C ncalmente a 10º C são colocados 200g de um líqudo de calor específco 0,40 cal/g. o C. Verfca-se que o equlíbro térmco se estabelece a 50º C. Determne
Solução numérica de equações diferenciais ordinárias. Problema de valor inicial (PVI)
 Solução numérca de equações derencas ordnáras Problema de valor ncal PVI 4 5 Inrodução 4 5 Uma equação derencal ordnára é denda como uma equação que envolve uma unção ncógna e algumas das suas dervadas
Solução numérca de equações derencas ordnáras Problema de valor ncal PVI 4 5 Inrodução 4 5 Uma equação derencal ordnára é denda como uma equação que envolve uma unção ncógna e algumas das suas dervadas
3 Análise de Demanda Condicionada
 3 Análse de Demanda Condconada 3.1 Inrodução A análse Condconada da Demanda é uma écnca que quebra o consumo resdencal em pares, cada uma assocada a um uso fnal ou a um deermnado equpameno em parcular.
3 Análse de Demanda Condconada 3.1 Inrodução A análse Condconada da Demanda é uma écnca que quebra o consumo resdencal em pares, cada uma assocada a um uso fnal ou a um deermnado equpameno em parcular.
5 Apreçamento de ESOs com preço de exercício fixo
 5 Apreçameno de ESOs com preço de exercíco fxo Ese capíulo rá explorar os prncpas modelos de apreçameno das ESOs ulzados hoje em da. Neses modelos a regra de decsão é esruurada em orno da maxmzação do
5 Apreçameno de ESOs com preço de exercíco fxo Ese capíulo rá explorar os prncpas modelos de apreçameno das ESOs ulzados hoje em da. Neses modelos a regra de decsão é esruurada em orno da maxmzação do
di L Ri v V dt + + = (1) dv dt
 Experiência Circuio RLC érie Regime DC Aluno: Daa: / /. Objeivos de Aprendizagem dese Experimeno A experiência raa de circuios ransiórios de segunda ordem. O objeivo dese experimeno é: Analisar as diferenes
Experiência Circuio RLC érie Regime DC Aluno: Daa: / /. Objeivos de Aprendizagem dese Experimeno A experiência raa de circuios ransiórios de segunda ordem. O objeivo dese experimeno é: Analisar as diferenes
CAPÍTULO 1 REPRESENTAÇÃO E CLASSIFICAÇÃO DE SISTEMAS. Sistema monovariável SISO = Single Input Single Output. s 1 s 2. ... s n
 1 CAPÍTULO 1 REPREENTAÇÃO E CLAIFICAÇÃO DE ITEMA 1.1. Represenação de ssemas 1.1.1. semas com uma enrada e uma saída (IO) e sema monovarável IO = ngle Inpu ngle Oupu s e = enrada s = saída = ssema 1.1..
1 CAPÍTULO 1 REPREENTAÇÃO E CLAIFICAÇÃO DE ITEMA 1.1. Represenação de ssemas 1.1.1. semas com uma enrada e uma saída (IO) e sema monovarável IO = ngle Inpu ngle Oupu s e = enrada s = saída = ssema 1.1..
CIRCUITOS ELÉTRICOS EXERCÍCIOS ) Para o circuito da figura, determinar a tensão de saída V out, utilizando a linearidade.
 FISP CIRCUITOS ELÉTRICOS EXERCÍCIOS RESOLVIDOS 00 CIRCUITOS ELÉTRICOS EXERCÍCIOS 00 Para o crcuo da fgura, deermnar a ensão de saída V ou, ulzando a lneardade. Assumremos que a ensão de saída seja V ou
FISP CIRCUITOS ELÉTRICOS EXERCÍCIOS RESOLVIDOS 00 CIRCUITOS ELÉTRICOS EXERCÍCIOS 00 Para o crcuo da fgura, deermnar a ensão de saída V ou, ulzando a lneardade. Assumremos que a ensão de saída seja V ou
Neo-fisherianos e teoria fiscal do nível de preços
 Anono Lcha 4/março/07 Neo-fsheranos e eora fscal do nível de preços O objevo desas noas é desacar os prncpas elemenos da abordagem neofsherana e da eora fscal do nível de preços. Desacamos 4 pequenos modelos
Anono Lcha 4/março/07 Neo-fsheranos e eora fscal do nível de preços O objevo desas noas é desacar os prncpas elemenos da abordagem neofsherana e da eora fscal do nível de preços. Desacamos 4 pequenos modelos
Aprendizagem Estatística de Dados. Francisco Carvalho
 Aprendzagem Esaísca de Dados Francsco Carvalho A função de Densdade Normal Valor Esperado Caso conínuo [ f ] Caso dscreo f p d [ f ] f p D A função de Densdade Normal Caso Unvarado função de densdade p
Aprendzagem Esaísca de Dados Francsco Carvalho A função de Densdade Normal Valor Esperado Caso conínuo [ f ] Caso dscreo f p d [ f ] f p D A função de Densdade Normal Caso Unvarado função de densdade p
RESULTADOS TEÓRICOS PARA TURBULÊNCIA GERADA POR DUAS GRELHAS OSCILANTES
 RESULTADOS TEÓRICOS PARA TURBULÊNCIA GERADA POR DUAS GRELHAS OSCILANTES Harry Edmar Schulz Fazal Hussan Chaudhry USP - Escola de Engenhara de São Carlos, Deparameno de Hdráulca e Saneameno Laboraóro de
RESULTADOS TEÓRICOS PARA TURBULÊNCIA GERADA POR DUAS GRELHAS OSCILANTES Harry Edmar Schulz Fazal Hussan Chaudhry USP - Escola de Engenhara de São Carlos, Deparameno de Hdráulca e Saneameno Laboraóro de
Universidade Estadual do Sudoeste da Bahia
 Unversdade Estadual do Sudoeste da Baha Departamento de Cêncas Exatas e Naturas 5 - Rotações, Centro de Massa, Momento, Colsões, Impulso e Torque Físca I Ferrera Índce 1. Movmento Crcular Unformemente
Unversdade Estadual do Sudoeste da Baha Departamento de Cêncas Exatas e Naturas 5 - Rotações, Centro de Massa, Momento, Colsões, Impulso e Torque Físca I Ferrera Índce 1. Movmento Crcular Unformemente
PROF. DR. JACQUES FACON LIMIARIZAÇÃO POR ENTROPIA DE WULU
 1 PUCPR- Ponfíca Unversdade Caólca Do Paraná PPGIA- Programa de Pós-Graduação Em Informáca Aplcada PROF. DR. JACQUES FACON IMIARIZAÇÃO POR ENTROPIA DE WUU Resumo: Uma nova écnca de marzação baseada em
1 PUCPR- Ponfíca Unversdade Caólca Do Paraná PPGIA- Programa de Pós-Graduação Em Informáca Aplcada PROF. DR. JACQUES FACON IMIARIZAÇÃO POR ENTROPIA DE WUU Resumo: Uma nova écnca de marzação baseada em
5.1 O Processo TAR. é definida como um processo limiar auto-regressivo com h. regimes se puder ser representada por (5) ). Os termos ,...
 5 O Modelo Não-Lnear Como vso no capíulo aneror, há espaço para uma análse mas profunda da função de reação do Banco Cenral do Brasl. Auores como Clarda, Gal e Gerler (2000) e Cogley e Sargen (2001) examnam
5 O Modelo Não-Lnear Como vso no capíulo aneror, há espaço para uma análse mas profunda da função de reação do Banco Cenral do Brasl. Auores como Clarda, Gal e Gerler (2000) e Cogley e Sargen (2001) examnam
Análise de Projectos ESAPL / IPVC
 Análse de Proecos ESAPL / IPV Tempo, apal, Juro e Taxa de Juro Juros Smples e Juros omposos apalzação e Facor de apalzação Descono e Facor de Acualzação As aplcações do rendmeno onsumo Não Geram Rendmenos
Análse de Proecos ESAPL / IPV Tempo, apal, Juro e Taxa de Juro Juros Smples e Juros omposos apalzação e Facor de apalzação Descono e Facor de Acualzação As aplcações do rendmeno onsumo Não Geram Rendmenos
MATEMÁTICA A - 12o Ano N o s Complexos - Potências e raízes Propostas de resolução
 MATEMÁTICA A - 1o Ano N o s Complexos - Potêncas e raízes Propostas de resolução Exercícos de exames e testes ntermédos 1. Smplfcando a expressão de z na f.a., como 5+ ) 5 1 5, temos: z 1 + 1 ) + 1 1 1
MATEMÁTICA A - 1o Ano N o s Complexos - Potêncas e raízes Propostas de resolução Exercícos de exames e testes ntermédos 1. Smplfcando a expressão de z na f.a., como 5+ ) 5 1 5, temos: z 1 + 1 ) + 1 1 1
Análise da Confiabilidade de Componentes Não Reparáveis
 Análse da onfabldade de omponenes Não Reparáves. omponenes versus Ssemas! Ssema é um conjuno de dos ou mas componenes nerconecados para a realzação de uma ou mas funções! A dsnção enre ssema, sub-ssema
Análse da onfabldade de omponenes Não Reparáves. omponenes versus Ssemas! Ssema é um conjuno de dos ou mas componenes nerconecados para a realzação de uma ou mas funções! A dsnção enre ssema, sub-ssema
Instituto de Física USP. Física V - Aula 26. Professora: Mazé Bechara
 Insiuo de Física USP Física V - Aula 6 Professora: Mazé Bechara Aula 6 Bases da Mecânica quânica e equações de Schroedinger. Aplicação e inerpreações. 1. Ouros posulados da inerpreação de Max-Born para
Insiuo de Física USP Física V - Aula 6 Professora: Mazé Bechara Aula 6 Bases da Mecânica quânica e equações de Schroedinger. Aplicação e inerpreações. 1. Ouros posulados da inerpreação de Max-Born para
defi departamento de física
 defi departamento de física Laboratórios de Física www.defi.isep.ipp.pt Interferómetro de Michelson Instituto Superior de Engenharia do Porto Departamento de Física Rua Dr. António Bernardino de Almeida,
defi departamento de física Laboratórios de Física www.defi.isep.ipp.pt Interferómetro de Michelson Instituto Superior de Engenharia do Porto Departamento de Física Rua Dr. António Bernardino de Almeida,
MEDIDA DO TEMPO DE RESPOSTA DOS MEDIDORES DE PRESSÃO DO SPR DA U.N.A. A. A. - UNIDADE I UTILIZANDO O MÉTODO DE MEDIDA DIRETA
 MEDIDA DO TEMPO DE RESPOSTA DOS MEDIDORES DE PRESSÃO DO SPR DA U.N.A. A. A. - UNIDADE I UTILIZANDO O MÉTODO DE MEDIDA DIRETA Sergo Rcardo Perera Perllo *, Irac Maríne Perera Gonçalves *, Robero Carlos
MEDIDA DO TEMPO DE RESPOSTA DOS MEDIDORES DE PRESSÃO DO SPR DA U.N.A. A. A. - UNIDADE I UTILIZANDO O MÉTODO DE MEDIDA DIRETA Sergo Rcardo Perera Perllo *, Irac Maríne Perera Gonçalves *, Robero Carlos
5 Programação Matemática Princípios Básicos
 5 Programação Maemáca Prncípos Báscos 5. Consderações Geras Ese capíulo em por objevo apresenar os conceos báscos de Programação Maemáca (PM), necessáros à compreensão do processo de omzação de dmensões,
5 Programação Maemáca Prncípos Báscos 5. Consderações Geras Ese capíulo em por objevo apresenar os conceos báscos de Programação Maemáca (PM), necessáros à compreensão do processo de omzação de dmensões,
Propagação de dano no modelo de Ising unidimensional
 Capíulo 4 Propagação de dano no modelo de Isng undmensonal 4. Propagação de dano O méodo da propagação de dano é uma écnca relavamene nova, nroduzda por Kauffman 68 no conexo dos auômaos celulares, que
Capíulo 4 Propagação de dano no modelo de Isng undmensonal 4. Propagação de dano O méodo da propagação de dano é uma écnca relavamene nova, nroduzda por Kauffman 68 no conexo dos auômaos celulares, que
Arco-Íris, Miragens e
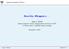 Insttuto Superor Técnco, e Jorge C. Romão Insttuto Superor Técnco, Departamento de Físca & CFTP A. Rovsco Pas 1, 1049-001 Lsboa, Portugal December 6, 2011 Jorge C. Romão Sldes EO 1 Arco Írs Jorge C. Romão
Insttuto Superor Técnco, e Jorge C. Romão Insttuto Superor Técnco, Departamento de Físca & CFTP A. Rovsco Pas 1, 1049-001 Lsboa, Portugal December 6, 2011 Jorge C. Romão Sldes EO 1 Arco Írs Jorge C. Romão
2 Sistemas de Reconhecimento de Voz
 2 Ssemas de Reconhecmeno de Voz O desenvolvmeno de nerfaces homem-máquna conroladas pela voz vsa subsur, em ceras aplcações, as nerfaces radconas as como eclados, panés e dsposvos smlares. Nese cenáro
2 Ssemas de Reconhecmeno de Voz O desenvolvmeno de nerfaces homem-máquna conroladas pela voz vsa subsur, em ceras aplcações, as nerfaces radconas as como eclados, panés e dsposvos smlares. Nese cenáro
2003/2004. então o momento total das forças exercidas sobre o sistema é dado por. F ij = r i F (e)
 Resolução da Frequênca de Mecânca Clássca I/Mecânca Clássca 2003/2004 I Consdere um sstema de N partículas de massas m, =,..., N. a Demonstre que, se a força nterna exercda sobre a partícula pela partícula
Resolução da Frequênca de Mecânca Clássca I/Mecânca Clássca 2003/2004 I Consdere um sstema de N partículas de massas m, =,..., N. a Demonstre que, se a força nterna exercda sobre a partícula pela partícula
3 Dados e Modelo Econométrico 3.1. A amostra de funcionários públicos
 3 Dados e Modelo Economérco 3.1. A amosra de funconáros públcos Os dados usados nese esudo êm como fone a Pesqusa Naconal de Amosra por Domcílo (PNAD, uma pesqusa domclar realzada anualmene no Brasl pelo
3 Dados e Modelo Economérco 3.1. A amosra de funconáros públcos Os dados usados nese esudo êm como fone a Pesqusa Naconal de Amosra por Domcílo (PNAD, uma pesqusa domclar realzada anualmene no Brasl pelo
Inserção de Variáveis Ambientais no Planejamento da Operação de Sistemas Hidrotérmicos
 Inserção de Varáves Ambenas no Planejameno da Operação de Ssemas Hdroérmcos VALLE, Ana Cláuda Marques, Escola de Engenhara Elérca e de Compuação, UFG, douoranda em Cencas Ambenas, PRPPG, UFG AGUIAR, Mara
Inserção de Varáves Ambenas no Planejameno da Operação de Ssemas Hdroérmcos VALLE, Ana Cláuda Marques, Escola de Engenhara Elérca e de Compuação, UFG, douoranda em Cencas Ambenas, PRPPG, UFG AGUIAR, Mara
PME 2556 Dinâmica dos Fluidos Computacional. Aula 9 - Modelo k-ε Standard
 ME 556 Dnâmca dos Fldos Compaconal Ala 9 - Modelo - Sandard Decomposção de Reynolds Decomposção de Reynolds Eqações de Reynolds (1) ( ) ( ) p Eqação de Naver-Soes na forma conservava para m fldo ncompressível:
ME 556 Dnâmca dos Fldos Compaconal Ala 9 - Modelo - Sandard Decomposção de Reynolds Decomposção de Reynolds Eqações de Reynolds (1) ( ) ( ) p Eqação de Naver-Soes na forma conservava para m fldo ncompressível:
EN2607 Transformadas em Sinais e Sistemas Lineares Lista de Exercícios Suplementares 1 2 quadrimestre 2011
 EN67 Transformadas em Sinais e Sisemas Lineares Lisa de Exercícios Suplemenares quadrimesre Figura Convolução (LATHI, 998) (N) (HAYKIN; VEEN,, p 79) O pulso rapezoidal x( ) da figura a seguir é aplicado
EN67 Transformadas em Sinais e Sisemas Lineares Lisa de Exercícios Suplemenares quadrimesre Figura Convolução (LATHI, 998) (N) (HAYKIN; VEEN,, p 79) O pulso rapezoidal x( ) da figura a seguir é aplicado
Resistores. antes de estudar o capítulo PARTE I
 PARTE I Undade B 6 capítulo Resstores seções: 61 Consderações ncas 62 Resstênca elétrca Le de Ohm 63 Le de Joule 64 Resstvdade antes de estudar o capítulo Veja nesta tabela os temas prncpas do capítulo
PARTE I Undade B 6 capítulo Resstores seções: 61 Consderações ncas 62 Resstênca elétrca Le de Ohm 63 Le de Joule 64 Resstvdade antes de estudar o capítulo Veja nesta tabela os temas prncpas do capítulo
ELECTROMAGNETISMO. EXAME 1ª Chamada 22 de Junho de 2009 RESOLUÇÕES
 ELECTROMAGNETISMO EXAME 1ª Chamada de Junho de 00 RESOLUÇÕES As esposas à mao pae das pegunas devem se acompanhada de esquemas lusavos, que não são epoduzdos aqu. 1. a. As ês paículas e o pono (.00, 0.00)
ELECTROMAGNETISMO EXAME 1ª Chamada de Junho de 00 RESOLUÇÕES As esposas à mao pae das pegunas devem se acompanhada de esquemas lusavos, que não são epoduzdos aqu. 1. a. As ês paículas e o pono (.00, 0.00)
APÊNDICE A. Rotação de um MDT
 APÊNDICES 7 APÊNDICE A Roação de um MDT 8 Os passos seguidos para a realização da roação do MDT foram os seguines: - Deerminar as coordenadas do cenro geomérico da região, ou pono em orno do qual a roação
APÊNDICES 7 APÊNDICE A Roação de um MDT 8 Os passos seguidos para a realização da roação do MDT foram os seguines: - Deerminar as coordenadas do cenro geomérico da região, ou pono em orno do qual a roação
Física IV - Laboratório REFLEXÃO E REFRAÇÃO (Parte 2)
 Física IV - Laboratório REFLEXÃO E REFRAÇÃO (Parte 2) O que acontece quando uma onda luminosa que se propaga em um meio 1 encontra a super@cie de um meio 2? Vetores unitários ˆk i direção da onda incidente
Física IV - Laboratório REFLEXÃO E REFRAÇÃO (Parte 2) O que acontece quando uma onda luminosa que se propaga em um meio 1 encontra a super@cie de um meio 2? Vetores unitários ˆk i direção da onda incidente
Física E Semiextensivo V. 4
 Físca E Semextensvo V. 4 Exercícos 0) E I força (vertcal, para cma) II força (perpendcular à folha, sando dela) III F (horzontal, para a dreta) 0) 34 03) 68 S N S N força (perpendcular à folha, entrando
Físca E Semextensvo V. 4 Exercícos 0) E I força (vertcal, para cma) II força (perpendcular à folha, sando dela) III F (horzontal, para a dreta) 0) 34 03) 68 S N S N força (perpendcular à folha, entrando
PCA e IMPCA. Capítulo. 5.1 Considerações Iniciais
 Capíulo 5 PCA e IMPCA 5. Consderações Incas A análse de componenes prncpas (PCA) [URK, M. A. & PENLAND, A. P. (99)] é uma ransformação lnear orogonal de um espaço q-dmensonal para um espaço n-dmensonal,
Capíulo 5 PCA e IMPCA 5. Consderações Incas A análse de componenes prncpas (PCA) [URK, M. A. & PENLAND, A. P. (99)] é uma ransformação lnear orogonal de um espaço q-dmensonal para um espaço n-dmensonal,
ESTUDO COMPARATIVO DE SISTEMAS DE AERAÇÃO PARA A ESTAÇÃO DE TRATAMENTO DE ESGOTOS SUZANO
 ESTUDO COMPARATIVO DE SISTEMAS DE AERAÇÃO PARA A ESTAÇÃO DE TRATAMENTO DE ESGOTOS SUZANO Roque Passos Pvel Escola Polécnca da Unversdade de São Paulo - EPUSP Pedro Alem Sobrnho Escola Polécnca da Unversdade
ESTUDO COMPARATIVO DE SISTEMAS DE AERAÇÃO PARA A ESTAÇÃO DE TRATAMENTO DE ESGOTOS SUZANO Roque Passos Pvel Escola Polécnca da Unversdade de São Paulo - EPUSP Pedro Alem Sobrnho Escola Polécnca da Unversdade
Capítulo 24: Potencial Elétrico
 Capítulo 24: Potencal Energa Potencal Elétrca Potencal Superfíces Equpotencas Cálculo do Potencal a Partr do Campo Potencal Produzdo por uma Carga Pontual Potencal Produzdo por um Grupo de Cargas Pontuas
Capítulo 24: Potencal Energa Potencal Elétrca Potencal Superfíces Equpotencas Cálculo do Potencal a Partr do Campo Potencal Produzdo por uma Carga Pontual Potencal Produzdo por um Grupo de Cargas Pontuas
Modulações digitais. Espaços de sinal e regiões de decisão. Funções ortogonais. Ortogonalização de Gram-Schmidt
 Modulaçõe dga Epaço de nal e regõe de decão Funçõe orogona Orogonalzação de Gram-Schmd Uma perpecva geomérca do na e ruído (Koelnkov) Um epaço orogonal de dmenõe é caracerzado por um conjuno de ψ () funçõe
Modulaçõe dga Epaço de nal e regõe de decão Funçõe orogona Orogonalzação de Gram-Schmd Uma perpecva geomérca do na e ruído (Koelnkov) Um epaço orogonal de dmenõe é caracerzado por um conjuno de ψ () funçõe
Experiência V (aulas 08 e 09) Curvas características
 Experênca (aulas 08 e 09) Curvas característcas 1. Objetvos 2. Introdução 3. Procedmento expermental 4. Análse de dados 5. Referêncas 1. Objetvos Como no expermento anteror, remos estudar a adequação de
Experênca (aulas 08 e 09) Curvas característcas 1. Objetvos 2. Introdução 3. Procedmento expermental 4. Análse de dados 5. Referêncas 1. Objetvos Como no expermento anteror, remos estudar a adequação de
Antenas e Propagação Folha de exercícios nº2 Conceitos Fundamentais
 Antenas e Propagação Folha de eercícos nº2 Concetos Fundamentas 1. Uma onda electromagnétca plana e unforme propaga-se em meo lvre. O campo magnétco H é dado por: 1 jk H e ( ˆ 2 yˆ) 120 a) Determne o campo
Antenas e Propagação Folha de eercícos nº2 Concetos Fundamentas 1. Uma onda electromagnétca plana e unforme propaga-se em meo lvre. O campo magnétco H é dado por: 1 jk H e ( ˆ 2 yˆ) 120 a) Determne o campo
F-128 Física Geral I. Aula exploratória-10b UNICAMP IFGW
 F-18 Físca Geral I Aula exploratóra-10b UNICAMP IFGW username@f.uncamp.br O teorema dos exos paralelos Se conhecermos o momento de nérca I CM de um corpo em relação a um exo que passa pelo seu centro de
F-18 Físca Geral I Aula exploratóra-10b UNICAMP IFGW username@f.uncamp.br O teorema dos exos paralelos Se conhecermos o momento de nérca I CM de um corpo em relação a um exo que passa pelo seu centro de
FEDERAL DE UBERLÂNDIA
 º POSMC Smpóso do Programa de Pós-graduação UNIVRSIDAD FDRAL D UBRLÂNDIA Faculdade de ngenhara Mecânca Programa de Pós-graduação em ngenhara Mecânca www.posgrad.mecanca.ufu.br MODLAGM POR LMNOS FINIOS
º POSMC Smpóso do Programa de Pós-graduação UNIVRSIDAD FDRAL D UBRLÂNDIA Faculdade de ngenhara Mecânca Programa de Pós-graduação em ngenhara Mecânca www.posgrad.mecanca.ufu.br MODLAGM POR LMNOS FINIOS
Modelo de Precificação de Capital: Segmento de Commodities Agrícola
 Modelo de Precfcação de Capal: Segmeno de Commodes Agrícola Capal Asse Prcng Model: Secor of Agrculural Commodes Táco Auguso Faras 1 Luz Eduardo Nascmeno Fgueredo Fábo Rodrgues Moura 3 Resumo: O objevo
Modelo de Precfcação de Capal: Segmeno de Commodes Agrícola Capal Asse Prcng Model: Secor of Agrculural Commodes Táco Auguso Faras 1 Luz Eduardo Nascmeno Fgueredo Fábo Rodrgues Moura 3 Resumo: O objevo
Capítulo 3. Dinâmica crítica do modelo de Baxter-Wu. 3.1 O Modelo
 Capíulo 3 Dnâmca críca do modelo de Baxer-Wu 3.1 O Modelo O modelo de Baxer-Wu fo nroduzdo por Wood e Grffhs 56 e resolvdo exaameno no conexo de mecânca esaísca de equlíbro por R.J. Baxer e F.Y.Wu em 1973
Capíulo 3 Dnâmca críca do modelo de Baxer-Wu 3.1 O Modelo O modelo de Baxer-Wu fo nroduzdo por Wood e Grffhs 56 e resolvdo exaameno no conexo de mecânca esaísca de equlíbro por R.J. Baxer e F.Y.Wu em 1973
SC de Física I Nota Q Nota Q2 Nota Q3 NOME: DRE Teste 1
 SC de Físca I - 2017-2 Nota Q1 88888 Nota Q2 Nota Q3 NOME: DRE Teste 1 Assnatura: Questão 1 - [3,5 pontos] Uma partícula de massa m se move sobre uma calha horzontal lsa com velocdade constante de módulo
SC de Físca I - 2017-2 Nota Q1 88888 Nota Q2 Nota Q3 NOME: DRE Teste 1 Assnatura: Questão 1 - [3,5 pontos] Uma partícula de massa m se move sobre uma calha horzontal lsa com velocdade constante de módulo
LISTA DE EXERCÍCIOS ENGENHARIA DE RESERVATÓRIOS
 PÓS-GRADUAÇÃO EM ENGENHARIA DE PETRÓLEO E GÁS NATURAL LISTA DE EXERCÍCIOS ENGENHARIA DE RESERVATÓRIOS 1. Consdere o esquema de searação FLASH mosrado na fura a seur que reresena o rocesso que ocorre em
PÓS-GRADUAÇÃO EM ENGENHARIA DE PETRÓLEO E GÁS NATURAL LISTA DE EXERCÍCIOS ENGENHARIA DE RESERVATÓRIOS 1. Consdere o esquema de searação FLASH mosrado na fura a seur que reresena o rocesso que ocorre em
2ª PARTE Estudo do choque elástico e inelástico.
 2ª PARTE Estudo do choque elástco e nelástco. Introdução Consderemos dos corpos de massas m 1 e m 2, anmados de velocdades v 1 e v 2, respectvamente, movmentando-se em rota de colsão. Na colsão, os corpos
2ª PARTE Estudo do choque elástco e nelástco. Introdução Consderemos dos corpos de massas m 1 e m 2, anmados de velocdades v 1 e v 2, respectvamente, movmentando-se em rota de colsão. Na colsão, os corpos
Óptica Óptica de Sólidos Aula 2. Daniel Schneider Tasca, CURSO DE ÓPTICA DA PÒS-GRAD. DO IF-UFRJ, 2007, Prof: Paulo H. S.
 Óptca 7 Óptca de Sóldos Aula Danel Schneder Tasca, CURSO DE ÓPTICA DA PÒS-GRAD. DO IF-UFRJ, 7, Prof: Paulo H. S. Rbero Sumáro da apresentação Equações de Maxwell Propagação da luz em meos condutores Dspostvos
Óptca 7 Óptca de Sóldos Aula Danel Schneder Tasca, CURSO DE ÓPTICA DA PÒS-GRAD. DO IF-UFRJ, 7, Prof: Paulo H. S. Rbero Sumáro da apresentação Equações de Maxwell Propagação da luz em meos condutores Dspostvos
Local branching aplicado ao problema de dimensionamento de lotes
 SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP Daa de Depóso: Assnaura: Local branchng aplcado ao problema de dmensonameno de loes Renao Andrade de Pava Orenadora: Franklna Mara Bragon de Toledo Dsseração apresenada
SERVIÇO DE PÓS-GRADUAÇÃO DO ICMC-USP Daa de Depóso: Assnaura: Local branchng aplcado ao problema de dmensonameno de loes Renao Andrade de Pava Orenadora: Franklna Mara Bragon de Toledo Dsseração apresenada
Dissertação submetida à
 UIVERSIDADE FEDERAL DE SATA CATARIA PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA MECÂICA SIMULAÇÃO DE PROCESSOS DE DESLOCAMETO IMISCÍVEL UTILIZADO MODELOS DE GÁS EM REDE COM MEDIADORES DE CAMPO Dsseração submeda
UIVERSIDADE FEDERAL DE SATA CATARIA PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA MECÂICA SIMULAÇÃO DE PROCESSOS DE DESLOCAMETO IMISCÍVEL UTILIZADO MODELOS DE GÁS EM REDE COM MEDIADORES DE CAMPO Dsseração submeda
Página 293. w1 w2 a b i 3 bi a b i 3 bi. 2w é o simétrico do dobro de w. Observemos o exemplo seguinte, em que o afixo de 2w não
 Preparar o Exame 0 0 Matemátca A Págna 9. Se 5 5 é o argumento de z, é argumento de z e 5 5. Este ângulo é gual ao ângulo de ampltude 5 é argumento de z.. Resposta: D w w a b b a b b. a b a a b b b bem
Preparar o Exame 0 0 Matemátca A Págna 9. Se 5 5 é o argumento de z, é argumento de z e 5 5. Este ângulo é gual ao ângulo de ampltude 5 é argumento de z.. Resposta: D w w a b b a b b. a b a a b b b bem
Curso de extensão, MMQ IFUSP, fevereiro/2014. Alguns exercício básicos
 Curso de extensão, MMQ IFUSP, feverero/4 Alguns exercíco báscos I Exercícos (MMQ) Uma grandeza cujo valor verdadero x é desconhecdo, fo medda três vezes, com procedmentos expermentas dêntcos e, portanto,
Curso de extensão, MMQ IFUSP, feverero/4 Alguns exercíco báscos I Exercícos (MMQ) Uma grandeza cujo valor verdadero x é desconhecdo, fo medda três vezes, com procedmentos expermentas dêntcos e, portanto,
Instituto de Física USP. Física Moderna. Aula 23. Professora: Mazé Bechara
 Insiuo de Física USP Física Moderna Aula 3 Professora: Mazé Bechara Aula 3 Bases da Mecânica quânica e equações de Schroedinger: para odos os esados e para esados esacionários. Aplicação e inerpreações.
Insiuo de Física USP Física Moderna Aula 3 Professora: Mazé Bechara Aula 3 Bases da Mecânica quânica e equações de Schroedinger: para odos os esados e para esados esacionários. Aplicação e inerpreações.
MATEMÁTICA LISTA DE EXERCÍCIOS NÚMEROS COMPLEXOS
 MATEMÁTICA LISTA DE EXERCÍCIOS NÚMEROS COMPLEXOS PROF: Claudo Saldan CONTATO: saldan.mat@gmal.com PARTE 0 -(MACK SP/00/Janero) Se y = x, sendo x= e =, o valor de (xy) é a) 9 9 9 9 e) 9 0 -(FGV/00/Janero)
MATEMÁTICA LISTA DE EXERCÍCIOS NÚMEROS COMPLEXOS PROF: Claudo Saldan CONTATO: saldan.mat@gmal.com PARTE 0 -(MACK SP/00/Janero) Se y = x, sendo x= e =, o valor de (xy) é a) 9 9 9 9 e) 9 0 -(FGV/00/Janero)
Espectro da radiação electromagnética
 specro da radiação elecromagnéica specro da radiação elecromagnéica A Naureza da Luz Carácer corpuscular Isaac Newon (643-77) Carácer ondulaório Chrisiaan Huygens(69-695) Carácer corpuscular não eplica
specro da radiação elecromagnéica specro da radiação elecromagnéica A Naureza da Luz Carácer corpuscular Isaac Newon (643-77) Carácer ondulaório Chrisiaan Huygens(69-695) Carácer corpuscular não eplica
