Algumas Possibilidades do Uso do GeoGebra nas Aulas de Matemática
|
|
|
- Alice Castanho Vasques
- 7 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE VIÇOSA III Semana Acadêmica de Matemática Algumas Possibilidades do Uso do GeoGebra nas Aulas de Matemática Profª Lahis Braga Souza Profª Thais Sena de Lanna Profª Cristiane Neves Mello Profª Bárbara Cunha Fontes Viçosa
2 UNIVERSIDADE FEDERAL DE VIÇOSA III Semana Acadêmica de Matemática Sumário Atividade 1 - Teorema de Pitágoras...3 Atividade 2 - Construção de prismas e pirâmides no GeoGebra 3D...4 Atividade 3 - Estudo das funções quadráticas...6 Atividade 4 - Funções trigonométricas...7 Atividade 5 - Trabalhando com triângulos de mesma área...8 Atividade 6 Noção intuitiva de limite e continuidade de uma função...9 Parte Parte Atividade 7- Construindo o gráfico da derivada...10
3 Atividade 1 - Teorema de Pitágoras Objetivo: Formalizar e compreender o conceito do Teorema de Pitágoras. Roteiro de Construção: Esconda o Eixo e a Malha para melhor visualização. Clique na ferramenta Controle Deslizante e clique sobre a janela de visualização. Na janela que abrirá, digite Cateto1 no campo destinado ao Nome e deixe o intervalo entre 0 e 15 com incremento de 1. Com a ferramenta Segmento com Comprimento Fixo, construa um segmento de comprimento Cateto1 (nome dado ao controle deslizante). Clique com o botão direito do mouse sobre o segmento formado e clique em renomear. No campo Nome, digite Cateto1. Selecione a ferramenta Reta Perpendicular e clique sobre o segmento criado no passo anterior e posteriormente sobre o ponto A. Faça agora o passo 2, nomeando o controle deslizante para cateto 2 Construa uma circunferência de centro A e raio Cateto2 (nome dado ao controle deslizante), com a ferramenta Círculo dados Centro e Raio. Com a ferramenta Intersecção de Dois Objetos, clique na circunferência formada no passo anterior e na reta perpendicular que passa pelo ponto A. Com a ferramenta Exibir/Esconder Objeto, esconda: a reta perpendicular, um dos pontos de intersecção entre a reta perpendicular e a circunferência e a circunferência. Construa os segmentos AD e DB (Cateto e Hipotenusa respectivamente). Clique com o botão direito do mouse sobre os segmentos AD e clique em renomear. No campo nome digite Cateto2. Faça o mesmo para o segmento DB renomeando para Hipotenusa. Selecione a ferramenta Polígono Regular e clique sobre os pontos D e B (No sentido horário), na janela que aparecerá digite 4 e clique em OK na janela que aparecerá. Com a mesma ferramenta, clique sobre os pontos A, D (no sentido horário) e por fim nos pontos B, A nessa ordem, digite 4 e clique em Ok na janela que aparecerá. Selecione a ferramenta Área, e clique sobre os três quadrados feitos anteriormente. Questões: 1) Clique em Exibir -> Planilha. Na planilha que aparecerá digite: (lembre-se há diferença com letras minúsculas e maiúscula no GeoGebra) 3
4 Nas células A1, A2, A3 digite db=, ba=, ad= Nas células B1,B2,B3 digite DB, BA, AD Nas células A5, A6, A7 digite (db)²=, (ba)²=, (ad)²= Nas células B5, B6, B7 digite (DB)², (BA)², (AD)² Movendo os controles deslizantes, o que pode observar em relação a área dos quadrados com os dados apresentados na planilha? 2) Digite nas células A9 e A10 digite (db)²=, (ba)² + (ad)²=. nas células abaixo digite (DB)² e (BA)²+(AD)² a) Movimentos os controles deslizantes, o que pode observar? b) Qual a relação as áreas dos quadrados? Atividade 2 - Construção de prismas e pirâmides no GeoGebra 3D Objetivo Compreender as características de um prisma e uma pirâmide no GeoGebra 3D. Roteiro de Construção Clicar em exibir, depois em janela de visualização 3D. Na janela de visualização 2 D, crie dois controles deslizantes com intervalo de 0 a 10, e incremento 0.1, renomeie os dois, o primeiro passando a ser h e o outro passando a ser l. Em seguida, clique em segmento com comprimento fixo, e selecione o comprimento l. Depois, clique em polígono regular, e clique nesses dois pontos do segmento, selecione 4 vértices. Um quadrado de lado l deverá ser formado tanto na janela de visualização 2D, quanto na janela de visualização 3D. Em seguida, clique em segmento com comprimento fixo, e selecione o comprimento l. Depois, clique em polígono regular, e clique nesses dois pontos do segmento, selecione 3 vértices. Um triângulo de lado l deverá ser formado tanto na janela de visualização 2D, quanto na janela de visualização 3D. Em seguida, na janela 3D, clique na sexta janela da direita para a esquerda e selecione a opção fazer extrusão para prisma ou cilindro, aí clique no quadrado, aí dará a opção de altura, coloque h nesse campo. 4
5 Em seguida, na janela 3D, clique na sexta janela da direita para a esquerda e selecione a opção fazer extrusão para pirâmide ou cone, aí clique no triângulo, aí dará a opção de altura, coloque h nesse campo. A figura deverá ficar parecida com esta, utilizando a primeira janela da direita para a esquerda, gire a janela de visualização 3D e explore a figura formada, mude também as cores se assim desejar: Atividade 3 - Estudo das funções quadráticas Objetivo Compreender os significados de cada parâmetro das funções quadráticas. Roteiro de Construção Criar os controles deslizantes a, b e c: Digitar no campo de entrada a função f(x) = ax^2 + bx + c. Mude a cor da parábola se desejar. Nesse momento, já poderia ser solicitado aos alunos que 5
6 manipulassem os parâmetros (com foco no a e c) para que conjecturassem sobre o que acontece. Depois, no campo de entrada, vamos localizar a coordenada do vértice, digitando no campo de entrada: V = ((-b) / (2a), (-(b² - 4a c)) / (4a)). Em seguida, habilite o rastro de V, movimente o controle b, e solicite aos alunos que conjecturem sobre o que estão visualizando. Os alunos devem concluir que a variação do parâmetro b faz com que a parábola se desloque tanto na parte positiva do eixo x quanto na parte negativa, bem como para cima e para baixo. Além disso, a trajetória do vértice traça uma parábola invertida. Atividade 4 - Funções trigonométricas Objetivo: Analisar o valor das funções seno, cosseno e tangente em triangulo retângulo. Roteiro de Construção Clicar na segunda janelinha superior (da direita para a esquerda) controle deslizante, e variar de -5 a 5. Digitar no campo de entrada y = ax, manter a positivo. 6
7 Clicar no segundo ícone da esquerda para a direita, e clicar em ponto sobre objeto, clicar na reta da função. Clicar no quarto ícone da esquerda para a direita, depois clicar em reta perpendicular, depois clicar no ponto A e no eixo x. Na interseção entre o eixo x e a reta perpendicular, colocar um outro ponto B, clicando novamente em ponto sobre objeto. Na interseção da reta com os eixos (na origem), coloque o ponto C, clicando mais uma vez em ponto sobre objeto. Clicando no quinto ícone da direita para a esquerda, clique em ângulo, depois clique (nessa ordem) em B, C, A, aparecerá a medida do ângulo interno correspondente ao vértice C. No campo de entrada, digite Distância[ A, B ], você terá a medida do cateto oposto ao ângulo criado. Será representado por d. No campo de entrada, digite Distância[ A, C ], você terá a medida da hipotenusa do triângulo. Será representado por e. No campo de entrada, digite Distância[ B, C ], você terá a medida do cateto adjacente ao ângulo criado. Será representado por f. No campo de entrada, digite d/e, e você terá a medida do seno do triângulo. Será representado por g. No campo de entrada, digite f/e, e você terá a medida do cosseno do triângulo. Será representado por h. No campo de entrada, digite d/f, e você terá a medida da tangente do triângulo. Será representado por i. Questões: 1) O que acontece com g, h e i quando variamos os pontos A? Justifique baseado na visualização e no que aprendeu em sala de aula. 2) Variando o controle deslizante a, altere as medidas do ângulo correspondente ao vértice C. O que acontece com as medidas de g, h e i, em cada ângulo que aparece, quando deslizamos o ponto A? Justifique. Atividade 5 - Trabalhando com triângulos de mesma área Objetivo: Trabalhar com os alunos os diferentes tipos de triângulo com mesma área. Formalizando a relação para o cálculo de área. 7
8 Roteiro de Construção: Construa uma reta a. Construa com a ferramenta Reta Paralela uma reta b paralela a reta a. Marque usando a ferramenta Ponto em Objeto os pontos D e E sobre a reta b Com a ferramenta Polígono construa os triângulos ABD e ABE. Com a ferramenta Área calcule a área do triângulo ABD e ABE. Questões: 1) O que você pode observar em relação as áreas desses triângulos? Você acha que isto acontece por que? 2) Movimente os pontos D e E, e descreva o que acontece com as medidas das áreas desses triângulos e se possível justifique o por que acontece. 3) Com a ferramenta Ângulo meça os ângulos do triângulo ABE. Quanto vale a soma de todos os ângulos internos? Use a ferramenta Entrada. 4) Com a ferramenta Mover, mova o ponto E. O que acontece com a soma dos ângulos internos do triângulo ABE? Atividade 6 Noção intuitiva de limite e continuidade de uma função Objetivo: Introduzir o assunto de limite de uma função visualizando graficamente, estudar a existência ou não do limite e verificar a continuidade de uma função em um ponto. Parte 1 Roteiro de Construção: Verifique que a janela de visualização esteja aparecendo os eixos coordenados e a malha. Caso contrário, clique com o botão direito do mouse e selecione as opções: Eixos e Malha. Insira na caixa de entrada a seguinte função f ( x)= { x ², x<1 2 x 3, x 1 com o seguinte comando: Se[<Condição>, <Então>, <Senão>] e aperte Enter. Crie um ponto A sobre o eixo x. Crie uma reta perpendicular ao eixo horizontal que passa por A. 8
9 Encontre o ponto B de interseção da reta a perpendicular com a função. Oculte a reta perpendicular. Crie uma reta perpendicular ao eixo y que passe pelo ponto B. Encontre o ponto C de interseção da reta b perpendicular com o eixo vertical. Oculte a reta b e o ponto B. Crie os segmentos AB e BC. Questões: 1) O que acontece com os valores de y quando os valores de x tendem a 1 pela direita? f (x )= x 1 + lim 2) O que acontece com os valores de y quando os valores de x tendem a 1 pela esquerda? f ( x)= x 1 lim 3) De acordo com os itens anteriores, o limite de f existe quando x=1? Justifique. 4) De acordo com o que já foi analisado até o momento, o que você diria sobre a Parte 2 continuidade dessa função? Justifique. Roteiro de Construção: Clique na ferramenta Controle Deslizante e clique sobre a janela de visualização. Na janela que abrirá, digite k no campo destinado ao Nome e deixe o intervalo entre -5 e 5. Clique duas vezes na função criada inicialmente e insira k, ao lado de x 2. Mova o número com a função. k no controle deslizante e observe o que acontece Questão: 9
10 1) Movendo o número k, no controle deslizante, é possível investigar para qual valor de k a função é contínua? 2) De acordo com o gráfico, para k= 1, o que acontece com a função nessa situação? 3) Existe o limite de f quando x tende a -1? Justifique sua resposta. Atividade 7- Construindo o gráfico da derivada Objetivo: Compreender a ideia de função derivada e construir o gráfico da função derivada a partir da função principal. Roteiro de Construção: Insira a função f ( x)=x ³ 4 x+2 na caixa de entrada. Clique na ferramenta Controle Deslizante e clique sobre a janela de visualização. Na janela que abrirá, digite a no campo destinado ao Nome e deixe o intervalo entre -5 e 5. Insira o ponto A=(a,f (a)) na caixa de entrada, em seguida tecle Enter. Utilizando a ferramenta reta tangente, tecle no gráfico da função e no ponto A. Dessa forma, obterá uma reta tangente ao gráfico no ponto A. Na opção inclinação, tecle na reta tangente, obtendo o valor da inclinação da reta tangente no ponto A. Renomeie a inclinação para m. Oculte a inclinação. Insira na caixa de entrada o ponto B=(a,m) Com o botão direito do mouse selecione a opção: habilitar rastro. Clique sobre o ponto B com o botão direito do mouse, selecione Propriedades e escolha uma cor para o ponto. Movimente o parâmetro a e observe a curva obtida pelo rastro deixado.. Questões: 10
11 1) Quais grandezas estão variando para gerar a curva? Elas estão em correspondência biunívoca? 2) A curva resultante da união dos pontos deixados pelo rastro corresponde ao gráfico de uma função? Se sim, qual? 11
Sumário. Educação Matemática: Oficinas Didáticas com GeoGebra 2012
 Sumário A Interface do GeoGebra...2 O menu do GeoGebra...3 Ferramentas de construção...4 LIÇÃO 1: Polígonos e ângulos...7 LIÇÃO 2: Retas perpendiculares e paralelas...11 LIÇÃO 3: Construindo gráficos...18
Sumário A Interface do GeoGebra...2 O menu do GeoGebra...3 Ferramentas de construção...4 LIÇÃO 1: Polígonos e ângulos...7 LIÇÃO 2: Retas perpendiculares e paralelas...11 LIÇÃO 3: Construindo gráficos...18
POTENCIALIDADES DO SOFTWARE GEOGEBRA NO ENSINO E APRENDIZAGM DE TRIGONOMETRIA
 1 UNIVERSIDADE FERDERAL DO RIO GRANDE DO NORTE UFRN CENTRO DE ENSINO SUPERIOR DO SERIDÓ CERES Departamento de Ciências Exatas e Aplicadas DCEA Programa Institucional de Iniciação à Docência PIBID/UERN
1 UNIVERSIDADE FERDERAL DO RIO GRANDE DO NORTE UFRN CENTRO DE ENSINO SUPERIOR DO SERIDÓ CERES Departamento de Ciências Exatas e Aplicadas DCEA Programa Institucional de Iniciação à Docência PIBID/UERN
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA
 APROPRIAÇÃO DE TECNOLOGIAS DIGITAIS: Um Estudo de Caso sobre Formação Continuada com Professores de Matemática PRODUTO DA DISSERTAÇÃO SEQUÊNCIA DIDÁTICA EVELIZE MARTINS KRÜGER PERES Porto Alegre 2015 A
APROPRIAÇÃO DE TECNOLOGIAS DIGITAIS: Um Estudo de Caso sobre Formação Continuada com Professores de Matemática PRODUTO DA DISSERTAÇÃO SEQUÊNCIA DIDÁTICA EVELIZE MARTINS KRÜGER PERES Porto Alegre 2015 A
DIRETORIA DE PESQUISA E PÓS-GRADUAÇÃO PROJETO: TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO E APRENDIZAGEM DE MATEMÁTICA
 DIRETORIA DE PESQUISA E PÓS-GRADUAÇÃO PROJETO: TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO E APRENDIZAGEM DE MATEMÁTICA NOME: DATA: / / Software GeoGebra 5.0 versão desktop 1ª Parte Conhecendo
DIRETORIA DE PESQUISA E PÓS-GRADUAÇÃO PROJETO: TECNOLOGIAS DE INFORMAÇÃO E COMUNICAÇÃO NO PROCESSO DE ENSINO E APRENDIZAGEM DE MATEMÁTICA NOME: DATA: / / Software GeoGebra 5.0 versão desktop 1ª Parte Conhecendo
Atividade 19: Espiral Logarítmica Objetivo: Apresentar o comando Curva.
 Atividade 19: Espiral Logarítmica Objetivo: Apresentar o comando Curva. Construir a espiral logarítmica. A espiral logarítmica é uma espiral cuja equação polar é dada por r=ae bt, onde r é a distância
Atividade 19: Espiral Logarítmica Objetivo: Apresentar o comando Curva. Construir a espiral logarítmica. A espiral logarítmica é uma espiral cuja equação polar é dada por r=ae bt, onde r é a distância
PLANO DE AULA Autora: Descritor: Série: Número de aulas previstas: Conteúdos: Objetivos:
 PLANO DE AULA Autora: Professora Rosa Descritor: Identificar propriedades de triângulos pela comparação de medidas de lados e ângulos Série: 8º ano Número de aulas previstas: 15 aulas Conteúdos: Elementos
PLANO DE AULA Autora: Professora Rosa Descritor: Identificar propriedades de triângulos pela comparação de medidas de lados e ângulos Série: 8º ano Número de aulas previstas: 15 aulas Conteúdos: Elementos
AULA 3 Atividade 06 Atividade 07 Atividade Complementar 8: Triângulos e seus ângulos internos
 AULA 3 Atividade 06 Segmento, ponto médio, mediatriz, paralelas e perpendiculares a) Construa um segmento com uma extremidade em (3, 4) e medida 3,5 (lembre-se: no lugar de vírgula devemos colocar o ponto).
AULA 3 Atividade 06 Segmento, ponto médio, mediatriz, paralelas e perpendiculares a) Construa um segmento com uma extremidade em (3, 4) e medida 3,5 (lembre-se: no lugar de vírgula devemos colocar o ponto).
CURSO DE CAPACITAÇÃO O USO DE FERRAMENTAS TECNOLÓGICAS E AS POSSIBILIDADES PEDAGÓGICAS NA FORMAÇÃO DOS DOCENTES NA REDE MUNICIPAL DE GURUPI TO
 CURSO DE CAPACITAÇÃO O USO DE FERRAMENTAS TECNOLÓGICAS E AS POSSIBILIDADES PEDAGÓGICAS NA FORMAÇÃO DOS DOCENTES NA REDE MUNICIPAL DE GURUPI TO A UTILIZAÇÃO DO SOFTWARE GEOGEBRA COMO FERRAMENTA DE ENSINO
CURSO DE CAPACITAÇÃO O USO DE FERRAMENTAS TECNOLÓGICAS E AS POSSIBILIDADES PEDAGÓGICAS NA FORMAÇÃO DOS DOCENTES NA REDE MUNICIPAL DE GURUPI TO A UTILIZAÇÃO DO SOFTWARE GEOGEBRA COMO FERRAMENTA DE ENSINO
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO PUC/SP ROSANA PERLETO DOS SANTOS
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO PUC/SP ROSANA PERLETO DOS SANTOS AS DIFICULDADES E POSSIBILIDADES DE PROFESSORES DE MATEMÁTICA AO UTILIZAREM O SOFTWARE GEOGEBRA EM ATIVIDADES QUE ENVOLVEM
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO PUC/SP ROSANA PERLETO DOS SANTOS AS DIFICULDADES E POSSIBILIDADES DE PROFESSORES DE MATEMÁTICA AO UTILIZAREM O SOFTWARE GEOGEBRA EM ATIVIDADES QUE ENVOLVEM
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO PAMPA - UNIPAMPA - BAGÉ PROGRAMA INSTITUCIONAL DE INICIAÇÃO À DOCÊNCIA SUBPROJETO DE MATEMÁTICA PIBID
 MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO PAMPA - UNIPAMPA - BAGÉ PROGRAMA INSTITUCIONAL DE INICIAÇÃO À DOCÊNCIA SUBPROJETO DE MATEMÁTICA PIBID Atividade nº 2 Oficina de Geometria Analítica com uso
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DO PAMPA - UNIPAMPA - BAGÉ PROGRAMA INSTITUCIONAL DE INICIAÇÃO À DOCÊNCIA SUBPROJETO DE MATEMÁTICA PIBID Atividade nº 2 Oficina de Geometria Analítica com uso
CONHECENDO E EXPLORANDO O GEOGEBRA
 CONHECENDO E EXPLORANDO O GEOGEBRA Bárbara Cunha Fontes 1 Cristiane Neves Mello 2 Marli Regina dos Santos 3 1 Universidade Federal de Viçosa / Departamento de Matemática, barbaracfontes@hotmail.com 2 Universidade
CONHECENDO E EXPLORANDO O GEOGEBRA Bárbara Cunha Fontes 1 Cristiane Neves Mello 2 Marli Regina dos Santos 3 1 Universidade Federal de Viçosa / Departamento de Matemática, barbaracfontes@hotmail.com 2 Universidade
Roteiro. Tela de entrada. Texto: Deive Barbosa Alves. Carlos Roberto Lopes Edinei Leandro dos Reis. Construindo Relações trigonométricas
 Roteiro Título da animação: Construindo Relações Tela de entrada Construindo Relações Botão entrar: o aluno irá para a próxima tela. No rodapé da página conterá o nome do objeto. 1 Tela de apresentação
Roteiro Título da animação: Construindo Relações Tela de entrada Construindo Relações Botão entrar: o aluno irá para a próxima tela. No rodapé da página conterá o nome do objeto. 1 Tela de apresentação
Minicurso GeoGebra CIME
 UNIVERSIDADE FEDERAL DE ALAGOAS CAMPUS DO SERTÃO PET ENGENHARIAS/MEC/SESu Minicurso GeoGebra CIME 2013.1 Delmiro Gouveia - AL, 15 de junho de 2013. NESTE CURSO TRATAREMOS SOBRE Apresentação geral do programa;
UNIVERSIDADE FEDERAL DE ALAGOAS CAMPUS DO SERTÃO PET ENGENHARIAS/MEC/SESu Minicurso GeoGebra CIME 2013.1 Delmiro Gouveia - AL, 15 de junho de 2013. NESTE CURSO TRATAREMOS SOBRE Apresentação geral do programa;
ESTUDO DAS CÔNICAS POR MEIO DA DEFINIÇÃO UNIFICADA E A UTILIZAÇÃO DO GEOGEBRA
 ESTUDO DAS CÔNICAS POR MEIO DA DEFINIÇÃO UNIFICADA E A UTILIZAÇÃO DO GEOGEBRA Juracélio Ferreira Lopes Instituto Federal de Minas Gerais Ouro Preto Juracelio.lopes@ifmg.edu.br Wladimir Seixas Universidade
ESTUDO DAS CÔNICAS POR MEIO DA DEFINIÇÃO UNIFICADA E A UTILIZAÇÃO DO GEOGEBRA Juracélio Ferreira Lopes Instituto Federal de Minas Gerais Ouro Preto Juracelio.lopes@ifmg.edu.br Wladimir Seixas Universidade
A UTILIZAÇÃO DO SOFTWARE GEOGEBRA NA FORMAÇÃO DE EDUCADORES DE MATEMÁTICA NO ENSINO FUNDAMENTAL
 A UTILIZAÇÃO DO SOFTWARE GEOGEBRA NA FORMAÇÃO DE EDUCADORES DE MATEMÁTICA NO ENSINO FUNDAMENTAL GT 05 Educação Matemática: tecnologias informáticas e educação à distância Prof a. Dr a. Julhane A. Thomas
A UTILIZAÇÃO DO SOFTWARE GEOGEBRA NA FORMAÇÃO DE EDUCADORES DE MATEMÁTICA NO ENSINO FUNDAMENTAL GT 05 Educação Matemática: tecnologias informáticas e educação à distância Prof a. Dr a. Julhane A. Thomas
Adilson Ortiz Bittencourt. O Ensino da Trigonometria no Ciclo Trigonométrico, por meio do Software Geogebra
 PRÓ-REITORIA DE PÓS-GRADUAÇÃO, PESQUISA E EXTENSÃO ÁREA DE CIÊNCIAS TECNOLÓGICAS CURSO DE MESTRADO PROFISSIONALIZANTE EM ENSINO DE FÍSICA E DE MATEMÁTICA Adilson Ortiz Bittencourt O Ensino da Trigonometria
PRÓ-REITORIA DE PÓS-GRADUAÇÃO, PESQUISA E EXTENSÃO ÁREA DE CIÊNCIAS TECNOLÓGICAS CURSO DE MESTRADO PROFISSIONALIZANTE EM ENSINO DE FÍSICA E DE MATEMÁTICA Adilson Ortiz Bittencourt O Ensino da Trigonometria
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior
 Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 08 ATIVIDADE 01 Seja ABCD um quadrilátero convexo inscrito em um círculo de
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 08 ATIVIDADE 01 Seja ABCD um quadrilátero convexo inscrito em um círculo de
Introdução ao software GeoGebra Por Meio de Atividades de Geometria
 Adriano Lima Teixeira Introdução ao software GeoGebra Por Meio de Atividades de Geometria O objetivo deste trabalho é de iniciar o uso do software GeoGebra por meio de atividades de Geometria, possibilitando
Adriano Lima Teixeira Introdução ao software GeoGebra Por Meio de Atividades de Geometria O objetivo deste trabalho é de iniciar o uso do software GeoGebra por meio de atividades de Geometria, possibilitando
ESTUDANDO MATEMÁTICA COM O AUXÍLIO DO GEOGEBRA UTILIZANDO AS JANELAS CAS E 3D
 ESTUDANDO MATEMÁTICA COM O AUXÍLIO DO GEOGEBRA UTILIZANDO AS JANELAS CAS E 3D Ministrantes: Bruno Santos Pereira, Ellen Cristina Barbosa dos Santos, Marrythiely Rodrigues Oliveira, Lucas Diêgo de Lima,
ESTUDANDO MATEMÁTICA COM O AUXÍLIO DO GEOGEBRA UTILIZANDO AS JANELAS CAS E 3D Ministrantes: Bruno Santos Pereira, Ellen Cristina Barbosa dos Santos, Marrythiely Rodrigues Oliveira, Lucas Diêgo de Lima,
Conhecendo o GeoGebra
 Conhecendo o GeoGebra Capítulo 1: Conhecendo o GeoGebra Passos Iniciais A figura a seguir apresenta a tela do GeoGebra 3.2. Barra de Menu Barra de Ferramentas Janela de Visualização Janela de Álgebra Campo
Conhecendo o GeoGebra Capítulo 1: Conhecendo o GeoGebra Passos Iniciais A figura a seguir apresenta a tela do GeoGebra 3.2. Barra de Menu Barra de Ferramentas Janela de Visualização Janela de Álgebra Campo
Assessores: Celço Luiz de Araújo Rubens Junior Schwalemberg. Trigonometria no GeoGebra
 NÚCLEO REGIONAL DE EDUCAÇÃO DE CASCAVEL CRTE COORDENAÇÃO REGIONAL DE TECNOLOGIA NA EDUCAÇÃO Av. Brasil, 2040. Bairro São Cristóvão. CEP:85816-290. Fone:(45) 3218-7895. Assessores: Celço Luiz de Araújo
NÚCLEO REGIONAL DE EDUCAÇÃO DE CASCAVEL CRTE COORDENAÇÃO REGIONAL DE TECNOLOGIA NA EDUCAÇÃO Av. Brasil, 2040. Bairro São Cristóvão. CEP:85816-290. Fone:(45) 3218-7895. Assessores: Celço Luiz de Araújo
UNIVERSIDADE REGIONAL DO NOROESTE DO ESTADO DO RIO GRANDE DO SUL DEPARTAMENTO DE FÍSICA, ESTATÍSTICA E MATEMÁTICA
 UNIVERSIDADE REGIONAL DO NOROESTE DO ESTADO DO RIO GRANDE DO SUL DEPARTAMENTO DE FÍSICA, ESTATÍSTICA E MATEMÁTICA GEOGEBRA Tânia Michel Pereira Juliane Sbaraine Costa Ijuí, setembro de 2009. Para acessar
UNIVERSIDADE REGIONAL DO NOROESTE DO ESTADO DO RIO GRANDE DO SUL DEPARTAMENTO DE FÍSICA, ESTATÍSTICA E MATEMÁTICA GEOGEBRA Tânia Michel Pereira Juliane Sbaraine Costa Ijuí, setembro de 2009. Para acessar
Geometria Dinâmica utilizando o Software Geogebra
 1 Geometria Dinâmica utilizando o Software Geogebra Gilmara Teixeira Barcelos Silvia Cristina Freitas Batista 2013 2 Licenciatura em Matemática Educação Matemática e Tecnologias 1º Período / / Nome: _
1 Geometria Dinâmica utilizando o Software Geogebra Gilmara Teixeira Barcelos Silvia Cristina Freitas Batista 2013 2 Licenciatura em Matemática Educação Matemática e Tecnologias 1º Período / / Nome: _
Revisão de Pré-Cálculo PÁRABOLAS. Prof. Dr. José Ricardo de Rezende Zeni Departamento de Matemática, FEG, UNESP Lc. Ismael Soares Madureira Júnior
 Revisão de Pré-Cálculo PÁRABOLAS Prof. Dr. José Ricardo de Rezende Zeni Departamento de Matemática, FEG, UNESP Lc. Ismael Soares Madureira Júnior Guaratinguetá, SP, Março, 2018 Direitos reservados. Reprodução
Revisão de Pré-Cálculo PÁRABOLAS Prof. Dr. José Ricardo de Rezende Zeni Departamento de Matemática, FEG, UNESP Lc. Ismael Soares Madureira Júnior Guaratinguetá, SP, Março, 2018 Direitos reservados. Reprodução
SEQUENCIA DIDÁTICA. Aula 1: Momento introdutório Duração: 1 hora aula Material necessário: lanterna e diferentes objetos tridimensionais.
 SEQUENCIA DIDÁTICA Aula : Momento introdutório Duração: hora aula Material necessário: lanterna e diferentes objetos tridimensionais. Objetivos: Instigar os estudantes sobre o aparecimento de figuras planas
SEQUENCIA DIDÁTICA Aula : Momento introdutório Duração: hora aula Material necessário: lanterna e diferentes objetos tridimensionais. Objetivos: Instigar os estudantes sobre o aparecimento de figuras planas
Geometria Dinâmica utilizando o Software Geogebra
 Geometria Dinâmica utilizando o Software Geogebra Gilmara Teixeira Barcelos Silvia Cristina Freitas Batista Campos dos Goytacazes 2008 Software GeoGebra 1ª Parte - Conhecendo o Software GeoGebra 1 Trata-se
Geometria Dinâmica utilizando o Software Geogebra Gilmara Teixeira Barcelos Silvia Cristina Freitas Batista Campos dos Goytacazes 2008 Software GeoGebra 1ª Parte - Conhecendo o Software GeoGebra 1 Trata-se
GeoGebra Quickstart Um rápido guia de referência sobre o GeoGebra
 GeoGebra Quickstart Um rápido guia de referência sobre o GeoGebra Geometria dinâmica, álgebra e cálculo formam juntos o GeoGebra, um software educativo premiado freqüentemente, que combina geometria e
GeoGebra Quickstart Um rápido guia de referência sobre o GeoGebra Geometria dinâmica, álgebra e cálculo formam juntos o GeoGebra, um software educativo premiado freqüentemente, que combina geometria e
Atividade 1. Construindo um prisma
 Atividade 1. Construindo um prisma 1- Clique em Unidades = Poliedro = Prisma (ver Figura 3). Abre-se uma janela na qual você pode escolher o número de lados do polígono (regular), o comprimento de cada
Atividade 1. Construindo um prisma 1- Clique em Unidades = Poliedro = Prisma (ver Figura 3). Abre-se uma janela na qual você pode escolher o número de lados do polígono (regular), o comprimento de cada
Relembrando: Ângulos, Triângulos e Trigonometria...
 Relembrando: Ângulos, Triângulos e Trigonometria... Este texto é apenas um resumo. Procure estudar esses assuntos em um livro apropriado. Ângulo é a região de um plano delimitada pelo encontro de duas
Relembrando: Ângulos, Triângulos e Trigonometria... Este texto é apenas um resumo. Procure estudar esses assuntos em um livro apropriado. Ângulo é a região de um plano delimitada pelo encontro de duas
FORMAÇÃO CONTINUADA EM MATEMÁTICA CECIERJ / SEEDUC RJ PLANO DE TRABALHO TRIGONOMETRIA NA CIRCUNFERÊNCIA MATEMÁTICA 1º ANO E.M. 4º BIMESTRE / 2012
 FORMAÇÃO CONTINUADA EM MATEMÁTICA CECIERJ / SEEDUC RJ PLANO DE TRABALHO TRIGONOMETRIA NA CIRCUNFERÊNCIA MATEMÁTICA 1º ANO E.M. 4º BIMESTRE / 2012 Cursista: LUCIENE CHIAPINI PEREIRA Matrícula(SEEDUC): 283746-6
FORMAÇÃO CONTINUADA EM MATEMÁTICA CECIERJ / SEEDUC RJ PLANO DE TRABALHO TRIGONOMETRIA NA CIRCUNFERÊNCIA MATEMÁTICA 1º ANO E.M. 4º BIMESTRE / 2012 Cursista: LUCIENE CHIAPINI PEREIRA Matrícula(SEEDUC): 283746-6
FUNDAÇÃO CECIERJ FORMAÇÃO CONTINUADA 1ª SÉRIE DO ENSINO MÉDIO PLANO DE TRABALHO FUNÇÕES TRIGONOMÉTRICAS PROFESSORA: EDILEIZER DA SILVA PEREIRA
 FUNDAÇÃO CECIERJ FORMAÇÃO CONTINUADA 1ª SÉRIE DO ENSINO MÉDIO PLANO DE TRABALHO FUNÇÕES TRIGONOMÉTRICAS PROFESSORA: EDILEIZER DA SILVA PEREIRA COLÉGIO ESTADUAL PEDRO BAPTISTA DE SOUZA TUTOR: RODOLFO GREGÓRIO
FUNDAÇÃO CECIERJ FORMAÇÃO CONTINUADA 1ª SÉRIE DO ENSINO MÉDIO PLANO DE TRABALHO FUNÇÕES TRIGONOMÉTRICAS PROFESSORA: EDILEIZER DA SILVA PEREIRA COLÉGIO ESTADUAL PEDRO BAPTISTA DE SOUZA TUTOR: RODOLFO GREGÓRIO
UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA
 UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA CADERNO DE EXERCÍCIOS ELABORADOS PELOS PARTICIPANTES DOS MINICURSOS SOBRE OS SOFTWARES
UNIVERSIDADE FEDERAL DE SANTA MARIA CENTRO DE CIÊNCIAS NATURAIS E EXATAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA CADERNO DE EXERCÍCIOS ELABORADOS PELOS PARTICIPANTES DOS MINICURSOS SOBRE OS SOFTWARES
Introdução à Astronomia Semestre:
 Introdução à Astronomia Semestre: 2015.1 Sergio Scarano Jr 22/10/2013 Horário de Atendimento do Professor Professor: Sergio Scarano Jr Sala: 119 Homepage: http://www.scaranojr.com.br/ * E-mail: scaranojr.ufs@gmail.com**
Introdução à Astronomia Semestre: 2015.1 Sergio Scarano Jr 22/10/2013 Horário de Atendimento do Professor Professor: Sergio Scarano Jr Sala: 119 Homepage: http://www.scaranojr.com.br/ * E-mail: scaranojr.ufs@gmail.com**
AULA 4. Atividade Complementar 10: Sistemas lineares 2x2 e sua interpretação geométrica 31
 AULA 4 Atividade Complementar 10: Sistemas lineares 2x2 e sua interpretação geométrica 31 Conteúdos Estruturantes: Números e Álgebra / Geometrias Conteúdo Básico: Sistemas lineares / Geometria espacial
AULA 4 Atividade Complementar 10: Sistemas lineares 2x2 e sua interpretação geométrica 31 Conteúdos Estruturantes: Números e Álgebra / Geometrias Conteúdo Básico: Sistemas lineares / Geometria espacial
DESENHO GEOMÉTRICO 9º ANO Prof. Danilo A. L. Pereira. Atividades básicas no GEOGEBRA. Polígonos Regulares
 Exercícios Polígonos Regulares 1 - Calcular a área de um triângulo. Para construção da figura você irá clicar no ícone que tem um triângulo, para fazer um polígono clique no ícone indicado por polígono,
Exercícios Polígonos Regulares 1 - Calcular a área de um triângulo. Para construção da figura você irá clicar no ícone que tem um triângulo, para fazer um polígono clique no ícone indicado por polígono,
CÍRCULO DADO O DIÂMETRO
 52 O GeoGebra oferece em sua instalação padrão um conjunto de ferramentas acessíveis por meio da Barra de Ferramentas e um conjunto com comandos que permitem construir objetos, realizar transformações,
52 O GeoGebra oferece em sua instalação padrão um conjunto de ferramentas acessíveis por meio da Barra de Ferramentas e um conjunto com comandos que permitem construir objetos, realizar transformações,
Roteiro. Título da animação: Ampliando as noções trigonométricas Autor: Equipe Rived Matemática/UFU Texto: Tela 1: Apresentação dos componentes
 Roteiro Título da animação: Ampliando as noções Texto: Tela 1: Apresentação dos componentes 1) Ampliando as noções 2) Equipe Rived Matemática/UFU 3) Componentes: Lóren Grace Kellen Maia Amorim Arlindo
Roteiro Título da animação: Ampliando as noções Texto: Tela 1: Apresentação dos componentes 1) Ampliando as noções 2) Equipe Rived Matemática/UFU 3) Componentes: Lóren Grace Kellen Maia Amorim Arlindo
18/06/13 REVISTA DO PROFESSOR DE MATEMÁTICA - SOCIEDADE BRASILEIRA DE MATEMÁTICA
 COMPUTADOR NA SALA DE AULA Estudo das cônicas com Geometria Dinâmica José Carlos de Souza Jr. Andréa Cardoso Unifal MG COMPUTADOR NA SALA DE AULA A exploração de softwares de Geometria Dinâmica nos permite
COMPUTADOR NA SALA DE AULA Estudo das cônicas com Geometria Dinâmica José Carlos de Souza Jr. Andréa Cardoso Unifal MG COMPUTADOR NA SALA DE AULA A exploração de softwares de Geometria Dinâmica nos permite
Tema da atividade: Teorema de Tales
 1 Tema da atividade: Teorema de Tales Objetivo: Explorar a Proporcionalidade do Teorema de Tales com suas representações Aritmética, Geométrica e Algébrica Aluno(a): Turma: Data: / / 1. 1 Abra um novo
1 Tema da atividade: Teorema de Tales Objetivo: Explorar a Proporcionalidade do Teorema de Tales com suas representações Aritmética, Geométrica e Algébrica Aluno(a): Turma: Data: / / 1. 1 Abra um novo
Geometria Analítica Plana
 Softwares Para o Ensino da Matemática Geometria Analítica Plana Nome do programa: EUKLID Descrição: Software de geometria dinâmica e construções em régua e compasso para criação de figuras geométricas.
Softwares Para o Ensino da Matemática Geometria Analítica Plana Nome do programa: EUKLID Descrição: Software de geometria dinâmica e construções em régua e compasso para criação de figuras geométricas.
Resolução de equações do 2º grau no Cabri-Géomètre II
 Resolução de equações do º grau no Cabri-Géomètre II Para resolver equações do º grau, provavelmente você já aprendeu várias estratégias que usavam sempre a álgebra (parte da matemática que estuda equações
Resolução de equações do º grau no Cabri-Géomètre II Para resolver equações do º grau, provavelmente você já aprendeu várias estratégias que usavam sempre a álgebra (parte da matemática que estuda equações
Resposta de alguns exercícios pares do Simmons - Capítulo 1
 Seção 2 Ex. 2a x < 0 ou x > 1. Ex. 2b. -1 < x < 0 ou 0 < x < 1. Ex. 2c. -2 < x < 1. Ex. 2d. x -1 ou x 2. Ex. 2e. x = 0 ou x 1. Ex. 2f. x = -1/2 ou x -1. Ex. 2g. x < -7 ou x > 3. Ex. 2h. -3/2 < x < 1. Ex.
Seção 2 Ex. 2a x < 0 ou x > 1. Ex. 2b. -1 < x < 0 ou 0 < x < 1. Ex. 2c. -2 < x < 1. Ex. 2d. x -1 ou x 2. Ex. 2e. x = 0 ou x 1. Ex. 2f. x = -1/2 ou x -1. Ex. 2g. x < -7 ou x > 3. Ex. 2h. -3/2 < x < 1. Ex.
Rosely Ouais Pestana Bervian José Benício dos Anjos França
 UNEB UNIVERSIDADE DO ESTADO DA BAHIA NEAD NÚCLEO DE EDUCAÇÃO A DISTÂNCIA DEPARTAMENTO DE EDUCAÇÃO CAMPUS I CURSO DE LICENCIATURA EM MATEMÁTICA A DISTÂNCIA DISCIPLINA: GEOMETRIA PLANA PROFESSORA FORMADORA:
UNEB UNIVERSIDADE DO ESTADO DA BAHIA NEAD NÚCLEO DE EDUCAÇÃO A DISTÂNCIA DEPARTAMENTO DE EDUCAÇÃO CAMPUS I CURSO DE LICENCIATURA EM MATEMÁTICA A DISTÂNCIA DISCIPLINA: GEOMETRIA PLANA PROFESSORA FORMADORA:
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA O Desenvolvimento de Hábitos de Pensamento: Um Estudo de Caso a partir de Construções
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA O Desenvolvimento de Hábitos de Pensamento: Um Estudo de Caso a partir de Construções
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSICA PROGRAMA DE PÓS-GRADUACÃO EM ENSINO DE MATEMÁTICA
 1 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSICA PROGRAMA DE PÓS-GRADUACÃO EM ENSINO DE MATEMÁTICA Daniel Rodrigues Topanotti TRIGONOMETRIA, RELAÇÃO ENTRE MOVIMENTOS CIRCULARES
1 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSICA PROGRAMA DE PÓS-GRADUACÃO EM ENSINO DE MATEMÁTICA Daniel Rodrigues Topanotti TRIGONOMETRIA, RELAÇÃO ENTRE MOVIMENTOS CIRCULARES
UM RELATO DO PROCESSO DE ELABORAÇÃO DE ATIVIDADE COM O GEOGEBRA
 UM RELATO DO PROCESSO DE ELABORAÇÃO DE ATIVIDADE COM O GEOGEBRA Marcela Souza Silva Graduada em Matemática (Licenciatura e Bacharelado) - Universidade Estadual Paulista Júlio Mesquita Filho São José do
UM RELATO DO PROCESSO DE ELABORAÇÃO DE ATIVIDADE COM O GEOGEBRA Marcela Souza Silva Graduada em Matemática (Licenciatura e Bacharelado) - Universidade Estadual Paulista Júlio Mesquita Filho São José do
No desenvolvimento deste guião, procure sempre colocar as denominações referidas em cada ponto.
 1 Este 3º guião contém atividades elementares com a finalidade de favorecer o reconhecimento e a consolidação das funções de algumas ferramentas do programa de geometria dinâmica Geogebra. Neste guião,
1 Este 3º guião contém atividades elementares com a finalidade de favorecer o reconhecimento e a consolidação das funções de algumas ferramentas do programa de geometria dinâmica Geogebra. Neste guião,
JANELA DE VISUALIZAÇÃO 3D
 31 Neste texto abordamos como exibir e explorar a Janela de Visualização 3D do GeoGebra. Abordamos como construir objetos como prismas e pirâmides. Em seguida, exploramos alguns comandos de 3D disponível
31 Neste texto abordamos como exibir e explorar a Janela de Visualização 3D do GeoGebra. Abordamos como construir objetos como prismas e pirâmides. Em seguida, exploramos alguns comandos de 3D disponível
Material do Professor. Tema: Roteiro de construção para a atividade Porcentagem
 1 Material do Professor Tema: Roteiro de construção para a atividade Porcentagem Objetivo: Dar suporte ao professor para fazer as construções necessárias à atividade Porcentagem ATIVIDADE 1: Construção
1 Material do Professor Tema: Roteiro de construção para a atividade Porcentagem Objetivo: Dar suporte ao professor para fazer as construções necessárias à atividade Porcentagem ATIVIDADE 1: Construção
Geometria e seus Artefatos
 Geometria e seus Artefatos Prof. Mário Selhorst Construção dos conceitos básicos de Geometria Analítica 1 SUMÁRIO (Use os links para acessar diretamente aos exemplos e o ícone 1. Perpendicular por um ponto
Geometria e seus Artefatos Prof. Mário Selhorst Construção dos conceitos básicos de Geometria Analítica 1 SUMÁRIO (Use os links para acessar diretamente aos exemplos e o ícone 1. Perpendicular por um ponto
1. Verifique se as seguintes igualdades são válidas, seja por integração ou por. + (a + b)x3 3 + abx2 2 + c. + c. + c
 Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática a Lista MAT - Cálculo I 7/II. Verifique se as seguintes igualdades são válidas, seja por integração ou por derivação:
Universidade Federal de Viçosa Centro de Ciências Eatas Departamento de Matemática a Lista MAT - Cálculo I 7/II. Verifique se as seguintes igualdades são válidas, seja por integração ou por derivação:
Minicurso de GeoGebra
 UNIVERSIDADE FEDERAL DE SANTA MARIA - RS GRUPO PET MATEMÁTICA DA UFSM Minicurso de GeoGebra Andréia luisa Friske Bernardo Abreu da Cruz Bruno Simões Gomes Dioggo Codein Dresch Dominiki Ribas dos Santos
UNIVERSIDADE FEDERAL DE SANTA MARIA - RS GRUPO PET MATEMÁTICA DA UFSM Minicurso de GeoGebra Andréia luisa Friske Bernardo Abreu da Cruz Bruno Simões Gomes Dioggo Codein Dresch Dominiki Ribas dos Santos
MARCIANE LINHARES CARLOS
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA MESTRADO PROFISSIONALIZANTE EM ENSINO DE MATEMÁTICA MARCIANE LINHARES CARLOS
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA MESTRADO PROFISSIONALIZANTE EM ENSINO DE MATEMÁTICA MARCIANE LINHARES CARLOS
Estudando Cônicas com Auxílio do Software Wingeom
 Estudando Cônicas com Auxílio do Software Wingeom Flávio de Freitas Afonso Bolsista PIBIC/CNPq Licenciando em Matemática CEFET-Campos Gilmara Teixeira Barcelos Professora do CEFET Campos - Mestre em Ciências
Estudando Cônicas com Auxílio do Software Wingeom Flávio de Freitas Afonso Bolsista PIBIC/CNPq Licenciando em Matemática CEFET-Campos Gilmara Teixeira Barcelos Professora do CEFET Campos - Mestre em Ciências
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ Matemática 3ºE.M 3º Bimestre/2013 Plano de Trabalho 2 Geometria Analítica Tarefa 2 Cursista: Vinícius Bento Ferro Tutora: Maria
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ Matemática 3ºE.M 3º Bimestre/2013 Plano de Trabalho 2 Geometria Analítica Tarefa 2 Cursista: Vinícius Bento Ferro Tutora: Maria
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA 120 PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA Registros Dinâmicos de Representação e Aprendizagem de Conceitos de
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA 120 PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA Registros Dinâmicos de Representação e Aprendizagem de Conceitos de
FUNDAÇÃO CECIERJ/CONSÓRCIO CEDERJ FORMAÇÃO CONTINUADA EM MATEMÁTICA 1º SÉRIE 2º BIMESTRE/2014 PLANO DE TRABALHO 2
 FUNDAÇÃO CECIERJ/CONSÓRCIO CEDERJ FORMAÇÃO CONTINUADA EM MATEMÁTICA 1º SÉRIE 2º BIMESTRE/2014 PLANO DE TRABALHO 2 RAZÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO Por: William Duarte de Carvalho Tutor: Rodolfo
FUNDAÇÃO CECIERJ/CONSÓRCIO CEDERJ FORMAÇÃO CONTINUADA EM MATEMÁTICA 1º SÉRIE 2º BIMESTRE/2014 PLANO DE TRABALHO 2 RAZÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO Por: William Duarte de Carvalho Tutor: Rodolfo
Figura 1 - Interface do GeoGebra
 O GeoGebra é um software de matemática dinâmica livre. Foi desenvolvido por Markus Hohenwarter e, posteriormente, modificado devido às contribuições de colaboradores do mundo todo. Já foi traduzido para
O GeoGebra é um software de matemática dinâmica livre. Foi desenvolvido por Markus Hohenwarter e, posteriormente, modificado devido às contribuições de colaboradores do mundo todo. Já foi traduzido para
ÂNGULOS EM UM TRIÂNGULO: SOMA DOS ÂNGULOS INTERNOS E TEOREMA DO ÂNGULO EXTERNO.
 UNIJUÍ - Universidade Regional do Noroeste do Estado do Rio Grande do Sul DCEEng - Departamento de Ciências Exatas e Engenharias PIBEX - PROGRAMA INSTITUCIONAL DE BOLSAS DE EXTENSÃO Projeto: Desenvolvimento
UNIJUÍ - Universidade Regional do Noroeste do Estado do Rio Grande do Sul DCEEng - Departamento de Ciências Exatas e Engenharias PIBEX - PROGRAMA INSTITUCIONAL DE BOLSAS DE EXTENSÃO Projeto: Desenvolvimento
Neste texto abordamos como construir um dado com a possibilidade de ser planificado e, além disso, ser lançado em um sorteio aleatório.
 59 Neste texto abordamos como construir um dado com a possibilidade de ser planificado e, além disso, ser lançado em um sorteio aleatório. Seguem os passos dessa construção. Construa um controle deslizante
59 Neste texto abordamos como construir um dado com a possibilidade de ser planificado e, além disso, ser lançado em um sorteio aleatório. Seguem os passos dessa construção. Construa um controle deslizante
Neste texto abordamos como construir um dado com a possibilidade de ser planificado e, além disso, ser lançado em um sorteio aleatório.
 72 Neste texto abordamos como construir um dado com a possibilidade de ser planificado e, além disso, ser lançado em um sorteio aleatório. Seguem os passos dessa construção. Construa um controle deslizante
72 Neste texto abordamos como construir um dado com a possibilidade de ser planificado e, além disso, ser lançado em um sorteio aleatório. Seguem os passos dessa construção. Construa um controle deslizante
Excel INTERMEDIÁRIO. Prof. Cassiano Isler Turma 3
 INTERMEDIÁRIO Gráficos Prof. Cassiano Isler 2017.1 - Turma 3 por Prof. Cassiano Isler INTERMEDIÁRIO - Aula 1 2 / 67 por GÓMEZ, Luis Alberto. para engenheiros. Visual Books, 2009. Capítulo 2. Disponível
INTERMEDIÁRIO Gráficos Prof. Cassiano Isler 2017.1 - Turma 3 por Prof. Cassiano Isler INTERMEDIÁRIO - Aula 1 2 / 67 por GÓMEZ, Luis Alberto. para engenheiros. Visual Books, 2009. Capítulo 2. Disponível
Estudando Trigonometria com applets desenvolvidos no software GeoGebra
 Estudando Trigonometria com applets desenvolvidos no software GeoGebra Elaborada por: Larissa de Sousa Moreira e Cíntia da Silva Gomes Orientada por: Gilmara Teixeira Barcelos e Silvia Cristina Freitas
Estudando Trigonometria com applets desenvolvidos no software GeoGebra Elaborada por: Larissa de Sousa Moreira e Cíntia da Silva Gomes Orientada por: Gilmara Teixeira Barcelos e Silvia Cristina Freitas
Resolvendo inequações: expressões com desigualdades (encontrar os valores que satisfazem a expressão)
 R é ordenado: Se a, b, c R i) a < b se e somente se b a > 0 (a diferença do maior com o menor será positiva) ii) se a > 0 e b > 0 então a + b > 0 (a soma de dois números positivos é positiva) iii) se a
R é ordenado: Se a, b, c R i) a < b se e somente se b a > 0 (a diferença do maior com o menor será positiva) ii) se a > 0 e b > 0 então a + b > 0 (a soma de dois números positivos é positiva) iii) se a
EXERCÍCIOS RESOLVIDOS TRIÂNGULOS
 1 EXERCÍCIOS RESOLVIDOS TRIÂNGULOS 1. CONSTRUIR UM TRIÂNGULO ESCALENO DE BASE 10 CM E ÂNGULOS ADJASCENTES À BASE DE 75 E 45. Sejam dados a base AB e os ângulos adjacentes à base. Primeiro transporte o
1 EXERCÍCIOS RESOLVIDOS TRIÂNGULOS 1. CONSTRUIR UM TRIÂNGULO ESCALENO DE BASE 10 CM E ÂNGULOS ADJASCENTES À BASE DE 75 E 45. Sejam dados a base AB e os ângulos adjacentes à base. Primeiro transporte o
FRACTAIS. Iteração: é um conjunto de procedimentos repetidos em série para construir um fractal. (NUNES, 2006, f. 30).
 Revisado por: A. Patrícia Grajales Spilimbergo e Cláudia Piva FRACTAIS Algumas definições... Fractal: Um fractal é um objeto que pode ser obtido geometricamente ou aleatoriamente através de processos recursivos,
Revisado por: A. Patrícia Grajales Spilimbergo e Cláudia Piva FRACTAIS Algumas definições... Fractal: Um fractal é um objeto que pode ser obtido geometricamente ou aleatoriamente através de processos recursivos,
POSSIBILIDADES DO USO DO GEOGEBRA NAS AULAS DE GEOMETRIA DO ENSINO FUNDAMENTAL II
 POSSIBILIDADES DO USO DO GEOGEBRA NAS AULAS DE GEOMETRIA DO ENSINO FUNDAMENTAL II Lahis Braga Souza¹ Marcela Souza Silva² ¹ Universidade Estadual Paulista Júlio Mesquita Filho Rio Claro/ Departamento de
POSSIBILIDADES DO USO DO GEOGEBRA NAS AULAS DE GEOMETRIA DO ENSINO FUNDAMENTAL II Lahis Braga Souza¹ Marcela Souza Silva² ¹ Universidade Estadual Paulista Júlio Mesquita Filho Rio Claro/ Departamento de
O uso do GeoGebra na formalização de conteúdos matemáticos
 O uso do GeoGebra na formalização de conteúdos matemáticos Geane dos Santos Santana / UFS geanesanttana@yahoo.com.br V Bienal da SBM / Outubro 2010 O uso do GeoGebra na formalização de conteúdos matemáticos
O uso do GeoGebra na formalização de conteúdos matemáticos Geane dos Santos Santana / UFS geanesanttana@yahoo.com.br V Bienal da SBM / Outubro 2010 O uso do GeoGebra na formalização de conteúdos matemáticos
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior jc
 Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 10 Reproduza as seguintes figuras no SuperLogo: ATIVIDADE 01 ATIVIDADE 02 Reproduza
Informática no Ensino de Matemática Prof. José Carlos de Souza Junior http://www.unifal-mg.edu.br/matematica/?q=disc jc Aula 10 Reproduza as seguintes figuras no SuperLogo: ATIVIDADE 01 ATIVIDADE 02 Reproduza
Minicurso GEOGEBRA Barra de Menu Barra de Ferramentas Janela Algébrica: Janela de entrada de dados
 UNIVERSIDADE FEDERAL DA PARAÍBA PRÓREITORIA DE GRADUAÇÃO PROJETO PIBID/LICENCIATURA MATEMÁTICA Prof. Antônio Joaquim Rodrigues Feitosa. Minicurso GEOGEBRA Introdução: Neste minicurso apresentaremos as
UNIVERSIDADE FEDERAL DA PARAÍBA PRÓREITORIA DE GRADUAÇÃO PROJETO PIBID/LICENCIATURA MATEMÁTICA Prof. Antônio Joaquim Rodrigues Feitosa. Minicurso GEOGEBRA Introdução: Neste minicurso apresentaremos as
Aula 1. Exercício 1: Exercício 2:
 Aula 1 Exercício 1: Com centro em A e raio de medida m achamos dois pontos B e C na reta, esses dois pontos são os centros das circunferências pedidas (2 soluções ). Exercício 2: Com centro em B e raio
Aula 1 Exercício 1: Com centro em A e raio de medida m achamos dois pontos B e C na reta, esses dois pontos são os centros das circunferências pedidas (2 soluções ). Exercício 2: Com centro em B e raio
MINI-CURSO Geometria Espacial com o GeoGebra Profa. Maria Alice Gravina Instituto de Matemática da UFRGS
 MINI-CURSO Geometria Espacial com o GeoGebra Profa. Maria Alice Gravina gravina@mat.ufrgs.br Instituto de Matemática da UFRGS Neste minicurso vamos trabalhar com os recursos do GeoGebra 3D e discutir possibilidades
MINI-CURSO Geometria Espacial com o GeoGebra Profa. Maria Alice Gravina gravina@mat.ufrgs.br Instituto de Matemática da UFRGS Neste minicurso vamos trabalhar com os recursos do GeoGebra 3D e discutir possibilidades
Provas de Acesso ao Ensino Superior Para Maiores de 23 Anos
 Provas de Acesso ao Ensino Superior Para Maiores de 23 Anos Candidatura de 207 EXAME DE MATEMÁTICA Tempo para realização da prova: 2 horas Tolerância: 30 minutos Material admitido: material de escrita
Provas de Acesso ao Ensino Superior Para Maiores de 23 Anos Candidatura de 207 EXAME DE MATEMÁTICA Tempo para realização da prova: 2 horas Tolerância: 30 minutos Material admitido: material de escrita
Atividades com Geogebra para o ensino de Cálculo
 Frank Victor Amorim Instituto Federal de Educação Ciência e Tecnologia do Rio Grande do Norte Brasil frank.amorim@ifrn.edu.br Giselle Costa de Sousa Universidade Federal do Rio Grande do Norte Brasil giselle@ccet.ufrn.br
Frank Victor Amorim Instituto Federal de Educação Ciência e Tecnologia do Rio Grande do Norte Brasil frank.amorim@ifrn.edu.br Giselle Costa de Sousa Universidade Federal do Rio Grande do Norte Brasil giselle@ccet.ufrn.br
Coordenadas Cartesianas
 1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
1 Coordenadas Cartesianas 1.1 O produto cartesiano Para compreender algumas notações utilizadas ao longo deste texto, é necessário entender o conceito de produto cartesiano, um produto entre conjuntos
Mini Curso GeoGebra. Download do GeoGebra: Java: / Divisão.
 Mini Curso GeoGebra Etapa I: Apresentação do Software; O GeoGebra é um software dinâmico, muito usado em conteúdos de Geometria, Álgebra, Estatística e Cálculo. É um programa livre e de código aberto;
Mini Curso GeoGebra Etapa I: Apresentação do Software; O GeoGebra é um software dinâmico, muito usado em conteúdos de Geometria, Álgebra, Estatística e Cálculo. É um programa livre e de código aberto;
Tarefa 2: Trigonometria no círculo
 FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ CURSO: MATEMÁTICA 1º ANO do ENSINO MÉDIO 3º BIMESTRE DE 2013 Tarefa 2: Trigonometria no círculo Cursista: Waine Vieira Junior
FORMAÇÃO CONTINUADA PARA PROFESSORES DE MATEMÁTICA FUNDAÇÃO CECIERJ/SEEDUC-RJ CURSO: MATEMÁTICA 1º ANO do ENSINO MÉDIO 3º BIMESTRE DE 2013 Tarefa 2: Trigonometria no círculo Cursista: Waine Vieira Junior
araribá matemática Quadro de conteúdos e objetivos Quadro de conteúdos e objetivos Unidade 1 Potências Unidade 2 Radiciação
 Unidade 1 Potências 1. Recordando potências Calcular potências com expoente natural. Calcular potências com expoente inteiro negativo. Conhecer e aplicar em expressões as propriedades de potências com
Unidade 1 Potências 1. Recordando potências Calcular potências com expoente natural. Calcular potências com expoente inteiro negativo. Conhecer e aplicar em expressões as propriedades de potências com
No triângulo formado pelos ponteiros do relógio e pelo seguimento que liga suas extremidades apliquemos a lei dos cossenos: 3 2
 COLÉGIO ANCHIETA-BA a AVALIAÇÃO de MATEMÁTICA _UNIDADE IV_ o ANO EM PROVA ELABORADA POR PROF OCTAMAR MARQUES. PROFA. MARIA ANTONIA CONCEIÇÃO GOUVEIA 0. Os ponteiros de um relógio têm comprimentos iguais
COLÉGIO ANCHIETA-BA a AVALIAÇÃO de MATEMÁTICA _UNIDADE IV_ o ANO EM PROVA ELABORADA POR PROF OCTAMAR MARQUES. PROFA. MARIA ANTONIA CONCEIÇÃO GOUVEIA 0. Os ponteiros de um relógio têm comprimentos iguais
CANDIDATO: DATA: 20 / 01 / 2010
 UNIVERSIDADE ESTADUAL DO CEARÁ - UECE SECRETARIA DE EDUCAÇÃO A DISTÂNCIA - SEaD Universidade Aberta do Brasil UAB LICENCIATURA PLENA EM MATEMÁTICA SELEÇÃO DE TUTORES PRESENCIAIS CANDIDATO: DATA: 0 / 0
UNIVERSIDADE ESTADUAL DO CEARÁ - UECE SECRETARIA DE EDUCAÇÃO A DISTÂNCIA - SEaD Universidade Aberta do Brasil UAB LICENCIATURA PLENA EM MATEMÁTICA SELEÇÃO DE TUTORES PRESENCIAIS CANDIDATO: DATA: 0 / 0
Matemática. Nesta aula iremos aprender as. 1 Ponto, reta e plano. 2 Posições relativas de duas retas
 Matemática Aula 5 Geometria Plana Alexandre Alborghetti Londero Nesta aula iremos aprender as noções básicas de Geometria Plana. 1 Ponto, reta e plano Estes elementos primitivos da geometria euclidiana
Matemática Aula 5 Geometria Plana Alexandre Alborghetti Londero Nesta aula iremos aprender as noções básicas de Geometria Plana. 1 Ponto, reta e plano Estes elementos primitivos da geometria euclidiana
Nesse texto vamos abordar como construir dois jogos utilizando os recursos gráficos, funções matemáticas e comandos internos do GeoGebra.
 66 Nesse texto vamos abordar como construir dois jogos utilizando os recursos gráficos, funções matemáticas e comandos internos do GeoGebra. COMANDO SE O comando Se, ou condicional, será muito útil no
66 Nesse texto vamos abordar como construir dois jogos utilizando os recursos gráficos, funções matemáticas e comandos internos do GeoGebra. COMANDO SE O comando Se, ou condicional, será muito útil no
E.E.M.FRANCISCO HOLANDA MONTENEGRO PLANO DE CURSO ENSINO MÉDIO
 E.E.M.FRANCISCO HOLANDA MONTENEGRO PLANO DE CURSO ENSINO MÉDIO DISCIPLINA: GEOMETRIA SÉRIE: 1º ANO (B, C e D) 2015 PROFESSORES: Crislany Bezerra Moreira Dias BIM. 1º COMPETÊNCIAS/ HABILIDADES D48 - Identificar
E.E.M.FRANCISCO HOLANDA MONTENEGRO PLANO DE CURSO ENSINO MÉDIO DISCIPLINA: GEOMETRIA SÉRIE: 1º ANO (B, C e D) 2015 PROFESSORES: Crislany Bezerra Moreira Dias BIM. 1º COMPETÊNCIAS/ HABILIDADES D48 - Identificar
Pontos correspondentes: A e D, B e E, C e F; Segmentos correspondentes: AB e DE, BC e EF, AC e DF.
 Teorema de Tales O Teorema de Tales possui diversas aplicações no cotidiano, que devem ser demonstradas a fim de verificar sua importância. O Teorema diz que retas paralelas, cortadas por transversais,
Teorema de Tales O Teorema de Tales possui diversas aplicações no cotidiano, que devem ser demonstradas a fim de verificar sua importância. O Teorema diz que retas paralelas, cortadas por transversais,
Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano
 Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú - UVA Curso de Licenciatura em Matemática marcio@matematicauva.org
Matemática Básica II - Trigonometria Nota 01 - Sistema de Coordenadas no Plano Márcio Nascimento da Silva Universidade Estadual Vale do Acaraú - UVA Curso de Licenciatura em Matemática marcio@matematicauva.org
3ª Igor/ Eduardo. Competência Objeto de aprendizagem Habilidade
 Matemática 3ª Igor/ Eduardo 9º Ano E.F. Competência Objeto de aprendizagem Habilidade C3 - Espaço e forma Números racionais. Números irracionais. Números reais. Relações métricas nos triângulos retângulos.
Matemática 3ª Igor/ Eduardo 9º Ano E.F. Competência Objeto de aprendizagem Habilidade C3 - Espaço e forma Números racionais. Números irracionais. Números reais. Relações métricas nos triângulos retângulos.
O USO DO SOFTWARE GeoGebra PARA O ESTUDO DE PROBLEMAS DE OTIMIZAÇÃO NO ENSINO MÉDIO
 2018, NÚMERO 1 VOLUME 6 ISSN 219-02X O USO DO SOFTWARE GeoGebra PARA O ESTUDO DE PROBLEMAS DE OTIMIZAÇÃO NO ENSINO MÉDIO RESUMO Josenildo da Cunha Lima EEEFM Min. José A. de Almeida e EMEIF João César
2018, NÚMERO 1 VOLUME 6 ISSN 219-02X O USO DO SOFTWARE GeoGebra PARA O ESTUDO DE PROBLEMAS DE OTIMIZAÇÃO NO ENSINO MÉDIO RESUMO Josenildo da Cunha Lima EEEFM Min. José A. de Almeida e EMEIF João César
PRODUTO DA DISSERTAÇÃO
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA MESTRADO PROFISSIONAL EM ENSINO DE MATEMÁTICA PRODUTO DA DISSERTAÇÃO GEOGEBRA
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL INSTITUTO DE MATEMÁTICA E ESTATÍSTICA PROGRAMA DE PÓS-GRADUAÇÃO EM ENSINO DE MATEMÁTICA MESTRADO PROFISSIONAL EM ENSINO DE MATEMÁTICA PRODUTO DA DISSERTAÇÃO GEOGEBRA
Solid Edge ST6. Tutorial 13. Modelando uma Hélice
 Solid Edge ST6 Tutorial 13 Modelando uma Hélice Neste tutorial serão introduzidos os conceitos de modelação, onde você verá a aplicação prática de features 3D através do comando Lofted Protrusion e a divisão
Solid Edge ST6 Tutorial 13 Modelando uma Hélice Neste tutorial serão introduzidos os conceitos de modelação, onde você verá a aplicação prática de features 3D através do comando Lofted Protrusion e a divisão
Introdução ao Cálculo Vetorial
 Introdução ao Cálculo Vetorial Segmento Orientado É o segmento de reta com um sentido de orientação. Por exemplo AB onde: A : origem e B : extremidade. Pode-se ter ainda o segmento BA onde: B : origem
Introdução ao Cálculo Vetorial Segmento Orientado É o segmento de reta com um sentido de orientação. Por exemplo AB onde: A : origem e B : extremidade. Pode-se ter ainda o segmento BA onde: B : origem
Seja AB = BC = CA = 4a. Sendo D o ponto de interseção da reta s com o lado AC temos, pelo teorema de Tales, AD = 3a e DC = a.
 GABARITO MA1 Geometria I - Avaliação 2-201/2 Questão 1. (pontuação: 2) As retas r, s e t são paralelas, como mostra a figura abaixo. A distância entre r e s é igual a e a distância entre s e t é igual
GABARITO MA1 Geometria I - Avaliação 2-201/2 Questão 1. (pontuação: 2) As retas r, s e t são paralelas, como mostra a figura abaixo. A distância entre r e s é igual a e a distância entre s e t é igual
CONCURSO DE ADMISSÃO AO COLÉGIO MILITAR DO RECIFE - 99 / 00 PROVA DE CIÊNCIAS EXATAS DA. 1 a é equivalente a a
 13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
13 1 a PARTE - MATEMÁTICA MÚLTIPLA ESCOLHA ESCOLHA A ÚNICA RESPOSTA CERTA, ASSINALANDO-A COM X NOS PARÊNTESES À ESQUERDA Item 01. Se a R e a 0, a expressão: 1 a é equivalente a a a.( ) 1 b.( ) c.( ) a
Caderno 1: 35 minutos. Tolerância: 10 minutos. (é permitido o uso de calculadora)
 Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/1.ª Fase Caderno 1: 7 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
Prova Final de Matemática 3.º Ciclo do Ensino Básico Decreto-Lei n.º 139/2012, de 5 de julho Prova 92/1.ª Fase Caderno 1: 7 Páginas Duração da Prova (Caderno 1 + Caderno 2): 90 minutos. Tolerância: 30
EXERCÍCIOS RESOLVIDOS TANGÊNCIA
 1 Resumo. Maria Bernadete Barison apresenta exercícios e resoluções sobre TANGÊNCIA em Desenho Geométrico. Geométrica vol.1 n.6c. 2005. Desenhos construídos por: Enéias de A. Prado. EXERCÍCIOS RESOLVIDOS
1 Resumo. Maria Bernadete Barison apresenta exercícios e resoluções sobre TANGÊNCIA em Desenho Geométrico. Geométrica vol.1 n.6c. 2005. Desenhos construídos por: Enéias de A. Prado. EXERCÍCIOS RESOLVIDOS
POLÍGONOS REGULARES CAD
 1 1. INTRODUÇÃO. POLÍGONOS REGULARES CAD Nesta aula você aprenderá a construir polígonos regulares e a medir o valor de seu ângulo interno. Além disso, aprenderá a traçar polígonos estrelados utilizando
1 1. INTRODUÇÃO. POLÍGONOS REGULARES CAD Nesta aula você aprenderá a construir polígonos regulares e a medir o valor de seu ângulo interno. Além disso, aprenderá a traçar polígonos estrelados utilizando
Ordenar ou identificar a localização de números racionais na reta numérica.
 Ordenar ou identificar a localização de números racionais na reta numérica. Estabelecer relações entre representações fracionárias e decimais dos números racionais. Resolver situação-problema utilizando
Ordenar ou identificar a localização de números racionais na reta numérica. Estabelecer relações entre representações fracionárias e decimais dos números racionais. Resolver situação-problema utilizando
Como obter o retângulo inscrito de maior área
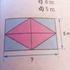 Como obter o retângulo inscrito de maior área Julio Omar Henrique da Silva 1 Dentro de todo triângulo retângulo se pode inserir um retângulo, a este se dá o nome de retângulo inscrito. O retângulo inscrito
Como obter o retângulo inscrito de maior área Julio Omar Henrique da Silva 1 Dentro de todo triângulo retângulo se pode inserir um retângulo, a este se dá o nome de retângulo inscrito. O retângulo inscrito
Trigonometria no Triângulo Retângulo
 Trigonometria no Triângulo Retângulo Prof. Márcio Nascimento marcio@matematicauva.org Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina:
Trigonometria no Triângulo Retângulo Prof. Márcio Nascimento marcio@matematicauva.org Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina:
APÊNDICE D SEQUÊNCIA DIDÁTICA
 APÊNDICE D SEQUÊNCIA DIDÁTICA ENCONTRO 1 Atividades de familiarização do menu do GeoGebra Apresentação de um PowerPoint com as informações sobre o curso e um vídeo desenvolvido no GeoGebra para estabelecermos
APÊNDICE D SEQUÊNCIA DIDÁTICA ENCONTRO 1 Atividades de familiarização do menu do GeoGebra Apresentação de um PowerPoint com as informações sobre o curso e um vídeo desenvolvido no GeoGebra para estabelecermos
