Faculdade de Engenharia Investigação Operacional. Prof. Doutor Engº Jorge Nhambiu
|
|
|
- Mariana Soares Pais
- 7 Há anos
- Visualizações:
Transcrição
1 1
2 Aula 2 Definição de Problemas de Investigação Operacional Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2
3 Problemas de Investigação Operacional Problemas de Investigação Operacional Programação Matemática Programação Linear Programação Não Linear 3
4 Problemas de Investigação Operacional O que são problemas de Investigação Operacional? Os problemas de Investigação Operacional são problemas de maximização ou minimização de funções de variáveis, designadas por objecto, que dependem de um número finito de variáveis. Estas variáveis podem ser independentes umas das outras, ou podem estar relacionadas através de uma ou mais restrições. 4
5 Problemas de Programação Matemática O que são problemas de Programação Matemática? Os problemas de Programação Matemática são uma classe particular de problemas de Investigação Operacional, que surgem na década de quarenta, aplicados nos campos da organização e da gestão económica, em que o objectivo e as restrições são dados como funções matemáticas e relações funcionais. 5
6 Programação Matemática Programação Matemática Planeamento de actividades O problema pode ser representado por um modelo matemático 6
7 Modelo matemático do problema de Programação Matemática maximizar f (x 1, x 2,, x N ) (minimizar) satisfazendo g 1 (x 1, x 2,, x N ) {, =, } b 1 g M (x 1, x 2,, x N ) {, =, } b M onde: x 1, x 2,, x N - N variáveis de decisão, f(x 1, x 2,, x N ) - função objectivo e g 1, g 2,, g M - M restrições do modelo 7
8 Classificação dos problemas de Programação Matemática Os problemas de Programação Matemática podem ser classificados em: lineares: se f (x 1, x 2,, x N ), gi (x 1, x 2,, x N ), i=1 M, são funções lineares PROGRAMAÇÃO LINEAR não lineares: se alguma das relações f (x 1, x 2,, x N ), g i (x 1, x 2,, x N ), i=1 M, for uma função não linear PROGRAMAÇÃO NÃO LINEAR 8
9 Programação Linear O que são problemas de Programação Linear? Os problemas de Programação Linear são uma classe particular de Problemas de Programação Matemática (PM), onde a função objectivo e as restrições podem ser representadas por funções lineares. A Programação Linear determina o planeamento óptimo de actividades, ou seja, um plano óptimo que represente a melhor solução entre todas as alternativas possíveis. 9
10 Programação Linear Programação Linear Planeamento de actividades O problema é representado matematicamente pelo modelo de PM onde todas as funções f (x 1, x 2,, x N ), g i (x 1, x 2,, x N ), i=1 M são lineares. 10
11 Modelo matemático do problema de Programação Linear maximizar f (x 1, x 2,, x N ) (minimizar) satisfazendo g 1 (x 1, x 2,, x N ) {, =, } b 1 g M (x 1, x 2,, x N ) {, =, } b M onde: x 1, x 2,, x N - variáveis de decisão, f(x 1, x 2,, x N ) - função objectivo LINEAR, g 1, g 2,, g M - restrições do modelo LINEARES 11
12 Exemplo Protótipo A empresa Nova Linha produz artigos de vidro de alta qualidade: janelas e portas, em três secções de produção: Secção de Serralharia: para produzir as estruturas de alumínio; Secção de Carpintaria: para produzir as estruturas de madeira; Secção de Vidro e Montagem: para produzir vidro e montar as portas e janelas. Devido à diminuição dos lucros, o gerente geral decidiu reorganizar a produção, e propõe produzir só 2 produtos que têm uma melhor aceitação entre os clientes. Estes produtos são: Produto 1: uma porta de vidro com estrutura de alumínio; Produto 2: uma janela grande com estrutura de madeira. 12
13 Exemplo Protótipo O Departamento de Marketing concluiu que a empresa pode vender tanto de qualquer dos dois produtos, tendo em conta a capacidade de produção disponível. Como ambos os produtos partilham a capacidade de produção da secção Nº3, o gerente solicitou ao Departamento de Investigação Operacional da empresa a resolução deste problema. O Departamento de IO para realizar a formulação do problema, procurou os seguintes dados: A capacidade de produção por minuto de cada secção a ser utilizada na produção de ambos os produtos; A capacidade de produção por minuto de cada secção, a ser utilizada para produzir uma unidade de cada produto; Os lucros unitários para cada produto. 13
14 Exemplo Protótipo Estes dados estão resumidos na seguinte tabela: Capacidade utilizada por unidade de produção Secção Nº Produto 1 Produto 2 Capacidade disponível Lucro unitário (em milhares de Mt)
15 Exemplo Protótipo: Formulação Maximizar Z = 3x 1 + 5x 2, sujeito a x 1 4 2x x 1 + 2x 2 18 x 1 0, x 2 0 x 1, x 2 - o número de unidades do produto 1 e 2 produzidas por minuto. Z o lucro total por minuto. 15
16 I. Identificar os valores de (x 1, x 2 ) que satisfaçam todas as restrições (região de admissibilidade) Exemplo Protótipo: Solução gráfica (I) x 2 1º x 1 0, x 2 0 (x 1, x 2 ) estão no 1º Quadrante 2º x 1 4 (x 1, x 2 ) estão situados à esquerda ou sobre a recta x 1 = x 1 = 4 x 2 = 6 3º 2 x 2 12 x 2 6 (x 1, x 2 ) estão situados abaixo ou sobre a recta x 2 = 6 2 Região de admissibilidade 4º 3 x x 2 18 (x 1, x 2 ) estão situados abaixo ou sobre a recta 3x 1 + 2x 2 = x 1 16
17 II. Determinar a solução Exemplo Protótipo: Solução gráfica (II) x 2 A função objectivo Z = 3x 1 + 5x 2 define uma recta que pode ser deslocada paralelamente no sentido do seu gradiente (garantindo o crescimento de Z), até se tornar tangente à região admissível. Neste caso o ponto de tangência (2,6) optimiza a função objectivo, pelo que a solução pretendida é x 1 = 2, x 2 = 6. O valor óptimo é Região das soluções admissíveis (2,6) é a solução x 1 Nova Linha deve fabricar duas portas (Produto 1) e seis janelas (Produto 2) por minuto obtendo um lucro de 36 Mil Mts por minuto. 17
18 Exemplo Protótipo: 3 recursos limitados a distribuir entre 2 actividades Capacidade de produção das 3 secções Recursos: M Produtos a produzir: 2 produtos Total de produtos a produzir por minutos: x 1 e x 2 Lucro por minuto: Z Actividades: N Nível da actividade j : x j Medida da vantagem: Z 18
19 Exemplo Protótipo (II) A empresa Filtros de Napipine Ltd, dedica-se a produção de três tipos de filtros para automóveis a saber: filtros de óleo, de gasolina e de ar. A manufactura de cada filtro requer o processamento em cada uma das duas máquinas que a empresa possui, que estão disponíveis 40 horas por mês. O tempo de processamento (em horas) e o lucro unitário de cada Filtro sobressalente (em Mt) apresenta-se na tabela seguinte: 19
20 Exemplo Protótipo (II) Capacidade utilizada por unidade de produção Máquina Filtros de óleo Filtros de ar Filtros de gasolina 1 0,02 0,03 0,05 2 0,05 0,02 0,04 Lucro unitário (em Mt) O problema consiste em determinar as quantidades de cada tipo de filtros a produzir por mês de modo a obter um lucro máximo. 20
21 Exemplo Protótipo (II) Maximizar Z = 250x x x 3 sujeito a: 0,02 x 1 + 0,03x 2 + 0,05x ,05 x 1 + 0,02x 2 + 0,04x 3 40 x 1 0, x 2 0, x 3 0 x 1, x 2, x 3 - o número filtros de óleo, ar e gasolina. Z o lucro total mensal. 21
22 Exemplo Protótipo (II): 2 recursos limitados a distribuir entre 3 actividades Capacidade de produção das 2 máquinas Recursos: M Produtos a produzir: 3 produtos Total de produtos a produzir por mês: x 1,x 2 e x 3 Lucro por mês: Z Actividades: N Nível da actividade j : x j Medida da vantagem: Z 22
23 O modelo de PL. Os parâmetros do modelo de PL para um problema onde estão envolvidas N actividades e M recursos podem ser definidos utilizando a seguinte tabela: Recursos Actividades M Utilização do recurso por actividade N Total de recurso disponível a 11 a a 1N. a 21 a a 2N a M1 a M2... a MN Lucro unitário c 1 c 2... c N Nível de actividade x 1 x 2... x N onde a i j, b i e c j são constantes, x j variáveis de decisão ( i=1,2,,m, j=1,2,,n ) b 1 b 2..,. b M 23
24 Formulação Matemática do Modelo de PL. Função objectivo Maximizar(minimizar) Z= c 1 x 1 + c 2 x c N x N sujeito a coluna j restrições linha i a 11 x 1 + a 12 x a 1 j x j + + a 1N x N {, =, } b 1 a 21 x 1 + a 22 x a 2 j x j + + a 2N x N {, =, } b 2 a i 1 x 1 + a i 2 x a i j x j + + a i N x N {, =, } b i a M 1 x 1 + a M 2 x a M j x j + + a M N x N {, =, } b M x 1, x 2,, x j,, x N 0 Condições de não negatividade onde a i j, b i e c j ( i=1,2,,m, j=1,2,,n ) são constantes e em cada restrição apenas se verifica uma e só uma das relações {, =, }. 24
25 I- TRANSPORTE: Exemplos clássicos de PL Suponha que um sistema de distribuição alimenta N armazéns a partir de M grandes unidades produtoras. Conhecendo os custos de transporte, a procura prevista para cada armazém e as capacidades (máximas) de produção de cada unidade, determinar o programa de distribuição com menor custo. II- COMPOSIÇÃO: Conhecendo os conteúdos calóricos e vitamínicos de diversos alimentos, bem como os seus preços, optimizar a composição da dieta a adoptar de modo a minimizar o seu custo e a satisfazer níveis mínimos de calorias e vitaminas. 25
26 Exemplos clássicos de PL III- PRODUÇÃO: Suponha que uma fábrica é capaz de produzir N produtos distintos utilizando M recursos limitados, os quais podem ser : horas de trabalho, tempos de operação de várias máquinas, matérias primas, serviços, etc. Conhecendo o lucro unitário, as quantidades de recurso utilizada para cada produto, e as quantidades de recursos disponíveis, determinar o plano óptimo de produção (com maior lucro). 26
27 O modelo de PL: Conclusões Os problemas de Programação Linear podem ser formulados de acordo com um modelo matemático geral, que consiste na determinação de valores não negativos para as variáveis x 1, x 2,, x j,, x N, a satisfazer um sistema de M equações (inequações) lineares que maximizem ou minimizem uma função (real) linear dessas variáveis. 27
Faculdade de Engenharia Investigação Operacional. Prof. Doutor Engº Jorge Nhambiu
 1 Aula 3 Definição de Problemas de Investigação Operacional (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema
1 Aula 3 Definição de Problemas de Investigação Operacional (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Aula 3 Definição de Problemas de Optimização (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema 3.1 Uma empresa
1 Aula 3 Definição de Problemas de Optimização (Prática) Construção de um modelo matemático de PL. Programação Matemática(PM) e Programação Linear(PL). Exemplos clássicos de PL. 2 Problema 3.1 Uma empresa
Recursos críticos disponíveis: Madeira 300 metros Horas de trabalho 110 horas
 I. Programação Linear (PL) 1. Introdução A Programação Linear é, no campo mais vasto da Programação Matemática, uma das variantes de aplicação generalizada em apoio da Decisão. O termo "Programação" deve
I. Programação Linear (PL) 1. Introdução A Programação Linear é, no campo mais vasto da Programação Matemática, uma das variantes de aplicação generalizada em apoio da Decisão. O termo "Programação" deve
Programação linear I João Carlos Lourenço
 Fundamentos de Investigação Operacional Programação linear I João Carlos Lourenço joao.lourenco@ist.utl.pt Ano lectivo 2011/2012 Leituras recomendadas: Nova, A.P., Lourenço, J.C., 2011, Apontamentos de
Fundamentos de Investigação Operacional Programação linear I João Carlos Lourenço joao.lourenco@ist.utl.pt Ano lectivo 2011/2012 Leituras recomendadas: Nova, A.P., Lourenço, J.C., 2011, Apontamentos de
Investigação Operacional
 Investigação Operacional Licenciatura em Gestão 3.º Ano Ano Lectivo 2013/14 Programação Linear Texto elaborado por: Maria João Cortinhal (Coordenadora) Anabela Costa Maria João Lopes Ana Catarina Nunes
Investigação Operacional Licenciatura em Gestão 3.º Ano Ano Lectivo 2013/14 Programação Linear Texto elaborado por: Maria João Cortinhal (Coordenadora) Anabela Costa Maria João Lopes Ana Catarina Nunes
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 15. Dualidade Interpretação económica. Problema dual: preços sombra e perdas de oportunidade. Propriedade dos desvios complementares 2 Formulação do Problema de PL em termos
1 Programação Linear (PL) Aula 15. Dualidade Interpretação económica. Problema dual: preços sombra e perdas de oportunidade. Propriedade dos desvios complementares 2 Formulação do Problema de PL em termos
EAD 350 Pesquisa Operacional Aula 01 Parte 2
 EAD 350 Pesquisa Operacional Aula 01 Parte 2 Profa. Daielly M. N. Mantovani Profa. Adriana Backx Noronha Viana Prof. Cesar Alexandre de Souza daielly@usp.br FEA/USP Elaboração de Modelos de PO Definição
EAD 350 Pesquisa Operacional Aula 01 Parte 2 Profa. Daielly M. N. Mantovani Profa. Adriana Backx Noronha Viana Prof. Cesar Alexandre de Souza daielly@usp.br FEA/USP Elaboração de Modelos de PO Definição
EAD 350 Pesquisa Operacional Aula 01 Parte 2
 EAD 350 Pesquisa Operacional Aula 01 Parte 2 Prof. Adriana Backx Noronha Viana (Material: Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Problema... Vocês foram contratados pela Wyndor Glass Company
EAD 350 Pesquisa Operacional Aula 01 Parte 2 Prof. Adriana Backx Noronha Viana (Material: Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Problema... Vocês foram contratados pela Wyndor Glass Company
Palavras e frases chave: Programação Linear; Tomada de decisões; Objectivos. Clasificação AMS: (opcional)
 VI Congreso Galego de Estatística e Investigación de Operacións Vigo 5-7 de Novembro de 2003 PROGRAMAÇÃO LINEAR: TOMADA DE DECISÕES, UMA NOVA ABORDAGEM NO ENSINO SECUNDÁRIO Maria José Teixeira do Nascimento
VI Congreso Galego de Estatística e Investigación de Operacións Vigo 5-7 de Novembro de 2003 PROGRAMAÇÃO LINEAR: TOMADA DE DECISÕES, UMA NOVA ABORDAGEM NO ENSINO SECUNDÁRIO Maria José Teixeira do Nascimento
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Forma geral de um problema Em vários problemas que formulamos, obtivemos: Um objetivo de otimização
Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Forma geral de um problema Em vários problemas que formulamos, obtivemos: Um objetivo de otimização
Faculdade de Ciência e Tecnologia da Universidade de Coimbra Departamento de Matemática
 Faculdade de Ciência e Tecnologia da Universidade de Coimbra Departamento de Matemática 2002/2003 1 Trabalho realizado no âmbito da cadeira de Fundamentos e Ensino da Álgebra por: Carla Sofia Monteiro
Faculdade de Ciência e Tecnologia da Universidade de Coimbra Departamento de Matemática 2002/2003 1 Trabalho realizado no âmbito da cadeira de Fundamentos e Ensino da Álgebra por: Carla Sofia Monteiro
Programação Linear. Rosa Canelas 2010
 Programação Linear Rosa Canelas 2010 Problemas de Optimização São problemas em que se procura a melhor solução (a que dá menor prejuízo, maior lucro, a que é mais eficiente, etc.) Alguns destes problemas
Programação Linear Rosa Canelas 2010 Problemas de Optimização São problemas em que se procura a melhor solução (a que dá menor prejuízo, maior lucro, a que é mais eficiente, etc.) Alguns destes problemas
Investigação Operacional
 Modelos de Programação Linear (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Modelação Matemática As técnicas e algoritmos
Modelos de Programação Linear (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas 1 Modelação Matemática As técnicas e algoritmos
Investigação Operacional
 Investigação Operacional Programação Linear Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território Problema Uma firma fabrica dois produtos P e P em três máquinas M, M e M. P é processado
Investigação Operacional Programação Linear Licenciatura em Engenharia Civil Licenciatura em Engenharia do Território Problema Uma firma fabrica dois produtos P e P em três máquinas M, M e M. P é processado
Pesquisa Operacional Aula 3 Modelagem em PL
 Pesquisa Operacional Aula 3 Modelagem em PL Prof. Marcelo Musci aula@musci.info www.musci.info Programação Linear Programação Linear: Preocupação em encontrar a melhor solução para problemas associados
Pesquisa Operacional Aula 3 Modelagem em PL Prof. Marcelo Musci aula@musci.info www.musci.info Programação Linear Programação Linear: Preocupação em encontrar a melhor solução para problemas associados
AULA 03 MODELOS DE PROGRAMAÇÃO LINEAR. Eduardo Camargo de Siqueira PESQUISA OPERACIONAL TECNÓLOGO EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS
 AULA 03 MODELOS DE PROGRAMAÇÃO LINEAR Eduardo Camargo de Siqueira PESQUISA OPERACIONAL TECNÓLOGO EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS PROGRAMAÇÃO LINEAR A PL usa um modelo matemático para descrever
AULA 03 MODELOS DE PROGRAMAÇÃO LINEAR Eduardo Camargo de Siqueira PESQUISA OPERACIONAL TECNÓLOGO EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS PROGRAMAÇÃO LINEAR A PL usa um modelo matemático para descrever
Universidade da Beira Interior Departamento de Matemática. Ficha de exercícios nº4 Pós-Optimização e Análise de Sensibilidade
 Ano lectivo: 2008/2009 Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº4 Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia 1.
Ano lectivo: 2008/2009 Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº4 Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia 1.
Investigação Operacional
 Ano lectivo: /6 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia. Uma fábrica
Ano lectivo: /6 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Pós-Optimização e Análise de Sensibilidade Cursos: Gestão e Economia. Uma fábrica
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios. Cap. IV Modelo Dual
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. IV Modelo Dual António Carlos Morais da Silva Professor de I.O. i Cap. IV - Modelo Dual - Exercícios IV. Modelo Problema Dual 1. Apresente o
Pesquisa Operacional aula 3 Modelagem PL. Profa. Alessandra Martins Coelho
 Pesquisa Operacional aula 3 Modelagem PL Profa. Alessandra Martins Coelho agosto/2013 Exercício Considerando que x j representa as variáveis de decisão, classificar os problemas a seguir em uma das categorias:
Pesquisa Operacional aula 3 Modelagem PL Profa. Alessandra Martins Coelho agosto/2013 Exercício Considerando que x j representa as variáveis de decisão, classificar os problemas a seguir em uma das categorias:
Otimização Aplicada à Engenharia de Processos
 Otimização Aplicada à Engenharia de Processos Aula 4: Programação Linear Felipe Campelo http://www.cpdee.ufmg.br/~fcampelo Programa de Pós-Graduação em Engenharia Elétrica Belo Horizonte Março de 2013
Otimização Aplicada à Engenharia de Processos Aula 4: Programação Linear Felipe Campelo http://www.cpdee.ufmg.br/~fcampelo Programa de Pós-Graduação em Engenharia Elétrica Belo Horizonte Março de 2013
Pesquisa Operacional. Introdução à Pesquisa Operacional Programação Linear
 Pesquisa Operacional Introdução à Pesquisa Operacional Programação Linear 1 Sumário Modelagem e limitações da Programação Linear. Resolução Gráfica. Forma padrão de um modelo de Programação Linear. Definições
Pesquisa Operacional Introdução à Pesquisa Operacional Programação Linear 1 Sumário Modelagem e limitações da Programação Linear. Resolução Gráfica. Forma padrão de um modelo de Programação Linear. Definições
Pesquisa Operacional Modelos, Conceitos Básicos para PL. Prof. Ricardo Santos
 Pesquisa Operacional Modelos, Conceitos Básicos para PL Prof. Ricardo Santos Problema do Transporte Centros de produção de produtos são denominados origens Mercados consumidores são denominados destinos
Pesquisa Operacional Modelos, Conceitos Básicos para PL Prof. Ricardo Santos Problema do Transporte Centros de produção de produtos são denominados origens Mercados consumidores são denominados destinos
sujeito a: 30x x (madeira) 5x x (horas de trabalho) x 1, x 2 0
 IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não tendo pois qualquer interesse prático. O método gráfico permite visualizar um conjunto
IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não tendo pois qualquer interesse prático. O método gráfico permite visualizar um conjunto
Optimização/Matemática II (Eco)
 Optimização/Matemática II (Eco) Frequência/ Exame 1ª Época 1º Ano 2º Semestre 2013 / 2014 Licenciaturas em Gestão, Finanças e Contabilidade, Gestão de Marketing e Economia 02-06-2014 Duração da Frequência:
Optimização/Matemática II (Eco) Frequência/ Exame 1ª Época 1º Ano 2º Semestre 2013 / 2014 Licenciaturas em Gestão, Finanças e Contabilidade, Gestão de Marketing e Economia 02-06-2014 Duração da Frequência:
Gestão de Operações II. Prof. Marcio Cardoso Machado. Método Gráfico para Solução de Problemas de Programação Linear
 Gestão de Operações II Prof. Marcio Cardoso Machado Método Gráfico para Solução de Problemas de Programação Linear Será apresentada a resolução de um exercício e o gabarito dos demais. Exercício resolvido
Gestão de Operações II Prof. Marcio Cardoso Machado Método Gráfico para Solução de Problemas de Programação Linear Será apresentada a resolução de um exercício e o gabarito dos demais. Exercício resolvido
Investigação Operacional
 Ano lectivo: 0/06 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Algoritmo Simplex Cursos: Gestão e Economia. Considere o seguinte conjunto
Ano lectivo: 0/06 Universidade da Beira Interior - Departamento de Matemática Investigação Operacional Ficha de exercícios n o Algoritmo Simplex Cursos: Gestão e Economia. Considere o seguinte conjunto
Modelos em Programação Linear Inteira
 Modelos em Programação Linear Inteira Maria João Cortinhal a, Anabela Dias Costa a, Maria João Lopes a, Ana Catarina Nunes a a Departamento de Métodos Quantitativos, ISCTE-IUL 13 de Setembro de 2013 1
Modelos em Programação Linear Inteira Maria João Cortinhal a, Anabela Dias Costa a, Maria João Lopes a, Ana Catarina Nunes a a Departamento de Métodos Quantitativos, ISCTE-IUL 13 de Setembro de 2013 1
No eixo das ordenadas o ponto B tem abcissa nula (x 1 = 0) pelo que a equação se reduz a 20x 2 = 300. Madeira. C(10,10) não é admissível.
 IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não sendo pois de considerar para resolução de problemas da vida real. Porque a determinação
IV. MÉTODO GRÁFICO O método gráfico só permite resolver problemas de PL de pequena dimensão (duas ou três variáveis) não sendo pois de considerar para resolução de problemas da vida real. Porque a determinação
PROGRAMAÇÃO LINEAR 11º ANO MATEMÁTICA A
 PROGRAMAÇÃO LINEAR 11º ANO MATEMÁTICA A Prof.ª: Maria João Mendes Vieira ESC 11MatA 2012/2013 PROGRAMAÇÃO LINEAR A programação linear é uma "ferramenta" matemática que permite encontrar a solução ótima
PROGRAMAÇÃO LINEAR 11º ANO MATEMÁTICA A Prof.ª: Maria João Mendes Vieira ESC 11MatA 2012/2013 PROGRAMAÇÃO LINEAR A programação linear é uma "ferramenta" matemática que permite encontrar a solução ótima
Resolução de PL usando o método Simplex
 V., V.Lobo, EN / ISEGI, 28 Resolução de PL usando o método Simplex Método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 947 Muito utilizado Facilmente implementado como
V., V.Lobo, EN / ISEGI, 28 Resolução de PL usando o método Simplex Método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 947 Muito utilizado Facilmente implementado como
Pesquisa Operacional aplicada ao Planejamento e Controle da Produção e de Materiais Programação Linear
 Pesquisa Operacional aplicada ao Planejamento e Controle da Produção e de Materiais Programação Linear Introdução à Pesquisa Operacional Origens militares Segunda guerra mundial Aplicada na alocação de
Pesquisa Operacional aplicada ao Planejamento e Controle da Produção e de Materiais Programação Linear Introdução à Pesquisa Operacional Origens militares Segunda guerra mundial Aplicada na alocação de
Modelos de planeamento e gestão de recursos hídricos. 19 de Novembro
 Modelos de planeamento e gestão de recursos hídricos 19 de Novembro Metodologias de análise Sistema real vs sistema simplificado Modelação Matemática; Física; Análise de sistemas: Simulação; Optimização:
Modelos de planeamento e gestão de recursos hídricos 19 de Novembro Metodologias de análise Sistema real vs sistema simplificado Modelação Matemática; Física; Análise de sistemas: Simulação; Optimização:
Método Simplex V 1.1, V.Lobo, EN / ISEGI, 2008
 .,.Lobo, EN / ISEGI, 8 Método Simplex Resolução de PL usando o método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 97 Muito utilizado Facilmente implementado como programa
.,.Lobo, EN / ISEGI, 8 Método Simplex Resolução de PL usando o método Simplex Algoritmo para resolver problemas de programação linear George Dantzig, 97 Muito utilizado Facilmente implementado como programa
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 10: Método Simplex Técnica das variáveis artificias Método das penalidades ( Big M ). Método das duas fases. 2 Modificando o Exemplo Protótipo. Suponha-se que é modificado
1 Programação Linear (PL) Aula 10: Método Simplex Técnica das variáveis artificias Método das penalidades ( Big M ). Método das duas fases. 2 Modificando o Exemplo Protótipo. Suponha-se que é modificado
Otimização Linear. Profª : Adriana Departamento de Matemática. wwwp.fc.unesp.br/~adriana
 Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Problema da Mistura minimizar f ( 1, 2,..., n ) = c 1 1 + c 2 2 +... + c n n Sujeito a: a 11 1
Otimização Linear Profª : Adriana Departamento de Matemática adriana@fc.unesp.br wwwp.fc.unesp.br/~adriana Problema da Mistura minimizar f ( 1, 2,..., n ) = c 1 1 + c 2 2 +... + c n n Sujeito a: a 11 1
Programação Linear (PL)
 Programação Linear (PL) Prof. Paulo Cesar F. De Oliveira, BSc, PhD 07/08/15 P C F de Oliveira 2014 1 Características Técnicas mais utilizadas na abordagem de problemas em PO Técnica de solução programável
Programação Linear (PL) Prof. Paulo Cesar F. De Oliveira, BSc, PhD 07/08/15 P C F de Oliveira 2014 1 Características Técnicas mais utilizadas na abordagem de problemas em PO Técnica de solução programável
PROGRAMAÇÃO LINEAR. Tipo de problemas: cálculo do plano óptimo de distribuição de mercadorias; minimiação de desperdícios no corte de materiais;
 PROGRAMAÇÃO LINEAR Atribuição de recursos limitados a actividades concorrentes de modo a atingir-se um objectivo. Tipo de problemas: estrutura ideal das fabricações atendendo ao equipamento, mão de obra,
PROGRAMAÇÃO LINEAR Atribuição de recursos limitados a actividades concorrentes de modo a atingir-se um objectivo. Tipo de problemas: estrutura ideal das fabricações atendendo ao equipamento, mão de obra,
Programação Linear. Gabriel Ferreira Gabriel Tutia Gabriel Yida Thiago Ferraz
 Programação Linear Gabriel Ferreira 8989404 Gabriel Tutia 8989085 Gabriel Yida 8989432 Thiago Ferraz 8989001 O que é? É um caso especial de programação matemática ou otimização matemática Método para encontrar
Programação Linear Gabriel Ferreira 8989404 Gabriel Tutia 8989085 Gabriel Yida 8989432 Thiago Ferraz 8989001 O que é? É um caso especial de programação matemática ou otimização matemática Método para encontrar
Otimização. Modelagem e Solução Gráfica. Paulo Henrique Ribeiro Gabriel Faculdade de Computação Universidade Federal de Uberlândia
 Otimização Modelagem e Solução Gráfica Paulo Henrique Ribeiro Gabriel phrg@ufu.br Faculdade de Computação Universidade Federal de Uberlândia 2016/1 Paulo H. R. Gabriel (FACOM/UFU) GSI027 2016/1 1 / 49
Otimização Modelagem e Solução Gráfica Paulo Henrique Ribeiro Gabriel phrg@ufu.br Faculdade de Computação Universidade Federal de Uberlândia 2016/1 Paulo H. R. Gabriel (FACOM/UFU) GSI027 2016/1 1 / 49
Programação Linear. (2ª parte) Informática de Gestão Maria do Rosário Matos Bernardo 2016
 Programação Linear (2ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Representação e resolução gráfica dos problemas de programação linear Problema de minimização Problema
Programação Linear (2ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Representação e resolução gráfica dos problemas de programação linear Problema de minimização Problema
PESQUISA OPERACIONAL I
 PESQUISA OPERACIONAL I Professor: Dr. Edwin B. Mitacc Meza edwin.professor@gmail.com www.engenharia-puro.com.br/edwin O Processo de Modelagem Modelagem Matemática É possível, de uma forma bastante geral,
PESQUISA OPERACIONAL I Professor: Dr. Edwin B. Mitacc Meza edwin.professor@gmail.com www.engenharia-puro.com.br/edwin O Processo de Modelagem Modelagem Matemática É possível, de uma forma bastante geral,
* O que originou a designação Operational Research no Reino Unido, A origem da Investigação Operacional (IO)?
 A origem da Investigação Operacional (IO)? A IO surgiu no final da II Guerra Mundial quando os Aliados se viram confrontados com problemas (relativamente aos recursos logísticos e às operações* das forças
A origem da Investigação Operacional (IO)? A IO surgiu no final da II Guerra Mundial quando os Aliados se viram confrontados com problemas (relativamente aos recursos logísticos e às operações* das forças
Universidade da Beira Interior Departamento de Matemática. Ficha de exercícios nº3: Dualidade. Interpretação Económica.
 Ano lectivo: 2008/2009; Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº3: Dualidade. Interpretação Económica. Cursos: Economia 1. Formule o problema
Ano lectivo: 2008/2009; Universidade da Beira Interior Departamento de Matemática INVESTIGAÇÃO OPERACIONAL Ficha de exercícios nº3: Dualidade. Interpretação Económica. Cursos: Economia 1. Formule o problema
II. Programação Linear (PL)
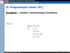 II. Programação Linear (PL) Dualidade revisão e interpretação econômica Seja o pl max Z x x x x 4 x, x 5x x 0 8 000-00 Prof.ª Gladys Castillo Formulação do Problema de PL em termos de Atividades. Exemplo
II. Programação Linear (PL) Dualidade revisão e interpretação econômica Seja o pl max Z x x x x 4 x, x 5x x 0 8 000-00 Prof.ª Gladys Castillo Formulação do Problema de PL em termos de Atividades. Exemplo
Problemas de Fluxos em Redes
 Investigação Operacional Problemas de Fluxos em Redes Slide Transparências de apoio à leccionação de aulas teóricas Problemas de fluxos em redes Rede: Conjunto de pontos (vértices) ligados por linhas ou
Investigação Operacional Problemas de Fluxos em Redes Slide Transparências de apoio à leccionação de aulas teóricas Problemas de fluxos em redes Rede: Conjunto de pontos (vértices) ligados por linhas ou
Pesquisa Operacional. Prof. José Luiz
 Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Pesquisa Operacional Prof. José Luiz Prof. José Luiz Função Linear - Introdução O conceito de função é encontrado em diversos setores da economia, por exemplo, nos valores pagos em um determinado período
Técnicas de Planeamento e Gestão. Folha nº. 1 Introdução à Programação Linear 2007/08
 Técnicas de Planeamento e Gestão Folha nº. 1 Introdução à Programação Linear 2007/08 1- A fábrica de gelados Derretem-se na Boca SARL fabrica duas qualidades de gelados: cassata de nozes (C) e pistachio
Técnicas de Planeamento e Gestão Folha nº. 1 Introdução à Programação Linear 2007/08 1- A fábrica de gelados Derretem-se na Boca SARL fabrica duas qualidades de gelados: cassata de nozes (C) e pistachio
Investigação Operacional
 Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Análise de Sensibilidade, Formulação Dual (Mestrado) Engenharia Industrial http://dps.uminho.pt/pessoais/zan - Escola de Engenharia Departamento de Produção e Sistemas Uma das tarefas mais delicadas no
Professor João Soares 20 de Setembro de 2004
 Teoria de Optimização (Mestrado em Matemática) Texto de Apoio 2A Universidade de Coimbra 57 páginas Professor João Soares 20 de Setembro de 2004 Optimização Linear Considere o problema (1) abaixo, que
Teoria de Optimização (Mestrado em Matemática) Texto de Apoio 2A Universidade de Coimbra 57 páginas Professor João Soares 20 de Setembro de 2004 Optimização Linear Considere o problema (1) abaixo, que
max z = 10x 1 + 4x 2 s.a x 1 + x x 1 + 4x x 1 + 6x 2 300
 Escola Superior de Tecnologia de Tomar Área de Matemática Investigação Operacional / Técnicas de Optimização e Decisão Engenharia Química, Engenharia do Ambiente, Engenharia Informática e Engenharia Civil
Escola Superior de Tecnologia de Tomar Área de Matemática Investigação Operacional / Técnicas de Optimização e Decisão Engenharia Química, Engenharia do Ambiente, Engenharia Informática e Engenharia Civil
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Linear (PL) Aula 8 : O método Simplex. Casos particulares. Empate no critério de entrada. Óptimo não finito. Soluções óptimas alternativas. Degenerescência. INÍCIO Forma Padrão Faculdade
1 Programação Linear (PL) Aula 8 : O método Simplex. Casos particulares. Empate no critério de entrada. Óptimo não finito. Soluções óptimas alternativas. Degenerescência. INÍCIO Forma Padrão Faculdade
EAD 350 Pesquisa Operacional Aula 04 Parte 1 Resolução de Exercícios
 EAD 350 Pesquisa Operacional Aula 04 Parte 1 Resolução de Exercícios Profa. Adriana Backx Noronha Viana (Adapt. Material Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Aula 3 Enunciado 4 Uma pequena
EAD 350 Pesquisa Operacional Aula 04 Parte 1 Resolução de Exercícios Profa. Adriana Backx Noronha Viana (Adapt. Material Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Aula 3 Enunciado 4 Uma pequena
Slide 1. c 2000, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP
 Construção de Modelos de Programação Linear e Inteira Slide 1 Transparências de apoio à leccionação de aulas teóricas Versão 2 c 2000, 1998 Construção de Modelos de Programação Linear e Inteira 1 Modelização
Construção de Modelos de Programação Linear e Inteira Slide 1 Transparências de apoio à leccionação de aulas teóricas Versão 2 c 2000, 1998 Construção de Modelos de Programação Linear e Inteira 1 Modelização
MÓDULO 3 - PROBLEMAS DE TRANSPORTE
 UNESA Sistemas de Transportes Currículo 08 / 009- MÓDULO 3 - PROBLEMAS DE TRANSPORTE. PROBLEMA CLÁSSICO DE TRANSPORTE O Problema de Transporte constitui uma das principais aplicações da PL para auxiliar
UNESA Sistemas de Transportes Currículo 08 / 009- MÓDULO 3 - PROBLEMAS DE TRANSPORTE. PROBLEMA CLÁSSICO DE TRANSPORTE O Problema de Transporte constitui uma das principais aplicações da PL para auxiliar
Métodos de Pesquisa Operacional
 Métodos de Pesquisa Operacional Programação Linear é a parte da Pesquisa Operacional que trata da modelagem e resolução de problemas formulados com funções lineares. Programação Linear } Métodos de Resolução
Métodos de Pesquisa Operacional Programação Linear é a parte da Pesquisa Operacional que trata da modelagem e resolução de problemas formulados com funções lineares. Programação Linear } Métodos de Resolução
EAD 350 Pesquisa Operacional Aula 03 Parte 2
 EAD 350 Pesquisa Operacional Aula 03 Parte 2 Profa. Adriana Backx Noronha Viana (Participação Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Método Simplex (item 4.1 do Hillier e Lieberman) - apenas
EAD 350 Pesquisa Operacional Aula 03 Parte 2 Profa. Adriana Backx Noronha Viana (Participação Prof. Cesar Alexandre de Souza) backx@usp.br FEA/USP Método Simplex (item 4.1 do Hillier e Lieberman) - apenas
Investigação Operacional 2004/05 2º Mini-teste Extra. 9 de Dezembro, 11:00h 12:30h
 Investigação Operacional 00/0 º Mini-teste Extra 9 de Dezembro, :00h :0h Sem consulta, sem máquina de calcular Justifique todas as respostas Departamento de Engenharia Civil Secção de Planeamento do Território
Investigação Operacional 00/0 º Mini-teste Extra 9 de Dezembro, :00h :0h Sem consulta, sem máquina de calcular Justifique todas as respostas Departamento de Engenharia Civil Secção de Planeamento do Território
PESQUISA OPERACIONAL. Fabiano F. T. dos Santos. Instituto de Matemática e Estatística
 PESQUISA OPERACIONAL Fabiano F. T. dos Santos Instituto de Matemática e Estatística Dualidade em Programação Linear Todo problema de programação linear, que chamaremos de primal, traz consigo um segundo
PESQUISA OPERACIONAL Fabiano F. T. dos Santos Instituto de Matemática e Estatística Dualidade em Programação Linear Todo problema de programação linear, que chamaremos de primal, traz consigo um segundo
Transparências de apoio à lecionação de aulas teóricas. c 2012, 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP
 Programação Linear Transparências de apoio à lecionação de aulas teóricas Versão 4 c 2012, 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear Problema de planeamento
Programação Linear Transparências de apoio à lecionação de aulas teóricas Versão 4 c 2012, 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear Problema de planeamento
Programação Linear. (1ª parte) Informática de Gestão Maria do Rosário Matos Bernardo 2016
 Programação Linear (1ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Introdução O modelo de programação linear: Problema de minimização Exemplo Formalização Problema
Programação Linear (1ª parte) Informática de Gestão 61020 Maria do Rosário Matos Bernardo 2016 Conteúdos Introdução O modelo de programação linear: Problema de minimização Exemplo Formalização Problema
Introdução à Pesquisa Operacional - Otimização Linear
 Introdução à Pesquisa Operacional - Otimização Linear Professora: Maristela Oliveira dos Santos - mari@icmc.usp.br Auxilio 2009: Victor C.B. Camargo Auxilio 2010 - PAE: Marcos Mansano Furlan - L-1007 Instituto
Introdução à Pesquisa Operacional - Otimização Linear Professora: Maristela Oliveira dos Santos - mari@icmc.usp.br Auxilio 2009: Victor C.B. Camargo Auxilio 2010 - PAE: Marcos Mansano Furlan - L-1007 Instituto
Métodos e Medidas II
 Métodos e Medidas II Disciplina: 1 Prof. Álvaro José Periotto ajperiotto@uem.br 3. Método Gráfico (conjunto de soluções/ponto ótimo) 1. Entendimento do Enunciado 2 Início Entendimento do Enunciado do P.P.L.
Métodos e Medidas II Disciplina: 1 Prof. Álvaro José Periotto ajperiotto@uem.br 3. Método Gráfico (conjunto de soluções/ponto ótimo) 1. Entendimento do Enunciado 2 Início Entendimento do Enunciado do P.P.L.
Simplex. Investigação Operacional José António Oliveira Simplex
 18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
18 Considere um problema de maximização de lucro relacionado com duas actividades e três recursos. Na tabela seguinte são dados os consumos unitários de cada recurso (A, B e C) por actividade (1 e 2),
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. VII Interpretação económica do modelo de PL António Carlos Morais da Silva Professor de I.O. i Cap. VII - Interpretação económica do modelo de
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. VII Interpretação económica do modelo de PL António Carlos Morais da Silva Professor de I.O. i Cap. VII - Interpretação económica do modelo de
Modelagem Matemática de Problemas de Programação Linear
 Capítulo 1 Modelagem Matemática de Problemas de Programação Linear 1.1. Introdução Neste Capítulo analisamos brevemente a estratégia usada para encontrar a modelagem matemática de um problema de programação
Capítulo 1 Modelagem Matemática de Problemas de Programação Linear 1.1. Introdução Neste Capítulo analisamos brevemente a estratégia usada para encontrar a modelagem matemática de um problema de programação
Pesquisa Operacional
 Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Pesquisa Operacional Análise de Sensibilidade Algébrica Profa. Sheila Morais de Almeida DAINF-UTFPR-PG abril - 016 1 Análise de Sensibilidade Algébrica Variações do Lado Direito Variações na Função Objetivo
Cap ıtulo 1 Exerc ıcios de Formula c Enunciados
 Capítulo 1 Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo se não houver atrasos.
Capítulo 1 Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo se não houver atrasos.
CAPÍTULO 4. Teoria da Dualidade
 CAPÍTULO 4 1. Introdução Uma dos conceitos mais importantes em programação linear é o de dualidade. Qualquer problema de PL tem associado um outro problema de PL, chamado o Dual. Neste contexto, o problema
CAPÍTULO 4 1. Introdução Uma dos conceitos mais importantes em programação linear é o de dualidade. Qualquer problema de PL tem associado um outro problema de PL, chamado o Dual. Neste contexto, o problema
Cap ıtulo 1 Exerc ıcios de Formula c ao Enunciados
 Capítulo 1 Exercícios de Formulação Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo
Capítulo 1 Exercícios de Formulação Enunciados Enunciados 2 Problema 1 Publicações Polémicas vai publicar uma autobiografia de um político controverso, e admite que a 1 a edição vai ser vendida por completo
Programação. Linear (PL) Exemplos Típicos de Aplicação da PL
 Programação Linear (PL) Exemplos Típicos de Aplicação da PL Planeamento de produção Problema de Transporte Programa de Investimento Programação Sequencial da Produção (Scheduling) Problema de Transexpedição
Programação Linear (PL) Exemplos Típicos de Aplicação da PL Planeamento de produção Problema de Transporte Programa de Investimento Programação Sequencial da Produção (Scheduling) Problema de Transexpedição
Exemplos de modelos de PL ou PI
 Exemplos de modelos de PL ou PI Prof. Eduardo Uchoa http://www.logis.uff.br/~uchoa/poi/ 1 Como funciona a PO? Toda a PO está baseada na construção de modelos matemáticos para representar de forma simplificada
Exemplos de modelos de PL ou PI Prof. Eduardo Uchoa http://www.logis.uff.br/~uchoa/poi/ 1 Como funciona a PO? Toda a PO está baseada na construção de modelos matemáticos para representar de forma simplificada
Pesquisa Operacional Aula 4 Solução Gráfica em Programação Linear
 Pesquisa Operacional Aula 4 Solução Gráfica em Programação Linear Prof. Marcelo Musci aula@musci.info www.musci.info Aplicável para modelos com 02 variáveis de decisão Útil para a ilustração de alguns
Pesquisa Operacional Aula 4 Solução Gráfica em Programação Linear Prof. Marcelo Musci aula@musci.info www.musci.info Aplicável para modelos com 02 variáveis de decisão Útil para a ilustração de alguns
DECISÕES ESTRATÉGICAS DE CURTO PRAZO: Programação Linear
 DECISÕES ESTRATÉGICAS DE CURTO PRAZO:! O que é?! Como a pode ajudar na maximização da lucratividade?! Como a pode ajudar na minimização dos custos?! Como determinar um mix de produção através da Programação
DECISÕES ESTRATÉGICAS DE CURTO PRAZO:! O que é?! Como a pode ajudar na maximização da lucratividade?! Como a pode ajudar na minimização dos custos?! Como determinar um mix de produção através da Programação
Aulas 2 e 3 - Modelos de Programação Linear
 Aulas 2 e 3 - Modelos de Programação Linear Pesquisa Operacional I Prof. Marcos Roboredo marcos.producao.uff@gmail.com http://www.logis.uff.br/~roboredo/po1.html Programação Matemática Um modelo de programação
Aulas 2 e 3 - Modelos de Programação Linear Pesquisa Operacional I Prof. Marcos Roboredo marcos.producao.uff@gmail.com http://www.logis.uff.br/~roboredo/po1.html Programação Matemática Um modelo de programação
Programação Linear M É T O D O S : E S T A T Í S T I C A E M A T E M Á T I C A A P L I C A D A S D e 1 1 d e m a r ç o a 2 9 d e a b r i l d e
 Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
Programação Linear A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Existe um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento
PROGRAMAÇÃO LINEAR E APLICAÇÕES
 E APLICAÇÕES Faculdade de Tecnologia de Ourinhos Tecnologia em Análise e Desenvolvimento de Sistemas Prof. Dr. Sidney C. Ferrari Pesquisa Operacional Notas Históricas Os caminhos da PO podem ser traçados
E APLICAÇÕES Faculdade de Tecnologia de Ourinhos Tecnologia em Análise e Desenvolvimento de Sistemas Prof. Dr. Sidney C. Ferrari Pesquisa Operacional Notas Históricas Os caminhos da PO podem ser traçados
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010
 DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
DISCIPLINA: Investigação Operacional ANO LECTIVO 2009/2010 Exame de Recurso Dep. Econ. Gestão e Engª Industrial 14 de Julho de 2010 duração: 2h30 (80) 1. Considere o modelo seguinte, de Programação Linear
Complementos de Investigação Operacional. Folha nº 1 Programação Inteira 2006/07
 Complementos de Investigação Operacional Folha nº Programação Inteira 2006/07 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Complementos de Investigação Operacional Folha nº Programação Inteira 2006/07 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Pesquisa Operacional
 Faculdade de Engenharia - Campus de Guaratinguetá Pesquisa Operacional Fabrício Maciel fabricio@feg.unesp.br Departamento de Produção 1 Programação linear Sumário Modelagem e limitações da Programação
Faculdade de Engenharia - Campus de Guaratinguetá Pesquisa Operacional Fabrício Maciel fabricio@feg.unesp.br Departamento de Produção 1 Programação linear Sumário Modelagem e limitações da Programação
α ( u 1 - u 2 ) = u 3 - u 2.
 2- NOÇÕES DE CONVEXIDADE E FORMULAÇÃO MATEMÁTICA DE PROBLEMAS DE PROGRAMAÇÃO LINEAR 21 Noções de Convexidade 211 - Combinação Convexa de pontos ponto b = αx 1 Considere C um conjunto contendo os pontos
2- NOÇÕES DE CONVEXIDADE E FORMULAÇÃO MATEMÁTICA DE PROBLEMAS DE PROGRAMAÇÃO LINEAR 21 Noções de Convexidade 211 - Combinação Convexa de pontos ponto b = αx 1 Considere C um conjunto contendo os pontos
de fevereiro de 2002
 15.053 12 de fevereiro de 2002 A Geometria de Programas Lineares - a geometria de LPs ilustrada em GTC Distribuir: Anotações da Aula 1 Mas, primeiro, o problema de Pigskin (de Ciência de Gerenciamento
15.053 12 de fevereiro de 2002 A Geometria de Programas Lineares - a geometria de LPs ilustrada em GTC Distribuir: Anotações da Aula 1 Mas, primeiro, o problema de Pigskin (de Ciência de Gerenciamento
Programação Matemática /2011
 Programação Matemática - 2010/2011 Ficha de exercícios n o 1 Exercício 1 Resolva o seguinte problema de optimização por metas: min Z = s + 1 ; s 2 ; s 3 + s+ 3 s.a x 1 + 2x 2 +s 1 s + 1 = 20 4x 1 x 2 +s
Programação Matemática - 2010/2011 Ficha de exercícios n o 1 Exercício 1 Resolva o seguinte problema de optimização por metas: min Z = s + 1 ; s 2 ; s 3 + s+ 3 s.a x 1 + 2x 2 +s 1 s + 1 = 20 4x 1 x 2 +s
Complementos de Investigação Operacional. Folha nº 1 Programação Inteira 2007/08
 Complementos de Investigação Operacional Folha nº Programação Inteira 2007/08 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Complementos de Investigação Operacional Folha nº Programação Inteira 2007/08 - A Eva e o Adão pretendem dividir entre eles as tarefas domésticas (cozinhar, lavar a louça, lavar a roupa, fazer as compras)
Problemas de Transportes e de Afectação
 CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
CAPÍTULO 6 Problemas de Transportes e de Afectação 1. Problema de Transporte Este problema, que é um dos particulares de PL, consiste em determinar a forma mais económica de enviar um bem disponível, em
Simplex. Transparências de apoio à leccionação de aulas teóricas. c 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP
 Simplex Transparências de apoio à leccionação de aulas teóricas Versão 3 c 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear abordagem algébrica max sujeito a: n
Simplex Transparências de apoio à leccionação de aulas teóricas Versão 3 c 2011, 2009, 1998 José Fernando Oliveira, Maria Antónia Carravilla FEUP Programação Linear abordagem algébrica max sujeito a: n
PESQUISA OPERACIONAL. Prof. Carlos Norberto Vetorazzi Jr.
 PESQUISA OPERACIONAL Prof. Carlos Norberto Vetorazzi Jr. 1. INTRODUÇÃO Definições : Método científico de tomada de decisão Conjunto de técnicas e ferramentas de apoio à decisão, através da modelagem matemática
PESQUISA OPERACIONAL Prof. Carlos Norberto Vetorazzi Jr. 1. INTRODUÇÃO Definições : Método científico de tomada de decisão Conjunto de técnicas e ferramentas de apoio à decisão, através da modelagem matemática
Dualidade e Análise de Sensibilidade
 Dualidade e Análise de Sensibilidade 33. Considere o seguinte problema de programação linear: Min Z = 4x 1 + 3x 2 + 6x 3 2x 1 + 2x 2 + 3x 3 4 3x 1 + x 2 + 3x 3 3 x 1, x 2, x 3 0 a) Escreva o dual associado
Dualidade e Análise de Sensibilidade 33. Considere o seguinte problema de programação linear: Min Z = 4x 1 + 3x 2 + 6x 3 2x 1 + 2x 2 + 3x 3 4 3x 1 + x 2 + 3x 3 3 x 1, x 2, x 3 0 a) Escreva o dual associado
Complementos de Investigação Operacional. Folha nº 2 Programação Multiobjectivo 2006/07
 Complementos de Investigação Operacional Folha nº 2 Programação Multiobjectivo 2006/07 1- x2 D(7,6) C(4,5) E(11,5) F(12,4) B(2,3) X G(13,2) A(1,1) H(10,1) max f 1 (x) = x 1 max f 2 (x) = x 2 (a) Represente
Complementos de Investigação Operacional Folha nº 2 Programação Multiobjectivo 2006/07 1- x2 D(7,6) C(4,5) E(11,5) F(12,4) B(2,3) X G(13,2) A(1,1) H(10,1) max f 1 (x) = x 1 max f 2 (x) = x 2 (a) Represente
Aplicações de PL possíveis até o momento
 Universidade Federal de Itajubá Instituto de Engenharia de Produção e Gestão Pesquisa Operacional Síntese Problemas Interessantes Prof. Dr. José Arnaldo Barra Montevechi Aplicações de PL possíveis até
Universidade Federal de Itajubá Instituto de Engenharia de Produção e Gestão Pesquisa Operacional Síntese Problemas Interessantes Prof. Dr. José Arnaldo Barra Montevechi Aplicações de PL possíveis até
PESQUISA OPERACIONAL I
 PESQUISA OPERACIONAL I Professor: Dr. Edwin B. Mitacc Meza edwin@engenharia-puro.com.br www.engenharia-puro.com.br/edwin/po-i.html Dualidade Introdução Uma das mais importantes descobertas no início do
PESQUISA OPERACIONAL I Professor: Dr. Edwin B. Mitacc Meza edwin@engenharia-puro.com.br www.engenharia-puro.com.br/edwin/po-i.html Dualidade Introdução Uma das mais importantes descobertas no início do
Investigação Operacional
 Investigação Operacional Victor Lobo Sumário Introdução Programa da cadeira Bibliografia Horário de dúvidas e contactos Avaliação O que é Investigação Operacional? Investigar as operações da empresa, embora
Investigação Operacional Victor Lobo Sumário Introdução Programa da cadeira Bibliografia Horário de dúvidas e contactos Avaliação O que é Investigação Operacional? Investigar as operações da empresa, embora
Investigação Operacional 2005/06 Ficha 6 Teoria da Dualidade e Problema de Transportes
 Investigação Operacional 2005/06 Ficha 6 Teoria da Dualidade e Problema de Transportes Departamento de Engenharia Civil Secção de Planeamento do Território e Ambiente 1. Problema da Pedreira III A empresa
Investigação Operacional 2005/06 Ficha 6 Teoria da Dualidade e Problema de Transportes Departamento de Engenharia Civil Secção de Planeamento do Território e Ambiente 1. Problema da Pedreira III A empresa
Disciplina que estuda métodos analíticos para auxiliar na tomada de decisões.
 Edgard Jamhour Disciplina que estuda métodos analíticos para auxiliar na tomada de decisões. Procura encontrar soluções ótimas ou próximo de ótimas para problemas de engenharia industrial, economia e finanças,
Edgard Jamhour Disciplina que estuda métodos analíticos para auxiliar na tomada de decisões. Procura encontrar soluções ótimas ou próximo de ótimas para problemas de engenharia industrial, economia e finanças,
Índice. Prefácio Os modelos de programação linear e a investigação operacional 17
 Índice Prefácio 13 Capítulo 1 Introdução 1. Os modelos de programação linear e a investigação operacional 17 2. O problema de programação linear 18 2.1. O problema de programação linear em substituição
Índice Prefácio 13 Capítulo 1 Introdução 1. Os modelos de programação linear e a investigação operacional 17 2. O problema de programação linear 18 2.1. O problema de programação linear em substituição
INVESTIGAÇÃO OPERACIONAL. Programação Linear. Exercícios. Cap. X Programação por Metas
 INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. X Programação por Metas António Carlos Morais da Silva Professor de I.O. i Cap. X Programação por Metas - Exercícios X. Programação por Metas.
INVESTIGAÇÃO OPERACIONAL Programação Linear Exercícios Cap. X Programação por Metas António Carlos Morais da Silva Professor de I.O. i Cap. X Programação por Metas - Exercícios X. Programação por Metas.
PESQUISA OPERACIONAL. UNIDADE 2 Visão Geral do Modelo
 PESQUISA OPERACIONAL UNIDADE 2 Visão Geral do Modelo Prof. Me. Carlos Guimarães 1 / 13 Objetivo Introduzir os elementos de um modelo de pesquisa operacional por meio da apresentação: Do conceito de modelo;
PESQUISA OPERACIONAL UNIDADE 2 Visão Geral do Modelo Prof. Me. Carlos Guimarães 1 / 13 Objetivo Introduzir os elementos de um modelo de pesquisa operacional por meio da apresentação: Do conceito de modelo;
Tópicos Especiais em Computação I
 Tópicos Especiais em Computação I Pesquisa Operacional Exercícios (Simplex) Prof. Fabio Henrique N. Abe Fabio.henrique.abe@gmail.comd Método Simplex Desenvolvido por George Dantzig em 1947 É um procedimento
Tópicos Especiais em Computação I Pesquisa Operacional Exercícios (Simplex) Prof. Fabio Henrique N. Abe Fabio.henrique.abe@gmail.comd Método Simplex Desenvolvido por George Dantzig em 1947 É um procedimento
PCC173 - Otimização em Redes
 PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 15 de maio de 2017 Marco Antonio M. Carvalho
PCC173 - Otimização em Redes Marco Antonio M. Carvalho Departamento de Computação Instituto de Ciências Exatas e Biológicas Universidade Federal de Ouro Preto 15 de maio de 2017 Marco Antonio M. Carvalho
