Emerson Marcos Furtado
|
|
|
- Eduarda Botelho Arantes
- 7 Há anos
- Visualizações:
Transcrição
1 Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde Professor do Curso Positivo de Curitiba desde Professor da Universidade Positivo de 2000 a Autor de livros didáticos destinados a concursos públicos nas áreas de matemática, matemática financeira, raciocínio lógico e estatística. Sócio-diretor do Instituto de Pesquisas e Projetos Educacionais Praxis de 2003 a Professor sócio do Colégio Positivo de Joinville desde Sócio-diretor da Empresa Teorema Produção de Materiais Didáticos Ltda. desde Autor de material didático para sistemas de ensino do Grupo Positivo de 2005 a Professor do Concursos e Editora de Curitiba (CEC) desde 1992, lecionando as disciplinas de raciocínio lógico, estatística, matemática e matemática financeira. Consultor da Empresa Result Consultoria em Avaliação de Curitiba de 1998 a Consultor em Estatística Aplicada com projetos de pesquisa desenvolvidos nas áreas socioeconômica, qualidade, educacional, industrial e eleições desde Membro do Instituto de Promoção de Capacitação e Desenvolvimento (Iprocade) desde Autor de questões para concursos públicos no estado do Paraná desde 2003.
2
3 Termo geral de uma sequência Observe a sequência: Qual é o próximo termo? (1, 3, 5,..., ) A sequência apresentada é a de números ímpares positivos. O próximo termo é igual a 7, em seguida, vem o 9, e assim por diante: (1, 3, 5, 7, 9,..., ) É costume se representar os termos de uma sequência pela letra a provida de um índice que indica a posição do termo na correspondente sequência. Por exemplo, na sequência mostrada anteriormente, podemos escrever: a 1 = 1 o 1.º termo é igual a 1. a 2 = 3 o 2.º termo é igual. = 5 o 3.º termo é igual a 5. a 4 = 7 o 4.º termo é igual a 7. a 5 = 9 o 5.º termo é igual a 9. Como poderíamos descobrir, por exemplo, o décimo termo dessa sequência? Poderíamos continuar escrevendo os números ímpares consecutivamente até atingirmos o 10.º termo. Talvez não seja uma tarefa tão trabalhosa. Mas, e se quiséssemos o centésimo termo, valeria a pena construir a sequência até se obter o centésimo número ímpar positivo? Nessas situações, não compensa escrever tantos números e fazer tantas contas. 107
4 O ideal é se compreender a lei de formação dos termos da sequência. Se a sequência é de números ímpares, um novo número é o anterior adicionado a duas unidades. Assim, começando com o número 1, o termo geral da sequência é dado por: Termo geral da sequência: = 2. n 1 Par = 1 a 1 = = 1 Par = 2 a 2 = = 3 Par = 3 = = 5 Par = 4 a 4 = = 7 O centésimo termo da sequência seria obtido substituindo-se n = 100 na expressão do termo geral: = 2. n 1 Par = 100 a 100 = = 199 Fica claro que para respondermos questões sobre sequências numéricas, tudo fica muito mais fácil quando conhecemos o termo geral da sequência. Existem sequências que têm características importantes e, por isso, ocupam lugar de destaque na Matemática. As principais são a progressão aritmética e a progressão geométrica. Progressão aritmética Uma Progressão Aritmética (PA) é uma sequência de números em que cada termo, a partir do segundo, é igual ao anterior somado a uma constante. Essa constante é denominada razão da PA e será representada pela letra r. Exemplo 1: A sequência (1, 4, 7, 10,...) é uma PA cuja razão é r = 3 (r > 0). 108
5 a 1 = 1 a = = 4 = a = = 7 a 4 = + 3 = = 10 Cada termo é igual ao anterior mais 3. Exemplo 2: A sequência (10, 8, 6, 4,...) é uma PA cuja razão é r = 2 (r < 0). a 1 = 10 a 2 2 = 10 2 = 8 = a 2 2 = 8 2 = 6 a 4 = 2 = 6 2 = 4 Cada termo é igual ao anterior menos 2. Exemplo 3: A sequência (5, 5, 5, 5,...) é uma PA cuja razão é r = 0. a 1 = 5 a = = 5 = a = = 5 a 4 = + 0 = = 5 Cada termo é igual ao anterior. De acordo com a razão, existem três tipos de PA: r > 0 a PA é crescente. r < 0 a PA é decrescente. r = 0 a PA é constante. Exemplo: Vamos verificar se a sequência definida pela fórmula +1 = + 4 e a 1 = 1 é uma Progressão Aritmética. a 1 = 1 +1 =
6 n = 1 a a 2 = = 5 n = 2 a 2+1 = a = = 9 n = 3 +1 = + 4 a 4 = = 13 Cada termo é igual ao anterior adicionado à constante 4. Logo, podemos afirmar que a sequência (1, 5, 9, 13,...) é uma PA. Termo geral da PA Para descobrir um termo qualquer de uma PA, não é necessário escrever todos os termos precedentes para encontrá-lo. Com a fórmula do termo geral, podemos obter qualquer termo de uma sequência conhecendo a sua posição. Considere uma progressão aritmética (a 1, a 2,, a 4,...,,...) de razão r. A partir do segundo, qualquer termo é igual ao anterior adicionado à razão, logo: a 2 + r = a 2 + r a 4 = + r a 5 = a 4 + r = -1 + r Essa última fórmula permite obter um termo qualquer de ordem n em função do termo anterior, de ordem n 1. Para relacionar um termo de ordem n em função do 1.º termo a 1, temos: a 2 + r = a 2 + r = (a 1 + r) + r + 2r a 4 = + r = (a 1 + 2r) + r + 3r a 5 = a 4 + r = (a 1 + 3r) + r + 4r = -1 + r = [a 1 + (n 2).r] + r + (n 1). r 110
7 A fórmula do termo geral da PA é dada por: + (n 1). r Quando conhecemos a fórmula do termo geral, podemos representar qualquer termo de uma sequência em função do primeiro termo e da razão. Exemplos: 8.º termo : n = 8 a 8 + 7r 16.º termo : n = 16 a r 30.º termo : n = r Soma dos termos de uma PA Há uma história curiosa ocorrida em uma pequena escola de uma cidade do interior da Alemanha, no século XVIII, que passou a fazer parte da história do desenvolvimento da Matemática. Um professor de Matemática solicitou aos próprios alunos que somassem os cem primeiros números inteiros positivos. O professor imaginava que os alunos levariam um bom tempo para encontrar a soma dos elementos dessa sequência. Passados alguns instantes, um aluno levanta-se e crava a resposta: O professor, acreditando que se tratava de uma brincadeira, repreende-o e pede para que tentasse realmente fazer as contas. O precoce aluno explica ao professor que a soma é igual a 50 vezes a soma do primeiro com o último termo, ou seja, = Acompanhe um possível raciocínio do aluno: S = reescrevendo em ordem contrária: S = Adicionando membro a membro as igualdades: 2S = ( ) + (2 + 99) + (3 + 98) (99 + 2) + ( ) 111
8 2S = S = S = S = O espantado professor, que nem sequer havia feito a conta, compreende a explicação e parabeniza o aluno pelo raciocínio magistral. Alguns anos depois, inclusive, presenteia-o com um livro sobre cálculos. O humilde aluno, que na época tinha cerca de oito anos, era filho de jardineiros e chamava-se Carl Friedrich Gauss ( ). Anos mais tarde, dedicou-se à Matemática e à Física, desenvolvendo trabalhos nos campos da teoria dos números, geometria diferencial, magnetismo, astronomia, geodésia e ótica. Para muitos é considerado, incontestavelmente, o maior matemático de toda a história, sendo conhecido como o Príncipe dos Matemáticos. O desenvolvimento utilizado por Gauss pode ser generalizado da seguinte maneira: Se (a 1, a 2,,..., -1, ) é uma progressão aritmética, então: + a (I) = a 2 + a 1 (II) Fazendo (I) + (II), temos: 2 = (a 1 + ) + (a ) + ( + -2 ) (-1 + a 2 ) + ( + a 1 ) A soma dos dois termos extremos é igual à soma de dois termos equidistantes dos extremos, de modo que é possível escrever: 2 = (a 1 + ) + (a 1 + ) + (a 1 + ) (a 1 + ) + (a 1 + ) 2 = (a 1 + ). n a = Exemplo 1. n 112 Obtenha a soma dos termos da PA ( 10, 5, 0, 5, 10, 15, 20), formada por sete termos.
9 = a n = a 1 + a S 7 = S 7 = 35 Exemplo 2 Calcule a soma dos 20 primeiros termos da PA (1, 3, 5,...). + (n 1). r a 20 = r a 20 = = S 20 = a a 1 + a n. 20 a 20 = 39 S 20 = S 20 = 400 Progressão geométrica Imagine que você tem duas propostas para um novo emprego. Em uma delas, seu salário inicial será de R$3.500,00, mas sofrerá aumentos anuais de 10% em relação ao salário do ano anterior. Na outra proposta, seu salário inicial será de R$4.000,00 e será aumentado a uma taxa de 8% ao ano, em relação ao ano anterior. Considerando-se apenas o valor do salário ao final do quarto ano, qual é a melhor proposta de emprego? Vamos verificar qual proposta é a mais vantajosa calculando os valores salariais ano a ano, até o quarto ano: 113
10 Salários da proposta 1 Salários da proposta 2 Ano 0: R$3.500,00 Ano 1: R$3.500,00. 1,10 = R$3.850,00 Ano 2: R$3.850,00. 1,10 = R$4.235,00 Ano 3: R$4.235,00. 1,10 = R$4.658,50 Ano 4: R$4.658,50. 1,10 = R$5.124,35 Ano 0: R$4.000,00 Ano 1: R$4.000,00. 1,08 = R$4.320,00 Ano 2: R$4.320,00. 1,08 = R$4.665,60 Ano 3: R$4.665,60. 1,08 = R$5.038,85 Ano 4: R$5.038,85. 1,08 = R$5.441,31 Os valores dos salários de cada proposta aumentam o mesmo percentual em relação ao valor anterior, ou seja, aumentam à uma taxa constante. Por isso, ao longo do tempo, tais valores constituem uma progressão geométrica. Progressão Geométrica (PG) é uma sequência de números ou expressões em que cada termo, a partir do segundo, é igual ao anterior multiplicado por uma constante. Essa constante é denominada razão da PG e será representada pela letra q. Exemplos: Uma PG pode ser classificada em crescente, decrescente, oscilante ou constante. (5, 5, 5, 5,...) PG constante cuja razão é q = 1 (ou uma PA de razão igual a 0). (1, 2, 4, 8,...) PG crescente cuja razão é q = 2. (27, 9, 3, 1,...) PG decrescente cuja razão é q = (1, 3, 9, 27,...) PG oscilante cuja razão é q = Termo geral de uma PG Numa PG, por meio da fórmula do termo geral, é possível encontrar qualquer termo da sequência sem ecessidade de se calcular todos os termos que o precedem. Considere uma progressão geométrica (a 1, a 2,, a 4,...,,...) de razão q. A partir do segundo termo, qualquer outro termo é igual ao anterior multiplicado pela razão, então: 114
11 a 2. q = a 2. q a 4 =. q a 5 = a 4. q = -1. q Essa última fórmula permite obter um termo qualquer de ordem n em função do termo anterior, de ordem n 1. Podemos relacionar um termo qualquer (de ordem n) com o 1.º termo de uma PG. Essa relação pode ser representada do seguinte modo: a 2. q = a 2. q = (a 1. q). q.q 2 a 4 =. q = (a 1. q 2 ). q.q 3 a 5 = a 4. q = (a 1. q 3 ). q.q 4 = -1. q = (a 1. q n 2 ). q. q n 1 Assim, podemos escrever:. q n 1 Conhecendo a fórmula do termo geral, podemos representar qualquer termo de uma PG em função do primeiro termo e da razão. Observe alguns exemplos: 7.º termo: n = 7 a 7. q 6 13.º termo: n = 13 a 13. q º termo: n = 48 a 48. q 47 Soma dos termos de uma PG finita Considere a PG finita cuja razão é q = 5, formada pelos seis seguintes números: 115
12 (8, 40, 200, 1 000, 5 000, ) Representando por S 6 a soma dos seis primeiros termos dessa PG, podemos escrever: S 6 = Efetuando as adições necessárias, obtemos o valor da soma correspondente: S 6 = Entretanto, em vez de calcularmos o valor da soma adicionando termo a termo, é possível obtê-la por meio de um procedimento simples. Retornando à soma, observe: S 6 = (I) Multiplicando a equação (I), membro a membro, pela razão q = 5, obtemos: 5. S 6 = Como os termos estão em PG, o produto de um termo qualquer pela razão resulto termo posterior, ou seja: 5. S 6 = (II) Subtraindo uma equação da outra, isto é, fazendo (II) (I), obtemos: 5. S 6 S 6 = S 6 = S 6 = 4 S 6 = Esse procedimento pode ser utilizado em qualquer PG, observe: Se (a 1, a 2,,..., -1, ) é uma progressão geométrica de razão q 1 e é a soma destes n termos, então: + a (I) Multiplicando membro a membro por q, temos:. q. q + a 2. q +. q q +. q 116
13 . q = a a q (II) Fazendo (II) (I), temos:. q =. q a 1. (q 1) =. q a 1 a = n. q a 1 q 1 Essa última fórmula é utilizada para calcular a soma dos n primeiros termos de uma PG finita em função do primeiro termo, do último termo e da razão da PG. Limite da soma dos termos de uma PG infinita Para encontrar a expressão do valor do limite da soma dos termos de qualquer PG infinita, podemos partir de uma soma finita e considerarmos que o n-ésimo termo tende a zero: =. q a 1 q 1 = 0 S = 0. q a 1 q 1 = a 1 q 1 Multiplicando por 1 o numerador e o denominador da última fração, obtemos: S = a 1 1 q, sendo q < 1 Dica de estudo O estudo das progressões matemáticas inicia-se com o conceito de termo geral. É necessário, antes de qualquer coisa, compreender-se a relação que permite obter qualquer termo de uma sequência. Isso vale para progressões aritméticas e progressões geométricas. A partir daí, as demais fórmulas podem ser desenvolvidas com êxito. Pratique a resolução de muitos exercícios para ganhar agilidade e eficiência nesse assunto. 117
14 Resolução de questões 1. (Cesgranrio) Em uma PA de 41 termos e de razão 9, a soma do termo central com o seu antecedente é igual ao último termo. Então, o termo central é: a) 369 b) 189 c) 201 d) 171 e) (FCC) Dispõe-se de uma caixa com 100 palitos de fósforos, todos inteiros, com os quais pretende-se construir quadrados da seguinte forma: no primeiro, o lado deverá medir 1 palito; no segundo, 2 palitos; no terceiro, 3 palitos, e assim sucessivamente. Seguindo esse padrão, ao construir-se o maior número possível de quadrados a) serão usados exatamente 92 palitos da caixa. b) sobrarão 8 palitos da caixa. c) serão usados todos os palitos da caixa. d) sobrarão 16 palitos da caixa. e) serão usados exatamente 96 palitos da caixa. 3. (FCC) Os termos da sucessão seguinte foram obtidos considerando uma lei de formação. (0, 1, 3, 4, 12, 13,...) Segundo essa lei, o décimo terceiro termo dessa sequência é um número: a) menor que 200. b) compreendido entre 200 e 400. c) compreendido entre 500 e 700. d) compreendido entre 700 e e) maior que
15 4. (Cesgranrio) Uma sequência de números (a 1, a 2,,..., ) é tal que a soma dos n primeiros termos é dada pela expressão = 3n 2 + n. O valor do 51.º termo é: a) 300 b) 301 c) 302 d) 303 e) (Cesgranrio) Quantos números múltiplos de 7 ou de 11 há entre 1 e 1 000? a) 90 b) 142 c) 220 d) 229 e) (FGV) A sequência (3m; m + 1; 5) é uma PA. Sua razão é: a) 3 b) 3 c) 7 d) 7 e) impossível de se determinar. 7. (Cesgranrio) Se S 3 = 0 e S 4 = 6 são, respectivamente, as somas dos três e quatro primeiros termos de uma progressão aritmética, então a soma S 5 dos cinco primeiros termos vale: a) 6 b) 9 c) 12 d) 15 e)
16 8. (Esaf) Uma progressão aritmética é uma sequência de números a 1, a 2,,...,, cuja lei de formação de cada um dos termos dessa sequência é dada por uma soma, conforme representação a seguir: a 2 + r, = a 2 + r, a 4 = + r,... = 1 + r, onde r é uma constante, denominada razão da progressão aritmética. Uma progressão geométrica é uma sequência de números g 1, g 2, g 3,..., g n, cuja lei de formação de cada um dos termos dessa sequência é dada por um produto, conforme representação a seguir: g 2 = g 1. q, g 3 = g 2. q, g 4 = g 3. q,...g n = g n 1. q, onde q é uma constante, denominada razão da progressão geométrica. Os números A, B e 10 formam, nessa ordem, uma progressão aritmética. Os números 1, A e B formam, nessa ordem, uma progressão geométrica. Com essas informações, pode-se afirmar que um possível valor para o produto entre r e q é igual a: a) 12 b) 15 c) 10 d) 12 e) 8 9. (FCC) Considere todos os números inteiros dispostos sucessivamente, em linhas e colunas, da forma como é mostrado a seguir. 1.ª coluna 2.ª coluna 3.ª coluna 4.ª coluna 5.ª coluna 6.ª coluna 7.ª coluna 1.ª linha ª linha Se fosse possível completar essa tabela, então, na terceira coluna e na tricentésima quadragésima sexta linha apareceria o número: a) b)
17 c) d) e) (FCC) Se a é um número inteiro positivo, define-se uma operação & como a & = 3a 2. Considere a sequência (a 1, a 2,,...,,...) cujo termo geral é = (n & ) &, para todo n = 1, 2, 3,.... A soma do terceiro e quinto termos dessa sequência é igual a: a) 42 b) 46 c) 48 d) 52 e) 56 Referências ASIMOV, Isaac. Antologia Volume 1 ( ). 2. ed. Rio de Janeiro: Nova Fronteira, Antologia Volume 2 ( ). 2. ed. Rio de Janeiro: Nova Fronteira, BOYER, Carl B. História da Matemática. 12. ed. São Paulo: Edgard Blücher Ltda., DANTE, Luiz Roberto. Matemática contexto e aplicações. São Paulo: Ática, v. 1. Edição reformulada. EVES, Howard. Introdução à História da Matemática. Campinas: Unicamp, GAERTNER, Rosinete (Org.). Tópicos de Matemática para o Ensino Médio. Blumenau: FURB. (Coleção Aritthmos 2.) GARBI, G. Gilberto. O Romance das Equações Algébricas. São Paulo: Makron Books,
18 . A Rainha das Ciências um passeio histórico pelo maravilhoso mundo da Matemática. São Paulo: Livraria de Física, IEZZI, Gelson et al. Matemática ciência e aplicações. 4. ed. São Paulo: Atual, LIMA, Elon Lages. Meu Professor de Matemática e outras Histórias. Rio de Janeiro: Sociedade Brasileira de Matemática, LIMA, Elon Lages et al. A Matemática do Ensino Médio. Rio de Janeiro: SociedadeBrasileira de Matemática, v. 1, 2 e 3.. Temas e Problemas Elementares. Rio de Janeiro: Sociedade Brasileira de Matemática, LINTZ, Rubens G. História da Matemática. Blumenau: FURB, v. 1. MORGADO, Augusto C.; CESAR, Benjamin. Matemática Financeira. Rio de Janeiro: Campus, MORGADO, Augusto C. et. al. Progressões e Matemática Financeira. Rio de Janeiro: Sociedade Brasileira de Matemática, Análise Combinatória e Probabilidade. Rio de Janeiro: Sociedade Brasileira de Matemática, TAHAN, Malba. O Homem que Calculava. 40. ed. Rio de Janeiro: Record, Gabarito 1. Se a PA possui 41 termos, o termo central é o vigésimo primeiro e, consequentemente, o seu antecedente é o vigésimo termo. Se a soma do termo central com o seu antecedente é igual ao último, então: a 21 + a 20 = a 41 Vamos escrever tudo em função de a 21, ou seja: a 20 = a r e a 41 = a r 122
19 Logo, substituindo as expressões de a 20 e a 41, temos: a 21 + a 20 = a 41 a 21 + (a r) = (a r) 2a 21 r = a r 2a 21 a 21 = 20r + r a 21 = 21r Substituindo r = 9, temos: a 21 = a 21 = 189 Portanto, o termo central é igual a 189. Resposta: B 2. Qualquer quadrado possui quatro lados iguais. Logo, para a construção de um quadrado cujo lado mede 1 palito são necessários: 4. 1 = 4 palitos Para o quadrado cujo lado mede 2 palitos são necessários: 4. 2 = 8 palitos Para o quadrado cujo lado mede 3 palitos são necessários: 4. 3 = 12 palitos Observe que a quantidade de palitos necessária para a construção de cada quadrado segue uma progressão aritmética cuja razão é igual a 4: (4, 8, 12,...) PA Dispondo-se de 100 palitos, deseja-se descobrir quantos palitos serão efetivamente utilizados para a construção dos quadrados. A quantidade de palitos utilizada é igual à soma dos termos de uma progressão aritmética de primeiro termo igual a 4 e razão também igual a 4. O termo geral dessa PA é dado por: 123
20 + (n 1). r = 4 + (n 1). 4 = 4 + 4n 4 = 4n A soma dos n primeiros termos dessa PA é dada por: = a n = 4 + 4n 2 = (2 + 2n). n = 2n. (n + 1). n Para que sejam utilizados, no máximo, 100 palitos, deve-se ter < 100, ou seja: 2n. (n + 1) < 100 Dividindo ambos os membros por 2, temos: n. (n + 1) < 50 Já que n é um número inteiro, pois representa a quantidade de quadrados, vamos analisar as possíveis soluções da inequação por verificação: n = 7 7. (7 + 1) = 7. 8 = 56 > 50 Logo, sete quadrados ou mais não podem ser construídos com os 100 palitos. n = 6 6. (6 + 1) = 6. 7 = 42 < 50 Portanto, seis é o número máximo de quadrados que podem ser construídos com os 100 palitos disponíveis. Assim, substituindo-se n = 6 na expressão da soma dos n primeiros termos da PA, temos: 124
21 = 2n. (n + 1) S 6 = (6 + 1) S 6 = S 6 = 84 Como serão utilizados 84 palitos para a construção de seis quadrados, necessariamente sobrarão = 16 palitos na caixa. Resposta: D 3. A sequência é construída de modo que, a partir do primeiro termo, adiciona-se 1 unidade para obter o próximo termo e, em seguida, multiplica-se por 3 para obter o próximo. Ou seja, são apenas duas operações distintas para se construir a sucessão de termos: adicionar 1 unidade e multiplicar por 3. Para encontrar o décimo terceiro termo, não vamos utilizar o termo geral de uma progressão aritmética, nem o termo geral de uma progressão geométrica, pois a sucessão não satisfaz as definições de PA ou PG. Logo, vamos obter os termos progressivamente por meio das duas operações mencionadas: a 1 = 0 a = = 1 = a 2. 3 = 1. 3 = 3 a 4 = + 1 = = 4 a 5 = a 4. 3 = 4. 3 = 12 a 6 = a = = 13 a 7 = a 6. 3 = = 39 a 8 = a = = 40 a 9 = a 8. 3 = = 120 a 10 = a = = 121 a = = 363 a = = 364 a = = >
22 Logo, o décimo terceiro termo da sucessão é maior que Resposta: E 4. Em qualquer sequência, a soma dos 51 primeiros termos é igual à soma dos 50 primeiros termos adicionada ao quinquagésimo primeiro termo, ou seja: S 51 = S 50 + a 51 Assim, o termo a 51 é igual à diferença entre a soma dos 51 primeiros termos e a soma dos 50 primeiros termos: a 51 = S 51 S 50 Se a soma dos n primeiros termos da sequência é dada por = 3n 2 + n, par natural não nulo, então, para se calcular a soma dos 51 primeiros termos, basta substituir n = 51: n = 51 S 51 = E para se calcular a soma dos 50 primeiros termos, basta substituir n = 50: n = 50 S 50 = Logo, temos: a 51 = S 51 S 50 Substituindo as expressões para S 51 e S 50, temos: a 51 = ( ) ( ) a 51 = 3. ( ) + (51 50) Utilizando o produto notável a 2 b 2 = (a + b). (a b), podemos escrever: a 51 = 3. ( ). (51 50) + 1 a 51 = 3. (101). (1) + 1 a 51 = a 51 = 304 Resposta: E 126
23 5. O primeiro múltiplo de 7 entre 1 e é igual a 7, o segundo é 14, o terceiro é 21. Os múltiplos de 7 entre 1 e constituem uma progressão aritmética em que o primeiro termo é igual a 7, cuja razão também é igual a 7. Observe que, ao dividir por 7, obtemos = Logo, não é divisível por 7, pois o resto é igual a 6. Porém, = 994 = , ou seja, 994 é múltiplo de 7 e é também o último múltiplo de 7 menor que Vamos utilizar o termo geral de uma PA para calcular a quantidade de múltiplos de 7 entre 1 e 1 000: + (n 1). r 994 = 7 + (n 1) = 7 + 7n = 7n n = 142 Assim, existem, exatamente, 142 múltiplos de 7 entre 1 e O raciocínio é análogo para os múltiplos de 11, que formam uma progressão aritmética de primeiro termo igual a 11 cuja razão é igual a 11. O último múltiplo de 11 até é o número 990. Logo, temos: + (n 1). r 990 = 11 + (n 1) = n = 11n n = 90 Logo, existem exatamente 90 múltiplos de 11 entre 1 e Porém, no conjunto dos múltiplos de 7 e no conjunto dos múltiplos de 11 existem múltiplos comuns. Tais números são múltiplos de 77. Assim, é preciso calcular os múltiplos de 77 entre 1 e O primeiro é igual a 77 e o último é igual a 924. Utilizando novamente a fórmula do termo geral de uma progressão aritmética, temos: 127
24 + (n 1). r 924 = 77 + (n 1) = n = 77n n = 12 Portanto, para se determinar a quantidade de múltiplos de 7 ou 11 entre 1 e 1 000, podemos adicionar a quantidade de múltiplos de 7 à quantidade de múltiplos de 11 e, da soma obtida, subtrair a quantidade de múltiplos de 77, pois essa quantidade já foi contabilizada uma vez entre os múltiplos de 7 e outra vez entre os múltiplos de 11. Assim, temos: = 220 Portanto, existem exatamente 220 números que são múltiplos de 7 ou de 11 entre 1 e Resposta: C 6. Se (a, b, c) formam, nessa ordem, uma progressão aritmética, então: b a = c b De forma análoga, se (3m; m + 1; 5) forma uma PA, então: (m + 1) 3m = 5 (m + 1) m + 1 3m = 5 m 1 1 2m = 4 m 1 4 = 2m m m = 3 Substituindo m = 3 na sequência, temos: ( 9; 2; 5) Logo, a razão é igual à diferença entre dois termos consecutivos, ou seja: r = 5 ( 2) = = 7 Resposta: C 128
25 7. A diferença entre a soma dos quatro primeiros termos e a soma dos três primeiros termos é igual ao quarto termo, ou seja: a 4 = S 4 S 3 a 4 = 6 0 a 4 = 6 Observando que a 2 + r, que = a 2 + r e que a soma dos três primeiros termos é igual a zero, temos: S 3 = 0 a 1 + a 2 + = 0 (a 2 r) + a 2 + (a 2 + r) = 0 3a 2 = 0 a 2 = 0 Além disso, podemos também escrever: a 4 = a 2 + 2r 6 = 0 + 2r r = 3 Por outro lado: a 5 = a 4 + r a 5 = 6 + ( 3) a 5 = 9 Se a soma dos cinco primeiros termos é igual à soma dos quatro primeiros termos mais o quinto termo, então: S 5 = S 4 + a 5 S 5 = 6 + ( 9) S 5 = 15 Resposta: D 129
26 8. Se (A, B, 10) formam, nessa ordem, uma PA, então: B A = 10 B A = 2B 10 (I) Se (1, A, B) formam, nessa ordem, uma PG, então: A 1 = B A A 2 = B (II) Substituindo (I) em (II), temos: (2B 10) 2 = B (2B) B = B 4B 2 40B B = 0 4B 2 41B = 0 B = ( 41) ± ( 41) ± 81 B = 8 B = 41 ± 9 8 B 1 = = B 2 = = 32 8 = 6,25 = 4 Por (I), se B = 6,25, então A = 2,50. Nesse caso, as possíveis sequências são: (2,50; 6,25; 10) PA cuja razão é igual a r = 6,25 2,50 = 3,75 e (1; 2,50; 6,25) PG cuja razão é igual a q = 2,50 / 1 = 2,50 Um valor possível para o produto entre r e q é igual a r. q = 3,75. 2,50 = 9,
27 Por (I), se B = 4, então A = 2. Então: ( 2; 4; 10) PA cuja razão é igual a r = 10 4 = 6 e (1; 2; 4) PG cuja razão é igual a q = 2 / 1 = 2 Um valor possível para o produto entre r e q é igual a: r. q = 6. ( 2) = 12 Portanto, um dos valores possíveis para o produto entre r e q é igual a 12. Resposta: A 9. Observe que os números de qualquer coluna constituem uma progressão aritmética cuja razão é igual a 7, pois a tabela é composta por 7 colunas cujos números são consecutivos. A diferença substancial entre as progressões aritméticas formadas em cada coluna está no primeiro termo da sequência, que é igual a 1 na 1.ª coluna, igual a 2 na 2.ª coluna, igual n.ª coluna e assim sucessivamente, até ser igual a 7 na 7.ª coluna. A progressão aritmética desenvolvid.ª coluna é dada por: (3, 10, 17, 24, 31,...) A numeração da linha fornece a posição do termo na correspondente progressão aritmética, ou seja, o número da 1.ª linha é o 1.º termo da PA, o número da 2.ª linha é igual ao 2.º termo da PA, o número d.ª linha é igual ao 3.º termo da PA, e assim sucessivamente, até o número da tricentésima quadragésima sexta linha (346.ª linha) ser o termo 346.º da PA. Assim, deseja-se encontrar o 346.º termo da progressão aritmética (3, 10, 17, 24, 31,...). Logo: r 46 = = 2418 Resposta: B 131
28 10. Para se encontrar o terceiro termo da sequência basta considerar n = 3 no termo geral: = (n & ) & = (3 & ) & Como a & = 3a 2, temos: = (3. 3 2) & = (7) & = (3. 7 2) = 19 Para se encontrar o quinto termo da sequência, basta considerar n = 5 no termo geral: = (n & ) & a 5 = (5 & ) & Observando que a & = 3a 2, temos: a 5 = (3. 5 2) & a 5 = (13) & a 5 = ( ) a 5 = 37 Portanto: + a 5 = = 56 Resposta: E 132
29
30
Emerson Marcos Furtado
 Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
CURSO ON-LINE MATEMÁTICA E RACIOCÍNIO LÓGICO - SENADO PROFESSOR: GUILHERME NEVES
 Conteúdo 1. Apresentação.... Progressão Aritmética... 3. Relação das questões comentadas... 1 4. Gabaritos... 7 1 1. Apresentação Seja bem vindo ao Ponto dos Concursos. Esta é a aula demonstrativa de Matemática
Conteúdo 1. Apresentação.... Progressão Aritmética... 3. Relação das questões comentadas... 1 4. Gabaritos... 7 1 1. Apresentação Seja bem vindo ao Ponto dos Concursos. Esta é a aula demonstrativa de Matemática
MATEMÁTICA FINANCEIRA
 MATEMÁTICA FINANCEIRA Progressão Aritmética e Geométrica Progressão Aritmética Uma sucessão de números na qual a diferença entre dois termos consecutivos é constante, é denominada progressão aritmética,
MATEMÁTICA FINANCEIRA Progressão Aritmética e Geométrica Progressão Aritmética Uma sucessão de números na qual a diferença entre dois termos consecutivos é constante, é denominada progressão aritmética,
MATEMÁTICA A - 11.o Ano. Propostas de resolução
 MATEMÁTICA A -.o Ano Sucessões Propostas de resolução Exercícios de exames e testes intermédios. Designado por a o maior dos dois termos considerados da progressão geométrica, e por b 0 menor, como a razão
MATEMÁTICA A -.o Ano Sucessões Propostas de resolução Exercícios de exames e testes intermédios. Designado por a o maior dos dois termos considerados da progressão geométrica, e por b 0 menor, como a razão
MATEMÁTICA 1º BIM MÉDIO INT. EM AGRONEGÓCIO 2º ANO
 Postado em 04 / 03 / 13 SEQUÊNCIAS NUMÉRICAS E PROGRESSÃO ARITMÉTICA Aluno(a): TURMA: 1- SEQUÊNCIAS O estudo das sequencias lógicas despertou o interesse de vários estudiosos/pesquisadores Um deles foi
Postado em 04 / 03 / 13 SEQUÊNCIAS NUMÉRICAS E PROGRESSÃO ARITMÉTICA Aluno(a): TURMA: 1- SEQUÊNCIAS O estudo das sequencias lógicas despertou o interesse de vários estudiosos/pesquisadores Um deles foi
Seqüências Numéricas
 Seqüências Numéricas É uma seqüência composta por números que estão dispostos em uma determinada ordem pré-estabelecida. Alguns exemplos de seqüências numéricas: (,, 6, 8, 0,,... ) (0,,, 3,, 5,...) (,,
Seqüências Numéricas É uma seqüência composta por números que estão dispostos em uma determinada ordem pré-estabelecida. Alguns exemplos de seqüências numéricas: (,, 6, 8, 0,,... ) (0,,, 3,, 5,...) (,,
Para simplificar a notação, também usamos denotar uma sequência usando apenas a imagem de :
 Sequências Uma sequência é uma função f de em, ou seja. Para todo número natural i associamos um número real por meio de uma determinada regra de formação. A sequencia pode ser denotada por: Ou, por meio
Sequências Uma sequência é uma função f de em, ou seja. Para todo número natural i associamos um número real por meio de uma determinada regra de formação. A sequencia pode ser denotada por: Ou, por meio
Emerson Marcos Furtado
 Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Aula demonstrativa Apresentação... 2 Relação das Questões Comentadas... 8 Gabaritos... 11
 Aula demonstrativa Apresentação... Relação das Questões Comentadas... 8 Gabaritos... 11 1 Apresentação Olá pessoal! Saiu o edital para o TJ-SP. A banca organizadora é a VUNESP e esta é a aula demonstrativa
Aula demonstrativa Apresentação... Relação das Questões Comentadas... 8 Gabaritos... 11 1 Apresentação Olá pessoal! Saiu o edital para o TJ-SP. A banca organizadora é a VUNESP e esta é a aula demonstrativa
RACIOCÍNIO LÓGICO QUANTITATIVO PARA AFRFB PROFESSOR: GUILHERME NEVES
 Aula 5 Parte 1 Progressão Aritmética... Progressão Geométrica... 13 Cálculo da razão.... 14 Termo Geral.... 14 Soma dos termos de uma Progressão Geométrica finita... 15 Soma dos termos de uma Progressão
Aula 5 Parte 1 Progressão Aritmética... Progressão Geométrica... 13 Cálculo da razão.... 14 Termo Geral.... 14 Soma dos termos de uma Progressão Geométrica finita... 15 Soma dos termos de uma Progressão
... Onde usar os conhecimentos os sobre s?...
 Manual de IV Matemática SEQÜÊNCIA OU SUCESSÃO Por que aprender Progr ogressõe ssões? s?... O estudo das Progressões é uma ferramenta que nos ajuda a entender fenômenos e fatos do cotidiano, desde situações
Manual de IV Matemática SEQÜÊNCIA OU SUCESSÃO Por que aprender Progr ogressõe ssões? s?... O estudo das Progressões é uma ferramenta que nos ajuda a entender fenômenos e fatos do cotidiano, desde situações
 01/06/015 MATEMÁTICA PROFESSOR: CRISTIANO JORGE PROGRESSÃO ARITMÉTICA (PA) 1 01/06/015 Sequência ou sucessão: A palavra seqüência sugere a ideia de termos sucessivos e pode ser finita ou infinita. Toda
01/06/015 MATEMÁTICA PROFESSOR: CRISTIANO JORGE PROGRESSÃO ARITMÉTICA (PA) 1 01/06/015 Sequência ou sucessão: A palavra seqüência sugere a ideia de termos sucessivos e pode ser finita ou infinita. Toda
Sequências. 1. (Uem 2013) Seja r um número inteiro positivo fixado. Considere a sequência numérica definida por 1 r
 Sequências. (Uem 03) Seja r um número inteiro positivo fixado. Considere a sequência numérica a definida por r e assinale o que for correto. an an a 0) A soma dos 50 primeiros termos da sequência (a, a,
Sequências. (Uem 03) Seja r um número inteiro positivo fixado. Considere a sequência numérica a definida por r e assinale o que for correto. an an a 0) A soma dos 50 primeiros termos da sequência (a, a,
Emerson Marcos Furtado
 Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Plano de Trabalho 1. Regularidades Numéricas: Sequências. Matemática 2º Ano 2º Bimestre/2014. Tarefa 1
 Matemática 2º Ano 2º Bimestre/2014 Plano de Trabalho 1 Regularidades Numéricas: Sequências Tarefa 1 Mônica Cristina Martins Pereira Tutor: Susi Cristine Britto Ferreira 1 SUMÁRIO INTRODUÇÃO...03 DESENVOLVIMENTO/ATIVIDADES...04
Matemática 2º Ano 2º Bimestre/2014 Plano de Trabalho 1 Regularidades Numéricas: Sequências Tarefa 1 Mônica Cristina Martins Pereira Tutor: Susi Cristine Britto Ferreira 1 SUMÁRIO INTRODUÇÃO...03 DESENVOLVIMENTO/ATIVIDADES...04
Matemática PROGRESSÕES. Professor Dudan
 Matemática PROGRESSÕES Professor Dudan Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos:
Matemática PROGRESSÕES Professor Dudan Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos:
Matemática E Extensivo V. 6
 Etensivo V. 6 Eercícios ) a) P() é sempre igual à soma dos coeficientes de P(). b) P() é sempre igual ao termo independente de P(). c) P() é a raiz de P(), pois P() =. a) P() = ³ + 7. ² 7. P() = + 7 7
Etensivo V. 6 Eercícios ) a) P() é sempre igual à soma dos coeficientes de P(). b) P() é sempre igual ao termo independente de P(). c) P() é a raiz de P(), pois P() =. a) P() = ³ + 7. ² 7. P() = + 7 7
Emerson Marcos Furtado
 Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Emerson Marcos Furtado Mestre em Métodos Numéricos pela Universidade Federal do Paraná (UFPR). Graduado em Matemática pela UFPR. Professor do Ensino Médio nos estados do Paraná e Santa Catarina desde 1992.
Caderno de Acompanhamento Progressão Aritmética e Função Afim Escola Estadual Judith Vianna. Estudante: Turma:
 Estudante: Turma: Sequências A natureza apresenta padrões e regularidades. Dessa forma, muitas teorias matemáticas são desenvolvidas a partir do estudo desses padrões e regularidades. Por exemplo, o estudo
Estudante: Turma: Sequências A natureza apresenta padrões e regularidades. Dessa forma, muitas teorias matemáticas são desenvolvidas a partir do estudo desses padrões e regularidades. Por exemplo, o estudo
MATEMÁTICA E SUAS TECNOLOGIAS PROGRESSÕES
 PROGRESSÕES A cada 76 anos o cometa Halley pode ser visto da Terra. Ele passou por aqui, pela última vez em 986 e deverá reaparecer no ano de 06. Depois em 38,, 90... e assim sucessivamente. Os números
PROGRESSÕES A cada 76 anos o cometa Halley pode ser visto da Terra. Ele passou por aqui, pela última vez em 986 e deverá reaparecer no ano de 06. Depois em 38,, 90... e assim sucessivamente. Os números
MATEMÁTICA. Sequências Numéricas P.A e P.G. Professor : Dêner Rocha
 MATEMÁTICA Sequências Numéricas P.A e P.G Professor : Dêner Rocha Sequência Podemos observar facilmente que o termo sequencia é facilmente encontrado no nosso dia-adia. Vejamos alguns explos: a) As notas
MATEMÁTICA Sequências Numéricas P.A e P.G Professor : Dêner Rocha Sequência Podemos observar facilmente que o termo sequencia é facilmente encontrado no nosso dia-adia. Vejamos alguns explos: a) As notas
Trabalho apresentado no Curso de Formação Continuada da Fundação CECIERJ Consórcio CEDERJ
 Trabalho apresentado no Curso de Formação Continuada da Fundação CECIERJ Consórcio CEDERJ Orientador: Paulo Alexandre Alves de Carvalho Grupo: 4 Série: 2ª série do Ensino Médio Cursista: Jozilaine Moreira
Trabalho apresentado no Curso de Formação Continuada da Fundação CECIERJ Consórcio CEDERJ Orientador: Paulo Alexandre Alves de Carvalho Grupo: 4 Série: 2ª série do Ensino Médio Cursista: Jozilaine Moreira
Aula 00 Aula Demonstrativa
 Aula 00 Aula Demonstrativa Apresentação... Progressão Aritmética... 3 Cálculo da razão... 3 Termo Geral... 4 Soma dos Termos... 6 Exercícios... 7 Questões IDECAN... 17 Relação das questões comentadas...
Aula 00 Aula Demonstrativa Apresentação... Progressão Aritmética... 3 Cálculo da razão... 3 Termo Geral... 4 Soma dos Termos... 6 Exercícios... 7 Questões IDECAN... 17 Relação das questões comentadas...
1. Progressão aritmética Resumo e lista
 Colégio Estadual Conselheiro Macedo Soares ª ano do Ensino Médio Atividade de Matemática do 1º bimestre de 019 Conteúdo: Progressão aritmética, Progressão geométrica Aluno(s):... N o(s) :... Aluno(s):...
Colégio Estadual Conselheiro Macedo Soares ª ano do Ensino Médio Atividade de Matemática do 1º bimestre de 019 Conteúdo: Progressão aritmética, Progressão geométrica Aluno(s):... N o(s) :... Aluno(s):...
Séries Numéricas 2,10,12,16,17,18,19,? 2,4,6,8,10,? 2,4,8,16,32,?
 SÉRIES NUMÉRICAS Séries Numéricas Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos: 2,10,12,16,17,18,19,?
SÉRIES NUMÉRICAS Séries Numéricas Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos: 2,10,12,16,17,18,19,?
Material Teórico - Módulo Progressões Aritméticas. Definição e Lei de Formação de uma PA. Primeiro Ano
 Material Teórico - Módulo Progressões Aritméticas Definição e Lei de Formação de uma PA Primeiro Ano Autor: Prof. Ulisses Lima Parente Revisor: Prof. Antonio Caminha M. Neto 1 Sequências elementares e
Material Teórico - Módulo Progressões Aritméticas Definição e Lei de Formação de uma PA Primeiro Ano Autor: Prof. Ulisses Lima Parente Revisor: Prof. Antonio Caminha M. Neto 1 Sequências elementares e
a 1 a 2 = a 7 = a 31 = a 44 = a 51 = Podemos escrever qualquer termo de uma PA se soubermos o 1º termo e a razão desta PA. n ln.
 1.6. Progressão Aritmética (PA). Observe as sequências abaixo: (a n) = (1, 4, 7, 10, 13,...) (b n) = ( -7, -5, -3, -1, 1, 3,...) (c n) = (2016, 2012, 2008, 2004,...) Elas possuem um padrão semelhante.
1.6. Progressão Aritmética (PA). Observe as sequências abaixo: (a n) = (1, 4, 7, 10, 13,...) (b n) = ( -7, -5, -3, -1, 1, 3,...) (c n) = (2016, 2012, 2008, 2004,...) Elas possuem um padrão semelhante.
NÚCLEO EDUCAFRO KALUNGA DISCIPLINA DE MATEMÁTICA PROFESSOR DEREK PAIVA
 NÚCLEO EDUCAFRO KALUNGA DISCIPLINA DE MATEMÁTICA PROFESSOR DEREK PAIVA NOTAS DE AULA: REPRESENTAÇÕES DECIMAIS A representação decimal é a forma como escrevemos um número em uma única base, e como essa
NÚCLEO EDUCAFRO KALUNGA DISCIPLINA DE MATEMÁTICA PROFESSOR DEREK PAIVA NOTAS DE AULA: REPRESENTAÇÕES DECIMAIS A representação decimal é a forma como escrevemos um número em uma única base, e como essa
Ao final de 10 anos, o número de exames por imagem aumentou de 40 milhões por ano para 94 milhões por ano. Isso
 Resposta da questão 1: [C] a1 = 6 an = 4 n = número de dias r = 4 = 6 + (n 1) 18 = n 1 n = 19 (6 + 4) 19 48 19 S = = S = 456km Resposta da questão : [C] Tem-se que os elementos de uma mesma coluna estão
Resposta da questão 1: [C] a1 = 6 an = 4 n = número de dias r = 4 = 6 + (n 1) 18 = n 1 n = 19 (6 + 4) 19 48 19 S = = S = 456km Resposta da questão : [C] Tem-se que os elementos de uma mesma coluna estão
Aulas particulares. Conteúdo
 Conteúdo Capítulo 4...2 Capitalização Simples...2 Exercícios...6 Resposta... 14 Capitalização Composta... 16 Exercícios... 17 Respostas... 19 Capitulo 5... 20 Progressões... 20 Progressão Aritmética (P.
Conteúdo Capítulo 4...2 Capitalização Simples...2 Exercícios...6 Resposta... 14 Capitalização Composta... 16 Exercícios... 17 Respostas... 19 Capitulo 5... 20 Progressões... 20 Progressão Aritmética (P.
Matemática E Intensivo V. 1
 GABARITO Matemática E Intensivo V. Exercícios 0) 5 0) 5 Seja o termo geral = 3n, então: Par =, temos: a = 3. = 3 = Par =, temos: a = 3. = 6 = 5 Par = 3, temos: a 3 = 3. 3 = 9 = 8 Então a + a + a 3 = +
GABARITO Matemática E Intensivo V. Exercícios 0) 5 0) 5 Seja o termo geral = 3n, então: Par =, temos: a = 3. = 3 = Par =, temos: a = 3. = 6 = 5 Par = 3, temos: a 3 = 3. 3 = 9 = 8 Então a + a + a 3 = +
Aula 00 Aula Demonstrativa
 Aula 00 Aula Demonstrativa Apresentação... Relação das questões comentadas... 10 Gabarito... 1 www.pontodosconcursos.com.br 1 Apresentação Olá, pessoal! Tudo bem com vocês? Esta é a aula demonstrativa
Aula 00 Aula Demonstrativa Apresentação... Relação das questões comentadas... 10 Gabarito... 1 www.pontodosconcursos.com.br 1 Apresentação Olá, pessoal! Tudo bem com vocês? Esta é a aula demonstrativa
Tópico D mtm B PROGRESSÃO GEOMÉTRICA
 Tópico D mtm B PROGRESSÃO GEOMÉTRICA Definição Progressão geométrica é uma sequência numérica em que cada termo, a partir do segundo, é igual ao anterior, multiplicado por uma constante chamada razão da
Tópico D mtm B PROGRESSÃO GEOMÉTRICA Definição Progressão geométrica é uma sequência numérica em que cada termo, a partir do segundo, é igual ao anterior, multiplicado por uma constante chamada razão da
José Wammes. Coordenação Editorial: Osmar Antonio Conte. Editoração: José Wammes. Ficha Catalográfica: Rute Teresinha Schio - CRB 1095
 1 José Wammes Coordenação Editorial: Osmar Antonio Conte Editoração: José Wammes Ficha Catalográfica: Rute Teresinha Schio - CRB 1095 Direitos desta edição reservados à: José Wammes Av. Ministro Cirne
1 José Wammes Coordenação Editorial: Osmar Antonio Conte Editoração: José Wammes Ficha Catalográfica: Rute Teresinha Schio - CRB 1095 Direitos desta edição reservados à: José Wammes Av. Ministro Cirne
2ª Série 2016 MATEMÁTICA E SUAS TECNOLOGIAS
 ª Série 6 MATEMÁTICA E SUAS TECNOLOGIAS ) A sequência (, 4, 8, 6,...) é uma: a) Função constante b) Progressão aritmética c) Progressão geométrica d) Função exponencial e) Funcão implícita ) O valor de
ª Série 6 MATEMÁTICA E SUAS TECNOLOGIAS ) A sequência (, 4, 8, 6,...) é uma: a) Função constante b) Progressão aritmética c) Progressão geométrica d) Função exponencial e) Funcão implícita ) O valor de
1ª série do Ensino Médio Turma 1º Bimestre de 2017 Data / / Escola Aluno
 AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 1ª série do Ensino Médio Turma 1º Bimestre de 2017 Data / / Escola Aluno EM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Avaliação da Aprendizagem em Processo
AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 1ª série do Ensino Médio Turma 1º Bimestre de 2017 Data / / Escola Aluno EM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Avaliação da Aprendizagem em Processo
PROGRESSÕES - INTENSIVO
 PROGRESSÕES - INTENSIVO Progressão Aritmética Definição Sequência numérica em que cada termo, a partir do segundo, é igual ao anterior somado com uma constante chamada razão da progressão aritmética. Exemplo
PROGRESSÕES - INTENSIVO Progressão Aritmética Definição Sequência numérica em que cada termo, a partir do segundo, é igual ao anterior somado com uma constante chamada razão da progressão aritmética. Exemplo
MATEMÁTICA. Docente: Marina Mariano de Oliveira
 MATEMÁTICA Docente: Marina Mariano de Oliveira MATEMÁTICA Docente: Marina Mariano de Oliveira Bacharelado em Meteorologia (incompleto) Instituto de Astronomia, Geofísica e Ciências Atmosféricas da Universidade
MATEMÁTICA Docente: Marina Mariano de Oliveira MATEMÁTICA Docente: Marina Mariano de Oliveira Bacharelado em Meteorologia (incompleto) Instituto de Astronomia, Geofísica e Ciências Atmosféricas da Universidade
LISTA DE EXERCÍCIOS 2º ANO GABARITO
 º ANO GABARITO Questão Matemática I 8 9 7 a9 = = 7 9 6 a8 = = 6 9 55 a7 = = Portanto, a média aritmética dos últimos termos será dada por: 8 7 6 55 + + + 7 7 M = = = 6 Questão O número de vigas em cada
º ANO GABARITO Questão Matemática I 8 9 7 a9 = = 7 9 6 a8 = = 6 9 55 a7 = = Portanto, a média aritmética dos últimos termos será dada por: 8 7 6 55 + + + 7 7 M = = = 6 Questão O número de vigas em cada
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se
 Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios
Critérios de divisibilidade Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios
segundo elemento, a diferença entre qualquer um deles e seu antecessor é igual a uma constante r que será
 MATEMÁTICA ENSINO MÉDIO MÓDULO DE REFORÇO - EAD PROGRESSÕES Progressão Aritmética I) PROGRESSÃO ARITMÉTICA ( PA) Uma Progressão Aritmética é uma sequência de elementos (a 1, a 2, a 3,, a n-1, a n,, ) tal
MATEMÁTICA ENSINO MÉDIO MÓDULO DE REFORÇO - EAD PROGRESSÕES Progressão Aritmética I) PROGRESSÃO ARITMÉTICA ( PA) Uma Progressão Aritmética é uma sequência de elementos (a 1, a 2, a 3,, a n-1, a n,, ) tal
Fundamentos Tecnológicos
 Fundamentos Tecnológicos Equações Algébricas e Equação de 1º Grau Início da aula 06 Equações Algébricas Expressões Algébricas - Definição Expressões algébricas são expressões matemáticas que apresentam
Fundamentos Tecnológicos Equações Algébricas e Equação de 1º Grau Início da aula 06 Equações Algébricas Expressões Algébricas - Definição Expressões algébricas são expressões matemáticas que apresentam
Portal da OBMEP. Material Teórico - Módulo Progressões Geométricas. Primeiro Ano
 Material Teórico - Módulo Progressões Geométricas Progressões Geométricas: Definição e Lei de Formação Primeiro Ano Autor: Prof. Ulisses Lima Parente Revisor: Prof. Antonio Caminha M. Neto Progressões
Material Teórico - Módulo Progressões Geométricas Progressões Geométricas: Definição e Lei de Formação Primeiro Ano Autor: Prof. Ulisses Lima Parente Revisor: Prof. Antonio Caminha M. Neto Progressões
Monster. Concursos. Matemática 1 ENCONTRO
 Monster Concursos Matemática 1 ENCONTRO CONJUNTOS NUMÉRICOS Conjuntos numéricos podem ser representados de diversas formas. A forma mais simples é dar um nome ao conjunto e expor todos os seus elementos,
Monster Concursos Matemática 1 ENCONTRO CONJUNTOS NUMÉRICOS Conjuntos numéricos podem ser representados de diversas formas. A forma mais simples é dar um nome ao conjunto e expor todos os seus elementos,
Raciocínio Lógico. Números. Professor Edgar Abreu.
 Raciocínio Lógico Números Professor Edgar Abreu www.acasadoconcurseiro.com.br Raciocínio Lógico QUESTÕES ENVOLVENDO SEQUÊNCIA DE NÚMEROS É comum aparecer em provas de concurso questões envolvendo sequências
Raciocínio Lógico Números Professor Edgar Abreu www.acasadoconcurseiro.com.br Raciocínio Lógico QUESTÕES ENVOLVENDO SEQUÊNCIA DE NÚMEROS É comum aparecer em provas de concurso questões envolvendo sequências
Séries Numéricas 2,10,12,16,17,18,19,? 2,4,6,8,10,? 2,4,8,16,32,?
 SÉRIES NUMÉRICAS Séries Numéricas Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos: 2,10,12,16,17,18,19,?
SÉRIES NUMÉRICAS Séries Numéricas Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos: 2,10,12,16,17,18,19,?
Matemática. Progressão Geométrica. Professor Dudan.
 Matemática Progressão Geométrica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROGRESSÃO GEOMÉTRICA Uma progressão geométrica (abreviadamente, P. G.) é uma sequência numérica em que cada termo,
Matemática Progressão Geométrica Professor Dudan www.acasadoconcurseiro.com.br Matemática PROGRESSÃO GEOMÉTRICA Uma progressão geométrica (abreviadamente, P. G.) é uma sequência numérica em que cada termo,
Meu nome: Minha Instituição:
 Meu nome: Minha Instituição: . O Teorema Fundamental da Aritmética enuncia que todo número natural maior que ou é primo ou pode ser escrito de forma única, a menos da ordem dos fatores, como produto de
Meu nome: Minha Instituição: . O Teorema Fundamental da Aritmética enuncia que todo número natural maior que ou é primo ou pode ser escrito de forma única, a menos da ordem dos fatores, como produto de
Matemática E Extensivo V. 6
 Etensivo V. 6 Eercícios ) a) P() é sempre igual à soma dos coeficientes de P(). b) P() é sempre igual ao termo independente de P(). c) P() é a raiz de P(), pois P() =. ) D a) P() = ³ + 7. ² 7. P() = +
Etensivo V. 6 Eercícios ) a) P() é sempre igual à soma dos coeficientes de P(). b) P() é sempre igual ao termo independente de P(). c) P() é a raiz de P(), pois P() =. ) D a) P() = ³ + 7. ² 7. P() = +
Progressão Geométrica
 Progressão Aritmética E Progressão Geométrica David Armando Zavaleta Villanueva Departamento de Matemática-CCET-UFRN 1 1 villanueva@ccet.ufrn.br Progressão Aritmética Definição 1 Chamamos de progresão
Progressão Aritmética E Progressão Geométrica David Armando Zavaleta Villanueva Departamento de Matemática-CCET-UFRN 1 1 villanueva@ccet.ufrn.br Progressão Aritmética Definição 1 Chamamos de progresão
TÓPICOS DE REVISÃO MATEMÁTICA I SEQUÊNCIAS E PROGRESSÕES. Prof. Rogério Rodrigues
 0 TÓPICOS DE REVISÃO MATEMÁTICA I SEQUÊNCIAS E PROGRESSÕES Prof. Rogério Rodrigues 1 1) SEQUÊNCIA NUMÉRICA: 1.1) Definição: È toda relação que associa cada um dos números naturais n (n 0) a um número real
0 TÓPICOS DE REVISÃO MATEMÁTICA I SEQUÊNCIAS E PROGRESSÕES Prof. Rogério Rodrigues 1 1) SEQUÊNCIA NUMÉRICA: 1.1) Definição: È toda relação que associa cada um dos números naturais n (n 0) a um número real
Rodada #1 Matemática
 Rodada #1 Matemática Professor Guilherme Neves Assuntos da Rodada 1. Estruturas Lógicas.. Lógica de Argumentação. 3. Diagramas Lógicos. 4. Trigonometria. 5. Matrizes, Determinantes e Solução de Sistemas
Rodada #1 Matemática Professor Guilherme Neves Assuntos da Rodada 1. Estruturas Lógicas.. Lógica de Argumentação. 3. Diagramas Lógicos. 4. Trigonometria. 5. Matrizes, Determinantes e Solução de Sistemas
MÉDIA ARITMÉTICA SIMPLES E PODERADA EXERCÍCIOS DE FIXAÇÃO
 MÉDIA ARITMÉTICA SIMPLES E PODERADA EXERCÍCIOS DE FIXAÇÃO 1) E0628 Em uma fábrica, a média salarial das mulheres é R$ 880,00; para os homens, a média salarial é R$ 1.020,00. Sabe-se, também, que a média
MÉDIA ARITMÉTICA SIMPLES E PODERADA EXERCÍCIOS DE FIXAÇÃO 1) E0628 Em uma fábrica, a média salarial das mulheres é R$ 880,00; para os homens, a média salarial é R$ 1.020,00. Sabe-se, também, que a média
MATEMÁTICA - 3o ciclo Sequências e sucessões (7 o ano) Propostas de resolução
 MATEMÁTICA - 3o ciclo Sequências e sucessões (7 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Verificando que em cada termo: o número de cubos cinzentos é igual à
MATEMÁTICA - 3o ciclo Sequências e sucessões (7 o ano) Propostas de resolução Exercícios de provas nacionais e testes intermédios 1. Verificando que em cada termo: o número de cubos cinzentos é igual à
Progressão Aritmética
 CEFET - Centro Federal de Educação Tecnológica Celso Suckow da Fonseca Definição Uma (P.A.) é uma sequência de números (a 1, a 2,..., a n,...) (n N) na qual a diferença entre cada termo a n+1 e o seu antecessor
CEFET - Centro Federal de Educação Tecnológica Celso Suckow da Fonseca Definição Uma (P.A.) é uma sequência de números (a 1, a 2,..., a n,...) (n N) na qual a diferença entre cada termo a n+1 e o seu antecessor
Centro Estadual de Educação de Jovens e Adultos de Votorantim
 Centro Estadual de Educação de Jovens e Adultos de Votorantim PROGRESSÕES PROGRESSÃO NUMÉRICA - é uma seqüência ou sucessão de números que obedecem a um raciocínio lógico. Sequências: Considere um campeonato
Centro Estadual de Educação de Jovens e Adultos de Votorantim PROGRESSÕES PROGRESSÃO NUMÉRICA - é uma seqüência ou sucessão de números que obedecem a um raciocínio lógico. Sequências: Considere um campeonato
CÂMARA MUNICIPAL DE GOIÂNIA. Matemática Progressão Aritmética e Progressão Geométrica
 CÂMARA MUNICIPAL DE GOIÂNIA Matemática JOSIMAR PADILHA Professor do Gran Cursos Online. Ministra aulas presenciais, telepresenciais e online de Matemática Básica, Raciocínio Lógico, Matemática Financeira
CÂMARA MUNICIPAL DE GOIÂNIA Matemática JOSIMAR PADILHA Professor do Gran Cursos Online. Ministra aulas presenciais, telepresenciais e online de Matemática Básica, Raciocínio Lógico, Matemática Financeira
Recorrências - Parte I
 Polos Olímpicos de Treinamento Curso de Álgebra - Nível Prof. Marcelo Mendes Aula 4 Recorrências - Parte I Na aula anterior, vimos alguns exemplos de sequências. Em alguns deles, os termos são dados em
Polos Olímpicos de Treinamento Curso de Álgebra - Nível Prof. Marcelo Mendes Aula 4 Recorrências - Parte I Na aula anterior, vimos alguns exemplos de sequências. Em alguns deles, os termos são dados em
x 1. Em cada uma das figuras, eles são apenas os primeiros elementos dos
 0) Nas figuras a seguir, a curva é o gráfico da função x retângulos hachurados para infinitos que possuem as mesmas características. f x. Observe atentamente o que ocorre com os x. Em cada uma das figuras,
0) Nas figuras a seguir, a curva é o gráfico da função x retângulos hachurados para infinitos que possuem as mesmas características. f x. Observe atentamente o que ocorre com os x. Em cada uma das figuras,
Progressões aritméticas
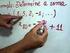 A UUL AL A Progressões aritméticas Quando escrevemos qualquer quantidade de números, um após o outro, temos o que chamamos de seqüência. As seqüências são, freqüentemente, resultado da observação de um
A UUL AL A Progressões aritméticas Quando escrevemos qualquer quantidade de números, um após o outro, temos o que chamamos de seqüência. As seqüências são, freqüentemente, resultado da observação de um
Matemática SÉRIES NUMÉRICAS. Professor Dudan
 Matemática SÉRIES NUMÉRICAS Professor Dudan Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos:
Matemática SÉRIES NUMÉRICAS Professor Dudan Uma série numérica é uma sequencia de números que respeita uma regra, uma lei de formação. Sendo assim todos foram produzidos à partir de uma mesma ideia. Exemplos:
Progressão aritmética e progressão geométrica
 Progressão aritmética e progressão geométrica Qualquer conjunto cujos elementos obedecem a uma ordem é uma sequência. No cotidiano, encontramos várias sequências: a lista de chamada de uma turma, as palavras
Progressão aritmética e progressão geométrica Qualquer conjunto cujos elementos obedecem a uma ordem é uma sequência. No cotidiano, encontramos várias sequências: a lista de chamada de uma turma, as palavras
PLANO DE TRABALHO I GOVERNO DO ESTADO DO RIO DE JANEIRO SECRECTARIA ESTADUAL DE EDUCAÇÃO METROPOLITANA I
 PLANO DE TRABALHO I GOVERNO DO ESTADO DO RIO DE JANEIRO SECRECTARIA ESTADUAL DE EDUCAÇÃO METROPOLITANA I PROJETO SEEDUC FORMAÇÃO CONTINUADA DE PROFESSORES COLÉGIO ESTADUAL MARECHAL JUAREZ TÁVORA GRUPO
PLANO DE TRABALHO I GOVERNO DO ESTADO DO RIO DE JANEIRO SECRECTARIA ESTADUAL DE EDUCAÇÃO METROPOLITANA I PROJETO SEEDUC FORMAÇÃO CONTINUADA DE PROFESSORES COLÉGIO ESTADUAL MARECHAL JUAREZ TÁVORA GRUPO
PROGRESSÃO ARITMÉTICA
 Hewlett-Packard PROGRESSÃO ARITMÉTICA Aulas 01 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 018 Sumário Progressão Aritmética... 1 PRELIMINAR 1... 1 Definição de progressão aritmética
Hewlett-Packard PROGRESSÃO ARITMÉTICA Aulas 01 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 018 Sumário Progressão Aritmética... 1 PRELIMINAR 1... 1 Definição de progressão aritmética
Numa PA, qualquer termo, a partir do segundo, é a média aritmética do seu antecessor e do seu sucessor.
 EEAR/AFA/EFOMM 0-0-015 FELIPE MATEMÁTICA Progressão aritmética ( PA ) Definição Consideremos a seqüência (, 4, 6, 8, 10, 1, 14, 16). Observamos que, a partir do segundo termo, a diferença entre qualquer
EEAR/AFA/EFOMM 0-0-015 FELIPE MATEMÁTICA Progressão aritmética ( PA ) Definição Consideremos a seqüência (, 4, 6, 8, 10, 1, 14, 16). Observamos que, a partir do segundo termo, a diferença entre qualquer
SEQUÊNCIA DIDÁTICA PODCAST ÁREA CIÊNCIAS DA NATUREZA I MATEMÁTICA - ENSINO MÉDIO
 SEQUÊNCIA DIDÁTICA PODCAST ÁREA CIÊNCIAS DA NATUREZA I MATEMÁTICA - ENSINO MÉDIO Título do Podcast Área Segmento Duração Progressão Geométrica Ciências da Natureza I Matemática Ensino médio 5min34seg Habilidades:
SEQUÊNCIA DIDÁTICA PODCAST ÁREA CIÊNCIAS DA NATUREZA I MATEMÁTICA - ENSINO MÉDIO Título do Podcast Área Segmento Duração Progressão Geométrica Ciências da Natureza I Matemática Ensino médio 5min34seg Habilidades:
SEQUÊNCIAS E PROGRESSÕES. Iva Emanuelly Rafael Carvalho
 SEQUÊNCIAS E PROGRESSÕES Iva Emanuelly Rafael Carvalho Conceituando... SEQUÊNCIAS Em muitas situações da vida diária aparece a ideia de sequência ou sucessão. Exemplos de sequências: a) A sequência dos
SEQUÊNCIAS E PROGRESSÕES Iva Emanuelly Rafael Carvalho Conceituando... SEQUÊNCIAS Em muitas situações da vida diária aparece a ideia de sequência ou sucessão. Exemplos de sequências: a) A sequência dos
ADIÇÃO E SUBTRAÇÃO DE ARCOS ADIÇÃO E SUBTRAÇÃO DE ARCOS EXERCÍCIOS DE FIXAÇÃO
 ADIÇÃO E SUBTRAÇÃO DE ARCOS AULA ESCRITA EXERCÍCIOS DE FIXAÇÃO ADIÇÃO E SUBTRAÇÃO DE ARCOS EXERCÍCIOS DE FIXAÇÃO E0176 Calcule o seno de 345º. RESOLUÇÃO CONJUNTOS AULA ESCRITA EXERCÍCIOS DE FIXAÇÃO EXERCÍCIOS
ADIÇÃO E SUBTRAÇÃO DE ARCOS AULA ESCRITA EXERCÍCIOS DE FIXAÇÃO ADIÇÃO E SUBTRAÇÃO DE ARCOS EXERCÍCIOS DE FIXAÇÃO E0176 Calcule o seno de 345º. RESOLUÇÃO CONJUNTOS AULA ESCRITA EXERCÍCIOS DE FIXAÇÃO EXERCÍCIOS
Estrada em obras PROGRESSÃO GEOMÉTRICA CONTEÚDOS
 PROGRESSÃO GEOMÉTRICA CONTEÚDOS Progressão geométrica (PG) Razão de uma PG Progressão geométrica crescente Progressão geométrica decrescente Progressão geométrica oscilante Progressão geométrica constante
PROGRESSÃO GEOMÉTRICA CONTEÚDOS Progressão geométrica (PG) Razão de uma PG Progressão geométrica crescente Progressão geométrica decrescente Progressão geométrica oscilante Progressão geométrica constante
EXERCÍCIOS EXTRAS MATEMÁTICA (P.A) PROF.: PITI
 EXERCÍCIOS EXTRAS MATEMÁTICA (P.A) PROF.: PITI 1. Escreva os 4 primeiros termos da seqüência a n = 3n + 2; n IN*. 2. Verifique, em cada seqüência, se é uma P.A. Em caso afirmativo, determine a razão e
EXERCÍCIOS EXTRAS MATEMÁTICA (P.A) PROF.: PITI 1. Escreva os 4 primeiros termos da seqüência a n = 3n + 2; n IN*. 2. Verifique, em cada seqüência, se é uma P.A. Em caso afirmativo, determine a razão e
RACIOCÍNIO LÓGICO - MATEMÁTICA
 RACIOCÍNIO LÓGICO MATEMÁTICO WWW.CONCURSOVIRTUAL.COM.BR 1 QUESTÕES - RACIOCINIO LÓGICO 12. Uma sequência de números segue a seguinte lei de formação: se um número N dessa sequência é par, adicione a ele
RACIOCÍNIO LÓGICO MATEMÁTICO WWW.CONCURSOVIRTUAL.COM.BR 1 QUESTÕES - RACIOCINIO LÓGICO 12. Uma sequência de números segue a seguinte lei de formação: se um número N dessa sequência é par, adicione a ele
EXERCÍCIOS COMPLEMENTARES DE MATEMÁTICA 1ª Série do E. M. 4º Bimestre
 EXERCÍCIOS COMPLEMENTARES DE MATEMÁTICA 1ª Série do E. M. 4º Bimestre 01. Interpolando-se sete termos aritméticos entre os números 10 e 98, obtém-se uma progressão aritmética cujo termo central é: a) 45.
EXERCÍCIOS COMPLEMENTARES DE MATEMÁTICA 1ª Série do E. M. 4º Bimestre 01. Interpolando-se sete termos aritméticos entre os números 10 e 98, obtém-se uma progressão aritmética cujo termo central é: a) 45.
Caro(a) aluno(a), Coordenadoria de Estudos e Normas Pedagógicas CENP Secretaria da Educação do Estado de São Paulo Equipe Técnica de Matemática
 Caro(a) aluno(a), Você saberia representar a soma dos n primeiros números naturais a partir do 1? Neste Caderno você terá a oportunidade de conhecer esse e outros casos que envolvem sequências e resolvê-los
Caro(a) aluno(a), Você saberia representar a soma dos n primeiros números naturais a partir do 1? Neste Caderno você terá a oportunidade de conhecer esse e outros casos que envolvem sequências e resolvê-los
Por exemplo, vamos obter os termos de uma progressão geométrica de razão 2, partindo do número 3.
 Definição: Progressão geométrica (ou simplesmente PG) é uma seqüência de números não nulos em que cada um deles, multiplicado por um número fixo, fornece o próximo elemento da seqüência. Esse número fixo
Definição: Progressão geométrica (ou simplesmente PG) é uma seqüência de números não nulos em que cada um deles, multiplicado por um número fixo, fornece o próximo elemento da seqüência. Esse número fixo
MATEMÁTICA Sequência & Progressões 1. Professor Marcelo Gonsalez Badin
 MATEMÁTICA Sequência & Progressões 1 Professor Marcelo Gonsalez Badin Seqüência Série Sucessão {2, 3, 5, 10} = {3, 10, 2, 5} Num conjunto não importa a ordem na qual os elementos são apresentados Conjunto
MATEMÁTICA Sequência & Progressões 1 Professor Marcelo Gonsalez Badin Seqüência Série Sucessão {2, 3, 5, 10} = {3, 10, 2, 5} Num conjunto não importa a ordem na qual os elementos são apresentados Conjunto
Binómio de Newton. De modo análogo, podemos calcular as quintas e sextas potências e, de modo geral, obter o
 Binómio de Newton Introdução Pelos produtos notáveis, sabemos que (a+b)² = a² + 2ab + b². Se quisermos calcular (a + b)³, podemos escrever: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 Se quisermos calcular,
Binómio de Newton Introdução Pelos produtos notáveis, sabemos que (a+b)² = a² + 2ab + b². Se quisermos calcular (a + b)³, podemos escrever: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 Se quisermos calcular,
2º Trimestre ÁLGEBRA. Aula 7 _ Progressão Aritmética Professor Luciano Nóbrega. Maria Auxiliadora
 2º Trimestre 1 ÁLGEBRA Aula 7 _ Progressão Aritmética Professor Luciano Nóbrega Maria Auxiliadora SEQUÊNCIA NUMÉRICA 2 SEQUÊNCIA NUMÉRICA Denominamos por Sequência Numérica uma função f, cujo domínio é
2º Trimestre 1 ÁLGEBRA Aula 7 _ Progressão Aritmética Professor Luciano Nóbrega Maria Auxiliadora SEQUÊNCIA NUMÉRICA 2 SEQUÊNCIA NUMÉRICA Denominamos por Sequência Numérica uma função f, cujo domínio é
MATEMÁTICA ELEMENTAR II:
 Marcelo Gorges Olímpio Rudinin Vissoto Leite MATEMÁTICA ELEMENTAR II: situações de matemática do ensino médio no dia a dia 2009 2009 IESDE Brasil S.A. É proibida a reprodução, mesmo parcial, por qualquer
Marcelo Gorges Olímpio Rudinin Vissoto Leite MATEMÁTICA ELEMENTAR II: situações de matemática do ensino médio no dia a dia 2009 2009 IESDE Brasil S.A. É proibida a reprodução, mesmo parcial, por qualquer
MATEMÁTICA 1ºANO Ementa Objetivos Geral Específicos
 DADOS DA COMPONENTE CURRICULAR Nome da Disciplina: MATEMÁTICA Curso: Ensino Técnico Integrado Controle Ambiental Série: 1ºANO Carga Horária: 100h Docente Responsável: GILBERTO BESERRA Ementa Conjuntos
DADOS DA COMPONENTE CURRICULAR Nome da Disciplina: MATEMÁTICA Curso: Ensino Técnico Integrado Controle Ambiental Série: 1ºANO Carga Horária: 100h Docente Responsável: GILBERTO BESERRA Ementa Conjuntos
Notação e fórmula. O teorema do binômio de Newton se escreve como segue: são chamados coeficientes binomiais e são definidos como:
 Introdução Em matemática, binômio de Newton permite escrever na forma canônica o polinómio correspondente à potência de um binómio. O nome é dado em homenagem ao físico e matemático Isaac Newton. Entretanto
Introdução Em matemática, binômio de Newton permite escrever na forma canônica o polinómio correspondente à potência de um binómio. O nome é dado em homenagem ao físico e matemático Isaac Newton. Entretanto
Geometria e Medida. Números e Operações. Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação. - Atenção.
 Conselho de Docentes do 3º Ano PLANIFICAÇÃO Anual de Matemática Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Geometria e Medida Localização e orientação no espaço Coordenadas
Conselho de Docentes do 3º Ano PLANIFICAÇÃO Anual de Matemática Domínios/Subdomínios Objetivos gerais Descritores de desempenho Avaliação Geometria e Medida Localização e orientação no espaço Coordenadas
PROGRESSÃO ARITMÉTICA
 Hewlett-Packard PROGRESSÃO ARITMÉTICA Aulas 01 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 019 Sumário Progressão Aritmética... 1 PRELIMINAR 1... 1 Definição de progressão aritmética
Hewlett-Packard PROGRESSÃO ARITMÉTICA Aulas 01 a 04 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 019 Sumário Progressão Aritmética... 1 PRELIMINAR 1... 1 Definição de progressão aritmética
Universidade do Estado do Rio Grande do Norte
 Universidade do Estado do Rio Grande do Norte Faculdade de Ciências Exatas e Naturais Departamento de Matemática e Estatística Disciplina: Princípios da Contagem Semestre: 205.2 Prof.:Laudelino Gomes Ferreira
Universidade do Estado do Rio Grande do Norte Faculdade de Ciências Exatas e Naturais Departamento de Matemática e Estatística Disciplina: Princípios da Contagem Semestre: 205.2 Prof.:Laudelino Gomes Ferreira
Método de Gauss-Jordan e Sistemas Homogêneos
 Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
Método de Gauss-Jordan e Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2017.1 14 de agosto
Série: 2º ano Nível: Ensino Médio Turma: 2. Subtemas: Sequências, Progressões Aritméticas e Progressões Geométricas.
 PLANO DE AULA Dados de identificação 1-ESCOLA DE ENSINO MÉDIO MACÁRIO BORBA Município: Sombrio, SC Disciplina: Matemática Série: º ano Nível: Ensino Médio Turma: Professora: Erodíades Daboit Possamai Tempo
PLANO DE AULA Dados de identificação 1-ESCOLA DE ENSINO MÉDIO MACÁRIO BORBA Município: Sombrio, SC Disciplina: Matemática Série: º ano Nível: Ensino Médio Turma: Professora: Erodíades Daboit Possamai Tempo
Matemática. Nas mesmas condições, juntando 16 mesas, o número de pessoas que poderão ser acomodadas é: a) 32 b) 40 c) 36 d) 38 e) 34
 Matemática 01- A negação da proposição Ana viu uma assombração ou Bia não ficou assustada é equivalente a: a) Ana não viu uma assombração ou Bia ficou assustada. b) Ana viu uma assombração ou Bia não ficou
Matemática 01- A negação da proposição Ana viu uma assombração ou Bia não ficou assustada é equivalente a: a) Ana não viu uma assombração ou Bia ficou assustada. b) Ana viu uma assombração ou Bia não ficou
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 CONJUNTOS NUMÉRICOS
 CONJUNTO DOS NÚMEROS NATURAIS... 2 RETA NUMERADA... 2 CONJUNTO DOS NÚMEROS INTEIROS... 4 SUBCONJUNTOS DE Z... 5 NÚMEROS OPOSTOS... 5 VALOR ABSOLUTO DE UM NÚMERO INTEIRO... 6 CONJUNTO DOS NÚMEROS RACIONAIS...
CONJUNTO DOS NÚMEROS NATURAIS... 2 RETA NUMERADA... 2 CONJUNTO DOS NÚMEROS INTEIROS... 4 SUBCONJUNTOS DE Z... 5 NÚMEROS OPOSTOS... 5 VALOR ABSOLUTO DE UM NÚMERO INTEIRO... 6 CONJUNTO DOS NÚMEROS RACIONAIS...
E essa procura pela abstração da natureza foi fundamental para a evolução, não só, mas também, dos conjuntos numéricos
 A história nos mostra que desde muito tempo o homem sempre teve a preocupação em contar objetos e ter registros numéricos. Seja através de pedras, ossos, desenhos, dos dedos ou outra forma qualquer, em
A história nos mostra que desde muito tempo o homem sempre teve a preocupação em contar objetos e ter registros numéricos. Seja através de pedras, ossos, desenhos, dos dedos ou outra forma qualquer, em
a) Falsa. Por exemplo, para n = 2, temos 3n = 3 2 = 6, ou seja, um número par.
 Matemática Unidade I Álgebra Série - Teoria dos números 01 a) Falsa. Por exemplo, para n =, temos 3n = 3 = 6, ou seja, um número par. b) Verdadeira. Por exemplo, para n = 1, temos n = 1 =, ou seja, um
Matemática Unidade I Álgebra Série - Teoria dos números 01 a) Falsa. Por exemplo, para n =, temos 3n = 3 = 6, ou seja, um número par. b) Verdadeira. Por exemplo, para n = 1, temos n = 1 =, ou seja, um
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional
 Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA12 Matemática Discreta Avaliação - GABARITO AV 3 - MA 12 13 de julho de 2013 1. (2,0) Seja (a n ) uma progressão
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA12 Matemática Discreta Avaliação - GABARITO AV 3 - MA 12 13 de julho de 2013 1. (2,0) Seja (a n ) uma progressão
Matéria: Matemática Assunto: Progressão Aritmética Prof. Dudan
 Matéria: Matemática Assunto: Progressão Aritmética Prof. Dudan Matemática PROGRESSÃO ARITMÉTICA Definição Uma progressão aritmética (abreviadamente, P. A.) é uma sequência numérica em que cada termo,
Matéria: Matemática Assunto: Progressão Aritmética Prof. Dudan Matemática PROGRESSÃO ARITMÉTICA Definição Uma progressão aritmética (abreviadamente, P. A.) é uma sequência numérica em que cada termo,
Propostas de resolução. Capítulo 1 Números racionais Avalia o que sabes
 Capítulo Números racionais 0 + 0 Avalia o que sabes Pág. 8. Analisemos cada uma das seguintes opções: Opção A: Se a é múltiplo de b, então existe um número natural n tal que a n b. Logo, a b. Exclui-se
Capítulo Números racionais 0 + 0 Avalia o que sabes Pág. 8. Analisemos cada uma das seguintes opções: Opção A: Se a é múltiplo de b, então existe um número natural n tal que a n b. Logo, a b. Exclui-se
Matemática PROFESSOR: Francisco Monteiro OBJETIVO GERAL
 ANO DE ESCOLARIDADE: 8º ano (A e B matutino e A vespertino) DISCIPLINA: Matemática PROFESSOR: Francisco Monteiro OBJETIVO GERAL Resolver situações-problema, construindo estratégias e fazendo uso de diversas
ANO DE ESCOLARIDADE: 8º ano (A e B matutino e A vespertino) DISCIPLINA: Matemática PROFESSOR: Francisco Monteiro OBJETIVO GERAL Resolver situações-problema, construindo estratégias e fazendo uso de diversas
Aula Inaugural Curso Alcance 2017
 Aula Inaugural Curso Alcance 2017 Revisão de Matemática Básica Professores: Me Carlos Eurico Galvão Rosa e Me. Márcia Mikuska Universidade Federal do Paraná Campus Jandaia do Sul cegalvao@ufpr.br 06 de
Aula Inaugural Curso Alcance 2017 Revisão de Matemática Básica Professores: Me Carlos Eurico Galvão Rosa e Me. Márcia Mikuska Universidade Federal do Paraná Campus Jandaia do Sul cegalvao@ufpr.br 06 de
Veja exemplos de sequências finitas e infinitas: Sequência finita: (5, 7, 9, 11, 13, 15, 17, 19) Sequência infinita (3, 5, 7, 11, 13, 17,...
 SEQUÊNCIAS NUMÉRICAS Sequência numérica é uma sequência ou sucessão que tem como contradomínio (conjunto de chegada) o conjunto dos números reais. As sequências numéricas podem ser finitas, quando é possível
SEQUÊNCIAS NUMÉRICAS Sequência numérica é uma sequência ou sucessão que tem como contradomínio (conjunto de chegada) o conjunto dos números reais. As sequências numéricas podem ser finitas, quando é possível
9º Ano do Ensino Fundamental II:
 Conteúdos para III Simulado SDP/Outubro/2010 MATEMÁTICA 9º Ano do Ensino Fundamental II: CAPÍTULO I - NOÇÕES ELEMENTARES DE ESTATÍSTICA 1. Organizando os dados 2. Estudando gráficos 3. Estudando médias
Conteúdos para III Simulado SDP/Outubro/2010 MATEMÁTICA 9º Ano do Ensino Fundamental II: CAPÍTULO I - NOÇÕES ELEMENTARES DE ESTATÍSTICA 1. Organizando os dados 2. Estudando gráficos 3. Estudando médias
Números complexos na forma algébrica
 Números complexos na forma algébrica A gênese do complexos Durante dois mil anos a matemática cresceu sem se importar com o fato de que as raízes quadradas dos negativos não podiam ser calculadas. Os gregos,
Números complexos na forma algébrica A gênese do complexos Durante dois mil anos a matemática cresceu sem se importar com o fato de que as raízes quadradas dos negativos não podiam ser calculadas. Os gregos,
MATEMÁTICA SEGUNDO ANO
 O único lugar onde o sucesso vem antes do trabalho é no dicionário Albert Einstein MATEMÁTICA SEGUNDO ANO NOME COMPLETO: TURMA: TURNO: ANO: PROFESSORA: Progressão Aritmética Conceito; Termo Geral; Soma
O único lugar onde o sucesso vem antes do trabalho é no dicionário Albert Einstein MATEMÁTICA SEGUNDO ANO NOME COMPLETO: TURMA: TURNO: ANO: PROFESSORA: Progressão Aritmética Conceito; Termo Geral; Soma
SISTEMA DECIMAL. No sistema decimal o símbolo 0 (zero) posicionado à direita implica em multiplicar a grandeza pela base, ou seja, por 10 (dez).
 SISTEMA DECIMAL 1. Classificação dos números decimais O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para
SISTEMA DECIMAL 1. Classificação dos números decimais O sistema decimal é um sistema de numeração de posição que utiliza a base dez. Os dez algarismos indo-arábicos - 0 1 2 3 4 5 6 7 8 9 - servem para
Desenho e Projeto de Tubulação Industrial Nível II
 Desenho e Projeto de Tubulação Industrial Nível II Módulo I Aula 02 EQUAÇÕES Pense no seguinte problema: Uma mulher de 25 anos é casada com um homem 5 anos mais velho que ela. Qual é a soma das idades
Desenho e Projeto de Tubulação Industrial Nível II Módulo I Aula 02 EQUAÇÕES Pense no seguinte problema: Uma mulher de 25 anos é casada com um homem 5 anos mais velho que ela. Qual é a soma das idades
