Matemática IV. Textos de Apoio

Transcrição

1 Matemática IV 2 o semestre do ano lectivo 2004/2005 Engenharias de Materiais e Química Textos de Apoio Cristina Caldeira

2 A grande maioria dos exercícios presentes nestes textos de apoio foram recolhidos de folhas práticas elaboradas ao longo dos anos por vários docentes do epartamento de Matemática da FCTUC.

3 Índice 1 Funções vectoriais Limites, continuidade e matriz Jacobiana Exercícios Curvas no espaço. Comprimento de uma curva do espaço Recta tangente a uma curva no espaço Plano tangente e recta normal a uma superfície Exercícios Cálculo integral Superfícies quádricas Elipsóide Hiperbolóide de uma folha Hiperbolóide de duas folhas Cone elíptico Parabolóide elíptico Parabolóide hiperbólico Cilindro elíptico Cilindro hiperbólico Cilindro parabólico Exercícios Integral duplo efinição Interpretação do integral duplo como volume de um sólido quando f assume apenas valores não negativos Algumas propriedades dos integrais duplos Cálculo de integrais duplos-integrais iterados Exercícios Integrais duplos em coordenadas polares Exercícios Aplicações do integral duplo Cálculo de volumes Exercícios Cálculo de áreas de superfícies Exercícios Massa, centro de massa e momentos duma figura plana Exercícios i

4 2.4 Integral triplo efinição e propriedades Exercícios Integral triplo em coordenadas cillíndricas e esféricas Exercícios Algumas aplicações do integral triplo Exercícios Integral curvilíneo de campos de vectores efinição, cálculo e aplicação ao cálculo do trabalho Exercícios Campos conservativos. Independência do caminho Exercícios Teorema de Green Exercícios Integral de superfície Integral de superfície de funções escalares Exercícios Integral de superfície de campos de vectores Exercícios Teorema de Stokes e teorema da divergência Exercícios Soluções dos exercícios 149 Bibliografia 155

5 Capítulo 1 Funções vectoriais 1.1 Limites, continuidade e matriz Jacobiana Uma função vectorial em n variáveis reais é uma função de domínio contido em R n e que toma valores em R m, com m > 1, f : R n R m. Exemplo f : R 2 \ {(0, 0)} R ( 3 ) x (x, y) x 2 + y, 3y 2 2 x 2 + y, x y 2 é uma função vectorial de 2 variáveis reais. Considere-se uma função vectorial f : R n R m (x 1, x 2,..., x n ) f(x 1, x 2,..., x n ). Para (x 1, x 2,..., x n ), f(x 1, x 2,..., x n ) R m, logo f(x 1, x 2,..., x n ) = (f 1 (x 1, x 2,..., x n ), f }{{} 2 (x 1, x 2,..., x n ),..., f }{{} m (x 1, x 2,..., x n )). }{{} R R R As m funções reais de n variáveis reais f i : R n R (x 1, x 2,..., x n ) f i (x 1, x 2,..., x n ), i = 1, 2,..., m são as chamadas funções componentes de f. No caso da função do exemplo anterior as funções componentes são f 1 : R 2 \ {(0, 0)} R x (x, y), x 2 + y 2 f 2 : R 2 \ {(0, 0)} R (x, y) 3y2 x 2 + y 2 e f 3 : R 2 \ {(0, 0)} R (x, y) x y. 1

6 2 Textos de Apoio de Matemática IV-2004/2005 Sejam f : R n R m x f(x) = (f 1 (x), f 2 (x),..., f m (x)) e a um ponto de acumulação de. iz-se que existe o limite de f no ponto a se existem os limites das m funções componentes em a e define-se ( ) lim f(x) = lim f 1(x), lim f 2 (x),..., lim f m (x). x a x a x a x a Se a é um ponto de acumulação de, diz-se que fé contínua em a se existe o limite de f quando x tende para a e este limite é igual a f(a). Se a é um ponto isolado de (a pertence a mas não é ponto de aumulação de ), por definição, f é contínua em a. Verifica-se facilmente que f é contínua em a se e só se todas as funções componentes são contínuas em a. iz-se que uma função f : R n R m é de classe C k num conjunto aberto S se as funções componentes de f são de classe C k em S. Sejam f : f R n R m e g : g R n R m duas funções vectoriais. Seja ainda α um número real. A soma de f e g é a função f + g : f g R n R m x f(x) + g(x). O produto de α pela função f é a função α f : f R n R m x α f(x). Proposição Nas condições anteriores, seja a um ponto de acumulação de f e de g. Suponha-se que existem os limites de f e g no ponto a e que a é um ponto de acumulação do domínio de f + g. Então: 1. Existe o limite de f + g no ponto a e lim x a (f + g)(x) = lim x a f(x) + lim x a g(x); 2. Existe o limite de α f no ponto a e lim x a (α f)(x) = α lim x a f(x); Proposição Nas condições anteriores, se f e g são contínuas em a f g, então a função f + g é contínua em a. Proposição Sejam f : A R n R m e g : B R m R k duas funções com f(a) B e seja a um ponto de A tal que f é contínua em a. Suponha-se ainda que g é contínua em f(a). Então a função g f é contínua em a. Sejam f : R n R m e a = (a 1, a 2,..., a n ) um ponto de. Suponha-se que f tem componentes f 1, f 2,..., f m, todas admitindo derivadas parciais de primeira ordem em a.

7 Cristina Caldeira 3 À matriz m n f 1 x 1 (a) f 2 x 1 (a). f m x 1 (a) f 1 x 2 (a) f 2 x 2 (a).... f m x 2 (a) f 1 x n (a) f 2 x n (a). f m x n (a) chama-se matriz Jacobiana de f no ponto a e representa-se por J f (a). Exemplo Considere-se a função As funções componentes de f são f 1 : R 2 R (x, y) x 2 y Assim, para todo o (x, y) R 2, [ J f (x, y) = 1.2 Exercícios f : R 2 R 2 (x, y) (x 2 y, cos(xy)). e f 2 : R 2 R (x, y) cos(xy). 2xy x 2 y sin(xy) x sin(xy) 1. Considere o campo de vectores definido por ( f(x, y) = (x 2 + 2y 2 ) sin 1 xy, 3x 2 y x 2 + 2y + 1, ) x 2 + y 2 2 Mostre que lim f(x, y) = (0, 1, 0). (x,y) (0,0) 2. Calcule as matrizes Jacobianas das seguintes funções: (a) f(x, y) = (x 2 + y 2, sin x), (x, y) R 2 ; (b) g(x, y, z) = (x 2 + y 2, sin x), (x, y, z) R 3 ; (c) h(t) = cos t î + sin t ĵ, 3. Considere a função vectorial Calcule J f (1, 0). t [0, 2π]. ]. f : R 2 R 3 (x, y) (x + y 2, xy, e y )..

8 4 Textos de Apoio de Matemática IV-2004/ Curvas no espaço. Comprimento de uma curva do espaço Suponha-se que se tem uma função vectorial r : [a, b] R R 3 t r(t) = (r 1 (t), r 2 (t), r 3 (t)) = r 1 (t)î + r 2 (t)ĵ + r 3 (t)ˆk, contínua em [a, b]. Considere-se fixado em R 3 um referencial ortonormado OXY Z. Quando t varia de a para b, a extremidade do vector r(t) (aplicado na origem) descreve uma curva no espaço, C. As equações Fig x = r 1 (t) y = r 2 (t) z = r 3 (t), t [a, b] dizem-se equações paramétricas de C. O ponto A da curva C tal que OA = r(a) é o ponto inicial da curva e o ponto B tal OB = r(b) é o ponto final. Para simplificar a linguagem muitas vezes confundiremos o ponto P da curva tal que OP = r(t) com o vector r(t) aplicado na origem e do qual P é a extremidade. Assim, abreviadamente diz-se que r(a) é o ponto inicial e r(b) é o ponto final. A multiplicidade de um ponto P da curva C é o número de elementos do conjunto {t [a, b] : r(t) = OP }. Supondo a 0 podemos interpretar a curva C como sendo a trajectória do ponto material que no instante t tem coordenadas (r 1 (t), r 2 (t), r 3 (t)), no referencial OXY Z. Considerem-se duas funções vectoriais contínuas, e r : [a, b] R R 3 t r(t) = (x(t), y(t), z(t)) s : [c, d] R R 3 u s(u) = (x 1 (u), y 1 (u), z 1 (u)).

9 Cristina Caldeira 5 Estas duas funções dizem-se duas parametrizações de uma mesma curva C se existe uma função bijectiva e contínua, h : [a, b] [c, d] tal que h(a) = c, h(b) = d e r(t) = s(h(t)), para todo o t [a, b], ou seja, x(t) = (x 1 h)(t) y(t) = (y 1 h)(t) z(t) = (z 1 h)(t), t [a, b]. Ao longo deste curso uma curva no espaço não será vista meramente como um conjunto de pontos. Uma curva tem um sentido, um ponto inicial, um ponto final, e cada ponto da curva tem uma multiplicidade. Vejamos alguns exemplos. Exemplo Considere-se a curva de equações paramétricas x = t cos(2t) y = t sin(2t), t [0, 2π]. z = t 1. O ponto inicial é (0, 0, 0), o ponto final é (2π, 0, 2π) e todos os pontos têm multiplicidade Fig Exemplo Seja C a curva de equações paramétricas x = cos t y = sin t, t [0, 2π]. z = 0 O ponto inicial e o ponto final coincidem com (1, 0, 0). Todos os pontos de C têm multiplicidade 1, com excepção do ponto (1, 0, 0) que tem multiplicidade 2. As equações x = cos(2t) y = sin(2t), t [0, π] z = 0 são também equações paramétricas de C, porque a função h : [0, 2π] [0, π], definida por h(t) = t/2, é bijectiva, contínua e, além disso, verifica h(0) = 0 e h(2π) = π.

10 6 Textos de Apoio de Matemática IV-2004/2005 A curva de equações paramétricas x = cos t y = sin t z = 0, t [0, 4π] não é C, porque neste caso todos os pontos têm multiplicidade 2, com excepção do ponto (1, 0, 0) que tem multiplicidade 3. Também a curva de equações paramétricas x = sin t y = cos t z = 0, t [0, 2π] não é C, porque esta curva tem ponto inicial (0, 1, 0) e o ponto inicial de C é (1, 0, 0). Seja C uma curva do espaço que admite uma parametrização de classe C 1 r : [a, b] R R 3 t r(t) = (x(t), y(t), z(t)). (Abreviadamente diz-se que a curva é de classe C 1.) Seja n um inteiro positivo e considere-se uma partição do intervalo [a, b] em n intervalos do mesmo comprimento, a = t 0 < t 1 < < t n 1 < t n = b. Assim t i t i 1 = (b a)/n, para i = 1, 2,..., n. Considerem-se os n + 1 pontos de C, P 0, P 1,..., P n, onde OP i = r(t i ), i = 0, 1,..., n. A linha poligonal que se obtém justapondo os n segmentos de recta P i 1 P i, i = 1, 2,..., n tem por comprimento n P i 1 P i. i=1 Fig

11 Cristina Caldeira 7 Se existir lim n + n P i 1 P i ao seu valor chama-se comprimento da curva C e representa-se por l(c). i=1 Proposição Nas condições anteriores, l(c) = b a r (t) dt = b a x (t) 2 + y (t) 2 + z (t) 2 dt. Observe-se que na definição que demos de comprimento de arco e na expressão para esse comprimento, presente na proposição anterior, intervém a parametrização da curva que estamos a considerar. Será então natural perguntar se, considerando duas parametrizações distintas de uma mesma curva, se obtém o mesmo valor para o comprimento de arco. e facto assim é, como veremos de seguida. Considerem-se duas funções vectoriais de classe C 1 e r : [a, b] R R 3 t r(t) = (x(t), y(t), z(t)) s : [c, d] R R 3 u s(u) = (x 1 (u), y 1 (u), z 1 (u)). Suponha-se que r e s são duas parametrizações de uma mesma curva C. Isto é, existe uma função bijectiva e de classe C 1, h : [a, b] [c, d] tal que h(a) = c, h(b) = d e r(t) = s(h(t)), para todo o t [a, b], ou seja, Então x(t) = (x 1 h)(t) y(t) = (y 1 h)(t) z(t) = (z 1 h)(t), t [a, b]. b a r (t) dt = = = b a b a b a x (t) 2 + y (t) 2 + z (t) 2 dt [x 1(h(t)) h (t)] 2 + [y 1(h(t)) h (t)] 2 + [z 1(h(t)) h (t)] 2 dt x 1 (h(t)) 2 + y 1(h(t)) 2 + z 1(h(t)) 2 h (t) dt. Sendo h contínua, bijectiva e verificando h(a) = c e h(b) = d, h tem de ser crescente e portanto h (t) = h (t). Então, efectuando a mudança de variável h(t) = u no integral anterior obtém-se

12 8 Textos de Apoio de Matemática IV-2004/2005 b a r (t) dt = = d c d c x 1 (u) 2 + y 1(u) 2 + z 1(u) 2 du s (u) du. Recorde-se que uma curva no espaço não é meramente um conjunto de pontos. Uma curva tem um sentido, um ponto inicial, um ponto final, e cada ponto da curva tem uma multiplicidade. Assim l(c) pode não coincidir com o comprimento do conjunto de pontos que é o contradomínio da parametrização r. Vejamos um exemplo. Exemplo Calculemos o comprimento da curva C que admite como parametrização O comprimento de C é r : [0, 4π] R R 3 t r(t) = (cos t, 0, sin t). l(c) = = 4π 0 4π 0 = 4π. r (t) dt sin 2 t + cos 2 t dt O contradomínio de r é o conjunto de pontos da circunferência do plano XOZ de raio 1 e centro na origem. Verifica-se assim que o comprimento de C é o dobro do perímetro desta circunferência. Isto deve-se ao facto dos pontos da curva (com excepção do ponto (1, 0, 0)) terem multiplicidade Recta tangente a uma curva no espaço Considere-se uma função vectorial r : [a, b] R R 3 t r(t) = (r 1 (t), r 2 (t), r 3 (t)) e suponha-se que as funções componentes de r, r 1, r 2 e r 3, são diferenciáveis em t 0 ]a, b[. A matriz Jacobiana de r em t 0 é o vector dr 1 dt (t 0) J r (t 0 ) = dr 2 dt (t 0) dr 3 dt (t 0)

13 Cristina Caldeira 9 ( lim h 0 ) r 3 (t 0 + h) r 3 (t 0 ), lim h 0 h r 1 (t 0 + h) r 1 (t 0 ) r 2 (t 0 + h) r 2 (t 0 ) =, lim h h 0 h 1 = lim h 0 h [(r 1(t 0 + h), r 2 (t 0 + h), r 3 (t 0 + h)) (r 1 (t 0 ), r 2 (t 0 ), r 3 (t 0 ))] r(t 0 + h) r(t 0 ) = lim. h 0 h Assim, esta matriz Jacobiana costuma ser representada por r (t 0 ) ou d r dt (t 0). Vejamos qual o significado geométrico de r (t 0 ). Seja C a curva de equações paramétricas (x, y, z) = r(t), t [a, b]. Considere-se h 0. Sejam P 0 e Q os pontos de C tais que OP 0 = r(t 0 ) e OQ = r(t 0 + h). Considere-se ainda o vector Fig r h = r(t 0 + h) r(t 0 ) h Se h > 0, r h tem a direcção e o sentido de r(t 0 + h) r(t 0 ). Se h < 0, r h tem a direcção de r(t 0 + h) r(t 0 ) mas o sentido contrário. Fazendo h tender para zero o vector OQ aproxima-se de OP 0 e r h aproxima-se de um vector paralelo à recta tangente a C em P 0. Assim, desde que seja não nulo, o vector r (t 0 ) é paralelo à recta tangente a C no ponto P 0. Então, se r (t 0 ) 0, uma equação da recta tangente a C no ponto P 0 é. (x, y, z) = P 0 + λ r (t 0 ), λ R. (1.1) Exemplo Seja C a curva no espaço com equações paramétricas x = t y = t 2, 0 t 1. z = 2t Escreva-se uma equação da recta tangente a C no ponto P 0 = (1/2, 1/4, 1). Seja r(t) = (t, t 2, 2t). Então P 0 = r(1/2) e uma equação da recta tangente a C em P 0 é (x, y, z) = P 0 + λ r (1/2), λ R = (1/2, 1/4, 1) + λ(1, 1, 2), λ R.

14 10 Textos de Apoio de Matemática IV-2004/ Plano tangente e recta normal a uma superfície Usando o conhecimento de como determinar uma equação da recta tangente, num ponto, a uma curva no espaço vamos ver como determinar uma equação do plano tangente, num ponto, a uma superfície de nível de uma função real de 3 variáveis reais. Considere-se uma função real de 3 variáveis reais de classe C 1, f : R 3 R (x, y, z) f(x, y, z). Seja k pertencente ao contradomínio de f, S = {(x, y, z) : f(x, y, z) = k}, (isto é, S é a superfície de nível de f de valor k) e P 0 = (x 0, y 0, z 0 ) um ponto de S. O plano tangente a S em P 0 é o plano (caso exista) que contém P 0 e é paralelo a todas as rectas que sejam tangentes, em P 0, a curvas do espaço que estejam contidas em S e que passem em P 0. Fig Seja C uma curva do espaço que está contida na superfície S e que contém P 0 e considere-se uma função vectorial que parametriza C, r : [a, b] R R 3 t r(t) = (r 1 (t), r 2 (t), r 3 (t)). Suponha-se que r(t 0 ) = OP 0 (t 0 [a, b]), que r(t) é diferenciável em t 0 e que r (t 0 ) 0. Recorde-se que o vector gradiente de f em P 0 é ( f f(p 0 ) = x (x 0, y 0, z 0 ), f y (x 0, y 0, z 0 ), f ) z (x 0, y 0, z 0 ). Uma vez que a curva C está contida na superfície S tem-se f(r 1 (t), r 2 (t), r 3 (t)) = k, t [a, b]. erivando ambos os membros em ordem a t em t 0 (regra da cadeia) obtém-se f x (x 0, y 0, z 0 ) dr 1 dt (t 0) + f y (x 0, y 0, z 0 ) dr 2 dt (t 0) + f z (x 0, y 0, z 0 ) dr 3 dt (t 0) = 0,

15 Cristina Caldeira 11 ou seja, f(p 0 ) r (t 0 ) = 0, onde designa o produto interno usual em R 3. Verificou-se assim que o vector gradiente de f em P 0 é ortogonal à recta tangente a C em P 0. Isto acontece para toda a curva contida em S e que passe em P 0. Então, se f(p 0 ) 0, a superfície S admite plano tangente em P 0 e esse plano tangente é perpendicular a f(p 0 ). Assim, se f(p 0 ) 0, uma equação do plano tangente a S em P 0 é (x x 0, y y 0, z z 0 ) f(p 0 ) = 0. (1.2) Se f(p 0 ) 0, a recta normal a S em P 0 é a recta que passa em P 0 e é paralela a f(p 0 ). Uma equação vectorial desta recta é (x, y, z) = P 0 + λ f(p 0 ), λ R. Exemplo Considerem-se a superfície de R 3 de equação z = x 2 + y 2 2 e o ponto de S, P 0 = (0, 0, 2). eterminemos equações paramétricas para a recta normal a S em P 0 e uma equação cartesiana do plano tangente a S em P 0. Considere-se a função real de 3 variáveis reais de domínio R 3 definida por f(x, y, z) = x 2 + y 2 z. S é a superfície de nível de f de valor 2. O vector gradiente de f em (x, y, z) é f(x, y, z) = (2x, 2y, 1), logo f(p 0 ) = (0, 0, 1). Então as equações x = 0 y = 0 z = 2 λ, λ R são equações paramétricas da recta normal a S em P 0, concluindo-se que essa recta coincide com o eixo dos ZZ. Uma equação cartesiana do plano tangente a S em P 0 é 1.6 Exercícios (x 0, y 0, z + 2) (0, 0, 1) = 0 z = etermine uma equação da recta tangente à curva C com equações paramétricas dadas, no ponto P 0 indicado. x = cos t (a) C : y = 2 sin t, t [0, 2π]; P 0 = ( 1, 0, π); z = t (b) C : x = t 2 y = 2, t [0, 2]; P 0 = (1, 2, 1). z = t 3 2. etermine a equação do plano tangente às seguintes superfícies nos pontos indicados: (a) z = x 2 + y 2 no ponto P 0 = (1, 2, 5); (b) (x 1) 2 + (y 2) 2 + z 2 = 3 no ponto P 0 = (0, 1, 1);

16 12 Textos de Apoio de Matemática IV-2004/2005 (c) x y2 9 z2 8 = 0 no ponto P 0 = (4, 3, 4); (d) z 2 = x 2 + y 2 no ponto P 0 = (1, 1, 2); (e) x 2 + y 2 = 25 no ponto P 0 = (3, 4, 2). 3. Mostre que as superfícies de equação são tangentes no ponto (0, 1, 1). x y2 = z 2 e x 2 + y 2 + (z 2) 2 = 2 4. Prove que toda a recta normal a uma esfera passa no seu centro. 5. etermine os pontos da superfície de equação z = 4x 2 +9y 2 onde a normal à superfície é paralela à recta que passa por P ( 2, 4, 3) e Q(5, 1, 2).

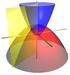
17 Capítulo 2 Cálculo integral 2.1 Superfícies quádricas Uma superfície quádrica é um subconjunto de R 3 constituído por todos os pontos de R 3 que satisfazem uma equação com a forma Ax 2 + By 2 + Cz 2 + xy + Eyz + F xz + Gx + Hy + Iz + J = 0, onde A, B,..., J são constantes reais e A, B,..., F não todas nulas. Pode provar-se que, para toda a superfície quádrica, existe um referencial ortonormado de R 3 em relação ao qual a equação da quádrica assume uma forma mais simples, a chamada forma canónica. Vejamos então quais são as equações das quádricas na forma canónica Elipsóide Um elipsóide é uma quádrica cuja equação na forma canónica é com a, b, c R +. x 2 a 2 + y2 b 2 + z2 c 2 = 1, Esta superfície é simétrica relativamente a cada um dos planos coordenados e relativamente à origem. A intersecção de um elipsóide na forma canónica com um plano paralelo a um dos planos coordenados é uma elipse, um ponto ou o conjunto vazio. Se a = b = c o elipsóide é uma superfície esférica de centro na origem e raio a. Na figura seguinte estão representados alguns elipsóides. 13

18 14 Textos de Apoio de Matemática IV-2004/2005 Fig Hiperbolóide de uma folha Um hiperbolóide de uma folha é uma quádrica cuja equação na forma canónica é de uma das formas: x 2 a 2 + y2 b 2 z2 c 2 = 1, x2 a 2 + y2 b 2 + z2 c 2 = 1 ou x 2 a 2 y2 b 2 + z2 c 2 = 1.

19 Cristina Caldeira 15 x 2 a 2 + y2 b 2 z2 c 2 = 1 Fig x2 a 2 + y2 b 2 + z2 c 2 = 1 x 2 a 2 y2 b 2 + z2 c 2 = 1 Fig O hiperbolóide de uma folha representado na figura é uma superfície simétrica relativamente a cada um dos planos coordenados. As secções por planos paralelos ao plano XOY são elipses. As secções por planos paralelos a XOZ ou a Y OZ são hipérboles Hiperbolóide de duas folhas Um hiperbolóide de duas folha é uma quádrica cuja equação na forma canónica é de uma das formas: x2 a y2 2 b + z2 2 c = 1, 2 x 2 a 2 y2 b 2 z2 c 2 = 1 ou x2 a 2 + y2 b 2 z2 c 2 = 1.

20 16 Textos de Apoio de Matemática IV-2004/2005 x2 a 2 y2 b 2 + z2 c 2 = 1 Fig x 2 a 2 y2 b 2 z2 c 2 = 1 x2 a 2 + y2 b 2 z2 c 2 = 1 Fig O hiperbolóide de duas folhas representado na figura é uma superfície simétrica em relação a cada um dos planos coordenados. As secções por planos paralelos a XOY são ou o conjunto vazio, ou um ponto ou uma elipse. As secções por plano paralelos a Y OZ ou a XOZ são hipérboles.

21 Cristina Caldeira Cone elíptico Um cone elíptico é uma quádrica cuja equação na forma canónica é de uma das formas: x 2 a 2 + y2 b 2 z2 c 2 = 0, x2 a 2 + y2 b 2 + z2 c 2 = 0 ou x 2 a 2 y2 b 2 + z2 c 2 = 0. x 2 a 2 + y2 b 2 z2 c 2 = 0 Fig x2 a 2 + y2 b 2 + z2 c 2 = 0 x 2 a 2 y2 b 2 + z2 c 2 = 0 Fig O cone representado na figura é uma superfície simétrica em relação a cada um dos planos coordenados. As secções por planos paralelos a XOY são elipses no caso de planos distintos de XOY e um ponto no caso do plano XOY. As secções por plano estritamente paralelos a Y OZ ou a XOZ são hipérboles. A intersecção com o plano XOZ é constituída por duas rectas, assim como a intersecção com o plano Y OZ.

22 18 Textos de Apoio de Matemática IV-2004/ Parabolóide elíptico Um parabolóide elíptico é uma quádrica cuja equação na forma canónica é de uma das formas: x 2 a + y2 2 b = 2pz, 2 y 2 b 2 + z2 c 2 = 2px ou x 2 a 2 + z2 c 2 = 2py, com p 0. x 2 a + y2 2 b = 2pz com p > 0 x 2 2 a + y2 = 2pz com p < 0 2 b2 Fig y 2 b + z2 2 c = 2px com p > 0 x 2 2 a + z2 = 2py com p > 0 2 c2 Fig

23 Cristina Caldeira 19 y 2 b + z2 2 c = 2px com p < 0 x 2 2 a + z2 = 2py com p < 0 2 c2 Fig Os parabolóides representados na figura são simétricos em relação aos planos XOZ e Y OZ. As secções por planos paralelos a XOY são o vazio, um ponto ou uma elipse. As secções por planos paralelos a Y OZ ou a XOZ são parábolas Parabolóide hiperbólico Um parabolíode hiperbólico é uma quádrica cuja equação na forma canónica é de uma das formas: x 2 a y2 2 b = 2pz, 2 y 2 b 2 z2 c 2 = 2px ou x 2 a 2 z2 c 2 = 2py, com p 0. x 2 a y2 = 2pz com p > 0 2 b2 Fig

24 20 Textos de Apoio de Matemática IV-2004/2005 x 2 a y2 = 2pz com p < 0 2 b2 Fig Os parabolóides hiperbólicos representados nas figuras e são simétricos relativamente aos planos XOZ e Y OZ. As intersecções com XOY são constituídas, para cada hiperbolóide, por duas rectas. As intersecções com planos estritamente paralelos a XOY são hiérboles e as intersecções com planos paralelos a XOZ ou Y OZ são parábolas Cilindro elíptico Um cilindro elíptico é uma quádrica cuja equação na forma canónica é de uma das formas: x 2 a 2 + y2 b 2 = 1, y 2 b 2 + z2 c 2 = 1 ou x 2 a 2 + z2 c 2 = 1. Para cada um destes cilindros, se as duas quantidades a e b ou b e c ou a e c são iguais, o cilindro diz-se circular recto. x 2 a 2 + y2 b 2 = 1, com a < b Fig

25 Cristina Caldeira 21 y 2 b 2 + z2 c 2 = 1 com b > c x 2 a 2 + z2 c 2 = 1 com a < c Fig O cilindro elíptico representado na figura é uma superfície simétrica relativamente a cada um dos planos coordenados. As secções por planos paralelos ao plano XOY são elipses. As secções por planos paralelos a XOZ ou a Y OZ são duas rectas, uma recta ou o vazio Cilindro hiperbólico Um cilindro hiperbólico é uma quádrica cuja equação na forma canónica é de uma das formas: x 2 a 2 y2 b 2 = 1, x2 a 2 + y2 b 2 = 1, y 2 b 2 z2 c 2 = 1, y2 b 2 + z2 c 2 = 1, x 2 a z2 = 1, ou 2 x2 c2 a + z2 2 c = 1. 2 x 2 a 2 y2 b 2 = 1, com a < b Fig

26 22 Textos de Apoio de Matemática IV-2004/2005 x2 a 2 + y2 b 2 = 1 x 2 a 2 z2 c 2 = 1 Fig O cilindro hiperbólico representado na figura é uma superfície simétrica relativamente a cada um dos planos coordenados. As secções por planos paralelos ao plano XOY são hipérboles. As secções por planos paralelos a XOZ são duas rectas. As secções por planos paralelos a Y OZ são duas rectas, uma recta ou o vazio Cilindro parabólico Um cilindro parabólico é uma quádrica cuja equação na forma canónica é de uma das formas: com a 0. y = az 2, y = ax 2, x = az 2, x = ay 2, z = ay 2, ou z = ax 2, y = az 2, com a > 0 Fig

27 Cristina Caldeira 23 x = az 2, com a < 0 z = ax 2, com a > 0 Fig O cilindro parabólico representado na figura é uma superfície simétrica relativamente aos planos coordenados XOY e Y OZ. As secções por planos paralelos ao plano Y OZ são parábolas. As secções por planos paralelos a XOZ são duas rectas, uma recta ou o vazio. As secções por planos paralelos a XOY são rectas. 2.2 Exercícios 1. Identifique e esboce as seguintes superfícies quádricas: (a)x 2 + 2y 2 + z 2 = 1 ; (b)x 2 + z 2 = 9 ; (c)x 2 + y 2 + z 2 = 2z ; (d)x 2 + y 2 = 4 z ; (e)(z 4) 2 = x 2 + y 2 ; (f)y = x 2 ; { z = 2 + y 2 (g) x 2 ; (h)x 2 + y = 0 ; (i)x 2 + 2y 2 z 2 = 1 ; (j)x 2 y 2 z 2 = Represente geometricamente o sólido S definido pelas condições: (a) x 2 + y 2 z 2 x 2 y 2 ; (b) x 2 + y 2 4 e x 2 + y 2 (z 6) 2 ; (c) x 2 + y 2 1 e 0 z x + y; (d) 0 z 2 e x 2 + y 2 z Faça o esboço gráfico dos seguintes subconjuntos de R 3 : (a) S = {(x, y, z) R 3 : x 0, y 0, z 0, e 6x + 3y + 2z 12}; (b) S = {(x, y, z) R 3 : x 2 + y 2 = 6y e x 2 + y 2 + z 2 36}; (c) S = {(x, y, z) R 3 : 4 + z x 2 + y 2 e 2 z x 2 + y 2 }.

28 24 Textos de Apoio de Matemática IV-2004/ Integral duplo efinição Seja R um rectângulo fechado de R 2, isto é, R = [a, b] [c, d] = {(x, y) R 2 : a x b e c y d}, com a < b e c < d. Considere-se uma partição do intervalo [a, b], P 1 = {x 0, x 1,..., x m }, com a = x 0 < x 1 < < x m 1 < x m = b, e uma partição do intervalo [c, d], P 2 = {y 0, y 1,..., y k }, com c = y 0 < y 1 < < y k 1 < y k = d. Tem-se assim uma decomposição da região rectangular R em mk rectângulos W i j = [x i 1, x i ] [y j 1, y j ], i = 1, 2,..., m, j = 1, 2,..., k, onde os rectângulos W ij se intersectam 2 a 2 quando muito nas respectivas fronteiras. Esta decomposição de R num número finito de rectângulos diz-se uma partição de R. Representemos por P esta partição de R. A norma (ou diâmetro) de P é a medida do maior dos comprimentos das diagonais de todos os rectângulos W ij, i = 1, 2,..., m, j = 1, 2,..., k e será representada por P ou δ P. Assim, { } P = máx (x i x i 1 ) 2 + (y j y j 1 ) 2 : i = 1,..., m, j = 1,..., k. Na figura seguinte está representada uma partição de uma região rectangular em 20 rectângulos. A norma desta partição é a medida do comprimento da diagonal assinalada. Fig

29 Cristina Caldeira 25 Para evitar o uso de dois índices chamaremos R 1, R 2,..., R n (com n = mk) aos mk rectângulos W ij, i = 1, 2,..., m, j = 1, 2,..., k. Seja f : R R (x, y) f(x, y) uma função real definda no rectângulo R. Seja P = {R 1, R 2,..., R n } uma partição de R em rectângulos. Represente-se por A i a área do rectângulo R i, para i = 1, 2,..., n. Uma soma de Riemann da função f relativamente à partição P é uma soma do tipo n f(u i, v i ) A i, i=1 onde (u i, v i ) é um ponto arbitrário de R i, para i = 1, 2,..., n. iz-se que f é integrável sobre R se existe um número real I para o qual é válido o seguinte: para todo o ε > 0 existe δ > 0 tal que, para toda a partição, P = {R i }, de R num número finito de rectângulos com P < δ, se tem f(u i, v i ) A i I < ε, i para qualquer escolha de (u i, v i ) R i. (2.1) Prova-se que, se existe um número real I verificando (2.1), então ele é único. Chama-se- -lhe integral duplo de f sobre R e representa-se por f(x, y) da ou f(x, y) dxdy. R Observação Intuitivamente (2.1) significa que as somas de Riemann de f se aproximam de I quando se consideram partições de R de norma cada vez mais pequena. Como saber se uma dada função é integrável sobre um dado rectângulo R? Prova-se que se f é contínua num rectângulo fechado R então f é integrável em R. Podemos garantir ainda a integrabilidade, sobre um rectângulo, de determinado tipo de funções, não necessariamente contínuas, o que nos permitirá também definir a noção de integral de uma função sobre regiões não necessariamente rectangulares. Considere-se uma função f : R 2 R (x, y) f(x, y), onde é um subconjunto fechado e limitado de R 2 cuja fronteira é uma união finita de conjuntos definidos por equações da forma x = ϕ(y) ou y = ψ(x), com ϕ e ψ funções R

30 26 Textos de Apoio de Matemática IV-2004/2005 contínuas em intervalos reais fechados e limitados. Suponha-se ainda que f é contínua em. Seja R = [a, b] [c, d] um rectângulo fechado de R 2 (a < b e c < d), que contém. efina-se uma função em todo o rectângulo R por g : R R 2 R { f(x, y) se (x, y) (x, y) 0 se (x, y). Pode provar-se que esta nova função, apesar de não ser contínua em R, é integrável sobre R. iz-se então que f é integrável sobre e define-se f(x, y) dxdy = R g(x, y) dxdy. Vamos agora considerar dois tipos especiais de regiões de R 2. Uma região de R 2 fechada e limitada diz-se verticalmente simples ou de tipo I se é da forma = {(x, y) R 2 : a x b e g 1 (x) y g 2 (x)}, com a < b, g 1 e g 2 funções contínuas em [a, b], distintas e verificando g 1 (x) g 2 (x), x [a, b]. Região verticalmente simples Fig Uma região de R 2 fechada e limitada diz-se horizontalmente simples ou de tipo II se é da forma = {(x, y) R 2 : c y d e h 1 (y) x h 2 (y)}, com c < d, h 1 e h 2 funções contínuas em [c, d], distintas e verificando h 1 (y) h 2 (y), y [c, d].

31 Cristina Caldeira 27 Região horizontalmente simples Fig Prova-se que se é um subconjunto fechado e limitado de R 2 cuja fronteira é uma união finita de conjuntos definidos por equações da forma x = ϕ(y) ou y = ψ(x), com ϕ e ψ funções contínuas em intervalos reais fechados e limitados, então é união de um número finito de regiões de R 2 que são, cada uma delas, de um dos tipos I ou II. Mais, estas regiões de tipos I ou II podem ser escolhidas de modo a que, duas a duas, se intersectem quando muito nas respectivas fronteiras. Será sobre regiões destas, que são união de um número finito de regiões de tipos I ou II, que iremos calcular integrais duplos. Observação efinimos a noção de integral duplo considerando partições da região de integração,, em rectângulos. A noção de integral duplo pode ser definida, de modo inteiramente análogo, considerando partições da região de integração em subregiões de outros tipos. No caso geral, o diâmetro de uma partição de em subregiões 1, 2,..., n é a maior das distâncias entre 2 pontos de que pertençam a um mesmo i. Tudo o resto funciona como no caso de uma partição em rectângulos Interpretação do integral duplo como volume de um sólido quando f assume apenas valores não negativos Comecemos por supôr que temos um rectângulo R = [a, b] [c, d] e uma função f : R R 2 R (x, y) f(x, y), contínua em R e tal que f(x, y) 0 para todo o (x, y) R. Efectue-se uma partição de R em rectângulos, P = {R 1, R 2,..., R n }, e considere-se uma soma de Riemann de f relativamente à partição P, n f(u i, v i ) A i, onde (u i, v i ) R i e A i designa a área de R i, para i = 1, 2,..., n. i=1

32 28 Textos de Apoio de Matemática IV-2004/2005 Seja E o sólido de R 3 que é delimitado pela região R, pelos planos x = a, x = b, y = c, y = d e pelo gráfico de f, isto é, E = {(x, y, z) R 3 : (x, y) R e 0 z f(x, y)}. A partição P determina a decomposição de E em n sólidos E 1, E 2,..., E n onde E i = {(x, y, z) R 3 : (x, y) R i e 0 z f(x, y)}, i = 1,..., n. Na figura seguinte estão representados a região R, a partição P, o sólido E e um dos sólidos menores, E i. Fig Vejamos o que se passa em cada um dos sólidos E i. Fixe-se i {1, 2,..., n}. f(u i, v i ) A i é igual ao volume do paralelipípedo de base R i e altura f(u i, v i ). Quanto mais pequena for a medida do comprimento das diagonais de R i mais o volume deste paralelipípedo se aproxima do volume do sólido E i. P i = (u i, v i, 0), Q i = (u i, v i, f(u i, v i )) Fig A soma de Riemann n f(u i, v i ) A i i=1

33 Cristina Caldeira 29 dá o volume da reunião de n paralelipípedos, de bases R 1, R 2,..., R n e alturas f(u 1, v 1 ), f(u 2, v 2 ),..., f(u n, v n ), respectivamente. O volume desta reunião de paralelipípedos dá uma aproximação para o volume do sólido E, aproximação essa que será tanto melhor quanto menor for a norma da partição. Este raciocínio que acabámos de expôr dá uma ideia intuitiva de porque é válido o resultado seguinte. Proposição Seja uma região de R 2 que é união de um número finito de regiões de R 2 que são, cada uma delas, de um dos tipos I ou II e f uma função definida e contínua em e verificando ainda f(x, y) 0, (x, y). Então o volume do sólido E = {(x, y, z) R 3 : (x, y) e 0 z f(x, y)}. é V (E) = f(x, y) dxdy Algumas propriedades dos integrais duplos Teorema Sejam uma região de R 2 que é união de um número finito de regiões de R 2 que são, cada uma delas, de um dos tipos I ou II e f e g funções reais integráveis em. Então 1. f + g é integrável em e [f(x, y) + g(x, y)] dxdy = f(x, y) dxdy + 2. Para todo o c R, a função c f é integrável em e cf(x, y) dxdy = c f(x, y) dxdy ; 3. Se f(x, y) g(x, y), para todo o (x, y), f(x, y) dxdy g(x, y) dxdy ; g(x, y) dxdy ; 4. Se = 1 2 onde 1 e 2 são duas regiões de R 2 que se intersectam, quando muito, nas suas fronteiras e cada uma delas é união de um número finito de regiões dos tipos I ou II, então f(x, y) dxdy = f(x, y) dxdy + f(x, y) dxdy. 1 2

34 30 Textos de Apoio de Matemática IV-2004/2005 emonstração : Faremos apenas a demonstração da parte (a) do teorema e no caso da região de integração ser um rectângulo. Considerem-se I 1 = f(x, y) dxdy, I 2 = g(x, y) dxdy e I = I 1 + I 2. Seja ε > 0, qualquer. Existe δ 1 > 0 tal que, para toda a partição, P = {R i }, de num número finito de rectângulos com P < δ 1, se tem f(u i, v i ) A i I 1 < ε/2, i para qualquer escolha de (u i, v i ) R i. o mesmo modo, existe δ 2 > 0 tal que, para toda a partição, P = {R i }, de num número finito de rectângulos com P < δ 2, se tem g(u i, v i ) A i I 2 < ε/2, i para qualquer escolha de (u i, v i ) R i. Sejam δ = min{δ 1, δ 2 } e P = {R i } uma qualquer partição de num número finito de rectângulos verificando P < δ. Para qualquer escolha de (u i, v i ) R i tem-se [f(u i, v i ) + g(u i, v i )] A i I i ( ) ( ) = f(u i, v i ) A i I 1 + g(u i, v i ) A i I 2 i i f(u i, v i ) A i I 1 + g(u i, v i ) A i I 2 i < ε/2 + ε/2 < ε. Então f + g é integrável em e [f(x, y) + g(x, y)] dxdy = I = I 1 + I 2. i Cálculo de integrais duplos-integrais iterados Suponha-se que R = [a, b] [c, d] é uma região rectangular fechada de R 2 e que f é uma função real contínua em R. esigne-se por I o integral de f sobre R. Fixe-se x 0 [a, b]. A função [c, d] R y f(x 0, y)

35 Cristina Caldeira 31 é contínua em [c, d] e portanto é integrável em [c, d]. O valor do seu integral depende de x 0. efina-se e considere-se a função A(x 0 ) = d c f(x 0, y) dy, para x 0 [a, b] A : [a, b] R x A(x). Vejamos qual o significado geométrico de A(x 0 ), para x 0 [a, b], no caso de se ter f(x, y) 0, (x, y) R. Fixe-se x 0 [a, b] e considere-se a curva C que se obtém intersectando a superfície {(x, y, z) R 3 : (x, y) R e z = f(x, y)} com o plano x = x 0. esigne-se por E(x 0 ) a região plana situada no plano x = x 0 e que é delimitada pela curva C e pelas rectas { { { x = x0 x = x0 x = x0, e. z = 0 y = c y = d Isto é, E(x 0 ) é a região a tracejado na figura seguinte. Então A(x 0 ) = d c Fig f(x 0, y) dy é a medida da área de E(x 0 ). x 0 [a, b]. Assim, intuitivamente, vemos que b a A(x) dx é a soma das áreas de todas as regiões planas da forma Isto é válido para todo o E(u) = {(x, y, z) R 3 : x = u, c y d e 0 z f(u, y)}, u [a, b]. Mas a soma dessas áreas é o volume do sólido E delimitado pela região R, pelos planos x = a, x = b, y = c, y = d e pela superfície de equação z = f(x, y). Mas já vimos que o volume de E é f(x, y) dxdy. R Intuitivamente verificámos assim o chamado teorema de Fubini (para o caso em que f(x, y) 0, (x, y) R.)

36 32 Textos de Apoio de Matemática IV-2004/2005 Teorema (Teorema de Fubini) Seja f uma função real de duas variáveis contínua no rectângulo R = [a, b] [c, d]. Então R f(x, y) dxdy = = b d a c d b c a f(x, y) dy dx f(x, y) dx dy. emonstração : Provemos que a função A é integrável em [a, b] e que o seu integral é I. Seja ε > 0 qualquer. Sendo f integrável em R existe δ > 0 tal que, para toda a partição P = {R i }, de R num número finito de rectângulos com P < δ, se tem f(u i, v i ) A i I < ε, (2.2) i para qualquer escolha de (u i, v i ) R i. Seja c = y 0 < y 1 < < y k = d uma partição de [c, d] verificando máx {y j y j 1 : j = 1,..., k} < δ 2. Seja a = x 0 < x 1 < < x m = b uma partição de [a, b] verificando máx {x l x l 1 : l = 1,..., m} < δ 2. Para l {1, 2,..., m} seja u l [x l 1, x l ], arbitrário. A(u l) = d c f(u l, y) dy = k j=1 yj y j 1 f(u l, y) dy. Usando o teorema do valor médio do cálculo integral, conclui-se que existem v 1,l, v 2,l,..., v k,l tais que v j,l [y j 1, y j ] e para j = 1, 2,..., k. Então yj y j 1 f(u l, y) dy = (y j y j 1 )f(u l, v j,l), A(u l) = k f(u l, vj,l)(y j y j 1 ). j=1 Considere-se a partição de R nos km rectângulos [x l 1, x l ] [y j 1, y j ], l = 1,..., m, j = 1,..., k.

37 Cristina Caldeira 33 A norma desta partição é { } máx (x l x l 1 ) 2 + (y j 1 y j ) 2 : l = 1,..., m, j = 1,..., k < δ. esignem-se por R 1, R 2,..., R n (com n = mk) os rectângulos desta partição e se R i = [x l 1, x l ] [y j 1, y j ] designe-se por (u i, v i ) o par (u l, v j,l ). Seja A i a área de R i. e (2.2) conclui-se que m A(u l)(x l x l 1 ) I l=1 Provou-se assim que O integral dx diz-se um integral iterado e será também representado por b a ( d c b a ( d c ) f(x, y) dy = = < ε. m k f(u l, vj,l)(y j y j 1 )(x l x l 1 ) I l=1 j=1 n f(u i, v i ) A i I i=1 ) f(x, y) dy dx = b a = I = R A(x) dx (2.3) f(x, y) dxdy. b d a c f(x, y) dy dx. Se em vez de termos fixado x = x 0 tivéssemos considerado y constante obtínhamos outro integral iterado d ( b ) d b f(x, y) dx dy = f(x, y) dx dy. c a O teorema de Fubini generaliza-se para regiões vertical ou horizontalmente simples. Teorema c a 1. Seja f uma função definida e contínua numa região verticalmente simples = {(x, y) R 2 : a x b e g 1 (x) y g 2 (x)}, sendo a < b, g 1 e g 2 funções contínuas em [a, b], distintas e verificando g 1 (x) g 2 (x), para todo o x em [a, b]. Então ( b ) g2 (x) f(x, y) dxdy = f(x, y) dy dx. a g 1 (x)

38 34 Textos de Apoio de Matemática IV-2004/ Seja f uma função definida e contínua numa região horizontalmente simples = {(x, y) R 2 : c y d e h 1 (y) x h 2 (y)}, sendo c < d, h 1 e h 2 funções contínuas em [c, d], distintas e verificando h 1 (y) h 2 (y), para todo o y em [c, d]. Então ( d ) h2 (y) f(x, y) dxdy = f(x, y) dx dy. c h 1 (y) Exemplo Calculemos xy dxdy, sendo = {(x, y) R 2 : x 2 + y 2 9 e 0 y 3 x}. Comecemos por representar a região. Fig Verifica-se facilmente que { = (x, y) R 2 : 0 y 3 e } 9 y 2 x 3 y. Então é horizontalmente simples e xy dxdy = = = ( 3 y xy dx 9 y 2 ] 3 y ) dy [ x 2 y dy 2 9 y ( 2 ) 9 6y + y y 2 y dy 2

39 Cristina Caldeira 35 = = 3 0 [ y 4 (y 3 3y 2 ) dy 4 y3 = Exemplo Calculemos x dxdy, sendo = {(x, y) R 2 : y x, x 2 + y 2 4 e xy 0}. ] 3 0 Fig Neste caso não é verticalmente simples nem horizontalmente simples. Mas = 1 2, sendo 1 = {(x, y) R 2 : 2 y 0 e 4 y 2 x y} e 2 = {(x, y) R 2 : 0 x 2 e x y 4 x 2 }. 1 é horizontalmente simples, 2 é verticalmente simples, e estas duas regiões intersectamse apenas na sua fronteira. Assim, x dxdy = x dxdy + x dxdy, 1 2 ( 0 ) y ( 2 ) 4 x 2 = x dx dy + x dy dx 2 4 y 2 0 x 0 ( y 2 = 2 4 ) y2 2 ( ) dy + x 4 x2 x dx 2 2 0

40 36 Textos de Apoio de Matemática IV-2004/ Exercícios 1. Calcule = [ y 3 3 2y ] 0 = f(x, y) da, sendo: 2 + [ 13 ] (4 x2 ) 3/2 x (a) f(x, y) = x 2 + y 2 e = [0, 1] x [0, 1]; (b) f(x, y) = { 1 x y se x + y 1 0 se x + y > 1 e = [0, 1] x [0, 1]; (c) f(x, y) = x y 1 e a região de R 2 definida por y x 2 e x y 2 ; (d) f(x, y) = sin x e a região de R 2 definida por y sin x, πy 2x e x 0; (e) f(x, y) = x 2 y 2 e o subconjunto do 1 o quadrante de R 2 determinado por y 1 x, y 2 x y x, y 2x ; (f) f(x, y) = x + y e = {(x, y) R 2 : x 1, y 1}; (g) f(x, y) = 1 2a x e = {(x, y) R 2 : (x a) 2 + (y a) 2 a 2, 0 x a, 0 y a}; (h) f(x, y) = y x 2 e = [ 1, 1] [0, 2]. 2. Inverta a ordem de integração e calcule, nos casos relevantes, os seguintes integrais: (a) (b) x e y2 dy dx; y sin(x 3 ) dx dy;

41 Cristina Caldeira 37 (c) (d) e ln x y dy dx; x x 2 2 f(x, y) dy dx; (e) r 0 2rx x 2 dx f(x, y) dy; x (f) (g) 1 x π sin x 0 f(x, y) dy dx + sin( x 2 ) f(x, y) dy dx x 2 0 f(x, y) dy dx; Integrais duplos em coordenadas polares Seja O um ponto fixo do plano e considere-se um semi-eixo com origem em O. iz-se que O é o pólo e que o semi-eixo é o eixo polar. Seja P um ponto do plano distinto do pólo O e considerem-se a distância, r, de P a O e o ângulo, θ, orientado no sentido anti-horário e medido em radianos que o eixo polar faz com OP. Fig Sendo r = OP, com P O, tem-se r > 0. Impondo que π < θ π o par (r, θ) assim definido é único e representa o ponto P. iz-se que (r, θ) são as coordenadas polares de P O. Todo o par da forma (0, θ), com θ ] π, π] é uma representação do pólo O. Uma vez imposta a restrição θ ] π, π] todos os pontos do plano, com excepção do pólo O, têm uma e uma só representação em coordenadas polares. Suponha-se que no plano se considera também, além do pólo O e do eixo polar, um referencial ortonormado XOY em que a origem coincide com o pólo e o semi-eixo positivo ȮX coincide com o eixo polar. Se um ponto P do plano tem coordenadas cartesianas (x, y) e coordenadas polares (r, θ), então { x = r cos θ y = r sin θ.

42 38 Textos de Apoio de Matemática IV-2004/2005 Fig Um rectângulo polar é uma região R do plano que em coordenadas polares é da forma R = {(r, θ) : a r b e α θ β}, (2.4) sendo b > a 0 e π < α < β π. Fig A área de um sector circular de raio r e ângulo ao centro θ (em radianos) é r2 θ 2.

43 Cristina Caldeira 39 A área do sector S é r2 θ 2. Fig Então a área do rectângulo polar definido em (2.4) é 1 2 b2 (β α) 1 2 a2 (β α) = 1 2 (b2 a 2 )(β α). Seja f uma função definida e contínua no rectângulo polar R dado por (2.4). R é uma região fechada e limitada de R 2 que é união de um número finito de regiões vertical ou horizontalmente simples. e acordo com o visto na subsecção 2.3.1, f é integrável em R. Pretendemos calcular I = f(x, y) dxdy. Efectuemos uma partição do intervalo [a, b] e uma partição do intervalo [α, β]: R a = r 0 < r 1 < < r k 1 < r k = b ; α = θ 0 < θ 1 < < θ m 1 < θ m = β. Estas duas partições determinam uma partição P 1 do rectângulo [a, b] [α, β] em n = km rectângulos, [r j 1, r j ] [θ l 1, θ l ], j = 1, 2,..., k, l = 1, 2,..., m. esignem-se estes n = km rectângulos por R 1, R 2,..., R n. Para i = 1, 2,..., n seja (ri, θi ) o ponto médio de R i. Então, para i = 1, 2,..., n, [ R i = ri r i 2, r i + r ] [ i θi θ i 2 2, θ i + θ ] i, 2 onde r i designa a amplitude do intervalo que é a projecção ortogonal de R i sobre o eixo dos XX e θ i designa a amplitude do intervalo que é a projecção ortogonal de R i sobre o eixo dos Y Y. A área de cada R i é r i θ i, a norma de P 1 é { P 1 = máx ( θi ) 2 + ( r i ) 2 : i = 1, 2,..., n}

44 40 Textos de Apoio de Matemática IV-2004/2005 e P 1 0, quando ( r i, θ i ) (0, 0), i = 1, 2,..., n. As duas partições efectuadas em [a, b] e [α, β] determinam também uma decomposição P 2 do rectângulo polar R em n rectângulos polares. Fig Para i = 1, 2,..., n designe-se por R i o rectângulo polar que em coordenadas polares é { (r, θ) : ri r i 2 r r i + r i e θi θ i 2 2 θ θ i + θ } i. 2 As coordenadas polares do ponto médio de R i são então (r i, θ i ). Fig As coordenadas cartesianas de (r i, θ i ) são { x i = r i cos θ i y i = r i sin θ i A área de R i é A i = 1 2 [ ( ri + r ) 2 ( i ri r ) ] 2 i θ i = ri r i θ i. 2 2.

45 Cristina Caldeira 41 O diâmetro ou norma de P 2 é a medida do comprimento da maior das diagonais dos rectângulos polares R 1, R 2,..., R n. esigne-se por P 2. Efectuando alguns cálculos obtém-se que P 2 = máx { 4(r i )2 sin 2 ( θi 2 ) ( ) θi + ( r i ) 2 cos 2 2 : i = 1, 2,..., n Observe-se que, atendendo a que o conjunto {r 1, r 2, r 3,...} é limitado (porque R é limitado), P 2 0, quando ( r i, θ i ) (0, 0), para todo o i. Considere-se a soma de Riemann para f, associada à decomposição P 2, que se obtém escolhendo o ponto médio em cada rectângulo polar, }. n f(x i, yi ) A i = i=1 n f(ri cos θi, ri sin θi ) ri r i θ i. (2.5) i=1 Considere-se a função e (2.5) obtém-se que g : [a, b] [α, β] R (r, θ) rf(r cos θ, r sin θ). n f(x i, yi ) A i = i=1 n g(ri, θi ) r i θ i (2.6) i=1 e o segundo membro desta igualdade é uma soma de Riemann da função g relativamente à partição P 1 de [a, b] [α, β] nos n rectângulos R 1 R 2,..., R n e onde em cada rectângulo se escolheu o ponto médio. A função g é contínua em [a, b] [α, β] e portanto é integrável. Seja I = [a,b] [α,β] g(r, θ) drdθ. Vamos provar que I = I. Seja ε > 0 qualquer. Efectuando partições de [a, b] e [α, β] em sub-intervalos de amplitudes suficientemente pequenas, isto é, considerando todos os r i e todos os θ i suficientemente pequenos, as normas de P 1 e P 2 são suficientemente pequenas para que (observação e definição de integral num rectângulo) e f(x i, yi ) A i I < ε/2 i g(ri, θi ) r i θ i I < ε/2. i

46 42 Textos de Apoio de Matemática IV-2004/2005 Então de (2.6) obtém-se ( ) ( I I = g(ri, θi ) r i θ i I + f(x i, yi ) A i + I) i i g(ri, θi ) r i θ i I + f(x i, yi ) A i I < ε. i Uma vez que isto é válido para todo o ε > 0 conclui-se que I = I, isto é, que f(x, y) dxdy = g(r, θ) drdθ R [a,b] [α,β] = f(r cos θ, r sin θ) r drdθ = = [a,b] [α,β] b a β α i ( β ) r f(r cos θ, sin θ) dθ dr α ( b ) r f(r cos θ, sin θ) dr dθ. Seja R uma região do plano que em coordenadas polares é da forma {(r, θ) : α θ β e h 1 (θ) r h 2 (θ)}, com π < α < β π, h 1 e h 2 funções contínuas e distintas em [α, β] e verificando h 1 (θ) h 2 (θ), θ [α, β]. iz-se que R é uma região polar de tipo I. a Região polar de tipo I Fig

47 Cristina Caldeira 43 Se em coordenadas polares R é da forma {(r, θ) : a r b e g 1 (r) θ g 2 (r)}, onde 0 a < b, g 1 e g 2 funções contínuas e distintas em [a, b] e verificando g 1 (r) g 2 (r), r [a, b], diz-se que R é uma região polar de tipo II. Região polar de tipo II Fig No resultado seguinte está descrita a mudança de coordenadas cartesianas para coordenadas polares no caso da região de integração ser uma região polar de tipo I ou de tipo II. Proposição (i) Sejam R = {(r, θ) : α θ β e h 1 (θ) r h 2 (θ)} uma região polar de tipo I e f uma função contínua em R. Então ( β ) h2 (θ) f(x, y) dxdy = rf(r cos θ, r sin θ) dr R α h 1 (θ) dθ. (ii) Sejam R = {(r, θ) : a r b e g 1 (r) θ g 2 (r)} uma região polar de tipo II e f uma função contínua em R. Então ( b ) g2 (r) f(x, y) dxdy = rf(r cos θ, r sin θ) dθ dr. R a g 1 (r)

48 44 Textos de Apoio de Matemática IV-2004/2005 Exemplo Calcular o volume do sólido E limitado superiormente pela superfície de equação z = x 2 + y 2 e inferiormente pela região R = {(x, y) R 2 : 1 x 2 + y 2 4 e x 0}. Fig Em coordenadas polares, R = {(r, θ) : 1 r 2 e π 2 θ π 2 }. Então Volume de E = = = = = π (x 2 + y 2 ) dxdy ( π ) 2 r(r 2 cos 2 θ + r 2 sin 2 θ) dθ R [ r 4 = π 4 = 15π 4. π 2 ( π 2 π 2 r 3 [θ] π 2 π 2 r 3 dr ] 2 1 r 3 dθ dr ) dr dr

49 Cristina Caldeira Exercícios 1. Calcule os seguintes integrais passando a coordenadas polares: (a) x dxdy onde = {(x, y) R 2 : y x, x 0, x 2 + y 2 9 e x 2 + y 2 4}; (b) dxdy onde = {(x, y) R 2 : 1 x 2 + y 2 4}; (c) (d) (e) (f) 2 4 x x (x 2 + y 2 ) 3 2 dy dx; e x2 + y 2 dy dx; 2xy (x 2 + y 2 ) x 2 y 2 dxdy sendo a região do 10 quadrante de R 2 limitada por y = 0, y = 3 3 x, x2 + y 2 = 1 4 e x2 y 2 = 1 ; dxdy onde = {(x, y) R 2 : x 2 + y 2 2x 0, x 2 + y 2 4 e y 3x} Aplicações do integral duplo Cálculo de volumes Vimos, na proposição 2.3.1, que se é uma região de R 2 que é união de um número finito de regiões de R 2 que são, cada uma delas, de um dos tipos I ou II, e f é uma função contínua em verificando f(x, y) 0, (x, y), então o volume do sólido E = {(x, y, z) R 3 : (x, y) e 0 z f(x, y)} é Se f for tal que então o volume do sólido V (E) = f(x, y) dxdy. f(x, y) 0, (x, y), {(x, y, z) R 3 : (x, y) e f(x, y) z 0} é f(x, y) dxdy.

50 46 Textos de Apoio de Matemática IV-2004/2005 O resultado da proposição pode ainda ser usado para calcular volumes de sólidos da forma E = {(x, y, z) R 3 : (x, y) e g(x, y) z f(x, y)}, onde f e g são funções contínuas em, distintas e verificando e Considerem-se os sólidos 0 g(x, y) f(x, y), (x, y). E 1 = {(x, y, z) R 3 : (x, y) e 0 z g(x, y)} E 2 = {(x, y, z) R 3 : (x, y) e 0 z f(x, y)}. Fig Então o volume de E é V (E) = V (E 2 ) V (E 1 ) = f(x, y) dxdy = [f(x, y) g(x, y)] dxdy. g(x, y) dxdy Exemplo Calculemos o volume do sólido E = {(x, y, z) R 3 : z 3/2 e x 2 + y 2 + (z 1) 2 1}. Fig

51 Cristina Caldeira 47 Uma vez que, { { x 2 + y 2 + (z 1) 2 = 1 x z = y 2 = 3 4 z = 3, 2 2 { a projecção de E sobre XOY é R = (x, y) R 2 : x 2 + y 2 3 } e o volume de E é 4 V (E) = Mudando para coordenadas polares, Exercícios V (E) = = = π R π π π π π = 2π 5 48 = 5π 24. [ x 2 y 2 3 ] 2 3/2 0 3/2 0 dxdy. ( r 2 3 ) r dr dθ 2 ( 1 r2 1 ) r dr dθ 2 [ 1 4 r2 1 3 (1 r2 ) 3/2 1. Usando integrais duplos, calcule o volume dos seguintes subconjuntos de R 3 : ] dθ (a) { x 2 + y z x + y ; (f) { x 2 + y 2 2z x 2 + y 2 + z 2 3 ; (b) x 2 + y 2 z 2 x 2 y 2 ; (c) x y2 1 1 z 12 3x 4y ; (g) y x 2 x y 2 0 z 3 ; (h) x2 a 2 + y2 b 2 + z2 c 2 1 com a, b, c R+ ; (d) { x 2 + y 2 z z 1 ; (i) { (z 16) 2 x 2 + y 2 x 2 + y 2 4 ; (e) { x 2 + y 2 + z 2 4 x 2 + y 2 2x ; (j) { z 2 (x 2 + y 2 ) y + z 2.