aula DISTRIBUIÇÃO NORMAL - PARTE I META OBJETIVOS PRÉ-REQUISITOS Apresentar o conteúdo de distribuição normal
|
|
|
- Flávio Furtado Caetano
- 7 Há anos
- Visualizações:
Transcrição
1 DISTRIBUIÇÃO NORMAL - PARTE I 4 aula META Apresentar o conteúdo de distribuição normal OBJETIVOS Ao final desta aula, o aluno deverá: determinar a média e a variância para uma função contínua; padronizar uma variável; determinar intervalos de confiança. PRÉ-REQUISITOS O aluno deverá saber interpretar os histogramas como representação da distribuição de valores de uma amostra.
2 Quimiometria INTRODUÇÃO Na aula anterior, vimos que quando precisamos obter informações sobre uma população, referentes a um determinado dado que varia dentro dessa população, podemos manipular dados de uma amostra representativa. Vimos também que um número relativamente grande de dados pode ser analisado com muita clareza através de uma representação gráfica conhecida como histograma. Nesta aula, veremos que as características básicas da distribuição representadas pelo histograma, ou seja, sua localização no eixo horizontal (faixa de valores possíveis) e sua dispersão dentro desta faixa, podem ser abreviadas por várias grandezas ou parâmetros estatísticos. Dentre essas grandezas, as mais estudadas nas ciências físicas são a média aritmética e o desvio padrão. 40
3 Distribuição normal - parte I Amédia aritmética de um conjunto de dados, que indica sua localização ou tendência central no histograma, é simplesmente a soma de todos os valores divididos pelo número total de elementos do conjunto. Este é o conceito de média que a maioria das pessoas conhece, mesmo intuitivamente. Utilizamos aqui este mesmo conceito e, muitas vezes, simplesmente nos referimos a ele como média, dispensando a qualificação 4aula MÉDIA ARITMÉTICA de média aritmética, pois caso seja necessário definir outro tipo de média, as definições serão destacadas apropriadamente. Resumindo a forma matemática destes parâmetros temos: média (normalmente traz uma barra sobre a letra x): x i = i-ésima observação N = Número total de observações na amostra Lembre-se de que na nossa amostra de 140 alturas, a média foi de 1,70 m. Se, no caso, obtivemos essa média a partir de uma amostra de uma população, trata-se da média amostral e não da média populacional. Para expressar a dispersão dos valores medidos em torno da média, calculamos o parâmetro chamado de desvio padrão. Para calcular o desvio padrão, primeiro calculamos a diferença, ou simplesmente desvio, de cada valor individual em relação à média de todos os valores da amostra. Desvio é uma medida do afastamento de cada ponto em relação à média. Em seguida, somamos os quadrados de todos os desvios e dividimos o total por N-1. O resultado é a variância, que é uma medida do espalhamento das observações em torno da média. 41
4 Quimiometria Variância s 2 : Note que a variância é uma espécie de média dos quadrados dos desvios. Enquanto a média tem as mesmas unidades das medidas originais, as unidades da variância são, pela própria definição, o quadrado das unidades originais. Para que as medidas de dispersão e de posição tenham as mesmas unidades, costuma-se substituir a variância pela sua raiz quadrada, que é chamada de desvio padrão. Desvio padrão também é uma medida do espalhamento entre os diversos valores obtidos. O desvio padrão é geralmente utilizado para definir intervalos em torno da média. Na nossa amostra, o desvio padrão foi de 0, O intervalo definido por um desvio padrão em torno da média tem como limites, portanto, 1,66596 e 1, Obtemos o limite inferior, 1,66596, subtraindo o desvio padrão 0,03641 da média 1,70237; e o limite superior, somando o desvio padrão ao valor da média. A região compreendida entre estes dois valores corresponde a 66,6% da área total do histograma ou 2/3 de todos os valores. Já a região definida por dois desvios padrão tem como limites 1,62955 e 1,77519 e contém 96,8% da área total. A boa notícia é que você não vai precisar calcular todas estas somatórias, pois qualquer calculadora científica já vem programada para calcular estes parâmetros estatísticos ao 42
5 Distribuição normal - parte I toque de uma tecla. Como tarefa, descubra como fazer isto usando sua calculadora preferida (use, para isto, o manual do fabricante). Agora que definimos as grandezas estatísticas mais comuns, obtidas para a descrição estatística de amostras, voltemos um pouco nossa atenção para a forma do histograma obtido. Vimos que ele representa graficamente a distribuição de valores ao longo da amostra e que esses valores se distribuíram dentro de uma faixa. Nos limites desta faixa as freqüências foram baixas e aumentaram simetricamente até um certo valor, na região central. Nosso próximo passo é classificar os tipos de distribuição, partindo justamente do tipo observado em nossa amostra que, aliás, é a distribuição mais comum, e por isso recebeu a denominação de distribuição normal. 4aula A DISTRIBUIÇÃO NORMAL Vamo-nos concentrar na nossa amostra de pessoas que efetivamente tiveram sua altura medida e esquecer um pouco a população total. Nessa amostra, conhecemos a distribuição exata de valores, então vamos tratá-la como uma nova população e buscar um modelo matemático que descreva a distribuição de valores dentro desta população. Imaginemos que temos à nossa disposição um modelo que possa ser adequado para isto. O procedimento a ser adotado inicialmente é testar esse modelo, ou seja, verificar se ele realmente representa nossos dados de forma adequada. Em caso positivo, usamos esse modelo, caso contrário, procuramos um novo modelo. Um dos modelos estatísticos mais importantes é a distribuição normal ou Gaussiana, que é uma distribuição de probabilidades de ocorrência de erros em medições, proposta no início do século XIX por Carl F. Gauss. Tantos foram e são os dados adequadamente descritos por ele que se chegou a pensar que os conjuntos de dados que não o seguissem estavam errados com relação ao modo como 43
6 Quimiometria foram medidos. É daí que vem o nome de distribuição normal. Hoje já se conhecem exceções à obediência da distribuição normal. A distribuição normal é uma distribuição contínua, ou seja, uma distribuição em que a variável pode assumir qualquer valor dentro de uma faixa como, por exemplo, pesos de um legume qualquer. Por exemplo, podemos ter, dentro de um pacote de batatas, tubérculos pesando desde 100 a 650 g, com quaisquer outros valores possíveis dentro deste intervalo. O agora, lembre-se agora novamente do nosso histograma. Nele há intervalos de valores que ocorreram mais do que outros (aqueles valores cujos blocos são mais altos ). Por outro lado, os valores próximos às extremidades estão associados a blocos mais baixos, ou seja, ocorreram menos. Podemos associar esta freqüência relativa à probabilidade de ocorrência dos referidos valores, pois os valores que ocorrem mais são conseqüentemente mais prováveis. Uma distribuição da variável contínua x é definida pela sua densidade de probabilidade f(x), que é uma expressão matemática que relaciona, no caso da distribuição normal, a probabilidade de ocorrência com parâmetros como a média e a variância populacionais. Não vamos deduzir a expressão específica a seguir, mas sim somente apresentá-la. Contudo, a dedução completa pode ser encontrada em livros de estatística. Distribuição Normal: em que f(x) é a densidade de probabilidade associada a ocorrência de um certo valor; f(x)dx é a probabilidade de ocorrência de um valor da variável no intervalo que vai de x a x+dx; m é a média populacional; 44
7 Distribuição normal - parte I s 2 é a variância populacional. 4aula A equação anterior é especificamente a forma da função matemática que reproduz a curva de distribuição estatística da variável. O que chamamos de curva de distribuição estatística da variável ou distribuição de freqüência é uma curva como esta abaixo, que nos mostra a variação das probabilidades dos valores possíveis para a referida variável. Não se preocupe qual seria esta variável do exemplo, somente veja que a probabilidade é máxima na média, que é igual a zero neste exemplo. Quando uma variável aleatória (com média dada por m e variância ó) se distribui de acordo com a distribuição normal, usamos a seguinte notação: x H N(m,ó 2 ). O sinal H aqui significa: distribui-se de acordo com. No exemplo acima, x H N(0,1) e veremos na próxima aula que na distribuição normal, praticamente toda a área da curva está contida dentro do intervalo entre ± 3 ó (desvios-padrão) em torno da média (3 acima e 3 abaixo). Por fim, o fato de termos os valores de m = 0 e ó = 1 permite que este exemplo possa ser classificado como uma situação especial de distribuição normal: a distribuição normal padronizada, que é o assunto da nossa próxima aula. 45
8 Quimiometria Como conclusão desta aula, podemos destacar que existe um tipo de distribuição estatística capaz de descrever um número tão grande de conjuntos de dados e CONCLUSÃO populações diferentes que ficou conhecida como distribuição normal. A própria distribuição se relaciona com a probabilidade de ocorrência de valores e ambas podem ser representadas por expressões matemáticas. (Fonte: 46
9 Distribuição normal - parte I RESUMO Quando precisamos obter informações sobre uma população, referentes a um determinado dado que varia dentro dela, podemos manipular dados de uma amostra representativa desta população e que um número relativamente grande de dados pode ser analisado com muita clareza através de uma representação gráfica conhecida como histograma. Nele, a ocorrência de valores é maior quanto mais próximos de um determinado valor, e vemos que os valores que apareceram vão de um certo valor mais baixo até um mais alto. Assim, começamos a ver que, olhando para o modo como os valores se distribuem, podemos começar a encontrar maneiras de descrever a nossa amostra: há um valor que, quanto mais próximo a ele, maior a ocorrência; todos os valores que foram observados estão dentro de um limite que vai do valor menor que foi observado até o maior; próximo destes limites há cada vez menos ocorrência. Estas características são próprias daquela população e podem ser usadas para qualificá-la. Aqui podemos introduzir os conceitos de média e desvios. O conceito de média que a maioria das pessoas conhece, mesmo intuitivamente, é simplesmente a soma de todos os valores divididos pelo número total de elementos do conjunto. Este conceito está correto. Os desvios dão uma medida do afastamento de cada ponto em relação à média. A forma do histograma que vimos também é muito importante. Nele há intervalos de valores que ocorreram mais do que outros (aqueles valores cujos blocos são mais altos ). Por outro lado, os valores próximos às extremidades estão associados a blocos mais baixos, ou seja, ocorreram menos. Este comportamento é muito comum para tipos muito diferentes de dados, como por exemplo, dados científicos, demográficos etc., tão comum que foi batizado de distribuição normal. 4aula 47
10 Quimiometria A DISTRIBUIÇÃO NORMAL REALMENTE É MUITO UTILIZADA? Para dar uma idéia do quanto a distribuição normal é considerada válida, ela é utilizada para se comparar as ocorrências médias de uma determinada doença, em uma dada população, em períodos anteriores àquele para o qual seja necessário identificar a possível ocorrência de uma epidemia. Estes são os chamados diagramas de controle e são utilizados para se estabelecer um intervalo de variação considerado normal. Para saber mais, acesse a página: saude_e_cidadania/ed_07/pdf/09_04.pdf (Acessada em 07/ 02/2008). PRÓXIMA AULA Na próxima aula iremos aprender a usar a forma matemática da distribuição normal para calcular a probabilidade de que um certo valor ou intervalo de valores ocorram a partir da densidade de probabilidade. REFERÊNCIAS BARROS NETO, B.; SCARMINIO, I. E.; BRUNS. R. E.; Planejamento e otimização de experimentos. Editora da Unicamp, BOX, G. E. P.; HUNTER, W. G.; HUNTER, J. S. Statistics for experimenters. An introduction to design, data analysis and model building. New York, Wiley: BUSSAB, W. O.; MORETIN, P. A. Estatística básica, São Paulo: Ed. Atual,
aula ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES
 ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
ANÁLISE DO DESEMPENHO DO MODELO EM REGRESSÕES 18 aula META Fazer com que o aluno seja capaz de realizar os procedimentos existentes para a avaliação da qualidade dos ajustes aos modelos. OBJETIVOS Ao final
aula INTERPRETAÇÃO DOS DADOS DO PLANEJAMENTO FATORIAL 2 2 META conhecer fundamentos do planejamento fatorial, vistos na aula anterior
 INTERPRETAÇÃO DOS DADOS DO PLANEJAMENTO FATORIAL 2 2 META conhecer fundamentos do planejamento fatorial, vistos na anterior OBJETIVOS Ao final desta, o aluno deverá: capacitar o aluno a manipular os dados
INTERPRETAÇÃO DOS DADOS DO PLANEJAMENTO FATORIAL 2 2 META conhecer fundamentos do planejamento fatorial, vistos na anterior OBJETIVOS Ao final desta, o aluno deverá: capacitar o aluno a manipular os dados
aula PLANEJAMENTO FATORIAL 2 2 META OBJETIVOS PRÉ-REQUISITOS
 PLANEJAMENTO FATORIAL 2 2 10 aula META apresentar ao aluno aspectos fundamentais dos planejamentos fatoriais através da exemplificação com um planejamento 2 2. OBJETIVOS Ao final desta aula, o aluno deverá:
PLANEJAMENTO FATORIAL 2 2 10 aula META apresentar ao aluno aspectos fundamentais dos planejamentos fatoriais através da exemplificação com um planejamento 2 2. OBJETIVOS Ao final desta aula, o aluno deverá:
aula AJUSTE POR MÍNIMOS QUADRADOS
 AJUSTE POR MÍNIMOS QUADRADOS META Conduzir o aluno a aplicar o método de ajuste por mínimos quadrados, efetuando uma regressão linear e oferecer ao aluno uma oportunidade de praticar a aplicação do método
AJUSTE POR MÍNIMOS QUADRADOS META Conduzir o aluno a aplicar o método de ajuste por mínimos quadrados, efetuando uma regressão linear e oferecer ao aluno uma oportunidade de praticar a aplicação do método
Estatística (MAD231) Turma: IGA. Período: 2018/2
 Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
Estatística (MAD231) Turma: IGA Período: 2018/2 Aula #04 de Probabilidade: 26/10/2018 1 Variáveis Aleatórias Contínuas De modo informal as variáveis aleatórias são contínuas quando resultam de algum tipo
)XQGDPHQWRVGHSUREDELOLGDGHHHVWDWtVWLFD
 )XQGDPHQWRVGHUREDELOLGDGHHHVWDWtVWLFD,QWURGXomR A história da estatística pode ser dividida em três fases. De acordo com PEANHA (00), a estatística inicialmente não mantinha nenhuma relação com a probabilidade,
)XQGDPHQWRVGHUREDELOLGDGHHHVWDWtVWLFD,QWURGXomR A história da estatística pode ser dividida em três fases. De acordo com PEANHA (00), a estatística inicialmente não mantinha nenhuma relação com a probabilidade,
Estatística Descritiva. Objetivos de Aprendizagem. 6.1 Sumário de Dados. Cap. 6 - Estatística Descritiva 1. UFMG-ICEx-EST. Média da amostra: Exemplo:
 6 ESQUEMA DO CAPÍTULO Estatística Descritiva 6.1 IMPORTÂNCIA DO SUMÁRIO E APRESENTAÇÃO DE DADOS 6.2 DIAGRAMA DE RAMO E FOLHAS 6.3 DISTRIBUIÇÕES DE FREQUÊNCIA E HISTOGRAMAS 6.4 DIAGRAMA DE CAIXA 6.5 GRÁFICOS
6 ESQUEMA DO CAPÍTULO Estatística Descritiva 6.1 IMPORTÂNCIA DO SUMÁRIO E APRESENTAÇÃO DE DADOS 6.2 DIAGRAMA DE RAMO E FOLHAS 6.3 DISTRIBUIÇÕES DE FREQUÊNCIA E HISTOGRAMAS 6.4 DIAGRAMA DE CAIXA 6.5 GRÁFICOS
12/06/14. Estatística Descritiva. Estatística Descritiva. Medidas de tendência central. Medidas de dispersão. Separatrizes. Resumindo numericamente
 Resumindo numericamente Para resumir numericamente dados quantitativos o objetivo é escolher medidas apropriadas de locação (``qual o tamanho dos números envolvidos?'') e de dispersão (``quanta variação
Resumindo numericamente Para resumir numericamente dados quantitativos o objetivo é escolher medidas apropriadas de locação (``qual o tamanho dos números envolvidos?'') e de dispersão (``quanta variação
Estatística Descritiva
 Estatística Descritiva ESQUEMA DO CAPÍTULO 6.1 IMPORTÂNCIA DO SUMÁRIO E APRESENTAÇÃO DE DADOS 6.2 DIAGRAMA DE RAMO E FOLHAS 6.3 DISTRIBUIÇÕES DE FREQUÊNCIA E HISTOGRAMAS 6.4 DIAGRAMA DE CAIXA 6.5 GRÁFICOS
Estatística Descritiva ESQUEMA DO CAPÍTULO 6.1 IMPORTÂNCIA DO SUMÁRIO E APRESENTAÇÃO DE DADOS 6.2 DIAGRAMA DE RAMO E FOLHAS 6.3 DISTRIBUIÇÕES DE FREQUÊNCIA E HISTOGRAMAS 6.4 DIAGRAMA DE CAIXA 6.5 GRÁFICOS
aula PLANEJAMENTO FATORIAL 2 3 META OBJETIVOS PRÉ-REQUISITOS
 PLANEJAMENTO FATORIAL 2 3 12 aula META Mostrar aos alunos que os planejamentos fatoriais podem ser expandidos com respeito ao número de fatores OBJETIVOS Ao final desta aula, o aluno deverá: elaborar um
PLANEJAMENTO FATORIAL 2 3 12 aula META Mostrar aos alunos que os planejamentos fatoriais podem ser expandidos com respeito ao número de fatores OBJETIVOS Ao final desta aula, o aluno deverá: elaborar um
Unidade I ESTATÍSTICA APLICADA. Prof. Mauricio Fanno
 Unidade I ESTATÍSTICA APLICADA Prof. Mauricio Fanno Estatística indutiva Estatística descritiva Dados no passado ou no presente e em pequena quantidade, portanto, reais e coletáveis. Campo de trabalho:
Unidade I ESTATÍSTICA APLICADA Prof. Mauricio Fanno Estatística indutiva Estatística descritiva Dados no passado ou no presente e em pequena quantidade, portanto, reais e coletáveis. Campo de trabalho:
aula PARÂMETROS ESTATÍSTICOS Introdução à Quimiometria META Apresentar os Parâmetros Estatística.
 Introdução à Quimiometria PARÂMETROS ESTATÍSTICOS 2 aula META Apresentar os Parâmetros Estatística. OBJETIVOS Ao final desta aula, o aluno deverá: diferenciar exatidão de precisão; construir e interpretar
Introdução à Quimiometria PARÂMETROS ESTATÍSTICOS 2 aula META Apresentar os Parâmetros Estatística. OBJETIVOS Ao final desta aula, o aluno deverá: diferenciar exatidão de precisão; construir e interpretar
Distribuição Normal. Prof. Eduardo Bezerra. (CEFET/RJ) - BCC - Inferência Estatística. 25 de agosto de 2017
 padrão - padronização Distribuição Normal Prof. Eduardo Bezerra (CEFET/RJ) - BCC - Inferência Estatística 25 de agosto de 2017 Eduardo Bezerra (CEFET/RJ) Distribuição Normal Março/2017 1 / 32 Roteiro Distribuições
padrão - padronização Distribuição Normal Prof. Eduardo Bezerra (CEFET/RJ) - BCC - Inferência Estatística 25 de agosto de 2017 Eduardo Bezerra (CEFET/RJ) Distribuição Normal Março/2017 1 / 32 Roteiro Distribuições
Aula 00 Aula Demonstrativa
 Aula 00 Modelos de questões comentadas CESPE-UnB... 3 Relação das questões comentadas... 12 Gabaritos... 13 1 Olá, pessoal. Como vocês já sabem, saiu o edital para o concurso do TCE-SC. Esta é a aula demonstrativa
Aula 00 Modelos de questões comentadas CESPE-UnB... 3 Relação das questões comentadas... 12 Gabaritos... 13 1 Olá, pessoal. Como vocês já sabem, saiu o edital para o concurso do TCE-SC. Esta é a aula demonstrativa
Lucas Santana da Cunha 12 de julho de 2017
 DISTRIBUIÇÃO NORMAL Lucas Santana da Cunha http://www.uel.br/pessoal/lscunha/ Universidade Estadual de Londrina 12 de julho de 2017 Distribuição Normal Dentre todas as distribuições de probabilidades,
DISTRIBUIÇÃO NORMAL Lucas Santana da Cunha http://www.uel.br/pessoal/lscunha/ Universidade Estadual de Londrina 12 de julho de 2017 Distribuição Normal Dentre todas as distribuições de probabilidades,
14. Distribuição de Probabilidade para Variáveis Aleatórias Contínuas
 4. Distribuição de Probabilidade para Variáveis Aleatórias Contínuas Os valores assumidos por uma variável aleatória contínua podem ser associados com medidas em uma escala contínua como, por exemplo,
4. Distribuição de Probabilidade para Variáveis Aleatórias Contínuas Os valores assumidos por uma variável aleatória contínua podem ser associados com medidas em uma escala contínua como, por exemplo,
Cálculo das Probabilidades e Estatística I
 Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Distribuição Normal Motivação: Distribuição
Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Distribuição Normal Motivação: Distribuição
Lucas Santana da Cunha de junho de 2018 Londrina
 Distribuição Normal Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 25 de junho de 2018 Londrina 1 / 17 Distribuição Normal Dentre todas as distribuições de probabilidades,
Distribuição Normal Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 25 de junho de 2018 Londrina 1 / 17 Distribuição Normal Dentre todas as distribuições de probabilidades,
Lucas Santana da Cunha de junho de 2018 Londrina
 Variável aleatória contínua: Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 13 de junho de 2018 Londrina 1 / 26 Esperança e variância de Y Função de distribuição acumulada
Variável aleatória contínua: Lucas Santana da Cunha email: lscunha@uel.br http://www.uel.br/pessoal/lscunha/ 13 de junho de 2018 Londrina 1 / 26 Esperança e variância de Y Função de distribuição acumulada
Medidas de Dispersão ou variabilidade
 Medidas de Dispersão ou variabilidade A média - ainda que considerada como um número que tem a faculdade de representar uma série de valores - não pode, por si mesma, destacar o grau de homogeneidade ou
Medidas de Dispersão ou variabilidade A média - ainda que considerada como um número que tem a faculdade de representar uma série de valores - não pode, por si mesma, destacar o grau de homogeneidade ou
Cálculo das Probabilidades e Estatística I
 Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Variáveis Aleatórias Ao descrever um espaço
Cálculo das Probabilidades e Estatística I Prof a. Juliana Freitas Pires Departamento de Estatística Universidade Federal da Paraíba - UFPB juliana@de.ufpb.br Variáveis Aleatórias Ao descrever um espaço
Estatística Descritiva
 Estatística Descritiva ESQUEMA DO CAPÍTULO 6.1 IMPORTÂNCIA DO SUMÁRIO E APRESENTAÇÃO DE DADOS 6.2 DIAGRAMA DE RAMO E FOLHAS 6.3 DISTRIBUIÇÕES DE FREQUÊNCIA E HISTOGRAMAS 6.4 DIAGRAMA DE CAIXA 6.5 GRÁFICOS
Estatística Descritiva ESQUEMA DO CAPÍTULO 6.1 IMPORTÂNCIA DO SUMÁRIO E APRESENTAÇÃO DE DADOS 6.2 DIAGRAMA DE RAMO E FOLHAS 6.3 DISTRIBUIÇÕES DE FREQUÊNCIA E HISTOGRAMAS 6.4 DIAGRAMA DE CAIXA 6.5 GRÁFICOS
MAE 116 Distribuição Normal FEA - 2º Semestre de 2018
 MAE 116 Distribuição Normal FEA - 2º Semestre de 2018 1 Introdução Até aqui estudamos variáveis aleatórias discretas que são caracterizadas por ter uma distribuição de probabilidade dada por uma tabela
MAE 116 Distribuição Normal FEA - 2º Semestre de 2018 1 Introdução Até aqui estudamos variáveis aleatórias discretas que são caracterizadas por ter uma distribuição de probabilidade dada por uma tabela
( x) = a. f X. = para x I. Algumas Distribuições de Probabilidade Contínuas
 Probabilidade e Estatística I Antonio Roque Aula Algumas Distribuições de Probabilidade Contínuas Vamos agora estudar algumas importantes distribuições de probabilidades para variáveis contínuas. Distribuição
Probabilidade e Estatística I Antonio Roque Aula Algumas Distribuições de Probabilidade Contínuas Vamos agora estudar algumas importantes distribuições de probabilidades para variáveis contínuas. Distribuição
Aula 3 MEDIDAS DE DISPERSÃO, ASSIMETRIA E CURTOSE.
 MEDIDAS DE DISPERSÃO, ASSIMETRIA E CURTOSE. Aula META Mensurar a dimensão média do afastamento dos valores de um conjunto de dados em relação à determinada Medida de Tendência Central, bem como de que
MEDIDAS DE DISPERSÃO, ASSIMETRIA E CURTOSE. Aula META Mensurar a dimensão média do afastamento dos valores de um conjunto de dados em relação à determinada Medida de Tendência Central, bem como de que
Estatística Aplicada Professor: André Luiz Araújo Cunha. Moda. Media
 Estatística Aplicada Professor: André Luiz Araújo Cunha Moda Define-se moda como sendo: o valor que surge com mais freqüência se os dados são discretos, ou, o intervalo de classe com maior freqüência se
Estatística Aplicada Professor: André Luiz Araújo Cunha Moda Define-se moda como sendo: o valor que surge com mais freqüência se os dados são discretos, ou, o intervalo de classe com maior freqüência se
Mecânica experimental Lima Junior, P.; Silva, M.T.X.; Silveira, F.L.
 ATIVIDADE 02 Texto de Apoio I Desvio Padrão da Média e Intervalos de Confiança Variabilidade e desvio padrão Quando realizamos uma série de observações do mesmo mensurando sob as mesmas condições, podemos
ATIVIDADE 02 Texto de Apoio I Desvio Padrão da Média e Intervalos de Confiança Variabilidade e desvio padrão Quando realizamos uma série de observações do mesmo mensurando sob as mesmas condições, podemos
AULA 5 MEDIDAS DESCRITIVAS DOCENTE: CIRA SOUZA PITOMBO
 UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA MEAU- MESTRADO EM ENGENHARIA AMBIENTAL URBANA ENG C 18 Métodos de Pesquisa Quantitativos e Qualitativos AULA 5 MEDIDAS DESCRITIVAS DOCENTE: CIRA SOUZA PITOMBO
UNIVERSIDADE FEDERAL DA BAHIA ESCOLA POLITÉCNICA MEAU- MESTRADO EM ENGENHARIA AMBIENTAL URBANA ENG C 18 Métodos de Pesquisa Quantitativos e Qualitativos AULA 5 MEDIDAS DESCRITIVAS DOCENTE: CIRA SOUZA PITOMBO
Inferência Estatística: Conceitos Básicos I
 Inferência Estatística: Conceitos Básicos I Introdução, Medidas de Tendência Central, Medidas de Variabilidade, Distribuições de Frequência e Probabilidade Flávia F. Feitosa BH1350 Métodos e Técnicas de
Inferência Estatística: Conceitos Básicos I Introdução, Medidas de Tendência Central, Medidas de Variabilidade, Distribuições de Frequência e Probabilidade Flávia F. Feitosa BH1350 Métodos e Técnicas de
Distribuições Discretas
 META: Estudar o comportamento das Variáveis Aleatórias Discretas, bem como das Distribuições Binomial e Poisson e suas aplicações. Entender o comportamento de uma Variável aleatória Contínua. OBJETIVOS:
META: Estudar o comportamento das Variáveis Aleatórias Discretas, bem como das Distribuições Binomial e Poisson e suas aplicações. Entender o comportamento de uma Variável aleatória Contínua. OBJETIVOS:
Aula 4 Conceitos Básicos de Estatística
 Aula 4 Conceitos Básicos de Estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa e interpreta informações numéricas para
Aula 4 Conceitos Básicos de Estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa e interpreta informações numéricas para
Introdução à Probabilidade e Estatística I
 Introdução à Probabilidade e Estatística I População e Amostra Medidas resumo Prof. Alexandre G Patriota Sala: 298A Email: patriota@ime.usp.br Site: www.ime.usp.br/ patriota Passos iniciais O primeiro
Introdução à Probabilidade e Estatística I População e Amostra Medidas resumo Prof. Alexandre G Patriota Sala: 298A Email: patriota@ime.usp.br Site: www.ime.usp.br/ patriota Passos iniciais O primeiro
Disciplina: Prof. a Dr. a Simone Daniela Sartorio. DTAiSeR-Ar
 Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo dos números
Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo dos números
b) Variáveis Aleatórias Contínuas
 Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
Disciplina: 1171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
b) Variáveis Aleatórias Contínuas
 Disciplina: 221171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
Disciplina: 221171 b) Variáveis Aleatórias Contínuas Prof. a Dr. a Simone Daniela Sartorio de Medeiros DTAiSeR-Ar 1 Uma variável aleatória é contínua (v.a.c.) se seu conjunto de valores é qualquer intervalo
Unidade III ESTATÍSTICA. Prof. Fernando Rodrigues
 Unidade III ESTATÍSTICA Prof. Fernando Rodrigues Medidas de dispersão Estudamos na unidade anterior as medidas de tendência central, que fornecem importantes informações sobre uma sequência numérica. Entretanto,
Unidade III ESTATÍSTICA Prof. Fernando Rodrigues Medidas de dispersão Estudamos na unidade anterior as medidas de tendência central, que fornecem importantes informações sobre uma sequência numérica. Entretanto,
BIOESTATISTICA. Unidade IV - Probabilidades
 BIOESTATISTICA Unidade IV - Probabilidades 0 PROBABILIDADE E DISTRIBUIÇÃO DE FREQUÊNCIAS COMO ESTIMATIVA DA PROBABILIDADE Noções de Probabilidade Após realizar a descrição dos eventos utilizando gráficos,
BIOESTATISTICA Unidade IV - Probabilidades 0 PROBABILIDADE E DISTRIBUIÇÃO DE FREQUÊNCIAS COMO ESTIMATIVA DA PROBABILIDADE Noções de Probabilidade Após realizar a descrição dos eventos utilizando gráficos,
Estatística Aplicada II. } Revisão: Probabilidade } Propriedades da Média Amostral
 Estatística Aplicada II } Revisão: Probabilidade } Propriedades da Média Amostral 1 Aula de hoje } Tópicos } Revisão: } Distribuição de probabilidade } Variáveis aleatórias } Distribuição normal } Propriedades
Estatística Aplicada II } Revisão: Probabilidade } Propriedades da Média Amostral 1 Aula de hoje } Tópicos } Revisão: } Distribuição de probabilidade } Variáveis aleatórias } Distribuição normal } Propriedades
Medidas de Dispersão. Prof.: Joni Fusinato
 Medidas de Dispersão Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com 1 Dispersão Estatística As medidas de posição (média, mediana, moda) descrevem características dos valores numéricos
Medidas de Dispersão Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com 1 Dispersão Estatística As medidas de posição (média, mediana, moda) descrevem características dos valores numéricos
Introdução à probabilidade e à estatística II. Prof. Alexandre G Patriota Sala: 298A Site:
 Introdução à probabilidade e à estatística II Revisão Prof. Alexandre G Patriota Sala: 298A Email: patriota@ime.usp.br Site: www.ime.usp.br/ patriota Estatística Estatística: É uma ciência que se dedica
Introdução à probabilidade e à estatística II Revisão Prof. Alexandre G Patriota Sala: 298A Email: patriota@ime.usp.br Site: www.ime.usp.br/ patriota Estatística Estatística: É uma ciência que se dedica
Aula 2 A distribuição normal
 Aula 2 A distribuição normal Objetivos: Nesta aula você estudará a distribuição normal, que é uma das mais importantes distribuições contínuas. Você verá a definição geral desta distribuição, mas, nesse
Aula 2 A distribuição normal Objetivos: Nesta aula você estudará a distribuição normal, que é uma das mais importantes distribuições contínuas. Você verá a definição geral desta distribuição, mas, nesse
Conceito de Estatística
 Conceito de Estatística Estatística Técnicas destinadas ao estudo quantitativo de fenômenos coletivos, observáveis. Unidade Estatística um fenômeno individual é uma unidade no conjunto que irá constituir
Conceito de Estatística Estatística Técnicas destinadas ao estudo quantitativo de fenômenos coletivos, observáveis. Unidade Estatística um fenômeno individual é uma unidade no conjunto que irá constituir
2.1 Variáveis Aleatórias Discretas
 4CCENDMMT02-P PROBABILIDADE E CÁLCULO DIFERENCIAL E INTEGRAL Girlan de Lira e Silva (1),José Gomes de Assis (3) Centro de Ciências Exatas e da Natureza /Departamento de Matemática /MONITORIA Resumo: Utilizamos
4CCENDMMT02-P PROBABILIDADE E CÁLCULO DIFERENCIAL E INTEGRAL Girlan de Lira e Silva (1),José Gomes de Assis (3) Centro de Ciências Exatas e da Natureza /Departamento de Matemática /MONITORIA Resumo: Utilizamos
Modelos Lineares Distribuições de Probabilidades Distribuição Normal Teorema Central do Limite. Professora Ariane Ferreira
 Distribuições de Probabilidades Distribuição Normal Teorema Central do Limite Professora Ariane Ferreira Modelos Probabilísticos de v.a. continuas Distribuição de Probabilidades 2 IPRJ UERJ Ariane Ferreira
Distribuições de Probabilidades Distribuição Normal Teorema Central do Limite Professora Ariane Ferreira Modelos Probabilísticos de v.a. continuas Distribuição de Probabilidades 2 IPRJ UERJ Ariane Ferreira
Probabilidade e Estatística
 Probabilidade e Estatística Aula 6 Distribuições Contínuas (Parte 02) Leitura obrigatória: Devore, Capítulo 4 Chap 6-1 Distribuições de Probabilidade Distribuições de Probabilidade Distribuições de Probabilidade
Probabilidade e Estatística Aula 6 Distribuições Contínuas (Parte 02) Leitura obrigatória: Devore, Capítulo 4 Chap 6-1 Distribuições de Probabilidade Distribuições de Probabilidade Distribuições de Probabilidade
AULA 07 Inferência a Partir de Duas Amostras
 1 AULA 07 Inferência a Partir de Duas Amostras Ernesto F. L. Amaral 10 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola,
1 AULA 07 Inferência a Partir de Duas Amostras Ernesto F. L. Amaral 10 de setembro de 2012 Faculdade de Filosofia e Ciências Humanas (FAFICH) Universidade Federal de Minas Gerais (UFMG) Fonte: Triola,
AST203-CVR 4-1 AST203-CVR. Observação eletromagnética. Processamento de sinais importante em várias áreas, além da astronomia telecomunicações
 Bloco 4 Estatística Atualizado: 2012 4-1 Bibliografia Lena Cap. 4 (parte) - só a inspiração... Wall & Jenkins, Practical statistics for astronomers Brandt Statistical and computacional methods in data
Bloco 4 Estatística Atualizado: 2012 4-1 Bibliografia Lena Cap. 4 (parte) - só a inspiração... Wall & Jenkins, Practical statistics for astronomers Brandt Statistical and computacional methods in data
Planejamento e Otimização de Experimentos
 Planejamento e Otimização de Experimentos Um Pouco de Estatística Prof. Dr. Anselmo E de Oliveira anselmo.quimica.ufg.br anselmo.disciplinas@gmail.com Populações, Amostras e Distribuições População Amostra
Planejamento e Otimização de Experimentos Um Pouco de Estatística Prof. Dr. Anselmo E de Oliveira anselmo.quimica.ufg.br anselmo.disciplinas@gmail.com Populações, Amostras e Distribuições População Amostra
Distribuições de Probabilidade
 Distribuições de Probabilidade 7 6 5 4 3 2 1 0 Normal 1 2 3 4 5 6 7 8 9 10 11 Exemplos: Temperatura do ar 20 18 16 14 12 10 8 6 4 2 0 Assimetrica Positiva 1 2 3 4 5 6 7 8 9 10 11 Exemplos: Precipitação
Distribuições de Probabilidade 7 6 5 4 3 2 1 0 Normal 1 2 3 4 5 6 7 8 9 10 11 Exemplos: Temperatura do ar 20 18 16 14 12 10 8 6 4 2 0 Assimetrica Positiva 1 2 3 4 5 6 7 8 9 10 11 Exemplos: Precipitação
UNIVERSIDADE FEDERAL DA PARAÍBA. Variáveis Aleatórias. Departamento de Estatística Luiz Medeiros
 UNIVERSIDADE FEDERAL DA PARAÍBA Variáveis Aleatórias Departamento de Estatística Luiz Medeiros Introdução Como sabemos, características de interesse em diversas áreas estão sujeitas à variação; Essa variabilidade
UNIVERSIDADE FEDERAL DA PARAÍBA Variáveis Aleatórias Departamento de Estatística Luiz Medeiros Introdução Como sabemos, características de interesse em diversas áreas estão sujeitas à variação; Essa variabilidade
Aula de hoje. administração. São Paulo: Ática, 2007, Cap. 3. ! Tópicos. ! Referências. ! Distribuição de probabilidades! Variáveis aleatórias
 Aula de hoje! Tópicos! Distribuição de probabilidades! Variáveis aleatórias! Variáveis discretas! Variáveis contínuas! Distribuição binomial! Distribuição normal! Referências! Barrow, M. Estatística para
Aula de hoje! Tópicos! Distribuição de probabilidades! Variáveis aleatórias! Variáveis discretas! Variáveis contínuas! Distribuição binomial! Distribuição normal! Referências! Barrow, M. Estatística para
Aula 9 Intervalo de confiança para a média da N(μ; σ 2 ), σ 2 desconhecida
 Aula 9 Intervalo de confiança para a média da N(μ; σ 2 ), σ 2 desconhecida Nesta aula você completará seu estudo básico sobre intervalos de confiança, analisando o problema de estimação da média de uma
Aula 9 Intervalo de confiança para a média da N(μ; σ 2 ), σ 2 desconhecida Nesta aula você completará seu estudo básico sobre intervalos de confiança, analisando o problema de estimação da média de uma
De onde vêm as expressões para variâncias e desvios padrão? 37
 APÊNDICE 03 Uma questão de estatística De onde vêm as expressões para variâncias e desvios padrão? 37 Conforme já foi antecipado no primeiro texto de apoio da segunda atividade experimental prevista neste
APÊNDICE 03 Uma questão de estatística De onde vêm as expressões para variâncias e desvios padrão? 37 Conforme já foi antecipado no primeiro texto de apoio da segunda atividade experimental prevista neste
Distribuição Normal. Prof. Herondino
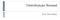 Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
Distribuição Normal Prof. Herondino Distribuição Normal A mais importante distribuição de probabilidade contínua em todo o domínio da estatística é a distribuição normal. Seu gráfico, chamado de curva
Inferência Estatística: Conceitos Básicos II
 Inferência Estatística: Conceitos Básicos II Distribuição Amostral e Teorema do Limite Central Análise Exploratória de dados no SPSS Flávia F. Feitosa BH1350 Métodos e Técnicas de Análise da Informação
Inferência Estatística: Conceitos Básicos II Distribuição Amostral e Teorema do Limite Central Análise Exploratória de dados no SPSS Flávia F. Feitosa BH1350 Métodos e Técnicas de Análise da Informação
Probabilidade II. Departamento de Estatística. Universidade Federal da Paraíba
 Probabilidade II Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Distribuição t de Student 02/14 1 / 1 A distribuição t de Student é uma das distribuições
Probabilidade II Departamento de Estatística Universidade Federal da Paraíba Prof. Tarciana Liberal (UFPB) Aula Distribuição t de Student 02/14 1 / 1 A distribuição t de Student é uma das distribuições
Termo-Estatística Licenciatura: 3ª Aula (06/03/2013)
 Termo-Estatística Licenciatura: 3ª Aula (06/03/2013) Prof. Alvaro Vannucci RELEMBRANDO Probabilidade condicional: P( X / Y) P( X Y) PY ( ) Se dois eventos (A e B) forem independentes: P( A B) P( A) P(
Termo-Estatística Licenciatura: 3ª Aula (06/03/2013) Prof. Alvaro Vannucci RELEMBRANDO Probabilidade condicional: P( X / Y) P( X Y) PY ( ) Se dois eventos (A e B) forem independentes: P( A B) P( A) P(
Adilson Cunha Rusteiko
 Janeiro, 2015 Estatística , A Estatística Estatística: É a parte da matemática aplicada que fornece métodos para coleta, organização, descrição, análise e interpretação
Janeiro, 2015 Estatística , A Estatística Estatística: É a parte da matemática aplicada que fornece métodos para coleta, organização, descrição, análise e interpretação
ESTATÍSTICA PROFESSOR: ALEXSANDRO DE SOUSA
 E.E. Dona Antônia Valadares MATEMÁTICA ENSINO MÉDIO - 3º ANO ESTATÍSTICA PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net ESTATÍSTICA Origem no latim Status (estado) + isticum
E.E. Dona Antônia Valadares MATEMÁTICA ENSINO MÉDIO - 3º ANO ESTATÍSTICA PROFESSOR: ALEXSANDRO DE SOUSA http://donaantoniavaladares.comunidades.net ESTATÍSTICA Origem no latim Status (estado) + isticum
Universidade Federal de Lavras Departamento de Estatística Prof. Daniel Furtado Ferreira 4 a Aula Prática Medidas de Dispersão
 Universidade Federal de Lavras Departamento de Estatística Prof. Daniel Furtado Ferreira 4 a Aula Prática Medidas de Dispersão 1) Os dados apresentados a seguir referem-se ao levantamento dos intervalos
Universidade Federal de Lavras Departamento de Estatística Prof. Daniel Furtado Ferreira 4 a Aula Prática Medidas de Dispersão 1) Os dados apresentados a seguir referem-se ao levantamento dos intervalos
- desvio padrão, caracteriza a dispersão dos resultados
 O resultado da experiência, então, pode ser expresso na forma < x > ± x n (veja a explicação mais adiante) - desvio padrão, caracteriza a dispersão dos resultados Histograma de frequências Histograma
O resultado da experiência, então, pode ser expresso na forma < x > ± x n (veja a explicação mais adiante) - desvio padrão, caracteriza a dispersão dos resultados Histograma de frequências Histograma
Universidade Federal do Paraná Seminário de Bioestatistica. Teste de Wilcoxon. Danielle Pierin Olivia Cleto
 Universidade Federal do Paraná Seminário de Bioestatistica Teste de Wilcoxon Danielle Pierin Olivia Cleto Teste de Postos com Sinais de Wilcoxon para Pares Combinados Esse teste é usado com dados amostrais
Universidade Federal do Paraná Seminário de Bioestatistica Teste de Wilcoxon Danielle Pierin Olivia Cleto Teste de Postos com Sinais de Wilcoxon para Pares Combinados Esse teste é usado com dados amostrais
AULA 17 - Distribuição Uniforme e Normal
 AULA 17 - Distribuição Uniforme e Normal Susan Schommer Introdução à Estatística Econômica - IE/UFRJ Distribuições Contínuas Em muitos problemas se torna matematicamente mais simples considerar um espaço
AULA 17 - Distribuição Uniforme e Normal Susan Schommer Introdução à Estatística Econômica - IE/UFRJ Distribuições Contínuas Em muitos problemas se torna matematicamente mais simples considerar um espaço
Distribuições Amostrais
 Distribuições Amostrais 1 Da população, com parâmetro, retira-se k amostras de tamanho n e calcula-se a estatística. Estas estatísticas são as estimativas de. As estatísticas, sendo variáveis aleatórias,
Distribuições Amostrais 1 Da população, com parâmetro, retira-se k amostras de tamanho n e calcula-se a estatística. Estas estatísticas são as estimativas de. As estatísticas, sendo variáveis aleatórias,
3 3. Variáveis Aleatórias
 ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
ÍNDICE 3. VARIÁVEIS ALEATÓRIAS...49 3.. VARIÁVEIS ALEATÓRIAS UNIDIMENSIONAIS...49 3.2. VARIÁVEIS DISCRETAS FUNÇÃO DE PROBABILIDADE E FUNÇÃO DISTRIBUIÇÃO DE PROBABILIDADE...50 3.2.. Função de probabilidade...50
Aplicações de. Integração
 Aplicações de Capítulo 6 Integração APLICAÇÕES DE INTEGRAÇÃO Neste capítulo exploraremos algumas das aplicações da integral definida, utilizando-a para calcular áreas entre curvas, volumes de sólidos e
Aplicações de Capítulo 6 Integração APLICAÇÕES DE INTEGRAÇÃO Neste capítulo exploraremos algumas das aplicações da integral definida, utilizando-a para calcular áreas entre curvas, volumes de sólidos e
Distribuições Amostrais
 Estatística II Antonio Roque Aula Distribuições Amostrais O problema central da inferência estatística é como fazer afirmações sobre os parâmetros de uma população a partir de estatísticas obtidas de amostras
Estatística II Antonio Roque Aula Distribuições Amostrais O problema central da inferência estatística é como fazer afirmações sobre os parâmetros de uma população a partir de estatísticas obtidas de amostras
1 Estatística Descritiva
 1 Estatística Descritiva A estatística descritiva é parte da estatística que lida com a organização, resumo e apresentação de dados. Esta é feita por meio de: Tabelas; Gráficos; Medidas Descritivas (média,
1 Estatística Descritiva A estatística descritiva é parte da estatística que lida com a organização, resumo e apresentação de dados. Esta é feita por meio de: Tabelas; Gráficos; Medidas Descritivas (média,
PROBABILIDADE E ESTATÍSTICA. Profa. Dra. Yara de Souza Tadano
 PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 4 09/2014 Estatística Descritiva Medidas de Variação Probabilidade e Estatística 3/42 Medidas de Variação Vamos
PROBABILIDADE E ESTATÍSTICA Profa. Dra. Yara de Souza Tadano yaratadano@utfpr.edu.br Aula 4 09/2014 Estatística Descritiva Medidas de Variação Probabilidade e Estatística 3/42 Medidas de Variação Vamos
Variáveis Aleatórias Contínuas
 Variáveis Aleatórias Contínuas Bacharelado em Administração - FEA - Noturno 2 o Semestre 2017 MAE0219 (IME-USP) Variáveis Aleatórias Contínuas 2 o Semestre 2017 1 / 35 Objetivos da Aula Sumário 1 Objetivos
Variáveis Aleatórias Contínuas Bacharelado em Administração - FEA - Noturno 2 o Semestre 2017 MAE0219 (IME-USP) Variáveis Aleatórias Contínuas 2 o Semestre 2017 1 / 35 Objetivos da Aula Sumário 1 Objetivos
Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine)
 Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine) Statistics for Managers Using Microsoft Excel, 5e 2008 Pearson Prentice-Hall, Inc. Chap 6-1 Objetivos: Neste capítulo, você aprenderá:
Revisão de distribuições de probabilidades contínuas (Capítulo 6 Levine) Statistics for Managers Using Microsoft Excel, 5e 2008 Pearson Prentice-Hall, Inc. Chap 6-1 Objetivos: Neste capítulo, você aprenderá:
Probabilidade e Estatística I Antonio Roque Aula 2. Tabelas e Diagramas de Freqüência
 Tabelas e Diagramas de Freqüência Probabilidade e Estatística I Antonio Roque Aula 2 O primeiro passo na análise e interpretação dos dados de uma amostra consiste na descrição (apresentação) dos dados
Tabelas e Diagramas de Freqüência Probabilidade e Estatística I Antonio Roque Aula 2 O primeiro passo na análise e interpretação dos dados de uma amostra consiste na descrição (apresentação) dos dados
08/12/97 Luiz Feijó Jr.
 Cálculo da Incerteza da medição guia prático A Medição A palavra medição tem múltiplos significados: pode ser o processo de quantificação pode ser o número resultante Resultado de uma medição Para um leigo:
Cálculo da Incerteza da medição guia prático A Medição A palavra medição tem múltiplos significados: pode ser o processo de quantificação pode ser o número resultante Resultado de uma medição Para um leigo:
aula EXEMPLO DE APLICAÇÃO DE REGRESSÃO Análise do desempenho do modelo em regressões
 Análise do desempenho do modelo em regressões EXEMPLO DE APLICAÇÃO DE REGRESSÃO META Apresentar ao aluno um exemplo de aplicação de regressão, que necessite de um termo quadrático OBJETIVOS Ao final desta
Análise do desempenho do modelo em regressões EXEMPLO DE APLICAÇÃO DE REGRESSÃO META Apresentar ao aluno um exemplo de aplicação de regressão, que necessite de um termo quadrático OBJETIVOS Ao final desta
Teste Anova. Prof. David Prata Novembro de 2016
 Teste Anova Prof. David Prata Novembro de 2016 Tipo de Variável Introduzimos o processo geral de teste de hipótese. É hora de aprender a testar a sua própria hipótese. Você sempre terá que interpretar
Teste Anova Prof. David Prata Novembro de 2016 Tipo de Variável Introduzimos o processo geral de teste de hipótese. É hora de aprender a testar a sua própria hipótese. Você sempre terá que interpretar
ESTATÍSTICA. x(s) W Domínio. Contradomínio
 Variáveis Aleatórias Variáveis Aleatórias são funções matemáticas que associam números reais aos resultados de um Espaço Amostral. Uma variável quantitativa geralmente agrega mais informação que uma qualitativa.
Variáveis Aleatórias Variáveis Aleatórias são funções matemáticas que associam números reais aos resultados de um Espaço Amostral. Uma variável quantitativa geralmente agrega mais informação que uma qualitativa.
Estimação de valores. Luiz Carlos Terra
 Luiz Carlos Terra Nesta aula, você conhecerá a parte mais importante da estatística, que é conhecida como inferência estatística, ou seja, você aprenderá como usar os dados de uma amostra para estimar
Luiz Carlos Terra Nesta aula, você conhecerá a parte mais importante da estatística, que é conhecida como inferência estatística, ou seja, você aprenderá como usar os dados de uma amostra para estimar
Tutorial para o desenvolvimento das Oficinas
 Tutorial para o desenvolvimento das Oficinas 1 Métodos Quantitativos Profa. Msc. Regina Albanese Pose 2 Objetivos Objetivo Geral Este tutorial tem como objetivo parametrizar o desenvolvimento da oficina
Tutorial para o desenvolvimento das Oficinas 1 Métodos Quantitativos Profa. Msc. Regina Albanese Pose 2 Objetivos Objetivo Geral Este tutorial tem como objetivo parametrizar o desenvolvimento da oficina
ESTATÍSTICA DESCRITIVA
 ESTATÍSTICA DESCRITIVA O principal objectivo da ESTATÍSTICA DESCRITIVA é a redução de dados. A importância de que se revestem os métodos que visam exprimir a informação relevante contida numa grande massa
ESTATÍSTICA DESCRITIVA O principal objectivo da ESTATÍSTICA DESCRITIVA é a redução de dados. A importância de que se revestem os métodos que visam exprimir a informação relevante contida numa grande massa
PROBABILIDADES: VARIÁVEL ALEATÓRIA CONTÍNUA E DISTRIBUIÇÃO NORMAL
 PROBABILIDADES: VARIÁVEL ALEATÓRIA CONTÍNUA E DISTRIBUIÇÃO NORMAL Aula 6 META Estudar o comportamento e aplicação das Variáveis Aleatórias Contínuas, bem como da Distribuição Normal. OBJETIVOS Ao final
PROBABILIDADES: VARIÁVEL ALEATÓRIA CONTÍNUA E DISTRIBUIÇÃO NORMAL Aula 6 META Estudar o comportamento e aplicação das Variáveis Aleatórias Contínuas, bem como da Distribuição Normal. OBJETIVOS Ao final
Medidas Descritivas de Posição, Tendência Central e Variabilidade
 Medidas Descritivas de Posição, Tendência Central e Variabilidade Prof. Gilberto Rodrigues Liska UNIPAMPA 29 de Agosto de 2017 Material de Apoio e-mail: gilbertoliska@unipampa.edu.br Local: Sala dos professores
Medidas Descritivas de Posição, Tendência Central e Variabilidade Prof. Gilberto Rodrigues Liska UNIPAMPA 29 de Agosto de 2017 Material de Apoio e-mail: gilbertoliska@unipampa.edu.br Local: Sala dos professores
DA PARAÍBA. Variáveis Aleatórias. Departamento de Estatística Luiz Medeiros
 UNIVERSIDADE FEDERAL DA PARAÍBA Variáveis Aleatórias Departamento de Estatística Luiz Medeiros Introdução Como sabemos, características de interesse em diversas áreas estão sujeitas à variação Essa variabilidade
UNIVERSIDADE FEDERAL DA PARAÍBA Variáveis Aleatórias Departamento de Estatística Luiz Medeiros Introdução Como sabemos, características de interesse em diversas áreas estão sujeitas à variação Essa variabilidade
Física Geral - Laboratório. Aula 2: Organização e descrição de dados e parâmetros de dispersão e correlação
 Física Geral - Laboratório Aula 2: Organização e descrição de dados e parâmetros de dispersão e correlação 1 Física Geral - Objetivos Ao final do período, o aluno deverá ser capaz de compreender as principais
Física Geral - Laboratório Aula 2: Organização e descrição de dados e parâmetros de dispersão e correlação 1 Física Geral - Objetivos Ao final do período, o aluno deverá ser capaz de compreender as principais
Exercícios de programação
 Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
Exercícios de programação Estes exercícios serão propostos durante as aulas sobre o Mathematica. Caso você use outra linguagem para os exercícios e problemas do curso de estatística, resolva estes problemas,
FÍSICA EXPERIMENTAL C ( )
 FÍSICA EXPERIMENTAL C (4323301) REPRESENTAÇÃO DE INCERTEZAS EM RESULTADOS EXPERIMENTAIS Medida, erro e incerteza Qualquer medida física possui sempre um valor verdadeiro, que é sempre desconhecido, e um
FÍSICA EXPERIMENTAL C (4323301) REPRESENTAÇÃO DE INCERTEZAS EM RESULTADOS EXPERIMENTAIS Medida, erro e incerteza Qualquer medida física possui sempre um valor verdadeiro, que é sempre desconhecido, e um
PARTE 2- MEDIDAS DE TENDÊNCIA CENTRAL VERSÃO: JANEIRO DE 2017
 COMUNICAÇÃO SOCIAL E MARKETING CENTRO DE CIÊNCIAS SOCIAIS APLICADAS UNIVERSIDADE CATÓLICA DE PETRÓPOLIS ESTATÍSTICA APLICADA PARA PESQUISA EM MARKETING E COMUNICAÇÃO (BASEADO NO MATERIAL DE AULA DO PROFESSOR
COMUNICAÇÃO SOCIAL E MARKETING CENTRO DE CIÊNCIAS SOCIAIS APLICADAS UNIVERSIDADE CATÓLICA DE PETRÓPOLIS ESTATÍSTICA APLICADA PARA PESQUISA EM MARKETING E COMUNICAÇÃO (BASEADO NO MATERIAL DE AULA DO PROFESSOR
1 Noções de Probabilidade
 Noções de Probabilidade Já vimos que para se obter informações sobre alguma característica da população, podemos utilizar uma amostra. Estudaremos agora a probabilidade, que é uma ferramenta usada e necessária
Noções de Probabilidade Já vimos que para se obter informações sobre alguma característica da população, podemos utilizar uma amostra. Estudaremos agora a probabilidade, que é uma ferramenta usada e necessária
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) INTRODUÇÃO AOS MÉTODOS ESTATÍSTICOS EM ENGENHARIA
 PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) INTRODUÇÃO AOS MÉTODOS ESTATÍSTICOS EM ENGENHARIA VARIABILIDADE NA MEDIDA DE DADOS CIENTÍFICOS Se numa pesquisa, desenvolvimento de um processo ou produto, o valor
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) INTRODUÇÃO AOS MÉTODOS ESTATÍSTICOS EM ENGENHARIA VARIABILIDADE NA MEDIDA DE DADOS CIENTÍFICOS Se numa pesquisa, desenvolvimento de um processo ou produto, o valor
Capítulo 5 Distribuições de probabilidade normal Pearson Prentice Hall. Todos os direitos reservados.
 Capítulo 5 Distribuições de probabilidade normal slide 1 Descrição do capítulo 5.1 Introdução à distribuição normal e distribuição normal padrão 5.2 Distribuições normais: encontrando probabilidades 5.3
Capítulo 5 Distribuições de probabilidade normal slide 1 Descrição do capítulo 5.1 Introdução à distribuição normal e distribuição normal padrão 5.2 Distribuições normais: encontrando probabilidades 5.3
5- Variáveis aleatórias contínuas
 5- Variáveis aleatórias contínuas Para variáveis aleatórias contínuas, associamos probabilidades a intervalos de valores da variável. Exemplo 5.1 Seja a variável correspondente ao tempo até a cura de pacientes
5- Variáveis aleatórias contínuas Para variáveis aleatórias contínuas, associamos probabilidades a intervalos de valores da variável. Exemplo 5.1 Seja a variável correspondente ao tempo até a cura de pacientes
Variáveis Aleatórias - VA
 Variáveis Aleatórias - VA cc ck kc kk 0 1 2 1/4 1/2 Prof. Adriano Mendonça Souza, Dr. Departamento de Estatística - PPGEMQ / PPGEP - UFSM - Introdução Se entende por VA ou V. indicadoras uma lista de valores
Variáveis Aleatórias - VA cc ck kc kk 0 1 2 1/4 1/2 Prof. Adriano Mendonça Souza, Dr. Departamento de Estatística - PPGEMQ / PPGEP - UFSM - Introdução Se entende por VA ou V. indicadoras uma lista de valores
Universidade Federal de Mato Grosso - UFMT Probabilidade e Estatística
 Universidade Federal de Mato Grosso - UFMT Probabilidade e Estatística 1 Introdução Definição: Estatística é um conjunto de conceitos e métodos científicos para coleta, organização, descrição, análise
Universidade Federal de Mato Grosso - UFMT Probabilidade e Estatística 1 Introdução Definição: Estatística é um conjunto de conceitos e métodos científicos para coleta, organização, descrição, análise
Tópico 3. Estudo de Erros em Medidas
 Tópico 3. Estudo de Erros em Medidas A medida de uma grandeza é obtida, em geral, através de uma experiência, na qual o grau de complexidade do processo de medir está relacionado com a grandeza em questão
Tópico 3. Estudo de Erros em Medidas A medida de uma grandeza é obtida, em geral, através de uma experiência, na qual o grau de complexidade do processo de medir está relacionado com a grandeza em questão
Variáveis Aleatórias Discretas e Distribuição de Probabilidade
 Variáveis Aleatórias Discretas e Distribuição de Probabilidades 01 de Abril de 2014 Objetivos Ao final deste capítulo você deve ser capaz de: Determinar probabilidades a partir de funções de probabilidade
Variáveis Aleatórias Discretas e Distribuição de Probabilidades 01 de Abril de 2014 Objetivos Ao final deste capítulo você deve ser capaz de: Determinar probabilidades a partir de funções de probabilidade
CAPÍTULO 4 DESCRIÇÃO E EXPLORAÇÃO DOS DADOS 2ª parte
 CAPÍTULO 4 DESCRIÇÃO E EXPLORAÇÃO DOS DADOS 2ª parte 4.3 Medidas de posição 4.4 Medidas de dispersão 4.5 Separatrizes Prof. franke 2 Vimos que a informação contida num conjunto de dados pode ser resumida
CAPÍTULO 4 DESCRIÇÃO E EXPLORAÇÃO DOS DADOS 2ª parte 4.3 Medidas de posição 4.4 Medidas de dispersão 4.5 Separatrizes Prof. franke 2 Vimos que a informação contida num conjunto de dados pode ser resumida
Distribuição de Probabilidade. Prof.: Joni Fusinato
 Distribuição de Probabilidade Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Variáveis Aleatórias Contínuas Distribuição de Probabilidade Contínua Modelo Normal Modelo t de Student
Distribuição de Probabilidade Prof.: Joni Fusinato joni.fusinato@ifsc.edu.br jfusinato@gmail.com Variáveis Aleatórias Contínuas Distribuição de Probabilidade Contínua Modelo Normal Modelo t de Student
Aula 7 Intervalos de confiança
 Aula 7 Intervalos de confiança Nesta aula você aprenderá um método muito importante de estimação de parâmetros. Na aula anterior, você viu que a média amostral X é um bom estimador da média populacional
Aula 7 Intervalos de confiança Nesta aula você aprenderá um método muito importante de estimação de parâmetros. Na aula anterior, você viu que a média amostral X é um bom estimador da média populacional
