ANÁLISE DE ALGORITMOS DE NAVEGAÇÃO PARA UM SISTEMA GPS DIFERENCIAL EM TEMPO REAL
|
|
|
- Ana Luiza Garrau da Costa
- 8 Há anos
- Visualizações:
Transcrição
1 INPE TDI/1040 ANÁLISE DE ALGORITMOS DE NAVEGAÇÃO PARA UM SISTEMA GPS DIFERENCIAL EM TEMPO REAL Leandro Baroni Dissertação de Mestrado do Curso de Pós-Graduação em Engenharia e Tecnologia Espaciais/Mecânica Espacial e Controle, orientada pelo Dr. Helio Koiti Kuga, aprovada em 27 de agosto de INPE São José dos Campos 2006
2 : Baroni, L. Análise de algoritmos de navegação para um sistema GPS diferencial em tempo real / L. Baroni. São José dos Campos: Instituto Nacional de Pesquisas Espaciais (INPE), p.; - (INPE TDI/1040) 1.Navegação. 2.Sistemas de navegação por satélites. 3.Sistema de posicionamento global. 4.Filtro de Kalman. 5. Método de mínimos quadrados. I. Título.
3
4
5 Algo só é impossível até que alguém duvida disso e acaba provando o contrário. Albert Einstein
6
7 A meus pais, ARNALDO BARONI e NEIDE MARTIN BARONI e minha irmã LUCIANA BARONI
8
9 AGRADECIMENTOS Ao Dr. Hélio Koiti Kuga por sua competência, compreensão e dedicação na orientação deste trabalho. À Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), pelo auxílio financeiro de bolsa de mestrado, processo número 02/ Ao Instituto Nacional de Pesquisas Espaciais pela oportunidade de estudos e pelos meios concedidos para a realização deste trabalho. Aos membros da banca examinadora pela predisposição em analisar e discutir este trabalho e pelas sugestões recebidas. Aos professores do DMC/INPE que transmitiram conhecimento e deram incentivos ao longo do curso. À minha família pela ajuda e apoio constantes que foram de grande importância ao longo deste trabalho. Aos amigos Alex, Bráulio, Carmen, Edmundo, Gilberto, Leandro, Vivian, Yasser que compartilharam do meu tempo neste mestrado e para Maria Cecilia, um sonho que se realizou, que deu sentido a tudo.
10
11 RESUMO O Sistema de Posicionamento Global (GPS) é um sistema de navegação baseado em satélites que permite ao usuário determinar sua posição e tempo com alta precisão. A determinação de posição do GPS é baseada no conceito de tempo de chegada do sinal, o qual está sujeito a diversas fontes de erros em sua medida. O efeito combinado destes erros na propagação do sinal causa uma degradação na precisão do posicionamento. Entretanto, existem métodos de melhorar a precisão do posicionamento, como o GPS diferencial (DGPS) e o posicionamento por dupla diferença, que tentam compensar, atenuar ou eliminar várias fontes de erros. Neste trabalho são analisados algoritmos que permitam navegação precisa em tempo real, através de técnicas de GPS diferencial. Algoritmos de GPS diferencial foram desenvolvidos, implementados e testados através da realização de posicionamento em tempo real para um usuário com a utilização de três métodos: DGPS na posição, DGPS nas medidas de pseudodistância e posicionamento por dupla diferença. Estes algoritmos foram testados em dois casos: estático, no qual ambos os receptores são mantidos fixos; e dinâmico, no qual o receptor usuário está se movendo. Os dados em ambos os casos foram coletados por dois receptores Ashtech Z12. O desempenho dos algoritmos no teste estático foi comparado com a linha de base conhecida, enquanto que o desempenho dos algoritmos no teste dinâmico foi comparado com uma trajetória de referência pós-processada e analisado em termos das precisões obtidas.
12
13 NAVIGATION ALGORITHM ANALYSIS FOR A REAL TIME DIFFERENTIAL GPS SYSTEM ABSTRACT The Global Positioning System (GPS) is a satellite-based navigation system that allows user to determine position and time with high precision. The position determination with GPS is based on the concept of signal time of arrival, which is affected by several errors sources in measurements. The combined effects of these errors at signal propagation cause degradation in the positioning accuracy. However, there are methods to improve the positioning accuracy, like differential GPS (DGPS) and double difference positioning, which try to compensate, attenuate or eliminate several error sources. In this work algorithms that allow precise real time navigation, through differential GPS techniques are analyzed. Differential GPS algorithms were developed, implemented and tested by the real time positioning for an user through three methods: DGPS on position, DGPS on pseudorange measurements and double difference measurements. These algorithms were tested in two cases: static, in which both receivers are fixed; and dynamic, in which the user receiver is moving. The data in both cases were collected by two Ashtech Z12 receivers. The algorithms performance in the static test was compared with a known baseline, while the algorithm performance in the dynamic test were compared with a post-processed reference trajectory and analyzed in terms of accuracies attained.
14
15 SUMÁRIO LISTADE FIGURAS LISTADETABELAS LISTADESÍMBOLOS LISTADESIGLASEABREVIATURAS CAPÍTULO1 INTRODUÇ ÃO Motivação eobjetivos Organização do Trabalho Revisão Bibliográfica CAPÍTULO2 FUNDAMENTOS DO GPS OSistema Navstar-GPS Segmento Espacial Segmento de Controle Segmento Usuário Determinação da Posição etempo Observáveis Pseudodistância Fase da Portadora Fontes de Erros Erros dos Relógios dos Satélites Erro Devido àtroposfera Erro Devido àionosfera Multicaminho Erro do Centro de Fase da Antena CAPÍTULO3 METODOLOGIA Método de Mínimos Quadrados Filtro de Kalman Sintonização do filtro Propagação... 50
16 3.2.3 Atualização Filtro de Kalman Estendido Posicionamento Absoluto Posicionamento Diferencial GPS Diferencial Observações de Simples Diferença Observações de Dupla Diferença CAPÍTULO4 ALGORITMOS DE GPS DIFERENCIAL GPS Diferencial na Posição GPS Diferencial na Pseudodistância Correções na Pseudodistância Estimação da Posição do Usuário Posicionamento por Dupla Diferença Branqueamento de Erros de Observação Inversão da Matriz R DD Fatoração de Cholesky Suavização Cálculo do Ruído Dinâmico Γ k QΓ T k CAPÍTULO5 APLICAÇ ÃO DOS ALGORITMOS EM POSICIONA- MENTO ESTÁTICO GPS Diferencial na Posição GPS Diferencial na Pseudodistância Resultados Modelagem das Observáveis por Dupla Diferença Modelagem Usando Filtro de Kalman Modelagem Usando Mínimos Quadrados Resultados Utilizando Dados do Código C Resultados Utilizando Dados do Código P Tempo de Execução dos Programas CAPÍTULO6 APLICAÇ ÃO DOS ALGORITMOS EM NAVEGAÇ ÃO Aplicação do GPS Diferencial na Posição Aplicação do GPS Diferencial na Pseudodistância... 96
17 6.2.1 Correções Resultados Resultados Usando Medidas de Dupla Diferença Modelagem por Filtro de Kalman Modelagem por Mínimos Quadrados Resultados para ofiltro de Kalman Resultados para omínimos Quadrados Tempo de Execução dos Programas CAPÍTULO7 CONCLUSÃO Conclusões Trabalhos Futuros REFERÊNCIAS BIBLIOGRÁFICAS 115
18
19 LISTA DE FIGURAS 2.1 Representação da constelação de satélites GPS Segmentos do GPS Conceito de GPS diferencial Geometria de uma observação Configuração do experimento Variação do GDOP, PDOP, TDOP e número de satélites visíveis durante a observação Erro da posição do usuário para DGPS na posição Resíduos da pseudodistância Erro da posição do usuário para DGPS na pseudodistância Erro do posicionamento do usuário sem suavização Erro do posicionamento do usuário com suavização de 10s Erro do posicionamento do usuário com suavização de 30s Erro do posicionamento do usuário com suavização de 50s Erro do posicionamento do usuário com suavização de 100s Erro do posicionamento do usuário sem suavização Erro do posicionamento do usuário com suavização de 10s Erro do posicionamento do usuário com suavização de 30s Erro do posicionamento do usuário com suavização de 50s Erro do posicionamento do usuário com suavização de 100s Trajetória da aeronave Altitude da aeronave em função do tempo Variação do número de satélites visíveis e GDOP, PDOP e TDOP em função do tempo Erro da posição da aeronave nas componentes leste, norte e vertical Erro horizontal da aeronave Resíduos das medidas para o método de DGPS na pseudodistância Erros da posição para o método de DGPS na pseudodistância Trajetória e altitude da aeronave entre 1575 e 1875s
20 6.9 Erros horizontal e vertical para o método de DGPS na pseudodistância entre 1575 e 1875s Erro horizontal para o método de DGPS na pseudodistância Comportamento dos resíduos durante o teste Erro da posição da aeronave nas componentes leste, norte e vertical para a solução por filtro de Kalman Erro horizontal para o filtro de Kalman Erro da posição da aeronave nas componentes leste, norte e vertical para a solução por mínimos quadrados Erro horizontal para o método de dupla diferença usando mínimos quadrados
21 LISTA DE TABELAS 3.1 Balanço de Erros do GPS (SA Destivada) Balanço de Erros do DGPS Valores iniciais da posição, desvio e deriva e suas covariâncias para o filtro de Kalman Estatística dos resíduos para o método de DGPS na pseudodistância Médias e desvios-padrão para a solução por filtro de Kalman nas medidas em C Médias e desvios-padrão para a solução por mínimos quadrados nas medidas em C Médias e desvios-padrão para a solução por filtro de Kalman nas medidas em P Médias e desvios-padrão para a solução por mínimos quadrados nas medidas em P Tempo total e médio de execução dos algoritmos Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para o método de DGPS na posição Valores iniciais dos estados e suas covariâncias para o filtro de Kalman Estatística dos resíduos para o método de DGPS na pseudodistância Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para o método de DGPS na pseudodistância Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para as épocas entre 1575s e 1875s para o método de DGPS na pseudodistância Média e desvio-padrão dos resíduos para o filtro de Kalman Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para a solução por filtro de Kalman Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para as épocas entre 1575s e 1875s usando o filtro de Kalman Média e desvio-padrão dos resíduos para os mínimos quadrados Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para a solução por mínimos quadrados Tempo total e médio de execução dos algoritmos
22
23 ẋ u, ẏ u, ż u ˆD i u A B D F G H H k I I ono K k L 1 P P k P ub Q R i R DD R ρ R k R s S T W P k P ub x k x ub ẋ ˆP 0 ˆP k ˆP ub ˆr u ˆx ˆx 0 ˆx k ˆx ub ˆx u LISTA DE SÍMBOLOS Componentes da velocidade de u Distância geométrica calculada entre o receptor u e o satélite i Matriz de formação da covariância Termo de contribuição do desvio do relógio do satélite Matriz que relaciona as pseudodistância e observações de dupla diferença Matriz do sistema dinâmico Matriz de adição de ruído Matriz de relação entre as medidas e os parâmetros Matriz de relação entre as medidas e os estados Matriz identidade Termo de contribuição do erro ionosférico Ganho de Kalman Matriz raiz quadrada de R 1 DD Matriz de covariância dos parâmetros Matriz de covariância dos estados Matriz de covariância de x ub Matriz de densidade espectral de potência dos ruídos dinâmicos Vetor posição do i-ésimo satélite GPS Matriz de covariância das observações de dupla diferença Matriz de covariância dos erros de medida da pseudodistância Matriz de covariância do ruído das medidas Matriz contendo as posições dos satélites visíveis Matriz contendo as linhas de visadas para os satélites visíveis Termo de contribuição do erro troposférico Matriz de pesos Matriz de covariância dos estados propagada Matriz de covariância propagada de x ub Vetor de estados propagado Vetor linha de base propagado Derivada temporal de x Matriz de covariância dos estados inicial estimada Matriz de covariância dos estados estimada Matriz de covariância estimada de x ub Vetor posição estimado do receptor u Vetor de parâmetros estimado Vetor de estados incial estimado Vetor de estados estimado Vetor linha de base estimado Vetor de estados estimado de u
24 ẑ DD H z DD b f h k r b r g r u v u x x 0 x k x ref x ub x u y k z DD z ρ E a a f0, a f1, a f2 B i b u c d u Du i E e I i u J L L 1, L 2, L 5 m M n Nu i q b q r r Vetor contendo as observações de dupla diferença calculadas Transformação de H por branqueamento Transformação de z DD por branqueamento Termo de contribuição do desvio do relógio do receptor Função não-linear que relaciona os estados à sua derivada temporal Função não-linear que relaciona os estados às observações Vetor posição do receptor b Posição geométrica Vetor posição do receptor u Vetor velocidade do receptor u Vetor de parâmetros Vetor de estados inicial Vetor de estados no instante t k Vetor com as coordenadas da base de referência Vetor linha de base entre os receptores Vetor de estados do receptor u Vetor de medidas no instante t k Vetor contendo as observações de dupla diferença Vetor contendo as medidas de pseudodistância Operador esperança Semi-eixo maior Coeficientes de correção do relógio do satélite Desvio do relógio do satélite i Desvio do relógio do receptor u Velocidade de propagação da luz Deriva do relógio do receptor u Distância geométrica entre o receptor u e o satélite i Anomalia excêntrica Excentricidade Erro devido à ionosfera Janela de suavização Índice de desempenho dos mínimos quadrados Freqüências do sinal GPS Número de medidas Satélite mestre Número de estados Ambigüidade no número de comprimentos de onda Densidade espectral de potência de ω b Densidade espectral de potência de ω r Número de ruídos na modelagem dinâmica
25 t t i t k t oc Tu i X i, Y i, Z i x b, y b, z b x ref, y ref, z ref x u, y u, z u y i r x ub x u ρ i u t R t i Γ k QΓ T k ɛ ν ν k ω ω b ω r ω u ρ b ρ u ν δ(t τ) δρ δρ i δ kl δt δx, δẋ, δy k δx, δy, δz δx, δy, δz ɛ i φ,u ɛ i ρ,u ɛ i ϕ,u ˆρ i u λ Tempo GPS Tempo de transmissão do sinal no relógio do satélite i Instante da k-ésima observação Tempo de referência das efemérides Erro devido à troposfera Coordenadas da posição do satélite i Coordenadas de posição do receptor b Coordenadas de posição da base de referência Coordenadas da posição do receptor u i-ésimo elemento de y Correções diferenciais na posição Incremento na linha de base Resíduo do vetor de estados Resíduo da medida de pseudodistância Correção relativística na relógio do satélite Termo de correção do relógio do satélite i Discretização de Q na propagação Contribuição dos erros não modelados Ruído na observação de dupla diferença Ruído no vetor de medidas Ruídos brancos da modelagem da dinâmica Ruído na modelagem da dinâmica do relógio Ruído na modelagem da dinâmica da posição Ruído na modelagem dinâmica Vetor contendo as pseudodistância medida pela base Vetor contendo as pseudodistância medida pelo usuário Transformação de ν por branqueamento Função delta de Dirac Vetor de correções diferenciais Correção diferencial na pseudodistância referente ao satélite i Função delta de Kronecker Intervalo de tempo entre as medidas Desvio definidos na linearização Coordenadas da linha de base Variação da linha de base Ruído de medida na pseudodistância via fase Ruído de medida na pseudodistância via código Ruído de medida na fase da portadora Pseudodistância calculada Comprimento de onda da portadora
26 Φ k+1,k Matriz de transição entre os instantes t k e t k+1 µ Parâmetro gravitacional da Terra φ i ub Observável de simples diferença em fase φ i u Pseudodistância via fase ρ i u Pseudodistância via código entre o receptor u e o satélite i ρ i corr,u Pseudodistância corrigida ρ ij ub Observável de dupla diferença em código ρ i ub Observável de simples diferença em código σ 0 Desvio-padrão do erro de medida da pseudodistância τ Tempo de percurso do sinal ϕ i u Fase da onda portadora 1 i b Matriz linha de visada entre o receptor b e o satélite i i i-ésimo satélite GPS j j-ésimo satélite GPS M Satélite meste T Transposto b Receptor b u Receptor u DD Observações de dupla diferença ref Base de referência ρ Medidas de pseudodistância Vetor ou matriz propagado ˆ Vetor ou matriz estimado/calculado Vetor ou matriz transformada
27 LISTA DE SIGLAS E ABREVIATURAS C/A Coarse/Aquisition code DGPS Differential Global Positioning System DoD Department of Defense DOP Dilution of Precision ECEF Earth Centered Earth Fixed Embraer Empresa Brasileira de Aeronáutica FK Filtro de Kalman GDOP Geometric Dilution of Precision GLONASS Global Navigation Satellite System GNSS Global Navigation Satellite System GPS Global Positioning System HDOP Horizontal dilution of precision IBGE Instituto Brasileiro de Geografia e Estatística IMU Inertial Motion Units INPE Istituto Nacional de Pesquisas Espaciais MCS Master Control Station MQ Mínimos quadrados NIMA National Imagery Mapping Agency P Precise code PDOP Position Dilution of Precision PPS Precise Positioning Service PRN Pseudorandom noise RINEX-2 Receiver Independent Exchange Format versão 2.10 RMS Root Mean Square RTCM Radio Technical Commission for Maritime Services SA Selective Availability SD Selective Denial SPS Standard Positioning Service SV Space Vehicle TDOP Time Dilution of Precision TOA Time of arrival UERE User Equivalent Range Error UFPR Universidade Federal do Paraná USNO United States Naval Observatory VDOP Vertical dilution of precision WADGPS Wide Area Differential Global Positioning System WGS-84 World Geodetic System of 1984
28
29 CAPÍTULO 1 INTRODUÇÃO O Sistema de Posicionamento Global (conhecido como Navstar-GPS, Global Positioning System) é um sistema de radionavegação por satélites, fornecendo a usuários no mundo todo posição, velocidade e determinação de tempo precisa. Os satélites do sistema transmitem sinais em radiofreqüência, contendo as informações requeridas para que o equipamento do usuário compute sua solução de navegação (posição, velocidade e tempo). O sistema foi projetado, desenvolvido e ainda é operado pelo Departamento de Defesa dos Estados Unidos, mas é parcialmente aberto a usuários civis. A determinação de posição através do GPS é baseada no conceito de tempo de chegada do sinal (TOA, time of arrival) (Kaplan, 1996). O conceito de TOA consiste em transmitir um sinal em um tempo conhecido e medir o tempo de chegada (recepção) deste sinal em um tempo posterior conhecido. Este intervalo de tempo é então multiplicado pela velocidade de propagação do sinal para obter a distância entre o emissor e o receptor. Através da medição do tempo de propagação de sinais de vários emissores em posições conhecidas, o receptor pode calcular sua posição. Cada distância medida pode ser relacionada a três coordenadas de posição. Dada as medidas de distância de três emissores, pode-se obter a solução para estas três incógnitas. A medida de tempo deve ser muito precisa, ou o posicionamento não será possível. Cada satélite carrega relógios atômicos de césio e rubídio, enquanto que os receptores usam osciladores de quartzo. A fim de medir o tempo real de percurso do sinal do satélite ao receptor, os relógios do satélite e do receptor devem ser mantidos em sincronismo. O desvio no relógio do receptor do usuário afeta a medida de tempo de percurso de todos os satélites igualmente, logo esse desvio se torna a quarta incógnita a ser estimada, juntamente com as três de posição. Assim, o usuário necessita de um mínimo de quatro satélites para determinar suas coordenadas (Misra e Enge, 2001). A precisão com que os erros de propagação do sinal são compensados é de extrema importância. No sistema GPS, as medidas de pseudodistância, que são as medidas de distância entre o satélite e o receptor mais os efeitos dos erros de propagação do 29
30 sinal, são freqüentemente usadas para estimar as coordenadas de posição e desvio do relógio. Infelizmente, há uma variedade de erros nas medidas que impedem o sistema GPS de alcançar alta precisão exigida por certas aplicações. O efeito combinado dos erros na propagação do sinal causa uma degradação na exatidão do posicionamento de cerca de 10m na posição horizontal e 13m na vertical (Axelrad e Brown, 1996). A fim de obter uma exatidão no posicionamento da ordem de metros, são necessários métodos mais complexos para reduzir esses erros. Um método de reduzir os erros nas medidas do GPS comumente utilizado é o chamado GPS diferencial (DGPS, Differential GPS). Um receptor GPS estacionário é colocado em um ponto de referência, com coordenadas conhecidas, geralmente chamado base. Assim, é possível calcular o valor verdadeiro da medida. Comparando-se o valor medido com o verdadeiro obtém-se a correção diferencial, que deve ser aplicada às medidas do receptor usuário. Este procedimento elimina os erros que são comuns a ambos os receptores. Assim, a técnica de GPS diferencial consiste de dois passos: gerar correções diferenciais na base de referência; aplicar essas correções no receptor usuário. Outro método utilizado é o posicionamento por simples diferença ou dupla diferença. As medidas do receptor base são combinadas com as medidas coletadas pelo receptor usuário, formando medidas diferenciais. Estas medidas são usadas para calcular a posição do usuário relativa à base. Esta técnica é capaz de eliminar erros comuns a ambos os receptores. Dada a proximidade da base e do usuário, o sinal de radio do GPS percorrerá caminhos próximos. Assim, o princípio destas técnicas diferenciais supõe que os efeitos ambientais (troposfera e ionosfera principalmente) são os mesmos em ambos os receptores para linhas de base próximas, pois estes efeitos são espacialmente correlacionados, isto é, a magnitude do erro é dependente da linha de base. Com isso, efeitos de modelagem complexa são minimizados e a técnica dá origem a um posicionamento relativo de grande precisão. No entanto deve-se tomar o cuidado de usar apenas os satélites visíveis em ambos os receptores (Martínez et al., 2000). 30
31 1.1 Motivação e Objetivos Durante os processos de desenvolvimento e certificação, as aeronaves necessitam determinar com precisão sua posição. Ao longo dos anos vários sistemas capazes de fornecer estes dados foram desenvolvidos, e entre eles, pode-se citar: cineteodolitos, sistemas de rádio, radar tracking e laser tracking. Entretanto, o GPS trouxe novas possibilidades em termos de precisão, facilidade de acesso aos dados e portabilidade. Em particular, o uso do GPS associado a técnicas diferenciais (DGPS) trouxe grande precisão, aliada às demais características do GPS, e se transformou numa ferramenta muito útil para posicionamento de aeronaves. A Embraer (Empresa Brasileira de Aeronáutica) usa um sistema DGPS para a determinação da trajetografia (posicionamento no tempo em um sistema de coordenadas solidário a pista) de suas aeronaves em ensaios de decolagem e pouso. Entretanto, a empresa ressente-se de vários aspectos, quanto ao emprego do DGPS: O sistema demanda um processamento pós-vôo que consome tempo e requer um operador altamente especializado; Não se dispõe a bordo de informações da posição presente da aeronave relativa a um ponto fixo (cabeceira da pista, pontos no solo etc.), o qual seria de grande valia nos ensaios de ruído, para atender os padrões americanos de certificação de aeronaves, bem como no suporte aos ensaios de pouso e decolagem; Não se dispõe de forma permanente os dados provenientes do DGPS junto com os demais dados de vôo provenientes da instrumentação, de forma a poderem ser acessados por qualquer usuário, como ocorre com os demais parâmetros medidos em vôo; O sistema DGPS tem um componente instalado na aeronave e outro, a base fixa, instalado em terra. Cada componente gera arquivos de dados os quais devem ser integrados e pós-processados para a obtenção das posições com a precisão desejada. Este pós-processamento tira a flexibilidade de uso do equipamento. Necessita-se portanto integrar as duas bases de dados na aeronave e seu processa- 31
32 mento em tempo real de forma a dispor da posição presente a bordo da aeronave, permitindo fornecer esta informação ao piloto e gravá-la com os demais dados de vôo para posterior uso. Para tal é preciso enviar, por telemetria, os dados da base fixa (de terra) para a aeronave, e processá-los em tempo real, gerando a posição presente a qual deverá ser armazenada e apresentada ao piloto. A utilização do procedimento de GPS diferencial se justifica a partir do fato de inexistirem outros métodos para se obter em tempo real as precisões necessárias para certificação de aeronaves. Neste trabalho, dentro do escopo de um projeto para desenvolvimento de sistema de GPS diferencial em tempo real e para navegação de aeronaves, serão analisados algoritmos que permitam navegação precisa em tempo real, através de técnicas de GPS diferencial. Uma análise preliminar revela que os seguintes itens devem ser considerados para realização do projeto: Concepção do sistema DGPS; Compilação, análise e escolha dos algoritmos de navegação via DGPS; Desenvolvimento do pacote de software necessário para navegação em tempo real via DGPS; Análise de erros e de desempenho e qualificação do software sob condições realísticas. Em vista das motivações expostas, os seguintes tipos de algoritmos foram investigados: Posicionamento absoluto e precisões possíveis; GPS diferencial usando correções direto nas coordenadas de posição; GPS diferencial usando correções nas medidas de pseudodistância; 32
33 GPS diferencial usando dupla diferença das medidas de pseudodistância. Os algoritmos de GPS diferencial foram desenvolvidos e implementados para testes, em duas situações. Na primeira situação, ambos os receptores permaneceram estáticos sobre marcos com coordenadas precisamente conhecidas. Na segunda situação, o receptor usuário estava a bordo de uma aeronave em um ensaio de vôo. Em ambas as situações foram testados as seguintes técnicas: DGPS na posição, DGPS nas medidas de pseudodistância e posicionamento por dupla diferença. A técnica de DGPS na posição consiste em gerar e aplicar correções diferenciais diretamente nas coordenadas de posição calculada pelos receptores. Usando as medidas de pseudodistância, cada receptor (base e usuário) calcula sua posição através de um mesmo método. Comparando-se então a posição calculada pela base com a posição do marco de referência, é possível gerar correções, que são aplicadas na posição calculada pelo usuário. Na técnica de DGPS nas medidas de pseudodistância, as correções diferenciais são aplicadas diretamente nas medidas de pseudodistância. Conhecendo-se as coordenadas da base, pode-se calcular o valor da pseudodistância verdadeira para cada satélite, levando em consideração os erros do relógio do satélite e receptor. A correção consiste então na diferença entre a pseudodistância verdadeira e a medida pela base. Ela é então somada à pseudodistância medida pelo usuário, e sua posição é calculada a partir da pseudodistância corrigida. Este método utiliza o filtro de Kalman para estimar a posição do usuário, utilizando as medidas de pseudodistância corrigidas. O posicionamento por dupla diferença utiliza as medidas de pseudodistância em ambos os receptores para gerar os observáveis de dupla diferença. Estes observáveis podem ser escritos como função da linha de base entre os receptores, de modo que a solução é a posição relativa dos receptores. A posição do usuário é obtida somando-se a linha de base com a posição da referência, que é previamente conhecida. 1.2 Organização do Trabalho Este trabalho está organizado da seguinte forma: 33
34 O Capítulo 1 traz uma introdução sobre a motivação, os objetivos e um resumo das investigações realizadas neste trabalho. Apresenta também uma revisão bibliográfica sobre trabalhos com GPS e técnicas de estimação. O Capítulo 2 apresenta uma descrição do sistema GPS, apresentando sua composição em segmentos, seus observáveis e fontes de erros. O Capítulo 3 faz uma revisão dos métodos de estimação, como o filtro de Kalman e mínimos quadrados, utilizados no desenvolvimento dos algoritmos testados. Faz também uma breve discussão dos métodos de posicionamento apresentados neste trabalho. O Capítulo 4 descreve a aplicação dos métodos mostrados no capítulo 3 nas técnicas de posicionamento descritas. O Capítulo 5 mostra resultados obtidos com a aplicação dos métodos descritos no capítulo 4 para o caso de um receptor usuário estático. O Capítulo 6 mostra resultados obtidos para o caso de um receptor usuário em movimento. O Capítulo 7 traz as conclusões deste trabalho, juntamente com as sugestões de trabalhos futuros. 1.3 Revisão Bibliográfica As referências Leick (1995), Parkinson (1996a) e Hofmann-Wellenhof et al. (1996) contêm informações sobre a história do sistema GPS, desde sua concepção e desenvolvimento até os dias atuais. O modelamento dos observáveis do GPS, como pseudodistância e ciclos, estão descritas em Spilker Jr. e Parkinson (1996). Esta referência mostra o desenvolvimento dessas equações, bem como o modelamento dos erros de medidas. A técnica de GPS diferencial e alguns métodos de obtenção da solução de navegação são mostrados em Strang e Borre (1997). Segundo esta referência, o uso de técnicas 34
35 de GPS diferencial associado à dupla diferença aumenta a exatidão do posicionamento. Parkinson e Enge (1996) e Hofmann-Wellenhof et al. (1996) também mostram como o DGPS pode melhorar a precisão da solução de navegação. Strang e Borre (1997) fornecem a álgebra envolvida nas aplicações do GPS, indicando pacotes de software em linguagem MATLAB na Internet. Misra e Enge (2001) fazem uma abordagem prática das características dos sinais, modelos das medidas e técnicas de processamento, fornecendo dados GPS para realização de experimentos. Todos abordam, em maior ou menor grau, técnicas de GPS diferencial. Trabalhos no INPE utilizando técnicas de estimação de estados em tempo real foram apresentados principalmente para determinação de órbita e atitude de satélites artificiais. No trabalho de Kuga (1982) implementou-se e testou-se procedimentos de estimação com o objetivo de verificar a possibilidade de sua utilização na determinação de órbita, em tempo real, de satélites artificiais. Em seu trabalho, o procedimento de estimação consiste de um filtro de Kalman associado a uma técnica adaptativa. Kuga (1989) apresenta um trabalho para determinação de órbitas de satélites artificiais terrestres através de através de técnicas de estimação combinadas a técnicas de suavização de estado. Em seu trabalho foi proposto um processo de estimação de órbita utilizando o filtro de Kalman em conjunto com técnicas adaptativas para prevenir da divergência e aumentar a robustez do filtro. Outros trabalhos foram realizados no INPE com respeito a estimação adaptativa, como Rios Neto e Kuga (1982, 1986). Na UFPR existem trabalhos sobre a utilização do DGPS no posicionamento de trens e navios. Krueger (1994) apresenta um estudo sobre o posicionamento cinemático de trens em tempo real utilizando o sistema DGPS. Massinhan (1997) utiliza uma técnica de posicionamento por GPS para ajudar a efetuar o controle de tráfego de trens. Saatkamp (2003) desenvolveu e experimentou um formato que permite a disponibilização de um serviço de transmissão de correções diferenciais para DGPS, fazendo uso de emissoras de radiodifusão sonora em freqüência modulada (FM). No trabalho de Briones (2001) investigou o posicionamento baseado nas ERDGPS, que são diversas estações de referência DGPS implantadas no litoral brasileiro. 35
36 Maybeck (1979) faz uma análise teórica das propriedades de técnicas de estimação, como o filtro de Kalman. Gelb et al. (1974) e Brown e Hwang (1996) são referências sobre técnicas de estimação por filtro de Kalman, mas com uma abordagem mais prática. Welch e Bishop (2001) apresenta uma introdução prática ao filtro de Kalman discreto. Esta introdução inclui uma descrição e uma discussão breve do filtro de Kalman discreto, derivação e exemplos, bem como noções da teoria de probabilidades. Em Lopes e Kuga (1988) e posteriormente em Lopes e Kuga (1997) é apresentado um algoritmo (ORBEST) para a determinação de órbitas baseado em medidas GPS. Tal algoritmo processa medidas de pseudodistância de todos os satélites GPS visíveis utilizando um método de otimização equivalente ao mínimos quadrados. É constatado como a precisão melhora com o número de satélites visíveis e conseqüentemente apresenta melhores resultados que aqueles que selecionam um PDOP ótimo com apenas quatro satélites. Outras referências também trazem algoritmos de navegação, como Bancroft (1985) e Kleusberg (2003). Saalfeld (1999) e Janssen (2001) propõem métodos de maximizar o número de observáveis de dupla diferença linearmente independentes dentro de uma rede permanente de monitoramento, pois um subconjunto de observações linearmente independentes contém toda informação do conjunto. Soon et al. (2003) apresenta os tipos de melhorias que podem ser alcançadas por um sistema de pseudolitos/dgps suavizado por medidas de fase da portadora. Os resultados mostrados são pós-processados e se referem a um teste em veículos terrestres. Os erros obtidos para o caso de GPS diferencial suavizado foram 0,627m, 0,380m e 1,790m para os erros norte, leste e vertical, respectivamente, enquanto que para o GPS diferencial sem suavização foram 1,167m, 1,007m e 4,591m. O trabalho de Hwang e Brown (1990) propõe uma forma de integrar as medidas de código e fase do GPS para prover soluções de posição altamente precisas. Este artigo apresenta dois esquemas distintos de integração baseado no filtro de Kalman. Martínez et al. (2000) usa um método de GPS diferencial na posição utilizando apenas três satélites GPS visíveis, escolhidos pelo critério de melhor DOP, para um 36
37 posicionamento em duas dimensões. A precisão horizontal obtida para este método é de cerca de 5m. Este resultado é comparado com um receptor de melhor precisão trabalhando em modo diferencial, com correções RTCM (Radio Technical Commission for Maritime Services). A revisão bibliográfica aqui apresentada tenta cobrir minimamente o escopo de investigação realizada, mas não tem a pretensão de exaurir o tema. Na realidade, tem-se observado um número crescente de pesquisas relacionadas ao GPS e mais recentemente com o sistema europeu GALILEO proposto. Trabalhos recentes já usam a terminologia GNSS (Global Navigation Satellite System) para se referir a este tipo de tecnologia (GPS, GALILEO, GLONASS). 37
38 38
39 CAPÍTULO 2 FUNDAMENTOS DO GPS 2.1 O Sistema Navstar-GPS O Sistema de Posicionamento Global (GPS) foi concebido pelo Departamento de Defesa dos Estados Unidos (DoD, Department of Defense) no início da década de 1970 e desenvolvido para apoiar a navegação e sincronização de tempo para uso militar (Spilker Jr. e Parkinson, 1996). Os objetivos de desempenho a serem atingidos pelo GPS são: Alta precisão na determinação da posição, velocidade e tempo para usuários militares; Boa precisão para usuários civis; Disponibilidade contínua de dados de navegação com cobertura global e regional; Independência das condições meteorológicas; Resistência a interferências externas no sinal; Uso de equipamentos práticos e baratos pelo usuário; O GPS utiliza como técnica de navegação a medição unidirecional de distância dos satélites GPS, que também transmitem sua posição (Spilker Jr. e Parkinson, 1996). As distâncias com relação a cada satélite são medidas fazendo-se a correlação entre o sinal recebido e uma réplica gerada pelo usuário. O usuário é capaz de diferenciar cada satélite através da porção do código PRN (Pseudorandom noise) que cada satélite transmite. Medindo a distância com relação a quatro satélites o usuário pode determinar as quatro incógnitas: três coordenadas de posição e a correção no relógio. O sistema GPS é dividido nos segmentos espacial, controle e usuário, descritos a seguir. 39
40 2.1.1 Segmento Espacial A configuração padrão deste segmento consiste de 24 satélites operacionais distribuídos em seis planos orbitais igualmente espaçados e com inclinação de 55 o e período orbital de um dia sideral (cerca de 12h). Tais satélites são denominados de satélites GPS. Os satélites transmitem em duas freqüências: L 1, de 1575,42MHz e L 2, de 1227,6MHz moduladas com dois tipos de códigos (código-c/a e código-p) e com uma mensagem de navegação. O Serviço de Posicionamento Padrão (SPS, Standard Positioning Service), disponível ao usuário civil é baseado no código-c/a, enquanto que usuários autorizados pelo DoD têm acesso ao Serviço de Posicionamento Preciso (PPS, Precise Positioning Service), o qual possui um maior grau de precisão, através do código-p, que é criptografado. Há uma nova freqüência em discussão, L 5 de 1176,45MHz, para uso civil, a ser incorporada na modernização dos satélites GPS, a partir de 2010 (Hatch et al., 2000; McDonald e Hegarty, 2000). A SA (Selective Availability), que é uma degradação intencional da precisão do GPS para uso civil, foi desativada em 2000, porém existe uma nova técnica chamada SD (Selective Denial), que consiste em bloquear todo o sinal do GPS em uma certa região instalando transmissores de interferência no local. Os sinais transmitidos fornecem dados sobre as efemérides dos satélites GPS (mensagem de navegação) bem como informações de tempo atômico GPS e outras informações consideradas relevantes (saúde dos satélites, almanaque, deriva dos relógios de bordo etc.) Segmento de Controle Este segmento tem a função de gerar o tempo GPS e as efemérides dos satélites. É também responsável pelo gerenciamento dos satélites atualizando periodicamente as informações que são transmitidas a cada um, como efemérides, status, dados de relógio e almanaque. Para isso, existe a Estação Mestre de Controle (MCS, Master Control Station) localizada na base de Schriever (antigamente Falcon) Air Force, Colorado, Estados Unidos. Juntamente com esta existem outras estações de monitoramento localizadas em Colorado Springs, Havaí, Kwajalein, Diego Garcia e Ascención Island. Com o desenvolvimento e aprimoramento do sistema foram integradas a este segmento sete estações pertencentes ao NIMA (National Imagery 40
41 Figura 2.1 Representação da constelação de satélites GPS. Fonte: Dana (2000). Mapping Agency) que estão localizadas no Equador, Argentina, Inglaterra, Bahrein, Austrália, China e USNO (United States Naval Observatory) Segmento Usuário O segmento usuário consiste basicamente de receptores militares e civis projetados especialmente para decodificar e processar os sinais que recebem dos satélites. O receptor computadorizado grava as transmissões de vários satélites e aplica algoritmos de solução para obtenção de posição, velocidade e tempo (solução de navegação). Figura 2.2 Segmentos do GPS. 41
42 2.2 Determinação da Posição e Tempo Um receptor GPS mede a diferença de tempo entre a transmissão do sinal pelo satélite e a recepção. Essa diferença multiplicada pela velocidade da luz resulta na distância com relação ao satélite. Como a posição do satélite é conhecida através da mensagem de navegação, o receptor deve então estar localizado em uma esfera de raio igual à distância medida centrada no satélite. Medindo a distância com relação a três satélites, a localização do receptor se reduz a dois pontos definidos pela interseção das esferas referentes a cada satélite. O ponto que coincide com a superfície da Terra é a posição do receptor e o outro é chamado ponto-espelho. A determinação precisa do tempo é um fator crítico, já que a distância é medida a partir de diferenças de tempo. Portanto, todos os elementos do sistema devem manter uma sincronização de tempo. Os satélites possuem relógios atômicos a bordo para manter a sincronização com o tempo GPS, que são monitorados pela MCS e seus desvios com relação ao tempo GPS são repassados ao usuário juntamente com a mensagem de navegação (Leick, 1995). Inicialmente, o relógio do receptor não está sincronizado com o tempo GPS. Logo, sua sincronização deve ser tomada como parte da solução de navegação. Este desvio do relógio causa um erro na medida de distância, que é o mesmo para cada satélite. Se o receptor rastreia quatro satélites simultaneamente, o desvio do relógio pode ser estimado juntamente com as três coordenadas de posição. Portanto, o problema básico de posicionamento por GPS envolve a sincronização de relógio juntamente com a determinação das coordenadas de posição. 2.3 Observáveis O sinal do GPS é composto de um código de baixa freqüência (código-c/a, código- P) modulado em uma onda portadora de alta freqüência (L 1, L 2 ). Há vários tipos de medidas que podem ser obtidas dos componentes de código e de fase do sinal. Os dois principais observáveis do GPS são pseudodistância e fase da portadora. 42
43 2.3.1 Pseudodistância A pseudodistância é uma medida da distância entre o satélite, no instante de envio do sinal, e a antena do receptor no instante de recepção, obtida através da medida do tempo de percurso do sinal. O tempo de percurso é medido através da correlação entre o código PRN recebido do satélite e uma réplica do código gerado internamente pelo receptor. A diferença de tempo que sincroniza a réplica com o código recebido é a medida do tempo de percurso do sinal entre o satélite e o receptor. Os relógios do satélite e do receptor possuem desvios do tempo GPS, que fazem a distância medida ser diferente da distância geométrica. Além dos erros de relógio, a distância medida é afetada também por outros fatores como desvios ionosférico e troposférico, multicaminho, erros internos do receptor, entre outros, e por isso é chamada de pseudodistância. Assim, o modelo matemático para a pseudodistância ρ i u entre o satélite i e o receptor u tem a forma: (Leick, 1995; Parkinson, 1996b) ρ i u = D i u + c (b u B i ) + T i u + I i u + ɛ i ρ,u (2.1) onde Du i = R i r u é a distância geométrica, R i é a posição do satélite, r u é a posição da antena do receptor, b u é o desvio do relógio do receptor, B i é o desvio do relógio do satélite i, Tu i é o erro troposférico, Iu i é o erro ionosférico, ɛ i ρ,u representa os outros erros e c é a velocidade da luz, m/s. Esta medida é também chamada de pseudodistância via código Fase da Portadora A medida da fase é a diferença entre a fase da onda portadora recebida do satélite e a fase gerada internamente no receptor. Esta medida não leva em conta o número de comprimentos de onda entre o receptor e o satélite. A fase da portadora ϕ i u é escrita como: (Leick, 1995; Parkinson, 1996b) ϕ i u = 1 λ [ ] D i u + c (b u B i ) + Tu i Iu i + N i u + ɛ i ϕ,u (2.2) 43
44 onde λ é o comprimento de onda da portadora e Nu i denota a ambigüidade no número de comprimentos de onda. O termo Iu i troca de sinal com relação à pseudodistância via código e ɛ i ϕ,u representa um erro aleatório na medida e é menor que o erro da pseudodistância via código. A medida de pseudodistância via fase φ i u é obtida multiplicando-se a fase ϕ i u pelo comprimento de onda λ: φ i u = λ ϕ i u = Du i + c (b u B i ) + Tu i Iu i + λ Nu i + ɛ i φ,u (2.3) 2.4 Fontes de Erros Erros dos Relógios dos Satélites O tempo GPS é gerado pelo segmento de controle através de redes de relógios atômicos em suas bases de rastreamento. Cada satélite GPS carrega a bordo dois relógios atômicos de césio e rubídio, que eventualmente apresentam desvios com relação ao tempo GPS e necessitam de correção. Para o relógio do receptor, a correção é parte integrante da solução de navegação. Os dados das efemérides do satélite, transmitidos através da mensagem de navegação, são relativos ao tempo GPS t. O relógio dos satélites, porém, possuem desvios com relação a este tempo de referência. Assim, cada satélite transmite as efemérides em seu próprio sistema de tempo t i, diferente do tempo GPS, t = t i t i. A correção t i é obtida usando coeficientes transmitidos pelo satélite na mensagem de navegação. O termo de correção do relógio do satélite é aproximado pelo polinômio: t i = a f0 + a f1 (t i t oc ) + a f2 (t i t oc ) 2 + t R (2.4) onde a f0, a f1 e a f2 são os coeficientes transmitidos na mensagem de navegação, t oc é o tempo de referência das efemérides e t R é uma correção relativística devido à velocidade relativa entre o satélite e o receptor, dada em função do semi-eixo maior a, da excentricidade e da órbita e da anomalia excêntrica E por t R = 2 c 2 aµ e sen E (2.5) 44
45 onde µ é o parâmetro gravitacional da Terra e c é a velocidade da luz Erro Devido à Troposfera O erro troposférico é causado pelo atraso no percurso do sinal devido à refração do sinal na troposfera. A maior parte desse erro é causada pelo chamado componente seco da atmosfera (gases como N 2, O 2 etc.). A outra parte (componente úmido) é causada pelo vapor de água presente na atmosfera. O componente seco do erro é função da pressão na superfície e da temperatura e é estável e previsível, com precisão de 2-5%. Este componente contribui com cerca de 90% do total da refração. O erro causado pelo vapor de água é menor, mas muito menos estável, pois varia em função da umidade relativa ou do deslocamento do receptor. Nas freqüências de operação do GPS, a troposfera é não-dispersiva, isto é, o desvio não depende da freqüência. Assim, este desvio não pode ser eliminado através de medidas em duas freqüências (Spilker Jr., 1996). Sendo dependente das condições atmosféricas locais, este erro não é compensado por nenhum parâmetro transmitido na mensagem de navegação. O erro troposférico é compensado por métodos definidos pelo usuário que geralmente dependem da altitude, ângulo de elevação dos satélites e às vezes da temperatura e umidade. Alguns modelos de correção são descritos em Goad e Goodman (1974); Black (1978) e Hopfield (1979) Erro Devido à Ionosfera A ionosfera é uma região de gases ionizados na atmosfera que afetam o sinal GPS. É uma região altamente variável produzida pela radiação ionizante do sol. Desse modo, o erro ionosférico pode variar rapidamente de alguns metros a várias dezenas de metros no zênite durante curtos períodos de tempo. A ionosfera é um meio dispersivo, ou seja, o índice de refração depende da freqüência da onda portadora. Assim, podese utilizar medidas em ambas as freqüências L 1 e L 2 para medir e corrigir os efeitos gerados na propagação do sinal (Klobuchar, 1996). A mensagem de navegação contem um modelo de correção ionosférico para usuários de freqüência única, mas sua eficiência é bastante reduzida em condições anormais, 45
46 como em picos de atividade solar (Yuan e Ou, 2001). Os principais efeitos causados pela ionosfera no sinal são atraso de grupo, avanço de fase e cintilação da amplitude (Christie et al., 1998) Multicaminho Multicaminho é o fenômeno no qual um sinal chega à antena do receptor através de vários caminhos atribuídos a reflexão e difração. Esse efeito distorce as modulações dos códigos C/A e P e observações de fase. Os sinais provenientes do multicaminho estão sempre atrasados comparados com o sinal direto devido à maior distância percorrida causada pela reflexão. O impacto do multicaminho nas medidas de pseudodistância ou fase da portadora depende de uma variedade de fatores, como potência e atraso do sinal refletido comparado com o sinal direto, características de atenuação da antena e sofisticação do receptor (Braasch, 1996) Erro do Centro de Fase da Antena Para uma dada antena de GPS, o centro de fase mudará com a mudança da direção do sinal de um satélite. Idealmente, a maior parte da variação do centro depende da elevação do satélite. O procedimento de calibração normalmente envolve a colocação de uma antena de referência em duas diferentes posições e diferenciando os dados para determinar o desvio do centro de fase (Stolk e Brown, 2003). 46
47 CAPÍTULO 3 METODOLOGIA Este Capítulo aborda os métodos de estimação por mínimos quadrados e filtro de Kalman, utilizados neste trabalho. Os conceitos básicos de posicionamento por GPS e GPS diferencial também são descritos. 3.1 Método de Mínimos Quadrados O método de mínimos quadrados é um algoritmo para estimar parâmetros, ou seja, estimar valores que são constantes ao longo do processo. É necessário medir direta ou indiretamente o que se deseja estimar de modo que para começar o processo de estimação necessita-se de um conjunto de medidas que esteja relacionada ao parâmetro. Desse modo torna-se fundamental a modelagem de como essas medidas se relacionam aos parâmetros a serem estimados (Kuga, 2002). A equação que relaciona as medidas aos parâmetros é formulada como uma equação linear: y = Hx (3.1) Formalmente, o algoritmo trata de minimizar um índice de desempenho do quadrado dos resíduos na forma: L = (y Hx) T W(y Hx) (3.2) onde y representa o vetor contendo m medidas, x representa o vetor de n parâmetros a serem estimados, e H é uma matriz m n que relaciona as medidas aos parâmetros e W é uma matriz de peso que pondera os diferentes tipos de erros. O valor estimado de x para m n e sua covariância P para o processamento em lotes, isto é, que processa as medidas todas de uma só vez, são dados por: ˆx = (H T WH) 1 H T Wy P = (H T WH) 1 (3.3) Este processamento também pode ser feito de forma recursiva, também chamada de forma de Kalman, na qual processa uma medida por vez. As equações para 47
48 i = 1... m são: K i = P i 1 H T i (H i P i 1 H T i + 1/w i ) 1 P i = (I K i H i )P i 1 ˆx i = ˆx i 1 + K i (y i H iˆx i 1 ) onde w i é o i-ésimo elemento da diagonal de W e y i é o i-ésimo elemento de y. (3.4) Para que o método de mínimos quadrados possa ser um estimador de estados, deve-se incluir no processo de estimação um modelo para a evolução dos estados no tempo. A equação que descreve essa evolução é dada, no caso discreto, por: x k+1 = Φ k+1,k x k (3.5) onde Φ k+1,k é a matriz de transição que relaciona os estados entre os instantes t k e t k+1. Assim, a estimativa de ˆx k é dada em função da estimativa inicial do estado ˆx 0 por ˆx k = Φ k,0ˆx 0 (3.6) pois Φ k+1,k 1 = Φ k+1,k Φ k,k 1. Desse modo pode-se reescrever a Equação (3.1) em função de ˆx 0 : com y = y 1 y 2. y = Hˆx 0 (3.7) H 1 Φ 1,0 e H = H 2 Φ 2,0.. y k H k Φ k,0 3.2 Filtro de Kalman O filtro de Kalman é um conjunto de equações matemáticas que fornece uma solução recursiva do problema de estimar o estado de um sistema baseado em medidas de dados com ruídos. Ele combina todas as medidas, o conhecimento a priori da dinâmica do sistema e equipamentos de medidas, estatísticas do ruído do sistema dinâmico e erros de medidas, além de informações da condição inicial para produzir uma estimativa do estado, de tal maneira que o erro é minimizado estatisticamente (Maybeck, 1979). Esse filtro é um estimador linear, ou seja, supõe-se que as equações de dinâmica e de observações sejam funções lineares do estado. Desse modo, existem técnicas que permitem que o filtro seja usado em problemas não-lineares, como o 48
49 filtro de Kalman estendido (Gelb et al., 1974; Stovall, 1997). A equação da dinâmica, que descreve a evolução do estado no tempo, é modelada pela equação diferencial linear: ẋ = Fx + Gω (3.8) onde x é o vetor com n estados, F é a matriz do sistema n n e pode ser função do tempo t, ω é um vetor de r ruídos brancos da modelagem da dinâmica e G é uma matriz n r de adição de ruído, com E[ω(t)] = 0 E[ω(t)ω(τ) T ] = Q(t)δ(t τ) (3.9) O operador E[ ] significa o operador esperança, Q é a matriz de densidade espectral de potência de ω e δ(t τ) é a função delta de Dirac. As observações são geralmente discretas e modeladas pela equação linear discreta no tempo: y k = H k x k + ν k (3.10) onde y k é um vetor contendo m observações, H k é uma matriz m n que relaciona o vetor de estado com as observações e ν k é uma seqüência branca, de dimensão m, que representa o ruído nas medidas, com E[ν k ] = 0 E[ν k ν T l ] = R kδ kl (3.11) onde R k é a matriz de covariância dos ruídos das medidas e δ kl e a função delta de Kronecker. Os ruídos da dinâmica ω e de observação ν são não-correlacionados entre si e nãocorrelacionados com o estado inicial x(t 0 ) (Brown e Hwang, 1996), ou seja, E[ω(t k )ν T k ] = 0 E[x(t 0 )ν T k ] = 0 E[x(t 0 )ω T (t)] = 0 (3.12) 49
50 No início do processo, é necessário ter uma estimativa do estado ˆx 0 e sua covariância ˆP 0. Esse estado inicial e sua covariância são então propagados até o instante da medida através da equação de modelo de dinâmica. O estado ˆx k e covariância ˆP k atualizados são formados a partir da combinação dos estado e covariância propagados do instante anterior para o instante atual com as informações das medidas processadas. A estimação dos estados consiste, assim, de duas fases: propagação e atualização. O método tem, portanto, natureza recursiva e não necessita armazenar as medidas previamente em grandes matrizes, sendo bastante útil para aplicações em tempo real (Gelb et al., 1974; Kuga, 2002) Sintonização do filtro O grau de otimização do filtro de Kalman está ligado à qualidade da informação a priori sobre as covariâncias dos ruídos de medidas R k e da densidade espectral do ruído da dinâmica Q k. Estes fatores descrevem a precisão do conhecimento desses modelos. Em muitas aplicações, essas covariâncias são conhecidas antes da operação do filtro e mantêm-se constantes durante o processo. Se estas informações são inadequadas, a estimação pode gerar resultados com desvios ou podem levar à divergência do filtro (Kuga, 1989; Hu et al., 2001). A covariância do ruído das medidas R k é geralmente obtida através de algumas amostras da medida, tomadas antes do início da operação do filtro. A densidade espectral do ruído do processo Q k é mais difícil de se obter, pois não é possível medir o processo diretamente. Pode-se obter resultados aceitáveis introduzindo incerteza suficiente na dinâmica. Outro modo de determinar Q k é utilizar algoritmos adaptativos (Rios Neto e Kuga, 1982; Rios Neto e Kuga, 1986; Brown e Hwang, 1996; Welch e Bishop, 2001) Propagação As equações da fase de propagação do instante k 1 para o instante k para o estado são dadas por: x = F x Φ = FΦ (3.13) 50
51 onde Φ k,k 1 é a matriz de transição de estado entre os instantes k 1 e k. A barra significa estado propagado antes de ser atualizado e o circunflexo indica estado atualizado. Estas equações são resolvidas através de algum método de integração numérica, com condições iniciais x k 1 = ˆx k 1 e Φ k 1,k 1 = I, onde I é a matriz identidade. A matriz de transição Φ descreve a evolução do erro de estimação entre instantes diferentes. No caso de F ser constante, a matriz de transição pode ser calculada analiticamente por: Φ k,k 1 = e Fδt = I + Fδt + 1 2! (Fδt) (3.14) onde δt é o intervalo de tempo entre os instantes das medidas (Brown e Hwang, 1996). A propagação da matriz de covariância é dada pela equação: P k = Φ k,k 1 ˆP k 1 Φ T k,k 1 + Γ k QΓ T k (3.15) onde Γ k QΓ T k = k k 1 Φ τ,k 1 G(τ)Q(τ)G T (τ)φ T τ,k 1dτ Atualização Após a estimativa do estado e covariância serem propagados até o instante da observação atual k, faz-se a atualização a partir das seguintes equações: K k = P k H T k (H k P k H T k + R k) 1 ˆx k = x k + K k (y k H k x k ) (3.16) ˆP k = (I K k H k ) P k onde K k é o ganho de Kalman e R k é a matriz de covariância dos erros de observação e I é a matriz identidade Filtro de Kalman Estendido Assume-se agora que a dinâmica do estado e as observações são descritas por equações não-lineares com relação ao estado: 51
52 ẋ = f(x, t) + Gω (3.17) e y k = h k (x k ) + ν k (3.18) Estas equações devem então ser linearizadas para a utilização no filtro. A linearização é feita através de uma expansão em série de Taylor em torno da melhor estimativa do estado disponível. Assim, linearização da função f truncada no termo linear fica: [ ] f f = f( x, t) + (x x) (3.19) x x= x [ ] f Definindo-se os desvios δx = x x, δẋ = ẋ x = ẋ f( x, t) e F = tem-se x x= x então: δẋ = Fδx + Gω (3.20) A equação das observações é linearizada expandindo-se h k em série de Taylor e truncando no termo linear: [ ] hk y k = h k ( x) + (x x) + ν k (3.21) x x= x [ ] hk Definindo-se o desvio δy k = y k h k ( x k ) e H k = tem-se a equação das x x= x observações linearizada: δy k = H k δx k + ν k (3.22) Assim, as equações da fase de propagação do estado e da matriz de transição são: x = f( x, t) Φ = FΦ (3.23) A matriz de covariância é propagada através de: P k = Φ k 1,k ˆP k 1 Φ T k 1,k + Γ k QΓ T k (3.24) A fase de atualização então toma a forma (Brown e Hwang, 1996; Kuga, 2001, 2002): 52
53 K k = P k H T k (H k P k H T k + R k) 1 ˆx k = x k + K k [y k h k ( x k )] (3.25) ˆP k = (I K k H k ) P k 3.3 Posicionamento Absoluto O posicionamento absoluto consiste na obtenção da solução de navegação de um receptor. Basicamente isso pode ser feito através da linearização da equação da pseudodistância (Equação 2.1) em torno da estimativa de posição atual: ρ i u = ρ i u ˆρ i u = = [ Xi ˆx u ρ i u Y i ŷ u ρ i u Zi ẑ u ρ i u x u ] 1 y u z u c Bi + Tu i + Iu i + ɛ i c b u (3.26) onde ρ i u é a pseudodistância medida, ˆρ i u é a pseudodistância calculada com base [ ] T na estimativa ˆx u, ρ i u é o resíduo da observação, X i = X i Y i Z i é a posição [ ] T do satélite GPS, x = x u y u z u c b u é um vetor contendo as coordenadas de posição (x u, y u, z u ) e o desvio do relógio (c b u ) do receptor, x u = x u ˆx u e o circunflexo representa estimativa da variável (Axelrad e Brown, 1996). O processo é iterativo e, dada uma condição inicial de posição do usuário (e.g. via Bancroft, 1985), obtém-se convergência por algum dos algoritmos citados nas seções anteriores (seções 3.1 e 3.2) ou outro método. Nota-se desta forma que os erros representados pelo vetor de ruído impactam a precisão do resultado. Outro algoritmo (Lopes e Kuga, 1988) propõe o processamento de medidas de todos os satélites GPS, sem restringir-se aos 4 melhores satélites GPS escolhidos normalmente pelo critério geométrico de melhor DOP (Dilution of Precision). A Tabela 3.1 mostra a contribuição de cada fonte de erro na precisão da estimativa da posição para o posicionamento absoluto. 53
54 Tabela 3.1 Balanço de Erros do GPS (SA Destivada). Fonte de erro Sistemático (m) Aleatório (m) Total (m) Efemérides GPS 2,1 0,0 2,1 Relógio do GPS 2,0 0,7 2,1 Ionosfera 4,0 0,5 4,0 Troposfera 0,7 0,5 0,7 Multicaminho 1,0 1,0 1,4 Medida do receptor 0,5 0,2 0,5 UERE (RMS) 5,1 1,4 5,3 UERE Filtrado (RMS) 5,1 0,4 5,1 1 sigma vertical VDOP = 2,5 12,8 1 sigma horizontal HDOP = 2,0 10,2 Fonte: Parkinson (1996b). 3.4 Posicionamento Diferencial Esta seção descreve os princípios básicos utilizados para o posicionamento via GPS diferencial GPS Diferencial O GPS diferencial (DGPS, differential GPS) é uma técnica que aumenta significativamente a precisão do posicionamento do usuário. O princípio básico do posicionamento por DGPS consiste em colocar um receptor num local fixo, comumente denominado de base, onde as suas coordenadas são precisamente conhecidas. Se as coordenadas da base são conhecidas, pode-se calcular quais deveriam ser os valores verdadeiros das medidas de pseudodistância. A comparação do valor verdadeiro com aquele que foi medido fornece os valores de correção que devem ser aplicadas a cada pseudodistância provinda de cada satélite GPS. A Figura 3.1 mostra o conceito do GPS diferencial. A aplicação desta técnica deve obedecer algumas hipóteses: O usuário deve estar próximo da base de referência (até cerca de 150km); A correção calculada na base para a pseudodistância de um dado satélite deve 54
55 ser aplicada à pseudodistância medida pelo usuário com relação ao mesmo satélite; As estimativas da base estimam os erros de variação lenta (em geral os erros atmosféricos e de relógio). Figura 3.1 Conceito de GPS diferencial. Fonte: Parkinson e Enge (1996). Para distâncias maiores, existe a técnica de WADGPS (Wide Area Differential GPS). Esta técnica calcula as correções baseadas em uma rede de bases de referência amplamente distribuída. O problema da distância do usuário à base de referência não é crítico e as correções são válidas para uma grande região geográfica. Desde que as correções são baseadas em uma rede de pontos de referência, as incertezas associadas com o uso das correções de uma única base são efetivamente removidas. Em síntese, o DGPS consiste em duas fases bem definidas: Gerar correções na base de referência; Aplicar correções no receptor usuário. A correção deve ser calculada diretamente na base de referência. A Equação (2.1) pode ser escrita na forma (Parkinson, 1996b; Parkinson e Enge, 1996): ρ b + δρ = SR s Hx ref (3.27) 55
56 onde ρ b é o vetor contendo as m pseudodistâncias medidas pela base referentes 1 T 1 0 R 1 a cada satélite, δρ corresponde às correções, S =..., R s =., 0 1 T m R m [ ] ˆxref X i ŷ ref Y i ẑ ref Z i H = 1 e x ref é o vetor com as coordenadas da ˆρ i b base de referência. ˆρ i b ˆρ i b Assim, as correções podem ser calculadas por: δρ = SR s Hx ref ρ b (3.28) Essa correção corresponde às correções individuais que devem ser aplicadas às medidas de pseudodistância do usuário. Portanto, o usuário remoto dispõe agora da seguinte equação para resolver o problema, dadas as suas medidas de pseudodistância coletadas: Hx u = SR s ρ u δρ (3.29) que deverá ser resolvida pelos métodos descritos anteriormente. Os seguintes cuidados devem ser tomados (Farrell e Givargis, 2000): Ambos, a base e o usuário, não devem aplicar a correção ionosférica provinda da mensagem de navegação do GPS; Ambos devem utilizar o mesmo conjunto de efemérides dos satélites GPS mesmo que algum deles disponha já de uma atualização; A base deve tentar não introduzir erros que não são mensuráveis pelo usuário, por exemplo, o multicaminho; O tempo da correção deve ser passado ao usuário, já que poderá existir uma latência devido ao enlace de rádio utilizado para transmitir as correções; As medidas da pseudodistância devem ser simultâneas. As correções diferenciais são bastante efetivas com relação a erros de relógio porque sua validade contra estes erros diminui apenas com o tempo, e não com a distância. Assim, o erro do posicionamento por DGPS cresce com a idade das correções. Neste 56
57 método, a magnitude do erro residual da ionosfera na pseudodistância depende principalmente da separação do usuário e a base e do ângulo de elevação dos satélites (Parkinson e Enge, 1996) e, que para linhas de base muito grandes, deve-se aplicar correções também para o erro da ionosfera (Kee e Yun, 2002). A Tabela 3.2 fornece um balanço de erros compreendendo os diversos tipos de erros que afetam a precisão do DGPS, usando-se as medidas de pseudodistância. A nomenclatura para as siglas é a seguinte: RMS (Root Mean Square) é a raiz média quadrática, UERE (User Equivalent Range Error) é o erro em distância equivalente ao usuário, e DOP (Dilution of Precision) é a diluição de precisão na vertical (VDOP) ou na horizontal (HDOP). O DOP representa o traço de uma matriz de covariância dos erros a menos de um fator de escala, e valores padrão de VDOP e HDOP são dados na Tabela 3.2. Tabela 3.2 Balanço de Erros do DGPS para Usuários a 50km da Base de Referência (SA desativada). Fonte de erro Sistemático (m) Aleatório (m) Total (m) Efemérides GPS 0,0 0,0 0,0 Relógio do GPS 0,0 0,7 0,7 Ionosfera 0,0 0,5 0,5 Troposfera 0,0 0,5 0,5 Multicaminho 1,0 1,0 1,4 Medida do receptor 0,0 0,2 0,2 Base de referência 0,3 0,2 0,4 UERE (RMS) 1,0 1,4 1,8 UERE Filtrado (RMS) 1,0 0,4 1,1 1 sigma vertical VDOP = 2,5 2,8 1 sigma horizontal HDOP = 2,0 2,2 Fonte: Parkinson e Enge (1996) Observações de Simples Diferença O observável chamado simples diferença é formado tomando-se a diferença das medidas em dois receptores em uma mesma época. A simples diferença para a medida 57
58 de pseudodistância é dada por (Misra e Enge, 2001): ρ i ub = ρ i u ρ i b = (Du i Db) i + (b u b b ) + (Tu i Tb) i + (Iu i Ib) i + (ɛ i ρ,u ɛ i ρ,b) = Dub i + b ub + Tub i + Iub i + ɛ i ρ,ub (3.30) onde ( ) ub = ( ) u - ( ) b, o índice u se refere ao usuário e o índice b se refere à base. O termo de desvio do relógio do satélite B i, que é comum às duas medidas, é cancelado. Os termos troposféricos e ionosféricos são diferenças dos desvios correspondentes nos dois receptores. A magnitude destes termos depende principalmente da distância de separação dos receptores (linha de base). Quando a distância entre os receptores for pequena, os resíduos ionosféricos e troposféricos se tornam pequenos em comparação com os erros devido ao multicaminho e ruídos do receptor. Desse modo, para uma linha de base pequena, a medida de simples diferença para a pseudodistância via código é ρ i ub = Dub i + b ub + ɛ i ρ,ub (3.31) Analogamente, a simples diferença correspondente à pseudodistância via fase é φ i ub = Dub i + b ub + λ Nub i + ɛ i φ,ub (3.32) onde Nub i = N u N i b i é a diferença entre as ambigüidades inteiras de ambos receptores e λ é o comprimento de onda da portadora Observações de Dupla Diferença O termo do desvio de relógio relativo b ub é comum a todas as medidas de simples diferença de todos os satélites em cada época. Este termo pode então ser eliminado através de medidas de dupla diferença, que são formadas através da subtração de duas simples diferença relativos a dois satélites distintos i e j. ρ ij ub = ρi ub ρ j ub (3.33) 58
59 Com a Equação (3.31) tem-se ρ ij ub = (Di ub D j ub ) + (ɛi ρ,ub ɛ j ρ,ub ) = Dij ub + ɛij ρ,ub (3.34) onde ( ) ij ub = ( )i ub - ( )j ub. Em particular, ρij ub pode ser formado por: ρ ij ub = (ρi u ρ i b) (ρ j u ρ j b ) (3.35) Esta observável é freqüentemente utilizada por eliminar todos os termos que geram erros de relógio, de atmosfera, atenuando por vezes o efeito do multicaminho. Por outro lado, nota-se que a precisão desse tipo de medida é deteriorada, além de introduzir correlações entre medidas realizadas no mesmo instante (seção 4.3). 59
60 60
61 CAPÍTULO 4 ALGORITMOS DE GPS DIFERENCIAL 4.1 GPS Diferencial na Posição Esta técnica de GPS diferencial consiste em calcular as correções no receptor base e aplicá-las no usuário utilizando a solução de navegação de ambos os receptores. Neste método de DGPS, cada receptor (base e usuário) calcula sua posição independentemente através de um mesmo algoritmo, por exemplo, um método de mínimos quadrados. É necessário que os dois receptores utilizem o mesmo conjunto de satélites. Deste modo, a contribuição de cada satélite para o erro é praticamente a mesma em ambos os receptores (Martínez et al., 2000). A Equação (2.1) define a medida de pseudodistância para o receptor u como função da posição [ ] T r u = x u y u z u e do desvio do relógio bu. Esta equação deve ser linearizada, resultando em [ ρ i u = ρ i u ˆρ i ˆxu X i u = onde R i = ˆρ i u ŷ u Y i ˆρ i u ẑ u Z i ˆρ i u x u ] 1 y u z u + ɛi ρ,u (4.1) c b u [ ] T ] T X i Y i Z i é o vetor posição do satélite i e xu = [x u y u z u c b u é o vetor de estados a ser estimado, contendo a posição e o desvio do relógio do receptor u. O modelo de medidas não apresenta os termos de erros atmosféricos, pois assume-se que estes serão eliminados com a aplicação das correções. A correção é calculada na base diretamente por comparação entre as coordenadas calculadas e as coordenadas da referência: onde δr é a correção diferencial, r ref = coordenada calculada pela base. δr = r ref r b (4.2) [ ] T [ ] T x ref y ref z ref e rb = x b y b z b é a 61
62 A posição do usuário r u pode ser modelada, em analogia com a Equação (2.1) da pseudodistância, por r u = r g + b B + T + I ono + ɛ (4.3) onde r g é a posição geométrica, b é o termo de desvio do relógio do receptor, que faz parte da solução de navegação, B é o termo de desvio do relógio do satélite, transmitido na mensagem de navegação, T e I são os termos de erros troposféricos e ionosféricos e ɛ são erros não modelados (multicaminho, atrasos internos do receptor etc.) assumido ruído branco. Como a linha de base entre os receptores é pequena, assume-se que os erros troposféricos e ionosféricos são os mesmos para ambos. Assim, a correção calculada pela base pode ser aplicada diretamente: ˆr u = r u + δr (4.4) onde ˆr u é a posição corrigida e r u é a posição calculada a partir das pseudodistâncias medidas pelo receptor usuário. 4.2 GPS Diferencial na Pseudodistância Neste método, as correções diferenciais são aplicadas diretamente nas medidas de pseudodistância. Este método baseia-se no fato de que se as coordenadas da base são conhecidas, pode-se calcular o valor da pseudodistância verdadeira para cada satélite, levando em consideração os erros do relógio do satélite e receptor. A correção consiste na diferença entre a pseudodistância verdadeira e a medida pela base (Equação 4.6). A pseudodistância corrigida é obtida somando-se a correção na pseudodistância medida e esta é então usada para calcular a posição do receptor. Os termos de erros atmosféricos não devem ser incorporados no cálculo da pseudodistância verdadeira, pois tomarão parte na correção diferencial Correções na Pseudodistância A pseudodistância verdadeira entre a base e o i-ésimo satélite GPS ˆρ i b é calculada baseando-se na Equação (2.1), mas desconsiderando os termos troposférico e ionosférico, ou seja, ˆρ i b = ˆD b i + c b b (4.5) 62
63 O termo ˆD i b = Ri r ref corresponde à distância geométrica e é calculado através das efemérides satélite na época da transmissão do sinal e das coordenadas de referência da base. A posição dos satélites GPS é requerida no instante da transmissão, porém, o instante da recepção é usado para computá-la. Isto é feito subtraindo-se o tempo de percurso τ do sinal do instante de recepção. O tempo de percurso é calculado através de um processo iterativo que inicia assumindo um valor de τ médio (Chiaradia et al., 2000). Então, a posição é interpolada para a época t τ que é usada para computar a distância geométrica. A correção δρ i gerada na base é simplesmente a diferença entre a pseudodistância calculada com as coordenadas da referência ˆρ i b e a pseudodistância medida pela base ρ i b : δρ i = ˆρ i b ρ i b (4.6) Esta correção cobre, na maior parte, os erros atmosféricos devido à proximidade entre os receptores e os erros na modelagem do relógio Estimação da Posição do Usuário A correção da base δρ i é usada para corrigir a medida de pseudodistância do satélite correspondente no usuário: ρ i corr,u = ρ i u + δρ i (4.7) onde ρ i corr,u é a pseudodistância corrigida e ρ i u é a pseudodistância medida. A posição do usuário é então computada a partir do processamento deste conjunto de medidas corrigidas. O receptor obedece ao modelo dinâmico, descrito por: ẋ u = Fx u + Gω u (4.8) onde F é a matriz que relaciona o estado e sua derivada linearmente, ω u é a matriz contendo os ruídos da modelagem dinâmica e G é a matriz de adição de ruído. ω u 63
64 é assumido ruído branco, logo: E[ω u ] = 0 E[ω u (t)ω T u (τ)] = Q(t)δ(t τ) (4.9) onde Q é a densidade espectral de potência do processo branco. A matriz de transição de estados do tempo k 1 para k correspondente a este modelo, de acordo com a Equação (3.14), e assumindo que o intervalo de tempo δt é pequeno, é dada por: Φ k,k 1 = I + Fδt (4.10) Desse modo a propagação do estado e sua covariância do tempo k 1 para k é feita através das equações: x u,k = Φ k,k 1ˆx u,k 1 P u,k = Φ k,k 1 ˆP u,k 1 Φ T k,k 1 + Γ kqγ T k (4.11) onde Γ k QΓ T k é a matriz de adição de ruído dinâmico na propagação do estado, e pode ser calculada pelo método da seção 4.4. A obtenção do modelo de medidas, no instante k, para este método pode ser obtida a partir da linearização Equação (2.1). Realizando uma expansão de Taylor em torno da estimativa do estado atual, o resíduo das medidas pode ser escrito como uma função linear do erro do estado estimado: ρ i u = H k x + ɛ u (4.12) [ ] D i onde H k = u, ρ i u = ρ i corr,u ˆρ i u consiste no resíduo das medidas e x u x=ˆx x u = x u ˆx u. Utilizando este modelo, a fase de atualização deste filtro tem a forma: K u,k = P u,k H T k (H k P u,k H T k + R ρ) 1 ˆx u,k = x u,k + K u,k (ρ corr,u ˆρ u ) (4.13) ˆP u,k = (I K u,k H k ) P u,k onde R ρ é a matriz de covariância dos erros de medida. As medidas de pseudo- 64
65 distância são assumidas não-correlacionadas entre si, de modo que R ρ tem a forma diagonal. 4.3 Posicionamento por Dupla Diferença Este método de posicionamento combina as medidas de pseudodistância provenientes de ambos os receptores para gerar os observáveis de dupla diferença (seção 3.4.3). As observações de dupla diferença são construídas escolhendo-se um satélite mestre M, geralmente pelo critério de maior elevação no início do período de observações e realizando as subtrações com as outras medidas. Este procedimento garante um conjunto de dupla diferenças linearmente independentes (Saalfeld, 1999; Janssen, 2001). O conjunto de medidas é então formado por: ρ Mi ub = (ρ M u ρ M b ) (ρ i u ρ i b), i = 1... m, i M (4.14) onde m é o número de satélites visíveis. Assim, tem-se um conjunto de m 1 medidas de dupla diferença. Esta equação também pode ser escrita, de acordo com a Equação (3.34), em função das distâncias geométricas ρ Mi ub = (D M u D M b ) (D i u D i b) + ɛ Mi ub (4.15) Considerando que a linha de base é menor que a distância entre os receptores e os satélites por ordens de magnitude, pode-se definir a seguinte relação, com base na Figura 4.1: onde 1 i b = [ xb X i ρ i b Dub i = Du i Db i = 1 i b x ub (4.16) ] y b Y i z b Z i é o vetor unitário apontando da base para ρ i b o satélite i e x ub representa a linha de base entre os receptores. ρ i b Utilizando a aproximação descrita, a Equação (4.15) se torna linear com relação à linha de base x ub : ρ Mi ub = (1 M b 1 i b)x ub + ɛ Mi ub (4.17) Esta equação constitui o modelo de medidas a ser considerado para a resolução do problema. Portanto, a aplicação do método de dupla diferença realiza um posicionamento relativo, pois permite a estimação da linha de base entre os receptores. 65
66 Figura 4.1 Geometria de uma observação. Fonte: Misra e Enge (2001). Como as observações de dupla diferença consistem de combinações entre as medidas de pseudodistância, o valor da matriz de covariância dessas observações pode ser calculado colocando-se a Equação (4.14) na forma matricial: z DD = D z ρ (4.18) [ ] T onde z DD = ρ M1 ub ρ Mm 1 ub é um vetor contendo as m 1 medidas de dupla diferença, z ρ = ρ M u ρ M b ρ 1 u ρ 1 b ρ m 1 u ρ m 1 b é um vetor contendo as [ ] T 2m medidas de pseudodistância observadas pelo usuário e pela base, dispostas alternadamente. A matriz D, de dimensões (m 1) (2m), é definida de modo a relacionar as pseudodistâncias observadas com as medidas de dupla diferença. Esta matriz assume então a seguinte forma: D = (4.19) Cada pseudodistância é medida com um erro cuja variância vale σ 2 0. Assim, a matriz 66
67 de covariâncias de z ρ é diagonal com a forma: cov[z ρ ] = σ 2 0 I (4.20) onde I é a matriz identidade de ordem 2m. De acordo com a Lei de Propagação de Covariâncias (Strang e Borre, 1997), a covariância de z DD, com relação à covariância de z ρ, é dada pela equação: R DD = cov[z DD ] = D cov[z ρ ] D T = D σ 2 0 D T (4.21) A matriz 2A = D D T, possui os elementos da diagonal principal com valor 4 e os elementos fora da diagonal com valor 2, logo: A =..... (4.22) Portanto a matriz R DD é dada pela expressão: R DD = 2σ0A 2 = 2σ (4.23) Branqueamento de Erros de Observação É bastante conveniente que a matriz R seja diagonal para fins de processamento seqüencial via filtro de Kalman. Este processo de diagonalização recebe usualmente o nome de branqueamento (Bierman, 1977). Neste caso, tem-se o seguinte modelo de medidas, dada pela Equação (4.17): z DD = Hx ub + ν (4.24) onde H = 1 M b 1i b e ν é um erro de observação com média zero, mas possui correlação 67
68 entre as medidas, isto é, E[ν] = 0 e E[νν T ] = R DD (4.25) com R DD sendo uma matriz positiva definida. Ao multiplicar a Equação (4.24) por L 1, com R 1 DD = L 1 L T, L 1 sendo triangular inferior, obtém-se um novo conjunto de observações, agora independentes, mas equivalentes ao conjunto antigo (Bierman, 1977): z DD = Hx ub + ν (4.26) com z DD = L 1 z DD, H = L 1 H e ν = L 1 ν. Este novo conjunto possui erro de observação com covariância unitária, pois E[ ν ν T ] = E[L 1 νν T L T ] = L 1 E[νν T ]L T = L 1 R DD L T = L 1 LL T L T = I (4.27) pois R 1 DD = (L 1 L T ) = (L T L) 1. A matriz L 1 pode ser obtida pela fatoração de R 1 DD Cholesky: pelo método de fatoração de R 1 DD = L 1 L T (4.28) A aplicação da fatoração de Cholesky nessa forma exige que R DD seja invertido. Entretanto, o formato de R DD na observação de dupla diferença possui inversa cujo valor pode ser calculado explicitamente Inversão da Matriz R DD R DD é uma matriz (m 1) (m 1) cujos elementos da diagonal principal têm o valor 4σ 2 0 e os elementos fora da diagonal têm o valor 2σ 2 0, dada pela Equação (4.23). 68
69 A matriz inversa do termo A =..... é dada por: A 1 = 1 m m.... (4.29) 1... m 1 Este resultado pode ser verificado calculando-se AA 1 = I Com isso, a matriz inversa de R DD é R 1 DD = 1 A 1 = 1 2σ0 2 2σ0m 2 m (4.30) 1... m Fatoração de Cholesky Se A é uma matriz n n positiva definida, então A pode ser fatorada na forma A = L L T (4.31) onde L é uma matriz triangular inferior com elementos das diagonais positivos. Essa fatoração é conhecida como fatoração de Cholesky (Ruggiero e Rocha, 1997) e pode feita através do seguinte algoritmo (Bierman, 1977): Para j = 1... n 1, executa-se o conjunto ordenado de equações recursivas: L j,j := A 1/2 j,j L k,j := A k,j /L j,j, k = j n A i,k := A i,k L i,j L k,j { k = j n i = k... n (4.32) e por fim L n,n := An,n 1/2, onde := em notação computacional significa o membro do lado esquerdo receber o valor do membro do lado direito. 69
70 4.3.4 Suavização Em comparação com ruídos da pseudodistância, ruídos de alta freqüência nas medidas de fase da portadora são muito pequenos, enquanto que seus erros de baixafreqüência (erros atmosféricos, ambigüidades etc.) tem características que levam a instabilidades na solução. Conseqüentemente, com uma eficiente combinação da informação fornecida pela fase da portadora com a da pseudodistância, uma redução significante do erro de estimação pode ser conseguida (Hwang e Brown, 1990). As medidas de fase permitem medidas precisas e sem ambigüidades da variação da pseudodistância entre duas épocas. Com isso, torna-se possível explorar esta característica para suavizar as medidas de pseudodistância (Misra e Enge, 2001). No entanto, a duração da janela de observação deve ser criteriosamente escolhida para o problema. Baseado na Equação (2.1), define-se a pseudodistância livre de erros ionosféricos ρ : ρ = D + c (b B) + T (4.33) As medidas de código e fase (equações 2.1 e 2.3) escritas em termos desta definição têm a forma: ρ(t) = ρ (t) + I(t) + ɛ ρ (t) (4.34) φ(t) = ρ (t) I(t) + λ N + ɛ φ (t) Tomando a diferença das medidas de pseudodistância via código ( ρ) e fase ( φ) entre duas épocas t i e t i 1 tem-se ρ(t i ) = ρ(t i ) ρ(t i 1 ) = ρ (t i ) + I(t i ) + ɛ ρ (t i ) φ(t i ) = φ(t i ) φ(t i 1 ) = ρ (t i ) I(t i ) + ɛ φ (t i ) (4.35) onde ρ é a mudança na pseudodistância livre de erros ionosféricos, I é a mudança no erro ionosférico e ɛ é a mudança dos termos de erros. Se as épocas são próximas, I(t i ) é pequeno e pode ser desprezado. Pode-se usar φ(t i ) como uma estimativa precisa de ρ (t i ). Pode-se então obter uma estimativa de ρ(t 0 ) em cada época: ˆρ(t 0 ) i = ρ(t i ) [φ(t i ) φ(t 0 )] (4.36) 70
71 Fazendo-se uma média de ˆρ(t 0 ) i sobre n épocas: ρ(t 0 ) = 1 ˆρ(t 0 ) i (4.37) n Com a estimativa de ρ(t 0 ), pode-se reconstruir o conjunto de pseudodistâncias suavizadas como sendo ρ(t i ) = ρ(t 0 ) + [φ(t i ) φ(t 0 )] (4.38) Uma implementação da suavização acima consiste em um filtro recursivo com duração de J épocas: i ρ(t i ) = 1 J ρ(t i) + J 1 [ ρ(t i 1 ) + ( φ(t i ) φ(t 0 ) )] J ρ(t 0 ) = ρ(t 0 ) (4.39) 4.4 Cálculo do Ruído Dinâmico Γ k QΓ T k A matriz de ruído dinâmico Γ k Q k Γ T k de Kalman é dada pela integral: necessária à propagação da covariância no filtro Γ k Q k Γ T k = k k 1 Φ k,τ G(τ)Q(τ)G T (τ)φ T k,τdτ (4.40) A integral da Equação (4.40) é resolvida pela regra do trapézio. Para isso, define-se (Ruggiero e Rocha, 1997): I 1 = Φ k,k GQG T Φ T k,k I 2 = Φ k,k 1 GQG T Φ T k,k 1 (4.41) com Φ k,k = I. Com isso, a integral é dada por: e é válida para δt pequenos. Γ k Q k Γ k = 1 2 (I 1 + I 2 )δt (4.42) 71
72 72
73 CAPÍTULO 5 APLICAÇÃO DOS ALGORITMOS EM POSICIONAMENTO ESTÁTICO Os algoritmos de GPS diferencial e dupla diferença descritos foram implementados para a realização de experimentos de posicionamento estático em tempo real para um receptor usuário. Neste teste ambos os receptores permaneceram estáticos, em posições precisamente conhecidas, para verificar a qualidade dos algoritmos propostos. Os dados utilizados foram coletados por dois receptores GPS Ashtech Z12 de dupla freqüência e qualidade geodésica, durante uma campanha de cerca de uma hora, gravados com uma freqüência de amostragem de 1Hz. O receptor base foi colocado sobre um marco de referência com coordenadas ECEF (Earth Centered Earth Fixed) no sistema WGS-84 dadas por x ref = ,0762m, y ref = ,0341m e z ref = ,2210m, ou ,40928 S, ,38152 W e 612,0274m no sistema geodésico, medidos pelo IBGE. O receptor usuário foi colocado a 5,20m de distância do receptor base (Figura 5.1). Os dados de navegação e observação de ambos os receptores foram coletados nos modos C1 (código C/A civil) e P1 (código-p preciso) e foram gravados no formato RINEX-2 (Gurtner, ). Estes arquivos foram editados de modo que o tempo total da medição e o conjunto de satélites fossem o mesmo para ambos os receptores. Durante o período de observação havia sempre 5 ou 6 satélites visíveis. O gráfico da Figura 5.2 mostra a variação do GDOP, PDOP, TDOP e número de satélites visíveis durante a observação para as medidas de pseudodistância em C1 e P1. Esses valores foram obtidos utilizando-se apenas os satélites visíveis em ambos os receptores simultaneamente. Os resultados são analisados em termos de um erro de posição com relação à linha de base entre os receptores, ou seja, a diferença entre a linha de base calculada a partir da solução do usuário e da posição de referência com a distância de 5,20m. Essa distância foi medida utilizando-se uma fita métrica. Todos os algoritmos foram implementados em rotinas escritas em linguagem FORTRAN. 73
74 Figura 5.1 Configuração do experimento. (a) Medidas em C1 (b) Medidas em P1 Figura 5.2 Variação do GDOP, PDOP, TDOP e número de satélites visíveis durante a observação. 5.1 GPS Diferencial na Posição Primeiramente, através de um método de mínimos quadrados, obtém-se, independentemente para cada receptor, a posição e o desvio do relógio para cada instante a partir dos dados medidos. Com isso, a base calcula a correção dada pela Equação (4.2). Esta correção é então somada à posição do usuário. A linha de base é obtida a partir da posição corrigida do usuário e da posição de referência da base. A Figura 5.3 mostra o erro da posição do usuário com respeito à linha de base de 5,20m. O erro permanece menor que 3m a maior parte do tempo, porém com alguns 74
75 picos de até 7m, devido ao alto valor do GDOP no final do experimento. Porém este resultado está dentro da precisão esperada para a técnica de DGPS mostrado na Tabela 3.2, com erro 1-sigma horizontal de 2,2m e erro 1-sigma vertical de 2,8m. Estes dados apresentaram um erro médio de 0,53m com desvio padrão de 1,34m. Figura 5.3 Erro da posição do usuário com relação à linha de base de 5,20m para DGPS na posição. 5.2 GPS Diferencial na Pseudodistância Este método de DGPS foi implementado de acordo com o descrito na seção 4.2. Por se tratar de receptores estáticos, o estado a ser considerado consiste de: onde r u = x u = [ r u b u d u ] T (5.1) [ x u y u z u ] T é a posição, bu e d u são o desvio e a deriva do relógio do receptor respectivamente, sendo ḃu = d u. Sendo assim, o modelo dinâmico é dado por: ẋ u = x u + Gω u (5.2)
76 onde ω u = [ ω r ω b ] T é a matriz contendo os ruídos da modelagem dinâmica da posição ω r e do relógio ω b e G é a matriz de adição de ruído, dada por [ ] T I G =. ω u é assumido ruído branco, logo: E[ω u ] = 0 E[ω u (t)ω T u (τ)] = Q(t)δ(t τ) (5.3) A matriz de transição de estados do tempo k 1 para k correspondente a este modelo, de acordo com a Equação (3.14), é dada por: I Φ k,k 1 = 0 1 δt (5.4) Desse modo a propagação do estado e sua covariância é feita através das equações: x u,k = Φ k 1,kˆx u,k 1 P u,k = Φ k 1,k ˆP u,k 1 Φ T k 1,k + Γ kqγ T k (5.5) onde Γ k QΓ T k é a matriz de adição de ruído dinâmico na propagação do estado, calculado pelo método da seção 4.4. O modelo de medidas para o estado considerado foi obtido a partir da Equação (2.1), que pode ser escrita explicitamente em termos dos elementos de x u, a menos dos termos de erros atmosféricos, pois assume-se que estes erros são eliminados com a aplicação da correção: ρ i corr,u = [ (X i x u ) 2 + (Y i y u ) 2 + (Z i z u ) 2] 1/2 + c bu c B i + ɛ u (5.6) onde R i é o vetor com as coordenadas de posição do satélite i. O procedimento de linearização descrito pela Equação (4.12) aplicado à Equação (5.6) resulta no seguinte modelo de medidas: 76
77 ρ u = ρ i corr,u ˆρ i u = H k x u + ɛ u = x u [ ] y ˆxu X i ŷ u Y i ẑ u Z i u = 1 0 ˆρ i u ˆρ i u ˆρ i z u (5.7) + ɛ u u b u d u Dessa forma, a fase de atualização deste filtro tem a forma: K u,k = P u,k H T k (H k P u,k H T k + R ρ) 1 ˆx u,k = x u,k + K u,k ρ u (5.8) ˆP u,k = (I K u,k H k ) P u,k onde ρ u é um vetor contendo os resíduos de observação em uma época e R ρ é a matriz de covariância dos erros de medida. As medidas de pseudodistância são assumidas não-correlacionadas entre si, de modo que R ρ tem a forma diagonal. A implementação computacional das equações de atualização (equações 5.8) na forma matricial requer uma inversão de matriz de ordem igual ao número de componentes do vetor de estados. Equivalentemente a esta inversão, pode-se realizar m atualizações do estado e sua covariância, onde m é o número de observações, na qual é processada uma pseudodistância por atualização, desde que R ρ seja diagonal. Assim, a inversão de matriz se transforma em m inversões de um escalar (Sorenson, 1980; Kuga, 1982) Resultados As coordenadas iniciais da posição para o filtro são as mesmas da referência. O valor do desvio do relógio foi obtido do primeiro instante de observação do arquivo RINEX. A Tabela 5.1 mostra os valores iniciais do vetor de estado. A covariância foi inicializada com um valor de (100m) 2 para a posição e desvio do relógio e de (10m/s) 2 para a deriva, de modo que tem-se a matriz de covariâncias iniciais: 77
78 ˆP u = (5.9) Tabela 5.1 Valores iniciais da posição, desvio e deriva e suas covariâncias para o filtro de Kalman. Estado Valor inicial Desvio-padrão x u [m] , y u [m] , z u [m] , b u [m] 98584, d u [m/s] 0 10 As pseudodistâncias são medidas pelo receptor com um erro de variância σ 2 0 = (3m) 2, de modo que R ρ é uma matriz diagonal de ordem m m dada por: σ R ρ =..... (5.10) 0... σ0 2 O valor das densidades espectrais de potência do ruído dinâmico da posição (q r ) e da deriva do relógio (q b ) são dadas por: q r = E[ω r ω T r ] = 0,009 2 m 2 /s 3 q b = E[ω b ω T b ] = (5.11) 0,92 m 2 /s 5 Estes valores foram ajustados off-line de modo a obter a melhor convergência do filtro. Assim, Q vale: [ ] qr I Q = (5.12) q b a qual é usada para calcular Γ k QΓ T k de acordo com o método da seção
79 O gráfico da Figura 5.4 mostra o comportamento dos resíduos da pseudodistância durante o tempo do experimento. Após a convergência do filtro, os resíduos permanecem menores que 1m. Figura 5.4 Resíduos da pseudodistância. A Tabela 5.2 mostra a média e o desvio-padrão dos resíduos do filtro para cada satélite visível. Nota-se pela tabela que os resíduos apresentam médias em torno de zero e desvios-padrão menores que 1,6m. Tabela 5.2 Estatística dos resíduos para o método de DGPS na pseudodistância. Satélite Média [m] Desvio-padrão [m] 1-0,071 0, ,487 0, ,733 1, ,066 0, ,036 0, ,446 1, ,132 0,655 O gráfico da Figura 5.5 mostra o erro da posição para este método, juntamente com 79
80 o erro de estimação de ±1-sigma dado pelo traço da matriz de covariância. Uma boa estimativa para a posição inicial do usuário são as coordenadas da base, o que gera o erro inicial de 4m. Após a convergência do filtro, a estimativa permanece com erro médio de 0,11m e desvio-padrão de 0,29m. Este método tem um comportamento mais suave e apresenta uma precisão melhor que o método de DGPS na posição (seção 5.1). Figura 5.5 Erro da posição do usuário com relação à linha de base de 5,20m para DGPS na pseudodistância. 5.3 Modelagem das Observáveis por Dupla Diferença Esta seção mostra os resultados da aplicação da técnica de posicionamento por dupla diferença, descrita na seção Os testes foram feitos utilizando filtro de Kalman e mínimos quadrados, ambos com ausência de rotina de suavização da pseudodistância e com suavização (seção 4.3.4) de janelas de 10, 30, 50 e 100 segundos Modelagem Usando Filtro de Kalman O vetor de estados x ub para o posicionamento por dupla diferença consiste apenas da posição relativa dos receptores (linha de base), visto que o desvio do relógio é 80
81 eliminado na construção dos observáveis, tal que x ub = [ δx δy δz] T (5.13) A propagação do estado e sua covariância são feitas com base no modelo de dinâmica considerando os receptores parados: onde G = ẋ ub = 0 + Gω r (5.14) [ 1 1 1] T e ωr é um ruído branco nas coordenadas da linha de base com densidade espectral Q. Assim, a matriz de transição Φ k,k 1 se reduz à matriz identidade. Das equações (3.13) e (3.15) tem-se que: x ub,k = ˆx ub,k 1 P ub,k = ˆP ub,k 1 + Γ k QΓ T k (5.15) Este filtro utiliza-se do modelo de medidas obtido após o processo de branqueamento (Equação 4.26). Sendo assim, a atualização é feita pelo conjunto de equações (3.16), utilizando o processamento seqüencial: K k = P ub,k H T k ( H k P ub,k H T k + I) 1 ˆx ub,k = x ub,k + K k ( z DD ẑ DD ) (5.16) ˆP ub,k = (I K k H k ) P ub,k onde ẑ DD é o vetor contendo as observações de dupla diferença calculadas com base nas pseudodistâncias preditas Modelagem Usando Mínimos Quadrados A solução por mínimos quadrados local foi obtida com o processamento das medidas em lotes, ou seja, processando todas as medidas de uma só vez em cada época, através das equações (Kuga, 2002): P = (H T WH) 1 x ub = PH T W z DD (5.17) 81
82 onde W é uma matriz de ponderação, dada por W = R 1 DD, z DD = z DD ẑ DD é o resíduo das medidas de dupla diferença e x ub e o incremento na linha de base. O valor da linha de base estimada ˆx ub é então calculada por: ˆx ub = x ub + x ub (5.18) Resultados Utilizando Dados do Código C1 O filtro de Kalman foi implementado de acordo com o descrito na seção 5.3.1, em conjunto com o algoritmo de suavização das medidas citado na seção Os valores iniciais da linha de base e da covariância do filtro foram: ˆx ub = 0 (m) e ˆP ub = (m 2 ) (5.19) O valor atribuído à variância dos erros de medida é σ0 2 = (3m) 2. Com isso, de acordo com a Equação (4.23), a matriz de covariância das observações de dupla diferença, de ordem (m 1) (m 1), vale R DD = (m2 ) (5.20) A suavização foi implementada utilizando janelas de 0 (ausência de suavização), 10, 30, 50 e 100 segundos. O valor da densidade espectral de potência do ruído dinâmico Q foi sintonizado de modo a obter a convergência do filtro e foi mantido constante durante o experimento. Com isso, Q assume os valores: Q = 0,001 2 m 2 /s 3 para o filtro sem suavização e Q = 0, m 2 /s 3 para o filtro com suavização. (5.21) 82
83 (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.6 Erro do posicionamento do usuário sem suavização. Os gráficos da Figura 5.6 mostram a solução em termos do erro de posicionamento da linha de base com relação a distância de referência de 5,20m na ausência de suavização, juntamente com as curvas de ±1-sigma de erro de estimação. As Figuras 5.7 a 5.10 mostram os resultados para diferentes graus de suavização. As Figuras 5.7a a 5.10a (esquerda) mostram o erro para a solução com o filtro de Kalman, juntamente com o erro de estimação de ±1-sigma dado pelo traço da matriz de covariância. As Figuras 5.7b a 5.10b (direita) mostram o erro de posicionamento referente à solução para o método de mínimos quadrados. (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.7 Erro do posicionamento do usuário com suavização de 10s. Uma boa estimativa para a posição inicial do usuário em um sistema de DGPS são 83
84 (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.8 Erro do posicionamento do usuário com suavização de 30s. (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.9 Erro do posicionamento do usuário com suavização de 50s. as coordenadas da base, ou seja, linha de base nula. Isto gera o erro inicial de cerca de 2m no filtro de Kalman. Após a convergência do filtro, a estimativa permanece com desvio dentro de 0,5m. Este método tem um comportamento bastante suave e permaneceu estável sob GDOP maior. A variação do GDOP e do número de satélites visíveis durante o experimento são mostrados no gráfico da Figura 5.2a. Os gráficos das Figuras 5.7 a 5.10 mostram que o aumento da duração da janela de suavização efetivamente levou a uma progressiva diminuição da magnitude do erro, após um ligeiro aumento na janela de 10s, tanto para a solução por filtro de Kalman quanto por mínimos quadrados, como pode ser visto nas Tabelas 5.3 e
85 (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.10 Erro do posicionamento do usuário com suavização de 100s. Na solução por mínimos quadrados, a diminuição da covariância entre 89 e 219s se deve à entrada de um sexto satélite em visibilidade durante este período. Nota-se que a suavização foi capaz de eliminar a descontinuidade em 89s, mas não em 219s. A partir de 1400s, nota-se que as medidas começaram a se degradar, devido ao aumento do valor do GDOP durante o experimento (Figura 5.2a). Nessa região, a suavização foi capaz de diminuir grandes oscilações. A Tabela 5.3 mostra a média e o desvio-padrão do erro de posicionamento para a solução por filtro de Kalman para as medidas em C1, tomadas a partir da convergência do filtro, assumido após 300s de experimento. Os valores mostram que a suavização leva o erro de posicionamento a diminuir, assim como o desvio-padrão. Tabela 5.3 Médias e desvios-padrão para a solução por filtro de Kalman nas medidas em C1. Janela [s] Média [m] Desvio padrão [m] 0 0,271 0, ,312 0, ,270 0, ,229 0, ,182 0,079 A precisão dos resultados em ambos os métodos é similar, exceto pelo fato de que a 85
86 solução por mínimos quadrados é feita ponto a ponto, ou seja, a solução é obtida a cada instante e sem modelo dinâmico. A solução por filtro de Kalman é recursiva, obtida através do aprimoramento da solução das épocas anteriores com as medidas da época atual. Isto gera um resultado mais estável que a solução ponto a ponto. A Tabela 5.4 apresenta os valores do erro e desvio-padrão para a solução por mínimos quadrados. Tabela 5.4 Médias e desvios-padrão para a solução por mínimos quadrados nas medidas em C1. Janela [s] Média [m] Desvio padrão [m] 0 0,695 1, ,866 1, ,595 1, ,437 1, ,327 1, Resultados Utilizando Dados do Código P1 O filtro de Kalman foi inicializado com os valores da linha de base e da covariância do filtro idênticos aos da seção anterior. O valor atribuído à variância dos erros de medida é σ0 2 = (0,5m) 2, pois estas medidas são obtidas através do código-p, teoricamente mais preciso. Assim, a matriz de covariância das observações vale: R DD = 0, (m2 ) (5.22) A suavização foi implementada utilizando janelas de 0 (ausência de suavização), 10, 30, 50 e 100 segundos. O valor da densidade espectral do ruído dinâmico Q foi sintonizado em: Q = 0,1 2 m 2 /s 3 para o filtro sem suavização e Q = 0,02 2 m 2 /s 3 para o filtro com suavização. (5.23) 86
87 (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.11 Erro do posicionamento do usuário sem suavização. O gráfico da Figura 5.11 mostra o erro de posicionamento para a solução por filtro de Kalman (Fig. 5.11a) e por mínimos quadrados (Fig. 5.11b) em P1 na ausência de suavização. O erro inicial está em cerca de 2,5m devido provavelmente a um rastreamento ainda não estabelecido devidamente. O valor do erro após 1200s de experimento aumenta, chegando a picos de 4m, pois o valor do GDOP nesse instante atinge cerca de 9, com picos de 14 nos momentos em que há diminuição de um satélite sendo rastreado. A Figura 5.2b mostra o valor do GDOP e o número de satélites em rastreamento durante o experimento. (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.12 Erro do posicionamento do usuário com suavização de 10s. As Figuras 5.12 a 5.15 mostram o erro de posicionamento com a aplicação de suavização com janelas de 10, 30, 50 e 100 segundos, respectivamente. A suavização 87
88 (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.13 Erro do posicionamento do usuário com suavização de 30s. (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.14 Erro do posicionamento do usuário com suavização de 50s. levou a um aumento progressivo da duração do pico de erro inicial. As Tabelas 5.5 e 5.6 mostram o valor da média e do desvio-padrão para o erro de posicionamento para a solução por filtro de Kalman e mínimos quadrados, respectivamente. Estes valores para o filtro foram calculados após a convergência do filtro e eliminado o pico inicial, de modo que para as janelas de 0, 10 e 30s foram tomados valores a partir de 300s de experimento e para as janelas de 50 e 100s, a partir de 400s. Na solução por mínimos quadrados, para a janela de 0, 10 e 30s foram tomados valores a partir de 200s e para 50 e 100s, a partir de 300s. 88
89 (a) Filtro de Kalman (b) Mínimos quadrados Figura 5.15 Erro do posicionamento do usuário com suavização de 100s. Tabela 5.5 Médias e desvios-padrão para a solução por filtro de Kalman nas medidas em P1. Janela [s] Média [m] Desvio padrão [m] 0-0,446 0, ,439 0, ,430 0, ,486 0, ,470 0,321 Tabela 5.6 Médias e desvios-padrão para a solução por mínimos quadrados nas medidas em P1. Janela [s] Média [m] Desvio padrão [m] 0 0,120 0, ,147 0, ,179 0, ,174 0, ,132 0,936 Os experimentos desta etapa mostram que o processo de suavização de medidas pode atenuar a média do erro, mas não afeta significativamente seu desvio-padrão. As várias janelas de suavização utilizadas (10, 30, 50, 100s) não modificaram con- 89
90 sideravelmente a precisão final e assim sendo torna-se discutível sua utilização em ambiente de tempo real, o que aumentaria a complexidade do código sem grandes benefícios. Provavelmente benefícios maiores são conseguidos para aplicações estáticas sem requisitos de tempo real. O filtro de Kalman proporcionou precisões melhores que o mínimos quadrados quando se utilizou medidas em C1, tanto no erro médio quanto no desvio-padrão. No entanto, ao utilizar-se medidas em P1 (teoricamente mais precisas), o filtro de Kalman produziu erros médios maiores e desvios-padrão menores que o procedimento de mínimos quadrados. 5.4 Tempo de Execução dos Programas A Tabela 5.7 mostra o tempo de execução total e o tempo de execução médio, que corresponde ao tempo de processamento das medidas de cada época, dos algoritmos testados. Os algoritmos de posicionamento por dupla diferença foram realizados utilizando o filtro de Kalman (FK) e mínimos quadrados (MQ), com suavização de duração indicada na tabela. Estes valores foram obtidos para um computador Pentium III de 1GHz, com 512Mb de memória RAM e Windows 2000 e as rotinas escritas em linguagem FORTRAN. Tabela 5.7 Tempo total e médio de execução dos algoritmos. Algoritmo Tempo total [s] Tempo médio [s] DGPS na posição ,0009 DGPS na pseudodistância ,0011 Dupla diferença (FK) 0s ,0010 Dupla diferença (FK) 10s ,0010 Dupla diferença (FK) 30s ,0010 Dupla diferença (FK) 50s ,0009 Dupla diferença (FK) 100s ,0010 Dupla diferença (MQ) 0s ,0010 Dupla diferença (MQ) 10s ,0012 Dupla diferença (MQ) 30s ,0012 Dupla diferença (MQ) 50s ,0012 Dupla diferença (MQ) 100s ,
91 Nota-se que o método de DGPS na posição, que utiliza mínimos quadrados, foi mais rápido que o método de DGPS na pseudodistância, que utiliza filtro de Kalman. O mesmo não ocorre com o método de dupla diferença. Estes valores mostram também que os algoritmos com suavização aparentemente não levaram mais tempo na execução, sendo assim, sua complexidade está apenas na implementação do código. 91
92 92
93 CAPÍTULO 6 APLICAÇÃO DOS ALGORITMOS EM NAVEGAÇÃO Os algoritmos de posicionamento descritos nos capítulos anteriores foram aplicados em dados de vôo provenientes de um usuário móvel e uma base fixa. Os dados foram coletados por um receptor instalado em uma aeronave e um receptor fixo, em um ensaio realizado no dia 16 de abril de 2002, durante cerca de 50min. As coordenadas de posição da base são dadas por ,9859 S, ,4615 W e 686,227m ou x ref = ,8649m, y ref = ,8146m e z ref = ,8289m em coordenadas ECEF no sistema WGS-84. As Figuras 6.1 e 6.2 reproduzem a trajetória horizontal da aeronave e sua altitude em função do tempo. Figura 6.1 Trajetória da aeronave. Os arquivos de dados foram coletados no formato RINEX-2 (Gurtner, ) e editados de forma que o conjunto de satélites visíveis e o tempo de observação fossem os mesmos para ambos os receptores. Todos os algoritmos foram implementados em rotinas escritas em linguagem FORTRAN. A variação do número de satélites visíveis e GDOP, PDOP e TDOP durante o tempo de observação está mostrada no gráfico da Figura 6.3. Será utilizada para comparação dos resultados uma trajetória pós-processada da aeronave, com precisão da ordem de centímetros. Para efeitos de comparação, esta 93
94 Figura 6.2 Altitude da aeronave em função do tempo. trajetória de referência é considerada suficientemente precisa. (a) Número de satélites (b) GDOP, PDOP e TDOP Figura 6.3 Variação do número de satélites visíveis e GDOP, PDOP e TDOP em função do tempo. 6.1 Aplicação do GPS Diferencial na Posição Este método de DGPS implementado está descrito na seção 4.1. A solução por este método é apenas a posição da aeronave, pois a dinâmica não entra na formulação do método. Os gráficos da Figura 6.4 mostram as componentes do erro na direção leste, norte e vertical. 94
95 A Tabela 6.1 traz as estatísticas dos erros. O erro horizontal (leste e norte) tem praticamente a mesma precisão (cerca de 0,2m), enquanto que o erro vertical é menos preciso (0,7m), e sua média está em torno de 2m. (a) Erro leste (b) Erro norte (c) Erro vertical Figura 6.4 Erro da posição da aeronave nas componentes leste, norte e vertical. Nota-se que esse método de posicionamento produz uma solução precisa, mas com uma acurácia não tão boa, pois pode-se ver pelo gráfico da Figura 6.5 que o erro horizontal não está distribuído em torno de zero. O resultado deste método apresenta uma solução horizontal com precisão de cerca de 0,25m, utilizando todos os satélites visíveis. Para comparação, Martínez et al. (2000) obtém uma solução em duas dimensões com um método semelhante, mas utilizando apenas três satélites, escolhidos pelo critério de DOP. A solução tem uma precisão de cerca de 5m. 95
96 Tabela 6.1 Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para o método de DGPS na posição. Média Desvio-padrão Erro leste [m] -0,429 0,265 Erro norte [m] 0,615 0,293 Erro vertical [m] -2,080 0,782 Figura 6.5 Erro horizontal da aeronave. 6.2 Aplicação do GPS Diferencial na Pseudodistância O modelo utilizado para descrever a trajetória da aeronave consiste em estimar a posição, velocidade e termos de relógio. O modelo dinâmico correspondente é dado por: ṙ u = v u v u = ω r ḃ u = d u d u = ω b (6.1) Assim, o vetor de estados a ser considerado consiste de 8 elementos: x = [ r u v u b u d u ] T (6.2) 96
97 [ ] T onde r u = x u y u z u são as coordenadas de posição do usuário, vu = [ ] T ẋ u ẏ u ż u são as coordenadas de velocidade e (bu, d u ) são o desvio e deriva do relógio do receptor, respectivamente. Dessa forma, a dinâmica da aeronave é representada pela seguinte equação de estados: I [ ] ẋ = x + G ω r (6.3) ω b 0 0 [ ] T I onde G = é a matriz de adição de ruídos dinâmicos Desse modo, pela Equação (3.14), a matriz de transição de estados assume a forma: I 3 3 δt I Φ k,k 1 = I δt (6.4) onde δt corresponde ao intervalo de tempo entre as medidas. A matriz H k, que relaciona o vetor de estado com as medidas, descrito na Equação (4.12), é dado por: [ ˆxu X i H k = ˆρ i u ŷ u Y i ˆρ i u ẑ u Z i ˆρ i u ] (6.5) Correções As pseudodistâncias corrigidas são calculadas pela equação: ρ i corr,u = ρ i u + (ˆρ i b ρ i b) (6.6) onde ρ i corr,u é a pseudodistância corrigida, ˆρ i b é a pseudodistância calculada com base nas coordenadas da referência e ρ i u e ρ i b são as pseudodistâncias medidas pelo usuário 97
98 e pela base respectivamente. A estimação do vetor de estado do usuário é realizada pelo filtro, processando as pseudodistâncias corrigidas, através das equações (4.11) e (4.13). O processamento das equações de atualização é feito de forma seqüencial Resultados O valor inicial dos componentes do vetor de estado e suas covariâncias estão mostrados na Tabela 6.2. Tabela 6.2 Valores iniciais dos estados e suas covariâncias para o filtro de Kalman. Estado Valor inicial Desvio-padrão x u [m] , y u [m] , z u [m] , ẋ u [m/s] 0 10 ẏ u [m/s] 0 10 ż u [m/s] 0 10 b u [m] 2362, d u [m/s] 0 10 A matriz de covariância das medidas R ρ é uma matriz diagonal de ordem m m, com m sendo o número de satélites visíveis, com os valores: R ρ =..... (m)2 (6.7) pois as pseudodistâncias são medidas com um erro de variância (3m) 2. Para este teste, m varia entre 7 e 8 satélites (Figura 6.3a). O filtro foi sintonizado com o valor da matriz de densidade espectral de potência 98
99 [ ] q r I Q = constante, onde q b E[ω r ω T r ] = q r I 3 3 δ(t τ) E[ω b ω T b ] = q bδ(t τ) (6.8) são dados por q r = 0,8 2 m 2 /s 5 e q b = 0,1 2 m 2 /s 5. O gráfico da Figura 6.6 mostra o comportamento dos resíduos das medidas de pseudodistância durante o tempo de processamento. Os resíduos apresentam média em torno de zero e desvios-padrão de até cerca de 2,5m, como pode ser visto na Tabela 6.3. Estes valores indicam que o filtro convergiu para um resultado coerente. Figura 6.6 Resíduos das medidas para o método de DGPS na pseudodistância. Os gráficos da Figura 6.7 mostra os erros de posição obtido com este método. A Tabela 6.4 traz as médias e desvios-padrão dos erros nas componentes leste, norte e vertical. Os erros apresentam picos, da ordem de 6m para a componente leste e 10m para a componente norte. Esses picos ocorrem no momento em que a aeronave realiza mudanças na sua trajetória. Este fato indica que o modelo de dinâmica implementado não é preciso o suficiente para responder a rápidas mudanças da trajetória da aeronave. 99
100 Tabela 6.3 Estatística dos resíduos para o método de DGPS na pseudodistância. Satélite Média [m] Desvio-padrão [m] 1-0,156 1, ,434 2, ,685 1, ,084 2, ,745 1, ,035 1, ,881 2, ,207 0,797 Tabela 6.4 Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para o método de DGPS na pseudodistância. Média Desvio-padrão Erro leste [m] -0,308 2,313 Erro norte [m] 0,541 2,905 Erro vertical [m] -2,058 1,374 Os valores do desvio-padrão dos erros horizontais (leste e norte) mostram-se maiores que o desvio-padrão do erro vertical devido aos picos mencionados. O erro vertical não apresenta tantos picos como os erros horizontais, provavelmente pelo fato de que componente vertical da trajetória não sofrer variações tão bruscas quanto a horizontal (ver Figuras 6.1 e 6.2). Considerando apenas um trecho retilíneo da trajetória, entre 1575s e 1875s do teste, conforme Figuras 6.8a e 6.8b, a média do erro e seu desvio-padrão estão mostrados na Tabela 6.5 e o comportamento do erro na Figura 6.9. Isto mostra que se a dinâmica for melhor ajustada, a solução por este método torna-se comparável à do método de DGPS na posição. A Figura 6.10 mostra o erro horizontal para todo o período, onde se nota a concentração em torno de zero, diferente do resultado de algoritmo de DGPS na posição. O erro na componente vertical permanece da mesma ordem de grandeza. 100
101 (a) Erro norte (b) Erro leste (c) Erro vertical Figura 6.7 Erros da posição para o método de DGPS na pseudodistância. (a) Trajetória da aeronave entre (b) Altitude da aeronave em função do tempo Figura 6.8 Trajetória e altitude da aeronave entre 1575 e 1875s. 101
102 (a) Erro horizontal (b) Erro vertical Figura 6.9 Erros horizontal e vertical para o método de DGPS na pseudodistância entre 1575 e 1875s. Tabela 6.5 Erro médio e desvio-padrão da posição em coordenadas leste-nortevertical para as épocas entre 1575s e 1875s para o método de DGPS na pseudodistância. Média Desvio-padrão Erro leste [m] -0,029 0,319 Erro norte [m] 0,570 0,639 Erro vertical [m] -2,283 0,691 Figura 6.10 Erro horizontal para o método de DGPS na pseudodistância. 102
103 6.3 Resultados Usando Medidas de Dupla Diferença Esta seção mostra o resultado do posicionamento utilizando observáveis de dupla diferença, obtido com filtro de Kalman e mínimos quadrados Modelagem por Filtro de Kalman A implementação deste método por filtro de Kalman assume como estados a serem estimados a linha de base (δx, δy, δz) e a variação da linha de base ( δx, δy, δz). Logo, o vetor de estado a ser considerado fica: x ub = [ δx δy δz δx δy δz] T (6.9) A equação de dinâmica da aeronave, considerando o vetor de estado dado, é escrita como: ẋ ub = [ 03 3 I ] x ub + Gω r (6.10) onde ω r é o ruído em ( δx, δy, δz), ] T com densidade espectral Q e G = [0 3 3 I 3 3 é a matriz de adição de ruído. Com base nesse modelo, a matriz de transição assume a forma: [ ] I3 3 δt I 3 3 Φ k,k 1 = I 3 3 (6.11) A matriz que relaciona o vetor de estado e a medida de dupla diferença é dada por: H = [ ] 1 M b 1 i b (6.12) onde 1 i b é o vetor de linha de visada entre o receptor b e o satélite i M e M indica o satélite mestre. Esta matriz passa pelo processo de branqueamento, descrito na seção 4.3.1, juntamente com o vetor de medidas para ser utilizado com o filtro de Kalman. 103
104 6.3.2 Modelagem por Mínimos Quadrados A solução por mínimos quadrados foi obtida com o processamento das medidas em lotes, ou seja, processando todas as medidas de uma só vez em cada época, através das equações (Kuga, 2002): P = (H T WH) 1 x ub,k = PH T W z DD (6.13) onde W é uma matriz de ponderação, dada por W = R 1 DD, z DD = z DD ẑ DD é o resíduo das medidas de dupla diferença e x ub e o incremento na linha de base. O valor da linha de base estimada ˆx ub,k, no instante k, é então calculada por: ˆx ub,k = ˆx ub,k 1 + x ub (6.14) Resultados para o Filtro de Kalman Os valores iniciais do vetor de estado ˆx ub são 0m para a linha de base e 0m/s para a variação da linha de base, enquanto que sua covariância ˆP ub é uma matriz diagonal, com os valores correspondentes à linha de base sendo (100m) 2 e (10m/s) 2 correspondendo à variação da linha de base, ou seja: ˆx ub = e ˆP 2 ub =.. (6.15) A matriz de covariância dos ruídos de medidas R DD vale, de acordo com a Equação (4.23): R DD = (m2 ) (6.16)
105 O filtro foi sintonizado com valor de Q, mantido constante durante todo o intervalo em Q = 1,1 2 I 3 3 m 2 /s 5. O gráfico da Figura 6.11 mostra o comportamento dos resíduos durante o tempo do teste. Os resíduos apresentam média em torno de zero e desvio-padrão de até cerca de 0,6m. A Tabela 6.6 mostra as estatísticas desses resíduos. O satélite mestre escolhido foi o SV 11. Figura 6.11 Comportamento dos resíduos durante o teste. Tabela 6.6 Média e desvio-padrão dos resíduos para o filtro de Kalman. Satélites Média [m] Desvio-padrão [m] M - 1 0,030 0,524 M - 2 0,074 0,519 M ,098 0,467 M ,102 0,808 M ,121 0,612 M ,312 0,427 M ,321 0,300 A Tabela 6.7 mostra os valores médios e os desvios-padrão do erro da posição da aeronave em coordenadas leste-norte-vertical usando a solução por filtro de Kalman. Os gráficos da Figura 6.12 mostram estes erros. As médias das componentes horizontais, isto é, leste e norte, permanecem em torno de zero, mas os desvios-padrão 105
Posicionamento por Satélite. Tecnologia em Mecanização em Agricultura de Precisão Prof. Esp. Fernando Nicolau Mendonça
 Posicionamento por Satélite Tecnologia em Mecanização em Agricultura de Precisão Prof. Esp. Fernando Nicolau Mendonça O Sistema GPS - Características Básicas O sistema GPS é composto por três segmentos:
Posicionamento por Satélite Tecnologia em Mecanização em Agricultura de Precisão Prof. Esp. Fernando Nicolau Mendonça O Sistema GPS - Características Básicas O sistema GPS é composto por três segmentos:
GNSS: CONCEITOS, MODELAGEM E PERSPECTIVAS FUTURAS DO POSICIONAMENTO POR SATÉLITE
 GNSS: CONCEITOS, MODELAGEM E PERSPECTIVAS FUTURAS DO POSICIONAMENTO POR SATÉLITE Prof. Dra. Daniele Barroca Marra Alves Departamento de Cartografia SUMÁRIO Posicionamento Sistemas de Posicionamento GPS,
GNSS: CONCEITOS, MODELAGEM E PERSPECTIVAS FUTURAS DO POSICIONAMENTO POR SATÉLITE Prof. Dra. Daniele Barroca Marra Alves Departamento de Cartografia SUMÁRIO Posicionamento Sistemas de Posicionamento GPS,
Sistema GNSS. (Global Navigation Satellite System)
 Sistema GNSS (Global Navigation Satellite System) POSICIONAR UM OBJETO NADA MAIS É DO QUE LHE ATRIBUIR COORDENADAS O Sol, os planetas e as estrelas foram excelentes fontes de orientação, por muito tempo.
Sistema GNSS (Global Navigation Satellite System) POSICIONAR UM OBJETO NADA MAIS É DO QUE LHE ATRIBUIR COORDENADAS O Sol, os planetas e as estrelas foram excelentes fontes de orientação, por muito tempo.
GPS Global positioning system
 GPS Global positioning system O Sistema de Posicionamento Global GPS-NAVSTAR (Navigation Satellite Time And Ranging) foi concebido inicialmente para substituir o sistema NNNS/TRANSIT que apresentava várias
GPS Global positioning system O Sistema de Posicionamento Global GPS-NAVSTAR (Navigation Satellite Time And Ranging) foi concebido inicialmente para substituir o sistema NNNS/TRANSIT que apresentava várias
GPS (Global Positioning System) Sistema de Posicionamento Global
 GPS (Global Positioning System) Sistema de Posicionamento Global 1 Sistema de Posicionamento Global é um sistema de posicionamento por satélite que permite posicionar um corpo que se encontre à superfície
GPS (Global Positioning System) Sistema de Posicionamento Global 1 Sistema de Posicionamento Global é um sistema de posicionamento por satélite que permite posicionar um corpo que se encontre à superfície
PPP PÓS PROCESSADO E EM TEMPO REAL. Prof. Dr. Haroldo Antonio Marques - UFPE Prof. Dr. João Francisco Galera Monico - UNESP
 PPP PÓS PROCESSADO E EM TEMPO REAL Prof. Dr. Haroldo Antonio Marques - UFPE Prof. Dr. João Francisco Galera Monico - UNESP Introdução Posicionamento GNSS em tempo real (ex.: RTK e DGPS): RTPPP (Real Time
PPP PÓS PROCESSADO E EM TEMPO REAL Prof. Dr. Haroldo Antonio Marques - UFPE Prof. Dr. João Francisco Galera Monico - UNESP Introdução Posicionamento GNSS em tempo real (ex.: RTK e DGPS): RTPPP (Real Time
GA119 MÉTODOS GEODÉSICOS
 Universidade Federal do Paraná Curso de Engenharia Cartográfica e de Agrimensura GA119 MÉTODOS GEODÉSICOS Profa. Regiane Dalazoana 4 Métodos baseados em Geodésia Espacial 4.1 Métodos Celestes da Geodésia
Universidade Federal do Paraná Curso de Engenharia Cartográfica e de Agrimensura GA119 MÉTODOS GEODÉSICOS Profa. Regiane Dalazoana 4 Métodos baseados em Geodésia Espacial 4.1 Métodos Celestes da Geodésia
Unesp UNIVERSIDADE ESTADUAL PAULISTA. Física 1 PRINCIPIOS DE FUNCIONAMENTO DO GPS
 Unesp Física 1 UNIVERSIDADE ESTADUAL PAULISTA UNIDADE DIFERENCIADA - SOROCABA/IPERÓ Veja também os sites: www.fis.puc-rio.br/fis-intr/gps.htm www.gpsglobal.com.br/artigos/ita12ahtml PRINCIPIOS DE FUNCIONAMENTO
Unesp Física 1 UNIVERSIDADE ESTADUAL PAULISTA UNIDADE DIFERENCIADA - SOROCABA/IPERÓ Veja também os sites: www.fis.puc-rio.br/fis-intr/gps.htm www.gpsglobal.com.br/artigos/ita12ahtml PRINCIPIOS DE FUNCIONAMENTO
Normas e especificações para levantamentos GPS
 Normas e especificações para levantamentos GPS IBGE- DGC - Coordenação de Geodésia IBGE- UE/SC Gerência de Geodésia e Cartografia IV CONFEGE - 21/08/06 a 25/08/06 - Rio de Janeiro/RJ Conteúdo Introdução:
Normas e especificações para levantamentos GPS IBGE- DGC - Coordenação de Geodésia IBGE- UE/SC Gerência de Geodésia e Cartografia IV CONFEGE - 21/08/06 a 25/08/06 - Rio de Janeiro/RJ Conteúdo Introdução:
Sistema de Posicionamento por Satélite
 Implantação de Faixa de Dutos Sistema de Posicionamento por Satélite Resumo dos conhecimentos necessários para o entendimento e uso dos Sistemas de s e seus equipamentos. 1 Introdução Os sistemas de posicionamento
Implantação de Faixa de Dutos Sistema de Posicionamento por Satélite Resumo dos conhecimentos necessários para o entendimento e uso dos Sistemas de s e seus equipamentos. 1 Introdução Os sistemas de posicionamento
Sincronização de Relógios
 Sistemas de Tempo Real: Sincronização de Relógios Rômulo Silva de Oliveira Departamento de Automação e Sistemas DAS UFSC romulo@das.ufsc.br http://www.das.ufsc.br/~romulo 1 Sincronização de Relógios Motivação
Sistemas de Tempo Real: Sincronização de Relógios Rômulo Silva de Oliveira Departamento de Automação e Sistemas DAS UFSC romulo@das.ufsc.br http://www.das.ufsc.br/~romulo 1 Sincronização de Relógios Motivação
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP - LABTOP Topografia 1. Sistema de Posicionamento por Satélite
 UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP - LABTOP Topografia 1 Sistema de Posicionamento por Satélite Recife, 2014 Sistema de Coordenadas Geográficas O globo é dividido
UNICAP Universidade Católica de Pernambuco Laboratório de Topografia de UNICAP - LABTOP Topografia 1 Sistema de Posicionamento por Satélite Recife, 2014 Sistema de Coordenadas Geográficas O globo é dividido
1 Problemas de transmissão
 1 Problemas de transmissão O sinal recebido pelo receptor pode diferir do sinal transmitido. No caso analógico há degradação da qualidade do sinal. No caso digital ocorrem erros de bit. Essas diferenças
1 Problemas de transmissão O sinal recebido pelo receptor pode diferir do sinal transmitido. No caso analógico há degradação da qualidade do sinal. No caso digital ocorrem erros de bit. Essas diferenças
Comparação entre dois métodos de GPS diferencial implementados através do filtro de Kalman
 Resumo Comparação entre dois métodos de GPS diferencial implementados através do filtro de Kalman Leandro Baroni Hélio Koiti Kuga, Divisão de Mecânica Espacial e Controle, Instituto Nacional de Pesquisas
Resumo Comparação entre dois métodos de GPS diferencial implementados através do filtro de Kalman Leandro Baroni Hélio Koiti Kuga, Divisão de Mecânica Espacial e Controle, Instituto Nacional de Pesquisas
RBMC-IP. Rede Brasileira de Monitoramento Contínuo dos Sistemas GNSS em Tempo Real. Diretoria de Geociências DGC Coordenação de Geodésia - CGED
 RBMC-IP Rede Brasileira de Monitoramento Contínuo dos Sistemas GNSS em Tempo Real Diretoria de Geociências DGC Coordenação de Geodésia - CGED 06 de Maio de 2009 Sumário Sistema GPS Técnica de Posicionamento
RBMC-IP Rede Brasileira de Monitoramento Contínuo dos Sistemas GNSS em Tempo Real Diretoria de Geociências DGC Coordenação de Geodésia - CGED 06 de Maio de 2009 Sumário Sistema GPS Técnica de Posicionamento
ANEXO L RESUMO ESPECIFICAÇÕES INCRA
 ANEXO L RESUMO ESPECIFICAÇÕES INCRA 1 Metodologia A metodologia utilizada para a determinação dos pontos de divisa, seguiu a metodologia para georreferenciamento de imóveis rurais do emitido pelo INCRA
ANEXO L RESUMO ESPECIFICAÇÕES INCRA 1 Metodologia A metodologia utilizada para a determinação dos pontos de divisa, seguiu a metodologia para georreferenciamento de imóveis rurais do emitido pelo INCRA
CAPÍTULO 2 SISTEMA DE POSICIONAMENTO GLOBAL (GPS)
 CAPÍTULO 2 SISTEMA DE POSICIONAMENTO GLOBAL (GPS) 2.1 Introdução A utilização de ondas de rádio e satélites artificiais em navegação teve início na década de 60 com o desenvolvimento do Navy Navigational
CAPÍTULO 2 SISTEMA DE POSICIONAMENTO GLOBAL (GPS) 2.1 Introdução A utilização de ondas de rádio e satélites artificiais em navegação teve início na década de 60 com o desenvolvimento do Navy Navigational
GPS. Sistema de Posicionamento por Satélites Artificiais. Sumário. O que é o GPS? Sumário
 Sumário GPS Sistema de Posicionamento por Satélites Artificiais P r o f. Ti a g o B a d r e M a r i n o G e o p r o c e s s a m e n t o D e p a r t a m e n t o d e G e o c i ê n c i a s I n s t i t u t
Sumário GPS Sistema de Posicionamento por Satélites Artificiais P r o f. Ti a g o B a d r e M a r i n o G e o p r o c e s s a m e n t o D e p a r t a m e n t o d e G e o c i ê n c i a s I n s t i t u t
Ivan Guilhon Mitoso Rocha. As grandezas fundamentais que serão adotadas por nós daqui em frente:
 Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Rumo ao ITA Física Análise Dimensional Ivan Guilhon Mitoso Rocha A análise dimensional é um assunto básico que estuda as grandezas físicas em geral, com respeito a suas unidades de medida. Como as grandezas
Faculdade de Engenharia Optimização. Prof. Doutor Engº Jorge Nhambiu
 1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
1 Programação Não Linear Aula 25: Programação Não-Linear - Funções de Uma única variável Mínimo; Mínimo Global; Mínimo Local; Optimização Irrestrita; Condições Óptimas; Método da Bissecção; Método de Newton.
Aula 19 TENDÊNCIAS DA CARTOGRAFIA: NOÇÕES DE GEODÉSIA. Antônio Carlos Campos. META Apresentar as tendências e perspectivas atuais da cartografia.
 Aula 19 TENDÊNCIAS DA CARTOGRAFIA: NOÇÕES DE GEODÉSIA META Apresentar as tendências e perspectivas atuais da cartografia. OBJETIVOS Ao final desta aula, o aluno deverá: determinar o GPS de navegação relacionando
Aula 19 TENDÊNCIAS DA CARTOGRAFIA: NOÇÕES DE GEODÉSIA META Apresentar as tendências e perspectivas atuais da cartografia. OBJETIVOS Ao final desta aula, o aluno deverá: determinar o GPS de navegação relacionando
As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
1 As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia e não têm a intenção de substituir o livro-texto, nem qualquer outra bibliografia. Introdução O Cálculo Numérico
- Global Positioning System - - Sistema de Posicionamento Global -
 - Global Positioning System - - Sistema de Posicionamento Global - É um sistema de navegação com base em satélites artificiais que emitem, em intervalos de 1 ms, sinais rádio, diferente de satélite para
- Global Positioning System - - Sistema de Posicionamento Global - É um sistema de navegação com base em satélites artificiais que emitem, em intervalos de 1 ms, sinais rádio, diferente de satélite para
CARTOGRAFIA TEMÁTICA e GPS
 CARTOGRAFIA TEMÁTICA e GPS Orientação e Forma Diversidade = A visibilidade é variável Ordem = As categorias se ordenam espontaneamente Proporcionalidade = relação de proporção visual Cores convencionais
CARTOGRAFIA TEMÁTICA e GPS Orientação e Forma Diversidade = A visibilidade é variável Ordem = As categorias se ordenam espontaneamente Proporcionalidade = relação de proporção visual Cores convencionais
LOGO FQA. Unidade 1 de FQA Nível 2. GPS e MCU. Satélites e Movimento Circular Uniforme. Marília Peres e Rosa Pais
 LOGO FQA Unidade 1 de FQA Nível 2 GPS e MCU Satélites e Movimento Circular Uniforme Marília Peres e Rosa Pais Índice 1 GPS - Sistema de Posicionamento Global 2 3 Coordenadas e Relógios Satélites Geoestacionários
LOGO FQA Unidade 1 de FQA Nível 2 GPS e MCU Satélites e Movimento Circular Uniforme Marília Peres e Rosa Pais Índice 1 GPS - Sistema de Posicionamento Global 2 3 Coordenadas e Relógios Satélites Geoestacionários
computador-cálculo numérico perfeita. As fases na resolução de um problema real podem, de modo geral, ser colocadas na seguinte ordem:
 1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções
 Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
Tópico 11. Aula Teórica/Prática: O Método dos Mínimos Quadrados e Linearização de Funções 1. INTRODUÇÃO Ao se obter uma sucessão de pontos experimentais que representados em um gráfico apresentam comportamento
GPS GLOBAL POSITION SYSTEM
 FUNDAMENTOS DA NAVEGAÇÃO ELETRÔNICA GPS GLOBAL POSITION SYSTEM ECOBATÍMETRO FISHFINDER AUTOR: PROF. DR. FABIO GONÇALVES DOS REIS UNIVERSIDADE ESTADUAL DE CAMPINAS UNICAMP EDIÇÃO REVISADA BRASIL 2004 6
FUNDAMENTOS DA NAVEGAÇÃO ELETRÔNICA GPS GLOBAL POSITION SYSTEM ECOBATÍMETRO FISHFINDER AUTOR: PROF. DR. FABIO GONÇALVES DOS REIS UNIVERSIDADE ESTADUAL DE CAMPINAS UNICAMP EDIÇÃO REVISADA BRASIL 2004 6
Introdução a Propagação Prof. Nilton Cesar de Oliveira Borges
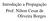 Introdução a Propagação Prof. Nilton Cesar de Oliveira Borges Como a luz, uma onda de rádio, perderia-se no espaço, fora do nosso planeta, se não houvesse um fenômeno que provocasse sua curvatura para
Introdução a Propagação Prof. Nilton Cesar de Oliveira Borges Como a luz, uma onda de rádio, perderia-se no espaço, fora do nosso planeta, se não houvesse um fenômeno que provocasse sua curvatura para
IW10. Rev.: 02. Especificações Técnicas
 IW10 Rev.: 02 Especificações Técnicas Sumário 1. INTRODUÇÃO... 1 2. COMPOSIÇÃO DO IW10... 2 2.1 Placa Principal... 2 2.2 Módulos de Sensores... 5 3. APLICAÇÕES... 6 3.1 Monitoramento Local... 7 3.2 Monitoramento
IW10 Rev.: 02 Especificações Técnicas Sumário 1. INTRODUÇÃO... 1 2. COMPOSIÇÃO DO IW10... 2 2.1 Placa Principal... 2 2.2 Módulos de Sensores... 5 3. APLICAÇÕES... 6 3.1 Monitoramento Local... 7 3.2 Monitoramento
1.1. Viagens com GPS. Princípios básicos de funcionamento de um GPS de modo a obter a posição de um ponto na Terra.
 1.1. Viagens com GPS Princípios básicos de funcionamento de um GPS de modo a obter a posição de um ponto na Terra. O que é o GPS? Como funciona o GPS? Qual é a precisão do GPS? O sistema de satélites do
1.1. Viagens com GPS Princípios básicos de funcionamento de um GPS de modo a obter a posição de um ponto na Terra. O que é o GPS? Como funciona o GPS? Qual é a precisão do GPS? O sistema de satélites do
Introdução ao Projeto de Aeronaves. Aula 39 Relatório de Projeto Técnicas de Estruturação
 Introdução ao Projeto de Aeronaves Aula 39 Relatório de Projeto Técnicas de Estruturação Tópicos Abordados Relatório de Projeto. Técnicas de Estruturação para uma boa Avaliação. Elaboração do Relatório
Introdução ao Projeto de Aeronaves Aula 39 Relatório de Projeto Técnicas de Estruturação Tópicos Abordados Relatório de Projeto. Técnicas de Estruturação para uma boa Avaliação. Elaboração do Relatório
Análise e Projeto Orientados por Objetos
 Análise e Projeto Orientados por Objetos Aula 02 Análise e Projeto OO Edirlei Soares de Lima Análise A análise modela o problema e consiste das atividades necessárias para entender
Análise e Projeto Orientados por Objetos Aula 02 Análise e Projeto OO Edirlei Soares de Lima Análise A análise modela o problema e consiste das atividades necessárias para entender
6. Geometria, Primitivas e Transformações 3D
 6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
MÓDULO 4 Meios físicos de transmissão
 MÓDULO 4 Meios físicos de transmissão Os meios físicos de transmissão são compostos pelos cabos coaxiais, par trançado, fibra óptica, transmissão a rádio, transmissão via satélite e são divididos em duas
MÓDULO 4 Meios físicos de transmissão Os meios físicos de transmissão são compostos pelos cabos coaxiais, par trançado, fibra óptica, transmissão a rádio, transmissão via satélite e são divididos em duas
UNIVERSIDADE DO EXTREMO SUL CATARINENSE. Correção geométrica de imagens
 Correção geométrica de imagens O georreferenciamento descreve a relação entre os parâmetros de localização dos objetos no espaço da imagem e no sistema de referência, transformando as coordenadas de cada
Correção geométrica de imagens O georreferenciamento descreve a relação entre os parâmetros de localização dos objetos no espaço da imagem e no sistema de referência, transformando as coordenadas de cada
Filtros de sinais. Conhecendo os filtros de sinais.
 Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Hardware (Nível 0) Organização. Interface de Máquina (IM) Interface Interna de Microprogramação (IIMP)
 Hardware (Nível 0) Organização O AS/400 isola os usuários das características do hardware através de uma arquitetura de camadas. Vários modelos da família AS/400 de computadores de médio porte estão disponíveis,
Hardware (Nível 0) Organização O AS/400 isola os usuários das características do hardware através de uma arquitetura de camadas. Vários modelos da família AS/400 de computadores de médio porte estão disponíveis,
SINCRONISMO USANDO GPS
 SINCRONISMO USANDO GPS Mario Piai Júnior Diretor Técnico da empresa TESC Sistemas de Controle Ltda mpiai@tesc.com.br Várias aplicações exigem que eventos, que acontecem fisicamente distantes entre si,
SINCRONISMO USANDO GPS Mario Piai Júnior Diretor Técnico da empresa TESC Sistemas de Controle Ltda mpiai@tesc.com.br Várias aplicações exigem que eventos, que acontecem fisicamente distantes entre si,
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Projetos. Universidade Federal do Espírito Santo - UFES. Mestrado em Informática 2004/1. O Projeto. 1. Introdução. 2.
 Pg. 1 Universidade Federal do Espírito Santo - UFES Mestrado em Informática 2004/1 Projetos O Projeto O projeto tem um peso maior na sua nota final pois exigirá de você a utilização de diversas informações
Pg. 1 Universidade Federal do Espírito Santo - UFES Mestrado em Informática 2004/1 Projetos O Projeto O projeto tem um peso maior na sua nota final pois exigirá de você a utilização de diversas informações
MÓDULO 7 Modelo OSI. 7.1 Serviços Versus Protocolos
 MÓDULO 7 Modelo OSI A maioria das redes são organizadas como pilhas ou níveis de camadas, umas sobre as outras, sendo feito com o intuito de reduzir a complexidade do projeto da rede. O objetivo de cada
MÓDULO 7 Modelo OSI A maioria das redes são organizadas como pilhas ou níveis de camadas, umas sobre as outras, sendo feito com o intuito de reduzir a complexidade do projeto da rede. O objetivo de cada
Processamento Sísmico:
 Processamento Sísmico: Até aqui vimos que um pulso sísmico artificial atravessa as camadas e parte de sua energia é refletida em cada superfície de contraste de impedância acústica. A fração da amplitude
Processamento Sísmico: Até aqui vimos que um pulso sísmico artificial atravessa as camadas e parte de sua energia é refletida em cada superfície de contraste de impedância acústica. A fração da amplitude
GPS RTK. Fabiano Cucolo 13/08/2015
 GPS RTK Fabiano Cucolo 13/08/2015 Um pouco sobre o palestrante Fabiano Cucolo fabiano@soloverdi.com.br 11-98266-0244 (WhatsApp) Consultor de Geotecnologias. Geógrafo e Mestre pela Unesp, dissertação e
GPS RTK Fabiano Cucolo 13/08/2015 Um pouco sobre o palestrante Fabiano Cucolo fabiano@soloverdi.com.br 11-98266-0244 (WhatsApp) Consultor de Geotecnologias. Geógrafo e Mestre pela Unesp, dissertação e
O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:
![O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]:](/thumbs/27/10931177.jpg) 4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
4 Tornado de Projeto O tornado de projeto é admitido, para fins quantitativos, com as seguintes características [15]: Tornado do tipo F3-médio; Velocidade máxima de 233km/h = 64,72m/s; Velocidade translacional
Capítulo 3. Avaliação de Desempenho. 3.1 Definição de Desempenho
 20 Capítulo 3 Avaliação de Desempenho Este capítulo aborda como medir, informar e documentar aspectos relativos ao desempenho de um computador. Além disso, descreve os principais fatores que influenciam
20 Capítulo 3 Avaliação de Desempenho Este capítulo aborda como medir, informar e documentar aspectos relativos ao desempenho de um computador. Além disso, descreve os principais fatores que influenciam
RECEPTOR AM DSB. Transmissor. Circuito Receptor AM DSB - Profº Vitorino 1
 RECEPTOR AM DSB Transmissor Circuito Receptor AM DSB - Profº Vitorino 1 O receptor super-heteródino O circuito demodulador que vimos anteriormente é apenas parte de um circuito mais sofisticado capaz de
RECEPTOR AM DSB Transmissor Circuito Receptor AM DSB - Profº Vitorino 1 O receptor super-heteródino O circuito demodulador que vimos anteriormente é apenas parte de um circuito mais sofisticado capaz de
ISO/IEC 12207: Gerência de Configuração
 ISO/IEC 12207: Gerência de Configuração Durante o processo de desenvolvimento de um software, é produzida uma grande quantidade de itens de informação que podem ser alterados durante o processo Para que
ISO/IEC 12207: Gerência de Configuração Durante o processo de desenvolvimento de um software, é produzida uma grande quantidade de itens de informação que podem ser alterados durante o processo Para que
Palavras-Chave: Sistema de Posicionamento Global. Sistemas de Localização Espacial. Equação de Superfícies Esféricas.
 METODOS MATEMÁTICOS PARA DEFINIÇÃO DE POSICIONAMENTO Alberto Moi 1 Rodrigo Couto Moreira¹ Resumo Marina Geremia¹ O GPS é uma tecnologia cada vez mais presente em nossas vidas, sendo que são inúmeras as
METODOS MATEMÁTICOS PARA DEFINIÇÃO DE POSICIONAMENTO Alberto Moi 1 Rodrigo Couto Moreira¹ Resumo Marina Geremia¹ O GPS é uma tecnologia cada vez mais presente em nossas vidas, sendo que são inúmeras as
Medida da velocidade de embarcações com o Google Earth
 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Física Programa de Pós-Graduação em Ensino de Física Mestrado Profissional em Ensino de Física Medida da velocidade de embarcações com o Google Earth
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO Instituto de Física Programa de Pós-Graduação em Ensino de Física Mestrado Profissional em Ensino de Física Medida da velocidade de embarcações com o Google Earth
CHECK - LIST - ISO 9001:2000
 REQUISITOS ISO 9001: 2000 SIM NÃO 1.2 APLICAÇÃO A organização identificou as exclusões de itens da norma no seu manual da qualidade? As exclusões são relacionadas somente aos requisitos da sessão 7 da
REQUISITOS ISO 9001: 2000 SIM NÃO 1.2 APLICAÇÃO A organização identificou as exclusões de itens da norma no seu manual da qualidade? As exclusões são relacionadas somente aos requisitos da sessão 7 da
ESCOLA SUPERIOR DE TECNOLOGIA
 ESCOLA SUPERIOR DE TECNOLOGIA SISTEMA DE POSICIONAMENTO GLOBAL GONÇALO PRATES Engenheiro Geógrafo ABRIL 2004 1 Sistema de Posicionamento Global Em 1973, o Departamento de Defesa dos Estados Unidos iniciou
ESCOLA SUPERIOR DE TECNOLOGIA SISTEMA DE POSICIONAMENTO GLOBAL GONÇALO PRATES Engenheiro Geógrafo ABRIL 2004 1 Sistema de Posicionamento Global Em 1973, o Departamento de Defesa dos Estados Unidos iniciou
UNIVERSIDADE FEDERAL DA BAHIA - UFBA
 UNIVERSIDADE FEDERAL DA BAHIA - UFBA Instituto de Ciências Ambientais e Desenvolvimento Sustentável Geoprocessamento Prof. Pablo Santos 08 a Aula Global Positioning System-GPS Uma utilidade pública Uma
UNIVERSIDADE FEDERAL DA BAHIA - UFBA Instituto de Ciências Ambientais e Desenvolvimento Sustentável Geoprocessamento Prof. Pablo Santos 08 a Aula Global Positioning System-GPS Uma utilidade pública Uma
O que são satélites? Existem 2 tipos de satélite, são os satélites naturais e satélites artificiais.
 O que são satélites? Existem 2 tipos de satélite, são os satélites naturais e satélites artificiais. Satélites naturais são: a Lua que gravita em torno da Terra. Satélites artificiais são: dispositivos,
O que são satélites? Existem 2 tipos de satélite, são os satélites naturais e satélites artificiais. Satélites naturais são: a Lua que gravita em torno da Terra. Satélites artificiais são: dispositivos,
Multiplexador. Permitem que vários equipamentos compartilhem um único canal de comunicação
 Multiplexadores Permitem que vários equipamentos compartilhem um único canal de comunicação Transmissor 1 Receptor 1 Transmissor 2 Multiplexador Multiplexador Receptor 2 Transmissor 3 Receptor 3 Economia
Multiplexadores Permitem que vários equipamentos compartilhem um único canal de comunicação Transmissor 1 Receptor 1 Transmissor 2 Multiplexador Multiplexador Receptor 2 Transmissor 3 Receptor 3 Economia
Telecomunicações. Prof. André Y. Kusumoto andre_unip@kusumoto.com.br
 Telecomunicações Prof. André Y. Kusumoto andre_unip@kusumoto.com.br Satélites Satélite é o elemento comum de interligação das estações terrenas, atuando como estação repetidora. Devido a sua altitude,
Telecomunicações Prof. André Y. Kusumoto andre_unip@kusumoto.com.br Satélites Satélite é o elemento comum de interligação das estações terrenas, atuando como estação repetidora. Devido a sua altitude,
PROPOSTA DE RASTREAMENTO E MONITORAMENTO HÍBRIDO SATELITAL
 PROPOSTA DE RASTREAMENTO E MONITORAMENTO HÍBRIDO SATELITAL Solução Tecnologia Monitoramento Instalação SOLUÇÃO A solução de rastreamento Unepxmil foi desenvolvida para atender as principais necessidades
PROPOSTA DE RASTREAMENTO E MONITORAMENTO HÍBRIDO SATELITAL Solução Tecnologia Monitoramento Instalação SOLUÇÃO A solução de rastreamento Unepxmil foi desenvolvida para atender as principais necessidades
Comunicações móveis por Satélite. slide 1
 Comunicações móveis por Satélite slide 1 Satélite de Comunicações São satélites colocados em órbita da terra com a missão de transportarem repetidores de sinais de telecomunicações. Os satélites podem
Comunicações móveis por Satélite slide 1 Satélite de Comunicações São satélites colocados em órbita da terra com a missão de transportarem repetidores de sinais de telecomunicações. Os satélites podem
RBMC e RBMC-IP: Rede GNSS ativa como apoio aos levantamentos de campo. Sonia Maria Alves Costa
 RBMC e RBMC-IP: Rede GNSS ativa como apoio aos levantamentos de campo Sonia Maria Alves Costa Mundogeo#Connect 2014 São Paulo, 8 de maio de 2014 Sumário Status da Rede Serviço RBMC-IP Acesso ao Serviço
RBMC e RBMC-IP: Rede GNSS ativa como apoio aos levantamentos de campo Sonia Maria Alves Costa Mundogeo#Connect 2014 São Paulo, 8 de maio de 2014 Sumário Status da Rede Serviço RBMC-IP Acesso ao Serviço
Tabela de roteamento
 Existem duas atividades que são básicas a um roteador. São elas: A determinação das melhores rotas Determinar a melhor rota é definir por qual enlace uma determinada mensagem deve ser enviada para chegar
Existem duas atividades que são básicas a um roteador. São elas: A determinação das melhores rotas Determinar a melhor rota é definir por qual enlace uma determinada mensagem deve ser enviada para chegar
Calibração de Equipamentos
 Vídeo Conferência Calibração de Equipamentos Instituto de Pesos e Medidas do Estado do Paraná Junho/2014 Diferença entre calibração e a verificação metrológica Calibração Estabelece o erro de medição e
Vídeo Conferência Calibração de Equipamentos Instituto de Pesos e Medidas do Estado do Paraná Junho/2014 Diferença entre calibração e a verificação metrológica Calibração Estabelece o erro de medição e
PÓS GRADUAÇÃO EM CIÊNCIAS DE FLORESTAS TROPICAIS-PG-CFT INSTITUTO NACIONAL DE PESQUISAS DA AMAZÔNIA-INPA. 09/abril de 2014
 PÓS GRADUAÇÃO EM CIÊNCIAS DE FLORESTAS TROPICAIS-PG-CFT INSTITUTO NACIONAL DE PESQUISAS DA AMAZÔNIA-INPA 09/abril de 2014 Considerações Estatísticas para Planejamento e Publicação 1 Circularidade do Método
PÓS GRADUAÇÃO EM CIÊNCIAS DE FLORESTAS TROPICAIS-PG-CFT INSTITUTO NACIONAL DE PESQUISAS DA AMAZÔNIA-INPA 09/abril de 2014 Considerações Estatísticas para Planejamento e Publicação 1 Circularidade do Método
Gerenciamento de Projetos Modulo II Ciclo de Vida e Organização do Projeto
 Gerenciamento de Projetos Modulo II Ciclo de Vida e Organização do Projeto Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com PMBoK Organização do Projeto Os projetos e o gerenciamento
Gerenciamento de Projetos Modulo II Ciclo de Vida e Organização do Projeto Prof. Walter Cunha falecomigo@waltercunha.com http://waltercunha.com PMBoK Organização do Projeto Os projetos e o gerenciamento
GPS. Global Positioning System
 GPS Global Positioning System Microsoft PowerPoint Johnny F. Crivellaro João Elinaldo GPS Global Positioning System Navegador portátil que identifica informações de satélites e define através de calculo
GPS Global Positioning System Microsoft PowerPoint Johnny F. Crivellaro João Elinaldo GPS Global Positioning System Navegador portátil que identifica informações de satélites e define através de calculo
DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE
 DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE Mariane Alves Gomes da Silva Eliana Zandonade 1. INTRODUÇÃO Um aspecto fundamental de um levantamento
DESENVOLVIMENTO DE UM SOFTWARE NA LINGUAGEM R PARA CÁLCULO DE TAMANHOS DE AMOSTRAS NA ÁREA DE SAÚDE Mariane Alves Gomes da Silva Eliana Zandonade 1. INTRODUÇÃO Um aspecto fundamental de um levantamento
Referências internas são os artefatos usados para ajudar na elaboração do PT tais como:
 Plano de Teste (resumo do documento) I Introdução Identificador do Plano de Teste Esse campo deve especificar um identificador único para reconhecimento do Plano de Teste. Pode ser inclusive um código
Plano de Teste (resumo do documento) I Introdução Identificador do Plano de Teste Esse campo deve especificar um identificador único para reconhecimento do Plano de Teste. Pode ser inclusive um código
5.2 MAN s (Metropolitan Area Network) Redes Metropolitanas
 MÓDULO 5 Tipos de Redes 5.1 LAN s (Local Area Network) Redes Locais As LAN s são pequenas redes, a maioria de uso privado, que interligam nós dentro de pequenas distâncias, variando entre 1 a 30 km. São
MÓDULO 5 Tipos de Redes 5.1 LAN s (Local Area Network) Redes Locais As LAN s são pequenas redes, a maioria de uso privado, que interligam nós dentro de pequenas distâncias, variando entre 1 a 30 km. São
O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2
 3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
3.2 O Espaço Nulo de A: Resolvendo Ax = 0 11 O ESPAÇO NULO DE A: RESOLVENDO AX = 0 3.2 Esta seção trata do espaço de soluções para Ax = 0. A matriz A pode ser quadrada ou retangular. Uma solução imediata
Considerações Finais. Capítulo 8. 8.1- Principais conclusões
 Considerações Finais Capítulo 8 Capítulo 8 Considerações Finais 8.1- Principais conclusões Durante esta tese foram analisados diversos aspectos relativos à implementação, análise e optimização de sistema
Considerações Finais Capítulo 8 Capítulo 8 Considerações Finais 8.1- Principais conclusões Durante esta tese foram analisados diversos aspectos relativos à implementação, análise e optimização de sistema
UNIVERSIDADE CATÓLICA DE PETRÓPOLIS CENTRO DE ENGENHARIA E COMPUTAÇÃO
 UNIVERSIDADE CATÓLICA DE PETRÓPOLIS CENTRO DE ENGENHARIA E COMPUTAÇÃO Amanda 5ª Atividade: Codificador e codificação de linha e seu uso em transmissão digital Petrópolis, RJ 2012 Codificador: Um codoficador
UNIVERSIDADE CATÓLICA DE PETRÓPOLIS CENTRO DE ENGENHARIA E COMPUTAÇÃO Amanda 5ª Atividade: Codificador e codificação de linha e seu uso em transmissão digital Petrópolis, RJ 2012 Codificador: Um codoficador
Cálculo Numérico Aula 1: Computação numérica. Tipos de Erros. Aritmética de ponto flutuante
 Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Cálculo Numérico Aula : Computação numérica. Tipos de Erros. Aritmética de ponto flutuante Computação Numérica - O que é Cálculo Numérico? Cálculo numérico é uma metodologia para resolver problemas matemáticos
Gerenciamento de Riscos do Projeto Eventos Adversos
 Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
Gerenciamento de Riscos do Projeto Eventos Adversos 11. Gerenciamento de riscos do projeto PMBOK 2000 PMBOK 2004 11.1 Planejamento de gerenciamento de riscos 11.1 Planejamento de gerenciamento de riscos
6 Construção de Cenários
 6 Construção de Cenários Neste capítulo será mostrada a metodologia utilizada para mensuração dos parâmetros estocásticos (ou incertos) e construção dos cenários com respectivas probabilidades de ocorrência.
6 Construção de Cenários Neste capítulo será mostrada a metodologia utilizada para mensuração dos parâmetros estocásticos (ou incertos) e construção dos cenários com respectivas probabilidades de ocorrência.
4 Arquitetura básica de um analisador de elementos de redes
 4 Arquitetura básica de um analisador de elementos de redes Neste capítulo é apresentado o desenvolvimento de um dispositivo analisador de redes e de elementos de redes, utilizando tecnologia FPGA. Conforme
4 Arquitetura básica de um analisador de elementos de redes Neste capítulo é apresentado o desenvolvimento de um dispositivo analisador de redes e de elementos de redes, utilizando tecnologia FPGA. Conforme
Introdução ao Sistema de Posicionamento Global (GPS)
 Prof. Dr. Gilberto Pessanha Ribeiro Universidade Federal Fluminense Instituto de Geociências gilberto@vm.uff.br gilbertopessanha@yahoo.com www.geomatica.eng.uerj.br/gilberto Introdução O Sistema de foi
Prof. Dr. Gilberto Pessanha Ribeiro Universidade Federal Fluminense Instituto de Geociências gilberto@vm.uff.br gilbertopessanha@yahoo.com www.geomatica.eng.uerj.br/gilberto Introdução O Sistema de foi
Sincronização em SDs I. Bruno M. Carvalho Sala: 3B2 Horário: 35T34
 Sincronização em SDs I Bruno M. Carvalho Sala: 3B2 Horário: 35T34 Introdução Sincronização em SDs consiste na aplicação de técnicas que fazem com que os processos concordem com o tempo ou a ordem de ocorrência
Sincronização em SDs I Bruno M. Carvalho Sala: 3B2 Horário: 35T34 Introdução Sincronização em SDs consiste na aplicação de técnicas que fazem com que os processos concordem com o tempo ou a ordem de ocorrência
DETERMINAÇÃO DE EPICENTROS E HIPOCENTROS
 DETERMINAÇÃO DE EPICENTROS E HIPOCENTROS TREINAMENTO TÉCNICO: DA TEORIA A PRÁTICA Apostila de Treinamento (IAG-SISMO-042010) Elaborado por: Afonso Emidio de Vasconcelos Lopes Marcelo Assumpção SÃO PAULO
DETERMINAÇÃO DE EPICENTROS E HIPOCENTROS TREINAMENTO TÉCNICO: DA TEORIA A PRÁTICA Apostila de Treinamento (IAG-SISMO-042010) Elaborado por: Afonso Emidio de Vasconcelos Lopes Marcelo Assumpção SÃO PAULO
APLICAÇÕES DA DERIVADA
 Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Descobertas do electromagnetismo e a comunicação
 Descobertas do electromagnetismo e a comunicação Porque é importante comunicar? - Desde o «início dos tempos» que o progresso e o bem estar das sociedades depende da sua capacidade de comunicar e aceder
Descobertas do electromagnetismo e a comunicação Porque é importante comunicar? - Desde o «início dos tempos» que o progresso e o bem estar das sociedades depende da sua capacidade de comunicar e aceder
RECEPTOR GPS ME-1513R TUTORIAL PARA PROGRAMAÇÃO DO ARM7LPC2138. 1 ME Componentes e Equipamentos Eletrônicos Ltda
 RECEPTOR GPS ME-1513R TUTORIAL PARA PROGRAMAÇÃO DO ARM7LPC2138 1 ME Componentes e Equipamentos Eletrônicos Ltda Prefácio Obrigado por escolher o Receptor GPS ME-1513R. Este manual mostra o código fonte
RECEPTOR GPS ME-1513R TUTORIAL PARA PROGRAMAÇÃO DO ARM7LPC2138 1 ME Componentes e Equipamentos Eletrônicos Ltda Prefácio Obrigado por escolher o Receptor GPS ME-1513R. Este manual mostra o código fonte
Método de Posicionamento Relativo por Satélite GPS com Correção do Efeito do Multicaminho em. Resultados e Análises 1
 TEMA Tend. Mat. Apl. Comput., 9, No. 1 (2008), 133-142. c Uma Publicação da Sociedade Brasileira de Matemática Aplicada e Computacional. Método de Posicionamento Relativo por Satélite GPS com Correção
TEMA Tend. Mat. Apl. Comput., 9, No. 1 (2008), 133-142. c Uma Publicação da Sociedade Brasileira de Matemática Aplicada e Computacional. Método de Posicionamento Relativo por Satélite GPS com Correção
muito como cartas náuticas faça para o watercraft, ou o a mapa rodoviário para excitadores. Usando estas cartas e outras ferramentas pilotos possa
 Carta Aeronáutica é a mapa projetou ajudar dentro navegação de avião, muito como cartas náuticas faça para o watercraft, ou o a mapa rodoviário para excitadores. Usando estas cartas e outras ferramentas
Carta Aeronáutica é a mapa projetou ajudar dentro navegação de avião, muito como cartas náuticas faça para o watercraft, ou o a mapa rodoviário para excitadores. Usando estas cartas e outras ferramentas
1 INTRODUÇÃO Internet Engineering Task Force (IETF) Mobile IP
 1 INTRODUÇÃO Devido ao crescimento da Internet, tanto do ponto de vista do número de usuários como o de serviços oferecidos, e o rápido progresso da tecnologia de comunicação sem fio (wireless), tem se
1 INTRODUÇÃO Devido ao crescimento da Internet, tanto do ponto de vista do número de usuários como o de serviços oferecidos, e o rápido progresso da tecnologia de comunicação sem fio (wireless), tem se
Receptor GNSS Navcom SF 3040 com tecnologia StarFire
 Receptor GNSS Navcom SF 3040 com tecnologia StarFire Webinar MundoGeo/Alezi Teodolini Um novo paradigma para os receptores GNSS: precisão de 5 cm com apenas um equipamento e sem utilizar bases Algumas
Receptor GNSS Navcom SF 3040 com tecnologia StarFire Webinar MundoGeo/Alezi Teodolini Um novo paradigma para os receptores GNSS: precisão de 5 cm com apenas um equipamento e sem utilizar bases Algumas
Arquitetura de Rede de Computadores
 TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
TCP/IP Roteamento Arquitetura de Rede de Prof. Pedro Neto Aracaju Sergipe - 2011 Ementa da Disciplina 4. Roteamento i. Máscara de Rede ii. Sub-Redes iii. Números Binários e Máscara de Sub-Rede iv. O Roteador
1. Introdução. 1.1 Introdução
 1. Introdução 1.1 Introdução O interesse crescente dos físicos na análise do comportamento do mercado financeiro, e em particular na análise das séries temporais econômicas deu origem a uma nova área de
1. Introdução 1.1 Introdução O interesse crescente dos físicos na análise do comportamento do mercado financeiro, e em particular na análise das séries temporais econômicas deu origem a uma nova área de
ARCO - Associação Recreativa dos Correios. Sistema para Gerenciamento de Associações Recreativas Plano de Desenvolvimento de Software Versão <1.
 ARCO - Associação Recreativa dos Correios Sistema para Gerenciamento de Associações Recreativas Versão Histórico da Revisão Data Versão Descrição Autor Página
ARCO - Associação Recreativa dos Correios Sistema para Gerenciamento de Associações Recreativas Versão Histórico da Revisão Data Versão Descrição Autor Página
ORIENTAÇÕES DO SISMMAC SOBRE O NOVO PLANO DE CARREIRA
 ORIENTAÇÕES DO SISMMAC SOBRE O NOVO PLANO DE CARREIRA 1. VALE A PENA ADERIR AO NOVO PLANO DE CARREIRA? Avaliamos que para a maioria dos professores valerá a pena aderir ao novo Plano, pois através da nossa
ORIENTAÇÕES DO SISMMAC SOBRE O NOVO PLANO DE CARREIRA 1. VALE A PENA ADERIR AO NOVO PLANO DE CARREIRA? Avaliamos que para a maioria dos professores valerá a pena aderir ao novo Plano, pois através da nossa
4 Avaliação Econômica
 4 Avaliação Econômica Este capítulo tem o objetivo de descrever a segunda etapa da metodologia, correspondente a avaliação econômica das entidades de reservas. A avaliação econômica é realizada a partir
4 Avaliação Econômica Este capítulo tem o objetivo de descrever a segunda etapa da metodologia, correspondente a avaliação econômica das entidades de reservas. A avaliação econômica é realizada a partir
CAPÍTULO 1 INTRODUÇÃO, OBJETIVOS, JUSTIFICATIVAS E ORGANIZAÇÃO DO TRABALHO
 CAPÍTULO 1 INTRODUÇÃO, OBJETIVOS, JUSTIFICATIVAS E ORGANIZAÇÃO DO TRABALHO 1.1 - INTRODUÇÃO Com o aumento da demanda de serviços de tecnologia e também buscando atender às necessidades atuais do progresso
CAPÍTULO 1 INTRODUÇÃO, OBJETIVOS, JUSTIFICATIVAS E ORGANIZAÇÃO DO TRABALHO 1.1 - INTRODUÇÃO Com o aumento da demanda de serviços de tecnologia e também buscando atender às necessidades atuais do progresso
Manual SAGe Versão 1.2 (a partir da versão 12.08.01)
 Manual SAGe Versão 1.2 (a partir da versão 12.08.01) Submissão de Relatórios Científicos Sumário Introdução... 2 Elaboração do Relatório Científico... 3 Submissão do Relatório Científico... 14 Operação
Manual SAGe Versão 1.2 (a partir da versão 12.08.01) Submissão de Relatórios Científicos Sumário Introdução... 2 Elaboração do Relatório Científico... 3 Submissão do Relatório Científico... 14 Operação
Dadas a base e a altura de um triangulo, determinar sua área.
 Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
Disciplina Lógica de Programação Visual Ana Rita Dutra dos Santos Especialista em Novas Tecnologias aplicadas a Educação Mestranda em Informática aplicada a Educação ana.santos@qi.edu.br Conceitos Preliminares
ENQUALAB 2013 QUALIDADE & CONFIABILIDADE NA METROLOGIA AUTOMOTIVA. Elaboração em planos de Calibração Interna na Indústria Automotiva
 ENQUALAB 2013 QUALIDADE & CONFIABILIDADE NA METROLOGIA AUTOMOTIVA Elaboração em planos de Calibração Interna na Indústria Automotiva Joel Alves da Silva, Diretor Técnico JAS-METRO Soluções e Treinamentos
ENQUALAB 2013 QUALIDADE & CONFIABILIDADE NA METROLOGIA AUTOMOTIVA Elaboração em planos de Calibração Interna na Indústria Automotiva Joel Alves da Silva, Diretor Técnico JAS-METRO Soluções e Treinamentos
)HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR
 6LPXODomR GH6LVWHPDV )HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR #5,6. Simulador voltado para análise de risco financeiro 3RQWRV IRUWHV Fácil de usar. Funciona integrado a ferramentas já bastante conhecidas,
6LPXODomR GH6LVWHPDV )HUUDPHQWDV &RPSXWDFLRQDLV SDUD 6LPXODomR #5,6. Simulador voltado para análise de risco financeiro 3RQWRV IRUWHV Fácil de usar. Funciona integrado a ferramentas já bastante conhecidas,
MANUAL RASTREAMENTO 2013
 MANUAL RASTREAMENTO 2013 Visão Geral O menu geral é o principal módulo do sistema. Através do visão geral é possível acessar as seguintes rotinas do sistema: Sumário, localização, trajetos, últimos registros.
MANUAL RASTREAMENTO 2013 Visão Geral O menu geral é o principal módulo do sistema. Através do visão geral é possível acessar as seguintes rotinas do sistema: Sumário, localização, trajetos, últimos registros.
Multiplexação. Multiplexação. Multiplexação - FDM. Multiplexação - FDM. Multiplexação - FDM. Sistema FDM
 Multiplexação É a técnica que permite a transmissão de mais de um sinal em um mesmo meio físico. A capacidade de transmissão do meio físico é dividida em fatias (canais), com a finalidade de transportar
Multiplexação É a técnica que permite a transmissão de mais de um sinal em um mesmo meio físico. A capacidade de transmissão do meio físico é dividida em fatias (canais), com a finalidade de transportar
NOTA TÉCNICA. Sistema Geodésico de Referência: Figura geométrica da superfície terrestre: Época de referência das coordenadas:
 NOTA TÉCNICA TÉRMINO DO PERÍODO DE TRANSIÇÃO PARA ADOÇÃO NO BRASIL DO SISTEMA DE REFERÊNCIA GEOCÊNTRICO PARA AS AMÉRICAS (SIRGAS), EM SUA REALIZAÇÃO DE 2,4 (SIRGAS2) A definição, implantação e manutenção
NOTA TÉCNICA TÉRMINO DO PERÍODO DE TRANSIÇÃO PARA ADOÇÃO NO BRASIL DO SISTEMA DE REFERÊNCIA GEOCÊNTRICO PARA AS AMÉRICAS (SIRGAS), EM SUA REALIZAÇÃO DE 2,4 (SIRGAS2) A definição, implantação e manutenção
SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO
 SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO Respostas breves: 1.1) 9,063 N 1.2) norte, pois é positiva. 1.3) São José (Costa Rica). 2) Não, porque Santa Maria não está localizada sobre ou entre os dois
SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO Respostas breves: 1.1) 9,063 N 1.2) norte, pois é positiva. 1.3) São José (Costa Rica). 2) Não, porque Santa Maria não está localizada sobre ou entre os dois
Universidade Federal de Goiás (CMEC/EEC/UFG), ds.andrade@hotmail.com; 2 Professor Titular do CMEC/EEC/UFG, epazini@eec.ufg.br
 CORRELAÇÃO ENTRE A VELOCIDADE DA ONDA ULTRASSÔNICA E A RESISTÊNCIA À COMPRESSÃO E O MÓDULO DE DEFORMAÇÃO DE TESTEMUNHOS DE CONCRETO EXTRAÍDOS DE UMA ESTRUTURA DE 60 ANOS: ESTUDO DE CASO DO ESTÁDIO MARACANÃ
CORRELAÇÃO ENTRE A VELOCIDADE DA ONDA ULTRASSÔNICA E A RESISTÊNCIA À COMPRESSÃO E O MÓDULO DE DEFORMAÇÃO DE TESTEMUNHOS DE CONCRETO EXTRAÍDOS DE UMA ESTRUTURA DE 60 ANOS: ESTUDO DE CASO DO ESTÁDIO MARACANÃ
PROIMRAD X.01: NOVO CÓDIGO PARA GERENCIAMENTO DE REJEITOS RADIOATIVOS
 PROIMRAD X.01: NOVO CÓDIGO PARA GERENCIAMENTO DE REJEITOS RADIOATIVOS Alexandre França Velo 1*, Joel Mesa Hormaza 1, Gilberto Ribeiro Furlan 2, Walter Siqueira Paes 2 1* Departamento de Física e Biofísica
PROIMRAD X.01: NOVO CÓDIGO PARA GERENCIAMENTO DE REJEITOS RADIOATIVOS Alexandre França Velo 1*, Joel Mesa Hormaza 1, Gilberto Ribeiro Furlan 2, Walter Siqueira Paes 2 1* Departamento de Física e Biofísica
