Estudo Prévio de um Tabuleiro em Arco Superior do tipo Bowstring
|
|
|
- Patrícia Rita César de Abreu
- 8 Há anos
- Visualizações:
Transcrição
1 Estudo Prévio de um Tabuleiro em Arco Superior do tipo Bowstring Pedro Pereira Clemente Andrade Gonçalves Dissertação para obtenção do Grau de Mestre em Engenharia Civil Júri Presidente: Prof. Doutor José Manuel Matos Noronha da Câmara Orientador: Prof. Doutor José Joaquim Costa Branco de Oliveira Pedro Vogal: Prof. Doutor João Sérgio Nobre Duarte Cruz Dezembro de 2012
2
3 RESUMO Na presente dissertação de Mestrado apresenta-se o Estudo Prévio de uma ponte em arco superior do tipo Bowstring, com tabuleiro misto aço-betão. Realiza-se inicialmente uma pesquisa sobre o contexto histórico e construtivo das pontes de arco superior, que permitiu a construção de uma base de dados das obras deste tipo construídas até ao presente, e que inclui informação geral sobre as obras, as suas características geométricas e quantidades de materiais utilizadas. Apresenta-se o estudo preliminar de várias soluções deste tipo, com o intuito de escolher e pré-dimensionar a solução a adoptar no Estudo Prévio, de uma alternativa à solução de dois tabuleiros de betão armado pré-esforçados, executados por avanços sucessivos, adoptada na Ponte sobre o Rio Sorraia. Procede-se ao dimensionamento dos vários elementos que compõem o tabuleiro, nomeadamente a laje de tabuleiro, as vigas de sustentação do mesmo, o arco e os pendurais, e realiza-se as verificações de segurança de Estudo Prévio, a partir de um modelo de análise estrutural tridimensional de elementos finitos, utilizando o software SAP2000. Por fim, são efectuadas medições das principais quantidades de materiais adoptadas na solução proposta, assim como a correspondente estimativa orçamental, comparando-a com outras soluções de arco superior do tipo Bowstring e com uma solução em caixão de betão armado pré-esforçado construída, e apresenta-se as principais conclusões relativamente às vantagens e desvantagens associadas a este tipo de solução estrutural. Palavras-chave: pontes de arco superior, ponte Bowstring, pendurais, dimensionamento de pontes, análise de tabuleiros, instabilidade de arcos i
4 ii
5 ABSTRACT The present study aims the Preliminary Design for a Bowstring tied-arch solution for a bridge s deck. A research about the historical context and construction methods of tied-arch bridges was initially conducted, and a data base with an extensive list of the constructed Bowstring bridges up to date was assembled, with the compilation of the i) general layout information, ii) geometric characteristics and iii) main steel / concrete quantities. A Preliminary Study of several Bowstring deck solutions was performed, as alternative solutions for a real highway double box-girder bridge deck erected by the balanced cantilever method, in order to choose one of them, to perform the deck pre-design. The pre-design of the deck was then performed, namely the deck slab, the steel girders, the steel arch and the hanger sections, as well as the installed forces. The required and relevant safety verifications were performed at Preliminary Study level, supported by a tridimensional structural analysis model, using the software SAP2000. To finish, main quantities and estimated cost were evaluated for the proposed deck, solution and a comparison of these results with other Bowstring tied-arch bridges and with the erected box-girder bridges was performed. Conclusions about the advantages and disadvantages of the proposed solution were finally discussed. Keywords: tied-arch bridges, Bowstring bridge, hangers, bridge design, deck analysis, arch instability iii
6 iv
7 AGRADECIMENTOS Em primeiro lugar, gostaria de agradecer ao professor José Oliveira Pedro por me ter ajudado, auxiliado e aturado ao longo deste ano de muito trabalho e dedicação. Sem ele obviamente nada disto teria sido possível. Realço que foi graças ao seu acompanhamento que posso afirmar que me sinto hoje mais preparado para o mundo do trabalho, do que se tivesse concluído os estudos há um ano. Em segundo lugar, não posso deixar de agradecer à minha mãe e ao meu pai, que estiveram sempre presentes na minha vida, de uma forma geral não directamente no trabalho levado a cabo para a realização desta dissertação de Mestrado, mas nos entretantos ou no durante, a suportar as minhas oscilações de humor, assim como as minhas necessidades básicas. Não posso deixar de exprimir a minha gratitude para com os meus amigos que estiveram mais perto de mim e que, apesar de me solicitarem vezes e vezes sem conta para festas, copos e paródia, conseguiram reconhecer a importância deste trabalho e apoiarem-me a 100%. Não vou enumerar nomes porque eles sabem quem são. Um muito obrigado a todos. v
8 vi
9 ÍNDICE Capítulo 1 - INTRODUÇÃO E OBJECTIVOS CONSIDERAÇÕES GERAIS OBJECTIVOS ESTRUTURA DO TRABALHO... 3 Capítulo 2 - ESTUDO DAS SOLUÇÕES CONSTRUÍDAS INTRODUÇÃO HISTÓRICA E EVOLUÇÃO ESTRUTURAL ESTÉTICA E FUNCIONALIDADE TIPOS DE PONTES DE ARCO SUPERIOR BOWSTRING OBRAS CONSTRUÍDAS RELAÇÕES DIMENSIONAIS DAS OBRAS CONSTRUÍDAS PRINCIPAIS QUANTIDADES DAS OBRAS CONSTRUÍDAS Capítulo 3 - CASO DE ESTUDO A SOLUÇÃO CONSTRUÍDA ESTUDO PRELIMINAR DE SOLUÇÕES DO TIPO BOWSTRING PROCESSO CONSTRUTIVO Capítulo 4 - ESTUDO DO COMPORTAMENTO ESTRUTURAL PRÉ-DIMENSIONAMENTO LAJE DO TABULEIRO VIGAS LONGITUDINAIS VIGAS TRANSVERSAIS ARCO PENDURAIS FIXAÇÕES/ANCORAGENS MATERIAIS ACÇÕES ACÇÕES PERMANENTES SOBRECARGAS VERIFICAÇÃO DE SEGURANÇA DA LAJE ANÁLISE TRANSVERSAL DA LAJE ANÁLISE LONGITUDINAL DA LAJE VERIFICAÇÃO DE SEGURANÇA DOS PENDURAIS COEFICIENTES DE INFLUÊNCIA ACERTO DAS FORÇAS DE PUXE RESISTÊNCIA DOS PENDURAIS FADIGA vii
10 4.6 VERIFICAÇÃO DE SEGURANÇA DO ARCO SECÇÃO FLEXÃO COMPOSTA ESTABILIDADE DO ARCO PILARES E FUNDAÇÕES Capítulo 5 - ANÁLISE COMPARATIVA DAS SOLUÇÕES QUANTIDADES DE MATERIAIS BETÃO AÇO ESTRUTURAL E PENDURAIS ARMADURAS ESTIMATIVA ORÇAMENTAL COMPARAÇÃO COM UMA SOLUÇÃO EM CAIXÃO DE BETÃO ARMADO PRÉ-ESFORÇADO ( CASO DE ESTUDO) COMPARAÇÃO COM OUTRAS SOLUÇÕES DE ARCO SUPERIOR DO TIPO BOWSTRING Capítulo 6 - CONCLUSÕES ANEXOS Anexo A Base de Dados Anexo B Peças desenhadas Anexo C Cálculos auxiliares de pré-dimensionamento Anexo D Medições e orçamento detalhado das soluções viii
11 ÍNDICE DE FIGURAS FIGURA 1.1 PONTE EM ARCO DO TIPO NET EM STEINKJER, NORUEGA. VÃO PRINCIPAL COM 80 M. [3] 2 FIGURA 1.2 PONTE BOLSTADSTRAUMEN NA NORUEGA. VÃO PRINCIPAL COM 84 M. [3] 2 FIGURA 1.3 PONTE FERROVIÁRIA DE VIA DUPLA EM ROTERDÃO, HOLANDA SOBRE O CANAL HARTEL. VÃO PRINCIPAL COM 170 M. 2 FIGURA 1.4 PONTE SOBRE O RIO SADO EM PORTUGAL. VÃOS PRINCIPAIS COM 160 M. 2 FIGURA 1.5 PONTE DEPOT STREET DO TIPO NET, EM OREGON, NOS ESTADOS UNIDOS. VÃO PRINCIPAL COM 93 M. 2 FIGURA 1.6 PONTE PENTELE EM DUNAÚJVÁROS, HÚNGRIA. VÃO PRINCIPAL COM 308 M. [2] 2 FIGURA 2.1 ESQUEMA DE UMA PONTE DE ARCO INFERIOR [4] 6 FIGURA 2.2 ESQUEMA DE UMA PONTE DE ARCO SUPERIOR DO TIPO TWO-HINGED [4] 6 FIGURA 2.3 ESQUEMA DE UMA PONTE DE ARCO SUPERIOR DO TIPO BOWSTRING [4] 6 FIGURA 2.4 PONTE ŽELEZNIČNÍ EM ROPICE, REPÚBLICA CHECA. VÃO COM 62 M. 8 FIGURA 2.5 PONTE EM SALIES-DU-SALAT, FRANÇA. VÃO COM 56 M. 8 FIGURA 2.6 PONTE REINA SOFÍA EM PALMA DEL RÍO, ESPANHA. VÃO PRINCIPAL COM 130 M. 8 FIGURA 2.7 VIADUTO DE BRIARE EM FRANÇA. VÃO PRINCIPAL COM 86 M. 9 FIGURA 2.8 PONTE NORDRING EM MARKTHEIDENFELD, ALEMANHA. VÃO PRINCIPAL COM 135 M. 9 FIGURA 2.9 PONTE DE L OBSERVATOIRE EM LIÈGE, BÉLGICA. VÃO PRINCIPAL COM 82 M. 9 FIGURA 2.10 PONTE UJINA EM HIROSHIMA, JAPÃO. VÃO PRINCIPAL COM 103 M. 9 FIGURA 2.11 PONTE DE LA PERALEDA EM TOLEDO, ESPANHA. VÃO COM 127 M. 9 FIGURA 2.12 PONTE SICKINGMÜHLEN EM MARL, ALEMANHA. VÃO COM 55.8 M. 10 FIGURA 2.13 PONTE MERIVALE EM BRISBANE, AUSTRÁLIA. VÃO PRINCIPAL COM 132 M. 10 FIGURA 2.14 PONTE CENTRALE EM REGGIO NELL EMILIA, ITÁLIA. VÃO COM 221 M. 10 FIGURA 2.15 PAVELETSKY RAILROAD OVERPASS EM MOSCOVO, RÚSSIA. VAO PRINCIPAL COM 110 M. 10 FIGURA 2.16 PONTE MAREXHE EM LIÈGE, BÉLGICA. VÃO COM 100M. 10 FIGURA 2.17 RELAÇÃO ALTURA DO ARCO/VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS 17 FIGURA 2.18 RELAÇÃO ALTURA DO TABULEIRO/VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS 18 FIGURA 2.19 RELAÇÃO ENTRE O PESO DE AÇO NO ARCO E NOS PENDURAIS POR M 2 DE ÁREA DO TABULEIRO EM FUNÇÃO DO VÃO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS 19 FIGURA 2.20 RELAÇÃO QUANTIDADE DE AÇO TOTAL POR M 2 DE ÁREA DO TABULEIRO EM FUNÇÃO DO VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS 19 FIGURA 2.21 RELAÇÃO QUANTIDADE DE AÇO TOTAL POR M 2 DE ÁREA DO TABULEIRO EM FUNÇÃO DO VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS 20 FIGURA 3.1 PONTE SOBRE O RIO SORRAIA, EM PORTUGAL, QUE FAZ PARTE DA AUTOESTRADA A13: (A) VISTA GERAL; (B) PONTE DE AVANÇOS SUCESSIVOS DURANTE A CONSTRUÇÃO; (C) SECÇÕES TRANSVERSAIS TIPO DO TABULEIRO EM CAIXÃO 21 FIGURA 3.2 EXEMPLO ESQUEMÁTICO DA SOLUÇÃO PROPOSTA, FACE À SOLUÇÃO EM VIGOR 22 FIGURA 3.3 SOLUÇÃO A 24 FIGURA 3.4 SOLUÇÃO B 24 FIGURA 3.5 SOLUÇÃO C 25 FIGURA 3.6 SOLUÇÃO D 25 FIGURA 3.7 SOLUÇÃO E 26 FIGURA 3.8 SOLUÇÃO F 26 FIGURA 4.1 ALÇADO E SECÇÃO TRANSVERSAL PARA A SOLUÇÃO PROPOSTA DE TABULEIRO DO TIPO BOWSTRING 29 FIGURA 4.2 ESQUEMA DA ESPESSURA DEFINIDA PARA A LAJE DE TABULEIRO 30 FIGURA 4.3 SECÇÕES TRANSVERSAIS INICIAL E FINAL DA VIGA LONGITUDINAL PRINCIPAL 32 FIGURA 4.4 SOLUÇÕES PARA A GEOMETRIA DA VIGA LONGITUDINAL PRINCIPAL 33 FIGURA 4.5 SOLUÇÃO INICIAL E FINAL PROPOSTAS COMO VIGAS LONGITUDINAIS SECUNDÁRIAS 34 FIGURA 4.6 PONTE DE LA EXPOSICIÓN EM VALENCIA, ESPANHA. VÃO PRINCIPAL COM 130 M. 35 FIGURA 4.7 PUENTE PUERTO EM ONDARROA, ESPANHA. VÃO COM 71.5 M. 35 FIGURA 4.8 SECÇÕES TRANSVERSAIS MÍNIMA E MÁXIMA DAS ESPINHAS 36 ix
12 FIGURA 4.9 PERFIL TRANSVERSAL DO TABULEIRO ESQUIÇO DA SOLUÇÃO PRÉ-DIMENSIONADA 37 FIGURA 4.10 SECÇÃO TRANSVERSAL DO ARCO 38 FIGURA 4.11 SECÇÕES DE APOIO ADOPTADAS NAS SOLUÇÃO PROPOSTA 39 FIGURA 4.12 GABARITO MÍNIMO CONDICIONANTE DA GEOMETRIA DOS PENDURAIS 40 FIGURA 4.13 ALTERNATIVAS PARA O TRAÇADO DOS PENDURAIS 41 FIGURA 4.14 EXEMPLO DE FIXAÇÕES DO MESMO ESTILO DAS USADAS NA SOLUÇÃO PROPOSTA, EXECUTADAS EM AÇO VAZADO PARA O TABULEIRO DA NOVA TRAVESSIA DO RIO SADO EM ALCÁCER DO SAL 42 FIGURA 4.15 DISTRIBUIÇÃO DE MOMENTOS E ARMADURAS NUM PAINEL DE LAJE 45 FIGURA 4.16 DISTRIBUIÇÃO DE ARMADURAS TRANSVERSAIS NUM PAINEL TIPO DE LAJE 46 FIGURA 4.17 DISTRIBUIÇÃO DE ARMADURAS LONGITUDINAIS NUM PAINEL TIPO DE LAJE 47 FIGURA 4.18 POSSÍVEIS CENÁRIOS ADOPTADOS DE ACÇÃO DAS SOBRECARGAS RODOFIVÁRIAS 48 FIGURA 4.19 MODELO DE CÁLCULO REALIZADO NO PROGRAMA SAP FIGURA 4.20 DESLOCAMENTOS VERTICAIS NOS PONTOS DE FIXAÇÃO DOS PENDURAIS, NA EXTREMIDADE DA DIREITA 52 FIGURA 4.21 DESLOCAMENTOS VERTICAIS NOS PONTOS DE FIXAÇÃO DOS PENDURAIS, NA EXTREMIDADE DA ESQUERDA 53 FIGURA 4.22 ENQUADRAMENTO DE ENUMERAS PONTES DO TIPO BOWSTRING, 62 FIGURA 4.23 GEOMETRIAS DE APLICAÇÃO DA SOBRECARGA ADOPTADAS PARA ESTUDO DA ESTABILIDADE DO ARCO 64 FIGURA 4.24 PRIMEIRO MODO DE INSTABILIDADE DO ARCO (FACTOR DE ESCALA IGUAL A +500) 65 FIGURA 5.1 RELAÇÃO ALTURA DO ARCO/VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS E PARA A SOLUÇÃO PROPOSTA 74 FIGURA 5.2 RELAÇÃO ALTURA DO TABULEIRO/VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS E PARA A SOLUÇÃO PROPOSTA 74 FIGURA 5.3 RELAÇÃO ENTRE O PESO DE AÇO NO ARCO E NOS PENDURAIS POR M 2 DE ÁREA DO TABULEIRO EM FUNÇÃO DO VÃO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS E PARA A SOLUÇÃO PROPOSTA 75 FIGURA 5.4 RELAÇÃO QUANTIDADE DE AÇO TOTAL POR M 2 DE ÁREA DO TABULEIRO EM FUNÇÃO DO VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS E PARA A SOLUÇÃO PROPOSTA 75 FIGURA 5.5 RELAÇÃO QUANTIDADE DE AÇO TOTAL POR M 2 DE ÁREA DO TABULEIRO EM FUNÇÃO DO VÃO DO TABULEIRO, PARA PONTES DO TIPO BOWSTRING RODOVIÁRIAS E FERROVIÁRIAS CONSTRUÍDAS E PARA A SOLUÇÃO PROPOSTA 76 x
13 ÍNDICE DE QUADROS QUADRO 2.1 LAYOUT DO QUADRO 2.2 FICHA DA BASE DE DADOS CONSTRUÍDA 11 QUADRO 2.2 FICHA-TIPO DA BASE DE DADOS CONSTRUÍDA SOBRE AS PONTES DO TIPO BOWSTRING 12 QUADRO 4.1 CARACTERÍSTICAS DO BETÃO ARMADO 43 QUADRO 4.2 PESOS VOLÚMICOS DO BETÃO BETUMINOSO, BETÃO LEVE E BETONILHA 43 QUADRO 4.3 CARACTERÍSTICAS DOS AÇOS PARA ARMADURAS 43 QUADRO 4.4 CARACTERÍSTICAS DOS AÇOS PARA BARRAS PRÉ-ESFORÇADAS 43 QUADRO 4.5 CARACTERÍSTICAS DOS AÇOS PARA PERFIS DE AÇO 43 QUADRO 4.6 ARMADURAS TRANSVERSAIS DISTRIBUÍDAS PELAS ZONAS ARBITRADAS E MOMENTOS FLECTORES ACTUANTES 46 QUADRO 4.7 ARMADURAS LONGITUDINAIS DISTRIBUÍDAS PELAS ZONAS ARBITRADAS E MOMENTOS FLECTORES ACTUANTES 47 QUADRO 4.8 DESLOCAMENTOS NOS PONTOS DE FIXAÇÃO DOS PENDURAIS 54 QUADRO 4.9 ESFORÇOS AXIAIS NOS PENDURAIS RELATIVOS AOS ELU 55 QUADRO 4.10 ESFORÇOS AXIAIS NOS PENDURAIS RELATIVOS À FADIGA 57 QUADRO 4.11 ESFORÇOS DE DIMENSIONAMENTO DO ARCO 58 QUADRO 4.12 FACTOR Λ PARA OS VÁRIOS CARREGAMENTOS ADOPTADOS 64 QUADRO 4.13 CÁLCULO DO COEFICIENTE DE ENCURVADURA 65 QUADRO 4.14 VALORES DOS FACTORES DE INTERACÇÃO 66 QUADRO 4.15 CÁLCULO DO COEFICIENTE DE ENCURVADURA (PARA UM ARCO DE D = 3000 MM) 66 QUADRO 4.16 VALORES DOS FACTORES DE INTERACÇÃO (PARA UM ARCO DE D = 3000 MM) 66 QUADRO 5.1 QUANTIDADE DE BETÃO DA LAJE DE TABULEIRO DA SOLUÇÃO PROPOSTA 70 QUADRO 5.2 QUANTIDADES DE AÇO DOS VÁRIOS ELEMENTOS DA SOLUÇÃO PROPOSTA 70 QUADRO 5.3 QUANTIDADES DE ARMADURA LONGITUDINAL SUPERIOR 71 QUADRO 5.4 QUANTIDADES DE ARMADURA LONGITUDINAL INFERIOR 71 QUADRO 5.5 QUANTIDADES DE ARMADURA TRANSVERSAL SUPERIOR 71 QUADRO 5.6 QUANTIDADES DE ARMADURA TRANSVERSAL INFERIOR 71 QUADRO 5.7 QUANTIDADES DE ARMADURA TOTAIS 72 QUADRO 5.8 ESTIMATIVA ORÇAMENTAL DA SOLUÇÃO PROPOSTA 72 QUADRO A.1 GEOMETRIA DOS ELEMENTOS DO TABULEIRO EM BETÃO E DERIVADOS 116 QUADRO A.2 MOMENTOS LONGITUDINAIS DE DIMENSIONAMENTO DAS CARGAS PERMAMENTES DA LAJE DE TABULEIRO 116 QUADRO A.3 MOMENTOS TRANSVERSAIS DE DIMENSIONAMENTO DAS CARGAS PERMAMENTES DA LAJE DE TABULEIRO 116 QUADRO A.4 MOMENTOS LONGITUDINAIS DE DIMENSIONAMENTO DAS SOBRECARGAS DA LAJE DE TABULEIRO 116 QUADRO A.5 MOMENTOS TRANSVERSAIS DE DIMENSIONAMENTO DAS SOBRECARGAS DA LAJE DE TABULEIRO 116 QUADRO A.6 ESFORÇO AXIAL NOS PENDURAIS DEVIDO À ACÇÃO DAS SOBRECARGAS, NAS VÁRIAS POSIÇÕES ADMITIDAS 117 QUADRO A.7 ESFORÇO AXIAL NOS PENDURAIS DEVIDO À ACÇÃO DE TEMPERATURA DE -1000ºC, ACTUANDO ISOLADAMENTE EM CADA PENDURAL, UM A UM 119 QUADRO A.8 DESLOCAMENTOS NOS PONTOS DE FIXAÇÃO DOS PENDURAIS AO TABULEIRO DEVIDO À ACÇÃO DE TEMPERATURA DE -1000ºC, ACTUANDO ISOLADAMENTE EM CADA PENDURAL, UM A UM 123 QUADRO A.9 ESFORÇO AXIAL NOS PENDURAIS DEVIDO ÀS VÁRIAS POSIÇÕES DE SOBRECARGA DO MODELO LM3 127 QUADRO A.10 VALORES DOS VÁRIOS PARÂMETROS USADOS NO CÁLCULO DOS DESLOCAMENTOS DE TENSIONAMENTO 129 QUADRO A.11 VALORES DOS ESFORÇOS AXIAIS E DAS VERIFICAÇÕES AOS ELS NOS PENDURAIS 129 QUADRO A.12 ORÇAMENTO DO CASO DE ESTUDO 130 QUADRO A.13 ORÇAMENTO DA SOLUÇÃO PROPOSTA 131 xi
14 SIMBOLOGIA diâmetro médio de um varão diâmetro de um varão RHS Rectangular Hollow Section (Secção Tubular Rectangular) CHS Circular Hollow Section (Secção Tubular Circular) h altura total de uma secção transversal b largura de uma secção transversal t espessura D diâmetro exterior da secção tubular circular de um perfil de aço L comprimento total da ponte B largura total da ponte f y e r u x u y u z f ck f cd f ctm E c,(28) γ c f yk f yd E s γ s f u α tensão de cedência espessura da laje de betão raio interior da secção tubular circular de um perfil de aço deslocamento segundo a direcção do eixo x deslocamento segundo a direcção do eixo y deslocamento segundo a direcção do eixo z valor característico da tensão de rotura do betão à compressão aos 28 dias de idade valor de cálculo da tensão de rotura do betão à compressão valor médio da tensão de rotura do betão à tracção simples módulo de elasticidade tangente na origem, σ c = 0, para um betão de massa volúmica normal aos 28 dias de idade coeficiente parcial relativo ao betão valor característico da tensão de cedência à tracção do aço das armaduras para betão armado valor de cálculo da tensão de cedência à tracção do aço das armaduras para betão armado valor de cálculo do módulo de elasticidade do aço de uma armadura para betão armado coeficiente parcial relativo ao aço das armaduras para betão armado ou de préesforço tensão última coeficiente de dilatação térmica linear LM1 Load Model 1 (Modelo de Carregamento 1) m i jj m ELU μ ω A s momento flector de laje na secção i, segundo a direcção j momento flector em Estado Limite Último momento flector reduzido percentagem mecânica de armadura área de armadura xii
15 pp peso próprio rcp restantes cargas permanentes sob sobrecargas Δ pp Δ rcp Δ tens Δ perm γ G γ Q γ P γ R N pp N rcp N sob N tens N total F Ed F Rd1 F Rd2 F Rd Δσ c γ Mf deslocamento devido à acção do peso próprio deslocamento devido à acção das restantes cargas permanentes deslocamento devido ao tensionamento dos pendurais deslocamento das cargas permanentes (pp + rcp + tens) coeficiente de segurança relativo às cargas permanentes coeficiente de segurança relativo às sobrecargas coeficiente de segurança relativo ao pré-esforço factor de minoração da força de rotura esforço axial actuante num pendural devido à acção do peso próprio esforço axial actuante num pendural devido à acção das restantes cargas permanentes esforço axial actuante num pendural devido à acção das sobrecargas esforço axial actuante num pendural devido ao tensionamento dos pendurais esforço axial actuante num pendural de serviço esforço axial actuante num pendural em Estado Limite Último força característica de rotura de uma barra força resistente de uma barra menor valor entre a força característica de rotura de uma barra e a força resistente de uma barra tensão de resistência à fadiga (não minorada) factor parcial de minoração LM3 Load Model 3 (Modelo de Carregamento 3) ΔN Ed Δσ LM3 Δσ E N Ed A M y,ed W PL γ M0 M z,ed P V y V z V MAX T M y esforço axial actuante devido à acção de fadiga tensão residual devido ao carregamento do modelo LM3 tensão residual devido à acção de fadiga (minorada) esforço axial de dimensionamento área da secção momento flector actuante segundo o eixo principal y momento plástico da secção factor de segurança para perfis metálicos momento flector actuante segundo o eixo principal z esforço axial esforço transverso segundo y esforço transverso segundo z esforço transverso máximo momento torsor momento flector segundo y xiii
16 M z M MAX E pp E rcp E tens E sob E ELU ΧLT Χ Φ α momento flector segundo x momento flector máximo esforço axial actuante no arco devido à acção do peso próprio esforço axial actuante no arco devido à acção das restantes cargas permanentes esforço axial actuante no arco devido ao tensionamento dos pendurais esforço axial actuante no arco devido à acção das sobrecargas esforço axial actuante no arco em Estado Limite Último coeficiente de redução devido à encurvadura lateral coeficiente de redução devido à encurvadura como coluna esbelteza normalizada parâmetro de encurvadura factor de imperfeição parâmetro que corresponde ao número de vezes que a acção aplicada inicialmente, necessita de ser incrementada para que a estrutura instabilize LM4 Load Model 4 (Modelo de Carregamento 4) N FE,el L TRANS L LONG A LONG A TRANS carga crítica comprimento do varão na direcção transversal comprimento do varão na direcção longitudinal armadura segundo a direcção longitudinal armadura segundo a direcção transversal xiv
17 Capítulo 1 - INTRODUÇÃO E OBJECTIVOS 1.1 CONSIDERAÇÕES GERAIS As pontes foram desde sempre consideradas obras de arte no domínio da Engenharia de Estruturas. De entre elas, as pontes com Arco Superior destacam-se pela sua qualidade estética incomparável. De entre as pontes com arco superior têm sido projectadas e construídas, nos últimos trinta anos, inúmeras obras do tipo Bowstring. O termo bowstring resulta do funcionamento estrutural adoptado por este tipo de obras. O arco superior bow, sempre fortemente comprimido, é interiormente autoequilibrado pelo tabuleiro traccionado, que funciona como um tirante daí o termo string. Da conjugação dos dois elementos resulta o tabuleiro com arco superior do tipo Bowstring arco com tirante. Um dos principais impulsionadores desta solução, conjugando-a com uma suspensão do tipo Net (caracterizada por ter pendurais cruzados em rede ) tem sido o Engenheiro norueguês Per Tveit. Desde a sua primeira obra construída em Steinkjer, Noruega, em 1963 (Figura 1.1) até à espantosamente leve e esbelta Ponte Bolstadstraumen, construída também em 1963 a 60 km a noroeste de Bergen, Noruega (Figura 1.2), foram abundantes as obras por si projectadas. Igualmente, no domínio das pontes ferroviárias, pontes do tipo Bowstring têm sido construídas. Embora menos esbelto que as obras rodoviárias do mesmo tipo, este tipo de tabuleiros permite vencer vãos superiores a 100 m, sem necessidade de recurso a apoios intermédios. Diversas obras ferroviárias, mesmo para as linhas de alta velocidade da Europa, China e Japão têm, por isso, adoptado soluções de tabuleiro superior do tipo Bowstring (Figura 1.3). Também em Portugal têm vindo a ser construídas pontes deste tipo nos últimos anos, especialmente no domínio das obras ferroviárias e pedonais. Possivelmente a obra mais significativa seja a recentemente inaugurada nova travessia ferroviária do Rio Sado (Figura 1.4). Trata-se de uma obra singular dado que conjuga duas vias ferroviárias com um caixão contínuo de 480 m suspenso por três arcos superiores centrais de 160 m [1]. No domínio das pontes rodoviárias são inúmeras as realizações recentes, sendo uma solução que se adapta bem quer a pequenos vãos, como a grandes obras de autoestradas. Dois casos muito recentes consistem na Ponte Depot Street, concluída nos Estados Unidos em 2006, para atravessamento do Rio Rogue (Figura 1.5), e na Ponte Pentele, concluída na Hungria em 2007, para atravessamento do Rio Danúbio pela nova autoestrada M8 (Figura 1.6) [2]. A primeira trata-se de uma ponte com tabuleiro e arco em betão armado pré-esforçado, com suspensão em Net e um vão de 93 m, a segunda de uma ponte com tabuleiro misto aço-betão e um arco metálico, com suspensão lateral inclinada e um vão de 308 m, e que evidenciam bem as potencialidades deste tipo de soluções estruturais, quer para vãos médios, quer para vãos acima dos 300 m. 1
18 Figura 1.1 Ponte em arco do tipo Net em Steinkjer, Noruega. Vão principal com 80 m. [3] Figura 1.2 Ponte Bolstadstraumen na Noruega. Vão principal com 84 m. [3] Figura 1.3 Ponte ferroviária de via dupla em Roterdão, Holanda sobre o Canal Hartel. Vão principal com 170 m. Figura 1.4 Ponte sobre o Rio Sado em Portugal. Vãos principais com 160 m. Figura 1.5 Ponte Depot Street do tipo Net, em Oregon, nos Estados Unidos. Vão principal com 93 m. Figura 1.6 Ponte Pentele em Dunaújváros, Húngria. Vão principal com 308 m. [2] Têm sido igualmente construídas diversas pontes pedonais com tabuleiros do tipo Bowstring. Estas pontes possuem características particulares dado que as cargas de serviço são muito menores, sendo a sua concepção porventura muito mais influenciada por razões estéticas e arquitectónicas, do que por critérios técnicos ou económicos. Deste modo, torna-se difícil a tipificação das pontes Bowstring pedonais e o seu estudo em conjunto com as pontes rodoviárias e ferroviárias do mesmo tipo, razão pela qual não se lhe faz referência no presente trabalho. 2
19 1.2 OBJECTIVOS Os objectivos identificados para esta dissertação de Mestrado, com vista à realização de um Estudo Prévio de um tabuleiro em arco superior do tipo Bowstring, foram os seguintes: 1. Elaboração de uma base de dados, de modo a ter uma visão de conjunto das pontes rodoviárias e ferroviárias construídas com esta tipologia em todo o mundo, assim como criar um guia de consulta deste tipo de pontes, para estudos futuros, e ter noções sobre o pré-dimensionamento de soluções; 2. Estudo preliminar das diversas soluções estruturais possíveis, para tabuleiros do tipo arco superior, e pré-dimensionamento dos elementos estruturais principais do tabuleiro para a solução proposta; 3. Estudo do comportamento estrutural de um tabuleiro deste tipo, para as acções condicionantes de projecto de acordo com os Eurocódigos; 4. Medições e Estimativa de Custo da solução estudada, e Análise Comparativa da solução proposta com obras construídas do mesmo tipo; e 5. Apresentação das conclusões que resumam as vantagens e desvantagens deste tipo de tabuleiro, em relação a outras soluções possíveis. 1.3 ESTRUTURA DO TRABALHO A dissertação de Mestrado apresenta uma estrutura que se enquadra de forma genérica nos objectivos identificados. No segundo Capítulo expõe-se uma designação e enquadramento histórico das pontes de arco superior do tipo Bowstring, em conjunto com uma vasta lista de obras do tipo, realizadas por todo o mundo. Com esta investigação pretende-se obter princípios de boa prática e noções sobre pré-dimensionamento. Seguidamente, no Capítulo 3, procede-se a um estudo preliminar de soluções, de forma a concluir sobre qual a solução mais viável para o desenvolvimento do estudo. No Capítulo 4, é realizada uma análise do comportamento da estrutura proposta, apresentando-se sucessivamente os modelos de análise e as principais verificações de segurança. No Capítulo 5 é apresentada uma medição e estimativa de custo da solução proposta e efectuada uma comparação dos resultados obtidos com um caso de estudo, com obras construídas do mesmo tipo e de outras soluções possíveis para o tabuleiro da solução proposta, nomeadamente 3
20 adoptando um caixão de betão armado pré-esforçado realizado pela técnica construtiva dos avanços sucessivos. Por fim, no Capítulo 6, mostram-se as conclusões que resumem as vantagens e desvantagens associadas às pontes de arco superior do tipo Bowstring, reportando-se à situação do caso de estudo. Apresentam-se igualmente neste capítulo linhas de desenvolvimento possíveis do trabalho realizado. 4
21 Capítulo 2 - ESTUDO DAS SOLUÇÕES CONSTRUÍDAS 2.1 INTRODUÇÃO HISTÓRICA E EVOLUÇÃO ESTRUTURAL Desde sempre que a construção de pontes com recurso ao arco é uma solução das mais utilizadas. Exemplo disso são as antigas pontes romanas de alvenaria em pedra, onde se pode encontrar um arco inferior que suporta o tabuleiro e as respectivas sobrecargas, transmitindo as cargas verticais para o solo. Aliás, o arco destaca-se como um dos elementos mais relevantes em todas as obras de Engenharia Civil. O seu formato exprime toda a capacidade que possui para encaminhar as cargas verticais aplicadas ao tabuleiro sobre um vale ou rio, para as suas fundações, nas margens ou nas encostas. A beleza do arco como solução estrutural advém precisamente da forma simples como se compreende o seu funcionamento em termos estruturais, seja para grandes pontes ou para pequenos vãos. Dos arcos de pedra passou-se para o uso de materiais mais resistentes e com melhores propriedades, como o ferro, o aço e o betão armado. Todavia, para o tipo de obras de arte existentes até ao início do século XX, em que predominavam os arcos inferiores, a adopção destes novos materiais não traziam grandes vantagens e conduziram a elevados custos, principalmente para pequenos vãos, levando a que se tornasse menos corrente a sua construção. Contudo, em sua substituição surgiram outras soluções estruturais que tiraram melhor partido das propriedades destes novos materiais, com menores custos de construção. [4] Porém, a evolução dos processos de construção e de dimensionamento devolveu novamente à solução estrutural em arco, a posição relevante que sempre teve na Engenharia das Pontes. Para além das pontes em arco inferior, surgiram mais recentemente as pontes de arco superior, que vieram trazer enumeras vantagens em muitos casos. Referem-se, por exemplo, as situações onde o terreno apresenta características de planície, sendo necessário um gabarito reduzido abaixo do tabuleiro e se torna impossível a colocação de um arco inferior compatível, ou quando é preciso um gabarito mínimo sobre um rio ou canal navegável pouco largo (entre 100 a 200 m). Contudo, o conceito estrutural principal do arco superior é o mesmo, ou seja, o arco continua a ser o elemento principal, sujeito a elevados esforços. No entanto, enquanto nas pontes de arco inferior o seu comportamento era muito intuitivo, sendo as cargas completamente descarregadas no arco através de pilares de ligação, nas pontes de arco superior o funcionamento torna-se mais complexo e menos compreensível (Figura 2.1). As cargas são transmitidas ao arco por pendurais, verticais ou inclinados, estando em princípio estes elementos de aço sempre à tracção. O arco encontra-se, tal como nos arcos inferiores, sempre muito comprimido, tendo tanto menor flexão, quanto maior o número de pendurais que lhe transmitem a carga vertical do tabuleiro. O apoio nas extremidades do tabuleiro é realizado através de colunas que constituem os encontros ou os pilares 5
22 de transição, e podem apresentar-se sobre diversas formas e diferentes materiais, embora as soluções de betão armado predominem. Referem-se ainda soluções em que se conjugam o arco superior com a passagem deste elemento para baixo do tabuleiro, passando a funcionar com um arco inferior tradicional (Figura 2.2). Trata-se de uma solução com algumas particularidades, dado que esta transição do tabuleiro tem que ser bem analisada em termos estruturais. Contudo, permite eliminar ou reduzir o impacto visual dos pilares/encontros que são necessários para o apoio do tabuleiro, no caso de um tabuleiro com um arco exclusivamente superior (Figura 2.3). No presente trabalho são estudadas as soluções de pontes com arco superior particular do tipo Bowstring, excluíndo todas as pontes de arco inferior ou misto, e também as pontes de arco superior com duplo suporte ( two-hinged ). Como se referiu no Capítulo 1 -, o termo bowstring resulta do funcionamento estruturalmente auto-equilibrado exibido por este tipo específico de tabuleiro com o arco superior. Refere-se este termo dado que este tipo de estruturas é equilibrada interiormente, sendo transmitidas para o exterior (entenda-se pilares ou encontros) apenas as cargas verticais aplicadas no tabuleiro, o que não acontece com os arcos tradicionais. De facto, o que se verifica, de forma simples, é que o arco superior bow, sempre fortemente comprimido, é interiormente autoequilibrado em termos de forças horizontais geradas pela força do arco, pelo tabuleiro traccionado, que funciona como um tirante daí o termo string. Da conjugação dos dois elementos resulta o tabuleiro com arco superior do tipo bowstring arco com tirante (Figura 2.3). Figura 2.1 Esquema de uma ponte de arco inferior [4] Figura 2.2 Esquema de uma ponte de arco superior do tipo Two-hinged [4] Figura 2.3 Esquema de uma ponte de arco superior do tipo Bowstring [4] 6
23 2.2 ESTÉTICA E FUNCIONALIDADE Estes são os aspectos fundamentais na fase de pré-dimensionamento de qualquer ponte, sendo de muito maior relevância quando se projecta as pontes com arco superior, pelo motivo claro do impacto que a dimensão e a geometria dos arcos produz. Relativamente à estética da obra, destaca-se dois aspectos principais que abrangem praticamente no seu todo, a beleza e integração paisagística de uma obra de arte deste tipo. O primeiro aspecto está ligado à relação entre a altura do arco e o vão da ponte. Da análise das pontes construídas é possível afirmar que se pode construir arcos superiores até uma relação de 1/12, ou seja, uma ponte com um vão de 120 m poderá ter um arco tão baixo como 10 m de altura. Quanto mais baixa for esta relação, mais harmonioso e esbelto será o desenho da ponte, sendo claro que deve haver um equilíbrio entre a estrutura e a envolvente, devendo existir um limite máximo de altura do arco, para que a obra de arte não se sobreponha à envolvente. O outro factor importante a ter em conta está directamente relacionado com as espessuras adoptadas para o arco e para as vigas de suporte do tabuleiro, principalmente as vigas longitudinais. Mais uma vez, quanto maiores as secções de qualquer um dos elementos, menos esbelta será a obra. Mas, mais importante que isso, é a relação entre as duas espessuras. Se se tiver um arco muito espesso face a uma laje e vigas muito esbeltas, o arco é destacadamente o elemento de suporte mais marcante da estrutura, especialmente quando se observa a obra a grande distância. Mas, se por outro lado forem de grandes dimensões as vigas de suporte do tabuleiro e o arco apresentar grande esbelteza, o papel inverte-se e passa o tabuleiro a ser o elemento principal, mais relevante da estrutura. Cada uma destas alternativas pode ser boa proposta consoante o que se queira dar entender e o que for praticável. Devem evitar-se, se for possível, situações em que não existam diferenças marcantes entre os dois elementos tabuleiro/arco, pois poderá tornar-se nesse caso uma ponte menos compreensível e mais pardacenta, podendo não cumprir os conceitos estéticos que se pretende. Quanto à funcionalidade dos vários elementos que compõem as pontes de arco superior excluindo o próprio arco, poder-se-á também destacar dois conceitos importantes. Um deles está ligado à rigidez das vigas longitudinais que suportam a laje de tabuleiro. Quanto mais rígidas forem estas vigas, menores serão os esforços no arco. Obviamente que esta influência pode ser maior ou menor em cada caso concreto, podendo não ser até um aspecto significativo. Verificam-se assim obras construídas que seguem este conceito, adoptando um tabuleiro bastante rígido suspenso de um arco relativamente esbelto (Figura 2.4), enquanto outras adoptam tabuleiros muito esbeltos suportados por arcos mais rígidos (Figura 2.5). O segundo aspecto a destacar tem a ver com a inclinação dos pendurais. O modelo mais tradicional consiste em adoptar pendurais verticais nas duas direcções. No entanto, ao longo dos anos foram adoptados outros tipos de soluções, envolvendo a inclinação dos tirantes de variadas formas, caracterizadas na secção seguinte. Esta concepção veio trazer vantagens ao nível dos esforços actuantes no arco. Dependendo do grau de inclinação, do número e da geometria dos pendurais, os seus efeitos sobre o arco têm tendência a diminuir. Um estudo deste efeito é 7
24 apresentado pelo Engenheiro norueguês Per Tveit [3], que demonstra que a variação dos esforços no arco é muito dependente do andamento dos pendurais, e nomeadamente que os esforços de flexão são minimizados quando se adopta um tipo de distribuição dos pendurais denominada Net (Figura 2.6), em que os pendurais são muito numerosos, inclinados e cruzados, funcionando como uma rede de apoios do tabuleiro e de transmissão quase contínua de forças ao arco. Com este tipo de suspensão têm sido projectados arcos e tabuleiros com esbeltezas extremamente elevadas. Figura 2.4 Ponte Železniční em Ropice, República Checa. Vão com 62 m. Figura 2.5 Ponte em Salies-du-Salat, França. Vão com 56 m. Figura 2.6 Ponte Reina Sofía em Palma del Río, Espanha. Vão principal com 130 m. 2.3 TIPOS DE PONTES DE ARCO SUPERIOR BOWSTRING As pontes de arco superior do tipo Bowstring podem ser classificadas de acordo com três aspectos associados à sua geometria: 1. Com base nos arcos; 2. Com base no tipo de suspensão; e 3. Com base no traçado dos pendurais. Com base na localização dos arcos (em qualquer uma das soluções os arcos poderão ser perfeitamente verticais ou inclinados): Central, podendo existir mais do que um arco (Figura 2.7); Laterais (em geral dois arcos ligados entre si por contraventamentos) (Figura 2.8); Diagonal atravessamento completo em planta do tabuleiro (Figura 2.9); 8
25 Figura 2.7 Viaduto de Briare em França. Vão principal com 86 m. Figura 2.8 Ponte Nordring em Marktheidenfeld, Alemanha. Vão principal com 135 m. Figura 2.9 Ponte de l Observatoire em Liège, Bélgica. Vão principal com 82 m. Com base no tipo de suspensão: Central pendurais fixos no centro do tabuleiro (Figura 2.10); Lateral pendurais fixos nas extremidades do tabuleiro (Figura 2.11); Figura 2.10 Ponte Ujina em Hiroshima, Japão. Vão principal com 103 m. Figura 2.11 Ponte de la Peraleda em Toledo, Espanha. Vão com 127 m. 9
26 Com base na geometria dos pendurais, ou seja, no tipo de inclinação que os pendurais apresentam na ligação arco-tabuleiro: Verticais (Figura 2.12); Inclinados, segundo a direcção transversal (Figura 2.13); Em leque (Figura 2.14); Triangulares (Figura 2.15); Em Net (Figura 2.16). Figura 2.12 Ponte Sickingmühlen em Marl, Alemanha. Vão com 55.8 m. Figura 2.13 Ponte Merivale em Brisbane, Austrália. Vão principal com 132 m. Figura 2.14 Ponte Centrale em Reggio nell Emilia, Itália. Vão com 221 m. Figura 2.15 Paveletsky Railroad Overpass em Moscovo, Rússia. Vao principal com 110 m. Figura 2.16 Ponte Marexhe em Liège, Bélgica. Vão com 100m. Todas estas configurações são possíveis e têm sido adoptadas em obras construídas, constituindo opções do Projectista. A variedade de opções de geometria dos arcos e dos sistemas de 10
27 suspensão associadas aos tabuleiros do tipo Bowstring, contribui de forma decisiva para tornar estas obras tão diversificadas e atraentes. 2.4 OBRAS CONSTRUÍDAS No Anexo A apresenta-se uma Base de Dados das pontes de arco superior do tipo Bowstring construídas em todo o mundo. Esta lista inclui diversos parâmetros que as caracterizam, obtidos a partir da consulta de numerosas fontes bibliográficas, artigos de congressos e sítios da internet, e como resultado de uma extensa pesquisa. De referir que pontes pedonais do tipo Bowstring não foram incluídas na base de dados visto que a sua tipologia é muito diferente e variada, sendo mais condicionada por aspectos arquitectónicos que condicionantes estruturais, dado que as solicitações são muito distintas (sobrecargas actuantes e larguras de tabuleiro muito menores). Quadro 2.1 Layout do Quadro 2.2 Ficha da base de dados construída Imagem da ponte TÍTULO DA PONTE Localização Data de conclusão Gabinete de engenharia/designer Utilização Método Construtivo Tabuleiro Secção transversal Material Largura [m] Altura [m] Esbelteza Arco Tipo Secção transversal Pendurais Material Vão [m] Altura [m] Rácio Altura/Vão Peso dos materiais Aço Betão Pendurais Arco Tabuleiro Arco Tabuleiro Publicações relevantes O objectivo desta recolha de informação consistiu em ter uma percepção geral das características gerais das obras construídas deste tipo. Contudo, revelou-se particularmente difícil a recolha informação para todas as obras por não se encontrar disponível ou estar muito dispersa. No futuro, tem todo o interesse procurar completar e manter actualizada esta base de dados, de forma a servir de auxílio para projectos da mesma natureza. Como esse não foi o objectivo principal do presente trabalho, as tabelas apresentam alguma falta de informação no que respeita nomeadamente a pormenores do tabuleiro e a quantidades de materiais utilizados. De modo a dar uma ideia geral do que já foi realizado e que se torna possível adoptar como base de partida para obras futuras, apresenta-se nas páginas seguintes alguns exemplos relevantes de obras construídas, que procuram de algum modo abranger todo o tipo de casos estruturais encontrados. 11
28 Quadro 2.2 Ficha-tipo da Base de Dados construída sobre as pontes do tipo Bowstring PONT D HENRIOUS La Blégude Blanche/Estoublon, França [5] 1927 [5] Rodoviária [5] Laterais Vigada Verticais Betão Armado Betão Armado [5] 6,00 [5] 25 [5] [6] BIG CREEK BRIDGE Lane County, Oregon, EUA [7] 1931 [7] Conde Balcom McCullough (designer) [7] Rodoviária [7] Laterais Maciça Rectangular Verticais Betão Armado Betão Armado [7] 8,23 [8] 37 [8] [9], [10], [11] BALCLUTHA ROAD BRIDGE Balclutha, Nova Zelândia [12] 1935 [12] W.L.Newnham (designer) [12] Rodoviária [12] Laterais Rectangular Verticais Betão Armado Betão Armado [12] 11,80 [12] 6 x 37 [12] 9,2 [13] 1/ [13] [14], [15] PONT D ENGIS Engis, Bélgica [16] 1950 [16] Rodoviária [16] Lateral Vigada Rectangular Verticais Misto Aço-Betão Betão Armado [16] 7 [16] 3 x 48 [16] 9,0 [16] 1/5 [17] 12
29 BRÜCKE DER SOLIDARITÄT Duisburg, Alemanha [18] 1950 [18] Krupp Stahlbau Hannover [18] Rodoviária [18] Lateral Vigada Caixão Rectangular Verticais Aço Aço [18] 14, [18] 4,32 [19] 35,5 [19] 3,4 1/7 - [20], [21], [22], [23] HERNANDO DE SOTO BRIDGE Arkansas/Tennessee, Estados Unidos [24] 1972 [24] Rodoviária [24] Laterais Treliçada 3D Verticais Aço [24] 27,00 2 x 274 [24] - [25] PONT DE MILSAUCY Liège, Bélgica [26] 1990 [26] Rodoviária [26] Elevação com grua Laterais Vigada Caixão Rectangular Network Misto Aço-Betão Aço [26] 15,46 [27] 145 [27] 1,28 24,0 [27] 12,1 1/6 - [28], [29] WESERBRÜCKE HOLZMINDEN Holzminden, Alemanha [30] 1996 [30] Ingenieurbüro Meyer + Winter [30] Rodoviária [30] Laterais Vigada Caixão Rectangular Verticais Misto Aço-Betão Aço [30] 14,50 [30] 89 [30] 450 (estrutural) [30] [30] [31] 13
30 AAREBRÜCKE Arch/Grenchen, Suíça [32] 1997 [32] Rodoviária [32] Laterais Caixão Hexagonal Triangular/Inclinados Betão Armado Aço [32] 13, [32] - [33] BOWSTRING D'AVIGNON-SUD Bonpas, França [34] 1998 [34] Société d'études R. Foucault et Associés [34] Ferroviária AV [34] Laterais Vigada Caixão Rectangular Verticais Misto Aço-Betão Aço [34] 124 [34] 2650 (estrutural) [34] - [35], [36], [37], [38] BRÜCKE HEBBELSTRASSE (Nr. 234) Hannover, Alemanha [39] 1999 [39] S.E.H. Stahlbau Engineering Hannover [39] Rodoviária [39] Laterais Treliçada 3D Verticais Aço [39] 9,10 [39] 58 [39] 270 (estrutural) [39] - [40], [41] VIADUC DE MORNAS Duisburg, Alemanha [42] 1999 [42] Bureau d'études Greisch [41] Ferroviária AV [42] Laterais Vigada Caixão Trapezoidal [41] Verticais Misto Aço-Betão [41] Aço [41] 17,50 [41] 119 [41] 2,30 [41] 30,0 [41] 7,6 1/ [42] 2650 [42] - [43], [44], [45], [46], [47], [48] 14
31 VIADUC DE LA GARDE-ADHÉMAR (VIADUC DE DONZÈRE) Pierrelatte, França [49] 2000 [49] Marc Mimram [49] Ferroviária AV [49] Laterais Caixão Trapezoidal [41] Verticais Misto Aço-Betão [41] Aço [41] 20,00 [41] 2 x 110 [41] 2,60 [41] 18,0 [41] 7,7 1/ [49] - [50], [51], [52], [53], [54], [55], [56], [57], [58], [59] ENNEÜS HEERMA BRIDGE Amesterdão, Holanda [60] 2001 [60] WS Atkins&Partners Overseas [60] Rodoviária/Ferroviária Ligeira [60] Central/Laterais Inclinados Betão Armado [60] Aço [60] 2 x 20,00 [60] 2 x 75 [60] 26,0 [61] 1/ (estrutural) [60] [60] [62], [63], [64], [65], [66] PUENTE BOLOGNESI Piura, Peru [67] 2002 [67] Rodoviária [67] Laterais Vigada Caixão Rectangular Leque Misto Aço-Betão Aço [67] 22,70 [67] 150 [67] 30,0 [67] 1/5 - [68], [69], [70] DZIWNA MOST Wolin, Polónia [71] 2003 [71] Rodoviária [71] Laterais Vigada Caixão Rectangular Net/Inclinados Misto Aço-Betão Aço [71] 12,80 [71] 180 [71] 25,0 [71] 1/7 - [72], [73] 15
32 JAMES JOYCE BRIDGE Dublin, Irlanda [74] 2003 [74] Santiago Calatrava SA (designer), Roughan & O'Donovan [74] Rodoviária [74] Laterais Tubular Inclinados Misto Aço-Betão Aço [74] 21,00 [74] 40 [74] - [74] MOST APOLLO Bratislava, Eslováquia [75] 2005 [75] Dopravoprojekt a.s. (designer) [75] Rodoviária [75] Laterais Caixão Leque/Inclinados Misto Aço-Betão Aço [75] 19,20 [76] 231 [75] 36,0 [75] 1/ [75] - [77], [78], [79], [80], [81], [82] PUENTE AL TERCER MILENIO Zaragoza, Espanha [83] 2008 [83] Juan José Arenas de Pablo (designer) [83] Rodoviária [83] Cimbre ao solo Central Vigada Rectangular Inclinados Betão Armado [83] Betão Armado [83] 43,00 [83] 216 [83] 36,0 [83] 1/6 [84], [85], [86], [87], [88], [89], [90], [91], [92], [93] DE GASPERI BRIDGE Milão, Itália [94] 2009 [94] Metropolitana Milanese SPA (designer) [94] Rodoviária [94] Laterais Vigada Tubular Circular [94] Leque/Inclinados Misto Aço-Betão [95] Aço [94] 13,65 [95] 80 [94] 2,25 [96] 11,6 [94] 6,1 1/7 - [97] 16
33 Altura do arco [m] 2.5 RELAÇÕES DIMENSIONAIS DAS OBRAS CONSTRUÍDAS A informação recolhida das várias pontes de arco superior do tipo Bowstring permitiu construir gráficos que relacionam a altura do arco e o vão do tabuleiro, em função do tipo de materiais adoptados no tabuleiro (betão armado, betão armado pré-esforçado, aço, misto aço-betão) e à utilização da ponte (rodoviária, ferroviária, ferroviária de alta velocidade, mista rodo-ferroviária). Estes gráficos permitem uma análise das soluções construídas bem como, no final do dimensionamento da solução estudada ao longo do trabalho, a sobreposição nestes gráficos dos valores finais obtidos, de modo a confrontar a solução estudada com as obras construídas. Os resultados do gráfico da Figura 2.17 permitem igualmente concluir que existe uma altura do arco crescente e aproximadamente linear com o vão do tabuleiro, e que o facto de a obra ser ferroviária ou rodoviária não altera esta relação de forma relevante. Esta conclusão é interessante na medida em que mostra que a maior rigidez do tabuleiro, que normalmente é necessária nas obras ferroviárias é, no caso das pontes Bowstring, conseguida sem aumentar a altura do arco, mas antes aumentando a rigidez do próprio tabuleiro e as quantidades de aço utilizadas, tanto no tabuleiro, como no arco e nos pendurais, como se torna evidente dos resultados das Figura 2.18 a Figura Rodoviária Ferroviária Ferroviária AV Rodoviária/Ferroviária Rodoviária/Ferroviária Ligeira Vão [m] Figura 2.17 Relação altura do arco/vão do tabuleiro, para pontes do tipo Bowstring rodoviárias e ferroviárias construídas 17
34 Altura do tabuleiro [m] 5 4,5 4 3,5 3 Rodoviária Ferroviária 2,5 2 1,5 1 Ferroviária AV Rodoviária/Ferroviária Ligeira 0, Vão [m] Figura 2.18 Relação altura do tabuleiro/vão do tabuleiro, para pontes do tipo Bowstring rodoviárias e ferroviárias construídas 2.6 PRINCIPAIS QUANTIDADES DAS OBRAS CONSTRUÍDAS O mesmo exercício que se realizou na secção anterior pode ser, analogamente, realizado para as quantidades de materiais usados, em relação ao vão do tabuleiro e, mais uma vez, aos materiais usados no tabuleiro da ponte, em função da sua utilização. De acrescentar que, devido à pouca informação obtida principalmente a nível das quantidades dos materiais, quer totais, quer por elementos, os gráficos apresentados correspondem apenas às pontes cujos arcos são metálicos, e que a quantidade de aço total diz respeito à soma dos pesos respectivos do arco, dos pendurais e do tabuleiro, dividida pela área em planta do tabuleiro. 18
35 Quantidade de aço total/m 2 de tabuleiro [kg/m 2 ] Quantidade de aço no arco e nos pendurais/m 2 de tabuleiro [kg/m 2 ] Rodoviária Ferroviária AV Vão [m] Figura 2.19 Relação entre o peso de aço no arco e nos pendurais por m 2 de área do tabuleiro em função do vão tabuleiro, para pontes do tipo Bowstring rodoviárias e ferroviárias construídas Rodoviária Ferroviária Ferroviária AV Rodoviária/Ferroviária Rodoviária/Ferroviária Ligeira Vão [m] Figura 2.20 Relação quantidade de aço total por m 2 de área do tabuleiro em função do vão do tabuleiro, para pontes do tipo Bowstring rodoviárias e ferroviárias construídas 19
36 Quantidade de aço total/m 2 de tabuleiro [kg/m 2 ] Aço Betão Armado BAPE Misto Aço-Betão Vão [m] Figura 2.21 Relação quantidade de aço total por m 2 de área do tabuleiro em função do vão do tabuleiro, para pontes do tipo Bowstring rodoviárias e ferroviárias construídas Estes gráficos mostram que, embora com grande dispersão, o uso de aço varia de forma crescente com o vão do tabuleiro, e se encontra maioritariamente entre os 100 kg/m 2 e os 1000 kg/m 2 para tabuleiros rodoviários, e valores superiores no caso de tabuleiros ferroviários. De realçar que existe uma grande incerteza na análise destes gráficos, comparativamente com a Figura 2.17, devido às varianças de largura de tabuleiro e tipos de suspensão, que são relevantes para as quantidades de aço usadas. Para uma melhor análise será necessário obter mais informação sobre as pontes incluídas na base de dados para que, dessa forma, seja possível obter gráficos mais esclarecedores, divididos por utilização em função do tipo e largura do tabuleiro, e daí se poder retirar algumas conclusões que possam ajudar ao pré-dimensionamento e à avaliação da solução estudada. 20
37 Capítulo 3 - CASO DE ESTUDO 3.1 A SOLUÇÃO CONSTRUÍDA O Estudo Prévio desenvolvido neste trabalho, constitui uma solução variante em relação à Ponte sobre o Rio Sorraia, em Portugal, que faz parte da autoestrada A13, em funcionamento. Trata-se de uma obra com dois tabuleiros em paralelo em viga contínua de três tramos, com tabuleiro em caixão de altura variável (Figura 3.1). (a) (b) (c) Figura 3.1 Ponte sobre o Rio Sorraia, em Portugal, que faz parte da autoestrada A13: (a) Vista geral; (b) Ponte de avanços sucessivos durante a construção; (c) secções transversais tipo do tabuleiro em caixão 21
38 Esta obra é constituída por dois viadutos e a ponte central. Cada viaduto é constituído por dois tabuleiros paralelos, em laje vigada pré-esforçada com m de largura e 2.55 m de altura. Excepto os vãos extremos, junto dos encontros, todos os restantes têm 43.7 m, e foram executados com cimbre auto-lançável inferior. A ponte central é composta por um tabuleiro com dois vãos de 75 m laterais e um central de 120 m, com secção transversal com uma variação de altura entre os 2.55 m e os 6.0 m. Pretende-se estudar a possibilidade de extender os viadutos de acesso até à zona dos vãos laterais da ponte com dois vãos adicionais de 43.7 m e 31.3 m, em cada um dos viadutos de aproximação e, em relação ao tramo central de 120 m, pretende-se estudar uma solução de arco superior do tipo Bowstring, o que permitiria evitar a necessidade de recorrer à técnica construtiva dos avanços sucessivos, facilitando desta forma a construção do tabuleiro sobre o Rio Sorraia (Figura 3.2). Figura 3.2 Exemplo esquemático da solução proposta, face à solução em vigor De acordo com a Memória Descritiva do Projecto [98] : O perfil transversal, contempla duas faixas de rodagem para 4 vias de tráfego com 3.75 m cada, que traduz a solução habitual das auto-estradas da BRISA. As bermas direita e esquerda têm respectivamente 3 m e 1 m de largura. A obra de arte integra os seguintes elementos no seu tabuleiro: pavimento, passeios exteriores sobrelevados, lancis elevados, guardas de segurança na protecção dos passeios e do separador entre faixas de rodagem, guarda corpos nas extremidades exteriores do tabuleiro, vigas de bordadura nos passeios exteriores e sistema de drenagem. O revestimento do tabuleiro, na zona da faixa de rodagem é constituído por uma camada de desgaste em betão betuminoso com 4 cm de espessura sobre uma camada de betão betuminoso de regularização também com 4 cm de espessura. Adoptam-se os mesmos passeios, com 1.05 m de largura, integram uma camada de enchimento em betão leve, com cerca de 20 cm de altura, na qual estão embebidos três tubos de 22
39 40 mm de diâmetro e dois tubos de 90 mm de diâmetro, em PVC rígido, para passagem de serviços. A superfície dos passeios será constituída por uma camada de 2 cm de betonilha esquartelada. São protegidos por uma guarda de segurança, ligada ao tabuleiro por intermédio de prumos metálicos distanciados de 2 m entre si. Os prumos metálicos são fixados por intermédio de chumbadouros. Prevê-se também a colocação no separador de uma guarda de segurança, ligada ao tabuleiro por intermédio de prumos metálicos distanciados de 2 m entre si. As vigas de bordadura, em betão armado, são pré-fabricadas em troços de 1.5 m, sendo a sua fixação ao tabuleiro efectuada pelo processo indicado nos desenhos de projecto. Quanto ao sistema de drenagem do tabuleiro, está prevista a colocação de sumidouros constituídos por tubos de PVC com 12,5 mm de diâmetro, afastados em geral de 10 m. Alguns dos elementos integrantes do acabamento do tabuleiro serão modificados devido a uma necessidade face ao dimensionamento estabelecido, não alterando as dimensões daqueles que estão pré-definidos por razões rodoviárias e de segurança, ou seja, largura das bermas, das faixas de rodagem e dos passeios. 3.2 ESTUDO PRELIMINAR DE SOLUÇÕES DO TIPO BOWSTRING De forma a procurar soluções completamente diferentes com criatividade e inovação, o Estudo Prévio da ponte de arco superior do tipo Bowstring para o caso de estudo iniciou-se com o desenvolvimento de vários esboços, partindo da investigação das soluções construídas apresentada no Capítulo 2 -. Apresentam-se nas figuras da presente página, alguns esquemas das soluções imaginadas. Procurou-se explorar os sistemas estruturados possíveis no domínio dos tabuleiros do tipo Bowstring, quer a nível dos arcos (laterais, centrais, inclinados), como ao nível dos pendurais (suspensão central, lateral, inclinada, tipo leque, tipo network, com suspensão rígida). 23
40 Figura 3.3 Solução A Figura 3.4 Solução B 24
41 Figura 3.5 Solução C Figura 3.6 Solução D 25
42 Figura 3.7 Solução E Figura 3.8 Solução F 26
43 Após uma avaliação sumária com comportamento das várias propostas estruturais acima apresentadas, optou-se pela Solução A, que apresenta várias características principais relevantes tanto ao nível estético, como ao nível do comportamento estrutural e viabilidade construtiva. Refere-se nomeadamente as seguintes características: Configuração mais clara quer em termos conceptuais como construtivos (arco metálico único, de secção constante e andamento parabólico ou circular); Apresenta um comportamento estrutural bem definido (suspensão lateral); Acrescenta uma certa inovação (arco enviesado na planta do tabuleiro). Tendo então a concepção definida, foi necessário pré-dimensionar um tabuleiro totalmente diferente do construído. Optou-se então por adoptar um tabuleiro misto aço-betão, com vigas longitudinais em caixão e vigas de alma cheia transversais. Estas vigas pretendem formar uma grelha onde se apoia a laje de betão, e são fixos os pendurais laterais de suspensão em direcção ao arco. O caso de estudo tem um perfil transversal definido, dividido em dois tabuleiros individuais. Para evitar dois arcos em paralelo e dois tabuleiros em paralelo, optou-se por uma laje de tabuleiro única, suspensa por um único arco superior do tipo Bowstring, o que permitiu reduzir a largura do separador central, substituído por separadores New Jersey. Esta decisão permitiu ganhar o espaço nos passeios laterais para inserção dos pendurais e, por outro lado, reduzir a inclinação destes por forma a cumprir o gabarito vertical mínimo de circulação sobre os passeios. De acrescentar que duas outras das soluções concebidas, as soluções B e C, podem ser objecto de estudo de futuros trabalhos semelhantes, visto se considerar terem também bom comportamento estrutural e viabilidade. 3.3 PROCESSO CONSTRUTIVO Qualquer que seja a solução do tipo bowstring a adoptar, o processo construtivo do tabuleiro tem que ser muito bem avaliado. Podem identificar-se as seguintes cinco operações principais do processo construtivo, por ordem sequencial de realização: Montagem por lançamento da estrutura metálica do tabuleiro com um apoio provisório central ou, em alternativa, montagem da estrutura metálica com auxilio de duas gruas, uma em cada margem do rio; Montagem e levantamento do arco, com auxilio de uma grua e colunas provisórias apoiadas no tabuleiro; Fixação dos pendurais do tabuleiro ao arco; Betonagem da laje de tabuleiro por troços com uma cofragem móvel apoiada na parte metálica do tabuleiro, realizando troços de 10 a 12 m, e posterior execução dos acabamentos; Acerto das forças nos pendurais, para cumprir a geometria do tabuleiro. Neste caso específico, uma solução possível para colocar a estrutura metálica do tabuleiro consiste em adoptar um processo de lançamento incremental, que consiste na montagem sequencial 27
44 da parte metálica do tabuleiro, ao mesmo tempo que esta é lançada sobre o rio, com um nariz metálico e um apoio provisório a dividir o vão de 120 m em dois vãos de 60 m, para efeitos de lançamento. Este apoio pode constituir uma dificuldade dado a existência do rio, podendo por isso encarar-se como uma boa alternativa a montagem do tabuleiro metálico, previamento assemblado na margem, com recurso a duas gruas móveis de grande capacidade. Parte-se de seguida para montagem do arco que, necessariamente por motivos económicos e construtivos, será transportado em segmentos de dimensões reduzidas e previamente soldado em troços de 20 a 30 m, os quais são ligados entre si já sobre o tabuleiro com recurso a colunas provisórias apoiadas no tabuleiro. Segue-se para a fixação dos pendurais ao longo do arco e junto ao tabuleiro, nas extremidades das espinhas transversais. Nesta fase não se efectua ainda o tensionamento dos pendurais, apenas se realiza a amarração das barras. Por fim, executa-se a betonagem total da laje de tabuleiro por troços de 10 a 12 m, após colocação de todas as armaduras transversais e longitudinais. Adopta-se um sistema de cofragem apoiado num cimbre móvel que se apoia nas próprias vigas do tabuleiro. Após esta fase executam-se os acabamentos do tabuleiro. Finalmente, quando o betão já tiver adquirido características resistentes suficientes, é possível proceder-se à montagem dos macacos hidráulicos junto ao ponto de fixação dos pendurais adjacente ao tabuleiro, para então se efectuar o acerto de cada pendural com uma força de puxe correspondente a um determinado deslocamento obtido no processo de dimensionamento. Este acerto permitirá ao tabuleiro ajustar-se à geometria da rasante de projecto. 28
45 Capítulo 4 - ESTUDO DO COMPORTAMENTO ESTRUTURAL 4.1 PRÉ-DIMENSIONAMENTO Neste capítulo efectua-se o pré-dimensionamento dos elementos principais da solução estrutural proposta para o tabuleiro, de modo a realizar a análise do seu comportamento e as principais verificações de segurança. Esse pré-dimensionamento inclui a laje do tabuleiro, as vigas longitudinais, as vigas transversais, os pendurais e o arco. No Anexo B são incluídos os desenhos com a definição geral da solução proposta e que dos quais se apresentam na Figura 4.1 um alçado e uma secção transversal tipo. Figura 4.1 Alçado e secção transversal para a solução proposta de tabuleiro do tipo Bowstring 29
46 4.1.1 LAJE DO TABULEIRO A primeira decisão a tomar refere-se à espessura da laje de betão e. Adoptou-se uma espessura de 30 cm com base no comprimento e largura vão, no tipo de tráfego e no tipo de sistema estrutural. Segundo [99], para pontes metálicas vigadas, uma boa regra de dimensionamento consiste em considerar uma espessura mínima de 15 cm para a laje de betão, em pontes rodoviárias. Se se admitir que se tem 4 cm de recobrimento (que traduz um cenário de agressividade ambiental média, correspondendo à corrosão induzida por carbonatação de Classe XC4 segundo a EN 206-1) na superfície superior e inferior, e 2 cm proporcionais a duas vezes a metade de um diâmetro médio de um varão (admite-se que ), tem-se um mínimo total de 25 cm (Figura 4.2). Visto o caso de estudo apresentar um perfil transversal do tabuleiro de 29 m relativamente largo e sujeito a rodados do veículo tipo concentrados, optou-se por adoptar a espessura de 30 cm acima mencionada. Φ Φ Figura 4.2 Esquema da espessura definida para a laje de tabuleiro O segundo passo consiste em estimar a armadura transversal e longitudinal, inferior e superior, nas secções principais da laje do tabuleiro. Para tal, recorreu-se a cálculos simples, considerando painéis de laje de 13.55x5 m, para estimar os momentos flectores actuantes. Numa fase mais avançada, utilizou-se um programa de análise estrutural com o qual se construiu um modelo tridimensional de laje (SAP2000), de forma a obter os esforços de dimensionamento mais aproximados, especialmente relevante para as acções das cargas concentradas dos veículos tipo regulamentares. Partindo destes valores, determinou-se as várias secções de armadura, e avaliou-se a maior ou menor susceptibilidade da laje à fissuração em serviço. As dimensões dos painéis de laje foram tendo sucessivas alterações, devido às mudanças no perfil transversal e à inclusão de vigas longitudinais laterais. Estes dois aspectos fizeram passar a maior dimensão da laje para 11.5 m, reduzindo assim a relação comprimento/largura, proporcionando um melhor funcionamento da laje de tabuleiro. Na fase de pré-dimensionamento colocou-se apoios verticais rígidos nos pontos de fixação dos pendurais, dado que se desconhecia a sua secção. Em termos reais, o mais correcto seria admitir molas elásticas com deformação axial segundo o eixo dos pendurais mas, como a rigidez destas 30
47 seria elevada, uma boa aproximação nesta fase foi conseguida com os referidos apoios, que impedem apenas os deslocamentos verticais VIGAS LONGITUDINAIS Entende-se como vigas principais as vigas longitudinais, que servem de sustentação das vigas secundárias ( espinhas transversais). Estando perante uma estrutura mista aço-betão, é óbvia a adopção de perfis metálicos como vigas de sustentação da laje de betão do tabuleiro SECÇÃO DA VIGA PRINCIPAL Admitiu-se a priori um perfil RHS (Rectangular Hollow Section Secção Tubular Rectangular) para a viga central que liga as carlingas de extremidade do tabuleiro, com 1000 mm de altura, 300 mm de largura e espessura de 20 mm (Figura 4.3). Realizou-se um conjunto de cálculos simples para avaliar qual seria a resistência à tracção com flexão para esta secção, variando apenas a largura e a espessura da parede, entre 300 mm/400 mm/500 mm e 20 mm/30 mm/40 mm respectivamente, e verificou-se que, através da análise directa dos esforços devido às cargas permanentes, com auxílio ao modelo tridimensional construído em SAP2000, a resistência de um perfil deste tipo não era suficiente para resistir às cargas actuantes. Foi então que se decidiu adoptar uma secção CHS (Circular Hollow Section Secção Tubular Circular) inicial, de secção constante, com 1000 mm de diâmetro e 20 mm de espessura, fazendo variar a partir destes valores, quer o diâmetro quer a espessura, em função das necessidades de resistência que eram requeridas. A alteração para uma secção circular deveu-se também a razões estéticas, e ao facto de se pretender vir também a adoptar na secção do arco uma secção tubular circular. Para averiguar o efeito da variação da secção nos esforços actuantes e no comportamento global da laje de betão, realizou-se vários ensaios, da mesma natureza que aqueles realizados anteriormente para secções RHS, de forma a poder obter a melhor solução de secção do tubo, isto é, o diâmetro e a espessura necessários. Após várias análises, pode-se concluir que as secções condicionantes do tubo encontram-se na zona central do tabuleiro (como seria de esperar), dado que esta viga se comporta praticamente como uma viga simplesmente apoiada, e que as variações de secção desta viga principal não alteram de forma significativa o comportamento do tabuleiro nas duas direcções. 31
48 Figura 4.3 Secções transversais inicial e final da viga longitudinal principal Posto isto, adoptou-se como solução final uma viga com 1250 mm de diâmetro e 25 mm de espessura (o que correspondeu a um ligeiro aumento quer do diâmetro da secção, quer da sua espessura, em relação à primeira secção tubular circular adoptada), sendo o suficiente para permitir um suporte central das espinhas transversais e resistir, principalmente, aos momentos flectores provocados pelas cargas permamentes e sobrecargas sobre o tabuleiro. De realçar que o resultado estruturalmente mais eficiente seria adoptar uma viga de secção variável, com esta a aumentar substancialmente das extremidades para o centro do tabuleiro. Mas, como é claro, tal seria pouco económico de se concretizar devido às maiores dificuldades de criação dos vários troços da viga tubular e iria reflectir-se nos custos adicionais em termos de montagem e soldadura, além de dificultar muito a tipificação das ligações às vigas transversais GEOMETRIA DA VIGA PRINCIPAL Outro estudo importante correspondeu ao andamento desta viga principal. Considerou-se à partida três soluções possíveis: uma viga única central a ligar as carlingas mas não ligada às nascenças dos arcos, duas vigas em V partindo das carlingas de extremidade e fazendo a junção numa viga central, e uma viga diagonal acompanhando o andamento do arco em planta e, portanto, ligando as nascenças dos arcos (Figura 4.4). 32
49 Figura 4.4 Soluções para a geometria da viga longitudinal principal Para esta análise teve-se o mesmo resultado que aquele observado na variação da secção. Os esforços são semelhantes nas três configurações, sendo máximos os momentos flectores nas zonas de meio vão, e não variam os esforços normais com a geometria adoptada. Assim, a solução em V não traz quaisquer vantagens, antes pelo contrário, dificulta muito a geometria e ligações das vigas transversais. A decisão a tomar encontrava-se então entre a i) viga central e a ii) viga diagonal. Do ponto de vista estético e de suporte dos elevados esforços axiais transmitidos pelo arco, a solução ii) é vantajosa. Do ponto de vista de simplicidade da solução de ligação e geometria das espinhas, e de comportamento da laje, a opção i) tem claros benefícios. No Capítulo 4 - acerca do dimensionamento do arco, foi possível verificar que existindo também vigas principais laterais (consideradas necessárias conforme se introduz a seguir), a importância da viga diagonal principal na absorção dos esforços normais de tracção transmitidos pelo arco é muito menor. Quer-se com isto dizer que as grandes forças de compressão que se instalam no arco, irão ser absorvidas pelas vigas principais laterais. Sendo assim, adoptou-se uma viga principal central ao longo de todo o comprimento do tabuleiro, com a secção definida na secção VIGAS SECUNDÁRIAS LATERAIS Finalmente, decidiu-se adoptar duas vigas laterais em caixão com cinco finalidades principais (Figura 4.5): Equilíbrio das elevadas forças de tracção transmitidas pelo arco ao tabuleiro; 33
50 Suporte das cargas concentradas dos passeios, seja de todo o equipamento extra-estrutural (condutas de drenagem, guardas de segurança, lancis, equipamento eléctrico), seja das sobrecargas (manutenção, tráfego de peões, estruturas inferiores de inspecção do tabuleiro). Melhor inserção e amarração dos tirantes que suportam o tabuleiro; Melhorar o comportamento da laje de betão, conferindo-lhe mais um apoio e eliminando assim o seu bordo livre; Reduzir a deformabilidade do bordo do tabuleiro na zona em que não possui suspensão lateral. Numa primeira abordagem adoptaram-se perfis HEB300 sob a laje de betão, no alinhamento dos lancis dos passeios. O facto de se alinhar com os lancis deve-se às cargas elevadas que o peso próprio dos mesmos impõem. Esta solução cumpria a função de uniformizar o comportamento da laje, constituindo um apoio desta. No entanto, após análise pormenorizada desta hipótese, observou-se que devido aos elevados esforços locais transmitidos pelas fixações dos pendurais e aos elevados esforços transmitidos pelo arco, seria preferível adoptar uma secção bastante rígida em caixão trapezóidal, que acompanhe a variação de altura das espinhas transversais, que contenha a sua parede interna sobre o lancil, e uma parede externa com inclinação escolhida para fixação dos pendurais. Figura 4.5 Solução inicial e final propostas como vigas longitudinais secundárias As dimensões adoptadas para estas vigas foram obtidas com os princípios anteriormente estabelecidos, admitindo-se uma espessura de 50 mm. Trata-se naturalmente de uma viga de muito maiores dimensões que o perfil inicialmente admitido, mas que reduz a importância da viga tubular central na grelha de apoios do tabuleiro, conforme se pretendia para um tabuleiro com suspensão central. Tal tornava-se igualmente importante para limitar as deformações verticais do bordo da laje na zona em que não tinha suspensão. Como a geometria da secção destas vigas laterais está dependente do dimensionamento de vários elementos e por facilidade de modelação, foram admitidas vigas em caixão rectangular, alinhadas com o centro do passeio (passeio + lancis + vigas de bordadura), com a largura do mesmo 34
51 (1.55 m) e com uma altura de 1.10 m, sendo este valor o aproximado à altura média dos caixões laterais VIGAS TRANSVERSAIS Optou-se por escolher vigas em I de alma cheia por serem de uso corrente, fácil construção e fácil colocação em obra. Esta escolha teve por base casos existentes das vigas transversais do tabuleiro atirantado da Ponte Vasco da Gama, ou mesmo algumas obras como, por exemplo, a Puente de la Exposición em Valencia (Figura 4.6) e a Puente Puerto em Ondarroa (Figura 4.7), do famoso arquitecto Santiago Calatrava. Figura 4.6 Ponte de la Exposición em Valencia, Espanha. Vão principal com 130 m. Figura 4.7 Puente Puerto em Ondarroa, Espanha. Vão com 71.5 m. Antes do pré-dimensionamento destas vigas, tomou-se uma decisão quanto ao afastamento entre estas espinhas. Considerou-se um afastamento de 5 m face à largura do tabuleiro (aproximadamente 27 m). Como mostra a experiência, esta distância, admitindo a existência de uma viga central principal e vigas laterais sobre o lancil, vai permitir que a laje tenha o comportamento adequado, diminuindo ao máximo a quantidade de armadura adoptada, respeitando a baixa espessura de pré-dimensionamento da laje do tabuleiro que foi adoptada e que é importante para tornar a solução do tabuleiro globalmente relativamente leve. Esta dimensão corresponderia também ao afastamento entre pendurais que também se encontra normalmente nas pontes deste tipo entres os 4 m e os 6 m. A primeira aproximação foi feita admitindo um perfil de secção constante com uma altura de 1 m, banzos iguais com uma largura de 500 mm e espessura de 30 mm, e espessura da alma de 20 mm. No entanto, verificou-se logo numa abordagem inicial que tal geometria seria insuficiente para suportar as acções actuantes, assim como permitir o apoio rígido esperado para a laje do tabuleiro. Optou-se então por fazer variar a secção das vigas transversais, mantendo o banzo superior alinhado com a laje e as espessuras dos elementos, fazendo variar a altura da alma e a largura dos banzos. A adopção de vigas de secção variável foi natural e deveu-se à diferença de esforços que estas vigas vão estar submetidas,e que encontra reflexo na análise das soluções construídas do mesmo tipo. 35
52 Realizaram-se vários testes e análises da mesma natureza que aqueles que foram realizados para as vigas principais, não com uma preocupação principal a nível de segurança das espinhas, mas procurando avaliar a influência da variação do perfil no comportamento longitudinal do tabuleiro de betão. Estas análises conduziram à conclusão que era necessário aumentar consideravelmente a altura máxima do perfil para 1.5 m a 2 m, consoante a secção mínima adoptada, para obter o comportamento desejável na laje do tabuleiro. Decidiu-se então adoptar uma altura máxima da secção igual a 2 m, na ligação à viga longitudinal central, e uma secção mínima na ligação às vigas longitudinais laterais que assegure os objectivos pretendidos, ou seja, com uma altura de 1 m (Figura 4.8). Figura 4.8 Secções transversais mínima e máxima das espinhas No modelo de análise, definiu-se a espinha transversal tipo com um perfil em I de altura varíavel (máxima = 2 m, mínima = 1 m), banzos iguais e de largura variável com a altura da secção (largura máxima = 800 mm, largura minima = 400 mm) e espessura constante de 40 mm em todos os elementos. Apesar de se ter diminuído a largura do perfil transversal do tabuleiro para que fosse possível enquadrar a geometria dos pendurais na solução apresentada, não foi o suficiente para garantir o gabarito na zona do passeio (Figura 4.9). De forma a resolver este problema, as espinhas foram prolongadas para fora do tabuleiro, de modo a garantir o cumprimento do gabarito mínimo sobre os passeios. 36
53 VVI IIGGAA LOONNGGI L IITTUUDDI IINNAAL L PPRRI II NNCCI IIPPAAL L CCAAI IIXXÃÃOO LAATTEE L RRAAL L EE SSPPI IINNHHAA EE SSPPI IINNHHAA CCAAI IIXXÃÃOO LAATTEE L RRAAL L Figura 4.9 Perfil transversal do tabuleiro esquiço da solução pré-dimensionada ARCO GEOMETRIA DO ARCO Começando pelo traçado do arco, podem destacar-se duas fortes opções tomadas. A primeira relaciona-se com o andamento em planta do arco. Como foi anteriormente afirmado, tratou-se de uma opção em primeiro lugar estética, pelo facto de ser pouco comum, mas também um desafio estrutural, visto não ser claro o funcionamento de toda a obra de arte como este tipo de suspensão, em que até o traçado dos pendurais é totalmente influenciado pela opção escolhida para o arco (Figura 3.3). Quanto à geometria do arco é necessário definir o seu tipo de curva, ou seja, se se adopta um arco parabólico ou circular, a sua secção transversal e a sua altura máxima acima do tabuleiro. Segundo Tveit [3], para arcos de aço o andamento deve ser circular SECÇÃO TRANSVERSAL DO ARCO Em segundo lugar e antes de definir dimensões da secção do arco, é necessário decidir que tipo de secção adoptar. Visto se propor um arco com um andamento pouco comum e com os pendurais inclinados em ambas as direcções, logo introduzindo forças verticais e horizontais importantes, é vantajoso a nível do dimensionamento adoptar uma secção cujas resistências à flexão sejam iguais em todas as direcções. Com esta ideia de concepção, optou-se por adoptar uma secção tubular circular. Tendo em consideração os elevados esforços que o arco estará sujeito, dado tratar-se de um arco único a suportar um tabuleiro de 120 m de vão e aproximadamente 27 m de largura, começou por admitir-se uma secção com 2 m de diâmetro e 50 mm de espessura. 37
54 Quando se realizou a verificação de segurança da secção do arco (apresentada mais à frente), observou-se que a mesma não era suficiente para garantir resistências superiores aos esforços actuantes. Tendo então de redefinir a secção, optou-se por baixar a espessura para um máximo de 40 mm, aumentando o seu diâmetro e utilizando um aço da classe S420 NH. Esta decisão teve por base o EC3 Parte 1-1 Quadro 3.1 [100], onde são apresentados os valores nominais da tensão de cedência e da tensão última para os vários tipos de aço e para a variação da espessura, sendo os 40 mm um limite máximo para tirar um maior partido da resistência do aço que esteja a ser utilizado. Repetiu-se todo o processo de dimensionamento e, mesmo assim, não foi possível garantir a segurança estrutural do arco. Tomou-se então a decisão de adoptar uma espessura de 80mm, e aumentar a qualidade do aço, de modo a não se perder capacidade resistente na redução da tensão de cedência devido ao aumento de espessura, em comparação com o aço da gama inferior (S460 NH/NLH para t = 80 mm f y = 430 MPa, vs. S420 NH/NLH para t = 40 mm f y = 420 MPa). Figura 4.10 Secção transversal do arco ALTURA DO ARCO Finalmente torna-se também necessário definir a altura do arco. Tendo por base o estudo feito no Capítulo 2 -, consegue-se observar e atribuir um limite máximo para o rácio altura/vão do arco, sendo este valor aproximadamente igual a 1/4. O caso de estudo em análise apresenta um vão de sensivelmente 120 m, o que conduz a um valor máximo de 30 m para o ponto mais alto do arco. Obviamente que quanto mais elevado for este valor, maior poderá ser a esbelteza do tabuleiro. Caso se pretendesse um arco de menor impacto, então o limite mínimo altura do arco / vão do tabuleiro situa-se normalmente na ordem de 1/9 (o que conduzia a uma altura mínima na ordem dos 13 m/14 m). 38
55 Contudo, quando se estudou a geometria dos pendurais, apresentada no Sub-Capítulo 4.1.5, verificou-se ser necessário subir o arco o mais possível. Decidiu-se portanto adoptar um arco com uma altura máxima de 30 m CONDIÇÕES DE APOIO DO ARCO E DO TABULEIRO Verificou-se ser muito importante a definição das condições de apoio do tabuleiro (Figura 4.11). Colocou-se três apoios em cada extremidade do tabuleiro, um a meio e os outros dois sobre os caixões laterais longitudinais. Todos eles apenas não permitem o deslocamento vertical. Aqueles que se encontram sobre as nascenças do arco, um deles impede os deslocamentos nas duas direcções sobre um plano horizontal, sendo fixo, enquanto o outro é um apoio móvel em ambas as direcções. O apoio de extremidade da carlinga fixa é unidireccional na direcção transversal, permitindo portanto os deslocamentos transversais da temperatura, mas restringindo os deslocamentos da frenagem, aceleração e sismos longitudinais. Na extremidade contrária, coloca-se um apoio unidireccional, guiado na direcção de permitir os deslocamentos longitudinais resultantes das deformações impostas da temperatura, mas travando o tabuleiro na direcção transversal no caso de uma acção sísmica. Figura 4.11 Secções de apoio adoptadas nas solução proposta Ter em atenção que, numa análise mais avançada da acção da variação de temperatura, da acção do vento e da acção sísmica, o tipo de apoios a considerar nas duas extremidades terá de ser repensado, de forma a que o tabuleiro tenha um comportamento desejado e vantajoso consoante o tipo de deformações a que a estrutura estiver sujeita. 39
56 4.1.5 PENDURAIS A decisão do traçado dos pendurais não se baseou na facilidade de dimensionamento, mas sim na margem de manobra que o andamento do arco e a largura do tabuleiro permitiram, levando a que estes sejam inclinados visto tratar-se de um tabuleiro com suspensão lateral. O objectivo principal e inicial foi adoptar tirantes do tipo Net ao longo de todo o comprimento do tabuleiro. Com um modelo tridimensional realizado no AutoCAD foram estudadas várias configurações tridimensionais, concluindo-se que não era fácil cumprir a regra do gabarito mínimo de 5.50 m sobre o lancil entre os passeios e as faixas de rodagem (Figura 4.12). Figura 4.12 Gabarito mínimo condicionante da geometria dos pendurais O facto de se pretender manter um arco não muito alto por razões estéticas, tornou necessária a realização de alguns ajustamentos locais do traçado em planta, procurando-se reduzir a largura do separador central e aumentando a distância dos pontos de amarração dos pendurais à custa do prolongamento do comprimento das espinhas transversais. As várias modificações executadas conduziram ao perfil transversal final onde a laje de tabuleiro apresenta 26.1 m de largura, mas a largura total é de 28.1 m. Estes 2 m a mais encontram-se divididos em dois, e fazem parte da extensão das espinhas transversais (Figura 4.9) 40
57 Figura 4.13 Alternativas para o traçado dos pendurais Foi então que se escolheu a opção 4 (Figura 4.13) em cima apresentada, tendo em conta que a inclinação dos tirantes não poderia ser excessivamente baixa (de forma a cumprir o gabarito mínimo), a proximidade da ancoragem dos mesmos no arco teria de ter um espaçamento mínimo razoável (admitiu-se um espaçamento de 1.25 m entre fixações de pendurais), devido aos esforços elevados e mal distribuídos que poderia provocar, e que a simetria em relação ao arco traria vantagens em relação ao seu dimensionamento. Apesar da simetria estabelecida para os pendurais em relação ao arco, esta distribuição não equilibra simetricamente as cargas permanentes, levando posteriormente a um dimensionamento menos esbelto e esforços mais elevados no arco. Pelo mesmo motivo o efeito da suspensão em Net adoptada não terá totalmente o efeito desejado [3]. Tendo então à partida uma solução geometricamente exequível, tornava-se necessário decidir sobre o tipo de pendurais a colocar e as respectivas fixações, o que será feito no Sub-Capítulo 4.5. Uma opção de base consiste na opção por adoptar cabos pré-esforçados de aço ou barras maciças. Visto os primeiros necessitarem de ancoragens de maiores dimensões e mais complexa a sua instalação, tal não seria viável perante as opções tomadas para o resto dos elementos que compõem a solução em estudo. Por outro lado, dado que a resistência dos cabos de pré-esforço é superior à do aço das barras, seríamos conduzidos a menores secções de aço nos pendurais, o que os tornava indesejavelmente mais flexíveis. Por estas razões é muitas vezes adoptado nas pontes do tipo Bowstring barras de pré-esforço em vez de cabos. Tendo em conta as dimensões do tabuleiro, foi feito um pré-dimensionamento dos esforços a transmitir aos pendurais, adoptando-se um valor base para o diâmetro do pendural igual a 100 mm. Este valor corresponde ao limite do catálogo da maioria dos fornecedores de barras pré-esforçadas, 41
58 dependendo também do tipo de aço a utilizar. Mais à frente neste capítulo, ver-se-á que devido à geometria dos pendurais e à distribuição de esforços gerada pela mesma, algumas das barras estarão sujeitas a forças menores, sendo possível optimizar a solução tipo adoptada de início. Contudo, por uma questão de uniformidade de apoio do tabuleiro e de simplicidade no estudo das ligações tanto ao arco como ao tabuleiro, consideraram-se todos os tirantes com a mesma secção transversal FIXAÇÕES/ANCORAGENS O tipo de fixações das barras atirantadas é fundamental pois para além de estas estarem sujeitas a esforços axiais muito elevados, devido à acção do vento e deformações do tabuleiro e do arco, podem estar igualmente sujeitas a esforços de flexão que induzem preocupantes fenómenos de fadiga localizados junto das ancoragens. Devido a estes efeitos decidiu-se libertar as rotações das barras em ambas as direcções, de modo a que os pendurais apenas tenham esforços axiais. Para que esta hipótese admitida possa ser posta em prática, é necessário colocar fixações/rótulas esféricas na zona da junção das espinhas transversais com o caixão longitudinal, do lado de fora do tabuleiro. No arco libertam-se as rotações das barras na direcção do arco, o que conduz a adoptar rótulas cilíndricas na ligação das barras ao arco (Figura 4.14). A força de tracção actuante em cada barra, será o resultado dos efeitos somados das cargas permanentes de todo o tabuleiro (pesos próprios mais restantes cargas permanentes), do pior cenário possível para as sobrecargas definidas segundo o EC1 Parte 2 [101], e da força de puxe que será aplicada a cada pendural isolado. Figura 4.14 Exemplo de fixações do mesmo estilo das usadas na solução proposta, executadas em aço vazado para o tabuleiro da nova travessia do Rio Sado em Alcácer do Sal 42
59 4.2 MATERIAIS Nos materiais adoptados na solução alternativa proposta procura-se seguir o que foi definido para a solução construída. Nesse sentido, a classe de betão adoptada C35/45 foi a mesma da solução construída, assim como as armaduras A500NR. O mesmo se aplica para os enchimentos de betonilha e betuminosos dos elementos integrantes do tabuleiro. Quanto ao aço estrutural adoptou-se um aço de elevada resistência S420NL ou NH para todos os elementos metálicos do tabuleiro e S460NH no arco. Nos pendurais foram adoptados aços S460 na maioria dos casos, mas também S355 nalguns pendurais de extremidade menos esforçados. O quadro seguinte dá-nos as características de referência dos respectivos materiais. Quadro 4.1 Características do betão armado Tipo Classe f ck [MPa] f cd [MPa] f ctm [MPa] E c,(28) [GPa] γ c [kn/m 3 ] Armado C35/ ,3 3, Quadro 4.2 Pesos volúmicos do betão betuminoso, betão leve e betonilha Tipo γ c [kn/m 3 ] Leve 18 Betuminoso 24 Betonilha 20 Quadro 4.3 Características dos aços para armaduras Classe f yk [MPa] f yd [MPa] E s [GPa] γ s [kn/m 3 ] A Quadro 4.4 Características dos aços para barras pré-esforçadas Classe f y [MPa] f u [MPa] E s [GPa] γ s [kn/m 3 ] α [/ºC] S * ,17E-06 S * * Valores das tensões últimas do aço retiradas do catálogo da MKT [102] Quadro 4.5 Características dos aços para perfis de aço Classe t 40 mm 40 mm t 80 mm f y [MPa] f u [MPa] f y [MPa] f u [MPa] S420 (NH/NLH) 420* 540* 390* 520* S460 (NH/NLH) 460* 560* 430* 550* E s [GPa] γ s [kn/m 3 ] α [/ºC] ,17E-06 * Valores recolhidos do EC3 Parte 1-1 [100], segundo a EN EC1 Parte 1-1, Quadro A.4 do Anexo A, valor do peso volúmico do aço a considerar entre 77.0 e
60 4.3 ACÇÕES ACÇÕES PERMANENTES O estudo corresponde a uma variante da obra existente e, como tal, também as acções respeitantes às cargas permanentes advêm da mesma. No caso do recobrimento betuminoso, foi necessário ajustar o valor devido às alterações no perfil transversal do tabuleiro. O mesmo acontece com o facto de se ter admitido um tabuleiro só, levando à adopção de separadores do tipo New Jersey para separar as faixas de rodagem. Os valores para cada carga, usados no dimensionamento são os seguintes: Peso específico do betão armado 25 kn/m 3 Peso específico do betão leve 18 kn/m 3 Peso específico do pavimento betuminoso 24 kn/m 3 Restantes cargas permanentes: - Passeio (betão leve) 2.25 kn/m - Enchimento (betonilha) 2.50 kn/m - Lancil 5.75 kn/m (x2) - Separador New Jersey 5.15 kn/m - Guarda de segurança 0.50 kn/m (x2) - Guarda-corpos 0.75 kn/m (x2) - Viga de bordadura 2.50 kn/m (x2) - Conduta longitudinal de drenagem 1.00 kn/m (x2) SOBRECARGAS As sobrecargas consideradas no estudo são de três tipos diferentes. Uma referente à acção do tráfico rodoviário, correspondente à utilização do modelo de carregamento LM1 estipulado no Ponto do EC1 Parte 2 [101], outra ligada ao ensaio dinâmico de fadiga e, finalmente, uma acção que diz respeito à análise de estabilidade do arco. Todas elas estão definidas nos respectivos Sub-Capítulos. De referir que, numa fase mais avançada do projecto, devem ser consideradas também as acções da temperatura, do vento e da chuva na verificação da segurança, nomeadamente dos pendurais. 44
61 4.4 VERIFICAÇÃO DE SEGURANÇA DA LAJE Como já afirmado anteriormente, foram obtidos os esforços dum painel de laje com as dimensões de 5x11.5 m, por acção de todas as cargas permanentes e respectivas sobrecargas. O efeito das sobrecargas rodoviárias foi obtido inicialmente através de superfícies de influência, usando o modelo de carregamento LM1, com três veículos concentrados de 600 kn, 400 kn e 200 kn, nas lanes 1, 2 e 3 respectivamente, com três metros de largura cada, como princípio de dimensionamento. No início admitiu-se quatro secções de dimensionamento, correspondendo aos momentos positivos e negativos, nas duas direcções. Visto a primeira abordagem ter sido elaborada com análises estruturais simplificadas, na etapa seguinte, onde se modelou tridimensionalmente a laje do tabuleiro, obteve-se onze secções para quantificação das quantidades de armadura. Figura 4.15 Distribuição de momentos e armaduras num painel de laje De realçar que na escolha de distribuição de armaduras esteve sempre em vigor regras de boa prática, nomeadamente: Escolha de quantidade de armadura o mais próxima da dimensionada; Utilização máxima de dois diâmetros diferentes; Utilização de diâmetros próximos; Variação de distribuição de armadura realizada definindo uma disposição base com espaçamento suficiente, para que os acrescentos sejam feitos nos intervalos médios. 45
62 4.4.1 ANÁLISE TRANSVERSAL DA LAJE Como abordado no ponto anterior, começou-se a análise com modelos simples. Para este caso, admitiu-se um painel de laje em consola com comprimento igual a metade da largura transversal do tabuleiro, sendo as cargas de área, como a camada de betuminoso, definidas como cargas distribuídas, e as cargas de faca, como as guardas de seguranças, definidas como cargas pontuais. A razão pela qual se escolheu adoptar um encastramento rígido prende-se não só pela simplificação de dimensionamento, como também pelo facto de este modelo se aproximar perto da verdade, visto ter-se uma viga longitudinal de enorme rigidez e conexão com a laje (perfil metálico com conectores de ligação à laje de betão). Após construção do modelo o mais próximo do real, onde já se incluíu as vigas longitudinais laterais, verificou-se uma ligeira diminuição dos esforços obtidos anteriormente, como seria de esperar. Apesar de se ter efectuado vários estudos quanto à geometria e andamento das vigas longitudinais, o efeito destas variações teve pouca influência nos esforços finais transversais. Em seguida apresentam-se os resultados obtidos. Quadro 4.6 Armaduras transversais distribuídas pelas zonas arbitradas e momentos flectores actuantes m m 2-11 m m m 6-11 m ELU [knm/m] μ 0,108 0,193 0,145 0,060 0,056 ω 0,120 0,231 0,166 0,064 0,060 A s [cm 2 /m] 16,04 30,93 22,18 8,59 7,99 Solução Φ16//0,10 Φ20 // 0,10 Φ16//0,20 + Φ20//0,20 Φ16 // 0,20 Φ20 // 0,20 A s [cm 2 /m] 20,11 31,42 25,76 10,05 15,71 Figura 4.16 Distribuição de armaduras transversais num painel tipo de laje ANÁLISE LONGITUDINAL DA LAJE Esta análise necessitou que se considerasse as dimensões da espinhas, isto porque a rigidez destas tem uma grande preponderância no comportamento longitudinal da laje. Foram realizados 46
63 vários testes até se obter a melhor solução, para a qual se apresentam os momentos flectores actuantes e as armaduras da laje de betão. Quadro 4.7 Armaduras longitudinais distribuídas pelas zonas arbitradas e momentos flectores actuantes m m 1-11 m m 3-11 m m 5-11 m ELU [knm/m] μ 0,069 0,110 0,163 0,047 0,026 0,069 ω 0,074 0,122 0,190 0,049 0,027 0,074 A s [cm 2 /m] 9,87 16,41 25,48 6,60 3,55 9,85 Solução Φ16//0,20 Φ16//0,10 Φ16//0,20 + Φ20//0,20 Φ16//0,20 Φ16//0,20 Φ16//0,20 A s [cm 2 /m] 10,05 20,11 25,76 10,05 10,05 10,05 Figura 4.17 Distribuição de armaduras longitudinais num painel tipo de laje Como não é claro qual o pior cenário para colocação das sobrecargas rodoviárias concentradas para as várias secções da laje, admitiu-se várias alternativas para a localização das mesmas, sendo estas apresentadas de seguida para melhor visualização. 47
64 Figura 4.18 Possíveis cenários adoptados de acção das sobrecargas rodofivárias As três posições foram importantes, uma para cada secção da laje, sendo a posição B a mais penalizante em termos globais. 4.5 VERIFICAÇÃO DE SEGURANÇA DOS PENDURAIS Primeiramente, antes de se efectuar a verificação da segurança dos pendurais, é necessário estabelecer um método que apresente a repartição do efeito dos esforços de um pendural para com os restantes, para assim se ter um pré-dimensionamento das forças permanentes a instalar no conjunto dos pendurais e dos respectivos acertos de geometria a que isso corresponde. O método a usar consiste numa série de passos apresentados no ponto seguinte, que têm o intuito de achar uma força de puxe para cada par de pendurais (dada a simetria em relação ao andamento do arco da ponte), de modo a verificar que o esforço axial permanente em cada pendural verifique as seguintes regras: Não exceda 50% da resistência à rotura da barra (EC3 Parte 1-11 Ponto 7.2 [103] ); Seja sempre uma força de tracção e nunca de compressão; Para cada cenário de acção da sobrecarga (acção positiva e negativa), se observe os dois pontos acima descritos. Entenda-se como esforço axial permanente o resultado da soma das acções do peso próprio, restantes cargas permanentes, sobrecargas e forças de puxe ou tensionamento. 48
65 Em simultâneo, os deslocamentos verticais a que a ponte ficará sujeita foram analisados considerando todas as acções, incluindo a força de tensionamento dos tirantes, e que permitem determinar as contraflechas de fabrico para que o tabuleiro se encontre no final da construção na rasante de projecto. Torna-se finalmente necessário efectuar um conjunto de verificações de segurança à fadiga, pois é um factor fundamental no dimensionamento deste tipo de elementos estruturais COEFICIENTES DE INFLUÊNCIA O primeiro passo consistiu na obtenção do esforço axial em cada tirante, devido à acção do peso próprio e das restantes cargas permanentes, através do modelo estrutural realizado no programa SAP2000 (Figura 4.19), que inclui um arco com uma secção base de 2 m de diâmetro e 50 mm de espessura, como destacado anteriormente. Todos os cálculos apresentados dizem respeito à solução proposta (arco com D = 2500 mm e t = 80 mm), visto ter-se efectuado essa alteração quando se realizou as verificações de segurança do arco, e esta ter influência directa no dimensionamento dos pendurais. 49
66 Figura 4.19 Modelo de cálculo realizado no programa SAP2000 De seguida, aplica-se a acção da sobrecarga rodoviária. Mais uma vez, a posição das sobrecargas mais condicionante para cada pendural não é simples de obter e, por isso, foram necessárias sucessivas posições para obter os esforços mais elevados em cada pendural. Foram admitidas posições a meio dos painéis de laje, sobre as espinhas transversais e adjacentes às mesmas. Verificando-se que a zona de aplicação das cargas onde os esforços nos pendurais mais solicitados são maiores, é a posição centrada com o painel de laje entre vigas longitudinais e transversais, alargou-se esta acção ao longo de todo o comprimento do tabuleiro, para poder assim obter os valores mais elevados de tracção e compressão nos tirantes, devido à acção das sobrecargas rodoviárias. Obtidas as forças nos pendurais para estas acções, pretendeu-se obter as forças de tensionamento a aplicar em cada tirante, de forma a que a soma das forças instaladas em cada pendural cumpra as regras referidas no ponto anterior. Montou-se então um sistema inicial para visualizar a influência da aplicação de carga num pendural, sobre os restantes quarenta e cinco. Para isso, aplicou-se sucessivamente a cada pendural uma acção de uma variação negativa de temperatura de -1000ºC, e registou-se o esforço axial resultante em todos os pendurais. O valor de 50
DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES
 DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES EXEMPLO DE APLICAÇÃO Carlos Moutinho FEUP, Maio de 2002 1. Dados Gerais - Laje destinada a zona comercial (Q = 4 kn/m 2 ) - Peso de revestimentos e paredes
DIMENSIONAMENTO DE LAJES ARMADAS EM DUAS DIRECÇÕES EXEMPLO DE APLICAÇÃO Carlos Moutinho FEUP, Maio de 2002 1. Dados Gerais - Laje destinada a zona comercial (Q = 4 kn/m 2 ) - Peso de revestimentos e paredes
MEMÓRIA DESCRITIVA PÓRTICO METÁLICO COM PONTE GRUA
 MEMÓRIA DESCRITIVA PÓRTICO METÁLICO COM PONTE GRUA INSTITUTO POLITÉCNICO DE BRAGANÇA! "# $&%(')*&,+ -.,/!0 1 2 23 Índice: 1- Informações gerais sobre o projecto e cálculo...1 2- Tipologia estrutural...2
MEMÓRIA DESCRITIVA PÓRTICO METÁLICO COM PONTE GRUA INSTITUTO POLITÉCNICO DE BRAGANÇA! "# $&%(')*&,+ -.,/!0 1 2 23 Índice: 1- Informações gerais sobre o projecto e cálculo...1 2- Tipologia estrutural...2
SISMO BUILDING TECHNOLOGY, TECNOLOGIA DE CONSTRUÇÃO ANTI-SISMICA: APLICAÇÕES EM PORTUGAL
 SÍSMICA 2007 7º CONGRESSO DE SISMOLOGIA E ENGENHARIA SÍSMICA 1 SISMO BUILDING TECHNOLOGY, TECNOLOGIA DE CONSTRUÇÃO ANTI-SISMICA: APLICAÇÕES EM PORTUGAL M.T. BRAZ CÉSAR Assistente IPBragança Bragança Portugal
SÍSMICA 2007 7º CONGRESSO DE SISMOLOGIA E ENGENHARIA SÍSMICA 1 SISMO BUILDING TECHNOLOGY, TECNOLOGIA DE CONSTRUÇÃO ANTI-SISMICA: APLICAÇÕES EM PORTUGAL M.T. BRAZ CÉSAR Assistente IPBragança Bragança Portugal
www.ferca.pt Pré-esforço Aderente
 www.ferca.pt Pré-esforço Aderente Princípios O sistema T TM tension technology foi desenvolvido no âmbito da criação de um conceito integrado de soluções na área do pré-esforço com aplicação em obras de
www.ferca.pt Pré-esforço Aderente Princípios O sistema T TM tension technology foi desenvolvido no âmbito da criação de um conceito integrado de soluções na área do pré-esforço com aplicação em obras de
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny
 Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Estudo Comparativo de Cálculo de Lajes Analogia de grelha x Tabela de Czerny Junior, Byl F.R.C. (1), Lima, Eder C. (1), Oliveira,Janes C.A.O. (2), 1 Acadêmicos de Engenharia Civil, Universidade Católica
Os desenhos do projecto devem incluir desenhos de dimensionamento e desenhos de pormenorização de armaduras.
 9.7 Notas sobre Desenhos de Projecto 9.7.1 Observações Gerais Os desenhos do projecto devem incluir desenhos de dimensionamento e desenhos de pormenorização de armaduras. Os desenhos de dimensionamento
9.7 Notas sobre Desenhos de Projecto 9.7.1 Observações Gerais Os desenhos do projecto devem incluir desenhos de dimensionamento e desenhos de pormenorização de armaduras. Os desenhos de dimensionamento
e-mail: ederaldoazevedo@yahoo.com.br
 Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
Centro de Ensino Superior do Amapá-CEAP Curso: Arquitetura e Urbanismo Assunto: Cálculo de Pilares Prof. Ederaldo Azevedo Aula 4 e-mail: ederaldoazevedo@yahoo.com.br Centro de Ensino Superior do Amapá-CEAP
Índice. Página. 1.1. Redes de Segurança... 2 1.2. Guarda-corpos... 4 1.3. Andaimes metálicos... 4 1.4. Bailéus... 5
 !""#$!""%&'( Índice Página 1.1. Redes de Segurança... 2 1.2. Guarda-corpos..... 4 1.3. Andaimes metálicos...... 4 1.4. Bailéus........ 5 EPC 1/6 EQUIPAMENTOS DE PROTECÇÃO COLECTIVA (texto provisório) 1.1
!""#$!""%&'( Índice Página 1.1. Redes de Segurança... 2 1.2. Guarda-corpos..... 4 1.3. Andaimes metálicos...... 4 1.4. Bailéus........ 5 EPC 1/6 EQUIPAMENTOS DE PROTECÇÃO COLECTIVA (texto provisório) 1.1
ESTRUTURAS DE COBERTURA PARA GRANDES VÃOS
 ESTRUTURAS DE COBERTURA PARA GRANDES VÃOS Travamentos e Contraventamentos Estruturas de Coberturas Elementos Principais vencem o vão Elementos Secundários Exemplo: Planta geral da cobertura Planta da cobertura
ESTRUTURAS DE COBERTURA PARA GRANDES VÃOS Travamentos e Contraventamentos Estruturas de Coberturas Elementos Principais vencem o vão Elementos Secundários Exemplo: Planta geral da cobertura Planta da cobertura
CAPÍTULO 3 PROBLEMA 3.1
 PÍTULO 3 PROLM 3.1 onsidere a placa em forma de L, que faz parte da fundação em ensoleiramento geral de um edifício, e que está sujeita às cargas indicadas. etermine o módulo, a direcção, o sentido e o
PÍTULO 3 PROLM 3.1 onsidere a placa em forma de L, que faz parte da fundação em ensoleiramento geral de um edifício, e que está sujeita às cargas indicadas. etermine o módulo, a direcção, o sentido e o
LIGAÇÕES DE PEÇAS METÁLICAS AO BETÃO COM BUCHAS CONCEPÇÃO E PORMENORIZAÇÃO
 SEMINÁRIO INTERNACIONAL SOBRE LIGAÇÕES ESTRUTURAIS REFORÇO DE ESTRUTURAS E ESTRUTURAS MISTAS LIGAÇÕES ENTRE DIFERENTES MATERIAS ESTRUTURAIS LIGAÇÕES DE PEÇAS METÁLICAS AO BETÃO COM BUCHAS ENG. TIAGO ABECASIS
SEMINÁRIO INTERNACIONAL SOBRE LIGAÇÕES ESTRUTURAIS REFORÇO DE ESTRUTURAS E ESTRUTURAS MISTAS LIGAÇÕES ENTRE DIFERENTES MATERIAS ESTRUTURAIS LIGAÇÕES DE PEÇAS METÁLICAS AO BETÃO COM BUCHAS ENG. TIAGO ABECASIS
ESTRUTURAS MISTAS: AÇO - CONCRETO
 ESTRUTURAS MISTAS: AÇO - CONCRETO INTRODUÇÃO As estruturas mistas podem ser constituídas, de um modo geral, de concreto-madeira, concretoaço ou aço-madeira. Um sistema de ligação entre os dois materiais
ESTRUTURAS MISTAS: AÇO - CONCRETO INTRODUÇÃO As estruturas mistas podem ser constituídas, de um modo geral, de concreto-madeira, concretoaço ou aço-madeira. Um sistema de ligação entre os dois materiais
Nº2 JUNHO 2002 PAREDES DIVISÓRIAS DE PAINÉIS LEVES
 Nº2 JUNHO 2002 PAREDES DIVISÓRIAS DE PAINÉIS LEVES Catarina Aguiar Bentes A monografia apresentada foi realizada no âmbito da cadeira de Tecnologias da Construção de Edifícios do 11º Mestrado em Construção
Nº2 JUNHO 2002 PAREDES DIVISÓRIAS DE PAINÉIS LEVES Catarina Aguiar Bentes A monografia apresentada foi realizada no âmbito da cadeira de Tecnologias da Construção de Edifícios do 11º Mestrado em Construção
CAMARGUE PÉRGOLA PARA TERRAÇOS COM LÂMINAS ORIENTÁVEIS E COM LATERAIS COSTUMIZÁVEIS APLICAÇÕES
 PÉRGOLA PARA TERRAÇOS COM LÂMINAS ORIENTÁVEIS E COM LATERAIS COSTUMIZÁVEIS. Proteção solar com sistema de drenagem incluído e invisível;. Proteção solar e ventilação com lâminas de alumínio orientáveis;.
PÉRGOLA PARA TERRAÇOS COM LÂMINAS ORIENTÁVEIS E COM LATERAIS COSTUMIZÁVEIS. Proteção solar com sistema de drenagem incluído e invisível;. Proteção solar e ventilação com lâminas de alumínio orientáveis;.
Cypecad Cálculo de esforços de uma estrutura com introdução manual de acções verticais e horizontais
 Cypecad Cálculo de esforços de uma estrutura com introdução manual de acções verticais e horizontais CAD 2 Rua Comendador Santos da Cunha, 304, Ap. 2330 4701-904 Braga Tel: 00 351 253 20 94 30 Fax: 00
Cypecad Cálculo de esforços de uma estrutura com introdução manual de acções verticais e horizontais CAD 2 Rua Comendador Santos da Cunha, 304, Ap. 2330 4701-904 Braga Tel: 00 351 253 20 94 30 Fax: 00
Profª. Angela A. de Souza DESENHO DE ESTRUTURAS
 DESENHO DE ESTRUTURAS INTRODUÇÃO A estrutura de concreto armado é resultado da combinação entre o concreto e o aço. Porém, para a sua execução, não é suficiente apenas a presença desses dois materiais;
DESENHO DE ESTRUTURAS INTRODUÇÃO A estrutura de concreto armado é resultado da combinação entre o concreto e o aço. Porém, para a sua execução, não é suficiente apenas a presença desses dois materiais;
ANÁLISE DE PROGRAMAS DE CÁLCULO PARA ESTRUTURAS DE ALVENARIA RESISTENTE. Ivone Maciel 1 Paulo Lourenço 2 ivone@civil.uminho.pt pbl@civil.uminho.
 ANÁLISE DE PROGRAMAS DE CÁLCULO PARA ESTRUTURAS DE ALVENARIA RESISTENTE Ivone Maciel 1 Paulo Lourenço 2 ivone@civil.uminho.pt pbl@civil.uminho.pt 1 Mestranda e Bolseira de investigação do Departamento
ANÁLISE DE PROGRAMAS DE CÁLCULO PARA ESTRUTURAS DE ALVENARIA RESISTENTE Ivone Maciel 1 Paulo Lourenço 2 ivone@civil.uminho.pt pbl@civil.uminho.pt 1 Mestranda e Bolseira de investigação do Departamento
2.1. Considerações Gerais de Lajes Empregadas em Estruturas de Aço
 23 2. Sistemas de Lajes 2.1. Considerações Gerais de Lajes Empregadas em Estruturas de Aço Neste capítulo são apresentados os tipos mais comuns de sistemas de lajes utilizadas na construção civil. 2.1.1.
23 2. Sistemas de Lajes 2.1. Considerações Gerais de Lajes Empregadas em Estruturas de Aço Neste capítulo são apresentados os tipos mais comuns de sistemas de lajes utilizadas na construção civil. 2.1.1.
Prevenção de risco de queda em altura no setor da construção mediante a utilização de andaimes. Pedro Vasco AECOPS - OPWAY
 Prevenção de risco de queda em altura no setor da construção mediante a utilização de andaimes Pedro Vasco AECOPS - OPWAY A prevenção do risco de queda em altura na construção, e para o caso específico
Prevenção de risco de queda em altura no setor da construção mediante a utilização de andaimes Pedro Vasco AECOPS - OPWAY A prevenção do risco de queda em altura na construção, e para o caso específico
OE Seminário Aplicação do Eurocódigo 8 ao Projecto de Edifícios Projecto de estruturas para resistência aos sismos EC8-1
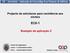 Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 2 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
Projecto de estruturas para resistência aos sismos EC8-1 Exemplo de aplicação 2 Ordem dos Engenheiros Lisboa 11 de Novembro de 2011 Porto 18 de Novembro de 2011 António Costa EXEMPLO EDIFÍCIO COM ESTRUTURA
INSPECÇÃO E REABILITAÇÃO DO SEMINÁRIO CONCILIAR DE BRAGA
 Encontro Nacional Betão Estrutural 2004 1 INSPECÇÃO E REABILITAÇÃO DO SEMINÁRIO CONCILIAR DE BRAGA P.B. LOURENÇO Prof. Associado EEUM Guimarães J. BARBOSA LOURENÇO Eng. Civil GPBL, Lda Porto D.V. OLIVEIRA
Encontro Nacional Betão Estrutural 2004 1 INSPECÇÃO E REABILITAÇÃO DO SEMINÁRIO CONCILIAR DE BRAGA P.B. LOURENÇO Prof. Associado EEUM Guimarães J. BARBOSA LOURENÇO Eng. Civil GPBL, Lda Porto D.V. OLIVEIRA
GereComSaber. Desenvolvimento de Sistemas de Software. Universidade do Minho Conselho de Cursos de Engenharia Licenciatura em Engenharia Informática
 Universidade do Minho Conselho de Cursos de Engenharia Licenciatura em Engenharia Informática Desenvolvimento de Sistemas de Software Ano Lectivo de 2009/10 GereComSaber Ana Duarte, André Guedes, Eduardo
Universidade do Minho Conselho de Cursos de Engenharia Licenciatura em Engenharia Informática Desenvolvimento de Sistemas de Software Ano Lectivo de 2009/10 GereComSaber Ana Duarte, André Guedes, Eduardo
APLICABILIDADE DE ESTRUTURAS EM AÇO EM EDIFÍCIO RESIDENCIAL VERTICAL DE MÉDIO PADRÃO NO MUNICÍPIO DE PRESIDENTE PRUDENTE-SP
 APLICABILIDADE DE ESTRUTURAS EM AÇO EM EDIFÍCIO RESIDENCIAL VERTICAL DE MÉDIO PADRÃO NO MUNICÍPIO DE PRESIDENTE PRUDENTE-SP Autores: Nayra Yumi Tsutsumoto (1); Cesar Fabiano Fioriti (2) (1) Aluna de Graduação
APLICABILIDADE DE ESTRUTURAS EM AÇO EM EDIFÍCIO RESIDENCIAL VERTICAL DE MÉDIO PADRÃO NO MUNICÍPIO DE PRESIDENTE PRUDENTE-SP Autores: Nayra Yumi Tsutsumoto (1); Cesar Fabiano Fioriti (2) (1) Aluna de Graduação
REFORÇO COM PRÉ-ESFORÇO EXTERIOR
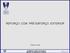 REFORÇO COM PRÉ-ESFORÇO EXTERIOR António Costa REFORÇO COM PRÉ-ESFORÇO EXTERIOR Aplicação Alteração do sistema estrutural Aumento da capacidade resistente Correcção do comportamento em serviço Exemplos
REFORÇO COM PRÉ-ESFORÇO EXTERIOR António Costa REFORÇO COM PRÉ-ESFORÇO EXTERIOR Aplicação Alteração do sistema estrutural Aumento da capacidade resistente Correcção do comportamento em serviço Exemplos
Manual de Instalção Version n. 01 of 14/06/2013
 Manual Técnico Manual de Instalção Version n. 01 of 14/06/2013 pag. 2 Index Index... 2 Introdução e informações gerais... 3 Guia Flexível... 3 DESCRIÇÃO... 3 MATERIAL... 3 CERTIFICADOS... 3 MEDIDAS...
Manual Técnico Manual de Instalção Version n. 01 of 14/06/2013 pag. 2 Index Index... 2 Introdução e informações gerais... 3 Guia Flexível... 3 DESCRIÇÃO... 3 MATERIAL... 3 CERTIFICADOS... 3 MEDIDAS...
Teoria das Estruturas
 Teoria das Estruturas Aula 02 Morfologia das Estruturas Professor Eng. Felix Silva Barreto ago-15 Q que vamos discutir hoje: Morfologia das estruturas Fatores Morfogênicos Funcionais Fatores Morfogênicos
Teoria das Estruturas Aula 02 Morfologia das Estruturas Professor Eng. Felix Silva Barreto ago-15 Q que vamos discutir hoje: Morfologia das estruturas Fatores Morfogênicos Funcionais Fatores Morfogênicos
Rua Dianópolis, 122-1º andar CEP: 03125-100 - Parque da Mooca - São Paulo / SP - Brasil Telefone: 55 (11) 2066-3350 / Fax: 55 (11) 2065-3398
 Frefer System Estruturas Metálicas Rua Dianópolis, 122-1º andar CEP: 03125-100 - Parque da Mooca - São Paulo / SP - Brasil Telefone: 55 (11) 2066-3350 / Fax: 55 (11) 2065-3398 www.frefersystem.com.br A
Frefer System Estruturas Metálicas Rua Dianópolis, 122-1º andar CEP: 03125-100 - Parque da Mooca - São Paulo / SP - Brasil Telefone: 55 (11) 2066-3350 / Fax: 55 (11) 2065-3398 www.frefersystem.com.br A
1. INTRODUÇÃO CRAVADAS ESTACAS CRAVADAS ESTACAS CAP. XV. Processos de Construção Licenciatura em Engenharia Civil
 CAP. XV ESTACAS CRAVADAS 1/47 1. INTRODUÇÃO 2/47 1 1. INTRODUÇÃO Pré-fabricadas Estacas cravadas Fundações indirectas (profundas) Alternativa às estacas moldadas 3/47 1. INTRODUÇÃO Processo pouco utilizado
CAP. XV ESTACAS CRAVADAS 1/47 1. INTRODUÇÃO 2/47 1 1. INTRODUÇÃO Pré-fabricadas Estacas cravadas Fundações indirectas (profundas) Alternativa às estacas moldadas 3/47 1. INTRODUÇÃO Processo pouco utilizado
Diagrama de transição de Estados (DTE)
 Diagrama de transição de Estados (DTE) O DTE é uma ferramenta de modelação poderosa para descrever o comportamento do sistema dependente do tempo. A necessidade de uma ferramenta deste tipo surgiu das
Diagrama de transição de Estados (DTE) O DTE é uma ferramenta de modelação poderosa para descrever o comportamento do sistema dependente do tempo. A necessidade de uma ferramenta deste tipo surgiu das
PLANO DE SINALIZAÇÃO TEMPORÁRIA
 PST. PLANO DE SINALIZAÇÃO TEMPORÁRIA (Descrição da Obra) Empreitada: descrição da empreitada Dono da Obra: identificação do dono da obra Edição / Revisão / Código: PST. Entidade Executante/Construtor:
PST. PLANO DE SINALIZAÇÃO TEMPORÁRIA (Descrição da Obra) Empreitada: descrição da empreitada Dono da Obra: identificação do dono da obra Edição / Revisão / Código: PST. Entidade Executante/Construtor:
www.catari.net uma marca diferente.
 www.catari.net uma marca diferente. cofragem modular perfeita! Com uma vasta gama de dimensões, permite solucionar todas as suas necessidades de cofragem vertical, em qualquer tipo de construção. O combro
www.catari.net uma marca diferente. cofragem modular perfeita! Com uma vasta gama de dimensões, permite solucionar todas as suas necessidades de cofragem vertical, em qualquer tipo de construção. O combro
CONSOLIDAÇÃO ESTRUTURAL DO CORO ALTO DA IGREJA DO PÓPULO EM BRAGA
 A Intervenção no Património. Práticas de Conservação e Reabilitação 173 CONSOLIDAÇÃO ESTRUTURAL DO CORO ALTO DA IGREJA DO PÓPULO EM BRAGA ESMERALDA PAUPÉRIO Engenheira IC-FEUP ANÍBAL COSTA Engenheiro Prof.
A Intervenção no Património. Práticas de Conservação e Reabilitação 173 CONSOLIDAÇÃO ESTRUTURAL DO CORO ALTO DA IGREJA DO PÓPULO EM BRAGA ESMERALDA PAUPÉRIO Engenheira IC-FEUP ANÍBAL COSTA Engenheiro Prof.
Rev.1 18.01.2013. Estantes cantoneira
 18.01.2013 Estantes cantoneira O sistema de estantes em cantoneira foi concebido para satisfazer as necessidades de armazenagem nas indústrias, oficinas, armazéns, etc, tendo em vista uma solução económica.
18.01.2013 Estantes cantoneira O sistema de estantes em cantoneira foi concebido para satisfazer as necessidades de armazenagem nas indústrias, oficinas, armazéns, etc, tendo em vista uma solução económica.
ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE
 ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE FUNDAÇÕES Todo projeto de fundações
ESTADO DE MATO GROSSO SECRETARIA DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP DEPARTAMENTO DE ENGENHARIA CIVIL PROJETO DE FUNDAÇÕES Todo projeto de fundações
Bastidores para fibra óptica
 Apresentação A gama de armários para fibra óptica Olirack foi concebida para a instalação, protecção e isolamento de terminadores e repartidores ópticos. A fibra óptica é um filamento feito de vidro ou
Apresentação A gama de armários para fibra óptica Olirack foi concebida para a instalação, protecção e isolamento de terminadores e repartidores ópticos. A fibra óptica é um filamento feito de vidro ou
Centro Universitário Católico Salesiano Auxilium Araçatuba / SP
 CONCURSO PONTE DE MACARRÃO Objetivo Geral O objetivo geral do trabalho proposto é motivar nos alunos o desenvolvimento de habilidades que lhes permitam: Aplicar conhecimentos básicos de Mecânica e Resistência
CONCURSO PONTE DE MACARRÃO Objetivo Geral O objetivo geral do trabalho proposto é motivar nos alunos o desenvolvimento de habilidades que lhes permitam: Aplicar conhecimentos básicos de Mecânica e Resistência
MEMÓRIA DESCRITIVA E JUSTIFICATIVA
 MEMÓRIA DESCRITIVA E JUSTIFICATIVA LOCALIZAÇÃO DA OBRA Neste projecto é proposta a ligação entre o bloco de aulas da Faculdade de Engenharia do Porto (FEUP), e o novo edifício da Associação de Estudantes
MEMÓRIA DESCRITIVA E JUSTIFICATIVA LOCALIZAÇÃO DA OBRA Neste projecto é proposta a ligação entre o bloco de aulas da Faculdade de Engenharia do Porto (FEUP), e o novo edifício da Associação de Estudantes
CHAPAS COLABORANTES PERFIL AL65
 CHAPAS COLABORANTES PERFIL AL65 ÍNDICE Introdução....................................................... 2 Características mecânicas dos diferentes materiais das lajes mistas...... 3 Condições de apoio................................................
CHAPAS COLABORANTES PERFIL AL65 ÍNDICE Introdução....................................................... 2 Características mecânicas dos diferentes materiais das lajes mistas...... 3 Condições de apoio................................................
CAIXA GERAL DE DEPÓSITOS GLOSSÁRIO DE TERMINOLOGIA ARQUIVISTIVA 1
 CAIXA GERAL DE DEPÓSITOS GLOSSÁRIO DE TERMINOLOGIA ARQUIVISTIVA 1 1 Zacarias Dias GCD, 2005 GLOSSÁRIO DE TERMINOLOGIA ARQUIVISTICA 1. Sem ter a pretensão de ser exaustivo na teoria arquivística, o presente
CAIXA GERAL DE DEPÓSITOS GLOSSÁRIO DE TERMINOLOGIA ARQUIVISTIVA 1 1 Zacarias Dias GCD, 2005 GLOSSÁRIO DE TERMINOLOGIA ARQUIVISTICA 1. Sem ter a pretensão de ser exaustivo na teoria arquivística, o presente
( Curso Dimensionamento de Estruturas de Aço CBCA módulo 3)
 GALPÕES (Projeto proposto) A ligação mais imediata que se faz da palavra galpão é com o uso industrial. No entanto galpões podem ser usados para as mais diversas atividades, tais como, hangares, espaços
GALPÕES (Projeto proposto) A ligação mais imediata que se faz da palavra galpão é com o uso industrial. No entanto galpões podem ser usados para as mais diversas atividades, tais como, hangares, espaços
Comprovação ao Fogo Tricalc 7.2 realiza a comprovação completa ao fogo das estruturas de betão, aço, madeira e alvenarias
 Home Comprovação ao Fogo Tricalc 7.2 realiza a comprovação completa ao fogo das estruturas de betão, aço, madeira e alvenarias Introdução A versão Tricalc 7.2 oferece, entre outras novidades, uma apresentação
Home Comprovação ao Fogo Tricalc 7.2 realiza a comprovação completa ao fogo das estruturas de betão, aço, madeira e alvenarias Introdução A versão Tricalc 7.2 oferece, entre outras novidades, uma apresentação
ZS Rest. Manual Profissional. BackOffice Mapa de Mesas. v2011
 Manual Profissional BackOffice Mapa de Mesas v2011 1 1. Índice 2. Introdução... 2 3. Iniciar ZSRest Backoffice... 3 4. Confirmar desenho de mesas... 4 b) Activar mapa de mesas... 4 c) Zonas... 4 5. Desenhar
Manual Profissional BackOffice Mapa de Mesas v2011 1 1. Índice 2. Introdução... 2 3. Iniciar ZSRest Backoffice... 3 4. Confirmar desenho de mesas... 4 b) Activar mapa de mesas... 4 c) Zonas... 4 5. Desenhar
Departamento de Engenharia Civil, Materiais de Construção I 3º Ano 1º Relatório INDÍCE
 INDÍCE 1- Introdução/ Objectivos... 2- Análise Granulométrica... 2.1- Introdução e descrição dos ensaios... 2.2- Cálculos efectuados, resultados encontrados e observações... 2.3- Conclusão... 3- Ensaio
INDÍCE 1- Introdução/ Objectivos... 2- Análise Granulométrica... 2.1- Introdução e descrição dos ensaios... 2.2- Cálculos efectuados, resultados encontrados e observações... 2.3- Conclusão... 3- Ensaio
O conhecimento das dimensões permite determinar os vãos equivalentes e as rigidezes, necessários no cálculo das ligações entre os elementos.
 PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
PRÉ-DIMENSIONAMENTO CAPÍTULO 5 Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos 3 abr 2003 PRÉ-DIMENSIONAMENTO O pré-dimensionamento dos elementos estruturais é necessário para que se possa calcular
Avaliação do desempenho estrutural de pontes
 Avaliação do desempenho estrutural de pontes Luís Oliveira Santos Laboratório Nacional de Engenharia Civil Seminário Gestão da Segurança e da Operação e Manutenção de Redes Rodoviárias e Aeroportuárias
Avaliação do desempenho estrutural de pontes Luís Oliveira Santos Laboratório Nacional de Engenharia Civil Seminário Gestão da Segurança e da Operação e Manutenção de Redes Rodoviárias e Aeroportuárias
A VISTA BACKSTAGE PRINCIPAIS OPÇÕES NO ECRÃ DE ACESSO
 DOMINE A 110% ACCESS 2010 A VISTA BACKSTAGE Assim que é activado o Access, é visualizado o ecrã principal de acesso na nova vista Backstage. Após aceder ao Access 2010, no canto superior esquerdo do Friso,
DOMINE A 110% ACCESS 2010 A VISTA BACKSTAGE Assim que é activado o Access, é visualizado o ecrã principal de acesso na nova vista Backstage. Após aceder ao Access 2010, no canto superior esquerdo do Friso,
Mestrado em Engenharia Civil Apresentação do novo Plano de Estudos
 Mestrado em Engenharia Civil Apresentação do novo Plano de Estudos CCMEC, 8 de Junho de 2015 1 Sumário 1 Introdução 2 Estrutura curricular do novo plano Tronco comum Perfil de Edificações Perfil de Estruturas
Mestrado em Engenharia Civil Apresentação do novo Plano de Estudos CCMEC, 8 de Junho de 2015 1 Sumário 1 Introdução 2 Estrutura curricular do novo plano Tronco comum Perfil de Edificações Perfil de Estruturas
Os caracteres de escrita
 III. Caracteres de Escrita Os caracteres de escrita ou letras técnicas são utilizadas em desenhos técnicos pelo simples fato de proporcionarem maior uniformidade e tornarem mais fácil a leitura. Se uma
III. Caracteres de Escrita Os caracteres de escrita ou letras técnicas são utilizadas em desenhos técnicos pelo simples fato de proporcionarem maior uniformidade e tornarem mais fácil a leitura. Se uma
PADRONIZAÇÃO DE PAINÉIS EM LIGHT STEEL FRAME
 PADRONIZAÇÃO DE PAINÉIS EM LIGHT STEEL FRAME ANITA OLIVEIRA LACERDA - anitalic@terra.com.br PEDRO AUGUSTO CESAR DE OLIVEIRA SÁ - pedrosa@npd.ufes.br 1. INTRODUÇÃO O Light Steel Frame (LSF) é um sistema
PADRONIZAÇÃO DE PAINÉIS EM LIGHT STEEL FRAME ANITA OLIVEIRA LACERDA - anitalic@terra.com.br PEDRO AUGUSTO CESAR DE OLIVEIRA SÁ - pedrosa@npd.ufes.br 1. INTRODUÇÃO O Light Steel Frame (LSF) é um sistema
Escola de Engenharia de São Carlos - Universidade de São Paulo Departamento de Engenharia de Estruturas. Alvenaria Estrutural.
 Alvenaria Estrutural Introdução CONCEITO ESTRUTURAL BÁSICO Tensões de compressão Alternativas para execução de vãos Peças em madeira ou pedra Arcos Arco simples Arco contraventado ASPECTOS HISTÓRICOS Sistema
Alvenaria Estrutural Introdução CONCEITO ESTRUTURAL BÁSICO Tensões de compressão Alternativas para execução de vãos Peças em madeira ou pedra Arcos Arco simples Arco contraventado ASPECTOS HISTÓRICOS Sistema
Modelo Cascata ou Clássico
 Modelo Cascata ou Clássico INTRODUÇÃO O modelo clássico ou cascata, que também é conhecido por abordagem top-down, foi proposto por Royce em 1970. Até meados da década de 1980 foi o único modelo com aceitação
Modelo Cascata ou Clássico INTRODUÇÃO O modelo clássico ou cascata, que também é conhecido por abordagem top-down, foi proposto por Royce em 1970. Até meados da década de 1980 foi o único modelo com aceitação
Professora: Engª Civil Silvia Romfim
 Professora: Engª Civil Silvia Romfim PARTES CONSTITUINTES DE UMA COBERTURA Pode-se dizer que a cobertura é subdividida em cinco principais partes: 1. Pelo telhado, composto por vários tipos de telhas;
Professora: Engª Civil Silvia Romfim PARTES CONSTITUINTES DE UMA COBERTURA Pode-se dizer que a cobertura é subdividida em cinco principais partes: 1. Pelo telhado, composto por vários tipos de telhas;
Prof. Vinícius C. Patrizzi ESTRADAS E AEROPORTOS
 Prof. Vinícius C. Patrizzi ESTRADAS E AEROPORTOS GEOMETRIA DE VIAS Elementos geométricos de uma estrada (Fonte: PONTES FILHO, 1998) 1. INTRODUÇÃO: Após traçados o perfil longitudinal e transversal, já
Prof. Vinícius C. Patrizzi ESTRADAS E AEROPORTOS GEOMETRIA DE VIAS Elementos geométricos de uma estrada (Fonte: PONTES FILHO, 1998) 1. INTRODUÇÃO: Após traçados o perfil longitudinal e transversal, já
MICROSOFT ACCESS MICROSOFT ACCESS. Professor Rafael Vieira Professor Rafael Vieira
 MICROSOFT ACCESS MICROSOFT ACCESS Professor Rafael Vieira Professor Rafael Vieira - Access - Programa de base de dados relacional funciona em Windows Elementos de uma Base de Dados: Tabelas Consultas Formulários
MICROSOFT ACCESS MICROSOFT ACCESS Professor Rafael Vieira Professor Rafael Vieira - Access - Programa de base de dados relacional funciona em Windows Elementos de uma Base de Dados: Tabelas Consultas Formulários
O concreto armado tem inúmeras aplicações: estruturas, pavimentos, paredes, fundações, barragens, reservatórios.
 AS ESTRUTURAS DE CONCRETO ARMADO. Concreto armado - é um material da construção civil que se tornou um dos mais importantes elementos da arquitetura do século XX. É usado nas estruturas dos edifícios.
AS ESTRUTURAS DE CONCRETO ARMADO. Concreto armado - é um material da construção civil que se tornou um dos mais importantes elementos da arquitetura do século XX. É usado nas estruturas dos edifícios.
PRÉ-DIMENSIONAMENTO DA ESTRUTURA
 ECC 1008 ESTRUTURAS DE CONCRETO PRÉ-DIMENSIONAMENTO DA ESTRUTURA (Aulas 9-12) Prof. Gerson Moacyr Sisniegas Alva Algumas perguntas para reflexão... É possível obter esforços (dimensionamento) sem conhecer
ECC 1008 ESTRUTURAS DE CONCRETO PRÉ-DIMENSIONAMENTO DA ESTRUTURA (Aulas 9-12) Prof. Gerson Moacyr Sisniegas Alva Algumas perguntas para reflexão... É possível obter esforços (dimensionamento) sem conhecer
INSTALAÇÃO DE UM NOVO SISTEMA DE DRENAGEM PLUVIAL NO VIADUTO DO LOUREIRO
 INSTALAÇÃO DE UM NOVO SISTEMA DE DRENAGEM PLUVIAL NO VIADUTO DO LOUREIRO Manuel Lorena 1 1 COBA, Consultores de Engenharia e Ambiente, Serviço de Vias de Comunicação, Núcleo Rodoviário Av. 5 de Outubro
INSTALAÇÃO DE UM NOVO SISTEMA DE DRENAGEM PLUVIAL NO VIADUTO DO LOUREIRO Manuel Lorena 1 1 COBA, Consultores de Engenharia e Ambiente, Serviço de Vias de Comunicação, Núcleo Rodoviário Av. 5 de Outubro
Cotagens especiais. Você já aprendeu a interpretar cotas básicas
 A UU L AL A Cotagens especiais Você já aprendeu a interpretar cotas básicas e cotas de alguns tipos de elementos em desenhos técnicos de modelos variados. Mas, há alguns casos especiais de cotagem que
A UU L AL A Cotagens especiais Você já aprendeu a interpretar cotas básicas e cotas de alguns tipos de elementos em desenhos técnicos de modelos variados. Mas, há alguns casos especiais de cotagem que
N.25 Fevereiro 2006 BETÃO COM VARÕES DE FIBRA DE VIDRO PROCESSOS DE CONSTRUÇÃO. Fernando Oliveira Marcelo Rodrigues Inês Santos João Dias
 N.25 Fevereiro 2006 BETÃO COM VARÕES DE FIBRA DE VIDRO PROCESSOS DE CONSTRUÇÃO Fernando Oliveira Marcelo Rodrigues Inês Santos João Dias EDIÇÃO: CONSTRULINK PRESS A monografia apresentada foi realizada
N.25 Fevereiro 2006 BETÃO COM VARÕES DE FIBRA DE VIDRO PROCESSOS DE CONSTRUÇÃO Fernando Oliveira Marcelo Rodrigues Inês Santos João Dias EDIÇÃO: CONSTRULINK PRESS A monografia apresentada foi realizada
GALPÃO. Figura 87 instabilidade lateral
 9 CONTRAVENTAMENTO DE ESTRUTURAS DE MADEIIRA 9..1 Generalliidades 11 As estruturas reticuladas são normalmente constituídas por elementos planos. Quando são estruturas espaciais (não planas), tendem a
9 CONTRAVENTAMENTO DE ESTRUTURAS DE MADEIIRA 9..1 Generalliidades 11 As estruturas reticuladas são normalmente constituídas por elementos planos. Quando são estruturas espaciais (não planas), tendem a
EXERCÍCIOS DE ESTRUTURAS DE MADEIRA
 UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA CIVIL,ARQUITETURA E URBANISMO Departamento de Estruturas EXERCÍCIOS DE ESTRUTURAS DE MADEIRA RAFAEL SIGRIST PONTES MARTINS,BRUNO FAZENDEIRO DONADON
UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA CIVIL,ARQUITETURA E URBANISMO Departamento de Estruturas EXERCÍCIOS DE ESTRUTURAS DE MADEIRA RAFAEL SIGRIST PONTES MARTINS,BRUNO FAZENDEIRO DONADON
AVALIAÇÃO DO EFEITO DO PAVIMENTO NO RUÍDO DE TRÁFEGO RODOVIÁRIO.
 AVALIAÇÃO DO EFEITO DO PAVIMENTO NO RUÍDO DE TRÁFEGO RODOVIÁRIO. CARLOS GUERRA AUTO-ESTRADAS DO ATLANTICO, S.A.. FERNANDO PALMA RUIVO DIRECTOR TÉCNICO, CERTIPROJECTO, Lda. DIVISÃO DE ACÚSTICA APLICADA
AVALIAÇÃO DO EFEITO DO PAVIMENTO NO RUÍDO DE TRÁFEGO RODOVIÁRIO. CARLOS GUERRA AUTO-ESTRADAS DO ATLANTICO, S.A.. FERNANDO PALMA RUIVO DIRECTOR TÉCNICO, CERTIPROJECTO, Lda. DIVISÃO DE ACÚSTICA APLICADA
 1/6 1 2 "SUPORTE RETRÁTIL PARA INSTALAÇÃO DE TELA FACHADEIRA". Apresentação Refere-se a presente invenção ao campo técnico de suportes para telas fachadeiras de edifícios em construção ou em reformas,
1/6 1 2 "SUPORTE RETRÁTIL PARA INSTALAÇÃO DE TELA FACHADEIRA". Apresentação Refere-se a presente invenção ao campo técnico de suportes para telas fachadeiras de edifícios em construção ou em reformas,
Estruturas de Concreto Armado. Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com
 Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
Estruturas de Concreto Armado Eng. Marcos Luís Alves da Silva luisalves1969@gmail.com unip-comunidade-eca@googlegroups.com 1 CENTRO TECNOLÓGICO DEPARTAMENTO DE ENGENHARIA CIVIL EA 851J TEORIA EC6P30/EC7P30
ESTRUTURA METÁLICA Vantagens da Construção em Aço. Maior limpeza de obra: Devido à ausência de entulhos, como escoramento e fôrmas.
 ESTRUTURA METÁLICA Vantagens da Construção em Aço Menor tempo de execução: A estrutura metálica é projetada para fabricação industrial e seriada, de preferência, levando a um menor tempo de fabricação
ESTRUTURA METÁLICA Vantagens da Construção em Aço Menor tempo de execução: A estrutura metálica é projetada para fabricação industrial e seriada, de preferência, levando a um menor tempo de fabricação
Normas Europeias para Projecto de Estruturas Metálicas
 CENFIM, Trofa 6 de Maio de 2014 Normas Europeias para Projecto de Estruturas Metálicas Rui Ferreira Alves O Sector da Construção no contexto da União Europeia Sector estratégico: relevante para promover
CENFIM, Trofa 6 de Maio de 2014 Normas Europeias para Projecto de Estruturas Metálicas Rui Ferreira Alves O Sector da Construção no contexto da União Europeia Sector estratégico: relevante para promover
Características do Sistema
 Características do Sistema O emprego de lajes nervuradas nas estruturas de concreto armado ganhou grande impulso nos últimos anos graças às modernas técnicas construtivas e ao desenvolvimento dos programas
Características do Sistema O emprego de lajes nervuradas nas estruturas de concreto armado ganhou grande impulso nos últimos anos graças às modernas técnicas construtivas e ao desenvolvimento dos programas
Planificação anual de 3º ciclo de Educação Tecnológica 7º e 8º ano
 Planificação anual de 3º ciclo de Educação Tecnológica 7º e 8º ano Domínios TECNOLOGIA E SOCIEDADE Subdomínios/Sugestões de Exploração Tecnologia e necessidades Humanas: Tecnologia como resposta às necessidades
Planificação anual de 3º ciclo de Educação Tecnológica 7º e 8º ano Domínios TECNOLOGIA E SOCIEDADE Subdomínios/Sugestões de Exploração Tecnologia e necessidades Humanas: Tecnologia como resposta às necessidades
Módulo 6 Pilares: Estados Limites Últimos Detalhamento Exemplo. Imperfeições Geométricas Globais. Imperfeições Geométricas Locais
 NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
NBR 68 : Estados Limites Últimos Detalhamento Exemplo P R O O Ç Ã O Conteúdo Cargas e Ações Imperfeições Geométricas Globais Imperfeições Geométricas Locais Definições ELU Solicitações Normais Situações
Outras Soluções Fichas de Aplicação
 Outras Soluções Fichas de Aplicação Cofragem Perdida Painel Perfurado Painel Sandwich Consulte o Dossier Técnico Viroc disponível em www.viroc.pt, na página de Downloads. Outros Suplementos de Soluções
Outras Soluções Fichas de Aplicação Cofragem Perdida Painel Perfurado Painel Sandwich Consulte o Dossier Técnico Viroc disponível em www.viroc.pt, na página de Downloads. Outros Suplementos de Soluções
Simplos. Estantes para cargas ligeiras
 Simplos Estantes para cargas ligeiras Estantes Simplos Estantes Simplos O sistema de armazenagem Simplos proporciona a melhor solução às mais diversas necessidades de armazenagem de cargas médias e ligeiras,
Simplos Estantes para cargas ligeiras Estantes Simplos Estantes Simplos O sistema de armazenagem Simplos proporciona a melhor solução às mais diversas necessidades de armazenagem de cargas médias e ligeiras,
[VIII CONCURSO DE PONTES DE ESPARGUETE]
![[VIII CONCURSO DE PONTES DE ESPARGUETE] [VIII CONCURSO DE PONTES DE ESPARGUETE]](/thumbs/27/12139840.jpg) [VIII CONCURSO DE PONTES DE ESPARGUETE] Regulamento do Concurso INCRIÇÕES 24 de fevereiro a 2 de março de 2015 MONTAGEM 4,5 e 9 a 12 de março de 2015 ROTURA - 14 de Março (13ª Mostra da UP) Página 1 de
[VIII CONCURSO DE PONTES DE ESPARGUETE] Regulamento do Concurso INCRIÇÕES 24 de fevereiro a 2 de março de 2015 MONTAGEM 4,5 e 9 a 12 de março de 2015 ROTURA - 14 de Março (13ª Mostra da UP) Página 1 de
NORMALIZAÇÃO. desenho técnico
 NORMALIZAÇÃO desenho técnico 2004/2005 II Formatos do papel (NP 48) Normalização No mundo actual cada vez mais é necessário haver um conjunto de regras ou normas que permitam uma uniformização, quer nos
NORMALIZAÇÃO desenho técnico 2004/2005 II Formatos do papel (NP 48) Normalização No mundo actual cada vez mais é necessário haver um conjunto de regras ou normas que permitam uma uniformização, quer nos
ISF 219: PROJETO DE PASSARELA PARA PEDESTRES. O Projeto de passarela para pedestres será desenvolvido em duas fases:
 ISF 219: PROJETO DE PASSARELA PARA PEDESTRES 1. OBJETIVO Definir e especificar os serviços constantes do Projeto de Passarela para Pedestres em Projetos de Engenharia Ferroviária. 2. FASES DO PROJETO O
ISF 219: PROJETO DE PASSARELA PARA PEDESTRES 1. OBJETIVO Definir e especificar os serviços constantes do Projeto de Passarela para Pedestres em Projetos de Engenharia Ferroviária. 2. FASES DO PROJETO O
Influência do tipo de laje nos custos de um edifício em aço
 ArtigoTécnico Ygor Dias da Costa Lima 1 Alex Sander Clemente de Souza 2 Silvana De Nardin 2 1 Mestre em Construção Civil pela Pós-Graduação em Construção Civil PPGCiv/UFSCar 2 Prof. Dr. Pós-Graduação em
ArtigoTécnico Ygor Dias da Costa Lima 1 Alex Sander Clemente de Souza 2 Silvana De Nardin 2 1 Mestre em Construção Civil pela Pós-Graduação em Construção Civil PPGCiv/UFSCar 2 Prof. Dr. Pós-Graduação em
Guia de Estudo Folha de Cálculo Microsoft Excel
 Tecnologias da Informação e Comunicação Guia de Estudo Folha de Cálculo Microsoft Excel Estrutura geral de uma folha de cálculo: colunas, linhas, células, endereços Uma folha de cálculo electrónica ( electronic
Tecnologias da Informação e Comunicação Guia de Estudo Folha de Cálculo Microsoft Excel Estrutura geral de uma folha de cálculo: colunas, linhas, células, endereços Uma folha de cálculo electrónica ( electronic
SAMUO APP: MANUAL DO ADMINISTRADOR
 as novas tecnologias ao serviço do desenvolvimento de projectos w w w. i m a d i p. c o m CABO VERDE: REALIZAÇÃO DE UMA ACÇÃO- PILOTO PARA A MELHORIA DA GESTÃO NUM GABINETE TÉCNICO SELECCIONADO OFITEC
as novas tecnologias ao serviço do desenvolvimento de projectos w w w. i m a d i p. c o m CABO VERDE: REALIZAÇÃO DE UMA ACÇÃO- PILOTO PARA A MELHORIA DA GESTÃO NUM GABINETE TÉCNICO SELECCIONADO OFITEC
1. Equilíbrio de corpos rígidos
 1. Equilíbrio de corpos rígidos No capítulo anterior foi referido que as forças exteriores que actuam num corpo rígido podem ser reduzidas a um sistema equivalente força/binário. Quando a força e o binário
1. Equilíbrio de corpos rígidos No capítulo anterior foi referido que as forças exteriores que actuam num corpo rígido podem ser reduzidas a um sistema equivalente força/binário. Quando a força e o binário
Qualificação de Procedimentos
 Qualificação de Procedimentos Os equipamentos em geral são fabricados por meio de uniões de partes metálicas entre si empregando-se soldas. Há, portanto a necessidade de se garantir, nestas uniões soldadas,
Qualificação de Procedimentos Os equipamentos em geral são fabricados por meio de uniões de partes metálicas entre si empregando-se soldas. Há, portanto a necessidade de se garantir, nestas uniões soldadas,
INTRODUÇÃO objectivo
 INTRODUÇÃO O tema central deste trabalho é o sistema de produção just-in-time ou JIT. Ao falarmos de just-in-time surge de imediato a ideia de produção sem stocks, inventários ao nível de zero, produção
INTRODUÇÃO O tema central deste trabalho é o sistema de produção just-in-time ou JIT. Ao falarmos de just-in-time surge de imediato a ideia de produção sem stocks, inventários ao nível de zero, produção
Análise das conseqüências do tráfego de CVC s sobre o comportamento estrutural das obras de arte da rede viária do DER-SP
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA DE ESTRUTURAS Análise das conseqüências do tráfego de CVC s sobre o comportamento estrutural das obras de arte da
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA DE ESTRUTURAS Análise das conseqüências do tráfego de CVC s sobre o comportamento estrutural das obras de arte da
SUPERESTRUTURA estrutura superestrutura infra-estrutura lajes
 SUPRSTRUTUR s estruturas dos edifícios, sejam eles de um ou vários pavimentos, são constituídas por diversos elementos cuja finalidade é suportar e distribuir as cargas, permanentes e acidentais, atuantes
SUPRSTRUTUR s estruturas dos edifícios, sejam eles de um ou vários pavimentos, são constituídas por diversos elementos cuja finalidade é suportar e distribuir as cargas, permanentes e acidentais, atuantes
Viadutos da Rib.ª de S. Braz e da Rib.ª da Várzea Concepção, Projecto e Obra
 Encontro Nacional BETÃO ESTRUTURAL - BE2012 FEUP, 24-26 de outubro de 2012 Viadutos da Rib.ª de S. Braz e da Rib.ª da Várzea Concepção, Projecto e Obra António Costa 1 Nuno Travassos 2 Júlio Appleton 3
Encontro Nacional BETÃO ESTRUTURAL - BE2012 FEUP, 24-26 de outubro de 2012 Viadutos da Rib.ª de S. Braz e da Rib.ª da Várzea Concepção, Projecto e Obra António Costa 1 Nuno Travassos 2 Júlio Appleton 3
DEOP DIRETORIA DE ENGENHARIA E OPERAÇÕES EPE PLANEJAMENTO E ENGENHARIA MANUAL DE TUBULAÇÕES TELEFÔNICAS PREDIAIS
 CAPÍTULO 2: ESQUEMA GERAL DA TUBULAÇÃO TELEFÔNICA. RECOMENDAÇÕES A tubulação telefônica é dimensionada em função da quantidade de pontos telefônicos previsto para cada parte do edifício. Cada ponto telefônico
CAPÍTULO 2: ESQUEMA GERAL DA TUBULAÇÃO TELEFÔNICA. RECOMENDAÇÕES A tubulação telefônica é dimensionada em função da quantidade de pontos telefônicos previsto para cada parte do edifício. Cada ponto telefônico
Prevenção e Segurança na Construção Ferroviária: Execução de Passagens Superiores à Via Férrea em Exploração
 Prevenção e Segurança na Construção Ferroviária: Execução de Passagens Superiores à Via Férrea em Exploração Anabela Canelas: Coordenadora de SHST na WS Atkins, Portugal (ar-canelas@netcabo.pt) Mafalda
Prevenção e Segurança na Construção Ferroviária: Execução de Passagens Superiores à Via Férrea em Exploração Anabela Canelas: Coordenadora de SHST na WS Atkins, Portugal (ar-canelas@netcabo.pt) Mafalda
2 Sistema de Lajes com Forma de Aço Incorporado
 2 Sistema de Lajes com Forma de Aço Incorporado 2.1. Generalidades As vantagens de utilização de sistemas construtivos em aço são associadas à: redução do tempo de construção, racionalização no uso de
2 Sistema de Lajes com Forma de Aço Incorporado 2.1. Generalidades As vantagens de utilização de sistemas construtivos em aço são associadas à: redução do tempo de construção, racionalização no uso de
2 Materiais e Métodos
 1 ANÁLISE DO COMPORTAMENTO DE VIGAS REFORÇADAS POR ACRÉSCIMO DE CONCRETO À FACE COMPRIMIDA EM FUNÇÃO DA TAXA DE ARMADURA LONGITUDINAL TRACIONADA PRÉ-EXISTENTE Elias Rodrigues LIAH; Andréa Prado Abreu REIS
1 ANÁLISE DO COMPORTAMENTO DE VIGAS REFORÇADAS POR ACRÉSCIMO DE CONCRETO À FACE COMPRIMIDA EM FUNÇÃO DA TAXA DE ARMADURA LONGITUDINAL TRACIONADA PRÉ-EXISTENTE Elias Rodrigues LIAH; Andréa Prado Abreu REIS
DESCRITIVO TÉCNICO - EST 1
 DESCRITIVO TÉCNICO - EST 1 1 DESCRITIVO TÉCNICO 1.1 CONSIDERAÇÕES INICIAIS Todos os cálculos e detalhamentos estão de acordo com o prescrito nas normas NBR 6118:2014 Projeto de Estruturas de Concreto -
DESCRITIVO TÉCNICO - EST 1 1 DESCRITIVO TÉCNICO 1.1 CONSIDERAÇÕES INICIAIS Todos os cálculos e detalhamentos estão de acordo com o prescrito nas normas NBR 6118:2014 Projeto de Estruturas de Concreto -
PROPOSTA # 7 CICLOVIA DO CARREGADO AO TEJO
 ORÇAMENTO PARTICIPATIVO DE ALENQUER ǀ OPA 2015 CICLOVIA DO CARREGADO AO TEJO Divisão de Obras Municipais Departamento Operativo 1 DESCRIÇÃO DA PROPOSTA 2 FOTOGRAFIA AÉREA / PLANTA DE LOCALIZAÇÃO Com esta
ORÇAMENTO PARTICIPATIVO DE ALENQUER ǀ OPA 2015 CICLOVIA DO CARREGADO AO TEJO Divisão de Obras Municipais Departamento Operativo 1 DESCRIÇÃO DA PROPOSTA 2 FOTOGRAFIA AÉREA / PLANTA DE LOCALIZAÇÃO Com esta
Construtora do Tâmega, SA Controlo e execução a parir de modelo digital 3D
 Construtora do Tâmega, SA Controlo e execução a parir de modelo digital 3D A Construtora do Tâmega empresa que sempre acompanhou a evolução das técnicas da construção e tudo o que a ela diz respeito não
Construtora do Tâmega, SA Controlo e execução a parir de modelo digital 3D A Construtora do Tâmega empresa que sempre acompanhou a evolução das técnicas da construção e tudo o que a ela diz respeito não
Miguel C. Branchtein, Delegacia Regional do Trabalho no Rio Grande do Sul
 DETERMINAÇÃO DE CONDIÇÃO DE ACIONAMENTO DE FREIO DE EMERGÊNCIA TIPO "VIGA FLUTUANTE" DE ELEVADOR DE OBRAS EM CASO DE QUEDA DA CABINE SEM RUPTURA DO CABO Miguel C. Branchtein, Delegacia Regional do Trabalho
DETERMINAÇÃO DE CONDIÇÃO DE ACIONAMENTO DE FREIO DE EMERGÊNCIA TIPO "VIGA FLUTUANTE" DE ELEVADOR DE OBRAS EM CASO DE QUEDA DA CABINE SEM RUPTURA DO CABO Miguel C. Branchtein, Delegacia Regional do Trabalho
TÍTULO: DESENVOLVIMENTO DE APLICATIVO PARA AVALIAÇÃO DOS ESFORÇOS EM LAJES
 TÍTULO: DESENVOLVIMENTO DE APLICATIVO PARA AVALIAÇÃO DOS ESFORÇOS EM LAJES CATEGORIA: CONCLUÍDO ÁREA: ENGENHARIAS E ARQUITETURA SUBÁREA: ENGENHARIAS INSTITUIÇÃO: CENTRO UNIVERSITÁRIO DO INSTITUTO MAUÁ
TÍTULO: DESENVOLVIMENTO DE APLICATIVO PARA AVALIAÇÃO DOS ESFORÇOS EM LAJES CATEGORIA: CONCLUÍDO ÁREA: ENGENHARIAS E ARQUITETURA SUBÁREA: ENGENHARIAS INSTITUIÇÃO: CENTRO UNIVERSITÁRIO DO INSTITUTO MAUÁ
Projeto de Rede Telefônica
 Projeto de Rede Telefônica Prof. Manoel Henrique Sequencia Definições e materiais. Caixas de distribuição Blocos de terminais Caixas de passagem Tubulação Entrada Primária Secundária Cabos telefônicos
Projeto de Rede Telefônica Prof. Manoel Henrique Sequencia Definições e materiais. Caixas de distribuição Blocos de terminais Caixas de passagem Tubulação Entrada Primária Secundária Cabos telefônicos
COMPORTAMENTO DE ESTRUTURAS DE AÇO ENFORMADAS A FRIO E DIMENSIONAMENTO
 COMPORTAMENTO DE ESTRUTURAS DE AÇO ENFORMADAS A FRIO E DIMENSIONAMENTO DE ACORDO COM O EC3-1-3 NUNO SILVESTRE DINAR CAMOTIM Departamento de Engenharia Civil e Arquitectura Instituto Superior Técnico RESUMO
COMPORTAMENTO DE ESTRUTURAS DE AÇO ENFORMADAS A FRIO E DIMENSIONAMENTO DE ACORDO COM O EC3-1-3 NUNO SILVESTRE DINAR CAMOTIM Departamento de Engenharia Civil e Arquitectura Instituto Superior Técnico RESUMO
CADEX. Consultoria em Logística Interna. Layout de armazém. Objectivos. Popularidade. Semelhança. Tamanho. Características
 CADEX Consultoria em Logística Interna Layout de armazém fonte: Wikipédia O layout de armazém é a forma como as áreas de armazenagem de um armazém estão organizadas, de forma a utilizar todo o espaço existente
CADEX Consultoria em Logística Interna Layout de armazém fonte: Wikipédia O layout de armazém é a forma como as áreas de armazenagem de um armazém estão organizadas, de forma a utilizar todo o espaço existente
Tipos de Fundações. Tipos de Fundações. Fundações. Tubulões à ar comprimido - exemplos:
 Universidade Federal do Espírito Santo Centro Tecnológico Departamento de Engenharia Civil Tecnologia da Construção Civil I Tubulões à ar comprimido - exemplos: Fundações Profa. Geilma Lima Vieira geilma.vieira@gmail.com
Universidade Federal do Espírito Santo Centro Tecnológico Departamento de Engenharia Civil Tecnologia da Construção Civil I Tubulões à ar comprimido - exemplos: Fundações Profa. Geilma Lima Vieira geilma.vieira@gmail.com
Estrutura Dupla Plana
 Estrutura Dupla Plana Plurigas Solar, Energias LDA. @2013 Instruções de Leia atentamente as instruções de segurança. As nossas estruturas foram concebidas especificamente para a suportar a montagem de
Estrutura Dupla Plana Plurigas Solar, Energias LDA. @2013 Instruções de Leia atentamente as instruções de segurança. As nossas estruturas foram concebidas especificamente para a suportar a montagem de
II EDIÇÃO DO CONCURSO GESTÃO DE IDEIAS PARA ECONOMIZAR
 II EDIÇÃO DO CONCURSO GESTÃO DE IDEIAS PARA ECONOMIZAR APRESENTAÇÃO DO CONCURSO: O concurso Gestão de Ideias para Economizar representa uma oportunidade para os estudantes se prepararem, em pequenos grupos,
II EDIÇÃO DO CONCURSO GESTÃO DE IDEIAS PARA ECONOMIZAR APRESENTAÇÃO DO CONCURSO: O concurso Gestão de Ideias para Economizar representa uma oportunidade para os estudantes se prepararem, em pequenos grupos,
COMPILAÇÃO FOTOGRÁFICA COMENTADA
 COMPILAÇÃO FOTOGRÁFICA COMENTADA CONSIDERAÇÕES As fotografias apresentadas foram registadas pelo autor deste trabalho ao longo de oito anos em obras sobre a sua responsabilidade e outras por onde passava
COMPILAÇÃO FOTOGRÁFICA COMENTADA CONSIDERAÇÕES As fotografias apresentadas foram registadas pelo autor deste trabalho ao longo de oito anos em obras sobre a sua responsabilidade e outras por onde passava
