CAPÍTULO IV - POSIÇÕES RELATIVAS DE UMA RETA E UM PLANO E DE DUAS RETAS

Transcrição

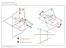
1 CAÍTULO IV - OSIÇÕES RELATIVAS DE UMA RETA E UM LANO E DE DUAS RETAS 41 sições elativas de uma eta e um plan As psições de uma eta a) paalela a ( // ) :X = R + t v, t IR R e um plan sã: v n // v n = 0 e R n R v v n = 0 e R b) cntida em ( ) c) e cncentes ( = {} ) v n = {} v n 0 14

2 Cas paticula: v n Exempls: 1 Detemine a inteseçã da eta cm plan, ns seguintes cass: a) : X = (1,6,2) + t (1,1,1) ; t IR : x z 3 = 0 b) c) : x 1= y 2 = 2 (z 1) :X = h(6,2,1) + t (1,2,1); = t : y = t ; t IR = t : x + y + 2z 1= 0 t, h IR Sluçã: a) v n = (11,,1) (1,0, 1) = 0, lg, = u = φ Cm R(1,6,2) é um pnt de, veificams que R Lg = φ 1 b) Send v = 1,1, e n = (6,2,1) (1,2,1) = (0, 5,10), tems que 2 v n = 0 Lg, = u = φ Cm R(1,2,1) é um pnt de, veificams que R Lg e cnsequentemente = 15

3 b) De v n = (1,3, 1) (11,,2) = 2 0 cncluíms que e sã cncentes Seja = {} = {(a,b,c)} Tems entã: (1) a + b + 2c 1= 0 (2) a = t b = t, c = t paa algum escala t De (1) e (2) btems t = 2 e (2,3, 2) 2 Detemine uma equaçã da eta que passa pel pnt A(1,0, 2) e é paalela as plans α: 2x y + 2 = 0 e β : x + z 3 = 0 Sluçã: Cm // α e // β, tems v nα e v nβ Send n α e nβ tems que // n α n Assim pdems cnsidea v β LI, v = nα nβ = (1,01) (2, 1,0) = (1,2, 1) Daí uma equaçã vetial da eta é: : X = (1,0, 2) + t (1,2, 1); t IR 42 sições elativas de duas etas Se duas etas estã cntidas n mesm plan dizems que sã cplanaes Cas cntái sã denminadas evesas As etas cplanaes pdem se paalelas (distintas u cincidentes) u cncentes 16

4 Resumind, duas etas 1 e 2 pdem se: Cplanaes Cncentes : { } 1 2 = 1 2 aalelas: Distintas : 1 2 = φ Cincidentes : Revesas 1 2 Estabeleceems a segui cndições paa a identificaçã da psiçã elativa de duas etas Cnsidee as etas : X = R + h v e s :X = S + t v ; h, t IR Se e s sã cplanaes entã s vetes RS, v s e v s [ RS,v,vs ] = sã cplanaes e ptant [ RS,v,vs ] = 0 Recipcamente, se 0 pdems te: i) v // vs, nesse cas e s sã paalelas, lg cplanaes 17

5 ii) v e vs LI, nesse cas RS, v e v s sã LD Cm v e lineamente independentes, entã pdems esceve RS cm cmbinaçã linea de v e vs Lg, existem escalaes h e t tais que S = R + hv + tvs Assim, plan β : X = R + h v + t v s ; h, t IR, cntém as etas e s, que ptant sã cplanaes Obsevems ainda que, neste cas as etas sã cncentes vs sã Um cas paticula de etas cncentes sã as etas pependiculaes Obsevems que se duas etas e s sã pependiculaes entã v v 0 s = v s v s Exempls 1 Estude a psiçã elativa ds seguintes paes de etas: 2x y z + 2 = 0 a) : e s : X = (1,0,2) + h (1, 3,7); h IR x + 3y z + 2 = 0 = h 1 x y b) : y = 1 h ; h IR e s : = = z = 4 + 4h x 3 c) : X = ( 2,1,3) + t( 10, 2, 18) ; t IR e s : = y 2 = 5 = 4 d) : X = (4, 3,1) + h(0,2,1); h IR e s : y = 1 2t ; t IR = 3 t z 12 9 Sluçã: a) Cm v // (2, 1, 1) (1,3, 1) = (4,1,7) e vs // (1, 3,7) tems que as etas e s sã cncentes u evesas Vams entã cnsidea R(0,0,2) e S(1,0,2) pnts de e s, espectivamente Assim, 18

6 [ RS,v,vs ] = = 28 0 tant, as etas e s sã evesas c) Cm v // (1, 1,4) e vs // ( 2,3,1) tems que as etas e s sã cncentes u evesas Vams entã cnsidea R(0,1,4) e S(1,0,8) pnts de e s, espectivamente Assim, [ RS,v,vs ] = = Lg as etas e s sã cncentes c) Cm v // ( 10, 2, 18) e vs // (5,1,9) tems que as etas e s sã paalelas (distintas u cincidentes) Além diss, pnt R( 2,1,3 ) petence às etas e s Assim, pdems cnclui que as etas e s sã cincidentes d) Cm v // (0,2,1) e vs // (0, 2, 1) tems que as etas e s sã paalelas (distintas u cincidentes) Obsevems que pnt R(4, 3,1) petence à eta, n entant nã petence à eta s, pis sistema 4 = 4 3 = 1 2 t nã tem sluçã 1= 3 t Assim, pdems cnclui que as etas e s sã paalelas distintas 2 Dê uma equaçã da eta que passa pel pnt ( 1,1,1 ) e é paalela à eta s: 2x y+ 4z + 3 = 0 x + 5y z + 6 = 0 19

7 Sluçã: Send e s etas paalelas pdems cnsidea v = vs Cm // (2, 1,4) (1,5, 1) = ( 19,6,11) as equações siméticas de s sã: v s x + 1 = 19 y 1 = 6 z 1 11 = 4 + t 3 Mste que as etas : x 2 = y = z 1 e s : y = 2 t; t IR = 3 sã cncentes e detemine pnt de inteseçã Sluçã: Sejam v = (1, 1,1), vs = (1, 1,0) e R(2,0,1) e S(4, 2,3) s, pnts de e espectivamente Entã v,v,rs] = [ s = e assim cncluíms que e s sã cplanaes Cm nã sã paalelas pis v e vs sã vetes LI, tems que as etas sã cncentes Seja = (x, y, z ) = { } { } s Entã, x 2 = y = z 1 e Daí, t = 0 e = (4, 2,3) y = 4 + t = 2 t = 3 4 Detemine uma equaçã da eta que passa pel pnt (1,2,3), é cncente cm a eta s : X = ( 1,3,5) + h (2,5,1); h IR, e tem vet dieçã v tgnal a vet u = (0,1, 4) 20

8 Sluçã: Seja { } = s Entã existe um eal h, tal que ( 1 + 2h,3 + 5h,5 + h ) Cnsideems v = Cm v é tgnal a u, tems que ( 2 + 2h,1 + 5h,2 + h) (0,1, 4) = 0 Lg, h = 7 Assim, = (13,18,12) e : X = (1,2,3) + t (2,5,1); t IR 5 Detemine uma cndiçã necessáia e suficiente paa que uma eta seja paalela a eix OX Sluçã: O eix OX tem vet dieçã i = (1,0,0) Entã, uma eta é paalela a eix OX se, e smente se, v é paalel a vet i = (1,0,0) 6 Detemine uma equaçã da eta que passa pel pnt = (1,0,2), é cncente cm a eta s : X = (1,0,1) + t (2,1,1);t IR e é paalela a plan : 2x 3y + 4z 6 = 0 Sluçã: 0 s Seja { } s = entã, existe t IR tal que = (1 + 2t, t,1 + t) e = (2t, t, t 1) Cm // tems ( 2t,t,t 1) (2, 3,4) = 0 Assim, t = 5 4 Cnsideand = (8,4, 1), uma equaçã vetial de é: v : X = (1,0,2) + t (8,4, 1); t IR 21